吉林省辽源一中2018_2019学年高一数学上学期期末考试试题
吉林省2018-2019学年高一第一学期期末考试 数学

2018-2019学年吉林省高一(上)期末数学试卷一、选择题(本大题共12小题,共48.0分)1. 若集合,,则A. B. C. D.2. 已知角的终边与单位圆交于点,则A. B. C. D.3. 把化为的形式是A. B. C. D.4. 时针走过2时40分,则分针转过的角度是A. B. C. D.5. 已知,,,则a,b,c的大小关系为A. B. C. D.6. 要得到函数的图象,只需将函数的图象上所有的点A. 横坐标伸长到原的倍纵坐标不变,再向左平行移动个单位长度B. 横坐标缩短到原的2倍纵坐标不变,再向右平行移动个单位长度C. 横坐标缩短到原的倍纵坐标不变,再向左平行移动个单位长度D. 横坐标伸长到原的2倍纵坐标不变,再向右平行移动个单位长度7. 已知函数,则的解析式为A. B.C. D.8. 若,,,,则A. B. C. D.9. 已知函数对任意,都有,的图象关于对称,且,则A. 0B.C.D.10. 已知是上的减函数,则a的取值范围是A. B. C. D.11. 若函数满足且时,,函数,则函数在区间内的与x轴交点的个数为A. 5B. 7C. 8D. 1012. 己知函数,图象关于y轴对称,且在区间上不单调,则的可能值有A. 7个B. 8个C. 9 个D. 10个二、填空题(本大题共4小题,共16.0分)13. 函数的定义域是______.14. 已知函数的部分图象如图所示:则函数的解析式为______.15. ______.16. 如图,C为半圆内一点,O为圆心,直径AB长为2cm,,,将绕圆心O逆时针旋转至,点在OA上,则边BC扫过区域图中阴影部分的面积为______.三、解答题(本大题共6小题,共56.0分)17. 若,求的值.计算:18. 已知函数求:Ⅰ函数的对称轴方程;Ⅱ函数在区间上的最值.19. 已知是R上的奇函数,且当时,;求的解析式;作出函数的图象不用列表,并指出它的增区间.20. 已知求的最小正周期;求的单调减区间;若函数在区间上没有零点,求m的取值范围.21. 如图,已知AB是一幢6层的写字楼,每层高均为3m,在AB正前方36m处有一建筑物CD,从楼顶A处测得建筑物CD的张角为.求建筑物CD的高度;一摄影爱好者欲在写字楼AB的某层拍摄建筑物已知从摄影位置看景物所成张角最大时,拍摄效果最佳问:该摄影爱好者在第几层拍摄可取得最佳效果不计人的高度?22. 设函数且是定义域为R的奇函数.求k值;若,试判断函数单调性并求使不等式恒成立的t的取值范围;若,且在上的最小值为,求m的值.。
2018-2019学年吉林省吉林市第一中学高一上学期期末考试数学(理)试题(解析版)

2018-2019学年吉林省吉林市第一中学高一上学期期末考试数学(理)试题一、单选题1.已知集合,集合,则()A.B.C.D.【答案】B【解析】解出集合Q的元素,由集合的交集运算得到结果.【详解】集合,集合,则.故答案为:B.【点睛】这个题目考查了集合的交集的运算,题目简单.2.下列各组函数是同一函数的是()A.,B.,C.,D.,【答案】D【解析】依次判断函数的定义域和对应法法则,判断是否为同一函数.【详解】对于A:定义域是R,定义域内不包含x=0,故不是同一函数;对于B,,x的取值范围是,中x的取值范围是;对于C,,中x的范围是,中x的范围是,故不为同一函数;D. ,定义域和对应法则相同,故是同一函数.故答案为:D.【点睛】本题考查同一函数的判断与应用,是基础题.判断函数是否为同一函数主要看两个函数定义域和对应法则,值域是否相同.解题时要认真审题,仔细解答.3.函数与的图象交点的横坐标所在区间为()A.B.C.D.【答案】B【解析】该问题可转化为方程ln(x+1)=的解的问题,进一步可转化为函数f(x)=ln(x+1)﹣的零点问题.【详解】令f(x)=ln(x+1)﹣,是增函数,∵f(2)=ln3﹣f(1)=ln2﹣1<lne﹣1=0,又函数f(x)在(1,2)上的图象是一条连续不断的曲线,∴函数f(x)在区间(1,2)内有零点,即ln(x+1)=有解,此解即为函数y=ln(x+1)与y=的图象交点的横坐标.故选:B.【点睛】本题考查函数零点的存在问题,本题中函数y=ln(x+1)与y=的图象交点的横坐标,可转化为函数f(x)=ln(x+1)﹣的零点.注意函数与方程思想、转化与化归思想的运用.4.函数的图象的大致形状是()A.B.C.D.【答案】B【解析】根据指数函数的图象和性质,当a>1时,x>0时,为增函数,排除C,D,再讨论x<0的单调性,即可得到答案.【详解】当x>0时,y=a x,因为a>1,所以是增函数,排除C、D,当x<0时,y=-a x,是减函数,所以排除A.故选:B.【点睛】本题考查了指数函数的图象和性质,需要分类讨论,去绝对值,属于基础题.5.,为两个不同的平面,,为两条不同的直线,下列命题中正确的是()①若,,则;②若,,则;③若,,,则④若,,,则. A.①③ B.①④ C.②③ D.②④【答案】B【解析】在①中,由面面平行的性质定理得m∥β;在②中,m与n平行或异面;在③中,m与β相交、平行或m⊂β;在④中,由n⊥α,m⊥α,得m∥n,由n⊥β,得m⊥β.【详解】由α,β为两个不同的平面,m,n为两条不同的直线,知:在①中,若α∥β,m⊂α,则由面面平行的性质定理得m∥β,故①正确;在②中,若m∥α,n⊂α,则m与n平行或异面,故②错误;在③中,若α⊥β,α∩β=n,m⊥n,则m与β相交、平行或m⊂β,故③错误;在④中,若n⊥α,m⊥α,则m∥n,由n⊥β,得m⊥β,故④正确.故选:B.【点睛】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想,是中档题. 6.如图为某几何体的三视图,则该几何体的表面积为( )A .B .C .D .【答案】B【解析】该几何体是一个正方体与半圆柱的组合体,表面积为,故选B .7.点P 在正方形ABCD 所在平面外,PD ⊥平面ABCD ,PD=AD ,则PA 与BD 所成角的度数为( )A.30°B.45°C.60°D.90° 【答案】C 【解析】PD分别取AC.PC 中点O.E.连OE,DE;则OE//PA,所以DOE ∠(或其补角)就是PA 与BD 所成的角;因PD ⊥平面ABCD ,所以PD ⊥DC,PD ⊥AD.设正方形ABCD 边长为2,则PA=PC=BD=所以,DOE ∆是正三角形。
2018-2019学年吉林省高中高一(上)期末数学试卷(解析版)

2018-2019学年吉林省高中高一(上)期末数学试卷一、选择题本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的1.(5分)已知角α的终边上有一点P(﹣3,m),且cosα=﹣,则m=()A.4B.5C.﹣4D.±42.(5分)已知集合A={x|﹣1<x﹣3≤2},B={x|3≤x<4},则∁A B=()A.(2,3)∪(4,5)B.(2,3]∪(4,5]C.(2,3)∪[4,5]D.(2,3]∪[4,5]3.(5分)已知函数f(x)=a﹣x+2+1,若f(﹣1)=9,则a=()A.2B.﹣2C.8D.﹣84.(5分)已知向量=(2,﹣1),=(k,2).若∥,则k=()A.﹣1B.1C.﹣4D.45.(5分)sin 20°cos 10°+sin 10°sin 70°的值是()A.B.C.D.6.(5分)设函数f(x)=log2x,若f(a+1)<2,则a的取值范围为()A.(﹣1,3)B.(﹣∞,3)C.(﹣∞,1)D.(﹣1,1)7.(5分)设函数f(x)=,若f(a)=1,则a=()A.3B.±3C.﹣3或1D.±3或18.(5分)已知函数f(x)=log2(x+1)+3x+m的零点在区间(0,1]上,则m的取值范围为()A.(﹣4.0)B.(﹣∞,﹣4)∪(0,+∞)C.(﹣∞,﹣4]∪(0,+∞)D.[﹣4,0)9.(5分)如图,在△ABC中,3BD=DC,AB=3,AC=2,∠BAC=60°,则=()A.﹣B.C.﹣D.10.(5分)函数f(x)=的部分图象大致为()A.B.C.D.11.(5分)已知函数f(x)=﹣3cos(2x﹣),则()A.f(x)在(0,)单调递减B.f(x)的图象关于(,0)对称C.f(x)在(0,]上的最大值为3D.f(x)的图象的一条对称轴为x=12.(5分)已知函数f(x)=3sin(2x﹣),若函数y=f2(x)﹣(m﹣1)f(x)﹣m在[0,]上有3个零点,则m的取值范围为()A.[,3)B.[﹣,3)C.[﹣,)D.[,3]二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上13.(5分)函数f(x)=log4(5﹣x)+的定义域为.14.(5分)定义在[﹣5,5]上的奇函数f(x),当x∈(0,5]时,f(x)=6x,则f(0)+f(﹣1)=.15.(5分)若cos(+)=,则cos(α+)=.16.(5分)已知函数f(x)=log a(﹣x+1)(a>0且a≠1)在[﹣2,0]上的值域是[﹣1,0].若函数g(x)=a x+m﹣3的图象不经过第一象限,则m的取值范围为.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤17.(10分)已知集合A={x|m﹣2<x≤m+1},B={x|log2(x﹣3)<2}.(1)当m=3时,求A∩B.(2)若A∩B=A,求m的取值范围.18.(12分)已知=1.(1)求tanα的值;(2)求的值.19.(12分)已知向量,不共线,向量=﹣,=+2,=3﹣.(1)若(+2)∥(+k),求k的值;(2)若,为相互垂直的单位向量,且(t+)⊥,求t的值.20.(12分)已知函数f(x)=A cos(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示.(1)求f(x)的解析式;(2)当x∈[﹣,]时,求f(x)的值域21.(12分)已知函数f(x)=4x﹣a•2x﹣2.(1)当a=2时,求方程f(x)=6的解;(2)若y=f(x)在[0,2]上有零点,求a的取值范围.22.(12分)已知向量=(,2sin x),=(sin2x,sin x),函数f(x)=•.(1)若||=2,x∈[0,π],求x的值;(2)若对任意x∈[,π],f(x)≤2m3+lgm恒成立,求m的取值范围.2018-2019学年吉林省高中高一(上)期末数学试卷参考答案与试题解析一、选择题本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的1.【解答】解:∵角α的终边上有一点P(﹣3,m),且cosα=﹣,∴x=﹣3,y=m,r =|OP|,由三角函数定义,可得==﹣,∴r=5,即=25,∴m=±4,故选:D.2.【解答】解:A={x|2<x≤5};∴∁A B={x|2<x<3,或4≤x≤5}=(2,3)∪[4,5].故选:C.3.【解答】解:∵函数f(x)=a﹣x+2+1,f(﹣1)=9,∴f(﹣1)=a3+1=9,解得a=2.故选:A.4.【解答】解:∵;∴4+k=0;∴k=﹣4.故选:C.5.【解答】解:sin 20°cos 10°+sin 10°sin 70°=cos70°cos10°+sin70°sin10°=cos(70°﹣10°)=cos60°=.故选:C.6.【解答】解:由题意知,log2(a+1)<2,即log2(a+1)<log24,所以0<a+1<4,解得﹣1<a<3.a的取值范围是(﹣1,3).故选:A.7.【解答】解:∵函数f(x)=,f(a)=1,∴当a>0时,f(a)=log3a=1,解得a=3;当a≤0时,f(a)=a2+2a﹣2=1,解得a=﹣3或a=1,(舍去).综上a=±3.故选:B.8.【解答】解:因为f(x)=log2(x+1)+3x+m在区间(0,1]上是单调递增,函数f(x)=log2(x+1)+3x+m的零点在区间(0,1]上,所以,即,解得﹣4≤m<0.故选:D.9.【解答】解:由题意可得,====,=,∴==﹣==﹣,故选:C.10.【解答】解:当x=2时,f(2)==﹣<0,排除B,C 当x=﹣2时,f(﹣2)==>0,故排除D,故选:A.11.【解答】解:函数f(x)=﹣3cos(2x﹣)=3sin(2x+),对于A:令2x+可得∴f(x)在(0,)单调递减不对;则A不对;对于B,D选项:令x=,可得f()=3sin(+)=3sin2π=0,∴f(x)的图象关于(,0)对称;则B选项对,D选项错误;对于C:令2x+=,可得x=,k∈Z则x=和时取得最大值3,∴在(0,]上取不得最大值为3;故选:B.12.【解答】解:由题意函数f(x)=t=3sin(2x﹣),∵x∈[0,]上,∴2x﹣∈[,];设t1,t2是函数y=f2(x)﹣(m﹣1)f(x)﹣m=0的根.可得t1=﹣1,t2=m;函数y=f2(x)﹣(m﹣1)f(x)﹣m在[0,]上有3个零点,当t1=﹣1时,对于的x值只有一个解;那么t2=m对于的x值有两个解;∴,即;故选:A.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上13.【解答】解:要使函数f(x)有意义,则;解得0≤x<5;∴f(x)的定义域为[0,5).故答案为:[0,5).14.【解答】解:根据题意,f(x)为定义在[﹣5,5]上的奇函数,则f(0)=0,f(﹣1)=﹣f(1),当x∈(0,5]时,f(x)=6x,则f(1)=61=6,则f(﹣1)=﹣f(1)=﹣6;则f(0)+f(﹣1)=﹣6;故答案为:﹣6.15.【解答】解:∵cos(+)=,∴cos(α+)=2cos2(+)﹣1=2×()2﹣1=﹣.故答案为:﹣.16.【解答】解:∵函数f(x)=log a(﹣x+1)(a>0且a≠1)在[﹣2,0]上的值域是[﹣1,0],而f(0)=0,∴f(﹣2)=log a3=﹣1,∴a=,即函数f(x)=(﹣x+1).若函数g(x)=﹣3的图象不经过第一象限,令g(x)=0,求得x=﹣m﹣1,则﹣m﹣1≤0,求得m≥﹣1,故答案为:[﹣1,+∞).三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤17.【解答】解:(1)当m=3时,A={x|1<x≤4},B={x|log2(x﹣3)<2}={x|3<x<7},∴A∩B={x|3<x≤4}.(2)∵A∩B=A,∴A⊆B,∵集合A={x|m﹣2<x≤m+1},B={x|3<x<7},∴,解得5≤m<6.∴m的取值范围是[5,6).18.【解答】解:(1)由=1,得,∴2sinα=cosα,则tan;(2)===.19.【解答】解:(1)∵=﹣,=+2,=3﹣,∴=3,=(1+3k)+(2﹣k),∵(+2)∥(+k),由向量共线定理可得,存在实数λ使得λ(+2)=+k,则解可得,k=;(2)∵=﹣,=+2,∴t+=(t+1)+(2﹣t),∵(t+)⊥,∴(t+)•=0,即+(t﹣2)=0,∵,为相互垂直的单位向量,∴=0,,∴2t﹣1=0,∴t=.20.【解答】解:(1)根据函数f(x)=A cos(ωx+φ)(A>0,ω>0,|φ|<)的部分图象,可得•=﹣,∴ω=2.再根据五点法作图,可得2•+φ=,∴φ=﹣,∴函数f(x)=A cos(2x﹣).再把点(0,2)代入,可得A cos(﹣)=2,∴A=4,故函数f(x)=4cos(2x ﹣).(2)当x∈[﹣,]时,2x﹣∈[﹣,],故cos(2x﹣)∈[﹣,1],∴f(x)∈[﹣2,4].21.【解答】解:(1)当a=2时,f(x)=4x﹣2•2x﹣2.因为f(x)=6,所以4x﹣2•2x﹣8=0,即(2x﹣4)(2x+2)=0,解得2x=4,即x=2.(2)设t=2x∈[1,4],则y=t2﹣at﹣2.y=f(x)在[0,2]上有零点等价于t2﹣at﹣2=0在[1,4]上有解,即a=t﹣在[1,4]上有解.令g(t)=t﹣,t∈[1,4],则g(t)在[1,4]上单调递增,所以g(1)min=g(1)=1﹣2=﹣1,g(t)min=g(4)=4﹣=.故a的取值范围为:[﹣1,].22.【解答】解:(1)向量=(,2sin x),=(sin2x,sin x),∴||=,又||=2,∴=2,∴sin2x=,解得sin x=±,又x∈[0,π],∴x=或x=;(2)向量=(,2sin x),=(sin2x,sin x),∴函数f(x )=•=sin2x+2sin2x =sin2x﹣cos2x+1=2sin(2x ﹣)+1,又x∈[,π],∴2x ﹣∈[,],∴sin(2x ﹣)∈[﹣1,],∴f(x)∈[﹣1,2];若对任意x∈[,π],f(x)≤2m3+lgm恒成立,则2m3+lgm≥f(x)max=2,设函数g(x)=2x3+lgx,则g(x)在(0,+∞)内是单调增函数,且g(1)=2,∴不等式g(m)≥2,可得出m≥1,即m的取值范围是[1,+∞).第11页(共11页)。
2018-2019学年吉林省吉林市第一中学高一上学期期末考试数学(理)试题

吉林一中2018-2019学年度上学期期末考试高一数学(理科)试卷★祝考试顺利★注意事项:1、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每个小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
3、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。
5、保持卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
6、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,集合,则()A. B. C. D.【答案】B【解析】【分析】解出集合Q的元素,由集合的交集运算得到结果.【详解】集合,集合,则.故答案为:B.【点睛】这个题目考查了集合的交集的运算,题目简单.2.下列各组函数是同一函数的是()A. ,B. ,C. ,D. ,【答案】D【解析】【分析】依次判断函数的定义域和对应法法则,判断是否为同一函数.【详解】对于A:定义域是R,定义域内不包含x=0,故不是同一函数;对于B,,x的取值范围是,中x的取值范围是;对于C,,中x的范围是,中x的范围是,故不为同一函数;D. ,定义域和对应法则相同,故是同一函数.故答案为:D.【点睛】本题考查同一函数的判断与应用,是基础题.判断函数是否为同一函数主要看两个函数定义域和对应法则,值域是否相同.解题时要认真审题,仔细解答.3.函数与的图象交点的横坐标所在区间为()A. B. C. D.【答案】B【解析】【分析】该问题可转化为方程ln(x+1)=的解的问题,进一步可转化为函数f(x)=ln(x+1)﹣的零点问题.【详解】令f(x)=ln(x+1)﹣,是增函数,∵f(2)=ln3﹣f(1)=ln2﹣1<lne﹣1=0,又函数f(x)在(1,2)上的图象是一条连续不断的曲线,∴函数f(x)在区间(1,2)内有零点,即ln(x+1)=有解,此解即为函数y=ln(x+1)与y=的图象交点的横坐标.故选:B.【点睛】本题考查函数零点的存在问题,本题中函数y=ln(x+1)与y=的图象交点的横坐标,可转化为函数f(x)=ln(x+1)﹣的零点.注意函数与方程思想、转化与化归思想的运用.4.函数的图象的大致形状是()A. B. C. D.【答案】B【解析】【分析】根据指数函数的图象和性质,当a>1时,x>0时,为增函数,排除C,D,再讨论x<0的单调性,即可得到答案.【详解】当x>0时,y=a x,因为a>1,所以是增函数,排除C、D,当x<0时,y=-a x,是减函数,所以排除A.故选:B.【点睛】本题考查了指数函数的图象和性质,需要分类讨论,去绝对值,属于基础题.5.,为两个不同的平面,,为两条不同的直线,下列命题中正确的是()①若,,则;②若,,则;③若,,,则④若,,,则.A. ①③B. ①④C. ②③D. ②④【答案】B【解析】【分析】在①中,由面面平行的性质定理得m∥β;在②中,m与n平行或异面;在③中,m与β相交、平行或m⊂β;在④中,由n⊥α,m⊥α,得m∥n,由n⊥β,得m⊥β.【详解】由α,β为两个不同的平面,m,n为两条不同的直线,知:在①中,若α∥β,m⊂α,则由面面平行的性质定理得m∥β,故①正确;在②中,若m∥α,n⊂α,则m与n平行或异面,故②错误;在③中,若α⊥β,α∩β=n,m⊥n,则m与β相交、平行或m⊂β,故③错误;在④中,若n⊥α,m⊥α,则m∥n,由n⊥β,得m⊥β,故④正确.故选:B.【点睛】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想,是中档题.6.如图为某几何体的三视图,则该几何体的表面积为()A. B. C. D.【答案】B【解析】该几何体是一个正方体与半圆柱的组合体,表面积为,故选B.7. 点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为()A. 30°B. 45°C. 60°D. 90°【答案】C【解析】分别取AC.PC中点O.E.连OE,DE;则OE//PA,所以(或其补角)就是PA与BD所成的角;因PD⊥平面ABCD,所以PD⊥DC,PD⊥AD.设正方形ABCD边长为2,则PA=PC=BD=所以OD=OE=DE=,是正三角形。
吉林省辽源一中2018-2019学年高三上学期期末考试试题理(数学)
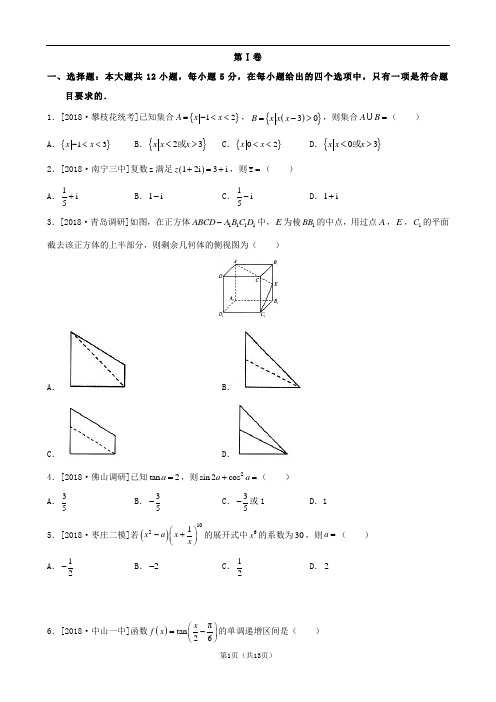
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2018·攀枝花统考]已知集合{}12A x x =-<<,(){}30B x x x =->,则集合AB =( ) A .{}13x x -<< B .{}23x x x <>或C .{}02x x <<D .{}03x x x <>或 2.[2018·南宁三中]复数z 满足()12i 3i z +=+,则z =( )A .1i 5+B .1i -C .1i 5-D .1i +3.[2018·青岛调研]如图,在正方体1111ABCD A B C D -中,E 为棱1BB 的中点,用过点A ,E ,1C 的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )A .B .C .D .4.[2018·佛山调研]已知tan 2a =,则2sin 2cos a a +=( )A .35B .35-C .35-或1 D .1 5.[2018·枣庄二模]若()1021x a x x ⎛⎫-+ ⎪⎝⎭的展开式中6x 的系数为30,则a =( ) A .12- B .2- C .12 D .26.[2018·中山一中]函数()πtan 26x f x ⎛⎫=- ⎪⎝⎭的单调递增区间是( )A .2π4π2π,2π33k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z B .2π4π2π,2π33k k ⎛⎫-+ ⎪⎝⎭,k ∈Z C .2π4π4π,4π33k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z D .2π4π4π,4π33k k ⎛⎫-+ ⎪⎝⎭,k ∈Z 7.[2018·山师附中]函数()f x 是R 上的偶函数,且()()1f x f x +=-,若()f x 在[]1,0-上单调递减,则函数()f x 在[]3,5上是( )A .增函数B .减函数C .先增后减的函数D .先减后增的函数8.[2018·棠湖中学]已知两点(),0A a ,()(),00B a a ->,若曲线22230x y y +--+=上存在点P ,使得90APB ∠=︒,则正实数a 的取值范围为( )A .(]0,3B .[]1,2C .[]2,3D .[]1,39.[2018·优创名校]函数()211ln 22f x x x =+-的图象大致为( ) A . B .C .D .10.[2018·南海中学]已知双曲线()222210,0x y a b a b-=>>的右焦点为F ,点A 在双曲线的渐近线上,OAF △是边长为2的等边三角形(O 为原点),则双曲线的方程为( )A .2213x y -=B .2213y x -=C .221412x y -= D .221124x y -=11.[2018·黄陵中学]在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =,c =,tan 21tan A c B b+=,则C ∠=( )A .π6B .π4C .π4或3π4D .π312.[2018·开封月考]已知空间四边形ABCD ,2π3BAC ∠=,AB AC ==6BD CD ==,且平面ABC ⊥平面BCD ,则空间四边形ABCD 的外接球的表面积为( )A .60πB .36πC .24πD .12π第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2018·南康模拟]已知单位向量a ,b 的夹角为60︒,则()()23+⋅-=a b a b ________. 14.[2018·曲靖统测]随机变量ξ服从正态分布()2,N ξμσ~,若()20241P μξμ-<≤=.,则()2P ξμ>+=__________.15.[2018·高新区月考]若实数x ,y 满足不等式组00220y x y x y ≥⎧⎪-≥⎨⎪--≥⎩,则11y w x -=+的取值范围是__________. 16.[2018·盐城期中]已知函数()2221f x x ax a =-+-,()2g x x a =-,[]11,1x ∀∈-,[]21,1x ∃∈-,使()()21f x g x =,则实数a 的取值范围是__________.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.17.(12分)[2018·华侨中学]已知数列{}n a 的前n 项和为n S ,且22n S n n =+.(1)求数列{}n a 的通项公式;(2)求数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T .18.(12分)[2018·唐山摸底]甲、乙两位工人分别用两种不同工艺生产同一种零件,已知尺寸在[]223,228(单位:mm )内的零件为一等品,其余为二等品,测量甲乙当天生产零件尺寸的茎叶图如图所示:。
2018-2019学年吉林省辽源市田家炳高级中学高一上学期期末联考(理)数学试题(答案+解析)

吉林省辽源市田家炳高级中学2018-2019学年高一上学期期末联考数学(理)试题一、选择题:(在每小题给出四个选项中,只有一项是符合题目要求的。
)1.计算cos(-780°)的值是()A. -B. -C.D.[答案]C[解析]cos(-780°)=cos780°=cos60°=.故选:C.2.下列函数中,既是奇函数又是增函数的是()A. B. C. D.[答案]B[解析]A.非奇非偶函数;B.奇函数且是单调递增函数;C.奇函数但在定义域上不是增函数;D. 奇函数,单调递减函数;故选B.3.已知a=(1,1),b=(1,-1),则a-b等于()A. (-1,2)B. (1,-2)C. (-1,-2)D. (1,2)[答案]A[解析]根据题意可得,故选A.4.已知是幂函数,且在第一象限内是单调递减的,则m的值为()A. -3B. 2C. -3或2D. 3[答案]A[解析]由y=(m2+m-5)x m是幂函数,知m2+m-5=1,解得m=2或m=-3.∵该函数在第一象限内是单调递减的,∴m<0.故m=-3.故选:A.5.若,,,则a,b,c之间的大小关系是()A. c>b>aB. c>a>bC. a>c>bD. b>a>c[答案]C[解析]∵a=22.5>1,<0,,∴a>c>b,故选:C.6.要得到函数y=cos的图象,只需将函数y=cos2的图象()A. 向左平移个单位长度B. 向左平移个单位长度C. 向右平移个单位长度D. 向右平移个单位长度[答案]B[解析]∵,∴要得到函数的图像,只需将函数的图像向左平移个单位.选B.7.函数的定义域为()A. {|≠}B. {|≠-}C. {|≠+kπ,k∈Z }D. {|≠+kπ,k∈Z }[答案]D[解析]由,k∈Z,即≠+kπ,k∈Z,即函数的定义域为{|≠+kπ,k∈Z },故选D.8.方程的解所在的区间为()A. (0,2 )B. (1,2 )C. (2,3 )D. (3,4 )[答案]C[解析]令,则在上单调递增.且,所以方程的解所在的区间为.故选C.9.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则()A. B.C. D.[答案]D[解析]由题意:.本题选择D选项.10.若函数的图象如图所示,其中a,b为常数,则函数的图象大致是( )A. B.C. D.[答案]D[解析]由于函数图像的单调性底数a小于1,则函数也是单调递减,则排除A,B,然后因为的定义域x>-1,则说明b=1,从而过点(0,2),排除C,选D.11.在△ABC中,若A=,cos B=,则sin C等于()A. B. -C. D. -[答案]A[解析]∵cos B=,∴B为锐角,则,则故选A. 12.在△ABC中,点M是BC的中点,AM=1,点P在AM上,且满足AP=2PM,则等于()A. -B. -C.D.[答案]B[解析]∵M是BC的中点,知AM是BC边上的中线,又由点P在AM上且满足,∴P是三角形ABC的重心,∴又∵AM=1,∴,∴.故选:B.二、填空题.13.已知函数,则的值为___.[答案]6[解析]令x-1=2,可得x=3,故f(2)=32-3=6,故答案为6.14.设函数=,若,则x0的取值范围是____.[答案](-∞,-1)∪(3,+∞)[解析]若x02,f(x0)>1即为>1,即>2,可得x0>3,;若,f(x0)>1即为>1,解得x0-1.综上可得,x0的取值范围是即答案为15.=________.[答案][解析]即答案为.16.给出下列命题:①函数=cos(+)是奇函数;②若α,β是第一象限角且α<β,则tanα<tanβ;③=2sin 在区间[-,]上的最小值是-2,最大值是;④=是函数=sin(2+π)的一条对称轴.其中正确命题的序号是________.[答案]①④[解析]①中,函数是奇函数,所以是正确的;②中,若、是第一象限角且,取时,则,所以不正确;③中,在区间上的最小值是,最大值是,所以不正确;④中,当时,函数,所以是函数的一条对称轴是正确的,故选①④.三、解答题(解答应写出文字说明、证明过程或演算步骤)17.已知集合A={|=},B={|<- 4或>2}.(1) 若m= -2, 求A∩(∁R B) ;(2)若A∪B=B,求实数m的取值范围.解:(1)m=-2,A={x|y=}={x|x≤-1},∁R B={x|-4≤x≤2},∴A∩(∁R B)={x|-4≤x≤-1}.(2)若A∪B=B,则A⊆B.∵A={x|x≤1+m},B={x|x<-4或x>2},∴1+m<-4.∴m<-5.18.已知函数.(1)求的值;(2)求的最大值和最小值.解:(1).(2)==,,因为,所以,当时,取最大值6;当时,取最小值. 19.已知向量m=(cos,sin ),n=(2+sin x,2-cos),函数=m·n,x∈R.(1) 求函数的最大值;(2) 若且=1,求的值.解:(1)因为f(x)=m·n=cos x(2+sin x)+sin x·(2-cos x)=2(sin x+cos x)=4sin(x∈R),所以f(x)的最大值是4.(2)因为f(x)=1,所以sin=.又因为x∈,即x+∈.所以cos=-,cos=cos=cos cos-sin sin=-×-×=-. 20.设函数是定义域(0,+∞)上的增函数,且=.(1)求的值;(2)若=1,求不等式的解集.解:(1)令,则.(2)令,即,且,即,由,得;又因为是定义在(0,+∞)上的增函数,所以,即,解得,即的解集为.21.设函数.(1)求函数的最大值及此时x的取值集合;(2)设A,B,C为△ABC的三个内角,已知cos B=,,且C为锐角,求sin A的值.解:(1),时,.此时的取值集合为.(2),,为锐角,,由,.22.已知函数=(1)写出该函数的单调区间;(2)若函数=-m恰有3个不同零点,求实数m的取值范围;(3)若≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.解:(1)函数f(x)的图象如图所示,则函数f(x)的单调递减区间是(0,1),单调递增区间是(-∞,0)及(1,+∞) .(2)作出直线y=m,函数g(x)=f(x)-m恰有3个不同零点等价于直线y=m与函数f(x)的图象恰有三个不同交点.根据函数f(x)=的图象,且f(0)=1,f(1)=,∴m∈.故实数m的取值范围为.(3)∵f(x)≤n2-2bn+1对所有x∈[-1,1]恒成立,∴[f(x)]ma x≤n2-2bn+1,又[f(x)]ma x=f(0)=1,∴n2-2bn+1≥1,即n2-2bn≥0在b∈[-1,1]上恒成立.令h(b)=-2nb+n2,∴h(b)=-2nb+n2在b∈[-1,1]上恒大于等于0.∴即由①得解得n≥0或n≤-2.同理由②得n≤0或n≥2.∴n∈(-∞,-2]∪{0}∪[2,+∞).故n的取值范围是(-∞,-2]∪{0}∪[2,+∞).。
【全国百强校】吉林省2018-2019学年高一上学期期末考试数学试题

吉林省2018-2019学年高一上学期期末考试数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
考试结束后,将答题卡交回。
注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5. 保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷一、选择题:本题共12小题,每小题 5分,共60 分(在每小题给出的四个选项中,只有一项是符合题目要求的)1.的值为()A. B. C. D.2.已知集合,,则()A. B. C. D.3.函数在下列区间一定有零点的是()A. B. C. D.4.下列函数中,与函数相同的是()A. B. C. D.5.下列函数中,在上为减函数的是()A. B. C. D.6.对于函数,下列命题正确的是()A. 周期为的偶函数B. 周期为的奇函数C. 周期为的偶函数D. 周期为的奇函数7.设则()A. B. C. D.8.将函数的图象上所有点向左平移个单位,再将所得的图象的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象对应的解析式是()A. B.C. D.9.已知,,那么的值是()A. B. C. D.10.函数的图象关于原点成中心对称,则等于()A. B. C. D.11.已知是奇函数,且时,,则当时,的表达式是()A. B. C. D.12.已知函数的定义域为,当时,,当时,,当时,,则()A. B. C. D.第Ⅱ卷二、填空题:(本题共4小题,每小题5分,共20分)13.若角的终边经过点,则的值为_____.14.函数且的图象必过定点_______________.15.已知,则______________;16.若函数的定义域为,则函数的定义域为____________.三、解答题:解答应写出文字说明、证明过程或演算步骤。
吉林省辽源市田家炳高级中学2018_2019学年高一数学上学期期末联考试卷理(含解析)

吉林省辽源市田家炳高级中学2018-2019学年高一数学上学期期末联考试卷理(含解析)注意事项:1.答题前,考生必须将自己的姓名、准考证号填写清楚,并将条形码粘贴到指定区域。
2.选择题必须用2B铅笔填涂;非选择题必须用0.5毫米黑色中性笔书写,字体工整,笔迹清楚。
3.按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄皱、弄破,不准使用涂改液,修正带,刮纸刀。
第Ⅰ卷选择题一、选择题:(在每小题给出四个选项中,只有一项是符合题目要求的。
)1.计算cos(-780°)的值是 ( )A. -B. -C.D.【答案】C【解析】【分析】直接利用诱导公式以及特殊角的三角函数求解即可.【详解】cos(-780°)=cos780°=cos60°=.故选:C.【点睛】本题考查余弦函数的应用,三角函数的化简求值,考查计算能力.2.下列函数中,既是奇函数又是增函数的是 ( )A. B. C. D.【答案】B【解析】【分析】根据奇函数定义先判断出奇偶性,然后根据单调性定义判断单调性即可.【详解】A.非奇非偶函数;B.奇函数且是单调递增函数;C.奇函数但在定义域上不是增函数;D. 奇函数,单调递减函数;【点睛】本题主要考查函数的奇偶性和单调性,结合初等函数的奇偶性和单调性判断出原函数的性质,主要考查了推理能力。
3.已知a=(1,1),b=(1,-1),则a-b等于 ( )A. (-1,2)B. (1,-2)C. (-1,-2)D. (1,2)【答案】A【解析】【分析】直接利用向量的坐标运算计算即可.【详解】根据题意可得故选A.【点睛】本题考查向量的坐标运算属基础题.4.已知是幂函数,且在第一象限内是单调递减的,则m的值为( )A. -3B. 2C. -3或2D. 3【答案】A【解析】【分析】根据幂函数的定义判断即可.【详解】由y=(m2+m-5)x m是幂函数,知m2+m-5=1,解得m=2或m=-3.∵该函数在第一象限内是单调递减的,∴m<0.故m=-3.故选:A.【点睛】本题考查了幂函数的定义以及函数的单调性问题,属于基础题.5.若,,,则a,b,c之间的大小关系是()A. c>b>aB. c>a>bC. a>c>bD. b>a>c【答案】C【解析】利用指数函数与对数函数的单调性即可得出.【详解】∵a=22.5>1,<0,,∴a>c>b,故选:C.【点睛】本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.6.要得到函数y=cos的图象,只需将函数y=cos2的图象( )A. 向左平移个单位长度B. 向左平移个单位长度C. 向右平移个单位长度D. 向右平移个单位长度【答案】B【解析】∵,∴要得到函数的图像,只需将函数的图像向左平移个单位.选B.7.函数的定义域为( )A. {|≠}B. {|≠-}C. {|≠+kπ,k∈Z }D. {|≠+kπ,k∈Z }【答案】D【解析】【分析】根据正切函数的定义域可求函数的定义域.【详解】由,k∈Z,即≠+kπ,k∈Z,即函数的定义域为{|≠+kπ,k∈Z }故选D.【点睛】熟练掌握正切函数的定义域是解题的关键..8.方程的解所在的区间为( )A. (0,2 )B. (1,2 )C. (2,3 )D. (3,4 )【答案】C【解析】【分析】判断,则在上单调递增.根据函数的零点存在性定理得出答案.【详解】令,则在上单调递增.且,所以方程的解所在的区间为.故选C.【点睛】本题考查了函数的单调性,函数零点的判断,方程解所在的区间,属于中档题.9.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则( )A. B.C. D.【答案】D【解析】由题意:.本题选择D选项.10.若函数的图象如图所示,其中a,b为常数,则函数的图象大致是( )A. B. C. D.【答案】D【解析】解:由于函数图像的单调性底数a小于1,则函数也是单调递减,则排除A,B,然后因为的定义域x>-1,则说明b=1,从而过点(0,2),排除C,选D。
吉林省辽源市高一上学期期末考试数学试题

吉林省辽源市高一上学期期末考试数学试题姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分) (2019高二下·玉林月考) 若集合,集合,则()A .B .C .D .2. (2分)已知函数f(x)=在R上单调递增,则实数a的取值范围是()A . 0<a≤3B . a≥2C . 2≤a≤3D . 0<a≤2或a≥33. (2分) (2019高一下·吉林期末) 下列命题中正确的是()A .B .C .D .4. (2分) (2018高三上·永春期中) 将函数的图象向左平移个单位,得到函数的图象,则下列说法不正确的是A .B . 在区间上是增函数C . 是图象的一条对称轴D . 是图象的一个对称中心5. (2分)已知实数a,b,c满足 =3,log3b=﹣, c,则实数a,b,c的大小关系为()A . a<b<cB . a<c<bC . c<a<bD . b<c<a6. (2分) (2018高一上·深圳月考) 若函数与图象上存在关于轴对称的点,则的取值范围是()A .B .C .D .7. (2分) (2018高二上·黑龙江期末) 下列说法错误的是()A . “函数为奇函数”是“ ”的充分不必要条件B . 已知三点不共线,若则点是△ 的重心C . 命题“ ,”的否定是:“ ,”D . 命题“若,则”的逆否命题是:“若,则”8. (2分)(2017·武邑模拟) 已知函数f(x)= (ω>0,|φ|<,a∈R)在区间[﹣3,3]上的图象如图所示,则可取()A . 4πB . 2πC . πD .9. (2分) (2016高一上·嘉兴期末) 如图,在等腰直角三角形ABC中,AB=AC= ,D,E是线段BC上的点,且DE= BC,则的取值范围是()A .B .C .D .10. (2分) (2020高二下·长沙期末) 已知函数,则函数的图象可能是()A .B .C .D .二、填空题 (共7题;共7分)11. (1分) (2019高一上·如东月考) 计算: =________12. (1分) (2019高一上·大庆期中) 函数的单调增区间是________;13. (1分)已知函数,若函数g(x)=f(x)﹣m有3个零点,则实数m的取值范围是________14. (1分) (2020高一上·柳州期末) 在梯形中,已知,,,,,则 ________.15. (1分)已知函数f(x)=lnx+ ,对任意x1 ,x2∈[1,2],x1≠x2 ,都有<﹣1,则实数b的取值范围是________.16. (1分) (2020高二上·六安开学考) 已知,角的终边上有一点,则________.17. (1分) (2019高一上·宁波期中) 已知,则 ________, ________.三、解答题 (共5题;共35分)18. (10分) (2019高一上·包头月考) 已知不等式的解集为A,不等式的解集为B.(1)求A∩B;(2)若不等式的解集为A∩B,求的值.19. (10分)化简求值(1)计算﹣cos π•tan(﹣π).(2)已知tan α= ,求下列各式的值:① ;②sin αcos α.20. (5分) (2020高三上·湖北月考) 将函数的图象向左平移个单位长度,再将所得图象各点的横坐标变为原来的2倍,纵坐标不变,得到函数的图象.已知的部分图象如图所示,且.(1)求的解析式;(2)设函数,求在上的值域.21. (5分)设不等式log3x<0的解集为M.(1)求集合M;(2)若a,b∈M,试比较ab+1与a+b的大小.22. (5分)(2017·江西模拟) 已知函数f(x)=ln(x+2a)﹣ax,a>0.(Ⅰ)求f(x)的单调区间;(Ⅱ)记f(x)的最大值为M(a),若a2>a1>0且M(a1)=M(a2),求证:;(Ⅲ)若a>2,记集合{x|f(x)=0}中的最小元素为x0 ,设函数g(x)=|f(x)|+x,求证:x0是g(x)的极小值点.参考答案一、单选题 (共10题;共20分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:二、填空题 (共7题;共7分)答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:答案:17-1、考点:解析:三、解答题 (共5题;共35分)答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、考点:解析:考点:解析:。
吉林省辽源一中2018_2019学年高一数学上学期期末考试试题

2018-2019学年上学期高一期末考试数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2018·五省联考]已知全集U =R ,则下列能正确表示集合{}0,1,2M =和{}220N x x x +==关系的韦恩(Venn )图是( )A .B .C .D .2.[2018·三明期中]已知函数()lg ,011,0x x f x x x >⎧=⎨+≤⎩,则()()1f f -=( )A .2-B .0C .1D .1-3.[2018·重庆八中]下列函数中,既是偶函数,又在(),0-∞内单调递增的为( ) A .22y x x =+B .2xy =C .22x xy -=-D .12log 1y x =-4.[2018·大庆实验中学]已知函数()32x f x a x=--的一个零点在区间()1,3内,则实数a 的取值范围是( ) A .51,2⎛⎫- ⎪⎝⎭B .5,72⎛⎫⎪⎝⎭C .()1,7-D .()1,-+∞5.[2018·金山中学]某三棱锥的三视图如图所示,则该三棱锥的各个面中,最大的面积是( )A .62B .22C .1D .646.[2018·黄山八校联考]若m ,n 是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )A .若αβ⊥,m β⊥,则//m αB .若//m α,n m ⊥,则n α⊥C .若//m α,//n α,m β⊂,n β⊂,则//αβD .若//m β,m α⊂,n αβ=I ,则//m n7.[2018·宿州期中]已知直线1:30l mx y -+=与211:22l y x =-+垂直,则m =( ) A .12-B .12C .2-D .28.[2018·合肥九中]直线l 过点()0,2,被圆22:4690C x y x y +--+=截得的弦长为23,则直线l 的方程是( )A .423y x =+ B .123y x =-+ C .2y =D .423y x =+或2y = 9.[2018·南宁模拟]如图,棱长为a 的正方体1111ABCD A B C D -中,M 为BC 中点,这直线1D M 与平面ABCD 所成角的正切值为( )此卷只装订不密封 班级 姓名 准考证号 考场号 座位号A .32B .55C .255D .1210.[2018·东城期末]已知圆22:4C x y +=,直线():l x y m m +=∈R ,设圆C 上到直线l 的距离为1的点的个数为S ,当032m ≤<时,则S 的可能取值共有( ) A .2种B .3种C .4种D .5种11.[2018·云天化中学]如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E 、F ,且12EF =.则下列结论中正确的个数.....为( )①AC BE ⊥; ②EF ∥平面ABCD ;③三棱锥A BEF -的体积为定值; ④AEF △的面积与BEF △的面积相等. A .1B .2C .3D .412.[2018·湛江调研]点A 、B 、C 、D 在同一个球的球面上,3AB BC AC ===, 若四面体ABCD 体积的最大值为3,则这个球的表面积为( ) A .169π16B .289π16C .25π16D .8π第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2018·华东师大附中]已知()214f x x +=-,则()f x 的解析式为__________.14.[2018·嘉兴三中]已知点()2,1A ,()2,3B -,()0,1C ,则ABC △中,BC 边上中线所在的直线方程为________.15.[2018·赣州期中]设某几何体的三视图如图所示,则该几何体的表面积是__________.主视图 左视图 俯视图16.[2018·嘉兴一中]若函数()224422f x x ax a a =-+-+在区间[]0,2上有两个零点,则实数a 的取值范围是_______.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(10分)[2018·安庆期中]设全集{}1,2,3,4,5,6U =,A ,B 都是U 的子集,{}1,2A =,(){}4,6UA B =Ið,(1)写出所有符合题意的集合B ; (2)计算:341lg2lg 3lg5log 2log 94-+-⋅.18.(12分)[2018宜昌期中·]设a 是实数,()2221x xa a f x ⋅+-=+, (1)证明:()f x 是增函数;(2)试确定a 的值,使()f x 为奇函数.19.(12分)[2018·华安一中]已知点()2,3A ,()4,1B ,ABC △是以AB 为底边的等腰 三角形,点C 在直线:220l x y -+=上.(1)求AB 边上的高CE 所在直线的方程;(结果写成直线方程的一般式) (2)求ABC △的面积.20.(12分)[2018·定远月考]如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x 的内接圆柱.(1)试用x 表示圆柱的高;(2)当x 为何值时,圆柱的侧面积最大,最大侧面积是多少?21.(12分)[2018·泸化中学]如图,四棱锥P ABCD -中,底面ABCD 是矩形,22AB AD ==,PD ⊥底面ABCD ,E ,F 分别为棱AB ,PC 的中点.(1)求证:EF ∥平面PAD ; (2)求证:平面PDE ⊥平面PEC .22.(12分)[2018·陕西四校联考]如图,直三棱柱111ABC A B C -的所有棱长都是2,D ,E 分别是AC ,1CC 的中点.(1)求证:AE ⊥平面1A BD ;(2)求三棱锥11B A BD -的体积.2018-2019学年上学期高一期末考试数学答案第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】A【解析】N 为220x x +=的解集,解220x x +=可得,0x =或2-,则{}2,0N =-,{}0M N =≠∅I ,由选项中的Venn 图可得选项A 符合题意,故选A . 2.【答案】C【解析】由题意得()111110f -=-+=,∴()()()110lg101f f f -===.故选C .3.【答案】D【解析】根据奇偶性的定义知A 即不是奇函数也不是偶函数,C 是奇函数,B 、D 是偶函数,在(),0-∞上B 是减函数,D 是增函数.故选D . 4.【答案】C【解析】函数()32x f x a x=--是增函数,且一个零点在区间()1,3内,根据零点存在 定理得到()()1030f f <>⎧⎪⎨⎪⎩解得a 的范围是()1,7-.故答案为C .5.【答案】A【解析】画出直观图如下图所示,计算各面的面积为122122ABC S =⨯⨯=△,12112ABD BCD S S ==⨯⨯=△△,16232ACD S =⨯⨯=△,故最大面积为6,所以选A .6.【答案】D【解析】对于A ,若αβ⊥,m β⊥,则//m α或m α⊂,故A 错误; 对于B ,若//m α,n m ⊥,则n α⊥或n α⊂或n 与α相交,故B 错误; 对于C ,若//m α,//n α,m β⊂,n β⊂,则//αβ或α、β相交,故C 错误; 对于D ,若//m β,m α⊂,n αβ=I ,由线面平行的性质定理,可得//m n , 故D 正确,故选D . 7.【答案】D【解析】很明显直线的斜率存在,直线方程即3y mx =+,1122y x =-+, 由直线垂直的充分必要条件可得:112m -⨯=-,解得2m =.本题选择D 选项. 8.【答案】D【解析】因为直线l 被圆22:4690C x y x y +--+=,()()22234x y -+-=截得的弦长为3()2431-=,设直线l 的方程为2y kx =+,(斜率不存在时不满足题意)223211k k -+=+,0k ∴=或43k =,即直线l 的方程是423y x =+或2y =,故选D . 9.【答案】C【解析】连接DM ,因为几何体是正方体,所以1D MD ∠就是直线1D M 与平面ABCD 所成角,1125tan 5DD D MD DM a∠===,故选C . 10.【答案】B【解析】因为圆C 上到直线l [)0,32m ,12m =时,圆C 上到直线l 的距离为1的点的个数为3;()1,32m 时,圆C 上到直线l 的距离为1的点的个数为2;[)0,12m 时,圆C 上到直线l 的距离为1的点的个数为4;因此S 的可能取值共有3种,故选B .11.【答案】C【解析】连结BD ,则AC ⊥平面11BB D D ,11BD B D ∥.AC BE ∴⊥,EF ∥平面ABCD ,从而①②正确,又BEF △面积为定值,A 到平面11BB D D 距离为定值,所以三棱锥A BEF -的体积为定值,从而③正确,因为A 到11B D 的距离不等于1BB .所以AEF △的面积与BEF △的面积不相等,④错误. 故选C . 12.【答案】B【解析】根据题意知,ABC △是一个等边三角形,其面积为334,外接圆的半径为1,小圆的圆心为Q ,由于底面积ABC S △不变,高最大时体积最大,所以DQ 与面ABC 垂直时体积最大,最大值为133ABC S DQ ⨯=△,∴4DQ =,设球心为O ,半径为R ,则在直角AQO △中,222OA AQ OQ =+, 即()22214R R =+-,∴178R =, 则这个球的表面积为217289π4π816S ⎛⎫== ⎪⎝⎭,故选B .第Ⅱ卷二、填空题:本大题共4小题,每小题5分. 13.【答案】()223f x x x =--【解析】因为()214f x x +=-,∴令1x t +=,则1x t =-,()()()2211423f x f t t t t ∴+==--=--,∴函数()f x 的解析式为()223f x x x =--,故答案为()223f x x x =--.14.【答案】350x y +-=【解析】设BC 中点为(),D x y ,已知()2,3B -,()0,1C ,则()1,2D -, 因为()121213AD k -==---,所以BC 边上中线所在的直线方程为350x y +-=.15.【答案】36【解析】由几何体的三视图可知,该几何体是一个长、宽、高分别为4,2,2的长方体截去一个三棱锥1D ACD -后剩下的部分(如图所示).∵1AD C △的三边长分别分225511223262AD C S =⨯=△. 故该几何体的表面积111422242424222636222S =⨯+⨯+⨯+⨯⨯+⨯⨯+⨯⨯+=.16.【答案】(1,57-【解析】由题意,要使函数()224422f x x ax a a =-+-+在区间[]0,2上有两个零点,只要()()002002202f f a a f ≥≥<<⎛⎧⎪⎪⎪⎨⎫< ⎪⎝⎭⎪⎪⎪⎩,即2222010180022220a a a a a a -+≥-+≥<⎧⎪⎪⎪<⎨-+<⎪⎪⎪⎩,解得(1,57a ∈,故答案为(1,57. 三、解答题:解答应写出文字说明、证明过程或演算步骤. 17.【答案】(1){}4,6,{}1,4,6,{}2,4,6,{}1,2,4,6;(2)2. 【解析】(1)集合B 为{}4,6,{}1,4,6,{}2,4,6,{}1,2,4,6. (2)341lg2lg3lg5log 2log 94-+-⋅ 232lg 2lg 23lg 5log 2log 3-=-+-⋅lg22lg23lg51=++-()3lg2lg51=+-3lg101=-312=-=.18.【答案】(1)见解析;(2)1.【解析】(1)证明:设1x 、2x ∈R 且12x x <,()()()()()121212122222*********x x x x x x f x f x a a -⎛⎫⎛⎫-=---= ⎪ ⎪++++⎝⎭⎝⎭, 又由2xy =在R 上为增函数,则120x>,220x >,由12x x <,可得12220x x-<,则()()120f x f x -<,故()f x 为增函数,与a 的值无关,即对于任意a ,()f x 在R 为增函数. (2)若()f x 为奇函数,且其定义域为R ,必有有()()f x f x -=-,即222121x x a a -⎛⎫-=-- ⎪++⎝⎭,变形可得()2212221x xa +==+, 解可得,1a =,即当1a =时,()f x 为奇函数. 19.【答案】(1)10x y --=;(2)2. 【解析】(1)由题意可知,E 为AB 的中点,13142AB k -==--, ∴()3,2E ,且11CE ABk k =-=,∴CE 所在直线方程为23y x -=-,即10x y --=. (2)由22010x y x y -+=--=⎧⎨⎩,得43x y =⎧⎨⎩=,∴()4,3C ,∴2AC BC ==,22AB =,∴AC BC ⊥,∴122ABC S AC BC =⋅=△.20.【答案】(1)33h x =-;(2)当12x =时,它的侧面积最大为3π2.【解析】(1)设所求的圆柱的底面半径为x ,它的轴截面如图,1BO =,3PO =,圆柱的高为h ,由图,得313x h-=,即33h x =-. (2)∵()()22π2π336πS hx x x x x =-=-=圆柱侧,当12x =时,圆柱的侧面积取得最大值为3π2. ∴当圆柱的底面半径为12时,它的侧面积最大为3π2.21.【答案】(1)见解析;(2)见解析.【解析】(1)证明:如图,取PD 的中点G ,连接AG ,FG . 因为F ,G 分别是PC ,PD 的中点,所以GF DC ∥,且12GF DC =. 又E 是AB 的中点,所以AE DC ∥,且12AE DC =, 所以GF AE ∥,且GF AE =,所以四边形AEFG 是平行四边形,故EF AG ∥.又AG ⊂平面PAD ,EF ⊄平面PAD ,所以EF ∥平面PAD .(2)因为PD ⊥底面ABCD ,CE ⊂底面ABCD ,所以CE PD ⊥. 因为四边形ABCD 是矩形,且2AB AD =,所以AD AE =,BC BE =,所以45AED BEC ∠=∠=︒,DE CE ⊥.又PD DE D =I ,PD ⊂平面PDE ,DE ⊂平面PDE ,所以CE ⊥平面PDE , 又CE ⊂平面PEC ,所以平面PDE ⊥平面PEC . 22.【答案】(1)见解析;(2)33. 【解析】(1)∵AB BC CA ==,D 是AC 的中点,∴BD AC ⊥,∵直三棱柱111ABC A B C -中1AA ⊥平面ABC ,∴平面11AA C C ⊥平面ABC , ∴BD ⊥平面11AAC C ,∴BD AE ⊥.又∵在正方形11AAC C 中,D ,E 分别是AC ,1CC 的中点,∴1A D AE ⊥. 又1A D BD D =I ,∴AE ⊥平面1A BD . (2)连结1AB 交1A B 于O ,∵O 为1AB 的中点,∴点1B 到平面1A BD 的距离等于点A 到平面1A BD 的距离. ∴1111111132133323B A BD A A BD B AA D AA D V V V S BD ---===⨯⨯=⨯⨯⨯=△.。
吉林省吉林市第一中学2018-2019学年高一上学期期末考试数学(理)试题(精品解析)

吉林一中2018-2019学年度上学期期末考试高一数学(理科)试卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,集合,则()A. B. C. D.【答案】B【解析】【分析】解出集合Q的元素,由集合的交集运算得到结果.【详解】集合,集合,则.故答案为:B.【点睛】这个题目考查了集合的交集的运算,题目简单.2.下列各组函数是同一函数的是()A. ,B. ,C. ,D. ,【答案】D【解析】【分析】依次判断函数的定义域和对应法法则,判断是否为同一函数.【详解】对于A定义域是R,定义内不包含x=0,故不是同一函数;对于B,,x的取值范围是,中x的取值范围是;对于C,,中x的范围是,中x的范围是,故不为同一函数;D. ,定义域和对应法则相同,故是同一函数.故答案为:D.【点睛】本题考查同一函数的判断与应用,是基础题.判断函数是否为同一函数主要看两个函数定义域和对应法则,值域是否相同.解题时要认真审题,仔细解答.3.函数与的图象交点的横坐标所在区间为()A. B. C. D.【答案】B【解析】【分析】该问题可转化为方程ln(x+1)=的解的问题,进一步可转化为函数f(x)=ln(x+1)﹣的零点问题.【详解】令f(x)=ln(x+1)﹣,是增函数,∵f(2)=ln3﹣f(1)=ln2﹣1<lne﹣1=0,又函数f(x)在(1,2)上的图象是一条连续不断的曲线,∴函数f(x)在区间(1,2)内有零点,即ln(x+1)=有解,此解即为函数y=ln(x+1)与y=的图象交点的横坐标.故选:B.【点睛】本题考查函数零点的存在问题,本题中函数y=ln(x+1)与y=的图象交点的横坐标,可转化为函数f(x)=ln(x+1)﹣的零点.注意函数与方程思想、转化与化归思想的运用.4.函数的图象的大致形状是()A. B. C. D.【答案】B【解析】【分析】根据指数函数的图象和性质,当a>1时,x>0时,为增函数,排除C,D,再讨论x<0的单调性,即可得到答案.【详解】当x>0时,y=a x,因为a>1,所以是增函数,排除C、D,当x<0时,y=-a x,是减函数,所以排除A.故选:B.【点睛】本题考查了指数函数的图象和性质,需要分类讨论,去绝对值,属于基础题.5.,为两个不同的平面,,为两条不同的直线,下列命题中正确的是()①若,,则;②若,,则;③若,,,则④若,,,则.A. ①③B. ①④C. ②③D. ②④【答案】B【解析】【分析】在①中,由面面平行的性质定理得m∥β;在②中,m与n平行或异面;在③中,m与β相交、平行或m⊂β;在④中,由n⊥α,m⊥α,得m∥n,由n⊥β,得m⊥β.【详解】由α,β为两个不同的平面,m,n为两条不同的直线,知:在①中,若α∥β,m⊂α,则由面面平行的性质定理得m∥β,故①正确;在②中,若m∥α,n⊂α,则m与n平行或异面,故②错误;在③中,若α⊥β,α∩β=n,m⊥n,则m与β相交、平行或m⊂β,故③错误;在④中,若n⊥α,m⊥α,则m∥n,由n⊥β,得m⊥β,故④正确.故选:B.【点睛】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力、推理论证能力,考查化归与转化思想,是中档题.6.如图为某几何体的三视图,则该几何体的表面积为()A. B. C. D.【答案】B【解析】该几何体是一个正方体与半圆柱的组合体,表面积为,故选B.7. 点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为()A. 30°B. 45°C. 60°D. 90°【答案】C【解析】分别取AC.PC中点O.E.连OE,DE;则OE//PA,所以(或其补角)就是PA与BD所成的角;因PD⊥平面ABCD,所以PD⊥DC,PD⊥AD.设正方形ABCD边长为2,则PA=PC=BD=所以OD=OE=DE=,是正三角形。
吉林省辽源一中2019届上学期高三期末考试理数学含答案

2019届上学期高三期末理数学一、单项选择题每题5分 1.[2018·攀枝花统考]已知集合,,则集合( )A .B .C .D .2.[2018·南宁三中]复数满足,则( ) A .B .C .D .3.[2018·青岛调研]如图,在正方体中,为棱的中点,用过点,,的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )A .B .C .D .4.[2018·佛山调研]已知,则( )A .B .C .或1D .15.[2018·枣庄二模]若的展开式中的系数为,则( ) A .B .C .D .6.[2018·中山一中]函数的单调递增区间是( ) A ., B ., C ., D ., 7.[2018·山师附中]函数是上的偶函数,且,若在上单调递减,则函数在上是( ) A .增函数B .减函数C .先增后减的函数D .先减后增的函数8.[2018·棠湖中学]已知两点,,若曲线上存在点,使得,则正实数的取值范围为( )A .B .C .D .9.[2018·优创名校]函数的图象大致为( ) A . B .C .D .10.[2018·南海中学]已知双曲线的右焦点为,点在双曲线的渐近线上,是边长为2的等边三角形(为原点),则双曲线的方程为( )A .B .C .D .11.[2018·黄陵中学]在中,角,,所对的边分别为,,,已知,,,则( ){}12A x x =-<<(){}30B x x x =->AB ={}13x x -<<{}23x x x <>或{}02x x <<{}03x x x <>或z ()12i 3iz +=+z =1i 5+1i -1i 5-1i +1111ABCD A B C D -E 1BB A E 1C tan 2a =2sin 2cos a a +=3535-35-()1021x a x x ⎛⎫-+ ⎪⎝⎭6x 30a =12-2-122()πtan 26x f x ⎛⎫=- ⎪⎝⎭2π4π2π,2π33k k ⎡⎤-+⎢⎥⎣⎦k ∈Z 2π4π2π,2π33k k ⎛⎫-+ ⎪⎝⎭k ∈Z 2π4π4π,4π33k k ⎡⎤-+⎢⎥⎣⎦k ∈Z 2π4π4π,4π33k k ⎛⎫-+ ⎪⎝⎭k ∈Z ()f x R ()()1f x f x +=-()f x []1,0-()f x []3,5(),0A a ()(),00B a a ->22230x y y +--+=P 90APB ∠=︒a (]0,3[]1,2[]2,3[]1,3()211ln 22f x x x =+-()222210,0x y a b a b -=>>F A OAF △O 2213x y -=2213y x -=221412x y -=221124x y -=ABC △A B C a bc a=c =tan 21tan A cB b +=C ∠=πππ3ππ12.[2018·开封月考]已知空间四边形,,,且平面平面,则空间四边形的外接球的表面积为( ) A .B .C .D .第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2018·南康模拟]已知单位向量,的夹角为,则________.14.[2018·曲靖统测]随机变量服从正态分布,若,则__________.15.[2018·高新区月考]若实数,满足不等式组,则的取值范围是__________.16.[2018·盐城期中]已知函数,,,,使,则实数的取值范围是__________.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.17.(12分)[2018·华侨中学]已知数列的前项和为,且.(1)求数列的通项公式; (2)求数列的前项和.18.(12分)[2018·唐山摸底]甲、乙两位工人分别用两种不同工艺生产同一种零件,已知尺寸在(单位:)内的零件为一等品,其余为二等品,测量甲乙当天生产零件尺寸的茎叶(1)从甲、乙两位工人当天所生产的零件中各随机抽取1个零件,求抽取的2个零件等级互不相同的概率;(2)从工人甲当天生产的零件中随机抽取3个零件,记这3个零件中一等品数量为,求的分布列和数学期望.19.(12分)[2018·长沙一中]在边长为的菱形中,,点,分别是边,的中点,,沿将翻折到,连接,,,得到如图的五棱锥,且(1)求证:平面平面;(2)求直线与平面所成的角的正弦值.ABCD 2π3BAC ∠=AB AC ==6BD CD ==ABC ⊥BCD ABCD 60π36π24π12πa b 60︒()()23+⋅-=a b a b ξ()2,N ξμσ~()20241P μξμ-<≤=.()2P ξμ>+=x y 00220y x y x y ≥⎧⎪-≥⎨⎪--≥⎩11y w x -=+()2221f x x ax a =-+-()2g x x a=-[]11,1x ∀∈-[]21,1x ∃∈-()()21f x g x =a {}n a n n S 22n S n n =+{}n a11n n a a+⎧⎫⎨⎬⎩⎭n n T []223,228mm 4ABCD 60DAB ∠=︒E F CD CB ACEF O =EF CEF △PEF △PA PB PD PB =PEF ⊥POA PE PAB20.(12分)[2018·成都实验中学]已知椭圆的中心在原点,焦点在轴上,焦距为,离心率为.(1)求椭圆的方程;(2)设直线经过点,且与椭圆交于,两点,若,求直线的方程.21.(12分)[2018·大庆实验中学]设函数.(1)当时,求函数的极值.(2)若函数在区间上有唯一的零点,求实数的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】[2018·南昌模拟]在平面直角坐标系中,直线的参数方程为(为参数).以原点为CxCL()0,1M C A B2AM MB=L()21ln22xf x a x=--1a=()f x()f x[]1,e ax yO l212x ty t=+⎧⎨=+⎩t极点,轴正半轴为极轴建立极坐标系,的极坐标方程为.(1)求的参数方程; (2)求直线被截得的弦长.23.(10分)【选修4-5:不等式选讲】 [2018·安康中学]已知函数.(1)解不等式;(2)设函数的最小值为,若,均为正数,且,求的最小值.x C 24sin 120ρρθ--=C l C ()11f x x x =-++()2f x ≤()f x m a b 14m a b +=a b +2018-2019学年上学期高三期末考试理科数学答案第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】B 【解析】集合,∵,∴,故选B .2.【答案】D【解析】∵,∴,∴.故选D .3.【答案】C【解析】取中点,连接,.平面为截面.如下图:∴故选C . 4.【答案】D【解析】∵, 又∵,∴.故选D .5.【答案】D【解析】由题意二项式的展开式为,展开式的为,∴, 解得,故选D . (){}{}3003B x x x x x x =->=<>或{}12A x x =-<<{}23A B x x x =<>或()12i 3iz +=+()()()()3i 12i 3i55i 1i 12i 12i 12i 5z +-+-====-++-z 1i =+1DD FAF 1C F 1AFC E 222222sin cos cos 2tan 1sin 2cos sin cos tan 1ααααααααα+++==++tan 2a =22221sin 2cos 121αα⨯++==+101x x ⎛⎫+ ⎪⎝⎭10102110101C C rr r r rr T x x x --+⎛⎫== ⎪⎝⎭6x ()2342632610101010C C C C x x a x a x -⋅=-⋅321010C C 30a -⋅=2a =6.【答案】B【解析】由题意,函数, 令,,解得,, 即函数单调递增区间是,,故选B . 7.【答案】D 【解析】已知,则函数周期,∵函数是上的偶函数,在上单调递减,∴函数在上单调递增,即函数在先减后增的函数.故选D .8.【答案】D【解析】∵,∴点在圆,又点还在圆,故,解不等式有,故选D .9.【答案】C 【解析】由,得为偶数,图象关于轴对称,排除;,排除;,排除,故选C .10.【答案】B【解析】双曲线的右焦点为,点在双曲线的渐近线上,是边长为2的等边三角形(为原点), 可得,,,解得,双曲线的焦点坐标在轴,所得双曲线的方程为,故选B .11.【答案】B()πtan 26x f x ⎛⎫=- ⎪⎝⎭πππππ2262x k k -+<-<+k ∈Z 2π4π2π2π33k x k -<<+k ∈Z ()f x 2π4π2π,2π33k k ⎛⎫-+ ⎪⎝⎭k ∈Z ()()1f x f x +=-2T =()f x R []1,0-()f x []0,1[]3,590APB ∠=︒P 222x y a +=P (()2211x y -+-=121a a -≤≤+13a ≤≤()()f x f x -=()f x y D 21310e 22ef ⎛⎫=-+< ⎪⎝⎭A ()211e e 022f =+>B ()222210,0x y a b a b -=>>F A OAF△O 2c =b a =223b a =2223c a a -=1a =b =x 2213y x -=【解析】利用正弦定理,同角三角函数关系,原式可化为:,去分母移项得:,∴,∴.由同角三角函数得:,由正弦定理,解得,∴或(舍).故选B . 12.【答案】A【解析】由余弦定理得,∴,由正弦定理得,∴的外接圆半径为.设外接球的球心为,半径为,球心到底面的距离为,设三角形的外接圆圆心为,的中点为,过点作, 连接,,. 在直角中,(1),在直角中,(2),解(1)(2)得.∴外接球的表面积为.故选A .第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.【答案】 【解析】,,,故答案为.14.【答案】 【解析】∵,∴..故答案为. 15.【答案】 sin cos 2sin 1cos sin sin A B CA B B +=sin cos sin cos 2sin cos B A A B C A +=()sin sin 2sin cos A B C C A+==1cos 2A =sin A =sin sin a c A C =sin C =π4C ∠=3π42112122362BC ⎛⎫=+-⋅-= ⎪⎝⎭6BC =62sin120r=︒r =ABC O R h ABC E BC F O OG DF ⊥DO BE OE OBE △(222R h =+DOG △()22R h=+h =R =4π60π=72-1==a b 111122⋅=⨯⨯=a b ()()2257232532322+⋅-=--=--=-a b a b a ab b 72-0.259()2,N ξμσ~()()221220.518P P μμξμ+=--<≤=()20.259P ξμ>+=0.2591,12⎡⎫-⎪⎢⎣⎭【解析】∵实数,满足,对应的平面区域如图所示:则表示可行域内的点到的两点的连线斜率的范围, 由图可知的取值范围为. 16.【答案】 【解析】,,使,即的值域是的子集,,,,当时,,即,,解得;当时,,即,,不等式组无解; 当时,,即,,不等式组无解;当时,,即,,不等式组无解; 综上所述,的范围为.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.17.【答案】(1);(2).【解析】(1)当时,;当时,.当时,也符合上式, x y 00220y x y x y ≥⎧⎪-≥⎨⎪--≥⎩11y w x -=+(),x y ()1,1-11y w x -=+1,12⎡⎫-⎪⎢⎣⎭[]2,1--[]11,1x ∀∈-[]21,1x ∃∈-()()21f x g x =()g x ()f x ()[]2,2g x a a ---∈()2221f x x ax a =-+-[]1,1x ∈-1a ≤-()222,2f x a a a a ⎡⎤∈+-⎣⎦222a a a +≤--222a a a -≤-[]2,1a ∈--10a -<≤()21,2f x a a ⎡⎤∈--⎣⎦12a -≤--222a a a -≤-01a <≤()21,2f x a a +⎡⎤∈-⎣⎦12a -≤--222a a a ≤+-1a >()222,2f x a a a a ⎡⎤∈-+⎣⎦222a a a -≤--222a a a -≤+a []2,1--()21n a n n *=+∈N ()323nn +1n =113a S ==2n ≥()()221212121n n n a S S n n n n n -⎡⎤=-=+--+-=+⎣⎦1n =故.(2)∵,故.18.【答案】(1);(2).【解析】(1)由茎叶图可知,甲当天生产了10个零件,其中4个一等品,6个二等品;乙当天生产了10个零件,其中5个一等品,5个二等品,∴抽取的2个零件等级互不相同的概率;(2)X 可取0,1,2,3. ,,,,的分布列为∴随机变量的期望. 19.【答案】(1)证明见解析;(2).【解析】(1)∵点,分别是边,的中点,∴, ∵菱形的对角线互相垂直,∴,,,, ∵平面,平面,,∴平面,又∵平面,∴平面平面. (2)设,连接,∵,∴为等边三角形,∴,,在中,中,,()21n a n n *=+∈N ()()111111212322123n n a a n n n n +⎛⎫==- ⎪++++⎝⎭()11111111112355721232323323n n T n n n n ⎛⎫⎛⎫=-+-+⋯+-=-= ⎪ ⎪++++⎝⎭⎝⎭12654565110102P ⨯+⨯==⨯()0346310C C 106C P X ===()1246310C C 112C P X ===()2146310C C 3210C P X ===()3046310C C 1330C P X ===X X ()01236210305E X =⨯+⨯+⨯+⨯=E F CD CB BDEF ∥ABCD BD AC ⊥EF AC ⊥EF AO ⊥EF PO ⊥AO ⊂PAO PO ⊂PAO AOPO O =EF ⊥PAO EF ⊂PEF PEF ⊥POA AOBD H =BO 60DAB ∠=︒ABD △4BD =2BH =HA =HO PO ==Rt BHO △BO ==PBO △22210BO PO PB +==∴,∴,,∴平面,以为原点,,,所在直线分别为,,轴,建立空间直角坐标系,则,,,,∴,,,设平面的一个法向量为,由,得, 令,得,设直线与平面所成的角为, 则.20.【答案】(1);(2). 【解析】(1)设椭圆方程为,∵,∴,,所求椭圆方程为.(2)由题得直线的斜率存在,设直线方程为, 则由得,且.PO BO ⊥PO EF ⊥EF BO O =PO ⊥BFED O OF AO OP x y z O xyz -()0,A -()2,B (P ()1,0,0E -(AP =()2,AB =(1,0,PE =-PAB (),,x y z =n n AP ⊥n AB ⊥020x ⎧=⎪⎨+=⎪⎩1y =()3=-n PE PAB θsin cos PE PE PE θ⋅=⋅===n n n221164x y +=1y =+()222210x y a b a b +=>>c =c e a ==4a =2b =221164x y +=L L 1y kx =+2211164y kx x y =+⎧⎪⎨+=⎪⎩()22148120k x kx ++-=0∆>设,,则由,得,又,,∴,,消去解得,, ∴直线的方程为. 21.【答案】(1)极小值为,无极大值;(2). 【解析】(1)时,函数的定义域为, ,令解得或(舍)时,,单调递减;时,,单调递增 列表如下∴时,函数的极小值为,函数无极大值.(2),其中, 当时,恒成立,单调递增, 又∵,∴函数在区间上有唯一的零点,符合题意. 当时,恒成立,单调递减, 又∵,∴函数在区间上有唯一的零点,符合题意. 当时,时,,单调递减,又∵,∴函数在区间上有唯一的零点;时,,单调递增,()11,A x y ()22,B x y 2AM MB =122x x =-122814k x x k +=-+1221214x x k =-+22814k x k --+=22212214x k --+=2x 2320k =k =L 1y =+02e 112x a a ⎧⎫-⎪⎪≤>⎨⎬⎪⎪⎩⎭或1a =()21ln 22x f x x =--()0,+∞()211x f x x x x -'=-=()0f x '=1x =1x =-01x <<()0f x '<()f x 1x >()0f x '>()f x 1x =()2a x a f x x x x -'=-=[]1,e x ∈1a ≤()0f x '≥()f x ()10f =()f x []1,e 2e a ≥()0f x '≤()f x ()10f =()f x []1,e 21e a <<1x ≤()0f x '<()f x ()10f =()f x ⎡⎣e x ≤()0f x '>()f x又∵,∴当时符合题意,即,∴时,函数在区间上有唯一的零点; ∴的取值范围是. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.【答案】(1)的参数方程为(为参数);(2)【解析】(1)∵的极坐标方程为,∴的直角坐标方程为,即, ∴的参数方程为(为参数).(2)∵直线的参数方程为(为参数),∴直线的普通方程为,∴圆心到直线的距离,∴直线被截得的弦长为23.【答案】(1);(2).【解析】(1)∵, ∴或或,∴,∴不等式解集为; (2)∵,∴, 又,,,∴,∴, 0f <()e 0f <2e 1022a --<2e 12a ->()f x ⎡⎣a 2e 112x a a ⎧⎫-⎪⎪≤>⎨⎬⎪⎪⎩⎭或C 4cos 24sin x y θθ=⎧⎨=+⎩θC 24sin 120ρρθ--=C 224120x y y +--=()22216x y +-=C 4cos 24sin x y θθ=⎧⎨=+⎩θl 212x t y t =+⎧⎨=+⎩t l 230x y --=l d ==l C =[]1,1-92()212,112,1x x f x x x x -≤-⎧⎪=-<≤⎨⎪>⎩,122x x ≤-⎧⎨-≤⎩1122x -<≤⎧⎨≤⎩122x x >⎧⎨≤⎩11x -≤≤[]1,1-()()11112x x x x -++≥--+=2m =142a b +=0a >0b >1212a b +=()125259222222a b a b a b a b b a ⎛⎫+=++=++≥+= ⎪⎝⎭当且仅当,即时取等号,∴.1422a b b a ⎧+=⎪⎨⎪=⎩323a b ⎧=⎪⎨⎪=⎩()min 92a b +=。
吉林省辽源市2019年高一上学期数学期末考试试卷A卷

吉林省辽源市2019年高一上学期数学期末考试试卷A卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)集合U={1,2,3,4,5,6},S={1,4,5},T={2,3,4},则S∩(∁UT)等于()A . {1,4,5,6}B . {1,5}C . {4}D . {1,2,3,4,5}2. (2分) (2016高二上·铜陵期中) 若直线过点P(11,1)且在两坐标轴上的截距相等,则这样的直线有()A . 1条B . 2条C . 3条D . 以上都有可能3. (2分)函数的定义域为()A .B .C .D .4. (2分)若,则当x>1时,a、b、c的大小关系是()A .B .C .D .5. (2分)如果直线l沿x轴负方向平移3个单位再沿y轴正方向平移1个单位后,又回到原来的位置,那么直线l的斜率是()A .B . -3C .D . 36. (2分)已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是()A .B .C .D .7. (2分) (2016高一上·潍坊期末) 已知函数f(x)=(x﹣a)(x﹣b)(其中a>b)的图象如图所示,则函数g(x)=b+logax的图象大致是()A .B .C .D .8. (2分)在正三棱柱ABC﹣A1B1C1中,若AB1⊥BC1 ,则下列关于直线A1C和AB1 , BC1的关系的判断正确的为()A . A1C和AB1 , BC1都垂直B . A1C和AB1垂直,和BC1不垂直C . A1C和AB1 , BC1都不垂直D . A1C和AB1不垂直,和BC1垂直9. (2分)若直线l1:y=kx+k+2与l2:y=﹣2x+4的交点在第一象限,则实数k的取值范围是()A . k>﹣B . k<2C . ﹣<k<2D . k<﹣或k>210. (2分) (2016高一下·沙市期中) 若三直线2x+3y+8=0,x﹣y﹣1=0和x+ky=0相交于一点,则k=()A . ﹣2B . -C . 2D .11. (2分) (2015高一下·衡水开学考) 正方体ABCD﹣A1B1C1D1中,P、Q、R分别是AB、AD、B1C1的中点.那么,正方体的过P、Q、R的截面图形是()A . 三角形B . 四边形C . 五边形D . 六边形12. (2分) (2019高二上·汇川期中) 已知函数f(x)=2x-1,g(x)=1-x2 ,规定:当|f(x)|≥g(x)时,h(x)=|f(x)|;当|f(x)|<g(x)时,h(x)=-g(x),则h(x)()A . 有最小值-1,最大值1B . 有最大值1,无最小值C . 有最小值-1,无最大值D . 有最大值-1,无最小值二、填空题 (共4题;共4分)13. (1分) (2018高一上·海南期中) lg20+lg5=________.14. (1分)(2017·山东模拟) 某几何体的三视图如图,则该几何体的体积为________.15. (1分) (2017高二上·南通开学考) 已知直线l1的方程为3x+4y-7=0,直线l2的方程为6x+8y+1=0,则直线l1与l2的距离为________.16. (1分) a为实数,函数在区间上的最大值记为. 当________ 时,的值最小.三、解答题 (共6题;共55分)17. (5分)已知集合A={x|4≤x<8,x∈R},B={x|6<x<9,x∈R},C={x|x>a,x∈R}.(1)求A∪B;(2)(∁UA)∩B;(3)若A∩C=∅,求a的取值范围.18. (15分) (2017高二上·常熟期中) 已知平行四边形ABCD的三个顶点的坐标为A(﹣1,5),B(﹣2,﹣1),C(2,3).(1)求平行四边形ABCD的顶点D的坐标;(2)在△ACD中,求CD边上的高所在直线方程;(3)求四边形ABCD的面积.19. (10分)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD上的点,且AB=2,∠BAD=60°.(1)求证:平面PBD⊥平面PAC;(2)当OM∥平面PAB且三棱锥M﹣BCD的体积等于时,求点C到面PBD的距离.20. (5分) (2017高二下·雅安期末) 已知函数f(x)= .(Ⅰ)求函数f(x)的定义域;(Ⅱ)判定f(x)的奇偶性并证明;(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.21. (10分) (2017高一下·启东期末) 已知三条直线l1:ax﹣y+a=0,l2:x+ay﹣a(a+1)=0,l3:(a+1)x﹣y+a+1=0,a>0.(1)证明:这三条直线共有三个不同的交点;(2)求这三条直线围成的三角形的面积的最大值.22. (10分)(2020·普陀模拟) 某居民小区为缓解业主停车难的问题,拟对小区内一块扇形空地进行改建.如图所示,平行四边形区域为停车场,其余部分建成绿地,点在围墙弧上,点和点分别在道路和道路上,且米,,设.(1)求停车场面积关于的函数关系式,并指出的取值范围;(2)当为何值时,停车场面积最大,并求出最大值(精确到平方米).参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分) 17-1、18-1、18-2、18-3、19-1、19-2、20-1、21-1、21-2、22-1、22-2、。
2018-2019学年吉林省辽源市田家炳高级中学高一上学期期末联考数学(文)试题(解析版)

2018-2019学年吉林省辽源市田家炳高级中学高一上学期期末联考数学(文)试题一、单选题1.已知集合U= {1,3,5,7,9},A = {1,5,7},则∁U A= ()A.{1,3 } B.{3, 7,9 }C.{3,5,9} D.{3,9}【答案】D【解析】根据补集定义求解结果.【详解】因为U= {1,3,5,7,9},A = {1,5,7},所以∁U A={3,9},选D.【点睛】本题考查补集定义,考查基本求解能力,属基本题.2.函数y=2的最大值、最小值分别是()A.2,-2 B.1,-3 C.1,-1 D.2,-1【答案】B【解析】根据余弦函数有界性确定最值.【详解】因为,所以,即最大值、最小值分别是1,-3,选B.【点睛】本题考查余弦函数有界性以及函数最值,考查基本求解能力,属基本题.3.函数f(x)=的图象关于()A.y轴对称B.直线y=-x对称C.坐标原点对称D.直线y=x对称【答案】C【解析】试题分析:显然函数定义域为,且函数为奇函数,所以图像关于坐标原点对称.故选C.【考点】奇函数图像的对称性.4.若向量=(2,3),=(4,7),则=()A.(-2,-4) B.(2,4) C.(6,10 ) D.(-6,-10)【答案】A【解析】试题分析:=(-2,-4).【考点】向量是加减运算。
点评:注意:向量的加减运算的结果仍然是一个向量。
属于基础题型。
5.已知扇形的周长为6cm,面积为2cm2,则扇形的圆心角的弧度数为()A.1 B.4 C.1或4 D.2或4【答案】C【解析】试题分析:设扇形的圆心角为,半径为,则解得或,故选C.【考点】1、弧度制的应用;2、扇形的面积公式.6.方程的解所在的区间为()A.(0,2 ) B.(1,2 ) C.(2,3 ) D.(3,4 )【答案】C【解析】判断,则在上单调递增.根据函数的零点存在性定理得出答案.【详解】令,则在上单调递增.且,所以方程的解所在的区间为.故选C.【点睛】本题考查了函数的单调性,函数零点的判断,方程解所在的区间,属于中档题.7.已知α∈(,π),sinα=,则tan(α+)等于()A.B.7 C.-D.-7【答案】A【解析】解:因为,选A8.在(0,2π)内,使成立的x的取值范围是()A.B.C.D.【答案】D【解析】先化成基本三角函数形式,再根据正弦函数性质解不等式.【详解】因为,所以,即,因此,,因为,所以或,选D.【点睛】本题考查三角函数配角公式以及正弦函数性质,考查基本求解能力,属基本题.9.设,,,则()A.y3 > y1 > y2 B.y2 >y1 >y3 C.y1>y2 > y3 D.y1 > y3 >y2【答案】D【解析】试题分析:利用指数函数比较大小.,因为在上单增,所以有,故选D.【考点】指数函数的单调性.10.已知角α的终边上有一点P (1,3),则的值为()A.1 B.-C.-1 D.-4【答案】A【解析】试题分析:根据三角函数的定义可知,根据诱导公式和同角三角函数关系式可知:,故选A.【考点】1、三角函数的定义;2、诱导公式和同角三角函数关系.【方法点晴】本题是一个三角函数的定义、三角函数诱导公式及同角三角函数关系式方面的综合性问题,属于中档题.解决本题的基本思路及其切入点是,首先根据三角函数的诱导公式将被求式进行整理与化简,再由点的坐标,根据三角函数的定义求出角的有关三角函数值,进而可得到所求结果.11.已知a > 0,且a≠1,函数与的图象只能是下图中的() A.B.C.D.【答案】B【解析】略12.设点D为△ABC中BC边上的中点,O为AD边上靠近点A的三等分点,则() A.=-+B.=-+C.=-D.=-【答案】B【解析】根据向量表示求结果.【详解】因为O为AD边上靠近点A的三等分点,所以=+,因为点D 为△ABC 中BC 边上的中点,=+=-+-+,选B. 【点睛】本题考查向量表示,考查基本分析化简能力,属基本题.二、填空题13.函数的单调递减区间是____.【答案】【解析】试题分析:函数由,其中是减函数,在上是减函数,在上是增函数,由复合函数单调性可知函数的减区间为【考点】复合函数单调性14.如果幂函数的图象过点, 那么(64)=____.【答案】【解析】设幂函数,∵幂函数f (x )的图象过点,故,解得:,∴,故,故答案为:.15.设α为钝角,且3sin 2α=cosα,则sinα=_______.【答案】【解析】根据二倍角正弦公式化简即得结果.【详解】因为,所以,因为为钝角,所以.【点睛】本题考查二倍角正弦公式,考查基本分析化简求解能力,属基本题.16.关于平面向量有下列三个命题:①若a·b=a·c,则b=c;②已知a=(k,3),b=(-2,6),若a∥b,则k=-1;③=0.其中正确的命题为______.(写出所有正确命题的序号)【答案】②③【解析】根据向量运算法则、向量数量积以及向量平行坐标表示化简求值,再作出判断.【详解】,①错;②对;,所以③对.【点睛】本题考查向量运算法则、向量数量积以及向量平行坐标表示,考查基本分析化简求解能力,属基本题.三、解答题17.设U= R,A={x |≤1},B= {x |2<x<5},C= {x|a≤x≤a+ 1}(a为实数).(1)求A∩B;(2)若B∪C=B,求a的取值范围.【答案】(1) (2)【解析】试题分析:(Ⅰ)根据指数函数的性质化简,然后利用交集的定义求解即可;(Ⅱ)由得,根据包含关系列出关于的不等式组求解,即可得到的取值范围.试题解析:(Ⅰ)∵∴∴(Ⅱ)由得∴即∴18.已知函数的图象上相邻最高点和最低点的横坐标相差,初相为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018-2019学年上学期高一期末考试数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2018·五省联考]已知全集U =R ,则下列能正确表示集合{}0,1,2M =和{}220N x x x +==关系的韦恩(Venn )图是( )A .B .C .D .2.[2018·三明期中]已知函数()lg ,011,0x x f x x x >⎧=⎨+≤⎩,则()()1f f -=( )A .2-B .0C .1D .1-3.[2018·重庆八中]下列函数中,既是偶函数,又在(),0-∞内单调递增的为( ) A .22y x x =+ B .2xy =C .22x xy -=-D .12log 1y x =-4.[2018·大庆实验中学]已知函数()32xf x a x=--的一个零点在区间()1,3内,则实数a 的取值范围是( ) A .51,2⎛⎫- ⎪⎝⎭B .5,72⎛⎫⎪⎝⎭C .()1,7-D .()1,-+∞5.[2018·金山中学]某三棱锥的三视图如图所示,则该三棱锥的各个面中,最大的面积是( )A.2B.2C .1 D.46.[2018·黄山八校联考]若m ,n 是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( )A .若αβ⊥,m β⊥,则//m αB .若//m α,n m ⊥,则n α⊥C .若//m α,//n α,m β⊂,n β⊂,则//αβD .若//m β,m α⊂,n αβ=,则//m n7.[2018·宿州期中]已知直线1:30l mx y -+=与211:22l y x =-+垂直,则m =( ) A .12-B .12C .2-D .28.[2018·合肥九中]直线l 过点()0,2,被圆22:4690C x y x y +--+=截得的弦长为直线l 的方程是( )A .423y x =+ B .123y x =-+ C .2y =D .423y x =+或2y = 9.[2018·南宁模拟]如图,棱长为a 的正方体1111ABCD A BC D -中,M 为BC 中点,这直线1D M 与平面ABCD 所成角的正切值为( )此卷只装订不密封 班级 姓名 准考证号 考场号 座位号ABCD .1210.[2018·东城期末]已知圆22:4C x y +=,直线():l x y m m +=∈R ,设圆C 上到直线l 的距离为1的点的个数为S,当0m ≤<S 的可能取值共有( ) A .2种B .3种C .4种D .5种11.[2018·云天化中学]如图,正方体1111ABCD A BC D -的棱长为1,线段11B D 上有两个动点E 、F ,且12EF =.则下列结论中正确的个数.....为( )①AC BE ⊥; ②EF ∥平面ABCD ;③三棱锥A BEF -的体积为定值; ④AEF △的面积与BEF △的面积相等. A .1B .2C .3D .412.[2018·湛江调研]点A 、B 、C 、D在同一个球的球面上,AB BC AC === 若四面体ABCD) A .169π16B .289π16C .25π16D .8π第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2018·华东师大附中]已知()214f x x +=-,则()f x 的解析式为__________.14.[2018·嘉兴三中]已知点()2,1A ,()2,3B -,()0,1C ,则ABC △中,BC 边上中线所在的直线方程为________.15.[2018·赣州期中]设某几何体的三视图如图所示,则该几何体的表面积是__________.主视图 左视图 俯视图16.[2018·嘉兴一中]若函数()224422f x x ax a a =-+-+在区间[]0,2上有两个零点,则实数a 的取值范围是_______.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(10分)[2018·安庆期中]设全集{}1,2,3,4,5,6U =,A ,B 都是U 的子集,{}1,2A =,(){}4,6UA B =ð,(1)写出所有符合题意的集合B ; (2)计算:341lg2lg 3lg5log 2log 94-+-⋅.18.(12分)[2018宜昌期中·]设a 是实数,()2221x xa a f x ⋅+-=+, (1)证明:()f x 是增函数;(2)试确定a 的值,使()f x 为奇函数.19.(12分)[2018·华安一中]已知点()2,3A ,()4,1B ,ABC △是以AB 为底边的等腰 三角形,点C 在直线:220l x y -+=上.(1)求AB 边上的高CE 所在直线的方程;(结果写成直线方程的一般式) (2)求ABC △的面积.20.(12分)[2018·定远月考]如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x 的内接圆柱.(1)试用x 表示圆柱的高;(2)当x 为何值时,圆柱的侧面积最大,最大侧面积是多少?21.(12分)[2018·泸化中学]如图,四棱锥P ABCD -中,底面ABCD 是矩形,22AB AD ==,PD ⊥底面ABCD ,E ,F 分别为棱AB ,PC 的中点.(1)求证:EF ∥平面PAD ; (2)求证:平面PDE ⊥平面PEC .22.(12分)[2018·陕西四校联考]如图,直三棱柱111ABC A B C -的所有棱长都是2,D ,E 分别是AC ,1CC 的中点.(1)求证:AE ⊥平面1A BD ;(2)求三棱锥11B A BD -的体积.2018-2019学年上学期高一期末考试数学答案第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】A【解析】N 为220x x +=的解集,解220x x +=可得,0x =或2-, 则{}2,0N =-,{}0M N =≠∅,由选项中的Venn 图可得选项A 符合题意,故选A .2.【答案】C【解析】由题意得()111110f -=-+=,∴()()()110lg101f f f -===.故选C .3.【答案】D【解析】根据奇偶性的定义知A 即不是奇函数也不是偶函数,C 是奇函数,B 、D 是偶函数,在(),0-∞上B 是减函数,D 是增函数.故选D . 4.【答案】C【解析】函数()32xf x a x=--是增函数,且一个零点在区间()1,3内,根据零点存在 定理得到()()1030f f <>⎧⎪⎨⎪⎩解得a 的范围是()1,7-.故答案为C .5.【答案】A【解析】画出直观图如下图所示,计算各面的面积为1122ABC S ==△,12112ABD BCD S S ==⨯⨯=△△,12ACD S ==△A .6.【答案】D【解析】对于A ,若αβ⊥,m β⊥,则//m α或m α⊂,故A 错误; 对于B ,若//m α,n m ⊥,则n α⊥或n α⊂或n 与α相交,故B 错误; 对于C ,若//m α,//n α,m β⊂,n β⊂,则//αβ或α、β相交,故C 错误; 对于D ,若//m β,m α⊂,n αβ=,由线面平行的性质定理,可得//m n ,故D 正确,故选D . 7.【答案】D【解析】很明显直线的斜率存在,直线方程即3y mx =+,1122y x =-+, 由直线垂直的充分必要条件可得:112m -⨯=-,解得2m =.本题选择D 选项. 8.【答案】D【解析】因为直线l 被圆22:4690C x y x y +--+=,()()22234x y -+-=截得的弦长为1=,设直线l 的方程为2y kx =+,(斜率不存在时不满足题意)1=,0k ∴=或43k =,即直线l 的方程是423y x =+或2y =,故选D . 9.【答案】C【解析】连接DM ,因为几何体是正方体,所以1D MD ∠就是直线1D M 与平面ABCD所成角,11tan 5DD D MD DM ∠===,故选C . 10.【答案】B【解析】因为圆C 上到直线l[)0,3,1=时,圆C 上到直线l 的距离为1的点的个数为3;()1,3时,圆C 上到直线l 的距离为1的点的个数为2;[)0,1时,圆C 上到直线l 的距离为1的点的个数为4;因此S 的可能取值共有3种,故选B .11.【答案】C【解析】连结BD ,则AC ⊥平面11BB D D ,11BD B D ∥.AC BE ∴⊥,EF ∥平面ABCD ,从而①②正确,又BEF △面积为定值,A 到平面11BB D D 距离为定值,所以三棱锥A BEF -的体积为定值,从而③正确,因为A 到11B D 的距离不等于1BB .所以AEF △的面积与BEF △的面积不相等,④错误. 故选C . 12.【答案】B【解析】根据题意知,ABC △1,小圆的圆心为Q ,由于底面积ABC S △不变,高最大时体积最大,所以DQ 与面ABC垂直时体积最大,最大值为13ABC S DQ ⨯=△4DQ =,设球心为O ,半径为R ,则在直角AQO △中,222OA AQ OQ =+,即()22214R R =+-,∴178R =, 则这个球的表面积为217289π4π816S ⎛⎫== ⎪⎝⎭,故选B .第Ⅱ卷二、填空题:本大题共4小题,每小题5分. 13.【答案】()223f x x x =--【解析】因为()214f x x +=-,∴令1x t +=,则1x t =-,()()()2211423f x f t t t t ∴+==--=--,∴函数()f x 的解析式为()223f x x x =--,故答案为()223f x x x =--.14.【答案】350x y +-=【解析】设BC 中点为(),D x y ,已知()2,3B -,()0,1C ,则()1,2D -, 因为()121213AD k -==---,所以BC 边上中线所在的直线方程为350x y +-=.15.【答案】36【解析】由几何体的三视图可知,该几何体是一个长、宽、高分别为4,2,2的长方体截去一个三棱锥1D ACD -后剩下的部分(如图所示).∵1AD C △的三边长分别分1162AD C S =⨯=△. 故该几何体的表面积111422242424222636222S =⨯+⨯+⨯+⨯⨯+⨯⨯+⨯⨯+=.16.【答案】(1,5-【解析】由题意,要使函数()224422f x x ax a a =-+-+在区间[]0,2上有两个零点,只要()()002002202f f a a f ≥≥<<⎛⎧⎪⎪⎪⎨⎫< ⎪⎝⎭⎪⎪⎪⎩,即2222010180022220a a a a a a -+≥-+≥<⎧⎪⎪⎪<⎨-+<⎪⎪⎪⎩,解得(1,5a ∈-,故答案为(1,5. 三、解答题:解答应写出文字说明、证明过程或演算步骤. 17.【答案】(1){}4,6,{}1,4,6,{}2,4,6,{}1,2,4,6;(2)2. 【解析】(1)集合B 为{}4,6,{}1,4,6,{}2,4,6,{}1,2,4,6. (2)341lg2lg3lg5log 2log 94-+-⋅ 232lg2lg23lg5log 2log 3-=-+-⋅lg22lg23lg51=++-()3lg2lg51=+-3lg101=-312=-=.18.【答案】(1)见解析;(2)1.【解析】(1)证明:设1x 、2x ∈R 且12x x <,()()()()()121212122222*********x x x x x x f x f x a a -⎛⎫⎛⎫-=---= ⎪ ⎪++++⎝⎭⎝⎭, 又由2x y =在R 上为增函数,则120x>,220x >,由12x x <,可得12220xx-<,则()()120f x f x -<,故()f x 为增函数,与a 的值无关,即对于任意a ,()f x 在R 为增函数. (2)若()f x 为奇函数,且其定义域为R ,必有有()()f x f x -=-,即222121x x a a -⎛⎫-=-- ⎪++⎝⎭,变形可得()2212221x xa +==+, 解可得,1a =,即当1a =时,()f x 为奇函数. 19.【答案】(1)10x y --=;(2)2. 【解析】(1)由题意可知,E 为AB 的中点,13142AB k -==--, ∴()3,2E ,且11CE ABk k =-=,∴CE 所在直线方程为23y x -=-,即10x y --=. (2)由22010x y x y -+=--=⎧⎨⎩,得43x y =⎧⎨⎩=,∴()4,3C ,∴2AC BC ==,AB =,∴AC BC ⊥,∴122ABC S AC BC =⋅=△.20.【答案】(1)33h x =-;(2)当12x =时,它的侧面积最大为3π2.【解析】(1)设所求的圆柱的底面半径为x ,它的轴截面如图,1BO =,3PO =,圆柱的高为h ,由图,得313x h-=,即33h x =-. (2)∵()()22π2π336πS hx x x x x =-=-=圆柱侧,当12x =时,圆柱的侧面积取得最大值为3π2. ∴当圆柱的底面半径为12时,它的侧面积最大为3π2.21.【答案】(1)见解析;(2)见解析.【解析】(1)证明:如图,取PD 的中点G ,连接AG ,FG . 因为F ,G 分别是PC ,PD 的中点,所以GF DC ∥,且12GF DC =. 又E 是AB 的中点,所以AE DC ∥,且12AE DC =, 所以GF AE ∥,且GF AE =,所以四边形AEFG 是平行四边形,故EF AG ∥.又AG ⊂平面PAD ,EF ⊄平面PAD ,所以EF ∥平面PAD .(2)因为PD ⊥底面ABCD ,CE ⊂底面ABCD ,所以CE PD ⊥. 因为四边形ABCD 是矩形,且2AB AD =,所以AD AE =,BC BE =,所以45AED BEC ∠=∠=︒,DE CE ⊥. 又PDDE D =,PD ⊂平面PDE ,DE ⊂平面PDE ,所以CE ⊥平面PDE ,又CE ⊂平面PEC ,所以平面PDE ⊥平面PEC . 22.【答案】(1)见解析;(2)3. 【解析】(1)∵AB BC CA ==,D 是AC 的中点,∴BD AC ⊥,∵直三棱柱111ABC A B C -中1AA ⊥平面ABC ,∴平面11AAC C ⊥平面ABC , ∴BD ⊥平面11AAC C ,∴BD AE ⊥. 又∵在正方形11AAC C 中,D ,E 分别是AC ,1CC 的中点,∴1A D AE ⊥. 又1A D BD D =,∴AE ⊥平面1A BD .(2)连结1AB 交1A B 于O ,∵O 为1AB 的中点,∴点1B 到平面1A BD 的距离等于点A 到平面1A BD 的距离.∴1111111121332B A BD A A BD B AA D AA D V V V S BD ---===⨯⨯=⨯⨯⨯=△.。
