2015年东北大学数学建模校内选拔赛

合集下载

2015年全国大学生数学建模竞赛(吉林赛区)评审结果

长春理工大学长春理工大学长春理工大学长春理工大学长春理工大学
马文联成丽波成丽波成丽波周林华蔡志丹施三支刘振文刘振文吕堂红杨华李喆王姝娜咸巍荀刘邢谷董王曹立铭蕾阔博珺蕾杜润梅
一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖
张泽健郭豪杰杨丽娟李敏郭豪杰
B201507006024 魏干植索洪伟郎海立北华大学
一等奖指导教师组一等奖指导教师组一等奖指导教师组一等奖宋云飞张杰一等奖一等奖指导教师组一等奖指导教师组一等奖指导教师组一等奖指导教师组一等奖
A201507007015 贾英贺刘世涛张广陆东北电力大学 A201507007007 靳大鹏李双林王明超东北电力大学 B201507007001 黄群王虹皓潘国良 B201507007010 沐禄严杰煜何泊延 B201507007011 肖遥刘鹏博于浩 B201507007013 夏佳军郭占超叶辉东北电力大学东北电力大学东北电力大学东北电力大学 B201507007008 彭烨秋张崇山霍彤彤东北电力大学
2015年全国大学生数学建模竞赛吉林赛区获奖名单(排名不分先后）普通本科院校报名代码参加队员学校名称指导教师获奖等级
A201507001236 陈泽宇张文婷王姝吉林大学 A201507001208 郑晓月杨钦瑞程水木吉林大学 A201507001199 赵铮张昕荻吉林大学 A201507001184 何书琤陶星明张昕冉吉林大学 A201507001177 冯少飞任钊民王浩成吉林大学 A201507001169 付豪杨倩张运昌 A201507001164 胡国荣-沈江平-孟磊吉林大学吉林大学吕显瑞董天邹永魁李立明何玲王蕊王蕊黄庆道吕显瑞侯秉喆王德辉魏元鸿吕悦包连璋吕显瑞张远航魏元鸿刘长春刘明姬伍铁如王彩玲朱复康张然梁树青邹永魁朱森许志国许志国王彩玲孙旭阳孙铭会曹阳韩月才一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖一等奖

东北大学学生荣获国际大学生数学建模竞赛19项一等奖

东北大学学生荣获国际大学生数学建模竞赛19项一等奖
2015年国际大学生数学建模竞赛（MCM/ICM）成绩近日揭晓，东北大学学生在本次竞赛中荣获74项大奖，包括19项国际一等奖（Meritorious Winner），55项国际二等奖（Honorable Mention），同级别获奖数量在全国高校名列前茅。

竞赛于2015年2月6日9时至2月10日9时（北京时间）举行，东北大学共计177支参赛队参赛。

经过四天四夜96个小时的不懈努力，东北大学学生最终以19项国际一等奖、55项国际二等奖再创佳绩。

其中获奖参赛队员分别来自工商管理学院、理学院、资源与土木工程学院、材料与冶金学院、机械工程与自动化学院、信息科学与工程学院、软件学院、中荷生物医学与信息工程学院；一等奖获奖参赛队分别由陈大力、宋叔尼、潘峰、崔建江、王琪、贾同、杨连平、赵秋月、郝丽娜、张云洲、王斐、覃文军、孙涛、朱和贵、翟丁老师指导。

国际大学生数学建模竞赛（MCM/ICM）始于1985年，是由美国数学学会、美国工业与应用数学学会等举办的国际性大学生数学建模竞赛。

作为世界范围内最具影响力的数学建模竞赛，竞赛要求参赛队员具备综合运用数学知识、计算机技术、英语写作以及其他相关知识，同时需要队员之间密切合作，集体发挥队员的创造性思维能力和分析问题、解决问题的综合能力。

为此，参赛队员必须经过从基础知识拓展、技能实训到实战演练的历时一整年的系列培训，才有可能在四天四夜的竞技中脱颖而出。

2015年东北三省数学建模联赛辽宁赛区暨沈阳理工大学校赛通知

关于举办沈阳理工大学第六届数学建模竞赛暨2015年东北三省数学建模联赛选拔赛的通知为了提高学生的综合素质，培养学生应用数学知识解决工程问题的能力，激发学生的创新实践热情，经研究决定举办我校第六届大学生数学建模竞赛暨2015年东北三省大学生数学建模竞赛选拔赛。

本次竞赛由理学院承办，现将竞赛组织工作的有关事项通知如下，欢迎各学院同学踊跃报名参赛。

一、报名条件：全日制在校本科学生。

二、报名时间及报名方式1、报名时间：2014年4月17日——2014年4月24日2、报名方式：本次竞赛采取网上报名。

请大家登陆网络报名系统/nemcm，注册登陆后填写队员及指导报名信息。

3、竞赛要求：竞赛以队为单位参赛，每支队伍由三名学生组成，学生自愿组合，年级、专业不限。

组队时要考虑优势互补(创新思维、专业基础、计算机应用等)。

4、竞赛内容与形式（1）竞赛题目及下载网址：本次联赛采用“2015年全国大学生数学建模夏令营”题目，下载网址为：。

按规定时间由网上下载，从中任选一道题作为参赛试题。

（2）按规定的时间提交一篇论文作为答卷。

（3）竞赛期间参赛队员可使用各种图书资料、计算机和软件以及网络以检索有关资料。

（4）论文提交日期为2014年5月15日。

5、竞赛时间：各参赛队伍请于5月15日16:00前将写好的论文发至理学院数学建模协会邮箱：slgsxjmjs@，并注明队伍编号。

6、奖项设置：本次竞赛设一等奖、二等奖、三等奖及优秀奖若干个，获奖的队伍将有机会代表学校参加2015年东北三省数学建模联赛和“高教社”杯全国大学生数学建模竞赛。

7、联系人：崔鹏展联系电话：139********王迪迪联系电话：139********沈阳理工数学建模讨论群：125449480三、答卷要求（1）答卷写成论文形式，用A4打印纸计算机打印，边距为2.5厘米；（2）论文第一页、第二页请直接下载（见附件2）。

论文题目直接用竞赛试题的标题，不要自行拟定，必须标明所选题目的英文字母（A、B、C、D之一），封面信息填写务必完整准确；（3）论文从第三页开始编页码，第三页打印论文题目、摘要、关键词，第四页开始打印论文；（4）不要页眉，从第三页开始不要有任何答题人身份的信息，否则答卷无效；（5）一级标题用4号，论文其他内容用小4号宋体字、单倍行距，左侧装订；（6）引用他人的成果或资料，在文后的参考文献中列出，正文、变量、公式、图、表、参考文献等格式参见科技类期刊中的标准形式；四、参赛费用（评审费）1、每份参加东三省数学建模联赛的作品需缴纳150元评审费。

2015年数学建模竞赛

2015年数学建模竞赛2015年的数学建模竞赛是一场备受期待的盛事，吸引了来自全国各地的优秀学子参与。

这场竞赛的主题是“城市规划与交通流量优化”，旨在通过数学建模的方式解决现实生活中城市交通拥堵问题，提高城市交通效率。

竞赛中，参赛者需要利用数学模型和算法，分析城市交通的特点和问题，提出合理的解决方案。

首先，他们要通过收集相关数据和实地调研，了解城市的交通状况、交通流量以及交通拥堵的原因。

其次，他们需要运用数学建模的方法，将城市交通系统抽象成数学模型，通过建立数学方程来描述交通流量、交通规划、交通信号灯等因素之间的关系。

在建模过程中，参赛者需要运用各种数学工具和理论，如概率统计、最优化理论、图论等，来解决问题。

他们需要运用概率统计的方法，对交通流量进行预测和分析，找出交通拥堵的概率分布；利用最优化理论，设计出交通信号灯的最优控制策略，使交通流量得到合理分配；应用图论的知识，分析道路网络的拓扑结构，找出最短路径和最优路径等。

参赛者在解题过程中需要进行大量的计算和仿真实验，利用计算机编程技术，实现数学模型的求解和优化。

他们需要运用MATLAB、Python等工具，编写程序来求解数学模型，通过模拟实验来验证模型的有效性和稳定性。

竞赛还要求参赛者能够对自己的研究成果进行有效的表达和展示。

他们需要撰写一份完整的报告，将自己的研究过程、结果和结论进行清晰、准确的描述。

在报告中，他们需要运用恰当的段落和标题，使文章结构清晰，易于阅读。

同时，他们还需要进行口头陈述，向评委和其他参赛者介绍自己的研究成果，并回答评委的提问。

2015年的数学建模竞赛为参赛者提供了一个锻炼自己数学建模能力和解决实际问题能力的机会。

通过参与竞赛，他们不仅可以提高自己的数学水平，还能培养团队合作能力、创新思维和解决问题的能力。

同时，竞赛也为城市交通规划和交通流量优化提供了新的思路和方法，为解决城市交通拥堵问题提供了有益的借鉴和启发。

2015年的数学建模竞赛是一场富有挑战性和创新性的比赛，通过数学建模的方式解决现实生活中的问题。

获奖名单-东三省数模竞赛2015

学校鞍山师范学院鞍山师范学院鞍山师范学院鞍山师范学院鞍山师范学院
大连大学大连大学大连大学大连大学大连大学大连东软信息学院大连东软信息学院大连东软信息学院大连东软信息学院大连东软信息学院大连海事大学大连海事大学大连海事大学大连海事大学大连海事大学大连海事大学大连海事大学大连海洋大学大连海洋大学大连海洋大学大连海洋大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连理工大学大连民族大学大连民族大学大连民族大学大连民族大学大连民族大学东北财经大学辽宁大学辽宁工程技术大学辽宁工程技术大学辽宁工程技术大学辽宁工程技术大学辽宁工程技术大学
队员一刘莹周伟邓利平刘彦宁孟楠楠刘员京房本旭杨祖莨杨晓赵志伟田家顺徐天宇管青企刘辉林志华李泓明侯大伟王九峥王嘉媛吴英恺彭琳廖海任于艳鑫王许洁申海洋冯燕曲芝萍孙耘龙王冠楚孙鸿博陈子谦王志宇刘博洋马鸣晨申星孙晨翔赵猛徐彦彤赵春宇陈红磊王新鹏夏文齐丁强吕思凡刘春艳贾思远孙海涵许鹭萍周定宁肖井礼张宏根赵维真张婷周鑫赵丹
3
张清香潘鑫杨柳欣 3
李翠玲代玉吴明运 1
汤林灿王国峰姚瀚晨 1
陈茜孙长明何艳
2
梁思越杨玲玲权家乐 3
刘书廷金姿秀张羽如 3
田智勇王轶婷刘祥平 1
滕秋霖汪晓玉曲国富 2
龚涛时杨杨康斌会 2
周罗杰顾秉焕陈志远 3
张建华刘美程王传博 3

2015年数学建模竞赛题目

2015年数学建模竞赛题目（原创实用版）目录1.2015 年数学建模竞赛概述2.竞赛题目分类及解析3.竞赛题目解答思路及方法4.竞赛对学生的意义和影响正文【2015 年数学建模竞赛概述】2015 年数学建模竞赛，即全国大学生数学建模竞赛，是我国面向全国大学生的一项重要的学科竞赛活动。

该竞赛旨在激发大学生学习数学的积极性，提高他们的创新意识和运用数学知识解决实际问题的综合能力，推动大学数学教学体系、教学内容和方法的改革。

【竞赛题目分类及解析】2015 年数学建模竞赛共有 A、B、C 三个题目，分别涉及不同的领域。

A 题：飞行器设计优化题目要求：根据给定的飞行器参数，建立数学模型，并求解最优设计方案。

解析：此题属于优化问题，需要运用线性规划、非线性规划等相关知识。

B 题：水质监测与评价题目要求：分析给定的水质监测数据，建立评价模型，对水质进行评价。

解析：此题涉及数据处理、统计分析、模糊评价等知识。

C 题：智能家居系统题目要求：设计一个智能家居系统，满足给定的功能需求。

解析：此题需要了解图论、动态规划等知识，以解决网络拓扑结构、任务调度等问题。

【竞赛题目解答思路及方法】1.对题目进行仔细阅读，理解题意，明确题目要求。

2.分析题目涉及的领域和知识点，确定解题思路。

3.利用相关数学方法和工具，建立数学模型。

4.求解模型，得到结果。

5.对结果进行分析和检验，撰写论文。

【竞赛对学生的意义和影响】参加数学建模竞赛，对学生具有重要的意义和影响。

首先，它可以激发学生学习数学的兴趣，提高他们的数学素养。

其次，通过解决实际问题，学生可以锻炼自己的创新能力和团队协作能力。

最后，竞赛成绩优秀的学生，还有机会获得奖学金、保研等优惠政策。

总之，2015 年数学建模竞赛题目涉及多个领域，对参赛学生的知识储备和解题能力提出了较高的要求。

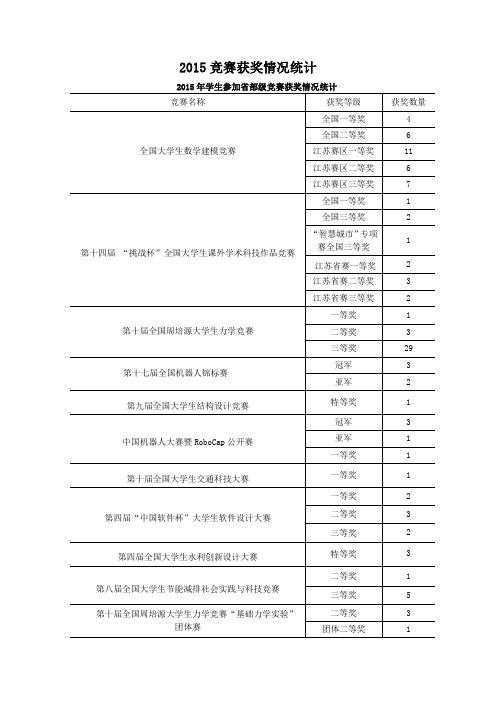
2015竞赛获奖情况统计

全国二等奖
1
全国三等奖
1
华东赛区特等奖
3
华东赛区一等奖
3
“创新创业杯”全国管理决策模拟大赛
特等奖
1
二等奖
8
全国高等院校企业竞争模拟大赛
特等奖
1
一等奖
1
二等奖
2
全国大学生创业综合模拟大赛
二等奖
1
第六届全国大学生数学竞赛
全国二等奖
1
省一等奖
20
省二等奖
33
省三等奖
23
第六届中国大学生服务外包创新创业大赛
三等奖
1
全国大学生英语竞赛
全国三等奖
1
江苏赛区特等奖
2
江苏赛区一等奖
16
江苏赛区二等奖
46
江苏赛区三等奖
88
第一届全国高校云计算应用创新大赛
二等奖
2
第六届“蓝桥杯”全国软件和信息技术专业人才大赛
全国选拔赛创业团队赛一等奖
1
全国选拔赛创业团队赛二等奖
2
全国总决赛创业团队赛二等奖
1
全国二等奖
13
全国三等奖
2
江苏赛区一等奖
4
江苏赛区二等奖
6
江苏赛区三等奖
1
第七届全国大学生广告艺术设计大赛
全国三等奖
2
省一等奖
1
省二等奖
2
省三等奖
7
第九届江苏省大学生力学竞赛
特等奖
6
一等奖
56
二等奖
91
团体特等奖
1
第九届江苏省大学生力学竞赛“基础力学实验”团体赛
特等奖
2
一等奖
1

2015全国大学生数学建模竞赛

在数据的原始坐标系 c’中相邻两个时刻��+1和��的竿影夹角变化记为：
Δ��′(�� ); 由向量内积关系可以得到：
cos (Δ��′(�� ))
=
��⃗⃗��⃗��⃗⃗��⃗⃗(⃗��⃗⃗��⃗⃗��⃗��) ∙⃗��⃗��⃗⃗��⃗⃗��⃗(⃗⃗��⃗⃗��⃗⃗��⃗��⃗+⃗⃗⃗1⃗⃗) |��⃗⃗��⃗��⃗⃗��⃗(⃗⃗⃗��⃗⃗��⃗⃗��⃗��) |∙ |⃗��⃗��⃗⃗��⃗⃗��⃗(⃗⃗��⃗⃗��⃗⃗��⃗��⃗+⃗⃗⃗1⃗⃗)
下面确定�� 及�� ：由所给的数据表格可以计算出：当天的第一组数据时，太阳直射点在 10.5N,79.5E;最后一组数据
时，太阳直射点在 10.5N,64.5E; 由于太阳照射不到的地区不可能有竿的阴影，故而目标点的经度区域为 10.5W,154.5E;
对于问题四，本文将视频材料等时间间隔采样（截图），依据针孔相机成像机理及空间坐标变换理论，将截图中竿顶端的像素坐标数据转化为大地坐标系中的坐标数据，继进而通过公式演算得到竿影夹角差分的正切比值仅与时刻有关的结论，从而引用网格搜索模型求解对应的经纬度坐标点。
关键词：网格搜索多目标最优化拟合针孔相机标定
|；p
为竿影的顶点
则由原始数据即可得到Δ��′(�� )与时刻的关系，也可以得到��′(�� )与时刻的关系

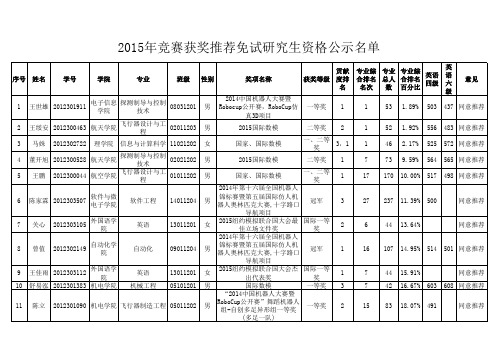
2015年竞赛获奖推荐免试研究生资格公示名单

1 2 3 4 5
电子信息探测制导与控制王世雄 2012301911 08031201 学院技术王绥安 2012300463 航天学院马姝 2012302722 飞行器设计与工 02011203 程
男男女男男
437 同意推荐 483 同意推荐 572 同意推荐 565 同意推荐 498 同意推荐
2015年竞赛获奖推荐免试研究生资格公示名单
序号姓名学号学院专业班级性别奖项名称 2014中国机器人大赛暨 Robocup公开赛，RoboCup仿真3D项目 2015国际数模国家、国际数模 2015国际数模国家、国际数模贡献获奖等级度排名一等奖二等奖 1 2 专业综专业专业综英语合排名总人合排名四级名次数百分比 1 1 1 7 17 53 52 46 73 170 1.89% 1.92% 2.17% 9.59% 10.00% 503 556 525 564 517 英语六级意见
冠军
1
50
137
36.50%
545
同意推荐
冠军
2
22
59
37.29%
441
同意推荐
特等奖第一名
2 1
8 68
20 170
40.00% 40.00%
456 502
同意推荐 462 同意推荐
一等奖
1
24
49
48.98%
494
472 参加答辩
一等奖二等奖二等奖特等奖二等奖二等奖二等奖
4 1 2 4 3 4 3
男
国际数模 “2014中国机器人大赛暨 RoboCup公开赛”舞蹈机器人组-自创多足异形组冠军(多足二队) 国际数模 “2014中国机器人大赛暨 RoboCup公开赛”舞蹈机器人组-自创双足人形组一等奖（双足二队）国家数模国际数模国际数模第四届全国海洋航行器设计与制作大赛-“仿生水黾机器人” 第四届全国海洋航行器设计与制作大赛-“遥控式水上救援器” “2014中国机器人大赛暨 RoboCup公开赛”RoboCup救援机器人组自主运行冠军(探索者队) “2014中国机器人大赛暨 RoboCup公开赛”舞蹈机器人组-常规双足人形组一等奖 (常规二队)

2015东三省赛建模

统健康响应评价--------------------20 2.3 权重的确定-----------------------------------------------21 第三章基于 PSR 模型的深圳福田红树林生态系统健康评价 3.1 压力子系统评价结果---------------------------------------25 3.1.1 自然压力----------------------------------------------25 3.1.1.1 年极端温度天气------------------------------------25 3.1.1.2 年台风和风暴潮次数--------------------------------25 3.1.1.3 赤潮发生的次数------------------------------------25 3.1.1.4 入侵物种种数数量----------------------------------26 3.1.1.5 红树林病虫害--------------------------------------26 3.1.2 人类压力----------------------------------------------26 3.1.2.1 人口密度------------------------------------------26 3.1.2.2 污染物排放----------------------------------------26 3.1.2.3 围填海--------------------------------------------27 3.1.2.4 噪声污染------------------------------------------27 3.2 状态子系统评价结果---------------------------------------27 3.2.1 环境质量----------------------------------------------27 3.2.1.1 水环境质量----------------------------------------27 3.2.1.2 沉积物质量----------------------------------------29 3.2.2 生物与生态--------------------------------------------29 3.2.2.1 浮游植物------------------------------------------30 3.2.2.2 浮游动物------------------------------------------31 3.2.2.3 潮间带大型底栖动物--------------------------------31 3.2.2.4 珍稀鸟类------------------------------------------32 3.2.3 生物生产力--------------------------------------------32 3.2.3.1 初级生产力----------------------------------------32 3.2.3.2 营养级间的总转换效率------------------------------32 3.2.3.3 总初级生产力/总呼吸量-----------------------------33 3.2.4 生境质量----------------------------------------------33

2015年吉林省数学建模竞赛成绩(各校按名次排序)

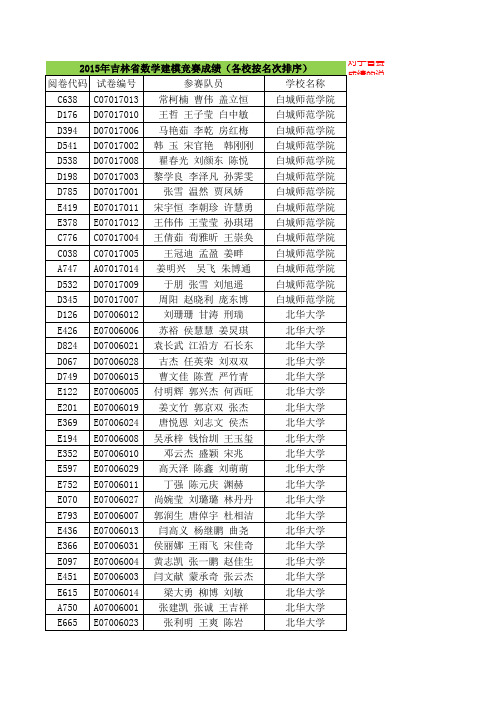
D538 D07017008 翟春光刘颜东陈悦
白城师范学院
D198 D07017003 黎学良李泽凡孙霁雯白城师范学院
D785 D07017001 张雪温然贾凤娇
白城师范学院
E419 E07017011 宋宇恒李朝珍许慧勇白城师范学院
E378 E07017012 王伟伟王莹莹孙琪珺白城师范学院
E195 E556 E132 E057 E177 E231 C794 D455 D373 E699 D218 D496 E034 E025 E170 E687 C344 C110 C114 B187 A498 A783 D399 D828 C502 C465 C661 C685 B655 A796 A521 E279 E461 D022 D475 E333 C803
C776 C07017004 王倩茹荀雅昕王崇奂白城师范学院
C038 C07017005 王冠迪孟盈姜畔
白城师范学院
A747 A07017014 姜明兴吴飞朱博通白城师范学院
D532 D07017009 于朋张雪刘旭遥
白城师范学院
D345 D07017007 周阳赵晓利庞东博
白城师范学院
D126 D07006012 刘珊珊甘涛刑瑞
北华大学
E426 E07006006 苏裕侯慧慧姜炅琪
北华大学
D824 D07006021 袁长武江沿方石长东
北华大学
D067 D07006028 古杰任英荣刘双双
北华大学
D749 D07006015 曹文佳陈萱严竹青
北华大学
E097 E07006004 黄志凯张一鹏赵佳生
北华大学

2015年全国大学生数学建模竞赛(吉林赛区)评审结果

A201507001072 刘芳宏周禹佳李胜男吉林大学 A201507001062 白济豪陈天霸庞安琪吉林大学 A201507001061 何雯夏昌伟许桂桂 A201507001053 黄小磊李阳张玉红 A201507001050 牛康龙邓华杰陈泱 A201507001043 于帅段宏英南萌吉林大学吉林大学吉林大学吉林大学
A201507001124 李纯翰郭钰生张开元吉林大学
A201507001081 薛笑阳鲁普之宋泽良吉林大学
A201507001042 牛冕尚楚宁邓心禹吉林大学
A201507001026 胡尚民陈建霖柳青秀吉林大学 A201507001018 王潇旸王寒松谢龙锋吉林大学 A201507001006 柏丛明许建文路千惠吉林大学 B201507001003 许志营潘健李卉冉 B201507001065 杨文昌王裕迟杨吉林大学吉林大学
吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学
王德辉聂元元曹春玲黄庆道杨泰山包连璋董志山王彩玲赵世舜吕显瑞史少云柴世民许志国吕显瑞曹春玲钟翠萍董天董天徐晓伟史少云徐晓伟纪友清赵世舜董和平董和平徐旭曹春玲吕显瑞吕显瑞包连璋于晓峰程开东吕悦李强柴世民张凯
吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学吉林大学
柴世民周倩程明曹春玲王继利史少云王继利聂元元邹永魁韩玉柱王继利梁树青董和平罗宏文刘长春曹春玲罗宏文任长宇张然朱复康曹阳罗宏文吕显瑞魏元鸿罗宏文梁树青杨泰山张然徐晓伟王德辉吕显瑞徐旭朱森韩玉柱韩玉柱张远航

2015高教社杯全国大学生数学建模竞赛获奖名单

闫庆伦闫庆伦李雷姜月萍闫庆伦来鹏程国胜程国胜吕红张正军建模教练组王小才王璞刘守生数模组数模组
88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120
三明学院闽南师范大学厦门大学厦门大学厦门大学福州大学福建工程学院福建农林大学九江学院东华理工大学江西理工大学江西理工大学南昌大学南昌大学山东大学山东大学山东大学山东大学山东女子学院山东财经大学山东财经大学山பைடு நூலகம்科技大学山东科技大学山东科技大学山东理工大学中国海洋大学中国海洋大学中国海洋大学齐鲁工业大学青岛大学青岛科技大学青岛科技大学青岛科技大学 5 / 62
东南大学东南大学东南大学扬州大学扬州大学江南大学河海大学河海大学河海大学河海大学南京工业大学南京工业大学南京工业大学南京大学南京大学南京大学南京师范大学南京邮电大学南京邮电大学南京邮电大学南京邮电大学南京邮电大学南京信息工程大学南京信息工程大学南京信息工程大学南京信息工程大学南京理工大学常州大学淮阴工学院解放军理工大学解放军理工大学中国计量学院中国计量学院 3 / 62
154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186
山东山东山东山东山东山东山东山东山东河南河南河南河南河南河南河南河南河南河南河南湖北湖北湖北湖北湖北湖北湖北湖北湖北湖北湖北湖北湖北

2015年数学建模竞赛

2015年数学建模竞赛2015年，数学建模竞赛再度吸引了广大数学爱好者的参与。

这场竞赛旨在通过解决实际问题的数学建模，培养学生的创新思维和解决实际问题的能力。

本文将为您介绍2015年数学建模竞赛的一些亮点和成果。

2015年数学建模竞赛的题目设计更加贴近实际，涉及的领域更加广泛。

竞赛题目涉及到了经济、环境、生物、物理等多个领域，使得参赛者需要具备多学科的知识和技能。

这样的设计能够激发参赛者的兴趣，同时也能培养他们的跨学科思维能力。

2015年数学建模竞赛注重团队合作和实践操作。

竞赛要求参赛者组成团队进行合作，团队成员之间需要充分交流和协作，共同解决问题。

这样的设计能够培养学生的团队合作意识和能力，提高他们的解决问题的效率。

2015年数学建模竞赛在评分标准上更加注重创新和实用性。

竞赛评委将根据参赛者的解题思路、模型建立的合理性以及解决问题的实用性等方面进行评分。

这样的评分标准鼓励参赛者在解决问题过程中提出创新的方法和思路，同时也要求他们的解决方案具有实际可行性。

在2015年数学建模竞赛中，参赛者们展现出了出色的数学建模能力和创新思维。

例如，有的参赛者通过建立合适的数学模型，成功解决了城市交通拥堵问题，提出了优化路网规划和交通信号控制策略的方案。

还有的参赛者通过建立人口增长模型，预测了未来人口变化趋势，为城市规划和资源分配提供了科学依据。

总的来说，2015年数学建模竞赛以其实际性、创新性和团队合作性受到了广大数学爱好者的关注和参与。

通过这场竞赛，参赛者们不仅提高了数学建模的能力，培养了创新思维和团队合作能力，还为实际问题的解决提供了有价值的思路和方案。

相信在未来的数学建模竞赛中，参赛者们会继续展现出更多的才华和创造力，为社会发展和科学进步做出更大的贡献。

第四届全国大学生数学竞赛东北大学校内选拔赛通知

东北大学第三届大学生数学竞赛暨第四届全国大学生数学竞赛校内选拔赛报名通知根据全国大学数学竞赛委员会工作安排，第四届大学生数学竞赛辽宁赛区预赛将于2012年10月27日举行。

为了更好地参加辽宁赛区的比赛，特组织东北大学校内选拔赛，现将具体事宜通知如下：一、参赛对象大学本科二年级或二年级以上的在校大学生。

竞赛分为非数学专业组和数学专业组(含数学与应用数学、信息与计算科学专业的学生)。

数学专业学生不得参加非数学专业组的竞赛。

二、竞赛内容非数学专业组竞赛内容为本科高等数学内容（高等数学内容为理工科本科教学大纲规定的高等数学的教学内容）。

数学专业组竞赛内容含数学分析、高等代数和解析几何（均为数学专业本科教学大纲规定的教学内容），所占比重分别为50%、35%及15%左右。

三、竞赛时间东北大学校内选拔赛竞赛时间定于9月15日上午9:00-11:30在东北大学举行（具体考试地点报名结束后发布到学生创新中心网站）。

请各位参赛同学提前做好相关准备。

相关考试信息请大家及时关注学生创新中心网站。

四、竞赛报名参加竞赛的同学请于2012年9月11日（周二）前登陆学生创新中心网站http://202.118.31.239进行网上报名。

网上报名需先注册，具体报名流程请查看网站中“使用帮助”。

五、竞赛形式以个人为单位参赛。

竞赛采用闭卷考试的形式，参加竞赛的学生必须遵守东北大学考试规则。

六、奖项设置本次竞赛设一等奖、二等奖和三等奖，一等奖比例为全体参赛数量的10%，二等奖比例为全体参赛数量的20%，三等奖比例为全体参赛数量的30%。

学校根据本次竞赛最终结果择优推荐参赛者参加辽宁赛区竞赛。

七、其他如有不明事宜请咨询学生创新中心王世远老师，联系电话83690577。

附：中国大学生数学竞赛竞赛大纲东北大学学生创新中心二○一二年八月三十一日附：中国大学生数学竞赛竞赛大纲(初稿)为了进一步推动高等学校数学课程的改革和建设，提高大学数学课程的教学水平，激励大学生学习数学的兴趣，发现和选拔数学创新人才，更好地实现“中国大学生数学竞赛”的目标，特制订本大纲。

2015全国大学生数学建模竞赛A

5.1.2 直杆太阳影子长度的变化曲线根据题目条件可得，日期为 2015 年 10 月 22 号，日期序号 n 295 ，时间T 的取值
范围为 9:00-15:00，地理纬度 39 54'26'' ，直杆长度 H 3m 。
图 2 直杆影子长度随时间的变化曲线
由图 2 可以看出：在 9:00——15:00 时间段内，直杆的太阳影子长度先减小后增大。这种影子长度的变化说明太阳在地平线以上高度的变化。在 9:00——12:00 时间段内，
5.2.1 直杆所处地点经度的确定已知东八区的经度为120 E 。假设直杆的影子长度最短时为当地时间正午 12:00，与
4．附件 4 为一根直杆在太阳下的影子变化的视频，并且已通过某种方式估计出直杆的高度为 2 米。请建立确定视频拍摄地点的数学模型，并应用你们的模型给出若干个可能的拍摄地点。
如果拍摄日期未知，你能否根据视频确定出拍摄地点与日期？
二、问题分析
本文是利用影子的变化轨迹确定视频拍摄的地点和日期。所以要在视频拍摄地点或者日期缺失的情况下，通过分析直杆的影子的变化轨迹补全缺失的信息。
，计算得出模型预估数据的误
差率为 6.25%，精度为 93.75%，所以问题一建立的影子长度变化模型能够准确的对影子长度进行预测，反映直杆影子长度变化趋势。
5.2 问题二模型建立及求解问题二要求根据附件 1 中给出的影子顶点坐标数据确定直杆所处的地点。结合问题
一影子长度变化模型中的赤纬、时角和太阳高度角、太阳方位角之间的数学关系，确定直杆所处地点的纬度和经度，从而确定直杆所处的地点。
23.45sin
2
284
365
n
(1)
时角表示地球与地球子午圈的角距离，可以通过时间衡量，小时作为计量单位。正

数学建模校内选拔赛的评比问题

数学建模校内选拔赛的评阅问题摘要：对于像全国数学建模竞赛这样的大型活动，竞赛后的评阅试卷过程往往需要很大的人力物力，如何评阅最少的试卷与又能体现出最大的公平度就能将优胜者选出是本文解决的关键问题。

为了实现兼顾公平，效率优先，我们制定如下两个指标：一是公平度，即必须保证评阅过程以及评阅结果公平、合理，必须避免因为评阅者的偏好不同或其它因素而对参赛论文造成误判；二是高效率，即面对大量答卷，既要在尽量短时间内完成阅卷，又要减少每位评阅者的阅卷数量，即使每位评阅者的工作量越少越好。

然后我们根据上述指标对题中所给方案进行合理性和缺点评价。

相对于理想情况，每个评阅者评阅所有答卷的方法，题中所述评阅方案评阅时间、评阅人数相对减少，评阅效率相对提高，但相对公平度较低。

于是由以上两个指标我们建立了圆桌模型，以此来实现阅卷过程中的公平度与高效率，并借助计算机仿真出每一轮评分中每一位阅卷者所给的分数，用大量数据来检验模型的合理性与准确性。

而题目中用到的四个变量、、、，我们通过查阅大量权威资料，对其之间存在的意义关系进行深入分析，试图建立其相关量间的规划模型。

在此过程中，假设每位评阅者阅卷量相同，采用计算机仿真，通过具体数据得到每位阅卷者所评阅的答卷总份数W。

但是在建立模型时，考虑的都是理想条件下的情况，与实际的情况可能会有出入。

所以可以根据现实生活中的改卷情况，构建系统偏差模型。

假设评阅人数与系统偏差呈线性关系，依据现实情况把线性关系表示出来，通过计算机进行模拟赋值，确定线性关系中的变量。

在重复问题（c）中模型方案，但要考虑到系统偏差。

最后在最优的1.2N 中选出优秀的N份。

关键词：公平度，高效，仿真，圆桌模型，系统偏差一问题重述某师范学院从2003年开始组队参加全国数学建模竞赛，由于此项活动不断发展，参赛者数量较大，（一般情况下，参加比赛的大约有200个队）。

选拔的方式主要是模仿全国赛，根据题目完成一篇科技论文。

评阅者主要根据论文来完成对其成绩的评定。