九年级数学直角三角形的边考试题
九年级数学下册 第一章直角三角形的边角关系单元综合检测2 试题

第一章 直角三角形的边角关系本卷贰O 贰贰年贰月捌日编写; 出题人:令狐学复;欧阳化语;令狐理总。
单元测试时间是:90分钟,满分是:100分一、选择题〔每一小题3分,一共30分,请把答案填入答卷相应的表格内〕1. 有一山坡程度方向前进了40米,就升高了20米,那么这个山坡的坡度是〔 〕A .1:2B .2:1C .D2. 假设A ∠为锐角,且1cos 3A =,那么〔 〕 A .0°< A ∠<30° B .30°<A ∠<45° C .45°<A ∠<60° D .60°<A ∠<90°3. 比拟tan 46,cos 29,sin 59︒︒︒的大小关系是〔 〕A .tan 46cos 29sin 59︒<︒<︒B .tan 46sin 59cos 29︒<︒<︒C .sin 59tan 46cos 29︒<︒<︒D .sin 59cos 29tan 46︒<︒<︒ 4. 在Rt ABC △中,90C ∠=°,假设1sin 2A =,那么A ∠的度数是〔 〕 A .60°B .45°C .30°D .无法确定5. 同一时刻,身高2.26m 的姚明在阳光下影长为1.13m ;小林浩在阳光下的影长为0.64m ,那么小林浩的身高为〔 〕6. 如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB 、CD 分别表示一楼、二楼地面的程度线,∠ABC =150°,BC 的长是8 m ,那么乘电梯从点B 到点C 上升的高度h 是〔 〕 Am B .4 m C. mD .8 mAB7. tan 45sin 452sin 30cos 45tan 30︒︒-︒︒+︒=〔 〕A .12B .22C .32D .338. 如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的程度间隔 为5米,那么这两树在坡面上的间隔 AB 为〔 〕A . αcos 5B . αcos 5C . αsin 5D .αsin 59. 将宽为2cm 的长方形纸条折叠成如下图的形状,那么折痕PQ 的长是〔 〕 A .233cm B .433cm C .5cm D .2cm 10.2tan 302tan 301tan 30︒-︒++︒=〔 〕A .233 B .2313- C .231- D .1 单元测试答卷班级___________学号_________ 姓名____________〔时间是:90分钟,满分是:100分〕一、选择题〔每一小题3分,一共30分,请把答案填入相应的表格内〕 题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题〔每空3分,一共30分〕 题号 11 12 13 14 15 答案题号16171819α5米AB60°P Q2cm答案11. 在Rt ABC △中,90C ∠=°,sinA=45,BC=20,那么ABC △的周长为__________ 12. 在Rt ABC △中,9032C AB BC ∠===°,,,那么cos A 的值是 .13. 如图,某游乐场内滑梯的滑板与地面所成的角∠A = 35°,滑梯的高度BC = 2米,那么滑板AB 的长约为_________米〔准确到0.1〕.14. 如图,小明从A 地沿北偏30向走1003m 到B 地,再从B 地向正南方向走200m 到C 地,此时小明离A 地 m .15. 如图,将以A 为直角顶点的等腰直角三角形ABC 沿直线BC 平移得到△C B A ''',使点B '与C 点重合,连结B A ',那么C B A ''∠tan 的值是 .16. 某校初三〔一〕班课外活动小组为了测得旗杆的高度,他们在离旗杆6米的A B 处的仰角为60°,如下图,那么旗杆的高度为 米.〔3 1.732≈,结果准确到0.1米〕17. 如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开场时绳子与水面的夹角为30°,此人以BCAAC (B ′)BA ′C ′ACDEB60°每秒0.5米收绳.问:未开场收绳子的时候,图中绳子BC 的长度是__________米;收绳8秒后船向岸边挪动了____________米?〔结果保存根号〕18. 小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如下图,把一张长方形卡片ABCD 放在每格宽度为12mm 的横格纸中,恰好四个顶点都在横格线上,α=36°,那么长方形卡片的周长为________.〞〔准确到1mm 〕19. 〔参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75〕20. 公园里有一块形如四边形ABCD 的草地,测得10BC CD ==米,120B C ∠=∠=°,45A ∠=°.那么这块草地的面积为__________.三、 解答题〔一共40分〕 21. 〔6分〕计算:22009(21)86sin 45(1)--+-+-°.CDABαl12mmDCBA22. 〔7分〕如图,AC 是我某大楼的高,在地面上B 点处测得楼顶A 的仰角为45º,沿BC 方向前进18米到达D 点,测得tan ∠ADC = 53.现打算从大楼顶端A 点悬挂一幅庆贺建国60周年的大型标语,假设标语底端距地面15m ,请你计算标语AE 的长度应为多少?23. 〔7分〕如图,两条笔直的公路AB CD 、相交于点O ,AOC ∠为36°,指挥中心M 设在OA 路段上,与O 地的间隔 为18千米.一次行动中,王警官带队从O 地出发,沿OC 方向行进,王警官与指挥中心均配有对讲机,两部对讲机只能在10千米之内进展通话,通过计算判断王警官在行进过程中能否实现与指挥中心用对讲机通话.【参考数据:sin 360.59cos360.81tan 360.73===°,°,°.】23. 〔10分〕如图,在航线l 的两侧分别有观测点A 和B ,点A 到航线l 的间隔 为2km ,点B 位于点A 北偏东60°方向且与A 相距10km 处.现有一艘轮船从位于点B 南偏西76°方向的C 处,正沿该航线自西向东航行,5min 后该轮船行至点A 的正北方向的D 处. 〔1〕求观测点B 到航线l 的间隔 ;B〔2〕求该轮船航行的速度〔结果准确到0.1km/h 〕.1.73,sin 760.97°≈,cos 760.24°≈,tan 76 4.01°≈〕24.〔10分〕花园小区有一朝向为正南方向的居民楼〔如图〕,该居民楼的一楼是高4米的小区商场,商场以上是居民住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与程度线的夹角为35°时,问:〔1〕商场以上的居民住房采光是否有影响,为什么?〔2〕假设要使商场采光不受影响,两楼应相距多少 米?〔结果保存一位小数〕〔参考数据:sin 350.57≈°,cos350.82≈°,tan 350.70≈°〕参考答案一、选择题 1. A 2. D 3. D 4. C 5. A 6. B 7. D 8. B 9. B 10. D 二、填空题 11. 6012. 13.14. 100 15.31 16.17. 解〔1〕如图,在Rt △ABC 中,BCAC=sin30° ∴ BC =︒sin305=10米 〔2〕收绳8秒后,绳子BC 缩短了4米,只有6米,这时,船到河岸的间隔 为1125365622=-=-米.故挪动间隔为.18. 解:作BE l ⊥于点E ,DF l ⊥于点F .18018090909036.DAF BAD ADF DAF ADF αα+∠=-∠=-=∠+∠=︒∴∠==︒°°°°,,根据题意,得BE =24mm ,DF =48mm. 在Rt ABE △中,sin BEABα=, 2440sin 360.60BE AB ∴===°mm在Rt ADF △中,cos DFADF AD∠=,4860cos360.80DF AD ∴===°mm .∴矩形ABCD 的周长=2〔40+60〕=200mm .19. 解:连接BD ,过C 作CE BD ⊥于E ,10120BC DC ABC BCD ==∠=∠=,°, 123090ABD ∴∠=∠=∴∠=°,°.5CE BE ∴=∴=,452A AB BD BE ∠=∴===°,ABD BCD ABCD S S S ∴=+△△四边形CE BD BD AB •+•=21212115(15022m =⨯+⨯=+. 三、解答题 20.解:)2200916sin 45(1)--+-︒+-=21+-=21)1++--ClD CBAE 1 2=211+++-=2+21. 解:在Rt ABC △中,90ACB ∠=°,45ABC ∠=°,Rt ABC ∴△是等腰直角三角形,AC BC =.在Rt ADC △中,90ACD ∠=°,tan AC ADC DC ∠=53=, 35DC AC ∴=, BC DC BD -=,即3185AC AC -=.45AC ∴=.那么451530AE AC EC =-=-=. 答:标语AE 的长度应为30米. 22. 解:过点M 作MH OC ⊥于点H . 在Rt MOH △中,sin MHMOH OM∠= 18OM =,36MOH ∠=°,18sin 36180.5910.6210MH ∴=⨯=⨯=>°.即王警官在行进过程中不能实现与指挥中心用对讲机通话. 23. 解:〔1〕设AB 与l 交于点O .在Rt AOD △中,6024cos 60ADOAD AD OA ∠====°,,°.又106AB OB AB OA =∴=-=,.在Rt BOE △中,)(360cos ,60km OB BE OAD OBE =︒=∴︒=∠=∠∴观测点B 到航线l 的间隔 为3km .〔2〕在Rt AOD △中,3260tan =︒=AD OD .B在Rt BOE △中,3360tan =︒=BE OE .DE OD OE ∴=+=.在Rt CBE △中,︒=∠=∴=︒=∠76tan 3tan ,3,76CBE BE CE BE CBE .3tan 76 3.38CD CE DE ∴=-=-°.15min h 12=,1212 3.3840.6112CDCD ∴==⨯≈〔km/h 〕.24. 解:〔1〕如图,光线交CD 于点E ,过点E 作EF BD ∥交AB 于点F . 设DE x =米,那么(18)AF x =-米在Rt AFE △中,35AEF ∠=°,tan 35AFEF ∴=° 180.7016x-=, 6.8x = 6.84>,∴居民住房的采光有影响.〔2〕如图,在Rt ABD △中tan ABADB BD ∠= 18tan 35BD =°,1825.7125.80.70BD =≈≈ 答:两楼相距25.8米.本卷贰O 贰贰年贰月捌日编写; 出题人:令狐学复;欧阳化语;令狐理总。
2021-2022学年北师大版九年级数学《第1章直角三角形的边角关系》单元综合达标测试(附答案)

2021-2022学年北师大版九年级数学上册《第1章直角三角形的边角关系》单元综合达标测试(附答案)一.选择题(共6小题,满分30分)1.如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD=3,CD=2,则tan B的值为()A.B.C.D.2.在△ABC中,BC=2,AC=2,∠A=30°,则AB的长为()A.B.2C.或4D.2或43.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD 的正切值是()A.B.C.D.4.如图,在Rt△ABC中,∠C=90°,AC=4,tan A=,则BC的长度为()A.2B.8C.D.5.如图,在边长为1的正方形网格中,连接格点D、N和E、C,DN和EC相交于点P,tan ∠CPN为()A.1B.2C.D.6.某水库大坝的横断面是梯形,坝内斜坡的坡度,坝外斜坡的坡度i=1:1,则两个坡角的和为()A.90°B.60°C.75°D.105°二.填空题(共10小题,满分50分)7.如图,△ABC的顶点都在正方形网格的格点上,则sin∠ACB的值为.8.如图,点D在钝角△ABC的边BC上连接AD,∠B=45°,∠CAD=∠CDA,CA:CB =5:7,则∠BAD的余弦值为.9.已知△ABC中,AB=10,AC=2,∠B=30°,则△ABC的面积等于.10.如图所示的网格是正方形网格,∠BAC∠DAE.(填“>”,“=”或“<”)11.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC=.12.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tan A=,则CD=.13.如图,一架长为10米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC 的长度约为米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)14.2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为米.(参考数据:sin20°≈0.34)15.如图,某中学综合楼入口处有两级台阶,台阶高AD=BE=15cm,深DE=30cm,在台阶处加装一段斜坡作为无障碍通道,设台阶起点为A,斜坡的起点为C,若斜坡CB的坡度i=1:9,则AC的长为cm.16.如图,一幢居民楼OC临近坡AP,山坡AP的坡度为i=1:(tanα=),小亮在距山坡坡脚A处测得楼顶C的仰角为60°,当从A处沿坡面行走6米到达P处时,测得楼顶C的仰角刚好为45°,点O,A,B在同一直线上,则该居民楼的高度为(结果保留根号).三.解答题(共5小题,满分40分)17.已知:Rt△ACB中,∠C=90°,∠A=60°,CD⊥AB于点D,CD=,解这个直角三角形.18.如图,△ABC中,∠A=30°,AC=2,tan B=,求AB的长.19.如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,BD平分∠ABC,DE⊥AB于点E,AE=6,cos A=.(1)求CD的长;(2)求tan∠DBC的值.20.如图,在△ABD中,∠ABD=∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,分别连接BC,DC,AC,记AC与BD的交点为O.(1)补全图形,求∠AOB的度数并说明理由;(2)若AB=5,cos∠ABD=,求BD的长.21.如图,一艘海轮位于灯塔P的南偏东30°方向,距离灯塔100海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.(1)问B处距离灯塔P有多远?(结果精确到0.1海里)(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔150海里的点O处.圆形暗礁区域的半径为60海里,进入这个区域,就有触礁的危险.①请判断海轮到达B处是否有触礁的危险?并说明理由.②如果海伦从B处继续向正北方向航行,是否有触礁的危险?直接写出结论,不用说明理由.(参考数据:≈1.414,≈1.732)参考答案一.选择题(共6小题,满分30分)1.解:∵∠BAC=90°,∴∠BAD+∠CAD=90°,又∠B+∠BAD=90°,∴∠CAD=∠B,∴tan∠B=,tan∠CAD=,∴=,即AD2=BD•CD=3×2=6.∴AD=.故tan∠B==.故选:D.2.解:作CD⊥AB交AB的延长线于点D,当B2C=2时,∵∠A=30°,∠ADC=90°,AC=2,∴CD=,∴AD==3,B2D==1,∴AB2=3﹣1=2,同理可得,AB1=3+1=4,即AB的长为2或4,故选:D.3.解:∵CD是AB边上的中线,∴CD=AD,∴∠A=∠ACD,∵∠ACB=90°,BC=6,AC=8,∴tan∠A=,∴tan∠ACD的值.故选:D.4.解:∵在Rt△ABC中,∠C=90°,AC=4,∴tan A===,∴BC=2.故选:A.5.解:连接格点MN、DM,如图所示:则四边形MNCE是平行四边形,△DAM和△MBN都是等腰直角三角形,∴EC∥MN,∠DMA=∠NMB=45°,DM=AD=2,MN=BM=,∴∠CPN=∠DNM,∴tan∠CPN=tan∠DNM,∵∠DMN=180°﹣∠DMA﹣∠NMB=180°﹣45°﹣45°=90°,∴tan∠CPN=tan∠DNM===2,故选:B.6.解:如图所示,∵ED:AE=1:,∴∠A=30°.∵CF:BF=1:1,∴∠B=45°.∴∠A+∠B=30°+45°=75°.故选:C.二.填空题(共10小题,满分50分)7.解:作如图所示的辅助线,则BD⊥AC,∵BC=,BD=,∴sin∠ACB=,故答案为.8.解:如图作AH⊥BC于H,DE⊥AB于E,设AC=CD=5k,BC=7k,∵∠B=45°,∠AHB=90°,∴AH=BH,设AH=BH=x,在Rt△ACH中,∵AH2+HC2=AC2,∴x2+(7k﹣x)2=(5k)2,解得x=3k或4k(舍弃与钝角三角形矛盾),当x=3k时,∴BH=AH=3k,DH=k,AD=k,DE=BE=k,AE=2k,∴cos∠BAD===,故答案为.9.解:作AD⊥BC交BC(或BC延长线)于点D,①如图1,当AB、AC位于AD异侧时,在Rt△ABD中,∵∠B=30°,AB=10,∴AD=AB sin B=5,BD=AB cos B=5,在Rt△ACD中,∵AC=2,∴CD===,则BC=BD+CD=6,∴S△ABC=•BC•AD=×6×5=15;②如图2,当AB、AC在AD的同侧时,由①知,BD=5,CD=,则BC=BD﹣CD=4,∴S△ABC=•BC•AD=×4×5=10.综上,△ABC的面积是15或10,故答案为15或10.10.解:在Rt△ABC中,tan∠BAC==,在Rt△ADE中,可表示tan∠DAE===1,∵tan∠BAC<tan∠DAE,∴∠BAC<∠DAE,故答案为:<.11.解:∵∠B=90°,sin∠ACB=,∴=,∵AB=2,∴AC=6,∵AC⊥CD,∴∠ACD=90°,∴AD===10,∴cos∠ADC==.故答案为:.12.解:延长AD和BC交于点E.∵在直角△ABE中,tan A==,AB=3,∴BE=4,∴EC=BE﹣BC=4﹣2=2,∵△ABE和△CDE中,∠B=∠EDC=90°,∠E=∠E,∴∠DCE=∠A,∴直角△CDE中,tan∠DCE=tan A==,∴设DE=4x,则DC=3x,在直角△CDE中,EC2=DE2+DC2,∴4=16x2+9x2,解得:x=,则CD=.故答案是:.13.解:由题意可得:∵∠ABO=70°,AB=10m,∴sin70°=,解得:AO=9.4(m),∵∠CDO=50°,DC=10m,∴sin50°=≈0.77,解得:CO=7.7(m),则AC=9.4﹣7.7=1.70(m),答:AC的长度约为1.70米.故答案为:1.70.14.解:过点A作AE⊥BD于点E,过点B作BG⊥CF于点G,在Rt△ABE中,∵sinα=,∴AE=AB×sin20°≈68米,在Rt△BCG中,∵sinβ=,∴BG=BC×sin45°≈142米,∴他下降的高度为:AE+BG=210米,故答案为:21015.解:过B作BF⊥AC,由题可知BF=30cm,AF=30cm.∵tan∠BCA==,∴CF=270cm,∴AC=CF﹣AF=270﹣30=240(cm).故答案为:240.16.解:如图,过点P作PE⊥OB于点E,PF⊥CO于点F,∵山坡AP的坡度为i=1:=tanα==,AP=6米,∴α=30°,∵PE⊥OB,∴PE=AP=3(米),AE=PE=3(米),∵PF⊥OC,∠CPF=45°,∴△PCF是等腰直角三角形,∴CF=PF,设CF=PF=m米,则OC=(m+3)米,OA=(m﹣3)米.在Rt△AOC中,∠OAC=60°,∴∠ACO=30°,∴OC=OA,即m+3=(m﹣3),解得:m=6+6,∴OC=6+6+3=(6+9)米,即该居民楼的高度为(6+9)米,故答案为:(6+9)米.三.解答题(共5小题,满分40分)17.解:∵∠C=90°,∠A=60°.∴∠B=30°.又CD⊥AB于D.∴BC=2CD=2.,∴BD===3.在直角三角形ACD中,∠A=60°,CD=∴AD===1,AC=2AD=2,∴AB=BD+AD=4.18.解:过C点作CD⊥AB于D,如图,在Rt△ACD中,∵sin A=,cos A=,即sin30°=,cos30°=,∴CD=×2=,AD=×2=3,在Rt△BCD中,∵tan B=,∴BD==2,∴AB=AD+BD=3+2=5.19.解:(1)在Rt△ADE中,∠AED=90°,AE=6,cos A=,∴AD==10,∴==8.∵BD平分∠ABC,DE⊥AB,DC⊥BC,∴CD=DE=8;(2)由(1)AD=10,DC=8,∴AC=AD+DC=18,在△ADE与△ABC中,∵∠A=∠A,∠AED=∠ACB,∴△ADE∽△ABC,∴,即=,∴BC=24,∴.20.解:(1)补全的图形,如图所示,可得出∠AOB=90°,理由如下:证明:由题意可知BC=AB,DC=AB,∵在△ABD中,∠ABD=∠ADB,∴AB=AD,∴BC=DC=AD=AB,∴四边形ABCD为菱形,∴AC⊥BD,∴∠AOB=90°;(2)∵四边形ABCD为菱形,∴OB=OD.在Rt△ABO中,∠AOB=90°,AB=5,cos∠ABD=,∴OB=AB•cos∠ABD=3,∴BD=2OB=6.21.解:(1)过点P作PD⊥AB于点D.依题意可知,P A=100海里,∠APD=90°﹣30°=60°,∠BPD=45°.∴∠A=90°﹣60°=30°.∴PD=P A=50(海里),在Rt△PBD中,∠BPD=45°,∴△PBD是等腰直角三角形,∴PB=PD=50(海里)≈70.7(海里).答:B处距离灯塔P约70.7海里.(2)①海轮到达B处没有触礁的危险,理由如下:依题意知:OP=150海里,PB=50海里,∴OB=OP﹣PB=(150﹣50)海里≈79.3海里>60海里,∴海轮到达B处没有触礁的危险.②过点O作OE⊥AB与E,交AB延长线于点E,则∠OEB=90°,∵∠OBE=∠PBD=45°,∴OE=OB sin∠OBE=(150﹣50)×=75﹣50≈56.07<60,∴海轮从B处继续向正北方向航行,有触礁的危险.。
北师大新版数学九年级下册第1章 直角三角形的边角关系(练习题)
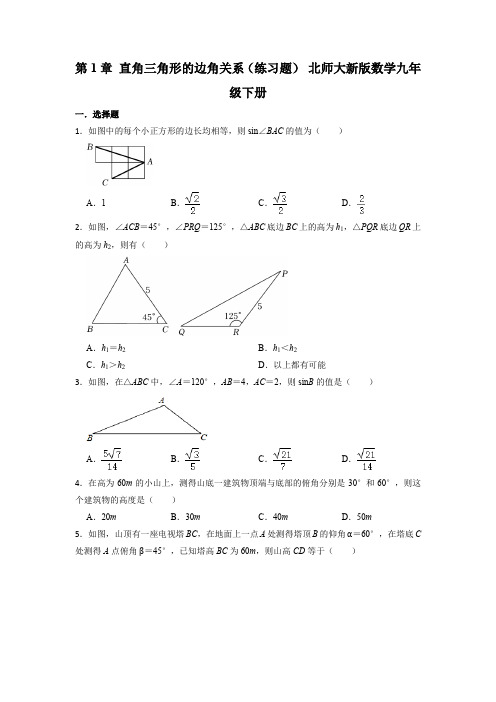
第1章直角三角形的边角关系(练习题)北师大新版数学九年级下册一.选择题1.如图中的每个小正方形的边长均相等,则sin∠BAC的值为()A.1B.C.D.2.如图,∠ACB=45°,∠PRQ=125°,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有()A.h1=h2B.h1<h2C.h1>h2D.以上都有可能3.如图,在△ABC中,∠A=120°,AB=4,AC=2,则sin B的值是()A.B.C.D.4.在高为60m的小山上,测得山底一建筑物顶端与底部的俯角分别是30°和60°,则这个建筑物的高度是()A.20m B.30m C.40m D.50m5.如图,山顶有一座电视塔BC,在地面上一点A处测得塔顶B的仰角α=60°,在塔底C 处测得A点俯角β=45°,已知塔高BC为60m,则山高CD等于()A.m B.m C.30m D.m 6.北京2022年冬奥会计划于2月4日开幕,2月20闭幕.如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为40°,底端点C与顶端点B的距离为50米.则赛道AB 的长度为()A.50sin40°米B.50cos40°米C.米D.米7.在△ABC中,AB=4,BC=5,sin B=,则△ABC的面积等于()A.15B.C.6D.8.如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于cos B 的是()A.B.C.D.9.如图,小东在教学楼距地面8米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.5米处,若国旗随国歌声冉冉升起,并在国歌播放46秒结束时到达旗杆顶端,则国旗匀速上升的速度为()米/秒.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)A.0.3B.0.2C.0.25D.0.3510.在如图所示的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,连接AB,AC,则sin∠BAC的值为()A.B.C.D.二.填空题11.如图,在Rt△ABD中,AB=6,tan∠ADB=,点C为斜边BD的中点,P为AD上任一点,过点P作PE⊥AC于点E,PF⊥BD于点F,则PE+PF=.12.如果一个斜坡的坡度i=1:,那么该斜坡的坡角为度.13.2cos45°﹣(π+1)0=.14.在Rt△ABC中,∠C=90°,sin A=,BC=6,则AB=.15.某滑雪运动员沿着坡比为1:的斜坡向下滑行了100米,则运动员下降的垂直高度为米.三.解答题16.学好数学,就是为能更好解决生活中遇到的问题,如图所示,为了测量山的高度AC,在水平面E处测得山顶A的仰角为30°,AC⊥EC,自E沿着EC方向向前走100m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)17.如图,在离铁塔20m的A处,用测倾仪测得塔顶的仰角为53°,测倾仪高AD为1.52m.求铁塔高BC(参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).18.如图,在高度为100米的小山上竖直建有一座铁塔,小明为测得铁塔的高度,先在山脚C处测得铁塔底部B的仰角为30°,后沿坡度i=1:2的山坡向上行走10米到达点D处,在点D处测得铁塔顶部A的仰角为30°,求铁塔AB的高度.19.如图,九年级数学兴趣小组要测量嵌在某大楼前面的电子屏高度CD.在该大楼正前方的A处测得电子屏CD顶端C的仰角为45°,底端D的仰角为30°.从A处沿水平地面向正前方走18米到达B处,测得顶端C的仰角为68.2°.求电子屏的高度CD.(结果保留整数)参考数据:sin68.2°≈0.93,≈1.41,cos68.2°≈0.37,≈1.73,tan68.2°≈2.5020.如图,小兵同学利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C 处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为120米,且AB垂直于桥面.(点A,B,C,M在同一平面内)(1)求大桥主架在桥面以上的高度AM;(结果保留根号)(2)求大桥主架在水面以上的高度AB.(结果精确到1米)(参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,≈1.73)。
北师大版九年级数学下册 第一章 直角三角形的边角关系 测试题 (含答案)

直角三角形的边角关系 测试题一、选择题1.如图,在Rt △ABC 中,∠B =90°,cos A =1213,则tan A 的值为( )A.125B.1312C.1213D.512第1题图 第2题图 第3题图 第4题图2.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D .若AC =5,BC =2,则sin ∠ACD 的值为( )A.53 B.255 C.52 D.233.如图,在△ABC 中,点E 在AC 上,点G 在BC 上,连接EG ,AE =EG =5,过点E 作ED ⊥AB ,垂足为D ,过点G 作GF ⊥AC ,垂足为F ,此时恰有DE =GF =4.若BG =25,则sin B 的值为( )A.2510B.510C.255D.55 4.如图,直线y =-33x +2与x 轴、y 轴分别交于A ,B 两点,把△AOB 沿直线AB 翻折后得到△AO ′B ,则点O ′的坐标是( )A .(3,3)B .(3,3)C .(2,23)D .(23,4) 5.tan45°的值为( ) A.12 B .1 C.22D.2 6.如图所示,△ABC 的顶点是正方形网格的格点,则sin B 的值为( ) A.12 B.22 C.32D .1第6题图 第7题图7.如图,在Rt △ABC 中,斜边AB 的长为m ,∠A =35°,则直角边BC 的长是( ) A .m sin35° B .m cos35° C.m sin35° D.mcos35°8.在△ABC 中,若⎪⎪⎪⎪sin A -12+⎝⎛⎭⎫33-tan B 2=0,则∠C 的度数为( )A .30°B .60°C .90°D .120° 二、填空题9.运用科学计算器计算:317sin73°52′≈________(结果精确到0.1). 10.计算:cos30°-sin60°=________.11.如图,铁路的路基的横断面为等腰梯形,其腰的坡度为1∶1.5,上底宽为6m ,路基高为4m ,则路基的下底宽为________m.12.如图,△ABC 中,∠ACB =90°,tan A =43,AB =15,AC =________.第11题图 第12题图 第13题图 第14 题图13.如图,Rt △ABC 中,∠ACB =90°,CM 为AB 边上的中线,AN ⊥CM ,交BC 于点N .若CM =3,AN =4,则tan ∠CAN 的值为________.14.如图,一艘渔船位于灯塔P 的北偏东30°方向,距离灯塔18海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东55°方向上的B 处,此时渔船与灯塔P 的距离约为________海里(结果取整数,参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).三、解答题15.如图,CD 是一高为4米的平台,AB 是与CD 底部相平的一棵树,在平台顶C 点测得树顶A 点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E ,在点E 处测得树顶A 点的仰角β=60°,求树高AB (结果保留根号).16.某地的一座人行天桥如图所示,天桥高为6米,坡面BC 的坡度为1∶1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面AC 的坡度为1∶ 3.(1)求新坡面的坡角α;(2)原天桥底部正前方8米处(PB 的长)的文化墙PM 是否需要拆除?请说明理由.17.在一个三角形中,各边和它所对角的正弦的比相等,即asin A=bsin B=csin C,利用上述结论可以求解如下题目,如:在△ABC中,若∠A=45°,∠B=30°,a=6,求b的值.解:在△ABC中,∵asin A=bsin B,∴b=a sin Bsin A=6sin30°sin45°=6×1222=3 2.解决问题:如图,甲船以每小时302海里的速度向正北方航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟后到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距102海里.(1)判断△A1A2B2的形状,并给出证明;(2)乙船每小时航行多少海里?参考答案与解析1.D2.A3.C 解析:在Rt △ADE 与Rt △EFG 中,⎩⎪⎨⎪⎧AE =EG ,DE =GF , ∴Rt △ADE ≌Rt △EFG (HL),∴∠A =∠GEF .∵∠A +∠AED =90°,∴∠GEF +∠AED=90°,∴∠DEG =90°.过点G 作GH ⊥AB 于点H ,则四边形DEGH 为矩形,∴GH =DE =4.在Rt △BGH 中,sin B =GH BG =425=255.故选C.4.A 解析:过点O ′作O ′C ⊥x 轴于点C .∵直线y =-33x +2与x 轴、y 轴分别交于A ,B 两点,∴点A ,B 的坐标分别为(23,0),(0,2),∴tan ∠BAO =OB OA =223=33,∴∠BAO=30°.∵把△AOB 沿直线AB 翻折后得到△AO ′B ,∴O ′A =OA =23,∠O ′AO =60°,∴CA =12O ′A =3,O ′C =O ′A ·sin ∠O ′AC =23×32=3,∴OC =OA -CA =23-3=3,∴点O ′的坐标为(3,3).故选A. 5.B 6.B 7.A 8.D 9.11.9 10.0 11.18 12.913.23 解析:∵∠ACB =90°,CM 为AB 边上的中线,∴AB =2CM =6,CM =BM ,∴∠B =∠MCB .∵AN ⊥CM ,∴∠CAN +∠ACM =90°.又∵∠ACM +∠MCB =90°,∴∠CAN =∠MCB ,∴∠B =∠CAN .又∵∠ACN =∠BCA ,∴△CAN ∽△CBA ,∴CN CA =AN BA =46=23,∴tan ∠CAN =CN AC =23.14.11 解析:过点P 作PC ⊥AB 于点C .依题意可得∠A =30°,∠B =55°.在Rt △P AC 中,∵P A =18海里,∠A =30°,∴PC =12P A =12×18=9(海里).在Rt △PBC 中,∵PC =9海里,∠B =55°,∴PB =PC sin B ≈90.8≈11(海里).15.解:过点C 作CF ⊥AB 于点F ,则BF =CD =4米,CF =BD .设AF =x 米.在Rt △ACF 中,tan ∠ACF =AF CF ,∠ACF =α=30°,则CF =AF tan30°=3x 米.在Rt △ABE 中,AB =AF +BF =(x +4)米,tan ∠AEB =AB BE ,∠AEB =β=60°,则BE =AB tan60°=33(x +4)米.∵CF =BD =DE +BE ,∴3x =3+33(x +4),解得x =33+42.则AB =33+42+4=33+122(米). 答:树高AB 是33+122米.16.解:(1)∵新坡面的坡度为1∶3,∴tan α=13=33,∴α=30°; (2)文化墙PM 不需要拆除.理由如下:过点C 作CD ⊥AB 于点D ,则CD =6米.∵坡面BC 的坡度为1∶1,新坡面AC 的坡度为1∶3,∴BD =CD =6米,AD =3CD =63米,∴AB =AD -BD =(63-6)米<8米,∴文化墙PM 不需要拆除.17.解:(1)△A 1A 2B 2是等边三角形.证明如下:由题意可得A 2B 2=102海里,A 1A 2=302×2060=102(海里),∴A 1A 2=A 2B 2.又∵∠A 1A 2B 2=180°-120°=60°,∴△A 1A 2B 2是等边三角形;(2)由(1)可知△A 1A 2B 2是等边三角形,∴A 1B 2=A 1A 2=102海里,∠A 2A 1B 2=60°,∴∠B 1A 1B 2=105°-60°=45°.由题意可知∠CB 1A 1=180°-105°=75°,∴∠B 2B 1A 1=75°-15°=60°.在△A 1B 2B 1中,由正弦定理得B 1B 2sin45°=A 1B 2sin60°,∴B 1B 2=A 1B 2sin60° ·sin45°=10232×22=2033(海里).乙船的速度为2033÷2060=203(海里/时). 答:乙船每小时航行203海里.。
【小初高学习】九年级数学下册第一章直角三角形的边角关系专题训练(二)解直角三角形应用中的六种基本模型

专题训练(二) 解直角三角形应用中的六种基本模型►模型一“独立”型1.如图2-ZT-1,一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好遇见渔船,那么救援船航行的速度为( )图2-ZT-1A.10 3海里/时B.30海里/时C.20 3海里/时D.30 3海里/时2.2017·台州如图2-ZT-2是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为1.2米,当车门打开角度∠AOB 为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)图2-ZT-2►模型二“背靠背”型3.如图2-ZT-3,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120 m,则这栋楼的高度为( )图2-ZT-3A.160 3 m B.120 3 mC.300 m D.160 2 m4.如图2-ZT-4,湖中的小岛上有一标志性建筑物,其底部有一点A,某人在岸边的点B处测得点A在点B的北偏东30°的方向上,然后沿岸边直行4千米到达点C处,再次测得点A在点C的北偏西45°的方向上(其中点A,B,C在同一平面上).求这个标志性建筑物底部上的点A到岸边BC的最短距离.图2-ZT-4►模型三“母抱子”型5.如图2-ZT-5,某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在点C 处仰望建筑物顶端A处,测得仰角为48°,再往建筑物的方向前进6米到达点D处,测得建筑物顶端A的仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:sin48°≈710,tan48°≈1110,sin64°≈910,tan64°≈2)图2-ZT-56.2017·内江如图2-ZT-6,某人为了测量小山顶上的塔ED的高,他在山下的点A 处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)图2-ZT-6►模型四“拥抱”型7.如图2-ZT-7,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1 m(即BD=1 m)到达CD位置时,它与地面所成的角∠CDO=51°18′,求梯子的长.(参考数据:sin51°18′≈0.780,cos51°18′≈0.625,tan51°18′≈1.248)图2-ZT-7►模型五梯形类8.如图2-ZT-8,梯形ABCD是拦水坝的横断面示意图,图中i=1∶3是指坡面的铅直高度DE与水平宽度CE的比,∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果精确到0.1.参考数据:3≈►模型六“斜截”型9.“蘑菇石”是贵州省著名自然保护区梵净山的标志,小明从山脚点B处先乘坐缆车到达与BC平行的观景平台DE处观景,然后再沿着坡角为29°的斜坡由点E步行到达“蘑菇石”点A处,“蘑菇石”点A到水平面BC的垂直距离为1790 m.如图2-ZT-9,DE∥BC,BD=1700 m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1 m,参考数据:sin80°≈0.9848,sin29°≈0.4848)详解详析1.[解析] D 由“B 在海岛A 的南偏东20°方向”和“海岛C 在海岛A 的南偏西10°方向”得∠BAC =30°,同理得∠ABC =60°,∴∠ACB =90°.∵AB =20海里,∴BC =10海里,AC =10 3海里,再由“救援船由海岛A 开往海岛C 用时20分钟”可求得救援船航行的速度为30 3海里/时.故选D.2.解:车门不会碰到墙.理由如下:如图,过点A 作AC ⊥OB ,垂足为C .在Rt △ACO 中,∵∠AOC =40°,AO ∴AC =AO ·sin∠AOC ≈1.2×0.64=0.768(米).∵汽车靠墙一侧OB 与墙MN 平行且距离为0.8米,0.8>0.768, ∴车门不会碰到墙.3.[解析] A 过点A 作AD ⊥BC 于点D , 则∠BAD =30°,∠CAD =60°,AD =120 m. 在Rt △ABD 中,BD =AD ·tan30°=120×33=40 3(m). 在Rt △ACD 中,CD =AD ·tan60°=120×3=120 3(m), ∴BC =BD +CD =40 3+120 3=160 3(m).4.解:过点A 作AD ⊥BC 于点D ,则AD 的长度就是点A 到岸边BC 的最短距离.在Rt △ACD 中,∠ACD =45°,设AD =x 千米,则CD =AD =x 千米. 在Rt △ABD 中,∠ABD =60°, 因为tan ∠ABD =AD BD ,即tan60°=x BD,所以BD =x tan60°=33x 千米.又因为BC =4千米, 所以BD +CD =4千米,即33x +x =4, 解得x =6-2 3,所以这个标志性建筑物底部上的点A 到岸边BC 的最短距离为(6-2 3)千米. 5.解:根据题意,得∠ADB =64°,∠ACB =48°. 在Rt △ADB 中,tan64°=AB BD ,则BD =AB tan64°≈12AB ,在Rt △ACB 中,tan48°=AB CB,则CB =ABtan48°≈1011AB ,∴CD =CB -BD ,即6=1011AB -12AB ,解得AB =1329≈14.7(米),∴建筑物的高度约为14.7米.6.[解析] 先求出∠DBE =30°,∠BDE =30°,得出BE =DE ,设EC =x ,则BE =2x ,DE =2x ,DC =3x ,BC =3x ,再根据∠DAC =45°,可得AC =DC ,列出方程求出x 的值,即可求出塔DE 的高度.解:由题意知,∠DBC =60°,∠EBC =30°, ∴∠DBE =∠DBC -∠EBC =60°-30°=30°. 又∵∠BCD =90°,∴∠BDC =90°-∠DBC =90°-60°=30°, ∴∠DBE =∠BDE ,∴BE =DE .设EC =x m ,则DE =BE =2EC =2x m ,DC =EC +DE =3x m , BC =BE 2-EC 2=3x m.由题意可知,∠DAC =45°,∠DCA =90°,AB =60 m , ∴△ACD 为等腰直角三角形,∴AC =DC , ∴3x +60=3x . 解得x =30+10 3.答:塔ED 的高度为(30+10 3)m. 7.解:设梯子的长为x m.在Rt △ABO 中,cos ∠ABO =OBAB,∴OB =AB ·cos∠ABO =x ·cos60°=12x m.在Rt △CDO 中,cos ∠CDO =OD CD, ∴OD =CD ·cos∠CDO =x ·cos51°18′≈0.625x m. ∵BD =OD -OB ,∴0.625x -12x =1,解得x =8.答:梯子的长约为8 m.8.解:过点A 作AF ⊥BC ,垂足为F . 在Rt △ABF 中,∠B =60°,AB =6, ∴AF =AB sin B =6sin60°=3 3, BF =AB cos B =6cos60°=3. ∵AD ∥BC ,AF ⊥BC ,DE ⊥BC , ∴四边形AFED 是矩形,∴DE =AF =3 3,FE =AD =4.在Rt △CDE 中,i =DE CE =13,∴CE =3DE =3×3 3=9,∴BC =BF +FE +CE =3+4+9=16, ∴S 梯形ABCD =12(AD +BC )·DE=12×(4+16)×3 3 ≈52.0.答:拦水坝的横断面ABCD 的面积约为52.0.9.解:过点D 作DF ⊥BC 于点F ,延长DE 交AC 于点M ,由题意,得EM ⊥AC , ∴四边形DMCF 为矩形, ∴DF =MC .在Rt △DFB 中,sin80°=DF BD ,则DF =BD ·sin80°=1700×sin80°(m), ∴AM =AC -MC =AC -DF =(1790-1700×sin80°)m. 在Rt △AME 中,sin29°=AM AE, 则AE =AMsin29°=1790-1700×sin80°sin29°≈238.9(m).答:斜坡AE 的长度约为238.9 m.。
北师大版九年级数学下册第一章直角三角形的边角关系综合题训练

北师大版九年级数学下册第一章直角三角形的边角关系综合压轴题专项训练试题1、如图,MN是表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心,500 米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400米,通过计算回答,如果不改变方向,输水路线是否会穿过居民区?2、如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D 是BC的中点,且AD⊥BC.(1)求sin B的值;(2)现需要加装支架DE,EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F.求支架DE的长.3、如图,拦水坝的横断面为等腰梯形ABCD,坝顶宽BC为6 m,坝高为3.2 m,为了提高水坝的拦水能力需要将水坝加高2 m,并且保持坝顶宽度不变,迎水坡CD的坡度不变,但是背水坡的坡度由原来的1∶2变成1∶2.5(坡度是坡高与坡的水平长度的比).求加高后的坝底HD的长为多少.4、小红家的阳台上放置了一个晒衣架(如图∶),图∶是晒衣架的侧面示意图,立杆AB,CD相交于点O ,B ,D 两点立于地面,经测量:AB =CD =136 cm ,OA =OC =51 cm ,OE =OF =34 cm ,现将晒衣架完全稳固张开,扣链EF 成一条线段,且EF =32 cm (参考数据:sin 61.9°≈0.882,cos 61.9°≈0.471,tan 28.1°≈0.534).(1)求证:AC ∶BD .(2)求扣链EF 与立杆AB 的夹角∶OEF 的度数(结果精确到0.1°).(3)小红的连衣裙穿在晒衣架上的总长度达到122 cm ,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.5、如图,在电线杆上的C 处引拉线CE ,CF 固定电线杆,拉线CE 和地面成60°角,在离电线杆6米的点B 处安置测角仪,在点A 处测得电线杆上C 处的仰角为30°.已知测角仪高AB 为1.5米,求拉线CE 的长(结果保留根号).6、如图,两条笔直的公路AB CD 、相交于点O ,AOC ∠为36°,指挥中心M 设在OA 路段上,与O 地的距离为18千米.一次行动中,王警官带队从O 地出发,沿OC 方向行进,王警官与指挥中心均配有对讲机,两部对讲机只能在10千米之内进行通话,通过计算判断王警官在行进过程中能否实现与指挥中心用对讲机通话.【参考数据:sin360.59cos360.81tan360.73===°,°,°.】7、在建筑楼梯时,设计者要考虑楼梯的安全程度和占地面积,如图1—136(1)所示,虚线为楼梯的斜度线,斜度线与地板的夹角为锐角θ,一般情况下,锐角θ愈小,楼梯的安全程度愈高,但占地面积较多,如图l—136(2)所示,为提高安全程度,把倾角由θ1减至θ2,这样楼梯占用地板的长度由d1增加到d2,已知d1=4 m,θ1=40°,θ2=36°,求楼梯占用地板的长度增加了多少.(精确到0.01 m,参考数据:sin36°≈0.5878,cos36°≈0.8090,tan 36°≈0.7265,sin 40°≈0.6428,cos 40°≈0.7660,tan 40°≈0.8391)8、在旧城改造中,要拆除一烟囱AB,如图1—137所示,在地面上事先划定以B为圆心,半径与AB等长的圆形区域为危险区,现在从与B地水平距离相距(BD=21米)21米远的建筑物CD的顶端C点测得A点的仰角为45°,B点的俯角为30°,现在离B点25米远的地方有一受保护的文物,则该文物是否在危险区内?试说明理由.,精确到0.01米)9、通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图1,在∶ABC中,AB =AC ,顶角A 的正对记作sadA ,这时sadA =底边腰=BC AB .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1)sad 60°=____________;(2)对于0°<∶A <180°,∶A 的正对值sadA 的取值范围是____________;(3)如图2,已知sinA =35,其中∶A 为锐角,试求sadA 的值. 10、根据道路管理规定,在羲皇大道秦州至麦积段上行驶的车辆,限速60千米/时.已知测速站点M 距离羲皇大道l (直线)的距离MN 为30米(如图8所示).现有一辆汽车由秦州向麦积方向匀速行驶,测得此车从点A 行驶到点B 所用时间为6秒,∠AMN =60°,∠BMN =45°.(1)计算AB 的长;(2)通过计算判断此车是否超速.11、如图所示,港口B 位于港口O 正西方向120 km 处,小岛C 位于港口O 北偏西60°的方向.一艘游船从港口O 出发,沿OA 方向(北偏西30°)以v km /h 的速度驶离港口O ,同时一艘快艇从港口B 出发,沿北偏东30°的方向以60 km /h 的速度驶向小岛C ,在小岛C 用1 h 加装补给物资后,立即按原来的速度给游船送去.(1)快艇从港口B 到小岛C 需要多长时间?(2)若快艇从小岛C 到与游船相遇恰好用时1 h ,求v 的值及相遇处与港口O 的距离.12、如图,修公路遇到一座山,于是要修一条隧道,为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C 在AB 的延长线上,设想过C 点作直线AB 的垂线l ,过点B 作一直线(在山的旁边经过),与l 相交于D 点,经测量∶ABD =135°,BD =800米,求直线l 上距离D 点多远的C 处开挖?(2≈1.414,结果精确到1米)13、已知:如图,在山脚的C 处测得山顶A 的仰角为 45°,沿着坡度为30°的斜坡前进400米到D 处(即 ∠,CD =400米),测得A 的仰角为,求山的高度AB .14、如图,在南北方向的海岸线MN 上,有A ,B 两艘巡逻船,现均收到故障船C 的求救信号.已知A ,B 两船相距1003+1)海里,船C 在船A 的北偏东60°方向上,船C 在船B 的东南方向上,MN 上有一观测点D ,测得船C 正好在观测点D 的南偏东75°方向上.(1)分别求出A 与C ,A 与D 间的距离AC 和AD (如果运算结果有根号,请保留根号).(2)已知距观测点D 处100海里范围内有暗礁,若巡逻船A 沿直线AC 去营救船C ,在23≈1.73)6015、如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1∶,且AB=30 m,李亮同学在大堤上A点处用高1.5 m的测量仪测出高压电线杆CD顶端D的仰角为30°,已知地面BC宽30 m,求高压电线杆CD的高度.(结果保留三位有效数字,≈1.732)16、如图,为了测量出楼房AC的高度,从距离楼底C处60米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1∶的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈,计算结果用根号表示,不取近似值).17、如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6 m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.(1)求∠BP Q的度数;(2)求该电线杆PQ的高度(结果精确到1 m).(参考数据:≈1.7,≈1.4)18、乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示).建造前工程师用以下方式做了测量:无人机在A处正上方97 m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测).无人机飞行到B处正上方的D处时能看到C处,此时测得C处的俯角为80°36′.(1)求主桥AB的长度;(2)若两观察点P,D的连线与水平方向的夹角为30°,求引桥BC的长度.(长度均精确到1 m,参考数据:3≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)。
鲁教版五四制 初中数学九年级上册 第二章 直角三角形的边角关系 复习习题 (含答案解析)

学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,某地修建高速公路,要从A地向B地修一条隧道(点A、B在同一水平面上).为了测量A、B两地之间的距离,一架直升飞机从A地出发,垂直上升800米到达C处,在C处观察B地的俯角为α,则A、B两地之间的距离为( )
A.800sinα米B.800tanα米C. 米D. 米
2.如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为6 cm,AB=6 cm,则阴影部分的面积为( )
A. B.
C. D.
3.如图,点D、E分别在AB、AC上,BE、CD相交于点F,设S四边形EADF=S1,S△BDF=S2,S△BCF=S3,S△CEF=S4,则S1S3与S2S4的大小关系是( )
A.14 mB.17 mC.20 mD.22 m
14.在△ABC中,若cosA= ,tanB= ,则这个三角形一定是()
A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形
15.如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方位角为北偏东80°,测得C处的方位角为南偏东25°,航行1h后到达C处,在C处测得A的方位角为北偏东20°,则C到A的距离是( )
A. B. C. D.
12.如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8 m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是()m.
A.8 +24B.8 +8C.24+8 D.8+8
(好题)初中数学九年级数学下册第一单元《直角三角形的边角关系》检测卷(含答案解析)

一、选择题1.在Rt ABC ∆中,90C ∠=︒,若5sin 13A =,则cos A 的值为( ) A .512 B .813 C .1312 D .12132.如图,传送带和地面所成斜坡AB 的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )A .5米B .5米C .25米D .45米 3.如图,在矩形ABCD 中,点E 是CD 的中点,点F 是BC 上一点,且FC=2BF ,连接AE ,EF .若AB=2,AD=3,则cos ∠AEF 的值是( )A .12B .1C .22D .324.在Rt ABC 中,∠C =90º,下列关系式中错误的是( )A .BC =AB•sinAB .BC =AC•tanA C .AC =BC•tanBD .AC =AB•cosB 5.如图,在Rt ABC △中,90ABC ∠=︒,4AB =,8BC =,D ,E 分别为边AB ,BC 上一点,且满足:1:3AD DB =.连接DE ,将ADBE 沿DE 翻折,点B 的对应点F 恰好落在边AC 上,则CF 的长度为( )A .1952055B .275C .52055D .3156.Rt ABC 中,90C ∠=︒,2AC =,1BC =,sin A =( )A .55B .2C .32D .127.如图,直线123////l l l ,ABC 的三个顶点分别落在123,,l l l 上,AC 交2l 于点D ,设1l 与2l 的距离为12,h l 与3l 的距离为2h .若12,:1:2AB BC h h ==,则下列说法正确的是( )A .:2:3ABD ABC S S =B .:1:2ABD ABC S S =△△C .sin :sin 2:3ABD DBC ∠∠=D .sin :sin 1:2ABD DBC ∠∠= 8.在ABC 中,90,13,12C AB BC ∠=︒==,则sin B 的值为( )A .1213B .512 C .513 D .1359.在Rt ABC 中,90C ∠=︒,5AB =,4BC =,则tan A 的值为( ) A .35 B .45 C .34 D .4310.如图,在正方形ABCD 中,边长为2的等边三角形AEF 的顶点E 、F 分别在BC 和CD 上,下列结论:①CE CF =;②75AEB ∠=︒;③BE DF EF +=;④正方形对角线:13AC =+,其中正确的序号是( )A .①②④B .①②C .②③④D .①③④ 11.如图,直线y =-33x +2与x 轴、y 轴分别交于A 、B 两点,把△AOB 绕点A 顺时针旋转60°后得到△AO'B',则点B'的坐标是( ) A .(4,23)B .(23,4)C .(3,3)D .(23+2,2) 12.如图,在边长相同的小正方形组成的网格中,点A B C D 、、、都在这些小正方形的顶点上,AB CD 、相交于点P ,则tan APD ∠=( ).A .5B .3C .10D .2二、填空题13.如图,测角仪CD 竖直放在距建筑物AB 底部8m 的位置,在D 处测得建筑物顶端A 的仰角为50°.若测角仪CD 的高度是1.5m ,则建筑物AB 的高度约为_____m .(结果精确到个位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)14.如图,在Rt ABC 中,90B ∠=︒,2AB =,1BC =.将ABC 绕点A 按逆时针方向旋转90︒得到''AB C ,连接'B C ,则tan 'ACB ∠=__________.15.如图,在Rt ABC △中,90A ∠=︒,AB AC =,BD 是AC 边上的中线,则tan ADB ∠的值是______.16.如图,点P (m ,1)是反比例函数3y x=图象上的一点,PT ⊥x 轴于点T ,把△PTO 沿直线OP 翻折得到△PT O ',则点T '的坐标为_______________.17.ABC ∆中,67.5A ,8BC =,BE AC ⊥交AC 于E ,CF AB ⊥交AB 于F ,点D 是BC 的中点.以点F 为原点,FD 所在的直线为x 轴构造平面直角坐标系,则点E 的横坐标为________.18.如图,四边形ABCD 中,AB=BC=3,∠A=∠C=90°,∠ABC=120°,点E 是对角线BD 上的一个动点,过点E 分别作AB ,BC ,CD ,AD 的垂线,垂足分别为点F ,H ,I ,G ,连结FG 和HI ,则FG+HI 的最小值为________.19.如图所示,在四边形ABCD 中,90B ∠=︒,2AB =,8CD =.连接AC ,AC CD ⊥,若1sin 3ACB ∠=,则AD 长度是_________.20.在Rt ABC ∆中,90A ∠=︒,3AB =,4BC =则cos B =______.三、解答题21.计算:20210+|﹣3|﹣2sin60°.22.如图,根据道路管理规定,在某笔直的大道AB 上行驶的车辆,限速60千米/时,已知测速站点M 距大道AB 的距离MN 为30米,现有一辆汽车从A 向B 方向匀速行驶,测得此车从A 点行驶到B 点所用时间为6秒,已知60AMN ∠=︒,45BMN ∠=︒.(参考数据:3 1.732≈,2 1.414≈)(1)计算AB 的长度(结果保留整数);(2)试判断此车是否超速,并说明理由.23.图①是一辆登高云梯消防车的实物图,图②是其工作示意图,起重臂AC 是可伸缩的(10m 20m AC ),且起重臂AC 可绕点A 在一定范围内转动,张角为()90150CAE CAE ∠∠︒︒,转动点A 距离地面BD 的高度AE 为3.5m .(1)当起重臂AC 长度为12m ,张角CAE ∠为120︒时,求云梯消防车最高点C 距离地面的高度CF ;(2)某日、一居民家突发险情,该居民家距离地面的高度为18m ,请问该消防车能否实3 1.732≈)24.如图在平面直角坐标系xOy 中,一次函数()0y kx b k =+≠的图象与反比例函数()0m y m x=≠的图象交于第二、四象限内的A 、B 两点,与x 轴交于C 点,点B 的坐标为()6,n .线段5OA =,E 为x 轴上一点,且4sin 5AOE ∠=.(1)求该反比例函数和一次函数的解析式;(2)求AOB的面积;25.(1)解方程:22360x x--=(2)计算:12cos301tan602sin30︒--︒+︒26.为了方便市民出行,县政府决定从“七星广场”河堤到对岸修建一座便民桥.为测量河的宽度,在河的对岸取一点A,在广场河边取两点,O B测得点A在点O的北偏东60︒方向,测得点A在点B北偏东45︒方向,量得OB长为50米,求河的宽度AC(结果保留根号)【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】由三角函数的定义可知sinBCAAB=,可设BC=5k,AB=13k由勾股定理可求得12AC k=,再利用余弦的定义代入计算即可.【详解】解:如图:在Rt ABC 中,sin BC A AB =,可设BC=5k ,AB=13k . 由勾股定理可求得()()222213512AC AB BC k k k =-=-=. 所以,1212cos =1313AC k A AB k ==. 故选:D .【点睛】 本题主要考查三角函数的定义,掌握正弦、余弦函数的定义是解题的关键.2.C解析:C【分析】作BC ⊥底面于点C ,根据坡度的概念、勾股定理列式计算即可;【详解】作BC ⊥底面于点C ,设BC x =,∵传送带和底面所成斜坡AB 的坡度为1∶2,∴2AC x =,由勾股定理得:222AC BC AB +=,即()222210x x +=,解得:25x =,即25BC =.故答案选C .【点睛】本题主要考查了解直角三角形的应用-坡度坡角问题,准确计算是解题的关键. 3.C解析:C【分析】连接AF ,根据题意可分别求出BF 、FC 、DE 的长,再利用勾股定理分别求出AF 、AE 、EF 的长,利用勾股定理的逆定理判断出AEF 为等腰直角三角形,再利用三角函数即可求得答案.【详解】如图:连接AF ,四边形ABCD 是矩形∴2,3AB DC AD BC ====∴∠B=∠C=∠D=90°FC=2BF∴BF=1,FC=2E 是CD 的中点∴DE=CE=1∴BF=CE=1在Rt ABF 中22222215AF AB BF =+=+=在Rt EFC 中22222215EF FC CE =+=+=在Rt ADE △中222223110AE AD DE =+=+=∴222AE EF AF =+且AF=EF∴△AEF 为等腰直角三角形∴∠AFE=90°,∠AEF=∠EAF=45°∴cos ∠AEF=cos45°=22故选:C .【点睛】本题考查了矩形的性质,勾股定理及其逆定理的运用,特殊角的三角函数值,解题关键是利用勾股定理逆定理判断出AEF 为等腰直角三角形. 4.D解析:D【分析】根据三角函数的定义即可作出判断.【详解】解:A 、∵sin BC A AB=, ∴sin BC AB A =, 故正确,不符合题意;B 、∵tanA= BC AC, ∴BC=AC•tanA ,故正确,不符合题意;C 、∵tanB=AC BC, ∴AC=BC•tanB , 故正确,不符合题意;D 、∵cos BC B AB=, ∴cos BC AB B =,故错误,符合题意;故选:D .【点睛】本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.5.A解析:A【分析】如图,过D 作DM AC ⊥于,M 根据已知条件先求解:,,,AD BD AC 再利用A ∠的三角函数求解,,AM DM 由对折得到:,DF 再利用勾股定理求解MF ,从而由CF AC AM MF =--可得答案.【详解】解:如图,过D 作DM AC ⊥于,M4:1:3,AB AD DB ==,13AD DB ∴==,,90ABC ∠=︒,4AB =,8BC =,22224845,AC AB BC ∴=+=+=1,AD DM AC =⊥,sin ,45DM BC A AD AC ∴=== 255DM ∴=, 同理:5cos ,545AM AB A AD AC ==== 55AM ∴=, 由对折可得:3,DF DB == 22222520535MF DF DM ⎛⎫∴=-=-= ⎪ ⎪⎝⎭,520519520545CF AC AM MF -∴=--== 故选:.A【点睛】 本题考查的是轴对称的性质,勾股定理的应用,锐角三角函数的应用,掌握以上知识是解题的关键.6.A解析:A【分析】求出斜边AB ,再求∠A 的正弦值.【详解】解:∵90C ∠=︒,2AC =,1BC =,∴2222215AB AC BC +=+= 5sin 5BC A AB ===, 故选:A .【点睛】本题考查了勾股定理和锐角的正弦函数值的求法,解题关键是求出斜边长,熟知正弦的意义.7.D解析:D【分析】作2⊥AE l ,2⊥CF l ,如图,则1AE h =,2CF h =,利用三角形面积公式可得到12::1:2ABD BCD S S h h ∆∆==,则可对A 、B 进行判断;利用正弦的定义得到1sin h ABD AB ∠=,2sin h DBC BC∠=,利用AB CB =可对C 、D 进行判断. 【详解】 解:作2⊥AE l ,2⊥CF l ,如图,则1AE h =,2CF h =,11122ABD S BD AE BD h ∆==,21122BCE S BD CF BD h ∆==, 12::1:2ABD BCD S S h h ∆∆∴==,:1:3ABD ABC S S ∆∆∴=,所以A 、B 选项错误;在Rt ABE ∆中,1sin h AE ABD AB AB ∠==, 在Rt BCF ∆中,2sin h CF DBC BC BC∠==, 而AB CB =,12sin :sin :1:2ABD DBC h h ∴∠∠==,所以C 选项错误,D 选项正确. 故选:D .【点睛】本题考查了考查了解直角三角形,也考查了平行线之间的距离和等腰直角三角形的性质,难度一般.8.C解析:C【分析】先根据勾股定理求得AC ,再根据正弦的定义求解即可;【详解】∵在ABC 中,90C ∠=︒,13AB =,12BC =,∴2213125AC =-=,∴5sin 13AC B AB ==; 故答案选C .【点睛】本题主要考查了勾股定理与解直角三角形,准确理解计算是解题的关键.9.D解析:D【分析】由勾股定理算出AC 的值,然后根据正切函数的定义即可得到解答.【详解】 解:由勾股定理可得:2222543AC AB BC =-=-=,∴tanA=43BC AC =, 故选D .【点睛】 本题考查解直角三角形,熟练掌握勾股定理及三角函数的定义是解题关键.10.A解析:A【分析】证明()Rt ABE Rt ADF HL ≅△△即可证明①正确,由①的结论得到三角形CEF 是等腰直角三角形,即可证明②正确,根据AC 垂直平分EF 可以判断③错误,利用锐角三角函数值求出AC 的长度证明④正确.【详解】解:∵四边形ABCD 是正方形,∴AB AD =,90B D ∠=∠=︒,∵AEF 是等边三角形,∴AE AF =, 在Rt ABE △和Rt ADF 中,AE AF AB AD =⎧⎨=⎩, ∴()Rt ABE Rt ADF HL ≅△△,∴BE DF =,∵BC CD =,∴BC BE CD DF -=-,即CE CF =,故①正确;∵CE CF =,90C ∠=︒,∴45CEF ∠=︒,∵60AEF ∠=︒,∴180604575AEB ∠=︒-︒-︒=︒,故②正确;如图,连接AC ,交EF 于点G ,∵AE AF =,CE CF =,∴AC 是EF 的垂直平分线,∵CAF DAF ∠≠∠,∴DF FG ≠,同理BE EG ≠,∴BE DF EF +≠,故③错误;∵AEF 是边长为2的等边三角形,ACB ACD ∠=∠,∵AC EF ⊥,EG FG =, ∴3sin 6023AG AE =⋅︒==112CG EF ==, ∴13AC AG CG =+=+,故④正确.故选:A .【点睛】本题考查四边形综合题,解题的关键是掌握正方形的性质,等边三角形的性质,解直角三角形的方法.11.B解析:B【分析】根据直线解析式求出点A 、B 的坐标,从而得到OA 、OB 的长度,再求出∠OAB =30°,利用勾股定理列式求出AB ,然后根据旋转角是60°判断出AB′⊥x 轴,再写出点B′的坐标即可.【详解】令y =0,则−3x +2=0,解得x =,令x =0,则y =2,所以,点A (0),B (0,2),所以,OA =OB =2,∵tan ∠OAB =OB OA ==, ∴∠OAB =30°,由勾股定理得,AB 4==, ∵旋转角是60°,∴∠OAB′=30°+60°=90°,∴AB′⊥x 轴,∴点B′(4).故选:B .【点睛】本题考查了坐标与图形性质−旋转,一次函数图象上点的坐标特征,勾股定理的应用,三角函数的应用,求出AB′⊥x 轴是解题的关键. 12.B解析:B【分析】设小正方形的边长为1,根据勾股定理可得AD 、AC 的值,进而可得△ADC 是等腰直角三角形,进而可得AD ⊥CD ,根据相似三角形的判定和性质可得PC =2DP ,根据等量代换和线段和差可得AD =CD =3DP ,继而即可求解.【详解】解析 设小正方形的边长为1,由图形可知,2AD DC AC ===,ADC ∴是等腰直角三角形,AD DC ∴⊥.//AC BD ,2AC CP BD DP∴==, 2PC DP ∴=,3AD DC DP ∴==,tan 3AD APD DP∴∠==.故选B.【点睛】本题考查了正方形的性质、等腰直角三角形的判定、勾股定理、相似三角形的判定及其性质以及锐角三角函数.此题难度适中,注意转化思想与数形结合思想的应用.二、填空题13.11【分析】根据题意作辅助线DE⊥AB然后根据锐角三角函数可以得到AE 的长从而可以求得AB的长本题得以解决【详解】解:作DE⊥AB于点E由题意可得DE=CD=8m∵∠ADE=50°∴AE=DE•ta解析:11【分析】根据题意,作辅助线DE⊥AB,然后根据锐角三角函数可以得到AE的长,从而可以求得AB 的长,本题得以解决.【详解】解:作DE⊥AB于点E,由题意可得,DE=CD=8m,∵∠ADE=50°,∴AE=DE•tan50°≈8×1.19=9.52(m),∵BE=CD=1.5m,∴AB=AE+BE=9.52+1.52=11.2≈11(m),故答案为:11.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,解答本题的关键是明确题意,利用数形结合的思想解答.14.【分析】如图延长与的延长线交于点证明四边形为正方形再求解过作于利用等面积法求解再利用勾股定理求解从而可得答案【详解】解:如图由题意得:延长与的延长线交于点则四边形为正方形过作于故答案为:【点睛】本题解析:4 3【分析】如图,延长C B''与BC的延长线交于点,G证明四边形ABGB'为正方形,再求解,B C AC ',过A 作AM B C '⊥于M , 利用等面积法求解,AM 再利用勾股定理求解,MC 从而可得答案.【详解】解:如图,由题意得:9090BAB B AB C '''∠=︒∠=∠=︒,, 2AB AB '==, 1BC =,22215,AC ∴=+=延长C B ''与BC 的延长线交于点,G 则90AB G '∠=︒,∴ 四边形ABGB '为正方形, 2211B G BG CG BG BC '∴===-=-=,,90B GB '∠=︒, 22215,B C '∴=+=过A 作AM B C '⊥于M ,11,22AB C S AB AB B C AM '''∴== 54AM =, 4555AM ∴==, ()224355555MC ⎛⎫∴=-= ⎪⎝⎭, 4545tan '.3355AM ACB MC ∴∠=== 故答案为:4.3【点睛】本题考查的是勾股定理的应用,旋转的性质,正方形的判定与性质,锐角三角函数的应用,掌握以上知识是解题的关键. 15.2【分析】由题意得到则结合角的正切值即可得到答案【详解】解:∵是边上的中线∴∴∵∴∵在中∴;故答案为:2【点睛】本题考查了求角的正切值三角形中线的性质解题的关键是掌握三角形中线的性质正确得到解析:2【分析】由题意,得到12AD AC =,则2AC AD =,结合角的正切值tan AB ADB AD∠=,即可得到答案.【详解】 解:∵BD 是AC 边上的中线,∴12AD AC =, ∴2AC AD=, ∵AB AC =,∴2AB AD=, ∵在Rt ABD 中,90A ∠=︒, ∴tan 2AB ADB AD ∠==; 故答案为:2.【点睛】本题考查了求角的正切值,三角形中线的性质,解题的关键是掌握三角形中线的性质,正确得到2AB AD=. 16.【分析】连接过点作于点C 先根据反比例函数解析式求出点P 坐标根据的正切值得到它的度数再根据折叠的性质证明是等边三角形再解直角三角形得到OC 和的长即可求出的坐标【详解】解:如图连接过点作于点C ∵点P(m解析:33,2⎛⎫ ⎪ ⎪⎝⎭【分析】连接TT ',过点T '作T C OT '⊥于点C ,先根据反比例函数解析式求出点P 坐标,根据POT ∠的正切值得到它的度数,再根据折叠的性质证明TOT '是等边三角形,再解直角三角形得到OC 和CT '的长,即可求出T '的坐标.【详解】解:如图,连接TT ',过点T '作T C OT '⊥于点C ,∵点P (m ,1)是反比例函数y x =图象上的一点,∴1=m ,∴OT =,1PT =,∵tan 3POT ∠=, ∴30POT ∠=︒,由折叠的性质得:30,POT POT OT OT ∠=∠=︒='='∴60TOT '∠=︒,又∵OT OT '=,∴TOT '是等边三角形,∵T C OT '⊥,∴12OC OT ==,3sin 2CT OT TOT '''=⋅∠==,∴322T ⎛⎫' ⎪ ⎪⎝⎭.故答案为:322⎛⎫ ⎪⎪⎝⎭. 【点睛】本题考查反比例函数与几何,解题的关键是掌握反比例函数的性质,利用锐角三角函数值得到特殊角的度数,然后解直角三角形. 17.【分析】连接DE 过E 作EH ⊥OD 于H 求得∠EDO =45°即可得到Rt △DEH 中求得DH 进而得出OH 即可求解【详解】如图所示连接过作于于于是的中点中点的横坐标是【点睛】本题主要考查了直角三角形斜边上中 解析:4-【分析】连接DE ,过E 作EH ⊥OD 于H ,求得∠EDO =45°,即可得到Rt △DEH 中,求得DH ,进而得出OH ,即可求解.【详解】如图所示,连接DE ,过E 作EH OD ⊥于H ,BE CA ⊥于E ,CF AB ⊥于F ,D 是BC 的中点,142DE DC BC DO DB ∴=====, DCE DEC ∴∠=∠,DBO DOB ∠=∠,67.5A ∴∠=︒,112.5ACB ABC ∴∠+∠=︒,18021802()()CDE BDO DCE DBO ∴∠+∠=︒-∠+︒-∠ 3602()DCE DBO =︒-∠+∠3602112.5=︒-⨯︒135=︒,45EDO ∴∠=︒,Rt DEH ∴∆中,cos 4522DH DE =︒⨯=422OH OD DH ∴=-=-点E 的横坐标是422-【点睛】本题主要考查了直角三角形斜边上中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.解决问题的关键是作辅助线构造等腰直角三角形.18.3【分析】先证明得到再证明:四边形四边形为矩形得到所以只要求的最小值即可当时最小再利用锐角三角函数可得答案【详解】解:AB=BC=3∠A=∠C=90°由过点E 分别作ABBCCDAD 的垂线垂足分别为点 解析:3【分析】先证明,Rt ABD Rt CBD ≌得到60,30,ABD CBD GDE IDE ∠=∠=︒∠=∠=︒再证明:,FG HI =四边形,AFEG 四边形CHEI 为矩形,得到AE FG =,所以只要求AE 的最小值即可,当AE BD ⊥时,AE 最小,再利用锐角三角函数可得答案.【详解】 解: AB=BC=3,∠A=∠C=90°,,120,BD BD ABC =∠=︒,Rt ABD Rt CBD ∴≌60,30,ABD CBD GDE IDE ∴∠=∠=︒∠=∠=︒由过点E 分别作AB ,BC ,CD ,AD 的垂线,垂足分别为点F ,H ,I ,G ,,,EF EH EG EI ∴== 四边形,AFEG 四边形CHEI 为矩形,90,FEG HEI ∴∠=∠=︒,FEG HEI ∴≌∴ ,FG HI =当FG 最小,则FG HI +最小,四边形AFEG 为矩形,,AE FG ∴=所以:当AE BD ⊥时,AE 最小,3,60,AB ABE =∠=︒sin 60,AE AB ∴︒= 3333,AE ∴=⨯= 所以:FG 的最小值是:33, 所以:FG HI +的最小值是:3323 3.⨯= 故答案为:3 3.【点睛】本题考查的是点到直线的距离垂线段最短,三角形全等的判定与性质,矩形的判定与性质,锐角三角函数的应用,掌握以上知识是解题的关键.19.10【分析】根据直角三角形的边角间关系先计算再在直角三角形中利用勾股定理即可求出【详解】解:在中∵∴在中故答案为:10【点睛】本题考查了解直角三角形和勾股定理利用直角三角形的边角间关系求出AC 是解决 解析:10【分析】根据直角三角形的边角间关系,先计算AC ,再在直角三角形ACD 中,利用勾股定理即可求出AD .【详解】解:在Rt ABC 中,∵12,sin3ABAB ACBAC=∠==,∴1263AC=÷=.在Rt ADC中,22AD AC CD=+2268=+10=.故答案为:10.【点睛】本题考查了解直角三角形和勾股定理,利用直角三角形的边角间关系,求出AC是解决本题的关键.20.【分析】根据题意画出图形进而得出cosB=求出即可【详解】解:∵∠A=90°AB=3BC=4则cosB==故答案为:【点睛】本题考查了锐角三角函数的定义正确把握锐角三角函数关系是解题的关键解析:3 4【分析】根据题意画出图形,进而得出cosB=ABBC求出即可.【详解】解:∵∠A=90°,AB=3,BC=4,则cosB=ABBC=34.故答案为:34.【点睛】本题考查了锐角三角函数的定义,正确把握锐角三角函数关系是解题的关键.三、解答题21.1【分析】直接利用特殊角的三角函数值以及绝对值的性质、零指数幂的性质分别化简得出答案.【详解】解:原式=12×2=1=1.【点睛】本题主要考查了实数的混合运算,结合特殊角三角函数中、零指数幂计算是解题的关键. 22.(1)82米;(2)不超速,见解析【分析】(1)已知MN=30m ,∠AMN=60°,∠BMN=45°求AB 的长度,可以转化为解直角三角形; (2)求得从A 到B 的速度,然后与60千米/时≈16.66米/秒,比较即可确定答案.【详解】解:(1)由题意可得在Rt AMN △中,30MN =米,60AMN ∠=︒, ∴tan AN MN AMN =⋅∠=在Rt BMN 中,∵45BMN ∠=︒,∴30BN MN ==(米). ∴3082AB AN BN =+=≈(米).(2)此车不超速,理由如下:由题意可得,汽车从A 到B 为匀速行驶,用时为6秒,且82AB =米,则汽车的速度为()306513.66÷=≈(米/秒).∵60千米/时≈16.67米/秒,13.6616.67<,∴此车不会超速.【点睛】本题考查了勾股定理以及解直角三角形的应用,解题的关键是从题目中抽象出直角三角形,难度不大.23.(1)9.5m ;(2)可以有效救援.【分析】(1)过点C 作CF ⊥BD ,垂足为F ,过点A 作AG ⊥CF ,垂足为G ,解直角三角形ACG 即可;(2)当起重臂最长,张角最大时,计算远臂点距离地面的最大高度,比较判断即可.【详解】(1)如图1,过点C作CF⊥BD,垂足为F,过点A作AG⊥CF,垂足为G,∵AE⊥BD,∴四边形AEFG是矩形,∴∠EAG=90°,FG=AE=3.5,∴∠CAG=30°,∵AC=12,∴CG=ACsin30°=12×1=6,2∴CF=CG+FG=6+3.5=9.5(米);(2)如图2,过点C作CF⊥BD,垂足为F,过点A作AG⊥CF,垂足为G,∵AE⊥BD,∴四边形AEFG是矩形,∴∠EAG=90°,FG=AE=3.5,∴∠CAG=60°,∵AC=20,∴CG=ACsin60°3,∴CF=CG+FG=17.32+3.5=20.82>18;∴能有效救援.【点睛】本题考查了生活实际问题中的解直角三角形,熟练把生活问题转化数学解直角三角形模型问题是解题的关键.24.(1)12y x =-,223y x =-+;(2)9 【分析】(1)过点A 作AH ⊥x 轴于H 点,由4sin 5AH ACE AO∠==,OA=5,根据正弦的定义可求出AH ,再根据勾股定理得到OH ,即得到A 点坐标(-3,4),把A (-3,4)代入y= ,确定反比例函数的解析式为y=- ;将B (6,n )代入,确定点B 点坐标,然后把A 点和B 点坐标代入y=kx+b (k≠0),求出k 和b .(2)先令y=0,求出C 点坐标,得到OC 的长,然后根据AOB BOC AOC SS S =+计算△AOB 的面积即可.【详解】解:(1)过A 作AH x ⊥轴交x 轴于H ,∴4sin 5AH ACE AO∠==,5OA =, ∴4AH =,∴223OH OA AH ,∴()3,4A -,将()3,4A -代入m y x=,得12=-m , ∴反比例函数的解析式为12y x =-, 将()6,B n 代入12y x=-,得2n =-, ∴()6,2B -, 将()3,4A -和()6,2B -分别代入()0y kx b k =+≠,得3462k b k b -+=⎧⎨+=-⎩,解得232k b ⎧=-⎪⎨⎪=⎩, ∴直线解析式:223y x =-+; (2)在直线223y x =-+中,令0y =,则有2203x -+=,解得3x =, ∴()3,0C ,即3OC =,∴13462AOC S =⨯⨯=△; 同理3BOC S =△,则9AOB BOC AOC S S S =+=△△△.【点睛】本题考查了反比例函数的综合运用.关键是作x 轴的垂线,解直角三角形求A 点坐标,用待定系数法求直线,双曲线的解析式.25.(1)134x +=,234x =;(2)5【分析】(1)用公式法解方程即可;(2)先求特殊角三角函数值,再进行实数计算.【详解】解:(1)22360x x --=, 2a =,3b =-,6c =-∴224(3)42(6)570b ac -=--⨯⨯-=>∴332224b x a -===⨯∴134x =,234x -=(2)原式)1122=-+⨯311=+5=-【点睛】本题考查了一元二次方程的解法和含有特殊角三角函数值的实数计算,解题关键是选择恰当的方法解一元二次方程和熟记特殊角三角函数值并熟练进行计算.26.河的宽度AC 为(25+米【分析】根据点A 在点B 北偏东45°方向,结合方位角的知识可证AC BC =,利用三角函数解直角三角形,列关出方程,解方程即可.【详解】根据题意,有30,45AOC ABC ∠=︒∠=︒, 又90ACB ∠=︒所以BC AC =, 在Rt AOC ∆中,tan AC AOC OC ∠=,即tan 30AC OC ︒= 设AC x =米,则BC x =米,由题意得503x x =+ 解得x =化简得25x =+∴河的宽度AC 为(25+米.【点睛】本题考查了解直角三角形的实际应用,熟记特殊角的三角函数值,灵活运用方位角的知识,规范解直角三角形是解题关键.。
九年级数学下册《直角三角形的边角关系》单元测试卷(附答案)

九年级数学下册《直角三角形的边角关系》单元测试卷(附答案)一.选择题(共10小题,满分30分)1.已知在Rt△ABC中,∠C=90°,AC=3,BC=4,则tan A的值为()A.B.C.D.2.在Rt△ABC中,各边的长度都扩大2倍,那么锐角A的正切值()A.都扩大2倍B.都扩大4倍C.没有变化D.都缩小一半3.在直角坐标系中,P是第一象限内的点,OP与x轴正半轴的夹角α的正切值是,则cos α的值是()A.B.C.D.4.计算sin45°的值等于()A.B.C.D.5.在Rt△ABC中,∠C=90°,AB=5,BC=3,则tan A的值是()A.B.C.D.6.在Rt△ABC中,∠C=90°,若sin A=,则cos B的值是()A.B.C.D.7.已知tan A=0.85,用计算器求∠A的大小,下列按键顺序正确的是()A.B.C.D.8.若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是()A.B.C.D.9.在△ABC中,已知∠C=90°,AC=4,sin A=,那么BC边的长是()A.2B.8 C.4D.1210.α为锐角,若sinα+cosα=,则sinα﹣cosα的值为()A.B.±C.D.0二.填空题(共10小题,满分30分)11.如图,在平面直角坐标系内有一点P(5,12),那么OP与x轴正半轴的夹角α的余弦值.12.若α为锐角,且,则m的取值范围是.13.用科学计算器计算: tan16°15′≈(结果精确到0.01)14.如果3sinα=+1,则∠α=.(精确到0.1度)15.计算:sin225°+cos225°﹣tan60°=.16.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,且c=3a,则tan A 的值为.17.在Rt△ABC中,∠C=90°,如果AC=4,sin B=,那么AB=.18.已知∠A是锐角,且tan A=2,那么cos A=.19.已知∠A+∠B=90°,若,则cos B=.20.化简=.三.解答题(共7小题,满分60分)21.如图,在Rt△ABC中,∠C=90°,BC=6,tan A=.求AB的长和sin B的值.22.已知cos45°=,求cos21°+cos22°+…+cos289°的值.23.计算下列各题:(1);(2)sin60°•cos60°﹣tan30°tan60°+sin245°+cos245°.24.在△ABC中,∠C=90°,BC=3,AB=5,求sin A,cos B,tan A的值.25.如图,在所示的直角坐标系中,P是第一象限的点,其坐标是(6,y),且OP与x轴的正半轴的夹角α的正切值是,求角α的正弦值.26.如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.(1)求证:DE是⊙O的切线;(2)若⊙O的半径为2,BE=1,求cos A的值.27.如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA、BC的距离为PE、PF.(1)若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.参考答案与解析一.选择题1.解:如图所示:∵在Rt△ABC中,∠C=90°,AC=3,BC=4,∴tan A==.故选:B.2.解:根据锐角三角函数的定义,知各边的长度都扩大2倍,那么锐角A的大小不变,所以其正切值不变.故选:C.3.解:如图:过点P作PE⊥x轴于点E,∵tanα=,∴设PE=4x,OE=3x,在Rt△OPE中,由勾股定理得OP=,∴cosα=.故选:C.4.解:sin45°=故选:C.5.解:∵∠C=90°,AB=5,BC=3,∴AC===4,∴tan A==,故选:D.6.解:Rt△ABC中,∠C=90°,∴∠A+∠B=90°,∴cos B=sin A=,故选:C.7.解:根据计算器功能键,先按反三角2ndF,再按正切值.故选:A.8.解:若用我们数学课本上采用的科学计算器计算sin42°16′,按键顺序正确的是.故选:C.9.解:由sin A==,不妨设BC=2k,则AB=3k,由勾股定理得,AC2+BC2=AB2,即(4)2+(2k)2=(3k)2,解得k=4(取正值),所以BC=2k=8,故选:B.10.解:∵sinα+cosα=,∴(sinα+cosα)2=2,即sin2α+cos2α+2sinαcosα=2.又∵sin2α+cos2α=1,∴2sinαcosα=1.∴(sinα﹣cosα)2=sin2α+cos2α﹣2sinαcosα=1﹣2sinαcosα=1﹣1=0.∴sinα﹣cosα=0.故选:D.二.填空题(共10小题,满分30分)11.解:过P作PA⊥OA,∵P点坐标为(5,12),∴OA=5,PA=12,由勾股定理得,OP===13.∴cosα==.故答案为:.12.解:∵0<cosα<1,∴0<<1,解得,故答案为:.13.解: tan16°15′≈0.71,故答案为:0.71.14.解:∵3sinα=+1,∴sinα=,解得,∠α≈65.5°,故答案为:65.5°.15.解:∵sin225°+cos225°=1,tan60°=,∴sin225°+cos225°﹣tan60°=1﹣,故答案为:1﹣.16.解:在Rt△ABC中,∠C=90°,c=3a,∴b===2a,∴tan A===,故答案为:.17.解:∵sin B=,∴AB===6.故答案是:6.18.解:设∠A所在的直角三角形为△ABC,∠C=90°,∠A、∠B、∠C所得的边为a,b,c,∵tan A=2,即=2,设b=k,则a=2k,∴c==k,∴cos A==,故答案为:.19.解:由∠A+∠B=90°,若,得cos B=,故答案为:.20.解:∵tan30°=<1,∴原式=1﹣tan30°=1﹣=.三.解答题(共7小题,满分60分)21.解:∵在Rt△ABC中,∠C=90°,BC=6,tan A==,∴AC=12,∴AB===6,∴sin B===.22.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245 =(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245=44+()2=44.23.解:(1)=(2×﹣)+=2﹣+=2;(2)sin60°•cos60°﹣tan30°tan60°+sin245°+cos245°.=×﹣×+()2+()2=﹣1++=.24.解:∵在△ABC中,∠C=90°,BC=3,AB=5,根据勾股定理可得:AC=4,∴sin A=,cos B==,tan A==.25.解:作PC⊥x轴于C.∵tanα=,OC=6∴PC=8.则OP=10.则sinα=.26.(1)证明:法一、连接AD、OD,∵AC是直径,∴AD⊥BC,∵AB=AC,∴D是BC的中点,又∵O是AC的中点,∴OD∥AB,∵DE⊥AB,∴OD⊥DE,∴DE是⊙O的切线.法二、连接OD,∵OC=OD,∴∠OCD=∠ODC,∵AB=AC,∴∠OCD=∠B,∴∠B=∠ODC,∴OD∥AB,∵DE⊥AB,∴OD⊥DE,∴DE是⊙O的切线.(2)解:由(1)知OD∥AE,∴∠FOD=∠FAE,∠FDO=∠FEA,∴△FOD∽△FAE,∴,∴,∴,解得FC=2,∴AF=6,∴Rt△AEF中,cos∠FAE====.27.解:(1)在Rt△BPE中,sin∠EBP==sin40°在Rt△BPF中,sin∠FBP==sin20°又sin40°>sin20°∴PE>PF;(2)根据(1)得sin∠EBP==sinα,sin∠FBP==sinβ又∵α>β∴sinα>sinβ∴PE>PF.。
鲁教版-数学-九年级上册-第二章 直角三角形的边角关系单元测试
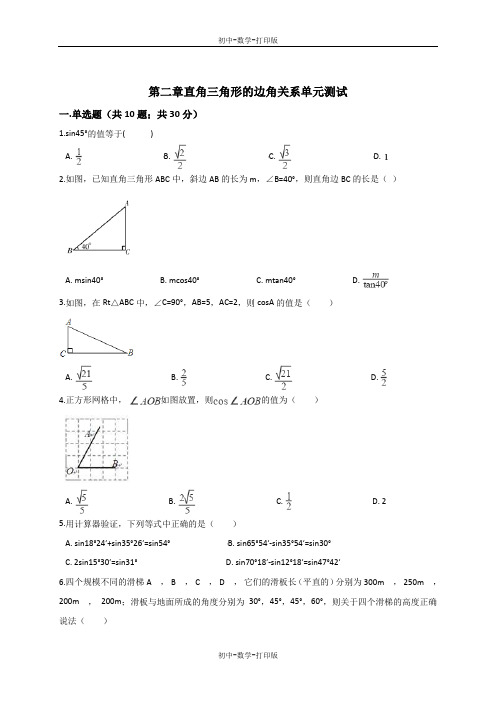
第二章直角三角形的边角关系单元测试一.单选题(共10题;共30分)1.sin45°的值等于( )A. B. C. D.2.如图,已知直角三角形ABC中,斜边AB的长为m,∠B=40°,则直角边BC的长是()A. msin40°B. mcos40°C. mtan40°D.3.如图,在Rt△ABC中,∠C=90°,AB=5,AC=2,则cosA的值是()A. B. C. D.4.正方形网格中,如图放置,则的值为()A. B. C. D. 25.用计算器验证,下列等式中正确的是()A. si n18°24′+sin35°26′=sin54°B. sin65°54′-sin35°54′=sin30°C. 2sin15°30′=sin31°D. sin70°18′-sin12°18′=sin47°42′6.四个规模不同的滑梯A ,B ,C ,D ,它们的滑板长(平直的)分别为300m ,250m ,200m ,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法()A. A的最高B. B的最高C. C的最高D. D的最高7.(2015•巴彦淖尔)如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是()A. 20海里B. 40海里C. 20海里D. 40海里8.若cosα=,则锐角α的大致范围是()A. 0°<α<30°B. 30°<α<45°C. 45°<α<60°D. 0°<α<90°9.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是()A. msin35°B. mcos35°C.D.10.(2014•泰州)如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是()A. 1,2,3B. 1,1,C. 1,1,D. 1,2,二.填空题(共8题;共24分)11.如图,当太阳光与地面成55°角时,直立于地面的玲玲测得自己的影长为1.25m,则玲玲的身高约为________ m.(精确到0. 01m)(参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.428).12.如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度是________ 米.(结果保留根号)13.如果α是锐角,且tanα=cot20°,那么α=________度.14.小虎同学在计算a+2cos60°时,因为粗心把“+”看成“﹣”,结果得2006,那么计算a+2cos60°的正确结果应为________15.小明乘滑草车沿坡比为1:2.4的斜坡下滑130米,则他下降的高度为________ 米.16.在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是________17.(2016•荆州)全球最大的关公塑像矗立在荆州古城东门外.如图,张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′,测得塑像顶部A处的仰角为45°,点D在观测点C正下方城墙底的地面上,若CD=10米,则此塑像的高AB约为________米(参考数据:ta n78°12′≈4.8).18.cos240°+cos2α=1,则锐角α=________度.三.解答题(共6题;共42分)19.(2015•泸州)如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A 的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).20.如图,某人在一栋高层建筑顶部C处测得山坡坡脚A处的俯角为60°,又测得山坡上一棵小树树干与坡面交界P处的俯角为45°,已知OA=50米,山坡坡度为12(即tan∠PAB=12,其中PB⊥AB ),且O、A、B在同一条直线上.(1)求此高层建筑的高度OC.(结果保留根号形式.);(2)求坡脚A处到小树树干与坡面交界P处的坡面距离AP的长度. (人的高度及测量仪器高度忽略不计,结果保留3个有效数字.)21.已知,如图Rt△ABC中,AB=8,BC=6,求sin∠A和tan∠A.22.如图,为了测量河宽,在河的一边沿岸边选取B、C两点,在对岸岸边选择点A.测得∠B=45°,∠C=60°,BC=30米.求这条河的宽度(这里指点A到直线BC的距离).(结果精确到1米,参考数据2≈1.4,3≈1.7)23.如图分别是某型号跑步机的实物图和示意图,已知踏板CD长为2米,支架AC长为0.8米,CD 与地面的夹角为12°,∠ACD=80°,(AB‖ED),求手柄的一端A离地的高度h.(精确到0.1米,参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,t an68°≈2.48)24.小明想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.(结果保留三位有效数字,参考数据:2 ≈1.414;3 ≈1.732.)答案解析一.单选题1.【答案】B【考点】特殊角的三角函数值【解析】【分析】根据即可求解.【解答】.故选:B.【点评】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.2.【答案】B【考点】解直角三角形【解析】【分析】根据锐角三角函数的定义解答即可.【解答】∵cos40°=,∴BC=AB•cos40°=mcos40°.故选B.【点评】本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.3.【答案】B【考点】锐角三角函数的定义【解析】【分析】根据锐角三角函数的概念直接解答即可.【解答】∵Rt△ABC中,∠C=90°,AB=5,AC=2,∴cosA==.故选B.【点评】本题考查锐角三角函数的概念:在直角三角形中,正弦等于对边比斜边;余弦等于邻边比斜边;正切等于对边比邻边.4.【答案】A【考点】锐角三角函数的定义【解析】【分析】作EF⊥OB,则求cos∠AOB的值的问题就可以转化为直角三角形边的比的问题.如图,作EF⊥OB,则EF=2,OF=1,由勾股定理得,OE=.=故选A.【点评】本题通过构造直角三角形,利用勾股定理和锐角三角函数的定义求解.5.【答案】D【考点】计算器—三角函数【解析】【解答】利用计算器分别计算出各个三角函数的数值,进行分别检验.正确的是sin70°18′-sin12°18′=sin47°42′ .故选D.【分析】本题考查三角函数的加减法运算.6.【答案】B【考点】解直角三角形的应用-坡度坡角问题【解析】【解答】A.的高度为:300×sin30°=150(米).B.的高度为:250×sin45°=125 ≈176.75(米).C.的高度为:200×sin45°=100 ≈141.4(米).D.的高度为:200×sin60°=100 ≈173.2(米).所以B的最高.故选:B.【分析】利用所给角的正弦值求出每个滑板的高度,比较即可.7.【答案】C【考点】解直角三角形的应用-方向角问题【解析】【解答】根据题意可知∠CAD=30°,∠CBD=60°,∵∠CBD=∠CAD+∠ACB,∴∠CAD=30°=∠ACB,∴AB=BC=40海里,在Rt△CBD中,∠BDC=90°,∠DBC=60°,sin∠DBC=,∴sin60°=,∴CD=40×sin60°=40×=20(海里).故选:C.【分析】根据方向角的定义及余角的性质求出∠CAD=30°,∠CBD=60°,再由三角形外角的性质得到∠CAD=30°=∠ACB,根据等角对等边得出AB=BC=20,然后解Rt△BCD,求出CD即可解答.8.【答案】C【考点】锐角三角函数的增减性【解析】【解答】解:∵cos30°=,cos45°=,cos60°=,且<<,∴cos45°<cosα<cos60°,∴锐角α的范围是:45°<α<60°.故选C.【分析】理解几个特殊角的度数以及余弦值,根据余弦函数随角度的增大而减小即可作出判断.9.【答案】A【考点】锐角三角函数的定义【解析】【解答】解:sin∠A= ,∵AB=m,∠A=35°,∴BC=msin35°,故选:A.【分析】根据正弦定义:把锐角A的对边a与斜边c的比叫做∠A的正弦可得答案.10.【答案】D【考点】解直角三角形【解析】【解答】解:A、∵1+2=3,不能构成三角形,故选项错误;B、∵12+12=()2,是等腰直角三角形,故选项错误;C、底边上的高是= ,可知是顶角120°,底角30°的等腰三角形,故选项错误;D、解直角三角形可知是三个角分别是90°,60°,30°的直角三角形,其中90°÷30°=3,符合“智慧三角形”的定义,故选项正确.故选:D.【分析】A、根据三角形三边关系可知,不能构成三角形,依此即可作出判定;B、根据勾股定理的逆定理可知是等腰直角三角形,依此即可作出判定;C、解直角三角形可知是顶角120°,底角30°的等腰三角形,依此即可作出判定;D、解直角三角形可知是三个角分别是90°,60°,30°的直角三角形,依此即可作出判定.二.填空题11.【答案】1.79【考点】解直角三角形的应用【解析】【解答】玲玲的身高=影长×tan55°=1.25×1.428≈1.79(m)。
(北师大版)佛山市九年级数学下册第一单元《直角三角形的边角关系》测试(答案解析)

一、选择题1.下列不等式成立的是( ) A .sin60°<sin45°<sin30° B .cos30°<cos45°<cos60° C .tan60°<tan45°<tan30°D .sin30°<cos45°<tan60°2.如图,在ABC ∆中,AC BC ⊥,30ABC ︒∠=,点D 是CB 延长线上的一点,且AB BD =,则tan DAC ∠的值为( )A .33B .23C .23+D .23-3.在RtΔABC 中,若∠C=90°,cosA=35,则sinA 的值为( ) A .35B .45 C .34D .544.三角形在正方形网格纸中的位置如图所示,则sinα的值是( )A .34B .43C .35D .45 5.在Rt △ABC 中,∠C =90°,AB =3BC ,则sin B 的值为( ) A .12B .22C .32D .236.如图,某建筑物AB 在一个坡度为1:0.75i =的山坡CE 上,建筑物底部点B 到山脚点C 的距离20BC =米,在距山脚点C 右侧水平距离为60米的点D 处测得建筑物顶部点A的仰角是24°,建筑物AB 和山坡CE 的剖面的同一平面内,则建筑物AB 的高度约为( )(参考数据:sin 240.41︒≈,cos240.91︒≈,tan 240.45︒≈)A .32.4米B .20.4米C .16.4米D .15.4米7.如图,矩形ABCD 的四个顶点分别在直线3l ,4l ,2l ,1l 上,若直线1234//////l l l l 且间距相等,3AB =,2BC =,则tan α的值为( )A .38B .13C .5 D .15158.△ABC 中,∠C=90°,∠A ,∠B ,∠C 的对边分别是a ,b ,c ,且22440c ac a -+=,则sinA+cosA 的值为( ) A .13+ B .122C .23+ D .29.在ΔABC 中,∠C =90º,AB =5,BC =3,则cos A 的值是( ) A .34B .43C .35D .4510.如图,△ABC 、△FED 区域为驾驶员的盲区,驾驶员视线PB 与地面BE 的央角∠PBE =43°,视线PE 与地面BE 的夹角∠PEB =20°,点A ,F 为视线与车窗底端的交点,AF //BE ,AC ⊥BE ,FD ⊥BE .若A 点到B 点的距离AB =1.6m ,则盲区中DE 的长度是( )(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)A .2.6mB .2.8mC .3.4mD .4.5m11.如图,河堤横断面迎水坡AB 的坡比是1:34BC m =,则坡面AB 的长度是( )A .433m B .43m C .23m D .8m12.如图,在Rt △ABC 中,∠ACB=90°,若5AC ,BC=2,则sin ∠A 的值为( )A .52B .53C .23D .255二、填空题13.正方形ABCD 、正方形FECG 如图放置,点E 在BC 上,点G 在CD 上,且BC =3EC ,则tan ∠FAG =_____.14.如图,矩形ABCD 中,AE =13AD ,将△ABE 沿BE 折叠后得到△GBE ,延长BG 交CD 于F 点,若CF =FD =3,则BC 的长为_____.15.如图,矩形ABCD 的四个顶点分别在直线3421,,,l l l l 上.若这四条直线相互平行且相邻直线的间距均为1,若α=30°,则矩形ABCD 的面积为_________.16.如图,直角坐标系原点O 为Rt ABC ∆斜边AB 的中点,()90,5,0ACB A ∠=︒-,且1tan 2A =,反比例函数(0)k y k x=≠经过点C ,则k 的值是_______.17.如图,C ,D 是两个村庄,分别位于一个湖的南,北两端A 和B 的正东方向上,且点D 位于点C 的北偏东60°方向上,CD=12km ,则AB=_______km18.在ABC 中,若213sin tan 02A B ⎛⎫-+-= ⎪ ⎪⎝⎭,则C ∠的度数为__________. 19.如图,在Rt ABC △中,90ABC ∠=︒,30ACB ∠=︒,2AB =,点E 为AC 上任意一点(不与点A 、C 重合),连结EB ,分别过点A 、B 作BE 、AE 的平行线交于点F ,则EF 的最小值为__________.20.如图,在菱形ABCD 中,4AB =,45ABC ∠=︒,菱形ABCD 的对角线交于点O ,则ABO 的面积为__________.三、解答题21.计算:()2202012330tan -++︒22.计算:12+(12)-1﹣2cos30°﹣313. 23.如图,根据道路管理规定,在某笔直的大道AB 上行驶的车辆,限速60千米/时,已知测速站点M 距大道AB 的距离MN 为30米,现有一辆汽车从A 向B 方向匀速行驶,测得此车从A 点行驶到B 点所用时间为6秒,已知60AMN ∠=︒,45BMN ∠=︒.(参考数据:3 1.732≈,2 1.414≈)(1)计算AB 的长度(结果保留整数); (2)试判断此车是否超速,并说明理由.24.吴兴区某中学开展研学实践活动,来到了“两山”理论发源地—一安吉余村,看到了“两山”纪念碑.如图,想测量纪念碑AB 的高度,小明在纪念碑前D 处用测角仪测得顶端A 的仰角为60︒,底端B 的俯角为45︒;小明又在同一水平线上的E 处用测角仪测得顶端A 的仰角为30,已知8m DE =,求该纪念碑AB 的高度.(3 1.7≈,结果精确到0.1m )25.(1)解方程:x 2﹣4x =12; (2)计算:sin30°3tan45°.26.(1)计算:()1012sin 45tan 5012-⎛⎫-︒--︒-+ ⎪⎝⎭(2)已知4cos60x =︒,先化简,再求2221111x x x x ++---的值.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】根据特殊角三角函数值,可得答案. 【详解】解:A 、sin60°sin45°=2,sin30°=12 ,故A 不成立;B 、cos30°cos45°=2,cos60°=12,故B 不成立;C 、tan60°,tan45°=1,tan30°,故C 不成立;D 、sin30°=12,cos45°,tan60°D 成立; 故选:D . 【点睛】本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题的关键.2.C解析:C 【分析】设AC=x ,根据三角函数可得,,AB=2x ,求出DC 即可. 【详解】 解:设AC=x ,∵AC BC ⊥,30ABC ︒∠=, tan ∠ABC=ACBC,3AC BC =,, sin ∠ABC=ACAB, 12AC AB =, AB=2x , BD=2x ,=(2x +,tan ∠DAC=2DC AC ==, 故选:C . 【点睛】本题考查了特殊角的三角函数和求三角函数值,解题关键是根据三角函数的定义,利用特殊角,表示出相关线段长.3.B解析:B 【分析】根据正弦和余弦的平方和等于1求解. 【详解】解:∵()()22sin cos 1A A +=,∴4sin 5A ===,故选B . 【点睛】本题考查锐角三角函数的性质,熟练掌握正弦函数与余弦函数的平方和等于1的性质是解题关键.4.C解析:C 【分析】将α∠转换成β∠去计算正弦值. 【详解】解:如图,βα∠=∠,4AB =,3BC =, ∴5AC =, 则3sin sin 5BC AC αβ===. 故选:C .【点睛】本题考查正弦值的求解,解题的关键是掌握网格图中三角函数值的求解.5.D解析:D 【分析】设BC=a ,则AB=3a ,根据勾股定理求出AC ,再根据正弦的定义求sin B . 【详解】解:设BC=a ,则AB=3a ,2222922AC AB BC a a a -=-=,sin B =222233AC a AB a ==, 故选:D . 【点睛】本题考查了三角函数,勾股定理,解题关键是明确三角函数的意义,通过设参数,求出需要的边长.6.C解析:C 【分析】延长AB 交CD 反向延长线于F .根据题意可知43BF FC =,则设BF=4x ,FC=3x .由正切可求出AF 的长.再在Rt BFC △中,由勾股定理可求出x 的值.最后即可利用=AB AF BF -求出AB 长. 【详解】如图延长AB 交CD 反向延长线于F ,由题意可知BF DF ⊥. ∵建筑物AB 在一个坡度为i =1:0.75的山坡CE 上, ∴10.75BF FC =,即43BF FC =. 设BF=4x 米,则FC=3x 米,DF=(60+3x )米, ∵24D ∠=︒, ∴tan tan 240.45AFD DF∠=︒==,∴0.45(603)(27 1.35)AF x x =+=+米.在Rt BFC △中,222BF FC BC +=,即222(4)(3)20x x +=, ∴1244x x ==-,(舍).∴4416BF =⨯=米,27 1.354=32.4AF =+⨯米. ∴=32.4-16=16.4AB AF BF -=米.故选:C . 【点睛】本题考查解直角三角形的实际应用和勾股定理.作出常用的辅助线是解答本题的关键.7.B解析:B 【分析】根据题意,可以得到BG 的长,再根据∠ABG=90°,AB=3,可以得到∠BAG 的正切值,再根据平行线的性质,可以得到∠BAG=∠α,从而可以得到tanα的值. 【详解】解:作CF ⊥l 4于点F ,交l 3于点E ,设CB 交l 3于点G ,由已知可得,GE ∥BF ,CE=EF , ∴△CEG ∽△CFB , ∴CE CGCF CB =, ∵12CE CF =, ∴12CG CB =, ∵BC=2, ∴GB=1,∵l 3∥l 4, ∴∠α=∠GAB ,∵四边形ABCD 是矩形,AB=3, ∴∠ABG=90°, ∴1tan 3BG BAG AB ∠==, ∴tanα的值为13, 故选:B . 【点睛】本题考查矩形的性质,解直角三角形,解答本题的关键是明确题意,利用数形结合的思想解答.8.A解析:A 【分析】由22440c ac a -+=得2c a =,则1sin 2a A c ==,即可得到30A ∠=︒,利用特殊角的三角函数值就可以求出结果. 【详解】解:∵22440c ac a -+=, ∴()220c a -=,即2c a =,∵90C ∠=︒,∴1sin 2a A c ==, ∴30A ∠=︒,∴cos 2A =,∴1sin cos 2A A +=. 故选:A . 【点睛】本题考查锐角三角函数,解题的关键是掌握特殊角的三角函数值.9.D解析:D 【分析】利用勾股定理可求出AC 的长,根据余弦函数的定义即可得答案. 【详解】∵∠C=90°,AB=5,BC=3,∴=4,∴cosA=ACAB =45.故选:D.【点睛】考查勾股定理及锐角三角函数的定义,在直角三角形中,锐角的余弦是角的邻边与斜边的比;熟练掌握各三角函数的定义是解题的关键.10.B解析:B【分析】首先证明四边形ACDF是矩形,利用∠PBE的正弦值可求出AC的长,即可得DF的长,利用∠PEB的正切值即可得答案.【详解】∵FD⊥AB,AC⊥EB,∴DF∥AC,∵AF∥EB,∴四边形ACDF是平行四边形,∵∠ACD=90°,∴四边形ACDF是矩形,∴DF=AC,在Rt△ACB中,∵∠ACB=90°,∠ABE=43°,∴AC=AB•sin43°≈1.6×0.7=1.12(m),∴DF=AC=1.12(m),在Rt△DEF中,∵∠FDE=90°,∠PEB=20°,∴tan∠PEB=DFDE≈0.4,∴D E≈1.120.4=2.8(m),故选:B.【点睛】本题考查解直角三角形的应用及矩形的判定与性质,熟练掌握各三角函数的定义是解题关键.11.D解析:D【分析】直接利用坡比的定义得出AC的长,进而利用勾股定理得出答案.【详解】∵河堤横断面迎水坡AB的坡比是∴BC AC = ∴4AC =解得:AC =故AB 8(m ),故选:D .【点睛】此题主要考查了解直角三角形的应用,正确掌握坡比的定义是解题关键.12.C解析:C【分析】先利用勾股定理求出AB 的长,然后再求sin ∠A 的大小.【详解】解:∵在Rt △ABC 中,AC =BC=2∴3=∴sin ∠A=23BC AB = 故选:C .【点睛】 本题考查锐角三角形的三角函数和勾股定理,需要注意求三角函数时,一定要是在直角三角形当中.第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题13.【分析】根据题意可以设EC=a 然后即可得到ADDG 和AG 的长然后作FH ⊥AG 利用锐角三角函数和勾股定理可以得到AH 和FH 的长从而可以得到tan ∠FAG 的值【详解】解:作FH ⊥AG 于点H ∵正方形FEC 解析:15【分析】根据题意,可以设EC=a ,然后即可得到AD 、DG 和AG 的长,然后作FH ⊥AG ,利用锐角三角函数和勾股定理可以得到AH 和FH 的长,从而可以得到tan ∠FAG 的值.【详解】解:作FH ⊥AG 于点H ,∵正方形FECG ,设EC=FG=a,则BC=AD=CD=3a,∵四边形ABCD是正方形,∴∠D=90°,DG=BE=2a,∴AG=22AD DG=13a,∴sin∠DAG=13a =21313,∵AD∥GF,∴∠HGF=∠DAG,∴sin∠HGF=213,∵sin∠HGF=HFGF,∴HFa =21313,解得HF=213a,∴HG=313a,∴AH=AG﹣HG=13a﹣313a=1013a,∴tan∠FAH=FHAH =213131013aa=15,即tan∠FAG=15,故答案为:15.【点睛】本题考查正方形的性质、锐角三角形函数,解答本题的关键是明确题意,利用数形结合的思想解答.14.6【分析】延长BF 交AD 的延长线于点H 证明△BCF ≌△HDF (AAS )由全等三角形的性质得出BC =DH 由折叠的性质得出∠A =∠BGE =90°AE =EG 设AE =EG =x 则AD =BC =DH =3x 得出EH解析:66【分析】延长BF 交AD 的延长线于点H ,证明△BCF ≌△HDF (AAS ),由全等三角形的性质得出BC =DH ,由折叠的性质得出∠A =∠BGE =90°,AE =EG ,设AE =EG =x ,则AD =BC =DH =3x ,得出EH =5x ,由锐角三角函数的定义及勾股定理可得出答案.【详解】解:延长BF 交AD 的延长线于点H ,∵四边形ABCD 是矩形,∴AD =BC ,AD ∥BC ,∠A =∠BCF =90°,∴∠H =∠CBF ,在△BCF 和△HDF 中,CBF H BCF FDH CF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BCF ≌△HDF (AAS ),∴BC =DH ,∵将△ABE 沿BE 折叠后得到△GBE ,∴∠A =∠BGE =90°,AE =EG ,∴∠EGH =90°,∵AE =13AD , ∴设AE =EG =x ,则AD =BC =DH =3x ,∴ED =2x ,∴EH =ED +DH =5x ,在Rt △EGH 中,sin ∠H =155EG x EH x ==, ∴sin ∠CBF =15CF BF =, ∴315BF =,∴BF =15,∴BC =222215366BF CF -=-=,故答案为:66.【点睛】本题考查了折叠的性质,矩形的性质,全等三角形的判定及性质,要注意折叠的图形中的相等的角和相等的线段,解题关键是利用倍长中线法正确作出辅助线证△BCF ≌△HDF . 15.【分析】过B 点作直线EF 与平行线垂直与l2交于点E 与l3交于点F 得AB=2进而求得矩形的面积;【详解】解:如图过B 作于E 点交于F 点∵∴∠又∵相邻直线的间距均为1∴BF=EF=1则∴又∵矩形ABCD 中解析:83 【分析】过B 点作直线EF 与平行线垂直,与l 2交于点E ,与l 3交于点F .得AB=2,43BC =.进而求得矩形的面积; 【详解】解:如图,过B 作2BE l ⊥于E 点,交2l 于F 点∵34//l l∴∠=30BAF α∠=︒又∵相邻直线的间距均为1,∴BF=EF=1则1sin 2BF AB α== ∴2212AB BF ==⨯=又∵矩形ABCD 中,∠90ABC =° 而∠+90ABF α∠=︒∴30EBC α∠=∠=︒,且BE=2 ∴3cos 2BE EBC BC ∠== ∴3432233BC BE =÷==则S 矩形ABCD=AB×BC=4832333⨯= 故答案为:83 【点睛】 本题考查了矩形的性质、直角三角形中三角函数的应用,锐角三角函数值的计算等知识,根据平行线之间的距离构造全等的直角三角形是关键.16.【分析】作CD ⊥AB 于点D 由可设BC=xAC=2x 根据勾股定理即可求出BC 和AC 的值利用面积法求出CD 的值再利用勾股定理求出BD 的值得到点C 的坐标然后可求出k 的值【详解】如图作CD ⊥AB 于点D ∵为斜解析:12【分析】作CD ⊥AB 于点D .由1tan 2A =可设BC=x ,AC=2x ,根据勾股定理即可求出BC 和AC 的值,利用面积法求出CD 的值,再利用勾股定理求出BD 的值,得到点C 的坐标,然后可求出k 的值. 【详解】如图,作CD ⊥AB 于点D .∵()5,0A -,O 为Rt ABC ∆斜边AB 的中点,∴()5,0B ,∴OB=5,AB=10.∵1tan 2A ==BC AC , ∴可设BC=x ,AC=2x ,由勾股定理得x 2+(2x)2=102,∴x=25∴BC=25AC=45∵1122AC BC AB CD ⋅=⋅, ∴254510CD =,∴CD=4,∴2==, ∴OD=5-2=3,∴C(3,4).反比例函数(0)k y k x=≠经过点C , ∴k=3×4=12.故答案为:12.【点睛】本题考查了勾股定理,面积法求线段的长,锐角三角函数的定义,以及反比例函数图象上点的坐标特征,求出点C 的坐标是解答本题的关键. 17.【分析】过点C 作CE ⊥BD 于E 构造直角三角形由方位角确定∠ECD=60°在Rt △CED 中利用三角函数AB=CD•cos ∠ECD 即可【详解】过点C 作CE ⊥BD 于E 由湖的南北两端A 和B ∴∠EBA=∠BA解析:【分析】过点C 作CE ⊥BD 于E 构造直角三角形,由方位角确定∠ECD=60°,在Rt △CED 中利用三角函数AB=CD•cos ∠ECD 即可.【详解】过点C 作CE ⊥BD 于E ,由湖的南,北两端A 和B∴∠EBA=∠BAC=90º,又∠BEC=90º则四边形ABCE 为矩形,∴AB=CE∵点D 位于点C 的北偏东60°方向上,∴∠ECD=60°,∵CD=12km ,在Rt △CED 中,∴CE=CD•cos ∠ECD=12×12=6km , ∴AB=CE=6km .故答案为:6.【点睛】本题考查解直角三角形的应用,通过辅助线,将问题转化矩形和三角形中,利用三角函数与矩形性质便可解决是关键.18.120º【分析】根据绝对值和平方的非负数性质可得sinA=tanB=根据特殊角的三角函数值可得出∠A∠B的度数根据三角形内角和定理即可得答案【详解】∵∴sinA-=0-tanB=0∴sinA=tan解析:120º【分析】根据绝对值和平方的非负数性质可得sinA=12,3出∠A、∠B的度数,根据三角形内角和定理即可得答案.【详解】∵213sin tan023A B⎫-+-=⎪⎪⎝⎭,∴sinA-12=03,∴sinA=12,tanB=33,∴∠A=30°,∠B=30°,∠C=180°-30°-30°=120°,故答案为:120°【点睛】本题考查了特殊角的三角函数值、非负数的性质及三角形内角和定理,根据非负数性质得出sinA=12,tanB=33,并熟记特殊角的三角函数值是解题关键.19.【分析】由题意过点B作BH⊥AC于H先解直角三角形求出BH再根据垂线段最短进行分析即可求解【详解】解:如图过点B作BH⊥AC于H在Rt△ABC中∵∠ABC=90°AB=2∠C=30°∴AC=2AB=解析:3【分析】由题意过点B作BH⊥AC于H,先解直角三角形求出BH,再根据垂线段最短进行分析即可求解.【详解】解:如图,过点B作BH⊥AC于H,在Rt△ABC中,∵∠ABC=90°,AB=2,∠C=30°,∴AC=2AB=4,BC=AB•cos30°=23,∵∠BHC=90°,∴BH=1BC=3,2∵BF//AC,∵当EF⊥AC时,EF的值最小,最小值=BH=3.故答案为:3.【点睛】本题考查解直角三角形的应用和平行线的性质以及垂线段最短等知识,解题的关键是理解题意,灵活运用所学知识解决问题.20.【分析】过A作AE⊥BC于点E则由题意可得AE的值进一步可求得△ABO 的面积【详解】解:如图过A作AE⊥BC于点E∵AB=4∠ABC=45°∴AE=AB=∴故答案为【点睛】本题考查菱形性质和解直角三解析:22【分析】过A作AE⊥BC于点E,则由题意可得AE的值,进一步可求得△ABO的面积.【详解】解:如图,过A作AE⊥BC于点E,∵AB=4,∠ABC=45°,∴AE=AB sin 45︒=42⨯=∴1111·42224ABO ABC S S BC AE ==⨯=⨯⨯=故答案为 .【点睛】本题考查菱形性质和解直角三角形的综合应用,熟练掌握菱形的性质是解题关键.三、解答题21.1+【分析】根据算术平方根,任何非零数的零次幂等于1以及特殊角的三角函数值计算即可.【详解】解:)02020330tan +︒=133+⨯=1+=1+【点睛】此题主要考查了实数运算,正确化简各数是解题关键.22.2【分析】分别根据特殊角的三角函数值、负整数指数幂及算术平方根的性质计算出各数,再根据实数混合运算的法则.【详解】+(12)-1﹣2cos30°﹣=23--==2.【点睛】本题考查的是实数的运算,熟记负整数指数幂、算术的性质及特殊角的三角函数值是解答此题的关键.23.(1)82米;(2)不超速,见解析【分析】(1)已知MN=30m ,∠AMN=60°,∠BMN=45°求AB 的长度,可以转化为解直角三角形;(2)求得从A 到B 的速度,然后与60千米/时≈16.66米/秒,比较即可确定答案.【详解】解:(1)由题意可得在Rt AMN △中,30MN =米,60AMN ∠=︒, ∴tan AN MN AMN =⋅∠=在Rt BMN 中,∵45BMN ∠=︒,∴30BN MN ==(米). ∴3082AB AN BN =+=≈(米).(2)此车不超速,理由如下:由题意可得,汽车从A 到B 为匀速行驶,用时为6秒,且82AB =米,则汽车的速度为()306513.66÷=≈(米/秒).∵60千米/时≈16.67米/秒,13.6616.67<,∴此车不会超速.【点睛】本题考查了勾股定理以及解直角三角形的应用,解题的关键是从题目中抽象出直角三角形,难度不大.24.8m【分析】设CD=x m ,解Rt △ACD 与Rt △DCB ,用含x 的代数式表示出AC 、CB ,然后根据△ACE 是含30度角的直角三角形列出方程,解方程即可求x 的值,进而可得AB .【详解】解:设CD=x m ,∵∠ADC=60°,∠CDB=45°,∴,CB=x•tan45°=x (m ),∵∠AED=30°,DE=8m ,∴, ∴,解得x=4(m ),∴(m ).答:该纪念碑AB 的高度约为10.8m .【点睛】本题考查的是解直角三角形的应用-仰角俯角问题,理解仰角俯角的概念、熟记锐角三角函数的概念是解题的关键.25.(1)x 1=6,x 2=﹣2;(2)1【分析】(1)采用分解因式法解方程;(2)将特殊角度的三角函数值代入计算即可.【详解】解:(1)x 2﹣4x ﹣12=0,(x ﹣6)(x +2)=0,x ﹣6=0或x +2=0,所以x 1=6,x 2=﹣2;(2)原式=112, 13=22+, =1.【点睛】本题考查一元二次方程的解法,特殊三角函数值的计算,掌握一元二次方程的解法,特殊三角函数值的计算,熟记特殊角度的三角函数值是关键.26.(1)0;(2)1x x -,2. 【分析】(1)原式先根据绝对值的代数意义,特殊角的三角函数值,负整数指数幂,零次幂以及算术平方根进行化简,再求出答案即可;(2)先求出x 的值,再根据异分母分式的减法进行通分并化简,最后把x 的代入化简结果中求值即可.【详解】解:(1)()1012sin 45tan 5012-⎛⎫︒--︒- ⎪⎝⎭=2213--+=213-+=0;(2)2221111x x x x ++--- =2211(1)(1)x x x x x ++--+- =(1)(1)(1)x x x x ++- =1x x - ∵14cos60=4=22x =︒⨯,∴原式=2221=-. 【点睛】 本题考查了分式的化简求值,绝对值,特殊角的三角函数值,负整数指数幂,零次幂以及算术平方根等知识点,能灵活运用知识点进行计算和化简是解此题的关键.。
2023年鲁教版(五四制)九年级数学上册《第2章直角三角形的边角关系》单元综合优生辅导测评(附答案)

2022-2023学年鲁教版(五四学制)九年级数学上册《第2章直角三角形的边角关系》单元综合优生辅导测评(附答案)一.选择题(共8小题,满分40分)1.在Rt△ABC中,cos A=,那么sin A的值是()A.B.C.D.2.如图,梯子(长度不变)跟地面所成的锐角为∠α,关于∠α的三角函数值与梯子的倾斜程度之间,叙述正确的是()A.sinα的值越大,梯子越陡B.cosα的值越大,梯子越陡C.tanα的值越小,梯子越陡D.陡缓程度与∠α的函数值无关3.如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为()A.B.C.D.4.如图,△ABC、△FED区域为驾驶员的盲区,驾驶员视线PB与地面BE的夹角∠PBE =43°,视线PE与地面BE的夹角∠PEB=20°,点A,F为视线与车窗底端的交点,AF∥BE,AC⊥BE,FD⊥BE.若A点到B点的距离AB=1.6m,则盲区中DE的长度是()(参考数据:sin43°≈0.7,tan43°≈0.9,sin20°≈0.3,tan20°≈0.4)A.2.6m B.2.8m C.3.4m D.4.5m5.无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135m的A处测得试验田右侧边界N 处俯角为43°,无人机垂直下降40m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为()(参考数据:tan43°≈0.9,sin43°≈0.7,cos35°≈0.8,tan35°≈0.7,结果保留整数)A.188m B.269m C.286m D.312m6.在正方形网格中,△ABC在网格中的位置如图,则cos B的值为()A.B.C.D.27.如图,两个高度相等且底面直径之比为1:2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是()A.cm B.6cm C.8cm D.10cm8.如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)()A.136.6米B.86.7米C.186.7米D.86.6米二.填空题(共8小题,满分40分)9.在Rt△ABC中,若∠C=90°,AC=5,BC=12,则sin A的值为.10.在Rt△ABC中,∠C=90°,AB=2,BC=,则sin=.11.如图,在△ABC中,∠ACB=90°,点D为AB边的中点,连接CD,若BC=4,CD =3,则cos∠DCB的值为.12.在△ABC中,若∠A、∠B满足|cos A﹣|+(sin B﹣)2=0,则∠C=.13.如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1:,则斜坡AB的长是米.14.数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为40米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,则旗杆的高度约为米.(结果精确到1米,参考数据:≈1.41,≈1.73)15.如图,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,则大厅两层之间的高度为米.(结果保留两个有效数字)【参考数据;sin31°=0.515,cos31°=0.857,tan31°=0.601】16.如图,一架长为6米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC 的长度约为米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)三.解答题(共6小题,满分40分)17.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.18.小军同学想利用所学的“锐角三角函数”知识测量一段两岸平行的河流宽度.他先在河岸设立A,B两个观测点,然后选定对岸河边的一棵树记为点M.测得AB=50m,∠MAB =22°,∠MBA=67°.请你依据所测数据求出这段河流的宽度(结果精确到0.1m).参考数据:sin22°≈,cos22°≈,tan22°≈,sin67°≈,cos67°≈,tan67°≈.19.无人机在实际生活中应用广泛.如图所示,小明利用无人机测量大楼的高度,无人机在空中P处,测得楼CD楼顶D处的俯角为45°,测得楼AB楼顶A处的俯角为60°.已知楼AB和楼CD之间的距离BC为100米,楼AB的高度为10米,从楼AB的A处测得楼CD的D处的仰角为30°(点A、B、C、D、P在同一平面内).(1)填空:∠APD=度,∠ADC=度;(2)求楼CD的高度(结果保留根号);(3)求此时无人机距离地面BC的高度.20.从2019年底以来,新冠疫情一直困扰着我们的日常生活,今年为进一步加强疫情防控工作,某公司决定安装红外线体温检测仪,这种设备的原理是采用非接触式测温法,只要用红外体温测试仪的镜头对准被测对象进行扫描,其体温就可立刻在显示屏上显示出来,从而有效地避免了其他常规测温法所可能造成的交叉感染,测温区域示意图如图所示,已知最大探测角∠P AO=75°,最小探测角∠PBO=30°.(参考数据:=1.414,=1.732,=2.236)(1)若该设备安装在离水平地面距离为2.2m的P处,即OP=2.2m,请求出图中OB的长度;(结果精确到0.1m)(2)若该公司要求测温区域AB的长度为4m,请求出该设备的安装高度OP的高度.(结果精确到0.1m)21.如图,某种路灯灯柱BC垂直于地面,与灯杆AB相连.已知直线AB与直线BC的夹角是76°,在地面点D处测得点A的仰角是53°,点B仰角是45°,点A与点D之间的距离为3.5米.求:(1)点A到地面的距离;(2)AB的长度.(精确到0.1米)(参考数据:sin53°≈0.8,cos53°≈0.6,sin76°≈0.97,cos76°≈0.24)22.郑州二七纪念塔位于郑州市二七广场,是为纪念京汉铁路工人大罢工中牺牲的烈士,发扬“二七”革命传统而修建的纪念性建筑.如图,某综合实践小组为测量塔顶旗杆的高度,在马路对面建筑物楼下选取了与二七塔的底部C在同一水平线上的测量点D,在建筑物楼上选取测量点E,DE⊥CD.已知,塔身BC高63m,ED=18m,在D处测得旗杆顶部A的仰角为58°,在E处测得旗杆底部B的仰角为45°,求旗杆AB的高度(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6).参考答案一.选择题(共8小题,满分40分)1.解:∵Rt△ABC中,cos A=,∴sin A==,故选:B.2.解:根据锐角三角函数的变化规律,知sinα的值越大,∠α越大,梯子越陡.故选:A.3.解:连接BF,∵CE是斜边AB上的中线,EF⊥AB,∴EF是AB的垂直平分线,∴S△AFE=S△BFE=5,∠FBA=∠A,∴S△AFB=10=AF•BC,∵BC=4,∴AF=5=BF,在Rt△BCF中,BC=4,BF=5,∴CF==3,∵CE=AE=BE=AB,∴∠A=∠FBA=∠ACE,又∵∠BCA=90°=∠BEF,∴∠CBF=90°﹣∠BFC=90°﹣2∠A,∠CEF=90°﹣∠BEC=90°﹣2∠A,∴∠CEF=∠FBC,∴sin∠CEF=sin∠FBC==,故选:A.4.解:∵FD⊥EB,AC⊥EB,∴DF∥AC,∵AF∥EB,∴四边形ACDF是平行四边形,∵∠ACD=90°,∴四边形ACDF是矩形,∴DF=AC,在Rt△ACB中,∵∠ACB=90°,∴AC=AB•sin43°≈1.6×0.7=1.12(m),∴DF=AC=1.12(m),在Rt△DEF中,∵∠FDE=90°,∴tan∠E=,∴DE≈=2.8(m),故选:B.5.解:由题意得:∠N=43°,∠M=35°,AO=135m,BO=AO﹣AB=95m,在Rt△AON中,tan N==tan43°,∴NO=≈150m,在Rt△BOM中,tan M==tan35°,∴MO=≈135.7m,∴MN=MO+NO=135.7+150≈286m.故选:C.6.解:在直角△ABD中,BD=2,AD=4,则AB===2,则cos B===.故选:A.7.解:甲液体的体积等于液体在乙中的体积.设乙杯中水深为x,则π×12×16=π×48×x,解得x=4.在直角△ABP中,已知AP=4cm,AB=8cm,∴BP=12cm.根据三角形的面积公式可知直角△ABP斜边上的高是6cm,所以乙杯中的液面与图中点P的距离是16﹣6﹣4=6(cm).故选:B.8.解:如图作DH⊥AB于H,延长DE交BC于F.在Rt△ADH中,AD=130米,DH:AH=1:2.4,∴DH=50(米),∵四边形DHBF是矩形,∴BF=DH=50(米),在Rt△EFB中,∠BEF=45°,∴EF=BF=50(米),在Rt△EFC中,FC=EF•tan60°,∴CF=50×≈86.6(米),∴BC=BF+CF=136.6(米).故选:A.二.填空题(共8小题,满分40分)9.解:如图所示:∵∠C=90°,AC=5,BC=12,∴AB==13,∴sin A=.故答案为:.10.解:∵sin A==,∴∠A=60°,∴sin=sin30°=.故答案为:.11.解:∵在△ABC中,∠ACB=90°,点D为AB边的中点,∴AD=BD=CD=AB,又∵CD=3,∴AB=6,∴cos∠DCB=cos∠B===,故答案为:.12.解:∵|cos A﹣|+(sin B﹣)2=0,∴cos A﹣=0,sin B﹣=0,∴cos A=,sin B=,∴∠A=60°,∠B=45°,则∠C=180°﹣∠A﹣∠B=180°﹣60°﹣45°=75°,故答案为:75°.13.解:如图所示:过点A作AF⊥BC于点F,∵斜面坡度为1:,∴tan∠ABF===,∴∠ABF=30°,∵在P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,∴∠HPB=30°,∠APB=45°,∴∠HBP=60°,∴∠PBA=90°,∠BAP=45°,∴PB=AB,∵PH=30m,sin60°===,解得:PB=20(m),故AB=20m,故答案为:20.14.解:过O点作OC⊥AB于C点,∵当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为30°,∴AC=45米,∠CAO=30°,∴OC=AC•tan30°=(米),∴旗杆的高度=40﹣15≈14(米),故答案为:14.15.解:在Rt△ABC中,∵∠ACB=90°,∴BC=AB•sin∠BAC=12×0.515≈6.2(米),答:大厅两层之间的距离BC的长约为6.2米.故答案为:6.2.16.解:由题意可得:∵∠ABO=70°,AB=6m,∴sin70°==≈0.94,解得:AO=5.64(m),∵∠CDO=50°,DC=6m,∴sin50°=≈0.77,解得:CO=4.62(m),则AC=5.64﹣4.62=1.02(m),答:AC的长度约为1.02米.故答案为:1.02.三.解答题(共6小题,满分40分)17.解:过点B作BM⊥FD于点M,在△ACB中,∠ACB=90°,∠A=60°,AC=10,∴∠ABC=30°,BC=AC×tan60°=10,∵AB∥CF,∴BM=BC×sin30°=10×=5,CM=BC×cos30°=15,在△EFD中,∠F=90°,∠E=45°,∴∠EDF=45°,∴MD=BM=5,∴CD=CM﹣MD=15﹣5.18.解:过点M作MN⊥AB,垂足为N,设MN=x米,在Rt△ANM中,∠MAB=22°,∴AN=≈=x(米),在Rt△MNB中,∠MBN=67°,∴BN=≈=x(米),∵AB=50米,∴AN+BN=50,∴x+x=50,∴x≈17.1,∴这段河流的宽度约为17.1米.19.解:(1)∵∠MP A=60°,∠NPD=45°,∴∠APD=180°﹣∠MP A﹣∠NPD=75°.过点A作AE⊥CD于点E.则∠DAE=30°,∴∠ADC=180°﹣90°﹣30°=60°.故答案为:75;60.(2)由题意可得AE=BC=100米,EC=AB=10米,在Rt△AED中,∠DAE=30°,tan30°=,解得DE=,∴CD=DE+EC=(+10)米.∴楼CD的高度为(+10)米.(3)过点P作PG⊥BC于点G,交AE于点F,则∠PF A=∠AED=90°,FG=AB=10米,∵MN∥AE,∴∠P AF=∠MP A=60°,∵∠ADE=60°,∴∠P AF=∠ADE,∵∠DAE=∠30°,∴∠P AD=30°,∵∠APD=75°,∴∠ADP=75°,∴∠ADP=∠APD,则AP=AD,∴△APF≌△DAE(AAS),∴PF=AE=100米,∴PG=PF+FG=100+10=110(米).∴此时无人机距离地面BC的高度为110米.20.解:(1)在Rt△OPB中,OP=2.2m,∠PBO=30°,∴OB===2.2≈3.8(m),∴OB的长度为3.8m;(2)过点A作AC⊥BP,垂足为C,在Rt△ACB中,∠PBO=30°,AB=4m,∴AC=AB=2(m),BC=AC=2(m),∵∠P AO=75°,∴∠APB=∠P AO﹣∠PBA=45°,在Rt△P AC中,PC===2(m),∴PB=PC+BC=(2+2)m,在Rt△POB中,∠PBO=30°,∴OP=PB=1+≈2.7(m),∴该设备的安装高度OP的高度为2.7m.21.解:(1)过点A作AF⊥CD,垂足为F,在Rt△AFD中,AF=AD sin53°=3.5×0.8=2.8米,答:点A到地面的距离为2.8米;(2)过点A作AG⊥EC,垂足为G,则AF=GC,AG=CF,在Rt△AFD中,DF=AD cos53°=3.5×0.6=2.1米,设CF为x米,则CD为(2.1+x)米,在Rt△BCD中,BC=CD tan45°=(2.1+x)米,∴GB=GC﹣BC=2.8﹣(2.1+x)=(0.7﹣x)米,在Rt△AGB中,tan76°=,∴tan76°=,∴,解得:x≈0.56,∴CF=AG=0.56米,∴AB==≈0.6米.22.解:过点E作EF⊥AC,垂足为F,则DE=FC=18m,EF=CD,∵BC=63m,∴BF=BC﹣CF=45(m),在Rt△BFE中,∠BEF=45°,∴EF===45(m),∴EF=CD=45m,在Rt△ACD中,∠ADC=58°,∴AC=CD tan58°≈45×1.6=72(m),∴AB=AC﹣BC=72﹣63=9(m),∴旗杆AB的高度约为9m.。
精品试题北师大版九年级数学下册第一章直角三角形的边角关系综合测评试题(含解析)

九年级数学下册第一章直角三角形的边角关系综合测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、已知在Rt △ABC 中,∠C =90°,∠A =60°,则 tan B 的值为( )A B .1 C D .22、在Rt ABC 中,∠C =90°,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,则下列式子一定成立的是( )A .sin a cB =⋅ B .cos a c B =⋅C .tan a c B =D .sin c a A =⋅3、如图要测量小河两岸相对的两点P ,A 的距离,点P 位于点A 正北方向,点C 位于点A 的北偏西46°,若测得PC =50米,则小河宽PA 为( )A .50sin44°米B .50cos44°C .50tan44°米D .50tan46°米4、tan 45︒的值为( )A .1B .2CD .5、某人沿坡度1:2i =的斜坡向上前进了10米,则他上升的高度为( )A .5米B .C .D .6、如图,在四边形ABCD 中,AD BC ∥,90ABC ∠=︒,O 为对角线BD 的中点,2OA =,5BC =,3CD =,则tan DCB ∠等于( )A .43B .34C .45 D .357、如图,某建筑物AB 在一个坡度为i =1:0.75的山坡BC 上,建筑物底部点B 到山脚点C 的距离BC =20米,在距山脚点C 右侧同一水平面上的点D 处测得建筑物顶部点A 的仰角是42°,在另一坡度为i =1:2.4的山坡DE 上的点E 处测得建筑物顶部点A 的仰角是24°,点E 到山脚点D 的距离DE =26米,若建筑物AB 和山坡BC 、DE 的剖面在同一平面内,则建筑物AB 的高度约为( )(参考数据:sin 24°≈0.41,cos 24°≈0.91,tan 24°≈0.45,sin 42°≈0.67.cos 42°≈0.74,tan 42°≈0.90)A .36.7米B .26.3 米C .15.4米D .25.6 米8、如图,E 是正方形ABCD 边AB 的中点,连接CE ,过点B 作BH ⊥CE 于F ,交AC 于G ,交AD 于H ,下列说法:①AH HG AB BG =; ②点F 是GB 的中点;③AG AB =;④S △AHG =16S △ABC .其中正确的结论的序号是( )A .①②③B .①③C .②④D .①③④ 9、在△ABC 中,∠C =90°,BC =2,sin A =23,则边AC 的长是( )A B .3 C .43 D 10、如图,在平面直角坐标系xoy 中,直线14y k x =+与y 轴交于点C ,与反比例函数2k y x =在第一象限内的图象交于点B ,连接BO ,若2OBC S ∆=,1tan 5BOC ∠=,则2k 的值是( )A .-20B .20C .-5D .5第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、等腰ABC ,底角是30ABC 的周长是_____________2、如图,矩形ABCD 中,DE ⊥AC 于点E ,∠ADE =α,cosα=35,AB =4,AD 长为_____.3、cos30°的相反数是 _____.4、构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图,在Rt△ABC 中,∠C =90°,∠ABC =30°,延长CB 至D ,使BD =AB ,连接AD ,得∠D =15°,所以tan15°AC CD ====2tan22.5°的值为 _____.5、如图, 在 Rt ABC △ 中, 390,tan ,2ACB BAC CD ∠∠== 是斜边 AB 上的中线, 点 E 是直线 AC 左侧一点, 联结 AE CE ED 、、, 若 ,EC CD EAC B ∠∠⊥=, 则 CDEABC SS 的值为______.三、解答题(5小题,每小题10分,共计50分)1、如图,平地上两栋建筑物AB 和CD 相距30m ,在建筑物AB 的顶部测得建筑物CD 底部的俯角为26.6°,测得建筑物CD顶部的仰角为45°.求建筑物CD 的高度.(参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50)2、如图,等腰Rt△ABC 中,AB =AC ,D 为线段BC 上的一个动点,E 为线段AB 上的一个动点,使得CD=.连接DE ,以D 点为中心,将线段DE 顺时针旋转90°得到线段DF ,连接线段EF ,过点D 作射线DR ⊥BC 交射线BA 于点R ,连接DR ,RF .(1)依题意补全图形;(2)求证:△BDE ≌△RDF ;(3)若AB =AC =2,P 为射线BA 上一点,连接PF ,请写出一个BP 的值,使得对于任意的点D ,总有∠BPF 为定值,并证明.3、小明周末沿着东西走向的公路徒步游玩,在A 处观察到电视塔在北偏东37度的方向上,5分钟后在B 处观察到电视塔在北偏西53度的方向上.已知电视塔C 距离公路AB 的距离为300米,求小明的徒步速度.(精确到个位,sin370.6︒≈,cos370.8︒≈,sin530.8︒≈,cos530.6︒≈,tan370.75︒≈,tan53 1.3︒≈)4、如图, 在 ABC 中,90,3C AC BC ∠===, 点 D E 、 分别在 AC 边和 AB 边上,沿着直线 DE 翻折 ADE ,点 A 落在 BC 边上,记为点 F ,如果 1CF =,则 BE =_______.5、计算:(1)22390x x +-=;(21016sin 453)2-⎛⎫+- ⎪⎝⎭︒.-参考答案-一、单选题1、A【分析】根据直角三角形的两个锐角互余即可求得30B ∠=︒,根据特殊角的三角函数值即可求解【详解】∵∠C =90°,∠A =60°,∴30B ∠=︒又tan 30︒=故选A【点睛】本题考查了直角三角形的两个锐角互余,求特殊角的三角函数值,理解特殊角的三角函数值是解题的关键.2、B【分析】根据题意,画出直角三角形,再根据锐角三角函数的定义对选项逐个判断即可.【详解】解:由题意可得,如下图:sinaAc=,则sina c A=⋅,A选项错误,不符合题意;cosaBc=,则cosa c B=⋅,B选项正确,符合题意;tanbBa=,则tanacB≠,C选项错误,不符合题意;sinaAc=,则sinacA=,D选项错误,不符合题意;故选B,【点睛】此题考查了锐角三角函数的定义,解题的关键是画出图形,根据锐角三角函数的定义进行求解.3、C【分析】先根据AP⊥PC,可求∠PCA=90°-46°=44°,在Rt△PCA中,利用三角函数AP=tan4450tan44PC︒⨯=︒米即可.【详解】解:∵AP⊥PC,∴∠PCA+∠A=90°,∵∠A=46°,∴∠PCA=90°-46°=44°,在Rt△PCA中,tan∠PCA=APCP,PC=50米,∴AP=tan4450tan44PC︒⨯=︒米.故选C.【点睛】本题考查测量问题,掌握测量问题经常利用三角函数求边,熟悉锐角三角函数定义是解题关键.4、A【分析】直接求解即可.【详解】解:tan45︒=1,故选:A.【点睛】本题考查特殊角的三角函数值,熟记特殊角的三角函数值是解答的关键.5、B【分析】由坡度定义可得位置升高的高度即为坡角所对的直角边.根据题意可得BC:AC=1:2,AB=10m,可解出直角边BC,即得到位置升高的高度.【详解】解:由题意得,BC:AC=1:2.∴设BC=x,则AC=2x.∵AB=10,BC2+ AC2=AB2,∴x2+ (2x)2=102,解得:x=.故选:B.【点睛】本题主要考查了坡度的定义和解直角三角形的应用,注意画出示意图会使问题具体化.6、A【分析】先根据平行线的性质和直角三角形斜边上的中线等于斜边的一半求出BD ,再根据勾股定理的逆定理判断出∠BDC =90°,由正切定义求解即可.【详解】解:∵AD ∥BC ,∠ABC =90°,∴∠BAD =90°,∵O 为对角线BD 的中点,OA =2,∴BD =2OA =4,∵BC =5,CD =3,∴BD 2+CD 2=BC 2,∴∠BDC =90°,∴tan∠DCB =BD CD =43, 故选:A .【点睛】本题考查平行线的性质、直角三角形的斜边中线性质、勾股定理的逆定理、正切,熟练掌握勾股定理的逆定理是解答的关键.7、D【分析】如图所示,过E 点做CD 平行线交AB 线段为点H ,标AB 线段和CD 线段相交点为G 和H 由坡度为i =1:0.75,BC =20可得BG =16,GC =12,由坡度为 i =1:2.4,DE =26可得DF =24,EF =10,分别在在AGB 中满足tan 42AG GD =︒,在AEH △中满足tan 24AH HE =︒化简联立得AB =25.6.【详解】如图所示,过E 点做CD 平行线交AB 线段为点H ,标AB 线段和CD 线段相交点为G 和H∵在BGC 中BC =20,坡度为i =1:0.75,∴222BG GC BC +=, ∴2223()4BG BG BC +=, ∴222916BG BG BC +=, ∴22252016BG =, ∴22540016BG =, ∴21640025BG =⨯, ∴2256BG =,∴16BG =, ∴3124CG BG ==. 在BGC 中DE =26,坡度为 i =1:2.4,∴222DF EF DE +=, ∴22212()5EF EF DE +=, ∴22214425EF EF DE +=, ∴221692625EF =, ∴225676169EF =⨯,∴2100EF =,∴10EF =, ∴12245DF EF ==, ∴在AGB 中满足tan 42AG GD =︒,在AEH △中满足tan 24AH HE =︒, 即0.9AB BG GC CD +=+,0.45AB BH GC CD DF+=++ 其中BG =16、BG =12、BH =BG -EF =6、DF =24,代入化简得160.9(12)60.45(36)AB CD AB CD +=+⎧⎨+=+⎩①②, 令2②-①有2261620.45360.91220.450.9AB AB CD CD -+⨯-=⨯⨯-⨯+⋅⋅-∴421.6AB -=,∴AB =25.6.故选:D .【点睛】本题考查了解直角三角形的应用,利用三角形的坡度和斜边长通过勾股定理可以求得三角形各边长度,再根据角度列含两个未知数的二元一次方程组,正确的列方程求解是解题的关键.8、D 【分析】①先证明△ABH≌△BCE,得AH=BE,则1122AH AD BC==,即12AHAB=,再根据平行线分线段成比例定理得:12HGBG=即可判断;②设BF=x,CF=2x,则BC,计算FG=23x即可判断;③根据等腰直角三角形得:AC,根据①中得:13AGAC=即可判断;④根据11,22HG AGBG CG==,可得同高三角形面积的比,然后判断即可.【详解】解:①∵四边形ABCD是正方形,∴AB=BC,∠HAB=∠ABC=90°,∵CE⊥BH,∴∠BFC=∠BCF+∠CBF=∠CBF+∠ABH=90°,∴∠BCF=∠ABH,∴△ABH≌△BCE,∴AH=BE,∵E是正方形ABCD边AB的中点,∴BE=12AB,∴1122AH AD BC==,即12AHAB=∵AH//BC,∴12 AH HG BC BG==∴AH HGAB BG=,故①正确;②1 tan tan2AH BF ABH BCFAB CF ∠=∠===设BF=x,CF=2x,则BC,∴AHx∴52 BH x=∴552263x x xFG BH GH BF x BF=--=--=≠,故②不正确;③∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,∴AC,∵12 AG AH CG BC==∴13 AG AC=∴13AG AC AB==,故③正确;④∵12GH AG BG CG==∴11,22 AHG ABGABG BCGS SS S∆∆∆∆==∴13 ABGABCSS∆∆=∴16AHG ABCS S=,故④正确.故选D.【点睛】本题属于四边形综合题,主要考查了正方形的性质、全等三角形的判定和性质、勾股定理等知识点,灵活应用相关知识点成为解答本题的关键.9、A【分析】先根据BC=2,sin A=23求出AB的长度,再利用勾股定理即可求解.【详解】解:∵sin A=BCAB =23,BC=2,∴AB=3,∴AC故选:A.【点睛】本题考查正弦的定义、勾股定理等知识,是重要考点,难度较小,掌握相关知识是解题关键.10、D【分析】先根据直线解析式求得点C的坐标,然后根据△BOC的面积求得BD的长,然后利用正切函数的定义求得OD的长,从而求得点B的坐标,利用待定系数法将点B坐标代入即可求得结论.【详解】解:∵直线y=k1x+4与x轴交于点A,与y轴交于点C,∴点C的坐标为(0,4),∴OC=4,过B作BD⊥y轴于D,∵S △OBC =2, ∴114222OC BD BD ⋅=⨯⋅=, ∴BD =1,∵tan∠BOC =15, ∴15BD OD =, ∴OD =5,∴点B 的坐标为(1,5), ∵反比例函数2k y x=在第一象限内的图象交于点B , ∴k 2=1×5=5.故选:D .【点睛】本题考查了反比例函数与一次函数的交点坐标,锐角三角函数,三角形面积,待定系数法求分别列函数解析式,解题的关键是作辅助线构造直角三角形.二、填空题140 【分析】设腰长为x ,则等腰三角形的高为2x ,三角形的面积为122x ⨯=x 的值,进而求出周长2x +的值.【详解】解:设等腰三角形的腰长为x ,高为sin 302x x ︒=,底边长为2cos30x ︒=122x S ∴=⨯=解得x =∴周长为240x =40+. 【点睛】 本题考查了锐角三角函数值,等腰三角形.解题的关键在于利用三角函数值将边长表示出来. 2、163【分析】将已知角度的三角函数转换到所需要的三角形中,得到∠ADE =∠DCE =α,求出AC 的值,再由勾股定理计算即可.【详解】∵∠ADC =∠AED =90°,∠DAE +∠ADE =∠ADE +∠CDE =90°∴∠DAE =∠CDE又∵∠DCE +∠CDE =90°∴∠ADE =∠DCE =α∴cosα=35=CD AC又∵矩形ABCD中AB=CD=4∴AC=20 3在ADC中满足勾股定理有163AD=故答案为:163.【点睛】本题考查了已知余弦长求边长,将已知余弦长转换到所需要的三角形中是解题的关键.3、【分析】先将特殊角的三角函数值代入求解,再求出其相反数.【详解】所以其相反数为故答案为:【点睛】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值以及相反数的概念.41##【分析】在等腰直角△ABC 中,∠C =90°,延长CB 至点D ,使得AB =BD ,则∠BAD =∠D .设AC =1,求出CD ,可得结论.【详解】解:如图,在等腰直角△ABC 中,∠C =90°,延长CB 至点D ,使得AB =BD ,则∠BAD =∠D .∵∠ABC =45°,∴45°=∠BAD +∠D =2∠D ,∴∠D =22.5°,设AC =1,则BC =1,AB =∴1CD CB BD CB AB =+=+=∴tan 22.5tan 1AC D CD ︒====.1.【点睛】本题考查解直角三角形,分母有理化,特殊直角三角形的性质,三角函数等知识,解题的关键是学会利用特殊直角三角形解决问题.5、1336【分析】先证明Rt AED Rt CED ≌,则AED CED S S =,进而证明DAE BCA ∽,据3tan 2BAC ∠=求得相似比,根据面积比等于相似比的平方即可求解【详解】解:CD 是Rt ABC 斜边 AB 上的中线, 12CD AB AD ∴== DCA DAC ∴∠=∠ 90ACB ∠=︒90CAB B ∴∠+∠=︒ EAC B ∠=∠90EAC DAC ∴∠+∠=︒ 即90EAD ∠=︒ 又EC CD ⊥90ECD ∴∠=︒EAD ECD ∴∠=∠ Rt AED Rt CED ∴≌ AED CED S S ∴= ,DA DC EA EC == ED AC ∴⊥又90ACB ∠=︒ BC AC ∴⊥//ED BC ∴ADE B ∴∠=∠又90EAD ACB ∠=∠=︒ DAE BCA ∴∽2ADC ABC S AD S BC ⎛⎫∴= ⎪⎝⎭ 3tan 2BAC ∠= 32CB CA ∴= 设3CB k =,则2AC k =AB ∴=12AD AB ∴== AED CED S S =2CDE ADC ABC ABC SS AD S SBC ⎛⎫∴== ⎪⎝⎭2132336k ⎛⎫ ⎪ ⎪== ⎪ ⎪⎝⎭故答案为:1336【点睛】 本题考查了解直角三角形,三角形全等的性质与判定,相似三角形的性质与判定,直角三角形斜边上的中线等于斜边的一半,垂直平分线的性质与判定,正切的定义,证明AED CED SS =是解题的关键. 三、解答题1、建筑物CD 的高度约为45m .【分析】如图所示,过点A 作AE ⊥CD 于E ,先证明AE =CE ,然后证明四边形ABDE 是矩形,则AE =BD =30m ,CE =AE =30m ,tan =30tan26.615m DE AE EAD =⋅︒≈∠,由此即可得到答案.【详解】解:如图所示,过点A作AE⊥CD于E,∴∠AEC=∠AED=90°,∵∠CAE=45°,∴∠C=45°,∴∠C=∠CAE,∴AE=CE,∵AB⊥BD,CD⊥BD,∴∠ABD=∠BDE=90°,∴四边形ABDE是矩形,∴AE=BD=30m,∴CE=AE=30m,tan=30tan26.615m∠,=⋅︒≈DE AE EAD∴CD=CE+DE=45m,答:建筑物CD的高度约为45m.【点睛】本题主要考查了矩形的性质与判定,等腰直角三角形的性质与判定,解直角三角形,解题的关键在于能够正确作出辅助线求解.2、(1)见解析;(2)见解析;(3)当4BP=,使得对于任意的点D,总有∠BPF为定值,证明见解析【分析】(1)根据题意作出图形连接,DR RF ;(2)根据BDR EDF ∠=∠可得BDE RDF ∠=∠,证明BRD 是等腰直角三角,可得BD DR =,根据旋转的性质可得ED DR =,进而根据边角边即可证明△BDE ≌△RDF ;(3)当24PB AB ==时,设DE a =,则CD =,分别求得,FR RP ,根据1tan 22RF a BPF RP a ∠===即可求解【详解】(1)如图,(2)DR ⊥BC90RDB ∴∠=︒将线段DE 顺时针旋转90°得到线段DF ,90,EDF ED FD ∴∠=︒=BDR EDF ∴∠=∠即BDE EDR EDR RDF ∠+∠=∠+∠BDE RDF ∴∠=∠ ABC 是等腰直角三角形45B ∴∠=︒90BDR ∠=︒45BRD ∴∠=︒BRD∴是等腰直角三角形∴=BD DR∴△BDE≌△RDF;(2)如图,当24==时,使得对于任意的点D,总有∠BPF为定值,证明如下,PB ABAB AC==ABC是等腰直角三角形,2∴=BCDC==,则CD,设DE a△BDE≌△RDF,==DR BD∴==,FR BR aABC是等腰直角三角形,∴∠=︒45EBD⊥DR BC∴∠=︒BRD45∴是等腰直角三角形,BDR∴==-BR a42()∴=-=--=4422PR BP BR a a△BDE ≌△RDF ,45FRD EBD ∴∠=∠=︒90BRF BRD DRF ∴∠=∠+∠=︒即FR AB ⊥1tan 22RF a BPF RP a ∴∠=== BPF ∴∠为定值【点睛】本题考查了等腰直角三角形的性质,全等三角形的性质,正切的定义,旋转的性质,掌握以上知识是解题的关键.3、126米/分钟【分析】过C 作CD AB ⊥于D ,则300CD =米,由解直角三角形求出AD 和BD 的长度,则求出AB 的长度,即可求出小明的速度.【详解】解:过C 作CD AB ⊥于D ,则300CD =米,∴903753CAD ∠=︒-︒=︒, ∴300tan tan 53 1.3CAD AD∠=︒=≈, ∴231AD ≈,同理:400BD ≈631AB AD BD =+=速度:631÷5≈126(米/分钟).【点睛】本题考查了解直角三角形的应用,以及解直角三角形,解题的关键是正确求出AD 和BD 的长度.4【分析】过点F 作FG AB ⊥于点G ,设BE x =,则AE x =,EG BE BG x =-=EGF △即可求得x ,即BE 的值【详解】解:如图,过点F 作FG AB ⊥于点G在 ABC 中,90,3C AC BC ∠===,AB ∴=tan 1AC B BC ==45A B ∠FGB ∴是等腰直角三角形BG FG ∴==sin FB B ⋅=设BE x =,则AE x =,EG BE BG x =-=沿着直线DE 翻折ADE ,点A 落在BC 边上,记为点F ,EA EF ∴=x在Rt EFG 中,222EF EG FG =+即()(222x x =+解得x =【点睛】本题考查了勾股定理,轴对称的性质,解直角三角形,根据题意构造直角三角形是解题的关键.5、(1)123,32x x ==-;(2)1 【分析】(1)用公式法求解即可;(2)根据特殊角的三角函数值、零指数幂和负整数指数幂、二次根式的性质计算即可.【详解】(1)∵2a =,3b =,9c =-24972810b ac -=+=>,∴x ==∴123,32x x ==-.(2)原式621=-01=+1=. 【点睛】 本题考查了解一元二次方程,特殊角的三角函数值、零指数幂和负整数指数幂、二次根式的性质等知识,熟练掌握并灵活运用这些知识是关键.。
(必考题)初中数学九年级数学下册第一单元《直角三角形的边角关系》测试卷(包含答案解析)(3)

一、选择题1.如图,在Rt ABC 中,90,4,3ACB AC BC ∠=︒==,将ABC 绕直角边AC 的中点O 旋转,得到DEF ,连接AD ,若DE 恰好经过点C ,且DE 交AB 于点G ,则tan DAG ∠的值为( )A .524B .513C .512D .7242.如图,在ABC 中,90C ∠=︒,设A ∠,B ,C ∠所对的边分别为a ,b ,c ,则下面四个等式一定成立的是( )A .sin c bB =⋅ B .cos a c B =⋅C .tan a b B =⋅D .tan b c B =⋅ 3.三角形在正方形网格纸中的位置如图所示,则sinα的值是( )A .34B .43 C .35D .45 4.在Rt ABC 中,90,3,2C BC AC ∠=︒==,则sin A 的值为( )A .32B .23C .21313D .31313 5.在Rt ABC 中,90,2,6C AC AB ∠=︒==,则下列结论正确的是( ) A .1sin 3A = B .2cos 4B = C .tan 22A = D .22tan 3B = 6.如图,边长为23的等边三角形AOB 的顶点B 在x 轴的正半轴上,点C 为AOB 的中心,将AOB 绕点O 以每秒60︒的速度逆时针旋转,则第2021秒,AOB 的中心C 的对应点2021C 的坐标为( )A .()0,2-B .()3,1-C .()1,3D .()1,3- 7.Rt ABC 中,90C ∠=︒,2AC =,1BC =,sin A =( )A .5B .2C .3D .128.如图,在直角△BAD 中,延长斜边BD 到点C ,使得BD=2DC ,连接AC ,如果5tanB 3=,则tan CAD ∠的值是( )A 3B 3C .13D .15 9.在ABC 中,90C ∠=︒,tan 2A =,则sin A 的值是( ) A .23 B .13 C 25 D 5 10.如图,在44⨯的正方形方格图形中,小正方形的顶点称为格点,ABC 的顶点都在格点上,则BAC ∠的正弦值是( )A .12B .55C .255D .无法确定 11.在Rt △ABC 中,∠C =90°,若1cos 2B =,则sin A 的值为( ) A .1 B .12 C .32 D .3312.如图,在Rt △ABC 中,∠ACB=90°,若5AC =,BC=2,则sin ∠A 的值为( )A .5B .5C .23D .25 二、填空题13.江堤的横断面如图,堤高BC 10=米,迎水坡AB 的坡比是1:3,则堤脚AC 的长是______.14.如图,在平面直角坐标系中,点B 在第一象限,BA x ⊥轴于点A ,反比例函数()0k y x x=>的图象与线段AB 相交于点C ,且C 是线段AB 的中点,点C 关于直线y x =的对称点'C 的坐标为()()1,1n n ≠,若OAB 的面积为4.则下列结论:①2n =;②4k =;③不等式k x x <的解集是2x >;④tan 2ABO ,其中正确结论的序号是________.15.如图,在Rt ABC △中,90A ∠=︒,AB AC =,BD 是AC 边上的中线,则tan ADB ∠的值是______.16.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D ,AB =9,AC =6,则cos ∠DCB =________________ .17.如图,在△ABC 中,∠A =30°,∠B =45°,BC =6cm ,则AB 的长为_____.18.如图,在菱形ABCD 中,4AB =,45ABC ∠=︒,菱形ABCD 的对角线交于点O ,则ABO 的面积为__________.19.在菱形ABCD 中,AB=4cm ,AB=BD ,则菱形ABCD 的面积是______.20.2sin30°+tan60°×tan30°=_____.三、解答题21.如图,在河流的右岸边有一高楼AB ,左岸边有一坡度1:2i =的山坡CF ,点C 与点B 在同一水平面上,CF 与AB 在同一平面内.某数学兴趣小组为了测量楼AB 的高度,在坡底C 处测得楼顶A 的仰角为45︒,然后沿坡面CF 上行了205米(即205CD =米)到达点D 处,此时在D 处测得楼顶A 的仰角为26.7︒.(参考数据:sin26.70.45︒≈,cos26.70.89︒≈,tan26.70.50︒≈)(1)求点C 到点D 的水平距离CE 的长;(2)求楼AB 的高度. 22.如图,已知四边形ABCD 和四边形DEFG 为正方形,点E 在线段DC 上,点,,A D G 在同一直线上,且5,3AD DE ==,连接,,AC CG AE ,并延长AE 交CG 于点H .(1)求sin EAC ∠的值.(2)求线段AH 的长.23.如图,建设“五化东安”,打造“绿色发展样板城市”.在数学课外实践活动中,小薇在紫水河北岸的自行车绿化道AC 上,在A 处测得对岸的吴公塔D 位于南偏东60°方向,往东走300米到达B 处,测得对岸的吴公塔D 位于南偏东30°方向.(1)求吴公塔D 到紫水河北岸AC 的距离约为多少米?(精确到13≈1.73)(2)小薇继续向东走到轮船码头C 处,测得对岸的吴公塔D 位于西南方向.已知小薇的平均速度为每小时5千米,小薇从B 处到轮船码头大约几分钟?(精确到1分钟) 24.某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥AB 是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥AB 上方150米的点C 处悬停,此时测得桥两端,A B 两点的俯角分别为65°和45°,求桥AB 的长度.(参考数据:sin650.91︒≈,cos650.42︒≈,tan65 2.14︒≈;结果精确到0.1米)25.如图,在东西方向的海岸线l 上有长为300米的码头海岸AB ,在码头的最西端A 处测得轮船M 在它的北偏东45︒方向上;同一时刻,在A 处正东方向距离A 处50米的C 处测得轮船M 在北偏东37︒方向上.(1)求轮船M 到海岸线l 的距离;(结果保留整数米)(2)如果轮船M 沿着南偏东22︒的方向就行,那么该轮船能否行至码头海岸AB 靠岸?请说明理由.(参考数据:sin370.60︒≈,tan370.75︒≈,sin 220.37︒≈,tan220.40︒≈)26.(1)计算:230360245sin tan cos ︒+-︒.(2)已知32a b =,求22a b a b -+的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】连接OG ,由勾股定理求出AB=5,由直角三角形的性质求出CG ,CD ,AD 的长,由锐角三角函数的定义可得出答案.【详解】解:连接OG ,在Rt△ABC中,∠C=90°,AC=4,BC=3,∴222243AC BC+=+,∵点O是AC边的中点,∴OC=OA=OD=12AC=2,∴∠GCO=∠ODC=∠BAC,∠ADC=90°,∴AG=CG,∴OG⊥AC,在Rt△ABC中,sin∠BAC=35BCAB=,cos∠BAC=45ACAB=,∴sin∠OCG=35,cos∠OCG=45,在Rt△OCG中,CG=5 cos2OCOCG=∠,在Rt△ACD中,CD=AC•cos∠OCG=165,AD=AC•sin∠OCG=125,∴DG=CD-CG=165-52=710,∴tan∠DAG=771012245DGAD==.故选:D.【点睛】本题考查了旋转的性质,锐角三角函数的定义,勾股定理,直角三角形的性质,正确的作出辅助线构造直角三角形是解题的关键.2.B解析:B【分析】根据∠B的正弦、余弦、正切的定义列式,根据等式的性质变形,判断即可.【详解】解:在△ABC 中,∠C=90°,∵sinB=b c , ∴c=sin b B,A 选项等式不成立; ∵cosB=a c , ∴a=c•cosB ,B 选项等式成立;∵tanB=b a , ∴a=tan b B,C 选项等式不成立; ∵tanB=b a , ∴b=a•tanB ,D 选项等式不成立;故选:B .【点睛】本题考查了锐角三角函数的定义,掌握锐角是三个三角函数的定义是解题的关键. 3.C解析:C【分析】将α∠转换成β∠去计算正弦值.【详解】解:如图,βα∠=∠,4AB =,3BC =,∴5AC =,则3sin sin 5BC AC αβ===. 故选:C .【点睛】本题考查正弦值的求解,解题的关键是掌握网格图中三角函数值的求解.4.D解析:D【分析】根据勾股定理求出斜边AB ,再根据锐角三角函数的意义求出结果即可;【详解】在Rt ABC 中,由勾股定理可得,AB ==∴sinBC A AB === 故答案选D .【点睛】本题主要考查了锐角三角函数的定义,准确计算是解题的关键.5.C解析:C【分析】根据勾股定理求出BC =【详解】∵在Rt ABC 中,90C ∠=︒,2AC =,6AB =, ∴BC =∴sin 63BC A AB ===,故A 错误;cos sin B A ==,故B 错误;tan ===BC A AC C 正确;tan===AC B BC ,故D 错误; 故选:C .【点睛】本题主要考查了解直角三角形,结合勾股定理进行计算是解题的关键.6.B解析:B【分析】通过计算画出第2021秒,AOB 的位置,过C′作C′D ⊥x 轴于点D ,连接OC′,BC′,求出DC′的长,即可求解.【详解】∵360°÷60°=6,∴AOB 的位置6秒一循环,而2021=6×336+5,∴第2021秒,AOB 的位置如图所示,设点C 的对应点C′,过C′作C′D ⊥x 轴于点D ,连接OC′,BC′,则∠DOC′=30°,OD=DB=3, ∴DC′=OD∙tan ∠DOC′=3×tan30°=3×33=1, ∴C′()3,1-. 故选B .【点睛】本题主要考查图形于=与坐标,等边三角形的性质,锐角三角函数,找到图形的变化规律,画出图形,是解题的关键.7.A解析:A【分析】求出斜边AB ,再求∠A 的正弦值. 【详解】解:∵90C ∠=︒,2AC =,1BC =,∴2222215AB AC BC +=+= 5sin 5BC A AB ===, 故选:A . 【点睛】 本题考查了勾股定理和锐角的正弦函数值的求法,解题关键是求出斜边长,熟知正弦的意义.8.D解析:D【分析】延长AD ,过点C 作CE ⊥AD ,垂足为E ,由5tanB 3=,即53AD AB =,设AD =5x ,则AB =3x ,利用相似三角形的判定可证△CDE ∽△BDA ,由相似三角形的性质可得:12CE DE CD AB AD BD ===,进而可得CE =32x ,DE =52x ,从而可求得tan ∠CAD 的值.解:如图,延长AD ,过点C 作CE ⊥AD ,垂足为E ,∵5tanB 3=,即53AD AB =, ∴设AD =5x ,则AB =3x , ∵∠CDE =∠BDA ,∠CED =∠BAD ,∴△CDE ∽△BDA , ∴12CE DE CD AB AD BD ===, ∴CE =32x ,DE =52x , ∴AE =152x , ∴tan ∠CAD =15CE AE =. 故选:D .【点睛】 本题考查了锐角三角函数的定义、相似三角形的判定和性质等知识,解题的关键是:正确添加辅助线,将∠CAD 放在直角三角形中.9.C解析:C【分析】由tanA=BC AC=2,设BC=2x ,可得AC=x ,Rt △ABC 中利用勾股定理算出5x ,然后利用三角函数在直角三角形中的定义,可算出sinA 的值.【详解】解:由tanA=BC AC=2,设BC=2x ,则AC=x , ∵Rt △ABC 中,∠C=90°,∴根据勾股定理,得()222225BC AC x x x +=+=, 因此,sinA=255BC AB x== 故选:C .本题已知正切值,求同角的正弦值.着重考查了勾股定理、三角函数的定义等知识,属于基础题.10.B解析:B【分析】先根据勾股定理的逆定理判断出ABC 的形状,再由锐角三角函数的定义即可得出结论.【详解】解:2223425AB =+=,2222420AC =+=,222125BC =+=,222AC BC AB ∴+=,ABC ∴为直角三角形,且90ACB ∠=︒,则sin BC BAC AB ∠==, 故选:B .【点睛】本题考查的是勾股定理的逆定理以及锐角三角函数的定义,熟知在一个三角形中,如果两条边长的平方之和等于第三边长的平方,那么这个三角形是直角三角形是解答此题的关键. 11.B解析:B【分析】根据互余角的三角函数间的关系:sin (90°-α)=cosα,cos (90°-α)=sinα解答即可.【详解】解:解:∵在△ABC 中,∠C=90°,∴∠A+∠B=90°,∴sinA= cosB=12, 故选:B .【点睛】本题考查了互余两角的三角函数关系式,掌握当∠A+∠B=90°时, sinA= cosB 是解题的关键. 12.C解析:C【分析】先利用勾股定理求出AB 的长,然后再求sin ∠A 的大小.【详解】解:∵在Rt △ABC 中,AC =BC=2∴3=∴sin ∠A=23BC AB = 故选:C .【点睛】 本题考查锐角三角形的三角函数和勾股定理,需要注意求三角函数时,一定要是在直角三角形当中.第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题13.米【分析】在Rt △ABC 中已知了坡面AB 的坡比是铅直高度BC 和水平宽度AC 的比值据此即可求解【详解】解:根据题意得:BC :AC=1:解得:AC=BC=10(米)故答案为:10米【点睛】本题考查了解直解析:【分析】在Rt △ABC 中,已知了坡面AB 的坡比是铅直高度BC 和水平宽度AC 的比值,据此即可求解.【详解】解:根据题意得:BC :AC=1解得:故答案为:【点睛】本题考查了解直角三角形的应用——坡度坡角问题,理解坡度坡角定义是关键. 14.②④【分析】根据对称性求出C 点坐标进而得OA 与AB 的长度再根据已知三角形的面积列出n 的方程求得n 进而用待定系数法求得k 再利用相关性质即可判断【详解】解:∵点C 关于直线y=x 的对称点C 的坐标为(1n ) 解析:②④【分析】根据对称性求出C 点坐标,进而得OA 与AB 的长度,再根据已知三角形的面积列出n 的方程求得n ,进而用待定系数法求得k ,再利用相关性质即可判断.【详解】解:∵点C 关于直线y=x 的对称点C'的坐标为(1,n )(n≠1),∴C (n ,1),∴OA=n ,AC=1,∴AB=2AC=2,∵△OAB 的面积为4,2解得,n=4,故①不正确;∴C(4,1),B(4,1),∴k=4×1=4,故②正确;解方程组4y xyx=⎧⎪⎨=⎪⎩,得:22xy=⎧⎨=⎩(负值已舍),∴直线y=x反比例函数(0)ky xx=>的图象的交点为(2,2),观察图象,不等式kxx<的解集是02x<<,故③不正确;∵B(4,1),∴OA=4,AB=2,∴tan ABO2OAAB∠==,故④正确;故答案为:②④.【点睛】本题是反比例函数图象与一次函数图象的交点问题,主要考查了一次函数与反比例函数的性质,对称性质,正切函数等,关键是根据对称求得C点坐标及由三角形的面积列出方程.15.2【分析】由题意得到则结合角的正切值即可得到答案【详解】解:∵是边上的中线∴∴∵∴∵在中∴;故答案为:2【点睛】本题考查了求角的正切值三角形中线的性质解题的关键是掌握三角形中线的性质正确得到解析:2【分析】由题意,得到12AD AC=,则2ACAD=,结合角的正切值tanABADBAD∠=,即可得到答案.【详解】解:∵BD是AC边上的中线,∴12AD AC=,AD∵AB AC =, ∴2AB AD=, ∵在Rt ABD 中,90A ∠=︒, ∴tan 2AB ADB AD ∠==; 故答案为:2.【点睛】本题考查了求角的正切值,三角形中线的性质,解题的关键是掌握三角形中线的性质,正确得到2AB AD=. 16.【分析】首先利用等角的余角得到∠A=∠DCB 然后根据余弦的定义求出cosA 即可【详解】解:在Rt △ABC 中∵CD ⊥AB ∴∠DCB+∠B=90°∵∠ACB =90°∴∠A+∠B=90°∴∠A=∠DCB 而 解析:23【分析】首先利用等角的余角得到∠A=∠DCB ,然后根据余弦的定义求出cosA 即可.【详解】解:在Rt △ABC 中,∵CD ⊥AB ,∴∠DCB+∠B=90°,∵∠ACB =90°,∴∠A+∠B=90°,∴∠A=∠DCB ,而cosA=AC AB =69=23, ∴cos ∠DCB=23. 故答案为:23. 【点睛】 本题考查了锐角三角函数的定义:在Rt △ABC 中,∠C=90°,我们把锐角A 的邻边a 与斜边c 的比叫做∠A 的余弦,记作cosA .17.【分析】根据题意过点C 作CD ⊥AB 根据∠B =45°得CD =BD 根据勾股定理和BC =得出BD 再根据∠A =30°得出AD 进而分析计算得出AB 即可【详解】解;过点C 作CD ⊥AB 交AB 于D ∵∠B =45°∴C 解析:33+【分析】根据题意过点C 作CD ⊥AB ,根据∠B =45°,得CD =BD ,根据勾股定理和BC =6得出BD ,再根据∠A =30°,得出AD ,进而分析计算得出AB 即可.【详解】解;过点C 作CD ⊥AB ,交AB 于D .∵∠B =45°,∴CD =BD ,∵BC 6,∴BD 3∵∠A =30°, ∴tan30°=CD AD, ∴AD =30CD tan ︒33=3, ∴AB =AD+BD =33.故答案为:33.【点睛】本题考查解直角三角形,熟练应用三角函数的定义是解题的关键.18.【分析】过A 作AE ⊥BC 于点E 则由题意可得AE 的值进一步可求得△ABO 的面积【详解】解:如图过A 作AE ⊥BC 于点E ∵AB=4∠ABC=45°∴AE=AB=∴故答案为【点睛】本题考查菱形性质和解直角三解析:2【分析】过A 作AE ⊥BC 于点E ,则由题意可得AE 的值,进一步可求得△ABO 的面积.【详解】解:如图,过A 作AE ⊥BC 于点E ,∵AB=4,∠ABC=45°,∴AE=AB sin 45︒=24222⨯= ∴1111·422222224ABO ABC S S BC AE ==⨯=⨯⨯= 故答案为22 .【点睛】 本题考查菱形性质和解直角三角形的综合应用,熟练掌握菱形的性质是解题关键. 19.【分析】根据菱形的性质结合AB=BD 得到△ABD 是等边三角形再利用锐角三角函数关系得出BE 的长即可得出菱形的面积【详解】∵在菱形ABCD 中AB=BD ∴AB=AD=BD=4(cm)∴△ABD 是等边三角解析:283cm【分析】根据菱形的性质结合AB=BD ,得到△ABD 是等边三角形,再利用锐角三角函数关系得出BE 的长,即可得出菱形的面积..【详解】∵在菱形ABCD 中,AB=BD ,∴AB=AD=BD=4(cm),∴△ABD 是等边三角形,∴∠A=60°,过点B 作BE ⊥AD 于E ,∴BE=AB•sin60°=433=, ∴菱形ABCD 的面积S=AD×BE 42383=⨯=(2cm ),故答案为:283cm【点睛】本题主要考查了菱形的性质,等腰直角三角形的判定和性质,特殊角的三角函数值,得出BE 的长是解题关键.20.2【分析】特殊值:sin30°=tan60°=tan30°=本题是特殊角将特殊角的三角函数值代入求解【详解】解:2sin30°+tan60°×tan30°=2×+×=1+1=2【点睛】本题考查了特殊解析:2【分析】特殊值:sin 30° =12,ta n 60°ta n 30°本题是特殊角,将特殊角的三角函数值代入求解.【详解】解:2sin30°+ta n60°×ta n30°=2×123=1+1=2【点睛】 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.三、解答题21.(1)40米;(2)楼AB 的高度为80米.【分析】(1)由CF 的坡度1:2i =,,DE CE ⊥可得1,2DE CE = 设,DE x = 则2,CE x = 由勾股定理可得,CD == = 解方程可得答案; (2)如图,过D 作DH AB ⊥于,H 先证明四边形DEBH 是矩形,可得2040,BH DE DH BE CE BC BC ====+=+, 设,AB m = 证明,BC AB m == 可得20,40,AH m DH m =-=+ 由26.7,ADH ∠=︒ 建立方程,再解方程检验即可得到答案.【详解】解:(1) CF 的坡度1:2i =,,DE CE ⊥1,2DE CE ∴= 设,DE x = 则2,CE x =,CD ∴===20,x ∴=240.CE x ∴==(2)如图,过D 作DH AB ⊥于,H,,DE BE AB BE ⊥⊥∴ 四边形DEBH 是矩形,2040,BH DE DH BE CE BC BC ∴====+=+,设,AB m =45,ACB AB BE ∠=︒⊥,45,ACB BAC ∴∠=∠=︒,BC AB m ∴==20,40,AH m DH m ∴=-=+由26.7,ADH ∠=︒tan 26.7,AH DH ∴︒=200.5,40m m -∴=+ 解得:80.m =经检验:80m =符合题意,所以:建筑物AB 的高为:80米.【点睛】本题考查的是解直角三角形的实际应用,坡度的含义,掌握利用解直角三角形测量建筑物的高是解题的关键.22.(1)1717;(2)3417【分析】 (1)作EM AC ⊥于M ,根据sin EM EAM AE∠=求出EM 、AE 即可解决问题. (2)先证明GDC EDA ∆≅∆,得GCD EAD ∠=∠,推出AH GC ⊥,再根据1122AGC S AG DC GC AH ∆=⋅⋅=⋅⋅,即可解决问题. 【详解】解:(1)作EM AC ⊥于M .四边形ABCD 是正方形,90ADC ∴∠=︒,5AD DC ,45DCA ∠=︒,∴在RT ADE ∆中,90ADE ∠=︒,5AD =,3DE =, 2234AE AD DE∴=+=,在RT EMC ∆中,90EMC ∠=︒,45ECM ∠=︒,2EC =,2EM CM ∴==, ∴在RT AEM ∆中,217sin 34EM EAC AE ∠===.(2)在GDC ∆和EDA ∆中,DG DE GDC EDA DC DA =⎧⎪∠=∠⎨⎪=⎩,GDC EDA ∴∆≅∆, GCD EAD ∴∠=∠,34GC AE =90DAE AED ∠+∠=︒,DEA CEH ∠=∠,90DCG HEC ∴∠+∠=︒,90EHC ∴∠=︒,AH GC ∴⊥,1122AGC S AG DC GC AH ∆=⋅⋅=⋅⋅, ∴11853422AH ⨯⨯=, 2034AH ∴=【点睛】本题考查正方形的性质、全等三角形的判定和性质、勾股定理、三角形面积等知识,添加常用辅助线是解决问题的关键,学会用面积法求线段,属于中考常考题型.23.(1)260,(2)5;【分析】(1)如图,过点D 作DH ⊥AC 于点H .设DH=x 米,通过解直角三角形列方程,得到DH 的长度.(2)求出BC 长,再求时间即可.【详解】解:过点D 作DH ⊥AC 于点H .由题意可知,∠HBD=60°,∠DAC=30°,AB=300,设DH=x米,在直角△BHD中,tan60°=DH BH,BH= 3x,tan30°=DH AH,AH=3x,300=3x-3x,解得,x=1503,∴DH=1503≈150×1.73≈260.答:求吴公塔D到紫水河北岸AC的距离约为260米.(2)由(1)可知,BH=150米,小薇继续向东走到轮船码头C处,测得对岸的吴公塔D位于西南方向,可知DH=HC=260米,BC=150+260=410(米),410米=0.41千米,小薇从B处到轮船码头的时间为0.410.0825(小时),0.082×60=4.92≈5(分钟),小薇从B处到轮船码头的时间为5分钟.【点睛】本题考查解直角三角形的应用,解题关键是构造直角三角形,熟练运用解直角三角形的知识进行计算.24.1米【分析】过点C作CD⊥AB,垂足为D,根据在C处测得桥两端A,B两点的俯角分别为60°和45°,可得∠CAD=∠MCA=65°,∠CBD=∠NCB=45°,利用角的三角函数求解即可.【详解】解:如图,过点C 作CD AB ⊥,垂足为D ,由题意得65MCA A ∠=∠=︒,45NCB B ∠=∠=︒,150CD =(米),在Rt ACD ∆中,015070.1tan 65 2.14CD AD ==≈(米), 在Rt BCD ∆中,45CBD ∠=︒, ∴150BD CD ==(米)∴70.1150220.1AB AD BD =+=+=(米)答:桥AB 的长度约为220.1米.【点睛】本题考查了三角函数的运算,构造直角三角形,利用解直角三角形求边是解题的关键. 25.(1)轮船M 到海岸线l 的距离为200米;(2)该轮船能行至码头海岸AB 靠岸【分析】(1)过点M 作MD ⊥AC 交AC 的延长线于D ,设DM=x ,解直角三角形即可得到结论; (2)作∠DMF=22°,交l 于点F .解直角三角形即可得到结论.【详解】解:(1)过点M 作MD ⊥AC 交AC 的延长线于D ,设DM=x ,∵在Rt △CDM 中,CD=DM•tan ∠CMD=x•tan37°,又∵在Rt △ADM 中,∠MAC=45°,∴AD=DM ,∵AD=AC+CD=50+x•tan37°,∴50+x•tan37°=x ,∴50502001tan 3710.75x ︒=≈=--, 答:轮船M 到海岸线l 的距离约为200米;(2)作∠DMF=22°,交l 于点F ,在Rt △DMF 中,DF=DM•tan ∠FMD=DM•tan22°≈200×0.40=80(米),∴AF=AC+CD+DF=DM+DF≈200+80=280<300,所以该轮船能行至码头AB 靠岸.【点睛】本题考查了解直角三角形的应用-方向角问题,读懂题目信息并作出辅助线构造成直角三角形是解题的关键.26.(1)3;(2)47【分析】(1)将这些特殊角的三角函数值代入求解即可;(2)将比例式转换为等积式后得到a 、b 之间的关系,然后求得两个的比值即可.【详解】(1)23060245sin cos ︒+-︒1222=⨯+ 131=+-3=;(2)设32a x b x ==,,则26242347a b x x a b x x --==++. 【点睛】本题考查了特殊角的三角函数值,比例的基本性质以及实数的运算,解题的关键是熟记这些特殊角的三角函数值.。
北师版初中九年级下册数学精品教学课件 第一章 直角三角形的边角关系 中考真题挑战

答案
6.【解析】
设楼高CE为x米.
在Rt△AEC中,∠CAE=45°,∴AE=CE=x米.
∵AB=20米,∴BE=(x-20)米.
在Rt△BEC中,CE=BE·tan 63.4°=tan 63.4°(x-20)米.
24
25
即cos∠ABE的值为 .
=
24
5
5
24
= 25,
6.[2020山东聊城模拟]某数学兴趣小组要测量实验大楼部分楼体的高度(如图1所示,CD部分),在起点A处测得大楼部
分楼体CD的顶端C点的仰角为45°,底端D点的仰角为30°,在同一剖面沿水平地面向前走20米到达B处,测得顶端C的仰
角为63.4°(如图2所示),求大楼部分楼体CD的高度约为多少米.
2.[2020四川凉山州中考]如图所示,△ABC的顶点在正方形网格的格点上,则tan A的值为 (
1
2
A.2
B. 2
C.2
D.2 2
答案
2.A 【解析】 如图,连接BD,根据勾股定理的逆定理可得BD⊥AC,在Rt△ABD中,
1
tan A= = 2.故选A.
)
5
3.[2019湖南湘西州中考]如图,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=7,则
熨烫台的高度.
(1)如图2-1,若AB=CD=110 cm,∠AOC=120°,求h的值;
(2)爱动脑筋的小明发现,当家里这种升降熨烫台的高度为120 cm时,两根支撑杆的夹角∠AOC是74°(如图2-2).求该熨
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省枣庄市峄城区城郊中学第一章测试题一.选择题1.如图,已知△ABC 为直角三角形,∠C =90°,若沿图中虚线剪去∠C ,则∠1+∠2等于( )A .270°B .135°C .90°D . 315° 2.如图,将一个等腰直角三角形按图示方式依次翻折,若DE =a ,则下列说法正确的个数有( )①DC ′平分∠BDE ;②BC 长为a )22( ;③△B C ′D 是等腰三角形;④△CED 的周长等于BC 的长。
A . 1个;B .2个;C .3个;D .4个。
3.如图,△ABC 中,∠C=90°,AC=BC ,AD 平分∠CAB 交BC 于点D ,DE ⊥AB ,垂足为E ,且AB=6cm ,则△DEB 的周长为( ) A .4cm B .6cm C .8 cm D .10cm 4.如图,EA ⊥AB ,BC ⊥AB ,EA=AB=2BC ,D 为AB 中点,有以下结论:(1)DE=AC ;(2)DE ⊥AC ;(3)∠CAB=30°;(4)∠EAF=∠ADE 。
其中结论正确的是( )CCA.(1),(3) B.(2),(3) C.(3),(4) D.(1),(2),(4)5.如图,△ABC中,∠ACB=90°,BA的垂直平分线交CB边于D,若AB=10,AC=5,则图中等于60°的角的个数为()A.2 B.3 C.4 D.56等腰三角形底边长为7,一腰上的中线把其周长分成两部分的差为3,则腰长是()A.4 B.10 C.4或10 D.以上答案都不对7.如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为()A.30° B.36° C.45° D.70°8.如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有()A.1个 B.2个 C.3个 D.4个9.边长为2的等边三角形的内有一点0,那么0到三角形各边的距离之和为 ( )A.3 B.23 C.2 D.4310.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,则∠ABC的大小是()A.40° B.45° C.50° D.60°二.填空题1.如图,在Rt△ABC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于D点,则∠BCD的度数为。
2.如图,△ABC中,∠C=Rt∠,AD平分∠BAC交BC于点D,BD∶DC=2∶1,BC=7.8cm,则D到AB的距离为 cm。
3.一辆汽车沿30°角的山坡从山底开到山顶,共走了4000米,那么这座山的高度为米.4.如图,在等腰直角三角形ABC中,AD⊥BC,PE⊥AB,PF⊥AC,则△DEF是三角形。
5.如图,∠E=∠F=90°,∠B=∠C.AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM。
其中正确的结论是(注:将你认为正确的结论都填上).6.如图,ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD= 。
7.“有两角和其中一边对应相等的两个三角形全等”的逆命题是.是命题。
(真或假)8.如图,在△ABC中,∠ABC、∠ACB的平分线交于点F,过F 作DE ∥BC ,分别交AB 、AC 于D 、E ,已知△ADE 的周长为24cm ,且BC = 8cm ,则△ABC 的周长= 。
三.解答题1.如图,已知AB=AC ,AD 是中线,BE=CF . (1)求证:△BDE ≌△COF;(2)当∠B =60°时,过AB 的中点G ,作GH∥BD, 求证:GH=41AB .2.如图,ABC △中,90ACB = ∠,AC BC =,CO 为中线.现将一直角三角板的直角顶点放在点O 上并绕点O 旋转,若三角板的两直角边分别交AC CB ,的延长线于点G H ,.(1)试写出图中除AC BC OA OB OC ===,外其他所有相等的线段; (2)请任选一组你写出的相等线段给予证明. 我选择证明 = . 证明:ABC DHG3.如图,在△ABC中,AB=AC,D是BC边上的一点,DE⊥AB,DF⊥AC,垂足分别为E、F,添加一个条件,使DE= DF,并说明理由.解:需添加条件是.理由是:4.将一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆放成如下右图的形式,使点B、F、C、D在同一条直线上.(1)求证:AB ED⊥;(2)若PB BC,请找出图中与此条件有关的一对全等三角形,并给F C DDF5.已知:如图,△ABC是边长3cm的等边三角形,Array动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答下面的问题:当t为何值时,△PBQ是直角三角形?6.如图,P是等边三角形ABC内的一点,连结PA PB PC,,,以BP为边作60PBQ∠= ,且BQ BP=,连结CQ.(1)观察并猜想AP 与CQ 之间的大小关系,并证明你的结论. (2)若::3:4:5PA PB PC =,连结PQ ,试判断PQC △的形状,并说明理由.拓展延伸7.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等.那么在什么情况下,它们会全等? (1)阅读与证明:对于这两个三角形均为直角三角形,显然它们全等.对于这两个三角形均为钝角三角形,可证它们全等(证明略). 对于这两个三角形均为锐角三角形,它们也全等,可证明如下: 已知:ABC △,111A B C △均为锐角三角形,11AB A B =,11BC B C =,1C C ∠=∠. 求证:111ABC A B C △≌△.(请你将下列证明过程补充完整.)证明:分别过点1B B ,作BD CA ⊥1D 则11190BDC B D C ∠=∠= ,QCPAB11BC B C = ,1C C ∠=∠, 111BCD B C D ∴△≌△, 11BD B D ∴=.(2)归纳与叙述:由(1)可得到一个正确结论,请你写出这个结论.山东省枣庄市峄城区城郊中学附答案 一.选择题1.A 2.C 3.B 4.D 5.C 6.C 7.B 8.D 9.A 10.B 二.填空题1.10° 2.2.6cm 3.2000 4.等腰直角 5.①②③ 6.37.三边对应相等的三角形是全等三角形,是真命题。
8.32cm 三.解答题1.证明:(1)因为AB=AC ,所以∠B=∠C , 在△BDE 和△CDF 中所以△BDE ≌△CDF(2)因为G 是AB 的中点,且GH∥BD,所以GH 是△ABD 的中位线,所以GH=21DB ,根据直角三角形中30°对的直角边等于斜边的一半可知,BE=21DB ,BD=21AB ,所以GH=41AB .2.解:(1)CG BH AG CH OG OH ===,, (2)90ACB AC BC AO BO === ∠,,,45CO OB CO AB ABC ∴=⊥= ,,∠. 9090COG GOB BOH GOB +=+= ∠∠,∠∠, COG BOH ∴=∠∠.又4518045135ABC OCB OBH ==∴=-=∠∠,∠,9045135GCO =+= ∠, GCO OBH∴=∠∠. GCO HBO ∴△≌△CG BH ∴=.3.解:需添加的条件是:BD =CD ,或BE =CF . 添加BD =CD 的理由:如图,因为AB =AC ,所以∠B =∠C .又因为DE ⊥AB ,DF ⊥AC ,所以∠BED =∠CFD .所以△BDE ≌△CDF (AAS). 所以DE = DF .添加BE=CF的理由:如图,因为AB=AC,所以∠B=∠C.因为DE⊥AB,DF⊥AC,所以∠BED=∠CFD.又因为BE=CF,所以△BDE≌△CDF (ASA).所以DE= DF.4.(1)证明:由题意得90A B A D∠+∠=∠=∠,,90D B∠+∠=∴.AB DE∴⊥.(2)若PB BC=,则有Rt△ABC≌Rt△DBP.B B A D BP BC∠=∠∠=∠=∵,,,∴ Rt△ABC≌Rt△DBP.说明:图中与此条件有关的全等三角形还有如下几对:Rt△APN≌ Rt△DCN、Rt△DEF≌ Rt△DBP、Rt△EPM≌ Rt△BFM.5.解:根据题意:AP=t cm,BQ=t cm.△ABC中,AB=BC=3cm,∠B=60°,∴BP=(3-t ) cm.△PBQ中,BP=3-t,BQ=t,若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°.当∠BQP=90°时,BQ=12BP.即t=12(3-t ),t=1 (秒).F C D由莲山课件提供/ 资源全部免费由莲山课件提供/ 资源全部免费当∠BPQ=90°时,BP =12BQ .3-t =12t ,t =2 (秒). 答:当t =1秒或t =2秒时,△PBQ 是直角三角形.6.解:(1)猜想:AP CQ =证明:在ABP △与CBQ △中,AB CB =∵,BP BQ =,60ABC PBQ ∠=∠=ABP ABC PBC PBQ PBC CBQ ∠=∠-∠=∠-∠=∠∴ABP CBQ ∴△≌△AP CQ =∴(2)由::3:4:5PA PB PC = 可设3PA a =,4PB a =,5PC a = 连结PQ ,在PBQ △中,由于4PB BQ a ==,且60PBQ ∠= PBQ ∴△为正三角形 4PQ a =∴于是在PQC △中,22222216925PQ QC a a a PC +=+==∵ PQC ∴△是直角三角形7.解:(1)又11AB A B = ,11190ADB A D B ∠=∠= ,111ADB A D B ∴△≌△,1A A ∴∠=∠,又111C C BC B C ∠=∠= ,,111ABC A B C ∴△≌△.(2)若ABC △,111A B C △均为锐角三角形或均为直角三角形或均为钝角三角形,11AB A B =,11BC B C =,1C C ∠=∠,则111ABC A B C △≌△.。
