人教版八年级数学《平行四边形》导学案
认识平行四边形.导学案

底
底
底
3、填一填
①两组对边( )的四边形叫平行四边形。
②从平行四边形一条边上的一点到它的对边的( )是平行四边形的( )。
③平行四边形有( )的特性。三角形具有( )的特性
4、判断。
(1)平行四边形是长方形。 ( )
(2)平行四边形只有一条高。 ( )
(3)两个完全相同的三角形能拼成一个平行四边形。 ( )
7、从平行四边形一条边上的一点到它的对边的( )是平行四边形的高。
这条对边是平行四边形的( )。
8、你能再做两条这样的高吗?
平行四边形的高有( )条
9、平行四边形有什么特性? ( )
10、生活中哪些地方用到这一特性?
二、练习
1、下面图形中,是平行四边形的在( )中打“√”
( ) ( ) ( )
( ) ( )
导学案
学习内容
认识平行四边形
学习目标
1、经历在对简单图形分类、观察、比较、交流的活动过程,认识平行四边形。
2、学会用不同方法做出一个平行四边形,会在方格纸上画平行四边形,能正确判断一个平面图形是不是平行四边形,能测量或画出平行四边形的高。
3、在学习中感受数学与生活的联系。
学习重点难点
认识平行四边形,探究平行四边形的基本特征及认识平行四边形的高,能够画出并测量平行四边形的高
三、 提升练习
1、给下面图形加一条线段使其变成一个平行四边形和一个三角形
2、 在两条平行线之间画出两个等底等高的平行四边形
四、总结 通过学习知道了:
什么特征?”
长方形和正方形的对边()且();四个角都是()角。
2、平行四边形也有( )条边,特征是( )
2023年春八下数学 18-1-3 平行四边形的判定(1) 导学案(人教版)

人教版初中数学八年级下册18.1.3 平行四边形的判定(1) 导学案一、学习目标:1.经历平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路;2.掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理论证.重点:掌握平行四边形的判定定理.难点:综合运用平行四边形的性质与判定解决问题.二、学习过程:课前自测平行四边形的性质:边:_____________________________;∵ _______________________________∴ _______________________________角:_____________________________;∵ _______________________________∴ _______________________________对角线:_____________________________;∵ _______________________________∴ _______________________________自主学习思考:反过来,对边相等,或对角相等,或对角线互相平分的四边形是平行四边形吗?也就是说,平行四边形的性质定理的逆命题成立吗?逆命题1:____________________________________________.逆命题2:____________________________________________.逆命题3:____________________________________________.逆命题1:(证明过程)如图,在四边形ABCD中,AB=CD,AD=CB.求证:四边形ABCD是平行四边形.【归纳】平行四边形判定定理1:_________________________________________. 几何符号语言:∵ _______________________,∴ _________________________.逆命题2:(证明过程)如图,在四边形ABCD中,∠A=∠C,∠B=∠D.求证:四边形ABCD是平行四边形.【归纳】平行四边形判定定理2:_________________________________________. 几何符号语言:∵ _______________________,∴ _________________________.逆命题3:(证明过程)如图,在四边形ABCD中,OA=OC,OB=OD.求证:四边形ABCD是平行四边形.【归纳】平行四边形判定定理3:_________________________________________.几何符号语言:∵ _______________________,∴ _________________________.典例解析例1.如图,以△ABC的各边向同侧作正三角形,即等边△ABD、等边△ACE、等边△BCF,连接DF,EF.求证:四边形AEFD是平行四边形.【针对练习】如图,将□ABCD的四边DA,AB,BC,CD分别延长至点E,F,G,H,使得AE=CG,BF=DH,连接EF,FG,GH,HE.求证:四边形EFGH为平行四边形.例2.如图,四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.(1)求∠D的度数;(2)求证:四边形ABCD是平行四边形.【针对练习】如图,在□ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形.例3.如图,□ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.【针对练习】变式1:若E、F继续移动至OA、OC的延长线上,仍使AE=CF,则结论还成立吗?为什么?变式2:问题中AE=CF,过点O作一直线分别交AB、CD于G、H,则四边形GFHE 是平行四边形吗?为什么?达标检测1.下面给出四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )A.1:2:3:4B.2:3:2:3C.2:3:3:2D.1:2:2:32.如图,在四边形ABCD中,AB=CD,BC=AD.若∠D=120°,则∠C的度数为( )A.60°B.70°C.80°D.90°3.如图,在□ABCD中,对角线AC、BD交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE= ∠CBF;④∠ABE= ∠CDF.其中不能判定四边形DEBF是平行四边形的有( )A.0个B.1个C.2个D.3个4.四边形ABCD中,AB=9cm,BC=6cm,CD=9cm,当AD=____cm时,四边形ABCD 是平行四边形.5.如图,在□ABCD中,点E,F分别在边AD,BC上,且BE//DF,若AE=5,则CF=_____.6.如图,线段AB,CD相交于点O,且图上各点把线段AB,CD四等分,这些点可以构成平行四边形的个数是_____.7.如图,在□ABCD的各边AB、BC、CD、DA上,分别取点K、L、M、N,使AK=CM、BL=DN,求证:四边形KLMN为平行四边形.8.如图,在□ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.求证:四边形ACDF是平行四边形.9.如图,在四边形ABCD中,AB∥CD,AD⊥CD,∠B=45°,延长CD到点E,使DE=DA,连接AE.(1)求证:AE=BC;(2)若AB=3,CD=1,求四边形ABCE的面积.10.如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?说说你的理由.。
(完整版)最新人教版八年级数学下册第十八章平行四边形导学案(全章)

18.1.1 平行四边形及其性质(一)学习目标:理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.学习重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.学习难点:运用平行四边形的性质进行有关的论证和计算.学习过程:一、自主预习(10分钟)1. 由_____ 条线段首尾顺次连接组成的多边形叫四边形;四边形有__________ 条边,_个角,四边形的内角和等于________ 度;2. 如图AB与BC叫_______ 边,AB与CD叫______ 边;ZA与/B叫 ____ 角,/D与/B叫______ 角; 3多边形中不相邻顶点的连线叫对角线,如图四边形ABCD中对角线有_______ 条,它们是—自学课本1. 有两组对边__________________ 的四边形叫平形四边形,平行四边形用“ _________ ”表示,平行四边形ABCD记作 _______________ 。
2. 如图CABCD中,对边有________ 组,分别是____________________ ,对角有______ ,分别是你能归纳ABCD的边、角各有什么关系吗?并证明你的结论,寸角线有条,它们是二、合作解疑(15分钟)如图,小明用一根36 m 长的绳子围成了一个平行四边形的场地,其中一条边 AB 长为8m ,其他三条边各长多少?个平行四边形的一个外角是38。
,这个平行四边形的各个内角的度数分别是: ____________ (3) ___________________________________________________________________________ _ ABCD 有一个内角等于40。
,则另外三个内角分别为: ______________________________________ (4) ________________________________________________________________________ 平行四边形的周长为50cm ,两邻边之比为2 :3,则两邻边分别为: _____________________________ 1. - ABCD 中,Z A : ZB : ZC :ZD 的值可以是()A.1 : 2 : 3: 4B.3 : 4 : 4 : 3C.3 : 3 : 4: 4 2. AABCD 的周长为40cm ,△ABC 的周长为27cm,AC 的长为 A.13cm B.3 cm C.7 cmD.11.5cm ___________________三、综合应用拓展(5分钟)1. 如图,AD //BC , AE //CD ,BD 平分Z ABC ,求证 AB=CE.四、当堂检测(10分钟) (一)填空:1•在-ABCD 中,Z A= 50,贝UZ B= ______ 度, Z C= ____ 度, Z D= _____ 度.2 •两组对边分别 ______ _ 勺四边形叫做平行四边形•它用符号“ □'表示,平行四边形ABCDD.3 : 4: 3: 4( )记作__________ 。
初二数学平行四边形(1)导学案

9.3平行四边形(1)导学案【学习目标】1、以中心对称为主线,探究平行四边形的性质;2、经历探索平行四边形的概念、性质的过程,在活动中发展探究意识和有条理的表达能力。
探究活动探究活动一探索平行四边形的概念1.图片欣赏:3张图片(见课件)中有你熟悉的图形吗?是平行四边形。
表示方法:平行四边形用符号“□”表示,例如:平行四边形ABCD 可记做“□ABCD”.2.巩固应用:如图,A′B′∥AB,B′C′∥BC,C′A′∥CA。
图中有几个平行四边形?将它们表示出来。
探究活动二探索平行四边形的性质O 是□ABCD 对角线AC 的中点.用透明纸覆盖在下图,描出□ABCD 及其对角线AC ,再用大头针钉在点O 处,将透明纸上的□ABCD 旋转180°.问题:□ABCD 绕点O 旋转180°后,①AB 旋转到什么位置?②∠BAD 旋转到什么位置?③猜想:对角线AC 与BD 有什么性质?你有什么发现?发现:□ABCD 绕点O 旋转180°后与原来的图形重合平行四边形是图形,对角线的交点是它的。
平行四边形的对边;平行四边形的对角;平行四边形的对角线。
CBAA ′B ′C ′符号语言:∵四边形ABCD是平行四边形∴AB=CD,BC=AD∵四边形ABCD是平行四边形∴∠A=∠C,∠B=∠D∵四边形ABCD是平行四边形∴AO=CO,BO=DO试一试:1.如果平行四边形ABCD的周长为32cm,且AB=5cm,那么BC=cm,CD=cm,DA=cm.2.如图,在□ABCD中,∠B=50°,求这个四边形的其他内角的度数,并说明理由.变式:在□ABCD中,若∠A=3∠B,则∠A=,∠D=;若∠A=∠B+∠D,则∠A=,∠B=。
3.如图,在□ABCD中,对角线相交于点O,BC=7cm,BD=10cm,AC=6cm.求△AOD的周长.变式:在□ABCD中,对角线AC与BD相交于O,AC=6,BD=12,则AD长度x的取值范围是()A.2<x<6 B.3<x<9 C.1<x<9 D.2<x<8。
人教版八年级数学下册 第18章 平行四边形 导学案

八年级(下)数学导学案 18.1.1 平行四边形的性质(1)导学目标:知识与技能:理解并掌握平行四边形的相关概念和性质,培养学生初步应用这些 知识解决问题的能力。
过程与方法:通过观察、实验、猜想、验证、推理、交流等数学活动进一步发展学生的演绎推理能力和发散思维能力。
情感态度与价值观:学生亲自经历探索平行四边形有关概念和性质的过程,体会 解决问题策略的多样性.导学重点:理解并掌握平行四边形的概念及其性质.导学难点:运用平移、旋转的图形变换思想探究平行四边形的性质. 导学过程:一、创设情境,引入新知探究活动(一)探索平行四边形的定义平行四边形是我们常见的图形,小区的伸缩门,庭院的竹篱笆,载重汽车的防护栏等都是平行四边形的形象。
1、定义:有两组对边__________________的四边形叫平形四边形,请你用几何语言 给平行四边形下个定义:∵ ∥ , ∥ ∴四边形ABCD 是平行四边形 2、表示:平行四边形用符号“______”表示,右上图的平行四边形记作_____ 注意:表示平行四边形时,一般按一定的方向依次写出各顶点字母3、对角线的定义:平行四边形 两个顶点连成的 ,叫做它的对角线。
4、如图ABCD 中,对边有______组,分别是___________________,对角有_____组,分别是____________,对角线有____条,它们是___________ 二、自主学习,探究新知。
探究活动(二)探索平行四边形的性质1、拼一拼:由两个全等三角形一边重合拼成的四边形 ABCD 平行四边形吗?请说明理由。
2、量一量:用直尺、量角器测量如图ABCD 的边、角。
AB= ____;DC=____; AD=____ ;BC= ____ ∠A= ____;∠C=____; ∠B=____;∠D=____3、猜一猜:仔细分析上面的测量结果,你能发现平行四边形的对边与对角有什么数量关系? 猜想: 4、证一证:我们需推理证明猜想的正确性,你能完成证明吗? 已知:如图,求证: AB=CD,AD=BC, ∠A=∠C, ∠B=∠D 证明:AB C ED FABCDA BCA BC归纳:平行四边形的性质1:平行四边形。
《平行四边形的认识》导学案

《平行四边形的认识》导学案平行四边形的认识导学案第一部分:引入目标- 了解平行四边形的定义和性质- 能够确定平行四边形的特征- 掌握标记和表示平行四边形的方法话题简介在几何学中,平行四边形是一种特殊的四边形,具有独特的性质和特征。
通过研究平行四边形的认识,我们可以更好地理解和应用几何学中的概念和原理。
第二部分:概念解释平行四边形的定义平行四边形是指有两对对边相互平行的四边形。
换句话说,平行四边形的对边两两平行,且对边长度相等。
平行四边形的性质平行四边形具有以下性质:1. 对边两两平行;2. 对角线彼此平分;3. 相邻角互补,即相邻内角的和为180度;4. 同位角相等,即位于同一边界的两个内角相等。
第三部分:特征判断判断平行四边形的特征确定一个四边形是否为平行四边形时,可以根据以下特征进行判断:1. 观察其对边是否平行;2. 测量对边长度是否相等;3. 判断相邻角是否互补;4. 检查同位角是否相等。
第四部分:标记和表示方法标记方法为了方便表示和讨论平行四边形,我们可以使用以下标记方法:- 一般用大写字母ABCD表示四边形的顶点;- 使用小写字母a、b、c、d表示四边形的边长;- 使用小写字母m、n表示对角线。
表示方法平行四边形可以用如下表示方法呈现:ABCD 或 ABCD第五部分:练题1. 下图中的四边形是否为平行四边形?为什么?请在此插入图片并提供答案2. 给定ABCD为平行四边形,若AD=6cm,BC=8cm,AC=10cm,请问BD的长度是多少?请提供你的答案和解题步骤结束语通过本导学案的学习,我们希望你能够清楚地理解平行四边形的定义和性质,并能够熟练运用判断和表示平行四边形的方法。
如果你还有任何问题,请随时向老师提问。
祝愉快学习!。
18.1 平行四边形导学案

A B D C 第18章平行四边形第1课时 18.1.1 平行四边形的性质导学案(1)【学习目标】1、理解平行四边形的定义及有关概念;2、能根据定义探索并掌握平行四边形的对边相等、对角相等的性质;3、能根据平行四边形的性质进行简单的计算和证明;【学习重点】平行四边形的定义,平行四边形对角、对边相等的性质;【学习难点】如何添加辅助线将平行四边形问题转化为三角形问题解决的思想方法;一、学前预习认真学习课本83页至84页的内容。
1、叫做平行四边形。
平行四边形用符号“”来表示。
2、阅读以下文字并填空:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.如上图,在ABCD中,AB的对边是,AB的邻边是,AD是BC 的边。
∠C的邻角是,∠C的邻对角是。
二、探索思考探究(一)通过观察、测量,我们可以发现:①平行四边形的对边;②平行四边形的对角;请你用我们学过的知识证明(需要你自己作图、写已知、求证,最后证明。
)练习一1、(1)在ABCD中,∠A=50°,求∠B、∠C、∠D的度数。
2、已知:ABCD中,AB=5,BC=3,求它的周长探索(二)a // b,作AD // GH // BC,若a // b,DA、GH、CB垂直于a,1、上面两图中AD、GH、BC相等吗?为什么?2、两条平行线间的距离:两条平行线间的距离和点与点之间的距离、点到直线的距离有何联系与区别:三、典例分析例1:在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E、F,求证:AE=CF四、当堂反馈1、.判断题:(1)平行四边形两组对边分别平行且相等. ( ) (2)平行四边形的四个内角都相等. ( )(3)平行四边形的相邻两个内角的和等于180°( )(4)如果平行四边形相邻两边长分别是2cm和3cm,那么周长是10cm. ( )2、在平行四边形ABCD中,如果∠A=42°,那么∠B= ,∠C=3、在□ ABCD中,∠A:∠B=2:3,则∠A= _____ ,∠B= ______,∠C= ______,∠D= _______.4、已知□ ABCD的周长为20cm,且AD-AB=1cm,求AD,CD5、如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.五、学习反思:(1)知识点:(2)数学方法:A BDCFEa ab bA AB BC CD DGHGHABCDO第2课时 18.1.1 平行四边形的性质导学案(2)【学习目标】1、理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.2、能运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题.3、培养学生的推理论证能力和逻辑思维能力. 【学习重点】掌握平行四边形对角线互相平分的性质【学习难点】能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题 一、学前预习1. 如图,若要使四边形ABCD 是平行四边形,可以添加条件: , 添加的理由是 2、平行四边形的性质:如图∵四边形ABCD 是平行四边形∴ , ( ) 二、探索思考探究(一)1、如图,在□ABCD 中,画出对角线, 对角线能画 条,分是 . 2、新出现的线段之间有什么关系?新出现的三角形之间有什么关系?理由是什么?3、由以上关系你发现平行四边形的对角线有什么性质?4、请证明;平行四边形的对角线互相平分.已知: 求证:5、性质定理3的符号语言表示:∵∴ ( ) 练习一 1、如图,在ABCD 中,B C =10cm ,A C =8cm ,B D =14cm ,△AOD 的周长是多少?△ABC 与△DBC 的周长那个长?长多少?.三、典例分析例1、已知四边形ABCD 是平行四边形,AB =20cm ,AD =16cm ,AC ⊥BC , 求BC 、CD 、AC 、OA 的长以及ABCD 的面积.练习二、已知四边形ABCD 是平行四边形,BC =4cm ,BD =10cm ,AC=6cm, 求AB 、CD 的长以及ABCD 的面积.例2、已知:如图ABCD 的对角线AC 、BD 相交于点O ,EF 过点O 与AB 、CD 分别相交于点E 、F .求证:OE =OF ,AE=CF ,BE=DF .四、当堂反馈1. 如图,□ABCD 的两条对角线相交于点O, 已知AB=8cm,BC=6cm,△AOB 的周长是18cm ,那么△AOD 的周长是 .2.如图,在□ABCD 中,AB=3,BC=5,对角线AC ,BD 相交于点O , 则OA 的取值范围是 .3、如图:ABCD 的对角线AC 、BD 相交于点O ,EF 过点O 与AB 、CD 分别相交于点E 、F .①求证:OE =OF ,AE=CF ,BE=DF .②若其他条件都不变,将EF 转动到图b 的位置,那么①中结论是否成立?若将EF 向两方延长与平行四边形的两对边的延长线分别相交(图c 和图d ),①中结论是否成立?说明你的理由.五、学习反思:(1)知识点: (2)数学方法BDA CBDA CCBADOB DCA OABCDO第3课时 18.1.2平行四边形的判定导学案(1)【学习目标】1.在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法. 2.会综合运用平行四边形的判定方法和性质来解决问题. 3.体会用类比、逆向联想及运动的思维方法来研究问题. 【学习重点】平行四边形的判定方法及应用【学习难点】平行四边形的判定定理与性质定理的灵活应用一、学前准备1.平行四边形的定义是2.平行四边形的性质:边的性质角的性质: :对角线的性质: 符号语言:如图∵∴(边) ,(角) (对角线二、探索思考探究(一)请写出平行四边形边、角、对角线的性质定理的逆命题:有关边的: 有关角的:有关对角线的:例1、如图, ABCD 的对角线AC 、BD 相交于点O ,E ,F 是AC 上的两点,并且AE=CF. 求证:四边形BFDE 是平行四边形.四、当堂反馈1、如图,AB=DC=EF ,AD=BC ,DE=CF ,图中有哪些互相平行的线段?并说明理由2、已知:如图,ABCD 中,点E 、F 分别在CD 、AB 上,DF ∥BE ,EF 交BD于点O .求证:EO=OF .3、已知□ABCD 中,AC 、BD 相交于O ,E 、F 是BO 、DO 的中点求证:AE ∥CF五、学习反思:(1)知识点: (2)数学方法:这些命题正确吗?如果正确,请证明A BCDEF第4课时 18.1.2平行四边形的判定导学案(2)【学习目标】1.掌握用一组对边平行且相等来判定平行四边形的方法.2.会综合运用平行四边形的四种判定方法和性质来证明问题.3.通过平行四边形的性质与判定的应用,启迪学生的思维,提高分析问题的能力.【学习重点】平行四边形各种判定方法及其应用,尤其是根据不同条件能正确地选择判定方法.【学习难点】平行四边形的判定定理与性质定理的综合应用一、学前准备1、平行四边形的性质:如图1∵∴(边),( )(角) ,( )如图2∵(对角线)∴ ( )2、平行四边形的判定:如图1 (1)定义∵∴四边形ABCD是平行四边形. ( )如图1 (2)∵∴四边形ABCD是平行四边形. ( )如图1 (3)∵∴四边形ABCD是平行四边形. ( )如图2(4)∵∴四边形ABCD是平行四边形. ( )二、探索思考探究(一)1、请同学们猜想一下,如果只考虑四边形的一组对边,当它满足什么条件时这个四边形是平行四边形?(据以下4个问题,写出一个你认为正确的猜想,并证明你的猜想)问题1:一组对边平行的四边形是平行四边形吗?如果是请给出证明,如果不是请举出反例说明.问题2:满足一组对边相等的四边形是平行四边形吗?问题3:如果一组对边平行,而另一组对边相等的四边形是平行四边形吗?问题4:一组对边平行且相等的四边形是平行四边形吗?例1如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.练习1 已知:如图,在四边形ABCD中,对角线AC和BD相交于O,AO=OC,BA⊥AC,DC⊥AC. 求证:四边形ABCD是平行四边形.四、当堂反馈1、如图,点EF是平行四边形ABCD边AD、BC上两点,AE=CF求证:BE∥DF2、已知:如图,ABCD中,E、F分别是AC上两点,且BE⊥AC于E,DF⊥AC于F.求证:四边形BEDF是平行四边形.3、已知:如图,A′B′∥BA,B′C′∥CB,C′A′∥AC.求证:①∠ABC=∠B′,∠CAB=∠A′,∠BCA=∠C′;②△ABC的顶点分别是△B′C′A′各边的中点.五、学习反思:(1)知识点:(2)数学方法:BD AC图1ACD 图2BO第5课时 18.1.2平行四边形的判定导学案(3)【学习目标】1、会综合运用平行四边形的四种判定方法和性质来证明问题.2、理解三角形中位线的概念,掌握三角形中位线的性质【学习重点】三角形中位线的概念和性质【学习难点】证明三角形中位线定理一、学前准备平行四边形的判定:如图1 (1)定义∵∴四边形ABCD是平行四边形. ( )如图1 (2)∵∴四边形ABCD是平行四边形. ( )如图1 (3)∵∴四边形ABCD是平行四边形. ( )如图1 (3)∵∴四边形ABCD是平行四边形. ( )如图2(5)∵∴四边形ABCD是平行四边形. ( )二、探索思考探究(一)1、请按要求画图:(1)在右框画任意△ABC中,(2)画AB、AC边中点D、E,连接DE.2、定义:像DE这样,连接三角形两边中点的线段叫做.3、问题1:一个三角形有几条中位线?问题2:三角形中位线与三角形中线有什么区别?问题3:通过观察、测量,DE与BC有怎样的关系?4、尝试证明你的猜想5、三角形中位线定理:符号语言:∵∴2. 如图,△ABC中,D、E分别是AB、AC中点.(1)若DE=5,则BC= .(2)若∠B=65°,则∠ADE= °.(3)若DE+BC=12,则BC= .三、典例分析例:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.求证:四边形EFGH是平行四边形.四、当堂反馈1、如图,A、B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样量出A、B两点间的距离?根据是什么?2、如图,ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,求△DOE的周长3、如图,ABCD的对角线AC,BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,求证:四边形EFGH是平行四边形五、学习反思:(1)知识点:(2)数学方法:BDAC图1ACD图2BEGFHB CDAABCAB CDOEGHF【学习目标】 【学习重点】 【学习难点】 一、学前准备二、探索思考 探究(一)三、典例分析四、当堂反馈五、学习反思:(1)知识点: (2)数学方法:1、在四边形ABCD 中:从下列条件(1)AB ∥CD ; (2)AD ∥BC ; (3)AD =BC ,(4)∠A =∠C ,选择两个条件,能判定四边形ABCD 是平行四边形的共有 种2、指出下列条件中,哪些一定能判定四边形ABCD 是平行四边形?(1). AB=BC, A D ∥BC (2). AB=CD,O A =OC (O 是对角线交点) (3). ∠A=∠B, ∠C=∠D (4).AB ∥CD, ∠A=∠C 3、如图,BD 是□ABCD 的对角线,点E 、F 在BD 上, 要使四边形AECF 是平行四边形,还需要增加的一个条 件是 (填上你认为正确的一个即可)。
人教版-数学-八年级下册- -19.1平行四边形 导学案

19.1平行四边形学习目标、重点、难点【学习目标】1、理解平行四边形的定义,能根据定义探究平行四边形的性质.2、了解平行四边形在生活中的应用实例,能根据平行四边形的性质解决有关的问题.【重点难点】平行四边形性质的探究及应用;平行四边形性质的探究.知识概览图新课导引平行四边形是我们常见的图形,小区的伸缩门、庭院的竹篱笆、载重汽车的防护栏等,都是平行四边形的形象。
平行四边形在生活中比比皆是,那么它有什么样的性质?又如何判断一个四边形是平行四边形呢?教材精华知识点1 平行四边形的概念有两组对边分别平行的四边形叫做平行四边形.表示方法:平行四边形用“”表示,如图19-1所示,平行四边形ABCD记作“ABCD”,其中表示顶点的字母要按顺时针或逆时针的顺序排列.相关概念:对边有AD和BC,AB和CD;对角有∠DAB和∠DCB,∠ABC和∠ADC;对角线是AC和BD.知识点2 平行四边形的性质(1)平行四边形的对边相等.(2)平行四边形的对角相等.(3)平行四边形的对角线互相平分.知识点3 平行四边形的面积平行四边形的面积等于平行四边形的底与底边上的高的积。
用式子可表示为S a h =⋅,其中a 为底边长,h 为底边上的高(即相应的两条平行线之间的距离).如图19-3所示,ABCD S BC AE CD AF =⋅=⋅Y知识点4 平行四边形的判定(1) 两组对边分别相等的四边形是平行四边形.(2) 对角线互相平分的四边形是平行四边形.(3) 两组对角分别相等的四边形是平行四边形.(4) 一组对边平行且相等的四边形是平行四边形.知识点5 三角形的中位线概念连接三角形两边中点的线段叫做三角形的中位线.如图19-6所示,若点D ,E ,F 分别为△ABC 的边AB ,BC ,CA 的中点,则线段DE ,EF ,DF 均是△ABC 的中位线.知识点6 三角形的中位线定理三角形的中位线平行于三角形的第三边,且等于第三边的一半.如图19-6所示,若D ,E ,F 分别为△ABC 的边AB ,BC ,CA 的中点,则DE12AC ,EF 12AB ,DF 12BC . 【方法拓展】(1)三角形的中位线定理在同一条件下具有两个结论;一个定性的是平行于第三边,另一个定量的就是等于第三边的一半,此结论用途比较广泛,又因为中位线具有平移角度、倍分转化的功能,因此当遇到中点或三角形中线时,应考虑是否作中位线,这种思想方法就是我们常说的“遇到中点想中位线”.知识点7 两条平行线间的距离两条平行线间最短的线段的长度叫做两条平行线间的距离.课堂检测基本概念题1、如图19-10所示,小明用一根36m长的绳子围成了一个平行四边形的场地,一条边AB的长为8m,则其他三边的长度各是多少?基础知识应用题2、平行四边形不一定具有的性质是()A. 对边平行B. 对边相等C. 对角线互相垂直D. 对角线互相平分V的周长是28cm,AC与BD交于点O,△OAB的周长3、如图19-11所示,已知ABCD比△OBC的周长大4cm,则AB=cm,BC=cm.综合应用题4、已知平行四边形的一边长为14,则下列各组数据中,能分别作为它的两条对角线长的是()A. 10和16B. 12和16C. 20和22D. 10和405、如图19-16所示,已知D,E,F分别在△ABC的边BC,AB,AC上,且DE∥AF,DF=AF,将FD延长到G,使FG=2DF,连接AG,求证:ED,AG互相平分.探索创新题6、如图19-20所示,在四边形ABCD中AD∥BC,且AD>BC,BC=6cm,P,Q分别从A,C同时出发,P以1cm/s的速度由A向D运动,Q 以2cm/s 的速度由C 向B 运动,几妙后四边形ABQP 是平行四边形?体验中考1、(09·威海)如图19-22所示,在四边形ABCD 中,E 是BC 边的中点,连接DE 并延长,交AB 的延长线于点F ,AB =BF ,添加一个条件,使四边形ABCD 是平行四边形,你认为下面四个条件中可选择的是 ( )A. AD =BCB. CD =BFC. ∠A =∠CD. ∠F =∠CDE2、(08·贵阳)如图19-23所示,在ABCD Y 中,E ,F 分别为边AB ,CD 的中点,连接DE ,BF ,BD.(1) 求证△ADE ≌△CBF ;(2) 若AD ⊥BD ,则四边形BFDE 是什么特殊四边形?请证明你的结论.学后反思附: 课堂检测及体验中考答案课堂检测1、解:因为四边形ABCD 是平行四边形,所以AB =CD ,AD =BC.又因为AB =8m ,所以CD =8m.因为AB+BC+CD+DA =36m ,所以AD ==11(3682)2010().22AD BC m ==⨯-⨯=⨯= 所以8,10.CD m AD BC m ===2、C3、9 54、C5、解:连接AD ,EG.因为DE =AF ,DF ∥AF ,所以四边形AEDF 为平行四边形,所以AEFD.因为FG =2DF ,所以GD =DF ,所以AE =DG ,即AE DG.所以四边形AEGD 为平行四边形.所以ED ,AG 互相平分6、解:设经过x 秒后,AP =BQ ,则AP =x ,BQ=BC-CQ=6-2x ,所以x =6-2x ,所以x =2 。
0118.1.1平行四边形学案

4.有两组对边__________________的四边形叫平形四边形,平行四边形用“______”表示,平行四边形ABCD记作__________。
5.如图□ABCD中,对边有______组,分别是___________________,对角有_____组,分别是_________________,对角线有______条,它们是___________________。
八年级数学导学案
班级:姓名:
课题
平行四边形
课型
新授
课时
1
周次
4
学习目标
1.理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2.会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
重点
难点
平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
难点是运用平行四边形的性质进行有关的论证和计算.
5.若□ABCD的对角线AC平分∠DAB,则对角线AC与BD的位置关系是______.
6.如图,□ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE=______.
盘点收获
3.. ABCD的周长为40cm,△ABC的周长为27cm,AC的长为()
A.13cmB.3 cmC.7 cmD.11.5cm
4.如图,AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.
巩固提升
自主完成下列练习:
1.两组对边分别______的四边形叫做平行四边形.它用符号“□”表示,平行四边形ABCD记作__________。
2.平行四边形的两组对边分别______且______;平行四边形的两组对角分别______;两邻角______;平行四边形的对角线______;平行四边形的面积=底边长×______.
【最新】人教版八年级数学下册《平行四边形》导学案

新人教版八年级数学下册《平行四边形》导学案【知识点精讲】1.【多边形】定义 由一些线段首尾顺次相接组成的图形叫做多边形(Polygon ).如果延长多边形的任一条边,整个多边形都在这条延长边的一侧,那么这样的多边形就叫做凸多边形,否则称为凹多边形.如无特别声明,中学里所说的多边形均指凸多边形,各边相等,各角也相等的多边形叫正多边形.多边形的内(外)角和定理 任意n 边形的内角和等于︒⋅-180)2(n ,外角和等于360°. 推论 ①n 边形的每个内角的取值范围是)180,0(︒︒;②正n 边形的每个内角均等于︒⋅-180)2(n n ; ③n 边形中至少有一个内角︒⋅-≥180)2(n n ;也至少有一个内角︒⋅-≤180)2(nn ; ④n 边形的n 个内角中,最多有3个是锐角;⑤n 边形的n 个外角中,最多有3个是钝角.四边形定义 在平面内由首尾相连的四条线段组成的封闭图形,叫做四边形(Quadrilateral ). 四边形具有四个顶点和四条边,我们一般只研究凸四边形,即将每条边延长后,其余各边都在各边所在直线的同一侧.四边形中没有公共顶点的两条边叫做对边,没有公共边的两个角叫做对角,对角顶点的联结线段叫做四边形的对角线. 2.【平行四边形】定义 两组对边分别平行的四边形叫做平行四边形. 平行四边形有一系列的性质定理和判定定理,掌握平行四边形的性质定理和判定定理,是研究平行四边形问题的基础. 性质定理 在平行四边形中, (1)对角分别相等; (2)对边分别相等; (3)对角线互相平分;(4)对角线的平方和等于四条边平方之和.判定定理 四边形中,若有下列条件之一成立,则这个四边形是平行四边形. (1)对角分别相等; (2)对边分别相等;(3)一组对边平行且相等; (4)对角线互相平分;(5)对角线的平方和等于四边的平方和. 推论三角形两边的平方和等于第三边上中线的平方与第三边之半的平方和的2倍.即222222a a b c m ⎛⎫⎛⎫+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭.欧拉定理四边形各边的平方之和等于其对角线的平方和加上两对角线中点连结线段的平方之四倍.已知 四边形ABCD ,M ,N 分别是对角线AC 、BD 的中点.求证:22222224MN AC BD DA CD BC AB ++=+++证明: 如图连结MD ,MB ,利用上述推论,得2222222222,22AMDM CD AD AM BM BC AB +=++=+两式相加,得22222224)(2AM DM BM DA CD BC AB ++=+++……①因为222222MN BN DM BM +=+,224AC AM =,224BD BN =. 由①式,得.444442222222222222MN AC BD ACMN BD AM MN BN DA CD BC AB ++=++=++=+++【例题精讲】a【夯实基础】【例1】(2011 广西玉林市)如图,在 ABCD 中,∠B =80°,AE 平分∠BAD 交BC 于点E ,CF ∥AE 交AD 于点F ,则∠BCF =( )A 、40°B 、50°C 、60°D 、80°【例2】如图所示,设P 为平行四边形ABCD 内的一点,PAB ∆,PBC ∆,PDC ∆,PDA ∆的面积分别记为1S ,2S ,3S ,4S ,则有( )A .14S S =B .1234S S S S +=+C .1324S S S S +=+D .以上都不对 【例3】如图,在平行四边形ABCD 中,E 为BC 中点,AE 的延长线与DC 的延长线相交于点F ,(1)证明:FAB DFA ∠=∠; (2)证明:FCE ABE ∆≅∆.【例4】(2010 厦门)如图,已知△ABC 是等边三角形,点D 、F 分别在线段BC 、AB 上,∠EFB = 60°,DC = EF .(1)求证:四边形EFCD 是平行四边形;(2)若BF = EF ,求证:AE = AD .【例5】如图,在ABC ∆中,90ACB ∠=︒,CD AB ⊥,D 为垂足,ABC ∠的平分线BE 交CD 于G ,交AC 于E ,//GF AB ,交AC 于F . 求证:AF CG =.【能力提高】【例6】下面有四个命题:(1)一组对边相等且一组对角相等的四边形是平行四边形;(2)一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;(3)一组对角相等且连结这一组对角顶点的对角线平分另一条对角线的四边形是平行四边形;(4)一组对角相等且连结这一组对角顶点的对角线被另一条对角线所平分的四边形是平行四边形.其中正确的个数是( )A 、1B 、2C 、3D 、4 (1988年全国初中数学联赛一试试题)【例7】若四边形ABCD 中,222222BD AC DA CD BC AB +=+++.求证:ABCD 是平行四边形.【例8】设正方形ABCD 的中点为,E F 是CE 的中点,求证:12DAE BAF ∠=∠.【例9】如图,在直角梯形ABCD中,AB∥CD,∠BCD=90°,AB = AD =10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm 的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q 运动停止,设运动时间为t.(1)求CD的长;(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.【例10】(2007 黑龙江)在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.请直接应用上述信息解决下列问题:当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.【挑战竞赛】【例11】如图,在正方形ABCD 的边AD 的延长线上取点E ,F 使DE = AD ,DF = BD ,连结BF 分别交CD ,CE 于H ,G .求证:△GHD 是等腰三角形.【例12】如图所示,在平行四边形ABCD 中,BC = 2AB ,M 为AD 的中点,CE ⊥AB 于E ,求证:∠DME =3∠AEM .【例13】如图,在平行四边形ABCD 中,,,,,AE BC AF CD EM AF FM AE ⊥⊥⊥⊥若,,EF a AC b ==求AM 的长.【例14】四边形ABCD 中,AB ,BC ,CD ,DA 的中点分别为M 、P 、N 、Q ,且MN + PQ =)(21DA CD BC AB +++,求证:四边形ABCD 是平行四边形.。
人教版八年级数学第十八章平行四边形导学案(定稿)

18.1.1平行四边形的性质(1)课前预习:1.四边形的内角和.2.有两组对边分别平行的四边形叫做.3.平行四边形的面积公式为:.4.平行四边形用符号“”表示,平行四边形ABCD记作“”.5.平行四边形的性质:(1)平行四边形的对边.(2)平行四边形的对角.6.两条平行线之间的平行线段都相等.7.两条平行线中,一条直线上到另一条直线的,叫做这两条平行线之间的距离.课内探究:探究1.在探究平行四边形性质的过程中,体会研究平行四边形性质的基本方法是什么?探究2●平行四边形的边角性质例1.如图,□ABCD的周长为60cm,A E⊥BC,AF⊥CD,垂足分别为E、F(1)若∠BAD=120°,求∠EAF的度数;(2)已知A E︰AF=4︰6,求□ABCD的各边的长变式训练:1.如图,□ABCD中,E为BC上的一点,AF⊥DE于F,∠DAF=62°,求∠BED的度数2.如图,□ABCD中,AE平分∠BAD交DC于点E,AD=8cm,AB=5cm,求EC的长探究2●平行四边形与全等三角形的综合应用例2.如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.(1)求证:△ABE≌△CDFABE≌△CDF外其余两对全等三角形(不再添加辅助线)变式训练:1、如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F,求证:AE=CF.2、如图,分别延长□ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.求证:△AEF≌△CHG.限时训练1.如图,已知在□ABCD中,AD=3cm,AB=2cm,则□ABCD的周长等于()A.10cmB.6cmC.5cmD.4cm第2题2.如图,□ABCD的面积是12,点E、F在BD上,且BE=EF=FD,则△CEF的面积为()A.2B.3C.4D.63.如图,平行四边形ABCD中,AB=AD,∠D=70°,BE⊥AC于E,则∠ABE等于()A.20°B.25°C.30°D.35°4.如图,平行四边形ABCD中,AE⊥BC于E,AF⊥DC于F,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积等于()A.87.5B.80C.75D.72.5第4题第5题第6题5.如图,直线l1∥l2,A、C、F在l1上,B、D、E在L2上,且AB∥CD,CE⊥l2,FG⊥l2,则下列说法不正确的是()A.AB=CDB.A、B两点之间的距离就是线段AB的长C.EC=FGD.直线l1、l2的距离就是线段CD的长6.如图,在平行四边形ABCD中,过对角线AC上一点P作EF∥AD,GH∥AB,与各边交点分别为E、F、G、H,则图中面积相等的平行四边形的对数为()A.3B.4C.5D.67.如图,已知平行四边形ABCD,E是AB延长线上一点,连接DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,这个条件是(只第7题第8题8.如图,在平行四边形ABCD中,∠A=130°,在AD上取DE=DC,则∠ECB的度数是度.自主训练1.一个平行四边形的周长为70cm,两组对边之间的距离为10cm和4cm,则这个平行四边形的各边长分别为2.如图,□ABCD中AB=13,AD=5,AC⊥BC,则S□ABCD=3.如图,四边形ABCD是平行四边形,△AB’C和△ABC关于AC所在直线对称,AD和B’C相交于点O,连接BB’.(1)请直接写出图中所有的等腰三角形(不添加字母);(2)求证:△AB’O≌△CDO.18.1.1平行四边形的性质(2)课前预习:1.平行四边形的对边且,对角 .2.两条平行线之间的距离处处3.平行四边形的对角线课内探究探究1平行四边形的两条对角线将平行四边形分成了四个三角形,你知道这四个三角形的面积有怎样的关系吗?你是怎样想的?与同学交流.探究2●平行四边形的对角线性质例1.已知:如图,□ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长多8cm,求这个平行四边形各边的长.变式训练如图,平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为()A.4cmB.5cmC.6cmD.8cm●平行四边形的性质的综合应用例2.如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠CAD=45°,AC=2,求BD的长.变式训练□ABCD的一边为6cm,一条对角线为8cm,则另一条对角线的取值范围为限时训练1.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1=()A.40°B.50°C.60°D.80°2.如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是()A.6B.8C.9D.10第2题第3题第4题3.如图为一个平行四边形ABCD,其中H、G两点分别在BC、CD上,AH⊥BC,AG⊥CD,且AH、AC、AG将∠BAD分成∠1、∠2、∠3、∠4四个角.若AH=5,AG=6,则下列关系正确的是()A.∠1=∠2B.∠3=∠4C.BH=GDD.HC=CG4.如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1等于()A.40°B.50°C.60°D.80°5.如图,在□ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,当点E、F 满足下列哪个条件时,四边形DEBF不一定是平行四边形()A.OE=OFB.DE=BF D.∠ABE=∠CDF第5题第6题第7题6.如图,点D、E、F分别为△ABC三边的中点,若△DEF的周长为10,则△ABC的周长为()A.5.B.10C.20D.407.如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是8.在□ABCD中,已知∠A=110°,则∠D= .9.如图,□ABCD中,对角线AC、BD相交于O,OE⊥DC,OF⊥AB,垂足分别是E、F.求证:OE=OF.自主训练1.如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,求平行四边形ABCD的周长.2.如图,点E 是□ABCD 的对角线AC 上任意一点,则S △ABE =S △ADE 是否正确?请说明理由.3.如图,在□ABCD 中,E 为BC 边上的一点,且AB=AE.(1)求证:△ABC ≌△EAD ;(2)若AE 平分∠DAB ,∠EAC=25°,求∠AED 的度数.18.1.1平行四边形的性质(3)课前预习1.在□ABCD 中,AC 、BD 交于点O ,已知AB =8cm ,BC =6cm ,△AOB 的周长是18cm ,那么△AOD 的周长是_____________.2. □ABCD 的对角线交于点O ,S △AOB =2cm 2,则S □ABCD =__________.3. □ABCD 的周长为60cm ,对角线交于点O ,△BOC 的周长比△AOB 的周长小8cm ,则AB =______cm ,BC =_______cm .4. □ABCD 中,对角线AC 和BD 交于点O ,若AC =8,AB =6,BD =m ,那么m 的取值范围是____________.课内探究例1. □ABCD 中,E 、F 在AC 上,四边形DEBF 是平行四边形.求证:AE=CF .F E D B A例2.如图,田村有一口四边形的池塘,在它的四角A 、B 、C 、D 处均有一棵大桃树.田村准备开挖养鱼,想使池塘的面积扩大一倍,并要求扩建后的池塘成平行四边形形状,请问田村能否实现这一设想?若能,画出图形,说明理由.D BA例3、已知:如下图, ABCD 的对角AC ,BD 交与点O.E ,F 分别是OA 、OC 的中点。
20年春人教版八年级数学《第18章平行四边形》导学案

20年春人教版八年级数学《第18章平行四边形》导学案18.1.1 平行四边形的性质第1课时平行四边形的边、角特征学习目标:1.掌握平行四边形的对边相等、对角相等的两条性质;2.根据平行四边形的性质进行简单的计算和证明;3.经历“实验—猜想—验证—证明”的过程,发展学生的思维水平.重点:掌握平行四边形的对边相等、对角相等的两条性质.难点:根据平行四边形的性质进行简单的计算和证明.一、知识回顾1.平行四边形的定义是什么?如何表示一个平行四边形?2.如图,DC∥GH ∥AB,DA∥EF∥CB,图中的平行四边形有多少个?将它们表示出来.一、要点探究探究点1:平行四边形的边、角的特征量一量1.画一个平行四边形ABCD,用尺子等工具度量它的四条边,并记录下数据,你能发现AB与DC,AD 与BC之间的数量关系吗?2.再用量角器等工具度量它的四个角,并记录下数据,你能发现∠A与∠C,∠B与∠D之间的数量关系吗?思考你发现了什么规律?证一证已知:四边形ABCD是平行四边形.求证:AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC.证明:如图,连接AC.∵四边形ABCD是平行四边形,∴AD___BC,AB___CD,∴∠1___∠2,∠3___∠4.又∵AC是△ABC和△CDA的公共边,∴△ABC____△CDA,∴AD___BC,AB___CD,∠ABC___∠ADC.∵∠BAD=∠1+∠4,∠BCD=∠2+∠3,∴∠BAD___∠BCD.思考不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?自主学课堂探要点归纳:平行四边形的对边____________;平行四边形的对角___________.典例精析例1如图,在平行四边形ABCD中.(1)若∠A =32°,求其余三个角的度数.(2)连接AC,已知平行四边形ABCD的周长等于20 cm,AC=7cm,求△ABC的周长.变式题(1)在平行四边形ABCD中,∠A:∠B=2:3,求各角的度数.(2)若平行四边形ABCD的周长为28cm,AB:BC=3:4,求各边的长度.方法总结:已知平行四边形的边角的比例关系求其他边角时,常会用到方程思想,结合平行四边形的性质列方程.例2如图,在平行四边形ABCD中,E,F是对角线AC上的两点,并且AE=CF,求证:BE=DF.针对训练1.如图,在平行四边形ABCD中.(1)若∠A=130°,则∠B=______ ,∠C=______ ,∠D=______.(2)若AB=3,BC=5,则它的周长= ______.(3)若∠A+ ∠C= 200°,则∠A=_____,∠B=______.2.如图,在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=_________.3.剪两张对边平行的纸条随意交叉叠放在一起,重合部分构成了一个四边形,转动其中一张纸条,线段AD 和BC的长度有什么关系?为什么?探究点2:平行线间的距离想一想:如图,若m // n,作AB // CD // EF,分别交m于A、C、E,交n于B、D、F.由________________________易知四边形ABCD,CDEF均为__________________.由平行四边形的性质得AB______CD_______EF.填一填:如图,在平行四边形ABCD中,DE⊥AB,BF⊥CD,垂足分别是E,F.求证:DE=BF.证明:∵四边形ABCD是平行四边形,∴∠A_____∠C,AD______CB.又∠AED= ∠CFB=90°,∴△ADE____△CBF(_____),∴AE_____CF.要点归纳:1.两条平行线之间的任何平行线段都__________.2.两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的_________.3.两条平行线间的距离__________.典例精析例3 如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.二、课堂小结平行四边形内容定义两组对边分别平行的四边形1.判断题(对的在括号内填“√”,错的填“×”):(1)四平行四边形两组对边分别平行且相等 ( )(2)平行四边形的四个内角都相等 ( )(3)平行四边形的相邻两个内角的和等于180° ( )(4)如果平行四边形相邻两边长分别是2cm和3cm,那么周长是10cm ( )(5)在平行四边形ABCD中,如果∠A=42°,那么∠B=48° ( )(6)在平行四边形ABCD中,如果∠A=35°,那么∠C=145°( )2.在平行四边形ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是()A .45° B. 55° C. 65° D. 75°3.如图,D、E、F 分别在△ABC的边AB、BC、AC上,且DE∥AC,DF∥BC,EF∥AB,则图中有_____个平行四边形.4.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为____________.5.已知在平行四边形ABCD中,DE平分∠ADC,BF平分∠ABC.求证:AE=CF.6.有一块形状如图所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?7.如图,在△ABC中,AD平分∠BAC,点M,E,F分别是AB,AD,AC上的点,四边形BEFM是平行四边形.求证:AF=BM.第十八章平行四边形18.1.1 平行四边形的性质第2课时平行四边形的对角线的特征学习目标:1.掌握平行四边形对角线互相平分的性质;2.经历对平行四边形性质的猜想与证明的过程,渗透转化思想,体会图形性质探究的一般思路.重点:掌握平行四边形对角线互相平分的性质.难点:经历对平行四边形性质的猜想与证明的过程,渗透转化思想,体会图形性质探究的一般思路.一、知识回顾1.你能说出平行四边形边、角的特征吗?平行四边形对边互相___________;平行四边形对边__________;平行四边形对角__________.二、要点探究探究点1:平行四边形的对角线的性质猜一猜如图,在□ABCD中,连接AC,BD,并设它们相交于点O. OA与OC,OB与OD有什么关系?证一证已知:如图,□ABCD的对角线AC、BD相交于点O.求证:OA=OC,OB=OD.证明:∵四边形ABCD是平行四边形,∴ AD___BC,AD___BC,∴∠1___∠2,∠3___∠4,∴△AOD___△COB(______),∴ OA____OC,OB____OD.要点归纳:平行四边形的性质:平行四边形的对角线互相_________.应用格式:∵四边形ABCD是平行四边形,∴ OA=OC,OB=OD.典例精析例1如图,已知平行四边形ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA 的周长长5cm,求这个平行四边形各边的长.方法总结:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.变式题如图,在平行四边形ABCD中,对角线AC、BD相交于点O,平行四边形ABCD的周长是100cm,△AOB与△BOC的周长的和是122cm,且AC:DB= 2:1,求AC和BD的长.课堂探例2如图,平行四边形ABCD 的对角线AC,BD 交于点O.点O 作直线EF,分别交AB,CD 于点E ,F.求证:OE=OF.变式题请判断下列图中,OE=OF 还成立么?方法总结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等. 1.如图,平行四边形ABCD 的对角线AC ,BD 交于点O ,若AD=16,AC=24,BD=12,则△OBC 的周长为 ( ) A.26 B.34 C.40 D.522.如图,在□ABCD 中,对角线AC 和BD 相交于点O ,△AOB 的周长为15,AB=6,则对角线AC 、BD 的长度的和是 ( )A.9B.18C.27D.363.如图,平行四边形ABCD 中,AC 、BD 交于O 点,点E 、F 分别是AO 、CO 的中点,试判断线段BE 、DF的关系并证明你的结论.探究点2:平行四边形的面积例3 如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.方法总结:已知平行四边形的高DE,DF,根据“等面积法”及平行四边形性质列方程求解.例4平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?方法总结:平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.例5如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?变式题如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?面积.1.如图,ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是()A. 10B. 14C. 20D. 222.如图,在平行四边形ABCD中,下列结论中错误的是()A.∠ABO=∠CDO B.∠BAD=∠BCDC.AO=CO D.AC⊥BD3.在□ABCD中,AC=24,BD=38,AB=m, 则m的取值范围是 ( )A. 24<m<39B.14<m<62C.7<m<31D.7<m<124.如图,□ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为()A.16B.14C.12D.105.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.8.如图,已知O是平行四边形ABCD的对角线的交点,AC=24,BD=18,AB=16,求△OCD的周长及AD 边的取值范围.第十八章平行四边形18.1.2 平行四边形的判定第1课时平行四边形的判定(1)学习目标:1.经历平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路;2.掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理论证.重点:经历平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路.难点:掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理论证.一、知识回顾1.平行四边形的定义是什么?有什么作用?2.除了两组对边分别平行,平行四边形还有哪些性质?3.平行四边形上面的三条性质的逆命题各是什么?三、要点探究探究点1:两组对边分别相等的四边形是平行四边形猜一猜将两长两短的四根细木条用小钉固定在一起,任意拉动,所得的四边形是平行四边形吗?证一证已知:四边形ABCD中,AB=DC,AD=BC.求证:四边形ABCD是平行四边形.证明:连接AC,在△ABC和△CDA中,AB=CD ,AC=CA,∴△ABC_____△CDA(________).BC=DA,∴∠1____∠4 , ∠ 2_____∠3,∴AB_____CD , AD_____BC,∴四边形ABCD是________________.自主学课堂探要点归纳:平行四边形的判定定理:两组对边分别_________的四边形是平行四边形.几何语言描述:在四边形ABCD中,∵AB=CD,AD=BC,∴四边形ABCD是_________________.典例精析例1如图,在Rt△MON中,∠MON=90°.求证:四边形PONM是平行四边形.例2如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形.针对训练如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.探究点2:两组对角分别相等的四边形是平行四边形猜一猜对于两组对角分别相等的四边形的形状你的猜想是什么?证一证已知:四边形ABCD中,∠A=∠C,∠B=∠D,求证:四边形ABCD是平行四边形.证明:∵∠A+∠C+∠B+∠D=_______°,又∵∠A=∠C,∠B=∠D,∴___∠A+___∠B=_______°,即∠A+∠B=______°,∴ AD_____BC.同理得 AB_____CD,∴四边形ABCD是________________.要点归纳:平行四边形的判定定理:两组对角分别________的四边形是平行四边形.几何语言描述:在四边形ABCD中,∵∠A=______,∠B=______,∴四边形ABCD是_______________.典例精析例3 如图,在四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.(1)求∠D的度数;(2)求证:四边形ABCD是平行四边形.针对训练1.判断下列四边形是否为平行四边形:2.能判定四边形ABCD是平行四边形的条件:∠A:∠B:∠C:∠D的值为()A. 1:2:3:4B. 1:4:2:3C. 1:2:2:1D. 3:2:3:2探究点3:对角线互相平分的四边形是平行四边形猜一猜如图,将两根细木条AC、BD的中点重叠,用小钉固定在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗?证一证已知:四边形ABCD中,OA=OC,OB=OD.求证:四边形ABCD是平行四边形.证明:在△AOB和△COD中,OA=OC,∠AOB=∠COD,∴△AOB______△COD(________).OB=OD,∴∠BAO_____∠OCD , ∠ ABO_____∠CDO,∴AB_____CD , AD_____BC,∴四边形ABCD是________________.要点归纳:平行四边形的判定定理:对角线互相________的四边形是平行四边形.几何语言描述:在四边形ABCD中,∵AO_____CO,DO_____BO,∴四边形ABCD是______________.典例精析例4(教材P46例3变式题)如图,AC是平行四边形ABCD的一条对角线,BM⊥AC于M,DN⊥AC于N,四边形BMDN是平行四边形吗?说说你的理由.例5昨天李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来?然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢(A,B,C为三顶点,即找出第四个顶点D)?(请用多种方法)针对训练1.根据下列条件,不能判定四边形为平行四边形的是()A.两组对边分别相等B.两条对角线互相平分C.两条对角线相等D.两组对边分别平行2.如图,在四边形ABCD中,AC与BD交于点O.如果AC=8cm,BD=10cm,那么当AO=_____cm,BO=_____cm时,四边形ABCD是平行四边形.二、课堂小结内容平行四边形的判定(1)定义法:两组对边分别平行的四边形叫平行四边形.两组对边分别相等的四边形是平行四边形.两组对角分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形.1.判断对错:(1)有一组对边平行的四边形是平行四边形. ( )(2)有两条边相等,并且另外的两条边也相等的四边形一定是平行四边形( )(3)对角线互相平分的四边形是平行四边形()(4)一条对角线平分另一条对角线的四边形是平行四边形( )(5)有一组对角相等且一组对边平行的四边形是平行四边形( )2.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形()A.OA=OC,OB=OD B.AB=CD,AO=COC.AB=CD,AD=BC D.∠BAD=∠BCD,AB∥CD3.如图,在四边形ABCD中,(1)如果AB∥CD,AD∥BC,那么四边形ABCD是 __________.(2)如果∠A:∠B:∠ C:∠D=a:b:a:b(a,b为正数),那么四边形ABCD是__________.(3)如果AD=6cm,AB=4cm,那么当BC=_______cm,CD=_____cm时,四边形ABCD为平行四边形.4.如图,五边形ABCDE是正五边形,连接BD、CE,交于点P.求证:四边形ABPE是平行四边形.5.如图,已知E,F,G,H分别是平行四边形ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.当堂检第2题图第3题图6.如图,AB 、CD 相交于点O ,AC ∥DB ,AO =BO ,E 、F 分别是OC 、OD 的中点.求证: (1)△AOC ≌△BOD ;(2)四边形AFBE 是平行四边形.7. 学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能 组成一个平行四边形,你觉得第四棵树应该栽在哪里?第十八章 平行四边形18.1.2 平行四边形的判定第2课时 平行四边形的判定(2)学习目标:1.掌握“一组对边平行且相等的四边形是平行四边形”的判定方法.2.会进行平行四边形的性质与判定的综合运用.重点:“一组对边平行且相等的四边形是平行四边形”的判定方法. 难点:平行四边形的性质与判定的综合运用.一、知识回顾1.上节课我们学习了判定一个四边形为平行四边形的方法有哪几种?四、要点探究探究点1:一组对边平行且相等的四边形是平行四边形想一想我们知道,两组对分别平行或相等的是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?对于这个问题,有以下两种猜想:猜想1:一组对边相等的四边形是平行四边形;猜想2:一组对边平行的四边形是平行四边形.这两种猜想对吗?如果不对,你能举出反例吗?活动如图,将线段AB向右平移BC长度后得到线段CD,连接AD,BC,由此你能猜想四边形ABCD的形状吗?猜一猜经历了上面的活动,你现在能猜出,一组对边满足什么条件的四边形是平行四边形吗?一组对边平__________________的四边形是平行四边形.证一证如图,在四边形ABCD中,AB=CD且AB∥CD,求证:四边形ABCD是平行四边形.证明:连接AC.∵AB∥CD,∴∠1=∠2.在△ABC和△CDA中,AB=CD,∠1=∠2,∴△ABC_____△CDA(________).AC=CA,∴ BC=DA.又∵AB= CD,∴四边形ABCD是________________.要点归纳:平行四边形的判定定理:一组对边________________的四边形是平行四边形.几何语言描述:在四边形ABCD中,∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形.典例精析例1如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.课堂探变式题如图,点C是AB的中点,AD=CE,CD=BE.(1)求证:△ACD≌△CBE;(2)求证:四边形CBED是平行四边形.针对训练1.已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是()A.AB∥CD,AB=CDB.AB∥CD,BC∥ADC.AB∥CD,BC=ADD.AB=CD,BC=AD2.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.探究点2:平行四边形的性质与判定的综合运用典例精析例2 如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?例3如图,将▱ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.方法总结:此题利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,再结合平行四边形的判定及性质进行解题.针对训练1.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )A.3种B.4种C.5种D.6种2.如图,在▱ABCD中,E,F分别是AB,CD的中点,连接DE,EF,BF,写出图中除▱ABCD以外的所有的平行四边形.二、课堂小结件,这个条件不可以是()A.AF=CE B.AE=CFC.∠BAE=∠FCD D.∠BEA=∠FCE2.已知四边形3:2,则较大边的长度是()A.8cm B.10cmC.12cm D.14cm3.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,则图中的平行四边形的个数共有____个.4.如图,点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.当堂检平行四边形的判定(2)平行四边形的性质与判定的综合运用一组对边平行且相等的四边形是平行四边形.第1题图第3题图5. 如图,△ABC 中,AB=AC=10,D 是BC 边上的任意一点,分别作DF ∥AB 交AC 于F ,DE ∥AC 交AB 于E ,求DE+DF 的值.能力提升6.如图,在四边形ABCD 中,AD ∥BC ,AD=12cm ,BC=15cm ,点P 自点A 向D 以1cm/s 的速度运动,到D 点即停止.点Q 自点C 向B 以2cm/s 的速度运动,到B 点即停止,点P ,Q 同时出发,设运动时间为t(s).(1)用含t 的代数式表示:AP=_____; DP=________; BQ=________;CQ=________;(2)当t 为何值时,四边形APQB 是平行四边形? (3)当t 为何值时,四边形PDCQ 是平行四边形?第十八章 平行四边形18.1.2 平行四边形的判定第3课时 三角形的中位线学习目标:1.理解三角形中位线的概念,掌握三角形的中位线定理;2.能利用三角形的中位线定理解决有关证明和计算问题.重点:理解三角形中位线的概念,掌握三角形的中位线定理. 难点:能利用三角形的中位线定理解决有关证明和计算问题.一、知识回顾1.平行四边形的性质和判定有哪些?边:①AB ∥CD,AD____BC ②AB=CD,AD____BC 平行四边形ABCD ③AB ∥CD,AB_____CD角:∠BAD____∠BCD ,∠ABC____∠ADC对角线:AO____CO,DO____BO自主学课堂探性 质判 定五、要点探究探究点1:三角形的中位线定理概念学习 三角形中位线:连接三角形两边中点的线段.如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,连接DE.则线段DE 就称为△ABC 的中位线.想一想 1.一个三角形有几条中位线?你能在△ABC 中画出它所有的中位线吗?2.三角形的中位线与中线有什么区别?猜一猜 如图,DE 是△ABC 的中位线,DE 与BC 有怎样的位置关系,又有怎样的数量关系? 猜想:三角形的中位线________三角形的第三边且________第三边的________.量一量 度量一下你手中的三角形,看看是否有同样的结论? 证一证 如图,在△ABC 中,点D,E 分别是AB,AC 边的中点.1.2DE BC DE BC =求证:∥,分析:证法1:证明:延长DE 到F ,使EF=DE .连接AF 、CF 、DC . ∵AE=EC ,DE=EF ,∴四边形ADCF 是_______________. ∴CF ∥AD ,CF=AD ,∴CF_____BD ,CF_____BD ,∴四边形BCFD 是________________, ∴DF_____BC ,DF_______BC , 12DE DF =又∵,∴DE_____BC ,DE=______BC. 证法2:证明:延长DE 到F ,使EF=DE .连接FC .∵∠AED=∠CEF ,AE=CE ,∴△ADE_____△CFE .∴∠ADE=∠_____,AD=_______, ∴CF______AD,∴BD______CF.∴四边形BCFD 是___________________. ∴DF_______BC. 12DE DF =又∵,倍长DE 至F DF 与AC 互相平分构造全等 三角形 角、边相等平行四边形线段相等、平行∴DE_____BC ,DE=______BC.要点归纳:三角形中位线定理:三角形的中位线平行于三角形的第三边且等于第三边的一半.符号语言:△ABC 中,若D 、E 分别是边AB 、AC 的中点, 12=.DE BC DE BC 则,重要结论:①中位线DE 、EF 、DF 把△ABC 分成四个全等的三角形;有三组共边的平行四边形,它们是四边形ADFE 和BDEF ,四边形BFED 和CFDE ,四边形ADFE 和DFCE.②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.面积等于原三角形面积的四分之一. 典例精析例1如图,在△ABC 中,D 、E 分别为AC 、BC 的中点,AF 平分∠CAB ,交DE 于点F.若DF =3,求AC的长.例2 如图,在四边形ABCD 中,AB=CD ,M 、N 、P 分别是AD 、BC 、BD 的中点,∠ABD=20°,∠BDC=70°,求∠PMN 的度数.例3 如图,在△ABC 中,AB =AC ,E 为AB 的中点,在AB 的延长线上取一点D ,使BD =AB ,求证:CD =2CE.方法总结:恰当地构造三角形中位线是解决线段倍分关系的关键.1. 如图,△ABC 中,D 、E 分别是AB 、AC 中点. (1) 若DE=5,则BC=________.(2) 若∠B=65°,则∠ADE=_________°. (3) 若DE+BC=12,则BC=_________.2. 如图,A ,B ,并分别找出AC 和BC 的中点M ,N ,如果测得MN=20m ,那么A ,B 两点间的距离为______m . 探究点2:三角形的中位线的与平行四边形的综合运用 例4 如图,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 中点.求证:四边形EFGH 是平行四边形.方法总结:顺次连结四边形四条边的中点,所得的四边形是平行四边形.变式题 如图,E 、F 、G 、H 分别为四边形ABCD 四边之中点.求证:四边形EFGH 为平行四边形.例5 如图,等边△ABC 的边长是2,D 、E 分别为AB 、AC 的中点,延长BC 至点F ,使CF=12BC ,连接CD和EF .(1)求证:DE=CF ; (2)求EF 的长.EGFHBC D A针对训练1.如图,在△ABC中,AB=6,AC=10,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为 ( )A.8B.10C.12D.162.如图,▱ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.二、课堂小结()当堂检三角形的中位线定理的应用三角形的中位线定理三角形中位线平行于第三边,并且等于它的一半三角形的中位线A.1B.2C.4D.82.如图,在▱ABCD中,AD=8,点E,F分别是BD,CD的中点,则EF等于()A.2B.3C.4D.53.如图,点 D、E、F 分别是△ABC 的三边AB、BC、AC的中点.(1)若∠ADF=50°,则∠B=____________°;(2)已知三边AB、BC、AC分别为12、10、8,则△ DEF的周长为_____________.4.在△ABC中,E、F、G、H分别为AC、CD、 BD、 AB的中点,若AD=3,BC=8,则四边形EFGH的周长是______________.5. 如图,在△ABC中,AB=6cm,AC=10cm,AD平分∠BAC,BD⊥AD于点D,BD的延长线交AC于点F,E为BC的中点,求DE的长.6.如图,E为▱ABCD中DC边的延长线上一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于O,连接OF,判断AB与OF的位置关系和大小关系,并证明你的结论.7.如图,在四边形ABCD中,AC⊥BD,BD=12,AC=16,E,F分别为AB,CD的中点,求EF的长.第1题图第2题图第3题图第十八章平行四边形18.2.1 矩形第1课时矩形的性质学习目标:1.理解矩形的概念,知道矩形与平行四边形的区别与联系;2.会证明矩形的性质,会用矩形的性质解决简单的问题;3.掌握直角三角形斜边中线的性质,并会简单的运用.重点:理解矩形的概念,知道矩形与平行四边形的区别与联系;掌握直角三角形斜边中线的性质,并会简单的运用.难点:会证明矩形的性质,会用矩形的性质解决简单的问题.一、知识回顾1.平行四边形是什么?它有哪些性质?2.你还记得长方形是什么吗?二、新知预习1.如图,现有一个活动的平行四边形,使它的一个内角变化,当内角变化为90°时,这是我们学过的哪个图形?2.自主学习:(1)矩形的定义:有一个角是直角的平行四边形叫做_________,也就是长方形.(2)矩形是特殊的平行四边形,平行四边形_________是矩形.三、自学自测1.矩形是常见的图形,你能举出一些生活中的实例吗?2.矩形是特殊的平行四边形,你能根据平行四边形的性质,说出3条矩形的性质吗?四、我的疑惑____________________________________________________________六、要点探究探究点1:矩形的性质思考因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?活动准备素材:直尺、量角器、橡皮擦、课本、铅笔盒等.(1)请同学们以小组为单位,测量身边的矩形(如书本,课桌,铅笔盒等)的四个角度数和对角线的长度,并记录测量结果.AC BD∠BAD∠ADC∠ABC∠BCD 橡皮擦课本桌子(2)根据测量的结果,你有什么猜想?猜想1 矩形的四个角都是_________.猜想2 矩形的对角线__________.证一证如图,四边形ABCD是矩形,∠B=90°.求证:∠B=∠C=∠D=∠A=90°.证明:∵四边形ABCD是矩形,∴∠B____∠D,∠C____∠A, AB____DC.∴∠B+∠C=_____°.又∵∠B = 90°,∴∠C =____°.∴∠B=∠C=∠D=∠A =_____°.如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相较于点O.求证:AC=DB.证明:∵四边形ABCD是矩形,∴AB____DC,∠ABC=∠DCB=_____°,在△ABC和△DCB中,∵AB=DC,∠ABC=∠DCB,BC= CB,∴△ABC____△DCB.∴AC____DB.思考请同学们拿出准备好的矩形纸片,折一折,观察并思考.矩形是不是轴对称图形?如果是,那么对称轴有几条?要点归纳:矩形除了具有平行四边形所有性质,还具有的性质有:课堂探1.矩形的四个角都是_______.矩形的对角线________.2.矩形是_________图形,它有_____条对称轴.几何语言描述:在矩形ABCD中,对角线AC与DB相交于点O.∠ABC=∠BCD=∠CDA=∠DAB =90°,AC=DB.典例精析例1如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证:DF=DC.例2如图,将矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,求△BED的面积.针对训练1.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是()A.AB∥DC B.AC=BDC.AC⊥BD D.OA=OB2.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD 面积的_________.3.如图,在矩形ABCD中,AE⊥BD于E,∠DAE:∠BAE=3:1,求∠BAE和∠EAO的度数.第1题图第2题探究点2:直角三角形斜边上的中线的性质活动 如图,一张矩形纸片,画出两条对角线,沿着对角线AC 剪去一半.问题 Rt △ABC 中,BO 是一条怎样的线段?它的长度与斜边AC 有什么关系? 猜想 直角三角形斜边上的中线等于斜边的________.证一证 如图,在Rt △ABC 中,∠ABC=90°,BO 是AC 上的中线.1.2BO AC =求证:证明:延长BO 至D, 使OD=BO,连接AD 、DC.∵AO=OC, BO=OD ,∴四边形ABCD 是____________. ∵∠ABC=90°,∴平行四边形ABCD 是________, ∴AC_______BD ,∴BO=_____BD=_____AC.要点归纳:直角三角形的性质:直角三角形斜边上的_______等于斜边的________. 典例精析例3 如图,在△ABC 中,AD 是高,E 、F 分别是AB 、AC 的中点. (1)若AB =10,AC =8,求四边形AEDF 的周长; (2)求证:EF 垂直平分AD.。
新人教版数学八年级下册平行四边形导学案

18.1.1 平行四边形的性质(1) 导学案一、学习目标1、理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.2、会用平行四边形的性质解决简单的平行四边形的计算问题。
3、通过学生动手体验、探索、归纳等获取知识的途径,从而培养学生对学习数学的兴趣。
二、自学探究1.请自学课本P 41至43页内容,思考下列问题: 活动一:1、观察平行四边形与一般的四边形有什么异同?2、归纳平行四边形概念:3、平行四边形记法:如图“ 平行四边形 ” 可用符号“ ”表示。
平行四边形ABCD 记作: ABCD活动二:1、观察上面这个四边形,它除具有四边形的性质和两组对边分别平行外以,它的边和角之间有什么关系?度量一下,是不是和你猜想的一致?2、证明你的猜想:已知:如图ABCD ,求证:AB =CD ,CB =AD ,∠B =∠D ,∠BAD =∠BCD .(分析:作ABCD 的对角线AC ,它将平行四边形分成△ABC 和△CDA ,证明这两个三角形全等即可得到结论)由此得到:平行四边形性质1 平行四边形的 . 平行四边形性质2 平行四边形的 . 三、达标训练 1.填空:(1)在ABCD 中,∠A= 50,则∠B= 度,∠C= 度,∠D= 度.(2)如果ABCD 的周长为28cm ,且AB :BC=2∶5,那么AB= cm ,BC= cm , CD= cm ,CD= cm . 2.在ABCD 中,如果EF ∥AD ,GH ∥CD ,EF 与GH 相交与点O ,那么图中的平行四边形一共有( ).(A )4个 (B )5个 (C )8个 (D )9个 3、平行四边形两角之比是2:3 ,各角都是多少度?ABCDAB CD4、、如图小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?四、小结提升1.在平行四边形ABCD中,∠A=50°,则∠B= °,∠D= °2、如果平行四边形ABCD的周长为28cm,且AB:BC=2∶5,那么AB= cm,BC= cm,CD= cm,CD= cm3、如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.4、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形.(1)线段AD和BC的长度有什么关系?为什么?若这个四边形的一个外角∠α=38°,这个四边形的每个内角的度数分别是多少?为什么?五、课后反思通过学习你学会了什么?还有什么问题不明白?在小组内讨论并解决疑难.六、课后作业18.1.1 平行四边形的性质(2) 导学案责任学校 小街中学 设计教师 许宽 日期 一、学习目标1、理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质。
平行四边形的性质(2)导学案
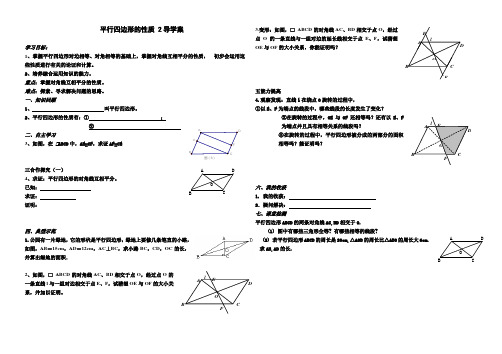
平行四边形的性质 2导学案学习目标:1、掌握平行四边形对边相等、对角相等的基础上,掌握对角线互相平分的性质,初步会运用这些性质进行有关的论证和计算。
2、培养综合运用知识的能力。
重点:掌握对角线互相平分的性质。
难点:探索、寻求解决问题的思路。
一、知识回顾1、叫平行四边形。
2、平行四边形的性质有:①;②二、自主学习3、如图,在 ABCD中,AE=CF,求证AF=CE三合作探究(一)4、求证:平行四边形的对角线互相平分。
已知:求证:证明:四、典型示范1.公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图,AB=15cm,AD=12cm,AC⊥BC,求小路BC,CD,OC的长,并算出绿地的面积.2、如图,□ABCD的对角线AC、BD相交于点O,经过点O的一条直线l与一组对边相交于点E、F,试猜想OE与OF的大小关系,并加以证明。
3.变形:如图,□ABCD的对角线AC、BD相交于点O,经过点O的一条直线与一组对边的延长线......相交于点E、F,试猜想OE与OF的大小关系,你能证明吗?五能力提高4.观察发现:直线l在绕点O旋转的过程中,①以E、F为端点的线段中,哪些线段的长度发生了变化?②在旋转的过程中,OE与OF还相等吗?还有以E、F为端点并且具有相等关系的线段吗?③在旋转的过程中,平行四边形被分成的两部分的面积相等吗?能证明吗?六、我的收获1. 我的收获:2.疑问解决:七、课堂检测平行四边形ABCD的两条对角线AC,BD相交于O.(1) 图中有哪些三角形全等? 有哪些相等的线段?(2) 若平行四边形ABCD的周长是20cm,△AOD的周长比△ABO的周长大6cm.求AB,AD的长.图(6)FEDCBAC DBAOCDBAOEAB CDOFlAB C DO l EFAB CDOl EF。
八年级人教版数学平行四边形导案

实验外校八年级数学导学案课题:平行四边形的性质(1)设计人:周青青审核人:李红飞学习目标:1、理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.2、会用平行四边形的性质解决简单的平行四边形的计算,并会进行有关的论证.学习重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.学习难点:运用平行四边形的性质进行有关的论证和计算..一、知识衔接二、预习导航1.有两组对边_______ 的四边形叫平形四边形,平行四边形用“_______”表示,平行四边形ABCD记作_______ 。
2.如图□ABCD中,对边有_______ 组,分别是_______,对角有_______ 组,分别是_______ ,对角线有_______ 条,它们是_______ 。
你能归纳ABCD的边、角各有什么关系吗?并证明你的结论。
三、课堂探究1、如果四边形ABCD是平行四边形,AB=6,且AB的长是□ABCD周长的,那么BC的长是多少?四、达标检测1.在ABCD中,∠A= 40°,则∠B= _______ 度,∠C= _______ 度,∠D= _______ 度.2.两组对边分别_______ 的四边形叫做平行四边形.它用符号“□”表示,平行四边形ABCD记作_______ 。
3.平行四边形的两组对边分别_______ ;平行四边形的两组对角分别_______ ;两邻角_______ ;平行4、平行四边形两邻边分别为24和16,若两长边间的距离为8,则两短边间的距离为( ).(A)5 (B)6 (C)8 (D)125.□ABCD中,两邻角之比为1∶2,则它的四个内角的度数分别是?6、如图,在一束平行光线中插入一张对边平行的纸板.如果光线与纸板右下那么光线与纸板左上方所成的∠2是多少度?为什么?五、知识小结:六、学习反思:。
人教版八年级数学《平行四边形》导学案

八年级数学《平行四边形的性质》(1)【学习目标】1•理解并掌握平行四边形的性质定理;2•应用用平行四边形的性质定理,求解与对角线有关问题;【学习重点】探索和证明平行四边形的性质,平行四边形的性质的简单应用.【学习难点】平行四边形的性质的探索和应用,用规范数学语言的表达.【学习过程】课前导学:1. _____________________________________________ 平行四边形的定义:叫做平行四边形。
记作: _____________________读作: _____________________几何语言表述:••• AB CD,AD BC, 二四边形ABCD是练习:如图:在口ABCD中,如果EF // AD , GH // CD, EF与GH相交与点0,那么图中的平行四边形一共有().A、4个B、5个C、8个D、9个2. 平行四边形的性质:①从边方面:平行四边形_______________________________________②从角方面:平行四边形_______________________________________用几何语言表述:••• U ABCD,_____________________ ? ________________________________________ -练习⑴•已知在—ABCD中,AB=8,周长等24,贝U CD= _________________, AD= ________ ,BC= ______⑵•已知在口-ABCD 中,Z A= 50°,则Z B=______ , Z C= ______, Z D=___.⑶.在乙」ABCD 中,若Z A: Z B=4: 5,则Z C= ________ ,Z D= _________.3•平行线之间的距离:两条平行中,一条直线上任意一点到 ________________________________________ ,叫做这两条平行线的距离4. ____________________________________ [结论】两条平行线之间的距离__________________________ ;两条平行线之间的任何两条平行线段 __________________思考:两平行线之间的距离和点与点之间的距离,点到直线的距离有何联系与区别?二、合作、交流、展示:例题1、在.口ABCD 中,AE丄BC,于E, AF丄CD 于F,/ EAF=60,求各内角的度数?三、巩固与应用1 .在匚ABCD中,/ A: / B: / C: / D的值可以是()A.1:2:3:4B.2:2:1:1C.2:1:2:1D.1:2:2:12 .若口ABCD的对角线AC平分/ DAB,则对角线AC与BD的位置关系是 __________________3 .若平行四边形的两个内角之比为 1 : 2,则其中较小的内角是( )度.A、90B、60C、120D、454. 如图AD // BC , AE // CD, BD 平分/ ABC,求证AB = CE.5. 如图所示,在ABCD 中,/ BAC=68°,/ ACB=32°,求/ D和/ BCD的度数?拓展:6.已知A、B、C三点不共线,以A、B、C为顶点画平行四边形, 你能求出第四个顶点D吗?有几个?7.剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学《平行四边形的性质》)(1【学习目标】理解并掌握平行四边形的性质定理;1. 2.应用用平行四边形的性质定理,求解与对角线有关问题;探索和证明平
【学习重点】平行四边形的性质的探索和应用,行四边形的性质,平行四边形的性质的简单应用.
用规范数学语言的表达.【学习难点】D
A
【学习过程】B
C
.课前导学:一 1. 平行四边形的定义:叫做平行四边形。
记作:
读作:
几何语言表述:∵AB CD,AD BC,∴四边形ABCD 是.
练习:如图:在□ABCD中,如果EF∥AD,GH∥CD,EF与GH相交
与点O,那么图中的平行四边形一共有().
A、4个
B、5个
C、8个
D、9个
2.平行四边形的性质:
①从边方面:平行四边形
②从角方面:平行四边形
用几何语言表述:
∵ABCD,
∴;.
练习⑴.已知在ABCD中,AB=8,周长等24,则CD=,AD= , BC=. ∠∠,∠,∠D=___.
°,则.已知在 B=____中ABCD,C=____A= 50⑵∠∠∠∠D= .
B=4:5,则C= 在⑶.中ABCD, 若A:,
3.平行线之间的距离:
两条平行中,一条直线上任意一点到,叫做这两条平行线的距离4.【结论】两条平行线之间的距离;两条平行线之间的任何两条平行线段;思考:两平行线之间的距离和点与点之间的距离,点到直线的距离有何联系与区别?
1
二、合作、交流、展示:⊥BC例题1、,于E,AF中,⊥AECD于F在,ABCD AD∠EAF=60°,求各内角的度数?
F CBE
三、巩固与应用
)的值可以是(中,∠1.在ABCDA:∠B:∠C:∠D A.1:2:3:4 B.2:2:1:1
C.2:1:2:1
D.1:2:2:1
□ABCD的对角线AC平分∠DAB,则对角线AC与BD的位置关系是2.若______.
3.若平行四边形的两个内角之比为1∶2,则其中较小的内角是()度.
A、90
B、60
C、120
D、45
4.如图AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.
A
D
ACB=32°,如图所示,在ABCD 中,∠BAC=68°,∠5.求∠D 和∠BCD的度数?
B
C
C为顶点画平行四边形,、、C三点不共线,以A、B、:拓展6.已知AB D吗?有几个?你能求出第四个顶点
剪两张对边平行的纸条,随意交叉叠放在一起,转动.7 其中一张,重合的部分构成了一个四边形。
BC的长度有什么关系?为什么?和(1)线段AD这个四边形的每个38°若这个四边形的一个外角∠α=,(2)
?
为什么度数分别是多少内角的?
2
平行四边形的性质()2】【学习目标理解并掌握平行四边形的性质定理;1. 2.应用用平行四边形的性质定理,求解与对角线有关问题;探索和证明平行四边形的性质,平行四边形的性质的简单应用.】【学习重点平行四边形的性质的探索和应用,用规范数学语言的表达.【学习难点】【】学习过程
课前导学:一.平行四边形的性质定理1 :平行四边形的;1.
. 平行四边形的性质定理2:平行四边形的
;∴几何语言叙述:∵ABCD
(从边方面)
(从角方面)
2.如图1,若L∥L,AB和CD是L和L之间任意两条平行线段则AB CD;2211
如图2,若在L1取点A、B,作AB⊥L于点B, DC⊥L于点C,则AB CD.
22A D LA D L 1 1
LL B C
2
2
C
B 图2
图1
A
D
3.平行四边形的性质定理3:平行四边形的对角线.
O
、BDOABCD,AC相交于点几何语言叙述:∵ B
C
∴。
那么AC=______4cmcm,cm,已知OA,OB的长度分别为3,O4.如图,ABCD的两条对角线相交于点
BD=_____cm,边AD长的取值范是_________ .
5. . 15和BD相交于O,△AOB的周长为,AB=6,对角线AC+BD=AC在ABC中,
二、合作、交流、展示:
ACBDO。
和的对角线交于点【例题:1.探究平行四边形的性质定理3】:如图,ABCD OA 与OB,OC与OD,有什么关系?试证明你的结论.
①观察、、、△COD之间的面积关系是BOCAOD②图中△△AOB△.
A
D
O
B
C
3
例题1、公园有一片绿地,它的形状是平行四边形,绿地上要修几条,BC=12m,AC⊥BC,求小路笔直的小路,如图,AB=15m,AD
OC的长,并算出绿地的面积CD,
O,ACBDO E和、交于点BC经过点的对角线于点的直线l分别交边AD 例题2、如图,ABCD,O、、旋转时OE关系是否会变化?OF)试探究OEOF关系;当直线l绕点和F,(1O、、)中的结论是否成立,1F,,与边CDEAB或它们的延长线相交于点试问((2)绕点旋转直线l为什么?FDA
O
EBC
三、巩固与应用
__.
的取值范围是__________,BD=m那么m=8AC1.
ABCD中,对角线和BD交于点O,若AC,AB=6,
已知,则AB2.10O的周长等于ABCD48,对角线AC、BD交于点,△AOD与△AOB的周长的差是==,AD .
SS=
AC上任意一点,求证:P3.如图所示,在ABCD中,是ABP??APD 4
.____ ___cm的周长是则△OBC,,中,.如图,ABCDAE⊥BC∠EAD=60°,AE=2cm,
AC+BD=14cm
A DP CB
5 第3题第4题第题SSSS+S
;
则上任意一点的边如图5., P是ABCDDC, ___
ABP△BCPABCDADP△ABP△△
、引两条高、向,由钝角顶点的周长是6.拓展:如图:ABCD36AABBCAEAF,D=60°EAF,求∠的度数)若∠(1
AF=5 ,)若2(AE= 4 ,求这个平行四边形的面积
4。
