第9章振动与波动9[1].1-9.3
大学物理振动波动PPT课件

b. 和t 求解
如 :
旋转矢量法
解析法 由 x00.0 40.0c8os
π
3
旋矢法
v 由0 旋 矢A 图si n 0 判s 断 i n 0 π3
A π
x/m
知 π
.
3
o
3
0.04 0.0158
15.
[例2] 一简谐运动的 x – t 曲线,如图所示,求:
(1) 初相 ;(2) 求运动方程,并用旋矢表示之;
讨论: a. 所含各种情况
= 0 , 直线(谐振动)
y A1 x A2
= /2 , 3/2 正椭圆 如 A1=A2 圆
— 其他情况 斜椭圆
b. 右旋与左旋
如 = 2 - 1>0
y 超前x 顺时针旋转(右旋)
如 = 2 - 1<0
x超前y 逆时针旋转(左旋).
28
28.
*三 .多个同方向同频率简谐运动的合成
两边对 t 求导
d(1mv21kx2)0 dt 2 2
.
d2x k x 0 dt2 m
21
21.
[例] 求图示系统的振动频率 .设轻绳与定滑轮
间无相对滑动.
分析:
k
J,r
a. 寻找平衡位置 , 建立图示坐标系 mgkx0
b. Ⅰ法 动力学法
m
o
x0
偏离x 平动与转动隔离
对m : mgFT ma
对J : F Trk(x0x)J
Fr 2mr2
at
5 (Rr)
d2
dt2
at r
d2
dt 2
2
(sin)
R FT c r
F
mg
T 2π 7(Rr)l
高二物理竞赛课件:振动和波动

dt
23
t 0 , v 3 (m / s) , a 2 / 2(m / s 2 )
2)振动曲线:
x
A
o
t
-A
T
振幅:旋转矢量的模A
圆频率:旋转矢量的角速度 位相:旋转矢量与Ox轴的夹角t+
y
M
A
t
M0
P
O
x
x
4.简谐振动的速度和加速度
x Acos(t )
v dx A sin(t ) A cos(t )
dt
2
a dv A 2 cos(t ) A 2 cos(t )
dt
➢ 速度和加速度作与位移同频率的简谐振动
➢ vm A , am A 2
➢ 速度位相比位移位相超前/2;加速度位相比 位移位相超前。
2A ωAA
a v
x
OO
t
A
T
例 9-1 已知某质点的振动曲线如图所示,求: (1)质点的振动表达式; (2) t 0 时质点的速度和加速度。
x(cm)
4
时间按余弦(或正弦)规律随时间变化:
x Acos(t )
则物体的运动为简谐振动。
2.描述简谐振动的物理量
x Acos(t )
2.1 周期和频率
T 2 , 1
T 2
2.2 振幅 A
2.3 位相与初相
t 时刻的位相: t+ 初相:
3.简谐振动的表示
1)振动表达式:x A cos(t )
§9-1 简谐振动的描述 §9-2 简谐振动的动力学特征 §9-3 简谐振动的合成 *§9-4 阻尼振动 受迫振动 共振
1.简谐振动的定义
1.1 机械振动 物体在一定位置附近作来回往复的运动。
《振动和波动的关系》课件

波长公式
波长与振动的速度和频率有 关: λ=v/f
单位
振动的单位是赫兹(Hz), 波动的单位是米(m)。
振动和波动的应用领域
1 医学
超声波用于医学成像和治 疗。
2 通信
无线电波和光纤传输用于 信息传输。
3 工程
振动传感器和结构动力学 用于工程设计。
振动和波动的实验和观测方法
1
实验
利用弹簧和质量系统进行振动实验。
2
观测方法
使用光学或电子仪器进行波动的观测。
3
数据分析
通过记录数据并应用相关分析方法来研究振动和波动现象。
振动和波动的未来发展趋势
技术创新
新技术的发展将推动振动和波动在各个领域的应用。
科学研究
对振动和波动现象的深入研究将带来新的发现和理 解。
振动和波动的关系
振动和波动是物理学中重要的概念,它们描述了物体或系统中的能量传播和 振动的特性。本课件将探讨振动和波动的定义、特点、公式和应用领域。
振动和波动的定义
1 振动
物体在时间内往复运动的过程。
2 波动
能量在介质中传输的过程,通常以波的形式呈现。Biblioteka 振动和波动的特点频率
振动的周期或波动的频率是描 述其快慢的特征。
振幅
振动或波动过程中的最大偏离 或变化。
波长
波动中相邻两个相位相同点之 间的距离。
振动和波动的相同点和不同点
相同点
都是描述物体或系统中能量传播和振动的过程。
不同点
振动是指物体自身的周期或往复运动,而波动是能 量在介质中传输的过程。
振动和波动的公式和单位
振动公式
振动的周期和频率可以用以 下公式描述: T=1/f
第九章-振动与波动基础PPT课件

单位:弧度每秒(rad/s)
T、γ、ω反映了振动的快慢,由简谐振动系统的物理 性质决定,故称它们为固有周期、固有频率、固有 圆频率
对弹簧振子:
T 2 m
k 3 相位
1 k 2 m
k m
相位 (ω t +φ): 初相位 φ :
决定物体在任意时刻的振动状态 决定初始时刻振动物体的运动状态
注意 相位既可以决定物体的振动状态
x=9.810-2cos(10t+3/2) m
固有频率
对同一谐振动取不同的计时起点不同,但、A不变
例题2 如图所示,振动系统由一倔强系数为k的 轻弹 簧、一半径为R、转动惯量为I的 定滑轮和一质量为 m的 物体所组成。使物体略偏离平衡位置后放手,任 其振动,试证物体作简谐振动,并求其周期T.
解:取位移轴ox,m在平 衡位置时,设弹簧伸长量
0 arc(tgvx00 )0,
m
O
x
由x0=Acos0=-0.098<0 cos0<0, 取0=
振动方程为:x=9.810-2cos(10t+) m
X
(2)按题意 t=0 时 x0=0,v0>0
1 g
x0=Acos0=0 , cos0=0 0=/2 ,3/2 2 2 l
v0=-Asin>0 , sin 0 <0, 取0=3/2 1.6Hz
x
写出振动方程,并计算振动频率。
解:⑴ 确定平衡位置 mg=k l 取为原点
X
k=mg/ l
令向下有位移 x, 则 f=mg-k(l +x)=-kx
作简谐振动 设振动方程为
xA cos t (0)
k m
gl
9.8 1r0a/d s 0.098
振动和波动

G为介质的切变弹性模量; 为质量密度。 在同一种固体介质中,由于固体材料切变弹性模量G 小于杨氏弹性模量Y,所以横波波速比纵波波速小。 ④ 在液体和气体只能传播纵波,其波速为:
v K
K为介质的容变弹性模量; 为质量密度。
三、平面简谐波的波动方程
简谐波:简谐振动在空间传播所形成的波叫简谐波。
0
4
8
12
16
20
结论:
(1) 质元并未“随波逐流” ,波的传播不是介质质元的传播。 (2) “上游”的质元依次带动“下游”的质元振动。 (3) 某时刻某质元的振动状态将在较晚时刻于“下游”某 处出现---波是振动状态的传播。
(4) 同相点----质元的振动状态相同。
3.波是相位的传播。 沿波的传播方向,各质元的相位依次落后。
的频率等于波源振动频率。
6.物体的弹性和波速 机械波的传播速度完全取决于介质的弹性性质和惯 性性质。即介质的弹性模量和介质的密度。 ① 对于柔软的绳索和弦线中横波波速为: T 为绳索或弦线中张力; 为质量线密度。 ② 细长的棒状介质中纵波波速为:
v Y
v
T
G
Y为介质的杨氏弹性模量; 为质量密度。 ③ 各向同性均匀固体介质横波波速:
波速--某一定的振动状态(或振动相位)在单位时间内所传 播的距离,称为波的相速,简称波速,用 v 表示。 频率—波在单位时间内前进的距离中所含完整波的数目, 或单位时间内,通过波射线上一点整波的数目。
1 --表示波在空间中的周期性 --表示波在时间上的周期性 T 由于波源作一次全振动,波前进一个波长的距离,所以波 v
x 2 A2 cos(t 2 )
( t 2 ) ( t 1 ) 2 1
复旦大学大学物理 1-9 第9章 波动

y T y u 2 2 t l x 2 2 y 1 y 2 2 x u t2
2 2
T
l
2. 细棒中的纵波波速
u
Y
Y 杨氏模量,密度
F L 胡克定理 Y S L
F L 由 胡克定理 Y S L F y Y y为x处的微小形变 S x
1 2 2 I A u 2
SI : W m
2
[例]在截面积为S的圆管中,有一列平面简谐波,其波动的 表达式为 量密度为
y A cos(t 2 πx / )
。管中波的平均能
w ,则通过截面S的平均能量是多少?
P w uS
T
u
2π
2π
P
2π
wS
空间周期性
u
x
T
k
相位差和波程差的关系:
2 π
k x
[例 ]已知:波向右传播,波速为u, a点的振动式为: 如图建立坐标,求波动式及b点振动式。 y a
xa
ya A cost
u o l b x
y A cost k x xa
二、平面简谐波
简谐波:波源作简谐振动,在波传到的区域,媒质中的 质元均作简谐振动 。 设
yo A cos(t )
u
y
波速 u
任一点p
假设:媒质无吸收(质元振幅均为A) x o 图中p点比o点落后时间:
x x
x o: t p: t u
则
x y A cos t u
x A sin t kx E Sx Sx
物理振动与波动教学

振动与波动在音乐中的应用:音乐通过振动与波动产生声音,使人们享受美妙的旋律。
振动与波动在通讯中的应用:无线电波的传输利用了振动与波动的原理,实现了远距离的信息 传递。
振动与波动在医疗领域的应用:超声波诊断技术利用振动与波动的原理,能够无创检测人体内 部结构。
振动与波动在建筑领域的应用:地震工程通过研究振动与波动对建筑的影响,提高建筑的抗震 性能。
波动能量的概念:波动能量是指波动过程中所传 递的能量,包括机械能、电磁能等。
波动能量的传播方式:波动能量的传播方式包括 机械波的传播和电磁波的传播。机械波的传播需 要介质,而电磁波的传播不需要介质。
波动能量的传播速度:波动能量的传播速 度与介质有关。对于机械波,其传播速度 取决于介质的性质;对于电磁波,其传播 速度为光速。
水波:水波是水面的振动现象,水波在传播过程中会遇到各种障碍物,发生反射、折射和干 涉等现象,可以用于水下探测和海洋科学研究。
理论教学:讲解 物理原理、公式 和概念,帮助学 生建立基础知识 体系。
实践教学:通过 实验、演示和互 动,让学生亲身 体验物理现象, 加深对理论知识 的理解。
结合方式:交替 进行理论教学和 实践教学,相互 补充,提高教学 效果。
波动能量的应用:波动能量的应用非常广泛,例 如声波可以用于通信、探测和成像等,电磁波可 以用于无线通信、卫星通信、雷达和遥感等。
波动方程的建立: 基于物理原理和数 学推导
求解方法:分离变 量法、积分变换法 等
实例分析:不同类 型波动方程的求解 过程
实际应用:波动方 程在物理、工程等 领域的应用
振动与波动在机 械工程中的应用: 用于检测机械设 备的振动和位移, 提高设备的稳定 性和可靠性。
振动是一种能量传 递方式
振动与波动基础

振动与波动基础振动与波动是物理学中重要的基础概念,它们在我们日常生活中无处不在,并且在各个领域都有着广泛的应用。
本文将介绍振动与波动的概念、特性以及其在自然界和科学研究中的应用。
一、振动的概念与特性振动是物体在某一固定点周围的周期性往复运动。
振动有以下几个基本特性:1. 振动的周期性:振动是具有周期性的运动,即在一定时间内,物体会重复经历相同的运动过程。
例如,钟摆在沿着一定路径来回摆动时,就是一种周期性的振动。
2. 振动的频率与周期:振动的频率指的是单位时间内振动完成的次数,单位为赫兹(Hz)。
而周期是指振动完成一个完整往复运动所需要的时间,单位为秒(s)。
频率与周期之间满足倒数关系,即频率等于1除以周期。
3. 振幅:振幅是指振动过程中物体离开平衡位置的最大距离。
振幅越大,物体的振动范围就越大;振幅越小,物体的振动范围就越小。
4. 谐振与非谐振:谐振是指振动中所受迫力与振动频率相同的情况。
当一个物体受到与其振动频率相同的外力作用时,会出现谐振现象,此时振幅会不断增大。
非谐振则是指振动中所受迫力与振动频率不同的情况。
二、波动的概念与特性波动是物理学中描述能量在空间传播的过程。
波动有以下几个基本特性:1. 波长与周期:波长是指在一个完整波动过程中,波的长度。
波长的单位通常是米(m),常用符号是λ。
周期是指波的一个完整循环所需要的时间,单位是秒(s)。
波长与周期之间满足长度与时间的倒数关系。
2. 频率与波速:频率是指波动中单位时间内波的个数,单位是赫兹(Hz)。
波速是指波动中波传播的速率,单位是米每秒(m/s)。
频率与波速之间满足长度与时间的正比关系。
3. 波的振幅:波的振幅是指波动中波的最大偏离程度。
波的振幅越大,波动的能量传递越强。
4. 波的传播方式:波动可以分为机械波和电磁波两种类型。
机械波是需要介质媒介传播的波动,如水波、声波等;电磁波则是不需要介质传播的波动,如光波、无线电波等。
三、振动与波动在自然界和科学研究中的应用振动与波动在自然界和科学研究中有着广泛的应用。
大学物理第九章振动学基础习题答案

第九章 振动学习题9-1 一小球与轻弹簧组成的振动系统,按(m) 3ππ8cos 05.0⎪⎭⎫ ⎝⎛+=t x ,的规律做自由振动,试求(1)振动的角频率、周期、振幅、初相、速度最大值和加速度最大值;(2)t=1s ,2s ,10s 等时刻的相位;(3)分别画出位移、速度和加速度随时间变化的关系曲线。
解:(1)ω=8πs -1,T=2π/ω=0.25s ,A=0.05m ,ϕ0=π/3,m A ω=v ,2m a A ω=(2)π=8π3t φ+ (3)略9-2 一远洋货轮质量为m ,浮在水面时其水平截面积为S 。
设在水面附近货轮的水平截面积近似相等,水的密度为ρ,且不计水的粘滞阻力。
(1)证明货轮在水中做振幅较小的竖直自由运动是谐振动;(2)求振动周期。
解:(1)船处于静止状态时gSh mg ρ=,船振动的一瞬间()F gS h y mg ρ=-++ 得F gSy ρ=-,令k gS ρ=,即F ky =-,货轮竖直自由运动是谐振动。
(2)ω==,2π2T ω==9-3 设地球是一个密度为ρ的均匀球体。
现假定沿直径凿通一条隧道,一质点在隧道内做无摩擦运动。
(1)证明此质点的运动是谐振动;(2)计算其振动周期。
解:以球心为原点建立坐标轴Ox 。
质点距球心x 时所受力为324433x mF G G mx x πρπρ=-=-令43k G m πρ=,则有F kx =-,即质点做谐振动。
(2)ω==2πT ω== 9-4 一放置在水平桌面上的弹簧振子,振幅A =2.0 ×10-2 m ,周期T s 。
当t =0时,(1)物体在正方向端点;(2)物体在平衡位置,向负方向运动;(3)物体在x ×10-2m 处,向负方向运动;(4)物体在x =-×10-2 m 处,向正方向运动。
求以上各种情况的振动方程。
解:ω=2π/T=4πs -1(1)ϕ0=0,0.02cos4(m)x t π=(2)ϕ0=π/2,0.02cos 4(m)2x t ππ⎛⎫=+ ⎪⎝⎭(3)ϕ0=π/3,0.02cos 4(m)3x t ππ⎛⎫=+ ⎪⎝⎭(4)ϕ0=4π/3,40.02cos 4(m)3x t ππ⎛⎫=+ ⎪⎝⎭9-5 有一弹簧,当其下端挂一质量为m 的物体时,伸长量为9.8 ×10-2 m 。
第9章-振动和波

恢复力与弹性力
图中的“弹簧振子”有一个平衡位置 O,在那个位 置,弹簧既没有伸长也没有缩短,对物体不施加作用力, 物体得以平衡。试把物体从平衡位置移开,例如移到P点, 然后放手,拉长的弹簧有收缩的趋势,它施加于物体的 作用力驱使物体向平衡位置移动。这种驱使物体向平衡 位置移动的力叫作恢复力。
恢复力和惯性这一对矛盾 不断斗争,它们的作用交替消 长,力学系统就在平衡位置左 右一定范围内来回振动。
(2) 2 1 (2k 1) , k 0, 1, 2,
则 A | A1 A2 |
(3) 2 1 为一般值
则 | A1 A2 | A A1 A2
2. 方向相同,频率不同的两个简 谐振动的合成
设
x1 x2
A1 cos(1 t 1) A2 cos(2 t 2
)
为简单起见,设
A1 A2 A
2. 因为 F 的数值大小正比于位移 x 的大小,所以物体 偏离平衡位置越远,则它受到的拉回平衡点的力也 越大。
恢复力与弹性力
重力也可以成为恢复力。如 图所示的单摆,如将小球从 平衡位置拉到P点再松手,小 球将在平衡位置O点附近往 复摆动。它的结构虽与上述 弹簧振子完全不同,但它们 的运动性质是十分相似的。
的质量为 m,弹簧的倔强系
数为 k,选取 x 轴,以平衡
位置 O 为原点,则振子的运
动方程为:
mx kx
令:
2 k
m
解为: x A cos( t 0 )
其中 A, 0 为待定常数,由初始条件确定。称这种运
动为简谐振动。
简谐振动的描述
2. 简谐振动的特征参量
x A cos( t 0 )
描绘一个简谐振动的特征参量有三个:振幅、角频 率和相位。
大学物理物理学课件振动与波动

大学物理物理学课件振动与波动一、教学内容本节课的教学内容来自于大学物理教材的“振动与波动”章节。
具体内容包括:振动的基本概念、简谐振动的特点、周期性波动的特性、波的传播与干涉、衍射等现象。
二、教学目标1. 使学生了解振动与波动的基本概念,理解简谐振动的特点,掌握周期性波动的特性。
2. 培养学生运用物理知识分析问题、解决问题的能力。
3. 培养学生的团队合作意识,提高学生的实践操作能力。
三、教学难点与重点1. 教学难点:振动与波动的数学表达式及其物理意义。
2. 教学重点:简谐振动的特点,周期性波动的特性,波的传播与干涉、衍射现象。
四、教具与学具准备1. 教具:多媒体课件、振动实验仪、波动演示仪。
2. 学具:笔记本、笔、实验报告册。
五、教学过程1. 实践情景引入:通过展示生活中常见的振动与波动现象,如音叉振动、水波传播等,引发学生对振动与波动的兴趣。
2. 知识讲解:介绍振动与波动的基本概念,讲解简谐振动的特点,阐述周期性波动的特性。
3. 例题讲解:分析振动与波动的数学表达式及其物理意义,通过示例题目,引导学生理解并掌握相关知识。
4. 随堂练习:布置具有代表性的题目,让学生现场解答,巩固所学知识。
5. 实验操作:分组进行振动实验和波动演示,使学生直观地了解振动与波动现象。
6. 课堂讨论:引导学生探讨振动与波动在现实生活中的应用,激发学生的学习兴趣。
7. 知识拓展:介绍振动与波动的研究领域及其发展前景,激发学生的学术追求。
六、板书设计板书内容主要包括振动与波动的基本概念、简谐振动的特点、周期性波动的特性、波的传播与干涉、衍射等现象的关键词和公式。
七、作业设计1. 题目一:振动与波动的基本概念答案:振动是指物体围绕其平衡位置做周期性的往复运动;波动是指振动在介质中传播的现象。
2. 题目二:简谐振动的特点答案:简谐振动是指物体在恢复力作用下,围绕平衡位置做周期性的往复运动,且满足胡克定律。
3. 题目三:周期性波动的特性答案:周期性波动是指波动过程中,质点振动的形式和振幅不变,周期性变化的物理量随时间呈正弦或余弦函数变化。
波动_大学物理

2
1
1 2
[1 cos 2(t kx)]d(t kx) 1 2
w
2 A 2
中国人民大学物理系徐靖编
w y
A
2 2
u
w
A 0
2
能量“一堆 一堆”地传 播
x
y 0 处,w w max ,y A 处,w 0 ,
中国人民大学物理系徐靖编
二. 能流密度
•波函数:振动量Ψ 随时间、空间的变化规律
Ψ Ψ ( x、y、z、t)
•建立波函数的依据
波的空间、时间周期性
沿波传播方向各质点振动状态(相位)相继落后 (滞后效应)
中国人民大学物理系徐靖编
•只讨论一维情况:
对平面简谐行波建立Ψ Ψ ( x , t )的数学形式
已知: 波线上任一点O的振动方程
波前(波阵面): 传在最前面的波面
波面
波 线
平面波
球面波
中国人民大学物理系徐靖编
二、波的特征量 波的特征:空间和时间上的周期性
1. 周期T、频率
即介质中各质点振动的周期和频率,由波源振动 情况决定。
描述波动的时间周期性
2. 波长
1 T
时间频率
同一波线上,相邻的相位差为 2 的两点间的距离 描述波动的空间周期性
周期T. 振幅A 某时刻 v
初相 0 该时刻各质点位移 波长 , 振幅A
其方向参看下一时刻状况 特征
某质点 v 方向参看前一质点
曲线形状随t 向前平移
只有t=0时刻波形才能提供初相
对确定质点曲线形状一定
中国人民大学物理系徐靖编
四.波函数(波动方程的积分形式)
简谐振动:微分方程 平面简谐波:积分形式 积分形式 微分方程
《振动和波动》课件

由摩擦力或阻尼器对振动物体的影响。
波动的类型——机械波、电磁波、声 波等
1 机械波
需要媒质传播的波动。
3 声波
由物体振动产生的机械波。
2 电磁波
不需要媒质传播的波动。
波动的传播——波的速度、波长与频 率的关系
1 波速
波动传播的速度。
2 波长
波动中相邻两个点之间的距离。
3 频率
波动在单位时间内重复的次数。
振动物体复位受力与位移成正比。
2 非线性振动
振动物体复位受力与位移不成正比。
自由振动和受迫振动
1 自由振动
物体在没有外力作用下的振动。
2 受迫振动
物体在外部力作用下的振动。
ቤተ መጻሕፍቲ ባይዱ
振动的频率和周期
1 频率
振动在单位时间内重复的次数。
2 周期
振动完成一个完整循环的时间。
谐振和阻尼振动
1 谐振
物体在外界周期性作用力下产生共振现象。
《振动和波动》PPT课 件 什么是振动和波动
振动是物体周围的来回运动,而波动则是物质在空间传递的起伏运动。了解 振动和波动的基本概念对深入研究其它相关领域至关重要。
振动和波动的区别
振动
是物体周围的来回运动。
波动
是物质在空间传递的起伏运动。
区别
振动是局部的,波动是传递的。
线性振动和非线性振动
1 线性振动
第九章 振动 习题册解答 (1)
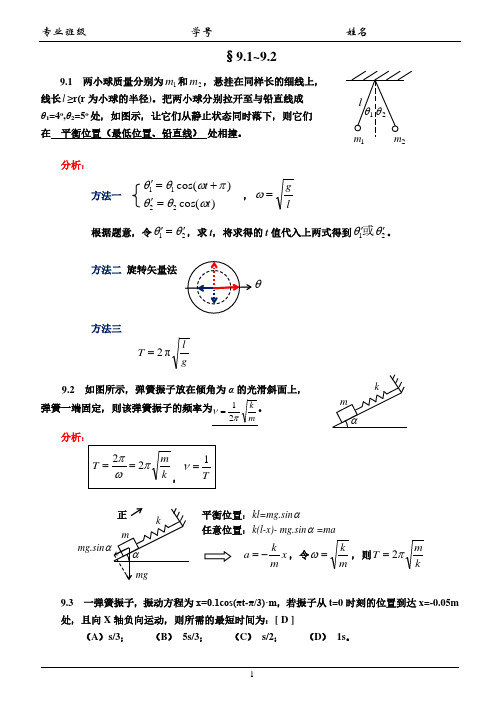
分析:总能量: E = 1 k A2 2
势能:
E P1
=
1 2
k
(A)2 3
=
1 9
E;
动能:
E k1
=
E
-
E P1
=
8 9
E;
E P2
=
1 2
k
(A)2 2
=
1 4
E
E k2
=
E - EP2
=
3 4
E
9.8 把单摆小球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ,然后 由静止释放,使其摆动。从放手时开始计时,若用余弦函数表示运动方程,则该单摆振动的初 相位为:[ B ]
(m)
§9.3~9.7
9.6 一个弹簧振子,作简谐振动,已知此振子势能的最大值为 100J。当振子处于最大位移
的一半处时其动能瞬时值为:[ C ]
(A) 25J; (B) 50J; (C) 75J; (D) 100J。
分析:总能量 E = 1 k A2 = 100J 2
振子处于最大位移一半时,势能为 EP
2π m
分析:
T = 2π = 2π ω
m ν=1 k, T
k m
α
正
k
m
mg.sinα α
mg
平衡位置:kl=mg.sin α 任意位置:k(l-x)- mg.sinα =ma
a = − k x ,令ω = k ,则T = 2π m
m
m
k
9.3 一弹簧振子,振动方程为 x=0.1cos(πt-π/3)·m,若振子从 t=0 时刻的位置到达 x=-0.05m 处,且向 X 轴负向运动,则所需的最短时间为:[ D ]
大学物理下册目录
第十章 波动
10 - 1 机械波的几个概念 10 - 2 平面简谐波的波函数 10 - 3 波的能量 能流密度 10 - 4 惠更斯原理 波的衍射和干涉 10 - 5 驻波 10 - 6 多普勒效应 10 - 7 平面电磁波
第9章振动与波动

第九章振动与波动【教学目的】让学生理解简谐振动中各振动参量的物理意义,掌握同方向、同频率的简谐振动合成方法。
理解简谐波的波动方程及其各波动参量的物理意义,了解干涉现象并掌握其规律。
【教学要求】一、了解简谐振动的特征及其运动方程;二、掌握描述简谐振动的物理量——振幅、周期、频率和相位;三、了解简谐振动的旋转矢量表示法;四、了解简谐振动的能量;掌握同方向、同频率简谐振动的合成方法。
五、掌握描述波动的物理量——波长、频率和波速;六、理解简谐波的波动方程和波动的能量;七、了解惠更斯原理,理解波的叠加原理和波的干涉。
【教学重点】一、简谐振动方程、描述简谐振动的各物理量;二、同方向、同频率的两个简谐振动的合成。
三、简谐波的波动方程及描述波动的各物理量;四、波的干涉。
【教学难点】振动相位的概念,波动方程的物理意义【教学方法】讲授【教学内容】第一讲:(2课时,共3讲)引言:2 振动是产生波动的起因,波动是振动在空间的传播振动——某物理量在一定值附近作周期性的变化。
有机械振动、电磁振荡波动——某种振动在空间的传播。
有机械波、电磁波无论是机械的,还是电磁的振动或波动,虽然在本质上各不相同,但遵从的运动规律具有共同性。
§9-1 简谐振动一、简谐振动的运动方程 弹簧谐振子——理想模型由虎克定律可得谐振子的运动方程222d 0d xx tω+= ——谐振动的微分方程 其通解为:0cos()x A t ωϕ=+ 或 0sin()x A t ωϕ'=+ ——谐振动的运动方程,其中的A 、ϕ(ϕ')由振动的初始条件确定说明:1.振动参量——描述振动的特征2. 振动的速度、加速度3.A 、 ϕ0 的确定 二、谐振动的能量k p E E E =+22220111===222mA kA m ωv1.在振动过程中,动能和势能不断地相互转化,但总能量保持不变;2.总能量E ∝A 2ω23.E K (t )、E P (t )的变化周期为T /2 三、谐振动的特征1. F =-kx ——动力学特征2. a =-ω2x ——运动学特征3. 动能势能相互转化,其和不变——能量特征三者相关,满足其一即为谐振动——判定谐振动的方法 四、旋转矢量法表示谐振动矢量A 以w 逆时针转动时,端点在x 轴上的投影——谐振动物理学Ⅲ教案山西农业大学物理系 郭 锐3(用动画说明之) 说明:(1)各振动参量与旋转矢量A 的对应关系 (2)旋转矢量A 本身不作谐振动(3)应用:①比较两振动的相位差 ∆ϕ= ϕ2-ϕ1②用来确定振动的初相 ③讨论振动的合成§9-2 简谐振动的合成一、同方向的两个简谐振动的合成 1. 同方向、同频率的合成1101cos()x A t ωϕ=+,2202cos()x A t ωϕ=+则合振动12x x x =+0cos()A t ωϕ=+——谐振动其中A =1012020101202sin sin arctgcos cos A A A A ϕϕϕϕϕ+=+用旋转矢量法合成:振动1、2的ω相同,相位差保持不变,则合矢量A 亦以ω转动——合成结果同上(用动画说明)。
2024版大学物理物理学课件振动与波动

01振动定义02振动分类物体在平衡位置附近所做的往复运动。
根据振动的性质可分为简谐振动、阻尼振动、受迫振动等。
振动定义及分类简谐振动模型建立弹簧振子模型由质量块和弹簧组成的系统,在忽略摩擦等阻力的情况下,可视为简谐振动模型。
单摆模型在重力作用下,细线悬挂的小球绕固定点做小幅度的摆动,可视为简谐振动模型。
简谐振动方程与特征量简谐振动方程描述物体简谐振动的数学表达式,如$x(t) = Acos(omega t + varphi)$。
特征量包括振幅$A$、角频率$omega$、初相位$varphi$ 等,分别表示振动的幅度、频率和初始状态。
简谐振动能量转换动能与势能转换在简谐振动过程中,物体的动能和势能不断相互转换,总能量保持不变。
机械能守恒在理想情况下,简谐振动的机械能(动能与势能之和)是守恒的,即不随时间变化。
阻尼振动的特点振幅逐渐减小;振动能量逐渐转化为其他形式的能量。
振动周期不变;阻尼振动的定义:阻尼振动是指振幅逐渐减小的振动,由于振动系统受到摩擦或其他阻力而产生。
阻尼振动现象及特点•受迫振动的定义:受迫振动是指系统在周期性外力的作用下产生的振动。
01受迫振动的产生条件02存在周期性外力;03外力频率与系统固有频率不同。
01受迫振动的规律02受迫振动的频率等于外力频率;03当外力频率接近系统固有频率时,振幅急剧增大,产生共振现象。
•共振现象的定义:当受迫振动的外力频率等于系统固有频率时,振幅达到最大值的现象称为共振。
共振的危害对建筑物、桥梁等结构造成破坏;对机器设备造成损坏;01对人体健康造成影响,如引起头晕、恶心等症状。
02共振的防范措施03避免使系统固有频率与外界频率相等;0102采用隔震、减震措施;提高系统阻尼,降低振幅。
实际应用举例乐器中的受迫振动01乐器中的弦、膜等部件在周期性外力的作用下产生受迫振动,发出美妙的声音。
建筑结构中的阻尼振动02在建筑结构设计中,通过增加阻尼材料或结构,减小地震等外力对建筑物的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
o
x
19
C、当 ∆ϕ为其他值时,称两振动不同相。 、 为其他值时,称两振动不同相。 ∆ϕ > 0 则X2比X1 的位相超前。 的位相超前。 ∆ϕ < 0 则X2比X1 的位相落后。 的位相落后。 用振幅矢量分析位相的关系 注意: 注意: ∆ϕ 的取值范围在 π 内。
x2
∆ϕ
x1
∆ϕ
x1
x2
o
x
o
x
-0.5 -1
x1 + x 2
2
1
20 -1
40
60
80
100
120
-2
设分振动 合振动
x1=Acosω 1 t ω x2=Acosω 2t ω x = x1+ x2
2
1
20 -1
40
60
80
100
120
-2
ω1 − ω 2 ω1 + ω 2 x = 2 A cos( t ) cos( t) 2 2
24
2 A = A2 + A2 + 2A A2 cos(ϕ2 −ϕ1 ) 1 1
讨论: 讨论:两种特殊情况 (1)若两分振动同相 若两分振动同相 ϕ 2−ϕ 1=±2kπ ± π (k=0,1,2,…)
v A
v A1
v A2
则 A = A1 + A2 ,合振幅最大。 合振幅最大。 X1 t X2 t 25
单位是 S-1 或 赫兹 Hz
6
3)、 初始条件 )、 初始时刻( )振动小球的位移X 和速度V 初始时刻(t=0)振动小球的位移 0和速度 0的 取值称为初始条件。 取值称为初始条件。
x 0 = A co s ϕ
v0 = − Aω sin ϕ
联立求得
2 A = x0 + 2 v0
ω2
■
v0 tan ϕ = − ω x0
2、 旋转矢量图和复数表示 、
1)、 旋转矢量表示法 )、
t
x = A cos(ωt + ϕ )
A
ωt A
ϕ
ω
0时刻
o
x
A 振幅矢量 ω 圆频率 ϕ 初相 ■
x
16
利用旋转矢量很容易求出简谐振动的位相和运动状态 例. 已知位相求状态 问状态? 如:位相 ωt1 + ϕ = π 3 ,问状态? 且向 负向运动。 x = A 2 ,且向x 负向运动。
31
2.∆ϕ =− π
π 2
右旋 y2 x2 + 2 = 1 正椭圆 2 A1 A 2 左旋
A1 = A2 圆
2
斜椭圆
3.Δ =其它值 ϕ
ϕ Δ 在0 Δ 在0 ϕ
y
A2
π 之间为右旋
−π
之间为左旋
− A1
− A2
A1
x
32
∆ϕ 为任意值时,合振动的轨迹一般为椭圆 为任意值时,
∆ϕ = 0
π
4
π
2 -0.2
4
6
8
10
12
x
t
k m o x x
4
简谐振动势能、 简谐振动势能、动能一个周期内平均值 动能
Ek 1 = T
T
∫
0
T
kA E k dt = 4
2
( 2 sin 2 α = 1 − cos 2α )
势能
E
p
1 = T
∫
0
kA E p dt = 4
2
( 2 cos 2 α = 1 + cos 2α )
v A2
v A
ω
ω
vω A1
ϕ1
t =0
ϕ2 ϕ
x2
x1
x
X
合振动是简谐振动, 其频率仍为ω 合振动是简谐振动 其频率仍为ω,
24
合振动 x =A cos(ω t+ϕ ) ω ϕ
v A2
ω
vω A1
ϕ1
v A
ω
t =0
ϕ2 ϕ
其中
x2
x1
x
X
2 A = A2 + A2 + 2A A2 cos(ϕ2 −ϕ1 ) 1 1 A sinϕ1 + A2 sinϕ2 tgϕ = 1 A cosϕ1 + A2 cosϕ2 1
-1
3
描述简谐振动的基本量 由 x = A cos( ωt + ϕ )
A, ω , ϕ .
A
ω
振幅(最大位移的绝对值)。 振幅(最大位移的绝对值)。
或者 圆频率 。单位 rad/s 或者/s 由系统性质决定(故称固有频率)。 由系统性质决定(故称固有频率)。
ω =
k m
( ωt + ϕ )
ϕ
位相(决定振动状态的物理量)。 位相(决定振动状态的物理量)。 称初位相。由时间零点决定。 称初位相。由时间零点决定。
21
3、简谐振动的能量 、
1 E k = mv 2 动能 2 1 = mA 2 ω 2 sin 2 (ω t + ϕ ) 2
E p Ek
1 0.8 0.6 0.4 0.2
势能
总能
1 E p = kx 2 2 1 = kA 2 cos 2 (ω t + ϕ ) 2 E = Ek + E p
1 1 2 = mv + kx 2 2 2 1 1 2 = kA = m ( A ω ) 2 2 2 守恒! 守恒! ■
x2 = A2 cos(ωt + ϕ 2 )
他们的位相差为
x2
∆ϕ = ϕ2 − ϕ1
∆ϕ
■
ϕ2
o
ϕ1
x1
x
18
A、当 ∆ϕ 为0或者 2π的整数倍 、 或者 两个简谐振动的振动矢量始终同向。 两个简谐振动的振动矢量始终同向。 同相。 称两振动同相 称两振动同相。
o
x
19
B、当 ∆ϕ为 π 或者π 的奇数倍 、 两个简谐振动的振动矢量始终反向。 两个简谐振动的振动矢量始终反向。 反相。 称两振动反相 称两振动反相。
6
总结: 总结: 凡是运动方程具有以下形式 运动方程
d dt
2
x
2
+ ω
2
x = 0
或振动方程具有以下形式 振动方程
x = A cos( ω t + ϕ )
都是简谐振动。 都是简谐振动。 ■
3
4)、 单摆也是简谐振动 )、 单摆的长为L,摆球的质量为 , 单摆的长为 ,摆球的质量为m, 当摆球的角位移 θ 很小时
25
2. 两同方向不同频率(相差较小)的简谐振动的合成 两同方向不同频率(相差较小)
ω1 ≈ ω 2
合振幅时强时弱的现象称为拍 拍频
∆ν = ν 1 −ν 2 = 0.1HZ
20 40 60 80 100 120
x1
1 0.5
-0.5 -1
t t t
28
x2
1 0.5 20 40 60 80 100 120
讨论: 的关系。 讨论:位相 ( ωt + ϕ )和位移 x 的关系。 ■ 5
另外两个重要的物理量---周期和频率 另外两个重要的物理量 周期和频率 周期
T=
2π
ω
单位是 S
振动往返一次的时间。 振动往返一次的时间。
1 ω = 频率 ν = T 2π
单位时间内振动的次数。 单位时间内振动的次数。■
第10章 章
动画
内容
§1 简谐振动 §2 两个简谐振动的合成 §3 阻尼振动 受迫振动 共振 §4 简谐波 §5 惠更斯原理 §6 波的叠加 干涉 驻波 §7 多普勒效应
机械振动 物体在平衡位置附近作往复周期性运动, 物体在平衡位置附近作往复周期性运动,称为机械 振动。 振动。 最简单机械振动是简谐振动。 最简单机械振动是简谐振动。 平衡位置(速度最大 ,最大位移(速度 平衡位置 速度最大),最大位移 速度 速度最大 为0),回复力 , 电磁量( 电磁量(如I 、V、 E、 B) 、 、 电磁振动 ■
2
3π π
4
π
π
5π π
4
3π π
7π π 2
5
2π
33
4.不同频率垂直方向简谐振动的合成 4.不同频率垂直方向简谐振动的合成 一般轨迹曲线复杂,且不稳定。 一般轨迹曲线复杂,且不稳定。 • 两振动的频率成整数比时,合成轨迹稳定, 两振动的频率成整数比时 合成轨迹稳定, 整数比 称为李萨如图形 李萨如图形。 称为李萨如图形。如: 1 y
1 2 1 因此: 因此: Ek = E p = kA = E 4 2
■
4
两个简谐振动的合成 §2 两个简谐振动的合成 1. 两同方向同频率的简谐振动的合成 ω1 = ω 2 x1=A1cos(ω t+ϕ 1) ω ϕ 分振动 : x =A cos(ω t+ϕ ) ω ϕ2 2 2 合振动 : x = x1+ x2 由矢量合成法 可得 x =A cos(ω t+ϕ ) ω ϕ
θ0
θ T
Fτ
d 2θ g + θ=0 2 l dt
振动方程
θ = θ 0 cos(ωt + ϕ )
o
■ 所以,单摆是简谐振动。 所以,单摆是简谐振动。
θ
mg
13
• 例10.1 一质点沿 轴作简谐振动,振幅 一质点沿X轴作简谐振动 轴作简谐振动, A=0.10m,周期 ,周期T=2s,当t=0时,质点相 , 时 对平衡位置的位移为x 对平衡位置的位移为 0=0.05,并向 的正 ,并向x的正 方向运动, 方向运动,求 1、质点位移的表达式 、 2、t=0.5s时,质点的位移,速度和加速 、 时 质点的位移, 度。
