立体几何证明方法——证面面垂直
空间几何线面平行面面平行线面垂直面面垂直的证明方法

空间几何线面平行面面平行线面垂直面面垂直的证明方法空间几何中,线、面、平行面、面平行线、面垂直面等概念是非常重要的。
在证明这些概念时,我们需要掌握一些基本的证明方法。
下面,我将介绍一些证明方法,帮助大家更好地理解这些概念。
一、线与面的关系1. 线与平面的关系线与平面的关系有两种情况:线在平面内或线与平面相交。
对于线在平面内的情况,我们可以通过以下证明方法来证明:(1)假设线与平面不在同一平面内,那么这条线必然与平面相交,与已知矛盾。
(2)假设线与平面在同一平面内,但不在同一直线上,那么这条线必然与平面相交,与已知矛盾。
(3)假设线与平面在同一直线上,但不在同一点上,那么这条线必然与平面相交,与已知矛盾。
因此,我们可以得出结论:线与平面必然在同一平面内且相交于一点或在平面内。
2. 线与直线的关系线与直线的关系有三种情况:相交、平行、重合。
对于线与直线相交的情况,我们可以通过以下证明方法来证明:(1)假设两条线不相交,那么这两条线必然平行,与已知矛盾。
(2)假设两条线重合,那么这两条线必然相交,与已知矛盾。
因此,我们可以得出结论:两条不同的线必然相交于一点或平行。
二、面与面的关系1. 平行面的关系平行面的关系有两种情况:平行或重合。
对于平行面的情况,我们可以通过以下证明方法来证明:(1)假设两个平面不平行,那么这两个平面必然相交,与已知矛盾。
(2)假设两个平面重合,那么这两个平面必然平行,与已知矛盾。
因此,我们可以得出结论:两个不同的平面必然平行或相交于一条直线。
2. 面垂直面的关系面垂直面的关系有两种情况:相交于一条直线或垂直。
对于面垂直的情况,我们可以通过以下证明方法来证明:(1)假设两个面不垂直,那么这两个面必然相交于一条直线,与已知矛盾。
(2)假设两个面相交于一条直线,那么这两个面必然不垂直,与已知矛盾。
因此,我们可以得出结论:两个不同的面必然相交于一条直线或垂直。
三、面平行线的关系面平行线的关系有两种情况:平行或相交。
高一数学必修2立体几何 面面垂直的判定与性质

求证:平面A1C⊥平面B1D
E、F分别是AB、BC的中点, 求证: 平面A1C1FE⊥平面B1D G是BB1的中点 求证: 平面A1C1G⊥平面B1D
A1
D1 A D C
F
E B G G G G C1 B1
三、两个平面垂直的性质定理: 1.如果两个平面垂直,则在一个平面 内垂直于它们的交线的直线垂直于另 一个平面.
你发现了什么?
二、两个平面垂直的判定定理: 如果一个平面经过了另一个平面的一 条垂线,那么这两个平面互相垂直.
符号: l
l
α
β l A
线面垂直,则面面垂直
线线垂直线面垂直来自面面垂直应 用 于 生 活
建筑工人砌墙时, 如何使所砌的墙和水平面垂直?
例1:在正方体ABCD—A1B1C1D1中,
面面垂直的判定与性质
淮北一中高一数学备课组
学习目标
1、掌握平面和平面垂直的定义; 2、掌握平面和平面垂直的判定定理;
3、掌握平面和平面垂直的性质定理; 4、掌握判定定理和性质定理的应用。
一、两个平面垂直的定义:
如果两个平面所成的二面角是直角 (即成直二面角),就说这两个平面 互相垂直.
观 察 生 活
证明:过A点作AD⊥SB于D点. ∵平面SAB ⊥ 平面SBC, ∴ AD⊥平面SBC, ∴ AD⊥BC. 又∵ SA ⊥ 平面ABC, ∴SA ⊥ BC. AD∩SA=A ∴BC ⊥ 平面SAB. ∴BC ⊥AB.
S
D A B C
【总结一下★成竹在胸】
为作辅助线提 供了理论依据
三、两个平面垂直的性质定理:
2.如果两个平面垂直,那么经过第一个 平面的一点垂直于第二个平面的直线, 在第一个平面内.
立体几何线面与面面垂直的证明

那么另一条也垂直于这个平 a 的无数条直线”是“ I 丄a B.必要不充分条件线面垂直与面面垂直专题复习【知识点】一.线面垂直(1) 直线与平面垂直的定义:如果直线l 和平面a 的 __________________ 一条直线都垂直,我们就说直线 I 与平面a 垂直,记作 _____________ .重要性质: ____________________________________________________________________________(2) 直线与平面垂直的判定方法:①判定定理:一条直线与一个平面的两条 ___________________ 都垂直,那么这条直线就垂直于这 个平面.用符号表示为:②常用结论:如果两条平行直线中的一条垂直于一个平面, 面.用符号可表示为:(3)直线与平面垂直的性质:① 由直线和平面垂直的定义知:直线与平面垂直,则直线垂直于平面的 ________ 直线.② 性质定理:垂直于同一平面的两条直线平行.用符号可表示为: 二、面面垂直(1) 平面与平面垂直的定义:两平面相交,如果它们所成的二面角是 _____________________ ,就说这两个平面互相垂直.(2) 平面与平面垂直的判定定理:如果一个平面经过另一个平面的一条 _____________________ ,那么这两个平面互相垂直.简述为 "线面垂直,则面面垂直”,用符号可表示为:(3)平面与平面垂直的性质:如果两个平面互相垂直,那么在一个平面垂直于它们交线的直线垂直于另一个平面. 用符号可表示为:【题型总结】 题型一小题:判断正误1. “直线I 垂直于平面 A.充分不必要条件C.充要条件D.既不充分又不必要条件2. 已知如图,六棱锥 P — ABCDE 的底面是正六边形, 下列结论不正确的是( ).A.CD// 平面 PAFB. DF 丄平面 PAFC. CF//平面 PAB 2.设m n, I 是三条不同的直线,,,是三个不同的平面,判断命题正误:理科数学复习专题立体几何①m,m ,则//⑥m n, m// ,则n②m,// ,则m⑦m n,n 1,则m//l③m,m//n,则n⑧, ,则〃④m,n ,则m//n⑨m n,n//I,则m 1⑤m,m n,则n//⑩,//,则题型「二证明线面垂直P归纳:①证明异面直线垂直的常用方法:_________________________________________②找垂线(线线垂直)的方法一:______________________________________________ 2.四棱锥P ABCD中,底面ABCD的边长PD PB 4, BAD 600, E 为PA 中点•1如图,四棱锥P-ABCD中,底面ABCD为平行四边形,/ DAB = 60° AB= 2AD, PD 丄底面ABCD .(1)证明:BD丄面PAD (2)证明:PA丄BD;求证:BD 平面PAC ;4的菱形,归纳:找垂线(线线垂直)的方法找垂线(线线垂直)的方法三:3、如图,AB是圆0的直径,C是圆0上不同于A, B的一点,PA 平面ABC , E是PC 的中点,AB 3 , PA AC 1.求证:AE PB•Z归纳:找垂线(线线垂直)的方法四:____________________________________4.如图,在三棱锥P ABC中,PA 底面ABC, BCA 900,AP=AC,点D , E分别为棱PB、PC的中点,且BC〃平面ADE求证:DE丄平面PAC ;归纳:_____________________________________________________________________________________ 题型三面面垂直的证明(关键:找线面垂直)1、如图所示,四边形ABCD是菱形,O是AC与BD 的交点,SA 平面ABCD.求证:平面SAC 平面SBD ;2. (2016理数)如图,在以A,B,C,D,E,F为顶点的五面体中面ABEF 为正方形,AF=2FD, AFD 90:,证明:平面ABEF 平面EFDC ;题型四面面垂直的性质(注意:交线)1、如图所示,平面EAD 平面ABCD , ADE是等边三角形,ABCD是矩形,F是AB的中点,G是AD的中点, 求证:EG 平面ABCD ;2、如图,平行四边形ABCD中,CD 1, BCD 600, BD CD,正方形ADEF,且面ADEF 面ABCD •求证:BD 平面ECD ;综合运用如图所示,PA丄矩形ABCD所在平面,M、N分别是AB、PC的中点.(1) 求证:MN //平面PAD.(2) 求证:MN丄CD.⑶若/ PDA = 45 °求证:面BMN丄平面PCD.【练习】1.设M表示平面,a、b表示直线,给出下列四个命题:金a〃b a M a M a//M① b M ②a//b ③b/ M ④b± Ma Mb M a b a b其中正确的命题是( )A.①②B.①②③C.②③④D.①②④2.给出以下四个命题:CD如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
证明面面垂直的方法

证明面面垂直的方法在日常生活和工作中,我们经常会遇到需要证明物体表面是否垂直的情况。
无论是在建筑工程、家具安装还是科学实验中,确保物体表面垂直是十分重要的。
那么,如何准确地证明一个物体表面是否垂直呢?接下来,我将介绍几种常用的方法来证明面面垂直的有效性。
首先,我们可以使用水平仪来证明物体表面是否垂直。
水平仪是一种测量工具,通常用于检查水平面的水平度。
在证明物体表面垂直时,我们可以将水平仪放置在需要检测的表面上,然后观察水平仪指针的指向。
如果指针指向中心位置,则表明该表面是垂直的;如果指针偏离中心位置,则表明该表面不是垂直的。
通过使用水平仪,我们可以快速、准确地证明物体表面是否垂直。
其次,我们还可以使用垂直尺来证明物体表面是否垂直。
垂直尺是一种具有垂直度量功能的测量工具,通常用于测量墙面、柱子等垂直表面的垂直度。
在证明物体表面垂直时,我们可以将垂直尺放置在需要检测的表面上,然后观察垂直尺的指示。
如果指示在垂直位置,则表明该表面是垂直的;如果指示偏离垂直位置,则表明该表面不是垂直的。
通过使用垂直尺,我们可以有效地证明物体表面是否垂直。
另外,我们还可以使用激光水平仪来证明物体表面是否垂直。
激光水平仪是一种利用激光技术进行水平和垂直测量的仪器,通常用于建筑、装修等领域。
在证明物体表面垂直时,我们可以将激光水平仪放置在需要检测的表面上,然后观察激光线的指向。
如果激光线垂直于地面,则表明该表面是垂直的;如果激光线不垂直于地面,则表明该表面不是垂直的。
通过使用激光水平仪,我们可以快速、精确地证明物体表面是否垂直。
除了以上介绍的方法外,我们还可以通过使用测量工具如测量尺、角尺等来证明物体表面是否垂直。
这些工具在实际工作中都有着重要的应用价值,能够帮助我们准确地证明物体表面是否垂直。
总的来说,证明物体表面是否垂直是一项重要的工作,它涉及到建筑、装修、科学实验等诸多领域。
通过使用水平仪、垂直尺、激光水平仪以及其他测量工具,我们可以有效地证明物体表面是否垂直,从而保证工作的准确性和可靠性。
怎么证明面面垂直

怎么证明面面垂直怎么证明面面垂直证明一个面上的一条线垂直另一个面;首先可以转化成一个平面的垂线在另一个平面内,即一条直线垂直于另一个平面然后转化成一条直线垂直于另一个平面内的两条相交直线也可以运用两个面的法向量互相垂直。
这是解析几何的方法。
证:连接AC,BD.PD垂直面ABCD=>PD垂直AC.ABCD为正方形=>AC垂直BD.而BD是PB在面ABCD内的射影=>PB垂直AC.PD垂直AC=>AC垂直面PBD.AC属于面ACE=>面PBD垂直面ACE21利用直角三角形中两锐角互余证明由直角三角形的定义与三角形的内角和定理可知直角三角形的两个锐角和等于90°,即直角三角形的两个锐角互余。
2勾股定理逆定理3圆周角定理的推论:直径所对的圆周角是直角,一个三角形的一边中线等于这边的一半,则这个三角形是直角三角形。
二、高中部分线线垂直分为共面与不共面。
不共面时,两直线经过平移后相交成直角,则称两条直线互相垂直。
1向量法两条直线的方向向量数量积为02斜率两条直线斜率积为-13线面垂直,则这条直线垂直于该平面内的所有直线一条直线垂直于三角形的两边,那么它也垂直于另外一边4三垂线定理在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
5三垂线定理逆定理如果平面内一条直线和平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
3高中立体几何的证明主要是平行关系与垂直关系的证明。
方法如下(难以建立坐标系时再考虑):Ⅰ.平行关系:线线平行:1.在同一平面内无公共点的两条直线平行。
2.公理4(平行公理)。
3.线面平行的性质。
4.面面平行的性质。
5.垂直于同一平面的两条直线平行。
线面平行:1.直线与平面无公共点。
2.平面外的一条直线与平面内的一条直线平行。
3.两平面平行,一个平面内的任一直线与另一平面平行。
面面平行:1.两个平面无公共点。
2017年__高二年级立体几何垂直证明题常见模型和方法

立体几何垂直证明题常见模型及方法垂直转化:线线垂直线面垂直面面垂直;基础篇类型一:线线垂直证明(共面垂直、异面垂直)(1) 共面垂直:实际上是平面内的两条直线的垂直 (只需要同学们掌握以下几种模型)○1 等腰(等边)三角形中的中线○2 菱形(正方形)的对角线互相垂直 ○3勾股定理中的三角形 ○4 1:1:2 的直角梯形中 ○5 利用相似或全等证明直角。
例:在正方体1111ABCD A BC D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1AO OE ⊥(2) 异面垂直 (利用线面垂直来证明,高考中的意图) 例1 在正四面体ABCD 中,求证AC BD ⊥变式 1 如图,在四棱锥ABCD P -中,底面A B C D 是矩形,已知60,22,2,2,3=∠====PAB PD PA AD AB .证明:AD PB ⊥;变式2 如图,在边长为2的正方形ABCD 中,点E 是AB 的中点,点F 是BC 的中点,将△AED,△DCF 分别沿,DE DF 折起,使,A C 两点重合于'A. 求证:'A D EF ⊥;类型二:线面垂直证明BE 'ADFG方法○1 利用线面垂直的判断定理例2:在正方体1111ABCD A BC D -中,O 为底面ABCD 的中心,E 为1CC ,求证:1AO BDE ⊥平面变式1:在正方体1111ABCD A BC D -中,,求证:11AC BDC ⊥平面 变式2:如图:直三棱柱ABC -A 1B 1C 1中, AC =BC =AA 1=2,∠ACB =90︒.E 为BB 1的中点,D 点在AB 上且DE = 3 .求证:CD ⊥平面A 1ABB 1;变式3:如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的中点,AD BC ∥,90ABC ∠=°,PA ⊥平面ABCD .3PA =,2AD =,AB =,6BC =C○2 利用面面垂直的性质定理 例3:在三棱锥P-ABC 中,PA ABC ⊥底面,PAC PBC ⊥面面,BC PAC ⊥求证:面。
《空间中垂直关系的证明——面面垂直》教学设计

(1) 能以相关的定义、公理和定理为出发点ꎬ认识和
理解空间中线面垂直、面面垂直的判定与性质定理.
(2) 会运用线面垂直、面面垂直的判定及性质定理证
明一些简单空间图形的垂直关系问题.
(3) 灵活处理好“ 线线、线面、面面” 三种垂直关系的
相互转化ꎬ为后续计算相关的角度问题与距离问题奠定
逻辑推理基础ꎬ积累逻辑推理经验.
ACC1 A1 ⊥平面 A1 BD.
面垂直.
关键问题:线面垂直.
问题 6 还有没有其它的
证明方法?
证明:记直线 AC 与 BD 的
交点为点 O. 连接 A1 O
∵ 平 面 ABCD 为 正 方 形ꎬ
∴ AO⊥BD
又 ∵ A1 D = A1 Bꎬ ∴ BD ⊥
图5
A1 Oꎬ且 A1 O∩AO = O
证明 ∵ 平面 AC 为正方形ꎬ∴ AC⊥BD
又∵ AA1 ⊥平面 ABCDꎬ∴ AA1 ⊥BD
∴ BD⊥平面 AA1 C1 Cꎬ且 BD⫋平面 BB1 D1 D
∴ 平面 AA1 C1 C⊥平面 BB1 D1 D
问题 5 问题 1 与问题 4 的证明过程有什么区别与联
系? (变与不变)总结证明面面垂直的关键问题是什么?
成立. 其中的垂直关系并没有变.
设计说明 研究面面垂直模型ꎬ以及面面垂直模型
的关键问题和本质. ( 线面垂直和线线垂直) 以及如何在
面面垂直模型中找准( 线面垂直) .
板块三:拓模与升华
问题 9: 如图 1ꎬ要使平面 PAD⊥平面 ABCDꎬ需要添
加什么条件?
图 3 图 4
收稿日期:2021 - 01 - 25
作者简介:邓丽(1981. 10 - ) ꎬ女ꎬ四川省南充人ꎬ硕士ꎬ中学高级教师ꎬ从事中学数学教学研究.
如何证明面面垂直(精选多篇)

如何证明面面垂直(精选多篇)第一篇:如何证明面面垂直如何证明面面垂直设p是三角形abc所在平面外的一点,p到a,b,c 三点的距离相等,角bac为直角,求证:平面pcb垂直平面abc过p作pq⊥面abc于q,则q为p在面abc的投影,因为p到a,b,c的距离相等,所以有qa=qb=qc,即q为三角形abc的中心,因为角bac为直,所以q在线段bc上,所以在面pcb上有线段pq⊥平面abc,故平面pcb⊥平面abc2证明一个面上的一条线垂直另一个面;首先可以转化成一个平面的垂线在另一个平面内,即一条直线垂直于另一个平面然后转化成一条直线垂直于另一个平面内的两条相交直线也可以运用两个面的法向量互相垂直。
这是解析几何的方法。
2一、初中部分1利用直角三角形中两锐角互余证明由直角三角形的定义与三角形的内角和定理可知直角三角形的两个锐角和等于90°,即直角三角形的两个锐角互余。
2勾股定理逆定理3圆周角定理的推论:直径所对的圆周角是直角,一个三角形的一边中线等于这边的一半,则这个三角形是直角三角形。
二、高中部分线线垂直分为共面与不共面。
不共面时,两直线经过平移后相交成直角,则称两条直线互相垂直。
1向量法两条直线的方向向量数量积为02斜率两条直线斜率积为-13线面垂直,则这条直线垂直于该平面内的所有直线一条直线垂直于三角形的两边,那么它也垂直于另外一边4三垂线定理在平面内的一条直线,如果和穿过这个平面的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
5三垂线定理逆定理如果平面内一条直线和平面的一条斜线垂直,那么这条直线也垂直于这条斜线在平面内的射影。
3高中立体几何的证明主要是平行关系与垂直关系的证明。
方法如下(难以建立坐标系时再考虑):ⅰ.平行关系:线线平行:1.在同一平面内无公共点的两条直线平行。
2.公理4(平行公理)。
3.线面平行的性质。
4.面面平行的性质。
5.垂直于同一平面的两条直线平行。
面面垂直的判定与性质

本题题目文字少,但有一定难度.只有真正 对面面垂直的性质定理熟练掌握后才能得心应 手.面面垂直的性质定理的核心是“垂直于交线, 则垂直于平面”,所以已知面面垂直,首先应找 交线,看是否在某个平面内存在直线垂直于交线, 若无,肯定要向交线作垂线.在不同平面内向交 线作垂线都能解决问题,但难度显然不同,做题 前应认真分析.本题的方法1较简单,但方法2将 平行和垂直的位置关系的判定和性质考查得淋漓 尽致,不失为一个训练的好题.
【例3】 如图所示,在直四棱柱ABCD- A1B1C1D1 中 , DB = BC , DB⊥AC,点M是棱BB1上一点. (1)求证:MD⊥AC; (2)试确定点M的位置,使得平面 DMC1⊥平面CC1D1D.
与垂直有关的探 索性问题
【证明】1 证明:因为BB1 平面ABCD,AC 平面ABCD,所以BB1 AC. 又因为BD AC,且BD BB1=B, 所以AC 平面BB1D. 而MD 平面BB1D,所以MD AC.
面面垂直的性质的理解中三个条件也 不可缺少,即: ①两个平面垂直; ②其中一个平面内的直线; ③垂直于交线.所以无论何时见到已知两 个平面垂直,都要首先找其交线,看是否 存在直线垂直于交线来决定是否该作辅助 线,这样就能目标明确,事半功倍.
1. (2011淮阴中学、姜堰中学、前黄中学第一次 联考) m、n是两条不同的直线,、、 是三 设 个不同的平面,有下面四个命题: / / ① / / ; ② m ; / / m / / m m / / n ③ ;④ m / / ; m / / n 其中真命题的序号是 ________ .
1.若l为一条直线,、、 为三个互不重合 的平面,给出下面三个命题: ① , ; ② , ; ③l ,l .
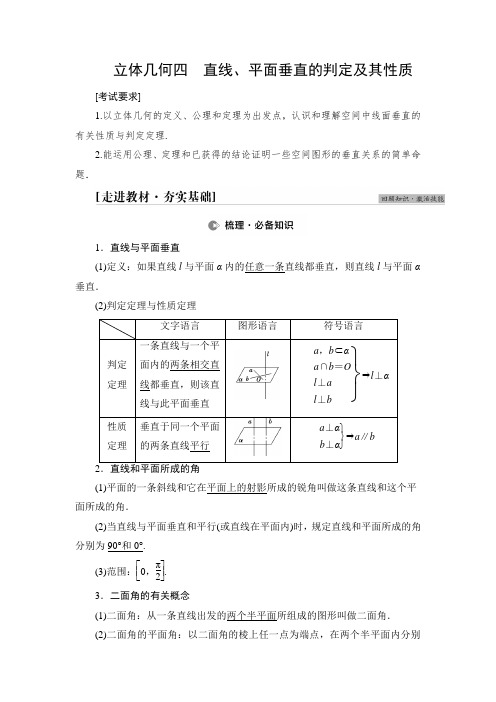
立体几何四 直线、平面垂直的判定及其性质
立体几何四 直线、平面垂直的判定及其性质[考试要求]1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线面垂直的有关性质与判定定理.2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题.1.直线与平面垂直(1)定义:如果直线l 与平面α内的任意一条直线都垂直,则直线l 与平面α垂直.(2)判定定理与性质定理文字语言 图形语言符号语言判定 定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎬⎫a ,b ⊂αa ∩b =Ol ⊥a l ⊥b⇒l ⊥α 性质 定理垂直于同一个平面的两条直线平行⎭⎬⎫a ⊥αb ⊥α⇒a ∥b (1)平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角.(2)当直线与平面垂直和平行(或直线在平面内)时,规定直线和平面所成的角分别为90°和0°.(3)范围:⎣⎢⎡⎦⎥⎤0,π2. 3.二面角的有关概念(1)二面角:从一条直线出发的两个半平面所组成的图形叫做二面角. (2)二面角的平面角:以二面角的棱上任一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.(3)范围:[0,π].4.平面与平面垂直(1)定义:如果两个平面所成的二面角是直二面角,就说这两个平面互相垂直.(2)判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面垂直⎭⎬⎫l⊥αl⊂β⇒α⊥β性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直⎭⎬⎫α⊥βl⊂βα∩β=al⊥a⇒l⊥α[常用结论]直线与平面垂直的五个结论(1)若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意直线.(2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.(3)垂直于同一条直线的两个平面平行.(4)一条直线垂直于两平行平面中的一个,则这条直线与另一个平面也垂直.(5)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.一、易错易误辨析(正确的打“√”,错误的打“×”)(1)垂直于同一个平面的两平面平行.()(2)若α⊥β,a⊥β⇒a∥α.()(3)若两平面垂直,则其中一个平面内的任意一条直线垂直于另一个平面.()(4)若平面α内的一条直线垂直于平面β内的无数条直线,则α⊥β.()[答案](1)×(2)×(3) ×(4)×二、教材习题衍生1.下列命题中错误的是()A.如果平面α⊥平面β,且直线l∥平面α,则直线l⊥平面βB.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面βC.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βD.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γA[A错误,l与β可能平行或相交,其余选项均正确.]2.如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中必有()A.SG⊥△EFG所在平面B.SD⊥△EFG所在平面C.GF⊥△SEF所在平面D.GD⊥△SEF所在平面A[四面体S-EFG如图所示:由SG⊥GE,SG⊥GF.且GE∩GF=G得SG⊥△EFG所在的平面.故选A.]3.如图所示,已知P A⊥平面ABC,BC⊥AC,则图中直角三角形的个数为________.4[∵P A⊥平面ABC,∴P A⊥AB,P A⊥AC,P A⊥BC,则△P AB,△P AC为直角三角形.由BC⊥AC,且AC∩P A=A,∴BC⊥平面P AC,从而BC⊥PC.因此△ABC,△PBC也是直角三角形.]考点一直线与平面垂直的判定与性质判定线面垂直的四种方法[典例1](1)(2019·北京高考)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:________.(2)如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=13DB,点C为圆O上一点,且BC=3AC,PD⊥平面ABC,PD=DB.求证:P A⊥CD.(1)②③⇒①或①③⇒②[(1)已知l,m是平面α外的两条不同直线,由①l⊥m与②m∥α,不能推出③l⊥α,因为l可以与α平行,也可以相交不垂直;由①l⊥m与③l⊥α能推出②m∥α;由②m∥α与③l⊥α可以推出①l⊥m.故正确的命题是②③⇒①或①③⇒②.](2)[证明]因为AB为圆O的直径,所以AC⊥CB,在Rt△ACB中,由3AC =BC,得∠ABC=30°.设AD=1,由3AD=DB,得DB=3,BC=23,由余弦定理得CD2=DB2+BC2-2DB·BC cos 30°=3,所以CD2+DB2=BC2,即CD⊥AB.因为PD⊥平面ABC,CD⊂平面ABC,所以PD⊥CD,由PD∩AB=D,得CD⊥平面P AB,又P A⊂平面P AB,所以P A⊥CD.点评:通过本例(2)的训练我们发现:判定定理与性质定理的合理转化是证明线面垂直的基本思想;另外,在解题中要重视平面几何知识,特别是正余弦定理及勾股定理的应用.[跟进训练]如图所示,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是CC1上一点.当CF=2时,证明:B1F⊥平面ADF.[证明]因为AB=AC,D是BC的中点,所以AD⊥BC.在直三棱柱ABC-A1B1C1中,因为BB1⊥底面ABC,AD⊂底面ABC,所以AD⊥B1B.因为BC∩B1B=B,BC,B1B⊂平面B1BCC1,所以AD⊥平面B1BCC1.因为B1F⊂平面B1BCC1,所以AD⊥B1F.法一:在矩形B1BCC1中,因为C1F=CD=1,B1C1=CF=2,所以Rt△DCF≌Rt△FC1B1,所以∠CFD=∠C1B1F,所以∠B1FD=90°,所以B1F⊥FD.因为AD∩FD=D,AD,FD⊂平面ADF,所以B1F⊥平面ADF.法二:在Rt△B1BD中,BD=CD=1,BB1=3,所以B1D=BD2+BB21=10.在Rt△B1C1F中,B1C1=2,C1F=1,所以B1F=B1C21+C1F2= 5.在Rt△DCF中,CF=2,CD=1,所以DF=CD2+CF2= 5.显然DF 2+B 1F 2=B 1D 2, 所以∠B 1FD =90°.所以B 1F ⊥FD .因为AD ∩FD =D ,AD ,FD ⊂平面ADF , 所以B 1F ⊥平面ADF .考点二 面面垂直的判定与性质证明面面垂直的两种方法[典例2] (2020·雅安模拟)如图,菱形ABCD 与正三角形BCE 的边长均为2,它们所在平面互相垂直,FD ⊥平面ABCD .(1)求证:平面ACF ⊥平面BDF ;(2)若∠CBA =60°,求三棱锥E -BCF 的体积. [解] (1)证明:在菱形ABCD 中,AC ⊥BD , ∵FD ⊥平面ABCD ,∴FD ⊥AC . 又∵BD ∩FD =D ,∴AC ⊥平面BDF . 而AC ⊂平面ACF ,∴平面ACF ⊥平面BDF . (2)取BC 的中点O ,连接EO ,OD , ∵△BCE 为正三角形,∴EO ⊥BC , ∵平面BCE ⊥平面ABCD 且交线为BC , ∴EO ⊥平面ABCD . ∵FD ⊥平面ABCD ,∴EO ∥FD ,得FD ∥平面BCE . ∴V E -BCF =V F -BCE =V D -BCE =V E -BCD .∵S △BCD =12×2×2×sin 120°=3,EO = 3. ∴V E -BCF=13S △BCD ×EO =13×3×3=1.点评:抓住面面垂直的性质,实现面面与线面及线线垂直间的转化是求解本题的关键,另外在第(2)问求解体积时等体积法的应用,是破题的另一要点,平时训练要注意灵活应用.[跟进训练](2020·广州模拟)如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC,且AC=BC=2,O,M分别为AB,VA的中点.(1)求证:平面MOC⊥平面VAB;(2)求三棱锥B-VAC的高.[解](1)证明:∵AC=BC,O 为AB的中点,∴OC⊥AB.∵平面VAB⊥平面ABC,平面VAB∩平面ABC=AB,OC⊂平面ABC,∴OC⊥平面VAB.∵OC⊂平面MOC, ∴平面MOC⊥平面VAB.(2)在等腰直角△ACB中,AC=BC=2,∴AB=2,OC=1,∴等边△VAB的面积为S△VAB =12×22×sin 60°=3,又∵OC⊥平面VAB,∴OC⊥OM,在△AMC中,AM=1,AC=2,MC=2,∴S△AMC =12×1×72=74,∴S△VAC=2S△MAC=72,由三棱锥V-ABC的体积与三棱锥C-VAB的体积相等,即13S△VAC·h=13S△VAB·OC, ∴h=3×172=2217,即三棱锥B-VAC的高为221 7.考点三平行与垂直的综合问题1.对命题条件的探索的三种途径途径一:先猜后证,即先观察与尝试给出条件再证明.途径二:先通过命题成立的必要条件探索出命题成立的条件,再证明充分性.途径三:将几何问题转化为代数问题.2.解决平面图形翻折问题的关键是抓住“折痕”,准确把握平面图形翻折前后的两个“不变”.(1)与折痕垂直的线段,翻折前后垂直关系不改变;(2)与折痕平行的线段,翻折前后平行关系不改变.探索性问题中的平行和垂直关系[典例3-1](2019·北京高考)如图,在四棱锥P-ABCD中,P A⊥平面ABCD,底面ABCD为菱形,E为CD的中点.(1)求证:BD⊥平面P AC;(2)若∠ABC=60°,求证:平面P AB⊥平面P AE;(3)棱PB上是否存在点F,使得CF∥平面P AE?说明理由.[解](1)证明:因为P A⊥平面ABCD,所以P A⊥BD.因为底面ABCD为菱形,所以BD⊥AC.又P A∩AC=A,所以BD⊥平面P AC.(2)证明:因为P A⊥平面ABCD,AE⊂平面ABCD,所以P A⊥AE.因为底面ABCD为菱形,∠ABC=60°,且E为CD的中点,所以AE⊥CD,所以AB⊥AE.又AB∩P A=A,所以AE⊥平面P AB.因为AE⊂平面P AE,所以平面P AB⊥平面P AE.(3)棱PB上存在点F,使得CF∥平面P AE.取F为PB的中点,取G为P A的中点,连接CF,FG,EG.则FG∥AB,且FG=12AB.因为底面ABCD为菱形,且E为CD的中点,所以CE∥AB,且CE=12AB.所以FG∥CE,且FG=CE.所以四边形CEGF为平行四边形.所以CF∥EG.因为CF⊄平面P AE,EG⊂平面P AE,所以CF∥平面P AE.点评:(1)处理空间中平行或垂直的探索性问题,一般先根据条件猜测点的位置,再给出证明.探索点存在问题,点多为中点或n等分点中的某一个,需根据相关的知识确定点的位置.(2)利用向量法,设出点的坐标,结论变条件,求出点的坐标,并指明点的位置.折叠问题中的平行与垂直关系[典例3-2](2018·全国卷Ⅰ)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=23DA,求三棱锥Q-ABP的体积.[解](1)证明:由已知可得,∠BAC=90°,即BA⊥AC.又BA⊥AD,AD∩AC=A,AD,AC⊂平面ACD,所以AB⊥平面ACD.又AB⊂平面ABC,所以平面ACD⊥平面ABC.(2)由已知可得,DC=CM=AB=3,DA=3 2.又BP=DQ=23DA,所以BP=2 2.如图,过点Q作QE⊥AC,垂足为E,则QE∥DC且QE=13DC.由已知及(1)可得,DC⊥平面ABC,所以QE⊥平面ABC,QE=1.因此,三棱锥Q-ABP的体积为V Q-ABP=13×S△ABP×QE=13×12×3×22sin 45°×1=1.点评:本例第(1)问是垂直关系证明问题,求解的关键是抓住“BA⊥AC”折叠过程中始终不变;本例第(2)问是计算问题,求解的关键是抓住“∠ACM=90°”折叠过程中始终不变.即折叠问题的处理可采用:不变的关系可在平面图形中处理,而对于变化的关系则要在立体图形中解决.[跟进训练]1.(2020·梧州模拟)如图,四边形ABCD中,AB=AD=CD=1,BD=2,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′-BCD,使平面A′BD⊥平面BCD,则下列结论正确的是()A.A′C⊥BDB.∠BA′C=90°C.CA′与平面A′BD所成的角为30°D.四面体A′-BCD的体积为1 3B[若A成立可得BD⊥A′D,产生矛盾,故A错误;由题设知:△BA′D 为等腰直角三角形,CD⊥平面A′BD,得BA′⊥平面A′CD,于是B正确;由CA′与平面A′BD所成的角为∠CA′D=45°知C错误;V A′-BCD=V C-A′BD=16,故D错误,故选B.]2.如图,直三棱柱ABC-A1B1C1中,D,E分别是棱BC,AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.(1)求证:C1E∥平面ADF;(2)设点M在棱BB1上,当BM为何值时,平面CAM⊥平面ADF? [解](1)证明:连接CE交AD于O,连接OF.因为CE,AD为△ABC的中线,则O为△ABC的重心,故CFCC1=COCE=23,故OF∥C1E,因为OF⊂平面ADF,C1E⊄平面ADF,所以C1E∥平面ADF.(2)当BM=1时,平面CAM⊥平面ADF.证明如下:因为AB=AC,D为BC的中点,故AD⊥BC.在直三棱柱ABC-A1B1C1中,BB1⊥平面ABC,BB1⊂平面B1BCC1,故平面B1BCC1⊥平面ABC.又平面B1BCC1∩平面ABC=BC,AD⊂平面ABC,所以AD⊥平面B1BCC1,又CM⊂平面B1BCC1,故AD⊥CM.又BM=1,BC=2,CD=1,FC=2,故Rt△CBM≌Rt△FCD.易证CM⊥DF,又DF∩AD=D,DF,AD⊂平面ADF,故CM⊥平面ADF.又CM⊂平面CAM,故平面CAM⊥平面ADF.。
立体几何中的面面垂直

硕果累累
1、本节课的主讲内容是: 2、学生的学习状态(收获与不足) 3、针对学生的不足之处,老师的一个合理化建议是什么
(2)当 P 为 AM 的中点时,MC∥平面 PBD. 证明如下:如图,连接 AC 交 BD 于 O.
因为 ABCD 为矩形,所以 O 为 AC 中点.连接 OP,因为 P 为 AM 中点,所 以 MC∥OP.MC⊄平面 PBD,OP⊂平面 PBD,所以 MC∥平面 PBD.
课后练习
2.(2017·全国卷Ⅰ)如图,在四棱锥 P-ABCD 中,AB∥CD,且∠BAP=∠CDP =90°。
(1)证明:平面 PAB⊥平面 PAD; (2)若 PA=PD=AB=DC,∠APD=90°,且四棱锥 P-ABCD 的体积为83,求 该四棱锥的侧面积.
[解] (1)证明:由已知∠BAP=∠CDP=90°, 得 AB⊥AP,CD⊥PD. 由于 AB∥CD,故 AB⊥PD,从而 AB⊥平面 PAD. 又 AB⊂平面 PAB, 所以平面 PAB⊥平面 PAD.
(2)在线段 AM 上是否存在点 P,使得 MC∥平面 PBD?说明理由.
[解] (1)证明:由题设知,平面 CMD⊥平面 ABCD,交线为 CD.因为 BC⊥ CD,BC⊂平面 ABCD,所以 BC⊥平面 CMD,故 BC⊥DM.
因为 M 为C︵D上异于 C,D 的点,且 DC 为直径,所以 DM⊥CM. 又 BC∩CM=C,所以 DM⊥平面 BMC. 而 DM⊂平面 AMD,故平面 AMD⊥平面 BMC.
(2)找二面角的平面角的方法 ①垂面法:由二面角的平面角的定义知,只需作与棱垂直的平面,则该平面与 两个半平面的交线构成的角即二面角的平面角. ②定义法:先分别在两个半平面内找一条垂直于棱的射线,然后平移到一起, 两射线的夹角即二面角的平面角.
高中数学必修2立体几何专题-线面、面面垂直专题总结

4.从一条直线出发的两个半平面所组成的图形叫 做 二面角 .这条直线叫做 二面角的棱,这两个半平 面叫做 二面角的面 .棱为l,面分别为α,β的二面角 记作二面角α—l—β.在二面角α—l—β的棱l上任取一 点O,以点O为垂足,在半平面α和β内分别作垂直 于棱l的射线OA和OB,则射线OA和OB构成的 二面角的平面角.二面角的大小可 ∠AOB叫做 平面角 以用它的 来度量,二面角的平面角是多 少度,就说这个二面角是多少度.平面角是 直角 的二面角叫做直二面角.一般地,两个平面相
在三棱锥O—ABC中,三条棱OA,OB,OC两两 互相垂直,且OA=OB=OC,M是AB边的中点,则 OM与平面ABC所成角的正切值是 .
(如图,连接MC,则 ∠OMC为所求.在Rt△OMC
中,OM=
OC 则tan∠OMC= = 2 .) OM
2 2
OA,
学点三
面面垂直的判定
如图1-10-3所示,过点S引三条不 共面的直线,使∠BSC=90°, ∠ASB=∠ASC=60°,若截取
1.直线与直线垂直
两直线垂直是指它们的交角或平移后的交角为直角,两条 直线不一定相交.
在平面几何中,两直线垂直时,它们一定相交.
2.直线和平面垂直
(1)直线和平面垂直的定义可以用来判定线线垂直,即 当直线和平面垂直时,该直线就垂直于这个平面内的任何 直线,可以把它作为线线垂直的判定定理. (2)要判定一条直线是否和一个平面垂直,取决于在这 个平面内能否找出两条相交直线和已知直线垂直,至于这 两条相交直线是否和已知直线有公共点,则无关紧要.
AC2 - CD2
=
2 2
2 2
a,
a,
∴AD2+SD2=SA2,即AD⊥SD.
8.7空间向量在立体几何中的应用——证明平行与垂直

1.用向量表示直线或点在直线上的位置(1)给定一个定点A 和一个向量a ,再任给一个实数t ,以A 为起点作向量AP →=t a ,则此向量方程叫做直线l 以t 为参数的参数方程.向量a 称为该直线的方向向量.(2)对空间任一确定的点O ,点P 在直线l 上的充要条件是存在唯一的实数t ,满足等式OP →=(1-t )OA →+tOB →,叫做空间直线的向量参数方程. 2.用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ,与平面α共面的两个不共线向量v 1和v 2,则l ∥α或l ⊂α⇔存在两个实数x ,y ,使v =x v 1+y v 2.(3)设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔v ⊥u . (4)设平面α和β的法向量分别为u 1,u 2,则α∥β⇔u 1 ∥u 2. 3.用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2=0. (2)设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔v ∥u . (3)设平面α和β的法向量分别为u 1和u 2,则α⊥β⇔u 1⊥u 2⇔u 1·u 2=0. 【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)直线的方向向量是唯一确定的.( × ) (2)平面的单位法向量是唯一确定的.( × ) (3)若两平面的法向量平行,则两平面平行.( √ ) (4)若两直线的方向向量不平行,则两直线不平行.( √ ) (5)若a ∥b ,则a 所在直线与b 所在直线平行.( × )(6)若空间向量a 平行于平面α,则a 所在直线与平面α平行.( × )1.平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k ),若α∥β,则k 等于( ) A.2 B.-4 C.4 D.-2 答案 C解析 ∵α∥β,∴两平面法向量平行, ∴-21=-42=k-2,∴k =4. 2.已知A (1,0,0),B (0,1,0),C (0,0,1),则下列向量是平面ABC 法向量的是( ) A.(-1,1,1) B.(1,-1,1) C.(-33,-33,-33) D.(33,33,-33) 答案 C解析 设n =(x ,y ,z )为平面ABC 的法向量, 则⎩⎪⎨⎪⎧n ·AB →=0,n ·AC →=0,化简得⎩⎪⎨⎪⎧-x +y =0,-x +z =0,∴x =y =z .故选C.3.已知直线l 的方向向量为v =(1,2,3),平面α的法向量为u =(5,2,-3),则l 与α的位置关系是____________. 答案 l ∥α或l ⊂α解析 ∵v ·u =0,∴v ⊥u ,∴l ∥α或l ⊂α.4.(教材改编)设u ,v 分别是平面α,β的法向量,u =(-2,2,5),当v =(3,-2,2)时,α与β的位置关系为________;当v =(4,-4,-10)时,α与β的位置关系为________. 答案 α⊥β α∥β解析 当v =(3,-2,2)时,u ·v =(-2,2,5)·(3,-2,2)=0⇒α⊥β. 当v =(4,-4,-10)时,v =-2u ⇒α∥β.5.(教材改编)如图所示,在正方体ABCD -A 1B 1C 1D 1中,O 是底面正方形ABCD 的中心,M 是D 1D 的中点,N 是A 1B 1的中点,则直线ON ,AM 的位置关系是________. 答案 垂直解析 以A 为原点,分别以AB →,AD →,AA 1→所在直线为x ,y ,z 轴,建立空间直角坐标系,设正方体棱长为1,则A (0,0,0),M (0,1,12),O (12,12,0),N (12,0,1),AM →·ON →=(0,1,12)·(0,-12,1)=0, ∴ON 与AM 垂直.题型一 利用空间向量证明平行问题例1 如图所示,平面P AD ⊥平面ABCD ,ABCD 为正方形,△P AD 是直角三角形,且P A =AD =2,E ,F ,G 分别是线段P A ,PD ,CD 的中点.求证:PB ∥平面EFG . 证明 ∵平面P AD ⊥平面ABCD ,且ABCD 为正方形,∴AB ,AP ,AD 两两垂直,以A 为坐标原点,建立如图所示的空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (2,2,0),D (0,2,0),P (0,0,2),E (0,0,1),F (0,1,1),G (1,2,0). ∴PB →=(2,0,-2),FE →=(0,-1,0),FG →=(1,1,-1), 设PB →=sFE →+tFG →,即(2,0,-2)=s (0,-1,0)+t (1,1,-1), ∴⎩⎪⎨⎪⎧t =2,t -s =0,-t =-2,解得s =t =2.∴PB →=2FE →+2FG →,又∵FE →与FG →不共线,∴PB →,FE →与FG →共面. ∵PB ⊄平面EFG ,∴PB ∥平面EFG . 引申探究本例中条件不变,证明平面EFG ∥平面PBC . 证明 ∵EF →=(0,1,0),BC →=(0,2,0), ∴BC →=2EF →,∴BC ∥EF .又∵EF ⊄平面PBC ,BC ⊂平面PBC , ∴EF ∥平面PBC ,同理可证GF ∥PC ,从而得出GF ∥平面PBC . 又EF ∩GF =F ,EF ⊂平面EFG ,FG ⊂平面EFG , ∴平面EFG ∥平面PBC .思维升华 (1)恰当建立空间直角坐标系,准确表示各点与相关向量的坐标,是运用向量法证明平行和垂直的关键.(2)证明直线与平面平行,只需证明直线的方向向量与平面的法向量的数量积为零,或证直线的方向向量与平面内的不共线的两个向量共面,或证直线的方向向量与平面内某直线的方向向量平行,然后说明直线在平面外即可.这样就把几何的证明问题转化为向量运算.如图,在四面体A -BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =22,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ=3QC .证明:PQ ∥平面BCD .证明 方法一 如图,取BD 的中点O ,以O 为原点,OD 、OP 所在射线分别为y 、z轴的正半轴,建立空间直角坐标系Oxyz .由题意知,A (0,2,2),B (0,-2,0),D (0,2,0). 设点C 的坐标为(x 0,y 0,0). 因为AQ →=3QC →,所以Q ⎝⎛⎭⎫34x 0,24+34y 0,12.因为M 为AD 的中点,故M (0,2,1). 又P 为BM 的中点,故P ⎝⎛⎭⎫0,0,12, 所以PQ →=⎝⎛⎭⎫34x 0,24+34y 0,0.又平面BCD 的一个法向量为a =(0,0,1),故PQ →·a =0. 又PQ ⊄平面BCD ,所以PQ ∥平面BCD .方法二 在线段CD 上取点F ,使得DF =3FC ,连接OF ,同方法一建立空间直角坐标系,写出点A 、B 、C 的坐标,设点C 坐标为(x 0,y 0,0). ∵CF →=14CD →,设点F 坐标为(x ,y,0),则(x -x 0,y -y 0,0)=14(-x 0,2-y 0,0),∴⎩⎨⎧x =34x 0y =24+34y∴OF →=(34x 0,24+34y 0,0)又由方法一知PQ →=(34x 0,24+34y 0,0),∴OF →=PQ →,∴PQ ∥OF .又PQ ⊄平面BCD ,OF ⊂平面BCD , ∴PQ ∥平面BCD .题型二 利用空间向量证明垂直问题 命题点1 证线面垂直例2 如图所示,正三棱柱ABC —A 1B 1C 1的所有棱长都为2,D 为CC 1的中点.求证:AB 1⊥平面A 1BD .证明 方法一 设平面A 1BD 内的任意一条直线m 的方向向量为m .由共面向量定理,则存在实数λ,μ,使m =λBA 1→+μBD →.令BB 1→=a ,BC →=b ,BA →=c ,显然它们不共面,并且|a |=|b |=|c |=2,a ·b =a·c =0,b·c =2,以它们为空间的一个基底,则BA 1→=a +c ,BD →=12a +b ,AB 1→=a -c ,m =λBA 1→+μBD →=⎝⎛⎭⎫λ+12μa +μb +λc , AB 1→·m =(a -c )·⎣⎡⎦⎤⎝⎛⎭⎫λ+12μa +μb +λc =4⎝⎛⎭⎫λ+12μ-2μ-4λ=0.故AB 1→⊥m ,结论得证. 方法二 如图所示,取BC 的中点O ,连接AO . 因为△ABC 为正三角形, 所以AO ⊥BC .因为在正三棱柱ABC —A 1B 1C 1中,平面ABC ⊥平面BCC 1B 1, 所以AO ⊥平面BCC 1B 1.取B 1C 1的中点O 1,以O 为原点,分别以OB →,OO 1→,OA →所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,则B (1,0,0),D (-1,1,0),A 1(0,2,3), A (0,0,3),B 1(1,2,0).设平面A 1BD 的法向量为n =(x ,y ,z ),BA 1→=(-1,2,3),BD →=(-2,1,0). 因为n ⊥BA 1→,n ⊥BD →,故⎩⎪⎨⎪⎧n ·BA 1→=0,n ·BD →=0,⇒⎩⎨⎧-x +2y +3z =0,-2x +y =0,令x =1,则y =2,z =-3,故n =(1,2,-3)为平面A 1BD 的一个法向量, 而AB 1→=(1,2,-3),所以AB 1→=n ,所以AB 1→∥n , 故AB 1⊥平面A 1BD . 命题点2 证面面垂直例3 如图,在三棱锥P ABC 中,AB =AC ,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上.已知BC =8,PO =4,AO =3,OD =2. (1)证明:AP ⊥BC ;(2)若点M 是线段AP 上一点,且AM =3.试证明平面AMC ⊥平面BMC . 证明 (1)如图所示,以O 为坐标原点,以射线OP 为z 轴的正半轴建立空间直角坐标系Oxyz .则O (0,0,0),A (0,-3,0), B (4,2,0),C (-4,2,0),P (0,0,4).于是AP →=(0,3,4), BC →=(-8,0,0),∴AP →·BC →=(0,3,4)·(-8,0,0)=0, 所以AP →⊥BC →,即AP ⊥BC . (2)由(1)知|AP |=5,又|AM |=3,且点M 在线段AP 上, ∴AM →=35AP →=⎝⎛⎭⎫0,95,125, 又BC →=(-8,0,0),AC →=(-4,5,0),BA →=(-4,-5,0), ∴BM →=BA →+AM →=⎝⎛⎭⎫-4,-165,125, 则AP →·BM →=(0,3,4)·⎝⎛⎭⎫-4,-165,125=0, ∴AP →⊥BM →,即AP ⊥BM ,又根据(1)的结论知AP ⊥BC ,且BM ∩BC =C , ∴AP ⊥平面BMC ,于是AM ⊥平面BMC . 又AM ⊂平面AMC ,故平面AMC ⊥平面BCM . 思维升华 证明垂直问题的方法(1)利用已知的线面垂直关系构建空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)其一证明直线与直线垂直,只需要证明两条直线的方向向量垂直;其二证明线面垂直,只需证明直线的方向向量与平面内不共线的两个向量垂直即可,当然 ,也可证直线的方向向量与平面法向量平行;其三证明面面垂直:①证明两平面的法向量互相垂直;②利用面面垂直的判定定理,只要能证明一个平面内的一条直线的方向向量为另一个平面的法向量即可.(1)如图所示,已知直三棱柱ABC —A 1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D 、E 、F 分别为B 1A 、C 1C 、BC 的中点.求证: ①DE ∥平面ABC ; ②B 1F ⊥平面AEF .证明 ①如图建立空间直角坐标系Axyz , 令AB =AA 1=4,则A (0,0,0),E (0,4,2),F (2,2,0),B (4,0,0),B 1(4,0,4). 取AB 中点为N ,连接CN , 则N (2,0,0),C (0,4,0),D (2,0,2), ∴DE →=(-2,4,0),NC →=(-2,4,0),∴DE →=NC →,∴DE ∥NC ,又∵NC ⊂平面ABC ,DE ⊄平面ABC . 故DE ∥平面ABC .②B 1F →=(-2,2,-4),EF →=(2,-2,-2),AF →=(2,2,0). B 1F →·EF →=(-2)×2+2×(-2)+(-4)×(-2)=0, B 1F →·AF →=(-2)×2+2×2+(-4)×0=0.∴B 1F →⊥EF →,B 1F →⊥AF →,即B 1F ⊥EF ,B 1F ⊥AF , 又∵AF ∩EF =F ,∴B 1F ⊥平面AEF .(2)如图所示,在四棱锥P -ABCD 中,PC ⊥平面ABCD ,PC =2,在四边形ABCD 中,∠B =∠C =90°,AB =4,CD =1,点M 在PB 上,PB =4PM ,PB 与平面ABCD 成30°角.①求证:CM ∥平面P AD ; ②求证:平面P AB ⊥平面P AD .证明 ①以C 为坐标原点,分别以CB 所在直线为x 轴,CD 所在直线为y 轴,CP 所在直线为z 轴建立如图所示的空间直角坐标系Cxyz , ∵PC ⊥平面ABCD ,∴∠PBC 为PB 与平面ABCD 所成的角, ∴∠PBC =30°.∵PC =2,∴BC =23,PB =4.∴D (0,1,0),B (23,0,0),A (23,4,0),P (0,0,2), M (32,0,32), ∴DP →=(0,-1,2),DA →=(23,3,0),CM →=(32,0,32),令n =(x ,y ,z )为平面P AD 的一个法向量, 则⎩⎪⎨⎪⎧DP →·n =0,DA →·n =0,即⎩⎨⎧-y +2z =0,23x +3y =0,∴⎩⎨⎧z =12y ,x =-32y ,令y =2,得n =(-3,2,1).∵n ·CM →=-3×32+2×0+1×32=0,∴n ⊥CM →,又CM ⊄平面P AD , ∴CM ∥平面P AD .②取AP 的中点E ,则E (3,2,1),BE →=(-3,2,1). ∵PB =AB ,∴BE ⊥P A .又∵BE →·DA →=(-3,2,1)·(23,3,0)=0, ∴BE →⊥DA →,∴BE ⊥DA ,又P A ∩DA =A ,∴BE ⊥平面P AD , 又∵BE ⊂平面P AB , ∴平面P AB ⊥平面P AD .题型三 利用空间向量解决探索性问题例4 如图,棱柱ABCD -A 1B 1C 1D 1的所有棱长都等于2,∠ABC 和∠A 1AC 均为60°,平面AA 1C 1C ⊥平面ABCD . (1)求证:BD ⊥AA 1;(2)求二面角D -A 1A -C 的余弦值;(3)在直线CC 1上是否存在点P ,使BP ∥平面DA 1C 1,若存在,求出点P 的位置,若不存在,请说明理由. (1)证明 设BD 与AC 交于点O ,则BD ⊥AC ,连接A 1O ,在△AA 1O 中,AA 1=2,AO =1,∠A 1AO =60°,∴A 1O 2=AA 21+AO 2-2AA 1·AO cos 60°=3, ∴AO 2+A 1O 2=AA 21, ∴A 1O ⊥AO .由于平面AA 1C 1C ⊥平面ABCD ,∴A 1O ⊥平面ABCD .以OB ,OC ,OA 1所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则A (0,-1,0),B (3,0,0),C (0,1,0),D (-3,0,0),A 1(0,0,3),C 1(0,2,3). 由于BD →=(-23,0,0),AA 1→=(0,1,3), AA 1→·BD →=0×(-23)+1×0+3×0=0, ∴BD →⊥AA 1→,即BD ⊥AA 1. (2)解 由于OB ⊥平面AA 1C 1C ,∴平面AA 1C 1C 的一个法向量为n 1=(1,0,0). 设n 2=(x ,y ,z )为平面DAA 1D 1的一个法向量, 则⎩⎪⎨⎪⎧n 2·AA 1→=0,n 2·AD →=0, 即⎩⎨⎧y +3z =0,-3x +y =0,取n 2=(1,3,-1),则〈n 1,n 2〉即为二面角D -A 1A -C 的平面角,∴cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=55,所以,二面角D -A 1A -C 的余弦值为55. (3)解 假设在直线CC 1上存在点P ,使BP ∥平面DA 1C 1,设CP →=λCC 1,P (x ,y ,z ),则(x ,y -1,z )=λ(0,1,3). 从而有P (0,1+λ,3λ),BP →=(-3,1+λ,3λ). 设n 3=(x 3,y 3,z 3)⊥平面DA 1C 1,则⎩⎪⎨⎪⎧n 3⊥A 1C 1→,n 3⊥DA 1→,又A 1C 1→=(0,2,0),DA 1→=(3,0,3),则⎩⎨⎧2y 3=0,3x 3+3z 3=0,取n 3=(1,0,-1),因为BP ∥平面DA 1C 1,则n 3⊥BP →, 即n 3·BP →=-3-3λ=0,得λ=-1, 即点P 在C 1C 的延长线上,且C 1C =CP .思维升华 对于“是否存在”型问题的探索方式有两种:一种是根据条件作出判断,再进一步论证;另一种是利用空间向量,先设出假设存在点的坐标,再根据条件求该点的坐标,即找到“存在点”,若该点坐标不能求出,或有矛盾,则判定“不存在”.在四棱锥P —ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E 、F 分别是AB 、PB 的中点. (1)求证:EF ⊥CD ;(2)在平面P AD 内求一点G ,使GF ⊥平面PCB ,并证明你的结论. (1)证明 如图,分别以DA 、DC 、DP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,设AD =a ,则D (0,0,0), A (a,0,0),B (a ,a,0), C (0,a,0),E ⎝⎛⎭⎫a ,a2,0, P (0,0,a ),F ⎝⎛⎭⎫a 2,a 2,a 2.EF →=⎝⎛⎭⎫-a 2,0,a 2,DC →=(0,a,0). ∵EF →·DC →=0,∴EF →⊥DC →,即EF ⊥CD .(2)解 设G (x,0,z ),则FG →=⎝⎛⎭⎫x -a 2,-a 2,z -a 2, 若使GF ⊥平面PCB ,则由FG →·CB →=⎝⎛⎭⎫x -a2,-a 2,z -a 2·(a,0,0) =a ⎝⎛⎭⎫x -a 2=0,得x =a2;由FG →·CP →=⎝⎛⎭⎫x -a2,-a 2,z -a 2·(0,-a ,a ) =a 22+a ⎝⎛⎭⎫z -a 2=0,得z =0. ∴G 点坐标为⎝⎛⎭⎫a 2,0,0,即G 点为AD 的中点.17.利用向量法解决立体几何问题典例 (12分)(2014·湖北)如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ ;(2)是否存在λ,使平面EFPQ 与平面PQMN 所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由. 规范解答解 以D 为原点,射线DA ,DC ,DD 1分别为x ,y ,z 轴的正半轴,建立如图所示的空间直角坐标系Dxyz .[1分]由已知得B (2,2,0),C 1(0,2,2),E (2,1,0),F (1,0,0),P (0,0,λ),M (2,1,2),N (1,0,2),BC 1→=(-2,0,2),FP →=(-1,0,λ),FE →=(1,1,0),MN →=(-1,-1,0),NP →=(-1,0,λ-2).[3分] (1)证明 当λ=1时,FP →=(-1,0,1), 因为BC 1→=(-2,0,2), 所以BC 1→=2FP →,即BC 1∥FP .而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ , 故直线BC 1∥平面EFPQ .[7分](2)解 设平面EFPQ 的一个法向量为n =(x ,y ,z ),则由⎩⎪⎨⎪⎧ FE →·n =0,FP →·n =0,可得⎩⎪⎨⎪⎧x +y =0,-x +λz =0. 于是可取n =(λ,-λ,1).[9分]同理可得平面PQMN 的一个法向量为m =(λ-2,2-λ,1).若存在λ,使平面EFPQ 与平面PQMN 所成的二面角为直二面角,则m ·n =(λ-2,2-λ,1)·(λ,-λ,1)=0,即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±22.[11分] 故存在λ=1±22,使平面EFPQ 与平面PQMN 所成的二面角为直二面角.[12分] 温馨提醒 (1)利用向量法证明立体几何问题,可以建坐标系或利用基底表示向量;(2)建立空间直角坐标系时,要根据题中条件找出三条互相垂直的直线;(3)利用向量除了可以证明线线平行、垂直,线面、面面平行、垂直外,还可以利用向量求夹角、距离,从而解决线段长度问题、体积问题等.[方法与技巧]1.用向量法解决立体几何问题,是空间向量的一个具体应用,体现了向量的工具性,这种方法可把复杂的推理证明、辅助线的作法转化为空间向量的运算,降低了空间想象演绎推理的难度,体现了由“形”转“数”的转化思想.2.两种思路:(1)选好基底,用向量表示出几何量,利用空间向量有关定理与向量的线性运算进行判断.(2)建立空间直角坐标系,进行向量的坐标运算,根据运算结果的几何意义解释相关问题.[失误与防范]用向量知识证明立体几何问题,仍然离不开立体几何中的定理.如要证明线面平行,只需要证明平面外的一条直线和平面内的一条直线平行,即化归为证明线线平行,用向量方法证明直线a ∥b ,只需证明向量a =λb (λ∈R )即可.若用直线的方向向量与平面的法向量垂直来证明线面平行,仍需强调直线在平面外.A 组 专项基础训练(时间:40分钟)1.若直线l 的方向向量为a =(1,0,2),平面α的法向量为n =(-2,0,-4),则( )A.l ∥αB.l ⊥αC.l ⊂αD.l 与α相交答案 B解析 ∵n =-2a ,∴a 与α的法向量平行,∴l ⊥α.2.已知平面α内有一点M (1,-1,2),平面α的一个法向量为n =(6,-3,6),则下列点P 中,在平面α内A.P (2,3,3)B.P (-2,0,1)C.P (-4,4,0)D.P (3,-3,4)答案 A解析 逐一验证法,对于选项A ,MP →=(1,4,1),∴MP →·n =6-12+6=0,∴MP →⊥n ,∴点P 在平面α内,同理可验证其他三个点不在平面α内.3.若AB →=λCD →+μCE →,则直线AB 与平面CDE 的位置关系是( )A.相交B.平行C.在平面内D.平行或在平面内答案 D解析 ∵AB →=λCD →+μCE →,∴AB →、CD →、CE →共面,∴AB 与平面CDE 平行或在平面CDE 内.4.如图,正方形ABCD 与矩形ACEF 所在平面互相垂直,AB =2,AF =1,M 在EF 上,且AM ∥平面BDE ,则M 点的坐标为( )A.(1,1,1)B.(23,23,1) C.(22,22,1) D.(24,24,1) 答案 C解析 设M 点的坐标为(x ,y,1),AC ∩BD =O ,则O (22,22,0), 又E (0,0,1),A (2,2,0),∴OE →=(-22,-22,1),AM →=(x -2,y -2,1), ∵AM ∥平面BDE ,∴OE →∥AM →,∴⎩⎨⎧ x -2=-22,y -2=-22,⇒⎩⎨⎧ x =22,y =22.5.已知平面α内的三点A (0,0,1),B (0,1,0),C (1,0,0),平面β的一个法向量n =(-1,-1,-1),则不重合的两个平面α与β的位置关系是___________________________________.解析 设平面α的法向量为m =(x ,y ,z ),由m ·AB →=0,得x ·0+y -z =0⇒y =z ,由m ·AC →=0,得x -z =0⇒x =z ,取x =1,∴m =(1,1,1),m =-n ,∴m ∥n ,∴α∥β.6.已知点P 是平行四边形ABCD 所在的平面外一点,如果AB →=(2,-1,-4),AD →=(4,2,0),AP →=(-1,2,-1).对于结论:①AP ⊥AB ;②AP ⊥AD ;③AP →是平面ABCD 的法向量;④AP →∥BD →.其中正确的是________.答案 ①②③解析 ∵AB →·AP →=0,AD →·AP →=0,∴AB ⊥AP ,AD ⊥AP ,则①②正确.又AB →与AD →不平行,∴AP →是平面ABCD 的法向量,则③正确.∵BD →=AD →-AB →=(2,3,4),AP →=(-1,2,-1),∴BD →与AP →不平行,故④错误.7.如图,四棱锥P -ABCD 的底面为正方形,侧棱P A ⊥底面ABCD ,且P A =AD=2,E ,F ,H 分别是线段P A ,PD ,AB 的中点.求证:(1)PB ∥平面EFH ;(2)PD ⊥平面AHF .证明 建立如图所示的空间直角坐标系Axyz .∴A (0,0,0),B (2,0,0),C (2,2,0),D (0,2,0),P (0,0,2),E (0,0,1),F (0,1,1),H (1,0,0).(1)∵PB →=(2,0,-2),EH →=(1,0,-1),∴PB →=2EH →,∴PB ∥EH .∵PB ⊄平面EFH ,且EH ⊂平面EFH ,∴PB ∥平面EFH .(2)PD →=(0,2,-2),AH →=(1,0,0),AF →=(0,1,1),∴PD →·AF →=0×0+2×1+(-2)×1=0,PD →·AH →=0×1+2×0+(-2)×0=0,∴PD ⊥AF ,PD ⊥AH ,又∵AF ∩AH =A ,∴PD ⊥平面AHF .8.如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,PD ∥QA ,QA =AB =12PD .证明:平面PQC ⊥平面DCQ .证明 如图,以D 为坐标原点,线段DA 的长为单位长,射线DA 、DP 、DC 分别为x 轴、y 轴、z 轴的正半轴建立空间直角坐标系Dxyz .依题意有Q (1,1,0),C (0,0,1),P (0,2,0),则DQ →=(1,1,0),DC →=(0,0,1),PQ →=(1,-1,0).∴PQ →·DQ →=0,PQ →·DC →=0.即PQ ⊥DQ ,PQ ⊥DC ,又DQ ∩DC =D ,∴PQ ⊥平面DCQ ,又PQ ⊂平面PQC ,∴平面PQC ⊥平面DCQ .9.如图,在底面是矩形的四棱锥P -ABCD 中,P A ⊥底面ABCD ,E ,F 分别是PC ,PD 的中点,P A =AB =1,BC =2.(1)求证:EF ∥平面P AB ;(2)求证:平面P AD ⊥平面PDC .证明 以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴,建立如图所示的空间直角坐标系,则A (0,0,0),B (1,0,0),C (1,2,0),D (0,2,0),P (0,0,1),∴E (12,1,12),F (0,1,12),EF →=(-12,0,0),PB →=(1,0,-1),PD →=(0,2,-1),AP →=(0,0,1),AD →=(0,2,0),DC →=(1,0,0),AB →=(1,0,0).(1)∵EF →=-12AB →,∴EF →∥AB →,即EF ∥AB , 又AB ⊂平面P AB ,EF ⊄平面P AB ,∴EF ∥平面P AB .(2)∵AP →·DC →=(0,0,1)·(1,0,0)=0,AD →·DC →=(0,2,0)·(1,0,0)=0,∴AP →⊥DC →,AD →⊥DC →,即AP ⊥DC ,AD ⊥DC .又AP ∩AD =A ,∴DC ⊥平面P AD .∵DC ⊂平面PDC ,∴平面P AD ⊥平面PDC .B 组 专项能力提升(时间:25分钟)10.如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别是棱BC ,DD 1上的点,如果B 1E ⊥平面ABF ,则CE 与DF 的和的值为________.答案 1解析 以D 1A 1,D 1C 1,D 1D 分别为x ,y ,z 轴建立空间直角坐标系,设CE =x ,DF =y ,则易知E (x,1,1),B 1(1,1,0),F (0,0,1-y ),B (1,1,1),∴B 1E →=(x -1,0,1),∴FB →=(1,1,y ),由于B 1E ⊥平面ABF ,∴FB →·B 1E →=(1,1,y )·(x -1,0,1)=0⇒x +y =1.11.在正方体ABCD —A 1B 1C 1D 1中,P 为正方形A 1B 1C 1D 1四边上的动点,O 为底面正方形ABCD 的中心,M ,N 分别为AB ,BC 的中点,点Q 为平面ABCD 内一点,线段D 1Q与OP 互相平分,则满足MQ →=λMN →的实数λ有________个.答案 2解析 建立如图的空间直角坐标系,设正方体的边长为2,则P (x ,y,2),O (1,1,0),∴OP 的中点坐标为⎝⎛⎭⎫x +12,y +12,1, 又知D 1(0,0,2),∴Q (x +1,y +1,0),而Q 在MN 上,∴x Q +y Q =3,∴x +y =1,即点P 坐标满足x +y =1.∴有2个符合题意的点P ,即对应有2个λ.12.如图,在长方体ABCD -A 1B 1C 1D 1中,AA 1=AD =1,E 为CD 的中点.(1)求证:B 1E ⊥AD 1;(2)在棱AA 1上是否存在一点P ,使得DP ∥平面B 1AE ?若存在,求AP 的长;若不存在,说明理由.(1)证明 以A 为原点,AB →,AD →,AA 1→的方向分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图).设AB =a ,则A (0,0,0),D (0,1,0),D 1(0,1,1),E ⎝⎛⎭⎫a 2,1,0,B 1(a,0,1),故AD 1→=(0,1,1),B 1E →=⎝⎛⎭⎫-a 2,1,-1,AB 1→=(a,0,1),AE →=⎝⎛⎭⎫a 2,1,0. ∵B 1E →·AD 1→=-a 2×0+1×1+(-1)×1=0, ∴B 1E ⊥AD 1.(2)解 假设在棱AA 1上存在一点P (0,0,z 0).使得DP ∥平面B 1AE ,此时DP →=(0,-1,z 0).又设平面B 1AE 的法向量n =(x ,y ,z ).∵n ⊥平面B 1AE ,∴n ⊥AB 1→,n ⊥AE →,得⎩⎪⎨⎪⎧ ax +z =0,ax 2+y =0. 取x =1,得平面B 1AE 的一个法向量n =⎝⎛⎭⎫1,-a 2,-a . 要使DP ∥平面B 1AE ,只要n ⊥DP →,有a 2-az 0=0, 解得z 0=12. 又DP ⊄平面B 1AE ,∴存在点P ,满足DP ∥平面B 1AE ,此时AP =12. 13.如图所示,四棱锥S —ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱SD 上的点.(1)求证:AC ⊥SD .(2)若SD ⊥平面P AC ,则侧棱SC 上是否存在一点E ,使得BE ∥平面P AC .若存在,求SE ∶EC 的值;若不存在,试说明理由.(1)证明 连接BD ,设AC ∩BD =O ,则AC ⊥BD .由题意知SO ⊥平面ABCD .以O 为坐标原点,OB →,OC →,OS →分别为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系,如图.设底面边长为a ,则高SO =62a , 于是S ⎝⎛⎭⎫0,0,62a ,D ⎝⎛⎭⎫-22a ,0,0, B ⎝⎛⎭⎫22a ,0,0,C ⎝⎛⎭⎫0,22a ,0,OC →=⎝⎛⎭⎫0,22a ,0, SD →=⎝⎛⎭⎫-22a ,0,-62a ,则OC →·SD →=0. 故OC ⊥SD .从而AC ⊥SD .(2)解 棱SC 上存在一点E ,使BE ∥平面P AC .理由如下:由已知条件知DS →是平面P AC 的一个法向量,且DS →=⎝⎛⎭⎫22a ,0,62a ,CS →=⎝⎛⎭⎫0,-22a ,62a ,BC →=⎝⎛⎭⎫-22a ,22a ,0. 设CE →=tCS →,则BE →=BC →+CE →=BC →+tCS → =⎝⎛⎭⎫-22a ,22a (1-t ),62at , 而BE →·DS →=0⇔t =13. 即当SE ∶EC =2∶1时,BE →⊥DS →.而BE 不在平面P AC 内,故BE ∥平面P AC .∴存在一点E ,使得BE ∥平面P AC ,此时SE ∶EC =2.。
立体几何线面垂直的证明

立体几何证明【知识梳理】1.直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行⇒线面平行”)相交,那么这条直线和交线平行.(“线面平行⇒线线平行”)2..直线与平面垂直判定定理一如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直⇒线面垂直”)判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.性质1.如果一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线。
(线面垂直⇒线线垂直)性质2:如果两条直线同垂直于一个平面,那么这两条直线平行.三。
平面与平面空间两个平面的位置关系:相交、平行.1.平面与平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(“线面平行⇒面面平行”)2. 两个平面垂直判定定理:如果一条直线与一个平面垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直⇒面面垂直”)性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.(面面垂直⇒线面垂直)知识点一 【例题精讲】1.在棱长为2的正方体1111D C B A ABCD -中,E 、F 分别为1DD 、DB 的中点。
(1)求证:EF//平面11D ABC ;(2)求证: 平面B 11D C C B 1⊥ EF C B 1⊥; (3)求三棱锥EFC B -1的体积V.2.如图所示, 四棱锥P -ABCD 底面是直角梯形,,,2,BA AD CD AD CD AB PA ⊥⊥=⊥底面ABCD , E 为PC 的中点, PA =AD =AB =1. (1)证明: //EB PAD 平面; (2)证明: BE PDC ⊥平面; (3)求三棱锥B -PDC 的体积V .3、如图所示,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点,证明:(1)AE⊥CD(2)PD⊥平面ABE.4、.如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°(Ⅰ)证明:AB⊥A1C;练习1、如图,菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°.(Ⅰ)证明:AD⊥PB;(Ⅱ)求三棱锥C﹣PAB的高.2.如图14所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.求证:EF⊥平面BCG;3.如图11所示,三棱柱ABCA1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B;4、如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.(Ⅰ)求证:BF⊥平面ACFD;(Ⅱ)求直线BD与平面ACFD所成角的余弦值.5、三棱锥P﹣ABC中,∠BAC=90°,PA=PB=PC=BC=2AB=2,(1)求证:面PBC⊥面ABC6.已知四棱锥P-ABCD中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC的中点.(1)求证:PA∥平面EDB;(2)求证:平面EDB⊥平面PBC;7、如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.(1)求证:AP∥平面BDE;2.求证BE 垂直平面PAC8、将如图一的矩形ABMD沿CD翻折后构成一四棱锥M﹣ABCD(如图二),若在四棱锥M﹣ABCD中有MA=.(1)求证:AC⊥MD;(2)求四棱锥M﹣ABCD的体积.作业1、如图1,菱形ABCD的边长为12,∠BAD=60°,AC交BD于点O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M,N分别是棱BC,AD 的中点,且DM=6.(Ⅰ)求证:OD⊥平面ABC;2、如图,在斜三棱柱ABC﹣A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.(Ⅰ)求证:A1B⊥AC1;3、如图所示,四棱锥P﹣ABCD的侧面PAD是边长为2的正三角形,底面ABCD 是∠ABC=60°的菱形,M为PC的中点,PC=.(Ⅰ)求证:PC⊥AD;AD,E,4、如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=12F分别为线段AD,PC的中点.(Ⅰ)求证:AP∥平面BEF;(Ⅱ)求证:BE⊥平面PAC.5、如图,四棱锥S﹣ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=.(1)证明:CD⊥SD;6.如图,四棱锥S ﹣ABCD 中,△ABD 是正三角形,CB=CD ,SC ⊥BD .(Ⅰ)求证:SB=SD ;(Ⅱ)若∠BCD=120°,M 为棱SA 的中点,求证:DM ∥平面SBC .7、如图,在矩形ABCD 中,点E 为边AD 上的点,点F 为边CD 的中点,234A E D B A A ===,现将ABE ∆沿BE 边折至PBE ∆位置,且平面PBE ⊥平面BCDE .(1)求证:平面PBE ⊥平面PEF ;8、如图5.在椎体P-ABCD 中,ABCD 是边长为1的棱形, 且∠DAB=60︒,2PA PD ==,PB=2,E,F 分别是BC,PC 的中点.(1) 证明:AD ⊥平面DEF;AB CDEBCDEFP9、在如图所示的多面体ABCDEF 中,ABCD 为直角梯形,//AB CD ,90DAB ∠=︒,四边形ADEF 为等腰梯形,//EF AD ,已知AE EC ⊥,2AB AF EF ===,4AD CD ==.(Ⅰ)求证:平面ABCD ⊥平面ADEF10.如图,在底面为平行四边形的四棱锥P ABCD -中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点. (Ⅱ)求证://PB 平面AEC ;11.棱长为2的正方体ABCD﹣A1B1C1D1中,M是棱AA1的中点,过C、M、D1作正方体的截面,则截面的面积是。
高中数学必修2立体几何专题线面垂直方法总结

线垂直还是选择面面垂直;要证明结论或要得
到哪个结论,就必须满足什么条件等.
4
【变式练习1】 如图,E,F分别为直角三角形ABC的直角 边 AC 和 斜 边 AB 的 中 点 , 沿 EF 将 △ AEF 折 起 到 △ A1EF 的 位 置 , 连 结 A1B , A1C. 求 证 : (1)EF⊥平面A1EC; (2)AA1⊥平面A1BC.
又 E F B C, 所 以 A A1 B C,
又 A1C B C= C , 所 以 A A1 平 面 A1B C .
6
用线面垂直的性质 定理证明线线垂直
【例2】 已知在直三棱柱ABC-A1B1C1中,ACB=90, CB=1,CA=3,,C1C=6,M是CC1的中点, 求证:A1BAM.
7
2
因为E是PC的中点,所以AE⊥PC. 由(1)知,AE⊥CD,且PC∩CD=C, 所以AE⊥平面PCD. 而PD 平面PCD,所以AE⊥PD. 又因为PA⊥底面ABCD,所以PA⊥AB. 由已知得AB⊥AD,且PA∩AD=A,所以AB⊥ 平面PAD. 又PD 平面PAD,所以AB⊥PD. 因为AB∩AE=A,所以PD⊥平面ABE.
3
本题考查直线及直线垂直、直线及平面垂
直等基础知识,考查空间想象能力和推理论证
能力.立体几何的证明关键是学会分析和掌握
一些常规的证明方法.如:已知中点证明垂直
时要首先考虑等腰三角形中的“三线合一”;
已知线段或角度等数量关系较多时最好标示出
来,充分进行计算,从而发现蕴含的垂直等关
系;已知线面垂直时会有哪些结论,是选择线
11
2 当
B1P =1时 PB
,
PO
平面
D1AC .
立体集合中证明面面垂直的条件

立体集合中证明面面垂直的条件《立体几何中证明面面垂直的条件》话说我们班呢,有个叫小明的同学。
那天呢,老师在黑板上画了一个很复杂的立体图形,然后问大家怎么证明图里的两个面是垂直的。
这可把小明给难住了,脸皱得像苦瓜一样。
我呢,就小声跟他说:“这证明面面垂直啊,其实是有好些个条件的。
”从这事儿呢,咱们今天就好好唠唠立体几何中证明面面垂直的条件。
首先呢,最常见的一个条件就是,如果一个平面内有一条直线垂直于另一个平面,那这两个平面就垂直。
就好比啊,你看一面墙(看成一个平面),地上竖着一根直杆子(看成一条直线),如果杆子垂直于地面,然后杆子又在另一面墙(另一个平面)上,那这两面墙肯定就是垂直的关系。
这是一种很直观的思路。
比如说在一个长方体里,侧面的一条棱垂直于底面,那侧面就跟底面垂直了。
还有呢,如果我们能证明二面角是直二面角,这两个面也是垂直的。
这就像一个张开成直角的折纸,这两片纸就可以看成两个面嘛。
但是这个证明二面角是直二面角有时候也不简单哦。
通常我们需要找到二面角的平面角,然后证明这个角是90°。
那怎么找这个平面角呢?这就需要我们利用三垂线定理之类的方法啦。
就像是在迷宫里找线索一样,要通过一些几何关系的推导去找到这个神秘的平面角。
另外,从向量的角度来看,如果我们能找出两个平面的法向量,当这两个法向量垂直的时候,也就是法向量的数量积为0的时候,对应的两个平面也是垂直的。
这就好比两个互相攻击的小怪兽(法向量),他们攻击的方向要是正正好好成直角的话,那就说明他们守护的两个平面也是垂直的。
我觉得呀,要想很好地掌握证明面面垂直的条件呢,一定要多做练习题。
你就像练武功一样,光知道招式(条件)没用,还得通过实战(做练习题)来提高自己的反应能力。
而且呢,要多画一些立体图形,把图形印在自己的脑子里,这样一遇到问题,就能快速地想出解题的思路了。
总的来说啊,立体几何中证明面面垂直就是从直线与平面垂直、二面角为直二面角、法向量垂直这些方面入手。
立体几何基本知识总结和线面垂直平行六种关系的证明方法

立体几何基本知识总结I. 基础知识要点 一、 平面.1. 经过不在同一条直线上的三点确定一个面.注:两两相交且不过同一点的四条直线必在同一平面内.2. 两个平面可将平面分成3或4部分.(①两个平面平行,②两个平面相交)3. 过三条互相平行的直线可以确定1或3个平面.(①三条直线在一个平面内平行,②三条直线不在一个平面内平行)[注]:三条直线可以确定三个平面,三条直线的公共点有0或1个. 4. 三个平面最多可把空间分成 8 部分.(X 、Y 、Z 三个方向) 二、 空间直线.1. 空间直线位置分三种:相交、平行、异面. 相交直线—共面有反且有一个公共点;平行直线—共面没有公共点;异面直线—不同在任一平面内[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(可能两条直线平行,也可能是点和直线等) ②直线在平面外,指的位置关系:平行或相交③若直线a 、b 异面,a 平行于平面α,b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.(×)(射影不一定只有直线,也可以是其他图形) ⑥在同一平面内的射影长相等,则斜线长相等.(×)(并非是从平面外一点..向这个平面所引的垂线段和斜线段) ⑦b a ,是夹在两平行平面间的线段,若b a =,则b a ,的位置关系为相交或平行或异面.2. 异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)3. 平行公理:平行于同一条直线的两条直线互相平行.4. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如下图). (二面角的取值范围[]180,0∈θ)(异面直线所成角(] 90,0∈θ)(斜线与平面成角()90,0∈θ)(直线与平面所成角[]90,0∈θ)(向量与向量所成角])180,0[ ∈θ推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等. 5. 两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面) 三、 直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种:相交、平行、在平面内.2. 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)[注]:①直线a 与平面α内一条直线平行,则a ∥α. (×)(平面外一条直线) ②直线a 与平面α内一条直线相交,则a 与平面α相交. (×)(平面外一条直线)③若直线a 与平面α平行,则α内必存在无数条直线与a 平行. (√)(不是任意一条直线,可利用平行的传递性12方向相同12方向不相同证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内) ⑤平行于同一直线的两个平面平行.(×)(两个平面可能相交) ⑥平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面) ⑦直线l 与平面α、β所成角相等,则α∥β.(×)(α、β可能相交)3. 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直. ● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理),得不出α⊥PO . 因为a ⊥PO ,但PO 不垂直OA .●三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面. 推论:如果两条直线同垂直于一个平面,那么这两条直线平行. [注]:①垂直于同一平面....的两个平面平行.(×)(可能相交,垂直于同一条直线.....的两个平面平行) ②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√) 5. ⑴垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短. [注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上四、 平面平行与平面垂直.1. 空间两个平面的位置关系:相交、平行.2. 平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,哪么这两个平面平行.(“线面平行,面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行. [注]:一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行,线线平行”)4. 两个平面垂直性质判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直性质判定二:如果一个平面与一条直线垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直,面面垂直”)注:如果两个二面角的平面对应平面互相垂直,则两个二面角没有什么关系.5. 两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面.证明:如图,找O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.6. 两异面直线任意两点间的距离公式:θcos 2222mn d n m l +++=(θ为锐角取加,θ为钝取减,综上,都POAaPαβθM AB O取加则必有⎥⎦⎤⎝⎛∈2,0πθ)7. ⑴最小角定理:21cos cos cos θθθ=(1θ为最小角,如图) ⑵最小角定理的应用(∠PBN 为最小角)简记为:成角比交线夹角一半大,且又比交线夹角补角一半长,一定有4条. 成角比交线夹角一半大,又比交线夹角补角小,一定有2条. 成角比交线夹角一半大,又与交线夹角相等,一定有3条或者2条. 成角比交线夹角一半小,又与交线夹角一半小,一定有1条或者没有. 五、 棱锥、棱柱. 1. 棱柱.⑴①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的. ②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.⑵{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱柱}⊃{正方体}. {直四棱柱}⋂{平行六面体}={直平行六面体}.⑶棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全.等的矩形..... ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形.注:①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×) (直棱柱不能保证底面是钜形可如图) ②(直棱柱定义)棱柱有一条侧棱和底面垂直.⑷平行六面体:定理一:平行六面体的对角线交于一点.............,并且在交点处互相平分. [注]:四棱柱的对角线不一定相交于一点.定理二:长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.推论一:长方体一条对角线与同一个顶点的三条棱所成的角为γβα,,,则1cos cos cos 222=++γβα. 推论二:长方体一条对角线与同一个顶点的三各侧面所成的角为γβα,,,则2cos cos cos 222=++γβα. [注]:①有两个侧面是矩形的棱柱是直棱柱.(×)(斜四面体的两个平行的平面可以为矩形) ②各侧面都是正方形的棱柱一定是正棱柱.(×)(应是各侧面都是正方形的直.棱柱才行) ③对角面都是全等的矩形的直四棱柱一定是长方体.(×)(只能推出对角线相等,推不出底面为矩形)④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交,可能不相交,若两条边相交,则应是充要条件)2. 棱锥:棱锥是一个面为多边形,其余各面是有一个公共顶点的三角形. [注]:①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V Sh V ==.图1θθ1θ2图2⑴①正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心. [注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形) ii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ③棱锥的侧面积与底面积的射影公式:αcos 底侧S S =(侧面与底面成的二面角为α)附: 以知c ⊥l ,b a =⋅αcos ,α为二面角b l a --.则l a S ⋅=211①,b l S ⋅=212②,b a =⋅αcos ③ ⇒①②③得αcos 底侧S S =. 注:S 为任意多边形的面积(可分别多个三角形的方法). ⑵棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高). ②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心. ⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心. ⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径; ⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)ii. 若一个三角锥,两条对角线互相垂直,则第三对角线必然垂直. 简证:A B ⊥CD ,AC ⊥BD ⇒ BC ⊥AD. 令b AC c AD a AB ===,,得c a c b AD BC c AD a b AB AC BC -=⋅⇒=-=-=,,已知()()0,0=-⋅=-⋅c a b b c a0=-⇒c b c a 则0=⋅AD BC .iii. 空间四边形OABC 且四边长相等,则顺次连结各边的中点的四边形一定是矩形. iv. 若是四边长与对角线分别相等,则顺次连结各边的中点的四边是一定是正方形. 简证:取AC 中点'O ,则⊥⇒⊥'⊥'AC AC O B AC o o ,平面=∠⇒⊥⇒'FGH BO AC B O O 90°易知EFGH 为平行四边形⇒EFGH 为长方形.若对角线等,则EFGH FG EF ⇒=为正方形. 3. 球:⑴球的截面是一个圆面. ①球的表面积公式:24R S π=. ②球的体积公式:334R V π=. l ab c FEH GBCDAO'⑵纬度、经度:①纬度:地球上一点P 的纬度是指经过P 点的球半径与赤道面所成的角的度数.②经度:地球上B A ,两点的经度差,是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数,特别地,当经过点A 的经线是本初子午线时,这个二面角的度数就是B 点的经度. 附:①圆柱体积:h r V 2π=(r 为半径,h 为高) ②圆锥体积:h r V 231π=(r 为半径,h 为高) ③锥形体积:Sh V 31=(S 为底面积,h 为高) 4. ①内切球:当四面体为正四面体时,设边长为a ,a h 36=,243a S =底,243a S =侧 得a a a R R a R a a a 46342334/424331433643222=⋅==⇒⋅⋅+⋅=⋅. 注:球内切于四面体:h S R S 313R S 31V 底底侧ACD B ⋅=⋅+⋅⋅⋅=- ②外接球:球外接于正四面体,可如图建立关系式.构造以半径为斜边的直角三角形线面垂直平行六种关系的证明方法总结一、线线平行的证明方法:1、利用平行四边形。
立体几何垂直证明题常见模型及方法总结计划x

立体几何垂直证明题常见模型及方法总结计划x 标准文档立体几何垂直证明题常见模型及方法证明空间线面垂直需注意以下几点:①由已知想性质,由求证想判定,即分析法与综合法相结合寻找证题思路。
②立体几何论证题的解答中,利用题设条件的性质适当添加辅助线(或面)是解题的常用方法之一。
③明确何时应用判定定理,何时应用性质定理,用定理时要先申明条件再由定理得出相应结论。
垂直转化:线线垂直线面垂直面面垂直;基础篇类型一:线线垂直证明(共面垂直、异面垂直)( 1)共面垂直:实际上是平面内的两条直线的垂直(只需要同学们掌握以下几种模型)○1 等腰(等边)三角形中的中线2 菱形(正方形)的对角线互相垂直○3 勾股定理中的三角形○○41:1:2 的直角梯形中○5 利用相似或全等证明直角。
例:在正方体 ABCD A1B1C1D1 中, O 为底面 ABCD 的中心, E 为 CC1 ,求证: A1O OE2)异面垂直(利用线面垂直来证明,高考中的意图)例 1 在正四面体ABCD中,求证 AC BD变式1 如图,在四棱锥PABCD中,底面A B C D是矩形,已知AB3, AD 2, PA 2, PD2 2, PAB60 .证明: ADPB;实用文案标准文档变式 2 如图,在边长为2 的正方形 ABCD 中,点 E 是 AB 的中点,点 F 是 BC 的中点,将△ AED, △ DCF 分别沿 DE , DF 折起,使 A,C 两点重合于 A' .A '求证 : A'DEF;EDBGF变式 3 如图,在三棱锥P ABC 中,⊿ PAB 是等边三角形,∠PAC=∠ PBC=90 o证明:AB⊥ PC类型二:线面垂直证明方法○1 利用线面垂直的判断定理例 2:在正方体ABCD A1B1C1D1 中, O 为底面 ABCD 的中心, E 为CC1 ,求证:A1O 平面 BDE变式 1:在正方体 ABCDA1B1C1D1 中, ,求证: AC1平面 BDC1变式 2:如图:直三棱柱ABC- A1B1C1 中, AC=BC=AA1=2,∠ ACB=90 .E 为 BB 1 的中点, D 点在 AB 上且 DE = 3 .求证:CD ⊥平面 A1ABB 1;实用文案标准文档变式3:如图,在四面体ABCD中, O 、 E分别是BD 、 BC的中点,CACBCDBD 2 , ABAD2.A求证:AO平面 BCD;DOBEC变式 4 如图,在底面为直角梯形的四棱锥P ABCD 中,AD ∥ BC ,ABC 90°, PA平面 ABCD . PA 3, AD2 , AB2 3 , BC61 求证: BD平面 PACPADE○利用面面垂直的性质定理BC2例 3:在三棱锥 P-ABC 中, PA底面 ABC , 面 PAC面 PBC ,求证: BC面 PAC 。
