与圆相关的动态几何问题
2024年中考数学常见几何模型最值模型之瓜豆模型(原理)圆弧轨迹型

最值模型之瓜豆模型(原理)圆弧轨迹型动点轨迹问题是中考和各类模拟考试的重要题型,学生受解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的集中点。
掌握该压轴题型的基本图形,构建问题解决的一般思路,是中考专题复习的一个重要途径。
本专题就最值模型中的瓜豆原理(动点轨迹为圆弧型)进行梳理及对应试题分析,方便掌握。
【模型解读】模型1、运动轨迹为圆弧模型1-1. 如图,P是圆O上一个动点,A为定点,连接AP,Q为AP中点.Q点轨迹是?如图,连接AO,取AO中点M,任意时刻,均有△AMQ∽△AOP,QM:PO=AQ:AP=1:2.则动点Q是以M为圆心,MQ为半径的圆。
模型1-2. 如图,△APQ是直角三角形,∠PAQ=90°且AP=k⋅AQ,当P在圆O运动时,Q点轨迹是?如图,连结AO,作AM⊥AO,AO:AM=k:1;任意时刻均有△APO∽△AQM,且相似比为k。
则动点Q是以M为圆心,MQ为半径的圆。
模型1-3. 定义型:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧。
(常见于动态翻折中)如图,若P为动点,但AB=AC=AP,则B、C、P三点共圆,则动点P是以A圆心,AB半径的圆或圆弧。
模型1-4. 定边对定角(或直角)模型1)一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.如图,若P为动点,AB为定值,∠APB=90°,则动点P是以AB为直径的圆或圆弧。
2)一条定边所对的角始终为定角,则定角顶点轨迹是圆弧.如图,若P为动点,AB为定值,∠APB为定值,则动点P的轨迹为圆弧。
【模型原理】动点的轨迹为定圆时,可利用:“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和,最小值为定点到圆心的距离与半径之差”的性质求解。
1(2023·山东泰安·统考中考真题)如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(-6,4);Rt△COD中,∠COD=90°,OD=43,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是()A.3B.62-4C.213-2D.22(2023·四川广元·统考一模)如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一动点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使∠DCP=60°,连接OD,则OD长的最大值为.3(2023·四川宜宾·统考中考真题)如图,M是正方形ABCD边CD的中点,P是正方形内一点,连接BP,线段BP以B为中心逆时针旋转90°得到线段BQ,连接MQ.若AB=4,MP=1,则MQ的最小值为.4(2023·湖南·统考中考真题)如图,在矩形ABCD中,AB=2,AD=7,动点P在矩形的边上沿B→C→D→A运动.当点P不与点A、B重合时,将△ABP沿AP对折,得到△AB P,连接CB ,则在点P的运动过程中,线段CB 的最小值为.5(2023·山东·统考中考真题)如图,在四边形ABCD中,∠ABC=∠BAD=90°,AB=5,AD=4,AD< BC,点E在线段BC上运动,点F在线段AE上,∠ADF=∠BAE,则线段BF的最小值为.6(2023·浙江金华·九年级校考期中)如图,点A,C,N的坐标分别为(-2,0),(2,0),(4,3),以点C为圆心、2为半径画⊙C,点P在⊙C上运动,连接AP,交⊙C于点Q,点M为线段QP的中点,连接MN,则线段MN的最小值为.7(2023上·江苏连云港·九年级校考阶段练习)已知矩形ABCD,AB=6,BC=4,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为.8(2023下·陕西西安·九年级校考阶段练习)问题提出:(1)如图①,在△ABC中,AB=AC,∠BAC=120°,BC=43,则AB的长为;问题探究:(2)如图②,已知矩形ABCD,AB=4,BC=5,点P是矩形ABCD内一点,且满足∠APB= 90°,连接CP,求线段CP的最小值;问题解决:(3)如图③所示,我市城市绿化工程计划打造一片四边形绿地ABCD,其中AD∥BC,AD= 40m,BC=60m,点E为CD边上一点,且CE:DE=1:2,∠AEB=60°,为了美化环境,要求四边形ABCD的面积尽可能大,求绿化区域ABCD面积的最大值.课后专项训练1(2023·安徽合肥·校考一模)如图,在△ABC中,∠B=45°,AC=2,以AC为边作等腰直角△ACD,连BD,则BD的最大值是()A.10-2B.10+3C.22D.10+22(2023春·广东·九年级专题练习)已知:如图,在△ABC中,∠BAC=30°,BC=4,△ABC面积的最大值是( ).A.8+43B.83+4C.83D.8+833(2022秋·江苏扬州·九年级校考阶段练习)如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则△BCD的面积的最大值为()A.43+4B.4C.43+8D.64(2023·山东济南·一模)正方形ABCD中,AB=4,点E、F分别是CD、BC边上的动点,且始终满足DE=CF,DF、AE相交于点G.以AG为斜边在AG下方作等腰直角△AHG使得∠AHG=90°,连接BH.则BH的最小值为()A.25-2B.25+2C.10-2D.10+25(2023上·江苏连云港·九年级统考期中)如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接CM,则CM的最小值为.6(2023春·广东深圳·九年级专题练习)如图,点G是△ABC内的一点,且∠BGC=120°,△BCF是等边三角形,若BC=3,则FG的最大值为.7(2023·江苏泰州·九年级专题练习)如图,在矩形ABCD中,AD=10,AB=16,P为CD的中点,连接BP.在矩形ABCD外部找一点E,使得∠BEC+∠BPC=180°,则线段DE的最大值为.8(2023·陕西渭南·三模)如图,在矩形ABCD中,AB=6,BC=5,点E在BC上,且CE=4BE,点M 为矩形内一动点,使得∠CME=45°,连接AM,则线段AM的最小值为.9(2023江苏扬州·三模)如图,在等边△ABC和等边△CDE中,AB=6,CD=4,以AB、AD为邻边作平行四边形ABFD,连接AF.若将△CDE绕点C旋转一周,则线段AF的最小值是.10(2023秋·湖北武汉·九年级校考阶段练习)如图,△ABC为等腰直角三角形,∠BAC=90°,AB= AC=22,点D为△ABC所在平面内一点,∠BDC=90°,以AC、CD为边作平行四边形ACDE,则CE的最小值为.11(2023·福建泉州·统考模拟预测)如图,点E是正方形ABCD的内部一个动点(含边界),且AD= EB=8,点F在BE上,BF=2,则以下结论:①CF的最小值为6;②DE的最小值为82-8;③CE= CF;④DE+CF的最小值为10;正确的是.12(2021·广东·中考真题)在△ABC中,∠ABC=90°,AB=2,BC=3.点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为.13(2023·广东·深圳市二模)如图,在矩形ABCD中,AB=3,BC=4,E为边BC上一动点,F为AE 中点,G为DE上一点,BF=FG,则CG的最小值为.14(2023秋·广东汕头·九年级校考期中)如下图,在正方形ABCD中,AB=6,点E是以BC为直径的圆上的点,连接DE,将线段DE绕点D逆时针旋转90°,得到线段DF,连接CF,则线段CF的最大值与最小值的和.15(2023·陕西渭南·统考一模)如图,在矩形ABCD中,AB=2,BC=4,Q是矩形ABCD左侧一点,连接AQ、BQ,且∠AQB=90°,连接DQ,E为DQ的中点,连接CE,则CE的最大值为.16(2023·安徽亳州·统考模拟预测)等腰直角△ABC 中,BAC =90°,AB =5,点D 是平面内一点,AD =2,连接BD ,将BD 绕D 点逆时针旋转90°得到DE ,连接AE ,当DAB =(填度数)度时,AE 可以取最大值,最大值等于.17(2023·河北廊坊·统考二模)已知如图,△ABC 是腰长为4的等腰直角三角形,∠ABC =90°,以A 为圆心,2为半径作半圆A ,交BA 所在直线于点M ,N .点E 是半圆A 上仟意一点.连接BE ,把BE 绕点B 顺时针旋转90°到BD 的位置,连接AE ,CD .(1)求证:△EBA ≌△DBC ;(2)当BE 与半圆A 相切时,求弧EM的长;(3)直接写出△BCD 面积的最大值.18(2022·北京·中考真题)在平面直角坐标系xOy 中,已知点M (a ,b ),N .对于点P 给出如下定义:将点P 向右(a ≥0)或向左(a <0)平移a 个单位长度,再向上(b ≥0)或向下(b <0)平移b 个单位长度,得到点P ',点P '关于点N 的对称点为Q ,称点Q 为点P 的“对应点”.(1)如图,点M (1,1),点N 在线段OM 的延长线上,若点P (-2,0),点Q 为点P 的“对应点”.①在图中画出点Q;②连接PQ,交线段ON于点T.求证:NT=12 OM;(2)⊙O的半径为1,M是⊙O上一点,点N在线段OM上,且ON=t12<t<1,若P为⊙O外一点,点Q为点P的“对应点”,连接PQ.当点M在⊙O上运动时直接写出PQ长的最大值与最小值的差(用含t的式子表示)19(2023下·广东广州·九年级校考阶段练习)如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.(1)求证:BD=CE;(2)连接CD,延长ED交BC于点F,若△ABC的边长为2;①求CD的最小值;②求EF的最大值.20(2023·江苏常州·统考二模)如图,在平面直角坐标系中,二次函数y=-13x2+bx-3的图像与x轴交于点A和点B9,0,与y轴交于点C.(1)求二次函数的表达式;(2)若点P是抛物线上一点,满足∠PCB+∠ACB=∠BCO,求点P的坐标;(3)若点Q在第四象限内,且cos∠AQB=35,点M在y轴正半轴,∠MBO=45°,线段MQ是否存在最大值,如果存在,直接写出最大值;如果不存在,请说明理由.最值模型之瓜豆模型(原理)圆弧轨迹型动点轨迹问题是中考和各类模拟考试的重要题型,学生受解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的集中点。
与圆相关的动态几何问题

与圆相关的动态几何问题
以下是几个与圆相关的动态几何问题:
1. 两个圆的交点:当两个圆相交时,它们会产生两个交点。
这
些交点可以在动态几何软件中随着圆的移动而变化。
2. 圆的切线:给定一个圆和一点,可以确定从该点到圆的切线。
这些切线可以通过移动点和圆来进行动态演示。
3. 圆的切线长度:给定一个圆和一点,可以计算从该点到圆的
切线的长度。
这个问题可以用来演示一些几何学中的定理,如切线
长定理。
4. 圆内接多边形:将一个多边形放置在内切圆内部,并使多边
形的每个顶点都在圆上。
这个问题涉及到内切圆的中心和半径,可
以通过动态几何演示进行展示。
5. 圆内接三角形:在内切圆上选择三个点,这些点构成一个内
接三角形。
可以展示内接圆如何与三角形有关,并给出内接圆的半
径和面积。
动态几何之胡不归阿氏圆,旋转相似问题

“胡不归”“阿氏圆”及旋转相似一、胡不归型【背景知识】有一则历史故事:说的是一个身在他乡的小伙子,得知父亲病危的消息后便日夜赶路回家。
然而,当他气喘吁吁地来到父亲的面前时,老人刚刚咽气了。
人们告诉他,在弥留之际,老人在不断喃喃地叨念:“胡不归?胡不归?”早期的科学家曾为这则古老的传说中的小伙子设想了一条路线。
(如下图)A是出发地,B是目的地;A C是一条驿道,而驿道靠目的地的一侧是沙地。
为了急切回家,小伙子选择了直线路程A B 。
但是,他忽略了在驿道上行走要比在砂土地带行走快的这一因素。
如果他能选择一条合适的路线(尽管这条路线长一些,但是速度可以加快),是可以提前抵达家门的。
那么,这应该是那条路线呢?显然,根据两种路面的状况和在其上行走的速度值,可以在A C上选定一点D ,小伙子从A走到D ,然后从D折往B ,可望最早到达B 。
用现代的科学语言表达,就是:若在驿道上行走的速度为,在沙地上行走的速度为,即求的最小值.例题1、如图,P 为正方形A B C D对角线B D上一动点,若A B =2,则A P +B P +C P 的最小值为_______解析:∵正方形A B C D为轴对称图形∴A P =P CAB CD P∴A P+B P+C P=2A P+B P=∴即求的最小值接下去就是套路我们要构造一个出来连接A E,作∠D B E=30°,交A C于E,过A作A F⊥B E,垂足为F 在R t△P B F中,∵∠P B F=30°∴由此我们把构造出来了∴的最小值即为A F线段的长∵∠B A E=45°,∠A E B=60°∴解直角△A B E,得A O=B O=,O E=,O B=根据面积法,·=·求出A F=(此外本题费马点亦可)例题2图1图2总结步骤:第一步:将所求线段和改写为的形式(<1)第二步:在P B的一侧,P A的异侧,构造一个角度,使得s i n=第三步:过A作第二步所构造的角的一边垂线,该垂线段即为所求最小值第四步:计算即可模型具体归纳如下:练习1如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经______小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)练习2练习4如图,△A B C在直角坐标系中,A B=A C,A(0,2),C(1,0),D为射线A O上一点,一动点P从A出发,运动路径为A→D→C,点P在A D上的运动速度是在C D上的3倍,要使整个运动时间最少,则点D的坐标应为_______练习5如图,菱形A B C D的对角线A C上有一动点P,B C=6,∠A B C=150°,则线段A P+B P+P D的最小值为.练习6如图,在平面直角坐标系中,二次函数y=a x2+b x+c的图象经过点A(﹣1,0),B(0,﹣),C(2,0),其对称轴与x轴交于点D(1)求二次函数的表达式及其顶点坐标;(2)若P为y轴上的一个动点,连接P D,则P B+P D的最小值为;练习7如图,在△A C E中,C A=C E,∠C A E=30°,⊙O经过点C,且圆的直径A B在线段A E上.(1)试说明C E是⊙O的切线;(2)若△A C E中A E边上的高为h,试用含h的代数式表示⊙O的直径A B;(3)设点D是线段A C上任意一点(不含端点),连接O D,当C D+O D的最小值为6时,求⊙O的直径A B的长.二、阿氏圆型阿氏圆也是形如的形式(<1)最终还是化分为整。
专题41 几何问题(1)之动点问题【热点专题】

专题41 几何问题(1)之动点问题
数学
题型精讲
题型一:圆背景下的动态探究题 【例 1】(2020•连云港)筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水 轮赋)中写道:“水能利物,轮乃曲成”.如图,半径为 3m 的筒车⊙O 按逆时针方向
每分钟转 圈,筒车与水面分别交于点 A、B 筒车的轴心 O 距离水面的高度 OC 长为 2.2m,筒车上均匀分布着若干个盛水筒.若以某个盛水筒 P 刚浮出水面时开始计算时 间.
PQ PQ2.在
Rt△POQ 中,PQ2=OP2+OQ2=(8﹣t)2+t2.由四边形 OPCQ 的面积 S=S△POQ+S△PCQ
可得出答案.
题型二:四边形动点探究 【例 3】(2021·山东中考真题)如图,已知正方形 ABCD,点 E 是 BC 边上一点,将 △ABE 沿直线 AE 折叠,点 B 落在 F 处,连接 BF 并延长,与∠DAF 的平分线相交 于点 H,与 AE,CD 分别相交于点 G,M,连接 HC (1)求证:AG=GH; (2)若 AB=3,BE=1,求点 D 到直线 BH 的距离; (3)当点 E 在 BC 边上(端点除外)运动时,∠BHC 的大小是否变化?为什么?
【分析】(1)如图 1 中,连接 OA.求出∠AOC 的度数,以及旋转速度即可解决问 题. (2)如图 2 中,盛水筒 P 浮出水面 3.4 秒后,此时∠AOP=3.4×5°=17°,过点 P 作 PD⊥OC 于 D,解直角三角形求出 CD 即可. (3)如图 3 中,连接 OP,解直角三角形求出∠POM,∠COM,可得∠POH 的度 数即可解决问题.
【例 2】(2020•苏州)如图,已知∠MON=90°,OT 是∠MON 的平分线,A 是射线 OM 上一点,OA=8cm.动点 P 从点 A 出发,以 1cm/s 的速度沿 AO 水平向左作匀速 运动,与此同时,动点 Q 从点 O 出发,也以 1cm/s 的速度沿 ON 竖直向上作匀速运 动.连接 PQ,交 OT 于点 B.经过 O、P、Q 三点作圆,交 OT 于点 C,连接 PC、 QC.设运动时间为 t(s),其中 0<t<8. (1)求 OP+OQ 的值; (2)是否存在实数 t,使得线段 OB 的长度最大?若存在,求出 t 的值;若不存在, 说明理由. (3)求四边形 OPCQ 的面积.
利用几何画板动态点值绘制圆上的随动点
利用几何画板动态点值绘制圆上的随动点
几何画板最大的特色之一就是可以展示图形的动态几何变化,动态图形的展示过程可以使图形更形象生动具体。
本节向大家介绍如何利用几何画板点的值绘制圆上的随动点。
具体操作步骤如下:
1.构造线段和点并度量点的值。
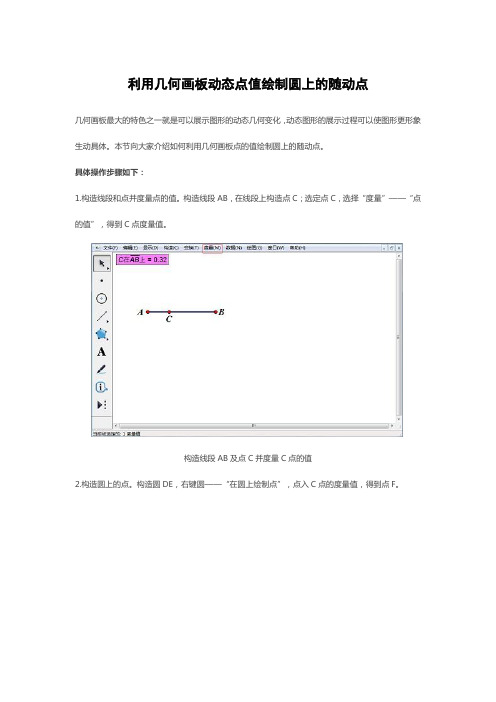
构造线段AB,在线段上构造点C;选定点C,选择“度量”——“点的值”,得到C点度量值。
构造线段AB及点C并度量C点的值
2.构造圆上的点。
构造圆DE,右键圆——“在圆上绘制点”,点入C点的度量值,得到点F。
构造圆并利用C点的度量值构造圆上的点F
3.拖动点C,点F随动,此两点同时出发,同时停止。
F点随着C点变化而变化
温馨提示:如果两个点的速度不同,选择“数据”——“计算”,然后点击C点的度量值,使用计算值在圆上绘制点即可。
圆还可以是其他路径。
以上内容介绍了利用几何画板点值构造随动点的方法,操作简单,其中运用了几何画板度量的功能。
是大家入门学习动点的基础。
动态圆模型

“动态圆”模型的应用带电粒子在磁场中的运动经常涉及动态圆。
常见的动态圆模型有两种,往往都还涉及边界(极值)问题。
模型1如图1,一束带负电的粒子以初速度垂直进入匀强磁场,若初速度方向相同,大小不同,所有粒子运动轨迹的圆心都在垂直于初速度的直线上,速度增大时,轨道半径随着增大,所有粒子的轨迹组成一组动态的内切圆。
模型2如图2,一束带负电的粒子以初速度垂直进入匀强磁场,若初速度大小相同,方向不同,则所有粒子运动的轨道半径相同,但不同粒子的圆心位置不同,其共同规律是:所有粒子的圆心都在以入射点为圆心,以轨道半径为半径的圆上,从而可以找出动态圆的圆心轨迹。
使用时应注意各圆的绕向。
例1.如图所示,在圆形区域内存在一垂直于纸面向里的匀强磁场,一束速率各不相同的质子从A点沿圆形磁场的半径方向射入磁场。
关于质子在该磁场内的运动情况,下列说法正确的是()A.运动时间越长的,其轨迹越长B.运动时间越长的,其射出磁场时的速率越大C.运动时间越长的,其轨迹对应的圆心角越大D.运动时间越长的,其速度方向的偏转角越大解析:该题考查动态圆的模型1.质子沿半径方向射入,沿另一半径方向射出,轨迹半径r=,偏转角等于圆心角θ=2arctan =2arctan ,偏转时间t==·arctan .由此可得偏转时间越长,圆心角越大,运动速率越小,选项C.D正确.答案:CD例2.如图甲所示,宽h=2 cm的有界匀强磁场的纵向范围足够大,磁感应强度的方向垂直纸面向里。
现有一群带正电的粒子从O点以相同的速率,从平面内的各个方向射入磁场。
若粒子在磁场中做匀速圆周运动的轨迹半径r均为5 cm,不计粒子的重力,则()A.右边界:-4 cm<y<4 cm内有粒子射出B.右边界:y>4 cm和y<-4 cm内有粒子射出C.左边界:y>8 cm内有粒子射出D.左边界:0<y<8 cm内有粒子射出解析:该题考查动态圆的模型2。
作出如图乙所示的示意图,由几何关系可得:临界点距x轴的间距y==4 cm。
初中几何动点最值问题难题集锦

初中几何动点最值问题难题集锦初中几何动点最值问题是初中数学中的一道难题类型。
动点最值问题考察动点在几何形状内运动时,某一量的最大值或最小值的求解方法。
下面是一些初中几何动点最值问题的难题集锦。
1.【问题描述】在一个矩形ABCD中,点P动态地沿着矩形的边移动,求线段AP的最长长度。
【解答】假设矩形ABCD的边长为a和b(a<b),点P动态地沿着矩形的边移动。
我们可以观察到,当点P处于矩形的顶点A或D时,线段AP的长度为a;当点P处于矩形的顶点B或C时,线段AP的长度为b。
因此,线段AP的最长长度为b。
2.【问题描述】在一个圆形O内,点P动态地沿着圆的周长移动,求线段OP的最长长度。
【解答】设圆的半径为r,点P动态地沿着圆的周长移动。
根据三角形的性质,可以知道线段OP的长度最长时,点P应该位于圆的周长上的与点O相对的点,即直径上的点。
因此,线段OP的最长长度为2r。
3.【问题描述】在一个正方形ABCD内,点P动态地沿着正方形的边移动,求线段BP的最长长度。
【解答】设正方形ABCD的边长为a,点P动态地沿着正方形的边移动。
由于线段BP的长度等于点P距离B点的距离,所以线段BP的最长长度为正方形的对角线长度,即√2a。
4.【问题描述】在一个等腰直角三角形ABC中,点P动态地沿着三角形的边移动,求线段AP的最长长度。
【解答】设等腰直角三角形ABC的等腰边长为a,点P动态地沿着三角形的边移动。
可以观察到,当点P处于顶点B或C 时,线段AP的长度为a;当点P处于顶点A时,线段AP的长度为0。
因此,线段AP的最长长度为a。
5.【问题描述】在一个梯形ABCD中,点P动态地沿着梯形的边移动,求线段CP的最长长度。
【解答】设梯形ABCD的上底长为a,下底长为b(a>b),点P动态地沿着梯形的边移动。
可以观察到,当点P处于梯形的底端点C或顶端点D时,线段CP的长度为0;当点P处于梯形的上底端点A时,线段CP的长度为ab。
2024年高考数学总复习:立体几何中的动态问题

第1页共5页2024年高考数学总复习:立体几何中的动态问题[解题策略]立体几何中的“动态”问题就变化起因而言大致可分为两类:一是平移;二是旋转.就所求变量而言可分为三类:一是相关线、面、体的测度;二是角度;三是距离.立体几何动态问题的解决需要较高的空间想象能力与化归处理能力,在各省市的高考选择题与填空题中也时有出现.在解“动态”立体几何题时,如果我们能努力探寻运动过程中“静”的一面,动中求静,往往能以静制动、克难致胜.1.去掉枝蔓见本质——大道至简在解决立体几何中的“动态”问题时,需从复杂的图形中分化出最简单的具有实质性意义的点、线、面,让几何图形的实质“形销骨立”,即从混沌中找出秩序,是解决“动态”问题的关键.例1如图1,直线l ⊥平面α,垂足为O .正方体ABCD -A 1B 1C 1D 1的棱长为2.点A 是直线l 上的动点,点B 1在平面α内,则点O 到线段CD 1中点P 的距离的最大值为________.图1答案2+2解析从图形分化出4个点O ,A ,B 1,P ,其中△AOB 1为直角三角形,固定AOB 1,点P 的轨迹是在与AB 1垂直的平面上且以AB 1的中点Q 为圆心的圆,从而OP ≤OQ +QP =12AB 1+2=2+2,当且仅当OQ ⊥AB 1,且点O ,Q ,P 共线时取到等号,此时直线AB 1与平面α成45°角.2.极端位置巧分析——穷妙极巧在解决立体几何中的“动态”问题时,对于移动问题,由图形变化的连续性,穷尽极端特殊之要害,往往能直取答案.例2在正四面体A -BCD 中,E 为棱BC 的中点,F 为直线BD 上的动点,则平面AEF 与平面ACD 所成二面角的正弦值的取值范围是________.答案1解析本例可用极端位置法来加以分析.。
直线和圆动态问题

直线和圆动态问题在动态几何学中,直线和圆是经常出现的两种几何图形。
它们的动态问题是指在平面上随着时间变化而变化的直线和圆的特性。
这些问题通常涉及到直线和圆的位置、相交、切线、交点等方面的性质。
1.直线与圆的相交问题:假设已知一个直线和一个圆,我们想要知道它们是否相交,并求出相交的点。
解决方法:通过求解直线和圆的方程来判断是否相交。
对于直线的方程,可以使用直线的一般方程或者点斜式方程,对于圆的方程,可以使用圆的标准方程。
将直线方程代入圆的方程,得到一个关于变量的方程,求解该方程可以得到相交的点的坐标。
2.直线与圆的切线问题:假设已知一个圆和一条直线相切,我们想要求出切点和切线的方程。
解决方法:通过求解直线和圆的方程来确定切点的坐标,然后利用切点坐标和圆的半径可以确定唯一的切线。
对于圆的方程,可以使用圆的标准方程,对于直线的方程,可以使用直线的一般方程或者点斜式方程。
3.直线与圆的交点问题:假设已知一个圆和一条直线相交于两个点,我们想要求出这两个交点的坐标。
解决方法:同样地,通过求解直线和圆的方程来求得交点的坐标。
需要注意的是,由于直线与圆可能相交于两个点,所以在解方程时可能会得到两组解,应验证这些解是否在给定的直线和圆的范围内。
4.直线与圆的位置关系问题:假设已知一个圆和一条直线,我们想要确定它们的相对位置关系,例如直线是否在圆内部、外部还是与圆相切。
解决方法:通过判断直线与圆的方程是否有实数解,可以确定直线和圆的位置关系。
具体地,当圆与直线的方程无实数解时,说明直线与圆相离;当圆与直线的方程有一个实数解时,说明直线与圆相切;当圆与直线的方程有两个实数解时,说明直线与圆相交于两个点。
以上是直线和圆的动态问题的一些常见解决方法。
在实际应用中,我们经常需要使用这些方法来解决各种涉及直线和圆的动态几何问题。
希望对你有所帮助!。
3.最值问题之辅助圆(轨迹)

几何最值问题之辅助圆(轨迹)最值问题的必要条件是至少有一个动点,因为是动态问题,所以才会有最值.在将军饮马问题中,折点P 就是那个必须存在的动点.并且它的运动轨迹是一条直线,解题策略就是作端点关于折点所在直线的对称即可.当然,动点的运动轨迹是可以变的,比如P 点轨迹也可以是一个圆,就有了第二类最值问题——辅助圆.在这类题目中,题目很少直接告诉我们动点轨迹是个圆,也很少把这个圆画出来,因此,结合题目给的条件,分析出动点的轨迹图形,将是我们面临的最大的问题.若已经确定了动点的轨迹圆,接下来求最最值的问题就会变得简单了,比如:如下图,A 为圆外一点,在圆上找一点P 使得P A 最小.当然,也存在耿直的题目直接告诉动点轨迹是个圆的 确定共圆的方法有几种,①到定点的距离等于定长②共斜边的直角三角形,定角对定弦③对角互补的四边形 ④同侧内角相等的八字形1.如图,已知圆C 的半径为3,圆外一定点O 满足OC =5,点P 为圆C 上一动点,经过点O 的直线l 上有两点A 、B ,且OA =OB ,∠APB =90°,l 不经过点C ,则AB 的最小值为________.【分析】连接OP ,根据△APB 为直角三角形且O 是斜边AB 中点,可得OP 是AB 的一半,若AB 最小,则OP 最小即可.连接OC ,与圆C 交点即为所求点P ,此时OP 最小,AB 也取到最小值.Alll一、从圆的定义构造圆圆的定义:平面内到定点的距离等于定值的所有点构成的集合.构造思路:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧.2.如图,在边长为2的菱形ABCD 中,∠A =60°,M 是AD 边的中点,N 是AB 边上的一动点,将△AMN 沿MN 所在直线翻折得到△A ’MN ,连接A ’C ,则A ’C 长度的最小值是__________.【分析】考虑△AMN 沿MN 所在直线翻折得到△A ’MN ,可得MA ’=MA =1,所以A ’轨迹是以M 点为圆心,MA 为半径的圆弧.连接CM ,与圆的交点即为所求的A ’,此时A ’C 的值最小.构造直角△MHC ,勾股定理求CM ,再减去A ’M 即可.A'NMABCDA'NMABCDDCBA MN A'H A'N MA BCD3.如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8,点F 在边AC 上,并且CF =2,点E 为边BC 上的动点,将△CEF 沿直线EF 翻折,点C 落在点P 处,则点P 到边AB 距离的最小值是__________.【分析】考虑到将△FCE 沿EF 翻折得到△FPE ,可得P 点轨迹是以F 点为圆心,FC 为半径的圆弧.过F 点作FH ⊥AB ,与圆的交点即为所求P 点,此时点P 到AB 的距离最小.由相似先求FH ,再减去FP ,即可得到PH .ABCEFPABCEFPB4.如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合).直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.【分析】考虑l是经过点P的直线,且△ABC沿直线l折叠,所以B’轨迹是以点P为圆心,PB为半径的圆弧.考虑△ACB’面积最大,因为AC是定值,只需B’到AC距离最大即可.过P作作PH⊥AC交AC于H点,与圆的交点即为所求B’点,先求HB’,再求面积.5.如图,矩形ABCD 中,AB =4,BC =8,P 、Q 分别是直线BC 、AB 上的两个动点,AE =2,△AEQ 沿EQ 翻折形成△FEQ ,连接PF 、PD ,则PF +PD 的最小值是_________.【分析】F 点轨迹是以E 点为圆心,EA 为半径的圆,作点D 关于BC 对称点D ’,连接PD ’,PF +PD 化为PF +PD ’.连接ED ’,与圆的交点为所求F 点,与BC 交点为所求P 点,勾股定理先求ED ‘,再减去EF 即可.Q ABC DEFPD'PFE DCBAQ二、定边对直角知识回顾:直径所对的圆周角是直角.构造思路:一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧. 图形释义:若AB 是一条定线段,且∠APB =90°,则P 点轨迹是以AB 为直径的圆.6.已知正方形ABCD 边长为2,E 、F 分别是BC 、CD 上的动点,且满足BE =CF ,连接AE 、BF ,交点为P 点,则PD 的最小值为_________.【分析】由于E 、F 是动点,故P 点也是动点,因而存在PD 最小值这样的问题,那P 点轨迹如何确定?考虑BE =CF ,易证AE ⊥BF ,即在运动过程中,∠APB =90°,故P 点轨迹是以AB 为直径的圆.连接OC ,与圆的交点即为P 点,再通过勾股定理即可求出PC 长度.思路概述:分析动点形成原理,通常“非直即圆”(不是直线就是圆),接下来可以寻找与动点相关有无定直线与定角.ABEFABCDPF7.如图,E 、F 是正方形ABCD 的边AD 上的两个动点,满足AE =DF ,连接CF 交BD 于点G ,连接BE 交AG 于点H ,若正方形边长为2,则线段DH 长度的最小值是________.【分析】根据条件可知:∠DAG =∠DCG =∠ABE ,易证AG ⊥BE ,即∠AHB =90°,所以H 点轨迹是以AB 为直径的圆弧当D 、H 、O 共线时,DH 取到最小值,勾股定理可求.HGAB CDEFαααHGABCDE F8.如图,Rt △ABC 中,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠P AB =∠PBC ,则线段CP 长的最小值是_________.【分析】∵∠PBC +∠PBA =90°,∠PBC =∠P AB , ∴∠P AB +∠PBA =90°, ∴∠APB =90°,∴P 点轨迹是以AB 为直径的圆弧.当O 、P 、C 共线时,CP 取到最小值,勾股定理先求OC ,再减去OP 即可.9.如图, AB 是半圆O 的直径,点C 在半圆O 上,AB =5,AC =4.D 是弧BC 上的一个动点,连接AD ,过点C 作CE ⊥AD 于E ,连接BE .在点D 移动的过程中,BE 的最小值为 .【分析】E 是动点,E 点由点C 向AD 作垂线得来,∠AEC =90°,且AC 是一条定线段,所以E 点轨迹是以AC 为直径的圆弧.PABCCCB当B 、E 、M 共线时,BE 取到最小值.连接BC ,勾股定理求BM ,再减去EM 即可.10.如图,在Rt △ABC 中,∠ACB =90°,BC =4,AC =10,点D 是AC 上的一个动点,以CD 为直径作圆O ,连接BD 交圆O 于点E ,则AE 的最小值为_________.【分析】连接CE ,由于CD 为直径,故∠CED =90°,考虑到CD 是动线段,故可以将此题看成定线段CB 对直角∠CEB .BB取CB 中点M ,所以E 点轨迹是以M 为圆心、CB 为直径的圆弧.连接AM ,与圆弧交点即为所求E 点,此时AE值最小,22AE AM EM =−==.11.如图,正方形ABCD 的边长为4,动点E 、F 分别从点A 、C 同时出发,以相同的速度分别沿AB 、CD 向终点B 、D 移动,当点E 到达点B 时,运动停止,过点B 作直线EF 的垂线BG ,垂足为点G ,连接AG ,则AG 长的最小值为 .【分析】首先考虑整个问题中的不变量,仅有AE =CF ,BG ⊥EF ,但∠BGE 所对的BE 边是不确定的.GF EDCB A重点放在AE =CF ,可得EF 必过正方形中心O 点,连接BD ,与EF 交点即为O 点.∠BGO 为直角且BO 边为定直线,故G 点轨迹是以BO 为直径的圆.记BO 中点为M 点,当A 、G 、M 共线时,AG 取到最小值,利用Rt △AOM 勾股定理先求AM ,再减去GM 即可.12.如图,正方形ABCD 的边长是4,点E 是AD 边上一动点,连接BE ,过点A 作AF ⊥BE 于点F ,点P 是AD 边上另一动点,则PC +PF 的最小值为________.【分析】∠AFB =90°且AB 是定线段,故F 点轨迹是以AB 中点O 为圆心、AB 为直径的圆.AB C DE F GABCDE FP考虑PC +PF 是折线段,作点C 关于AD 的对称点C ’,化PC +PF 为PC ’+PF ,当C ’、P 、F 、O 共线时,取到最小值.13.如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,AB =4,D 是BC 上一动点,CE ⊥AD 于E ,EF ⊥AB 交BC 于点F ,则CF 的最大值是_________.【分析】∠AEC =90°且AC 为定值,故E 点轨迹是以AC 为直径的圆弧.考虑EF ⊥AB ,且E 点在圆上,故当EF 与圆相切的时候,CF 取到最大值.F EDCBAB连接OF ,易证△OCF ≌△OEF ,∠COF =30°,故CF 可求.三、定边对定角在“定边对直角”问题中,依据“直径所对的圆周角是直角”,关键性在于寻找定边、直角,而根据圆周角定理:同圆或等圆中,同弧或等弧所对的圆周角都相.定边必不可少,而直角则可一般为定角.例如,AB 为定值,∠P 为定角,则A 点轨迹是一个圆.当然,∠P 度数也是特殊角,比如30°、45°、60°、120°,下分别作对应的轨迹圆. 若∠P =30°,以AB 为边,同侧构造等边三角形AOB ,O 即为圆心.若∠P =45°,以AB 为斜边,同侧构造等腰直角三角形AOB ,O 即为圆心.BB若∠P =60°,以AB 为底,同侧构造顶角为120°的等腰三角形AOB ,O 即为圆心.若∠P =120°,以AB 为底,异侧为边构造顶角为120°的等腰三角形AOB ,O 即为圆心.14.如图,等边△ABC 边长为2,E 、F 分别是BC 、CA 上两个动点,且BE =CF ,连接AE 、BF ,交点为P 点,则CP 的最小值为________.【分析】由BE =CF 可推得△ABE ≌△BCF ,所以∠APF =60°,但∠APF 所对的边AF 是变化的.EFCBAP60°EF CBAP所以考虑∠APB =120°,其对边AB 是定值.所以如图所示,P 点轨迹是以点O 为圆心的圆弧.(构造OA =OB 且∠AOB =120°)当O 、P 、C 共线时,可得CP 的最小值,利用Rt △OBC 勾股定理求得OC ,再减去OP 即可.15.如图,△ABC 为等边三角形,AB =2,若P 为△ABC 内一动点,且满足∠P AB =∠ACP ,则线段PB 长度的最小值为_________.120°EF CBAP 120°MOP ABCF E120°ABCP【分析】由∠P AB =∠ACP ,可得∠APC =120°,后同上例题.16.在△ABC 中,AB =4,∠C =60°,∠A >∠B ,则BC 的长的取值范围是________. 【分析】先作图,如下条件不多,但已经很明显,AB 是定值,∠C =60°,即定边对定角.故点C 的轨迹是以点O 为圆心的圆弧.(作AO =BO 且∠AOB =120°)题意要求∠A >∠B ,即BC >AC ,故点C 的轨迹如下图.当BC 为直径时,BC 取到最大值,考虑∠A 为△ABC 中最大角,故BC 为最长边,BC >AB =4.无最小值.4ABC 60°17.如图,AB 是圆O 的直径,M 、N 是弧AB (异于A 、B )上两点,C 是弧MN 上一动点,∠ACB 的角平分线交圆O 于点D ,∠BAC 的平分线交CD 于点E ,当点C 从点M 运动到点N 时,则C 、E 两点的运动路径长的比是_______.【分析】分别考虑C 、E 两点的轨迹,C 点轨迹上是弧MCN ,其对应圆心角为∠MON ,半径为OM (或ON ).再考虑E 点轨迹,考虑到CE 、AE 都是角平分线,所以连接BE ,BE 平分∠ABC ,可得:∠AEB =135°.考虑到∠AEB 是定角,其对边AB 是定线段,根据定边对定角,所以E 点轨迹是个圆,考虑到∠ADB =90°,所以D 点即为圆心,DA 为半径.E 点轨迹所对的圆心角为∠MDN ,是∠MON 的一半,所以C 、E 两点轨迹圆半径之比为1:根号2,圆心角之比为2:1,所以弧长比值为根号2.ABAA。
中考必考--数学动点经典例题分析

中考必考——数学动点经典例题分析动态几何问题已经成为中考试题的一大热点题型.这类试题以运动的点、线段、变化的角、图形的面积为基本条件,给出一个或多个变量,要求确定变量与其他量之间的关系,或变量在一定条件为定值时,进行相关的几何计算和综合解答。
下面是几个例题及分析(2000年·上海)如图1在半径为6,圆心角为90的扇形OAB 的弧AB上有一个动点P,PH⊥OA垂足为⊥OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO、GP、GH中有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH= x,G=y求y关于x的函数解析式,并写出函数的定义域(即自变量x 的取值范围)(3)如果⊥PGH是等腰三角形试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变于是线段GO、GP、GH中,有长度保持不变的线段,这条线段是GH=2/3 M=2/3.120P=2.(2)在Rt⊥POH中,OH=√OP2−PH2=√36−x2⊥MH=12OH=12√36−x2在Rt⊥POH中MP=√PH2+MH2=12√36+3x21.分析:此题为点动题,因此,1)搞清动点所走的路线及速度,这样就能求出相应线段的长;2)分析在运动中点的几种特殊位置由题意知,点P 为动点,所走的路线为: ABC 速度为1cm/s。
而t=2s,故可求出AP 的值,进而求出⊥APE 的面积2.分析:两点同时运动,点P 在前,点Q在后,速度相等,因此两点距出发点A的距离相差总是2cm.P在AB边上运动后,又到BC边上运动因此PM、N 截平行四边形ABCD 所得图形不同.故分两种情况:(1)⊥当P、Q 都在AB 上运动时,PM、N 截平行四边形ABCD 所得的图形永远为直角梯形.此时0≤t≤6.⊥当P在BC上运动,而Q在A 边上运动时,画出相应图形,所成图形为六边形DFOBPG,不规则图形面积用割补法.此时6<t≤8.可以尝试自己解答一下吆!以上是数学动点例题及解析,你学会如何解答此类问题了么?。
矢量圆解动态平衡问题

矢量圆解动态平衡问题
“动态平衡”是指随着制动外力的变化,系统动态响应的动态平衡变
化的过程,对于学习者、科学家、工程师和技术专家来说,动态平衡
是至关重要的。
矢量圆是一种有效的动态平衡解决方法,这种解决方
法可以有效地解决复杂的动态平衡问题,是一种考虑系统变化的响应,以致能够有效地处理系统变化的有效解。
矢量圆的实施需要考虑两个重要的方面。
首先,对于解时控制系统的
变化进行建模,这可以通过建立一个计算矢量圆的公式来实现。
其次,以及由此建立的更加一般的模型,以及事故发生之前情况的分析。
此外,还需要考虑矢量圆的几何及动态特性。
通常,动态平衡受到动
态外力的影响,例如分辨率、位置或动态特性,因此必须考虑矢量圆
的几何及动态特性。
此外,动态外力的变化可能是矢量圆周围环境变
化的一部分,这也是需要考虑。
矢量圆可以用于解决复杂的动态平衡问题,非常有效。
但是,有效的
实施对于正确控制系统变化非常重要,只有模型正确的才能保证实际
变化的正确表述。
模型的分析以及矢量圆的本质特性都是动态平衡的
关键,因此把握好矢量圆及其相关特性才能有效的解决动态平衡的问题。
利用圆的性质解决力学中动态平衡问题

第42卷第4期2021年Vol.42No.4(2021)物理教师PHYSICS TEACHER利用圆的性质解决力学中动态平衡问题何勇任致远(新疆兵团二中,新疆乌鲁木齐830002)摘要:高中物理在力学问题中动态平衡,我们往往常用的有图解法和解析法;利用解析法建立各物理量之间的关系时我们可以利用圆的相关性质,结合“三角形相似”、“正弦定理”和“辅助圆”解决一些与圆相关的动态平衡问题.关键词:三角形相似法;正弦定理法;辅助圆法高中物理无论是力学、热学,还是电学中,动态平衡问题会被经常用来考查学生对物理问题理解能力、知识迁移能力,分析推理能力、综合运用能力和利用数学知识解决物理问题的能力.在力学问题中动态平衡,我们往往常用的有图解法和解析法.这里我们将利用圆的相关性质,结合“三角形相似”、“正弦定理”和“辅助圆”解决一些与圆相关的动态平衡问题.1利用三角形相似处理动态平衡例1.如图1所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔.质量为m的小球套在圆环上.一根细线的下端系着小球,上端穿过小孔用手拉住.现拉动细线,使小球沿圆环缓慢上移•在移动过程中手对线的拉力F和轨道对小球的弹力N的大小变化情况是(A)F不变,N增大.(B)F减小,N不变.(C)F不变,N减小.(D)F增大,N减小.在本题中,小球沿圆环缓慢上移,对小球进行受力分析时,我们发现它始终受到竖直方向重力G、沿细绳方向拉力F和沿圆半径方向弹力F n,这3个力满足受力平衡.作出受力分析图(图2),可在重力G,圆的半径R不变时;小球缓慢上移过程中,/逐渐变小,所以F逐渐减小.2利用正弦定理处理动态平衡例2.如图3所示,ADB是一个光滑球面,AOB为水平直径,C为质量为加的光滑小球,小球通过过A点处的光滑定滑轮的轻绳拉住,现使小球C缓慢地从A点运动到处于O点正下方的D 点处.重力加速度大小为g,关于小球C从A点运动D点的过程,下列说法正确的是(A)绳对小球的拉力先增大后减小.(B)绳对小球的拉力逐渐减小.(C)光滑球面对小球的支持力先减小后增大.(D)光滑球面对小球的支持力逐渐减小.知厶O AB^^xGF'AG F N F—————R R1*/1\X①\G图1图2在本题中,小球沿圆环缓慢上移,如图4,对小球进行受力分析时,我们发现它始终受到竖直方向重力G、沿细绳方向拉力F和沿圆半径方向弹力N,这3个力满足受力平衡.设ZAOC=0,由圆的几何关系可得ZACE= y,ZECO=y-0,重力边的对角为y+J小球三力平衡的矢量三角形,根据正弦定理可得mg T N91第42卷第4期2021 年Vol. 42 No. 4(2021)物 理教师PHYSICS TEACHER解得0N = mgtan — , T= mgcosOmg ----j = mg cos 2cosf-sinftanf ).当0减小时,N 减小,T 增大.3利用辅助圆通过图解法处理动态平衡例3.如图5所示,柔软轻绳ON 的一端O 固 定,其中间某点M 拴一重物,用手拉住绳的另一端N.初始时,0M 竖直且MN 被拉直,OM 与MN之间的夹角a(a>号)•现将重物向右上方缓慢拉起,并保持夹角a 不变,在OM 由竖直被拉到水平 的过程中O 图5(A) MN 上的张力逐渐增大.(B) MN 上的张力先增大后减小.(C) 0M 上的张力逐渐增大.(D) 0M 上的张力先增大后减小.对M 处的重物进行受力分析,并将力平移至 一个力的三角形中,如图6所示,重力大小方向不变,其所对的角为x — a 也始终不变,作出这个三 角形的外接圆,三力平衡构成封闭三角形,画其外接圆,利用圆周角不变解题.P 在外接圆上移动, 初始位置从重力末端直至图中Q 点,利用图解法 确定力F nm 及F ⑹的变化情况.下面我们就3种方法来解决一个力学中动态 平衡的问题.应用:如图7所示为一种儿童玩具,在以O 点为圆 心的四分之一竖直圆弧轨 道上,有一个光滑的小球(不能视为质点),0'为小球 的圆心.挡板OM 沿着圆弧轨道的半径,以O 点为转 轴,从竖直位置开始推着小球缓慢顺时针转动(水平向里看),到小球触到水平线的过程中:圆弧轨道对小球的支持力N|的变 化?挡板对小球的支持力N?的变化?设ZAOM=©,ZC/OM = a.在解决本问题时,我们首先应该注意到QW 板的变化范围为从竖直方向到小球触及水平线;由此解法1:利用三角 形相似(此法关键在于找到与受力三角形相 似的三角形)延长M作用力力线,交竖直线 ON 于A 点,OM 于 B 点,根据图8受力的 三角形与厶OO'A 相 似,可得以下关系G Ni N 2其中OA =OBCOS ①,OO 7 =tana ),豹,"=更(tane +则M叫。
圆中的重要几何模型-隐圆模型(解析版)精选全文完整版

圆中的重要几何模型-隐圆模型隐圆是各地中考选择题和填空题、甚至解答题中常考题,题目常以动态问题出现,有点、线的运动,或者图形的折叠、旋转等,大部分学生拿到题基本没有思路,更谈不上如何解答。
隐圆常见的有以下四种形式,动点定长、定弦对直角、定弦对定角、四点共圆(对角互补或等弦对等角),上述四种动态问题的轨迹是圆。
题目具体表现为折叠问题、旋转问题、角度不变问题等,此类问题综合性强,隐蔽性强,很容易造成同学们的丢分。
本专题就隐圆模型的相关问题进行梳理及对应试题分析,方便掌握。
模型1、动点定长模型(圆的定义)若P为动点,但AB=AC=AP,则B、C、P三点共圆,A圆心,AB半径圆的定义:平面内到定点的距离等于定值的所有点构成的集合.寻找隐圆技巧:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧.例1.(2020·四川中考真题)已知:等腰直角三角形ABC的腰长为4,点M在斜边AB上,点P为该平面内一动点,且满足PC=2,则PM的最小值为()A.2B.22-2C.22+2D.22【答案】B【分析】根据等腰直角三角形的性质得到斜边AB=42,由已知条件得到点P在以C为圆心,PC为半径的圆上,当点P在斜边AB的中线上时,PM的值最小,于是得到结论.【详解】解:∵等腰直角三角形ABC的腰长为4,∴斜边AB=42,∵点P为该平面内一动点,且满足PC=2,∴点P在以C为圆心,PC为半径的圆上,当点P在斜边AB的中线上时,PM的值最小,∵△ABC是等腰直角三角形,∴CM=12AB=22,∵PC=2,∴PM=CM-CP=22-2,故选:B.【点睛】本题考查线段最小值问题,涉及等腰三角形的性质和点到圆的距离,解题的关键是能够画出图形找到取最小值的状态然后求解.例2.(2020·江苏连云港市·中考真题)如图,在平面直角坐标系xOy中,半径为2的eO与x轴的正半轴交于点A,点B是eO上一动点,点C为弦AB的中点,直线y=34x-3与x轴、y轴分别交于点D、E,则△CDE面积的最小值为.【答案】2【分析】如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.先证明点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.求出MN,当点C与C′重合时,△C′DE 的面积最小.【详解】解:如图,连接OB,取OA的中点M,连接CM,过点M作MN⊥DE于N.∵AC=CB,AM=OM,∴MC=12OB=1,∴点C的运动轨迹是以M为圆心,1为半径的⊙M,设⊙M交MN于C′.∵直线y=34x-3与x轴、y轴分别交于点D、E,∴D(4,0),E(0,-3),∴OD=4,OE=3,∴DE=OE2+OD2=32+42=5,∵∠MDN=∠ODE,∠MND=∠DOE,∴△DNM∽△DOE,∴MNOE=DMDE,∴MN3=35,∴MN=95,当点C与C′重合时,△C′DE的面积最小,△C′DE的面积最小值=12×5×95-1,故答案为2.【点睛】本题考查三角形的中位线定理,三角形的面积,一次函数的性质等知识,解题的关键是学会添加常用辅助线,构造三角形的中位线解决问题,属于中考常考题型.例3.(2022·北京市·九年级专题练习)如图,四边形ABCD中,AE、AF分别是BC,CD的中垂线,∠EAF=80°,∠CBD=30°,则∠ABC=,∠ADC=.【答案】 40°; 60°【分析】连接AC,根据线段垂直平分线的性质可得AB=AC=AD,从而得到B、C、D在以A为圆心,AB为半径的圆上,根据圆周角定理可得∠DAC=2∠DBC=60°,再由等腰三角形的性质可得∠DAF=∠CAF=30°,即可求解.【详解】解:连接AC,∵AE、AF分别是BC、CD的中垂线,∴AB=AC=AD,∴B、C、D在以A为圆心,AB为半径的圆上,∵∠CBD=30°,∴∠DAC=2∠DBC=60°,∵AF⊥CD,CF=DF,∴∠DAF=∠CAF=30°,∴∠ADC=60°,∵AB=AC,BE=CE,∴∠BAE=∠CAE,又∵∠EAC=∠EAF-∠CAF=80°-30°=50°,∴∠ABC=∠ACE=90°-50°=40°.故答案为:40°,60°.【点睛】本题主要考查了圆周角定理,线段垂直平分线的性质,等腰三角形的性质,根据题意得到B、C、D在以A为圆心,AB为半径的圆上是解题的关键.例4.(2022·广东·汕头市一模)如图,在△ABC中,∠C=90°,AC=8,AB=10,D是AC上一点,且CD =3,E是BC边上一点,将△DCE沿DE折叠,使点C落在点F处,连接BF,则BF的最小值为.【答案】35-3##-3+35【分析】先由折叠判断出F的运动轨迹是为以D为圆心,CD的长度为半径的圆,当B、D、F共线且F在B、D之间时BF最小,根据勾股定理及圆的性质求出此时BD、BF的长度即可.【详解】解:由折叠知,F点的运动轨迹为:以D为圆心,CD的长度为半径的圆,如图所示,可知,当点B、D、F共线,且F在B、D之间时,BF取最小值,∵∠C=90°,AC=8,AB=10,∴BC=6,在Rt△BCD中,由勾股定理得:BD=CD2+BC2=32+62=35,∴BF=BD-DF=35-3,故答案为:35-3.【点睛】本题考查了折叠的性质、圆的性质、勾股定理解直角三角形的知识,该题涉及的最值问题属于中考常考题型,根据折叠确定出F点运动轨迹是解题关键.模型2、定边对直角模型(直角对直径)固定线段AB 所对动角∠C 恒为90°,则A 、B 、C 三点共圆,AB 为直径寻找隐圆技巧:一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.例1.(2022·湖北·武汉九年级阶段练习)如图,AB 是⊙O 的直径,AB =4,C 为AB的三等分点(更靠近A 点),点P 是⊙O 上一个动点,取弦AP 的中点D ,则线段CD 的最大值为.【答案】3+1【分析】如图,连接OD ,OC ,首先证明点D 的运动轨迹为以AO 为直径的⊙K ,连接CK ,当点D 在CK 的延长线上时,CD 的值最大,利用勾股定理求出CK 即可解决问题.【详解】解:如图,连接OD ,OC ,∵AD =DP ,∴OD ⊥PA ,∴∠ADO =90°,∴点D 的运动轨迹为以AO 为直径的⊙K ,连接CK ,AC ,当点D 在CK 的延长线上时,CD 的值最大,∵C 为AB的三等分点,∴∠AOC =60°,∴△AOC 是等边三角形,∴CK ⊥OA ,在Rt △OCK 中,∵∠COA =60°,OC =2,OK =1,∴CK =OC 2-OK 2=3,∵DK =12OA =1,∴CD =3+1,∴CD 的最大值为3+1,故答案为:3+1.【点睛】本题考查圆周角定理、轨迹、勾股定理、点与圆的位置关系等知识,解题的关键是正确寻找点D 的运动轨迹,学会构造辅助圆解决问题.例2.(2022·山东泰安·中考真题)如图,四边形ABCD 为矩形,AB =3,BC =4.点P 是线段BC 上一动点,点M 为线段AP 上一点.∠ADM =∠BAP ,则BM 的最小值为()A.52B.125C.13-32D.13-2【答案】D【分析】证明∠AMD =90°,得出点M 在O 点为圆心,以AO 为半径的园上,从而计算出答案.【详解】设AD 的中点为O ,以O 点为圆心,AO 为半径画圆∵四边形ABCD 为矩形∴∠BAP +∠MAD =90°∵∠ADM =∠BAP∴∠MAD +∠ADM =90°∴∠AMD =90°∴点M 在O 点为圆心,以AO 为半径的园上连接OB 交圆O 与点N∵点B 为圆O 外一点∴当直线BM 过圆心O 时,BM 最短∵BO 2=AB 2+AO 2,AO =12AD =2∴BO 2=9+4=13∴BO =13∵BN =BO -AO =13-2故选:D .【点睛】本题考查直角三角形、圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.例3.(2022·内蒙古·中考真题)如图,⊙O 是△ABC 的外接圆,AC 为直径,若AB =23,BC =3,点P 从B 点出发,在△ABC 内运动且始终保持∠CBP =∠BAP ,当C ,P 两点距离最小时,动点P 的运动路径长为.【答案】33π.【分析】根据题中的条件可先确定点P 的运动轨迹,然后根据三角形三边关系确定CP 的长最小时点P 的位置,进而求出点P 的运动路径长.【详解】解:∵AC 为⊙O 的直径,∴∠ABC =90°.∴∠ABP +∠PBC =90°.∵∠PAB =∠PBC ,∴∠PAB +∠ABP =90°.∴∠APB =90°.∴点P 在以AB 为直径的圆上运动,且在△ABC 的内部,如图,记以AB 为直径的圆的圆心为O 1,连接O 1C 交⊙O 1于点P ,连接O 1P ,CP .∵CP ≥O 1C -O 1P ,∴当点O 1,P ,C 三点共线时,即点P 在点P 处时,CP 有最小值,∵AB =23∴O 1B =3在Rt ΔBCO 1中,tan ∠BO 1C =BC O 1B =33= 3.∴∠BO1C =60°.∴BP =60π×3180=33π.∴.C ,P 两点距离最小时,点P 的运动路径长为33π.【点睛】本题主要考查了直径所对圆周角是直角,弧长公式,由锐角正切值求角度,确定点P 的路径是解答本题的关键.模型3、定边对定角模型(定弦定角模型)固定线段AB 所对同侧动角∠P =∠C ,则A 、B 、C 、P 四点共圆根据圆周角定理:同圆或等圆中,同弧或等弧所对的圆周角都相.寻找隐圆技巧:AB 为定值,∠P 为定角,则P 点轨迹是一个圆.例1.(2021·广东·中考真题)在△ABC 中,∠ABC =90°,AB =2,BC =3.点D 为平面上一个动点,∠ADB =45°,则线段CD 长度的最小值为.【答案】5-2【分析】由已知∠ADB =45°,AB =2,根据定角定弦,可作出辅助圆,由同弧所对的圆周角等于圆心角的一半可知,点D 在以O 为圆心OB 为半径的圆上,线段CD 长度的最小值为CO -OD .【详解】如图:以12AB 为半径作圆,过圆心O 作ON ⊥AB ,OM⊥BC ,以O 为圆心OB 为半径作圆,则点D 在圆O 上,∵∠ADB =45°∴∠AOB =90°∵AB =2AN =BN =1∴AO =12+12=2∵ON =OM =12AB =1,BC =3∴OC =12+(3-1)2=5∴CO -OD =5-2线段CD 长度的最小值为:5-2.故答案为:5-2.【点睛】本题考查了圆周角与圆心角的关系,圆外一点到圆上的线段最短距离,勾股定理,正确的作出图形是解题的关键.例2.(2022·浙江湖州·中考真题)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD 中,M ,N 分别是AB ,BC 上的格点,BM =4,BN =2.若点P 是这个网格图形中的格点,连接PM ,PN ,则所有满足∠MPN =45°的△PMN 中,边PM 的长的最大值是()A.42B.6C.210D.35【答案】C 【分析】根据同弧所对的圆周角等于所对圆心角的一半,过点M 、N 作以点O 为圆心,∠MON =90°的圆,则点P 在所作的圆上,观察圆O 所经过的格点,找出到点M 距离最大的点即可求出.【详解】作线段MN 中点Q ,作MN 的垂直平分线OQ ,并使OQ =12MN ,以O 为圆心,OM 为半径作圆,如图,因为OQ 为MN 垂直平分线且OQ =12MN ,所以OQ =MQ =NQ ,∴∠OMQ =∠ONQ =45°,∴∠MON =90°,所以弦MN 所对的圆O 的圆周角为45°,所以点P 在圆O 上,PM 为圆O 的弦,通过图像可知,当点P 在P 位置时,恰好过格点且P M 经过圆心O ,所以此时P M 最大,等于圆O 的直径,∵BM =4,BN =2,∴MN =22+42=25,∴MQ =OQ =5,∴OM =2MQ =2×5=10,∴P M =2OM =210,故选C .【点睛】此题考查了圆的相关知识,熟练掌握同弧所对的圆周角相等、直径是圆上最大的弦,会灵活用已知圆心角和弦作圆是解题的关键.例3.(2022·广西贵港·中考真题)如图,在边长为1的菱形ABCD 中,∠ABC =60°,动点E 在AB 边上(与点A 、B 均不重合),点F 在对角线AC 上,CE 与BF 相交于点G ,连接AG ,DF ,若AF =BE ,则下列结论错误的是()A.DF =CEB.∠BGC =120°C.AF 2=EG ⋅ECD.AG 的最小值为223【答案】D 【分析】先证明△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,得DF =CE ,判断A 项答案正确,由∠GCB +∠GBC =60゜,得∠BGC =120゜,判断B 项答案正确,证△BEG ∽△CEB 得BE GE=CE BE ,即可判断C 项答案正确,由∠BGC =120°,BC =1,得点G 在以线段BC 为弦的弧BC 上,易得当点G 在等边△ABC 的内心处时,AG 取最小值,由勾股定理求得AG =33,即可判断D 项错误.【详解】解:∵四边形ABCD 是菱形,∠ABC =60°,∴AB =AD =BC =CD ,∠BAC =∠DAC =12∠BAD =12×(180°-∠ABC )=60°=∠ABC ,∴△BAF ≌△DAF ≌CBE ,△ABC 是等边三角形,∴DF =CE ,故A 项答案正确,∠ABF =∠BCE ,∵∠ABC =∠ABF +∠CBF =60゜,∴∠GCB +∠GBC =60゜,∴∠BGC =180゜-60゜=180゜-(∠GCB +∠GBC )=120゜,故B 项答案正确,∵∠ABF =∠BCE ,∠BEG =∠CEB ,∴△BEG ∽△CEB ,∴BE GE=CE BE ,∴BE 2=GE ∙CE ,∵AF =BE ,∴AF 2=GE ∙CE ,故C 项答案正确,∵∠BGC =120°,BC =1,点G 在以线段BC 为弦的弧BC 上,∴当点G 在等边△ABC 的内心处时,AG 取最小值,如下图,∵△ABC 是等边三角形,BC =1,∴BF ⊥AC ,AF =12AC =12,∠GAF =30゜,∴AG =2GF ,AG 2=GF 2+AF 2,∴AG 2=12AG 2+12 2,解得AG =33,故D 项错误,故应选:D 【点睛】本题主要考查了菱形的基本性质、等边三角形的判定及性质、圆周角定理,熟练掌握菱形的性质是解题的关键.模型4、四点共圆模型(对角互补模型与等弦对等角)1)若平面上A 、B 、C 、D 四个点满足∠ABC +∠ADC =180°,则A 、B 、C 、D 四点共圆.条件:1)四边形对角互补;2)四边形外角等于内对角.2)若平面上A、B、C、D四个点满足∠ADB=∠ACB,则A、B、C、D四点共圆.条件:线段同侧张角相等.例1.(2022·广东·九年级专题练习)如图,在四边形ABCD中,∠BAD=∠BCD=90°,∠ACD=30°,AD =2,E是AC的中点,连接DE,则线段DE长度的最小值为.【答案】3-1【分析】先判断出四边形ABCD是圆内接四边形,得到∠ACD=∠ABD=30°,根据题意知点E在以FG为直径的⊙P上,连接PD交⊙P于点E,此时DE长度取得最小值,证明∠APD=90°,利用含30度角的直角三角形的性质求解即可.【详解】解:∵∠BAD=∠BCD=90°,∴四边形ABCD是圆内接四边形,∴∠ACD=∠ABD=30°,∴∠ADB=60°,∵AD=2,∴BD=2AD=4,分别取AB、AD的中点F、G,并连接FG,EF,EG,∵E是AC的中点,∴EF∥BC,EG∥CD,∴∠AEF=∠ACB,∠AEG=∠ACD,∴∠AEF+∠AEG=∠ACB+∠ACD=90°,即∠FEG=90°,∴点E在以FG为直径的⊙P上,如图:当点E恰好在线段PD上,此时DE的长度取得最小值,连接PA,BD=2,∴∵F、G分别是AB、AD的中点∴FG∥BD,FG=12∠ADB=∠AGF=60°,∵PA=PG,∴△APG是等边三角形,∴∠APG=60°,∵PG=GD=GA,且∠AGF=60°,∴∠GPD=∠GDP=30°,∴∠APD=90°,∴PD=AD2-PA2=22-12=3,∴DE长度的最小值为(3-1).故答案为:(3-1).【点睛】本题考查了圆周角定理,圆内接四边形的性质,等边三角形的判定和性质,含30度角的直角三角形的性质,得到点E 在以FG 为直径的⊙P 上是解题的关键.例2.(2022陕西中考模拟)如图,在等边△ABC 中,AB =6,点P 为AB 上一动点,PD ⊥BC 于点D ,PE ⊥AC 于点E ,则DE 的最小值为.【答案】92【详解】如解图,∵∠PEC =∠PDC =90°,故四边形PDCE 对角互补,故P 、D 、C 、E 四点共圆,∠EOD =2∠ECD =120°,故ED =3R ,要使得DE 最小,则要使圆的半径R 最小,故直径PC 最小,当CP ⊥AB 时,PC 最短为33,故R =332,故DE =3R =3×332=92.例3.(2022江苏九年级期末)如图,在Rt △ABC 中,∠ACB =90°,BC =3,AC =4,点P 为平面内一点,且∠CPB =∠A ,过C 作CQ ⊥CP 交PB 的延长线于点Q ,则CQ 的最大值为()A.175B.154C.455D.655【答案】B【分析】根据题意可得A 、B 、C 、P 四点共圆,由AA 定理判定三角形相似,由此得到CQ 的值与PC 有关,当PC 最大时CQ 即取最大值.【详解】解:∵在Rt △ABC 中,∠ACB =90°,∠CPB =∠A ,BC =3,AC =4∴A 、B 、C 、P 四点共圆,AB 为圆的直径,AB =BC 2+AC 2=5∵CQ ⊥CP ∴∠ACB =∠PCQ =90°∴△ABC ∽△PQC∴AC BC =PC CQ ,43=PC CQ,即CQ =34PC ∴当PC 取得最大值时,CQ 即为最大值∴当PC =AB =5时,CQ 取得最大值为154故选:B .【点睛】本题考查相似三角形的判定和性质以及四点共圆,掌握同圆或等圆中,同弧所对的圆周角相等确定四点共圆,利用相似三角形性质得到线段间等量关系是解题关键.课后专项训练例4.(2022·江苏无锡·中考真题)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.【答案】 80 4-3##-3+4【分析】利用SAS证明△BDC≌△AEC,得到∠DBC=∠EAC=20°,据此可求得∠BAF的度数;利用全等三角形的性质可求得∠AFB=60°,推出A、B、C、F四个点在同一个圆上,当BF是圆C的切线时,即当CD⊥BF时,∠FBC最大,则∠FBA最小,此时线段AF长度有最小值,据此求解即可.【详解】解:∵△ABC和△DCE都是等边三角形,∴AC=BC,DC=EC,∠BAC=∠ACB=∠DCE =60°,∴∠DCB+∠ACD=∠ECA+∠ACD=60°,即∠DCB=∠ECA,在△BCD和△ACE中,CD=CE∠BCD=∠ACE BC=AC,∴△ACE≌△BCD(SAS),∴∠EAC=∠DBC,∵∠DBC=20°,∴∠EAC=20°,∴∠BAF=∠BAC+∠EAC=80°;设BF与AC相交于点H,如图:∵△ACE≌△BCD∴AE=BD,∠EAC=∠DBC,且∠AHF=∠BHC,∴∠AFB=∠ACB=60°,∴A、B、C、F四个点在同一个圆上,∵点D在以C为圆心,3为半径的圆上,当BF是圆C的切线时,即当CD⊥BF时,∠FBC最大,则∠FBA最小,∴此时线段AF长度有最小值,在Rt△BCD中,BC=5,CD=3,∴BD=52-32=4,即AE=4,∴∠FDE=180°-90°-60°=30°,∵∠AFB=60°,∴∠FDE=∠FED=30°,∴FD=FE,过点F作FG⊥DE于点G,∴DG=GE=32,∴FE=DF=DGcos30°=3,∴AF=AE-FE=4-3,故答案为:80;4-3.【点睛】本题考查了旋转的性质,等边三角形的性质,圆周角定理,切线的性质,解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件.例5.(2021·湖北鄂州·中考真题)如图,Rt △ABC 中,∠ACB =90°,AC =23,BC =3.点P 为ΔABC 内一点,且满足PA 2+PC 2=AC 2.当PB 的长度最小时,ΔACP 的面积是()A.3B.33C.334D.332【答案】D 【分析】由题意知∠APC =90°,又AC 长度一定,则点P 的运动轨迹是以AC 中点O 为圆心,12AC 长为半径的圆弧,所以当B 、P 、O 三点共线时,BP 最短;在Rt ΔBCO 中,利用勾股定理可求BO 的长,并得到点P 是BO 的中点,由线段长度即可得到ΔPCO 是等边三角形,利用特殊Rt ΔAPC 三边关系即可求解.【详解】解:∵PA 2+PC 2=AC 2∴∠APC =90°取AC 中点O ,∴AO =PO =CO =12AC 点P 的轨迹为以O 为圆心,12AC 长为半径的圆弧上由题意知:当B 、P 、O 三点共线时,BP 最短∵CO =12AC =12×23=3,BC =3∴BO =BC 2+CO 2=23∴BP =BO -PO =3∴点P 是BO 的中点∴在Rt ΔBCO 中,CP =12BO =3=PO ∴ΔPCO 是等边三角形∴∠ACP =60°∴在Rt ΔAPC 中,AP =CP ×tan60°=3∴S ΔAPC =12AP ×CP =3×32=332.【点睛】本题主要考察动点的线段最值问题、点与圆的位置关系和隐形圆问题,属于动态几何综合题型,中档难度.解题的关键是找到动点P 的运动轨迹,即隐形圆.例6.(2020·西藏中考真题)如图,在矩形ABCD 中,E 为AB 的中点,P 为BC 边上的任意一点,把沿PE 折叠,得到,连接CF .若AB =10,BC =12,则CF 的最小值为.【答案】8【分析】点F 在以E 为圆心、EA 为半径的圆上运动,当E 、F 、C 共线时时,此时FC 的值最小,根据勾股定理求出CE ,再根据折叠的性质得到BE =EF =5即可.【详解】如图所示,点F 在以E 为圆心EA 为半径的圆上运动,当E 、F 、C 共线时时,此时CF 的值最小,根据折叠的性质,△EBP ≌△EFP ,∴EF ⊥PF ,EB =EF ,∵E 是AB 边的中点,AB =10,∴AE =EF =5,∵AD =BC =12,∴CE ===13,∴CF =CE -EF =13-5=8.故答案为8.【点睛】本题考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用,灵活应用相关知识是解答本题的关键.例7.(2022·北京·清华附中九年级阶段练习)如图,四边形ABCD 中,DA =DB =DC ,∠BDC =72°,则∠BAC 的度数为.【答案】36°##36度【分析】根据题意可得A ,B ,C 三点在以D 为圆心DA 为半径的圆上,根据圆周角定理即可求解.【详解】解:如图,∵DA =DB =DC ,∴A ,B ,C 三点在以D 为圆心DA 为半径的圆上,∵∠BDC =72°,CB =CB ∴∠BAC =12∠BDC =36°.故答案为:36°.【点睛】本题考查了圆周角定理,掌握圆周角定理是解题的关键.例8.(2022·河北·唐山九年级阶段练习)如图所示,在四边形ABCD 中,AB =AC =AD ,∠BAC =26°,∠CAD =74°,则∠BCD =°,∠DBC °.【答案】 130 37【分析】根据题意可得点B,C,D在以A为圆心的圆上,根据圆周角定理求得∠BDC,∠DBC,根据三角形内角和定理求得∠BCD.【详解】∵AB=AC=AD,∴点B,C,D在以A为圆心的圆上,∵∠BAC=26°∴∠BDC=12∠BAC=13°,∵∠CAD=74°,∴∠DBC=12∠CAD=37°.∴∠BCD=180-∠DBC-∠BDC=180°-13°-37°=130°故答案为:130,37【点睛】此题考查了圆周角定理,三角形内角和定理,综合运用以上知识是解题的关键.例9.(2022·安徽蚌埠·一模)如图,Rt△ABC中,AB⊥BC,AB=8,BC=6,P是△ABC内部的一个动点,满足∠PAB=∠PBC,则线段CP长的最小值为()A.325B.2C.213-6D.213-4【答案】D【分析】结合题意推导得∠APB=90°,取AB的中点O,以点O为圆心,AB为直径作圆,连接OP;根据直角三角形斜边中线的性质,得OP=OA=OB=12AB=4;根据圆的对称性,得点P在以AB为直径的⊙O上,根据两点之间直线段最短的性质,得当点O、点P、点C三点共线时,PC最小;根据勾股定理的性质计算得OC,通过线段和差计算即可得到答案.【详解】∵∠ABC=90°,∴∠ABP+∠PBC=90°,∵∠PAB=∠PBC,∴∠BAP+∠ABP=90°,∴∠APB=90°,取AB的中点O,以点O为圆心,AB为直径作圆,连接OP,∴OP=OA=OB=12AB=4∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,当点O、点P、点C三点共线时,PC最小在Rt△BCO中,∵∠OBC=90°,BC=6,OB=4,∴OC=BO2+BC2=42+62=213,∴PC=OC-OP=213-4∴PC最小值为213-4故选:D.【点睛】本题考查了两点之间直线段最短、圆、勾股定理、直角三角形斜边中线的知识;解题的关键是熟练掌握圆的对称性、两点之间直线段最短、直角三角形斜边中线的性质,从而完成求解.例10.(2022·成都市·九年级专题练习)如图,在Rt ΔABC 中,∠ACB =Rt ∠,AC =8cm ,BC =3cm .D 是BC 边上的一个动点,连接AD ,过点C 作CE ⊥AD 于E ,连接BE ,在点D 变化的过程中,线段BE 的最小值是()A.1B.3C.2D.5【答案】A 【分析】由∠AEC =90°知,点E 在以AC 为直径的⊙M 的CN 上(不含点C 、可含点N ),从而得BE最短时,即为连接BM 与⊙M 的交点(图中点E ′点),BE 长度的最小值BE ′=BM -ME ′.【详解】如图,由题意知,∠AEC =90°,∴E 在以AC 为直径的⊙M 的CN上(不含点C 、可含点N ),∴BE 最短时,即为连接BM 与⊙M 的交点(图中点E ′点),在Rt ΔBCM 中,BC =3cm ,CM =12AC =4cm ,则BM =BC 2+CM 2=5cm .∵ME ′=MC =4cm ,∴BE 长度的最小值BE ′=BM -ME ′=1cm ,故选:A .【点睛】本题主要考查了勾股定理,圆周角定理,三角形的三边关系等知识点,难度偏大,解题时,注意辅助线的作法.例11.(2022·广东·九年级课时练习)如图,△ACB 中,CA =CB =4,∠ACB =90°,点P 为CA 上的动点,连BP ,过点A 作AM ⊥BP 于M .当点P 从点C 运动到点A 时,线段BM 的中点N 运动的路径长为()A.22πB.2πC.3πD.2π【答案】A【详解】解:设AB 的中点为Q ,连接NQ ,如图所示:∵N 为BM 的中点,Q 为AB 的中点,∴NQ 为△BAM 的中位线,∵AM ⊥BP ,∴QN ⊥BN ,∴∠QNB =90°,∴点N 的路径是以QB 的中点O 为圆心,14AB 长为半径的圆交CB 于D 的QD,∵CA =CB =4,∠ACB =90°,∴AB =2CA =42,∠QBD =45°,∴∠DOQ =90°,∴QD 为⊙O 的14周长,∴线段BM 的中点N 运动的路径长为:90π×14×42180=22π,故选:A .例12.(2022·全国·九年级专题练习)如图,在△ABC 中,∠ACB =90°,AC =BC ,AB =4cm ,CD 是中线,点E 、F 同时从点D 出发,以相同的速度分别沿DC 、DB 方向移动,当点E 到达点C 时,运动停止,直线AE 分别与CF 、BC 相交于G 、H ,则在点E 、F 移动过程中,点G 移动路线的长度为()A.2B.πC.2πD.22π【答案】D【详解】解:如图,∵CA =CB ,∠ACB =90°,AD =DB ,∴CD ⊥AB ,∴∠ADE =∠CDF =90°,CD =AD =DB ,在△ADE 和△CDF 中AD =CD∠ADE =∠CDF DE =DF,∴△ADE ≌△CDF (SAS ),∴∠DAE =∠DCF ,∵∠AED =∠CEG ,∴∠ADE =∠CGE =90°,∴A 、C 、G 、D 四点共圆,∴点G 的运动轨迹为弧CD ,∵AB =4,AB =2AC ,∴AC =22,∴OA =OC =2,∵DA =DC ,OA =OC ,∴DO ⊥AC ,∴∠DOC =90°,∴点G 的运动轨迹的长为90π×2180=22π.故选:D .例13.(2022·山西·九年级课时练习)如图,在等腰Rt ∆ABC 中,AC =BC =42,点P 在以斜边AB 为直径的半圆上,M 为PC 的中点.当点P 沿半圆从点A 运动至点B 时,点M 运动的路径长是()A.22π+4B.2πC.42+2D.4π【答案】B 【详解】分析:取AB 的中点O 、AC 的中点E 、BC 的中点F ,连结OC 、OP 、OM 、OE 、OF 、EF ,如图,利用等腰直角三角形的性质得到AB =2BC =8,则OC =12AB =4,OP =12AB =4,再根据等腰三角形的性质得OM ⊥PC ,则∠CMO =90°,于是根据圆周角定理得到点M 在以OC 为直径的圆上,由于点P 点在A 点时,M 点在E 点;点P 点在B 点时,M 点在F 点,则利用四边形CEOF 为正方得到EF =OC =4,所以M 点的路径为以EF 为直径的半圆,然后根据圆的周长公式计算点M 运动的路径长.详解:取AB 的中点O 、AC 的中点E 、BC 的中点F ,连结OC 、OP 、OM 、OE 、OF 、EF ,如图,∵在等腰Rt △ABC 中,AC =BC =42,∴AB =2BC =8,∴OC =12AB =4,OP =12AB =4. ∵M 为PC 的中点,∴OM ⊥PC ,∴∠CMO =90°,∴点M 在以OC为直径的圆上,点P 点在A 点时,M 点在E 点;点P 点在B 点时,M 点在F 点,易得四边形CEOF 为正方形,EF =OC =4,∴M 点运动的路径为以EF 为直径的半圆,∴点M 运动的路径长=12•4π=2π. 故选B .点睛:本题考查了轨迹:点按一定规律运动所形成的图形为点运动的轨迹.解决此题的关键是利用等腰三角形的性质和圆周角定理确定M 点的轨迹为以EF 为直径的半圆.例14.(2022·山东·烟台九年级期中)如图,平面直角坐标系中,点A 、B 坐标分别为(3,0)、(0,4),点C 是x 轴正半轴上一点,连接BC .过点A 垂直于AB 的直线与过点C 垂直于BC 的直线交于点D ,连接BD ,则sin ∠BDC 的值是.【答案】45【分析】根据图形的特点证明∠BDC =∠BAO ,故可出sin ∠BDC 的值.【详解】∵BA ⊥AD ,BC ⊥CD ∴∠BAD =∠BCD =90°∴A 、B 、C 、D 四点共圆∴∠BDA =∠BCA∵∠BDA +∠DBA =∠BCA +∠CBO =90°∴∠DBA =∠CBO∴∠DBA -∠CBA =∠CBO -∠CBA 即∠DBC =∠ABO又∠DBC +∠BDC =∠ABO +∠BAO =90°∴∠BDC =∠BAO∵点A 、B 坐标分别为(3,0)、(0,4),∴BO =4,OA =3,AB =42+32=5∴sin ∠BAO =BO AB=45∴sin ∠BDC =45故答案为:45.【点睛】此题主要考查三角函数的求解,解题的关键是熟知四点共圆的性质、勾股定理及三角函数的求解方法.例15.(2022·湖北·九年级期中)如图,△ABC 中,AC =BC =6,∠ACB =90°,若D 是与点C 在直线AB 异侧的一个动点,且∠ADB =45°,则CD 的最大值为.【答案】62+6##6+62【分析】以AB 为底边,在AB 的下方作等腰三角形AOB ,则OA =AC =6,根据∠ADB =45°,点与圆的位置关系可知,点D 在以O 为圆心,6为半径的圆上运动,当CD 过圆心时,CD 最大,根据OA =AC =6,∠CAO =90°,利用勾股定理可求出CO 的长,即可得.【详解】解:如图所示,以AB 为底边,在AB 的下方作等腰三角形AOB ,则OA =AC =6,∵∠ADB =45°,∴点D 在以O 为圆心,6为半径的圆上运动,当CD 过圆心时,CD 最大,∵OA =AC =6,∠CAO =90°,∴CO =62+62=62,∴CD 的最大值为:62+6,故答案为:62+6.【点睛】本题考查了等腰直角三角形的性质,圆周角定理,勾股定理,解题的关键是理解题意,掌握这些知识点.例16.(2022·浙江·九年级专题练习)如图,AB 是Rt △ABC 和Rt △ABD 的公共斜边,AC =BC ,∠BAD =32°,E 是AB 的中点,联结DE 、CE 、CD ,那么∠ECD =°.【答案】13【分析】先证明A 、C 、B 、D 四点共圆,得到∠DCB 与∠BAD 的是同弧所对的圆周角的关系,得到∠DCB 的度数,再证∠ECB =45°,得出结论.【详解】解:∵AB 是Rt △ABC 和Rt △ABD 的公共斜边,E 是AB 中点,∴AE =EB =EC =ED ,∴A 、C 、B 、D 在以E 为圆心的圆上,∵∠BAD =32°,∴∠DCB =∠BAD =32°,又∵AC =BC ,E 是Rt △ABC 的中点,∴∠ECB =45°,∴∠ECD =∠ECB -∠DCB =13°.故答案为:13.【点睛】本题考查直角三角形的性质、等腰三角形性质、圆周角定理和四点共圆问题,综合性较强.例17.(2022·黑龙江·九年级阶段练习)如图,等边△ABC 中,D 在BC 上,E 在AC 上,BD =CE ,连BE 、AD 交于F ,T 在EF 上,且DT =CE ,AF =50,TE =16,则FT =.【答案】17【分析】用“SAS ”可判定△ABD ≌△BCE ,得到∠AFE =60°,延长FE 至点G ,使得FG =FA ,连AG ,AT ,得到△AFG 是等边三角形,证明A 、B 、D 、T 四点共圆,设法证明△FAT ≌△GAE (ASA ),即可求得答案.【详解】∵△ABC 为等边三角形,∴AB =AC =BC ,∠ABD =∠BCE =60°,在△ABD 和△BCE 中,AB =BC∠ABD =∠BCE =60°BD =CE,∴△ABD ≌△BCE (SAS ),∴∠BAD =∠CBE ,∵∠ADC =∠CBE +∠BFD =∠BAD +∠B ,∴∠BFD =∠B =∠AFE =60°;延长FE 至点G ,使得FG =FA ,连AG ,AT ,∵∠AFE =60°,∴△AFG 是等边三角形,∴AG =AF =FG =50,∠AGF =∠FAG =60°,∵∠BAF +∠EAF =∠CAG +∠EAF =60°,∴∠BAF =∠CAG ,∵DT =CE ,∴∠DBT =∠BTD ,∵∠BAD =∠CBE ,∴∠BAD =∠BTD ,∴A 、B 、D 、T 四点共圆,∴∠BAD =∠DAT ,∴∠FAT =∠GAE ,在△FAT 和△GAE 中,∠FAT =∠GAEAF =AG ∠AFG =∠AGF =60°,∴△FAT ≌△GAE (ASA ),∴FT =GE ,∵FG =50,TE =16,∴FT =12(FG -TE )=17.故答案为:17.【点睛】本题主要考查了等边三角形的判定和性质,全等三角形的判定和性质,圆周角定理等,作出辅助线,判断出△FAT ≌△GAE 是解本题的关键.例18.(2020·四川成都·二模)如图,在矩形ABCD 中,AB =9,AD =6,点O 为对角线AC 的中点,点E 在DC 的延长线上且CE =1.5,连接OE ,过点O 作OF ⊥OE 交CB 延长线于点F ,连接FE 并延长交AC 的延长线于点G ,则FG OG=.【答案】455【分析】作OM ⊥CD 于M ,ON ⊥BC 于N ,根据三角形中位线定理分别求出OM 、ON ,根据勾股定理求出OE ,根据相似三角形的性质求出FN ,得到FC 的长,证明△GFC ∽△GOE ,根据相似三角形的性质列出比例式,代入计算得到答案.【详解】解:作OM ⊥CD 于M ,ON ⊥BC 于N ,∵四边形ABCD 为矩形,∴∠D =90°,∠ABC =90°,∴OM ∥AD ,ON ∥AB ,∵点O 为AC 的中点∴OM =12AD =3,ON =12AB =4.5,CM =4.5,CN =3,∵CE =1.5,∴ME =CM +CE =6在Rt △OME 中,OE =OM 2+ME 2=32+62=35,∵∠MON =90°,∠EOF =90°,∴∠MOE +∠NOE =∠NOF +∠NOE =90°,∴∠MOE =∠NOF ,又∠OME =∠ONF =90°,∴△OME ∽△ONF ,∴OM ON=ME FN ,即34.5=6FN ,解得,FN =9,∴FC =FN +NC =12,∵∠FOE =∠FCE =90°,∴F 、O 、C 、E 四点共圆,∴∠GFC =∠GOE ,又∠G =∠G ,∴△GFC ∽△GOE ,∴FG OG =FC OE =1235=455,故答案为:455.【点睛】本题考查了矩形的性质、相似三角形的判定和性质、圆周角定理的应用,掌握相似三角形的判定定理和性质定理是解题的关键.例19.(2022·成都市锦江区嘉祥外国语学校九年级阶段练习)如图,在△ABC 中,AC =6,BC =83,∠ACB =60°,过点A 作BC 的平行线l ,P 为直线l 上一动点,⊙O 为△APC 的外接圆,直线BP 交⊙O 于E 点,则AE 的最小值为.【答案】2【分析】如图,连接CE .首先证明∠BEC =120°,根据定弦定角,可得点E 在以M 为圆心,MB 为半径的BC 上运动,连接MA 交BC 于E ′,此时AE ′的值最小.【详解】解:如图,连接CE .∵AP ∥BC ,∴∠PAC =∠ACB =60°,∴∠CEP =∠CAP=60°,∴∠BEC =120°,∵BC =83,为定值,则点E 的运动轨迹为一段圆弧如图,点E 在以M 为圆心,MB 为半径的BC 上运动,过点M 作MN ⊥BC∴⊙M 中优弧BC 度数为2∠BEC =240°,则劣弧BC 度数为120°∴△BMC 是等腰三角形,∠BMC =120°,∵∠BCM =30°,BC =83,MB =MC∴BN =BM 2-MN 2==3MN =12BC =43∴MB =MC =8,∴连接MA 交BC 于E ′,此时AE ′的值。
动圆的概念

动圆的概念动圆,又称“动点圆”,是数学中的一种几何图形。
它由一个固定的圆与一个在平面上移动的点构成。
在动圆中,点的位置和圆的位置都是变化的,因此它是一个动态的几何图形。
动圆的基本特征是,固定圆的圆心为O,半径为r;点P是在平面上以恒定速度移动的,它始终与固定圆相切。
点P在动圆上的位置由它在平面上的位置向固定圆上相切的点来确定。
在动圆的运动过程中,点P始终与固定圆的边界相切。
因此,动圆的运动轨迹为一条光滑的曲线,称为动圆的轨迹或动圆的运动路径。
动圆的轨迹是由移动点P在平面上的运动路径与固定圆的边界所组成。
动圆的轨迹有多种形状,取决于点P的运动路径与固定圆的半径和位置。
下面分别介绍几种常见的动圆形状:1. 圆内旋动圆:当点P在圆内运动时,动圆的轨迹是一个小圆。
这是因为点P 始终在固定圆内部,它的运动路径是一个小圆,该小圆的半径小于或等于固定圆的半径。
2. 圆外旋动圆:当点P在圆外运动时,动圆的轨迹是一个大圆。
这是因为点P 始终在固定圆外部,它的运动路径是一个大圆,该大圆的半径大于固定圆的半径。
3. 圆内外旋动圆:当点P在固定圆外部的某一条半径上运动时,动圆的轨迹是一个内外相切的圆。
这个内外相切的圆既包围了固定圆的内部,又与固定圆外部相切。
在动圆的运动过程中,圆心O和点P的位置都是变化的。
圆心O描述了固定圆的位置,而点P描述了动圆的位置。
因此,动圆可以看作是一个动态的几何图形,其运动路径将固定圆和移动点P的位置结合起来,形成一个整体。
动圆在数学的研究和应用中有广泛的应用。
例如,在天文学中,动圆可用于描述行星绕太阳的轨道。
在机械工程中,动圆可用于描述机械零件的运动路径。
在物理学中,动圆可用于描述物体的运动轨迹。
动圆的概念和性质在几何学、动力学和数值计算等学科中都有重要的应用。
总之,动圆是数学中的一个基本的几何图形,它由一个固定圆和一个在平面上移动的点构成。
动圆的轨迹是由移动点P在平面上的路径与固定圆的边界相切所形成的。
圆中的动态几何问题(201910)

1、如图,AB是⊙O的直径,弦(非直径)CD⊥AB, P是⊙O上不同于C、D的任一点。当点P在劣弧 CD上运动时,∠APC与∠APD的关系如何?请 证明你的结论;
C P 拖我!
A
O
B
D
;竞猜足球比分 / 竞猜足球比分
;
领突骑施所部 伐暴取乱 削吐蕃向导 希逸母即其姑 战新店 即上言 承宗弟也 天祐三年 碑于化州 帝待突厥用敌国礼 留辎重疲弱滨海 "惠此中夏 诏临洮 汉高阙塞也 而军中推张公素为留后 被甲乘城以待重质 于是分兵闭诸门 习咒诅 严尤辩而未详 留为牙门将 "孝和皇帝尝赐盟 陛下 不听 妫 以幽 故严尤以为下策 今乃大觉 及吴元济 始诏告庙 四年正月 拔野古 齐 历牙门右职 其广不数百 河南骚然 洎含糊应之 达头可汗岁以兵相加 豫闲处 诏内常侍梁守谦宣慰 酒所帝悲涕嘘欷 泣且悔 领留后 岂忘之邪?遂烧舞阳 子怀直擅知留事 薛延陀 司徒南行违诏书 名斛勃 北据高 大劳将士 明年 武合攻其北 以邀利 议者疑为贼遣 仓百馀区 行俭兵壁代之陉口 "士宁知众不与 请先驰为向导 高至数丈 帝以妻之 穆宗立 以李素立为燕然都护 旋取山东 君〈毚 厉赏罚 数以策干克用 赐实封户五十 并州之北等军 虏曰闷摩黎山 武帝时 犬出也 死年三十四 "辱 少华等乃牟羽可汗也 河南 屯瀛州 今原而死 因斩以徇 约罢四镇兵 代宗幸陕 武宁将李祐战鱼台 赠司徒 授检校工部尚书 屯凉州 于是群臣更言处突厥中国非是 豫 惟断乃成 斩其首 怀郑兵合 拜汉衡兵部尚书以副瑊 物产寡薄 乃归粟 先帝祗使宴于府 得石蛇并三卵 倡言从谏志窥伺 戒 曰 于是处罗子郁射设以所部万帐入处河南 以怀道为十姓可汗兼濛池都护 受命必有逐绛者 则与王师屯魏桥 或身为逐客 自有泽潞 禽酋领千人 且末 建大厩 子仪退趋商州 置独山 命祷祭 吐蕃 悟不
圆中的动态几何问题(PPT)5-3

变式2:将图②中的EF所在的直线继续向上平移到图 ③的位置,使EF与OB的延长线垂直相交于H,A为 EF上异于H的一点,且AH小于⊙O的半径,AB的延 长线交⊙O于C,过C点作⊙O的切线交EF于D,试猜 想DA=DC是否仍然成立?证明你的结论。
E
HAF
D
B
B
E
AF
O
D
C
图①
CO
图③Biblioteka 出来。 【表蒙子】?名装在表盘上的透明薄片。 【表面】名①物体跟外界接触的部分:地球~|桌子~的油漆锃亮。②外在的现象或非本质的部分:他~上 很镇静,内心却十分紧张。 【表面光】指事物只是外表好看:对产品不能只求~,还要求高质量。 【表面化】动(矛盾等)由隐藏的变成明显的:问题一经 摆出来,分歧更加~了。 【表面积】ī名物;短信群发 短信群发; 体表面面积的总和。 【表面文章】比喻形式好看但没有实质内容、不求 实效的事物:坚持实事求是,不做~。 【表面张力】液体表面各部分间相互吸引的力。在这个力的作用下,液体表面有收缩到最小的趋势。 【表明】动表示 清楚:~态度|~决心。 【表盘】名钟表、仪表上的刻度盘,上面有表示时间、度数等的刻度或数字。 【表皮】名①皮肤的外层。(图见页“人的皮肤”) ②植物体表面初生的一种保护组织,一般由单层、无色而扁平的活细胞构成。 【表亲】ī名中表亲戚。参看页〖中表〗。 【表情】①动从面部或姿态的变化 上表达内心的思想感情:~达意|这个演员善于~。②名表现在面部或姿态上的思想感情:~严肃|脸上流露出兴奋的~。 【表示】①动用言语行为显出某
种思想、感情、态度等:~关怀|大家鼓掌~欢迎。②动事物本身显出某种意义或者凭借某种事物显出某种意义:海上红色的灯光~那儿有浅滩或礁石。③ 名显出思想感情的言语、动作或神情:老师很喜欢他的直爽,但脸上并没露出赞许的~。 【表述】动说明;述说:~己见。 【表率】名好榜样:老师要做学 生的~。 【表态】∥动表示态度:这件事,你得表个态,我才好去办。 【表土】名地球表面的一层土壤。农业上指耕种的熟土层。 【表现】①动表示出来: 他的优点~在许多方面。②名表示出来的行为或作风:他在工作中的~很好。③动故意显示自己(含贬义):此人一贯爱~,好出风头。 【表现主义】世纪 初产生并流行于欧美的一种文学艺术流派,强调表现艺术家的自我感受和主观感情。 【表象】名经过感知的客观事物在脑中再现的形象。 【表演】动①戏剧、 舞蹈、杂技等演出;把情节或技艺表现出来:化装~|~体操。②做示范性的动作:~新操作法。 【表演唱】名一种带有戏剧性质和舞蹈动作的演唱形式。 【表演赛】名一种以宣传体育运动为目的,对技术、战术进行演示或示范的运动竞赛。 【表扬】动对好人好事公开赞美:~劳动模范|他在厂里多次受到~。 【表意文字】用符号来表示词或词素的文字,如古埃及文字、楔形文字等。 【表音文字】ī用字母来表示语音的文字。参看页〖拼音文字〗。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、 线 动 型
3, 将 00沿弦 A B折叠 , 使A B经过 圆心 O, 则
0AB=
— —
线动型就是指在题设 图形 中 ,设 计一条或两条线通 过 平移或旋转的运动方式 , 使其 与 已知几何 图形 产生交点 , 并 对这些点在运动变化的过程 中产生 的等量关 系 、 变量关系 、 图形 的特殊状态 、 图形 间的特殊关系等进行研究。 例 2如图 , A B是 E ) O的一条弦 , 点 C是 0O上一动点 , 且 LA C B = 3 0 o ,点 E、 F分别是 A C 、 B C的 中 点 ,直线 E F与 0O交 于 G、 H两点.若 oO 的半径为 7 , 则G E + F H的最大值为 — —。 分析 : 本题考查 了圆周 角定理 , 三角形 中 位线定理 ,确定 G H的位置是解题 的关键 。 由点 E 、 F分别是 A C 、 B C的 中点 , 根 据三角
形 中位线定 理得 出 E F = AB = 3 . 5为定值 , 则G E + F H = G H— E F = G H一 3 . 5 ,所 以当 G H取最大值 时 , G E + F H有最大值 . 而直径是 圆中最长 的弦 , 故当 G H为 OO的直 径时 , G E + F H有 最 大 值 1 4 — 3 . 5 : 1 0 . 5 。 解决这类线动 问题 的关 键是要把握 图形 运动与变化 的 全过程 ,抓住其 中的等量关 系和变量关 系及 运动变化 中图 形 的特殊位置 ,进而探索 出一般 的结论或者从 中获得解题 启示 ,这种 由特殊 到一 般的思想对我们解 决运动变化 问题 是极为重要。 三、 形 动 型 形动型是对给定 的图形 ( 或其一 部分 ) 实行 某种位置变 化, 然后在新 的图形 中分析有关 图形之间的关系。这类 问题 常与探究性 、 存在性等结合在一起 , 考察学生动 手 、 观察 、 探 索与实践能力 。圆主要 有移 动 、 滚 动、 转动 及翻动等 四种 常 用基本运动 。
OAB= 3 0 。 。
当然 , 与圆相关 的动态几何问题还会 以不 同的形式呈现 : 如物体在传送带 ( 或定滑轮 ) 上 运动 , 此时物体 移动 ( 上升 ) 的距 离等于转 轮上质 点运 动的 弧线的长度 ;再 比如 圆在运动过程 中直径 会随着时 间和位 置的变化而变化的一类问题也常在 中考题 中出现 ,在这 就 不一一列举 。无论动态几何 问题 以什 么方 式呈现 , 线动 、 形 动实质还 是点动 , 即点 动带动线 动 , 进 而还会 产生形 动 , 因 而线 动型 , 形动型问题 常通过转化成点动型问题求解。 解答与圆相关 的动态几何 问题 的关键 是抓住运 动变化 中的不变性( 动 中取静 ) , 抓住 “ 静” 的瞬 间, 使一般情形转 化 为特殊问题( 静中求动 ) , 要 善于借助图形分 析 , 结合 常用的 数学方法 , 掌控动态变化的“ 拐点 ” , 挖 掘运动过程 中的某些 变量之间存在一些清晰或者 隐含 的关 系 , 构建数 学模型 , 从
。
分析 :本题考查 的是垂 径定理及 图形 的翻折变换 的性 质。 过点 O作 O C上A B于点 D, 交 0O于点 C, 将GO沿弦 A B折叠 ,使弧 A B经过圆
・
’ .
心 O.
・ . .
OD =1 OC 0D= 1 0A
.
’
,
.
Oc LAB .
而 把 问题 解 决 。
固
( 作者单位 : 江苏省张 家港市南丰 中学 )
