保温训练1
人教版五年级上册科学保温和散热(第一课时)(课件)

保温材料
材料:泡沫、毛线、皮革,棉花、羽绒以及其中的空 气等材料都是热的不良导体,能降低热传递的 速度,到达保温的效果。
2.保温大作战
想什么办法能使一瓶热 水的温度保持更持久?
(1)设保温箱
请你选用下面提供的材料制作一个保温箱 。
规则: (1)小组合作,将设计图画在实验单上,标明使用材料
和注意事项。
为什么这些物品和材料能保温?它们有什么特点?
(1)暖水瓶保温的方法
保温瓶(杯) 内胆是真空的
为什么这些物品和材料能保温?它们有什么特点?
(2)保温杯和餐食盒保温的方法
玻璃杯是双层的
(2)保温杯和餐食盒保温的方法
用来保温的物品或材料大多使用热的不良导体制成,有的杯子是双层 的,这样做的目的是:
小结:保温物品(材料)的作用
保温物品内的温度﹥外界的温度时:减缓保温
物品温度降落的速度。
保温物品内的温度﹤外界的温度时:减缓杯内水
的温度升高的速度。
3.生活中的保温
◆窗户上安双层玻璃,有什么好处? ◆许多房屋的墙壁有保温层,这样做有什么好处?
双层玻璃中间是空气 ,空气是热的不良导 体,减缓热的传递。
人教鄂教版 五年级上
保和蔼散热
第一课时 怎样保温
➢平时烧好的热水需要装到暖水瓶里,喝水的时候需倒到杯子里。 这是为什么?
在生产、生活中,有时需要保温,有时需要散热。说一说,家里在 什么情况下需要保温?什么情况下需要散热?
一、怎样保温
1.保温材料特点
生活中人们用来保温的物品和材料知道哪些?
生活中人们用来保温的物品和材料知道哪些?
(2)从实验盒中选择原材料,也可以自行补充安全、易 操作的原材料。 (3)保温箱的设计要科学、实用、美观,易于操作。
2013届高考历史总复习 精典例题+详细解析 考前保温训练一

考前保温训练(一)(限时:45分钟满分:100分)一、选择题(本大题共12小题,每小题5分,共60分)1.“任天者定,任人者争;定之以天,争乃不生。
”这句话充分说明了西周宗法制度的精神。
其中的“天”是指( )A.确定继统人选的天子B.决定嫡庶身份的天命C.辨别是非善恶的天理D.表现自然主义的天道解析:选B 题干材料的意思是宗法制下按嫡庶身份的规定决定继承关系就不会出现争斗,如果由人决定则会发生争斗。
由此可知答案为B项。
2.(2012·无锡一模)有学者指出,古代小农的供给行为具有双重性,即在满足自我家庭消费的同时,又积极向市场提供剩余农产品和主动以市场为导向安排生产活动。
对上述观点理解准确的是( ) A.古代小农生产具有多种经营的特点B.市场需求是影响古代小农生产的决定性因素C.古代小农具有强烈的商品生产意识D.古代小农主要通过市场交换获得生活必需品解析:选A 材料认为小农经济在自给自足的同时,并不排斥商品生产。
说明古代小农经济具有多种经营的特点。
3.有人认为董仲舒的“天人感应”学说继承了儒家思想的“仁政”思想。
这一观点主要是看到了董仲舒( )A.主张“民为贵,社稷次之,君为轻”B.提出“君者舟也,庶人者水也;水则载舟,水则覆舟”C.认为天子受命于天,地位不可动摇D.认为人君要爱护百姓,如果残暴,天将降灾祸于他解析:选D 本题只有C、D两项符合董仲舒的思想,其中D项体现董仲舒“天人感应”思想继承了儒家“仁政”思想。
4.(2012·湛江模拟)右图是清末上海《神州画报》上的漫画《此之谓中国之独立》,其中场景最早可能出现在( )A.《南京条约》之后B.《北京条约》之后C.《马关条约》之后D.《辛丑条约》之后解析:选C 本题考查《马关条约》的影响。
《马关条约》的签订,大大刺激了列强侵略中国的野心,随后列强掀起瓜分中国的狂潮,与图的寓意吻合,故选C项。
5.(2012·广东六校第二次联考)下表是小王同学在学习了“近代前期中国人民反侵略、求民主的斗争”之后的一个小结。
陕西省2014届高三高考考前 数学30天保温训练1(集合)Word版含解析

2014年高三数学考前30天保温训练1(集合)一.选择题(共18小题)1.设集合,,如果把b﹣a叫做集合{x|a≤x≤b}的“长度”,B2.(2014•温州一模)已知集合A={1,2,3},B={(x,y)|x∈A,y∈A,x+y∈A},则B中28.(2011•广东模拟)已知a,b∈R,且集合{1,﹣b,2a+2﹣a}={2b,﹣1,a+b},则b﹣a=222213.(2013•江西)已知集合M={1,2,zi},i 为虚数单位,N={3,4},M ∩N={4},则复数15.(2013•山东)已知集合A 、B 全集U={1、2、3、4},且∁U (A ∪B )={4},B={1,2},17.(2009•广东)已知全集U=R ,则正确表示集合M={﹣1,0,1}和N={x|x 2+x=0}关系的 B . . 18.(2014•洛阳二模)已知集合U={x ∈N|0<x ≤8},A={2,3,4,5},B={3,5,7},则如图所示的韦恩图中阴影部分表示的集合为( )2014年高三数学考前30天保温训练1(集合)参考答案与试题解析一.选择题(共18小题)1.设集合,,如果把b﹣a叫做集合{x|a≤x≤b}的“长度”,B解:∵,,是2.(2014•温州一模)已知集合A={1,2,3},B={(x,y)|x∈A,y∈A,x+y∈A},则B中28.(2011•广东模拟)已知a,b∈R,且集合{1,﹣b,2a+2﹣a}={2b,﹣1,a+b},则b﹣a=≥2,解得2有2213.(2013•江西)已知集合M={1,2,zi},i为虚数单位,N={3,4},M∩N={4},则复数15.(2013•山东)已知集合A、B全集U={1、2、3、4},且∁U(A∪B)={4},B={1,2},16.(2013•唐山一模)设集合A={1,2},则满足A∪B={1,2,3,4}的集合B的个数是()17.(2009•广东)已知全集U=R,则正确表示集合M={﹣1,0,1}和N={x|x2+x=0}关系的B..18.(2014•洛阳二模)已知集合U={x∈N|0<x≤8},A={2,3,4,5},B={3,5,7},则如图所示的韦恩图中阴影部分表示的集合为()。
防火防爆安全措施有毒有害气体防护防冻保温安全措施考试题 1

防火防爆安全措施、有毒有害气体防护、防冻保温安全措施考试题1、承包商应按照相关法律、法规和安全技术规范的规定制定防火防爆管理制度、应急预案。
对(正确答案)错2、现场作业前,承包商应组织开展防火防爆应急演练,演练合格后方可作业。
对(正确答案)错3、呈气体、蒸汽、气溶胶(粉尘、烟、雾)状态的毒物均可经呼吸道进入人体。
对(正确答窠)错4、凡有爆炸和火灾危险的区域,操作人员必须穿防静电鞋、防静电工作服。
对错5、含硫化氢油井井场应与周围环境隔离,应设立实体围墙。
O对错6、含硫化氢油井应建立在低洼处或相对封闭区域内。
()对7、目前,油田企业油井中发现含硫化氢现象比较少见。
O对■错8、含硫化氢天然气井井场阀门应采用平板阀。
O对错9、在硫化氢环境中对非金属材料无特殊要求。
()对错10、呼吸器报警器完好,使用时无须注意气瓶的压力值。
O对错Ik硫化氢对生命或健康有立即危险的浓度时300PPM。
O对错12、固定式空气呼吸站是一个远距离空气供应装置,可以同时供多人使用。
O 对错13、硫化氢气体比空气轻,所以它漂浮在空气的上层,易随风飘散。
O对错14、承包商制定操作规程时应考虑防火防爆因素,并组织本单位人员按照不少于()次/月的频率,进行安全操作、事故事件、应急处置等方面的安全培训。
A、1B、2C、3D、415、分离器距离井口应不小于Om,距离计量罐应不小于()m oA、IOm20mC、30m.1D、40m16、热交换器(加热炉)距井口距离应不小于Om,距离计量罐应不小于OmOA^IOmB、20mC、30m;1D、40m17、数采房距离井口应不小于Om,距离计量罐应不小于Om oA^IOmB、20mC、30mD、40m18、计量罐、储油罐距井口应不小于()m,距井队发电房应不小于()m oA、IOmB、20mC、30m ID、40m19、压井管线、掺稀注入设备接口距井口距离应不小于()moA、IOmB、15mC、20m∣1D、25m20、计量罐区域设施在正常接地基础上,应增加阵列式静电接地措施,试油流程中()及()以下法兰应进行静电跨接。
供热蒸汽管道保温方案(一)

供热蒸汽管道保温方案1. 保温材料的选择- 蒸汽管道保温需要选择耐高温、隔热性好的保温材料,如岩棉、玻璃棉、硅酸钙板等。
- 考虑到蒸汽管道的使用环境,保温材料还需具有防腐蚀、耐磨损等特性,以确保长期有效的保温效果。
2. 施工工艺- 在进行蒸汽管道保温施工前,需要对管道进行清洁、防腐处理,确保保温层能够牢固粘附在管道表面。
- 采用专业的施工工艺,如预制保温套管、喷涂保温等方式,确保保温材料能够紧密包裹管道,不存在空隙。
3. 保温层厚度的确定- 根据蒸汽管道的工作温度、环境温度等因素,结合保温材料的导热系数,确定保温层的厚度,以达到预期的保温效果。
- 同时,还需考虑到管道的结构特点、安全要求等因素,确保保温层的厚度能够满足工程的实际需求。
4. 防火安全考虑- 蒸汽管道保温方案需要考虑防火安全,保温材料和保温层的防火等级需符合相关标准要求,以确保在发生火灾时能够起到有效的阻燃作用。
- 同时,还需要配备防火检测设备,定期对蒸汽管道的保温层进行检测和维护,确保防火安全措施的有效性。
5. 节能环保要求- 在选择保温材料和施工工艺时,需要考虑节能环保要求,选择符合国家标准的环保保温材料,并采用节能的施工工艺,以减少能源消耗和对环境的影响。
- 同时,还可以考虑利用可再生能源、回收利用废弃保温材料等方式,进一步降低对环境的影响,实现可持续发展。
6. 维护保养措施- 完成蒸汽管道保温后,需要制定定期的维护保养计划,对保温层进行检测和维护,及时发现和处理保温层存在的问题,确保保温效果持久稳定。
- 同时,还需要配备专业的维护保养人员,进行定期的维护保养工作,确保蒸汽管道保温方案的长期有效性。
7. 监测与评估- 实施蒸汽管道保温方案后,需要建立监测评估体系,对保温效果进行定期监测和评估,及时发现问题并作出调整,确保保温效果符合设计要求。
- 同时,还需对蒸汽管道保温方案的整体效果进行评估,包括节能效果、环保效益、安全性等方面的评估,为后续改进和优化提供参考。
建筑工程施工中的外墙保温技术_1

建筑工程施工中的外墙保温技术发布时间:2022-07-27T02:38:27.427Z 来源:《工程建设标准化》2022年37卷6期作者:刘照楠[导读] 以建筑物外立面作为主要建筑材料的外墙围护结构,不但对建筑物外形构造有很大影响,同时也对提高建筑物的保温性能,以及调节室内外温度都有很大影响。
刘照楠陵县华建置业有限公司山东德州 253500摘要:以建筑物外立面作为主要建筑材料的外墙围护结构,不但对建筑物外形构造有很大影响,同时也对提高建筑物的保温性能,以及调节室内外温度都有很大影响。
外墙保温技术的使用,不仅可以有效防止在夏季不同时房间温度的温差变动得很大,降低了房屋能耗,而且也可以增强房屋的实用性和舒适度。
外墙保温技术在具体使用过程中,还必须满足相应的节能环境条件,在减少暖通空调系统能量的基础上,进一步发挥保温建筑物的功能。
关键词:建筑工程;外墙保温技术;工程施工引言随着国家经济发展的水平日益提高,人民的生活品质也愈来愈好,因此他们对建筑工程的品质也有了越来越高的要求。
外墙保温材料是建筑材料工程施工中的主要部分,其施工效率和我们的生活密切相关。
采用外墙保温材料不仅可以使建筑材料的保温性能有所改善,还能够起到节能减排的效果。
所以在进行建筑项目施工时,就必须对外墙保温施工的技术加以不断优化,从而改善建筑项目施工的总体品质。
基于此,论文将对外墙保温技术在建设工程施工中的运用展开深入研究,希望能够为相关工作人员提供帮助。
1外墙保温技术的优势1.1增强保温效果外墙保温性能技术通过涂层法对墙面进行涂层,因此它可以减少在墙面中发生的热桥情况,使保温层的连续性得到了改善。
对建筑物的保温效果加以提高,从而使建筑工程能够更加符合人们的需求,为我们的生活提供服务。
1.2延长建筑寿命在施工中使用外墙保温施工技术能够提高建筑物结构耐久性,即使存在温差很大的情形,外墙保温板材也能够有效减少其对施工的影响,能够有效防止由于温差过大造成建筑物构件发生变形甚至墙面发生开裂,从而延长建筑物使用寿命。
专练10七道选择题有机化学基础综合题-2023年高考化学考前手感保温训练(全国卷)(原卷版)
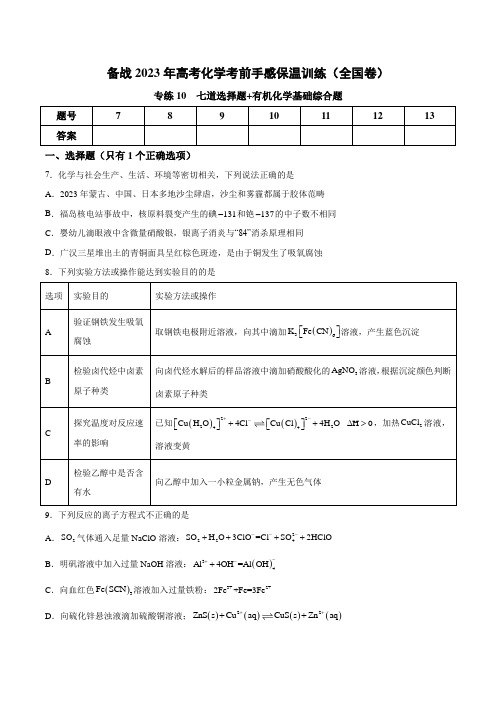
备战2023年高考化学考前手感保温训练(全国卷)专练10 七道选择题+有机化学基础综合题题号 7 8 9 10 11 12 13 答案一、选择题(只有1个正确选项)7.化学与社会生产、生活、环境等密切相关,下列说法正确的是 A .2023年蒙古、中国、日本多地沙尘肆虐,沙尘和雾霾都属于胶体范畴 B .福岛核电站事故中,核原料裂变产生的碘131-和铯137-的中子数不相同 C .婴幼儿滴眼液中含微量硝酸银,银离子消炎与“84”消杀原理相同 D .广汉三星堆出土的青铜面具呈红棕色斑迹,是由于铜发生了吸氧腐蚀 8.下列实验方法或操作能达到实验目的的是 选项实验目的 实验方法或操作A验证钢铁发生吸氧腐蚀取钢铁电极附近溶液,向其中滴加()36K Fe CN ⎡⎤⎣⎦溶液,产生蓝色沉淀B检验卤代烃中卤素原子种类向卤代烃水解后的样品溶液中滴加硝酸酸化的3AgNO 溶液,根据沉淀颜色判断卤素原子种类C探究温度对反应速率的影响 已知()()222244Cu H O 4ClCu Cl 4H O +--⎡⎤⎡⎤++⎣⎦⎣⎦ H 0∆>,加热2CuCl 溶液,溶液变黄D检验乙醇中是否含有水向乙醇中加入一小粒金属钠,产生无色气体9.下列反应的离子方程式不正确的是A .2SO 气体通入足量NaClO 溶液:2224SO H O 3ClO =Cl SO 2HClO ---++++B .明矾溶液中加入过量NaOH 溶液:()34Al 4OH =Al OH -+-+ C .向血红色()3Fe SCN 溶液加入过量铁粉:3+2+2Fe +Fe=3Fe D .向硫化锌悬浊液滴加硫酸铜溶液;()()()()22ZnS s Cuaq CuS s Zn aq ++++10.下列关于有机物的说法不正确的是A .苯环上的一氯代物有7种B .化学式为C 5H 12O 2的二元醇有多种同分异构体,主链上有3个碳原子的二元醇,其同分异构体数目是(不包括1个碳原子上连接2个羟基的化合物): 1种 C .化学式为C 9H 12含有苯环的同分异构体有8种D .研究表明禽流感病毒H7N9在沸水中两分钟就能被杀死,是因为病毒所含蛋白质受热变性11.短周期主族元素X 、Y 、Z 、W 原子序数依次增大,其中X 、Y 、Z 可形成的化合物是一种具有发展前景的“绿色”化工产品( 如图所示),W 是短周期中金属性最强的元素,下列说法正确的是A .简单氢化物的稳定性: Y<ZB .原子半径: X<Y<Z<WC .X 2Z 2、W 2Z 2中所含化学键类型完全相同D .W 的最高价氧化物的水化物是一种弱碱12.利用电化学原理消除污染,还可获得电能,下面是一种处理垃圾渗透液的装置工作原理图。
保温练习1

高三物理保温练习(一)1.下列说法正确的是( )A.伽利略探究物体下落规律的过程所用的科学方法是:问题→猜想→数学推理→实验验证→合理外推→得出结论B.打雷时,呆在木屋里比呆在汽车里更安全C.牛顿在寻找万有引力的过程中,他没有利用牛顿第二定律,但他用了牛顿第三定律D.在不需要考虑物体本身的大小和形状时,建立质点概念是应用近似替代法2. 如图所示,质量分别为m1、m2的两个物体通过轻弹簧连接,在力F的作用下一起沿水平方向做匀加速直线运动(m1在光滑地面上,m2在空中)。
已知力F与水平方向的夹角为0。
则m1的加速度大小为( )A. B. C. D.3. 如图所示,虚线a、b、c是电场中的三个等势面,相邻等势面间的电势差相同,实线为一个带正电的质点仅在电场力作用下,通过该区域的运动轨迹,P、Q是轨迹上的两点。
下列说法中正确的是()A. 三个等势面中,等势面c的电势最高B. 带电质点一定是从P点向Q点运动C. 带电质点通过P点时的加速度比通过Q点时小D.带电质点通过P点时的动能比通过Q点时小4. —条足够长的浅色水平传送带自左向右匀速运行。
现将一块木炭无初速地放在传送带的最左端,木炭在传送带上将会留下一段黑色的径迹。
下列说法中正确的是 ( )A. 黑色的径迹将出现在木炭的左侧B. 木炭的质量越大,径迹的长度越短C. 传送带运动的速度越大,径迹的长度越短D. 木炭与传送带间动摩擦因数越大,径迹的长度越短5.质量为1kg的物体,放在动摩擦因数为0.2的水平面上,在水平拉力的作用下由静止开始运动.水平拉力做的功W和物体发生的位移s之间的关系如图所示,重力加速度为10m/s2。
则下列说法正确的是( )A.s=3m/sB.s=9m时物体的速度大小为/sC.OA段物体的加速度大小为3 m/s2D.AB段物体的加速度大小为3m/s26.(9分)要测定一个自感系数很大的线圈L 的直流电阻,实验室提供下列器材:① 待测线圈L ,阻值约为2Ω,额定电流为2A (符号)② 电流表1A 量程为0.6A ,内阻为0.2Ω(符号) ③ 电流表2A 量程为3A ,内阻约为0.2Ω(符号)④ 变阻器1R 阻值为0~10Ω,变阻器2R 阻值为0~l k Ω(符号)⑤ 电池E ,电动势为9V ,内阻很小(符号) ⑥ 定值电阻3410,100R R =Ω=Ω(符号)⑦ 开关12,S S (符号)要求实验时,改变变阻器的阻值,可使在尽可能大的范围内测得多组1A 表、2A 表的读数1I 、2I ,然后利用12I I -的图象,求出电感线圈的电阻.(1)实验中定值电阻应选用 ,变阻器应选用 . (2)请在方框内画出电路图.(3)实验结束时应先断开开关 .(4)实验测得数据如图21I I -所示,则电感线圈的直流电阻值为 Ω.(保留两位有效数字)高三物理保温练习(二)1. 一名宇航员在某星球上完成自由落体运动实验,让一个质量为2 kg 的小球从一定的高度自由下落,测得在第5 s 内的位移是18 m ,则:A .物体在2 s 末的速度是20 m/sB .物体在第5 s 内的平均速度是3.6 m/sC .物体在第2 s 内的位移是20 mD .物体在5 s 内的位移是50 m2.如图所示,一光滑小球静止放置在光滑半球面的最底端,利用竖直放置的光滑挡板水平向右缓慢地推动小球,则在小球运动的过程中(该过程小球未脱离球面),木板对小球的推力F 1、半球面对小球的支持力F 2的变化情况正确的是:A . F 1增大、F 2减小B .F 1增大、F 2增大C . F 1减小、F 2减小D .F 1减小、F 2增大3. 如图,光滑斜面固定于水平面,滑块A 、B 叠放后一起冲上斜面,且始终保持相对静止,A 上表面水平。
人教鄂教版小学科学五年级上册一单元4课《保温和散热》第1课时教案

学生活动:
- 完成作业:认真完成老师布置的课后作业,巩固学习效果。
- 拓展学习:利用老师提供的拓展资源,进行进一步的学习和思考。
- 反思总结:对自己的学习过程和成果进行反思和总结,提出改进建议。
教学方法/手段/资源:
- 自主学习法:引导学生自主完成作业和拓展学习。
学具准备
多媒体
课型
新授课
教法学法
讲授法
课时
第一课时
步骤
师生互动设计
二次备课
教学资源准备
1. 教材:确保每位学生都有《人教鄂教版小学科学五年级上册》一单元4课《保温和散热》的教材,以便学生能够跟随教学进度进行学习和复习。
2. 辅助材料:准备与教学内容相关的图片、图表、视频等多媒体资源。例如,可以准备不同保温材料的图片,展示各种保温材料的特点和应用场景。还可以准备热量散发的动画视频,帮助学生直观地理解热量散发的过程。
总体来说,本节课的教学效果较好,学生在知识、技能、情感态度等方面都有所收获和进步。然而,我深知教学是一门艺术,需要不断学习和探索。针对教学中存在的问题和不足,我将在今后的教学中采取以下改进措施:
1. 在教学方法上,进一步加强启发式教学,引导学生主动思考和探究,提高学生对知识点的理解和掌握程度。
2. 在教学策略上,及时给予学生针对性的指导和反馈,帮助学生解决学习中的困惑,提高学习效果。
2. 科学思维:培养学生运用观察、实验和分析等方法,形成科学思维的习惯。
3. 科学态度:培养学生对科学探究的兴趣和热情,培养学生的团队合作意识和勇于尝试的精神。
4. 科学知识:让学生了解和掌握保温和散热的原理及相关知识,培养学生运用科学知识解决实际问题的能力。
2017年高考数学保温试题(1)理(含解析)

2017北京市朝阳区高考数学保温试卷(理科)(1)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知集合A={x|x>2},B={x|(x﹣1)(x﹣3)<0},则A∩B=()A.{x|x>1} B.{x|2<x<3} C.{x|1<x<3} D.{x|x>2或x<1}2.若a,b∈R,i为虚数单位,且(a+i)i=b+i则()A.a=1,b=1 B.a=﹣1,b=1 C.a=1,b=﹣1 D.a=﹣1,b=﹣13.下面四个条件中,使a>b成立的充分而不必要的条件是()A.a>b+1 B.a>b﹣1 C.a2>b2D.a3>b34.执行如图所示的程序框图,如果输入的a=1,b=1,那么输出的值等于()A.21 B.34 C.55 D.895.在的二项展开式中,x2的系数为()A.B.C.D.6.在△ABC中,角A,B,C所对的边分别为a,b,c,若sin(A+B)=,a=3,c=4,则sinA=()A.B.C.D.7.设圆C的圆心在双曲线﹣=1(a>0)的右焦点且与此双曲线的渐近线相切,若圆C 被直线l:x﹣y=0截得的弦长等于2,则a的值为()A.B.C.2 D.38.定义在R上的偶函数f(x)满足f(x+2)﹣f(x)=0,且在[﹣1,0]上单调递增,设a=f(log32),b=f(log2),c=f(),则a,b,c的大小关系是()A.a>b>c B.a>c>b C.b>c>a D.c>b>a二、填空题:本大题共6小题,每小题5分,共30分.9.抛物线y2=4x与直线x=1围成的封闭区域的面积为.10.若x,y满足约束条件,则x+2y的取值范围是.11.若非零向量,满足|+|=||+||,则向量,的夹角为.12.在等差数列{a n}中,若a5+a7=4,a6+a8=﹣2,则数列{a n}的公差等于;其前n项和S n的最大值为.13.直线与圆x2+y2=1相交于A、B(其中a、b为实数),且∠AOB=(O是坐标原点),则点P(a,b)与点(1,0)之间距离的最大值为.14.正方体ABCD﹣A1B1C1D1中,M,N分别是棱BC,CC1上不与正方体顶点重合的动点,用平面AMN截正方体,下列关于截面的说法正确的有.①若BM=C1N,则截面为等腰梯形②若BM=CM,且时,截面为五边形③截面的面积存在最大值④截面的面积存在最小值.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:该公司从注册的会员中,随机抽取了100位统计他们的消费次数,得到数据如下:假设汽车美容一次,公司成本为150元.根据所给数据,解答下列问题:(Ⅰ)估计该公司一位会员至少消费两次的概率;(Ⅱ)某会员仅消费两次,求这两次消费中,公司获得的平均利润;(Ⅲ)假设每个会员最多消费5次,以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为X元,求X的分布列和数学期望E(X).16.已知函数y=2cos(ωx+θ)(x∈R,ω>0,0≤θ≤)的图象与y轴相交于点M(0,),且该函数的最小正周期为π.(1)求θ和ω的值;(2)已知点A(,0),点P是该函数图象上一点,点Q(x0,y0)是PA的中点,当y0=,x0∈[,π]时,求x0的值.17.如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.(Ⅰ)求证:AD⊥平面PQB;(Ⅱ)点M在线段PC上,PM=tPC,试确定t的值,使PA∥平面MQB;(Ⅲ)若PA∥平面MQB,平面PAD⊥平面ABCD,求二面角M﹣BQ﹣C的大小.18.已知平面上两个定点、,P为一个动点,且满足.(1)求动点P的轨迹C的方程;(2)若A、B是轨迹C上的两个不同动点.分别以A、B为切点作轨迹C的切线,设其交点为Q,证明为定值.19.设函数f(x)=x﹣﹣alnx(a∈R).(Ⅰ)讨论函数f(x)的单调性.(Ⅱ)若f(x)有两个极值点x1,x2,记过点A(x1,f(x1)),B(x2,f(x2))的直线斜率为k.问:是否存在a,使得k=2﹣a?若存在,求出a的值;若不存在,请说明理由.20.如图,设A是由n×n个实数组成的n行n列的数表,其中a u(i,j=1,2,3,…,n)表示位于第i行第j列的实数,且a u∈{1,﹣1}.记S(n,n)为所有这样的数表构成的集合.对于A∈S(n,n),记r i(A)为A的第i行各数之积,c j(A)为A的第j列各数之积.令l(A=(A)+(A)).(Ⅰ)请写出一个A∈s(4,4),使得l(A)=0;(Ⅱ)是否存在A∈S(9,9),使得l(A)=0?说明理由;(Ⅲ)给定正整数n,对于所有的A∈S(n,n),求l(A)的取值集合.2017北京市朝阳区高考数学保温试卷(理科)(1)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知集合A={x|x>2},B={x|(x﹣1)(x﹣3)<0},则A∩B=()A.{x|x>1} B.{x|2<x<3} C.{x|1<x<3} D.{x|x>2或x<1}【考点】1E:交集及其运算.【分析】求出B中不等式的解集确定出B,找出A与B的交集即可.【解答】解:由B中不等式解得:1<x<3,即B={x|1<x<3},∵A={x|x>2},∴A∩B={x|2<x<3},故选:B.2.若a,b∈R,i为虚数单位,且(a+i)i=b+i则()A.a=1,b=1 B.a=﹣1,b=1 C.a=1,b=﹣1 D.a=﹣1,b=﹣1【考点】A3:复数相等的充要条件.【分析】根据所给的关于复数的等式,整理出等式左边的复数乘法运算,根据复数相等的充要条件,即实部和虚部分别相等,得到a,b的值.【解答】解:∵(a+i)i=b+i,∴ai﹣1=b+i,∴a=1,b=﹣1,故选C.3.下面四个条件中,使a>b成立的充分而不必要的条件是()A.a>b+1 B.a>b﹣1 C.a2>b2D.a3>b3【考点】29:充要条件.【分析】利用不等式的性质得到a>b+1⇒a>b;反之,通过举反例判断出a>b推不出a>b+1;利用条件的定义判断出选项.【解答】解:a>b+1⇒a>b;反之,例如a=2,b=1满足a>b,但a=b+1即a>b推不出a>b+1,故a>b+1是a>b成立的充分而不必要的条件.故选:A.4.执行如图所示的程序框图,如果输入的a=1,b=1,那么输出的值等于()A.21 B.34 C.55 D.89【考点】EF:程序框图.【分析】根据已知的程序框图可得,该程序的功能是利用循环结构计算并输出变量b的值,模拟程序的运行过程,可得答案.【解答】解:模拟程序的运行,可得a=1,b=1,执行循环体,a=2,b=3,不满足条件b>50,执行循环体,a=5,b=8不满足条件b>50,执行循环体,a=13,b=21,不满足条件b>50,执行循环体,a=34,b=55,满足条件b>50,退出循环,输出的值为55.故选:C.5.在的二项展开式中,x2的系数为()A.B.C.D.【考点】DA:二项式定理.【分析】利用二项展开式的通项公式求出展开式的通项,令x的指数为2,求出展开式中,x2的系数,即得答案.【解答】解:展开式的通项为T r+1=(﹣1)r22r﹣6C6r x3﹣r令3﹣r=2得r=1所以项展开式中,x2的系数为﹣故选C6.在△ABC中,角A,B,C所对的边分别为a,b,c,若sin(A+B)=,a=3,c=4,则sinA=()A.B.C.D.【考点】HP:正弦定理.【分析】由内角和定理及诱导公式知sin(A+B)=sinC=,再利用正弦定理求解.【解答】解:∵A+B+C=π,∴sin(A+B)=sinC=,又∵a=3,c=4,∴=,即=,∴sinA=,故选B.7.设圆C的圆心在双曲线﹣=1(a>0)的右焦点且与此双曲线的渐近线相切,若圆C被直线l:x﹣y=0截得的弦长等于2,则a的值为()A.B.C.2 D.3【考点】KJ:圆与圆锥曲线的综合.【分析】圆C的圆心C(,0),双曲线的渐近线方程为x±ay=0,再由C到渐近线的距离可求出圆C方程+y2=2.由l被圆C截得的弦长是2及圆C的半径为可知=1,由此能求出a的值.【解答】解:圆C的圆心C(,0),双曲线的渐近线方程为x±ay=0,C到渐近线的距离为d==,故圆C方程+y2=2.由l被圆C截得的弦长是2及圆C的半径为可知,圆心C到直线l的距离为1,即=1,∴a=.故选A.8.定义在R上的偶函数f(x)满足f(x+2)﹣f(x)=0,且在[﹣1,0]上单调递增,设a=f(log32),b=f(log2),c=f(),则a,b,c的大小关系是()A.a>b>c B.a>c>b C.b>c>a D.c>b>a【考点】3Q:函数的周期性;3F:函数单调性的性质.【分析】推导出f(x)的周期为2,在[0,1]上单调递减,log2=﹣log32,<<log32<1,由此能求出结果.【解答】解:∵定义在R上的偶函数f(x)满足f(x+2)﹣f(x)=0,且在[﹣1,0]上单调递增,∴f(x)的周期为2,在[0,1]上单调递减,log2=﹣log32,<<log32<1,∴c=f()=f(﹣)=f(),b=f(log2)=f(﹣)=f(),f()=f(﹣)=f(),∵<<<log32,∴b>c>a.故选:C.二、填空题:本大题共6小题,每小题5分,共30分.9.抛物线y2=4x与直线x=1围成的封闭区域的面积为.【考点】K8:抛物线的简单性质.【分析】方法一:求得交点坐标,对x积分,根据定积分的运算,即可求得答案;方法二:求得交点坐标,对y积分,根据定积分的运算,即可求得答案.【解答】解:方法一:,解得:,,则A(1,2),B(1,﹣2),∴S=2dx=2×=,∴抛物线y2=4x与直线x=1围成的封闭区域的面积,故答案为:.方法二:,解得:,,则A(1,2),B(1,﹣2),S=dy=2dy=2×=,∴抛物线y2=4x与直线x=1围成的封闭区域的面积,故答案为:.10.若x,y满足约束条件,则x+2y的取值范围是[3,7] .【考点】7C:简单线性规划.【分析】利用已知条件画出可行域,关键目标函数的几何意义求最值.【解答】解:由约束条件得到可行域如图:设z=x+2y则y=,当此直线经过图中A(1,1)时直线在y轴的截距最小,z最小,经过C(1,3)时,直线在y轴的截距最大,z最大,所以x+2y的最小值为1+2=3,最大值为1+2×3=7,所以x+2y的取值范围为:[3,7];故答案为:[3,7].11.若非零向量,满足|+|=||+||,则向量,的夹角为0°.【考点】9R:平面向量数量积的运算.【分析】把已知向量等式两边平方,化简可得向量,的夹角.【解答】解:由|+|=||+||,两边平方得:,∴,得,∴,得cos<>=1,则向量,的夹角为0°.故答案为:0°.12.在等差数列{a n}中,若a5+a7=4,a6+a8=﹣2,则数列{a n}的公差等于﹣3 ;其前n项和S n的最大值为57 .【考点】85:等差数列的前n项和;84:等差数列的通项公式.【分析】等差数列{a n}中,由a5+a7=4,a6+a8=﹣2,解得a1=17,d=﹣3,由此求出S n=﹣n2+,再用配方法能够求出S n的最大值.【解答】解:等差数列{a n}中,∵a5+a7=4,a6+a8=﹣2,∴,解得a1=17,d=﹣3,∴S n=17n+=17n﹣+=﹣n 2+=﹣(n ﹣)2+,∴当n=6时,S n 取最大值S 6=﹣=57.故答案为:﹣3,57.13.直线与圆x 2+y 2=1相交于A 、B (其中a 、b 为实数),且∠AOB=(O 是坐标原点),则点P (a ,b )与点(1,0)之间距离的最大值为.【考点】J9:直线与圆的位置关系.【分析】根据直线和圆的位置关系以及两点间的距离公式即可得到结论.【解答】解:∵∠AOB=(O 是坐标原点),∴∴圆心到直线ax+by=的距离d=.即,整理得2a 2+b 2=3, 则点P(a,b)与点Q(1,)之间距离d 1====则点P (a ,b )与点(1,0)之间距离的最大值为.故答案为:14.正方体ABCD ﹣A 1B 1C 1D 1中,M ,N 分别是棱BC ,CC 1上不与正方体顶点重合的动点,用平面AMN 截正方体,下列关于截面的说法正确的有 ①② . ①若BM=C 1N ,则截面为等腰梯形②若BM=CM ,且时,截面为五边形③截面的面积存在最大值 ④截面的面积存在最小值. 【考点】L2:棱柱的结构特征.【分析】画出正方体,根据动点M ,N 的不同位置动点不同 的截面;M ,N 分别是棱BC ,CC 1上不与正方体顶点重合的动点,考虑极限位置时的截面形状以及面积极限判断.【解答】解:对于①,如图1,若BM=C1N,则MN∥AD1,D1N=AM,截面AMND1为等腰梯形,故①正确;对于②,如图2,若BM=CM,且时,设截面与棱C1D1的交点为R,延长DD1,使DD1∩NR=N1,连接AN1交A1D1于S,连接SR,可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1N:D1N1,截面为五边形故②正确;对于③,当BM=C1N→0时,过点A,M,N的截面→矩形,其面积接近最大,∵M,N分别是棱BC,CC1上不与正方体顶点重合的动点,∴BM=C1N≠0,∴截面的面积不存在最大值,故③错误;对于④,当BM→BC时CN→0时,截面→等边三角形,边长为→,面积→,又M,N分别是棱BC,CC1上不与正方体顶点重合的动点,所以截面面积不存在最小值;故④错误;故答案为:①②三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:该公司从注册的会员中,随机抽取了100位统计他们的消费次数,得到数据如下:假设汽车美容一次,公司成本为150元.根据所给数据,解答下列问题: (Ⅰ)估计该公司一位会员至少消费两次的概率;(Ⅱ)某会员仅消费两次,求这两次消费中,公司获得的平均利润;(Ⅲ)假设每个会员最多消费5次,以事件发生的频率作为相应事件发生的概率,设该公司为一位会员服务的平均利润为X 元,求X 的分布列和数学期望E (X ).【考点】CH :离散型随机变量的期望与方差;CG :离散型随机变量及其分布列. 【分析】(I )根据频数计算频率,得出概率; (II )根据优惠标准计算平均利润;(III )求出各种情况对应的X 的值和概率,得出分布列,从而计算出数学期望. 【解答】解:(I )随机抽取的100位会员中,至少消费两次的会员有20+10+5+5=40, ∴该公司一位会员至少消费两次的概率为P==.(II )第一次消费时,公司获取利润为200﹣150=50元, 第二次消费时,公司获取利润为200×0.95﹣150=40元, ∴求这两次消费中,公司获得的平均利润为=45元.(III )若会员消费1次,平均利润为50元, 若会员消费2次,平均利润为45元, 若会员消费3次,平均利润为为40元, 若会员消费4次,平均利润为35元, 若会员消费5次,平均利润为30元, ∴X 的可能取值为50,45,40,35,30,∴P (X=50)=,P (X=45)=,P (X=40)=,P (X=35)=,P (X=30)=.∴X 的分布列为:∴E (X )=50×+45×+40×+35×+30×=46.25.16.已知函数y=2cos (ωx+θ)(x ∈R ,ω>0,0≤θ≤)的图象与y 轴相交于点M (0,),且该函数的最小正周期为π. (1)求θ和ω的值;(2)已知点A (,0),点P 是该函数图象上一点,点Q (x 0,y 0)是PA 的中点,当y 0=,x 0∈[,π]时,求x 0的值.【考点】HK :由y=Asin (ωx+φ)的部分图象确定其解析式.【分析】(1)将M 坐标代入已知函数,计算可得得cos θ,由θ范围可得其值,由ω=结合已知可得ω值;(2)由已知可得点P 的坐标为(2x 0﹣,).代入y=2cos (2x+)结合x 0∈[,π]和三角函数值得运算可得.【解答】解:(1)将x=0,y=代入函数y=2cos (ωx+θ)得cos θ=,∵0≤θ≤,∴θ=.由已知周期T=π,且ω>0,∴ω===2(2)∵点A (,0),Q (x 0,y 0)是PA 的中点,y 0=,∴点P 的坐标为(2x 0﹣,).又∵点P 在y=2cos (2x+)的图象上,且x 0∈[,π],∴cos (4x 0﹣)=,≤4x 0﹣≤,从而得4x 0﹣=,或4x 0﹣=,解得x 0=或17.如图,在四棱锥P ﹣ABCD 中,底面ABCD 为菱形,∠BAD=60°,Q 为AD 的中点,PA=PD=AD=2. (Ⅰ)求证:AD ⊥平面PQB ;(Ⅱ)点M 在线段PC 上,PM=tPC ,试确定t 的值,使PA ∥平面MQB ; (Ⅲ)若PA ∥平面MQB ,平面PAD ⊥平面ABCD ,求二面角M ﹣BQ ﹣C 的大小.【考点】MR :用空间向量求平面间的夹角;LS :直线与平面平行的判定;LW :直线与平面垂直的判定.【分析】(Ⅰ)证明AD ⊥BQ ,AD ⊥PQ ,利用线面垂直的判定,可得AD ⊥平面PQB .; (Ⅱ)利用PA ∥平面MQB ,可得MN ∥PA ,利用比例关系,即可得到结论;(Ⅲ)证明PQ ⊥平面ABCD ,建立空间直角坐标系,求出平面MQB 的法向量=,取平面ABCD 的法向量=(0,0,1),利用向量的夹角公式,即可求得二面角M ﹣BQ ﹣C 的大小. 【解答】(Ⅰ)证明:连接BD .因为四边形ABCD 为菱形,∠BAD=60°,所以△ABD 为正三角形. 又Q 为AD 中点,所以AD ⊥BQ .因为PA=PD,Q为AD的中点,所以AD⊥PQ.又BQ∩PQ=Q,所以AD⊥平面PQB.(Ⅱ)解:当时,PA∥平面MQB.下面证明:连接AC交BQ于N,连接MN.因为AQ∥BC,所以.因为PA∥平面MQB,PA⊂平面PAC,平面MQB∩平面PAC=MN,所以MN∥PA,所以,所以,即.(Ⅲ)解:因为PQ⊥AD,平面PAD⊥平面ABCD,交线为AD,所以PQ⊥平面ABCD.以Q为坐标原点,分别以QA,QB,QP所在的直线为x,y,z轴,建立如图所示的空间直角坐标系Q﹣xyz.由PA=PD=AD=2,则有A(1,0,0),,.设平面MQB的法向量为=(x,y,z),由,且,,可得令z=1,得.所以=为平面MQB的一个法向量.取平面ABCD的法向量=(0,0,1),则=,故二面角M﹣BQ﹣C的大小为60°.18.已知平面上两个定点、,P为一个动点,且满足.(1)求动点P的轨迹C的方程;(2)若A、B是轨迹C上的两个不同动点.分别以A、B为切点作轨迹C的切线,设其交点为Q,证明为定值.【考点】J3:轨迹方程;K6:抛物线的定义;KH:直线与圆锥曲线的综合问题.【分析】(1)先设P(x,y),欲动点P的轨迹C的方程,即寻找x,y之间的关系,结合向量的坐标运算即可得到.(2)先设出A,B两点的坐标,利用向量关系及向量运算法则,用A,B的坐标表示出,最后看其是不是定值即可.【解答】解:(I)设P(x,y).由已知,∵∴4y+8=4整理,得x2=8y即动点P的轨迹C为抛物线,其方程为x2=8y.(II)由已知N(0,2).即得(﹣x1,2﹣y1)=λ(x2,y2﹣2)将(1)式两边平方并把x12=8y1,x22=8y2代入得y1=λ2y2解(2)、(3)式得,且有x1x2=﹣λx22=﹣8λy2=﹣16.抛物线方程为.所以过抛物线上A、B两点的切线方程分别是,即y=解出两条切线的交点Q的坐标为所以=所以为定值,其值为0.19.设函数f(x)=x﹣﹣alnx(a∈R).(Ⅰ)讨论函数f(x)的单调性.(Ⅱ)若f(x)有两个极值点x1,x2,记过点A(x1,f(x1)),B(x2,f(x2))的直线斜率为k.问:是否存在a,使得k=2﹣a?若存在,求出a的值;若不存在,请说明理由.【考点】6B:利用导数研究函数的单调性;6C:函数在某点取得极值的条件.【分析】(Ⅰ)求导,令导数等于零,解方程,跟据f′(x)f(x)随x的变化情况即可求出函数的单调区间;(Ⅱ)假设存在a,使得k=2﹣a,根据(I)利用韦达定理求出直线斜率为k,根据(I)函数的单调性,推出矛盾,即可解决问题.【解答】解:(I)f(x)定义域为(0,+∞),f′(x)=1+,令g(x)=x2﹣ax+1,△=a2﹣4,①当﹣2≤a≤2时,△≤0,f′(x)≥0,故f(x)在(0,+∞)上单调递增,②当a<﹣2时,△>0,g(x)=0的两根都小于零,在(0,+∞)上,f′(x)>0,故f(x)在(0,+∞)上单调递增,③当a>2时,△>0,g(x)=0的两根为x1=,x2=,当0<x<x1时,f′(x)>0;当x1<x<x2时,f′(x)<0;当x>x2时,f′(x)>0;故f(x)分别在(0,x1),(x2,+∞)上单调递增,在(x1,x2)上单调递减.(Ⅱ)由(I)知,a>2.因为f(x1)﹣f(x2)=(x1﹣x2)+﹣a(lnx1﹣lnx2),所以k==1+﹣a,又由(I)知,x1x2=1.于是k=2﹣a,若存在a,使得k=2﹣a,则=1,即lnx1﹣lnx2=x1﹣x2,亦即(*)再由(I)知,函数在(0,+∞)上单调递增,而x2>1,所以>1﹣1﹣2ln1=0,这与(*)式矛盾,故不存在a,使得k=2﹣a.20.如图,设A是由n×n个实数组成的n行n列的数表,其中a u(i,j=1,2,3,…,n)表示位于第i行第j列的实数,且a u∈{1,﹣1}.记S(n,n)为所有这样的数表构成的集合.对于A∈S(n,n),记r i(A)为A的第i行各数之积,c j(A)为A的第j列各数之积.令l(A=(A)+(A)).(Ⅰ)请写出一个A∈s(4,4),使得l(A)=0;(Ⅱ)是否存在A∈S(9,9),使得l(A)=0?说明理由;(Ⅲ)给定正整数n,对于所有的A∈S(n,n),求l(A)的取值集合.【考点】57:函数与方程的综合运用.【分析】(Ⅰ)可以取第一行都为﹣1,其余的都取1,即满足题意;(Ⅱ)不存在A∈S(9,9),使得l(A)=0.可用反证法证明假设存在,得出矛盾,从而证明结论;(Ⅲ)通过分析正确得出l(A)的表达式,及从A0如何得到A1,…依此类推即可得到A k.【解答】(Ⅰ)解:答案不唯一,如图所示数表符合要求.(Ⅱ)解:不存在A∈S(9,9),使得l(A)=0.证明如下:假设存在A∈S(9,9),使得l(A)=0.因为r i(A)∈{1,﹣1},c j(A)∈{1,﹣1},(i,j=1,2,3,…,9),所以r1(A),…,r9(A);c1(A),…,c9(A),这18个数中有9个1,9个﹣1.令M=r1(A)•…r9(A)c1(A)…c9(A).一方面,由于这18个数中有9个1,9个﹣1,从而M=﹣1.①另一方面,r1(A)•…r9(A)表示数表中所有元素之积(记这81个实数之积为m);c1(A)•…c9(A)也表示m,从而M=m2=1.②①、②相矛盾,从而不存在A∈S(9,9),使得l(A)=0.(Ⅲ)解:记这n2个实数之积为P.一方面,从“行”的角度看,有P=r1(A)•r2(A)…r n(A);另一方面,从“列”的角度看,有P=c1(A)c2(A)…c n(A).从而有r1(A)•r2(A)…r n(A)=c1(A)c2(A)…c n(A).③注意到r i(A)∈{1,﹣1},c j(A)∈{1,﹣1},(i,j=1,2,3,…,n),下面考虑r1(A),…,r n(A);c1(A),…,c n(A),这些数中﹣1的个数:由③知,上述2n个实数中,﹣1的个数一定为偶数,该偶数记为2k(0≤k≤n);则1的个数为2n﹣2k,所以l(A)=(﹣1)×2k+1×(2n﹣2k)=2(n﹣2k).对数表A0:a ij=1,(i,j=1,2,3,…,n),显然l(A0)=2n.将数表A0中的a11由1变为﹣1,得到数表A1,显然l(A1)=2n﹣4.将数表A1中的a22由1变为﹣1,得到数表A2,显然l(A2)=2n﹣8.依此类推,将数表A k﹣1中的a kk由1变为﹣1,得到数表A k.即数表A k满足:a11=a22=…=a kk=﹣1(1≤k≤n),其余a ij=1.所以 r1(A)=r2(A)=…=r k(A)=﹣1,c1(A)=c2(A)=…=c k(A)=﹣1.所以l(A k)=2[(﹣1)×k+(n﹣k)]=2n﹣4k.由k的任意性知,l(A)的取值集合为{2(n﹣2k)|k=0,1,2,…n}.。
heat训练方法

heat训练方法"Heat"训练方法是一种针对运动员的体能训练方法,主要目的是提高运动员的耐热能力和减少在高温环境下的身体疲劳。
下面将详细介绍这种训练方法。
首先,我们需要明确"Heat"训练的基本概念和原理。
人体在高温环境下运动时,会出现一系列的生理变化,如心率加快、出汗增多等。
这些变化不仅影响运动员的运动表现,还可能引发一些健康问题。
因此,"Heat"训练的主要目的是通过模拟高温环境,使运动员逐渐适应这种环境,从而提高其耐热能力。
在进行"Heat"训练时,需要注意以下几点:逐步增加训练强度:一开始,运动员可以在相对较低的温度下进行训练,然后逐渐提高温度和训练强度。
这样可以帮助运动员逐步适应高温环境,避免突然的高温环境对身体造成过大的负担。
保持适当的补水:在高温环境下运动时,人体会大量出汗,导致水分和电解质的流失。
因此,运动员需要及时补充水分和电解质,以维持身体的正常功能。
合理安排训练时间:为了避免中暑等健康问题,建议在清晨或傍晚时段进行"Heat"训练。
这些时段气温相对较低,可以减少运动员在高温环境下的暴露时间。
结合其他训练方法:除了"Heat"训练外,运动员还可以结合其他训练方法,如力量训练、有氧训练等,以提高全面的身体素质。
通过以上介绍,我们可以看出,"Heat"训练方法是一种针对运动员的体能训练方法,旨在提高运动员的耐热能力和减少在高温环境下的身体疲劳。
在进行这种训练时,需要注意逐步增加训练强度、保持适当的补水、合理安排训练时间以及结合其他训练方法。
通过这些措施,运动员可以逐渐适应高温环境,提高运动表现,并减少健康问题的发生。
大象版科学五上 结构与保温 (1)

大象版 五年级上
新知讲解
观察下图玻璃的结构
新知讲解
提出问题
观察双层玻璃窗的结构,想一想为什么要这么设计,尝试从事物的结构角度
提出我们可以探究的科学问题。
玻璃窗为什么要做成双层玻璃的? 这样加工起来不是很麻烦吗? 和单层的玻璃窗比起来,这样设 计有什么优点?
新知讲解
打算研究的问题: 相同材料做成的双层结构和单层结构的物体, 在相同时间内,哪一个保温效果好?
新知讲解
迁移应用
冰淇淋冷藏箱的保温效果与哪些因素有关?我们还有什么问题需要
继续研究?尝试自己设计实验方案并进行研究。
要是把冷藏箱做 成几层,每层做 成一个一个的小
格子……
外包装的颜 色会不会和吸收
热辐射有关?
我想试试外面加 一层锡纸能不能 更好地防止热辐
射……
把我们的探究结 论都整理好,准 备设计一个冰淇 淋冷藏箱吧!
新知讲解
实验方案
实验目的:…… 我的假设:在相同时间内,双层结构温度变化幅度小。 相同条件:塑料瓶、水的多少和初始温度、时间…… 不同条件:单层结构与双层结构。
新知讲解
实验步骤: 1.用大塑料瓶套小瓶的方法,制作双层结构瓶。 2. 分别在双层瓶和单层瓶内倒入同样多的温水,记录初始温度。 3. 用橡皮泥将温度计固定在测量位置…… 4.每2分钟观察并记录一次温度数据,共观察10分钟。
双层玻璃每层玻璃内外表面的温差都相对减小,加上采用合适的间隔可以有 效防止夹层中空气的对流,静止的空气是热的不良导体,因此保温效果大大 增加。
新知讲解
保温瓶的原理
保温瓶的软木塞是热的不良导体,减慢了热的传导。 双层结构的夹层被抽成真空,最大限度地减少了热传导和热 对流,再加上水银镀层,又尽可能地阻止了热辐射。 多种方式同时使用,大大减缓了热传递的速度,起到了良好 的保温作用。
大象版科学五上 材料与保温 (1)

新知讲解
事实证据
选择一个问题,制订好研究计划,开始研究吧。注意及时记录实验数据。
不同材料勺子上黄油熔化快慢实验图
不同材料长条棒上火柴掉落快慢实验图
新知讲解
材料超市
酒精灯 蜡环或火柴 白凡士林或冻黄油 大小和形状相同而材质不同的勺子 粗细相同而材质不同的长条棒 (如玻璃棒、塑料棒、木棒、铁棒、铜棒等) 热水 冰块 棉被 烧杯 温度计 ……
打算研究的问题: 1. 同时加热不同材料做的 物体,哪些物体传递热的 速度更慢?
为什么冰糕箱上要裹棉被? 裹上棉被的冰块融化得慢吗?
2.相同时间内,裹上棉被的 冰块比不裹棉被的冰块温 度上升得慢吗?
新知讲解
小贴士
一般来说,可探究的科学问题中所涉及的两个 或多个条件都是可以观察或测量的。
像“它可以发挥什么作用”“用或不用它可能 导致什么结果”这样的问题就是从事物的功 能 角 度 提 出的问题。
新知讲解
安全提示
可以在木棒、塑料棒一端裹上一些 锡纸再加热,以防被点燃或烧坏。
新知讲解
裹棉被对冰块融化快慢的影响实验计划
相同条件 不同条件 实验步骤 观察内容
冰块大小及数量……
裹棉被与不裹棉被
……
1. 测量相同时间内冰 块温度的变化。 2. 观察相同时间内冰 块状态的变化
新知讲解
得出结论
热的良导体和不良导体 什么材料的勺子上黄油熔化得最慢? 什么材料的长条棒上的火柴掉落得最慢? 裹着棉被的冰块比不裹棉被的冰块温度上升得吗? …… 比较分析各小组的实验结果,总结物体的材料对热传递 的快慢有什么影响。
科学上使用“导热系 数”来描述物质的导 热性,我们可以上网搜 索一下常见材料的导
热系数……
小学科学23科学擂台——保温物品大比拼(一)(教案)

小学科学23科学擂台——保温物品大比拼(一)(教案)标题:小学科学23科学擂台——保温物品大比拼(一)在小学科学教学中,科学擂台活动是一种常见的教学形式,它能够激发学生的学习兴趣,培养学生的科学研究能力和动手能力。
本文将为大家介绍一期小学科学科学擂台活动的具体内容,即保温物品大比拼。
一、任务目标本次科学擂台活动的目标是让学生了解保温物品的作用和原理,培养学生的观察能力和实验设计能力。
通过比较不同保温物品的保温效果,让学生学会选择合适的保温物品。
二、教学步骤1. 介绍保温物品的作用和原理首先,教师向学生介绍保温物品的作用和原理。
保温物品常常用于保持食物或饮品的温度,使其在一段时间内保持热或冷。
保温物品一般由具有良好绝热性能的材料制成,例如保温杯、保冷袋等。
学生通过观察实际例子和讨论,理解保温物品的作用和原理。
2. 学生分组进行实验设计将学生分为若干小组,每个小组包括4-5名学生。
每个小组将负责设计一个保温装置的实验。
他们可以选择不同的材料和结构设计,以测试保温效果。
教师在设计实验的过程中提供指导和帮助。
3. 实验步骤每个小组按照自己的设计制作保温装置,并编写实验步骤和观察记录表。
实验步骤大致包括:准备保温材料、装置结构设计、测量初始温度、注入一定温度的水或其他液体、记录温度变化等。
4. 实施实验学生按照设计好的实验步骤,进行实验操作。
在实验过程中,他们需要观察保温物品的保温效果,并记录所测得的温度变化。
5. 数据整理与分析实验结束后,学生需要整理实验数据并进行分析。
他们可以使用表格、图表等方式展示实验结果,并讨论保温物品的保温效果。
教师可以指导学生从实验数据中发现规律和问题,并帮助他们进行进一步思考。
6. 结果总结与展示每个小组在教室内展示自己的实验结果,并进行简单的讲解。
学生可以通过实验结果的比较,总结出保温物品的保温效果与材料及结构的关系,并给出自己的观察和结论。
三、评价方式教师可以根据学生的实验设计、实验操作、数据分析和结果总结等方面进行综合评价。
冀人版小学科学五上-第二十三课 保温物品大比拼(一)教案

23.科学擂台——保温物品大比拼(一)教学目标科学知识能列举出生活中常用的保温物品。
科学探究1.能根据不同任务,明确要解决的主要问题。
2.能通过多种方式进行调研,搜集与问题有关的信息。
3.能按照分析、构思、呈现的过程设计制作方案,并运用概念图呈现出来。
科学态度1.能对制作保温物品表现出探究兴趣。
2.能接受别人的意见和建议,反思、调整自己的方案。
3.能采用新的思路、新的材料和新的方法设计制作方案。
4.能与他人分工合作、沟通交流,综合考虑大家意见,形成集体观点。
科学、技术、社会与环境(STSE)能说出人们的实际需求促进了保温技术的发展。
教学重点能列举出生活中常用的保温物品。
教学难点能对制作保温物品表现出探究兴趣。
教学准备教师准备保温盒、保温袋、课件等。
学生准备课前搜集保温物品资料,《科学学生活动手册》,笔,等等。
教学建议课时安排:建议安排2课时。
第一课时完成“任务”和“调研”。
第二课时完成“设计”。
教学过程第一课时(一)明确任务1引导:生活中我们经常会遇到这样的情景(出示教科书中的两幅图片),请说出两幅图各描述的是什么。
你们在生活中有没有遇见过类似的事情?我们怎样解决呢?要解决这个问题需要按照这样的流程进行(出示齿轮图)。
2.讨论:确定要完成的任务是什么?面临的主要问题是什么?3.小结:我们面临的任务是:制作一个保温箱,储存300克冰块,要求在半小时内尽量少融化;制作一个保温袋、储存刚出锅的5个馒头,要求在半小时内保持较高的温度。
面临的主要问题是:制作保温物品的材料有哪些?保温物品的结构是什么样的?保温物品怎样携带?4提示:根据小组成员的意见,选择一个感兴趣的任务。
(二)制订计划1.引导:根据活动中面临的主要问题,我们可以通过实地观察、专家咨询、查阅图书资料、收听收看广播电视、浏览互联网等途径进行调研,获取相关信息。
调研之前需要先制订一个小组活动计划。
计划内容包括调研主题、主要问题、调研方法、记录信息等。
冬季户外活动,保暖有妙招

冬季户外活动,保暖有妙招
在冬季进行户外活动时,保持身体的温暖是非常重要的,以下是一些建议:1.穿着合适的服装:选择轻便、保暖、防水的服装,可以避免感冒和其他健
康问题。
同时,佩戴帽子、手套等保暖用品,可以减少身体暴露在寒冷环境中的部分。
2.穿着鞋底厚实的鞋子:可以增加脚的保暖度。
3.使用暖宝宝等保暖用品:在户外活动时,可以使用暖宝宝等保暖用品,特
别是对身体容易受寒的部位,如脚底、腰部等。
4.喝温水:在冬季进行户外活动时,需要喝温水来保持身体温暖和舒适。
5.逐渐适应寒冷环境:在进行户外活动时,需要逐渐适应寒冷环境,避免一
开始就进行过量的运动或暴露在极端的寒冷环境中。
6.合理安排户外活动时间:选择合适的时间进行户外活动,避免在早晨和晚
上气温较低的时候进行活动。
7.注意呼吸系统保护:在进行户外活动时,需要注意呼吸系统的保护,采用
鼻腔呼吸或口鼻结合呼吸的方法,以减轻寒冷天气对呼吸道的刺激。
8.饮食注意:冬季天气寒冷,身体需要更多的能量来抵御寒冷,因此需要注
意饮食,增加身体的营养和能量。
总的来说,冬季进行户外活动时,需要注意保持身体的温暖,可以选择合适的服装、使用保暖用品、喝温水、逐渐适应寒冷环境、合理安排户外活动时间、注意呼吸系统保护和饮食注意等方面来保持身体温暖。
冀人版五年级科学上册 第23课《保温物品大比拼(一)》(课件)(课件)共13张

我们可以采用组合法从材料、结构、携带中各选取一项,比如 选择厚纸板、棉花、双层、方形、胶带连接、提手携带,就可 以构思出一副样图。
呈现 为了使构思更加清晰,我们可以采用画草图的形 式将构思呈现出来
评价和改进
向同学们介绍自己的设计方案 (1)我们的设计意图是什么? (2)我们设计的保温物品其保温效果可能会怎样? (3)我们设计的保温物品成本是多少,能否做成?
思考:我们要完成该任务面临的主要问题是什么?
2 开展调研
保温箱具有保温性好,密封,保鲜,环保等特点, 保温箱的种类有:泡沫类、防水布类、塑料类、金 属类、木质类等
调研之前,先制定一个调研计划,调研计划的内容包 括研究主题、主要问题、调研方法和记录信息。
如第一小组调研计划如下: 调研主题:如何制作一个保温箱 主要问题:(1)制作保温箱的材料有哪些? (2)保温箱的结构是什么样的? (3)保温箱怎么携带? 调研方法:实地考察、查阅资料、浏览互联网等 记录信息:可以采用拍照、绘图和文字记录等方法。
通过调研,我们对保温物品的结构和特点有了一定的认 识,按照主要问题,收集到的信息,我们应该怎样设计 自己的保温物品呢?
3 进行设计
设计是研发保温物品的主要过程。设计将从分析、 构思、呈现和评价几个方面进行
分析
分析调研中获得的信息,根据任务要求,从形状、材 料、结构和颜色等方面进行设计分析,并通过概念图 的方式记录下来。
讨论: (1)如何选择材料? (选用热的不良导体;选用易加工的材料) (2)如何使结构有利于保温? (采用双层容器;缩小内胆外部面积) (3)如何便于携带? (尽量缩小体积;采用拆装式)
构思
为了解决设计分析中的三个关键性问题,采用头脑 风暴法,提出解决问题的多个设想,并把结果通过 概念图的形式记录下来。
新教科版五年级下册4-7 做个保温杯 一课一练(含答案解析)

7 做个保温杯一、填空题。
1.热的良导体吸热_________,散热也_________;热的不良导体吸热_________,散热也_________。
2.把同样多、相同温度的热水分别放在相同大小的陶瓷杯和不锈钢杯中,五分钟后,_________杯中的水温度更低。
3.我们可以选用热的_________作为保温的材料。
二、选择题。
(把正确答案的序号填在括号里)1.夏天,有些小卖部会在冰柜玻璃上盖一层棉被,是因为( )。
A.让冰柜里的温度更低B.棉被会使冰棍儿融化C.棉被可以减缓热量进入冰箱2.向容量差不多的不锈钢杯、陶瓷杯、塑料杯中,分别倒入同样多、温度相同的热水,摸一下外壁发现( )A.不锈钢杯先热B.陶瓷杯先热C.塑料杯先热3.下列物体中最适合做保温材料的是( )。
A.陶瓷B.泡沫塑料C.不锈钢4.保温杯做成双层、真空的原因是( )。
A.双层防护,类似穿两层衣服B.真空无法产生热对流和热传导C.不锈钢内胆比较保温三、判断题。
(正确的画“√”,错误的画“X”)1.很多保温杯都是用不锈钢制作的,因为不锈钢是热的良导体,可以保温。
( )2.保温杯只能保热不能保冷。
( )3.保温瓶的瓶口--般做得很小,是为了减慢热的传递。
( )4.太阳照在我们身上,我们之所以感觉很热,是因为空气是热的良导体。
( )四、综合题。
1.小明和同学探究不同情况下杯子里的热水变凉的情况,利用温度计测量水杯中的水温随时间变化的情况并记录,如下表所示。
保温效果记录表(1)该实验中,需要保持相同的条件有________、________等。
(2)保温效果最好的是________号,保温效果最差的是________号。
(3)如果要研究有没有盖对保温效果的影响,可以选择________号和________号;如果要研究毛巾和泡沫塑料对保温效果的影响,可以选择________号和________号。
2.阅读资料并解答问题。
石墨散热石墨散热是目前最常见的一种散热方式,如手机内部的散热依靠的就是石墨非常好的导热性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
保温训练(一)(时间:60分钟分值:100分)第Ⅰ卷(选择题共42分)一、选择题(本大题共7个小题,每小题6分,共42分,每小题给出的四个选项中,只有一项符合题目要求)1.下列各组离子在溶液中按括号内的物质的量之比混合,得到无味、酸性、澄清溶液的是()。
A.Fe3+、Na+、Cl-、S2-(1∶2∶3∶1)B.NH+4、Ba2+、OH-、Cl-(1∶1∶1∶2)C.K+、H+、I-、HCO-3(1∶2∶2∶1)D.Na+、Al3+、Cl-、OH-(4∶1∶3∶4)解析A中:2Fe3++S2-===2Fe2++S↓,产生浑浊,过量的S2-水解呈碱性;B中生成氨水呈碱性;C中H++HCO-3===H2O+CO2↑,H+过量呈酸性,D 中生成AlO-2水解呈碱性。
答案 C2.下列实验操作与预期目的或所得结论一致的是()。
该钠盐可能是硫酸钠或硫酸氢钠或亚硫酸钠或亚硫酸氢钠;选项C不正确,向裂化汽油中加入酸性高锰酸钾溶液,振荡,紫色褪去,说明该汽油中可能含有不饱和烃或苯的同系物;选项D,向含有少量的FeBr2的FeCl2溶液中,加入适量氯水,此时首先是Fe2+转变为Fe3+,并不能保证除去了Br-。
答案 B3.(2013·黔江区调研)金银花中能提取出有很高的药用价值的绿原酸(如图),下列说法不正确的是()。
A.绿原酸分子中有3个手性碳原子B.绿原酸能发生取代、加成、消去和氧化反应C.1 mol绿原酸与NaOH溶液反应,最多消耗4 mol NaOH D.绿原酸水解的一种产物能与FeCl3发生显色反应解析A项左侧连接羟基的3个碳和连接酯基的碳均为手性碳,错误。
C项1 mol绿原酸含有2 mol酚羟基和1 mol酯基1 mol羧基1 mol,能消耗4 molNaOH,正确;D项绿原酸水解产物如下图,右侧产物含有酚羟基,能与FeCl3显紫色,正确。
B项醇羟基、酯基、羧基和酚羟基邻对位均能发生取代,醇羟基、酚羟基和C—C键均易被氧化,C—C键和苯环均能与H2发生加成;醇羟基能发生消去反应,正确。
答案 A4.(2013·合肥高三质检)化学反应中的能量变化是由化学反应中旧化学键断裂时吸收的能量与新化学键形成时放出的能量不同引起的。
如下图为N2(g)和O2(g)反应生成NO(g)过程中的能量变化:下列说法正确的是()。
A.1 mol N2(g)和1 mol O2(g)反应放出的能量为180 kJB.1 mol N2(g)和1 mol O2(g)具有的总能量小于2 mol NO(g)具有的总能量C.通常情况下,N2(g)和O2(g)混合能直接生成NOD.NO是一种酸性氧化物,能与NaOH溶液反应生成盐和水解析根据图示可以看出,拆开1 mol N2和1 mol O2需要吸收的能量分别为946 kJ和498 kJ,生成2 mol NO(g)放出的能量=2 mol×632 kJ·mol-1,故反应吸收的热量为180 kJ;选项B,N2和O2的反应是吸热反应,反应物的总能量小于生成物的总能量;选项C,N2与O2在高压放电时才能化合生成NO;选项D,NO不是酸性氧化物,不能与NaOH溶液反应。
答案 B5.V、W、X、Y均是元素周期表中短周期元素,在周期表中的相对位置关系如表所示:Z素。
V的最简单氢化物为甲,W的最简单氢化物为乙,甲、乙混合时有白烟生成。
下列说法正确的是()。
A.原子半径:X>Y>V>WB.X、W的质子数之和与最外层电子数之和的比值为2∶1C.甲、乙混合时所生成的白烟为离子化合物,但其中含有共价键D.少量Z的单质与过量W的单质可化合生成ZW2解析根据V、W的最简单氢化物的性质,结合题图信息,可以推断甲为NH3、乙为HCl,V为N、W为Cl,从而可以确定Y为C,X为Al;根据Z 是人体血液中血红蛋白最重要的组成金属元素,知Z为Fe。
选项A,原子半径:X>W>Y>V,A项错。
选项B,Al、Cl的质子数之和为30,最外层电子数之和为10,二者之比为3∶1,B项错。
选项C,白烟为NH4Cl,是离子化合物,其中N、H原子之间的化学键是共价键,C项正确。
选项D,少量的Fe与过量的Cl2化合生成的是FeCl3,D项错。
答案 C6.(2013·重庆调研)某化学科研小组研究在其他条件不变时,改变某一条件对化学平衡的影响,得到如下变化规律(图中p表示压强,T表示温度,n表示物质的量)。
根据以上规律判断,下列结论正确的是()。
A.反应Ⅰ:ΔH>0,p2>p1B.反应Ⅱ:ΔH<0,T1<T2C.反应Ⅲ:ΔH>0,T2>T1或ΔH<0,T2<T1D.反应Ⅳ:ΔH<0,T2>T1解析反应Ⅰ中温度降低,A的平衡转化率升高,说明平衡向正反应方向移动,故正反应是放热反应,ΔH<0,压强增大平衡向正反应方向移动,A的转化率升高,故p2>p1,A错;反应Ⅱ中T1温度下反应先达平衡,说明T1>T2,温度降低,n(C)增大,说明平衡向正反应方向移动,故正反应是放热反应,ΔH<0,B错;反应Ⅳ中,若T2>T1,则温度高,A的平衡转化率增大,说明平衡向正反应方向移动,正反应是吸热反应,ΔH>0,D错。
答案 C7.下列说法正确的是()。
A.反应A(g)2B(g)ΔH,若正反应的活化能为E a kJ·mol-1,逆反应的活化能为E b kJ·mol-1,则ΔH=(E a-E b) kJ·mol-1B.标准状况下,向0.1 mol·L-1的氨水中加入少量氯化铵晶体,若混合溶液pH=7,则c(NH+4)=c(Cl-)C.足量的锌铜合金与100 mL pH=1稀硫酸反应,反应3 s时测得pH=2,假设反应前后溶液的体积保持不变,则3 s内产生氢气的平均速率是33.6 mL·s -1D.将浓度为0.1 mol·L-1 HF溶液加水不断稀释过程中,电离平衡常数K a(HF)保持不变,c(F-)c(H+)始终保持增大解析A项,正反应的活化能可理解为断裂旧化学键吸收的能量,而逆反应的活化能可理解为形成新化学键放出的能量,二者的差值即为反应的热效应,正确;B项,标准状况下,pH=7的溶液不为中性,错误;C项,没指明气体所处的状态为标准状况,错误;D项,当无限稀释时,c(H+)为常数,而c(F-)却不断减小,故c(F-)c(H+)减小,D项错误。
答案 A第Ⅱ卷(非选择题共58分)二、非选择题(本大题共4个小题,共58分)8.(14分)(2013·重庆高三月考)铝是地壳中含量最高的金属元素,铝及其化合物在生产生活中的应用日趋广泛。
(1)铝元素所在周期的各元素形成的简单离子中半径最小的是________。
(填离子符号),铝元素与氯元素所形成化合物中化学键类型为________,其晶体类型为________。
(2)明矾[KAl(SO4)2]是一种混凝剂,次氯酸钠是一种常用的消毒剂,二者的水溶液混合时产生白色沉淀,写出反应的离子方程式__________。
(3)氮化铝(AlN)和氮化硼结构相似,都是具有优良性能的新型材料,二者相比较,熔点较高的是________。
(4)工业上常用铝土矿(含SiO 2等杂质)生产铝。
从Na 2SiO 3和NaAlO 2混合溶液中制得Al(OH)3,需要从下列试剂中选择两种,选用的试剂组合最好的是________。
a .NaOH 溶液b .氨水c .CO 2d .盐酸(5)四氢铝锂(LiAlH 4)是有机合成中重要的还原剂,溶解于NaOH 溶液时产生一种无色气体,请完成下列离子方程式。
LiAlH 4+__________________===______________。
(6)某Mg-Al 合金是一种潜在的贮氢材料。
73.2 g 该合金恰好溶解于1.4 L 5.0 mol·L -1 HCl 溶液,则合金中Mg 和Al 的物质的量之比为________。
解析 (1)铝元素所在周期为第三周期,当简单离子核外电子数相同时,可根据“径大序小”规律可知各元素形成的简单离子半径大小顺序为S 2->Cl ->Na +>Mg 2+>Al 3+,所以离子半径最小的是Al 3+,铝与氯形成共价键,形成晶体为分子晶体。
(2)KAl(SO 4)2溶液中含有能水解的阳离子Al 3+,NaClO 溶液中含有能水解的阴离子ClO -,两者相遇能发生水解相互促进反应;(3)硼与铝位于同主族,硼的原子半径小于铝的原子半径,氮硼键键能大于氮铝键键能,因而熔点较高的为BN ;(4)向混合溶液中加入足量盐酸,生成H 2SiO 3、AlCl 3和NaCl ,过滤除去H 2SiO 3,然后向滤液中加入足量氨水,生成Al(OH)3和NH 4Cl ,过滤可得到Al(OH)3;(5)LiAlH 4中H 为-1价,具有还原性,H 2O 中H 为+1价,产生的无色气体为H 2,根据原子守恒,得失电子守恒和电荷守恒配平离子方程式;(6)设合金中Mg 的物质的量为x ,Al 的物质的量为y ,则⎩⎨⎧ 24 g·mol -1×x +27 g·mol -1×y =73.2 g 2x +3y =1.4 L ×5.0 mol·L -1=7.0 mol 解得⎩⎨⎧x =1.7 mol y =1.2 mol ,则合金中Mg 和Al 的物质的量之比为17∶12。
答案 (1)Al 3+ 共价键 分子晶体(2)Al 3++3ClO -+3H 2O===Al(OH)3↓+3HClO(3)氮化硼 (4)bd(5)2H2O Li++AlO-2+4H2↑(6)17∶129.(15分)(2013·重庆名校联考)某小组同学以碳棒为电极电解CuCl2溶液时,发现阴极碳棒上除了有红色物质析出外,还有少量白色物质析出。
为探究阴极碳棒上的产物,同学们阅读资料并设计了如下过程:Ⅰ.有关资料:铜的化合物颜色性质如下(1)提出假设①红色物质一定有铜,还可能有Cu2O;②白色物质为铜的化合物,其化学式可能为__________________________。
(2)实验验证取电解CuCl2溶液后的阴极碳棒,洗涤、干燥,连接下列装置进行实验,验证阴极产物,①实验前,检查装置A 气密性的方法是_____________________________。
②实验时,各装置从左至右的连接顺序为A →________→________→B →________→________。
(3)观察现象,得出结论实验结束后,碳棒上的白色物质变为红色,F 中物质不变色,D 中出现白色沉淀,根据现象①碳棒上的红色物质是否有Cu 2O________(填“是”或“否”),理由是_________________________;②装置________(填上图中装置编号)中________的现象说明提出假设②中的白色物质一定存在;③写出装置B 中发生反应的化学方程式__________________。
