第五章无失真信源编码

合集下载

第5章无失真信源编码定理

如果我们要对信源的N次扩展信源进行编码，也必须满足
qN rl ，两边取对数得： l log q
l
N log r
N 表示平均每个信源符号所需的码符号个数。
5.2 等长码
例：对英文电报得32个符号进行二元编码，根据上述关系：
l log 32 5 log 2
我们继续讨论上面得例子，我们已经知道英文的极限熵是1.4bit,远小于5bit，也就是说，5个二元码符号只携带 1.4bit的信息量，实际上，5个二元符号最多可以携带5bit 信息量。我们可以做到让平均码长缩短，提高信息传输率
0.8112
0.4715
若采用等长二元编码，要求编码效率 0.96 ，允许错误率
105 ，则： N 4.13107
也就是长度要达到4130万以上。
5.5 变长码
1、唯一可译变长码与及时码
信源符号出现概率码1
码2
码3
码4
s1
1/2
0
0
1
1
s2
1/4
11
10
10
01
s3
1/8
00
00
密码：是以提高通信系统的安全性为目的的编码。通常通过加密和解密来实现。从信息论的观点出发，“加密”可视为增熵的过程，“解密”可视为减熵的过程。
5.1 编码器
信源编码理论是信息论的一个重要分支，其理论基础是信源编码的两个定理。无失真信源编码定理：是离散信源/数字信号编码的基础；限失真信源编码定理：是连续信源/模拟信号编码的基础。
5.1 编码器
信源编码：以提高通信有效性为目的的编码。通常通过压缩信源的冗余度来实现。采用的一般方法是压缩每个信源符号的平均比特数或信源的码率。即同样多的信息用较少的码率传送，使单位时间内传送的平均信息量增加，从而提高通信的有效性。

信息论基础与应用-李梅-第五章无失真信源编码解析

s1 s1s1 s 2 s1s2 s3 s1s3 s16 s4 s4
二次扩展码码字 w j ( j 1, 2,...,16)
w1 w1w1 00 w 2 w1w2 001 w3 w1w3 0001 w16 w4 w4 111111
第五章：无失真信源编码
一、信源编码的相关概念
4. 关于编码的一些术语

编码器输出的码符号序列 wi称为码字；长度 li 称为码字长度，简称码长；全体码字的集合C称为码。若码符号集合为X={0,1}，则所得的码字都是二元序列，称为二元码。

将信源符号集中的每个信源符号
si 固定的映射成某
一个码字 wi ，这样的码称为分组码。
码字与信源符号一一对应
2) 不同的信源符号序列对应不同的码字序列
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续2）
例1：
1) 奇异码
s1 s2 s3 s4
0 11 00 Байду номын сангаас1
译码 11
s2 s4
奇异码一定不是唯一可译码
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续3）
译码 0 0 0 1 1 0 1 1
s1s2 s3 s4
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续5）
4)
唯一可译码 1 1 0 1 0 0 1 0 0 0 0
s1 s2
1 10
1 0
1
s2 / s3 ?
s3 100 s4 1000

为非即时码
第五章：无失真信源编码
一、信源编码的相关概念

《信息论与编码原理》孟放-第五八章无失真信源编码（编码定理编码算法）-2016-打印版

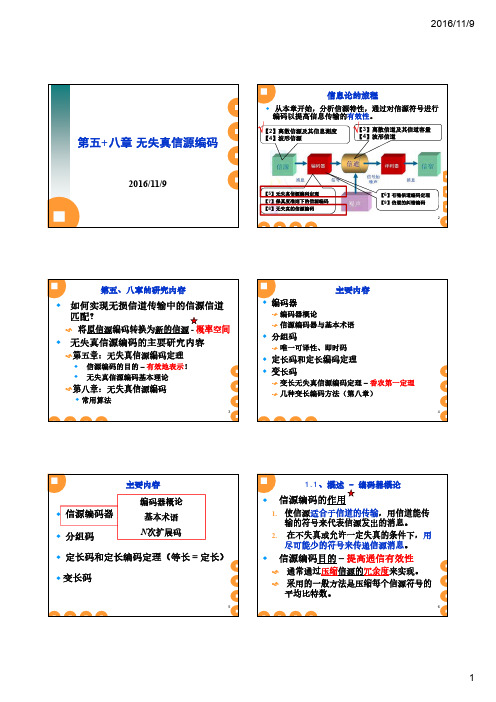
【5】无失真信源编码定理【7】保真度准则下的信源编码【8】无失真的信源编码【6】有噪信道编码定理【9】信道的纠错编码271.1、概述–编码器概论（续）✹信源编码理论是信息论的一个重要分支，其理论基础：无失真信源编码定理；限失真信源编码定理。

✹本章主要介绍无失真信源编码，它实质上是一种统计匹配编码，根据信源的不同概率分布而选用与之相匹配的码。

✹信源的统计剩余度主要决定于以下两个因素无记忆信源中，符号概率分布的非均匀性。

有记忆信源中，符号间的相关性及符号概率分布的非均匀性。

81.1、概述–信源编码器模型✹信源编码：将信源符号序列按一定的数学规律映射成码符号序列的过程。

信宿信道信源编码器译码器X ’XSS ’信源编码器模型{}qs s s S ,,,21 =12{,,,}r X x x x = 91.1、概述–信源编码器模型（续）✹将信源符号集中的符号（或者长为N 的信源符号序列）映射成由码符号组成的长度为的一一对应的码符号序列。

{}q W W W C ,,,21 =编码器},...,,{:21r x x x X {}q s s s S ,,,21 ={}ili i i i x x x W 21=i x i s il i W 101.2、概述–基本术语{}q W W W C ,,,21 =编码器},...,,{:21r x x x X {}q s s s S ,,,21 ={}il i i i i x x x W 21=信源符号集码符号集码字码元/ 码符号代码组C / 码Cr 元码定长码、变长码；奇异码、非奇异码平均码长()∑=ii i l s p L 11信源符号出现概率码字码1码2码3S 1p (S 1)W 10000S 2p (S 2)W 2010111S 3p (S 3)W 31000100S 4p (S 4)W 411111111.2、概述–基本术语–例题5.1()()()()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡43214321s p s p s p s p s s s s P S 例题：设有二元信道的信源编码器，其概率空间如右：定长码：变长码：非奇异码：奇异码：码1码2、码3码1、码2码3121.3、概述–N 次扩展码✹实际接收：N 次无记忆扩展信源--〉N 次扩展码{}q W W W C ,,,21 ={}qs s s S ,,,21 =is {}12,,,NN q S ααα= },,,{21N q N C W W W =12Nj j j js s s α= Nq j ,,2,1 =qj j j N ,,2,1,,,21 =iW Nj j j j W W W 21=W131.3、概述–N 次扩展码✹例题5.1 -续()16,,2,1 =j j W 00111==W W W 001212==W W W 二次扩展信源符号二次扩展码码字(1,2, (16)j j α=111s s α=212s s α=313s s α=1644s s α=0001313==W W W 1111114416==W W W 信源符号码字码2S 1W 10S 2W 201S 3W 3001S 4W 411114✹信源编码器✹分组码✹定长码和定长编码定理✹变长码主要内容定义唯一可译性即时码的判别与构造152.1、分组码✹分组码：将信源符号集中的每个信源符号映射成一个固定的码字。

第五章信源编码与编码定理

时分复用与时分多址接入技术tdmtdma频分复用与频分多址接入技术fdmfdma码分复用与码分多址接入技术cdmcdma波分复用wdm空分复用sdm统计复用statisticalmultiplex编码问题的一般概念与定义以上四类编码技术都有其专门的学科论述而信息论中仅定性定量地给出各种编码方法的理论极限和性能界限
log n = H0 ≥ H1 ≥ H2 ≥ ⋯ ≥ Hm+1 ≥ ⋯ ≥ H∞
§5. 2 定长编码及定长编码定理
上式表明对信源特性了解越多，则所需传输的信息量就越少。因此我们对Hm感兴趣，若把L个消息符号排成一个序列，不论其是否有记忆，只要统计出Hm的值，就对压缩序列的冗余有利。我们可以仅从符号间相互独立的序列中看到这一特点。从数学的大数定律中可以证明这样一个结论，如果对L个消息符号可构成无记忆序列，则按每一个序列的出现概率可将所有序列分成两大类：一类是高概率序列类高概率序列类；另一类是低概率序列类低概率序列类。高概率序列类低概率序列类所谓高概率序列是指属于此集合的元素，大体上将以几乎相同的概率出现。一般称为渐近等概率集合渐近等概率集合，记AL。而且L越大这种等渐近等概率集合等概率特性越明显。另一类集合中的序列，它的出现概率很低，几概率特性越明显 C 乎为零。所以我们把这一部分序列集合称为低概率集合低概率集合，记为 AL 低概率集合
§5. 1 编码问题的一般概念与定义
⒉ 限失真信源编码(Source coding with finite distortion) 此编码方式不能构成可逆编码，即编码后的码字序列经解码(反变换)处理后，所恢复的消息序列与发端的原消息序列存在有一定的失真。这种编码适合于连续信源模拟信号的编码，因为对连续信源的信号无论做何种处理，都无法避免信息的损失。比如语音信号，即使采用64Kbit/s 以上的速率量化，也会有相当的信息产生丢失，只不过有时人耳察觉不到而已。实际工程中失真大量存在，而且在允许失真的限度下进行编码处理对于大多数用户都是可以接受的。因此对于信息量无限大的连续变量来说，按照熵编码的原则压缩，信息丢失的程度应该是最小。

第5章信源编码第1讲无失真信源编码定长编码定理 2016

00 01 10 11
0 01 001 111
12/62
余映云南大学
5.1 编码的定义
• 采用分组编码方法，需要分组码具有某些属性，以保证在接收端能够迅速准确地将码译出。 • 下面讨论分组码的属性：
余映云南大学
13/62
5.1 编码的定义
• (1) 奇异码和非奇异码
– 若信源符号和码字是一一对应的，则该码为非奇异码；反之为奇异码。 – 例如表中码1是奇异码，其他是非奇异码。
信源符号出现概率码1 码2 码3 码4
A B C D
1/2 1/4 1/8 1/8
0 11 00 11
余映云南大学
0 10 00 01
1 10 100 1000
1 01 001 0001
18/62
5.1 编码的定义
• (3) 即时码和非即时码
– 唯一可译码又分为非即时码和即时码。 – 即时码是一种没有一个码字构成另一码字前缀的码。在译码时没有延迟，收到一个完整码字后就能立即译码。 – 如果收到一个完整码字后，不能立即译码，还需等下一个码字开始接收后才能判断是否可以译码，这样的码叫做非即时码。
信源符号
出现概率
码1
码2
码3
码4
a1 a2 a3 a4
1/2 1/4 1/8 1/8
0 11 00 11
余映云南大学
0 10 00 01
1 10 100 1000
1 01 001 0001
14/62
5.1 编码的定义
• (2) 唯一可译码和非唯一可译码
– 若任意有限长的码元序列，只能被唯一地分割成一个个的码字，则称为唯一可译码。 – 例如{0, 10, 11}是一种唯一可译码。 – 因为任意一串有限长码序列， – 如100111000

第五章信源编码LVRH1010

解：将信源通过一个二元信道传输，就必须把信源符号si变换成由0，1符号组成的码符号序列，即进行编码。可以用不同的二元码符号序列与信源符号一一对应，就得到不同的码。
信源符号 P(si) s1 s2 s3 s4 P(s1) P(s2) P(s3) P(s4) 码1 00 01 10 11 码2 0 01 001 111 5.1 编码的定义定长码变长码二次扩展信源符号二次扩展码字 S1=S1S1 s2=S1S2 …… s4=S4S4 00 001 …… 111111
l ≥ log r q = 5
分析：考虑到符号出现的概率以及符号之间的相关性后，实际平均每分析个英文电报符号所提供的信息量约1.4bit，远小于5bit，因此定长编码后，每个码字只载1.5bit信息，5个二进制符号最大能载5bit信息，因此，定长编码的信息传输效率低。解决方案: 解决方案 (1)对于不会出现的符号序列不予编码，这样不会造成误差； (2)对于概率非常小的信源符号序列不予编码，这样可能会造成一定误差，但当信源符号序列N足够大，误差概率非常小
第五章信源编码五
问题
• 对信源有两个重要问题 1. 信源输出的信息量的度量问题度量问题；度量问题 2. 如何更有效地有效地表示信源输出的问题输出的问题；有效地输出的问题
信源输出的符号序列，经过信源编码，变换成适合信道传输的符号序列，同时，在不失真或允许一定失真的条件下，用尽可能少的码符号来传递信源消息，提高信息传输的效率。
i =1 8
a7 0.05
a8 , 0.04
HL (X ) 2 .55 得K = = 2.83bit / 符号 90 % K 即每个符号用 2.83bit 进行定长二元编码，共有 2 2.83 = 7.11种可能性若取 L = 1，据 η = 根据 η = H( X ) = 0.9 ⇒ ε = 0 .28 H (X ) + ε

(信息论)第5章无失真信源编码

这就是说，每个英文电报符号至少要用5位二元符号进行编码才能得到唯一可译码。 12
定长编码定理
定长信源编码定理讨论了编码的有关参数对译码差错的限制关系
sq p s q
定理 5.3.1 设离散无记忆信源
S s1 P p s 1 p s 2 s2
的熵为H S ，其 N 次扩展信源为
S N 1 p 1 P
2 q p 2 p q

N N

现在用码符号集 X x1 , x2 ,, xr 对N次扩展信源 S N 进行长度为 l 的定长编码，对于 0, 0 ，只要满足
l H S N log r
则当 N 足够大时，译码错误概率为任意小，几乎可以实现无失真编码。反之，若满足
l H S 2 N log r
则不可能实现无失真编码。而当N足够大时，译码错误概 14 率近似等于1。

以上的定理5.3.1 和定理5.3.2实际上说明的是一个问题，虽然该定理是在平稳无记忆离散信源的条件下证明的，但它也同样适合于平稳有记忆信源，只要要 2 求有记忆信源的极限熵 H S 和极限方差存在即可。对于平稳有记忆信源，式(5.6)和式(5.7 ) 中 H S 应该为极限熵 H S 。
变长码(可变长度码)
2
奇异码：若码中所有码字都不相同，则称此码为非
奇异码。反之，称为奇异码。
同价码：每个码符号所占的传输时间都相同的码。定
长码中每个码字的传输时间相同。而变长码中的每个码字的传输时间不一定相等。
表 5.1
信源符号si
信源符号出现概率 si p

第五章编码定理 PPT课件

S2 0.18
S3 0.1
S4 S5 0.1 0.07
S6 0.06
S7 0.05
S8 0.04
可以求得H(S)=2.5524比特/符号及方差
（2 S） 7.82
若信可要源见设求符，译编号差码码序错差效列率错率长与N为（为度编2：1必码9SH00）H须效%-(26NS2(（(，2S满率7)S.)1S)8H即足要0）2H-(26S2：求(0(S7)S.2.)0并N)88（.72292不.10S8H0）.2高21H0可-(268S20.(79(S2时7).S解8.6))821，可2得001必解.620088.须得792.18N0把021可.820118解H0600.H82-(得26个S28(1(S)0S符)8) 0号.02.8208.792.821可
当 N→∞时，由④式得： N 2
r M
→1ex0p( N2N(无S2绝))对大应部的分码在字，A译中码的一序定列出已错
在N→∞时，由①式得 P(A ) →1 P( Ac ) 0
全部序列几乎都落入 A 集，且无对应的码字，故译
码错误概率趋于1。完成逆定理的证明。
第五章编码定理
第五章编码定理
3、变换编码特点：将原来的信号空间变换为另外一个空间。如Fourier（傅里叶）变换、Haar（哈尔）变换、
Walsh-Hadamard（阿达玛）变换（简称DWHT）、 Slant变换、Cosine变换、Sine变换、 Hotelling 变换等 4、识别编码特点：关联识别（与样本比较识别），逻辑识别（利用逻辑表达式判断识别）。
aN A
aN A
M exp[(H (S) )N ]
P(A ) P(aN ) M min P(aN )

第五章无失真信源编码13

H ( S ) LN H ( S ) 1 log r N log r N
N 其中，为 S中每个信源符号序列编码所对应的码字的平均 LN i 码长。
LN p( i )i , i为 i 所对应的码字的长度
i 1
qN
LN : 离散无记忆信源 S中每个信源符号 S i 所对应的平均码长 N
li r 1 i 1 q
(kraft不等式）
2.McMillan不等式
在满足kraft不等式的条件下，唯一可译码存在的充要条 q 件是：
li r 1 i 1
( McMillan 不等式）
三.唯一可译码判断准则
设S0为原始码字的集合。再构造一系列集合S1,S2,…Sn。构造S1,S2,… Sn的方法： 1、首先考察S0中所有的码字。若码字Wj是码字Wi的前缀，即Wi = WjA，则将后缀A列为S1中的元素，S1就是由所有具有这种性质的A构成的集合。 2、当n>1，则将S0于Sn-1比较，看是否S0中的码字是Sn-1的前缀，如果是，则取后缀为Sn中元素，且看Sn-1中码字是否为S0中码字的前缀，如果是，则取后缀为Sn中元素，如此构成集合Sn。
3.编码器的数学模型
信源发出的消息符号集
S S1 , S 2 ,..., S q

信源编码器
信道的基本符号集合
输出的码字集合C（代码组）
C W1 ,W2 ,...,Wq

X x1 , x2 ,..., xq

其中：Wi称为码字，如果码字由N个码元组成，则码长为N。
xi 称为码元,或码符号
第二节离散无记忆信源的定长编码
一.离散无记忆信源的唯一可译码存在条件

无失真信源编码

∑ 其中 z = (z1, z2,
所以，
zN )
，z
=
E( 1 N
N i=1
zi )
，σ
2
= Var(zi )
pr
⎧⎨x ⎩
:
log p(x) N
+
H(X)
≥
δ
⎫ ⎬
≤
⎭
σ2 Nδ 2
（5. 2. 10）
其中，自信息的方差
σ 2 = Var [log p ( x i )]
q
∑ = E⎡⎣log2 p(xi)⎤⎦ − H2(X) = pi log2 pi − H2(X) （5. 2. 11） i=1
（5. 2.6）
因为信源是无记忆的，所以 p(x) = p(x1 )
得到
N
log p(x) = ∑ log p(xi )
i =1
将（5. 2. 7）代入（5. 2. 6），得
p(xN ) ，
（5. 2. 7）
∑ 1
N
N
log p(xi ) + H ( X )
i =1
≥δ
（5. 2. 8）
14
令 zi = log p ( xi ) , 可得 E(zi ) = −H ( X ) , 所以
第五章无失真信源编码
中山大学信息科学与技术学院
主要内容
本章主要介绍无失真信源编码定理与一些重要的无失真信源编码方法
一、概述二、定长码三、变长码四、哈夫曼编码五、几种实用的信源编码方法
1
信源编码：将信源符号序列按一定的数学规律映射成由码符号组成的码序列的过程。
信源译码：根据码序列恢复信源序列的过程。无失真信源编码：即信源符号可以通过编码序列

信息论无失真信源编码

含义：无论码由多少个码字组成，总是能够正确译码，不存在二义性。
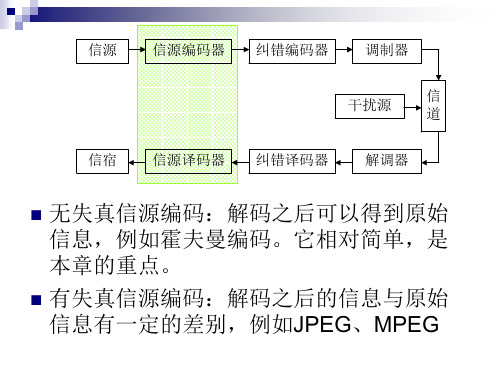
即时码
ABCD 1 10 100 1000
ABCD 1 01 001 0001
10110 010 →BACB
10110 0 01→ABAD
无需知道下一个码字的码符号，即可译码，这样的唯一可译码成为即时码。
命题5.2.1 一个唯一可译码成为即时码的充要条件是其中任何一个码字都不是其他码字的前缀。
信源信源编码器纠错编码器调制器
干扰源
信道
信宿信源译码器纠错译码器解调器
无失真信源编码：解码之后可以得到原始信息，例如霍夫曼编码。它相对简单，是本章的重点。
有失真信源编码：解码之后的信息与原始信息有一定的差别，例如JPEG、MPEG
5.1 编码器
S=(s1,s2,…,sq) 编码器 C=编码，编码器的映射必须是一一对应、可逆的。
码的分类
根据码长
固定长度码（定长码）：所有码字的长度相同。可变长度码（变长码）：码字长短不一。
码字是否相同
非奇异码：所有码字都不相同。奇异码：存在相同的码字。
5.2 分组码
s1,…,si-1 si si+1,…,sq
无关
无关
5.3 定长码
编码速率：R
l
log N
r
，其中l是码字长度，r是码符号的个
数，N代表N次扩展信源。
编码效率：η=H(S)/R，其中H(S)是扩展之前信源的熵。
例如：S={A,B,C}, 等概率出现，N=2, SN={AA,…,CC}，对 SN进行二元编码，则r=2，编码方式如下，则l=4。
AA AB AC BA BB BC CA CB CC

信息论第5章无失真信源编码

若码长l1, l2, …, lq 不满足Kraft不等式à 不是惟一可译码；反之， l1, l2, …, lq 满足Kraft不等式的码，不一定是惟一可译码。结论：不能用克拉夫特不等式，只能根据定义判断码C是否是惟一可译码。判别依据：非惟一可译变长码有限长的码符号序列能译成两种不同的码字序列。
66
香农第一定理的物理意义
无失真信源编码的实质：对离散信源进行变换变换后信源符号(信道的输入信源)尽可能为等概率分布新信源符号平均所含的信息量达到最大 à 使信道的信息传输率R达到信道容量C，实现信源与信道理想的统计匹配。无失真信源编码定理通常又称为无噪信道编码定理。表述为：若信道的信息传输率R不大于信道容量C，总能对信源的输出进行适当的编码，使得在无噪无损信道上能无差错地以最大信息传输率C传输信息，但要使信道的信息传输率R大于C 而无差错地传输信息则是不可能的。
62
63
64
65
定理4.8（香农信息论的主要定理之一）的结论：
要做到无失真的信源编码，编码每个信源符号平均所需最少的r元码元数为信源的熵Hr(S) 。即Hr(S) 是无失真信源压缩的极限值。若编码的平均码长小于信源的熵值Hr(S) ，则惟一可译码不存在，在译码或反变换时必然要带来失真或差错。通过对扩展信源进行变长编码，当N ∞时，平均码长 Hr(S) 。
4
几个术语：信源符号：信源输入S={s1,s2,…,sq} 码符号 (码元)：X={x1,x2,…,xr} 码字Wi：由xj (j=1,2,…,r)组成的长度为 li 的序列，Wi与si一一对应。码字长度 (码长)： Wi的长度li 码 (码书)：码字Wi的集合 C={W1,W2,…,Wq} 编码器：将信源符号si变换成Wi的设备

第5章2无失真和限失真信源编码

i 1 2
28
5.2.3
最佳变长编码
最佳变长编码凡是能载荷一定的信息量，且码字的平均长度最短，可分离的变长码的码字集合称为最佳变长码。
29
5.2.3
最佳变长编码
能获得最佳码的编码方法主要有：

香农（Shannon）

费诺（Fano）
哈夫曼（Huffman）等
30
5.2.3
最佳变长编码
2
2.83
7.11
Pe＝0.04 太大
16
5.2.1
定长编码定理
0.28
H(X ) ＝ 0.90, H(X )
2 8 i 1
( X ) D[ I ( xi )] pi (log pi ) 2 [ H ( X )]2 7.82(bit) 2
若要求译码错误概率 10－6
对于平均符号熵为 HL(X) 的离散平稳无记忆信源，必存在一种无失真编码方法，使平均信息率满足不等式
H L (X) K H L (X)
其中为任意小正数。
20
5.2.2
变长编码定理
用变长编码来达到相当高的编码效率，一般所要求的符号长度 L可以比定长编码小得多。编码效率的下界:
编码。
12
5.2.1
定义
定长编码定理

H L ( X) K
为编码效率，即信源的平均符号熵为H(X)，采用平均符号码长为来编码，所得的效 K 率。编码效率总是小于1，且最佳编码效率为
H L ( X) , 0 H L ( X)
13
5.2.1
定长编码定理
编码定理从理论上阐明了编码效率接近1的理想编码器的存在性，它使输出符号的信息率与信源熵之比接近于1，即

信息论：第5章无失真信源编码定理

19
(4)非奇异码若一组码中所有码字都不相同(即所有信源符号映射到不同的码符号序列)，则称为非奇异码。
si s j Wi W j
则称码C为非奇异码。
si , s j S Wi ,W j C
20
（5）奇异码
若一组码中有相同的码字，则为奇异码。
si s j Wi W j
30
即时码（异前缀码）一定是唯一可译码。因为，如果没有一个码字是其他码字的前缀，则在译码过程中，当收到一个完整码字的码符号序列时，无需考虑下一个符号，就能直接把它译成对应的码字或信源符号。
31
32
33
5.2
等长码
一般说来，若要实现无失真的编码，这不但要求信源符号与码字是一一对应的，而且要求码符号序列的反变换也是唯一的。也就是说，所编的码必须是唯一可译码。否则，所编的码不具有唯一可译码性，就会引起译码带来的错误与失真。
11
超过信宿的灵敏度和分辨力所传送的信息是毫无意义的，也是完全没有必要的。比如话声信源，界别过多的划分，人耳就很难分辨。图像信源亦是如此，人们看电影，当图片超过每秒25张以上时，人眼就能将离散的照片在人脑内反映成连续画面。
此时，就应该引入限定失真条件下的信源编码问题。
12
5.1
编码器
32272781179同样可以求得信源序列长度增加到3和4时进行变长编码所得的编码效率和信息传输率分别为如果对这一信源采用等长二元码编码要求编码效率达到96允许译码错误概率105则可以算出自信息方差为98580需要的信源序列长度为可以看出使用等长编码时为了使编码效率较高96需要对非常长的信源序列进行编码且总存在译码差错
此式表明，只有当 l长的 S s1 , , sq ，有 q 个符号，那么它的N次扩展信码符号序列数大于或等于N次源 S N 1 , , N 共有 q N 个符号。 q 扩展信源的符号数时，才可

第五章：无失真编码1

实际信源举例

对于数字型图像信号，可以采用马氏链模型
1 2 X x 2 N 1

1
2 N 1
1 1
而
为相邻像素之间的相关系数。实际信源举例2）语音信源可以近似用一个一维随机过程U(ω, t)表示。严格的讲，它是一个非平稳过程，但是对于短时段(5-50ms)可认为是平稳的，且某些是随机噪声（清辅音）而某些时段则呈现周期性特征（浊音），还有一些短时段是二者的混合。

无记忆信源

在某些简单的离散平稳信源情况下，信源先后发出的一个个符号彼此是统计独立的。也就是说信源输出的随机矢量 X=(X１X２…XＮ）中，各随机变量 Xi (i=1,2,…N) 之间是无依赖的、统计独立的，则 N 维随机矢量的联合概率分布满足 P(X)=P １（Ｘ１） P２（Ｘ２）…PＮ（ＸＮ）我们称由信源空间［X，P(x)］描述的信源X为离散无记忆信源。这信源在不同时刻发出的符号之间是无依赖的，彼此统计独立的。
可能取值。
离散序列信源

例：最简单 L=3 的三位 PCM 信源：这时 L=3, n=2, 即i={0,1}，则有：
U 3 U 000, U 001,, U 111 3 2 3 p(u ) p , p p , p 0 0 1 1

离散序列信源总结
离散无记忆信源离散序列信源离散有记忆信源
一般无记忆平稳无记忆平稳序列信源时齐马氏链信源
随机波形信源

更一般地说，实际信源输出的消息常常是时间和取值都是连续的。例如，语音 X(t)、热噪声信号n(t)、电视图像信号X(x0,y0,t)等时间连续函数。同时，在某一固定时间t０，它们的可能取值又是连续的和随机的。对于这种信源输出的消息，可用随机过程来描述。称这类信源为随机波形信源。分析一般随机波形信源比较复杂和困难。常见的随机波形信源输出的消息是时间上或频率上为有限的随机过程。根据取样定理，只要是时间上或频率上受限的随机过程，都可以把随机过程用一系列时间(或频率)域上离散的取样值来表示，而每个取样值都是连续型随机变量。这样，就可把随机过程转换成时间(或频率)上离散的随机序列来处理。甚至在某种条件下可以转换成随机变量间统计独立的随机序列。如果随机过程是平稳的随机过程，时间离散化后可转换成平稳的随机序列。这样，随机波形信源可以转换成连续平稳信源来处理。若再对每个取样值(连续型的)经过分层(量化)，就可将连续的取值转换成有限的或可数

第五章无失真编码2

无失真信源编码■无失真编码概述■变长信源编码■实用的无失真信源编码方法举例■定长信源编码有q个源字母5=(5,...\)总组合数：qN 入---- ►信源编码出有I•个码字母--------- ► C = (Cj... Cr)总码组合数：§5.1无失真编码器一1—-- --------离散、无失真、无记忆信源编码的一般模型:§5.1无失真编码器一2■问题；能否讲行无失真编码,怎样进行无失真编码S:不考虑信源统计特性：■应满足条件订无失真：有效：q77 >/ 7由qW：皿N logr •结论：①当q=r时JNN不有效。

②当1 =N时,r>q ,亦不满足有效性相互矛盾!q N <r•解决办法：引入信源统计特性。

§5.1无失真编码器一3■考察无失真条件：q—I JogqN logr需分别表示等概条件下的消息爛H(S) = logq 与码字//(C) = logr之比, "考虑信源的实际统计特性(非等概)，实际消息爛为：H(S)二-为口logp 代入无失真条件得：/〉H(S) '~N _ logr此时：即使q=r;只要logr >/f(S)就有可能实现IvN。

即无失真与有效性同时满足。

■具体实现时：定长与变长编码£ 5.2分组码（几个码类的概念）・非奇异码：■每一个码字仅对应信源中的一个信源符号（序列）O■编码是单义的。

编码II■反之为奇异码或非单义码。

编码I£ 5.2分组码（几个码类的概念）■唯一可译码■编码单义、译码单义■对任何一个有限长度的信源字母序列，如果编码得到的码字母序列不与其他任何信源字母序列所对应的码字母序列相同。

编码I编码u」j 5.2分组码（几个码类的概念）・即时码（前缀码）■是一类唯一可译码■在一个变长码中，没有任何一个码字是其他码字的前缀。

■译码时无需参考后续的码符号就能立即作出判断，进行无延时译码。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6. 唯一可译性(续2) 唯一可译性(续2
例1: 1) 奇异码
s1 0 s2 11 s3 00 s4 11
译码
s2
11
s4
奇异码一定不是唯一可译码
第五章: 第五章:无失真信源编码
6. 唯一可译性(续3) 唯一可译性(续3
2) 非奇异码
s1 0 s2 10 s3 00 s4 01
信源的统计剩余度主要决定于以下两个因素 : 1)无记忆信源中,符号概率分布的非均匀性; )无记忆信源中,符号概率分布的非均匀性; 2)有记忆信源中,符号间的相关性及符号概率分布 )有记忆信源中,符号间的相关性及符号概率分布的非均匀性. 的非均匀性. 怎样压缩信源的冗余度? 怎样压缩信源的冗余度? 1) 去除码符号间的相关性. 去除码符号间的相关性. 2) 使码符号等概分布. 使码符号等概分布.
{
q ≤r
N
l
}
X : {x1 , x2 ,..., xr }
l 当r=2 时, ≥ log q N 当N=1 时, l ≥ log q
第五章: 第五章:无失真信源编码
1. 唯一可译定长码存在的条件(续2) 唯一可译定长码存在的条件(续2
例2:英文字母表中,每一字母用定长编码转换成二进制表示,码字的最短长度是多少?
二次扩展码码字 w j ( j =1,2,...,16)
w1 = ww = 00 1 1 w2 = ww2 = 001 1 w3 = ww3 = 0001 1
s16 = s4s4
w16 = w4w4 =111111
第五章: 第五章:无失真信源编码
4. 关于编码的一些术语
编码器输出的码符号序列 wi称为码字码字;长度 li 称为码码字字长度,简称码长码长;全体码字的集合C称为码. 码长码若码符号集合为X={0,1},则所得的码字都是二元序列,称为二元码二元码. 二元码将信源符号集中的每个信源符号 si 固定的映射成某一个码字 wi ,这样的码称为分组码分组码. 分组码若一个码中所有码字的码长都相等,则称为定长码定长码; 定长码否则为变长码变长码. 变长码
三进制完全树
三进制满树
第五章: 第五章:无失真信源编码
8. 即时码的构造方法(续3) 即时码的构造方法(续3
用树图法可以方便地构造即时码.树中每个中间节点都伸出1至r个树枝,将所有的码字都安排在终端节点上就可以得到即时码. 每个中间节点都正好有r个分枝的树称为完完全树. 全树. 所有终端节点的阶数都相等的树为整树整树满树) (满树)
w j = wj1 wj2 wjN
s j = s j1 s j2 s jN
j =1,2,, qN
j1, j2 ,, jN =1,2,, q
第五章: 第五章:无失真信源编码
3. N次扩展码(续1) N次扩展码(续1
二次扩展信源符号 s j ( j =1,2,...,16)
s1 = s1s1 s2 = s1s2 s3 = s1s3
第五章: 第五章:无失真信源编码
2. 信源编码器模型
信源编码:将信源符号序列按一定的数学规律映射成码符号序列的过程. X = {x1, x2,, xr} S
信源
X 编码器
信道
Y 译码器
S'
信宿
S = {s1, s2 , sq} ,
图1 信源编码器模型
第五章: 第五章:无失真信源编码
2. 信源编码器模型(续1) 信源编码器模型(续1
信源符号si s1 s2 s3 s4 码1 0 11 00 11 码2 0 10 00 01 码3 0 10 110 111
第五章: 第五章:无失真信源编码
6. 唯一可译性(续1) 唯一可译性(续1
唯一可译码应当满足的条件 1) w (i =1,2,..., q) si (i =1,2,..., q) i 码字与信源符号一一对应 2) 不同的信源符号序列对应不同的码字序列
110 1110 1111
s5
s6
第五章: 第五章:无失真信源编码
8. 即时码的构造方法
用树图法可以方便地构造即时码.树中每个中间节点都伸出1至r个树枝,将所有的码字都安排在终端将所有的码字都安排在终端节点上就可以得到即时码. 节点上
第五章: 第五章:无失真信源编码
8. 即时码的构造方法(续1) 即时码的构造方法(续1
第五章: 第五章:无失真信源编码
5. 奇异性
若信源符号和码字是一一对应的,则该码为非奇异非奇异奇异码. 码.反之为奇异码奇异码
信源符号si s1 s2 s3 s4 码1 0 11 00 11 码2 0 10 00 01
第五章: 第五章:无失真信源编码
6. 唯一可译性
若任意一串有限长的码符号序列只能被唯一地译为对应的信源符号序列,则称此码为唯一可译码唯一可译码. 唯一可译码
五:实用的无失真信源编码方法
第五章: 第五章:无失真信源编码
1. 唯一可译定长码存在的条件
对于定长码,非奇异码一定是唯一可译码. 所谓非奇异码,即信源符号集中的每一个信源符号 si 与码中的某一个码字 wi一一对应. 设信源符号集中共有q个符号, = {s1, s2,, sq} , S 码符号集中共有 r种码元,X :{x1, x2 ,..., xr } , 定长码码长为 l ,则要满足非奇异性必然有
第五章: 第五章:无失真信源编码
6. 唯一可译性(续5) 唯一可译性(续5
4) 唯一可译码 1 1 0 1 0 0 1 0 0 0 0 1 0 1
s1 s2
1 10
s2 / s3 ?
s3 100 s4 1000
∴
为非即时码
第五章: 第五章:无失真信源编码
6. 唯一可译性(续6) 唯一可译性(续6
7. 即时码(续3) 即时码(续3
消息
A
000 010 011 100 101 111
B
010 011 000 011 101 100 0
C
1 00
D
00 01 10
E
F
00 01 100 101 110 111
s1
s2
s3
s4
10 1110 1111 1100 1101
0110 0111 0100 0101
s4 p ( s4 )
码2 0 10 110 111
信源符号si s1 s2 s3 s4
第五章: 第五章:无失真信源编码
3. N次扩展码 N次扩展码
S = s1, s2,, sq
{
}
si
C = {w , w2 ,, wq} 1
wi
S = s1, s2 ,, sqN
N
{
}
CN = {w1, w2 ,, wqN }
q≤r
l
该条件是必要条件,而不是充分条件. 该条件是必要条件,而不是充分条件.
第五章: 第五章:无失真信源编码
1. 唯一可译定长码存在的条件(续1) 唯一可译定长码存在的条件(续1
如果对N次扩展信源 sN 进行定长编码,要满足非奇异性,须满足条件
N 其中 S = s1 , s 2 , , s q N
无失真信源编码定理限失真信源编码定理
本章主要介绍无失真信源编码,它实质上是一种统本章主要介绍无失真信源编码,它实质上是一种统计匹配编码, 计匹配编码,根据信源符号的不同概率分布而选用与之相匹配的码. 之相匹配的码.
第五章: 第五章:无失真信源编码
1. 信源编码概述(续2) 信源编码概述(续2
第五章: 第五章:无失真信源编码
8. 即时码的构造方法(续4) 即时码的构造方法(续4
将码与码树建立"一一对应"关系: 将码与码树建立"一一对应"关系: 树根码字起点树枝数码的进制数节点码字或码字的一部分终止节点码字节数码长非满树变长码满树等长码
第五章: 第五章:无失真信源编码
译码 0 10 00 01 0 译码 01 00 00 10
s1s2s3s4s1
s4s3s3s2
第五章: 第五章:无失真信源编码
6. 唯一可译性(续4) 唯一可译性(续4
3) 等长码
+
非奇异码
唯一可译码
s1 00 s2 01 s3 10 s4 11
译码 0 0 0 1 1 0 1 1
s1s2s3s4
第五章:无失真信源编码
一:信源编码的相关概念二:定长码及定长信源编码定理
三:变长码及变长信源编码定理四:变长码的编码方法
五:实用的无失真信源编码方法
第五章: 第五章:无失真信源编码
1. 信源编码概述
信源编码的作用: 信源编码的作用:
使信源适合于信道的传输, 使信源适合于信道的传输,用信道能传输的符号来代表信源发出的消息; 表信源发出的消息; 在不失真或允许一定失真的条件下, 在不失真或允许一定失真的条件下,用尽可能少的符号来传递信源消息,提高信息传输率. 号来传递信源消息,提高信息传输率.
5) 唯一可译码
s1 s2
1 01
1 0 1 0 0 1 0 0 0 1 0 1
→
即时
s3 001 s4 0001
s2
∴
为即时码
任何一个码字不是其它码字的延长或前缀
第五章: 第五章:无失真信源编码
7. 即时码
若某个唯一可译码在接收到一个完整的码字时无需参考后续的码符号就能立即译码,则称此码为即时码即时码. 即时码问题: 1) 判断下面的码是否即时码? 0 10 110 111 2) 等长码是否即时码?
∑P(s ) =1
i=1 i
4
而其依赖关系为:
P(s2 / s1) = P(s1 / s2 ) = P(s4 / s3 ) = P(s3 / s4 ) =1, 其余P(s j / si ) = 0

第五章 无失真信源编码

第5章无失真信源编码定理

信息论基础与应用-李梅-第五章 无失真信源编码解析

《信息论与编码原理》孟放-第五八章无失真信源编码（编码定理编码算法）-2016-打印版

第五章 信源编码与编码定理

第5章 信源编码 第1讲 无失真信源编码 定长编码定理 2016

第五章 信源编码LVRH1010