改进型CIC抽取滤波器设计与FPGA实现
一种性能良好的高效CIC抽取滤波器的设计

一
种 性 能 良好 的 高 效 C C抽 取 滤 波 器 的 设 计 I
叶 和 忠 ,赵 利 ,彭 小 卫 ,周 胜 源
( 林 电 子 科技 大 学 信 息 与 通 信 学 院 , 西 桂 林 桂 广 510) 4 0 4
摘 要 : 对 传 统 C C 抽 取 滤 波 器 性 能 和 结 构 存 在 的 问 题 , 用 一 个 I O 针 I 利 S P滤 波 器 和 余 弦 滤 波 器 对 C C抽 取 滤 波 器 I
Y e H e hong,Zha ,Pe a z o Li ng Xiow e ,Zho i u She gy n n ua
( c o l f n o ma in a d C m m u ia in E g n e ig,Gul nv ri f e t nc T c n lg ,Gu l 4 0 4, S ho fr t n o o I o nc t n ie rn o in U ie st o c r i e h oo y i y El o i n 5 1 0 Chn ) i ia
表 明 : 设 计 方 法使 得 C C 抽 取 滤 波 器 性 能 得 到 改 善 , 现 结 构 高 效 , 实 际 工 程 中 有 很 大 的应 用 价 值 。 该 I 实 在
CIC滤波器的原理及FPGA实现

com ber: p rocess (clk_ com b) b eg in if (clk_ com b’even t and clk_ com b= ’1’) then
x ≤x_ in; - - x_ in 是 8 位输入 i0 ≤i0+ conv_ in teger (sx tx) ; i1 ≤i1+ i0; - - 累加 i2 ≤i2+ i1; i3 ≤i3+ i2; - - i3 为第四级积分器输出
……… End if; End p rocess in tegra to r;
大。鉴于此, 当前的专用DDC 芯片中, 都采用了一种 高 效的滤波器—— C IC 滤波器 (C IC 滤 波 器 是 由 Hogenauer E. B. 于 1981 年提出的, 因此又被称为 Hogenauer 滤波器) 作为第一级滤波器, 实现抽取、 低 通滤波; 第二级则采用一般的 F IR 或者 F IR 实现 的特殊滤波器 (如半带滤波器) , 此时它们工作在较 低的频率下, 且滤波器的参数得到了优化, 因此更容 易以较低的阶数实现, 节省资源, 降低功耗。 本文在研究C IC 滤波器基本原理的基础上, 对 其进行了 FPGA 仿真、综合, 并最终应用在工程中, 达到了设计要求。
resou rces and can p lay w ell in h igher frequency. B a sed on the theo ry of C IC filter, I have
FPGA的CIC滤波器的设计

FPGA的CIC滤波器的设计1.原理概述CIC滤波器由差分器、积分器和组合器三部分组成,可有效实现信号的重采样和滤波功能。
其基本原理是将输入信号通过差分器进行差分运算,然后经过积分器进行累积运算,最后通过组合器实现滤波和重采样。
CIC滤波器的特点是具有高的通带增益和截止频率,且不需要乘法器和存储器,适合在FPGA中实现。
2.设计步骤(1)确定CIC滤波器的设计参数,包括增益因子、积分阶数、截止频率等。
(2)根据设计参数计算滤波器的结构参数,包括输入和输出数据宽度、积分器的阶数和阶间差值等。
(3)根据计算结果,设计CIC滤波器的硬件结构,包括差分器、积分器和组合器的实现方法。
(4) 使用HDL语言(如Verilog或VHDL)编写FPGA的CIC滤波器的代码,同时进行功能仿真和波形仿真。
(5)在FPGA开发板上进行综合、布局布线和验证,实现CIC滤波器的硬件设计。
3.设计关键技术(1)差分器设计:差分器实现差分运算,可以简单采用异或门或加减器实现。
需要注意输入信号的幅度范围和差分器的输出范围。
(2)积分器设计:积分器实现累积运算,需要考虑积分阶数、数据宽度和溢出等问题。
可以采用寄存器与加法器的串行或并行结构实现。
(3)组合器设计:组合器实现滤波和重采样功能,需要根据设计参数确定组合器的截止频率和增益系数。
可以采用多级组合器结构实现。
(4)输入输出接口设计:FPGA的CIC滤波器需要与外部系统进行数据交换,因此需要设计合适的输入输出接口,包括数据接口、时钟接口和控制接口等。
4.实现优化技术(1)折叠积分器:为了减少资源占用和延迟,可以采用折叠积分器结构,将多级积分器合并为一个积分器实现。
(2)级联结构:为了增加滤波器的阶数和降低截止频率,可以采用级联结构,将多个CIC滤波器级联实现。
(3)变系数设计:为了实现可调节的滤波参数,可以设计可变系数的CIC滤波器,在运行时动态调整增益因子和积分阶数。
综上所述,FPGA的CIC滤波器设计是一项复杂的数字信号处理任务,需要深入理解CIC滤波器的原理和设计方法,结合FPGA的硬件实现技术进行设计和优化。
(完整版)CIC滤波器的原理与设计
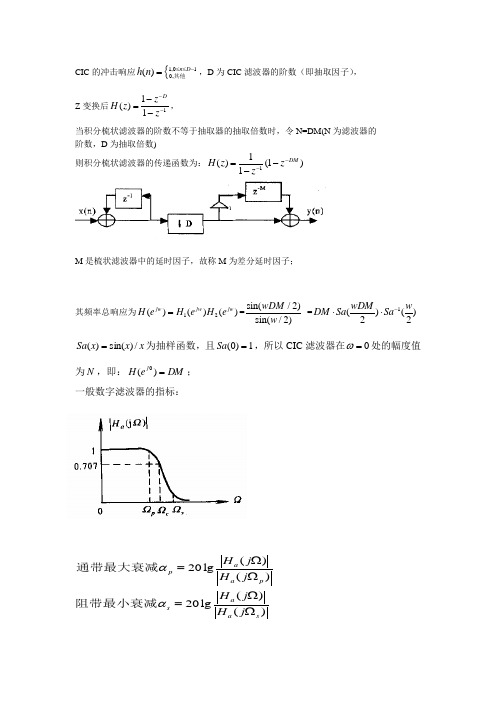
CIC 的冲击响应{1,010,()n D h n ≤≤-=其他,D 为CIC 滤波器的阶数(即抽取因子),Z 变换后11()1Dz H z z ---=-,当积分梳状滤波器的阶数不等于抽取器的抽取倍数时,令N=DM(N 为滤波器的 阶数,D 为抽取倍数)则积分梳状滤波器的传递函数为:)1(11)(1DM z zz H ----=M 是梳状滤波器中的延时因子,故称M 为差分延时因子;其频率总响应为12()()()jw jw jwH e H e H e ==sin(/2)sin(/2)wDM w =1()()22wDM wDM Sa Sa -⋅⋅x x x Sa /)sin()(=为抽样函数,且1)0(=Sa ,所以CIC 滤波器在0=ω处的幅度值为N ,即:DM e H j =)(0; 一般数字滤波器的指标:()20lg()()20lg ()a pa p a s a s H j H j H j H j ααΩ=ΩΩ=Ω通带最大衰减阻带最小衰减即:CIC 幅频特性响应曲线图由其频率响应函数可以看出其主瓣电平最大为D ,旁瓣电平为21.51()sin(3/2)/sin(3/2)sin(3/2)j DMH e DM DM ωπωπππ=⋅==,旁瓣与主瓣的差值 (用dB 数表示)为: dB A DM s 46.1323lg 20lg201===πα 可计算出旁瓣与主瓣的差值约为13.46,意味着阻带衰减很差,单级级联时旁瓣电平很大,为降低旁瓣电平,增加阻带衰减采用级联的方式,N 级频率响应为:)2()2()()2/sin()2/sin()(ωωωωωQ Q Q Qj Q Sa DM Sa DM DM e H -⋅⋅=⎥⎦⎤⎢⎣⎡=, 可得到N 级CIC 的旁瓣抑制 dB Q Q A DM Q Qs )46.13(23lg 20)lg(201⨯=⋅==πα 分析一下发现在Q 级联时多出了Q DM 这个处理增益,因此分析一下尽量减少带内容差(通带衰减),即,在通带内,幅度应尽量平缓;下面就它的幅平响应曲线来分析:00()20lg ()()20lg()ps j a p jw a j a s jw a H e H eH e H e αα==1、设在红线w1处抽取的信号带宽很窄,为无混叠信号的带宽,能很好的对窄带信号进行滤波,去除掉高频信号噪声;且在绿线w2=2pi/DM-w1处衰减值足够大,则在其信号带宽内,红线到绿线,信号给CIC 滤波器带来的混叠就可以忽略,计算此时阻带衰减:)2/sin()2/sin(lg 20()(lg 2022012w DM w DM e H e H A jw j ==·引入带宽比例因子b=B/(fs/DM ), B 为抽取信号的带宽,D 为抽取因子,M 为延时因子;fs 为输入端采样率,则w1=b*2pi/DM ;带入可化简得:b A lg 201-≈; (假设b=0.01;即fs=100MHz ,D=20,信号带宽为50khz,此时衰减为40dB);可见单级的CIC 滤波器的无混叠信号带宽内的阻带衰减能达到40dB;;并不怎么大,适用于较粗略的滤波,适合放在第一级抽取;如果采用级联的方式可以加大无混叠信号带宽;但是满足的通带不够窄;2、在红线w1处幅度不能下降太多,通带内幅值容差不能太大,否则会引起高频失真;设该带内容差为s δ,则,)()(lg 2010jw j s e H e H =δ将w1带入可简化得)sin(lg 20b bs ππδ≈,当N 级时,其带内容差也会增大;由上面分析可知,阻带衰减和带内容差,只与带宽比例因子b 有关,Df Bb s /=,分析可知,在信号带宽一定的前提下,应尽可能采用小的抽取因子,或增大输入采样率;故一般把它放在抽取系统的第一级,所以在配置CIC 时,信号带宽,采样率,抽取因子,综合考虑,下面是阻带衰减和通带衰减的一个表:表1:大抽取因子下的通带衰减由CIC频幅响应图可以发现,幅频特性的零点位于1/M处(M取值为整数),这说明差分因子M决定了零点的位置;抽取因子D狭定了抽取后信号的采样频率,它同差分延时因子M一起还决定了主瓣和旁瓣的宽度;级数Q可以用来控制阻带衰减,Q越大阻带衰减越大,通带内的混叠就越小,但Q越大,通带内主瓣衰减也越大,所以Q不可太大,不宜超过5级。
Hogenauer CIC滤波器算法研究及FPGA设计实现

果 4 ( l o ∞ 5 ( O 1 一 Oo ) 一 一 11)
㈨
㈨
∞
+
则 在 计 算 6 4 (l 0 (L O (0 0 一 2山 现 + 一 O 1 )+ O O )一 11 )=
从 上 述 计 算 过 程 , 以 看 出 : 的 运 算 都 是 基 丁 2 可 所有 进 Ⅲ 行 运 算 的 , 果 最 终 的 结 果 在 有 效 范 围 内 , 对 于 中间 过 程 所 如 则
黻 l 号
为
为 了 快 速 准 确 地 设 计 C C滤 波 器 , 常 首二 进 制 补 码 形 式 , 上述 各 数 可 以 表示 为 : ) 故
6 ( l o 一 O1)
仿 真 , 后 利 用 Vei gHD 然 ro L进 行 硬 件 描 述 。在算 法仿 真 中 , l Malb中所 提 供 的 数 据 类 型 与 实 际 数 字 系 统 所 采 用 的 数 制 t a
定 的 参 考 价值 。
关键 词 : C; ta Ve i g; 进 制 补码 ; 据 抽 取 CI Ma lb; rl 二 o 数
中图 分 类 号 : N7 7T 1 2 T 1 . ; N9 17 3
文献标识码 : A
高分解 速率滤波 器的一种非 常有 效的结构 就是 由
H g n u r引 入 的 “ 联 积 分 器 梳 状 ” c sa e itg ao o ea e 级 f cd nertr a
。
,
如下 形 式 :
一
2 1 单 级 C C 滤 波 器 . I
∑ x“ 2
X 一
一
( ) x o
() 1
c 滤 器 两个 本的 节 I 波 是由 基 环 组成, 图1 示, 别 c 如 所 分
新型CIC滤波器的优化设计及其仿真

( 解放军信息工程 大学通信工程系 , 河南 郑州 40 0 ) 50 2 摘要 : I CC滤波器 的优点在于非常容易用硬件实现 , 然而它具有 一对矛盾一阻带衰减和 通带波动。文中针对 由这对 矛盾引 起 的通频带过窄的不足 , 提出了一种适用于 D B—T系统接收机的新 型 CC滤波器的设计方法 。该方法 结合典型的补偿滤 V I 波器 , 设计了一种全局可调的多级 CC滤波器 , I 统一优化滤波器 中的参 数, 抽象出了此问题的数学模型 , 并采用 网格搜 索法 进行求解。最后用 Maa6 5和 Q a u 15 1 tb. l un sI . 平台进行了联合仿真 , 并和其它设计方法 的仿真结果进行 了对比。仿 真结 果 表明新型 cc滤波器在满足阻带衰减指标 的要求下 , I 最小化 了通带波动 , 达到了更优异的性能 , 同时也证明了硬件电路的正
CIC抽取滤波器的高效改进算法研究

H( :[ ( =[ ) n (
一
) ]
Mi
() 2
壶 (
其 中 M。 。 =1
) ( 3 )
收 稿 日期 :0 6一t 20 O一1 ; 回 日期 :0 7— 4—1 6修 20 0 2
作者简介 : 余
磊 (9 2一) 男 , 18 , 河南信 阳人 , 信息工程大学硕 士研究 生, 主要研究方 向为软件无线电。
一
种高效 的算 法结构 , 改善 了通 带损耗 , 增大 了阻带 衰减 , C C滤 波器 的 实 际应 用和 深 入研 对 I
究 有着现 实 意义 。
关键 词 : I C C滤 波器 ; 弦预 滤波器 ; 余 多相 滤 波 中 图分 类号 :N 1 T 73 文 献标识 码 : A 文章编 号 :6 1— 6 3 2 0 ) 2— 2 0— 3 17 0 7 ( 0 7 0 0 1 0
r s o s a e b ane y u i g a c s a d c snep ei ra h le h r e i p r a h o e p n e h sbe n o ti d b sn a c de o i r fhe nd t ef trs a p nnga p o c f i
维普资讯
第 8卷 第 2期
20 0 7年 6月
信 息 工 程 fr t n E g n e i g U i e s y o r a o n o mai n i e r n v r i o n t
V0 . . 1 8 No 2
维普资讯
A b t a t T s p pe r p s d a fiin tucu e f rt e r aiai n o o c main fle . s r c : hi a rp o o e n efce t sr t r o h e lz to fa c mb de i t tr o i Usn oy h s e o o iin,t e f tr c n b p r td a o rr t . Th mp o e a nt de i g a p l p a e d c mp st o h le a e o e a e tlwe ae i ei rv d m g i u
改进型CIC抽取滤波器设计与FPGA实现

改进型CIC抽取滤波器设计与FPGA实现作者:张杰戴宇杰张小兴吕英杰来源:《现代电子技术》2009年第10期摘要:为了改善级联积分梳状(CIC)滤波器通带不平和阻带衰减不足的缺点,给出一种改进型CIC滤波器。
该滤波器在采用COSINE滤波器提高阻带特性的基础上,级联了一个SINE滤波器,补偿了其通带衰减。
硬件实现时,采用新的多相分解方法结合非递归结构,不仅大大减少了存储单元数量,还使电路结构更加规则。
经仿真和FPGA验证,改进型CIC滤波器使用较少硬件,实现了阻带衰减100.3 dB,通带衰减仅为0.000 1 dB。
关键词:CIC抽取滤波器;COSINE滤波器;SINE滤波器;设计优化;FPGA中图分类号:TP368.1文献标识码:A文章编号:1004-373X(2009)10-022-03Design of Modified CIC Decimation Filter and FPGA ImplementationZHANG Jie,DAI Yujie,ZHANG Xiaoxing,LV Yingjie(Institute of Microelectronics,Nankai University,Tianjin,300071,China)Abstract:A modified Cascaded Integral Comb(CIC) filter which improves the passband and stopband characteristics respect to the CIC filter is presented in this paper.A cascaded SINE filter is introduced after the COSINE one which improves the stopband characteristics to compensate the passband drop.Applying the new poly-phase decomposition as well as no-recursive structure,this filter not only greatly decreases the amount of memory,but also makes the circuit more regular.Simulation and FPGA verification result indicates that the stopband attenuation is up to 100.3 dB and the passband attenuation is only 0.000 1 dB.Keywords:CIC decimation filter;COSINE filter;SINE filter;optimization design;FPGA抽取滤波器是Σ-Δ模/数转换器中的重要组成部分,积分梳状滤波器经常作为第一级滤波器,用以实现抽取和低通滤波[1]。
基于FPGA的CIC抽取滤波器设计与实现

( ) 4
C I C 抽取滤波器的幅频特性如图 2 所示 。 / 其中 [ 为其 主 瓣, 其 它 的 区 间 为 旁 瓣。由 图 0. 2 DM ] π 可见 , 随着频率的增 大 , 旁 瓣 电 平 不 断 减 小, 但旁瓣电平相 对主瓣电平较大 , 阻带衰减较差 。 为降低 旁 瓣 电 平 , 可以采 用多级 C I C 滤波器级联的办法来实现 。
总第 2 6 7期 2 0 1 2 年第 1 期
计算机与数字工程 C o m u t e r &D i i t a l E n i n e e r i n p g g g
V o l . 4 0N o . 1 1 3 7
基于 F P G A的C I C 抽取滤波器设计与实现
雷能芳
( ) 渭南师范学院物理与电气工程学院 渭南 7 1 4 0 0 0
[ 2] / 可以由 F P GA C P L D 开发工具 Q u a r t u s Ⅱ来完成 。采用 比直接采用 该方法进行数字信 号 处 理 系 统 的 F P GA 设 计 ,
图 5 测试电路
在Q 对测试电路进行编译 , 下载到 c u a r t u s Ⅱ 环境中 , - y 就可以对硬件进行测 c l o n e系列 E P 1 C 1 2 Q 2 4 0 C 8 器 件 后, / 经D 试 。 调制器 的 输 出 信 号 为 数 字 信 号 , A 转换后可以通 过示波器进行测试 , 也可以直接采用 Q u a r t u s Ⅱ 软件中的 嵌
图 3 3 级 C I C 抽取滤波器模型图
滤波器常结合半带滤波器来完成采样速 率 的 抽 取 功 能 。 滤 波时只做加法运算 , 大大简化了计算量 , 从而降低后续电路 的处理速度 。 本文的创新之 处 在 于 : 应用现代 D S P技术设计 C I C抽 取滤波 器 , 图 形 化 界 面 使 设 计 简 单 易 行, 避免了繁琐的 设计者甚至 不 需 要 了 解 F VHD L 语言编程 ; P GA 和 硬 件 描 述语言 , 真正实现了电子系统设计的黑盒 子 化 、 积木化和简
基于FPGA的CIC抽取滤波器设计与实现

计算机与数字工程
Co ue mp tr& Dii l gn eig gt a En ie r n
Vo . 0 No 1 14 .
1 37
2 1 年第 1 02 期
基 于 F GA 的 C C抽 取 滤 波器 设 计 与 实现 P I
雷能 芳
( 渭南师范学 院物理与电气工程学 院 渭南 740) 1 0 0
v rf db o t r i uain a dh r wa ets. eii y s fwa esm lt n a d r et e o
Ke ors CI f tr e i to yW d C i e ,d cma in,FPGA,DS i e l P Bul r d Cls a s Numbe TN7 3 r 1
1 引 言
在数字信号处理 中, 随着采样速率 的提高 , 采样 后的数 据流 的速率变得很高 , 会导致后续 的信号 处理速度跟不 上 , 因此有必要对 A/ D后 的数 据流进 行 降速处理 。实现采 样 速率变换 ( 抽取 和内插 ) 的关键问题是如何实现抽取前 和 内 个 Nhomakorabea成的 。
图 1 单 级 C C抽 取 滤 波器 框 图 I
单级 C C抽取 滤波 器积 分 部分 是单 极 点 的 I I I R滤波 器, 其传输 函数为 :
H () F I - z
() 1 z = 一
( 1 )
() 2
梳状部分是一个对称 的 FR滤波器 , I 其传 输函数 为 :
Abs rc Fil o rm ma eGa eAra ( GA )d vcsi d l s di h il fdgtlsg a r c sig,bu ti c mpiae O ta t edPr g a bl t r y FP e ie swieyu e nt ef do iia in lp o e sn e ti s o lct dt d sg sn e in u ig VH DL rVe i gH DL.Fo hemu t r t i a r c sigt c n o y i o t r a o,t sp p rp p e c e o m— o rl o rt li a esgn lp o e sn e h olg ns fwaerdi hi a e orosdas h mef ri — pe e a ino sa eI tg a o m bd cma in fle a e n FP lm ntto fCa c d n e r t rCo e i to i rb s do GA n t a d DSP Bule .Th oret e sa dfa iii ft ed sg S i r d ec rcn s n e sblt o h e in i y
一种改进的cic滤波器设计方法

体验到 了快乐之后 , 还利用周末的时间 . 主动从 自我封闭的家庭 、 自行 组织 起 了健 身娱 乐 活 动 呢 ! 要. 回 去准 备 材 料 。 由于 想 制 作 的 动物 不 同 , 它 们 的 牙齿 不 同 , 制 幼儿 园 两 点一 线 中走 出 来 , ● 解 放 空 间 作 的方 法 不 同 .所 以需 要 的材 料 也 不 同 .孩 子们 准 备 得 格 外 带 劲 . 整个活动从材料的准备到设计再到制作 . 没 有 成 人 的 帮 助 或 案例 : 姚 老 师 的一 节 社 会 活 动 《 到小兔 家作客》 通 过 层 层 选 十扰, 存 制作时他们是 那么的认真 : 多 了一 份 耐 心 、 多 了一 份 自 拔. 获 得 了市 级 一 等 奖 的 喜 人 成 绩 , 消 息 一 经 传 出来 , 大 家 都 不 信 , 因此 所 作 作 品 真是 创 意 多 多 : 发箍成 了小兔头上 的饰品 ; 白 免 为 她 高 兴 :已 到 中 年 的 她 根 本 就 不 想 也 不 敢 参 加 如 此 竞 争 激
儿. 让 他们 先欣 赏 画册 上 的动 物 来 刷 牙 画 面 . 大 概 了解 一下 动 物 周 一 到 周 五 分 别 开展 不 同 的活 动 : 或跳舞 、 或踢 毽子 、 或 打 羽 毛 牙齿 的 不 同做 法 ( 注意 : 欣 赏 的 时 间不 要 太 长 , 以免 束 缚 幼 儿 的 球 、 或 跑 步 … … 时 间哪 怕 只有 - s j , 会儿 . 机 会 哪 怕 只 有 一点 点 , 但 经小年轻带动了, 她们 便 有 了不 竭 的热 情 和 干劲 , 为此 , 她 们 在 思维 1 然后告诉 他们 . 我 们 明天 也 要 做 手 工 “ 动物来 刷牙” , 好 朋 友 讨 论讨 论 , 然 后 根据 自己 的需
FPGA的CIC滤波器的设计

FPGA的CIC滤波器的设计CIC滤波器是一种高效的滤波结构,主要用于在数字信号处理中降低采样率。
它的结构包括一个或多个级联的积分器和组合器。
积分器用于对输入信号进行累加,组合器用于将积分结果进行减法运算并输出。
设计FPGA上的CIC滤波器需要以下步骤:1.确定滤波器的规格:首先,你需要确定滤波器的采样率和通带、阻带的频率要求。
这将决定你需要设计多少级的CIC滤波器以及每级的系数。
2.确定滤波器的结构:根据滤波器的规格,你可以确定CIC滤波器的级数和输出信号的截止频率。
CIC滤波器的级数决定了降采样的比率,输出信号的截止频率将决定滤波器的性能。
3.设计CIC滤波器的系数:CIC滤波器的系数由积分器和组合器的阶数决定。
你可以使用公式来计算系数,也可以通过在FPGA上进行仿真来获得最佳的系数。
4. 实现CIC滤波器:一旦你确定了CIC滤波器的系数,你可以开始在FPGA上实现该滤波器。
你可以选择使用HDL (Hardware Description Language) 编写滤波器的代码,也可以使用可视化编程工具来设计滤波器。
5.测试和优化滤波器性能:一旦滤波器被实现,你可以使用测试向量对其进行性能测试。
你可以通过观察输出信号的频谱特性来评估滤波器的效果,并根据需要进行优化。
设计FPGA上的CIC滤波器需要一些基本的信号处理和FPGA编程知识。
你需要熟悉CIC滤波器的原理和性能特点,以及FPGA的编程语言和开发工具。
此外,你还需要掌握一些数字信号处理的基本概念,如离散时间系统、采样定理等。
总结起来,设计FPGA上的CIC滤波器需要先确定滤波器的规格和结构,然后设计滤波器的系数,最后在FPGA上实现并测试滤波器。
这个过程需要一些基本的信号处理和FPGA编程知识,但随着你的实践和学习,你将能够设计出高性能的CIC滤波器。
FPGA的CIC滤波器的设计

FPGA的CIC滤波器的设计CIC滤波器的设计主要涉及滤波器的参数确定、级联结构的设计、数据格式的选择和实现细节。
首先,CIC滤波器的参数包括滤波器阶数、滤波器响应和抽取/插值比例。
滤波器阶数决定了滤波器的截止频率和滤波器的响应速度。
滤波器响应可以是低通、高通或带通响应,根据实际需求选择。
抽取/插值比例决定了滤波器的抽取/插值功能,可以根据需要选择。
其次,CIC滤波器采用级联结构,每个级联包括一个积分器和一个信号延迟器。
级联结构的数量决定了滤波器的阶数,阶数越高滤波器的性能越好。
级联结构还可以根据需求进行扩展或压缩。
然后,对于FPGA的CIC滤波器设计,数据格式的选择非常重要。
常见的数据格式有定点(Fixed-Point)和浮点(Floating-Point)两种。
定点数据格式可以节省硬件资源,但需要进行定点数的运算和溢出处理。
浮点数据格式计算精度高,但需要更多的硬件资源。
根据实际需求选择合适的数据格式。
最后,实现细节包括CIC滤波器的硬件资源分配、时钟分配和时序约束等。
硬件资源分配需要根据滤波器的参数确定所需要的积分器、延迟器和加法器等硬件资源。
时钟分配需要合理分配时钟信号,以满足滤波器的运算速度和性能需求。
时序约束能够帮助设计人员解决时序问题,确保滤波器的正确性和稳定性。
总的来说,FPGA的CIC滤波器设计涉及滤波器参数选择、级联结构设计、数据格式选择和实现细节。
通过合理的设计和优化,可以实现快速、高效的滤波功能,满足各种信号处理需求。
CIC抽取滤波器的MATLAB设计及FPGA实现

CIC抽取滤波器的MATLAB设计及FPGA实现杨翠娥【摘要】CIC抽取滤波器是无线通信中的常用模块,一般用于数字下变频(DDC)系统中.它可以在降低采样速率的同时,完成低通滤波的作用.本论文介绍了CIC抽取滤波器的工作原理,并给出了CIC滤波器的MATLAB程序及仿真结果.最后,利用FPGA高速、高稳定性的特点,在QUAR-TUS设计环境下进行了CIC滤波器的HDL模块设计.【期刊名称】《山西电子技术》【年(卷),期】2017(000)001【总页数】3页(P46-48)【关键词】CIC;抽取;MATLAB;FPGA【作者】杨翠娥【作者单位】太原工业学院,山西太原030008【正文语种】中文【中图分类】TN911.4随着数字通信技术的发展,信号传输的速度越来越快。
这就对数字信号处理提出了更高的要求。
多速率信号处理技术可以在一个数字信号处理系统中采用多个不同的采样率,同时可以实现不同采样率之间的相互转换。
这种技术在降低高速数字系统的复杂度,减少存储量及提高灵活性等方面具有较好的性能。
数字信号的速率可以通过内插和抽取来改变,其中,内插用于上变频系统中,抽取用于下变频系统中。
无论抽取还是内插,都需要设计一个满足抽取或内插(抗混叠)要求的数字滤波器。
该滤波器性能的好坏将影响取样速率变换的效果以及实时处理的能力。
为此,积分级联梳状(CIC)滤波器得到了广泛的应用。
本文将以单级CIC抽取滤波器的设计为例进行CIC抽取滤波器的MATLAB分析设计及FPGA的实现。
积分级联梳状(CIC)抽取滤波器即实现对输入信号采样率的抽取和低通滤波,以完成信号的降速处理。
在数字下变频系统中得到了广泛应用。
CIC抽取滤波器包括积分和梳状两个基本组成部分。
如图1所示。
以单级CIC抽取系统为例,取级数N=1。
积分器实际上是单极点的FIR滤波器,反馈系数为1时的状态方程如下:根据z变换,积分器的传输函数可以表示为:梳状器也是一个对称FIR滤波器,其状态方程可以表示为:式中,D为设计参数,称为微分延迟,其传输函数为:则单级CIC滤波器的传递函数为:其传递函数的幅频特性为:如图2所示为单级CIC滤波器的幅频特性。
基于FPGA的CIC滤波器的优化设计

基于FPGA的CIC滤波器的优化设计李怡琳;肖顺文;易欢;杨湲【摘要】针对在数字下变频系统中单独应用CIC滤波器实现抽取滤波时,因高阶CIC滤波器通带衰减过大的问题,在原有的CIC滤波器后级联一补偿滤波器以达到降低采样率,防止频率混叠的目的.仿真结果表明,改进后的CIC滤波器通带波纹数减少,通带衰减降幅明显.%This paper talks about the problem of large passband attenuation caused by the high order of CIC filter when it is individually applied in the DDC system to achieve decimation and filtration.Because of that,a compensation filter is attached to the original CIC filter to reduce the sampling rate and avoid aliasing frequency.The simulation results show that the improved CIC filter has much fewer ripples and the passband attenuation is obviously decreased.【期刊名称】《西华师范大学学报(自然科学版)》【年(卷),期】2017(038)001【总页数】5页(P106-110)【关键词】FPGA;数字下变频;CIC滤波器;ISOP滤波器【作者】李怡琳;肖顺文;易欢;杨湲【作者单位】西华师范大学电子信息工程学院,四川南充 637009;西华师范大学电子信息工程学院,四川南充 637009;西华师范大学电子信息工程学院,四川南充637009;西华师范大学电子信息工程学院,四川南充 637009【正文语种】中文【中图分类】TN92软件无线电中的数字接收机前端所接收到的数字信号由于高频采样,数据量较大,所以对数据进行采样后的处理就显得尤为重要。
一种改进型CIC抽取滤波器的实现方法

一种改进型CIC抽取滤波器的实现方法谢海霞;孙志雄【摘要】针对传统CIC抽取滤波器处理宽带信号时,阻带衰减满足要求,通带衰减过大的问题,提出了一种改进CIC抽取器的设计方法;在分级抽取滤波器的基础上用锐化技术改善滤波器通阻带衰减,采用内插二阶多项补偿函数对通带进行额外补偿,使带内更平坦,并利用多相分解的方法降低了抽取滤波器采样率;仿真验证了改进型滤波器具有更好的通、阻带特性.最后在FPGA上实现这个改进型CIC滤波器的设计,并进行了时序仿真和综合验证.【期刊名称】《电子设计工程》【年(卷),期】2018(026)014【总页数】5页(P162-166)【关键词】CIC抽取滤波器;内插二阶多项式;多相分解;FPGA【作者】谢海霞;孙志雄【作者单位】海南热带海洋学院电子通信工程学院,海南三亚572022;海南热带海洋学院电子通信工程学院,海南三亚572022【正文语种】中文【中图分类】TN911.72数字上、下变频器所涉及的抽取和内插存在着混叠、镜频等问题,抽取、内插后如何分离出需要的信号,关键在于抽取前和内插后的抗混叠高效数字滤波器设计。
由于CIC滤波器结构只有乘法运算,便于提高实时性和简化硬件,故常用它作为抗混叠高效数字滤波器。
经典CIC抽取器一般用来处理窄带信号,而处理宽带信号时,幅频响应很不理想,满足带外衰减指标时,通带衰减过大,难以满足抗混叠性能要求。
因此,如何更好地增大滤波器的零点抑制同时又不影响其通带性能一直是CIC滤波器研究的热点[1-5]。
1 CIC抽取器的设计CIC抽取器结构简单,主要由积分部分、抽取部分和梳状部分组成[6]。
其结构如图1所示。
图1 单级CIC抽取滤波器框图式(1)为单级CIC抽取器传输函数。
由于单级CIC的过渡带的衰减性能不是很好,所以实际应用中,通常是由多个单级CIC滤波器级联方法来加大过渡带和阻带的衰减。
多级传输函数为式(2):其中,M为大于1的整数,称为抽取因子,决定了CIC的通带大小;K为级联数,对旁瓣抑制比起到加大作用。
CIC插值滤波器的FPGA设计与实现

CIC插值滤波器的FPGA设计与实现摘要:基于多速率信号处理原理,设计了用于下变频的CIC插值滤波器,由于CIC 滤波器结构只用到加法器和延迟器,没有乘法器,很适合用FPGA来实现,所以本文分析了CIC滤波器的原理,性能及影响参数,借助MATLAB设计符合系统要求CIC 滤波器,并利用Modelsim软件建模仿真,验证CIC滤波器性能是否达到要求。
(一)CIC滤波器基本原理A.CIC滤波器的基本单元CIC滤波器主要由积分滤波Integrator和梳状滤波Comb两个基本单元部分构成。
典型的CIC滤波器的结构,它由两个基本单元I(积分滤波器)和C(梳状滤波器)级联构成。
本设计主要针对插值滤波器,所以插值滤波器的结构示意图如图1-1所示:图 1-1 3级级联的CIC插值滤波器结构示意图积分器和梳状滤波器之间是一个采样率转换器,对于CIC插值器而言,它完成在每一个样值后补上R-1个0值的工作,,对于CIC抽取器来说,它完成在实际的抽取工作,每R个样值中取样一个。
R(插值倍数),M(延迟因子,一般取1或者2)以及N(级联级数)是影响CIC 滤波器的三个参数,它们的值需根据通带性能的需求而设定。
(二)CIC插值滤波器的设计流程根据CIC滤波器的原理,本设计的流程如图2-1所示:图2-1 CIC 插值滤波器的设计流程图(三)模型的建立和测试A .位宽策略对于数字滤波器,一个不得不考虑的问题是为防止溢出每一级所需的位宽。
对于抽取器来说,CIC 滤波器的输出增益为(*)NG R M = (3-1)所以,在全精度的情况下,最后一级输出的位宽为2log (*)out in B B N R M =+ (3-2)其中in B 表示输入数据的宽度,为了保证精度,每一个积分器和梳状滤波器的输入输出位宽都为out B 。
对于插值器而言,输出增益为212,1,2,....2(*)/,1, 2......2i i N i N i N G R M R i N N N --⎛⎫== ⎪ ⎪=++⎝⎭ (3-3)因此,第i 级为避免溢出所需要的位宽为2log ()i in i W B G =+ (3-4)最后一级输出位宽为22log (*)log out in B B N R M R =+- (3-5)在实际当中,当差分延时M=1时,为保证稳定,所有积分器的位宽在理论值的基础上加一。
改进的高性能CIC抗混叠滤波器

2012年第07期,第45卷 通 信 技 术 Vol.45,No.07,2012 总第247期 Communications Technology No.247,Totally改进的高性能CIC抗混叠滤波器皇甫文斌, 朱 江, 王世练(国防科学技术大学 电子科学与工程学院,湖南 长沙410073)【摘 要】这里对一种旋转锐化级联积分梳状滤波器(RSCIC,Rotated Sharpening Cascaded Integrator Comb Filter)进行了研究,RSCIC由锐化级联积分梳状滤波器(SCIC,Sharpening Cascaded Integrator Comb Filter)和旋转内插滤波器(Rotated Sinc Filter)两部分构成。
RSCIC可有效地提高传统积分梳状滤波器(CIC, Cascaded Integrator Comb Filter)的通带和阻带传输性能,特别适合采样率转化。
仿真表明,在同等条件下,RSCIC滤波器的阻带衰减性能比传统的CIC滤波器提高了22 dB,通带抗衰减性能比传统的CIC滤波器提高了0.5 dB。
【关键词】采样率转换;积分梳状滤波器;锐化级联积分梳状滤波器;旋转内插滤波器【中图分类号】TN911.72 【文献标识码】A 【文章编号】1002-0802(2012)07-0119-03 Improved High Performance CIC FilterHUANGFu Wen-bin, ZHU Jiang, WANG Shi-lian(School of Electronic Science and Engineering, National University of Defense Technology,Changsha Hunan 410073, China)【Abstract】CIC(Cascaded Integrator Comb) filter, for its simple hardware, is a most commonly-used multistate filter. However, the large distortion of the pass-band and the attenuation of the stop-band limit its applications, a new cascade structure is studied and proposed. Simulation shows that the proposed structure could improves the stop-band attenuation by 30dB as compared with the traditional CIC Filter. The new structure is quite good in the sampling rate conversion.【Key words】sample rate conversion;CIC;sharpening CIC;rotating sharpening CIC0 引言积分梳状滤波器CIC [1]结构简单,不使用乘法器,且不需要预先存储滤波器系数,是目前用于采样率转换常用的滤波器,但是,单一积分梳状滤波器通带和阻带性能相对较差,无法满足实际应用要求[2]。
cic滤波器的fpga实现

cic滤波器的FPGA实现发布时间:2016-01-26 15:07:21技术类别:CPLD/FPGA一、关于多采样率数字滤波器很明显从字面意思上可以理解,多采样率嘛,就是有多个采样率呗。
前面所说的FIR,IIR滤波器都是只有一个采样频率,是固定不变的采样率,然而有些情况下需要不同采样频率下的信号,具体例子我也不解释了,我们大学课本上多速率数字信号处理这一章也都举了不少的例子。
按照传统的速率转换理论,我们要实现采样速率的转换,可以这样做,假如有一个有用的正弦波模拟信号,AD采样速率是f1,现在我需要用到的是采样频率是f2的信号,传统做法是将这个经过f1采样后的信号进行DA转换,再将转换后的模拟信号进行以f2采样频率的抽样,得到采样率为f2的数字信号,至此完成采样频率的转换但是这样的做法不仅麻烦,而且处理不好的话会使信号受到损伤,所以这种思想就被淘汰了,现在我们用到的采样率转换的方法就是抽取与内插的思想。
二、抽取先来总体来解释一下抽取的含义:前面不是说,一个有用的正弦波模拟信号经采样频率为f1的抽样信号抽样后得到了数字信号,很明显这个数字信号序列是在f1频率下得到的,现在,假如我隔几个点抽取一个信号,比如就是5吧,我隔5个点抽取一个信号,是不是就是相当于我采用了1/5倍f1的采样频率对模拟信号进行采样了?所以,抽取的过程就是降低抽样率的过程,但是我们知道,这是在时域的抽样,时域的抽样等于信号在频域波形的周期延拓,周期就是采样频率,所以,为了避免在频域发生频谱混叠,抽样定理也是我们要考虑的因素下面来具体来介绍如上图所示,假如上面就是某一有用信号经采样频率f1抽样得到的频谱,假设这时候的采样频率为8Khz ,可以通过数格子得到,从0到F1处有8个空格,每个空格代表1Khz,有些朋友可能会问,这不是在数字频域吗,单位不是π吗,哪来的hz?是的,这里是数字频域,采样频率F1处对应的是2π,这里只是为了好解释,我们用模拟频率来对应数字频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
处理后每级表达式都可以与非递归算法结构的表达式 合并 , 既可以使 CCOS 滤波器部分电路工作在低频降 低功耗又可以大大减少存储单元数量 。CCOS 滤波器 实现结构如图 4 ( a ) 所示 , 图 4 ( b ) 为对 CCOS 滤波器抽 取改进后整体改进型滤波器的结构 。
为了进一步提高 CCOS 的通带特性 ,对文献 [ 4 ] 提 出的 CCOS 进 行 改 进 , 在 其 后 级 联 一 个 SIN E 滤 波 器 [ 5 ] ,其幅频特性与传输函数如下 :
集成电路设计
张 杰等 : 改进型 CIC 抽取滤波器设计与 FP GA 实现
改进型 CIC 抽取滤波器设计与 FPGA 实现
张 杰 ,戴宇杰 ,张小兴 ,吕英杰
( 南开大学 南开大学微电子所 天津 300071)
摘 要 : 为了改善级联积分梳状 ( CIC) 滤波器通带不平和阻带衰减不足的缺点 ,给出一种改进型 CIC 滤波器 。该滤波器 在采用 COSIN E 滤波器提高阻带特性的基础上 ,级联了一个 SIN E 滤波器 ,补偿了其通带衰减 。硬件实现时 ,采用新的多相 分解方法结合非递归结构 ,不仅大大减少了存储单元数量 ,还使电路结构更加规则 。经仿真和 FP GA 验证 ,改进型 CIC 滤波 器使用较少硬件 ,实现了阻带衰减 100. 3 dB ,通带衰减仅为 0. 000 1 dB 。 关键词 :CIC 抽取滤波器 ;COSIN E 滤波器 ; SIN E 滤波器 ; 设计优化 ; FP GA 中图分类号 : TP368. 1 文献标识码 :A 文章编号 :10042373X ( 2009) 102022203
jω H SIN ( e ) = e
ω -j M
2
2 ω/ 4) ] [ 1 + sin ( M
- M
( 9) ( 10)
图4 改进型 CIC 实现框图
H SIN ( z ) =
1பைடு நூலகம்4
- 1 + 6z
2
- z
- M
式中 : M 必须为偶数 , 这样才能避免分数延时 。出于节 省功耗的目的 , 取 M 为抽取值的 2 倍 ,这样 SIN E 滤波 器即可在提取到抽取之后 , 将计算量降为原来的 1/ M , 该结构通过移位和加法即可实现 ,无需乘法器 。 图 3 为改进型 CIC ( 取 M = 64) 与 CCOS ,CIC 的幅 频特性曲线比较 , 可以看出改进的 CIC 滤波器的通带 特性得到明显改善 。由于补偿滤波器的引入 ,阻带衰减 为100. 3 dB ,但通带衰减仅为 0. 000 1 dB 。
参 考 文 献
构使电路设计和版图设计变得更加容易[ 10212 ] 。
SIN E 滤波器放在最后一级如图 5 所示 。
图 5 SIN E 滤波器的实现结构
[ 1 ] Jovanovic G ,Dolecek ,Mit ra S K. A New Two2stage Shar2 pened Co mb Decimator [ J ] . IEEE Trans. on Circuit s and Systerms2I ,2005 ,52 (7) :1 41621 420. [2 ] Laddomada M. Generalized Comb Decimation Filter for Sigma Delta A/ D Converter : Analysis and Design [J ]. IEEE Trans . on Circuits and Systerms2I ,2007 ,54 (5) :99421 005. [3 ] Hogenauer E B. An Economical Class of Digital Filter for Deci2 mation and Interpolation [J ]. IEEE Trans . on Acoustics ,Speech and Signal Processing ,1981 ,ASSP229 (2) :1552162. [ 4 ] Dolecek G J ,Carmo na J D. A New Cascaded Modified CIC2 Co sine Decimatio n Filter [J ]. IEEE Circuit s and Systems , 2005 ( 4) :2182333. [ 5 ] Dolecek G J ,Mit ra S K. A New Two2stage CIC2based Deci2 mation Filter[ A ] . Image and Signal Processing and Analysis [ C ] . Istanbul Turkey ,2007 :2182333. [ 6 ] J ang Y , Yang S. No n2recursive Cascaded Integrator2Comb Decimation Filters wit h Integer Multiple Factors [J ] . IEEE Midwest Symp . Circuit s and Systems ,2001 ( 1) :1302133. [ 7 ] Meyer2Baese U ,Rao S ,Ramirez J , et al . Co st2effective Hoge2 nauer Cascaded Integrato r Co mb Decimato r Filter Design for Custom ICs [ J ] . IEEE Elect ronic Journal , 2005 , 41 ( 3 ) : 1582160. [ 8 ] Shahana T K ,J ames K R. Poly2p hase Implementatio n of Nov - recursive Co mb Decimato rs fo r Sigma Delta A/ D Co nvert2
k1 k2 2 k3 8 H MCCOS ( z ) = H1 ( z ) H2 ( z ) H3 ( z ) ・
1 - z- M ・ M 1 - z- 1 1
K
( 1)
式中 : 参数 M 为降频因子 , 决定了 CIC 的通带大小 ;
K 为 滤波器的阶数 , 对阻带衰减起到加深作用 。频率
响应为 :
收稿日期 :2008208207
22
《现代电子技术》 2009 年第 10 期总第 297 期
n1 8 n2 4 n3 2 H1 ( z ) H2 ( z ) H3 ( z )
集成电路
( 5) ( 6) ( 7) ( 8)
H1 ( z ) = ( 1 / 2 ) [ ( 1 - z ) / ( 1 - z ) ]
k3 = 2 ; n1 = 2 , n2 = n3 = 4 。 从图 2 中可以看出 CIC 滤
按照式 ( 5 ) 中 CCOS 各级联部分的关系 , 文献 [ 4 ] 中给出一种电路实现结构图 ,通过抽取使部分电路工作 在更低频率 。为了进一步提高滤波器设计的功耗使用 效率 ,减小占用芯片的面积 ,对文献 [ 4 ] 的结构进行再次 改进和优化 。通过改变算法运算的具体步骤 ,来减少运 算的步数 ,从而提高滤波器的效率 。
图1 CIC 滤波器实现框图
2 改进的 CIC 结构
经典的抽取滤波器为 Hogenauer [ 3 ] CIC 滤波器 ,其 传输函数表达式为 :
H ( z) =
为了改善 CIC 抽取滤波器阻带衰减不足的缺点 , 采用一种新型 COSIN E 滤波器 [ 4 ] ,其传输函数为 : N - 2N - N 2 ( 3) HCOS ( z ) = 0 . 125 ( 1 + z ) ( 1 + z ) 幅频特性具有 COSIN E 函数的形式 : ω jN 2 | H COS ( e ) | = ( 1/ 2 ) | co s Nω + co s Nω | ( 4 ) 当 N 取不同值时 ,幅频响应如图 2 ( a) 所示 。 把不同 N 值的 COSIN E 滤波器级联 , 幅频响应会 呈现低 通 特 性 , 因 此 文 献 [ 4 ] 采 用 CIC 滤 波 器 级 联 COSIN E滤波器的结构来改善传统 CIC 滤波器的幅频 特性 。令 N i = M/ 2 i+1 , 此时 COSIN E 滤波器第一个零 点与 CIC 滤波器的第一个零点重合 , 增加了第一个零 点附近旁瓣的衰减 。取 M = 32 ,传输函数为 :
H2 ( z ) = H3 ( z ) =
-4 1 1 - z -1 4 1 - z -4 1 1 - z -1 4 1 - z
= =
1 ( 1 + z 2 ) ( 1 + z ) ( 12) 4 1 ( 1 + z 2 ) ( 1 + z ) ( 13) 4
其次把 CCOS 滤波器的部分电路再次抽取降频 ,
1 CIC 抽取滤波器原理
jω H (e ) =
1
M
e- j
- 1) ω( M2
sin (ω M / 2) sin (ω / 2)
K
( 2)
滤波电路由积分模块与差分模块组成 ,根据置换原 则将抽取因子提到差分模块之前 , 使其工作在较低频 率 ,并节省了 M - 1 个存储单元 ,框图如图 1 所示 。
23
集成电路设计
张 杰等 : 改进型 CIC 抽取滤波器设计与 FP GA 实现 中 ,对文献 [ 4 ] 中的结构进行优化 ,使部分电路工作在更 低的频率下 ,大大降低了功耗 ; 采用非递归结构 ,结合传 输函数自身的特性合并部分分式 , 降低了电路复杂性 ; 在每级处理时仅采用加法器和延时单元 ,节省了硬件资 源 ,提高了实用性 。
Design of Modif ied CIC Decimation Filter and FPGA Implementation
