2016年襄城区中考适应性考试数学答题卡-答题卡
中考数学答题卡(定稿)

x2 1 2x . x 1 1 x
(2)
注 意 事 项
1. 选择题部分必须使用 2B 铅笔填涂;非选择题部分必须使用 0.5 毫米的黑 色签字笔书写,字体工整、笔迹清楚。 2. 请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案 无效;在草稿纸、试题卷上答题无效。 3. 保持卡面清洁,不要折叠、不要弄破,禁用涂改液,涂改胶条。 正确填涂 错误填涂
18. (本题 8 分) (1)
填涂样例
缺考标记 21. (本题 10 分) (1)
A A A A A B B B B B C C C C C D D D D D
卷Ⅰ(选择题)
1 2 3 4 5
A A A A A B B B B B C C C C C D D D D D
6 7 8 9 10
卷Ⅱ(11-16 为填空题,17-24 为解答题)
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效 22. (本题 10 分) (1)
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效 (2)
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效 (3)在点 P 在整个运动过程中. ①
y
C
A D
B
A
(3)
O
x
B
(第 22 题)
湖北省襄阳市2016年中考适应性考试数学试卷含答案 (2)

2016年九年级适应性考试数学试卷一、选择题(每小题3分,共计30分) ( )1.2016-的倒数的绝对值为:A. 2016-B.20161-C.2016D. 20161,结果如下表: A.众数是2元 B.中位数是2元 C.极差是5元 D.平均数是2.45元 ( )3.下列运算正确的是:A.532a a a =+B.ab b a 624=+C.1)11(02=+a D.10)52(2= ( )4.如图,AB ∥DE,AC ⊥CD,并且∠A=35º,则∠D 的度数为:A.55ºB.45ºC.30ºD.60º( )5.已知函数44)1(2+--=x x k y 与x 轴只有一个交点,则k 的取值范围是:A.2≤k 且1≠kB. 2<k 且1≠kC.2=kD. 2=k 或1( )6. PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.已知1微米相当于1米的一百万分之一,则2.5微米用科学记数可表示为 A. 7105.2-⨯米 B.6105.2-⨯ 米 C. 7105.2⨯米 D. 6105.2⨯米 ( )7.如图所示的是由一些正方体小木块搭成的几何体的主视图与俯视图,它最多需要小木块的块数是:A.8B. 7C.6D.5( )8.如图,在△ABC 中,分别以点A 和点B 为圆心,大于21AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC 于点D,连接AD,若△ADC 的周长为8,AB=6, 则△ABC 的周长为:A.20B.22C.14D.16 ( )9.已知抛物线c bx ax y ++=2的图像如图所示, 则直线b ax y -=一定不经过:A.第一象限B. 第二象限C. 第三象限D. 第四象限( )10.如图,在矩形ABCD 中,点E 是AD 的中点,∠EBC 的平分线交CD 于点F,将△DEF 沿EF 折叠,点D 恰好落在BE 上M 点处,延长BC,EF 交于点N.有下列四个结论: ①BF 垂直平分EN;②BF 平分∠MFC;③△DEF ∽△FEB;④tan ∠N=3.其中,将正确结论的序号全部选对的是:ABCDE第4题图主视图俯视图AB C DMN Ox yA. ①②③B. ①②④C. ②③④D. ①②③④二、填空题(每小题3分,共计18分)11.计算: 6)272483(÷-=________________.12.如图,点P 是反比例函数在第二象限上的一点,且矩形PEOF 的面积为5,则反比例函数的表达式为_____________. 13.若关于x 的不等式组⎩⎨⎧>+≥-0630x x m 的整数解恰好有三个,则m 的取值范围是____________.14.盒子里装有大小形状相同,质地均匀的4个白球和3个红球,搅匀后从中摸出一个球,放回搅匀后,再摸出第二个球,则两次取出的均是红球的概率是___________.15. 如图四边形ABCD 是⊙O 的内接四边形,已知∠BOD=120°则∠BCD 的度数为___________16.已知□ABCD 的周长为40㎝,AE ⊥BC 于点E,AF ⊥CD 于点F,若AE=4㎝,AF=6㎝,则CE+CF=_________㎝. 三、解答题(共72分) 17.(6分)先化简,再求值:222)11(yxy x yy x y x +-÷+-- 其中145sin 21-︒=x ,230sin 2-︒=y18. (6分)从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟, 从乙地到甲地需42分钟.甲地到乙地全程是多少千米?19. (6分)如图,点E 是□ABCD 的边AD 上一点,连接CE 并延长交BA 的延长线于点F,若BG=DE,并且∠AEF=70º.求∠AGB 的度数.A BCDE F G20. (7分)为响应襄阳市创建“全国卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A,B,C,D 四等.从中随机抽取了部分学生成绩进行统计,绘制成如图两幅不完整的统计图表,根据图表信息,解答下列问题:A BCD O(1)被抽取的学生总数是_____人,C 等在样本中所占的百分比是_____; (2) D 等在扇形统计图所对应的圆心角是多少度?并补全左侧的条形图; (3)估计全校校生成绩为A 等的大约有多少人?21. (6分)在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B 两个凉亭之间的距离.现测得AC=50m,BC=100m, ∠CAB=120º,请计算A,B 两个凉亭之间的距离.22. (7分)如图,AB 是⊙O 的直径,C 是⊙O 上的一点,AD 和过点C 的切线互相垂直,垂足为D ,AD 交⊙O 于E. (1)求证:AC 平分∠DAB ; (2)连接CE ,若CE=6,AC=8,求⊙O 的直径的长.23. (10分)为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y (台)与补贴款额x (元)之间大致满足如图所示的一次函数关系.随着补贴款额x 的不断增大,销售量也不断增加,但每台彩电的收益p (元)会相应降低且满足:11051+-=x p(0≥x ).(1)在政府补贴政策实施后,求出该商场销售彩电台数y 与政府补贴款额x 之间的函数关系式;(2)在政府未出台补贴措施之前,该商场销售彩电的总收益额为多少元?(3)要使该商场销售彩电的总收益最大,政府应将每台补贴款额x 定为多少?并求出总收益的最大值.100014000100200y(台)x(元)24. (12分)已知:将一副三角板(Rt △ABC 和Rt △DEF)如图①摆放,点E,A,D,B 在一条直线上,且D 是AB 的中点.将Rt △DEF 绕点D 顺时针方向旋转角α(︒<<︒900α),在旋转过程中,直线DE,AC 相交于点M,直线DF,BC 相交于点N,分别过点M,N 作直线AB 的垂线,垂足为G ,H.(1)当︒=30α时(如图②),求证:AG=DH;(2) 当︒=60α时(如图③),(1)中的结论是否成立?请写出你的结论,并说明理由; (3)当︒<<︒900α(如图④)时,求证:DH GD HB AG ⋅=⋅.25. (12分)如图,抛物线与直线相交于A,B 两点,若点A 在x 轴上,点B 的坐标是(2,4),抛物线与x 轴另一交点为D,并且△ABD 的面积为6,直线AB 与y 轴的交点的坐标为(0,2).点P 是线段AB(不与A,B 重合)上的一个动点,过点P 作x 轴的垂线,交抛物线与点Q. (1)分别求出抛物线与直线的解析式; (2)求线段PQ 长度的最大值;(3)当PQ 取得最大值时, 在抛物线上是否存在M 、N 两点(点M 的横坐标小于N 的横坐标),使得P 、D 、M 、N 为顶点的四边形是平行四边形?若存在,求出MN 的坐标;若不存在,请说明理由.参考答案一.选择题二.填空题11.23 12.x y 5-= 13.21<≤m 14.499 15.120º 16.31020+或324+ 三.解答题17.yx y x y y x y x y x y y y x y x y x y x y x y x y x +-=-⋅-+=-⋅-+---++=)(2)())((2)(]))(())(([:22原式解 ……………………3分由1212112221145sin 21+=-=-⨯=-︒=x ,212212230sin 2-=-⨯=-︒=y 得: 2,22=+=-y x y x ……………………5分∴原式=222222=⨯ ……………………6分 18.解:设从甲地到乙地时上坡段的路程为x 千米,平路段的路程为y 千米,根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+604245605443y x y x ……………………3分解得⎩⎨⎧==6.15.1y x ……………………4分1.36.15.1=+=+y x ……………………5分答:甲地到乙地的全程是3.1千米. ……………………6分19.解: ∵四边形ABCD 是平行四边形∴AB=CD, ∠B=∠D ……………………2分 又∵BG=DE∴△ABG ≌△CDE ……………………3分 ∴∠AGB=∠CED ……………………4分 ∵∠CED=∠AEF=70º ……………………5分 ∴∠AGB=70º ……………………6分20.解:(1)200,10% ……………………………………………………2分 (2)36º (补全图略)………………………………………………………………4分 (3)9002001201500=⨯……………………………………………………6分 答:全校学生成绩为A 等的大约有900人. ……………………………7分 21.解: 过点C 作CD ⊥AB 于D在Rt △CDA 中∠CAD=180º-∠CAB=180º-120º =60º…………………………………1分 ∵ACCDCAD =∠sin ∴325235060sin =⨯=︒⋅=AC CD ………………………………………………2分 同理:25215060cos =⨯=︒⋅=AC AD ………………………………………………3分 在Rt △CBD 中,1325)325(1002222=-=-=CD BC BD ………………4分∴AB=BD-AD=251325- ………………………………………………5分 答:AB 之间的距离是(251325-)m. ………………………………………………6分 22.(1)证明:如图,连接OC∵CD 是⊙O 的切线 ∴OC ⊥CD ∴∠OCF=90º ∵AD ⊥CD∴∠D=∠OCF=90º (2)分∴OC ∥AD∴∠1=∠3 ……………………………………3分 ∵OA=OC ∴∠2=∠3 ∴∠1=∠2即AC 平分∠DAB ……………………………………4分 (2)如右图,连接OE∵∠1=∠2, ∠1=EOC ∠21,∠2=BOC ∠21∴BOC EOC ∠=∠∴BC=CE=6 …………………………5分 ∵AB 是⊙O 的直径 ∴∠ACB=90º 在Rt △ABC 中10682222=+=+=BC AC AB …………………………6分∴⊙O 的直径的长为10. …………………………7分 23.(1)解:根据题意,可设b kx y += 将(100,1000),(200,1400)代入上式,得:⎩⎨⎧=+=+14002001000100b k b k ………………………2分 解得⎩⎨⎧==6004b k ………………………3分∴所求作的函数关系式为:6004+=x y . ………………………4分 (2) ∵在6004+=x y 中,当0=x 时,600=y在11051+-=x p 中,当0=x 时,110=p ………………5分 ∴66000110600=⨯答: 在政府未出台补贴措施之前,该商场销售彩电的总收益额为66000元. ……6分 (3)设总收益为W 元,则W=)11051)(6004(+-+x x ………………7分 =66000320542++-x x =98000)200(542+--x ………………8分∵ 054<-=a∴W 存在最大值∴当x=200时W 有最大值98000. ………………9分答: 政府应将每台补贴款额定为200元时,可获得最大利润98000元. ………………10分 24、(1)∵∠A=∠MDA=α=30º∴MA=MD 又∵MG ⊥AD∴AG=21AD ………………1分 ∵∠FDB=90º -α=90º -30º =60º ,∠B=60º ∴△CDB 是等边三角形 又∵CH ⊥BD ∴DH=21BD ………………2分 ∵D 为AD 的中点∴AD=BD ………………3分 ∴AG=DH ………………4分 (2)∵∠A=∠NDB ,AD=BD ,∠B=∠MDA=α=60º∴△AMD ≌△DNB ………………5分 ∴AM=DN又∵∠A=∠NDH=90º -α=90º -60º =30º,∠AGM=∠DHN=90º ∴△AGM ≌△DHN ………………7分 ∴AG=DH ………………8分 (3)在Rt △AGM 中,∠A=30º∴∠AMG=90º -30º =60º =∠B又∵∠AGM=∠NHB=90º∴△AGM ∽△NHB ………………9分∴NHHBAG MG =∴MG ·NH=AG ·HB ………………10分 ∵∠GMD+∠GDM=90º,∠HDN+∠GDM=90º ∴∠GMD=∠HDN又∵∠MGD=∠DHN=90º ∴△MGD ∽△DHN ∴DHHNMG GD =∴MG ·NH=GD ·DH ………………11分 ∴AG ·HB=GD ·GH ………………12分25、(1)解:设直线的解析式为: b kx y += 将点B(2,4),点(0,2)代入上式得:⎩⎨⎧==+242b b k 解得⎩⎨⎧==21b k ∴所求直线的解析式为:2+=x y . ………………2分当0=y 时,2-=x ,即点A 的坐标为(-2,0) ∵S △ABD =64)]2([21||21=⨯--⨯=⋅D B x y AD ∴1=D x∴点D 的坐标(1,0)设抛物线的解析式为:)1)(2(-+=x x a y 将点B(2,4)代入上式得:1=a∴所求抛物线的解析式为:)1)(2(-+=x x y即22-+=x x y ………………4分(2)设点P 的横坐标为t ,则点P 为(t ,t+2),点Q 为(t ,22-+t t )………………5分 ∴PQ=t+2-(22-+t t )=42+-t ………………7分 ∵a=-1<0∴PQ 有最大值4 ………………8分 (3)由(2)知点P 坐标为(0,2) ………………9分 ①以PD 为平行四边形的边时,设点M 坐标为(m ,n )则点N 为(m+1,n-2) ∵点M 、N 均在抛物线上∴ n=m 2+m-2n-2=(m+1)2+m+1-2 解得 m=-2n=0∴M(-2,0),N (-1,-2) …………10分 ②以PD 为平行四边形的对角线时,设点M 为(m,n )则点N 为(1-m,2-n )同(1)理得M (-1,-2)N (2,4) …………11分 综上所述存在M (-2,2),N (-1,-2)和M (-1,-2),N (2,4)满足题意。
数学答题卡2
贴条形码区
(此处贴条形码)
缺考考生,由监考员用 2B 铅笔 填涂右面的缺考标记
40 20 0.05 0.35 0.65 0.95 1.25 1.55 视力
考生禁填
24%
0.35~0.65
填 正确填涂 涂 错误填涂 样 √ × Ο 例 ●
注 意 事 项
1、 答题前, 考生先将自己的姓名、 准考证号填写清楚, 并认真核准条形码 上的准考证号、姓名。 2、 选择题部分必须使用 2B 铅笔填涂:非选择题部分必须使用 0.5 毫米及 以上书写黑色字迹的钢笔或签字笔作答,字体工整、笔迹清楚。 3、 请按照题号顺序在各题目的答题区域内作答, 超出答题区域书写的答案 无效;在草稿纸、试卷上答题无效。 4、 保持卡面清洁,不折叠,不破损。
9 [ A ][ B ][ C ][ D ] 10 [ A ][ B ][ C ][ D ]
(1)________,________,________ (2) (3)
(2)
二、填空题(每小题 3 分,共 18 分) 11 15 ; 12 . 16 ; 13 . , 三、解答题(8 小题共 72 分) ; 14 .
1.25~1.55 ≤0.35
一、选择题(每小题 3 分,共 30 分)
███ ███ ███ ███
1 2 3 4
[ A ][ B ][ C ][ D ] [ A ][ B ][ C ][ D ] [ A ][ B ][ C ][ D ] [ A ][ B ][ C ][ D ]
5 [ A ][ B ][ C ][ D ] 6 [ A ][ B ][ C ][ D ] 7 [ A ][ B ][ C ][ D ] 8 [ A ][ B ][ C ][ D ]
襄城区2016年九年级适应性考试数学试卷参考答案
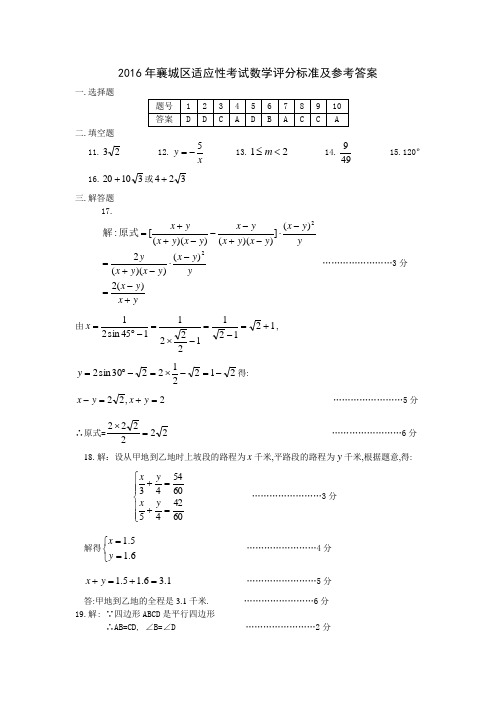
2016年襄城区适应性考试数学评分标准及参考答案一.选择题题号 1 2 3 4 5 6 7 8 9 10 答案D D C A D B A C CA二.填空题11.23 12.x y 5-= 13.21<≤m 14.499 15.120º 16.31020+或324+ 三.解答题17.yx y x y y x y x y x y y y x y x y x y x y x y x y x +-=-⋅-+=-⋅-+---++=)(2)())((2)(]))(())(([:22原式解 ……………………3分由1212112221145sin 21+=-=-⨯=-︒=x ,212212230sin 2-=-⨯=-︒=y 得: 2,22=+=-y x y x ……………………5分∴原式=222222=⨯ ……………………6分 18.解:设从甲地到乙地时上坡段的路程为x 千米,平路段的路程为y 千米,根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+604245605443y x y x ……………………3分解得⎩⎨⎧==6.15.1y x ……………………4分1.36.15.1=+=+y x ……………………5分答:甲地到乙地的全程是3.1千米. ……………………6分19.解: ∵四边形ABCD 是平行四边形∴AB=CD, ∠B=∠D ……………………2分又∵BG=DE∴△ABG ≌△CDE ……………………3分 ∴∠AGB=∠CED ……………………4分 ∵∠CED=∠AEF=70º ……………………5分 ∴∠AGB=70º ……………………6分20.解:(1)200,10% ……………………………………………………2分 (2)36º (补全图略)………………………………………………………………4分 (3)9002001201500=⨯……………………………………………………6分 答:全校学生成绩为A 等的大约有900人. ……………………………7分 21.解: 过点C 作CD ⊥AB 于D在Rt △CDA 中∠CAD=180º-∠CAB=180º-120º =60º…………………………………1分 ∵ACCDCAD =∠sin ∴325235060sin =⨯=︒⋅=AC CD ………………………………………………2分 同理:25215060cos =⨯=︒⋅=AC AD ………………………………………………3分 在Rt △CBD 中,1325)325(1002222=-=-=CD BC BD ………………4分∴AB=BD-AD=251325- ………………………………………………5分 答:AB 之间的距离是(251325-)m. ………………………………………………6分 22.(1)证明:如图,连接OC∵CD 是⊙O 的切线 ∴OC ⊥CD ∴∠OCF=90º ∵AD ⊥CD∴∠D=∠OCF=90º……………………………………2分 ∴OC ∥AD∴∠1=∠3 ……………………………………3分 ∵OA=OC ∴∠2=∠3 ∴∠1=∠2即AC 平分∠DAB ……………………………………4分 (2)如右图,连接OE∵∠1=∠2, ∠1=EOC ∠21,∠2=BOC ∠21∴BOC EOC ∠=∠∴BC=CE=6 …………………………5分 ∵AB 是⊙O 的直径 ∴∠ACB=90ºABC D E OF123ABC D E OF123在Rt △ABC 中10682222=+=+=BC AC AB …………………………6分∴⊙O 的直径的长为10. …………………………7分 23.(1)解:根据题意,可设b kx y += 将(100,1000),(200,1400)代入上式,得:⎩⎨⎧=+=+14002001000100b k b k ………………………2分 解得⎩⎨⎧==6004b k ………………………3分∴所求作的函数关系式为:6004+=x y . ………………………4分 (2) ∵在6004+=x y 中,当0=x 时,600=y在11051+-=x p 中,当0=x 时,110=p ………………5分 ∴66000110600=⨯答: 在政府未出台补贴措施之前,该商场销售彩电的总收益额为66000元. ……6分 (3)设总收益为W 元,则W=)11051)(6004(+-+x x ………………7分 =66000320542++-x x =98000)200(542+--x ………………8分∵ 054<-=a∴W 存在最大值∴当x=200时W 有最大值98000. ………………9分答: 政府应将每台补贴款额定为200元时,可获得最大利润98000元. ………………10分 24、(1)∵∠A=∠MDA=α=30º∴MA=MD 又∵MG ⊥AD∴AG=21AD ………………1分 ∵∠FDB=90º -α=90º -30º =60º ,∠B=60º ∴△CDB 是等边三角形 又∵CH ⊥BD ∴DH=21BD ………………2分 ∵D 为AD 的中点∴AD=BD ………………3分 ∴AG=DH ………………4分 (2)∵∠A=∠NDB ,AD=BD ,∠B=∠MDA=α=60º∴△AMD ≌△DNB ………………5分 ∴AM=DN又∵∠A=∠NDH=90º -α=90º -60º =30º,∠AGM=∠DHN=90º ∴△AGM ≌△DHN ………………7分 ∴AG=DH ………………8分 (3)在Rt △AGM 中,∠A=30º∴∠AMG=90º -30º =60º =∠B又∵∠AGM=∠NHB=90º∴△AGM ∽△NHB ………………9分∴NHHBAG MG = ∴MG ·NH=AG ·HB ………………10分 ∵∠GMD+∠GDM=90º,∠HDN+∠GDM=90º ∴∠GMD=∠HDN又∵∠MGD=∠DHN=90º ∴△MGD ∽△DHN ∴DHHNMG GD = ∴MG ·NH=GD ·DH ………………11分 ∴AG ·HB=GD ·GH ………………12分25、(1)解:设直线的解析式为: b kx y += 将点B(2,4),点(0,2)代入上式得:⎩⎨⎧==+242b b k 解得⎩⎨⎧==21b k ∴所求直线的解析式为:2+=x y . ………………2分 当0=y 时,2-=x ,即点A 的坐标为(-2,0) ∵S △ABD =64)]2([21||21=⨯--⨯=⋅D B x y AD ∴1=D x∴点D 的坐标(1,0)设抛物线的解析式为:)1)(2(-+=x x a y 将点B(2,4)代入上式得:1=a∴所求抛物线的解析式为:)1)(2(-+=x x y即22-+=x x y ………………4分(2)设点P 的横坐标为t ,则点P 为(t ,t+2),点Q 为(t ,22-+t t )………………5分 ∴PQ=t+2-(22-+t t )=42+-t ………………7分 ∵a=-1<0∴PQ 有最大值4 ………………8分 (3)由(2)知点P 坐标为(0,2) ………………9分 ①以PD 为平行四边形的边时,设点M 坐标为(m ,n )则点N 为(m+1,n-2) ∵点M 、N 均在抛物线上∴ n=m 2+m-2n-2=(m+1)2+m+1-2 解得 m=-2n=0∴M(-2,0),N (-1,-2) …………10分 ②以PD 为平行四边形的对角线时,设点M 为(m,n )则点N 为(1-m,2-n )同(1)理得M (-1,-2)N (2,4) …………11分 综上所述存在M (-2,2),N (-1,-2)和M (-1,-2),N (2,4)满足题意。
襄阳市襄城区九年级适应性考试数学试卷

襄阳市襄城区2016年九年级适应性考试数学试卷一、选择题(每小题3分,共计30分) ( )1.2016-的倒数的绝对值为:A. 2016-B.20161-C.2016D. 20161,结果如下表: 每天使用零花钱(单位:元)12345 人数 2 56 4 21关于这20名同学每天使用的零花钱,下列说法错误的是:A.众数是2元B.中位数是2元C.极差是5元D.平均数是元 ( )3.下列运算正确的是:A.532a a a =+B.ab b a 624=+C.1)11(02=+a D.10)52(2= ( )4.如图,AB ∥DE,AC ⊥CD,并且∠A=35º,则∠D 的度数为:º º º º( )5.已知函数44)1(2+--=x x k y 与x 轴只有一个交点,则k 的取值范围是:A.2≤k 且1≠kB. 2<k 且1≠kC.2=kD. 2=k 或1( )6. 是指大气中直径小于或等于微米的颗粒物,也称为可入肺颗粒物.已知1微米相当于1米的一百万分之一,则微米用科学记数可表示为A. 7105.2-⨯米B.6105.2-⨯ 米C. 7105.2⨯米D. 6105.2⨯米 ( )7.如图所示的是由一些正方体小木块搭成的 几何体的主视图与俯视图,它最多需要小木块的块数是:B. 7( )8.如图,在△ABC 中,分别以点A 和点B 为圆心,大于21AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC 于点D,连接AD,若△ADC 的周长为8,AB=6, 则△ABC 的周长为:( )9.已知抛物线c bx ax y ++=2的图像如图所示, 则直线b ax y -=一定不经过:A.第一象限B. 第二象限C. 第三象限D. 第四象限 ( )10.如图,在矩形ABCD 中,点E 是AD 的中点,∠EBC 的平分线交CD 于点F,将△DEF 沿EF 折叠,点D 恰好落在BE 上M 点处,延长BC,EF 交于点N.有下列四个结论: ①BF 垂直平分EN;②BF 平分∠MFC;③△DEF ∽△FEB;④tan ∠N=3.其中,将正确结论的序号全部选对的是:ABCDE第4题图主视图俯视图AB C DMN Ox yA. ①②③B. ①②④C. ②③④D. ①②③④二、填空题(每小题3分,共计18分)11.计算: 6)272483(÷-=________________.12.如图,点P 是反比例函数在第二象限上的一点,且矩形PEOF 的面积为5,则反比例函数的表达式为_____________. 13.若关于x 的不等式组⎩⎨⎧>+≥-0630x x m 的整数解恰好有三个,则m 的取值范围是____________.14.盒子里装有大小形状相同,质地均匀的4个白球和3个红球,搅匀后从中摸出一个球,放回搅匀后,再摸出第二个球,则两次取出的均是红球的概率是___________.15. 如图四边形ABCD 是⊙O 的内接四边形,已知∠BOD=120°则∠BCD 的度数为___________16.已知□ABCD 的周长为40㎝,AE ⊥BC 于点E,AF ⊥CD 于点F,若AE=4㎝,AF=6㎝,则CE+CF=_________㎝. 三、解答题(共72分) 17.(6分)先化简,再求值:222)11(yxy x yy x y x +-÷+-- 其中145sin 21-︒=x ,230sin 2-︒=y18. (6分)从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟, 从乙地到甲地需42分钟.甲地到乙地全程是多少千米19. (6分)如图,点E 是□ABCD 的边AD 上一点,连接CE 并延长交BA 的延长线于点F,若BG=DE,并且∠AEF=70º.求∠AGB 的度数.A BCDE F G20. (7分)为响应襄阳市创建“全国卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A,B,C,D 四等.从中随机抽取了部分学生成绩进行统计,绘制成如图两幅不完整的统计图表,根据图表信息,解答下列问题:A BCD O等级人数ABCD5020A 等60%B 等25%C 等D 等(1)被抽取的学生总数是_____人,C 等在样本中所占的百分比是_____; (2) D 等在扇形统计图所对应的圆心角是多少度并补全左侧的条形图; (3)估计全校校生成绩为A 等的大约有多少人21. (6分)在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B 两个凉亭之间的距离.现测得AC=50m,BC=100m, ∠CAB=120º,请计算A,B 两个凉亭之间的距离.22. (7分)如图,AB 是⊙O 的直径,C 是⊙O 上的一点,AD 和过点C 的切线互相垂直,垂足为D ,AD 交⊙O 于E. (1)求证:AC 平分∠DAB ; (2)连接CE ,若CE=6,AC=8,求⊙O 的直径的长.23. (10分)为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y (台)与补贴款额x (元)之间大致满足如图所示的一次函数关系.随着补贴款额x 的不断增大,销售量也不断增加,但每台彩电的收益p (元)会相应降低且满足:11051+-=x p (0≥x ).(1)在政府补贴政策实施后,求出该商场销售彩电台数y 与政府补贴款额x 之间的函数关系式;(2)在政府未出台补贴措施之前,该商场销售彩电的总收益额为多少元(3)要使该商场销售彩电的总收益最大,政府应将每台补贴款额x 定为多少并求出总收益的最大值.A BCDE O100014000100200y(台)x(元)24. (12分)已知:将一副三角板(Rt △ABC 和Rt △DEF)如图①摆放,点E,A,D,B 在一条直线上,且D 是AB 的中点.将Rt △DEF 绕点D 顺时针方向旋转角α(︒<<︒900α),在旋转过程中,直线DE,AC 相交于点M,直线DF,BC 相交于点N,分别过点M,N 作直线AB 的垂线,垂足为G,H. (1)当︒=30α时(如图②),求证:AG=DH;(2) 当︒=60α时(如图③),(1)中的结论是否成立请写出你的结论,并说明理由; (3)当︒<<︒900α(如图④)时,求证:DH GD HB AG ⋅=⋅.25. (12分)如图,抛物线与直线相交于A,B 两点,若点A 在x 轴上,点B 的坐标是(2,4),抛物线与x 轴另一交点为D,并且△ABD 的面积为6,直线AB 与y 轴的交点的坐标为(0,2).点P 是线段AB(不与A,B 重合)上的一个动点,过点P 作x 轴的垂线,交抛物线与点Q. (1)分别求出抛物线与直线的解析式; (2)求线段PQ 长度的最大值;(3)当PQ 取得最大值时, 在抛物线上是否存在M 、N 两点(点M 的横坐标小于N 的横坐标),使得P 、D 、M 、N 为顶点的四边形是平行四边形若存在,求出MN 的坐标;若不存在,请说明理由.2016年襄城区适应性考试数学评分标准及参考答案一.选择题题号1 2 3 4 5 6 7 8 9 10答案 D D C A D B A C C A二.填空题11.23 12.x y 5-= 13.21<≤m 14.499 º 16.31020+或324+ 三.解答题17.yx y x y y x y x y x y y y x y x y x y x y x y x y x +-=-⋅-+=-⋅-+---++=)(2)())((2)(]))(())(([:22原式解 ……………………3分由1212112221145sin 21+=-=-⨯=-︒=x ,212212230sin 2-=-⨯=-︒=y 得: 2,22=+=-y x y x ……………………5分∴原式=222222=⨯ ……………………6分 18.解:设从甲地到乙地时上坡段的路程为x 千米,平路段的路程为y 千米,根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+604245605443y x y x ……………………3分解得⎩⎨⎧==6.15.1y x ……………………4分1.36.15.1=+=+y x ……………………5分答:甲地到乙地的全程是千米. ……………………6分19.解: ∵四边形ABCD 是平行四边形∴AB=CD, ∠B=∠D ……………………2分 又∵BG=DE∴△ABG ≌△CDE ……………………3分 ∴∠AGB=∠CED ……………………4分 ∵∠CED=∠AEF=70º ……………………5分 ∴∠AGB=70º ……………………6分20.解:(1)200,10% ……………………………………………………2分 (2)36º (补全图略)………………………………………………………………4分 (3)9002001201500=⨯……………………………………………………6分 答:全校学生成绩为A 等的大约有900人. ……………………………7分 21.解: 过点C 作CD ⊥AB 于D在Rt △CDA 中∠CAD=180º-∠CAB=180º-120º =60º…………………………………1分 ∵ACCDCAD =∠sin ∴325235060sin =⨯=︒⋅=AC CD ………………………………………………2分 同理:25215060cos =⨯=︒⋅=AC AD ………………………………………………3分 在Rt △CBD 中,1325)325(1002222=-=-=CD BC BD ………………4分∴AB=BD-AD=251325- ………………………………………………5分 答:AB 之间的距离是(251325-)m. ………………………………………………6分 22.(1)证明:如图,连接OC∵CD 是⊙O 的切线 ∴OC ⊥CD ∴∠OCF=90º ∵AD ⊥CD∴∠D=∠OCF=90º (2)分∴OC ∥AD∴∠1=∠3 ……………………………………3分 ∵OA=OC ∴∠2=∠3 ∴∠1=∠2即AC 平分∠DAB ……………………………………4分 (2)如右图,连接OE∵∠1=∠2, ∠1=EOC ∠21,∠2=BOC ∠21∴BOC EOC ∠=∠∴BC=CE=6 …………………………5分 ∵AB 是⊙O 的直径 ∴∠ACB=90º 在Rt △ABC 中10682222=+=+=BC AC AB …………………………6分∴⊙O 的直径的长为10. …………………………7分 23.(1)解:根据题意,可设b kx y += 将(100,1000),(200,1400)代入上式,得:⎩⎨⎧=+=+14002001000100b k b k ………………………2分 解得⎩⎨⎧==6004b k ………………………3分∴所求作的函数关系式为:6004+=x y . ………………………4分 (2) ∵在6004+=x y 中,当0=x 时,600=y在11051+-=x p 中,当0=x 时,110=p ………………5分 ∴66000110600=⨯答: 在政府未出台补贴措施之前,该商场销售彩电的总收益额为66000元. ……6分 (3)设总收益为W 元,则W=)11051)(6004(+-+x x ………………7分 =66000320542++-x x =98000)200(542+--x ………………8分∵ 054<-=a∴W 存在最大值∴当x=200时W 有最大值98000. ………………9分答: 政府应将每台补贴款额定为200元时,可获得最大利润98000元. ………………10分 24、(1)∵∠A=∠MDA=α=30º∴MA=MD 又∵MG ⊥AD∴AG=21AD ………………1分 ∵∠FDB=90º -α=90º -30º =60º ,∠B=60º ∴△CDB 是等边三角形 又∵CH ⊥BD ∴DH=21BD ………………2分 ∵D 为AD 的中点∴AD=BD ………………3分 ∴AG=DH ………………4分 (2)∵∠A=∠NDB ,AD=BD ,∠B=∠MDA=α=60º∴△AMD ≌△DNB ………………5分 ∴AM=DN又∵∠A=∠NDH=90º -α=90º -60º =30º,∠AGM=∠DHN=90º ∴△AGM ≌△DHN ………………7分 ∴AG=DH ………………8分 (3)在Rt △AGM 中,∠A=30º∴∠AMG=90º -30º =60º =∠B又∵∠AGM=∠NHB=90º∴△AGM ∽△NHB ………………9分∴NHHBAG MG =∴MG ·NH=AG ·HB ………………10分 ∵∠GMD+∠GDM=90º,∠HDN+∠GDM=90º ∴∠GMD=∠HDN又∵∠MGD=∠DHN=90º ∴△MGD ∽△DHN ∴DHHNMG GD =∴MG ·NH=GD ·DH ………………11分 ∴AG ·HB=GD ·GH ………………12分25、(1)解:设直线的解析式为: b kx y += 将点B(2,4),点(0,2)代入上式得:⎩⎨⎧==+242b b k 解得⎩⎨⎧==21b k ∴所求直线的解析式为:2+=x y . ………………2分当0=y 时,2-=x ,即点A 的坐标为(-2,0) ∵S △ABD =64)]2([21||21=⨯--⨯=⋅D B x y AD ∴1=D x ∴点D 的坐标(1,0)设抛物线的解析式为:)1)(2(-+=x x a y 将点B(2,4)代入上式得:1=a∴所求抛物线的解析式为:)1)(2(-+=x x y即22-+=x x y ………………4分(2)设点P 的横坐标为t ,则点P 为(t ,t+2),点Q 为(t ,22-+t t )………………5分 ∴PQ=t+2-(22-+t t )=42+-t ………………7分 ∵a=-1<0∴PQ 有最大值4 ………………8分 (3)由(2)知点P 坐标为(0,2) ………………9分 ①以PD 为平行四边形的边时,设点M 坐标为(m ,n )则点N 为(m+1,n-2) ∵点M 、N 均在抛物线上 ∴ n=m 2+m-2n-2=(m+1)2+m+1-2 解得 m=-2n=0∴M(-2,0),N (-1,-2) …………10分 ②以PD 为平行四边形的对角线时,设点M 为(m,n )则点N 为(1-m,2-n )同(1)理得M (-1,-2)N (2,4) …………11分综上所述存在M (-2,2),N (-1,-2)和M (-1,-2),N (2,4)满足题意。
2016年襄阳市襄城区中考适应性考试数学试卷含答案

襄阳市襄城区2016年九年级适应性考试数学试卷一、选择题(每小题3分,共计30分) ( )1.2016-的倒数的绝对值为:A. 2016-B.20161-C.2016D. 20161,结果如下表: A.众数是2元 B.中位数是2元 C.极差是5元 D.平均数是2.45元 ( )3.下列运算正确的是:A.532a a a =+B.ab b a 624=+C.1)11(02=+a D.10)52(2= ( )4.如图,AB ∥DE,AC ⊥CD,并且∠A=35º,则∠D 的度数为:A.55ºB.45ºC.30ºD.60º( )5.已知函数44)1(2+--=x x k y 与x 轴只有一个交点,则k 的取值范围是:A.2≤k 且1≠kB. 2<k 且1≠kC.2=kD. 2=k 或1( )6. PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.已知1微米相当于1米的一百万分之一,则2.5微米用科学记数可表示为 A. 7105.2-⨯米 B.6105.2-⨯ 米 C. 7105.2⨯米 D. 6105.2⨯米 ( )7.如图所示的是由一些正方体小木块搭成的 几何体的主视图与俯视图,它最多需要小木块的块数是:A.8B. 7C.6D.5( )8.如图,在△ABC 中,分别以点A 和点B 为圆心,大于21AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC 于点D,连接AD,若△ADC 的周长为8,AB=6, 则△ABC 的周长为:A.20B.22C.14D.16 ( )9.已知抛物线c bx ax y ++=2的图像如图所示, 则直线b ax y -=一定不经过:A.第一象限B. 第二象限C. 第三象限D. 第四象限( )10.如图,在矩形ABCD 中,点E 是AD 的中点,∠EBC 的平分线交CD 于点F,将△DEF 沿EF 折叠,点D 恰好落在BE 上M 点处,延长BC,EF 交于点N.有下列四个结论: ①BF 垂直平分EN;②BF 平分∠MFC;③△DEF ∽△FEB;④tan ∠N=3.其中,将正确结论的序号全部选对的是:ABCDE第4题图主视图俯视图AB C DMN Ox yA. ①②③B. ①②④C. ②③④D. ①②③④二、填空题(每小题3分,共计18分)11.计算: 6)272483(÷-=________________.12.如图,点P 是反比例函数在第二象限上的一点,且矩形PEOF 的面积为5,则反比例函数的表达式为_____________. 13.若关于x 的不等式组⎩⎨⎧>+≥-0630x x m 的整数解恰好有三个,则m 的取值范围是____________.14.盒子里装有大小形状相同,质地均匀的4个白球和3个红球,搅匀后从中摸出一个球,放回搅匀后,再摸出第二个球,则两次取出的均是红球的概率是___________.15. 如图四边形ABCD 是⊙O 的内接四边形,已知∠BOD=120°则∠BCD 的度数为___________16.已知□ABCD 的周长为40㎝,AE ⊥BC 于点E,AF ⊥CD 于点F,若AE=4㎝,AF=6㎝,则CE+CF=_________㎝. 三、解答题(共72分) 17.(6分)先化简,再求值:222)11(yxy x yy x y x +-÷+-- 其中145sin 21-︒=x ,230sin 2-︒=y18. (6分)从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟, 从乙地到甲地需42分钟.甲地到乙地全程是多少千米?19. (6分)如图,点E 是□ABCD 的边AD 上一点,连接CE 并延长交BA 的延长线于点F,若BG=DE,并且∠AEF=70º.求∠AGB 的度数.A BCDE F G20. (7分)为响应襄阳市创建“全国卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A,B,C,D 四等.从中随机抽取了部分学生成绩进行统计,绘制成如图两幅不完整的统计图表,根据图表信息,解答下列问题:A BCDO(1)被抽取的学生总数是_____人,C 等在样本中所占的百分比是_____; (2) D 等在扇形统计图所对应的圆心角是多少度?并补全左侧的条形图; (3)估计全校校生成绩为A 等的大约有多少人?21. (6分)在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B 两个凉亭之间的距离.现测得AC=50m,BC=100m, ∠CAB=120º,请计算A,B 两个凉亭之间的距离.22. (7分)如图,AB 是⊙O 的直径,C 是⊙O 上的一点,AD 和过点C 的切线互相垂直,垂足为D ,AD 交⊙O 于E. (1)求证:AC 平分∠DAB ; (2)连接CE ,若CE=6,AC=8,求⊙O 的直径的长.23. (10分)为了拉动内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y (台)与补贴款额x (元)之间大致满足如图所示的一次函数关系.随着补贴款额x 的不断增大,销售量也不断增加,但每台彩电的收益p (元)会相应降低且满足:11051+-=x p(0≥x ).(1)在政府补贴政策实施后,求出该商场销售彩电台数y 与政府补贴款额x 之间的函数关系式;(2)在政府未出台补贴措施之前,该商场销售彩电的总收益额为多少元?(3)要使该商场销售彩电的总收益最大,政府应将每台补贴款额x 定为多少?并求出总收益的最大值.100014000100200y(台)x(元)24. (12分)已知:将一副三角板(Rt △ABC 和Rt △DEF)如图①摆放,点E,A,D,B 在一条直线上,且D 是AB 的中点.将Rt △DEF 绕点D 顺时针方向旋转角α(︒<<︒900α),在旋转过程中,直线DE,AC 相交于点M,直线DF,BC 相交于点N,分别过点M,N 作直线AB 的垂线,垂足为G ,H.(1)当︒=30α时(如图②),求证:AG=DH;(2) 当︒=60α时(如图③),(1)中的结论是否成立?请写出你的结论,并说明理由; (3)当︒<<︒900α(如图④)时,求证:DH GD HB AG ⋅=⋅.25. (12分)如图,抛物线与直线相交于A,B 两点,若点A 在x 轴上,点B 的坐标是(2,4),抛物线与x 轴另一交点为D,并且△ABD 的面积为6,直线AB 与y 轴的交点的坐标为(0,2).点P 是线段AB(不与A,B 重合)上的一个动点,过点P 作x 轴的垂线,交抛物线与点Q. (1)分别求出抛物线与直线的解析式; (2)求线段PQ 长度的最大值;(3)当PQ 取得最大值时, 在抛物线上是否存在M 、N 两点(点M 的横坐标小于N 的横坐标),使得P 、D 、M 、N 为顶点的四边形是平行四边形?若存在,求出MN 的坐标;若不存在,请说明理由.2016年襄城区适应性考试数学评分标准及参考答案一.选择题二.填空题11.23 12.x y 5-= 13.21<≤m 14.499 15.120º 16.31020+或324+ 三.解答题17.yx y x y y x y x y x y y y x y x y x y x y x y x y x +-=-⋅-+=-⋅-+---++=)(2)())((2)(]))(())(([:22原式解 ……………………3分由1212112221145sin 21+=-=-⨯=-︒=x ,212212230sin 2-=-⨯=-︒=y 得: 2,22=+=-y x y x ……………………5分∴原式=222222=⨯ ……………………6分 18.解:设从甲地到乙地时上坡段的路程为x 千米,平路段的路程为y 千米,根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+604245605443y x y x ……………………3分解得⎩⎨⎧==6.15.1y x ……………………4分1.36.15.1=+=+y x ……………………5分答:甲地到乙地的全程是3.1千米. ……………………6分19.解: ∵四边形ABCD 是平行四边形∴AB=CD, ∠B=∠D ……………………2分 又∵BG=DE∴△ABG ≌△CDE ……………………3分 ∴∠AGB=∠CED ……………………4分 ∵∠CED=∠AEF=70º ……………………5分 ∴∠AGB=70º ……………………6分20.解:(1)200,10% ……………………………………………………2分 (2)36º (补全图略)………………………………………………………………4分 (3)9002001201500=⨯……………………………………………………6分 答:全校学生成绩为A 等的大约有900人. ……………………………7分 21.解: 过点C 作CD ⊥AB 于D在Rt △CDA 中∠CAD=180º-∠CAB=180º-120º =60º…………………………………1分 ∵ACCDCAD =∠sin ∴325235060sin =⨯=︒⋅=AC CD ………………………………………………2分 同理:25215060cos =⨯=︒⋅=AC AD ………………………………………………3分 在Rt △CBD 中,1325)325(1002222=-=-=CD BC BD ………………4分∴AB=BD-AD=251325- ………………………………………………5分 答:AB 之间的距离是(251325-)m. ………………………………………………6分 22.(1)证明:如图,连接OC∵CD 是⊙O 的切线 ∴OC ⊥CD ∴∠OCF=90º ∵AD ⊥CD∴∠D=∠OCF=90º (2)分∴OC ∥AD∴∠1=∠3 ……………………………………3分 ∵OA=OC ∴∠2=∠3 ∴∠1=∠2即AC 平分∠DAB ……………………………………4分 (2)如右图,连接OE∵∠1=∠2, ∠1=EOC ∠21,∠2=BOC ∠21∴BOC EOC ∠=∠∴BC=CE=6 …………………………5分 ∵AB 是⊙O 的直径 ∴∠ACB=90º 在Rt △ABC 中10682222=+=+=BC AC AB …………………………6分∴⊙O 的直径的长为10. …………………………7分 23.(1)解:根据题意,可设b kx y += 将(100,1000),(200,1400)代入上式,得:⎩⎨⎧=+=+14002001000100b k b k ………………………2分 解得⎩⎨⎧==6004b k ………………………3分∴所求作的函数关系式为:6004+=x y . ………………………4分 (2) ∵在6004+=x y 中,当0=x 时,600=y在11051+-=x p 中,当0=x 时,110=p ………………5分 ∴66000110600=⨯答: 在政府未出台补贴措施之前,该商场销售彩电的总收益额为66000元. ……6分 (3)设总收益为W 元,则W=)11051)(6004(+-+x x ………………7分 =66000320542++-x x =98000)200(542+--x ………………8分∵ 054<-=a∴W 存在最大值∴当x=200时W 有最大值98000. ………………9分答: 政府应将每台补贴款额定为200元时,可获得最大利润98000元. ………………10分 24、(1)∵∠A=∠MDA=α=30º∴MA=MD 又∵MG ⊥AD∴AG=21AD ………………1分 ∵∠FDB=90º -α=90º -30º =60º ,∠B=60º ∴△CDB 是等边三角形 又∵CH ⊥BD ∴DH=21BD ………………2分 ∵D 为AD 的中点∴AD=BD ………………3分 ∴AG=DH ………………4分 (2)∵∠A=∠NDB ,AD=BD ,∠B=∠MDA=α=60º∴△AMD ≌△DNB ………………5分 ∴AM=DN又∵∠A=∠NDH=90º -α=90º -60º =30º,∠AGM=∠DHN=90º ∴△AGM ≌△DHN ………………7分 ∴AG=DH ………………8分 (3)在Rt △AGM 中,∠A=30º∴∠AMG=90º -30º =60º =∠B又∵∠AGM=∠NHB=90º∴△AGM ∽△NHB ………………9分∴NHHBAG MG =∴MG ·NH=AG ·HB ………………10分 ∵∠GMD+∠GDM=90º,∠HDN+∠GDM=90º ∴∠GMD=∠HDN又∵∠MGD=∠DHN=90º ∴△MGD ∽△DHN ∴DHHNMG GD =∴MG ·NH=GD ·DH ………………11分 ∴AG ·HB=GD ·GH ………………12分25、(1)解:设直线的解析式为: b kx y += 将点B(2,4),点(0,2)代入上式得:⎩⎨⎧==+242b b k 解得⎩⎨⎧==21b k ∴所求直线的解析式为:2+=x y . ………………2分当0=y 时,2-=x ,即点A 的坐标为(-2,0) ∵S △ABD =64)]2([21||21=⨯--⨯=⋅D B x y AD ∴1=D x∴点D 的坐标(1,0)设抛物线的解析式为:)1)(2(-+=x x a y 将点B(2,4)代入上式得:1=a∴所求抛物线的解析式为:)1)(2(-+=x x y即22-+=x x y ………………4分(2)设点P 的横坐标为t ,则点P 为(t ,t+2),点Q 为(t ,22-+t t )………………5分 ∴PQ=t+2-(22-+t t )=42+-t ………………7分 ∵a=-1<0∴PQ 有最大值4 ………………8分 (3)由(2)知点P 坐标为(0,2) ………………9分 ①以PD 为平行四边形的边时,设点M 坐标为(m ,n )则点N 为(m+1,n-2) ∵点M 、N 均在抛物线上∴ n=m 2+m-2n-2=(m+1)2+m+1-2 解得 m=-2n=0∴M(-2,0),N (-1,-2) …………10分 ②以PD 为平行四边形的对角线时,设点M 为(m,n )则点N 为(1-m,2-n )同(1)理得M (-1,-2)N (2,4) …………11分 综上所述存在M (-2,2),N (-1,-2)和M (-1,-2),N (2,4)满足题意。
襄城区2016中考适应性考试训练题答案

2016年襄城区适应性考试训练题参考答案一.选择题二.填空题11.)2)(2(-+x x x 12.1->k 且0≠k 13.221<≤-x 14.50º 15.3 16. 22 三.解答题17.解:原式x x -+=)2(3 ………………………………………………1分x x -+=63 ………………………………………………2分62+=x ………………………………………………3分由︒-=30sin 3x ,得23-=x . ……………………………………4分 ∴原式36)23(2=+-⨯= . ……………………………………………5分 18.证明: ∵AB ∥DE∴∠B=∠EDF ………………………………………………2分∴在△ABC 与△FDE 中⎪⎩⎪⎨⎧∠=∠=∠=∠F A DFAB EDF B ……………………………………………5分 ∴△ABC ≌△FDE ……………………………………………7分∴BC=DE ……………………………………………8分19.解:(1)∵在3+=kx y 中,当0=x 时,3=y∴点D 的坐标为(0,3) ……………………………………………1分∴BD=3-(-6)=9又∵S △DBP =27∴27||21=⋅P x BD 即27||921=⨯⨯P x ∴6||=P x∵点P 在第四象限且PB ⊥y 轴于点B∴点P 的坐标为(6,-6) ……………………………………………2分将点P(6,-6)分别代入3+=kx y 与xm y =得:一次函数的表达式为:323+-=x y 反比例函数的表达式为:xy 36-= ……………………………………………3分 (2) ∵在323+-=x y 中, 当0=y 时,2=x ∴点C 的坐标为(2,0) ……………………………………………4分∴S △DOQ =21S △COD =322121⨯⨯⨯=23 ∴23||21=⋅Q x OD 即23||321=⨯⨯Q x ∴ 1||=Q x ……………………………………………5分将1=x 或1-=x 代入323+-=x y 得23=y 或29=y ∴点Q 的坐标为(1,23)或(-1,29) ……………………………………………6分 20.解:(1)金刚酥10人(图略)……………………………………………2分 (2)60050103000=⨯ ……………………………………………3分 答:全校同学中最喜爱金刚酥的同学有600人.…………………………4分(3) 用树状图如图所示: AA BC D B A B C D C A B C D D A B C D …………5分 共有16种等可能情况,恰好两次都摸到A 的有1种.…………6分∴恰好两次都摸到A 的的概率是161.……………………7分 21.解:设购买一个手电峝用x 元,则购买一个台灯用(x+20)元,根据题意,得:xx 1604520400⨯=+ ……………………1分 解得20=x ……………………2分经检验20=x 是原分式方程的解. ……………………3分设神火公司可购买m 个该品牌的台灯, 根据题意,得:1540)82(2040≤++m m ……………………4分 解得4117≤m ……………………5分 ∵m 取正整数∴m 可取的最大值是17 ……………………6分答: 神火公司最多可购买17个该品牌的台灯. ……………………7分22.(1)证明:连接OD∵DE ⊥MN∴∠DEM=90º……………………1分∵AD 平分∠CAM∴∠OAD=∠DAM又∵OD=OA∴∠OAD=∠ODA∴∠ODA=∠DAM∴OD ∥AE ……………………2分∴∠ODE=∠DEM=90º∴OD ⊥DE ……………………3分∴DE 是⊙O 的切线. ……………………4分(2)连接CD在Rt △DEA 中52242222=+=+=AE DE DA ……………………5分∵AC 是直径∴∠ADC=∠AED=90º又∵∠DAE=∠CAD∴△DAE ∽△CAD ……………………6分∴ACAD AD AE = 即AC52522= ∴AC=10……………………7分即⊙O 的直径是10㎝. ……………………8分23.解:(1)批发量不少于20㎏但少于60㎏时,批发单价为5元/㎏;批发量不少于60㎏时, 批发单价为4元/㎏. ……………………………………………2分(2)当6020<≤m 时,m w 5=;当60≥m 时, m w 4=…………………………………………4分图略…………………………………………5分显然当300240≤<w 时,两种批发方式产生了交集,此时批发单价为4元/㎏,可以批发到较多数量的这种蔬菜. …………………………………………6分(3)设最高销量y(㎏)与零售价x(元)的函数关系式为:b kx y +=将(6,80),(7,40)代入上式得:⎩⎨⎧=+=+407806b k b k 解得⎩⎨⎧=-=32040b k ∴32040+-=x y …………………………………………7分设每天获得的利润为z 元,由题意得:)32040)(40(+--=x x z1280480402-+-=x x160)6(402+--=x …………………………………………8分∵040<-=a∴当6=x 时,z 有最大值160当6=x 时,80320640=+⨯-=y …………………………………………9分答:进货80㎏且销售单价为6元/㎏时,每日获得的利润最大. ……………………10分 24.(1)32 ……………………………………2分(2)由题意可知: ∠A=∠B=90º, ∠AMP=∠BNQ=60º,AP=BQ∴△AMP ≌△BNQ∴S △AMP =S △BNQ …………………………………3分∴要满足题目要求,只需S △AMP =S △EMN 即可.设点E 向平移的距离为x,则AP=x,根据题意,得S △AMP =AP AM ⋅21=x x ⋅⨯3321263x = S △EMN =)33)(33(33221x x --⨯=2)33(33x - ∴22)33(3363x x -=…………………………………5分 解得6336-=x 或66336>+=x (不合题意,舍去)∴点E 向右平移6336-时, △AMP,△BNQ,△EMN 三个三角形的面积相等.……6分(3)由题意可知,当PQ ∥AB 时,AP=BQ 可以产生如图所示的以下两种情况:A BC D O(E)P QA B C D O (E)QP 1图2图H 如图1∵PQ ∥AB,PQ=AB=6∴四边形APQB 是平行四边形∴AP=BQ ………………………8分过点O 作OH ⊥AB 于N根据正方形ABCD 与等边△EPQ 的轴对称性可知:∠AOH=45º, ∠POH=30º∴∠AOP=∠AOH-∠POH=45º-30º=15º………………………9分同理可得图2中的∠AOP=165º综上所述,当AP=BQ 时, ∠AOP 的度数为15º或165º………………………10分25.(1)解:由0822=--x x 解得:2-=x 或4∵x 1>x 2∴点A,B 的坐标分别为(4,0),(-2,0) ……………………1分∴可设所求的抛物线的解析式为:)4)(2(-+=x x a y将点C(0,4)代入上式得:21-=a ……………………2分 ∴)4)(2(21-+-=x x y 即4212++-=x x y ……………………3分 (2)设点P 的坐标为(m,0)由A(4,0),C(0,4)可知AC 所在直线为:4+-=x y由B(-2,0),C(0,4)可知AC 所在直线为:42+=x y ……………………4分 ∵PE ∥AC∴可设PE 所在直线为: b x y +-=将点P(m,0)代入上式得:m b =∴PE 所在直线为: m x y +-=由⎩⎨⎧+=+-=42x y m x y 解得⎪⎪⎩⎪⎪⎨⎧+=-=34234m y m x 即点E 的坐标为(342,34+-m m ) 同理点F 的坐标为: (328,342m m -+)……………………5分 ∵S 四边形PECF =S △ABC - S △EBP - S △FPA =||21||2121F E y AP y BP OC AB ⋅-⋅-⋅ 328)4(21342)2(214621m m m m -⋅--+⋅+-⨯⨯= 31634322++-=m m 6)1(322+--=m ……………………6分∵032<-=a ∴当1=m 时,四边形PECF 的面积取得最大值6 ∴当四边形PECF 的面积最大时,点P 的坐标为(1,0) ……………………7分(3)存在点Q 使得△QAC 为等腰三角形,点Q 的坐标为: (0,0),(0,-4),(0,244+), (0,244-) ……………………11分(每写对一个加1分)。
襄阳市襄州区2016-2017学年中考适应性考试数学试题含答案

襄州区2016—2017学年度九年级适应性考试数 学 试 题(本试题共4页,满分120分,考试时间120分钟)★祝考试顺利★一、选择题(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将序号在答题卡上涂黑作答. 1.2017的相反数是( )A .﹣2017B .2017C .20171 D.201712.实数5的值在( ) A .1和2之间B .2和3之间C .3和4之间D .4和5之间3.下列计算正确的是( )A.3a +4b =7abB.(ab 3)3=ab 6C .x 12÷x 6=x 6D.(a +2)2=a 2+4 4.如图,AB ∥CD ,射线AE 交CD 于点F ,若∠1=125°,则∠2的度数是( )A .55°B .65°C .75°D .85°5.2017年4月8日,中国财经新闻报道中国3月外汇储备30090.9亿,这个数据用科学计 数法表示为( )A .3.00909×104 B .3.00909×105 C .3.00909×1012 D .3.00909×1013 6.如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( )A .B .C .D .7.某校九年级(1)班全体学生2017年初中毕业体育考试的成绩统计如表:根据表中的信息判断,下列结论中错误的是( ) A .该班一共有50名同学B .该班学生这次考试成绩的众数是30分成绩(分) 25 29 26 24 27 28 30 人数(人) 66981056C .该班学生这次考试成绩的中位数是27分D .该班学生这次考试成绩的平均数是26.8分8.如图,在▱ABCD 中,BF 平分∠ABC ,交AD 于点F ,CE 平分∠BCD ,交AD 于点E ,AB=6, EF=2,则BC 长为( )A .8B .10C .12D .149.如图,△ABC 中,D 为AB 上一点,E 为BC 上一点,且AC=CD=BD=BE ,∠A=50°,则∠CDE 的度数为( ) A .50° B .51°C .51.5°D .52.5°10.如图,在Rt △AOB 中,∠AOB=90°,OA=2,OB=1,将Rt △AOB 绕点O 顺时针旋转90°后 得Rt △FOE ,将线段EF 绕点E 逆时针旋转90°后得线段ED ,分别以O ,E 为圆心,OA 、 ED 长为半径画弧AF 和弧DF ,连接AD ,则图中阴影部分面积是( ) A .π B .5+π C .414π- D .410π- 二、填空题(本大题共6个小题,每小题3分,共18分)把答案填在答题卡的相应位置上. 11.分解因式:m 3-4m =_____________.12.已知x ﹣2y =3,那么代数式3+2x-4y 的值是________.13.某校在甲、乙两名同学中选拔一人参加襄阳广播电台举办“国学风,少年颂”襄阳首届少 年儿童经典诵读大赛.在相同的测试条件下,两人3次测试成绩(单位:分)如下: 甲:79,86,82;乙:88,79,90.从甲、乙两人3次的成绩中各随机抽取一次成绩进 行分析,求抽到的两个人的成绩都大于80分的概率是_______.14.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,请你添加一个适当的条件 ______________________使其成为菱形(只填一个即可).15.若点O 是等腰△ABC 的外心,且∠BOC=60°,底边BC=2,则△ABC 的面积 为____________________.16.如图,在正方形ABCD 中,△APBC 是等边三角形,连接PD ,DB ,则.___________=∆ABCDBPD S S 正方形三、解答题(本大题共9个小题,共72分.解答应写出文字说明、证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.) 17.(本小题满分6分) 化简求值:122)12124(22+-+÷+--+x x x x x x ,其中12-=x .18.(本小题满分6分)某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)这次调查的学生共有多少名?(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数. (3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法, 求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次 记为A 、B 、C 、D 、E ). 19.(本小题满分6分)如图,一次函数b kx y +=1(k <0)与反比例函数xmy =2的图象相交于A 、B 两点, 一次函数的图象与y 轴相交于点C ,已知点A (4,1),B (n,2))(1)求反比例函数和一次函数的解析式;(2)写出1y>2y时,x的取值范围;20.(本小题满分6分)某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.(1)求购买一个甲种足球、一个乙种足球各需多少元;(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?21.(本小题满分6分)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M.(1)求证:△AEC≌△ADB;(2)若BC=2,∠BAC=30°,当四边形ADFC是菱形时,求BF的长.22.(本小题满分8分)如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O 于点E.(1) 求证:AC平分∠DAB;xyOA BCAB CDEF(2) 连接CE ,若CE=6,AC=8,求AE 的长.23.(本小题满分11分) 某淘宝店专销某种品牌的运动服,每套进价70元,售价120元/套.为了促销,淘宝店决定凡是一次购买数量不超过10套的,按原价每套120元购买;10套以上的,每多买1套,每套降价1元,每多买2套,每套降价2元…^(例如,某人一次性购买15套运动服,多出5套,按每套降价5元购买,共需(15×115)元;但是最低价90元/套. (1)求顾客一次至少买多少套,才能以最低价购买?,(2)写出当一次购买x (x >10)件时,利润w (元)与购买量x (件)之间的函数关系式;(3)有一天,一位顾客买了35套运动服,另一位顾客买了40套运动服,淘宝店发现卖了 40套反而比卖35套赚的钱少!为了使每次卖的数量多赚的钱也多,在其它促销条件 不变的情况下,最低价为90元/套至少要提高到多少?为什么?24.(本小题满分11分) 如图,将矩形ABCD 沿AH 折叠,使得顶点B 落在CD 边上的P 点处.折痕与边BC 交于点 H, 已知AD=8,HC:HB=3:5. (1)求证:△H CP∽△PDA;(2) 探究AB 与HB 之间的数量关系,并证明你的结论;(3)连结BP ,动点M 在线段AP 上(点M 与点P 、A 不重合),动点N 在线段AB 的延长 线上,且BN=PM ,连结MN 交PB 于点F ,作ME⊥BP 于点E .试问当点M 、N 在移动过 程中,线段EF 的长度是否发生变化?若变化,说明理由;说明理由;若不变,求 出线段EF 的长度.25.(本小题满分12分)已知,△ABC 在平面直角坐标系中的位置如图①所示,A 点坐标为(﹣4,0),B 点坐标 为(6,0),点D 为BC 的中点,点E 为线段AB 上一动点,连接DE 经过点A 、B 、C 三点 的抛物线的解析式为28y ax bx =++.(1)求抛物线的解析式;(2)如图①,将△ADE 以DE 为轴翻折,点A 的对称点为点G ,当点G 恰好落在抛物线的 对称轴上时,求G 点的坐标;(3)如图②,当点E 在线段AB 上运动时,抛物线28y ax bx =++的对称轴上是否存在点F ,使得以C 、D 、E 、F 为顶点的四边形为平行四边形?若存在,请直接写出点E\F 的坐标;若不存在,请说明理由.襄州区2017年适应性考试数学 参考答案题号 1 2 3 4 5 6 7 8 9 10 答案 A B C A C ABBDD11. )2)(2(-+m m m ; 12. 9; 13.94; 14. AC ⊥BD(答案不唯一,只要正确,均给分);15.32+或32-; 16.413-. 三、解答题(共72分) 17.(本小题6分)解:122)12124(22+-+÷+--+x x x x x x=2)1()1)(1()2(22+-•-++x x x x x ………………2分=1221)1(2+-=+-x x x x ………………4分当12-=x 时,原式=112)112(2+--- =222-…………6分 18.(本小题6分)解:(1)56÷20%=280(名),答:这次调查的学生共有280名;………………1分 (2)互助:280×15%=42(名),进取:280﹣42﹣56﹣28﹣70=84(名),………………2分 补全条形统计图,如图所示,………………3分(3)由(2)中调查结果知:学生关注最多的两个主题为“进取”和“感恩” 用树状图为:………………4分如图,共有20个等可能结果,恰好选到“C ”和“E ”有2个,……5分 ∴恰好选到“进取”和“感恩”两个主题的概率是.……………6分19.(本小题6分)解:(1)∵点A (4,1)在反比例函数y=的图象上, ∴m=4×1=4,∴反比例函数的解析式为y=.………………1分 ∵点B 在反比例函数y=的图象上,∴将点B 的坐标为(n ,2)代入y=得n=2. ∴B (2,2), ………………2分 将点A (4,1),B (2,2)分别代入y=kx+b , 用待定系数法可求得一次函数解析式为321+-=x y ;………………4分(2)由图象可知,当1y >2y 时,x <0或42<<x .…………6分20.(本小题6分)解:(1)设购买一个甲种足球需x 元,则购买一个乙种足球需(x +20)元, 由题意得:20216002400+⨯=x x .………………1分 解得:x =60.………………2分 经检验,x =60是原方程的解.x +20=80答:购买一个甲种足球需60元,购买一个乙种足球需80元..…………3分 (2)设这所学校可购买y 个甲种足球,由题意得: )50(8060y y -+≤3500,.………………4分 解得:y ≥25.………………5分答:这所学校此次最少可购买25个甲种足球..………………6分解:(1)由旋转的性质得:△ABC ≌△ADE ,且AB=AC , ∴AE=AD ,AC=AB ,∠BAC=∠DAE ,.………………1分 ∴∠BAC+∠BAE=∠DAE+∠BAE ,即∠CAE=∠DAB , ∴△AEC ≌△ADB (SAS );.………………2分 (2)过点B 作BM ⊥EC 于点M ,∵∠BAC=30°AB=AC, ∴∠ABC=∠ACB=75°.…………3分 ∵当四边形ADFC 是菱形时,AC ∥DF, ∴∠FBA=∠BAC=30°, ∵AB=AD,∴∠ADB=∠ABD=30°,∴∠ACE=∠ADB=30°,∴∠FCB=45°.…………4分 ∵BM ⊥EC ,∴∠MBC=45°, ∴BM=MC=BCsin45°=22×2=2,.………………5分 ∵∠ABC =75°,∠ABD =30°,∠FCB=45° ∴∠BFC =180°-75°-45°-30°=30°, ∴BF=2BM=22..………………6分 22.(本小题8分)(1)证明:连接OC ,则OC ⊥CD ,又AD ⊥CD ,∴∠ADC=∠OCD=90°, ∴AD ∥OC ,∴∠CAD =∠OCA ,..………………1分 又OA =OC ,∴∠OCA =∠OAC ,∴∠CAD =∠CAO ,∴AC 平分∠DAB ...………………2分 (2)解:连接BC 、OB,∵∠EOA =2∠CAD ,∠COB=2∠CAO ∵∠CAD =∠CAO,∴∠EOA =∠COB ∴BC=EC=6………………3分 ∵AB 是⊙O 的直径,∴∠ACB=90°,又AC=8,勾股定理易得AB=10,………………4分 ∵∠DAC =∠CAB,∠ADC =∠ACB=90°,∴△ADC ∽△ACB,∴ABACAC AD =, ∴AD=1086⨯=4.8,………………6分又∠DEC=∠ABC,同理可得DE=3.6, ∴AE=AD-DE=6.4-3.6=2.8.………………8分解:(1)由题意得:(120-90)÷1+10=40(套);………………2分 (2)当10<x ≤40时,w =x (60-x )=x x 602+-;………………4分 当x >40时,w =(90-70)x =20x ………………5分 (3)当x >40时,w =20x ,w 随x 的增大而增大,符合题意; ………………6分 当10<x ≤40时,w =x x 602+-=900)30(2+--x ………………8分 ∵a =﹣1<0,∴抛物线开口向下.对称轴是直线x=30∴ 10<x ≤30,w 随着x 的增大而增大,………………9分 而当x =30时,w 最大值=900; ………………10分∵要求卖的数量越多赚的钱越多,即w 随x 的增大而增大, ∴由以上可知,当x =30,最低售价为120﹣(30﹣10)=100元.……11分24.(本小题11分)解:(1)由折叠的性质可知,∠APH=∠B=90°, ∴∠APD+∠HPC=90°, 又∠PHC+∠HPC=90°, ∴∠APD=∠PHC ,………………1分 又∠D=∠C=90°,∴△HCP ∽△PDA ;………………2分(2) AB=2BH.∵HC:HB=3:5,设HC=3x ,则HB=5x ,在矩形ABCD 中,BC=AD=8 ,∴HC=3,则HB=5 ……3分 由折叠的性质可知HP=HB=5,AP=AB,在Rt △HCP,易得PC=4,∵△HCP ∽△PDA∴HP CP AP AD =,∴10458=⨯=AP ………………5分 ∴AB=AP=10=2BH,即AB=2BH.………………6分(3)EF 的长度不变. ………………7分作MQ ∥AB 交PB 于Q , ∴∠MQP=∠ABP , 由折叠的性质可知,∠APB=∠ABP ,∴∠MQP=∠APB ,∴MP=MQ ,又BN=PM ,∴MQ=BN ,∵MQ ∥AB ,∴BNMQ FB QF =, ∴QF=FB ,………………8分∵MP=MQ ,ME ⊥BP , ∴PE=QE ,∴EF=21PB , ………………9分 由(2)得,PC=4,BC=8,∴PB=22BC PC +=54,………………10分 ∴EF=52 .………………11分25.(本小题12分)解:(1)∵抛物线28y ax bx =++经过点A (﹣4,0),B (6,0),∴⎩⎨⎧=++=+-0863608416b a b a , ………………2分 解得⎪⎩⎪⎨⎧=-=3231b a ,………………3分 ∴抛物线的解析式是:832312++-=x x y ;………………4分 (2)如图,作DM ⊥抛物线的对称轴于点M ,设G 点的坐标为(1,n ),由翻折的性质,可得AD=DG , ∵A (-4,0),C (0,8),点D 为AC 的中点, ∴点D 的坐标是(-2,4),………………6分∴点M 的坐标是(﹣1,4),DM=2﹣(﹣1)=3, ∵B (6,0),C (0,8),∴AC=2248+=45,∴AD=25,………………7分在Rt △GDM 中,222MG DM DG +=32+(4﹣n )2=20,解得n=411±,………………8分 ∴G 点的坐标为(1,411+)或(1,411-);………………9分(3)存在.符合条件的点E 、F 的坐标为:1E (-1,0) ,1F (1,4);………………10分 2E (3,0),2F (1,-4);………………11分 3E (-3,0),3F (1,12).………………12分。
最新襄阳市襄州区-学年中考适应性考试数学试题含答案.doc

襄州区2016—2017学年度九年级适应性考试数 学 试 题(本试题共4页,满分120分,考试时间120分钟)★祝考试顺利★一、选择题(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将序号在答题卡上涂黑作答. 1.2017的相反数是( )A .﹣2017B .2017C .20171D .201712.实数5的值在( ) A .1和2之间B .2和3之间C .3和4之间D .4和5之间3.下列计算正确的是( )A.3a +4b =7abB.(ab 3)3=ab 6C .x 12÷x 6=x 6D.(a +2)2=a 2+4 4.如图,AB ∥CD ,射线AE 交CD 于点F ,若∠1=125°,则∠2的度数是( )A .55°B .65°C .75°D .85°5.2017年4月8日,中国财经新闻报道中国3月外汇储备30090.9亿,这个数据用科学计 数法表示为( )A .3.00909×104B .3.00909×105C .3.00909×1012D .3.00909×10136.如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( )A .B .C .D .7.某校九年级(1)班全体学生2017年初中毕业体育考试的成绩统计如表:根据表中的信息判断,下列结论中错误的是( ) A .该班一共有50名同学B .该班学生这次考试成绩的众数是30分C .该班学生这次考试成绩的中位数是27分D .该班学生这次考试成绩的平均数是26.8分8.如图,在▱ABCD 中,BF 平分∠ABC ,交AD 于点F ,CE 平分∠BCD ,交AD 于点E ,AB=6, EF=2,则BC 长为( )A .8B .10C .12D .149.如图,△ABC 中,D 为AB 上一点,E 为BC 上一点,且AC=CD=BD=BE ,∠A=50°,则∠CDE 的度数为( ) A .50° B .51°C .51.5°D .52.5°10.如图,在Rt △AOB 中,∠AOB=90°,OA=2,OB=1,将Rt △AOB 绕点O 顺时针旋转90°后 得Rt △FOE ,将线段EF 绕点E 逆时针旋转90°后得线段ED ,分别以O ,E 为圆心,OA 、 ED 长为半径画弧AF 和弧DF ,连接AD ,则图中阴影部分面积是( ) A .π B .5+π C .414π- D .410π- 二、填空题(本大题共6个小题,每小题3分,共18分)把答案填在答题卡的相应位置上. 11.分解因式:m 3-4m =_____________.12.已知x ﹣2y =3,那么代数式3+2x-4y 的值是________.13.某校在甲、乙两名同学中选拔一人参加襄阳广播电台举办“国学风,少年颂”襄阳首届少 年儿童经典诵读大赛.在相同的测试条件下,两人3次测试成绩(单位:分)如下: 甲:79,86,82;乙:88,79,90.从甲、乙两人3次的成绩中各随机抽取一次成绩进 行分析,求抽到的两个人的成绩都大于80分的概率是_______.14.如图,平行四边形ABCD 的对角线AC ,BD 相交于点O ,请你添加一个适当的条件______________________使其成为菱形(只填一个即可).15.若点O 是等腰△ABC 的外心,且∠BOC=60°,底边BC=2,则△ABC 的面积 为____________________.16.如图,在正方形ABCD 中,△APBC 是等边三角形,连接PD ,DB ,则.___________=∆A B C DBPDS S 正方形 三、解答题(本大题共9个小题,共72分.解答应写出文字说明、证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.) 17.(本小题满分6分) 化简求值:122)12124(22+-+÷+--+x x x x x x ,其中12-=x .18.(本小题满分6分)某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)这次调查的学生共有多少名?(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数. (3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法, 求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次 记为A 、B 、C 、D 、E ). 19.(本小题满分6分)如图,一次函数b kx y +=1(k <0)与反比例函数xmy =2的图象相交于A 、B 两点, 一次函数的图象与y 轴相交于点C ,已知点A (4,1),B (n,2))(1)求反比例函数和一次函数的解析式;(2)写出1y>2y时,x的取值范围;20.(本小题满分6分)某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.(1)求购买一个甲种足球、一个乙种足球各需多少元;(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?21.(本小题满分6分)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F,BD交AE于M.(1)求证:△AEC≌△ADB;(2)若BC=2,∠BAC=30°,当四边形ADFC是菱形时,求BF的长.22.(本小题满分8分)如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.(1) 求证:AC平分∠DAB;xCE(2) 连接CE ,若CE=6,AC=8,求AE 的长.23.(本小题满分11分) 某淘宝店专销某种品牌的运动服,每套进价70元,售价120元/套.为了促销,淘宝店决定凡是一次购买数量不超过10套的,按原价每套120元购买;10套以上的,每多买1套,每套降价1元,每多买2套,每套降价2元…^(例如,某人一次性购买15套运动服,多出5套,按每套降价5元购买,共需(15×115)元;但是最低价90元/套. (1)求顾客一次至少买多少套,才能以最低价购买?,(2)写出当一次购买x (x >10)件时,利润w (元)与购买量x (件)之间的函数关系式;(3)有一天,一位顾客买了35套运动服,另一位顾客买了40套运动服,淘宝店发现卖了 40套反而比卖35套赚的钱少!为了使每次卖的数量多赚的钱也多,在其它促销条件 不变的情况下,最低价为90元/套至少要提高到多少?为什么?24.(本小题满分11分) 如图,将矩形ABCD 沿AH 折叠,使得顶点B 落在CD 边上的P 点处.折痕与边BC 交于点 H, 已知AD=8,HC:HB=3:5. (1)求证:△H CP∽△PDA;(2) 探究AB 与HB 之间的数量关系,并证明你的结论;(3)连结BP ,动点M 在线段AP 上(点M 与点P 、A 不重合),动点N 在线段AB 的延长 线上,且BN=PM ,连结MN 交PB 于点F ,作ME⊥BP 于点E .试问当点M 、N 在移动过 程中,线段EF 的长度是否发生变化?若变化,说明理由;说明理由;若不变,求 出线段EF 的长度.25.(本小题满分12分)已知,△ABC 在平面直角坐标系中的位置如图①所示,A 点坐标为(﹣4,0),B 点坐标 为(6,0),点D 为BC 的中点,点E 为线段AB 上一动点,连接DE 经过点A 、B 、C 三点 的抛物线的解析式为28y ax bx =++.(1)求抛物线的解析式;(2)如图①,将△ADE 以DE 为轴翻折,点A 的对称点为点G ,当点G 恰好落在抛物线的 对称轴上时,求G 点的坐标;(3)如图②,当点E 在线段AB 上运动时,抛物线28y ax bx =++的对称轴上是否存在 点F ,使得以C 、D 、E 、F 为顶点的四边形为平行四边形?若存在,请直接写出点E\F 的坐标;若不存在,请说明理由.襄州区2017年适应性考试数学 参考答案11. )2)(2(-+m m m ; 12. 9; 13.94; 14. AC ⊥BD(答案不唯一,只要正确,均给分);15.32+或32-; 16.413-. 三、解答题(共72分) 17.(本小题6分)解:122)12124(22+-+÷+--+x x x x x x=2)1()1)(1()2(22+-∙-++x x x x x ………………2分=1221)1(2+-=+-x x x x ………………4分当12-=x 时,原式=112)112(2+--- =222-…………6分 18.(本小题6分)解:(1)56÷20%=280(名),答:这次调查的学生共有280名;………………1分 (2)互助:280×15%=42(名),进取:280﹣42﹣56﹣28﹣70=84(名),………………2分 补全条形统计图,如图所示,………………3分(3)由(2)中调查结果知:学生关注最多的两个主题为“进取”和“感恩” 用树状图为:………………4分如图,共有20个等可能结果,恰好选到“C ”和“E ”有2个,……5分∴恰好选到“进取”和“感恩”两个主题的概率是.……………6分19.(本小题6分)解:(1)∵点A (4,1)在反比例函数y=的图象上, ∴m=4×1=4,∴反比例函数的解析式为y=.………………1分∵点B 在反比例函数y=的图象上,∴将点B 的坐标为(n ,2)代入y=得n=2. ∴B (2,2), ………………2分 将点A (4,1),B (2,2)分别代入y=kx+b , 用待定系数法可求得一次函数解析式为 321+-=x y ;………………4分 (2)由图象可知,当1y >2y 时,x <0或42<<x .…………6分20.(本小题6分)解:(1)设购买一个甲种足球需x 元,则购买一个乙种足球需(x +20)元, 由题意得:20216002400+⨯=x x .………………1分解得:x =60.………………2分 经检验,x =60是原方程的解.x +20=80答:购买一个甲种足球需60元,购买一个乙种足球需80元..…………3分 (2)设这所学校可购买y 个甲种足球,由题意得: )50(8060y y -+≤3500,.………………4分 解得:y ≥25.………………5分答:这所学校此次最少可购买25个甲种足球..………………6分21.(本小题6分)解:(1)由旋转的性质得:△ABC ≌△ADE ,且AB=AC , ∴AE=AD ,AC=AB ,∠BAC=∠DAE ,.………………1分 ∴∠BAC+∠BAE=∠DAE+∠BAE ,即∠CAE=∠DAB , ∴△AEC ≌△ADB (SAS );.………………2分 (2)过点B 作BM ⊥EC 于点M ,∵∠BAC=30°AB=AC, ∴∠ABC=∠ACB=75°.…………3分 ∵当四边形ADFC 是菱形时,AC ∥DF, ∴∠FBA=∠BAC=30°, ∵AB=AD,∴∠ADB=∠ABD=30°,∴∠ACE=∠ADB=30°,∴∠FCB=45°.…………4分 ∵BM ⊥EC ,∴∠MBC=45°, ∴BM=MC=BCsin45°=22×2=2,.………………5分 ∵∠ABC =75°,∠ABD =30°,∠FCB=45° ∴∠BFC =180°-75°-45°-30°=30°, ∴BF=2BM=22..………………6分 22.(本小题8分)(1)证明:连接OC ,则OC ⊥CD ,又AD ⊥CD ,∴∠ADC=∠OCD=90°, ∴AD ∥OC ,∴∠CAD =∠OCA ,..………………1分 又OA =OC ,∴∠OCA =∠OAC ,∴∠CAD =∠CAO ,∴AC 平分∠DAB ...………………2分 (2)解:连接BC 、OB,∵∠EOA =2∠CAD ,∠COB=2∠CAO ∵∠CAD =∠CAO,∴∠EOA =∠COB ∴BC=EC=6………………3分 ∵AB 是⊙O 的直径,∴∠ACB=90°,又AC=8,勾股定理易得AB=10,………………4分 ∵∠DAC =∠CAB,∠ADC =∠ACB=90°,∴△ADC ∽△ACB,∴ABACAC AD =, ∴AD=1086⨯=4.8,………………6分又∠DEC=∠ABC,同理可得DE=3.6,∴AE=AD-DE=6.4-3.6=2.8.………………8分 23.(本小题11分)解:(1)由题意得:(120-90)÷1+10=40(套);………………2分 (2)当10<x ≤40时,w =x (60-x )=x x 602+-;………………4分 当x >40时,w =(90-70)x =20x ………………5分 (3)当x >40时,w =20x ,w 随x 的增大而增大,符合题意; ………………6分 当10<x ≤40时,w =x x 602+-=900)30(2+--x ………………8分 ∵a =﹣1<0,∴抛物线开口向下.对称轴是直线x=30∴ 10<x ≤30,w 随着x 的增大而增大,………………9分 而当x =30时,w 最大值=900; ………………10分∵要求卖的数量越多赚的钱越多,即w 随x 的增大而增大, ∴由以上可知,当x =30,最低售价为120﹣(30﹣10)=100元.……11分24.(本小题11分)解:(1)由折叠的性质可知,∠APH=∠B=90°, ∴∠APD+∠HPC=90°, 又∠PHC+∠HPC=90°, ∴∠APD=∠PHC ,………………1分 又∠D=∠C=90°,∴△HCP ∽△PDA ;………………2分(2) AB=2BH.∵HC:HB=3:5,设HC=3x ,则HB=5x ,在矩形ABCD 中,BC=AD=8 ,∴HC=3,则HB=5 ……3分 由折叠的性质可知HP=HB=5,AP=AB,在Rt △HCP,易得PC=4,∵△HCP ∽△PDA∴HP CP AP AD =,∴10458=⨯=AP ………………5分 ∴AB=AP=10=2BH,即AB=2BH.………………6分(3)EF 的长度不变. ………………7分作MQ ∥AB 交PB 于Q , ∴∠MQP=∠ABP , 由折叠的性质可知,∠APB=∠ABP ,∴∠MQP=∠APB ,∴MP=MQ ,又BN=PM ,∴MQ=BN ,∵MQ ∥AB ,∴BNMQ FB QF =, ∴QF=FB ,………………8分∵MP=MQ ,ME ⊥BP , ∴PE=QE ,∴EF=21PB , ………………9分 由(2)得,PC=4,BC=8,∴PB=22BC PC +=54,………………10分 ∴EF=52 .………………11分25.(本小题12分)解:(1)∵抛物线28y ax bx =++经过点A (﹣4,0),B (6,0),∴⎩⎨⎧=++=+-0863608416b a b a , ………………2分 解得⎪⎩⎪⎨⎧=-=3231b a ,………………3分 ∴抛物线的解析式是:832312++-=x x y ;………………4分 (2)如图,作DM ⊥抛物线的对称轴于点M ,设G 点的坐标为(1,n ),由翻折的性质,可得AD=DG , ∵A (-4,0),C (0,8),点D 为AC 的中点, ∴点D 的坐标是(-2,4),………………6分∴点M 的坐标是(﹣1,4),DM=2﹣(﹣1)=3, ∵B (6,0),C (0,8),∴∴AD=………………7分在Rt △GDM 中,222MG DM DG +=32+(4﹣n )2=20,解得n=4,………………8分 ∴G 点的坐标为(1,4)或(1,4………………9分(3)存在.符合条件的点E 、F 的坐标为:1E (-1,0) ,1F (1,4);………………10分 2E (3,0),2F (1,-4);………………11分 3E (-3,0),3F (1,12).………………12分。
2016初三中考适应性试卷数学答题卡201604
|
最大最全最精的教育资源网
(2)
(3)
全国中小学教育资源门户网站
| 天量课件、教案、试卷、学案 免费下载
|
最大最全最精的教育资源网
28.(10 分) (1) A y
E H C
(
,
)
最大最全最精的教育资源网
25.(8 分) (1)
(2)
26.(10 分) (1) , (2)补全甲的图像。 (3)
,
450 310
y(cm) C
A
30 O
B
15 17 t
x(秒)
(第 26 题)
27.(10 分) (1)
全国中小学教育资源门户网站
| 天量课件、教案、试卷、学案 免费下载
抽测成绩(次)
24.(10 分) (1)
全国中小学教育资源门户网站
| 天量课件、教案、试卷、学案 免费下载
|
最大最全最精的教育资源网
(2)
(3)
全国中小学教育资源门户网站
| 天量课件、教案、试卷、学案 免费下载
|
最大最全最精的教育资源网
2016 年春季初三中考适应性试卷 数学试题
1 [A] [B] [C] [D] 2 [A] [B] [C] [D] 3 [A] [B] [C] [D] 4 [A] [B] [C] [D] 5 [A] [B] [C] [D] 6 [A] [B] [C] [D] 7 [A] [B] [C] [D] 8 [A] [B] [C] [D] 9 [A] [B] [C] [D]
16.___________ 17.____________
三、解答题(本大题共 10 小题,共 84 分) . 19.(8 分) 计算: (1) (2)
襄城区九年级适应性考试数学试卷参考答案
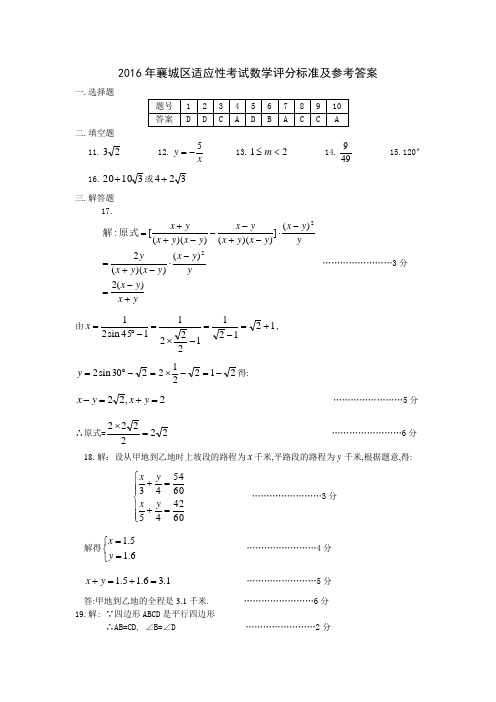
2016年襄城区适应性考试数学评分标准及参考答案一.选择题二.填空题11.23 12.x y 5-= 13.21<≤m 14.499 15.120º 16.31020+或324+ 三.解答题17.yx y x y y x y x y x y y y x y x y x y x y x y x y x +-=-⋅-+=-⋅-+---++=)(2)())((2)(]))(())(([:22原式解 ……………………3分由1212112221145sin 21+=-=-⨯=-︒=x ,212212230sin 2-=-⨯=-︒=y 得: 2,22=+=-y x y x ……………………5分∴原式=222222=⨯ ……………………6分 18.解:设从甲地到乙地时上坡段的路程为x 千米,平路段的路程为y 千米,根据题意,得:⎪⎪⎩⎪⎪⎨⎧=+=+604245605443y x y x ……………………3分解得⎩⎨⎧==6.15.1y x ……………………4分1.36.15.1=+=+y x ……………………5分答:甲地到乙地的全程是3.1千米. ……………………6分19.解: ∵四边形ABCD 是平行四边形∴AB=CD, ∠B=∠D ……………………2分又∵BG=DE∴△ABG ≌△CDE ……………………3分 ∴∠AGB=∠CED ……………………4分 ∵∠CED=∠AEF=70º ……………………5分 ∴∠AGB=70º ……………………6分20.解:(1)200,10% ……………………………………………………2分 (2)36º (补全图略)………………………………………………………………4分 (3)9002001201500=⨯……………………………………………………6分 答:全校学生成绩为A 等的大约有900人. ……………………………7分 21.解: 过点C 作CD ⊥AB 于D在Rt △CDA 中∠CAD=180º-∠CAB=180º-120º =60º…………………………………1分 ∵ACCDCAD =∠sin ∴325235060sin =⨯=︒⋅=AC CD ………………………………………………2分 同理:25215060cos =⨯=︒⋅=AC AD ………………………………………………3分 在Rt △CBD 中,1325)325(1002222=-=-=CD BC BD ………………4分∴AB=BD-AD=251325- ………………………………………………5分 答:AB 之间的距离是(251325-)m. ………………………………………………6分 22.(1)证明:如图,连接OC∵CD 是⊙O 的切线 ∴OC ⊥CD ∴∠OCF=90º ∵AD ⊥CD∴∠D=∠OCF=90º……………………………………2分 ∴OC ∥AD∴∠1=∠3 ……………………………………3分 ∵OA=OC ∴∠2=∠3 ∴∠1=∠2即AC 平分∠DAB ……………………………………4分 (2)如右图,连接OE∵∠1=∠2, ∠1=EOC ∠21,∠2=BOC ∠21∴BOC EOC ∠=∠∴BC=CE=6 …………………………5分 ∵AB 是⊙O 的直径 ∴∠ACB=90º在Rt △ABC 中10682222=+=+=BC AC AB …………………………6分∴⊙O 的直径的长为10. …………………………7分 23.(1)解:根据题意,可设b kx y += 将(100,1000),(200,1400)代入上式,得:⎩⎨⎧=+=+14002001000100b k b k ………………………2分 解得⎩⎨⎧==6004b k ………………………3分∴所求作的函数关系式为:6004+=x y . ………………………4分 (2) ∵在6004+=x y 中,当0=x 时,600=y在11051+-=x p 中,当0=x 时,110=p ………………5分 ∴66000110600=⨯答: 在政府未出台补贴措施之前,该商场销售彩电的总收益额为66000元. ……6分 (3)设总收益为W 元,则W=)11051)(6004(+-+x x ………………7分 =66000320542++-x x =98000)200(542+--x ………………8分∵ 054<-=a∴W 存在最大值∴当x=200时W 有最大值98000. ………………9分答: 政府应将每台补贴款额定为200元时,可获得最大利润98000元. ………………10分 24、(1)∵∠A=∠MDA=α=30º∴MA=MD 又∵MG ⊥AD∴AG=21AD ………………1分 ∵∠FDB=90º -α=90º -30º =60º ,∠B=60º ∴△CDB 是等边三角形 又∵CH ⊥BD ∴DH=21BD ………………2分 ∵D 为AD 的中点∴AD=BD ………………3分 ∴AG=DH ………………4分 (2)∵∠A=∠NDB ,AD=BD ,∠B=∠MDA=α=60º∴△AMD ≌△DNB ………………5分 ∴AM=DN又∵∠A=∠NDH=90º -α=90º -60º =30º,∠AGM=∠DHN=90º ∴△AGM ≌△DHN ………………7分 ∴AG=DH ………………8分 (3)在Rt △AGM 中,∠A=30º∴∠AMG=90º -30º =60º =∠B又∵∠AGM=∠NHB=90º∴△AGM ∽△NHB ………………9分∴NHHBAG MG = ∴MG ·NH=AG ·HB ………………10分 ∵∠GMD+∠GDM=90º,∠HDN+∠GDM=90º ∴∠GMD=∠HDN又∵∠MGD=∠DHN=90º ∴△MGD ∽△DHN ∴DHHNMG GD = ∴MG ·NH=GD ·DH ………………11分 ∴AG ·HB=GD ·GH ………………12分25、(1)解:设直线的解析式为: b kx y += 将点B(2,4),点(0,2)代入上式得:⎩⎨⎧==+242b b k 解得⎩⎨⎧==21b k ∴所求直线的解析式为:2+=x y . ………………2分 当0=y 时,2-=x ,即点A 的坐标为(-2,0) ∵S △ABD =64)]2([21||21=⨯--⨯=⋅D B x y AD ∴1=D x∴点D 的坐标(1,0)设抛物线的解析式为:)1)(2(-+=x x a y 将点B(2,4)代入上式得:1=a∴所求抛物线的解析式为:)1)(2(-+=x x y即22-+=x x y ………………4分(2)设点P 的横坐标为t ,则点P 为(t ,t+2),点Q 为(t ,22-+t t )………………5分 ∴PQ=t+2-(22-+t t )=42+-t ………………7分 ∵a=-1<0∴PQ 有最大值4 ………………8分 (3)由(2)知点P 坐标为(0,2) ………………9分 ①以PD 为平行四边形的边时,设点M 坐标为(m ,n )则点N 为(m+1,n-2) ∵点M 、N 均在抛物线上∴ n=m 2+m-2n-2=(m+1)2+m+1-2 解得 m=-2n=0∴M(-2,0),N (-1,-2) …………10分 ②以PD 为平行四边形的对角线时,设点M 为(m,n )则点N 为(1-m,2-n )同(1)理得M (-1,-2)N (2,4) …………11分 综上所述存在M (-2,2),N (-1,-2)和M (-1,-2),N (2,4)满足题意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年襄城区中考适应性考试
数学答题卡
考场/座位号:
姓 名: 班 级:
注意事项1.答题前,请将姓名、班级、考场、
座位号、准考证号填写清楚。
2.客观题答题,必须使用2B铅笔填涂,修改时用橡皮擦干净。
3.主观题使用黑色签字笔书写。
4.必须在题号所对应的答题区域内作答,超出答题区域书写无效。
5.保持答卷清洁、完整。
正确填涂缺考标记准考证号
[0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0][1][2][3][4][5][6][7][8][9][0]
[1]
[2]
[3][4]
[5][6]
[7][8]
[9]
一、选择题(每小题3分,共计30分)
1 [A ] [B ] [C ] [D ]
2 [A ] [B ] [C ] [D ]
3 [A ] [B ] [C ] [D ]
4 [A ] [B ] [C ] [D ]
5 [A ] [B ] [C ] [D ]
6 [A ] [B ] [C ] [D ]
7 [A ] [B ] [C ] [D ]
8 [A ] [B ] [C ] [D ]
9 [A ] [B ] [C ] [D ]
10 [A ] [B ] [C ] [D ]
二、填空题(每小题3分,共计18分)11、 12、
13、 14、
15、 16、
三、解答题(共72
分)
17、(6分)成绩查询:登录或扫描二维码下载App (用户名和初始密码均为准考证号)
18、(6分)
19、(6分)
20、(7分)21、(6分)
22、(7分)
23、(10分)
24、(12分)
25、(12分)。
