2013年一模分类汇编----四边形
2013年全国各地中考模拟卷分类汇编:相似图形(12页)

2013年全国各地中考模拟卷分类汇编--相似形一、选择题1、(2013年湖北荆州模拟题)如图, △ABC 中,DE ∥BC ,AD=5,BD=10,AE=3,则CE 的值为( ▲ )A.9B.6C.3D.4 答案:B2. (2013年湖北荆州模拟题)已知矩形ABCD 中,AB =1,在BC 上取一点E ,沿AE 将△ABE 向上折叠,使B 点落在AD 上的F 点,若四边形EFDC 与矩形ABCD 相似,则AD 为( ▲ ) A .215- B .215+ C . 3D .2答案:B3.(2013年北京平谷区一模)如图,点D E F ,,分别是ABC △三边的中点,若ABC △的周长为20cm ,则DEF △ 的周长为 A .15cm B .20cm 3C .5cmD .10cm答案:D4、如图是小明设计用手电来测量某古城墙高度的示意图.点P 处放一水平的平面镜, 光线从点A 出发经平面镜反射后刚好射到古城墙CD 的顶端C 处,已知 AB ⊥BD ,CD ⊥BD , 且测得AB =1.2米,BP =1.8米,PD =12米,那么该古城墙的高度是( B ) A. 6米 B. 8米 C. 18米 D.24米5、(2013云南勐捧中学二模)如图,DE 是ABC △的中位线, 则ADE △与ABC △的面积之比是( ) A .1:1 B .1:2 C .1:3 D .1:4【答案】DBPBC 第1题图6、(2013年广东省中山市一模)如图,DE 与ABC △的边AB AC ,分别相交于D E ,两点,且DE BC ∥.若AD :BD=3:1, DE=6,则BC 等于( ).A. 8B.92C. 35D. 2答案:A7、(2013宁波五校联考二模)如图,ABC ∆中,D 、E 是BC 边上的点,1:2:3::=EC DE BD ,M 在AC 边上,2:1:=MA CM ,BM 交AD 、AE 于H 、G ,则GM HG BH ::等于 ( )A .1:2:3B .1:3:5C .5:12:25D .10:24:51 答案:D8、(2013山东德州特长展示)如图,为了测量某棵树的高度,小明用长为2m 的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距6m ,与树相距15m ,则树的高度为 ( ) A .9m B .7mC .4mD .5m B9. (2013上海黄浦二摸)如图,E 、F 分别是平行四边形ABCD 边BC 、CD 的中点,AE 、AF 交BD 于点G 、H ,若△AGH 的面积为1,则五边形CEGHF 的面积是 (A )1 (B )2(C )3(D )4二、填空题1、(2013年上海奉贤区二模)如图,已知∠E =∠C ,如果再增加一个条件就可以得到DEBCAD AB =,那么这个条件可以是 ▲ (只要写出一个即可).A B C DE 第1题图A D BFE12答案:∠B =∠D (等);2、(2013年上海长宁区二模)已知,△ABC 的重心G 到BC 边中点D 的距离是2,则BC 边上的中线长是 . 答案: 63、(2013年江苏南京一模)根据图中所给两个三角形的角度和边长,可得x = ▲ .4、如图,Rt △ABC 中,∠B =Rt ∠,点D 在边AB 上,过点D 作DG ∥AC 交BC 于点G ,分别过点D ,G 作DE ∥BC ,FG ∥AB ,DE 与FG 交于点O .当阴影面积等于梯形ADOF 的面积时,则阴影面积与△ABC 的面积之比为516▲ .5、(2013云南勐捧中学三模)已知△ABC ∽△C B A ''',且A B C S ∆∶C B A S ''''∆=16∶9,若AB=2,则B A ''= .【答案】1.5第13题图(第1题)45°81°754°81° 3x4.2D6、 (2013珠海市文园中学一模)如图,平行四边形ABCD 中,5AB =,3AD =,AE 平分DAB ∠交BC 的延长线于F 点,则CF =___________. 答案:2;三、解答题1.(2013年北京龙文教育一模)在Rt △ABC 中,∠ACB =90°,tan ∠BAC =12. 点D 在边AC 上(不与A ,C 重合),连结BD ,F 为BD 中点.(1)若过点D 作DE ⊥AB 于E ,连结CF 、EF 、CE ,如图1. 设CF kEF =,则k = ; (2)若将图1中的△ADE 绕点A 旋转,使得D 、E 、B 三点共线,点F 仍为BD 中点,如图2所示.求证:BE -DE =2CF ;(3)若BC =6,点D 在边AC 的三等分点处,将线段AD 绕点A 旋转,点F 始终为BD 中点,求线段CF 长度的最大值.答案:解:(1)k =1;…………………1分(2)如图2,过点C 作CE 的垂线交BD 于点G ,设BD 与AC 的交点为Q . 由题意,tan ∠BAC =12, ∴12BC DE AC AE ==. ∵ D 、E 、B 三点共线, ∴ AE ⊥DB .∵ ∠BQC =∠AQD ,∠ACB =90°, ∴ ∠QBC =∠EAQ.∵ ∠ECA+∠ACG =90°,∠BCG+∠ACG =90°,B CADE FB DEA FCBAC1图2图备图2图BDEAFCGQ∴ ∠ECA =∠BCG . ∴ BCG ACE △∽△. ∴12BC GB AC AE ==. ∴ GB =DE. ∵ F 是BD 中点, ∴ F 是EG 中点.在Rt ECG △中,12CF EG =,∴ 2BE DE EG CF -==. .……………4分(3)情况1:如图,当AD =13AC 时,取AB 的中点M ,连结MF 和CM ,∵∠ACB =90°, tan ∠BAC =12,且BC = 6, ∴AC =12,AB=∵M 为AB 中点,∴CM=∵AD =13AC ,∴AD =4.∵M 为AB 中点,F 为BD 中点, ∴FM =12AD = 2. ∴当且仅当M 、F 、C 三点共线且M 在线段CF 上时CF 最大,此时CF =CM +FM=2+.…………………………….……………………………5分 情况2:如图,当AD =23AC 时,取AB 的中点M , 连结MF 和CM ,类似于情况1,可知CF的最大值为4+综合情况1与情况2,可知当点D 在靠近点C 的 三等分点时,线段CF的长度取得最大值为4+2、(2013年聊城莘县模拟)如图,平行四边形ABCD 中,E 是CD 的延长线上一点,BE与BAD 交于点F ,DE =CD 。
人教中考数学一模试题分类汇编——平行四边形综合含答案解析

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图,在平行四边形ABCD中,AD⊥DB,垂足为点D,将平行四边形ABCD折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度2.如图1,在△ABC中,AB=AC,AD⊥BC于D,分别延长AC至E,BC至F,且CE=EF,延长FE交AD的延长线于G.(1)求证:AE=EG;(2)如图2,分别连接BG,BE,若BG=BF,求证:BE=EG;(3)如图3,取GF的中点M,若AB=5,求EM的长.【答案】(1)证明见解析(2)证明见解析(3)5 2【解析】【分析】(1)根据平行线的性质和等腰三角形的三线合一的性质得:∠CAD=∠G,可得AE=EG;(2)作辅助线,证明△BEF≌△GEC(SAS),可得结论;(3)如图3,作辅助线,构建平行线,证明四边形DMEN是平行四边形,得EM=DN=12AC,计算可得结论.【详解】证明:(1)如图1,过E作EH⊥CF于H,∵AD⊥BC,∴EH∥AD,∴∠CEH=∠CAD,∠HEF=∠G,∵CE=EF,∴∠CEH=∠HEF,∴∠CAD=∠G,∴AE=EG;(2)如图2,连接GC,∵AC=BC,AD⊥BC,∴BD=CD,∴AG是BC的垂直平分线,∴GC=GB,∴∠GBF=∠BCG,∵BG=BF,∴GC=BE,∵CE=EF,∴∠CEF=180°﹣2∠F,∵BG=BF,∴∠GBF=180°﹣2∠F,∴∠GBF=∠CEF,∴∠CEF=∠BCG,∵∠BCE=∠CEF+∠F,∠BCE=∠BCG+∠GCE,∴∠GCE=∠F,在△BEF 和△GCE 中,CE GCE F CG BF EF =⎧⎪∠=∠⎨⎪=⎩,∴△BEF ≌△GEC (SAS ),∴BE =EG ;(3)如图3,连接DM ,取AC 的中点N ,连接DN ,由(1)得AE =EG ,∴∠GAE =∠AGE ,在Rt △ACD 中,N 为AC 的中点,∴DN =12AC =AN ,∠DAN =∠ADN , ∴∠ADN =∠AGE ,∴DN ∥GF ,在Rt △GDF 中,M 是FG 的中点, ∴DM =12FG =GM ,∠GDM =∠AGE , ∴∠GDM =∠DAN ,∴DM ∥AE ,∴四边形DMEN 是平行四边形, ∴EM =DN =12AC , ∵AC =AB =5, ∴EM =52. 【点睛】 本题是三角形的综合题,主要考查了全等三角形的判定与性质,直角三角形斜边中线的性质,等腰三角形的性质和判定,平行四边形的性质和判定等知识,解题的关键是作辅助线,并熟练掌握全等三角形的判定方法,特别是第三问,辅助线的作法是关键.3.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF 与BE交于点O.(1)求证:△AOB和△AOE是“友好三角形”;(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的,请直接写出△ABC的面积.【答案】(1)见解析;(2)12;探究:2或2.【解析】试题分析:(1)利用一组对边平行且相等的四边形是平行四边形,得到四边形ABFE是平行四边形,然后根据平行四边形的性质证得OE=OB,即可证得△AOE和△AOB是友好三角形;(2)△AOE和△DOE是“友好三角形”,即可得到E是AD的中点,则可以求得△ABE、△ABF的面积,根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解.探究:画出符合条件的两种情况:①求出四边形A′DCB是平行四边形,求出BC和A′D推出∠ACB=90°,根据三角形面积公式求出即可;②求出高CQ,求出△A′DC的面积.即可求出△ABC的面积.试题解析:(1)∵四边形ABCD是矩形,∴AD∥BC,∵AE=BF,∴四边形ABFE是平行四边形,∴OE=OB,∴△AOE和△AOB是友好三角形.(2)∵△AOE和△DOE是友好三角形,∴S△AOE=S△DOE,AE=ED=AD=3,∵△AOB与△AOE是友好三角形,∴S△AOB=S△AOE,∵△AOE≌△FOB,∴S△AOE=S△FOB,∴S△AOD=S△ABF,∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2××4×3=12.探究:解:分为两种情况:①如图1,∵S△ACD=S△BCD.∴AD=BD=AB,∵沿CD折叠A和A′重合,∴AD=A′D=AB=×4=2,∵△A′CD与△ABC重合部分的面积等于△ABC面积的,∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC,∴DO=OB,A′O=CO,∴四边形A′DCB是平行四边形,∴BC=A′D=2,过B作BM⊥AC于M,∵AB=4,∠BAC=30°,∴BM=AB=2=BC,即C和M重合,∴∠ACB=90°,由勾股定理得:AC=,∴△ABC的面积是×BC×AC=×2×2=2;②如图2,∵S△ACD=S△BCD.∴AD=BD=AB,∵沿CD折叠A和A′重合,∴AD=A′D=AB=×4=2,∵△A′CD与△ABC重合部分的面积等于△ABC面积的,∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC,∴DO=OA′,BO=CO,∴四边形A′BDC是平行四边形,∴A′C=BD=2,过C作CQ⊥A′D于Q,∵A′C=2,∠DA′C=∠BAC=30°,∴CQ=A′C=1,∴S△ABC=2S△ADC=2S△A′DC=2××A′D×CQ=2××2×1=2;即△ABC的面积是2或2.考点:四边形综合题.4.如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.(1)求证:△AEF≌△DCE.(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.【答案】(1)证明见解析;(2)6cm.【解析】分析:(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.详解:(1)证明:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.在Rt△AEF和Rt△DEC中,∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.∴△AEF≌△DCE.(2)解:∵△AEF≌△DCE.AE=CD.AD=AE+4.∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32.解得,AE=6(cm).答:AE的长为6cm.点睛:此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握,难易程度适中,是一道很典型的题目.5.点P是矩形ABCD对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F,点O为AC的中点.(1)如图1,当点P与点O重合时,请你判断OE与OF的数量关系;(2)当点P运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;(3)若点P在射线OA上运动,恰好使得∠OEF=30°时,猜想此时线段CF,AE,OE之间有怎样的数量关系,直接写出结论不必证明.【答案】(1)OE =OF .理由见解析;(2)补全图形如图所示见解析,OE =OF 仍然成立;(3)CF =OE+AE 或CF =OE ﹣AE .【解析】【分析】(1)根据矩形的性质以及垂线,即可判定()AOE COF AAS ∆≅∆,得出OE =OF ; (2)先延长EO 交CF 于点G ,通过判定()AOE COG ASA ∆≅∆,得出OG =OE ,再根据Rt EFG ∆中,12OF EG =,即可得到OE =OF ; (3)根据点P 在射线OA 上运动,需要分两种情况进行讨论:当点P 在线段OA 上时,当点P 在线段OA 延长线上时,分别根据全等三角形的性质以及线段的和差关系进行推导计算即可.【详解】(1)OE =OF .理由如下:如图1.∵四边形ABCD 是矩形,∴ OA =OC .∵AE BP ⊥,CF BP ⊥,∴90AEO CFO ∠=∠=︒.∵在AOE ∆和COF ∆中,AEO CFO AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AOE COF AAS ∆≅∆,∴ OE =OF ;(2)补全图形如图2,OE =OF 仍然成立.证明如下:延长EO 交CF 于点G .∵AE BP ⊥,CF BP ⊥,∴ AE //CF ,∴EAO GCO ∠=∠.又∵点O 为AC 的中点,∴ AO =CO .在AOE ∆和COG ∆中,EAO GCO AO CO AOE COG ∠=∠⎧⎪=⎨⎪∠=⎩,∴()AOE COG ASA ∆≅∆,∴ OG =OE ,∴Rt EFG ∆中,12OF EG =,∴ OE =OF ; (3)CF =OE +AE 或CF =OE -AE . 证明如下:①如图2,当点P 在线段OA 上时.∵30OEF ∠=︒,90EFG ∠=︒,∴60OGF ∠=︒,由(2)可得:OF =OG ,∴OGF ∆是等边三角形,∴ FG =OF =OE ,由(2)可得:AOE COG ∆≅∆,∴ CG =AE .又∵ CF =GF +CG ,∴ CF =OE +AE ;②如图3,当点P 在线段OA 延长线上时.∵30OEF ∠=︒,90EFG ∠=︒,∴60OGF ∠=︒,同理可得:OGF ∆是等边三角形,∴ FG =OF =OE ,同理可得:AOE COG ∆≅∆,∴ CG =AE .又∵ CF =GF -CG ,∴ CF =OE -AE .【点睛】本题属于四边形综合题,主要考查了矩形的性质、全等三角形的性质和判定以及等边三角形的性质和判定,解决问题的关键是构建全等三角形和证明三角形全等,利用矩形的对角线互相平分得全等的边相等的条件,根据线段的和差关系使问题得以解决.6.猜想与证明:如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.拓展与延伸:(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为.(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF 的中点,试证明(1)中的结论仍然成立.【答案】猜想:DM=ME,证明见解析;(2)成立,证明见解析.【解析】试题分析:延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(1)、延长EM交AD于点H,根据ABCD和CEFG为矩形得到AD∥EF,得到△FME和△AMH全等,得到HM=EM,根据Rt△HDE得到HM=DE,则可以得到答案;(2)、连接AE,根据正方形的性质得出∠FCE=45°,∠FCA=45°,根据RT△ADF中AM=MF得出DM=AM=MF,根据RT△AEF中AM=MF得出AM=MF=ME,从而说明DM=ME.试题解析:如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH(ASA)∴HM=EM,在RT△HDE中,HM=DE,∴DM=HM=ME,∴DM=ME.(1)、如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH(ASA)∴HM=EM,在RT△HDE中,HM=EM∴DM=HM=ME,∴DM=ME,(2)、如图2,连接AE,∵四边形ABCD和ECGF是正方形,∴∠FCE=45°,∠FCA=45°,∴AE和EC在同一条直线上,在RT△ADF中,AM=MF,∴DM=AM=MF,在RT△AEF中,AM=MF,∴AM=MF=ME,∴DM=ME.考点:(1)、三角形全等的性质;(2)、矩形的性质.7.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.【答案】(1)AG2=GE2+GF2(2)【解析】试题分析:(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,MN=x,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(2x+x)2,解得x=,推出BN=,再根据BG=BN÷cos30°即可解决问题.试题解析:(1)结论:AG2=GE2+GF2.理由:连接CG.∵四边形ABCD是正方形,∴A、C关于对角线BD对称,∵点G在BD上,∴GA=GC,∵GE⊥DC于点E,GF⊥BC于点F,∴∠GEC=∠ECF=∠CFG=90°,∴四边形EGFC是矩形,∴CF=GE,在Rt△GFC中,∵CG2=GF2+CF2,∴AG2=GF2+GE2.(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,∴∠AMN=30°,∴AM=BM=2x,MN=x,在Rt△ABN中,∵AB2=AN2+BN2,∴1=x2+(2x+x)2,解得x=,∴BN=,∴BG=BN÷cos30°=.考点:1、正方形的性质,2、矩形的判定和性质,3、勾股定理,4、直角三角形30度的性质8.如图1所示,(1)在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P 是BC延长线上一点,N是∠ACP的平分线上一点,若∠AMN=60°,求证:AM=MN.(2)若将(1)中“正三角形ABC”改为“正方形ABCD”,N是∠DCP的平分线上一点,若∠AMN=90°,则AM=MN是否成立?若成立,请证明;若不成立,说明理由.(3)若将(2)中的“正方形ABCD”改为“正n边形A1A2…A n“,其它条件不变,请你猜想:当∠A n﹣2MN=_____°时,结论A n﹣2M=MN仍然成立.(不要求证明)【答案】0 (2)180 nn【解析】分析:(1)要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.(2)同(1),要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.详(1)证明:在边AB上截取AE=MC,连接ME.在正△ABC中,∠B=∠BCA=60°,AB=BC.∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAE,BE=AB-AE=BC-MC=BM,∴∠BEM=60°,∴∠AEM=120°.∵N是∠ACP的平分线上一点,∴∠ACN=60°,∴∠MCN=120°.在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,∴△AEM≌△MCN(ASA),∴AM=MN.(2)解:结论成立;理由:在边AB上截取AE=MC,连接ME.∵正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE,BE=AB-AE=BC-MC=BM,∴∠BEM=45°,∴∠AEM=135°.∵N是∠DCP的平分线上一点,∴∠NCP=45°,∴∠MCN=135°.在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,∴△AEM≌△MCN(ASA),∴AM=MN.(3)由(1)(2)可知当∠A n-2MN等于n边形的内角时,结论A n-2M=MN仍然成立;即∠A n-2MN=()02180nn-时,结论A n-2M=MN仍然成立;故答案为[()02180nn-].点睛:本题综合考查了正方形、等边三角形的性质及全等三角形的判定,同时考查了学生的归纳能力及分析、解决问题的能力.难度较大.9.如图1,在菱形ABCD中,ABC=60°,若点E在AB的延长线上,EF∥AD,EF=BE,点P 是DE的中点,连接FP并延长交AD于点G.(1)过D作DH AB,垂足为H,若DH=,BE=AB,求DG的长;(2)连接CP,求证:CP FP;(3)如图2,在菱形ABCD中,ABC=60°,若点E在CB的延长线上运动,点F在AB的延长线上运动,且BE=BF,连接DE,点P为DE的中点,连接FP、CP,那么第(2)问的结论成立吗?若成立,求出的值;若不成立,请说明理由.【答案】(1)1;(2)见解析;(3).【解析】试题分析:(1)根据菱形得出DA∥BC,CD=CB,∠CDG=∠CBA=60°,则∠DAH=∠ABC=60°,根据DH⊥AB得出∠DHA=90°,根据Rt△ADH的正弦值得出AD的长度,然后得出BE的长度,然后证明△PDG≌△PEF,得出DG=EF,根据EF∥AD,AD∥BC 得出EF∥BC,则说明△BEF为正三角形,从而得出DG的长度;(2)连接CG、CF,根据△PDG≌△PEF得出PG=PF,然后证明△CDG≌△CBF,从而得到CG=CF,根据PG=PF得出垂直;(3)过D作EF的平行线,交FP延长于点G,连接CG、CF证△PEF≌△PDG,然后证明△CDG≌△CBF,从而得出∠GCE=120°,根据Rt△CPF求出比值.试题解析:(1)解:∵四边形ABCD为菱形∴DA∥BC CD="CB" ∠CDG=∠CBA=60°∴∠DAH=∠ABC=60°∵DH⊥AB ∴∠DHA=90°在Rt△ADH中 sin∠DAH=∴AD=∴BE=AB=×4=1 ∵EF∥AD ∴∠PDG=∠PEB ∵P为DE的中点∴PD=PE∵∠DPG=∠EPF ∴△PDG≌△PEF ∴DG=EF ∵EF∥AD AD∥BC ∴EF∥BC∴∠FEB=∠CBA=60°∵BE=EF ∴△BEF为正三角形∴EF=BE=1 ∴DG=EF=1、证明:连接CG、CF由(1)知△PDG≌△PEF ∴PG=PF在△CDG与△CBF中易证:∠CDG=∠CBF=60° CD=CB BF=EF=DG ∴△CDG≌△CBF∴CG=CF ∵PG=PF ∴CP⊥GF(3)如图:CP⊥GF仍成立理由如下:过D作EF的平行线,交FP延长于点G连接CG、CF证△PEF≌△PDG ∴DG=EF=BF ∵DG∥EF ∴∠GDP=∠EFP ∵DA∥BC∴∠ADP=∠PEC∴∠GDP-∠ADP=∠EFP-∠PEC ∴∠GDA=∠BEF=60°∴∠CDG=∠ADC+∠GDA=120°∵∠CBF=180°-∠EBF=120°∴∠CBF=∠CDG ∵CD=BC DG=BF ∴△CDG≌△CBF∴CG=CF ∠DCG=∠FCE ∵PG=PF ∴CP⊥PF ∠GCP=∠FCP∵∠DCP=180-∠ABC=120°∴∠DCG+∠GCE=120°∴∠FCE+∠GCE=120°即∠GCE=120°∴∠FCP=∠GCE=60°在Rt△CPF中 tan∠FCP=tan60°==考点:三角形全等的证明与性质.10.(本题满分10分)如图1,已知矩形纸片ABCD中,AB=6cm,若将该纸片沿着过点B的直线折叠(折痕为BM),点A恰好落在CD边的中点P处.(1)求矩形ABCD的边AD的长.(2)若P为CD边上的一个动点,折叠纸片,使得A与P重合,折痕为MN,其中M在边AD上,N在边BC上,如图2所示.设DP=x cm,DM=y cm,试求y与x的函数关系式,并指出自变量x的取值范围.(3)①当折痕MN的端点N在AB上时,求当△PCN为等腰三角形时x的值;②当折痕MN的端点M在CD上时,设折叠后重叠部分的面积为S,试求S与x之间的函数关系式【答案】(1)AD=3;(2)y=-其中,0<x<3;(3)x=;(4)S=.【解析】试题分析:(1)根据折叠图形的性质和勾股定理求出AD的长度;(2)根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式;(3)过点N作NQ⊥CD,根据Rt△NPQ 的勾股定理进行求解;(4)根据Rt△ADM的勾股定理求出MP与x的函数关系式,然后得出函数关系式.试题解析:(1)根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得:AD=3.(2)由折叠可知AM=MP,在Rt△MPD中,∴∴y=-其中,0<x<3.(3)当点N在AB上,x≥3,∴PC≤3,而PN≥3,NC≥3.∴△PCN为等腰三角形,只可能NC=NP.过N点作NQ⊥CD,垂足为Q,在Rt△NPQ中,∴解得x=.(4)当点M在CD上时,N在AB上,可得四边形ANPM为菱形.设MP=y,在Rt△ADM中,,即∴ y=.∴ S=考点:函数的性质、勾股定理.。
2013年全国各地中考模拟卷分类汇编:圆有关的性质(共16页)

第1题图2013年全国各地中考模拟卷分类汇编--圆有关的性质一、选择题1、(2013年湖北荆州模拟题)如图,AB 是⊙O 的直径,弦BC =2cm ,F 是弦BC 的中点,∠ABC =60°.若动点E 以2cm /s 的速度从A 点出发沿着A →B →A 的方向运动,设运动时间为t (s )(0≤t <3),连接EF ,当△BEF 是直角三角形时,t 的值为( ▲ )A . 47B . 1C . 47或1D . 47或1或49答案:D2. (2013年安徽凤阳模拟题二)如图,AB 是⊙O 的直径,点D 在AB 的延长线上,DC 切⊙O 于C .若∠A =25°,则∠D 等于( )A .40°B .50°C .60°D .70° 答案:A3(2013年安徽凤阳模拟题三).已知AB 是⊙O 的直径,过点A 的弦AD 平行于半径OC , 若∠A =70°,则∠B 等于( ) (A )30° (B )35° (C )40° (D )60°答案:B4.(2013年安徽初中毕业考试模拟卷一)如图,△ABC 是⊙O 的内接三角形,BD 为直径,若∠DBC =18,则∠A 的度数是( ).A .36B .72C .60D .无法确定 答案:B第3题图5.(2013北京房山区一模)如图,四边形ABCD 是⊙O 的内接正方形,点P 是劣弧上不同于点C 的任意一点,则∠BPC 的度数是( ) A .45° B .60° C .75° D .90° 答案:A6、(2013年安徽省模拟六)如图,是⊙O 的直径AB =8,⊿ABC 为正三角形,则图中阴影部 分的面积之和为……【 】 A .B . 2C .D答案:D7、(2013年安徽省模拟七)如图,直径为10的⊙A 经过点C (0,5)和点O (0,0),B 是y 轴右侧⊙A 优弧上一点,则tan OBC 的值为………………………【 】 A .12 BCD答案:C8、(2013年安徽省模拟八)一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是………【 】 A .0.5 B .1 C .2 D .4 答案:B9、(2013年聊城莘县模拟)如图,已知O 是四边形ABCD 内一点,OA =OB =OC ,∠ABC =∠ADC =70°,则∠DAO +∠DCO 的大小是( )第2题图第1题图A .70°B .110°C .140°D .150° 答案:D10、(2013届宝鸡市金台区第一次检测)如图,在半径为5的圆O 中,AB ,CD 是互相垂直的两条弦,垂足为P ,且AB =CD =4,则OP 的长为( )A .1B .2C .2D .22答案:B11.(2013浙江东阳吴宇模拟题)如图,AB 是⊙O 的直径,C ,D 为圆上两点,若∠AOC =130°,则∠D 等于 ( )(A ) 20 (B ) 25° (C ) 35° (D ) 50° 答案:B12.(2013浙江省宁波模拟题)如图,圆内接四边形ABCD 是由四个全等的等腰梯形组成,AD 是⊙O 的直径,则∠BEC 的度数为( )A .15°B .30°C .45°D .60°答案:B13. (2013沈阳一模)如图,在半径为5的圆O 中,AB ,CD 是互相垂直的两条弦,垂足为P ,且AB =CD =8,则OP 的长为( ).第10题 D BOAC第8题图2A .3B .4 C. D .24 答案:C14.(2013盐城市景山中学模拟题)已知:如图2,OA ,OB 是⊙O 的两条半径,且OA ⊥OB ,点C 在⊙O 上则∠ACB 的度数为( ◆ )A .45°B .35°C .25°D .20° 答案:A15.已知AB 是⊙O 的直径,过点A 的弦AD 平行于半径OC , 若∠A =70°,则∠B 等于( B ) (A )30° (B )35° (C )40° (D )60°16. 如图,AB 为⊙O 的直径,弦CD ⊥AB 于点E ,已知CD =12, EB =2,则⊙O 的直径为( D )A . 8B . 10C .16D .2017、(2013河南南阳市模拟)如图,⊙O 是△ABC 的外接圆,∠B =60°,OP ⊥AC 于点P ,OP =2,则⊙O 的半径为( )DC第5题【答案】A18、(2013云南勐捧中学一模)如图,点A 、B 、C 在⊙O 上,若∠BAC =20º,则∠BOC 的度数为( )A .20ºB .30ºC .40ºD .70º【答案】C19、(2013云南勐捧中学二模) 已知两圆的半径分别为1和2,圆心距为5,那么这两个圆的位置关系是 ( )A .内切B .相交C .外离D .外切 【答案】C20、(2013年广州省惠州市模拟)如图,AB 是⊙O 的直径,C .D 是⊙O 上一点,∠CDB =20°,过点C 作⊙O 的切线交AB 的延长线于点E ,则∠E 等于( )A .40°B 50°C .60°D 70° 答案:B21、(2013年广东省珠海市一模)已知⊙O 的半径为3cm ,点A 到圆心O 的距离为4cm ,则点A 与⊙O 的位置关系是22、(2013年广东省中山市一模)如图,△ABC 内接于⊙O ,AD 是⊙O 的直径,∠ABC =25°,则∠CAD 的度数是( ) A .25°B . 60°C .65°D .75°答案:C23、(2013浙江台州二模)5.如图,四个边长为1的小正方形拼成一个大正方形,A 、B 、O 是小正方形顶点,⊙O 的半径为1,P 是⊙O 上的点,且位于右上方的小正方形内, 则sin ∠APB 等于( )A .12B . 2 2C . 3 2D .1【答案】B24、(2013宁波五校联考一模)如图,四边形ABCD 是⊙O 的内接四边形,AC ⊥BD 于点E ,若AB =4,CD =3,则⊙O的半径为( )A .3B C .2.5D 答案:C25、(2013年湖北宜昌调研)如图,AB 是半圆的直径,弦CD ∥AB ,∠A =65°,∠BCD 的度数是( ) (A )25°(B )35°(C )55°(D )65°(第1题)ACB第1题26. (2013年吉林沈阳模拟)如图,在半径为5的圆O 中,AB ,CD 是互相垂直的两条弦,垂足为P ,且AB =CD =8,则OP 的长为( ).A .3B .4 C. D .24 答案:C二、填空题1、(2013年湖北荆州模拟题)如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠CDB =30°,CD =则阴影部分图形的面积为为 ▲ . 2π32.(2013年安徽模拟二)如图所示,A 、B 、C 、D 是圆上的点,00168,40A ∠=∠=,则D ∠= .答案:0283.(2013北京平谷区一模)如图,⊙O 的半径OA =6,弦AB =8,P 为AB 上一动点,则点P 到圆心O 的最短距离为 .答案:4、(2013年湖北荆州模拟5)如图,已知AB 是⊙O 的直径,C 是⊙O 上的一点,连接AC ,过点C 作直线CD ⊥AB 交AB 于点D ,E 是OB 上一点,直线CE 与⊙O 交于点F ,连接AF 交第2题图O PBA第1题图直线CD于G,AC=22,AG=2,则AF长为▲ . 答案:4图,⊙O是等腰三角形的5、(2013年聊城莘县模拟)如外接圆,,,为⊙的直径,,连结,则,答案:45,26、(2013年聊城莘县模拟)如图,⊙O的半径为5,弦AB=8,OC⊥AB于C,则OC的长等于__________.答案:37、(2013年江苏南京一模)如图,在平面直角坐标系中,一个圆与两坐标轴分别交于A、B、C、D四点.已知()20A,,()60B-,,()03C,,则点D的坐标为.B ADCOyx答案:(0,-4)AB第1题图8、(2013年江苏南京一模)工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm ,测得钢珠顶端离零件表面的距离为8mm ,如图所示,则这个小圆孔的宽口AB 的长度为 ▲ mm . 答案:8mm9、(2013年江苏南京一模)如图,在半径为R 的⊙O 中,和度数分别为36°和108°,弦CD 与弦AB 长度的差为 ▲ (用含有R 的代数式表示). 答案:16.10、如图,△ABC 三个顶点的坐标分别为A (-1,3)、B (-2,-2)、C (4,-2), 则△ABC 外接圆半径的长为____.11. 如图,△ABC 内接于⊙O ,半径为5,BC =6,CD ⊥AB 于D 点,则tan ∠ACD 的值为__43___.12、(2013河南南阳市模拟)如图,量角器的直径与直角三角板ABC 的斜边AB 重合,其中量角器0刻度线的端点N 与点A 重合,射线CP 从CA 处出发沿顺时针方向以每秒2度的速度旋转,CP 与量角器的半圆弧交于点E ,第35秒时,点E 在量角器上对应的读数是 度.(第3题)【答案】14013、(2013云南勐捧中学模拟)如图,A ,B ,C 是⊙O 上的三点,∠BAC =30°, 则∠BOC = 度.【答案】60第11题图14、(2013年广州省惠州市模拟)⊙O 的半径为1㎝,弦AB =2㎝,AC =3㎝,则∠BAC的度数为 . 答案:150或72015、(2013浙江台州二模)14.如图AB 、AC 是O ⊙的两条弦,A ∠=30°,过点C 的切线与OB 的延长线交于点D ,则D ∠【答案】30°16.(2013江西饶鹰中考模拟)在⊙O 中,点B 在⊙O 上,四边形AOCB 是矩形,对角线AC的长为5,则⊙O 的半径长为 . 答案:517. (2013宁波五校联考二模)如右图,△ABC 内接于⊙O ,BC = a ,CA = b ,∠A -∠B = 90°,则⊙O 的半径为(第2题图)答案:2221b a + 18、(2013河南沁阳市九年级第一次质量检测)长度等于圆的半径的弦所对的圆周角的度数为 .30°或150°19、(2013河南沁阳市九年级第一次质量检测)如图,Rt △ABC 中0030,90=∠=∠A C ,在AC 边上取点O 画圆使⊙O 经过A 、B 两点,下列结论中:①CO AO 2=;②BC AO =;③以O 为圆心,以OC 为半径的圆与AB 相切;④延长BC 交⊙O 与D ,则A 、B 、D 是⊙O 的三等分点.正确的序号是 (多填或错填不给分).①③④20. (2013年唐山市二模)如图,⊙O 是⊿ABC 的外接圆,∠BAC =500,点P 在AO 上(点P 不点A .O 重合)则∠BPC 可能为 度 (写出一个即可). 答案:70 (答案不唯一,大于50小于100都可)21. (2013年广西钦州市四模)如图6,AB 为半圆O 的直径,OC AB OD ⊥,平分BOC ∠,交半圆于点D ,AD 交OC 于点E ,则AEO ∠的度数是____________. 答案:67.522.(2013年广西梧州地区一模)已知在⊙O 中,直径AB 为10 cm ,弦AC 为6 cm ,∠ACB 的平分线交⊙O 于D ,交AB 于E ,则 CD 的长是 ★ 。
2013年全国各地中考模拟卷分类汇编:整式(含答案)

2013年全国各地中考模拟卷分类汇编---整 式一、选择题1.(2013浙江东阳吴宇模拟题)下列运算正确的是( ) (A )1243a a a =⋅ (B )743)(a a = (C )3632)(b a b a = (D )a a a =÷432、7.(2013盐城市景山中学模拟题)对于非零的实数a 、b ,规定a ★b = 1 b - 1a .若2★(2x-1)=1,则x =( ◆ )A . 5 6B . 5 4C . 3 2D .- 16答案:A3、(2013浙江锦绣·育才教育集团一模)下列运算正确的是( ▲ )A .b a b a --=--2)(2B .b a b a +-=--2)(2C .b a b a 22)(2--=--D .b a b a 22)(2+-=--答案:D4、(2013年安徽模拟二)下列计算正确的是 ( ).答案:B6.(2013年安徽模拟二)观察下列图形(每幅图中最小..的三角形都是全等的),则第n 个图形中最小..的三角形的个数是( ).答案:B7. (2013年安徽凤阳模拟题二)下列运算正确的是( )A .5510x x x +=B .5510·x x x =C .5510()x x = D .20210x x x ÷=答案:B8.(2013年安徽初中毕业考试模拟卷一)下列计算正确的是 ( ).A.3= B .236()m m -=- C .44()mn mn = D .824m m m ÷=第1个图 第2个图第3个图第4个图第3题图答案:B9.(2013年北京顺义区一模)下列计算正确的是A .235a a a +=B .236a a a ⋅= C. 235()a a = D. 532a a a ÷= 答案:D10、(2013年安徽省模拟七)下列运算正确的是………………………………【 】A .236·a a a =B .1122-⎛⎫=- ⎪⎝⎭C4=±D .|6|6-=答案:D11、(2013年安徽省模拟八)下列运算正确的是………………………………………【 】 A .(a 3)2=a 9 B .a 2+a 3=a 5 C .a 6÷a 2=a 3 D .a 3·a 4=a 7 答案:D12、(2013年湖北荆州模拟5)下列运算中,正确的是 ( ▲ ) A .5a -2a =3 B .()22224x y x y +=+ C .842x x x ÷=D .41)2(2=-- 答案: D13、(2013年湖北荆州模拟5)如图(1),把一个长为m 、宽为n 的长方形(m n >)沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( ▲ ) A .2m n - B .m n - C .2mD .2n 答案: A14、(2013年湖北荆州模拟6)下列各式计算正确的是( ▲ )A .()11132-⎛⎫--=- ⎪⎝⎭B= C .2a 2+4a 2=6a 4 D .(a 2)3=a 6答案:D 15、(2013年聊城莘县模拟)计算的结果是( )A .B .C .D .答案:Am nn(2)(1)第4题图16、(2013届金台区第一次检测)下列计算正确的是( )A .a 3+a 2=a 5B .a 3-a 2=aC .a 3·a 2=a 6D .a 3÷a 2=a答案:D17、(2013年上海长宁区二模)下列各式中,运算正确的是( ).A. 523a a a =+B. a a a 2=-3C. 523a a a =⋅D. 2323a a a =÷ 答案:C18、(2013年江苏南京一模)下列运算正确的是 ( )A .a 2+a 3=a 5B .a 2•a 3=a 6C .a 3÷a 2=aD .(a 2)3=a 8答案:C19.(2013年江苏南京一模)下列计算正确的是( )A .a 3+a 3=a 6B .a 6÷a 3=a 2C .(a 2)3=a 8D .a 2·a 3=a 5 答案:D20、下列运算中,计算正确的是( A )A .236()a a = B .3362a a a += C .632a a a ÷= D .3332a a a ⋅= 21. 下列运算错误的是【 B 】 A. -(a -b )=-a + bB. a 2·a 3=a 6C. a 2-2ab+b 2=(a -b )2D. 3a -2a =a22. 对任意实数x ,多项式1062-+-x x 的值是【 A 】 A. 负数B. 非负数C. 正数D. 无法确定23. 下列计算中,结果正确的是( )A.632a a a =⋅B.a a a 632=⋅C. 632)(a a =D.326a a a =÷24、(2013杭州江干区模拟)已知x 是实数,且(2)(0x x --=,则21x x ++的值为( )A .13B . 7C . 3D . 13或7或3 【答案】C25、(2013河南南阳市模拟)下列各式:①x 2+x 3=x 5 ;②a 3•a 2=a 6 ;③;④;⑤(π﹣1)0=1,其中正确的是( )【答案】A26、(2013云南勐捧中学一模)下列选项中,与xy 2是同类项的是( ) A .—2xy 2 B .2x 2yC .xyD .x 2y 2【答案】A27.(2013云南勐捧中学三模)下列计算正确的是( )A .a 5+a 3=a 8B .2×3= 6C .2-2=-4 D .x 2·x 3=x 6【答案】B28、(2013年广东省佛山市模拟) 已知的值等于则822263,3)()(b a b a b a =÷( ) (原创)A.6B.9C.12D.81 答案:B29、(2013年惠州市惠城区模拟)下列运算中,正确的是( )A. 2322=-a aB. 532)(a a = C. 963a a a =⋅ D. (4222)2a a = 答案:C30、(2013年广东省珠海市一模)在下列运算中,计算正确的是答案:C31、(2013年广东省中山市一模)下列运算正确的是( )A .x·x 2 = x 2 B. (xy )2 = xy 2 C. (x 2)3 = x 6 D.x 2 +x 2 = x 4 答案:C32、(2013北仑区一模)3.下列运算不正确...的是( ▲ ). A.-(a -b )=-a + b B. a 2·a 3=a 6 C.a 2-2ab+b 2=(a -b )2 D.3a -2a =a 【答案】B33.(2013北仑区一模)11. 世界上著名的莱布尼茨三角形如图所示,则排在第10行从左边数第3个位置上的数是( ▲ ).A.1321 B. 3601 C. 4951 D. 6601 【答案】B34、(2013浙江永嘉一模)7.下列运算中,计算正确的是( ▲ )A .236()a a = B .3362a a a += C .632a a a ÷= D .3332a a a ⋅= 【答案】A35、(2013重庆一中一模)2.计算32)a b (的结果是A . 33a bB .35a bC .36a bD .6ab 【答案】C36. (2013重庆一中一模)已知一个多项式与23x x +的和等于2341x x +-,则这个多项 式是A .31x -+B . 31x --C . 31x +D .31x - 【答案】D37. (2013重庆一中一模)10.如图所示,已知等边三角形ABC 的边长为1,按图中所示的规律,在同一平面内用2013个这样的三角形拼接而成的四边形的周长是第2题A .2015B .2016C .2017D .2018 【答案】A38、(2013年江苏南京一模)下列各式中,计算结果为a 6的是( ) A .a 2+a 4B .a 8-a 2C .a 2·a 3D .a 7÷a答案:D39. (2013江西饶鹰中考模拟)下列运算错误..的是 A.6332a a a =+ B.936a a a =÷- C.633a a a =⋅ D.6328)2(a a -=-答案:A40、(2013凤阳县县直义教教研中心)下列运算正确的是( ).A. 22232x x x -= B .22(2)2a a -=- C .222()a b a b +=+D .()2121a a --=--A41、(2013年湖北宜昌调研)下列计算正确的是( ) (A )32a a a =+ (B )22a a -=- (C )236a a a =÷ (D )623)(a a =-答案:D 42.(2013年江苏无锡崇安一模)下列运算正确的是…………………………( ▲ )A .3a +2a =5a 2B .(2a )3=6a 3C .(x +1)2=x 2+1D .x 2-4=(x +2)(x -2)答案:D43.(2013年江苏东台第二学期阶段检测)下列运算中正确的是A .2325a a a +=B .23622a a a ⋅=C .22(2)(2)4a b a b a b +-=-D .222(2)4a b a b +=+ 答案:C44.(2013年杭州拱墅区一模)下列因式分解正确的是( )A .222()a b a b -=-B .222168(4)a ab b a b -+=-CAB┅┅C .222()a ab b a b ++=+D .22()x y xy xy xy x y ++=+ 答案:B45. (2013珠海市文园中学一模)下列运算正确的是( ) A .2222a a a += B .()339a a = C .248a a a ⋅= D .632a a a ÷=答案:B46. (2013年广西钦州市四模)下列二次三项式是完全平方式的是: (A)2816x x -- (B)2816x x ++ (C)2416x x -- (D)2416x x ++ 答案:B47.(2013年广西梧州地区一模)下列各式计算正确的是 (A) 10a 6÷5a 2=2a 4 ( B) 553223=+ (C) 2(a 2)3=6a 6 ( D) (a -2)2=a 2-4 答案:A48.(2013年广西梧州地区一模)已知12-=-b a ,则124+-b a 的值为 (A) 1- ( B ) 0 (C ) (D ) 3 答案:A二、填空题1、(2013年聊城莘县模拟)当时,代数式的值为答案:2、(2013年上海奉贤区二模)计算:26a a ÷= ▲ ; 答案:4a3、(2013年江苏南京一模)课本上,公式(a -b )2=a 2-2ab +b 2是由公式(a +b )2=a 2+2ab +b 2推导得出的,该推导过程的第一步...是:(a -b )2= ▲ . 答案:[a +(-b )]2(注:写a 2+2a ·(-b )+(-b )2也可)4、(2013年江苏南京一模)常见的“幂的运算”有:①同底数幂的乘法,②同底数幂的除法,③幂的乘方,④积的乘方.在“()()2223510a a a a ⋅==”的运算过程中,运用了上述幂的运算中的 (填序号) . 答案:①③5、我县开展“四边三化”工作,某街道产生m 立方米的拆违垃圾需要清理,某工程队承包了清理工作,计划每天清理60立方米,考虑到还有其他地方的垃圾需要清理,该工程队决定增加人手以提高50%的清理效率,则完成整个任务的实际时间比原计划时间少用了180m天(用含m 的代数式表示) 6、(2013云南勐捧中学二模)计算:(a 2b )3的结果是_ . 【答案】36b a7. (2013江西饶鹰中考模拟)化简:)12(2--a a = . 答案:18、(2013年吉林沈阳模拟)若m 为实数,且13m m -=,221m m-则= . 答案:±1339. (2013年唐山市二模)随着电子技术的发展,手机价格不断降低,某品牌手机按原价降低m 元后,又降低20%,此时售价为n 元,则该手机原价为 元. 答案:54n m +; 10..(2013年杭州拱墅区一模)计算:=-⋅)2(3a a ;=32)2(ab ; 答案: 26a -;368a b三、解答题1.(2013年北京房山区一模)已知a 是关于x 的方程240x -=的解,求代数式()()7112---++a a a a 的值.答案:解法一: ∵a 是关于x 的方程240x -=的解∴42=a . ------------------1分 ∵()()7112---++a a a a=71222---+++a a a a a ------------3分=622-a -------4分当42=a 时,原式=2 ----5分 解法二: ()()7112---++a a a a=71222---+++a a a a a ---------------2分 =622-a -----3分∵a 是关于x 的方程240x -=的解∴2=a 或2-=a -----------------4分 当2±=a 时,原式=2 -----------5分2.(2013年北京平谷区一模)已知2250x x --=,求21(21)(2)(2)4()2x x x x x -++---的值.答案:解:12(21)(2)(2)4()2x x x x x -++---222441442x x xx x =-++--+ …………………………………………………… 3分 223x x =-- ………………………………………………………………………… 4分∵ 2250,x x --=∴ 当 225x x -=时, 原式 2=. …………………… …………………………… 5分 =mn 2………………………1分当2-=mn 时,原式=4)2(22-=-⨯=mn ………………………2分 5、(2013年福州市初中毕业班质量检查) (每小题7分,共14分)(1) 计算:(π+3)0―|―2013|+64×18解: 原式=1-2013+8×18……3分=1-2013+1 ……4分 =-2011 ……7分(2) 已知a 2+2a =-1,求2a (a +1)-(a +2)(a -2)的值. 解:原式=2a 2+2a -a 2+4 ……3分= a 2+2a +4 ……4分∵a 2+2a =-1∴原式=-1+4=3 ……7分另解:∵a 2+2a =-1 ∴a 2+2a +1=0 ∴(a +1)2=0∴a =-1 ……3分 原式=2×(-1)×(-1+1)-(-1+2)×(-1-2)=3 ……7分6. (2013年广西钦州市四模)先化简,再求值:()()()322484a b a b ab a b ab +-+-÷,其中a =2,1b =.解:(1)()()()322484a b a b ab a b ab +-+-÷=2222a b b ab -+-……………………………………………………………(3分) =22a ab -………………………………………………………………………(4分) 当2a =,1b =时,原式=22221-⨯⨯………………………………………(5分) =44-=0…………………………………(6分)。
2013年全国各地中考模拟卷分类汇编 二次函数的图像和性质(共38页)

10、 (2013 年湖北荆州模拟 5)如图, 抛物线 y = x2 + 1 与双曲线 y = 则关于 x 的不等式 A.x > 1 k + x2 + 1 < 0 的解集是 ( ▲ ) x B.x < −1 C.0 < x < 1
k 的交点 A 的横坐标是 1, x
D.−1 < x <0
答案: D 11、(2013 年湖北荆州模拟 6)抛物线 y x 2 6 x 5 的顶点坐标为( ▲ ) A.(3,﹣4) 答案:A 12、(2013 届宝鸡市金台区第一次检测)二次函数 y x 2 1的图象与 x 轴交于 A、B 两 点,与 y 轴交于点 C,下列说法错误 的是( .. A.点 C 的坐标是(0,1) C.△ABC 是等腰直角三角形 答案:D 13.(2013 浙江锦绣· 育才教育集团一模)如图,已知点 A(12,0),O 为坐标原点,P 是 线段 OA 上任意一点(不含端点 O,A),过 P、O 两点的二次函数 y1 和过 P、A 两点的 二次函数 y2 的图象开口均向下, 它们的顶点分别为 B、 C, 射线 OB 与 AC 相交于点 D. 当 OD=AD=8 时,这两个二次函数的最大值之和等于( A.5 B. 2 7 C.8 ▲ ) D.6 ) B.(3,4) C.(﹣3,﹣4) D. (﹣3, 4)
2.(2013 年 安 徽 模 拟 二 ) 二次函数 y ax2 bx c 的图象如图所示,则一次函数
y bx b2 4ac 与反比例函数 y
( y O A. 答案:D x ). y O B. x
abc 在同一坐标系内的图象大致为 x
y O C. x
y O D. x
2014届高三数学北京各区模拟分类汇编-立体几何(文科)
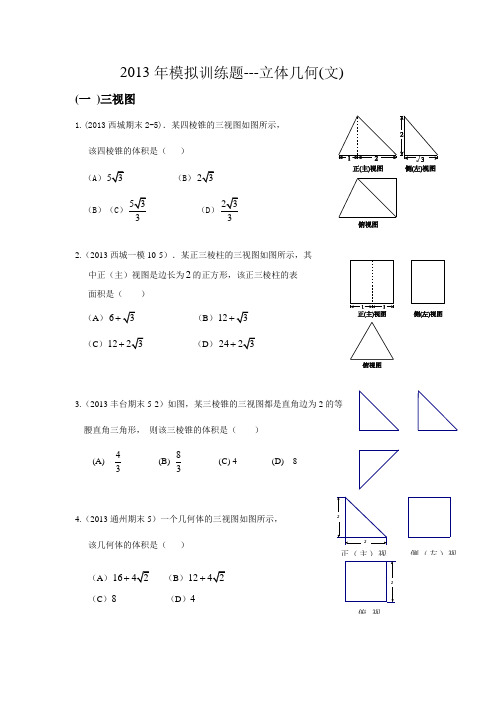
2013年模拟训练题---立体几何(文)(一 )三视图1.(2013西城期末2-5).某四棱锥的三视图如图所示, 该四棱锥的体积是( ) (A )53 (B )23(B )(C )533(D )2332.(2013西城一模10-5).某正三棱柱的三视图如图所示,其 中正(主)视图是边长为2的正方形,该正三棱柱的表 面积是( )(A )63+ (B )123+ (C )1223+ (D )2423+3.(2013丰台期末5-2)如图,某三棱锥的三视图都是直角边为2的等腰直角三角形, 则该三棱锥的体积是( )(A)43 (B) 83(C) 4 (D) 84.(2013通州期末5)一个几何体的三视图如图所示,该几何体的体积是( )(A )1642+ (B )1242+ (C )8 (D )4222正(主)视侧(左)视俯视5.(2013东城期末3-11)一个几何体的三视图如图所示,则该几何体的体积为 .6.(2013海淀一模8-11).某几何体的三视图如图所示,则它的体积为______.7.(2013东城一模12-5)已知一个几何体的三视图如图所示(单位:cm),那么这个几何体的侧.面积是( ) (A )2(1+2)cm(B )2(3+2)cm(C )2(4+2)cm (D )2(5+2)cm8.(2013东城二模13-4)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )A .1B .2C .3D .49.(2013昌平期末5)已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积为( )A. 4 B .8 C. 12 D. 24B.10.(2013海淀二模9-4).某空间几何体的三视图如右图所示, 则该几何体的表面积为( )俯视图24侧视图主视图22244666左视图5俯视图主视图俯视图侧(左)视图正(主)视图A.180B.240C. 276D.300 11.(2013海淀期末1-13). 三棱锥D ABC 及其三视图中的主视图和左视图如图所示,则棱BD 的长为______.12.(2013朝阳二模15-7)某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.16 B.13 C.12D.113.(2013朝阳期末4-6). 已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )A .34 B .32C .34D .114.(2013石景山期末6-7).某三棱锥的三视图如图所示,该三棱锥的体积是( )A .38 B .4 C .2 D .3415.(2013丰台二模17-6).某几何体的三视图如图所示,则该 几何体的表面积为( )DABC22主视图234左视图31正视图俯视图正(主)视图侧(左)视图俯视图22 3231俯视图1侧视图1正视图1(A )24 (B ) 20+42 (C )28 (D )24+ 4216.(2013房山期末6). 若正三棱柱的三视图如图所示,该三棱柱的表面积是( ) A. 3 B.932C. 63+D. 623+17.(2013房山二摸7).一个几何体的三视图如图所示,则这个几何体的表面积为( )A .9182+ B. 1893+ C. 1832+ D. 918.(2013朝阳一模14-7)某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为( )A. 4B. 22C. 203D. 819.(2013石景山一模7).某四棱锥的三视图如图所示,则最长的一条侧棱长度是( )A .13B .2222221 1 1正视图侧视俯视336俯视图侧(左)视图正(主视图)C .5D .2920.(2013房山一模7).某三棱椎的三视图如图所示,该三棱锥的四个面的面积中,最大的是( ) A. 43 B. 8 C. 47 D. 8321.(2013昌平二模7)已知四棱锥P ABCD -的三视图如图所示,则此四棱锥的四个侧面的面积中最大的是( )A. 2B. 3C.13 D. 3222.(2013顺义二模12).一个几何体的三视图如图所示,若该几何体的表面积为292m ,则______h m =.23.(2013西城二模11-6).对于直线m ,n 和平面α,β,使m ⊥α成立的一个充分 条件是( ) (A )m n ⊥,n ∥α(B )m ∥β,⊥βα (C )m ⊥β,n ⊥β,n ⊥α (D )m n ⊥,n ⊥β,⊥βα主视图3 3 22侧视图俯视图俯视图h452正(主)视图侧(左)视图(二)综合小题1.(2013海淀期末1-8). 如图,在棱长为1的正方体1111ABCD A B C D -中,点, E F 分别是棱1,BC CC 的中点,P 是侧面11BCC B 内一点,若1//A P 平 面,AEF 则线段1A P 长度的取值范围是( )A .5[1,]2 B. 325[,]42C. 5[,2]2D. [2,3]2.(2013西城一模10-8).如图,正方体1111ABCD A B C D -中, E 是棱11B C 的中点,动点P 在底面ABCD 内,且11PA A E =, 则点P 运动形成的图形是( )(A )线段 (B )圆弧(C )椭圆的一部分 (D )抛物线的一部分B 1C 1D 1A 1FE BC DA(三)位置关系证明1.(2013海淀期末1-17)如图,在直三棱柱111ABC A B C -中,90BAC ∠=︒,1AB AC AA ==, 且E 是BC 中点.(I )求证:1//A B 平面1AEC ;(Ⅱ)求证:1B C ⊥平面1AEC .2.(2013东城一模12-16)(本小题共14分)如图,已知AD ⊥平面ABC ,CE ⊥平面ABC , F 为BC 的中点,若12AB AC AD CE ===.(Ⅰ)求证://AF 平面BDE ; (Ⅱ)求证:平面BDE ⊥平面BCE .3.(2013东城二模13-17)如图,BCD △是等边三角形,AB AD =,90BAD ∠=︒,M ,N ,G 分别是BD ,BC ,AB 的中点,将BCD △沿BD 折叠到BC D '△的位置,使得AD C B '⊥.⑴ 求证:平面GNM ∥平面ADC ';⑵ 求证:C A '⊥平面ABD .G NMDCB A GN MDCBAEC 1B 1A 1CBAABC DEF4.(2013西城二模11-17).(本小题满分14分)如图1,在四棱锥ABCD P -中,⊥PA 底面ABCD ,面ABCD 为正方形,E 为侧棱PD 上一点,F 为AB 上一点.该四棱锥的正(主)视图和侧(左)视图如图2所示.(Ⅰ)求四面体PBFC 的体积; (Ⅱ)证明:AE ∥平面PFC ; (Ⅲ)证明:平面PFC ⊥平面PCD .5.(2013丰台期末5-17)如图,三棱柱111C B A ABC —中,⊥1AA 平面ABC ,AB ⊥BC , 点M , N 分别为A 1C 1与A 1B 的中点.(Ⅰ)求证:MN //平面 BCC 1B 1;(Ⅱ)求证:平面A 1BC ⊥平面A 1ABB 1.6.(2013丰台二模17).如图,多面体EDABC 中,AC ,BC ,CE 两两垂直,AD //CE ,EDDC ⊥,12AD CE =,M 为BE 中点.(Ⅰ)求证:DM //平面ABC ;(Ⅱ)求证:平面BDE ⊥平面BCD.N MC 1B 1ABC A 17.(2013通州期末16)如图,在三棱柱ABC -A 1B 1C 1中,CC 1⊥底面ABC ,AC =BC =2,22AB =,CC 1=4,M 是棱CC 1上一点.(Ⅰ)求证:BC ⊥AM ;(Ⅱ)若M ,N 分别为CC 1,AB 的中点,求证:CN //平面AB 1M8.(2013房山一模16)在四棱锥P ABCD -中,底面ABCD 为直角梯形,BC //AD ,90ADC ∠=︒,12BC CD AD ==,PA PD =,E F ,为AD PC ,的中点.(Ⅰ)求证:PA //平面BEF ;(Ⅱ)求证:AD PB ⊥.9.(2013房山二模16).如图,ABCD 是正方形, DE ⊥平面ABCD ,DE AF //,22===AF DA DE .(Ⅰ) 求证:AC ⊥平面BDE ;(Ⅱ) 求证://AC 平面BEF ;(Ⅲ) 求四面体BDEF 的体积.N MB 1A 1C 1CBAPABCEFDFEDCBAD是等边三角形,D是BC的10(2013大兴一模17)如图直三棱柱ABC—A1B1C1中,ABC中点(Ⅰ)求证:直线A1D⊥B1C1(Ⅱ)判断A1B与平面ADC1的位置关系,并证明你的结论.A 1B 1CBD 1C 1ADE(四)是否存在问题1.(2013东城期末3-17)如图,在菱形ABCD 中, MA ⊥平面ABCD ,且四边形ADNM 是平行四边形.(Ⅰ)求证:AC ⊥BN (Ⅱ)当点E 在AB 的什么位置时,使得//AN 平面MEC ,并加以证明.2.(2013西城一模10-16)在如图所示的几何体中,面CDEF 为正方形,面ABCD 为等腰梯形,AB //CD ,3AC =,22AB BC ==,AC FB ⊥.(Ⅰ)求证:⊥AC 平面FBC ; (Ⅱ)求四面体FBCD 的体积; (Ⅲ)线段AC 上是否存在点M ,使EA //平面FDM ? 证明你的结论.3.(本小题满分14分)在长方体1111ABCD-A B C D 中,12AA=AD=,E 是棱CD 上的一点. (Ⅰ)求证:1AD ⊥平面11A B D (Ⅱ)求证:11B E AD ⊥;(Ⅲ)若E 是棱CD 的中点,在棱1AA 上是否存在点P ,使得DP ∥平面1B AE ?若存在,求出线段AP 的长;若不存在,请说明理由.ABCDENM4.(2013海淀一模8-17)在四棱锥P ABCD -中,PA ⊥平面ABCD ,ABC ∆是正三角形,AC 与BD 的交点M 恰好是AC 中点,又30CAD ∠= ,4PA AB ==,点N 在线段PB 上,且13PN NB =.(Ⅰ)求证:BD PC ⊥;(Ⅱ)求证://MN 平面PDC ; (Ⅲ)设平面PAB 平面PCD =l ,试问直线l 是否与直线CD 平行,请说明理由.5.(2013海淀二模9-17)如图1,在直角梯形ABCD 中,//AD BC ,90ADC ∠=︒,BA BC =. 把BAC ∆沿AC 折起到PAC ∆的位置,使得P 点在平面ADC 上的正投影O 恰好落在线段AC 上, 如图2所示. 点,E F 分别为棱,PC CD 的中点.(I ) 求证:平面//OEF 平面APD ; (Ⅱ)求证:CD ⊥平面POF ; (Ⅲ) 在棱PC 上是否存在一点M ,使得M 到点,,,P O C F 四点距离相等?请说明理由.6.(2013石景山一模17)如图,在底面为直角梯形的四棱锥P -ABCD 中,AD ∥BC ,∠ABC=90o ,PD ⊥平面ABCD ,AD =1,AB=3,BC =4。
2013年5月全国各地名校最新初三试卷分类汇编 直角三角形与勾股定理

直角三角形与勾股定理一、选择题1、(2013年湖北荆州模拟5)小正方形边长为1,连接小正方形的三个顶点,可得△ABC ,则AC 边上的高是( ▲ ). ABCD 答案: C2、 (2013年江苏南京一模)如图,直线上有三个正方形3和4,则b 的面积为( ) A .3 B .4 C .5 D .7答案:73、(2013年广东省佛山市模拟)设a ,b ,c 分别是△ABC 的三条边,且∠A =60º,那么ca bb ac +++的值是( ) (原创) A.1 B.0.5 C.2 D.3 答案:A4、(2013北仑区一模)12. 如图,四边形ABCD 中,∠BAD =∠ACB =90°,AB =AD ,AC =4BC ,设CD 的长为x ,四边形ABCD 的面积为y ,则y 与x 之间的函数关系式是 ( ▲ ).A .225y x =B .2425y x =C .2225y x =D .245y x =【答案】A5.(2013郑州外国语预测卷)如图,两个等圆⊙A 、⊙B 分别与直线l 相切于点C 、D ,连接AB 与直线l 相交于点O ,∠AOB =30°,连接AC 、BD ,若AB =4,则这两个等圆的半径为( )ABC 第1题图 lABC DA .21B .1C .3D .2 答案:B6.(2013辽宁葫芦岛一模)已知:直线l 1∥l 2,一块含30°角的直角三角板如图所示放置,∠1=25°,则∠2等于( ) A .30°B .35°C .40°D .45°答案:B7.(2013宁波五校联考一模)如图,已知∠AOM=60°,在射线OM 上有点B ,使得AB与OB 的长度都是整数,由此称B 是“完美点”,若OA=8,则图中完美点B 的个数为 ( )A . 1B . 2C . 3D . 4答案:B8.(2013宁波五校联考一模)如图,已知∠AOM=60°,在射线OM 上有点B ,使得AB 与OB 的长度都是整数,由此称B 是“完美点”,若OA=8,则图中完美点B 的个数为 ( )A . 1B . 2C . 3D . 4答案:A9.如图,在Rt △ABC 中,AB=BC=6,点E ,F 分别在边AB ,BC 上,AE=3,CF=1,P 是斜边AC 上的一个动点,则△PEF 周长的最小值为 .510、(2013年福州市初中毕业班质量检查) “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示)若针扎到小正方形(阴影部分)的概率是19,则大、小两个正方形的边长之比是A .3∶1 B .8∶1 C .9∶1 D .22∶1A1 2 l 1 l 2ABCD FG第4题第5题 BEF第6题1题图11、 (2013年广西钦州市四模)图1中,每个小正方形的边长为1,ABC 的三边a ,b ,c 的大小关系是:(A)a<c<b (B)a<b <c (C)c<a<b (D)c<b<a 答案:C12. (2013年广西钦州市四模)如图2所示,在Rt ABC △中,90A ∠=°,BD 平分6. 如图是某几何体的三视图及相关数据,请写出一个a,b,c,关系的等式 a 2+b 2=c 2且∠DAE =450,将△ADC 绕点A 顺时针旋转900后,得到△AFB ,连接EF ,下列结论:(1)△AED ≌△AEF ;(2)△ABE ∽△ACD ;(3)BE +DC =DE ;(4)2BE +2DC =2DE .其中正确的是 ▲ .第8题图【答案】(1) (4)9(2013河南南阳市模拟)如图,△ABC 中,∠ACB=90°,AB=8cm ,D 是AB 的中点.现将△BCD 沿BA 方向平移1cm ,得到△EFG ,FG 交AC 于H ,则GH 的长等于cm .第9题图 【答案】310、(2013温州模拟)16.将一副三角尺如图拼接:含30°角的三角尺(△ABC )的长直角边与含45°角的三角尺(△ACD )的斜边恰好重合.已知AB=23,E 是AC 上的一点(AE>CE),且DE=BE ,则AE 的长为 ▲ .【答案】7511、(2013浙江永嘉一模)14.如图,在△ABC中,∠ACB =90°,∠A =30°,点D 是AB 的中点,连结CD .若AC,则图中长度等于1cm的线段有 ▲ 条.12.(2013郑州外国语预测卷)如图,l ∥m ,等腰直角三角形ABC 的直角顶点C 在直线m 上,若∠β=20°,则∠α的度数为 度.答案:2513.(2013江西饶鹰中考模拟)小红在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为4、8、6,则原直角三角形纸片的斜边长是 .答案:20或58(第1题)(第2题图) AB Cl mαβ第1题图ABCDE14、. (2013河南沁阳市九年级第一次质量检测)如图,Rt△ABC 中0030,90=∠=∠A C ,在AC 边上取点O 画圆使⊙O 经过A 、B 两点,下列结论中:①CO AO 2=;②BC AO =;③以O 为圆心,以OC 为半径的圆与AB 相切;④延长BC 交⊙O 与D ,则A 、B 、D 是⊙O 的三等分点.正确的序号是 (多填或错填不给分).①③④三、解答题1、(2013浙江锦绣·育才教育集团一模)(本小题满分8分)如图,在Rt △ABC 中,∠BAC =90°,AC =2AB ,点D 是AC 的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A 、D 重合,连结BE 、EC .试猜想线段BE 和EC 的关系,并证明你的猜想.答案:解:数量关系为:BE =EC ,位置关系是:BE ⊥EC .----------1分 证明:∵△AED 是直角三角形,∠AED =90°,且有一个锐角是45°, ∴∠EAD =∠EDA =45°, ∴AE =DE , ∵∠BAC =90°,∴∠EAB =∠EAD +∠BAC =90°+45°=135°, ∠EDC =∠ADC -∠EDA =180°-45°=135°, ∴∠EAB =∠EDC , ∵D 是AC 的中点, ∴AD = AB , ∵AC =2AB , ∴AB =DC , ∴△EAB ≌△EDC ,A∴EB =EC ,且∠AEB =∠AED =90°, ∴∠DEC +∠BED =∠AED =∠BED =90°,∴BE ⊥ED .---------------8分(中间过程酌情给分)2.(2013年北京平谷区一模)已知:如图,四边形ABCD 中,90︒,120D ∠=︒,E 是AD 上一点,∠BED=135°,BE =DC =2DE =求 (1)点C 到直线AD 的距离; (2)线段BC 的长.答案:解:(1)作CF ⊥AD 交AD 的延长线于F . ..1分 ∵ ∠ADC =120°, ∴ ∠CDF =60°.在Rt △CDF中,sin60 3.FC CD =⋅︒==………………………………………2分 即点C 到直线AD 的距离为3. (2)∵ ∠BED=135°,BE = ∴ ∠AEB =45°. ∵ 90A ∠=︒, ∴ ∠ABE =45°.∴ 2.AB AE == ………………………………………………………………………3分 作BG ⊥CF 于G .可证四边形ABGF 是矩形. ∴ FG =AB =2,CG =CF -FG =1. ∵ 12DF CD =∴22 4.BG AF AE ED DF ==++=+ ………………………………..4分 ∴ BC ……………………………………………… 5分 3.(2013郑州外国语预测卷)如图,等边△ABC 中,AO 是∠BAC 的角平分线,D 为AO 上一点,以CD 为一边且在CD 下方作等边△CDE ,连结BE . (1) 求证:△ACD ≌△BCE ; (2) 延长BE 至Q , P 为BQ 上一点,连结CP 、CQ 使CP =CQ =5, 若BC =8时,求PQ 的长.A 第2题图答案:证明:△ABC 和△CDE 均为等边三角形,∴AC =BC , CD =CE 且∠ACB =∠DCE =60° ∵∠ACD +∠DCB =∠DCB +∠BCE =60° ∴∠ACD =∠BCE ∴△ACD ≌△BCE(2)解:作CH ⊥BQ 交BQ 于H , 则PQ =2HQ在Rt △BHC 中 ,由已知和(1)得 ∠CBH =∠CAO =30° ∴ CH =4, 在Rt △CHQ 中,HQ =345CH CQ 2222=-=-∴PQ =2HQ =64. (2013江西饶鹰中考模拟)某校九年级(1)班数学兴趣小组开展了一次活动,过程如下: 如图1,在等腰直角△ABC 中,AB =AC ,∠BAC =90°,小明将一块直角三角板的直角顶点放在斜边BC 边的中点O 上,从BC 边开始绕点A 顺时针旋转,其中三角板两条直角边所在的直线分别AB 、AC 于点E 、F .(1)小明在旋转中发现:在图1中,线段AE 与CF 相等。
2013年北京市数学中考一、二模拟题分类汇编:几何综合
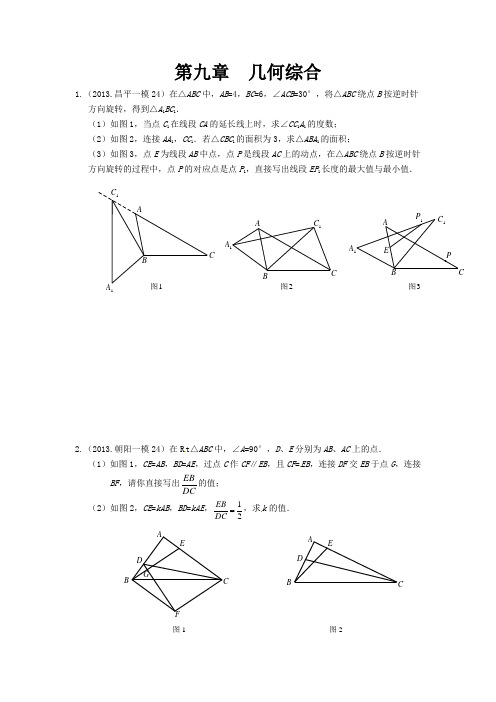
第九章 几何综合1.(2013.昌平一模24)在△ABC 中,AB =4,BC =6,∠ACB =30°,将△ABC 绕点B 按逆时针方向旋转,得到△A 1BC 1.(1)如图1,当点C 1在线段CA 的延长线上时,求∠CC 1A 1的度数; (2)如图2,连接AA 1,CC 1.若△CBC 1的面积为3,求△ABA 1的面积;(3)如图3,点E 为线段AB 中点,点P 是线段AC 上的动点,在△ABC 绕点B 按逆时针方向旋转的过程中,点P 的对应点是点P 1,直接写出线段EP 1长度的最大值与最小值.C 1C BA 1A图2A 1C 1ABC图1图3A2.(2013.朝阳一模24)在R t △ABC 中,∠A =90°,D 、E 分别为AB 、AC 上的点. (1)如图1,CE =AB ,BD =AE ,过点C 作CF ∥EB ,且CF =EB ,连接DF 交EB 于点G ,连接BF ,请你直接写出EBDC的值; (2)如图2,CE =kAB ,BD =kAE ,12EB DC ,求k 的值.图2B 图 1FB3.(2013.大兴一模24)如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;(3)设AP为x,四边形EF GP的面积为S,请直接写..S...出.S与x的函数关系式,并求出的最小值.4.(2013.东城一模24)问题1:如图1,在等腰梯形ABCD中,AD∥BC,AB=BC=CD,点M,N分别在AD,CD上,若∠MBN=12∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;问题2:如图2,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M,N分别在DA,CD的延长线上,若∠MBN=12∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明.5.(2013.房山一模24)(1)如图1,△ABC和△CDE都是等边三角形,且B、C、D三点共线,联结AD、BE相交于点P,求证:BE = AD.(2)如图2,在△BCD中,∠BCD<120°,分别以BC、CD和BD为边在△BCD外部作等边三角形ABC、等边三角形CDE和等边三角形BDF,联结AD、BE和CF交于点P,下列结论中正确的是(只填序号即可)①AD=BE=CF;②∠BEC=∠ADC;③∠DPE=∠EPC=∠CPA=60°;(3)如图2,在(2)的条件下,求证:PB+PC+PD=BE.6.(2013.海淀一模24)在△ABC中,∠ACB=90︒.经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于ABC∠,分别过点C、点A作直线l的垂线,垂足分别为点D、点E.(1)若45ABC∠=︒,CD=1(如图),则AE的长为;(2)写出线段AE、CD之间的数量关系,并加以证明;(3)若直线CE、AB交于点F,56CFEF=,CD=4,求BD的长.ABB第24题图1第24题图2AD7.(2013.怀柔一模24)如图,△ABC 中,∠ACB=90°,AD=AC,AB=AN,连结CD 、BN,CD 的延长线交BN 于点F .(1)当∠A DN 等于多少度时,∠ACE=∠EBF,并说明理由;(2)在(1)的条件下,设∠ABC=α,∠CAD =β,试探索α、β满足什么关系时,△ACE ≌△FBE ,并说明理由.8.(2013.门头沟一模24)已知:在△ABC 中,AB =AC ,点D 为BC 边的中点,点F 是AB 边上一点,点E 在线段DF 的延长线上,点M 在线段DF 上,且∠BAE =∠BDF ,∠ABE =∠DBM .(1) 如图1,当∠ABC =45°时,线段 DM 与AE 之间的数量关系是 ; (2) 如图2,当∠ABC =60°时,线段 DM 与AE 之间的数量关系是 ;(3)① 如图3,当ABC α∠=(0<<90α︒︒)时,线段 DM 与AE 之间的数量关系是;② 在(2)的条件下延长BM 到P ,使MP =BM ,连结CP ,若AB =7,AE=求sin ∠ACP 的值.AB CDEF M MFED CA ACD EF M 图1图2图39.(2013.密云一模24)如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC ∥交CD 于点F .46AB BC ==,, 60B =︒∠. (1)点E 到BC 的距离为 ;(2)点P 为线段EF 上的一个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,连结PN ,设EP x =.①点N 在线段AD 上时(如图2),PMN △的形状是否发生改变?若不变,求出PMN △的周长;若改变,请说明理由;②当点N 在线段DC 上时(如图3),是否存在点P ,使PMN △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.C(备用)A D EB F CA DE BF CP N10.(2013.平谷一模24)(1)如图(1),△ABC 是等边三角形,D 、E 分别是AB 、BC 上的点,且BD CE =,连接AE 、CD 相交于点P .请你补全图形,并直接写出∠APD 的度数;= (2)如图(2),Rt △ABC 中,∠B =90°,M 、N 分别是AB 、BC 上的点,且,AM BC =BM CN =,连接AN 、CM 相交于点P ,请你猜想∠APM = °,并写出你的推理过程.11.(2013.石景山一模24)如图,△ABC 中,∠90ACB =︒, 2=AC ,以AC 为边向右侧作等边三角形ACD .(1)如图24-1,将线段AB 绕点A 逆时针旋转︒60,得到线段1AB ,联结1DB ,则与1DB 长度相等的线段为 (直接写出结论);(2)如图24-2,若P 是线段BC 上任意一点(不与点C 重合),点P 绕点A 逆时针旋转︒60得到点Q ,求ADQ ∠的度数;(3)画图并探究:若P 是直线BC 上任意一点(不与点C 重合),点P 绕点A 逆时针旋转︒60得到点Q ,是否存在点P ,使得以 A 、 C 、 Q 、 D 为顶点的四边形是梯形,若存在,请指出点P 的位置,并求出PC 的长;若不存在,请说明理由.12.(2013.西城一模24)在Rt △ABC 中,∠ACB =90°,∠ABC =α,点P 在△ABC 的内部.(1) 如图1,AB =2AC ,PB =3,点M 、N 分别在AB 、BC 边上,则cos α=_______, △PMN 周长的最小值为_______;(2) 如图2,若条件AB =2AC 不变,而PA =2,PB =10,PC =1,求△ABC 的面积; (3) 若PA =m ,PB =n ,PC =k ,且cos sin k m n αα==,直接写出∠APB 的度数.图24-1 图24-2DB 1ABCD备用图ACD备用图ACD13.(2013.顺义一模24)如图1,将三角板放在正方形ABCD 上,使三角板的直角顶点E 与正方形ABCD 的顶点A 重合.三角板的一边交CD 于点F ,另一边交CB 的延长线于点.G(1)求证:EF EG =;(2)如图2,移动三角板,使顶点E 始终在正方形ABCD 的对角线AC 上,其他条件不变, (1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)如图3,将(2)中的“正方形ABCD ”改为“矩形ABCD ”,且使三角板的一边经过点B ,其他条件不变,若AB a =,BC b =,求EFEG的值.14.(2013.通州一模24)已知:2AD =,4BD =,以AB 为一边作等边三角形ABC .使C 、D两点落在直线AB 的两侧.(1)如图,当∠ADB=60°时,求AB 及CD 的长;(2)当∠ADB 变化,且其它条件不变时,求CD 的 最大值,及相应∠ADB 的大小.15.(2013.海淀二模24)如图1,在△ABC 中,AB =AC ,ABC α∠=. 过点A 作BC 的平行线与∠ABC 的平分线交于点D ,连接CD .图1 图2 (1)求证:AC AD =;(2)点G 为线段CD 延长线上一点,将射线GC 绕着点G 逆时针旋转β,与射线BD 交于点E .①若βα=,2GD AD =,如图2所示,求证:2DEG BCD S S ∆∆=; ②若2βα=,GD kAD =,请直接写出DEGBCDS S ∆∆的值(用含k 的代数式表示).第九章 几何综合参考答案1.(2013.昌平一模24)解:(1)如图1,依题意得:△A 1C 1B ≌△ACB .……… 1分∴BC 1=BC ,∠A 1C 1B =∠C =30°. ∴∠BC 1C = ∠C =30°.∴∠CC 1A 1 = 60°.…………………………… 2分A DB CA 1C 1ABC图1(2)如图2,由(1)知:△A 1C 1B ≌△ACB .∴A 1B = AB ,BC 1 = BC ,∠A 1BC 1 =∠ABC . ∴∠1 = ∠2,114263A B AB C B BC === ∴ △A 1BA ∽△C 1BC ………………… 3分 ∴112ΔΔ2439A BA C BCS S ⎛⎫== ⎪⎝⎭. ………………4分∵1Δ3C BC S =, ∴1Δ43A BA S =. ……………………………5分(3)线段EP 1长度的最大值为8,EP 1长度的最小值1. ………… 7分2.(2013.朝阳一模24)解:(1)EB DC =. ………………………………………………………………………2分 (2)过点C 作CF ∥EB 且CF =EB ,连接DF 交EB 于点G , 连接BF .∴四边形EBFC 是平行四边形. …………………………………………………3分 ∴CE ∥BF 且CE =BF . ∴∠ABF =∠A =90°. ∵BF =CE =kAB .∴BFk AB=. ∵BD =kAE ,∴BDk AE=.… ……………………………………………………………………4分 ∴BF BD AB AE=.∴DBF ∆∽EAB ∆. ……………………………………………………………5分 ∴DFk BE=,∠GDB=∠AEB . ∴∠DGB =∠A =90°. ∴∠GFC =∠BGF =90°. ∵12CF EB DC DC ==. 21C 1CBA 1A图2B∴DF DFEB CF==∴k…………………………………………………………………………7分3.(2013.大兴一模24)(1)证明: ∵PE=BE , ∴∠EBP=∠EPB . 又∵∠EPH=∠EBC=90°, ∴∠EPH-∠EPB=∠EBC-∠EBP . 即∠PBC=∠BPH . 又∵AD ∥BC , ∴∠APB=∠PBC .∴∠APB=∠BPH . ………………………………………2分 (2)△PHD 的周长不变,为定值 8 ………………………3分 证明:过B 作BQ ⊥PH ,垂足为Q 由(1)知∠APB=∠BPH 又∵ ∠A=∠BQP=90°,BP=BP ∴ △ABP ≌△QBP ∴ AP=QP , AB=BQ 又∵ AB=BC ∴ BC = BQ又∵ ∠C=∠BQH=90°,BH=BH ∴ △BCH ≌△BQH ∴ CH=QH∴ △PHD 的周长为:PD+DH+PH =AP+PD+DH+HC =AD+CD =8………………5分(3)21282S x x =-+ 配方得,21(2)62S x =-+,∴当x =2时,S 有最小值6 …………………………………7分4.(2013.东城一模24)(本小题满分7分)AB CDEF G H PQ=180°,=180°.BN5.(2013.房山一模24)(1)证明:∵△ABC 和△CDE 都是等边三角形 ∴BC=AC ,CE=CD ,∠ACB=∠DCE=60° ∴∠BCE=∠ACD∴△BCE ≌△ACD (SAS )∴BE=AD --------------1分 (2)①②③都正确 --------------4分 (3)证明:在PE 上截取PM=PC ,联结CM由(1)可知,△BCE ≌△ACD (SAS ) ∴∠1=∠2设CD 与BE 交于点G,,在△CGE 和△PGD 中 ∵∠1=∠2,∠CGE=∠PGD∴∠DPG=∠ECG=60°同理∠CPE=60° ∴△CPM 是等边三角形--------------5分 ∴CP=CM ,∠PMC=60° ∴∠CPD=∠CME=120°∵∠1=∠2,∴△CPD ≌△CME (AAS )---6分 ∴PD=ME∴BE=PB+PM+ME=PB+PC+PD. -------7分即PB+PC+PD=BE .6.(2013.海淀一模24)(1)2AE =.………………………1分(2)线段AE 、CD 之间的数量关系为2AE CD =.………………………2分 证明:如图1,延长AC 与直线l 交于点G . 依题意,可得∠1=∠2. ∵∠ACB =90︒, ∴∠3=∠4. ∴BA BG =.∴CA =CG .………………………3分∵AE ⊥l ,CD ⊥l , ∴CD ∥AE . ∴△GCD ∽△GAE . ∴12CD GC AE GA ==. ∴2AE CD =.………………………4分AACB(3)解:当点F 在线段AB 上时,如图2, 过点C 作CG ∥l 交AB 于点H ,交AE 于点G . ∴∠2=∠HCB . ∵∠1=∠2, ∴∠1=∠HCB . ∴CH BH =. ∵∠ACB =90︒,∴∠3+∠1=∠HCB +∠4 =90︒. ∴∠3=∠4. ∴CH AH BH ==. ∵CG ∥l ,∴△FCH ∽△FEB . ∴56CF CH EF EB ==. 设5,6CH x BE x ==,则10AB x =.∴在△AEB 中,∠AEB =90︒,8AE x =. 由(2)得,2AE CD =. ∵4CD =, ∴8AE =. ∴1x =.∴10,6,5AB BE CH ===. ∵CG ∥l ,∴△AGH ∽△AEB . ∴12HG AH BE AB ==. ∴3HG =.………………………5分 ∴8CG CH HG =+=. ∵CG ∥l ,CD ∥AE , ∴四边形CDEG 为平行四边形. ∴8DE CG ==.∴2BD DE BE =-=.……………………6分 当点F 在线段BA 的延长线上时,如图3, 同理可得5CH =,3GH =,6BE =. ∴DE =2CG CH HG =-=. ∴ 8BD DE BE =+=.∴2BD =或8.……………………7分7.(2013.怀柔一模24)(1)解:图3图2当∠ADN 等于90度时,∠ACE=∠EBF. ……………………………1分 理由如下:∵∠ACB=∠ADN =90°, ∴△ABC 和△AND 均为直角三角形 又∵AC=AD ,AB=AN∴△ABC ≌△AND ……………………………2分 ∴∠CAB=∠DAN∴∠CAD=∠BAN 又∠ACD=∠ADC, ∠ABN=∠ANB∴∠ACD= ∠ABN 即∠ACE=∠EBF……………………………3分(2)解:当2βα=时,△ACE ≌△FBE . ……………………………4分在△ACD 中,∵AC=AD ,∴αβ-=-=∠-=∠ 9021802180CAD ACD ……………………………5分在Rt △ABC 中,∠ACD+∠BCE=90°,即9090BCE α︒-+∠=︒,∴∠BCE=α.∵∠ABC=α,∴∠ABC=∠BCE ……………………6分 ∴CE=BE由(1)知:∠ACE=∠EBF,又∠AEC=∠BEF∴△ACE ≌△FBE .………………………7分8.(2013.门头沟一模24)解:(1)DM AE =.………………………………………………………………………2分(2)12DM AE =. ………………………………………………………………3分 (3)① cos DM AE =α. …………………………………………………………4分② 如图,连结AD 、EP . ∵AB =AC ,∠ABC =60°, ∴△ABC 为等边三角形.又∵D 为BC 的中点,∴AD ⊥BC ,∠DAC =30°,BD =DC =12BC =72. ∵∠BAE =∠BDM ,∠ABE =∠DBM ,∴△ABE ∽△DBM . ∴12BM DB BE AB ==.∴EB =2BM . 又∵PB =2BM ,∴EB =PB .∵60EBP ABE ABP PBC ABP ABC ∠=∠+∠=∠+∠=∠=︒, ∴△BEP 为等边三角形. ∴EM ⊥BP .∴∠BMD =90°.∵D 为BC 的中点,M 为BP 的中点,∴DM ∥PC .∴∠BPC =∠BMD = 90°. ∵AB CB =,BE BP =,∠ABE =∠DBM , ∴△ABE ≌△CBP .∴BCP BAE ∠=∠,∠BPC =∠BEA = 90°.在Rt △AEB 中,∵∠BEA =90°,AE=AB =7,∴cos EAB ∠=∴cos cos PCB BAE ∠=∠=5分 在Rt △ABD中,sin AD AB ABD =⋅∠= 在Rt △NDC中,cos DC CN NCD =∠∴ND =∴NA AD ND =-=. 过点N 作NH ⊥AC 于H .∴12NH AN ==6分∴sin NH ACP CN ∠==……………………………………………………7分9.(2013.密云一模24)(1)如图1,过点E 作EG ⊥BC 于点G . ∵E 为AB 的中点,HP ACEF M N 图2①当点N 在线段AD 上运动时,周长不变.∵PM ⊥EF ,EG ⊥EF , ∴PM ∥EG . ∵EF ∥BC ,同理MN=AB=4.如图2,过点P 作PH ⊥MN 于H , ∵MN ∥AB ,∴∠NMC=∠B=60°,∠PMH=30度. ②当点N 上运动时,存在.M N=2MR=310.(2013.平谷一模24)解:(1)60°……………..1分 (2)45° ………………………………..2分证明:作AE ⊥AB 且AE CN BM ==.可证EAM MBC ∆≅∆. ……………………………..3分 ∴ ,.ME MC AME BCM =∠=∠∵ 90,CMB MCB ∠+∠=︒∴ 90.CMB AME ∠+∠=︒ ∴ 90.EMC ∠=︒∴ EMC ∆是等腰直角三角形,45.MCE ∠=︒ ...................5分 又△AEC ≌△CAN (s , a , s ).. (6)分∴ .ECA NAC ∠=∠ ∴ EC ∥AN. ∴45.APM ECM ∠=∠=︒…………………………………………………………………..7分11.(2013.石景山一模24)解:(1) BC …………………………… 1分 (2由作图知AQ AP =,∠︒=06PAQ ∵△ACD 是等边三角形.∴AD AC =,PAQ CAD ∠=︒=∠06 ∴QAD PAC ∠=∠ 在△PAC 和△QAD 中⎪⎩⎪⎨⎧=∠=∠=AD AC QAD PAC AQ AP ∴△PAC ≌△QAD∴︒=∠=∠90ACP ADQ …………………………… 3分 (3)如图3,同①可证△PAC ≌△QAD ,︒=∠=∠90ACP ADQ图3 图4AB CDPQD BQPCA当AD ∥CQ 时,︒=∠-︒=∠90180ADQ CQD∵︒=∠60ADC ∴︒=∠30QDC ∵2==AC CD∴31==DQ CQ ,∴3==DQ PC 且AD CQ ≠…………………………… 5分∴此时四边形ACQD 是梯形.如图4,同理可证△PAC ≌△QAD ,︒=∠=∠90ACP ADQ 当AQ ∥CD 时,︒=∠=∠60ADC QAD ,︒=∠30AQD∵2==AC AD∴4AQ DQ ==,∴PC DQ ==此时DQ 与AC 不平行,四边形ACDQ 是梯形.综上所述,这样的点P 有两个,分别在C 点两侧,当P 点在C 点左侧时,3=PC ;当P 点在C点右侧时,PC =…………………………… 7分12.(2013.西城一模24)解:(1)cos α,△PMN 周长的最小值为 3 ; …………2分(2)分别将△PAB 、△PBC 、△PAC 沿直线AB 、BC 、AC 翻折,点P 的对称点分别是点D 、E 、F ,连接DE 、DF ,(如图6)则△PAB ≌△DAB ,△PCB ≌△ECB ,△PAC ≌△FAC . ∴AD =AP =AF , BD =BP =BE ,CE =CP =CF .∵由(1)知∠ABC =30°,∠BAC =60°,∠ACB =90°, ∴∠DBE =2∠ABC =60°,∠DAF =2∠BAC =120°, ∠FCE =2∠ACB =180°.∴△DBE 是等边三角形,点F 、C 、E 共线.∴DE =BD =BP EF =CE +CF =2CP =2. ∵△ADF 中,AD =AF ,∠DAF =120°, ∴∠ADF =∠AFD =30°.∴DF .∴22210EF DF DE +==.∴∠DFE =90°. ………………………………………………………4分PBAC DE F图6∵2ABC DBE DFE DAF BDAFE S S S S S ∆∆∆∆==++多边形,∴2112222ABC S ∆=++=∴ABC S ∆=. ……………………………………………5分 (3)∠APB =150°. ………………………………………………………… 7分 说明:作BM ⊥DE 于M ,AN ⊥DF 于N .(如图7) 由(2)知∠DBE =2α,∠DAF =1802α- . ∵BD =BE=n ,AD =AF=m , ∴∠DBM =α,∠DAN =90α- . ∴∠1=90α- ,∠3=α. ∴DM =sin n α,DN =cos m α. ∴DE =DF =EF . ∴∠2=60°.∴∠APB =∠BDA =∠1+∠2+∠3=150°.13.(2013.顺义一模24)(1)证明:∵9090GEB BEF DEF BEF ∠+∠=∠+∠=°,°,∴.DEF GEB ∠=∠ 又∵ED BE =,∴Rt Rt FED GEB △≌△.∴.EF EG = ………………………………………………………2分(2)成立.证明:如图,过点E 分别作BC CD 、的垂线,垂足分别为H I 、,则90EH EI HEI =∠=,°.∵9090GEH HEF IEF HEF ∠+∠=∠+∠=°,°,∴.IEF GEH ∠=∠∴Rt Rt FEI GEH △≌△.∴.EF EG = …………………………………4分321NMPACD EFB图7(3)解:如图,过点E 分别作BC CD 、的垂线,垂足分别为M N 、,则90MEN ∠=°,.EM AB EN AD ∥,∥∴.EM CE EN AB CA AD == ∴.EM AD a EN AB b ==…………………………………5分 ∴9090GME MEF FEN MEF ∠+∠=∠+∠=°,°, ∴.MEN GEM ∠=∠∴Rt Rt FEN GEM △∽△. ∴.EF EN b EG EM a ==…………………………………7分14.(2013.通州一模24)解:(1)过点A 作AG BC ⊥于点G . ∵∠ADB=60°,2AD =, ∴1DG =,AG =∴ 3GB =,∴tan AG ABG BG ∠==, ∴30ABG ∠=o,AB = ……………… 1分; ∵ △ABC 是等边三角形,∴ 90DBC ∠=o,BC =, ……………… 2分;由勾股定理得:CD ===…… 3分;(2)作60EAD ∠=o ,且使AE AD =,连接ED 、EB . ………… 4分; ∴△AED 是等边三角形, ∴AE AD =,60EAD ∠=o ,∵ △ABC 是等边三角形, ∴AB AC =,60BAC ∠=o ,∴EAD DAB BAC DAB ∠+∠=∠+∠, 即EAB DAC ∠=∠,∴△EAB ≌△DAC . ……………… 5分;∴EB =DC .G第24题图D CBA 第24题图ECBA当点E 、D 、B 在同一直线上时,EB 最大,∴246EB =+=, ……………… 6分; ∴ CD 的最大值为6,此时120ADB ∠=o . ……………… 7分. 另解:作60DBF ∠=o ,且使BF BD =,连接DF 、AF . 参照上面解法给分.15.(2013.海淀二模24)解:(1) ∵BD 平分ABC ∠,∴12∠=∠. ∵AD ∥BC , ∴23∠=∠.∴13∠=∠.---------------1分 ∴AB AD =. ∵AB AC =,∴AC AD =.---------------2分 (2)①证明:过A 作AH BC ⊥于点H .∴90AHB ∠=.∵AB AC =,ABC α∠=, ∴ACB ABC α∠=∠=. ∴1802BAC α∠=︒-. 由(1)得=AB AC AD =.∴点B 、C 、D 在以A 为圆心,AB 为半径的圆上.∴12BDC BAC ∠=∠. ∴90GDE BDC α∠=∠=︒-.----------3分∵G ∠=β=αABC =∠, ∴90G GDE ∠+∠=︒. ∴90DEG AHB ∠=∠=︒.∴△DEG ∽△AHB .------------------4分 ∵2GD AD =,AB AD =,FA BCD第24题图∴22DEG AHB S GD S BA ∆∆==4. ∵AD ∥BC ,∴2BCD ABC AHB S S S ∆∆∆==.∴2DEG BCD S S ∆∆=.----------------------5分 ②2=DEG BCDS k S ∆∆. -------------------------7分。
2013年全国名校初三模拟数学试卷分类汇编:23 线段 角与相交线

2题图线段,角与相交线一、选择题1、(2013安徽芜湖一模)下面四个图形中,∠1=∠2一定成立的是( ).答案:B2、(2013江苏扬州弘扬中学二模)如图,直线a ,b 被c 所截,a ∥b ,若∠1=35°,则∠2的大小为( )A . 35°B . 145° C. 135° D. 125°答案:B3、(2013·湖州市中考模拟试卷3)如果50α∠=,那么α∠的补角等于 . 答案: 134、(广东省2013初中学业水平模拟六)若α∠补角是α∠余角的3倍,则α∠= . 答案:45度5、(广东省2013初中学业水平模拟一)如图1,AOC ∠和BOD ∠都是直角,且︒=∠30DOC ,则=∠AOB ( ). A .︒30 B .︒60 C .︒120 D .︒150 答案:D6、(广东省2013初中学业水平模拟一)︒28的补角是( ). A .︒58 B .︒72 C .︒62D .︒152答案:C7、(广州海珠区2013毕业班综合调研)如图,∠1与∠2是同位角,若∠2=65°,则∠1的大小是( )A .25°B .65°C .115°D .不能确定答案:D8、(2013湛江调研测试)∠A=20°,则∠A 的余角为A .20°B .70°C .80°D .160°AO DCB图1第4题图21答案:B二、填空题1、(广州海珠区2013毕业班综合调研)如图,AB 为⊙O 的直径,点C 在⊙O 上,若︒=∠20C ,则=∠BOC °.答案:40°2、(2013广西钦州市模拟)如图,点B 是线段AC 上的点, 点D 是线段BC 的中点,若AB=4cm ,AC =10cm ,则CD= ▲ cm . 第1题 答案:33、(2013年孝感模拟)如图, 直线AB 、CD 相交于点E ,EF ⊥AB 于E ,若∠CEF =59°,则∠AED 的度数为 .答案: ︒1494、(2013年孝感模拟)在一次夏令营活动中,小明同学从营地A 出发,要到A 地的北偏东60°方向的C 处,他先沿正东方向走了200m 到达B 地,再沿北偏东30°方向走,恰能到达目的地C (如图),那么,由此可知,B C 、两地相距 m .答案: 2005、(2013年犍为县五校联考)某同学在纸上画了四个点,如果把这四个点彼此连接,连成第1题图BOCAABCD一个图形,则这个图形中会有 个三角形出现。
2013年全国各地中考模拟卷分类汇编:动态综合型问题(共40页)

DCBA2013年全国各地中考模拟卷分类汇编--动态综合型问题一、选择题1、(2013年湖北荆州模拟题)如图,正方形ABCD的边长为4cm,动点P、Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为(▲)A.B.C.D.答案:B2.(2013年北京房山区一模)如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是答案:B3.(2013年北京顺义区一模)如图,AB为半圆的直径,点P为AB上一动点,动点P从点A出发,沿AB匀速运动到点B,运动时间为,分别以AP和PB为直径作半圆,则图中阴影部分的面积S与时间t之间的函数图象大致为A.B.C.D.答案:DPDCBA第2题图4、(2013年安徽省模拟六)如图所示,矩形ABCD 的长、宽分别为8cm 和4cm ,点E 、F 分别在AB 、BC 上,且均从点B 开始,以1cm /s 的速度向B -A -D 和B -C -D 的方向运动,到达D 点停止.则线段EF 的长ycm 关于时间ts 函数的大致图象是……【 】答案:A5、(2013年湖北荆州模拟6)如图,已知A 、B 是反比例函数ky x(k >0,x >0)图象上的两点,BC ∥x 轴,交y 轴于点C .动点P 从坐标原点O 出发,沿O →A →B →C 匀速运动,终点为C .过点P 作PM ⊥x 轴,PN ⊥y 轴,垂足分别为M 、N .设四边形OMPN 的面积为S ,点P 运动的时间为t ,则S 关于t 的函数图象大致为( ▲ )A B C D 答案:A6、(2013年广东省佛山市模拟)如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t ,正方形除去圆部分的面积为S (阴影部分),则S 与t 的大致图象为( )答案:A7、(2013浙江台州二模)9.如图,已知Rt △ABC 的直角边AC =24,斜边AB =25,一个以点P 为圆心、半径为1的圆在△ABC 内部沿顺时针方向滚动,且运动过程中⊙P 一直保持与△ABC 的边相切,当点P 第一次回到 它的初始位置时所经过路径的长度是( )A .563B . 25C .1123D . 56 tA BtCtD第1题图第2题图(第1题)【答案】C8、(2013年杭州拱墅区一模)如图,在△ABC 中,已知∠C =90°,AC =BC =4,D 是AB的中点,点E 、F 分别在AC 、BC 边上运动(点E 不与点A 、C 重合),且保持AE =CF ,连接DE 、DF 、EF .在此运动变化的过程中,有下列结论:①四边形CEDF 有可能成为正方形;②△DFE 是等腰直角三角形; ③四边形CEDF 的面积是定值;④点C 到线段EF. 其中正确的结论是( )A .①④B .②③C .①②④D .①②③④ 答案:D二、填空题1、(2013年湖北荆州模拟6)如图,在等腰梯形ABCD 中,AB ∥CD ,BC =4,AD=B =45°,直角三角板含45°角的顶点E 在边BC 上移动,一直角边始终经过点A ,斜边与CD 交于点F ,若△ABE 为等腰三角形,则CF = ▲. 答案: 2.5或3或3点出发,以1cm /s 的速度沿着A →B →C →D 的方向不停移动,直到点P 到达点D 后才停止.已知△PAD 的面积S (单位:cm 2)与点P 移动的时间(单位:s )的函数如图②所示,则点P 从开始移动到停止移动一共用了 秒(结果保留根号).第15题图 【答案】(4+2)第1题图A CFD EB2、(2013年广东省佛山市模拟)如图△ABC 中,∠ACB =90°,BC =6 cm ,AC =8cm ,动点P 从A 出发,以2 cm / s 的速度沿AB 移动到B ,则点P 出发 s 时,△BCP 为等腰三角形.(原创)答案: 2,2.5,1. 43.(2013郑州外国语预测卷)如图在平行四边形ABCD 中,点E 在CD 边上运动(不与C 、D 两点重合),连接AE 并延长与BC 的延长线交于点F 。
2013年全国名校初三模拟数学试卷分类汇编:3 整式

整式一、选择题1、(2013山西中考模拟六)已知2243a b x y x y x y -+=-,则a +b 的值为( )A. 1B. 2C. 3D. 4 答案:B2、(2013·吉林中考模拟)下列计算正确的是( )A 、a +2a =3a 2B 、a ·a 2=a 3C 、(2a )2=2a 2D 、(-a 2)3=a 6 答案:B3、(2013·湖州市中考模拟试卷3)下列运算正确的是( ).A. a 2+a 3=a 5B. 235a a a ⋅=C. (a 2)3=a 5D. a 10÷a 2=a 5 答案:B4、(2013·湖州市中考模拟试卷8)下列计算中,不正确...的是 ( ) A . 23a a a -+= B . ()2555xy xy xy -÷=C .()326326x y x y -=-D . ()22233ab a a b ∙-=-答案:C5、(2013·湖州市中考模拟试卷10)下列运算正确的是( )A .23a a a +=B .22(3)6a a =C .623a a a ÷=D .34aa a =· 答案:D二、填空题1、(2013温州市一模)某商品按标价八折出售仍能盈利b 元,若此商品的进价为a 元,则该商品的标价为 元.(用含,a b 的代数式表示) 答案:54+a b () 2、(2013·吉林中考模拟)已知x +y =﹣5,xy =6,则x 2+y 2= _________ . 答案:13三、解答题1、(2013·湖州市中考模拟试卷3)先化简,再求值:2(2)(4)a a a -++,其中a =答案:解:原式=22444a a a a-+++ …………………………4分 =224a + …………………………6分当a =,原式=24+ …………………………7分 =10 …………………………8分。
2013年全国各地中考模拟卷分类汇编:实数的有关概念(含答案)

2013年全国各地中考模拟卷分类汇编--实数的有关概念一、选择题1、(2013年上海奉贤区二模)与无理数3最接近的整数是( )A .1;B .2 ;C .3;D .4; 答案:B2、(2013届宝鸡市金台区第一次检测)下列四个数中最小的一个数是( )A .-2B .-0.1C .0D .|-1|答案:A3、(2013年上海长宁区二模)下列各数中,无理数是( ). A.21B. 3.14C. 3D. 38 答案:C4.(2013浙江东阳吴宇模拟题)下列各数中,比-2小1的数是( ) A. -1 B. 1C. -4D. -3答案:D5.(2013浙江省宁波模拟题)下列各数中是负数的是 ( )A .0.5B . 2C . -1D . 2 答案:C6.(2013浙江省宁波模拟题)《泰囧》上映15天, 累计票房达802000000元,创国产片票房新纪录;预计28日即可超过《变形金刚3》创下的2595.39万观影人数纪录。
用科学记数法表示802000000元正确的是( )A .8 02×105元B .80.2×106元C .0.802×107元D .8.02×108元 答案:D7.(2013浙江省宁波模拟题)实数-8的立方根是______________. 答案:-28.(2013沈阳一模)在下列实数中无理数有( )个.,,,2843 2.020020002……,πº,tan 30°.A.2B.3C.4D.5 答案:B9.(2013沈阳一模)明天数学课要学―勾股定理‖,小敏在―百度‖搜索引擎中输入―勾股定理‖,能搜索到与之相关的结果个数约为12 500 000,这个数用科学记数法表示为( ). A. 1.25×105 B.1.25×106 C.1.25×107 D.0.125×108 答案:C10.(2013浙江锦绣·育才教育集团一模)太阳内部高温核聚变反应释放的辐射能功率为33.8102⨯千瓦,到达地球的仅占20亿分之一,到达地球的辅射能功率为( ▲ )千瓦.(用科学计数法表示,保留2个有效数字) A .141.910⨯ B .142.010⨯C .157.610⨯D .151.910⨯答案:A11、(2013年江苏南京一模)如果a 与-3互为相反数,那么a 等于 A .3B .-3C .13D .-13答案:A12、(2013年江苏南京一模)2013年元宵节正值周末,观灯人数也创下历史新高.据统计,当天有520000游客在夫子庙地区观灯闹元宵,将520000用科学记数法表示为 A .0.52×105 B .5.2×104C .5.2×105D .5.2×106答案:C13、(2013年江苏南京一模)下面的数中,与2-的和为0的是 ( ▲ )A.2B.2-C.21D. 21- 答案:A14、(2013年江苏南京一模)一种花瓣的花粉颗粒直径约为0.0000065米,0.0000065用科学记数法表示为( ▲ ) A .56.510-⨯ B .66.510-⨯C .76.510-⨯D .66510-⨯答案:B15.(2013年江苏南京一模) 3的相反数为 ( )A .3B .-3C .31D . 31-答案:B16、(2013年江苏南京一模)在学雷锋活动中,我市青少年积极报名争当―助人为乐志愿者‖,仅一个月就有107000人报名,将107000用科学记数法表示为 ( ) A .4107.10⨯ B .51007.1⨯C .60.10710⨯D .61.0710⨯答案:B17、(2013年江苏南京一模)如果向北走3 km 记作+3 km ,那么向南走5 km 记作 A .-5 km B .-2 km C .+5 km D .+8 km 答案:A18、如果a 与1互为相反数,则|2|a +等于( C ) A .2B .2-C .1D .1-19.在下列实数中,最小的数是(D )A .0B .3C .2D .π- 20.股市有风险,投资需谨慎。
备战中考数学一模试题分类汇编——平行四边形综合及详细答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到到B′的位置,AB′与CD交于点E.(1)求证:△AED≌△CEB′(2)若AB = 8,DE = 3,点P为线段AC上任意一点,PG⊥AE于G,PH⊥BC于H.求PG + PH的值.【答案】(1)证明见解析;(2).【解析】【分析】(1)由折叠的性质知,,,,则由得到;(2)由,可得,又由,即可求得的长,然后在中,利用勾股定理即可求得的长,再过点作于,由角平分线的性质,可得,易证得四边形是矩形,继而可求得答案.【详解】(1)四边形为矩形,,,又,;(2),,,,在中,,过点作于,,,,,,,、、共线,,四边形是矩形,,.【点睛】此题考查了折叠的性质、矩形的性质、角平分线的性质、等腰三角形的判定与性质以及勾股定理等知识.此题难度较大,注意掌握折叠前后图形的对应关系,注意掌握辅助线的作法,注意数形结合思想的应用.2.阅读下列材料:我们定义:若一个四边形的一条对角线把四边形分成两个等腰三角形,则这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如正方形就是和谐四边形.结合阅读材料,完成下列问题:(1)下列哪个四边形一定是和谐四边形.A.平行四边形B.矩形C.菱形D.等腰梯形(2)命题:“和谐四边形一定是轴对称图形”是命题(填“真”或“假”).(3)如图,等腰Rt△ABD中,∠BAD=90°.若点C为平面上一点,AC为凸四边形ABCD 的和谐线,且AB=BC,请求出∠ABC的度数.【答案】(1) C ;(2)∠ABC的度数为60°或90°或150°.【解析】试题分析:(1)根据菱形的性质和和谐四边形定义,直接得出结论.(2)根据和谐四边形定义,分AD=CD,AD=AC,AC=DC讨论即可.(1)根据和谐四边形定义,平行四边形,矩形,等腰梯形的对角线不能把四边形分成两个等腰三角形,菱形的一条对角线能把四边形分成两个等腰三角形够.故选C.(2)∵等腰Rt△ABD中,∠BAD=90°,∴AB=AD.∵AC为凸四边形ABCD的和谐线,且AB=BC,∴分三种情况讨论:若AD=CD,如图1,则凸四边形ABCD是正方形,∠ABC=90°;若AD=AC,如图 2,则AB=AC=BC,△ABC是等边三角形,∠ABC=60°;若AC=DC,如图 3,则可求∠ABC=150°.考点:1.新定义;2.菱形的性质;3.正方形的判定和性质;4.等边三角形的判定和性质;5.分类思想的应用.3.菱形ABCD中、∠BAD=120°,点O为射线CA上的动点,作射线OM与直线BC相交于点E,将射线OM绕点O逆时针旋转60°,得到射线ON,射线ON与直线CD相交于点F.(1)如图①,点O与点A重合时,点E,F分别在线段BC,CD上,请直接写出CE,CF,CA三条段段之间的数量关系;(2)如图②,点O在CA的延长线上,且OA=13AC,E,F分别在线段BC的延长线和线段CD的延长线上,请写出CE,CF,CA三条线段之间的数量关系,并说明理由;(3)点O在线段AC上,若AB=6,BO=27,当CF=1时,请直接写出BE的长.【答案】(1)CA=CE+CF.(2)CF-CE=43AC.(3)BE的值为3或5或1.【解析】【分析】(1)如图①中,结论:CA=CE+CF.只要证明△ADF≌△ACE(SAS)即可解决问题;(2)结论:CF-CE=43AC.如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.只要证明△FOG≌△EOC(ASA)即可解决问题;(3)分四种情形画出图形分别求解即可解决问题.【详解】(1)如图①中,结论:CA=CE+CF.理由:∵四边形ABCD是菱形,∠BAD=120°∴AB=AD=DC=BC,∠BAC=∠DAC=60°∴△ABC,△ACD都是等边三角形,∵∠DAC=∠EAF=60°,∴∠DAF=∠CAE,∵CA=AD,∠D=∠ACE=60°,∴△ADF≌△ACE(SAS),∴DF=CE,∴CE+CF=CF+DF=CD=AC,∴CA=CE+CF.(2)结论:CF-CE=43 AC.理由:如图②中,如图作OG∥AD交CF于G,则△OGC是等边三角形.∵∠GOC=∠FOE=60°,∴∠FOG=∠EOC,∵OG=OC,∠OGF=∠ACE=120°,∴△FOG≌△EOC(ASA),∴CE=FG,∵OC=OG,CA=CD,∴OA=DG,∴CF-EC=CF-FG=CG=CD+DG=AC+13AC=43AC,(3)作BH⊥AC于H.∵AB=6,AH=CH=3,∴BH=33,如图③-1中,当点O在线段AH上,点F在线段CD上,点E在线段BC上时.∵OB=27,∴OH=22OB BH=1,∴OC=3+1=4,由(1)可知:CO=CE+CF,∵OC=4,CF=1,∴CE=3,∴BE=6-3=3.如图③-2中,当点O在线段AH上,点F在线段DC的延长线上,点E在线段BC上时.由(2)可知:CE-CF=OC,∴CE=4+1=5,∴BE=1.如图③-3中,当点O在线段CH上,点F在线段CD上,点E在线段BC上时.同法可证:OC=CE+CF,∵OC=CH-OH=3-1=2,CF=1,∴CE=1,∴BE=6-1=5.如图③-4中,当点O在线段CH上,点F在线段DC的延长线上,点E在线段BC上时.同法可知:CE-CF=OC,∴CE=2+1=3,∴BE=3,综上所述,满足条件的BE的值为3或5或1.【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,等边三角形的性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.4.(感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.(应用)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,菱形CEFG的面积是_______.(只填结果)【答案】见解析【解析】试题分析:探究:由四边形ABCD 、四边形CEFG 均为菱形,利用SAS 易证得△BCE ≌△DCG ,则可得BE=DG ;应用:由AD ∥BC ,BE=DG ,可得S △ABE +S △CDE =S △BEC =S △CDG =8,又由AE=3ED ,可求得△CDE 的面积,继而求得答案.试题解析:探究:∵四边形ABCD 、四边形CEFG 均为菱形,∴BC=CD ,CE=CG ,∠BCD=∠A ,∠ECG=∠F .∵∠A=∠F ,∴∠BCD=∠ECG .∴∠BCD-∠ECD=∠ECG-∠ECD ,即∠BCE=∠DCG .在△BCE 和△DCG 中,BC CD BCE DCG CE CG ⎧⎪∠∠⎨⎪⎩=== ∴△BCE ≌△DCG (SAS ),∴BE=DG .应用:∵四边形ABCD 为菱形,∴AD ∥BC ,∵BE=DG ,∴S △ABE +S △CDE =S △BEC =S △CDG =8,∵AE=3ED ,∴S △CDE =1824⨯= , ∴S △ECG =S △CDE +S △CDG =10∴S 菱形CEFG =2S △ECG =20.5.如图,现将平行四边形ABCD 沿其对角线AC 折叠,使点B 落在点B ′处.AB ′与CD 交于点E .(1)求证:△AED≌△CEB′;(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.【答案】(1)见解析(2)见解析【解析】【分析】(1)由题意可得AD=BC=B'C,∠B=∠D=∠B',且∠AED=∠CEB',利用AAS证明全等,则结论可得;(2)由△AED≌△CEB′可得AE=CE,且EF⊥AC,根据等腰三角形的性质可得EF垂直平分AC,∠AEF=∠CEF.即AF=CF,∠CEF=∠AFE=∠AEF,可得AE=AF,则可证四边形AECF是菱形.【详解】证明:(1)∵四边形ABCD是平行四边形∴AD=BC,CD∥AB,∠B=∠D∵平行四边形ABCD沿其对角线AC折叠∴BC=B'C,∠B=∠B'∴∠D=∠B',AD=B'C且∠DEA=∠B'EC∴△ADE≌△B'EC(2)四边形AECF是菱形∵△ADE≌△B'EC∴AE=CE∵AE=CE,EF⊥AC∴EF垂直平分AC,∠AEF=∠CEF∴AF=CF∵CD∥AB∴∠CEF=∠EFA且∠AEF=∠CEF∴∠AEF=∠EFA∴AF=AE∴AF=AE=CE=CF∴四边形AECF是菱形【点睛】本题考查了折叠问题,全等三角形的判定和性质,平行四边形的性质,菱形的判定,熟练掌握这些性质和判定是解决问题的关键.6.如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.(1)求证:△AEF≌△DCE.(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.【答案】(1)证明见解析;(2)6cm.【解析】分析:(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.详解:(1)证明:∵EF⊥CE,∴∠FEC=90°,∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,∴∠AEF=∠ECD.在Rt△AEF和Rt△DEC中,∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.∴△AEF≌△DCE.(2)解:∵△AEF≌△DCE.AE=CD.AD=AE+4.∵矩形ABCD的周长为32cm,∴2(AE+AE+4)=32.解得,AE=6(cm).答:AE的长为6cm.点睛:此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握,难易程度适中,是一道很典型的题目.7.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.【答案】(1)AG2=GE2+GF2(2)【解析】试题分析:(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,MN=x,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(2x+x)2,解得x=,推出BN=,再根据BG=BN÷cos30°即可解决问题.试题解析:(1)结论:AG2=GE2+GF2.理由:连接CG.∵四边形ABCD是正方形,∴A、C关于对角线BD对称,∵点G在BD上,∴GA=GC,∵GE⊥DC于点E,GF⊥BC于点F,∴∠GEC=∠ECF=∠CFG=90°,∴四边形EGFC是矩形,∴CF=GE,在Rt△GFC中,∵CG2=GF2+CF2,∴AG2=GF2+GE2.(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,∴∠AMN=30°,∴AM=BM=2x,MN=x,在Rt△ABN中,∵AB2=AN2+BN2,∴1=x2+(2x+x)2,解得x=,∴BN=,∴BG=BN÷cos30°=.考点:1、正方形的性质,2、矩形的判定和性质,3、勾股定理,4、直角三角形30度的性质8.(1)问题发现如图1,点E. F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;(2)类比引申如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E. F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系时,仍有EF=BE+DF;(3)联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC 满足的等量关系,并写出推理过程。
2013年全国各地中考模拟卷分类汇编:分式

1 1 ………………………………………(4 分) x 1 x 1
x 1 x 1 ………………………(6 分) ( x 1)( x 1) ( x 1)( x 1)
-2-
( x 1) ( x 1) ……………………………(6 分) ( x 1)( x 1)
mn 2
mn mn
C、
2mn mn
D、
mn mn
答案:C 二、填空题 1 . ( 2013 年 北 京 平 谷 区 一 模 ) 如 果 分 式 _____________ 2、(2013 沈阳一模)化简(x- 答案:x-1 x 3、(2013 年江苏南京一模)若分式 有意义,则 x 的取值范围是 ▲ . 1-x 答案: x≠1
= =
2 1 (x 2) x 1 ………1 分 x 2 x 1 x2
x 2 x 1 ……2 分 x 1 x 2
x 2 4 x 2 +1 3 = = ( x 1)( x 2) ( x 1)( x 2)
=
3 .…….3 分 x 3x
a mn
3.(2013 辽宁葫芦岛一模)化简 A. x +1 答案:D B.
x2 x 的结果是 x 1 1 x
C.— x
) D.
x -1
x
4、(2013 年湖北宜昌调研)若分式 (A)a=2 答案:A (B)a=0
a 无意义,则( a2
(C)a>2
)
(D)a>0
5、 (2013 年江苏东台第二学期阶段检测)小明通常上学时走上坡路,通常的速度为 m 千米 /时,放学回家时,沿原路返回,通常的速度为 n 千米/时,则小明上学和放学路上的平均 速度为( A、 )千米/时 B、
2013年北京市数学中考一、二模拟题分类汇编:操作探究

操作探究1.(2013.昌平一模22)(1)人教版八年级数学下册92页第14题是这样叙述的:如图1,□ABCD中,过对角线BD上一点P作EF∥BC,HG∥AB,图中哪两个平行四边形的面积相等?为什么?根据习题背景,写出面积相等的一对平行四边形的名称为和;(2)如图2,点P为□ABCD内一点,过点P分别作AD、AB的平行线分别交□ABCD的四边于点E、F、G、H. 已知S□BHPE = 3,S□PFDG = 5,则;(3)如图3,若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重复、无缝隙).已知①②③④四个平行四边形面积的和为14,四边形ABCD的面积为11,则菱形EFGH的周长为.2.(2013.燕山一模22)阅读下列材料:问题:如图⑴,已知正方形ABCD中,E、F分别是BC、CD边上的点,且∠EAF =45°.判断线段BE、EF、FD之间的数量关系,并说明理由.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△DAF绕点A顺时针旋转90°,得到△BAH,然后通过证明三角形全等可得出结论.请你参考小明同学的思路,解决下列问题:⑴图⑴中线段BE、EF、FD之间的数量关系是;⑵如图⑵,已知正方形ABCD边长为5,E、F分别是BC、CD边上的点,且∠EAF=45°,AG⊥EF于点G,则AG的长为,△EFC的周长为;⑶如图⑶,已知△AEF中,∠EAF=45°,AG⊥EF于点G,且EG=2,GF=3,则△AEF的面积为.3.(2013.朝阳一模22)阅读下面材料:小雨遇到这样一个问题:如图1,直线l1∥l2∥l3,l1与l2之间的距离是1,l2与l3之间的距离是2,试画出一个等腰直角三角形ABC,使三个顶点分别在直线l1、l2、l3上,并求出所画等腰直角三角形ABC的面积.小雨是这样思考的:要想解决这个问题,首先应想办法利用平行线之间的距离,根据所求图形的性质尝试用旋转的方法构造全等三角形解决问题.具体作法如图2所示:在直线l1任取一点A,作AD⊥l2于点D,作∠DAH=90°,在AH上截取AE=AD,过点E作EB⊥AE交l3于点B,连接AB,作∠BAC=90°,交直线l2于点C,连接BC,即可得到等腰直角三角形ABC.请你回答:图2中等腰直角三角形ABC的面积等于.参考小雨同学的方法,解决下列问题:如图3,直线l1∥l2∥l3,l1与l2之间的距离是2,l2与l3之间的距离是1,试画出一个等边三角形ABC,使三个顶点分别在直线l1、l2、l3上,并直接写出所画等边三角形ABC的面积(保留画图痕迹).4.(2013.海淀一模22)问题:如图1,、、、是同一平面内的一组等距平行线(相邻平行线间的距离为1).画出一个正方形,使它的顶点、、、分别在直线、、、上,并计算它的边长.图1 图2小明的思考过程:他利用图1中的等距平行线构造了的正方形网格,得到了辅助正方形,如图2所示, 再分别找到它的四条边的三等分点、、、,就可以画出一个满足题目要求的正方形.请回答:图2中正方形的边长为 .请参考小明的方法,解决下列问题:(1)请在图3的菱形网格(最小的菱形有一个内角为,边长为1)中,画出一个等边△,使它的顶点、、落在格点上,且分别在直线a、b、c上;(3)如图4,、、是同一平面内的三条平行线,、之间的距离是,、之间的距离是,等边△的三个顶点分别在、、上,直接写出△的边长.图3 图45.(2013.东城一模22)如图,在菱形纸片ABCD中,AB=4cm,∠ABC=120°,按下列步骤进行裁剪和拼图:第一步:如图1,在线段AD上任意取一点E,沿EB,EC剪下一个三角形纸片EBC(余下部分不再使用);第二步:如图2,沿三角形EBC的中位线GH将纸片剪成两部分,并在线段GH上任意取一点M,线段BC上任意取一点N,沿MN将梯形纸片GBCH剪成两部分;第三步:如图3,将MN左侧纸片绕G点按顺时针方向旋转180°,使线段GB与GE重合,将MN右侧纸片绕H点按逆时针方向旋转180°,使线段HC与HE重合,再与三角形纸片EGH拼成一个与三角形纸片EBC面积相等的四边形纸片.(注:裁剪和拼图过程均无缝且不重叠)(1)请你在图3中画出拼接成的四边形;(2)直接写出拼成的四边形纸片周长的最小值为________cm,最大值为________cm.6.(2013.怀柔一模22)理解与应用:我们把对称中心重合、四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度相等.....一条直线l与方形环的边线有四个交点、、、.小明在探究线段与的数量关系时,从点、向对边作垂线段、,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:(1)直线l与方形环的对边相交时(22题图1),直线l分别交、、、于、、、,小明发现与相等,请你帮他说明理由;(2)直线l与方形环的邻边相交时(22题图2),l分别交、、、于、、、,l与的夹角为,请直接写出的值(用含的三角函数表示).7.(2013.门头沟一模22)操作与探究:在平面直角坐标系xOy中,点P从原点O出发,且点P只能每次向上平移2个单位长度或向右平移1个单位长度.(1)实验操作:在平面直角坐标系xOy中,点P从原点O出发,平移1次后可能到达的点的坐标是,;点P从原点O出发,平移2次后可能到达的点的坐标是,,;点P从原点O出发,平移3次后可能到达的点的坐标是;(2)观察发现:任一次平移,点P可能到达的点在我们学过的一种函数的图象上,如:平移1次后在函数的图象上;平移2次后在函数的图象上,….若点P平移5次后可能到达的点恰好在直线上,则点P的坐标是;(3)探究运用:点P从原点O出发经过次平移后,到达直线上的点Q,且平移的路径长不小于30,不超过32,求点Q的坐标.8.(2013.平谷一模22)对于平面直角坐标系中的任意两点,我们把叫做两点间的直角距离,记作.(1)已知点,那么两点间的直角距离=_____________;(2)已知O为坐标原点,动点满足,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有满足条件的图形;(3)设是一定点,是直线上的动点,我们把的最小值叫做点到直线的直角距离.试求点到直线的直角距离..9.(2013.石景山一模22)问题解决:已知:如图,为上一动点,分别过点、作于点,于点,联结、.(1)请问:点满足什么条件时,的值最小?(2)若,,,设.用含的代数式表示的长(直接写出结果).拓展应用:参考上述问题解决的方法,请构造图形,并求出代数式的最小值.来源:学,科,网]10.(2013.顺义一模22)如图1,在四边形中,,分别是的中点,连结并延长,分别与的延长线交于点,则(不需证明).小明的思路是:在图1中,连结,取的中点,连结,根据三角形中位线定理和平行线性质,可证得.问题:如图2,在中,,点在上,,分别是的中点,连结并延长,与的延长线交于点,若,连结,判断的形状并证明.11.(2013.通州一模22)如图所示,在4×4的菱形斜网格图中(每一个小菱形的边长为1,有一个角是60°),菱形的边长为2,是的中点,沿将菱形剪成①、②两部分,用这两部分可以分别拼成直角三角形、等腰梯形、矩形,要求所拼成图形的顶点均落在格点上.(1)在下面的菱形斜网格中画出示意图;(2)若所拼成的直角三角形、等腰梯形、矩形的面积分别记为、、,周长分别记为、、,判断所拼成的三种图形的面积、周长的大小关系(用“=”、“>”、“<”、“≤”或“≥”连接):面积关系是;周长关系是.12.(2013.西城一模22)先阅读材料,再解答问题:小明同学在学习与圆有关的角时了解到:在同圆或等圆中,同弧(或等弧)所对的圆周角相等.如图,点A、B、C、D均为⊙O上的点,则有∠C=∠D.小明还发现,若点E在⊙O外,且与点D在直线AB同侧,则有∠D>∠E.请你参考小明得出的结论,解答下列问题:(1) 如图1,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0) .①在图1中作出△ABC的外接圆(保留必要的作图痕迹,不写作法);②若在轴的正半轴上有一点D,且∠ACB =∠ADB,则点D的坐标为;(2) 如图2,在平面直角坐标系xOy中,点A的坐标为(0,m),点B的坐标为(0,n),其中m>n>0.点P为轴正半轴上的一个动点,当∠APB达到最大时,直接写出此时点P的坐标.13.(2013.延庆一模22)阅读下面材料:将正方形ABCD(如图1)作如下划分:第1次划分:分别联结正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;第2次划分:将图2左上角正方形AEMH按上述方法再作划分,得图3,则图3中共有_______个正方形;若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有_______个正方形;继续划分下去,能否将正方形ABCD划分成有2013个正方形的图形?需说明理由.14.(2013.昌平二模22)(1)【原题呈现】如图,要在燃气管道l上修建一个泵站分别向A、B两镇供气. 泵站修在管道的什么地方,可使所用的输气管线最短?解决问题:请你在所给图中画出泵站P的位置,并保留作图痕迹;(2)【问题拓展】已知a>0,b>0,且a+b=2,写出的最小值;(3)【问题延伸】已知a>0,b>0,写出以、、为边长的三角形的面积.15.(2013.朝阳二模22)阅读下列材料:小华遇到这样一个问题,如图1, △ABC中,∠ACB=30º,BC=6,AC=5,在△ABC内部有一点P,连接PA、PB、PC,求PA+PB+PC的最小值.小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD、BE,则BE的长即为所求.(1)请你写出图2中,PA+PB+PC的最小值为;(2)参考小华的思考问题的方法,解决下列问题:①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长.16.(2013.大兴二模22)在三角形纸片ABC中,已知∠ABC=90°,AB=6,BC=8.过点A作直线平行于BC,折叠三角形纸片ABC,使直角顶点B 落在直线上的T处,折痕为MN.当点T 在直线上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动(点M可以与点A重合,点N可以与点C重合),求线段AT长度的最大值与最小值的和(计算结果不取近似值).17.(2013.东城二模22)阅读并回答问题:数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:作法:①在OA,OB上分别截取OD,OE,使OD=OE.②分别以D,E为圆心,以大于为半径作弧,两弧在内交于点C.③作射线OC,则OC就是的平分线小聪只带了直角三角板,他发现利用三角板也可以作角平分线,方法如下:作法: ①利用三角板上的刻度,在OA ,OB 上分别截取OM ,ON ,使OM =ON .②分别过以M ,N 为OM ,ON 的垂线,交于点P.③作射线OP ,则OP 就是的平分线.小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.根据以上情境,解决下列问题:(1) 小聪的作法正确吗?请说明理由;(2) 请你帮小颖设计用刻度尺作平分线的方法.(要求:不与小聪方法相同,请画出图形,并写出画图的方法,不必证明).18.(2013.房山二模22)如图1,在矩形MNPQ 中,点E ,F ,G ,H 分别在边NP ,PQ ,QM ,MN 上,当时,我们称四边形EFGH 为矩形MNPQ 的反射四边形.已知:矩形ABCD 的四个顶点均为边长为1的正方形网格的格点,请解决下列问题: (1)在图2中,点E ,F 分别在BC ,CD 边上,请作出矩形ABCD 的反射四边形EFGH ,并求出反射四边形EFGH 的周长.(2)在图3中作出矩形ABCD 的所有反射四边形,并判断它们的周长之间的关系.19.(2013.密云二模22)实践与操作:如图1是以正方形两顶点为圆心,边长为半径,画两段相等的圆弧而成的轴对称图形,图2是以图1为基本图案经过图形变换拼成的一个中心对称图形.(1)请你仿照图1,用两段相等圆弧(小于或等于半圆),在图3中重新设计一个不同的轴对称图形.(2)以你在图3中所画的图形为基本图案,经过图形变换在图4中拼成一个中心对称图形.20.(2013.石景山二模22)如图,在矩形ABCD中,AB=3,BC=4,点M、N、分别在BC、AB上,将矩形ABCD沿MN折叠,设点B的对应点是点E.(1)若点E在AD边上,BM=,求AE的长;(2)若点E在对角线AC上,请直接写出AE的取值范围:.解:21.(2013.丰台二模22)操作探究:一动点沿着数轴向右平移5个单位,再向左平移2个单位,相当于向右平移3个单位.用实数加法表示为 5+()=3.若平面直角坐标系xOy中的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”.规定“平移量”{a,b}与“平移量”{c,d}的加法运算法则为.(1)计算:{3,1}+{1,2};(2)若一动点从点A(1,1)出发,先按照“平移量”{2,1}平移到点B,再按照“平移量”{-1,2}平移到点C;最后按照“平移量”{-2,-1}平移到点D,在图中画出四边形ABCD,并直接写出点D的坐标;(3)将(2)中的四边形ABCD以点A为中心,顺时针旋转90°,点B旋转到点E,连结AE、BE若动点P从点A出发,沿△AEB的三边AE、EB、BA 平移一周.请用“平移量”加法算式表示动点P的平移过程.22.(2013.海淀二模22)如图1,四边形ABCD中,、为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为,如果在点的运动过程中,的值不变,则我们称四边形ABCD为“四边形”,此时的值称为它的“值”.经过探究,可得矩形是“四边形”.如图2,矩形ABCD中,若AB=4,BC=3,则它的“值”为.图1 图2 图3(1)等腰梯形(填“是”或“不是”)“四边形”;(2)如图3,是⊙O的直径,A是⊙O上一点,,点为上的一动点,将△沿的中垂线翻折,得到△.当点运动到某一位置时,以、、、、、中的任意四个点为顶点的“四边形”最多,最多有个.23.(2013.怀柔二模22)探究与应用已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y = 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有..两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.(1)如图,若反比例函数解析式为y= ,P点坐标为(1, 0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1;(2)请你通过改变P点坐标,对直线M1 M的解析式y﹦kx+b进行探究可得 k﹦,若点P的坐标为(m,0)时,则b﹦;(3)依据(2)的规律,如果点P的坐标为(6,0),请你直接写出点M1和点M的坐标.解:(1)如图(2)k﹦,b﹦;(3)M1的坐标为(,),M的坐标为(,).24.(2013.西城二模22)在平面直角坐标系xOy中,点经过变换得到点,该变换记作,其中为常数.例如,当,且时,.(1) 当,且时,= ;(2) 若,则= ,= ;(3) 设点是直线上的任意一点,点经过变换得到点.若点与点重合,求和的值.第七章操作探究参考答案1.(2013.昌平一模22)解:(1)□AEPH 和□PGCF或□ABGH 和□EBCF 或□AEFD 和□HGCD . … 1分(2)1. ……………………………… 2分(3)24.……………………………… 4分2.(2013.燕山一模22)⑴线段BE、EF、FD之间的数量关系是EF=BE+FD; (1)分⑵AG的长为 5 ,△EFC的周长为 10 ;………………………3分⑶△AEF的面积为 15 .………………………5分3.(2013.朝阳一模22)解: 5;……………………………………………2分如图;………………………………………3分. ………………………………………5分4.(2013.海淀一模22)(1).………………………2分(2)①如图:(答案不唯一) …4分②.………………………5分5.(2013.东城一模22)解:(1)拼接成的四边形所图虚线所示;………………2分(2);. …………………………5分(注:通过操作,我们可以看到最后所得的四边形纸片是一个平行四边形,其上下两条边的长度等于原来菱形的边AB=4,左右两边的长等于线段MN的长,当MN垂直于BC时,其长度最短,等于原来菱形的高的一半,于是这个平行四边形的周长的最小值为2(+4)=;当点E与点A重合,点M与点G重合,点N与点C重合时,线段MN最长,等于,此时,这个四边形的周长最大,其值为.)6.(2013.怀柔一模22)理解与应用:…………………1分=∠N’NF……………………2分………………3分)……………………………5分7.(2013.门头沟一模22)解:(1)(0,6),(1,4),(2,2),(3,0).………………………2分(2)平移5次后P在y=-2x+10上,又在y=3x上,联立方程组即可。
2013年全国名校初三模拟数学试卷分类汇编:29矩形 菱形 正方形

矩形、菱形、正方形一、选择题1、(2013江苏射阴特庸中学)如图,菱形ABCD 的周长是16,∠A =60°,则对角线BD 的长度为( )A .2B .2 3C .4D .4 3 答案:B2、(2013江苏扬州弘扬中学二模)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( ). A .2+10 B .2+210 C .12 D .18 答案:B3、 (2013山西中考模拟六)在下列命题中,正确的是( )A .一组对边平行的四边形是平行四边形B .有一个角是直角的四边形是矩形C .有一组邻边相等的平行四边形是菱形D .对角线互相垂直平分的四边形是正方形 答案:C4、(2013·湖州市中考模拟试卷1)如图,在菱形ABCD 中,点E 、 F 分别是AB 、AC 的中点,如果EF =3,那么菱形ABCD 的周长是( )A. 24B. 18C. 12D. 6 答案:A5、(2013·湖州市中考模拟试卷7)正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,正方形BEFG 的边长为4,则D E K △的面积为( ) 10题图A.10B.12C.14D.16答案:D6、(2013·湖州市中考模拟试卷10)如图,四边形ABCD 的对角线互相平分,要使它成为矩形,那么需要添加的条件是()A.CD AB =B.BC AD =C.BC AB =D.BD AC = 答案:D7、6.(2013年河北省一摸)|下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是A .①②③B .①②C .①③D .②③答案:B8、(2013年河北二摸)如图,在菱形ABCD 中,DE ⊥AB ,3cos 5A =,AE =3,则tan ∠DBE 的值是A .12B .2 C.2 D.5 答案:B9、(2013年河北三摸)一个正方形的面积等于10,则它的边长a 满足A. 3<a <4B. 5<a <6C.7<a <8D. 9<a <10 答案:A10、(2013年河北三摸)如图,矩形ABCD 的对角线AC ⊥OF ,边CD 在OE 上,∠BAC =70°,则 ∠EOF 等于 A. 10° B. 20° C. 30° D. 70° 答案:B11、(2013年河北三摸)如图,在正方形ABCD 中,AB =3㎝.动第8题图DAB CE点M 自A 点出发沿AB 方向以每秒1㎝的速度运动,同时动点N 自A 点出发沿折线AD —DC —CB 以每秒3㎝的速度运动,到达B 点时运动同时停止.设△AMN 的面积为y (㎝2),运动时间为x (秒),则下列图象中能大致反映y 与x 之间函数关系的是答案:B12、(2013年河北四摸)如图,小聪在作线段AB 的垂直平分线时,他是这样操作的:分别以A 和B 为圆心,大于12AB 的长为半径画弧,两弧相交于C 、D ,则直线CD 即为所求.根据他的作图方法可知四边形ADBC 一定是...A .矩形B .菱形C .正方形D .等腰梯形答案:B二、填空题1、(2013山东省德州一模)如图,四边形ABCD 中,E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点.请你添加一个条件,使四边形EFGH 为矩形,应添加的条件是 .答案:AC BD2、(2013温州市一模)如图,在正方形ABCD 的外侧,作等边△ADE ,则∠AEB= .答案:15°3、(2013·曲阜市实验中学中考模拟)如图,菱形ABCD 的对角线的长分别为2和5,P 是对AD H G F BE 第1题(第2题) CAB D MNBACD7题角线AC 上任一点(点P 不与点A 、C 重合),且PE ∥BC 交AB 于E ,PF ∥CD 交AD 于F ,则阴影部分的面积是_______.答案:2.54、(2013·温州市中考模拟)将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一边上,则∠1+∠2=______. 1 25题图 6题图7、2013年温州一摸)如图,以O 为顶点的两条抛物线分别经过正方形的四个顶点A 、B 、C 、D ,则阴影部分的面积为______ 答案:18、(2013年温州一摸)将两张矩形纸片如图所示摆放,使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一边上,则∠1+∠2=______. (2) 若BC =10,∠BAC =90°,且四边形AECF 是菱形,求BE 的长.答案证:(1)由□ABCD ,得AD=BC,AD ∥BC. ……2分由BE=DF,得AF=CE, ∴AF=CE,AF ∥CE. ……3分 ∴四边形AECF 是平行四边形; ……4分(2)由菱形AECF,得AE=EC ,∴∠EAC=∠ACE. ……5分由∠BAC=90°,得∠BAE=∠B ,∴AE=EB. ……7分FEDCBA∴BE=AE=EC , BE=5. ……8分2、(2013江苏射阴特庸中学)小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片ABCD 放在每格宽度为12mm 的横格纸中,恰好四个顶点都在横格线上,已知∠α=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(结果精确到1mm )答案:解:作BE ⊥l 于点E ,DF ⊥l 于点F . ……2分 ∵∠α+∠DAF=180°-∠BAD=180°-90°=90°,∠ADF+∠DAF=90°, ∴∠ADF=∠α=36°.根据题意,得BE=24mm, DF=48mm . ……4分 在Rt △ABE 中,sin α=BE/AB ,∴AB=BE/sin36°=40(mm).……6分 在Rt △ADF 中,cos ∠ADF=DF/AD ,∴AD=DF/COS36°=60(mm ).8分 ∴矩形ABCD 的周长=2(40+60)=200(mm). ……10分3、(2013江苏射阴特庸中学)如图,△AEF 中,∠EAF =45°,AG ⊥EF 于点G ,现将△AEG 沿AE 折叠得到△AEB ,将△AFG 沿AF 折叠得到△AFD ,延长BE 和DF 相交于点C . (1)求证:四边形ABCD 是正方形;(2)连接BD 分别交AE 、AF 于点M 、N ,将△ABM 绕点A 逆时针旋转,使AB 与AD 重合,得到△ADH ,试判断线段MN 、ND 、DH 之间的数量关系,并说明理由. (3)若EG =4,GF =6,BM =32,求AG 、MN 的长.答案:(1)由∠BAD=∠ABC=∠ADC=90°,得矩形ABCD, ……2分由AB=AD ,得四边形ABCD 是正方形. ……3分 (2)MN 2=ND 2+DH 2. ……4分理由:连接NH ,由△ABM ≌△ADH ,得AM=AH ,BM=DH ,∠ADH=∠ABD=45°, ∴∠NDH=90°, ……6分 再证△AMN ≌△AHN ,得MN=NH , ……7分 ∴MN 2=ND 2+DH 2. ……8分 (3)设AG=x ,则EC=x-4,CF=x-6,由Rt △ECF ,得(x-4)2+(x-6)2=100,x 1=12,x 2=-2(舍去) ∴AG=12.……10分 由AG=AB=AD=12,得BD=122,∴MD=92,FE H G N M FE DCB A设NH=y,由Rt △NHD,得y 2=(92-y)2+(32)2,y=52,即MN=5 2. ……12分 4、(2013山西中考模拟六) 如图,在ABC △中,90ACB = ∠,2AC =,3BC =.D 是BC 边上一点,直线DE BC ⊥于D ,交AB 于E ,CF AB ∥交直线DE 于F .设CD x =.(1)当x 取何值时,四边形EACF 是菱形?请说明理由; (2)当x 取何值时,四边形EACD 的面积等于2?答案:解:(1)90ACB = ∠,AC BC ∴⊥,又DE BC ⊥,EF AC ∴∥.又AE CF ∥,∴四边形EACF 是平行四边形. 当CF AC =时,四边形ACFE 是菱形. 此时,2CF AC ==,3BD x =-,2tan 3B =∠, ()2tan 33ED BD B x ==- ∠.∴()222333DF EF ED x x =-=--=. 在Rt CDF △中,222CD DF CF +=,∴222223x x ⎛⎫+= ⎪⎝⎭∴x =即当x =时,四边形ACFE 是菱形.(2)由已知得,四边形EACD 是直角梯形,212142233EACD S x x x x ⎛⎫=⨯-=-+ ⎪⎝⎭ 梯形,依题意,得21223x x -+=. 整理,得2660x x -+=.解之,得13x =,23x =.33x BC =+>=,∴3x =+3x =EACD 的面积等于2.5、(2013·曲阜市实验中学中考模拟)如图,在矩形ABCD 中,AE 平分∠DAB 交DC 于点E ,连接BE ,过E 作EF ⊥BE 交AD 于F.ED FBCA(1)∠DEF 和∠CBE 相等吗?请说明理由;(2)请找出图中与EB 相等的线段(不另添加辅助线和字母),并说明理由. 答案:解:(1)相等. 理由如下: ……1分∵四边形ABCD 是矩形 ∴∠C=∠D=90°∴∠BEC+∠CBE=90° ∵EF ⊥BE ∴∠BEF=90° ∴∠DEF+∠BEC=90°∴∠DEF=∠CBE ………3分 (2)BE=EF.理由如下: ………4分∵AE 平分∠DAB ∴∠DAE=∠BAE∵AB ∥CD ∴∠BAE=∠DEA ∴∠DAE=∠DEA ∴AD=ED=BCA ∵∠C=∠D=90° ∠DEF=∠CBE∴△DEF ≌△CBE (ASA )∴BE=EF …………8分6、(2013·湖州市中考模拟试卷3)已知:在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE =2. (1)如图①,当四边形EFGH 为正方形时,求△GFC 的面积;(2)如图②,当四边形EFGH 为菱形,且BF =a 时,求△GFC 的面积(用含a 的代数式表示);(3)在(2)的条件下,△GFC 的面积能否等于2?请说明理由.解:(1)如图①,过点G 作G M B C ⊥于M .在正方形EFGH 中,90,H E F E H E F ∠==. ………………………1分B ACD EF90.90,.A E HB E F A E H A H E A H E B E F ∴∠+∠=∠+∠=∴∠=∠又∵90A B ∠=∠= , ∴⊿AHE ≌⊿BEF . ………………………2分同理可证:⊿MFG ≌⊿BEF . ………………………3分∴GM=BF=AE =2.∴FC=BC-BF =10. ………………………4分 (2)如图②,过点G 作G M B C⊥于M .连接HF . //,.//,.A DBC A H F M F H E H F G E H F G F H ∴∠=∠∴∠=∠.A H EM F G ∴∠=∠ ………………………5分 又90,,A G M F E H G F ∠=∠==∴⊿AHE ≌⊿MFG . ………………………6分 ∴GM=AE =2. ………………………7分11(12)12.22G F C S F CG M a a ∴=⋅=-=- ………………………8分 (3)⊿GFC 的面积不能等于2. ………………………9分∵若2,G F C S = 则12- a =2,∴a =10. 此时,在⊿BEF 中,……………10分在⊿AHE 中,12>.…11分 ∴AH >AD .即点H 已经不在边AB 上.故不可能有2.G F C S = ………………………………………12分 解法二:⊿GFC 的面积不能等于2. ………………………9分 ∵点H 在AD 上,∴菱形边长EH的最大值为.∴BF的最大值为 ………………………10分 又因为函数12G F CS a =- 的值随着a 的增大而减小, 所以GFC S的最小值为12-. ………………………11分又∵122>,∴⊿GFC 的面积不能等于2. ………………12分EO D C BA7、20. (2013年深圳育才二中一摸) 如图,四边形ABCD 是矩形,对角线AC 、BD 相交于点O ,BE ∥AC 交DC 的延长线于点E . (1)求证:BD =BE ;(2)若∠DBC =30︒,BO =4,求四边形ABED 的面积. (1)证明:∵四边形ABCD 是矩形,∴AC =BD ,AB ∥CD ,…………………………2分∵BE ∥AC∴四边形ABEC 是平行四边形。
2013年北京市数学中考一、二模拟题分类汇编:四边形

四边形1.(2013顺义一模19)已知:如图,四边形ABCD 中,对角线AC 、BD 相交于点E ,BD DC ⊥,45ABD ∠=︒,30ACD ∠=︒,AD CD ==,求AC 和BD的长.2.(2013石景山一模19)已知:如图,在四边形ABCD 中,AD DC ⊥,△DBC 是等边三角形,︒=∠45ABD ,2=AD .求四边形ABCD 的周长.3.(2013西城一模19)如图,平行四边形ABCD 的对角线AC 、BD 交于点O , AC ⊥AB ,AB =2,且AC ︰BD =2︰3. (1) 求AC 的长; (2) 求△AOD 的面积.DCBADCBAEA4.(2013平谷一模19)已知:如图,四边形ABCD 中,90A ∠=︒,120D ∠=︒,E是AD 上一点,∠BED=135°,BE =DC =2DE = 求(1)点C 到直线AD 的距离; (2)线段BC 的长.5.(2013通州一模20)如图,在矩形ABCD 中,AB =3,BC ,△DCE 是等边三角形,DE交AB 于点F ,求△BEF 的周长.6.(2013密云一模19)如图,已知菱形ABCD ,AB=AC ,E 、F 分别是BC 、AD的中点,连接AE 、CF(1)证明:四边形AECF 是矩形; (2)若AB=8,求菱形的面积。
DA DFEB C7.(2013门头沟一模19)如图,在四边形ABCD 中,∠A =∠ADC =120º,AB =AD ,E 是BC 的中点,DE =15,DC =24,求四边形ABCD 的周长.8.(2013丰台一模19)如图,四边形ABCD 中,AB = AD ,∠BAD =90°,∠CBD =30°,∠BCD =45°, 若AB =22.求四边形ABCD 的面积.9.(2013海淀一模19)如图,在四边形ABCD 中,对角线AC ,BD 相交于点E ,DAB ∠=CDB ∠=90︒,ABD ∠=45︒,∠DCA =30︒,AB =.求AE 的长和△ADE 的面积.ABCDDCE AB10.(2013怀柔一模19)将一副三角板如图拼接:含30°角的三角板(△ABC)的长直角边与含45°角的三角板(△ACD)的斜边恰好重合.已知AB=23,P是AC上的一个动点,连接DP.(1)当点P运动到∠ABC的平分线上时,求DP的长;(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;11.(2013房山一模19)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,A C=10,试求CD的长.12.(2013朝阳一模19)如图,在四边形ABCD中,∠D=90°,∠B=60°,AD=6,AB=3,AB⊥AC,在CD上选取一点E,连接AE,将△ADE沿AE翻折,使点D落在AC上的点F处.求(1)CD的长;(2)DE的长.第19题图13.(2013昌平一模21)已知:如图,在□ABCD 中,∠BAD ,∠ADC 的平分线AE ,DF 分别与线段BC 相交于点E ,F ,AE 与DF 相交于点G .(1)求证:AE ⊥DF ;(2)若AD =10,AB =6,AE =4,求DF 的长.GA EBCDF14.(2013大兴一模19)已知:如图,过正方形ABCD 的顶点B 作直线BE 平行于对角线AC ,AE=AC (E ,C 均在AB 的同侧).求证:∠CAE=2∠BAE .15.(2013东城一模20)如图,四边形ABCD 是矩形,点E 在线段CB 的延长线上,连接DE 交AB 于点F ,∠AED =2∠CED ,点G 是DF 的中点. (1)求证:∠CED =∠DAG ;(2)若BE =1,AG =4,求sin AEB 的值.EDCBA16.(2013燕山一模19)如图,四边形ABCD中,∠ADC=∠B=90°,∠C=60°,AD=3,E为DC 中点,AE∥BC.求BC的长和四边形ABCD的面积.第五章四边形参考答案1.(2013顺义一模19)解:∵BD DC⊥∴90BDC∠=︒∵30ACD∠=︒,AD CD==,∴60,30,DEC DAC ACD∠=︒∠=∠=︒tan302DE CD=⋅︒==EBACD∴ 24EC DE == ,30ADE ∠=︒ …………………………………………1分∴ 2AE DE == ……………………………………………………… 2分- ∴ 246AC AE EC =+=+= ………………………………………………3分过点A 作AM BD ⊥,垂足为M ∵ 60AEB DEC ∠=∠=︒∴sin 602AM AE =⋅︒== 1cos60212ME AE =︒=⨯= ………………………………………………4分 ∵45ABD ∠=︒∴BM AM ==∴123BD BM ME DE =++=+=+…………………………5分2.(2013石景山一模19)解:过点A 作BD AE ⊥于点E ………1分∵AD DC ⊥ ∴︒=∠90ADC ∵△DBC 是等边三角形 ∴︒=∠60BDC∴︒=∠30ADB ………………… 2分 在Rt △AED 中,2=AD ∴121==AD AE 由勾股定理得:3=DE ………………………………3分在Rt △AEB 中,︒=∠45ABD ∴1==AE BE∴2=AB ………………………………4分∴31+=BD∴31+===BD BC DC∴322432222++=+++=+++AD CD BC AB …………5分即四边形ABCD 的周长为3224++.3.(2013西城一模19)解:(1)如图2.∵平行四边形ABCD 的对角线AC 、BD 交于点O∴OA = 12 AC ,OB = 12 BD . …………… 1分 ∵AC ︰BD =2︰3, ∴OA ︰OB =2︰3 .设OA =2x (x >0),则OB =3x .ABCDE∵AC ⊥AB ,∴∠BAC =90°.在Rt △OAB 中,OA 2+AB 2=OB 2. …………………………………… 2分 ∵AB =2,∴(2x )2+22=(3x )2. 解得x =±255(舍负).∴AC =2OA = 855. …………………………………………………… 3分(2)∵平行四边形ABCD 的对角线AC 、BD 交于点O ,∴OB =OD .∴S △AOD = S △AOB = 12 AO ²AB = 12³455³2= 455. ……………………… 5分4.(2013平谷一模19)解:(1)作CF ⊥AD 交AD 的延长线于F . …………..1分 ∵ ∠ADC =120°, ∴∠CDF =60°.在Rt △CDF 中,sin 60 3.2FC CD =⋅︒==………………………………………2分 即点C到直线AD 的距离为3. (2)∵ ∠BED=135°,BE = ∴ ∠AEB =45°. ∵ 90A ∠=︒, ∴ ∠ABE =45°.∴ 2.AB AE == ……………………3分 作BG ⊥CF 于G .可证四边形ABGF 是矩形. ∴ FG =AB =2,CG =CF -FG =1. ∵12DFCD ==∴ 22 4.BG AF AE ED DF ==++=+………………………………..4分∴ BC ==……………………………………………… 5分5.(2013通州一模20) 解法一:∵矩形ABCD ,△DCE 是等边三角形,∴30ADF ECB ∠=∠=o ,3ED EC ==,在Rt △ADF 中,90A ∠=o ,AD =,G A BDEF∴tan AFADF AD∠=,tan 30==o∴1AF =,∴312FB AB AF =-=-=,2FD =, ……………… 1分; ∴321EF ED DF =-=-=, ……………… 2分; 过点E 作EG CB ⊥,交CB 的延长线于点G . ……………… 3分; 在Rt △ECG 中,90EGC ∠=o ,3EC =,30ECG ∠=o , ∴1322EG EC ==,cos GCECG EC∠=,cos 303GC ==o∴GC =∴GB GC BC =-== 由勾股定理得,222EB EG GB =+,∴EB = ……………… 4分;∴△BEF 的周长=3EF FB EB ++=……………… 5分. 解法二:∵矩形ABCD ,△DCE 是等边三角形,∴60EDC ECD ∠=∠=o ,3ED EC ==,过点E 作EH CD ⊥交CD 于点H ,交AB 于点G . ……………… 1分; ∴点H 是DC 的中点,点G 是AB 的中点,30FEG ∠=o ,GH AD ==,在Rt △EHD 中,90EHD ∠=o ,3ED =, ∴sin EH EDH ED∠=,sin 603EH ==o∴EH =∴EG EH GH =-== 在Rt △EGF 中,90EGF ∠=o ,60EFG ∠=o , ∴sin EGEFG EF∠=,sin 60==o∴1EF =, ……………… 2分;∴1122FG EF ==,∵点G 是AB 的中点,3AB =,∴1322GB AB ==,∴13222FB FG GB =+=+=, ……………… 3分;由勾股定理得,222EB EG GB =+,∴EB = ……………… 4分; ∴△BEF 的周长=3EF FB EB ++=……………… 5分.解法三:∵矩形ABCD ,△DCE 是等边三角形, ∴30ADF ECB ∠=∠=o ,3ED EC ==, 在Rt △ADF 中,90A ∠=o,AD =,∴tan AFADF AD∠=,tan 30==o∴1AF =,∴312FB AB AF =-=-=,2FD =, ……………… 1分; ∴321EF ED DF =-=-=, ……………… 2分; 过点B 作BG CE ⊥,交CE 于点G . ……………… 3分; 在Rt △BCG 中,90BGC ∠=o,BC =,30ECB ∠=o ,∴12BG BC ==,cos GC BCG BC∠=, H F E D BA第20题图GG 第20题图ABCDEFcos 30==o∴32GC =, ∴33322GE EC GC =-=-=, 由勾股定理得,222EB EG GB =+,或BG 是线段EC 的垂直平分线,∴EB =BE =BC , ………… 4分; ∴△BEF 的周长=3EF FB EB ++=……………… 5分.AD 、四边形AECF 是矩形………………………3分 3=8s ∴⨯菱形5分7.(2013门头沟一模19)解:如图,过点A 作AF ⊥BD 于F .∵∠BAD =120°,AB =AD ,∴∠ABD =∠ADB =30°.∵∠ADC =120°, ∴∠BDC =∠ADC -∠ADB =12030︒-︒=90°. 在Rt △BDC 中,∠BDC =90°,DE =15,E 是BC 的中点,DC =24, ∴BC=2DE =30.…………………………………2分 ∴18BD ==.………3分 ∵AD =AB ,AF ⊥BD ,∴1118922DF BD ==⨯=. F BAECD在Rt △AFD 中,∵∠AFD =90°,∠ADB =30°,∴9cos cos 30DF DF AD AB ADB =====∠︒……………………………………4分∴四边形ABCD 的周长=AB +AD +DC +BC 243054=+=+ ………5分8.(2013丰台一模19)解:过点C 作CE ∥DB ,交AB 的延长线于点E .∴∠ACE =∠COD =60°. -----------------1分 又∵DC ∥AB , ∴四边形DCEB 为平行四边形.---------------- 2分 ∴BD =CE ,BE = DC =3,AE =AB +BE =8+3=11. ---------------- 3分 又∵DC ∥AB ,AD =BC , ∴DB =AC =CE .∴△ACE 为等边三角形.∴AC =AE =11, ∠CAB =60°. ----------- 4分过点C 作CH ⊥AE 于点H .在Rt △ACH 中, CH =AC ²sin ∠CAB =11³23.∴梯形ABCD ------------- 5分9.(2013海淀一模19) 解:过点A 作AF ⊥BD 于F . ∵∠CDB =90°,∠1=30°,∴∠2=∠3=60°. ………………………1分 在△AFB 中,∠AFB =90°.∵∠4=45°,AB =,∴AF =BF ………………………2分 在△AFE 中,∠AFE =90°.∴1,2EF AE ==.………………………3分 在△ABD 中,∠DAB =90°.∴DB =∴1DE DB BF EF =--=-.………………………4分∴1131)222ADE S DE AF ∆-=⋅==………………………5分10.(2013怀柔一模19)解:(1)在Rt△ABC 中,AB =23,∠BAC=30°∴BC=3,AC =3. 如图(1),作DF⊥AC ∵Rt△ACD 中,AD =CD ∴DF=AF =CF =23………………………………………… 1分 ∵BP 平分∠ABC ∴∠PBC=30° ∴CP=BC²tan30°=1 ∴PF=21 ∴DP=22DF PF =210. ………………………………………… 2分(2)当P 点位置如图(2)所示时,根据(1)中结论,DF =23,∠ADF=45° 又PD =BC =3∴cos∠PDF=PDDF =23∴∠PDF=30°………………………………………… 3分∴∠PDA=∠ADF-∠PDF=15°………………………………………… 4分 当P 点位置如图(3)所示时,同(2)可得∠PDF=30°.∴∠PDA=∠ADF+∠PDF=75°………………………………………… 5分11.(2013房山一模19)解:过点B 作BM ⊥FD 于点M . -------------------------1分在△ACB 中,∠ACB =90°, ∠A =60°,AC =10,∴∠ABC =30°, BC =AC 分 ∵AB ∥CF ,∴∠BCM =30°.∴1sin 302BM BC =⋅︒==分cos3015CM BC =⋅︒==-------4分 在△EFD 中,∠F =90°, ∠E =45°, ∴∠EDF =45°,∴MD BM ==∴15CD CM MD =-=-. ----------5分12.(2013朝阳一模19)解:(1)∵AB ⊥AC ,∴∠BAC =90°. ∵∠B =60°,AB=3, ∴AC =10. ………………………………………………………………………1分 ∵∠D =90°,AD =6,∴CD =8. ………………………………………………………………………2分 (2)由题意,得∠AFE =∠D=90°,AF=AD =6, EF=DE .∴∠EFC =90°,∴FC =4. … ……………………………………………………………………3分 设DE =x ,则EF=x ,CE=8-x .在Rt △EFC 中,由勾股定理,得 2224(8)x x +=-.………………………4分 解得x =3.所以DE =3. ……………………………………………………………………5分13.(2013昌平一模21)(1)证明:∵四边形ABCD 是平行四边形, ∴AB ∥DC .∴∠BAD +∠ADC=180°. ……………………………1分∵AE 、DF 分别平分∠BAD 、∠ADC ,∴111,222BAD ADC ∠=∠∠=∠ .∴112()902BAD ADC ∠+∠=∠+∠=︒ .∴∠AGD=90°.∴AE ⊥DF . ……………………………………………2分(2)由(1)知:AD ∥BC ,且BC= AD = 10,DC =AB =6,∠1=∠3,∠2=∠4 .∴∠1=∠AEB ,∠2=∠DFC .4321GAE B CDF∴∠3=∠AEB ,∠4=∠DFC . ∴BE=AB =6,CF=DC =6. ∴BF =4.∴EF =2. ……………………………………3分 ∵AD ∥BC ,∴△EFG ∽△ADG . ∴15EGEFAG AD ==.∴145EG EG =-. ∴EG=23.∴AG=103. ……………………………………4分由(1)知∠FGE=∠AGD=90°,由勾股定理,得DG=3,FG=3.∴DF=. ……………5分14.(2013大兴一模19)证明:过A 作AG ⊥BE 于G ,连结BD 交AC 于点O ,………………1分∴ AGBO 是正方形.………………………………………………………2分∴ AG=AO=21AC =21AE∴ ∠AEG=30°. ………………………………………………………3分∵ BE∥AC,∴ ∠CAE =∠AEG = 30 º.∴ ∠BAE = 45º – 30º = 15º . ∴ ∠CAE = 2∠BAE .……………………………………………………5分15.(2013东城一模20)(本小题满分5分) 解:(1)证明:∵ 矩形ABCD ,∴ AD ∥BC . ∴ ∠CED =∠ADE . 又∵点G 是DF 的中点, ∴ AG =DG . ∴ ∠DAG =∠ADE .∴ ∠CED =∠DAG . …………………………2分(2) ∵ ∠AED =2∠CED ,∠AGE =2∠DAG , ∴ ∠AED =∠AGE .∴ AE =AG . ∵ AG =4, ∴ AE =4.在Rt △AEB 中,由勾股定理可求AB∴ sin AB AEB AE ∠==…………………………5分∴DE =3360tan =︒AD =1,AE =︒60sin AD =2. ………………………1分又∵E 为DC 中点,∴CE =DE =1, 在Rt △CEF 中,∠CFE =90°,∠C =60°, ∴CF =CE ²cos 60°=21,EF =CE ²sin 60°=23.………………………2分∴BC =BF +CF =AE +CF =2+21=25. ………………………3分 ∴四边形ABCD 的面积ABCD S 四边形=ADE S ∆+ABCE S 梯形 =21AD ²DE +21(AE + BC )²EF =21³3³1+21³(2+25)³23=8313. ………………………5分。
全国名校2013年中考数学模拟试卷分类汇编33 图形的变换
图形的变换(图形的平移、旋转与轴对称)一、选择题1、(2013安徽芜湖一模)下列图形既是轴对称图形,又是中心对称图形的是 ( ).A B C D[w#~@ww*.zzste&] 答案:D2、(2013江苏东台实中)下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是( ).答案:D3、(2013江苏扬州弘扬中学二模)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( ).A .2+10B .2+210C .12D .18 答案:B4、(2013·吉林中考模拟)下列图形中,既是轴对称图形,又是中心对称图形的是( )答案:B5、(2013·曲阜市实验中学中考模拟)李刚同学设计了四种正多边形的瓷砖图案,在这四种瓷砖中,用一种瓷砖可以密铺平面的是( )10题图A. (1)(2)(4)B. (2)(3)(4)C. (1)(3)(4)D. (1)(2)(3)答案:A6、(2013·温州市中考模拟)将一圆形纸片对折后再对折,得到图1,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是()答案:C7、(2013·湖州市中考模拟试卷1)下列交通标志中,既是中心对称图形,又是轴对称图形的是()答案:D8、(2013·湖州市中考模拟试卷3)下列图形中,既是中心对称图形又是轴对称图形的是( ).A. 等边三角形B. 等腰直角三角形C. 菱形D. 等腰梯形答案:C9、(2013·湖州市中考模拟试卷7)如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为60︒的菱形,剪口与折痕所成的角α的度数应为()A.15︒或30︒ B.30︒或45︒ C.45︒或60︒ D.30︒或60︒答案:D10、(2013年深圳育才二中一摸)下列平面图形,既是中心对称图形,又是轴对称图形的是( )A .等腰三角形B .正五边形C .平行四边形D .矩形 答案:D11、(2013年深圳育才二中一摸)如图,将△ABC 绕着点C 顺时针旋转50°后得到△'''C B A . 若∠A =40°. ∠'B =110°,则∠'BCA 的度数是( ) A .110° B.80° C.40° D.30° 答案:B12、(2013年广西南丹中学一摸)如图,在边长为1的正方形组成的网格中,△ABC 的顶点都在格点上,将△ABC绕点C 顺时针旋转60°,则顶点A 所经过的路径长为 A .10πBCD .π答案:C13、(2013年河南西华县王营中学一摸)下列图形中,既是轴对称图形又是中心对称图形的是( )答案:D14、(2013年河北四摸)如图,点A 、B 、C 、D 、O 都在方格纸的格点上,若△COD 是由△AOB 绕点O 按逆时针方向旋转而得,则旋转的角度为( ) (A )30° (B )45° (C )90° (D )135°答案:C第11题图/B15、(2013年温州一摸)将一圆形纸片对折后再对折,得到图1,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是( ) 答案:C二、填空题1、(2013吉林镇赉县一模)如图所示,在△ABC 中,∠CAB 绕点A 逆时针旋转到△A′B ′C ′的位置,使CC ′∥AB ,则∠BAB 答案:30°2、(2013山西中考模拟六) 已知△ABC 的面积为36,将△ABC 沿BC 平移到△A ´B ´C ´,使B ´和C重合,连结AC ´交AC 于D ,则△C ´DC 的面积为________.答案:183、(2013·温州市中考模拟)如图,五角星绕中心旋转一定角度后能与自身完全重合,则其旋转的角度至少为____º答案:72º4、(2013·湖州市中考模拟试卷3)如图,将一块含45角的直角三角尺ABC 在水平桌面A B C D上绕点B 按顺时针方向旋转到11A BC 的位置,若AB =8cm ,那么点A 旋转到1A 所经过的路线长为_ cm .(结果保留π)答案:65、(2013·湖州市中考模拟试卷8)一个长方形的长与宽分别为和16cm ,绕它的对称中心旋转一周所扫过的面积是2cm ;旋转90度时, 扫过的面积是 2cm .答案:256π,6401283π+ 6、(2013年河北三摸)两个全等的梯形纸片如图(1)摆放,将梯形纸片ABCD 沿上底AD 方向向右平移得到图(2).已知AD =4,BC =8,若阴影部分的面积是四边形A ′B ′CD 的面积的13,则图(2)中平移距离A ′A =________.答案:37、(2013年河北四摸)如图4,将∆ABC 沿直线AB 向右平移后到达∆BDE 的位置,若∠CAB =50°,∠ABC =100°,则∠CBE 的度数为 . 答案:30︒8、(2013年温州一摸)如图,五角星绕中心旋转一定角度后能与自身完全重合,则其旋转的角度至少为____º 答案:721 2 题图三、解答题1、(2013安徽芜湖一模)如图,已知ABC △的三个顶点的坐标分别为(23)A -,、(60)B -,、(10)C -,.(1)经过怎样的平移,可使ABC △的顶点A 与坐标原点O 重合,并直接写出此时点C 的对应点1C 坐标;(不必画出平移后的三角形)(2)将ABC △绕坐标原点O 逆时针旋转90°,得到△A ′B ′C ′,画出△A ′B ′C ′.答案:解:(1)1C (1,-3);………………………………………………………………(3分)(2)图形略;……………………………………………………………………… (8分) 2、(2013安徽芜湖一模)如图1,△ABC 是等腰直角三角形,四边形ADEF 是正方形,D 、F分别在AB 、AC 边上,此时BD =CF ,BD ⊥CF 成立. (1)当正方形ADEF 绕点A 逆时针旋转θ(090θ<<)时,如图2,BD =CF 成立吗?若成立,请证明;若不成立,请说明理由.(2)当正方形ADEF 绕点A 逆时针旋转45°时,如图3,延长BD 交CF 于点G .① 求证:BD ⊥CF ;② 当AB =4,ADBG 的长.图1 图2 图3答案:(本小题满分12分)解(1)BD =CF 成立.理由:∵△ABC 是等腰直角三角形,四边形ADEF 是正方形,∴AB =AC ,AD =AF ,∠BAC =∠DAF =90°,∵∠BAD =DAC BAC ∠-∠,∠CAF =DAC DAF ∠-∠,∴∠BAD =∠CAF ,∴△BAD ≌△CAF .第18题图图13.3图13.2图13.145°θG CDEFFEDCF E DCBA∴BD =CF.……………………………………………………………………(4分)(2)①证明:设BG 交AC 于点M .∵△BAD ≌△CAF (已证),∴∠ABM =∠GCM . ∵∠BMA =∠CMG ,∴△BMA ∽△CMG .∴∠BGC =∠BAC =90°.∴BD ⊥CF .……………………………………(7分)②过点F 作FN ⊥AC 于点N .∵在正方形ADEF 中,AD =2, ∴AN =FN =121=AE . ∵在等腰直角△ABC 中,AB =4, ∴CN =AC -AN =3,BC =2422=+AC AB .Rt △FCN ∽Rt △ABM ,∴ABCNAM FN = ∴AM ==⨯AB 3134.∴CM =AC -AM =4-34=38,310422=+=AM AB BM .…… (9分)∵△BMA ∽△CMG ,∴CGCMBA BM =. ∴CG 3843104=. ∴CG =5104.…………………………………… (11分) ∴在Rt △BGC 中,=-=22CG BC BG 5108. ……………… (12分) 3、(2013温州市一模)如图,正比例函数(0)y kx k =≠经过点A (2,4), AB ⊥x 轴于点B .(1)求该正比例函数的解析式.(2)将△ABO 绕点A 逆时针旋转90︒得到△ADC ,写出点C 的坐标,试判断点C 是否在直线113y x =+的图象上,并说明理由.答案:解:(1)∵正比例函数(0)y kx k =≠经过点A (2,4) ∴42k =2k ∴=2y x ∴=MN FE DCG 45°图13.3D OBACyx(第22题)(2) ∵A (2,4),AB ⊥x 轴于点B∴2,4OB AB ==∵△ABO 绕点A 逆时针旋转90︒得到△ADC ∴2,4DC OB AD AB ==== ∴C (6,2)∵当6x =时,161323y =⨯+=≠ ∴点C 不在直线113y x =+的图象上4、(2013·湖州市中考模拟试卷1)在如图的方格纸中,每个小方格都是边长为1个单位的正方形,A B C △的三个顶点都在格点上(每个小方格的顶点叫格点).(1)画出A B C △绕点C 顺时针旋转90后的11ABC △;(2)求边AB 旋转时所扫过区域的面积答案:(1)画图(略) ………………………………4分 (2)72π…………………………‥4分 5、(2013年上海市)(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)数学课上,张老师出示图1和下面框中条件:(1)①当点C 与点F 重合时,如图2所示,可得DM的值为 ▲ ; 如图1,两块等腰直角三角板ABC 和DEF 有一条边在同一条直线l 上,∠ABC =∠DEF = 90°,AB = 1,DE = 2.将直线EB 绕点E 逆时针旋转45°,交直线AD 于点M .将图1中的三角板ABC 沿直线l 向右平移,设C 、E 两点间的距离为x .(第25题图1)C E F l B (第25题图2)E F (C ) B l②在平移过程中,AMDM的值为▲(用含x的代数式表示);(2)艾思轲同学将图2中的三角板ABC绕点C逆时针旋转,原题中的其他条件保持不变.当点A落在线段DF上时,如图3所示,请你帮他补全图形,并计算AMDM的值;(3)艾思轲同学又将图1中的三角板ABC绕点C逆时针旋转m度,090m<≤,原题中的其他条件保持不变.请你计算AMDM的值(用含x的代数式表示).答案:解:(1)① 1.………………………………………………………………………(2分)②2x.………………………………………………………………………(2分)(2)联结AE,补全图形如图1所示.…………………………………………(1分)∵△ABC和△DEF是等腰直角三角形,∠ABC =∠DEF = 90°,AB = 1,DE = 2,∴BC = 1,EF = 2,∠DFE =∠ACB= 45°.∴AC=DF=,∠EFB = 90°.∴AD DF AC=-=A为DF的中点.………………………(1分)∴EA⊥DF,EA平分∠DEF.∴∠MAE = 90°,∠AEF = 45°,AE=∵∠MEB =∠AEF= 45°,∴∠MEA =∠BEF.∴Rt△MAE∽Rt△BFE.……………………………………………………(1分)∴AM AEBF EF=,∴AM=.……………………………………………(1分)∴DM AD AM=-==,∴1AMDM=.……………………(1分)(第25题备用图)E F l(第25题图3)E F(C) l(3)如图2,过点B 作BE 的垂线交直线EM 于点G ,联结AG .∵∠EBG = 90°,∠BEM = 45°,∴∠BGE = 45°.∴BE = BG .…………………………………………………………………(1分) ∵∠ABC =∠EBG = 90°,∴∠ABG =∠CBE .……………………………(1分) 又∵BA = BC ,∴△ABG ≌△CBE .………………………………………(1分) ∴AG = CE = x ,∠AGB =∠CEB .∵∠AGB +∠AGM =∠CEB +∠DEM = 45°,∴∠AGM =∠DEM ,∴AG ∥DE .…………………………………………(1分) ∴2AM AG xDM DE ==.…………………………………………………………(1分) 注:第(3)小题直接写出结果不得分。
2013年全国各地中考模拟卷分类汇编:平行四边形(共12页)

(1)将梯形纸片剪拼成平行四边形:请在下图中画出示意图,要求用两种不同的画法,
并简要说明如何剪拼和变换的;
(2)如图,将四边形ABCD剪拼成平行四边形.在下图中画出示意图.
4、两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC不动,将△DEF进行如下操作:
A. 2 B.3 C. D. 6
答案:B
3.(2013年北京平谷区一模)如图,在□ 中, , 为垂足.
如果 ,则
A. B. C. D.
答案:C
4、(2013年湖北荆州模拟6)如图,已知一张纸片□ , ,点 是 的中点,点 是 上的一个动点,沿 将纸片折叠,使点 落在纸片上的点 处,连结 ,则下列各角中与 不一定相等的是(▲)
(1)如图△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
(2)如图,当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.
(3)如图,△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinα的值.
解:(1)过C点作CG⊥AB于G,
在Rt△AGC中,∵sin60°= ,∴ 1分
∵AB=2,∴S梯形CDBF=S△ABC= 3分
(2)菱形5分
∵CD∥BF,FC∥BD,∴四边形CDBF是平行四边形6分
∵DF∥AC,∠ACD=90°,∴CB⊥DF7分
∴四边形CDBF是菱形8分
(判断四边形CDBF是平行四边形,并证明正确,记2分)
2013年全国各地中考模拟卷分类汇编:因式分解

2013年全国各地中考模拟卷分类汇编---因式分解一、选择题1、(2013年聊城莘县模拟)把a 3-ab 2分解因式的正确结果是( )A 、(a +ab ) (a -ab )B 、a (a 2-b 2)C 、a (a +b )(a -b )D 、a (a -b )2答案:C2、(2013温州模拟)5.下列式子中是完全平方式的是( ▲ )A .22b ab a ++B .222++a aC .222b b a +-D .122++a a 【答案】D3.(2013年上海静安区二摸)下列式子中,从左到右的变形为多项式因式分解的是(A ))2)(2(22-+=-x x x (B )2)2)(2(2-=-+x x x(C ))2)(2(4-+=-x x x (D )4)2)(2(-=-+x x x 答案:A4、10.(2013年唐山市二模)已知a 、b 、c 是△ABC 的三边长,且满足223223ac b a b bc ab a ++=++,则△ABC 的形状是 ( )A .等腰三角形B .直角三角形C .等腰三角形或直角三角形D .等腰直角三角形答案:C二、填空题1、(2013年安徽凤阳模拟题二)分解因式:x 3− 4x = .答案:.x (x +2)(x -2)2(2013年安徽凤阳模拟题三).分解因式:29xy x -= .答案:x (y +3)(y -3)3.(2013年安徽初中毕业考试模拟卷一)因式分解3233a ab -= . 答案:3()()a a b a b +-4.(2013年北京房山区一模)分解因式:3x y xy -= .答案:(1)(1)xy x x +-5.(2013年北京龙文教育一模)分解因式:2212123b ab a +-= 答案:()223b a -6.(2013年北京平谷区一模)分解因式:324a ab -=__________ .答案:(2)(2)a a b a b +-7.(2013年北京顺义区一模)分解因式:231212ab ab a -+= . 答案:23(2)a b -8、(2013年安徽省模拟六)因式分解:3a+12a 2+12a 3= .答案:23(21)a a +9、(2013年安徽省模拟八)分解因式xy 2-x = .答案:x (y -1)(y +1)10、(2013年湖北荆州模拟5)分解因式 x (x -1)-3x +4= ▲ .答案: (x -2)211、(2013年湖北荆州模拟6)分解因式:xy 2-x =______▲____.答案:x (y +1)(y -1)12、(2013年上海奉贤区二模)分解因式:1682+-x x = ▲ ;答案:2)4(-x ;13、(2013届宝鸡市金台区第一次检测)分解因式:269mn mn m ++= 答案:m (n +3) 214、(2013年上海长宁区二模)在实数范围内分解因式:32-m = .答案:(m +3)(m -3)15.(2013浙江省宁波模拟题)因式分解:x 2y -y =______________.答案:y (x +1)(x -1)16. (2013沈阳一模)分解因式x 3-6x 2+9x =__________.答案:x (x -3)217. (2013沈阳一模)若m 为实数,且13m m -=,221m m-则= .答案:±13318.(2013盐城市景山中学模拟题)分解因式: x 2-36= ◆ .答案:(x +6)(x -6);19、(2013年江苏南京一模)分解因式:224a b -= .【答案】.(m +1)(m -1)31、(2013浙江东阳吴宇模拟题)分解因式:182x -8= .答案:2(3x -2)(3x +2)32. (2013上海黄浦二摸)分解因式:123+++x x x = ▲ .答案:()()211x x ++33.(2013年上海闵行区二摸)因式分解:2x y x y -= ▲ .答案:(1)x y x -34.(2013郑州外国语预测卷)分解因式:3m (2x -y )2-3mx 2= . 答案:3m (x -y )(3x -y ); 35、(2013凤阳县县直义教教研中心)分解因式:3ax 2+6axy +3ay 2=______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(海淀)19.如图,在四边形A B C D 中,对角线A C ,B D 相交于点
E
,D A B ∠=C D B ∠=90︒,A B D ∠=45︒,∠D C A =30︒,6
A B
=.求A E 的长和
△A D E 的面积.
2.(东城)19. 如图,四边形ABCD 是矩形,点E 在线段CB 的延长线上,连接DE 交AB 于点F , ∠AED =2∠CED ,点G 是DF 的中点. (1)求证:∠CED =∠DAG ;
(2)若BE =1,AG =4,求sin A E B ∠的值.
3.(西城)19.如图,平行四边形ABCD 的对角线AC 、BD 交于点O , AC ⊥AB ,AB =2,且AC ︰BD =2︰3. (1) 求AC 的长; (2) 求△AOD 的面积.
4.(朝阳) 19. 如图,在四边形ABCD 中,∠D =90°,∠B =60°,AD =6,
AB =
103
3
,AB ⊥AC ,在CD 上选取一点E ,连接AE ,将△ADE 沿AE 翻折,
使点D 落在AC 上的点F 处. 求(1)CD 的长; (2)DE 的长.
F E
B
A
D
C
5.(丰台)19.如图,四边形ABCD 中,AB = AD ,∠BAD =90°, ∠CBD =30°,∠BCD =45°, 若AB =2
2
.求四边形A B C D 的面积.
6.(石景山)19. 已知:如图,在四边形ABCD 中,AD
DC ⊥,△D B C
是等边三角形,︒
=∠45ABD ,2
=AD
.求四边形ABCD 的周长.
7.(昌平)21. 已知:如图,在□ABCD 中,∠BAD ,∠ADC 的平分线
AE ,DF 分别与线段BC 相交于点E ,F ,AE 与DF 相交于点G .
(1)求证:AE ⊥DF ;
(2)若AD =10,AB =6,AE =4,求DF 的长.
G
A E
B
C
D
F
8.(顺义)19.已知:如图,四边形ABCD 中,对角线
AC 、BD 相交于点E ,B D
D C
⊥,45A B D ∠=︒,30A C D ∠=︒,
2
3
A D C D ==,求AC 和BD 的长.
9.(通州)19.如图,在矩形ABCD 中,AB =3,BC =3
,△DCE 是等
边三角形,DE 交AB 于点F ,求△BEF 的周长.
A
B
C
D
D
C
B
A
D
C B
A
E
A D
F
E
B C
D
A
C
B
10.(大兴)19.已知:如图,过正方形ABCD 的顶点B 作直线BE 平行于对角线AC ,AE=AC (E ,C 均在AB 的同侧).
求证:∠CAE=2∠BAE .
11.(怀柔)19.
将一副三角板如图拼接:含30°角的三角板
(△ABC )的长直角边与含45°角的三角板(△ACD )的斜边恰好重合.已知AB =23
,P 是AC 上的一个动点,连
接DP .
(1)当点P 运动到∠ABC 的平分线上时,求DP 的长;
(2)当点P 在运动过程中出现PD =BC 时,求此时∠PDA 的度数; 12.(密云)19.如图,已知菱形ABCD ,AB=AC ,E 、F 分别是BC 、AD 的中点,连接AE 、CF
(1)证明:四边形AECF 是矩形; (2)若AB=8,求菱形的面积。
13.(平谷)19.已知:如图,四边形ABCD 中,90A ∠=︒,
120D ∠=︒
,E 是AD 上一点,∠BED=135°,22
B E
=,23
D C
=,23
D E
=-.
求(1)点C 到直线AD 的距离; (2)线段BC 的长.
D
C
E A
B E
D
C
B
A
D
C
A
B
D
E
14.(门头沟)19.如图,在四边形ABCD 中,∠A =∠ADC =120º,
AB =AD ,E 是BC 的中点,DE =15,DC =24,
求四边形ABCD 的周长.
15.(房山)19.一副直角三角板如图放置,点C 在FD 的延长线上,
AB ∥CF ,∠F =∠ACB =90°,∠E =45°,∠A =60°,A C=10,试求CD 的长.
16.(延庆)19. 如图,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上F 点处,已知CE=6cm ,AB=16cm ,求BF 的长.
17.(燕山)19.如图,四边形ABCD 中,∠ADC =∠B =90°, ∠C = 60°,AD =
3
,E 为DC 中点,AE ∥BC .
求BC 的长和四边形ABCD 的面积.
F
E D
C
B
A
第19题图
E
B
A
C
D。
