2011年普通高等学校招生全国统一考试数学试题(北京卷) 理 (精校版无答案)
2011年北京市高考理科数学试题及标准答案

2011年普通高等学校招生全国统一考试数 学(理)(北京卷)本试卷共5页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合2{|1}P x x =≤,{}M a =.若PM P =,则a 的取值范围是(A)(,1]-∞-(B)[1,)+∞(C )[1,1]-(D)(,1][1,)-∞-+∞ (2)复数212i i-=+ (A )i (B)i - (C)4355i -- (D)4355i -+ (3)在极坐标系中,圆2sin ρθ=-的圆心的极坐标是(A )(1,)2π (B )(1,)2π- (C )(1,0) (D)(1,)π(4)执行如图所示的程序框图,输出的s 值为(A)3-(B)12- (C)13(D)2(5)如图,,,AD AE BC 分别与圆O 切于点,,D E F ,延长AF 与圆O 交于另一点G 。
给出下列三个结论:① AD AE AB BC CA +=++;② AF AG AD AE ⋅=⋅;③ AFB ADG ∆∆其中,正确结论的序号是(A)① ② (B )② ③(C )① ③ (D )① ② ③(6)根据统计,一名工人组装第x 件某产品所用的时间(单位:分钟)为()x A f x x A <=≥(,A c 为常数)。
已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟, 那么c 和A 的值分别是(A )75,25 (B )75,16 (C )60,25 (D)60,16 (7)某四面体的三视图如图所示,该四面体四个面的面积中 最大的是(A ) 8(B)(C) 10(D)(8)设(0,0)A ,(4,0)B ,(4,4)C t +,(,4)D t (t R ∈),记()N t 为平行四边形内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数()N t 的 值域为(A ){9,10,11} (B){9,10,12} (C){9,11,12} (D ){10,11,12}A G俯视图。
2011年普通高等学校招生全国统一考试(北京卷word版本)

2011年普通高等学校招生全国统一考试(北京卷word 版本)理科综合能力测试本部分共20小题,每小题6分,共120分,在每小题列出的四个选项中,选出最符合题目要求的一项。
1.下列生命过程中,没有..发生细胞分化的是A .断尾壁虎长出新尾巴B .砍伐后的树桩上长出新枝条C .蝌蚪尾巴消失的过程D .胚胎发育中出现造血干细胞 2.在生态学研究中,下列方法与研究目的不相符...的是 A .给海龟安装示踪起调查其洄游路线 B .给大雁佩戴标志环调查其迁徙路线C .用样方法研究固着在岩礁上贝类的种群关系D .用标志重捕法调查鸟尔黄鼠的丰富度 3.下列与细胞内物质运输有关的叙述,正确的是 A .叶绿体合成的ATP 通过核孔进入细胞核 B .氢离子可以通过扩散作用进入液泡内 C .溶液体内的酶由内质网形成的小泡运入D .内质网的膜结构成分可以转移到细胞膜中4.胰岛素的A ,B 两条肽链是由一个基因编码的:下列有关胰岛素的叙述,正确的是 A .胰岛素基因的两条DNA 单链分别编码A ,B 两条肽链 B .沸水浴加热之后,构成胰岛素的肽链充分伸展并断裂 C .胰岛素的功能取决于氨基酸的序列,与空间结构无关D .核糖体合成的多肽链需经蛋白酶的作用形成胰岛素5.一次性过量饮水会造成人体细胞肿胀,功能受损。
可用静脉滴注高浓度盐水(1.8%NaCl溶液)对患者进行治疗。
其原理是 A .升高细胞外液的离子浓度 B .促进抗利尿激素的分泌 C .降低细胞内液的离子浓度 D .减少细胞外液液体总量 6.垃圾分类有利于资源回收利用。
下列垃圾归类不合理...的是7.下列说法不正确...的是 A .麦芽糖及其水解产物均能发生银镜反应B .用溴水即可鉴别苯酚溶液,2,4-已二烯和甲苯C .在酸性条件下,18325C H C O O C H 的水解产物是183C H C O O H 和25C H O HD .用甘氨酸()和丙氨酸()缩合最多可形成4种二肽8.结合右图判断,下列叙述正确的是A .Ⅰ和Ⅱ中正极均被保护B .Ⅰ和Ⅱ中负极反应均是Fe —2e —=Fe 2+C .Ⅰ和Ⅱ中正极反应均是O 2+2H 2O+4e —=4OH—D .Ⅰ和Ⅱ中分别加入少量K 3[Fe (CN )6]溶液,均有蓝色沉淀9.下列与处理方法对应的反应方程式不正确...的是 A .用Na 2S 去除废水中的Hg 2+:Hg 2++S 2-=HgS ↓B .用催化法处理汽车尾气中的CO 和NO :CO+NO −−−→催化剂C+NO 2C .向污水中投放明矾,生成能凝聚悬浮物的胶体:Al 3++3H 2O Al(OH)3(胶体)+3H+D .用高温催化氧化法去除烃类废气(C x H y ):C x H y +()4y x +O 2−−−→催化剂高温xCO 2+2y H 2O10.25℃、101kPa 下:下列说法正确的是 A .①和②产物的阴阳离子个数比不相等B .①和②生成等物质的量的产物,转移电子数不同C .常温下Na 与足量O 2反应生成Na 2O ,随温度升高生成Na 2O 的速率逐渐加快D .25℃、101kPa 下:Na 2O 2(s )+2 Na (s )= 2Na 2O (s ) H ∆=-317kJ/mol11.下列实验方案中,不能测定Na 2CO 3和NaCHO 3,混合物中Na 2CO 3质量分数的是 A .取a 克混合物充分加热,减重b 克 B .取a 克混合物与足量稀盐酸充分反应,加热、蒸干、灼烧,得b 克固体 C .取a 克混合物与足量稀硫酸充分反应,逸出气体用碱石灰吸收,增重b 克D .取a 克混合物与足量Ba (OH )2溶液充分反应,过滤、洗涤、烘干,得b 克固体12.已知反应:2CH 3COCH 3(l ) 催化剂CH 3COCH 2COH (CH 3)2(l )。
2011年普通高等学校招生全国统一考试(北京卷)

2011年普通高等学校招生全国统一考试理科综合能力测试化学试题(北京卷)本试卷分共14页,满分300分。
考试时长150分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
以下数据可供解题时参考:可用到的相对原子质量:H 1 C 12 O 16 Na 23 S 32 Cl 35.5第一部分(选择题,共120分)本部分共20小题,每小题6分,共120分,在每小题列出的四个选项中,选出最符题目要求的一项。
7.下列说法不正确...的是A.麦芽糖及其水解产物均能发生银镜反应B.用溴水即可鉴别苯酚溶液、2,4-已二烯和甲苯C.在酸性条件下,CH3CO18OC2H5的水解产物是CH3CO18OH和C2H5OHD.用甘氨酸()和丙氨酸()缩合最多可形成4种二肽8.结合下图判断,下列叙述正确的是A.Ⅰ和Ⅱ中正极均被保护B. Ⅰ和Ⅱ中负极反应均是Fe-2e-=Fe2+C. Ⅰ和Ⅱ中正极反应均是O2+2H2O+4e-=4OH-D. Ⅰ和Ⅱ中分别加入少量K3Fe(CN)6溶液,均有蓝色沉淀10. 25℃、101kPa 下:①2Na(s)+1/2O2(g)=Na2O(s) △H1=-414KJ/mol②2Na(s)+O2(g)=Na2O2(s) △H2=-511KJ/mol下列说法正确的是A.①和②产物的阴阳离子个数比不相等B.①和②生成等物质的量的产物,转移电子数不同C.常温下N a与足量O2反应生成Na2O,随温度升高生成Na2O的速率逐渐加快D.25℃、101kPa 下,Na2O2(s)+2 Na(s)= 2Na2O(s)△H=-317kJ/mol12.已知反应:2CH3COCH3(l)催化剂CH3COCH2COH(CH3)2(l)。
取等量CH3COCH3,分别在0℃和20℃下,测得其转化分数随时间变化的关系曲线(Y-t)如下图所示。
下列说法正确的是A.b代表0℃下CH3COCH3的Y-t曲线B.反应进行到20min 末,H 3COCH 3的(0)1(20)v C v C ︒>︒C.升高温度可缩短反应达平衡的时间并能提高平衡转化率D.从Y=0到Y=0.113,CH 3COCH 2COH(CH 3)2的(0)1(20)n C n C ∆︒=∆︒第二部分(非选择题 共180分)本部分共11小题,共180分。
2011年北京高考数学理科试卷(带详解)

2011年普通高等学校招生全国统一考试(北京卷)数学(理)第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}{}2|1,P x x M a ==….若P M P = ,则a 的取值范围是( )A .(], 1-∞-B .[1, +∞)C .[11]?-,D .][1 1-∞-+∞ (,,)【测量目标】集合的基本运算,并集.【考查方式】描述法,列举法表示出集合,根据两集合并集为其中一集合,求参数取值范围. 【难易程度】容易 【参考答案】C【试题解析】2{|1}{|11}P x x x x ==-剟?,[1,1]P M P a =⇒∈- ,选C.2.复数i 212i-=+( )A .iB .i -C .43i 55-- D .43i 55-+ 【测量目标】复数的代数运算.【考查方式】直接求复数的代数式的值. 【难易程度】容易 【参考答案】A【试题解析】22i 2(i 2)(12i)2i i i 242(1)2412i (12i)(12i)141i ii i 4(1)-----+---+====++----,选A. 3.在极坐标系中,圆2sin ρθ=-的圆心的极坐标是( )A .π(1,)2B .π(1,)2-C .()1,0D .(1π),【测量目标】坐标系和参数方程.【考查方式】给出参数方程,化为圆的标准方程得到圆心,进而得到圆心极坐标. 【难易程度】容易 【参考答案】B【试题解析】222sin (1)1x y ρθ=-⇒++=,圆心直角坐标为0,1-(),极坐标为π(1,)2-,选B.4.执行如图所示的程序框图,输出的s 值为( )第4题图A .3-B .12- C .13 D .2【测量目标】循环结构的程序框图. 【考查方式】看懂程序框图内的逻辑,代数关系,求值. 【难易程度】容易 【参考答案】D【试题解析】循环操作4次时S 的值分别为11,,3,232--,选D. 5.如图,,,AD AE BC 分别与圆O 切于点,,D E F 延长AF 与圆O 交于另一点G .给出下列三个结论: ①CA BC AB AE AD ++=+; ②AF AG AD AE = ③ADG AFB ∽△△ 其中正确结论的序号是( )第5题图A .①②B .②③C .①③D .①②③【测量目标】圆的性质.【考查方式】给出图形,根据圆的性质,判断命题的正确性. 【难易程度】中等 【参考答案】A【试题解析】①正确.由条件可知BD BF =,CF CE =,可得CA BC AB AE AD ++=+. ②正确.通过条件可知AD AE =.由切割定理可得2AF AG AD AD AE == . ③错误.连接FD ,若ADG AFB ∽△△,则有ABF DGF ∠=∠.通过图像可知 2ABF BFD BDF DGF ∠=∠+∠=∠,因而错误.答案选A.6.根据统计,一名工作组装第x 件某产品所用的时间(单位:分钟)为,()x A f x x A <=…(A ,c 为常数).已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟,那么c 和A的值分别是 ( ) A .75,25 B .75,16 C .60,25 D .60,16 【测量目标】分段函数,函数的应用.【考查方式】将分段函数应用到实际问题中,进行分段求解. 【难易程度】中等 【参考答案】D【试题解析】由条件可知,x A …时所用时间为常数,所以组装第4件产品用时必然满足第一个分段函数,即(4)3060f c ==⇒=,()1516f A A ==⇒=,选D. 7.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )第7题图A .8 B. C .10 D.【测量目标】空间三视图的表面积.【考查方式】已知四面体的三视图,通过三视图还原几何体,求最大面的面积. 【难易程度】容易 【参考答案】C【试题解析】由三视图还原几何体如下图,该四面体四个面的面积中最大的是PAC △,面积为10,选C.第7题图8.设()0,0A ,()4,0B ,()4,4C t +,()(),4D t t ∈R .记()N t 为平行四边形ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数()N t 的值域为 ( )A .{}9,10,11B .{}9,10,12C .{}9,11,12D .{}10,11,12【测量目标】平行四边形的定义,直角坐标系.【考查方式】根据已给的两点和含参的两点,在直角坐标系中确定平行四边形,得到坐标,求出参数.【难易程度】较难 【参考答案】C【试题解析】如下图,分别对应点为12,9,11,选C.第8题图第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分. 9.在ABC △中.若b =5,π4B ∠=, tan A =2,则sin A =____________;a =_______________. 【测量目标】正弦定理,同角三角函数的基本关系.【考查方式】给出一角和其对应边的大小以及另一角的正切值,根据正弦定理和同角关系求角A 正弦值和对应边长. 【难易程度】中等【参考答案】5,【试题解析】由tan 2A =⇒sin 12cos sin cos 2A A A A =⇒=,又22sin cos 1A A +=所以 221sin sin 14A A +=解得sin A =55,πsin 4a ==a =10.已知向量a =1),b =(0,-1),c =(k.若2-a b 与c 共线,则k =________. 【测量目标】向量的坐标和线性运算.【考查方式】给出两向量的具体坐标和一向量参数坐标,根据共线关系,求参数值. 【难易程度】容易 【参考答案】1【试题解析】2-=a b 由2-a b 与c31k k =⇒= 11.在等比数列{n a }中,1a =12,44a =-,则公比q =______________;12...n a a a +++=____________.【测量目标】等比数列通项以及前n 项和.【考查方式】给出等比数列两项,利用等比数列的通项求公比,继而求出前n 绝对值的和. 【难易程度】中等 【参考答案】2-,1122n --【试题解析】由{}n a 是等比数列得341a a q =,又141,4,2a a ==- 所以31422q q -=⇒=-,{||}n a 是以12为首项,以2为公比的等比数列,1121||||||22n n a a a -+++=- .12.用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有__________个.(用数字作答)【测量目标】排列,组合及其应用. 【考查方式】通过排列组合计算个数. 【难易程度】容易 【参考答案】14【试题解析】个数为42214-=.13.已知函数32,2()(1),2x f x x x x ⎧⎪=⎨⎪-<⎩… 若关于x 的方程()f x k =有两个不同的实根,则实数k 的取值范围是_______【测量目标】利用函数单调性求参数的范围.【考查方式】已知函数的解析式和条件,求参数的取值范围. 【难易程度】中等 【参考答案】(0,1) 【试题解析】2()(2)f x x x=…单调递减且值域为(0,1],3()(1)(2)f x x x =-<单调递增且值域为(,1)-∞,()f x k =有两个不同的实根,则实数k 的取值范围是(0,1).14.曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >的点的轨迹.给出下列三个结论: ① 曲线C 过坐标原点; ② 曲线C 关于坐标原点对称;③若点P 在曲线C 上,则12F PF △的面积不大于212a . 其中,所有正确结论的序号是 . 【测量目标】命题的正确性.【考查方式】给出已知条件,判断命题的正确性. 【难易程度】较难 【参考答案】②③【试题解析】①曲线C 经过原点,这点不难验证是错误的,如果经过原点,即么1a =,与条件不符;②曲线C 关于原点对称,这点显然正确,如果在某点处212||||,PF PF a =关于原点的对称点处也一定符合212||||;PF PF a =③三角形12F F P 的面积invm S 12=12||||PF PF 121sin 2F PF ∠…12||||PF PF =22a三、解答题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分) 已知函数π()4cos sin()16f x x x =+-.(Ⅰ)求()f x 的最小正周期:(Ⅱ)求()f x 在区间ππ,64⎡⎤-⎢⎥⎣⎦上的最大值和最小值. 【测量目标】函数sin()y A x ωϕ=+的图像及其变换,两角和的正弦.【考查方式】将已给的解析式通过两角和的正弦化为sin()y A x ωϕ=+形式,得到周期; 根据函数图像及性质求最值.【难易程度】中等【试题解析】(Ⅰ)因为π()4cos sin()16f x x x =+-1)cos 21sin 23(cos 4-+=x x x (步骤1) 1cos 22sin 32-+=x x x x 2cos 2sin 3+=π2sin(2)6x =+(步骤2)所以)(x f 的最小正周期为π(步骤3)(Ⅱ)因为ππππ2π,2.64663x x --+所以剟剟 于是,当πππ2,626x x +==即时,)(x f 取得最大值2;(步骤4)当πππ2,,()666x x f x +=-=-即时取得最小值1-.(步骤5)16.(本小题共14分)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,2,60AB BAD =∠= . (I )求证:BD ⊥平面;PAC(Ⅱ)若,PA AB =求PB 与AC 所成角的余弦值;(Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.第16题图【测量目标】空间中线线,线面,面面的位置关系,二面角,空间向量及其运算. 【考查方式】建立合适的空间直角坐标系,得到各个点的坐标,使立体几何问题成为代数问题,从而证明线面垂直,二面角的余弦值,以及空间内长度. 【难易程度】中等 【试题解析】(Ⅰ)因为四边形ABCD 是菱形,所以AC BD ⊥.(步骤1)又因为PA ABCD ⊥平面. 所以PA BD ⊥.所以BD PAC ⊥平面.(步骤2) (Ⅱ)设AC BD O = .因为602BAD PA PB ∠=︒==,,所以1BO AO CO ===,3.(步骤3)如图,以O 为坐标原点,建立空间直角坐标系O xyz -,则(0,(0,(1,0,0),P A B C .(步骤4)所以 设PB 与AC 所成角为θ,则cos ||||PB AC PB AC θ=== . (步骤5)(Ⅲ)由(Ⅱ)知).0,3,1(-=设(0,),P t (0t >),则(1,)BP t =-设平面PBC 的法向量(,,)x y z =m ,则0,0BC BP ==m m (步骤6)所以0,0x x tz ⎧-+⎪⎨--+=⎪⎩令,3=y 则.6,3t z x ==所以6)t=m (步骤7)同理,平面PDC的法向量6()t=-n因为平面PCB PDC ⊥平面, 所以0 m n =,即03662=+-t , 解得6=t ,所以PA =6(步骤8)第16题图17.本小题共13分以下茎叶图记录了甲、乙两组个四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X 表示.第17 题图 (Ⅰ)如果8X =,求乙组同学植树棵树的平均数和方差; (Ⅱ)如果9X =,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y 的分布列和数学期望. (注:方差()()()2222121n s x x x x x x n⎡⎤=-+-++-⎢⎥⎣⎦ ,其中x 为1x ,2x ,…… n x 的平均数) 【测量目标】茎叶图,离散型随机事件的分布列和期望.【难易程度】中等【考查方式】直接根据茎叶图求平均数和方差;继而求事件的分布列和期望.【试题分析】当8X =时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,所以平均数为 8891035;44x +++==(步骤1)方差为 .1611])43510()4359()4358()4358[(4122222=-+-+-+-=s (步骤2) (Ⅱ)当9X =时,由茎叶图可知,甲组同学的植树棵树是:9,9,11,11;乙组同学的植树棵数是:9,8,9,10.分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能的结果,这两名同学植树总棵数Y 的可能取值为17,18,19,20,21事件“17Y =”等价于“甲组选出的同学植树9棵,乙组选出的同学植树8棵”所以该事件有2种可能的结果,因此((17)P Y =)=.81162=(步骤3) 同理可得;41)18(==Y P ;41)19(==Y P .81)21(;41)20(====Y P Y P (步骤4)(步骤5)17171818191920202121EY P Y P Y P Y P Y P Y =⨯=+⨯=+⨯=+⨯=+⨯=()()()()()1111117181920211984448=⨯+⨯+⨯+⨯+⨯=(步骤6)18.(本小题共13分) 已知函数2()()e xkf x x k =-. (Ⅰ)求()f x 的单调区间;(Ⅱ)若对于任意的(0,)x ∈+∞,都有1()ef x …,求k 的取值范围. 【测量目标】利用导数求函数的单调区间,利用导数解决不等式问题.【考查方式】给出含参数的函数解析式,利用导数求其单调区间;根据最值和不等式解出参数的取值范围.【难易程度】较难【试题解析】(Ⅰ)221()()e .xk f x x k k'=-(步骤1)令()0f x '=,得k x ±=.当0k >时,)()(x f x f '与的情况如下所以,)(x f 的单调递增区间是(k -∞-,)和),(+∞k ;单调递减区间是),(k k -当0k <时,)()(x f x f '与的情况如下所以,)(x f 的单调递减区间是(k -∞-,)和),(+∞k ;单调递增区间是(,)k k -(步骤3)(Ⅱ)当0k >时,因为11(1)e ek kf k ++=>所以不会有1(0,),().e x f x ∀∈+∞…(步骤4)当0k <时,由(Ⅰ)知)(x f 在(0,+∞)上的最大值是24().e k f k -= 所以1(0,),()e x f x ∀∈+∞…等价于241().e ek f k -=…(步骤5) 解得102k -<…. 故当1(0,),()e x f x ∀∈+∞…时,k 的取值范围是).0,21[-(步骤6) 19.(本小题共14分) 已知椭圆22:14x G y +=过点,0m ()作圆221x y +=的切线l 交椭圆G 于A B ,两点. (I )求椭圆G 的焦点坐标和离心率;(II )将AB 表示为m 的函数,并求AB 的最大值.【测量目标】椭圆的简单几何性质,直线与圆的位置关系,两点间的距离公式.【考查方式】已知椭圆的标准方程,求椭圆的焦点和离心率;过定点的直线与圆相切,与椭圆有两个交点,求两交点距离的最大值. 【难易程度】较难【试题解析】(Ⅰ)由已知得,1,2==b a 所以c ==(步骤1)所以椭圆G 的焦点坐标为)0,3(),0,3(-,离心率为.23==a c e (步骤2) (Ⅱ)由题意知,||1m ….当1=m 时,切线l 的方程1=x ,点A B 、的坐标分别为),23,1(),23,1(- 此时3||=AB (步骤3)当1m =-时,同理可得3||=AB当1||>m 时,设切线l 的方程为),(m x k y -=(步骤4) 由0448)41(.14),(2222222=-+-+⎪⎩⎪⎨⎧=+-=m k mx k x k y x m x k y 得 设A B 、两点的坐标分别为),)(,(2211y x y x ,则2222122214144,418km k x x k m k x x +-=+=+(步骤5) 又由l 与圆.1,11||,1222222+==+=+k k m k km y x 即得相切 所以212212)()(||y y x x AB -+-=]41)44(4)41(64)[1(2222242k m k k m k k +--++=2 .3||342+=m m (步骤6) 由于当3±=m 时,,3||=AB 所以),1[]1,(,3||34||2+∞--∞∈+= m m m AB .(步骤7)因为||2,||||AB m m ==+ 且当3±=m 时,||2AB =,所以||AB 的最大值为2. (步骤8)20.(本小题共13分)若数列12,,...,(2)n n A a a a n =…满足111(1,2,...,1)n a a k n +-==-,数列n A 为E 数列,记()n S A =12...n a a a +++.(Ⅰ)写出一个满足150a a ==,且5()S A >0的E 数列n A ;(Ⅱ)若112a =,2000n =,证明:E 数列n A 是递增数列的充要条件是n a =2011; (Ⅲ)对任意给定的整数2n n ()…,是否存在首项为0的E 数列n A ,使得()n S A =0?如果存在,写出一个满足条件的E 数列n A ;如果不存在,说明理由.【测量目标】数列的概念和通项公式,等差数列的综合应用,归纳推理.【考查方式】已知数列的的条件,写出符合该条件的一般数列;知道首项和项数利用归纳推理判断充要条件;探究深层次的数列问题.【难易程度】较难【试题解析】(Ⅰ)0,1,2,1,0是一具满足条件的E 数列5A .(步骤1) (答案不唯一,0,1,0,1,0也是一个满足条件的E 的数列5A )(Ⅱ)必要性:因为E 数列5A 是递增数列,所以)1999,,2,1(11 ==-+k a a k k .所以5A 是首项为12,公差为1的等差数列. (步骤2)所以2000122000112011a =+-⨯=().充分性,由于20001999211,1a a a a -⋯⋯-……,所以200012000119991999a a a a -+,即剟.(步骤3)又因为12000122011a a ==,,所以200011999a a =+.故n n n A k a a 即),1999,,2,1(011 =>=-+是递增数列. (步骤4)综上,结论得证.(Ⅲ)令.1),1,,2,1(011±=-=>=-=+A k k k c n k a a c 则 (步骤5)因为2111112c c a a c a a ++=++=… ,1211+++++=n n c c c a a所以13211)3()2()1()(-++-+-+-+=n n c c n c n c n na A S)].1()2)(1()1)(1[(2)1(121--++--+----=n c n c n c n n (步骤6) 因为1,1k k c c =±-所以为偶数(1,,1).k n =-所以12(1)(1)(1)(2)(1)n c n c n c --+--++- 为偶数,所以要使()0,n S A =必须使(1)2n n -为偶数, 即4整除(1),n n -亦即4n m =或*41()n m m =+∈N .(步骤7)当*41(),n m m =+∈N 时E 数列n A 的项满足4141420,1,k k k a a a +--===-14=k a ),,2,1(m k =时,有;0)(,01==n A S a;0)(,0,0),,,2,1(11144=====+n k k A S a a m k a 有时当*41(),n n m m E A =+∈N 时数列的项满足,,1,0243314-===---k k k a a a当*4243(),(1)n m n m m n m =+=+∈-N 或时不能被4整除,此时不存在E 数列n A , 使得.0)(,01==n A S a (步骤8)。
2011年普通高等学校招生全国统一考试数学理试题(全国卷,含答案).doc

2011 年普通高等学校招生全国统一考试数学理试题(全国卷,含答案)本试卷分第Ⅰ卷 ( 选择题 ) 和第Ⅱ卷 ( 非选择题 ) 两部分。
第Ⅰ卷 1 至 2 页。
第Ⅱ卷 3 至 4 页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答题前, 考生在答题卡上务必用直径0.5 毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用 橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
..........3.第Ⅰ卷共 l2 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是 符合题目要求的。
一、选择题(1) 复数 z 1i , z 为 z 的共轭复数,则 zz z 1( A ) 2i( B ) i( C ) i( D ) 2i【答案】 B(2) 函数 y 2 x( x 0) 的反函数为( A ) yx 2( x R)( B )4( C )y 4x 2( x R)( )Dyx 2( x 0)4y 4x 2 ( x 0) 【答案】 B(3) 下面四个条件中,使 a b 成立的充分而不必要的条件是( A ) a >b 1( B ) a >b 1(C ) a 2> b 2( D ) a 3> b 3【答案】 A(4) 设 S n 为等差数列a n 的前 n 项和,若 a 1 1,公差 d2 , S k 2 S k 24 ,则 k( A ) 8 (B ) 7( C ) 6( D ) 5【答案】 D(5) 设函数 f ( x) cos x(0) ,将 yf ( x) 的图像向右平移个单位长度后,所得的图3像与原图像重合,则的最小值等于( A )1(B ) 3(C ) 6( D ) 93【答案】 C(6) 已知直二面角l , 点 A , AC l , C 为垂足 , B , BD l , D 为垂足.若 AB2, AC BD 1,则 D 到平面 ABC 的距离等于2 (B) 36 (D) 1(A)3 (C)33【答案】 CA(7) 某同学有同样的画册 2 本,同样的集邮册 3 本,从中取出 4 本赠送给 4 位朋友每位朋友 1 本,则不同的赠送方法共有(A) 4 种(B)10 种(C)18 种(D)20 种lD【答案】 BCB E(8) 曲线 y e 2 x1在点 (0,2) 处的切线与直线 y 0 和 y x 围 成的三角形的面积为(A)1(B)1 (C)2 (D)1323【答案】 A(9) 设 f ( x) 是周期为 2 的奇函数,当 0x 1 时, f (x)2x(1 x) , 则 f (5 )11112(A) -(B)(C)(D)2442【答案】 A(10) 已知抛物线C : y 24x 的焦点为 F ,直线 y2x 4 与 C 交于 A , B 两点.则cos AFB(A)4(B)3 (C)3 (D)4 5555【答案】 D(11) 已知平面 α截一球面得圆 M ,过圆心 M 且与 α 成 600 二面角的平面 β 截该球面得圆 N .若该球面的半径为 4,圆 M 的面积为 4 ,则圆 N 的面积为(A) 7 (B) 9(C)11(D)13【答案】 D(12) r r rr rr r 1 rr r rr设向量 a , b , c 满足 | a | | b |1, agb, ac,bc60 ,则 | c | 的最大值2等于(A) 2 (B)3(c)2(D) 1【答案】 AB绝密★启用前2011 年普通高等学校招生全国统一考试ACD理科数学 ( 必修 +选修 II)第Ⅱ卷注意事项:1 答题前,考生先在答题卡上用直径0. 5 毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,然后贴好条形码。
2011年北京高考数学答案解析(理科)
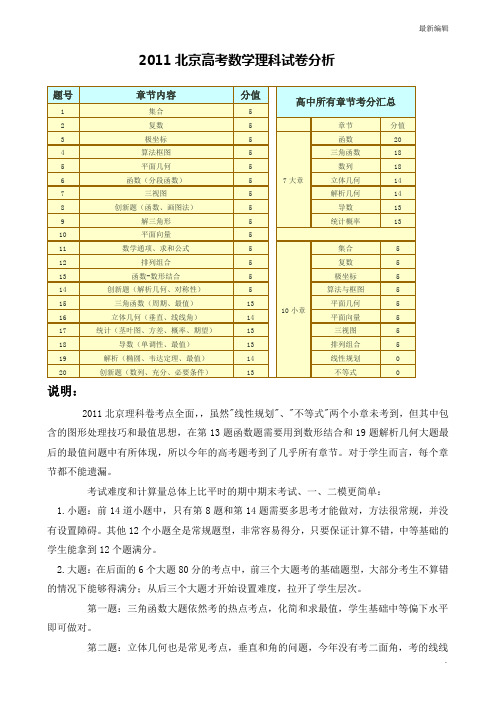
2011北京高考数学理科试卷分析说明:2011北京理科卷考点全面,,虽然"线性规划"、"不等式"两个小章未考到,但其中包含的图形处理技巧和最值思想,在第13题函数题需要用到数形结合和19题解析几何大题最后的最值问题中有所体现,所以今年的高考题考到了几乎所有章节。
对于学生而言,每个章节都不能遗漏。
考试难度和计算量总体上比平时的期中期末考试、一、二模更简单:1.小题:前14道小题中,只有第8题和第14题需要多思考才能做对,方法很常规,并没有设置障碍。
其他12个小题全是常规题型,非常容易得分,只要保证计算不错,中等基础的学生能拿到12个题满分。
2.大题:在后面的6个大题80分的考点中,前三个大题考的基础题型,大部分考生不算错的情况下能够得满分;从后三个大题才开始设置难度,拉开了学生层次。
第一题:三角函数大题依然考的热点考点,化简和求最值,学生基础中等偏下水平即可做对。
第二题:立体几何也是常见考点,垂直和角的问题,今年没有考二面角,考的线线角更简单,基础弱的学生甚至可以用几何向量法做出这三问,顺利拿到14分。
第三题:是统计题,没有像以前一样设计难度,考点全部是基础型,茎叶图、期望值、方差等在平时的小题考试中经常出现,求的概率甚至可以用数数的方法做出来。
从第四题开始,就要求中等以上基础了。
第四题:导数题一开始便求导,却是个复合函数,学生平时练少了就会疏忽此处而算错,此题就完全丢分。
到求单调性和最值的部分就是常规方法,但第一问就需要讨论参数,用画表格,讨论的方法能顺利解出两问,计算没有难度,中等偏上水平学生能拿到分。
平时学习只要求做到第一问的学生可能在讨论时会卡住,对于学习浅的同学第一问的分数也很难拿到。
第五题:解析几何考的是椭圆,第一问考基础知识是送分题,一般学生都能拿到分。
第二问考的是常规方法,只需要联立方程,用韦达定理求弦长公式,最后求最值即可做出。
计算量一如既往是整份试卷中最大的一题,也是决定能否过140分的关键一题,让很多学生畏惧,基础好的学生勇于一试。
2011北京高考数学真题(理科)及答案

2011北京高考数学真题(理科)一.选择题1.已知集合2{|1}P x x =≤,{}M a =.若PM P =,则a 的取值范围是 ( )A .(,1]-∞-B .[1,)+∞C .[1,1]-D .(,1][1,)-∞-+∞2.复数212i i-=+ ( ) A .i B .i - C .4355i -- D . 4355i -+3.在极坐标系中,圆的圆心的极坐标是 ( )A .(1,)2π B .(1,)2π- C .(1,0) D .(1,)π4.执行如图所示的程序框图,输出的s 值为 ( )A .3-B .12- C .13 D .25.如图,AD ,AE ,BC 分别与圆O 切于点D ,E ,F ,延长AF 与圆O 交于另一点G .给出下列三个结论: ①AD AE AB BC CA +=++; ②AF AG AD AE ⋅=⋅; ③AFB ADG △△∽.其中正确结论的序号是 ( )A .①②B .②③C .①③D .①②③6.根据统计,一名工人组装第x 件某产品所用的时间(单位:分钟)为,,(),cx A xf x cx A x⎧<⎪⎪=⎨⎪≥⎪⎩(A ,c 为常数),已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟,那么c 和A 的值分别是( )A .75, 25B .75, 16C .60, 25D .60,16 7.某四面体的三视图如图所示,该四面体四个面的面积中最大的是( ) A .8 B .62 C .10 D .8211s s s -=+0,2i s ==4i <1i i =+s输出开始结束第4题CB F AODEG第5题俯视图侧(左)视图正(主)视图3448.设(0,0)A ,(4,0)B ,(4,4)C t +,(,4)D t (t R ∈).记()N t 为平行四边形ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数()N t 的值域为 ( ) A .{9,10,11} B .{9,10,12} C .{9,11,12} D .{10,11,12}二.填空题9.在ABC △中,若5b =,4B π∠=,tan 2A =,则sin A =_________;a =________.10.已知向量(3,1)a =,(0,1)b =-,(,3)c k =.若2a b -与c 共线,则k =______. 11.在等比数列{}n a 中,若112a =,44a =-,则公比q = ;12||||||n a a a +++= .12.用数字2,3组成四位数,且数字2,3 至少都出现一次,这样的四位数共有 个(用数字作答).13.已知函数32, 2,()(1), 2.x f x x x x ⎧≥⎪=⎨⎪-<⎩若关于x 的方程()f x k =有两个不同的实根,则实数k 的取值范围是 .14.曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2a (1a >)的点的轨迹,给出下列三个结论:①曲线C 过坐标原点;②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则12F PF △的面积不大于212a .其中,所有正确结论的序号是 .三.解答题15.(13分)已知函数()4cos sin()16f x x x π=+-.(1)求()f x 的最小正周期; (2)求()f x 在区间[,]64ππ-上的最大值和最小值.16.(14分)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,2AB =,60BAD ∠=.(1)求证BD ⊥平面PAC ;(2)若PA AB =,求PB 与AC 所成角的余弦值; (3)当平面PBC 与平面PDC 垂直时,求PA 的长.17.(13分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X 表示.(1)如果8X =,求乙组同学植树棵数的平均数和方差;(2)如果9X =,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y 的分布列和数学期望.999X 008111甲组 乙组 C A B D P18.(13分)已知函数2()()x kf x x k e =-. (1)求()f x 的单调区间;(2)若对于任意的(0,)x ∈+∞,都有1()f x e≤,求k 的取值范围.19.(14分)已知椭圆22:14x G y +=,过点(,0)m 作圆221x y +=的切线l 交椭圆G 于A ,B 两点. (1)求椭圆G 的焦点坐标和离心率;(2)将||AB 表示为m 的函数,并求||AB 的最大值.20.(13分)若数列n A :12,,,n a a a (2n ≥)满足1||1k k a a +-=(1,2,,1k n =-),则称n A 为E 数列.记12()n n S A a a a =+++.(1)写出一个满足150a a ==,且5()0S A >的E 数列5A ;(2)若112a =,2000n =.证明:E 数列n A 是递增数列的充要条件是2011n a =;(3)对任意给定的整数n (2n ≥),是否存在首项为0的E 数列n A ,使得()0n S A =?若果存在,写出一个满足条件的E 数列n A ;如果不存在,说明理由.参考答案及试题解析。
2011年北京市高考数学试卷(理科)答案与解析

2011年北京市高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)21.(5分)(2011•北京)已知集合P={x|x≤1},M={a}.若P∪M=P,则a 的取值范围是()A.(﹣∞,﹣1] B.[1,+∞)C.[﹣1,1] D.(﹣∞,﹣1]∪[1,+∞)【考点】集合关系中的参数取值问题.【专题】集合.【分析】通过解不等式化简集合P;利用P∪M=P⇔M⊆P;求出a 的范围.2【解答】解:∵P={x|x≤1},∴P={x|﹣1≤x≤1} ∵P∪M=P ∴M⊆P ∴a∈P ﹣1≤a≤1 故选:C.【点评】本题考查不等式的解法、考查集合的包含关系:根据条件P∪M=P⇔M⊆P是解题关键.2.(5分)(2011•北京)复数=()A.i B.﹣i C. D.【考点】复数代数形式的混合运算.【专题】数系的扩充和复数.2【分析】将分子、分母同乘以1﹣2i,再按多项式的乘法法则展开,将i用﹣1代替即可.【解答】解:==i 故选A 【点评】本题考查复数的除法运算法则:分子、分母同乘以分母的共轭复数;再按多项式的乘法法则展开即可. 3.(5分)(2011•北京)在极坐标系中,圆ρ=﹣2sinθ的圆心的极坐标系是()A. B. C.(1,0) D.(1,π)【考点】简单曲线的极坐标方程.【专题】直线与圆;坐标系和参数方程.【分析】先在极坐标方程ρ=﹣2sinθ的两边同乘以ρ,再利用直角坐标与极坐标间的关系,222即利用ρcosθ=x,ρsinθ=y,ρ=x+y,进行代换即得直角坐标系,再利用直角坐标方程求解即可.【解答】解:将方程ρ=﹣2sinθ两边都乘以p得:2ρ=﹣2ρsinθ,化成直角坐标方程为 122x+y+2y=0.圆心的坐标(0,﹣1).∴圆心的极坐标故选B.【点评】本题考查点的极坐标和直角坐标的互化,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互,能在极坐标系中用极坐标刻画点的位置.4.(5分)(2011•北京)执行如图所示的程序框图,输出的s值为()A.﹣3 B.﹣ C. D.2 【考点】循环结构.【专题】算法和程序框图.【分析】i=0,满足条件i<4,执行循环体,依此类推,当i=4,s=2,此时不满足条件i<4,退出循环体,从而得到所求.【解答】解:i=0,满足条件i<4,执行循环体,i=1,s= 满足条件i<4,执行循环体,i=2,s=﹣满足条件i<4,执行循环体,i=3,s=﹣3 满足条件i<4,执行循环体,i=4,s=2 不满足条件i<4,退出循环体,此时s=2 故选:D 【点评】根据流程图计算运行结果是算法这一模块的重要题型,处理的步骤一般为:分析流程图,从流程图中即要分析出计算的类型,又要分析出参与计算的数据建立数学模型,根据第一步分析的结果,选择恰当的数学模型解模.算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题. 5.(5分)(2011•北京)如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:①AD+AE=AB+BC+CA;②AF•AG=AD•AE③△AFB~△ADG 其中正确结论的序号是() 2A.①② B.②③ C.①③ D.①②③ 【考点】与圆有关的比例线段.【专题】直线与圆.【分析】根据从圆外一点引圆的两条切线,切线长相等,得到第一个说法是正确的,根据切割线定理知道第二个说法是正确的,根据切割线定理知,两个三角形△ADF~△ADG,得到第三个说法错误.【解答】解:根据从圆外一点引圆的两条切线,切线长相等,有CE=CF,BF=BD,∴AD+AE=AB+BC+CA,故①正确,∵AD=AE,2AE=AF•AG,∴AF•AG=AD•AE,故②正确,根据切割线定理知△ADF~△ADG 故③不正确,综上所述①②两个说法是正确的,故选A.【点评】本题考查与圆有关的比例线段,考查圆的切线长定理,考查圆的切割线定理,考查切割线构成的两个相似的三角形,本题是一个综合题目.6.(5分)(2011•北京)根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为(A,C为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是() A.75,25 B.75,16 C.60,25 D.60,16 【考点】函数解析式的求解及常用方法.【专题】函数的性质及应用.【分析】首先,x=A的函数值可由表达式直接得出,再根据x=4与x=A的函数值不相等,说明求f(4)要用x<A对应的表达式,将方程组联解,可以求出C、A的值.【解答】解:由题意可得:f(A)==15,所以c=15 而f(4)==30,可得出=30 故=4,可得A=16 从而c=15=60 故答案为D 3【点评】分段函数是函数的一种常见类型,解决的关键是寻找不同自变量所对应的范围,在相应区间内运用表达式加以解决.7.(5分)(2011•北京)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是()A.8 B. C.10 D.【考点】由三视图求面积、体积.【专题】立体几何.【分析】三视图复原的几何体是一个三棱锥,根据三视图的图形特征,判断三棱锥的形状,三视图的数据,求出四面体四个面的面积中,最大的值.【解答】解:三视图复原的几何体是一个三棱锥,如图,四个面的面积分别为:8,6,,10,显然面积的最大值,10.故选C.【点评】本题是基础题,考查三视图复原几何体的知识,考查几何体的面积,空间想象能力,计算能力,常考题型.8.(5分)(2011•北京)设A (0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为()A.{9,10,11} B.{9,10,12} C.{9,11,12} D.{10,11,12} 【考点】集合的含义.【专题】集合.【分析】分别由t=0,1,2求出N(t),排除错误选项A,B,D,从而得到正确选项.【解答】解:当t=0时,▱ABCD的四个顶点是A(0,0),B(4,0),C(4,4),D(0,4),符合条件的点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共九个,N(t)=9,故选项D不正确.当t=1时,▱ABCD的四个顶点是A(0,0),B(4,0),C(5,4),D(1,4), 4同理知N(t)=12,故选项A不正确.当t=2时,▱ABCD的四个顶点是A(0,0),B(4,0),C(6,4),D(2,4),同理知N(t)=11,故选项B不正确.故选C.【点评】本题考查集合的性质和应用,解题时要注意排除法的合理运用.本题中取整点是个难点,常用的方法是,先定横(或纵)坐标,在定纵(横)坐标,以确定点的个数,如果从图形上看,就是看直线x=r(r是整数)上有几个整点在四边形内.二、填空题(共6小题,每小题5分,满分30分)9.(5分)(2011•北京)在△ABC中.若b=5,,tanA=2,则sinA= ;a= 2 .【考点】正弦定理;同角三角函数间的基本关系.【专题】解三角形.【分析】由tanA的值,利用同角三角函数间的基本关系求出cosA的平方,然后由A的范围,再利用同角三角函数的基本关系求出sinA的值,然后再利用正弦定理,由sinA,sinB及b的值即可求出a的值.2【解答】解:由tanA=2,得到cosA==,由A∈(0,π),得到sinA==,根据正弦定理得:=,得到a===2.故答案为:;2 【点评】此题考查学生灵活运用同角三角函数间的基本关系以及正弦定理化简求值,是一道中档题.10.(5分)(2011•北京)已知向量=(,1),=(0,﹣1),=(k,).若与共线,则k= 1 . 5【考点】平面向量共线(平行)的坐标表示.【专题】平面向量及应用.【分析】利用向量的坐标运算求出的坐标;利用向量共线的坐标形式的充要条件列出方程,求出k的值.【解答】解:∵与共线,∴解得k=1.故答案为1.【点评】本题考查向量的坐标运算、考查向量共线的坐标形式的充要条件:坐标交叉相乘相等.11.(5分)(2011•北京)在等比数列{a}中,a=,a=﹣4,则公比q= ﹣2 ;|a|+|a|+…+|a|= n1412n.【考点】等比数列的性质;等比数列的前n项和.【专题】等差数列与等比数列.【分析】先利用等比数列的通项公式求得公比;|a|是以a为首项,|q|为公比,进而利用等n1比数列的求和公式求解.【解答】解:q===﹣2,|a|+|a|+…+|a|== 12n故答案为:﹣2,【点评】本题主要考查了等比数列的性质.考查了对等比数列的通项公式和求和公式的灵活运用.12.(5分)(2011•北京)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有14 个.(用数字作答)【考点】计数原理的应用.【专题】算法和程序框图.【分析】本题是一个分类计数问题,首先确定数字中2和3 的个数,当数字中有1个2,3个3时,当数字中有2个2,2个3时,当数字中有3个2,1个3时,写出每种情况的结果数,最后相加.【解答】解:由题意知本题是一个分类计数问题,首先确定数字中2和3 的个数,1当数字中有1个2,3个3时,共有C=4种结果,4 62当数字中有2个2,2个3时,共有C=6种结果,41当数字中有3个2,1个3时,共有有C=4种结果,4根据分类加法原理知共有4+6+4=14种结果,故答案为:14 【点评】本题考查分类计数原理,是一个数字问题,这种问题一般容易出错,注意分类时要做到不重不漏,本题是一个基础题,也是一个易错题,易错点在数字中重复出现的数字不好处理.13.(5分)(2011•北京)已知函数若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是(0,1).【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】要求程f(x)=k有两个不同的实根是数k的取值范围,根据方程的根与对应函数零点的关系,我们可以转化为求函数y=f(x)与函数y=k交点的个数,我们画出函数的图象,数形结合即可求出答案.【解答】解:函数的图象如下图所示:由函数图象可得当k∈(0,1)时方程f(x)=k有两个不同的实根,故答案为:(0,1)【点评】本题考查的知识点是根的存在性及根的个数判断,其中根据方程的根与对应函数零点的关系,将方程问题转化为函数问题是解答的关键. 14.(5分)(2011•北京)曲线C是平面内与两个定点F(﹣1,0)和F(1,0)的距离的122积等于常数a(a>1)的点的轨迹.给出下列三个结论: 7①曲线C过坐标原点;②曲线C关于坐标原点对称;2③若点P在曲线C上,则△FPF的面积不大于a.12其中,所有正确结论的序号是②③ .【考点】轨迹方程.【专题】圆锥曲线的定义、性质与方程.【分析】由题意曲线C是平面内与两个定点F(﹣1,0)和F(1,0)的距离的积等于常122数a (a>1),利用直接法,设动点坐标为(x,y),及可得到动点的轨迹方程,然后由方程特点即可加以判断.【解答】解:对于①,由题意设动点坐标为(x,y),则利用题意及两点间的距离公式的得:22224⇔[(x+1)]•[(x﹣1)]=a+y+y(1)将原点代入验证,此方程不过原点,所以①错;对于②,把方程中的x被﹣x代换,y被﹣y 代换,方程不变,故此曲线关于原点对称.②正确;对于③,由题意知点P在曲线C上,则△FPF的面积1222=asin∠FPF,≤a,所以③正确.12故答案为:②③.【点评】此题重点考查了利用直接法求出动点的轨迹方程,并化简,利用方程判断曲线的对称性及利用解析式选择换元法求出值域.三、解答题(共6小题,满分80分)15.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间上的最大值和最小值.【考点】三角函数的周期性及其求法;两角和与差的余弦函数;三角函数的最值.【专题】三角函数的图像与性质.【分析】(Ⅰ)利用两角和公式和二倍角公式对函数的解析式进行化简整理后,利用正弦函数的性质求得函数的最小正周期.(Ⅱ)利用x的范围确定2x+的范围,进而利用正弦函数的单调性求得函数的最大和最小值.【解答】解:(Ⅰ)∵,=4cosx()﹣1 2=sin2x+2cosx﹣1 =sin2x+cos2x ), =2sin(2x+ 8所以函数的最小正周期为π;(Ⅱ)∵﹣≤x≤,∴﹣≤2x+≤,=时,f(x)取最大值2,∴当2x+,即x==﹣时,f(x)取得最小值﹣1.当2x+时,即x=﹣【点评】本题主要考查了三角函数的周期性及其求法,三角函数的最值.解题的关键是对函数解析式的化简整理.16.(14分)(2011•北京)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若PA=AB,求PB与AC所成角的余弦值;(Ⅲ)当平面PBC与平面PDC 垂直时,求PA的长.【考点】直线与平面垂直的判定;点、线、面间的距离计算;用空间向量求直线间的夹角、距离.【专题】空间位置关系与距离.【分析】(I)由已知条件可得ACBD,PABD,根据直线与平面垂直的判定定理可证(II)结合已知条件,设AC与BD的交点为O,则OB⊥OC,故考虑分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系,设PB与AC所成的角为θ,则,代入公式可求(III)分别求平面PBC的法向量,平面PDC的法向量由平面PBC⊥平面PDC可得从而可求t即PA 【解答】解:(I)证明:因为四边形ABCD是菱形,所以AC⊥BD, 9又因为PA⊥平面ABCD,所以PA⊥BD,PA∩AC=A 所以BD⊥平面PAC (II)设AC∩BD=O,因为∠BAD=60°,PA=AB=2,所以BO=1,AO=OC=,以O为坐标原点,分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系O﹣xyz,则P(0,﹣,2),A(0,﹣,0),B(1,0,0),C(0,,0)所以=(1,,﹣2),设PB与AC所成的角为θ,则cosθ=| (III)由(II)知,设,则设平面PBC的法向量=(x,y,z)则=0,所以令,平面PBC的法向量所以,同理平面PDC的法向量,因为平面PBC⊥平面PDC,所以=0,即﹣6+=0,解得t=,所以PA=.【点评】本小题主要考查空间线面关系的垂直关系的判断、异面直线所成的角、用空间向量的方法求解直线的夹角、距离等问题,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力17.(13分)(2011•北京)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差,其中为x,1x, (x)的平均数)2n 10【考点】茎叶图;众数、中位数、平均数;极差、方差与标准差;离散型随机变量的期望与方差.【专题】概率与统计.【分析】(Ⅰ)根据所给的数据,把所有数据相加再除以4写出这组数据的平均数,再利用所给的方差的公式,做出这组数据的方差.(Ⅱ)根据所给的变量写出随机变量可能的取值,结合变量对应的事件写出变量的概率,写出分布列,做出期望值.【解答】解:(Ⅰ)当X=8,乙组同学植树棵数是8,8,9,10,平均数是=,方差为+=;(Ⅱ)当X=9时,甲组同学的植树棵数是9,9,11,11;乙组同学的植树棵数是9,8,9,10,分别从甲和乙两组中随机取一名同学,共有4×4=16种结果,这两名同学植树的总棵数Y可能是17,18,19,20,21,事件Y=17,表示甲组选出的同学植树9棵,乙组选出的同学植树8棵,∴P(Y=17)= P(Y=18)= P(Y=19)= P(Y=20)=,P(Y=21)= Y 17 18 19 20 21 P 0.125 0.25 0.25 0.25 0.125 =19.∴随机变量的期望是EY=【点评】本题考查一组数据的平均数和方差,考查离散型随机变量的分布列和期望值,考查等可能事件的概率,本题是一个概率与统计的综合题目.18.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的单调区间; 11(Ⅱ)若对于任意的x∈(0,+∞),都有f(x)≤,求k的取值范围.【考点】利用导数研究函数的单调性;导数在最大值、最小值问题中的应用.【专题】函数的性质及应用;导数的概念及应用.【分析】(I)求导,令导数等于零,解方程,跟据f′(x),f(x)随x的变化情况即可求出函数的单调区间;(Ⅱ)根据若对于任意的x∈(0,+∞),都有f(x)≤,利用导数求函数f(x)在区间(0,+∞)的最大值,即可求出k的取值范围.【解答】解:(Ⅰ)=,令f′(x)=0,得x=±k 当k>0时,f′(x)f(x)随x的变化情况如下:x k (﹣∞,﹣﹣k (﹣k,k)(k,+∞) k)0 0 + f′(x) + ﹣21﹣ 0 f(x)递增递增递减4ke 所以,f(x)的单调递增区间是(﹣∞,﹣k),和(k,+∞),单调递减区间是(﹣k,k);当k<0时,f′(x)f(x)随x的变化情况如下: x k (﹣∞,k)(k,﹣k)﹣k (﹣k,+∞)0 + 0 f′(x)﹣﹣21﹣ 0 f(x)递减递增递减 4ke 所以,f(x)的单调递减区间是(﹣∞,k),和(﹣k,+∞),单调递增区间是(k,﹣k);(Ⅱ)当k>0时,有f(k+1)=,不合题意,,当k<0时,由(I)知f(x)在(0,+∞)上的最大值是f(﹣k)=∴任意的x∈(0,+∞),f(x)≤,⇔f(﹣k)=≤,解得﹣,故对于任意的x∈(0,+∞),都有f(x)≤,k 的取值范围是﹣.【点评】此题是个难题.考查利用导数研究函数的单调性和在闭区间上的最值问题,对方程f'(x)=0根大小进行讨论,体现了分类讨论的思想方法,特别是(II)的设置,有关恒成立问题一般转化为求函数的最值问题,体现了转化的思想,增加了题目的难度.2219.(14分)(2011•北京)已知椭圆.过点(m,0)作圆x+y=1的切线I交椭圆G于A,B 两点.(Ⅰ)求椭圆G的焦点坐标和离心率; 12(Ⅱ)将|AB|表示为m的函数,并求|AB|的最大值.【考点】圆与圆锥曲线的综合.【专题】圆锥曲线的定义、性质与方程;圆锥曲线中的最值与范围问题.【分析】(I)由题意及椭圆和圆的标准方程,利用椭圆离心率的定义和点到直线的距离公式即可求解;(II)由题意即m得取值范围分m=1时,m=﹣1及当m≠±1三大类求出|AB|的长度,利用直线方程与椭圆方程进行联立,利用根与系数的关系得到k与m之间关系等式,利用直线与圆相切的条件即可.【解答】解:(I)由题意得a=2,b=1,所以c= ∴椭圆G的焦点坐标离心率e=.(II)由题意知:|m|≥1,当m=1时,切线l的方程为x=1,点A(1,)点B(1,﹣)此时|AB|=;当m=﹣1时,同理可得|AB|=;22222当|m|>1时,设切线l的方程为:y=k(x﹣m),由⇒(1+4k)x﹣8kmx+4km﹣4=0,设A(x,y),B(x,y)则x+x= 112212222又由l与圆x+y=1相切∴圆心到直线l的距离等于圆的半径即=1⇒m=,所以|AB|= =]=,由于当m=±1时,|AB|=,当m≠±1时,|AB|=,此时m∈(﹣∞,﹣1]∪[1,+∞)又|AB|=≤2(当且仅当m=±时,|AB|=2),所以,|AB|的最大值为2.故|AB|的最大值为2.【点评】此题重点考查了椭圆及圆的标准方程,还考查了点到直线的距离公式,对于第二问,重点考查了利用m的范围分裂进行讨论,联立直线与椭圆的方程利用整体代换的思想建立m与k的关系等式,还考查两点间的距离公式及又m的范围解出|AB|的最值. 1320.(13分)(2011•北京)若数列A=a,a,…,a(n≥2)满足|a﹣a|=1(k=1,2,…,n12nk+1k n﹣1),数列A为E数列,记S (A)=a+a+…+a.nn12n(Ⅰ)写出一个满足a=a=0,且S(A)>0的E数列A;1ssn(Ⅱ)若a=12,n=2000,证明:E数列A是递增数列的充要条件是a=2011;1nn(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列A,使得S(A)=0?如nn果存在,写出一个满足条件的E数列A;如果不存在,说明理由.n【考点】数列的应用.【专题】等差数列与等比数列;点列、递归数列与数学归纳法.【分析】(Ⅰ)根据题意,a=±1,a=±1,再根据|a﹣a|=1给出a的值,可以得出符合题24k+1k5的E数列A;5(Ⅱ)从必要性入手,由单调性可以去掉绝对值符号,可得是A公差为1的等差数列,再n证充分性,由绝对值的性质得出不等式,再利用同向不等式的累加,可得a﹣a=1>0,k+1k A是递增数列;n(Ⅲ)根据定义构造数列,再用等差数列求和公式求出S(A),最后通过讨论得出符合条n 件的S(A).n【解答】解:(Ⅰ)0,1,0,1,0是一个满足条件的E数列A 5(Ⅱ)必要性:因为E数列A是递增数列n 所以a﹣a=1(k=1,2,…,1999)k+1k所以A是首项为12,公差为1的等差数列.n所以a=12+(2000﹣1)×1=2011 2000充分性:由于a﹣a≤1 20001999 a﹣a≤1 19991998… a﹣a≤1,21所以a﹣a≤1999,即a≤a+1999 2000120001又因为a=12,a=2011 12000所以a=a+1999 20001故a﹣a=1>0(k=1,2,…,1999),即A是递增数列.k+1kn综上所述,结论成立.(Ⅲ)设c=a﹣a (k=1,2,…,n﹣1),则c=±1 kk+1kk因为a=a+c 211a=a+c+c 3112… a=a+c+c+…+c n112n1﹣所以S(A)=na+(n﹣1)c+(n﹣2)c+(n﹣3)c+...+c n1123n1﹣=(n﹣1)+(n﹣2)+ (1)[(1﹣c)(n﹣1)+(1﹣c)(n﹣2)+…+(1﹣c)] 12n1﹣= 因为c=±1,所以1﹣c为偶数(k=1,2,…,n﹣1))kk所以(1﹣c)(n﹣1)+(1﹣c)(n﹣2)+…+(1﹣c)为偶数12n1﹣所以要使S(A)=0,必须=使为偶数n*即4整除n(n﹣1),亦即n=4m或n=4m+1(m∈N) 14*当n=4m(m∈N)时,E数列A的项满足a=a=0,a=﹣1,a=1(k=1,2,…,n4k+14k14k24k﹣﹣n﹣1))此时,有a=0且S(A)=0成立1n*当n=4m+1(m∈N)时,E数列A的项满足a=a=0a=﹣1a=1(k=1,2,…,n n4k+14k14k24k﹣﹣﹣1))a=0时,亦有a=0且S(A)=0成立4m+11n**当n=4m+2或n=4m+3(m∈N)(m∈N)时,n(n﹣1)不能被4整除,此时不存在数列数列A,使得a=0且S(A)=0成立n1n【点评】本题以数列为载体,考查了不等式的运用技巧,属于难题,第三小问注意去绝对值,分类讨论思想的运用. 15。
2011年高考真题——理科数学(北京卷)Word版含答案

绝密★使用完毕前2011年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
考试时间长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合P={x ︱x 2≤1},M={a }.若P ∪M=P,则a 的取值范围是 (A )(-∞, -1] (B )[1, +∞) (C )[-1,1] (D )(-∞,-1] ∪[1,+∞)(2)复数212i i-=+ (A )i (B )-i (C )4355i -- (D )4355i -+(3)在极坐标系中,圆ρ=-2sin θ的圆心的极坐标系是(A) (1,)2π (B) (1,)2π- (C) (1,0)(D)(1,π)(4)执行如图所示的程序框图,输出的s 值为 (A )-3 (B )-12(C )13(D )2(5)如图,AD ,AE ,BC 分别与圆O 切于点D ,E ,F ,延长AF 与圆O 交于另一点G 。
给出下列三个结论:○1AD+AE=AB+BC+CA ;○2AF·AG=AD·AE③△AFB ~△ADG其中正确结论的序号是(A)①②(B)②③(C)①③(D)①②③(6)根据统计,一名工作组装第4件某产品所用的时间(单位:分钟)为(A,C为常数)。
已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么C和A的值分别是(A)75,25 (B)75,16 (C)60,25 (D)60,16(7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是(A) 8 (B) 62 (C)10 (D) 82(8)设()0,0A ,()4,0B ,()4,4C t +,()(),4D t t R ∈.记()N t 为平行四边形ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数()N t 的值域为(A ){}9,10,11 (B ){}9,10,12 (C ){}9,11,12 (D ){}10,11,12第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分。
2011年北京卷(理科数学)

2011年普通高等学校招生全国统一考试理科数学(北京卷)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}P x x 2=≤1,{}M a =,若P M P =U ,则a 的取值范围是 A.(,1]-∞- B.[1,)+∞C.[1,1]-D.(,1][1,)-∞-+∞U 2.复数212i i-=+ A.i B.i - C.4355i -- D.4355i -+3.在极坐标系中,圆2sin ρθ=-的圆心的极坐标系是A .(1,)2πB .(1,)2π- C .(1,0) D .(1,)π4.执行如图所示的程序框图,输出的s 值为A .3-B .1- C .1D .25.如图,AD ,AE ,BC 分别与圆O 切于点D ,E ,F ,延长AF 与圆O 交于另一点G .给出下列三个结论: ①AD AE AB BC CA +=++; ②AF AG AD AE ⋅=⋅ ③AFB ADG ∆∆: 其中正确结论的序号是A .①②B .②③C .①③D .①②③6.根据统计,一名工作组装第x 件某产品所用的时间(单位:分钟)为⎪⎪⎩⎪⎪⎨⎧≥<=Ax Ac Ax x c x f )((A ,C 为常数).已知工人组装第4件产品用时30分钟,组装第A 件产品用时15分钟,那么C 和A 的值分别是A .75,25B .75,16C .60,25D .60,16 7.某四面体的三视图如图所示,该四面体四个面的面积中,最大的是 A .8 B..10 D.8.设(0,0)A ,(4,0)B ,(4,4)C t +,(,4)D t (t R ∈).记()N t 为平行四边形ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数()N t 的值域为A .{9,10,11}B .{9,10,12}C .{9,11,12}D .{10,11,12} 二、填空题:共6小题,每小题5分,共30分. 9.在ABC ∆中,若5b =,4B π∠=,tan 2A =,则sin A = ;a = .10.已知向量a =r ,(0,1)b =-r,(c k =r.若2a b -r r 与c r 共线,则k = .11.在等比数列{}n a 中,112a =,44a =-,则公比q = ;12n a a a +++=L _ . 12.用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有 个.(用数字作答)13.已知函数322()(1)2x f x xx x ⎧≥⎪=⎨⎪-<⎩,若关于x 的方程()f x k =有两个不同的实正(主)视图侧(左)视图俯视图根,则数k 的取值范围是 .14.曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2a (1a >)的点的轨迹.给出下列三个结论: ①曲线C 过坐标原点; ②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则12F PF ∆的面积大于212a .其中,所有正确结论的序号 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分13分)已知函数()4cos sin()16f x x x π=+-.(Ⅰ)求()f x 的最小正周期: (Ⅱ)求()f x 在区间[,]64ππ-上的最大值和最小值. 16.(本小题满分14分) 如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,2AB =,60BAD ∠=o . (Ⅰ)求证:BD ⊥平面;PAC(Ⅱ)若PA AB =,求PB 与AC 所成角的余弦值; (Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.17.(本小题满分13分) 以下茎叶图记录了甲、乙两组各四名同学的植树棵树,乙组记录中有一个数据模糊,无法确认,在图中以X 表示.APDCB(Ⅰ)如果8X =,求乙组同学植树棵数的平均数和方差;(Ⅱ)如果9X =,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y 的分布列和数学期望.(注:方差2222121[()()()]n s x x x x x x n =-+-++-L ,其中x 为1x ,2x ,…n x 的平均数)18.(本小题满分13分) 已知函数2()()x kf x x k e =-. (Ⅰ)求()f x 的单调区间;(Ⅱ)若对于任意的(0,)x ∈+∞,都有1()f x e≤,求k 的取值范围.19.(本小题满分14分)已知椭圆G :2214x y +=,过点(,0)m 作圆221x y +=的切线l 交椭圆G 于A ,B 两点.(Ⅰ)求椭圆G 的焦点坐标和离心率;(Ⅱ)将AB 表示为m 的函数,并求AB 的最大值. 20.(本小题满分13分)若数列n A :1a ,2a ,L ,n a (2n ≥),满足111n a a +-=,(1,2,,1k n =-L ),则称数列n A 为E 数列,记12()n n S A a a a =+++L . (Ⅰ)写出一个满足10s a a ==,且5()0S A >的E 数列n A ;(Ⅱ)若112a =,2000n =,证明:E 数列n A 是递增数列的充要条件是2011n a =; (Ⅲ)对任意给定的整数n (2n ≥),是否存在首项为0的E 数列n A ,使得5()0S A =?如果存在,写出一个满足条件的E 数列n A ;如果不存在,说明理由.甲组 乙组0 119 9 18 9X。
2011年北京市高考数学试卷(理科)(含解析版)

;|a1|+|a2|+…+|an|=
.
12.(5 分)用数字 2,3 组成四位数,且数字 2,3 至少都出现一次,这样的四位数共有 数字作答)
个.(用
13.(5 分)已知函数
若关于 x 的方程 f(x)=k 有两个不同的实根,则数 k
16.(14 分)如图,在四棱锥 P﹣ABCD 中,PA⊥平面 ABCD,底面 ABCD 是菱形,AB=2,∠BAD=60°. (Ⅰ)求证:BD⊥平面 PAC; (Ⅱ)若 PA=AB,求 PB 与 AC 所成角的余弦值; (Ⅲ)当平面 PBC 与平面 PDC 垂直时,求 PA 的长.
20.(13 分)若数列 An=a1,a2,…,an(n≥2)满足|ak+1﹣ak|=1(k=1,2,…,n﹣1),数列 An 为 E 数列,记 S(An)=a1+a2+…+an.
(Ⅰ)写出一个满足 a1=as=0,且 S(As)>0 的 E 数列 An; (Ⅱ)若 a1=12,n=2000,证明:E 数列 An 是递增数列的充要条件是 an=2011; (Ⅲ)对任意给定的整数 n(n≥2),是否存在首项为 0 的 E 数列 An,使得 S(An)=0?如果存在,
.
三、解答题(共 6 小题,满分 80 分) 15.(13 分)已知 f(x)=4cosxsin(x+ )﹣1. (Ⅰ)求 f(x)的最小正周期; (Ⅱ)求 f(x)在区间[﹣ , ]上的最大值和最小值.
17.(13 分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊, 无法确认,在图中以 X 表示.
绝密★启用前
2011 年普通高等学校招生全国统一考试
①AD+AE=AB+BC+CA;②AF•AG=AD•AE③△AFB~△ADG 其中正确结论的序号是( )
2011年北京高考数学答案解析(理科)

2011北京高考数学理科试卷分析题号章节内容分值高中所有章节考分汇总1 集合 52 复数 5 章节分值3 极坐标 57大章函数204 算法框图5 三角函数185 平面几何 5 数列186 函数(分段函数) 5 立体几何147 三视图 5 解析几何148 创新题(函数、画图法) 5 导数139 解三角形 5 统计概率1310 平面向量 511 数学通项、求和公式 510小章集合 512 排列组合 5 复数 513 函数-数形结合 5 极坐标 514 创新题(解析几何、对称性) 5 算法与框图 515 三角函数(周期、最值)13 平面几何 516 立体几何(垂直、线线角)14 平面向量 517 统计(茎叶图、方差、概率、期望)13 三视图 518 导数(单调性、最值)13 排列组合 519 解析(椭圆、韦达定理、最值)14 线性规划020 创新题(数列、充分、必要条件)13 不等式0说明:2011北京理科卷考点全面,,虽然"线性规划"、"不等式"两个小章未考到,但其中包含的图形处理技巧和最值思想,在第13题函数题需要用到数形结合和19题解析几何大题最后的最值问题中有所体现,所以今年的高考题考到了几乎所有章节。
对于学生而言,每个章节都不能遗漏。
考试难度和计算量总体上比平时的期中期末考试、一、二模更简单:1.小题:前14道小题中,只有第8题和第14题需要多思考才能做对,方法很常规,并没有设置障碍。
其他12个小题全是常规题型,非常容易得分,只要保证计算不错,中等基础的学生能拿到12个题满分。
2.大题:在后面的6个大题80分的考点中,前三个大题考的基础题型,大部分考生不算错的情况下能够得满分;从后三个大题才开始设置难度,拉开了学生层次。
第一题:三角函数大题依然考的热点考点,化简和求最值,学生基础中等偏下水平即可做对。
第二题:立体几何也是常见考点,垂直和角的问题,今年没有考二面角,考的线线角更简单,基础弱的学生甚至可以用几何向量法做出这三问,顺利拿到14分。
2011北京高考数学真题(理科)及答案

个(用数字作答).
13.已知函数
f
(x)
2
x
,
x 2, 若关于 x 的方程 f (x) k 有两个不同的实根,则实数 k 的取值范围
(x 1)3, x 2.
是
.
14.曲线 C 是平面内与两个定点 F1(1, 0) 和 F2 (1, 0) 的距离的积等于常数 a2 ( a 1 )的点的轨迹,给出
b
(0,
1)
,
c
(k
,
3)
.若
a
2b
与
c
共线,则
k
______.
{an } 中
,
若
a1
1 2
,
a4 4 ,
则
公
比
q
;
| a1 | | a2 | | an |
.
12.用数字 2,3 组成四位数,且数字 2,3 至少都出现一次,这样的四位数共有
f
(x)
在区间[
,
] 上的最大值和最小值.
64
16.( 14 分 ) 如 图 , 在 四 棱 锥 P ABCD 中 , PA 平 面 ABCD , 底 面 ABCD 是 菱 形 , AB 2 ,
BAD 60 . P
(1)求证 BD 平面 PAC ; (2)若 PA AB ,求 PB 与 AC 所成角的余弦值; (3)当平面 PBC 与平面 PDC 垂直时,求 PA 的长.
下列三个结论:
①曲线 C 过坐标原点;
②曲线 C 关于坐标原点对称;
③若点
P
在曲线
C
2011年北京市高考数学试卷(理科)答案与解析

2011年北京市高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2011•北京)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是()A.(﹣∞,﹣1]B.[1,+∞)C.[﹣1,1]D.(﹣∞,﹣1]∪[1,+∞)【考点】集合关系中的参数取值问题.【专题】集合.【分析】通过解不等式化简集合P;利用P∪M=P⇔M⊆P;求出a的范围.【解答】解:∵P={x|x2≤1},∴P={x|﹣1≤x≤1}∵P∪M=P∴M⊆P∴a∈P﹣1≤a≤1故选:C.【点评】本题考查不等式的解法、考查集合的包含关系:根据条件P∪M=P⇔M⊆P是解题关键.2.(5分)(2011•北京)复数=()A.i B.﹣i C.D.【考点】复数代数形式的混合运算.【专题】数系的扩充和复数.【分析】将分子、分母同乘以1﹣2i,再按多项式的乘法法则展开,将i2用﹣1代替即可.【解答】解:==i故选A【点评】本题考查复数的除法运算法则:分子、分母同乘以分母的共轭复数;再按多项式的乘法法则展开即可.3.(5分)(2011•北京)在极坐标系中,圆ρ=﹣2sinθ的圆心的极坐标系是()A.B.C.(1,0)D.(1,π)【考点】简单曲线的极坐标方程.【专题】直线与圆;坐标系和参数方程.【分析】先在极坐标方程ρ=﹣2sinθ的两边同乘以ρ,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.【解答】解:将方程ρ=﹣2sinθ两边都乘以p得:ρ2=﹣2ρsinθ,化成直角坐标方程为x2+y2+2y=0.圆心的坐标(0,﹣1).∴圆心的极坐标故选B.【点评】本题考查点的极坐标和直角坐标的互化,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互,能在极坐标系中用极坐标刻画点的位置.4.(5分)(2011•北京)执行如图所示的程序框图,输出的s值为()A.﹣3 B.﹣C.D.2【考点】循环结构.【专题】算法和程序框图.【分析】i=0,满足条件i<4,执行循环体,依此类推,当i=4,s=2,此时不满足条件i<4,退出循环体,从而得到所求.【解答】解:i=0,满足条件i<4,执行循环体,i=1,s=满足条件i<4,执行循环体,i=2,s=﹣满足条件i<4,执行循环体,i=3,s=﹣3满足条件i<4,执行循环体,i=4,s=2不满足条件i<4,退出循环体,此时s=2故选:D【点评】根据流程图计算运行结果是算法这一模块的重要题型,处理的步骤一般为:分析流程图,从流程图中即要分析出计算的类型,又要分析出参与计算的数据建立数学模型,根据第一步分析的结果,选择恰当的数学模型解模.算法和程序框图是新课标新增的内容,在近两年的新课标地区高考都考查到了,这启示我们要给予高度重视,属于基础题.5.(5分)(2011•北京)如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:①AD+AE=AB+BC+CA;②AF•AG=AD•AE③△AFB~△ADG其中正确结论的序号是()A.①② B.②③ C.①③ D.①②③【考点】与圆有关的比例线段.【专题】直线与圆.【分析】根据从圆外一点引圆的两条切线,切线长相等,得到第一个说法是正确的,根据切割线定理知道第二个说法是正确的,根据切割线定理知,两个三角形△ADF~△ADG,得到第三个说法错误.【解答】解:根据从圆外一点引圆的两条切线,切线长相等,有CE=CF,BF=BD,∴AD+AE=AB+BC+CA,故①正确,∵AD=AE,AE2=AF•AG,∴AF•AG=AD•AE,故②正确,根据切割线定理知△ADF~△ADG故③不正确,综上所述①②两个说法是正确的,故选A.【点评】本题考查与圆有关的比例线段,考查圆的切线长定理,考查圆的切割线定理,考查切割线构成的两个相似的三角形,本题是一个综合题目.6.(5分)(2011•北京)根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为(A,C为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是()A.75,25 B.75,16 C.60,25 D.60,16【考点】函数解析式的求解及常用方法.【专题】函数的性质及应用.【分析】首先,x=A的函数值可由表达式直接得出,再根据x=4与x=A的函数值不相等,说明求f(4)要用x <A对应的表达式,将方程组联解,可以求出C、A的值.【解答】解:由题意可得:f(A)==15,所以c=15而f(4)==30,可得出=30故=4,可得A=16从而c=15=60故答案为D【点评】分段函数是函数的一种常见类型,解决的关键是寻找不同自变量所对应的范围,在相应区间内运用表达式加以解决.7.(5分)(2011•北京)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是()A.8 B. C.10 D.【考点】由三视图求面积、体积.【专题】立体几何.【分析】三视图复原的几何体是一个三棱锥,根据三视图的图形特征,判断三棱锥的形状,三视图的数据,求出四面体四个面的面积中,最大的值.【解答】解:三视图复原的几何体是一个三棱锥,如图,四个面的面积分别为:8,6,,10,显然面积的最大值,10.故选C.【点评】本题是基础题,考查三视图复原几何体的知识,考查几何体的面积,空间想象能力,计算能力,常考题型.8.(5分)(2011•北京)设A(0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为()A.{9,10,11} B.{9,10,12} C.{9,11,12} D.{10,11,12}【考点】集合的含义.【专题】集合.【分析】分别由t=0,1,2求出N(t),排除错误选项A,B,D,从而得到正确选项.【解答】解:当t=0时,▱ABCD的四个顶点是A(0,0),B(4,0),C(4,4),D(0,4),符合条件的点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共九个,N(t)=9,故选项D不正确.当t=1时,▱ABCD的四个顶点是A(0,0),B(4,0),C(5,4),D(1,4),同理知N(t)=12,故选项A不正确.当t=2时,▱ABCD的四个顶点是A(0,0),B(4,0),C(6,4),D(2,4),同理知N(t)=11,故选项B不正确.故选C.【点评】本题考查集合的性质和应用,解题时要注意排除法的合理运用.本题中取整点是个难点,常用的方法是,先定横(或纵)坐标,在定纵(横)坐标,以确定点的个数,如果从图形上看,就是看直线x=r(r是整数)上有几个整点在四边形内.二、填空题(共6小题,每小题5分,满分30分)9.(5分)(2011•北京)在△ABC中.若b=5,,tanA=2,则sinA= ;a= 2.【考点】正弦定理;同角三角函数间的基本关系.【专题】解三角形.【分析】由tanA的值,利用同角三角函数间的基本关系求出cosA的平方,然后由A的范围,再利用同角三角函数的基本关系求出sinA的值,然后再利用正弦定理,由sinA,sinB及b的值即可求出a的值.【解答】解:由tanA=2,得到cos2A==,由A∈(0,π),得到sinA==,根据正弦定理得:=,得到a===2.故答案为:;2【点评】此题考查学生灵活运用同角三角函数间的基本关系以及正弦定理化简求值,是一道中档题.10.(5分)(2011•北京)已知向量=(,1),=(0,﹣1),=(k,).若与共线,则k= 1 .【考点】平面向量共线(平行)的坐标表示.【专题】平面向量及应用.【分析】利用向量的坐标运算求出的坐标;利用向量共线的坐标形式的充要条件列出方程,求出k的值.【解答】解:∵与共线,∴解得k=1.故答案为1.【点评】本题考查向量的坐标运算、考查向量共线的坐标形式的充要条件:坐标交叉相乘相等.11.(5分)(2011•北京)在等比数列{a n}中,a1=,a4=﹣4,则公比q= ﹣2 ;|a1|+|a2|+…+|a n|=.【考点】等比数列的性质;等比数列的前n项和.【专题】等差数列与等比数列.【分析】先利用等比数列的通项公式求得公比;|a n|是以a1为首项,|q|为公比,进而利用等比数列的求和公式求解.【解答】解:q===﹣2,|a1|+|a2|+…+|a n|==故答案为:﹣2,【点评】本题主要考查了等比数列的性质.考查了对等比数列的通项公式和求和公式的灵活运用.12.(5分)(2011•北京)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有14 个.(用数字作答)【考点】计数原理的应用.【专题】算法和程序框图.【分析】本题是一个分类计数问题,首先确定数字中2和3 的个数,当数字中有1个2,3个3时,当数字中有2个2,2个3时,当数字中有3个2,1个3时,写出每种情况的结果数,最后相加.【解答】解:由题意知本题是一个分类计数问题,首先确定数字中2和3 的个数,当数字中有1个2,3个3时,共有C41=4种结果,当数字中有2个2,2个3时,共有C42=6种结果,当数字中有3个2,1个3时,共有有C41=4种结果,根据分类加法原理知共有4+6+4=14种结果,故答案为:14【点评】本题考查分类计数原理,是一个数字问题,这种问题一般容易出错,注意分类时要做到不重不漏,本题是一个基础题,也是一个易错题,易错点在数字中重复出现的数字不好处理.13.(5分)(2011•北京)已知函数若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是(0,1).【考点】根的存在性及根的个数判断.【专题】函数的性质及应用.【分析】要求程f(x)=k有两个不同的实根是数k的取值范围,根据方程的根与对应函数零点的关系,我们可以转化为求函数y=f(x)与函数y=k交点的个数,我们画出函数的图象,数形结合即可求出答案.【解答】解:函数的图象如下图所示:由函数图象可得当k∈(0,1)时方程f(x)=k有两个不同的实根,故答案为:(0,1)【点评】本题考查的知识点是根的存在性及根的个数判断,其中根据方程的根与对应函数零点的关系,将方程问题转化为函数问题是解答的关键.14.(5分)(2011•北京)曲线C是平面内与两个定点F1(﹣1,0)和F2(1,0)的距离的积等于常数a2(a >1)的点的轨迹.给出下列三个结论:①曲线C过坐标原点;②曲线C关于坐标原点对称;③若点P在曲线C上,则△F1PF2的面积不大于a2.其中,所有正确结论的序号是②③.【考点】轨迹方程.【专题】圆锥曲线的定义、性质与方程.【分析】由题意曲线C是平面内与两个定点F1(﹣1,0)和F2(1,0)的距离的积等于常数a2(a>1),利用直接法,设动点坐标为(x,y),及可得到动点的轨迹方程,然后由方程特点即可加以判断.【解答】解:对于①,由题意设动点坐标为(x,y),则利用题意及两点间的距离公式的得:⇔[(x+1)2+y2]•[(x﹣1)2+y2]=a4(1)将原点代入验证,此方程不过原点,所以①错;对于②,把方程中的x被﹣x代换,y被﹣y 代换,方程不变,故此曲线关于原点对称.②正确;对于③,由题意知点P在曲线C上,则△F1PF2的面积=a2sin∠F1PF2,≤a2,所以③正确.故答案为:②③.【点评】此题重点考查了利用直接法求出动点的轨迹方程,并化简,利用方程判断曲线的对称性及利用解析式选择换元法求出值域.三、解答题(共6小题,满分80分)15.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间上的最大值和最小值.【考点】三角函数的周期性及其求法;两角和与差的余弦函数;三角函数的最值.【专题】三角函数的图像与性质.【分析】(Ⅰ)利用两角和公式和二倍角公式对函数的解析式进行化简整理后,利用正弦函数的性质求得函数的最小正周期.(Ⅱ)利用x的范围确定2x+的范围,进而利用正弦函数的单调性求得函数的最大和最小值.【解答】解:(Ⅰ)∵,=4cosx()﹣1=sin2x+2cos2x﹣1=sin2x+cos2x=2sin(2x+),所以函数的最小正周期为π;(Ⅱ)∵﹣≤x≤,∴﹣≤2x+≤,∴当2x+=,即x=时,f(x)取最大值2,当2x+=﹣时,即x=﹣时,f(x)取得最小值﹣1.【点评】本题主要考查了三角函数的周期性及其求法,三角函数的最值.解题的关键是对函数解析式的化简整理.16.(14分)(2011•北京)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(Ⅰ)求证:B D⊥平面PAC;(Ⅱ)若PA=AB,求PB与AC所成角的余弦值;(Ⅲ)当平面PBC与平面PDC垂直时,求PA的长.【考点】直线与平面垂直的判定;点、线、面间的距离计算;用空间向量求直线间的夹角、距离.【专题】空间位置关系与距离.【分析】(I)由已知条件可得ACBD,PABD,根据直线与平面垂直的判定定理可证(II)结合已知条件,设AC与BD的交点为O,则OB⊥OC,故考虑分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系,设PB与AC所成的角为θ,则,代入公式可求(III)分别求平面PBC的法向量,平面PDC的法向量由平面PBC⊥平面PDC可得从而可求t即PA【解答】解:(I)证明:因为四边形ABCD是菱形,所以AC⊥BD,又因为PA⊥平面ABCD,所以PA⊥BD,PA∩AC=A所以BD⊥平面PAC(II)设AC∩BD=O,因为∠BAD=60°,PA=AB=2,所以BO=1,AO=OC=,以O为坐标原点,分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系O﹣xyz,则P(0,﹣,2),A(0,﹣,0),B(1,0,0),C(0,,0)所以=(1,,﹣2),设PB与AC所成的角为θ,则cosθ=|(III)由(II)知,设,则设平面PBC的法向量=(x,y,z)则=0,所以令,平面PBC的法向量所以,同理平面PDC的法向量,因为平面PBC⊥平面PDC,所以=0,即﹣6+=0,解得t=,所以PA=.【点评】本小题主要考查空间线面关系的垂直关系的判断、异面直线所成的角、用空间向量的方法求解直线的夹角、距离等问题,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力17.(13分)(2011•北京)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差,其中为x1,x2,…x n的平均数)【考点】茎叶图;众数、中位数、平均数;极差、方差与标准差;离散型随机变量的期望与方差.【专题】概率与统计.【分析】(Ⅰ)根据所给的数据,把所有数据相加再除以4写出这组数据的平均数,再利用所给的方差的公式,做出这组数据的方差.(Ⅱ)根据所给的变量写出随机变量可能的取值,结合变量对应的事件写出变量的概率,写出分布列,做出期望值.【解答】解:(Ⅰ)当X=8,乙组同学植树棵数是8,8,9,10,平均数是=,方差为+=;(Ⅱ)当X=9时,甲组同学的植树棵数是9,9,11,11;乙组同学的植树棵数是9,8,9,10,分别从甲和乙两组中随机取一名同学,共有4×4=16种结果,这两名同学植树的总棵数Y可能是17,18,19,20,21,事件Y=17,表示甲组选出的同学植树9棵,乙组选出的同学植树8棵,∴P(Y=17)=P(Y=18)=P(Y=19)=P(Y=20)=,P(Y=21)=∴随机变量的期望是EY==19.【点评】本题考查一组数据的平均数和方差,考查离散型随机变量的分布列和期望值,考查等可能事件的概率,本题是一个概率与统计的综合题目.18.(13分)(2011•北京)已知函数.(Ⅰ)求f(x)的单调区间;(Ⅱ)若对于任意的x∈(0,+∞),都有f(x )≤,求k的取值范围.【考点】利用导数研究函数的单调性;导数在最大值、最小值问题中的应用.【专题】函数的性质及应用;导数的概念及应用.【分析】(I)求导,令导数等于零,解方程,跟据f′(x),f(x)随x的变化情况即可求出函数的单调区间;(Ⅱ)根据若对于任意的x∈(0,+∞),都有f(x )≤,利用导数求函数f(x)在区间(0,+∞)的最大值,即可求出k的取值范围.【解答】解:(Ⅰ)=,令f′(x)=0,得x=±k当k>0时,f′(x)f(x)随x的变化情况如下:所以,f(x)的单调递增区间是(﹣∞,﹣k),和(k,+∞),单调递减区间是(﹣k,k);当k<0时,f′(x)f(x)随x的变化情况如下:所以,f(x)的单调递减区间是(﹣∞,k),和(﹣k,+∞),单调递增区间是(k,﹣k);(Ⅱ)当k>0时,有f(k+1)=,不合题意,当k<0时,由(I)知f(x)在(0,+∞)上的最大值是f(﹣k)=,∴任意的x∈(0,+∞),f(x)≤,⇔f(﹣k)=≤,解得﹣,故对于任意的x∈(0,+∞),都有f(x)≤,k的取值范围是﹣.【点评】此题是个难题.考查利用导数研究函数的单调性和在闭区间上的最值问题,对方程f'(x)=0根大小进行讨论,体现了分类讨论的思想方法,特别是(II)的设置,有关恒成立问题一般转化为求函数的最值问题,体现了转化的思想,增加了题目的难度.19.(14分)(2011•北京)已知椭圆.过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B 两点.(Ⅰ)求椭圆G的焦点坐标和离心率;(Ⅱ)将|AB|表示为m的函数,并求|AB|的最大值.【考点】圆与圆锥曲线的综合.【专题】圆锥曲线的定义、性质与方程;圆锥曲线中的最值与范围问题.【分析】(I)由题意及椭圆和圆的标准方程,利用椭圆离心率的定义和点到直线的距离公式即可求解;(II)由题意即m得取值范围分m=1时,m=﹣1及当m≠±1三大类求出|AB|的长度,利用直线方程与椭圆方程进行联立,利用根与系数的关系得到k与m之间关系等式,利用直线与圆相切的条件即可.【解答】解:(I)由题意得a=2,b=1,所以c=∴椭圆G的焦点坐标离心率e=.(II)由题意知:|m|≥1,当m=1时,切线l的方程为x=1,点A(1,)点B(1,﹣)此时|AB|=;当m=﹣1时,同理可得|AB|=;当|m|>1时,设切线l的方程为:y=k(x﹣m),由⇒(1+4k2)x2﹣8k2mx+4k2m2﹣4=0,设A(x1,y1),B(x2,y2)则x1+x2=又由l与圆x2+y2=1相切∴圆心到直线l的距离等于圆的半径即=1⇒m2=,所以|AB|==]=,由于当m=±1时,|AB|=,当m≠±1时,|AB|=,此时m∈(﹣∞,﹣1]∪[1,+∞)又|AB|=≤2(当且仅当m=±时,|AB|=2),所以,|AB|的最大值为2.故|AB|的最大值为2.【点评】此题重点考查了椭圆及圆的标准方程,还考查了点到直线的距离公式,对于第二问,重点考查了利用m 的范围分裂进行讨论,联立直线与椭圆的方程利用整体代换的思想建立m与k的关系等式,还考查两点间的距离公式及又m的范围解出|AB|的最值.20.(13分)(2011•北京)若数列A n=a1,a2,…,a n(n≥2)满足|a k+1﹣a k|=1(k=1,2,…,n﹣1),数列A n为E数列,记S(A n)=a1+a2+…+a n.(Ⅰ)写出一个满足a1=a s=0,且S(A s)>0的E数列A n;(Ⅱ)若a1=12,n=2000,证明:E数列A n是递增数列的充要条件是a n=2011;(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列A n,使得S(A n)=0?如果存在,写出一个满足条件的E数列A n;如果不存在,说明理由.【考点】数列的应用.【专题】等差数列与等比数列;点列、递归数列与数学归纳法.【分析】(Ⅰ)根据题意,a2=±1,a4=±1,再根据|a k+1﹣a k|=1给出a5的值,可以得出符合题的E数列A5;(Ⅱ)从必要性入手,由单调性可以去掉绝对值符号,可得是A n公差为1的等差数列,再证充分性,由绝对值的性质得出不等式,再利用同向不等式的累加,可得a k+1﹣a k=1>0,A n是递增数列;(Ⅲ)根据定义构造数列,再用等差数列求和公式求出S(A n),最后通过讨论得出符合条件的S(A n).【解答】解:(Ⅰ)0,1,0,1,0是一个满足条件的E数列A5(Ⅱ)必要性:因为E数列A n是递增数列所以a k+1﹣a k=1(k=1,2, (1999)所以A n是首项为12,公差为1的等差数列.所以a2000=12+(2000﹣1)×1=2011充分性:由于a2000﹣a1999≤1a1999﹣a1998≤1…a2﹣a1≤1,所以a2000﹣a1≤1999,即a2000≤a1+1999又因为a1=12,a2000=2011所以a2000=a1+1999故a k+1﹣a k=1>0(k=1,2,…,1999),即A n是递增数列.综上所述,结论成立.(Ⅲ)设c k=a k+1﹣a k(k=1,2,…,n﹣1),则c k=±1因为a2=a1+c1a3=a1+c1+c2…a n=a1+c1+c2+…+c n﹣1所以S(A n)=na1+(n﹣1)c1+(n﹣2)c2+(n﹣3)c3+…+c n﹣1=(n﹣1)+(n﹣2)+…+1﹣[(1﹣c1)(n﹣1)+(1﹣c2)(n﹣2)+…+(1﹣c n﹣1)]=因为c k=±1,所以1﹣c k为偶数(k=1,2,…,n﹣1))所以(1﹣c1)(n﹣1)+(1﹣c2)(n﹣2)+…+(1﹣c n﹣1)为偶数所以要使S(A n)=0,必须=使为偶数即4整除n(n﹣1),亦即n=4m或n=4m+1(m∈N*)当n=4m(m∈N*)时,E数列A n的项满足a4k+1=a4k﹣1=0,a4k﹣2=﹣1,a4k=1(k=1,2,…,n﹣1))此时,有a1=0且S(A n)=0成立当n=4m+1(m∈N*)时,E数列A n的项满足a4k+1=a4k﹣1=0a4k﹣2=﹣1a4k=1(k=1,2,…,n﹣1))a4m+1=0时,亦有a1=0且S(A n)=0成立当n=4m+2或n=4m+3(m∈N*)(m∈N*)时,n(n﹣1)不能被4整除,此时不存在数列数列A n,使得a1=0且S(A n)=0成立【点评】本题以数列为载体,考查了不等式的运用技巧,属于难题,第三小问注意去绝对值,分类讨论思想的运用.。
(完整版)年北京市高考数学试卷(理科)

2011年北京市高考数学试卷(理科)一、选择题(共8小题,每小题5分,满分40分)1.(5分)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是()A.(﹣∞,﹣1] B.[1,+∞) C.[﹣1,1] D.(﹣∞,﹣1]∪[1,+∞)2.(5分)复数=()A.i B.﹣i C.D.3.(5分)在极坐标系中,圆ρ=﹣2sinθ的圆心的极坐标是()A. B.C.(1,0) D.(1,π)4.(5分)执行如图所示的程序框图,输出的s值为()A.﹣3 B.﹣C.D.25.(5分)如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:①AD+AE=AB+BC+CA;②AF•AG=AD•AE③△AFB~△ADG其中正确结论的序号是()A.①②B.②③C.①③D.①②③6.(5分)根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为(A,C为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A 的值分别是()A.75,25 B.75,16 C.60,25 D.60,167.(5分)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是()A.8 B.C.10 D.8.(5分)设A(0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为平行四边形ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为( )A.{9,10,11} B.{9,10,12} C.{9,11,12} D.{10,11,12}二、填空题(共6小题,每小题5分,满分30分)9.(5分)在△ABC 中.若b=5,,tanA=2,则sinA= ;a= .10.(5分)已知向量=(,1),=(0,﹣1),=(k ,).若与共线,则k= .11.(5分)在等比数列{a n }中,a 1=,a 4=﹣4,则公比q= ;|a 1|+|a 2|+…+|a n |= . 12.(5分)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有 个.(用数字作答)13.(5分)已知函数若关于x 的方程f (x )=k 有两个不同的实根,则数k的取值范围是 .14.(5分)曲线C 是平面内与两个定点F 1(﹣1,0)和F 2(1,0)的距离的积等于常数a 2(a >1)的点的轨迹.给出下列三个结论: ①曲线C 过坐标原点; ②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则△F 1PF 2的面积不大于a 2. 其中,所有正确结论的序号是 .三、解答题(共6小题,满分80分)15.(13分)已知f(x )=4cosxsin (x+)﹣1. (Ⅰ)求f (x )的最小正周期;(Ⅱ)求f (x)在区间[﹣,]上的最大值和最小值.16.(14分)如图,在四棱锥P ﹣ABCD 中,PA ⊥平面ABCD,底面ABCD 是菱形,AB=2,∠BAD=60°.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若PA=AB,求PB与AC所成角的余弦值;(Ⅲ)当平面PBC与平面PDC垂直时,求PA的长.17.(13分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差,其中为x1,x2, (x)n的平均数)18.(13分)已知函数.(Ⅰ)求f(x)的单调区间;(Ⅱ)若对于任意的x∈(0,+∞),都有f(x)≤,求k的取值范围.19.(14分)已知椭圆.过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B两点.(Ⅰ)求椭圆G的焦点坐标和离心率;(Ⅱ)将|AB|表示为m 的函数,并求|AB |的最大值.20.(13分)若数列A n =a 1,a 2,…,a n (n≥2)满足|a k+1﹣a k |=1(k=1,2,…,n ﹣1),数列A n 为E 数列,记S(A n )=a 1+a 2+…+a n .(Ⅰ)写出一个满足a 1=a s =0,且S (A s )>0的E 数列A n ;(Ⅱ)若a 1=12,n=2000,证明:E 数列A n 是递增数列的充要条件是a n =2011;(Ⅲ)对任意给定的整数n (n≥2),是否存在首项为0的E 数列A n ,使得S (A n )=0?如果存在,写出一个满足条件的E 数列A n ;如果不存在,说明理由.2011年北京市高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)已知集合P={x|x2≤1},M={a}.若P∪M=P,则a的取值范围是()A.(﹣∞,﹣1] B.[1,+∞)C.[﹣1,1] D.(﹣∞,﹣1]∪[1,+∞)【解答】解:∵P={x|x2≤1},∴P={x|﹣1≤x≤1}∵P∪M=P∴M⊆P∴a∈P﹣1≤a≤1故选:C.2.(5分)复数=()A.i B.﹣i C.D.【解答】解:==i故选A3.(5分)在极坐标系中,圆ρ=﹣2sinθ的圆心的极坐标是()A. B.C.(1,0)D.(1,π)【解答】解:将方程ρ=﹣2sinθ两边都乘以p得:ρ2=﹣2ρsinθ,化成直角坐标方程为x2+y2+2y=0.圆心的坐标(0,﹣1).∴圆心的极坐标故选B.4.(5分)执行如图所示的程序框图,输出的s值为()A.﹣3 B.﹣C.D.2【解答】解:i=0,满足条件i<4,执行循环体,i=1,s=满足条件i<4,执行循环体,i=2,s=﹣满足条件i<4,执行循环体,i=3,s=﹣3满足条件i<4,执行循环体,i=4,s=2不满足条件i<4,退出循环体,此时s=2故选:D5.(5分)如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:①AD+AE=AB+BC+CA;②AF•AG=AD•AE③△AFB~△ADG其中正确结论的序号是()A.①②B.②③C.①③D.①②③【解答】解:根据从圆外一点引圆的两条切线,切线长相等,有CE=CF,BF=BD,∴AD+AE=AB+BC+CA,故①正确,∵AD=AE,AE2=AF•AG,∴AF•AG=AD•AE,故②正确,根据切割线定理知△ADF~△ADG故③不正确,综上所述①②两个说法是正确的,故选A.6.(5分)根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为(A,C为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是()A.75,25 B.75,16 C.60,25 D.60,16【解答】解:由题意可得:f(A)==15,所以c=15而f(4)==30,可得出=30故=4,可得A=16从而c=15=60故答案为D7.(5分)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是( )A.8 B.C.10 D.【解答】解:三视图复原的几何体是一个三棱锥,如图,四个面的面积分别为:8,6,,10,显然面积的最大值,10.故选C.8.(5分)设A(0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为()A.{9,10,11} B.{9,10,12}C.{9,11,12}D.{10,11,12}【解答】解:当t=0时,▱ABCD的四个顶点是A(0,0),B(4,0),C(4,4),D(0,4),符合条件的点有(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共九个,N(t)=9,故选项D不正确.当t=1时,▱ABCD的四个顶点是A(0,0),B(4,0),C(5,4),D(1,4),同理知N(t)=12,故选项A不正确.当t=2时,▱ABCD的四个顶点是A(0,0),B(4,0),C(6,4),D(2,4),同理知N(t)=11,故选项B不正确.故选C.二、填空题(共6小题,每小题5分,满分30分)9.(5分)在△ABC中.若b=5,,tanA=2,则sinA= ;a= 2.【解答】解:由tanA=2,得到cos2A==,由A ∈(0,π),得到sinA==,根据正弦定理得:=,得到a===2.故答案为:;210.(5分)已知向量=(,1),=(0,﹣1),=(k,).若与共线,则k= 1 .【解答】解:∵与共线,∴解得k=1. 故答案为1.11.(5分)在等比数列{a n }中,a 1=,a 4=﹣4,则公比q= ﹣2 ;|a 1|+|a 2|+…+|a n |= .【解答】解:q===﹣2,|a 1|+|a 2|+…+|a n |==故答案为:﹣2,12.(5分)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有 14 个.(用数字作答)【解答】解:由题意知本题是一个分类计数问题,首先确定数字中2和3 的个数,当数字中有1个2,3个3时,共有C 41=4种结果, 当数字中有2个2,2个3时,共有C 42=6种结果, 当数字中有3个2,1个3时,共有有C 41=4种结果, 根据分类加法原理知共有4+6+4=14种结果, 故答案为:1413.(5分)已知函数若关于x 的方程f (x )=k 有两个不同的实根,则数k的取值范围是 (0,1) .【解答】解:函数的图象如下图所示:由函数图象可得当k ∈(0,1)时 方程f (x )=k 有两个不同的实根, 故答案为:(0,1)14.(5分)曲线C 是平面内与两个定点F 1(﹣1,0)和F 2(1,0)的距离的积等于常数a 2(a >1)的点的轨迹.给出下列三个结论:①曲线C过坐标原点;②曲线C关于坐标原点对称;③若点P在曲线C上,则△F1PF2的面积不大于a2.其中,所有正确结论的序号是②③.【解答】解:对于①,由题意设动点坐标为(x,y),则利用题意及两点间的距离公式的得:⇔[(x+1)2+y2]•[(x﹣1)2+y2]=a4(1)将原点代入验证,此方程不过原点,所以①错;对于②,把方程中的x被﹣x代换,y被﹣y 代换,方程不变,故此曲线关于原点对称.②正确;对于③,由题意知点P在曲线C上,则△F1PF2的面积=a2sin∠F 1PF2,≤a2,所以③正确.故答案为:②③.三、解答题(共6小题,满分80分)15.(13分)已知f(x)=4cosxsin(x+)﹣1.(Ⅰ)求f(x)的最小正周期;(Ⅱ)求f(x)在区间[﹣,]上的最大值和最小值.【解答】解:(Ⅰ)∵,=4cosx()﹣1=sin2x+2cos2x﹣1=sin2x+cos2x=2sin(2x+),所以函数的最小正周期为π;(Ⅱ)∵﹣≤x≤,∴﹣≤2x+≤,∴当2x+=,即x=时,f(x)取最大值2,当2x+=﹣时,即x=﹣时,f(x)取得最小值﹣1.16.(14分)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(Ⅰ)求证:BD⊥平面PAC;(Ⅱ)若PA=AB,求PB与AC所成角的余弦值;(Ⅲ)当平面PBC与平面PDC垂直时,求PA的长.【解答】解:(I)证明:因为四边形ABCD是菱形,所以AC⊥BD,又因为PA⊥平面ABCD,所以PA⊥BD,PA∩AC=A所以BD⊥平面PAC(II)设AC∩BD=O,因为∠BAD=60°,PA=AB=2,所以BO=1,AO=OC=,以O为坐标原点,分别以OB,OC为x轴、y轴,以过O且垂直于平面ABCD的直线为z轴,建立空间直角坐标系O﹣xyz,则P(0,﹣,2),A(0,﹣,0),B(1,0,0),C(0,,0)所以=(1,,﹣2),设PB与AC所成的角为θ,则cosθ=|(III)由(II)知,设,则设平面PBC的法向量=(x,y,z)则=0,所以令,平面PBC的法向量所以,同理平面PDC的法向量,因为平面PBC⊥平面PDC,所以=0,即﹣6+=0,解得t=,所以PA=.17.(13分)以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.(Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差;(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差,其中为x1,x2, (x)n的平均数)【解答】解:(Ⅰ)当X=8,乙组同学植树棵数是8,8,9,10,平均数是=,方差为+=;(Ⅱ)当X=9时,甲组同学的植树棵数是9,9,11,11;乙组同学的植树棵数是9,8,9,10,分别从甲和乙两组中随机取一名同学,共有4×4=16种结果,这两名同学植树的总棵数Y可能是17,18,19,20,21,事件Y=17,表示甲组选出的同学植树9棵,乙组选出的同学植树8棵,∴P(Y=17)=P(Y=18)=P(Y=19)=P(Y=20)=,P(Y=21)=Y1718192021P0。
2011年高考北京数学试题(理科)

一、活动背景伴随着生物质能、风能、太阳能、水能、化石能、核能等的使用,人类逐步从原始文明走向农业文明和工业文明。
而随着全球人口和经济规模的不断增长,能源使用带来的环境问题及其诱因不断地为人们所认识,不止是烟雾、光化学烟雾和酸雨等的危害,大气中二氧化碳浓度升高将带来的全球气候变化,也已被确认为不争的事实。
在此背景下,“碳足迹”、“低碳经济”、“低碳技术”、“低碳发展”、“低碳生活方式”、“低碳社会”、“低碳城市”、“低碳世界”等一系列新概念、新政策应运而生。
而能源与经济以至价值观实行大变革的结果,可能将为逐步迈向生态文明走出一条新路,即摒弃20世纪的传统增长模式,直接应用新世纪的创新技术与创新机制,通过低碳经济模式与低碳生活方式,实现社会可持续发展。
西藏作为西部地区生态环境良好的地区,更有必要宣传低碳意识,保持这份优美的环境二、活动目的初步了解西藏的能源消耗方式,宣传低碳理念及节能小知识,并对西藏的整个经济社会及旅游资源环境做初步了解,帮助宣传西藏,促进民族团结三、活动规划:1.活动主题:低碳西藏行2.活动时间:2012年9月1号至2012年9月10日3.活动地点:西藏4.活动对象:西藏人民5.经费预算:见附表16.人员安排:见附表2四、活动亮点:1.活动形式:旅游采访,问卷调查2活动内容:具体活动安排见附表33活动后期:1)制作活动过程中积累的每日心得文字资料,拍摄的照片视频等。
2)召开队员总结会,总结此次活动的整体认识及收获和意义。
3)将相关实践心得及实践论文递交学校。
4)参与社会实践成果展,并参加优秀实践小组的评选。
5)给赞助企业和支持单位寄去感谢信以鸣谢他们对本次活动的支持。
4活动宣传:联系有关媒体,制作横幅及标语,通过学校网站及校报大力宣传。
五、活动流程1团队建设:1)组建团队,确定团队成员。
2)建立完善的组织制度、安全制度及财务制度等团队制度,确保实活动顺利进行。
2.实践团队职能分工:团队负责人:负责实践团队在实践期间的组织管理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年普通高等学校招生全国统一考试数学(理)(北京卷) 本试卷共5页,150分。
考试时间长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题 共40分)
一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合P={x ︱x 2≤1},M={a }.若P ∪M=P,则a 的取值范围是
(A )(-∞, -1] (B )[1, +∞) (C )[-1,1] (D )(-∞,-1] ∪[1,+∞)
(2)复数212i i
-=+ (A )i (B )-i (C )4355i -
- (D )4355i -+ (3)在极坐标系中,圆ρ=-2sin θ的圆心的极坐标系是 (A) (1,)2π (B) (1,)2π
- (C) (1,0) (D)(1,π) (4)执行如图所示的程序框图,输出的s 值为
(A )-3
(B )-
12 (C )13
(D )2
(5)如图,AD ,AE ,BC 分别与圆O 切于点D ,E ,F ,延长AF 与圆O 交于另一点G 。
给出下列三个结论:
○
1AD+AE=AB+BC+CA ; ○
2AF ·AG=AD ·AE ③△AFB ~△ADG
其中正确结论的序号是
(A )①② (B )②③
(C )①③ (D )①②③
(6)根据统计,一名工作组装第4件某产品所用的时间(单位:分钟)为
(A ,C 为常数)。
已知工人组装第4件产品用时30分钟,组装第A 件产
品用时15分钟,那么C 和A 的值分别是
(A )75,25 (B )75,16 (C )60,25 (D )60,16
(7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是
(A) 8 (B) (8)设()0,0A ,()4,0B ,()4,4C t +,()(),4D t t R ∈.记()N t 为平行四边形ABCD 内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数()N t 的值域为
(A ){}9,10,11 (B ){}9,10,12
(C ){}9,11,12 (D ){}10,11,12
第二部分 (非选择题 共110分)
二、填空题共6小题,每小题5分,共30分。
(9)在ABC ∆中。
若b=5,4B π
∠=,tanA=2,则sinA=____________;a=_______________。
(10)已知向量a =1),b =(0,-1),c =(k 。
若a -2b 与c 共线,则
k=___________________。
(11)在等比数列{a n }中,a 1=12
,a 4=-4,则公比q=______________;12...n a a a +++=_________________。
(12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有__________个。
(用数字作答)
(13)已知函数32,2()(1),2x f x x x x ⎧≥⎪=⎨⎪-<⎩
若关于x 的方程f(x)=k 有两个不同的实根,则数k
的取值范围是_______
(14)曲线C 是平面内与两个定点F 1(-1,0)和F 2(1,0)的距离的积等于常数 a 2 (a >1)的点的轨迹.给出下列三个结论:
① 曲线C 过坐标原点;
② 曲线C 关于坐标原点对称;
③若点P 在曲线C 上,则△F 1PF 2的面积大于2
1a 2。
其中,所有正确结论的序号是 。
三、解答题共6小题,共80分,解答应写出文字说明,演算步骤或证明过程。
(15)(本小题共13分) 已知函数()4cos sin()16f x x x π
=+-。
(Ⅰ)求()f x 的最小正周期:
(Ⅱ)求()f x 在区间,64ππ⎡⎤-⎢⎥⎣
⎦上的最大值和最小值。
(16)(本小题共14分)
如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,
2,60AB BAD =∠= .
(Ⅰ)求证:BD ⊥平面;PAC
(Ⅱ)若,PA AB =求PB 与AC 所成角的余弦值;
(Ⅲ)当平面PBC 与平面PDC 垂直时,求PA 的长.
(17)本小题共13分
以下茎叶图记录了甲、乙两组各四名同学的植树棵树。
乙组记录中有一个数据模糊,无法确认,在图中以X 表示。
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y 的分布列和数学期望。
(注:方差()()()
2222121n s x x x x x x n ⎡⎤=-+-++-⎢⎥⎣⎦ ,其中x 为1x ,2x ,…… n x 的平均数)
(18)(本小题共13分) 已知函数2()()x k f x x k e =-。
(Ⅰ)求()f x 的单调区间;
(Ⅱ)若对于任意的(0,)x ∈+∞,都有()f x ≤
1e
,求k 的取值范围。
(19)(本小题共14分)
已知椭圆2
2:14
x G y +=.过点(m ,0)作圆221x y +=的切线l 交椭圆G 于A ,B 两点. (I )求椭圆G 的焦点坐标和离心率;
(II )将AB 表示为m 的函数,并求AB 的最大值.
(20)(本小题共13分)
若数列12,,...,(2)n n A a a a n =≥满足11(1,2,...,1)k k a a k n +-==-,数列n A 为E 数列,记()n S A =12...n a a a +++.
(Ⅰ)写出一个满足10s a a ==,且()s S A 〉0的E 数列n A ; (Ⅱ)若112a =,n=2000,证明:E 数列n A 是递增数列的充要条件是n a =2011; (Ⅲ)对任意给定的整数n (n ≥2),是否存在首项为0的E 数列n A ,使得()n S A =0?如果存在,写出一个满足条件的E 数列n A ;如果不存在,说明理由。
