带电粒子在磁场中的运动(磁聚焦)
带电粒子在磁场中的运动(临界、极值、磁聚焦、扩散)_图文

A.
B.
2R
2R
O
O
B
M 2R R N
M R 2R
N
C.
2R D.
O
RM
O
M 2R
2R N M 2R
2R N
ON
……以速率 v 沿纸面各个方向由小孔O射入磁场
B
M
2R 2R
O
O
2R R
R 2R
A.
B.
ON
O
2R
2R
C.
2R
R
O
2R
2R
D.
例2、如图,质量为m、带电量为+q 的粒子以速度v 从O点
。
a y v0 M B
r 2R Or N
O
bx
二、磁聚焦和磁扩散原理
1、条件:圆形磁场区域半径与粒子轨道半径相等 2、特点:磁聚焦和次扩散具有可逆性
磁场区域半径 R 与运动半径 r 相等
C
B
r
四边形ABCD为菱形
R
D
AB//CD
Hale Waihona Puke A因为AB边竖直,则CD边竖直
从C点水平射出
磁扩散现象
一点发散成平行
沿y 轴正方向射入磁感应强度为 B 的圆形匀强磁场区域, 磁场方向垂直纸面向外,粒子飞出磁场区域后,从 b 处 穿过x轴,速度方向与 x 轴正方向的夹角为30º,不计重力 ,试求圆形匀强磁场区域的最小面积;
y o
y O2
x
A
v
p
60° 60° 30° b
O
O1
30°
v
x
以运动轨迹对应的弦长为直径的圆面积最小
带电粒子在磁场中的运动(临界、极值、磁聚 焦、扩散)_图文.ppt
带电粒子在磁场中的运动(磁聚焦和磁扩散)

θR O/
OM
x
图 (b)
(3)带电微粒在y轴右方(X> O)的区域离开磁场并做 匀速直线运动.靠近上端发射出来的带电微粒在穿出 磁场后会射向X轴正方向的无穷远处,靠近下端发射 出来的带电微粒会在靠近原点之处穿出磁场.所以, 这束带电微粒与X轴相交的区域范围是X> 0.
装带 置点
微 粒 发 射
Pv Cr
(2)这束带电微粒都通过坐标原点。 如图(b)所示,从任一点P水平进入磁场的 带电微粒在磁场中做半径为R 的匀速圆周运动,圆 心位于其正下方的Q点,设微粒从M 点离开磁 场.可证明四边形PO’ MQ是菱形,则M 点就是坐 标原点,故这束带电微粒都通过坐标原点0.
y
v AC
R O/
O
x
图 (a)
y
Pv R
y
D
C
v0
O
x
A
B
S=2(πa2/4-a2/2) =(π-2)a2/2
解:(1)设匀强磁场的磁感应强度的大小为B。令圆弧AEC是自C点垂直于 BC入射的电子在磁场中的运行轨道。依题意,圆心在A、C连线的中垂线上, 故B点即为圆心,圆半径为a,按照牛顿定律有 ev0B= mv02/a,得B= mv0/ea。 (2)自BC边上其他点入射的电子运动轨道只能在BAEC区域中。因而,圆弧 AEC是所求的最小磁场区域的一个边界。
(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区
域,并从坐标原点O沿y轴负方向离开,求电场强度和磁感
应强度的大小与方向。
y
(2)请指出这束带电微粒与x轴相 带
交的区域,并说明理由。
点 微
粒
(3)在这束带电磁微粒初速度变为
发 射
磁场中带电粒子的运动与电磁感应定律

添加标题
添加标题
添加标题
添加标题
粒子在磁场中的运动轨迹:圆周 运动或螺旋运动
影响因素:洛伦兹力的大小和方 向取决于粒子的电荷量、速度和 磁感应强度。
感谢观看
汇报人:XX
螺旋线运动:带电粒子在非 匀强磁场中做螺旋线运动,
轨迹为曲线
洛伦兹力:带电粒子在磁场 中受到的力,方向垂直于磁 场和速度方向
磁聚焦:带电粒子在磁场中 的聚焦现象,轨迹为直线
霍尔效应
霍尔效应的定义:指磁场中带电粒子受到洛伦兹力作用而发生偏转的现象。
霍尔效应的原理:带电粒子在磁场中运动时,会受到洛伦兹力的作用,使得粒子在垂直 于磁场的方向上发生偏转。
公式: F=qvBsinθ, 其中q为带电粒 子的电荷量,v 为带电粒子的速 度,B为磁感应 强度,θ为速度 与磁感应强度的 夹角
应用:带电粒子 在磁场中的运动 轨迹、霍尔效应 等
特点:洛伦兹力 始终不做功,只 改变带电粒子的 运动方向而不改 变其速度大小
带电粒子在磁场中的运动轨迹
匀速圆周运动:带电粒子在 匀强磁场中做匀速圆周运动, 轨迹为圆形
霍尔效应的应用:在电子学、磁学、物理学等领域有广泛应用,例如霍尔传感器等。
霍尔效应的意义:揭示了磁场与带电粒子之间的相互作用规律,为深入理解电磁场理论 奠定了基础。
磁场对带电粒子的影响
洛伦兹力:带电粒子在磁场中受到的力, 方向与磁场垂直,大小与粒子速度和磁感 应强度有关。
匀速圆周运动:带电粒子在磁场中做匀速 圆周运动,运动轨迹是一个圆,圆心在磁 场中心。
当带电粒子在磁场中做匀速圆周 运动时,洛伦兹力提供向心力, 磁场能量密度与带电粒子能量密 度之比等于向心加速度与带电粒 子速度平方之比。
高中物理 带电粒子在圆形有界磁场中的运动之磁聚焦与磁发散
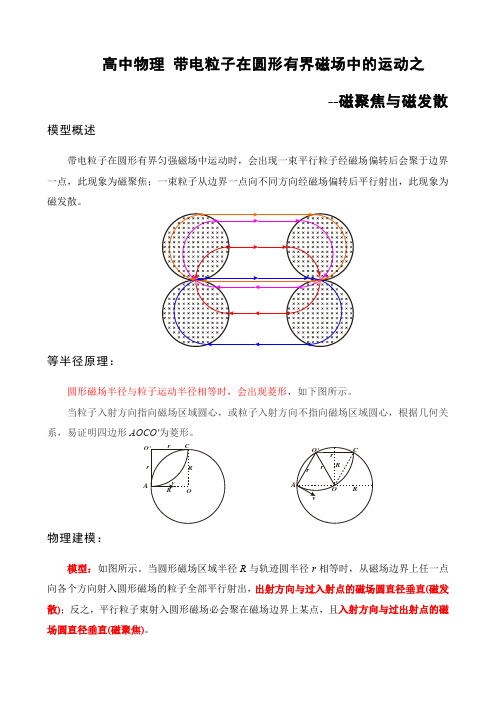
高中物理 带电粒子在圆形有界磁场中的运动之--磁聚焦与磁发散模型概述带电粒子在圆形有界匀强磁场中运动时,会出现一束平行粒子经磁场偏转后会聚于边界一点,此现象为磁聚焦;一束粒子从边界一点向不同方向经磁场偏转后平行射出,此现象为磁发散。
等半径原理:圆形磁场半径与粒子运动半径相等时,会出现菱形,如下图所示。
当粒子入射方向指向磁场区域圆心,或粒子入射方向不指向磁场区域圆心,根据几何关系,易证明四边形AOCO'为菱形。
物理建模:模型:如图所示。
当圆形磁场区域半径R 与轨迹圆半径r 相等时,从磁场边界上任一点向各个方向射入圆形磁场的粒子全部平行射出,出射方向与过入射点的磁场圆直径垂直(磁发散);反之,平行粒子束射入圆形磁场必会聚在磁场边界上某点,且入射方向与过出射点的磁场圆直径垂直(磁聚焦)。
O A证明:如图所示,任意取一带电粒子以速率v从A点射入时,粒子在磁场中的运动轨迹圆半径为R,有界圆形磁场的半径也为R,带电粒子从区域边界C点射出,其中O为有界圆形磁场的圆心,B为轨迹圆的圆心。
图中AO、OC、CO'、O'A的长度均为R,故AOCO'为菱形。
由几何关系可知CO'∥AO,即从C点飞出的粒子速度方向与OA垂直,因此粒子飞出圆形有界磁场时速度方向均与OA垂直。
反之也成立。
解题切入点:分析发现粒子轨道半径与磁场区域圆半径的关系,二者相等为磁聚焦或磁发散,否则不满足该关系,但满足怎么进入怎么出去的角度关系,借助几何关系解答。
【典例1】(磁聚焦)如图所示,x轴正方向水平向右,y轴正方向竖直向上。
在xOy平面内有与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。
在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m、电荷量q(q>0)和初速度v的带电微粒。
发射时,这束带电微粒分布在0<y<2R的区间内.已知重力加速度大小为g。
(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域,并从坐标原点O沿y轴负方向离开,求电场强度和磁感应强度的大小与方向。
带电粒子在磁场中的运动(磁聚焦)

例1、在xoy平面内有很多质量为m,电量为e的电子,从坐
标原点O不断以相同速率沿不同方向射入第一象限,如 图所示.现加一垂直于xOy平面向里、磁感强度为B的匀 强磁场,要求这些入射电子穿过磁场都能平行于x轴且 沿x轴正向运动,试问符合该条件的磁场的最小面积为 多大?(不考虑电子间的相互作用)
y
v0
例3放置在坐标原点O的粒子源,可以向第二象限内放射出质量为m、电荷量为q
的带正电粒子,带电粒子的速率均为v,方向均在纸面内,如图所示.若在某区域内
存在垂直于xOy平面的匀强磁场(垂直纸面向外),磁感应强度大小为B,则这些粒子
都能在穿过磁场区后垂直射到垂直于x轴放置的挡板PQ上,求:
(1)挡板PQ的最小长度; (2)磁场区域的最小面积.
On
x2 + (r-y)2=r2。
即所有出射点均在以坐标(0,r)为圆心的圆弧abO上,显然,
磁场分布的最小面积应是实线1和圆弧abO所围的面积,由几何
关系得
Smin
2(1 r2
4
1 2
r2)
(
2
1)( mv0 eB
)2
解2: 磁场上边界如图线1所示。
y
设P(x,y)为磁场下边界上的一 点,经过该点的电子初速度与x轴
子最后扩展到 -2H<y<2H 范围内,继续沿 x 轴正向平行地
Байду номын сангаас
以相同的速率 v0向远处射出。已知电子的电量为 e,质量为
m,不考虑电子间的相互作用。
y
v0
2H
v0
H
对称思想
O -H v0 -2H
x 图形象什么?
v0
蝴蝶
如图,在xoy平面上-H<y<H的范围内有一片稀疏的电子.从x轴的负半轴的
磁聚焦模型及其应用

带电粒子在磁场中的运动一.磁聚焦模型例题1.如图所示,圆O1的坐标为(0﹑R),半径为R的圆形区域内存在垂直向外的磁感应强度为B的匀强磁场,在坐标原点O处有一粒子源,可向的y>0区域各个方向发射质量为m电量为+q速度为v=qbR/m 的粒子,证明:粒子经过该磁场偏转后都能平行于x轴方向运动。
反过来,如果从右侧以平行x轴的速度射入题中的磁场中,粒子将向那个方向偏转?出射位置有何特点?模型:结论:1 . ;2. 。
例题2.如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场。
在直线y=a的上方和直线x=2a的左侧区域内,有一沿y轴负方向的匀强电场,场强大小为E。
一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当速度方向沿x轴正方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力。
(1)求磁感应强度B的大小;(2)粒子在第一象限内运动到最高点时的位置坐标;(3)若粒子以速度v从O点垂直于磁场方向射入第一象限,当速度方向沿x轴正方向的夹角=30°时,求粒子从射入磁场到最终离开磁场的时间t。
1、如右图所示,纸面内有宽为L水平向右飞行的带电粒子流,粒子质量为m,电荷量为-q,速率为v0,不考虑粒子的重力及相互间的作用,要使粒子都汇聚到一点,可以在粒子流的右侧虚线框内设计一匀强磁场区域,则磁场区域的形状及对应的磁感应强度()可以是(其中B0=mv0/qL,A、C、D选项中曲线均为半径是L的圆弧,B选项中曲线为半径是0.5L的圆)补充:如图,ABCD是边长为a的正方形。
质量为m、电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC变射入正方形区域。
在正方形内适当区域中有匀强磁场。
电子从BC边上的任意点入射,都只能从A 点射出磁场。
不计重力,求:(1)次匀强磁场区域中磁感应强度的方向和大小;(2)此匀强磁场区域的最小面积。
磁场中带电粒子的运动与磁力线分析

磁场中带电粒子的运动与磁力线分析磁场是一个无处不在的自然现象,它对带电粒子的运动产生了重要影响。
当带电粒子在磁场中运动时,它会受到磁场力的作用,从而使其运动轨迹发生偏转。
本文将通过分析带电粒子的运动和磁力线来探讨这一现象。
在磁场中,带电粒子的运动受到洛伦兹力的作用。
洛伦兹力的大小与粒子的电荷量、速度以及磁场的强度有关。
根据洛伦兹力的方向与带电粒子的速度方向垂直,带电粒子在磁场中会沿着一个弯曲的轨道运动。
在研究带电粒子的运动时,一个重要的概念是磁力线。
磁力线是用来描述磁场的一种方法,它表示了磁场中的力线的方向和分布。
在二维平面上,磁力线是封闭的曲线,而在三维空间中,磁力线是闭合的曲面。
磁力线的密度反映了磁场的强弱,磁力线越密集,说明磁场越强。
带电粒子在磁场中的运动轨迹与磁力线有着密切的关系。
当带电粒子在磁场中运动时,它会沿着磁力线进行螺旋状运动。
这是由于带电粒子受到洛伦兹力的作用,使其在垂直于速度方向的平面上发生偏转,并沿着磁力线方向旋转。
带电粒子的运动轨迹形状取决于粒子的速度和磁场的强度。
当粒子的速度较小或磁场较弱时,它的运动轨迹较为平缓,呈螺旋状。
而当粒子的速度较大或磁场较强时,它的运动轨迹变得更为复杂,可能会出现更多的波动和扭曲。
有时候,带电粒子在磁场中的运动会形成一个闭合的环形轨道,这种现象称为磁聚焦。
磁聚焦的原理是粒子在磁场中的力与它在运动过程中的离心力之间的平衡。
当磁场的强度恰好满足一定条件时,粒子将被磁力线束缚在一个环形轨道上,而不会偏离轨道。
除了磁聚焦,带电粒子的运动还可能受到其他因素的影响,例如电场的作用以及其他粒子之间的相互作用。
这些因素可以使带电粒子的轨迹变得更加复杂。
此外,带电粒子在磁场中的运动还可以产生诸如霍尔效应和磁共振等现象,这些现象在磁场应用和磁共振成像等领域具有重要应用价值。
总之,在磁场中带电粒子的运动与磁力线之间存在着紧密的联系。
洛伦兹力使带电粒子在磁场中发生偏转,并沿着磁力线方向旋转,形成螺旋状的轨迹。
带电粒子在电磁场中的运动

Fac
n
线圈所受合力矩大小为
M = Mac + Mbd = IBl1l 2 sin = IBS sin = Pm B sin
.8.
磁力矩定义: 磁力矩定义: 定义 注意: 注意
M = P ×B m
1. 上式对于在均匀磁场中任意形状的平面线圈均 成立; 成立 2. 带电粒子作圆或椭圆轨道运动及自旋运动时 其 带电粒子作圆或椭圆轨道运动及自旋运动时,其 磁力矩也可由上式计算. 磁力矩也可由上式计算 如果场点与平面线圈的距离远远大于平面线圈的平 均线度,则该线圈称为磁偶极子 磁偶极子. 均线度,则该线圈称为磁偶极子 磁偶极矩
Idl
二,安培定律的应用
1.直线电流所受安培力 F = I l × B 直线电流所受安培力
∫) Id l × B (
l
B
F I
l
θ
F = IBl sinθ
2.平行无限长载流直线 电流间的相互作用力 平行无限长载流直线
0 I2 dl1 dF12= I1dl1B12 = I 1 2π a dF 12 0 I 2 I1 dF 21 0 I 2 I1 = 同理 = dl1 2π a dl2 2π a
讨 论
1)en方向与 B 相同 ) 稳定平衡
+ + + + + +
2)方向相反 ) 不稳定平衡 . . . . . . . . .
3)方向垂直 ) 力矩最大
.I . . + + + + + + F . . .
+ F + + + + + + + + + +B+
高中物理磁聚焦原理

高中物理磁聚焦原理
磁聚焦原理是指利用磁场的作用对带电粒子进行聚焦的过程。
在高中物理中,磁聚焦原理通常用于解释质谱仪、电子显微镜等仪器的工作原理。
简单来说,磁聚焦原理是通过在磁场中放置带电粒子,利用磁场对带电粒子的力的作用,使这些带电粒子的运动得到控制和聚焦。
具体来说,磁场中一个带电粒子受到的洛伦兹力的大小与粒子的电荷、速度以及磁场的强度和方向有关。
当带电粒子在磁场中运动时,其受到的洛伦兹力的方向垂直于粒子的速度方向和磁场的方向,从而使带电粒子在磁场中做圆周运动。
在磁聚焦系统中,通常会使用一种特定形状的磁场,使得带电粒子在磁场中的圆周运动能够聚焦在一条轴线上。
通过调节磁场的强度和方向,可以控制带电粒子的轨迹,使其能够聚焦在想要的位置。
在实际的应用中,磁聚焦原理被广泛运用于粒子加速器、粒子探测器、质谱仪等设备中,用于研究微观粒子的性质和结构。
同时,磁聚焦原理也为一些成像技术(如电子显微镜)提供重要的技术支持。
总的来说,磁聚焦原理是利用磁场的作用对带电粒子进行聚焦的原理,通过这种原理可以控制粒子的运动轨迹,实
现粒子的聚焦和控制。
磁聚焦的原理和具体应用

磁聚焦的原理和具体应用1. 磁聚焦的原理磁聚焦是一种利用磁场来对粒子进行聚焦的技术,其原理基于磁场对带电粒子施加的力的影响。
当带电粒子通过磁场时,其运动轨迹会受到磁力的作用而发生偏转,从而实现粒子的聚焦效果。
磁聚焦原理的核心是通过调整磁场的强度和方向来控制粒子的运动轨迹,使其能够在特定位置进行聚焦。
2. 磁聚焦的具体应用2.1 粒子加速器粒子加速器是磁聚焦技术的主要应用领域之一。
通过在加速器中设置多个磁场,可以使带电粒子在一条直线上加速,并将其聚焦在特定的点上。
这种聚焦技术可以在科学研究领域以及工业应用中发挥重要作用。
例如,粒子加速器可用于核物理实验、粒子物理实验以及放射性同位素的生产等多个领域。
2.2 电子显微镜磁聚焦技术在电子显微镜中也发挥着重要作用。
电子显微镜是一种利用电子束来观察微观物体的仪器。
通过在电子显微镜中设置磁场,可以聚焦电子束,使其能够更好地对待观察物体进行成像。
磁聚焦技术的应用可以提高电子显微镜的分辨率和观察效果,使得显微镜在材料科学、生物科学等领域中有着广泛的应用。
2.3 等离子体聚焦磁聚焦技术还可以应用于等离子体聚焦。
等离子体聚焦是一种将等离子体束聚焦到高密度区域的技术,其可以在核聚变实验、等离子体物理研究以及工业等领域中发挥重要作用。
通过调整磁场的强度和方向,可以控制等离子体束的运动轨迹,实现对等离子体束的聚焦效果。
2.4 粒子束物理磁聚焦技术在粒子束物理研究中也有广泛的应用。
通过在粒子束物理实验中设置磁场,可以聚焦粒子束,使其能够更好地进行加速、传输和分析。
磁聚焦技术的应用可以提高粒子束的质量和聚集度,使得实验结果更加准确和可靠。
3. 总结磁聚焦技术利用磁场对带电粒子施加的力的影响,通过调整磁场的强度和方向来控制粒子的运动轨迹,实现对粒子的聚焦效果。
磁聚焦技术在粒子加速器、电子显微镜、等离子体聚焦和粒子束物理研究等领域中都有着重要的应用。
通过磁聚焦技术,科学家可以加速、聚焦和分析带电粒子,从而实现更加精确、深入的科学研究。
高中物理磁聚焦原理

高中物理磁聚焦原理:高中物理磁聚焦原理主要涉及带电粒子在磁场中的运动规律。
当一个带电粒子进入匀强磁场时,如果其速度方向与磁感应强度方向成任意角度θ,那么这个带电粒子的运动可以被分解为两个分量:一个平行于磁感应强度方向(V∥),另一个垂直于磁感应强度方向(V⊥)。
由于磁场的作用,垂直于磁感应强度的速度分量V⊥的大小不会改变,但其方向会不断改变。
因此,带电粒子在垂直于磁感应强度的平面内会作匀速圆周运动。
而平行于磁感应强度的速度分量V∥则保持不变,因此这部分的运动是沿磁感应强度方向的匀速直线运动。
这两种运动的合成,就形成了螺旋线运动。
螺旋线的半径(也称为电子在磁场中作圆运动的回旋半径)可以通过公式R=mv ⊥/(qB)来计算,其中m是带电粒子的质量,v⊥是垂直于磁感应强度的速度分量,q是带电粒子的电荷量,B是磁感应强度。
另外,粒子每转一周前进的距离称为螺距,其公式为h=v∥*T,其中T是粒子转过一周所需的时间,也称为回转周期。
当带电粒子的速度v与磁感应强度B的夹角很小,且各粒子速率v大致相同时,这些粒子在磁场中经过一个回转周期后,会各自经过不同的螺距轨道重新会聚到一点。
这种现象称为磁聚焦,与光束经光学透镜聚焦相类似。
磁发散和磁聚焦的原理

磁发散和磁聚焦的原理嘿,朋友们!今天咱来聊聊磁发散和磁聚焦,这可真是神奇又有趣的玩意儿啊!你想想看,那磁场就像一个神奇的魔法师,能把那些带电粒子指挥得团团转。
磁发散呢,就好像是把一群调皮的孩子给撒开了,让它们各奔东西,跑得漫无边际。
而磁聚焦呢,则像是把这些孩子又都给召集起来,让它们乖乖地聚到一块儿。
咱先说磁发散。
你就把它想象成是放烟花,那些带电粒子就像是烟花里的火星,从一个点“嗖”地一下就散开啦!它们在磁场的作用下,沿着不同的轨迹飞出去,可有意思啦!这在很多实际应用中可重要了呢,比如说一些特殊的仪器设备里,就靠这磁发散来实现各种奇妙的功能。
再来讲讲磁聚焦。
这就好比是你拿着一个放大镜,把阳光聚焦到一个小点上。
那些带电粒子呀,本来在磁场里乱跑,结果呢,经过一番神奇的“操作”,它们就都汇聚到一起啦!这可太神奇了,不是吗?在一些科学研究和技术领域,磁聚焦可是发挥了大作用呢!比如在电子显微镜里,它能让我们看清那些超级超级小的东西。
你说这磁发散和磁聚焦是不是特别酷?它们就像是磁场这位魔法师手中的魔法棒,轻轻一挥,就能带来各种令人惊叹的效果。
想象一下,如果没有磁发散和磁聚焦,我们的世界会变成什么样呢?很多高科技的东西可能就没法实现啦!那可不行,我们的生活可离不开这些神奇的原理呢。
所以啊,我们得好好感谢科学家们发现了这些神奇的原理,让我们能够利用它们来创造出更多有趣又有用的东西。
我们也要对这个世界充满好奇,去探索更多像磁发散和磁聚焦这样的奇妙现象,说不定哪天我们自己也能发现一些超级厉害的东西呢!这不就是科学的魅力所在吗?让我们一起在科学的海洋里畅游,去发现更多的神奇和惊喜吧!总之,磁发散和磁聚焦,它们真的是太重要、太有趣啦!我们可不能小瞧了它们哦!。
带电粒子在磁场中的运动

带电粒子在磁场中的运动 1.1 洛伦兹力
实验证明,静止的电荷在磁场中不受力的作用,运动的电荷才受到磁场的作用力。运动电荷在磁场 中受到的磁场力称为洛伦兹力。
洛伦兹力 f 的方向垂直于运动电荷的速度 v 与磁感应强度 B 所组成的平面且符合右手螺旋定则。当 q 0 时,f 的方向为 v B 的方向;当 q 0 时,f 的方向为 v B 的反方向。
F q(E v B)
可以看出,通过改变电场强度 E 和磁感应强度 B 在空间的分布可以实现对带电粒子运动的控制。
利用上述原理可制成滤速器。若粒子所带电荷量 q 0 ,则它受到竖直向下的电场力和竖直向上的洛伦 兹力的作用;若粒子所带电荷量 q 0 ,则它受到竖直向上的电场力和竖直向下的洛伦兹力的作用。
R
mv qB
我们把粒子运动一周所需时间称为回旋周期,用符号
T
的速率成正比,速率越大粒子的回旋半径越大,而回旋周期与粒子的速率及回 旋半径无关。
带电粒子在磁场中的运动
1.2 带电粒子在匀强磁场中的运动
2.带电粒子的初速度v与B成任意夹角
带电粒子同时参与这两个运动的结果是使其沿螺旋线向前运动,如图所示。可得螺旋线的半径
可知,洛伦兹力总是垂直于运动电荷的速度 v,因此洛伦兹力对运动电荷不做功,它只改变运动电荷 速度的方向,不改变速度的大小。
带电粒子在磁场中的运动
1.2 带电粒子在匀强磁场中的运动
1.带电粒子的初速度v垂直于B
洛伦兹力即为粒子做圆周运动的向心力,即
qvB
m
v2 R
由此得粒子做圆周运动的半径(回旋半径)为
这样这些带电粒子沿半径不同的螺旋线运动,但它们的螺距却是近似相等的,即经距离 d 后都 相交于同一点 A 。这个现象与光束通过光学透镜的现象很相似,故称为磁聚焦。
磁聚焦原理

磁聚焦原理
磁聚焦原理是指在磁场作用下,带电粒子运动的轨迹会因磁场的不同而发生偏转,这样在一定条件下,将粒子团体置于磁场中,就可以实现对带电粒子的聚焦和分离。
这种原理在物理学、化学和材料科学等领域中都有广泛的应用。
磁聚焦原理的具体描述是:当带电粒子通过垂直于磁场方向的区域时,它的运动轨迹会因磁场的不同而发生偏转。
偏转的方向由洛伦兹力决定,它与带电粒子速度方向垂直,且大小与粒子电量、速度、磁场的强度和方向有关。
在恰当的磁场强度下,粒子的偏转量可被控制,从而实现粒子的聚焦和分离。
磁聚焦原理具有很多优点,比如能够有效地聚焦和分离带电粒子,从而提高分离效率和分离纯度;能够实现对带电粒子的定向操纵和控制;操作简便,对于小颗粒、稀有粒子的分离具有显著优势;同时具有无损、无污染和低成本等特点。
磁聚焦原理的应用十分广泛,其中较为常见的包括质谱仪、离子注入、磁性纳米颗粒制备、生物医学等领域。
例如,在质谱仪中,磁场可以用来实现对不同离子种类的分离和鉴别;在离子注入中,磁聚焦可以实现对粒子束的定向传输和调节;在磁性纳米颗粒制备中,利用磁聚焦可以实现对颗粒的定向操纵和控制等。
总之,磁聚焦原理是物理学、化学和材料科学等领域中十分重要的一种原理,具有广泛的应用。
磁场的控制可以实现对带电粒子的定向操纵和聚焦,从而为相关领域的研究和实践提供了重要的技术支撑。
磁聚焦技术的原理和应用

磁聚焦技术的原理和应用1. 磁聚焦技术概述磁聚焦技术是一种基于磁场调控粒子运动的技术,通过利用磁场的力线分布特性,将粒子在磁场中聚焦或偏转,从而实现对粒子的控制和操纵。
磁聚焦技术被广泛应用于物理学、材料科学、生物医学等领域,具有重要的科学研究和工程应用价值。
2. 磁聚焦技术的原理磁聚焦技术的原理基于洛伦兹力和磁场力线分布的相互作用。
当带电粒子穿过磁场时,根据洛伦兹力的作用,粒子受到一个与速度和磁场强度、磁场方向相互垂直的力,从而在磁场中偏转。
在磁场力线分布的影响下,粒子可被磁场力束缚在一定的区域内,实现聚焦效果。
3. 磁聚焦技术的应用3.1 粒子加速器磁聚焦技术是粒子加速器中不可或缺的技术,通过对粒子束的磁聚焦,可以使粒子束的直径减小,能量变高,从而实现粒子加速的效果。
粒子加速器广泛应用于物理学研究、核工程等领域。
3.2 声波成像技术磁聚焦技术在声波成像技术中的应用非常重要。
在声波成像过程中,通过调控磁场的力线分布和磁场强度,可以实现对声波的聚焦和偏转,从而获得高质量的声波图像。
3.3 生物医学应用磁聚焦技术在生物医学领域的应用也较为广泛。
例如,在磁共振成像(MRI)中,通过调节磁场的力线分布和强度,可以实现对患者身体内部组织和器官的聚焦,从而获得高分辨率的图像。
此外,磁聚焦技术还被应用于药物传递系统中的靶向输送,通过磁场聚焦释放药物,提高治疗效果。
4. 磁聚焦技术的优势磁聚焦技术具有以下优势:•可以通过调节磁场的力线分布和强度,实现对粒子的聚焦和偏转,从而精确操纵和控制粒子的运动轨迹。
•与传统的机械聚焦技术相比,磁聚焦技术无需接触物体,不会对物体造成破坏,具有非接触性。
•磁聚焦技术具有较高的定位精度和操控精度,能够实现对微小、复杂结构的粒子和物体的精确操纵。
•磁聚焦技术可以在不同尺度上实现聚焦效果,从纳米尺度的粒子到宏观尺度的物体都可以通过磁场力线分布的操纵实现聚焦效果。
5. 结论磁聚焦技术是一种基于磁场力线分布的粒子操纵技术,具有广泛的应用前景。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【答案】(1);方向垂直于纸面向外(2)见解析 (3)与x同相交的区域范围是x>0. y
y
【解析】 略 【关键】 图示
v A
P v R R Q
θ O/ O
R
C
O/ O 图 (a)
x 图 (b)
x y
装带 置点 微 粒 发 射
P
v R
C
r
O/
Q
O 图 (c)
x
例、如图,在xOy平面内,有以O′(R,0)为圆心,R为半径的圆
2( ) 得:t = v0
MN d = R sin( ) sin
R′=mv/qB = d/cosθ。
以上3式联立求解得 CM=d cotα
例、如图,在直角坐标系 xOy 中,点M(0,1)处不断向 +y 方向
发射出大量质量为 m、带电量为 –q 的粒子,粒子的初速度 大小广泛分布于零到 v0之间。已知这些粒子此后所经磁场的 磁感应强度大小为 B,方向垂直于纸面向里,所有粒子都沿 +x 方向经过 b 区域,都沿 -y的方向通过点 N(3,0)。 (1)通过计算,求出符合要求的磁场范围的最小面积; (2)若其中速度为 k1v0 和 k2v0 的两个粒子同时到达 N 点 (1>k1>k2>0),求二者发射的时间差。
On
x2 + (r-y)2=r2。
即所有出射点均在以坐标(0,r)为圆心的圆弧abO上,显然, 磁场分布的最小面积应是实线1和圆弧abO所围的面积,由几何 关系得 mv 1 1 Smin 2( r 2 r 2 ) ( 1)( 0 ) 2
4 2 2 eB
解2: 磁场上边界如图线1所示。 设P(x,y)为磁场下边界上的一 点,经过该点的电子初速度与x轴 夹角为 ,则由图可知: x = rsin, y = r-rcos , 得: x2 + (y-r)2 = r2。
y (mv0/qB) 2 v0 1 M N O 1 2 3 x(mv0/qB) a b c
例、(1975 IPHO试题)质量均为m的一簇粒子在P点以同一
速度v向不同方向散开(如图),垂直纸面的匀强磁场B 将这些粒子聚焦于R点,距离PR=2a,离子的轨迹应是轴 y 对称的。试确定磁场区域的边界。
解答:在磁场B中,粒子受洛仑兹力作用
2 mvn B qd
n=1,2,3,…
磁透镜
O
M
z
例、如图所示,在 xOy平面上-H < y< H的范围内有一片
稀疏的电子,从 x 轴的负半轴的远外以相同的速率 v0 沿 x 轴正向平行地向 y 轴射来,试设计一个磁场区域,使
得:(1)所有电子都能在磁场力作用下通过原点 O; (2)
这一片电子最后扩展到 -2H<y<2H 范围内,继续沿 x 轴正向平行地以相同的速率 v0向远处射出。已知电子的 电量为 e,质量为 m,不考虑电子间的相互作用。质量为m电荷量ຫໍສະໝຸດ e的电子以大小为v0的初速度沿纸面垂
直于BC边射入正方形区域。在正方形内适当区域中有匀
强磁场,电子从BC边上的任意点入射,都只能从A点射 出磁场。不计重力,求: (1)此匀强磁场区域中磁感应强度的大小和方向; (2)此匀强磁场区域的最小面积。
y
D
C
v0 O x
A
B
解:(1)设匀强磁场的磁感应强度的大小为B。令圆弧AEC是自C点垂直于 BC入射的电子在磁场中的运行轨道。依题意,圆心在A、C连线的中垂线上, 故B点即为圆心,圆半径为a,按照牛顿定律有 ev0B= mv02/a,得B= mv0/ea。 (2)自BC边上其他点入射的电子运动轨道只能在BAEC区域中。因而,圆弧 AEC是所求的最小磁场区域的一个边界。 (3)设某射中A点的电子速度方向与BA的延长线夹 D 角为θ的情形。该电子的运动轨迹qpA如图所示。图中 圆弧Ap的圆心为O,pq垂直于BC边 ,圆弧Ap的半径 仍为a,在D为原点、DC为x轴、DA为y轴的坐标系中, A p点的坐标为(x,y),则 x=asinθ,y=-acosθ。 θ 由④⑤式可得:x2+y2=a2,这意味着在范围0≤θ≤π/2内, p点处在以D为圆心、a为半径的四分之一圆周AFC上, 它是电子做直线运动和圆周运动的分界线,构成所求 磁场区域的另一边界。 C E pq F B
磁
场
作半径为r的圆周运动: A(x,y) r 2 mv v = qvB = m r r qB v b 设半径为r的圆轨道上运动的粒子, a a R x O P 在点A (x,y)离开磁场,沿切线飞向R 点。由相似三角形得到: y-b a-x y x 同时,A作为轨迹圆上的点,应满足方程: x2+(y-b)=r2 消去(y-b),得到满足条件的A点的集合,因此,表示磁场边界 x (a-x) 的函数方程为: y= r2-x2
例、 (第二十届全国预赛试题)从 z轴上的O点发射一束电量为
q、质量为m的带正电粒子,它们速度方向分布在以O点 为顶点、z轴为对称轴的一个顶角很小的锥体内(如图所 示),速度的大小都等于v。试设计一种匀强磁场,能使 这束带电粒子会聚于z轴上的另一点M,M点离开O点的 距离为d。要求给出该磁场的方向、磁感应强度的大小和 最小值。不计粒子间的相互作用和重力的作用。
y 1
P (x,y)
v0
O
θ r
r
x
O
所以磁场区域的下边界也是半径为r,圆心为(0,r)的 圆弧应是磁场区域的下边界。 两边界之间图形的面积即为所求。图中的阴影区域面 积,即为磁场区域面积:
2 m2v0 1 2 r2 S 2( r ) ( 1) 2 2 4 2 2 eB
例、(2009· 海南· T16)如图,ABCD是边长为a的正方形。
O
因此,所求的最小匀强磁场区域,是分别以B和D为圆心、a为半径的两个四 分之一圆周AEC和AFC所围成的区域,其面积为S=2(πa2/4-a2/2) =(π-2)a2/2
磁聚焦概括:
迁移与逆向、对称的物理思想!
一点发散成平行
R
平行会聚于一点
r
R r
区域半径 R 与运动半径 r 相等
例、(2009年浙江卷)如图,在xOy平面内与y轴平行的匀强
电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。 在圆的左边放置一带电微粒发射装置,它沿x轴正方向发 射出一束具有相同质量m、电荷量q(q>0)和初速度v的带 电微粒。发射时,这束带电微粒分布在0<y<2R的区间内。 已知重力加速度大小为g。 (1)从A点射出的带电微粒平行于x轴从C点进入有磁场区 域,并从坐标原点O沿y轴负方向离开,求电场强度和磁感 应强度的大小与方向。 y (2)请指出这束带电微粒与x轴相 带 点 微 交的区域,并说明理由。 粒 R 发 v O/ (3)在这束带电磁微粒初速度变为 射 C 装 2v,那么它们与x轴相交的区域又在 置 O 哪里?并说明理由。 x
形磁场区域,磁感应强度大小为 B,方向垂直xOy平面向外, 在 y=R上方有范围足够大的匀强电场,方向水平向右,电场 强度大小为E。在坐标原点O处有一放射源,可以在xOy平面 内向 y 轴右侧(x >0)发射出速率相同的电子,已知电子在 y 该磁场中的偏转半径也为 R, E 电子电量为 e,质量为 m。 不计重力及阻力的作用。 R (1)求电子射入磁场时的速度大小; (2)速度方向沿x轴正方向射入磁场 的电子,求它到达y轴所需要的时间; O O′ x (3)求电子能够射到y轴上的范围。
解1: 电子由O点射入第Ⅰ象限做匀速
圆周运动
2 v0 mv0 ev0 B m r= r eB v0 所有电子的轨迹圆半径相等,且均过 O O点。这些轨迹圆的圆心都在以O为圆 心,半径为r的且位于第Ⅳ象限的四分 之一圆周上,如图所示。
y
O1 O2 O3 O5 O4
x
由图可知,a、b、c、d 等点就是各电 子离开磁场的出射点,均应满足方程
y 2H v0
v0
H O -H x
对称思想
v0
-2H
v0
例、(2008· 重庆高考)如图为一种质谱仪工作原理示意图。在
以O为圆心,OH为对称轴,夹角为2α的扇形区域内分布 着方向垂直于纸面的匀强磁场。对称于OH轴的C和D分 别是离子发射点和收集点。CM垂直磁场左边界于M,且 OM=d。现有一正离子束以小发散角(纸面内)从C射出, 这些离子在CM方向上的分速度均为v0。若该离子束中比 荷为q/m的离子都能会聚到D,试求: (1)磁感应强度的大小和方向(提示:可考虑沿CM方向运 动的离子为研究对象); (2)离子沿与CM成 θ 角的直线 CN进入磁场,其轨道半径和在 磁场中的运动时间; (3)线段CM的长度。
第三章 磁场
§6、带电粒子在磁场中的运动
(磁聚焦)
带电粒子在直边界磁场中的运动
当带电粒子从同一边界入射出 ——对称性 射时速度与边界夹角相同
磁聚焦原理图解
数学公式推理
• • • • • • • • • • • 设速度夹角为a,粒子运动半径为r,磁场半径 也为r,则粒子圆心的横纵坐标为 X=rsina Y=rcosa 显然,所有圆心的轨迹方程依然是圆 X2+y2=r2 圆心在坐标原点,半径为r 下面求粒子的出点坐标(x1,y1) 磁场圆的参数方程: X2+(y-r)2=r2 粒子的轨迹参数方程: (X-rsina)2+(y-rcosa)2=r2 将出点坐标代入两个方程解:x1=rsina,y1=r+rcosa 说明出点的和圆心在同一竖直线上,即出点水平。
例、在xoy平面内有很多质量为m,电量为e的电子,从坐
标原点O不断以相同速率沿不同方向射入第一象限,如
图所示.现加一垂直于xOy平面向里、磁感强度为B的匀 强磁场,要求这些入射电子穿过磁场都能平行于x轴且 沿x轴正向运动,试问符合该条件的磁场的最小面积为 多大?(不考虑电子间的相互作用)
