福建省福州八中2016—2017学年高一下学期期末考试数学试题 (word版含答案)
福建省福州市高一数学下学期期末考试试题(扫描版,无答案)

福建省福州市2016—2017学年高一数学下学期期末考试试题(扫描版,
无答案)
尊敬的读者:
本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
(全优试卷)版福建省福州市高一下学期期末联考试题数学Word版含答案
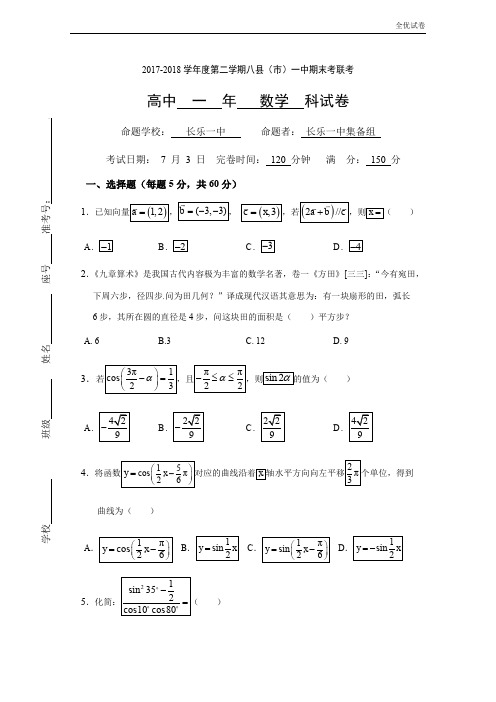
2017-2018学年度第二学期八县(市)一中期末考联考高中 一 年 数学 科试卷命题学校: 长乐一中 命题者: 长乐一中集备组 考试日期: 7 月 3 日 完卷时间: 120 分钟 满 分: 150 分 一、选择题(每题5分,共60分)1()1,2a=,)2//a b c +,则)ABC D .4-2.《九章算术》是我国古代内容极为丰富的数学名著,卷一《方田》[三三]:“今有宛田, 下周六步,径四步问为田几何?”译成现代汉语其意思为:有一块扇形的田,弧长 6步,其所在圆的直径是4步,问这块田的面积是( )平方步? A. 6B.3C. 12D. 93.)ABCD 4曲线为( )AB CD51352cos10cos80-=( ) 学校 班级 姓名 座号 准考号: .A B C D6( )A. B. C.7a b = 上的投影为( )A B C D .8 )A9.3a b =b a b =,( )A B C D10 )A B C D11.)A .2BC D12.的最大值为( )A B .2 C .5D二、填空题(每题5分,共20分)13.已知点P ⎝⎛⎭⎫sin 34π,cos 34π落在角θ的终边上,且θ∈[0,2π),则θ的值为 .14等于 .15________.16. ①;②③,④R 上是奇函数,其中命题正确的是___.三、解答题(共6大题,17题10分,18~22题每题12分,共70分)17.已知向量(3,OC=-OB=-(5OA=-,(6,(1)若点A,B,C能构成三角形,求实数m应满足的条件;(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.18.(1)(2)19扩大3倍,纵坐标扩大2(1)(2).20(1);(2),.21边界的中间部分为长1(1)(2)如图,平行四边形的一边在海岸线EF上,一边在半径OD上,另外一个顶点P在圆弧22(1)围,(2).2017---2018学年度第二学期八县(市)一中期末考联考高一数学参考答案一、选择题:(每小题5 分,共60 分)二、填空题:(每小题5 分,共20 分)13. 7π414. 15.16. ②③④三、解答题:(共6大题,17题10分,18~22题每题12分,共70分)17. 解:(1)若点A 、B 、C 能构成三角形,则这三点不共线, ………1分(3,1)AB OB OA -==(2AC OC OA -==-…………………3分3(1)m ∴- . ……………5分 (2)若△ABC 为直角三角形,且∠A 为直角,则AB AC⊥, ………7分…………………………9分…………10分 18.解:(1)4||a b b +3=………2分 229||6||91a a b b =++=⨯ ………4分(2)2-………6分 222(2)4||4||41a b a a b b =+=++=⨯ ………8分222(23)4||129||41b a b a b a =-=-+=⨯ ………10分||||7m n m n =⨯………12分 19. 解:(1) ………3分………5分 (2)………7分………9分 所以………11分…12分…………3分……………4分……………6分…………7分(2)…………8分…………9分…………11分……………………12分21. (1)…………1分………2分…………4分∴曲线段FGBC(2)5分解法一:……6分……8分(注:学过正弦定理可以采用解法二求线段OM的长度)(解法二:sin120)……8分2cos3OMθθ=-……11分……12分22. 解:(1…………………1分…………………4分……………………5分……………………6分(2……………………8分全优试卷,⎢⎣9分12①λ,1,与已知不符.10分②,……………11分③,矛盾.……………12分综上所述。
福建省福州八中2016—2017学年高二下学期期末考试数学(理)试题含答案

福州八中2016—2017学年第二学期期末考试高二数学(理)考试时间:120分钟 试卷满分:150分 2017.6。
10说明:本次数学考试不允许使用计算器,凡将计算器带入考场...........................者.,.即按舞弊论处......参考公式:1.用最小二乘法求线性回归方程系数公式1221ni ii n ii x y nx yb xnx==-=-∑∑,a y bx =-.2。
,))()()(()(22d b c a d c b a bc ad n K ++++-=其中d c b a n +++=为样本容量.3。
独立性检验的临界值表:第Ⅰ卷(100分)一、选择题(本大题共10小题,每小题4分,共40分.每题有且只有一个选项是正确的,请把答案填在答卷相应位置上) 1. 10×9×8×…×4可表示为 A 。
610AB.710AC 。
610C D 。
710C2.在极坐标系下,圆C :03sin 42=++θρρ的圆心坐标为A.)0,2(B.)2,2(πC 。
),2(π D.)2,2(π-3.已知随机变量8=+ηξ,若)6.0,10(~B ξ,则ηE ,ηD 分别是 A.2和2.4B.2和5.6C.6和5.6 D 。
6和2.44.已知盒中装有大小一样,形状相同的3个白球与7个黑球,每次从中任取一个球并不放回,则在第1次取到的白球条件下,第2次取到的是黑球的概率为 A 。
B.C.D 。
5.若6622106)21(x a x a x a a x ++++=- ,则6210a a a a++++ 的值为A 。
1 B.62C 。
53D 。
636.某校开设A 类选修课3门,B 类选修课3门,一位同学从中选3门.若要求两类课程中至少选一门,则不同的选法共有 A.18 B 。
9 C.6D.37.已知随机变量ξ服从正态分布(1,1)N ,若(3)0.977P ξ<=,则(13)P ξ-<<= A. 0。
福建省福州市高一数学下学期期末质量检测试题

2016年福州市高一第二学期期末质量检测数 学 试 题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.终边落在第二象限的角组成的集合为 ( ) A .{|,}2k k k Z παπαπ<<+∈ B .{|,}2k k k Z παπαππ+<<+∈C .{|22,}2k k k Z παπαπ<<+∈ D .{|22,}2k k k Z παπαππ+<<+∈2.AB BC AD +-= ( )A .ADB .DAC .CD D .DC3.若α为第四象限角,3cos ,5α=则tan α=( ) A .43- B .43 C .34- D .344.sin63cos33sin 27sin33︒︒-︒︒= ( )A .0B .12.15.点O 为正六边形ABCDEF 的中心,则可作为基底的一对向量是 ( ) A .,OA BC B .,OA CD C.,AB CF D .,AB DE6.点(tan 3,cos3)落在 ( )A .第一象限B .第二象限 C.第三象限 D .第四象限7.角α的终边与单位圆交于点43(,)55-,则cos()2πα-=( )A .35B . C.45 D .45-8.已知函数()sin 2()f x x ϕ=+,则 ( ) A .当4πϕ-=时,()f x 为奇函数 B .当0ϕ=时,()f x 为偶函数 C. 当2πϕ=时,()f x 为奇函数 D .当ϕπ=时,()f x 为偶函数9.若向量(4,3)a =,(1,2)b =--,则b 在a 方向上的投影为( )A .-2B .2 C.- D . 10.为得到cos y x =的图象,只需将sin()6y x π=+的图象 ( )A .向左平移6π个单位B .向右平移6π个单位 C. 向左平移6π个单位 D .向右平移3π个单位 11.如图,点P 是半径为1的半圆弧AB 上一点,若AP 长度为x,则直线AP 与半圆弧AB 所围成的图形的面积S 关于x 的函数图象为 ( )12.将函数()3cos()2f x x π=与()1g x x =-的所有交点从左到右依次记为123,,,,n A A A A ,若O 为坐标原点,则12n OA OA OA +++=( )A .0B .1 C.3 D .5第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知钝角α满足sin α=,则α= . 14.如图所示,在正方形ABCD 中,点E 为边AB 的中点,线段AC 与DE 交于点P ,则tan APD ∠= .15.将函数()sin(2)4f x x π=-的图象上所有点的横坐标缩小为原来的12倍(纵坐标不变)得到()g x 的图象,则()g x = .16.在△ABC 中,D 为BC 中点,直线AB 上的点M 满足:32(33)()AM AD AC R λλλ=+-∈,则AMMB= . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知四点A (-3,1),B (-1,-2),C (2,0),D (23,4m m +) (1)求证:AB BC ⊥; (2) //AD BC ,求实数m 的值. 18. 已知函数()sin(2)4f x x π=+(1)用“五点法”作出()f x 在长度为一个周期的闭区间上的简图; (2)写出()f x 的对称中心与单调递增区间; (3)求()f x 的最大值以及取得最大值时x 的集合.19. 已知函数44()cos sin cos cos 22x xf x x x x =-+ (1)求()f x 的周期; (2)若2()23f α=,求()3f πα+的值.20.在△ABC 中,AB=2,AC=23,∠BAC=60°,D 为△ABC 所在平面内一点,2BC CD = (1)求线段AD 的长; (2)求∠DAB 的大小.21.如图,点P 为等腰直角△ABC 内部(不含边界)一点,AB=BC=AP=1,过点P 作PQ//AB ,交AC 于点Q ,记,PAB APQ θ∠=∆面积为()S θ (1)求()S θ关于θ的函数;(2)求()S θ的最大值,并求出相应的θ值.22.已知函数()sin()(0,0)f x x ωϕωϕπ=+><<部分图象如图所示,点P 为()f x 与x 轴的交点,点A,B 分别为()f x 的图象的最低点与最高点,2PA PB PA ⋅= (1)求ω的值;(2)若[1,1]x ∈-,求()f x 的取值范围.试卷答案一、选择题1-5: DDABB 6-10: CBCAC 11、12:AD 二、填空题 13.23π 14. -3 15.sin(4)4x π- 16.1 三、解答题17.解:(1)依题意得,(2,3),(3,2)AB BC =-= 所以23(3)20AB BC ⋅=⨯+-⨯=所以AB BC ⊥.(2)2(33,3)AD m m =++,因为//AD BC所以23(3)2(33)0m m +-+= 整理得2210m m --= 所以,实数m 的值为12-或1. 18.(1)按五个关键点列表:描点并将它们用光滑的曲线连接起来,如下图所示:(2)由(1)图象可知, ()f x 图象的对称中心为1(,0),82k k Z ππ-+∈; 单调递增区间为3[,),88k k k Z ππππ-++∈ (3)max ()1f x =,此时x 组成的集合为{|}8x x k k Z ππ=+∈.19.2222()(cos sin )(cos sin )cos f x x x x x x x =+-+cos 222sin(2)6x xx π==+所以()f x 的周期22T ππ==. (2) 因2()2sin()263f απα=+=,所以,令6t πα=+,则6t πα=-,1sin 3t =所以,()2sin[2()]336f πππαα+=++22sin(2)22cos 22(12sin )149t t t π=+==-=20. 解:(1)依题意得:212cos 2323AB AC AB AC BAC ⋅=⋅∠=⨯⨯= 因为2BC CD =所以1113()2222AD AC CD AC BC AC AC AB AB AC =+=+=+-=-+ 所以22221319319432412244244923AD AB AC AB AC AB AC =-+=+-⋅=⨯+⨯-⨯=所以1AD =,即AD =1 (2)由(1)可知,221313132()212222223AD AB AB AC AB AB AC AB ⋅=-+⋅=-+⋅=-⨯+⨯=-所以,11cos ,122AD AB DAB AD AB⋅-∠===-⨯ 又因0180,DAB ︒<∠<︒ 所以120.DAB ∠=︒21. 解:(1)依题意得,∠CAB =4π,如图,过点A 作直线PQ 的垂线,垂足为E. 因为PQ//AB ,所以,,4EPA PAB EQA CAB πθ∠=∠=∠=∠=在RT △APE 中,cos cos ,sin sin EP AP EPA AE AP EPA θθ⋅∠==⋅∠== 在RT △AQE 中,因为,4EQA π∠=所以sin EQ AE θ==所以PE =PE -EQ =cos sin θθ-, 所以11()(cos sin )sin ((0,))224S PQ AE πθθθθθ=⋅=-∈(2)由(1)得,1()(cos sin )sin 2S θθθθ=-111cos 2sin 24221sin(2)444θθπθ-=-⋅=+-因为(0,)4πθ∈,所以32(,)444πππθ+∈ 所以当242ππθ+=,即8πθ=时,max 1()4S θ=22. 解:(1)设0(,0),()P x f x 最小正周期为T ,,则0013(,1),(,1)44A x TB x T +-+, 所以13(,1),(,1)44PA T PB T =-= 222311,11616PA PB T PA T ⋅=-=+,解得T =4,所以2.2T ππω==(2)由(1)知,()sin()2f x x πϕ=+,T =4,由22,222k x k k Z ππππϕπ-+≤+≤+∈ 得221414,k x k k Z ϕϕππ-+-≤≤+-∈所以()f x 的增区间为22[14,14]k k ϕϕππ-+-+-,减区间为22[14,34]()k k k Z ϕϕππ+-+-∈因为0ϕπ<<,所以2141414,k k k k Z ϕπ-+<-+-<+∈当0k =时,2111ϕπ-<-<所以()f x 在区间2[1,1]ϕπ--上为增函数,在区间2[1,1]ϕπ-为减函数,所以当[1,1]x ∈-时,max 2()(1)1f x f ϕπ=-=易知21x ϕπ=-为()f x 图象的一条对称轴.所以当221(1)1(1)ϕϕππ---≤--,即,min ()(1)sin()cos 2f x f πϕϕ==+= 当221(1)1(1)ϕϕππ--->--,即02πϕ<<时,min ()(1)sin()cos 2f x f πϕϕ=-=-+=-综上,当02πϕ<<,()f x 的值域为[cos ,1]ϕ-;当2πϕπ≤<时,()f x 的值域为[cos ,1].ϕ。
2016年福建省福州八中高一下学期期末数学试卷与解析答案

2015-2016学年福建省福州八中高一(下)期末数学试卷一、选择题(本大题共8小题,每小题5分,共40分.每题有且只有一个选项是正确的,请把答案填在答卷相应位置上)1.(5分)已知sinα=,且α是第二象限角,那么tanα的值为()A.B.C.D.2.(5分)一个半径为R的圆中,60°的圆心角所对的弧长为()A.60R B.R C.R D.R3.(5分)已知||=3,在方向上的投影为,则•=()A.3 B.C.2 D.4.(5分)已知向量,,满足||=1,||=2,=,⊥,则与的夹角等于()A.120°B.60°C.30°D.90°5.(5分)函数f(x)=cos2x+2sinx的最小值和最大值分别为()A.﹣3,1 B.﹣2,2 C.﹣3,D.﹣2,6.(5分)要将y=sin(2x+)的图象转化为某一个偶函数图象,只需将y=sin (2x+)的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位7.(5分)设M为平行四边形ABCD对角线的交点,O为平行四边形ABCD所在平面内任意一点,则等于()A.B.2 C.3 D.48.(5分)关于x的方程x2﹣(cosAcosB)x﹣cos2=0有一个根为1,则△ABC 一定是()二、填空题(本大题共4小题,每小题5分,共20分)9.(5分)计算:=.10.(5分)在△ABC中,已知∠BAC=60°,∠ABC=45°,BC=,则AC=.11.(5分)设平面向量=(﹣2,1),=(λ,﹣1),若与的夹角是钝角,则λ的范围是.12.(5分)tan70°+tan50°﹣=.三、解答题(本大题共有4个小题,共40分.解答应写出文字说明、演算步骤或证明过程.)13.(10分)已知非零向量,满足||=1,且(﹣)•(+)=.(1)求||;(2)当•=时,求向量与+2的夹角θ的值.14.(10分)已知向量=(sinθ,﹣2)与=(1,cosθ)互相垂直,其中θ∈(0,).(Ⅰ)求sinθ和cosθ的值;(Ⅱ)若sin(θ﹣φ)=,0<φ<,求cosφ的值.15.(10分)在锐角三角形ABC中,角A、B、C所对的边分别为a、b、c且(tanA ﹣tanB)=1+tanA•tanB.(1)求A﹣B的大小;(2)已知<B<,向量=(sinA,cosA),=(cosB,sinB),求|3﹣2|的取值范围.16.(10分)设函数f(x)=•,其中向量=(2cos x,1),=(cos x,sin 2x+m).(Ⅰ)求函数f(x)的最小正周期和在[0,π]上的单调递增区间.(Ⅱ)当时,﹣4<f(x)<4恒成立,求实数m的取值范围.四、选择题(本大题共4小题,每小题4分,共16分.每题有且只有一个选项是正确的,请把答案填在答卷相应位置上)A.B.C.2 D.418.(4分)在△ABC中,①若B=60°,a=10,b=7,则该三角形有且有两解;②若三角形的三边的比是3:5:7,则此三角形的最大角为120°;③若△ABC为锐角三角形,且三边长分别为2,3,x,则x的取值范围是.其中正确命题的个数是()A.0 B.1 C.2 D.319.(4分)如图,BC是单位圆A的一条直径,F是线段AB上的点,且BF=2FA,DE是圆A中绕圆心A运动的一条直径,则的值是()A.B.﹣ C.﹣ D.不确定20.(4分)已知f(x)=sin(2015x+)+cos(2015x﹣)的最大值为A,若存在实数x1、x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1﹣x2|的最小值为()A.B.C.D.五、填空题(本大题共2小题,每小题4分,共8分)21.(4分)四边形ABCD中,==(1,1),+=,则四边形ABCD的面积是.22.(4分)已知α,β∈(0,),=,且3sin β=sin(2α+β),则α+β=.六、解答题(本大题共有2个小题,共26分.解答应写出文字说明、演算步骤或23.(13分)已知向量=(sinx,cosx),=(cosx,cosx),=(2,1),且cosx≠0.(Ⅰ)若∥,求•的值;(Ⅱ)设△ABC的内角A,B,C的对边分别为a,b,c,,且,求函数f(A)的值域.24.(13分)岛A观察站发现在其东南方向有一艘可疑船只,正以每小时10海里的速度向东南方向航行(如图所示),观察站即刻通知在岛A正南方向B处巡航的海监船前往检查.接到通知后,海监船测得可疑船只在其北偏东75°方向且相距10海里的C处,随即以每小时10海里的速度前往拦截.(I)问:海监船接到通知时,距离岛A多少海里?(II)假设海监船在D处恰好追上可疑船只,求它的航行方向及其航行的时间.2015-2016学年福建省福州八中高一(下)期末数学试卷参考答案与试题解析一、选择题(本大题共8小题,每小题5分,共40分.每题有且只有一个选项是正确的,请把答案填在答卷相应位置上)1.(5分)已知sinα=,且α是第二象限角,那么tanα的值为()A.B.C.D.【解答】解:∵sinα=,且α是第二象限角∴cosα=﹣=即tanα=故选:A.2.(5分)一个半径为R的圆中,60°的圆心角所对的弧长为()A.60R B.R C.R D.R【解答】解:60°=rad,∴60°的圆心角所对的弧长=.故选:D.3.(5分)已知||=3,在方向上的投影为,则•=()A.3 B.C.2 D.【解答】解:∵已知||=3,在方向上的投影为,∴•=||||cos<>=3×=;故选:B.角等于()A.120°B.60°C.30°D.90°【解答】解:∵⊥,=,∴∴∴与的夹角等于1200故选:A.5.(5分)函数f(x)=cos2x+2sinx的最小值和最大值分别为()A.﹣3,1 B.﹣2,2 C.﹣3,D.﹣2,【解答】解:∵,∴当时,,当sinx=﹣1时,f min(x)=﹣3.故选:C.6.(5分)要将y=sin(2x+)的图象转化为某一个偶函数图象,只需将y=sin (2x+)的图象()A.向左平移个单位B.向左平移个单位C.向右平移个单位D.向右平移个单位【解答】解:设将函数y=sin(2x+)的图象向左平移m个单位,所得图象为偶函数.由于平移后函数图象所对应的函数解析式为:y=sin[2(x+m)+]=sin (2x+2m+),由于:所得图象为偶函数,解得:m=+,k∈Z,所以:当k=0时,m=,即将y=sin(2x+)的图象向左平移个单位,图象转化为某一个偶函数图象,故选:B.7.(5分)设M为平行四边形ABCD对角线的交点,O为平行四边形ABCD所在平面内任意一点,则等于()A.B.2 C.3 D.4【解答】解:∵O为任意一点,不妨把A点看成O点,则=,∵M是平行四边形ABCD的对角线的交点,∴=2=4故选:D.8.(5分)关于x的方程x2﹣(cosAcosB)x﹣cos2=0有一个根为1,则△ABC 一定是()A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形【解答】解:∵关于x的方程有一个根为1,∴1﹣cosAcosB﹣=0,∴cosC+2cosAcosB=1,∴﹣cosAcosB+sinAsinB+2cosAcosB=1,cosAcosB+sinAsinB=1,即cos(A﹣B)=1.∵﹣π<A﹣B<π,∴A﹣B=0,故△ABC一定是等腰三角形,故选:A.二、填空题(本大题共4小题,每小题5分,共20分)9.(5分)计算:=.故答案为:10.(5分)在△ABC中,已知∠BAC=60°,∠ABC=45°,BC=,则AC=.【解答】解:∵∠BAC=60°,∠ABC=45°,∴BC=由正弦定理可得,可得AC===故答案为:11.(5分)设平面向量=(﹣2,1),=(λ,﹣1),若与的夹角是钝角,则λ的范围是.【解答】解:∵与的夹角是钝角,∴=﹣2λ﹣1<0,且.解得,且λ≠2.故答案为:12.(5分)tan70°+tan50°﹣=﹣.【解答】解:因为:tan70°+tan50°﹣=tan(70°+50°)(1﹣tan70°tan50°)﹣tan70°tan50°=﹣(1﹣tan70°tan50°)﹣tan70°tan50°=﹣+tan70°tan50°﹣tan70°tan50°=﹣.故答案为:﹣.三、解答题(本大题共有4个小题,共40分.解答应写出文字说明、演算步骤或证明过程.)13.(10分)已知非零向量,满足||=1,且(﹣)•(+)=.(1)求||;(2)当•=时,求向量与+2的夹角θ的值.【解答】解:(1)因为(﹣)•(+)=,即﹣=,即||2﹣||2=,所以,||2=||2﹣=1﹣=,故||=.…(4分)(2)因为||2 =||2+4+|2|2=1﹣1+1=1,故||=1.…(6分)又因为•()=||2+2=1﹣=,…(8分)∴cos θ=═,…(10分)又0°≤θ≤180°,故θ=60°.…(12分)14.(10分)已知向量=(sinθ,﹣2)与=(1,cosθ)互相垂直,其中θ∈(0,).(Ⅰ)求sinθ和cosθ的值;(Ⅱ)若sin(θ﹣φ)=,0<φ<,求cosφ的值.【解答】解:(1)∵与互相垂直,则,即sinθ=2cosθ,代入sin2θ+cos2θ=1得,又,∴(2)∵0<φ<,,∴﹣<θ﹣φ<,则cos(θ﹣φ)==,∴cosφ=cos[θ﹣(θ﹣φ)]=cosθcos(θ﹣φ)+sinθsin(θ﹣φ)=.15.(10分)在锐角三角形ABC中,角A、B、C所对的边分别为a、b、c且(tanA ﹣tanB)=1+tanA•tanB.(1)求A﹣B的大小;(2)已知<B<,向量=(sinA,cosA),=(cosB,sinB),求|3﹣2|的取值范围.【解答】解:(1)∵(tanA﹣tanB)=1+tanA•tanB,又△ABC为锐角三角形∴=,即tan(A﹣B)==,∵0<A<,0<B<,∴﹣<A﹣B<,则A﹣B=.(2)∵=(sinA,cosA),=(cosB,sinB),∴||=1,||=1,•=sinAcosB+cosAsinB=sin(A+B),则|3﹣2|2=9||2+4||2﹣12•=13﹣12sin(A+B)=13﹣12sin(2B+),∵<B<,∴<2B+<,∴sin(2B+)∈(,1),12sin(2B+)∈(6,12),13﹣12sin(2B+)∈(1,7),则|3﹣2|∈(1,)∴|3﹣2|的取值范围是(1,).16.(10分)设函数f(x)=•,其中向量=(2cos x,1),=(cos x,sin 2x+m).(Ⅰ)求函数f(x)的最小正周期和在[0,π]上的单调递增区间.(Ⅱ)当时,﹣4<f(x)<4恒成立,求实数m的取值范围.【解答】解:(Ⅰ)函数=2cos2x+=cos2x++1=2sin (2x+)+m+1.故函数f(x)的最小正周期为=π.区间为[kπ﹣,kπ+],k∈z.故在[0,π]上的单调递增区间为[0,]、[,π].(Ⅱ)当时,≤2x+≤,故有≤sin(2x+)≤1,故m+2≤f(x)≤m+3.再由﹣4<f(x)<4恒成立,可得m+2>﹣4且m+3<4,解得﹣6<m<1,故实数m的取值范围为(﹣6,1).四、选择题(本大题共4小题,每小题4分,共16分.每题有且只有一个选项是正确的,请把答案填在答卷相应位置上)17.(4分)求值:cos cos=()A.B.C.2 D.4【解答】解:cos cos===.故选:A.18.(4分)在△ABC中,①若B=60°,a=10,b=7,则该三角形有且有两解;②若三角形的三边的比是3:5:7,则此三角形的最大角为120°;③若△ABC为锐角三角形,且三边长分别为2,3,x,则x的取值范围是.其中正确命题的个数是()A.0 B.1 C.2 D.3【解答】解:①如图示:,由=,得:sinA=,∴A=arcsin>60°,∴C只能是锐角,该三角形有且只有一个解,故①错误;②不妨设:三角形的三边是:a=3,b=5,c=7,∴∠C最大,由cosC==﹣,∠C=120°,故②正确;③由cosA>0,cosB>0且cosC>0,结合余弦定理知,正确,故选:C.19.(4分)如图,BC是单位圆A的一条直径,F是线段AB上的点,且BF=2FA,DE是圆A中绕圆心A运动的一条直径,则的值是()A.B.﹣ C.﹣ D.不确定【解答】解:∵=,=,∴=()•()=+++=+•()+.∵由题意可得=0,=﹣1,||=||=,∴=+0﹣1=﹣,故选:B.20.(4分)已知f(x)=sin(2015x+)+cos(2015x﹣)的最大值为A,若存在实数x1、x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1﹣x2|的最小值为()A.B.C.D.【解答】解:f(x)=sin(2015x+)+cos(2015x﹣)=sin2015xcos+cos2015xsin+cos2015xcos+sin2015xsin=sin2015x+cos2015x+cos2015x+sin2015x=sin2015x+cos2015x=2(sin2015x+cos2015x)=2sin(2015x+),∴f(x)的最大值为A=2;由题意得,|x1﹣x2|的最小值为=,∴A|x1﹣x2|的最小值为.故选:B.五、填空题(本大题共2小题,每小题4分,共8分)21.(4分)四边形ABCD中,==(1,1),+=,则四边形ABCD的面积是.【解答】解:∵==(1,1),∴四边形ABCD是平行四边形.又+=,∴四边形ABCD是菱形.上式两边平方可得:1+1+2cosB=3,∴cosB=.∴四边形ABCD的面积S===.故答案为:.22.(4分)已知α,β∈(0,),=,且3sin β=sin(2α+β),则α+β=.【解答】解:∵=,整理可得:tan2+4tan﹣1=0,解得tan=﹣2,∵α∈(0,),∈(0,),∴tan=﹣2.∵3sin β=sin(2α+β),可得:3sin[(α+β)﹣α]=sin[(α+β)+α],∴3sin (α+β)cosα﹣3cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα,∴可得:sin (α+β)cosα=2cos(α+β)sinα,∴可得:tan(α+β)=2tanα=2tan(2×)=2×=2×=1,∵α,β∈(0,),∴α+β∈(0,),∴α+β=.故答案为:.六、解答题(本大题共有2个小题,共26分.解答应写出文字说明、演算步骤或证明过程.)23.(13分)已知向量=(sinx,cosx),=(cosx,cosx),=(2,1),且cosx≠0.(Ⅰ)若∥,求•的值;(Ⅱ)设△ABC的内角A,B,C的对边分别为a,b,c,,且,求函数f(A)的值域.【解答】解:(Ⅰ)若,得sinx=2cosx,因为cosx≠0,所以tanx=2,所以,(Ⅱ)∵△ABC中,2sinAcosB+cosBsinC=﹣sinBcosC∴2sinAcosB=﹣(cosBsinC+sinBcosC)=﹣sin(B+C)=﹣sinA又sinA>0得:,因为0<B<π,所以.则.又.所以因为,所以,所以,所以,即函数f(A)的值域为.24.(13分)岛A观察站发现在其东南方向有一艘可疑船只,正以每小时10海里的速度向东南方向航行(如图所示),观察站即刻通知在岛A正南方向B处巡航的海监船前往检查.接到通知后,海监船测得可疑船只在其北偏东75°方向且相距10海里的C处,随即以每小时10海里的速度前往拦截.(I)问:海监船接到通知时,距离岛A多少海里?(II)假设海监船在D处恰好追上可疑船只,求它的航行方向及其航行的时间.【解答】解:(I)依题意得∠BAC=45°,∠ABC=75°,BC=10,∴∠ACB=60°,…2分在△ABC中,由正弦定理得:=…3分∴AB====5.答:海监船接到通知时,距离岛A5海里…5分(II)设海监船航行时间为t小时,则BD=10t,CD=10t,…6分又∵∠BCD=180°﹣∠ACB=180°﹣60°=120°,∴BD2=BC2+CD2﹣2BC•CDcos120°,…7分∴300t2=100+100t2﹣2×10×10t•(﹣),∴2t2+t﹣1=0,解得t=1或t=﹣(舍去)…9分∴CD=10,∴BC=CD,∴∠CBD=(180°﹣120°)=30°,∴∠ABD=75°+30°=105°,…11分答:海监船的方位角105°航行,航行时间为1个小时…12分赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC.(1)如图,当∠APB=90°时,若AC=5,PC=,求BC的长;(2)当∠APB=90°时,若AB=APBC的面积是36,求△ACB的周长.2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
2016-2017年福建省福州市八县(市)一中高一(下)期末数学试卷(解析版)

2016-2017学年福建省福州市八县(市)一中高一(下)期末数学试卷一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)若扇形的半径为6cm,所对的弧长为2πcm,则这个扇形的面积是()A.12πcm2B.6 cm2C.6πcm2D.4 cm22.(5分)在△ABC中,若,∠B=90°则m=()A.﹣B.C.﹣D.3.(5分)若,则tanα的值是()A.B.C.1D.以上答案都不对4.(5分)在△ABC中,角A,B,C所对的边分别是a,b,c,若sin A=sin C,b2﹣a2=ac,则∠A=()A.B.C.D.5.(5分)cos43°cos77°+sin43°cos167°的值是()A.B.C.D.6.(5分)以下关于向量说法的四个选项中正确的选项是()A.若任意向量共线且为非零向量,则有唯一一个实数λ,使得B.对于任意非零向量,若,则C.任意非零向量满足,则同向D.若A,B,C三点满足,则点A是线段BC的三等分点且离C点较近7.(5分)在△ABC中,利用正弦定理解三角形时,其中有两解的选项是()A.a=3,b=6,A=30°B.a=6,b=5,A=150°C.D.8.(5分)已知,则=()A.B.C.D.﹣9.(5分)已知△ABC满足,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则的值为()A.﹣B.C.﹣2D.10.(5分)若函数y=A sin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内的图象如图所示,且在y轴上的截距为,M,N分别是这段图象的最高点和最低点,则在方向上的投影为()A.B.C.﹣D.11.(5分)下列对于函数f(x)=2+2cos2x,x∈(0,3π)的判断不正确的是()A.对于任意x∈(0,3π),都有f(x1)≤f(x)≤f(x2),则|x1﹣x2|的最小值为B.存在a∈R,使得函数f(x+a)为偶函数C.存在x0∈(0,3π),使得f(x0)=4D.函数f(x)在区间内单调递增12.(5分)在平面内,定点A,B,C,D满足,,动点M,N满足、=,则的最小值是()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知角α的终边过点,则cosα的值为.14.(5分)平面上点O为坐标原点,A(0,2),B(1,0),C是平面上任意一点且满足,则C点坐标是.15.(5分)若,则sin2θ=.16.(5分)在下列五个命题中:①已知大小分别为1N与2N的两个力,要使合力大小恰为,则它们的夹角为;②已知,,则sinα<cosβ;③若A,B,C是斜△ABC的三个内角,则恒有tan A+tan B+tan C=tan A tan B tan C成立;④;⑤已知,则x的大小为;其中错误的命题有.(写出所有错误命题的序号)三、解答题:请在答题卡指定区域内作答,解答时应写出证明过程或演算步骤(17小题10分,18-22小题各12分,共70分).17.(10分)已知,且∥,设函数y=f(x)(Ⅰ)求函数y=f(x)的对称轴方程及单调递减区间;(Ⅱ)若,求函数y=f(x)的最大值和最小值并写出函数取最值时x的值.18.(12分)如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足=,=2,记,,试以为平面向量的一组基底.利用向量的有关知识解决下列问题;(Ⅰ)用来表示向量;(Ⅱ)若|AB|=3,|AD|=2,且|BF|=,求||.19.(12分)平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深y(米)是随着一天的时间t(0≤t≤24,单位小时)呈周期性变化,某天各时刻t的水深数据的近似值如表:(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从①y=A sin(ωt+ϕ),②y=A cos(ωt+φ)+b,③y=﹣A sinωt+b(A>0,ω>0,﹣π<φ<0).中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ)中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全.20.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.(Ⅰ)若b=6,求角C的余弦值;(Ⅱ)若点D,E在线段BC上,且BD=DE=EC,,求AD的长.21.(12分)设向量,函数.(Ⅰ)若ω是函数y=g(x)在上的零点,求sinω的值;(Ⅱ)设,,求sin(α+β)的值.22.(12分)已知O为坐标原点,对于函数f(x)=a sin x+b cos x,称向量为函数f(x)的伴随向量,同时称函数f(x)为向量的伴随函数.(Ⅰ)设函数,试求g(x)的伴随向量;(Ⅱ)记向量的伴随函数为f(x),求当且时sin x的值;(Ⅲ)由(Ⅰ)中函数g(x)的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移个单位长度得到h(x)的图象.已知A(﹣2,3)B(2,6),问在y =h(x)的图象上是否存在一点P,使得.若存在,求出P点坐标;若不存在,说明理由.2016-2017学年福建省福州市八县(市)一中高一(下)期末数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)若扇形的半径为6cm,所对的弧长为2πcm,则这个扇形的面积是()A.12πcm2B.6 cm2C.6πcm2D.4 cm2【解答】解:∵扇形的弧长l为l=2πcm,半径r为r6cm,∴扇形的面积为S=lr==6πcm2.故选:C.2.(5分)在△ABC中,若,∠B=90°则m=()A.﹣B.C.﹣D.【解答】解:由已知得到=3﹣2m=0,所以m=;故选:D.3.(5分)若,则tanα的值是()A.B.C.1D.以上答案都不对【解答】解:∵,可得:=2+,∴解得:tanα==.故选:A.4.(5分)在△ABC中,角A,B,C所对的边分别是a,b,c,若sin A=sin C,b2﹣a2=ac,则∠A=()A.B.C.D.【解答】解:∵在△ABC中,角A,B,C所对的边分别是a,b,c,sin A=sin C,∴由正弦定理得a=c,∵b2﹣a2=ac,∴b2=a2+c2,∴∠A=.故选:B.5.(5分)cos43°cos77°+sin43°cos167°的值是()A.B.C.D.【解答】解:cos43°cos77°+sin43°cos167°=cos43°cos77°+sin43°cos(90°+77°)=cos43°cos77°﹣sin43°sin77°=cos(43°+77°)=cos120°=﹣cos60°=﹣.故选:D.6.(5分)以下关于向量说法的四个选项中正确的选项是()A.若任意向量共线且为非零向量,则有唯一一个实数λ,使得B.对于任意非零向量,若,则C.任意非零向量满足,则同向D.若A,B,C三点满足,则点A是线段BC的三等分点且离C点较近【解答】解:对于A,共线且为非零向量,若=时,则不存在实数λ,使成立,∴A错误;对于B,对于任意非零向量,若,则﹣=0,即,∴B正确;对于C,任意非零向量满足,则它们夹角的余弦值cosθ=±1,∴同向或反向,C错误;对于D,如图所示,,∴+=+,∴(﹣)=(﹣),∴2=,∴点A是线段BC的三等分点且离B点较近,∴D错误.故选:B.7.(5分)在△ABC中,利用正弦定理解三角形时,其中有两解的选项是()A.a=3,b=6,A=30°B.a=6,b=5,A=150°C.D.【解答】解:对于A,由正弦定理可得:sin B===1,可得B为90°,C =60°,只有一解;对于B,由正弦定理可得:sin B===,b<a,可得B锐角,三角形只有一解;对于C,由正弦定理可得:sin B===2,可得这样的三角形无解;对于D,由正弦定理可得:sin B==,由b>a,可得B∈(30°,150°),有2解;故选:D.8.(5分)已知,则=()A.B.C.D.﹣【解答】解:∵已知=cos[﹣(﹣)]=cos(+),则=cos2(+)=2﹣1=2•﹣1=,故选:C.9.(5分)已知△ABC满足,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则的值为()A.﹣B.C.﹣2D.【解答】解:,可得•=4×2×cos=8×(﹣)=﹣4,由点D、E分别是边AB,BC的中点,可得=,由DE=2EF,可得==,则=(+)•(﹣)=(+)•(﹣)=﹣2+2+•=﹣×16+×4﹣×4=﹣4+3﹣=﹣.故选:A.10.(5分)若函数y=A sin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内的图象如图所示,且在y轴上的截距为,M,N分别是这段图象的最高点和最低点,则在方向上的投影为()A.B.C.﹣D.【解答】解:根据函数y=A sin(ωx+φ)在一个周期内的图象,可得==3﹣1,∴ω=.再根据五点法作图可得•1+φ=,∴φ=,函数的解析式为y=A sin(x+).由于该函数在,∴A sin=,∴A=2,故函数的解析式为y=2sin (x+).∴M(1,2)、N(5,﹣2),∴=5﹣4=1.设方向上的投影为a,∵=1=a•||=a,∴a=,故选:B.11.(5分)下列对于函数f(x)=2+2cos2x,x∈(0,3π)的判断不正确的是()A.对于任意x∈(0,3π),都有f(x1)≤f(x)≤f(x2),则|x1﹣x2|的最小值为B.存在a∈R,使得函数f(x+a)为偶函数C.存在x0∈(0,3π),使得f(x0)=4D.函数f(x)在区间内单调递增【解答】解:f(x)=2+2cos2x=2+cos2x+1=3+cos2x,对于A,函数f(x)的周期为,对于任意x∈(0,3π),都有f(x1)≤f(x)≤f (x2),可知f(x1)是函数的最小值,f(x2)是函数的最大值,|x1﹣x2|的最小值就是函数的半周期,故A正确;对于B,不妨取a=π,则函数f(x+a)=3+cos(2x+2π)=3+cos2x为偶函数,故B正确;对于C,x=π∈(0,3π),cos2x=1,f(x)=4,故存在x0∈(0,3π),使得f(x0)=4,故C正确;对于D,当x∈时,2x∈,此时函数不具备单调性,故D不正确.∴对于函数f(x)=2+2cos2x,x∈(0,3π)的判断不正确的是:D.故选:D.12.(5分)在平面内,定点A,B,C,D满足,,动点M,N满足、=,则的最小值是()A.B.C.D.【解答】解:平面内定点A,B,C,D满足,,可设:D(0,0),A(2,0),B(﹣1,),C(﹣1,﹣),∵动点M,N满足||=2,=,可设N(2+2cosθ,2sinθ),由=得M(+cosθ,﹣+sinθ),∴=(cosθ﹣,sinθ﹣),∴=+=cos2θ﹣3cosθ++sin2θ﹣sinθ+=4﹣3cosθ﹣sinθ=4﹣2sin(θ+)≥4﹣2,当且仅当sin(θ+)=1时取等号,∴的最小值是4﹣2.故选:A.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知角α的终边过点,则cosα的值为﹣.【解答】解:∵角α的终边过点,∴x=tan=﹣1,y=2,r=|OP|=,∴cosα===﹣,故答案为:.14.(5分)平面上点O为坐标原点,A(0,2),B(1,0),C是平面上任意一点且满足,则C点坐标是(1,2).【解答】解:由平面上点O为坐标原点,A(0,2),B(1,0),C是平面上任意一点,得=(0,﹣2)+2(1,0)+(﹣1,2)=(1,0),设C(x,y),A(0,2),则=(x,y﹣2)=(1,0),∴x=1,y=2.则C点坐标是:(1,2).故答案为:(1,2).15.(5分)若,则sin2θ=﹣.【解答】解:若=,则tanθ=﹣4,∴sin2θ====﹣,故答案为:.16.(5分)在下列五个命题中:①已知大小分别为1N与2N的两个力,要使合力大小恰为,则它们的夹角为;②已知,,则sinα<cosβ;③若A,B,C是斜△ABC的三个内角,则恒有tan A+tan B+tan C=tan A tan B tan C成立;④;⑤已知,则x的大小为;其中错误的命题有①②④⑤.(写出所有错误命题的序号)【解答】解:对于①,||=1,||=2,|+|=,∴||+2||×||cosθ+||=1+2×1×2×cosθ+4=6cosθ=,∴它们的夹角θ≠,①错误;对于②,,,且sin=cos(﹣)=cos,cos(﹣)=cos0<<<π,∴cos>cos,∴sinα>cosβ,②错误;对于③,斜△ABC中,A+B=π﹣C,∴tan(A+B)=tan(π﹣C),∴=﹣tan C,∴tan A+tan B+tan C=tan A tan B tan C,③正确;对于④,sin50°(1+tan10°)=sin50°•====1,∴④错误;对于⑤,(cos x+1)=sin x,∴sin x﹣cos x=,∴sin(x﹣)=,又x∈(0,),∴x﹣∈(﹣,),∴x﹣=或x﹣=,解得x=或x=π,⑤错误.综上,错误的命题是①②④⑤.故答案为:①②④⑤.三、解答题:请在答题卡指定区域内作答,解答时应写出证明过程或演算步骤(17小题10分,18-22小题各12分,共70分).17.(10分)已知,且∥,设函数y=f(x)(Ⅰ)求函数y=f(x)的对称轴方程及单调递减区间;(Ⅱ)若,求函数y=f(x)的最大值和最小值并写出函数取最值时x的值.【解答】解:(Ⅰ)∵,,且∥,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)由,得x=.由,得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∴,函数在[kπ+,kπ+],(k∈z)递减﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)∵∴,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)∴;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)18.(12分)如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足=,=2,记,,试以为平面向量的一组基底.利用向量的有关知识解决下列问题;(Ⅰ)用来表示向量;(Ⅱ)若|AB|=3,|AD|=2,且|BF|=,求||.【解答】解:(Ⅰ)∵在平行四边形ABCD中,,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)由(Ⅰ)可知:,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)∵|AB|=3,|AD|=2,且∴∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)∴=﹣+==9﹣6×+1=7∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)19.(12分)平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深y(米)是随着一天的时间t(0≤t≤24,单位小时)呈周期性变化,某天各时刻t的水深数据的近似值如表:(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从①y=A sin(ωt+ϕ),②y=A cos(ωt+φ)+b,③y=﹣A sinωt+b(A>0,ω>0,﹣π<φ<0).中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ)中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全.【解答】(满分12分)解:(Ⅰ)根据表中近似数据画出散点图,如图所示:依题意,选②y=A cos(ωt+ϕ)+b做为函数模型,∴,∵∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)又∵函数y=0.9cos(φ)+1.5的图象过点(3,2.4),∴2.4=0.9×cos(+φ)+1.5,∴cos(+φ)=1,∴sinφ=﹣1,又∵﹣π<φ<0,∴φ=﹣,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)(Ⅱ)由(Ⅰ)知:令y≥1.05,即∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)∴,∴12k﹣1≤t≤12k+7又∵5≤t≤18∵5≤t≤7或11≤t≤18﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)∴这一天可以安排早上5点至7点以及11点至18点的时间段组织训练,才能确保集训队员的安全.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)20.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.(Ⅰ)若b=6,求角C的余弦值;(Ⅱ)若点D,E在线段BC上,且BD=DE=EC,,求AD的长.【解答】(满分12分)解:(Ⅰ)∵由正弦定理得:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∵B=60°,c=4,b=6,∴,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)∵b>c∴∠B>∠C∴∠C为锐角﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)∵BD=DE=EC,,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)在,∵B=60°,∴,∴∠BAE=30°或150°(不合题意,舍去)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)∴,∴,∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)21.(12分)设向量,函数.(Ⅰ)若ω是函数y=g(x)在上的零点,求sinω的值;(Ⅱ)设,,求sin(α+β)的值.【解答】解:(Ⅰ)∵,函数,∴g(x)=•=4cos x•sin(x+)+1×(﹣1)=2sin x cos x+2cos2x﹣1=2sin(2x+)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)由得:∴又∵∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)∵,∴,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)22.(12分)已知O为坐标原点,对于函数f(x)=a sin x+b cos x,称向量为函数f(x)的伴随向量,同时称函数f(x)为向量的伴随函数.(Ⅰ)设函数,试求g(x)的伴随向量;(Ⅱ)记向量的伴随函数为f(x),求当且时sin x的值;(Ⅲ)由(Ⅰ)中函数g(x)的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移个单位长度得到h(x)的图象.已知A(﹣2,3)B(2,6),问在y =h(x)的图象上是否存在一点P,使得.若存在,求出P点坐标;若不存在,说明理由.【解答】解:(Ⅰ)∵,∴∴g(x)的伴随向量(Ⅱ)∵的伴随函数为f(x),且,∴又∵且sin2x+cos2x=1,∴(Ⅲ)由(Ⅰ)知:(用余弦表示也可以)将函数g(x)的图象(纵坐标不变)横坐标伸长为原来的2倍,得到函数再把整个图象向右平移个单位长得到h(x)的图象,得到设,∵A(﹣2,3)B(2,6),∴又∵,∴,∴(x+2)(x﹣2)+(2cos x﹣3)(2cos x﹣6)=0,,∴(*)∵,∴∴又∵,∴当且仅当x=0时,和同时等于,这时(*)式成立,∴.第21页(共21页)。
___2016-2017学年高一下学期期末考试数学试题+Word版含答案

___2016-2017学年高一下学期期末考试数学试题+Word版含答案福州一中2016-2017学年第二学期第四学段模块考试高一数学(必修4)模块试卷一、选择题(本题共10小题,每小题4分,共40分)1.设a=sin36°,b=cos(-52°),c=tan218°,则()A) a<b<cB) a<c<bC) b<c<aD) b<a<c2.△ABC内角A,B,C的对边分别为a,b,c,且a/b=b/c,则△ABC是()A) 等边三角形B) 有一个角是30°的直角三角形C) 等腰直角三角形D) 有一个角是30°的等腰三角形3.已知向量a,b不共线,且c=λa+μb,d=a+(2λ-1)b,若c 与d方向相反,则μ的值为()A) 1/2B) -1/4C) 1/4或-1/4D) -1/24.已知tanθ=2,则sin(θ+sin^-1(7/25))-cosθ=()A) -11/25B) 2/5C) 7/25D) 19/255.函数f(x)=(1-cos2x)cos^2(x/2),x∈R是()A) 最小正周期为π的偶函数B) 最小正周期为π的偶函数C) 最小正周期为π的奇函数D) 最小正周期为π的奇函数6.下列说法正确的是()A) 若a·b=c且a≠0,则b=c/aB) 若sinθ=1/3,cosθ=4/5,且θ∈[π/2,π],则tanθ=-3/4C) △ABC中,若AB>AC,则∠A>∠BD) 若f(x)是偶函数,则f(-x)也是偶函数7.已知tanα=tanβ/3,b=42,则∠B=45°是方程x^2+2πx+33+4=0的两根,α,β∈(π/3,π),则α+β=()A) π/3或4π/3B) 2π/3或5π/3C) π或2π/3D) π/3或4π/38.如图,在某地A第北偏西25°方向上有一条笔直的公路L,某天,A地收到在它___方向,距离24km的观测站C的报告:与C相距31km的公路L上的B处有一个人正以每小时5km的速度向A地进发。
福建省福州八中2016—2017学年高一下学期期末考试数学试题含答案

福州八中2016—2017学年第二学期期末考试高一数学 必修4考试时间:120分钟 试卷满分:150分 2017。
7.12Ⅰ卷一、选择题:(本大题共10小题,每小题5分,共50分) 1。
化简cos 15°cos 45°-cos 75°sin 45°的值为 A 。
12B. 32 C .-12D .-322.设a n =211111123n n n n n ++++++++(n ∈N *),则a3= A .13B 。
11113456+++ C . 19 D. 111349+++ 3.若AD 是△ABC 的中线,已知=,,则等于A 。
1()2a b -B 。
1()2a b + C 。
1()2a b -+ D 。
1()2a b -+ 4. 若递增等比数列{a n }的前n 项和为S n ,a 2=2,S 3=7,则公比q等于A 。
2 B.12C 。
2或12 D 。
无法确定5。
若将函数f (x )=2sinxcosx —2sin 2x +1的图象向右平移φ个单位,所得图象关于y 轴对称,则φ的最大负值是A 。
-8πB 。
-58πC .-38πD.-34π 6.已知12(2,1),(1,3),(1,2),ee a ===-若1122a e e λλ=+,则实数对(λ1,λ2)为A 。
(1,1) B.(—1,1) C.(—1,—1)D 。
无数对7.在△ABC 中,2cos ab C =,则这个三角形一定是 A 。
等腰三角形B 。
直角三角形C.等腰直角三角D.等腰或直角三角形8。
已知α为锐角,且3cos(),cos245παα+== A.2425B 。
725C 。
-2425 D.±24259. 已知x =12π是函数f (x )=3sin (2x +φ)+cos (2x +φ)(0<φ<π)图象的一条对称轴,将函数f (x )的图象向右平移34π个单位后得到函数g (x )的图象,则函数g (x )在[-4π,6π]上的最小值为A 。
2016-2017学年福建省福州市第八中学高一数学下期中试卷

2016-2017学年福建省福州八中高一(下)期中数学试卷
、选择题:(本大题共10小题,每小题5分,共50分,有且只有一个选项正确)
1 .如果cos X 0,且tan ©>0,则9是( )
B .第二象限的角C.第三象限的角 D .第四象限的角
2.①某高校为了解学生家庭经济收入情况,从来自城镇的150名学生和来自农村的150名
学生中抽取100名学生的样本;
②某车间主任从100件产品中抽取10件样本进行产品质量检验.
I.简单随机抽样法;
n .分层抽样法.
上述两问题和两方法配对正确的是()
A.①配I,②配n B .①配n ,②配I C.①配I,②配I D .①配n ,②配n
3.某研究机构对儿童记忆能力x和识图能力y进行统计分析,得到如下数据:
记忆能力x46810
识图能力y3568
A 4 A
由表中数据,求得线性回归方程为,二厂x+ .,若某儿童的记忆能力为11时,则他的识
图能力约为()
A. 8.5 B . 8.7
4.如果如图所示程序执行后输出的结果是
C. 8.9 D . 9
480,那么在程序UNTIL后面的条件”应为()
DO
i=i-2
S=s*i
LOOP UNTIL
PRINTS END
C. i v 8
B . i>=8
「,厂V:T,则sin (2 n-a)
1 Vs
B. :.
C.
D . i v =8
( )
D. !
6.天气预报说,在今后的三天中,每一天下雨的概率均为50% .现采用随机模拟试验的方
A .第一象限的角。
福建省福州八中2016-2017学年高一下学期期中数学试卷Word版含解析

2016-2017学年福建省福州八中高一(下)期中数学试卷一、选择题:(本大题共10小题,每小题5分,共50分,有且只有一个选项正确)1.如果cosθ<0,且tanθ>0,则θ是()A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角2.①某高校为了解学生家庭经济收入情况,从来自城镇的150名学生和来自农村的150名学生中抽取100名学生的样本;②某车间主任从100件产品中抽取10件样本进行产品质量检验.I.简单随机抽样法;Ⅱ.分层抽样法.上述两问题和两方法配对正确的是()A.①配I,②配ⅡB.①配Ⅱ,②配Ⅰ C.①配I,②配I D.①配Ⅱ,②配Ⅱ3.某研究机构对儿童记忆能力x和识图能力y进行统计分析,得到如下数据:由表中数据,求得线性回归方程为,=x+,若某儿童的记忆能力为11时,则他的识图能力约为()A.8.5 B.8.7 C.8.9 D.94.如果如图所示程序执行后输出的结果是480,那么在程序UNTIL后面的“条件”应为()A.i>8 B.i>=8 C.i<8 D.i<=85.若,,则sin(2π﹣α)=()A .B .C .D .6.天气预报说,在今后的三天中,每一天下雨的概率均为50%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用0,1,2,3,4表示下雨,用5,6,7,8,9表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 据此估计,这三天中恰有两天下雨的概率近似为( ) A .0.30 B .0.35 C .0.40 D .0.507.如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )A .B .C .D .8.若sinα=,cosα=﹣,则在角α终边上的点是( ) A .(﹣4,3) B .(3,﹣4) C .(4,﹣3) D .(﹣3,4)9.记集合A={x ,y )|x 2+y 2≤4}和集合B={(x ,y )|x ﹣y ﹣2≤0,x ﹣y +2≥0}表示的平面区域分别为Ω1、Ω2,若在区域Ω1内任取一点M (x ,y ),则点M 落在区域Ω2内的概率为( )A .B .C .D .10.当x=时,函数f (x )=Asin (x +φ)(A >0)取得最小值,则函数y=f (﹣x )是( )A .奇函数且图象关于直线x=对称B .偶函数且图象关于点(π,0)对称C .奇函数且图象关于(,0)对称D.偶函数且图象关于点(,0)对称二、填空题:(本大题有4小题,每小题5分,共20分.请将正确的答案填在横线上)11.已知扇形AOB的周长是6,中心角是2弧度,则该扇形的面积为.12.设a=sin33°,b=cos55°,c=tan35°,则a,b,c三数由大到小关系为.13.高一(9)班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:则统计表中的a•p=.14.已知函数f(x)=x+sinπx,则f()+f()+f()+…+f()的值为.三、解答题:(本大题有3个小题,共30分.请书写完整的解答过程)15.(10分)某中学调查了某班全部50名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)(I)从该班随机选1名同学,求该同学至少参加上述一个社团的概率;(II)在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A1,A2,A3,A4,A5,3名女同学B1,B2,B3,现从这5名男同学和3名女同学中各随机选1人,求A1被选中且B1未被选中的概率.16.(10分)某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200.220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.(Ⅰ)求直方图中x的值;(Ⅱ)求月平均用电量的众数和中位数;(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?17.(10分)已知:﹣<x<﹣π,tanx=﹣3.(Ⅰ)求sinx•cosx的值;(Ⅱ)求的值.四、选择题:(本大题共2小题,每小题5分,共15分,有且只有一个选项正确)18.现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为()A.B.C.D.19.函数y=,x∈(﹣,0)∪(0,)的图象可能是下列图象中的()A.B. C. D.五、填空题:(共5分.请将正确的答案填在横线上)20.将函数f(x)=2cos2x的图象向右平移个单位得到函数g(x)的图象,若函数g(x)在区间和上均单调递增,则实数a的取值范围是.六、解答题:(本大题有3个小题,共35分.请书写完整的解答过程)21.(11分)已知关于x的二次函数f(x)=ax2﹣4bx+1.(Ⅰ)设集合A={﹣1,1,2,3,4,5}和B={﹣2,﹣1,1,2,3,4},分别从集合A,B中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.(Ⅱ)设点(a,b)是区域内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.22.(12分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,﹣π<φ<0).(1)若f(x)的部分图象如图所示,求f(x)的解析式;(2)在(1)的条件下,求最小正实数m,使得函数f(x)的图象向左平移m 个单位后所对应的函数是偶函数;(3)若f(x)在[0,]上是单调递增函数,求ω的最大值.23.(12分)我们把平面直角坐标系中,函数y=f(x),x∈D上的点P(x,y),满足x∈N*,y∈N*的点称为函数y=f(x)的“正格点”.(Ⅰ)若函数f(x)=sinmx,x∈R,m∈(3,4)与函数g(x)=lgx的图象有正格点交点,求m的值,并写出两个函数图象的所有交点个数.(Ⅱ)对于(Ⅰ)中的m值,函数f(x)=sinmx,时,不等式log a x >sinmx恒成立,求实数a的取值范围.2016-2017学年福建省福州八中高一(下)期中数学试卷参考答案与试题解析一、选择题:(本大题共10小题,每小题5分,共50分,有且只有一个选项正确)1.如果cosθ<0,且tanθ>0,则θ是()A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角【考点】GC:三角函数值的符号.【分析】根据三角函数的符号,判断θ是哪一象限角即可.【解答】解:∵cosθ<0,∴θ是第二、第三象限角或x负半轴角,又tanθ>0,∴θ是第一或第三象限角,∴θ是第三象限角.故选:C.【点评】本题考查了根据三角函数值判断三角函数符号的应用问题,是基础题目.2.①某高校为了解学生家庭经济收入情况,从来自城镇的150名学生和来自农村的150名学生中抽取100名学生的样本;②某车间主任从100件产品中抽取10件样本进行产品质量检验.I.简单随机抽样法;Ⅱ.分层抽样法.上述两问题和两方法配对正确的是()A.①配I,②配ⅡB.①配Ⅱ,②配Ⅰ C.①配I,②配I D.①配Ⅱ,②配Ⅱ【考点】B3:分层抽样方法;B2:简单随机抽样.【分析】由题意知①的总体中个体明显分层两,用分层抽样,②的总体中个体的数目不大用简单分层抽样.【解答】解:①、总体中个体明显分层两层:来自城镇的学生和来自农村的学生,故用分层抽样来抽取样本;②,总体中个体的数目是100,不是很大,故用简单分层抽样来抽取样本.故选B.【点评】本题的考点是选择抽样方法,即根据总体的特征和抽样方法适用的条件进行选择最佳方法.3.某研究机构对儿童记忆能力x和识图能力y进行统计分析,得到如下数据:由表中数据,求得线性回归方程为,=x+,若某儿童的记忆能力为11时,则他的识图能力约为()A.8.5 B.8.7 C.8.9 D.9【考点】BK:线性回归方程.【分析】由表中数据计算、,根据线性回归方程过样本中心点求出,写出线性回归方程,利用回归方程计算x=11时的值.【解答】解:由表中数据,计算=×(4+6+8+10)=7,=×(3+5+6+8)=5.5,且线性回归方程=x+过样本中心点(,),∴=5.5﹣×7=﹣0.1=﹣,∴线性回归方程为=x﹣;当x=11时,=×11﹣=8.7,即某儿童的记忆能力为11时,他的识图能力约为8.7.故选:B.【点评】本题考查了线性回归方程过样本中心点的应用问题,是基础题.4.如果如图所示程序执行后输出的结果是480,那么在程序UNTIL后面的“条件”应为()A.i>8 B.i>=8 C.i<8 D.i<=8【考点】EA:伪代码.【分析】先根据输出的结果推出循环体执行的次数,再根据S=1×10×8×6=480得到程序中UNTIL后面的条件.【解答】解:因为输出的结果是480,即S=1×10×8×6,需执行3次,所以程序中UNTIL后面的“条件”应为i<8.故选:C.【点评】本题主要考查了直到型循环语句问题,语句的识别是一个逆向性思维过程,是基础题.5.若,,则sin(2π﹣α)=()A.B.C.D.【考点】GO:运用诱导公式化简求值.【分析】由条件利用诱导公式求得cosα的值,再根据α的范围求得sinα的值,可得要求式子的值.【解答】解:∵=﹣cosα,∴cosα=.又,∴sinα=﹣=﹣,∴sin(2π﹣α)=﹣sinα=,故选:B.【点评】本题主要考查同角三角函数的基本关系、诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.6.天气预报说,在今后的三天中,每一天下雨的概率均为50%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用0,1,2,3,4表示下雨,用5,6,7,8,9表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989据此估计,这三天中恰有两天下雨的概率近似为()A.0.30 B.0.35 C.0.40 D.0.50【考点】CE:模拟方法估计概率.【分析】由题意知模拟三天中恰有两天下雨的结果,分析所给的数据可得表示三天下雨的数据组数,根据概率公式,计算可得结果.【解答】解:根据题意,用随机模拟试验模拟三天中恰有两天下雨的结果,分析可得:20组数据中表示三天中恰有两天下雨的有191、271、932、812、393、027、730,共7组,则这三天中恰有两天下雨的概率近似为=0.35;故选:B.【点评】本题考查模拟方法估计概率,解题主要依据是等可能事件的概率,注意列举法在本题的应用.7.如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为()A.B.C.D.【考点】BA:茎叶图;CB:古典概型及其概率计算公式.【分析】根据茎叶图中的数据,求出甲乙两人的平均成绩,再求出乙的平均成绩不小于甲的平均成绩的概率,即可得到答案.【解答】解:由已知中的茎叶图得,甲的平均成绩为(88+89+90+91+92)=90;设污损的数字为x,则乙的平均成绩为(83+83+87+99+90+x)=88.4+,当x=9,甲的平均数<乙的平均数,即乙的平均成绩超过甲的平均成绩的概率为,当x=8,甲的平均数=乙的平均数,即乙的平均成绩等于甲的平均成绩的概率为,所以,甲的平均成绩超过乙的平均成绩的概率为1﹣﹣=.故选:D.【点评】本题考查了平均数,茎叶图,古典概型概率计算公式的应用问题,是基础题目.8.若sinα=,cosα=﹣,则在角α终边上的点是()A.(﹣4,3)B.(3,﹣4)C.(4,﹣3)D.(﹣3,4)【考点】G9:任意角的三角函数的定义.【分析】利用三角函数的定义有sinα=,cosα=,从而可知选项.【解答】解:由于sinα=,cosα=﹣,根据三角函数的定义:sinα=,cosα=,可知x=﹣4,y=3,故选:A.【点评】本题主要考查了三角函数的定义.考查了学生对三角函数基础知识的掌握.9.记集合A={x,y)|x2+y2≤4}和集合B={(x,y)|x﹣y﹣2≤0,x﹣y+2≥0}表示的平面区域分别为Ω1、Ω2,若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2内的概率为()A.B.C.D.【考点】CF:几何概型.【分析】分别求出集合A,B对应区域的面积,根据几何概型的概率公式即可得到结论.【解答】解:区域Ω1对应的面积S1=4π,作出平面区域Ω2,则Ω2对应的平面区域如图,则对应的面积S=2π+4,则根据几何概型的概率公式可知若在区域Ω1内任取一点M(x,y),则点M落在区域Ω2的概率为P==.故选;D【点评】本题主要考查几何概型的概率公式的计算,根据条件求出相应的面积是解决本题的关键.10.当x=时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f(﹣x)是()A.奇函数且图象关于直线x=对称B.偶函数且图象关于点(π,0)对称C.奇函数且图象关于(,0)对称D.偶函数且图象关于点(,0)对称【考点】HJ:函数y=Asin(ωx+φ)的图象变换;H2:正弦函数的图象.【分析】由题意可得sin(+φ)=﹣1,解得φ=2kπ﹣,k∈Z,从而可求y=f(﹣x)=﹣Asinx,利用正弦函数的图象和性质即可得解.【解答】解:由x=时函数f(x)=Asin(x+φ)(A>0)取得最小值,∴﹣A=Asin(+φ),可得:sin(+φ)=﹣1,∴+φ=2kπ﹣,k∈Z,解得:φ=2kπ﹣,k∈Z,∴f(x)=Asin(x﹣),∴y=f(﹣x)=Asin(﹣x﹣)=﹣Asinx,∴函数是奇函数,排除B,D,∵由x=时,可得sin取得最大值1,故C错误,图象关于直线x=对称,A 正确;故选:A.【点评】本题主要考查了正弦函数的图象和性质,考查了数形结合能力,属于基础题.二、填空题:(本大题有4小题,每小题5分,共20分.请将正确的答案填在横线上)11.已知扇形AOB的周长是6,中心角是2弧度,则该扇形的面积为.【考点】G8:扇形面积公式.【分析】由已知中,扇形AOB的周长是6cm,该扇形的中心角是2弧度,我们可设计算出弧长与半径的关系,进而求出弧长和半径,代入扇形面积公式,即可得到答案【解答】解:∵扇形圆心角2弧度,可得扇形周长和面积为整个圆的.弧长l=2πr•=2r,故扇形周长C=l+2r=4r=6,∴r=,扇形面积S=π•r2•=.故答案为:.【点评】本题考查的知识点是扇形面积公式,弧长公式,其中根据已知条件,求出扇形的弧长及半径,是解答本题的关键,属于基础题.12.设a=sin33°,b=cos55°,c=tan35°,则a,b,c三数由大到小关系为c>b >a.【考点】GA:三角函数线.【分析】分别作出三角函数线,比较可得.【解答】解:∵a=sin33°,b=cos55°,c=tan35°,作出三角函数线结合图象可得c>b>a,故答案为:c>b>a.【点评】本题考查三角函数线,数形结合是解决问题的关键,属基础题.13.高一(9)班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:则统计表中的a•p=65.【考点】B8:频率分布直方图.【分析】由频率=,得第一组人数为200,由频率分布直方图得第一组的频率为0.2,从而n=1000,进而a=1000×0.02×5=100,第二组人数为1000×[1﹣(0.04+0.04+0.03+0.02+0.01)×5]=300,求出P==0.65,由此能求出a•P.【解答】解:由频率=,得第一组人数为:=200,由频率分布直方图得第一组的频率为:0.04×5=0.2,n==1000,∴a=1000×0.02×5=100,第二组人数为1000×[1﹣(0.04+0.04+0.03+0.02+0.01)×5]=300,∴P==0.65,∴a•P=100×0.65=65.故答案为:65.【点评】本题考查频率率的求法及应用,是基础题,解题时要认真审题,注意频率=及频率分布直方图的合理运用.14.已知函数f(x)=x+sinπx,则f()+f()+f()+…+f()的值为4033.【考点】3O:函数的图象;3T:函数的值.【分析】根据题意,求出f(2﹣x)的解析式,分析可得f(x)+f(2﹣x)=2,将f()+f()+f()+…+f()变形可得[f()+f()]+[f()+f ()]+…[f ()+f ()]+f (1),计算可得答案.【解答】解:根据题意,f (x )=x +sinπx ,f (2﹣x )=(2﹣x )+sin [π(2﹣x )]=(2﹣x )﹣sinx ,则有f (x )+f (2﹣x )=2,f ()+f ()+f ()+…+f ()=[f ()+f ()]+[f ()+f ()]+…[f ()+f ()]+f (1)=4033;故答案为:4033.【点评】本题考查了利用函数的对称性求函数值的应用问题,关键是依据函数的解析式确定函数的对称中心.三、解答题:(本大题有3个小题,共30分.请书写完整的解答过程) 15.(10分)(2017春•台江区校级期中)某中学调查了某班全部50名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)(I )从该班随机选1名同学,求该同学至少参加上述一个社团的概率; (II )在既参加书法社团又参加演讲社团的8名同学中,有5名男同学A 1,A 2,A 3,A 4,A 5,3名女同学B 1,B 2,B 3,现从这5名男同学和3名女同学中各随机选1人,求A 1被选中且B 1未被选中的概率.【考点】CC :列举法计算基本事件数及事件发生的概率;B8:频率分布直方图.【分析】(Ⅰ)由调查数据可知,既未参加书法社团又未参加演讲社团的有30人,故至少参加上述一个社团的共有50﹣30=20(人),利用古典概率计算公式即可得出.(Ⅱ)从这5名男同学和3名女同学中各随机选1人,其一切可能的结果组成的基本事件有15个根据题意,这些基本事件的出现是等可能的,事件“A 1被选中且B 1未被选中”所包含的基本事件有:{A 1,B 2},{A 1,B 3},共2个,利用古典概率计算公式即可得出.【解答】解:(Ⅰ)由调查数据可知,既未参加书法社团又未参加演讲社团的有30人,故至少参加上述一个社团的共有50﹣30=20(人),所以从该班随机选1名同学,该同学至少参加上述一个社团的概率为P=.(4分)(Ⅱ)从这5名男同学和3名女同学中各随机选1人,其一切可能的结果组成的基本事件有:{A1,B1},{A1,B2},{A1,B3},{A2,B1},{A2,B2},{A2,B3},{A3,B1},{A3,B2},{A3,B3},{A4,B1},{A4,B2},{A4,B3},{A5,B1},{A5,B2},{A5,B3},共15个.…(6分)根据题意,这些基本事件的出现是等可能的,事件“A1被选中且B1未被选中”所包含的基本事件有:{A1,B2},{A1,B3},共2个.…(8分)因此,A1被选中且B1未被选中的概率为.…(10分)【点评】本题考查了古典概型及其概率计算公式、列举法,考查了推理能力与计算能力,属于中档题.16.(10分)(2017春•黄山期末)某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200.220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.(Ⅰ)求直方图中x的值;(Ⅱ)求月平均用电量的众数和中位数;(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?【考点】CC:列举法计算基本事件数及事件发生的概率;B8:频率分布直方图.【分析】(Ⅰ)由直方图的性质能求出直方图中x的值.(Ⅱ)由频率分布直方图能求出月平均用电量的众数和中位数.(Ⅲ)月平均用电量为[220,240]的用户有25户,月平均用电量为[240,260)的用户有15户,月平均用电量为[260,280)的用户有10户,由此能求出月平均用电量在[220,240)的用户中应抽取的户数.【解答】(本小题10分)解:(Ⅰ)由直方图的性质,可得(0.002+0.0095+0.011+0.0125+x+0.005+0.0025)×20=1得:x=0.0075,所以直方图中x的值是0.0075.…(3分)(Ⅱ)月平均用电量的众数是=230.…(4分)因为(0.002+0.0095+0.011)×20=0.45<0.5,所以月平均用电量的中位数在[220,240)内,设中位数为a,由(0.002+0.0095+0.011)×20+0.0125×(a﹣220)=0.5得:a=224,所以月平均用电量的中位数是224.…(6分)(Ⅲ)月平均用电量为[220,240]的用户有0.0125×20×100=25户,月平均用电量为[240,260)的用户有0.0075×20×100=15户,月平均用电量为[260,280)的用户有0.005×20×100=10户,…(8分)抽取比例==,所以月平均用电量在[220,240)的用户中应抽取25×=5户.…(10分)【点评】本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.17.(10分)(2017春•台江区校级期中)已知:﹣<x<﹣π,tanx=﹣3.(Ⅰ)求sinx•cosx的值;(Ⅱ)求的值.【考点】GH:同角三角函数基本关系的运用;GI:三角函数的化简求值.【分析】(Ⅰ)利用“切化弦”及其平方关系可得sinx•cosx的值;(Ⅱ)根据诱导公式化简,利用“弦化切”可得答案.【解答】解:(Ⅰ)∵tanx=﹣3,即=﹣3,且﹣<x<﹣π,sin2x+cos2x=1,∴cosx=﹣,sinx=.那么:sinx•cosx=.(Ⅱ)原式====﹣3.【点评】本题考查了“弦化切”及同角三角函数基本关系式,考查了计算能力,属于基础题.四、选择题:(本大题共2小题,每小题5分,共15分,有且只有一个选项正确)18.现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为()A.B.C.D.【考点】CB:古典概型及其概率计算公式.【分析】基本事件总数n=23=8,设两道题分别为A,B题,利用列举法求出满足恰有一男一女抽到同一题目的事件个数,由此能求出其中恰有一男一女抽到同一道题的概率.【解答】解:现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,基本事件总数n=23=8,设两道题分别为A,B题,所以抽取情况共有:AAA,AAB,ABA,ABB,BAA,BAB,BBA,BBB,其中第1个,第2个分别是两个男教师抽取的题目,第3个表示女教师抽取的题目,一共有8种;其中满足恰有一男一女抽到同一题目的事件有:ABA,ABB,BAA,BAB,共4种,故其中恰有一男一女抽到同一道题的概率为p=.故选:C.【点评】本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.19.函数y=,x∈(﹣,0)∪(0,)的图象可能是下列图象中的()A.B. C. D.【考点】3O:函数的图象.【分析】根据三角函数图象及其性质,利用排除法即可.【解答】解:因为y=是偶函数,排除A,当x=1时,y=>1,排除C,当x=时,y=>1,排除B、C,故选D.【点评】本题考查了三角函数的图象问题,注意利用函数图象的寄偶性及特殊点来判断.五、填空题:(共5分.请将正确的答案填在横线上)20.将函数f(x)=2cos2x的图象向右平移个单位得到函数g(x)的图象,若函数g(x)在区间和上均单调递增,则实数a的取值范围是[,] .【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【分析】根据函数y=Asin(ωx+φ)的图象变换规律,求得g(x)=2cos(2x﹣);再利用条件以及余弦函数的单调性,求得a的范围.【解答】解:将函数f(x)=2cos2x的图象向右平移个单位得到函数g(x)=2cos(2x﹣)的图象,若函数g(x)在区间和上均单调递增,∴a>0.由2kπ﹣π≤0﹣≤2kπ,且2kπ﹣π≤2•﹣≤2kπ,k∈Z,求得k=0,﹣π≤a≤①.由2nπ﹣π≤4a﹣≤2nπ,且2nπ﹣π≤2•﹣≤2nπ,求得n=1,≤a≤②,由①②可得,≤a≤,故答案为:.【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,余弦函数的单调性,属于中档题.六、解答题:(本大题有3个小题,共35分.请书写完整的解答过程)21.(11分)(2017春•黄山期末)已知关于x的二次函数f(x)=ax2﹣4bx+1.(Ⅰ)设集合A={﹣1,1,2,3,4,5}和B={﹣2,﹣1,1,2,3,4},分别从集合A,B中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.(Ⅱ)设点(a ,b )是区域内的随机点,求函数f (x )在区间[1,+∞)上是增函数的概率.【考点】CF :几何概型;CB :古典概型及其概率计算公式.【分析】(Ⅰ)分a=1,2,3,4,5 这五种情况来研究a >0,且≤1的取法共有16种,而所有的取法共有6×6=36 种,从而求得所求事件的概率.(Ⅱ)由条件可得,实验的所有结果构成的区域的面积等于S △OMN =×8×8=32,满足条件的区域的面积为S △POM =×8×=,故所求的事件的概率为 P=,运算求得结果.【解答】解:要使函数y=f (x )在区间[1,+∞)上是增函数,则a >0且,即a >0且2b ≤a .(Ⅰ)所有(a ,b )的取法总数为6×6=36个,满足条件的(a ,b )有(1,﹣2),(1,﹣1),(2,﹣2),(2,﹣1),(2,1),(3,﹣2),(3,﹣1),(3,1),(4,﹣2),(4,﹣1),(4,1),(4,2),(5,﹣2),(5,﹣1),(5,1),(5,2)共16个,所以,所求概率.…(6分)(Ⅱ)如图,求得区域的面积为.由,求得所以区域内满足a >0且2b ≤a 的面积为.所以,所求概率.【点评】本题考查了等可能事件的概率与二次函数的单调区间以及简单的线性规划问题相结合的问题,画出实验的所有结果构成的区域,Ⅰ是古典概型的概率求法,Ⅱ是几何概型的概率求法.22.(12分)(2017春•台江区校级期中)已知函数f(x)=Asin(ωx+φ)(A >0,ω>0,﹣π<φ<0).(1)若f(x)的部分图象如图所示,求f(x)的解析式;(2)在(1)的条件下,求最小正实数m,使得函数f(x)的图象向左平移m 个单位后所对应的函数是偶函数;(3)若f(x)在[0,]上是单调递增函数,求ω的最大值.【考点】HK:由y=Asin(ωx+φ)的部分图象确定其解析式;H5:正弦函数的单调性.【分析】(1)根据函数f(x)的部分图象,求出A、T、ω和φ的值,即可写出f(x)的解析式;(2)根据函数图象平移法则,写出f(x)左移m个单位后的函数解析式,根据函数y是偶函数,求出m的最小正数;(3)根据f(x)在[0,]上是单调递增函数,得出﹣≤φ≤ω+φ≤,求出ω≤﹣,再根据φ的取值范围求出ω的最大值.【解答】解:(1)根据函数f(x)=Asin(ωx+φ)的部分图象知,\A=3,=﹣=,∴T=π,ω==2;根据五点法画图知,2×+φ=,解得φ=﹣,∴f(x)=3sin(2x﹣);(2)f(x)=3sin(2x﹣),函数f(x)的图象向左平移m个单位后,所对应的函数是y=3sin[2(x+m)﹣]=3sin(2x+2m﹣)的图象,又函数y是偶函数,∴2m﹣=+kπ,k∈Z,解得m=+,k∈Z,∴m的最小正数是;(3)f(x)=Asin(ωx+φ)在[0,]上是单调递增函数,A>0,ω>0,∴﹣≤φ≤ω+φ≤,解得ω≤﹣;又﹣π<φ<0,∴﹣≤φ<0,∴0<﹣≤,∴ω≤+=3,即ω的最大值为3.【点评】本题考查了正弦型函数的图象与性质的应用问题,也考查了数形结合思想,是综合题.23.(12分)(2017春•台江区校级期中)我们把平面直角坐标系中,函数y=f (x),x∈D上的点P(x,y),满足x∈N*,y∈N*的点称为函数y=f(x)的“正格点”.(Ⅰ)若函数f(x)=sinmx,x∈R,m∈(3,4)与函数g(x)=lgx的图象有正格点交点,求m的值,并写出两个函数图象的所有交点个数.(Ⅱ)对于(Ⅰ)中的m值,函数f(x)=sinmx,时,不等式log a x >sinmx恒成立,求实数a的取值范围.【考点】3O:函数的图象.【分析】(I)根据正弦函数的性质可知正格点交点坐标为(10,1),从而求出m的值,根据图象判断交点个数.(II)令y=log a x的最小值大于f(x)的最大值即可.【解答】解:(Ⅰ)若y=sinmx与函数y=lgx的图象有正格点交点,则此交点必为(10,1),∴sin10m=1,即10m=+2kπ,m=+,k∈Z.∵m∈(3,4),∴.作出y=sinmx与y=lgx的函数图象,如图所示:根据图象可知:两个函数图象的所有交点个数为10个.(Ⅱ)由(Ⅰ)知,x∈(0,],i)当a>1时,不等式log a x<0,而sin>0,故不等式log a x>sinmx无解.ii)当0<a<1时,由图函数y=log a x在上为减函数,∵关于x的不等式log a x>sinmx在(0,]上恒成立,∴log a>1,解得:.综上,.【点评】本题考查了方程的解与函数图象的关系,函数恒成立问题与函数最值计算,属于中档题.。
最新版福建省福州市第八中学高一数学下学期期末考试试题

福州市2014-2015高一数学第二学期期末试题(带答案)必修4考试时间:120分钟 试卷满分:150分2015.7.7A 卷(共100分)一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知α为第二象限角,54sin =α,则=-)2sin(απ A .2425- B .2425 C .1225D .1225-2. 已知函数()=sin f x x ,下列结论中错误的是A .()f x 既偶函数,又是周期函数.B. ()f xC. ()y f x =的图像关于直线2x π=对称D. ()y f x =的图像关于(),0π中心对称3. 设向量(2,0),(1,1)a b ==,则下列结论中正确的是A .2=⋅b aB .||||a b =C .a b ⊥D .//a b4. 若a =(2,1),b =(3,4),则向量a 在向量b 方向上的投影为A .52B. 2C. 5D. 105.已知αtan ,且0απ∈-(,),则sin αα的值是A B .-3C D .36.函数()()1cos f x x x =的最小正周期为A .2πB .32π C .πD .2π 7.在△ABC 中,若tan A ·tan B <1,则△ABC 的形状是 A .锐角三角形 B .直角三角形 C .钝角三角形 D .可能是锐角三角形,也可能是钝角三角形 8.已知函数()()sin f x x ωϕ=A +(0A >,0ω>,2πϕ<)的部分图象如图所示,则ϕ=C A .6π B .3πC .6π-D .3π-9.如图,BC 是单位圆A 的一条直径, F 是线段AB 上的点,且2BF FA =,若DE 是圆A 中绕圆心A 运动的一条直径,则FE FD ∙的值是A.34- B. 89- C. 14- D. 不确定 10.设函数()()sin cos 0f x x x ωωω=+>的最小正周期为π,将()y f x =的图象向左平移8π个单位得函数()y g x =的图象,则A. ()02g x π⎛⎫ ⎪⎝⎭在,上单调递减B. ()344g x ππ⎛⎫⎪⎝⎭在,上单调递减C. ()02g x π⎛⎫ ⎪⎝⎭在,上单调递增D. ()344g x ππ⎛⎫⎪⎝⎭在,上单调递增二、填空题(本大题共4小题,每小题4分,共16分。
2016-2017年福建省福州八中高一(下)期末数学试卷(解析版)

2016-2017学年福建省福州八中高一(下)期末数学试卷一、选择题:(本大题共10小题,每小题5分,共50分)1.(5分)化简cos15°cos45°﹣cos75°sin45°的值为()A.B.C.﹣D.﹣2.(5分)设a n=(n∈N*),则a3=()A.B.C.D.3.(5分)若AD是△ABC的中线,已知=,,则等于()A.B.C.D.4.(5分)若递增等比数列{a n}的前n项和为S n,a2=2,S3=7,则公比q等于()A.2B.C.2或D.无法确定5.(5分)若将函数f(x)=2sin x cos x﹣2sin2x+1的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最大负值是()A.﹣B.﹣C.﹣D.﹣6.(5分)已知,若,则实数对(λ1,λ2)为()A.(1,1)B.(﹣1,1)C.(﹣1,﹣1)D.无数对7.(5分)在△ABC中,,则这个三角形一定是()A.等腰三角形B.直角三角形C.等腰直角三角D.等腰或直角三角形8.(5分)已知α为锐角,且,则cos2α=()A.B.C.D.9.(5分)已知x=是函数f(x)=sin(2x+φ)+cos(2x+φ)(0<φ<π)图象的一条对称轴,将函数f(x)的图象向右平移个单位后得到函数g(x)的图象,则函数g(x)在[﹣,]上的最小值为()A.﹣2B.﹣1C.﹣D.﹣10.(5分)平面上有四个互异点A、B、C、D,已知(,则△ABC的形状是()A.直角三角形B.等腰直角三角形C.等腰三角形D.无法确定二、填空题:(本大题4小题,每小题5分,共20分)11.(5分)已知tan(α+β)=3,tan(α﹣β)=2,则tan2α的值为.12.(5分)如图,一栋建筑物AB高(30﹣10)m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处测得对塔顶C的仰角为30°,则通信塔CD的高为m.13.(5分)D、E、F分别为△ABC的边BC、CA、AB上的中点,且,给出下列命题:①;②;③;④,其中正确命题的序号为.14.(5分)数列{a n}中,,则a10=.三、解答题:(本大题3个小题,共30分)15.(10分)已知向量,的夹角为120°,且||=2,||=3.求:(Ⅰ)•;(Ⅱ)|+2|.16.(10分)已知等差数列{a n}的前n项和S n满足S3=0,S5=﹣5.(1)求{a n}的通项公式;(2)求a1+a4+a7+…+a3n+1.17.(10分)在△ABC中,BC边上的中线AD长为3,且BD=2,sin B=.(Ⅰ)求sin∠BAD的值;(Ⅱ)求AC的长.一、选择题:(本大题2个小题,每小题5分,共10分)18.(5分)将石子摆成如图的梯形形状,称数列5,9,14,20,…为梯形数,根据图形的构成,此数列的第2 012项与5的差即a2012﹣5=()A.2 018×2 012B.2 018×2 011C.1 009×2 012D.1 009×2 01119.(5分)已知向量满足,若M为AB的中点,并且,则λ+μ的最大值是()A.B.C.D.二、填空题:(本大题5分)20.(5分)给出四个命题:(1)若sin2A=sin2B,则△ABC为等腰三角形;(2)若sin A=cos B,则△ABC为直角三角形;(3)若sin2A+sin2B+sin2C<2,则△ABC为钝角三角形;(4)若cos(A﹣B)cos(B﹣C)cos(C﹣A)=1,则△ABC为正三角形,以上正确命题的是.三、解答题:(本大题3个小题,共35分)21.(11分)已知等差数列{a n}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.(1)求{a n}的通项公式a n与前n项和公式S n;(2)令b n=,若{b n}是等差数列,求数列{}的前n项和T n.22.(12分)已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足a sin A﹣c sin C =b(sin A﹣sin B).(Ⅰ)求角C的大小;(Ⅱ)若边长c=4,求△ABC的周长最大值.23.(12分)已知=(sin x,cos x),=(cosφ,sinφ)(|φ|<).函数f(x)=•且f(﹣x)=f(x).(1)求f(x)的解析式及单调递增区间:(2)将f(x)的图象向右平移单位得g(x)的图象,若g(x)+1≤ax+cos x在x∈[0,]上恒成立,求实数a的取值范围.2016-2017学年福建省福州八中高一(下)期末数学试卷参考答案与试题解析一、选择题:(本大题共10小题,每小题5分,共50分)1.(5分)化简cos15°cos45°﹣cos75°sin45°的值为()A.B.C.﹣D.﹣【解答】解:cos15°cos45°﹣cos75°sin45°=cos15°cos45°﹣sin15°sin45°=cos(15°+45°)=cos60°=故选:A.2.(5分)设a n=(n∈N*),则a3=()A.B.C.D.【解答】解:由题意,a n=(n∈N*),可知当n=3时,可得a3=,故选:D.3.(5分)若AD是△ABC的中线,已知=,,则等于()A.B.C.D.【解答】解:∵AD是△ABC的中线,∴根据向量加法的四边形法则得,=,∵=,,∴=.故选:B.4.(5分)若递增等比数列{a n}的前n项和为S n,a2=2,S3=7,则公比q等于()A.2B.C.2或D.无法确定【解答】解:由题意可得,,化简可得2﹣5q+2q2=0,解得q=2,或q=(舍去),故选:A.5.(5分)若将函数f(x)=2sin x cos x﹣2sin2x+1的图象向右平移φ个单位,所得图象关于y轴对称,则φ的最大负值是()A.﹣B.﹣C.﹣D.﹣【解答】解:f(x)=2sin x cos x﹣2sin2x+1,=sin2x+cos2x,=,把函数的图象向右平移∅个单位,得到的图象关于y轴对称,令:﹣2∅+=(k∈Z),解得:∅=(k∈Z),当k=0时,∅=﹣,故选:A.6.(5分)已知,若,则实数对(λ1,λ2)为()A.(1,1)B.(﹣1,1)C.(﹣1,﹣1)D.无数对【解答】解:∵=(2λ1+λ2,λ1+3λ2),,∴,解得.∴实数对(λ1,λ2)=(﹣1,1).故选:B.7.(5分)在△ABC中,,则这个三角形一定是()A.等腰三角形B.直角三角形C.等腰直角三角D.等腰或直角三角形【解答】解:在△ABC中,,由正弦定理可得:sin A=2sin B cos C,又sin A=sin(B+C)=sin B cos C+cos B sin C,∴cos B sin C=sin B cos C,可得tan C=tan B,∴A=B.∴a=b.则这个三角形一定是等腰三角形.故选:A.8.(5分)已知α为锐角,且,则cos2α=()A.B.C.D.【解答】解:∵0<α<,,∴可得:<α+<,∴sin(α+)=,∴sinα=sin[(α+)﹣]=sin(α+)cos﹣cos(α+)sin=﹣=,∴cos2α=1﹣2sin2α=1﹣2×()2=.故选:A.9.(5分)已知x=是函数f(x)=sin(2x+φ)+cos(2x+φ)(0<φ<π)图象的一条对称轴,将函数f(x)的图象向右平移个单位后得到函数g(x)的图象,则函数g(x)在[﹣,]上的最小值为()A.﹣2B.﹣1C.﹣D.﹣【解答】解:已知x=是函数f(x)=sin(2x+φ)+cos(2x+φ)=2sin(2x+φ+)(0<φ<π)图象的一条对称轴,∴2×+φ+=kπ+,k∈Z,∴φ=,即f(x)=2sin(2x+).将函数f(x)=2sin(2x+)的图象向右平移个单位后,得到函数g(x)=2sin[2(x﹣)+]=2sin(2x﹣)=2sin(2x﹣)=﹣2sin (2x﹣)的图象,在[﹣,]上,2x﹣∈[﹣,],故当2x﹣=时,g(x)取得最小值为﹣1,故选:B.10.(5分)平面上有四个互异点A、B、C、D,已知(,则△ABC的形状是()A.直角三角形B.等腰直角三角形C.等腰三角形D.无法确定【解答】解:∵(,∴(+)•(﹣)=0,可得=.可得AB=AC.则△ABC的形状是等腰三角形.故选:C.二、填空题:(本大题4小题,每小题5分,共20分)11.(5分)已知tan(α+β)=3,tan(α﹣β)=2,则tan2α的值为﹣1.【解答】解:∵tan(α+β)=3,tan(α﹣β)=2,∴tan(2α)=tan[(α+β)+(α﹣β)]===﹣1.故答案为:﹣1.12.(5分)如图,一栋建筑物AB高(30﹣10)m,在该建筑物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处测得对塔顶C的仰角为30°,则通信塔CD的高为60 m.【解答】解:设AE⊥CD,垂足为E,则在△AMC中,AM==20,∠AMC=105°,∠C=30°,∴,∴AC=60+20,∴CE=30+10,∴CD=30﹣10+30+10=60,故答案为:60.13.(5分)D、E、F分别为△ABC的边BC、CA、AB上的中点,且,给出下列命题:①;②;③;④,其中正确命题的序号为②③④.【解答】解:①=,故①不正确;②==,故②正确;③=,故③正确;④将三个向量的结果代入知成立.故④正确.故②③④正确故答案为②③④.14.(5分)数列{a n}中,,则a10=.【解答】解:数列{a n}中,,取倒数可得:﹣=3,∴数列{}是等差数列,首项为,公差为3.则==.解得:a10=.故答案为:.三、解答题:(本大题3个小题,共30分)15.(10分)已知向量,的夹角为120°,且||=2,||=3.求:(Ⅰ)•;(Ⅱ)|+2|.【解答】解:(Ⅰ)=2×3×cos120°=﹣3.(Ⅱ)|+2|2=+4+4=28,∴|+2|=2.16.(10分)已知等差数列{a n}的前n项和S n满足S3=0,S5=﹣5.(1)求{a n}的通项公式;(2)求a1+a4+a7+…+a3n+1.【解答】解:(1)由等差数列的性质可得,解得a1=1,d=﹣1,则{a n}的通项公式a n=1﹣(n﹣1)=2﹣n;(2)∵{a n}为等差数列,∴a1+a4+a7+…+a3n+1以1为首项,以﹣3为公差的等差数列,∵(3n+1﹣1)+1=n+1∴a1+a4+a7+…+a3n+1=n+1+=17.(10分)在△ABC中,BC边上的中线AD长为3,且BD=2,sin B=.(Ⅰ)求sin∠BAD的值;(Ⅱ)求AC的长.【解答】(本小题10分)解:(Ⅰ)在△ABD中,BD=2,sin B=,AD=3,∴由正弦定理=,得sin∠BAD═==;…(4分)(Ⅱ)∵sin B=,∴cos B=,…(5分)∵sin∠BAD=,∴cos∠BAD=,…(6分)∴cos∠ADC=cos(∠B+∠BAD)=×﹣×=﹣,…(7分)∵D为BC中点,∴DC=BD=2,∴在△ACD中,由余弦定理得:AC2=AD2+DC2﹣2AD•DC cos∠ADC=9+4+3=16,…(9分)∴AC=4.…(10分)一、选择题:(本大题2个小题,每小题5分,共10分)18.(5分)将石子摆成如图的梯形形状,称数列5,9,14,20,…为梯形数,根据图形的构成,此数列的第2 012项与5的差即a2012﹣5=()A.2 018×2 012B.2 018×2 011C.1 009×2 012D.1 009×2 011【解答】解:由已知的图形我们可以得出图形的编号与图中石子的个数之间的关系为:n=1时,a1=2+3=×(2+3)×2;n=2时,a2=2+3+4=×(2+4)×3;…由此我们可以推断:a n=2+3+…+(n+2)=[2+(n+2)]×(n+1)∴a2012﹣5=×[2+(2012+2)]×(2012+1)﹣5=1 009×2 011.故选:D.19.(5分)已知向量满足,若M为AB的中点,并且,则λ+μ的最大值是()A.B.C.D.【解答】解:如图所示,∵向量满足=1,,不妨取A(1,0),B(0,1).∵M为AB的中点,∴M.∵=λ(1,0)+μ(0,1)=(λ,μ).∵,∴=1,设,μ=+sinθ,θ∈[0,2π).则λ+μ=1+sinθ+cosθ=1+,当=1时取等号.∴λ+μ的最大值是1+.故选:B.二、填空题:(本大题5分)20.(5分)给出四个命题:(1)若sin2A=sin2B,则△ABC为等腰三角形;(2)若sin A=cos B,则△ABC为直角三角形;(3)若sin2A+sin2B+sin2C<2,则△ABC为钝角三角形;(4)若cos(A﹣B)cos(B﹣C)cos(C﹣A)=1,则△ABC为正三角形,以上正确命题的是(3)(4).【解答】解:(1)若sin2A=sin2B,∵A,B∈(0,π),∴2A=2B,或2A+2B=π,解得A =B,或A+B=,则△ABC为等腰三角形或直角三角形,因此不正确;(2)若sin A=cos B=,∵A,B∈(0,π),∴A=﹣B,或A+﹣B=π,解得A+B=或,则△ABC为钝角三角形或直角三角形,因此不正确;(3)∵sin2A+sin2B+sin2C<2,∴++<2,化为cos2A+cos2B+cos2C>﹣1,∴2cos2A+2cos(B+C)cos(B﹣C)>0,∴cos A[﹣cos(B+C)﹣cos(B﹣C)]>0,∴cos A cos B cos C<0,因此△ABC为钝角三角形,正确;(4)若cos(A﹣B)cos(B﹣C)cos(C﹣A)=1,∵cos(A﹣B)∈(﹣1,1],cos(B﹣C)∈(﹣1,1],cos(C﹣A)∈(﹣1,1],可知:只有三个都等于1,又A,B,C∈(0,π),∴A﹣B=B﹣C=C﹣A=0,∴A=B=C,则△ABC为正三角形,正确.以上正确的命题是:(3)(4).故答案为:(3)(4).三、解答题:(本大题3个小题,共35分)21.(11分)已知等差数列{a n}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.(1)求{a n}的通项公式a n与前n项和公式S n;(2)令b n=,若{b n}是等差数列,求数列{}的前n项和T n.【解答】解:(1)∵a1+a4=14,∴2a1+3d=14,①∵a1,a2,a7成等比数列,∴,即,②由①②得d2=4a1d,∵d≠0,∴d=4a1,代入①解得d=4、a1=1,∴a n=a1+(n﹣1)d=4n﹣3,S n==2n2﹣n;(2)由(1)知,∵{b n}是为等差数列,∴2b2=b1+b3,即=,解得,或k=0(8分),①当时,即b n=2n,则∴=(10分)②当k=0时,b n=2n﹣1,则=,∴=,综上可得,T n=或.(12分)22.(12分)已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足a sin A﹣c sin C =b(sin A﹣sin B).(Ⅰ)求角C的大小;(Ⅱ)若边长c=4,求△ABC的周长最大值.【解答】解:(Ⅰ)已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足a sin A﹣c sin C=b(sin A﹣sin B).利用正弦定理得:a2﹣c2=b(a﹣b),整理得:,由于0<C<π,则:C=.(Ⅱ)由于:C=,c=4,A+B=,则:,整理得:,=,所以:a+b+c=4+,=,由于:,则:,解得:所以:△ABC的周长最大值为12.23.(12分)已知=(sin x,cos x),=(cosφ,sinφ)(|φ|<).函数f(x)=•且f(﹣x)=f(x).(1)求f(x)的解析式及单调递增区间:(2)将f(x)的图象向右平移单位得g(x)的图象,若g(x)+1≤ax+cos x在x∈[0,]上恒成立,求实数a的取值范围.【解答】解:(1)∵f(x)=•=sin x cosφ+cos x sinφ=sin(x+φ),再由f(﹣x)=f(x)可知函数f(x)的图象关于直线x=对称,∴+φ=+kπ,k∈Z,又|φ|<,∴φ=∴f(x)=sin(x+),由2kπ﹣≤x+≤2kπ+可得2kπ﹣≤x≤2kπ+,∴函数的递增区间为[2kπ﹣,2kπ+],k∈Z;(2)由图象平移易知g(x)=sin x,即sin x+1≤ax+cos x在x∈[0,]上恒成立.也即sin x﹣cos x≤ax﹣1在x∈[0,]上恒成立令h(x)=sin x﹣cos x=sin(x﹣),x∈[0,];φ(x)=ax﹣1如下图:h(x)的图象在φ(x)图象的下方,则:a≥k AB==,故a≥。
福建省福州八中高一下学期期末考试数学

福建省福州八中高一下学期期末考试数学集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#福州八中2008—2009学年第二学期期末考试高一数学 必修Ⅳ考试时间:120分钟 试卷满分:150分命题:尹慧仙 审核:陈文清 校对:郑敏 第Ⅰ卷(100分)一、选择题:(每小题5分,共50分) 1.下列等式中成立的是A .si n (2×360°-40°)=si n 40°B .cos (3π+4π)=cos 4πC .cos370°=cos (-350°)D .cos625π=cos (-619π)2.等腰梯形ABCD 中,对角线AC 与BD 交于点P ,点E 、F 分别在两腰,AD 、BCB.12上,EF 过点P ,且EF BC AD =BD AC =PF PE =PF EP =14 4.以下四个命题正确的序号是(1)若ABCD DC AB 则,=是平行四边形;(2)若四边形ABCD 是平行四边形,则DC AB =;(3)若c a c b b a ===则,,; (4)若.//,//,//c a c b b a 则 A.(1)(2)(3) B. (2)(3)C. (2)(3) (4)D.(1) (2)(3) (4)5. 函数y=ta n (x -4π)的定义域是 A. {x≠43π+kπ,k ∈Z}B. {x|x=43π+kπ,k ∈Z}C. {x|x≠43π+kπ} D. {x ∈R |x≠43π+kπ,k ∈Z}6.下列函数中,在区间02⎛⎫ ⎪⎝⎭π,上为增函数且以π为周期的函数是A .sin2xy = B .sin y x =C .tan2xy = D .cos 2y x =- 7. 已知221224(,),(x,x ),(x x,)=-==-a b c ,若//,⊥a b a c ,则x=A. x=0或x =-2或x =4B. x=0或x =-2C. x =-2或x =4D. x =-28.若3f (cos x )cos x,=则30f (sin )=A.-1C. 129.与向量a = (12,5) 平行的单位向量为 A .1251313⎛⎫ ⎪⎝⎭,-B .1251313⎛⎫- ⎪⎝⎭,-C .1251313⎛⎫ ⎪⎝⎭, 或1251313⎛⎫- ⎪⎝⎭,- D .1251313⎛⎫- ⎪⎝⎭, 或1251313⎛⎫ ⎪⎝⎭,- 10.已知函数1tan sin )(++=x b x a x f ,满足.7)5(=f 则)5(-f 的值为A .5B .-5C .6D .-6二、填空题(每空4分,共24分)11.如图,是函数()ϕω+=x A y sin (其中πϕπω<<->>,0,0A )的一个周期内的图象,则函数的解析式为 . 12.函数y =cos(4π-2x )的单调递增区间是 . 13. 已知33cos ,,tan 524⎛⎫=-<<- ⎪⎝⎭πθπθπθ则且= ,而且sin 2cos 3sin 5cos -+=αααα . 14.在△ABC 中,已知15,3,5,2AB CA AB AC BAC ⋅∠===则= ,那么向量AB 在向量AC 上的投影为 .三、解答题(第15题8分、第16题、第17题各9分,,共26题) 15.以填图方式解答变换方法或所得函数解析式.sin()5y x =-π函数sin y x =.sin(2)5y x π=-..第11题16. 已知向量a =(cos ,sin αα),b =(cos ,sin ββ).(1)求(2)⋅+a a b 的取值范围; (2)若3παβ-=,求2a b +.17.已知函数22()(sin cos )2cos f x x x x =++,(1)求函数f (x)的最小正周期;(2)求函数f (x)的最大值和最小值,以及取得最值时的x 的集合;(3)求函数f (x)的单调递减区间.第Ⅱ卷(50分)四、填空题(每空4分,共20分) 18. 右上程序执行后输出的结果是__ __. 19.函数223y cos(x )π=--的定义域 A= ; 若x ∈A ,则函数22233g(x )cos(x )sin (x )ππ=---+的最小值为 .20.已知腰BC=5,底边AC=6的等腰△ABC ,沿高BD 折起成直二面角,如图,则折成的几何体的体积为 ,二面角B -AC -D 的正切值为 . 五、解答题(每题10分,共30分)21. (本小题满分10分) △ABC 中三个内角为A 、B 、C ,若关于x 的方程22cos cos cos 02Cx x A B --=有一根为1,试判断△ABC 的形状,并证明你的结论. 22. (本小题满分10分)设ABC △的内角A B C ,,所对的边长分别为a b c ,,,且cos 3a B =,sin 4b A =. (Ⅰ)求tanB 和边长a ;(Ⅱ)若ABC △的面积10S =,求ABC △的周长l . 23. (本题满分10分)已知△ABC 的顶点坐标为A (1,0),B (5,8),C (7, -4),在边AB 上有一点P ,其横坐标为4. (1)设AB AP λ=,求实数λ;(2)在边AC 上求一点Q ,使线段PQ 把△ABC 分成面积相等的两部分.Luoying123福州八中2008—2009学年第二学期期末考试高一数学必修Ⅳ试卷参考答案及评分标准12cos cos cos()A B A B ⇒=-+…4分12cos cos cos cos sin sin 1cos cos sin sin A B A B A B A B A B ⇒=-+⇒=-…6分;1cos(A B )∴-=,…7分又0<A<π, -π<-B<0,得-π<A -B <π, 所以A -B=0,即A=B …….10分22.解:(1)由cos 3a B =与sin 4b A =两式相除,有:4sin sin sin tan 3cos cos cos b A A b B b B a Ba BbB====…2分又tan 0B >, 则3cos 5B =……4分,得5a =.……5分(2)3cos 5B =>0,得4sin 5B =, ……6分由1sin 2S ac B =,得到5c =(或11sin (sin )210522S bc A c b A c c ====⇒=).…7分;由222cos 2a c b B ac+-=,解得:25b =,……9分;所以1025l =+.……10分。
福建省福州八中2016—2017学年高二下学期期末考试数学(文)试题

福州八中2016—2017学年第二学期期末考试高二数学(文)考试时间:120分钟 试卷满分:150分2017.6.10第Ⅰ卷一、选择题(本大题共8小题,每小题5分,共40分.每题有且只有一个选项是正确的,请把答案填在答卷相应位置上) 1.已知集合A={x|x 2-3x-4≤0},B={x|-2<x≤2},那么A∩(∁R B)等于 A. (2,4]B. [-1,2]C. [-2,-1]∪[2,4]D. [-1,2)∪(2,4]2. 若函数f(x)=⎩⎨⎧x 2+1,x≤1,lg x ,x>1,则f(f(10))=A .lg101B .1C .2D .03.下列函数为奇函数的是 A .y =x 2+2xB .y =x 3sinxC .y =2cosx +1D .y =2x -12x 4.设a =log 37,b =21.1,c =0.83.1,则A .c<a<bB .b<a<cC .c<b<aD .a<c<b5.函数y =2log 4(1-x)的图象大致是6.如果函数f(x)=x 2+bx +c 对于任意实数t ,都有f(2+t)=f(2-t),那么A. f(2)<f(1)<f(4)B. f(1)<f(2)<f(4)C. f(2)<f(4)<f(1)D. f(4)<f(2)<f(1)7.指数函数y=f(x)的反函数的图象过点(2,-1),则此指数函数为 A. x y 3=B.x y 2=C. x y )21(=D.x y 10=8. 能够把圆O :x 2 +y 2= 16的周长和面积同时分为相等的两部分的函数称为圆O 的“和谐函数”,下列函数不是圆O 的“和谐函数”的是 A .()x x f x e e -=- B .()1[(4)(4)]f x n x x =-+C .3()f x x =D . ()tan2x f x = 二、填空题(本大题共4小题,每小题6分,共24分) 9. 函数f (x )=x log 219-的定义域为_____ ___ 10.若3log a 4=,则2a +2-a =___ _____ 11. 幂函数223()(1)mm f x m m x +-=--在(0,)+∞上为增函数,则m =12. 若函数f(x)是定义在R 上的偶函数,且在区间[0,+∞)上是单调增函数.如果实数t 满足f(ln t)+f ⎝⎛⎭⎫ln 1t <2f(1)时,那么t 的取值范围是____ __三、解答题(本大题共有3个小题,共36分.解答应写出文字说明、演算步骤或证明过程.)13.(本小题满分12分)(1)设x >0,求y =x +4x 2的最小值; (2)已知x +y =1,求2x 2+3y 2的最小值.14. (本小题满分 12 分)函数f(x)的定义域为(0,+∞),且对一切x>0,y>0都有f ⎝⎛⎭⎫xy =f(x)-f(y),当x>1时,有f(x)>0.(1)求f(1)的值;(2)判断f(x)的单调性并加以证明; (3)若f(4)=2,求f(x)在[1,16]上的值域.15.(本小题满分12分)已知函数f(x)=()kx 14log x 4++(k ∈R)是偶函数. (1)求k 的值;(2)设g(x)=⎪⎪⎭⎫⎝⎛-⋅a 342a log x 4,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a 的取值范围.第Ⅱ卷一、选择题(本大题共4小题,每小题4分,共16分.每题有且只有一个选项是正确的,请把答案填在答卷相应位置上)16. 定义在R 上的函数f(x)满足f(-x)=-f(x),f(x -2)=f(x +2),且x ∈(-1,0)时,f(x)=2x +15,则f(log 220)= A .1B.45C .-1D .-4517.若函数y=f(x)(x ∈R )满足f(x+2)=f(x),且x ∈(-1,1]时f(x)=1-x 2,函数g(x)=lg ,0,1,0,x x x ≠⎧⎨=⎩,则函数h(x)=f(x)-g(x)在区间[-5,10]内零点的个数为 A.15B.14C.13D.1218. 若2x +5y ≤2-y +5-x ,则有( ) A .x +y≥0B .x +y≤0C .x -y≤0D .x -y≥019. 已知e 为自然对数的底数,若对任意的1[,1]x e∈,总存在唯一的[1,1]y ∈-,使得2ln 1y x x a y e -++=成立,则实数a 的取值范围是 A. 2(,)e+∞ B. 21(,)e e e +C.1[,]e eD. 2(,]e e二、填空题(本大题共2小题,每小题4分,共8分) 20.若f(x)对于任意实数x 恒有2f(x)-f(-x)=3x +1,则f(x)=21. 对任意实数21,x x ,min(21,x x )表示21,x x 中较小的那个数,若x x g x x f =-=)(,2)(2,则))(),(min(x g x f 的最大值是__________三、解答题(本大题共有2个小题,共26分.解答应写出文字说明、演算步骤或证明过程.)22.(本小题满分13分)已知函数f(x)=sinx ,g(x)=mx -x 36(m 为实数). (1)求曲线y =f(x)在点P(π4,f(π4))处的切线方程; (2)求函数g(x)的单调递减区间;(3)若m =1,证明:当x>0时,f(x)<g(x)+x 36.23. (本小题满分13分)已知函数2(1)()()x x a f x x++=为偶函数. (1)求实数a 的值;(2)记集合E ={y|y =f(x),x ∈{-1,1,2}},λ=lg 22+lg2lg5+lg5-14,判断λ与E 的关系;(3)当x ∈[1m ,1n ](m>0,n>0)时,若函数f(x)的值域为[2-3m,2-3n],求m ,n 的值.福州八中2016—2017学年第二学期期末考试高二数学(文) 试卷参考答案及评分标准第Ⅰ卷一、选择题:本大题共8小题,每小题5分,共40分 1-8 ACDA CACB二、填空题:本大题共4小题,每小题6分,共24分 9. (0,3] 10. 433 11. 2 12. ⎝⎛⎭⎫1e ,e三、解答题:本大题共有3个小题,共36分 13.(本小题满分12分)解:(1) y =x +4x 2=x 2+x 2+4x 2≥3·3x 2·x 2·4x2=3, …………4分当且仅当x 2=4x 2时取“=”号. …………6分(2)由柯西不等式(2x 2+3y 2)·⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫132≥⎝⎛⎭⎪⎫2x ·12+3y·132= (x +y)2=1,…………10分所以2x 2+3y 2≥65,当且仅当2x =3y ,即x =35,y =25时,等号成立.所以2x 2+3y 2的最小值为65. …………12分14. (本小题满分12分) 解:(1)∵当x>0,y>0时,f ⎝ ⎛⎭⎪⎫x y =f(x)-f(y),∴令x =y>0,则f(1)=f(x)-f(x)=0. …………3分(2)设x 1,x 2∈(0,+∞),且x 1<x 2,则f(x 2)-f(x 1)=f ⎝ ⎛⎭⎪⎫x 2x 1,…………5分 ∵x 2>x 1>0.∴x 2x 1>1,∴f ⎝ ⎛⎭⎪⎫x 2x 1>0. …………6分 ∴f(x 2)>f(x 1),即f(x)在(0,+∞)上是增函数.…………7分 (3)由(2)知f(x)在[1,16]上是增函数.∴f(x)min =f(1)=0,f(x)max =f(16), …………9分∵f(4)=2,由f ⎝ ⎛⎭⎪⎫x y =f(x)-f(y),知f ⎝ ⎛⎭⎪⎫164=f(16)-f(4),∴f(16)=2f(4)=4,∴f(x)在[1,16]上的值域为[0,4]. …………12分15.(本小题满分12分)解: (1)由函数f(x)是偶函数可知,f(x)=f(-x),…………1分所以log 4(4x+1)+kx =log 4(4-x+1)-kx , 所以log 44x+14+1=-2kx ,…………3分即x =-2kx 对一切x∈R 恒成立,所以k =-12.…………5分(2)函数f(x)与g(x)的图象有且只有一个公共点,即方程log 4(4x+1)-12x =log 4⎝ ⎛⎭⎪⎫a·2x -43a 有且只有一个实根,即方程2x +12x =a·2x-43a 有且只有一个实根.…………6分令t =2x >0,则方程(a -1)t 2-43at -1=0有且只有一个正根.…………7分①当a =1时,则t =-34,不合题意;…………8分②当a≠1时,Δ=0,解得a =34或-3.若a =34,则t =-2,不合题意;若a =-3,则t =12;…………10分③若方程有一个正根与一个负根,即-1a -1<0,解得a>1. …………11分综上所述,实数a 的取值范围是{-3}∪(1,+∞).…………12分第Ⅱ卷高二数学(文)期末考试卷答案 第1页 共3页一、选择题:本大题共4小题,每小题4分,共16分 16-19 CBBD二、填空题:本大题共2小题,每小题4分,共8分 20. x +1 21. 1三、解答题: 本大题共有2个小题,共26分 22. (本小题满分13分)解: (1)由题意得所求切线的斜率k =f′(π4)=cos π4=22…………2分切点P(π4,22),则切线方程为y -22=22(x -π4), …………3分即x -2y +1-π4=0. …………4分(2)g′(x)=m -12x 2.①当m≤0时,g′(x)≤0,则g(x)的单调递减区间是(-∞,+∞);…………6分 ②当m>0时,令g′(x)<0,解得x<-2m 或x>2m ,则g(x)的单调递减区间是(-∞,-2m),(2m ,+∞).…………8分 (3)证明:当m =1时,g(x)=x -x36.令h(x)=x -sinx ,x ∈[0,+∞),h′(x)=1-cosx≥0,…………10分 则h(x)是[0,+∞)上的增函数.故当x>0时,h(x)>h(0)=0, …………12分 即sinx<x ,f(x)<g(x)+x36. …………13分23. (本小题满分13分)解: (1)∵f (x )为偶函数,∴f (x )=f (-x ),…………1分∴(x +1)(x +a )x 2=(-x +1)(-x +a )x 2, ∴2(a +1)x =0,∵x ∈R 且x ≠0,∴a =-1. …………4分(2)由(1)可知:f(x)=x 2-1x2,当x =±1时,f(x)=0;当x =2时,f(x)=34,∴E ={0,34}. …………6分∵λ=lg 22+lg2lg5+lg5-14=lg2(lg2+lg5)+lg5-14=lg2+lg5-14=lg10-14=34,∴λ∈E. …………8分(3)∵f (x )=x 2-1x 2=1-1x 2,x ∈[1m ,1n ],∴f ′(x )=2x 3>0,…………9分 ∴f (x )在[1m ,1n ]上单调递增. ∴⎩⎪⎨⎪⎧f (1m )=2-3m ,f (1n )=2-3n ,∴⎩⎨⎧1-m 2=2-3m ,1-n 2=2-3n .…………11分 ∴m ,n 为x 2-3x +1=0的两个根, 又由题意可知:1m <1n ,且m >0,n >0,∴m >n . ∴m =3+52,n =3-52. …………13分。
2016-2017学年福建省福州市八县(市)一中高一(下)期末数学试卷

2016-2017学年福建省福州市八县(市)一中高一(下)期末数学试卷一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)若扇形的半径为6cm,所对的弧长为2πcm,则这个扇形的面积是()A.12πcm2B.6 cm2C.6πcm2D.4 cm22.(5分)在△ABC中,若,∠B=90°则m=()A.﹣ B.C.﹣ D.3.(5分)若,则tanα的值是()A.B.C.1 D.以上答案都不对4.(5分)在△ABC中,角A,B,C所对的边分别是a,b,c,若sinA=sinC,b2﹣a2=ac,则∠A=()A.B.C.D.5.(5分)cos43°cos77°+sin43°cos167°的值是()A.B.C.D.6.(5分)以下关于向量说法的四个选项中正确的选项是()A.若任意向量共线且为非零向量,则有唯一一个实数λ,使得B.对于任意非零向量,若,则C.任意非零向量满足,则同向D.若A,B,C三点满足,则点A是线段BC的三等分点且离C点较近7.(5分)在△ABC中,利用正弦定理解三角形时,其中有两解的选项是()A.a=3,b=6,A=30°B.a=6,b=5,A=150°C.D.8.(5分)已知,则=()A.B.C.D.﹣9.(5分)已知△ABC满足,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则的值为()A.﹣ B.C.﹣2 D.10.(5分)若函数y=Asin(ωx+φ)在一个周期内的图象如图所示,且在,M,N分别是这段图象的最高点和最低点,则方向上的投影为()A.B.C.﹣D.11.(5分)下列对于函数f(x)=2+2cos2x,x∈(0,3π)的判断不正确的是()A.对于任意x∈(0,3π),都有f(x1)≤f(x)≤f(x2),则|x1﹣x2|的最小值为B.存在a∈R,使得函数f(x+a)为偶函数C.存在x0∈(0,3π),使得f(x0)=4D.函数f(x)在区间内单调递增12.(5分)在平面内,定点A,B,C,D满足,,动点M,N满足、=,则的最小值是()A.B.C. D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知角α的终边过点,则cosα的值为.14.(5分)平面上点O为坐标原点,A(0,2),B(1,0),C是平面上任意一点且满足,则C点坐标是.15.(5分)若,则sin2θ=.16.(5分)在下列五个命题中:①已知大小分别为1N与2N的两个力,要使合力大小恰为,则它们的夹角为;②已知,,则sinα<cosβ;③若A,B,C是斜△ABC的三个内角,则恒有tanA+tanB+tanC=tanAtanBtanC成立;④;⑤已知,则x的大小为;其中错误的命题有.(写出所有错误命题的序号)三、解答题:请在答题卡指定区域内作答,解答时应写出证明过程或演算步骤(17小题10分,18-22小题各12分,共70分).17.(10分)已知,且∥,设函数y=f(x)(Ⅰ)求函数y=f(x)的对称轴方程及单调递减区间;(Ⅱ)若,求函数y=f(x)的最大值和最小值并写出函数取最值时x的值.18.(12分)如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足=,=2,记,,试以为平面向量的一组基底.利用向量的有关知识解决下列问题;(Ⅰ)用来表示向量;(Ⅱ)若|AB|=3,|AD|=2,且|BF|=,求||.19.(12分)平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深y(米)是随着一天的时间t(0≤t≤24,单位小时)呈周期性变化,某天各时刻t的水深数据的近似值如表:(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从①y=Asin(ωt+ϕ),②y=Acos(ωt+ϕ)+b,③y=﹣Asinωt+b(A>0,ω>0,﹣π<ϕ<0).中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ)中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全.20.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.(Ⅰ)若b=6,求角C的余弦值;(Ⅱ)若点D,E在线段BC上,且BD=DE=EC,,求AD的长.21.(12分)设向量,函数.(Ⅰ)若ω是函数y=g(x)在上的零点,求sinω的值;(Ⅱ)设,,求sin(α+β)的值.22.(12分)已知O为坐标原点,对于函数f(x)=asinx+bcosx,称向量为函数f(x)的伴随向量,同时称函数f(x)为向量的伴随函数.(Ⅰ)设函数,试求g(x)的伴随向量;(Ⅱ)记向量的伴随函数为f(x),求当且时sinx的值;(Ⅲ)由(Ⅰ)中函数g(x)的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移个单位长度得到h(x)的图象.已知A(﹣2,3)B (2,6),问在y=h(x)的图象上是否存在一点P,使得.若存在,求出P点坐标;若不存在,说明理由.2016-2017学年福建省福州市八县(市)一中高一(下)期末数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)若扇形的半径为6cm,所对的弧长为2πcm,则这个扇形的面积是()A.12πcm2B.6 cm2C.6πcm2D.4 cm2【解答】解:∵扇形的弧长l为l=2πcm,半径r为r6cm,∴扇形的面积为S=lr==6πcm2.故选:C.2.(5分)在△ABC中,若,∠B=90°则m=()A.﹣ B.C.﹣ D.【解答】解:由已知得到=3﹣2m=0,所以m=;故选:D.3.(5分)若,则tanα的值是()A.B.C.1 D.以上答案都不对【解答】解:∵,可得:=2+,∴解得:tanα==.故选:A.4.(5分)在△ABC中,角A,B,C所对的边分别是a,b,c,若sinA=sinC,b2﹣a2=ac,则∠A=()A.B.C.D.【解答】解:∵在△ABC中,角A,B,C所对的边分别是a,b,c,sinA=sinC,∴由正弦定理得a=c,∵b2﹣a2=ac,∴b2=a2+c2,∴∠A=.故选:B.5.(5分)cos43°cos77°+sin43°cos167°的值是()A.B.C.D.【解答】解:cos43°cos77°+sin43°cos167°=cos43°cos77°+sin43°cos(90°+77°)=cos43°cos77°﹣sin43°sin77°=cos(43°+77°)=cos120°=﹣cos60°=﹣.故选:D.6.(5分)以下关于向量说法的四个选项中正确的选项是()A.若任意向量共线且为非零向量,则有唯一一个实数λ,使得B.对于任意非零向量,若,则C.任意非零向量满足,则同向D.若A,B,C三点满足,则点A是线段BC的三等分点且离C点较近【解答】解:对于A,共线且为非零向量,若=时,则不存在实数λ,使成立,∴A错误;对于B,对于任意非零向量,若,则﹣=0,即,∴B正确;对于C,任意非零向量满足,则它们夹角的余弦值cosθ=±1,∴同向或反向,C错误;对于D,如图所示,,∴+=+,∴(﹣)=(﹣),∴2=,∴点A是线段BC的三等分点且离B点较近,∴D错误.故选:B.7.(5分)在△ABC中,利用正弦定理解三角形时,其中有两解的选项是()A.a=3,b=6,A=30°B.a=6,b=5,A=150°C.D.【解答】解:对于A,由正弦定理可得:sinB===1,可得B为90°,C=60°,只有一解;对于B,由正弦定理可得:sinB===,b<a,可得B锐角,三角形只有一解;对于C,由正弦定理可得:sinB===2,可得这样的三角形无解;对于D,由正弦定理可得:sinB==,由b>a,可得B∈(30°,150°),有2解;故选:D.8.(5分)已知,则=()A.B.C.D.﹣【解答】解:∵已知=cos[﹣(﹣)]=cos(+),则=cos2(+)=2﹣1=2•﹣1=,故选:C.9.(5分)已知△ABC满足,点D、E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则的值为()A.﹣ B.C.﹣2 D.【解答】解:,可得•=4×2×cos=8×(﹣)=﹣4,由点D、E分别是边AB,BC的中点,可得=,由DE=2EF,可得==,则=(+)•(﹣)=(+)•(﹣)=﹣2+2+•=﹣×16+×4﹣×4=﹣4+3﹣=﹣.故选:A.10.(5分)若函数y=Asin(ωx+φ)在一个周期内的图象如图所示,且在,M,N分别是这段图象的最高点和最低点,则方向上的投影为()A.B.C.﹣D.【解答】解:根据函数y=Asin(ωx+φ)在一个周期内的图象,可得==3﹣1,∴ω=.再根据五点法作图可得•1+φ=,∴φ=,函数的解析式为y=Asin(x+).由于该函数在,∴Asin=,∴A=2,故函数的解析式为y=2sin (x+).∴M(1,2)、N(5,﹣2),∴=5﹣4=1.设方向上的投影为a,∵=1=a•||=a,∴a=,故选:B.11.(5分)下列对于函数f(x)=2+2cos2x,x∈(0,3π)的判断不正确的是()A.对于任意x∈(0,3π),都有f(x1)≤f(x)≤f(x2),则|x1﹣x2|的最小值为B.存在a∈R,使得函数f(x+a)为偶函数C.存在x0∈(0,3π),使得f(x0)=4D.函数f(x)在区间内单调递增【解答】解:f(x)=2+2cos2x=2+cos2x+1=3+cos2x,对于A,函数f(x)的周期为,对于任意x∈(0,3π),都有f(x1)≤f(x)≤f(x2),可知f(x1)是函数的最小值,f(x2)是函数的最大值,|x1﹣x2|的最小值就是函数的半周期,故A正确;对于B,不妨取a=π,则函数f(x+a)=3+cos(2x+2π)=3+cos2x为偶函数,故B 正确;对于C,x=π∈(0,3π),cos2x=1,f(x)=4,故存在x0∈(0,3π),使得f(x0)=4,故C正确;对于D,当x∈时,2x∈,此时函数不具备单调性,故D 不正确.∴对于函数f(x)=2+2cos2x,x∈(0,3π)的判断不正确的是:D.故选:D.12.(5分)在平面内,定点A,B,C,D满足,,动点M,N满足、=,则的最小值是()A.B.C. D.【解答】解:平面内定点A,B,C,D满足,,可设:D(0,0),A(2,0),B(﹣1,),C(﹣1,﹣),∵动点M,N满足||=2,=,可设N(2+2cosθ,2sinθ),由=得M(+cosθ,﹣+sinθ),∴=(cosθ﹣,sinθ﹣),∴=+=cos2θ﹣3cosθ++sin2θ﹣sinθ+=4﹣3cosθ﹣sinθ=4﹣2sin(θ+)≥4﹣2,当且仅当sin(θ+)=1时取等号,∴的最小值是4﹣2.故选:A.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知角α的终边过点,则cosα的值为﹣.【解答】解:∵角α的终边过点,∴x=tan=﹣1,y=2,r=|OP|=,∴cosα===﹣,故答案为:.14.(5分)平面上点O为坐标原点,A(0,2),B(1,0),C是平面上任意一点且满足,则C点坐标是(1,2).【解答】解:由平面上点O为坐标原点,A(0,2),B(1,0),C是平面上任意一点,得=(0,﹣2)+2(1,0)+(﹣1,2)=(1,0),设C(x,y),A(0,2),则=(x,y﹣2)=(1,0),∴x=1,y=2.则C点坐标是:(1,2).故答案为:(1,2).15.(5分)若,则sin2θ=﹣.【解答】解:若=,则tanθ=﹣4,∴sin2θ====﹣,故答案为:.16.(5分)在下列五个命题中:①已知大小分别为1N与2N的两个力,要使合力大小恰为,则它们的夹角为;②已知,,则sinα<cosβ;③若A,B,C是斜△ABC的三个内角,则恒有tanA+tanB+tanC=tanAtanBtanC成立;④;⑤已知,则x的大小为;其中错误的命题有①②④⑤.(写出所有错误命题的序号)【解答】解:对于①,||=1,||=2,|+|=,∴||+2||×||cosθ+||=1+2×1×2×cosθ+4=6cosθ=,∴它们的夹角θ≠,①错误;对于②,,,且sin=cos(﹣)=cos,cos(﹣)=cos0<<<π,∴cos>cos,∴sinα>cosβ,②错误;对于③,斜△ABC中,A+B=π﹣C,∴tan(A+B)=tan(π﹣C),∴=﹣tanC,∴tanA+tanB+tanC=tanAtanBtanC,③正确;对于④,sin50°(1+tan10°)=sin50°•====1,∴④错误;对于⑤,(cosx+1)=sinx,∴sinx﹣cosx=,∴sin(x﹣)=,又x∈(0,),∴x﹣∈(﹣,),∴x﹣=或x﹣=,解得x=或x=π,⑤错误.综上,错误的命题是①②④⑤.故答案为:①②④⑤.三、解答题:请在答题卡指定区域内作答,解答时应写出证明过程或演算步骤(17小题10分,18-22小题各12分,共70分).17.(10分)已知,且∥,设函数y=f(x)(Ⅰ)求函数y=f(x)的对称轴方程及单调递减区间;(Ⅱ)若,求函数y=f(x)的最大值和最小值并写出函数取最值时x的值.【解答】解:(Ⅰ)∵,,且∥,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)由,得x=.由,得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∴,函数在[kπ+,kπ+],(k∈z)递减﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)∵∴,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)∴;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)18.(12分)如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足=,=2,记,,试以为平面向量的一组基底.利用向量的有关知识解决下列问题;(Ⅰ)用来表示向量;(Ⅱ)若|AB|=3,|AD|=2,且|BF|=,求||.【解答】解:(Ⅰ)∵在平行四边形ABCD中,,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)由(Ⅰ)可知:,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)∵|AB|=3,|AD|=2,且∴∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)∴=﹣+==9﹣6×+1=7∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)19.(12分)平潭国际“花式风筝冲浪”集训队,在平潭龙凤头海滨浴场进行集训,海滨区域的某个观测点观测到该处水深y(米)是随着一天的时间t(0≤t≤24,单位小时)呈周期性变化,某天各时刻t的水深数据的近似值如表:(Ⅰ)根据表中近似数据画出散点图(坐标系在答题卷中).观察散点图,从①y=Asin(ωt+ϕ),②y=Acos(ωt+ϕ)+b,③y=﹣Asinωt+b(A>0,ω>0,﹣π<ϕ<0).中选择一个合适的函数模型,并求出该拟合模型的函数解析式;(Ⅱ)为保证队员安全,规定在一天中的5~18时且水深不低于1.05米的时候进行训练,根据(Ⅰ)中的选择的函数解析式,试问:这一天可以安排什么时间段组织训练,才能确保集训队员的安全.【解答】(满分12分)解:(Ⅰ)根据表中近似数据画出散点图,如图所示:依题意,选②y=Acos(ωt+ϕ)+b做为函数模型,∴,∵∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)又∵函数y=0.9cos(φ)+1.5的图象过点(3,2.4),∴2.4=0.9×cos(+φ)+1.5,∴cos(+φ)=1,∴sinφ=﹣1,又∵﹣π<φ<0,∴φ=﹣,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)(Ⅱ)由(Ⅰ)知:令y≥1.05,即∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)∴,∴12k﹣1≤t≤12k+7又∵5≤t≤18∵5≤t≤7或11≤t≤18﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)∴这一天可以安排早上5点至7点以及11点至18点的时间段组织训练,才能确保集训队员的安全.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)20.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.(Ⅰ)若b=6,求角C的余弦值;(Ⅱ)若点D,E在线段BC上,且BD=DE=EC,,求AD的长.【解答】(满分12分)解:(Ⅰ)∵由正弦定理得:﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)∵B=60°,c=4,b=6,∴,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)∵b>c∴∠B>∠C∴∠C为锐角﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)∵BD=DE=EC,,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)在,∵B=60°,∴,∴∠BAE=30°或150°(不合题意,舍去)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)∴,∴,∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)21.(12分)设向量,函数.(Ⅰ)若ω是函数y=g(x)在上的零点,求sinω的值;(Ⅱ)设,,求sin (α+β)的值.【解答】解:(Ⅰ)∵,函数,∴g(x)=•=4cosx•sin(x+)+1×(﹣1)=2sinxcosx+2cos2x﹣1=2sin(2x+)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)由得:∴又∵∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(Ⅱ)∵,∴,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)22.(12分)已知O为坐标原点,对于函数f(x)=asinx+bcosx,称向量为函数f(x)的伴随向量,同时称函数f(x)为向量的伴随函数.(Ⅰ)设函数,试求g(x)的伴随向量;(Ⅱ)记向量的伴随函数为f(x),求当且时sinx的值;(Ⅲ)由(Ⅰ)中函数g(x)的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移个单位长度得到h(x)的图象.已知A(﹣2,3)B (2,6),问在y=h(x)的图象上是否存在一点P,使得.若存在,求出P点坐标;若不存在,说明理由.【解答】解:(Ⅰ)∵,∴∴g(x)的伴随向量﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)(Ⅱ)∵的伴随函数为f(x),且,∴又∵且sin2x+cos2x=1,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)(Ⅲ)由(Ⅰ)知:(用余弦表示也可以)将函数g(x)的图象(纵坐标不变)横坐标伸长为原来的2倍,得到函数再把整个图象向右平移个单位长得到h(x)的图象,得到﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)设,∵A(﹣2,3)B(2,6),∴又∵,∴,,∴(*)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分),∴,∴,这时(*)式成立,∴.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福州八中2016—2017学年第二学期期末考试高一数学 必修4考试时间:120分钟 试卷满分:150分2017.7.12Ⅰ卷一、选择题:(本大题共10小题,每小题5分,共50分) 1. 化简cos 15°cos 45°-cos 75°sin 45°的值为 A.12B.32C .-12D .-322.设a n =211111123n n n n n++++++++ (n ∈N *),则a 3=A .13B. 11113456+++C. 19D. 111349+++3.若AD 是△ABC 的中线,已知=,,则等于A . 1()2a b -B. 1()2a b +C.1()2a b -+ D. 1()2a b -+4. 若递增等比数列{a n }的前n 项和为S n ,a 2=2,S 3=7,则公比q 等于A.2B.12C.2或12D.无法确定5.若将函数f (x )=2sinxcosx -2sin 2x +1的图象向右平移φ个单位,所得图象关于y 轴对称,则φ的最大负值是A .-8πB.-58πC.-38πD.-34π6.已知12(2,1),(1,3),(1,2),e e a ===- 若1122a e e λλ=+,则实数对(λ1,λ2)为A.(1,1)B.(-1,1)C.(-1,-1)D.无数对7.在△ABC 中,2cos ab C=,则这个三角形一定是 A.等腰三角形B.直角三角形C.等腰直角三角D.等腰或直角三角形8.已知α为锐角,且3cos(),cos245παα+==A.2425B. 725C. -2425D.±24259. 已知x =12π是函数f (x )(2x +φ)+cos (2x +φ)(0<φ<π)图象的一条对称轴,将函数f (x )的图象向右平移34π个单位后得到函数g (x )的图象,则函数g(x )在[-4π,6π]上的最小值为A.-2B.-1C.D.10.平面上有四个互异点A 、B 、C 、D ,已知((2)()0DB DC AD AB AC ++⋅-=,则△ABC 的形状是 A.直角三角形B.等腰直角三角形C.等腰三角形D.无法确定二、填空题:(本大题4小题,每小题5分,共20分)11.已知tan (α+β)=3,tan (α-β)=2,则tan 2α的值为 ______ . 12. 如图,一栋建筑物的高为(30-,在该建筑物的正东方向有一个通信塔CD .在它们之间的地面点M (B ,M ,D 三点共线)处测得楼顶A ,塔顶C 的仰角分别为15°和60°,在楼顶A 处测得塔顶C 的仰角为30°,则通信塔CD 的高为________ m.13.已知D ,E ,F 分别为△ABC 的边BC ,CA ,AB 的中点,且BC a = ,CA b = ,给出下列命题:①12AD a b =- ; ②12BE a b =+ ; ③1122CF a b =-+,④0A D B E C F ++= =0.其中正确命题的序号为________. 14.数列{a n }中,11,213nn na a a a +==+,则 a 10= ______ .三、解答题:(本大题3个小题,共30分)15.(本小题10分)已知向量,的夹角为120°,且||=2,||=3.求: (Ⅰ)•; (Ⅱ)|+2|.16. (本小题10分)已知等差数列{a n }的前n 项和S n 满足S 3=0,S 5 = -5.(Ⅰ)求{a n }的通项公式; (Ⅱ)求a 1+a 4+a 7+…+a 3n +1.17. (本小题10分)在△ABC 中,BC 边上的中线AD 长为3,且BD=2,sinB=8. (Ⅰ)求sin ∠BAD 的值;(Ⅱ)求AC 的长.Ⅱ卷一、选择题:(本大题2个小题,每小题5分,共10分)18. 将石子摆成如图的梯形形状,称数列5,9,14,20,…为梯形数,根据图形的构成,此数列的第2 012项与5的差即a 2 012-5=A .2 018×2 012B .2 018×2 011C .1 009×2 012D .1 009×2 01119. 已知向量满足,若M为AB 的中点,并且,则λ+μ的最大值是A.1B. 1D. 1 二、填空题:(本大题5分)20.给出四个命题:①若sin 2A=sin 2B ,则△ABC 为等腰三角形;②若sin A=cos B ,则△ABC为直角三角形;③若sin 2A+sin 2B+sin 2C <2,则△ABC 为钝角三角形;④若cos (A-B )cos (B-C )cos (C-A )=1,则△ABC 为正三角形,以上正确命题序号的是_____________________. 三、解答题:(本大题3 个小题,共35分)21. (本小题11分)已知等差数列{a n }中公差d ≠0,有a 1+a 4=14,且a 1,a 2,a 7成等比数列. (Ⅰ)求{a n }的通项公式a n 与前n 项和公式S n ;(Ⅱ)令b n =nS n k+ (k<0),若{b n }是等差数列,求数列{11n n b b +}的前n 项和T n .22. (本小题12分)已知△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足asin A-csin C=b(sinA -sin B ). (Ⅰ)求角C 的大小;(Ⅱ)若边长c=4,求△ABC 的周长最大值.23. (本小题12分)已知=(sinx ,cosx ),=(cos φ,sin φ)(|φ|<).函数f (x )=• 且f (3π-x )=f (x ). (Ⅰ)求f (x )的解析式及单调递增区间;(Ⅱ)将f (x )的图象向右平移3π单位得g (x )的图象,若g (x )+1≤ax +cosx 在x ∈[0,4π]上恒成立,求实数a 的取值范围.福州八中2016—2017学年第二学期期末考试高一数学必修4 试卷参考答案及评分标准Ⅰ卷一、选择题:(本大题共10小题,每小题5分,共50分)1. A2. D3. A4. A5. A6. B7.A8. A9. B 10. C二、填空题:(本大题4小题,每小题5分,共20分)11.-1 12. 60 13.②③④14.三、解答题:(本大题3个小题,共30分)15.(本小题10分)【解析】:(Ⅰ)•=…………2分;……5分(Ⅱ)|+|2==13,…………9分所以,|+|=.…………10分16.(本小题10分)【解析】:(Ⅰ)由等差数列的性质,可得,………………………2分解得a1=1,d=-1,……4分则{a n}的通项公式a n=1-(n-1)=2-n;…………………………5分(Ⅱ)∵{a n}为等差数列,∴a1+a4+a7+…+a3n+1以1为首项,以-3为公差的等差数列,…………8分∴a1+a4+a7+…+a3n+1=n+1+=…………10分17.(本小题10分)【解析】:(1)在△ABD中,BD=2,sin B=,AD=3,∴由正弦定理=,得sin∠BAD ═==;……4分(2)∵sin B=,∴cos B=,…………5分∵sin∠BAD=,∴cos∠BAD=,………………6分∴cos∠ADC=cos(∠B+∠BAD)=×-×=-,………………7分∵D为BC中点,∴DC=BD=2,∴在△ACD 中,由余弦定理得:AC2=AD2+DC2-2AD•DC cos∠ADC=9+4+3=16,…9分高一数学期末考试卷答案第1页共4页∴AC=4.…………10分Ⅱ卷一、选择题:(本大题2个小题,每小题5分,共10分)18.D 19. B二、填空题:(本大题5分)20.③④三、解答题:(本大题3 个小题,共35分)21.(本小题11分)【解析】:(Ⅰ)∵a1+a4=14,∴2a1+3d=14,①………………1分∵a1,a2,a7成等比数列,∴,即,②……………………2分由①②得d2=4a1d,∵d≠0,∴d=4a1,代入①解得d=4、a1=1,………………3分∴a n=a1+(n-1)d=4n-3,……………………4分S n==2n2-n;………………5分(Ⅱ)由(1)知,∵{b n}是为等差数列,∴2b2=b1+b3,即=,解得,或k=0,由条件知,,即b n=2n,………………7分则…………………………8分∴=……………………………………10分所以,T n=……………………………………………………11分22.(本小题10分)【解析】:(Ⅰ)由已知,根据正弦定理,asin A-csin C=(a-b)sin B 得,a2-c2= b(a-b),即a2+b2-c2=ab.………………2分由余弦定理得cos C==.又C∈(0,π).所以C=.……………………5分(Ⅱ)∵C=,,A+B=,………………6分∴,可得:a=sin A,b=sin B=sin(-A),………………8分∴a+b+c=+sin A+sin(-A)=+sin A+(cos A+sin A )=8sin (A+)+4……………………10分∵由0<A <可知,<A+<,可得:<sin (A+)≤1. ……11分∴△ABC 的周长a +b +c 的最大值为12. ……………………12分23.(本小题12分)【解析】:(Ⅰ)∵f (x )=•=sinxcos φ+cosxsin φ=sin (x +φ),…2分 再由f (-x )=f (x )可知函数f (x )的图象关于直线x =对称,∴+φ=+k π,k ∈Z ,又|φ|<,∴φ= …………4分∴f (x )=sin (x +),由2k π-≤ x +≤2k π+可得2k π-≤x ≤ 2k π+,∴函数的递增区间为[2k π-,2k π+],k ∈Z ; ………………6分(Ⅱ)由图象平移易知g (x )=sinx ,即sinx +1≤ax +cosx 在x ∈[0,]上恒成立.也即sinx -cosx ≤ax -1在x ∈[0,]上恒成立. …………8分令h (x )=sinx -cosx =sin (x -),x ∈[0,];φ(x )= ax -1 ………………10分如下图:h (x )的图象在φ(x )图象的下方, 则: a ≥k AB ==,故a ≥.………………12分高一数学期末考试卷答案 第3页 共4页。
