苏科初中数学九上《2.6 正多边形与圆》PPT课件 (4)
合集下载
《正多边形与圆》PPT课件 (公开课获奖)2022年苏科版 (4)
证明(1)
【能力检测】 2．今年五一节期间 ,||王老板在其 经营的服装店里卖出两件衣服 ,其中一件是裤子 售价为168元 ,盈利20％ ,一件是夹克衫售价也是 168元 ,但亏损20％ ,问||王老板在这次的交易过 程中是赚了还是亏了 ,如果是赚了 ,赚了多少 ?如 果是亏了 ,亏了多少 ?还是不赚不亏 ?
各边相等、各角相等的多边形叫正多边形 .
探索：正多边形的对称性
正多边形都是轴对称图形 ,正n边形有n条对称轴 , 每条对称轴都经过它的中|心 . 当n为偶数时 ,正n边形又是中|心对称图形 ,对称中| 心就是这个正多边形的中|心 .
2.6 正多边形与圆(1)
以下命题中 ,正确的说法有
〔填序号〕
①正多边形的各边相等；
形 ,能按图②恰好拼成13×5的矩形吗 ?动手试一
试!
3
5
3 5
8
5
8 3
5
5
5
3
3
3
5
（图①）
5
8
（图②）
请同学们再计算一以以以以下图①、图②的面积 ,
你发现了什么 ?
证明(1)
【数学实验二】如图 ,〔1〕画∠AOB＝90° ,并画
∠AOB的角平分线OC.
〔2〕将三角尺的直角顶点落在OC的任意一点P
A
C
B
D
请再量一量证实你的猜测．
证明(1)
【探究活动二 】图〔1〕中有曲线吗 ?请把图 〔2〕中编号相同的点用线段连接起来.
（图1）
1 2 3 4 5 6 7 8
12 345 678
（图2）
证明(1)
【感悟归纳 】 从以上两个探究活动中 ,你有什么感悟啊 ?
正多边形和圆公开课课件ppt
例 有一个亭子它的地基是半径为4m的正六边形,求地基的周长和面 积(精确到0.1平方米).
F A
B
E
.. O
D
rR
PC
由 于A B CDE F是 正 六 边 形 ， 所 以
它的中心角等于360 60，
6
F
OB C是 等 边 三 角 形 ， 从 而 正
六边形的边长等于它的半径. A
∴亭子的周长 L=6×4=24(m)
.
4．已知圆内接正方形的边长为2，则该圆 的内接正六边形边长为
__________．
5． 圆内接正六边形的边长是8 cm用么该正六边形的半径为________；
边心距为________．
6．以下有四种说法：①顺次连结对角线相等的四边形各边中点， 则所得的四边形是菱形；②等边三角形是轴对称图形，但不是中 心对称图形；③顶点在圆周上的角是圆周角；④边数相同的正多 边形都相似，其中正确的有（ ）
三. 正多边形有关的计算
正多边形的内角:
内角(n2)180 n
正多边形的半径:外接圆的半径
E
D
半径R
F 中心角 O
.
边心距r
C
正多边形的中心角:
A
B
中心角 360 n
正多边形的边心距： r
R
2
（
a
2
）
正多边形的面积：S
n(1ar) 2
1Lr 2
2
练习
完成下表中正多边形的计算(把计算结果填入表中)：
学习目标：
• 1.了解正多边形与圆的关系及正多边形的有关概念，会判定正多边形。 • 2.理解正多边形的中心、半径、边长、边心距、中心角之间的关系，并
苏科版数学九年级上册2.6《正多边形与圆》说课稿
苏科版数学九年级上册2.6《正多边形与圆》说课稿一. 教材分析《正多边形与圆》这一节内容，主要介绍了正多边形的定义、性质以及与圆的关系。
通过学习，学生能够理解正多边形的概念，掌握正多边形的性质，以及了解正多边形与圆之间的联系。
这一节内容是初中数学的重要内容，对于学生理解和掌握圆的性质，以及进一步学习圆的方程和其他相关知识具有重要作用。
二. 学情分析九年级的学生已经具备了一定的几何知识，对于图形的认知和理解有一定的基础。
但是，正多边形这一概念较为抽象，学生可能难以理解和接受。
因此，在教学过程中，需要引导学生从实际出发，通过观察和动手操作，逐步理解正多边形的概念和性质。
三. 说教学目标1.知识与技能：学生能够理解正多边形的定义，掌握正多边形的性质，了解正多边形与圆的关系。
2.过程与方法：通过观察、操作、思考、交流等活动，学生能够培养自己的空间想象能力和逻辑思维能力。
3.情感态度与价值观：学生能够体验到数学与实际生活的联系，增强对数学的兴趣和信心。
四. 说教学重难点1.重点：正多边形的定义和性质，正多边形与圆的关系。
2.难点：正多边形概念的理解，正多边形性质的证明。
五. 说教学方法与手段1.教学方法：采用问题驱动法、案例教学法、小组合作法等。
2.教学手段：利用多媒体课件、实物模型、几何画板等辅助教学。
六. 说教学过程1.导入新课：通过展示一些生活中的正多边形图片，如足球、骰子等，引导学生观察和思考，引出正多边形的概念。
2.自主学习：学生通过阅读教材，了解正多边形的定义和性质。
3.合作交流：学生分组讨论，分享自己对正多边形的理解和感悟。
4.教师讲解：针对学生的讨论，教师进行讲解，重点讲解正多边形的性质和与圆的关系。
5.练习巩固：学生进行课堂练习，巩固所学知识。
6.总结拓展：学生总结本节课所学内容，教师进行拓展讲解。
七. 说板书设计1.定义：各边相等，各角相等的多边形。
a.边数确定，形状唯一。
b.相邻两边夹角相等。
《正多边形和圆》圆PPT教学课件
E
课堂小结
正多边形的定义与对称性
正多边形
正多边形的有
关概念及性质
正多边形的
有关计算
①正多边形的内角和= (n 2) 180
②中心角=
360
n
添加辅助线的方法：
连半径，作边心距
n
.
（2）正n边形的每个中心角
如图，已知半径为4的圆内接正六边形ABCDEF：
60
①它的中心角等于
度 ；
F
=
② OC BC (填＞、＜或＝）；
A
③△OBC是 等边 三角形；
B
都等于
E
（3）正n边形的每个外角都
O
D
360°
等于
.
C
P
④圆内接正六边形的面积是
△OBC面积的
6
倍.
1
周长 边心距
2
A
A
F
D
E
B
E
O
O
O
·
90°
72°
·
A
D
·
60°
C
B
C
D
B
C
3.你能尺规作出正方形、正八边形吗？
只要作出已知⊙O的互相垂直的直径即
得圆内接正方形，再过圆心作各边的垂
线与⊙O相交，或作各中心角的角平分
线与⊙O相交，即得圆内接正八边形，
照此方法依次可作正十六边形、正三十
二边形、正六十四边形……
D
A
O
·
心对称图形吗？
新知讲解
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗？都是中心对称
图形吗？
正n边形都是轴对称图形，都有n条对称轴，只有边数为偶数的正多边形才是
九年级数学正多边形和圆课件ppt苏科版九年级上
A E F B G K
L H C
2.正多边形与圆的关系 思考： 1.已知圆，如何将这个圆的圆周 四等份？
2.顺次连接四等份点得到的四边 形是正多边形吗？为什么？
A
D
B
C
弦相等（多边形的边相等）
弧相等—
圆周角相等（多边形的角相等）
—多边形是正多边形
例2. 利用圆作出正六边形.
思考：用直尺和圆规如何作出 正八边形，正三角形和正十二 边形.
画正多边形 的方法 1.用量角器等分圆 2.尺规作图等分圆
2.正多边形与圆的关系
⑴我们可以借助量角器将一 个圆n(n≥3)等分,依次连接 各等分点所得的多边形是这 个圆的内接正多边形. ⑵这个圆是这个正多边形的 外接圆.正多边形的外接圆 的圆心叫做正多边形的中心， 每条边所对的圆心角叫做正 多边形的中心角。
例3：有一个亭子它的地基是半径为 4m的正六边形,求地基的周长和面积 (精确到0.1平方米).
F
B
P
E .Oຫໍສະໝຸດ A B.r R
D
C
巩固训练： （1）若一个正多边形的每个内角 为150度，则这个正多边形的边数 为 。
（2）将一个边长为1的正六边形 补成如图所示的矩形，这个正方 形的边长为 。
（3）已知正四边形的外接圆的半径 为R，则正四边形的周长是 。
2、正多边形与圆的关系 思考： 正多边形的中心角 与正多边形的外角 有什么关系？
2.正多边形与圆的关系 思考： 1.正三角形的内切圆与外接圆 有关系吗？
2.它们有怎样的关系？
哪些是轴对称图形？哪些是中心对称 图形？并画出对称轴；找出对称中心.
正多边形的性质:
1.正多边形的各边相等,各角相等. 2.正n边形是轴对称图形,有n对称轴; 当n是偶数时，它还是中心对称图形。
L H C
2.正多边形与圆的关系 思考： 1.已知圆，如何将这个圆的圆周 四等份？
2.顺次连接四等份点得到的四边 形是正多边形吗？为什么？
A
D
B
C
弦相等（多边形的边相等）
弧相等—
圆周角相等（多边形的角相等）
—多边形是正多边形
例2. 利用圆作出正六边形.
思考：用直尺和圆规如何作出 正八边形，正三角形和正十二 边形.
画正多边形 的方法 1.用量角器等分圆 2.尺规作图等分圆
2.正多边形与圆的关系
⑴我们可以借助量角器将一 个圆n(n≥3)等分,依次连接 各等分点所得的多边形是这 个圆的内接正多边形. ⑵这个圆是这个正多边形的 外接圆.正多边形的外接圆 的圆心叫做正多边形的中心， 每条边所对的圆心角叫做正 多边形的中心角。
例3：有一个亭子它的地基是半径为 4m的正六边形,求地基的周长和面积 (精确到0.1平方米).
F
B
P
E .Oຫໍສະໝຸດ A B.r R
D
C
巩固训练： （1）若一个正多边形的每个内角 为150度，则这个正多边形的边数 为 。
（2）将一个边长为1的正六边形 补成如图所示的矩形，这个正方 形的边长为 。
（3）已知正四边形的外接圆的半径 为R，则正四边形的周长是 。
2、正多边形与圆的关系 思考： 正多边形的中心角 与正多边形的外角 有什么关系？
2.正多边形与圆的关系 思考： 1.正三角形的内切圆与外接圆 有关系吗？
2.它们有怎样的关系？
哪些是轴对称图形？哪些是中心对称 图形？并画出对称轴；找出对称中心.
正多边形的性质:
1.正多边形的各边相等,各角相等. 2.正n边形是轴对称图形,有n对称轴; 当n是偶数时，它还是中心对称图形。
2.6正多边形与圆课件
边心距＝OD= 在Rt△ABD中,∠BAD=30°,
1 3 AD OA OD R R R， 2 2
1 R. 2
A
O · D
∴AB=
3R ？
∴S△ABC=
B 3 3R R 2 2 3 3R 2 4
C
二、对称性
正多边形都是轴对称图形，一个正n边形 共有n条对称轴，每条对称轴都通过n边形 的中心.
你能尺规作出正六边形、正三角形、正十 二边形吗？
以半径长在 圆周上截取六段 相等的弧，依次 连结各等分点， 则作出正六边形. 先作出正六 边形，则可作正 三角形，正十二 边形，正二十四 边形………
F
E O ·
A
D
B
C
延伸拓展
同圆的内接正三角形、正四边形、 正六边形的边长之比为 .
1、正方形ABCD的外接圆圆心O叫做正方形 中心 ． ABCD的______ 2、正方形ABCD的内切圆⊙O的半径OE叫做 边心距 正方形ABCD的______ ． 3、若正六边形的边长为1，那么正六边形的中 60 度，半径是___ 1 ，边心距是 3 ， 心角是____ 2 它的每一个内角是______ 120° ．面积是____ 中心 角 4、正n边形的一个外角度数与它的______ 的度数相等．
2.6 正多边形与圆
三条边相等， 三个角也相等（60°）
四条边都相等， 四个角也相等（90°）
正多边形：
各边相等，各角也相等的多边形叫做正多边形 .
如果一个正多边形有n条边，那么这个正 多边形叫做正n边形.
想一想：
菱形是正多边形吗？矩形是正多边形吗？为什么？
各边相等，各角也相等的多边形叫做正多边形.
5.正多边形一定是 轴 对称图形,一个正n边 形共有 n 条对称轴,每条对称轴都通 过 中心 ;如果一个正n边形是中心对称图 形,n一定是 偶 数.
1 3 AD OA OD R R R， 2 2
1 R. 2
A
O · D
∴AB=
3R ？
∴S△ABC=
B 3 3R R 2 2 3 3R 2 4
C
二、对称性
正多边形都是轴对称图形，一个正n边形 共有n条对称轴，每条对称轴都通过n边形 的中心.
你能尺规作出正六边形、正三角形、正十 二边形吗？
以半径长在 圆周上截取六段 相等的弧，依次 连结各等分点， 则作出正六边形. 先作出正六 边形，则可作正 三角形，正十二 边形，正二十四 边形………
F
E O ·
A
D
B
C
延伸拓展
同圆的内接正三角形、正四边形、 正六边形的边长之比为 .
1、正方形ABCD的外接圆圆心O叫做正方形 中心 ． ABCD的______ 2、正方形ABCD的内切圆⊙O的半径OE叫做 边心距 正方形ABCD的______ ． 3、若正六边形的边长为1，那么正六边形的中 60 度，半径是___ 1 ，边心距是 3 ， 心角是____ 2 它的每一个内角是______ 120° ．面积是____ 中心 角 4、正n边形的一个外角度数与它的______ 的度数相等．
2.6 正多边形与圆
三条边相等， 三个角也相等（60°）
四条边都相等， 四个角也相等（90°）
正多边形：
各边相等，各角也相等的多边形叫做正多边形 .
如果一个正多边形有n条边，那么这个正 多边形叫做正n边形.
想一想：
菱形是正多边形吗？矩形是正多边形吗？为什么？
各边相等，各角也相等的多边形叫做正多边形.
5.正多边形一定是 轴 对称图形,一个正n边 形共有 n 条对称轴,每条对称轴都通 过 中心 ;如果一个正n边形是中心对称图 形,n一定是 偶 数.
苏科版-数学-九年级上册- 正多边形和圆 参考课件
K
F
E 作法：1.在⊙O中作一条直径AD；
M
J
2.分别以A、D为圆心，⊙O的半径为
A
D 半径作弧，与⊙O相交于B、F和C、E；
3.依次连接A、B、C、D、E、就是所作的正六边形.
B
C
4.依次连接OB、OC、OE、OF，并分别
H
作边AB、BC、CD、DE、EF、FA所对圆心角的
③正多边形一定是中心对称图形;
④边数相同的正多边形一定相似.
A.1 B.2
C.3
D.4
7.如果一个正多边形绕它的中心旋转90°就和
原来的图形重合,那么这个正多边形是(C )
A.正三角形
B.正五边形
C.正方形
D.正六边形
课堂小结
1.正多边形的各边相等，各角相等.
2.正n边形是轴对称图形,有n条对称轴;但不一定是中心 对称, 当n是偶数时，既是轴对称图形又是中心对称图形．
18,则它们的周长之比为 2﹕3 ，面积之比 为 4﹕9 .
5.下列说法中正确的是( D ) A.平行四边形是正四边形 B.矩形是正四边形 C.菱形是正四边形 D.正方形是正四边形
๔ 巩固& 练习 ☞
6.下列命题中,真命题的个数是( A )
①各边都相等的多边形是正多边形;
②各角都相等的多边形是正多边形;
平分线，分别与⊙O相交于点G、H、I、J、K、
M，依次连接A、G、B、H、C、I、D、J、E、
K、F、M各点，十二边形AGBHCIDJEKFM就是
所作的正四边形.
๔ 巩固& 练习 ☞
见教材P144 练习
๔ 巩固& 练习 ☞
1.将一个正五边形绕它的中心旋转,至少要旋 转 72 度，才能与原来的图形位置重合.
《正多边形与圆》PPT课件 (同课异构)2022年苏科版 (5)
3x7
x 2, (10)x 5.
解:原不等式组的解集为
-7 -6 -5 -4 -3 -2 -1 0
5x2
x 1,
解:原不等式组的解集为
(11)x 4. -3 -2 -1 0 1 2 3 4 5
1x4
(12)xx
0, 4.
解:原不等式组的解集为
-6 -5 -4 -3 -2 -1 0 1
大小小大取中间
-5 -4 -3 -2 -1 0
x2
解:原不等式组的解集为
-5 -4 -3 -2 -1 0 1 2
x0
同大取大
探索. 求下列不等式组的解集:
x 3,
(5)
x
7.
解:原不等式组的解集为
0 1 2 3 45 6 7 89
x3
x 2,
(6)
x
5.
解:原不等式组的解集为
-7 -6 -5 -4 -3 -2 -1 0
正多边形与圆的关系
A
B
E
O
C
D
⊙O是正五边形的
.
正五边形是⊙O的
;
点O叫做正五边形的
.
AO叫做正五边形的
.
∠AOB叫做正五边形的
.
点A、B、C、D、E、F、G、H是
⊙O上的八等分点，则八边形
ABCDEFGH是
.
它的一个外角是 它的一个内角是 它的一个中心角是 把这个多边形绕它的中心至少要旋转 才能与它自身重合。
1. 同大取大， 2.同小取小；
3.大小小大取中间， 4.大大小小是无解。
(((57683(4(1)2)))))xxxx32xxxxxxxx3704,1.37,52.0641,.,2,.,4.
江苏地区数学学科正多边形和圆课件 (苏科版九年级上)
正多边形的概念： 各边相等,各角也相等的多边形叫做正 多边形.
思考：各边相等与各角相等必须同时成立吗？ 你能举例说明吗？
下列正多边形中，哪些是轴对称图形？哪些是中心 对称图形？哪些既是轴对称图形，又是中心对称图 形？ 如果是轴对称图形，画出它的对称轴；如果是中心对 称图形找出它的对称中心．
正多边形的性质:
1.正多边形的各边相等,各角相等.
2.正n边形是轴对称图形,有n条对称轴; 但不一定是中心对称, 当n是偶数时，既 是轴对称图形又是中心对称图形．
画正五边形
正多边形与圆的关系：
⑴我们可以借助量角器将一个圆n(n≥3)等分, 依次连接各等分点所得的多边形是这个圆的内 接正多边形.
⑵这个圆是这个正多边形的外接圆.正多边形 的外接圆的圆心叫做正多边形的中心．
刚刚我们画了五边 形，那么你会画五角 星吗？
1.正四边形 思考：如何作正八边形？
2．正六边形 思考：如何作正三边形，正十二边形呢？
3
1、正方形ABCD的外接圆圆心O叫 做正方形ABCD的_中__心___．
２.正多边形一定是 轴 对称图形, 一个正n边形共有 n 条对称轴,每条 对称轴都通过 中心 ;如果一个正n边 形是中心对称图形,n一定是 偶数 .
观察下列图案，里面有我们学过 的哪些图形呢？
我们已学过正三角形，正方形
这两个图形的边与角有什么特
点?
各边相等,各角也相等
日常生活中你还看 到哪些具有这两个 性质的多边形?
教学目标：
⒈了解正多边形的概念、正多边形 与圆的关系;
⒉会通过等分圆心角的方法等分圆 周，画出所需的正多边形；
⒊会用直尺和圆规画一些特殊的正 多边形.
３.将一个正五边形绕它的中心旋转,至少要 旋转 72 度,才能与原来的图形位置重合.
《正多边形与圆》PPT课件 (公开课获奖)2022年苏科版 (1)
E
结论一定成立吗 ?与同学交流 ．
O
F B
证明(1)
【能力检测 】 1．你认为大圆内的10个小圆的 周长之和与另一个大圆内的2个小圆的周长之和 哪一个大一些 ?请你猜一猜 ,并用学过的知识和 数学方法验证你的猜测．
证明(1)
【能力检测】 2．今年五一节期间 ,|王老板在其 经营的服装店里卖出两件衣服 ,其中一件是裤子 售价为168元 ,盈利20％ ,一件是夹克衫售价也是 168元 ,但亏损20％ ,问|王老板在这次的交易过程 中是赚了还是亏了 ,如果是赚了 ,赚了多少 ?如果 是亏了 ,亏了多少 ?还是不赚不亏 ?
发现了什么 ?
证明(1)
【数学实验二】如图 ,〔1〕画∠AOB＝90° ,并画
∠AOB的角平分线OC.
〔2〕将三角尺的直角顶点落在OC的任意一点P
上 ,使三角尺的两条直角边与∠AOB的两边分别交于
点E、F ,并比较PE、PF的长度；
A
〔3〕把三角尺绕点P旋转 ,
C
比较PE与PF的长度.
P
你能得到什么结论 ?你的
典型例题
例1 在等边三角形ABC中 ,E、F、G、H、L、
K分别是各边三等分点 ,试说明六边形EFGHLK是正
六边形．
A
E
K
F
L
B
C
GH
2.6 正多边形与圆(1)
总结拓展
思考：如何利用圆来画正多边形 ?
2.6 正多边形与圆(1)
请你画一画
1．如图 ,⊙O． 〔1〕用量角器把⊙O五等份 ,依次连接各等分 点 ,得五边形ABCDE； 〔2〕五边形ABCDE是正五边形吗 ?为什么 ?
12 345 678
（图2）
最新苏科版九年级数学上册精品课件-2.6正多边形与圆
M
1.连半径，得中心角；
2.作边心距，构造直角三角形.
2019/8/31
18
【单练习击】此处编母版标题样式
1. 填表
• 单•击正 形第多边此二边数处级 编半径辑母边版长文边本心样距式 周长
•3 第三级2
23
4 2 • 第四• 级2第五级
6
22
1 23
1
8
3
12
面积
33
4
63
2. 若正多边形的边心距与半径的比为1:2，则这个多边形 的边数是 3 .
• A单击此处E 编辑母版文B 本的样圆式心，称其为正多边形的中心.
• 第二级 R
• 第三级
• 第四级O
G
• 第五级 H
外接圆的半径叫做正多边形的半 径.
r
内切圆的半径叫做正多边形的边
DF
C
心距.
正多边形每一条边对应所对的外接圆的圆心角都相等， 叫做正多边形的中心角.
探单究归击纳 此处编母版标题样式
亭子地基的面积 S 1 l r 1 24 2 3 41.6(m2 ).
22
2019/8/31
17
单击此处编母版标题样式
方法归纳
圆•内单接击正此多处边编形的辑辅母助版线文本样式
• 第F二级 E
• 第三级
• 第四级
A
·O • 第五级 D
rR
半径R
B MC
C
边长一半
O
中心角一半 边心距r
把☉O进行5等分,依次连接各等分点得到五边形ABCDE .
•这单个击五边此形处A编BC辑DE母是版正文五本边形样吗式？简
单说• 说第理二由级.
B
• 第三级
1.连半径，得中心角；
2.作边心距，构造直角三角形.
2019/8/31
18
【单练习击】此处编母版标题样式
1. 填表
• 单•击正 形第多边此二边数处级 编半径辑母边版长文边本心样距式 周长
•3 第三级2
23
4 2 • 第四• 级2第五级
6
22
1 23
1
8
3
12
面积
33
4
63
2. 若正多边形的边心距与半径的比为1:2，则这个多边形 的边数是 3 .
• A单击此处E 编辑母版文B 本的样圆式心，称其为正多边形的中心.
• 第二级 R
• 第三级
• 第四级O
G
• 第五级 H
外接圆的半径叫做正多边形的半 径.
r
内切圆的半径叫做正多边形的边
DF
C
心距.
正多边形每一条边对应所对的外接圆的圆心角都相等， 叫做正多边形的中心角.
探单究归击纳 此处编母版标题样式
亭子地基的面积 S 1 l r 1 24 2 3 41.6(m2 ).
22
2019/8/31
17
单击此处编母版标题样式
方法归纳
圆•内单接击正此多处边编形的辑辅母助版线文本样式
• 第F二级 E
• 第三级
• 第四级
A
·O • 第五级 D
rR
半径R
B MC
C
边长一半
O
中心角一半 边心距r
把☉O进行5等分,依次连接各等分点得到五边形ABCDE .
•这单个击五边此形处A编BC辑DE母是版正文五本边形样吗式？简
单说• 说第理二由级.
B
• 第三级
正多边形和圆公开课PPT课件
弦心距OF叫正五边形ABCDE的________， 内切 它是正五边形ABCDE的________圆的半径。
边心距
8、∠AOB叫做正五边形ABCDE的_______角，
72度 它的度数是________
中心
D
E
A
第8页/共19页
C
.O
B F
9、图中正六边形ABCDEF的中心角是_______;
它的度数是_________;
QR=RS=ST=TP=2PA
第4页/共19页
二. 正多边形有关的概念
正多边形的中心: 一个正多边形的 外接圆的圆心.
E
半径R
. F O 中心角
D C
正多边形的半径: 外接圆的半径
边心距r
正多边形的中心角: 正多边形的每一条 边所对的圆心角.
正多边形的边心距： 中心到正多边形的 一边的距离.
第5页/共19页
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢？
思考1: 把一个圆4等分, 并依次连 接这些点,得到正多边形吗??
A
D
B
C
弦相等（多边形的边相等）
弧相等
圆周角相等（多边形的角相等）
—多边形是正多边形 第2页/共19页
思考2: 把一个圆5等分, 并依次连接这些点, 得到正多边形吗??
120 ∠BOC=_____度; ∠BOD=_____度.
中心 60
第6页/共19页
外接
A
.O
D
C
5、正方形ABCD的外接圆圆心O叫做 正方形ABCD的____________
中心
6、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的___________
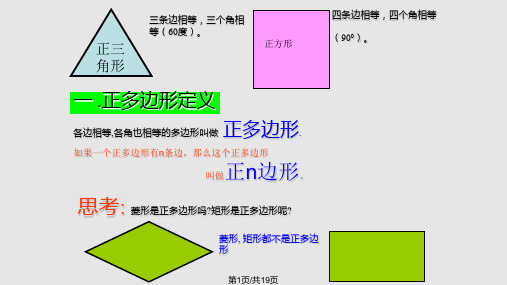
边心距
8、∠AOB叫做正五边形ABCDE的_______角，
72度 它的度数是________
中心
D
E
A
第8页/共19页
C
.O
B F
9、图中正六边形ABCDEF的中心角是_______;
它的度数是_________;
QR=RS=ST=TP=2PA
第4页/共19页
二. 正多边形有关的概念
正多边形的中心: 一个正多边形的 外接圆的圆心.
E
半径R
. F O 中心角
D C
正多边形的半径: 外接圆的半径
边心距r
正多边形的中心角: 正多边形的每一条 边所对的圆心角.
正多边形的边心距： 中心到正多边形的 一边的距离.
第5页/共19页
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢？
思考1: 把一个圆4等分, 并依次连 接这些点,得到正多边形吗??
A
D
B
C
弦相等（多边形的边相等）
弧相等
圆周角相等（多边形的角相等）
—多边形是正多边形 第2页/共19页
思考2: 把一个圆5等分, 并依次连接这些点, 得到正多边形吗??
120 ∠BOC=_____度; ∠BOD=_____度.
中心 60
第6页/共19页
外接
A
.O
D
C
5、正方形ABCD的外接圆圆心O叫做 正方形ABCD的____________
中心
6、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的___________
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
作业
《南通小题》76页
探索：正多边形的对称性
正多边形都是轴对称图形，正n边形有n条对称轴， 每条对称轴都经过它的中心。 当n为偶数时，正n边形又是中心对称图形，对称中 心就是这个正多边形的中心。
2.6 正多边形与圆(1)
下列命题中，正确的说法有
（填序号）
①正多边形的各边相等；
②各边相等的多边形是正多边形；
③正多边形的各角相等；
四边形ABCD就是所求作的正方形． 2、作正六边形
你会作正三角形、正八边形、正十六边形吗？
2.6 正多边形与圆(1)
课堂练习
1．正十二边形的每一个外角为
°，
每一个内角是
°，
该图形绕其中心至少旋转
°和本身重合．
2.6 正多边形与圆(2)
课堂练习
2．为增加绿化面积，某小区将原来正方形地 砖更换为如图所示的正八边形植草砖，更换后，图 中阴影部分为植草区域，设正八边形与其内部小正 方形的边长都为a，求阴影部分的面积．
初中数学 九年级(上册)
2.6 正多边形与圆 （1）
等边三角形 （正三角形）
正方形 （正四边形）
正五边形
正六边形
这些图形有什么共同点？ 各边相等 各角相等
各边相等、各角相等的多边形叫正多边形。
2.6 正多边形与圆(1)
大家议一议
各边相等的多边形是正多边形吗？ 各角相等的多边形是正多边形吗？
各边相等、各角相等的多边形叫正多边形。
④各角相等的多边形是正多边形；
⑤既是轴对称图形，又是中心对称的多边形是正多边形．
正多边形与圆的关系
A
B
E
O
C
D
⊙O是正五边形的
正五边形是⊙O的
点O叫做正五边形的
AO叫做正五边形
. .
.
2.6 正多边形与圆(1)
尺规作图： 1、作正方形
作法：（1）在⊙O中任作一直径AC． （2）过点O作直径BD，使BD⊥AC． （3）顺次连接A、B、C、D
典型例题
（1）如图1，已知△PAC是圆O的内接正三角形，那么 ∠OAC﹦_____ （2）如图2，设AB是圆O的直径，AC是圆的任意一条弦， ∠OAC﹦α ﹒ ①如果α ﹦45°，那么AC能否成为圆内接正多边形的一 条边？若有可能，那么此多边形是几边形？请说明理由 ②若AC是圆的内接正n边形的一边，则用含n的代数式表 示α 应为_______