大兴区高三数学文科参考答案与评分标准
2019~2020学年度北京市大兴区高三第一次综合练习参考答案

2019~2020学年度北京市大兴区高三第一次综合练习高三数学参考答案及评分标准一、选择题(共10小题,每小题4分,共40分)二、填空题(共5小题,每小题5分,共25分) (11)2-(12)答案不唯一,只要π02m <≤ (13)(2]-∞,(或{|2}a a ≤ (14)1;4(第一个空3分,第二个空2分)(15)①③ (不选或有错选得0分,只选对1个得3分,全部选对得5分.)三、解答题(共6小题,共85分) (16)(共14分) 解:(Ⅰ) 由于 1c =,2π3A =, 1sin 2ABC S bc A ∆=, ……2分所以2b =. ……3分 由余弦定理 2222cos a b c bc A =+-, ……5分 解得a =. ……6分(Ⅰ)①当1AD =时,在ABC ∆中,由正弦定理sin sin b BCB BAC=∠, ……2分即2sin B=,所以sin B =. ……4分 因为1AD AB ==,所以ADB B ∠=∠. ……6分 所以sin sin ADB B ∠=, ……7分即sin ADB ∠=. ……8分②当30CAD︒∠=时,在ABC∆中,由余弦定理知,222cos2AB BC ACBAB BC+-===⋅.……3分因为120A︒=,所以90DAB︒∠=,……4分所以π2B ADB∠+∠=,……5分所以sin cosADB B∠=,……7分即sin ADB∠=.……8分(17)(共14分)解:(Ⅰ)由频率分布直方图知,(0.0020.0020.006)1020m⨯++⨯=,……2分解得200m=. ……3分(Ⅱ)方法1:由图知,每位学生成绩不低于90分的频率为0.0110=0.1⨯,……1分由已知,X的所有可能取值为012,,,……2分则022(0)(10.1)0.81P X C==⋅-=,12(1)0.1(10.1)0.18P X C==⋅-=,222(2)0.10.01P X C==⋅=. ……5分所以X的分布列为……6分所以=00.81+10.1820.010.2EX⨯⨯+⨯=. ……7分方法2:由图知,每位学生成绩不低于90分的频率为0.0110=0.1⨯,……1分由已知(2,0.1)X B~,……2分则022(0)(10.1)0.81P X C==⋅-=,12(1)0.1(10.1)0.18P X C==⋅-=,222(2)0.10.01P X C==⋅=. ……5分所以X的分布列为……6分所以=20.10.2EX⨯=. ……7分P ABCDA 1B 1C 1E(Ⅲ)机构M 抽测的不达标率为200.1200= , ……1分 机构N 抽测的不达标率为200.2100=. ……2分 (以下答案不唯一,只要写出理由即可)①用机构M 测试的不达标率0.1估计A 校不达标率较为合理。
大兴区2023-2024学年第一学期期末检测高三数学试卷及答案

大兴区2023~2024学年度第一学期期末检测高三数学 2024.01本试卷共9页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题纸一并交回。
第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知全集{}1U x x =>,集合{}2A x x =≥,则U C A = A.{}12x x <≤ B.{}2x x < C.{}12x x <<D.{}1x x ≤2. 若复数z 满足i (i)1z ⋅+=,则复数z 的虚部是 A.2-B.2C.1-D.03. 在261()x x-的展开式中,常数项为A.15-B.15C.20-D.204. 设向量,a b ,若||1=a ,(3,4)=-b ,λ=b a (0)λ>,则=a A.43(,)55-B.43(,)55-C.34(,)55-D.34(,)55-5. 已知函数()21x f x =-,则不等式()f x x ≤的解集为 A.(,2]-∞ B.[0,1] C.[1,)+∞ D.[1,2]6. 在ABC △中,“π2C =”是“22sin sin 1A B +=”的 A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7. 已知定点(1,3)M 和抛物线2:8C x y =,F 是抛物线C 的焦点,N 是抛物线C 上的点,则||||NF NM +的最小值为A.3B.4C.5D.68. 已知0a b >>且10ab =,则下列结论中不正确的是 A.lg lg 0a b +> B.lg lg 0a b -> C.1lg lg 4a b ⋅<D.lg 1lg ab>9. 木楔在传统木工中运用广泛. 如图,某木楔可视为一个五面体,其中四边形ABCD 是边长为2的正方形,且ADE △,BCF △均为等边三角形,//EF CD ,4EF =,则该木楔的体积为B.C.3D.310. 设无穷等差数列{}n a 的公差为d ,集合{}*sin ,n T t t a n ==∈N . 则 A.T 不可能有无数个元素B.当且仅当0d =时,T 只有1个元素C.当T 只有2个元素时,这2个元素的乘积有可能为12D.当2πd k=,2k ≥,*k ∈N 时,T 最多有k 个元素,且这k 个元素的和为0第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分。
2023-2024学年北京市大兴区高三上学期期中考试检测数学试卷含详解

大兴区2023~2024学年度第一学期期中检测高三数学本试卷共4页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将答题卡交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}{}111,0,1A x x B =-<≤=-,,则A B = ()A.{}0B.{}1-C.{}1 D.{}0,12.在复平面内,复数z 对应的点的坐标是()1,1-,则z z ⋅=()A.1B.C.2D.3.下列函数中,既是偶函数又在区间()0,∞+上单调递增的是()A.2x y =B.1y x -=C.cos y x= D.ln ||y x =4.设x ∈R ,则“sin 0x =”是“cos 1x =”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.已知向量(10)(01)a b == ,,,,若()()a b a b λμ-⊥+,其中∈R ,λμ,则()A.1λμ+=-B.1λμ+=C.1λμ⋅=- D.1λμ⋅=6.在平面直角坐标系x O y 中,角α以O x 为始边,点(3,4)P -在角α终边上,则错误的是()A.4sin 5α=B.7cos 225α=C.1sin cos 5αα+=D.tan22α=7.在ABC 中,π,4,6A AB BC a ∠===,且满足该条件的ABC 有两个,则a 的取值范围是()A.()0,2 B.(C.()2,4 D.()8.已知12a =,5log 2b =,tan1c =,则()A .b a c<< B.a c b <<C.a b c<< D.c b a<<9.设函数()e ln x f x x =-的极值点为0x ,且0x M ∈,则M 可以是()A.10,2⎛⎫ ⎪⎝⎭B.12,23⎛⎫⎪⎝⎭C.2,13⎛⎫⎪⎝⎭D.()1,210.已知数列{}n a 满足1(1) n n n a a a +=-(n *∈N ),且101a <<.给出下列四个结论:①214a ≤;②12334n n a a a a +++++<;③m n *∀∈N ,,当n m >时,n m a a >;④k *∀∈N ,m *∃∈N ,当n m ≥时,1n a k<.其中所有正确结论的个数为()A.1B.2C.3D.4第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.2lg2lg25+=______.12.设函数()tan f x x =,则π()4f -=______;若()f x 满足对于定义域内的每一个x 都有()()f x T f x +=,0T >,则T 的最小值是______.13.等比数列{}n a 的前n 项和为n S ,能说明“若{}n a 为递增数列,则*1,N n n n S S +∀∈<”为假命题的一组1a 和公比q的值为1a =_______,q =_______.14.已知等边ABC 的边长为4,E F ,分别是,AB AC 的中点,则EF EA ⋅=_______;若M N ,是线段BC 上的动点,且1MN =,则EM EN ⋅的最小值为_______.15.已知函数1()22.xx a f x x x a ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩,,,①当0a =时,()f x 的值域为_______;②若关于x 的方程()()f x f x -=恰有2个正实数解,则a 的取值范围是_______.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.在ABC 中,2a =,2c b =.(1)若1sin 4B =,求C ∠;(2)若60A ︒∠=,求△ABC 的面积.17.已知等差数列{}n a 满足41a =,65a =.数列{}n b 满足15b a =,13n n bb +=.(1)求数列{}n a 的通项公式;(2)设数列{}n a 前n 项和n S 的最小值为m ,若4a ,m ,k b 构成等比数列,求k 的值.18.已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭,且()f x 图象的相邻两条对称轴之间的距离为π2.(1)求ω的值;(2)再从条件①、条件②、条件③这三个条件中选择两个作为已知,若()f x a ≥对ππ,42x ⎡⎤∈⎢⎣⎦恒成立,求a 的取值范围.条件①:()01f =-;条件②:()f x 的最大值为2;条件③:()f x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增.注:如果选择多组符合要求的条件分别解答,按第一组解答计分.19.已知函数32()1f x x ax =--.(1)若1a =,求()f x 的极值;(2)若()f x 在区间[2,0]-上的最小值为(2)f -,求a 的取值范围;(3)直接写出一个a 值使()f x 在区间[1,0]-上单调递减.20.设函数23()9(3)e ax f x x x =--,曲线()y f x =在点(0(0))f ,处的切线方程为27y =.(1)求a 的值;(2)求证:当(],3x ∈-∞时,()27f x ≥;(3)问存在几个点()00,()P x f x ,使曲线()y f x =在点P 处的切线平行于x 轴?(结论不要求证明)21.设数列12:,,,n A a a a (2)n ≥,如果1202024n a a a <<<< ≤,且i a *∈N ,(1,2,,)i n = ,对于2k ∀≥,11s t r k ∃-≤≤≤≤,使k s t r a a a a =++成立,则称数列A 为E 数列.(1)分别判断数列1,3,5,7和数列2,6,14,22是否是E 数列,并说明理由;(2)若数列A 是E 数列,且2023n a =,求n 的最小值;(3)若数列A 是E 数列,且2024n a =,求n 的最大值.大兴区2023~2024学年度第一学期期中检测高三数学第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}{}111,0,1A x x B =-<≤=-,,则A B = ()A.{}0B.{}1-C.{}1 D.{}0,1【答案】D【分析】利用集合,A B ,即可求出A B ⋂.【详解】由题意,{}{}111,0,1A x x B =-<≤=-,,∴{}0,1A B = ,故选:D.2.在复平面内,复数z 对应的点的坐标是()1,1-,则z z ⋅=()A.1B.C.2D.【答案】C【分析】根据复数的几何意义可得1i,z =-结合共轭复数的定义以及复数的乘法运算即可求解.【详解】由题意可得1i,z =-故1i z =+,进而()()1i 1i 2z z ⋅=+-=,故选:C3.下列函数中,既是偶函数又在区间()0,∞+上单调递增的是()A.2x y =B.1y x -=C.cos y x =D.ln ||y x =【答案】D【分析】分别判断各选项中函数的奇偶性和单调性即可.【详解】指数函数2x y =不是偶函数,A 选项错误;幂函数1y x -=是奇函数,B 选项错误;函数cos y x =是偶函数,但在()0,∞+上不单调,C 选项错误;函数ln y x =是偶函数,()0,x ∞∈+时ln y x =单调递增.故选:D4.设x ∈R ,则“sin 0x =”是“cos 1x =”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【分析】根据同角三角函数平方关系,结合必要不充分性的判断即可求解.【详解】由sin 0x =,则22sin 1cos 0cos 1x x x =-=⇒±=,故充分性不成立,由cos 1x =,则22cos 1sin 1sin 0x x x =-=⇒=,故必要性成立,故“sin 0x =”是“cos 1x =”的必要不充分条件,故选:B5.已知向量(10)(01)a b == ,,,,若()()a b a b λμ-⊥+,其中∈R ,λμ,则()A.1λμ+=-B.1λμ+=C.1λμ⋅=-D.1λμ⋅=【答案】D【分析】利用向量的线性运算和向量垂直的坐标运算求解.【详解】向量(10)(01)a b ==,,,,()1,a b λλ-=- ,()1,a b μμ+= ,()()a b a b λμ-⊥+ ,()()10a b a b λμλμ-⋅+=-⋅=,即1λμ⋅=.故选:D6.在平面直角坐标系x O y 中,角α以O x 为始边,点(3,4)P -在角α终边上,则错误的是()A.4sin 5α=B.7cos 225α=C.1sin cos 5αα+= D.tan22α=【答案】B【分析】根据任意角三角函数的定义求sin ,cos ,tan ααα,进而可以判断AC ;利用倍角公式判断B ;利用倍角公式结合象限角的三角函数值的符号判断D 【详解】由题意可知:4344sin ,tan 5533ααα-==-=--,故A 正确;且227cos 2cos sin 25ααα=-=-,故B 错误;431sin cos 555αα⎛⎫+=+-= ⎪⎝⎭,故C 正确;因为22tan42tan 31tan 2ααα==--,整理得22tan 3tan 2022αα--=,解得tan 22α=或1tan 22α=-,且π2π2ππ,2αk k k Z +<<+Î,则ππππ,422αk k k Z +<<+Î,可知k 为奇数时,2α为第三象限角,k 为偶数时,2α为第一象限角,综上所述:tan 02α>,即tan 22α=,故D 正确;故选:B.7.在ABC 中,π,4,6A AB BC a ∠===,且满足该条件的ABC 有两个,则a 的取值范围是()A.()0,2B.(2,C.()2,4D.()【答案】C【分析】由题意可知,画出A ∠和边长AB ,以B 为圆心,a 为半径作圆与AC 边有两个交点时即可求出a 的取值范围.【详解】根据题意如下图所示:易知当BC AC ⊥时,sin 302BC AB == ,若2a =满足条件的三角形只有一个;由题可知以B 为圆心,a 为半径的圆与AC 边有两个交点时,即图中12,C C 两点满足题意;所以可得BC a AB <<,即24a <<;即a 的取值范围是()2,4.故选:C8.已知12a =,5log 2b =,tan1c =,则()A.b a c <<B.a c b <<C.a b c <<D.c b a<<【答案】A【分析】根据正切函数的单调性可得1c <,根据对数的性质可得12b <,即可比较.【详解】πtan1tan 14c =>=,551log 2log 2b =<=,所以b ac <<,故选:A9.设函数()e ln x f x x =-的极值点为0x ,且0x M ∈,则M 可以是()A.10,2⎛⎫ ⎪⎝⎭B.12,23⎛⎫⎪⎝⎭C.2,13⎛⎫⎪⎝⎭D.()1,2【答案】B【分析】求导,再根据导函数的单调性结合极值点的定义及零点的存在性定理即可得出答案.【详解】()1()e 0xf x x x '=->,因为函数1e ,xy y x ==-在()0,∞+上都是增函数,所以函数1()e xf x x'=-在()0,∞+上是增函数,又213212333e 20,e 023222f f ⎛⎫⎛⎫''=-<=-=->-= ⎪ ⎪⎝⎭⎝⎭,所以存在唯一实数012,23x ⎛⎫∈⎪⎝⎭,使得()00f x '=,当00x x <<时,()0f x '<,当0x x >时,()0f x ¢>,所以函数函数()e ln x f x x =-又唯一极值点0x ,且012,23x ⎛⎫∈⎪⎝⎭,故M 可以是12,23⎛⎫ ⎪⎝⎭.故选:B.10.已知数列{}n a 满足1(1) n n n a a a +=-(n *∈N ),且101a <<.给出下列四个结论:①214a ≤;②12334n n a a a a +++++<;③m n *∀∈N ,,当n m >时,n m a a >;④k *∀∈N ,m *∃∈N ,当n m ≥时,1n a k<.其中所有正确结论的个数为()A.1B.2C.3D.4【答案】C【分析】根据二次函数的性质即可判定①,由放缩法即可求解②,根据数列的单调性即可判断③④【详解】由于2211111(1) =24a a a a ⎛⎫=---+ ⎪⎝⎭,且101a <<,所以214a ≤,故①正确,21(1) 0n n n n n n a a a a a a +-=--=-≤,由于101a <<,所以0n a <,故1n n a a +<,所以当2n ≥时,214n a a <≤,因此()()1231113111444n n a a a a a n n +++++<+-<+-=,故②正确,由于1n n a a +<,所以数列{}n a 为单调递减数列,所以m n *∀∈N ,,当n m >时,n m a a <;③错误,21(1) =n n n n n a a a a a +=--,故21(1) =n n n n n a a a a a +=--,则111n n na a a +=-,由于01n a <<,则011n a <-<,所以1111n n na a a +=>-,又21nn n a a a +=-,同除以21111n n n n n n n n n a a aa a a a a a ++++=-,所以1111n n n n a a a a ++=-,1112211111,,n n n n a a a a a a a a --=-=- ,相加可得11121111n n n n n a a a a a a a a -+++++=- ,故1111n n a a +->,进而可得111101n a n n a +<<<+,k *∀∈N ,m *∃∈N ,当1m k =+时,又数列{}n a 为单调递减数列,当n m ≥时,111n m a a m k≤<=-.故④正确故选:C【点睛】方法点睛:本题主要考查数列求和的应用,根据数列的递推关系,利用累加法求出数列的通项公式以及,利用裂项法进行求和是解决本题的关键;常见的数列求和的方法有公式法即等差等比数列求和公式,分组求和类似于n n n c a b =+,其中{}n a 和{}n b 分别为特殊数列,裂项相消法类似于()11n a n n =+,错位相减法类似于n n n c a b =⋅,其中{}n a 为等差数列,{}n b 为等比数列等.第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.2lg2lg25+=______.【答案】2【分析】通过同底对数的运算法则,求得结果.【详解】2lg2lg25lg4lg25lg1002+=+==本题正确结果:2【点睛】本题考查对数的运算,属于基础题.12.设函数()tan f x x =,则π()4f -=______;若()f x 满足对于定义域内的每一个x 都有()()f x T f x +=,0T >,则T 的最小值是______.【答案】①.1-②.π【分析】根据诱导公式直接计算π()4f -,根据最小正周期的概念求解即可;【详解】函数()tan f x x =,则πππ(tan(tan 1444f -=-=-=-,若()f x 满足对于定义域内的每一个x 都有()()f x T f x +=,0T >,则T 为函数()tan f x x =的一个正周期,又函数()tan f x x =的最小正周期为π,所以T 的最小值是π.故答案为:1-;π13.等比数列{}n a 的前n 项和为n S ,能说明“若{}n a 为递增数列,则*1,N n n n S S +∀∈<”为假命题的一组1a 和公比q的值为1a =_______,q =_______.【答案】①.1-②.12(答案不唯一)【分析】由题意,等比数列{}n a 为递增数列,且*1,0N n n a +∈≤∃,取一组符合条件的1a 和公比q 即可.【详解】“若{}n a 为递增数列,则*1,N n n n S S +∀∈<”为假命题,所以若{}n a 为递增数列,则*1,N n n n S S +∃∈≥,1n n S S +≥,则110n n n S S a ++-=≤,等比数列{}n a 为递增数列,且*1,0N n n a +∈≤∃,则11a =-和公比12q =,满足题意.故答案为:1-;1214.已知等边ABC 的边长为4,E F ,分别是,AB AC 的中点,则EF EA ⋅= _______;若M N ,是线段BC 上的动点,且1MN =,则EM EN ⋅的最小值为_______.【答案】①.2②.114##2.75【分析】第一空:通过()EF EA EA AF EA ⋅=+⋅ 展开整理,带入数据计算即可;第二空:设,03BN t t =≤≤,通过()()EM EN EB BM EB BN ⋅=+⋅+ 展开整理,带入数据然后配方求最值.【详解】()22222cos1202EF EA EA AF EA EA AF EA ⋅=+⋅=+⋅=+⨯⨯= ;若M N ,是线段BC 上的动点,且1MN =,不妨设N 点相对M 更靠近B 点,设,03BN t t =≤≤,()()()2EM EN EB BM EB BN EB BM BN EB BM BN ∴⋅=+⋅+=++⋅+⋅ ()()2221cos1201t t t t=+++++ 22111324t t t ⎛⎫=-+=-+ ⎪⎝⎭,当12t =时,EM EN ⋅ 取最小值,且为114.故答案为:2;114.15.已知函数1()22.xx a f x x x a ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩,,,①当0a =时,()f x 的值域为_______;②若关于x 的方程()()f x f x -=恰有2个正实数解,则a 的取值范围是_______.【答案】①.(0)+∞,②.[11)-,【分析】①当0a =时,分别判断两段的值域,取并集得()f x 的值域;②方程()()f x f x -=恰有2个正实数解,则y 轴左边的函数图像翻折到右边,与右边的图像有两个交点,作出图像判断a 的取值范围.【详解】①当0a =时,10()220.xx f x x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩,,,,0x ≤时,1()2x f x ⎛⎫= ⎪⎝⎭,函数单调递减,011()2f x ⎛⎫≥ ⎪⎝=⎭;0x >时,()2f x x =,函数单调递增,()0f x >,所以()f x 的值域为(0)∞+,;②函数1()22.xx a f x x x a ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩,,,关于x 的方程()()f x f x -=恰有2个正实数解,则y 轴左边的函数图像翻折到右边,与y 轴右边的图像有两个交点,分别作出函数12,,22xx y x y y ⎛⎫=== ⎪⎝⎭的图像,其中函数2y x =与2x y =的图像相交于点()1,2和()2,4结合图像可知方程()()f x f x -=恰有2个正实数解,为1x =和2x =,需要11a -≤<,所以a 的取值范围为[11)-,.故答案为:(0)∞+,;[11)-,.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.在ABC 中,2a =,2c b =.(1)若1sin 4B =,求C ∠;(2)若60A ︒∠=,求△ABC 的面积.【答案】(1)30C ︒∠=或150︒(2)233【分析】(1)根据正弦定理得到1sin 2C =即可得到答案;(2)根据余弦定理得到3b =,再根据三角形面积公式求解即可.【小问1详解】因为2c b =,所以由正弦定理sin sin c C b B =,得sin 2sin C B =,因为1sin 4B =,所以1sin 2C =,因为0180C ︒︒<∠<,所以30C ︒∠=或150︒【小问2详解】由余弦定理2222cos a b c bc A =+-,得2222(2)22cos60b b b b ︒=+-⨯⨯,解得3b =或233b =-(舍去),由△ABC 的面积1sin 2S bc A =,得212sin 63202S b b =⨯=⨯︒=17.已知等差数列{}n a 满足41a =,65a =.数列{}nb 满足15b a =,13n n b b +=.(1)求数列{}n a 的通项公式;(2)设数列{}n a 前n 项和n S 的最小值为m ,若4a ,m ,k b 构成等比数列,求k 的值.【答案】(1)27n a n =-;(2)4.【分析】(1)根据给定条件,求出等差数列的公差即可得解.(2)由(1)的信息,求出m ,再借助等比数列求解即可.【小问1详解】设等差数列{}n a 的公差为d ,则113155a d a d +=⎧⎨+=⎩,解得15a =-,2d =,所以数列{}n a 的通项公式1(1)27n a a n d n =+-=-.【小问2详解】由(1)知,1230a a a <<<,4560a a a <<<< ,从而{}n a 的前n 项和n S 的最小值33253292m S ⨯==-⨯+⨯=-,由4a ,m ,k b 构成等比数列,得2481k m b a ==,由27n a n =-,得53a =,即153b a ==,又13n n b b +=,则数列{}n b 是首项为3,公比3q =的等比数列,即有3k k b =,由381k =,解得4k =,所以k 的值是4.18.已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>><⎪⎝⎭,且()f x 图象的相邻两条对称轴之间的距离为π2.(1)求ω的值;(2)再从条件①、条件②、条件③这三个条件中选择两个作为已知,若()f x a ≥对ππ,42x ⎡⎤∈⎢⎣⎦恒成立,求a 的取值范围.条件①:()01f =-;条件②:()f x 的最大值为2;条件③:()f x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增.注:如果选择多组符合要求的条件分别解答,按第一组解答计分.【答案】(1)2ω=(2)条件选择见解析,1a ≤【分析】(1)根据题意求出函数()f x 的最小正周期,结合正弦型函数的周期公式可求得ω的值;(2)选①②,根据函数()f x 的最大值求出A 的值,根据()01f =-结合ϕ的取值范围,求出ϕ的值,可得出函数()f x 的解析式;选②③,根据函数()f x 的最大值求出A 的值,分析可知,π26f ⎛⎫-=- ⎪⎝⎭,结合ϕ的取值范围,可求出ϕ的值,可得出函数()f x 的解析式;选①③,分析可知,π6f A ⎛⎫-=- ⎪⎝⎭,结合ϕ的取值范围,可求出ϕ的值,再由()01f =-可得出A 的值,即可得出()f x 的解析式;再由ππ,42x ⎡⎤∈⎢⎥⎣⎦结合正弦型函数的基本性质可求出()f x 的最小值,即可得出实数a 的取值范围.【小问1详解】解:因为()f x 的图象的相邻两个对称轴的距离为π2,所以,函数()f x 的最小正周期为π2π2T =⨯=,所以2π2T ω==.【小问2详解】解:选择条件①②.因为()f x 的最大值为2,所以2A =,即()()2sin 2f x x ϕ=+.由()02sin 1f ϕ==-,得1sin 2ϕ=-,又因为2πϕ<,所以π6ϕ=-,所以函数()f x 的解析式为()π2sin 26f x x ⎛⎫=- ⎪⎝⎭.选择条件②③.因为()f x 的最大值为2,所以2A =,因为()f x 的最小正周期为πT =,且在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增,又因为区间ππ,63⎡⎤-⎢⎥⎣⎦的长度为πππ3622T ⎛⎫--== ⎪⎝⎭,所以π26f ⎛⎫-=- ⎪⎝⎭,即πsin 13ϕ⎛⎫-+=- ⎪⎝⎭,得()ππ2π32k k ϕ-=-∈Z ,则()π2π6k k ϕ=-∈Z ,又因为2πϕ<,所以π6ϕ=-.所以()f x 的解析式为()π2sin 26f x x ⎛⎫=-⎪⎝⎭.选择条件①③.因为()f x 的最小正周期为πT =,且在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增,又因为区间ππ,63⎡⎤-⎢⎥⎣⎦的长度为πππ3622T ⎛⎫--== ⎪⎝⎭,所以ππsin 63f A A ϕ⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭,即πsin 13ϕ⎛⎫-+=- ⎪⎝⎭,得()ππ2π32k k ϕ-=-∈Z ,则()π2π6k k ϕ=-∈Z ,又因为2πϕ<,所以π6ϕ=-.由()01f =-,得π1sin 162A A ⎛⎫-=-=- ⎪⎝⎭,所以2A =.所以()f x 的解析式为()π2sin 26f x x ⎛⎫=- ⎪⎝⎭.因为ππ,42x ⎡⎤∈⎢⎥⎣⎦,所以ππ5π2,636x ⎡⎤-∈⎢⎥⎣⎦所以π1sin 2,162x ⎛⎫⎡⎤-∈ ⎪⎢⎥⎝⎭⎣⎦,故()[]1,2f x ∈.当π2x =时,()f x 的最小值为1.因为ππ,42x ⎡⎤∈⎢⎥⎣⎦,()f x a ≥恒成立,则1a ≤,所以a 的取值范围为(],1-∞.19.已知函数32()1f x x ax =--.(1)若1a =,求()f x 的极值;(2)若()f x 在区间[2,0]-上的最小值为(2)f -,求a 的取值范围;(3)直接写出一个a 值使()f x 在区间[1,0]-上单调递减.【答案】(1)极大值为(0)1f =-,极小值为231327⎛⎫=- ⎪⎝⎭f (2)[2,)-+∞(3)2-(答案不唯一,3,2a ⎛⎤∈-∞- ⎥⎝⎦即可)【分析】(1)求导,利用导数判断原函数单调性和极值;(2)求导,分类讨论两根大小,利用导数判断原函数单调性和最值,列式求解即可;(3)由题意可得32a x ≤在[)1,0-内恒成立,根据恒成立问题分析求解.【小问1详解】当1a =时,32()1f x x x =--,函数()f x 的定义域为R ,则2()32f x x x ='-,令()0f x '=,解得0x =,或23x =,()f x '与()f x 在区间R 内的情况如下:x (,0)-∞020,3⎛⎫ ⎪⎝⎭232,+3⎛⎫∞ ⎪⎝⎭()f x '+0-0+()f x 单调递增极大值单调递减极小值单调递增所以()f x 的极大值为(0)1f =-,极小值为231327⎛⎫=- ⎪⎝⎭f .【小问2详解】由题意知,2()32(32)f x x ax x x a '=-=-.令()0f x '=,则0x =,23x a =,①当223a ≤-,即3a ≤-时,()0f x '≤在区间[2,0]-上恒成立,所以()f x 区间[2,0]-上单调递减,所以()f x 的最小值为(0)f ,与已知相矛盾,不符合题意;②当2203a -<<,即30a -<<时,()f x '与()f x 在区间(2,0)-上的变化情况如下:x 22,3⎛⎫- ⎪⎝⎭a 23a 2a,03⎛⎫ ⎪⎝⎭()f x '+0-()f x 单调递增极大值单调递减因为()f x 在区间[2,0]-上的最小值为(2)f -,所以(2)(0)f f -≤,即941a ---≤,解得2a ≥-,所以20a -≤<;③当203a ≥,即0a ≥时,()0f x '≥在区间[2,0]-上恒成立,所以()f x 在[2,0]-上单调递增,最小值为(2)f -,满足题意;综上所述:a 的取值范围是[2,)-+∞.【小问3详解】若()f x 在区间[1,0]-上单调递减,则2()320f x x ax '=-≤在[)1,0-内恒成立,可得32a x ≤在[)1,0-内恒成立,即32a ≤-,即a 的取值范围为3,2⎛⎤-∞- ⎥⎝⎦,所以a 的值可以为2-.20.设函数23()9(3)e ax f x x x =--,曲线()y f x =在点(0(0))f ,处的切线方程为27y =.(1)求a 的值;(2)求证:当(],3x ∈-∞时,()27f x ≥;(3)问存在几个点()00,()P x f x ,使曲线()y f x =在点P 处的切线平行于x 轴?(结论不要求证明)【答案】(1)1(2)证明见解析(3)2【分析】(1)求导,再根据导数的几何意义即可得解;(2)利用导数求出()f x 在(],3x ∈-∞上的最小值,即可得证;(3)曲线()y f x =在点P 处的切线平行于x 轴,即曲线()y f x =在点P 处的斜率为0,则点P 的个数即函数()y f x '=零点的个数,结合(2)即可得出答案.【小问1详解】因为23()9(3)e ax f x x x =--,所以23()183(3)e (3)e ax ax f x x x x a '=----,因为曲线()y f x =在点(0(0))f ,处的切线方程为27y =,所以所以(0)27270f a =-=',所以1a =;【小问2详解】由(1)知,2()(18e (3))x f x x x '=--,设2()18e (3)x g x x =--,所以()e (3)(1)x g x x x =---',当3x >或1x <时,()0g x '<,当13x <<时,()0g x '>,所以函数()g x 在()(),1,3,∞∞-+上单调递减,在()1,3上单调递增,所以当(],3x ∈-∞时,()()min 1184e 0g x g ==->,则当0x <时,()0f x '<,当03x <<时,()0f x ¢>,所以函数()f x 在(),0∞-上单调递减,在()0,3上单调递增,所以()()min 027f x f ==,所以当(],3x ∈-∞时,()27f x ≥;【小问3详解】曲线()y f x =在点P 处的切线平行于x 轴,即曲线()y f x =在点P 处的斜率为0,则点P 的个数即函数()y f x '=零点的个数,由题意可知点P 可以是()0,27,当00x ≠时,令2()(18e (3))0x f x x x '=--=,则218e (3)0x x --=由(2)得,2()18e (3)x g x x =--在()(),1,3,∞∞-+上单调递减,在()1,3上单调递增,()()1184e>0,318g g =-=,由当x →-∞时,()g x ∞→+,当x →+∞时,()g x →-∞,所以当3x <时,函数()g x 无零点,当3x >时,()g x 有且仅有一个零点,综上,函数()y f x '=有2个零点,即存在2个点()00,()P x f x ,使曲线()y f x =在点P 处的切线平行于x 轴【点睛】方法点睛:利用导数证明不等式问题,方法如下:(1)直接构造函数法:证明不等式()()f x g x >(或()()f x g x <)转化为证明()()0f x g x ->(或()()0f x g x -<),进而构造辅助函数()()()h x f x g x =-;(2)适当放缩构造法:一是根据已知条件适当放缩;二是利用常见放缩结论;(3)构造“形似”函数,稍作变形再构造,对原不等式同解变形,根据相似结构构造辅助函数.21.设数列12:,,,n A a a a (2)n ≥,如果1202024n a a a <<<< ≤,且i a *∈N ,(1,2,,)i n = ,对于2k ∀≥,11s t r k ∃-≤≤≤≤,使k s t r a a a a =++成立,则称数列A 为E 数列.(1)分别判断数列1,3,5,7和数列2,6,14,22是否是E 数列,并说明理由;(2)若数列A 是E 数列,且2023n a =,求n 的最小值;(3)若数列A 是E 数列,且2024n a =,求n 的最大值.【答案】(1)1,3,5,7是E 数列,2,6,14,22是E 数列,理由见解析(2)3(3)127【分析】(1)分别验证数列1,3,5,7和数列2,6,14,22中234,,a a a 是否满足E 数列性质即可得出结论;(2)利用反证法证明2n =不成立,取特例可知当3n =存在数列满足E 数列,即可得n 的最小值为3;(3)首先证明若1a 为奇数,则n a 必为奇数,又2024n a =可得1a 为偶数;利用E 数列性质可证明得出18a ≥,解不等式即可求出127n ≤.【小问1详解】①是E 数列.因为21113a a a a =++=,31121135a a a a =++=++=,41131157a a a a =++=++=,所以①是E 数列.②是E 数列.因为21116a a a a =++=,312226614a a a a =++=++=,4123261422a a a a =++=++=,所以②是E 数列.【小问2详解】首先证明n 不能为2.假设2n =,由数列A 为E 数列知,2111132023a a a a a =++==.所以120233a *=∉N ,与已知矛盾,故假设不成立.所以n 不能为2.因为数列A :2898672023,,满足211113867a a a a a =++==,31222898678672023a a a a =++=++=,此时A 是E 数列,所以n 的最小值为3.【小问3详解】(i )以下证明:若1a 为奇数,则n a 必为奇数.假设数列A 中存在偶数,设(2)k a k ≥是数列A 中第一个偶数,因为数列A 是E 数列,所以11s t r k ∃-≤≤≤≤,使k s t r a a a a =++.因为s t r a a a ,,均为奇数,所以k a 也为奇数,与k a 为偶数矛盾.所以若1a 为奇数,则n a 必为奇数.因为2024n a =为偶数,所以1a 不能为奇数,只能为偶数.(ii )以下证明:若1=2a ,则42n a p =+(p *∈N ).若不然,设k a (2k ≥)为第一个满足42k a p ≠+(p *∈N )的项,因为数列A 是E 数列,所以11s t r k ∃-≤≤≤≤,使k s t r a a a a =++.因为123424242s t r a p a p a p =+=+=+,,(123p p p *∈,,N ),所以k a ()123412p p p =++++,与42k a p ≠+(p *∈N )矛盾;所以若1=2a ,则42n a p =+(p *∈N ).而20244506042n a p ==⨯+≠+(p *∈N ),所以12a ≠.同理,若14a =,则84n a p =+(p *∈N ).而20248253084n a p ==⨯+≠+(p *∈N ).所以1a 4≠.同理,若16a =,则126n a p =+3p ='(p p *'∈N ,).而2024367423n a p '==⨯+≠(p *'∈N ),所以16a ≠.综上18a ≥.(3)当18a ≥时,因为数列A 是E 数列,所以111123288216316(2)16n n n n n a a a a a a a a n ----≥++≥++≥+⨯≥+⨯≥≥+-⨯ ()13216168a n n =+-⨯≥-由题意知,2024168n ≥-,解得127n ≤;所以n 的最大值为127.此时()1681,2,,127n a n n =-= 即为满足条件的E 数列【点睛】关键点点睛:本题关键在于求解第(3)问时,首先证明1a 只能为偶数,再利用数列性质分别验证1a 的最小偶数取值,构造不等式即可得出其最大值.。
北京市大兴区2022-2023学年高三上学期期末考试数学试题

大兴区2022~2023学年度第一学期期末检测试卷2022.12高三数学学校__________姓名__________班级__________考号__________考生须知1.本试卷共4页,共两部分,21道小题。
满分150分。
考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、班级、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题用2B 铅笔作答,其他题用黑色字迹签字笔作答。
(选择题 共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知集合{}12A x x =≤≤,则A =R( )A.{}1,2x x x <>或B.{}1,2x x x ≤≥或C.{}1,2x x x ≤>或D.{}1,2x x x <≥或2.下列函数中,既是奇函数又在定义域上是增函数的是( )A.ln y x =B.tan y x =C.3y x =D.1y x=-3.在()51x -展开式中,2x 的系数为 A.10B.5C.10-D.5-4.设n S 为等差数列{}n a 的前n 项和.已知33S =-,52a =,则( )A.{}n a 为递减数列B.30a =C.n S 有最大值D.60S =5.已知抛物线24y x =上一点M 与其焦点的距离为5,则点M 到x 轴的距离等于( ) A.3B.4C.5D.426.“0a =”是“直线210x ay a -+-=()a ∈R 与圆221x y +=相切”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件D.既不充分也不必要条件7.某圆锥曲线C 是椭圆或双曲线,若其中心为坐标原点,对称轴为坐标轴,且过()2,1A -和32,2B ⎛ ⎝⎭两点,则曲线C 的离心率等于( )A.12B.2236 8.已知数列{}n a 中,11a =,12n n n a a +⋅=,*n ∈N ,则下列结论错误..的是( ) A.22a =B.432a a -=C.{}2n a 是等比数列D.12122n n n a a +-+=9.“赵爽弦图”是我国古代数学的瑰宝,它是由四个全等的直角三角形和一个正方形构成.现仿照赵爽弦图,用四个三角形和一个小平行四边形构成如下图形,其中,E ,F ,G ,H 分别是DF ,AG ,BH ,CE 的中点,若AG x AB y AD =+,则2x y +等于( )A.25B.45 C.1 D.2 10.已知函数()2cos 23x f x x x π=-+,给出下列结论:①()f x 是周期函数;②()f x 的最小值是12-;③()f x 的最大值是12;④曲线()y f x =是轴对称图形,则正确结论的序号是( )A.①③1B.②④C.①②③D.②③④第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分。
北京市大兴区高三数学一模文科试题及答案
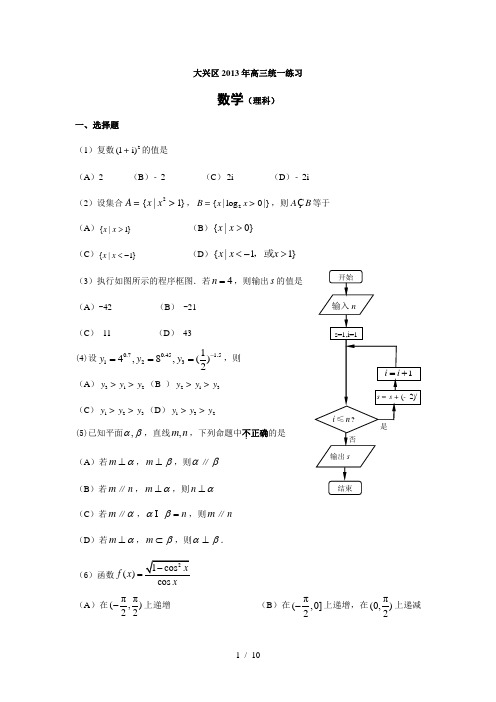
是否 结束开始s=1,i=1(2)i s s =+-1i i =+输入n输出si n ≤?大兴区2013年高三统一练习数学(理科)一、选择题(1)复数2(1i)+的值是(A )2 (B )2- (C )2i (D )2i -(2)设集合2{|1}=>A x x ,2{|log 0|}=>B x x ,则ÇA B 等于(A )}1|{>x x (B )}0|{>x x (C )}1|{-<x x(D ){|11},或x x x <-> (3)执行如图所示的程序框图.若4n =,则输出s 的值是 (A )-42 (B ) -21 (C ) 11 (D ) 43(4)设0.70.45 1.512314,8,()2y y y -===,则(A )312y y y >>(B )213y y y >> (C )123y y y >>(D )132y y y >>(5)已知平面βα,,直线n m ,,下列命题中不.正确的是 (A )若α⊥m ,β⊥m ,则α∥β (B )若m ∥n ,α⊥m ,则α⊥n (C )若m ∥α,n =βα ,则m ∥n (D )若α⊥m ,β⊂m ,则βα⊥.(6)函数21cos ()cos x f x x-=(A )在ππ(,)22-上递增 (B )在π(,0]2-上递增,在π(0,)2上递减(C )在ππ(,)22-上递减 (D )在π(,0]2-上递减,在π(0,)2上递增 (7)若实数,a b 满足221a b +≤,则关于x 的方程220x x a b -++=无.实数根的概率为 (A )14 (B ) 34(C )3π24π+ (D )π24π-(8)抛物线2(22)y x x =-≤≤绕y 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是(A )1 (B )2 (C )22 (D )4二、填空题(9)函数f x x x()s i nc o s =的最小正周期是 (10)已知中心在原点,焦点在x 轴上的双曲线的离心率为32,实轴长为4,则双曲线的方程是(11)已知矩形ABCD 中,2AB =,1AD =,E 、F 分别是BC 、CD 的中点,则()AE AF AC +?等于.(12)已知数列{}n a ,1+2n n a a +=,1=1a ,数列11n n a a +禳镲镲睚镲镲铪的前n 项和为1837,则n =. (13)已知函数⎪⎩⎪⎨⎧-=-2112)(xx f x 00>≤x x 在区间[1,]m -上的最大值是1,则m 的取值范围是.(14)已知函数()f x 是定义在(0,)+?上的单调递增函数,且*ÎN x 时,()*ÎN f x ,若[()]3f f n n =,则(2)=f ;(4)(5)f f +=三、解答题(15)(本小题满分13分)在∆A B C 中,角A ,B ,C 的对边分别为a ,b ,c ,3cos 5=A ,π4B =,2b =.(Ⅰ)求a 的值;(Ⅱ)求sin C 及∆A B C 的面积. (16)(本小题满分13分)一次考试结束后,随机抽查了某校高三(1)班5名同学的数学与物理成绩如下表: 学生 1A2A3A4A5A数学 89 91 93 95 97 物理8789899293(Ⅰ)分别求这5名同学数学与物理成绩的平均分与方差,并估计该班数学与物理成绩那科更稳定;(Ⅱ)从以上5名同学中选2人参加一项活动,求选中的学生中至少有一个物理成绩高于90分的概率.(17)(本小题满分13分)如图,直三棱柱ABC —A 1B 1C 1中,ABC D 是等边三角形,D 是BC 的中点. (Ⅰ)求证:直线A 1D ⊥B 1C 1;(Ⅱ)判断A 1B 与平面ADC 1的位置关系,并证明你的结论.(18)(本小题满分14分) 已知函数()(1)e x f x ax =+.(I )求函数()f x 的单调区间;(Ⅱ)当0a >时,求函数()f x 在区间[2,0]-上的最小值.19.(本小题满分14分)已知动点P 到点A (-2,0)与点B (2,0)的斜率之积为14-,点P 的轨迹为曲线C 。
北京市大兴区2022~2023学年度第二学期高三年级数学摸底检测(含参考答案)

大兴区2022~2023学年度第二学期高三年级摸底检测高三数学(答案在最后) 第一部分 (选择题 共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合{25}U x N x =∈-<<,集合{0,1,2}A =,则U C A =( )(A ){0,2,3} (B ){10,2,3}-, (C ){13,4}-,(D ){3,4}(2)若复数z 满足34i z i ⋅=-,则z =( )(A )1(B )5 (C )7(D )25(3)若α为任意角,则满足cos()cos 4k παα+⋅=的一个k 值为( )(A )2 (B )4 (C )6 (D )8(4)在人类中,双眼皮由显性基因A 控制,单眼皮由隐性基因a 控制.当一个人的基因型为AA 或Aa 时,这个人就是双眼皮,当一个人的基因型为aa 时,这个人就是单眼皮.随机从父母的基因中各选出一个A 或者a 基因遗传给孩子组合成新的基因.根据以上信息,则“父母均为单眼皮”是“孩子为单眼皮”的( ) (A )充分不必要条件 (B )必要不充分条件 (C )充要条件(D )既不充分也不必要条件(5)已知三个函数3y x =,3x y =,3log y x =,则( )(A )定义域都为R(B )值域都为R (C )在其定义域上都是增函数(D )都是奇函数(6)双曲线222:1y C x b-=的渐近线与直线1x =交于A ,B 两点,且|AB |=4,那么双曲线C的离心率为( ) (A 2 (B 3(C )2(D 5(7)设{}n a 是各项均为正数的等比数列,n S 为其前n 项和. 已知1316a a ⋅=,314S =,若存在0n 使得012,,,n a a a 的乘积最大,则0n 的一个可能值是( ) (A )4 (B )5 (C )6(D )7(8)一次数学考试共有8道判断题,每道题5分,满分40分.规定正确的画√,错误的画×.甲、乙、丙、丁四名同学的解答及得分情况如表所示,则m 的值为( )题号学生 1 2 3 4 5 6 7 8 得分 甲 × √ × √ × × √ × 30 乙 × × √ √ √ × × √ 25 丙 √ × × × √ √ √ × 25 丁×√×√√×√√m(A )35 (B )30 (C )25(D )20(9)点P 在函数y =e x 的图象上.若满足到直线y =x +a 的距离为2的点P 有且仅有3个,则实数a 的值为( ) (A )22 (B )23 (C )3(D )4(10)如图,正方体1111ABCD A B C D -的棱长为2,点O 为底面ABCD 的中心,点P 在侧面11BCC B 的边界及其内部运动.若1D O OP ⊥,则11D C P ∆面积的最大值为( )(A )255(B )455(C )5(D )25第二部分 (非选择题 共110分)二、填空题共5小题,每小题5分,共25分。
北京市大兴区2019届高三上学期期末检测文科数学试卷+Word版含解析

大兴区2018-2019学年度第一学期期末检测试卷高三数学(文)本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.设集合,,则等于( )A. B. C. D.【答案】C【解析】【分析】求解一元二次不等式化简集合B,然后直接利用交集运算得答案.【详解】解:∵x2﹣3x≤0,∴0≤x≤3,∴B=[0,3],A=(2,+∞),∴A∩B=(2,3].故选:C.【点睛】本题考查了交集及其运算,考查了一元二次不等式的解法,是基础题.2.已知,则下列不等式成立的是( )A. B. C. D.【答案】B【解析】【分析】利用不等式的基本性质、函数的单调性即可得出.【详解】解:∵a>b>0,∴,,lga>lgb,2﹣a<2﹣b.只有B正确.故选:B.【点睛】本题考查了不等式的基本性质、函数的单调性,考查了推理能力与计算能力,属于基础题.3.在复平面内,复数对应的点的坐标为,则等于( )A. B. C. D.【答案】A【解析】【分析】由已知可得z,代入(1+i)z,利用复数代数形式的乘除运算化简得答案.【详解】解:由已知得,z=2﹣i,∴(1+i)z=(1+i)(2﹣i)=3+i.故选:A.【点睛】本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.4.执行如图所示的程序框图,若输出的的值为,则输入的值为( )A. B. C. D.【答案】B【解析】【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.【详解】解:模拟程序的运行,可得S=0,n=1满足条件1<i,执行循环体,S,n=2满足条件2<i,执行循环体,S,n=3满足条件3<i,执行循环体,S,n=4满足条件4<i,执行循环体,S(1)+()+()+(),n=5由题意,此时应该不满足条件5<i,退出循环,输出S的值为,可得4<i≤5,可得i的值为5.故选:B.【点睛】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.5.已知奇函数是定义在上的增函数,则“”是“”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】C【解析】【分析】根据函数奇偶性和单调性之间的关系,结合充分条件和必要条件的定义即可得到结论.【详解】解:∵奇函数f(x)在R上为增函数,∴若a+b>0,得a>﹣b,则f(a)>f(﹣b),即f(a)>﹣f(b),则f(a)+f(b)>0成立,即充分性成立,若f(a)+f(b)>0,则f(a)>﹣f(b)=f(﹣b),∵函数f(x)在R上为增函数,∴a>﹣b,即a+b>0成立,即必要性成立,则“a+b>0”是“f(a)+f(b)>0”充分必要条件,故选:C.【点睛】本题主要考查充分条件和必要条件的判断,根据不等式的性质,结合函数奇偶性和单调性之间的性质是解决本题的关键.综合性较强.6.已知向量,,若,则()•()的最大值为( )A. B. C. D.【答案】D【解析】【分析】向量加法的坐标运算及及数量积的运算有:(1+cosθ,sinθ),(cosθ,1+sinθ),()•()=(1+cosθ)cosθ+sinθ(1+sinθ)由三角函数辅助角公式有:()•()=1sin(),再求最值即可.【详解】解:由||=1设(cosθ,sinθ),则(1+cosθ,sinθ),(cosθ,1+sinθ),所以()•()=(1+cosθ)cosθ+sinθ(1+sinθ)=1sin(),即()•()的最大值为:1,故选:D.【点睛】本题考查了向量的坐标运算及数量积的运算,三角函数辅助角公式及最值,属简单题.7.某三棱锥的三视图如图所示,则该三棱锥的体积为( )A. B. C. D.【答案】A【解析】【分析】由三视图还原原几何体,可知原几何体为三棱锥,再由棱锥体积公式求解.【详解】解:由三视图还原原几何体如图,该几何体为三棱锥P﹣ABC,则该几何体的体积V.故选:A.【点睛】本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.8.A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表:A品牌车型A1A2A3环比增长率-7.29% 10.47% 14.70%B品牌车B1B2B3型环比增长-8.49% -28.06% 13.25%率根据此表中的数据,有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多;②A品牌三种车型总销量环比增长率可能大于14.70%;③B品牌三款车型总销量环比增长率可能为正;④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率.其中正确结论的个数是( )A. B. C. D.【答案】B【解析】【分析】根据表中数据,对关于7月份销量的四个结论,分析正误即可.【详解】解:根据表中数据,对关于7月份销量的四个结论:对于①,A1车型销量增长率比B1车型销量增长率高,但销量不一定多,①错误;对于②,A品牌三种车型中增长率最高为14.70%,所以总销量环比增长率不可能大于14.70%,②错误;对于③,B品牌三款车型中有销量增长率为13.25%,所以它的总销量环比增长率也可能为正,③正确;对于④,由题意知A品牌三种车型总销量环比增长率,也可能小于B品牌三种车型总销量环比增长率,④正确;综上所述,其中正确的结论序号是③④.故选:B.【点睛】本题考查了合情推理与命题真假的判断,也考查了销售量与增长率的应用问题,是基础题.第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分。
2025届北京市大兴区魏善庄中学高三数学试题文下学期综合练习

2025届北京市大兴区魏善庄中学高三数学试题文下学期综合练习考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数21iz i+=-,i 是虚数单位,则下列结论正确的是 A .5z =B .z 的共轭复数为31+22i C .z 的实部与虚部之和为1D .z 在复平面内的对应点位于第一象限2.执行如图所示的程序框图,输出的结果为( )A .78B .158C .3116D .15163.设某大学的女生体重y (单位:kg )与身高x (单位:cm )具有线性相关关系,根据一组样本数据(x i ,y i )(i=1,2,…,n ),用最小二乘法建立的回归方程为ˆy=0.85x-85.71,则下列结论中不正确的是 A .y 与x 具有正的线性相关关系 B .回归直线过样本点的中心(x ,y )C .若该大学某女生身高增加1cm ,则其体重约增加0.85kgD .若该大学某女生身高为170cm ,则可断定其体重比为58.79kg4.函数cos 1ln(),1,(),1x x x f x xex π⎧->⎪=⎨⎪≤⎩的图象大致是( ) A . B .C .D .5.设椭圆E :()222210x y a b a b+=>>的右顶点为A ,右焦点为F ,B 、C 为椭圆上关于原点对称的两点,直线BF 交直线AC 于M ,且M 为AC 的中点,则椭圆E 的离心率是( ) A .23B .12C .13D .146.已知抛物线22(0)y px p =>上一点(5,)t 到焦点的距离为6,P Q 、分别为抛物线与圆22(6)1x y -+=上的动点,则PQ 的最小值为( )A 211B .525-C .5D .517.下列命题是真命题的是( )A .若平面α,β,γ,满足αγ⊥,βγ⊥,则//αβ;B .命题p :x R ∀∈,211x -≤,则p ⌝:0x R ∃∈,2011x -≤;C .“命题p q ∨为真”是“命题p q ∧为真”的充分不必要条件;D .命题“若()110xx e -+=,则0x =”的逆否命题为:“若0x ≠,则()110xx e -+≠”.8.已知椭圆C :()222210x y a b a b+=>>的左、右焦点分别为1F ,2F ,点()11,P x y ,()11,Q x y --在椭圆C 上,其中>0x ,0y >,若2PQ OF =,13QF ≥,则椭圆C 的离心率的取值范围为( )A .610,2⎡⎫-⎪⎢⎪⎣⎭B .(0,62⎤-⎦C .2,312⎛⎤- ⎥⎝⎦D .(0,31⎤-⎦9.已知双曲线22221(0)x y a b a b-=>>的右焦点为F ,过F 的直线l 交双曲线的渐近线于A B 、两点,且直线l 的倾斜角是渐近线OA 倾斜角的2倍,若2AF FB =,则该双曲线的离心率为( ) A .324B .233C .305D .5210.已知定义在R 上的函数()f x ,若函数()2y f x =+为偶函数,且()f x 对任意1x ,[)22,x ∈+∞ ()12x x ≠,都有()()21210f x f x x x -<-,若()()31f a f a ≤+,则实数a 的取值范围是( )A .13,24⎡⎤-⎢⎥⎣⎦B .[]2,1--C .1,2⎛⎤-∞- ⎥⎝⎦D .3,4⎛⎫+∞⎪⎝⎭11.若直线2y kx =-与曲线13ln y x =+相切,则k =( ) A .3 B .13C .2D .1212.2-31ii =+( ) A .15-22i B .15--22iC .15+22i D .15-+22i 二、填空题:本题共4小题,每小题5分,共20分。
北京市大兴区魏善庄中学2025届高三(最后冲刺)数学试卷含解析

北京市大兴区魏善庄中学2025届高三(最后冲刺)数学试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效. 5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.抛掷一枚质地均匀的硬币,每次正反面出现的概率相同,连续抛掷5次,至少连续出现3次正面朝上的概率是( ) A .14B .13C .532D .3162.已知双曲线()222210,0x y a b a b-=>>的左、右顶点分别是,A B ,双曲线的右焦点F 为()2,0,点P 在过F 且垂直于x 轴的直线l 上,当ABP ∆的外接圆面积达到最小时,点P 恰好在双曲线上,则该双曲线的方程为( )A .22122x y -=B .2213y x -=C .2213x y -=D .22144x y -=3.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知l 丈为10尺,该楔体的三视图如图所示,其中网格纸上小正方形边长为1,则该楔体的体积为( )A .10000立方尺B .11000立方尺C .12000立方尺D .13000立方尺4.已知数列{}n a 的通项公式是221sin 2n n a n π+⎛⎫=⎪⎝⎭,则12312a a a a +++⋅⋅⋅+=( ) A .0B .55C .66D .785.把函数2()sin f x x =的图象向右平移12π个单位,得到函数()g x 的图象.给出下列四个命题①()g x 的值域为(0,1] ②()g x 的一个对称轴是12x π=③()g x 的一个对称中心是1,32π⎛⎫⎪⎝⎭ ④()g x 存在两条互相垂直的切线 其中正确的命题个数是( ) A .1B .2C .3D .46.若直线2y x =-的倾斜角为α,则sin 2α的值为( ) A .45B .45-C .45±D .357. “2b =”是“函数()()2231f x b b x α=--(α为常数)为幂函数”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件8.函数()()()sin 0,02g x A x A ωϕϕπ=+><<的部分图象如图所示,已知()5036g g π⎛⎫==⎪⎝⎭,函数()y f x =的图象可由()y g x =图象向右平移3π个单位长度而得到,则函数()f x 的解析式为( )A .()2sin 2f x x =B .()2sin 23f x x π⎛⎫=+⎪⎝⎭C .()2sin f x x =-D .()2sin 23f x x π⎛⎫=- ⎪⎝⎭9.1x <是12x x+<-的( )条件 A .充分不必要B .必要不充分C .充要D .既不充分也不必要10.一个盒子里有4个分别标有号码为1,2,3,4的小球,每次取出一个,记下它的标号后再放回盒子中,共取3次,则取得小球标号最大值是4的取法有( ) A .17种B .27种C .37种D .47种11.设()y f x =是定义域为R 的偶函数,且在[)0,+∞单调递增,0.22log 0.3,log 0.3a b ==,则( ) A .()()(0)f a b f ab f +>> B .()(0)()f a b f f ab +>> C .()()(0)f ab f a b f >+>D .()(0)()f ab f f a b >>+12.已知双曲线22221(0)x y a b a b-=>>的右焦点为F ,过F 的直线l 交双曲线的渐近线于A B 、两点,且直线l 的倾斜角是渐近线OA 倾斜角的2倍,若2AF FB =,则该双曲线的离心率为( ) A .324B .233C .305D .52二、填空题:本题共4小题,每小题5分,共20分。
北京市大兴区旧宫中学2020年高三数学文期末试题含解析

北京市大兴区旧宫中学2020年高三数学文期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知已知f(x)是奇函数,且f(2﹣x)=f(x),当x∈[2,3]时,f(x)=log2(x﹣1),则f()=()A.log27﹣log23 B.log23﹣log27 C.log23﹣2 D.2﹣log23参考答案:C【考点】函数的周期性;函数奇偶性的性质;函数的图象.【分析】由f(x)是奇函数,且f(2﹣x)=f(x),可知f(4+x)=f(x),于是f()=f(4)=﹣f(2)=log23﹣2,从而可得答案.【解答】解:∵f(x)是奇函数,且f(2﹣x)=f(x),∴f(2+x)=f(﹣x)=﹣f(x),∴f(4+x)=f(x),即f(x)是以4为周期的函数;∴f()=f(4);又f(2﹣x)=f(x),∴f(﹣2)=f(4)=f();又当x∈[2,3]时,f(x)=log2(x﹣1),f(x)是奇函数,∴f(﹣2)=﹣f(2)=log23﹣2,∴f()=log23﹣2.故选C.【点评】本题考查函数的周期性与奇偶性,求得f()=﹣f(2)是关键,也是难点,考查综合分析与转化的能力,属于中档题.2. 将函数的图象按向量平移后得到图象对应的函数解析式是() A. B.C. D.参考答案:D略3. 下列有关命题的叙述,错误的个数为①若为真命题,则为真命题②“”是“”的充分不必要条件③命题,使得,则,使得④命题“若,则或”的逆否命题为“若或,则”A. 1B. 2C. 3D. 4参考答案:B若p q为真命题,则至少有有一个为真,所以不一定为真,所以①错误。
得或,所以“”是“”的充分不必要条件,②正确。
根据特称命题的否定式全称命题知③正确。
“若,则x=1或x=2”的逆否命题为“若4. 函数图像上的动点到直线的距离为,点到轴的距离为,则的值为()A. B. C.D.不确定的正数参考答案:C5. 设等差数列的前项和为,若,则等于()A.18 B.36 C.45 D.60参考答案:C6. 函数y=tan的单调增区间是()A.,k∈ZB.,k∈ZC.,k∈ZD.,k∈Z参考答案:A7. 对于函数,下列命题正确的是A.函数f(x)的图象恒过点(1,1)B.∈R,使得C.函数f(x)在R上单调递增D.函数f(x)在R上单调递减参考答案:A略8. 已知函数()参考答案:A略9. 设全集U={1,2,3,4,5},集合M={1,4},N={1,3,5},则N∩(?U M)=()A.{1,3}B.{1,5} C.{3,5} D.{4,5}参考答案:C1 0.参考答案:D二、填空题:本大题共7小题,每小题4分,共28分11. 设是定义在上的偶函数,对任意的,都有,且当时,,若关于的方程在区间内恰有三个不同实根,则实数的取值范围是 .参考答案:略12. 某天,小赵、小张、小李、小刘四人一起到电影院看电影,他们到达电影院之后发现,当天正在放映A,B,C,D,E五部影片,于是他们商量一起看其中的一部影片:小赵说:只要不是B就行;小张说:B,C,D,E都行;小李说:我喜欢D,但是只要不是C就行;小刘说:除了E之外,其他的都可以据此判断,他们四人可以共同看的影片为____参考答案:【知识点】集合运算. A1D解析:小赵可以看的电影的集合为:{A,C,D,E,},小张可以看的电影的集合为{B,C,D,E},小李可以看的电影的集合为:{A,B,D,E},小刘可以看的电影的集合为:{A,B,C,D},这四个集合的交集中只有元素D ,故填D .【思路点拨】分别找出小赵、小张、小李、小刘四人各自可以看的电影的集合,然后求这些集合的交集即可.13. 设若不等式对于任意的恒成立,则实数的取值范围是▲参考答案:14. 函数是周期函数,它的周期是__ .参考答案:【知识点】三角函数的周期.B4【答案解析】解析:解:由正切函数的周期公式可知,所以周期为.【思路点拨】由正切函数的周期公式可求出函数的周期.15. 已知变量x,y满足条件,若z=y﹣x的最小值为﹣3,则z=y﹣x的最大值为.参考答案:考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式对应的平面区域,利用线性规划的知识,先求出m的值,然后通过平移即可求z的最大值.解答:解:作出不等式组对应的平面区域如图:(阴影部分).由z=y﹣x得y=x+z,平移直线y=x+z,由图象可知当直线y=x+z经过点C时,直线y=x+z的截距最小,此时z最小,为﹣3,即z=y﹣x=﹣3,由,解得,即C(2,﹣1),C也在直线x+y=m上,∴m=2﹣1=1,即直线方程为x+y=1,当直线y=x+z经过点B时,直线y=x+z的截距最大,此时z最大,由,解得,即B(,),此时z=y﹣x=﹣=,故答案为:.点评:本题主要考查线性规划的应用,利用图象平行求得目标函数的最大值和最小值,利用数形结合是解决线性规划问题中的基本方法.16. 已知定义在R上的偶函数满足:,且当时,单调递减,给出以下四个命题:①;②直线为函数图象的一条对称轴;③函数在上单调递增;④若关于的方程在上的两根为,则。
2020年北京大兴区黄村第四中学高三数学文期末试卷含解析

2020年北京大兴区黄村第四中学高三数学文期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 函数,则的图象只可能是参考答案:C因为函数都为偶函数,所以也为偶函数,图象关于轴对称,排除A,D.当时,函数,所以当时,,所以选C.2. 在空间,下列命题正确的是()A.平行于同一平面的两条直线平行B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行参考答案:D【考点】空间中直线与直线之间的位置关系.【专题】空间位置关系与距离.【分析】利用空间中线线、线面、面面间的位置关系求解.【解答】解:平行于同一平面的两条直线平行、相交或异面,故A错误;平行于同一直线的两个平面平行或相交,故B错误;垂直于同一平面的两个平面平行或相交,故C错误;由直线与平面垂直的性质得:垂直于同一平面的两条直线平行,故D正确.故选:D.【点评】本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.3. 已知直线l1:(1﹣a)x+ay﹣2=0,l2:ax+(2a+1)y+3=0,则“a=﹣2”是“l1⊥l2”成立的()A.充分不变要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件参考答案:A考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据直线垂直的等价条件得到(1﹣a)a+a(2a+1)=0,然后利用充分条件和必要条件的定义进行判断即可.解答:解:若l1⊥l2,则(1﹣a)a+a(2a+1)=0,即a2+2a=0,解得a=0或a=﹣2,则“a=﹣2”是“l1⊥l2”成立的充分不必要条件,故选:A点评:本题主要考查充分条件和必要条件的判断,根据直线垂直的等价条件是解决本题的关键.4. 函数y=log sin(2x+)的单调减区间为( )A.(kπ﹣,kπ](k∈Z)B.(kπ﹣](k∈Z)C.(kπ﹣,kπ+](k∈Z)D.(kπ+,kπ+](k∈Z)参考答案:C考点:复合函数的单调性.专题:函数的性质及应用.分析:由题意可得,本题即求函数t=sin(2x+)在满足t>0时,函数t的增区间,结合正弦函数的图象可得2kπ+0<2x+≤2kπ+,k∈z,解得x的范围,可得结论.解答:解:函数y=log sin(2x+)的单调减区间,即函数t=sin(2x+)在满足t>0时,函数t的增区间,结合正弦函数的图象可得2kπ+0<2x+≤2kπ+,k∈z,解得kπ﹣<x≤kπ+,故在满足t>0的条件下,函数t的增区间为(kπ﹣,kπ+],k∈z,故选:C.点评:本题主要考查复合函数的单调性,对数函数、正弦函数的图象性质,体现了转化的数学思想,属于中档题.5. △ABC中A,B,C的对边分别是a,b,c,面积S=,则C的大小是( ) A.30°B.45°C.90°D.135°参考答案:B【考点】余弦定理.【专题】三角函数的求值.【分析】已知等式左边利用三角形面积公式化简,右边利用余弦定理化简,整理求出【解答】解:∵△ABC中,S=absinC,a2+b2﹣c2=2abcosC,且S=,∴absinC=abcosC,即tanC=1,则C=45°.故选:B.【点评】此题考查了余弦定理,以及三角形的面积公式,熟练掌握余弦定理是解本题的关键.6. 已知实数x,y满足,则的取值范围是()A.[-1,3] B.[-13,3] C.[3,11] D.[-5,11]参考答案:D画出不等式组表示的平面区域如图.当直线过点时,;过点时,.所以的取值范围是.7. 下列命题正确的是( )A.函数在内单调递增B.函数图象关于点对称C.函数的最小正周期为2πD.函数图象关于直线对称参考答案:B8. 一个六棱柱的底面是正六边形,侧棱垂直于底面,所有棱的长都为,顶点都在同一个球面上,则该球的体积为(A)(B)(C)(D)参考答案:D六棱柱的对角线长为:,球的体积为:V==9. 在中,=90°AC=4,则等于( )A. -16B. -8C.8 D.16参考答案:D10. 已知是不等式组表示的平面区域内的一点,,为坐标原点,则的最大值A.2B.3C.5D.6参考答案:D略二、填空题:本大题共7小题,每小题4分,共28分11. 已知中心为的正方形的边长为2,点、分别为线段、上的两个不同点,且,则的取值范围是▲ .参考答案:12. 平行四边形ABCD中,,则λ+μ=__________.参考答案:1 在平行四边形中,,且,则,所以;故填1.13. 设是空间中给定的个不同的点,则使成立的点的个数有_________个.参考答案:1【知识点】平面向量坐标运算解:设设,则因为,所以,所以因此,存在唯一的点M,使成立。
2021-2022学年北京大兴区黄村第七中学高三数学文联考试题含解析

2021-2022学年北京大兴区黄村第七中学高三数学文联考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 若平面四边形ABCD满足,则该四边形一定是A.正方形 B.矩形 C.菱形 D.直角梯形参考答案:C2. 如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为()A. B. C. D.参考答案:C略3. 设点是线段BC的中点,点A在直线BC外,,,则()A.2 B.4 C.6 D.8参考答案:略4. 设集合U={1,2,3,4},A={1,4},B={2},则B∪(?U A)=()A.{2} B.{2,3} C.{1,2,4} D.{2,3,4}参考答案:B【考点】交、并、补集的混合运算.【专题】计算题;集合.【分析】由全集U及A,求出A的补集,找出B与A补集的并集即可.【解答】解:∵U={1,2,3,4},A={1,4},B={2},∴?U A={2,3},则B∪(?U A)={2,3},故选:B.【点评】此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.5. 函数图象的对称轴为,则的值为A.B.C.D.参考答案:D6. 已知函数f(x)的定义域为R,f′(x)为函数f(x)的导函数,当x∈[0.+∞)时,2sinxcosx﹣f′(x)>0且?x∈R,f(﹣x)+f(x)+cos2x=1.则下列说法一定正确的是()A.﹣f(﹣)>﹣f(﹣)B.﹣f(﹣)>﹣f(﹣)C.﹣f()>﹣f()D.﹣f(﹣)>﹣f()参考答案:B【考点】导数的运算.【分析】令F(x)=sin2x﹣f(x),可得F′(x)=2sinxcosx﹣f′(x)>0,x∈[0.+∞)时.可得F (x)在x∈[0,+∞)上单调递增.又?x∈R,f(﹣x)+f(x)+cos2x=1.可得f(﹣x)=sin2x﹣2sin2x+f(x)=﹣[sin2x﹣f(x)],F(x)为奇函数.进而得出答案.【解答】解:令F(x)=sin2x﹣f(x),则F′(x)=2sinxcosx﹣f′(x)>0,x∈[0.+∞)时.∴F(x)在x∈[0,+∞)上单调递增.又?x∈R,f(﹣x)+f(x)+cos2x=1.∴f(﹣x)+f(x)=2sin2x,∴sin2(﹣x)﹣f(﹣x)=sin2x﹣2sin2x+f(x)=﹣[sin2x﹣f(x)],故F(x)为奇函数,∴F(x)在R上单调递增,∴>F.即>﹣F,故选:B.7. (5分)等差数列{a n}的前n项和为S n,已知a5=8,S3=6,则a9=()A. 8 B. 12 C. 16 D. 24参考答案:C【考点】:等差数列的通项公式;等差数列的前n项和.【专题】:等差数列与等比数列.【分析】:由给出的等差数列的第5项和前3项和代入通项公式及前n项和公式求等差数列的首项和公差,然后直接运用通项公式求a9.解:设等差数列{a n}的首项为a1,公差为d,则,解得:a1=0,d=2,所以a9=a1+8d=0+8×2=16.故选C.【点评】:本题考查了等差数列的通项公式和前n项和公式,考查了计算能力,此题属基础题.8. 设0≤α<2π,若sin α>cos α,则α的取值范围是()A.(,) B.(,π)C.(,) D.(,)参考答案:C9. 函数在上零点的个数是()A. 2个B. 3个C. 4个D. 5个参考答案:C【分析】令,即,即,解得,再由,即可求解,得到答案.【详解】由函数,令,即,即,所以,又由,所以,即函数在上有4个零点,故选C.【点睛】本题主要考查了函数与方程的应用,以及三角函数的化简求值问题,其中解答中熟记函数零点的定义,准确利用正切函数的性质求解是解答的关键,着重考查了运算与求解能力,属于基础题.10. 某几何体的三视图如图所示,则该几何体的体积是()A.6 B.7 C.8 D.9参考答案:A【考点】棱柱、棱锥、棱台的体积.【分析】根据三视图得出空间几何体是以俯视图为底面的四棱锥,代入锥体体积公式,可得答案.【解答】解:根据三视图得出空间几何体是以俯视图为底面的四棱锥,其底面面积S=×(2+4)×2=6,高h=3,故体积V==6,故选:A【点评】本题考查的知识点是棱锥的体积与表面积,简单几何体的三视图,难度中档.二、填空题:本大题共7小题,每小题4分,共28分11. 在△ABC中,角A,B,C所对的边分别为a,b,c,已知的面积为__________.参考答案:12. 已知线的方程为:,以坐标原点O为极点, x轴的芷半轴为极轴建立极坐标系,圆C的极坐标方程为,则直线被圆C截得的线段的最短长度为__________.参考答案:13. 若函数为偶函数,则实数参考答案:略14. 已知A,B,C,D四点在半径为的球面上,且AC=BD=4,AD=BC=,AB=CD,则三棱锥D-ABC的体积是__________.参考答案:15. (选修4-1:几何证明选讲)已知AB,BC是圆O的两条弦,AO BC,AB= , BC=,则圆O的半径等于________。
2022-2023学年北京市大兴区高三上学期期中考试数学试卷含答案

大兴区2022~2023学年度第一学期期中检测试题高三数学第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若复数i(1i)z =-,则z 在复平面内对应的点位于(A )第一象限(B )第二象限(C )第三象限(D )第四象限(2)已知集合{0123}A =,,,,集合{||2}B x x =≤,则A B =(A )[22]-,(B )[02],(C ){1,2}(D ){012},,(3)下列函数中,在(0)+∞,上单调递增,且值域为[0)+∞,的是(A )2x y =(B )1y x=-(C )y =(D )2log y x=(4)若命题“x ∃∈R ,220x x m ++≤”是真命题,则实数m 的取值范围是(A )1m <(B )1m ≤(C )1m >(D )1m ≥(5)“1a =”是“函数2()2x x af x a+=-具有奇偶性”的(A )充分不必要条件(B )必要不充分条件(C )充要条件(D )既不充分也不必要条件(6)在ABC ∆中,=90342C CA CB AD DB ∠=== ,,,,则=AC AD ⋅(A )3(B )5(C )6(D )10(7)已知函数1π()sin()26f x x =-,则结论正确的是(A )()f x 的图象关于点5π3(,0)中心对称(B )()f x 的图象关于直线π3x =-对称(C )()f x 在区间ππ(-,)内有2个零点(D )()f x 在区间[,0]2π-上单调递增(8)若0a b >>,则①11b a >;②11a ab b +>+->-.上述结论中,所有正确结论的序号是(A )①②(B )①③(C )②③(D )①②③(9)已知函数()32x x f x =-,则(A )()f x 在R 上单调递增(B )对x ∀∈R ,()1f x >-恒成立(C )不存在正实数a ,使得函数()xf x y a =为奇函数(D )方程()f x x =只有一个解(10)右图为某无人机飞行时,从某时刻开始15分钟内的速度()V x (单位:米/分钟)与时间x (单位:分钟)的关系.若定义“速度差函数”()v x 为无人机在时间段[0,]x 内的最大速度与最小速度的差,则()v x 的图象为(A )(B)(C )(D )第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分。
北京市大兴区高考数学解答题大全含解析

北京市大兴区高考数学解答题大全解答题含答案有解析1.如图所示,将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ,要求B 点在AM 上,D 点在AN 上,且对角线MN 过C 点,已知4AB =米,3AD =米.(1)要使矩形AMPN 的面积大于64平方米,则DN 的长应在什么范围内? (2)当DN 的长为多少时,矩形花坛AMPN 的面积最小?并求出最小值. 2.已知()()()23222f x x a x a a a R =-+++∈,.(1)若不等式()2f x >的解集为()()14-∞+∞,,,求a 的值; (2)解不等式()0f x ≤.3.如图,在以A 、B 、C 、D 、E 、F 为顶点的五面体中,面ABCD 是等腰梯形,//AB CD ,面ABFE 是矩形,平面ABFE ⊥平面ABCD ,BC CD AE a ===,60DAB ∠=.(1)求证:平面⊥BDF 平面ADE ;(2)若三棱锥B DCF -3a 的值. 4.如图所示,在三棱柱111ABC A B C -中,ABC 与111A B C △都为正三角形,且1AA ⊥平面ABC ,1F F ,分别是11AC A C ,的中点.求证:(1)平面11AB F ∥平面1C BF ; (2)平面11AB F ⊥平面11ACC A .5.已知函数()2sin 3sin cos f x wx wx wx =+(ω>0)的最小正周期为π.(Ⅰ)求ω的值和f (x )的单调递增区间; (Ⅱ)若关于x 的方程f (x )﹣m =0在区间[0,2π]上有两个实数解,求实数m 的取值范围. 6.已知324ππβα<<<,()3sin 5αβ+=-,()12cos 13αβ-=,求:cos 2β的值. 7.已知数列{}n a 中,12a =,()124,2n n a a n n N n *--+=∈≥.(1)求数列{}n a 的通项公式: (2)设121n n b a =-,求数列{}n b 的通项公式及其前n 项和n T .8.已知点(1,0)A 、(1cos 2,1)M x +、(2,3sin 22)N x m +(,x R m R ∈∈),且()f x AM AN =. (1)求函数()f x 的解析式; (2)如果当5,66x ππ⎡⎫∈-⎪⎢⎣⎭时,两个函数()f x 与()2g x =的图象有两个交点,求m 的取值范围. 9.已知向量()3,4a =,()4,2b =.(1)当k 为何值时,2ka b +与2a b -垂直?(2)若2AB a b =+,BC a b μ=+,且,,A B C 三点共线,求μ的值. 10.已知数列的前项和为.(1)求数列的通项公式;(2)设,求数列的前项和.11.已知函数()23sin 22cos 1f x x x =--,x ∈R(1)求函数()f x 的最小正周期;(2)设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且6c =,()0f C =,()sin sin 2sin 2C B A A +-=,求ABC ∆的面积.12.设数列{}n a 是等差数列,其前n 项和为()*n S n ∈N ;数列{}nb 是等比数列,公比大于0,其前n 项和为()*n T n ∈N.已知11b=,322b b =+,424b a a =+,5162b a a =+.(1)求数列{}n a 和数列{}n b 的通项公式;(2)设数列1 n n a b ⎧⎫⎨⎩-⎬⎭的前n 项和为n K ,若n K m <对任意的n *∈N 恒成立,求实数m 的取值范围. 13.已知()0,απ∈,1sin cos 5αα+=.求sin 2α和sin cos αα-的值. 14.已知f (α)=()()()322sin cos tan tan sin ππααπααπαπ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭----,其中α≠12kπ(k ∈Z ). (1)化简f (α); (2)若f (2π+β)=-33,β是第四象限的角,求sin (2β+6π)的值.15.手机支付也称为移动支付(Mobile Payment),是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图. 组数 第l 组第2组第3组第4组第5组分组 [15,25)[25,35)[35,45)[45,55)[55,65)频数203630104(1)求x ;(2)从第l ,3,4组中用分层抽样的方法抽取6人,求第l ,3,4组抽取的人数: (3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率. 16.设等比数列{}n a 的最n 项和n S ,首项11a =,公比()(1,0)1q f λλλλ==≠-+.(1)证明:(1)n n S a λλ=+-; (2)若数列{}n b 满足112b =,()()*1,2n n b f b n n -=∈≥N ,求数列{}n b 的通项公式; (3)若1λ=,记11n n n c a b ⎛⎫=- ⎪⎝⎭,数列{}n c 的前项和为n T ,求证:当2n ≥时,4n T <.17.已知数列{}n a 的前n 项和为n S ,且2,n a ,n S 成等差数列. (1)求数列{}n a 的通项公式;(2)若n n b n a =⋅,求数列{}n b 的前n 项和n T ; 18.设全集为R ,集合{|24}A x x ,集合{|3782}B x x x =-≥-.(Ⅰ)求AB ;(Ⅱ)若{|13},C x a x a A C A =-≤≤+⋂=,求实数a 的取值范围.19.(6分)已知直线1:2(1)20l mx m y -++=,2:230l x y -+=,3:10l x y -+=是三条不同的直线,其中m R ∈.(1)求证:直线1l 恒过定点,并求出该点的坐标;(2)若以2l ,3l 的交点为圆心,C 与直线1l 相交于,A B 两点,求AB 的最小值. 20.(6分)已知函数()2()log 2a f x x =+,(1)若3f =,求a 的值,并判断()f x 的奇偶性; (2)求不等式()(2)f x f x ≤+的解集.21.(6分)已知函数()2cos 2cos 1f x x x x =+-.(1)求函数()f x 的最小正周期;(2)求函数()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的值域.22.(8分)如图,在三棱锥A-BCD 中,AB ⊥AD ,BC ⊥BD ,平面ABD ⊥平面BCD ,点E ,F(E 与A ,D 不重合)分别在棱AD ,BD 上,且EF ⊥AD.求证:(1)EF ∥平面ABC ; (2)AD ⊥AC.23.(8分)己知函数()sin 3cos f x x x =-. (1)若(0,)x π∈,()0f x =,求x ;(2)当x 为何值时,()f x 取得最大值,并求出最大值.24.(10分)如图,在平行四边形ABCD 中,3AB =,2BC =,12,AB AD e e ABAD==,AB 与AD 的夹角为3π.(1)若12AC xe ye =+,求x 、y 的值; (2)求AC BD ⋅的值;(3)求AC 与BD 的夹角的余弦值.25.(10分)已知等差数列{}n a 的首项为1a ,公差为d ,前n 项和为n S ,且满足n mS n =,,()m nS m m n =≠. (1)证明4m n S +>;(2)若()222222333312sin cos cos cos sin sin sin 0p p p p p p p p a a a a a a a a ++++++-+-=+≠,()0,1d ∈,当且仅当9n =时,n S 取得最小值,求首项a 的取值范围.26.(12分)(Ⅰ)已知直线l 过点()2,3且与直线320x y ++=垂直,求直线l 的方程; (Ⅱ)求与直线21y x =+5.27.(12分)设数列{}n a 的首项1a ,为常数,且()*132nn n a a n N+=-∈(1)判断数列35n n a ⎧⎫-⎨⎬⎩⎭是否为等比数列,请说明理由;(2)n S 是数列{}n a 的前n 项的和,若{}n S 是递增数列,求1a 的取值范围.28.已知cosα,sin(α-β)=10,且α,β∈(0,2π).求: (1)cos(α-β)的值; (2)β的值.29.已知直线l 1:ax ﹣y ﹣2=0与直线l 2:(3﹣2a )x+y ﹣1=0(a ∈R ). (1)若l 1与l 2互相垂直,求a 的值:(2)若l 1与l 2相交且交点在第三象限,求a 的取值范围. 30.在等差数列{}n a 中,已知15a =,59113a a =. (1)求数列{}n a 的前n 项和n S 的最大值; (2)若n n b a =,求数列{}n b 前n 项和n T .参考答案解答题含答案有解析 1.(1)(0,1)(9,)+∞,(2)3DN =时,min ()48AMPN S =【解析】 【分析】(1)设DN x =,有题知DN DC DAAM=,得到4(3)x AM x+=,再计算矩形AMPN 的面积,解不等式即可.(2)首先将花坛AMPN 的面积化简为36424AMPN S x x=++,再利用基本不等式的性质即可求出面积的最小值. 【详解】(1)设DN x =,0x >. 因为四边形ABCD 为矩形,所以DN DC DAAM=.即:43x x AM =+,解得:4(3)x AM x+=.所以24(3)AMPNx S AN AM x+==,(0)x >. 所以24(3)64x x+>,21090x x -+>,解得9x >或1x <.因为0x >,所以9x >或01x <<. 所以DN 的长度范围是(0,1)(9,)+∞.(2)因为224(3)4(69)AMPNx x x S x x+++==364242448x x x x=++≥+=. 当且仅当364x x=,即3x =时取“=”. 所以当3DN =时,min ()48AMPN S =. 【点睛】本题第一问考查了函数模型,第二问考查了基本不等式,属于中档题.2.(1)1a =;(2)2a <时,解集为[2],2a a +,2a =时,解集为{4},2a >时解集为[2,2]a a +. 【解析】 【分析】(1)由一元二次不等式的解集一一元二次方程的解之间的联系求解; (2)按2a 和2a +的大小分类讨论. 【详解】(1)由题意22(32)2420x a x a a -+++->的解集为()()14-∞+∞,,, 则方程22(32)2420x a x a a -+++-=的解为1和4,∴2321424214a a a +=+⎧⎨+-=⨯⎩,解得1a =;(2)不等式()0f x ≤为(2)(2)0x a x a ---≤,22a a =+时,2a =,此时不等式解集为{4},2a >时,22a a >+,22a x a +≤≤,当2a <时,22a a <+,22a x a ≤≤+。
2023北京大兴高三(上)期末数学试卷及答案

2023北京大兴高三(上)期末数学第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合A={x|1≤x≤2},则∁R A=(A){x|x<1,或x>2}(B){x|x≤1,或x≥2}(C){x|x≤1,或x>2}(D){x|x<1,或x≥2}(2)下列函数中,既是奇函数又在定义域上是增函数的为(A)y=ln x(B)y=tan x(C)3y x(D)y=−1x(3)在(x−1)5展开式中,x2的系数为(A)10(B)5(C)−10(D)−5(4)记S n为等差数列{a n}的前n项和.已知S3=−3,a5=2,则(A){a n}为递减数列(B)a3=0(C)S n有最大值(D)S6=0(5)已知抛物线y2=4x上一点M与其焦点F的距离为5,则点M到x轴的距离等于(A)3(B)4(C)5(D)4√2(6)“a=0”是“直线x−ay+2a−1=0(a∈R)与圆x2+y2=1相切”的(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(7)某圆锥曲线C是椭圆或双曲线,若其中心为坐标原点,对称轴为坐标轴,且过A(−2,1)和B(32,−√24)两点,则曲线C的离心率等于(A)12(B)√22(C)√32(D)√62(8)已知数列{a n}中,a1=1,a n⋅a n+1=2n,n∈N∗,则下列结论错误的是(A)a2=2(B)a4−a3=2(C){a2n}是等比数列(D)a2n−1+a2n=2n+1(9)“赵爽弦图”是我国古代数学的瑰宝,它是由四个全等的直角三角形和一个正方形构成。
现仿照赵爽弦图,用四个三角形和一个小平行四边形构成如下图形,其中,E ,F ,G ,H 分别是DF ,AG ,BH ,CE 的中点,若AG ⃗⃗⃗⃗⃗ =xAB ⃗⃗⃗⃗⃗ +yAD ⃗⃗⃗⃗⃗ ,则2x +y 等于 (A )25 (B )45(C )1(D )2(10)已知函数f(x)=cos πx x 2−2x+3,给出下列结论:①f(x)是周期函数;②f(x)最小值是−12;③f(x)的最大值是12;④曲线y =f(x)是轴对称图形.则正确结论的序号是 (A )①③ (B )②④ (C )①②③ (D )②③④第二部分 (非选择题 共110分)二、填空题共5小题,每小题5分,共25分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大兴区2014~2015学年度第一学期期末检测
高三数学(文)参考答案及评分标准
一、选择题(每题5分,共40分)
二、填空题(每题5分,共30分) (9) 2e (10)
π2
(11) 1
(12)
3π4 (13) 1
4
(14) 1;11
(,)44
-(第一个空3分,第二个空2分) 三、解答题(共80分) (15)(本题满分13分) (Ⅰ)解:由π3cos()25θ-=
,得3
sin 5
θ=, ………………2分 又22sin cos 1θθ+=,所以216
cos 25
θ=
因为π(,π)2
θ∈,所以4cos 5
θ=- ………………5分
(Ⅱ)5
()cos sin cos 26
f x x x x θ=-
53
cos cos 265
x x x =-⨯
1
2cos 22
x x =
- ………………3分 π
sin(2)6x =- ………………5分
由πππ
2π22π,262k x k k --+∈Z ≤≤
得ππ
ππ63
k x k -
+≤≤, ………………7分 所以,函数()f x 的增区间是ππ
[π,π]()63
k k k -+∈Z . ………………8分
(16)(本题满分13分)
解:(Ⅰ)设{}n a 的公差为d ,则51411a a d =+=,113726a d a d +++= 解得13a =,d 2= ………………4分
所以12+=n a n ………………5分
(Ⅱ)2n a n b =n a -=)12(212+-+n n ………………2分 12n n S b b b =++
+
3521(222)[35(21)]n n +=+++-++++………………4分
32(14)321
142
n n n -++=-- ………………6分
2321
(28)23
n n n +=--- ………………8分
(17)(本题满分13分) 解(Ⅰ)样本均值是
574811121213
8
+++++++=9………………3分
(Ⅱ)有茎叶图提供的数据,在8人的样本数据中有4人分数大于9分,所以,样本中超
过9分的人数占样本总数的
1
2
, ………………2分 据此估计,高三年级300人中,估计有1
3002
⨯=150人超过9分。
………………5分
(Ⅲ)设从8人中随机抽取男、女生各一人的得分用(,)x y 表示,其中x 表示男生得分,y 表
示女孩是得分,则所有不同的情况是
(5,4),(5,8),(5,12),(5,13),(7,4),(7,8),(7,12),(7,13),(11,4),(11,8),(11,12),(11,13), (12,4),(12,8),(12,12),(12,13)共16种, ………………2分
其中,女生成绩不低于男生的有(5,8),(5,12),(5,13),(7,8),(7,12),(7,13),
(11,12),(11,13),(12,12),(12,13)共10种, ………………4分
所以,女生得分不低于男生得分的概率10
0.62516
P =
= ………………5分
(18)(本题满分14分)
解:(Ⅰ)连结OG , ………………..1分 因为四边形ABCD 是菱形, 所以,CO OA =,又CG GE =,
所以,OG 为三角形ACE ∆的中位线…………….2分 所以,OG AE ∥.
又OG ⊂平面DBE ,AE ⊄平面DBE
∴//AE 平面DBE ………………………4分 (Ⅱ)因为四边形ABCD 是菱形,所以BD AC ⊥。
又平面ABCD ⊥平面ACEF ,且交线AC
∴BD ⊥平面ACEF , ………………………2分 又 FC ⊂平面ACEF
∴BD ⊥CF ………………3分 在菱形ACEF ,CF AE ⊥,AE OG //
∴CF OG ⊥ ………………………4分 ⊂=OG BD O OG BD ,, 平面BGD
∴⊥CF 平面BGD ………………………5分 ∴BG CF ⊥ ………………………6分 (Ⅲ)由题知,AB BC AC ===2,故60ABC ∠=,
在三角形DAB 中,2AD AB ==,120DAB ∠=,所以BD =32.…………1分
又ABC FAC ∠=∠,所以60FAC ∠=,所以FCA ∆是等边三角形,
所以2,CF AE ==所以1
32
BDG S BD OG ∆=
⋅= ……………………2分 又CF ⊥面BDG ,所以,点C 到面BDG 的距离114
2
h CF ==
……………………3分
所以 1
1
32
E BDG A BDG C BDG BDG V V V S h ---∆===⋅=
……………4分
(19)(本题满分14分)
解:(Ⅰ)由题意,椭圆22
22:1(0)x y C a b a b
+=>>的一个顶点是(0,1),
所以1b = ………………………1分
B
2
3=a c ,222a b c =+ 解得 2=a , ………………………3分
故椭圆C 的方程式14
22
=+y x ………………………4分 (Ⅱ)当0=k 时,
如图,椭圆的外切矩形ABCD 面积为8. ………………1分 当0≠k 时,如图所示,
∵椭圆的外切矩形ABCD 的边AB 所在直线方程为y kx m =+ ∴直线BC 和AD 的斜率均为k
1
-
. 由⎩⎨⎧+==+m
kx y y x 4422 消去y 得 0448142
2
2
=-+++m kmx x k )( ………………2分
0441448222=-+-=∆))(()(m k km
化简得:142
2
+=k m ………………3分 所以,直线AB 方程为 142+-=k kx y
直线DC 方程为 142++=k kx y 直线AB 与直线DC 之间的距离为
1
1422
2++k k …………5分
同理,可求BC 与AD 距离为2
222142111
1
42k k k k ++=+-+-)()( …………6分
则矩形ABCD 的面积为:2
19
441421142222222+++
=++⋅++=k
k k k k k S 由均值定理 108≤<S ………………9分
仅当12
=k ,即1±=k 时S 有最大值10.
因此,当1±=k 时S 有最大值10;
当K =0时,S 有最小值8. ………………10分
(20)(本题满分13分)
解:(Ⅰ)因为),(,,),(+∞∈=0y x x y x G y
由3()(1,3)f x G x x =-,则有033
>-x x ………2分 所以 函数的定义域为),3()0,3(∞+- ………3分 (Ⅱ)因为),(,,),(+∞∈=0y x x y x G y
所以32322()(2,log (1))1g x G x ax bx x ax bx =+++=+++
0)1(log 232>+++bx ax x ,得023>++bx ax x .………2分
因为823)(2-=++='b ax x x g ,得8232---=ax x b .
所以082)823(2322323
>---=---++=++x ax x ax x x ax x bx ax x
存在]8,4[∈x 使0822
3
>---x ax x .
0822<++∴ax x ………4分
存在]8,4[∈x 使x
x a 8
2-
-<, 所以max )(x
x a 8
2-
-<, ………5分 由于8
2x x
--
在],[84∈x 上单调递减, 所以当4=x 时,x
x 8
2-
-有最大值为.10- ………6分 a 的取值范围是(,10).-∞- ………7分
(Ⅲ)当2≤∈∈x N y N x ,,*
*时,
21==y x ,, 或32==y x ,时,),(),(x y G y x G < ………1分
3x ≥时,),(),(x y G y x G > ………2分。
