物距u像距v焦距f
2个凸透镜成像规律

2个凸透镜成像规律引言凸透镜是一种常见的光学器件,广泛应用于摄影、眼镜、显微镜等领域。
了解凸透镜的成像规律对于正确使用和设计光学系统非常重要。
本文将详细探讨两个凸透镜的成像规律,并通过实例和图示进行解释。
凸透镜的基本概念在开始讨论成像规律之前,我们首先需要了解凸透镜的基本概念。
凸透镜是由两个球面构成的,其中至少一个球面是凸面。
凸透镜有一个光轴,光线垂直于光轴时不会发生偏折。
凸透镜的两个焦点分别是物距和像距相等时的位置,我们将在后面的内容中详细解释。
成像规律一:物距和像距的关系物距和像距是凸透镜成像过程中的重要参数。
物距是从物体到凸透镜的距离,通常用字母u表示;像距是从像到凸透镜的距离,通常用字母v表示。
根据凸透镜的成像规律,物距和像距之间存在以下关系:1.当物体位于凸透镜的一侧时(物距为正),像距可能为正、负或无穷大。
–当物体位于凸透镜的焦点前方时,像距为正,成像为实像。
–当物体位于凸透镜的焦点后方但在透镜的近焦点和光轴之间时,像距为负,成像为虚像。
–当物体位于凸透镜的近焦点上时,像距趋近于无穷大,成像为无穷远处的虚像。
2.当物体位于凸透镜的另一侧时(物距为负),像距为正,成像为实像。
3.当物体位于凸透镜的焦点上时,像距趋近于无穷大,成像为无穷远处的虚像。
成像规律二:物像距和焦距的关系焦距是凸透镜的一个重要参数,用字母f表示。
焦距是指物体与凸透镜之间的距离等于像距与凸透镜之间的距离时的数值。
根据凸透镜的成像规律,物像距和焦距之间存在以下关系:1.当物距u和像距v都为正时,焦距f为正。
2.当物距u为负,像距v为正时,焦距f为负。
3.当物距u为正,像距v为负时,焦距f为负。
4.当物距u和像距v都为负时,焦距f为正。
实例分析:成像规律在实际应用中的应用为了更好地理解凸透镜的成像规律,我们将通过几个实例来说明其在实际应用中的应用。
实例一:放大镜放大镜是一种常见的凸透镜应用。
当我们将放大镜放在物体前方时,通过调整距离可以观察到物体的放大或缩小的实像。
凸透镜 成像公式

凸透镜成像公式咱们来聊聊凸透镜成像公式哈。
你知道吗,凸透镜这玩意儿在咱们的生活中可太常见啦!就说我之前去博物馆参观的时候,看到了一个古老的望远镜,那里面就用到了凸透镜。
当时我好奇地凑近去看,透过那个小小的镜片,仿佛看到了一个全新的世界。
咱们先来说说凸透镜成像公式到底是啥。
它就是 1/f = 1/u + 1/v 。
这里的f 表示凸透镜的焦距,u 是物距,v 是像距。
这公式看起来挺简单,可里面的学问大着呢!比如说,当物距 u 大于 2 倍焦距 f 的时候,像距 v 就在 1 倍焦距 f和 2 倍焦距之间,这时候成的像是倒立缩小的实像。
想象一下,你拿着相机拍远处的高楼大厦,这就相当于物距很大,拍出来的照片里,那高楼就变小了,这就是倒立缩小实像的实际应用。
要是物距 u 等于 2 倍焦距 f 呢,像距 v 也等于 2 倍焦距 f ,成的像是倒立等大的实像。
我有一次在教室里做实验,用蜡烛、凸透镜和光屏,好不容易把物距调整到正好等于 2 倍焦距,看到那清晰等大的像出现在光屏上,心里那叫一个激动!当物距 u 在 1 倍焦距 f 和 2 倍焦距之间时,像距 v 就大于 2 倍焦距,成的像是倒立放大的实像。
投影仪就是利用这个原理,把小小的胶片上的图像放大,让咱们能在大屏幕上看到清晰的画面。
还有一种特殊情况,当物距 u 小于焦距 f 时,成的像是正立放大的虚像。
放大镜就是这样,你把小蚂蚁放在放大镜下面,看到的是一个比实际大很多的蚂蚁,可神奇啦!学习凸透镜成像公式,可不能光是死记硬背,得结合实际去理解。
就像我那次在公园里,用自己带的简易凸透镜观察花朵,通过调整距离,看到了不同大小和清晰度的花朵影像,这让我对凸透镜成像的原理有了更直观的感受。
其实,凸透镜成像公式不仅仅是个数学公式,它更是打开我们观察世界的一扇窗户。
通过它,我们能更好地理解光的折射,能明白为什么我们看到的东西有时大有时小,有时清晰有时模糊。
所以啊,同学们,别小看这个小小的凸透镜成像公式,它里面藏着大大的科学奥秘,等着我们去探索和发现呢!就像我在博物馆看到那个古老的望远镜,谁能想到一个小小的凸透镜,能让我们看到那么遥远的地方,能让我们对未知的世界充满好奇和向往。
透镜焦距的测量

透镜焦距的测量
透镜焦距的测量可以采取以下方法:
1. 焦距公式法:根据透镜成像公式1/f = 1/v - 1/u,其中f为透
镜焦距,v为物距,u为像距。
测量物体与透镜之间的距离和
像与透镜之间的距离,并代入公式计算焦距。
2. 平面镜法:将光线垂直入射于透镜上,透过透镜后会形成一条射线,用平面镜反射这条射线,使其再次经过透镜,将平面镜向透镜移动,当成像发生最大偏移时,此时的像距就是透镜的焦距。
3. 物齐截法:从透镜前方不同距离处,依次放置两个小物体,当两个物体的像恰好重合时,离透镜最近的物体距离就是透镜的焦距。
4. 背景法:在透镜前放置一条标尺,调整透镜距离标尺的距离,使标尺上某一值的数字清晰可见,调整透镜的位置,使背景清晰,此时透镜到标尺的距离即为透镜的焦距。
需要注意的是,以上方法在测量时都应考虑到透镜的形状和光线的入射角度等因素,尽可能减小误差。
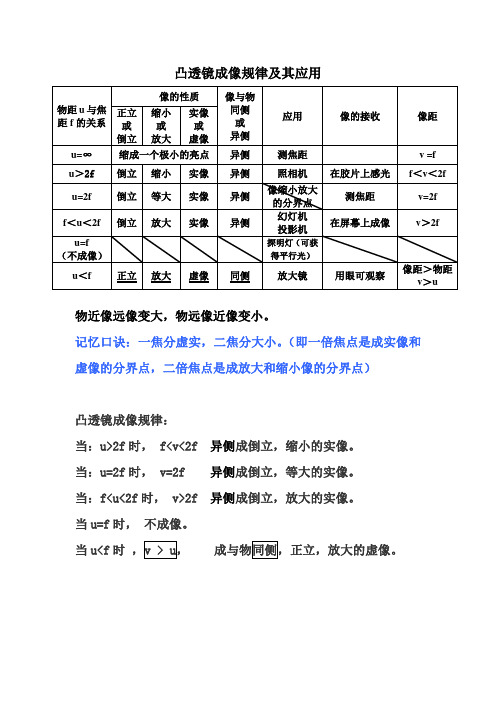
物距u与焦距f的关系
异侧 异侧 异侧
同侧
照相机
像缩小放大 的分界点 幻灯机 投影机
探明灯(可获 得平行光)
放大镜
在胶片上感光 测焦距
在屏幕上成像
用眼可观察
f<v<2f v=2f v>2f
像距>物距 v>u
物近像远像变大,物远像近像变小。 记忆口诀:一焦分虚实,二焦分大小。(即一倍焦点是成实像和 虚像的分界点,二倍焦点是成放大和缩小像的分界点)
凸透镜成像规律: 当:u>2f 时, f<v<2f 异侧成倒立,缩小的实像。 当:u=2f 时, v=2f 异侧成倒立,等大的实像。 当:f<u<2f 时, v>2f 异侧成倒立,放大的实像。 当 u=f 时, 不成像。 当 u<f 时 ,v > u, 成与物同侧,正立,放大的虚像。
凸透镜成像规律及其应用
物距 u 与焦 距 f 的关系
u=∞
像的性质
正立 或 倒立
缩小 或 放大
实像 或 虚像
缩成一个极小的亮点
u>2f 倒立 缩小 实像
u=2f 倒立 等大 实像
f<u<2f 倒立 放大
u=f (不成像)
u<f
正立 放大
实像 虚像
像与物 同侧
或 异侧
应用
像的接收
像距
异侧
测焦距
v =f
物距u与焦距f的关系
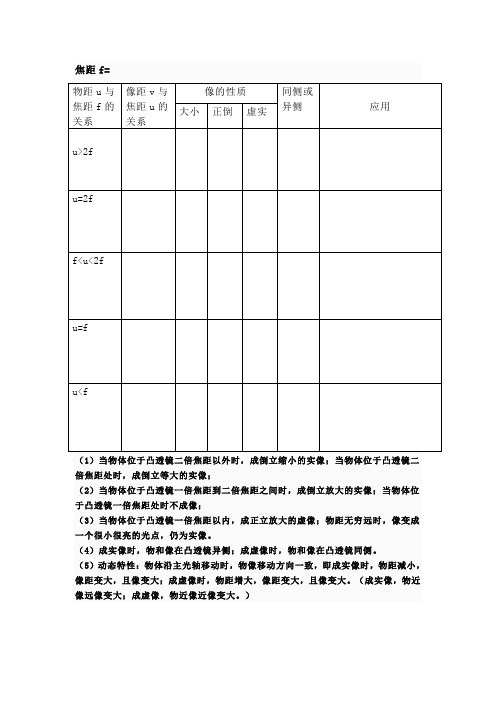
像距v与焦距u的关系
像的性质
同侧或
异侧
应用
大小
正倒
虚实
u>2fu=Βιβλιοθήκη ff<u<2f
u=f
u<f
焦距f=
(1)当物体位于凸透镜二倍焦距以外时,成倒立缩小的实像;当物体位于凸透镜二倍焦距处时,成倒立等大的实像;
(2)当物体位于凸透镜一倍焦距到二倍焦距之间时,成倒立放大的实像;当物体位于凸透镜一倍焦距处时不成像;
(3)当物体位于凸透镜一倍焦距以内,成正立放大的虚像;物距无穷远时,像变成一个很小很亮的光点,仍为实像。
(4)成实像时,物和像在凸透镜异侧;成虚像时,物和像在凸透镜同侧。
(5)动态特性:物体沿主光轴移动时,物像移动方向一致,即成实像时,物距减小,像距变大,且像变大;成虚像时,物距增大,像距变大,且像变大。(成实像,物近像远像变大;成虚像,物近像近像变大。)
初二物理物距

物距:u 像距:v 焦距:f 焦距是透镜的焦点到透镜中心的距离,物距是物体到透镜的距离,像距是所成的像到透镜的距离物距u>2f 时,f<V<2f.像是倒立、缩小的实像。
与物体在透镜的两侧。
(应用:照像机。
) 物距f<u<2f 时,V>2f 。
像是倒立的、放大的实像。
像与物在透镜的两侧。
(应用:投影仪) 物距v<f 时,像是正立、放大的虚像。
与物在镜的同侧。
(应用:放大镜)当物距u=f 时折射 光线彼此平行。
所以,此时不能成像。
当物距u=2f 时,成倒立 等大的实像,像与物在镜的两侧。
V=2f.1、2009年10月1日,在庄严的门广场举行了盛大的阅兵式。
在鲜艳的八一军旗引领下,阅兵分列式徒步方队迈着整齐步伐匀速行进在天安门广场。
已知天安门广场东、西两个华表之间距离为96m ,要求走过时间为66s ,求阅兵分列式徒步方队的行进速度。
(计算结果保留一位小数)分列式徒步方队的行进速度96m 1.5m/s 66ss v t ===2、一个空心铜球的质量为89g ,体积为30cm 3。
将它的空心部分注满某种液体后,总质量为361g 。
已知铜的密度38.9g/cm ρ=铜,求:(1)这个铜球空心部分的体积;(2)注入液体的密度。
(1)球壳(铜球所含铜)的体积3389g 10cm 8.9g/cm m V ρ===铜壳铜 空心部分的体积33330cm 10cm 20cm V V V =-=-=空心球壳(2)注入液体的质量361g 89g 272g m m m =-=-=总液球因为空心部分注满液体,则V V 空心=注入液体的密度33272g 13.6g/cm 20cmm V ρ===液液液3、峭壁前方的山路上有一辆汽车,在下列两种情况下,汽车鸣笛后都是经过3s 听到回声,分别求鸣笛时车和峭壁间的距离。
(空气中声速340m/s )(1)车向靠近峭壁的方向匀速行驶,速度为10m/s ;(2)车向远离峭壁的方向匀速行驶,速度为10m/s 。
物距、焦距、焦点关系
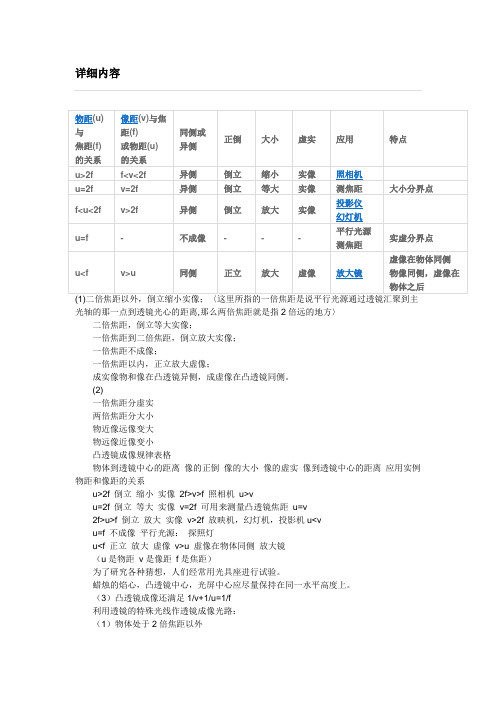
(2)物体处于2倍焦距和1倍焦距之间(3)物体处于一倍焦距以内(4)凸透镜成像光路实验研究凸透镜的成像规律是:当物距在一倍焦距以内时,得到正立、放大的虚像;在一倍焦距到二倍焦距之间时得到倒立、放大的实像;在二倍焦距以外时,得到倒立、缩小的实像。
该实验就是为了研究证实这个规律。
实验中,有下面这个表:物距像的性质像的位置与物同侧与异侧像距vu>2f 倒立缩小实像异侧f<v<2fu=2f 倒立等大实像异侧v=2f 此时物体与像的距离是最小的,即4倍焦距。
f<u<2f 倒立放大实像异侧v>2fu=f 不成像v无限大(平行光源,如:探照灯)u<f 正立放大虚像同侧u,v同侧这就是为了证实那个规律而设计的表格。
其实,透镜成像满足透镜成像公式:1/u(物距)+1/v(像距)=1/f(透镜焦距)照相机运用的就是凸透镜的成像规律镜头就是一个凸透镜,要照的景物就是物体,胶片就是屏幕照射在物体上的光经过漫反射通过凸透镜将物体的像成在最后的胶片上胶片上涂有一层对光敏感的物质,它在曝光后发生化学变化,物体的像就被记录在胶卷上至于物距、像距的关系与凸透镜的成像规律完全一样物体靠近时,像越来越远,越来越大,最后再同侧成虚像。
物距增大,像距减小,像变小;物距减小,像距增大,像变大。
一倍焦距分虚实,二倍焦距分大小。
凸透镜成像规律表:实像,物近像远像变大一焦分虚实,二焦分大小虚像,物远像远像变大实像皆倒立,物远像变小(4)当成虚像时,物、像的左右一致,上下一致;当成实像时,物、像的左右相反,上下相反.。
(5)凸透镜成像的两个分界点:2f点是成效放大缩小实像的分界点;f点是成实像虚像的分界点。
透镜的焦距的测量实验原理

透镜的焦距的测量实验原理透镜的焦距是指光线聚焦于透镜上某一点的距离,可以通过测量光线通过透镜后的聚焦距离来确定。
测量透镜焦距的实验原理主要有两种方法,分别是物距法和像距法。
物距法是通过改变物体到透镜的距离来测量透镜的焦距。
在实验中,首先固定一架准直光源,将光源与透镜之间的距离定义为物距。
然后调整透镜的位置,使得光线经过透镜后能够在屏幕上形成清晰的像。
这时,测量屏幕与透镜之间的距离,即可得到透镜的焦距。
原理是根据薄透镜成像方程:1/f = 1/v - 1/u,其中f为焦距,v为像距,u为物距。
在实验中,通过改变物距u,实验测量对应的像距v,并利用成像方程计算焦距f。
像距法是通过测量透镜成像的像距来测量透镜的焦距。
在实验中,首先将准直光源按一定距离放置在透镜的一侧,使得光线平行射入透镜。
然后调整屏幕的位置,使得透镜形成一个清晰的像。
测量屏幕与透镜之间的距离即为像距,即可得到透镜的焦距。
原理是当光线平行射入透镜时,透镜能够将光线聚焦于其焦点上。
于是根据薄透镜成像方程:1/f = 1/v - 1/u,其中f为焦距,v为像距,u则为无穷大。
在实验中,通过改变屏幕与透镜之间的距离v,实验测量对应的像距v,并利用成像方程计算焦距f。
无论是物距法还是像距法,都是利用透镜成像的特性来测量焦距。
在实验中,需要注意选择合适的光源和测量仪器,以确保实验的准确性。
此外,还需要进行多组实验数据的测量和处理,以提高实验结果的可靠性和精度。
总结起来,透镜焦距的测量可以通过物距法和像距法来实现。
实验原理是利用薄透镜成像方程,通过测量物距和像距之间的关系来计算焦距。
在实验中,光源的选择、测量仪器的使用以及实验数据的处理都对实验结果的准确性和精度产生重要影响。
凸透镜成像五个规律

凸透镜成像五个规律
凸透镜成像的五个规律是:
1. 物距-像距关系:物体与凸透镜之间的距离称为物距,像与凸透镜之间的距离称为像距。
物距和像距的关系可以用公式来表示:1/f = 1/v - 1/u,其中f为凸透镜的焦距,v为像距,u为物距。
根据这个关系,当物距增大时,像距也会增大,当物距减小时,像距也会减小。
2. 物象距离比例关系:根据物距-像距关系,可以推导出物体的高度与像高度之间的比例关系。
即h/v = h/u,其中h为物体的高度,v为像高度,u为物体的高度。
这个比例关系告诉我们,物体和像的大小与它们之间的距离是成反比的。
3. 放大率的定义:凸透镜成像时,物体的放大率定义为图片高度与物体高度的比值:|v/u| = |h'/h|,其中h'为图片的高度。
放大率告诉我们图片相对于物体的大小变化。
4. 倒立成像:对于凸透镜来说,如果物体是直立的,那么它的像是倒立的。
这个规律说明了为什么我们看到镜子中的图片是倒立的。
5. 实像和虚像:当物距小于凸透镜的焦距时,成像是一个正立的、放大的实像。
当物距大于焦距时,成像是一个倒立的、缩小的虚像。
如果物距等于焦距,成像距离无限远,成像是一个实像。
这些规律告诉我们在不同情况下成像的性质。
凸透镜成像规律 物距和像距反比

凸透镜成像规律:物距和像距反比一、引言在日常生活中,我们经常会接触到凸透镜,比如眼镜、相机镜头等。
凸透镜作为一种光学器件,能够对光线进行折射,从而形成物体的像。
而凸透镜成像规律中的物距和像距反比则是我们在研究凸透镜成像过程中不得不考虑的重要因素。
本文将深入探讨这一规律,并通过深度和广度兼具的方式,帮助读者更好地理解这一主题。
二、物距和像距的概念在讨论凸透镜成像规律中的物距和像距反比之前,我们首先要了解物距和像距的概念。
物距指的是物体与凸透镜之间的距离,通常用符号“u”表示;像距指的是像与凸透镜之间的距离,通常用符号“v”表示。
在凸透镜成像过程中,物体放置的位置和凸透镜的焦点位置会影响像的位置和大小,而物距和像距反比则是描述这种关系的重要规律。
三、物距和像距反比的数学表示根据凸透镜成像规律,物距和像距之间存在着一种反比的关系,可以用数学公式来表示:\[\frac{1}{f}=\frac{1}{u} + \frac{1}{v}\]其中,f表示凸透镜的焦距。
这个公式被称为透镜公式,它揭示了物距u、像距v和焦距f之间的定量关系。
从这个公式中可以看出,当物距u增大时,像距v会相应减小;反之,当物距u减小时,像距v会相应增大。
这就是物距和像距反比的数学表示。
四、反比关系引申出的光学效应物距和像距反比的数学规律不仅仅是一种定量关系,它还引申出了一些重要的光学效应。
1. 放大和缩小当物体与凸透镜的距离增大时,像将被放大;当物体与凸透镜的距离减小时,像将被缩小。
这一现象是由于物距和像距反比的规律所决定的。
2. 聚焦和发散当物体位于凸透镜的焦点之外时,光线经凸透镜折射后会聚焦于一点,形成实像;当物体位于凸透镜的焦点之内时,光线经凸透镜折射后会发散,形成虚像。
这一现象也是由物距和像距反比的规律所决定的。
五、个人观点和总结物距和像距反比是凸透镜成像规律中的重要概念,它揭示了物距、像距和焦距之间的定量关系。
通过深度和广度兼具的探讨,我们更好地理解了这一规律,并从中引申出了一些重要的光学效应。
透镜成像与物距的关系

透镜成像与物距的关系透镜是一种能够将光线折射的光学元件,它在摄影、眼镜等领域得到广泛应用。
而透镜成像的原理则是基于透镜折射光线的能力,在光学领域有着重要的地位。
本文将重点探讨透镜成像与物距的关系,并通过具体示例加深理解。
首先,我们需要了解透镜成像的基本原理。
透镜可以将光线聚焦或发散,形成实像或虚像。
当光线通过透镜折射时,会遵循折射定律,即入射角与折射角之比等于两种介质的折射率之比。
根据透镜的形状,主要有凸透镜和凹透镜两种。
对于凸透镜,当入射光线平行于主光轴,入射到透镜上时,折射光线会汇聚到透镜的焦点上,形成实像。
这个焦点称为物距,用符号u表示。
而当光线经过凸透镜后,若不平行于主光轴,则经过透镜后会呈现发散的趋势,产生虚像。
虚像的位置与物体的距离以及透镜的形状、焦距等因素有关。
接下来,我们来具体讨论透镜成像与物距之间的关系。
根据透镜成像的公式,可以得知物距(u)、像距(v)与透镜焦距(f)之间的关系。
这个公式可以表示为:1/f = 1/v - 1/u其中,f表示透镜的焦距,v表示像距,u表示物距。
当光线从无穷远处入射到透镜上时,即物距(u)为正无穷大时,我们可以推导出该情况下的透镜成像公式:1/f = 1/v这个公式即是透镜成像的主要依据。
从这个公式可以看出,在无穷远处的物体成像后,像距(v)等于透镜的焦距(f)。
这种情况下,透镜将光线聚焦在焦点上,形成清晰的实像。
当物体与透镜的距离变得有限时,物距(u)变为有限值,透镜成像的位置也会发生变化。
例如,当物体靠近透镜时,物距(u)变为负值,代入透镜成像公式理解具体情况。
如果物距(u)非常接近透镜,几乎与透镜接触,那么根据公式可以得知像距(v)也会趋近于负无穷大,也就是透镜的背面形成虚像。
以凸透镜为例,当物体与透镜的距离大于2倍的焦距时,透镜会将光线进一步聚焦,形成实像。
实像的位置取决于入射光线的倾斜角度以及物体与透镜的距离。
而如果物体与凸透镜的距离小于2倍的焦距,光线会在透镜的另一侧发散,出现虚像。
凸透镜成像的公式

凸透镜成像的公式好嘞,以下是为您生成的关于“凸透镜成像的公式”的文章:咱先来说说凸透镜成像这回事儿。
在物理学里,这可是个相当重要的知识点。
记得有一次,我给学生们上凸透镜成像的课。
那堂课上,有个小家伙特别积极,一直瞪着大眼睛,紧紧盯着我手里的凸透镜,好像那是个神秘的宝贝。
咱们先来讲讲凸透镜成像的公式,那就是 1/f = 1/u + 1/v 。
这里的 f表示凸透镜的焦距,u 表示物距,v 表示像距。
这个公式看着简单,可里面的门道多着呢!比如说,如果物距 u 很大很大,远远超过了焦距 f ,那像距 v 就会变得很小很小,这时候成的像就是缩小的实像。
就好像你用相机拍远处的大山,大山在相机里看起来就变小了,这就是因为物距很大。
再比如说,如果物距 u 比焦距 f 稍微大一点,那像距 v 就会比较大,成的像就是放大的实像。
这就好比你用放大镜看东西,离得不是特别远,看到的东西就变大了,这就是因为物距在一定范围内。
咱们回到那个小家伙身上。
我让大家做实验的时候,他特别认真,摆弄着蜡烛、凸透镜和光屏,嘴里还念念有词。
我走过去一听,原来他在念叨着公式,一边调整距离一边计算着。
还有啊,如果物距 u 等于焦距 f ,这时候是不成像的。
想象一下,光线通过凸透镜后,没法汇聚或者发散成像,是不是挺神奇的?要是物距 u 小于焦距 f ,这时候成的就是放大的虚像。
就像你透过放大镜看字,字变得很大,但这个像你在光屏上是找不到的,只能用眼睛直接看。
这个凸透镜成像的公式,在生活中的应用可多啦!比如咱们的眼睛,晶状体就相当于一个凸透镜。
看远处物体的时候,晶状体变薄,焦距变长;看近处物体的时候,晶状体变厚,焦距变短,这样才能让我们看清各种东西。
还有投影仪,也是利用了凸透镜成像的原理。
通过调整物距和像距,把小小的图像放大,投到屏幕上,让大家都能看得清楚。
在学习凸透镜成像公式的过程中,大家可别死记硬背,要多做实验,多观察,多思考。
就像那个认真的小家伙一样,通过自己的实践去理解和掌握。
镜头的焦距和像距的关系

镜头的焦距和像距的关系焦距和像距是摄影学中的两个重要概念。
了解和掌握焦距与像距之间的关系对于摄影师来说至关重要。
在本文中,我们将探讨焦距和像距之间的关系,并阐述如何通过调整焦距来实现不同的拍摄效果。
一、焦距的定义和测量方法焦距是指从透镜到成像平面(胶片或传感器)的距离,通常以毫米(mm)为单位来表示。
焦距较短时,拍摄的视场较宽,被摄物体呈现出广角效果;焦距较长时,拍摄的视场较窄,被摄物体呈现出望远效果。
测量焦距的一种常用方法是通过透镜的光学特性进行。
可以利用白光光源和物体,观察透镜在物体不同位置时的焦点,从而确定焦距的大小。
二、像距的定义和测量方法像距是指光线经过透镜后,在成像平面上的距离,即物体的像离透镜的距离。
像距可以分为物距(物体到透镜的距离)和像方距(图像到透镜的距离)两个部分。
当物距大于零时,像距亦为正数,表示实像;当物距小于零时,像距为负数,表示虚像。
测量像距的一个常用方法是通过调节物体和透镜的距离,然后观察透镜背后成像平面的位置,从而确定像距的大小。
三、焦距和像距的关系焦距和像距之间存在着一定的数学关系,即焦距与物距和像距之间的比例关系。
根据薄透镜公式,可以得到如下关系式:1/f = 1/v + 1/u其中,f表示焦距,v表示像距,u表示物距。
从上述公式可以得知,当物距等于焦距时,像距为无穷大,此时可以得到清晰焦点的无穷远景。
而当物距小于焦距时,像距为正数,表示实像;当物距大于焦距时,像距为负数,表示虚像。
四、不同焦距的拍摄效果不同焦距对于拍摄效果具有明显的影响。
在摄影中,广角、标准焦距和长焦距分别具有不同的特点和应用场景。
1. 广角拍摄广角镜头的焦距较短,通常小于50mm。
广角镜头具有宽广的视场和较大的景深,能够捕捉到更多的景物细节。
广角镜头适合拍摄大陆风光、建筑物等场景,可以营造出独特的空间感和透视效果。
2. 标准焦距拍摄标准焦距通常为50mm到70mm之间,视角与人眼相似,画面展现出较为真实的比例关系。
初中光学凸透镜成像规律

初中光学凸透镜成像规律一、凸透镜的定义和分类凸透镜是一种中央薄边厚的透镜,由两个球面或一个球面和一个平面组成。
根据其形状可分为双凸透镜和平凸透镜,根据其折射率与周围介质的大小关系可分为凸状物质与环境折射率相等的正常凸透镜和折射率大于周围介质的全息凸透镜。
二、光线追迹法光线追迹法是研究光学成像规律的重要方法。
它通过模拟光线在光学器件中传播的路径并运用光学公式来计算物体成像位置、大小等参数。
三、物距与像距物距指物体与透镜之间的距离,通常用符号u表示;像距指成像点与透镜之间的距离,通常用符号v表示。
四、焦距焦距是指使平行光线通过透镜后会聚于一点的位置到该点之间的距离。
焦距可分为前焦点和后焦点,分别用符号f1和f2表示。
五、成像规律1. 物距u、像距v和焦距f的关系:1/u + 1/v = 1/f2. 物体与像的大小关系:物体高度H与像高度h的比值等于物距u与像距v的比值,即H/h = u/v。
3. 成像位置:当物体到透镜的距离小于焦距时,成像位置为虚焦点;当物体到透镜的距离等于焦距时,成像位置为焦点;当物体到透镜的距离大于焦距时,成像位置为实焦点。
六、应用举例1. 平凸透镜成像规律当平凸透镜放置在光轴上时,其物方和像方均为平面。
根据成像规律可知,在平凸透镜上方放置一个实物,则其下方将出现一个倒立、缩小、实际的图像。
2. 双凸透镜成像规律双凸透镜在两侧均呈弧形。
根据成像规律可知,在双凸透镜上方放置一个实物,则其下方将出现一个倒立、放大、实际的图像。
当物体到达双凸透镜中心时,其图像将位于同一位置,即物距和像距相等。
3. 全息凸透镜成像规律全息凸透镜是一种特殊的凸透镜,其折射率大于周围介质。
根据成像规律可知,在全息凸透镜上方放置一个实物,则其下方将出现一个倒立、放大、虚拟的图像。
七、注意事项1. 在使用光学仪器进行实验时,应注意保持光路清洁,避免污染或损坏光学器件。
2. 在进行计算时,应根据实际情况选择合适的公式,并注意单位的转换。
凸透镜成像规律物体离焦点远成像位置的确定

凸透镜成像规律物体离焦点远成像位置的确定凸透镜是一种常用的光学元件,具有多种应用场景,比如摄影、相机镜头等。
了解凸透镜成像规律对于理解光学原理至关重要。
本文将探讨凸透镜成像规律中物体远离焦点的成像位置的确定方法。
1. 凸透镜成像规律回顾在讨论物体离焦点远成像位置的确定之前,我们需要先回顾凸透镜的成像规律。
凸透镜的成像规律可以用以下公式表示:1/f = 1/v + 1/u其中,f为透镜的焦距,v为像距,u为物距。
这个公式称为薄透镜公式。
2. 物体离焦点远成像位置的确定方法当物体离焦点较远时,我们可以采用以下方法确定其成像位置。
首先,我们需要确定物距u的值。
物距是指物体到透镜的距离。
当物体离焦点较远时,可近似认为物距u接近于无穷大。
这是因为无穷远处的物体光线基本平行,相对于透镜的曲率来说,可以认为是平面波。
其次,根据凸透镜成像规律中的薄透镜公式,我们可以得到以下关系:1/f = 1/v + 1/u由于物距u接近于无穷大,可以近似地将公式中的1/u近似为0。
这样,我们可以将薄透镜公式进一步简化为:1/f = 1/v将上述简化的公式进行变形,可以得到物像距之间的关系:v = f根据这个关系,当物体离焦点较远时,像距v的值与焦距f相等。
也就是说,凸透镜的焦点正好是物体远离焦点时的成像位置。
3. 实例分析为了更好地理解物体离焦点远成像位置的确定方法,我们可以通过一个实际例子进行分析。
假设透镜的焦距为20厘米,现有一个物体距离焦点的距离为50厘米。
根据上述方法,我们可以计算物体的成像位置。
根据物像距之间的关系v = f,我们知道像距v等于焦距f,即v = 20厘米。
因此,物体距离焦点50厘米处的成像位置就是距离透镜20厘米的地方。
4. 结论通过分析凸透镜成像规律中物体离焦点远成像位置的确定方法,我们可以总结得出结论:当物体离焦点较远时,凸透镜的成像位置就是透镜焦点位置。
凸透镜成像规律是光学中的重要概念,了解准确成像位置的确定方法对于实际应用具有重要意义。
物距与像距的关系

物距与像距的关系
物距:u,像距:v,焦距:f,关系:1/u+1/v=1/f。
光学中最基本的高斯成像公式:1/u+1/v=1/f,即物距的倒数加上像距的倒数等于焦距的倒数。
像距是由于物距和焦距决定的,而且像距小于焦距成实像的情况是不会发生的。
物距简介
在物理学中,物距就是指物体到透镜光心的距离。
物距的物理符号是u,单位为长度的国际单位米(m)。
对于透镜而言,通过光心且与光轴垂直的平面,即是物方主平面也是像方主平面重合。
物距与像距存在共轭关系,物距越远,像距越近;相反,物距越近,像距越远。
在进行光学计算时,严格地讲,物距应为被摄体平面与镜头前主面间的距离。
凸透镜成像规律u=f

凸透镜成像规律u=f
凸透镜成像规律是光学中非常重要的一个规律,涉及到透镜成像
的质量和成像位置等。
该规律的基本公式为:
u = f
其中,u表示物距,f表示透镜的焦距。
这个公式是凸透镜成像的
基本公式,也是凸透镜成像规律的中心公式。
我们来探究一下这个公式的含义和推导过程。
当凸透镜位于光源和观察者之间时,光线经过凸透镜后会聚在透
镜的同一侧。
根据光的传播规律,光线的传播速度与光线到凸透镜的
距离成反比,即速度的平方反比于距离。
因此,可以得到:
f = (2v/u)^(1/2)
其中,f表示透镜的焦距,v表示光线的传播速度。
将f代入u = f,得到:
u = (2v/u)^(1/2)
将u和f代入u = f,得到:
u = (2v/u)^(1/2) = (2/√2)f
这个公式可以理解为:透镜的物距与透镜的焦距的平方根成正比。
接下来,我们来探究一下凸透镜成像的基本特征。
根据凸透镜成像规律,当光线经过凸透镜时,会聚在透镜的同一侧,并且成的像会远离透镜。
这是因为凸透镜成像是由物距到像距的
直线路径变成曲线路径,并且成的像会远离透镜。
在凸透镜成像中,成的像的形状和物体的形状相同,只是大小不
同。
成的像的位置是在物距和像距之间,并且随着物距的增加,像距减小,像的位置逐渐靠近透镜。
凸透镜成像的规律可以用上述公式表示,即u = f,其中u表示物距,f表示透镜的焦距。
通过这个公式,我们可以计算出物距和像距之间的关系,并且判断凸透镜成像的形状和位置等。
焦距与成像大小的关系公式

焦距与成像大小的关系公式
焦距与成像大小的关系公式可以由薄透镜公式推导得出。
薄透镜公式为:
1/f = 1/v - 1/u
其中,f为透镜的焦距,v为物体到透镜的距离(像距),u为物体距离透镜的距离(物距)。
根据光学成像的规律,成像大小与物体到透镜的距离和物体距离透镜的距离有关,可以用物体的像高v'表示。
根据物像距离关系,可以得到:
v/u = v'/u'
由于v'为像高,可以用物体的高度h表示。
v' = h'/h
将v'代入上述物像距离关系中,可以得到:
v/u = h'/u'
将v/u代入薄透镜公式中,可以得到:
1/f = h'/u' - h/u
进一步整理化简可以得到:
h'/h = f/u - f/v
这就是焦距与成像大小的关系公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
凸透镜专题
1.当物体与凸透镜的距离稍大于透镜的焦距时,物体成()立的()像(填“虚”或“实”),
物体从较远处向透镜靠近时,像逐渐()(填“变大”或“变小”),像到凸透镜的距离逐渐()(填“变大”或“变小”)
答案:正;虚;变大;变大
2.小静同学取一焦距为12cm的凸透镜,把一支铅笔放在距透镜8cm的地方,那么她
得到的铅笔的像()
A、倒立缩小的实像
B、倒立放大的实像
C、正立缩小的虚像
D、正立放大的虚像
答案:D
3.小王同学把蜡烛从凸透镜前3倍焦距的地方移到1.5倍焦距的地方,凸透镜所成的
像()
A、始终是缩小的
B、始终是放大的
C、逐渐变大的
D、逐渐缩小的
答案:C
4.物体AB位于凸透镜的主光轴上且成实像,当将透镜遮住一半后,AB在光屏上的像
()
A、只有上半部,亮度不变
B、只有下半部,亮度不变
C、与原来的相同,亮度不变
D、与原来的相同,亮度变暗
分析:将透镜遮住一半,只影响物体处的光经过透镜后到达光屏上的光的多少,即影响成像的亮度,不会影响成像的形状的。
这一类题可以有许多种出法如:
1、小孔成像时,把小孔遮住一部分,所成的像如何变化?答:形状不变,亮度变
暗。
2、摄影师在给同学们照相时,一只苍蝇落在了镜头上,照出的相片上会不会有一
点苍蝇,或是有一个大的黑点呢?
答:不会,照出的相只会比没有苍蝇时稍暗些。
3、发生日食时,太阳被月亮挡住一部分,太阳变成了月牙形,这时做小孔成像,
所成的像是什么样的?
答:也是月牙形。
所成的像只与物体的形状有关。
5.某同学在做“凸透镜成像”实验时,在光屏上得到烛焰缩小的像,然后他把燃烧的蜡
烛和光屏互换位置,这时光屏上()
A、成倒立缩小的像
B、成倒立放大的像
C、成正立放大的像
D、不成像
分析:做这个题时不要想当然:根据光路是可逆的,还成倒立的缩小的像。
应该仔细看已知和要求的内容。
题中说把蜡烛和光屏互换位置,换位置后,根据光路是可逆的,知一定有成清析的像,是放大的还是缩小的,要想蜡烛在什么位置,光屏在什么位置(像的位置)?依题意知:原来蜡烛在二倍焦距外,像在二倍焦距内,一倍焦距外。
换位置后,蜡烛在二倍焦距内一倍焦距外,光屏(像)在二倍焦距外,所以所成的像是倒立放大的像。
答案:B
6.将蜡烛放在距凸透镜30cm处,在离凸透镜45cm的光屏上可以得到清晰的蜡烛的
像,则()
A、凸透镜的焦距是18cm,像是倒立缩小的
B、凸透镜的焦距是18cm,像是倒立放大的
C、凸透镜的焦距是30cm,像是正立放大的
D、凸透镜的焦距是45cm,像是正立缩小的
分析:依题意知物距在30cm时,像距为45cm,因成等大的像时,物距与像距相等,本题物距小于像距,可推测出成的像是倒立放大的实像。
也就是
2f>u(30cm)>f(1倍的焦距),v(45cm)>2f,这两个不等式可变形为:
45cm>2f>30cm,解得:22.5cm>f>15cm。
所以应选B。
知识扩展:焦距求法有一公式:1/u+1/v=1/f,把已知代入后,解得f=18cm
答案:B
7.将物体放在焦距为f的凸透镜主轴上,分别离透镜20cm、14cm和6cm时,各能
得到缩小的实像、放大的实像和放大的虚像,则该凸透镜的焦距f为()
A、10cm>f>6cm
B、10cm>f>7cm
C、14cm>f>10cm
D、20cm>f>14cm
分析:这一类题都是依据平面镜成像特点,得出不等式,再根据不等式,推算出结
果。
本题依题意知:20cm>2f , 2f>14cm>f , f>6cm。
把三个不等式组成不等式组,解得:10cm>f>7cm,图解为:
答案:B
8.“影”是我们日常生活中常见的光现象,如做光学游戏形成的“手影”、剧院放映的电
影、湖岸景色在水中的倒影、春游时留下美好记忆的照片——摄影等。
以下列出的“影”与物理知识对应关系不正确的是()
A、手影——光的直线传播
B、倒影——平面镜成像
C、摄影——凹透镜的成像
D、电影——凸透镜成像
答案:C
9.发光物体P从距凸透镜60cm的地方沿主光轴向透镜方向以v=5cm/s的速度开始
做匀速直线运动,已知凸透镜的焦距是10cm。
则当t为6s时成()像;当t为9s 时,成()像;当t为11s时成()像。
分析:当t为6s时,物体前进了5cm/s×6s=30cm,距凸透镜还有
60cm-30cm=30cm,此时物距u>2f,所以成缩小倒立的实像。
当t为9s时,物体前进了5cm/s×9s=45cm,距凸透镜还有60cm-45cm=15cm,此时物距2f>u>f,所以成放大倒立的实像。
当t为11s时,物体前进了5cm/s×11s=55cm,距凸透镜还有60cm-55cm=5cm,此时物距为u<f,所以成放大正立的虚像。
答案:缩小倒立的实像;放大倒立的实像;放大正立的虚像。
10.某摄影师在给顾客拍摄全身像后,准备让顾客不动,再用该相机给他拍摄半身像,
如果相机镜头焦距不变,则摄影师应将相机向_________移动;同时暗箱应
_________.(本空填“变长”、“不变”或“变短”).
分析:照完全身像,再照半身像,也就是像要变大,可以根据:物近像远像变大来做
答案:前;变长
11.照相机的镜头相当于一个凸透镜,胶卷相当于光屏.当你用照相机拍摄比原来远的
景物时,应使胶片离镜头_________一些;当改为拍摄人像时,人离镜头越近,在底片上成的像越_________.
分析:据“用照相机拍摄比原来远的景物时”知物体远了,根据:物远像近像变小,知胶片离镜头要近一些。
第二问是物近了,那么像应离凸透镜(镜头)远些,像也就变大了:物近像远像变大。
答案:近;大
12.小华参观展览会,在一个小展室里可见一个女导游在介绍商品,试着与她握手,却
发现是一个虚拟导游,可望不可及.后来他发现这个女导游只是在一个玻璃屏风后倒立的电视机屏幕上经过处理的一个形象而已,如图10-1所示.则这个玻璃屏风是()镜,这个虚拟导游是_____像(填“虚”、“实”),电视机屏幕与玻璃屏风的距离应满足的条件是()
【分析】倒立的电视机屏幕上的人像是倒立的,而通过玻璃屏风看到的人像是正立、放大的像.因此这个屏风是凸透镜,由于玻璃屏风成的像于电视机屏幕上的人像在凸透镜两侧,则这个虚拟导游是实像,根据凸透镜成像规律,物体应该在一倍焦距和二倍焦距之间.
【解答】凸透;实;一倍焦距和二倍焦距之间
【点评】掌握凸透镜成像的规律,并能解释具体问题十分重要.。
