物距像距和焦距的关系
凸透镜成像规律表格物距像距

凸透镜成像规律表格物距像距凸透镜是常用的光学器材之一,常常用于成像。
它可以将一束光线汇聚,从而形成清晰的像。
通常我们可以根据物距、像距、焦距等参数来描述凸透镜的成像规律。
下面将根据这些参数,分别对凸透镜成像规律进行表格化总结,以方便读者掌握相关知识。
一、光线走向分类光线走向分类分类规律平行光线经过凸透镜以后会汇聚于焦点上此时物距无穷大,像距为焦距凸透镜上的多束光线均匀地向外发散此时像距无穷大,物距为-焦距光线经过凸透镜以后呈现的是散射状此时物距和像距均不等于焦距二、物距、像距、焦距的关系焦距可以是一个重要的参考指标,可以用来计算物距和像距之间的关系。
下表列出了不同物距、像距和焦距的关系。
物距、像距和焦距关系物距像距焦距物距小于焦距,像距大于焦距有限实像正数值焦距为正物距等于焦距无穷远实像无穷大数值焦距为正物距大于焦距,像距小于焦距虚像负数值焦距为正三、物体放置位置和实际成像关系我们在实际应用中,往往需要考虑物体的放置位置和实际成像关系。
下表列举了不同情况下的物距、像距和成像情况。
物体放置位置和实际成像关系物距像距成像情况物体在凸透镜的焦点附近无穷大无穷大无法成像物体在凸透镜的后焦面上二倍焦距二倍焦距实像与物体等大物体在凸透镜的前面有限实物像无穷大物体放置距离越小,物体成像越大,距离凸透镜越近,成像越大。
物体在凸透镜前的焦平面上无穷大二倍焦距虚像,镜像高大以上是凸透镜成像规律的表格化总结。
读者可以根据这些表格,更加深入地了解凸透镜成像的相关知识。
同时,在实际应用中,也可以根据这些规律,进行合理的选择和操作,以达到最优的成像效果。
焦距、物距与像距 .

最长焦距/最短焦距=变焦倍数光学变焦镜头不单要看其变焦倍数,还要看其焦距范围,焦距越大,看的越远,视角范围越小之南宫帮珍创作玩单反的谁还在乎光学变焦的倍数呀?这倍数可是越大越狗头。
人家有钱的高烧们都自豪地宣称自己的镜头都是1倍的--定焦数码单反,镜头标识乘1。
5就是实际焦距变焦和焦距首先没有太大的区别其次,一般的普通数码相机的变焦要在7倍以上方可达到210以上的焦距能看物体的远近只和焦距有关系,比方4-88mm 的22倍镜头没有10-100mm10倍镜头看的远。
要想知道能看的最远距离就看最大焦距是多少,想知道能看的最大区域是多大,就看最小焦距是多少。
光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置,它通常是在镜头内。
表达光圈大小我们是用f值。
光圈f 值 = 镜头的焦距 / 镜头口径的直径从以上的公式可知要达到相同的光圈f值,长焦距镜头的口径要比短焦距镜头的口径大。
完整的光圈值系列如下: f1, f1。
4, f2, f2。
8, f4, f5。
6, f8, f11, f16, f22, f32, f44, f64 这里值得一题的是光圈f值愈小,在同一单位时间内的进光量便愈多,而且上一级的进光量刚是下一级的一倍,例如光圈从f8调整到f5.6,进光量便多一倍,我们也说光圈开大了一级。
您知道光圈大小对景深影响的原理吗?一个物点发出的光线通过镜头聚焦之后,所有光线形成一个圆锥形光束。
圆锥的顶角与光圈有关:光圈越大、顶角越大。
圆锥顶点与底片接触形成一个像点。
如果底片稍微前移或者后移一点固定距离,切割光束形成一个圆斑,圆斑的大小与顶角有关:顶角大则圆斑也大。
换句话说:底片偏离同样的距离,光圈大圆斑也大。
现在我们不要移动底片、而是移动物点,使得光束的顶点移动。
如果形成的光斑相同,较细的光束(意为着光圈较小)物点可以移动更大的距离,这就说明小光圈景深更大。
景深随着物距的增加而增加,随着焦距的增加而减少。
透镜成像规律口诀

透镜成像规律口诀透镜成像规律是光学学科中的基础知识之一。
透镜成像的规律可用以下口诀来概括:“物距离焦距,焦距距离物;像距离焦距,焦距距离像。
”这句口诀简洁明了地描述了透镜成像的规律,下面将进一步展开说明。
透镜成像涉及一些基本概念,包括物距、像距和焦距。
物距是指物体离透镜的距离,通常用符号u表示;像距是指成像后的像与透镜之间的距离,通常用符号v表示;焦距是指透镜的焦点到透镜的距离,通常用符号f表示。
根据透镜成像规律,物距、像距和焦距之间存在一定的关系。
口诀的第一句“物距离焦距”意味着物距u与焦距f之间的关系。
当物距与焦距相等时,即u = f,光线经过透镜后将呈现出特殊的成像效果,我们称之为“无穷远成像”。
在这种情况下,光线经透镜后将会汇聚到焦点上,形成一个清晰的像。
口诀的第二句“焦距距离物”意味着焦距f与物距u之间的关系。
当焦距等于物距时,即f = u,我们称之为“物距等于焦距成像”。
在这种情况下,光线经透镜后将会成为平行光,没有所谓的“聚焦”或“分散”。
接着,我们来看看下半句口诀。
口诀的第三句“像距离焦距”意味着像距v与焦距f之间的关系。
当像距与焦距相等时,即v = f,我们称之为“成像在焦点处”。
在这种情况下,光线经透镜后将会始终保持平行的状态。
最后一句口诀“焦距距离像”意味着焦距f与像距v之间的关系。
当焦距等于像距时,即f = v,我们称之为“像距等于焦距成像”。
在这种情况下,光线在透镜上发生折射后,将聚焦在无穷远处,形成一个非常小而清晰的像,称之为“实像”。
综上所述,通过透镜成像规律口诀,我们可以简单而系统地理解和记忆透镜成像规律。
这些基本规律为我们进一步研究和应用透镜提供了基础。
凸透镜成像规律经典练习题推导焦距与物距像距的关系

凸透镜成像规律经典练习题推导焦距与物距像距的关系在物理光学中,凸透镜是一种常见的光学器件,它具有将光线聚焦或者发散的特性。
对于凸透镜而言,焦距、物距和像距是重要的概念。
本文将通过经典的练习题,推导凸透镜的焦距与物距像距之间的关系。
首先,我们来看一个常见的问题:给定一个凸透镜,其焦距为f,物体位于凸透镜的物距为u,像位于凸透镜的像距为v。
我们的目标是推导出焦距与物距像距之间的关系。
我们先从凸透镜成像的规律入手。
根据凸透镜成像规律,我们知道以下关系式成立:1/u + 1/v = 1/f其中,u为物距,v为像距,f为焦距。
在推导焦距与物距像距之间的关系时,我们需要将上述关系式稍作变换。
首先,将上述方程两边同时乘以uvf,得到:vf + uf = uv接下来,我们将方程两边同时除以uvf,得到:1/f + 1/u = 1/v现在,我们已经得到了焦距与物距像距之间的关系式。
继续推导之前,我们可以对上述关系式再进行一些变换。
首先,我们可以将右边的1/v换成v/v,得到:1/f + 1/u = v/u进一步,我们可以将右边的v/u展开为1 - u/u,得到:1/f + 1/u = 1 - u/u继续变换,我们可以将右边的u/u化简为1,得到:1/f + 1/u = 1 - 1化简后可得:1/f + 1/u = 0将上式两边同时乘以fu,得到:u + f = 0继续变换,我们可以将上式写成:u = -f通过上述推导,我们得到了凸透镜焦距与物距像距之间的关系:物距u等于焦距f的相反数。
这意味着当物体位于焦距前方时,像位于焦距后方;当物体位于焦距后方时,像位于焦距前方。
以上是凸透镜成像规律经典练习题推导焦距与物距像距的关系。
通过这样的推导,我们可以更深入地理解凸透镜成像的规律,将其应用于实际问题的求解中。
总结一下,凸透镜的焦距与物距像距之间的关系由以下公式给出:1/f + 1/u = 1/v其中,f表示焦距,u表示物距,v表示像距。
凸透镜成像规律总结

凸透镜成像规律总结凸透镜成像规律总结凸透镜是一种常见的光学器件,它是由两个球面组成的,其中至少一个球面是凸起的。
凸透镜的成像规律是研究光线透过凸透镜后的成像情况的基本规律。
凸透镜成像规律主要有物距与像距、物高与像高的关系、放大率、透镜公式等几个方面。
首先,我们来讨论物距与像距的关系。
物距指的是物体与透镜之间的距离,记作u;像距指的是物体的像与透镜之间的距离,记作v。
根据凸透镜成像规律,物距、像距和焦距之间存在以下公式关系:1/u + 1/v = 1/f其中,f表示焦距。
当物体距离凸透镜的距离u变化时,像距v也会相应变化,但二者的倒数之和保持不变,其值等于焦距的倒数1/f。
其次,我们来讨论物高与像高的关系。
物高指的是物体的垂直高度,记作h1;像高指的是物体的像的垂直高度,记作h2。
根据凸透镜成像规律,物高与像高之间存在以下公式关系:h2/h1 = -v/u其中,符号“-”表示像放大与物体放大方向相反。
当像的垂直高度为正时,物体的垂直高度为负;当像的垂直高度为负时,物体的垂直高度为正。
接下来,我们来讨论凸透镜的放大率。
凸透镜的放大率指的是像的垂直高度与物体的垂直高度的比值,记作V。
根据凸透镜成像规律,放大率的计算公式为:V = -h2/h1 = v/u放大率的值可以是正值也可以是负值,当放大率为正值时,表示像与物体的高度方向相同放大;当放大率为负值时,表示像与物体的高度方向相反放大。
最后,我们来看一下透镜公式。
透镜公式是凸透镜成像规律的一个重要公式,用于求解物距、像距和焦距之间的关系。
透镜公式的表达式为:1/f = (n - 1) * (1/R1 - 1/R2)其中,n表示透镜的折射率;R1和R2分别表示透镜两个球面的曲率半径。
透镜公式可以用于计算焦距,也可以用于计算物距和像距中的任意两个未知量。
综上所述,凸透镜成像规律可以通过物距与像距、物高与像高的关系、放大率和透镜公式等几个方面来总结。
这些规律可以帮助我们理解和研究光线在凸透镜中的传播和成像情况,对于光学实验和应用具有重要的指导意义。
物距像距和焦距的关系

物距像距和焦距的关系
物距像距和焦距是光学中三个基本概念,也是图像成像的重要参数。
下面将分别介绍
这三个概念以及它们之间的关系。
1. 物距
物距是指距离物体到透镜或成像光学系统的距离。
物距通常用符号u来表示,单位是
米(m)。
物距是决定图像成像位置的重要参数,通常情况下,物距愈大,成像位置越远离透镜。
2. 像距
3. 焦距
物距、像距和焦距之间的关系可以通过透镜成像公式来描述:
1/f=1/v+1/u
式子中f表示透镜的焦距,u表示物距,v表示像距。
在透镜成像公式中,一个焦距值对应着一个光学系统的特定成像位置,当物距、像距
或焦距中任意一个量固定时,其他两个量之间的关系也是确定的。
例如,当一个物体在一个焦距为5cm的透镜前放置40cm处,成像位置应该是10cm处,因为:
1/0.1=1/0.05+1/0.4
因此,当物距u给定时,可以根据透镜成像公式计算出对应的像距v和焦距f,当焦距f给定时,可以反推物距u和像距v,当像距v给定时,可以计算出物距u和焦距f。
总之,物距、像距和焦距是光学成像中的重要概念,它们之间存在着密不可分的联系。
在实际的光学成像应用中,需要根据需要确定物距、像距和焦距的具体数值,以达到最佳
的成像效果。
成虚像时物距与像距的关系

成虚像时物距与像距的关系
虚像时物距与像距的关系:
1、物距与像距成正比:当物距按正比增加时,像距也同样增加,即用一定比
例可以换取恒定的像距。
2、焦距的变化无影响:即使焦距和成像手段的不同,物距与像距也仍然遵循
着正比关系。
3、焦距和物距的变化无关:当焦距变化的时候,像距并不会做出相应的变化,但物距会随焦距的变化而变化。
4、物不依赖像:随着物距的减小,像距也会相应减小。
但是,由于物距变化
无关像距,因此物距不因像距变化而改变。
5、焦距决定像距:焦距可以决定像距的大小,物距决定成像的大小,从而确
定像距的大小。
6、像距获取物距:若已知像距,可根据焦距以及图像尺寸计算出物距。
7、像距改变亦可获取物距:若更改像距,可根据焦距以及图像尺寸计算出新
的物距。
8、在逼近焦点时要保持相同的像距:逼近焦点时物距会变化,但像距不受物
距变化影响,应当保持其不变,以确保图像质量。
凹透镜焦距 公式法

凹透镜焦距公式法凹透镜焦距是描述凹透镜光学特性的一个重要参数,它代表了凹透镜能够将平行光线聚焦成的最小焦点距离。
凹透镜是一种中央较薄边缘较厚的透镜,通过光线的折射来实现对光线的聚焦。
凹透镜焦距的公式法是一种简单而经典的计算方法,可以用于准确计算凹透镜焦距的数值。
根据凹透镜焦距公式,焦距f与物距p和像距q之间存在着如下的关系:1/f=1/p+1/q。
在这个公式中,焦距f 的单位通常为米(m),物距p和像距q的单位则根据具体情况而定。
这个公式的推导基于光学的薄透镜假设,即透镜的厚度相对于其半径是非常小的。
这种假设使得光线在透镜上的折射行为可以简化为一次折射,从而使得计算变得相对容易。
通过这个公式,我们可以了解到物距和像距之间的关系与凹透镜焦距的大小密切相关。
当物距为无穷大时,即光线是平行的,我们可以得到焦距的一个特殊情况,即无穷远焦距。
在这种情况下,平行光线将会被凹透镜聚焦到焦点上。
此外,凹透镜焦距的正负号也非常重要。
根据公式,焦距为正表示透镜是凹透镜,即光线会在透镜后面汇聚;而焦距为负表示透镜是凸透镜,光线会在透镜前面汇聚。
这个正负号的意义在实际应用中具有重要指导意义。
凹透镜焦距的计算也可以通过实验来进行。
通过将物体放置在凹透镜的前方,然后移动一个屏幕来观察到物体所成的像。
通过测量物距和像距,我们可以使用焦距公式来计算凹透镜的焦距。
这种实验方法可以加深对凹透镜焦距概念的理解,并验证理论计算。
总结起来,凹透镜焦距公式法是一种非常有指导意义的方法,可以帮助我们计算凹透镜焦距,并深入理解凹透镜光学特性。
通过这个公式,我们可以了解到焦距与物距、像距的关系,以及透镜的类型。
同时,公式法也通过实验方法将理论知识与实际操作相结合,使得我们更加全面地理解和应用凹透镜焦距的概念。
凸透镜与凹透镜的成像规律与计算方法

凸透镜与凹透镜的成像规律与计算方法一、凸透镜成像规律1.物距与像距的关系:凸透镜成像时,物距(u)与像距(v)之间存在以下关系:1/f = 1/v - 1/u,其中f为凸透镜的焦距。
2.成像情况:根据物距与焦距的关系,凸透镜成像分为以下几种情况:(1)当u > 2f时,成倒立、缩小的实像,应用于照相机、摄像机等。
(2)当2f > u > f时,成倒立、放大的实像,应用于幻灯机、投影仪等。
(3)当u < f时,成正立、放大的虚像,应用于放大镜等。
二、凹透镜成像规律1.成像情况:凹透镜成像时,物距(u)与像距(v)之间存在以下关系:1/f = 1/v - 1/u,其中f为凹透镜的焦距。
根据物距与焦距的关系,凹透镜成像分为以下几种情况:(1)当u > f时,成倒立、缩小的实像。
(2)当u < f时,成正立、放大的虚像。
2.发散作用:凹透镜对光线具有发散作用,使通过透镜的光线推迟会聚。
三、凸透镜与凹透镜的计算方法1.凸透镜焦距的计算:当已知凸透镜成像时的物距(u)和像距(v)时,可以通过以下公式计算凸透镜的焦距(f):1/f = 1/v - 1/u2.凹透镜焦距的计算:当已知凹透镜成像时的物距(u)和像距(v)时,可以通过以下公式计算凹透镜的焦距(f):1/f = 1/v - 1/u四、凸透镜与凹透镜的应用1.凸透镜的应用:照相机、摄像机、幻灯机、投影仪、放大镜等。
2.凹透镜的应用:近视眼镜、防盗报警器、激光准直等。
综上所述,凸透镜与凹透镜的成像规律与计算方法是光学中的重要知识点。
掌握这些知识,有助于我们更好地理解和应用光学设备。
习题及方法:1.习题:一个凸透镜的焦距是10cm,一物体放在凸透镜前20cm处,求:a)成像情况b)像的大小c)由凸透镜成像规律可知,物距大于2f时,成倒立、缩小的实像。
d)物距为20cm,焦距为10cm,物距是焦距的二倍,所以成倒立、缩小的实像。
焦距、物距与像距 .

精心整理最长焦距/最短焦距=变焦倍数玩单反的谁还在乎光学变焦的倍数呀?这倍数可是越大越狗头。
人家有钱的高烧们都自豪地宣称自己的镜头都是1倍的--定焦数码单反,镜头标识乘1。
5就是实际焦距变焦和焦距首先没有太大的区别其次,一般的普通数码相机的变焦要在7倍以上方可达到210以上的焦距能看物体的远近只和焦距有关系,比如4-88mm的22倍镜头没有10-100mm10倍镜头看的远。
要想知道能看2.镜头不是“薄透镜”,计算对焦距离时我们可以把镜头简化为分裂成两个平面(两个主面)的薄透镜,两个平面的间距也就是虚拟透镜的厚度,这个厚度与镜头本身长度没有直接关系。
3.两个主面并不一定和镜头最前、最后的镜片重合,因此物距也不等于镜头前端到对焦物体的距离(工作距离)。
4.今天大部分镜头标注的焦距是其对无限远处对焦时的焦距,镜头对近处对焦时需要改变实际焦距。
红圈百微在对0.3m对焦时,焦距一定不到100mm。
此时镜头的主面位置也会变化,主点间距当然也在变。
这样我们就知道:1.镜头工作距离并不是真正的物距。
只有知道前主面的位置才能知道物距是多少。
2.对焦距离=物距+主点间距+焦距+焦像距(d=u+p+f+i)。
对焦距离和镜头工作距离、镜头长度没有直接关系。
3.根据相似三角形原理(图中浅红色两个三角形),放大倍率M=h':h=i:f。
只要我们知道了镜头在某一放大倍率M时的实际焦距f,带入透镜成像公式1/f=1/u+1/v,我们就能算出像距和物距,如果我们再知道此时镜头的主点间距p,就能算出镜头的对焦距离:不幸的是,厂家从不公布镜头某一放大倍率或某一对焦距离的主点间距是多少、实际焦距是多少,因此我们是不可能算出通过计算把对焦距离和放大倍率联系起来的。
一个悲哀的结局...。
焦距、物距与像距 .

最长焦距/最短焦距=变焦倍数光学变焦镜头不但要看其变焦倍数,还要看其焦距范围,焦距越大,看的越远,视角范围越小玩单反的谁还在乎光学变焦的倍数呀?这倍数可是越大越狗头。
人家有钱的高烧们都自豪地宣称自己的镜头都是1倍的--定焦数码单反,镜头标识乘1。
5就是实际焦距变焦和焦距首先没有太大的区别其次,一般的普通数码相机的变焦要在7倍以上方可达到210以上的焦距能看物体的远近只和焦距有关系,比如4-88mm的22倍镜头没有10-100mm10倍镜头看的远。
要想知道能看的最远距离就看最大焦距是多少,想知道能看的最大区域是多大,就看最小焦距是多少。
光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置,它通常是在镜头内。
表达光圈大小我们是用f值。
光圈f值= 镜头的焦距/ 镜头口径的直径从以上的公式可知要达到相同的光圈f值,长焦距镜头的口径要比短焦距镜头的口径大。
完整的光圈值系列如下:f1,f1。
4,f2,f2。
8,f4,f5。
6,f8,f11,f16,f22,f32,f44,f64这里值得一题的是光圈f值愈小,在同一单位时间内的进光量便愈多,而且上一级的进光量刚是下一级的一倍,例如光圈从f8调整到f5.6,进光量便多一倍,我们也说光圈开大了一级。
您知道光圈大小对景深影响的原理吗?一个物点发出的光线通过镜头聚焦之后,所有光线形成一个圆锥形光束。
圆锥的顶角与光圈有关:光圈越大、顶角越大。
圆锥顶点与底片接触形成一个像点。
如果底片稍微前移或者后移一点固定距离,切割光束形成一个圆斑,圆斑的大小与顶角有关:顶角大则圆斑也大。
换句话说:底片偏离同样的距离,光圈大圆斑也大。
现在我们不要移动底片、而是移动物点,使得光束的顶点移动。
如果形成的光斑相同,较细的光束(意为着光圈较小)物点可以移动更大的距离,这就说明小光圈景深更大。
景深随着物距的增加而增加,随着焦距的增加而减少。
一般而言,35mm相机的标准镜头焦长约是28-70mm,因此如果焦长高于70mm就代表支持望远效果,若是低于28mm就表示有广角拍摄能力。
物距相距焦距公式

物距相距焦距公式
以物距相距焦距公式为题,让我们来探讨一下这个有趣的数学公式吧。
焦距是光学中一个重要的概念,它是指光线经过透镜或凸面镜后会汇聚或发散的距离。
而物距则是指光线从物体发出到透镜或凸面镜的距离。
两者之间存在一种关系,即物距与像距满足焦距公式。
焦距公式可以表示为:1/f = 1/v - 1/u,其中f表示焦距,v表示像距,u表示物距。
这个公式告诉我们,当物体与透镜或凸面镜的距离发生变化时,像的位置也会相应地发生变化。
当物体距离透镜或凸面镜的距离u无限远时,像的位置v就是焦距f,这种情况下形成的像称为无穷远像。
而当物体距离透镜或凸面镜的距离u等于焦距f时,像的位置v会出现在无限远处,形成平行光。
当物体距离透镜或凸面镜的距离u小于焦距f时,像的位置v 会出现在透镜或凸面镜的同一侧,呈现放大的效果。
当物体距离透镜或凸面镜的距离u大于焦距f时,像的位置v会出现在透镜或凸面镜的另一侧,呈现缩小的效果。
焦距公式的应用非常广泛。
在摄影领域中,我们可以利用焦距公式计算出在不同物距下的焦点位置,从而调整相机镜头的焦距,使得拍摄的主体清晰、锐利。
在眼镜的制作中,焦距公式可以帮助我们根据患者的视力情况来定制合适的镜片,以达到矫正视力的效果。
焦距公式是光学中的重要工具,它帮助我们理解光线经过透镜或凸面镜后的行为,从而应用于各个领域。
通过深入研究焦距公式,我们能更好地掌握光学原理,为实际问题提供解决方案。
让我们一起感受这个公式的魅力吧!。
物距像距焦距的关系公式

物距像距焦距的关系公式
物距像距焦距的关系是摄影技术的重要基础,在没有相机的情况下,人们根据物距像距焦距的关系来调整拍摄距离,达到拍摄良好照片的目的。
物距像距焦距的关系是指物体到镜头的距离(物距)与镜头到感光元件的距离(像距)之间的关系。
一般情况下,当物距增加时,像距也会增加,但是当物距增加到一定程度时,像距就不会增加了,这时像距与物距之间的关系就变成了物距像距焦距的关系。
物距像距焦距的关系可以使用下面的公式来表示:
F = (d1 × d2)/(d1 + d2)
其中,F表示焦距,d1表示物距,d2表示像距。
物距像距焦距的关系是摄影中重要的基础,它可以帮助摄影师根据不同的拍摄距离来调整焦距,从而获得更好的拍摄效果。
比如,如果摄影师想要拍摄物体的细节,他可以使用较短的物距,从而将焦距调整到较长的值,从而获得更大的放大效果。
另外,物距像距焦距的关系也可以用来计算不同焦距的摄影镜头的拍摄距离,从而达到良好的拍摄效果。
总之,物距像距焦距的关系是摄影技术中重要的基础,并且可以帮
助摄影师在拍摄时进行有效的焦距调整,以获得更好的拍摄效果。
凸透镜成像规律
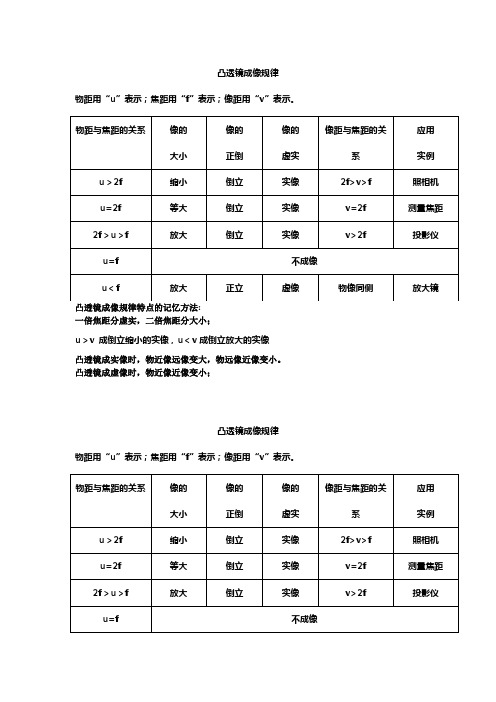
凸透镜成像规律
物距用“u”表示;焦距用“f”表示;像距用“v”表示。
凸透镜成像规律特点的记忆方法:
一倍焦距分虚实,二倍焦距分大小;
u>v 成倒立缩小的实像,u<v成倒立放大的实像
凸透镜成实像时,物近像远像变大,物远像近像变小。
凸透镜成虚像时,物近像近像变小;
凸透镜成像规律
物距用“u”表示;焦距用“f”表示;像距用“v”表示。
凸透镜成像规律特点的记忆方法:
一倍焦距分虚实,二倍焦距分大小;
u>v成倒立缩小的实像,u<v成倒立放大的实像
凸透镜成实像时,物近像远像变大,物远像近像变小。
凸透镜成虚像时,物近像近像变小;。
物距、焦距、焦点关系
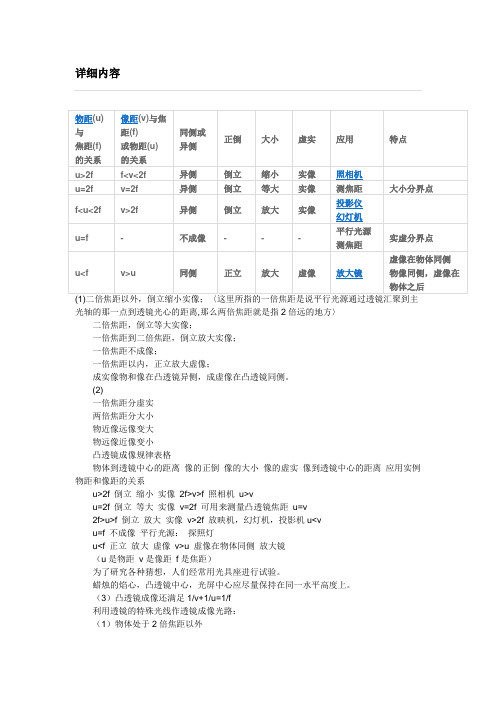
(2)物体处于2倍焦距和1倍焦距之间(3)物体处于一倍焦距以内(4)凸透镜成像光路实验研究凸透镜的成像规律是:当物距在一倍焦距以内时,得到正立、放大的虚像;在一倍焦距到二倍焦距之间时得到倒立、放大的实像;在二倍焦距以外时,得到倒立、缩小的实像。
该实验就是为了研究证实这个规律。
实验中,有下面这个表:物距像的性质像的位置与物同侧与异侧像距vu>2f 倒立缩小实像异侧f<v<2fu=2f 倒立等大实像异侧v=2f 此时物体与像的距离是最小的,即4倍焦距。
f<u<2f 倒立放大实像异侧v>2fu=f 不成像v无限大(平行光源,如:探照灯)u<f 正立放大虚像同侧u,v同侧这就是为了证实那个规律而设计的表格。
其实,透镜成像满足透镜成像公式:1/u(物距)+1/v(像距)=1/f(透镜焦距)照相机运用的就是凸透镜的成像规律镜头就是一个凸透镜,要照的景物就是物体,胶片就是屏幕照射在物体上的光经过漫反射通过凸透镜将物体的像成在最后的胶片上胶片上涂有一层对光敏感的物质,它在曝光后发生化学变化,物体的像就被记录在胶卷上至于物距、像距的关系与凸透镜的成像规律完全一样物体靠近时,像越来越远,越来越大,最后再同侧成虚像。
物距增大,像距减小,像变小;物距减小,像距增大,像变大。
一倍焦距分虚实,二倍焦距分大小。
凸透镜成像规律表:实像,物近像远像变大一焦分虚实,二焦分大小虚像,物远像远像变大实像皆倒立,物远像变小(4)当成虚像时,物、像的左右一致,上下一致;当成实像时,物、像的左右相反,上下相反.。
(5)凸透镜成像的两个分界点:2f点是成效放大缩小实像的分界点;f点是成实像虚像的分界点。
凸透镜成像规律归纳总结

凸透镜成像规律归纳总结凸透镜成像规律是指在光线经过凸透镜时,光线的传播方向和焦点的位置发生变化,从而形成图像的规律。
凸透镜成像规律涉及图像的位置、大小和性质等方面。
以下是凸透镜成像规律的完整总结。
1.凸透镜的焦点和焦距:凸透镜有两个焦点,分别是凸透镜前面的一个焦点和凸透镜后面的一个焦点。
焦点与透镜的曲率半径有关,曲率半径越小,焦点越靠近透镜。
焦距是从透镜中心到焦点的距离,可以由透镜的曲率半径计算得出。
2.物距、像距和焦距的关系:物距是指物体到透镜的距离,像距是指像到透镜的距离。
根据凸透镜成像规律可以得出以下关系式:1/f=1/v-1/u,其中f为焦距,v为像距,u为物距。
这个公式被称为薄透镜公式。
3.图像的位置和性质:根据凸透镜成像规律可以得出以下结论:-当物体位于透镜的远焦点之外时,图像位于透镜的近焦点之内。
图像是倒立的,放大的,位于透镜的同侧。
-当物体位于透镜的近焦点之外、远焦点之内时,图像位于透镜的远焦点之外,图像是倒立的,缩小的,位于透镜的同侧。
-当物体位于透镜的近焦点上时,图像位于无穷远处,图像是倒立的,实际上是一个平面波。
4.放大倍数:放大倍数是指图像的大小和物体的大小之间的比值。
根据凸透镜成像规律可以得出放大倍数的计算公式:放大倍数=,v/u。
当放大倍数大于1时,图像是放大的;当放大倍数小于1时,图像是缩小的;当放大倍数等于1时,图像和物体的大小相等。
5.球差:球差是凸透镜成像中一个重要的光学缺陷,导致像上不同位置至焦轴的距离不同,从而造成图像的模糊或色差。
为了减小球差的影响,可以采用复合透镜或附加光具来进行光学设计。
凸透镜成像规律是光学理论的基础,对于理解和应用光学设备和光学系统具有重要意义。
通过凸透镜成像规律的研究和应用,我们可以设计和制造出更加精确、高清晰度的光学器件和仪器。
焦距、物距与像距.

最长焦距/最短焦距=变焦倍数光学变焦镜头不但要看其变焦倍数,还要看其焦距范围,焦距越大,看的越远,视角范围越小玩单反的谁还在乎光学变焦的倍数呀?这倍数可是越大越狗头。
人家有钱的高烧们都自豪地宣称自己的镜头都是1倍的一一定焦数码单反,镜头标识乘1。
5就是实际焦距变焦和焦距首先没有太大的区别其次,一般的普通数码相机的变焦要在7倍以上方可达到210以上的焦距能看物体的远近只和焦距有关系,比如4-88mm 的22倍镜头没有10-100mm10 倍镜头看的远。
要想知道能看的最远距离就看最大焦距是多少,想知道能看的最大区域是多大,就看最小焦距是多少。
光圈是一个用来控制光线透过镜头,进入机身内感光面的光量的装置,它通常是在镜头内。
表达光圈大小我们是用f值。
光圈f值=镜头的焦距/镜头口径的直径从以上的公式可知要达到相同的光圈f值,长焦距镜头的口径要比短焦距镜头的口径大。
完整的光圈值系列如下:fl , fl o 4 , f2 , f2。
8, f4 , f5。
6, f8 , f11 , f16 , f22 , f32 , f44 , f64 这里值得一题的是光圈f值愈小,在同一单位时间内的进光量便愈多,而且上一级的进光量刚是下一级的一倍,例如光圈从f8调整到f5.6,进光量便多一倍,我们也说光圈开大了一级。
您知道光圈大小对景深影响的原理吗?一个物点发出的光线通过镜头聚焦之后,所有光线形成一个圆锥形光束。
圆锥的顶角与光圈有关:光圈越大、顶角越大。
圆锥顶点与底片接触形成一个像点。
如果底片稍微前移或者后移一点固定距离,切割光束形成一个圆斑,圆斑的大小与顶角有关:顶角大则圆斑也大。
换句话说:底片偏离同样的距离,光圈大圆斑也大。
现在我们不要移动底片、而是移动物点,使得光束的顶点移动。
如果形成的光斑相同,较细的光束(意为着光圈较小)物点可以移动更大的距离,这就说明小光圈景深更大。
景深随着物距的增加而增加,随着焦距的增加而减少。
凸透镜的焦距与物距、像距之间满足的关系。

凸透镜的焦距与物距、像距之间满足的关
系。
凸透镜的焦距与物距、像距之间满足的关系
凸透镜是一种广泛应用于光学系统中的光学元件,能够使光线通过折射而聚焦。
了解凸透镜的焦距与物距、像距之间的关系对于正确使用凸透镜至关重要。
凸透镜的焦距指的是光线通过凸透镜后的聚焦点与凸透镜的中心之间的距离。
焦距可以用于计算物体与凸透镜之间的距离以及像距与物距之间的关系。
对于凸透镜,有一个简单的公式可以用来计算焦距:
1 / f = 1 / v - 1 / u
其中,f表示凸透镜的焦距,v表示像距,u表示物距。
根据这个公式,我们可以看出以下几个关系:
1. 如果物距u增大,那么像距v也会增大。
这意味着物体离凸透镜越远,形成的像也会越远。
2. 当物距u无限大时,像距v等于焦距f。
这代表光线是平行射入凸透镜的,而凸透镜将它们聚焦在焦距处。
3. 当物距u等于焦距f时,像距v会变得非常大。
这是因为光线会通过凸透镜后呈现出与射入方向相反的方向,形成一个虚像。
综上所述,凸透镜的焦距与物距、像距之间满足的关系可以通过简单的公式来描述。
了解这些关系对于设计和使用光学系统中的凸透镜是非常重要的,可以帮助我们预测和控制光线的聚焦效果。
镜头的焦距和像距的关系

镜头的焦距和像距的关系焦距和像距是摄影学中的两个重要概念。
了解和掌握焦距与像距之间的关系对于摄影师来说至关重要。
在本文中,我们将探讨焦距和像距之间的关系,并阐述如何通过调整焦距来实现不同的拍摄效果。
一、焦距的定义和测量方法焦距是指从透镜到成像平面(胶片或传感器)的距离,通常以毫米(mm)为单位来表示。
焦距较短时,拍摄的视场较宽,被摄物体呈现出广角效果;焦距较长时,拍摄的视场较窄,被摄物体呈现出望远效果。
测量焦距的一种常用方法是通过透镜的光学特性进行。
可以利用白光光源和物体,观察透镜在物体不同位置时的焦点,从而确定焦距的大小。
二、像距的定义和测量方法像距是指光线经过透镜后,在成像平面上的距离,即物体的像离透镜的距离。
像距可以分为物距(物体到透镜的距离)和像方距(图像到透镜的距离)两个部分。
当物距大于零时,像距亦为正数,表示实像;当物距小于零时,像距为负数,表示虚像。
测量像距的一个常用方法是通过调节物体和透镜的距离,然后观察透镜背后成像平面的位置,从而确定像距的大小。
三、焦距和像距的关系焦距和像距之间存在着一定的数学关系,即焦距与物距和像距之间的比例关系。
根据薄透镜公式,可以得到如下关系式:1/f = 1/v + 1/u其中,f表示焦距,v表示像距,u表示物距。
从上述公式可以得知,当物距等于焦距时,像距为无穷大,此时可以得到清晰焦点的无穷远景。
而当物距小于焦距时,像距为正数,表示实像;当物距大于焦距时,像距为负数,表示虚像。
四、不同焦距的拍摄效果不同焦距对于拍摄效果具有明显的影响。
在摄影中,广角、标准焦距和长焦距分别具有不同的特点和应用场景。
1. 广角拍摄广角镜头的焦距较短,通常小于50mm。
广角镜头具有宽广的视场和较大的景深,能够捕捉到更多的景物细节。
广角镜头适合拍摄大陆风光、建筑物等场景,可以营造出独特的空间感和透视效果。
2. 标准焦距拍摄标准焦距通常为50mm到70mm之间,视角与人眼相似,画面展现出较为真实的比例关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u与f的关系 v与f的关系像的正倒像的大小像的虚实
u>2f f<v<2f 倒立缩小实像
u=2f v=2f 倒立等大实像
f<u<2f v>2f 倒立放大实像
u<f ***** 正立放大虚像
(****部分为没有,不存在,u是物距,v是像距,f是焦距)
结论:(1)焦点是成实像和虚像的分界点。
两倍焦距处是成放大像和缩小像的分界点。
(2)不论实像,虚像,物体离焦点越近所成的像越大,像离透镜也越远。
(3)实像总是倒立的,能呈现在光屏上;而虚像是正立的,不能呈现在光屏上。
探究目的:弄清凸透镜成的像的虚实、大小、正倒跟物距有什么关系?
器材:蜡烛、光具座和光屏.
步骤:我们可以把物体放在距凸透镜比较远的地方,然后逐渐移近,观察成像的情况.物距大到双面程度成实像,小到什么时候成虚像,大概不同的凸透镜会有不同,要有一个参照距离才便于研究.
不同的凸透镜,焦距的大小不同.我们就用焦距f作为参照距离.先把物体放在较远处,例如使物距u>2f,然后把物体移近些,使物距u=2f,再移动物体,使物距u在2f和f之间,即2f>u>f,继续移动物体,使物距u=f,最后使物距u<f.观察看看凸透镜成像的规律.(表格.数据如下表)
物距(u) 像距(v) 像的性质应用
倒正大小虚实
u>2f f<v<f 倒小实相机
u=2f v=2f 倒等实——
f<u<2f v>2f 倒大实幻灯机
u=f ——————————
u<f ——正大虚放大镜
结论:凸透镜成像的规律如下
1、一焦分虚实,二焦分大小
(一倍焦距以内是虚象,一倍以外是实象,不包括一倍焦距)
2、虚象同侧正,实象异侧倒
(虚象在同一侧,是正立的象,实象在异侧,是倒立的)
3、物小象变大,物大象变小
(物距变小,象变大,物距变大,象变小)。
