高中立体几何证明线面平行的常见方法

合集下载

立体几何常考定理的总结(八大定理)

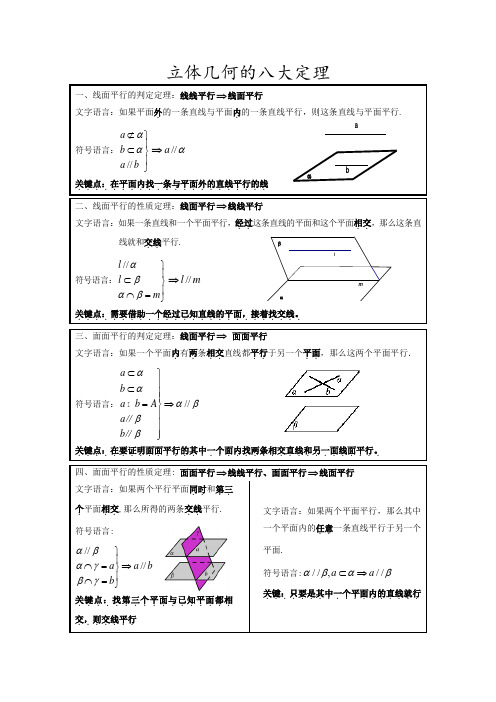
lmβααba立体几何的八大定理一、线面平行的判定定理：线线平行⇒线面平行文字语言：如果平面外．的一条直线与平面内．的一条直线平行，则这条直线与平面平行. 符号语言：//a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点：在平面内找一条与平面外的直线平行的线．．．．．．．．．．．．．．．．．．．．．．二、线面平行的性质定理：线面平行⇒线线平行文字语言：如果一条直线和一个平面平行，经过．．这条直线的平面和这个平面相交．．，那么这条直线就和交线．．平行. 符号语言：//l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点：需要借助一个经过已知直线的平面，接着找交线。

．．．．．．．．．．．．．．．．．．．．．．．．．．三、面面平行的判定定理：线面平行⇒ 面面平行文字语言：如果一个平面内．有两．条相交．．直线都平行．．于另一个平面．．，那么这两个平面平行．符号语言：//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点：在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行文字语言：如果两个平行平面同时．．和第三．．个．平面相交．．,那么所得的两条交线．．平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点：找第三个平面与已知平面都相．．．．．．．．．．．．．．．．．交，则交线平行．．．．．．．文字语言：如果两个平面平行，那么其中一个平面内的任意．．一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键：只要是其中一个平面内的直线就行．．．．．．．．．．．．．．．．．．nmAαaBA l βαaβα五、线面垂直的判定定理：线线垂直⇒线面垂直文字语言：如果一条直线和一个平面内．的两．条相交．．直线垂直．．，那么这条直线垂直于这个平面. 符号语言：,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点：在平面内找两条相交直线与所要证的直线垂直．．．．．．．．．．．．．．．．．．．．．．．．六、线面垂直的性质定理：线面垂直⇒线线垂直文字语言：若一条直线垂直于一个平面，则这条直线垂直平面内的任意．．一条直线. 符号语言：l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点：往往线面垂直中的线线垂直需要用这个定理推出．．．．．．．．．．．．．．．．．．．．．．．．．七、平面与平面垂直的判定定理：线面垂直⇒面面垂直文字语言：如果一个平面经过．．另一个平面的一条垂线，则这两个平面互相垂直. （如果一条直线垂直于一个平面，并且有另一个平面经过这条直线，那么这两个平面垂直）符号表示：a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点：．．．．在需要证明的两个平面中找线面垂直．．．．．．．．．．．．．．．．八、平面与平面垂直的性质定理：面面垂直⇒线面垂直文字语言：如果两个平面互相垂直，那么在一个平面内垂直．．于它们的交线．．的直线垂直于另一个平面.符号语言：l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点：先找交线，再在其中一个面内找与交线垂直的线。

立体几何线面平行垂直,线面角二面角的证明方法

APBCED一：线面平行的证明方法：1、用“近似平行法”先找到面上与已知直线平行的直线（一般为表示面的三角形的边界直线，或三角形某边上的中线）看找到的这条线与已知线的长度关系，1）若相等应该构造平行四边形；2）若不相等一般利用三角形中位线的性质（将这两个不相等的线段的端点连结并延长即会出现关键三角形）。

2、若既不能构造平行四边形也不能性用中位线性质，则应再构造一个此直线所在的平面，证明此平面与已知平面平行（先证面面平行，推出线面平行）例一：如图，已知菱形ABCD ，其边长为2，60BAD ∠= ，ABD ∆绕着BD 顺时针旋转120得到PBD ∆，M 是PC 的中点．（1）求证：//PA 平面MBD ；（2）求直线AD 与平面PBD 所成角的正弦值．例二：已知四棱锥P-ABCD ，底面ABCD 是60=∠A 、边长为a 的菱形，又ABCD PD 底⊥，且PD=CD ，点M 、N 分别是棱AD 、PC 的中点．（1）证明：DN//平面PMB ；（2）证明：平面PMB ⊥平面PAD ；（3）求点A 到平面PMB 的距离．例三：如图，已知点P 是平行四边形ABCD 所在平面外的一点，上的点且PE EA BF FD =∶∶，求证：EF //平面PBC ．二：线面垂直的证明方法：通过线线垂直，证明线面垂直1）利用勾股定理逆定理及三角形中两个角和为90°； 2）利用等边、等腰三角形（中线即高线），正方形、矩形邻边垂直，正方形菱形对角线垂直等；3）通过线面垂直，反推线线垂直；4）利用面面垂直的性质，证明垂直于交线即垂直于另一个平面。

例四：如图,四边形ABCD 为矩形，CF ⊥平面ABCD ，DE ⊥平面ABCD ， AB=4a ，BC= CF=2a,P 为AB 的中点.(1)求证：平面PCF ⊥平面PDE ； (2)求四面体PCEF 的体积.C例五：如图，在四棱锥ABCD P -中，ABCD 是矩形，ABCD PA 平面⊥， 3,1===AB AD PA ，点F 是PD 的中点，点E 在CD 上移动。

立体几何线面平行证明

立体几何线面平行证明要证明两个线面平行，一般可以通过以下几种方法来进行证明：方法一：使用平行线的性质假设我们有线面A和线面B，要证明A和B平行，可以通过以下步骤进行证明：1.假设线面A和线面B不平行，即存在一条线a与线面A不平行，又与线面B相交于一点P。

2.假设在线面A上存在一点Q，它与直线a上相交于一点R。

3.由于线a与线面B相交于P，所以线段PR必然属于线面B。

4.由于线a与线面A相交于R，所以线段PR必然属于线面A。

5.由于线面A和线面B都包含线段PR，所以它们必然相交。

6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。

方法二：使用支撑面的性质假设我们有线面A和线面B，要证明A和B平行，可以通过以下步骤进行证明：1.假设在线面A上存在一条直线a，它与线面B相交于一点P。

2.过直线a作平行于线面B的平面，该平面与线面A相交于线段QR。

3.由于直线a与线面B相交于点P，所以线段PR必然属于线面B。

4.由于平面上的任意两点可以确定一条直线，所以线段QR也属于线面B。

5.因此，线段QR同时属于线面A和线面B，所以它们不是平行的。

6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。

方法三：使用平行四边形的性质假设我们有线面A和线面B，要证明A和B平行1.假设在线面A上存在一条直线a，它与线面B相交于一点P。

2.在线面A上选择一点Q，并通过P点作一条平行于线面A的直线b。

3.连接直线a和直线b，得到平行四边形PQRD。

4.由于平行四边形的特性，相邻两边平行且长度相等，所以线段PD也是平行于线面A的，并且它必然属于线面B。

5.因此，线段PD同时属于线面A和线面B，所以它们不是平行的。

6.这与我们的假设相矛盾，因此假设不成立，即线面A和线面B是平行的。

以上三种方法是一些常用的证明线面平行的方法，根据实际问题的具体情况，可以选择适合的方法进行证明。

立体几何常见证明方法

立体几何方法归纳小结一、线线平行的证明方法1、根据公理4，证明两直线都与第三条直线平行。

2、根据线面平行的性质定理，若直线a平行于平面A ，过a的平面B与平面A相交于b ，则a//b。

3、根据线面垂直的性质定理，若直线a与直线b都与平面A垂直，则a//b 。

4、根据面面平行的性质定理，若平面A//平面B，平面C与平面A和平面B的交线分别为直线a与直线b，则a//b 。

二、线面平行的证明方法1、根据线面平行的定义，证直线与平面没有公共点。

2、根据线面平行的判定定理，若平面A内存在一条直线b与平面外的直线a平行，则a//A 。

(用相似三角形或平行四边形)3、根据平面与平面平行的性质定理，若两平面平行，则一个平面内的任一直线与另一个平面平行。

三、面面平行的证明方法1、根据定义，若两平面没有公共点，则两平面平行。

2、根据两平面平行的判定定理，一个平面内有两相交直线与另一平面平行，则两平面平行。

或根据两平面平行的判定定理的推论，一平面内有两相交直线与另一平面内两相交直线平行，则两平面平行。

3、垂直同一直线的两平面平行。

4、平行同一平面的两平面平行。

四、两直线垂直的证明方法1、根据定义,证明两直线所成的角为90°2、一直线垂直于两平行直线中的一条,也垂直于另一条.3、一直线垂直于一个平面,则它垂直于平面内的所有直线.4、根据三垂线定理及逆定理,若平面内的直线垂直于平面的一条斜线(或斜线在平面内的射影),则它垂直于斜线在平面内的射影(或平面的斜线).五、线面垂直的证明方法1、根据定义,证明一直线与平面内的任一(所有)直线垂直,则直线垂直于平面.2、根据判定定理,一直线垂直于平面内的两相交直线,则直线垂直于平面.3、一直线垂直于两平行平面中的一个,也垂直于另一个.4、两平行直线中的一条垂直于一个平面,另一条也垂直于这个平面.5、根据两平面垂直的性质定理,两平面垂直,则一个平面内垂直于它们交线的直线垂直于另一个平面.六、面面垂直的证明方法1、根据面面垂直的定义，两平面相交所成的二面角为直二面角，则两平面垂直。

高中立体几何证明线面平行的常见方法

高中立体几何证明线面平行的常见方法1.通过“平移”再利用平行四边形的性质题目1：四棱锥P-ABCD的底面是平行四边形，点E、F分别为棱AB、PD的中点。

证明AF∥平面PCE。

证明：将四棱锥P-ABCD平移，使其底面平移到平面PCE上，得到四棱锥P'-A'B'C'D'，其中A'B'C'D'与ABCD平行，且P'、E'、F'分别为A'B'、C'D'、A'D'的中点。

因为AF∥PD，所以AF'=PD'=C'F'，又因为AD'=C'D'/2=AB'/2=AF'/2，所以AD'∥B'C'。

因此，根据平行四边形的性质，AF'∥B'C'，即AF∥CE。

题目3：四棱锥P-ABCD底面是直角梯形，BA⊥AD，CD⊥AD，CD=2AB，E为PC的中点，证明EB∥平面PAD。

证明：连接PE，因为E为PC的中点，所以PE∥AD。

又因为CD⊥AD，所以CD∥PE。

又因为CD=2AB，所以AB∥PE。

因此，根据平行四边形的性质，EB∥PA，即EB∥平面PAD。

2.利用三角形中位线的性质题目4：四面体ABCD中，E、F、G、M分别是棱AD、CD、BD、BC的中点，证明AM∥平面EFG。

证明：连接EF、EG、FG，因为E、F、G分别为三角形BCD、ACD、ABD的中点，所以EF、EG、FG分别是这三个三角形的中位线。

因此，EF∥AD，EG∥BD，FG∥AC。

又因为M为BC的中点，所以AM∥FG。

因此，AM∥平面EFG。

3.利用平行四边形的性质题目7：正方体ABCD-A' B' C' D'中O为正方形ABCD的中心，M为B'B的中点，求证D'O∥平面A'BC'。

高中立体几何最佳解题方法及考题详细解答

高中立体几何最佳解题方法总结一、线线平行的证明方法1、利用平行四边形；2、利用三角形或梯形的中位线；3、如果一条直线和一个平面平行，经过这条直线的平面与这个相交，那么这条直线和交线平行。

（线面平行的性质定理）4、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

（面面平行的性质定理）5、如果两条直线垂直于同一个平面，那么这两条直线平行。

（线面垂直的性质定理）6、平行于同一条直线的两个直线平行。

7、夹在两个平行平面之间的平行线段相等。

二、线面平行的证明方法1、定义法：直线和平面没有公共点。

2、如果平面外的一条直线和这个平面内的一条直线平行，那么这条直线就和这个平面平行。

（线面平行的判定定理）3、两个平面平行，其中一个平面内的任意一条直线必平行于另一个平面。

4、反证法。

三、面面平行的证明方法1、定义法：两个平面没有公共点。

2、如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行。

（面面平行的判定定理）3、平行于同一个平面的两个平面平行。

4、经过平面外一点，有且只有一个平面与已知平面平行。

5、垂直于同一条直线的两个平面平行。

四、线线垂直的证明方法1、勾股定理；2、等腰三角形；3、菱形对角线;4、圆所对的圆周角是直角；5、点在线上的射影；6、如果一条直线和这个平面垂直，那么这条直线和这个平面内的任意直线都垂直。

7、在平面内的一条直线，如果和这个平面一条斜线垂直，那么它也和这条斜线的射影垂直。

（三垂线定理）8、在平面内的一条直线，如果和这个平面一条斜线的射影垂直，那么它也和这条斜线垂直。

9、如果两条平行线中的一条垂直于一条直线，那么另一条也垂直于这条直线。

五、线面垂直的证明方法：1、定义法：直线与平面内的任意直线都垂直；2、点在面内的射影；3、如果一条直线和一个平面内的两条相交直线垂直，那么这条直线就和这个平面垂直。

（线面垂直的判定定理）4、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线必垂直于另一个平面。

总结证明线面平行的常用方法

BC DA 1B 1C 1D 1图２AFE GαabA图1总结证明线面平行的常用方法空间直线与平面平行问题是立体几何的一个重要内容，也是高考考查的重点，下面就常见的线面平行的判定方法介绍如下：方法一、反证法【例1】求证：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．（直线与平面平行的判定定理）已知：,,a b a αα⊄⊂∥b ，如图1．求证：a ∥α．【分析】要证明直线与平面平行，可以从直线与平面平行的定义入手，但从定义来看，必须说明直线与平面无公共点，这一点直接说明是困难的，但我们可以借助反正法来证明．【证明】假设直线a 与平面α不平行，又∵a α⊄，∴a A α=．下面只要说明aA α=不可能即可．∵a ∥b ，∴a ，b 可确定一平面，设为β．又aA α=， ∴,A a A β∈∈．又b ,A αα⊂∈，∴平面α与平面β中含有相同的元素直线b ，以及不在直线b 上的点Ａ，由公理２的推论知，平面α与平面β重合． ∴a α⊂，这与已知a α⊄相矛盾． ∴a A α=不可能．故a ∥α．方法二、判定定理法【例2】正方体1AC 中，Ｅ、G 分别为BC 、11C D 的中点，求证：EG ∥平面11BDD B 【分析】要证明EG ∥平面11BDD B ，根据线面平行的判定定理，需在平面11BDD B 内找到一条与EG 平行的直线，充分借助Ｅ、G 为中点的条件．【证明】如图２，取BD 的中点为Ｆ，连结EF ，1D F ． ∵Ｅ为BC 的中点， ∴ EF ∥CD 且12EF CD =又∵G 为11C D 的中点， ∴ 1D G ∥CD 且112D G CD =∴ EF ∥1D G ，且1EF D G =B C DA 1B 1C 1D 1AＮＭE Ｆ图３故四边形1EFD G 为平行四边形．∴ 1D F ∥EG又1D F ⊂平面11BDD B ，且EG ⊄平面11BDD B ， ∴ EG ∥平面11BDD B 【评注】根据直线与平面平行的判定定理证明直线和平面平行的关键是在平面内找到一条直线和已知直线平行，常用到中位线定理、平行四边形的性质、成比例线段、平行转移法、投影法等.具体应用时,应根据题目条件而定.方法三、运用面面平行的性质定理【例3】在正方体1111ABCD A B C D -中，点N 在BD 上，点M 在1B C 上，且CM DN =，求证：MN ∥平面11AA BB ．【分析】若过MN 能作一个平面与平面11AA BB 平行，则由面面平行的性质定理，可得MN 与平面11AA BB 平行．【证明】如图3，作MP ∥1BB ，交BC 与点Ｐ，联结NP ． ∵ MP ∥1BB ，∴1CM CPMB PB=． ∵1BD B C =，DN CM =，∴1B M BN =， ∵1CM DN MB NB =，∴DN CPNB PB= ∴NP ∥CD ∥AB ， ∴面MNP ∥面11AA BB ． ∴MN ∥平面11AA BB【评注】本题借助于成比例线段，证明一个平面内的两条相交直线与另一个平面内的两条相交直线分别平行，得到这两个平面平行，进而得到线面平行，很好地体现了线面、线线、面面平行关系之间的转化思想．。

立体几何证明方法——证线面平行

如图,在正方体 ABCD-A1B1C1D1 中，点 M、N 在分别是 BC1、B1D1 的中点。求证:MN//平面 AA1B1B
D1
A1
面面平行则线面平行
D A
N
C1 G
B1
M C
B
.
7
此课件下载可自行编辑修改，此课件供参考！部分内容来源于网络，如有侵权请与我联系删除！
关键：构造三角形平面 D1 A1 四边形平面
面面平行
D
A
构造三角形平面 .
N
C1
B1
M C
B
5
方法演练二：
如图,在正方体 ABCD-A1B1C1D1 中，
点 M、N 在分别是 BC1、B1D1 的中点。
求证:MN//平面 AA1B1B
D1
构造平行
A1
G
四边形平面
D
A
N
C1
B1
HM C
B
.
6
方法演练二：
a
的一条平行于一个平面，
b
那么另一条直线也平行于这个平面。
a // b
推理过程： a //
b //
b
.
3
方法演练一：
如图，在三棱锥 S ABC 中，
E，F 分别是侧棱 SA，SB 的中点。
求证： EF // 平面ABC .
S
E A
F C
关键点：找三角形平面 B
.
4
方法演练二：
如图,在正方体 ABCD-A1B1C1D1 中，点 M、N 在分别是 BC1、B1D1 的中点。求证:MN//平面 AA1B1B
二如何证明直线与平面平行：
方法一：线线平行，则线面平行。

高考理科数学必考——几何证明与利用空间向量求线面角、面面角

高考理科数学必考——几何证明与利用空间向量求线面角、面
面角
时间过的飞快，距离高考的时间就只剩76天了，同学和老师也越来越紧张了，有些地方欠缺的同学开始寝食难安，老师也赶快奉献点干货来帮助几何证明欠缺的学生。

立体几何其实难度不大，只要你会空间向量，会建系，一切就自然而然水到渠成了。

在这先分析这些立体几何的解题思路。

在立体几何中，第一问一般会让你证明线面平行、线面垂直、面面平行、面面垂直
1、证明线面平行的方法1、平移的方法，找到直线与平面内一条直线平行
2、利用面面平行、证明线面平行
2、证明线面垂直的方法1、证明直线与平面内相交的两直线垂直
3、证明面面平行的方法1、证明一个平面内两相交的直线与另一个平面内两相交的直线互相平行
2、证明平面内两相交的直线分别平行另一个平面
4、证明面面垂直的方法1、先证明一条直线垂直于一个平面，这条直线还在另一个平面内
利用这些方法第一问就可以轻松解决了。

在立体几何第二中，会求线面角、面面角，在第二步中，利用空间向量解决就可以
利用空间向量解决第二问的步骤1、找三垂，建立空间直角坐标系
2、写出各个点的坐标
3、求出直线向量、面的法向量
4、利用夹角公式算出余弦值
下面通过两个例题说明一下这个空间几何。

立体几何中的向量方法——证明平行及垂直

立体几何中的向量方法(一)——证明平行与垂直1．直线的方向向量与平面的法向量确实定(1)直线的方向向量：在直线上任取一非零向量作为它的方向向量．(2)平面的法向量可利用方程组求出：设a ，b 是平面α两不共线向量，n 为平面α的法向量，则求法向量的方程组为⎩⎨⎧n ·a ＝0，n ·b ＝0.2．用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ，与平面α共面的两个不共线向量v 1和v 2，则l ∥α或l ⊂α⇔存在两个实数*，y ，使v ＝*v 1＋y v 2.(3)设直线l 的方向向量为v ，平面α的法向量为u ，则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1，u 2，则α∥β⇔u 1∥u 2.3．用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2＝0.(2)设直线l 的方向向量为v ，平面α的法向量为u ，则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2，则α⊥β⇔u 1⊥u 2⇔u 1·u 2＝0.【思考辨析】判断下面结论是否正确(请在括号中打"√〞或"×〞)(1)直线的方向向量是唯一确定的．()(2)平面的单位法向量是唯一确定的．()(3)假设两平面的法向量平行，则两平面平行．()(4)假设两直线的方向向量不平行，则两直线不平行．()(5)假设a ∥b ，则a 所在直线与b 所在直线平行．()(6)假设空间向量a 平行于平面α，则a 所在直线与平面α平行．()1．以下各组向量中不平行的是()A ．a ＝(1,2，－2)，b ＝(－2，－4,4)B ．c ＝(1,0,0)，d ＝(－3,0,0)C ．e ＝(2,3,0)，f ＝(0,0,0)D ．g ＝(－2,3,5)，h ＝(16,24,40)2．平面α有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则以下点P 中，在平面α的是()A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－3,4)3．AB →＝(1,5，－2)，BC →＝(3,1，z )，假设AB →⊥BC →，BP →＝(*－1，y ，－3)，且BP ⊥平面ABC ，则实数*，y ，z 分别为______________．4．假设A (0,2，198)，B (1，－1，58)，C (－2,1，58)是平面α的三点，设平面α的法向量n ＝(*，y ，z )，则*∶y ∶z ＝________.题型一证明平行问题例1(2013·改编)如图，在四面体A －BCD 中，AD ⊥平面BCD ，BC ⊥CD ，AD ＝2，BD ＝22，M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且AQ ＝3QC .证明：PQ ∥平面BCD .如图，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E ，F ，M ，N 分别是棱AB ，AD ，A 1B 1，A 1D 1的中点，点P ，Q 分别在棱DD 1，BB 1上移动，且DP ＝BQ ＝λ(0<λ<2)．(1)当λ＝1时，证明：直线BC 1∥平面EFPQ ；(2)是否存在λ，使平面EFPQ 与平面PQMN 所成的二面角为直二面角？假设存在，求出λ的值；假设不存在，说明理由．题型二证明垂直问题例2 如下图，正三棱柱(底面为正三角形的直三棱柱)ABC —A 1B 1C 1的所有棱长都为2，D 为CC 1的中点．求证：AB 1⊥平面A 1BD .如下图，在四棱锥P －ABCD 中，PC ⊥平面ABCD ，PC ＝2，在四边形ABCD 中，∠B ＝∠C ＝90°，AB ＝4，CD ＝1，点M 在PB 上，PB ＝4PM ，PB 与平面ABCD 成30°角．(1)求证：CM ∥平面PAD ；(2)求证：平面PAB ⊥平面PAD .题型三解决探索性问题例3 如图，棱柱ABCD－A1B1C1D1的所有棱长都等于2，∠ABC和∠A1AC均为60°，平面AA1C1C⊥平面ABCD.(1)求证：BD⊥AA1；(2)求二面角D－A1A－C的余弦值；(3)在直线CC1上是否存在点P，使BP∥平面DA1C1，假设存在，求出点P的位置，假设不存在，请说明理由．如下图，四棱锥S—ABCD的底面是正方形，每条侧棱的长都是底面边长的2倍，P为侧棱SD上的点．(1)求证：AC⊥SD.(2)假设SD⊥平面PAC，则侧棱SC上是否存在一点E，使得BE∥平面PAC.假设存在，求SE∶EC的值；假设不存在，试说明理由．利用向量法解决立体几何问题典例：如图，四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．(1)证明：PB∥平面AEC；(2)设二面角D－AE－C为60°，AP＝1，AD＝3，求三棱锥E－ACD的体积．A组专项根底训练1．假设直线l的方向向量为a＝(1,0,2)，平面α的法向量为n＝(－2,0，－4)，则()A．l∥αB．l⊥αC．l⊂αD．l与α相交2．假设AB→＝λCD→＋μCE→，则直线AB与平面CDE的位置关系是()A．相交B．平行C．在平面D．平行或在平面3．A(4,1,3)，B(2，－5,1)，C(3,7，－5)，则平行四边形ABCD的顶点D的坐标是() A．(2,4，－1) B．(2,3,1)C．(－3,1,5) D．(5,13，－3)4．a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，假设a，b，c三向量共面，则实数λ等于()A.627B.637C.607D.6575．如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝2，AA 1＝3，AD ＝22，P 为C 1D 1的中点，M 为BC 的中点．则AM 与PM 所成的角为()A ．60°B ．45°C ．90°D ．以上都不正确6．平面α的三点A (0,0,1)，B (0,1,0)，C (1,0,0)，平面β的一个法向量n ＝(－1，－1，－1)，则不重合的两个平面α与β的位置关系是________．7．设点C (2a ＋1，a ＋1,2)在点P (2,0,0)、A (1，－3,2)、B (8，－1，4)确定的平面上，则a ＝________.8．如图，在正方体ABCD —A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝2a 3，则MN 与平面BB 1C 1C 的位置关系是________． 9．如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ∥QA ，QA ＝AB＝12PD .证明：平面PQC ⊥平面DCQ . 10．如图，在底面是矩形的四棱锥P －ABCD 中，PA ⊥底面ABCD ，E ，F 分别是PC ，PD 的中点，PA ＝AB ＝1，BC ＝2.(1)求证：EF ∥平面PAB ；(2)求证：平面PAD ⊥平面PDC .B 组专项能力提升11．如图，正方形ABCD 与矩形ACEF 所在平面互相垂直，AB ＝2，AF ＝1，M 在EF 上，且AM ∥平面BDE ，则M 点的坐标为()A ．(1,1,1)B ．(23，23，1) C ．(22，22，1) D ．(24，24，1)12．设u ＝(－2,2，t )，v ＝(6，－4,4)分别是平面α，β的法向量，假设α⊥β，则t 等于()A ．3B ．4C ．5D ．613．在正方体ABCD —A 1B 1C 1D 1中，P 为正方形A 1B 1C 1D 1四边上的动点，O 为底面正方形ABCD 的中心，M ，N 分别为AB ，BC 的中点，点Q 为平面ABCD 一点，线段D 1Q 与OP 互相平分，则满足MQ →＝λMN→的实数λ有________个．14．如下图，直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝AA 1，D 、E 、F 分别为B 1A 、C 1C 、BC 的中点．求证：(1)DE ∥平面ABC ；(2)B 1F ⊥平面AEF .15．在四棱锥P —ABCD 中，PD ⊥底面ABCD ，底面ABCD 为正方形，PD ＝DC ，E 、F 分别是AB 、PB 的中点．(1)求证：EF ⊥CD ；(2)在平面PAD 求一点G ，使GF ⊥平面PCB ，并证明你的结论．。

立体几何3直线与平面的位置关系(平行、垂直、异面)-高考数学专题复习

立体几何—直线与平面的位置关系（平行、垂直、异面）知识精要1、证明直线与平面的平行的思考途径:（1）转化为直线与平面无公共点；（2）转化为线线平行；（3）转化为面面平行. 2、证明直线与平面垂直的思考途径:（1）转化为该直线与平面内任一直线垂直；（2）转化为该直线与平面内相交二直线垂直；（3）转化为该直线与平面的一条垂线平行；（4）转化为该直线垂直于另一个平行平面。

3、证明平面与平面的垂直的思考途径：（1）转化为判断二面角是直二面角；（2）转化为线面垂直；(3) 转化为两平面的法向量平行。

4、空间向量的直角坐标运算：设a ＝123(,,)a a a ，b ＝123(,,)b b b 则：(1) a ＋b ＝112233(,,)a b a b a b +++； (2) a －b ＝112233(,,)a b a b a b ---； (3)λa ＝123(,,)a a a λλλ (λ∈R)； (4) a ·b ＝112233a b a b a b ++； 5、夹角公式：设a ＝123(,,)a a a ，b ＝123(,,)b b b ，则2cos ,a b a <>=.6、异面直线间的距离：||||CD n d n ⋅=(12,l l 是两异面直线，其公垂向量为n ，C D 、是12,l l 上任一点，d 为12,l l 间的距离).7、点B 到平面α的距离：||||AB n d n ⋅=（n 为平面α的法向量，A α∈，AB 是α的一条斜线段）. 热身练习：1、A 、B 、C 表示不同的点，a 、l 表示不同的直线，α、β表示不同的平面，下列推理不正确的是（ C ）()A ααα⊂⇒∈∈∈∈l B l B A l A ,,,()B βα∈∈A A ,，AB B B =⇒∈∈βαβα ,直线 ()C αα∉⇒∈A l A l ,内不在()D α∈C B A ,,，β∈C B A ,,且C B A ,,不共线α⇒与β重合2、对于空间三条直线，有下列四个条件：①三条直线两两相交且不共点；②三条直线两两平行；③三条直线共点；④有两条直线平行，第三条直线和这两条直线都相交．其中，使三条直线共面的充分条件有（ B ）（1和4）()A 1个 ()B 2个 ()C 3个 ()D 4个3、在空间四边形ABCD 的边AB 、BC 、CD 、DA 上分别取点H G F E ,,,，如果EF 与HG 相交于一点M ，那么（ A ）()A M 一定在直线AC 上 ()B M 一定在直线BD 上 ()C M 可能在直线AC 上，也可能在直线BD 上 ()D M 既不在直线AC 上，也不在直线BD 上4、设ABCD 是空间四边形，E ，F 分别是AB ，CD 的中点，则,,满足（ B ）（A ）共线（B ）共面（C ）不共面（D ）可作为空间基向量正确答案：B 错因：学生把向量看为直线。

立体几何证明方法——证面面平行

立体几何证明方法——证面面平行立体几何中，证明面面平行是一个常见的问题，可以通过多种方法进行证明。

下面将介绍几种常用的证明方法。

1.使用直线面法相交性质证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，选择平面ABCD上的两条相交直线AE和BF，然后分别在这两条直线上选择两个点C和D。

根据直线面法相交性质，直线AE与平面ABCD相交于点E，直线AE与平面CDH相交于点C，同理，直线BF与平面ABCD相交于点F，直线BF与平面CDH相交于点D。

连接线段AD和BC，可以得到四边形ABCD。

然后，考察四边形ABCD，如果四边形ABCD是平行四边形，则线段AD与线段BC互相平行。

由直线平行与面平行的性质可知，平面ABCD与平面EFHG平行。

因此，我们只需要证明四边形ABCD为平行四边形即可。

接下来，通过证明线段AD与线段BC互相平行来证明四边形ABCD为平行四边形。

可采用向量法、等距向量法等方法进行证明，具体方法根据题目要求来选择。

2.使用距离法证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，在平面ABCD上选择一点P，在平面EFGH上选择一点Q。

然后，构造线段PQ，并将其延长，过点P和Q分别作平行于平面ABCD和EFGH的直线。

两条直线与平面ABCD和EFGH的交点分别为A、B和E、F。

由于点P、Q到平面ABCD的距离相等，点A、B到平面EFGH的距离相等，利用距离的定义可以推出直线AE与直线BF互相平行。

同理可以证明直线BE与直线AF互相平行。

因此，根据平行四边形的性质可知线段AD与线段BC平行。

由于线段AD与线段BC平行，所以平面ABCD与平面EFGH平行。

3.使用垂线法证明：设空间中有两个平面ABCD和EFGH，要证明这两个平面平行。

首先，选择平面ABCD上的两条垂线，可以是两个相交直线的垂线或两个平行直线的垂线。

然后，在平面EFGH中分别找到与这两条垂线相交的直线段，并将其延长。

立体几何中平行与垂直证明方法归纳

a ∥
a∥
α
a a
β
3) 利用定义：直线在平面外，且直线与平面没有公共点
（三）平面与平面平行的证明
常见证明方法：
1) 利用平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。
3
a ⊂ b ⊂
a ∩b P
a // b //
⇒ /性：如正方体的上下底面互相平行等
一条直线与一个平面内的两条相交直线都垂直，则该直线垂直于此平面。
a
b
ab
A
l
l a l b
l
b
Aa
4) 利用平面与平面垂直的性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。
5
l
a
a
a l
l
5) 利用常用结论：
① 一条直线平行于一个平面的一条垂线，则该直线也垂直于此平面。
在同一个平面内，垂直于同一条直线的两条直线互相平行。
8) 利用定义：在同一个平面内且两条直线没有公共点
（二）直线与平面平行的证明
1) 利用直线与平面平行的判定定理：
平面外的一条直线与此平面内的一条直线平行，则该直线与此平面平行。
a
a
b a∥
a∥b
b
2) 利用平面与平面平行的性质推论：
两个平面互相平行，则其中一个平面内的任一直线平行于另一个平面。
a b ba
b a
α
4) 利用平面与平面垂直的性质推论：
如果两个平面互相垂直，在这两个平面内分别作垂直于交线的直线，则这
两条直线互相垂直。
4
l a b al
bl
ab
β b

立体几何中的平行性的证明.

立体几何中的平行性的证明
一、证明两直线平行的方法：
1、定义法：同一平面内无公共点的两条直线（用反证法证明）。

2、判定定理：如果一条直线与一个平面平行，则经过这条直线的平面与这个平
面相交，直线与交线平行。

3、平行与同一直线的两条直线平行。

4、面面平行的性质定理：如果两个平行平面同时和第三个平面相交，则交线平
行。

5、向量法：如果两个直线的方向向量共线，则两直线平行。

6、垂直于同一平面的两直线平行。

二、证明直线和平面平行的方法：
1、定义法：证明直线与平面无公共点（反证法）。

2、判定定理：如果平面外的一条直线和平面内的一条直线平行，则直线和平面
平行。

3、面面平行的性质：如果两个平面平行，那么一个平面内的任何一条直线都平
行于另一个平面。

4、如果平面外的一条直线和平面的一条垂线垂直，那么这条直线和这个平面平
行。

5、如果平面外的一条直线和这个平面都垂直于同一个平面，那么这条直线和这
个平面平行。

三、证明平面与平面平行的方法：
1、定义法：证明两个平面没有公共点（反证法）。

2、判定定理：如果一个平面内的两条相交直线分别和另一个平面平行，那么这
两个平面相互平行。

3、推论：如果一个平面内的两条相交直线分别和另一个平面内的两条直线（相
交）平行，那么这两个平面相互平行。

4、垂直于同一直线的两个平面相互平行。

5、如果两个平面的法向量平行，那么这两个平面平行。

6、。

立体几何线面平行的判定

立体几何线面平行的判定
在立体几何中，线面平行的判定可以通过多种方法来进行。

首先，我们可以使用平行线的性质来判定线面的平行关系。

如果一条
直线与一个平面内的另一条直线平行，那么这两条直线与该平面平行。

这是因为平行线与同一平面的相交直线之间的对应角相等。

这
个性质可以帮助我们判定线面的平行关系。

另外，我们也可以利用垂直平分线的性质来判定线面的平行关系。

如果一条直线垂直于一个平面，并且平面内的另一条直线与这
条直线垂直，则这两条直线与该平面平行。

这是因为垂直平分线的
性质保证了这种平行关系成立。

此外，我们还可以利用平行四边形的性质来判定线面的平行关系。

如果一个四边形是平行四边形，那么它的对边是平行的。

因此，如果我们能够构造出一个平行四边形，就可以通过其性质来判定线
面的平行关系。

总之，线面平行的判定可以通过平行线的性质、垂直平分线的
性质以及平行四边形的性质来进行。

这些方法可以帮助我们在立体
几何中判定线面的平行关系，从而解决相关的几何问题。

立体几何证明平行和垂直

立体几何证明平行和垂直
在立体几何中，我们可以通过以下定理和性质来证明线段、平面、直线的平行和垂直关系：
1. 平行线定理：若两条直线与第三条直线交叉时，两个内角和等于180度，则这两条直线是平行的。

2. 垂直线定理：若两条直线相交时，相邻的内角是直角，则这两条直线是垂直的。

3. 垂直平分线定理：若一个直线通过一个线段的中点并与该线段垂直，则这条直线垂直于该线段。

4. 同位角定理：当一条直线与两条平行直线相交时，对应的同位角是相等的。

5. 垂直平分线性质：当一条直线垂直平分一条线段时，它同时垂直于该线段的两个中垂线。

6. 垂直平分线交角性质：当两条直线都垂直平分了同一条线段时，这两条直线是平行的。

根据以上定理和性质，我们可以利用构造图形、辅助线、角度计算等方法进行立体几何证明的平行和垂直关系。

这些证明通常涉及到直线与平面的交点、线段的中点、角度的大小等问题，需要根据给定的条件进行分析和推导。

需要注意的是，在立体几何证明中，除了以上的定理和性质，还可以利用立体几何中的其他相关定理和公式来辅助证明，具体证明方法也要根据具体情况灵活运用。

总之，立体几何的平行和垂直关系证明是一个比较重要的内容，需要熟悉相关定理和性质，并能够熟练运用各种证明方法来解决问题。

立体几何---线面平行

直线、平面平行的判定【要点梳理】要点一、直线和平面平行的判定文字语言：直线和平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.简记为：线线平行，则线面平行.符号语言：a a a、b u a,a//b n a//a.要点诠释：(1)用该定理判断直线a与平面a平行时，必须具备三个条件：①直线a在平面a外，即a a a；②直线b在平面a内，即b u a；③直线a,b平行，即a〃b.这三个条件缺一不可，缺少其中任何一个，结论就不一定成立．(2)定理的作用将直线和平面平行的判定转化为直线与直线平行的判定,也就是说,要证明一条直线和一个平面平行,只要在平面内找一条直线与已知直线平行即可．要点二、两平面平行的判定文字语言：如果一个平面内有两条相交直线与另一个平面平行,则这两个平面平行.图形语言：j n符号语言：若au a、b u a,ab=A，且a//p、b//p，则a//p.要点诠释：(1)定理中平行于同一个平面的两条直线必须是相交的.(2)定理充分体现了等价转化的思想，即把面面平行转化为线面平行，可概述为：线面平行n面面平行.要点三、判定平面与平面平行的常用方法1．利用定义：证明两个平面没有公共点,有时直接证明非常困难,往往采用反证法．2．利用判定定理：要证明两个平面平行,只需在其中一个平面内找两条相交直线,分别证明它们平行于另一个平面,于是这两个平面平行,或在一个平面内找到两条相交的直线分别与另一个平面内两条相交的直线平行．3．平面平行的传递性：即若两个平面都平行于第三个平面,则这两个平面互相平行．【典型例题】类型一、直线与平面平行的判定例1.已知AB,BC,CD是不在同一平面内的三条线段，E,F,G分别是AB,BC,CD的中点，求证：AC//平面EFG,BD//平面EFG.例2.已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内，P、Q分别为对角线AE、BD上的点，且AP=DQ,如右图.求证：PQ〃平面CBE.【变式1】在正方体ABCD—ABCD中，O是正方形ABCD的中心，求证：AO//面BCD.11111111111【变式2】已知P是平行四边形ABCD所在平面外一点，E、F分别为AB、PD的中点，求证：AF〃平面PEC.【变式3】如右图所示，在四棱锥P-ABCD中，底面ABCD是矩形，PA，平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.(1)证明：EF〃平面PAD；(2)求三棱锥E-ABC的体积V.类型二、平面与平面平行的判定例3.如右图，已知正方体ABCD—A1B1C1D1,求证：平面AB1D1〃平面BDC1.例4.如右图，正方体ABCD—A1B1C1D1中，M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点.求证：平面AMN〃平面EFDB.【变式1】点P是^ABC所在平面外一点，G,G,G分别是△PBC,△APC,△ABP的重心，求123证：面GGG//面ABC.123【变式2】如右图所示，在三棱柱ABC—A1B1c l中，点D,E分别是BC与B1C1的中点.求证：平面A1EB〃平面ADC1.【变式3】已知在正方体ABCD—A'B'C'D'中，M,N分别是A'D',A'B'的中点，在该正方体中作出过顶点且与平面AMN平行的平面，并证明你的结论.【巩固练习】1．下列说法中正确的是（）A.如果一个平面内有一条直线和另一个平面平行，那么这两个平面平行B.如果一个平面内有无数条直线和另一个平面平行，那么这两个平面平行C.如果一个平面内的任何一条直线都与另一个平面平行，那么这两个平面平行D.如果两个平面平行于同一直线，则这两个平面平行2.已知三条互相平行的直线a、b、c中，a u a,b,c u a，则平面a、p的位置关系是（）A.平行B.相交C.平行或相交D.重合3.已知m,n是两条不重合的直线，a、p是两个不重合的平面，给出下列三个命题：「m//p[m与n异面「m//n①\n m//n:②\n n与p相交；③\n m//a。

高中数学证明线面平行方法

高中数学证明线面平行方法一.线面平行判断方法(1)利用定义：证明直线与平面无公共点;(2)利用判定定理：从直线与直线平行得到直线与平面平行;(3)利用面面平行的性质：两个平面平行，则一个平面内的直线必平行于另一个平面。

注：线面平行通常采用构造平行四边形来求证。

>>>二.证明线面平行的方法一，面外一条线与面内一条线平行，或两面有交线强调面外与面内版二，面外一直线上不同两点到面的权距离相等，强调面外三，证明线面无交点四，反证法(线与面相交，再推翻)五，空间向量法，证明线一平行向量与面内一向量(x1x2-y1y2=0)>>>三.高中数学必考知识点必修一：1、集合与函数的概念 (这部分知识抽象，较难理解)2、基本的初等函数(指数函数、对数函数)3、函数的性质及应用 (比较抽象，较难理解)首先，在高中必考数学知识点归纳整理，集合的初步知识与其他知识点密切联系。

它们是学习、掌握和使用数学语言的基础，是高中数学学习的出发点。

所以同学在集合与函数的概念一定要学扎实。

同学们应该知道，函数在高中是最重要的基本概念之一，老师运用有关的概念和函数的性质，培养学生的思维能力。

必修二：1、立体几何(1)、证明：垂直(多考查面面垂直)、平行(2)、求解：主要是夹角问题，包括线面角和面面角。

立体几何这部分对高一同学是难点，因为需要同学立体意识较强。

在学习立体几何证明：垂直(多考查面面垂直)、平行在学习空间几何体、点、直线、平面之间的位置关系时，重点要帮助学生逐步形，逐步掌握解决立体几何的相关问题。

必修三：1、算法初步：高考必考内容，5分(选择或填空)2、统计：3、概率：高考必考内容。

在学习算法初步、统计等内容的时候，要注意顺序渐进，不可追求一步到位，特别要注意其思想的重要性。

必修四：1、基本初等函数(三角函数：图像、性质、高中重难点)这个是高考中占分最多的题目。

2、平面向量：高考不单独命题，易和三角函数、圆锥曲线结合命题。

立体几何中有关平行、垂直常用的判定方法

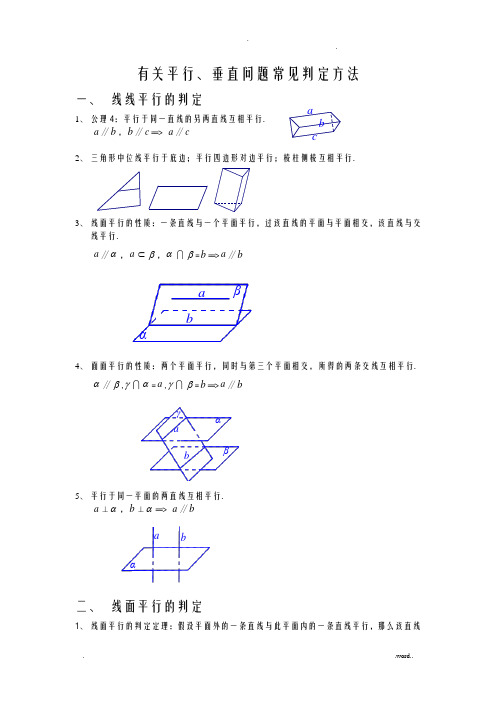
有关平行、垂直问题常见判定方法一、线线平行的判定1、公理4：平行于同一直线的另两直线互相平行. a ∥b ，b ∥c ==> a ∥c2、三角形中位线平行于底边；平行四边形对边平行；棱柱侧棱互相平行．3、线面平行的性质：一条直线与一个平面平行，过该直线的平面与平面相交，该直线与交线平行．a ∥α，a ⊂β，αβ=b ==>a ∥bβαba4、面面平行的性质：两个平面平行，同时与第三个平面相交，所得的两条交线互相平行．α∥β,γα=a ,γβ=b ==>a ∥bγβαb a5、平行于同一平面的两直线互相平行．a ⊥α，b ⊥α==> a ∥bαba二、线面平行的判定1、线面平行的判定定理：假设平面外的一条直线与此平面内的一条直线平行，那么该直线c b a与此平面平行．a ⊄α，b ⊂α，a ∥b ==> a ∥ααba2、假设两平面平行，那么一个平面内的任一直线与另一平面平行．α∥β，a ⊂α==> a ∥βαβa3、 α⊥β，a ⊥β，a ⊄α==> a ∥αβαa4、 a ⊥b ，b ⊥α，a ⊄α==> a ∥ααab三、面面平行的判定1、面面平行的判定定理：假设一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．a ⊂α，b ⊂α，a b =O ,a ∥β,b ∥β==> α∥βO αβa b αβa2、垂直于同一直线的两个平面互相平行．a ⊥α，a ⊥β==> α∥β (见上图)3、平行于同一平面的两个平面互相平行．α∥γ，β∥γ==> α∥βαγβ4、柱体的上下底面互相平行四、线线垂直1、线线垂直的定义：a 与b 所成的角为直角．2、线面垂直的定义：假设一条直线与一个平面垂直，那么该直线与平面内的任一直线都垂直．a ⊥α，b ⊂α==> a ⊥bαab3、a ⊥α，b ∥α==> a ⊥bαab4、三垂直定理及其逆定理l ⊥α( H 为垂足)，a ⊂α，HM 是斜线PM 在平面α内的射影三垂线定理〔垂影那么垂斜〕：a ⊥HM ==> a ⊥PM三垂线定理的逆定理〔垂斜那么垂影〕：a ⊥PM ==> a ⊥HMlM H Pαa5、a ⊥α，b ⊥β，α⊥β==> a ⊥bβαab五、线面垂直的判定1、线面垂直的判定定理：假设一直线和平面内的两相交直线都垂直，那么该直线与此平面垂直．a ⊂α，b ⊂α,ab =O , l ⊥a ,l ⊥b ==> l ⊥αlO αa b2、a∥b，a⊥α==> b⊥ααb a3、直棱柱的侧棱与底面垂直4、一条直线垂直于两平行平面中的一个平面，也垂直于另一个平面α∥β，a⊥α==> a⊥βαβa5、面面垂直性质：两平面垂直，一个平面内垂直于它们交线的直线垂直于另一个平面．α⊥β，αβ=l，a⊂α，a⊥l==> a⊥βlβαa5、两相交平面同时垂直于第三个平面，那么它们的交线也与第三个平面垂直．αβ=l ，α⊥γ,β⊥γ==> l ⊥γl γβα六、面面垂直的判定1、定义:两平面相交所成二面角为直二面角.2、判定定理:假设一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直.a ⊥β，a ⊂α ==> α⊥βl βαa2、a ∥α，a ⊥β==> α⊥ββαa。