四川省乐山市2017-2018学年高一数学上学期第一次月考试题
四川省乐山市高一数学上学期第一次月考试题

四川省乐山市2017-2018学年高一数学上学期第一次月考试题(时间:120分钟 满分:150分) 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如果1{|}A x x >-=,那么( )A .0⊆AB .{0}∈AC .∅∈AD .{0}⊆A 2.函数f (x )=x -1x -2的定义域为( ) A .(1,+∞) B .[1,+∞) C .[1,2)D .[1,2)∪(2,+∞)3.已知全集U =R ,集合P ={x ∈N *|x <7},Q ={x |x -3>0},那么图中阴影部分表示的集合是( )A .{1,2,3,4,5,6}B .{x |x >3}C .{4,5,6}D .{x |3<x <7}4.设函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤1,2x,x >1,则f (f (3))=( )A.15 B .3 C.23D.1395.已知集合A ={0,m ,m 2−3m +2},且2∈A ,则实数m 的值为( ) A .2 B .3 C .0或3 D .0或2或36.已知3x 212xf +=-)(,则f (6)的值为( ) A .15 B .7 C .31D .177. 下列各函数在其定义域中,既是奇函数又是增函数的是 ( ) A. 1x y += B. 3x y -= B. C. x1y -= D. x x y =8.二次函数f (x )=ax 2+2a 是区间[-a ,a 2]上的偶函数,又g (x )=f (x -1),则g (0),)(23g ,g (3)的大小关系为( ) A .)(23g <g (0)<g (3) B .g (0)<)(23g <g (3) C .)(23g <g (3)<g (0) D .g (3)<)(23g <g (0)9.设函数)(x f 是定义在R 上的奇函数,当0x ≥时,有b x 2x x f 2++=)(,(b 为常数)则)(1f -等于 ( )A. -3B. 3C.1D. -110.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x 万件时的生产成本为C (x )=12x 2+2x +20(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )A .36万件B .18万件C .22万件D .9万件11.已知函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤0,1,x >0.若f (x -4)>f (2x -3),则实数x 的取值范围是( )A .(-1,+∞)B .(-∞,-1)C .(-1,4)D .(-∞,1)12.定义在R 上的偶函数f (x )在),(+∞0上是增函数,且f (3)=0,则0x xf 2>-)(的解集为( )A .(0,3)B .(3,+∞)C .(-3,0)∪(3,+∞)D .(-∞,-3)∪(0,3)第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上) 13.如果集合A={x |ax 2+2x +1=0}中只有一个元素,则a 的值是 ________.14.已知函数⎩⎨⎧≤+>=0,10,2)(x x x x x f ,若f (a )+f (1)=0,则实数a 的值等于________.15.已知f (x )=ax 3+bx -4,其中a ,b 为常数,若f (-2)=2,则f (2)的值等于________.16.对R b a ∈,,记⎩⎨⎧<≥=ba b b a a b a ,,},max{,则函数)}(,max{)(R x 1x x 1x x f 2∈+-+=的最小值为________.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分) 已知全集U =R ,集合A ={y |y =3-x 2,x ∈R ,且x ≠0},集合B 是函数y =x -2+25-x的定义域,集合C ={x |5-a <x <a }.(1)求集合A ∪(∁U B );(2)若C ⊆(A ∩B ),求实数a 的取值范围.18.(本小题满分12分) 已知函数f (x )=2x +1x +1,(1)判断函数在区间(-1,+∞)上的单调性,并用定义证明你的结论; (2)求该函数在区间[1,4]上的最大值与最小值.19. (本小题满分12分) 已知奇函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x >0,0,x =0,x 2+mx ,x <0.(1)求实数m 的值,并画出)(x f y =的图像;(2)若函数f (x )在区间[-1,a -2]上单调递增,求实数a 的取值范围.20.(本小题满分12分)某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖挂4节车厢,一天能来回16次,如果该车每次拖挂7节车厢,则每天能来回10次.(1)若每天来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数的解析式; (2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每次拖挂多少节车厢才能使运营人数最多?并求出每天最多运营人数.21.(本小题满分12分)已知函数()21f x ax bx =++,(,a b 为实数),x R ∈,()()(),0,0f x x F x f x x >⎧⎪=⎨-<⎪⎩.(1)若()10f -=,且函数()f x 的值域为[)0,+∞,求()F x 的解析式;(2)在(1)的条件下,当[]2,2x ∈-时,()()g x f x kx =-是单调函数,求实数k 的取值范围.22. (本小题满分12分)奇函数f(x)的定义域为R ,且在[)+∞,0上为增函数,那么是否存在m ,使)()()(0f t 2m 4f 4t 2f 2>-+-对任意[]10t ,∈均成立?若存在,求出m 的取值范围;若不存在,说明理由。
乐山市第一高级中学2018-2019学年高三上学期11月月考数学试卷含答案

乐山市第一高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. 下列判断正确的是()A .①不是棱柱B .②是圆台C .③是棱锥D .④是棱台2. 设S n 为等比数列{a n }的前n 项和,已知3S 3=a 4﹣2,3S 2=a 3﹣2,则公比q=( )A .3B .4C .5D .63. 集合,是的一个子集,当时,若有,则称为的一个“孤立{}5,4,3,2,1,0=S A S A x ∈A x A x ∉+∉-11且x A 元素”.集合是的一个子集, 中含4个元素且中无“孤立元素”,这样的集合共有个B S B B B A.4 B. 5 C.6 D.74. 在抛物线y 2=2px (p >0)上,横坐标为4的点到焦点的距离为5,则该抛物线的准线方程为( )A .x=1B .x=C .x=﹣1D .x=﹣5. 圆上的点到直线的距离最大值是( )012222=+--+y x y x 2=-y x A .B .C .D .12+122+122+6. 已知2a =3b =m ,ab ≠0且a ,ab ,b 成等差数列,则m=( )A .B .C .D .67. 若则的值为( )⎩⎨⎧≥<+=-)2(,2)2(),2()(x x x f x f x)1(f A .8B .C . 2D .81218. 已知AC ⊥BC ,AC=BC ,D 满足=t +(1﹣t ),若∠ACD=60°,则t 的值为()A .B .﹣C .﹣1D.9. 设1m >,在约束条件,,1.y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值小于2,则m 的取值范围为()A .(1,1+B .(1)+∞C. (1,3)D .(3,)+∞10.函数f (x )的定义域为[﹣1,1],图象如图1所示:函数g (x )的定义域为[﹣2,2],图象如图2所示,方程f (g (x ))=0有m 个实数根,方程g (f (x ))=0有n 个实数根,则m+n=()班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A .14B .12C .10D .811.已知A ,B 是以O 为圆心的单位圆上的动点,且||=,则•=()A .﹣1B .1C .﹣D .12.如图甲所示, 三棱锥 的高 ,分别在P ABC -8,3,30PO AC BC ACB ===∠=o,M N BC和上,且,图乙的四个图象大致描绘了三棱锥的体积与PO (),203CM x PN x x ==∈(,N AMC -y 的变化关系,其中正确的是()A .B . C. D .1111]二、填空题13.已知z 是复数,且|z|=1,则|z ﹣3+4i|的最大值为 . 14.已知各项都不相等的等差数列,满足,且,则数列项中{}n a 223n n a a =-26121a a a =∙12n n S -⎧⎫⎨⎬⎩⎭的最大值为_________.15.等差数列中,,公差,则使前项和取得最大值的自然数是________.{}n a 39||||a a =0d <n S 16.抛物线y 2=4x 上一点M 与该抛物线的焦点F 的距离|MF|=4,则点M 的横坐标x= .17.已知两个单位向量满足:,向量与的夹角为,则.,a b r r 12a b ∙=-r r 2a b -r r cos θ=18.设是空间中给定的个不同的点,则使成立的点的个数有_________个.三、解答题19.已知中心在坐标原点O 的椭圆C 经过点A (2,3),且点F (2,0)为其右焦点.(1)求椭圆C 的方程;(2)是否存在平行于OA 的直线l ,使得直线l 与椭圆C 有公共点,且直线OA 与l 的距离等于4?若存在,求出直线l 的方程;若不存在,说明理由. 20.如图,正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,请在此正方体中取出四个顶点构成一个三棱锥,满足三棱锥的四个面都是直角三角形,并求此三棱锥的体积.21.已知函数f (x )=ax 3+2x ﹣a ,(Ⅰ)求函数f (x )的单调递增区间;(Ⅱ)若a=n 且n ∈N *,设x n 是函数f n (x )=nx 3+2x ﹣n 的零点.(i )证明:n ≥2时存在唯一x n 且;(i i )若b n =(1﹣x n )(1﹣x n+1),记S n =b 1+b 2+…+b n ,证明:S n <1.22.【常熟中学2018届高三10月阶段性抽测(一)】已知函数.()()2ln R f x x ax x a =-+-∈(1)若函数是单调递减函数,求实数的取值范围;()f x a (2)若函数在区间上既有极大值又有极小值,求实数的取值范围.()f x ()0,3a23.设函数f (x )=lg (a x ﹣b x ),且f (1)=lg2,f (2)=lg12(1)求a ,b 的值.(2)当x ∈[1,2]时,求f (x )的最大值.(3)m 为何值时,函数g (x )=a x 的图象与h (x )=b x ﹣m 的图象恒有两个交点. 24.(本小题满分10分)直线l 的极坐标方程为θ=α(ρ∈R ,ρ≠0),其中α∈[0,π),曲线C 1的参数方程为(t 为参数),圆C 2的普通方程为x 2+y 2+2x =0.{x =cos t y =1+sin t)3(1)求C 1,C 2的极坐标方程;(2)若l 与C 1交于点A ,l 与C 2交于点B ,当|AB |=2时,求△ABC 2的面积.乐山市第一高级中学2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题1. 【答案】C【解析】解:①是底面为梯形的棱柱;②的两个底面不平行,不是圆台;③是四棱锥;④不是由棱锥截来的,故选:C . 2. 【答案】B【解析】解:∵S n 为等比数列{a n }的前n 项和,3S 3=a 4﹣2,3S 2=a 3﹣2,两式相减得3a 3=a 4﹣a 3,a 4=4a 3,∴公比q=4.故选:B . 3. 【答案】C 【解析】试题分析:根据题中“孤立元素”定义可知,若集合B 中不含孤立元素,则必须没有三个连续的自然数存在,所有B 的可能情况为:,,,,,共6个。
XXX2017-2018学年第一学期期末考试高一数学试卷

XXX2017-2018学年第一学期期末考试高一数学试卷XXX2017-2018学年第一学期期末考试高一年级数学试卷第I卷(选择题共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知向量a=(2,1),b=(λ−1,2),若a+b与a−b共线,则λ=()A.−2B.−1C.1D.2改写:向量a=(2,1),向量b=(λ-1,2),若a+b和a-b共线,则λ=() A。
-2 B。
-1 C。
1 D。
22.已知3sinα+4cosα=2,则1-sinαcosα-cos2α的值是() A。
- B。
C。
-2 D。
2改写:已知3sinα+4cosα=2,求1-sinαcosα-cos2α的值,答案为() A。
- B。
C。
-2 D。
23.已知在△ABC中,AB=AC=1,BC=3,则AB·AC=() A。
1/33 B。
- C。
-2 D。
-改写:在△ABC中,AB=AC=1,BC=3,求XXX的值,答案为() A。
1/33 B。
- C。
-2 D。
-4.在△ABC中,若AB2=AB·AC+BA·BC+CA·CB,则△ABC是() A.锐角三角形B.钝角三角形C.直角三角形D.不确定改写:在△ABC中,如果AB2=AB·AC+BA·BC+CA·CB,则△ABC是() A.锐角三角形B.钝角三角形C.直角三角形D.不确定5.已知△ABC中,内角A,B,C所对边的边长分别为a,b,c,且c=7/11,a+b=22/3,XXX-tanA-tanB=3,则△ABC的面积为() A。
3/33 B。
- C。
3 D。
33/2改写:已知△ABC中,内角A,B,C所对边的边长分别为a,b,c,且c=7/11,a+b=22/3,XXX-tanB=3,求△ABC的面积,答案为() A。
3/33 B。
- C。
四川省乐山市2017-2018学年高一英语上学期第一次月考试题

四川省乐山市2017-2018学年高一英语上学期第一次月考试题第一部分:听力(共两节,满分30分)第一节:(共5小题;每小题1.5分, 满分7.5分)请听5下面对话,选出最佳选项。
1.Who painted the painting?A.The man,s son.B.The woman.C.The man.2.Which of the following is new?A.The shoes.B.The T-shirt.C.The jeans.3.Where does the conversation probably take place?A.At a travel agency.B.At a hotel.C.At a restaurant.4.What does the man want to do?A.Do sunbathing.B.Have dinner,C.Take a rest.5.What will the man do on Saturday night?A.Write his essay,B.Watch a DVD.C.Go clubbing.第二节(共15小题,每小题1.5分,满分22.5分)请听第6段材料,回答6、7题。
6.Why is the man going to Paris?A.To learn about fashion Paris?B.To visit his daughter.C.To see his wife.7.How long does the woman still have to wait?A.One and a half hours.B.An hour.C.Half an hour,请听第7段材料,回答第8、9题。
8. Who has a truck?A.George.B.Brian.C.David.9.What will the speakers probably not take with them?A.The tents.B.The guitar.C.The sleeping bags.请听第8段材料,回答第10至12题。
四川省乐山市高一上学期数学第一次月考试卷

四川省乐山市高一上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共14题;共28分)1. (2分)已知集合,,则()A .B .C .D .2. (2分) (2018高一上·海南期中) 下列函数中与函数y=x相等的函数是()A .B .C .D .3. (2分) (2019高一上·辽源期中) 函数的最大值与最小值之和()A . 1.75B . 3.75C . 4D . 54. (2分)已知函数则,,的大小关系为()A .B .C .D .5. (2分) (2018高二下·保山期末) 若函数在区间内单调递增,则实数的取值范围是()A .B .C .D .6. (2分) .定义在R上的函数y=f(x)是减函数,且函数y=f(x-1)的图象关于(1,0)成中心对称,若s,t满足不等式.则当时,的取值范围是()A .B .C .D .7. (2分) (2016高一上·杭州期中) ()A . (﹣∞,2]B . (0,+∞)C . [2,+∞)D . [0,2]8. (2分) (2018高二下·衡阳期末) 已知集合A={1,2,3,4},B={2,4,6,8},则A B中元素的个数为()A . 1B . 2C . 3D . 49. (2分)已知,则()A . lg2B . lg32C .D .10. (2分) (2018高一上·江苏期中) 已知函数,则()A . −2B . 4C . 2D . −111. (2分)(2016·山东理) 已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x>时,f(x+ )=f(x﹣).则f(6)=()A . ﹣2B . ﹣1C . 0D . 212. (2分) (2016高二下·长春期中) 求函数f(x)=﹣x2+4x﹣6,x∈[0,5]的值域()A . [﹣6,﹣2]B . [﹣11,﹣2]C . [﹣11,﹣6]D . [﹣11,﹣1]13. (2分) (2019高一上·焦作期中) 设函数,若,则实数a的取值范围是()A .B .C .D .14. (2分)已知函数.若f(﹣a)+f(a)≤2f(1),则a的取值范围是()A . [﹣1,0)B . [0,1]C . [﹣1,1]D . [﹣2,2]二、填空题 (共6题;共6分)15. (1分) (2018高一上·台州月考) 函数的定义域为________奇偶性为________.16. (1分) (2019高一上·松原月考) 已知一次函数,当时,,当时,,则 ________.17. (1分) (2016高一上·潍坊期中) 已知函数y=f(x)是R上的奇函数,当x>0时,f(x)= ,则f (﹣)=________18. (1分) (2018高一上·重庆期中) 已知函数,若对任意恒成立,则实数的最大值是________.19. (1分) (2017高三上·邳州开学考) 函数f(x)= 的值域为________.20. (1分) (2019高一上·静海月考) 函数的最小值为________.三、解答题 (共5题;共65分)21. (10分)已知集合P={x|x2+4x=0},集合Q={x|x2+2(m+1)x+m2﹣1=0},(1)若P⊆Q,求实数m的取值范围;(2)若Q⊆P,求实数m的取值范围.22. (10分) (2017高一上·长春期中) 已知函数.(1)求函数f(x)的定义域;(2)求f(1),f(﹣1),f(2),f(﹣2);(3)判断并证明f(x)的奇偶性.23. (15分) (2018高一上·大石桥期末) 已知函数 .(1)求函数的定义域;(2)若函数的最小值为,求的值.24. (15分) (2017高一上·桂林月考) 已知函数是定义在上的奇函数,且,(1)确定函数的解析式;(2)判断函数的单调性并用定义法证明;(3)解不等式:25. (15分) (2016高一上·杭州期中) 已知函数f(x)=2x+2ax+b ,且f(1)= 、f(2)= .(1)求a、b的值;(2)判断f(x)的奇偶性并证明;(3)先判断并证明函数f(x)在[0,+∞)上的单调性,然后求f(x)的值域.参考答案一、单选题 (共14题;共28分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、填空题 (共6题;共6分)15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共5题;共65分) 21-1、21-2、22-1、22-2、22-3、23-1、23-2、24-1、24-2、24-3、25-1、25-2、25-3、。
四川省乐山市高一上学期数学第一次月考试卷

四川省乐山市高一上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)(2017·湖南模拟) 已知集合A={x∈N|1<x<log2k},若集合A中至少有4个元素,则()A . k>32B . k≥32C . k>16D . k≥162. (2分)设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则()A . {2,3}B . {1,4,5}C . {4,5}D . {1,5}3. (2分) (2020高一上·昌平月考) 下列函数中,与函数y=x相同的是()A . y =B . y=()C . y=D . y=4. (2分) (2019高一上·河南月考) 已知函数由下表确定,若,则a的值为()A . 2B . 4C . 2或5D . 3或45. (2分) (2018高一上·安庆期中) 如图所示,是全集,是的子集,则阴影部分所表示的集合是()A .B .C .D .6. (2分) (2019高三上·湖南月考) 设集合,,则()A .B .C .D .7. (2分)已知函数,则使方程有解的实数的取值范围是()A .B .C .D .8. (2分) (2018高一上·漳平月考) 已知f(2x+1)=x2+x,则f(3)=()A .B .C .D .9. (2分)设集合S={x||x+3|+|x﹣1|>m},T={x|a<x<a+8},若存在实数a使得S∪T=R,则m∈()A . {m|m<8}B . {m|m≤8}C . {m|m<4}D . {m|m≤4}10. (2分)若a,b是任意实数,且a>b,则()A .B .C .D .11. (2分) (2019高一上·长春月考) f(x),则f[f(-1)]=()A . 2B . 6C .D .12. (2分) (2018高一上·大连期末) 对于每个实数x,设取,两个函数中的较小值.若动直线y=m与函数的图象有三个不同的交点,它们的横坐标分别为x1、x2、x3 ,则x1+x2+x3的取值范围是()A . (2,)B . (2,)C . (4,)D . (0,)二、填空题 (共4题;共4分)13. (1分) (2019高一上·鸡东月考) 已知集合A={x|2x+a>0},若1∉A,则实数a的取值范围是________.14. (1分) (2020高一上·北京期中) 若幂函数的图象经过点,则的值等于________.15. (1分) (2016高一下·汕头期末) 定义一种运算a⊗b= ,令f(x)=(3x2+6x)⊗(2x+3﹣x2),则函数f(x)的最大值是________.16. (1分)使不等式sin2x+acosx+a2≥1+cosx对一切x∈R恒成立的负数a的取值范围是________ .三、解答题 (共6题;共65分)17. (10分)作出y=x2﹣4x+3的图象,求f(2)、f(1)、f(0)的值,观察f(2)和f(0)的符号.18. (10分) (2019高一上·长春期中) 设集合,,全集,求.19. (5分) (2020高三上·怀宁月考) 设关于 x 的函数 f(x)=lg(x2﹣2x﹣3)的定义域为集合 A,函数g(x)=x﹣a,(0≤x≤4)的值域为集合 B.(1)求集合 A,B;(2)若集合 A,B 满足A∩B=B,求实数 a 的取值范围.20. (10分) (2020高一下·隆化期中) 已知函数不等式的解集为(1)求函数的解析式.(2)当关于的的不等式的解集为R时,求的取值范围.21. (15分) (2019高三上·襄阳月考) 已知函数.(1)当时,求不等式的解集;(2)当时,若对任意实数都成立,求的取值范围.22. (15分) (2016高一上·虹口期中) 定义实数a,b间的计算法则如下a△b= .(1)计算2△(3△1);(2)对0<x<z<y的任意实数x,y,z,判断x△(y△z)与(x△y)△z的大小,并说明理由;(3)写出函数y=(1△x)+(2△x),x∈R的解析式,作出该函数的图象,并写出该函数单调递增区间和值域(只需要写出结果).参考答案一、单选题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共65分)答案:17-1、考点:解析:答案:18-1、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、答案:21-2、考点:解析:答案:22-1、答案:22-2、答案:22-3、考点:解析:。
四川省乐山市高一数学下学期第一次月考试题

四川省乐山市2016-2017学年高一数学下学期第一次月考试题(全卷共22道题,满分150分,考试时间120分钟)一、选择题(每小题5分,共60分) 1、在△ABC 中,c=3,B=45°, C=60°,则b=( )A.22 B. 23 C. 223 D. 22、如果,是单位向量,那么下列四个结论中正确的是( )A. == C. ·=1 D. ∥3、在ABC ∆中,若A=60°,34=a ,24=b ,则B 等于( )A.45°B.135°C.45°或135°D.以上答案都不对 4、已知·= -64=3=,则在方向上的投影是( )A. 21-B. 23- C. -2 D. -65、下列命题中: (1=,则a =b 或a = -b ; (2)若a ∥b ,b ∥c ,则a ∥c ;(3)若a 、b 、c 是非零向量,且a ·c =b ·c ,则a =b ; 其中正确命题的个数是( ) A.3 B.2 C.1 D.06、已知点A (-1,-2),B (1,-1),C (x ,2),若A 、B 、C 三点共线,则x 的值为( )A.-4B.-3C. 2D.77、在△ABC 中,若4:3:2sin sin :sin =C B A :,则最大角的余弦值为( ) A. 94- B. 41- C. 121 D. 242181=2=,若b ⊥+(,则a 与b 的夹角为( )A. 30°B.60°C.120°D.150°9、在△ABC 中,D 是BC 中点,AB=8,AC=6,则AD · 的值是( )A.-14B.-28C.14D.2810、钝角三角形ABC 的面积是21,AB=1,BC=2,则AC=( )A.1B.2C.5 D.511、在△ABC 中,内角A 、B 、C 所对的边分别为c b a ,,,若bcosC+ccosB=asinA ,则△ABC 的形状是( )A.锐角三角形B.直角三角形C.钝角三角形D.不确定 12、已知向量,不共线,且对任意实数x-≥-立的是( )A. a ·b -2=0 B. -2·b =0 C. a ⊥b=二、填空题(每小题5分,共20分)13、设向量,不共线,)(b a +λ与(+2)共线,则实数λ的值为 14、在△ABC 中,AB=4,AC=3,·BC =1,则BC=15、在ABC ∆中,A=120°, c=5, a=7 , 则=CBsin sin 16、△ABC 的面积为4153,41cos -=B ,AC=4,则△ABC 的周长为三、解答题(共70分) 17、(本题满分10分)已知a =(1,-2),b =(3,2) (1)求+2 ; (2)设)2,9(-=,若n m +=,求n m 、的值。
高一数学上学期第一次月考试题18

2016—2017学年度九江一中高一第一次月考数学试卷第I 卷(选择题)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知I ={0,1,2,3,4,5,6,7,8,9},M ={1,2,4,5},N ={0,3,5,7},则()I C M N =( )A .{5,7}B .{6,8,9}C .{4,6,7}D .{1,3,5,6,8}2.集合{}2320A x x x =-+={}06,B x x x N =<<∈,则满足A C B ⊆⊆的集合C 的个数为( )A .6B .2C .8D .43.下列对应是集合A 到集合B 的映射的是( )A .A N = .+=NB .3:-→x x fB .{}平面内的圆=A .{}平面内的三角形=B .作圆的内接三角形:fC .{}20≤≤=x x A .{}60≤≤=y y B .x y x f 21:=→ D .{}0,14A =, .{}2,1,0,1,2B =-- .中的数开平方A f :4.函数254y x x =---的单调增区间是( )A.(,2]-∞-B.[5,2]--C.[2,)-+∞D.[2,1]-5.已知集合{}20,,58A m m m =-+且2A ∈,则实数m 的值为( )A .2B .3C .3或2D .0,3,26.在函数 ([2,2])y x x =∈-的图像上有一点(,)P t t ,此函数的图像与x 轴、直线2x =-及=x t 围成的图形(如图阴影部分)的面积为S ,则S 与t 的函数关系图像可表示为 ( )7.一元二次方程0122=-+-m mx x 的两个实数根分别是21,x x ,且221214x x +=,则m 的值是( )A .6B .-2C .-6D .6或-28.设函数⎪⎩⎪⎨⎧=≠-+=1,11,12)(x x x x x f 则1234031()()()()2016201620162016f f f f ++++的值为( ) A .2016 B .2015 C .4031 D .40329.已知函数247y x x =-+在闭区间[1,]m -上有最大值12,最小值3,则m 的取值范围是( )A .[2,+∞)B .[0,5]C .(-∞,5]D .[2,5] 10.若函数2(1)3,1()4,1a x ax a x f x ax x ⎧++-≥=⎨+<⎩是R 上的减函数,则实数a 的取值范围是( ) A .0a < B .1a <- C .21a -≤≤- D .312a -≤≤- 11.设A 是整数集的一个非空子集,对于A k ∈,如果1,1k A k A -∉+∉,那么k 是A 的一个“孤立元”给定{}1,2,3,4,5,6A =,则A 的所有子集中,全是“孤立元”的集合的个数为( )A .13B .20C .17D .1912.已知函数2()+2f x ax x a =+,()+2g x x =,若对于任意实数, ()x f x 与)(x g 至少有一个为正数,则实数a 的取值范围是 ( )A .112a <≤B .415a <≤C .45a > D .1a >第II 卷(非选择题)二、填空题(本大题共4小题,每小题5分)13.设集合{}22A x x =-≤<,{}B x x a =≤,若A B ≠∅,则实数a 的取值范围为________.14.若函数()f x 的定义域是[1,2]-,则函数()(2)f x f x +-的定义域为________.15.函数24 1 0() 1 0x x x f x x ⎧++≥=⎨<⎩,则满足不等式2(5)(42)f x x f x -<-的x 的取值范围是______16.设集合[0,1)A =,[1,2]B =,函数()1, ()22, x x A f x x x B +∈⎧=⎨-∈⎩,若0x A ∈,且[]0()f f x A ∈,则0x 的取值范围是__________三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.)17.(本小题10分)已知全集{}2150U x N x +=∈-<,{}1,3,5,7A =,{}27120B x x x =-+=(1)求A B ,A B ;(2)求U A C B (),U U C A C B ()().18. (本小题10分)已知()f x 是一次函数,且单调递减,若[()]94f f x x =+(1)求()f x 的解析式;(2)当0x ≥时,g(1)()x f x -=,求g()x 的解析式,并指出其定义域.19. (本小题12分)已知A B R ==,对应关系212f x x x a→++:,如果按对应关系f 能建立集合A 到集合B 的映射,(1)求实数a 的取值范围;(2)若B 中的元素15在A 中有两个原像,求实数a 的取值范围.20. (本小题12分)已知集合{}1A x ax =<,24B x y x x ⎧==++⎨⎬-⎩⎭(1)当12a =时,求A B ; (2)若B A ⊆,求实数a 的取值范围.21. (本小题12分)已知函数()f x 满足以下两个条件:①对任意实数,a b 都有()()()2f a b f a f b ab +=++;②对任意实数x 恒有2()f x x x ≥-.(1)若(0)=(1)f f ,求(1)f 和(2)f 的值;(2)证明:()f x 在1[,)2+∞上单调递增.22. (本小题14分已知2()4f x x x =-(1)画出()f x 的图像并写出其单调区间;(2)若方程()= f x t 有4个不等实根12341234,,, ( )x x x x x x x x <<<,记24()h t x x =+,求()h t 的解析式,并指出其定义域;(3)若()g x 在定义域内存在区间[,]m n ,使得()g x 在区间[,]m n 上的值域为[2,2]m n ,则称[,]m n 为()g x 的倍值区间. 在条件(2)下,若()()2k t h t a =+在定义域内存在倍值区间,求a 的范围.1-6 BCCDBB 7-12 BCDDBC13. 2a ≥- 14. [0,2] 15. (1,2)- 16. 1(,1)217. (1){}=3A B ,{}=1,3,4,57A B ,;(2){}=1,5,7U A C B (),{}=2,6U U C A C B ()(). 18. (1)()32f x x =--;(2)2g()=36 5 (1)x x x x ---≥-19. (1)1a >;(2)16a <<20. (1)[2,2)-; (2)11(,)24-21. (1)(1)0f =,(2)2f = 22. (1)增区间[2,0]-和[2,+)∞;减区间,2]-∞-(和[0,2] (2)()24h t t =+t (4,0)∈-(3)由于()242k t t a =+在定义域t (4,0)∈-内递增,所以()2()2k m m k n n =⎧⎨=⎩, 所以方程()422h t t a t =+=即22(21)40t a t a -++-=在 (4,0)-内有两个不同的根,则)4,417(--∈a。
四川省成都市2017-2018学年高一上学期期末调研考试数学试题

四川省成都市2017-2018学年高一上学期期末调研考试数学试题2017-2018学年度上期期末高一年级调研考试数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合$P=\{x|<x<2\}$,$Q=\{x|-1<x<1\}$,则$P\capQ=$()A。
$\{x|x<1\}$ B。
$\{x|<x<1\}$ C。
$\{x|-1<x<1\}$ D。
$\{\}$2.已知平面向量$a=(m+1,-2)$,$b=(-3,3)$,若$a//b$,则实数$m$的值为()A。
0 B。
-3 C。
1 D。
-13.函数$y=ax+1-3(a>且a≠1)$的图像一定经过的点是()A。
$(。
-2)$ B。
$(-1.-3)$ C。
$(。
-3)$ D。
$(-1.-2)$4.已知$\frac{\sin\theta+\cos\theta}{1}=\frac{1}{1+2\cos\theta}$,则$\tan\theta$的值为()A。
-4 B。
$-\frac{1}{11}$ C。
$\frac{1}{11}$ D。
45.函数$f(x)=\log_3|x-2|$的大致图像是()A。
B。
C。
D。
6.函数$f(x)=\frac{1}{\pi}\tan(x+\frac{\pi}{4})$的单调递增区间为()A。
$(2k-\frac{3\pi}{4},2k+\frac{\pi}{4}),k∈Z$ B。
$(2k-\frac{3\pi}{4},2k+\frac{\pi}{4}),k∈Z$C。
$(4k-\frac{3\pi}{4},4k+\frac{\pi}{4}),k∈Z$ D。
$(4k-\frac{3\pi}{4},4k+\frac{\pi}{4}),k∈Z$7.函数$f(x)=\ln(-x)-x-2$的零点所在区间为()A。
[推荐学习]2017-2018学年高一数学上学期第一次月考试题2
![[推荐学习]2017-2018学年高一数学上学期第一次月考试题2](https://img.taocdn.com/s3/m/c90f994525c52cc58bd6be9b.png)
第一师高级中学2017-2018学年第一学期高一年级第一次月考数学试卷第Ⅰ卷(选择题 共60分)一、选择题:(本大题共 12 小题,每小题 5 分,共 60 分.)1、若{}{}0,1,2,3,|3,A B x x a a A ===∈,则A B ⋂=(A ){}1,2 (B ){}0,1 (C ){}0,3 (D ){}32.下列四组函数,表示同一函数的是( ) (A )2)(x x f =,x x g =)( (B )x x f =)(,xx x g 2)(= (C )4)(2-=x x f ,22)(-⋅+=x x x g (D )1)(+=x x f ,⎩⎨⎧-<---≥+=1111)(x x x x x g 3.设集合A 和集合B 都是实数集R ,映射B A f →:是把集合A 中的元素x 映射到集合B 中的元素246x x -+,则在映射f 下,B 中的元素2在A 中所对应的元素组成的集合是( )A . {2}- B . {2} C . {2,2}- D . {0}4、设全集为R , 函数11)(+⋅-=x x x f 的定义域为M , 则C MR 为………………………… ( )(A) (-∞,1) (B) ),1[+∞ (C) ,1][1,)(∞-⋃+∞- D ,1)(1,)(∞-⋃+∞-5.设全集{},|-24,{|U R A x x B x y ==≤<=则图中阴影部分表示的集合为( ) 温馨提示: 1、本试卷分第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间120分钟 2、本试卷命题范围:数学必修一第一章集合与函数 3、正式开考前,请在规定位置填写班级、姓名、学号,正式开考后才允许答题。
A. {|2}x x ≤-B. {|2}x x >-C. {}|4x x ≥D.{|4}x x ≤6.若不等式组⎩⎨⎧->-≥+2210x x a x 无解,则实数a 的取值范围是( )A .a ≥一1B .a <-1C .a ≤1 D.a ≤-17.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数为 ( )A .y =1x 2B .y =1xC .y =x 2D .y =x 13 8. f (x )=2211,2,1,x x x x x ⎧-≤⎪⎨+-⎪⎩>则f 1(2)f ⎛⎫ ⎪⎝⎭的值为 A. 1516 B.1627- C. 89 D. 189.当0≤x ≤2时,a <-x 2+2x 恒成立,则实数a 的取值范围是 ( )A .(-∞,1]B .(-∞,0]C .(-∞,0)D .(0,+∞)10.已知函数y=f(x)与y=g(x)的图象如图,则y=f(x)·g(x)的大致图象为( )11.知函数()835+++=cx bx ax x f ,且()102=-f ,则函数()2f 的值为( )A. -2B.-6C.6D.812、对实数a 和b ,定义运算“◎”:a ◎b ()()⎩⎨⎧>-≤-11b a b b a a ,设函数()=x f (22-x )◎(2x x -),R x ∈。
普通高中2017_2018学年高一数学1月月考试题08(1)

广东省中山市普通高中2017-2018学年高一数学1月月考试题 满分150分,考试时间l20分钟。
第I 卷 选择题共60分)一、选择题:(本大题共12小题,每小题5分,共60分。
在各题所给出的四个选项中,有且只有一个是正确的,请将正确选项的代号填在答题卡上)1、设全集U={1,2,3,4,5,6},集合A={1,2},B={2,3},则A (U ðB)=A 、{4,5}B 、{2,3)C 、{1}D 、{2}2、下列四组函数中,表示同一函数的是A 、f (x )x )x ==B 、2x f (x )x,g(x )x ==C 、22f (x )ln x ,g(x )ln x ==D 、22x f (x )log ,g(x )==3、下列函数,在其定义域内既是奇函数又是增函数的是A 、3y x =B 、3x y =C 、2y log x =-D 、 1y x=- 4、函数f (x )是定义在R 上的奇函数,当x >0时,1f (x )x =-+,则当x <0时,f (x )等于A 、-x +lB 、-x -1C 、x +lD 、x -l5(式中a >0)指数幂形式为 A 、34a - B 、34a C 、43a - D 、43a6、函数1f (x )lg x=+ A 、(0,2] [B 、(0,2) C 、(01)(12],, D 、(2],-∞7、若231xlog ==1,则3x +9x 的值为A 、 6B 、3C 、52D 、128、设函数2020x log x,(x )f (x ),(x )>⎧=⎨<⎩,若12f (a )=,则实数a 的值是A 、-1 C 、14 D 、-19、设a >1,则020202a ..log a,.,a 的大小关系是A 、020202a ..log a .a <<B 、 020202.a .log a a .<<C 、020202a ...log a a <<D 、020202a ...a log a <<10、设方程322x x -=的解为0x ,则0x 所在的大致区间是A 、(0,1)B 、(1,2)C 、(2,3)D 、(3,4)11、定义运算a(a b )a b b(a b )≤⎧⊕=⎨>⎩,则函数12x f (x )=⊕的图象是12、阅读下列一段材料,然后解答问题:对于任意实数x ,符号[x ]表示“不超过x 的最大整数”,在数轴上,当x 是整数,[x ]就是x ,当x 不是整数时,[x ]是点x 左侧的第一个整数点,这个函数叫做“取整函数”,也叫高斯(Gauss)函数如[-2]=-2,[-1.5]=-2,[2.5]=2,则2222211[][]+[1]+[3]+[4]43log log log log log +的值为 A 、0 B 、-2 C 、-1 D 、l第Ⅱ卷 (共90分)二、填空题(本大题共4小题,每小题4分,共l6分,把答案填在答卷纸的相应位置上。
2017-2018学年度第一学期高一第一次月考成绩统计表
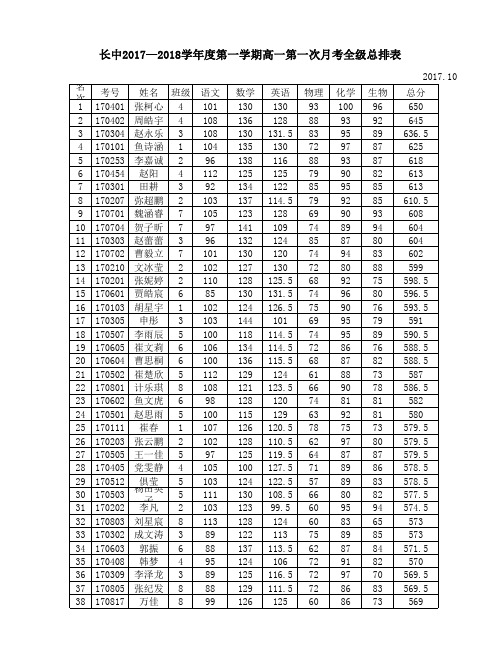
长中2017—018学年度第一学期高一第一次月考全级总排表
2017.10 名次 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 考号 170614 170104 170822 170712 170107 170834 170114 170115 170311 170708 171055 170318 170417 170815 170333 170519 170624 170217 170215 170308 170729 170514 170516 170617 170809 170811 170225 170711 170411 170610 170223 170406 170234 170108 170618 170211 170508 170616 姓名 班级 司梦晨 6 惠嘉康 1 胡叶叶 8 周逸飞 7 鱼朝阳 1 弥田 8 高金枝 1 尚甜甜 1 陈宝玲 3 李阳 7 杨广 10 杨扬 3 宇文雅 4 郭钾 8 黎佳昊 3 于莹莹 5 全宝婷 6 张晨 2 洪亦璇 2 李昭伟 3 解欣 7 陈雪彤 5 景凡 5 李一杰 6 党佳杰 8 尚国梁 8 罗睿青 2 剡心怡 7 梁娜 4 高星 6 曹亚鹏 2 曹锐洋 4 申岩 2 司帅 1 王帅 6 李煜 2 贾文丽 5 尚丁 6 语文 98 96 89 82 102 103 93 97 90 88 100 88 95 94 87 98 101 95 108 93 102 101 99 94 89 87 91 84 84 107 83 100 92 94 92 90 102 91 数学 117 126 117 119 101 126 112 109 107 120 118 101 103 119 113 115 124 92 97 108 120 116 111 113 138 118 114 123 118 125 123 98 111 102 133 113 112 110 英语 114 100 123.5 89.5 109 105.5 101.5 123 113 98.5 76 113 114.5 81.5 86.5 104 114.5 105.5 106.5 101.5 108 113 78 90.5 87 111.5 99 105 72 79.5 84.5 108.5 73 95.5 109.5 67.5 117 76 物理 57 60 67 67 70 48 66 50 58 65 64 61 63 62 80 59 42 69 47 45 56 42 62 55 44 57 65 56 74 50 62 69 80 68 56 70 52 67 化学 73 85 83 90 73 76 86 82 92 87 82 82 87 86 81 72 72 84 84 89 62 70 86 89 88 80 76 76 95 86 78 76 84 86 80 90 55 95 生物 77 68 54 86 78 74 74 71 71 72 89 83 64 84 79 78 72 79 79 85 72 78 84 78 73 65 72 73 73 68 84 62 73 67 42 82 74 73 总分 536 535 533.5 533.5 533 532.5 532.5 532 531 530.5 529 528 526.5 526.5 526.5 526 525.5 524.5 521.5 521.5 520 520 520 519.5 519 518.5 517 517 516 515.5 514.5 513.5 513 512.5 512.5 512.5 512 512
乐山市第一中学2018-2019学年上学期高三数学10月月考试题

乐山市第一中学2018-2019学年上学期高三数学10月月考试题班级__________ 座号_____ 姓名__________ 分数__________一、选择题1. 若集合A ={-1,1},B ={0,2},则集合{z|z =x +y ,x ∈A ,y ∈B}中的元素的个数为( )A5B4C3D22. 函数y=a x +2(a >0且a ≠1)图象一定过点( )A .(0,1)B .(0,3)C .(1,0)D .(3,0)3. 若复数在复平面内对应的点关于轴对称,且,则复数在复平面内对应的点在12,z z y 12i z =-12z z ()A .第一象限B .第二象限C .第三象限D .第四象限【命题意图】本题考查复数的几何意义、代数运算等基础知识,意在考查转化思想与计算能力.4. 已知不等式组表示的平面区域为,若内存在一点,使,则的取值⎪⎩⎪⎨⎧≥+≤+≥-1210y x y x y x D D 00(,)P x y 001ax y +<a 范围为()A .B .C .D .(,2)-∞(,1)-∞(2,)+∞(1,)+∞5. 一个多面体的直观图和三视图如图所示,点是边上的动点,记四面体的体M AB FMC E -积为,多面体的体积为,则( )1111]1V BCE ADF -2V =21V V A .B .C .D .不是定值,随点的变化而变化413121M 6. 执行如图所示的程序框图,如果输入的t =10,则输出的i =( )A .4B .5C .6D .77. 已知点A (0,1),B (﹣2,3)C (﹣1,2),D (1,5),则向量在方向上的投影为()A .B .﹣C .D .﹣8. 如图,在棱长为1的正方体中,为棱中点,点在侧面内运动,若1111ABCD A B C D -P 11A B Q 11DCC D ,则动点的轨迹所在曲线为( )1PBQ PBD ∠=∠QA.直线B.圆C.双曲线D.抛物线【命题意图】本题考查立体几何中的动态问题等基础知识,意在考查空间想象能力.9. 已知i 是虚数单位,则复数等于()A .﹣ +iB .﹣ +iC .﹣iD .﹣i10.某几何体的三视图如图所示,则该几何体的体积为( )A .B .C .D .16163π-32163π-1683π-3283π-【命题意图】本题考查三视图、圆柱与棱锥的体积计算,意在考查识图能力、转化能力、空间想象能力.11.为得到函数sin 2y x =-的图象,可将函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象()A .向左平移3π个单位B .向左平移6π个单位C.向右平移3π个单位D .向右平移23π个单位12.已知双曲线﹣=1的一个焦点与抛物线y 2=4x 的焦点重合,且双曲线的渐近线方程为y=±x ,则该双曲线的方程为( )A .﹣=1B .﹣y 2=1C .x 2﹣=1D .﹣=1二、填空题13.若正数m 、n 满足mn ﹣m ﹣n=3,则点(m ,0)到直线x ﹣y+n=0的距离最小值是 . 14.17.已知函数f (x )是定义在R 上的奇函数,且它的图象关于直线x=1对称.15.已知直线l 的参数方程是(t 为参数),曲线C 的极坐标方程是ρ=8cos θ+6sin θ,则曲线C 上到直线l 的距离为4的点个数有 个. 16.抛物线的焦点为,经过其准线与轴的交点的直线与抛物线切于点,则24x y =F y Q P FPQ ∆外接圆的标准方程为_________.三、解答题17.(本题满分15分)正项数列满足,.}{n a 121223+++=+n n n n a a a a 11=a (1)证明:对任意的,;*N n ∈12+≤n n a a (2)记数列的前项和为,证明:对任意的,.}{n a n n S *N n ∈32121<≤--n n S 【命题意图】本题考查数列的递推公式与单调性,不等式性质等基础知识,意在考查推理论证能力,分析和解决问题的能力.18.已知函数f (x )=.(1)求函数f (x )的最小正周期及单调递减区间;(2)当时,求f (x )的最大值,并求此时对应的x 的值.19.在直角坐标系中,已知一动圆经过点且在轴上截得的弦长为4,设动圆圆心的轨xOy (2,0)y 迹为曲线.C (1)求曲线的方程;111]C (2)过点作互相垂直的两条直线,,与曲线交于,两点与曲线交于,两点,(1,0)C A B C E F 线段,的中点分别为,,求证:直线过定点,并求出定点的坐标.AB EF M N MN P P20.已知椭圆C:+=1(a>b>0)的短轴长为2,且离心率e=,设F1,F2是椭圆的左、右焦点,过F2的直线与椭圆右侧(如图)相交于M,N两点,直线F1M,F1N分别与直线x=4相交于P,Q两点.(Ⅰ)求椭圆C的方程;(Ⅱ)求△F2PQ面积的最小值.21.已知函数f(x)的定义域为{x|x≠kπ,k∈Z},且对定义域内的任意x,y都有f(x﹣y)=成立,且f(1)=1,当0<x<2时,f(x)>0.(1)证明:函数f(x)是奇函数;(2)试求f(2),f(3)的值,并求出函数f(x)在[2,3]上的最值.22.19.已知函数f(x)=ln.乐山市第一中学2018-2019学年上学期高三数学10月月考试题(参考答案)一、选择题1. 【答案】C【解析】由已知,得{z|z =x +y ,x ∈A ,y ∈B}={-1,1,3},所以集合{z|z =x +y ,x ∈A ,y ∈B}中的元素的个数为3.2. 【答案】B【解析】解:由于函数y=a x(a >0且a ≠1)图象一定过点(0,1),故函数y=a x +2(a >0且a ≠1)图象一定过点(0,3),故选B .【点评】本题主要考查指数函数的单调性和特殊点,属于基础题. 3. 【答案】B 【解析】4. 【答案】A【解析】解析:本题考查线性规划中最值的求法.平面区域如图所示,先求的最小值,当D z ax y =+12a ≤时,,在点取得最小值;当时,,在点取12a -≥-z ax y =+1,0A ()a 12a >12a -<-z ax y =+11,33B ()得最小值.若内存在一点,使,则有的最小值小于,∴或1133a +D 00(,)P x y 001ax y +<z ax y =+1121a a ⎧≤⎪⎨⎪<⎩,∴,选A .1211133a a ⎧>⎪⎪⎨⎪+<⎪⎩2a <5. 【答案】B 【解析】考点:棱柱、棱锥、棱台的体积.6. 【答案】【解析】解析:选B.程序运行次序为第一次t =5,i =2;第二次t =16,i =3;第三次t =8,i =4;第四次t =4,i =5,故输出的i = 5.7. 【答案】D【解析】解:∵;∴在方向上的投影为==.故选D .【点评】考查由点的坐标求向量的坐标,一个向量在另一个向量方向上的投影的定义,向量夹角的余弦的计算公式,数量积的坐标运算.8. 【答案】C.【解析】易得平面,所有满足的所有点在以为轴线,以所在直//BP 11CC D D 1PBD PBX ∠=∠X BP 1BD线为母线的圆锥面上,∴点的轨迹为该圆锥面与平面的交线,而已知平行于圆锥面轴线的平面截圆Q 11CC D D 锥面得到的图形是双曲线,∴点的轨迹是双曲线,故选C.Q 9. 【答案】A【解析】解:复数===,故选:A .【点评】本题考查了复数的运算法则,属于基础题. 10.【答案】D【解析】由三视图知几何体为一个底面半径为2高为4的半圆柱中挖去一个以轴截面为底面高为2的四棱锥,因此该几何体的体积为,故选D .21132244428233V =π⨯⨯-⨯⨯⨯=π-11.【答案】C 【解析】试题分析:将函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象向右平移3π个单位,得2sin 2sin 233y x x ππ⎛⎫=--=- ⎪⎝⎭的图象,故选C .考点:图象的平移.12.【答案】B【解析】解:已知抛物线y 2=4x 的焦点和双曲线的焦点重合,则双曲线的焦点坐标为(,0),即c=,又因为双曲线的渐近线方程为y=±x ,则有a 2+b 2=c 2=10和=,解得a=3,b=1.所以双曲线的方程为:﹣y 2=1.故选B .【点评】本题主要考查的知识要点:双曲线方程的求法,渐近线的应用.属于基础题.二、填空题13.【答案】 .【解析】解:点(m ,0)到直线x ﹣y+n=0的距离为d=,∵mn ﹣m ﹣n=3,∴(m﹣1)(n﹣1)=4,(m﹣1>0,n﹣1>0),∴(m﹣1)+(n﹣1)≥2,∴m+n≥6,则d=≥3.故答案为:.【点评】本题考查了的到直线的距离公式,考查了利用基本不等式求最值,是基础题.14.【答案】【解析】解:∵f(x)=a x g(x)(a>0且a≠1),∴=a x,又∵f′(x)g(x)>f(x)g′(x),∴()′=>0,∴=a x是增函数,∴a>1,∵+=.∴a1+a﹣1=,解得a=或a=2.综上得a=2.∴数列{}为{2n}.∵数列{}的前n项和大于62,∴2+22+23+…+2n==2n+1﹣2>62,即2n+1>64=26,∴n+1>6,解得n>5.∴n的最小值为6.故答案为:6.【点评】本题考查等比数列的前n项和公式的应用,巧妙地把指数函数、导数、数列融合在一起,是一道好题.15.【答案】 2 【解析】解:由,消去t 得:2x ﹣y+5=0,由ρ=8cos θ+6sin θ,得ρ2=8ρcos θ+6ρsin θ,即x 2+y 2=8x+6y ,化为标准式得(x ﹣4)2+(y ﹣3)2=25,即C 是以(4,3)为圆心,5为半径的圆.又圆心到直线l 的距离是,故曲线C 上到直线l 的距离为4的点有2个,故答案为:2.【点评】本题考查了参数方程化普通方程,考查了极坐标方程化直角坐标方程,考查了点到直线的距离公式的应用,是基础题. 16.【答案】或()2212x y -+=()2212x y ++=【解析】试题分析:由题意知,设,由,则切线方程为,代入()0,1F 2001,4P x x ⎛⎫ ⎪⎝⎭1'2y x =()20001142y x x x x -=-得,则,可得,则外接圆以为直径,则()0,1-02x =±()()2,1,2,1P -PF FQ ⊥FPQ ∆PQ ()2212x y -+=或.故本题答案填或.1()2212x y ++=()2212x y -+=()2212x y ++=考点:1.圆的标准方程;2.抛物线的标准方程与几何性质.三、解答题17.【答案】(1)详见解析;(2)详见解析.18.【答案】【解析】解:(1)f(x)=﹣=sin2x+sinxcosx﹣=+sin2x﹣=sin(2x﹣)…3分周期T=π,因为cosx≠0,所以{x|x≠+kπ,k∈Z}…5分当2x﹣∈,即+kπ≤x≤+kπ,x≠+kπ,k∈Z时函数f(x)单调递减,所以函数f(x)的单调递减区间为,,k∈Z…7分(2)当,2x﹣∈,…9分sin(2x﹣)∈(﹣,1),当x=时取最大值,故当x=时函数f (x )取最大值为1…12分【点评】本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,三角函数最值的解法,属于基础题. 19.【答案】(1) ;(2)证明见解析;.24y x =(3,0)【解析】(2)易知直线,的斜率存在且不为0,设直线的斜率为,,,11(,)A x y 22(,)B x y 则直线:,,(1)y k x =-1212(,)22x x y y M ++由得,24,(1),y x y k x ⎧=⎨=-⎩2222(24)0k x k x k -++=,2242(24)416160k k k ∆=+-=+>考点:曲线的轨迹方程;直线与抛物线的位置关系.【易错点睛】导数法解决函数的单调性问题:(1)当不含参数时,可通过解不等式)(x f )0)((0)(''<>x f x f 直接得到单调递增(或递减)区间.(2)已知函数的单调性,求参数的取值范围,应用条件恒成立,解出参数的取值范围(一般可用不等式恒成立的理论求解),应注意),(),0)((0)(''b a x x f x f ∈≤≥参数的取值是不恒等于的参数的范围.)('x f 20.【答案】【解析】解:(Ⅰ)∵椭圆C :+=1(a >b >0)的短轴长为2,且离心率e=,∴,解得a 2=4,b 2=3,∴椭圆C 的方程为=1.(Ⅱ)设直线MN 的方程为x=ty+1,(﹣),代入椭圆,化简,得(3t 2+4)y 2+6ty ﹣9=0,∴,,设M(x1,y1),N(x2,y2),又F1(﹣1,0),F2(1,0),则直线F1M:,令x=4,得P(4,),同理,Q(4,),∴=||=15×||=180×||,令μ=∈[1,),则=180×,∵y==在[1,)上是增函数,∴当μ=1时,即t=0时,()min=.【点评】本题考查椭圆方程的求法,考查三角形面积的最小值的求法,是中档题,解题时要认真审题,注意韦达定理、直线方程、弦长公式、函数单调性、椭圆性质的合理运用.21.【答案】【解析】(1)证明:函数f(x)的定义域为{x|x≠kπ,k∈Z},关于原点对称.又f(x﹣y)=,所以f(﹣x)=f[(1﹣x)﹣1]======,故函数f(x)奇函数.(2)令x=1,y=﹣1,则f(2)=f[1﹣(﹣1)]==,令x=1,y=﹣2,则f(3)=f[1﹣(﹣2)]===,∵f(x﹣2)==,∴f(x﹣4)=,则函数的周期是4.先证明f(x)在[2,3]上单调递减,先证明当2<x<3时,f(x)<0,设2<x<3,则0<x﹣2<1,则f(x﹣2)=,即f(x)=﹣<0,设2≤x1≤x2≤3,则f(x1)<0,f(x2)<0,f(x2﹣x1)>0,则f(x1)﹣f(x2)=,∴f(x1)>f(x2),即函数f(x)在[2,3]上为减函数,则函数f(x)在[2,3]上的最大值为f(2)=0,最小值为f(3)=﹣1.【点评】本题主要考查了函数奇偶性的判断,以及函数的最值及其几何意义等有关知识,综合性较强,难度较大.22.【答案】【解析】解:(1)∵f(x)是奇函数,∴设x>0,则﹣x<0,∴f(﹣x)=(﹣x)2﹣mx=﹣f(x)=﹣(﹣x2+2x)从而m=2.(2)由f(x)的图象知,若函数f(x)在区间[﹣1,a﹣2]上单调递增,则﹣1≤a﹣2≤1∴1≤a≤3【点评】本题主要考查函数奇偶性的应用以及函数单调性的判断,利用数形结合是解决本题的关键.。
2017-2018学年四川省乐山市高一(上)期末数学试卷(解析版)

2017-2018学年四川省乐山市高一(上)期末数学试卷一、选择题(本大题共12小题,共60.0分)1.设集合A={1,2,3},集合B={-2,2},则A∩B=()A. B. C. D. 1,2,2.cos390°的值为()A. B. C. D.3.已知函数,则f(f(-2))=()A. B. 0 C. 1 D.4.角α终边上一点的坐标为(-1,2),则tan2α=()A. 2B.C.D.5.函数f(x)=x2-()|x|的零点个数为()A. 0B. 1C. 2D. 36.已知函数f(x)=x+tan x+1,若f(a)=-3,则f(-a)的值为()A. 0B. 3C. 4D. 57.函数f(x)=2sin(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,则ω,φ的值分别是()A.B.C.D.8.已知cos(-θ)=,则sin()的值是()A. B. C. D.9.已知,,且α,β均为锐角,则=()A. B. C. D.10.已知函数,对∀x1,x2∈(-∞,+∞),总有<(x1≠x2)成立,则实数a的取值范围是()A. B. C. D.11.已知函数f(x)=sin(ωx+φ)(其中ω>0|φ|<)图象相邻对称轴的距离为,一个对称中心为(-,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象()A. 向右平移个单位B. 向右平移个单位C. 向左平移个单位D. 向左平移个单位12.函数,,<<,若x1,x2,x3是函数y=f(x)+a三个不同的零点,则x1+x2+x3的范围是()A. B. C. D.二、填空题(本大题共4小题,共20.0分)13.计算(log29)•(log34)=______.14.已知幂函数y=f(x)的图象过点(,),则f(4)的值为______.15.已知集合A={x|-2≤x≤5},B={x|m+1<x<2m-1},若B⊆A,则实数m的取值范围是______.16.已知f(x)为偶函数,当x≥0时,,∈,,∈,,则不等式的解集为______.三、解答题(本大题共6小题,共70.0分)17.已知集合<,B={x|x<1或x>2},U=R.(1)求A∪B;(2)求A∩(∁U B).18.已知∈,,且.(1)求的值;(2)求的值.19.已知二次函数f(x)=x2+mx-3的两个零点为-1和n.(1)求m,n的值;(2)若f(3)=f(2a-5),求a的值.20.李庄村某社区电费收取有以下两种方案供农户选择:方案一:每户每月收管理费2元,月用电不超过30度,每度0.4元,超过30度时,超过部分按每度0.5元.方案二:不收管理费,每度0.48元.(1)求方案一收费L(x)元与用电量x(度)间的函数关系;(2)小李家九月份按方案一交费34元,问小李家该月用电多少度?(3)小李家月用电量在什么范围时,选择方案一比选择方案二更好?21.已知函数.(1)求的值;(2)求f(x)的单调递增区间;(3)当∈,时,求f(x)的值域.22.已知函数,其中x∈(-4,4)(1)判断并证明函数f(x)的奇偶性;(2)判断并证明函数f(x)在(-4,4)上的单调性;(3)是否存在这样的负实数k,使f(k-cosθ)+f(cos2θ-k2)≥0对一切θ∈R恒成立,若存在,试求出k取值的集合;若不存在,说明理由.答案和解析1.【答案】B【解析】解:∵集合A={1,2,3},集合B={-2,2},∴A∩B={2}.故选:B.找出A与B的公共元素即可求出交集.此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.【答案】D【解析】解:cos390°的=cos30°=.故选:D.直接利用诱导公式化简求解即可.本题考查诱导公式的应用,三角函数化简求值,考查计算能力.3.【答案】C【解析】解:根据题意,函数,则f(-2)=(-2)+12=10,则f(f(-2))=f(10)=lg10=1;故选:C.根据题意,由函数解析式可得f(-2)的值,进而计算f(f(-2))的值,即可得答案.本题考查分段函数的求值计算,注意分段函数的解析式的形式,属于基础题.4.【答案】D【解析】解:∵角α终边上一点的坐标为(-1,2),∴tanα==-2,则tan2α==,故选:D.由题意利用任意角的三角函数的定义求得tanα的值,再利用二倍角的正切公式求得tan2α的值.本题主要考查任意角的三角函数的定义,二倍角的正切公式,属于基础题.5.【答案】C【解析】解:∵f(-x)=x2-()|x|=f(x),∴函数f(x)=x2-()|x|是偶函数,易知f(x)在[0,+∞)上是增函数,而f(0)=-1,f(1)=>0,故f(x)在(0,1)上有一个零点,故f(x)共有2个零点,故选:C.可判断函数f(x)是偶函数且在[0,+∞)上是增函数,从而解得.本题考查了函数的性质的判断与应用.6.【答案】D【解析】解:根据题意,函数g(x)=f(x)-1=x+tanx,则g(-x)=(-x)+tan(-x)=-(x+tanx)=-g(x),则函数g(x)为奇函数,则g(a)+g(-a)=f(a)-1+f(-a)-1=0,又由f(a)=-3,则f(-a)=5,故选:D.根据题意,设g(x)=f(x)-1=x+tanx,分析可得g(x)为奇函数,结合奇函数的定义可得g(a)+g(-a)=f(a)-1+f(-a)-1=0,代入f(a)的值,即可得答案.本题考查函数奇偶性的性质应用,关键是理解函数奇偶性的定义,属于基础题.7.【答案】A【解析】解:由图象可得函数的周期T满足T=-(-)=,∴T=π,∴ω==2,∴f(x)=2sin(2x+φ),又函数图象经过点(,2),∴2sin(+φ)=2,∴+φ=2kπ+,∴φ=2kπ-,k∈Z∵|φ|<,∴当k=0时,φ=-故选:A.由图象和函数的周期公式可得ω,代入点的坐标结合角的范围可得φ值.本题考查三角函数的图象和解析式,数形结合是解决问题的关键,属中档题.8.【答案】A【解析】解:cos(-θ)=sin[-(-θ)]=sin()=,故选:A.由已知及诱导公式即可计算求值.本题主要考查了诱导公式在三角函数求值中的应用,属于基础题.9.【答案】A【解析】解:∵α,β均为锐角,∴α+β∈(0,π),∈(),由,,得sin(α+β)=,cos()=.∴=sin[(α+β)-()]=sin(α+β)cos()-cos(α+β)sin()]=.故选:A.由已知求得sin(α+β),cos()的值,再由=sin[(α+β)-()]展开两角差的正弦求解.本题考查三角函数的化简求值,考查同角三角函数基本关系式与两角差的正弦,是基础的计算题.10.【答案】C【解析】解:由题意,对∀x1,x2∈(-∞,+∞),总有(x1≠x2)成立,所以函数是减函数;可得:,解得,a≤,故选:C.判断函数是减函数,列出不等式组,从而解出实数a的取值范围.本题考查了分段函数的单调性,以及函数的单调性的求解方法,考查转化思想的应用,属于基础题.11.【答案】D【解析】解:由题意可得函数的最小正周期为=2×,∴ω=2.再根据-×2+φ=kπ,|φ|<,k∈z,可得φ=,f(x)=sin(2x+),故将f(x)的图象向左平移个单位,可得y=sin[2(x+)+]=sin(2x+)=cos2x的图象,故选:D.由周期求得ω,根据图象的对称中心求得φ的值,可得函数的解析式,再根据函数y=Asin(ωx+φ)的图象变换规律得出结论.本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.12.【答案】B【解析】解:函数,其图象(如下),通过图象可得,当1<-a<2时,函数y=-a与f(x)交点设为x1,x2,x3,不妨设x1<x2<x3,通过图象交点,可得x2+x3关于x=对称,∴x2+x3=,令,可得x=.∴<x1<0可得:x1+x2+x3.故选:B.根据函数,作出图象,函数y=-a与f(x)交点设为x1,x2,x3,不妨设x1<x2<x3,通过图象交点可得x2+x3是定值,求解x1的范围可得x1+x2+x3的范围.本题主要考查指数函数的图象和三角函数图象的应用,体现了数形结合和转化的数学思想,属于中档题.13.【答案】4【解析】解;(log29)•(log34)=(2log23)•(2log32)=.把真数写成幂的形式,然后运用对数式的性质化简计算.本题考查对数的运算性质,同时考查了换底公式,也可直接运用结论log a b×log b a=1运算.14.【答案】2【解析】解:设幂函数y=f(x)=xα,∵f(x)的图象过点(,),∴=,∴α=,∴f(x)=∴f(4)==2,故答案为:2.设幂函数y=f(x)=xα,根据f(x)的图象过点(,),求得α的值,可得函数f(x)的解析式,从而求得f(4)的值.本题主要考查幂函数的定义,用待定系数法求函数解析式,奇函数的值,属于基础题.15.【答案】(-∞,3]【解析】解:根据题意得,①B=Φ时,m+1≥2m-1∴m≤2;②B≠Φ时,解得2<m≤3综上m≤3.故答案为(-∞,3].运用分类讨论的思想和子集的概念可得结果.本题考查集合子集的概念.16.【答案】或【解析】解:根据题意,当x≥0时,,当0≤x≤时,f(x)=cosπx,f(x)≤即cosπx≤,又由0≤x≤,解可得≤x≤,当x>时,f(x)=2x-1,f(x)≤即2x-1≤,又由x>,解可得<x≤,综合可得:在[0,+∞)上,f(x)≤的解集为[,],又由函数f(x)为偶函数,则在R上,f(x)≤的解集为[-,-]∪[,];若不等式,必有-≤x-1≤-或≤x-1≤;解可得:≤x≤或≤x≤;即不等式的解集为;故答案为:.根据题意,由函数的解析式分段讨论f(x)≤的解集,结合函数的奇偶性可得在R上,f(x)≤的解集为[-,-]∪[,];对于不等式,必有-≤x-1≤-或≤x-1≤;解可得x的取值范围,即可得答案.本题考查分段函数的应用以及函数奇偶性的性质,注意函数解析式的形式.17.【答案】解:(1)∵集合<,B={x|x<1或x>2};∴∪或>.(2)∵U=R,B={x|x<1或x>2};∴C U B={x|1≤x≤2};∴.【解析】(1)进行并集的运算即可;(2)进行补集、交集的运算即可.考查描述法表示集合的概念,以及交集、并集和补集的运算.18.【答案】解:(1)∵∈,,,∴,则,∴ .(2)由==.【解析】(1)由已知利用同角三角函数基本关系式可求cosα,tanα,利用两角差的正切函数公式进而计算得解;(2)利用三角函数恒等变换的应用化简即可计算得解.本题主要考查了三角函数恒等变换的应用,考查了转化思想,属于基础题.19.【答案】解:(1)因为二次函数f(x)=x2+mx-3的两个零点为-1和n,则-1和n是方程x2+mx-3=0的两个根,则-1+n=-m,-1×n=-3,解得m=-2,n=3.(2)因为f(x)=x2+mx-3的图象对称轴为x=1,则由f(3)=f(2a-5)可得或3=2a-5,解得a=2或4.综上a=2或4.【解析】(1)根据题意,分析可得-1和n是方程x2+mx-3=0的两个根,由根与系数的关系分析可得-1+n=-m,-1×n=-3,解可得m、n的值,即可得答案;(2)根据题意,由二次函数的性质分析可得或3=2a-5,解可得a的值,即可得答案.本题考查二次函数的性质,关键是求出m、n的值,属于基础题.20.【答案】解:(1)当0≤x≤30时,L(x)=2+0.4x;当x>30时,L(x)=2+30×0.4+(x-30)×0.5=0.5x-1,∴L(x)=;(2)当0≤x≤30时,L(x)≤L(30)=14,故小李家九月份用电超过30度,由0.5x-1=34得:x=70,故小李家该月用电70度;(3)方案二收费E(x)=0.48x,x≥0,令L(x)<E(x),当0≤x≤30时,2+0.4x<0.48x,解得25<x≤30,当x>30时,0.5x-1<0.48x,解得:30<x<50,综上可得:小李家月用电量在(25,50)时,选择方案一比选择方案二更好.【解析】(1)根据方案一:每户每月收管理费2元,月用电不超过30度,每度0.4元,超过30度时,超过部分按每度0.5元,可得收费L(x)元与用电量x(度)间的函数关系;(2)由(1)可得小李家九月份用电超过30度,令0.5x-1=34,解得小李家该月用电度数;(3)方案二收费E(x)=0.48x,x≥0,令L(x)<E(x),解得答案.本题考查的知识点是根据实际问题选择函数类型,难度不大,属于基础题.21.【答案】解:(1)∵,∴,=.(2)由,=,=,令:,(k∈Z),解得:,(k∈Z)所以函数的单调增区间为,∈(3)∵ ∈,,∴,∴,故函数的值域为,.【解析】(1)直接利用函数的关系式求出函数的值.(2)利用三角函数的关系式的恒等变换求出函数的关系式为正弦型函数,进一步利用整体思想求出函数的单调区间.(3)利用函数的关系式,根据函数的定义域求出函数的值域.本题考查的知识要点:三角函数关系式的恒等变变换,正弦型函数的性质的应用,利用函数的定义域求函数的值域,主要考查学生的运算能力和转化能力,属于基础题型.22.【答案】解:(1)∵,∴f(x)是奇函数.…(4分)(2)任取,∈,,且<,=,∵16+4(x2-x1)-x1x2>16+4(x1-x2)-x1x2>0,∴>>>∴f(x)在(-4,4)上的减函数;…(8分)(3)∵f(k-cosθ)≥-f(cos2θ-k2)=f(k2-cos2θ),∵f(x)是(-4,4)上的减函数<<<<<对θ∈R恒成立由k-cosθ≤k2-cos2θ对θ∈R恒成立得:k-k2≤cosθ-cos2θ对θ∈R恒成立令,∵∈,∴∈,∴由-4<k-cosθ<4对θ∈R恒成立得:-3<k<3由-4<cos2θ-k2<4对θ∈R恒成立得:-2<k<2即综上所得:-2<k≤-1所以存在这样的k其范围为-2<k≤-1…(14分)【解析】(1)根据函数奇偶性的定义进行判断即可.(2)根据函数单调性定义进行判断.(3)根据函数奇偶性和单调性的关系将不等式进行转化,利用参数分离法进行求解即可.本题主要考查不等式恒成立以及函数奇偶性和单调性的判断,利用函数奇偶性和单调性的定义是解决本题的关键.。
四川省乐山市2017_2018学年高二数学上学期第一次月考试题

y'x'O'(C')B'A'2019届高二(上)第一次月考数学试题一选择题:本大题共12小题,每小题5分,共60分.1.下列命题正确的是( )A. 棱柱的侧面都是长方形B. 棱柱的所有面都是四边形C. 棱柱的侧棱不一定相等D. 一个棱柱至少有五个面2.下列说法不正确的....是 A. 空间中,一组对边平行且相等的四边形是一定是平行四边形;B. 同一平面的两条垂线一定共面;C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内D. 过一条直线有且只有一个平面与已知平面垂直3.圆柱底面圆的半径和圆柱的高都为2,则圆柱侧面展开图的面积为( )A. π4B. π24C. π8D. π284.水平放置的ABC ∆由“斜二测画法”画得的直观图如图所示,已知''3,''2A C B C ==,则AB 边的实际长度为( )(A(B )5 (C )52(D )25.已知为直线, 为平面, , ,则与之间的关系是( )A. 平行B. 垂直C. 异面D. 平行或异面6.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )(A )6 (B )9 (C )12 (D )184题图7.如图,在正方体1111D C B A ABCD -中,若E 是11C A 的中点,则直线CE 垂直于( )A .ACB .BDC .D A 1 D .11D A8.,αβ是两个平面,,m n 是两条直线,有下列四个命题:正确的命题有( )(1)如果m n ⊥,m α⊥,//n β,那么αβ⊥.(2)如果m α⊥,//n α,那么m n ⊥.(3)如果//αβ,m α⊂,那么//m β.4)如果//m n ,//αβ,那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有( )A ○1○2B ○1C ○2○3D ○2○3○49.把边长为1的正方形ABCD 沿对角线BD 折起,使得平面ABD ⊥平面CBD ,形成 三棱锥C -ABD 的正视图与俯视图如图所示,则侧视图的面积为 ( ) A.21 B. 22 C. 41 D. 429题图 11题图10.已知各顶点都在同一球面上的正四棱锥的高为3,体积为6,则这个球的表面积为( )A. π16;B. π20;C. π24;D. π32;11.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥底面ABCD ,E 是PC的中点,2,2AB AD PA ===,则异面直线BC 与AE 所成的角的大小为( )(A )π6 (B )π4(C )π3(D )π212.如图,正方体ABCD —A 1B 1C 1D 1的棱长为1,线段AC 1上有E D C B A P两个动点E ,F ,且EF .有下列四个结论:①CE ⊥BD ; ②三棱锥E —BCF 的体积为定值;③△BEF 在底面ABCD 内的正投影是面积为定值的三角形;④在平面ABCD 内存在无数条与平面DEA 1平行的直线,其中正确结论的个数是( )A .1B .2C .3D .4二填空题(每小题5分)13已知圆锥的母线长是,侧面展开图是半圆,则该圆锥的侧面积为_______14.正方体1111D C B A ABCD -中,直线1BC 与直线1AB 所成角的大小为_____15.某几何体的三视图如图所示,则该几何体的体积为.16.已知正三棱锥P ABC -,点P ,A ,B ,C 都在半径为3的球面上,若PA ,PB ,PC 两两相互垂直,则球心到截面ABC 的距离为______三、计算题17.如图,某几何体的下部分是长为8,宽为6,高为3的长方体,上部分是侧棱长都相等且高为3的四棱锥,求:(1)该几何体的体积;(2)该几何体的表面积.18、如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm)。
四川省眉山市2017_2018学年高一数学1月月考试题无答案2018011101156

四川省眉山市2017-2018学年高一数学1月月考试题(无答案)数学试题满分150分.考试时间120分钟.一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的.1.设全集U R =,集合0,1,2,4{4{}}1|A B x x ==<≤,,则A B =( )A .{}1,2,3,4B .{}2,3,4C .{}4,2D .{}14x x <≤2.一个扇形的面积为15π,弧长为5π,则这个扇形的中心角为( ) A.6π B. 3π C. 23πD.56π3.设 10()2,0xx f x x ⎧≥⎪=⎨<⎪⎩ ,则((2))f f -= ( ) A 1- B14 C 12 D 324.设方程lg 30x x +-=的实数解为0x ,则0x 所在的一个区间是( ) A.()3,+∞B.()2,3C.()1,2D.()0,15.设,M P 是两个非空集合,定义M 与P 的差集为:{}|,M P x x M x P -=∈∉且,则()M M P --=( ).A P.B M P .C M P .D M6.在()0,2π内,使sin cos x x ≥成立的x 取值范围是( )A .π7π,44⎡⎤⎢⎥⎣⎦ B .π5π,44⎡⎤⎢⎥⎣⎦ C 5π0,4⎡⎤⎢⎥⎣⎦ D .π7π0,,2π44⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦7.函数2sin y x =的图象是 ( )8. 同时具有性质“①最小正周期为π;②图象关于直线3x π=对称;③在(,)63ππ-上是增函数”的一个函数是 ( ) A sin()26x y π=+ B cos()26x y π=- C sin(2)6y x π=-D cos(2)3y x π=+9.函数()y f x =在(0,2)上是增函数,函数(2)y f x =+是偶函数,则下列结论正确的 ( )A .57(1)()()22f f f <<B .57()(1)()22f f f << C .75()()(1)22f f f <<D .75()(1)()22f f f <<10.将函数()2sin()(0)3f x x πωω=->的图象向左平移3πω个单位,得到函数()y g x =的图象.若()y g x =在0,4π⎡⎤⎢⎥⎣⎦上为增函数,则ω的最大值为 ( ) A .2 B . 4 C .5 D .6 11.若方程lg cos 0x x -=的解的个数为m ,则m 的值是 ( )A.3B.4C.5D.612. 定义在R 上的函数()f x 满足()(4)f x f x =+.当20x -≤<2()log ()f x x =-;当02x ≤<时,1()2x f x -=,则(1)(2)(3)...(2017)f f f f ++++=( )A.630B.1260C.1261D.3781二、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题卡上相应位置. 13.若lg 2,lg3a b ==,则用,a b 表示100log 12的表达式为 .14. 已知,44x ππ⎡⎤∈-⎢⎥⎣⎦,则函数f (x )=cos 2x +sin x 的最小值为 . 15.把函数2sin()6y x π=-图象上所有点的横坐标缩短为原来的21倍(纵坐标不变),再把所得函数图象向左平移3π个单位,得到图象对应的解析式为 . 16.设定义域为R 的函数2lg ,0()2,0x x f x x x x ⎧>=⎨--≤⎩ ,若关于x 的函数()()2221y f x bf x =++有8个不同的零点,则实数b 的取值范围是 .三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤. 17. (本题10分)(1)化简:sin()sin()2cos()sin(2)πααπαπα---+(2)已知角α的终边上一点)P m ,且1sin 2α=-,求cos ,tan αα的值18.(本题12分) 已知函数()xf x a =(0a >,且1a ≠).(1)若函数()f x 在[]2,1-上的最大值为2,求a 的值; (2)若1a >,求使得()2log 1f x <成立的x 的取值集合.19.(本题12分)如图所示是函数()sin()(0,0,)2f x A x A πωϕωϕ=+>><的图象(1)求,,A ωϕ的值;(2)当⎥⎦⎤⎢⎣⎡∈125,12ππx 时,求函数()f x 的值域及单调增区间,20.(本题12分) 已知某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产1百件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为5百件,产品销售数量为t (百件)时,销售所得的收入为21(5)2t t -万元. (1)该公司这种产品的年生产量为x 百件,生产并销售这种产品得到的利润为当年产量x 的函数()f x ,求()f x ;(2)当该公司的年产量为多大时当年所获得的利润最大?.21.(本题12分)已知定义域为R 的函数()1231x a f x =-++是奇函数. (1)求a 的值;(2)判断函数()f x 的单调性并证明;22.(本题12分) 对于函数()f x ,若存在R x ∈0,使00()f x x =成立,则称0x 为()f x 的不动点.已知函数2()(1)(1)(0)f x ax b x b a =+++-≠. (1)当1,2a b ==时,求函数()f x 的不动点;(2)若对任意实数b ,函数()f x 恒有两个相异的不动点,求a 的取值范围; (3)当01a <<,若()f x 的两个不动点为12,x x ,且()12221af x x a -+=+,求实数b 的取值范围.。
2017-2018学年四川省雅安中学高一(上)第一次月考数学试卷

2017-2018学年四川省雅安中学高一(上)第一次月考数学试卷一.选择题(本大题共12小题,每小题5分,共60分.)1.(5分)下列所给关系中正确的个数是()(1)π∈R;(2)∉Q;(3)0∈N;(4)|﹣4|∉N*;(5)∈Z.A.1 B.2 C.3 D.42.(5分)设集合A={x|x2﹣4x+3≥0},B={x|2x﹣3≤0},则A∪B=()A.(﹣∞,1]∪[3,+∞)B.[1,3]C. D.3.(5分)下列各组函数中表示同一函数的是()A.f(x)=x﹣1与g(x)= B.f(x)=x与g(x)=C.f(x)=x2﹣x与g(t)=t2﹣t D.f(x)=x﹣1与g(x)=4.(5分)已知f(x﹣1)=x2+4x﹣5,则f(x)的表达式是()A.f(x)=x2+6x B.f(x)=x2+8x+7 C.f(x)=x2+2x﹣3 D.f(x)=x2+6x﹣105.(5分)下列函数,既是奇函数,又在区间(0,+∞)上是减函数的是()A.f(x)=﹣x2B.f(x)=C.f(x)=D.f(x)=x36.(5分)已知f(x)是R上的奇函数,当x>0时,f(x)=x2﹣x,则当x<0时,f(x)=()A.﹣x2+x B.﹣x2﹣x C.x2+x D.x2﹣x7.(5分)若集合,,则()A.M=N B.M⊊N C.N⊊M D.M∩N=∅8.(5分)已知偶函数f(x)在区间[0,+∞)上是增函数,则f(﹣1)与f(a2﹣2a+3)的大小关系是()A.f(﹣1)≥f(a2﹣2a+3)B.f(﹣1)≤f(a2﹣2a+3)C.f(﹣1)>f (a2﹣2a+3)D.f(﹣1)<f(a2﹣2a+3)9.(5分)设函数f(x)=2x+1的定义域为[1,5],则函数f(2x﹣3)的定义域为()A.[1,5]B.[3,11] C.[3,7]D.[2,4]10.(5分)定义在R上的偶函数f(x)满足:对任意的x1,x2∈(﹣∞,0](x1≠x2),有<0,且f(2)=0,则不等式<0解集是()A.(﹣∞,﹣2)∪(2,+∞)B.(﹣∞,﹣2)∪(0,2)C.(﹣2,0)∪(2,+∞) D.(﹣2,0)∪(0,2)11.(5分)已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R 都满足f(x•y)=x•f(y)+y•f(x),则f(x)是()A.奇函数B.偶函数C.不是奇函数也不是偶函数D.既是奇函数又是偶函数12.(5分)已知定义在R上的函数f(x)满足f(﹣x)=﹣f(x),f(x﹣4)=﹣f(x),且在区间[0,2]上是减函数.若方程f(x)=k在区间[﹣8,8]上有四个不同的根,则这四根之和为()A.±4 B.±8 C.±6 D.±2二、填空题(本大题共4小题,每小题5分,共20分.)13.(5分)函数y=的定义域是.14.(5分)设函数f(x)=若f(x0)=1,则x0等于.15.(5分)已知函数y=的定义域是R,则实数m的取值范围.16.(5分)定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)•f(﹣a)≤0;②f(a)+f(b)≤f(﹣a)+f(﹣b);③f(b)•f(﹣b)≥0;④f(a)+f(b)≥f(﹣a)+f(﹣b).其中正确的是(把你认为正确的不等式的序号全写上).三、解答题(本大题共6小题,共70分.)17.(10分)已知全集U=R,集合A={x|2a≤x≤a+3},B={x|x<﹣1或x≥5}.(1)若a=﹣1时,求A∩B、(∁U B)∪A;(2)若A∩B=∅,求a的取值范围.18.(12分)已知集合A=,若:(1)B⊆A,B={x|m+1≤x≤2m﹣1},求实数m的范围;(2)A⊆B,B={x|m﹣6≤x≤2m﹣1,求实数m的范围.19.(12分)已知函数f(x)=,a∈(1,+∞),x∈(﹣1,+∞).(1)判断函数f(x)的单调性,并证明;(2)是否存在实数a,使得函数f(x)在[a,+∞)的最小值为a?若存在,求出a的值,若不存在,说明理由.20.(12分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式.(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润约为多少万元.(精确到1万元).21.(12分)已知函数f(x)的定义域为R,对任意的x,y∈R,都有f(x+y)=f(x)+f(y),且当x<0时,f(x)>0.(1)求证:f(x)是奇函数;(2)判断f(x)在R上的单调性,并加以证明;(3)解关于x的不等式f(x2)+3f(a)>3f(x)+f(ax),其中常数a∈R.22.(12分)已知函数f(x)=ax2﹣|x|+2a﹣1(a为实常数).(Ⅰ)若a=1,作函数f(x)的图象并写出单调区间;(Ⅱ)当a≥0时,设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;(Ⅲ)设h(x)=,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.2017-2018学年四川省雅安中学高一(上)第一次月考数学试卷参考答案与试题解析一.选择题(本大题共12小题,每小题5分,共60分.)1.(5分)下列所给关系中正确的个数是()(1)π∈R;(2)∉Q;(3)0∈N;(4)|﹣4|∉N*;(5)∈Z.A.1 B.2 C.3 D.4【分析】根据元素与集合的关系进行判断【解答】解:对于(1):π是一个元素,R是实数集,π∈R;正确.对于(2):是无理数,Q是有理数集;∉Q;正确.对于(3):0是一个元素,N是自然数集,0∈N;正确.对于(4):|﹣4|是一个元素,N是自然数集,|﹣4|∈N*;故不对;对于(5):是一个元素,一个分数,Z是整数集,﹣∉Z.故不对;故选:C.【点评】本题主要考查元素与集合的关系,属于基础题2.(5分)设集合A={x|x2﹣4x+3≥0},B={x|2x﹣3≤0},则A∪B=()A.(﹣∞,1]∪[3,+∞)B.[1,3]C. D.【分析】先分别求出集合A和B,由此能求出A∪B.【解答】解:∵集合A={x|x2﹣4x+3≥0}={x|x≤1或x≥3},B={x|2x﹣3≤0}={x|x≤},∴A∪B={x|x或x≥3}=(﹣∞,]∪[3,+∞).故选:D.【点评】本题考查集合的求法,是基础题,解题时要认真审题,注意并集定义和不等式性质的合理运用.3.(5分)下列各组函数中表示同一函数的是()A.f(x)=x﹣1与g(x)= B.f(x)=x与g(x)=C.f(x)=x2﹣x与g(t)=t2﹣t D.f(x)=x﹣1与g(x)=【分析】根据两个函数的定义域相同,对应关系也相同,判断它们是同一函数即可.【解答】解:对于A:f(x)=x﹣1与=|x﹣1|,定义域都是R,对应法则不同,∴不是同一函数;故A不对.对于B:f(x)=x的定义域是R,而的定义域x≥0,∴不是同一函数;故B不对.对于C:f(x)=x2﹣x与g(t)=t2﹣t它们的定义域相同,对应关系也相同,∴是同一函数;故C对.对于D:f(x)=x﹣1的定义域是R,而的定义域x≠1,∴不是同一函数;故D不对.故选:C.【点评】本题考查了判断两个函数是否为同一函数的问题,是基础题.4.(5分)已知f(x﹣1)=x2+4x﹣5,则f(x)的表达式是()A.f(x)=x2+6x B.f(x)=x2+8x+7 C.f(x)=x2+2x﹣3 D.f(x)=x2+6x﹣10【分析】【方法﹣】用换元法,设t=x﹣1,用t表示x,代入f(x﹣1)即得f(t)的表达式;【方法二】凑元法,把f(x﹣1)的表达式x2+4x﹣5凑成含(x﹣1)的形式即得f(x)的表达式;【解答】解:【方法﹣】设t=x﹣1,则x=t+1,∵f(x﹣1)=x2+4x﹣5,∴f(t)=(t+1)2+4(t+1)﹣5=t2+6t,f(x)的表达式是f(x)=x2+6x;【方法二】∵f(x﹣1)=x2+4x﹣5=(x﹣1)2+6(x﹣1),∴f(x)=x2+6x;∴f(x)的表达式是f(x)=x2+6x;故选:A.【点评】本题考查了函数解析式的常用求法的问题,是基础题.5.(5分)下列函数,既是奇函数,又在区间(0,+∞)上是减函数的是()A.f(x)=﹣x2B.f(x)=C.f(x)=D.f(x)=x3【分析】根据函数奇偶性和单调性的性质进行判断即可.【解答】解:A.f(x)=﹣x2是偶函数,不满足条件.B.f(x)=是偶函数,不满足条件.C.f(﹣x)=﹣=﹣f(x)是奇函数,当x>0时,f(x)==x﹣3是减函数,满足条件.D.f(x))=x3是奇函数,当x>0时,f(x)=x3是增函数,不满足条件.故选:C.【点评】本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的奇偶性和单调性的性质.6.(5分)已知f(x)是R上的奇函数,当x>0时,f(x)=x2﹣x,则当x<0时,f(x)=()A.﹣x2+x B.﹣x2﹣x C.x2+x D.x2﹣x【分析】设x<0,变形得到﹣x>0,根据x>0时的解析式,结合函数的奇偶性,可求得x<0时的函数解析式【解答】解:设x<0,则﹣x>0,∵当x>0时,f(x)=x2﹣x,∴f(﹣x)=(﹣x)2﹣(﹣x)=x2+x,又f(x)是定义在R上的奇函数,则f(﹣x)=﹣f(x),∴f(x)=﹣f(﹣x)=﹣x2﹣x,故选:B.【点评】本题考查了函数的性质,奇偶性的定义,属于容易题.7.(5分)若集合,,则()A.M=N B.M⊊N C.N⊊M D.M∩N=∅【分析】根据题意,对于集合M,N,2n+1属于奇数,n+2属于整数,分析可得答案.【解答】解:={x|x=(2n+1),n∈Z},={x|x=(n+2),n∈Z},2n+1属于奇数,n+2属于整数,∴M⊊N故选:B.【点评】本题考查集合间包含关系的判定,涉及集合的表示法,关键是分析集合M,N的元素.8.(5分)已知偶函数f(x)在区间[0,+∞)上是增函数,则f(﹣1)与f(a2﹣2a+3)的大小关系是()A.f(﹣1)≥f(a2﹣2a+3)B.f(﹣1)≤f(a2﹣2a+3)C.f(﹣1)>f (a2﹣2a+3)D.f(﹣1)<f(a2﹣2a+3)【分析】直接利用函数的单调性,推出不等式求解即可.【解答】解:a2﹣2a+3=(a﹣1)2+2≥2,f(﹣1)=f(1),偶函数f(x)在区间[0,+∞)上是增函数,可得:f(﹣1)<f(a2﹣2a+3).故选:D.【点评】本题考查函数的单调性的应用,函数是奇偶性的应用,考查计算能力.9.(5分)设函数f(x)=2x+1的定义域为[1,5],则函数f(2x﹣3)的定义域为()A.[1,5]B.[3,11] C.[3,7]D.[2,4]【分析】由题意知1≤2x﹣3≤5,求出x的范围并用区间表示,是所求函数的定义域.【解答】解:∵函数f(x)的定义域为[1,5],∴1≤2x﹣3≤5,解得2≤x≤4,∴所求函数f(2x﹣3)的定义域是[2,4].故选:D.【点评】本题的考点是抽象函数的定义域的求法,由两种类型:①已知f(x)定义域为D,则f(g(x))的定义域是使g(x)∈D有意义的x的集合,②已知f (g(x))的定义域为D,则g(x)在D上的值域,即为f(x)定义域.10.(5分)定义在R上的偶函数f(x)满足:对任意的x1,x2∈(﹣∞,0](x1≠x2),有<0,且f(2)=0,则不等式<0解集是()A.(﹣∞,﹣2)∪(2,+∞)B.(﹣∞,﹣2)∪(0,2)C.(﹣2,0)∪(2,+∞) D.(﹣2,0)∪(0,2)【分析】根据函数奇偶性和单调性之间的关系解不等式即可.【解答】解:∵对任意的x1,x2∈(﹣∞,0](x1≠x2),有<0,∴此时函数f(x)为减函数,∵f(x)是偶函数,∴当x≥0时,函数为增函数,则不等式<0等价为<0,即xf(x)<0,∵f(﹣2)=﹣f(2)=0,∴作出函数f(x)的草图:则xf(x)<0等价为或,即x<﹣2或0<x<2,故不等式的解集为(﹣∞,﹣2)∪(0,2).故选:B.【点评】本题主要考查不等式的解集,利用函数奇偶性和单调性之间的关系是解决本题的关键.11.(5分)已知f(x)是定义在R上的不恒为零的函数,且对任意的x,y∈R 都满足f(x•y)=x•f(y)+y•f(x),则f(x)是()A.奇函数B.偶函数C.不是奇函数也不是偶函数D.既是奇函数又是偶函数【分析】分别令y=﹣x与y=x,即可求得f(﹣x)+f(x)=0,从而得到答案.【解答】解:∵f(x•y)=x•f(y)+y•f(x),令x=y=﹣t得:f(t2)=﹣tf(﹣t)﹣tf(﹣t),①再令x=y=t得:f(t2)=tf(t)+tf(t),②由①②得:﹣tf(﹣t)﹣tf(﹣t)=tf(t)+tf(t),即2t[f(t)+f(﹣t)]=0,∵t不恒为0,∴f(t)+f(﹣t)=0,即f(x)+f(﹣x)=0,∴f(﹣x)=﹣f(x).∴f(x)是奇函数,故选:A.【点评】本题考查抽象函数及其应用,着重考查赋值法,属于中档题.12.(5分)已知定义在R上的函数f(x)满足f(﹣x)=﹣f(x),f(x﹣4)=﹣f(x),且在区间[0,2]上是减函数.若方程f(x)=k在区间[﹣8,8]上有四个不同的根,则这四根之和为()A.±4 B.±8 C.±6 D.±2【分析】由条件“f(﹣x)=﹣f(x)”函数为奇函数,由“f(x﹣4)=﹣f(x)”可得f(x+8)=f(x),即函数的周期为8,且在[0,2]上为减函数,画出示意图,由图解得答案.【解答】解:∵f(﹣x)=﹣f(x),∴f(x)为奇函数,∵f(x﹣4)=﹣f(x),即f(x+8)=f(x),∴f(x)是周期为8的周期函数,根据f(﹣x)=﹣f(x),f(x﹣4)=﹣f(x),可得f(x﹣4)=f(﹣x),∴f(x)关于直线x=﹣2对称,又根据题意知,f(x)在[0,2]上为减函数,结合以上条画出函数的示意图,由图看出,①当k>0时,四个交点中两个交点的横坐标之和为2×(﹣2)=﹣4,另两个交点的横坐标之和为2×6=12,所以四根之和为8;②当k<0时,四个交点中两个交点的横坐标之和为2×(﹣6)=﹣12,另两个交点的横坐标之和为2×2=4,所以四根之和为﹣8;综合①②可得,四根之和为±8.故选:B.【点评】本题考查了数形结合的数学思想方法.数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.二、填空题(本大题共4小题,每小题5分,共20分.)13.(5分)函数y=的定义域是{x|x>﹣2且x≠5} .【分析】根据二次根式以及分母不为0,求出函数的定义域即可.【解答】解:由题意得:,解得:x>﹣2且x≠5,故函数的定义域是{x|x>﹣2且x≠5},故答案为:{x|x>﹣2且x≠5}.【点评】本题考查了函数的定义域问题,考查二次根式的性质,是一道基础题.14.(5分)设函数f(x)=若f(x0)=1,则x0等于2或﹣1..【分析】分别由2x0﹣3=1,﹣2x0﹣2=1,求出对应的x0的值,判断即可.【解答】解:由2x0﹣3=1,解得:x0=2,符合题意,由﹣2x0﹣2=1,解得:x0=﹣1或x0=3(舍),故x0=2或﹣1,故答案为:2或﹣1.【点评】本题考查了分段函数问题,考查解方程,是一道基础题.15.(5分)已知函数y=的定义域是R,则实数m的取值范围[1,6] .【分析】通过讨论m的范围,结合二次函数的性质求出m的范围即可.【解答】解:m﹣1=0即m=1时,y=,符合题意;m﹣1≠0即m≠1时,由题意得:,解得:1<m≤6,综上,m∈[1,6],故答案为:[1,6].【点评】本题考查了二次函数的性质,考查分类讨论思想,是一道基础题.16.(5分)定义在R上的奇函数f(x)为减函数,若a+b≤0,给出下列不等式:①f(a)•f(﹣a)≤0;②f(a)+f(b)≤f(﹣a)+f(﹣b);③f(b)•f(﹣b)≥0;④f(a)+f(b)≥f(﹣a)+f(﹣b).其中正确的是①④(把你认为正确的不等式的序号全写上).【分析】根据奇函数的性质,可以证明对任意的x,都有f(x)•f(﹣x)=﹣[f (x)]2≤0,由此可得①正确而③不正确;再根据奇函数f(x)是定义在R上的减函数,结合a+b≤0可得f(a)≥f(﹣b),同理f(b)≥f(﹣a),相加即得:f(a)+f(b)≥f(﹣a)+f(﹣b),从而得到④正确而②不正确.【解答】解:∵函数f(x)为奇函数∴对任意的x∈R,都有f(﹣x)=﹣f(x),可得f(x)•f(﹣x)=﹣[f(x)]2≤0,由此可得①f(a)•f(﹣a)≤0正确,而③f(b)•f(﹣b)≥0不正确;∵a+b≤0,即a≤﹣b,且函数f(x)为定义在R上的减函数,∴f(a)≥f(﹣b),同理可得f(b)≥f(﹣a)两式相加,得:f(a)+f(b)≥f(﹣a)+f(﹣b).因此,④正确而②不正确.故答案为:①④【点评】本题给出抽象函数,在已知单调性和奇偶性的前提下,判断有关不等式是否正确,考查了函数的简单性质及其应用的知识点,属于基础题.三、解答题(本大题共6小题,共70分.)17.(10分)已知全集U=R,集合A={x|2a≤x≤a+3},B={x|x<﹣1或x≥5}.(1)若a=﹣1时,求A∩B、(∁U B)∪A;(2)若A∩B=∅,求a的取值范围.【分析】(1)a=﹣1时求出集合A,根据交集、补集和并集的定义,计算即可;(2)讨论集合A=∅和集合A≠∅,要使A∩B=∅成立求出满足条件的实数a的取值范围.【解答】解:(1)a=﹣1时,集合A={x|﹣2≤x≤2},B={x|x<﹣1或x≥5},则A∩B={x|﹣2≤x<﹣1},又全集U=R,∁U B={x|﹣1≤x<5},∴(∁U B)∪A={x|﹣2≤x<5};(2)①当2a>a+3,即a>3时,集合A=∅,A∩B=∅成立;②当a≤3时,集合A≠∅,要使A∩B=∅成立,则有,解得﹣≤a<5;综上,实数a的取值范围是{x|﹣≤a<2或a>3}.【点评】本题考查了交、并、补集的混合运算,以及集合间的包含关系判断及应用问题.18.(12分)已知集合A=,若:(1)B⊆A,B={x|m+1≤x≤2m﹣1},求实数m的范围;(2)A⊆B,B={x|m﹣6≤x≤2m﹣1,求实数m的范围.【分析】要使函数y=有意义,必需﹣x2+3x+10≥0,解得A={x|﹣2≤x≤5}.(1)B⊆A,B={x|m+1≤x≤2m﹣1},分类讨论:B=∅时,m+1>2m﹣1,解得m.B ≠∅时,,m+1≤2m﹣1,解得m范围.(2)A⊆B,B={x|m﹣6≤x≤2m﹣1},则,m﹣6≤2m﹣1,解得m范围.【解答】解:要使函数y=有意义,则﹣x2+3x+10≥0,化为:x2﹣3x ﹣10≤0,解得:﹣2≤x≤5.∴A={x|﹣2≤x≤5}.(1)B⊆A,B={x|m+1≤x≤2m﹣1},∴B=∅时,m+1>2m﹣1,解得m<﹣2.B≠∅时,,m+1≤2m﹣1,解得﹣2≤m≤3.综上可得:实数m的范围是(﹣∞,3].(2)A⊆B,B={x|m﹣6≤x≤2m﹣1},则,m﹣6≤2m﹣1,解得3≤m ≤4.∴实数m的取值范围是{m|3≤m≤4}.【点评】本题考查了集合与集合之间的关系、不等式的解法、分类讨论方法,考查了推理能力与计算能力,属于中档题.19.(12分)已知函数f(x)=,a∈(1,+∞),x∈(﹣1,+∞).(1)判断函数f(x)的单调性,并证明;(2)是否存在实数a,使得函数f(x)在[a,+∞)的最小值为a?若存在,求出a的值,若不存在,说明理由.【分析】(1)f(x)在(﹣1,+∞)上单调递增,利用导数证明即可,(2)由(1)可得f(x)在(﹣1,+∞)上单调递增,求出f(x)min=f(a)==a,解得a=1,结合a的范围,即可判断.【解答】解:(1)f(x)在(﹣1,+∞)上单调递增证明如下∵f(x)=,∴f′(x)=,∵a∈(1,+∞),∴f′(x)>0在(﹣1,+∞)上恒成立,∴f(x)在(﹣1,+∞)上单调递增;(2)由(1)可得f(x)在(﹣1,+∞)上单调递增,∵a∈(1,+∞),∴f(x)在[a,+∞)上单调递增,∴f(x)min=f(a)=,∵函数f(x)在[a,+∞)的最小值为a,∴=a,解得a=1,∵a∈(1,+∞),∴a的不存在.【点评】本题考查了导数和函数的单调性的关系,以及单调性和函数的最值的关系,属于基础题.20.(12分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式.(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润约为多少万元.(精确到1万元).【分析】(1)根据函数的模型设出函数解析式,从两个图中分别找出特殊点坐标,代入函数解析式求出两个函数解析式.(2)将企业获利表示成对产品B投资x的函数,再用换元法,将函数转化为二次函数,即可求出函数的最值.【解答】解:(1)投资为x万元,A产品的利润为f(x)万元,B产品的利润为g(x)万元,由题设f(x)=k1x,g(x)=k2,(k1,k2≠0;x≥0)由图知f(1)=,∴k1=又g(4)=,∴k2=从而f(x)=,g(x)=(x≥0)(2)设A产品投入x万元,则B产品投入10﹣x万元,设企业的利润为y万元y=f(x)+g(10﹣x)=,(0≤x≤10),令,∴(0≤t≤)当t=,y max≈4,此时x=3.75∴当A产品投入3.75万元,B产品投入6.25万元时,企业获得最大利润约为4万元.【点评】本题考查利用待定系数法求函数的解析式、考查将实际问题的最值问题转化为函数的最值问题.解题的关键是换元,利用二次函数的求最值的方法求解.21.(12分)已知函数f(x)的定义域为R,对任意的x,y∈R,都有f(x+y)=f(x)+f(y),且当x<0时,f(x)>0.(1)求证:f(x)是奇函数;(2)判断f(x)在R上的单调性,并加以证明;(3)解关于x的不等式f(x2)+3f(a)>3f(x)+f(ax),其中常数a∈R.【分析】(1)利用赋值法即可求f(0),根据函数f(x)的奇偶性的定义,利用赋值法即可得到结论;(2)根据函数单调性的定义即可判断f(x)的单调性;(3)将不等式进行等价转化,结合函数的奇偶性和单调性的性质即可得到结论.【解答】解:(1)∵f(x)对一切x,y∈R都有f(x+y)=f(x)+f(y),令x=y=0,得:f(0)=f(0)+f(0),∴f(0)=0,令y=﹣x,得f(x﹣x)=f(x)+f(﹣x)=f(0)=0,∴f(﹣x)=﹣f(x),∴f(x)是奇函数.(2)∵f(x)对一切x,y∈R都有f(x+y)=f(x)+f(y),当x<0时,f(x)>0.令x1>x2,则x2﹣x1<0,且f(x2﹣x1)=f(x2)+f(﹣x1)>0,由(1)知,f(x2)﹣f(x1)>0,∴f(x2)>f(x1).∴f(x)在R上是减函数.(3)f(2x)=f(x)+f(x)=2f(x),f(3x)=f(2x+x)=f(2x)+f(x)=3f(x),则不等式f(x2)+3f(a)>3f(x)+f(ax),等价为f(x2)+f(3a)>f(3x)+f (ax),即f(x2+3a)>f(3x+ax),∵f(x)在R上是减函数,∴不等式等价为x2+3a<3x+ax,即(x﹣3)(x﹣a)<0,当a=0时,不等式的解集为∅,当a>3时,不等式的解集为(3,a),当a<3时,不等式的解集为(a,3).(12分)【点评】本题主要考查抽象函数的应用,利用赋值法结合函数单调性和奇偶性的定义是解决本题的关键.22.(12分)已知函数f(x)=ax2﹣|x|+2a﹣1(a为实常数).(Ⅰ)若a=1,作函数f(x)的图象并写出单调区间;(Ⅱ)当a≥0时,设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;(Ⅲ)设h(x)=,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.【分析】(Ⅰ)当a=1时,利用分段函数作函数f(x)的图象并写出单调区间;(Ⅱ)当a≥0时,根据二次函数的图象和性质即可求g(a)的表达式;(Ⅲ)利用函数单调性的定义即可得到结论.【解答】解:(I)当a=1时,f(x)=x2﹣|x|+1=,作图如下单调减区间:(﹣∞,],[0,],单调增区间:[﹣,0],[,+∞),(II)当x∈[1,2]时,f(x)=ax2﹣x+2a﹣1.若a=0,则f(x)=﹣x﹣1在区间[1,2]上是减函数,g(a)=f(2)=﹣3.若a>0,则f(x)=a(x﹣)2+2a﹣﹣1,f(x)图象的对称轴是直线x=.当0<<1,即a>时,f(x)在区间[1,2]上是增函数,g(a)=f(1)=3a﹣2.当1≤≤2,即≤a≤时,g(a)=f=2a﹣﹣1.当>2,即0<a<时,f(x)在区间[1,2]上是减函数,g(a)=f(2)=6a﹣3.综上可得g(a)=.(III)当x∈[1,2]时,h(x)=ax+﹣1,在区间[1,2]上任取x1、x2,且x1<x2,则h(x2)﹣h(x1)==(x2﹣x1)=(x2﹣x1).…(11分)因为h(x)在区间[1,2]上是增函数,所以h(x2)﹣h(x1)>0.因为x2﹣x1>0,x1x2>0,所以ax1x2﹣(2a﹣1)>0,即ax1x2>2a﹣1.当a=0时,上面的不等式变为0>﹣1,即a=0时结论成立.当a>0时,x1x2>,由1<x1x2<4,得≤1,解得0<a≤1.当a<0时,x1x2<,由1<x1x2<4,得≥4,解得﹣≤a<0.所以实数a的取值范围为.【点评】本题主要考查函数单调性的判断和证明,综合考查函数的性质的应用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川省乐山市2017-2018学年高一数学上学期第一次月考试题(时间:120分钟 满分:150分) 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如果1{|}A x x >-=,那么( )A .0⊆AB .{0}∈AC .∅∈AD .{0}⊆A 2.函数f (x )=x -1x -2的定义域为( ) A .(1,+∞) B .[1,+∞) C .[1,2)D .[1,2)∪(2,+∞)3.已知全集U =R ,集合P ={x ∈N *|x <7},Q ={x |x -3>0},那么图中阴影部分表示的集合是( )A .{1,2,3,4,5,6}B .{x |x >3}C .{4,5,6}D .{x |3<x <7}4.设函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤1,2x,x >1,则f (f (3))=( )A.15 B .3 C.23D.1395.已知集合A ={0,m ,m 2−3m +2},且2∈A ,则实数m 的值为( ) A .2 B .3 C .0或3 D .0或2或36.已知3x 212xf +=-)(,则f (6)的值为( ) A .15 B .7 C .31D .177. 下列各函数在其定义域中,既是奇函数又是增函数的是 ( ) A. 1x y += B. 3x y -= B. C. x1y -= D. x x y =8.二次函数f (x )=ax 2+2a 是区间[-a ,a 2]上的偶函数,又g (x )=f (x -1),则g (0),)(23g ,g (3)的大小关系为( ) A .)(23g <g (0)<g (3) B .g (0)<)(23g <g (3) C .)(23g <g (3)<g (0) D .g (3)<)(23g <g (0)9.设函数)(x f 是定义在R 上的奇函数,当0x ≥时,有b x 2x x f 2++=)(,(b 为常数)则)(1f -等于 ( )A. -3B. 3C.1D. -110.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x 万件时的生产成本为C (x )=12x 2+2x +20(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )A .36万件B .18万件C .22万件D .9万件11.已知函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤0,1,x >0.若f (x -4)>f (2x -3),则实数x 的取值范围是( )A .(-1,+∞)B .(-∞,-1)C .(-1,4)D .(-∞,1)12.定义在R 上的偶函数f (x )在),(+∞0上是增函数,且f (3)=0,则0x xf 2>-)(的解集为( )A .(0,3)B .(3,+∞)C .(-3,0)∪(3,+∞)D .(-∞,-3)∪(0,3)第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上) 13.如果集合A={x |ax 2+2x +1=0}中只有一个元素,则a 的值是 ________.14.已知函数⎩⎨⎧≤+>=0,10,2)(x x x x x f ,若f (a )+f (1)=0,则实数a 的值等于________.15.已知f (x )=ax 3+bx -4,其中a ,b 为常数,若f (-2)=2,则f (2)的值等于________.16.对R b a ∈,,记⎩⎨⎧<≥=ba b b a a b a ,,},m a x {,则函数)}(,max{)(R x 1x x 1x x f 2∈+-+=的最小值为________.三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分) 已知全集U =R ,集合A ={y |y =3-x 2,x ∈R ,且x ≠0},集合B 是函数y =x -2+25-x的定义域,集合C ={x |5-a <x <a }. (1)求集合A ∪(∁U B );(2)若C ⊆(A ∩B ),求实数a 的取值范围.18.(本小题满分12分) 已知函数f (x )=2x +1x +1,(1)判断函数在区间(-1,+∞)上的单调性,并用定义证明你的结论; (2)求该函数在区间[1,4]上的最大值与最小值.19. (本小题满分12分) 已知奇函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x >0,0,x =0,x 2+mx ,x <0.(1)求实数m 的值,并画出)(x f y =的图像;(2)若函数f (x )在区间[-1,a -2]上单调递增,求实数a 的取值范围.20.(本小题满分12分)某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖挂4节车厢,一天能来回16次,如果该车每次拖挂7节车厢,则每天能来回10次.(1)若每天来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数的解析式; (2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每次拖挂多少节车厢才能使运营人数最多?并求出每天最多运营人数.21.(本小题满分12分)已知函数()21f x ax bx =++,(,a b 为实数),x R ∈,()()(),0,0f x x F x f x x >⎧⎪=⎨-<⎪⎩.(1)若()10f -=,且函数()f x 的值域为[)0,+∞,求()F x 的解析式;(2)在(1)的条件下,当[]2,2x ∈-时,()()g x f x kx =-是单调函数,求实数k 的取值范围.22. (本小题满分12分)奇函数f(x)的定义域为R ,且在[)+∞,0上为增函数,那么是否存在m ,使)()()(0f t 2m 4f 4t 2f 2>-+-对任意[]10t ,∈均成立?若存在,求出m 的取值范围;若不存在,说明理由。
沫若中学高一上期第一次月考数学试题答案(时间:120分钟 满分:150分) 第Ⅰ卷 (选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如果1{|}A x x >-=,那么( )A .0⊆AB .{0}∈AC .∅∈AD .{0}⊆A 【答案】D 2.函数f (x )=x -1x -2的定义域为( ) A .(1,+∞) B .[1,+∞) C .[1,2)D .[1,2)∪(2,+∞)解析:选D.根据题意有⎩⎪⎨⎪⎧x -1≥0,x -2≠0,解得x ≥1且x ≠2.3.已知全集U =R ,集合P ={x ∈N *|x <7},Q ={x |x -3>0},那么图中阴影部分表示的集合是( )A .{1,2,3,4,5,6}B .{x |x >3}C .{4,5,6}D .{x |3<x <7}答案: C P ={1,2,3,4,5,6},Q ={x |x >3},则阴影部分表示的集合是P ∩Q ={4,5,6}.4.设函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤1,2x,x >1,则f (f (3))=( )A.15 B .3 C.23D.139答案:D 由题意得f (3)=23,从而f (f (3))=f (23)=(23)2+1=139.5.已知集合A ={0,m ,m 2−3m +2},且2∈A ,则实数m 的值为( ) A .2 B .3 C .0或3 D .0或2或3【答案】B【解析】若m =2,则m 2−3m +2=0,与集合中元素的互异性矛盾,∴m ≠2,m 2−3m +2=2,则m =3或m =0(舍去).6.已知3x 212xf +=-)(,则f (6)的值为( ) A .15 B .7 C .31D .17解析:选C.令x 2-1=t ,则x =2t +2. 将x =2t +2代入3x 212xf +=-)(得f (t )=2(2t +2)+3=4t +7. 所以f (x )=4x +7,所以f (6)=4×6+7=31. 7.下列各函数在其定义域中,既是奇函数又是增函数的是 ( )A. 1x y +=B. 3x y -= C. x1y -= D. x x y = 答案: D8.二次函数f (x )=ax 2+2a 是区间[-a ,a 2]上的偶函数,又g (x )=f (x -1),则g (0),)(23g ,g (3)的大小关系为( ) A .)(23g <g (0)<g (3) B .g (0)<)(23g <g (3) C .)(23g <g (3)<g (0) D .g (3)<)(23g <g (0)解析:选A.由题意得⎩⎪⎨⎪⎧a ≠0,-a =-a 2,解得a =1,所以f (x )=x 2+2,所以g (x )=f (x -1)=(x -1)2+2.因为函数g (x )的图象关于直线x =1对称,所以g (0)=g (2). 又因为函数g (x )=(x -1)2+2在区间[1,+∞)上单调递增,所以g ⎝ ⎛⎭⎪⎫32<g (2)<g (3),所以g ⎝ ⎛⎭⎪⎫32<g (0)<g (3). 9.设函数)(x f 是定义在R 上的奇函数,当0x ≥时,有b x 2x x f 2++=)(,(b 为常数)则)(1f -等于 (A )A. -3B. 3C.1D. -110.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品x 万件时的生产成本为C (x )=12x 2+2x +20(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为 ( B )A .36万件B .18万件C .22万件D .9万件11.已知函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≤0,1,x >0.若f (x -4)>f (2x -3),则实数x 的取值范围是( )A .(-1,+∞)B .(-∞,-1)C .(-1,4)D .(-∞,1)解析:选C .f (x )的图象如图.由图知若f (x -4)>f (2x -3),则⎩⎪⎨⎪⎧x -4<0,x -4<2x -3,解得-1<x <4.故实数x 的取值范围是(-1,4).12.定义在R 上的偶函数f (x )在),(+∞0上是增函数,且f (3)=0,则0x xf 2>-)(的解集为( )A .(0,3)B .(3,+∞)C .(-3,0)∪(3,+∞)D .(-∞,-3)∪(0,3) 答案: C第Ⅱ卷 (非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上) 13.如果集合A={x |ax 2+2x +1=0}中只有一个元素,则a 的值是 ( B ) A .0 B .0 或1 C .1 D .不能确定14.已知函数f (x )=⎩⎪⎨⎪⎧2x ,x >0,x +1,x ≤0,若f (a )+f (1)=0,则实数a 的值等于________.解析:若a >0,则2a +2=0,得a =-1,与a >0矛盾,舍去;若a ≤0,则a +1+2=0,得a =-3,所以实数a 的值等于-3.答案:-315.已知f (x )=ax 3+bx -4,其中a ,b 为常数,若f (-2)=2,则f (2)的值等于________. 解析:设g (x )=ax 3+bx ,显然g (x )为奇函数,则f (x )=ax 3+bx -4=g (x )-4,于是f (-2)=g (-2)-4=-g (2)-4=2,所以g (2)=-6,所以f (2)=g (2)-4=-6-4=-10.答案:-1016.对R b a ∈,,记⎩⎨⎧<≥=ba b b a a b a ,,},m a x {,则函数)}(,max{)(R x 1x x 1x x f 2∈+-+=的最小值为________.答案:1三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分) 已知全集U =R ,集合A ={y |y =3-x 2,x ∈R ,且x ≠0},集合B 是函数y =x -2+25-x的定义域,集合C ={x |5-a <x <a }. (1)求集合A ∪(∁U B );(2)若C ⊆(A ∩B ),求实数a 的取值范围. 解:(1)由已知得A ={x |x <3},B ={x |2≤x <5},∴∁U B ={x |x <2,或x ≥5},∴A ∪(∁U B )={x |x <3,或x ≥5}=(-∞,3)∪[5,+∞). (2)由(1)知A ∩B ={x |2≤x <3},当C =∅时,满足C ⊆(A ∩B ),此时5-a ≥a ,解得a ≤52;当C ≠∅时,要满足C ⊆(A ∩B ), 则⎩⎪⎨⎪⎧5-a <a ,5-a ≥2,a ≤3,解得52<a ≤3.综上可得a ≤3.18.(本小题满分12分) 已知函数f (x )=2x +1x +1,(1)判断函数在区间(-1,+∞)上的单调性,并用定义证明你的结论; (2)求该函数在区间[1,4]上的最大值与最小值. 解:(1)函数f (x )在(-1,+∞)上是增函数. 任取x 1,x 2∈(-1,+∞),且x 1<x 2,f (x 1)-f (x 2)=2x 1+1x 1+1-2x 2+1x 2+1=x 1-x 2x 1+x 2+,∵x 1-x 2<0,(x 1+1)(x 2+1)>0, 所以f (x 1)-f (x 2) <0,即f (x 1)<f (x 2), 所以函数f (x )在(-1,+∞)上是增函数.(2)由(1)知函数f (x )在[1,4]上是增函数,最大值f (4)=95,最小值f (1)=32.19. (本小题满分12分) 已知奇函数f (x )=⎩⎪⎨⎪⎧-x 2+2x ,x >0,0,x =0,x 2+mx ,x <0.(1)求实数m 的值,并画出)(x f y =的图像;(2)若函数f (x )在区间[-1,a -2]上单调递增,求实数a 的取值范围.解:(1)当x <0时,-x >0,∴f (-x )=-(-x )2+2(-x )=-x 2-2x ,又f (x )是奇函数,∴f (-x )=-f (x ),于是当x <0时,f (x )=x 2+2x =x 2+mx ,∴m =2.(2)结合f (x )的图象(图略)可知,要使f (x )在[-1,a -2]上单调递增,需⎩⎪⎨⎪⎧a -2>-1,a -2≤1,解得1<a ≤3.故实数a 的取值范围为(1,3].20.(本小题满分12分)某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖挂4节车厢,一天能来回16次,如果该车每次拖挂7节车厢,则每天能来回10次.(1)若每天来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数的解析式; (2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每次拖挂多少节车厢才能使运营人数最多?并求出每天最多运营人数.解:(1)设每天来回y 次,每次拖挂x 节车厢,由题意设y =kx +b (k ≠0),当x =4时,y =16,当x =7时,y =10,得到16=4k +b ,10=7k +b ,解得k =-2,b =24,所以y =-2x +24.(2)设每天来回y 次,每次拖挂x 节车厢,由题意知,每天拖挂车厢最多时,运营人数最多,设每天拖挂S 节车厢,则S =xy =x (-2x +24)=-2x 2+24x =-2(x -6)2+72,所以当x =6时,S max =72,此时y =12,则每日最多运营人数为110×72=7 920(人).故这列火车每天来回12次,才能使运营人数最多,每天最多运营人数为7 920. 21.(本小题满分12分)设集合{}{}2|8150,|10A x x x B x ax =-+==-=.已知函数()21f x ax bx =++,(,a b 为实数),x R ∈,()()(),0,0f x x F x f x x >⎧⎪=⎨-<⎪⎩.(1)若()10f -=,且函数()f x 的值域为[)0,+∞,求()F x 的解析式;(2)在(1)的条件下,当[]2,2x ∈-时,()()g x f x kx =-是单调函数,求实数k 的取值范围.【答案】(1)()()()221,010x x F x x x ⎧+>⎪=⎨-+<⎪⎩,;(2)(][),26,-∞-+∞.【解析】∵当[]2,2x ∈-时,()()g x f x kx =-是单调函数, ∴222k -≤-或222k -≥,即2k ≤-或6k ≥, 则实数k 的取值范围为(][),26,-∞-+∞.22.(本小题满分12分)奇函数f(x)的定义域为R ,且在[)+∞,0上为增函数,那么是否存在m ,使)()()(0f t 2m 4f 4t 2f 2>-+-对任意[]10t ,∈均成立?若存在,求出m 的取值范围;若不存在,说明理由。
