中值定理证明
中值定理证明方法总结

设 f (x) , g(x) , h(x) 都在 (a , b) 上连续 , 且在 [a , b] 内可导, 证明至少存在一点 ξ ∈(a , b) , 使
f (a) f (b) f ′(ξ ) g(a) g(b) g′(ξ ) = 0 h(a) h(b) h′(ξ )
说明 若取 h(x) ≡1, g(x) = x , f (a) = f (b) ,即为罗尔定理; 若取 h(x) ≡1, g(x) = x , 即为拉格朗日中值定理; 若取 h(x) ≡1, g′(x) ≠ 0, 即为柯西中值定理; ( 自己验证 )
柯西 目录 上页 下页 返回 结束
f (b) − f (a) F(x) − f (x) 证: 作辅助函数 ϕ(x) = F(b) − F(a) 则 (x) 在[a,b]上 续, 在(a,b)内 导, 且 ϕ 连 可 f (b)F(a) − f (a)F(b) ϕ(a) = = ϕ(b) F(b) − F(a) 使 由罗尔定理知, 至少存在一点 即 f (b) − f (a) f ′(ξ ) = . F(b) − F(a) F′(ξ ) 思考: 思考 柯西定理的下述证法对吗 ? ∵ f (b) − f (a) = f ′(ξ )(b − a), ξ ∈(a, b) 两个 ξ 不 F(b) − F(a) = F′(ξ )(b − a), ξ ∈(a, b) 一定相同 上面两式相比即得结论. 错!
1 f (n) (x )(x − x )n +⋯+ 0 0 n!
f (b) − f (a) f ′(ξ ) = F(b) − F(a) F′(ξ )
证明中值定理的方法
直观分析 辅助函数法 逆向分析 例如, 证明拉格朗日定理 : f (b) − f (a) = f ′(ξ )(b − a) 要构造满足罗尔定理条件的辅助函数 . y = f (x) 方法1. 方法 直观分析 由图可知 , 设辅助函数
高等数学-中值定理证明
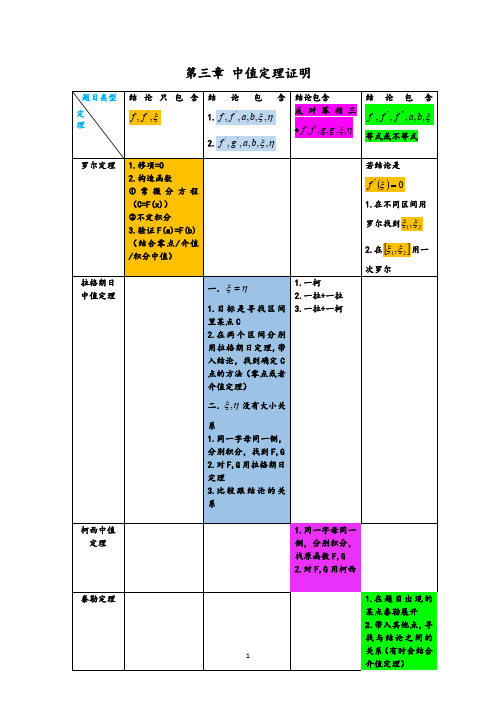
若结论是
f '' 0
1.在不同区间用
罗尔找到 1,2
2.在 1,2 用一
次罗尔
柯西中值 定理
1.同一字母同一 侧,分别积分, 找原函数 F,G 2.对 F,G 用柯西
泰勒定理
1.在 题 目 出 现 的
某点泰勒展开
2.带入其他点,寻
找与结论之间的
1
关系(有时会结合
介值定理)
1.闭区间上连续函数定理 ① ② ③ ④ 2.微分中值定理 ①
(1) 存在(0,1)内两个不同的点 , ,使得 f ' ( ) f ' () 2 .
(2)
存在(0,1)内两个不同的点 , ,使得
1 f ' ( )
1 f ' ()
2 .
(3) 存在(0,1)内两个不同的点 , ,使得 f ' ( ) f ' () 1 .
f ' ( ) (4) 存在(0,1)内两个不同的点 , 及大于零的常数 ,使得 f ' () (5) 对于任意的正整数 n,存在(0,1)内两个不同的点 , 及常数 0 ,
3
5.若 f (x) 在[0,1] 上可导,且当 x [0,1] 时有 0 f (x) 1,且 f (x) 1,证明:在 (0,1) 内有且仅有一个点 使得 f ( )
6.设 f (x) 在[0,1]上连续,在(0,1)内可导,且 f (0) = f (1) =0, f (1 ) =1。试证 2
②
③
④
3.积分中值定理 ① ②
不等式证明思路 构造函数(利用极值) 拉格朗日中值定理 函数凹凸性定义
2
1.若 f (x) 在 [a,b] 上连续,在 (a,b) 上可导, f (a) f (b) 0 ,证明: R , (a,b) 使得: f ( ) f ( ) 0
利用中值定理证明积分不等式

利用中值定理证明积分不等式
中值定理是计算积分的一种方法,它是以定积分为例进行证明的。
这句话可以简单理解为:如果一个函数在某一个闭区间上可以积分,那么该闭区间上这个函数的积分与函数在这个闭区间上的中值成正比。
假设函数f(x)在闭区间[a,b]上可以积分,那么可以用中值定理在区间[a,b]上证明积分不等式:
设置M即f(x)在[a,b]区间上的一阶导数的极值点,则根据中值定理可得:
∫a b f(x)dx=f(M)∫a b dx
即f(x)的积分∫a b f(x)dx等于函数在区间[a,b]上的中值f(M)乘以[a,b]区间的长度,此时由于f(M)为最大值,则记∫a b f(x)dx=M(b-a),于是得出结论:
∫a b f(x)dx≤M(b-a)
当然积分不等式也可以用最大值和最小值对函数f(x)进行比较来证明:
设置N即f(x)在[a,b]区间上的最小值,则根据最大值定理可得:
∫a b f(x)dx≥N(b-a)
有了以上两个结论,就可以推出:
N(b-a) ≤ ∫a b f(x)dx≤M(b-a)
由此可见,中值定理是一种有用的工具,它能够证明闭区间上某一函数的积分与该函数在闭区间上的中值成正比,也能证明积分不等式,即积分的最小值与该函数在闭区间上的最小值的乘积的一定不等于积分的最大值与该函数在闭区间上的最大值的乘积,这就是中值定理所证明的积分不等式。
一元函数的积分中值定理

一元函数的积分中值定理1.定理表述:对于连续函数f(x),如果它在区间[a,b]上连续,那么存在一个点c∈[a, b],使得积分值等于函数在该点的值与区间长度的乘积,即∫[a,b]f(x)dx = f(c)·(b - a)。
2.证明:根据连续函数的性质,在区间[a,b]上一定可以找到最大值M和最小值m。
从而有:m·(b - a) ≤ ∫[a,b]f(x)dx ≤ M·(b - a)如果f(x)是一个常数函数,那么不论c在区间[a,b]上的哪个位置,定理都成立。
因为常数函数的积分就是常数的倍数。
如果f(x)不是常数函数,那么在区间[a,b]上至少有一个点x0,使得f(x0)>m。
令c = x0,那么f(c)·(b - a) ≥ m·(b - a) ≤ ∫[a,b]f(x)dx 同理,可以找到另一个点x1,使得f(x1) < M。
令c = x1,有f(c)·(b - a) ≤ M·(b - a) ≥ ∫[a,b]f(x)dx因此,对于连续函数f(x),在区间[a,b]上,必然存在一些点c∈[a,b],使得积分值等于函数在该点的值与区间长度的乘积。
3.特殊情况:当积分值为0时,可以推论出函数在整个区间[a,b]上都为0。
4.应用:(1)利用积分中值定理,可以证明平均值定理:对于连续函数f(x),在区间[a,b]上,存在一些点c∈[a,b],使得f(c)等于函数在该区间上的平均值.(2) 积分中值定理是Rolle定理的推广,Rolle定理是积分中值定理在导数为0处的特殊情况。
(3) 应用积分中值定理,可以证明柯西-施瓦茨(Cauchy-Schwarz)不等式等一些重要的数学定理。
总结:积分中值定理是微积分中非常重要的定理,它建立了连续函数积分值与函数在其中一点的关系。
通过这一定理,我们可以推导出许多重要的数学定理,并且应用于实际问题的求解中,具有非常重要的意义。
高等数学常见中值定理证明及应用

中值定理首先我们来看看几大定理:1、 介值定理:设函数f(x)在闭区间[a,b]上连续,且在该区间的端点取不同的函数值f(a)=A及f(b)=B ,那么对于A 与B 之间的任意一个数C ,在开区间(a,b)内至少有一点ξ使得f(ξ)=C(a<ξ<b).Ps:c 是介于A 、B 之间的,结论中的ξ取开区间。
介值定理的推论:设函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有最大值M ,最小值m,若m ≤C ≤M,则必存在ξ∈[a,b], 使得f(ξ)=C 。
(闭区间上的连续函数必取得介于最大值M 与最小值m 之间的任何值。
此条推论运用较多)Ps :当题目中提到某个函数f(x),或者是它的几阶导函数在某个闭区间上连续,那么该函数或者其几阶导函数必可以在该闭区间上取最大值和最小值,那么就对于在最大值和最小值之间的任何一个值,必存在一个变量使得该值等于变量处函数值。
2、 零点定理:设函数f(x)在闭区间[a,b]上连续,且f(a)与f(b)异号,即f(a).f(b)<0,那么在开区间内至少存在一点ξ使得f(ξ)=0.Ps:注意条件是闭区间连续,端点函数值异号,结论是开区间存在点使函数值为0.3、 罗尔定理:如果函数f(x)满足:(1)、在闭区间[a,b]上连续; (2)、在开区间(a,b)内可导; (3)、在区间端点处函数值相等,即f(a)=f(b).那么在(a,b)内至少有一点ξ(<a ξ<b),使得f`(x)=0;4、 拉格朗日中值定理:如果函数f(x)满足:(1)、在闭区间[a,b]上连续; (2)、在开区间(a,b)内可导;那么在(a,b)内至少有一点ξ(<a ξ<b),使得 f(b)-f(a)=f`(ξ).(b-a).5、 柯西中值定理:如果函数f(x)及g(x)满足(1)、在闭区间[a,b]上连续; (2)、在开区间(a,b)内可导; (3)、对任一x(a<x<b),g`(x)≠0,那么在(a,b)内至少存在一点ξ,使得)`()`()()()()(ξξg f a g b g a f b f =--Ps :对于罗尔定理、拉格朗日中值定理、柯西中值定理结论都是开开区间内取值。
拉格朗日中值定理证明及其应用

拉格朗日中值定理证明及其应用拉格朗日中值定理是微积分中的一个重要定理,它指出了在一个区间上连续的函数中,存在一个点,该点的导数等于该函数在区间端点处的导数的平均值。
这个定理由法国数学家约瑟夫·路易·拉格朗日在18世纪提出并证明,成为微积分中的经典定理之一。
它在证明和应用中都具有重要的意义。
本文将重点介绍拉格朗日中值定理的证明方法和其在实际应用中的具体例子。
我们来看一下拉格朗日中值定理的表述:设函数f(x)在闭区间[a, b]上连续,在开区间(a, b)上可导,那么在区间(a, b)内至少存在一个点ξ,使得f(b)-f(a)=f'(ξ)(b-a)。
这个定理告诉我们,对于任意一个连续函数,在某个区间上一定存在某个点,该点的导数等于函数在该区间两端点处的导数的平均值。
这个平均值就是f(b)-f(a)/(b-a)。
那么,我们来看一下拉格朗日中值定理的证明方法。
我们可以通过定义函数g(x)=f(x)-((f(b)-f(a))/(b-a))(x-a),来说明g(x)在区间[a, b]上满足拉格朗日定理的条件。
然后,我们可以通过中值定理证明g(x)在[a, b]上满足罗尔定理的条件,即满足在区间[a, b]上可导,并且在端点处函数值相等。
然后根据罗尔定理,我们可以得出存在一点ξ,使得g'(ξ)=0,即f'(ξ)=(f(b)-f(a))/(b-a),这就是拉格朗日中值定理的结论。
拉格朗日中值定理的证明看似简单,但却包含了微积分中的许多重要思想和方法,如中值定理的迭代运用、利用辅助函数进行构造、间接证明等等,对于学习微积分的同学来说,是一个很好的练习和思考题目。
接下来,我们来看一下拉格朗日中值定理在实际应用中的具体例子。
我们可以通过该定理证明一些函数的性质,比如函数在某个区间内的增减性、凹凸性等。
该定理在求解一些实际问题时也具有重要作用,比如在物理学中来研究质点的位移、速度、加速度之间的关系时,就可以利用拉格朗日中值定理来进行分析。
重积分中值定理证明

重积分中值定理证明一、重积分中值定理内容(以二元函数为例)设 f(x,y) 在闭区域 D 上连续,D 的面积为S,则在 D 上至少存在一点(ξ,eta),使得∬_D f(x,y)dσ = f(ξ,eta)S二、证明过程(一)利用连续函数的性质1. 存在最大值和最小值- 因为 f(x,y) 在闭区域 D 上连续,根据闭区域上连续函数的性质,f(x,y) 在 D 上必能取得最大值 M 和最小值 m。
- 即对于任意(x,y)∈ D,有m≤slant f(x,y)≤slant M。
2. 估计积分值的范围- 由重积分的性质,对于∬_D f(x,y)dσ,有- mS≤slant∬_D f(x,y)dσ≤slant MS,其中S 是区域 D 的面积。
3. 应用介值定理- 因为mS≤slant∬_D f(x,y)dσ≤slant MS,所以(∬_D f(x,y)dσ)/(S)介于 m 和M 之间。
- 又因为 f(x,y) 在 D 上连续,根据连续函数的介值定理,在 D 上至少存在一点(ξ,eta),使得f(ξ,eta)=(∬_D f(x,y)dσ)/(S)。
- 即∬_D f(x,y)dσ = f(ξ,eta)S。
(二)以一元函数定积分中值定理为基础(拓展思路)1. 将重积分转化为累次积分(以矩形区域D = [a,b]×[c,d]为例)- 根据重积分化为累次积分的定理,∬_D f(x,y)dσ=∫_a^b dx∫_c^d f(x,y)dy。
- 对于固定的x∈[a,b],令F(x)=∫_c^d f(x,y)dy。
2. 应用一元函数定积分中值定理- 由于F(x) 在[a,b]上连续(因为f(x,y) 连续),根据一元函数定积分中值定理,存在ξ∈[a,b],使得∫_a^b F(x)dx = F(ξ)(b - a)。
- 即∫_a^b dx∫_c^d f(x,y)dy=∫_c^d f(ξ,y)dy(b - a)。
求中值定理证明的几种构造函数的方法

求中值定理证明的几种构造函数的方法1 原函数法此法是将结论变形并向罗尔定理的结论靠拢,凑出适当的原函数作为辅助函数,主要思想分为四点1)将要证的结论中的换成;(2)通过恒等变形将结论化为易消除导数符号的形式;(3)用观察法或积分法求出原函数(等式中不含导数符号),并取积分常数为零;(4)移项使等式一边为零,另一边即为所求辅助函数 . 例1:证明柯西中值定理分析:在柯西中值定理的结论中令,得,先变形为再两边同时积分得,令,有故为所求辅助函数. 例2:若, , ,…, 是使得的实数.证明方程在(0,1)内至少有一实根. 证:由于并且这一积分结果与题设条件和要证明的结论有联系,所以设(取),则 1)在[0,1]上连续 2)在(0,1)内可导 3) =0,故满足罗尔定理的条件,由罗尔定理,存在使,即亦即 . 这说明方程在(0,1)内至少有实根.2 积分法对一些不易凑出原函数的问题,可用积分法找相应的辅助函数. 例3:设在[1,2]上连续,在(1,2)内可导,, .证明存在使 . 分析:结论变形为,不易凑成 .我们将换为,结论变形为,积分得: ,即,从而可设辅助函数为,有 .本题获证. 例4:设函数,在上连续,在内可微, .证明存在,使得: . 证:将变形为,将换为,则,两边关于积分,得: ,所以,其中,由可得 .由上面积分的推导可知,为一常数,故其导数必为零,从整个变形过程知,满足这样结论的的存在是不成问题的.因而令,易验证其满足罗尔定理的条件,原题得证.3 几何直观法此法是通过几何图形考查两函数在区间端点处函数值的关系,从而建立适当的辅助函数. 例5:证明拉格朗日中值定理. 分析:通过弦两个端点的直线方程为,则函数与直线AB的方程之差即函数在两个端点处的函数值均为零,从而满足罗尔定理的条件故上式即为要做辅助函数. 例6:若在上连续且 .试证在内至少有一点,使 . 分析:由图可看出,此题的几何意义是说,连续函数的图形曲线必跨越这一条直线,而两者的交点的横坐标,恰满足 .进而还可由图知道,对上的同一自变量值,这两条曲线纵坐标之差构成一个新的函数,它满足 <0, >0,因而符合介值定理的条件.当为的一个零点时,恰等价于 .因此即知证明的关键是构造辅助函数 .4 常数k值法此方法构造辅助函数的步骤分为以下四点: 1)将结论变形,使常数部分分离出来并令为 . 2)恒等变形使等式一端为及构成的代数式,另一端为及构成的代数式. 3)观察分析关于端点的表达式是否为对称式.若是,则把其中一个端点设为,相应的函数值改为 . 4)端点换变量的表达式即为辅助函数 . 例7:设在上连续,在内可导,,试证存在一点,使等式成立. 分析:将结论变形为,令,则有,令,可得辅助函数 . 例8:设在上存在,在,试证明存在,使得 . 分析:令,于是有,上式为关于,,三点的轮换对称式,令(or: ,or: ),则得辅助函数 .5 分析法分析法又叫倒推法,就是从欲证的结论出发借助于逻辑关系导出已知的条件和结论. 例9:设函数在[0,1]上连续,在(0,1)内可导,证明在(0,1)内存在一点,使得 . 分析:所要证的结论可变形为: ,即,因此可构造函数,则对与在[0,1]上应用柯西中值定理即可得到证明. 例10:设函数在[0,1]上连续,在(0,1)内可导,且 =0,对任意有 .证明存在一点使(为自然数)成立. 分析:欲证其成立,只需证由于对任意有,故只需证: 即,于是引入辅助函数(为自然数). 例11:设函数在区间[0,+ ]上可导,且有个不同零点: .试证在[0,+ ]内至少有个不同零点.(其中,为任意实数)证明:欲证在[0,+ )内至少有个不同零点,只需证方程 =0在[0,+ ]内至少有个不同实根. 因为,,,故只需证方程在内至少有个不同实根. 引入辅助函数,易验证在区间[ ],[ ],…,[ ]上满足罗尔定理的条件,所以,分别在这个区间上应用罗尔定理,得,其中且以上说明方程在[ ] [ ] … [ ] [0,+ ]内至少有个不同实根,从而证明了方程 =0在[0,+ ]内至少有个不同实根。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中值定理首先我们来瞧瞧几大定理:1、 介值定理:设函数f(x)在闭区间[a,b]上连续,且在该区间的端点取不同的函数值f(a)=A 及f(b)=B,那么对于A 与B 之间的任意一个数C,在开区间(a,b)内至少有一点ξ使得f(ξ)=C(a<ξ<b)、Ps:c 就是介于A 、B 之间的,结论中的ξ取开区间。
介值定理的推论:设函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有最大值M,最小值m,若m ≤C ≤M,则必存在ξ∈[a,b], 使得f(ξ)=C 。
(闭区间上的连续函数必取得介于最大值M 与最小值m 之间的任何值。
此条推论运用较多)Ps :当题目中提到某个函数f(x),或者就是它的几阶导函数在某个闭区间上连续,那么该函数或者其几阶导函数必可以在该闭区间上取最大值与最小值,那么就对于在最大值与最小值之间的任何一个值,必存在一个变量使得该值等于变量处函数值。
2、 零点定理:设函数f(x)在闭区间[a,b]上连续,且f(a)与f(b)异号,即f(a)、f(b)<0,那么在开区间内至少存在一点ξ使得f(ξ)=0、Ps:注意条件就是闭区间连续,端点函数值异号,结论就是开区间存在点使函数值为0、3、 罗尔定理:如果函数f(x)满足:(1)、在闭区间[a,b]上连续; (2)、在开区间(a,b)内可导;(3)、在区间端点处函数值相等,即f(a)=f(b)、那么在(a,b)内至少有一点ξ(<a ξ<b),使得f`(x)=0;4、 拉格朗日中值定理:如果函数f(x)满足:(1)、在闭区间[a,b]上连续; (2)、在开区间(a,b)内可导;那么在(a,b)内至少有一点ξ(<a ξ<b),使得 f(b)-f(a)=f`(ξ)、(b-a)、5、 柯西中值定理:如果函数f(x)及g(x)满足(1)、在闭区间[a,b]上连续; (2)、在开区间(a,b)内可导; (3)、对任一x(a<x<b),g`(x)≠0,那么在(a,b)内至少存在一点ξ,使得)`()`()()()()(ξξg f a g b g a f b f =--Ps:对于罗尔定理、拉格朗日中值定理、柯西中值定理结论都就是开开区间内取值。
6、 积分中值定理:若函数f(x)在[a,b]上连续,则至少存在一点],[b a ∈ξ使得)()()(a b f dx x f ba-=⎰ξPs:该定理课本中给的结论就是在闭区间上成立。
但就是在开区间上也就是满足的,下面我们来证明下其在开区间内也成立,即定理变为:若函数f(x)在[a,b]上连续,则至少存在一点),(b a ∈ξ使得)()()(a b f dx x f ba-=⎰ξ证明:设⎰=xadx x f x F )()(,],[b a x ∈因为)(x f 在闭区间上连续,则)(x F 在闭区间上连续且在开区间上可导(导函数即为)(x f )。
则对)(x F 由拉格朗日中值定理有:),(b a ∈∃ξ使得ab dx x f ab a F b F F ba-=--=⎰)()()()`(ξ而)()`(ξξf F = 所以),(b a ∈∃ξ使得)()()(a b f dx x f ba-=⎰ξ。
在每次使用积分中值定理的时候,如果想在开区间内使用,我们便构造该函数,运用拉格朗日中值定理来证明下使其在开区间内成立即可。
千万不可直接运用,因为课本给的定理就是闭区间。
定理运用:1、设)(x f 在[0,3]上连续,在(0,3)内存在二阶导函数,且⎰+==2)3()2()()0(2f f dx x f f 、证明:(1))2,0(∈∃η使)0()(f f =η(2))3,0(∈∃ξ使0)``(=ξf证明:先瞧第一小问题:如果用积分中指定理似乎一下子就出来了,但有个问题就就是积分中值定理就是针对闭区间的。
有的人明知这样还硬就是这样做,最后只能就是0分。
具体证明方法在上面已经说到,如果要在开区间内用积分中指定理,必须来构造函数用拉格朗日中值定理证明其在开区间内符合。
(1)、令]2,0[),()(0∈=⎰x x F dt t f x则由题意可知)2,0(]2,0[)(上连续,在x F 内可导、则对)(x F 由拉格朗日中值定理有:2)0()2()`()2,0(F F F -=∈∃ηη使)2,0(),0(2)()(2∈==∴⎰ηηf dt t f f(2)、对于证明题而言,特别就是真题第一问证明出来的结论,往往在第二问中都会有运用,在做第二问的时候我们不要忘记了第一问证明出来的东西,我们要时刻注意下如何将第一问的东西在第二问中进行运用:第二问就是要证明存在点使得函数二阶倒数为0,这个很容易想到罗尔定理来证明零点问题,如果有三个函数值相等,运用两次罗尔定理那不就解决问题啦,并且第一问证明出来了一个等式,如果有f(a)=f(b)=f(c),那么问题就解决了。
第一问中已经在(0,2)内找到一点,那么能否在(2,3)内也找一点满足结论一的形式呢,有了这样想法,就得往下寻找了,)3()2()0(2f f f +=,瞧到这个很多人会觉得熟悉的,与介值定理很像,下面就来证明:]3,0[)(在x f Θ上连续,则在]3,2[上也连续,由闭区间上连续函数必存在最大值与最小值,分别设为M,m;则.)3(,)2(M f m M f m ≤≤≤≤ 从而,M f f m ≤+≤2)3()2(,那么由介值定理就有:)0(2)3()2()(],3,2[f f f c f c =+=∈∃使]3,2[),2,0(),()()0(∈∈==∴c c f f f ηη则有罗尔定理可知:0)`(),,0(11=∈∃ξηξf ,0)`(),,(22=∈∃ξηξf c 0)``(),3,0(),(21=⊆∈∃ξξξξfPs:本题记得好像就是数三一道真题,考察的知识点蛮多,涉及到积分中值定理,介值定理,最值定理,罗而定理,思路清楚就会很容易做出来。
2、设f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1、 证明:ξξξ-=∈∃1)()1,0()1(f 使得、1)`()`(),1,0()2(=⋅∈∃ηξξηf f 使得、两个不同点、 本题第一问较简单,用零点定理证明即可。
(1)、首先构造函数:]1,0[,1)()(∈-+=x x x f x F1)1()1(11)0()0(==-=-=f F f F01)1()0(<-=⋅F F Θ由零点定理知:ξξξξ-==∈∃1)(,0)()1,0(f F 即使得(2)、初瞧本问貌似无从下手,但就是我们始终要注意,对于真题这么严谨的题目,她的设问就是一问紧接一问,第一问中的结论或多或少总会在第二问中起到作用。
在想想高数定理中的就这么些定理,第一问用到的零点定理,从第二问的结论来瞧,也更本不涉及什么积分问题,证明此问题也只可能从三大中值定理出发,具体就是哪个定理,得瞧自己的情况,做题有时候就就是慢慢试,一种方法行不通,就换令一种方法,有想法才就是最重要的,对于一道题,您没想法,便无从下手。
另外在说一点,在历年证明题中,柯西中值定理考的最少。
本题结论都涉及一阶倒数,乘积之后为常数,很可能就是消去了变为1(您题目做多了,肯定就知道事实就就是这样)、并且第一问中0与1之间夹了个ξ,如果我们在0与ξ,ξ与1上对)(x f 运用拉格朗日中值定理似乎有些线索。
写一些简单步骤,具体详细步骤就不多写了:将第一问中)(ξf 代入即可。
)1,(,11)()1()`(),0(,1)0()()`(ξζξξξξζξηξξξξη∈-=--=∈-=-=f f f f f f)1,0()1,(),1,0(),0(,1)`()`(⊆∈⊆∈=⋅∴ξζξηηξf fPs:本题就是05年数一的一道真题,第一问就是基本问题,送分的,第二问有一定区分度,对定理熟练的会容易想到拉格朗日定理,不熟练的可能难以想到方法。
做任何题,最重要的不就是您一下子就能把题目搞出来,而就是您得有想法,有想法才就是最重要的,有了想法您才能一步步的去做,如果行不通了,在改变思路,寻求新的解法,如果您没想法,您就根本无从下手。
对于这道题的结论比较有意思,比较对称,另外一个就就是结论的条件,为何要把ηξ、放在两个范围内,不像上一题中直接来个)1,0(∈ξη、,这个分界点1/2 的作用就是干不的。
很可能也就是把1 /2当做某一个点就像上一题中的ξ,就是否要用到拉格朗日中值定理呢,这就是我们的一个想法。
那具体的函数如何来构造呢,这个得从结论出发,22)`()`(ηξηξ+=+f f 我们把等式变一下:0)`()`(22=-+-ηηξξf f ,2)`(ξξ-f 这个不就就是331)(ξξ-f 关于ξ的导数(而且题目中f(1)=1/3,貌似这样有点想法了),本题会不会也像上一题那样,运用拉格朗日中值定理后相互消掉变为0呢,有了这些 想法我们就要开始往下走了: 先来构造一个函数:)21(2211)21()1()`()21(221)0()21()`(,0)1(,0)0(,31)()(3F F F F F F F F F F x x f x F -=--==-===-=ηξ0)`()`(=+ξηF F 刚好证明出来。
Ps:本题就是近几年数二的一道真题,只有一问,有比较大区分度的,得从条件结论互相出发,如何构造出函数就是关键。
做出来之后我们反过来瞧这个1/2的作用就知道了,如果只给)1,0(∈ξη、,那就更难了 得自己找这个点,既然题中给了这个点,并且把两个变量分开在两个区间内,我们就对这两个变量在对应区间用相应定理。
说明真题出的还就是很有技巧的。
一般设计难一点的中值定理证明,往往得用拉格朗日定理来证明,两个变量,都涉及到导数问题,这就是因为拉格朗日中值定理条件要少些,只需连续,可导即可,不像罗尔定理得有式子相等才可进一步运用。
4、设f(x)在区间[-a,a](a>0)上具有二阶连续导数,f(0)=0 (1)、写出f(x)的带拉格朗日余项的一阶麦克劳林公式 (2)、证明在[-a,a]上至少存在一点η使得⎰-=aadx x f f a )(3)``(3η第一问课本上记住了写出来就行,考的很基础 (1)、22!2)``()0`(!2)``(!1)0`()0()(x f x f x f x f f x f ξξ+⋅=++= (2)、第二问先将第一问的式子f(x)代入瞧瞧有什么结果出来⎰⎰--⋅=aaaadx x f dx x f 22)``()(ξ,)``(ξf 此处不能直接拿到积分号外面,因为她不就是与x 无关的数。
做到这儿,我们想办法把她弄到积分号外面似乎就能出来,有了这样想法就得寻求办法。
