正方形的性质与判定经典例题练习
中考数学复习之正方形的性质与判定,考点过关与基础练习题
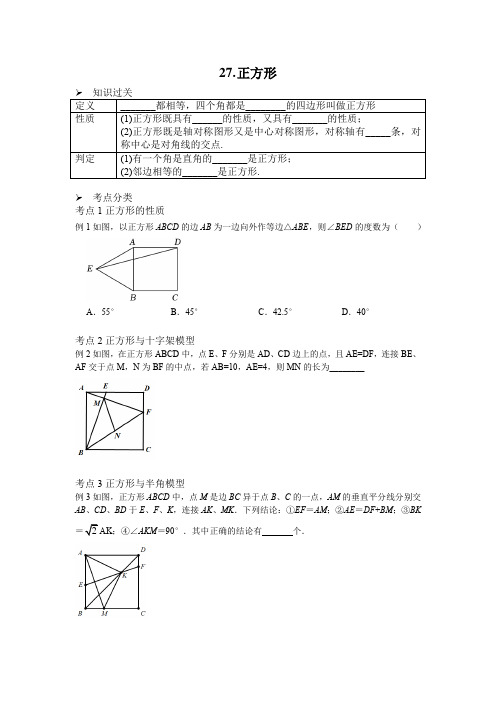
27.正方形➢考点分类考点1正方形的性质例1如图,以正方形ABCD的边AB为一边向外作等边△ABE,则∠BED的度数为()A.55°B.45°C.42.5°D.40°考点2正方形与十字架模型例2如图,在正方形ABCD中,点E、F分别是AD、CD边上的点,且AE=DF,连接BE、AF交于点M,N为BF的中点,若AB=10,AE=4,则MN的长为________考点3正方形与半角模型例3如图,正方形ABCD中,点M是边BC异于点B、C的一点,AM的垂直平分线分别交AB、CD、BD于E、F、K,连接AK、MK.下列结论:①EF=AM;②AE=DF+BM;③BKAK;④∠AKM=90°.其中正确的结论有个.➢ 真题演练1.如图,E 、F 分别是正方形ABCD 的边CD 、AD 上的点,且CE =DF ,AE 、BF 相交于点O ,下列结论:①AE =BF ;①AE ①BF ; ①AO =OE ;①S ①AOB =S四边形DEOF ,其中正确的有( )A .①①①B .①①①C .①①①D .①①①2.如图,E 、F 、H 分别为正方形ABCD 的边AB 、BC 、CD 上的点,连接DF ,HE ,且HE =DF ,DG 平分①ADF 交AB 于点G .若①BEH =52°,则①AGD 的度数为( )A .26°B .38°C .52°D .64°3.如图,在正方形ABCD 中,点E 、F 分别在边BC 、CD 上,连接AF 、EF ,过点E 作EH ①AD 交AD 于点H ,EG ①AF 交AD 于点G ,连接GF ,若BE =DF =1,且EF =2+√2,则sin①FGD 的值为( )A .√32B .√33C .√3−12D .12 4.如图,点E 为正方形ABCD 的对角线BD 上的一点,连接CE ,过点E 作EF ①CE 交AB 于点F ,交对角线AC 于点G ,且点G 为EF 的中点,若正方形的边长为4√2,则AG 的长为( )A .2B .3C .2√2D .43√25.如图,在正方形ABCD中,AB=2,点E是BC边的中点,连接DE,延长EC至点F,使得EF=DE,过点F作FG①DE,分别交CD、AB于N、G两点,连接CM、EG、EN,下列正确的是:①tan∠GFB=12;①MN=NC;①CMEG=12;①S四边形GBEM=√5+12()A.4B.3C.2D.16.如图,在正方形ABCD中,E为对角线AC上一点,连接DE,过点E作EF①DE,交BC 延长线于点F,以DE,EF为邻边作矩形DEFG,连接CG.在下列结论中:①DE=EF;①①DAE①①DCG;①AC①CG;①CE=CF.其中正确的是()A.①①①B.①①①C.①①①D.①①①7.如图,点E在正方形ABCD外,连结AE、BE、DE,过点A作AE的垂线交DE于点F.若AE=AF=4√2,BF=10,则下列结论:①△AFD≌△AEB;②EB⊥ED;③点B到直线AE的距离为3√2;④S△ABF+S△ADF=40.其中正确的结论是.(填写所有正确结论的序号)8.如图,边长为5的正方形ABCD中,点E、G分别在射线AB、BC上,F在边AD上,ED与FG交于点M,AF=1,FG=DE,BG>AF,则MC的最小值为.9.如图,在边长为4的正方形ABCD内有一动点P,且BP=√2.连接CP,将线段PC绕点P逆时针旋转90°得到线段PQ.连接CQ、DQ,则12DQ+CQ的最小值为.10.如图,小明同学将边长为5cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起,其中直角三角板的直角顶点落在点A处,两条直角边分别与CD交于点F,与CB延长线交于点E,则四边形AECF的面积是.11.已知四边形ABCD是正方形.(1)如图1所示,点O是正方形对角线的交点,连接OB,OC,若AB=4,求OB的长.(2)如图2所示,当点O是BC上一点,OC'⊥BC,连接BC',C'D,点M是C'D的中点,连接OM,CM,求证:CM=OM.12.如图,正方形ABCD 的对角线AC 、BD 相交于点O ,G 是CD 边上一点,连接BG 交AC 于E ,过点A 作AM ⊥BG ,垂足M ,AM 交BD 于点F .(1)求证:OE =OF .(2)若H 是BG 的中点,BG 平分∠DBC ,求证:DG =2OE .➢ 课后练习1.如图,在边长为8的正方形ABCD 中,E 、F 分别是边AB 、BC 上的点,且BE =CF =2,连接DE 、AF 交于点O ,过点F 作AF 的垂线段FG ,连接CG 使得①GCF =135°,连接AG 交DE 于点M ,则①GFM 的面积为( )A .24B .25C .25√22D .262.如图,在正方形ABCD 中,E 为BC 上一点,过点E 作EF ①CD ,交AD 于点F ,交对角线BD 于点G ,取DG 的中点H ,连接AH ,EH ,FH .下列结论:①FH ①AE ;①AH =EH 且AH ①EH ;①①BAH =①HEC ;①①EHF ①①AHD .其中正确的个数是( )A .4个B .3个C .2个D .1个3.如图,正方形ABCD 的边长为4,点E 在边AB 上,BE =1,①DAM =45°,点F 在射线AM 上,且AF =√2,过点F 作AD 的平行线交BA 的延长线于点H ,CF 与AD 相交于点G ,连接EC 、EG 、EF .下列结论:①CG =34√34;①①AEG 的周长为8;①①EGF 的面积为1710.其中正确的是( )A .①①①B .①①C .①①D .①①4.如图,E 为正方形ABCD 的边AB 的中点,过点E 作①GEF =90°,分别与边AD ,BC 交于点G ,F .若AG =2,BF =4,则GF 的长为( )A .4B .6C .8D .105.如图,在正方形ABCD 中,点E ,点F 分别是对角线BD ,AC 上的点,连接CE ,EF ,DF ,若EF ①BC ,且①CEF =15°,则①EDF 的度数为( )A .22.5°B .25°C .30°D .35°6.如图,在平面直角坐标系中,四边形ABCD 是边长为2的正方形,点A 在y 轴上运动,点B 在x 轴上运动,点E 为对角线的交点,在运动过程中点E 到y 轴的最大距离是( )A .√22B .1C .√2D .27.如图,在正方形ABCD中,O为对角线AC、BD的交点,E、F分别为边BC、CD上一点,且OE①OF,连接EF.若∠AOE=150°,DF=√3,则EF的长为()A.2√3B.2+√3C.√3+1D.38.如图,在正方形ABCD中,E、F分别是AB,BC的中点,CE,DF交于点G,连接AG,下列结论:①CE=DF;①CE①DF;①①AGE=①CDF;①①EAG=30°,其中正确的结论是()A.①①B.①①C.①①①D.①①①9.如图,在正方形ABCD中,AB=2,延长AD到点E,使得DE=1,EF⊥AE,EF=AE.分别连接AF,CF,M为CF的中点,则AM的长为.10.如图,在△ABC中,AC=BC=5,AB=6,以BC为边向外作正方形BCDE,连接AD,则AD=.11.如图,已知正方形ABCD的对角线AC与BD相交于点O,若AC=2√2cm,点E在DC 边的延长线上,若∠CAE=15°,则AE=cm.12.如图,点E在正方形ABCD边CD上,以CE为边向正方形ABCD外部作正方形CEFG,连接AF,P、Q分别是AF、AB的中点,连接PQ.若AB=7,CE=5,则PQ=.13.如图,正方形ABCD的边长为6.E,F分别是射线AB,AD上的点(不与点A重合),且EC⊥CF,M为EF的中点.P为线段AD上一点,AP=1,连接PM.当△PMF为直角三角形时,则AE的长为.14.如图,正方形ABCD中,点E为BC边上一点,点F为CD边上一点,且BE=CF,连接AE、BF交于点G.(1)求证:∠AGF=90°;(2)连接GC,若GC平分∠EGF,求证:AB=2CF;(3)在(2)的条件下,连接GD,过点E作EH∥GD交CD边于点H,交BF于点M,若FH=2,求线段FM的长.➢冲击A+如图1,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC 的中点,连接MH.(1)求证:MH为⊙O的切线.(2)若MH=32,ACBC=34,求⊙O的半径.(3)如图2,在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于点N,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段AO、CN、NQ的长度.。
正方形性质与判定练习题

正方形的性质与判断练习题一、填空1、如, E 是正方形 ABCD的角 BD 上一点,且 BE= BC,∠ ACE=°.2、如,四形 ABDC是正方形,延 CD 到点 E,使 CE=CB,∠ AEC=°.3、如,正方形 ABCD中,点 E 在 BC的延上, AE均分∠ DAC,以下:① ∠ E=°;② ∠AFC=°;③ ∠ ACE=135°;④ AC=CE;⑤ AD∶ CE=1∶ 2. 此中正确的有个.4、如,等△ EDC在正方形ABCD内, EA、 EB,∠ AEB=°;∠ ACE=°.第1题图第 2题图第 3题图第4题图5、已知正方形 ABCD,以 CD 作等△ CDE,∠ AED 的度数是° .6、如,四形 ABCD是正方形, E 是 CD 上一点,若△ AFB 逆旋角θ( 0°<θ< 180°)后,与△ AED重合,θ °.第 6题图第7题图第8题图第9题图7 、已知正方形ABCD中,点 E 在 DC上, DE = 2,EC = 1,把段 AE 点 A 旋,使点 E 落在直BC 上的点 F, F、C 两点的距离 ___________.8 、如,正方形ABCD的面12,△ ABE 是等三角形,点 E 在正方形 ABCD内,在角AC 上有一点P,使 PD+PE的和最小,个最小.9 、如,四形ABCD是9 的正方形片,将其沿MN 折叠,使点 B 落在 CD 上的B,点 A 点A ,且BC =3,CN=;AM的是.10、正方形的面是1,其角是________. 311、如,三个均 2 的正方形重叠在一同,O1、O2是此中两个正方形的中心,暗影部分的面是.12、如,将n 个都1cm 的正方形按如所示放,点A1、 A2、⋯、 A n分是正方形的中心,n 个的正方形重叠部分的面和.O2O1第 11题图第14题图第 12题图第13题图13、边长为 1 的正方形ABCD 绕点 A 逆时针旋转30°获得正方形 AB′ C′,D两′图叠成一个“蝶形风筝”(如下图重叠部分),则这个风筝的面积是.14、如图,边长为 1 的正方形ABCD绕点 A 逆时针旋转45 度后获得正方形AB′ C′,D边′B′与C′DC 交于点 O,则四边形 AB′OD 的周长是.15、如右图,正方形ABCD中, AB=6,点 E 在边 CD 上,且 CD=3DE.将△ ADE 沿 AE对折至△ AFE,延伸 EF 交边 BC 于点 G,连结 AG、 CF.以下结论:① △ ABG≌ △ AFG;② BG =GC;③ AG ∥ CF;④S△FGC= 3.此中正确的结论是.(填序号)16、如右图,四边形ABCD为正方形,以AB 为边向正方形外作等边△ABE, CE与 DB订交于点F,则AFD =。
正方形的性质与判定【十大题型】(举一反三)(浙教版)(原卷版)

专题5.3 正方形的性质与判定【十大题型】【浙教版】【题型1 正方形的性质(求角的度数)】 (1)【题型2 正方形的性质(求线段的长度)】 (3)【题型3 正方形的性质(求面积、周长)】 (4)【题型4 正方形的性质(探究数量关系)】 (6)【题型5 判定正方形成立的条件】 (10)【题型6 正方形判定的证明】 (12)【题型7 正方形的判定与性质综合】 (16)【题型8 探究正方形中的最值问题】 (19)【题型9 正方形在坐标系中的运用】 (20)【题型10 正方形中的多结论问题】 (23)【题型1 正方形的性质(求角的度数)】【例1】(2022春•建阳区期中)如图,在正方形ABCD中有一个点E,使三角形BCE是正三角形,求:(1)∠BAE的大小(2)∠AED的大小.【变式1-1】如图,已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2)连接FC,观察并猜测∠FCN的度数,并说明理由.【变式1-2】(2022•武威模拟)如图,在正方形ABCD中,点E是对角线AC上的一点,点F在BC的延长线上,且BE=EF,EF交CD于点G.(1)求证:DE=EF;(2)求∠DEF的度数.【变式1-3】(2022春•新市区校级期末)如图,在给定的正方形ABCD中,点E从点B出发,沿边BC方向向终点C运动,DF⊥AE交AB于点F,以FD,FE为邻边构造平行四边形DFEP,连接CP,则∠DFE+∠EPC的度数的变化情况是()A.一直减小B.一直减小后增大C.一直不变D.先增大后减小【题型2 正方形的性质(求线段的长度)】【例2】(2022春•牡丹江期末)如图,正方形ABCD的边长为10,点E,F在正方形内部,AE=CF=8,BE=DF=6,则线段EF的长为()A.2√2B.4C.4−√2D.4+√2【变式2-1】(2022春•巴南区期末)如图,四边形ABCD是边长为4的正方形,点E在边CD上,且DE =1,作EF∥BC分别交AC、AB于点G、F,P、H分别是AG,BE的中点,则PH的长是()A.2B.2.5C.3D.4【变式2-2】(2022•越秀区一模)将正方形ABCD与正方形BEFG按如图方式放置,点F、B、C在同一直线上,已知BG=√2,BC=3,连接DF,M是DF的中点,连接AM,则AM的长是()A.√102B.√3C.√132D.32【变式2-3】(2022春•吴中区校级期末)如图,在正方形ABCD中,AB=4√5.E、F分别为边AB、BC的中点,连接AF、DE,点N、M分别为AF、DE的中点,连接MN,则MN的长度为.【题型3 正方形的性质(求面积、周长)】【例3】(2022春•鄞州区期末)有两个正方形A,B.现将B放在A的内部得图甲,将A,B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,若三个正方形A和两个正方形B得图丙,则阴影部分的面积为()A.28B.29C.30D.31【变式3-1】(2022春•工业园区校级期中)如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE 为Rt△,∠CED=90°,OE=2√2,若CE•DE=3,则正方形ABCD的面积为()A.5B.6C.8D.10【变式3-2】(2022•台州)如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为.【变式3-3】(2022•江北区一模)如图,以Rt△ABC的各边为边分别向外作正方形,∠BAC=90°,连结DG,点H为DG的中点,连结HB,HN,若要求出△HBN的面积,只需知道()A.△ABC的面积B.正方形ADEB的面积C.正方形ACFG的面积D.正方形BNMC的面积【题型4 正方形的性质(探究数量关系)】【例4】(2022秋•中原区校级月考)如图,线段AB=4,射线BG⊥AB,P为射线BG上一点,以AP为边作正方形APCD,且点C、D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP,直线CE 与线段AB相交于点F(点F与点A、B不重合).(1)求证:△AEP≌△CEP;(2)判断CF与AB的位置关系,并说明理由;(3)请直接写出△AEF的周长.【变式4-1】(2022春•雁塔区校级期末)在正方形ABCD中,∠MAN=45°,该角可以绕点A转动,∠MAN的两边分别交射线CB,DC于点M,N.(1)当点M,N分别在正方形的边CB和DC上时(如图1),线段BM,DN,MN之间有怎样的数量关系?你的猜想是:,并加以证明.(2)当点M,N分别在正方形的边CB和DC的延长线上时(如图2),线段BM,DN,MN之间的数量关系会发生变化吗?证明你的结论.【变式4-2】(2022春•莆田期末)如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.(1)求证:AO=BO;(2)求证:∠HEB=∠HNB;(3)过A作AP⊥ED于P点,连BP,则PE−PA的值.PB【变式4-3】(2022春•鼓楼区校级期中)如图,正方形ABCD的对角线相交于点O.点E是线段DO上一点,连接CE.点F是∠OCE的平分线上一点,且BF⊥CF与CO相交于点G.点H是线段CE上一点,且CO=CH.(1)若OF=5,求FH的长;(2)求证:BF=OH+CF.【题型5 判定正方形成立的条件】【例5】(2022春•海淀区校级期中)已知四边形ABCD为凸四边形,点M、N、P、Q分别为AB、BC、CD、DA上的点(不与端点重合),下列说法正确的是(填序号).①对于任意凸四边形ABCD,一定存在无数个四边形MNPQ是平行四边形;②如果四边形ABCD为任意平行四边形,那么一定存在无数个四边形MNPQ是矩形;③如果四边形ABCD为任意矩形,那么一定存在一个四边形为正方形;④如果四边形ABCD为任意菱形,那么一定存在一个四边形为正方形.【变式5-1】(2022春•岳麓区校级月考)如图,E、F、G、H分别是AB、BC、CD、DA的中点.要使四边形EFGH是正方形,BD、AC应满足的条件是.【变式5-2】(2022春•汉寿县期中)如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F在AC 上,且OE=OF,连接DE并延长至点M,使DE=ME,连接MF,DF,BE.(1)当DF=MF时,证明:四边形EMBF是矩形;(2)当△DMF满足什么条件时,四边形EMBF是正方形?请说明理由.【变式5-3】(2022春•沛县期中)已知在△ABC中,D为边BC延长线上一点,点O是边AC上的一个动点,过O作直线MN∥BC,设MN与∠BCA的平分线相交于点E,与∠ACD的平分线相交于点F.(1)求证:OE=OF;(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.(3)在(2)的条件下,且△ABC满足条件时,矩形AECF是正方形?.【题型6 正方形判定的证明】【例6】(2022春•虹口区期末)如图,在四边形ABCD中,AB∥CD,AD=CD,E是对角线BD上的一点,且AE=CE.(1)求证:四边形ABCD是菱形;(2)如果AB=BE,且∠ABE=2∠DCE,求证:四边形ABCD是正方形.【变式6-1】(2022春•宜城市期末)如图,四边形ABCD是平行四边形,连接对角线AC,过点D作DE ∥AC与BC的延长线交于点E,连接AE交DC于F.(1)求证:BC=CE;(2)连接BF,若∠DAF=∠FBE,且AD=2CF,求证:四边形ABCD是正方形.【变式6-2】(2022秋•市南区期末)已知:在平行四边形ABCD中,分别延长BA,DC到点E,H,使得BE=2AB,DH=2CD.连接EH,分别交AD,BC于点F,G.(1)求证:AF=CG;(2)连接BD交EH于点O,若EH⊥BD,则当线段AB与线段AD满足什么数量关系时,四边形BEDH 是正方形?【变式6-3】(2022•上海)已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.(1)求证:四边形ABCD是菱形;(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.【题型7 正方形的判定与性质综合】【例7】(2022•威海)如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为cm2.【变式7-1】(2022•萧山区模拟)如图,P为正方形ABCD内的一点,画▱P AHD,▱PBEA,▱PCFB,▱PDGC,请证明:以E,F,G,H为顶点的四边形是正方形.【变式7-2】(2022•萧山区模拟)已知:如图,边长为4的菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.(1)求证:四边形ABCD是正方形.(2)E是OB上一点,BE=1,且DH⊥CE,垂足为H,DH与OC相交于点F,求线段OF的长.【变式7-3】(2022春•潜山市期末)如图,已知四边形ABCD为正方形,AB=3√2,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.【题型8 探究正方形中的最值问题】【例8】(2022春•沙坪坝区校级月考)如图,在正方形ABCD中,M,N是边AB上的动点,且AM=BN,连接MD交对角线AC于点E,连接BE交CN于点F,若AB=3,则AF长度的最小值为.【变式8-1】(2022•泰山区一模)如图,M、N是正方形ABCD的边CD上的两个动点,满足AM=BN,连接AC交BN于点E,连接DE交AM于点F,连接CF,若正方形的边长为2,则线段CF的最小值是()A.2B.1C.√5−1D.√5−2【变式8-2】(2022•青山区模拟)已知矩形ABCD,AB=2,AD=4AB=8,E为线段AD上一动点,以CE 为边向上构造正方形CEFG,连接BF,则BF的最小值是.【变式8-3】(2022•郧阳区模拟)如图,P A=2√2,PB=4√2,以AB为边作正方形ABCD,使得P、D两点落在直线AB的两侧,当∠APB变化时,则PD的最大值为.【题型9 正方形在坐标系中的运用】【例9】(2022春•市中区期末)在平面直角坐标系中,对于两个点P、Q和图形W,如果在图形W上存在点M、N(M、N可以重合)使得PM=QN,那么称点P与点Q是图形W的一对平衡点.已知正方形的边长为2,一边平行于x轴,对角线的交点为点O,点D的坐标为(2,0).若点E(x,2)与点D是正方形的一对平衡点,则x的取值范围为()A.﹣3≤x≤3B.﹣4≤x≤4C.﹣2≤x≤2D.﹣5≤x≤5【变式9-1】(2022秋•永新县期末)如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣2,0)、B(0,﹣2)、C(2,0)、D(0,2),求证:四边形ABCD是正方形.【变式9-2】(2022春•顺城区期末)如图,在平面直角坐标系xOy中,直线OC:yOC=3x与直线AC:yAC=﹣x+8相交于点C(2,6).(1)点M从点O出发以每秒1个单位长度的速度沿x轴向右运动,点N从点A出发以每秒3个单位长度的速度沿x轴向左运动,两点同时出发.分别过点M,N作x轴的垂线,分别交直线OC,AC于点P,Q,请你在图1中画出图形,猜想四边形PMNQ的形状(点M,N重合时除外),并证明你的猜想;(2)在(1)的条件下,当点M运动秒时,四边形PMNQ是正方形(直接写出结论).【变式9-3】(2022•河南模拟)如图,正方形OABC 中,点A (4,0),点D 为AB 上一点,且BD =1,连接OD ,过点C 作CE ⊥OD 交OA 于点E ,过点D 作MN ∥CE ,交x 轴于点M ,交BC 于点N ,则点M 的坐标为( )A .(5,0)B .(6,0)C .(254,0)D .(274,0) 【题型10 正方形中的多结论问题】【例10】(2022春•慈溪市期末)如图,正方形ABCD 中,点P 为BD 延长线上任一点,连结P A ,过点P 作PE ⊥P A ,交BC 的延长线于点E ,过点E 作EF ⊥BP 于点F .下列结论:(1)P A =PE ; (2)BD =2PF ;(3)CE =√2PD ; (4)若BP =BE ,则PF =(√2+1)DF .其中正确的个数为( )A .1B .2C .3D .4【变式10-1】(2022春•渝中区校级期中)如图,正方形ABCD 的边长为a ,点E 在边AB 上运动(不与点A ,B 重合),∠DAM =45°,点F 在射线AM 上,且AF =√2BE ,CF 与AD 相交于点G .连接EC 、EF 、EG .下列结论:①∠ECF =45°;②△AEG 的周长为(1+√22)a ;③BE 2+DG 2=EG 2;④当G 是线段AD的中点时,BE =13a .正确的个数是( )A.1个B.2个C.3个D.4个【变式10-2】(2022秋•三水区月考)如图,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G,下列结论:①HF=2HG;②∠GDH=∠GHD;③图中有8个等腰三角形;④S△CDG=S△DHF.其中正确的结论个数是()A.1个B.2个C.3个D.4个【变式10-3】(2022春•玉林期末)如图,正方形ABCD中,点E在边CD上,过点A作AF⊥AE交CB的延长线于点F,连接EF,AG平分∠F AE,AG分别交BC、EF于点G、H,连接EG、DH.则下列结论中:①BF=DE;②∠EGC=2∠BAG;③AD+DE=√3DH;④DE+BG=EH;⑤若DE=CE,则CE:CG:EG=3:4:5,其中正确的结论有.。
初中数学 习题3:正方形的性质与判定

正方形的性质与判定一、填空题1.正方形的一边长5cm,则周长为cm,面积为cm22.E是正方形ABCD对角线AC上一点,且AE=AB,则∠ABE=3.E是正方形ABCD内一点,且△EAB是等边三角形,则∠ADE=4.正方形ABCD中,对角线BD长为16cm,P是AB上任意一点,则点P到AC、BD的距离之和等于cm5.正方形有条对称轴.6.如图(1),在正方形ABCD的边BC的延长线上取一点E,使CE=AC,连结AE交CD于F,则∠AFC=(1) (2)7.如图(2),E是正方形ABCD内一点,如果△ABE是等边三角形,那么∠DCE=,如果DE的延长线交BC于G,则∠BEG=8.F是正方形ABCD的对角线AC上一点,AF=AD,FG⊥AC于F,交CD于G,那么∠DFG=9.如图(3),截去正方形ABCD的∠A、∠C后,∠ 1、∠2、∠3、∠4的和为(3)(4)10.如图(4),正方形的对角线相交于O,∠BAC的平分线交BD于E,若正方形的周长是20cm,则DE=二、选择题1.正方形具有而矩形不一定具有的特征是( )A.四个角都是直角B.对角线互相平分C.对角线互相垂直D.对角线相等2.如图(5),在正方形ABCD中,∠DAF=25°,AF交对角线BD于E 点,则∠BEC=( ) A.45°B.60°C. 70°D.75°(5) (6)3.下列图形中,既是轴对称图形,又是中心对称图形的是( )A.平行四边形B.等腰三角形C.等边三角形D.菱形4.如图(6),正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )A.30 B.34 C.36 D.405.如右图,以A、B为顶点作位置不同的正方形,一共可以作( )A.1个B.2个C.3个D.4个三、解答题(每题12分,共24分)1.图中的矩形是由六个正方形组成,其中最小的正方形的面积为1,求这个矩形的长和宽各是多少?2.如图,E是正方形ABCD外一点,AE=AD,∠ADE=75°,求∠AEB的度数.四、对于周长为20的矩形,通过填写下表,研究它的长、宽的变化对面积的影响.矩形的长……8 7 6 5 4 3 2 ……矩形的宽…………矩形的面积……观察数据,你有什么结论?五、如图,△ABC中,点O是AC上一动点,过点O作直线MN∥BC,设Mn交∠ACB的平分线于点E,交∠ACH的平分线于点F.⑴说明:EO=FO;⑵当点O运动到何处时,四边形AECF是矩形;⑶当O是AC上怎样的点,且AC与BC具有什么关系时,四边形AECF是正方形?参考答案一、1.20,25;2.°;3.75°;4.8;5.4;6.°7.15°,45°;8.° 9.540°10.5二、三、1.设中间最小正方形的边长为,则右下方正方形的边长为,左下方正方形的边长为,左上方正方形的边长为,右上方正方形的边长为,根据长方形的对边相等可列方程2(1)(2)(4)(3)x x x x+++=+++,解这个方程得,∴长方形的长为13,宽为11,面积为243;2.∵△ADE中,AE=AD,∠ADE=75°,∴∠AED=75°(等边对等角)∴∠EAD=180°-75°×2=30°又∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴△ABE中,AB=AE,∠BAE=120°∴∠AEB=1(1802°°)30=°四、在周长一定的情况下,当长方形的长与宽的差的绝对值越小,长方形的面积越大,当长与宽相等时,长方形的面积最大.五、⑴证OE OC OF==;⑵AC的中点;⑶当O是AC的中点,且AC⊥BC时,四边形AECF 是正方形.。
中考数学专项复习命题点5 正方形的性质与判定(必考)

解法4:如解图④,过点 作 于点 ,交 于点 ,由点 是 的中点,得 , 分别是 , 的中点,由中位线得 ,得 ,由 ,得 ,则 .
第15题解图④
第16题图
16.[2023安徽]如图,点 在正方形 的对角线 上, 于点 ,连接 并延长,交边 于点 ,交边 的延长线于点 .若 , ,则 ( )
, , .
第10题图
10.[2023河北]如图,在 中, ,点 是斜边 的中点,以 为边作正方形 .若 ,则 ( )
A. B. C. 12 D. 16
√
【解析】 四边形 是正方形,又 , , (负值已舍),在 中,点 是斜边 的中点, ,即 ,在 中, , , .
第15题解图①
解法2:如解图②,延长 交 的延长线于点 ,易得 ,由 ,点 是 的中点,得 ,由 垂直平分 ,得 , , , ,则 , .
第15题解图②
解法3:如解图③,过点 作 交 于点 ,过点 作 于点 ,易得四边形 是矩形,在 中求得 ,在 中求得 ,则 .
√
第9题图
9.(优质原创)如图,在正方形 中, , 分别在边 , 上,且 为等边三角形,若 ,则 的长为_ ________.
第9题图
【解析】 设 与 的交点为 , 为等边三角形,四边形 为正方形, , , , , , , 垂直平分 , , ,
第13题图
13.如图, 是正方形 的对角线, 平分 交 的延长线于点 ,交 于点 ,则 的值为( )
A. B. C. 2 D.
√
【解析】 四边形 是正方形, , , , ,, 平分 , , , , , , , .
第2题图
2.(新中考)如图,平行四边形 的对角线互相垂直,要使 成为正方形,还需添加的一个条件是_ _______________________.(只需添加一个即可)
正方形的性质与判定专题练习

正方形专题训练(含答案)一.选择题(共11小题)1.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为()2.)如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为()A.a2B.a2C.a2D.a23.如图,F是正方形ABCD的边CD上的一个动点,BF 的垂直平分线交对角线AC于点E,连接BE,FE,则∠EBF 的度数是()A.45°B.50°C.60°D.不确定4.平行四边形、矩形、菱形、正方形都具有的是()A.对角线互相平分B.对角线互相垂直C .对角线相等D.对角线互相垂直且相等5.正方形的一条对角线长为4,则这个正方形的面积是()6.(2014•福州)如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°7.顺次连接菱形各边的中点所形成的四边形是()A.等腰梯形B.矩形C.菱形D.正方形8.下列说法中,正确的是()A.相等的角一定是对顶角B.四个角都相等的四边形一定是正方形C.平行四边形的对角线互相平分D.矩形的对角线一定垂直9.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是()A.选①②B.选②③C.选①③D.选②④10.如图,在正方形ABCD中,CE=MN,∠MCE=35°,那么∠ANM等于()A.45°B.50°C.55°D.60°11.如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的面积为()A.9B.16 C.20 D.25二.填空题(共5小题)12.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=_________度.13.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是_________度.14.如图,四边形ABCD为正方形,△ADE为等边三角形.AC为正方形ABCD的对角线,则∠EAC=_________度.A.8B.4C.8D.1615.已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为_________.16.如图所示,正方形ABCD 的周长为16cm,顺次连接正方形ABCD各边的中点,得到四边形EFGH,则四边形EFGH的周长等于_________cm,四边形EFGH的面积等于_________cm.三.解答题(共6小题)17.如图,正方形ABCD中,E、F分别为BC、CD上的点,且AE⊥BF,垂足为点G.求证:AE=BF.18.如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC.19.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.(1)求证:AE=CF;(2)若∠ABE=55°,求∠EGC的大小.20.在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证:(1)BH=DE.(2)BH⊥DE.21.已知:如图,▱ABCD中,O是CD的中点,连接AO 并延长,交BC的延长线于点E.(1)求证:△AOD≌△EOC;(2)连接AC,DE,当∠B=∠AEB=_________°时,四边形ACED是正方形?请说明理由.22.(2014•随州)已知:如图,在矩形ABCD中,M、N 分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.(1)求证:△ABM≌△DCM;(2)填空:当AB:AD=_________时,四边形MENF 是正方形.一.选择题(共11小题)1.(2014•南充)如图,将正方形OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1,),则点C 的坐标为( )A . (﹣,1) B . (﹣1,) C . (,1) D . (﹣,﹣1)考点: 全等三角形的判定与性质;坐标与图形性质;正方形的性质.专题:几何图形问题. 分析: 过点A 作AD ⊥x 轴于D ,过点C 作CE ⊥x 轴于E ,根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD 和△OCE 全等,根据全等三角形对应边相等可得OE=AD ,CE=OD ,然后根据点C 在第二象限写出坐标即可.解答: 解:如图,过点A 作AD ⊥x 轴于D ,过点C 作CE ⊥x 轴于E ,∵四边形OABC 是正方形, ∴OA=OC ,∠AOC=90°, ∴∠COE+∠AOD=90°, 又∵∠OAD+∠AOD=90°, ∴∠OAD=∠COE, 在△AOD 和△OCE 中,,∴△AOD ≌△OCE (AAS), ∴OE=AD=,CE=OD=1,∵点C 在第二象限, ∴点C 的坐标为(﹣,1).故选:A .点评: 本题考查了全等三角形的判定与性质,正方形的性质,坐标与图形性质,作辅助线构造出全等三角形是解题的关键,也是本题的难点.2.(2014•山西)如图,点E 在正方形ABCD 的对角线AC 上,且EC=2AE ,直角三角形FEG 的两直角边EF 、EG 分别交BC 、DC 于点M 、N .若正方形ABCD 的边长为a,则重叠部分四边形EMCN 的面积为( )A . a 2B . a 2C . a 2D . a 2考点:全等三角形的判定与性质;正方形的性质.专题:几何图形问题. 分析: 作EP ⊥BC 于点P ,EQ ⊥CD 于点Q ,△EPM ≌△EQN,利用四边形EMCN 的面积等于正方形MCQE 的面积求解.解答:解:作EP ⊥BC 于点P,EQ ⊥CD 于点Q ,∵四边形ABCD是正方形,∴∠BCD=90°,又∵∠EPM=∠EQN=90°,∴∠PEQ=90°,∴∠PEM+∠MEQ=90°,∵三角形FEG是直角三角形,∴∠NEF=∠NEQ+∠MEQ=90°,∴∠PEM=∠NEQ,∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°,∴EP=EN,四边形MCQE是正方形,在△EPM和△EQN中,,∴△EPM≌△EQN(ASA)∴S△EQN=S△EPM,∴四边形EMCN的面积等于正方形MCQE的面积, ∵正方形ABCD的边长为a,∴AC=a,∵EC=2AE,∴EC=a,∴EP=PC=a,∴正方形MCQE的面积=a ×a=a2,∴四边形EMCN的面积=a2,故选:D.点评:本题主要考查了正方形的性质及全等三角形的判定及性质,解题的关键是作出辅助线,证出△EPM≌△EQN.3.(2014•台州)如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连接BE,FE,则∠EBF的度数是()A.45°B.50°C.60°D.不确定考点:全等三角形的判定与性质;正方形的性质.专题:几何图形问题.分析:过E作HI∥BC,分别交AB、CD于点H、I,证明Rt△BHE≌Rt△EIF,可得∠IEF+∠HEB=90°,再根据BE=EF即可解题.解答:解:如图所示,过E作HI∥BC,分别交AB、CD于点H、I,则∠BHE=∠EIF=90°,∵E是BF的垂直平分线EM上的点,∴EF=EB,∵E是∠BCD角平分线上一点,∴E到BC和CD的距离相等,即BH=EI,Rt△BHE和Rt△EIF中,,∴Rt△BHE≌Rt△EIF(HL),∴∠HBE=∠IEF , ∵∠HBE+∠HEB=90°, ∴∠IEF+∠HEB=90°, ∴∠BEF=90°, ∵BE=EF ,∴∠EBF=∠EFB=45°. 故选:A .点评: 本题考查了正方形角平分线和对角线重合的性质,考查了直角三角形全等的判定,全等三角形对应角相等的性质.4.(2014•郴州)平行四边形、矩形、菱形、正方形都具有的是( ) A . 对角线互相平分 B . 对角线互相垂直 C . 对角线相等 D . 对角线互相垂直且相等考点: 正方形的性质;平行四边形的性质;菱形的性质;矩形的性质.专题:证明题. 分析: 本题主要依据平行四边形、矩形、菱形、正方形都具有对角线相互平分的性质来判断.解答: 解:A 、对角线相等是平行四边形、矩形、菱形、正方形都具有的性质;B 、对角线互相垂直是菱形、正方形具有的性质;C 、对角线相等是矩形和正方形具有的性质;D 、对角线互相垂直且相等是正方形具有的性质. 故选:A .点评: 本题主要考查平行四边形、矩形、菱形、正方形的性质定理.5.(2014•来宾)正方形的一条对角线长为4,则这个正方形的面积是( )A . 8B . 4C . 8D . 16考点:正方形的性质.分析: 根据正方形的面积等于对角线乘积的一半列式计算即可得解.解答: 解:∵正方形的一条对角线长为4, ∴这个正方形的面积=×4×4=8.故选:A .点评: 本题考查了正方形的性质,熟记利用对角线求面积的方法是解题的关键.6.(2014•福州)如图,在正方形ABCD 的外侧,作等边三角形ADE ,AC 、BE 相交于点F ,则∠BFC 为( )A . 45°B . 55°C . 60°D .75°考点: 正方形的性质;等腰三角形的性质;等边三角形的性质.分析: 根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC . 解答: 解:∵四边形ABCD 是正方形, ∴AB=AD又∵△ADE 是等边三角形, ∴AE=AD=DE,∠DAE=60° ∴AD=AE∴∠ABE=∠AEB ,∠BAE=90°+60°=150° ∴∠ABE=(180°﹣150°)÷2=15° 又∵∠BAC=45° ∴∠BFC=45°+15°=60°故选:C .点评: 本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°.7.(2014•来宾)顺次连接菱形各边的中点所形成的四边形是( ) A . 等腰梯形 B . 矩形 C . 菱形D . 正方形考点:正方形的判定;三角形中位线定理;菱形的性质.分析:根据三角形的中位线定理以及菱形的性质即可证得. 解答: 解:∵E ,F 是中点, ∴EH ∥BD ,同理,EF ∥AC,GH ∥AC ,FG ∥BD , ∴EH ∥FG ,EF ∥GH ,则四边形EFGH 是平行四边形. 又∵AC ⊥BD , ∴EF ⊥EH ,∴平行四边形EFGH 是矩形. 故选:B .点评: 本题主要考查了矩形的判定定理,正确理解菱形的性质以及三角形的中位线定理是解题的关键.8.(2014•湘西州)下列说法中,正确的是( ) A . 相等的角一定是对顶角B . 四个角都相等的四边形一定是正方形C . 平行四边形的对角线互相平分D . 矩形的对角线一定垂直考点: 正方形的判定;对顶角、邻补角;平行四边形的性质;矩形的性质.分析: 根据对顶角的定义,正方形的判定,平行四边形的性质,矩形的性质对各选项分析判断利用排除法求解. 解答: 解:A 、相等的角一定是对顶角错误,例如,角平分线分成的两个角相等,但不是对顶角,故本选项错误;B 、四个角都相等的四边形一定是矩形,不一定是正方形,故本选项错误;C 、平行四边形的对角线互相平分正确,故本选项正确;D 、矩形的对角线一定相等,但不一定垂直,故本选项错误. 故选:C .点评: 本题考查了正方形的判定,平行四边形的性质,矩形的性质,对顶角的定义,熟记各性质与判定方法是解题的关键.9.(2014•株洲)已知四边形ABCD 是平行四边形,再从①AB=BC ,②∠ABC=90°,③AC=BD,④AC ⊥BD 四个条件中,选两个作为补充条件后,使得四边形ABCD 是正方形,现有下列四种选法,其中错误的是( ) A . 选①② B . 选②③ C . 选①③ D . 选②④考点:正方形的判定;平行四边形的性质.分析:要判定是正方形,则需能判定它既是菱形又是矩形. 解答: 解:A 、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD 是正方形,正确,故本选项不符合题意;B 、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD 是正方形,错误,故本选项符合题意;C 、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD 是正方形,正确,故本选项不符合题意; D 、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD 是正方形,正确,故本选项不符合题意. 故选:B .点评: 本题考查了正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个矩形有一个角为直角.③还可以先判定四边形是平行四边形,再用1或2进行判定.10.(2014•红桥区三模)如图,在正方形ABCD 中,CE=MN ,∠MCE=35°,那么∠ANM 等于( )A . 45°B .50° C .55° D .60°考点:全等三角形的判定与性质;正方形的性质. 分析: 过B 作BF ∥MN 交AD 于F,则∠AFB=∠ANM ,根据正方形的性质得出∠A=∠EBC=90°,AB=BC,AD ∥BC,推出四边形BFNM 是平行四边形,得出BF=MN=CE ,证Rt △ABF ≌Rt △BCE,推出∠AFB=∠ECB 即可.解答:解:过B 作BF ∥MN 交AD 于F , 则∠AFB=∠ANM , ∵四边形ABCD 是正方形,∴∠A=∠EBC=90°,AB=BC,AD ∥BC , ∴FN ∥BM,BE ∥MN ,∴四边形BFNM 是平行四边形, ∴BF=MN , ∵CE=MN , ∴CE=BF,在Rt △ABF 和Rt △BCE 中∴Rt △ABF ≌Rt △BCE (HL ), ∴∠AFB=∠ECB=35°, ∴∠ANM=∠AFB=55°, 故选C .点评: 本题考查了平行四边形的性质和判定,全等三角形的性质和判定,正方形的性质的应用,主要考查学生的推理能力.11.(2014•四会市一模)如图,菱形ABCD 中,∠B=60°,AB=5,则以AC 为边长的正方形ACEF 的面积为( )A . 9B . 16C . 20D . 25考点:菱形的性质;正方形的性质.分析: 据已知可求得△ABC 是等边三角形,从而得到AC=AB,从而求出正方形ACEF 的边长,进而可求出其面积.解答: 解:∵B=60°,AB=BC , ∴△ABC 是等边三角形,∴AC=AB=5,∴正方形ACEF 的边长为5, ∴正方形ACEF 的面积为25, 故选D .点评: 本题考查菱形与正方形的性质,属于基础题,对于此类题意含有60°角的题目一般要考虑等边三角形的应用.二.填空题(共5小题)12.(2009•江西模拟)如图,在正方形ABCD 的外侧,作等边三角形ADE ,则∠AEB= 15 度.考点:正方形的性质;等边三角形的性质. 分析: 由等边三角形的性质可得∠DAE=60°,进而可得∠BAE=150°,又因为AB=AE ,结合等腰三角形的性质,易得∠AEB 的大小.解答: 解:△ADE 是等边三角形;故∠DAE=60°, ∠BAE=90°+60°=150°,又有AB=AE,故∠AEB=30°÷2=15°; 故答案为15°.点评: 主要考查了正方形基本性质:①两组对边分别平行;四条边都相等;相邻边互相垂直;②四个角都是90°;③对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角.13.(2008•佛山)如图,已知P 是正方形ABCD 对角线BD 上一点,且BP=BC,则∠ACP 度数是 22.5 度.考点: 正方形的性质.专题:计算题. 分析: 根据正方形的性质可得到∠DBC=∠BCA=45°又知BP=BC,从而可求得∠BCP 的度数,从而就可求得∠ACP 的度数. 解答: 解:∵ABCD 是正方形, ∴∠DBC=∠BCA=45°,∵BP=BC ,∴∠BCP=∠BPC=(180°﹣45°)=67。
【精编版】中考数学专题训练——正方形的判定和性质

中考专题训练——正方形的判定和性质1.如图,在矩形ABCD中,点E,F分别在边AB,BC上,AF⊥DE,且AF=DE,AF与DE相交于点G.(1)求证:矩形ABCD为正方形:(2)若AE:EB=2:1,△AEG的面积为4,求四边形BEGF的面积.2.已知:如图,边长为4的菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.(1)求证:四边形ABCD是正方形.(2)E是OB上一点,BE=1,且DH⊥CE,垂足为H,DH与OC相交于点F,求线段OF的长.3.如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.(1)求证:∠HEA=∠CGF;(2)当AH=DG时,求证:菱形EFGH为正方形.4.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.5.如图①,在正方形ABCD中,点E,F分别在AB、BC上,且AE=BF.(1)试探索线段AF、DE的数量关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图②中补全图形,并说明理由.6.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.(1)求证:四边形MANP是正方形;(2)求证:EM=BN.7.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F 分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.8.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形;②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.9.平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;(2)如果四边形ABCD是正方形,四边形OBEC也是正方形吗?如果是,请给予证明;如果不是,请说明理由.10.如果P是正方形ABCD内的一点,且满足∠APB+∠DPC=180°,那么称点P是正方形ABCD的“对补点”.(1)如图1,正方形ABCD的对角线AC,BD交于点M,求证:点M是正方形ABCD 的对补点;(2)如图2,在平面直角坐标系中,正方形ABCD的顶点A(1,1),C(3,3).除对角线交点外,请再写出一个该正方形的对补点的坐标,并证明.11.已知:如图,E是正方形ABCD的对角线BD上的点,连接AE、CE.(1)求证:AE=CE;(2)若将△ABE沿AB翻折后得到△ABF,当点E在BD的何处时,四边形AFBE是正方形?请证明你的结论.12.如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.(1)试判断四边形PQEF是否是正方形,并证明;(2)PE是否总过某一定点,并说明理由.13.在平面直角坐标系xOy中,OEFG为正方形,点F的坐标为(1,1).将一个最短边长大于的直角三角形纸片的直角顶点放在对角线FO上.(1)如图,当三角形纸片的直角顶点与点F重合,一条直角边落在直线FO上时,这个三角形纸片与正方形OEFG重叠部分(即阴影部分)的面积为;(2)若三角形纸片的直角顶点不与点O,F重合,且两条直角边与正方形相邻两边相交,当这个三角形纸片与正方形OEFG重叠部分的面积是正方形面积的一半时,试确定三角形纸片直角顶点的坐标(不要求写出求解过程),并画出此时的图形.14.(1)如图矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.15.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图1,求证:矩形DEFG是正方形;(2)若AB=2,CE=,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.16.如图,在矩形ABCD中,AD=6,CD=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2,连接CF.(1)当DG=2时,求证:四边形EFGH是正方形;(2)当△FCG的面积为2时,求CG的值.17.已知,如图,矩形ABCD中,AD=6,DC=7,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.(1)若DG=2,求证四边形EFGH为正方形;(2)若DG=6,求△FCG的面积;(3)当DG为何值时,△FCG的面积最小.18.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.(1)∠EAF=°(直接写出结果不写解答过程);(2)①求证:四边形ABCD是正方形.②若BE=EC=3,求DF的长.(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是(直接写出结果不写解答过程).19.如图1,在正方形ABCD中,G为线段BD上一点,连接AG,过G作AG⊥GE交BC 于E,连接AE.(1)求证:BG=DG+BE;(2)如图2,AB=4,E为BC中点,P,Q分别为线段AB,AE上的动点,满足QE=AP,则在P,Q运动过程中,当以PQ为对角线的正方形PRQS的一边恰好落在△ABE 的某一边上时,直接写出正方形PRQS的面积.20.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图,求证:矩形DEFG是正方形;(2)若AB=2,CE=2,求CG的长;(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.参考答案;1.如图,在矩形ABCD中,点E,F分别在边AB,BC上,AF⊥DE,且AF=DE,AF与DE相交于点G.(1)求证:矩形ABCD为正方形:(2)若AE:EB=2:1,△AEG的面积为4,求四边形BEGF的面积.【分析】(1)根据矩形的性质得∠DAB=∠B=90°,由等角的余角相等可得∠ADE=∠BAF,利用AAS可得△ABF≌△DAE(AAS),由全等三角形的性质得AD=AB,即可得四边形ABCD是正方形;(2)根据相似三角形面积的比等于相似比的平方即可解决问题.【解答】(1)证明:∵四边形ABCD是矩形,∴∠DAB=∠B=90°,∵DE⊥AF,∴∠DAB=∠AGD=90°,∴∠BAF+∠DAF=90°,∠ADE+∠DAF=90°,∴∠BAF=∠ADE,在△ABF和△DAE中,,∴△ABF≌△DAE(AAS),∴AD=AB,∵四边形ABCD是矩形,∴四边形ABCD是正方形;(2)解:∵△ABF≌△DAE,∴BF=AE,∵AE:EB=2:1,设AE=2x,EB=x,∴BF=AE=2x,AB=3x,∴AF==x,∵∠EAG=∠F AB,∠AGE=∠B=90°,∴△AEG∽△AFB,∴△AEG的面积:△AFB的面积=AE2:AF2=4x2:13x2=4:13,∵△AEG的面积为4,∴△AFB的面积为13,∴四边形BEGF的面积=13﹣4=9.2.已知:如图,边长为4的菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.(1)求证:四边形ABCD是正方形.(2)E是OB上一点,BE=1,且DH⊥CE,垂足为H,DH与OC相交于点F,求线段OF的长.【分析】(1)由菱形的性质得出AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,得出∠BAD+∠ABC=180°,证出∠BAD=∠ABC,求出∠BAD=90°,即可得出结论;(2)由正方形的性质得出AC⊥BD,AC=BD,CO=AC,DO=BD,得出∠COB=∠DOC=90°,CO=DO,证出∠ECO=∠EDH,证明△ECO≌△FDO(ASA),即可得出结论.【解答】(1)证明:∵四边形ABCD是菱形,∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,∴∠BAD+∠ABC=180°,∵∠CAD=∠DBC,∴∠BAD=∠ABC,∴2∠BAD=180°,∴∠BAD=90°,∴四边形ABCD是正方形;(2)解:∵四边形ABCD是正方形,AB=BC=4,∴AC⊥BD,AC=BD=4,∴OB=CO=AC=2,DO=BD=2,∴∠COB=∠DOC=90°,CO=DO,∵DH⊥CE,垂足为H,∴∠DHE=90°,∠EDH+∠DEH=90°,∵∠ECO+∠DEH=90°,∴∠ECO=∠EDH,在△ECO和△FDO中,,∴△ECO≌△FDO(ASA),∴OE=OF.∵BE=1,∴OE=OF=OB﹣BE=2﹣1.3.如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.(1)求证:∠HEA=∠CGF;(2)当AH=DG时,求证:菱形EFGH为正方形.【分析】(1)连接GE,根据正方形的性质和平行线的性质得到∠AEG=∠CGE,根据菱形的性质和平行线的性质得到∠HEG=∠FGE,解答即可;(2)证明Rt△HAE≌Rt△GDH,得到∠AHE=∠DGH,证明∠GHE=90°,根据正方形的判定定理证明.【解答】证明:(1)连接GE,∵AB∥CD,∴∠AEG=∠CGE,∵GF∥HE,∴∠HEG=∠FGE,∴∠HEA=∠CGF;(2)∵四边形ABCD是正方形,∴∠D=∠A=90°,∵四边形EFGH是菱形,∴HG=HE,在Rt△HAE和Rt△GDH中,,∴Rt△HAE≌Rt△GDH(HL),∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∴菱形EFGH为正方形;4.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.【分析】(1)作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF即可;(2)同(1)的方法判断出△ADE≌△CDG得到CG=AE,即:CE+CG=CE+AE=AC =6.【解答】解:(1)如图,作EM⊥BC于M,EN⊥CD于N,∴∠MEN=90°,∵点E是正方形ABCD对角线上的点,∴EM=EN,∵∠DEF=90°,∴∠DEN=∠MEF,∵∠DNE=∠FME=90°,在△DEN和△FEM中,,∴△DEN≌△FEM(ASA),∴EF=DE,∵四边形DEFG是矩形,∴矩形DEFG是正方形;(2)CE+CG的值是定值,定值为6,理由如下:∵正方形DEFG和正方形ABCD,∴DE=DG,AD=DC,∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,在∴△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴AE=CG,∴CE+CG=CE+AE=AC=AB=×3=6是定值.5.如图①,在正方形ABCD中,点E,F分别在AB、BC上,且AE=BF.(1)试探索线段AF、DE的数量关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图②中补全图形,并说明理由.【分析】(1)根据已知利用SAS判定△DAE≌△ABF,由全等三角形的判定方法可得到AF=DE.(2)根据已知可得HK,KJ,IJ,HI都是中位线,由全等三角形的判定可得到四边形四边都相等且有一个角是直角,从而来可得到该四边形是正方形.【解答】解:(1)AF=DE.∵ABCD是正方形,∴AB=AD,∠DAB=∠ABC=90°,∵AE=BF,∴△DAE≌△ABF,∴AF=DE.(2)四边形HIJK是正方形.如下图,H、I、J、K分别是AE、EF、FD、DA的中点,∴HI=KJ=AF,HK=IJ=ED,∵AF=DE,∴HI=KJ=HK=IJ,∴四边形HIJK是菱形,∵△DAE≌△ABF,∴∠ADE=∠BAF,∵∠ADE+∠AED=90°,∴∠BAF+∠AED=90°,∴∠AOE=90°∴∠KHI=90°,∴四边形HIJK是正方形.6.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.(1)求证:四边形MANP是正方形;(2)求证:EM=BN.【分析】(1)根据有三个角是直角的四边形是矩形证明四边形MANP是矩形,再根据角平分线的性质得:PM=PN,可得结论;(2)证明△EPM≌△BPN,可得结论.【解答】证明:(1)∵四边形ABCD是正方形,∴∠DAB=90°,AC平分∠DAB,(1分)∵PM⊥AD,PN⊥AB,∴∠PMA=∠PNA=90°,∴四边形MANP是矩形,(2分)∵AC平分∠DAB,PM⊥AD,PN⊥AB,∴PM=PN,(3分)∴四边形MANP是正方形;(4分)(2)∵四边形ABCD是正方形,∴PM=PN,∠MPN=90°,∵∠EPB=90°,∴∠MPE+∠EPN=∠NPB+∠EPN=90°,∴∠MPE=∠NPB,(5分)在△EPM和△BPN中,∵,∴△EPM≌△BPN(ASA),(6分)∴EM=BN.(7分)7.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F 分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.【分析】(1)连接CD,根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD,结合AE=CF可证出△ADE≌△CDF(SAS),根据全等三角形的性质可得出DE=DF、ADE=∠CDF,通过角的计算可得出∠EDF=90°,再根据O为EF的中点、GO=OD,即可得出GD⊥EF,且GD=2OD=EF,由此即可证出四边形EDFG是正方形;(2)过点D作DE′⊥AC于E′,根据等腰直角三角形的性质可得出DE′的长度,从而得出2≤DE<2,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.【解答】(1)证明:连接CD,如图1所示.∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,∴∠A=∠DCF=45°,AD=CD.在△ADE和△CDF中,,∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴△EDF为等腰直角三角形.∵O为EF的中点,GO=OD,∴GD⊥EF,且GD=2OD=EF,∴四边形EDFG是正方形;(2)解:过点D作DE′⊥AC于E′,如图2所示.∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,∴DE′=BC=2,AB=4,点E′为AC的中点,∴2≤DE<2(点E与点E′重合时取等号).∴4≤S四边形EDFG=DE2<8.∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.8.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形;②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.【分析】(1)作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF即可;(2)同(1)的方法证出△ADE≌△CDG得到CG=AE,得出CE+CG=CE+AE=AC=4即可.【解答】①证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:∵正方形ABCD∴∠BCD=90°,∠ECN=45°∴∠EMC=∠ENC=∠BCD=90°且NE=NC,∴四边形EMCN为正方形∵四边形DEFG是矩形,∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°∴∠DEN=∠MEF,又∠DNE=∠FME=90°,在△DEN和△FEM中,,∴△DEN≌△FEM(ASA),∴ED=EF,∴矩形DEFG为正方形,②解:CE+CG的值为定值,理由如下:∵矩形DEFG为正方形,∴DE=DG,∠EDC+∠CDG=90°∵四边形ABCD是正方形,∵AD=DC,∠ADE+∠EDC=90°∴∠ADE=∠CDG,在△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴AE=CG∴AC=AE+CE=AB=×2=4,∴CE+CG=4 是定值.9.平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;(2)如果四边形ABCD是正方形,四边形OBEC也是正方形吗?如果是,请给予证明;如果不是,请说明理由.【分析】(1)由平行线可得四边形OBEC为平行四边形,又矩形对角线互相平分且相等,则可得四边形OBEC为菱形;(2)由平行线可得四边形OBEC为平行四边形,又正方形对角线互相垂直、平分且相等,则可得四边形OBEC为正方形.【解答】解:(1)四边形OBEC是菱形.证明:∵BE∥OC,CE∥OB,∴四边形OBEC为平行四边形.又∵四边形ABCD是矩形,∴OC=OB,∴平行四边形OBEC为菱形;(2)四边形OBEC是正方形.证明:∵BE∥OC,CE∥OB,∴四边形OBEC为平行四边形.又∵四边形ABCD是正方形,∴OC=OB,∠BOC=90°,∴平行四边形OBEC为正方形.10.如果P是正方形ABCD内的一点,且满足∠APB+∠DPC=180°,那么称点P是正方形ABCD的“对补点”.(1)如图1,正方形ABCD的对角线AC,BD交于点M,求证:点M是正方形ABCD 的对补点;(2)如图2,在平面直角坐标系中,正方形ABCD的顶点A(1,1),C(3,3).除对角线交点外,请再写出一个该正方形的对补点的坐标,并证明.【分析】(1)根据四边形ABCD是正方形,得到AC⊥BD,于是得到结论;(2)如图2,延长CD交y轴于E,延长CB交x轴于F,则四边形CEOF是正方形连接OC,EF交于P,推出A,C在直线y=x上,得到A在OC上,根据全等三角形的性质得到∠APD=∠APB,得到∠CPD+∠APB=180°,于是得到结论.【解答】解:(1)∵四边形ABCD是正方形,∴AC⊥BD,∴∠AMB=∠CMD=90°,∴∠AMB+∠CMD=180°,∴点M是正方形ABCD的对补点;(2)如图2,点P(,)是该正方形的对补点,延长CD交y轴于E,延长CB交x轴于F,则四边形CEOF是正方形连接OC,EF交于P,∵A(1,1),C(3,3),∴A,C在直线y=x上,∴A在OC上,在△APD与△APB中,,∴△APD≌△APB,∴∠APD=∠APB,∴∠DPE=∠BPF,∵∠EPC+∠APF=180°,∴∠CPD+∠APB=180°,∴P(,)是该正方形的对补点.11.已知:如图,E是正方形ABCD的对角线BD上的点,连接AE、CE.(1)求证:AE=CE;(2)若将△ABE沿AB翻折后得到△ABF,当点E在BD的何处时,四边形AFBE是正方形?请证明你的结论.【分析】(1)利用正方形的性质和SAS证明△ABE≌△CBE即可;(2)由折叠的性质得出∠F=∠AEB,AF=AE,BF=BE,由直角三角形斜边上的中线性质得出AE=BD=BE=DE,证出AE=BE=AF=BF,得出四边形AFBE是菱形,AE ⊥BD,即可得出结论.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=CB,∠BAD=∠ABC=90°,∠ABE=∠CBE=45°,在△ABE和△CBE中,,∴△ABE≌△CBE(SAS),∴AE=CE.(2)解:点E在BD的中点时,四边形AFBE是正方形;理由如下:由折叠的性质得:∠F=∠AEB,AF=AE,BF=BE,∵∠BAD=90°,E是BD的中点,∴AE=BD=BE=DE,∵BF=BE,∴AE=BE=AF=BF,∴四边形AFBE是菱形,E是正方形ABCD对角线的交点,∴AE⊥BD,∴∠AEB=90°,∴四边形AFBE是正方形.12.如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.(1)试判断四边形PQEF是否是正方形,并证明;(2)PE是否总过某一定点,并说明理由.【分析】(1)正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形,故可根据正方形的定义证明四边形PQEF是否使正方形.(2)证PE是否过定点时,可连接AC,证明四边形APCE为平行四边形,即可证明PE 过定点.【解答】解:(1)在正方形ABCD中,AP=BQ=CE=DF,AB=BC=CD=DA,∴BP=QC=ED=F A.又∵∠BAD=∠B=∠BCD=∠D=90°,∴△AFP≌△BPQ≌△CQE≌△DEF.∴FP=PQ=QE=EF,∠APF=∠PQB.∴四边形PQEF是菱形,∵∠FPQ=90°,∴四边形PQEF为正方形.(2)连接AC交PE于O,∵AP平行且等于EC,∴四边形APCE为平行四边形.∵O为对角线AC的中点,∴对角线PE总过AC的中点.13.在平面直角坐标系xOy中,OEFG为正方形,点F的坐标为(1,1).将一个最短边长大于的直角三角形纸片的直角顶点放在对角线FO上.(1)如图,当三角形纸片的直角顶点与点F重合,一条直角边落在直线FO上时,这个三角形纸片与正方形OEFG重叠部分(即阴影部分)的面积为;(2)若三角形纸片的直角顶点不与点O,F重合,且两条直角边与正方形相邻两边相交,当这个三角形纸片与正方形OEFG重叠部分的面积是正方形面积的一半时,试确定三角形纸片直角顶点的坐标(不要求写出求解过程),并画出此时的图形.【分析】(1)S=OE•EF=;(2)如图,正方形GFEO的面积为1,当重合的面积为正方形GFEO的面积的一半时,有两种情况:①四边形OSCB的面积为时,易证得四边形ACDO为正方形,△ABC≌△DSC,有四边形OSCB的面积与正方形ACDO的面积相等,故有OD=OA=即点C的坐标为(,).②四边形FSCB的面积为时,易证得四边形ACDF为正方形,△ABC≌△DSC,有四边形FSCB的面积与正方形ACDO的面积相等,故有AD=F A=即点C的坐标为(1﹣,1﹣).【解答】解:(1)S=OE•EF=;(2)如图,正方形GFEO的面积为1,当重合的面积为正方形GFEO的面积的一半时,有两种情况:①四边形OSCB的面积为时,易证得四边形ACOD为正方形,△ABC≌△DSC,有四边形OSCB的面积与正方形ACOD的面积相等,故有OD=OA=即点C的坐标为(,).②四边形FSCB的面积为时,易证得四边形ACDF为正方形,△ABC≌△DSC,有四边形FSCB的面积与正方形ACDO的面积相等,故有FD=F A=即点C的坐标为(1﹣,1﹣).14.(1)如图矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.【分析】(1)根据矩形的性质得出OD=OC,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据菱形的判定推出即可;(2)根据菱形的性质得出∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据矩形的判定推出即可;(3)根据正方形的性质得出OD=OC,∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据正方形的判定推出即可;【解答】解:(1)四边形CODP的形状是菱形,理由是:∵四边形ABCD是矩形,∴AC=BD,OA=OC=AC,OB=OD=BD,∴OC=OD,∵DP∥OC,DP=OC,∴四边形CODP是平行四边形,∵OC=OD,∴平行四边形CODP是菱形;(2)四边形CODP的形状是矩形,理由是:∵四边形ABCD是菱形,∴AC⊥BD,∴∠DOC=90°,∵DP∥OC,DP=OC,∴四边形CODP是平行四边形,∵∠DOC=90°,∴平行四边形CODP是矩形;(3)四边形CODP的形状是正方形,理由是:∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,OA=OC=AC,OB=OD=BD,∴∠DOC=90°,OD=OC,∵DP∥OC,DP=OC,∴四边形CODP是平行四边形,∵∠DOC=90°,OD=OC∴平行四边形CODP是正方形.15.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图1,求证:矩形DEFG是正方形;(2)若AB=2,CE=,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.(1)作EP⊥CD于P,EQ⊥BC于Q,证明Rt△EQF≌Rt△EPD,得到EF=ED,【分析】根据正方形的判定定理证明即可;(2)通过计算发现E是AC中点,点F与C重合,△CDG是等腰直角三角形,由此即可解决问题.(3)分两种情形考虑问题即可;【解答】(1)证明:作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA,∴EQ=EP,∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,在Rt△EQF和Rt△EPD中,,∴Rt△EQF≌Rt△EPD(ASA),∴EF=ED,∴矩形DEFG是正方形;(2)如图2中,在Rt△ABC中.AC=AB=2,∵EC=,∴AE=CE,∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=.(3)①当DE与AD的夹角为30°时,点F在BC边上,∠ADE=30°,则∠CDE=90°﹣30°=60°,在四边形CDEF中,由四边形内角和定理得:∠EFC=360°﹣90°﹣90°﹣60°=120°,②当DE与DC的夹角为30°时,点F在BC的延长线上,∠CDE=30°,如图3所示:∵∠HCF=∠DEF=90°,∠CHF=∠EHD,∴∠EFC=∠CDE=30°,综上所述,∠EFC=120°或30°.16.如图,在矩形ABCD中,AD=6,CD=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2,连接CF.(1)当DG=2时,求证:四边形EFGH是正方形;(2)当△FCG的面积为2时,求CG的值.【分析】(1)由于四边形ABCD为矩形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;(2)过F作FM⊥DC于M,根据AB∥CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,利用三角形面积解答即可.【解答】(1)证明:在矩形ABCD中,有∠A=∠D=90°,∴∠DGH+∠DHG=90°.在菱形EFGH中,EH=GH∵AH=2,DG=2,∴AH=DG,∴Rt△AEH≌Rt△DHG(HL).∴∠AHE=∠DGH.∴∠AHE+∠DHG=90°.∴∠EHG=90°.∴四边形EFGH是正方形.(2)过F作FM⊥DC于M,则∠FMG=90°.∴∠A=∠FMG=90°.连接EG.由矩形和菱形性质,知AB∥DC,HE∥GF,∴∠AEG=∠MGE,∠HEG=∠FGE,∴∠AEH=∠MGF.∵EH=GF,∴△AEH≌△MGF.∴FM=AH=2.∵S△FCG=,∴CG=2.17.已知,如图,矩形ABCD中,AD=6,DC=7,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.(1)若DG=2,求证四边形EFGH为正方形;(2)若DG=6,求△FCG的面积;(3)当DG为何值时,△FCG的面积最小.【分析】(1)由于四边形ABCD为矩形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于AB∥CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,从而有FM=HA=2(即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2),进而可求三角形面积;(3)先设DG=x,由第(2)小题得,S△FCG=7﹣x,在△AHE中,AE≤AB=7,利用勾股定理可得HE2≤53,在Rt△DHG中,再利用勾股定理可得x2+16≤53,进而可求x ≤,从而可得当x=时,△GCF的面积最小.【解答】解:(1)∵四边形ABCD为矩形,四边形HEFG为菱形,∴∠D=∠A=90°,HG=HE,又AH=DG=2,∴Rt△AHE≌Rt△DGH(HL),∴∠DHG=∠HEA,∵∠AHE+∠HEA=90°,∴∠AHE+∠DHG=90°,∴∠EHG=90°,∴四边形HEFG为正方形;(2)过F作FM⊥DC,交DC延长线于M,连接GE,∵AB∥CD,∴∠AEG=∠MGE,∵HE∥GF,∴∠HEG=∠FGE,∴∠AEH=∠MGF,在△AHE和△MFG中,∠A=∠M=90°,HE=FG,∴△AHE≌△MFG,∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,因此;(3)设DG=x,则由第(2)小题得,S△FCG=7﹣x,在△AHE中,AE≤AB=7,∴HE2≤53,∴x2+16≤53,∴x≤,∴S△FCG的最小值为,此时DG=,∴当DG=时,△FCG的面积最小为().18.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.(1)∠EAF=45°(直接写出结果不写解答过程);(2)①求证:四边形ABCD是正方形.②若BE=EC=3,求DF的长.(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是(直接写出结果不写解答过程).【分析】(1)根据平角的定义得到∠DFE+∠BEF=360°﹣90°=270°,根据角平分线的定义得到∠AFE=DFE,∠AEF=BEF,求得∠AEF+∠AFE=(∠DFE+∠BEF),根据三角形的内角和定理即可得到结论;(2)①作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,先证明四边形ABCD 是矩形,再由角平分线的性质得出AB=AD,即可得出四边形ABCD是正方形;②设DF=x,根据已知条件得到BC=6,由①得四边形ABCD是正方形,求得BC=CD =6,根据全等三角形的性质得到BE=EG=3,同理,GF=DF=x,根据勾股定理列方程即可得到结论;(3)把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ =2,得出MG=DG=MP=PH=6,GQ=4,设MR=HR=a,则GR=6﹣a,QR=a+2,在Rt△GQR中,由勾股定理得出方程,解方程即可.【解答】解:(1)∵∠C=90°,∴∠CFE+∠CEF=90°,∴∠DFE+∠BEF=360°﹣90°=270°,∵AF平分∠DFE,AE平分∠BEF,∴∠AFE=DFE,∠AEF=BEF,∴∠AEF+∠AFE=(∠DFE+∠BEF)=270°=135°,∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,故答案为:45;(2)①作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,∵AB⊥CE,AD⊥CF,∴∠B=∠D=90°=∠C,∴四边形ABCD是矩形,∵∠CEF,∠CFE外角平分线交于点A,∴AB=AG,AD=AG,∴AB=AD,∴四边形ABCD是正方形;②设DF=x,∵BE=EC=3,∴BC=6,由①得四边形ABCD是正方形,∴BC=CD=6,在Rt△ABE与Rt△AGE中,,∴Rt△ABE≌Rt△AGE(HL),∴BE=EG=3,同理,GF=DF=x,在Rt△CEF中,EC2+FC2=EF2,即32+(6﹣x)2=(x+3)2,解得:x=2,∴DF的长为2;(3)解:如图2所示:把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,∴MG=DG=MP=PH=5,∴GQ=3,设MR=HR=a,则GR=5﹣a,QR=a+2,在Rt△GQR中,由勾股定理得:(5﹣a)2+32=(2+a)2,解得:a=,即HR=;故答案为:.19.如图1,在正方形ABCD中,G为线段BD上一点,连接AG,过G作AG⊥GE交BC 于E,连接AE.(1)求证:BG=DG+BE;(2)如图2,AB=4,E为BC中点,P,Q分别为线段AB,AE上的动点,满足QE=AP,则在P,Q运动过程中,当以PQ为对角线的正方形PRQS的一边恰好落在△ABE 的某一边上时,直接写出正方形PRQS的面积.【分析】(1)过点G作GN⊥BC于点N,作GM⊥AB于点M,过点E作EF⊥BC,交BD于点F,先证明△AGM≌△EGN(ASA),从而AM=EN,再利用DG=BD﹣BG=AB﹣BM=AM,FG=BG﹣BF=BN﹣BE=EN,得出DG=FG,则BG =BF+FG=DG+BE;(2)分五种情况讨论,以点B为原点,BC所在直线为x轴,BA所在直线为y轴建立平面直角坐标系,分别求得AE和PQ的解析式,二者联立解得用含m的式子表示的点Q 的坐标,在Rt△QEF中,由勾股定理得出QE的表达式,然后结合QE=AP得出关于m的方程,解得m的值,则可得点Q的横坐标,从而可得正方形PRQS的面积,利用锐角三角函数和线段的和差关系列出方程,可求正方形的边长,即可求解.【解答】解:(1)证明:过点G作GN⊥BC于点N,作GM⊥AB于点M,过点E作EF ⊥BC,交BD于点F,如图所示:∵四边形ABCD是正方形,BD是对角线,∴BF=BE,GM=GN,∵AG⊥GE,GN⊥BC,GM⊥AB,∴∠AMG=∠ENG=90°,∠AGM+∠MGN=∠EGN+∠MGN,∴∠AGM=∠EGN,∴在△AGM和△EGN中,,∴△AGM≌△EGN(ASA),∴AM=EN,∵DG=BD﹣BG=AB﹣BM=AM,FG=BG﹣BF=BN﹣BE=EN,∴DG=FG,∴BG=BF+FG=DG+BE;(2)①若正方形PRQS的一边恰好落在AB上,如图2:当点P在点R的上方,∵AB=4,E为BC中点,∴A(0,4),E(2,0),设AE的解析式为y=kx+4,将(2,0)代入得:0=2k+4,∴k=﹣2,∴y=﹣2x+4,∵PQ与AB的夹角为45°,∴设PQ的解析式为y=﹣x+m,则P为(0,m),|AP|=4﹣m,由解得:Q(4﹣m,2m﹣4),过Q作QF⊥BC,则QF=2m﹣4,EF=m﹣2,∴在Rt△QEF中,由勾股定理得:QE==(m﹣2).∵QE=AP,∴(m﹣2)=(4﹣m),∴m=3,∴4﹣m=1,∴正方形PRQS的面积为1.如图2﹣1,当点P在点R的下方,∵tan∠RAQ==,∴AR=2RQ,∴AP=AR+RP=3RQ,∴AQ==RQ,∵BE=2,AB=4,∴AE===2,∵QE=AP,∴QE=3RQ,∴3RQ+RQ=2,∴RQ=,∴正方形PRQS的面积为.②当正方形PRQS的一边落在AE上,如图2﹣2,∵tan∠P AQ==,∴AS=2PS,∴AP==PS,∵QE=AP,∴QE=5PS,∵AE=AS+SQ+QE=2,∴2PS+PS+5PS=2,PS=,∴正方形PRQS的面积为,如图2﹣3,同理可得:AE=AR+RE=AR+QE﹣QR=(5+1)RP=2,∴PR=,∴正方形PRQS的面积为,当正方形PRQS与BC重合时,如图2﹣4,∵tan∠BAE==,∴AS=2SQ,∴AP=AS+SP=3SQ,∵sin∠AEB===,∵QE=QR,∴QE≠AP,∴这种情况不存在,故舍去,综上所述:正方形PRQS的面积为或1或或.20.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图,求证:矩形DEFG是正方形;(2)若AB=2,CE=2,求CG的长;(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.(1)作EP⊥CD于P,EQ⊥BC于Q,证明Rt△EQF≌Rt△EPD,得到EF=ED,【分析】根据正方形的判定定理证明即可;(2)通过计算发现E是AC中点,点F与C重合,△CDG是等腰直角三角形,由此即可解决问题.(3)分两种情形考虑问题即可;【解答】(1)证明:作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA,∴EQ=EP,∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,在Rt△EQF和Rt△EPD中,,∴Rt△EQF≌Rt△EPD(ASA),∴EF=ED,∴矩形DEFG是正方形;(2)如图2中,在Rt△ABC中,AC=AB=4,∵EC=2,∴AE=CE,∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=2;(3)①如图3,当DE与AD的夹角为40°时,∠DEC=45°+40°=85°,∵∠DEF=90°,∴∠CEF=5°,∵∠ECF=45°,∴∠EFC=130°,②如图4,当DE与DC的夹角为40°时,∵∠DEF=∠DCF=90°,∴∠EFC=∠EDC=40°,。
正方形的性质及判定典型题(精选)

、正方形的性质例1】正方形有条对称轴.例2】已知正方形BD EF 的边长是正方形ABCD 的对角线,则S正方形BDEF :S正方形ABCD例3】如图,已知正方形ABCD 的面积为256 ,点 F 在CD 上,点 E 在CB 的延长线上,且AE AF ,AF 20,则BE 的长为例4】如图,在正方形ABCD 中, E 为AB 边的中点,G , F 分别为AD ,BC 边上的点,若AG 1,BF 2 ,GEF 90 ,则GF 的长为.例5】将n 个边长都为1cm 的正方形按如图所示摆放,点A1,A2,...,A n分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为如图,正方形 ABCD 中, O 是对角线 A C ,B D 的交点,过点 O 作OE OF ,分别交 AB ,CD 于 E ,F ,若 AE 4,CF 3,则 EF如图,正方形 ABCD 的边长为 2cm ,以 B 为圆心, BC 长为半径画弧交对角线 BD 于点E ,连接C E , P 是C E 上任意一点, PM BC 于M ,PN BD 于N ,则PM PN 的值为如图所示,正方形 ABCD 对角线 AC 与BD 相交于 O ,MN ∥ AB ,且分别与 AO 、BO 交于 M 、N .试探讨 BM 与CN 之间的关系,写出你所得到的结论的证明过程.例 6】例 7】 例 8】 如图, E 是正方形 ABCD对角线 BD 上的一点,求证: AE C E . 例 9】 如图, P 为正方形ABCD对角线上一点, PE BC 于E ,PF CD 于F .求证: AP EF. 例 10】例 11】如图,已知 P 是正方形 ABCD 内的一点,且 ABP 为等边三角形,那么 DCP例 13】如图,已知 E 、 F 分别是正方形 ABCD 的边 BC 、 CD 上的点,AE于M 、N ,若 EAF 50 ,则 CME CNF例 14】 如图,四边形 ABCD 为正方形,以 AB 为边向正方形外作正方形则AF D例 12】 已知正方形 ABCD ,在AD 、 等腰直角三角形. AC 上分别取 E 、 F 两点,使 ED∶AD 2FC∶AC ,求证: BEF 是AF 分别与对角线 BD 相交ABE , CE 与 BD 相交于点 F ,D CB例15】如果点 E 、F 是正方形ABCD 的对角线BD 上两点,且BEDF 吗?并阐明理由.DF DE .D N AN ,求证KL M N ,K L M N例16】如图,正方形ABCD 中,在AD 的延长线上取点交CD ,CE 于H ,G .求证:GHD 是等腰三角形.例17】如图,过正方形顶点A 引AE ∥ BD连结BF 分别E ,F ,使DE AD , D F BD,且 B E BD .若BE 与AD 的延长线的交点为F ,求证,你能判断四边形AECF 的形状例18】如图所示,在正方形ABCD 中,AK 、AN 是 A 内的两条射线,BK AK ,BL AN ,D M AK ,D C第 5 页 共 10 页例19】如图,正方形 ABCD 的边 CD 在正方形 ECGF 的边CE 上,连接 BE , D G ,求证: BE DG .例 20】 ( 2007 年三帆中学期中考试)如图,在正方形 上的一点, CE CF , FD C 30 ,求 BEFABC D 中, 的度数 . E 为 CD 边上的一点,AF 为 BC 延长线DEBC F例21】已知:如图,在正方形 ABCD 中,G 是CD 上一点,延长 BC到E ,使CE CG ,连接 BG 并延 长交 D E 于 F .(1)求BC G ≌ D CE ;2)将 △ DCE 绕点 D 顺时针旋转 90 得到 DAE ,判断四边形 E BG D 是什么特殊四边形?并说明 理由.例22】若正方形 ABCD 的边长为 4,E 为BC 边上一点, BE 3,M 为线段 AE 上一点,射线 BM 交正 方形的一边于点 F ,且 BF AE ,则 BM 的长为 .例 23】如图 1,在正方形 ABCD 中, E 、 F 、 G 、 H 分别为边 AB 、 BC 、 CD 、 D A 上的点,HA EB FC GD ,连接 EG 、FH ,交点为 O .⑴ 如图 2,连接 EF ,FG ,GH ,H E ,试判断四边形 EFGH 的形状,并证明你的结论;⑵ 将正方形 ABCD 沿线段 EG 、HF 剪开,再把得到的四个四边形按图例 26】如图,正方形 ABCD 中, E ,F 是 AB ,BC 边上两点,且 EF AE FC ,DG EF 于 G ,求证:3 的方式拼接成一个 四边形.若正方形 ABCD 的边长为 3 cm ,H A EB FC GD 1cm ,则图 3 中阴影部分的面 积为 2cm例24】如图,正方形 ABCD 对角线相交于点 O ,点 P 、Q 分别是 BC CD 上的点, A Q D P ,求证:1)OP OQ ;(2)O P OQ. 例25】如图,在正方形 ABCD 中, E 、F 分别是 AB 、BC 的中点,求证:AM ADA EB 图2D G C图AD例27】如图,点 M ,N 分别在正方形 ABCD 的边 BC ,CD 上,已知 MCN 的周长等于正方形 ABCD 周长的一半,求 M AN 的度数例28】如图,设 EF ∥ 正方形 ABCD 的对角线 AC ,在D A 延长线上取一点 G ,使 AG AD ,EG 与DF交于 H ,求证: AH 正方形的边长.例29】把正方形 ABCD 绕着点 A ,按顺时针方向旋转得到正方形 AEFG ,边 FG 与 BC 交于点 H(如 图).试问线段 HG 与线段 HB 相等吗?请先观察猜想,然后再证明你的猜想.例30】如图所示,在直角梯形 ABCD 中, AD∥ BC , ADC 90 ,l 是 AD 的垂直平分线,交 AD 于点M ,以腰 AB 为边作正方形 ABFE ,作 EP l 于点 P ,求证 2EP AD 2CD.Fl例33】如图,已知平行四边形 ABCD 中,对角线 AC 、BD 交于点 O ,E 是BD 延长线上的点,且 ACE是等边三角形.⑴ 求证:四边形 ABCD 是菱形;⑵ 若 AED 2 EAD ,求证:四边形 ABCD 是正方形.例31】如图所示, A BC D 是正方形, E 为B F 上的一点,四边形 AEFC 恰好是一个菱形,、正方形的判定四边形 ABC D 的四个内角的平分线两两相交又形成一个四边形 ⑴四边形 EFG H 对角互补;⑵若四边形 ABCD 为平行四边形,则四边形 EFG H 为矩形. ⑶四边形 ABCD 为长方形,则四边形 EF GH 为正方形.例 32】EF GH ,求证:D则 EAB __________AB例34】已知:如图,在ABC 中,AB AC ,AD BC ,垂足为点 D ,AN 是ABC 外角CAM 的平分线,CE AN ,垂足为点 E .⑴ 求证:四边形AD CE 为矩形;⑵ 当ABC 满足什么条件时,四边形AD CE 是一个正方形?并给出证明.l例 35】如图,点 M 是矩形 ABCD 边 AD 的中点, 2AB AD ,点 P 是 BC 边上一动点, PE M C ,PF BM ,垂足分别为 E 、 F ,求点 P 运动到什么位置时,四边形 PEM F 为正方形.例36】如图, ABCD 是边长为 1的正方形, EFGH 是内接于 ABCD 的正方形, AE a ,AF b ,若 SEFGH 3,则b a =例37】如图, A 在线段 BG 上, ABCD 和 DEFG 都是正方形,面积分别为7cm 2和11cm 2,则 CDE的面积为例 38】如图,在正方形 ABCD 中,点 P ,P 1为正方形内的两点,且 PB PD ,P 1B AB , CBP P 1BP ,则 B P 1PDE第 11 页 共 10 页例40】已知: PA 2,PB 4,以 AB 为一边作正方形 ABCD ,使 P 、D 两点落在直线 AB 的两侧.(1)如图,当∠ APB= 45 °时,求 AB 及 PD 的长;( 2)当∠ APB 变化,且其它条件不变时,求 PD 的最大值,及相应∠ APB 的大小 .D C例 39】 如图,若在平行四边形 顶点组成一个正方形. ABC D 各边上向平行四边形的外侧作正方形,求证:以四个正方形中心为A DM。
正方形的性质与判定经典例题练习题

正方形第一课时一、自主学习●目标导学1、理解并掌握正方形的性质。
2、通过自学、合作、交流培养自己分析问题解决问题的能力。
●合作探究【探究一】正方形的定义1、正方形的定义:2、正方形与矩形和菱形的关系是【探究二】正方形的性质1、归纳正方形的性质:边角对角线对称性2、用几何语言叙述正方形的性质:【探究三】正方形的周长与面积边讲边练:①正方形与等腰三角形(等边三角形)结合1. 如图,E是正方形ABCD的对角线BD上一点,且BE=BC,则∠ACE=°2. 如图,四边形ABCD是正方形,延长CD到E,使CE=CB,则∠DBE=°.3. 如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:(1)∠E=22.5°;(2) ∠AFC=112.5°;(3) ∠ACE=135°;(4)AC=CE;(5) AD∶CE=1∶ 2.其中正确的有()A.5个 B.4个 C.3个 D.2个4. 如图,等边△EDC在正方形ABCD内,连结EA、EB,则∠AEB=°;∠ACE =°.5.已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是°.②正方形与旋转结合1.如图1,四边形ABCD是正方形,E是边CD上一点,若△AFB经过逆时针旋转角θ后与△AED重合,则θ的取值可能为()A.90°B.60°C.45°D.30°2.已知正方形ABCD中,点E在边DC上,DE = 2,EC = 1(如图2所示)把线段AE 绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为___________.3. 如图3,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.③正方形对角线的对称性1. 如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF= .可以用一句话概括:正方形边上的任意一点到两对角线的距离之和等于 .思考:如若P在AB的延长线时,上述结论是否成立?若不成立,请写出你的结论,并加以说明.2.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP =EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD= 2EC.其中正确结论的序号是.思考:当点P在DB的长延长线上时,请将备用图补充完整,并思考(1)正确结论是否依旧成立?若成立,直接写出结论;若不成立,请写出相应的结论.④正方形的折叠1.如图1,将边长为8cm的正方形纸片ABCD折叠,使点D落在BC边中点E处,点A 落在点F处,折痕为MN,则线段CN的长是.2.如图2,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD 边上的B'处,点A对应点为A',且CB'=3,则AM的长是 .3如图3,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE 对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是 .课后练习1、已知:如图,正方形ABCD中,CM=CD,MN⊥AC,连结CN,则∠DCN=_____=____∠B,∠MND=_______=_______∠B.2.在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,则△ABO的周长是()A.12+122 B.12+62 C.12+2 D.24+623.正方形的面积是31,则其对角线长是________.4. 如图,在正方形ABCD中,△PBC、△QCD是两个等边三角形,PB与DQ交于M,BP与CQ交于E,CP与DQ交于F.求证:PM = QM.P5. 如图4,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F,若正方形A′B′C′D′绕点O旋转某个角度后,OE=OF吗?两正方形重合部分的面积怎样变化?为什么?6.如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E 在射线BC上,且PE=PB.试判断PE与PB的关系.7. 如图,正方形ABCD的面积为12,△ADE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PB+PE的和最小,则这个最小值为 .8.如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.(1)如图②,若M为AD边的中点,①△AEM的周长=_____cm;②求证:EP=AE+DP;(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.正方形第二课时一、自主学习● 目标导学1、理解并掌握正方形的判定方法。
正方形的性质与判定(八大类型)(原卷版)

专题03 正方形的性质与判定(八大类型)【题型1 正方形的性质】【题型2 正方形的判定】【题型3 矩形的性质与判定综合运用】【题型4 正方形中最小值问题】【题型5 正方形-对角互模型】【题型6 正方形-半角互模型】【题型7 正方形-手拉手模型】【题型8 正方形-十字架模型】【题型1 正方形的性质】1.(2023春•增城区期中)如图,在正方形ABCD的外侧作等边三角形ADE,则∠AEB度数为()A.10°B.15°C.22.5°D.30°2.(2023春•鼓楼区期中)矩形、正方形都具有的性质是()A.对角线相等B.邻边相等C.对角线互相垂直D.对角线平分对角3.(2023春•张北县校级期中)四边形ABCD是正方形,E为CD.上一点,连接AE,过B作BF⊥AE于E,∠ABF=30°且,则正方形ABCD的周长为()A.B.C.24D.6 4.(2023•官渡区校级模拟)用四根长度相等的木条制作学具,先制作图(1)所示的正方形ABCD,测得BD=10cm,活动学具成图(2)所示的四边形ABCD,测得∠A=120°,则图(2)中BD的长是()A.cm B.cm C.cm D.cm 5.(2023•龙川县一模)如图,P为AB上任意一点,分别以AP,PB为边在AB 同侧作正方形APCD、正方形PBEF,连接AF,BC,设∠CBE=x°,∠AFP =y°,则y与x的关系为()A.y=x B.y=2x C.y=180﹣x D.y=90﹣x 6.(2023•巧家县一模)如图,在边长为4cm的正方形ABCD中,对角线AC,BD相交于点E,F为线段BC的中点,连接EF,则线段EF的长为()A.B.C.1D.2 7.(2023•新华区模拟)一个正方形和一个直角三角形的位置如图所示,若∠1=α,则∠2=()A.α﹣45°B.α﹣90°C.270°﹣αD.180°﹣α8.(2023春•苏州期中)如图,在正方形ABCD中,E为AD上一点,连接BE,BE交对角线于点F,连接DF,若∠ABE=35°,则∠CFD的度数为()A.80°B.70°C.75°D.45°9.(2023•碑林区校级二模)如图,在正方形ABCD中,点P在对角线BD上,PE⊥BC,PF⊥CD,E,F分别为垂足,连接AP,EF,若AP=5,则EF=()A.5B.5C.2.5D.10.(2023•五华区校级模拟)如图,有六根长度相同的木条,小明先用四根木条制作了能够活动的菱形学具,他先将该活动学具调成图1所示菱形,测得∠B=60°,对角线AC=10cm,接着将该活动学具调成图2所示正方形,最后用剩下的两根木条搭成了如图3所示的图形,连接BE,则图3中△BCE的面积为()A.cm2B.50cm2C.cm2D.25cm2 11.(2023春•天津期中)如图,在边长为4的正方形ABCD中,点E,点F分别是BC,AB上的点,连接DE,DF,EF,满足∠DEF=∠DEC.若AF=1,则EF的长为()A.B.C.D.12.(2022春•汉阴县期末)如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB =S四边形DEOF中,正确结论的个数为()A.4个B.3个C.2个D.1个13.(2022春•新泰市期中)如图,在正方形ABCD中,点O是对角线AC、BD 的交点,过点O作射线OM、ON分别交BC、CD于点E、F,且∠EOF=90°,OC、EF交于点G.给出下列结论:①△COE≌△DOF;②△OBE≌△OCF;③四边形CEOF的面积为正方形ABCD面积的;④DF2+CE2=EF2.其中正确的为.(将正确的序号都填入)14.(2022春•长春期末)小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得正方形的对角线AC=40cm,则图1中对角线AC的长为cm.【题型2 正方形的判定】15.(2023春•黄埔区期中)下列说法错误的是()A.对角线相等的菱形是正方形B.对角线互相平分且垂直的四边形是菱形C.对角线相等的平行四边形是矩形D.对角线垂直且相等的四边形是正方形16.(2023•雁塔区校级二模)如图,在矩形ABCD中,对角线AC,BD交于点O,要使该矩形成为正方形,则应添加的条件是()A.CD=AD B.OD=CD C.BD=AC D.∠AOB=60°17.(2022春•铁岭县期中)小明在学习了正方形以后,给同桌小文出了道题:从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选两个作为补充条件,使平行四边形ABCD为正方形.现有下列四种选法你认为错误的是()A.①②B.①③C.②③D.②④18.(2022•鼓楼区校级开学)如图,E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,则四边形EFMN的形状是()A.平行四边形B.矩形C.菱形D.正方形19.(2022春•河西区期末)如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE,则下列结论不一定正确的是()A.∠AFP=∠BPQB.EF∥QPC.四边形EFPQ是正方形D.四边形PQEF的面积是四边形ABCD面积的一半20.(2023•莱西市一模)四边形ABCD为矩形,E是AB延长线上的一点,AC =EC.(1)求证:△BCD≌△CBE;(2)△ACE添加一个条件,矩形ABCD为正方形.请说明理由.21.(2023春•鼓楼区校级月考)如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G、F、H分别是BE、BC、CE的中点.连接EF,若BE⊥EC,EF⊥BC,说明:四边形EGFH是正方形.22.(2022秋•皇姑区期末)如图,AD是△ABC的一条角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.(1)求证:四边形AEDF是菱形;(2)若∠B=35°,当∠C=度时,四边形AEDF为正方形(直接填空).23.(2022秋•东港市期末)如图,在△ABC中,∠ACB=90°,点D是边AB 的中点,连接CD,过点C作CE∥AB,过点B作BE∥CD,CE,BE交于点E.(1)判断四边形CDBE是什么特殊的四边形,并证明;(2)直接写出当△ABC再满足什么条件时,四边形CDBE是正方形.24.(2022春•隆阳区期中)如图,点B,C,F在同一条直线上,AC⊥BF于点C,且AC=BC,连接AB,取AB的中点D,连接CD,过点A作CE的垂线,垂足为E,已知点E到直线AC和CF的距离相等.求证:四边形ADCE是正方形.25.(2021秋•平远县期末)如图,在矩形ABCD中,M,N分别是边AD,BC 的中点,E,F分别是线段BM,CM的中点.(1)判断四边形MENF是什么特殊四边形,并证明你的结论;(2)当AD,AB满足什么条件时,四边形MENF是正方形.【题型3 正方形的性质与判定综合运用】26.(2023春•任城区校级月考)如图所示△ABC中,∠C=90°,∠A,∠B的平分线交于D点,DE⊥BC于点E,DF⊥AC于点F.(1)求证:四边形CEDF为正方形;(2)若AC=12,BC=16,求CE的长.27.(2022春•南谯区校级月考)如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.(1)求证:BE=DE;(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形;②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.28.(2022春•海阳市期末)如图,在矩形ABCD中,点E,F分别在边AB,BC上,AF⊥DE,且AF=DE,AF与DE相交于点G.(1)求证:矩形ABCD为正方形:(2)若AE:EB=2:1,△AEG的面积为4,求四边形BEGF的面积.29.(2022春•关岭县期末)如图,在△ABC中,∠BAC=90°,∠BAC的平分线交BC于点D,DE∥AB,交AC于点E,DF∥AC,交AB于点F.(1)求证:四边形AFDE是正方形;(2)若AD=3,求四边形AFDE的面积.30.(2022春•覃塘区期末)如图,在矩形ABCD中,点E,F分别在BC,CD 边上,且AE=AF,∠CEF=45°.(1)求证:四边形ABCD是正方形;(2)若,BE=1,求四边形ABCD的面积.31.(2022春•交口县期末)如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.(1)求证:AK=AH;(2)求证:四边形AKFH是正方形;(3)若四边形AKFH的面积为10,CE=1,求点A,E之间的距离.【题型4 正方形中最小值问题】32.(2021春•龙口市期末)如图,在边长为6的正方形ABCD中,点P为对角线AC上一动点,PE⊥AB于E,PF⊥BC于F,则EF的最小值为()A.B.C.4D.333.(河西区一模)如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为()A.2B.4C.D.234.(铜仁地区)以边长为2的正方形的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于A、B两点,则线段AB的最小值.35.(2021•威海)如图,在正方形ABCD中,AB=2,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G,连接BG.若AE=BF,则BG的最小值为.36.(2021秋•江汉区月考)已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并证明;(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;(3)如图3,连接BG,N为BG中点,若AB=13,CE=5,则MN的最大值为.【题型5 正方形-对角互模型】37.(2021秋•锦江区期末)如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC 于点M,N,记△AOM的面积为S1,△CON的面积为S2,若正方形的边长AB=10,S1=16,则S2的大小为()A.6B.7C.8D.938.(2021•重庆)如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为()A.1B.C.2D.2 39.(2022春•龙胜县期中)如图,两个边长相等的正方形ABCD和OEFG,若将正方形OEFG绕点O按逆时针方向旋转150°,则两个正方形的重叠部分四边形OMCN的面积()A.不变B.先增大再减小C.先减小再增大D.不断增大40.(2021春•正阳县期中)将n个边长都为1cm的正方形按如图所示的方法摆放,点A1、A2、…A n分别是正方形对角线的交点,则2021个正方形形成的重叠部分的面积和为()A.cm2 B.505cm2C.cm2 D.()2021cm2 41.(2020•呼伦贝尔)已知:如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F分别是边BC,CD上的点,且∠EOF=90°.求证:CE=DF.42.(2021•深圳模拟)如图,正方形ABCD的对角线交于点O,点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M,OF、AB的延长线交于点N,连接MN.(1)求证:OM=ON;(2)若正方形ABCD的边长为6,OE=EM,求MN的长.【题型6 正方形-半角互模型】43.(1)如图①,正方形ABCD①中,点E、F分别在边BC、CD上,∠EAF =45°,延长CD到点C,使DG=BE,连接EF、AG,求证:EF=FG;(2)如图②,在△ABC中,∠BAC=90°,点M、N在边BC上,且∠MAN =45°,若BM=2,AB=AC,CN=3,求MN的长.44.已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.(1)当∠MAN绕点A旋转到(如图1)时,求证:BM+DN=MN;(2)当∠MAN绕点A旋转到如图2的位置时,猜想线段BM,DN和MN之间又有怎样的数量关系呢?请直接写出你的猜想.(不需要证明)45.把一个含45°的三角板的锐角顶点与正方形ABCD的顶点A重合,然后把三角板绕点A顺时针旋转,它的两边分别交直线CB、DC于点M、N.(1)当三角板绕点A旋转到图(1)的位置时,求证:MN=BM+DN.(2)当三角板绕点A旋转到图(2)的位置时,试判断线段MN、BM、DN 之间具有怎样的等量关系?请写出你的猜想,并给予证明.【题型7 正方形-手拉手模型】46.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.(1)求证:EB=GD;(2)判断EB与GD的位置关系,并说明理由;(3)若AB=3,AG=,求EB的长.47.点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作正方形ACDE 和BCFG,连接AF、BD.(1)如图①,AF与BD的数量关系和位置关系分别为,;(2)将正方形BCFG绕着点C顺时针旋转α角(0°<α<360°),①如图②,第(1)问的结论是否仍然成立?请说明理由;②若AC=4,BC=,当正方形BCFG绕着点C顺时针旋转到点A、B、F三点共线时,求DB的长度.【题型8 正方形-十字架模型】48.(2022春•沙坪坝区校级月考)如图,F是正方形ABCD对角线BD上一点,连接AF,CF,并延长CF交AD于点E.若∠AFC=140°,则∠DEC的度数为()A.80°B.75°C.70°D.65°49.(2022•灞桥区校级模拟)如图,在正方形ABCD中,点E、点F分别在AD、CD上,且AE=DF,若四边形OEDF的面积是1,OA的长为1,则正方形的边长AB为()A.1B.2C.D.250.(2022春•孝南区期中)如图1,P为正方形ABCD的边BC上一动点(P 与B、C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E.(1)求证:AP⊥BQ;(2)当P运动到BC中点处时(如图2),连接DE,请你判断线段DE与AD 之间的关系,并说明理由;(3)如图3,在(2)的条件下,过A点作AM⊥DE于点H,交BQ、CD于点N、M,若AB=2,求QM的长度.51.(2021春•船营区校级期中)如图,在正方形ABCD中,E是边AB上的点,连接CE,过点D作DF⊥CE,分别交BC,CE于点F、G.(1)求证:CE=DF;(2)若AB=3,图中阴影部分的面积和与正方形ABCD的面积之比为2:3,则△DCG的面积为,CG+DG的长为.52.(2020秋•莲湖区期中)(1)如图1,在正方形ABCD中,AE、DF相交于点O且AE⊥DF则AE和DF的数量关系为.(2)如图2,在正方形ABCD中,E、F、G分别是边AD、BC、CD上的点,BG⊥EF,垂足为H.求证:EF=BG.(3)如图3,在正方形ABCD中,E、F、M分别是边AD、BC、AB上的点,AE=2,BF=5,BM=1,将正方形沿EF折叠,点M的对应点恰好与CD边上的点N重合,求CN的长度.。
正方形的性质与判定专题练习

正方形专题训练(含答案)一.选择题(共11小题)1.如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,),则点C的坐标为()2.)如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为()A.a2B.a2C.a2D.a23.如图,F是正方形ABCD的边CD上的一个动点,BF 的垂直平分线交对角线AC于点E,连接BE,FE,则∠EBF 的度数是()A.45°B.50°C.60°D.不确定4.平行四边形、矩形、菱形、正方形都具有的是()A.对角线互相平分B.对角线互相垂直C .对角线相等D.对角线互相垂直且相等5.正方形的一条对角线长为4,则这个正方形的面积是()6.(2014•福州)如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°7.顺次连接菱形各边的中点所形成的四边形是()A.等腰梯形B.矩形C.菱形D.正方形8.下列说法中,正确的是()A.相等的角一定是对顶角B.四个角都相等的四边形一定是正方形C.平行四边形的对角线互相平分D.矩形的对角线一定垂直9.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是()A.选①②B.选②③C.选①③D.选②④10.如图,在正方形ABCD中,CE=MN,∠MCE=35°,那么∠ANM等于()A.45°B.50°C.55°D.60°11.如图,菱形ABCD中,∠B=60°,AB=5,则以AC为边长的正方形ACEF的面积为()A.9B.16 C.20 D.25二.填空题(共5小题)12.如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB=_________度.13.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是_________度.14.如图,四边形ABCD为正方形,△ADE为等边三角形.AC为正方形ABCD的对角线,则∠EAC=_________度.A.8B.4C.8D.1615.已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为_________.16.如图所示,正方形ABCD 的周长为16cm,顺次连接正方形ABCD各边的中点,得到四边形EFGH,则四边形EFGH的周长等于_________cm,四边形EFGH的面积等于_________cm.三.解答题(共6小题)17.如图,正方形ABCD中,E、F分别为BC、CD上的点,且AE⊥BF,垂足为点G.求证:AE=BF.18.如图,在正方形ABCD中,P是对角线AC上的一点,连接BP、DP,延长BC到E,使PB=PE.求证:∠PDC=∠PEC.19.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.(1)求证:AE=CF;(2)若∠ABE=55°,求∠EGC的大小.20.在平面内正方形ABCD与正方形CEFH如图放置,连DE,BH,两线交于M.求证:(1)BH=DE.(2)BH⊥DE.21.已知:如图,▱ABCD中,O是CD的中点,连接AO 并延长,交BC的延长线于点E.(1)求证:△AOD≌△EOC;(2)连接AC,DE,当∠B=∠AEB=_________°时,四边形ACED是正方形?请说明理由.22.(2014•随州)已知:如图,在矩形ABCD中,M、N 分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.(1)求证:△ABM≌△DCM;(2)填空:当AB:AD=_________时,四边形MENF 是正方形.一.选择题(共11小题)1.(2014•南充)如图,将正方形OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1,),则点C 的坐标为( )A . (﹣,1) B . (﹣1,) C . (,1) D . (﹣,﹣1)考点: 全等三角形的判定与性质;坐标与图形性质;正方形的性质.专题:几何图形问题. 分析: 过点A 作AD ⊥x 轴于D ,过点C 作CE ⊥x 轴于E ,根据同角的余角相等求出∠OAD=∠COE,再利用“角角边”证明△AOD 和△OCE 全等,根据全等三角形对应边相等可得OE=AD ,CE=OD ,然后根据点C 在第二象限写出坐标即可.解答: 解:如图,过点A 作AD ⊥x 轴于D ,过点C 作CE ⊥x 轴于E ,∵四边形OABC 是正方形, ∴OA=OC ,∠AOC=90°, ∴∠COE+∠AOD=90°, 又∵∠OAD+∠AOD=90°, ∴∠OAD=∠COE, 在△AOD 和△OCE 中,,∴△AOD ≌△OCE (AAS), ∴OE=AD=,CE=OD=1,∵点C 在第二象限, ∴点C 的坐标为(﹣,1).故选:A .点评: 本题考查了全等三角形的判定与性质,正方形的性质,坐标与图形性质,作辅助线构造出全等三角形是解题的关键,也是本题的难点.2.(2014•山西)如图,点E 在正方形ABCD 的对角线AC 上,且EC=2AE ,直角三角形FEG 的两直角边EF 、EG 分别交BC 、DC 于点M 、N .若正方形ABCD 的边长为a,则重叠部分四边形EMCN 的面积为( )A . a 2B . a 2C . a 2D . a 2考点:全等三角形的判定与性质;正方形的性质.专题:几何图形问题. 分析: 作EP ⊥BC 于点P ,EQ ⊥CD 于点Q ,△EPM ≌△EQN,利用四边形EMCN 的面积等于正方形MCQE 的面积求解.解答:解:作EP ⊥BC 于点P,EQ ⊥CD 于点Q ,∵四边形ABCD是正方形,∴∠BCD=90°,又∵∠EPM=∠EQN=90°,∴∠PEQ=90°,∴∠PEM+∠MEQ=90°,∵三角形FEG是直角三角形,∴∠NEF=∠NEQ+∠MEQ=90°,∴∠PEM=∠NEQ,∵AC是∠BCD的角平分线,∠EPC=∠EQC=90°,∴EP=EN,四边形MCQE是正方形,在△EPM和△EQN中,,∴△EPM≌△EQN(ASA)∴S△EQN=S△EPM,∴四边形EMCN的面积等于正方形MCQE的面积, ∵正方形ABCD的边长为a,∴AC=a,∵EC=2AE,∴EC=a,∴EP=PC=a,∴正方形MCQE的面积=a ×a=a2,∴四边形EMCN的面积=a2,故选:D.点评:本题主要考查了正方形的性质及全等三角形的判定及性质,解题的关键是作出辅助线,证出△EPM≌△EQN.3.(2014•台州)如图,F是正方形ABCD的边CD上的一个动点,BF的垂直平分线交对角线AC于点E,连接BE,FE,则∠EBF的度数是()A.45°B.50°C.60°D.不确定考点:全等三角形的判定与性质;正方形的性质.专题:几何图形问题.分析:过E作HI∥BC,分别交AB、CD于点H、I,证明Rt△BHE≌Rt△EIF,可得∠IEF+∠HEB=90°,再根据BE=EF即可解题.解答:解:如图所示,过E作HI∥BC,分别交AB、CD于点H、I,则∠BHE=∠EIF=90°,∵E是BF的垂直平分线EM上的点,∴EF=EB,∵E是∠BCD角平分线上一点,∴E到BC和CD的距离相等,即BH=EI,Rt△BHE和Rt△EIF中,,∴Rt△BHE≌Rt△EIF(HL),∴∠HBE=∠IEF , ∵∠HBE+∠HEB=90°, ∴∠IEF+∠HEB=90°, ∴∠BEF=90°, ∵BE=EF ,∴∠EBF=∠EFB=45°. 故选:A .点评: 本题考查了正方形角平分线和对角线重合的性质,考查了直角三角形全等的判定,全等三角形对应角相等的性质.4.(2014•郴州)平行四边形、矩形、菱形、正方形都具有的是( ) A . 对角线互相平分 B . 对角线互相垂直 C . 对角线相等 D . 对角线互相垂直且相等考点: 正方形的性质;平行四边形的性质;菱形的性质;矩形的性质.专题:证明题. 分析: 本题主要依据平行四边形、矩形、菱形、正方形都具有对角线相互平分的性质来判断.解答: 解:A 、对角线相等是平行四边形、矩形、菱形、正方形都具有的性质;B 、对角线互相垂直是菱形、正方形具有的性质;C 、对角线相等是矩形和正方形具有的性质;D 、对角线互相垂直且相等是正方形具有的性质. 故选:A .点评: 本题主要考查平行四边形、矩形、菱形、正方形的性质定理.5.(2014•来宾)正方形的一条对角线长为4,则这个正方形的面积是( )A . 8B . 4C . 8D . 16考点:正方形的性质.分析: 根据正方形的面积等于对角线乘积的一半列式计算即可得解.解答: 解:∵正方形的一条对角线长为4, ∴这个正方形的面积=×4×4=8.故选:A .点评: 本题考查了正方形的性质,熟记利用对角线求面积的方法是解题的关键.6.(2014•福州)如图,在正方形ABCD 的外侧,作等边三角形ADE ,AC 、BE 相交于点F ,则∠BFC 为( )A . 45°B . 55°C . 60°D .75°考点: 正方形的性质;等腰三角形的性质;等边三角形的性质.分析: 根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC . 解答: 解:∵四边形ABCD 是正方形, ∴AB=AD又∵△ADE 是等边三角形, ∴AE=AD=DE,∠DAE=60° ∴AD=AE∴∠ABE=∠AEB ,∠BAE=90°+60°=150° ∴∠ABE=(180°﹣150°)÷2=15° 又∵∠BAC=45° ∴∠BFC=45°+15°=60°故选:C .点评: 本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°.7.(2014•来宾)顺次连接菱形各边的中点所形成的四边形是( ) A . 等腰梯形 B . 矩形 C . 菱形D . 正方形考点:正方形的判定;三角形中位线定理;菱形的性质.分析:根据三角形的中位线定理以及菱形的性质即可证得. 解答: 解:∵E ,F 是中点, ∴EH ∥BD ,同理,EF ∥AC,GH ∥AC ,FG ∥BD , ∴EH ∥FG ,EF ∥GH ,则四边形EFGH 是平行四边形. 又∵AC ⊥BD , ∴EF ⊥EH ,∴平行四边形EFGH 是矩形. 故选:B .点评: 本题主要考查了矩形的判定定理,正确理解菱形的性质以及三角形的中位线定理是解题的关键.8.(2014•湘西州)下列说法中,正确的是( ) A . 相等的角一定是对顶角B . 四个角都相等的四边形一定是正方形C . 平行四边形的对角线互相平分D . 矩形的对角线一定垂直考点: 正方形的判定;对顶角、邻补角;平行四边形的性质;矩形的性质.分析: 根据对顶角的定义,正方形的判定,平行四边形的性质,矩形的性质对各选项分析判断利用排除法求解. 解答: 解:A 、相等的角一定是对顶角错误,例如,角平分线分成的两个角相等,但不是对顶角,故本选项错误;B 、四个角都相等的四边形一定是矩形,不一定是正方形,故本选项错误;C 、平行四边形的对角线互相平分正确,故本选项正确;D 、矩形的对角线一定相等,但不一定垂直,故本选项错误. 故选:C .点评: 本题考查了正方形的判定,平行四边形的性质,矩形的性质,对顶角的定义,熟记各性质与判定方法是解题的关键.9.(2014•株洲)已知四边形ABCD 是平行四边形,再从①AB=BC ,②∠ABC=90°,③AC=BD,④AC ⊥BD 四个条件中,选两个作为补充条件后,使得四边形ABCD 是正方形,现有下列四种选法,其中错误的是( ) A . 选①② B . 选②③ C . 选①③ D . 选②④考点:正方形的判定;平行四边形的性质.分析:要判定是正方形,则需能判定它既是菱形又是矩形. 解答: 解:A 、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD 是正方形,正确,故本选项不符合题意;B 、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD 是正方形,错误,故本选项符合题意;C 、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD 是正方形,正确,故本选项不符合题意; D 、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD 是正方形,正确,故本选项不符合题意. 故选:B .点评: 本题考查了正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个矩形有一个角为直角.③还可以先判定四边形是平行四边形,再用1或2进行判定.10.(2014•红桥区三模)如图,在正方形ABCD 中,CE=MN ,∠MCE=35°,那么∠ANM 等于( )A . 45°B .50° C .55° D .60°考点:全等三角形的判定与性质;正方形的性质. 分析: 过B 作BF ∥MN 交AD 于F,则∠AFB=∠ANM ,根据正方形的性质得出∠A=∠EBC=90°,AB=BC,AD ∥BC,推出四边形BFNM 是平行四边形,得出BF=MN=CE ,证Rt △ABF ≌Rt △BCE,推出∠AFB=∠ECB 即可.解答:解:过B 作BF ∥MN 交AD 于F , 则∠AFB=∠ANM , ∵四边形ABCD 是正方形,∴∠A=∠EBC=90°,AB=BC,AD ∥BC , ∴FN ∥BM,BE ∥MN ,∴四边形BFNM 是平行四边形, ∴BF=MN , ∵CE=MN , ∴CE=BF,在Rt △ABF 和Rt △BCE 中∴Rt △ABF ≌Rt △BCE (HL ), ∴∠AFB=∠ECB=35°, ∴∠ANM=∠AFB=55°, 故选C .点评: 本题考查了平行四边形的性质和判定,全等三角形的性质和判定,正方形的性质的应用,主要考查学生的推理能力.11.(2014•四会市一模)如图,菱形ABCD 中,∠B=60°,AB=5,则以AC 为边长的正方形ACEF 的面积为( )A . 9B . 16C . 20D . 25考点:菱形的性质;正方形的性质.分析: 据已知可求得△ABC 是等边三角形,从而得到AC=AB,从而求出正方形ACEF 的边长,进而可求出其面积.解答: 解:∵B=60°,AB=BC , ∴△ABC 是等边三角形,∴AC=AB=5,∴正方形ACEF 的边长为5, ∴正方形ACEF 的面积为25, 故选D .点评: 本题考查菱形与正方形的性质,属于基础题,对于此类题意含有60°角的题目一般要考虑等边三角形的应用.二.填空题(共5小题)12.(2009•江西模拟)如图,在正方形ABCD 的外侧,作等边三角形ADE ,则∠AEB= 15 度.考点:正方形的性质;等边三角形的性质. 分析: 由等边三角形的性质可得∠DAE=60°,进而可得∠BAE=150°,又因为AB=AE ,结合等腰三角形的性质,易得∠AEB 的大小.解答: 解:△ADE 是等边三角形;故∠DAE=60°, ∠BAE=90°+60°=150°,又有AB=AE,故∠AEB=30°÷2=15°; 故答案为15°.点评: 主要考查了正方形基本性质:①两组对边分别平行;四条边都相等;相邻边互相垂直;②四个角都是90°;③对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角.13.(2008•佛山)如图,已知P 是正方形ABCD 对角线BD 上一点,且BP=BC,则∠ACP 度数是 22.5 度.考点: 正方形的性质.专题:计算题. 分析: 根据正方形的性质可得到∠DBC=∠BCA=45°又知BP=BC,从而可求得∠BCP 的度数,从而就可求得∠ACP 的度数. 解答: 解:∵ABCD 是正方形, ∴∠DBC=∠BCA=45°,∵BP=BC ,∴∠BCP=∠BPC=(180°﹣45°)=67。
《正方形的性质与判定》习题1

(2)你能找到哪两个图形可以通过旋转而相互得到,并指出旋转中心和旋转角。
《正方形的性质与判定》习题
1.如图,已知四边形ABCD是菱形,当满足条件______时,它成为正方形. (填上你认为正确的一个条件即可)
2.已知ABCD,对角线AC,BD交于O.
(1)若,则ABCD是_______;
(2)若,则ABCD是_______;
(3)若,则ABCD是_______;
(4若,且,则ABCD是_______.
3.如图,四边形ABCD是边长为2的正方形,P是ABCD的边CD上任意一点,且于E,于F,则______.
4.如图,是一块在电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成. 设中间最小的一个正方形边长为1,则这个矩形色块图的面积为_______.
5.如图,P是正方形ABCD内一点,将绕点B顺时针方向旋转能与重合,若,则_______.
6.如图,正方形ABCD,AB=a,M为AB的中点,ED=3AE,(1)求ME的长;(2)△EMC是直角三角形吗?为什么?
7.以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF;
正方形的性质及判定练习题

正方形的性质及判定练习题一、知识梳理:1、定义:一组邻边相等的矩形是正方形.2、正方形性质:(1)边的性质:对边平行,四条边都相等.(2)角的性质:四个角都是直角.(3)对角线的性质:两条对角线互相垂直平分且相等,•每条对角线平分一组对角.(4)对称性:既是轴对称图形,又是中心对称图形.3、判定:(1)一组邻边相等的矩形是正方形(2)对角线互相垂直的矩形是正方形(3)有一个是直角的菱形是正方形(4)对角线相等的菱形是正方形总结:矩形+(或)=正方形菱形+(或)=正方形二、基础训练:性质:1、如图,四边形ABCD是正方形,两条对角线相交于点O.(1)一条对角线把它分成_______个全等的________ 三角形;(2)两条对角线把它分成_______个全等的________三角形;图中一共有________个等腰直角三角形;(3)∠AOB=_____度,∠OAB=_____度.(4)AB: AO: AC=________.2、正方形具有而矩形不一定具有的性质是( )A、四个角相等B、对角线互相垂直平分C、对角互补D、对角线相等.3、正方形具有而菱形不一定具有的性质()A、四条边相等.B、对角线互相垂直平分C、对角线平分一组对角D、对角线相等.4、正方形对角线长6,则它的面积为_________ ,周长为________.5、如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.判定:F A B C D 1. 下列说法错误的是( )A.两条对角线相等的菱形是正方形 B.两条对角线相等且垂直平分的四边形是正方形C.两条对角线垂直且相等的四边形是正方形 D. 两条对角线垂直的矩形是正方形2.四个内角都相等的四边形一定是( )A .正方形B .菱形C .矩形D .平行四边形3.已知在□ABCD 中,∠A=90°,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( )A .∠D=90° B.AB=CD C. AD=BC D. BC=CD4.四边形ABCD 中,AC 、BD 相交于点O ,能判别这个四边形是正方形的条件是( )A. OA=OB=OC=OD ,AC ⊥BDB. AB ∥CD ,AC=BDC. AD ∥BC ,∠A=∠CD. OA=OC ,OB=OD ,AB=BC5.能使平行四边形ABCD 为正方形的两个条件是 ________ _________ ___________________________________________________________ .(最少填三组)三、【聚焦“中考”】例:如图,在△ABC 中,AB=AC ,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F . (1)求证:DE=DF .(2)只添加一个条件,使四边形EDFA 是正方形,•请你至少写出两种不同的添加方法.(不另外添加辅助线,无需证明)自我检测:1.如图,在ABC 中∠ACB=90°,CD 平分∠ACB,DE ⊥BC ,DF⊥AC,垂足分别为E 、F , 求证:四边形CFDE 为正方形2. 如图所示,在Rt ΔABC 中,∠C =90°,∠A 、∠B 的平分线交于点D ,DE ⊥BC 于E ,DF ⊥AC 于F ,试说明四边形CEDF 为正方形。
第03讲 正方形的性质与判定(知识解读+真题演练+课后巩固)(原卷版)

第3讲正方形的性质与判定1. 理解正方形的概念;2. 探索并证明正方形的性质定理和判定定理,并能运用它们进行证明和计算;3. 通过经历正方形的性质定理和判定定理的探索过程,丰富学生的数学活动经验和体验,进一步培养和发展学生的合情推理能力;4. 通过正方形的性质定理和判定定理以及相关问题的证明和计算,进一步培养和发展学生的演绎推理能力.知识点1:正方形的概念与性质正方形的定义:一组邻边相等的矩形叫做正方形。
※正方形的性质:正方形具有平行四边形、矩形、菱形的一切性质。
(正方形是轴对称图形,有两条对称轴)知识点2:正方形的判定※正方形常用的判定:有一个内角是直角的菱形是正方形;邻边相等的矩形是正方形;对角线相等的菱形是正方形;对角线互相垂直的矩形是正方形。
注意:正方形、矩形、菱形和平行边形四者之间的关系(如图3所示):【题型1:正方形的概念和性质】【典例1】(2021秋•萧县期末)矩形,菱形,正方形不同时具有的性质是()A.对边平行且相等B.对角相等C.对角线互相平分D.每条对角线平分一组对角【变式1-1】(2022春•双台子区期末)矩形、菱形、正方形都具有的性质是()A.对角线相等B.对角线互相平分C.对角线互相垂直D.对角线互相平分且相等【变式1-2】(2020秋•罗湖区校级期末)下列说法正确的是()A.矩形的对角线相等垂直B.菱形的对角线相等C.正方形的对角线相等D.菱形的四个角都是直角【典例2】(2022春•溆浦县期中)一个正方形的面积为8m²,则它的对角线长为()A.2cm B.2cm C.4cm D.3cm【变式2-1】(2022秋•临淄区期末)如图,小明用四根长度相同的木条制作能够活动的菱形学具,他先把活动学具做成图1所示的菱形,并测得∠B=60°,对角线AC=1cm,接着把活动学具做成图2所示的正方形,则图2中对角线AC的长为()A.cm B.2cm C.3cm D.4cm【变式2-2】(2022春•涿州市期末)如图,以正方形ABCD的中心为原点建立平面直角坐标系,点A的坐标为(2,2),则点D的坐标为()A.(2,2)B.(﹣2,2)C.(﹣2,﹣2)D.(2,﹣2)【变式2-3】(2022春•乌拉特前旗期末)如图,四边形ABCD是边长为10的正方形,点E在正方形内,且AE⊥BE,又BE=8,则阴影部分的面积是()A.76B.24C.48D.88【题型2:正方形的判定】【典例3】(2022秋•莱西市期末)下列说法错误的是()A.对角线相等的菱形是正方形B.对角线垂互相平分且垂直的四边形是菱形C.对角线相等的平行四边形是矩形D.对角线垂直且相等的四边形是正方形【变式3-1】(2022秋•金水区校级期中)已知四边形ABCD是平行四边形,下列结论中错误的有()①当AB=DC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.A.1个B.2个C.3个D.4个【变式3-2】(2022秋•济阳区期中)如图,在矩形ABCD中,对角线AC、BD 交于点O,添加下列一个条件,能使矩形ABCD成为正方形的是()A.BD=AC B.DC=AD C.∠AOB=60°D.OD=CD【变式3-3】(2022春•卫辉市期末)如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是()A.①②③④B.①②③C.①②④D.②③④【典例4】(2021秋•平远县期末)如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.(1)判断四边形MENF是什么特殊四边形,并证明你的结论;(2)当AD,AB满足什么条件时,四边形MENF是正方形.【变式4-1】(2022秋•郓城县期中)如图,在矩形ABCD中,点E,F分别在边AB,BC上,AF⊥DE,且AF=DE,AF与DE相交于点G.求证:矩形ABCD为正方形.【变式4-2】(2022春•宽城区期末)如图,在矩形ABCD中,点E、F分别在边AB、BC上,DE=AF,DE⊥AF于点G.(1)求证:△ABF≌△DAE.(2)求证:四边形ABCD是正方形.【变式4-3】(2022秋•二七区校级月考)如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.(1)求证:四边形ADCE为矩形;(2)当∠BAC=°时,四边形ADCE是一个正方形,并说明理由.【题型3:正方形的性质与判定综合】【典例5】(2022春•临沭县期末)如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF 为邻边作矩形DEFG,连接AG.(1)求证:矩形DEFG是正方形;(2)求AG+AE的值;(3)若F恰为AB中点,请直接写出正方形DEFG的面积.【变式5-1】(2022春•赣县区校级期末)如图,E、F、M、N分别是正方形ABCD 四条边上的点,且AE=BF=CM=DN(1)求证:四边形EFMN是正方形;(2)若AB=7,AE=3,求四边形EFMN的周长.【变式5-2】(2022春•覃塘区期末)如图,在矩形ABCD中,点E,F分别在BC,CD边上,且AE=AF,∠CEF=45°.(1)求证:四边形ABCD是正方形;(2)若,BE=1,求四边形ABCD的面积.【变式5-3】(2022春•交口县期末)如图,已知四边形ABCD和CEFG均是正方形,点K在BC上,延长CD到点H,使DH=BK=CE,连接AK,KF,HF,AH.(1)求证:AK=AH;(2)求证:四边形AKFH是正方形;(3)若四边形AKFH的面积为10,CE=1,求点A,E之间的距离.1.(2021•娄底)如图,点E、F在矩形ABCD的对角线BD所在的直线上,BE =DF,则四边形AECF是()A.平行四边形B.矩形C.菱形D.正方形2.(2022秋•漳州期末)如图,在矩形ABCD中,对角线AC、BD交于点O,添加下列一个条件,能使矩形ABCD成为正方形的是()A.BD=AC B.DC=AD C.∠AOB=60°D.OD=CD 3.(2022春•东莞市期中)下列给出的条件中,不能判断▱ABCD是正方形的是()A.AC=BD,AD=AB B.AD=AB,∠A=90°C.AC=BD,AC⊥BD D.AC⊥BD,AD=AB 4.(2022•什邡市校级二模)如图,四边形ABCD是平行四边形,下列结论中错误的是()A.当▱ABCD是矩形时,∠ABC=90°B.当▱ABCD是菱形时,AC⊥BDC.当▱ABCD是正方形时,AC=BDD.当▱ABCD是菱形时,AB=AC5.(2022春•河西区期末)如图,点E,F,P,Q分别是正方形ABCD的四条边上的点,并且AF=BP=CQ=DE,则下列结论不一定正确的是()A.∠AFP=∠BPQB.EF∥QPC.四边形EFPQ是正方形D.四边形PQEF的面积是四边形ABCD面积的一半6.(2021•玉林)一个四边形顺次添加下列条件中的三个条件便得到正方形:a.两组对边分别相等b.一组对边平行且相等c.一组邻边相等d.一个角是直角顺次添加的条件:①a→c→d②b→d→c③a→b→c则正确的是()A.仅①B.仅③C.①②D.②③7.(2022•邵阳)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.8.(2022•贵阳)如图,在正方形ABCD中,E为AD上一点,连接BE,BE的垂直平分线交AB于点M,交CD于点N,垂足为O,点F在DC上,且MF∥AD.(1)求证:△ABE≌△FMN;(2)若AB=8,AE=6,求ON的长.9.(2020•湘西州)如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.(1)求证:△BAE≌△CDE;(2)求∠AEB的度数.10.(2022•雅安)如图,E,F是正方形ABCD的对角线BD上的两点,且BE =DF.(1)求证:△ABE≌△CDF;(2)若AB=3,BE=2,求四边形AECF的面积.1.(2022春•张家川县期末)如图,在矩形ABCD中,对角线AC、BD交于点O,添加下列一个条件,能使矩形ABCD成为正方形的是()A.BD=AB B.DC=AD C.∠AOB=60°D.OD=CD 2.(2022春•平南县期末)下列说法中正确的是()A.对角线相等的四边形是矩形B.对角线相等且互相垂直的四边形是正方形C.对角线互相垂直的四边形是菱形D.菱形的面积为两条对角线长度乘积的一半3.(2022秋•铁西区期中)如图,已知正方形ABCD的面积为64平方厘米,DE =10厘米,则CE的长为()A.6B.12C.2D.2 4.(2022秋•朝阳区校级期末)如图,直线l过正方形ABCD的顶点A,BE⊥l 于点E,DF⊥l于点F.若BE=2,DF=4,则的EF长为.5.(2022秋•龙岗区校级期末)已知正方形ABCD的对角线长为6cm,则正方形ABCD的面积为cm2.6.(2022秋•茂南区期末)正方形的边长为5,则它的周长为.7.(2022秋•建邺区校级期中)如图,四边形ABCD是正方形,以CD为边向外作等边△CDE,则∠AEC=°.8.(2022秋•茂南区期末)如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连接CE、DF.求证:CE=DF.9.(2022春•寻乌县期末)如图,△ABC中,AD是∠BAC的平分线,作DE∥AB交AC于点E,DF∥AC交AB于点F.(1)求证:四边形AEDF是菱形;(2)当△ABC满足条件时,四边形AEDF是正方形.10.(2022春•江宁区期末)如图,△ABC的中线AF与中位线DE相交于点O.(1)求证:AF与DE互相平分;(2)当△ABC满足时,四边形ADFE是正方形.11.(2022•龙岗区模拟)如图,在△ABC中,∠BAC=90°,∠BAC的平分线交BC于点D,DE∥AB,DF∥AC.(1)求证:四边形AFDE为正方形;(2)若AD=2,求四边形AFDE的面积.12.(2021春•海淀区校级期末)如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.(1)求证:四边形BFEG是矩形;(2)求四边形EFBG的周长;(3)当AF的长为多少时,四边形BFEG是正方形?。
正方形的性质与判定

正方形的性质与判定一、选择题1. (2011天津)如图,将正方形纸片ABCD 折叠,使边AB 、CB 均落在对角线BD 上,得折痕BE 、BF ,则∠EBF 的大小为( ) A 、15° B 、30°C 、45°D 、60°故选C .2. (2011山东济南)如图,△ABC 中,∠ACB =90°,AC >BC ,分别以△ABC 的边AB 、BC 、CA 为一边向△ABC 外作正方形ABDE 、BCMN 、CAFG ,连接EF 、GM 、ND ,设△AEF 、△BND 、△CGM 的面积分别为S 1、S 2、S 3,则下列结论正确的是( )A .S 1=S 2=S 3B .S 1=S 2<S 3C .S 1=S 3<S 2D .S 2=S 3<S 1 故选A .3. (2011山东烟台)如图,三个边长均为2的正方形重叠在一起,O 1、O 2是其中两个正方形的中心,则阴影部分的面积是 . 故答案为2.4. (2011福建三明)如图,在正方形纸片ABCD 中,E ,F 分别是AD ,BC 的中点,沿过点B 的直线折叠,使点C 落在EF 上,落点为N ,折痕交CD 边于点M ,BM 与EF 交于点P ,再展开.则下列结论中:①CM=DM ;②∠ABN =30°;③AB 2=3CM 2;④△PMN 是等边三角形.正确的有( )A 、1个B 、2个C 、3个D 、4个故选C . 二、填空题5. (2011江苏南京)如图,E 、F 分别是正方形ABCD 的边BC 、CD 上的点,BE =CF ,连接AE 、BF .将△ABE 绕正方形的中心按逆时针方向旋转到△BCF ,旋转角为α( 0°<α<180°),则∠α= 90° .6. (2011•南通)已知:如图1,O 为正方形ABCD 的中心,分别延长OA 到点F ,OD 到点E ,使OF =2OA ,OE =2OD ,连结EF ,将△FOE 绕点O 逆时针旋转α角得到△''F OE (如图2).(1) 探究AE ′与BF'的数量关系,并给予证明; (2) 当α=30°时,求证:△AOE ′为直角三角形.7.(2011江苏宿迁)如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.(1)当t≠1时,求证:△PEQ≌△NFM;(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.8.(2011山东日照)正方形ABCD的边长为4,M、N分别是BC、CD上的两个动点,且始终保持AM⊥MN.当BM=2时,四边形ABCN的面积最大.9.(2011湖北孝感)已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是10.(2011辽宁沈阳)如图,正方形ABCD中,点E、F分别在边BC、CD上,且AE=EF=FA.下列结:①△ABE≌△ADF;②CE=CF;③∠AEB=75°;④BE+DF=EF;⑤S△ABE+S△ADF=S△CEF,其中正确的是①②③⑤(只填写序号).三、解答题11.(2011呼和浩特)如图所示,四边形ABCD是正方形,点E是边BC的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.(1)求证:EG=CF;(2)将△ECF绕点E逆时针旋转90°,请在图中直接画出旋转后的图形,并指出旋转后CF与EG的位置关系.12.(2011湖北咸宁)(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3求AG,MN的长.13.(2011广西防城港)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.(1)求证:EB=GD;(2)判断EB与GD的位置关系,并说明理由;(3)若AB=2,AG=2,求EB的长.14.(2011广西来宾)已知正方形ABCD的对角线AC 与BD交于点O,点,点E、F分别是OB、OC上的动点,(1)如果动点E、F满足BE=CF(如图).①写出所有以点E或F为顶点的全等三角形(不得添加辅助线)②证明:AE⊥BF(2)如果动点E、F满足BE=OF(如图),问AE⊥BF 时,点E在什么位置,并证明你的结论.(第24(2)题图)(第24(1)题图)B15. 2011天水)某校开展的一次动漫设计大赛,杨帆同学运用了数学知识进行了富有创意的图案设计,如图(1),他在边长为1的正方形ABCD内作等边△BC E,并与正方形的对角线交于点F、G,制作如图(2)的图标,请我计算一下图案中阴影图形的面积.H FEG D CB A。
正方形的性质与判定练习题

克,,
思 才只 在
能有科
成功就是99% 的血汗, 加上 1%的灵感。
达不 学
到畏上
光艰从
------爱迪生
辉险没 的勇 有
顶于 平
点攀坦
----登 的--
的
大
5、已知四边形 ABCD是平行四边形,对角线 AC、BD相交于点 O。
⑴若 AB=BC ,则四边形 ABCD 是( 菱形 ) ⑵若 AC=BD ,则四边形ABCD 是( 矩形 ) ⑶若∠BCD=90 0,则四边形ABCD 是( 矩形 )
⑷若 OA=OB ,则四边形 ABCD 是( 矩形 ) ⑸若AB=BC ,且AC=BD ,则四边形 ABCD 是
欲证∠ MFD =45°,由于
△MDF 是直角三角形 ,只须证 △MDF 是等腰三角形 ,即只要证
_____=_____
要证 MD =FD,大家只须证得哪两个三角形全等 ?
△CMD ≌△ADF
试一试
看能不能完成证明 ???
例4、已知:如图 (4)在正方形 ABCD 中, F为CD延长线上 一点,CE⊥AF于 E,交 AD于M, 求证:∠ MFD=45°
1正方形的一条对角线把正方形分成两个全等的等腰直角三角形3如果一个菱形的对角线相等那么它一定是正方形4如果一个矩形的对角线互相垂直那么它一定是正方形5四条边相等且有一个角是直角的四边形是正方形10正方形矩形菱形都是平行四边a四个角相等
1、判断题 :
(1) 正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( √ )
求证:四边形 ABCD 是正方形。
A
D
O
B
C
第十九章 四边形
13、长见识
数一数图中正方形的个数,你发现了什么 ?
正方形性质与判定练习(含答案)

C. 2
D. 5 1
18.如图,正方形 ABCD 中,AD 5,点 E 、F 是正方形 ABCD 内的两点,且 AE FC 4 ,
BE DF 3,则以 EF 为直径的圆的面积为 ( )
A. 1 2
B. 3 5
C. 3 4
D.
19.如图,在平面直角坐标系中,正方形 A1B1C1D1 、D1E1E2B2 、A2 B2C2 D2 、D2 E3E4 B3 、A3B3C3D3 ,
D.16
21.如图,在正方形 ABCD 中,对角线 AC ,BD 相交于点 O ,E ,F 分别在 OD ,OC 上,
且 DE CF ,连接 DF , AE , AE 的延长线交 DF 于点 M ,则下列四个结论中正确结 论的个数是 ( )
① AE DF ;
② AM DF ;
③ DAE CDF ;
.
38.如图,正方形 ABCD 中, AB 12 ,点 E 在边 CD 上,CD 3DE .将 ADE 沿 AE 对折
至 AFE ,延长 EF 交边 BC 于点 G ,连接 AG ,CF .则下列结论正确的是
.
① ABG AFG ; ② BG GC ;
为
.
31.如图,RtABC 中,C 90 ,AC 2 ,BC 1 ,以斜边为一边向右上方作正方形 ABDE ,
连接 CD ,则 CD 的长为
.
32.如图,将正方形 OABC 放在平面直角坐标系中, O 是坐标原点,点 A 的坐标是 (2,3) ,
则 C 点坐标是
.
33.如图,在平面直角坐标系中,点 A 的坐标是 (0,3) ,点 B 的坐标是 (4,0) ,以 AB 为边
正方形性质与判定练习
1.如果要证明平行四边形 ABCD 为正方形,那么我们需要在四边形 ABCD 是平行四边形的 基础上,进一步证明 ( )
正方形的性质和判定典型试题综合训练(含解析)

正方形的性质和判定典型试题综合训练(含解析)一.选择题(共15小题)1.关于▱ABCD的叙述,正确的是()A.若AB⊥BC,则▱ABCD是菱形B.若AC⊥BD,则▱ABCD是正方形C.若AC=BD,则▱ABCD是矩形D.若AB=AD,则▱ABCD是正方形2.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是()A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC3.如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是()A.AO=BO=CO=DO,AC⊥BD B.AC=BC=CD=DA C.AO=CO,BO=DO,AC⊥BD D.AB=BC,CD⊥DA 4.如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确...的是()A.B.C.D.5.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为()A.B.2C.+1 D.2+16.如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为()A.1 B.2 C.3 D.37.如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B 的度数为何?()A.50 B.55 C.70 D.758.如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…A n分别是正方形的中心,则这n个正方形重叠部分的面积之和是()A.n B.n﹣1 C.()n﹣1D.n9.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是()A.7 B.8 C.7D.710.正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点,正方形BEFG的边长为4,则△DEK的面积为()A.10 B.12 C.14 D.1611.如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是()A.B.C.D.12.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是()A.1或9 B.3或5 C.4或6 D.3或613.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF 的长为()A.1 B.4﹣2C.D.3﹣414.如图,在正方形ABCD中,点O为对角线AC的中点,过点O作射线OG、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下列结论中:(1)△OEF是等腰直角三角形;(2)图形中全等的三角形只有两对;(3)BE+BF=OA;(4)正方形ABCD的面积等于四边形OEBF面积的4倍,正确的结论有()A.1个B.2 个C.3个D.4个15.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是()A.()2014B.()2015C.()2015D.()2014二.填空题(共10小题)16.矩形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件,使其成为正方形(只填一个即可)17.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是.18.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=.19.如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为cm.20.如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是.21.如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF=AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有条.22.如图所示,E是正方形ABCD边BC上任意一点,EF⊥BO于F,EG⊥CO于G,若AB=10厘米,则四边形EGOF的周长是厘米.23.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB=.24.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为.25.如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=.三.解答题(共10小题)26.如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.(1)求证:四边形BEDF是菱形;(2)若正方形边长为4,AE=,求菱形BEDF的面积.27.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?28.已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.29.如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.30.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.31.如图,△ABC中,MN∥BD交AC于P,∠ACB、∠ACD的平分线分别交MN于E、F.(1)求证:PE=PF;(2)当MN与AC的交点P在什么位置时,四边形AECF是矩形,说明理由;(3)当△ABC满足什么条件时,四边形AECF是正方形.(不需要证明)32.如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.(1)求证:△ABF≌△CBE;(2)判断△CEF的形状,并说明理由.33.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.34.在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.35.已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.正方形的性质和判定典型试题综合训练参考答案与试题解析一.选择题(共15小题)1.关于▱ABCD的叙述,正确的是()A.若AB⊥BC,则▱ABCD是菱形B.若AC⊥BD,则▱ABCD是正方形C.若AC=BD,则▱ABCD是矩形D.若AB=AD,则▱ABCD是正方形【分析】由菱形的判定方法、矩形的判定方法、正方形的判定方法得出选项A、B、D错误,C正确;即可得出结论.【解答】解:∵▱ABCD中,AB⊥BC,∴四边形ABCD是矩形,不一定是菱形,选项A错误;∵▱ABCD中,AC⊥BD,∴四边形ABCD是菱形,不一定是正方形,选项B错误;∵▱ABCD中,AC=BD,∴四边形ABCD是矩形,选项C正确;∵▱ABCD中,AB=AD,∴四边形ABCD是菱形,不一定是正方形,选项D错误.故选:C.2.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是()A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC【分析】当BE平分∠ABC时,四边形DBFE是菱形,可知先证明四边形BDEF是平行四边形,再证明BD=DE 即可解决问题.【解答】解:当BE平分∠ABC时,四边形DBFE是菱形,理由:∵DE∥BC,∴∠DEB=∠EBC,∵∠EBC=∠EBD,∴∠EBD=∠DEB,∴BD=DE,∵DE∥BC,EF∥AB,∴四边形DBEF是平行四边形,∵BD=DE,∴四边形DBEF是菱形.其余选项均无法判断四边形DBEF是菱形,故选D.3.如图所示,已知四边形ABCD的对角线AC、BD相交于点O,则下列能判断它是正方形的条件是()A.AO=BO=CO=DO,AC⊥BD B.AC=BC=CD=DA C.AO=CO,BO=DO,AC⊥BD D.AB=BC,CD⊥DA 【分析】根据正方形的判定对角线互相垂直平分且相等的四边形是正方形,对各个选项进行分析从而得到最后的答案.【解答】解:A、正确,AC⊥BD且AC、BD互相平分可判定为菱形,再由AC=BD判定为正方形;B、错误,不能判定为正方形;C、错误,只能判定为菱形;D、错误,不能判定为正方形;故选A.4.如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确...的是()A.B.C.D.【分析】利用勾股定理求出正方形的对角线为10≈14,由此即可判定A不正确.【解答】解:选项A不正确.理由正方形的边长为10,所以对角线=10≈14,因为15>14,所以这个图形不可能存在.故选A.5.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边正方形EFGH的周长为()A.B.2C.+1 D.2+1【分析】由正方形的性质和已知条件得出BC=CD==1,∠BCD=90°,CE=CF=,得出△CEF是等腰直角三角形,由等腰直角三角形的性质得出EF的长,即可得出正方形EFGH的周长.【解答】解:∵正方形ABCD的面积为1,∴BC=CD==1,∠BCD=90°,∵E、F分别是BC、CD的中点,∴CE=BC=,CF=CD=,∴CE=CF,∴△CEF是等腰直角三角形,∴EF=CE=,∴正方形EFGH的周长=4EF=4×=2;故选:B.6.如图,四边形ABCD,AEFG都是正方形,点E,G分别在AB,AD上,连接FC,过点E作EH∥FC交BC于点H.若AB=4,AE=1,则BH的长为()A.1 B.2 C.3 D.3【分析】求出BE的长,再根据两组对边分别平行的四边形是平行四边形求出四边形EFCH平行四边形,根据平行四边形的对边相等可得EF=CH,再根据正方形的性质可得AB=BC,AE=EF,然后求出BH=BE即可得解.【解答】解:∵AB=4,AE=1,∴BE=AB﹣AE=4﹣1=3,∵四边形ABCD,AEFG都是正方形,∴AD∥EF∥BC,又∵EH∥FC,∴四边形EFCH平行四边形,∴EF=CH,∵四边形ABCD,AEFG都是正方形,∴AB=BC,AE=EF,∴AB﹣AE=BC﹣CH,∴BE=BH=3.故选:C.7.如图,有一平行四边形ABCD与一正方形CEFG,其中E点在AD上.若∠ECD=35°,∠AEF=15°,则∠B 的度数为何?()A.50 B.55 C.70 D.75【分析】由平角的定义求出∠CED的度数,由三角形内角和定理求出∠D的度数,再由平行四边形的对角相等即可得出结果.【解答】解:∵四边形CEFG是正方形,∴∠CEF=90°,∵∠CED=180°﹣∠AEF﹣∠CEF=180°﹣15°﹣90°=75°,∴∠D=180°﹣∠CED﹣∠ECD=180°﹣75°﹣35°=70°,∵四边形ABCD为平行四边形,∴∠B=∠D=70°(平行四边形对角相等).故选C.8.如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…A n分别是正方形的中心,则这n个正方形重叠部分的面积之和是()A.n B.n﹣1 C.()n﹣1D.n【分析】根据题意可得,阴影部分的面积是正方形的面积的,已知两个正方形可得到一个阴影部分,则n个这样的正方形重叠部分即为(n﹣1)个阴影部分的和.【解答】解:由题意可得一个阴影部分面积等于正方形面积的,即是×4=1,5个这样的正方形重叠部分(阴影部分)的面积和为:1×4,n个这样的正方形重叠部分(阴影部分)的面积和为:1×(n﹣1)=n﹣1.故选:B.9.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是()A.7 B.8 C.7D.7【分析】由正方形的性质得出∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,由SSS证明△ABE≌△CDF,得出∠ABE=∠CDF,证出∠ABE=∠DAG=∠CDF=∠BCH,由AAS证明△ABE≌△ADG,得出AE=DG,BE=AG,同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,得出EG=GF=FH=EF=7,证出四边形EGFH是正方形,即可得出结果.【解答】解:如图所示:∵四边形ABCD是正方形,∴∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,∴∠BAE+∠DAG=90°,在△ABE和△CDF中,,∴△ABE≌△CDF(SSS),∴∠ABE=∠CDF,∵∠AEB=∠CFD=90°,∴∠ABE+∠BAE=90°,∴∠ABE=∠DAG=∠CDF,同理:∠ABE=∠DAG=∠CDF=∠BCH,∴∠DAG+∠ADG=∠CDF+∠ADG=90°,即∠DGA=90°,同理:∠CHB=90°,在△ABE和△ADG中,,∴△ABE≌△ADG(AAS),∴AE=DG,BE=AG,同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,∴EG=GF=FH=EF=12﹣5=7,∵∠GEH=180°﹣90°=90°,∴四边形EGFH是正方形,∴EF=EG=7;故选:C.10.正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点,正方形BEFG的边长为4,则△DEK的面积为()A.10 B.12 C.14 D.16【分析】连DB,GE,FK,则DB∥GE∥FK,再根据等底等高的三角形面积相等,正方形BEFG的边长为4可求出S△DGE=S△GEB,S△GKE=S△GFE,再由S阴影=S正方形GBEF即可求出答案.【解答】解:连DB,GE,FK,则DB∥GE∥FK,在梯形GDBE中,S△GDB=S△EDB(同底等高)∴S△GDB﹣公共三角形=S△EDB﹣公共三角形即∴S△DGE=S△GEB,S△GKE=S△GFE同理S△GKE=S△GFE∴S阴影=S△DGE+S△GKE=S△GEB+S△GEF=S正方形GBEF=42=16 故选:D.11.如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是()A.B.C.D.【分析】根据旋转的性质及正方形的性质分别求得△ABC与△CD′E的面积,从而不难求得重叠部分的面积.【解答】解:∵绕顶点A顺时针旋转45°,∴∠D′CE=45°,∴CD′=D′E,∵ED′⊥AC,∴∠CD′E=90°,∵AC==,∴CD′=﹣1,∴正方形重叠部分的面积是×1×1﹣×(﹣1)(﹣1)=﹣1.故选:D.12.如图是由三个边长分别为6、9、x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是()A.1或9 B.3或5 C.4或6 D.3或6【分析】根据题意列方程,即可得到结论.【解答】解:如图,∵若直线AB将它分成面积相等的两部分,∴(6+9+x)×9﹣x•(9﹣x)=×(6+9+x)×9﹣6×3,解得x=3,或x=6,故选D.13.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF 的长为()A.1 B.4﹣2C.D.3﹣4【分析】在AF上取FG=EF,连接GE,可得△EFG是等腰直角三角形,根据等腰直角三角形的性质可得EG=EF,∠EGF=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BAE+∠AEG=∠EGF,然后求出∠BAE=∠AEG=22.5°,根据等角对等边可得AG=EG,再根据正方形的对角线平分一组对角求出∠ABD=45°,然后求出△BEF是等腰直角三角形,根据等腰直角三角形的性质可得BF=EF,设EF=x,最后根据AB=AG+FG+BF列方程求解即可.【解答】解:如图,在AF上取FG=EF,连接GE,∵EF⊥AB,∴△EFG是等腰直角三角形,∴EG=EF,∠EGF=45°,由三角形的外角性质得,∠BAE+∠AEG=∠EGF,∵∠BAE=22.5°,∠EGF=45°,∴∠BAE=∠AEG=22.5°,∴AG=EG,在正方形ABCD中,∠ABD=45°,∴△BEF是等腰直角三角形,∴BF=EF,设EF=x,∵AB=AG+FG+BF,∴4=x+x+x,解得x=2(2﹣)=4﹣2.故选B.14.如图,在正方形ABCD中,点O为对角线AC的中点,过点O作射线OG、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下列结论中:(1)△OEF是等腰直角三角形;(2)图形中全等的三角形只有两对;(3)BE+BF=OA;(4)正方形ABCD的面积等于四边形OEBF面积的4倍,正确的结论有()A.1个B.2 个C.3个D.4个【分析】(1)(3)(4)正确.只要证明△BOE≌△COF,即可解决问题,(2)图中全等三角形不止两对,故(2)错误.【解答】解:∵四边形ABCD是正方形,∴AB=BC,ABC=90°,∠BAO=∠ABO=∠OBC=45°,AC⊥BD,∵∠EOF=90°,∴∠BOE+∠BOF=90°,∵∠BOF+∠COF=90°,∴∠BOE=∠COF,在△BOE和△COF中,,∴△BOE≌△COF(ASA),∴OE=OF,BE=CF,∴△EOF是等腰直角三角形,故(1)正确,∴BE+BF=CF+BF=BC=OA,故(3)正确,∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=S正方形ABCD,∴S正方形ABCD=4S四边形OEBF故(4)正确;图中全等三角形有△BOE≌△COF,△AOB≌△AOD≌△DOC≌△BOC,故(2)错误.故选C.15.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是()A.()2014B.()2015C.()2015D.()2014【分析】利用正方形的性质结合锐角三角函数关系得出正方形的边长,进而得出变化规律即可得出答案.【解答】解:如图所示:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,∴D1E1=C1D1sin30°=,则B2C2=()1,同理可得:B3C3==()2,故正方形A n B n C n D n的边长是:()n﹣1.则正方形A2015B2015C2015D2015的边长是:()2014.故选:D.二.填空题(共10小题)16.矩形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件AB=BC(答案不唯一),使其成为正方形(只填一个即可)【分析】此题是一道开放型的题目答案不唯一,证出四边形ABCD是菱形,由正方形的判定方法即可得出结论.【解答】解:添加条件:AB=BC,理由如下:∵四边形ABCD是矩形,AB=BC,∴四边形ABCD是菱形,∴四边形ABCD是正方形,故答案为:AB=BC(答案不唯一).17.在平行四边形ABCD中,对角线AC与BD相交于点O,要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的序号是①③④.【分析】由矩形、菱形、正方形的判定方法对各个选项进行判断即可.【解答】解:∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形,又∵AB⊥AD,∴四边形ABCD是正方形,①正确;∵四边形ABCD是平行四边形,AB=BD,AB⊥BD,∴平行四边形ABCD不可能是正方形,②错误;∵四边形ABCD是平行四边形,OB=OC,∴AC=BD,∴四边形ABCD是矩形,又OB⊥OC,即对角线互相垂直,∴平行四边形ABCD是正方形,③正确;∵四边形ABCD是平行四边形,AB=AD,∴四边形ABCD是菱形,又∵AC=BD,∴四边形ABCD是矩形,∴平行四边形ABCD是正方形,④正确;故答案为:①③④.18.如图,将正方形纸片按如图折叠,AM为折痕,点B落在对角线AC上的点E处,则∠CME=45°.【分析】由正方形的性质和折叠的性质即可得出结果.【解答】解:∵四边形ABCD是正方形,∴∠B=90°,∠ACB=45°,由折叠的性质得:∠AEM=∠B=90°,∴∠CEM=90°,∴∠CME=90°﹣45°=45°;故答案为:45°.19.如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50cm2,则菱形的边长为13cm.【分析】根据正方形的面积可用对角线进行计算解答即可.【解答】解:因为正方形AECF的面积为50cm2,所以AC=cm,因为菱形ABCD的面积为120cm2,所以BD=cm,所以菱形的边长=cm.故答案为:13.20.如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是(2+,1).【分析】过点D作DG⊥BC于点G,根据四边形BDCE是菱形可知BD=CD,再由BC=2,∠D=60°可得出△BCD是等边三角形,由锐角三角函数的定义求出GD及CG的长即可得出结论.【解答】解:过点D作DG⊥BC于点G,∵四边形BDCE是菱形,∴BD=CD.∵BC=2,∠D=60°,∴△BCD是等边三角形,∴BD=BC=CD=2,∴CG=1,GD=CD•sin60°=2×=,∴D(2+,1).故答案为:(2+,1).21.如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF=AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有3条.【分析】能画3条:①与EF互相垂直且垂足为O,构建直角三角形,可以证明两直角三角形全等得EF=PQ;②在AD上截取AP=AD,连接PO延长得到PQ;③同理在AB了截取BQ=AB,连接QO并延长得到PQ.【解答】解:这样的直线PQ(不同于EF)有3条,①如图1,过O作PQ⊥EF,交AD于P,BC于Q,则PQ=EF;②如图2,以点A为圆心,以AE为半径画弧,交AD于P,连接PO并延长交BC于Q,则PQ=EF;③如图3,以B为圆心,以AE为半径画弧,交AB于Q,连接QO并延长交DC于点P,则PQ=EF.22.如图所示,E是正方形ABCD边BC上任意一点,EF⊥BO于F,EG⊥CO于G,若AB=10厘米,则四边形EGOF的周长是厘米.【分析】根据已知可得到△BFE,△CGE是等腰直角三角形,得到BF=EF,EG=GC,则四边形EGOF的周长OF+EF+OG+CG=OB+OC=BD【解答】解:∵EF⊥BO于F,EG⊥CO,∠BAC=∠ACB=45°∴△BFE,△CGE是等腰直角三角形∴BF=EF,EG=GC∴四边形EGOF的周长OF+EF+OG+CG=OB+OC=BD=10cm 故答案为10.23.如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=,AG=1,则EB=.【分析】首先连接BD交AC于O,由四边形ABCD、AGFE是正方形,即可得AB=AD,AE=AG,∠DAB=∠EAG,然后利用SAS即可证得△EAB≌△GAD,则可得EB=GD,然后在Rt△ODG中,利用勾股定理即可求得GD的长,继而可得EB的长.【解答】解:连接BD交AC于O,∵四边形ABCD、AGFE是正方形,∴AB=AD,AE=AG,∠DAB=∠EAG,∴∠EAB=∠GAD,在△AEB和△AGD中,,∴△EAB≌△GAD(SAS),∴EB=GD,∵四边形ABCD是正方形,AB=,∴BD⊥AC,AC=BD=AB=2,∴∠DOG=90°,OA=OD=BD=1,∵AG=1,∴OG=OA+AG=2,∴GD==,∴EB=.故答案为:.24.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为()n﹣1.【分析】首先求出AC、AE、HE的长度,然后猜测命题中隐含的数学规律,即可解决问题.【解答】解:∵四边形ABCD为正方形,∴AB=BC=1,∠B=90°,∴AC2=12+12,AC=;同理可求:AE=()2,HE=()3…,∴第n个正方形的边长a n=()n﹣1.故答案为()n﹣1.25.如图,在正方形ABCD中,O是对角线的交点,过点O作OE⊥OF,分别交AD,CD于E,F,若AE=6,CF=4,则EF=2.【分析】由正方形的性质得出∠ADC=90°,∠OAE=∠ODE=∠ODF=∠OCF=45°,OA=OB=OC=OD,AC⊥BD,证出∠AOE=∠DOF,由ASA证明△AOE≌△DOF,得出AE=DF=6,同理:DE=CF=4,由勾股定理求出EF即可.【解答】解:∵四边形ABCD是正方形,∴∠ADC=90°,∠OAE=∠ODE=∠ODF=∠OCF=45°,OA=OB=OC=OD,AC⊥BD,∴∠AOD=90°,∵OE⊥OF,∴∠EOF=90°,∴∠AOE=∠DOF,在△AOE和△DOF中,,∴△AOE≌△DOF(ASA),∴AE=DF=6,同理:DE=CF=4,∴EF===2.故答案为:2.三.解答题(共10小题)26.如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.(1)求证:四边形BEDF是菱形;(2)若正方形边长为4,AE=,求菱形BEDF的面积.【分析】(1)连接BD交AC于点O,则可证得OE=OF,OD=OB,可证四边形BEDF为平行四边形,且BD ⊥EF,可证得四边形BEDF为菱形;(2)由正方形的边长可求得BD、AC的长,则可求得EF的长,利用菱形的面积公式可求得其面积.【解答】(1)证明:如图,连接BD交AC于点O,∵四边形ABCD为正方形,∴BD⊥AC,OD=OB=OA=OC,∵AE=CF,∴OA﹣AE=OC﹣CF,即OE=OF,∴四边形BEDF为平行四边形,且BD⊥EF,∴四边形BEDF为菱形;(2)解:∵正方形边长为4,∴BD=AC=4,∵AE=CF=,∴EF=AC﹣2=2,∴S菱形BEDF=BD•EF=×4×2=8.27.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?【分析】(1)由DF=BE,四边形ABCD为正方形可证△CEB≌△CFD,从而证出CE=CF.(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG≌△FCG,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.【解答】(1)证明:在正方形ABCD中,∵,∴△CBE≌△CDF(SAS).∴CE=CF.(2)解:GE=BE+GD成立.理由是:∵由(1)得:△CBE≌△CDF,∴∠BCE=∠DCF,∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,又∵∠GCE=45°,∴∠GCF=∠GCE=45°.∵,∴△ECG≌△FCG(SAS).∴GE=GF.∴GE=DF+GD=BE+GD.28.已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.【分析】(1)由菱形的性质得出∠B=∠D,AB=BC=DC=AD,由已知和三角形中位线定理证出AE=BE=DF=AF,OF=DC,OE=BC,OE∥BC,由SAS证明△BCE≌△DCF即可;(2)由(1)得:AE=OE=OF=AF,证出四边形AEOF是菱形,再证出∠AEO=90°,四边形AEOF是正方形.【解答】(1)证明:∵四边形ABCD是菱形,∴∠B=∠D,AB=BC=DC=AD,∵点E,O,F分别为AB,AC,AD的中点,∴AE=BE=DF=AF,OF=DC,OE=BC,OE∥BC,在△BCE和△DCF中,,∴△BCE≌△DCF(SAS);(2)解:当AB⊥BC时,四边形AEOF是正方形,理由如下:由(1)得:AE=OE=OF=AF,∴四边形AEOF是菱形,∵AB⊥BC,OE∥BC,∴OE⊥AB,∴∠AEO=90°,∴四边形AEOF是正方形.29.如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.【分析】根据正方向的性质,可得∠ADF=CDE=90°,AD=CD,根据全等三角形的判定与性质,可得答案.【解答】证明:∵四边形ABCD是正方形,∴∠ADF=CDE=90°,AD=CD.∵AE=CF,∴DE=DF,在△ADF和△CDE中,∴△ADF≌△CDE(SAS),∴∠DAF=∠DCE,在△AGE和△CGF中,,∴△AGE≌△CGF(AAS),∴AG=CG.30.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.【分析】(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;(2)过点A作AH⊥BG,在Rt△ABH、Rt△AHG中,求出AH、HG即可解决问题.【解答】解:(1)结论:AG2=GE2+GF2.理由:连接CG.∵四边形ABCD是正方形,∴A、C关于对角线BD对称,∵点G在BD上,∴GA=GC,∵GE⊥DC于点E,GF⊥BC于点F,∴∠GEC=∠ECF=∠CFG=90°,∴四边形EGFC是矩形,∴CF=GE,在Rt△GFC中,∵CG2=GF2+CF2,∴AG2=GF2+GE2.(2)过点A作AH⊥BG,∵四边形ABCD是正方形,∴∠ABD=∠GBF=45°,∵GF⊥BC,∴∠BGF=45°,∵∠AGF=105°,∴∠AGB=∠AGF﹣∠BGF=105°﹣45°=60°,在Rt△ABH中,∵AB=1,∴AH=BH=,在Rt△AGH中,∵AH=,∠GAH=30°,∴HG=AH•tan30°=,∴BG=BH+HG=+.31.如图,△ABC中,MN∥BD交AC于P,∠ACB、∠ACD的平分线分别交MN于E、F.(1)求证:PE=PF;(2)当MN与AC的交点P在什么位置时,四边形AECF是矩形,说明理由;(3)当△ABC满足什么条件时,四边形AECF是正方形.(不需要证明)【分析】(1)根据CE平分∠ACB,MN∥BC,可知∠ACE=∠BCE,∠PEC=∠BCE,PE=PC,同理:PF=PC,故PE=PF.(2)根据矩形的性质可知当P是AC中点时四边形AECF是矩形.(3)当∠ACB=90°时四边形AECF是正方形.【解答】证明:(1)∵CE平分∠ACB,∴∠ACE=∠BCE.∵MN∥BC,∴∠PEC=∠BCE.∴∠ACE=∠PEC,PE=PC.同理:PF=PC.∴PE=PF.(2)当P是AC中点时四边形AECF是矩形,∵PA=PC,PF=PC,∴四边形AECF是平行四边形.∵PE=PC,∴AC=EF,四边形AECF是矩形.(3)当∠ACB=90°时,四边形AECF是正方形.32.如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.(1)求证:△ABF≌△CBE;(2)判断△CEF的形状,并说明理由.【分析】(1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB=135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=CB,∠ABC=90°,∵△EBF是等腰直角三角形,其中∠EBF=90°,∴BE=BF,∴∠ABC﹣∠CBF=∠EBF﹣∠CBF,∴∠ABF=∠CBE.在△ABF和△CBE中,有,∴△ABF≌△CBE(SAS).(2)解:△CEF是直角三角形.理由如下:∵△EBF是等腰直角三角形,∴∠BFE=∠FEB=45°,∴∠AFB=180°﹣∠BFE=135°,又∵△ABF≌△CBE,∴∠CEB=∠AFB=135°,∴∠CEF=∠CEB﹣∠FEB=135°﹣45°=90°,∴△CEF是直角三角形.33.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.【分析】(1)连接CD,根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD,结合AE=CF可证出△ADE≌△CDF(SAS),根据全等三角形的性质可得出DE=DF、ADE=∠CDF,通过角的计算可得出∠EDF=90°,再根据O为EF的中点、GO=OD,即可得出GD⊥EF,且GD=2OD=EF,由此即可证出四边形EDFG是正方形;(2)过点D作DE′⊥AC于E′,根据等腰直角三角形的性质可得出DE′的长度,从而得出2≤DE<2,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.【解答】(1)证明:连接CD,如图1所示.∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,∴∠A=∠DCF=45°,AD=CD.在△ADE和△CDF中,,∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴△EDF为等腰直角三角形.∵O为EF的中点,GO=OD,∴GD⊥EF,且GD=2OD=EF,∴四边形EDFG是正方形;(2)解:过点D作DE′⊥AC于E′,如图2所示.∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,∴DE′=BC=2,AB=4,点E′为AC的中点,∴2≤DE<2(点E与点E′重合时取等号).∴4≤S四边形EDFG=DE2<8.∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.34.在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.【分析】(1)根据正方形的性质可得AO=CO,OD=OF,∠AOC=∠DOF=90°,然后求出∠AOD=∠COF,再利用“边角边”证明△AOD和△COF全等,根据全等三角形对应边相等即可得证;(2)与(1)同理求出CF=AD,连接DF交OE于G,根据正方形的对角线互相垂直平分可得DF⊥OE,DG=OG=OE,再求出AG,然后利用勾股定理列式计算即可求出AD.【解答】解:(1)AD=CF.理由如下:在正方形ABCO和正方形ODEF中,AO=CO,OD=OF,∠AOC=∠DOF=90°,∴∠AOC+∠COD=∠DOF+∠COD,即∠AOD=∠COF,在△AOD和△COF中,,∴△AOD≌△COF(SAS),∴AD=CF;(2)与(1)同理求出CF=AD,如图,连接DF交OE于G,则DF⊥OE,DG=OG=OE,∵正方形ODEF的边长为,∴OE=OD=×=2,∴DG=OG=OE=×2=1,∴AG=AO+OG=3+1=4,在Rt△ADG中,AD===,∴CF=AD=.。
正方形的性质及判定典型题(精选)

一、正方形的性质【例1】 正方形有 条对称轴.【例2】 已知正方形BDEF 的边长是正方形ABCD 的对角线,则:BDEF ABCD S S =正方形正方形【例3】 如图,已知正方形ABCD 的面积为256,点F 在CD 上,点E 在CB 的延长线上,且20AE AF AF ⊥=,,则BE 的长为FE D CBA【例4】 如图,在正方形ABCD 中,E 为AB 边的中点,G ,F 分别为AD ,BC 边上的点,若1AG =,2BF =,90GEF ∠=︒,则GF 的长为 .【例5】 将n 个边长都为1cm 的正方形按如图所示摆放,点12...n A A A ,,,分别是正方形的中心,则n 个正方形重叠形成的重叠部分的面积和为A 5A 4A 3A 2A 1正方形的性质及判定【例6】 如图,正方形ABCD 中,O 是对角线AC BD ,的交点,过点O 作OE OF ⊥,分别交AB CD ,于E F ,,若43AE CF ==,,则EF =OFE DC BA【例7】 如图,正方形ABCD 的边长为2cm ,以B 为圆心,BC 长为半径画弧交对角线BD 于点E ,连接CE ,P 是CE 上任意一点,PM BC ⊥于M ,PN BD ⊥于N ,则PM PN +的值为PNME DC BA【例8】 如图,E 是正方形ABCD 对角线BD 上的一点,求证:AE CE =.EDCBA【例9】 如图,P 为正方形ABCD 对角线上一点,PE BC ⊥于E ,PF CD ⊥于F .求证:AP EF =.F EPDCB A【例10】 如图所示,正方形ABCD 对角线AC 与BD 相交于O ,MN ∥AB ,且分别与AO BO 、交于M N 、.试探讨BM 与CN 之间的关系,写出你所得到的结论的证明过程.M N CDO B A【例11】 如图,已知P 是正方形ABCD 内的一点,且ABP ∆为等边三角形,那么DCP ∠=PDCBA【例12】 已知正方形ABCD ,在AD 、AC 上分别取E 、F 两点,使2ED AD FC AC =∶∶,求证:BEF ∆是等腰直角三角形.GEHDFCBA【例13】 如图,已知E 、F 分别是正方形ABCD 的边BC 、CD 上的点,AE 、AF 分别与对角线BD 相交于M 、N ,若50EAF ∠=︒,则CME CNF ∠+∠= .NMFEDCBA【例14】 如图,四边形ABCD 为正方形,以AB 为边向正方形外作正方形ABE ,CE 与BD 相交于点F ,则AFD ∠=FEDCBA【例15】 如果点E 、F 是正方形ABCD 的对角线BD 上两点,且BE DF =,你能判断四边形AECF 的形状吗?并阐明理由.E CDFBA【例16】 如图,正方形ABCD 中,在AD 的延长线上取点E ,F ,使DE AD =,DF BD =.连结BF 分别交CD ,CE 于H ,G .求证:GHD ∆是等腰三角形.3142FE GHCDBA【例17】 如图,过正方形顶点A 引AE BD ∥,且BE BD =.若BE 与AD 的延长线的交点为F ,求证DF DE =.GFEBDA【例18】 如图所示,在正方形ABCD 中,AK 、AN 是A ∠内的两条射线,BK AK ⊥,BL AN ⊥,DM AK ⊥,DN AN ⊥,求证KL MN =,KL MN ⊥.K NMLB A【例19】 如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,连接,BE DG ,求证:BE DG =.GC FEDBA【例20】 (2007年三帆中学期中考试)如图,在正方形ABCD 中,E 为CD 边上的一点,F 为BC 延长线上的一点,CE CF =,30FDC ∠=︒,求BEF ∠的度数.BDCAEF【例21】 已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使CE CG =,连接BG 并延长交DE 于F .(1)求证:BCG DCE ∆∆≌;(2)将DCE △绕点D 顺时针旋转90︒得到DAE '∆,判断四边形E BGD '是什么特殊四边形?并说明理由.【例22】 若正方形ABCD 的边长为4,E 为BC 边上一点,3BE =,M 为线段AE 上一点,射线BM 交正方形的一边于点F ,且BF AE =,则BM 的长为 . ABCDEF E 'G【例23】 如图1,在正方形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 上的点,HA EB FC GD ===,连接EG 、FH ,交点为O . ⑴ 如图2,连接EF FG GH HE ,,,,试判断四边形EFGH 的形状,并证明你的结论;⑵ 将正方形ABCD 沿线段EG 、HF 剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD 的边长为3cm ,1cm HA EB FC GD ====,则图3中阴影部分的面积为_________2cm .图3图1图2H DGC FEBAOH GFEDC BA【例24】 如图,正方形ABCD 对角线相交于点O ,点P 、Q 分别是BC 、CD 上的点,AQ DP ⊥,求证:(1)OP OQ =;(2)OP OQ ⊥.BO D CAQP【例25】 如图,在正方形ABCD 中,E 、F 分别是AB 、BC 的中点,求证:AM AD =.MFEDCBA【例26】 如图,正方形ABCD 中,E F ,是AB BC ,边上两点,且EF AE FC DG EF =+⊥,于G ,求证: DG DA =G FEC DBA【例27】 如图,点M N ,分别在正方形ABCD 的边BC CD ,上,已知MCN ∆的周长等于正方形ABCD 周长的一半,求MAN ∠的度数NMDCBA【例28】 如图,设EF ∥正方形ABCD 的对角线AC ,在DA 延长线上取一点G ,使AG AD =,EG 与DF交于H ,求证:AH =正方形的边长.HEGCDFBA【例29】 把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H (如图).试问线段HG 与线段HB 相等吗?请先观察猜想,然后再证明你的猜想.GCHF EDB A【例30】 如图所示,在直角梯形ABCD 中,AD BC ∥,90ADC ∠=︒,l 是AD 的垂直平分线,交AD 于点M ,以腰AB 为边作正方形ABFE ,作EP l ⊥于点P ,求证22EP AD CD +=.lPM FE DC BA【例31】 如图所示,ABCD 是正方形,E 为BF 上的一点,四边形AEFC 恰好是一个菱形,则EAB ∠=______. ABCDEF二、正方形的判定【例32】 四边形ABCD 的四个内角的平分线两两相交又形成一个四边形EFGH ,求证:⑴四边形EFGH 对角互补;⑵若四边形ABCD 为平行四边形,则四边形EFGH 为矩形. ⑶四边形ABCD 为长方形,则四边形EFGH 为正方形.HEFG DCBA【例33】 如图,已知平行四边形ABCD 中,对角线AC 、BD 交于点O ,E 是BD 延长线上的点,且ACE∆是等边三角形.⑴ 求证:四边形ABCD 是菱形;⑵ 若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.OEDCBA【例34】 已知:如图,在ABC ∆中,AB AC =,AD BC ⊥,垂足为点D ,AN 是ABC ∆外角CAM ∠的平分线,CE AN ⊥,垂足为点E . ⑴ 求证:四边形ADCE 为矩形;⑵ 当ABC ∆满足什么条件时,四边形ADCE 是一个正方形?并给出证明.M ENCDBA【例35】 如图,点M 是矩形ABCD 边AD 的中点,2AB AD =,点P 是BC 边上一动点,PE MC ⊥,PF BM ⊥,垂足分别为E 、F ,求点P 运动到什么位置时,四边形PEMF 为正方形.PMF EDC BA【例36】 如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE a AF b ==,,若23EFGH S =,则b a -=H GFEDCBA【例37】 如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为27cm 和211cm ,则CDE∆ 的面积为GFEDCB A【例38】 如图,在正方形ABCD 中,点1P P ,为正方形内的两点,且11PB PD PB AB CBP PBP ==∠=∠,,,则1BPP ∠=P1PDCBA【例39】如图,若在平行四边形ABCD各边上向平行四边形的外侧作正方形,求证:以四个正方形中心为顶点组成一个正方形.P RQS NM FEDCBA【例40】已知:PA4PB=,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.(1)如图,当∠APB=45°时,求AB及PD的长;(2)当∠APB变化,且其它条件不变时,求PD 的最大值,及相应∠APB的大小.PDCBA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方形第一课时一、自主学习●目标导学1、理解并掌握正方形的性质。
2、通过自学、合作、交流培养自己分析问题解决问题的能力。
●合作探究【探究一】正方形的定义1、正方形的定义:2、正方形与矩形和菱形的关系是【探究二】正方形的性质1、归纳正方形的性质:边角对角线对称性2、用几何语言叙述正方形的性质:【探究三】正方形的周长与面积边讲边练:①正方形与等腰三角形(等边三角形)结合1. 如图,E是正方形ABCD的对角线BD上一点,且BE=BC,则∠ACE=°2. 如图,四边形ABCD是正方形,延长CD到E,使CE=CB,则∠DBE=°.3. 如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:(1)∠E=22.5°;(2) ∠AFC=112.5°;(3) ∠ACE=135°;(4)AC=CE;(5) AD∶CE=1∶ 2. 其中正确的有()A.5个 B.4个 C.3个 D.2个4. 如图,等边△EDC在正方形ABCD内,连结EA、EB,则∠AEB=°;∠ACE=°.5.已知正方形ABCD,以CD为边作等边△CDE,则∠AED的度数是°.②正方形与旋转结合1.如图1,四边形ABCD是正方形,E是边CD上一点,若△AFB经过逆时针旋转角θ后与△AED重合,则θ的取值可能为()A.90°B.60°C.45°D.30°2.已知正方形ABCD中,点E在边DC上,DE = 2,EC = 1(如图2所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为___________.3. 如图3,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.③正方形对角线的对称性1. 如图:正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于E,PF⊥BD于F,则PE+PF= .可以用一句话概括:正方形边上的任意一点到两对角线的距离之和等于.思考:如若P在AB的延长线时,上述结论是否成立?若不成立,请写出你的结论,并加以说明.2.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP =EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD= 2EC.其中正确结论的序号是.思考:当点P在DB的长延长线上时,请将备用图补充完整,并思考(1)正确结论是否依旧成立?若成立,直接写出结论;若不成立,请写出相应的结论.④正方形的折叠1.如图1,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的长是 .2. 如图2,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且C B '=3,则AM 的长是 .3如图3,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC =3.其中正确结论的个数是 .课后练习1、已知:如图,正方形ABCD 中,CM =CD ,MN ⊥AC ,连结CN ,则∠DCN =_____=____∠B ,∠MND =_______=_______∠B.2.在正方形ABCD 中,AB =12 cm ,对角线AC 、BD 相交于O ,则△ABO 的周长是( )A.12+122B.12+62C.12+2D.24+623.正方形的面积是31,则其对角线长是________. 4. 如图,在正方形ABCD 中,△PBC 、△QCD 是两个等边三角形,PB 与DQ 交于M ,BP 与CQ 交于E ,CP 与DQ 交于F .求证:PM = QM .P5. 如图4,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O 重合,A′B′交BC于点E,A′D′交CD于点F,若正方形A′B′C′D′绕点O旋转某个角度后,OE=OF吗?两正方形重合部分的面积怎样变化?为什么?6.如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.试判断PE与PB的关系.7. 如图,正方形ABCD的面积为12,△ADE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PB+PE的和最小,则这个最小值为.8.如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.(1)如图②,若M为AD边的中点,①△AEM的周长=_____cm;②求证:EP=AE+DP;(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.正方形第二课时一、自主学习●目标导学1、理解并掌握正方形的判定方法。
2、通过合作、探究、交流培养自己分析问题和解决问题的能力。
二、合作学习●合作探究根据正方形的定义如何判定一个四边形为正方形?练一练:1、判断:(1)四条边都相等的四边形是正方形。
()(2)两条对角线相等且互相垂直的四边形是正方形。
()(3)两条对角线分别平分一组对角的四边形是正方形。
()(4)两条对角线互相垂直的矩形是正方形。
()2.不能判定四边形是正方形的是()A.对角线互相垂直且相等的四边形 B.对角线互相垂直的矩形C.对角线相等的菱形 D.对角线互相垂直平分且相等的四边形3、四边形ABCD的对角线相交于点O,能判定它是正方形的条件是()A.AB=BC=CD=DA B.AO=CO,BO=DO,AC⊥BDC.AC=BD,AC⊥BD且AC、BD互相平分 D.AB=BC,CD=DA4、如图,已知四边形ABCD是菱形,则只须补充条件:(用字母表示)就可以判定四边形ABCD是正方形.精讲精练例1、已知Rt ABC 中,90C ∠=︒,CD 平分ACB ∠,交AB 于D ,DF//BC,DE//AC ,求证:四边形DECF 为正方形。
例2、已知:如图,在△ABC 中,AB =AC ,AD ⊥BC ,垂足为点D ,AN 是△ABC 外角∠CAM 的平分线,CE ⊥AN ,垂足为点E ,(1)求证:四边形ADCE 为矩形;(2)当△ABC 满足什么条件时,四边形ADCE 是一个正方形?并给出证明.例3如图,已知平行四边形ABCD 中,对角线AC BD ,交于点O ,E 是BD 延长线上的点,且ACE △是等边三角形.(1)求证:四边形ABCD 是菱形;(2)若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.DBAO A MNE例4、如图,△ABC 中,点O 是AC 边上一个动点,过点O 作直线MN ∥BC ,设MN 交∠BCA 的平分线于E ,交∠BCA 的外角平分线于点F .(1)求证:EO =FO(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论.(3) 当点O 运动到何处时,四边形AECF 是有可能是正方形?并证明你的结论.拓展探究(平行四边形与特殊平行四边形的综合运用)1、如图,正方形ABCD 中,E 、F 、G 分别是AD 、AB 、BC 上的点,且AE=FB=GC 。
试判断EFG 的形状,并说明理由。
2、如图,在正方形ABCD 中,P 为BC 上一点,Q 为CD 上一点,(1)若PQ=BP+DQ ,求PAQ ∠。
(2)若45PAQ ∠=︒,求证:PQ=BP+DQ.3、如图,菱形ABCD的边长为2,对角线BD=2,E、F分别是AD、CD上的动点,且满足≅.(2)判断BEF的形状。
AE+CF=2.(1)求证:BDE BCF(11 舟山)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点,得四边形EFGH.(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),①试用含α的代数式表示∠HAE;②求证:HE=HG;③四边形EFGH是什么四边形?并说明理由.∠例1、在正方形ABCD的边BC的延长线上取一点E,使CE=CA,连接AE交CD于F,求AFD 的度数。
变式:1、已知如下图,正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,CE=CF.(1)求证:△BEC≌△DFC;(2)若∠BEC=60°,求∠EFD的度数.例2:如图,E为正方形ABCD的BC边上的一点,CG平分∠DCF,连结AE,并在CG上取一点G,使EG=AE.求证:AE⊥EG.例3、P为正方形ABCD内一点,PA=1,PB=2,PC=3,求∠APB的度数.例4如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;1、如图,四边形ABCD 为正方形,以AB 为边向正方形外作等边三角形ABE ,CE 与DB 相交于点F ,则AFD = 。
2、(哈尔滨)若正方形ABCD 的边长为4,E 为BC 边上一点,BE=3,M 为线段AE 上一点,射线BM 交正方形的一边于点F ,且BF=AE ,则BM 的长为 。
4.E 为正方形ABCD 内一点,且△EBC 是等边三角形,求∠EAD 的度数.5、如图,正方形ABCD 与正方形OMNP 的边长均为10,点O 是正方形ABCD 的中心,正方形OMNP 绕O 点旋转,证明:无论正方形OMNP 旋转到何种位置,这两个正方形重叠部分的面积总是一个定值,并求这个定值.ABC P DE6、(2008义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.7、(大连)(1)如图,已知正方形ABCD和正方形CGEF(CG>BC),B、C、G在同一直线上,M为线段AE的中点。
