大一高数课件第七章 7-2-1
合集下载
第七章 2汉密尔顿图

只能邻接路上的结点为止。若 p=n,则汉密尔顿路找到了,否则 p<n,转 STEP 2。
L: v1
vp
2021/2/16
7-2 汉密尔顿图 2021/2/16
7-2 汉密尔顿图
如果 v p 不邻接于 vl1, vm1,..., v j1,..., vt1 中的任意一个结点,则 deg(vp ) p 1 k ,
deg(u)+deg(v)≥ n, 则G是汉密尔顿图。
2021/2/16
11
7-2 汉密尔顿图
设G=〈V ,E〉是有n个结点的简单图, (1) 如果任两结点u,v∈V, 均有
deg(u)+deg(v)≥ n-1, 则在G中存在一条汉密尔顿路;
(1)证明:首先证明图 G 连通。用反证法进行证明。假设图 G 不连通,则图 G 至少
deg(v1) k , deg(vp ) deg(v1) p 1 k k p 1 n 1 , 这 与 前 提 条 件
deg u +deg v n-1矛盾。因此 v p 必然邻接于 vl1, vm1,..., v j1,..., vt1 中的任意一个结
点。回路 L1 一定存在。 STEP 3:打开回路,得到基本路径 L2。
有两个连通分支 G1 和 G2 。G1=<V1, E1> ,G2=<V2 , E2> 。| V1 | n1 ,| V2 | n2 。在G1 中取 一 个 结 点 v1 , deg(v1) n1 1 , 在 G2 中 取 一 个 结 点 v2 , deg(v2 ) n2 1 。
deg(v1) deg(v2 ) n1 1 (n2 1) n1 n2 2 n 2 ,与 deg u+deg v n-1 矛
因此该定理不能证明彼得森图是非 汉密尔顿图。但彼得森图是非汉密尔 顿图。
L: v1
vp
2021/2/16
7-2 汉密尔顿图 2021/2/16
7-2 汉密尔顿图
如果 v p 不邻接于 vl1, vm1,..., v j1,..., vt1 中的任意一个结点,则 deg(vp ) p 1 k ,
deg(u)+deg(v)≥ n, 则G是汉密尔顿图。
2021/2/16
11
7-2 汉密尔顿图
设G=〈V ,E〉是有n个结点的简单图, (1) 如果任两结点u,v∈V, 均有
deg(u)+deg(v)≥ n-1, 则在G中存在一条汉密尔顿路;
(1)证明:首先证明图 G 连通。用反证法进行证明。假设图 G 不连通,则图 G 至少
deg(v1) k , deg(vp ) deg(v1) p 1 k k p 1 n 1 , 这 与 前 提 条 件
deg u +deg v n-1矛盾。因此 v p 必然邻接于 vl1, vm1,..., v j1,..., vt1 中的任意一个结
点。回路 L1 一定存在。 STEP 3:打开回路,得到基本路径 L2。
有两个连通分支 G1 和 G2 。G1=<V1, E1> ,G2=<V2 , E2> 。| V1 | n1 ,| V2 | n2 。在G1 中取 一 个 结 点 v1 , deg(v1) n1 1 , 在 G2 中 取 一 个 结 点 v2 , deg(v2 ) n2 1 。
deg(v1) deg(v2 ) n1 1 (n2 1) n1 n2 2 n 2 ,与 deg u+deg v n-1 矛
因此该定理不能证明彼得森图是非 汉密尔顿图。但彼得森图是非汉密尔 顿图。
大一高数课件第七章7-3-1

对角线的长为 |m n || ,m n |, n m n { 1 , 1 ,1 }m , n { 1 ,3 , 1 } m
|m n |3 , |m n |1,1
平 行 四 边 形 的 对 角 线 的 长 度 各 为3, 1.1
;
b0
=__________;
c0=____________;
5、一向量与xoy, yoz,zox三个坐标平面的夹角,,
满足cos2+cos2 +cos2 =____________ .
二、一向量的终点在点B(2,1,7),它在 X轴, Y轴 和Z轴上的投影依次为4,4和7,求这向量的 起点A的坐.标
zz1
(z2z)
zz1z2 1
,
M 为有向线段 AB的定比分点. M 为中点时,
x x1 x2 , 2
y y1 y2 , 2
z z1 z2 . 2
三、向量的模与方向余弦的坐标表示式
非零向量 a的方向角:
z
、、
非零向量与三条坐标轴的 正向的夹角称为方向角.
向向量量的的坐坐标 标: 表达ax式, :ay,a az ,{a x,a y,a z}
M 1 M 2 { x 2 x 1 ,y 2 y 1 ,z 2 z 1 } 特殊地: O M {x ,y ,z}
向量的加减法、向量与数的乘法运算的坐标表达式
a a b {{ a a x x , a b yx ,, a a zy } ,b y b , a { z b x b ,z b } y,b z},
空间两向量的夹角的概念:
a0,
b0,
向量a 与向量b 的夹角
|m n |3 , |m n |1,1
平 行 四 边 形 的 对 角 线 的 长 度 各 为3, 1.1
;
b0
=__________;
c0=____________;
5、一向量与xoy, yoz,zox三个坐标平面的夹角,,
满足cos2+cos2 +cos2 =____________ .
二、一向量的终点在点B(2,1,7),它在 X轴, Y轴 和Z轴上的投影依次为4,4和7,求这向量的 起点A的坐.标
zz1
(z2z)
zz1z2 1
,
M 为有向线段 AB的定比分点. M 为中点时,
x x1 x2 , 2
y y1 y2 , 2
z z1 z2 . 2
三、向量的模与方向余弦的坐标表示式
非零向量 a的方向角:
z
、、
非零向量与三条坐标轴的 正向的夹角称为方向角.
向向量量的的坐坐标 标: 表达ax式, :ay,a az ,{a x,a y,a z}
M 1 M 2 { x 2 x 1 ,y 2 y 1 ,z 2 z 1 } 特殊地: O M {x ,y ,z}
向量的加减法、向量与数的乘法运算的坐标表达式
a a b {{ a a x x , a b yx ,, a a zy } ,b y b , a { z b x b ,z b } y,b z},
空间两向量的夹角的概念:
a0,
b0,
向量a 与向量b 的夹角
高等数学教学资料-第七章

kx3 k2 x6
1
k k
2
,
y 0
ykx3
其值随k的不同而变化,
故极限不存在.
确定极限不存在的方法:
( 1 ) 令 P (x ,y ) 沿 y k 趋 向 x 于 P 0 (x 0 ,y 0 ), 若 极 限 值 与 k 有 关 , 则 可 断 言 极 限 不 存 在 ;
(2)找两种不同趋近方式,使limf(x,y)存在, xx0 yy0 但两者不相等,此时也可断言f(x,y)在点 P0(x0,y0)处极限不存在.
内点一定是聚点; 边界点可能是聚点;
例 {x ( ,y )|0 x 2 y 2 1 }
(0,0)既是边界点也是聚点.
点集E的聚点可以属于E,也可以不属于E.
例如, {x ( ,y )|0 x 2 y 2 1 }
(0,0) 是聚点但不属于集合.
例如, {x (,y)|x2y21 }
边界上的点都是聚点也都属于集合.
x x0 y y0
(或 f ( x, y) A ( 0)这里 | PP0 |).
说明:
(1)定义中PP0 的方式是任意的;
(2)二元函数的极限也叫二重极限 limf (x, y); xx0 yy0
(3)二元函数的极限运算法则与一元函数类似.
例2 求证lx i0m (x2y2)sin x2 1y20 y 0
正 数 , 总 存 在 正 数 , 使 得 对 于 适 合 不 等 式 0 | PP0 | ( x x0 )2 ( y y0 )2 的 一 切 点,都有| f ( x , y ) A | 成立,则称 A 为函数
z f ( x, y)当 x x0, y y0 时的极限, 记为 lim f ( x, y) A
《高等数学(上册)》 第七章

于是平面图形的面积为
S b[ f (x) g(x)]dx . a
7.2.1 平面图形的面积
类似地,由左右两条曲线 x (y) 与 x (y) 及上下两条直线 y d 与 y c 所围
成的平面图形(见下图)的面积为
S d [ ( y) ( y)]dy . c
7.2.1 平面图形的面积
即
V [ f (x)]2 dx ,
于是体积元素为
dV [ f (x)]2 dx ,
旋转体的体积为
V b[ f (x)]2 dx . a
7.2.2 立体的体积
同理,由连续曲线 x (y) ,直线 y c ,y d 以及 y 轴所围区域,绕 y 轴旋转
的旋转体(见下图)体积为
V d 2 ( y)dy . c
7.2.2 立体的体积
3
例 6 如图所示,求由曲线 y x2 与直线 x 4 , x 轴所围图形绕 x 轴旋转而成的
旋转体的体积.
解 所求旋转体的体积为
V
4
(
x
3 2
)
2
dx
0
1 4
4
x4
0
64 .
7.2.2 立体的体积
2
2
2
例 7 如图所示,求星形线 x3 y3 a3 所围成的图形绕 x 轴旋转所得旋转体的体积.
例 1 计算由抛物线 y x2 1 和 y x2 x 所围成的图形的面积.
解 (1)画图,如图所示;
(2)确定图形在
x
轴上的投影区间:
1 2
,1
;
(3)确定上下曲线, f上 (x) x2 1 ; f下 (x) x2 x ; (4)计算积分:
S
1 1
高等数学上册第七章课件.ppt
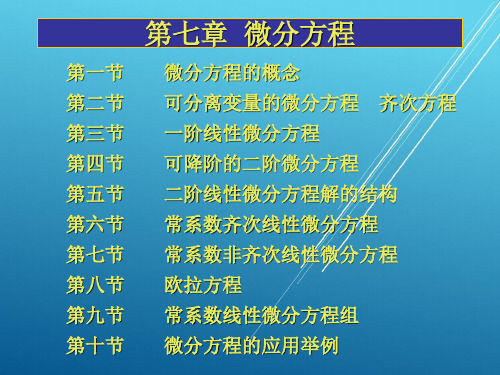
y C2 ex ,再利用 y (0) = 1 得 C2 1, 故所求曲线方程为
第四节 可降阶的二阶微分方程
小结 可降阶微分方程的解法 —— 降阶法
逐次积分
令 y p(x) ,
令 y p(y) ,
第五节 二阶线性微分方程解的结构
•n 阶线性微分方程的一般形式为
y(n) a1(x) y(n1) an1(x) y an (x) y f (x) f (x) 0 时, 称为非齐次方程 ; f (x) 0 时, 称为齐次方程.
第四节 可降阶的二阶微分方程
例 求解 解
代入方程得
则 y d p d p dy p d p dx dy dx dy
两端积分得 ln p ln y ln C1 , 即 p C1y,
(一阶线性齐次方程)
故所求通解为
第四节 可降阶的二阶微分方程
例
解初值问题
y e2y 0 y x 0 0 ,
y p(x) y q(x) y f (x), 为二阶线性微分方程.
复习: 一阶线性方程 y P(x) y Q(x)
通解:
y
C
e
P(x)d
x
eP(x)d x
Q(x) eP(x)d x dx
齐次方程通解Y 非齐次方程特解 y
第五节 二阶线性微分方程解的结构
•线性齐次方程解的结构
定理 若函数 y1(x), y2 (x) 是二阶线性齐次方程 y P(x) y Q(x) y 0
的两个解, 则 y C1y1(x) C2 y2 (x)
也是该方程的解. (叠加原理)
证 将 y C1y1(x) C2 y2 (x) 代入方程左边, 得 [C1y1 C2 y2 ] P(x)[C1y1 C2 y2 ]
《高等数学(下册)》课件 高等数学 第7章

列条件:
0) 满足下
(1)un1 un (n 1,2 ,3, ) ;(2)lnim un 0 , 则级数收敛,且其和 S u1 。
例2 判别以下级数的敛散性:
(1) (1)n
n 1
1 n
;(2)
n 1
(1)n1
n 2n 1
;
解
(1)该级数为交错级数。因为
un1
1 n 1
1 n
un
,且
lim
un
1 3n 2
1 3n
1
,而级数
是发散的,由比较审
n1 3n
敛法可知,级数 1 发散。
n1 3n 2
(2)因为
un
1 n2n
1 2n
,而几何级数
1 2n
n 1
是收敛的,由比
较审敛法可知,级数
1 n1 n2n
收敛。
1
1
(3)因为 un (n 1)(n 3) n2
1
,而
p-
级数
1 5
1 8
1 9
1 16
1 2k 1
1
1 2k 1
2
1 2k
1
1 2
1 2
1 2
1 2
1 1 k . 22
由于k可以任意大,所以数列Sk 无界,从而部分和数列Sk 也
无界,因此调和级数 1 是发散的。
n1 n
定理1
对于 p- 级数
1 np
n 1
( p 0),当
p 1
,1 3
,由性质2可知,
级数
1
发散。
n1 n 3
性质3(级数收敛的必要条件) 若级数 un 收敛,则它的一般项 n 1
0) 满足下
(1)un1 un (n 1,2 ,3, ) ;(2)lnim un 0 , 则级数收敛,且其和 S u1 。
例2 判别以下级数的敛散性:
(1) (1)n
n 1
1 n
;(2)
n 1
(1)n1
n 2n 1
;
解
(1)该级数为交错级数。因为
un1
1 n 1
1 n
un
,且
lim
un
1 3n 2
1 3n
1
,而级数
是发散的,由比较审
n1 3n
敛法可知,级数 1 发散。
n1 3n 2
(2)因为
un
1 n2n
1 2n
,而几何级数
1 2n
n 1
是收敛的,由比
较审敛法可知,级数
1 n1 n2n
收敛。
1
1
(3)因为 un (n 1)(n 3) n2
1
,而
p-
级数
1 5
1 8
1 9
1 16
1 2k 1
1
1 2k 1
2
1 2k
1
1 2
1 2
1 2
1 2
1 1 k . 22
由于k可以任意大,所以数列Sk 无界,从而部分和数列Sk 也
无界,因此调和级数 1 是发散的。
n1 n
定理1
对于 p- 级数
1 np
n 1
( p 0),当
p 1
,1 3
,由性质2可知,
级数
1
发散。
n1 n 3
性质3(级数收敛的必要条件) 若级数 un 收敛,则它的一般项 n 1
大一高数课件第七章

微分的概念
总结词
微分是导数的另一种表达方式,也是描 述函数在某一点附近的变化率的重要概 念。
VS
详细描述
微分表示函数在某一点处的增量与自变量 增量的比值当自变量增量趋于0时的极限 ,即函数在该点附近的变化率。微分与导 数的关系是微分等于导数与自变量增量的 乘积加上高阶无穷小量。微分具有线性性 质,即函数的微分满足线性运算规则。
洛必达法则
洛必达法则
如果函数f(x)与g(x)在某点x0的某个领域内 有定义,且f'(x0)=0或f'(x0)不存在,而 g'(x0)≠0,那么当x→x0时,lim (f(x)/g(x))=lim (f'(x0)/g'(x0))。
洛必达法则的应用条件
应用洛必达法则求极限时,需要满足三个条 件:分子和分母的导数都存在且分母的导数 不为零;所求极限的表达式是“0/0”或“ 无穷大/无穷大”的形式;通过等价无穷小 替换或有理化分母等方法将所求极限的表达 式化为“0/0”的形式。
03
导数与微分
导数的定义
总结词
导数是描述函数在某一点附近的变化率的重要概念。
详细描述
导数定义为函数在某一点处的切线的斜率,表示函数在该点附近的变化率。通过求导,可以分析函数 在某一点附近的增减性、极值等性质。
导数的性质
总结词
导数具有一些重要的性质,如可加性、可乘性、链式法则等 。
详细描述
导数具有可加性和可乘性,即对于两个函数的和或乘积求导 ,可以分别对每个函数求导后再进行相应的运算。链式法则 是指对复合函数的导数进行求导时,需要用到外层函数的导 数和内层函数的导数。
应用
微积分基本定理是计算定积分的 基石,通过它可以求出许多复杂 函数的定积分。
高等数学第七章.ppt

规
划
a11x1+a12x2+…+a1nxn=b1
(1)
的
a21x1+a22x2+…+a2nxn=b2
(2)
标
准
……
型
am1x1+am2x2+…+amnxn=bm
(m)
x1 ,x2 ,…xn≥0
第三节 单纯形法
其简缩形式为
一
max Z c1x1 c2 x2 cn xn
线 性
n
aij x j bi
ZA=300 ZB=175 ZC=110 ZD=150
x2 15 A
3x1+x2=15
可行域
10
B
x1+x2=10
5
C
O
5
10
A(0,15) B(2.5,7.5) C(9,1) D (15,0)
x1+6x2=15
D
15
x1
10x1+20x2=0
第三节 单纯形法
单纯形方法是一种较为完善的、步骤 化的线性规划问题求解方法。它的原理涉 及到较多的数学理论上的推导和证明,我 们在此仅介绍这种方法的具体操作步骤及 每一步的经济上的含义。为更好地说明问 题,我们仍结合实例介绍这种方法
第
一
节
线
《经济大词典》定义线性规划:一种
性
具有确定目标,而实现目标的手段又有
规
一定限制,且目标和手段之间的函数关
划 模 型
系是线性的条件下,从所有可供选择的 方案中求解出最优方案的数学方法。
的
基
本
原
理
二、线性规划三要素
第
大一高数课件第七章 7-8-1

( A1 A2 ) x ( B1 B2 ) y (C1 C2 )z ( D1 D2 ) 0
由于系数 A1 A2 , B1 B2 , C1 C2 因此上述方程表示一个平面。 不全为零,
该平面经过直线 L , 且对于不同来自 值,直线与平面的位置关系:
(1)
L
A B C . m n p
Am Bn Cp 0.
( 2) L //
x 1 y z 1 例 6 设直线 L : ,平面 : x y 2 z 3, 2 1 2 求直线与平面的夹角. 解 n {1,1, 2}, s {2,1, 2},
思考题解答
6 p 0 p 6, m 0, 2m 0 s 0, n 0,
故当 m 0, n 0, p 6时结论成立.
练 习 题
一、 填空题:
x3 z 1 1、 通过点 ( 4 ,1 , 3 ) 且平行于直线 y 2 5 的直线方程为______________; 5 x 3 y 3 z 9 0 2、 直线 与直线 3 x 2 y z 1 0 2 x 2 y z 23 0 的夹角的余弦为__________; 3 x 8 y z 18 0
^ ( s , n) 2
^ ( s , n) 2
sin cos cos . 2 2
sin | Am Bn Cp | A2 B 2 C 2 m 2 n 2 p 2
直线与平面的夹角公式
六、求与已知直线 L1 : x 3 y 5 z 及 2 3 1 x 10 y 7 z L2: 都相交且和 L3: x 2 y 1 z 3 5 4 1 8 7 1
大一上册微积分课件chapter7

s in n 1 x c o s x ( n 1) (1 s in 2 x ) s in n 2 x d x s in n 1 x c o s x ( n 1) s in n 2 x d x
(n 1) sin n xdx
T h erefo re
n s in n x d x c o s x s in n 1 x ( n 1) s in n 2 x d x
3x
2x 2 ln x 33
2 3
xdx
3
2x 2 ln x 4 x 2 C
3
9
Example6 x arctan xdx
arctan
xd
x2 2
arctan x x2 2
x2 2
1
1 x2
dx
x2 2
arctan
x
1 2
1
1
1 x
2
dx
x2 arctan x 1 x arctan x C
b
(
f
(x)g(x)
f
( x) g ( x))dx
a
a
f (x)g(x)]ba
b f (x)g(x)dx
a
b f (x)g(x)dx
a
b f (x)g(x)dx a
f (x)g(x)]ba
b f (x)g(x)dx
a
or
b a
udv
uv]ba
b
vdu
a
Exampe
1
arctan xdx.
Thus
s in n x d x 1 c o s x s in n 1 x n 1 s in n 2 x d x
n
n
s in n x d x s in n 1 x d c o s x s in n 1 x c o s x c o s x d s in n 1 x s in n 1 x c o s x ( n 1) c o s 2 x s in n 2 x d x s in n 1 x c o s x ( n 1) (1 s in 2 x ) s in n 2 x d x
高等数学第七章课件.ppt

a
(2) 三角形法则
b
向量的加法符合下列运算规律:
((12))交结换合律律::aa
b b
cb
(aa.
b)
c
a
a a
(b
b
c ).
多个向量相加,可以按照三角形法则.
负向量:大小相a 等但方向a相反的向量.
减法:a b a (b)
ab
b
a
ab
特例:a
(a)
0.
b
α φ1 = φ
=λ|α|cosφ
λα φ1=π- φ
=λPrjlα
λ<0
当λ<0时 φ1=π-φ
λα
Prj(λα)=|λ|.|α|cos(φ1) =-λ|α|(-cosφ)
λ >0 α
=λPrjlα; 当λ=0时
λα
φ1 = φ φ1=π- φ
Prj(λα)= 0 =λPrjlα;
λ<0
(二) 向量的坐标表示
单位向量:模长为1的向量. a0
或
M1 M 20
零向量:模长为0的向量. 0
自由向量:不考虑起点位置的向量.
相等向量:大小相等且方向相同的向量.
a
向量平行 方向相反或者方向b 相同的向量a
a//b
零向量和任何向量都平行.
三、向量的线性运算
(一) 向量的加 减法
加法:a b c
(1) 平行四边形法则
b c
a
b
c
a
(b )
ab
(向(二((123量))))aa向与000,,,量实aaa与数与 与数aa0的2同 的反a乘向乘向法,积,|| 记aa作|||a||12,a规a||a定 | a是一个向量.
高考数学(理科)大一轮复习课件:第七章 立体几何 第7章-第7节

D,E,F 分别为 B1A,C1C,BC 的中点.求
证:
核
(1)DE∥平面 ABC;
心
考 向
(2)B1F⊥平面 AEF.
课
图7-7-4
时
限
时
检
测
菜单
【证明】 如图建立空间直角坐标系 A-xyz,令 AB=AA1
=4,
基
础
则 A(0,0,0),E(0,4,2),F(2,2,0),
知
识 点
B(4,0,0),B1(4,0,4).
cos〈a,b〉=|aa|·|bb|
课
核
时
心 考
2.求直线与平面所成的角
限 时
向
检
设直线 l 的方向向量为 a,平面 α 的法向量为 n,直线 l 测
|a·n|
与平面 α 所成的角为 θ,则 sin θ=_|c_o_s_〈__a_,__n_〉__|_=__|a_|_|n_|_.
菜单
3.求二面角的大小
方 法 技 巧
A.a=(1,0,0),n=(-2,0,0)
B.a=(1,3,5),n=(1,0,1)
C.a=(0,2,1),n=(-1,0,-1)
核
D.a=(1,-1,3),n=(0,3,1)
课 时
心
限
考 向
【答案】 D
时 检
测
菜单
基 础 知 识 点
方
4.已知两平面的法向量分别为 m=(0,1,0),n=(0,1,1),
2.已知向量 m,n 分别是直线 l 和平面 α 的方向向量、 法向量,若 cos〈m,n〉=-12,则 l 与 α 所成的角为( )
方 法 技 巧
A.30°
大一高数课件第七章 7-7-1

的平面; 平行于 xoy 面 的平面 的平面; 平行于 yoz 面 的平面; 的平面. 平行于 zox 面 的平面
例 3 设平面过原点及点 ( 6,−3, 2) , 且与平面 4 x − y + 2 z = 8 垂 直,求此平面方程. 求此平面方程. 解 设平面为 Ax + By + Cz + D = 0,
三、两平面的夹角
定义 两平面法向量之间的夹角称 为两平面的夹角. 为两平面的夹角. (通常取锐角) 通常取锐角)
r n2
r n1
θ
Π2
Π 1 : A1 x + B1 y + C1 z + D1 = 0,
Π 2 : A2 x + B2 y + C 2 z + D2 = 0, r r n1 = { A1 , B1 , C 1 }, n 2 = { A2 , B 2 , C 2 },
设平面上的任一点为 M ( x , y , z ) r r 必有 M 0 M ⊥ n ⇒ M 0 M ⋅ n = 0
Q M 0 M = { x − x 0 , y − y0 , z − z 0 }
∴ A( x − x0 ) + B( y − y0 ) + C(z − z0 ) = 0
平面的点法式方程
n = (0, B,C) ⊥ i, 平面平行于 x 轴;
• Ax + Cz + D = 0 表示 平行于 y 轴的平面; 轴的平面; • Ax + By + D = 0 表示 平行于 z 轴的平面; 轴的平面;
• C z + D = 0 表示 • A x + D =0 表示 • B y + D =0 表示
高等数学 第七章

二、余子式与代数余子式
定义 1 三阶行列式中,把元素 aij (i 1,2,3 ;j 1,2 ,3) 所在行和列的元素删掉,剩下的 元 素 保 持 原 来 的 相 对 位 置 不 变 所 构 成 的 二 阶 行 列 式 称 为 元 素 aij 的 余 子 式 , 记 为 Mij .将 Aij (1)i j Mij 称为元素 aij 的代数余子式.
那么,我们称这样的矩阵为行最简阶梯形矩阵.
1 0 0 3 1 5 2 0
例如,
0
1
0
4
,
0
0
0
1
等都是行最简阶梯形矩阵.
0 0 1 4 0 0 0 0
0 0 0 0 0 0 0 0
三、方阵的行列式
定义 2 由 n 阶方阵 A 的元素按照原来的位置顺序构成的行列式称为方阵 A 的行列式,记为 | A | 或 det A .
行列式按行(或列)展开的方法可用来计算 n 阶行列式的值,这个方法称 为展开式法则.
第二节
行列式的性质及计算
一、行列式的性质
性质 1(转置性) 任一行列式 D 与其转置行列式的值都相等,即 D DT . 性质2(互换性) 互换行列式的某两行(列),行列式变号. 推论 若行列式某两行(列)元素对应相等,则行列式的值为零,反之不一定成立. 性质3(数乘性) 行列式的某一行(列)中所有元素都乘以同一个数 ,等于用数乘以行列式. 推论1 如果行列式中某一行(列)有公因子 ,则可以把公因子 提到行列式外. 推论2 如果行列式的某两行(列)对应元素成比例,则行列式的值为零.
二、矩阵的加减
定义 2 设 A (a ij )mn , B (bij )mn ,则规定 A B (aij bij )mn .
高等数学7.1—2章PPT课件

由初始条件得 C = 1, 故所求特解为
y x2 1 1
.
13
例3. 求下述微分方程的通解:
y sin2 (x y 1) 解: 令 u x y 1, 则
u 1 y
故有
1 u sin2 u
即
sec2 u du dx
解得
tan u x C
所求通解: tan(x y 1) x C ( C 为任意常数 )
这说明 x C1 cos k t C2 sin k t 是方程的解 . C1 ,C2 是两个独立的任意常数, 故它是方程的通解.
利用初始条件易得: C1 A,C2 0 , 故所求特解为
x Acos k t
.
7
例2. 已知曲线上点 P(x, y) 处的法线与 x 轴交点为 Q
且线段 PQ 被 y 轴平分, 求所满足的微分方程 .
g( (x))(x) dx f (x) dx
两边积分, 得 g( y) dy f (x) dx
则有
G( y)
F ( x)
G(y) F(x) C
②
当G(y) 与F(x) 可微且 G’(y) =g(y)≠0 时, 上述过程可逆,
说明由②确定的隐函数 y=(x) 是①的解. 同样,当F’(x) = f (x)≠0 时, 由②确定的隐函数 x=(y) 也是①的解.
.
14
例四 求方程 d y ex y 的通解. dx
解法 1 分离变量 e y d y ex dx
ey ex C
即
(ex C)ey 1 0 ( C < 0 )
解法 2 令u x y, 则u 1 y
故有 积分
u 1 eu
du
1 eu
xC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试用向量方法证明: 例2 试用向量方法证明:对角线互相平分的四边 D r 形必是平行四边形. 形必是平行四边形. C r a b 证 Q AM = MC
BM = MD
A
M
B
∴ AD = AM + MD = MC + BM = BC
平行且相等, 结论得证. AD 与 BC 平行且相等, 结论得证.
四、小结
r a
r b
负向量: 大小相等但方向相反的向量. 负向量: 大小相等但方向相反的向量.
r −a
r −a r a
向径: 向径: 空间直角坐标系中任一点 M 与原 点构成的向量. 点构成的向量OM .
二、向量的加减法 r r r 加法: [1] 加法:a + b = c
(平行四边形法则) 平行四边形法则)
按照向量与数的乘积的规定, 按照向量与数的乘积的规定, r a r0 r r r0 a =| a | a r =a . |a| 上式表明: 上式表明:一个非零向量除以它的模的结果是 一个与原向量同方向的单位向量. 一个与原向量同方向的单位向量.
r r r 1 r b − 3a 例1 化简 r a − b + 5 − b + 5 2 r r 解 r 1 r b − 3a r a − b + 5 − b + 5 2 5 1 r r r 5r = (1 − 3)a + − 1 − + ⋅ 5 b = −2a − b . 2 5 2
1 2 三、 D1 A = − ( c + a ) , D2 A = − ( c + a ) , 5 5 3 4 D3 A = − ( c + a ), D4 A = − ( c + a ). 5 5
分为同向和反向
r c
r r r | c |=| a | + | b |
r b
r a
r c r r r | c |= | a | − | b |
向量的加法符合下列运算规律: 向量的加法符合下列运算规律:
r r r r 交换律: (1)交换律: a + b = b + a . r r r r r r r r r 结合律: (2)结合律:a + b + c = (a + b ) + c = a + (b + c ). r r r a + ( − a ) = 0. (3) )
7、两向量___________,我们称这两个向量相等; 两向量___________,我们称这两个向量相等; ___________ 两个模相等、____________的向量互为逆向量 的向量互为逆向量; 8、两个模相等、____________的向量互为逆向量; 把空间中一切单位向量归结到共同的始点, 9、 把空间中一切单位向量归结到共同的始点, 则终 构成____________ ____________; 点构成____________;
用向量方法证明: 二 、用向量方法证明 :对角线互相平分的四边形是平 行四边形 .
三 、 把 ABC 的 BC 边 五 等 分 , 设 分 点 依 次 为 D1 , D2 , D3 , D4 , 再 把 各 分 点 与 点 A 连 接 , 试 以 AB = c , BC = a 表示向量 D1 A , D2 A , D3 A 和 D4 A .
10、 把平行于某一直线的一切单位向量归结到共同的 10、 始点,则终点构成____________________ ____________________; 始点,则终点构成 ____________________; r r r r r r 11、 成立, 应满足_______ 11、要使 a + b = a − b 成立,向量 a , b 应满足_______ _________________; _________________; r r r r r r 12、 成立, 应满足_______ 12、要使 a + b = a + b 成立,向量 a , b 应满足_______ ___________ .
1r − a 2
数与向量的乘积符合下列运算规律: 数与向量的乘积符合下列运算规律:
r r r λ 结合律: (1)结合律: ( µ a ) = µ ( λ a ) = (λµ )a r r r ( 分配律: (2)分配律: λ + µ )a = λ a + µ a r r r r λ (a + b ) = λ a + λ b
练习题答案
大小; 一、1、既有大小,又有方向; 既有大小,又有方向; 2、大小; 模等于零; 起点; 3、模等于 1; 4、模等于零; 5、起点; 共线向量,共面向量; 7、模相等且方向相同; 6、共线向量,共面向量; 7、模相等且方向相同; 方向相反; 的球面; 8、方向相反; 9、半径为 1 的球面; 10、 的两点; 10、距离等于r2 的两点; r r r 11、 12、 11、a 垂直于b ; 12、a 与b 同向 .
向量的概念
(注意与标量的区别) 注意与标量的区别)
向量的加减法 (平行四边形法则) 平行四边形法则) 向量与数的乘法
(注意数乘后的方向) 注意数乘后的方向)
思考题
已知平行四边形ABCD的对角线 的对角线 已知平行四边形
r r AC = a , BD = b r r 表示平行四边形四边上对应的向量. 试用 a , b 表示平行四边形四边上对应的向量
r [2] 减法 r r r a − b = a + (−b)
r b
r r a +b
r a
r r a −b
r r b a r r −b r −b c r r r c = a + (−b ) r r =a−b
三、向量与数的乘法 r r 是一个数, 设 λ 是一个数,向量 a 与 λ 的乘积 λa 规定为 r r r r (1) λ > 0, λa 与 a 同向, λa |= λ | a | | r 同向, a r r r 2a ( 2 ) λ = 0, λ a = 0 r r r r | 反向, ( 3) λ < 0, λa 与 a 反向,λa |=| λ | ⋅ | a |
两个向量的平行关系 v r v 定理 设向量 a ≠ 0,那末向量 b 平行于 a 的充 v r 分必要条件是: 分必要条件是:存在唯 一的实数 λ ,使 b = λ a .
证
充分性显然; 充分性显然; 必要性
r r 设 b‖ a
取
r r 取正值, 当b 与 a 同向时 λ 取正值, r r r r 取负值, . 当b 与 a 反向时 λ 取负值,即有 b = λ a r r r r b r r r Q 此时 b 与 λa 同向. 且 λa = λ a = r a = b .
思考题解答
A
D
r b
M
r a
B
C
1 r r BC = AD = AM + MD = ( a + b ). 2 1 r r DC = AB = AM + MB = ( a − b ). 2
练 习 题
填空: 一、 填空: 向量是_________的量; _________的量 1、 向量是_________的量; 向量的___________叫做向量的模; ___________叫做向量的模 2、 向量的___________叫做向量的模; ___________的向量叫做单位向量 的向量叫做单位向量; 3、 ___________的向量叫做单位向量; _____________的向量叫做零向量 的向量叫做零向量; 4、 _____________的向量叫做零向量; _____无关的向量称为自由向量 无关的向量称为自由向量; 5、 与_____无关的向量称为自由向量; 平行于同一直线的一组向量叫做_________ _________, 6、 平行于同一直线的一组向量叫做_________ , 三 个或三个以上平行于同一平面的一组向量叫做___ 个或三个以上平行于同一平面的一组向量叫做___ _________; _________;
a
r b λ = r, a
r r r r λ 的唯一性 . 设 b = λa, 又设 b = µa, r r r 两式相减, 两式相减,得 ( λ − µ )a = 0, 即 λ − µ a = 0,
r Q a ≠ 0, 故 λ − µ = 0, 即 λ = µ .
r0 r 同方向的单位向量, 设a 表示与非零向量 a 同方向的单位向量,
⋅M
1
单位向量:模长为1的向量. a 0 或 M M 0 单位向量:模长为1的向量. 1 2 r 零向量:模长为0的向量. 零向量:模长为0的向量. 0
自由向量: 不考虑起点位置的向量. 自由向量: 不考虑起点位置的向量. 相等向量: 大小相等且方向相同的向量. 相等向量: 大小相等且方向相同的向量.
一、向量的概念
向量: 既有大小又有方向的量. 向量: 既有大小又有方向的量. 向量表示:r 向量表示:a 或 M 1 M 2
为起点, 为终点的有向线段. 以 M 1 为起点, M 2 为终点的有向线段. r 向量的模:向量的大小. 向量的模:向量的大小.| a | 或 | M M |
1 2
M2 ⋅
r b
r c
(平行四边形法则有时也称为三角形法则) 平行四边形法则有时也称为三角形法则)
三角形法则可推广到多个向量相加 .
r a r r b c r a
r b
s = a1 + a2 + a3 + a4 + a5
a4
a5 a3
s
a2 a1
机动
目录
