20.几何图形的涂色问题
圆环涂色 数学问题

圆环涂色数学问题
一、几何学
圆环涂色问题在几何学中是一个经典的问题。
几何学是研究大小、形状、空间等概念的数学分支,而圆环涂色问题则涉及到平面图形的几何特性和染色方案。
通过对圆环的涂色,可以进一步探讨图形的染色性质和规律,加深对几何学基本概念的理解。
二、拓扑学
拓扑学是研究几何图形在连续变形下保持不变的性质的数学分支。
在圆环涂色问题中,拓扑学的思想可以应用于探讨涂色的方式和规律。
例如,可以通过拓扑等价的概念来研究不同的涂色方案是否等价,或者通过研究涂色的传递性质来探索染色问题的解法。
三、组合数学
组合数学是研究计数、排列、组合等问题的数学分支。
在圆环涂色问题中,组合数学的思想可以应用于计算不同染色方案的数量。
例如,可以通过组合数学中的排列组合公式来计算不同染色方案的数量,或者通过组合数学中的递归方法来探讨染色问题的解法。
四、计算机科学
计算机科学在圆环涂色问题中也有重要的应用。
计算机科学可以提供高效的算法和程序来求解染色问题。
例如,可
以使用计算机科学中的图论算法来求解圆环涂色问题,或者使用计算机科学中的优化算法来寻找最优的染色方案。
此外,计算机科学还可以通过模拟实验来验证染色方案的正确性和有效性。
总之,圆环涂色数学问题涉及到几何学、拓扑学、组合数学和计算机科学等多个领域的知识。
通过对这些领域知识的综合应用,可以深入探讨圆环涂色问题的性质和规律,为解决实际问题提供有效的工具和方法。
概率与统计微专题(涂色或染色问题培优版)

概率与统计微专题涂色(染色)问题【培优版】与涂色(染色)问题有关的试题新颖有趣,是近几年高考考查的热点、高频考点,其中包含着丰富的数学思想,解题方法技巧性强且灵活多变.本专题总结涂色(染色)计数问题的常见类型及求解方法,侧重于分类加法计数原理、分步乘法计数原理在涂色(染色)问题中的应用.一、涂色问题与染色问题涂色问题和染色问题都是数学中的组合数学问题,它们有一些相似之处,但严格来说涂色问题与染色问题是有区别的,举例如下:(1)涂色问题的例子:在一个方格纸上,按照一定的规律,如螺旋式或交替式,给每个方格涂色.给一个几何图形,如三角形、正方形等,用不同颜色进行涂色,使得满足某种对称或美观要求.(2)染色问题的例子:给定一个地图,能否用有限种颜色给各个国家或地区染色,使得相邻国家或地区颜色不同.在一个网络中,确定能否用有限种颜色给节点染色,使得相邻节点颜色不同.可以看出,涂色问题更注重颜色的排列和组合方式,以及如何达到特定的视觉效果;而染色问题更关注如何满足特定的限制条件,如相邻区域或节点的颜色不同.本文在中学范围内,探讨涂色问题与染色问题的解法,因此对它们不加以区别,认为它们是相同类型的问题.二、涂色(染色)问题主要类型在中学范围内,涂色(染色)问题主要有以下几种类型:(1)点线面染色问题:涉及对点、线、面的染色;(2)区域染色问题:将一个平面区域按照一定的规则进行染色;(3)图形染色问题:对各种几何图形进行染色,如三角形、正方形等;(4)染色方案问题:确定满足一定条件的染色方案的数量;(5)染色规律问题:寻找染色过程中的规律;(6)限定条件染色问题:在特定限制条件下进行染色,等等.三、涂色(染色)问题的常用解题策略选好分类标准,优化分类顺序的策略.分类讨论是一种重要的数学思想方法,当问题所给对象不能进行统一研究时,就需要对研究的对象进行分类,将整体问题划分为局部问题,把复杂问题转化为单一问题,然后分而治之、各个击破,最后综合各类的结果得到整个问题的解答.因此,采用分类策略解答染色问题时,我们可以从三个方面入手考虑,(1)从确定染色顺序入手根据染色问题的要求,先确定好区域的染色顺序,对各个区域分步染色,再由乘法原理计算出染色的种数,是处理这类问题最基本的方法.(2)从使用颜色的种类入手按照染色问题中的题设要求,从使用了多少种颜色分类讨论入手,分别计算出各种情形的种类,再用分类计数原理求出不同的染色方法的种数.(3)从相对区域是否同色入手从某两个不相邻区域同色与不同色入手,分别计算出两种情形的种数,再用分类计数原理求中不同的染色方法的种类.四、应用两个计数原理解决涂色(染色)问题的一般步骤(1)明确问题:仔细理解涂色染色问题的具体要求和限制条件;(2)分解步骤:将整个涂色染色过程分解为若干个相互独立的步骤;(3)分类或分步:①分类:根据不同的情况或条件进行分类,每类相互独立;②分步:按照一定的顺序进行分步操作.(4)确定方法数:在分类的情况下,分别计算每类的方法数;在分步的情况下,相乘得到总的方法数.(5)计算总数:如果既有分类又有分步,需要明确先分类再分步计算,还是先分步再分类计算;(6)检查结果:检查计算结果是否满足问题的限制条件.五、应用两个计数原理解决涂色(染色)问题注意事项应用分类加法计数原理和分步乘法计数原理解决涂色(染色)问题时,需要注意以下几点:(1)确保分类或分步的合理性和完整性,避免遗漏情况.(2)注意题目中的限制条件,不符合要求的方案应排除.(3)对于复杂的问题,可以通过列举部分情况来辅助理解和分析.当然,对于复杂的问题,可能需要建立模型,比如递推数列来解决问题.类型一点染色问题点染色问题,要注意对各点依次染色,主要方法有:(1)根据共用了多少种颜色分类讨论;(2)根据相对顶点是否同色分类讨论.【典例1】将一个四棱锥S ABCD−的每个顶点染上一种颜色,并使同一条棱的两端点异色,如果只有5种颜色可供使用,那么不同的染色方法的总数是多少?图1【解析】设想染色按S A B C D −−−−的顺序进行,对 , , S A B 染色,有54360⨯⨯=种染色方法.由于C 点的颜色可能与A 同色或不同色,这影响到D 点颜色的选取方法数,故分类讨论:C 与A 同色时(此时C 对颜色的选取方法唯一),D 与A ,C ,S 不同色,有3种选择;C 与A 不同色时,C 有2种选择的颜色,D 有2种颜色可供选择,从而对C ,D 染色有13227⨯⨯+=种染色方法.由乘法原理,总的染色方法数是607420⨯=种.【总结与反思】图1中的连接状况是本质条件,而是否空间图形则无关紧要.下面的两个问题,尽管与例题表述方式不同,但具有相同的数学模型,所以都可以转化为本例来解决.(1)如图2,用五种颜色给图中的5个车站的候车牌A 、B 、C 、D 、E 染色,要求相邻两个车站间的候车牌的颜色不同,有多少种不同的染色方法.图2(2)如图3所示为一张有5个行政区划的地图,今要用5种颜色给地图着色,要求相邻的区域不同色,共有多少种方案?图3【举一反三】(2023下广东河源高二期中考试)1.将一个三棱台的每个顶点染上一种颜色,并使同一条棱的两端点异色,如果只有5种颜色可供使用,那么不同的染色方法的总数是 .【答案】1920【分析】利用分步计数原理进行计算即可.【详解】设在三棱台ABC DEF −中,首先对,,A B C 着色,有543⨯⨯种;然后:D 点可以用B 或C 点的色,也可以用剩下的两种色.现分类:(1)用B 或C 点的色,由对称性,不妨设用B 点的色,则E 点有4种色可以选择,又分为两类:①E 与C 同色,则F 有3种色可选择;②与C 不同色,则F 有2种色可选择,共有2(1332)⨯⨯+⨯,(2)用剩下的两种色,则E 点有3种色可选择,又分为两类:①E 与C 同色,则F 有3种色可选择;②与C 不同色,则F 有2种色可选择,共有:()21322⨯⨯+⨯.所以不同的染色方法的总数是()()54321332213221920⎡⎤⨯⨯⨯⨯⨯+⨯+⨯⨯+⨯=⎣⎦. 故答案为:1920.类型二 线段染色问题【典例2】如图5,用红、黄、蓝、白、四种颜色染矩形ABCD 的四条边,每条边只染一种颜色,且使相邻两边染不同的颜色,如果颜色可能反复使用,共有多少种不同的染色方法.图5解法一:(1)使用四种颜色,每条边一种,应用分步乘法计数原理,有432124⨯⨯⨯=种; (2)使用三种颜色染色,则必须将一组对边染成同色,故有423248⨯⨯⨯=种; (3)使用两种颜色时,则两组对边必须分别同色,有4312⨯=种.因此,所求的染色方法数为24481284++=种.解法二: 染色按AB BC CD DA −−−的顺序进行,对 , AB BC 染色有4312⨯=种染色方法.由于CD 的颜色可能与AB 同色或不同色,这影响到DA 颜色的选取方法数,故分类讨论: 当CD 与AB 同色时,这时CD 对颜色的选取方法唯一,则DA 有3种颜色可供选择;当CD 与AB 不同色时,CD 有2种可供选择的颜色,DA 有2种可供选择的颜色,从而对CD ,DA 染色有13227⨯+⨯=种染色方法.由乘法原理,总的染色方法数为12784⨯=种.【总结与反思】要注意对各条线段依次讨论,主要方法有:(1)根据共用了多少种颜色分类讨论;(2)根据相对的线段是否同色分类讨论.【举一反三】(2023辽宁大连一中月考)2.正五边形ABCDE 中,若把顶点A ,B ,C ,D ,E 染上红、黄、绿、黑四种颜色中的一种,使得相邻顶点所染颜色不相同,则不同的染色方法共有 种.【答案】240【解析】根据题意,不妨先染顶点A ,再染B ,E ,讨论B 、E 同色,B 、E 不同色两种情况,结合分步乘法与分类加法计数原理,逐步计算,即可得出结果.【详解】由题意,不妨先染顶点A ,则有14C 种染法;再染B ,E ,当B ,E 同色时,B ,E 共有13C 种染法,则C ,D 共有2232C A 种染法;当B ,E 不同色时,B ,E 共有23A 种染法,则C ,D 的染色情况可以分以下三类: ①若C 与A 颜色相同,则D 有2种不同染色方法;②若D 与A 颜色相同,则C 有2种不同染色方法;③若C 、D 与A 颜色都不相同,则C 、D 有3种不同染色方法;综上,不同的染色方法有()1122243323223240C C C A A ⎡⎤+++=⎣⎦种. 故答案为:240.【点睛】思路点睛:解答排列、组合问题的角度:解答排列、组合应用题要从“分析”、“分辨”、“分类”、“分步”的角度入手;(1)“分析”就是找出题目的条件、结论,哪些是“元素”,哪些是“位置”;(2)“分辨”就是辨别是排列还是组合,对某些元素的位置有、无限制等;(3)“分类”就是将较复杂的应用题中的元素分成互相排斥的几类,然后逐类解决;(4)“分步”就是把问题化成几个互相联系的步骤,而每一步都是简单的排列、组合问题,然后逐步解决.类型三 面染色问题【典例3】如图6,将一个四棱锥的每一个面染上一种颜色,使每两个具有公共棱的面染成不同颜色,如果只有4种颜色可供使用,则不同的染色方法总数为( )图6A.36B.48C.72D.108【答案】C【分析】对面SAB 与面SDC 同色和不同色进行分类,结合分步乘法计算原理,即可得出答案.【解析】当面SAB 与面SDC 同色时,面ABCD 有4种方法,面SDC 有3种方法,面SAD 有2种方法,面SAB 有1种方法,面SBC 有2种方法,即4321248⨯⨯⨯⨯=种,当面SAB 与面SDC 不同色时,面ABCD 有4种方法,面SDC 有3种方法,面SAD 有2种方法,面SAB 有1种方法,面SBC 有1种方法,即4321124⨯⨯⨯⨯=种,即不同的染色方法总数为482472+=种,故选C .【总结与反思】应用两个计数原理解决面染色问题需要注意以下几点:(1)确定面的数量和颜色种类;(2)分析面之间的关联,找出相互独立的染色步骤;(3)对不同情况分类讨论,计算每一类的染色方法数.特别要注意:按相对的面是否同色,分情况讨论;(4)按照分步计数原理,将每一步的方法数相乘,得到总的染色方法数.【举一反三】3.如图所示的几何体由三棱锥−P ABC 与三棱柱111ABC A B C 组合而成,现用3种不同颜色对这个几何体的表面涂色(底面111A B C 不涂色),要求相邻的面均不同色,则不同的涂色方案共有( )A .6种B .9种C .12种D .36种【答案】C 【解析】三棱锥−P ABC 三个侧面的颜色各不相同,先进行染色,然后再给三棱柱111ABC A B C 的侧面染色,保证组合体中相邻的侧面颜色不同即可.【详解】先涂三棱锥−P ABC 的三个侧面,有1113216C C C =种情况,然后涂三棱柱的三个侧面,有1112112C C C =种情况,共有6212⨯=种不同的涂法.故选:C .类型四区域染色问题【典例4】要用四种颜色给四川、青藏、西藏、云南四省(区)的地图染色(图8)每一省(区)一种颜色,只要求相邻的省(区)不同色,则不同染色的方法有多少种?图8【解析】先给四川染色有4种方法,再给青海染色有3种方法,接着给西藏染色有2种方法,最后给云南染色有2种方法,根据乘法原理,不同的染色方法共有4×3×2×2=48种.【总结与反思】本例是分步乘法计数原理在染色中的应用.根据乘法原理,对各个区域分步染色,这是处理这类问题的基本的方法.【举一反三】(2024下山东滨州高二月考)4.如图,用4种不同的颜色,对四边形中的四个区域进行着色,要求有公共边的两个区域不能用同一种颜色,则不同的着色方法有()A.48B.56C.72D.256【答案】A【分析】先给四个区域标记,然后根据分步乘法计数原理求解出着色的方法数.A B C D,如下图所示:【详解】将四个区域标记为,,,第一步涂:4A 种涂法,第二步涂:3B 种涂法,第三步涂:2C 种涂法,第四步涂:2D 种涂法,根据分步乘法计数原理可知,一共有432248⨯⨯⨯=种着色方法.故选:A.【典例5】如图11,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同不同,且两端格子的颜色也不同,则不同的涂色方法共有 种(用数字作答).图11【答案】630【解析】不妨将图中的4个格子从左到右依次缩号为①②③④.第一类情况:①③同色.第一步,涂①有6种方法;第二步,涂②有5种方法;第三步,涂③只有1种方法;第四步,涂④也有5种方法.依分步乘法计数原理,有6515150⨯⨯⨯=种方法.第一类情况:①③不同色.涂②有6种方法;涂②有5种方法;涂③有4种方法;涂④时应与①③不同色,也有4种方法,依分步乘法计数原理,有6544480⨯⨯⨯=种方法.最后由分类加法计数原理,共有150480630+=种方法.【举一反三】(2023下山东济南高二期中考试)5.某公园设计了如图所示的观赏花坛,现有郁金香、玛格丽特、小月季、小杜鹃四种不同的花可供采购,要求相邻区域种不同种类的花,则不同的种植方案个数为( )A .24B .36C .48D .96【答案】C 【分析】由分步乘法计数原理求解即可.【详解】先种区域1有4种选择,区域2有3种选择,区域3有2种选择,区域4有1种选择,区域5有2种选择,区域6有1种选择,则共有:43212148⨯⨯⨯⨯⨯=种.故选:C.【典例6】如图13,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有 种.(以数字作答)图13【典型错解】按A B C D E →→→→的顺序分五步着色:(1)A 有4种染法;(2)B 与A 不同色,有3种染法;(3)C 与 , A B 不同色有2种染法;(4)D 与 , A C 不同色有2种染法;(5)E 与 , , A B D 不同色,有1种染法,因此不同的着色方法共有43221448⨯⨯⨯⨯=种.【错解剖析】上述解法犯了一个处理染色问题最常见的错误.事实上,在第五步,若 , D B 不同色,则E 有1种染法;若 , D B 同色,则E 有2种染法.可见D 的染色不同,E 的染色方法数不同.【启示】按某种顺序着色分步计算时,要注意考虑前一步的染法对后继染色的影响,谨防出错.请看下面几种正确解法.解法一:从相邻最多的区域开始分步计算受错解启发最后者一步可以将 , D E 两个区域合在一起,按的 , A B C D E →→→顺序分四步着色:(1)(2)(3)染法同上;(4) , D E 着色分两种情况:若D 与B 同色,则D 有1种染法,E 有2种染法;若D 与B 不同色,则 , D E 有1种染法,根据分步乘法计数原理,不同的着色方法共有:()432121172⨯⨯⨯⨯+⨯=种.【总结与反思】为了使前一步的每一种染法对后继染色的影响小一些,尽量降低出错机会,习惯上,第一步染色常常从相邻最多的区域开始,即最大相邻原则.解法二:从不相邻的区域入手分类计算以 , B D 是否同色为标准分类:(1)若 , B D 同色,按 , B D A C E →→→的顺序着色,则有432248⨯⨯⨯=种方法; (2)若 , B D 不同色,按 , B D A C E →→→的顺序着色,则有4321124⨯⨯⨯⨯=种方法, 所以不同的着色方法共有482472+=种.【总结与反思】在解法一,按某种顺序染色,前后染色关系繁杂难以理顺时,解法二往往是一种行之有效的方法.【分析】依题意至少要选用3种颜色,先分类,在每类中再利用分步乘法原理计数. 解法三:从被选用颜色的种数入手分类计算【解析】依题意至少要选用3种颜色,因此分如下三类:(1)第一类:当选用三种颜色时,区域 , B D 必须同色,区域 , C E 必须同色,由分步乘法原理可得,有43224⨯⨯=种;(2)当用四种颜色时,若区域 , B D 同色,则区域 , C E 不同色,有432124⨯⨯⨯=种;若区域 , C E 同色,则区域 , B D 不同色,有432124⨯⨯⨯=种,故用四种颜色时,共有22448⨯=种,由加法原理可知满足题意的着色方法共有:244872+=.解法四:去杂法(1)按A B C D E →→→→的顺序着色,先不考虑E 与B 不同色的限制,有4322296⨯⨯⨯⨯=种着色方法,但在这个计算中,包括E 与B 同色的情况,不符合条件,此时可把 , E B 合并为一个区域. (2)按()A B E C D →→→的顺序着色,得出不符合条件的着色方法有432124⨯⨯⨯=种, 因此符合条件的不同着色方法共有962472−=种.【总结与反思】解法三根据共用了多少种颜色分类讨论,分别计算出各种情形的种数,再用加法原理求出不同染色的方法总数.按颜色分类与按区域分步(区域也可以分类),对应着组合计数的加法原理与乘法原理,它们都是“通法”,都有独立存在的价值,并且相互之间有内在联系,还常常要交叉综合使用,没有必要厚此薄彼,也没有证据表明两种算法的一致性是“巧合”.【举一反三】(2023江苏盐城滨海三校高二下期中联考)6.如图,一个地区分为5个行政区域,现给地图涂色,要求相邻区域不得使用同一颜色.现有5种颜色可供选择,则不同的涂色方法的有( )种A .540B .360C .300D .420【答案】D 【分析】分②和④涂同种颜色和不同种颜色是讨论即可.【详解】分两种情况讨论即可:(i)②和④涂同种颜色时,从①开始涂,①有5种涂法,②有4种涂法,④有1种涂法,③有3种涂法,⑤有3种涂法,∴此时有5×4×1×3×3=180种涂法;(ii)②和④涂不同种颜色时,从①开始涂,①有5种涂法,②有4种涂法,④有3种涂法,③有2种涂法,⑤有2种涂法,∴此时有5×4×3×2×2=240种涂法;∴总共有180+240=420种涂色方法.故选:D﹒【典例7】(2024辽宁名校联盟联考)为迎接元宵节,某广场将一个圆形区域分成A B C D E五个部分(如图15所示),现用4种颜色的鲜花进行装扮(4种颜色均用到),,,,,每部分用一种颜色,相邻部分用不同颜色,则该区域鲜花的摆放方案共有()图15A.48种B.36种C.24种D.12种.【答案】A【分析】满足条件的涂色方案可分为,B D区域同色,且和其它区域不同色和,C E区域同色两类,且和其它区域不同色,结合分步乘法计数原理,分类加法计数原理求解即可【解析】满足条件的摆放方案可分为两类,第一类,B D区域同色,且和其它区域不同色的摆放方案,满足条件的方案可分四步完成,第一步,先摆区域A有4种方法,第二步,摆放区域,B D有3种方法,第三步,摆放区域C有2种方法,A B C不同色,且4种颜色都要用到,摆放区域E有1种方法,第四步,考虑到区域,,由分步乘法计数原理可得第一类中共有432124⨯⨯⨯=种方案,第二类,,C E区域同色两类,且和其它区域不同色的摆放方案,满足条件的方案可分四步完成,第一步,先摆区域A有4种方法,第二步,摆放区域B有3种方法,第三步,摆放区域,C E有2种方法,A B C不同色,且4种颜色都要用到,摆放区域D有1种方法,第四步,考虑到区域,,由分步乘法计数原理可得第一类中共有432124⨯⨯⨯=种方案,根据分步加法计数原理可得该区域鲜花的摆放方案共有48种,故选A.【总结与反思】本例根据某两个不相邻区域是否同色分类讨论.从某两个不相邻区域同色与不同色入手,分别计算出两种情形的种数,再用加法原理求出不同染色方法数.综合上面几例,我们可以总结出一类区域染色问题的解题程序,分三步叙述于下:第一步,进行几何结构的分析.主要是弄清一共有几块区域,区域与区域之间哪此存在相邻关系(异色),哪此不存在相邻关系(可同色,也可异色).为了简化图形并凸显关系,可将区域模型图对应为模式结构图.(从表层结构到深层结构)第二步,根据图形的深层结构各个击破,或分步计数或分类计数,或以区域为主计数或以颜色为主计数.在以区域为主分步计数时,要执行“最大相邻原则”,每次都从相邻最多的区域开始染色.第3步,反思回顾,“防假、防漏、防重”.为了防止在第二步计算中出现:渗杂了不合条件的染法,遗漏了符合条件的染法,或重复了符合条件的染法,反思回顾是一个必要步骤.根据解题的时间和环境,可采取画树树状图、多解对照、推进到一般等措施.同时,要注意积累成功的经验与失败的教训.【举一反三】(2023下江苏常州高二期中考试)7.如图所示的一圆形花圃,拟在A,B,C,D区域种植花苗,现有3种不同颜色的花苗,每个区域种植1种颜色的花苗,且相邻的2块区域种植颜色不同的花苗,则不同的种植方法总数为()A.12B.18C.24D.30【答案】B【分析】先对A区域种植,再对B区域种植,最后分两类:D块与B块相同、D块与B块不相同,对C 、D区域种植,根据计数原理即可求解.【详解】根据题意,分3步进行分析:(1)对于A 块,可以在3种不同的花中任选1种,有3种情况;(2)对于B 块,可以在剩下的2种不同的花中任选1种,有2种情况;(3)对于C 、D 块,分2种情况:若D 块与B 块相同,则C 块可以在其余的2种不同的花中任选1种,有2种情况, 若D 块与B 块不相同,则C 块有1种情况,D 块有1种情况,此时C 、D 有1种情况, 则C 、D 共有213+=种情况;综合可得:一共有32318⨯⨯=种不同的种法.故选:B类型五 区域种植问题近几年在各级各类考试中经常出现这类试题:在给定的几个区域中栽种植物,要求在相邻的区域中栽种不同的植物,求共有多少不同的栽种方法.这类问题实际上是一类染色问题(或地图着色问题).【典例8】在一个正六边形的6个区域栽种观赏植物,如图17,要求同一块中种同一种植物,相邻的两块种不同的植物.现有四种不同的植物可供选择,则有 种栽种方案.图17【解析】以A ,C ,E (相间)栽种植物情况作为分类标准:①考虑A ,C ,E 栽种同一种植物,有4种栽法;B ,D ,F 各有3种栽法,∴ 共有 4333108⨯⨯⨯=种栽法. ②考虑A ,C ,E 栽种同两种植物,此时种A ,C ,E 有343⨯⨯种,种B ,D ,F 有322⨯⨯种栽法(若A ,C 栽种同一种植物,则B 有3 种栽法,D ,F 各有2种栽法),因此,共有343322432⨯⨯⨯⨯⨯=种方法.③考虑A ,C ,E 种3种植物,有43224⨯⨯=种栽法;B ,D ,F 各有2种栽法,∴ 共有 2422192⨯⨯=种栽法.综合①、②、③三类,共有 108432192732++=种栽法.【总结与反思】进一步的,问题可以推广到一般的情形:用()2m m ≥种不同的颜色,给图18中()2n n ≥个彼此相连的区域12 , , , n A A A 染色,且任何相邻的2个区域染不同的颜色,则不同的涂色方案种数为:()()()111n n n a m m =−+−−.注意:上述问题中的m 种颜色是可供选择的,而不是全部都要用上的.图18【举一反三】8.如图,用5种不同颜色给图中标有1、2、3、4各部分涂色,每部分只涂一种颜色,且相邻两部分涂不同颜色,则不同的涂色方法共有( )A .160种B .240种C .260种D .360种【答案】C 【分析】按:1234→→→的顺序进行涂色,结合分类加法、分步乘法计数原理求得正确答案.【详解】先给第1部分涂色,有5种涂色方法;再给第2部分涂色,有4种涂色方法; 再给第3部分涂色:若第3部分颜色与第2部分相同,则第3部分只有1种涂色方法,再给第4部分涂色,有4种涂色方法;若第3部分颜色与第2部分不相同,则第3部分有3种涂色方法,再给第4部分涂色,有3种涂色方法.所以不同的涂色方法一共有54(1433)260⨯⨯⨯+⨯=种.故选:C【典例9】(2023四川绵阳南山中学高二月考)某城市在中心广场建造一个花圃,花圃分为6个部分,如图20所示.现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,则不同的栽种方法有( )图20A.80种B.120种C.160种D.240种【答案】B【分析】由题意,按照一定顺序,由1,2,3,5的顺序,在5号区域的选择上进行分情况,根据分类加法原理和分步乘法原理,可得答案.【解析】第一步,对1号区域,栽种有4种选择;第二步,对2号区域,栽种有3种选择; 第三步,对3号区域,栽种有2种选择;第四步,对5号区域,栽种分为三种情况, ①5号与2号栽种相同,则4号栽种仅有1种选择,6号栽种有2种选择,②5号与3号栽种相同,则6号栽种仅有1种选择,4号栽种有2种选择,③5号与2、3号栽种都不同,则4、6号只有1种;综上所述,()4322211120⨯⨯⨯++⨯=种.故选:B .【总结与反思】用()2m m ≥种不同的颜色,给图21中()()12n n +≥个彼此相连的车轮型区域012 , , , , n A A A A 染色,且任何相邻的2个区域染不同的颜色,则不同的涂色方案种数为:()()()212n n n a m m m ⎡⎤=−+−−⎣⎦.图21【举一反三】9.某广场中心建造一个花圃,花圃分成5个部分(如图),现有4种不同颜色的花可以栽种,若要求每部分必须栽种一种颜色的花且相邻部分不能栽种同样颜色的花,则不同的栽种方法有 种.(用数字作答)【答案】72【分析】根据题意,分析可得本题是分类计数问题,分2种情况讨论,当选3种颜色时,就是②④同色,③⑤同色,从4中颜色中选3中,在三个元素上排列;当4种颜色全用,只能②④或③⑤用一种颜色,先选出同色的一对,再用四种颜色全排列,由分类计数原理计算可得答案.【详解】由题意,分2种情况讨论:第一:当选用3种颜色时②④同色,③⑤同色,共有涂色方法3343C ?A 24=种, 第二:4色全用时涂色方法,即②④或③⑤用一种颜色,共有1424C ?A =48种, 根据分类加法原理知不同的着色方法共有24+48=72种.故答案为:72.。
涂色问题的常见解法及策略

解题篇经典题突破方法高二数学2019年5月涂色问题的常见解进及策曜■江苏省盐城市时杨中学刘长柏对于涂色问题的解法,拨云破雾、还其本来面目,就会发现实质是用分类或分步计数原理导航,通过深入缜密分析题意,将原题化归为熟悉的排列、组合或综合题型,逐类分步推理求解的。
涂色问题的常见解法:根据分步计数原理,对各个区域分步涂色;根据共用了多少颜色分类讨论;根据不相邻区域是否同色分类讨论等。
一・根据分步计数原理,对各个区域分步涂色伸I f用红黄绿三种颜色给图1中的5个带状格子涂色。
要求每格涂一种颜色且相邻格子不能涂同一种颜色•共有多少种不同的涂法?图1分析:根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
解:从满足一格一颜色、邻格不同色的限制条件入手,分成三类:一类是左边三个邻格从红黄绿中任取3色,涂法有A;种,且右面两相邻格涂法有A;种。
共有Aj・A;=12(种)。
二类是左起4格涂成红绿红绿的类似模式有A;种,末一格涂法有A;种,共有A;・A;=12(种)。
三类是左起4格涂成红绿红黄的类似模式有A:种,其中产生与一类重复的有6种(如红绿红黄绿与一类的红绿红黄绿)。
综上得:A;A;+A;A;+(A:—6)=42(种)。
点评:带状区域的涂色问题的解法,与推导排列数公式A;的思想方法类似,可构造排好顺序的m个空位(格),从n个不同元素中任取m Cm^n')个填充。
此类涂色题一般可转化成有限制条件的排列或组合问题。
练习1:用5种不同的颜色给图2中标①、②、③、④的各部分涂色,每部分只涂一种颜色•相邻部分涂不同颜色,则不同的涂色方法有多少种?解:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种•由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5X4X3X4=240(种)。
二、根据共用了多少颜色分类讨论制2如图3所示,花坛内有5个花池,有5种不同颜色的花卉可供栽种,每个花池内只能栽种同颜色的花卉,相邻两池的花卉颜色不同,则最图3多有多少种栽种方案?分析:本题要完成的事件是花池内栽种花卉;由于5种不同颜色的花卉可供选择,所以可选择3种、4种、5种不同颜色的花卉栽种•可见有3类方法可独立完成这件事,而每一类又不能“一次性”完成,所以分步进行。
20.几何图形的涂色问题

返回
20几何图形的涂色问题空间图形的涂色问题由于其空间位置的特点处理问题时容易受空间想像的限制使问题变得很不直观若利用欧拉定理的思想与方法通过图形的变换转化为平面图形的涂色问题可使一类空间涂色问题得以简化而使问题变得直观下面给出几例来看欧拉思想在涂色问题中的应用例1某城市在中心广场建造一个扇环形花圃花圃分为6个部分如右图现要栽种4种不同颜色的花每一部分栽种一种且相邻部分不能栽种同样颜色的花问有多少种不同的栽种方法解析利用欧拉思想进行拉伸变形可使图1变形为图2这两种图形的涂色其实质是一样的我们不妨用1234代表四种颜色在右侧图形中先在123区域涂上123三种颜色然后依次涂第456三个区域涂区域4可用24颜色图1图2若区域4涂颜色2则整个花圃有123243123234两种涂法若区域4涂颜色4则整个花圃有123434123424123423三种涂法即区域123颜色确定以后区域456有5种涂法所以共有不同的栽种方法为a345120种例2将一个四棱锥的每个顶点染上一种颜色并使同一条棱上的两端异色如果只有5种颜色可供使用求不同的涂色方法总数解析本题如果将棱锥的顶点往下作投影或者是将四棱锥看成是可以拉伸的薄膜状表面进行拉伸变成平面图形图1则空间图形的涂色就能变成平面图形的涂色继而将点扩展为平面区域则又可变为平面内圆形区域的涂色问题图2方法同例1解略有420种涂色方法例3用5种颜色给正方体abcda1b1c1d1各面涂色要求相邻两个面不同色现已将过顶点a的3个面涂了颜色那么其余3个面涂色方法有多少种解析分三类一是剩余三面的颜色与以a为顶点的三面的颜色相同则只能涂其对面颜色有1种涂法二是只有2种与所涂颜色相同则有c23种方式另一种颜色为剩余两种颜色中的一种故有6种涂法三是只有一种颜色与前面所涂相同有c13种剩余涂为两种其它颜色故也有6种涂法综上有13种例4现用4种颜色给三棱柱的6个顶点涂色要求同一条棱的两端点的颜色不同4种颜色全部用上问有多少种不同的涂色方案解析将左侧图形拉伸为右侧图形则中间三点不同色不妨为三颜色123又4种颜色全用上故外围三点中一定有一点涂第4种颜色在此情况下从其余三色中任挑两色另外两点都只有一种涂法故共有c34a33c13c23216种涂法返回
五年级:美妙数学之“正方体涂色问题”(0807五)

五年级:美妙数学之“正方体涂色问题”(0807五)
我们人教版五年级下册学过了探索图形,你还记得吗?
探索图形中的其中一类就是正方体涂色问题,把小正方体拼成大正方体,这样的大正方体的规格可以简单地表示成2×2×2,3×3×3……n×n×n,问,三面涂色,两面涂色,一面涂色的和没有涂色的小正方体各有几个?
大家回忆一下这样的问题我们一般怎样解决呢?
算三面涂色的小正方体的个数方法是这样的:三面涂色的小正方体都是大正方体的顶点所在的小正方体,大正方体一共有8个顶点也就是三面涂色的小正方体有8个;两面涂色的小正方体分布在大正方体的棱处,但要去掉头尾,所以两面涂色小正方体个数为(n-2)×12;一面涂色小正方体分布在大正方体的面上,但是要去掉面上一圈,也就是(n-2)×(n-2)×6;没有涂色的小正方体分布在内心,也就是要剥去大正方体华丽的外表,所以没有涂色的小正方体个数是(n-2)×(n-2)×(n-2)。
同学们想起来了吗?那我的问题来了,正方体是这样那长方体呢?敬请期待下一期的分享。
高考数学中涂色问题的常见解法及策略

高考数学中涂色问题的常见解法及策略整理:高三数学组 2009年4月与涂色问题有关的试题新颖有趣,近年已经在高考题中出现,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,因而这类问题有利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本文拟总结涂色问题的常见类型及求解方法一.区域涂色问题1、 根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、 用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?分析:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种,由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5434240⨯⨯⨯=2、 根据共用了多少种颜色讨论,分别计算出各种出各种情形的种数,再用加法原理求出不同的涂色方法种数。
例2、四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
分析:依题意只能选用4种颜色,要分四类: (1)②与⑤同色、④与⑥同色,则有44A ; (2)③与⑤同色、④与⑥同色,则有44A ; (3)②与⑤同色、③与⑥同色,则有44A ;(4)③与⑤同色、② 与④同色,则有44A ;(5)②与④同色、③与⑥同色,则有44A ;所以根据加法原理得涂色方法总数为544A =120例3、如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4 分析:依题意至少要用3种颜色1) 当先用三种颜色时,区域2与42) 区域3与5必须同色,故有34A 种; 3) 当用四种颜色时,若区域2与4同色,4) 则区域3与5不同色,有44A 种;若区域3有44A 种,故用四种颜色时共有244A 种。
由加法原理可知满足题意的着色方法共有34A +244A =24+2⨯24=723、 根据某两个不相邻区域是否同色分类讨论,从某两个不相邻区域同色与不同色入手,分别计算出两种情形的种数,再用加法原理求出不同涂色方法总数。
涂色问题的解题技巧

ʏ江苏省张家港中等专业学校 张 娴 韩文美排列组合中有一类常见问题涂色问题,此类问题基于两个计数原理与排列组合知识,关注图形的结构特征,解决方法技巧性强且灵活多变,有利于培养同学们的创新思维能力㊁分析问题与观察问题以及解决问题的能力,已成为数学命题中比较常见的一类基本题型,备受各方关注㊂1.直线型涂色问题图1例1 (2022 2023学年江苏省常州一中高二下学期段考数学试卷)现有6种不同的颜色,给图1中的5个格子涂色,每个格子涂一种颜色,要求最多使用4种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有种㊂分析:根据题设条件,选出的颜色可以是2种,3种或者4种,依次通过直线型的图形结构特征求出方法数,通过分类法求和,即可得以分析与求解㊂解:由题意选出的颜色可以是2种,3种或者4种,规定左边起为第一个空,不同情况如下㊂当选出2种颜色时,第一个空有2种选择,第一个空颜色确定后,其余空颜色就确定了,共有C 26ˑ2=30(种)方法㊂当选出3种颜色时,第一个空有3种选择,第二个空有2种选择,第三个空可分为与第一个空颜色相同和不同的情况,第四个空和第五个空都各有2种选择,但要去掉整体只用了2种颜色的情况,共有C 36C 13C 12㊃(C 12C 12+C 12C 12)-2C 36C 23=840(种)方法㊂当选出4种颜色时,必有2种颜色相同,可采用插空法,将这2种相同颜色去插入另外3种颜色形成的空,共有C 46C 14A 33C 24=2160(种)方法㊂综上分析,不同的涂色方法共有30+840+2160=3030(种)㊂点评:直线型涂色问题往往从第一个位置入手,逐一分析,在前一个已涂色的条件下涂下一个位置,注意对不同位置的分析加以合理分类讨论与分步处理,进而确定直线型涂色问题的种数㊂2.区域型涂色问题图2例2 (2022 2023学年湖北省武汉市高二下学期期中数学试卷)七巧板是古代劳动人民智慧的结晶㊂图2是某同学用木板制作的七巧板,它包括5个等腰直角三角形㊁一个正方形和一个平行四边形㊂若用四种颜色给各板块涂色,要求正方形板块单独一色,其余板块两块一种颜色,而且有公共边的板块不同色,则不同的涂色方案有种㊂分析:根据题设条件,先对七巧板中的不同区域加以合理标记,并通过画图分析其中四板块A ,B ,C ,D 必涂上不同颜色,再根据分类㊁分步计数原理计算剩下的部分即可得以分析与求解㊂解:由题意知,对七巧板中的不同区域加以合理标记,如图3所示㊂93解题篇 创新题追根溯源 高二数学 2024年3月图3由于一共4种颜色,板块A 需单独一色,剩下6个板块中每2个区域涂同一种颜色,且板块B ,C ,D 两两有公共边不能同色,故板块A ,B ,C ,D 必定涂不同的颜色㊂①当板块E 与板块C 同色时,则板块F ,G 与板块B ,D 或板块D ,B 分别同色,共有2种情况㊂②当板块E 与板块B 同色时,则板块F 只能与D 同色,板块G 只能与C 同色,共1种情况㊂又板块A ,B ,C ,D 颜色可排列,故共(2+1)ˑA 44=72(种)方案㊂点评:区域型涂色问题,应该给区域依次标上相应的序号,以便分析问题㊂在给各区域涂色时,要注意不同的涂色顺序,其解题就有繁简之分㊂在实际解答时,应按不同的涂色顺序多多尝试,看哪一种最简单㊂3.立体型涂色问题图4例3 (2024届上海市七宝中学高三上学期期中数学试卷)某数学兴趣小组用纸板制作正方体教具,如图4所示,现给图中的正方体展开图的6个区域涂色,有红㊁橙㊁黄㊁绿4种颜色可选,要求制作出的正方体相邻面所涂颜色均不同,共有种不同的涂色方法㊂分析:根据题设条件,由正方体展开图的平面图形回归正方体的立体图形,先从涂A 入手,再分C 与F 同色㊁C 与F 不同色两种情况讨论,利用分步㊁分类计数原理分析与运算可得答案㊂图5解:如图5所示,还原回正方体后,D ㊁B 为正方体的前后两个对面,A ㊁E 为正方体的左右两个对面,F ㊁C 为正方体的上下两个对面,先涂A有4种涂法㊂①当C 与F 同色时,涂C 有3种涂法,若D 与B 同色,则有2种涂法,最后涂E 有2种涂法;若D 与B 不同色,则有A 22种涂法,最后涂E 有1种涂法㊂则有4ˑ3ˑ(2ˑ2+A 22ˑ1)=72(种)涂法㊂②当C 与F 不同色时,涂C 有3种涂法,涂F 有2种涂法,此时D 与B 必同色且只有1种涂法,E 也只有1种涂法㊂则有4ˑ3ˑ2ˑ1ˑ1=24(种)涂法㊂综上分析可得,一共有72+24=96(种)不同的涂法㊂点评:立体型涂色问题,往往要同时考虑平面几何的结构特征,又要考虑立体几何的结构特征,综合 二维 与 三维 中的涂色要求与限制条件,全面考查同学们的空间想象能力与逻辑推理能力㊂4.环状型涂色问题图6例4 (2024届浙江省名校联盟高三上学期9月份月考数学试卷)五行是华夏民族创造的哲学思想,多用于哲学㊁中医学和占卜方面㊂五行学说是华夏文明重要的组成部分㊂古代先民认为,天下万物皆由五类元素组成,分别是金㊁木㊁水㊁火㊁土,彼此之间存在相生相克的关系㊂图6是五行图,现有5种颜色可供选择给五 行 涂色,要求五行相生不能用同一种颜色(例如金生火,水生木,不能同色),五行相克可以用同一种颜色(例如水克火,木克土,可以用同一种颜色),则不同的涂色方法种数为( )㊂A.3125 B .1000C .1040D .1020分析:根据题设条件,从数学文化场景中加以合理转化,抽象问题的本质与内涵,通过环状型涂色问题来转化,并加以分析,先根据不相邻区域是否同色进行分类,确定涂色顺序,再分步计数即可㊂解:依题可知五行相克可以用同一种颜4 解题篇 创新题追根溯源 高二数学 2024年3月色,也可以不用同一种颜色,即无限制条件而五行相生不能用同一种颜色,即相邻位置不能用同一种颜色㊂故问题转化为图7中A ,B ,C ,D ,E 5个区域,有5种不同的颜色可用,要求相邻区域不能涂同一种颜色,即5种颜色5个区域的环状涂色问题㊂图7分为以下两类情况㊂第一类,A ,C ,D 3个区域涂3种不同的颜色㊂第一步涂A ,C ,D 区域,从5种不同的颜色中选3种按顺序涂在不同的3个区域上,则有A 35种方法;第二步涂B 区域,由于A ,C 颜色不同,则有3种方法;第三步涂E 区域,由于A ,D 颜色不同,则有3种方法㊂由分步计数原理知,共有3ˑ3ˑA 35=540(种)方法㊂第二类,A ,C ,D 3个区域涂2种不同的颜色㊂C ,D 不能涂同种颜色,则A ,C 涂色相同,或A ,D 涂色相同,两种情况方法数相同㊂若A ,C 涂色相同,第一步涂A ,C ,D 区域,A ,C 可看成同一区域,且A ,D 区域不同色,即涂2个区域不同色,从5种不同的颜色中选2种按顺序涂在不同的2个区域上,则有A 25种方法;第二步涂B 区域,由于A ,C 颜色相同,则有4种方法;第三步涂E 区域,由于A ,D 颜色不同,则有3种方法㊂由分步计数原理知,共有4ˑ3ˑA 25=240(种)方法㊂若A ,D 涂一色,与A ,C 涂一色的方法数相同,则共有2ˑ240=480(种)方法㊂由分类计数原理可知,不同的涂色方法数为540+480=1020㊂选D ㊂点评:求解环状型涂色问题,是基于直线型涂色问题加以分析与处理,同时要考虑最后一个位置与原来第一个位置之间的限制,这样才能形成一个闭环,这也是解决问题中比较容易出错的一个环节,要加以高度重视㊂5.探究型涂色问题例5 (2023年吉林省长春市高考数学质检试卷)将圆分成n (n ȡ2,且n ɪN *)个扇形,每个扇形用红㊁黄㊁蓝㊁橙四色之一涂色,要求相邻扇形不同色,设这n 个扇形的涂色方法为a n 种,则a n 与a n -1的递推关系是㊂分析:根据题设条件,对n 个扇形依次加以编号,按n =2与n >2两种情况加以分类讨论a n 的情况,由分步计数原理得到a n 与a n -1之间的关系㊂解:将圆分成n 个扇形时,将n 个扇形依次设为T 1,T 2, ,T n ㊂设这n 个扇形的涂色方法为a n 种㊂当n =2时,a 2=4ˑ3=12㊂当n >2时,T 1有4种涂法,T 2有3种涂法,接着T 3,T 4, ,T n -1,T n ,依次有3种涂法,故共有4ˑ3n -1种涂法㊂但当T n 与T 1的颜色相同时,有a n -1种涂法,a n =4ˑ3n -1-a n -1㊂点评:求解探究型涂色问题,往往从最简单的图形入手,依次分析两个图形涂色之间的联系与差别,进而加以合理推理,构建相应的关系式,得以解决对应的探究性问题,从而实现问题的解决㊂对于涂色问题,抓住探究问题的本质,结合涂色图形的结构特征,以及涂色的种数与限制条件,从关键点入手,结合选取颜色加以分析,合理分类讨论,借助两个计数原理以及排列组合知识,注意 重 或者 漏 的情形,进而加以合理操作与计算㊂(责任编辑 徐利杰)14解题篇 创新题追根溯源 高二数学 2024年3月。
五年级下学期数学 长方体和正方体的染色问题 专项题型训练 后面带答案

长方体与正方体的染色问题【知识点总结】三个面都染色的在8个顶点处,两个面都染色的在12条棱的中间段(去掉每条横两头的各一个),一面有色的在各个面的中央,没有着色的在长方体的里面。
对于一个n×n×n的正方体,其涂色情况如下:三面涂色的:8块二面涂色的:(n-2)×12一面涂色的:(n-2)×(n-2)×6没有颜色的:(n-2)×(n-2)×(n-2)验算的方法:上面的总数=体积数对于一个a×b×c的长方体,其涂色情况如下:三面涂色的:8块二面涂色的:[(a-2)+(b-2)+(c-2)]×4一面涂色的:[(a-2)×(b-2)+(a-2)×(c-2)+(b-2)×(c-2)]×2 没有颜色的:(a-2)×(b-2)×(c-2)验算的方法:上面的总数=体积数【针对性训练】1、下图是一个表面被涂上红色的棱长为10厘米的正方体木块,如果把它洞虚线切成8个正方体,这些小正方体的所有表面的面积和是()平方厘米。
2、一个正方体形状的木块儿,棱长为1米,若沿着正方体的三个方向分别锯成3份,四份、五份,如下图,得到大大小小的长方体60块,这60块长方体的表面积的和是多少平方米?3、一个表面积为56平方厘米的长方体如图切成27个小长方体,这27个小长方体的表面积的和是多少平方厘米?4、(1)将一个长10厘米,宽5厘米,高4厘米的长方体表面全部染成红色,然后切割成棱长为1厘米的小正方体,所有的小正方体中有1面染色的有()个,2面染色的有()个,三面染色的有()个,0面染色的有()个。
(2)将一个棱长为8厘米的正方体表面全部染成红色,然后切割成棱长为1厘米的小正方体,所有的小正方体中有1面染色的有()个,2面染色的有()个,三面染色的有()个,0面染色的有()个5、(1)将一个表面涂有红色的长方体分割成若干个体积为1立方厘米的小正方体,其中一点红色没有涂的小立方体只有3块。
高中数学中涂色问题的解法

高中数学中涂色问题的解法涂色问题是高中数学中的一类比较复杂而且重要的问题,高考中多次涉及。
这种题目根据条件可分为颜色必须用完和不必用完两种。
根据需要涂色的图形可分为条状结构和环状结构两种。
解决问题的方法也有依次去涂和按所用颜色种数分类讨论两种。
作题时只要弄清条件和图形的结构,再把每种结构下解决问题的方法弄清楚,就可以了。
下面我们就用历年高考题中的涂色问题作为例子。
一、条状结构例1:将3种作物种植在5 块试验田里,每块种植一种作物且相邻的试验田不能种植同一种作物,共有多少种种植方法?分析:从数学角度上来看,这是一个条状结构且颜色必须用完的问题。
我们先用依次来涂的方法,再用所用颜色种数来讨论的方法。
解1:只管从左到右依次来种。
若三种作物可种完可不种完共有3·2·2·2·2=48 种方法,其中只种两种作物共有C23·2=6种方法,所以共有48-6=42 种方法。
解2:三种作物必须种完,那就不必讨论颜色种数。
(1)把这五块地分为3,1,1三组。
①③⑤必为一组,所以地块分组只有一种方法,再种上三种作物共有A33=6 种方法。
(2)把这五块地分为2,2,1 三组。
①③同组时,②④也可和⑤同组,有两种方法,同理①④同组时也有两种方法,①⑤同组时有1 种方法,①自己一组时有1 种方法,所以地块分组共有6 种方法,再种有6A33种方法。
由(1),(2)知共有42种方法。
可见:条状结构若不按颜色分类,只管依次去涂即可,非常简单,只要考虑清楚颜色必须用完还是可不用完即可。
若按颜色分类,颜色有几种就把图形中的区域分为几组,再往每组涂色即可,结果即是分组的办法数与Amn的积。
其中n 为全部可用颜色种数,m 为实际使用颜色种数。
变式:用5种不同的颜色给图中A,B,C,D 四个区域涂色,规定每个区域只能涂一种颜色,相邻区域颜色不同,求有多少种不同的涂色方法?分析:因为D 区域和其他三区域都相邻,A 和C 又不相邻,所以把D 涂完后,就是条状结构的问题。
有趣的几何问题解决关于几何形的有趣问题

有趣的几何问题解决关于几何形的有趣问题几何学是关于形状、大小、相对位置以及属性的学科,常常引发许多有趣的问题和挑战。
通过探索几何形,我们可以发现其中隐藏的规律和美妙之处。
本文将介绍一些有趣的几何问题,并给出解决方法。
问题一:等边三角形的内切圆在一个等边三角形中,三条边长相等,三个角度也相等。
我们可以探索等边三角形的内切圆,即与三角形的三条边相切的圆。
我们想知道这个内切圆的圆心位置是否有规律,并找到一种简单的方法来确定圆心。
解决方法:假设等边三角形的边长为a,可以证明内切圆的半径r等于a乘以根号3再除以6。
圆心与三角形顶点的连线垂直且平分三角形的顶角。
这个结果告诉我们,无论等边三角形的大小如何,内切圆的半径和圆心的位置都是固定的。
问题二:平行四边形的对角线相交问题平行四边形有两对相邻的边平行,我们想知道当两条对角线相交时,它们是否把平行四边形的中心分成两等份。
解决方法:通过简单的证明,我们可以得出结论:平行四边形的对角线交点会将平行四边形的中心分成两等份。
这意味着对角线交点离四个顶点的距离相等。
问题三:涂色问题给定一个几何图形,我们想知道用不同颜色涂色最少需要多少种颜色,使得相邻的部分不会有相同的颜色。
解决方法:涂色问题可以通过图论中的顶点着色问题来解决。
我们可以将几何图形映射为一个图,其中每个顶点代表一个区域,相邻的区域之间有一条边连接。
然后,我们可以使用图论中的算法来解决顶点着色问题,找到涂色所需的最小颜色数。
问题四:黄金分割问题黄金分割是一种特殊比例,它在数学、艺术和建筑中都有广泛应用。
我们想知道如何通过一个正方形构造出黄金矩形,并找到黄金矩形的特性。
解决方法:假设我们有一个边长为1的正方形,可以通过将它的一个边与另一个边长为1的正方形的对角线相交,得到一个长宽比为黄金分割比例(约为1.618)的长方形。
黄金矩形有许多有趣的特点,例如当我们将正方形从内部切割出一个黄金矩形时,剩余部分也是一个黄金矩形。
数学彩色涂色问题

数学彩色涂色问题数学彩色涂色问题是一类涉及图论和组合数学的问题,涉及到给定一个图,如何用不同的颜色对其进行涂色,使得相邻的节点颜色不同。
这个问题在许多领域都有应用,如地图着色、调度问题等。
本文将介绍数学彩色涂色问题的背景、解决方法以及一些相关应用。
背景介绍数学彩色涂色问题源于图论,图由节点和边组成。
在彩色涂色问题中,我们希望为图的每个节点选择一种颜色,使得任意相邻节点的颜色都不相同。
这里的相邻节点是指通过边连接的节点。
解决方法解决数学彩色涂色问题的方法有很多种,以下是一些常见的方法:1. 贪心算法:贪心算法是一种贪心思想的算法,它根据一定的规则进行选择。
在数学彩色涂色问题中,我们可以使用贪心算法来选择每个节点的颜色。
具体做法是从一个节点开始,依次向其相邻节点涂色,并保证相邻节点颜色不同。
2. 回溯算法:回溯算法是一种通过逐个尝试所有可能解的算法。
在数学彩色涂色问题中,我们可以使用回溯算法来逐个尝试给每个节点涂色,直到找到符合要求的解或者试探所有可能的情况。
3. 图染色算法:图染色算法是一种基于图的染色理论的算法。
在数学彩色涂色问题中,我们可以将图转化为一个染色图,然后使用染色图算法来对节点进行涂色。
应用领域数学彩色涂色问题在许多领域都有应用,如地图着色、调度问题等。
在地图着色问题中,我们希望给定一张地图,使得相邻的地区颜色不同。
数学彩色涂色问题可以帮助我们确定如何给地图上的每个地区选择颜色,以满足相邻地区颜色不同的要求。
在调度问题中,我们希望在给定一组任务和资源的情况下,找到一种合理的分配方案。
数学彩色涂色问题可以帮助我们确定如何将任务分配给资源,以使得任意相邻任务被分配给不同的资源。
结论数学彩色涂色问题是一个有趣且具有实际应用价值的问题。
通过合适的算法和技巧,我们可以有效地解决这类问题,并在实际应用中获得良好的效果。
希望本文对读者理解和解决数学彩色涂色问题提供一些帮助。
涂色问题的常见解法及策略

涂色问题的常见解法及策略涂色问题是数学中一个常见的问题,涉及到给定一定数量的区域,并使用有限数量的颜色对这些区域进行染色。
在这篇文章中,我将介绍一些常见的解法和策略,以及我对涂色问题的观点和理解。
在解决涂色问题时,最基本的策略之一是使用“回溯法”。
回溯法是一种通过不断尝试不同的选择,并撤销不合适的选择的方法。
在涂色问题中,我们可以从一个区域开始,选择一个颜色将其染色,然后递归地对相邻的区域进行染色。
如果在染色过程中发现无法继续染色,则回溯到上一个选择,并选择另一种颜色。
另一种常见的解法是使用“图论”的方法。
将涂色问题抽象成图论中的图模型,其中图的每个节点代表一个区域,边表示两个相邻区域之间的连接。
然后,我们可以使用图染色算法,如“图的着色问题算法”来解决涂色问题。
这些算法使用一系列的规则和策略来确定每个节点应该染哪种颜色,以确保相邻节点不具有相同的颜色。
除了这些基本的解法之外,还有许多高级的策略可供选择。
例如,“最小割算法”可以将复杂的涂色问题转化为图的最小割问题,并使用最小割算法来解决。
此外,还可以使用“启发式搜索”技术,通过估计每个选择的优先级来指导搜索过程。
这些策略通常需要更多的计算资源和算法知识,但在处理复杂的问题时可能会获得更好的结果。
从简单到复杂,由浅入深的方式来探讨涂色问题,可以帮助我们建立对问题的深刻理解。
我们可以从最基本的回溯法开始,逐渐引入图论的概念和算法。
了解不同解法的优缺点,并能够根据问题的具体情况选择合适的解法,这对于解决涂色问题至关重要。
总结起来,涂色问题是一个常见的数学问题,涉及到给定一定数量的区域,并使用有限数量的颜色对这些区域进行染色。
常见的解法和策略包括回溯法、图论算法、最小割算法和启发式搜索技术。
通过从简单到复杂的方式来探讨涂色问题,我们可以建立对问题的深刻理解,并能够灵活选择适合的解法。
一年级涂颜色数学题

一年级涂颜色数学题
一、题目示例。
1. 按要求给图形涂颜色。
把三角形涂成红色,圆形涂成蓝色,正方形涂成绿色。
(给出一些混合在一起的三角形、圆形、正方形的图案)
题目解析:
这道题主要考查一年级学生对不同图形的认识能力。
一年级的学生刚刚开始接触简单的几何图形,通过涂颜色这种直观的方式,帮助他们区分三角形、圆形和正方形的形状特征。
在解答时,学生需要仔细观察每个图形的形状,然后根据要求涂上相应的颜色。
这有助于加深他们对图形的记忆和理解,同时也锻炼了他们的观察力和动手能力。
2. 给数量是3的物体涂上黄色。
(图中有不同数量的各种物体,如花朵、气球等)
题目解析:
本题重点在于考查学生对数量的认识。
一年级学生正在学习数与量的对应关系,通过让他们找出数量是3的物体并涂色,能够强化他们对数3的概念理解。
学生需要先数出每个物体的数量,然后确定哪些是数量为3的物体,再进行涂色操作。
这道题既考验了学生的数数能力,也考验了他们根据数量特征进行分类的能力。
3. 根据算式涂颜色。
例如:2 + 1 =(),图中有五组小方块,每组有不同的数量,要求根据算式的结果给对应的小方块组涂颜色。
题目解析:
这类题目是将计算与图形结合起来考查一年级学生。
在这个例子中,首先要计算出2+1 = 3,然后在图中找到数量是3的小方块组并涂上颜色。
这有助于学生理解算
式的意义,将抽象的计算结果与具体的数量(图形)联系起来,是数与形结合思想在一年级数学中的初步体现,对学生后续学习数学有着重要的引导作用。
区域涂色问题公式

区域涂色问题公式
区域涂色问题通常是指在平面坐标系中给定一些区域的边界,计算或估计这些区域的面积。
对于简单的几何形状,可以使用基本的几何公式来计算。
但对于复杂的区域,我们可能需要使用积分来求解。
下面是一些常见的区域涂色问题的公式:
1.矩形区域:矩形的面积可以使用公式A = length × width(A
为面积,length为矩形的长度,width为矩形的宽度)来
计算。
2.正方形区域:正方形的面积可以使用公式A = side × side
(A为面积,side为正方形的边长)来计算。
3.圆形区域:圆的面积可以使用公式A = π × radius^2(A为
面积,π为圆周率,radius为圆的半径)来计算。
4.三角形区域:三角形的面积可以使用公式A = 0.5 × base ×
height(A为面积,base为底边长,height为高)来计算。
5.不规则形状的区域:对于不规则形状的区域,可以使用数
值积分或几何分割的方法来计算。
这需要将复杂的形状分
解为较小的几何形状,然后计算每个形状的面积,并将它
们加起来。
需要注意的是,对于复杂的区域,可能没有直接的公式可以使用,因此需要采用近似的方法来计算或估计面积。
这可能包括将区域分割为一系列小矩形或小三角形,并计算它们的面积之
和,以得到估计的区域面积。
几何图形的涂色问题

动态规划
它是将问题分解为更小的子问题, 并且分阶段地进 Nhomakorabea求解的方法。
回溯算法
它从某个状态开始,搜索所有可 能到达的状态,直到找到解决方 案。
涂色问题的应用
1
计算机图形学
图形学中最基本的问题之一是三角形网格着色。由这个问题可以推广到其他图形 渲染问题。
2
艺术设计
运用涂色问题的理论可以更好地指导数字绘画,特别是创新性的色彩设计。
问题与讨论
如果您有任何关于该问题的问题或者讨论想法,欢迎您在下面的评论区留言, 我们将有专业人员回答您的疑问。
一维涂色问题
最少需要几种颜色来染一条线,使 相邻两点颜色不同?
二维涂色问题
三维涂色问题
最少需要几种颜色来染一整个区域, 最少需要几种颜色来染一个立体图
使相邻两点颜色不同?
形,使相邻两点颜色不同?
涂色问题的解决方法
贪心算法
这种方法基于贪婪选择原则进行 求解问题,它每次考虑当前最优 的策略,并且不考虑以后的后果
3
地图着色
地图着色问题涉及在地图上给每个行政区划涂上颜色,以便于区别。这个问题也 可以归纳到涂色问题类型。
总结
涂色问题的重要性总结
涂色问题是一个既有理论意义又有实际应用的重要 问题,是此领域研究的基础。
未来研究的方向
随着计算机算法和技术的不断提高和挑战涂色问题 的新视角,研究方法也不断得到改善,我们有充分 理由相信涂色问题在未来的研究方向上仍然有大量 的探索空间。
几何图形的涂色问题
本演示文稿将向您介绍几何图形的涂色问题,包括其定义、解决方法和应用 领域。
问题介绍
什么是涂色问题?
涂色问题是要求对给定对象进行染色,要求相邻两点有着不同的颜色。
涂色问题解题技巧

涂色问题解题技巧介绍如下:
1.确定涂色方案:在解决涂色问题之前,需要明确涂色的方案,
例如每个对象只能染一种颜色或染多种颜色。
2.列出约束条件:在涂色问题中,通常存在一些约束条件,如相
邻的对象不能染相同的颜色等。
列出这些约束条件有助于确定可行的方案。
3.利用图形表示问题:将对象和约束条件用图形表示出来,可以
帮助理解问题,找到规律和解题思路。
4.利用递归算法:对于较为复杂的涂色问题,可以采用递归算法,
逐步将问题分解为简单的子问题,最终得到解决方案。
5.利用数学模型:对于一些涂色问题,可以建立数学模型,如图
论模型、矩阵模型等,通过数学方法解决问题。
6.尝试不同的方案:对于复杂的涂色问题,可能存在多个可行的
方案,需要尝试不同的方案,找到最优解。
总之,解决涂色问题需要综合运用数学、图形、逻辑等多种方法,找到最优的解决方案。
2023届新高考数学题型全归纳之排列组合专题06 染色问题含解析
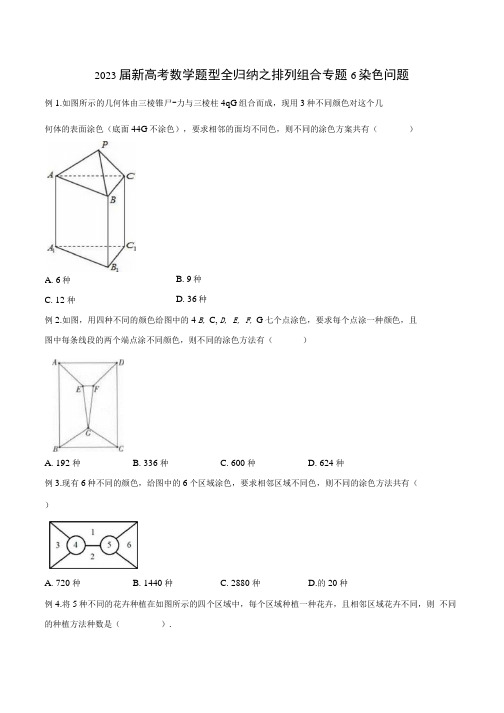
2023届新高考数学题型全归纳之排列组合专题6染色问题例1.如图所示的几何体由三棱锥尸-力与三棱柱4qG 组合而成,现用3种不同颜色对这个几何体的表面涂色(底面44G 不涂色),要求相邻的面均不同色,则不同的涂色方案共有( )B. 9种 D. 36种例2.如图,用四种不同的颜色给图中的4 B, C, D, E, F, G 七个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )A. 192 种B. 336 种C. 600 种D. 624 种例3.现有6种不同的颜色,给图中的6个区域涂色,要求相邻区域不同色,则不同的涂色方法共有()A. 720 种B. 1440 种C. 2880 种D.的20 种例4.将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则 不同的种植方法种数是( ).A. 6种C. 12 种/ D、A. 420B. 180C. 64D. 25例5.用红、黄、蓝、绿、橙五种不同颜色给如图所示的5块区域力、B、C、D、E涂色,要求同一区域用同一种颜色,有共公边的区域使用不同颜色,则共有涂色方法()A. 120 种B. 720 种C. 840 种D. 960 种例6.如图,某伞厂生产的太阳伞的伞篷是由太阳光的七种颜色组成,七种颜色分别涂在伞篷的八个区域内, 且恰有一种颜色涂在相对区域内,则不同颜色图案的此类太阳伞最多有().A. 40320 种B. 5040 种C. 20160 种D. 2520 种例7.如图所示,将四棱锥S-/4灰刀的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种色可供使用,则不同的染色方法种数为()A. 240B. 360C. 420D. 960例8.如图所示,将33x33方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为()例9.如图给三棱柱的顶点染色,定义由同一条棱连接的两个顶点叫相邻顶点,规定相邻顶点不得使用同•种颜色,现有4种颜色可供选择,则不同的染色方法有.例10.现用五种不同的颜色,要对如图中的四个部分进行着色,要求公共边的两块不能用同一种颜色,共 有 种不同着色方法例11.如图所示的五个区域中,中心区E 域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供 选择.要求每个区域只涂•种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为.例12.从红、黄、蓝、黑四种颜色中选出3种颜色,给如图所示的六个相连的圆涂色,若每种颜色只能涂 两个圆,且相邻两个圆所涂颜色不能相同,则不同的涂色方案的种数是.C. 64D. 7856oooooo例13.如图一个正方形花圃被分成5份.若给这5个部分种植花,要求相邻两部分种植不同颜色的花,已知现有红、黄、蓝、绿4种颜色不同的花,则不同的种植方法有种例14.现有五种不同的颜色,要对图形中的四个部分进行着色,要求有公共边的两块不能用同•种颜色,不同的涂色方法有种.例15.现将如图所示的5个小正方形涂上红、黄两种颜色,其中3个涂红色,2个涂黄色,若恰有两个相邻的小正方形涂红色,则不同的涂法共有种(用数字作答).例16.四色猜想是近代数学难题之一,四色猜想的内容是:“任何一张地图最多用四种颜色就能使具有共同边界的国家着上不同的颜色”,如图,一张地图被分成了五个区域,每个区域只使用一种颜色,现有4 种颜色可供选择(四种颜色不一定用完),则满足四色猜想的不同涂色种数为例17.如图,将标号为1, 2, 3, 4, 5的五块区域染上红、黄、绿三种颜色中的一种,使得相邻区域(有公共边)的颜色不同,则不同的染色方法有种・2例18.某城市在中心广场建造一个花圃,花阚分为6个部分.现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,则不同的栽种方法有种.(用数字作答)例19.给图中4 B, C, D, E尸六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有一种不同的染色方案.例20.如图,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色方法有种.(用数字作答)例21.给如图染色,满足条件每个小方格染•种颜色,有公共边的小方格颜色不能相同,则用4种颜色染色的方案有_种,用5种颜色染色的方案共有_种.例22.如图,用四种不同的颜色给三棱柱48C-48'C'的六个顶点涂色,要求每个点涂•种颜色.若每个底面的顶点涂色所使用的颜色不相同,则不同的涂色方法共有种;若每条棱的两个端点涂不同的颜色,则不同的涂色方法共有种.专题6染色问题例1.如图所示的几何体由三棱锥尸-48c与三棱柱48C-4qG组合而成,现用3种不同颜色对这个儿何体的表面涂色(底面431cl不涂色),要求相邻的面均不同色,则不同的涂色方案共有()A. 6种B. 9种C. 12种D. 36种【解析】先涂三棱锥尸一力8c的三个侧面,有C;C;C:=6种情况,然后涂三棱柱的三个侧面,有C;C:C;=2种情况,共有6x2 = 12种不同的涂法.故选:C.例2.如图,用四种不同的颜色给图中的4 B, C, D, E, F, G七个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有()A. 192 种B. 336 种C. 600 种D. 624 种【解析】由题意,点E F, G分别有4, 3, 2种涂法,(1)当力与尸相同时,力有1种涂色方法,此时/有2种涂色方法,①若。
表面涂色的正方体

CONTENTS
• 引言 • 表面涂色正方体的基本概念 • 表面涂色正方体的性质 • 表面涂色正方体的应用 • 表面涂色正方体的制作与展示 • 总结与展望
01
引言
目的和背景
研究正方体表面涂色问题的目的
正方体是一种常见的几何体,研究其表面涂色问题有助于深入理解几何形状和空间结构。此外,该问题在实际应 用中也具有广泛的意义,如建筑设计、艺术创作等领域。
表面涂色的定义
涂色范围
仅限于正方体的外表面,不包括内部。
涂色方式
可以是单一颜色,也可以是多种颜色的组 合或图案。
涂色目的
通常为了美观、标识或特殊功能需求。
正方体的面、棱和顶点
面
正方体有6个面,每个面都 是正方形,且面积相等。
棱
正方体有12条棱,每条棱 连接两个相邻的面。
顶点
正方体有8个顶点,每个顶 点由三条棱交汇而成。
涂色正方体的应用领域
表面涂色的正方体在数学、计算机科学、物理学等多个领域具有广泛的应用,如组合数 学中的计数问题、计算机图形学中的渲染技术、以及物理学中的晶体结构等。
涂色正方体的研究方法
研究表面涂色的正方体主要采用组合数学、图论、群论等方法,通过对涂色模式的分类 和计数,揭示其内在的数学结构和性质。
背景介绍
正方体表面涂色问题是一个经典的数学问题,涉及到组合数学、图论等多个领域。在过去的几十年里,许多数学 家和研究者对此进行了深入的研究,并提出了各种解决方案和算法。随着计算机技术的发展,该问题也得到了更 加广泛和深入的应用。
正方体的定义和性质
• 正方体的定义:正方体是一种特殊的立方体,它的所有棱长都 相等,且每个面都是正方形。在数学上,正方体可以用一个三 维坐标系中的点集来表示,其中每个点的坐标都满足一定的条 件。
高考数学中涂色问题常见解法及策略

高考数学中涂色问题的常见解法及策略与涂色问题有关的试题新颖有趣,近年已经在高考题中出现,其中包含着丰富的数学思想。
解决涂色问题方法技巧性强且灵活多变,因而这类问题有利于培养学生的创新思维能力、分析问题与观察问题的能力,有利于开发学生的智力。
本文拟总结涂色问题的常见类型及求解方法 一.区域涂色问题 1、 根据分步计数原理,对各个区域分步涂色,这是处理染色问题的基本方法。
例1、 用5种不同的颜色给图中标①、②、③、④的各部分涂色,每部分只涂一种颜色,相邻部分涂不同颜色,则不同的涂色方法有多少种?分析:先给①号区域涂色有5种方法,再给②号涂色有4种方法,接着给③号涂色方法有3种,由于④号与①、②不相邻,因此④号有4种涂法,根据分步计数原理,不同的涂色方法有5434240⨯⨯⨯=2、根据共用了多少种颜色讨论,分别计算出各种出各种情形的种数,再用加法原理求出不同的涂色方法种数。
例2、四种不同的颜色涂在如图所示的6个区域,且相邻两个区域不能同色。
分析:依题意只能选用4种颜色,要分四类: (1)②与⑤同色、④与⑥同色,则有44A ; (2)③与⑤同色、④与⑥同色,则有44A ;(3)②与⑤同色、③与⑥同色,则有44A ;(4)③与⑤同色、② 与④同色,则有44A ;(5)②与④同色、③与⑥同色,则有44A ;所以根据加法原理得涂色方法总数为544A =120例3、如图所示,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着方法共有多少种? 分析:依题意至少要用3种颜色1) 当先用三种颜色时,区域2与4必须同色,2) 区域3与5必须同色,故有34A 种;3) 当用四种颜色时,若区域2与4同色,4) 则区域3与5不同色,有44A 种;若区域3与5同色,则区域2与4不同色,有44A 种,故用四种颜色时共有244A 种。
由加法原理可知满足题意的着色方法共有34A +244A =24+2⨯24=72② ① ③④ 243 1 5①②③ ④⑤⑥3、根据某两个不相邻区域是否同色分类讨论,从某两个不相邻区域同色与不同色入手,分别计算出两种情形的种数,再用加法原理求出不同涂色方法总数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例 2】 将一个四棱锥的每个顶点 染上一种颜色,并使同一条棱上的 两端异色,如果只有 5 种颜色可供 使用,求不同的涂色方法总数.
解析
本题如果将棱锥的顶点往下作投影,Байду номын сангаас者是将
四棱锥看成是可以拉伸的薄膜状表面进行拉伸,变成 平面图形(图1),则空间图形的涂色就能变成平面图 形的涂色,继而将点扩展为平面区域,则又可变为平 面内圆形区域的涂色问题(图2).
返回
【例 4】 现用 4 种颜色给三棱柱的 6 个顶点涂色, 要求同一条棱的两端点的颜色不同,4 种颜色全 部用上,问有多少种不同的涂色方案?
解析 将左侧图形拉伸为右侧图形,则中间三点不 同色,不妨为三颜色1、2、3,又4种颜色全用上, 故外围三点中一定有一点涂第4种颜色,在此情况 下从其余三色中任挑两色,另外两点都只有一种涂 法. 故共有C3A3C1C2=216种涂法. 4 3 3 3
方法同例1,解略.有420种涂色方法.
【例 3】 用 5 种颜色给正方体 A BC D —A 1B 1C 1D 1 各 面涂色, 要求相邻两个面不同色, 现已将过顶点 A 的 3 个面涂了颜色,那么其余 3 个面涂色方法有 多少种?
解析 分三类,一是剩余三面的颜色与以A 为顶点 的三面的颜色相同,则只能涂其对面颜色,有1种 涂法,二是只有2种与所涂颜色相同,则有C2种方 3 式,另一种颜色为剩余两种颜色中的一种,故有6 种涂法,三是只有一种颜色与前面所涂相同,有C1 3 种,剩余涂为两种其它颜色,故也有6种涂法,综 上有13种.
图1
种同样颜色的花,问有多少种不同的栽种方法? 解析 利用欧拉思想进行拉伸变形,
可使图1变形为图2,这两种图形的涂 色其实质是一样的.我们不妨用1、2、 3、4代表四种颜色,在右侧图形中,先 在1、2、3区域涂上1、2、3三种颜色, 然后依次涂第4、5、6三个区域,涂区域 4可用2、4颜色.
图2
①若区域4涂颜色2,则整个花圃有123243、123234 两种涂法. ②若区域4涂颜色4,则整个花圃有123434、 123424、123423三种涂法. 即区域1、2、3颜色确定以后,区域4、5、6有5种 涂法,所以共有不同的栽种方法为A3×5=120种. 4
备课资讯 20 几何图形的涂色问题
空间图形的涂色问题由于其空间位置的特点, 处理问题时容易受空间想像的限制,使问题变得很 不直观,若利用欧拉定理的思想与方法,通过图形 的变换转化为平面图形的涂色问题,可使一类空间 涂色问题得以简化而使问题变得直观.下面给出几 例来看欧拉思想在涂色问题中的应用.
【例 1】 某城市在中心广场建造一个 扇环形花圃,花圃分为 6 个部分,如 右图,现要栽种 4 种不同颜色的花, 每一部分栽种一种且相邻部分不能栽
