业动量和角动量习题和答案
《大学物理I》作业-No.03 角动量与角动量守恒-A-参考答案

《大学物理I 》作业 No.03 角动量 角动量守恒定律 (A 卷)班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、选择题[ ]1、一质点沿直线做匀速率运动时,(A) 其动量一定守恒,角动量一定为零。
(B) 其动量一定守恒,角动量不一定为零。
(C) 其动量不一定守恒,角动量一定为零。
(D) 其动量不一定守恒,角动量不一定为零。
答案:B答案解析:质点作匀速直线运动,很显然运动过程中其速度不变,动量不变,即动量守恒;根据角动量的定义v m r L⨯=,质点的角动量因参考点(轴)而异。
本题中,只要参考点(轴)位于质点运动轨迹上,质点对其的角动量即为零,其余位置均不会为零。
故(B)是正确答案。
[ ]2. 两个均质圆盘A 和B 密度分别为A ρ和B ρ,若A ρ>B ρ,两圆盘质量与厚度相同,如两盘对通过盘心且垂直于盘面的轴的转动惯量各为A J 和B J ,则 (A) A J >B J(B) B J >A J(C) A J =B J(D) A J 、B J 哪个大,不能确定答案:B答案解析:设A 、B 联盘厚度为d ,半径分别为A R 和B R ,由题意,二者质量相等,即B B A A d R d R ρπρπ22=因为B A ρρ>,所以22B A R R <,由转动惯量221mR J =,则B A J J <。
[ ]3.对于绕定轴转动的刚体,如果它的角速度很大,则 (A) 作用在刚体上的力一定很大 (B) 作用在刚体上的外力矩一定很大(C) 作用在刚体上的力和力矩都很大 (D) 难以判断外力和力矩的大小答案:D 答案解析:由刚体质心运动定律和刚体定轴转动定律知:物体所受的合外力和合外力矩只影响物体运动的加速度和角加速度,因此无法通过刚体运动的角速度来判断外力矩的大小,正如无法通过速度来判断物体所受外力的大小一样。
02动量与角动量测试题

第二章 动量与角动量 测试题一、选择题1.一个静止的质点,在两个互成锐角的恒力1F 、2F ,作用下开始运动,经过一段时间以后,突然撤去一个力,则该质点在撤去该力前、后两个阶段的运动性质分别是 ( )(A )匀加速直线运动,匀减速直线运动(B )匀加速直线运动,匀变速曲线运动(C )匀变速曲线运动,匀速圆周运动(D )匀加速直线运动,匀速圆周运动2.质量为m 的质点沿x 轴方向运动,其运动方程为t A x ωcos =,式中A 、ω均为正的常量,则该质点所受的合外力为 ( )(A )x f 2ω= (B )x m f 2ω=(C )x m f ω-= (D )x m f 2ω-=3. 在下列关于力与运动关系的叙述中,正确的是 ( )(A )若质点从静止开始,所受合力恒定,则一定作匀加速直线运动(B )若质点所受合力的大小不变,则一定作匀加速直线运动(C )若质点所受合力恒定,肯定不会做曲线运动(D )若质点所受合力的方向不变,则一定作直线运动(E )若质点所受合力越大,则质点速度必定越大4、质量为m 的质点,以一恒定速率v 沿图中正三角形ABC 的光滑轨道运动,质点越过A 时,轨道作用于质点冲量的大小为 ( )(A) v m (B)v m 2 (C) v m 3 (D) v m 25. 如图所示,圆锥摆的摆球质量为m ,速率为v ,圆半径为R ,当摆球在轨道上运动半周时,摆球所受重力冲量的大小为( )(A) 2m v . (B) 22)/()2(v v R mg m π+(C) v /Rmg π.(D) 0.7.力i t F 12=(SI )作用在质量m=2 kg 的物体上,使物体由原点从静止开始运动,则它在3 s 末的动量应为 ( )(A )i 54-kg · m ·s -1(B )i 54kg · m ·s -1 (C )i 27-kg · m ·s -1 (D )i 27kg · m ·s -17、两块质量相同的木块1和2 ,从同一高度自由下落,在下落的途中,第1块物体被水平飞来的子弹击中,子弹陷于木块之中,那么这两块木块的落地情况是 ( )(A) 第1木块比第2木块先落地; (B) 两木块同时落地;(C) 第2木块比第1木块先落地; (D) 条件不足,无法判断8、质点m 在竖直平面内作匀速园周运动,如图所示,从A 点运动到B 点过程中 ( ) (A) )(,02i j Ra -=∆=∆v v ,角动量守恒 (B) R r R S 2,21=∆=∆ π, 动量守恒 (C) 重力的功 0,=∆=v mgRA , 机械能守恒 (D) )(),(j i j i R r +=∆-=∆v v ,合外力的功为零9、在过程中如果_____,则质点系对该点的角动量保持不变 ( )(A )外力矢量和始终为零(B )外力做功始终为零(C )外力对参考点力矩的矢量和始终为零(D )内力对参考点力矩的矢量和始终为零10、一长细绳上端固定,下端系一小球,在小球摆动过程中 ( )(A) 小球动量守恒 (B) 小球与地球系统机械能守恒(C) 小球动能守恒 (D) 小球对悬点角动量守恒二、计算题1. 一质量为m ,速度为0v 的摩托车,在关闭发动机以后沿直线滑行,它所受到的阻力v c f -=,式中c 为正常数。
ch2动力学(下)动量和角动量2012例题

快速拉动物体下方的细线时,上方的细线不会断, 原因如下:画出快速拉动下方细线时重物的受力图 . F是上方线对物体的作用力, f是下方线对物体的作 用力.根据动量定理,则有 (Mg f F)t (Mv)
v 或 F Mg (f M ) t
由于是快速拉动,因而意味着 Δt 很小,而 M 较大,结果, 在拉动中 M v 可以较大,以致使
解: (2)杆做匀减速转动 0 t
0 t
由转动定律得
0 0 l t 3g
1 mgl 3g M 4 1 I l 2 ml 12
[例5]计算质量为m,半径 为R的匀质球体绕其轴线 的转动惯量.
[例5]计算质量为m,半径 为R的匀质球体绕其轴线 的转动惯量.
[例3]如图所示,长为 l ,质量为m的均匀细杆两端各牢 固地连结一个质量为m的小球。整个可绕O点并垂直于杆 长的水平轴无摩擦地转动,当系统在水平位置时,试求 (1)系统所受的合外力矩; (2)系统对O轴的转动惯量; (3)系统的角加速度。
如图所示,长为 l ,质量为m的均匀细杆 两端各牢固地连结一个质量为m的小球。 整个可绕O点并垂直于杆长的水平轴无摩 擦地转动,当系统在水平位置时,试求 (1)系统所受的合外力矩; (2)系统对O轴的转动惯量; (3)系统的角加速度。
(Mg F N)t (Mv)
v 或 N Mg (F M ) t
t
• 注意到砧子质量M较大,而作用时间Δt 较短,故 v v 较大,以致会使 M FM 0
t
结果 N=Mg , 故打击时,人体受力不变,因而不 会受到伤害.
在锤击时间内,砧子运动是一 个向下加速运动的过程,锤子 结束后,砧子运动是一个减速运 动过程,此过程中F=0,由动量 定理知
03第三章 动量与角动量作业答案

第三次作业(第三章动量与角动量)一、选择题[A]1.(基础训练2)一质量为m0的斜面原来静止于水平光滑平面上,将一质量为m的木块轻轻放于斜面上,如图3-11(A) 保持静止.(B) 向右加速运动.(C) 向右匀速运动.(D) 向左加速运动.【提示】设m0相对于地面以V运动。
依题意,m静止于斜面上,跟着m0一起运动。
根据水平方向动量守恒,得:m V mV+=所以0V=,斜面保持静止。
[C]2.(基础训练3)如图3-12所示,圆锥摆的摆球质量为m,速率为v,圆半径为R,当摆球在轨道上运动半周时,摆球所受重力冲量的大小为(A) 2m v.(B) 22)/()2(vv Rmgmπ+(C) v/Rmgπ(D) 0.【提示】22TGTI mgdt mg==⨯⎰,而vRTπ2=[C ]3.(自测提高1)质量为m的质点,以不变速率v沿图3-16正三角形ABC的水平光滑轨道运动。
质点越过A点的冲量的大小为(A) m v.(B) .(C) .(D) 2m v.【提示】根据动量定理2121ttI fdt mv mv==-⎰,如图。
得:21I mv mv∴=-=[ B] 4.(自测提高2)质量为20 g的子弹,以400 m/s的速率沿图3-17所示的方向射入一原来静止的质量为980 g的摆球中,摆线长度不可伸缩。
子弹射入后开始与摆球一起运动的速率为(A) 2 m/s.(B) 4 m/s.(C) 7 m/s .(D) 8 m/s.【提示】相对于摆线顶部所在点,系统的角动量守恒:2sin30()mv l M m lV︒=+其中m为子弹质量,M为摆球质量,l为摆线长度。
解得:V=4 m/s(解法二:系统水平方向动量守恒:2sin30()mv M m V︒=+)图3-11图3-17二、填空题1、(基础训练7)设作用在质量为1 kg 的物体上的力F =6t +3(SI ).如果物体在这一力的作用下,由静止开始沿直线运动,在0到2.0 s 的时间间隔内,这个力作用在物体上的冲量大小I=18N s ⋅.【提示】2222(63)(33)18I Fdt t dt t t N s ==+=+=⋅⎰⎰2.(基础训练8)静水中停泊着两只质量皆为0m 的小船。
(上海交大)大学物理上册课后习题答案4动量和角动量

)s 习题44-1.如图所示的圆锥摆,绳长为l ,绳子一端固定,另一端系一质量为m 的质点,以匀角速ω绕铅直线作圆周运动,绳子与铅直线的夹角为θ。
在质点旋转一周的过程中,试求:(1)质点所受合外力的冲量I;(2)质点所受张力T 的冲量T I。
解:(1)设周期为τ,因质点转动一周的过程中,速度没有变化,12v v =,由I mv =∆ ,∴旋转一周的冲量0I =;(2)如图该质点受的外力有重力和拉力,且cos T mg θ=,∴张力T 旋转一周的冲量:2cos T I T j mg j πθτω=⋅=⋅所以拉力产生的冲量为2mgπω,方向竖直向上。
4-2.一物体在多个外力作用下作匀速直线运动,速度4/v m s =。
已知其中一力F方向恒与运动方向一致,大小随时间变化内关系曲线为半个椭圆,如图。
求:(1)力F在1s 到3s 间所做的功;(2)其他力在1s 到3s 间所做的功。
解:(1)半椭圆面积⋅====⋅=⎰⎰⎰⎰v t F v t Fv x F x F A d d d dJ 6.12540201214==⨯⨯⨯=ππ(2)由动能定理可知,当物体速度不变时,外力做的总功为零,所以当该F做的功为125.6J 时,其他的力 的功为-125.6J 。
4-3.质量为m 的质点在Oxy 平面内运动,运动学方程为cos sin r a t i b t j ωω=+,求:(1)质点在任一时刻的动量;(2)从0=t 到ωπ/2=t 的时间内质点受到的冲量。
解:(1)根据动量的定义:P mv = ,而drv dt== sin cos a t i b t j ωωωω-+ , ∴()(sin cos )P t m a t i b t j ωωω=-- ;(2)由2()(0)0I mv P P m b j m b j πωωω=∆=-=-= , 所以冲量为零。
4-4.质量为M =2.0kg 的物体(不考虑体积),用一根长为l =1.0m 的细绳悬挂在天花板上。
角动量练习题

角动量练习题角动量是物体绕某一点旋转时所具有的物理量,它是描述物体旋转状态的重要参数。
在本篇文章中,我们将通过一些练习题来巩固对角动量的理解和应用。
练习题一:质点角动量假设一个质点的质量为m,速度为v,沿着均匀圆周运动,半径为r。
计算此质点的角动量L。
解析:质点的角动量L可以通过以下公式进行计算:L = mvr其中,m表示质量,v表示速度,r表示半径。
练习题二:刚体的角动量现考虑一个自由刚体,该刚体绕自己的一个固定轴做匀速旋转。
刚体总质量为M,刚体质量分布与距离轴的距离的平方成正比,比例常数为k。
问刚体质心的角动量与旋转轴的角动量之比是多少?解析:对于这个刚体,质心的角动量L_cm可以通过以下公式计算:L_cm = I_cm * ω_cm其中,I_cm表示刚体绕质心的转动惯量,ω_cm表示质心的角速度。
而整个刚体绕轴的角动量L_axis可以通过以下公式计算:L_axis = I_axis * ω_axis其中,I_axis表示刚体绕轴的转动惯量,ω_axis表示轴的角速度。
根据转动惯量的定义可知,I_axis = kM,I_cm = (1/2)kM。
将以上结果代入计算,可得:L_cm / L_axis = (1/2) / 1 = 1 / 2练习题三:角动量守恒现有两个质量分别为m1、m2的质点,m1的速度为v1,m2的速度为v2,m1和m2的初始位置分别为r1和r2,它们在一个封闭系统中相互作用。
求系统的总角动量L_i和最后的总角动量L_f。
解析:系统的总角动量L_i可以通过以下公式计算:L_i = L1 + L2 = m1v1r1 + m2v2r2其中,L1和L2分别为两个质点的角动量。
根据角动量守恒定律可知,L_i = L_f。
因此,总角动量在系统内部相互作用过程中保持不变。
练习题四:转动惯量计算假设一个半径为R、质量均匀分布的圆环围绕其直径做匀速转动。
计算该圆环相对于转动轴的转动惯量I。
解析:对于一个质量均匀分布的圆环,其转动惯量I可以通过以下公式计算:I = (1/2)MR^2其中,M表示圆环的质量,R表示圆环的半径。
清华出版社《大学物理》专项练习及解析 03动量与角动量

清华出版社专项练习动量与角动量一、选择题 1、(0063A15)质量为m 的质点,以不变速率v 沿图中正三角形ABC 的水平光滑轨道运动.质点越过A 角时,轨道作用于质点的冲量的大小为(A) m v . (B) 2m v . (C) 3m v . (D) 2m v . [ ] 2、(0067B30)两辆小车A 、B ,可在光滑平直轨道上运动.第一次实验,B 静止,A 以0.5 m/s 的速率向右与B 碰撞,其结果A以 0.1 m/s 的速率弹回,B 以0.3 m/s 的速率向右运动;第二次实验,B 仍静止,A 装上1 kg 的物体后仍以0.5 m/s的速率与B 碰撞,结果A 静止,B 以0.5 m/s 的速率向右运动,如图.则A 和B 的质量分别为(A) m A =2 kg , m B =1 kg (B) m A =1 kg , m B =2 kg (C) m A =3 kg , m B =4 kg (D) m A =4 kg, m B =3 kg [ ]3、(0367A10)质量为20 g 的子弹沿X 轴正向以 500 m/s 的速率射入一木块后,与木块一起仍沿X 轴正向以50 m/s 的速率前进,在此过程中木块所受冲量的大小为(A) 9 N·s . (B) -9 N·s .(C)10 N·s . (D) -10 N·s . [ ] 4、(0368A10) 质量分别为m A 和m B (m A >m B )、速度分别为A v 和B v (v A > v B )的两质点A 和B ,受到相同的冲量作用,则(A) A 的动量增量的绝对值比B 的小.(B) A 的动量增量的绝对值比B 的大.(C) A 、B 的动量增量相等.(D) A 、B 的速度增量相等. [ ] 5、(0384A20)质量为20 g 的子弹,以400 m/s 的速率沿图示方向射入一原来静止的质量为980 g 的摆球中,摆线长度不可伸缩.子弹射入后开始与摆球一起运动的速率为 (A) 2 m/s . (B) 4 m/s . (C) 7 m/s . (D) 8 m/s . [ ]6、(0385B25)一质量为M 的斜面原来静止于水平光滑平面上,将一质量为m 的木块轻轻放于斜面上,如图.如果此后木块能静止于斜面上,则斜面将(A) 保持静止. (B) 向右加速运动. (C) 向右匀速运动. (D) 向左加速运动.[ ] 7、(0386A20) A 、B 两木块质量分别为m A 和m B ,且m B =2m A ,两者用一轻弹簧连接后静止于光滑水平桌面上,如图所示.若用外力将两木块压近使弹簧被压缩,然后将外力撤去,则此后两木块运动动能之比E KA /E KB 为C(A) 21. (B) 2/2. (C) 2. (D) 2. [ ]8、(0629C45)用一根细线吊一重物,重物质量为5 kg ,重物下面再系一根同样的细线,细线只能经受70 N 的拉力.现在突然向下拉一下下面的线.设力最大值为50 N ,则(A)下面的线先断. (B)上面的线先断.(C)两根线一起断. (D)两根线都不断. [ ] 9、(0632A10)质量为m 的小球,沿水平方向以速率v 与固定的竖直壁作弹性碰撞,设指向壁内的方向为正方向,则由于此碰撞,小球的动量增量为(A) v m . (B) 0.(C) v m 2. (D) v m 2-. [ ] 10、(0633A20)机枪每分钟可射出质量为20 g 的子弹900颗,子弹射出的速率为800 m/s ,则射击时的平均反冲力大小为(A) 0.267 N . (B) 16 N .(C)240 N . (D) 14400 N . [ ] 11、(0659A15)一炮弹由于特殊原因在水平飞行过程中,突然炸裂成两块,其中一块作自由下落,则另一块着地点(飞行过程中阻力不计)(A) 比原来更远. (B) 比原来更近.(C) 仍和原来一样远. (D) 条件不足,不能判定. [ ] 12、(0702B25)如图所示,圆锥摆的摆球质量为m ,速率为v ,圆半径为当摆球在轨道上运动半周时,摆球所受重力冲量的大小为(A) 2m v . (B) 22)/()2(v v R mg m π+(C) v /Rmg π. (D) 0.[ ]13、(0703A15)如图所示,砂子从h =0.8 m 高处下落到以3 m /s 向右运动的传送带上.取重力加速度g =10 m /s 2落到传送带上的砂子的作用力的方向为(A) 与水平夹角53°向下.(B) 与水平夹角53°向上. (C) 与水平夹角37°向上. (D) 与水平夹角37°向下. [ ]14、(0706B30) 如图所示.一斜面固定在卡车上,一物块置于该斜面上.在卡车沿水平方向加速起动的过程中,物块在斜面上无相对滑动.此时斜面上摩擦力对物块的冲量的方向(A) 是水平向前的. (B) 只可能沿斜面向上. (C) 只可能沿斜面向下.(D) 沿斜面向上或向下均有可能. [ ]15、(5260A20)动能为E K 的A 物体与静止的B 物体碰撞,设A 物体的质量为B 物体的二倍,m A =2m B .若碰撞为完全非弹性的,则碰撞后两物体总动能为(A) E K (B)K E 32. (C) K E 21. (D) K E 31. [ ] 16、(0405A20)人造地球卫星,绕地球作椭圆轨道运动,地球在椭圆的一个焦点上,则卫星的(A)动量不守恒,动能守恒.(B)动量守恒,动能不守恒.(C)对地心的角动量守恒,动能不守恒.(D)对地心的角动量不守恒,动能守恒. [ ]17、(0406B30) 人造地球卫星绕地球作椭圆轨道运动,卫星轨道近地点和远地点分别为A 和B .用L 和E K 分别表示卫星对地心的角动量及其动能的瞬时值,则应有(A) L A >L B ,E KA >E kB . (B) L A =L B ,E KA <E KB .(C) L A =L B ,E KA >E KB . (D) L A <L B ,E KA <E KB . [ ]18、(0407C45) 体重、身高相同的甲乙两人,分别用双手握住跨过无摩擦轻滑轮的绳子各一端.他们从同一高度由初速为零向上爬,经过一定时间,甲相对绳子的速率是乙相对绳子速率的两倍,则到达顶点的情况是(A)甲先到达. (B)乙先到达.(C)同时到达. (D)谁先到达不能确定. [ ]19、(5636A15) 一质点作匀速率圆周运动时,(A) 它的动量不变,对圆心的角动量也不变.(B) 它的动量不变,对圆心的角动量不断改变.(C) 它的动量不断改变,对圆心的角动量不变.(D) 它的动量不断改变,对圆心的角动量也不断改变. [ ]二、填空题:1、(0055A20) 质量为m 的小球自高为y 0处沿水平方向以速率v 0抛出,与地面碰撞后跳起的最大高度为21y 0,水平速率为21v 0,则碰撞过程中 (1) 地面对小球的竖直冲量的大小为 ________________________;(2)2、(0056B40) 质量m =10 kg 的木箱放在地面上,在水平拉力F 的作用下由静止开始沿直线运动,其拉力随时间的变化关系如图所示.若已知木箱与地面间的摩擦系数μ=0.2,那么在t = 4 s 时,木箱的速度大小为______________;在t =7 s 时,木箱的速度大小为______________.(g 取10 m/s 23、(0060A10) 一质量为m 的物体,原来以速率v 向北运动,它突然受到外力打击,变为向西运动,速率仍为v ,则外力的冲量大小为________________________,方向为____________________.4、(0061A10) y 21y有两艘停在湖上的船,它们之间用一根很轻的绳子连接.设第一艘船和人的总质量为250 kg ,第二艘船的总质量为500 kg ,水的阻力不计.现在站在第一艘船上的人用F =50 N 的水平力来拉绳子,则 5 s 后第一艘船的速度大小为_________;第二艘船的速度大小为______.5、(0062B30) 两块并排的木块A 和B ,质量分别为m 1和m 2 ,静止地放置在光滑的水平面上,一子弹水平地穿过两木块,设子弹穿过两木块所用的时间分别为∆t 1 和∆t 2 ,木块对子弹的阻力为恒力F ,则子弹穿出后,木块A 的速度大小为_________________________________,木块B 的速度大小为______________________.6、(0066A20) 两个相互作用的物体A 和B ,无摩擦地在一条水平直线上运动.物体A 的动量是时间的函数,表达式为P A =P 0-bt ,式中P 0 、b 分别为正值常量,t 是时间.在下列两种情况下,写出物体B 的动量作为时间函数的表达式:(1) 开始时,若B 静止,则P B 1=______________________;(2) 开始时,若B 的动量为-P 0,则P B 2=_____________.7、(0068A15) 一质量为m 的小球A ,在距离地面某一高度处以速度v 水平抛出,触地后反跳.在抛出t 秒后小球A 跳回原高度,速度仍沿水平方向,速度大小也与抛出时相同,如图.则小球A 与地面碰撞过程中,地面给它的冲量的方向为________________,冲量的大小为____________________.8、(0184A15) 设作用在质量为1 kg 的物体上的力F =6t +3(SI).如果物体在这一力的作用下,由静止开始沿直线运动,在0到 2.0 s 的时间间隔内,这个力作用在物体上的冲量大小I =__________________.9、(0222A20) 一物体质量M =2 kg ,在合外力i t F )23(+= (SI)的作用下,从静止开始运动,式中i 为方向一定的单位矢量,则当t =1 s 时物体的速度1v =__________.10、(0371A20) 一颗子弹在枪筒里前进时所受的合力大小为t F 31044005⨯-= (SI)子弹从枪口射出时的速率为300 m/s .假设子弹离开枪口时合力刚好为零,则(1)子弹走完枪筒全长所用的时间t =____________,(2)子弹在枪筒中所受力的冲量I =________________,(3)子弹的质量m =__________________.11、(0372A15) 水流流过一个固定的涡轮叶片,如图所示.水流流过叶片曲面前后的速率都等于v ,每单位时间流向叶片的水的质量保持不变且等于Q ,则水作用于叶片的力大小为______________,方向为_________.12、(0374B40) 图示一圆锥摆,质量为m 的小球在水平面内以角速度ω匀速转动.在小球转动一周的过程中,(1) 小球动量增量的大小等于__________________.(2) 小球所受重力的冲量的大小等于________________.(3) 小球所受绳子拉力的冲量大小等于_______________. 13、(0387B25) 质量为1 kg 的球A 以5 m/s 的速率和另一静止的、质量也为1 kg 的球B 在光滑水平面上作弹性碰撞,碰撞后球B 以2.5 m/s 的速率,沿与A 原先运动的方向成60°v的方向运动,则球A 的速率为____________,方向为______________________.14、(0393B25) 两球质量分别为m 1=2.0 g ,m 2=5.0 g ,在光滑的水平桌面上运动.用直角坐标OXY 描述其运动,两者速度分别为i 101=v cm/s ,)0.50.3(2j i v += cm/s .若碰撞后两球合为一体,则碰撞后两球速度v 的大小v =_________,v 与x 轴的夹角α=__________.15、(0630A10) 一质量m =10 g 的子弹,以速率v 0=500 m/s 沿水平方向射穿一物体.穿出时,子弹的速率为v =30 m/s ,仍是水平方向.则子弹在穿透过程中所受的冲量的大小为________,方向为_________.16、(0631A15) 一物体质量为10 kg ,受到方向不变的力F =30+40t (SI)作用,在开始的两秒内,此力冲量的大小等于________________;若物体的初速度大小为10 m/s ,方向与力F 的方向相同,则在2s 末物体速度的大小等于___________________.17、(0707B25) 假设作用在一质量为10 kg 的物体上的力,在4秒内均匀地从零增加到50 N ,使物体沿力的方向由静止开始作直线运动.则物体最后的速率v =_______________.18、(0708B35) 一质量为1 kg 的物体,置于水平地面上,物体与地面之间的静摩擦系数μ 0=0.20,滑动摩擦系数μ=0.16,现对物体施一水平拉力F =t +0.96(SI),则2秒末物体的速度大小v =______________.19、(0709A15) 质量为1500 kg 的一辆吉普车静止在一艘驳船上.驳船在缆绳拉力(方向不变)的作用下沿缆绳方向起动,在5秒内速率增加至5 m/s ,则该吉普车作用于驳船的水平方向的平均力大小为______________.20、(0710B30) 一吊车底板上放一质量为10 kg 的物体,若吊车底板加速上升,加速度大小为a =3+5t (SI),则2秒内吊车底板给物体的冲量大小I =___________;2秒内物体动量的增量大小P ∆=__________________.21、(0711A20) 粒子B 的质量是粒子A 的质量的4倍,开始时粒子A 的速度j i 43+=0A v ,粒子B 的速度j i 72-=0B v ;在无外力作用的情况下两者发生碰撞,碰后粒子A 的速度变为j i 47-=A v ,则此时粒子B 的速度B v =______________.22、(0715B30)有一质量为M (含炮弹)的炮车,在一倾角为θ 的光滑斜面上下滑,当它滑到某处速率为v 0时,从炮内射出一质量为m 的炮弹沿水平方向. 欲使炮车在发射炮弹后的瞬时停止下滑,则炮弹射出时对地的速率v =__________.23、(0717A10) 如图所示,质量为m 的子弹以水平速度0v 射入静止的木 块并陷入木块内,设子弹入射过程中木块M 不反弹,则墙壁 对木块的冲量=____________________.24、(0718A15) 一质量为30 kg 的物体以10 m·s -1的速率水平向东运动,另一质量为20 kg 的物体以20m·s -1的速率水平向北运动。
第四章动量和角动量答案

第四章 动量和角动量答案一.选择题 1.(C)2.(B)3.(C)4.(C)5.(C)6.(D)7.(C)8.(C)9.(A)10.(D)11.(A)12.(A)13.(B) 14. (B) 15.(B) 二.填空题:1.s N ⋅7.4; 与速度方向相反. 2.mM Mv V +=.3.s N ⋅18.4.)cos sin (j t b i t a m m Pωωωωυ+-==;零.5.s rad /36.6.不一定; 动量.7.s N ⋅140; s m /24.8.s 003.0; s N ⋅6.0; g 2. 9.s m /10; 北偏东087.36.10.c x 2311.0; k ab mω. 12.s cm /14.6; 05.35. 13.0. 14.Mk l 0;Mk nmM Ml +0. 15.RGMm 32; RG M m 3-.三. 计算题:1.解:由动量定理知质点所受外力的总冲量12)(v m v m v m I -=∆=由A→B1683.045cos -⋅⋅-=--=-=sm kg mvmv mvmv I AB AxBx x1283.045sin 0-⋅⋅-=-=-=sm kg mvmvI A Ayys N I I I y x ⋅=+=739.022方向:x y I I tg /1=θ,5.202=θ(与X轴正向夹角).2.解:(1)因穿透时间极短,故可认为物体未离开平衡位置.因此,作用于子弹、物体系统上的外力均在铅直方向,故系统在水平方向动量守恒.令子弹穿出时物体的水平速度为v ',有: v M mv mv '+=0s m M v v m v /13.3/)(0=-=' N l Mv Mg T 5.26/2=+=(2)s N mv mv t f ⋅-=-=∆7.40(0v方向为正,负号表示冲量与0v方向相反). 3.解:完全弹性碰撞,动量守恒,机械能守恒碰前:对A:gl v A 21= 方向向右,对B:01=B v ;碰后:对A:gh v A 22= 方向向左,对B:2B v ,方向向右. 动量守恒:221A A B B A A v m v m v m -= (1) 机械能守恒:222221212121B B A A A A v m v m v m +=(2)联立(1)、(2)两式解得: 2/321A A v v =, 2/22A B v v =而 s m gh v A /66.222==s m v A /41= s m v B /33.12= m l 8.0=;B克服阻力作的功为动能的减少,由动能定理: )(42.42/22J v m W B B f ==..4.解:∑∑<<in exii F F ==∴∑=ni i m p 1i v恒矢量0N νe =++p p p即αθep Np νp 又因为 νe p p ⊥)(212ν2e N p p p +=∴︒==9.61arctanνe p p α122N sm kg 1036.1--⋅⋅⨯=p 代入数据计算得系统动量守恒 , 即0N νe =++p p p 122e s m kg 102.1--⋅⋅⨯=p 123sm kg 104.6--⋅⋅⨯=νp。
第04章 动量和角动量 部分例题

(3) t=6 秒时刻木箱速度。 解:(1) 根据动量定理: 30
0
m
F/N
4
7
t/s
2
F/N 30
0 4 7 t/s
3
[例4-2] 一物体质量为m,受到方向不变的力F = a + bt 的作用, 求从开始到时刻 t1内,此力的冲量为多少?若物体的初速度 大小为v0,方向与力F相同,求在t1时刻的物体速度大小。
14
mv0 (m M )V
v2 (m M ) g (m M ) l 1 1 (m M )V 2 2(m M ) gl (m M )v 2 2 2
O l m M
解这三个方程式,得
mM v0 5 gl m 若m = 10g,M = 1kg,l = 0.5m,则有
0
x
x方向: y方向:
fdt Mv m(v u cos ) — (1) ( N Mg mg ) d t mu sin — ( 2 )
0
9
θ
10
讨论:
1. 若炮车与地面没有摩擦
2. 若炮车与地面有摩擦,但水平发射炮弹
3. 自锁现象,即 v=0 时
11
解: t1 1 冲量大小 I Fdt a bt dt at1 bt12 0 2 冲量等于动量的增量 I p2 p1 mv mv0
∴物体的速度大小 1 1 1 2 v p2 p1 v0 at1 bt1 v0 m m 2
0.01 1 v0 5 9.8 0.5 500(m / s) 0.01
15
[例4-13]考察如图示两物体间的碰撞,求弹簧对地面的最大压力。
03 力学:第三章 动量与角动量-课堂练习及部分习题解答

Zhang Shihui
题.设行星的质量为m,它绕太阳运动的角动量为L0,试 推导行星绕太阳运动的掠面速度(即行星的矢径单位时 间内扫过的面积)表达式 。 解:在dt的时间内,矢r 处的速度 v 同向 Δr v 与 夹角为 θ ,即 与 夹角为 θ r r Δ r r h θ Δr 顶点到 r 的距离 h = Δr sin θ 1 在dt的时间内,矢径扫过的面积 ΔS = r Δr sin θ 2 L0 1 1 dS 1 L= ΔtÆ0, dr = vdt 故 = r v sin θ = r × v = 2m 2m 2 dt 2
r
地心O
M = r ×F =0 r1 R + l1 因此,角动量守恒 r1mv1 = r2 mv2⇒ v2 = v1 = v1 r2 R + l2
v
因万有引力F始终沿地心指向卫星, 与矢径方向相同,故
学习指导·第三章 动量和角动量·典型例题第4题
Zhang Shihui
题. 匀质的柔软细绳铅直悬挂着,绳的下端刚好触到水平地 面上。如把绳的上端释放,绳将落到地面上。试证明:在 绳下落过程中,任意时刻作用于地面的压力(大小),等 于已落到地面上的绳重量的三倍。 解:设单位绳长的质量为λ。t时刻已经落到地面 的绳长为x,这部分绳子对地面的压力N0 = (λ x) g 此外,即将接触地面的质元dm对地面的冲量dp 会产生一个额外的冲力F (注:质元长dx,下落 的距离为x) 。设此瞬间质元的速度为v,则
m
解:水平方向M和m组成的系统所受合外 力为零,因此质心在水平方向不受外力作 用,质心水平方向分量保持不变,等于0
Μ
mΔx + M ΔX mx + MX ⇒ Δxc = =0 xc = m+M m+M
2-4动量与角动量(二)解答.ppt

1 m/s 1 N· m· s ,物体速度的大小v=______________ LB=____________ .
vB d O B
A
vA
物体受有心力作用,力对力心(圆心)的力矩为0, 所以角动量守恒
L L ; L L B A A B
r m v r m v A A B B
2.一力学系统由两个质点组成,他们之间只有万有引力 作用。若两质点所受外力的矢量和为零,则此系统
(A)动量、机械能及对一轴的角动量守恒
(B)动量、机械能守恒,但角动量是否守恒不能确定 (C)动量守恒,但机械能和角动量是否守恒不能确定 (D)动量和角动量守恒,但机械能是否守恒不能确定
角动量是否守恒决定于外力力矩的矢量和是否为0,机械能
p
mvd
o
5.两个滑冰运动员的质量各为70 kg,均以6.5 m/s的速率沿 相反的方向滑行,滑行路线间的垂直距离为10 m,当彼此
交错时,各抓住一10 m长的绳索的一端,然后相对旋转,
2275 kgm2· s-1 则抓住绳索之后各自对绳中心的角动量L=_______
它们各自收拢绳索,到绳长为5 m时,各自的速率
13 m· s-1。 v =________
1 2 角动量 L r P 角动量大小 L 5 70 6 . 5 22750 kgm s
由角动量守恒:半径减 小一半, 速率增大一倍 : v 13 m/ s
三、计算题
1.质量为1 kg的物体,它与水平桌面间的摩擦系数μ= 0.2 .现对物体施以F = 10t (SI)的力,(t表示时刻), 力的方向保持一定,如图所示.如t = 0时物体静止, 则t = 3 s时它的速度大小v 为多少?
动量和角动量例题和练习
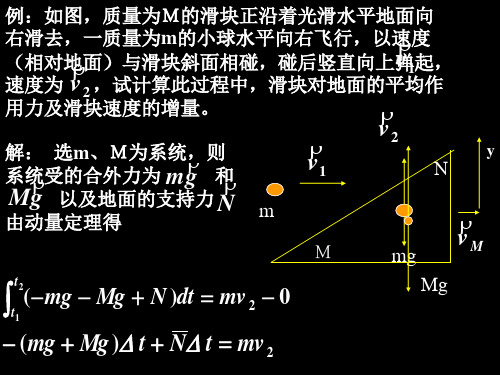
u
60
0
Y
u
v人
X
v
v人x = ucos 600 + v v人y = usin600
解:如图以人和车为研究系 统则水平方向的合外力为零, 统则水平方向的合外力为零, 因此水平方向动量守恒, 因此水平方向动量守恒,设 人跳车后相以地面的 速度 为 v人 ,车相对地面的速度 为 v 则: v人 = u + v
θ
α
X
3mvt
3vt = vB sinα + vc sinθ − vc cosθ + vB cosα = 0 又 vt = v0 − gt
解上述方程得: 解上述方程得:
α =θ
3m t v 3m(v0 − gt ) v1 = = 2sinα 2sinα
例:哈雷慧星绕太阳运动的轨道是一个椭圆,它离太阳 哈雷慧星绕太阳运动的轨道是一个椭圆, 10 v1 = 5.46×104 m/ s 最近的距离为 r = 8.75 ×10 m , 时 1 它距离太阳最远时, 它距离太阳最远时, v2 = 9.08×102 m/ s ,这时 r2 = ?
u
600
u
v人
v
v人x = ucos 600 + v v人y = usin600 (m2 + m1 )v0 = m1v + m2v人x (m2 + m1 )v0 = m1v + m2 (v + ucos 600 ) m2ucos 600 v = v0 − = 2.5m/ s m1 + m2
以人为研究对象,Y方向上受到车作用力的冲量为I 以人为研究对象,Y方向上受到车作用力的冲量为Iy ,Y方向上受到车作用力的冲量为 则
动量与角动量习题

习题4 4-1.如图所示的圆锥摆,绳长为l,绳子一端固定,另一端系一质量为m的质点,以匀角速ω绕铅直线作圆周运动,绳子与铅直线的夹角为θ。
在质点旋转一周的过程中,试求:(1)质点所受合外力的冲量I;(2)质点所受张力T的冲量TI。
解:(1)设周期为�8�3,因质点转动一周的过程中,速度没有变化,12vv�8�8,由Imv�8�8�8�5,∴旋转一周的冲量0I�8�8;(2)如图该质点受的外力有重力和拉力,且cosTmg�8�0�8�8,∴张力T旋转一周的冲量:2cosTITjmgj�8�9�8�0�8�3�8�6�8�8�8�2�8�8�8�2 所以拉力产生的冲量为2mg�8�9�8�6,方向竖直向上。
4-2.一物体在多个外力作用下作匀速直线运动,速度4/vms�8�8。
已知其中一力F方向恒与运动方向一致,大小随时间变化内关系曲线为半个椭圆,如图。
求:(1)力F 在1s到3s间所做的功;(2)其他力在1s到3s间所做的功。
解:(1)由于椭圆面积为Sab�8�9�8�8椭,∴�8�9�8�9�8�94042012121�8�8�8�7�8�7�8�7�8�8�8�2�8�8vabA (2)由动能定理可知,当物体速度不变时,外力做的总功为零,所以当该F做的功为125.6J时,其他的力的功为�8�2125.6J。
4-3.质量为m的质点在Oxy 平面内运动,运动学方程为cossinratibtj�8�6�8�6�8�8�8�0,求:(1)质点在任一时刻的动量;(2)从0�8�8t到�8�6�8�9/2�8�8t的时间内质点受到的冲量。
解:(1)根据动量的定义:Pmv�8�8,而drvdt�8�8�8�8sincosatibtj�8�6�8�6�8�6�8�6�8�2�8�0,∴sincosPtmatibtj�8�6�8�6�8�6�8�8�8�2�8�2 ;�8�0�8�6lmgTFN2010O23ts1 (2)由200ImvPPmbjmbj�8�9�8�6�8�6�8�6�8�8�8�5�8�8�8�2�8�8�8�2�8�8 ,所以冲量为零。
第3章动量角动量习题解答

第3章 动量 角动量3-1一架飞机以300m/s 的速度水平飞行,与一只身长0.20m 、质量0.50kg 的飞鸟相撞,设碰撞后飞鸟的尸身与飞机具有一样的速度,而原先飞鸟关于地面的速度很小,能够忽略不计。
试估量飞鸟对飞机的冲击力(碰撞时刻可用飞鸟身长被飞机速度相除来估算)。
依照此题计算结果,谈谈高速运动的物体(如飞机、汽车)与通常情形下不足以引发危害的物体(如飞鸟、小石子)相碰撞后会产生什么后果?解 飞鸟碰撞前速度能够忽略,碰撞进程中冲量的大小为:I m Ft υ==考虑到碰撞时刻可估算为 lt υ=即得飞鸟对飞机的冲击力2250.5300 2.2510(N)0.2m F l υ⨯===⨯由此可见飞机所受冲击力是相当大的,足以致使机毁人亡,后果很严峻。
3-2 水力采煤,是用高压水枪喷出的强力水柱冲击煤层。
如图,设水柱直径30mm D =,水速56m/s υ=,水柱垂直射在煤层表面上,冲击煤层后的速度为零,求水柱对煤的平均冲力。
解 △t 时刻内射向煤层的水柱质量为21π4m V D x ρρ∆=∆=∆ 煤层对水柱的平均冲击力(如图以向右为正方向)为211x x x m m m F t t υυυ∆-∆∆==-∆∆211π4x xD t ρυ∆=-∆3322311.010π(3010)562.2210(N)4-=-⨯⨯⨯⨯⨯⨯=-⨯水柱对煤层的平均冲力为'32.2210N F F =-=⨯,方向向右。
3-3 质量10kg m =的物体沿x 轴无摩擦地运动,设0t =时,物体位于原点,速度为零。
若是物体在作使劲()34N Ft =+的作用下运动了3秒,计算3秒末物体的速度和加速度各为多少?(题中F 作用线沿着x 轴方向)解 力F 在3秒内的冲量33d (34)d 27N s I F t t t ==+=⋅⎰⎰习题3-2图依照质点的动量定理 ()30m I υ-=得()3 2.7m/s Imυ== 加速度()()223153m/s 1.5m/s 10F a m === 3-4 质量为m 的物体,开始时静止,在时刻距离T t 20≤≤内,受力()2021t T F F T ⎡⎤-=-⎢⎥⎢⎥⎣⎦作用,试证明,在2t T =时物体的速度为043F Tm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
冲量:⎰=21ttdtFI为作用于物体上的力和作用时间之积求解方法:Ⅰ、若为恒力,则tFI∆=[C]1.(基础训练3)如图3-12所示,圆锥摆的摆球质量为m,速率为v,圆半径为R,当摆球在轨道上运动半周时,摆球所受重力冲量的大小为(A) 2m v.(B) 22)/()2(vv Rmgmπ+(C) v/Rmgπ. (D) 0.Ⅱ、若为变力,则①已知力的表达式,利用定义式⎰=21ttdtFI②已知动量的变化,利用动量定理⎰-==2112ttvmvmdtFI1、(自测提高6)质量为m的小球自高为y处沿水平方向以速率v抛出,与地面碰撞后跳起的最大高度为21y,水平速率为21v,如图3-17.(1)地面对小球的竖直冲量的大小为(1+(2)地面对小球的水平冲量的大小为12m v。
度为h处自由下落到倾角为30°的光滑固定斜面上。
设碰撞是完全弹性的,则小球对斜面的冲量的大小为,方向为垂直斜面向下。
⎰-==2112ttvmvmdtFI1.(自测提高7)一物体质量M=2 kg,在合外力(32)F t i=+(SI)的作用下,从静止开y21y始运动,式中i 为方向一定的单位矢量, 则当t=1 s 时物体的速度1v=2(/)i m s 。
【解法】用动量定理计算。
110()0Fdt mv mv =∆=-⎰[D ]2.(自测提高4)用一根细线吊一重物,重物质量为5 kg ,重物下面再系一根同样的细线,细线只能经受70 N 的拉力.现在突然向下拉一下下面的线.设力最大值为50 N ,则(A)下面的线先断. (B)上面的线先断. (C)两根线一起断. (D)两根线都不断. 3.(基础训练15)质量为m 的小球与桌面相碰撞,碰撞前、后小球的速率都是v ,入射方向和出射方向与桌面法线的夹角都是α,如图所示。
若小球与桌面作用的时间为∆t ,求小球对桌面的平均冲力。
【解法】由动量定理0()()t N mg dt mv ∆+=∆⎰N 为桌面对小球的作用力,mg为小球所受重力。
沿y 轴方向的分量形式为()()cos (cos )2cos t N mg dt N mg t mv mv mv ααα∆-=-∆=--=⎰tmv mg tmv N ∆≅+∆=ααcos 2cos 2小球对桌面的平均冲力为tmv N N ∆-=-=αcos 2'4.(自测提高12)如图3-23示,有两个长方形的物体A 和B 紧靠着静止放在光滑的水平桌面上,已知m A =2 kg ,m B =3 kg .现有一质量m =100 g 的子弹以速率v 0=800 m/s 水平射入长方体A ,经t = 0.01 s ,又射入长方体B ,最后停留在长方体B 内未射出.设子弹射入A 时所受的摩擦力为F= 3×103 N ,求: (1) 子弹在射入A 的过程中,B 受到A 的作用力的大小.(2) 当子弹留在B 中时,A 和B 的速度大小.【解法】从0t =s 到0.01t =s 对A 、B 用动量定理()0A B F t m m v ∆=+-代入题给数据得子弹出A 入B 瞬时A 、B 共同速度大小为v =6m/s 。
从0t =s 到0.01t =s 对子弹用动量定理,10F t m v m v -∆=-代入题给数据得子弹出A 入B 瞬时速度大小为1v =500m/s 。
(1)从0t =s 到0.01t =s 对B 用动量定理,0B f t m v ∆=-代入题给数据得子弹在射入A 的过程中,B 受到A 的作用力的大小1800f N =。
(2)子弹出A 入B 瞬时A 、B 共同速度大小即为子弹留在B 中时,A 的速度大小即 6/A v v m s ==。
用动量守恒定律可求得子弹留在B 中,子弹和B 的共同速度大小1()B B m v m v m m V +=+代入题给数据得子弹和B 的共同速度大小为V =22m/s 。
即 22/B v V m s ==。
4.(自测提高14)一质量为m 的匀质链条,长为L ,手持其上端,使下端离桌面的高度为h 。
现使链条自静止释放落于桌面,试计算链条落到桌面上的长度为l 时,桌面对链条的作用力。
[提示:可参考物理课本例题。
]【解法】取x 轴向下为正, 设t 时刻,落在桌面上的部分链条长为l m ,则有l m m l l Lλ==(m Lλ=为链条的质量线密度)此时在空中的链条的速度大小v =在d t 时间内,有dm vdt λ=链条元落在桌面上.根据动量定理()()0l m g f dt vdt v λ-=-()232l m l h gvdt m f m g v lg v dtLLλλ+=+=+=方向向上。
♫动量守恒定律:如果系统所受合外力的矢量和为零,则系统内各物体的动量矢量和保持不变。
2021012211v m v m v m v m+=+写出分量形式为:∑==ni ix F 10∑==ni ixiC vm 1∑==ni iy F 1∑==ni iyiC vm 1说明:有时虽然系统所受合外力不为零,但内力远大于外力,这时可忽略外力作用,近似认为系统的动量是守恒的。
如碰撞和打击这一类问题即是这样处理的。
[A] 1.(基础训练2)一质量为m 0的斜面原来静止于水平光滑平面上, 将一质量为m 的木块轻轻放于斜面上,如图.如果此后木块能静止 于斜面上,则斜面将(A) 保持静止 (B) 向右加速运动. (C) 向右匀速运动(D) 向左加速运动.【解法】假设斜面以V 向右运动。
由水平方向动量守恒得 0(cos )0m V m V v θ+-= ,而0v =,得0V =。
2.(基础训练8)静水中停泊着两只质量皆为0m 的小船.第一只船在左边,其上站一质量为m 的人,该人以水平向右速度v从第一只船上跳到其右边的第二只船上,然后又以同样的速率v 水平向左地跳回到第一只船上.此后 (1) 第一只船运动的速度为v1=02m vm m -+。
(2) 第二只船运动的速度为v2=02m v m。
(水的阻力不计,所有速度都相对地面而言)【解法】提示:第一跳 010m v m v '+= 02()m v m m v '=+第二跳 0101()m v m v m m v '-+=+0202()m m v m v m v '+=-+3.(自测提高8)两球质量分别为m 1=2.0 g ,m 2=5.0 g ,在光滑的水平桌面上运动.用直角坐标OXY 描述其运动,两者速度分别为vcm/s ,)0.50.3(v 2j i += cm/s .若碰撞后与x 轴的夹角α=35.5︒. (基础训练14)=19.6 m 处炸裂成质量相等的两块.其中一块在爆炸后1秒钟落到爆炸点正下方的地面上.设此处与发射点的距离S 1=1000 m ,问另一块落地点与发射地点间的距离是多少?(空气阻力不计,g =9.8 m/s 2) 【解法】因第一块爆炸后落在其正下方的地面上,说明它的速度方向是沿竖直方向的. 利用 2t g t h '+'=211v , 式中t '为第一块在爆炸后落到地面的时间. 可解得v 1=14.7 m/s ,竖直向下.取y 轴正向向上, 有v 1y =-14.7 m/s设炮弹到最高点时(v y =0),经历的时间为t ,则有S 1 = v x t (1) h=221gt (2)由(1)及(2)得 t =2 s , v x =500 m/s 以2v表示爆炸后第二块的速度,由爆炸前后的动量守恒得 x v v m m x =221 (3)0==+yy m m m vv v 1y 22121 (4)解出 v 2x =2v x =1000 m/s , v 2y =-v 1y =14.7 m/s再由斜抛公式 x 2= S 1 +v 2x t 2 (5) y 2=h +v 2y t 2-22gt 21(6)落地时 y 2 =0,可得 t 2 =4 s , t 2=-1 s (舍去) 故 x 2=5000 m♫质点对定点的角动量: v m r p r L ⨯=⨯=大小:=L αsin rmv 方向:(右手法则)与v r⨯同向力矩:F r M⨯=角动量定理:对同一参考点O ,质点所受的冲量矩等于质点角动量的增量。
12d 21L L t M t t-=⎰角动量守恒的条件:质点所受相对于参考点的力矩的矢量和等于零。
[B ]1. (自测提高2)质量为20 g 的子弹,以400 m/s 的速率沿图入一原来静止的质量为980 g 的摆球中,摆线长度不可伸缩.子弹射入后开始与摆球一起运动的速率为(A) 2 m/s . (B) 4 m/s . (C) 7 m/s . (D) 8 m/s .【解法】对摆线顶部所在点角动量守恒。
2sin 30()m v l M m lV ︒=+;其中m 为子弹质量,M 为摆球质量,l 为摆线长度。
2.(基础训练11)将一质量为m 的小球,系于轻绳的一端,绳的另一端穿过光滑水平桌面上的小孔用手拉住.先使小球以角速度ω1在桌面上做半径为r 1的圆周运动,然后缓慢将绳下拉,使半径缩小为r 2,在此过程中小球的动能增量是222111221(1)2r m r rω-。
附加题:1.(自测提高13)有一水平运动的皮带将砂子从一处运到另一处,砂子经一竖直的静止漏斗落到皮带上,皮带以恒定的速率v 水平地运动.忽略机件各部位的摩擦及皮带另一端的其它影响,试问:(1) 若每秒有质量为q m =d M /d t 的砂子落到皮带上,要维持皮带以恒定速率v 运动,需要多大的功率?(2) 若q m =20 kg/s ,v =1.5 m/s ,水平牵引力多大?所需功率多大? 【解法】(1) 设t 时刻落到皮带上的砂子质量为M ,速率为v ,t+d t 时刻,皮带上的砂子质量为M+d M ,速率也是v ,根据动量定理,皮带作用在砂子上的力F 的冲量为: v v v ⋅=⋅+-+=M M M M M t F d )0d ()d (d∴ m q t M F ⋅==v v /d d由牛顿第三定律,此力的大小等于砂子对皮带的作用力大小F ',即F '=F .由于皮带匀速运动,所需的水平牵引力大小为F ″= F ',因而, F " =F ,F "与v 同向,所需供给的功率为:22/d mP F M t v q =⋅=⋅= v v v d M d t =v d(2) 当q m =d M/d t=20 kg/s ,v =1.5 m/s 时,水平牵引力大小F "=v q m =30 N所需功率为 P=v 2q m =45 W。
