匀速圆周运动的加速度
圆周运动的速度和加速度

圆周运动的速度和加速度圆周运动是物体在圆周轨道上运动的一种形式。
它具有一定的速度和加速度,这些物理量对于描述和分析圆周运动非常重要。
速度是物体在单位时间内所走过的距离。
在圆周运动中,由于物体沿着圆周轨道运动,所以速度的方向也在不断变化。
我们可以用线速度来描述圆周运动的速度,线速度是物体沿着圆周轨道的路径长度与所用时间的比值。
假设物体在时间 t 内沿圆形轨道运动一周,圆的半径为 r,圆的周长为2πr,则物体所走过的距离就是圆的周长,即S=2πr。
因此,圆周运动的速度 v 可以表示为:v = S / t = (2πr)/ t加速度是物体速度变化的快慢程度。
在圆周运动中,由于速度的方向不断变化,所以加速度的方向也在不断变化。
我们称这种加速度为向心加速度,它的方向指向圆心,大小与速度的变化量有关。
根据物理学原理,向心加速度 a 的大小可以表示为:a = v^2 / r = ((2πr)/ t)^2 / r = 4π^2r / t^2其中,v 是圆周运动的速度,r 是圆的半径,t 是运动所用的时间。
通过以上公式,我们可以计算出圆周运动的速度和加速度。
在实际应用中,这些物理量的计算是非常重要的,它们可以帮助我们了解和分析物体在圆周运动中的行为。
在工程领域,圆周运动的速度和加速度在机械设计和动力学分析中扮演着重要的角色。
比如在车辆运动中,我们需要计算车轮的速度和加速度,来确定车辆的行驶性能和操控性。
总结:圆周运动的速度和加速度是描述物体在圆周轨道上运动的两个重要物理量。
速度是物体在单位时间内所走过的距离,而加速度是速度变化的快慢程度。
通过运用相关的公式,我们可以计算出圆周运动的速度和加速度,进而分析和了解物体在圆周运动中的行为。
在工程应用中,这些物理量对于机械设计和动力学分析具有重要意义。
力学中的圆周运动加速度

力学中的圆周运动加速度圆周运动是力学中的经典问题之一,它描述了物体在圆形轨道上运动的情况。
而圆周运动的加速度是一个关键概念,它描述了物体在圆周运动过程中速度的变化率。
本文将深入探讨力学中的圆周运动加速度,并解释其物理原理和相关公式。
1. 圆周运动的基本概念圆周运动指的是物体沿着一条圆形轨道运动的情况。
在圆周运动中,物体所受的合力始终指向轨道的中心,被称为向心力。
向心力是物体保持在轨道上的原因,它的大小与物体的质量和轨道的曲率半径有关。
2. 圆周运动的加速度定义加速度是速度的变化率,描述了物体在运动过程中速度增加或减少的程度。
对于圆周运动,加速度与速度的方向有关。
由于圆周运动的速度始终沿着轨道切线方向,而加速度则指向向心力的方向。
3. 圆周运动加速度的计算根据牛顿第二定律,物体的加速度与作用在物体上的合力成正比,反比于物体的质量。
在圆周运动中,物体所受的合力就是向心力,因此可以根据向心力来计算圆周运动的加速度。
圆周运动的加速度公式为:a = (v²) / r其中,a表示圆周运动的加速度,v表示物体的速度,r表示轨道的曲率半径。
4. 圆周运动加速度的特点根据圆周运动加速度的计算公式可知,加速度与速度平方成正比,与曲率半径成反比。
这意味着在圆周运动中,速度越大、曲率半径越小,加速度就越大。
相反,速度越小、曲率半径越大,加速度就越小。
5. 圆周运动加速度的应用圆周运动加速度在物理学和工程学中有广泛的应用。
例如,在机械工程中,我们可以利用圆周运动加速度来计算转子的旋转速度和转力。
在物理学中,我们可以通过圆周运动加速度来解释行星围绕太阳的运动以及颗粒在圆桶中的沉降过程。
总结:力学中的圆周运动加速度是一个重要的概念,它描述了物体在圆形轨道上运动时速度的变化率。
圆周运动的加速度与向心力密切相关,根据加速度的计算公式可知,它与速度平方成正比,与曲率半径成反比。
圆周运动加速度在物理学和工程学中有广泛的应用,它帮助我们理解和解释了许多自然现象和工程问题。
圆周运动的速度与加速度计算

圆周运动的速度与加速度计算在物理学中,圆周运动指的是物体沿着圆形路径运动的情况。
在圆周运动中,我们常常需要计算物体的速度和加速度,以了解其运动状态。
本文将介绍如何计算圆周运动的速度和加速度。
一、速度的计算在圆周运动中,速度是一个矢量量,表示物体在单位时间内沿圆周路径前进的距离。
根据定义,速度等于物体运动过的弧长除以时间。
因此,圆周运动的速度计算公式为:v = 2πr / T其中,v表示速度,r表示圆的半径,T表示物体运行一周所需的时间。
举例来说,假设有一个半径为5米的车轮,它的圆周运动周期为2秒。
我们可以利用上述公式来计算车轮的速度:v = 2π * 5 / 2 = 31.4 m/s所以,该车轮的速度为31.4 m/s。
二、加速度的计算在圆周运动中,加速度是一个矢量量,表示物体在单位时间内速度的变化量。
由于圆周运动中速度的方向随着位置的变化而变化,所以圆周运动的加速度不仅仅是大小,还有方向。
物体在圆周运动中的加速度的大小可以通过以下公式计算:a = v^2 / r其中,a表示加速度,v表示速度,r表示圆的半径。
与速度不同,加速度的大小决定了物体在圆周运动中的向心力。
向心力指的是指向圆心的力,使物体沿着圆周路径运动。
根据牛顿第二定律,向心力与加速度之间的关系可以通过以下公式计算:F = ma其中,F表示力,m表示物体的质量,a表示加速度。
举例来说,假设一个物体以30 m/s的速度在半径为10米的圆形路径上运动。
我们可以利用上述公式来计算物体的加速度:a = (30)^2 / 10 = 90 m/s^2所以,该物体在圆周运动中的加速度为90 m/s^2。
结论:圆周运动的速度和加速度计算可以通过特定的公式来得出。
速度的计算公式为v = 2πr / T,加速度的计算公式为a = v^2 / r。
对于圆周运动,加速度的存在意味着物体受到向心力的作用,该力向圆心的方向指引物体沿着圆周路径运动。
通过对速度和加速度的计算,我们可以更好地理解圆周运动的特性和物体的运动状态。
圆周运动中的速度与加速度计算

圆周运动中的速度与加速度计算圆周运动是物体沿着一个圆形轨道运动的过程,它在日常生活和科学研究中都有广泛的应用。
在圆周运动中,速度和加速度是两个重要的物理量,它们对于描述物体的运动状态和变化趋势起着关键作用。
本文将从速度和加速度的概念入手,详细探讨圆周运动中的速度与加速度的计算方法。
一、速度的计算速度是描述物体在单位时间内位移的变化量,它是一个矢量量纲。
在圆周运动中,物体的速度与它所处的位置和时间有关。
我们可以通过以下公式来计算圆周运动中的速度:v = rω其中,v表示速度,r表示物体的半径,ω表示物体的角速度。
在圆周运动中,物体的速度大小等于半径与角速度的乘积。
当物体的角速度增大时,其速度也会相应增大;当物体的半径增大时,其速度也会相应增大。
这说明速度与角速度和半径之间存在着直接的线性关系。
二、加速度的计算加速度是描述物体在单位时间内速度的变化量,也是一个矢量量纲。
在圆周运动中,物体的加速度与它的速度和时间有关。
我们可以通过以下公式来计算圆周运动中的加速度:a = rα其中,a表示加速度,r表示物体的半径,α表示物体的角加速度。
在圆周运动中,物体的加速度大小等于半径与角加速度的乘积。
当物体的角加速度增大时,其加速度也会相应增大;当物体的半径增大时,其加速度也会相应增大。
这说明加速度与角加速度和半径之间存在着直接的线性关系。
三、速度与加速度的关系在圆周运动中,速度和加速度之间存在着一定的关系。
根据速度和加速度的定义,我们可以得到以下公式:a = vω其中,a表示加速度,v表示速度,ω表示角速度。
这个公式说明了加速度与速度和角速度之间的关系。
当物体的速度增大时,其加速度也会相应增大;当物体的角速度增大时,其加速度也会相应增大。
这说明加速度与速度和角速度之间存在着直接的线性关系。
四、实际应用圆周运动的速度与加速度计算在实际应用中有着广泛的应用。
例如,在机械工程中,我们需要计算旋转机械的速度和加速度,以确定其工作状态和性能。
匀速圆周运动知识点解析

匀速圆周运动知识点解析1.匀速圆周运动的定义(1)轨迹是圆周的运动叫圆周运动。
(2)质点沿圆周运动,如果在相同时间里通过的弧长相等,这种运动叫匀速圆周运动。
(3)匀速圆周运动是最简单的圆周运动形式,也是最基本的曲线运动之一。
(4)匀速圆周运动是一种理想化的运动形式。
许多物体的运动接近这种运动,具有一定的实际意义。
一般圆周运动,也可以取一段较短的时间(或弧长)看成是匀速圆周运动。
2.周期(1)物体做匀速圆周运动时,运动一周所用的时间。
(2)周期用符号T表示,单位是秒。
(3)周期是反映重复性运动的运动快慢的物理量。
它从另一个角度描述了物体的运动。
3.线速度(1)物体做匀速圆周运动时,通过的弧长s跟通过这段弧长所用时间t的比值,叫运动物体线速度大小。
线速度的方向为圆周上某点的切线方向。
(2)线速度的计算公式:(3)线速度的意义:线速度实质上还是物体某一时刻的瞬时速度,虽然是用弧长和时间的比定义了速度大小,但当时间t趋于零时,弧长和为区别角速度而取名为线速度。
4.角速度转过这些角度所用时间t的比值,叫物体做匀速圆周运动的角速度。
(2)角速度计算公式:(3)角速度单位为:弧度/秒(rad/s)。
(4)角速度是矢量,方向为右手螺旋法则的大拇指的指向。
(5)角速度是描述转动快慢的物理量。
在描述转动效果时,它比用线速度描述更具有代表性。
5.向心加速度(1)匀速圆周运动的加速度方向匀速圆周运动的速度大小不变,速度的方向时刻在变,由于速度方向的变化,质点一定具有加速度,该加速度反映速度方向变化的快慢,该加速度的方向沿着半径指向圆心。
设质点沿半径是r的圆周做匀速圆周运动,在某时刻它处于A点,速度是vA,经过很短时间Δt后,运动到B点,速度为vB。
根据矢量合成的三角形法则可知,矢量vA与Δv之和等于vB,所以Δv是质点在A点时的加速度。
如图4-20。
时Δv便垂直于vA。
而vA是圆的切线,故Δv是指向圆心的。
即A点加速度指向圆心,所以匀速圆周运动的加速度又叫向心加速度。
高中物理公式推导(匀速圆周运动向心加速度、向心力)
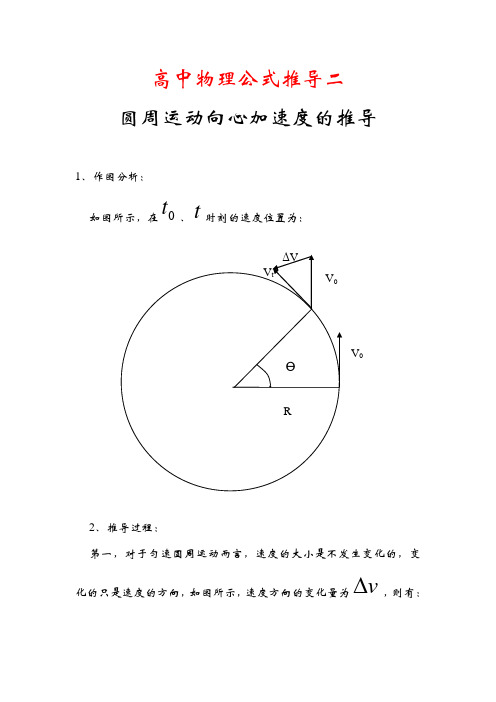
V tΔV 高中物理公式推导二 圆周运动向心加速度的推导1、作图分析: 如图所示,在0t、t 时刻的速度位置为:2、推导过程:第一,对于匀速圆周运动而言,速度的大小是不发生变化的,变化的只是速度的方向,如图所示,速度方向的变化量为v ,则有:RƟV 0V 0θθ∆=∆≈∆t v v v 0第二,根据加速度的定义:tv a ∆∆=则有:t v t v a n ∆∆=∆∆=θ0第三,根据圆周运动的相关关系知:Rv t =∆∆=θω是故,圆周运动的向心加速度为:Rv a n 2=第四,圆周运动的向心力的大小为:Rvmm a F n 2==3、意外收获:第一,对于圆周运动,我们应该理解速度、角速度、周期之间的关系。
具体为:R v =ωT πω2=vR πω2=第二,我们应该掌握极限的相关知识,合理利用极限来解决相关问题。
第三,如果我们谈论的不是匀速圆周运动,我们同样可以利用此方法进行谈论。
对于非匀速圆周运动(或者叫做曲线运动),不仅速度的方向发生了变化,而且速度的大小也发生了变化,所以, 不仅有向心加速度之外,应该也有使物体速度大小变化的加速度。
但是,在这种情况下,我们的向心加速度,叫做径向加速度,速度大小变化的加速度,叫做切向加速度。
故有:(1)向心加速度为:R v a n 2=(2)切向加速度为:t v a t ∆∆=(注意:这里的v∆是指切向速度方向速度的变化量,并不是指图上的v∆。
)4、注意事项:对于匀速圆周运动而言,需要掌握的知识点并不是很多,我们只要能够理解一些物理量之间的基本关系即可。
本篇的讨论只为学有余力的高中学生推荐,不过,物理推导讲究的是方法,并不是死记硬背公式,掌握了这一知识点的推导过程对以后了解其他物理知识会有很大的帮助。
匀速圆周运动推导加速度的公式

匀速圆周运动推导加速度的公式英文版Title: Derivation of Acceleration Formula for Uniform Circular MotionUniform circular motion, a fundamental concept in physics, refers to the movement of an object along a circular path with a constant speed. This motion is characterized by the object's constant angular velocity and the resulting acceleration, known as centripetal acceleration, which acts towards the center of the circle. In this article, we will derive the formula for centripetal acceleration in uniform circular motion.Let's consider an object moving in a circular path with a radius r and a constant speed v. The object completes one revolution in a time period T, resulting in an angular velocity ω (omega) given by ω = 2π/T. The linear speed v is related to the angular velocity and the radius by the formula v = ωr.Now, let's focus on the acceleration of the object. Since the speed is constant, the tangential acceleration is zero. However, there is a radial or centripetal acceleration acting towards the center of the circle. This acceleration is responsible for keeping the object in circular motion.To derive the formula for centripetal acceleration, we need to consider the change in velocity over time. In uniform circular motion, the velocity vector changes direction but not magnitude. Let's consider a small change in the velocity vector Δv after a time Δt. This change in velocity is perpendicular to the original velocity vector and指向圆心。
物体的匀速圆周运动和变速圆周运动

物体的匀速圆周运动和变速圆周运动物体的圆周运动是指物体围绕一个中心点以圆周轨迹运动的过程。
根据速度的变化情况,圆周运动可以分为匀速圆周运动和变速圆周运动两种。
一、匀速圆周运动匀速圆周运动是指物体在圆周轨迹上的速度大小保持不变的运动。
在匀速圆周运动中,物体的加速度与速度垂直,即物体始终保持恒定的速度,但方向不断改变,由于速度的方向与轨迹相切,因此产生向心加速度。
向心加速度的大小与速度的大小成正比,与运动物体离中心的距离成反比。
例如,当我们用线栓一端连接一个质点并保持恒定的长度时,将质点绕另一端作圆周运动。
此时质点的速度大小保持不变,但速度的方向不断改变,一直向中心指向。
二、变速圆周运动变速圆周运动是指物体在圆周轨迹上速度大小不断改变的运动。
在变速圆周运动中,物体的加速度不仅与速度的方向垂直,还会改变速度的大小,即物体会经历加速和减速阶段。
例如,当我们用弹簧连接一个质点,并使质点在水平面上做圆周运动,此时质点的速度大小会随着弹簧的伸缩而改变。
当弹簧伸长时,质点的速度增加;当弹簧缩短时,质点的速度减小。
因此,质点在变速圆周运动中速度的大小和方向都在不断变化。
总结:物体的圆周运动有两种形式,即匀速圆周运动和变速圆周运动。
匀速圆周运动是指物体在圆周轨迹上速度大小不变的运动,其加速度大小由向心加速度决定;变速圆周运动是指物体在圆周轨迹上速度大小不断改变的运动,其加速度既包括向心加速度,也包括改变速度大小的加速度。
理解物体的圆周运动对于解析和预测物体的运动状态具有重要意义,也有助于我们理解天体运动、车辆转弯等现象。
通过深入研究圆周运动,我们可以更好地理解物理学中的基本概念和原理,并应用于解决实际问题中。
匀速圆周运动加速度公式

匀速圆周运动加速度公式
匀速圆周运动:
1.线速度V=s/t=2πR/T
2.角速度ω=Φ/t=2π/T=2πf
3.向心加速度a=V2/R=ω2R=(2π/T)2R
4.向心力F心=mV2/R=mω2R=m(2π/T)2R
5.周期与频率T=1/f
6.角速度与线速度的关系V=ωR
7.角速度与转速的关系ω=2πn(此处频率与转速意义相同)
8.主要物理量及单位:
弧长(S):米(m)
角度(Φ):弧度(rad)
频率(f):赫(Hz)
周期(T):秒(s)
转速(n):r/s
半径(R):米(m)
线速度(V):m/s
角速度(ω):rad/s
向心加速度:m/s2
注:
(1)向心力可以由具体某个力提供,也可以由合力提供,还可以由分力提供,方向始终与速度方向垂直。
(2)做匀速度圆周运动的物体,其向心力等于合力,并且向心力只改变速度的方向,不改变速度的大小,因此物体的动能保持不变,但动量不断改变。
人教版高一物理必修第二册第六章《圆周运动》向心加速度

这[例个题力2]可能长沿为什L的么细方线向,?一端拴一质量为m的小球,一端固定于O点.
[这例个题力1]可自能行沿车什的么小方齿向轮?A、大齿轮B、后轮C是相互关联的三个转动部分,如图所示。
小质球点在 做水匀平速面圆内周做运匀动速,圆从周A运运动动到(这B,种线运速动度通从常v被A变称成为v“B圆,锥速摆度运的动变”化),量如Δ图v,甲如所何示表. 示?
Δv vA vB
B
O
A
当自Δt 行取车值正不常断骑变行小时,AΔ、v 的B、方C向三与轮v边A的缘方上向的关点系的如向何心变加化速?度的大小如何比较?
当Δt 取值不断变小,Δv 的方向与v 的方向关系如何变化? 受质到点指 做向匀太速阳圆的周引运力动作,用从A运动到B,线速度从vA变成vB,速度的变化量Δv,如何表示?
Δv 当你Δ能t足画够出小Δt,时v间A内,速vB度的变夹化角量θ 就Δv足吗够?小。
v [所例求题加2]速度长a为是Lt的A时细刻线的,瞬一时端加拴速一度质吗量?为得m的小球,一端固定于O点.
A 质此点时做θ 所匀对速的圆弦周长运和动弧,长从近A运似动相到等B。,线速度从vA变成vB,速度的变化量Δv,如何表示?
看,向心加速度与半径成正比;
匀速圆周运动的实质是什么?
当Δt足够小,Δv=v∙θ
受到指向太阳的引力作用
当Δt足够小,vA,vB的夹角θ 就足够小。
从公式
看,向心加速度与半径成反比;
从公式
看,向心加速度与半径成正比;
地球受到什么力的作用?
质点做匀速圆周运动,从A运动到B,线速度从vA变成vB,速度的变化量Δv,如何表示?
变速曲线运动 运动状态改变 这个力可能沿什么方向?
质点做匀速圆周运动,从A运动到B,线速度从vA变成vB,速度的变化量Δv,如何表示?
2023年新教材高中物理向心加速度讲义新人教版必修第二册

3.向心加速度(1)知道向心加速度的概念.(2)会用矢量图表示速度变化量与速度间的关系.(3)能运用数学方法,结合加速度定义式推导向心加速度的公式.一、匀速圆周运动的加速度方向1.定义:物体做匀速圆周运动时的加速度总指向圆心,把它叫作向心加速度(centripetal acceleration).2.方向:向心加速度的方向沿半径指向圆心,即向心加速度的方向与速度方向垂直. 导学:向心加速度与周期、转速、线速度、角速度关系的推导 由线速度与周期的关系v =2πππ代入a =π2π得a =4π2π2r .由T =1π(n 取r/s)代入a =4π2ππ2得a =4π2n 2r . 由v =ωr 代入a =π2π得a =π2π=v ·ππ=ωv .二、匀速圆周运动的加速度大小1.推导:向心加速度与向心力的关系符合牛顿第二定律,则有:F n =ma n =m π2π=mω2r . 2.向心加速度公式:a n =________=________.3.作用效果:只改变线速度的方向,不改变线速度的大小. 拓展:速度变化量的矢量图从同一点作出v A 和v B 的矢量,从v A 末端指向v B 末端的矢量,即Δv知识点一 向心加速度的方向及意义导学探究(1)图甲中的小球与图乙中的运动员正在做匀速圆周运动,是否具有加速度?(2)做匀速圆周运动的加速度方向如何确定?你的依据是什么?探究总结1.向心加速度的方向特点:(1)指向圆心:无论匀速圆周运动,还是变速圆周运动,向心加速度的方向都指向圆心,或者说与线速度的方向垂直.(2)时刻改变:无论向心加速度的大小是否变化,向心加速度的方向随线速度方向的改变而改变.所以一切圆周运动都是变加速曲线运动.2.匀速圆周运动中的“变”与“不变”:(1)“不变”量:匀速圆周运动的角速度、周期、转速不变;线速度、加速度这两个矢量的大小不变.(2)“变化”量:匀速圆周运动的线速度、加速度这两个矢量的方向时刻改变.3.物理意义:向心加速度描述圆周运动中线速度改变的快慢.典例示范【例1】下列关于向心加速度的说法中正确的是( )A.向心加速度表示做圆周运动的物体速率改变的快慢B.匀速圆周运动的向心加速度是不变的C.匀速圆周运动的向心加速度大小不变D.只要是圆周运动,其加速度都是不变的练1 荡秋千是儿童喜爱的一项体育运动,如图所示,当秋千荡到最高点时,小孩的加速度方向是图中的( )A.a方向B.b方向C.c方向D.d方向练2 (多选)关于匀速圆周运动和向心加速度,下列说法正确的是( )A.匀速圆周运动的速度大小保持不变,所以做匀速圆周运动的物体没有加速度B.做匀速圆周运动的物体,虽然速度大小不变,但方向时刻在变,所以必有加速度C.做匀速圆周运动的物体,向心加速度的大小保持不变,所以是匀变速曲线运动D.匀速圆周运动的向心加速度大小虽然不变,但方向始终指向圆心,时刻发生变化,所以匀速圆周运动不是匀变速运动知识点二向心加速度公式的理解与应用探究总结1.向心加速度公式,②a n=ω2r.(1)基本公式:①a n=π2πr,②a n=4π2n2r.(2)拓展公式:①a n=4π2π22.对向心加速度大小与半径关系的理解(1)当r一定时,a n∝v2,a n∝ω2..(2)当v一定时,a n∝1π(3)当ω一定时,a n∝r.3.向心加速度与半径的关系:典例示范题型一对向心加速度公式的理解【例2】(多选)如图所示为甲、乙两球在不同轨道上做匀速圆周运动的向心加速度随半径变化的图像,由图像可知( )A.甲球运动时,线速度大小保持不变B.甲球运动时,角速度大小保持不变C.乙球运动时,线速度大小保持不变D.乙球运动时,角速度大小保持不变题型二向心加速度公式的应用【例3】飞机在做俯冲拉起运动时,可以看成是做圆周运动,如图所示,若在最低点附近做半径为R=240 m的圆周运动,飞行员的质量m=60 kg,飞机经过最低点P时的速度为v=360 km/h,试计算:(1)此时飞机的向心加速度a的大小;(2)此时飞行员对座椅的压力F N是多大.(g取10 m/s2)题型三传动装置中向心加速度的分析【例4】如图所示,两轮用皮带传动,皮带不打滑.图中有A、B、C三点,这三点所在处半径关系为r A>r B=r C,则这三点的向心加速度a A、a B、a C之间的关系是( )A.a A=a B=a C B.a C>a A>a BC.a C<a A<a B D.a C=a B>a A思维方法:分析此类问题要“看”“找”“选”练3 如图所示为两级皮带传动装置,转动时皮带均不打滑,中间两个轮子是固定在一起的,轮1的半径和轮2的半径相同,轮3的半径和轮4的半径相同,且为轮1和轮2半径的一半,则轮1边缘的a点和轮4边缘的c点相比( )A.线速度之比为1∶4B.角速度之比为4∶1C.向心加速度之比为8∶1D.向心加速度之比为1∶8练4 A、B两艘快艇在湖面上做匀速圆周运动(如图),在相同时间内,它们通过的路程之比是4∶3,运动方向改变的角度之比是3∶2,则它们( )A.线速度大小之比为4∶3B.角速度大小之比为3∶4C.圆周运动的半径之比为2∶1D.向心加速度大小之比为1∶21.下列关于向心加速度的说法中正确的是( )A.向心加速度越大,物体速率变化越快B.向心加速度的大小与轨道半径成反比C.向心加速度的方向始终与线速度的方向垂直D.在匀速圆周运动中向心加速度是恒量2.转篮球是一项需要技巧的活动,如图所示,让篮球在指尖上匀速转动,指尖刚好静止在篮球球心的正下方.下列判断正确的是( )A.篮球上的各点做圆周运动的圆心均在指尖与篮球的接触处B.篮球上各点的向心力是由手指提供的C.篮球上各点做圆周运动的角速度相等D.篮球上各点离转轴越近,做圆周运动的向心加速度越大3.如图所示,一个凹形桥模拟器固定在水平地面上,其凹形轨道是半径为0.4 m的半圆,且在半圆最低点装有一个压力传感器(图中未画出).一质量为0.4 kg的玩具小车经过凹形轨道最低点时,传感器的示数为8 N,则此时小车的(g取10 m/s2)( )A.速度大小为1 m/sB.速度大小为4 m/sC.向心加速度大小为10 m/s2D.向心加速度大小为20 m/s24.如图所示,甲、乙、丙、丁四个可视为质点的小物体放置在匀速转动的水平转盘上,与转轴的距离分别为4r、2r、2r、r,甲、丙位于转盘的边缘处,两转盘边缘接触,靠摩擦传递动力,转盘与转盘之间、物体与盘面之间均未发生相对滑动,则向心加速度最大的是( )A.甲B.乙C.丙D.丁5.如图所示,自行车的小齿轮A、大齿轮B、后轮C是相互关联的三个转动部分,且半径R B=4R A、R C=8R A.当自行车正常骑行时,A、B、C三轮边缘的向心加速度的大小之比a A∶a B∶a C等于( )A.1∶1∶8B.4∶1∶4C.4∶1∶32D.1∶2∶43.向心加速度预习填空二、2.π2πw2r知识点精讲知识点一提示:(1)小球与运动员都具有加速度.(2)做匀速圆周运动的物体加速度方向与合力方向相同,依据是牛顿第二定律.【例1】【解析】圆周运动有两种情形:一是匀速圆周运动,二是非匀速圆周运动.在匀速圆周运动中,加速度的方向指向圆心,叫向心加速度,其大小不变,方向时刻改变;非匀速圆周运动中加速度可以分解为向心加速度和切向加速度,向心加速度改变线速度的方向,切向加速度改变线速度的大小.故选项C正确.【答案】 C练 1 解析:当秋千荡到最高点时,小孩的速度为零,沿半径方向的向心加速度为零,加速度方向沿圆弧的切线方向,即图中的b方向,B正确.答案:B练2 解析:做匀速圆周运动的物体,速度的大小不变,但方向时刻在变,所以必有加速度,且向心加速度大小不变,方向时刻指向圆心,向心加速度不恒定,因此匀速圆周运动不是匀变速运动,故A、C错误,B、D正确.答案:BD知识点二【例2】 【解析】 A 对,B 错:由a =π2π知,v 不变时,a 与R 成反比,图像为双曲线的一支.C 错,D 对:由a =ω2R 知,ω不变时,a 与R 成正比,图像为过原点的倾斜直线.【答案】 AD【例3】 【解析】 (1)v =360 km/h =100 m/s 则a =π2π=1002240 m/s 2=1253 m/s 2.(2)对飞行员进行受力分析,则飞行员在最低点受重力和座椅的支持力,向心力由二力的合力提供.所以F N -mg =ma 得F N =mg +ma代入数据得F N =3 100 N根据牛顿第三定律可知,飞行员对座椅的压力大小也为3 100 N . 【答案】 (1)1253m/s 2(2)3 100 N【例4】 【解析】 A 、B 两点通过同一条皮带传动,线速度大小相等,即v A =v B ,由于r A >r B ,根据a =v 2r 可知a A <a B ;A 、C 两点绕同一转轴转动,有ωA =ωC ,由于r A >r C ,根据a=ω2r 可知a C <a A ,所以a C <a A <a B ,故选项C 正确,A 、B 、D 错误.【答案】 C练3 解析:A 错:由题意知v a =v 3,v 2=v c ,又轮2与轮3同轴传动,角速度相同,v 2=2v 3,所以v a ∶v c =1∶2.B 错:角速度之比为ππππ=ππππ∶ππππ=14.C 错,D 对:设轮4的半径为r ,则a a =ππ2ππ=(0.5v c )22r=ππ28π=18a c ,即a a ∶a c =1∶8.答案:D练4 解析:由圆周运动公式有,通过的路程s =Rθ=vt ,转过的角度θ=ωt ,已知在相同的时间内,通过的路程之比是4∶3,转过的角度之比是3∶2,则A 、B 的线速度大小之比是4∶3,角速度大小之比是3∶2,则选项A 正确,B 错误;由R =s θ,得半径之比为ππππ=ππππ·ππππ=43×23=8∶9,由向心加速度a =ω2R ,得向心加速度大小之比为ππππ=ωA2ωB2·R A R B =3222×89=2∶1,选项C 、D 错误.答案:A随堂练习1.解析:A错:在匀速圆周运动中,速率不变.B错:向心加速度的大小可用a n=π2π或a n=ω2r表示,当v一定时,a n与r成反比;当ω一定时,a n与r成正比.可见a n与r的比例关系是有条件的.C对:向心加速度的方向始终与线速度的方向垂直.D错:在匀速圆周运动中,向心加速度的大小恒定,但方向始终指向圆心,即其方向时刻变化,所以向心加速度不是恒量.答案:C2.解析:A错:篮球上的各点做圆周运动的圆心在篮球的轴线上,类似于地球的自转轴.B错:手指并没有与篮球上别的点接触,不可能提供所有点的向心力.C对:篮球上各点做圆周运动的周期相等,角速度相等.D错:篮球上各点离转轴越近,由a=rω2可知,做圆周运动的向心加速度越小.答案:C3.解析:当小车经过最低点时,受到的支持力与重力的合力提供向心力,则F N-mg=mπ2π,代入数据得v=2 m/s,向心加速度a n=π2π=10 m/s2.答案:C4.解析:先根据a n=ω2r分析同一转盘上两物体的向心加速度关系,再根据a n=π2π分析不同转盘上两物体的向心加速度关系.所以选项C正确.答案:C5.解析:A、B的线速度大小相等,R A∶R B=1∶4,根据a=π2π知,a A∶a B=4∶1.A、C 的角速度大小相等,R A∶R C=1∶8,根据a=ω2r知,a A∶a C=1∶8,所以a A∶a B∶a C=4∶1∶32.答案:C。
加速度方向的判断方法

加速度方向的判断方法
加速度是物体在单位时间内速度改变的量。
它包括大小和方向两个方面。
判断加速度方向的方法有以下几种:
1.物体在直线运动中加速度方向判断:
-当物体的速度增大时,加速度的方向与速度方向相同;
-当物体的速度减小时,加速度的方向与速度方向相反。
2.物体在圆周运动中加速度方向判断:
-当物体做匀速圆周运动时,加速度的方向指向圆心;
-当物体做非匀速圆周运动时,加速度的方向既有径向分量,也有切
向分量。
它们的合力与速度方向不一致。
3.通过速度-时间图判断加速度方向:
-在速度-时间图中,加速度的方向可以通过速度曲线的变化率来判断。
如果速度曲线上升越来越陡,则加速度方向为正;如果速度曲线下降越来
越陡,则加速度方向为负。
4.刚体运动中的判断:
-对于刚体的平动运动和转动运动,加速度方向的判断需要考虑物体
的自由度和受力情况。
-对于平动运动而言,物体上各个部分的加速度方向都相同,取决于
合外力的方向;
-对于转动运动而言,物体上不同部分的加速度方向有可能不同,取决于合力矩和物体的惯性矩。
需要注意的是,以上方法都是基于经验和运动定律的推导得出的。
在具体问题中,还需要结合具体的物理模型和实验结果进行分析,以得到准确的加速度方向。
另外,通过使用物理学中的数学工具如矢量、向量、微积分等,可以更准确地描述和计算加速度的方向。
这些方法包括矢量分析、速度矢量和加速度矢量的瞬时关系等。
但这些方法需要具备一定的数学基础和物理知识支持。
匀速圆周运动平均加速度的关系

匀速圆周运动平均加速度的关系1.引言1.1 概述概述部分旨在简要介绍和概括匀速圆周运动平均加速度的关系这篇文章的主题和内容。
本篇文章将探讨匀速圆周运动的基本概念及特点,并重点分析匀速圆周运动平均加速度的定义以及与其他因素的关系。
通过深入研究并理解匀速圆周运动的平均加速度,我们可以更好地理解圆周运动中的物体在速度和加速度方面的特性。
通过掌握匀速圆周运动平均加速度的关系,我们能够更好地预测和描述物体在圆周运动中的行为。
进一步地,此文将在正文部分详细讨论圆周运动的基本概念和特点,以及匀速圆周运动的平均加速度定义与其他因素的关系。
在结论部分,文章将总结得出匀速圆周运动平均加速度的关系的重要结论。
通过阅读本文,读者将能够更深入地理解和应用匀速圆周运动平均加速度的概念,从而加强对圆周运动的理解和应用。
文章结构部分的内容可以按以下方式编写:1.2 文章结构本文将按照以下结构进行叙述:1. 引言:在引言部分,我们将概述匀速圆周运动平均加速度的关系,并明确文章的目的。
2. 正文:正文部分将介绍圆周运动的基本概念和匀速圆周运动的特点。
我们将详细解释圆周运动的定义、相关量的计算方法以及匀速圆周运动的特征和规律。
3. 结论:在结论部分,我们将给出匀速圆周运动的平均加速度的定义,并探讨它与其他因素的关系。
我们将通过分析实际案例和数学推导来阐释匀速圆周运动平均加速度的特点和影响因素。
通过上述结构,我们将全面而系统地介绍匀速圆周运动平均加速度的关系,帮助读者深入理解和应用相关知识。
1.3 目的本文的目的是探讨匀速圆周运动的平均加速度与其他因素的关系。
在物理学中,圆周运动是一种常见的运动形式,它涉及物体在一个圆形轨道上运动,并保持匀速运动的特点。
而加速度是描述物体加速度变化的物理量,它与物体的速度和时间变化有关。
我们希望通过研究匀速圆周运动的平均加速度,探讨以下问题:匀速圆周运动的平均加速度与半径的关系、与周期的关系、与线速度的关系等。
匀速圆周运动的加速度公式

匀速圆周运动的加速度公式《匀速圆周运动的加速度公式,你懂了吗?》嘿,朋友们!今天咱们来聊聊匀速圆周运动的加速度公式。
你想想,像游乐场里的旋转木马,是不是一直在做圆周运动呀?其实,任何做匀速圆周运动的物体,都有一个特定的加速度。
这个加速度公式就是:$a = v^2/r$ ,这里的$a$是加速度,$v$是线速度,$r$是圆周运动的半径。
比如说,有个小珠子在一个半径为 1 米的圆盘上,以 2 米每秒的线速度做匀速圆周运动。
那咱们算算,它的加速度就是$2^2÷1 = 4$米每秒平方。
怎么样,是不是感觉还挺简单的?只要记住这个公式,再找对线速度和半径,就能算出加速度啦!《搞懂匀速圆周运动的加速度公式,其实不难!》朋友们,咱们一起来看看匀速圆周运动的加速度公式!不知道大家有没有观察过时钟的指针,它就是在做匀速圆周运动。
那它的加速度怎么算呢?这就要用到咱们的公式啦。
公式是$a = v^2/r$。
比如说,一辆玩具车在圆形轨道上跑,线速度是 3 米每秒,轨道半径是 2 米。
那加速度就是$3^2÷2 = 4.5$米每秒平方。
就像这样,生活中有好多匀速圆周运动的例子,咱们都能用这个公式算出来它们的加速度。
多观察,多思考,这个公式就能轻松掌握啦!《匀速圆周运动的加速度公式,一学就会!》亲爱的小伙伴们,今天咱们来学学匀速圆周运动的加速度公式。
比如说,你在公园里玩那种旋转的秋千,这就是匀速圆周运动。
那怎么知道它的加速度呢?公式是$a = v^2/r$ 。
假设一个小球在半径为 0.5 米的圆圈里,以 1 米每秒的速度转,那加速度就是$1^2÷0.5 = 2$米每秒平方。
是不是一下子就明白了?只要记住这个公式,遇到类似的问题,都能迎刃而解!《轻松理解匀速圆周运动的加速度公式》小伙伴们,咱们来聊聊匀速圆周运动的加速度公式,别怕,很简单的!想象一下,一个自行车的轮子在转,这就是匀速圆周运动。
咱们的加速度公式是$a = v^2/r$ 。
匀变速率圆周运动切向加速度和法向加速度

匀变速率圆周运动切向加速度和法向加速度匀变速率圆周运动是物理学中比较常见的一种运动形式,它的特点是物体在圆周路径上做匀速运动,并且速度大小在不断变化。
针对这种运动形式,我们需要了解一些重要概念,其中包括切向加速度和法向加速度。
一、匀变速率圆周运动的概念匀变速率圆周运动是指物体在圆周路径上做匀速运动,并且速度大小在不断变化。
在这种运动中,物体沿着一个固定的圆周运动,所以它的运动轨迹可以用半径为r的圆周表示。
二、切向加速度和法向加速度的概念1. 切向加速度在匀变速率圆周运动中,物体的速度大小在不断变化,因此它有一个切向方向上的加速度,也就是切向加速度。
切向加速度的方向与速度变化的方向相同,它的大小可以根据公式at=v2/r来计算,其中v 表示速度大小,r表示圆周半径。
2. 法向加速度在匀变速率圆周运动中,物体始终沿着一个圆周路径运动,因此它还有一个与切向方向垂直的方向上的加速度,也就是法向加速度。
法向加速度的大小可以根据公式an=v2/r来计算,其中v表示速度大小,r表示圆周半径。
三、切向加速度和法向加速度的关系和意义1. 切向加速度和法向加速度的关系在匀变速率圆周运动中,切向加速度和法向加速度两者之间是相互独立的,但它们的合成结果却是物体的加速度方向和大小。
可以根据勾股定理来计算加速度大小,即a=√(at2+an2)。
2. 切向加速度和法向加速度的意义切向加速度和法向加速度分别决定了物体在匀变速率圆周运动中的速度大小和运动方向。
在现实生活中很多运动都属于匀变速率圆周运动,例如汽车在转弯时的运动、摩托车在曲线行驶时的运动等。
值得注意的是,在做匀变速率圆周运动时,切向加速度和法向加速度对物体运动的影响是不可或缺的,因此要对这两个概念有一个清晰的认识,才能更好地理解这种运动形式。
同时,它们在很多物理学应用中也是非常重要的概念,例如在地球上人的体重变化、星球运动及太阳系的运动等方面都有它们的应用。
匀速圆周运动的特点和计算

匀速圆周运动的特点和计算匀速圆周运动是指物体在圆周路径上以恒定速度运动的现象。
它具有以下特点:1.速度大小恒定:在匀速圆周运动中,物体沿圆周路径的速度大小保持不变。
2.速度方向变化:虽然速度大小不变,但物体在圆周路径上运动时,速度方向不断变化,始终指向圆心。
3.向心加速度:匀速圆周运动中,物体受到一个指向圆心的向心加速度,其大小为a=v²/r,其中v为速度大小,r为圆周半径。
4.向心力:向心加速度是由向心力引起的,其大小为F=m*a,其中m为物体的质量。
5.周期性:匀速圆周运动的物体每隔一定时间会回到起点,这个时间称为周期,用T表示。
6.角速度:匀速圆周运动的物体在单位时间内转过的角度称为角速度,用ω表示。
其大小为ω=2π/T。
匀速圆周运动的计算公式如下:1.线速度v与角速度ω、半径r的关系:v=ω*r。
2.向心加速度a与速度v、半径r的关系:a=v²/r。
3.向心力F与质量m、向心加速度a的关系:F=m*a。
4.周期T与角速度ω的关系:T=2π/ω。
5.角速度ω与频率f的关系:ω=2π*f,其中频率f是单位时间内圆周运动的次数。
以上是匀速圆周运动的特点和计算方法的详细介绍,希望能对您有所帮助。
习题及方法:一辆自行车以6m/s的速度在圆形路径上匀速运动,圆形路径的半径为6m,求自行车的向心加速度和向心力。
根据向心加速度公式a=v²/r,将速度v=6m/s和半径r=6m代入,得到向心加速度a=6²/6=6m/s²。
根据向心力公式F=m a,需要知道自行车的质量m,假设自行车质量为m=10kg,将向心加速度a=6m/s²和质量m=10kg代入,得到向心力F=106=60N。
一个物体在半径为5m的圆形路径上做匀速圆周运动,角速度为ω=4π/s,求物体的线速度和周期。
根据线速度公式v=ωr,将角速度ω=4π/s和半径r=5m代入,得到线速度v=4π5=20πm/s。
2022-2023学年高一物理人教版2019学案典例练习6.3向心加速度

6.3 向心加速度一、匀速圆周运动的加速度方向1.定义:物体做匀速圆周运动时的加速度总指向,这个加速度叫作.2.向心加速度的作用:向心加速度的方向总是与速度方向,故向心加速度只改变速度的,不改变速度的.二、匀速圆周运动的加速度大小:a n =或a n =.运动,也适用于运动. 【参考答案】圆心向心加速度垂直方向大小v 2r ω2r 匀速圆周非匀速圆周考点一:向心加速度的概念、公式和推导【例1】 下列关于向心加速度的说法错误的是( )A .向心加速度的方向始终与速度方向垂直B .向心加速度只改变线速度的方向,不改变线速度的大小C .物体做圆周运动时的加速度方向始终指向圆心D .物体做匀速圆周运动时的加速度方向始终指向圆心【答案】C【详解】A .向心加速度的方向沿半径指向圆心,速度方向则沿圆周的切线方向,向心加速度的方向始终与速度方向垂直,选项A 正确;B .向心加速度只改变线速度的方向,不改变线速度的大小,选项B 正确;CD .物体做匀速圆周运动时,只有向心加速度,加速度方向始终指向圆心,物体做变速圆周运动时,加速度的方向并不始终指向圆心,选项C 错误,D 正确。
故选C 。
【变式练习】1.对于匀速圆周运动,下列说法错误的是( )A .线速度不变B .角速度不变C .加速度发生变化D .周期不变【答案】A【详解】A .匀速圆周运动线速度的大小不变,方向时刻改变,故A 错误;BD .匀速圆周运动角速度不变,基础知识梳理典型例题分析根据2T πω=可知周期不变,故BD 正确;C .匀速圆周运动的加速度始终与速度方向垂直,加速度的大小不变,方向时刻改变,故C 正确。
本题选错误项,故选A 。
2.下列说法中正确的是( )A .向心加速度表示做圆周运动的物体速率改变的快慢B .向心加速度描述线速度方向变化的快慢C .在匀速圆周运动中,向心加速度是恒定的D .匀速圆周运动是匀变速曲线运动【答案】B【详解】AB .匀速圆周运动中速率不变,向心加速度描述线速度方向变化的快慢,故A 错误,B 正确;CD .匀速圆周运动中,向心加速度的大小不变,方向时刻变化,所以匀速圆周运动是变加速曲线运动,故CD 错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返回
知识学习 ——自主探究 合作学习
一、向心加速度
(1)方向:沿半径指向圆心
(2)大小:
a v2 r
a 2r
a
4 2
T2
r
返回
知识学习 ——自主探究 合作学习
做一做: 用一根细线系一个小球,使小球在水平面内做
匀速圆周运动。
观察并思考: 1.手所受的拉力情况如何? 2.小球的受力情况如何? 3.线的拉力方向有何特点? 4.一旦线断或者松手,结果如何?
返回
知识学习 ——自主探究 合作学习
二、向心力
⑴定义:做匀速圆周运动的物体受到的沿半径指向 圆心的力,这个力叫向心力。
⑵方向:总是指向圆心,与速度方向垂直。 ⑶特点:①只改变速度方向,不改变速度大小
②是根据作用效果命名的。
返回
知识学习 ——自主探究 合作学习
介绍向心力演示器 演示实验(利用控制变量法) ——演示向心力F与v、ω、r的关系
返回
疑难解答
这三道题模型尽管不同,但是在解题过程中似乎有相 同之处,请问老师,解答这类题目的一般思路是什么?
返回
疑难解答
这三道题模型尽管不同,但是在解题过程中似乎有相 同之处,请问老师,解答这类题目的一般思路是什么? 解答:这个问题问得好。 对于“匀速圆周运动,向心力是由合外力提供(充当)的”, 这一点很重要,所以在匀速圆周运动中,①明确研究对象, ②通过受力分析得到合外力后,也就得到了向心力,这是一 条重要的思路。
D.球A对筒壁的压力一定大于球B对筒
答案:AB
返回
家庭作业
1、甲乙两个质点绕同一圆心做匀速圆周运动,已知甲乙两 物体的质量之比为2:1,甲的转动半径是乙转动半径的的3/4, 当甲转了60周时,乙转了45周,则甲乙两质点的向心力之 比是多少?
2、内壁光滑的半球形容器,可绕过球 心O的竖直转轴O1O2转动,在容器中放 一个小物体p (可视为质点)。当容器 以某一角速度ω旋转时,物体P在图中所 示位置恰能保持相对静止。已知球的半 径为R,求角速度ω。
演示实验(利用控制变量法) (1)ω不变,r不同(2)v不变,r不同 (3) r相同, ω不同
返回
知识学习 ——自主探究 合作学习
(4)向心力公式
v2 F m
r
F m2r
F m 4 2 r
T2
返回
典型例题 ——自主探究 合作学习
例1:(课本22页第3题)一部机器由电动机带动,机器上的 皮带轮的半径是电动机皮带轮半径的3倍,如图所示,皮带与 两轮之间不发生滑动。已知机器皮带轮边缘上一点的向心加 速度为0.1m/s2。 (1)电动机皮带轮与机器皮带轮的转速比n1:n2是多少? (2)机器皮带轮上A点到转轴的距离为轮半径的一半,A点 的向心加速度是多少? (3)电动机皮带边缘上某点的向心加速度是多少?
向心加速度 向心力
淄博一中 物理组
学习目标 家庭作业
知识学习 挑战自我
典型例题 疑难解答
归纳总结
5分钟检测 (复习篇)
反馈训练
5分钟检测 (巩固篇)
学习目标
1. 理解向心力和向心加速度的概念。 2.知道向心力与向心加速度大小与哪些因素有关, 理解公式的确切含义,并能用来进行有关计算。 3.知道在变速圆周上某一点的向心力和加速度。
返回
挑战自我
有一种叫“飞椅”的游乐项目, 示意图如图所示,长为L的钢绳 一端系着座椅,另一端固定在半 径为r的水平转盘边缘,转盘可绕 穿过其中心的竖直轴转动。当转 盘以角速度ω匀速转动时,钢绳 与转轴在同一竖直平面内,与竖 直方向的夹角为θ,不计钢绳的 重力,求转盘转动的角速度ω与 夹角θ的关系。
答案:1:1:3;2:1:2;2:1:6
返回
反馈训练
2、如图所示,一个内壁光滑的圆锥形 筒的轴线垂直于水平面,圆锥筒固定不 动,两个质量相同的小球A和B紧贴着 内壁分别在图中所示的水平面内做匀速 圆周运动,则 A.球A的线速度一定大于球B的线速度 B.球A的角速度一定小于球B的角速度 C.球A的运动周期一定小于球B的运动
返回
5分钟检测——复习篇
A、B两轮通过皮带传动,C轮与A轮同轴,它们的半径 之比是RARBRC=1:2:3,如图所示,求 (1)三轮边缘的线速度之比vA:vB:vC (2)三轮角速度之比ωA:ωB:ωC
答案:1:1:3;2:1:2
返回
5分钟检测——巩固篇
如图所示,质量为1kg的小球用长为 0.5m的细线悬挂在O点,O点距地面高 度为1m,如果使小球绕OO/轴在水平面 内做圆周运动,若细线拉力为12.5N就 会拉断,g取10m/s2, 求:当小球的角速度多大时细线将断裂?
答案:5rad/s
返回
返回
典型例题 ——自主探究 合作学习
例2:(课本25页第3题)一个圆盘 在水平面内匀速转动,角速度为 4rad/s。盘面上距圆盘重心0.10m的 位置有一个质量为0.10kg的小物体在 随圆盘一起做匀速圆周运动,如图 所示。
(1)物体受到的摩擦力是静摩擦力还是滑动摩擦力? (2)关于小物体所受的向心力,甲乙两人有不同意见: “甲认为这个向心力等于圆盘对小物体的静摩擦力,指向 圆心;乙认为小物体有向前运动的趋势,静摩擦力方向和 相对运动方向相反,即向后,而不是与运动方向垂直,因 此向心力不可能是静摩擦力。你的意见是什么?说明理由。
返回
归纳总结
向心力加速度
a v2 r
a 2r
a
4 2
T2
r
由牛顿第 二定律
向心力
F m v2 r
F m2r
F
m
4 2T2rFra bibliotek返回反馈训练
1、A、B两轮通过皮带传动,C轮与A轮同轴,它们的半径 之比是RA:RB:RC=1:2:3,如图所示,求 (1)三轮边缘的线速度之比vA:vB:vC (2)三轮角速度之比ωA:ωB:ωC (3)三轮边缘的点的向心加速度aA:aB:aC
返回
知识学习 ——自主探究 合作学习
1、速度的变化量与初速度、末速度矢量图形关系。
2、匀速圆周运动的速度的变化量与初速度、末速度矢 量图形关系。 3、当速度的变化量无限减小时,其方向趋于指向圆心 吗?匀速圆周运动的加速度(瞬时)指向圆心吗? 4、匀速圆周运动的速度的变化量的大小如何用线速度 的大小和对应角去表示?用到那些数学知识和处理思想?
