2009-2010年1时间序列参考答案(A卷)

合集下载

时间序列考试A卷——答案 2

一、单项选择题1. t X 的k 阶差分是【 C 】（A ）k t t t k X X X -∇=- （B ）11k k k t t t k X X X ---∇=∇-∇ （C ）111k k k t t t X X X ---∇=∇-∇ （D ）1112k k k t t t X X X ----∇=∇-∇ 2. MA(2)模型121.10.24t t t t X εεε--=-+，则移动平均部分的特征根是【 A 】（A ）10.8λ=，20.3λ= （B ）10.8λ=-，20.3λ= （C ）10.8λ=-，20.3λ=- （D ）10.8λ=-，20.2λ= 3.关于差分121.30.40t t t X X X ---+=，其通解是【 D 】（A ）1(0.80.3)t t C + （B ） 1(0.80.5)t t C + （C ） 120.80.3t t C C + （D ）120.80.5t t C C +4. AR(2)模型121.10.24t t t t X X X ε--=-+，其中0.04t D ε=，则t t EX ε=【 B 】（A ）0 （B ） 0.04 （C ） 0.14 （D ）0.25. ARMA(2,1)模型1210.240.8t t t t t X X X εε-----=-，其延迟表达式为【 A 】（A ）2(10.24)(10.8)t t B B X B ε--=- （B ） 2(0.24)(0.8)t t B B X B ε--=- （C ）2(0.24)0.8t t B B X ε--=∇ （D ）2(10.24)t t B B X ε--=∇三、（15分）已知MA(2)模型为120.60.5t t t t X εεε--=-+，其中0.04t D ε=，（1）计算前3个逆函数，,1,2,3j I j =；----------------（8分）（2）计算()t Var X ；-----------------------------------（7分）解答：（1）t X 的逆转形式为：1t jt j t j X IX ε+∞-==+∑，或0()t j t j j I X ε+∞-==-∑------------（1分）将其代入原模型得：2212(10.60.5)(1)t t X B B I B I B X =-+----------（1分）比较B 的同次幂系数得：11:0.600.6B I I --=⇒=-———（2分）2212:0.60.500.14B I I I -++=⇒=———（2分） 33213:0.60.500.384B I I I I -++=⇒=———（2分）（2）12(0.60.5)0t t t t EX E εεε--=-+=———（1分）21212[(0.60.5)(0.60.5)]t t t t t t t EX E εεεεεε----=-+-+，———（2分）因为20,0.04,t s t s E t sεεεσ≠⎧=⎨==⎩———（2分）所以：222()(10.60.5)0.040.0644t t Var X EX ==++⨯=———（2分）四、（15分）已知AR(2)模型为(10.5)(10.3)t tB B X ε--=，20.5t D εεσ==。

时间序列试卷参考答案

时间序列试卷参考答案内蒙古财经学院2009——2010学年第一学期期末考试试卷《时间序列分析》试卷参考答案一、填空题（1分*20空=20分）1. 描述性2. 平稳性，白噪声3. 严平稳，宽平稳，宽平稳4. 时域分析方法，频域分析方法5. 纯随机性，2χ，1,:210>?==m H m ρρρ ，m k H k ≤≤≠?1,0:1ρ6. 否，一阶，12步，d(x,1,12)7. 差分运算，ARMA 模型8. 自回归9. t t x B ε=Φ)(二、不定项选择题（2分*5=10分）1 A C D ；2 A D ；3 A BD ；4 B ；5 A D三、判断并说明理由（10分）1.（5分）答：说法不完全正确。

模型的有效性检验指的是检验模型的有效性。

如果模型有效，则拟合残差应该不含有任何信息，即残差为纯随机序列；如果模型拟合不显著，则拟合残差应该残留未被模型提取充分的信息，即非纯随机序列。

所以模型的有效性检验等同于对残差进行纯随机性检验，而不是平稳性检验。

2.（5分）答：说法是错误的。

证明：2110110121)()()0,1,0(εσεεεεεεεεεt x Var x Var x x x x ARIMA t t t t t t t t t t t =+++=+++==++=+=----- 模型：例如即方差非齐次。

四、简答题：（第1小题15分，第2小题5分，本题共20分）1. 答：（1）平滑法是进行趋势分析和预测时常用的一种方法。

它是利用修匀技术，削弱短期随机波动对序列的影响，使序列平滑化，从而显示出长期趋势变化的规律（2）根据平滑技术的不同，平滑法可以具体分为移动平均法和指数平滑法。

移动平均法假定在一个比较短的时间间隔里，序列值之间的差异主要是由随机波动造成的。

根据这种假定，我们可以用一定时间间隔内的平均值作为某一期的估计值，具体公式为：++++++++++++=+-++---+--++----为偶数，为奇数，n x x x x x n n x x x x x n x n t n t t n t n t n t n t t n t n t t )2121(1)(1~2121222112112121 指数平滑法的思想是在实际生活中，我们会发现对大多数随机事件而言，一般都是近期的结果对现在的影响会大些，远期的结果对现在的影响会小些。

时间序列练习题答案

时间序列练习题答案一、选择题1. 时间序列分析中的自回归模型（AR）是指：A. 模型中的误差项B. 模型预测值依赖于自身过去的值C. 模型预测值依赖于其他变量的值D. 模型预测值依赖于未来的值2. 移动平均模型（MA）的主要特征是：A. 预测值依赖于过去的误差项B. 预测值依赖于过去的观测值C. 预测值依赖于未来的误差项D. 预测值依赖于未来的观测值3. 以下哪个不是时间序列分析中的平稳性检验方法？A. 单位根检验B. 协整检验C. KPSS检验D. 方差比检验4. 时间序列的差分操作通常用于：A. 消除季节性效应B. 消除趋势C. 消除周期性变化D. 消除随机波动5. 季节性调整的目的是：A. 消除随机波动B. 消除季节性效应C. 消除长期趋势D. 消除周期性变化二、简答题1. 简述自回归积分滑动平均模型（ARIMA）的基本组成部分。

2. 解释什么是时间序列的平稳性，并说明为什么在时间序列分析中需要考虑平稳性。

3. 描述季节性时间序列的特点，并说明如何识别和处理季节性效应。

三、计算题1. 给定以下时间序列数据：\[ y_t = \{10, 15, 20, 25, 30, 35, 40, 45, 50, 55\} \] 假设这是一个一阶自回归模型AR(1)，其中自回归系数φ=0.8。

请计算下一个时间点的预测值。

2. 假设一个时间序列模型的ACF（自相关函数）在滞后1时显著不为0，而在滞后2及以后时显著为0。

根据这个信息，推测该时间序列可能属于哪种类型的模型？四、案例分析题1. 某公司销售数据呈现明显的季节性变化，如何在时间序列分析中对数据进行季节性调整？2. 一个时间序列模型的ADF（Augmented Dickey-Fuller）检验结果表明存在单位根，这意味着什么？如何对数据进行处理以消除单位根？五、论述题1. 论述时间序列分析在金融领域中的应用，并举例说明。

2. 讨论时间序列分析中的因果关系检验方法，并说明在实际应用中如何选择合适的方法。

时间序列习题答案

时间序列习题答案时间序列习题答案时间序列分析是一种用来研究随时间变化的数据模式和趋势的方法。

它在经济学、金融学、统计学等领域中被广泛应用。

下面我将给出一些时间序列分析的习题，并附上详细的答案解析。

习题一：某公司过去一年的销售额如下：100, 120, 130, 140, 150, 160, 170, 180, 190, 200。

请计算该公司的平均销售额和年度增长率。

答案解析：首先，计算平均销售额的方法是将所有销售额相加，然后除以销售额的个数。

在这个例子中，销售额的个数为10，总销售额为100+120+130+140+150+160+170+180+190+200=1540。

因此，平均销售额为1540/10=154。

接下来，计算年度增长率的方法是将最后一年的销售额减去第一年的销售额，然后除以第一年的销售额，并乘以100%。

在这个例子中，最后一年的销售额为200，第一年的销售额为100。

因此，年度增长率为(200-100)/100*100%=100%。

习题二：某股票的每日收盘价如下：10.2, 10.5, 10.7, 10.9, 11.1, 11.3, 11.5, 11.7, 11.9, 12.1。

请计算该股票的平均收盘价和收益率。

答案解析：计算平均收盘价的方法与计算平均销售额的方法相同。

将所有收盘价相加，然后除以收盘价的个数。

在这个例子中，收盘价的个数为10，总收盘价为10.2+10.5+10.7+10.9+11.1+11.3+11.5+11.7+11.9+12.1=113.9。

因此，平均收盘价为113.9/10=11.39。

计算收益率的方法是将每日的收盘价减去前一日的收盘价，然后除以前一日的收盘价，并乘以100%。

在这个例子中，第二天的收盘价为10.5，第一天的收盘价为10.2。

因此，第二天的收益率为(10.5-10.2)/10.2*100%=2.94%。

习题三：某城市过去十年的月度平均气温如下：15, 18, 20, 22, 25, 28, 30, 29, 26, 23。

时间序列习题(含答案)

一、单项选择题 1．时间数列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的，后者是根据变量值大小排列的D 前者是根据变量值大小排列的，后者是根据时间顺序排列的 2．时间数列中，数值大小与时间长短有直接关系的是( )A 平均数时间数列B 时期数列C 时点数列D 相对数时间数列 3．发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数 4．计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平 5．某车间月初工人人数资料如下：则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( )A150万人 B150．2万人 C150．1万人 D 无法确定 7．由一个9项的时间数列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 8．采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度 9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为( )A 5%6.58 B 5%6.158 C 6%6.58 D 6%6.158 10．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( )A 简单平均法B 几何平均法C 加权序时平均法D 首末折半法 11、时间序列在一年内重复出现的周期性波动称为（）A 、长期趋势B 、季节变动C 、循环变动D 、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、B 二、多项选择题1．对于时间数列，下列说法正确的有( )A 数列是按数值大小顺序排列的B 数列是按时间顺序排列的C 数列中的数值都有可加性D 数列是进行动态分析的基础E 编制时应注意数值间的可比性 2．时点数列的特点有( )A 数值大小与间隔长短有关B 数值大小与间隔长短无关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的3．下列说法正确的有( )A 平均增长速度大于平均发展速度B 平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( )A %100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100％D %100⨯-=基期水平基期水平报告期水平增长速度E %100⨯=基期水平报告期水平增长速度 5．采用几何平均法计算平均发展速度的公式有( )A1231201-⨯⨯⨯⨯=n n a a a a a a a a nx Ba a nx n =C 1a a nx n= D nR x = E n xx ∑=6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有( )A 第二年的环比增长速度=定基增长速度=10％B 第三年的累计增长量=逐期增长量=200万元C 第四年的定基发展速度为135％D 第五年增长1％绝对值为14万元E 第五年增长1％绝对值为13．5万元 7．下列关系正确的有( )A 环比发展速度的连乘积等于相应的定基发展速度B 定基发展速度的连乘积等于相应的环比发展速度C 环比增长速度的连乘积等于相应的定基增长速度D 环比发展速度的连乘积等于相应的定基增长速度E 平均增长速度=平均发展速度-1 8．测定长期趋势的方法主要有( )A 时距扩大法B 方程法C 最小平方法D 移动平均法E 几何平均法9．关于季节变动的测定，下列说法正确的是( ) A 目的在于掌握事物变动的季节周期性 B 常用的方法是按月(季)平均法 C 需要计算季节比率D 按月计算的季节比率之和应等于400％E 季节比率越大，说明事物的变动越处于淡季 10．时间数列的可比性原则主要指( )A 时间长度要一致B 经济内容要一致C 计算方法要一致D 总体范围要一致E 计算价格和单位要一致1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．AE8．ACD 9．ABC 10．ABCDE 三、判断题1．时间数列中的发展水平都是统计绝对数。

(整理)《时间序列分析》试卷a答案.

2010—2011学年第一学期2007应用数学《时间序列分析》试卷A 答案一（18分，每空1分）1 112211t t t t t X X X a a ϕϕθ-----=-2 偏自相关函数；自相关函数3 矩估计法、最小二乘估计法、极大似然估计法4 B5 1ϕ；06 1,1,2,i i n λ<=7 m8利用序列图进行判断；利用样本自相关函数ˆk ρ进行平稳性检验；利用单位根检验进行判断9 12222011ˆ 1.96()t l a l X G G G σ+-±+++ 10 存在11 使得预测误差的均方値达到最小10 (1)S DB -二（8分，每小题1分）1 错；2错；3对；4对；5 错；6 错；7 错；8对三（12分，每小题2分）1 (1)2(10.80.5)t t X B B a =-+；(2) 21(10.5)(1 1.20.4)t t B X B B a --=-+2 (1) 稳定；（2）稳定3 （1）120.5,0.25G G ==; (2) 120.5,0G G =-=四（4分）AR{1}五（12分）（1）34321324321ˆ(1)(,,)([100.60.3],,)100.697.20.39696.12X E X X X X E X X a X X X ==+++=+⨯+⨯=；（2分）35321435321ˆ(2)(,,)([100.60.3],,)100.697.120.397.297.432X E X X X X E X X a X X X ==+++=+⨯+⨯=；（2分） 36321546321ˆ(3)(,,)([100.60.3],,)100.697.4320.397.1297.5952X E X X X X E X X a X X X ==+++=+⨯+⨯= （2分）（2）010110.6G G G ϕ===221/21/2011.96() 1.966 1.3613.7144G G σ+=⨯⨯=五月份销售额的 95%的置信区间为(83.7176,111.1464) （2分）六（50分）1 （1）AR(1)模型：10.667831t t t X X a -=+ （5分）疏系数的ARMA(1,6)模型：160.5578970.47526t t t t X X a a --=++ （5分）（2）上边AR(1)模型的AIC 值为-0.804969，第二个模型的AIC 值为-0.876542，根据AIC 准则可知，第二个模型拟合效果更好。

时间序列分析参考答案

时间序列分析参考答案时间序列分析参考答案时间序列分析是一种研究随时间变化的数据模式和趋势的统计方法。

它可以帮助我们理解数据的变化规律，预测未来的趋势，以及制定相应的决策。

在本文中，我们将探讨时间序列分析的基本概念、方法和应用。

一、时间序列分析的基本概念时间序列是按照时间顺序排列的一系列数据观测值。

它可以是连续的，比如每天的股票价格，也可以是离散的，比如每月的销售额。

时间序列分析的目标是找出数据中的模式和趋势，以便进行预测和决策。

时间序列分析的基本概念包括趋势、季节性和周期性。

趋势是指数据在长期内的整体变化方向，可以是上升、下降或平稳。

季节性是指数据在一年中周期性重复出现的变化模式，比如节假日销售额的增长。

周期性是指数据在较长时间内出现的波动，通常周期长度大于一年。

二、时间序列分析的方法时间序列分析的方法包括描述性分析、平稳性检验、模型建立和预测等。

描述性分析是对时间序列数据进行可视化和统计分析，以了解数据的基本特征。

常用的描述性分析方法包括绘制折线图、直方图和自相关图等。

折线图可以显示数据的整体趋势和季节性变化，直方图可以展示数据的分布情况，自相关图可以帮助我们发现数据的相关性。

平稳性检验是判断时间序列数据是否具有平稳性的方法。

平稳性是指数据的均值和方差在时间上保持不变。

常用的平稳性检验方法包括单位根检验和ADF检验等。

模型建立是根据时间序列数据的特征，选择合适的模型来描述数据的变化规律。

常用的模型包括AR模型、MA模型和ARMA模型等。

AR模型是自回归模型，表示当前观测值与过去观测值之间的线性关系；MA模型是移动平均模型，表示当前观测值与过去观测值的误差之间的线性关系；ARMA模型是自回归移动平均模型，综合考虑了自回归和移动平均的效果。

预测是利用已知的时间序列数据，通过建立模型来预测未来的观测值。

常用的预测方法包括滚动预测、指数平滑法和ARIMA模型等。

滚动预测是指根据当前观测值和过去观测值的模型，逐步预测未来的观测值；指数平滑法是基于历史数据的加权平均值，对未来的观测值进行预测；ARIMA模型是自回归移动平均差分整合模型，可以处理非平稳的时间序列数据。

时间序列分析习题答案

时间序列分析习题答案时间序列分析习题答案时间序列分析是一种广泛应用于统计学和经济学领域的方法，用于研究随时间变化的数据。

通过对时间序列数据的建模和分析，我们可以揭示数据背后的规律和趋势，从而进行预测和决策。

下面我将给出一些时间序列分析习题的答案，希望能对大家的学习和理解有所帮助。

1. 什么是时间序列？时间序列是按照时间顺序排列的一系列数据观测值。

它可以是连续的，比如每天的股票价格，也可以是离散的，比如每个月的销售额。

时间序列分析的目标是通过对这些数据的分析和建模，揭示数据背后的规律和趋势。

2. 时间序列分析的步骤是什么？时间序列分析一般包括以下几个步骤：- 数据收集：收集并整理时间序列数据，确保数据的准确性和完整性。

- 数据可视化：通过绘制时间序列图，观察数据的趋势、季节性和周期性等特征。

- 数据平稳性检验：通过统计检验方法，判断时间序列数据是否平稳。

如果不平稳，需要进行差分处理。

- 模型选择：根据数据的特征和目标，选择适合的时间序列模型，比如ARIMA模型、季节性ARIMA模型等。

- 模型拟合：利用选定的模型，对时间序列数据进行拟合和参数估计。

- 模型诊断：对拟合的模型进行诊断，检验模型的残差序列是否符合模型假设。

- 模型预测：利用已拟合的模型，对未来的数据进行预测。

3. 如何判断时间序列数据的平稳性？平稳性是时间序列分析的基本假设之一，它要求时间序列的均值、方差和自相关函数在时间上都是常数。

常用的平稳性检验方法有：- 绘制时间序列图：观察数据是否具有明显的趋势、季节性和周期性。

- 平稳性统计检验：常用的统计检验方法有ADF检验、KPSS检验等。

这些检验方法的原理是基于单位根检验，判断序列是否存在单位根，从而判断序列的平稳性。

4. 如何选择适合的时间序列模型？选择适合的时间序列模型需要考虑数据的特征和目标。

常用的时间序列模型有：- AR模型：自回归模型，利用过去的观测值对当前值进行预测。

- MA模型：移动平均模型，利用过去的白噪声误差对当前值进行预测。

《时间序列》试卷答案

《时间序列》试卷答案【篇一：时间序列分析试卷及答案3套】>一、填空题（每小题2分，共计20分）1. arma(p, q)模型_________________________________，其中模型参数为____________________。

2. 设时间序列?xt?，则其一阶差分为_________________________。

3. 设arma (2, 1)：xt?0.5xt?1?0.4xt?2??t?0.3?t?1则所对应的特征方程为_______________________。

4. 对于一阶自回归模型ar(1): xt?10＋?xt?1??t，其特征根为_________，平稳域是_______________________。

5. 设arma(2, 1):xt?0.5xt?1?axt?2??t?0.1?t?1，当a满足_________时，模型平稳。

6. 对于一阶自回归模型______________________。

7. 对于二阶自回归模型ar(2):xt?0.5xt?1?0.2xt?2??tma(1):xt??t?0.3?t?1，其自相关函数为则模型所满足的yule-walker方程是______________________。

8. 设时间序列?xt?为来自arma(p,q)模型：xt??1xt?1?l??pxt?p??t??1?t?1?l??q?t?q则预测方差为___________________。

9. 对于时间序列?xt?，如果___________________，则xt~i?d?。

10. 设时间序列?xt?为来自garch(p，q)模型，则其模型结构可写为_____________。

二、（10分）设时间序列?xt?来自arma?2,1?过程，满足1b0.5bx2t1?0.4bt,2其中??t?是白噪声序列，并且e??t??0,var??t。

（1）判断arma?2,1?模型的平稳性。

时间序列分析习题及答案

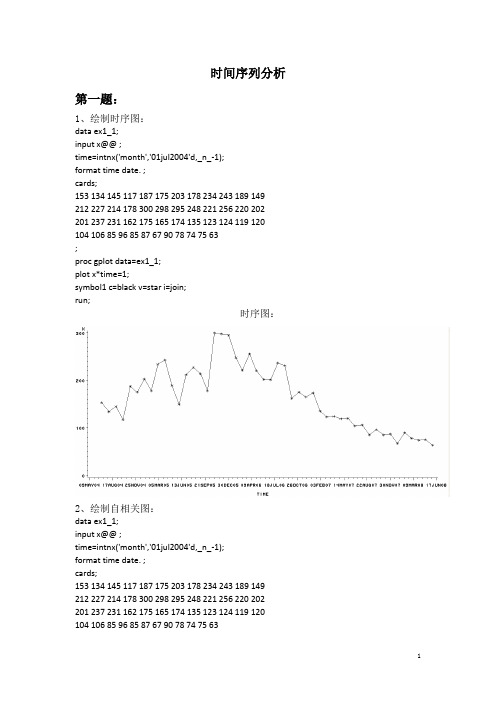
时间序列分析第一题：1、绘制时序图：data ex1_1;input x@@ ;time=intnx('month','01jul2004'd,_n_-1);format time date. ;cards;153 134 145 117 187 175 203 178 234 243 189 149 212 227 214 178 300 298 295 248 221 256 220 202 201 237 231 162 175 165 174 135 123 124 119 120 104 106 85 96 85 87 67 90 78 74 75 63;proc gplot data=ex1_1;plot x*time=1;symbol1 c=black v=star i=join;run;时序图：2、绘制自相关图：data ex1_1;input x@@ ;time=intnx('month','01jul2004'd,_n_-1);format time date. ;cards;153 134 145 117 187 175 203 178 234 243 189 149 212 227 214 178 300 298 295 248 221 256 220 202 201 237 231 162 175 165 174 135 123 124 119 120 104 106 85 96 85 87 67 90 78 74 75 63;proc arima data=ex1_1;identify var=x;run;样本自相关图：白噪声检验输出结果：因为P值小于α，所以该序列为非白噪声序列，根据时序图看出数据并不在一个常数值附近随机波动，后期有递减的趋势，所以不是平稳序列。

第二题：1、选择拟合模型方法一：首先绘制该序列的时序图，直观检验序列平稳性。

时间序列习题(含答案)

一、单项选择题1．时间数列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的，后者是根据变量值大小排列的D 前者是根据变量值大小排列的，后者是根据时间顺序排列的 2．时间数列中，数值大小与时间长短有直接关系的是( )A 平均数时间数列B 时期数列C 时点数列D 相对数时间数列 3．发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数 4．计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平5．某车间月初工人人数资料如下：则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( )A150万人 B150．2万人 C150．1万人 D 无法确定 7．由一个9项的时间数列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 8．采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度 9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为( )A 5%6.58 B 5%6.158 C 6%6.58 D 6%6.158 10．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( )A 简单平均法B 几何平均法C 加权序时平均法D 首末折半法 11、时间序列在一年内重复出现的周期性波动称为（）A 、长期趋势B 、季节变动C 、循环变动D 、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、B 二、多项选择题1．对于时间数列，下列说法正确的有( )A 数列是按数值大小顺序排列的B 数列是按时间顺序排列的C 数列中的数值都有可加性D 数列是进行动态分析的基础E 编制时应注意数值间的可比性 2．时点数列的特点有( )A 数值大小与间隔长短有关B 数值大小与间隔长短无关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的3．下列说法正确的有( )A 平均增长速度大于平均发展速度B 平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( )A %100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100％D %100⨯-=基期水平基期水平报告期水平增长速度E %100⨯=基期水平报告期水平增长速度 5．采用几何平均法计算平均发展速度的公式有( )A1231201-⨯⨯⨯⨯=n n a a a a a a a a nx Ba a nx n =C 1a a nx n= D nR x = E n x x ∑=6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有( )A 第二年的环比增长速度=定基增长速度=10％B 第三年的累计增长量=逐期增长量=200万元C 第四年的定基发展速度为135％D 第五年增长1％绝对值为14万元E 第五年增长1％绝对值为13．5万元 7．下列关系正确的有( )A 环比发展速度的连乘积等于相应的定基发展速度B 定基发展速度的连乘积等于相应的环比发展速度C 环比增长速度的连乘积等于相应的定基增长速度D 环比发展速度的连乘积等于相应的定基增长速度E 平均增长速度=平均发展速度-1 8．测定长期趋势的方法主要有( )A 时距扩大法B 方程法C 最小平方法D 移动平均法E 几何平均法9．关于季节变动的测定，下列说法正确的是( ) A 目的在于掌握事物变动的季节周期性 B 常用的方法是按月(季)平均法 C 需要计算季节比率D 按月计算的季节比率之和应等于400％E 季节比率越大，说明事物的变动越处于淡季 10．时间数列的可比性原则主要指( )A时间长度要一致 B经济内容要一致 C计算方法要一致 D总体范围要一致E计算价格和单位要一致1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．AE8．ACD 9．ABC 10．ABCDE三、判断题1．时间数列中的发展水平都是统计绝对数。

2010《时间序列分析》试卷A答案

2010—2011学年第一学期2007应用数学《时间序列分析》试卷A 答案一（18分，每空1分）1 112211t t t t t X X X a a ϕϕθ-----=-2 偏自相关函数；自相关函数3 矩估计法、最小二乘估计法、极大似然估计法4 B51ϕ；0 6 1,1,2,i i n λ<=7 m8利用序列图进行判断；利用样本自相关函数ˆk ρ进行平稳性检验；利用单位根检验进行判断9 12222011ˆ 1.96()t l a l X G G G σ+-±+++ 10 存在11 使得预测误差的均方値达到最小10 (1)S DB -二（8分，每小题1分）1 错；2错；3对；4对；5 错；6 错；7 错；8对三（12分，每小题2分）1 (1)2(10.80.5)t t X B B a =-+；(2) 21(10.5)(1 1.20.4)t t B X B B a --=-+2 (1) 稳定；（2）稳定3 （1）120.5,0.25G G ==; (2) 120.5,0G G =-=四（4分）AR{1}五（12分）（1）34321324321ˆ(1)(,,)([100.60.3],,)100.697.20.39696.12X E X X X X E X X a X X X ==+++=+⨯+⨯=；（2分）35321435321ˆ(2)(,,)([100.60.3],,)100.697.120.397.297.432X E X X X X E X X a X X X ==+++=+⨯+⨯=；（2分）36321546321ˆ(3)(,,)([100.60.3],,)100.697.4320.397.1297.5952X E X X X X E X X a X X X ==+++=+⨯+⨯= （2分）（2）010110.6G G G ϕ===221/21/2011.96() 1.966 1.3613.7144G G σ+=⨯⨯=五月份销售额的 95%的置信区间为(83.7176,111.1464) （2分）六（50分）1 （1）AR(1)模型：10.667831t t t X X a -=+ （5分）疏系数的ARMA(1,6)模型：160.5578970.47526t t t t X X a a --=++ （5分）（2）上边AR(1)模型的AIC 值为-0.804969，第二个模型的AIC 值为-0.876542，根据AIC 准则可知，第二个模型拟合效果更好。

时间序列分析试卷及答案

时间序列分析试卷1一、填空题（每小题2分，共计20分）1. ARMA(p, q)模型_________________________________，其中模型参数为____________________。

2. 设时间序列{}t X ，则其一阶差分为_________________________。

3. 设ARMA (2, 1)：1210.50.40.3t t t t t X X X εε---=++-则所对应的特征方程为_______________________。

4. 对于一阶自回归模型AR(1): 110t t t X X φε-=+＋，其特征根为_________，平稳域是_______________________。

5. 设ARMA(2, 1):1210.50.1t t t t t X X aX εε---=++-，当a 满足_________时，模型平稳。

6. 对于一阶自回归模型MA(1):10.3t t t X εε-=-，其自相关函数为______________________。

7. 对于二阶自回归模型AR(2):120.50.2t t t t X X X ε--=++则模型所满足的Yule-Walker 方程是______________________。

8. 设时间序列{}t X 为来自ARMA(p,q)模型：1111t t p t p t t q t q X X X φφεθεθε----=++++++L L则预测方差为___________________。

9. 对于时间序列{}t X ，如果___________________，则()~t X I d 。

10. 设时间序列{}t X 为来自GARCH(p ，q)模型，则其模型结构可写为_____________。

二、（10分）设时间序列{}t X 来自()2,1ARMA 过程，满足()()210.510.4ttB B X B ε-+=+,其中{}t ε是白噪声序列，并且()()2t t 0,E Var εεσ==。

时间序列分析试卷及答案

时间序列分析试卷1一、填空题（每小题2分，共计20分）1. ARMA(p, q)模型_________________________________，其中模型参数为____________________。

2. 设时间序列{}t X ，则其一阶差分为_________________________。

3. 设ARMA (2, 1)：1210.50.40.3t t t t t X X X εε---=++-则所对应的特征方程为_______________________。

4. 对于一阶自回归模型AR(1): 110t t t X X φε-=+＋，其特征根为_________，平稳域是_______________________。

5. 设ARMA(2, 1):1210.50.1t t t t t X X aX εε---=++-，当a 满足_________时，模型平稳。

6. 对于一阶自回归模型MA(1):10.3t t t X εε-=-，其自相关函数为______________________。

7. 对于二阶自回归模型AR(2):120.50.2t t t t X X X ε--=++则模型所满足的Yule-Walker 方程是______________________。

8. 设时间序列{}t X 为来自ARMA(p,q)模型：1111t t p t p t t q t q X X X φφεθεθε----=++++++则预测方差为___________________。

9. 对于时间序列{}t X ，如果___________________，则()~t X I d 。

10. 设时间序列{}t X 为来自GARCH(p ，q)模型，则其模型结构可写为_____________。

二、（10分）设时间序列{}t X 来自()2,1ARMA 过程，满足()()210.510.4ttB B X B ε-+=+,其中{}t ε是白噪声序列，并且()()2t t 0,E Var εεσ==。

内蒙古财经学院时间序列试卷答案

内蒙古财经学院2009——2010学年第一学期期末考试试卷《时间序列分析》试卷参考答案五、计算题：1.检验下列模型的平稳性和可逆性（3分+7分=10分）（1）1t t 1-t t 6.18x .0x -++=εε （2）2t 1t t 2t 1-t t 5.06.14x .18x .0x ---+++-=εεε 解：（1）16.16.118.08.011>=-=<==θφ，模型平稳、不可逆；（2）12.28.04.116.04.18.014.14.112122<-=--=-<-=-=+>=-=φφφφφ，所以模型非平稳；11.16.15.011.26.15.015.05.012122>=+-=-<-=--=+<=-=θθθθθ，所以模型不可逆，综合以上，该模型不平稳不可逆2. （1）对于任意常数c ，如下定义的无穷阶MA 序列一定是非平稳序列：（10分） ),0(~),(221εσεεεεW N C x t t t t t +++=--（2）{}t x 的一阶差分序列一定是平稳序列。

1--=t t t x x y 证明：（1）常数≠+++=+++==+++=----)())((0))((22222121 εεεσσσεεεεεεC C Var Varx C E Ex t t t t t t t t 所以序列是非平稳序列。

（2）1321211)1()()(--------+=+++-+++=-=t t t t t t t t t t t C C C x x y εεεεεεεε 常数=-+=-+==-+=--22211)1())1((0))1((εεσσεεεεC C Var Vary C E Ey t t t t t t所以一阶差分序列是平稳序列。

3.使用指数平滑法得到5~1=-t x ，26.5~1=+t x ，已知序列观察值25.5=t x ，5.51=+t x ，求指数平滑系数α。

应用时间序列A卷答案

优质文本一、填空题（24分，每题3分） 1.对任意的T t t n ∈,...1和任意的h 使得n i T h t i ,...,2,1,=∈+有()()()()h t X h t X h t X n +++,...,,21与()()()()n t X t X t X ,...,,21相同的联合分布；2.()()⎪⎩⎪⎨⎧=•<∀-+++=--0,,0...211t s t tp t p t t X E t s WN X X X εσεεφφ; 3. 231,231-+; 4. 拖尾; 5 连续型时间序列分析和离散型时间序列分析;6.频域分析和时域分析;7. 矩估计、极大似然估计和最小二乘估计 8 AIC 和SBC;二、简答题（共20分，每题10分）1．（本题10分）解：（1）时间序列分析方法强调变量值序列顺序的重要性；2分（2）时间序列各观察值之间存在一定的依存关系； 2分（3）时间序列分析根据自身的变化规律来预测未来； 2分（4）时间序列是一组随机变量的一次样本实现； 2分（5）时间序列分析和回归分析的建模思路不同。

2分2.（本题10分）解：（1）模型识别：即确定自回归模型阶数p 和移动平均模型阶数q 。

2 分（2）参数估计：即给出均值、自回归参数和移动平均参数，以与白噪音方差2σ的估计值。

3分（3）模型的检验和模型选择：对所选择的不同阶数p 和q 的值，重复估计步骤，直至选出最优模型为止。

3 分（4）应用信息准则法进行模型优化选择。

2 分三．证明题（共12分）证明：()t f 是具有周期T 的函数，因而是有界函数，ε是区间(0,T)上均匀分布的随机变量，因而()()()()011=+•+=•+=⎰⎰t d Tt f d Tt f X E TTεεεε 5分为常数，()()()()()()()()()[]()()[]()()⎩⎨⎧≠-=-=•=-•-=nTs t nTs t t X s X t X E s X E s X t X E t X E s t ,0,var ,γ 5分因而()t X 的二阶矩都存在，均值函数为常数，协方差函数只与t-s 有关，因而为宽平稳过程。

时间序列期末考试A卷答案

第(-)学期考试试卷课程代码6024000课程名称时间序列分析B(A卷)考试时间____________(注：匕｝为均值为零的白噪声序列)一、单项选择题(从下列各题四个备选答案中选出一个正确答案，并将其字母代号写在该题【1 内。

答案错选或未选者,该题不得分。

每小题4分,共20分。

)1.X,的k阶差分是【C】(A) Px严Xt—X.k(B) 丁X严P-'X厂p-'Xj(c) =v A-,x/-v A-'x/_1(D)v*x r=V A-,X,_1-V A-,X/_22.MA⑵模型X f=^-1.1£-Z_I+0.24^_2,则移动平均部分的特征根是【A】(A)人=0.8, /U=0.3 (B) =-0.8, /U=0.3(C)人=-0.8, = -0.3 (D) & =一0.8,入=0.23•关于差分X,—1.3Xi+0.4X一2=0,其通解是【D】(A) q(08+0.3‘)(B) q(o.&+o.5『)(C) qO.S+C/O.M (D) Cfi.S1+C20S4.AR(2)模型X, =£—l.lXj+0.24X_2，其中£>£=0.04,则EX 禺=[B 】(A) 0 (B) 0.04(C) 0.14 (D) 0.25.ARMA(2,l)tMgy X, -X,., -0.24X z_2 =^; -0.8^,.,,其延迟表达式为【A 】(A) (l-B-0.24B2)X, =(l-0.8BX (B) (B2-B-0.24)%, =(B-0.8X(C) (B2-B-0.24)X f =0.8V^ (D) (1 -B-0.24/?2)X f = Vf r二、简答题(10分)对于均值为零的平稳序列，其自相关系数存在两个估计量，请写出两个估计量，并说出它们各自优缺点。

三、（15 分）已知 MA （2）模型为 X r =^-0.6^_,+0.5^_2,其中 Ds, = 0.04 ,（1）计算前3个逆函数，/…; = 1,2,3; -------------------------- （8分）（2）计算Var{X t ）；------------------------------------ （7 分）解答：（1） X 」勺逆转形式为：或J 壬 --------------------------------------------------------- （1分） /■]J-0将其代入原模型得：X, = （1 -0.6B + 0.5B 2）（1 -I.B- I 2B 2 • • •）%, -------- （1 分）比较B 的同次幕系数得：B:-Z 1-0.6 = 0=>/l =-0.6 ---------------- （2 分） B 2:-Z 2 + 0.6/, + 0.5 = 0 Z 2 = 0.14 ---------------- （2 分）肝：一人+0・6厶+0・5人=0=>厶=0.384 ------ （2分）（2） EX t = E （s j -0.6^ + 0.5^_2） = 0 ---------- （1 分）EX ； = E[（£ _0・6吕-]+0・5名-2）（吕 _0・6吕-]+0・5爲_2）]（2分）所以：Var （X z ） = EX ； = （1 + 0.62 + 0.52）x0.04 = 0.0644 -- （2 分）四、（15 分）已知 AR （2）模型为（1—0・53）（1-0・33）/=爲 Ds. =a ；= 0.5（1）计算偏相关系数％伙=123）； -------------------------------- （8分）（2） W/r （XJ ； ----------------------------------------- （7 分）解答（1）（l-0・5B ）（l-0・3B ）X 『 =X 『—O ・8X"i+O ・15X_=£,所以：％ =0.=-0」5对于A&2）模型其系数满足2阶Yule-Walker 方程:姑金“69565 和/金+ *“40652,产生偏相关系数的相关序列为，相应Yule-Wolker 方程为:‘1 p\/ 、 '1 P\ V 0.8、（PC<P1 16l.Pi 1315丿4所以:（2分）当£ = 2时, P\ P\Po >2ij =rpi~他」一1因为0, m b ； = 0.04, t= s将其代入原模型得：（1-加-02肝）丘手一广吕一（1分）7-0比较B 的同次幕系数得：G° = lB :G\- %G ()= 0 => G] = (p 、= £ -------- ( 2 分)3’ ： G, — %G] +(P 、G Q = 0 => G? = --------- ( 2 分) 225 553G 3 —(pfi 2 一(p 2G } =0=>G 3= 〜0」6385 -------- (2 分)^7P\=(P\\P Q 即 ®I =ZV 所以(Pw= P\ 0.69565% =[。

2009-2010年1时间序列参考答案(A卷)

时间序列考试A卷——答案 2

时间序列试卷参考答案

时间序列练习题答案

时间序列习题答案

时间序列习题(含答案)

(整理)《时间序列分析》试卷a答案.

时间序列分析参考答案

时间序列分析习题答案

《时间序列》试卷答案

时间序列分析习题及答案

时间序列习题(含答案)

2010《时间序列分析》试卷A答案

时间序列分析试卷及答案

时间序列分析试卷及答案

最新-2009-01时间序列分析06级期末a卷答案

内蒙古财经学院时间序列试卷 答案

应用时间序列A卷答案

时间序列期末考试A卷答案

内蒙古财经学院时间序列试卷答案