浙教版数学九年级上册3.2 图形的旋转同步练习.docx

合集下载

九年级数学上册 3.2 图形的旋转同步习题 (新版)浙教版-(新版)浙教版初中九年级上册数学试题

3.2 图形的旋转一、选择题（共10小题；共50分）1. 如图所示，和都为等腰直角三角形，若经旋转后能与重合，下列说法正确的是( )A. 旋转中心为点，旋转角为B. 旋转中心为点，旋转角为C. 旋转中心为点，旋转角为D. 旋转中心为点，旋转角为2. 如图，在中，，在同一平面内，将绕点旋转到的位置，使得，则( )A. B. C. D.3. 如图，将（其中，）绕点按顺时针方向旋转到的位置，使得点，，在同一条直线上，那么旋转角等于( )A. B. C. D.4. 如图，将矩形绕点顺时针旋转到矩形的位置，旋转角为．若，则( )A. B. C. D.5. 如图，中，，，，把绕点旋转后得到，则点的坐标为( )A. B. 或C. 或D.6. 如图，绕点逆时针旋转得到，若，，则的度数是( )A. B. C. D.7. 如图所示，两个圆中的一个圆是由另一个圆旋转而得到的，则它的旋转中心有( )A. 个B. 个C. 无数个D. 无法确定8. 如图，边长为的正方形绕着点逆时针旋转到正方形，图中阴影部分的面积为( )A. B. C. D.9. 如图，中，，，，且在直线上，将绕点顺时针旋转到①，可得到点，此时；将位置①的三角形绕点顺时针旋转到位置②，可得到点，此时；将位置②的三角形绕点顺时针旋转到位置③，可得到点，此时；；按此规律继续旋转，直到点为止，则等于( )A. B. C. D.10. 在锐角中，，，（如图），将绕点按逆时针方向旋转得到（顶点、分别与、对应），当点在线段的延长线上时，则的长度为( )A. B. C. D.二、填空题（共10小题；共50分）11. 如图，绕点旋转后，顶点的对应点为，则，点的对应点分别为，图中相等的线段有组．12. 如图所示，绕点顺时针旋转至，，，，则，，度，度．13. 如图所示，若把绕点旋转一定的角度就得到，那么；对应边，，；对应角，，．14. 如图，中，．将绕点顺时针旋转得到，与交于，则．15. 如图，把绕点逆时针旋转，得到，点恰好落在边上，连接，则度．16. 如图，将边长为的正方形沿轴正方向连续翻转次，点依次落在点、、、、、的位置，则的横坐标．17. 如图，一段抛物线：，记为，它与轴交于点，；将绕点旋转得，交轴于点；将绕点旋转得，交轴于点；如此进行下去，直至得．若在第段抛物线上，则．18. 如图，在坐标系中，由绕点旋转得到，则点的坐标为．19. 如图，已知梯形中，，，，，，把线段绕点逆时针旋转到位置，连接，则的长为．20. 如图的平面直角坐标系中有一个正六边形，其中的坐标分别为和．若在无滑动的情况下，将这个六边形沿着轴向右滚动，则在滚动过程中，这个六边形的顶点中，会过点的是点．三、解答题（共5小题；共65分）21. 如图，不用量角器，在方格纸中画出绕点顺时针方向旋转后得到的．22. 如图，在三角形中，，将三角形绕顶点按顺时针方向旋转得到三角形，观察图并回答问题：Ⅰ ；（填“ ”或“ ”或“ ”）Ⅱ 此旋转过程中的旋转角是：；Ⅲ 求的余角的度数．23. 如图，试画出四边形绕点逆时针旋转之后的图形，的坐标是；．24. 如图，在中，，如果将该三角形绕点按顺时针方向旋转到的位置，点恰好落在边的中点处，求旋转角的大小．25. 在正方形中，点，，分别是边，，的中点，点是直线上一点．将线段绕点逆时针旋转，得到线段，连接．Ⅰ 如图 1，求证：，且；Ⅱ 如图 2，若点在线段的延长线上，猜想线段，，之间满足的数量关系，并证明你的结论．Ⅲ 若点在线段的反向延长线上，请在图 3中补全图形并直接写出线段，，之间满足的数量关系．答案第一部分1. D2. A3. C4. B5. B6. C7. C8. C9. B 10. B第二部分11. ，；12. ；；；；；；13. ，；，，；，，14.15.16.17.18.19.20.第三部分21. 如图即为所求．22. （1）（2）或（3）由将三角形绕点按顺时针方向旋转得到三角形得，．因为，所以，所以．23. 如图四边形即为所求．；24. 在中，点为的中点，，又由旋转的性质可得，，，是等边三角形，旋转角等于．25. （1）正方形，，，分别是边，，的中点，，，．，．．即．（2）；将线段绕点逆时针旋转，得到线段，，，，，，，在和中，，，，，．是等腰直角三角形，，，即．（3）word ．11 / 11。

浙教版九年级数学上册同步练习(PDF)版)：3.2 图形的旋转

第 1 页（共 7 页）
A. 4，30∘
B. 2，60∘
C. 1，30∘
D. 3，60∘
7. 如图，在 △ �� 中，∠�� = 70∘ ．在同一平面内，将 △ �� 绕点 �� 旋转到 △ ��ʹ��ʹ 的位置，使得 ��ʹ∥��，则 ∠��ʹ = ( )
C. 1 −
3 3
D. 1 −
3 4
9. 正方形 �� 在坐标系中的位置如图所示，将正方形 �� 绕 �� 点顺时针旋转 90∘ 后，�� 点的坐
A. −2,2
B. 4,1
C. 3,1
D. 4,0
C. 格点 ��
D. 格点 ��
3. 如图，在 △ �� 中，∠�� = 75∘ ，在同一平面内，将 △ �� 绕点 �� 旋转到 △ ��ʹ��ʹ 的位置，使得 ��ʹ∥��，则 ∠��ʹ = ( )
A. 60∘
B. 75∘
C. 85∘
D. 90∘
6. 如图，在 △ �� 中， �� = 4 ， �� = 6 ， ∠�� = 60∘ ，将 △ �� 沿射线 �� 的方向平移，得到 △ ��ʹ��ʹ��ʹ，再将 △ ��ʹ��ʹ��ʹ 绕点 ��ʹ 逆时针旋转一定角度后，点 ��ʹ 恰好与点 �� 重合，则平移的距离和旋转角的度数分别为 ( )

浙教版数学九年级上册(同步练习)《3.2图形的旋转》

《3.2图形的旋转》同步练习1.下列图形中，既是轴对称图形又是中心对称图形的是()2.对下列生活现象的解释，其数学原理运用错误的是()A. 把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理B. 木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中，垂线段最短”的原理C. 将自行车的车架设计为三角形是运用了“三角形的稳定性”的原理D. 将车轮设计为圆形是运用了“圆的旋转对称性”的原理3.如图，将一把含30°角的直角三角尺ABC绕点A旋转，使得点B，A，C′在同一条直线上，则三角尺ABC旋转的角度是()A. 60°B. 90°C. 120°D. 150°4.如图，把△ABC绕点C顺时针旋转35°得到△A′B′C，A′B′交AC于点D.若∠A′DC＝90°，则∠A的度数为()A. 45°B. 55°C. 65°D. 75°5.如图，将等边三角形ABC绕点C顺时针旋转120°得到△EDC，连结AD，B D.有下列结论：①AC＝AD；②BD⊥AC；③四边形ACED是菱形.其中正确的个数是()A. 0B. 1C. 2D. 36.如图，已知菱形OABC 的顶点O (0，0)，B (2，2)，若菱形绕点O 逆时针旋转，每秒旋转45°，则第60 s 时，菱形的对角线交点D 的坐标为( )A. (1，－1)B. (－1，－1) 0) D. (07.在如图所示的4×4的正方形网格中，△MNP 绕某点旋转一定的角度得到△M 1N 1P 1，则其旋转中心是( )A. 点AB. 点BC. 点CD. 点D8.如图，△ABC 的顶点坐标为A (－2，3)，B (－3，1)，C (－1，2)，以坐标原点O 为旋转中心，顺时针旋转90°，得到△A ′B ′C ′，点A ′，B ′，C ′分别是点A ，B ，C 的对应点.(1)求过点B ′的反比例函数的表达式.(2)求线段CC ′的长.9.如图，在平面直角坐标系中，∠AOB ＝90°，AB ∥x 轴，OB ＝2，反比例函数y ＝k x经过点B.将△AOB 绕点B 逆时针旋转，使点O 的对应点D 落在x 轴的正半轴上.若AB 的对应线段CB 恰好经过点O .(1)求点B 的坐标和反比例函数的表达式.(2)判断点C 是否在反比例函数的图象上，并说明理由.。

九年级数学上册第3章圆的基本性质 3.2 图形的旋转练习 (新版)浙教版

3.2图形的旋转(见A本23页)A 练就好基础基础达标1．下列现象中属于旋转的是( C)A．电梯的升降运动B．飞机起飞后冲向空中的过程C．汽车方向盘的转动D．笔直的铁轨上飞驰而过的火车2．如图所示，△ABC按顺时针方向旋转一个角度后得△A′B′C′，图中的旋转中心是( A)A．A点B．B点C．C点D．B′点2题图3题图3．如图所示，图中的每个阴影旋转一个角度后，能互相重合，这个角度可以是( C) A．30°B．45°C．120°D．90°4．如图所示，直角三角形ABC绕直角顶点C顺时针方向旋转90°后到达△A1B1C，延长AB交A1B1于点D，则∠ADA1的度数是( D)A．30°B．60°C．75°D．90°4题图第5题图5．如图所示，在Rt△ABC中，∠ACB＝90°，∠A＝35°，以C为旋转中心，将△ABC 旋转到△A′B′C的位置，点B在斜边A′B′上，则∠BDC为( D)A．70°B．90°C．100°D．105°6．如图所示，△ABC为等边三角形，D是△ABC内一点，若△ABD经过逆时针旋转后到△ACP位置，则旋转中心是__点A__，旋转角等于__60°__，△ADP是__等边__三角形．6题图7题图7．如图所示，已知点P的坐标为(1，1)，若将点P绕原点顺时针旋转45度，得到点P1，则点P1的坐标为(2，0) ．8．一个正方形绕着它的中心旋转一定角度后，就能与它自身重合，这个角度至少是__90°__．第9题图9．如图所示，△ABC是等边三角形，D是BC上的一点，△ABD经过逆时针旋转后到△ACE 的位置.(1)旋转中心是哪一点？(2)旋转了多少度？(3)如果M是AB的中点，经过上述旋转后，点M转到什么位置？解：(1)点A (2)60度(3)点M转到AC边的中点第10题图10．如图所示，在正方形ABCD中作∠EAF＝45°，分别交边BC，CD于点E，F(不与顶点重合)，把△ABE绕点A逆时针旋转90°落在△ADG的位置．(1)请你在图中画出△ADG(不写作法)；(2)试说明BE，DF与EF之间的数量关系．第10题答图解：(1)作图如图．(2)BE＋DF＝EF.证明：∵△ADG≌△ABE，∴AG＝AE，∠DAG＝∠BAE，DG＝BE，又∵∠EAF＝45°，即∠DAF＋∠BAE＝∠EAF＝45°，∴∠GAF＝∠FAE，∵在△GAF和△FAE中，AG＝AE，∠GAF＝∠FAE，AF＝AF，∴△AFG≌△AFE(SAS)．∴GF＝EF.又∵DG＝BE，∴GF＝BE＋DF，∴BE＋DF＝EF.B 更上一层楼能力提升11．在图形旋转中，下列说法错误的是( C)A．图形上各点的旋转角度相同B．对应点到旋转中心距离相等C．由旋转得到的图形也一定可以由平移得到D．旋转不改变图形的大小、形状第12题图12．2017·河南中考我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O.固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为( D) A．(3，1) B．(2，1) C．(1，3) D．(2，3)第13题图13．如图所示，将直角三角形ABC绕直角顶点C顺时针旋转90°，得到△A′B′C.连结AA′，若∠1＝20°，则∠B的度数是__65°__．第14题图14．金华中考在平面直角坐标系中，点A的坐标是(0，3)，点B在x轴上，将△AOB绕点A逆时针旋转90°得到△AEF，点O，B对应点分别是E，F.(1)若点B的坐标是(－4，0)，请在图中画出△AEF，并写出点E，F的坐标；(2)当点F落在x轴上方时，试写出一个符合条件的点B的坐标．解：(1)作图如图，∵△AOB绕点A逆时针旋转90°后得到△AEF，第14题答图∴AO⊥AE，AB⊥AF，BO⊥EF，AO＝AE，AB＝AF.∵EF＝OB＝4，∴点E的坐标是(3，3)，点F的坐标是(3，－1)．(2)∵点F落在x轴的上方，∴EF＜AO，BO＝EF，∵AO⊥AE，AO＝AE，∴点E的坐标是(3，3)．又∵EF＝OB，∴OB＜AO，AO＝3，∴OB＜3，∴一个符合条件的点B的坐标是(－2，0)．第15题图15．2017·徐州中考如图所示，已知AC⊥BC，垂足为C，AC＝4，BC＝33，将线段AC 绕点A按逆时针方向旋转60°得到线段AD，连结DC，DB.(1)线段DC＝__4__；(2)求线段DB的长度．解：(1)证△ACD是等边三角形，得CD＝4.第15题答图(2)作DE⊥BC于点E.∵△ACD是等边三角形，∴∠ACD＝60°，又∵AC⊥BC，∴∠DCE＝∠ACB－∠ACD＝90°－60°＝30°，∴Rt △CDE 中，DE ＝12DC ＝2，CE ＝DC·cos30°＝4×32＝23， ∴BE ＝BC －CE ＝33－23＝ 3.∴在Rt △BDE 中，BD ＝DE 2＋BE 2＝22＋（3）2＝7.C 开拓新思路拓展创新16．如图所示，将△ABC 绕点B 逆时针旋转α得到△DBE，点E 在AB 边上，DE 的延长线与AC 相交于点F ，连结DA ，BF ，∠ABC ＝α＝60°，BF ＝AF.(1)求证：DA∥BC.(2)猜想线段DF ，AF 的数量关系，并证明你的猜想．第16题图解：(1)证明：由旋转的性质可知：∠DBE＝∠ABC＝60°，BD ＝AB ， ∴△ABD 为等边三角形， ∴∠DAB ＝60°， ∴∠DAB ＝∠ABC， ∴DA ∥BC.第16题答图(2)猜想：DF ＝2AF ，证明如下：如图，在DF 上截取DG ＝AF ，连结BG ，由旋转的性质可知，DB ＝AB ，∠BDG ＝∠BAF，在△DBG 和△ABF 中， ⎩⎪⎨⎪⎧DB ＝AB ，∠BDG ＝∠BAF，DG ＝AF ，∴△DBG ≌△ABF(SAS)， ∴BG ＝BF ，∠DBG ＝∠ABF， ∵∠DBG ＋∠GBE＝α＝60°，∴∠GBE ＋∠ABF＝60°，即∠GBF＝α＝60°，又∵BG＝BF ，∴△BGF 为等边三角形， ∴GF ＝BF ，又∵BF＝AF，∴FG＝AF，∴DF＝DG＋FG＝AF＋AF＝2AF.。

初中数学浙教版九年级上册3.2图形的旋转同步练习

初中数学浙教版九年级上册3.2图形的旋转同步练习一、单选题（共10题；共20分）1.在绿色食品、回收、节能、节水四个标志中，是由某个基本图形经过旋转得到的是（）A. B. C. D.2.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是（）A. 逆时针旋转90°B. 顺时针旋转90°C. 逆时针旋转45°D. 顺时针旋转45°3.如图，在Rt△ABC中，∠BAC=90°，将Rt△ABC绕点C按逆时针方向旋转46°得到Rt△A′B′C，点A在边B′C 上，则∠ACB的大小为（）A. 23°B. 44°C. 46°D. 54°4.如图所示是一个旋转对称图形，若将它绕自身中心旋转一定角度之后不能与原图重合，则这个角度可能是A. B. C. D.5.如图，在平面直角坐标系中，△ABC的顶点都在方格线的格点上，将△ABC绕点P顺时针方向旋转90°，得到△A′B′C′，则点P的坐标为（）A. B. C. D.6.如图，在正方形网格中，线段A′B′是线段AB绕某点顺时针旋转一定角度所得，点A′与点A是对应点，则这个旋转的角度大小可能是（）A. 45°B. 60°C. 90°D. 135°7.如图，在6×4的方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是（）A. 点MB. 格点NC. 格点PD. 格点Q8.一辆模型赛车，先前进1m，然后沿原地逆时针方向旋转，旋转角为a(0<a<90°)，被称为一次操作，若五次操作后，发现赛车回到出发点，则旋转角a为（）A. 108°B. 120°C. 72 °D. 36°9.如图，教室里有一只倒地的装垃圾的灰斗，BC与地面的夹角为50°，∠C=25°，小贤同学将它绕点C旋转一定角度，扶起平放在地面上(如图)，则灰斗柄AB绕点C转动的角度为（）A. 75°B. 25°C. 115°D. 105°10.如图，在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB＝90°，直角边AO在x轴上，且AO＝1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O＝2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O＝2A1O……依此规律，得到等腰直角三角形A2 017OB2 017.则点B2 017的坐标（）A. （22 017，－22 017）B. （22 016，－22 016）C. （22 017，22 017）D. （22 016，22 016）二、填空题（共5题；共5分）11.如图，△ABC中，∠ACB=90°，∠ABC=32°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为________．12.如图，将△ABC绕点旋转到△AEF的位置，点E在BC边上，EF与AC交于点G.若∠B＝70°，∠C＝25°，则∠FGC＝________°.13.如图，把△ABC绕着点A顺时针方向旋转角度a(0°<a<90°)，得到△AB'C'，若B'，C，C'三点在同一条直线上，∠B'CB=46°，则a的度数是________。

九年级数学上册第3章圆的基本性质 3.2 图形的旋转同步练习 (新版)浙教版

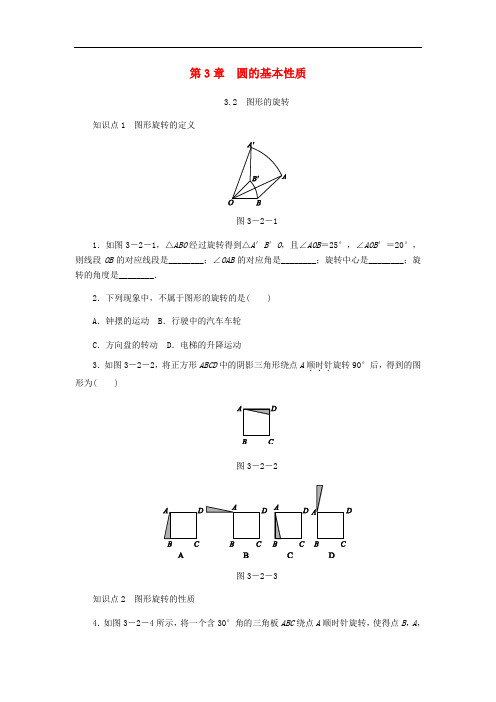
第3章圆的基本性质3.2 图形的旋转知识点1 图形旋转的定义图3－2－11．如图3－2－1，△ABO经过旋转得到△A′B′O，且∠AOB＝25°，∠AOB′＝20°，则线段OB的对应线段是________；∠OAB的对应角是________；旋转中心是________；旋转的角度是________．2．下列现象中，不属于图形的旋转的是( )A．钟摆的运动 B．行驶中的汽车车轮C．方向盘的转动 D．电梯的升降运动3．如图3－2－2，将正方形ABCD中的阴影三角形绕点A顺时针．．．旋转90°后，得到的图形为( )图3－2－2图3－2－3知识点2 图形旋转的性质4．如图3－2－4所示，将一个含30°角的三角板ABC绕点A顺时针旋转，使得点B，A，C′在同一条直线上，则三角板ABC旋转的角度是( )A．60° B．90°C．120° D．150°3－2－43－2－55．如图3－2－5，将△AOB绕点O按逆时针方向旋转45°后得到△COD，若∠AOB＝15°，则∠AOD的度数是________．图3－2－66．如图3－2－6，将△ABC绕点A顺时针旋转60°得到△AED.若线段AB＝3，则BE＝________．7．如图3－2－7，△ABC的三个顶点都在方格纸的格点上，其中点A的坐标是(－1，0)，现将△ABC绕点A顺时针旋转90°.(1)旋转后点C的坐标是________；(2)画出旋转后的三角形．图3－2－7知识点3 中心对称8．如图3－2－8，已知△ABC与△A′B′C′关于点O成中心对称，则下列判断不正确的是( )A．∠ABC＝∠A′B′C′ B．∠BOC＝∠B′A′C′C．AB＝A′B′ D．OA＝OA′3－2－83－2－99．如图3－2－9，在平面直角坐标系中，若△ABC与△A1B1C1关于点E成中心对称，则对称中心点E的坐标是________．10．2017·金华改编如图3－2－10，在平面直角坐标系中，△ABC各顶点的坐标分别为A(－2，－2)，B(－4，－1)，C(－4，－4)．作出△ABC关于原点O成中心对称的△A1B1C1.图3－2－1011．如图3－2－11，如果齿轮A以逆时针方向旋转，那么齿轮E旋转的方向是( )图3－2－11A．顺时针 B．逆时针C．顺时针或逆时针 D．不能确定12．如图3－2－12，E，F分别是正方形ABCD的边AB，BC上的点，且BE＝CF，连结CE，DF，将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置，则旋转角的度数为( )A．30° B．45° C．60° D．90°3－2－123－2－1313．如图3－2－13，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么点A(－2，5)的对应点A′的坐标是________．14．如图3－2－14所示，正方形ABCD的边BC上有一点E，∠DAE的平分线交CD于点F.求证：AE＝DF＋BE.图3－2－1415．创新学习问题：如图3－2－15①，点E，F分别在正方形ABCD的边BC，CD上，∠EAF＝45°，试判断BE，EF，FD之间的数量关系．[发现证明]小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF＝BE＋FD，请你利用图①证明上述结论．[类比引申]如图②，在四边形ABCD中，∠BAD≠90°，AB＝AD，∠B＋∠D＝180°，点E，F分别在边BC，CD上，则当∠EAF与∠BAD满足______关系时，仍有EF＝BE＋FD.[探究应用]如图③，在某公园的同一水平面上，四条道路围成四边形ABCD.已知AB＝AD＝80米，∠B＝60°，∠ADC＝120°，∠BAD＝150°，道路BC，CD上分别有景点E，F，且AE⊥AD，DF＝40(3－1)米，现要在E，F之间修一条笔直的道路，求道路EF的长(结果精确到1米，参考数据：2≈1.41，3≈1.73)．图3－2－15详解详析1．OB′∠OA′B′点O45°2．D 3.A4．D [解析] 旋转角是∠CAC′＝180°－30°＝150°.5．60°[解析] 由旋转可知∠BOD＝45°，∠AOB＝15°，∴∠AOD＝60°.6．3 [解析] ∵将△ABC绕点A顺时针旋转60°得到△AED，∴∠BAE＝60°，AB＝AE，∴△BAE是等边三角形，∴BE＝AB＝3.故答案为3.7．(1)(2，1) (2)略8．B [解析] 因为△ABC与△A′B′C′关于点O成中心对称，所以可得∠ABC＝∠A′B′C′，AB＝A′B′，OA＝OA′.故选B.9．(3，－1)10．解：如图，△A1B1C1就是所求作的图形．11．B [解析] 齿轮A以逆时针方向旋转，齿轮B以顺时针方向旋转，齿轮C以逆时针方向旋转，齿轮D以顺时针方向旋转，齿轮E以逆时针方向旋转．故选B.12．D [解析] 如图，连结OC，OD.∵O为正方形ABCD的中心，∴OD＝OC，OD⊥OC，∴∠DOC＝90°.由题意得点D的对应点为C，∠DOC即为旋转角，则将△DCF绕着正方形的中心O按顺时针方向旋转90°到△CBE的位置．故选D. 13．5，2)[解析] 如图，分别过点A，A′作AC⊥x轴于点C，A′C′⊥x轴于点C′.由旋转的性质可得AO＝A′O，∠AOA′＝90°，∴∠AOC＋∠A′OC′＝90°.∵∠C＝∠C′＝90°，∴∠A′OC′＋∠OA′C′＝90°，∴∠AOC＝∠OA′C′，∴△ACO≌△OC′A′，∴AC＝OC′，OC＝A′C′.∵A(－2，5)，∴OC′＝AC＝5，A′C′＝OC＝2，∴A′(5，2)．14证明：如图所示，将△ADF绕点A顺时针旋转90°得△ABF′，则∠3＝∠1，∠AFD＝∠F′，∠ABF′＝∠D，BF′＝DF.∵四边形ABCD为正方形，∴AB∥CD，∠ABC＝∠D＝90°，∴∠AFD＝∠FAB，∠ABF′＝∠D＝90°，∴∠ABF′＋∠ABC＝180°，∴F′，B，C三点共线．∵∠FAB＝∠2＋∠BAE，∴∠AFD＝∠2＋∠BAE.又∵∠DAE的平分线交CD于点F，∴∠1＝∠2，∴∠3＝∠2，∴∠AFD＝∠3＋∠BAE，∴∠F′＝∠3＋∠BAE.∵∠F′AE＝∠3＋∠BAE，∴∠F′AE＝∠F′，∴AE＝EF′＝BF′＋BE＝DF＋BE.15．解：[发现证明]证明：∵将△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，∴△ABE≌△ADG，∴∠BAE＝∠DAG，∠B＝∠ADG，AE＝AG，BE＝DG.∵∠BAE＋∠DAF＝90°－∠EAF＝45°，∴∠DAG＋∠DAF＝45°，即∠GAF＝45°.∵在正方形ABCD中，∠B＝∠ADF＝90°，∴∠ADG ＋∠ADF ＝180°，即点G ，D ，F 在一条直线上．在△EAF 和△GAF 中，⎩⎪⎨⎪⎧AE ＝AG ，∠EAF ＝∠GAF ＝45°，AF ＝AF ，∴△EAF ≌△GAF ， ∴EF ＝GF .又GF ＝DG ＋FD ＝BE ＋FD ， ∴EF ＝BE ＋FD .[类比引申]∠EAF ＝12∠BAD[探究应用]如图，连结AF ，延长BA ，CD 交于点O .在△AOD 中，∠ODA ＝180°－∠ADC ＝60°， ∠OAD ＝180°－∠BAD ＝30°，AD ＝80米， ∴∠AOD ＝90°，AO ＝40 3米，OD ＝40米． ∵OF ＝OD ＋DF ＝40＋40(3－1)＝40 3(米)， ∴AO ＝OF ，∴∠OAF ＝45°， ∴∠DAF ＝45°－30°＝15°， ∴∠EAF ＝90°－15°＝75°， ∴∠EAF ＝12∠BAD .由已知条件得∠B ＝60°，∠BAE ＝60°， ∴△ABE 是等边三角形，∴BE＝AB＝80米．再由[类比引申]的结论可得EF＝BE＋DF＝40(3＋1)≈109(米)．即道路EF的长约为109米．。

2018-2019学年浙教版九年级上3.2图形的旋转同步导学练(含答案)

3.2 图形的旋转旋转的三要素：旋转中心、旋转方向和旋转角度；旋转变换是全等变换，即旋转前后的两个图形全等，每一对对应点与旋转中心的连线所成的角就是旋转角度．1.如图所示，四边形ABCD为正方形，O为对角线AC，BD的交点，则△COD绕点O(C)可以得到△DOA.A.顺时针旋转90°B.顺时针旋转45°C.逆时针旋转90°D.逆时针旋转45°(第1题) （第2题）（第3题）(第4题)2.如图所示，正方形OABC在平面直角坐标系中，点A的坐标为(2，0)，将正方形OABC绕点O顺时针旋转45°，得到正方形OA′B′C′，则点C′的坐标为(A).A.(2，2)B.(-2，2)C.(2，-2)D.(22，22)3.如图所示，将△ABC绕点A逆时针旋转100°，得到△ADE.若点D在线段BC的延长线上，则∠B的大小为(B).A.30°B.40°C.50°D.60°4.如图所示，在△ABC中，已知∠ACB=90°，AC=BC，BC=2，若以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，则BB′的值是(B).A.5B.25C.3D.23(第5题)(第6题)(第7题) （第8题）5.如图所示，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连结AB′，且点A，B′，A′在同一条直线上，则AA′的长为(A).A.6B.43C.33D.36.如图所示，将△AOB绕点O按逆时针方向旋转60°后得到△COD，若∠AOB=15°，则∠AOD 的度数是45°．7.如图所示，在正方形ABCD中，AD=1，将△ABD绕点B顺时针旋转45°得到△A′BD′，此时A′D′与CD交于点E，则DE的长度为2-2．8.如图所示，点A的坐标为(-1，5)，点B的坐标为(3，3)，点C的坐标为(5，3)，点D的坐标为(3，-1)，小明发现：线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，这个旋转中心的坐标是 (1，1)或(4，4) .9.如图所示，在平面直角坐标系中，O 为坐标原点，每个小方格的边长为1个单位长度.正方形ABCD 顶点都在格点上．(1)若将正方形ABCD 绕点A 顺时针方向旋转90°，点B 到达点B 1，点C 到达点C 1，点D 到达点D 1，求点B 1，C 1，D 1的坐标．(2)若线段AC1的长度与点D1的横坐标的差恰好是一元二次方程x 2+ax+1=0的一个根，求a的值．(第9题)【答案】(1)B 1(2，-1)，C 1(4，0)，D 1(3，2). (2)AC1=2213+=10，∴线段AC1的长度与点D1的横坐标的差是10-3.∴(10-3)2+(10-3)a+1=0，解得a=-210.10.如图所示，在△ABC 中，∠ACB=135°，将△ABC 绕点A 顺时针旋转90°，得到△AED，连结CD ，CE ．(第10题)(1)求证：△ACD 为等腰直角三角形．(2)若BC=1，AC=2，求四边形ACED 的面积．【答案】(1)∵△AED 是△ABC 旋转90°得到的，∴△ABC ≌△AED.∴∠CAD=90°，AC=AD.∴△ACD 是等腰直角三角形.(2)∵△ACD 是等腰直角三角形∴∠ADC=∠ACD=45°，AC=AD=2.∴CD=22AD AC +=22.∵∠ADE=∠ACB=135°，∴∠CDE=∠ADE -∠ADC=90°.∵DE=BC=1，∴S 四边形ADEC =S △ACD +S △CDE =21×2×2+21×22×1=2+2.11.如图所示，P 是正方形ABCD 内一点，将△ABP 绕点B 顺时针旋转到与△CBP′重合，若PB=3，则PP′的长为(B ). A.22B.32C.3D.无法确定（第11题）(第12题)(第13题)12.如图所示，在Rt△ABC 中，∠ACB=90°，∠ABC=30°，将△ABC 绕点C 顺时针旋转至△A′B′C，使得点A′恰好落在AB 上，则旋转角度为(B ).A.30°B.60°C.90°D.150°13.如图所示，O 是正△ABC 内一点，OA=3，OB=4，OC=5，将线段BO 绕点B 逆时针旋转60°得到线段BO′，则下列结论：①△BO′A 可以由△BOC 绕点B 逆时针旋转60°得到；②点O 与O′的距离为4；③∠AOB=150°；④S=150°；④S 四边形AOBO ′=6+33；⑤S △AOC +S △AOB =6+493.其中正确的结论是(A ).A.①②③⑤B.①②③④C.①②③④⑤D.①②③14.如图所示，将正五边形ABCDE 的点C 固定，并依顺时针方向旋转，若要使新五边形A′B′CD′E′的顶点D′落在直线BC 上，则至少要旋转 72° ．(第14题)(第15题) （第16题）（第16题答图）15.如图所示，在正方形ABCD 中，E ，F 分别是边BC ，CD 上的点，∠EAF=45°，△ECF 的周长为4，则正方形ABCD 的边长为 2 ．16.如图所示，在Rt△ABC 中，∠B=90°，AB=BC=2，将△ABC 绕点C 顺时针旋转60°，得到△DEC，则AE 的长是 2+6 .【解析】如答图所示，连结AD.设AE 与CD 交于点O.由题意得CA=CD ，∠ACD=60°，∴△ACD 为等边三角形.∴AD=CA，∠DAC=∠DCA=∠ADC=60°.∵∠ABC=90°，AB=BC=2，∴CD＝AD=AC=22.∵AC=AD，CE=ED ，∴AE 垂直平分DC.∴EO=21DC=2.在Rt△AOD 中，AD ＝22，OD ＝21CD ＝2，∴OA＝22OD AD -＝()()22222-＝6.∴AE=EO+OA=2+6. 17.如图所示，在正方形ABCD 中，E ，F 是对角线BD 上两点，且∠EAF=45°，将△ADF 绕点A 顺时针旋转90°后，得到△ABQ，连结EQ ，求证：(1)EA 是∠QED 的平分线.(2)EF 2=BE 2+DF 2.（第17题）【答案】(1)∵将△ADF 绕点A 顺时针旋转90°后，得到△ABQ，∴QB=DF，AQ=AF ，∠BAQ=∠DAF. ∵∠EAF=45°，∴∠DAF+∠BAE=45°.∴∠QAE=45°.∴∠QAE=∠FAE.在△AQE 和△AFE 中，∵⎪⎩⎪⎨⎧=∠=∠=AE AE FAE QAE AE AQ ，∴△AQE≌△AFE(SAS).∴∠AEQ=∠AEF.∴EA 是∠QED 的平分线. (2)由(1)得△AQE≌△AFE，∴QE=EF.∵BD 是正方形ABCD 的对角线，∴∠ABD＝∠ADB＝45°.由旋转的性质得∠ABQ＝∠ADB＝45°.∴∠QBE＝∠ABQ+∠ABD＝90°.在Rt △QBE 中，QB 2+BE 2=QE 2，∵QB=DF，∴EF 2=BE 2+DF 2.18.如图1所示，将一个边长为2的正方形ABCD 和一个长为2、宽为1的长方形CEFD 拼在一起，构成一个大的长方形ABEF.现将小长方形CEFD 绕点C 顺时针旋转至CE′F′D′，旋转角为α．(1)当点D′恰好落在EF 边上时，求旋转角α的值．(2)如图2所示，G 为BC 中点，且0°＜α＜90°，求证：GD′=E′D．(3)小长方形CEFD 绕点C 顺时针旋转一周的过程中，△DCD′与△BCD′能否全等？若能，直接写出旋转角α的值；若不能，请说明理由．(第18题)【答案】(1)∵长方形CEFD 绕点C 顺时针旋转至CE′F′D′，∴CD′=CD=2.在Rt△CED′中，CD′=2，CE=1，∴∠CD′E =30°.∵CD∥EF，∴α=30°.(2)∵G 为BC 中点，∴CG=1.∴CG=CE.∵长方形CEFD 绕点C 顺时针旋转至长方形CE′F′D′， ∴∠D′CE′=∠DCE=90°，CE=CE′=CG.∴∠GCD′=∠DCE′=90°+α.在△GCD′和△E′CD 中，∵，∴△GCD′≌△E′CD.∴GD′=E′D.(3)能.旋转角α的值为135°或315°时，△DCD′与△BCD′全等.19.【聊城】如图所示，将△ABC 绕点C 顺时针旋转，使点B 落在AB 边上点B′处，此时，点A 的对应点A′恰好落在BC 边的延长线上.下列结论中，错误的是(C ).A.∠BCB ′=∠ACA ′B.∠ACB=2∠BC.∠B′CA=∠B′ACD.B′C 平分∠BB′A′（第19题）（第20题）20.【南宁】如图所示，把正方形铁片OABC 置于平面直角坐标系中，顶点A 的坐标为(3，0)，点P(1，2)在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至①位置，第二次旋转至②位置……则正方形铁片连续旋转2017次后，点P 的坐标为（6053，2） .21.如图所示，图1是电子屏幕的局部示意图，4×4网格的每个小正方形边长均为1，每个小正方形的顶点叫做格点，点A，B，C，D在格点上，光点P从AD的中点出发，按图2的程序移动.(1)请在图1中用圆规画出光点P经过的路径．(2)在图1中，所画图形是轴对称 (填“轴对称”或“中心对称”)图形，所画图形的周长是4π (结果保留π)．(第21题)【答案】(1)图略(2)轴对称4π22.(1)如图1所示，点P是正方形ABCD内的一点，把△ABP绕点B顺时针旋转，使点A与点C重合，点P的对应点是点Q.若PA=3，PB=22，PC=5，求∠BQC的度数．(2)如图2所示，点P是等边三角形ABC内的一点，若PA=12，PB=5，PC=13，求∠BPA的度数．（第22题）（第22题答图）【答案】(1)如答图1所示，连结PQ.由旋转可知：BQ=BP=22，QC=PA=3.∵四边形ABCD 是正方形，∴△ABP绕点B顺时针旋转90°，才能使点A与点C重合，即∠PBQ=90°.∴∠PQB=45°，PQ=4.在△PQC中，PQ=4，QC=3，PC=5，∴PC2=PQ2+QC2.∴∠PQC=90°.∴∠BQC=90°+45°=135°.(2)如答图2所示，将△ABP绕点B顺时针旋转，使点A与点C重合，此时点P的对应点是点P′.由旋转知，△APB≌△CP′B，∴∠BPA=∠BP′C，P′B=PB=5，P′C=PA=12.∵△ABC 是正三角形，∴△ABP绕点B顺时针旋转60°，才能使点A与点C重合，得∠PBP′=60°.∵P′B=PB=5，∴△PBP′是正三角形.∴∠PP′B=60°，PP′=5.在△PP′C中，PC=13，PP′=5，P′C=12.∴PC2=PP′2+P′C2.∴∠PP′C=90°.∴∠BPA=∠BP′C=60°+90°=150°.。

浙教版九年级数学上册32 图形的旋转同步练习

3.2 图形的旋转同步练习【练习1】一、填空题．1．如图所示，△ABC的∠BAC=90°，AB=AC=5cm．△ABC 按逆时针方向转动一个角度后成为△ACD，则图中________是旋转中心，旋转_______度，点B与点_____是对应点，点C与点______是对应点，∠ACD=______，AD=________．2．如图，E为正方形ABCD内一点，∠AEB=135°，BE=3cm，△AEB 按顺时针方向旋转一个角度后成为△CFB，图中_______是旋转中心，旋转_______度，点A 与点_________是对应点，点E与点________是对应点，△BEF是______三角形，∠CBF= ∠______，∠BFC=________度，∠EFC=_______度，BF=______cm．3．如图所示，△ABC、△ADE均是顶角为42°的等腰三角形，BC和DE 分别是底边，图中△______与△_______，可以通过以点________为旋转中心，旋转角度为________，其中∠BAD=∠________，CE=_______．二、解答题．4．如图所示，△ABO绕O点旋转后，G点是B的对应点，作出△AOB 旋转后的三角形．5．如图所示，任画一个直角△ABC，其中∠B=90°，取△ABC外一点P 为旋转中心，按逆时针方向旋转60°，作出旋转后的三角形．6．将图中，阴影部分的图形绕着点O按顺时针旋转90°，画出旋转后的图形．7．如图所示，香港特别行政区区徽是由五个同样的花瓣组成的，它可以看作是什么“基本图案”通过怎样的旋转而得到的？【练习1】参考答案一、1．A 90 C D ∠B AC2．B 90 C F 等腰三角形∠ABE（AEB）135 90 3cm 3．ABD ACE A 42°∠CAE BD二、4．略5．先找到图案中的关键点把关键点绕着O按顺时针方向转动60°，得到它各自的对应点，即可获得旋转后的图形．6～7．略【练习2】◆基础检测1、如图,过圆心O和圆上一点A连一条曲线,将曲线OA绕O点按同一方向连续旋转三次,每次旋转90°,把圆分成四部分,则（）A．这四部分不一定相等B．这四部分相等B．前一部分小于后一部分D．不能确2、如图是一个旋转对称图形，要使它旋转后与自身重合，至少应将它绕中心逆时针方向旋转的度数为（）A．30°B．60°C．120°D．180°3、如图所示的图形是旋转对称图形，它是绕它的旋转中心旋转_______度后与自身重合的？4、如图所示的五角星绕中心点旋转一定的角度后能与自身完全重合，则其旋转的角度至少为5、如上图案可以看做是哪个基本图形通过几次旋转得到的？每次旋转了多少度？旋转中心是哪个？◆典例分析我们在生活中可以看到不少图形绕着某一点旋转一定的角度后重合，如下图所示，这四个图形都是旋转对称图形．请大家观察上面的图形，然后说一说它们在旋转多少度后能与自身重合？解：图（1）绕着一点旋转180°后能与自身重合．图（2）绕着一点旋转120°或240°后能与自身重合．图（3）绕着一点旋转90°或180°或270°后能与自身重合．图（4）绕着一点旋转72°划144°或216°或288°后能与自身重合．●拓展提高1、如下四个图案，它们绕中心旋转一定的度数后都能和原来的图形相互重合，其中有一个图案与其余图案旋转的度数不同的是（）（A）（B）（C）（D）2、如图所示图形旋转一定角度能与自身重合，则旋转的角度可能是（）A．30°B．60°C．90°D．120°3、如图所示的图案是由两个边长相等的正方形组成的，把这个图案旋转一定角度后可以与原来的图案重合，则旋转的角度为（）A．45°或90°B．90°或180°C．180°或270°D．n·45°（1≤n≤8，且n为正整数）4、如图，已知等边三角形ABC和等边三角形DBC有公共的底边BC，以图中的某个点为旋转中心，旋转△DBC与△ABC重合，则旋转中心为（写出所有满足条件的点）．A5、如图，是某设计师设计的方桌布图案的一部分，请你运用旋转的方法，将该图案绕原点O顺时针依次旋转90°、180°、270°，并画出图形，你来试一试吧！但是涂阴影时，要注意利用旋转变换的特点，不要涂错了位置，否则你将得不到理想的效果，并且还要扣分的噢！6、已知如图，正方形ABCD中，E为CD边上一点，F为BC边上一点，CE=CF:（1）EBC∠与相等吗？FDC∠（2）△DCF能与△BCE重合吗？（3）BE与DF垂直吗？●体验中考1、如图，△ABC的直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP=3，求PP′的长．【练习2】参考答案◆基础检测1、B.旋转对称图形:绕着某电脑旋转一定的角度与自身重合，本题是旋转o 902、B 如果一幅旋转对称图形有n 个图案，那么这个图形至少旋转α=no360倍后，能与自身重合，即旋转倍后都能与自身重合．本题至少旋转︒=606360o3、等或或O o o 1359045 图形旋转n n o 45=α倍后，均能与自身重合．4、o72. o o725360= 5、本题图案可以看作由一个菱形通过6次旋转得到的，每次旋转o 60，旋转中心在图形的中心．●拓展提高1、B. A 、C 、D 都是旋转o 60与自身重合，而B 旋转o 120与自身重合．2、C ︒=904360o3、D4、B 、C 、BC 的中点5、基本图形是其中一个菱形，通过5次旋转得到．每次旋转了60度，旋转中心是整个图案的中心．6、解：∵CE=CF,BC=CD,∠DCF=∠DCB=90°,∴△DCF 可看作由△BCE 以点C 为旋转中心顺时针旋转90°得到的，所以（1）EBC FDC ∠=∠，（2）△DCF 能与△BCE 重合（3）延长BE 交DF 于点G,∵EBC FDC ∠=∠，F BEC ∠=∠在△BEG 中，︒=∠∴︒=∠+∠=∠+∠9090BGF BEC EBC F EBC即BE ⊥DF●体验中考1、∵△ABP绕点A逆时针旋转后，能与△ACP′重合，∴AP′=AP，∠CAP′=∠BAP，∴∠PAP′=∠PAC+∠CAP′=∠PAC+∠BAP=∠BAC=90°，△PAP′为等腰直角三角形，PP′为斜边，∴PP′=AP=3．。

浙教版九年级数学上册 3.2 图形的旋转同步测试试题(无答案)

3.2 图形的旋转同步测试题（满分120分；时间：120分钟）班级____________姓名___________成绩_________一、选择题（本题共计10 小题，每题3 分，共计30分，）1. 如图，在Rt△ABC中，∠ACB=90∘，∠A=40∘，以直角顶点C为旋转中心，将△ABC旋转到△EFC的位置，其中E、F分别是A、B的对应点，且点B在斜边EF上，直角边EC交AB于点D，则旋转角等于（）A.70∘B.80∘C.60∘D.50∘2. 如图，点A,B,C,O都在方格纸的格点上，若△COD是由△AOB绕着点O按逆时针的方向旋转而得，则旋转角的度数是：()A.45∘B.90∘C.120∘D.135∘3. 下列图形旋转60∘后可与自身重合的是（）A.等边三角形B.正六边形C.正方形D.平行四边形4. 不能由基本图形1得到图形2的方法是（）A.旋转和平移B.中心对称和轴对称C.平移和轴对称D.中心对称5. 将一图形绕着点O顺时针方向旋转70∘后，再绕着点O逆时针方向旋转120∘，这时如果要使图形回到原来的位置，需要将图形绕着点O的运动为（）A.顺时针方向50∘B.逆时针方向50∘C.顺时针方向190∘D.逆时针方向190∘6. 如图，在平面直角坐标系中，点A的坐标为(√3, 1)，将OA绕原点O逆时针旋转90∘到OB的位置，则点B的坐标为（）A.(√3, −1)B.(−√3, 1)C.(1, −√3)D.(−1, √3)7. 如图，矩形OABC的顶点O为坐标原点，点A在x轴上，点B的坐标为(2, 1)．如果将矩形0ABC绕点O旋转180∘旋转后的图形为矩形OA1B1C1，那么点B1的坐标为（）A.(2, 1)B.(−2, 1)C.(−2, −1)D.(2, −l)8. 如图，在菱形OABC中，点A在x轴上，点B(4,2)将菱形OABC绕原点O逆时针旋转90∘，若点C的对应点是点C1，那么点C1坐标是()A.(−2, 4)B.(−2.5, 2)C.(−1.5, 2)D.(−2, 1.5)9. 如图，在Rt△ABC中，∠C=90∘，AC=6，BC=8，把△ABC绕AB边上的点D顺时针旋转90∘得到△A′B′C′，A′C′交AB于点E，若AD=BE，则△A′DE的面积是（）A.3B.5C.11D.610. 如图，在菱形OABC中，点A在x轴上，点B(4,2)将菱形OABC绕原点O逆时针旋转90∘，若点C的对应点是点C1，那么点C1坐标是()A.(−2, 4)B.(−2, 5.2)C.(−1, 5.2)D.(−2, 1.5)二、填空题（本题共计10 小题，每题3 分，共计30分，）11. 任意一个正整数旋转180∘如果，可以发现有趣的现象，如808旋转180∘后仍是808，169旋转180∘后成691，而37旋转180∘就不是数了，则所有的五位数中旋转180∘后，还是原来的五位数共有________个．12. 如图，将Rt△ABC（其中∠B=35∘，∠C=90∘）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C、A、B1在同一条直线上，那么旋转角的度数是________．13. 钟表上的时针绕其中心旋转一周是12小时，则时针经过4个小时所转过的角度为________，若时针从12时开始，绕中心旋转150∘，则它所指向的具体数字是________．14. 指令(s, θ)的意义：以原地原方向为基准，沿逆时针方向旋转θ角，再沿旋转后的方向行进s米，现有一位于A点处的机器人，面朝正东方向，按指令(5, 60∘)运动至B点，再按指令(5, 120∘)运动至C点，则AC=________米．15. 如图，△ABC与△ADE都是直角三角形，∠B与∠AED都是直角，点E在AC上，∠D=30∘，如果△ABC经过旋转后能与△AED重合，那么旋转中心是点________，逆时针旋转了________度．16. 已知点A的坐标为(a, b)，O为坐标原点，连接OA，将线段OA绕点O按逆时针方向旋转90∘得OA1，则点A1的坐标为________．17. 方格纸中，若三角形的3个顶点分别在小正方形的顶点（格点）上，这样的三角形叫格点三角形．在如图的方格纸中，画出与△ABC成中心对称的格点三角形．________．18. 如图，正三角形ABC绕其中心O至少旋转________度，可与其自身重合．19. 如图，Rt△AOB的斜边OA在y轴上，且OA=5，OB=4．将Rt△AOB绕原点O逆时针旋转一定的角度，使直角边OB落在x轴的负半轴上得到相应的Rt△A′OB′，则A′点的坐标是________．20. 如图，△ABC是等边三角形，点P是△ABC内一点．△APC沿逆时针方向旋转后与△AP′B 重合，最小旋转角等于________∘．三、解答题（本题共计6 小题，共计60分，）21. 如图，已知O是坐标原点，A、B两点的坐标分别为(3, −1)、(2, 1)．（1）以O点为旋转中心将△OAB逆时针旋转90∘得到△OA′B′，画出旋转前与旋转后的图形；（2）如果△OAB内部一点M的坐标为(x, y)，写出M的对应点M′的坐标．22. 图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成，面积为74的正方形．在Rt△ABC中，若直角边BC=5，将四个直角三角形中边长为5的直角边分别向外延长一倍，得到图乙所示的“数学风车”．（1）这个风车至少需要绕着中心旋转________才能和本身重合；（2）求这个风车的外围周长（图乙中的实线）．23. 有两块形状完全相同的不规则的四边形木板，如图所示，两位木匠工师傅通过测量可知∠B=∠D=90∘，AD=CD，现要将其拼成正方形，思考一段时间后，一位木工师傅说“我可以将这两块木板拼成一个正方形．”另一位木工师傅说“可以将一块木板拼成一个正方形，两块木板拼成两个正方形．”两位师傅把每一块木板都只分割一次，你知道他们是怎么做的吗？画出图形，并说明理由．24. 在正方形ABCD中，点E在BC上，点F在AB上，∠FDE=45∘，△DEC按顺时针方向旋转一个角度后成△DGA，如下图所示．（1）哪一个点是旋转中心旋转角度等于多少？（2）指出图中的对应线段和对应角；（3）求∠GDF的度数．25. 如图，已知△ABC和△AEF中，∠B=∠E，AB=AE，BC=EF，∠EAB=25∘，∠F=57∘；（1）请说明∠EAB=∠FAC的理由；（2）△ABC可以经过图形的变换得到△AEF，请你描述这个变换；（3）求∠AMB的度数．26. 把一副三角板如图①放置，其中∠ACB=∠DEC=90∘，∠A=45∘，∠D=30∘，斜边AB= 10cm，DC=17cm，把三角板DCE绕点C顺时针旋转15∘，得到△D1CE1，如图②，这时AB 与CD1相交于点O，与D1E1相交于点F．（1）求∠OFD1的度数；（2）求线段AD1的长；（3）若把△D1CE1绕着点C顺时针再旋转30∘，得△D2CE2，这时点B在△D2CE2的内部、外部，还是边上？请说明理由．。

浙教版九年级数学上册同步练习：3.2 图形的旋转

浙教版九年级数学上册同步练习：33.2图形的旋转知识点1图形旋转的定义图3－2－11．如图3－2－1，△ABO经过旋转失掉△A′B′O，且∠AOB＝25°，∠AOB′＝20°，那么线段OB的对应线段是________；∠OAB的对应角是________；旋转中心是________；旋转的角度是________．2．以下现象中，不属于图形的旋转的是()A．钟摆的运动B．行驶中的汽车车轮C．方向盘的转动D．电梯的升降运动3．如图3－2－2，将正方形ABCD中的阴影三角形绕点A顺时针．．．旋转90°后，失掉的图形为()图3－2－2图3－2－3知识点2图形旋转的性质4．如图3－2－4所示，将一个含30°角的三角板ABC绕点A顺时针旋转，使得点B，A，C′在同一条直线上，那么三角板ABC旋转的角度是()A．60°B．90°C．120°D．150°3－2－43－2－55．如图3－2－5，将△AOB绕点O按逆时针方向旋转45°后失掉△COD，假定∠AOB ＝15°，那么∠AOD的度数是________．图3－2－66．如图3－2－6，将△ABC绕点A顺时针旋转60°失掉△AED.假定线段AB＝3，那么BE＝________．7．如图3－2－7，△ABC的三个顶点都在方格纸的格点上，其中点A的坐标是(－1，0)，现将△ABC绕点A顺时针旋转90°.(1)旋转后点C的坐标是________；(2)画出旋转后的三角形．图3－2－7知识点3中心对称8．如图3－2－8，△ABC与△A′B′C′关于点O成中心对称，那么以下判别不正确的选项是()A．∠ABC＝∠A′B′C′ B．∠BOC＝∠B′A′C′C．AB＝A′B′ D．OA＝OA′3－2－83－2－99．如图3－2－9，在平面直角坐标系中，假定△ABC与△A1B1C1关于点E成中心对称，那么对称中心点E的坐标是________．10．2021·金华改编如图3－2－10，在平面直角坐标系中，△ABC各顶点的坐标区分为A(－2，－2)，B(－4，－1)，C(－4，－4)．作出△ABC关于原点O成中心对称的△A1B1C1.图3－2－1011．如图3－2－11，假设齿轮A以逆时针方向旋转，那么齿轮E旋转的方向是()图3－2－11A．顺时针B．逆时针C．顺时针或逆时针D．不能确定12．如图3－2－12，E，F区分是正方形ABCD的边AB，BC上的点，且BE＝CF，连结CE，DF，将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置，那么旋转角的度数为()A．30°B．45°C．60°D．90°3－2－123－2－1313．如图3－2－13，将线段AB绕点O顺时针旋转90°失掉线段A′B′，那么点A(－2，5)的对应点A′的坐标是________．14．如图3－2－14所示，正方形ABCD的边BC上有一点E，∠DAE的平分线交CD 于点F.求证：AE＝DF＋BE.图3－2－1415．创新学习效果：如图3－2－15①，点E，F区分在正方形ABCD的边BC，CD上，∠EAF＝45°，试判别BE，EF，FD之间的数量关系．[发现证明]小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF＝BE＋FD，请你应用图①证明上述结论．[类比引申]如图②，在四边形ABCD中，∠BAD≠90°，AB＝AD，∠B＋∠D＝180°，点E，F 区分在边BC，CD上，那么当∠EAF与∠BAD满足______关系时，仍有EF＝BE＋FD.[探求运用]如图③，在某公园的同一水平面上，四条路途围成四边形ABCD.AB＝AD＝80米，∠B ＝60°，∠ADC＝120°，∠BAD＝150°，路途BC，CD上区分有景点E，F，且AE⊥AD，DF＝40(3－1)米，现要在E，F之间修一条蜿蜒的路途，求路途EF的长(结果准确到1米，参考数据：2≈1.41，3≈1.73)．图3－2－15详解详析1．OB′∠OA′B′点O45°2．D 3.A4．D[解析] 旋转角是∠CAC′＝180°－30°＝150°.5．60°[解析] 由旋转可知∠BOD＝45°，∠AOB＝15°，∴∠AOD＝60°.6．3[解析] ∵将△ABC绕点A顺时针旋转60°失掉△AED，∴∠BAE＝60°，AB＝AE，∴△BAE是等边三角形，∴BE＝AB＝3.故答案为3.7．(1)(2，1)(2)略8．B[解析] 由于△ABC与△A′B′C′关于点O成中心对称，所以可得∠ABC＝∠A′B′C′，AB＝A′B′，OA＝OA′.应选B.9．(3，－1)10．解：如图，△A1B1C1就是所求作的图形．11．B[解析] 齿轮A以逆时针方向旋转，齿轮B以顺时针方向旋转，齿轮C以逆时针方向旋转，齿轮D以顺时针方向旋转，齿轮E以逆时针方向旋转．应选B.12．D[解析] 如图，连结OC，OD.∵O为正方形ABCD的中心，∴OD＝OC，OD⊥OC，∴∠DOC＝90°.由题意得点D的对应点为C，∠DOC即为旋转角，那么将△DCF绕着正方形的中心O按顺时针方向旋转90°到△CBE的位置．应选D. 13．5，2)[解析] 如图，区分过点A，A′作AC⊥x轴于点C，A′C′⊥x轴于点C′.由旋转的性质可得AO＝A′O，∠AOA′＝90°，∴∠AOC＋∠A′OC′＝90°.∵∠C＝∠C′＝90°，∴∠A′OC′＋∠OA′C′＝90°，∴∠AOC＝∠OA′C′，∴△ACO≌△OC′A′，∴AC＝OC′，OC＝A′C′.∵A(－2，5)，∴OC′＝AC＝5，A′C′＝OC＝2，∴A′(5，2)．14证明：如下图，将△ADF绕点A顺时针旋转90°得△ABF′，那么∠3＝∠1，∠AFD＝∠F′，∠ABF′＝∠D，BF′＝DF.∵四边形ABCD为正方形，∴AB∥CD，∠ABC＝∠D＝90°，∴∠AFD＝∠F AB，∠ABF′＝∠D＝90°，∴∠ABF′＋∠ABC＝180°，∴F′，B，C三点共线．∵∠F AB＝∠2＋∠BAE，∴∠AFD＝∠2＋∠BAE.又∵∠DAE的平分线交CD于点F，∴∠1＝∠2，∴∠3＝∠2，∴∠AFD＝∠3＋∠BAE，∴∠F ′＝∠3＋∠BAE .∵∠F ′AE ＝∠3＋∠BAE ，∴∠F ′AE ＝∠F ′，∴AE ＝EF ′＝BF ′＋BE ＝DF ＋BE .15．解：[发现证明]证明：∵将△ABE 绕点A 逆时针旋转90°至△ADG ，使AB 与AD 重合，∴△ABE ≌△ADG ，∴∠BAE ＝∠DAG ，∠B ＝∠ADG ，AE ＝AG ，BE ＝DG .∵∠BAE ＋∠DAF ＝90°－∠EAF ＝45°，∴∠DAG ＋∠DAF ＝45°，即∠GAF ＝45°.∵在正方形ABCD 中，∠B ＝∠ADF ＝90°，∴∠ADG ＋∠ADF ＝180°，即点G ，D ，F 在一条直线上．在△EAF 和△GAF 中，⎩⎨⎧AE ＝AG ，∠EAF ＝∠GAF ＝45°，AF ＝AF ，∴△EAF ≌△GAF ，∴EF ＝GF .又GF ＝DG ＋FD ＝BE ＋FD ，∴EF ＝BE ＋FD .[类比引申]∠EAF ＝12∠BAD [探求运用]如图，连结AF ，延伸BA ，CD 交于点O .在△AOD 中，∠ODA ＝180°－∠ADC ＝60°，∠OAD ＝180°－∠BAD ＝30°，AD ＝80米，∴∠AOD ＝90°，AO ＝40 3米，OD ＝40米．∵OF ＝OD ＋DF ＝40＋40(3－1)＝40 3(米)，∴AO ＝OF ，∴∠OAF ＝45°，∴∠DAF ＝45°－30°＝15°，∴∠EAF ＝90°－15°＝75°，∴∠EAF ＝12∠BAD . 由条件得∠B ＝60°，∠BAE ＝60°，∴△ABE 是等边三角形，∴BE ＝AB ＝80米．再由[类比引申]的结论可得EF ＝BE ＋DF ＝40(3＋1)≈109(米)．即路途EF 的长约为109米．。

浙教版数学九年级上册3.2 图形的旋转 同步练习.docx

九年级数学上册 3.2 图形的旋转同步习题 (新版)浙教版-(新版)浙教版初中九年级上册数学试题

浙教版九年级数学上册同步练习(PDF)版)：3.2 图形的旋转

浙教版数学九年级上册(同步练习)《3.2图形的旋转》

九年级数学上册 第3章 圆的基本性质 3.2 图形的旋转练习 (新版)浙教版

初中数学浙教版九年级上册3.2图形的旋转 同步练习

九年级数学上册 第3章 圆的基本性质 3.2 图形的旋转同步练习 (新版)浙教版