2011届上海市黄浦区高考一模数学1

合集下载

2011年上海市黄浦区高三一模语文试卷(附答案)

上海市黄浦区2011届第一学期高三期终基础学业测评（语文）试卷（150分钟完成，满分150分） 2011.1.11学生注意：1．答案与作文全都写在答卷上，写在试卷上不给分。

2．答题时注意试卷题号和答卷题号一一对应，不能错位。

一阅读 80分（一）阅读下文，完成第1—6题。

(16分)①朋友小聚，席间说起某些“讽一劝百”或只是炫耀“三俗”、谈不上“讽”与“劝”的热播连续剧，有人戏称之为“中产阶级堕落宝典”，当场被一时髦淑女善意提醒：“您老可别成了九斤老太啊！”于是哄堂大笑，话题很快切换，觥筹交错，言笑如仪。

②但我却不禁暗自浮想联翩起来。

盖哄笑之由，并非座中一客被誉为“九斤老太”，乃因说者自居时髦，却一本正经吐出一个很落伍的词，多少也有点幽默。

“九斤老太”是鲁迅小说《风波》里一笔带过的人物，曾经与阿Q、祥林嫂、闰土、假洋鬼子、孔乙己一道流行过，如今已颇为古旧，纵然比谌容《人到中年》里的“马列主义老太太”名气响一点，较之也曾奔赴鲁迅笔底、永远保鲜的“国骂”，就逊色多了。

现代文学一些“共名”（何其芳语）悄悄隐退，主要因为近一二十年大量新词涌现，□□了一度流行的旧词。

③新词迭出，表征社会进步。

比如“发扬”什么，自幼用惯，曾几何时已被“弘扬”取代。

上下一心，咸与“弘扬”，“发扬”就黯然失色。

有些场合改用“发扬”，反而不够庄重。

从红色年代过来的人都熟悉“光辉”一词，当时只觉臻乎其极，无以复加，孰料又有“辉煌”起来，百尺竿头，更进一步。

盛大场面若无“再造辉煌”，“共创辉煌”予以描写，加以烘托，就缺了什么。

相当长一段历史时期，“感情”单独使用，很可能变成“敏感词”。

文学中写不写感情，写到什么程度，主体是谁，悠悠万事，惟此为大，现在不也被风光无限的“情怀”代替了吗？……“四化”“小康”何其“辉煌”，几十年下来，乔治·奥威尔所谓“新说法”如雨后春笋，更新之速，惟房屋拆建道路翻修可以媲美。

再用旧词，若非“白头宫女在，闲坐说玄宗”，也只能是“谁爱风流高格调，共怜时世检梳妆”了。

黄浦区2011学年度第一学期期末高三测试答案

黄浦区2011学年度第一学期期终高三化学测试参考答案与评分标准2012.1.4一、本题共10分，每小题2 分二、本题共36分，每小题3分四、本题共13分，每空1分23．钠（Na）、氧（O）第三周期第ⅠA族、第二周期第ⅥA族Na+＜O2-24．熔融（或高温）强氧化25. Na2O2 + SO2 →Na2SO4，SO2具有还原性，易被强氧化剂Na2O2氧化（或者2Na2O2 + 2SO2 →2Na2SO3 + O2，SO2在物质类别和组成上与CO2相类似。

）26. 离子晶体碱性氧化物27．Cr2O3+2Al Al2O3+ 2Cr五、本题共6分28．3 6 1 3 1 3 （2分）29．KClO3﹥K2MnO4 （1分）30．紫（红）色（1分）Cl2 +2OH－→ClO－+ Cl－+ H2O或2Na2O2 + 2CO2 →2Na2CO3 + O2（2分）六、本题共8分31．247 kJ （1分） 32．增大（1分）N a+N a+2-33．反应③消耗了反应②中的产物H 2O ，使反应②的化学平衡向正反应方向移动（2分） 34．温度低于240℃时，CO 的转化率随着温度的升高而增大；温度高于240℃时，CO 的转化率随着温度的升高而减小。

（2分）在较低温时，各反应体系均未达到平衡，CO 的转化率主要受反应速率影响，随着温度的升高反应速率增大，CO 的转化率也增大；在较高温时，各反应体系均已达到平衡，CO 的转化率主要受反应限度影响，随着温度的升高平衡向逆反应方向移动，CO 的转化率减小。

（2分）七、本题共8 分35． a b d （答对一个得1分，全对得2分，答错一个得0分） 36．羧基、碳碳双键（2分，只讲双键扣1分） 37．或（任写一种，2分）38．（2分，没有H 2O 扣1分）八、本题共11 分39．C 10H 12O 2 ( 2分) 40．保护酚羟基（1分） 41．HCOOH （1分） 42．缩聚反应（1分） 43．（2分）44．（2分）45．（任写一种， 2分）九、本题共14分46．b、d（答对一个得1分，全对得2分，答错一个得0分）；47．防止倒吸（1分）48．a、d（答对一个得1分，全对得2分，答错一个得0分）；5Cl2 + I2 + 6H2O →2HIO3 + 10HCl（2分）49．a、c、d（答对一个得1分，全对得2分，答错一个得0分）；取少量试液加入KSCN溶液，不变红（或者加少量BaCl2溶液，有白色沉淀生成）（2分。

2011年全国统一高考数学真题试卷——上海市

作者：卫福山单位：上海市松江二中2011年普通高等学校招生全国统一考试(上海卷)理科数学考生注意：1．答卷前，考生务必在答题纸上将姓名、高考准考证号填写清楚，并在规定的区域内贴上条形码。

2．本试卷共23道试题，满分150分。

考试时间120分钟。

一．填空题（本答题满分56分）本大题共有14题，考生必须在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分。

1、函数1()2f x x =-的反函数为1()f x -= 。

2、若全集U R =，集合{|1}{|0}A x x x x =≥≤，则U C A = 。

3、设m 为常数，若点(0,5)F 是双曲线2219y x m -=的一个焦点，则m = 。

4、不等式13x x+≤的解为。

5、在极坐标系中，直线(2cos sin )2ρθθ+=与直线cos 1ρθ=的夹角大小为。

6、在相距2千米的A 、B 两点处测量目标C ，若075,60CAB CBA ∠=∠=，则A 、C 两点之间的距离是千米。

7、若圆锥的侧面积为2π，底面积为π，则该圆锥的体积为。

8、函数sin()cos()26y x x ππ=+-的最大值为。

9、马老师从课本上抄录一个随机变量ε的概率分布律如下表请小牛同学计算ε的数学期望，尽管“！”处无法完全看清，且两个“？”处字迹模糊，但能肯定这两个“？”处的数值相同。

据此，小牛给出了正确答案E ε= 。

?!?321P(ε=x )x10、行列式a b c d（,,,{1,1,2}a b c d ∈-）的所有可能值中，最大的是。

11、在正三角形ABC 中，D 是BC 上的点，3,1AB BD ==，则AB AD ⋅= 。

12、随机抽取9个同学中，至少有2个同学在同一月出生的概率是（默认每月天数相同，结果精确到0.001）。

13、设()g x 是定义在R 上、以1为周期的函数，若()()f x x g x =+在[3,4]上的值域为[2,5]-，则()f x 在区间[10,10]-上的值域为。

数学_2011年某校高考数学一模试卷(文科)(含答案)

2011年某校高考数学一模试卷（文科）一、选择题（本大题共12小题，每小题5分，共计60分）1. 设集合I ={−2, −1, 0, 1, 2}，A ={1, 2}，B ={−2, −1, 1, 2}，则A ∪(C I B)=( )A 1B 1，2C 2D 0，1，22. 函数f(x)=2√3x+12lg(1−x)的定义域是（）A (−13, +∞)B (−13, 1)C (−13,13) D (−∞,−13)3. 若p:|x +1|>2，q:x >2，则¬p 是¬q 成立的（）A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件4. 设a >1，函数y =a |x|的图象形状大致是（）A B C D5. 如图是一个几何体的三视图，则此三视图所描述几何体的表面积为（）A (12+4√3)πB (20+4√3)πC 20πD 28π6. 已知a →=(1, 2)，b →=(3, −1)且a →+b →与a →−λb →互相垂直，则实数的λ值为（）A −611B −116C 611D 116 7. 过点(√3，−2)的直线l 经过圆x 2+y 2−2y =0的圆心，则直线l 的倾斜角大小为（）A 30∘B 60∘C 150∘D 120∘8. 在△ABC 中，已知a =2bcosC ，那么这个三角形一定是（）A 等边三角形B 直角三角形C 等腰三角形D 等腰直角三角形9. f(x)={a x ，(x >1)(4−a2)x +2，(x ≤1)是R 上的单调递增函数，则实数a 的取值范围为( )A (1, +∞)B [4, 8)C (4, 8)D (1, 8)10. 2008年3月份开始实施的《个人所得税法》规定：全月总收入不超过2000元的免征个人工资、薪金所得税，超过2000元的部分需征税，设全月总收入金额为x元，前三级税率如下表：级数全月应纳税金额税率当全月总收入不超过4000元时，计算个人所得税的一个算法框图如上所示，则输出①，输出②分别为（）A 0.05x，0.1xB 0.05x，0.1x−225C 0.05x−100，0.1xD 0.05x−100，0.1x−22511. 若不等式组{x−y+5≥0y≥a0≤x≤3表示的平面区域是一个三角形，则a的取值范围是（）A a<5B a≥8C a<5或a≥8D 5≤a<812. 对于任意实数x，符号[x]表示x的整数部分，即[x]是不超过x的最大整数，例如[2]=2；[2.1]=2；[−2.2]=−3，这个函数[x]叫做“取整函数”，它在数学本身和生产实践中有广泛的应用．那么[log21]+[log22]+[log23]+...+[log264]的值为（）A 21B 76C 264D 642二、填空题（本大题共4小题，每小题5分，共计20分）13. 已知数列{a n}，其前n项和S n=n2+n+1，则a8+a9+a10+a11+a12=________．14. 函数y=x+√1−2x的值域________．15. 已知tan(α+β)=25,tan(β−π4)=14，则cosα+sinαcosα−sinα的值为________．16. 分别在区间[1, 6]和[2, 4]内任取一实数，依次记为m和n，则m>n的概率为________．三、解答题（本大题共5小题，共计70分）17. 已知集合A={x|x2−3x+2=0}，B={x|x2−mx+2=0}，且A∩B=B，求实数m 的取值范围．18. 已知函数f(x)=lg 1+x 1−x（1）求证：对于f(x)的定义域内的任意两个实数a ，b ，都有f(a)+f(b)=f(a+b 1+ab )；（2）判断f(x)的奇偶性，并予以证明．19. 为了研究某高校大学新生学生的视力情况，随机地抽查了该校100名进校学生的视力情况，得到频率分布直方图，如图．已知前4组的频数从左到右依次是等比数列{a n }的前四项，后6组的频数从左到右依次是等差数列{b n }的前六项．（1）求等比数列{a n }的通项公式；（2）求等差数列{b n }的通项公式；（3）若规定视力低于5.0的学生属于近视学生，试估计该校新生的近视率μ的大小．20. 一个四棱锥S −ABCD 的底面是边长为a 的正方形，且SA =a ，SB =SD =√2a ．（1）求证：SA ⊥平面ABCD ；（2）若SC 为四棱锥中最长的侧棱，点E 为AB 的中点．求直线SE 与平面SAC 所成角的正弦值．21. 已知向量a →=(sin(ωx +φ)，2)，b →=（1, cos(ωx +φ)），ω>0，0<φ<π4．函数f(x)=(a →+b →)•(a →−b →)，若y =f(x)的图象的一个对称中心与它相邻的一个对称轴之间的距离为1，且过点M(1, 72)． (I)求函数f(x)的表达式；(II)当−1≤x ≤1时，求函数f(x)的单调区间．四、选考题：请考生在第22、23、24题中任选一题作答，如果多做，则按所做的第一题记分．作答时用2B 铅笔在答题卡上把所选题目对应的题号涂黑．本题满分10分．22. 选修4−1：几何证明选讲如图，AB 是⊙O 的直径，AC 是弦，∠BAC 的平分线AD 交⊙O 于点D ，DE ⊥AC ，交AC 的延长线于点E ．OE 交AD 于点F ．（1）求证：DE 是⊙O 的切线；（2）若AC AB =35，求AF DF 的值．23. 选修4−4：几何证明选讲在曲线C 1:{x =1+cosθy =sinθ（θ为参数）上求一点，使它到直线C 2:{x =−2√2+12t y =1−12t（t 为参数）的距离最小，并求出该点坐标和最小距离．24. 选修4−5：不等式选讲已知|x −4|+|3−x|<a（1）若不等式的解集为空集，求a 的范围（2）若不等式有解，求a 的范围．2011年某校高考数学一模试卷（文科）答案1. D2. B3. A4. A5. C6. C7. D8. C9. B10. D11. D12. C13. 10014. (−∞, 1]15. 32216. 35 17. 解：化简条件得A ={1, 2}，A ∩B =B ⇔B ⊆A ，…根据集合中元素个数集合B 分类讨论，B =φ，B ={1}或{2}，B ={1, 2}当B =φ时，△=m 2−8<0∴ −2√2<m <2√2，…当B ={1}或{2}时，{△=01−m +2=0或4−2m +2=0， ∴ m 无解…当B ={1, 2}时，{1+2=m 1×2=2… ∴ m =3．…综上所述，m =3或−2√2<m <2√2．…18. 解：（1）证明：∵ f(x)=lg 1+x 1−x∴ f(a)+f(b)=lg 1+a 1−a +lg 1+b 1−b =lg(1+a 1−a ×1+b 1−b )=lg 1+a+b+ab 1−a−b+abf(a +b 1+ab )=lg 1+a +b 1+ab 1−a +b 1+ab =lg 1+a +b +ab 1−a −b +ab ∴ 对于f(x)的定义域内的任意两个实数a ，b ，都有f(a)+f(b)=f(a+b 1+ab )；（2）函数f(x)=lg 1+x 1−x 的定义域为(−1, 1)∵ f(−x)=lg 1−x 1+x =lg(1+x 1−x )−1=−lg 1+x 1−x =−f(x)∴ 函数f(x)是奇函数．19. 估计该校新生近视率为91%．20. 证明：（1）∵ SA =a ，SB =SD =√2a ．又∵ 四棱锥S −ABCD 的底面是边长为a 的正方形，由勾股定理可得SA ⊥AB ，SA ⊥AD又∵ AB ∩AD =A∴ SA ⊥平面ABCD ； …．解：（2）作EF ⊥AC 交于 F ，连接SF ，∵ EF ⊂平面ABCD ，SA ⊥平面ABCD∴ EF ⊥SA ，又∵ SA ∩AC =A∴ EF ⊥平面SAC （ 8分）∴ ∠ESF 是直线SE 与平面SAC 所成角．在Rt △ESF 中EF =14BD =√24a ，SE =√52a ∴ sin∠ESF =EF SE =√1010…． 21. 解：(1)f(x)=(a →+b →)•(a →−b →)=a →2−b →2=sin 2(ωx +φ)+4−1−cos 2(ωx +φ)，=−cos(2ωx +2φ)+3由题意得周期T =2π2ω=4，故ω=π4… 又图象过点M(1, 72)，所以72=3−cos(π2+2φ)即sin2φ=12，而0<φ<π4，所以2φ=π6∴ f(x)=3−cos(π2x +π6) (2)当−1≤x ≤1时，−π3≤π2x +π6≤2π3 ∴ 当−π3≤π2x +π6≤0时，即x ∈[−1, −13]时，f(x)是减函数当0≤π2x +π6≤2π3时，即x ∈[−13, 1]时，f(x)是增函数 ∴ 函数f(x)的单调减区间是[−1, −13]，单调增区间是[−13, 1]22. 解：（1）证明：连接OD ，得∠ODA =∠OAD =∠DAC ，…∴ OD // AE ，又AE ⊥DE ，…∴ DE ⊥OD ，又OD 为半径∴ DE 是的⊙O 切线 …（2）过D 作DH ⊥AB 于H ，则有∠DOH =∠CABcos∠DOH =cos∠CAB =AC AB =35，…设OD =5x ，则AB =10x ，OH =3x ，DH =4x ，∴ AH =8x ，AD 2=80x 2，由△AED ∽△ADB ，得AD 2=AE ⋅AB =AE ⋅10x ，∴ AE =8x ，…又由△AEF ∽△DOF ，得AF:DF =AE:OD =85，∴ AF DF =85．… 23. 解：直线C 2化成普通方程是x +y −2√2−1=0 …设所求的点为P(1+cosθ, sinθ)，…则C到直线C2的距离d=√2−1|√2…=|sin(θ+π4)+2|…当θ+π4=3π2时，即θ=5π4时，d取最小值1…此时，点P的坐标是(1−√22, −√22)…24. 解：（1）不等式|x−4|+|3−x|<a的解集为⌀⇔|x−3|+|x−4|<a的解集为⌀．又∵ |x−3|+|x−4|≥|x−3−(x−4)|=1，∴ |x−3|+|x−4|的最小值为1，|x−3|+|x−4|<a的解集为⌀．只须a小于等于|x−3|+|x−4|的最小值即可，a≤1，故a的范围为：(−∞, 1]．（2）若不等式有解，则a的范围为（1）中a的范围的补集．即a的范围为：a>1．。

数学_2011年上海市黄浦区高考数学一模试卷(文理合卷)_(含答案)

2011年上海市黄浦区高考数学一模试卷（文理合卷）一、选择题（每小题4分，满分16分）1. 函数f(x)=cos 2x −sin 2x(x ∈R)的最小正周期T =( ) A 2π B π C π4D π22. 已知关于x 、y 的二元一次线性方程组的增广矩阵是[13−λ1+λλ22λ]，则该线性方程组有无穷多组解的充要条件是λ=( )A 2B 1或2C 1D 0 3. 给出下列命题：(1)函数y =sinx +√3cosx 的图象可由y =sinx 的图象平移得到；(2) 已知非零向量a →、b →，则向量a →在向量b →的方向上的投影可以是a →⋅b→|b →|；(3)在空间中，若角α的两边分别与角β的两边平行，则α=β；(4)从总体中通过科学抽样得到样本数据x 1、x 2、x 3...x n (n ≥2, n ∈N +)，则数值S =√(x 1−x)2+(x 2−x)2+⋯+(x n −x)2¯¯¯n−1（x ¯为样本平均值）可作为总体标准差的点估计值．则上述命题正确的序号是[答]( )A (1)、(2)、(4)B (4)C (2)、(3)D (2)、(4) 4. 若数列{a n }满足a 1=2，a n+1=1+a n 1−a n(n ∈N ∗)，则该数列的前2011项的乘积a 1⋅a 2⋅a 3•…•a 2010⋅a 2011=( ) A 3 B −6 C −1 D 235. （文科）若函数y =4x 和y ＝|x −a|的图象有三个不同的公共点，则实数a 的取值范围是（）A a >−4B a ≤−4C a ≤4D a >4二、填空题（每小题4分，满分56分） 6. 函数y =lg(x+1)x的定义域是________．7. 已知函数y =f(x)与函数y =f −1(x)互为反函数，若函数f −1(x)=x−a x+a(x ≠−a, x ∈R)的图象过点(1, 3)，则f(4)=________．8. 已知命题A ：若x >1，则x +4x−1≥5且8−6x −32x ≤2成立．命题A 的逆否命题是________；该逆否命题是________．（填“真命题”或“假命题”）9. 已知全集U ={−2, −1, 0, 1, 2}，集合A ={x|log 2(x 2−12)=−1, x ∈R}，B ={x|4x −3⋅2x +2=0, x ∈R}，则A ∩(C u B)=________． 10. 不等|x|−5|x|+1>−2的解集是________．11. 方程sinx +cosx =−1的解集是________．12. 已知角α的顶点在原点，始边与平面直角坐标系x 轴的正半轴重合，点P(−2, √3)在角α的终边上，则sin(α+π3)=________．13.如图，正三棱柱ABC −A 1B 1C 1的所有棱的长度都为4，则异面直线AB 1与BC 1所成的角是________（结果用反三角函数值表示）．14.如图所示，正三棱柱ABC −A 1B 1C 1的所有棱的长度都为4，点D 是B 1C 1的中点，则异面直线AB 1与A 1D 所成的角是________（结果用反三角函数值表示）． 15. 已知某圆锥体的底面半径r =1，沿圆锥体的母线把侧面展开后可得到圆心角为2π3的扇形，则该圆锥体的体积是________．16. 已知e 1→、e 2→是两个不共线的平面向量，向量a →=2e 1→−e 2→，b→=e 1→+λe 2→(λ∈R)，若a → // b →，则λ=________．17. （理科）一副扑克牌（有四色，同一色有13张不同牌）共52张．现随机抽取3张牌，则抽出的3张牌有且仅有2张花色相同的概率为________（用数值作答）．18. （文科）一副扑克牌（有四色，同一色有13张不同牌）共52张．现随机抽取3张牌，则抽出的3张牌花色各不相同的概率为________（用数值作答）．19. 下面是用区间二分法求方程2sinx +x −1=0在[0, 1]内的一个近似解（误差不超过0.001）的算法框图，如图所示，则判断框内空白处应填入________，才能得到需要的解．20. 在数列{a n}中，如果对任意n∈N+都有a n+2−a n+1a n+1−a n=p（p为常数），则称数列{a n}为“等差比”数列，p叫数列{a n}的“公差比”．现给出如下命题：（1）等差比数列{a n}的公差比p一定不为零；（2）若数列{a n}(n∈N+)是等比数列，则数列{a n}一定是等差比数列；（3）若等比数列{a n}是等差比数列，则等比数列{a n}的公比与公差比相等．则正确命题的序号是________．21. （文科）计算limn→∞C22+C32+C42+⋯+C n2n3=________．22. （理科）若关于x的方程√4−x2−kx+2k=0有2个不同的实数根，则实数k的取值范围是________．23. 若数列{a n}满足a1=2，a n+1=1+a n1−a n(n∈N+)，则可得该数列的前2011项的乘积a1⋅a2⋅a3...a2010⋅a2011=________．三、解答题（共6小题，满分78分）24. 如图所示，已知三棱锥A−BCD中，AD⊥平面BCD点M、N、G、H分别是棱AB、AD、DC、CB的中点．（1）求证M、N、G、H四点共面；（2）已知DC＝1，CB=√2，AD=√6，AB是球M的大圆直径，点C在球面上，求球M的体积V．25. 定义：如果函数y=f(x)在定义域内给定区间[a, b]上存在x0(a<x0<b)，满足f(x0)=f(b)−f(a)b−a，则称函数y=f(x)是[a, b]上的“平均值函数”，x0是它的一个均值点．如y=x4是[−1, 1]上的平均值函数，0就是它的均值点．（1）判断函数f(x)=−x2+4x在区间[0, 9]上是否为平均值函数？若是，求出它的均值点；若不是，请说明理由；（2）若函数f(x)=−x2+mx+1是区间[−1, 1]上的平均值函数，试确定实数m的取值范围．26. 已知a、b∈R，向量e1→=(x, 1)，e2→=(−1, b−x)，函数f(x)=a−1e1→e2→是偶函数．（1）求b的值；（2）若在函数定义域内总存在区间[m, n](m<n)，使得y=f(x)在区间[m, n]上的函数值组成的集合也是[m, n]，求实数a的取值范围．27. 如图，某市拟在长为16km的道路OP的一侧修建一条自行车赛道，赛道的前一部分为曲线OSM，该曲线段为函数y=Asinωx(A>0, ω>0, x∈[0, 8]的图象，且图象的最高点为S(6, 4√3)．赛道的后一段为折线段MNP，为保证参赛队员的安全，限定∠MNP=120∘．（1）求实数A和ω的值以及M、P两点之间的距离；（2）连接MP，设∠NPM=θ，y=MN+NP，试求出用θ表示y的解析式；（3）（理科）应如何设计，才能使折线段MNP最长？（文科）求函数y的最大值．28. （理科）已知各项都为正数的数列{a n}满足a1=1，S n=12a n a n+1(n∈N+)，其中Sn是数列{a n}的前n项的和．（1）求数列{a n}的通项公式a n；（2）已知p(≥2)是给定的某个正整数，数列{b n}满足b n=1，b k+1b k =k−pa k+1(k=1, 2, 3…,p−1)，求b k；（3）化简b1+b2+b3+...+b p．29. （文科）在数列{a n}中，如果对任意n∈N+都有a n+2−a n+1a n+1−a n=p（p为非零常数），则称数列{a n}为“等差比”数列，p叫数列{a n}的“公差比”．（1）已知数列{a n}满足a n}=−3⋅2n+5(n∈N+)，判断该数列是否为等差比数列？（2）已知数列{b n}(n∈N+)是等差比数列，且b1=2，b2=4公差比p=2，求数列{b n}的通项公式b n；（3）记S n为（2）中数列{b n}的前n项的和，证明数列{S n}(n∈N+)也是等差比数列，并求出公差比p的值．2011年上海市黄浦区高考数学一模试卷（文理合卷）答案1. B2. C3. D4. A5. D6. (−1, 0)∪(0, +∞)7. −568. 若x+4x−1<5或8−6x−32x>2，则x≤1成立,真命题9. {−1}10. (−∞, −1)∪(1, +∞)11. {x|x=(2n−1)π或x=2nπ−π2, n∈Z}12. −√211413. acrcos1414. arccos√6415. 2√2π316. −1217. 23442518. 16942519. f(a)⋅f(x0)<020. （1）、（3）21. 1622. k≤023. 324. 连接MH，NG，∵ M、N、G、H分别是棱AB、AD、DC、CB的中点，∴ MH // AC，NG // AC，∴ MH // NG，根据两条平行线可以确定一个平面，∴ ∵ M、N、G、H四点共面．设球半径为R，∵ AB是球M大圆直径，点c在球面上，∴ MA＝MB＝MC＝R，且∠ACB＝90∘，∴ BC⊥AC，∵ AD⊥平面BCD，∴ AD⊥BC，∵ AC∩AD＝A，∴ BC⊥平面ACD，∴ BC⊥CD，∴ BD2＝BC2+CD2＝3，∵ AD=√6，∴ AB2＝3+6＝9，∴ AB＝3，∴ 球半径=32，∴ 球体积V=92π．25. 解：（1）由定义可知，关于x的方程−x2+4x=f(9)−f(0)9−0在(0, 9)内有实数根时，函数f(x)=−x2+4x在区间[0, 9]上是平均值函数．解−x2+4x=f(9)−f(0)9−0⇒x2−4x−5=0，可得x=5，x=−1．又−1∉(0, 9)，∴ x=5，所以函数f(x)=−x2+4x在区间[0, 9]上是平均值函数，5是它的均值点．（2）∵ 函数f(x)=−x2+mx+1是区间[−1, 1]上的平均值函数，∴ 关于x的方程−x2+mx+1=f(1)−f(−1)1−(−1)在(−1, 1)内有实数根．由−x2+mx+1=f(1)−f(−1)1−(−1)⇒x2−mx+m−1=0，解得x=m−1，x=1．又1∉(−1, 1)∴ x=m−1必为均值点，即−1<m−1<1⇒0<m<2．∴ 所求实数m的取值范围是0<m<2．26. 解（1）由已知可得，f(x)=a−1|2x−b|，且函数的定义域为D=(−∞,b2)∪(b2,+∞)．又y=f(x)是偶函数，故定义域D关于原点对称．于是，b=0．又对任意x∈D有f(x)=f(−x)因此所求实数b=0．（2）由（1）可知，f(x)=a−1|2x|(D=(−∞, 0)∪(0, +∞)．考察函数f(x)=a−1|2x|的图象，可知：f(x)在区间(0, +∞)上增函数．f(x)在区间(−∞, 0)上减函数因y =f(x)在区间[m, n]上的函数值组成的集合也是[m, n]，故必有m ，n 同号． ①当0<m <n 时，f(x)在区间[m, n]上是增函数有{a −12m =m a −12n =n ，即方程x =a −12x，也就是2x 2−2ax +1=0有两个不相等的正实数根，因此{2a >0△=4a 2−8>0，解得a >√2．②当m <n <0时，f(x)区间[m, n]上是减函数有{a +12m =na +12n =m ，化简得(m −n)a =0，解得a =0．综上所述，所求实数a 的取值范围a =0或a >√2． 27. 解（1）结合题意和图象，可知{2πω4=6Asin6ω=4√3，解此方程组，得{ω=π12A =4√3，于是y =4√3sin π12xx ∈[0,8]．进一步可得点M 的坐标为{x =8y =4√3sin 8π12=6．所以，MP =√(8−16)2+(6−0)2=10(km)．（2）在△MNP 中，∠MNP =120∘∠NPM =θ，故MN sinθ=NP sin(60∘−θ)=MP sin120∘．又MP =10，因此，y =√3√3∘−θ)(0∘<θ<60∘)．（3）（文）把y =√3√3∘−θ)进一步化为：y =√3∘+θ)(0∘<θ<60∘)．所以，当θ=30∘时y max =√3=20√33(km)．（理）把y =√3+√3∘−θ)进一步化为：y =√3∘+θ)(0∘<θ<60∘)．所以，当θ=30∘时y max =√3=20√33(km)．可以这样设计：连接MP ，分别过点M 、P 在MP 的同一侧作与MP 成30∘角的射线，记两射线的交点为N ，再修建线段NM 和NP ，就可得到满足要求的最长折线段MNP 赛道． 28. 解：（1）∵ s n =12a n ⋅a n+1，(n ∈N ∗)， ∴ s n−1=12a n−1⋅a n ．∴ a n =12a n (a n+1−a n−1)，即a n+1−a n−1=2(n ≥2)．∴ a 2，a 4，a 6，…a 2n 是首项为a 2，公差为2的等差数列； a 1，a 3，…a 2n−1是首项为a 1，公差为2的等差数列．又a 1=1，s 1=12a 1a 2，可得a 2=2．∴ a 2n =2n ，a 2n−1=2n −1(n ∈N ∗)．所以，所求数列的通项公式为：a n =n ．（2）∵ p 是给定的正整数(p ≥2)，b k+1b k=k−p a k+1(k =1, 2, 3,…p −1)，∴ 数列{b k }是项数为p 项的有穷数列． b 1=1，b k+1b k=k−pk+1(k =1, 2, 3,…p −1)，∴ b 2=(−1)p−12，b 3=(−1)2(p−1)(p−2)3⋅2，b 4=(−1)3(p−1)(p−2)(p−3)4⋅3⋅2，…，归纳可得b k =(−1)k−1(p−1)(p−2)(p−3)…(p−k+1)k!(k =1,2,3,…p)．（3）由（2）可知b k =(−1)k−1(p−1)(p−2)(p−3)…(p−k+1)k!(k =1,2,3,…p)，进一步可化为b k =−1p (−1)k C p k(k =1,2,3,…p)．所以，b 1+b 2+b 3+...+b p−1+b p=−1p[(−1)C p 1+(−1)2C p 2+(−1)3C p 3+⋯+(−1)p C p p ]=−1p [C p 0+(−1)C p 1+(−1)2C p 2+(−1)3C p 3+⋯+(−1)p C p p −1]=−1p [(1−1)p −1]=1p ．29. 解：（1）因为数列{a n }满足a n =−3⋅2n +5(n ∈N +)，所以a n+2−a n+1a n+1−a n=−3⋅2n+2+5+3⋅2n+1−5−3⋅2n+1+5+3⋅2n −5=2(n ∈N +)；所以，数列{a n }是等差比数列，且公差比p =2．（2）因为数列{b n }是等差比数列，且公差比p =2，所以，b n+1−b n b n −b n−1=2(n ≥2)，即数列{b n −b n−1}是以(b 2−b 1)为首项，公比为2的等比数列；b n −b n−1=(b 2−b 1)⋅2n−2=2n−1(n ≥2)；于是，b n −b n−1=2n−1，b n−1−b n−2=2n−2，…，b 2−b 1=2；将上述n −1个等式相加，得 b n −b 1=2+22+23+...+2n−1=2(1−2n−1)1−2=2n −2；∴ 数列{b n }的通项公式为b n =2n (n ∈N +)．（3）由（2）可知，s n =b 1+b 2+b 3+...+b n =2+22+23+...+2n =2n+1−2；于是，s n+2−s n+1s n+1−s n=2n+3−2−2n+2+22n+2−2−2n+1+2=2(n ∈N +)；所以，数列{s n}是等差比数列，且公差比为p=2．。

2011年高考第一次模拟考数学试卷(文)及答案

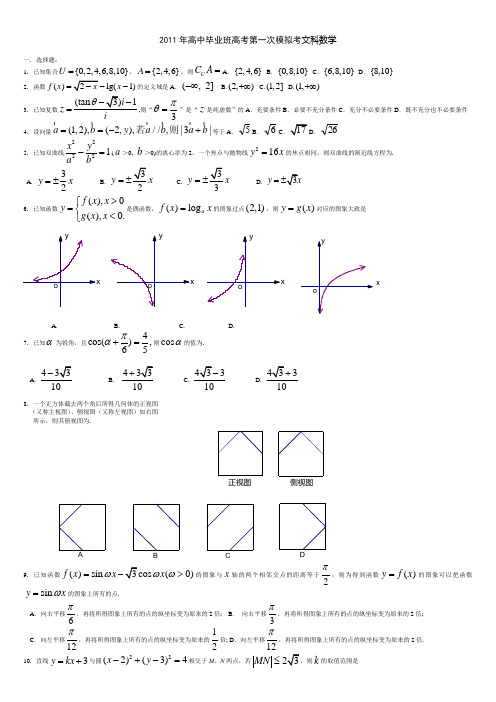
x侧视图正视图DCBA2011年高中毕业班高考第一次模拟考文科数学一. 选择题：1. 已知集合{0,2,4,6,8,10}U=，{2,4,6}A=，则UC A=A．{2,4,6}B．{0,8,10}C．{6,8,10}D．{8,10}2.函数()lg(1)f x x-的定义域是A．(, 2]-∞ B.(2,)+∞ C.(1,2] D.(1,)+∞3.已知复数(tan1iziθ-=,则“3πθ=”是“z是纯虚数”的A．充要条件B．必要不充分条件C．充分不必要条件D．既不充分也不必要条件4.设向量(1,2),(2,),//,|3|a b y a b a b==-+若则等于A．5B．6C．265.已知双曲线22221x ya b-=(a＞0, b＞0)的离心率为2，一个焦点与抛物线216y x=的焦点相同，则双曲线的渐近线方程为.A.32y x=±B.2y x=±C.3y x=±D. y=6. 已知函数(),0(),0.f x xyg x x>⎧=⎨<⎩是偶函数，()log af x x=的图象过点(2,1)，则()y g x=对应的图象大致是A. B. C. D.7.已知α为锐角，且4cos(),65πα+=则cosα的值为.A.410-B.410+C.310D.3108.一个正方体截去两个角后所得几何体的正视图（又称主视图）、侧视图（又称左视图）如右图所示，则其俯视图为.9.已知函数()sin cos(0)f x x xωωω=>的图象与x轴的两个相邻交点的距离等于2π，则为得到函数()y f x=的图象可以把函数siny xω=的图象上所有的点.A．向右平移6π，再将所得图象上所有的点的纵坐标变为原来的2倍; B．向右平移3π，再将所得图象上所有的点的纵坐标变为原来的2倍;C．向左平移12π，再将所得图象上所有的点的纵坐标变为原来的12倍; D．向左平移12π，再将所得图象上所有的点的纵坐标变为原来的2倍.0.08克)0.050.040.020.03频率/组距0.010.07产品重量（克）频数（490,495]（495,500]（500,505]（505,510]（510,515]481486DE ACB10. 直线3y kx =+与圆22(2)(3)4x y -+-=相交于M、N 两点，若MN ≤k的取值范围是 A．[B ．C．(,[)33-∞-+∞D．[,33-二. 填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（11～13题） 11. 已知1{1,,1,2}2α∈-，则使函数y x α=在[0,)+∞上单调递增的所有α值为 .12. 已知函数(),()f x g x 分别由下表给出：则满足(())(())f g x g f x =的x 值为．13. 某市新年第一个月前10天监测到空气污染指数如下表（主要污染物为可吸入颗粒物）：（第i天监测得到的数据记为i a ）在对上述数据的分析中，一部分计算见右图所示的算法流程图，则这10个数据的平均数a = ，输出的S 值是_ ，（二）选做题（14、15题，考生只能从中选做一题）14.（几何证明选做题）如图所示，圆的内接三角形ABC 的角平分线BD 与AC 交于点D ，与圆交于点E,连结AE ，已知ED=3,BD=6 , 则线段AE 的长＝ .15. (坐标系与参数方程选做题) 已知直线112,:()2.x t l t y kt =-⎧⎨=+⎩为参数，2,:12.x s l y s =⎧⎨=-⎩ （s 为参数），若1l //2l ，则k = ；若12l l ⊥，则k = ．16.（本小题满分12分）已知数列{}n a 是首项为２，公比为12的等比数列，n S 为{}n a 的前n 项和. （1）求数列{}n a 的通项n a 及n S ；（2）设数列{}n n b a +是首项为－２，公差为２的等差数列，求数列{}n b的通项公式及其前n 项和n T .17. (本小题满分12分)某食品厂为了检查甲乙两条自动包装流水线的生产情况，随即在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在(495,510]的产品为合格品，否则为不合格品．表1是甲流水线样本频数分布表，图１是乙流水线样本的频率分布直方图．第13题图第14题图HGDE FABC表１：（甲流水线样本频数分布表）图1：（乙流水线样本频率分布直方图）（1）根据上表数据在答题卡上作出甲流水线样本的频率分布直方图；（2）若以频率作为概率，试估计从两条流水线分别任取１件产品，该产品恰好是合格品的概率分别是多少；（3）由以上统计数据完成下面22⨯列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．附：下面的临界值表供参考：(参考公式：22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++)18.（本小题满分14分）已知如图：平行四边形ABCD 中，6BC =，正方形ADEF 所在平面与平面ABCD 垂直，G ，H 分别是DF ，BE 的中点．（１）求证：GH ∥平面CDE ；（２）若2,CDDB ==F-ABCD 的体积．19. (本小题满分1４分)如图，某人在塔的正东方向上的C 处在与塔垂直的水平面内沿南偏西60°的方向以每分钟100米的速度步行了１分钟以后，在点D 处望见塔的底端B 在东北方向上，已知沿途塔的仰角AEB ∠=α,α的最大值为60．（1）求该人沿南偏西60°的方向走到仰角α最大时，走了几分钟；（2）求塔的高AB.20.（本小题满分14分）在直角坐标系xoy 上取两个定点12(2,0),(2,0)A A -,再取两个动点1(0,),N m 2(0,)N n ,且3mn =.（1）求直线11A N 与22A N 交点的轨迹M 的方程；（2）已知点G (1,0)和'(1,0)G -，点P 在轨迹M 上运动，现以P 为圆心，PG 为半径作圆Ｐ，试探究是否存在一个以点'(1,0)G -为圆心的定圆，总与圆P 内切？若存在，求出该定圆的方程；若不存在，请说明理由.21.（本小题满分14分）已知函数321()(21)3(2)13f x x a x a a x =-++++，a R ∈．（1）当0a =时，求曲线()y f x =在点（3,(3)f ）处的切线方程；（2）当1a =-时，求函数()y f x =在[0,4]上的最大值和最小值；（3）当函数'()y f x =在0,4（）上有唯一的零点时，求实数a 的取值范围．D EACB揭阳市2011年高中毕业班高考第一次模拟考数学(文科)参考答案及评分说明一．选择题：BCCAD BDCAC解析： 3.(tan z i θ==+，当3πθ=时，z i =是纯虚数，反之当z 是纯虚数时，θ未必为3π，故选C.4. 4(1,2)a b y a b ⇒=-⇒=//3+||a b ⇒=3+，选A.5. 依题意得双曲线的半焦距4c =，由22ce a a==⇒=，∴b ==，∵双曲线的焦点在x轴，∴双曲线的渐近线方程为y =.选D.6. 依题意易得2()log f x x =（0x >）因函数的图象关于y 轴对称，可得2()log ()g x x =- （0x <）,选B.7. coscos 66ππαα⎡⎤⎛⎫=+-== ⎪⎢⎥⎝⎭⎣⎦310.选D.8. 依题意可知该几何体的直观图如右，其俯视图应选C. 9. 依题意知2ω=，故()2sin(2)3f x x π=-2sin 2()6x π=-，故选A.10.当|MN|=1，可求出k =，再结合图形可得答案C.或设圆心到直线3y kx =+的距离为d，则d =，由22||()42MN d =-且MN ≤231k k ≥⇒≥k ≤二. 填空题：11.1,1,22；12. 2, 4、； 13. 60、3.4、；14.15. 4、－１.解析： 12. 将1,2,3,4x =依次代入方程(())(())f g x g f x =检验，易得2,4x =14. ∵,E E EAD EBA ∠=∠∠=∠∴EDA ∆∽EAB ∆AE EDBE AE⇒=2AE ED BE ⇒=⋅39=⨯AE ⇒=15. 将1l 、2l 的方程化为直角坐标方程得：1:240l kx y k +--=，2:210l x y +-=，由1l //2l 得24211k k+=≠⇒4k =,由12l l ⊥得220k +=1k ⇒=-三．解答题：16. 解：（1）∵数列{}n a 是首项12a =，公比12q =的等比数列∴1212()22n n n a --=⋅=，12(1)124(1)1212n n nS -==--.（2）依题意得：22(1)24nn b a n n +=-+-=-∴224242n n n b n a n -=--=--设数列{}n n b a +的前ｎ项和为n P 则(224)(3)2nn n P n n -+-==- ∴221(3)4(1)3422n n n n nT P S n n n n -=-=---=--+ 17. 解：（１）甲流水线样本的频率分布直方图如下：HGDEFAC（２）由表１知甲样本中合格品数为814830++=，由图１知乙样本中合格品数为(0.060.090.03)54036++⨯⨯=，故甲样本合格品的频率为300.7540=乙样本合格品的频率为360.940=，据此可估计从甲流水线任取１件产品，该产品恰好是合格品的概率为0.75 从乙流水线任取１件产品，该产品恰好是合格品的概率为0.9.（３）22⨯列联表如下：------10分∵22()()()()()n ad bc K a b c d a c b d -=++++＝280(120360) 3.11766144040⨯-≈⨯⨯⨯ 2.706>∴有90％的把握认为产品的包装质量与两条自动包装流水线的选择有关．---------12分18．（1）证法１：∵//EF AD ,//AD BC ∴//EF BC 且EF AD BC ==∴四边形EFBC 是平行四边形 ∴H 为FC 的中点又∵G 是FD 的中点∴//HG CD ∵HG ⊄平面CDE ，CD ⊂平面CDE ∴GH ∥平面CDE证法２：连结EA ，∵ADEF 是正方形 ∴G 是AE 的中点∴在⊿EAB 中，//GH AB又∵AB ∥CD ，∴GH ∥CD ，∵HG ⊄平面CDE ，CD ⊂平面CDE ∴GH ∥平面CDE（2）∵平面ADEF ⊥平面ABCD ，交线为AD 且F A ⊥AD ，∴F A ⊥平面ABCD .∵6BC =, ∴6FA =又∵2,CD DB == ，222CD DB BC +=∴BD ⊥CD ∴ ABCD S CD BD =⋅＝∴ F ABCD V -=13ABCD S FA ⋅＝163⨯=19.解：（１）依题意知在△DBC中30BCD ∠= ,18045135DBC ∠=-=CD ＝100(ｍ),1801353015D ∠=--=，由正弦定理得sin sin CD BCDBC D=∠∠ ∴sin 100sin15sin sin135CD D BC⋅∠⨯==1001)==（ｍ）在Rt △ABE 中，tan ABBEα=∵AB 为定长 ∴当BE 的长最小时，α取最大值60°，这时BE CD ⊥当BE CD ⊥时，在Rt△BEC 中cosEC BC BCE =⋅∠1)25(3==(ｍ), 设该人沿南偏西60°的方向走到仰角α最大时，走了t 分钟，甲流水线乙流水线合计合格品 a =30b=36 66 不合格品 c =10d =414合计4040n =80则100EC t===（分钟）（２）由（１）知当α取得最大值60°时， BE CD ⊥，在Rt △BEC 中,sin BE BC BCD =⋅∠ ∴tan 60sin tan 60AB BE BC BCD =⋅=⋅∠⋅＝11)25(32⋅=-（m ）即所求塔高为25(3-m.20.解：（1）依题意知直线11A N 的方程为：(2)2m y x =+直线22A N 的方程为：(2)2ny x =-- 设(,)Q x y 是直线11A N 与22A N 交点，①×②得22(4)4mn y x =-- 由3mn = 整理得22143x y +=∵12,N N 不与原点重合 ∴点12(2,0),(2,0)A A -不在轨迹M 上∴轨迹M 的方程为22143x y +=（2x ≠±）(2)由（1）知，点G (1,0)和'(1,0)G -为椭圆22143x y +=的两焦点，由椭圆的定义得|'|||4PG PG +=,即|'|4||PG PG =-∴以'G 为圆心，以4为半径的圆与P 内切，即存在定圆'G ，该定圆与P 恒内切，其方程为：22(1)16x y ++=21．解：（1）当0a =时， 321()13f x x x =-+，∴(3)1f =， ∵2'()2f x x x =- 曲线在点(3,1)处的切线的斜率'(3)3k f == ∴所求的切线方程为13(3)y x -=-，即38y x =-（2）当1a =-时，函数321()313f x x x x =+-+∵2'()23f x x x =+-，令'()0f x =得121,3x x ==-2[0,4]x ∉，当(0,1)x ∈时，'()0f x <，即函数()y f x =在(0,1)上单调递减，当(1,4)x ∈时，'()0f x >，即函数()y f x =在(1,4)上单调递增∴函数()y f x =在[0,4]上有最小值，2()(1)3f x f ==-最小值，又1(0)1,(4)263f f ==∴当1a =-时，函数()y f x =在[0,4]上的最大值和最小值分别为1226,33-.-----8分(3) ∵2'()2(21)3(2)f x x a x a a =-+++(3)(2)x a x a =---∴123,2x a x a ==+①当12x x =时，32a a =+，解得1a =，这时123x x ==，函数'()y f x =在(0,4)上有唯一的零点，故1a =为所求； ②当12x x >时，即32a a >+1a ⇒>，这时12x x >3>，又函数'()y f x =在(0,4)上有唯一的零点，∴2134,324,424.3 4.3x a a x a <<<+<⎧⎧⇒⇒≤<⎨⎨≥≥⎩⎩，③当12x x <时，即1a <，这时12x x <3<又函数'()y f x =在(0,4)上有唯一的零点，∴120,30,200 3.02 3.x a a x a ≤≤⎧⎧⇒⇒-<≤⎨⎨<<<+<⎩⎩综上得当函数'()y f x =在(0,4)上有唯一的零点时，20a -<≤或423a ≤<或1a =.。

数学_2011年上海市高考数学模拟试卷1(理科)_(含答案)

2011年上海市高考数学模拟试卷1（理科）一、填空题（本大题满分56分）本大题共有14题，考生必须在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分． 1. 函数y =2x −x 2(1≤x ≤2)反函数是________．2. 若复数z 满足|1z−2zi |=3−2i （i 是虚数单位），则z =________．3. (x −1)(x −2)…(x −10)的展开式中，x 9的系数等于________．4. 直线y =−√3x +1的方向向量与x 轴的正方向上的单位向量i →的夹角是________． P x 0.1 0.3 y 6. 如图是一个算法的流程图，则输出S 的值是________．7. 在极坐标系中，直线ρsin(θ+π4)＝2被圆ρ＝4截得的弦长为________． 8. 设cos(−80∘)=k ，那么tan100∘=________．9. 设数列{a n }的前n 项和为b n ，数列{b n }的前n 项积为c n ，且恒有b n +c n =1，则数列{1a n }中最接近2011的是第________项．10. 已知函数f(x)=a +√x 2+ax +b （a ，b 为实常数），若f(x)的值域为[0, +∞)，则常数a ，b 应满足的条件________．11. 在△ABC 中，已知|AB|=2，|BC|2|CA|2=12，则△ABC 面积的最大值为________．12. 对于集合N ={1, 2, 3, ..., n}的每一个非空子集，定义一个“交替和”如下：按照递减的次序重新排列该子集，然后从最大数开始交替地减、加后继的数．例如集合{1, 2, 4, 6, 9}的交替和是9−6+4−2+1=6，集合{5}的交替和为5．当集合N 中的n =2时，集合N ={1, 2}的所有非空子集为{1}，{2}，{1, 2}，则它的“交替和”的总和S 2=1+2+(2−1)=4，请你尝试对n =3、n =4的情况，计算它的“交替和”的总和S 3、S 4，并根据其结果猜测集合N ={1, 2, 3, ..., n}的每一个非空子集的“交替和”的总和S n =________．13. 由曲线x 2=2y ，x 2=−2y ，x =2，x =−2围成的图形绕y 轴旋转一周所得的旋转体的体积为V 1；满足x 2+y 2≤4，x 2+(y −1)2≥1，x 2+(y +1)2≥1的点组成的图形绕y 轴旋转一周所得的旋转体的体积为V 2，试写出V 1与V 2的一个关系式________．14. 某人有两盒火柴，每盒都有n 根火柴，每次用火柴时他在两盒中任取一盒并从中抽出一根，求他发现用完一盒时另一盒还有r 根(1≤r ≤n)的概率________．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案．考生必须在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分． 15. 正方体ABCD −A 1B 1C 1D 1中，P 是面AA 1B 1B 上点，P 到平面A 1B 1C 1D 1距离是P 到BC 距离的2倍，则P 轨迹所在曲线是（）A 直线B 双曲线C 抛物线D 椭圆16. 记实数x 1，x 2，…x n 中的最大数为max{x 1, x 2, ...x n }，最小数为min{x 1, x 2, ...x n }．已知△ABC 的三边边长为a 、b 、c(a ≤b ≤c)，定义它的倾斜度为t =max{a b , bc , ca }⋅min{a b, bc, ca}，x ，则“t =1”是“△ABC 为等边三角形”的（）A 充分但不必要的条件B 必要而不充分的条件C 充要条件D 既不充分也不必要的条件17. 已知圆x 2+y 2=1与x 轴的两个交点为A 、B ，若圆内的动点P 使|PA|、|PO|、|PB|成等比数列，则PA →⋅PB →的取值范围为（）A (0,12] B [−12，0) C (−12，0) D [−1, 0)18. 已知实数a ，b ，c 成等差数列，点P(−1, 0)在直线ax +by +c =0上的射影是Q ，则Q 的轨迹方程是（）A x 2+(y +1)2=2B x 2+(y −1)2=2C (x +1)2+y 2=2D (x −1)2+y 2=2三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．19. 已知n 为自然数，实数a >1，解关于x 的不等式log a x −4log a 2x +12log a 3x −⋯+n(−2)n−1log a n x >1−(−2)n3log a (x 2−a)．20. 如图，在多面体ABCDEF 中，四边形ABCD 是正方形，EF // AB ，EF ⊥FB ，AB =2EF ，∠BFC =90∘，BF =FC ，H 为BC 的中点．（1）求证：FH // 平面EDB ；（2）求证：AC ⊥平面EDB ；（3）求二面角B −DE −C 的大小．21. 已知△ABC 三个内角满足A 、B 、C 成等差，设x =cos A−C 2，f(x)=cosB(1cosA +1cosC )．（1）求f(x)解析式及定义域；（2）讨论函数单调性，并证明；（3）求f(x)值域．22.（1）A(−2, 0)、B(2, 0)，M 满足MA →⋅MB →=0，求M 轨迹．（2）若（1）中的轨迹按向量(1, −1)平移后恰与x +ky −3=0相切，求k ．（3）如图，l 过x 2a 2+y 2b 2=1 (a >b >0)长轴顶点A 且与长轴垂直的直线，E 、F 是两焦点，P ∈l ，P 、A 不重合，若∠EPF =α，则有0<α≤arctan cb ，类比此结论到x 2a2−y 2b 2=1 (a >0, b >0)，l 是过焦点F 且垂直x 轴的直线，A 、B 是两顶点，P ∈l ，P 、F 不重合，∠APB =α，求α取值范围．23. 定义双曲正弦函数y =sin ℎx =12(e x −e −x )，双曲余弦函数y =cos ℎx =12(e x +e −x )．（1）各写出四条双曲正弦函数和双曲余弦函数的性质．（定义域除外）（2）给出双曲正切函数、双曲余切函数、双曲正割函数和双曲余割函数的定义式，探究并证明六者间的平方关系．（3）模仿三角函数中两角的和与差关系，探究并证明双曲正弦函数、双曲余弦函数和双曲正切函数的“两角”和与差关系．2011年上海市高考数学模拟试卷1（理科）答案1. y =√1−x +1x ∈[0, 1]2.4−7i 53. −554. 120∘或60∘5. 0.46. 637. 4√38. −√1−k 2k9. 4410. {a =0b ≤0或{a <0b =5a 24 11. 2√212. n ⋅2n−1 13. V 1=V 2 14. 2×C 2n−r−1n−r 22n−r15. D 16. B 17. B 18. A19. 解：利用对数换底公式，原不等式左端化为log a x −4⋅log a x log a a 2+12⋅log a x log a a 3++n(−2)n−1⋅log a x log a a n=[1−2+4++(−2)n−1]log a x =1−(−2)n3log a x故原不等式可化为1−(−2)n3log a x >1−(−2)n3log a (x 2−a)．①当n 为奇数时，1−(−2)n3>0，不等式①等价于log a x >log a (x 2−a)．②因为a >1，②式等价于{x >0x 2−a >0x >x 2−a ⇔{x >0|x >√a x 2−x −a <0⇔{x >√a1−√1+4a 2<x <1+√1+4a 2因为1−√1+4a2<0，1+√1+4a2>√4a2=√a ，所以，不等式②的解集为{x|√a <x <1+√1+4a2}．当n 为偶数时，1−(−2)n3<0，不等式①等价于log a x >log a (x 2−a)．③因为a >1，③式等价于{x >0x 2−a >0x <x 2−a ⇔{x >0|x >√a x 2−x −a >0⇔{x >√a x <1−√1+4a 2或{x >√ax >1+√1+4a 2因为1−√1+4a2<0，1+√1+4a2>√4a2=√a ，所以，不等式③的解集为{x|x >1+√1+4a2}．综合得：当n 为奇数时，原不等式的解集是{x|√a <x <1+√1+4a2}；当n 为偶数时，原不等式的解集是{x|x >1+√1+4a2}20. 证明：（1）设AC 于BD 交于点G ，则G 为AC 的中点，连接EG ，GH ，又H 为BC 的中点，∴ GH // AB 且GH =12AB ，又EF // AB 且EF =12AB ，∴ EF // GH 且EF =GH ，∴ 四边形EFHG 为平行四边形∴ EG // FH ，而EG ⊂平面EDB ，∴ FH // 平面EDB ．（2）由四边形ABCD 为正方形，有AB ⊥BC ，又EF // AB ，∴ EF ⊥BC 而EF ⊥FB ，∴ EF ⊥平面BFC ，∴ EF ⊥FH ，∴ AB ⊥FH ，又BF =FC ，H 为BC 的中点，∴ FH ⊥BC∴ FH ⊥平面ABCD ，∴ FH ⊥BC ，FH ⊥AC ，又FH // EG ，∴ AC ⊥EG 又AC ⊥BD ，EG ∩BD =G ， ∴ AC ⊥平面EDB ，（3）EF ⊥FB ，∠BFC =90∘，∴ BF ⊥平面CDEF ，在平面CDEF 内过点F 作FK ⊥DE 交DE 的延长线与k ，则 ∠FKB 为二面角B −DE −C 的一个平面角，设EF =1，则AB =2，FC =√2，DE =√3，又EF // DC ，∴ ∠KEF =∠EDC ， ∴ sin∠EDC =sin∠KEF =√2√3， ∴ FK =EFsin∠KEF =√2√3， tan∠FKB =BF FK=√3，∴ ∠FKB =60∘，∴ 二面角B −DE −C 为60∘． 21. 解：（1）由题意，∵ A 、B 、C 成等差 ∴ 2B =A +C ∴ 3B =180∘ ∴ B =60∘ ∴ f(x)=cosB(1cosA+1cosC)=12×cosA+cosC cosAcosC．∵ x =cosA−C 2，∴ f(x)=2x4x 2−3，(12<x <√32,√32<x ≤1)（2）f /(x)=−8x 2−6(4x 2−3)2<0，∴ 函数的单调减区间是(12，√32)，(√32,1] （3）由（2）知，f(12)=−12，f(1)=2，∴ f(x)值域为(−∞,−12)∪[2,+∞)．22. 解：（1）设M(x,y)，由MA →⋅MB →=0得x 2+y 2=4，所以点M 的轨迹方程为x 2+y 2=4．（2）将x 2+y 2=4向右平移一个单位，再向下平移一个单位后，得到圆(x −1)2+(y +1)2=4，因为圆平移后恰与x +ky −3=0相切，√k 2+1=2，得k =0或k =43．（3）由题意可得：不妨设P(c, t)(t >0)，则tan∠APF =a+c t，tan∠BPF =c−a t所以tanα=tan(∠APF −∠BPF)=a+c t −a−ct1+b 2t2=2at+b 2t≤ab所以0<tanα≤a b．显然α为锐角，即：0<α≤arctan a b所以α取值范围为：(0,arctan ab ]．23. 解：(1)sin ℎx =12(e x −e −x ) 奇函数，单调递增，无周期性，值域为R ．cos ℎx =12(e x +e −x ) 偶函数，R 上无单调，无周期性，值域为[1, +∞)．（2）tan ℎx =sinhxcoshx；cot ℎx =coshx sinhx；sec ℎx =1coshx；csc ℎx =1sinhx．cos ℎ2(x)−sin ℎ2(x)=1；cot ℎ2(x)−csc ℎ2(x)=1；tan ℎ2(x)+sec ℎ2(x)=1．（3）sin ℎ(x +y)=sin ℎ(x)⋅cos ℎ(y)+cos ℎ(x)⋅sin ℎ(y)， sin ℎ(x −y)=sin ℎ(x)⋅cos ℎ(y)−cos ℎ(x)⋅sin ℎ(y)， cos ℎ(x +y)=cos ℎ(x)⋅cos ℎ(y)+sin ℎ(x)⋅sin ℎ(y)， cos ℎ(x −y)=cos ℎ(x)⋅cos ℎ(y)−sin ℎ(x)⋅sin ℎ(y)， tan ℎ(x +y)=tanh(x)+tanh(y)1+tanh(x)⋅tanh(y)；tan ℎ(x −y)=tanh(x)−tanh(y)1−tanh(x)⋅tanh(y)．。

黄浦区2011年高考模拟考

黄浦区2011年高考模拟考英语试卷听力原文I. Listening ComprehensionSection A Short ConversationsDirections: In section A, you will hear ten short conversations between two speakers. At the end of each conversation, a question will be asked about what was said. The conversations and the questions will be spoken only once. After you hear a conversation and the question about it, read the four possible answers on your paper, and decide which one is the best answer to the question you have heard.1.W: Where did you say you found this dog?M: It was under a big tree between the library and the office building.Q: Where did the man find the dog?2.M: Can you tell me what time Flight 805 arrives?W: Yes, it is supposed to arrive at 9:30 a.m. The delay is expected to be two hours.Q: When is the airplane now expected to arrive?3.W: Have you taken Professor Fang’s exam before? I’m kind of nervous.M: Yes. Just concentrate on the important ideas he’s talked about in class, and ignore the details.Q: What’s the most probable relationship between the two speakers?4. M: How about joining me for a cup of coffee?W: I’d love to, but I’m exhausted. I stayed up till 3 this morning, writing a paper for my literature class.Q: Why does the woman decline the man’s invitation?5.W: Jane told us on the phone not to worry about her. Her right hand doesn’t hurt as much as itdid yesterday.M: S he’d better have it examined anyway. And I will call her about it this evening.Q: What does the man think Jane should do?6. M: The wall behind looks a bit grey and dull. What can we do to make it less ugly?W: I think we should paint it white so we can do some drawings on it.Q: What is the woman’s idea to make the wall look less ugly?7．W: You have been overworked for two weeks. I think you really need to go out and get some fresh air and sunshine.M: You are right. That’s just what I am thinking about.Q: What’s the man most probably going to do?8. M: I won a first prize in the School Writing Contest and I got this dictionary as an award.W: It’s a good dictionary! I had no idea you were such a marvelous writer.Q：What does the woman mean?9. W: There is a non-stop train for Washington and it leaves at 2:30.M: It’s faster than the 2 o’clock train. Besides, we can have something to eat before getting on the train.Q: What do we learn from the conversation?10. M: John missed class again, didn’t he? I wonder why.W: Well, I knew he had been absent all week. So I called him this afternoon to see if he wassick. It turned out that his wife was badly injured in a car accident.Q: What does the woman say about John?Section B PassagesDirections: In section B, you will hear two short passages, and you will be asked three questions on each of the passages. The passages will be read twice, but the questions will be spoken only once. When you hear a question, read the four possible answers on your paper and decide which one would be the best answer to the question you have heard.Questions 11 through 13 are based on the following passage.Life at college is filled with excitement and entertainment. However, most students do not know how to use their time wisely. The following advice should help you manage your time better and get more out of your college experience.Firstly, get organized. Organizing your work is necessary if you are going to be successful. Many students do not plan their routine, so unexpected problems can easily appear. Also, it can be very hard to clean up if you don’t organize your room and the things inside it. It is very important to keep yourself organized.The second thing you’d better to do is to find a hobby. Finding yourself a good hobby is a great way to avoid getting bored. Hobbies can fill up much of your free time and give you something to focus on. Choose something that is easy to organize and inexpensive. Many students also join clubs connected to their hobbies, which can be a good way to make new friends.What’s more, set clear goals. Setting goals for yourself is the first step towards success. Sometimes, college life can seem difficult and disappointing. If you give yourself clear and realistic goals, and work hard to achieve them, you will find everything a lot easier. Achieving your goals can be very satisfying, and will give you the confidence you need for life after graduation.11. What is the best way to avoid unexpected problems?12. What is the advantage of taking up a hobby?13. Who is the speaker talking to?Questions 14 through 16 are based on the following passage.Were you the first or the last child in your family? Or were you a middle or an only child? Some people think it matters where you were born in your family. But there are different ideas about what birth order means. Some people say that oldest children are smart and strong-willed. They are very likely to be successful. The reason for this is simple: parents have a lot of time for their first child, they give him or her a lot of attention. So this child is very likely to do well. An only child will succeed for the same reason. What happens to the other children in the family? Middle children don’t get so much attention, so they don’t feel that they’re important. If a family has many children, the middle one sometimes gets lost in the crowd. The youngest child, though, often gets special treatment. He or she is the baby. Often this child grows up to be funny and charming. Do you believe these ideas of birth order too? A recent study saw things quite differently. The study found that first children believed in family rules. They didn’t take manychances in their lives. They usually followed orders. Rules didn’t mea n as much to later children in the family. They went out and followed their own ideas. They took chances and they often did better in life.14. According to common belief, in what way are the first child and the only child alike?15. What do people usually say about middle children?16. What do we learn about later children in a family from a recent study of birth order?Section C Longer ConversationsDirections: In section C, you will hear two longer conversations. Each conversation will be read twice. After you hear the conversation, you are required to fill in the numbered blanks with the information you have heard. Write your answers on your answer sheet.Blanks 17 through 20 are based on the following conversation.M: Hey, Lisa. You’ve been to Spain, right?W: That’s right. Are you thinking of going there?M: Yeah, I’m thinking of going for Christmas.W: Hmm, I wouldn’t go over Christmas. That’s the rainy season.M: Yeah? Does it rain a lot?W: Every day. Not a good time, believe me.M: When does the rainy season end?W: Around April. And then it’s beautiful right up until around September.M: Hmm. What about May? Probably better, don’t you think?W: Sure. I really enjoy lying on the beach there.Complete the form. Write ONE WORD OR NUMBER for each answer.Blanks 21 through 24 are based on the following conversation.W:Oh, I’m fed up with my job.M: Hey, there is a perfect job for you in the paper today. You might be interested.W: Oh, what is it? What do they want?M: Wait a minute. Eh, here it is. The European Space Agency is looking for translators.W: The European Space Agency?M: Well, that’s what it says. They need an English translator to work from French or German. W: So they need a degree in French or German, I suppose. Well, I’ve got that. What’s more, I have plenty of experience. What else are they asking for?M: Just that. A university degree and three or four years’experience as a translator in a professional environment. They also say the person should have a lively and inquiring mind, effective communication skills and the ability to work individually or as a part of the team. W: Well, if I stay at my present job much longer, I won’t have any mind or skills left. I really want the job.Complete the form. Write NO MORE THAN THREE WORDS for each answer.黄浦区2011年高考模拟考英语试卷参考答案第I卷1-5 DDBAA 6-10 CABBD11-13 ACC 14-16 BDA17. Spain 18. Christmas 19. April 20. beach21. European Space 22. French or German23. Three or four 24. communication skills25-29 BDBBB 30-34 CDCDC 35-40 AADAAC41-45 JFBHI 46-49 CAGD50-54 BDADC 55-59 ACADC 60-64 BBDCA65-68 CCCD 69-71 CCB 72-75 BDCB76-80 DBFCA81. To improve pupils’ (poor) academic performance.82. “I have got something to do,” he said to them.83. pupils can/ may know how often they slip into the habit/ use slang84. they (should) speak and write standard English第II卷I. Translation1. Please avoid going to bed after 11 often.2. The information helped us (to) decide whether to hold the farewell party (ornot).3. It was the song that reminded me of the time we had spent together. 4．Knowing / Because he knew the city very well, he had no trouble (in) finding the restaurant (which had been) recommended by his friend.5.Students should be encouraged to express themselves / their (own) ideasfreely in (the) group discussion, for the process of thinking is far moreimportant than the right answer.2010学年第二学期普陀区高三英语质量调研4月19日听力测试现在开始Listening ComprehensionSection A Short ConversationsDirections: In section A, you will hear ten short conversations between two speakers. At the end of each conversation, a question will be asked about what was said. The conversations and the questions will be spoken only once. After you hear a conversation and the question about it, read the four possible answers on your paper, and decide which one is the best answer to the question you have heard.1. W: Hi! I'm calling about the three-bedroom house you advertised in yesterday'spaper. It sounds really nice.M: It is--especially if you have children.Q: What do we learn from the conversation?2. M: What's the time for departure?W: 5:30. That only leaves us 15 minutes to go through the customs and checkour baggage.Q: At what time did the conversation take place?3. M: Are there any more questions on this lecture? Yes, Mary.W: Dr.Baker, do you think an independent candidate could become president? Q: What most probably is Mary?4. M: I'd like to have a talk with your director sometime this week. Could youarrange it for me?W: He's rather busy these days. But I'll see what I can do.Q: What's the man asking the woman to do?5.W:I'd love to see a different type of movie for a change.I am tired of movies aboutromantic stories.M:I agree.Let's go to see a new movie at Rawl Theater .I hear its a real story oftwo present breakers.Q:What kind of movie does the woman find boring ?6.M: Why did Margaret call yesterday?W: She wanted to pick up some magazines she lent me.Q: What do we learn from the conversation?7. W: You seem to have a lot of work to do at your office. You're always staying lateand working overtime.M: That's true. But it's no bother to me. The work is interesting. I don'tmind extra hours at all.Q: How does the man feel about his job?8. M: Well, the holiday should soon be here.W: Yes, isn't it exciting by this time next week! We'll be on the plane.Q: What do we learn from the conversation?9: M: What happened to you? You are so late.W: The bus I took broke down in front of the hospital and I had to walkfrom there.Q: Why was the woman so late?10. M: Are you sure you have corrected all the typing errors in this paper?W: Perhaps, I'd better read it through again.Q: What's the woman going to do?Section B PassagesDirections:In section B, you will hear two short passages, and you will be asked three questions on each of the passages. The passages will be read twice but the questions will be spoken only once. When you hear a question, read the four possible answers in your paper, and decide which one would be the best answer to the question you have heard.Questions 11 through 13 are based on the following passage.When couples get married, they usually plan to have children. Sometimes, however, a couple cannot have a child of their own. In this case, they may decide to adopt a child. In fact, adoption is very common today. There are about 60,000 adoptions each year in the United States alone. Some people prefer to adopt infants; others adopt older children. Some couples adopt children from their own countries; others adopt children from foreign countries. In any case, they all adopt children for the same reason----they care about children and want to give their adopted child a happy life.Most adopted children know that they are adopted. Psychologists and child-care experts generally think this is a good idea. However, many adopted children or adoptees have very little information about their biological parents. As a matter of fact, it is often very difficult for adoptees to find out about their birth parentsbecause the birth records of most adoptees are usually sealed. The information is secret so no one can see it. Naturally, adopted children have different feelings about their birth parents. Many adoptees want to search for them, but others do not. The decision to search for birth parents is a difficult one to make. Most adoptees have mixed feelings about finding their biological parents. Even though adoptees do not know about their natural parents, they do know that their adopted parents want them, love them and will care for them.Questions11. According to the speaker, why do some couples adopt children?12. Why do many adoptees find it hard to make the decision to search for theirbirth parents?13. What can we infer from the passage?Questions 14 through 16 are based on the following passage.There are many reasons why family life in Britain has changed so much in the last fifty years. The liberation of women in the early part of the twentieth century and the social and economic effects of World War II had a great impact on traditional family life. Women became essential to industry and the professions. During the war they had worked in factories and proved their worth, now, with the loss of millions of men, their services were too important to the nation.More recently, great advances in scientific knowledge, and particularly in medicine, have had enormous social consequences.Children are better cared for and are far healthier. Infant death rate is low. Above all, parents can now plan the size of their family if they wish through more effective means of birth control.Different attitudes to religion, authority and tradition generally have also greatly contributed to changes in family life. But these developments have affected all aspects of society. It is particularly interesting to note that the concept of "the family" as a social unit has survived all these challenges.Questions14. What is this passage mainly about?15. Why did British women become so important to industry afterWorld War II?16. What remained unchanged in spite of all the challenges in family life?Section C Longer ConversationsDirections: In section C, you will hear a longer conversation. The conversation will be read twice. After you hear the conversation, you will be required to fulfill the task by filling in the numbered blanks with the information you have heard.Blanks 17 through 20 are based on the following conversation.W: Can I help you, sir?M: Yes, I have left a book on the train.W: Where and when did you on the train?M: I got on board the train at Park Station this morning, at around ten fifteen.W: I see. Do you remember all the details?M: It wasn’t very crowded when I got on the train. So I was able to find a seat and I was reading the book I lost. I got off the train at Preston at around 11 a.m.W: What is the name of the book?M: It’s Going to Asia.W: Okay, can you fill in this form please?M: Sure. Thanks.(Now listen again)Complete the form. Write NO MORE THAN ONE WORD for each answer.Blanks 21-24 are based on the following conversation:M: Excuse me. Have you been waiting long?W: About ten minutes.M: Did you notice whether the number eleven bus has gone by?W: Not while I’ve been standing here. I’m waiting for the number eleven myself. M: Good. Hot today, isn’t it?W: Yes, it is. I wish that it would rain and cool off.M: Me too. This is unusual for March. I don’t remember it ever being so hot and dry in March before.W: You’re from Florida then.M: Not really. I was born in New York, but I’ve lived here for ten years now.W: My mother and I have just moved here from Indiana.M: Pretty cold in Indiana, isn’t it?W: Yes. That’s why we moved. But we didn’t know that it would be so hot here.We should have gone to California. Do you think we’ve missed the bus?M: No. It’s always a little late.(Now listen again)Complete the form. Write NO MORE THAN THREE WORDS for each answer.听力测试到此结束，请继续答题。

上海市浦东新区2011数学一模(含答案)

浦东新区2010学年度第一学期期末质量抽测高三数学试卷（理科） 2011.1题号一二三总分 141-1815-19 20 21 22 23 得分注意：1. 答卷前，考生务必在试卷上指定位置将学校、班级、姓名、考号填写清楚. 2. 本试卷共有23道试题，满分150分，考试时间120分钟.一、填空题（本大题共有14题，满分56分）只要求直接填写结果，每个空格填对得4分，否则一律得零分.1．函数xx y --=21的定义域为__________________. 2．函数)1(log 3-=x y 的反函数是__________________.3．若五个数3,2,1,0,a 的平均数为1，则这五个数的方差等于__________________. 4．方程0cos sin sin cos =xx x x 的解为__________________.5．若“条件α：2x ≤4≤”是“条件β：31m x m -≤≤-”的充分条件，则m 的取值范围是__________________.6．从一个底面半径和高都是R 的圆柱中，挖去一个以圆柱的上底为底，下底面的中心为顶点的圆锥，得到一个如图（1）所示的几何体，那么这个几何体的体积是_________________. 7．在等差数列}{n a 中，18,0654321=++=++a a a a a a ，则数列}{n a 的通项公式为__________________.8．在ABC ∆中，60,4,13=∠==ACB BC AB ，则AC 的长等于__________________. 9．已知]32,6[ππα∈，则αsin 的取值范围是__________________.10．执行如图（2）所示的程序框图，若输入0=x ，则输出y 的值为__________________.11．已知方程)(04)4(2R a ai x i x ∈=++++有实数根b ，则复数=+bi a __________________.得分评卷人图（1）图（2）12．世博期间，5人去某地铁站参加志愿者活动，该地铁站有4个出口，要求每个出口都要有志愿者服务，不同安排方法有__________________种（用数值表示）.13．设定义*N 上的函数⎪⎩⎪⎨⎧=)()2()()(为偶数为奇数n n f n nn f ，)2()3()2()1(nn f f f f a ++++= ，那么=-+n n a a 1__________________.14．在某条件下的汽车测试中，驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息：注：油耗=加满油后已行驶距离加满油后已用油量，可继续行驶距离=当前油耗汽车剩余油量，平均油耗指定时间内的行驶距离指定时间内的用油量=.从上述信息可以推断在10∶00—11∶00这1小时内________ (填上所有正确判断的序号) .① 向前行驶的里程为80公里； ② 向前行驶的里程不足80公里； ③ 平均油耗超过9.6升/100公里； ④ 平均油耗恰为9.6升/100公里； ⑤ 平均车速超过80公里/小时．二、选择题(本大题共有4题，满分16分) 每小题都给出四个选项，其中有且只有一个选项是正确的，选对得 4分，否则一律得零分.15．若函数)sin()(ϕ+=x x f 是偶函数，则ϕ可取的一个值为（）A ．πϕ-=B ．2πϕ-=C ．4πϕ-=D ．8πϕ-=16．关于数列{a n }有以下命题，其中错误的命题为（）A ．若2≥n 且n n n a a a 211=+-+，则}{n a 是等差数列B ．设数列}{n a 的前n 项和为n S ，且n n a S +=12，则数列}{n a 的通项1)1(--=n n aC ．若2≥n 且211n n n a a a =-+，则}{n a 是等比数列D ．若}{n a 是等比数列，且k n m N k n m 2,=+∈*，，，则2k n m a a a =17．一颗骰子连续掷两次，朝上的点数依次为a 、b ，使复数)4)((ai b bi a -+为实数的概率是（）A ．31 B ．41 C ．61D ．121 18．点O 在ABC ∆所在平面内，给出下列关系式：（1）0=++OC OB OA ；（2）OA OC OC OB OB OA ⋅=⋅=⋅；（3）0=⎫⎛-⋅=⎫⎛-⋅BA BC OB AB AC OA ；（4）0)()(=⋅+=⋅+BC OC OB AB OB OA ．则点O 依次为ABC ∆的（）A ．内心、外心、重心、垂心B ．重心、外心、内心、垂心C ．重心、垂心、内心、外心D ．外心、内心、垂心、重心三、解答题（本大题共有5题，满分78分）解答下列各题必须写出必要的步骤．19．（本小题满分14分，第1小题满分6分，第2小题满分8分）已知向量),(),,(a a n a a m x x =-=，其中0>a 且1≠a ，（1）当x 为何值时，n m ⊥；（2）解关于x的不等式m <.20．（本小题满分14分，第1小题满分6分，第2小题满分8分）野营活动中，学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架ABC P -（如图3）进行野炊训练. 已知cm PC 130=，A 、B 两点间距离为cm 350.（1）求斜杆PC 与地面ABC 所成角的大小（用反三角函数值表示）；（2）将炊事锅看作一个点Q ，用吊绳PQ 将炊事锅吊起烧水（锅的大小忽略不计），若使炊事锅Q 到地面ABC 及各条斜杆的距离都不小于30cm ，试问吊绳PQ 长的取值范围.21．（本小题满分16分，第1小题满分6分，第2小题满分10分）已知]2,1[,3)(∈-+=x xbx x f (1) 2=b 时，求)(x f 的值域；(2) 2≥b 时，)(x f 的最大值为M ，最小值为m ，且满足：4≥-m M ，求b 的取值范围．图（3）22．（本小题满分16分，第1小题满分4分，第2小题满分5分，第3小题满分7分）（1）若对于任意的*∈N n ，总有1)1(2++=++n Bn A n n n 成立，求常数B A ,的值；（2）在数列}{n a 中，211=a ，)1(221+++=-n n n a a n n （2≥n ，*∈N n ），求通项n a ；（3）在（2）题的条件下，设2)1(21+++=n n a n n b ，从数列}{n b 中依次取出第1k 项，第2k 项，…第n k 项，按原来的顺序组成新的数列}{n c ，其中n k n b c =，其中m k =1，*+∈=-N r k k n n 1.试问是否存在正整数r m ,使S c c c n n =++++∞→)(lim 21 且131614<<S 成立？若存在，求正整数r m ,的值；不存在，说明理由.23．（本题满分18分，第1小题满分6分，第2小题满分6分，第3小题满分6分）已知函数)(x f ，如果存在给定的实数对（b a ,），使得b x a f x a f =-⋅+)()(恒成立，则称)(x f 为“S-函数”.（1）判断函数xx f x x f 3)(,)(21==是否是“S-函数”；（2）若x x f tan )(3=是一个“S-函数”，求出所有满足条件的有序实数对),(b a ；（3）若定义域为R 的函数)(x f 是“S-函数”，且存在满足条件的有序实数对)1,0(和)4,1(，当]1,0[∈x 时，)(x f 的值域为]2,1[，求当]2012,2012[-∈x 时函数)(x f 的值域.。

上海市黄浦区高三第一学期期

高中物理学习材料（马鸣风萧萧**整理制作）上海市黄浦区2011届高三第一学期期终基础学业测评物理试卷（完卷时间：120分钟满分：150分）2011年1月11日考生注意：1．答卷前，考生务必将姓名、准考证号等填写清楚。

2．本试卷共8页，满分150分。

考试时间120分钟。

考生应用蓝色或黑色的钢笔或圆珠笔将答案写在答题卷上。

3．第30、31、32、33、34题要求写出必要的文字说明、方程式和重要的演算步骤。

只写出最后答案，而未写出主要演算过程的不能得分。

有关物理量的数值计算问题，答案中必须明确写出数值和单位。

第I卷（共65分）一、单项选择题（45分）Ⅰ单项选择题。

（18分。

本题共9小题，每小题2分，每小题给出的四个答案中，只有一个是正确的。

把正确答案选出来，并将正确答案前面的字母填涂在答题卷相应的位置上。

）1．关于速度和加速度的关系，下列说法中正确的是（）A．速度变化量越大，加速度就越大B．速度变化得越快，加速度就越大C．加速度方向保持不变，速度方向也保持不变D．加速度大小不断变小，速度大小也不断变小2．如图所示，一个质量为m=1.2kg物体，放在倾角为θ=300的斜面上静止不动。

若用竖直向上的力F=6.0 N提物体，物体仍静止，下列说法中正确的是（）A．斜面受到的压力减少6.0NB．物体受到的合外力减少6.0 NC．物体受到的摩擦力减少6.0ND．物体对斜面的作用力减少6.0 N3．关于闭合电路，下列说法中正确的是（）A．闭合电路中，电流越大，电源的路端电压就越大B ．闭合电路中，外电阻越大，电源的路端电压就越大C ．闭合电路中，电流总是从电势高的地方流向电势低的地方D ．闭合电路中，电源的路端电压越大，电源的输出功率就越大4．如图所示为三个门电路符号，A 输入端全为“1”，B 输入端全为“0”。

下列正确的是（）A ．甲为“非”门，输出为“1”B ．乙为“或”门，输出为“0”C ．乙为“与”门，输出为“1”D ．丙为“或”门，输出为“1”5．对于一定质量的气体，下列说法中正确的是（）A.压强增大时，单位体积内气体分子数增加B.当温度升高时，气体分子的平均动能增大C.要使气体分子的平均动能增大，外界必须向气体传热D.温度升高时，分子间的平均距离一定增大6．M 和N 是绕在同一个环形铁芯上的两个线圈，绕法和线路如图所示。

上海市黄浦区2011届高三数学上学期期终基础学业测评文【会员独享】

图1ABC C 1A 1B 1D 黄浦区2010学年度第一学期期终基础学业测评高三数学试卷(文)考生注意：1．每位考生应同时收到试卷和答题卷两份材料，解答必须在答题卷上进行，写在试卷上的解答一律无效；2．答卷前，考生务必将姓名、准考证号等相关信息在答题卷上填写清楚； 3．本试卷共23道试题，满分150分；考试时间120分钟．一．填空题(本大题满分56分) 本大题共有14题，考生应在答题卷的相应编号的空格内直接填写结果，每题填对得4分，否则一律得零分．1．函数lg(1)x y x+=的定义域是 2．已知函数1()()y f x y f x -==与函数互为反函数，若函数1()x af x x a--=+ ()x a x R ≠-∈，的图像过点(23)，，则(4)f ＝．3．已知命题A ：若431586212x x x x x>+≥--≤-，则且成立．命题A 的逆否命题是；该逆否命题是．(填“真命题”或“假命题”)4．已知全集{}21012U =--，，，，，集合221|log ()12A x x x R ⎧⎫=-=-∈⎨⎬⎩⎭，，{}|43220x x B x x R =-⋅+=∈，，则()U A C B ⋂＝．5．不等式||52||1x x ->-+的解集是．6．方程sin cos 1x x +=-的解集是．7．已知角α的顶点在原点，始边与平面直角坐标系x 轴的正半轴重合，点(2P -在角α的终边上，则sin(3πα+＝．8．如图1所示，正三棱柱111ABC A B C -的所有棱的长度都为4，点11D B C 是的中点，则异面直线11AB A D 与所成的角是 (结果用反三角函数值表示)．9．已知某圆锥体的底面半径3r =，沿圆锥体的母线把侧面展开后可得到圆心角为23π的扇形，则该圆锥体的体积是．10．已知12e e 、是两个不共线的平面向量，向量12122()a e e b e e R λλ=-=+∈，，若//a b ，则λ＝．11．一副扑克牌(有四色，同一色有13张不同牌)共52张．现随机抽取3张牌，则抽出的3张牌花色各不相同的概率为 (用数值作答)．12．下面是用区间二分法求方程2sin 10x x +-=在[01]，内的一个近似解(误差不超过0.001)的算法框图，如图2所示，则判断框内空白处应填入，才能得到需要的解．13．计算22222343limnn C C C C n →∞++++＝．14．若{}*1112()1nn n na a a a n N a ++==∈-数列满足，，则可得该数列的前2011项的乘积12320102011a a a a a ⋅⋅⋅⋅⋅= ．二．选择题(本大题满分16分) 本大题共有4题，每题有且只有一个正确答案，考生应在答题卷的相应编号上，将代表答案的小方格涂黑，选对得4分，否则一律得零分．15．函数22()cos sin f x x x =-(x R ∈)的最小正周期T= [答]( )A ．2π．B ．π．C ．4π． D ．2π． 16．已知关于x 、y 的二元一次线性方程组的增广矩阵是13122λλλλ-+⎛⎫⎪⎝⎭，则该线性方程组有无穷多组解的充要条件是λ＝ [答]( ) A ．2． B ．1或2． C ．1． D ．0． 17．给出下列命题：(1)函数sin sin y x x y x =+=的图像可由的图像平移得到；(2) ||ba b a b a b ⋅已知非零向量、，则向量在向量的方向上的投影可以是； (3)在空间中，若角α的两边分别与角β的两边平行，则αβ=；(4)从总体中通过科学抽样得到样本数据123n x x x x 、、、、(*2n n N ≥∈，)，则数值S =(x 为样本平均值)可作为总体标准差的点估计值．则上述命题正确的序号是 [答]( ) A ．(1)、(2)、(4)． B ．(4)． C ．(2)、(3)． D ．(2)、(4)．18．若函数4||y y x a x==-和的图像有三个不同的公共点，则实数a 的取值范围是 [答]( )A ．4a >-．B ．4a ≤-．C ．4a ≤．D ．4a >．三．解答题(本大题满分78分)本大题共有5题，解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤．19．(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分．如图3所示，已知三棱锥A BCD -中，AD BCD ^平面，点M N G H 、、、分别是AB AD DC CB 棱、、、的中点．(1)求证M N G H 、、、四点共面；(2)已知1DC CB AD AB M ===，是球的大圆直径，点C 在球面上，求球M 的体积V ．20．(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分．定义：如果函数00()[]y f x a b x a x <b =<在定义域内给定区间，上存在()，满足0()()()f b f a f x b a-=-，则称函数()y f x =是[]a b ，上的“平均值函数”，0x 是它的一个均值点．如4[11]y x =-是，上的平均值函数，0就是它的均值点． (1)判断函数2()4f x x x =-+在区间[09]，上是否为平均值函数？若是，求出它的均值点；若不是，请说明理由；(2)若函数2()1[11]f x x mx =-++-是区间，上的平均值函数，试确定实数m 的取值范围． 21．(本题满分16分)本题共有2个小题，第1小题满分7分，第2小题满分9分．已知12((1)a b R e x e b x 、，向量，1)，，，?=--u ru r 121()||f x a e e 函数=-×u r u r 是偶函数．(1) 求b 的值；(2) 若在函数定义域内总存在区间[]m n ，(m <n )，使得()y f x =在区间[]m n ，上的函DACB·· · · M N GH图3数值组成的集合也是[]m n ，，求实数a 的取值范围．22．(本题满分16分)本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分5分．如图4,某市拟在长为16km 的道路OP 的一侧修建一条自行车赛道，赛道的前一部分为曲线OSM ，该曲线段为函数sin (00[08])y A x A x ωω=>>∈，，，的图像，且图像的最高点为(6S .赛道的后一段为折线段MNP ，为保证参赛队员的安全，限定120MNP ∠=.(1)求实数A ω和的值以及M 、P 两点之间的距离；(2)联结MP ，设NPM y MN NP θ∠==+，，试求出用y θ表示的解析式； (3)求函数y 的最大值．23．(本题满分18分)本题共有3个小题，第1小题满分6分，第2小题满分7分，第3小题满分5分．在数列{}*211n n n n na a a n N p a a +++-∈=-中，如果对任意都有(p 为非零常数)，则称数列{}n a 为“等差比”数列，p 叫数列{}n a 的“公差比”．(1) 已知数列{}n a 满足*325()n n a n N =-⋅+∈，判断该数列是否为等差比数列？(2) 已知数列{}n b *()n N ∈是等差比数列，且1224b b ==，，公差比2p =，求数列{}n b 的通项公式n b ；(3)记n S 为(2)中数列{}n b 的前n 项的和，证明数列{}n S *()n N ∈也是等差比数列，并求出公差比p 的值．黄浦区2010学年度第一学期期终基础学业测评数学试卷(文理合卷)(2011年1月12日) 参考答案和评分标准一、填空题1、(10)(0)-??，，；2、53；3、435862112x x x x x+<-->?-若或，则成立；真命题 (每空2分) ；4、{}1-；5、(1)(1)-???，，；6、|(21)22x x n x n n Z p p p 禳镲=-=-?睚镲镲铪或，；7、-；8、(理科)1arccos 4，(文科)arccos 4；9；10、12- ；11、(理科)234425，(文科)169425；12、0()()0f a f x ?；13、(理科)(1)、(3) ，(文科)16 ； 14、(理科)49k <-，(文科) 3．二、选择题： 15、B 16、C 17、D 18、(理科)A(文科)D三、解答题19、(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分．解(1)M N G H 点、、、是三棱锥所在棱的中点，//////M N B D G H B D M N G H∴，，进一步有． M NG H M N G H ∴、、、在直线和所确定的平面内．于是，M N G H 、、、四点共面． (2)AB M C 是球的大圆直径，点在球面上，A B C ∴⊥、、是大圆上的三点，且有BC AC ． AD ⊥⊥由平面BCD ，可得BC 平面ADC ． BC DC ∴⊥．13DC CB AD AB ====由，．3439()322V ππ∴==球． 20．(本题满分14分) 本题共有2个小题，第1小题满分7分，第2小题满分7分．解(1)由定义可知，关于x 的方程2(9)(0)490f f x x --+=-在(09)，内有实数根时，函数2()4[09]f x x x =-+是，上的平均值函数．解22(9)(0)445090f f x x x x --+=--=-，即，可得1251x x ==-或．又125(09)(1(09))x x =∈=-∉，，，故舍去，所以，2()4[09]f x x x =-+是，上的平均值函数，5是它的均值点． (2)2()1-11f x x mx =-++是[，]上的平均值函数，2(1)(1)11(1)f f x x mx --∴++=--关于的方程-在(11)-，内有实数根．22(1)(1)1101(1)f f x mx x mx m --++=-+-=--由-，得，解得1211x m x =-=或．又21(1)x =∉-，1，11x m ∴=-必为均值点，即111m -<-<． ∴所求实数02m m <<的取值范围是．21．(本题满分16分)本题共有2个小题，第1小题满分7分，第2小题满分9分．解(1)由已知可得，1()|2|f x a x b =--，且函数的定义域为D =()()22b b-∞⋃+∞，，．又()y f x =是偶函数，故定义域D 关于原点对称．于是，b =0(22b bb D D D ≠∈∉否则，当0时，有-且，即必不关于原点对称)．又对任意()()0.x D f x f x b ∈=-=，有，可得因此所求实数b =0． (2) 由(1)可知，1()((0)(0))2||f x a D x =-=-∞⋃+∞，，．考察函数1()2||f x a x =-的图像，可知：()(0)f x +∞在区间，上是增函数，()()f x -∞在区间，0上是减函数．因()y f x =在区间[]m n ，上的函数值组成的集合也是[]m n ，，故必有m n 、同号．①当0m n <<时，()[]f x m n 在区间，上是增函数，有1212a m ma n n ⎧-=⎪⎪⎨⎪-=⎪⎩，即方程12x a x =-，也就是22210x ax -+=有两个不相等的正实数根，因此220480a a >⎧⎨∆=->⎩，解得2()2210)a m n m n x ax ><-+=此时，、取方程的两根即可．②当0m n <<时，()[]f x m n 在区间，上是减函数，有1212a n ma m n ⎧+=⎪⎪⎨⎪+=⎪⎩，化简得()0m n a -=，解得10(()0)2a m n m n mn m n =<=<<此时，、的取值满足，且即可．综上所述，所求实数0a a a =>的取值范围是或．22．(本题满分16分)本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分5分．解(1)结合题意和图像，可知264sin 6A πωω⎧⎪⎪=⎨⎪=⎪⎩，解此方程组，得12A πω⎧=⎪⎨⎪=⎩，于是([08])12y x x =∈π，．进一步可得点M的坐标为88612x y π=⎧⎪⎨==⎪⎩．所以，10MP ==(km )．(2)在120MNP MNP NPM θ∆∠=∠=中，，，故sin sin(60)sin120MN NP MPθθ==-．又10MP =，因此，)y θθ=-(060θ<<)． (3)把)y θθ=-进一步化为：)y θ=+(060θ<<)．所以，当max 30y θ===时，(km )．可以这样设计：联结MP ，分别过点M 、P 在MP 的同一侧作与MP 成30角的射线，记两射线的交点为N ，再修建线段NM 和NP ，就可得到满足要求的最长折线段MNP 赛道．23．(本题满分18分)本题共有3个小题，第1小题满分6分，第2小题满分7分，第3小题满分5分．(理科)解(1)112n n n S a a +=，0n a >*()n N ∈，1112n n n S a a --∴=． 11111()2(2)2n n n n n n a a a a a a n +-+-∴=--=≥，即．24682n a a a a a ∴、、、、、是首项为2a ，公差为2的等差数列；135721n a a a a a -、、、、、是首项为1a ，公差为2的等差数列．又1112112a a a ==，S ，可得22a =．∴*221221()n n a n a n n N -==-∈，．所以，所求数列的通项公式为*()n a n n N =∈．(2)p 是给定的正整数(2p ≥)，11(1231)k k k b k pk p b a ++-==-，，，，， ∴数列{}k b 是项数为p 项的有穷数列．又111(1231)1k kbk pb k p b k +-===-+，，，，，．23234(1)(1)(2)(1)(2)(3)(1)(1)(1)232432p p p p p p b b b ------∴=-=-=-⋅⋅⋅，，,… 归纳可得1(1)(2)(3)(1)(1)(123)!k k p p p p k b k p k -----+=-=，，，，．(3)由(2)可知，1(1)(2)(3)(1)(1)(123)!k k p p p p k b k p k -----+=-=，，，，进一步可化为：1(1)(123)k k k p b C k p p=--=，，，，．所以，1223312311[(1)(1)(1)(1)]p pp p p p p p b b b b b C C C C p-+++++=--+-+-++-0122331[(1)(1)(1)(1)1]p pp p p p p C C C C C p=-+-+-+-++--1[(11)1]p p=--- 1p=． (文科){}*21*2111(1)325()32322()3232nn n n n n n n nn n a a n N a a n N a a ++++++=-??--??\==?--??Q 解数列满足，． ∴数列{}n a 是等差比数列，且公差比p =2．(2)∵数列{}n b 是等差比数列，且公差比p =2，112(2)n nn n b b n b b +--∴=≥-，即数列{}121)2n n b b b b ---是以(为首项，公比为的等比数列． 21121()22(2)n n n n b b b b n ---\-=-??．于是，112n n n b b ---=， 2122n n n b b ----=，…212b b -=．将上述1n -个等式相加，得211222n n b b --=+++L .∴数列{}n b 的通项公式为*2()n n b n N =∈．(3)由(2)可知，123n n S b b b b =++++L 2122222nn +=+++=-L ．于是，32*21211222()22n n n n n n n n S S n N S S +++++++--==∈--．所以，数列{}n S 是等差比数列，且公差比为2p =．。

数学_2011上海市某校高考数学模拟试卷(理科)_(含答案) (3)

2011上海市某校高考数学模拟试卷（理科）一、填空题（本题共14小题，每小题4分，共56分） 1. 函数y =√1−lgx 的定义域为________．2. 过P(1, 2)，以n →=(3,4)为法向量的点法向式直线方程为________． 3. 若复数z 满足|z1−ii|=−1+2i ，则z 等于________． 4. 设集合A ={x|−2<x <1}，B ={x|x −a <0}，若A ⊊B ，则a 的取值范围为________． 5. 若函数f(x)=2+sin 2ωx(ω>0)的最小正周期与函数g(x)=tan x2的最小正周期相等，则正实数ω的值为________．6. 现有2010年上海世博会各展览馆卡片5张，卡片正面分别是中国馆、台湾馆、沙特馆、日本馆、韩国馆，每张卡片大小、质地和背面图案均相同，将卡片正面朝下反扣在桌子上，从中一次性随机抽出两张，则抽到台湾馆的概率是________．7. 若(2x +√3)4=a 0+a 1x +a 2x 2+a 3x 2+a 3x 3+a 4x 4，则(a 0+a 2+a 4)2−(a 1+a 3)2的值为________．8. 已知xy >0，且xy −x −y =0，则x +y 的最小值为________． 9. 已知|a →|=|b →|=2，a →与b →的夹角为π3，则a →+b →在a →上的投影为________．10. 在锐角△ABC 中，角B 所对的边长b =10，△ABC 的面积为10，外接圆半径R =13，则△ABC 的周长为________．且其数学期望Eξ=1.5，则a −b =________．12. 如右图所示，已知0为矩形ABCD 的边CD 上一点，以直线CD 为旋转轴，旋转这个矩形所得的几何体体积为1，其中以OA 为母线的圆锥体积为14，则以OB 为母线的圆锥体积为________．13. 在正整数数列中，由1开始依次按如下规则将某些数染成红色：先染1，再染两个偶数2、4；再染4后面最邻近的三个连续奇数5、7、9；再染9后面最邻近的四个连续偶数10、12、14、16；再染此后最邻近的五个连续奇数17、19、21、23、25；按此规则一直染下去，得到一红色子数列1，2，4，5，7，9，10，12，14，16，17，…．则在这个红色子数列中，由1开始的第2011个数是________．14. 我们把形如y =b|x|−a (a >0,b >0)的函数因其图象类似于汉字“囧”字，故生动地称为“囧函数”，并把其与y 轴的交点关于原点的对称点称为“囧点”，以“囧点”为圆心凡是与“囧函数”有公共点的圆，皆称之为“囧圆”，则当a =1，b =1时，所有的“囧圆”中，面积的最小值为________．二、选择题（本题共4小题，每小题5分，共20分）15. “α=2kπ+β，k∈Z”是“sinα=sinβ”的（）A 充分不必要条件B 必要不充分条件C 充要条件D 既非充分又非必要条件16. 某流程图如图所示，现输入如下四个函数，则可以输出的函数是（）A f(x)=x2B f(x)=|x|x C f(x)=e x−e−xe x+e−xD f(x)=√x17. 已知函数f(x)=sinπx的图象的一部分如左图，则右图的函数图象所对应的函数解析式为（）A y=f(2x−12) B y=f(2x−1) C y=f(x2−1) D y=f(x2−12)18. 数列{a n}满足a1=1，a n+1⋅√1a n2+4=1(n∈N∗)，记S n=a12+a22+...+a n2，若S2n+1−S n≤m30对n∈N∗恒成立，则正整数m的最小值为（）A 10B 9C 8D 7三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤．19. 如图，直三棱柱ABC−A1B1C1中，CA=CB=2，∠BCA=90∘，AA1=4，E是A1B1的中点．（1）求CE与平面ACB所成的角．（2）求异面直线BA1与CB1所成的角．20. 设f(x)=2sin(π2−x 2)sin(π+x 2)+cos 2(π2−x 2)−cos 2(π+x2)（1）若x ∈(0,π2)，求f(x)的最小值；（2）设g (x)=f(2x −π4)+2m ，x ∈[π4,7π8]，若g (x)有两个零点，求实数m 的取值范围．21. 在平面直角坐标系中，直线L:y =mx +3−4m ，m ∈R 恒过一定点，且与以原点为圆心的圆C 恒有公共点．（1）求出直线L 恒过的定点坐标；（2）当圆C 的面积最小时，求圆C 的方程；（3）已知定点Q(−4, 3)，直线L 与（2）中的圆C 交于M 、N 两点，试问QM →⋅QN →⋅tan∠MQN 是否存在最大值，若存在则求出该最大值，并求出此时直线L 的方程，若不存在请说明理由．22. 已知点P n (a n , b n )满足a n+1=a n b n+1，b n+1=b n1−a n2，且P 0(13,23)(n ∈N)．（1）求点P 1坐标，并写出过点P 0，P 1的直线L 的方程；（2）猜测点P n (n ≥2)与直线L 的位置关系，并加以证明；（3）求数列{a n }与{b n }的通项公式，并求OP n →⋅OP n+1→的最小值（其中O 为坐标原点，n ∈N ∗）．23. 已知函数f 1(x)=e |x−2a+1|，f 2(x)=e |x−a|+1，x ∈R ．（1）若a =2，求f(x)=f 1(x)+f 2(x)在x ∈[2, 3]上的最小值；（2）若|f 1(x)−f 2(x)|=f 2(x)−f 1(x)对于任意的实数x ∈R 恒成立，求a 的取值范围；（3）当4≤a ≤6时，求函数g(x)=f 1(x)+f 2(x)2−|f 1(x)−f 2(x)|2在x ∈[1, 6]上的最小值．2011上海市某校高考数学模拟试卷（理科）答案1. (0, 10]2. 3(x −1)+4(y −2)=03. 1+i4. a ≥15. 126. 257. 18. 49. 310. 10+10√3 11. 0 12. 11213. 395914. 3π15. A16. C17. B18. A19. 解：（1）过点E作EH垂直于AB于H，连接CH，则∠ECH就是所求的CE与平面ACB所成的角∵ EH=4，CH=√2∠ECH=arctan2√2即CE与平面ACB所成的角为arctan2√2；（2）在直三棱柱的下方补上一个全等的直三棱柱∵ CB1 // C2B∴ ∠A1BC2或其补角就是异面直线BA1与CB1所成的角∵ BA1=2√6，C2B=2√5，A1C2=2√17∴ 在△A1BC2中，由余弦定理可得∠A1BC2=arccos(−√3010)∴ 异面直线BA1与CB1所成的角为arccos√3010．20. 解：（1）∵ f(x)=2sin(π2−x2)sin(π+x2)+cos2(π2−x2)−cos2(π+x2)=−2cos 12xsin12x+sin212x−cos212x∴ f(x)=−sinx−cosx=−√2sin(x+π4)∵ π4<x+π4<3π4∴ x=π4，f min=−√2（2）设g(x)=−√2sin2x+2m，x∈[π4,7π8]∵ 函数g(x)有两个零点∴ 方程−√2sin2x+2m=0当x∈[π4,7π8]时有两个解∴ y =2m 与y =√2sin2x ，x ∈[π4,7π8]图象有两个交点则−√2<2m ≤−1 ∴ −√22<m ≤−1221. 解：（1）直线L:y =mx +3−4m 可化简为y =m(x −4)+3 所以直线恒过定点T(4, 3)（2）由题意，要使圆C 的面积最小，定点T(4, 3)在圆上，所以圆C 的方程为x 2+y 2=25．（3）QM →⋅QN →⋅tan∠MQN=|QM →||QN →|⋅cos∠MQN ⋅tan∠MQN =|QM →|⋅|QN →|⋅sin∠MQN =2S △MQN （10分）由题意得直线L 与圆C 的一个交点为M(4, 3)，又知定点Q(−4, 3)，直线L MQ :y =3，|MQ|=8，则当N(0, −5)时S MQN 有最大值32．即QM →⋅QN →×tan∠MQN 有最大值为64，此时直线L 的方程为2x −y −5=0． 22. 解：（1）由a 0=13，b 0=23，得a 1=14，b 1=34，得P 1坐标为(14,34)…2′显然直线L 的方程为x +y =1 ...4′ （2）由a 1=14，b 1=34，得a 2=15，b 2=45，∴ 点P 2∈L ，猜想点P n (n ≥2, n ∈N)在直线L 上，…6′ 以下用数学归纳法证明：当n =2时，点P 2∈L当n =k(k ≥2)时，点P k ∈L ，即a k +b k =1，则当n =k +1时，a k+1+b k+1=a k b k+1+b k+1=(1+a k )⋅b k 1−a k2=bk1−a k=1，∴ 点P k+1∈L ，∴ 点P n ∈L(n ≥2)…10′ （3）由a n+1=a n b n+1，b n+1=bn1−a n2，a n +b n =1，得a n+1=a n b n1−a n2=a n1−a n1−a n2=a n 1+a n(a n ≠0)∴1a n+1=1a n+1...12′∴ {1a n}是等差数列，∴ 1a n=1a 0+n =n +3，∴ a n =1n+3，b n =n+2n+3 (14)′OP n →⋅OP n+1→=a n a n+1+b n b n+1=1−2n +5n 2+7n +12...16′令2n +5=t 则n =t−52，上式可化简化1−4tt 2+4t+3=1−4t+3t+4由单调性可得当t =7， n =1时，上式有最小值为1320所以1−2n+5n 2+7n+12(n ∈N ﹡)的最小值为1320． ...18′23. 解：（1）对于a =2，x ∈[2, 3]，f(x)=e |x−3|+e |x−2|+1=e 3−x +e x−1≥2√e 3−x ⋅e x−1=2e ，当且仅当e 3−x =e x−1，即x =2时等号成立，∴ f(x)min =2e ．（2）|f 1(x)−f 2(x)|=f 2(x)−f 1(x)对于任意的实数x 恒成立，即f 1(x)≤f 2(x)对于任意的实数x 恒成立，亦即e |x−2a+1|≤e |x−a|+1对于任意的实数x 恒成立， ∴ |x −2a +1|≤|x −a|+1，即|x −2a +1|−|x −a|≤1对于任意的实数x 恒成立．又|x −2a +1|−|x −a|≤|(x −2a +1)−(x −a)|=|−a +1|对于任意的实数x 恒成立，故只需|−a +1|≤1，解得0≤a ≤2，∴ a 的取值范围为0≤a ≤2．（3）g(x)=f 1(x)+f 2(x)2−|f 1(x)−f 2(x)|2={f 1(x)，f 1(x)≤f 2(x)f 2(x)，f 1(x)>f 2(x)∵ f 1(x)与f 2(x)的底数都同为e ，外函数都单调递增∴ 比较f 1(x)与f 2(x)的大小关系，只须比较|x −2a +1|与|x −a|+1的大小关系令F 1(x)=|x −2a +1|，F 2(x)=|x −a|+1，G(x)={F 1(x)，F 1(x)≤F 2(x)F 2(x)，F 1(x)>F 2(x)其中4≤a ≤6，x ∈[1, 6]∵ 4≤a ≤6∴ 2a −1≥a ≥1，令2a −1−x =1，得x =2a −2，由题意可以如下图象：当4≤a≤6时，a≤6≤2a−2，G(x)min=F2(a)=1，g(x)min=e1=e；。

黄浦区高三数学一模解析

x 2 + y 2 x 2 + y 2黄浦区高三一模数学解析一. 填空题〔本大题共 12 题，1-6 每题 4 分，7-12 每题 5 分，共 54 分〕 1. 集合 A = {x , x 2} 〔 x ∈ R 〕，假设1∈ A ，那么 x = . 【考点】集合【解析】 x = 1 时， x 2 = 1 ，不满足集合元素的互异性，舍去；当 x 2 = 1 ⇒ x = ±1 ，经检验 x = 1 舍去，故 x = -1 2. 函数 f (x ) = lg1- x，那么该函数的定义域是 .1+ x【考点】函数的概念【解析】由对数函数定义可知1 - x> 0 ⇒ -1 < x < 1，故其定义域为(-1,1)1 + x3. sin(π -θ ) = - 1 ，那么cos(π-θ ) = .32【考点】诱导公式【解析】由sin(π -θ ) = - 1⇒ sin θ = - 1 ，那么cos(π-θ ) = sin θ = - 133 2 34. 幂函数 y = f (x ) 的图像过点 1，那么 f (x ) = .【考点】幂函数(4, ) 2αα1 1-1【解析】由幂函数概念可设 f (x ) = x ⇒ f (4) = 4 = ⇒ α = - ，那么 f (x ) = x 22 25. x 是-2 和 8 的等差中项， y 2 是 32 和 8 的等比中项，那么 = .【考点】等差等比数列【解析】易得 x =-2 + 8 = 3, y 2 = 2= 16 ，那么 = 56. 直线l 过点 P (-2,1) ，直线l 的一个方向向量d = (-3, 2) ，那么直线l 的点方向式方程是 .【考点】直线点方向式方程【解析】由直线点方向式方程公式 x - x 0 = y - y 0 ⇒ x + 2 = y - 1u v -3 232 ⨯ 82 (3 2 )2 - ( 2)2 = ()9-r - rr -9 7 5 2 5 2 57. 某圆锥体的底面圆的半径长为的体积是 . 【考点】圆锥，其侧面展开图是圆心角为 2π 的扇形，那么该圆锥体 3【解析】设圆锥母线长为l ，由圆锥展开图可得2π ⨯ = 2π ⨯ l ⇒ l = 3 3，那么圆锥的高为h = = 4 ，那么其体积V = 1 π ( 2 )2 ⨯ 4 = 8 π8. ( 1 - x3 3 x )9的二项展开式中的常数项的值是a ，假设3i ⋅ z + a - 6i = 72 + 3i 〔其中i 是虚数单位〕，那么复数 z 的模| z |= 〔结果用数值表示〕【考点】二项式定理、复数【解析】由二项式定理展开式T⎛ 1 ⎫r C r x -1 x 23 = C r (-1) x 2 ，当r +1 9 ⎪ 9 ⎝ ⎭3r - 9 = 0 ⇒ r = 6 ⇒ a = 84 ，那么 z = 9i -12= 3 + 4i ⇒ z = 5 2 3i 9. 假设关于 x 、 y 的二元一次线性方程组⎧a 1x + b 1 y =c 1的增广矩阵是⎛ m1 3 ⎫，且⎨a x +b y =c 0 2 n ⎪⎩ 2 2 2⎝ ⎭-1 0 1⎧x = 1⎨ y = -1 是该线性方程组的解，那么三阶行列式 0 3 m 中第 3 行第 2 列的元素的代数⎩2 n 1余子式的值是 .【考点】矩阵行列式【解析】由矩阵知识得⎧m - 1 = 3 ⇒ ⎧m = 4，那么 n 的代数余子式为(-1)3+2-11= m = 4⎨-2 = n ⎨n = -2 0 m ⎩ ⎩10. 某高级中学欲从本校的 7 位古诗词爱好者〔其中男生 2 人、女生 5 人〕中随机选取 3 名同学作为学校诗词朗读比赛的主持人，假设要求主持人中至少有一位是男同学，那么不同选取方法的种数是〔结果用数值表示〕【考点】排列组合【解析】这题用正难那么反比较容易：所有情况减去没有男同学的情况即可，即C 3 - C 3= 25 ；或者直接求解：有 1 名男生和 2 名男生两种情况： C 1 ⋅ C 2 + C 2 ⋅ C 1 = 252 25 5 -6k + 4k - 255 11. 平面向量 a 、b 满足| a |= 5 ， | b |= 1， a ⋅ b = 3 ，向量c = λ ⋅ a + (1- λ) ⋅ b 〔 λ ∈ R 〕，且对任意λ ∈ R ，总有| c + k a |≥ 2 5 成立，那么实数k 的取值范围是 .【考点】平面向量【解析】不妨设b = OB = (1, 0) ，由a ⋅ b = a b cos θ ⇒ cos θ = 3⇒ a = OA = (3, 4) ，由c = OC = λOA + (1 - λ )OB 可知5C 点落在直线 AB : y = 2x - 2 上，故设C (m , 2m - 2) ⇒ c = (m , 2m - 2) ，故c + k a ≥ 2 5 ⇒ ≥ 2 ，其几何意义为点(-3k , -4k ) 到直线 AB : y = 2x - 2 大于等于2 ，即 ≥ 2 ⇒ k ≤ -6或k ≥12. a ,b ∈ R ，函数 f (x 2 2 - ax - b | 〔 x ∈ R 〕，假设函数 f (x ) 的最小值为2b 2，那么实数b 的取值范围是 .【考点】函数最值f ( x ) ⎧⎪x 2,x 2 ≥ ax + b 【解析】设 g (x ) = = ⎨ ，，即将 f (x ) 的最小值为2b 2 转化为 g (x ) 的最小值为b 2 ，其中2 ⎪⎩ax + b , x 2< ax + b g (x ) = max {x 2 , ax + b }1.当 y = x 2 与 y = ax + b 没有交点或交点在 y 轴同侧时，此时即 g (x )min = b 2 = 0 ⇒ b = 02.当 y = x 2 与 y = ax + b 没有交点或交点在 y 轴异侧时，那么b > 0① 当a ≥ 0 时，最低点交点坐标为(-b , b 2 )，此时b 2 = -ab + b ⇒ b = -a + 1 ≤ 1 ⇒ 0 < b ≤ 1 ② 当a < 0 时，最低点交点坐标为(b , b 2 )，此时b 2 = ab + b ⇒ b = a + 1 < 1 ⇒ 0 < b < 1 综上，实数b 的取值范围是[0,1]二. 选择题〔本大题共 4 题，每题 5 分，共 20 分〕13. a 、b 、l 是空间中三条直线，其中直线 a 、b 在平面α 上，那么“ l ⊥ a 且l ⊥ b 〞是“ l ⊥ 平面α 〞的〔〕A.充分非必要条件B.必要非充分条件C.充要条件D.非充分也非必要条件(m + 3k )2+ (2m - 2 + 4k )2【考点】立体几何【解析】直线与平面垂直的判定定理是直线与平面内两条相交的直线垂直，当 a 与b 不想交时不能由l ⊥a 且l ⊥b 推出l ⊥平面α，但l ⊥平面α时，l 垂直于平面α内所有直线，应选 B14.为了得到函数y = sin x - 3 cos x 〔x ∈R 〕的图像，可以将函数y = 2sin x 〔x ∈R 〕的图像〔〕A.向右平移π 6C. 向右平移π3个单位 B. 向左平移π3 个单位 D. 向左平移π6个单位个单位【考点】三角函数【解析】 y = sin x -3 cos x = 2sin(x -π) ，应选 C315.某企业欲做一个介绍企业开展史的铭牌，铭牌的截面形状是如下列图的扇形环面〔由扇形OAD 挖去扇形OBC 后构成〕，OA =10 米，OB =x 米〔0 <x <10 〕，线段BA 、线段CD 、弧BC 、弧AD 的长度之和为30 米，圆心角为θ弧度，那么θ关于x 的函数解析式是〔〕A. θ=2x +10 x +10C. θ=10 -x 10 +x【考点】三角函数【解析】AB B. θ=D. θ=x +102x +1010 -x2x +10;那么2(10，应选 ACD 10 x,BC x,CD 10x) 10x3010 2x10xkx ⎩ 1 11 16. k ∈ R ，函数 f (x ) =| x2 - 4 | +x 2 + kx 的定义域为 R ，假设函数 f (x ) 在区间(0, 4) 上有两个不同的零点，那么k 的取值范围是〔〕A. -7 < k < -2B. k < -7 或 k > -2C. -7 < k < 0D. -2 < k < 0【考点】三角函数【解析】| x 2 - 4 | +x 2 + kx = 0 ⇒| x 2 - 4 | +x 2 = -kx ，那么y =| x 2 - 4 | +x 2 = ⎧4, x ∈ (0, 2)⎨2x 2 - 4, x ∈[2, 4)由图像分析可得： y 过点A (2, 4) 时， k当： y 故 7k过点A (4, 28) 时， k 2 ，选 A三. 解答题〔本大题共 5 题，共 14+14+14+16+18=76 分〕17. 正方体 ABCD - A 1B 1C 1D 1 的棱长为 4，点 E 是侧面CDD 1C 1 的中心. 〔1〕联结 A 1D ，求三棱锥 A 1 - DED 1 的体积V A -DED 的数值；〔2〕求异面直线 A 1E 与 AD 所成角的大小〔结果用反三角函数值表示〕. 【考点】立体几何【解析】(1) 正方体 ABCD - A 1B 1C 1D 1 的棱长为 4，点 E 是侧面CDD 1C 1 的中心，∴ AD ⊥ 平面 DCC D ， S= 1 S = 4 .1 11 1∆DED 14 正方形DCC 1D 1∴ V A 1 -DED 1= 1 ⋅ S 3 ∆DED ⋅ A 1D 1 = 1 ⨯ 4⨯ 4 = 163 3(2) ABCD - A 1B 1C 1D 1 是正方体，∴ AD ∥ A 1D 1 ， A 1D 1 ⊥ 平面 DCC 1D 1 .∴ ∠EA 1D 1 就是异面直线 A 1E 与 AD 所成的角(或补角)， A 1D 1 ⊥ D 1E .2kx 7 yA Ox2 ∴ D E = 1 D C = 142 + 42 = 2 .12 1 2∴ tan ∠EA D = D 1E =2 ，即∠EA D = arctan 2 .A 1D 1 21 122所以，所求异面直线 A 1E 与 AD 所成的角的大小是arctan 2.18. 在△ ABC 中，内角 A 、 B 、C 所对的边分别为a 、b 、c ，假设 A 为钝角，且2a sin B - 2b = 0 . 〔1〕求角 A 的大小；〔2〕记 B = x ，求函数 f (x ) = cos x + cos(π+ x ) 的值域.3【考点】三角比与三角函数【解析】(1) ∆ABC 的内角 A 、B 、C 所对的边分别为a 、b 、c ， 2a sin B - 2b = 0 ，∴根据正弦定理：a sin A =b sin B = csin C= 2R ，2a s in B - 2b = 0 可化为2 ⋅ 2R sin A sin B - 2 ⋅ 2R sin B = 0(0 < B < π , sin B ≠ 0) ．∴ sin A =2.A 为钝角，即 π < A < π ，∴ A = 3π .2 2 4(2) B = x ， A + B + C = π ，∴C = π - x - 3 π = π - x ，且0 < x < π.4 4 4∴ f (x ) = cos x + cos(π + x ) = cos x + 1 cos x - 3sin x = 3 sin(π - x ) .3 又 0 < x < π ，可得 π 2 2 3π π < - x < .4 12 6 3考察函数 y = sin x 的图像，可知sin π < sin(π - x ) < 3.12 3 21 11- x 1+ x 1- x 1 1 1 x x x 2 0, 0, 0. 因此，3 sin π < 3 sin(π - x ) < 3 .12 3 2所以函数 f (x ) 的值域是( 3 sin π , 3) .(写成(, 3) 也可以)12 2 19. 实数 a 、b 是常数，函数 f (x ) = (4 2 + + a )( + b ) .〔1〕求函数 f (x ) 的定义域，判断函数的奇偶性，并说明理由；〔2〕假设a = -3 ， b = 1 ，设t = + ，记t 的取值组成的集合为 D ，那么函数 f (x ) 的值域与函数 g (t ) = 1(t 3 - 3t 2 ) 〔 t ∈ D 〕的值域相同，试解决以下问题：2① 求集合 D ；② 研究函数 g (t ) = 1(t 3 - 3t 2 ) 在定义域 D 上是否具有单调性？假设有，请用函数单调性定义2加以证明，假设没有，请说明理由，并利用你的研究结果进一步求出函数 f (x ) 的最小值.【解析】(1) 实数a 、b 是常数，函数 f (x ) ( 1 x 1 xa )( 1 x 2b ) ，由解得 1 x 1 .函数的定义域是[ 1,1] .对于任意x[ 1,1]，有 x [ 1,1] ，且f ( 即 f ( x )f (x ) 对x [ 1,1]都成立. (又 f (x )不恒为零)所以，函数 f (x )是偶函数.(该函数是偶函数不是奇函数也可以)(2)a3,b1 ，f (x )( 1 x1 x3)( 1 x 21).( 1 x1 xa )( 1 x 2b ) f (x ) ，6 - 2 1+ x 1- x 2x ) ( 1 ( x )1 ( x ) a )( 1 ( x )2 b )1 x 1 x2 2 1 x 2 t 2设t( 1 x 1 )，那么t 2 .0 1 x 21 ，2 t 24(t0)，即 2 t2 .于是， g (t ) 1 (t 33t 2 )的定义域为D [ 2,2] .对于任意的t 、tD ，且t，有2 g (t 1 ) 1 211 (t t )[t (t2) t (t 2) 1t (t2) 1 t (t2)] .2 121 12 2 2 1 222 1又t 10,t 2 0,t 1 t 20 ，且t 12 0, t 2 20 (这里二者的等号不能同时成立)，1 (t t )[t (t2) t (t2)1t (t 2)1 t (t 2)] 0 ，即2 121 12 221 2 22 1g (t 1) g (t 2 ) 0, g (t 1) g (t 2 ).函数g (t ) 在D 上是减函数.(g (t ))ming (2)1 (2323 22 )2 .又函数 f (x )的值域与函数g (t )函数 f (x )的最小值为 2 .1 (t 323t 2 )的值域相同，2 1 [(t 1 t )(t 2 2 1 t t t 2) 1 2 2 3(t 1 t )(t 2 1 t )] 2 D[ 2,2].2 1 (t 1 t )[(t 22 12t ) (t 21 22t ) (1t t 2 2 1 2t ) (1 t t 1 2 1 2t )] 2 g (t ) 2 2 1[t 3 1 3t 2 1 (t 3 2 3t 2 )] 22 3 2 3 x 2 4 x y 2 2 2 . 3 1,2 3 x 2 y 2 2 2a 2b 2 20. 定义：椭圆 a 2 + b 2 = 1 〔 a > b > 0 〕，把圆 x + y = a 2 + b2称为该椭圆的协同圆，设椭圆 x 2 y 2C : + = 1 的协同圆为圆O 〔 O 为坐标系原点〕，试解决以下问题： 4 2〔1〕写出协同圆圆O 的方程；〔2〕设直线l 是圆O 的任意一条切线，且交椭圆C 于 A 、 B 两点，求OA ⋅ OB 的值；〔3〕设 M 、 N 是椭圆C 上的两个动点，且OM ⊥ ON ，过点O 作OH ⊥ MN ，交直线MN 于 H 点，求证：点 H 总在某个定圆上，并写出该定圆的方程.x 2 y 2 2 2【解析】(1)由椭圆C : 1 ，可知a4 24,b 2 .根据协同圆的定义，可得该椭圆的协同圆为圆O : x 2y 2 4 . 3(2) 设点A (x 1,y 1)、B (x 2,y 2 ) ，那么OA OB x 1x 2 不存在两种情况加以讨论：①当直线l 的斜率不存在时，直线l : x .y 1y 2 .因为直线l 为圆O 的切线，故分直线l 的斜率存在和假设l : x ，由可解得此时，OA OB x 1x 2 y 1y 2②当直线l 的斜率存在时，设l : y 4 4 0 . 当l : x 时，同理可得：OA OB 0 . 3 3 .x 2 y 2由 4 2 y kx t . 1, 得(1 2k 2 )x 24ktx 2t 24 0 .于是，xy 2 , 3 2 . 3 kx t x 1 2x 4kt ,1 2k 2x 1x 2. 1 2k 22t 24ONk 1x1xk1x 2 4yy22k1x.1,x 2141 2k 2,2y24k1112k 2.31进一步算得y1y2又由于直线l 是圆O 的切线，故，可算得3t2.4k2 4 .2t2 4t2 4k 23t24k 2 4所以，x1x2y1y2 1 2k 2 1 2k 2 1 2k 20 ，即OA OB 0 .综上，总有OA OB 0 .证明(3) M、N 是椭圆C 上的两个动点，且OM .设M(x1,y1)、N(x2,y2 )，那么x1x2 y1y2 0 ．下面分直线OM、ON 中有一条直线的斜率不存在和两条直线的斜率都存在两种情况加以讨论.假设直线ON 的斜率不存在，即点N 在y 轴上，那么点M 在x 轴上，有x 2 4,y2 2 ．1 2由S1|OM | |ON |1|OH | | MN | ，可解得|OH |2．OMN 2 2 3假设直线OM、ON 的斜率都存在，设OM : y ，那么ON : y ．1 k 2由得可算得|OM | 2 1 ．1 2k 21 k2 3(1k 2 )2同理可得|ON | 2 1 ．于是，| MN | |OM |2|ON |22 1 ．2 k 2(1 2k 2 )(2 k 2 )1 1 1由S1|OM | |ON |1|OH | | MN | ，可解得|OH |2．OMN 2 2 3因此，总有|OH |2，即点H 在圆心为坐标系原点，半径为23的圆上．所以该定圆的方程为圆x 2y2 4 . 3(kx1t)(kx2t)k x x221 2kt(x1x2)tt214k 22k 2 | k 010 t |k 223n n n -1 n n -1 n +1 n n n -1 n +1 n n n -1 21. 函数 y = f (x ) 的定义域为R ，数列{a } 〔 n ∈ N * 〕满足a ≠ a ， a = f (a) ， n2 1 n n -1f (a ) + kf (a ) = t (a + ka ) 〔 n ≥ 2 ， n ∈ N * 〕〔实数k 、t 是非零常数〕.n n -1 n n -1〔1〕假设k = -1 ，且数列{a } 〔n ∈ N * 〕是等差数列，求实数t 的值；〔2〕假设a+ ka ≠ 0 ，数列{b }〔 n ∈ N * 〕满足b = a + ka 〔 n ∈ N * 〕，求通项公式b ；2 1 nn n +1 n n 〔3〕假设k = -1 ， t ≠ 1，数列{a } 〔 n ∈ N *〕是等比数列，且a = a 〔 a ≠ 0 ， a ∈ R 〕，n 1 a 2 ≠ a 1 ，试证明： f (a ) = t ⋅ a .【考点】数列综合【解析】解数列{a }(n ∈ N *) 满足a ≠ a ， a = f (a ) ， n 2 1 n n -1f (a ) + kf (a ) = t (a + ka )(n ≥ 2,n ∈ N * ) ， ∴a + ka = t (a + ka )(n ≥ 2,n ∈ N * ) ． (1) 数列{a }(n ∈ N *) 是等差数列， a ≠ a ， k = -1 ，n 2 1 记公差为d ，那么公差d ≠ 0 ．∴ a n +1 - a n = t (a n - a n -1 ) ，即d = td .∴ t = 1．(2) a + ka ≠ 0 数列{b }(n ∈ N * ) 满足b = a + ka (n ∈ N * ) ，2 1 n n n +1 n∴ b = a + ka ≠ 0 b = tb(n ≥ 2, n ∈ N * ) ．1 2 1n n -1 ∴数列{b }(n ∈ N * ) 是首项为b ，公比为t 的等比数列．n 1∴ b = (a + ka )tn -1 (n ∈ N * ) ．n 2 1 证明(3) k = -1，t ≠ 1 ， a 2 ≠ a 1 ，∴ a - a = t (a - a )(n ≥ 2,n ∈ N * ) ．根据(2)，可知当k = -1 时， b = (a - a )t n -1 (n ∈ N * ) ．n 2 1 ∴ a n = (a n - a n -1 ) + (a n -1 - a n -2 ) + + (a 2 - a 1 ) + a 1n b (1- t n -1 ) = b n -1 + b n -2 + + b 1 + a 1 = 1 + a ．(利用累加法也可以求出a n ) 1- t (a - a )(1- t n -1 ) a - a (a - a ) n -1 *∴ a n = 2 + a = a + 2 - t (n ∈ N ) ．1- t 1- t 1- t数列{a }(n ∈ N *) 是等比数列，∴ (a 2 - a ) + a = 0 ，解得a = ta ．(利用a 2 = a ⋅ a 也可以)1- t2 2 1 3又 a 2 = f (a 1 ) = f (a ) ，∴ f (a ) = ta .。