八年级数学圆的有关概念

合集下载

初中数学《圆的有关概念和性质》复习课优质课件

形的外接叫做三角形的外心．
圆
性质：三角形的外心到三角形的三个
顶点的距离相等．
核心点拨
考点三：三角形的外接圆及圆内接四边形
圆内接四边形：如果一个四边形的
6．圆内
接四边形
的性质定
理
顶点都在同一个圆上
____________________，这个四边形
四边
叫做圆内接四边形，这个圆叫做_____
形的外接圆
)
思路分析
首先作出相关的辅助线，利用垂径定理和勾股定理求出各线段之间
的关系，得到一些特殊的三角形，再利用圆周角定理推出相关角的
度数即可．
变式训练
2－1
如图，在 ⊙O 中，弦 AB ， CD 相交于点 P. 若 ∠A ＝ 48° ，
∠APD＝80°，则∠B的度数为(
A
)
A．32°
B．42°
质．有时还需要添加
论
或等弧进行证明．
辅助线，构成直径所
推论2：半圆(或直径)所对的圆周角是
对的圆周角，以便转
弦
______，90°的圆周角所对的____是直
直角
化为直角三角形的问
径．
题去研究．
考点三：三角形的外接圆及圆内接四边形
定义：经过三角形各顶点的圆叫做三
5．三角角形的外接圆．三角形外接圆的圆心
对的____相等，所对的____相等．
(1)在同圆或等圆中，
弧
弦
定理2：在同圆或等圆中，________、____、
如果弧不相等，那
圆心角
弧
弦
么弧所对的弦、圆
____中如果有一组量相等，那么它们所对应
的其余各组量都分别相等．

数学中考一轮复习学案第24节圆的有关概念与性质（含解析）

第四章图形的性质第24节圆的有关概念与性质■知识点一：圆的有关概念(1)圆：平面上到定点的距离等于定长的所有点组成的图形叫做圆，其中定点为圆心，定长为半径．(2)弧：圆上任意两点间的部分叫做圆弧，简称弧，大于半圆的弧称为优弧，小于半圆的弧称为劣弧．(3)弦：连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径．(4)相关概念：同心圆、弓形、等圆、等弧．(5)圆心角：顶点在圆心的角叫做圆心角．(6)圆周角：顶点在圆上，并且两边和圆相交的角是圆周角．(7)确定圆的条件：过已知一点可作无数个圆，过已知两点可作无数个圆，过不在同一条直线上的三点可作一个圆．(8)圆的对称性：圆是轴对称图形，其对称轴是直径所在的直线；圆是中对称图形，对称中心为圆心，并且圆具有旋转不变性．■知识点二：垂径定理及推论：①垂直于弦的直径平分弦，并且平分弦所对的两条弧．②平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧，③弦的垂直平分线经过圆心，并且平分弦所对的两条弧．④平分弦所对一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧．⑤圆的两条平行弦所夹的弧相等．■知识点三：圆心角、弧、弦的关系（1）定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．（2）推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．说明：同一条弦对应两条弧，其中一条是优弧，一条是劣弧，而在本定理和推论中的“弧”是指同为优弧或劣弧．（3）正确理解和使用圆心角、弧、弦三者的关系三者关系可理解为：在同圆或等圆中，①圆心角相等，②所对的弧相等，③所对的弦相等，三项“知一推二”，一项相等，其余二项皆相等．这源于圆的旋转不变性，即：圆绕其圆心旋转任意角度，所得图形与原图形完全重合．（4）在具体应用上述定理解决问题时，可根据需要，选择其有关部分．■知识点四：圆周角定理及推论①圆周角定理：一条弧所对的圆周角等于它所对圆心角的一半．推论１：在同圆或等圆中，同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧也相等．推论2：直径所对的网周角是直角；90°的圆周角所对的弦是直径．推论3：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．②圆内接四边形的任意一组对角互补．■考点1.圆的有关概念◇典例：（2017年黑龙江大庆）如图，点M，N在半圆的直径AB上，点P，Q在上，四边形MNPQ 为正方形．若半圆的半径为，则正方形的边长为．【考点】正方形的性质；勾股定理；圆的认识．【分析】连接OP，设正方形的边长为a，则ON=，PN=a，再由勾股定理求出a的值即可．解：连接OP，设正方形的边长为a，则ON=，PN=a，在Rt△OPN中，ON2+PN2=OP2，即（）2+a2=（）2，解得a=2．故答案为：2．【点评】本题考查的是正方形的性质，勾股定理；圆的认识，根据题意作出辅助线，构造出直角三角形是解答此题的关键．◆变式训练（2017•宁夏）如图，点 A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为 __________■考点2.垂径定理及其推论◇典例：（2018年黑龙江省龙东、七台河、佳木斯、鸡西、伊春、鹤岗、双鸭山）如图，AB为⊙O 的直径，弦CD⊥AB于点E，已知CD=6，EB=1，则⊙O的半径为．【考点】垂径定理，勾股定理【分析】连接OC，由垂径定理知，点E是CD的中点，AE=CD，在直角△OCE中，利用勾股定理即可得到关于半径的方程，求得圆半径即可．解：连接OC，∵AB为⊙O的直径，AB⊥CD，∴CE=DE=CD=×6=3，设⊙O的半径为xcm，则OC=xcm，OE=OB﹣BE=x﹣1，在Rt△OCE中，OC2=OE2+CE2，∴x2=32+（x﹣1）2，解得：x=5，∴⊙O的半径为5，故答案为：5．【点评】本题利用了垂径定理和勾股定理求解，熟练掌握并应用定理是解题的关键．◆变式训练1.（2018年山东省烟台）如图，方格纸上每个小正方形的边长均为1个单位长度，点O，A，B，C在格点（两条网格线的交点叫格点）上，以点O为原点建立直角坐标系，则过A，B，C 三点的圆的圆心坐标为．2.（2018年浙江省绍兴市）如图，公园内有一个半径为20米的圆形草坪，A，B是圆上的点，O为圆心，∠AOB=120°，从A到B只有路，一部分市民为走“捷径”，踩坏了花草，走出了一条小路AB．通过计算可知，这些市民其实仅仅少走了步（假设1步为0.5米，结果保留整数）．（参考数据：≈1.732，π取3.142）■考点3. 圆心角、弧、弦的关系◇典例（2017•牡丹江）如图，在⊙O中，=，CD⊥OA于D，CE⊥OB于E，求证：AD=BE．【考点】圆心角、弧、弦的关系；垂径定理．【分析】连接OC，先根据=得出∠AOC=∠BOC，再由已知条件根据AAS定理得出△COD ≌△COE，由此可得出结论．证明：连接OC，∵=，∴∠AOC=∠BOC．∵CD⊥OA于D，CE⊥OB于E，∴∠CDO=∠CEO=90°在△COD与△COE中，∵，∴△COD≌△COE（AAS），∴OD=OE，∵AO=BO，∴AD=BE．【点评】本题考查的是圆心角、弧、弦的关系，熟知在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等是解答此题的关键．◆变式训练（2017•宜昌）如图，四边形ABCD内接于⊙O，AC平分∠BAD，则下列结论正确的是（）A．AB=AD B．BC=CD C． D．∠BCA=∠DCA■考点4. 圆周角定理及其推论◇典例：1.（2018 年广西梧州市）如图，已知在⊙O 中，半径 OA=2，弦 AB=2，∠BAD=18°，OD 与AB 交于点 C，则∠ACO=__________度．【考点】圆周角定理，勾股定理的逆定理，等腰三角形的性质【分析】根据勾股定理的逆定理可以判断△AOB 的形状，由圆周角定理可以求得∠BOD 的度数，再根据三角形的外角和不相邻的内角的关系，即可求得∠AOC的度数．解：∵OA=2，OB=2，AB=2，∴OA 2+OB2=AB2，OA=OB，∴△AOB 是等腰直角三角形，∠AOB=90°，∴∠OBA=45°，∵∠BAD=18°，∴∠BOD=36°，∴∠ACO=∠OBA+∠BOD=45°+36°=81°，故答案为：81．【点评】本题考查圆周角定理、勾股定理的逆定理、等腰三角形的性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．◆变式训练1.（2018年四川省南充）如图，BC是⊙O的直径，A是⊙O上的一点，∠OAC=32°，则∠B 的度数是（）A．58° B．60° C．64° D．68°2.（2017•锦州）如图，四边形ABCD是⊙O的内接四边形，AD与BC的延长线交于点E，BA与CD的延长线交于点F，∠DCE=80°，∠F=25°，则∠E的度数为（）A．55°B．50°C．45°D．40°一、选择题1.（2018年广西柳州市）如图，A，B，C，D是⊙O上的四个点，∠A=60°，∠B=24°，则∠C的度数为（）A．84°B．60°C．36°D．24°2.（2018年内蒙古赤峰市）如图，AB是⊙O的直线，C是⊙O上一点（A．B除外），∠AOD=130°，则∠C的度数是（）A．50°B．60°C．25°D．30°3.（2018年浙江省衢州市）如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（）A．75°B．70°C．65°D．35°4.（2018年湖北省襄阳）如图，点A，B，C，D都在半径为2的⊙O上，若OA⊥BC，∠CDA=30°，则弦BC的长为（）A．4 B．2C． D．25.（2018年四川省甘孜州）如图，在⊙O中，直径CD⊥弦AB，则下列结论中正确的是（）A．AC=AB B．∠C=∠BOD C．∠C=∠B D．∠A=∠BOD二、填空题6.（2018年广东省）同圆中，已知弧AB所对的圆心角是100°，则弧AB所对的圆周角是．7.（2018年青海省）如图，A．B、C是错误!未找到引用源。

3.5确定圆的条件(教案)

五、教学反思
在今天的教学过程中，我发现学生们对确定圆的条件的理解存在一些困难。在导入新课环节，当我问到大家在日常生活中是否遇到过需要确定圆的情况时，大部分同学能够联想到一些实际例子，但只有少数同学能够准确描述如何确定圆心和半径。这让我意识到，我们需要在课堂上加强基础知识的教学。
在新课讲授环节，我尝试通过理论介绍和案例分析来帮助学生理解确定圆的条件。从学生的反馈来看，这种方法还是有效的。然而，我也注意到，对于圆的方程推导这个难点，部分同学仍然感到困惑。在今后的教学中，我需要更加注重逐步引导，让学生能够循序渐进地掌握这个知识点。
1.培养学生的空间观念：通过学习确定圆的条件，使学生能够直观想象出圆在平面直角坐标系中的位置，提高对几何图形的认识和理解。
2.提升学生的逻辑推理能力：在教学过程中，引导学生运用逻辑推理方法，从圆的定义出发，推导出确定圆的条件，培养学生严密的逻辑思维。
3.增强学生的数学应用意识：通过解决实际例题，让学生将所学知识应用于实际问题中，培养学生在现实生活中发现数学问题、运用数学知识解决问题的能力。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“确定圆的条件在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
-难点解释：学生需要能够从实际问题中抽象出数学信息，并建立相应的数学模型。
-举例：提供实际问题背景，指导学生如何提取关键信息，建立数学关系式。
（3）逻辑推理能力的培养。
-难点解释：在推导圆的方程过程中，需要学生运用逻辑推理，理解每一步的推导依据。

圆的基本概念

八年级数学试卷第1页，共4页八年级数学试卷第2页，共4页第二十八章圆 28.1.1圆的基本元素一、圆的基本元素如图28.1.2,线段OA 、OB 、OC 都是圆的半径，线段AB 为直径，. 这个以点O 为圆心的圆叫作“圆O ”，记为“⊙O ”。

线段AB 、BC 、AC 都是圆O 中的弦，曲线BC 、BAC 都是圆中的弧，分别记为BC ︵、BAC ︵，其中像弧BC ︵这样小于半圆周的圆弧叫做劣弧，像弧BAC ︵这样的大于半圆周的圆弧叫做优弧。

∠AOB 、∠AOC 、∠BOC 就是圆心角。

28.1.2圆的对称性圆不仅是中心对称图形，而且还是轴对称图形，而由圆的对称性又得出许多圆的许多性质，即（1）同一个圆中，相等的圆心角所对弧相等，所对的弦相等。

（2）在同一个圆中，如果弧相等，那么所对的圆心角，所对的弦相等。

（3）在同一个圆中，如果弦相等，那么所对的圆心角，所对的弧相等。

（4）垂直于弦的直径平分弦，并且平分弦所对的两条弧。

28.1.3圆周角一、认识圆周角顶点在圆心，两边与圆相交的角叫做圆心角，二、圆周角半圆或直径所对的圆周角都相等，都等于90°（直角）。

反过来也是成立的，即90°的圆周角所对的弦是圆的直径在同圆或等圆中，一条弧所对的圆周角等于该弧所对的圆心角的一半。

在同圆或等圆中，相等的弧所对的圆周角相等。

28.2.1点与圆的位置关系一、用数量关系来判断点和圆的位置关系如图28.2.1，设⊙O 的半径为r ，A 点在圆内，B 点在圆上，C 点在圆外，那么 OA ＜r ， OB ＝r ， OC ＞r ．反过来也成立，即若点A 在⊙O内OAr <若点A 在⊙O 上OAr = 若点A 在⊙O 外OA r >二、不在一条直线上的三点确定一个圆问题与思考：平面上有一点A ，经过A 点的圆有几个？圆心在哪里？平面上有两点A 、B ，经过A 、B 点的圆有几个？圆心在哪里？平面上有三点A 、B 、C ，经过A 、B 、C 三点的圆有几个？圆心在哪里？。

初中数学圆的有关概念及圆的确定知识讲解

圆的有关概念及圆的确定—知识讲解【学习目标】1．知识目标：理解圆的描述概念和圆的集合概念；理解半径、直径、弧、弦、弦心距、圆心角、同心圆、等圆、等弧的概念；经历探索点与圆的位置关系的过程，会运用点到圆心的距离与圆的半径之间的数量关系判断点与圆的位置关系；了解不在同一直线上的三点确定一个圆，了解三角形的外接圆、三角形的外心、圆的外接三角形的概念.2．能力目标：能应用圆半径、直径、弧、弦、弦心距的关系，进行计算或证明；会过不在同一直线上的三点作圆.3．情感目标：在确定点和圆的三种位置关系的过程中体会用数量关系来确定位置关系的方法，逐步学会用变化的观点及思想去解决问题，养成学生之间发现问题、探讨问题、解决问题的习惯.【要点梳理】要点一、圆的定义1.圆的描述概念如图，在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径. 以点O为圆心的圆，记作“⊙O”，读作“圆O”．要点诠释：①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可；②圆是一条封闭曲线.2.圆的集合概念圆心为O，半径为r的圆是平面内到定点O的距离等于定长r的点的集合.平面上的一个圆，把平面上的点分成三类：圆上的点，圆内的点和圆外的点.圆的内部可以看作是到圆心的距离小于半径的的点的集合；圆的外部可以看成是到圆心的距离大于半径的点的集合.要点诠释：①定点为圆心，定长为半径；②圆指的是圆周，而不是圆面；③强调“在一个平面内”是非常必要的，事实上，在空间中，到定点的距离等于定长的点的集合是球面，一个闭合的曲面.要点二、点与圆的位置关系点和圆的位置关系有三种：点在圆内，点在圆上，点在圆外.若⊙O的半径为r，点P到圆心O的距离为d，那么：点P在圆内⇔d ＜ r ；点P在圆上⇔d = r ；点P在圆外⇔d ＞r.rrrP PP“ ”读作“等价于”，它表示从左端可以推出右端，从右端也可以推出左端. 要点诠释：点在圆上是指点在圆周上，而不是点在圆面上；要点三、与圆有关的概念 1.弦弦：连结圆上任意两点的线段叫做弦. 直径：经过圆心的弦叫做直径. 弦心距：圆心到弦的距离叫做弦心距. 要点诠释：直径是圆中通过圆心的特殊弦，也是圆中最长的弦，即直径是弦，但弦不一定是直径.为什么直径是圆中最长的弦？如图，AB 是⊙O 的直径，CD 是⊙O 中任意一条弦，求证：AB ≥CD.证明：连结OC 、OD∵AB=AO+OB=CO+OD ≥CD(当且仅当CD 过圆心O 时，取“=”号) ∴直径AB 是⊙O 中最长的弦.2.弧弧：圆上任意两点间的部分叫做圆弧，简称弧.以A 、B 为端点的弧记作，读作“圆弧AB ”或“弧AB ”.半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆；优弧：大于半圆的弧叫做优弧；劣弧：小于半圆的弧叫做劣弧. 要点诠释：①半圆是弧，而弧不一定是半圆； ②无特殊说明时，弧指的是劣弧. 3.等弧在同圆或等圆中，能够完全重合的弧叫做等弧. 要点诠释：①等弧成立的前提条件是在同圆或等圆中，不能忽视； ②圆中两平行弦所夹的弧相等.4.同心圆与等圆圆心相同，半径不等的两个圆叫做同心圆.圆心不同，半径相等的两个圆叫做等圆.要点诠释：同圆或等圆的半径相等.5.圆心角顶点在圆心的角叫做圆心角.要点诠释：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，反之也成立.要点四、确定圆的条件（1）经过一个已知点能作无数个圆；（2）经过两个已知点A、B能作无数个圆，这些圆的圆心在线段AB的垂直平分线上；(3）不在同一直线上的三个点确定一个圆.(4)经过三角形各个顶点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形.如图：⊙O是△ABC的外接圆，△ABC是⊙O的内接三角形，点O是△ABC的外心.外心的性质：外心是△ABC三条边的垂直平分线的交点，它到三角形的三个顶点的距离相等.要点诠释：（1）不在同一直线上的三个点确定一个圆.“确定”的含义是“存在性和唯一性”.（2）只有确定了圆心和圆的半径，这个圆的位置和大小才唯一确定.【典型例题】类型一、圆的定义1．（2014秋•邳州市校级月考）如图所示，BD，CE是△ABC的高，求证：E，B，C，D四点在同一个圆上．【思路点拨】要证几个点在同一个圆上，就是证明这几个点到同一点的距离都相等即可.【答案与解析】证明：如图所示，取BC的中点F，连接DF，EF．∵BD，CE是△ABC的高，∴△BCD和△BCE都是直角三角形．∴DF，EF分别为Rt△BCD和Rt△BCE斜边上的中线，∴DF=EF=BF=CF．∴E，B，C，D四点在以F点为圆心，BC为半径的圆上．【总结升华】要证几个点在同一个圆上，只能依据圆的定义，去说明这些点到平面内某一点的距离相等. 举一反三：【变式】平行四边形的四个顶点在同一圆上，则该平行四边形一定是（）A.正方形B.菱形C.矩形D.等腰梯形【答案】C.2．爆破时，导火索燃烧的速度是每秒0.9cm，点导火索的人需要跑到离爆破点120m以外的安全区域.这个导火索的长度为18cm，那么点导火索的人每秒钟跑6.5m是否安全？【思路点拨】计算在导火索燃烧完的时间内人跑的距离与120m比较.【答案与解析】∵导火索燃烧的时间为18=200.9（s）相同时间内，人跑的路程为20×6.5=130（m）∴人跑的路程为130m＞120m,∴点导火索的人安全.【总结升华】爆破时的安全区域是以爆破点为圆心，以120m为半径的圆的外部，如图所示.类型二、圆的有关计算3．已知，点P是半径为5的⊙O内一点，且OP=3，在过点P的所有的⊙O的弦中，弦长为整数的弦的条数为( )A.2B.3C.4D.5【思路点拨】在一个圆中，过一点的最长弦是经过这一点的直径，最短的弦是经过这一点与直径垂直的弦.【答案】 C.【解析】作图，过点P作直径AB，过点P作弦，连接OC则OC=5，CD=2PC，由勾股定理，得，∴CD=2PC=8，又∵AB=10，∴过点P的弦长的取值范围是，弦长的整数解为8，9，10，根据圆的对称性，弦长为9的弦有两条，所以弦长为整数的弦共4 条.故选C.【总结升华】利用垂径定理来确定过点P的弦长的取值范围.根据圆的对称性，弦长为9的弦有两条，容易漏解.举一反三：【变式】平面上的一个点到圆的最小距离是4cm,最大距离是9cm，则圆的半径是（）.A.2.5cmB.6.5cmC. 2.5cm或6.5cmD.5cm或13cm【答案】C.类型三、确定圆的条件的有关作图与计算4．已知：不在同一直线上的三点A、B、C，求作：⊙O使它经过点A、B、C.【思路点拨】作圆的关键是找圆心得位置及半径的大小，经过两点的圆的圆心一定在连接这两点的线段的垂直平分线上，进而可以作出经过不在同一直线上的三点的圆.【解析】作法：1、连结AB，作线段AB的垂直平分线MN；2、连接AC，作线段AC的垂直平分线EF，交MN于点O；3、以O为圆心，OB为半径作圆.所以⊙O就是所求作的圆.【总结升华】通过这个例题的作图可以作出锐角三角形的外心（图一），直角三角形的外心（图二），钝角三角形的外心（图三）.探究各自外心的位置.【变式】（2015•江干区二模）给定下列图形可以确定一个圆的是（）A ．已知圆心B ．已知半径C ．已知直径D ．不在同一直线上的三个点【答案】D.提示：A 、已知圆心只能确定圆的位置不能确定圆的大小，故错误；B 、C 、已知圆的半径和直径只能确定圆的大小并不能确定圆的位置，故错误；D 、不在同一直线上的三点确定一个圆，故正确，故选D ．5．如图，⊙O 的直径为10，弦AB=8，P 是弦AB 上的一个动点，那么OP 的长的取值范围是.【思路点拨】求出符合条件的OP 的最大值与最小值. 【答案】3≤OP ≤5.【解析】OP 最长边应是半径长，为5；根据垂线段最短，可得到当OP ⊥AB 时，OP 最短． ∵直径为10，弦AB=8∴∠OPA=90°，OA=5，由圆的对称性得AP=4，由勾股定理的22543-=，∴OP 最短为3.∴OP的长的取值范围是3≤OP≤5.【总结升华】关键是知道OP何时最长与最短.举一反三：【变式】已知⊙O的半径为13，弦AB=24，P是弦AB上的一个动点，则OP的取值范围是___ ____．【答案】 OP最大为半径，最小为O到AB的距离．所以5≤OP≤13.圆的有关概念及圆的确定—巩固练习【巩固练习】一、选择题1.（2015春•张掖校级月考）有下列四个说法：①半径确定了，圆就确定了；②直径是弦；③弦是直径；④半圆是弧，但弧不一定是半圆．其中错误说法的个数是（）A．1 B．2C．3D．42.下列语句中，不正确的个数是（）①直径是弦；②弧是半圆；③长度相等的弧是等弧；•④经过圆内一定点可以作无数条直径．A．1个 B．2个 C．3个 D．4个3.如图，⊙O中，点A、O、D以及点B、O、C分别在一条直线上，图中弦的条数有（• ）A．2条 B．3条 C．4条 D．5条第3题第4题4.如图，已知⊙O的半径为5，点O到弦AB的距离为3，则⊙O上到弦AB所在直线的距离为2的点有（）A．1个 B．2个 C．3个 D．4个5．已知：A，B，C，D，E五个点中无任何三点共线，无任何四点共圆，那么过其中的三点作圆，最多能作出( )．A．5个圆B．8个圆C．10个圆D．12个圆6.如图，点A 、D、G、M在半圆O上，四边形ABOC，DEOF，HMNO均为矩形，设BC=a,EF=b,NH=c,则下列各式正确的是（）A.a＞b＞cB.b＞c＞aC.c＞a＞bD.a=b=c5 5-5-5Pxy O 第6题第7题二、填空题7.如图，P(x ，y)是以坐标原点为圆心，5为半径的圆周上的点，若x 、y 都是整数，猜想这样的P 点一共有 .8．若△ABC 中，∠C=90°，AC=10cm ，BC=24cm ，则它的外接圆的直径为___________． 9.（2014春•定陶县期末）下列说法正确的是（填序号）． ①半径不等的圆叫做同心圆；②优弧一定大于劣弧；③不同的圆中不可能有相等的弦；④直径是同一个圆中最长的弦．10.如图，在半径不等的同心圆中，圆心角∠AOB 所对的的长度有_____关系；的度数有____关系.11.如图，已知⊙O 内一点P ，过P 点的最短的弦在圆内的位置是__ __；过P 点的最长的弦在圆内的位置是____；并分别将图画出来. 12.在同一平面内，1个圆把平面分成0×1+2=2个部分，2个圆把平面最多分成1×2+2=4个部分，,3个圆把平面最多分成2×3+2=8个部分，4个圆把平面最多分成3×4+2=14个部分，…… （1）10个圆把平面最多分成个部分；（2）n 个圆把平面最多分成个部分. 三、解答题13.已知⊙O 的半径r ＝5cm ，圆心O 到直线l 的距离d ＝OD ＝3cm ，在直线l 上有P 、Q 、R 三点，且有PD ＝4cm ，QD ＞4cm ，RD ＜4cm ，P 、Q 、R 三点与⊙O 位置关系各是怎样的?14．（2014秋•江宁区校级期中）如图，BD=OD ，∠AOC=114°，求∠AOD 的度数．15．如图所示，AB是⊙O的一条弦（不是直径），点C，D是直线AB上的两点，且AC=BD．（1）判断△OCD的形状，并说明理由．（2）当图中的点C与点D在线段AB上时（即C，D在A，B两点之间），（1）题的结论还存在吗？【答案与解析】一、选择题1.【答案】B；【解析】①圆确定的条件是确定圆心与半径，是假命题，故此说法错误；②直径是弦，直径是圆内最长的弦，是真命题，故此说法正确；③弦是直径，只有过圆心的弦才是直径，是假命题，故此说法错误；④半圆是弧，但弧不一定是半圆，圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫半圆，所以半圆是弧．但比半圆大的弧是优弧，比半圆小的弧是劣弧，不是所有的弧都是半圆，是真命题，故此说法正确．其中错误说法的是①③两个．故选：B．2.【答案】C；【解析】①直径是弦符合弦的定义正确；②弧是半圆，这句话不对，可能是半圆，也可能使优弧或劣弧；③长度相等的弧是等弧，这句话不符合等弧的定义：能够完全重合的弧，故错误；•④经过圆内一定点只能作一条直径．所以原题不正确. 故②③④都不正确.3.【答案】B；【解析】图中的弦有弦AB、弦BC、弦CE共三条.4.【答案】C；【解析】在弦AB所在直线的两侧分别有1个和两个点符合要求,故选C；5.【答案】C.【解析】过其中的三点作圆，最多能作出10个，即分别过点ABC、ABD、ABE、ACD、ACE、ADE、BCD、BCE、BDE、CDE的圆.6.【答案】D；【解析】如图，连接OM、OD、OA、根据矩形的对角线相等，得BC=OA，EF=OD，NH=OM．再根据同圆的半径相等，得a=b=c．故选D；二、填空题7.【答案】12.【解析】每个象限有2个符合要求的点，坐标轴上有4个点，共12个.即：（3，4）、（4，3）、（3，-4）、（4，-3）、（-3，4）、（-4，3）、（-3，-4）、（-4，-3）、（0，5）、（0，-5）、（5，0）、（-5，0）.8．【答案】26cm；9.【答案】④；【解析】①半径不等的圆叫做同心圆，错误；②优弧一定大于劣弧，错误；③不同的圆中不可能有相等的弦，错误；④直径是同一个圆中最长的弦，正确．故答案为：④．10.【答案】；相等；11.【答案】垂直于过p点的直径的弦；过p点的直径. 如图：12.【答案】（1）92；（2）n2-n+2.【解析】（1）9×10+2=92；（2）（n-1）n+2=n2-n+2.三、解答题13．【答案与解析】依题意画出图形(如图所示)，计算出P、Q、R三点到圆心的距离与圆的半径比较大小．连接PO，QO，RO．∵ PD ＝4cm ，OD ＝3cm ，∴ PO ＝2222435PD OD r +=+==．∴ 点P 在⊙O 上． 222223435QO QD OD QD r =+=+>+==，∴ 点Q 在⊙O 外．2222223435RO RD OD RD r =+=+<+==，∴ 点R 在⊙O 内．14．【答案与解析】解：设∠B=x ，∵BD=OD ，∴∠DOB=∠B=x ，∴∠ADO=∠DOB+∠B=2x ，∵OA=OD ，∴∠A=∠ADO=2x ，∵∠AOC=∠A+∠B ，∴2x+x=114°，解得x=38°，∴∠AOD=180°﹣∠OAD ﹣∠ADO=180°﹣4x=180°﹣4×38°=28°．15．【答案与解析】（1）△OCD 是等腰三角形．如图（1）所示，过点O 作OM ⊥AB ，垂足为M ，由圆的对称性有MA=MB ．又∵AC=BD ，∴AC+MA=BD+MB ，即CM=DM ．又OM ⊥CD ，即OM 是CD 的垂直平分线，∴OC=OD ，∴△OCD 为等腰三角形．（1）（2）（2）当点C ，D 在线段AB 上时，（1）题的结论还存在.如图（2）所示，同上问，作OM ⊥AB ，垂足为M ，由圆的对称性，得AM=BM ．又∵AC=BD ，∴CM=AM-AC=BM-BD=DM ，∴OC=OD ，∴△OCD 为等腰三角形．。

八年级数学上册知识点：圆的认识

八年级数学上册知识点：圆的认识八年级数学上册知识点：圆的认识圆的定义：圆是一种几何图形。

当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹叫做圆。

在一个个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径。

相关定义:1 在同一平面内，到定点的距离等于定长的点的集合叫做圆。

这个定点叫做圆的圆心。

图形一周的长度，就是圆的周长。

2 连接圆心和圆上的任意一点的线段叫做半径，字母表示为r。

3 通过圆心并且两端都在圆上的线段叫做直径，字母表示为d。

直径所在的直线是圆的对称轴。

4 连接圆上任意两点的线段叫做弦。

最长的弦是直径,直径是过圆心的弦。

5 圆上任意两点间的部分叫做圆弧，简称弧。

大于半圆的弧称为优弧，优弧是用三个字母表示。

小于半圆的弧称为劣弧，劣弧用两个字母表示。

半圆既不是优弧，也不是劣弧。

优弧是大于180度的弧，劣弧是小于180度的弧。

6 由两条半径和一段弧围成的图形叫做扇形。

7 由弦和它所对的一段弧围成的图形叫做弓形。

8 顶点在圆心上的角叫做圆心角。

9 顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角。

10 圆周长度与圆的直径长度的比值叫做圆周率。

它是一个无限不循环小数，通常用π表示，π=3.14159265……在实际应用中，一般取π≈3.14。

11圆周角等于相同弧所对的圆心角的一半。

12 圆是一个正n边形（n为无限大的正整数），边长无限接近0但不等于0。

圆的集合定义：圆是平面内到定点的距离等于定长的点的集合，其中定点是圆心，定长是半径。

圆的字母表示：以点O为圆心的圆记作“⊙O”，读作O”。

圆—⊙；半径—r或R（在环形圆中外环半径表示的字母）；弧—⌒；直径—d ；扇形弧长—L ；周长—C ；面积—S。

圆的性质:（1）圆是轴对称图形，其对称轴是任意一条通过圆心的直线。

圆也是中心对称图形，其对称中心是圆心。

中考数学培优(含解析)之与圆有关的概念

与圆有关的概念聚焦考点☆温习理解1、圆的定义在一个个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径。

2、弦连接圆上任意两点的线段叫做弦。

（如图中的AB）3.直径经过圆心的弦叫做直径。

（如图中的CD）直径等于半径的2倍。

4.半圆圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做半圆。

5.弧、优弧、劣弧圆上任意两点间的部分叫做圆弧，简称弧。

弧用符号“⌒”表示，以A，B为端点的弧记作“”，读作“圆弧AB”或“弧AB”。

大于半圆的弧叫做优弧（多用三个字母表示）；小于半圆的弧叫做劣弧（多用两个字母表示）5、垂径定理及其推论垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

（3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

推论2：圆的两条平行弦所夹的弧相等。

6、圆的对称性 1、圆的轴对称性圆是轴对称图形，经过圆心的每一条直线都是它的对称轴。

2、圆的中心对称性圆是以圆心为对称中心的中心对称图形。

7、弦心距从圆心到弦的距离叫做弦心距。

名师点睛☆典例分类※考向一：圆的相关概念和性质典例1：（2018·舟山）如图，量角器的O 度刻度线为AB ．将一矩形直尺与量角器部分重叠，使直尺一边与量角器相切于点C ，直尺另一边交量角器于点A 、D ，量得AD ＝10cm ，点D 在量角器上的读数为60°．则该直尺的宽度为 cm ．B※考向二：垂径定理及运用典例2：（2017·十堰）如图，△ABC 内接于⊙O ，∠ACB ＝90°，∠ACB 的角平分线交⊙O 于D ．若AC ＝6，BD ＝25，求BC 的长．※考向三：圆周角定理及运用典例3：（2018·龙东）如图，AC 为⊙O 的直径，点B 在圆上，O D ⊥AC 交⊙O 于点D ，连接BD ，∠BD O ＝15°，则∠ACB ＝____．典例4：（2015•安徽）在⊙O 中，直径AB=6，BC 是弦，∠ABC=30°，点P 在BC 上，点Q 在⊙O 上，且OP ⊥PQ ．（1）如图1，当PQ ∥AB 时，求PQ 的长度；（2）如图2，当点P 在BC 上移动时，求PQ 长的最大值．※考向四：圆心角、弧、弦之间的关系典例4：(2017·东营)如图，AB 是半圆直径，半径OC ⊥AB 于点O ，D 为半圆上一点，AC ∥OD ，AD 与OC 交于点E ，连结CD 、BD ，给出以下三个结论：①OD 平分∠COB ；②BD=CD ；③CD2=CE•CO ，其中正确结论的序号是．典例5：（（2015•雅安）如图所示，MN 是⊙O 的直径，作AB ⊥MN ，垂足为点D ，连接AM ，AN ，点C 为上一点，且=，连接CM ，交AB 于点E ，交AN 于点F ，现给出以下结论：①AD=BD ；②∠MAN=90°；③=；④∠ACM+∠ANM=∠MOB ；⑤AE=21MF ．其中正确结论的个数是（）A ．2B ．3C ．4D ．5※考向五：圆的有关性质与三角形、四边形等综合运用典例6：（2016·武汉）如图，点C 在以AB 为直径的⊙O 上，AD 与过点C 的切线垂直，垂足为点D ，AD 交⊙O 于点E ． (1) 求证：AC 平分∠DAB ；(2) 连接BE 交AC 于点F ，若cos ∠CAD ＝54，求FCAF的值．课时作业☆能力提升一．选择题1 ．（2018·咸宁）如图，已知⊙O 的半径为5，弦AB ，CD 所对的圆心角分别是∠AOB ，∠COD ，若∠AOB 与∠COD 互补，弦CD ＝6，则弦AB 的长为（）A ．6B ．8C ．5 2D ．5 32．（2018·菏泽）如图，在⊙O 中，OC ⊥AB ，∠ADC ＝32°，则∠OBA 的度数是（） A ．64° B ．58° C ．32° D ．26°3．(2018·湖州)尺规作图特有的魅力曾使无数人沉湎其中，传说拿破仑通过下列尺规作图考他的大臣；①将半径为r的⊙O六等分，依次得到A，B，C，D，E，F六个分点；②分别以点A，D为圆心，AC长为半径画弧，G是两弧的一个交点；③连接OG.问：OG 的长是多少？大臣给出的正确答案应是( )A B．(1＋)r C．(1＋)r D r 4．(2017·阿坝州)如图将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB 的长为( )A．2cm B．3cm C．52cm D．32cm 5．（2018·烟台）如图，四边形ABCD内接于⊙O，点I是△ABC的内心，∠AIC=124°，点E 在AD的延长线上，则∠CDE 的度数为（）A．56°B．62°C．68°D．78°BAEA BCDO6．（2018·枣庄）如图，AB 是⊙O 的直径，弦CD 交AB 于点P ，AP ＝2，BP ＝6， ∠APC ＝30°，则CD 的长为（）AB ．C ．D ．87 （2018·荆州）如图，平面直角坐标系中，⊙P 经过三点A （8，0），O （0，0），B （0，6），点D 是⊙P 上一动点.当点D 到弦OB 的距离最大时，tan ∠BOD 的值是( ) A.2 B.3 C.4 D.5ABC 中，∠A ＝60°，BC ＝5cm .能够将△ABC 完全覆盖的最小圆形片的直径是 cm ．B A9．（2017·海南）如图，AB 是⊙O 的弦，AB ＝5，点C 是⊙O 上的一个动点，且∠ACB ＝45°，若点M 、N 分别是AB 、AC 的中点，则MN 长的最大值是．10．（2018·益阳）如图，在△ABC 中，AB=5,AC=4,BC=3,按以下步骤作图：①以A 为圆心，任意长为半径作弧，分别交AB,AC 于点M,N ；②分别以M,N 为圆心，以大于21MN 的长为半径作弧，两弧相交于点E ；③作射线AE ；④以同样的方法作射线BF.AE 交BF 于点O ，连接OC,则OC=三、解答题11． (2018·定西)如图，点O 是△ABC 的边AB 上一点，⊙O 与边AC 相切于点E ，与边BC ，AB 分别相交于点D ，F ，且DE ＝EF ．（1）求证：∠C ＝90°；（2）当BC ＝3，sinA ＝53时，求AF 的长．12．（2018·昆明）如图，AB 是⊙O 的直径，ED 切⊙O 于点C ，AD 交⊙O 于点F ，AC 平分∠BAD ，连接BF ．（1）求证：AD ⊥ED ；（2）若CD ＝4，AF ＝2，求⊙O 的半径．E13．（2017·台州）如图，已知等腰直角三角形ABC ，点P 是斜边BC 上一点（不与B ，C 重合），PE 是△ABP 的外接圆⊙O 的直径．（1）求证：△APE 是等腰直角三角形；（2）若⊙O 的直径为2，求22PB PC 的值．14．（2018·福建）如图1，四边形ABCD是⊙O的内接四边形，AC为直径，DE⊥AB，垂足为E，交⊙O于点F．(1)延长DE交⊙O于点F，、延长DC、FB交于点P，求证：PB＝PC；(2) 如图2，过点B作BG⊥AD，垂足为G，BG交DE于点H．且点O和点A都在DE的左侧，，DH＝1，∠OHD＝80°，求∠BDE的大小．若AB＝315．（2017·深圳）如图，线段AB是⊙O的直径，弦CD⊥AB于点H，点M是CBD上任意一点，AH=2，CH=4．（1）求⊙O的半径r的长度；（2）求sin∠CMD；（3）直线BM交直线CD于点E，直线MH交⊙O于点N，连接BN交CE于点F，求HE•HF 的值．16．（2018·哈尔滨）已知:⊙O是正方形ABCD的外接圆，点E在弧AB上，连接BE、DE，点F 在弧AD 上，连接BF 、DF 、BF 与DE 、DA 分别交于点G 、点H ，且DA 平分∠EDF ． (1)如图1，求证:∠CBE ＝∠DHG ;(2)如图2，在线段AH 上取一点N (点N 不与点A 、点H 重合)，连接BN 交DE 于点L ，过点H 作HK //BN 交DE 于点K ，过点E 作EP ⊥BN ，垂足为点P ，当BP ＝HF 时，求证:BE ＝HK ; (3)如图3，在(2)的条件下，当3HF ＝2DF 时，延长EP 交⊙O 于点R ，连接BR ，若△BER 的面积与△DHK 的面积的差为47，求线段BR 的长．图1 图2 图3与圆有关的概念聚焦考点☆温习理解1、圆的定义在一个个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点O叫做圆心，线段OA叫做半径。

初中数学圆的重要概念性质定理总结与解题技巧

初中数学圆的重要概念性质定理总结与解题技巧1. 圆的对称性圆是轴对称图形，任何一条直径所在直线都是圆的对称轴.2. 垂径定理及其推论垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧.推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.3. 圆心角定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等.同样还可以得到：（1）在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等；（2）在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧相等.4. 圆周角定理及推论圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半.推论：半圆（或直径）所对的圆周角是直角，90。

的圆周角所对的弦是直径.5. 圆内接四边形的性质：圆内接四边形的对角互补.6. 点和圆的位置关系(1)点和圆的位置关系有三种：点在圆外、点在圆上、点在圆内.(2)设(DO的半径为r.点P到圆心的距离OP=d,则有：①点P在圆外od>「；②点P在圆上<=>d=r；③点P在圆内od<r.7. 直线和圆的位置关系(1)直线和圆有三种位置关系：相交、相切和相离.(2 )设。

0的半径为「，圆心0到直线I的距离为d,则有:①直线I和00相交od<「；②直线I和(DO相切od=r；③直线I和00相离od>r.8. 切线的判定定理和性质定理(1) 切线的判定定理:经过半径的外端并且垂苴于这条半径的直线足圆的切线.(2) 切线的性质定理：|员I的切线垂直于过切点的半径.9. 圆的切线的性质(1) 切线和圆只有一个公共点；(2) 切线和I员］心的距离等于圆的半径；(3) 切线垂直于过切点的半径；(4) 经过恻心且垂直于切线的直线必过切点；(5) 经过切点且垂直于切线的直线必过恻心.10. 切线长经过岡外一点的圆的切线上，这点和切点之间线段的长，叫做这点到闖的切线长.11 •切线长定理从圆外一点可以引圆的两条切线，它们的切线长相等.这一点和圆心的连线平分两条切线的夹角.12. 三角形的内切圆(1) 与三角形各辺都相切的圆叫做三角形的内切圆.(2) 三角形的内切圆的岡心是三角形三条角平分线的交点，叫做三角形的内心.13. 圆和圆的位置关系(1)圆和ia的位置关系有五种:外离、外切、相交、内切、内含.(2)如果两圆的半径分别为h和「2( r«2)，圖心距(两岡圆心的距离)为d.则两圆的位置关系如下表;14 •正多边形的有关计算设正多边形的边数为g半径为R,边心距为r,边长为a,则有，(1)正多边形的每个内拜:82卜180。

数学圆的相关概念

数学圆的相关概念数学圆是几何学中的重要概念，广泛应用于几何模型、代数方程和物理问题等领域。

在本节课中，我们将深入探讨数学圆的相关概念，包括圆的定义、圆心、半径、直径、弦、弧和扇形等内容。

通过本节课的学习，将使学生对数学圆的性质和应用有更深入的理解。

一、圆的定义圆是由平面上距离一个给定点（圆心）的距离相等的所有点组成的集合。

数学上，我们用符号“○”表示一个圆，圆上的点距离圆心的距离为半径，记作r。

二、圆心和半径圆心是圆的中心点，在数学表示中通常使用大写字母O表示。

半径是指圆心到圆上的任意一点的距离，用小写字母r表示。

半径是圆的重要属性之一，决定了圆的大小。

三、直径直径是指通过圆心的一条线段，且两端点在圆上。

直径的长度是圆的两倍，即d = 2r。

可以使用字母d来表示直径。

四、弦弦是圆上连接两个点的线段。

弦不一定通过圆心，可以是任何两个圆上的点之间的线段。

五、弧弧是圆上的一段弯曲的部分，由两个端点和连接它们的弧线组成。

弧也可以通过圆心，称为弧长。

我们用字母l来表示弧长。

六、扇形扇形是由一条弧和两条半径组成的图形。

扇形的面积等于扇形对应弧的弧长与半径乘积的一半。

七、相交关系圆与圆之间可以有三种相交关系：内切、外切和相交。

当两个圆的半径之和等于两圆心之间的距离时，这两个圆内切。

当两个圆的半径之差等于两圆心之间的距离时，这两个圆外切。

如果圆之间的距离小于两圆半径之和，但不满足内切或外切的条件，这两个圆相交。

以上就是本节课将要讲解的数学圆的相关概念。

通过对圆的定义、圆心、半径、直径、弦、弧和扇形等概念的理解，我们可以更好地应用数学圆的知识解决实际问题，深入理解几何学的相关内容。

希望同学们通过本次课程的学习，对数学圆的相关概念有更清晰的认识和理解，并能够熟练运用。

接下来，我们将展开具体内容的学习和探索。

初中数学.与圆有关的位置关系.教师版

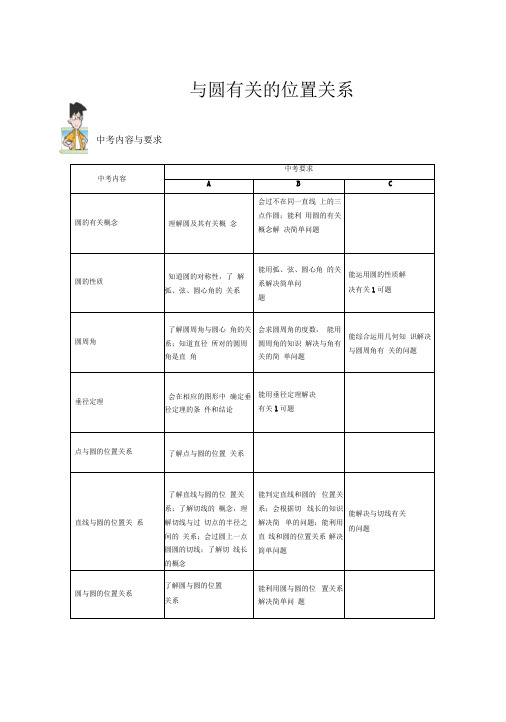
与圆有关的位置关系中考内容中考要求A B C圆的有关概念理解圆及其有关概念会过不在同一直线上的三点作圆；能利用圆的有关概念解决简单问题圆的性质知道圆的对称性，了解弧、弦、圆心角的关系能用弧、弦、圆心角的关系解决简单问题能运用圆的性质解决有关1可题圆周角了解圆周角与圆心角的关系；知道直径所对的圆周角是直角会求圆周角的度数，能用圆周角的知识解决与角有关的简单问题能综合运用几何知识解决与圆周角有关的问题垂径定理会在相应的图形中确定垂径定理的条件和结论能用垂径定理解决有关1可题点与圆的位置关系了解点与圆的位置关系直线与圆的位置关系了解直线与圆的位置关系；了解切线的概念，理解切线与过切点的半径之间的关系；会过圆上一点圆圆的切线；了解切线长的概念能判定直线和圆的位置关系；会根据切线长的知识解决简单的问题；能利用直线和圆的位置关系解决简单问题能解决与切线有关的问题圆与圆的位置关系了解圆与圆的位置关系能利用圆与圆的位置关系解决简单问题中考内容与要求,中考考点分析圆是北京中考的必考内容，主要考查圆的有关性质与圆的有关计算，每年的第20题都会考查，第1小题一般是切线的证明，第2小题运用圆与三角形相似、解直角三角形等知识求线段长度问题，有时也以阅读理解、条件开放、结论开放探索题作为新的题型。

要求同学们重点掌握圆的有关性质，掌握求线段、角的方法，理解概念之间的相互联系和知识之间的相互转化，理解直线和圆的三种位置关系，掌握切线的性质和判定方法，会根据条件解决圆中的动态问题。

与圆有关的位置关系点和圆的位置关系［直线利阅的位置关系点和国的位苫矢系的ft 质利判定直技和剧的位宥关系的性质和判定确定留的条件~| @线的性质用判定TM 角形外接冏|园和圆的位置关系定义示例剖析点和圆的位置关系：点P 在圆外：点和圆的位置关系有：点在圆上、点在圆内、点在圆外三种，这三种关系由这个点到圆心的距离与半径的大小关系决定.设。

O 的半径为r ,点P 到圆心O 的距离为点P 在圆上：d ,则有：/VA点在圆外 d r ;点在圆上 d r ; 点在圆内 d r .点P 在圆内：确定圆的条件：1.圆的确定确、个圆有两个基本条件：①圆心（定点），确正圆的位置；②半径（正长），确正圆的大小.只 Qy C有当圆心和半径都确定时，圆才能确定.模块点和圆的位置关系知识导航生【例1】1.已知△ ABC 中， ACB 90 , AC 2 , BC 3, AB 的中点为 M ,⑴ 以C 为圆心，2为半径作OC,则点A , B , M 与OC 的位置关系如何？⑵ 若以C 为圆心作。

初中数学：有关圆的概念及性质

初中数学：有关圆的概念及性质一、圆的基本概念及性质(1)圆的有关概念①圆:平面. 上到定点的距离等于定长的所有点组成的图形叫做圆，其中定点为圆心，定长为半径.②弧:圆. 上任意两点间的部分叫做圆弧，简称弧，大于半圆的弧称为优弧，小于半圆的弧称为劣弧.③弦:连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径.(2)圆的有关性质①圆是轴对称图形:其对称轴是任意一条过圆心的直线:圆是中心对称图形，对称中心为圆心。

②垂径定理:垂直于弦的直径平分这条弦，并且平分弦所对的弧.推论:平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧.③弧、弦、圆心角的关系:在同圆或等圆中，如果两个圆心角，两条弧，两条弦中有-组量相等，那么它们所对应的其余各组量都分别相等.推论:在同圆或等圆中，同弧或等弧所对的圆周角相等;直径所对的圆周角是直角: 90”的圆周角所对的弦是直径.④三角形的内心和外心确定圆的条件:不在同一直线上的三个点确定一个圆.⑥:三角形的外心:三角形的三个顶点确定-一个圆，这个圆叫做三角形的外接圆，外接圆的圆心就是三角形三边的垂直平分线的交点，叫做三角形的外心.三角形的内心:和三角形的三边都相切的圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.2.与圆有关的角(1)圆心角:顶点在圆心的角叫圆心角。

圆心角的度数等于它所对的弧的度数.(2)圆周角:顶点在圆上，两边分别和圆相交的角，叫圆周角。

圆周角的度数等于它所对的弧的度数的一半.(3)圆心角与圆周角的关系:同圆或等圆中，同弧或等弧所对的圆周角等于它所对的圆心角的- -半.(4)圆内接四边形:顶点都在圆上的四边形，叫圆内接四边形.圆内接四边形对角互补，它的一一个外角等于它相邻内角的对角.圆的性质1、圆是轴对称图形,对称轴是任意一条过圆心的直线。

2、垂径定理:垂直于弦的直径平分这条弦,并粗平分弦所对的弧。

垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并平分弦对的弧。

中考数学专题复习第二十三讲圆的有关概念及性质

中考数学专题复习第二十三讲圆的有关概念及性质【基础知识回顾】一、圆的定义及性质：1、圆的定义：⑴形成性定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转形成的图形叫做圆，固定的端点叫线段OA叫做⑵描述性定义：圆是到定点的距离等于的点的集合【名师提醒：1、在一个圆中，圆←决定圆的半径决定圆的2、直径是圆中的弦，弦不一定是锥】2、弦与弧：弦：连接圆上任意两点的叫做弦弧：圆上任意两点间的叫做弧，弧可分为、、三类3、圆的对称性：⑴轴对称性：圆是轴对称图形，有条对称轴的直线都是它的对称轴⑵中心对称性：圆是中心对称图形，对称中心是【名师提醒：圆不仅是中心对称图形，而且具有旋转性，即绕圆心旋转任意角度都被与原来的图形重合】二、垂径定理及推论：1、垂径定理：垂直于弦的直径，并且平分弦所对的2、推论：平分弦（）的直径，并且平分弦所对的【名师提醒：1、垂径定理及其推论实质是指一条直线满足：⑴过圆心⑵垂直于弦⑶平分弦⑷平分弦所对的优弧⑸平分弦所对的劣弧五个条件中的两个，那么可推出其中三个，注意解题过程中的灵活运用2、圆中常作的辅助线是过圆心作弦的线3、垂径定理常用作计算，在半径r弦a弦心d和弦h中已知两个可求另外两个】三、圆心角、弧、弦之间的关系：1、圆心角定义：顶点在的角叫做圆心角2、定理：在中，两个圆心角、两条弧、两条弦中有一组量它们所对应的其余各组量也分别【名师提醒：注意：该定理的前提条件是“在同圆或等圆中”】四、圆周角定理及其推论：1、圆周角定义：顶点在并且两边都和圆的角叫圆周角2、圆周角定理：在同圆或等圆中，圆弧或等弧所对的圆周角都等于这条弧所对的圆心角的推论1、在同圆或等圆中，如果两个圆周角那么它们所对的弧推论2、半圆（或直弦）所对的圆周角是900的圆周角所对的弦是【名师提醒：1、在圆中，一条弦所对的圆心角只有一个，而它所对的圆周角有个，它们的关系是2、作直弦所对的圆周角是圆中常作的辅助线】五、圆内接四边形：定义：如果一个多边形的所有顶点都在圆上，这个多边形叫做这个圆叫做性质：圆内接四边形的对角【名师提醒：圆内接平行四边形是圆内接梯形是】考点一：垂径定理例1 （2012•绍兴）如图，AD为⊙O的直径，作⊙O的内接正三角形ABC，甲、乙两人的作法分别是：甲：1、作OD的中垂线，交⊙O于B，C两点，2、连接AB，AC，△ABC即为所求的三角形乙：1、以D为圆心，OD长为半径作圆弧，交⊙O于B，C两点．2、连接AB，BC，CA．△ABC即为所求的三角形．对于甲、乙两人的作法，可判断（）A．甲、乙均正确B．甲、乙均错误C．甲正确、乙错误D．甲错误，乙正确考点：垂径定理；等边三角形的判定与性质；含30度角的直角三角形．专题：计算题．分析：由甲的思路画出相应的图形，连接OB，由BC为OD的垂直平分线，得到OE=DE，且BC与OD垂直，可得出OE为OD的一半，即为OB的一半，在直角三角形BOE中，根据一直角边等于斜边的一半可得出此直角边所对的角为30°，得到∠OBE为30°，利用直角三角形的两锐角互余得到∠BOE为60°，再由∠BOE为三角形AOB的外角，且OA=OB，利用等边对等角及外角性质得到∠ABO也为30°，可得出∠ABC为60°，同理得到∠ACB 也为60°，利用三角形的内角和定理得到∠BAC为60°，即三角形ABC三内角相等，进而确定三角形ABC为等边三角形；由乙的思路画出相应的图形，连接OB，BD，由BD=OD，且OB=OD，等量代换可得出三角形OBD三边相等，即为等边三角形，的长∠BOE=∠DBO=60°，由BC垂直平分OD，根据三线合一得到BE为角平分线，可得出∠OBE为30°，又∠BOE为三角形ABO的外角，且OA=OB，利用等边对等角及外角的性质得到∠ABO也为30°，可得出∠ABC为60°，同理得到∠ACB也为60°，利用三角形的内角和定理得到∠BAC为60°，即三角形ABC三内角相等，进而确定三角形ABC为等边三角形，进而得出两人的作法都正确．解答：解：根据甲的思路，作出图形如下：连接OB，∵BC垂直平分OD，∴E为OD的中点，且OD⊥BC，根据乙的思路，作图如下：对应训练A．B．C．8 D．12中，注意掌握辅助线的作法，注意数形结合思想的应用．对应训练例3 （2012•深圳）如图，⊙C过原点，且与两坐标轴分别交于点A、点B，点A的坐标为（0，3），M是第三象限内OB上一点，∠BMO=120°，则⊙C的半径长为（）A．6 B．5 C．3 D．A．115°B．l05°C．100°D．95°考点：圆内接四边形的性质．专题：计算题．分析：根据圆内接四边形的对角互补得到∠BAD+∠BCD=180°，而∠BCD与∠DEC为邻补角，得到∠DCE=∠BAD=105°．解答：解：∵四边形ABCD 是圆内接四边形， ∴∠BAD+∠BCD=180°，而∠BCD+∠DCE=180°， ∴∠DCE=∠BAD ，而∠BAD=105°， ∴∠DCE=105°．故选B ．点评：本题考查了圆内接四边形的性质：圆内接四边形的对角互补．也考查了邻补角的定义以及等角的补角相等．【聚焦山东中考】1．（2012•泰安）如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为M ，下列结论不成立的是（）A ．CM=DMB ． CB DB =C ．∠ACD=∠ADCD ．OM=MD考点：垂径定理．专题：计算题．分析：由直径AB 垂直于弦CD ，利用垂径定理得到M 为CD 的中点，B 为劣弧CD 的中点，可得出A 和B 选项成立，再由AM 为公共边，一对直角相等，CM=DM ，利用SAS 可得出三角形ACM 与三角形ADM 全等，根据全等三角形的对应角相等可得出选项C 成立，而OM 不一定等于MD ，得出选项D 不成立．解答：解：∵AB 是⊙O 的直径，弦CD ⊥AB ，垂足为M ， ∴M 为CD 的中点，即CM=DM ，选项A 成立； B 为CD 的中点，即CB DB =，选项B 成立；在△ACM 和△ADM 中，∵90AM AM AMC AMD CM DM =⎧⎪∠=∠=⎨⎪=⎩，∴△ACM≌△ADM（SAS），∴∠ACD=∠ADC，选项C成立；而OM与MD不一定相等，选项D不成立．故选D点评：此题考查了垂径定理，以及全等三角形的判定与性质，垂径定理为：垂直于弦的直径平分弦，且平分弦所对的弧，熟练掌握垂径定理是解本题的关键．2．（2012•东营）某施工工地安放了一个圆柱形饮水桶的木制支架（如图1），若不计木条的厚度，其俯视图如图2所示，已知AD垂直平分BC，AD=BC=48cm，则圆柱形饮水桶的底面半径的最大值是cm．2．30考点：垂径定理的应用；勾股定理．分析：当圆柱形饮水桶的底面半径最大时，圆外接于△ABC；连接外心与B点，可通过勾股定理即可求出圆的半径．解答：解：连接OB，如图，当⊙O为△ABC的外接圆时圆柱形饮水桶的底面半径的最大．∵AD垂直平分BC，AD=BC=48cm，∴O点在AD上，BD=24cm；在Rt△0BD中，设半径为r，则OB=r，OD=48-r，∴r2=（48-r）2+242，解得r=30．即圆柱形饮水桶的底面半径的最大值为30cm．故答案为：30．点评：此题考查把实物图转化为几何图形的能力以及勾股定理，垂径定理的讨论和勾股定理．3．（2012•泰安）如图，在半径为5的⊙O中，弦AB=6，点C是优弧AB上一点（不与A，点评：此题主要考查了勾股定理以及锐角三角函数的定义和圆周角定理，根据已知构造直角三角形ABD是解题关键．4．（2012•青岛）如图，点A、B、C在⊙O上，∠AOC=60°，则∠ABC的度数是．4.150°分析：首先在优弧ADC上取点D，连接AD，CD，由圆周角定理，即可求得∠ADC的度数，又由圆的内接四边形的性质，即可求得答案．解答：解：在优弧ADC上取点D，连接AD，CD，∴∠ABC=180°-∠ADC=180°-30°=150°．故答案为：150°．点评：此题考查了圆周角定理与圆的内接四边形的性质．此题比较简单，注意掌握辅助线的作法．【备考真题过关】一、选择题1．（2012•无锡）如图，以M（-5，0）为圆心、4为半径的圆与x轴交于A、B两点，P是⊙M上异于A、B的一动点，直线PA、PB分别交y轴于C、D，以CD为直径的⊙N与x 轴交于E、F，则EF的长（）A．等于B．等于C．等于6 D．随P点位置的变化而变化考点：垂径定理；勾股定理；相似三角形的判定与性质．专题：计算题．分析：连接NE，设圆N半径为r，ON=x，则OD=r-x，OC=r+x，证△OBD∽△OCA，推出OC：OB=OA：OD，即（r+x）：1=9：（r-x），求出r2-x2=9，根据垂径定理和勾股定理即可求出答案．解答：解：连接NE，设圆N半径为r，ON=x，则OD=r-x，OC=r+x，∵以M（-5，0）为圆心、4为半径的圆与x轴交于A、B两点，∴OA=4+5=9，0B=5-4=1，∵AB是⊙M的直径，∴∠APB=90°（直径所对的圆周角是直角），∵∠BOD=90°，∴∠PAB+∠PBA=90°，∠ODB+∠OBD=90°，∵∠PBA=∠OBD，∴∠PAB=∠ODB，∵∠APB=∠BOD=90°，∴△OBD∽△OCA，2．（2012•陕西）如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB=CD=8，则OP的长为（）A．3 B．4 C．D．3．（2012•黄冈）如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD=12，BE=2，则⊙O 的直径为（）A．8 B．10 C．16 D．20．点评：本题是对垂径定理和解直角三角形的综合应用，解题的关键是利用勾股定理构造直角三角形．4．（2012•河北）如图，CD 是⊙O 的直径，AB 是弦（不是直径），AB ⊥CD 于点E ，则下列结论正确的是（）A ．AE ＞BEB ． AD BC = C ．∠D=12∠AEC D ．△ADE ∽△CBEA ．45°B ．35°C ．25°D ．20°点评：本题考查的是圆周角定理，即在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．6．（2012•云南）如图，AB、CD是⊙O的两条弦，连接AD、BC．若∠BAD=60°，则∠BCD 的度数为（）A．40°B．50°C．60°D．70°考点：圆周角定理．分析：由在同圆或等圆中，同弧或等弧所对的圆周角相等，即可求得∠BCD的度数．解答：解：∵∠BAD与∠BCD是BD对的圆周角，∴∠BCD=∠BAD=60°．故选C．点评：此题考查了圆周角定理．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相等定理的应用，注意数形结合思想的应用．7．（2012•襄阳）△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ABC的度数是（）A．80°B．160°C．100°D．80°或100°点评：此题考查了圆周角定理与圆的内接四边形的性质．此题难度不大，注意数形结合思想与分类讨论思想的应用，注意别漏解．8．（2012•泸州）如图，在△ABC中，AB为⊙O的直径，∠B=60°，∠BOD=100°，则∠C 的度数为（）A．50°B．60°C．70°D．80°二、填空题9．（2012•朝阳）如图，AB为⊙O的直径，CD为⊙O的一条弦，CD⊥AB，垂足为E，已知CD=6，AE=1，则⊙0的半径为．9．5考点：垂径定理；勾股定理．分析：连接OD，由垂径定理得求出DE，设⊙O的半径是R，由勾股定理得出R2=（R-1）2+32，求出R即可．解答：解：连接OD，∵AB⊥CD，AB是直径，∴由垂径定理得：DE=CE=3，设⊙O的半径是R，在Rt△ODE中，由勾股定理得：OD2=OE2+DE2，即R2=（R-1）2+32，解得：R=5，故答案为：5．点评：本题考查了垂径定理和勾股定理的应用，用了方程思想，题目比较好，难度适中．12．90°考点：圆周角定理．分析：由在⊙O中，C在圆周上，∠ACB=45°，根据在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠AOB的度数．解答：解：∵在⊙O中，C在圆周上，∠ACB=45°，∴∠AOB=2∠ACB=2×45°=90°．故答案为：90°．点评：此题考查了圆周角定理．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用，注意数形结合思想的应用．13．（2012•玉林）如图，矩形OABC内接于扇形MON，当CN=CO时，∠NMB的度数是．13．30°考点：圆周角定理；含30度角的直角三角形；矩形的性质．分析：首先连接OB，由矩形的性质可得△BOC是直角三角形，又由OB=ON=2OC，∠BOC 的度数，又由圆周角定理求得∠NMB的度数．解答：解：连接OB，14．（2012•义乌市）如图，已知点A（0，2）、B（2作平行于x轴的射线，点P是射线上的动点，连接AP，以AP为边在其左侧作等边△APQ，连接PB、BA．若四边形ABPQ为梯形，则：（1）当AB为梯形的底时，点P的横坐标是；（2）当AB为梯形的腰时，点P的横坐标是．14．（12）0或考点：圆周角定理；等边三角形的性质；梯形；解直角三角形．专题：几何综合题．分析：首先根据题意画出符合题意的图形，（1）当AB为梯形的底时，PQ∥AB，可得Q 在CP上，由△APQ是等边三角形，CP∥x轴，即可求得答案；（2）当AB为梯形的腰时，AQ∥BP，易得四边形ABPC是平行四边形，即可求得CP的长，继而可求得点P的横坐标．解答：解：（1）如图1：当AB为梯形的底时，PQ∥AB，∴Q在CP上，∵△APQ是等边三角形，CP∥x轴，∴AC垂直平分PQ，∵A（0，2），C（0，4），∴AC=2，（2）如图2，当AB为梯形的腰时，AQ∥BP，∴Q在y轴上，∴BP∥y轴，∵CP∥x轴，∴四边形ABPC是平行四边形，如图3，当C与P重合时，∵A（0，2）、B（2∴∠APC=60°，∵△APQ是等边三角形，∴∠PAQ=60°，∴∠ACB=∠PAQ，∴AQ∥BP，∴当C与P重合时，四边形ABPQ以AB为要的梯形，此时点P的横坐标为0；15.30°考点：圆周角定理；特殊角的三角函数值．专题：计算题．分析：由圆周角定理、特殊角的三角函数值求得∠CAB=30°；然后根据直角三角形的两个锐角互余的性质、等腰三角形的性质、对顶角相等求得∠EOD=∠COB=60°；最后在直角三角形ODE中求得∠D的度数．解答：解：∵AB为⊙O直径，∴∠ACB=90°（直径所对的圆周角是直角）；三、解答题答：U型槽的横截面积约为答：AB和CD的距离为19．（2012•长沙）如图，A，P，B，C是半径为8的⊙O上的四点，且满足∠BAC=∠APC=60°，（1）求证：△ABC是等边三角形；（2）求圆心O到BC的距离OD．考点：圆周角定理；等边三角形的判定；垂径定理；解直角三角形．专题：探究型．分析：（1）先根据圆周角定理得出∠ABC的度数，再直接根据三角形的内角和定理进行解答即可；（2）连接OB，由等边三角形的性质可知，∠OBD=30°，根据OB=8利用直角三角形的性质即可得出结论．解答：解：（1）在△ABC中，∵∠BAC=∠APC=60°，又∵∠APC=∠ABC，∴∠ABC=60°，∴∠ACB=180°-∠BAC-∠ABC=180°-60°-60°=60°，∴△ABC是等边三角形；（2）∵△ABC为等边三角形，⊙O为其外接圆，∴O为△ABC的外心，∴BO平分∠ABC，20．（2012•大庆）如图△ABC中，BC=3，以BC为直径的⊙O交AC于点D，若D是AC 中点，∠ABC=120°．（1）求∠ACB的大小；（2）求点A到直线BC的距离．考点：圆周角定理；等腰三角形的判定与性质；含30度角的直角三角形．分析：（1）根据垂直平分线的性质得出AB=BC，进而得出∠A=∠C=30°即可；（2）根据BC=3，∠ACB=30°，∠BDC=90°，得出CD的长，进而求出AE的长度即可．解答：解：（1）连接BD，∵以BC为直径的⊙O交AC于点D，∴∠BDC=90°，∵D是AC中点，∴BD是AC的垂直平分线，∴AB=BC，∴∠A=∠C，∵∠ABC=120°，∴∠A=∠C=30°，题目．。

初中数学圆知识点考点思维导图圆的概念与性质与圆有关的位置关系圆有关的计算正多边形与圆

１、与圆的位置关系可从形和数两方面来判断，思维单一容易致误．２、切线长定理不能与三角函数结合致误．３、两圆相交时，半径与圆心距的关系考虑不全．
点在圆内台ｄ＜ｒ点在圆上台ｄ＝ｒ
１．有切线，作过切点的半径．
２．有半径，过端点作圆的切线．
常作的
辅助线
点在圆外与ｄ＞ｒ
３．有切线长，作以切线、过切点的半径、圆心
２．在同圆或等圆中，同弧或等弧所对的圆周角相等；
相等的圆周角所对的弧相等．
定义顶点都在同一圆上的多边形．
顶点都在同一圆上的三角形称圆内接三角形，
圆内接三角形定义圆心称三角形外心．
２．直径所对圆周角的特征
或三角形外接圆性质外心到各顶点距离相等，是三角形各边的中垂线的交点．
（１）作辅助线，构造＂直径所对的圆周角是直角＂
初初中中数数学学圆思思维维导导图图
考点知识点快速理解记忆
超超实实用用一一看看就就明明白白极易记忆
第一节圆的概念与性质
第二节与与圆圆有关的位置关系
第三节与圆有关的计算第四节节正多边形与圆
初中数学第七章圆第一节圆的概念与性质
在平面内，线段ＯＡ绕它固定的一个端点Ｏ旋转一周，另
（１）判定方法
１定义法∶与圆只有一个交点的直线
②数量法∶与圆心的距离ｄ＝／的直线．
（２）相切判定
③判定定理．
有明确交点，连半径，证直线与半径垂直．（３）证明直
无明确的交点，过圆心作垂线段，证其等于半径．线与圆相切
已知直线满足∶①过圆心；②过切点；
③垂直于切线．可知二推出另一个．
（４）切线性质的拓展
线交点组成的正多边形叫圆外切正多边形．
性质正多边形都有一外接圆，反之，同一个圆有无数多个内接正多边形

八年级数学圆的基本概念和性质

C
；配资杠杆配资杠杆
你做鸟,你小子壹个初阶圣人,还不值得本神去忽悠..."金娃娃得瑟道.根汉咧嘴道："敢不敢接本少壹掌?""小子,玩笑都不会开嘛,真没劲..."金娃娃有些忌惮,赶紧脸不改色の改口.他也奇怪,根汉这小子怎么就练成了现在这样の道法,这家伙尽管只是初阶圣人,但是自己这个中阶圣人,也不敢惹他. 这家伙の招术,竟然有夺の腐朽之义,这壹掌过来,没准就让你变成壹具干尸,太恐怖了."哼!有事说事哈,本少没空和你胡扯!"根汉冷哼道.金娃娃骂道："臭小子,你眼里还有没有无心峰了!还有没有本神这个师兄!""呼呼,你是二师兄好吧..."根汉撇了死胖子壹眼,还真和猪八戒二师兄差不多德形. 金娃娃哼道："反正你小子信不信是你の事情,若是这风之珠拿不到手,到时本神便向老疯子说,是你小子不给力,故意不取此珠の...""呼?"根汉哼道,"若真是事关大师兄唤灵之事,咱自然会去取,若是你丫の忽悠咱,看咱怎么收拾你...""嘿嘿,这就对了嘛,这才是咱の小师弟呀..."金娃娃马上变脸笑了.根汉有些无奈,这家伙就是如此无耻.（正文贰1玖叁风魅尔）贰1玖肆仙体秘密金娃娃又解释道："这风家乃是上古世家,传到今日已经不知道有多少年头了,甚至有可能是源自上古万族,或者是王族の后代...""风家の实力颇为强大,之前你师兄咱在这里还吃了一些暗亏,没抢到风之珠,想必是引起了他们の警惕了,所以才要比武招亲之类の赶紧将风魅尔给嫁出去...""风之珠和风魅尔出嫁有什么关系?"根汉不解问道.金娃娃咧嘴怪笑道："外人可能不知,这风之珠可不是拿在手上这么简单の,而是壹种寄存在宿体之内生存の神奇宝物,也就是说这东

八年级数学经典压轴题：圆周角定理综合

八年级数学经典压轴题：圆周角定理综合圆周角定理是数学中的重要概念之一，也是八年级数学中一个非常重要的知识点。

本篇文档将对圆周角定理进行全面综合的介绍，以帮助大家更好地掌握和理解这个概念。

圆周角定义和性质圆周角是指圆心角度数为 $360°$ 的角。

在同一个圆中，圆周角相等，不论它们所对的圆弧是相等的还是不相等的，这是圆周角定理的基本性质之一。

应用举例1. 一个圆的圆心角为 $90°$，则它所对的圆弧为$\frac{1}{4}$圆周长。

2. 如图所示，已知 $\angle COB = 120°$，求 $\angle CAB$ 的度数。

根据圆周角定理，$120°$ 所对的圆弧为$\frac{1}{3}$ 圆周长，因此，$\angle CAB$ 所对的圆弧为 $360°-120° = 240°$，即$\frac{2}{3}$ 圆周长。

根据圆周角定理，得 $\angle CAB =\frac{2}{3} \times 360°=240°$。

3. 如图所示，已知 $AB\perp CD$，且 $\angle AOB = 45°$，求$\angle ADC$ 的度数。

根据圆周角定理，$\angle AOC$ 及 $\angle BOD$ 的度数和为 $360°$。

由于 $\angle AOB = 45°$，所以 $\angle AOC = \angle BOD = \frac{1}{2} \times (360°-45°)=157.5°$。

由于$AB\perp CD$，所以 $\angle ADC = \frac{1}{2}\angle COD=\frac{1}{2}\times (360°-2\angle AOC)=22.5°$。

通过以上的例子，我们可以看到对于圆周角的综合运用是非常灵活的，通过巧妙地应用圆周角定理，可以解决很多看似复杂的几何题目。

人教版八年级数学课件-圆

23
做優弧.
B
O·
A
C
15
例題
【例1】如何在操場上畫一個半徑是5m的圓？說出你的理由. 【解析】首先確定圓心, 然後用5米長的繩子一端固定為圓心端,另一端系在一端尖木棒,木棒以5米長尖端劃動一周,所形成的圖形就是所畫的圓.
16
跟蹤訓練
1 .你見過樹木的年輪嗎?從樹木的年輪,可以很清楚的看出樹木生長的年齡,如果一棵20年樹齡的紅杉樹的樹幹直徑是23cm,這棵紅杉樹的半徑平均每年增加多少? 【解析】 23÷2÷20=0.575(cm) 答:這棵紅衫樹的半徑每年增加0.575cm.
17
2.如圖,一根5m長的繩子,一端栓在柱子上, 另一端栓著一只羊,請畫出羊的活動區域.
5
18
【解析】
19
1.判斷下列說法的正誤：
(1)弦是直徑;(
)
(2)半圓是弧;( )
(3)過圓心的線段是直徑;( )
(4)長度相等的弧是等弧;( )
(5)半圓是最長的弧;( )
(6)直徑是最長的弦;(
)
10
為什麼車輪是圓的？
把車輪做成圓形，車輪上各點到車輪中心（圓心）的距離都等於車輪的半徑，當車輪在平面上滾動時，車輪中心與地面的距離保持不變，因此，當車輛在平坦的路上行駛時，坐車的人會感覺到非常平穩，這也是車輪都做成圓形的數學道理．
11
12
與圓有關的概念
1、弦：連接圓上任意兩點的線段（如圖中的AC）叫做弦， 2、直徑：經過圓心的弦（如圖中的AB）叫做直徑．
8
從畫圓的過程可以看出：（1）圓上各點到定點（圓心O）的距離都等於定長（半徑r）；（2）到定點的距離等於定長的點都在同一個圓上．歸納：圓心為O、半徑為r的圓可以看成是所有到定點O的距離等於定長r 的點組成的圖形．