2.5第2课时
语文:2.5《华罗庚》第2课时课件(1)(粤教版必修1)

语》中提出来的文艺批评的话语的话,我想说,北 大的风范可用人们对杜甫诗的评论‘沉郁顿挫’ 来概括, 而对清华则可用杜甫对李白诗的评价‘清 新俊逸’来概括。 《漫谈北大派和清华派》 ”( )“清 新俊逸”,“沉郁顿挫”,季羡林清华毕业,北大 执教,在他身上,这两种风范是水乳交融、恰到好 处地搀和在一起的。 简言之, 他的清新俊逸似李白, 他的沉郁顿挫似杜甫,正所谓“清华其神,北大其 魂”。于是这八个字,成为解读季羡林的钥匙。
“神”、“魄”(对清华的依恋,对北大的情 思或爱国情怀);使文章真实可信,具有感染 力;为作者独特的解读提供了依据。
10.作者为什么认为“清华其神,北大其魂”成为 解读季羡林的钥匙?作者这样的解读方式,对我 们分析评判一个人有怎样的启示?(6 分) 答案 (1)大学期间清华园生活的生气勃勃、 充满
怎么锻炼;成就是抢不来的,有无功业,看你怎 么勤奋;荣耀是哭不来的,有无地位,看你怎么 拼搏。 爱情是买不来的,有无真心,看你怎么灌溉;幸 福是购不到的,可否如意,看你怎么呵护;永恒 是唤不出的,能否长久,看你如何浇铸。
12.在下面一段话后续写。要求:①先用一句话 写出自己的观点; ②然后至少写出两条理由; ③不超过 50 字。(6 分) 有报道说, 国家语委副主任王登峰近日对 媒体表示, 我国对地方台使用方言进行播音有 严格要求,播报新闻不能使用方言。对此,你 怎么看?
民主的气氛,科学的传统,始终占着主导的地位。 我同广大的清华校友一样,现在所以有一点点知 识, 难道不就是在清华园中打下的基础吗?离开清 华以后,我当然也学习了不少的新知识,但是在每 一个阶段,只要我感觉到学习有所收获,我立刻想 到清华园,没有在那里打下的基础,所有这一切都 是不可能的。” 1935 年, 季羡林得母校清华的栽培, 赴德留学。 1946 年回国, 又承清华教授陈寅恪的引荐, 进了北 大。季羡林执教北大,迄今已届六十年。他对清华 的依恋,已如前述。那么,他对北大又是一番什么 情思呢?1998 年北大百年校庆, 季羡林发表了一篇
2.5 有理数的乘方第2课时

有理数的乘方一、学生兴趣问题引入[师]假设一张厚度为0.09mm的纸连续对折始终是可能的,对折多少次后所得的厚度将超过你的身高?你能算吗?[生]1次对折后,厚度为0.09×2mm,2次对折后,厚度为0.09×2×2mm,14次对折后,厚度为0.09×2×2×2……×2≈1.47m。
14 2为了表示简便,我们把2×2×2……×2记为214。
14个2[师]如果对于几个相同的因数a相乘:a×a×a×a×……×a我们也将之记为a n。
n个a板书:求n个相同因数a的乘积的运算叫做乘方(Power),乘方的结果叫做幂(Power),a叫做底数(base number),n叫做指数(exponent)。
把a n读做a的n次方。
二、乘方的意义举例:1、几种常见的乘方[师]怎样表示图中正方形的面积,立方体的体积呢?[生]5×5平方单位,5×5×5立方单位。
[师]我们可以把5×5记做52,读作5的平方,5×5=52=25;5×5×5记作53,读作5的立方,即5×5×5=53=125。
注意:一个数可以看做这个数本身的一次方,例如,5就是51,指数1通常省略不写,二次方也叫做平方,如52通常读做5的平方;三次方也叫做立方,如53可读做5的立方。
做一做1、(口答)把下列相同因数的乘积写成幂的形式,并说出底数和指数。
(1)(-6)×(-6)×(-6)(2)23×23×23×232、把(-12)5写成几个相同因数相乘的形式。
10个(-2)32)×(-2)×(-2)×…×(-2[师]注意:幂的底数是分数或负数时,底数应该添上括号,如(-5)3,(23 )4三、利用乘方定义计算1、例1 计算:(1)(-3)2;(2)1.53;(3)(-43)4;(4)(-1)11;解:(1)(-3)2=(-3)×(-3)=9 (2)1.53=1.5×1.5×1.5=3.375(3)(-43)4=(-43)×(-43)×(-43)×(-43)=25681(4)(-1)11=-1(为什么?)。
2.5全等三角形 第2课时 全等三角形的判定1——“SAS”

凹槽问题
图形
巧妙地利用两边夹角构造出两个全等的三角形,将不 处理
可到达(不可测量)的两点间的距离,转化为可直接测 方法
量的两点间的距离,达到解决问题的目的.
第2课时 全等三角形的判定1——“SAS”
总结反思
小结 知识点 “SAS”
__两__边____及其夹__角______分别相等的两个三角形全等.通常可 简写成“边角边”或“SAS”.
解:测量步骤:如图,在平地上任找一点 O,连接 OA, OB,延长 AO 至点 C,使 CO=AO,延长 BO 至点 D,使 DO=BO,则 CD=AB.依据:△AOB≌△COD(SAS).
第2课时 全等三角形的判定1——“SAS”
【归纳总结】“SAS”的实际应用类型及处理方法:
类型
两点不能直达问题
即 AC=DF. AB=DE(已知),
在△ABC 和△DEF 中,∠A=∠D(已证), AC=DF(已证),
∴△ABC≌△DEF(SAS).
第2课时 全等三角形的判定1——“SAS”
【归纳总结】应用“SAS”判定两个三角形全等的三点注意: (1)对应:“SAS”包含“边”“角”两种元素,一定要注意元素的“对 应”关系; (2)顺序:在应用时一定要按边、角、边的顺序排列条件,绝不 能出现按边、边、角(或角、边、边)的顺序排列的错误,因为 边边角(或角边边)不能保证两个三角形全等; (3)注意挖掘题目中的隐含条件:公共边(角)相等;对顶角相等.
第2章 三角形
2.5 全等三角形
第2章 三角形
第2课时 全等三角形的 判定1——“SAS”
目标突破 总结反思
第2课时 全等三角形的判定1——“SAS”
目标突破
目标一 利用“SAS”证明三角形全等
湘教版数学七年级上册2.5整式的加法和减法第2课时去括号法则

初中数学试卷第2课时去括号法则要点感知1去括号法则:(1)括号前是“+”号,运用把括号去掉,原括号里各项的符号都.(2)括号前是“-”号,把括号和它前面的“-”号去掉,原括号里各项的符号都要.预习练习1-1下列去括号,正确的是( )A.a-(b+c)=a-b-c B.a+(b-c)=a+b+cC.a-(b+c)=a-b+c D.a-(b+c)=a+b-c1-2把3a-(2a-1)去括号,再合并同类项的结果是( )A.5a-1 B.5a+1 C.a-1 D.a+1要点感知2整式加减的实质就是和.一般地,几个整式相加减,如果有括号就先,然后再.预习练习2-1 计算:(1)(2x +1)+(-x +2);(2)(x +2)-(3-6x).知识点1 去括号1.下列去括号中正确的是( )A .x +(3y +2)=x +3y -2B .a 2-(3a 2-2a +1)=a 2-3a 2-2a +1C .y 2+(-2y -1)=y 2-2y -1D .m 3-(2m 2-4m -1)=m 3-2m 2+4m -12.下列各组式子中,互为相反数的有( )①a -b 与-a -b ;②a +b 与-a -b ;③a +1与1-a ;④-a +b 与a -b.A .①②④B .②④C .①③D .③④3.在-( )=-x 2+3x -2的括号里应填上的代数式是( )A .x 2-3x -2B .x 2+3x -2C .x 2-3x +2D .x 2+3x +24.下列各题去括号错误的是( )A .x -(3y -12)=x -3y +12B .m +(-n +a -b)=m -n +a -bC .-(-4x -6y +3)=4x -6y +3D .(a +12b)-(-13c +27)=a +12b +13c -27知识点2 整式的加减运算5.化简-(a -1)-(-a -2)+3的结果是( )A .4B .6C .0D .无法计算6.下列各式化简正确的是( )A.(3a-4b)-(5c-4b)=3a-8b-5cB.(a+b)-(3b-5a)=-2b-4aC.(2a-3b+c)-(2c-3b+a)=a+3cD.(2a-2b)-(3a+3b)=-a-5b7.把4a-(a-3b)去括号,并合并同类项的结果是 . 8.若m、n互为相反数,则8m+(8n-3)的值是 . 9.计算:(1)(3a+2b)+(a-2b);(2)(3x+6)-(2x-7);(3)-(2x2-xy)+(x2+xy-6);(4)ab-(4ab+3b2)-(2a2+2ab-b2).10.下列去括号正确的是( )A.a+(b-c-d)=a+b+c+d B.a-(b+c-d)=a-b-c+dC.a-(b-c-d)=a-b-c+d D.a+(b-c-d)=a-b+c+d11.化简a-(5a-3b)+(2b-a)的结果是( )A.7a-b B.-5a+5b C.7a+5b D.-5a-b12.已知a-2b=-2,则4-2a+4b的值是( )A.0 B.2 C.4 D.813.根据去括号的法则,在方框中填上“+”号或“-”号,正确的是( )①2x□(-y+2x)=4x-y;②(x2+2y2)□(x2+y2)=y2;③-(2x+3y)□(x-3y)=-3x;④a□(m+n-p+d)=a-m-n+p-d.A.+,+,-,-B.+,-,+,-C.+,-,-,+D.+,-,-,-14.(济南中考)计算:3(2x+1)-6x=.15.(吉林中考)若a-2b=3,则2a-4b-5=.16.计算:(1)(-x+3x2-2)-(-1+2x-3x2);(2)2a-(3a+4b)+(2a+b);(3)-(-3a2-2ab+9)-(5ab+4a2-6);(4)(2x2+x)-[2x+(1-x2)];(5)2x2-[x2-(3x2+2x-1)].17.(a+2)2+4|b-5|=0,求(7a+8b)-(-4a+6b)的值.18.在-3x2+2xy+y2-2x+y-1中,不改变代数式的值,把含字母x的项放在前面带“+”号的括号里,同时把不含字母x的项放在前面带“-”的括号里.挑战自我19.当x=1时,多项式ax2+bx+1的值为3,则多项式-(6a-2b)+(5a-3b)的值等于( ) A.0 B.1 C.2 D.-220.a,b在数轴上的位置如图,化简|b-a|-|a|+|a+b|.参考答案要点感知1(1)加法结合律,都不变.(2)改变.预习练习1-1 A1-2 D要点感知2去括号,合并同类项.去括号,合并同类项(1)原式=2x+1-x+2=x+3.(2)原式=x+2-3+6x=7x-1.1.C 2.B 3.C 4.C 5.B 6.D 7.3a+3b 8.-3 9.(1)原式=3a+2b+a-2b=4a.(2)原式=3x+6-2x+7=x+13.(3)原式=-2x2+xy+x2+xy-6=-x2+2xy-6.(4)原式=ab-4ab-3b2-2a2-2ab+b2=-2a2-5ab-2b2.10.B 12.D 13.D 14.3 15.116.(1)原式=-x+3x2-2+1-2x+3x2=6x2-3x-1.(2)原式=2a-3a-4b+2a+b=a-3b.(3)原式=3a2+2ab-9-5ab-4a2+6=-a2-3ab-3.(4)原式=2x2+x-(2x+1-x2)=2x2+x-2x-1+x2=3x2-x-1.(5)原式=2x2-(x2-3x2-2x+1)=2x2-x2+3x2+2x-1=4x2+2x-1. 17.根据题意,得a+2=0,b-5=0,则a=-2,b=5.原式=7a+8b+4a-6b=11a+2b=-22+10=-12.18.原式=(-3x2+2xy-2x)-(-y2-y+1).挑战自我19.D20.由题意得b-a>0,a<0,a+b<0,原式=(b-a)+a-(a+b)=b-a+a-a-b=-a.。
2020年秋九年级数学上册 第2章 2.5 一元二次方程的应用 第2课时 图形面积问题同步练习
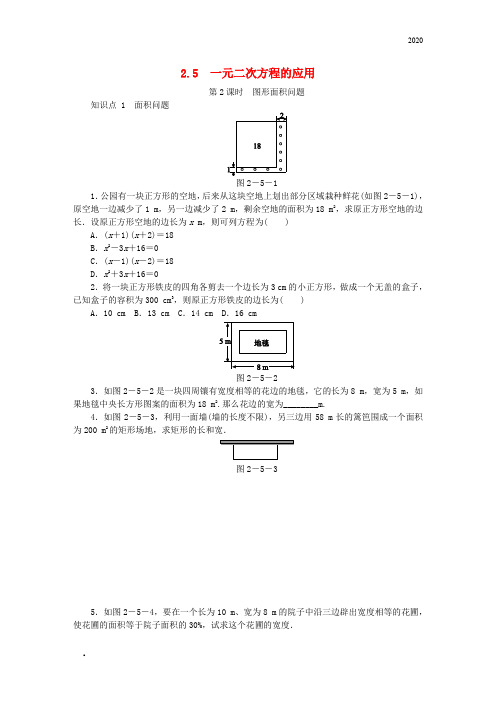
2.5 一元二次方程的应用第2课时图形面积问题知识点 1 面积问题图2-5-11.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图2-5-1),原空地一边减少了1 m,另一边减少了2 m,剩余空地的面积为18 m2,求原正方形空地的边长.设原正方形空地的边长为x m,则可列方程为( )A.(x+1)(x+2)=18B.x2-3x+16=0C.(x-1)(x-2)=18D.x2+3x+16=02.将一块正方形铁皮的四角各剪去一个边长为3 cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300 cm3,则原正方形铁皮的边长为( )A.10 cm B.13 cm C.14 cm D.16 cm图2-5-23.如图2-5-2是一块四周镶有宽度相等的花边的地毯,它的长为8 m,宽为5 m,如果地毯中央长方形图案的面积为18 m2.那么花边的宽为________m.4.如图2-5-3,利用一面墙(墙的长度不限),另三边用58 m长的篱笆围成一个面积为200 m2的矩形场地,求矩形的长和宽.图2-5-35.如图2-5-4,要在一个长为10 m、宽为8 m的院子中沿三边辟出宽度相等的花圃,使花圃的面积等于院子面积的30%,试求这个花圃的宽度.图2-5-4知识点 2 动点问题6.教材练习第2题变式如图2-5-5,在△ABC中,∠ABC=90°,AB=8 cm,图2-5-5BC=6 cm.动点P,Q分别从点A,B同时开始运动,点P的速度为1 cm/s,点Q的速度为2 cm/s,点Q运动到点C后停止运动,点P也随之停止运动.经过几秒后,能使△PBQ的面积为15 cm2?( )A.2 s B.3 s C.4 s D.5 s7.如图2-5-6,在Rt△ABC中,∠C=90°,点P,Q同时由A,B两点出发分别沿AC,BC方向向点C匀速运动,其速度均为2 cm/s,几秒后△PCQ的面积是△ABC面积的一半?图2-5-68.如图2-5-7,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米.图2-5-79.在△ABC中,∠B=60°,AB=24 cm,BC=16 cm,点P从点A开始沿AB边向点B以4 cm/s的速度运动,点Q从点C开始沿CB边向点B以2 cm/s的速度运动.它们同时出发,求几秒后,△PBQ的面积是△ABC面积的一半.10.2016·百色如图2-5-8,在直角墙角AOB(OA⊥OB,且OA,OB长度不限)中,要砌20 m长的墙,与直角墙角AOB围成地面为矩形的储仓,且矩形地面AOBC的面积为96 m2.(1)求矩形地面的长;(2)有规格为0.80 m×0.80 m和1.00 m×1.00 m的地板砖单价分别为55元/块和80元/块.若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?图2-5-811.如图2-5-9①,要设计一幅宽20 cm,长30 cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为2x cm,则每个竖彩条的宽为3x cm.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形ABCD.(1)结合以上分析完成填空:如图②:用含x的代数式表示:AB=________cm;AD=________cm;矩形ABCD的面积为________cm2.(2)列出方程并完成本题的解答.图2-5-9详解详析1.C [解析] 根据题意,可知剩余的长方形空地的长为(x-1)m,宽为(x-2)m,所以可列出方程为(x-1)(x-2)=18,故选C.2. D [解析] 设原正方形铁皮的边长是x cm,则做成的没有盖的长方体盒子的长、宽均为(x-3×2)cm,高为3 cm,根据题意列方程得(x-3×2)×(x-3×2)×3=300,解得x1=16,x 2=-4(不合题意,舍去).即原正方形铁皮的边长是16 cm.故选D.3.1 [解析] 设花边的宽为x m ,则地毯的长为(8-2x )m ,宽为(5-2x )m ,根据题意列方程得(8-2x )(5-2x )=18,解得x 1=1,x 2=5.5(不符合题意,舍去).故花边的宽为1 m.4.解:设垂直于墙的一边长为x m ,则平行与墙的一边长为(58-2x )m. 依题意得x (58-2x )=200, 解得x 1=25,x 2=4,58-2x 1=8,58-2x 2=50.答:矩形的长为25 m ,宽为8 m 或矩形的长为50 m ,宽为4 m. 5.解:设这个花圃的宽度为x m ,依题意,得 (10-2x )(8-x )=10×8×(1-30%), 解得x 1=12(不合题意,舍去),x 2=1. 答:这个花圃的宽度为1 m.6.B [解析] 设经过t s 后,能使△PBQ 的面积为15 cm 2, 则BP =(8-t )cm ,BQ =2t cm ,由三角形的面积计算公式列方程得12×(8-t )×2t =15,解得t 1=3,t 2=5(当t =5时,BQ =10,不合题意,舍去).故经过3 s 后,能使△PBQ 的面积为15 cm 2. 7.解:设t s 后△PCQ 的面积是△ABC 面积的一半,则可得此时PC =AC -AP =(12-2t )cm ,CQ =BC -BQ =(9-2t )cm ,∴△PCQ 的面积为12·PC ·CQ =12(12-2t )(9-2t )cm 2.∵△PCQ 的面积是△ABC 面积的一半,△ABC 的面积=12×12×9=54(cm 2),∴12(12-2t )(9-2t )=27,解得t =9或t =1.5.∵0≤t ≤4.5, ∴t =1.5,则1.5 s 后△PCQ 的面积是△ABC 面积的一半. 8.设AB =x 米,则BC =(100-4x )米. 根据题意得x (100-4x )=400,整理得x 2-25x +100=0,解得x 1=20,x 2=5. 当AB =20米时,BC =20米,符合题意; 当AB =5米时,BC =80米>25米,故舍去. 答:羊圈的边长AB ,BC 都为20米.9.解:设x s 后,△PBQ 的面积是△ABC 面积的一半,则12(24-4x )(16-2x )×32=12×12×24×16×32,解得x =2或x =12(舍去). 答:2 s 后,△PBQ 的面积是△ABC 面积的一半.10.解: (1)设矩形地面的长为x m ,则宽为(20-x )m ,由题意,得x (20-x )=96, 解得x 1=12,x 2=8(舍去). 答:矩形地面的长为12 m.(2)需要规格为0.80 m×0.80 m 的地板砖96÷(0.8×0.8)=150(块), 则总费用为55×150=8250(元);需要规格为1.00 m×1.00 m 的地板砖96÷(1.0×1.0)=96(块), 则总费用为80×96=7680(元).∵7680<8250,∴用规格为1.00 m×1.00 m 的地板砖费用较少.11. (1)(20-6x ) (30-4x ) (24x 2-260x +600)(2)根据题意,得24x 2-260x +600=(1-13)×20×30,整理,得6x 2-65x +50=0,解得x 1=56,x 2=10(不合题意,舍去),则2x =53,3x =52.答:每个横、竖彩条的宽度分别为53 cm ,52 cm.。
高中数学人教A版必修五优化练习:第二章 2.5 第2课时 等比数列的前n项和公式的性质及应用 含解析

[课时作业] [A 组 基础巩固]1.设首项为1,公比为23的等比数列{a n }的前n 项和为S n ,则( )A .S n =2a n -1B .S n =3a n -2C .S n =4-3a nD .S n =3-2a n解析:S n =a 1(1-q n )1-q =a 1-a n q1-q =3-2a n .答案:D2.设S n 为等比数列{a n }的前n 项和,8a 2-a 5=0,则S 4S 2=( )A .5B .8C .-8D .15解析:∵8a 2-a 5=0,∴8a 1q =a 1q 4,∴q 3=8,∴q =2,∴S 4S 2=1-q 41-q 2=1+q 2=5.答案:A3.已知在等比数列{a n }中,公比q 是整数,a 1+a 4=18,a 2+a 3=12,则此数列的前8项和为( ) A .514 B .513 C .512D .510解析:由已知得⎩⎪⎨⎪⎧a 1+a 1q 3=18,a 1q +a 1q 2=12,解得q =2或q =12.∵q 为整数,∴q =2.∴a 1=2,∴S 8=2(1-28)1-2=29-2=510.答案:D4.设{a n }是由正数组成的等比数列,S n 为其前n 项和,已知a 2a 4=1,S 3=7,则S 5=( ) A.152 B.314 C.334D.172解析:由a 2a 4=1⇒a 1=1q 2,又S 3=a 1(1+q +q 2)=7,联立得:⎝⎛⎭⎫1q +3⎝⎛⎭⎫1q -2=0,∴q =12,a 1=4, S 5=4⎝⎛⎭⎫1-1251-12=314.答案:B5.在数列{a n }中,a 1=2,a n +1=2a n ,S n 为{a n }的前n 项和,若S n =126,则n =________. 解析:∵a 1=2,a n +1=2a n ,∴数列{a n }是首项为2,公比为2的等比数列, ∴S n =2(1-2n )1-2=126,∴2n =64,∴n =6.答案:66.等比数列{a n }的公比q >0,已知a 2=1,a n +2+a n +1=6a n ,则{a n }的前4项和S 4=________. 解析:由a n +2+a n +1=6a n ,得q n +1+q n =6q n -1,即q 2+q -6=0,q >0,解得q =2, 又∵a 2=1,∴a 1=12,∴S 4=12·(1-24)1-2=152.答案:1527.设S n 为等比数列{a n }的前n 项和.若a 1=1,且3S 1,2S 2,S 3成等差数列,则a n =________. 解析:设等比数列{a n }的公比为q (q ≠0),依题意得a 2=a 1·q =q ,a 3=a 1q 2=q 2,S 1=a 1=1,S 2=1+q ,S 3=1+q +q 2,又3S 1,2S 2,S 3成等差数列,所以4S 2=3S 1+S 3,即4(1+q )=3+1+q +q 2,所以q =3(q =0舍去).所以a n =a 1q n -1=3n -1. 答案:3n -18.设{a n }是由正数组成的等比数列,S n 是其前n 项和,证明:log 0.5S n +log 0.5S n +2>2log 0.5S n +1.证明:设{a n }的公比为q ,由已知得a 1>0,q >0. ∵S n +1=a 1+qS n ,S n +2=a 1+qS n +1,∴S n S n +2-S 2n +1=S n (a 1+qS n +1)-(a 1+qS n )S n +1=S n a 1+qS n S n +1-a 1S n +1-qS n S n +1=a 1(S n -S n +1)=-a 1a n +1<0, ∴S n ·S n +2<S 2n +1.根据对数函数的单调性可以得到log 0.5(S n S n +2)>log 0.5S 2n +1, 即log 0.5S n +log 0.5S n +2>2log 0.5S n +1.9.设等比数列{a n }的公比q <1,前n 项和为S n ,已知a 3=2,S 4=5S 2,求{a n }的通项公式. 解析:由题设知a 1≠0,S n =a 1·(1-q n )1-q,则⎩⎪⎨⎪⎧a 1q 2=2, ①a 1·(1-q 4)1-q=5×a 1·(1-q 2)1-q , ② 由②得1-q 4=5(1-q 2),(q 2-4)(q 2-1)=0.(q -2)(q +2)(q -1)(q +1)=0, 因为q <1,解得q =-1或q =-2. 当q =-1时,代入①得a 1=2, 通项公式a n =2×(-1)n -1; 当q =-2时,代入①得a 1=12;通项公式a n =12×(-2)n -1.综上,当q =-1时,a n =2×(-1)n -1; 当q =-2时,a n =12×(-2)n -1.[B 组 能力提升]1.在等比数列{a n }中,公比q =2,log 2a 1+log 2a 2+log 2a 3+…+log 2a 10=35,则S 10=( ) A.1 0232B.1 0242C .235D.1 0222解析:由题意知log 2(a 1·a 2·…·a 10)=35, ∴a 1·a 2·a 3·…·a 10=235. ∴a 1·(a 1q )·(a 1q 2)·…·(a 1q 9)=235.∴a 101q1+2+3+…+9=235.∴a 101·245=235,即a 101=1210, ∴a 1=12.∴a 1+a 2+…+a 10=a 1(1-q 10)1-q =1 0232.答案:A2.已知{a n }是等差数列,公差d 不为零,前n 项和是S n ,若a 3,a 4,a 8成等比数列,则( ) A .a 1d >0,dS 4>0 B .a 1d <0,dS 4<0 C .a 1d >0,dS 4<0 D .a 1d <0,dS 4>0解析:因为{a n }是等差数列,a 3,a 4,a 8成等比数列, 所以(a 1+3d )2=(a 1+2d )(a 1+7d )⇒a 1=-53d ,所以S 4=2(a 1+a 4)=2(a 1+a 1+3d )=-23d ,所以a 1d =-53d 2<0,dS 4=-23d 2<0.答案:B3.一个项数是偶数的等比数列,它的偶数项的和是奇数项的和的两倍,它的首项为1,且中间两项的和为24,则此等比数列的项数为________. 解析:由题意可知q =2, 设该数列为a 1,a 2,a 3,…,a 2n , 则a n +a n +1=24,又a 1=1, ∴q n -1+q n =24,即2n -1+2n =24, 解得n =4,∴项数为8项. 答案:84.(2019·高考全国Ⅰ卷)设等比数列{a n }满足a 1+a 3=10,a 2+a 4=5,则a 1a 2…a n 的最大值为________.解析:设{a n }的公比为q , 于是a 1(1+q 2)=10,① a 1(q +q 3)=5,②联立①②得a 1=8,q =12,∴a n =24-n ,∴a 1a 2…a n =23+2+1+…+(4-n )=2-12n n 2+72n n =2-12 (n -72 )2+498≤26=64.∴a 1a 2…a n的最大值为64. 答案:645.已知等差数列{a n }的前n 项和为S n ,a 3=5,S 6=36, (1)求数列{a n }的通项公式;(2)设b n =2a n ,求数列{b n }的前n 项和T n .解析:(1)设{a n }的公差为d ,则⎩⎪⎨⎪⎧a 1+2d =5,6a 1+6×52d =36, 即⎩⎪⎨⎪⎧a 1+2d =5,a 1+52d =6,∴a 1=1,d =2. ∴a n =1+2(n -1)=2n -1,(n ∈N *). (2)∵b n =2a n =22n -1, ∴T n =21+23+25+…+22n -1 =2(1-4n )1-4=2(4n -1)3.6.已知数列{a n }的前n 项和为S n ,且S n =2a n -2(n ∈N *),数列{b n }中,b 1=1,点P (b n ,b n+1)在直线x -y +2=0上.(1)求数列{a n },{b n }的通项公式; (2)记T n =a 1b 1+a 2b 2+…+a n b n ,求T n .解析:(1)由S n =2a n -2得S n -1=2a n -1-2(n ≥2), 两式相减得a n =2a n -2a n -1,即a na n -1=2(n ≥2),又a 1=S 1=2a 1-2,∴a 1=2,∴{a n }是以2为首项,2为公比的等比数列. ∴a n =2n .∵点P (b n ,b n +1)在直线x -y +2=0上, ∴b n -b n +1+2=0,即b n +1-b n =2, ∴{b n }是等差数列. 又b 1=1,∴b n =2n -1.(2)∵T n =1×2+3×22+…+(2n -3)2n -1+(2n -1)·2n ,① ∴2T n =1×22+3×23+…+(2n -3)2n +(2n -1)2n +1.② ①-②,得-T n =1×2+2×(22+23+…+2n )-(2n -1)·2n +1 =2+2·22-2n ·21-2-(2n -1)2n +1=2+4·2n -8-(2n -1)2n +1=(3-2n )·2n +1-6. ∴T n =(2n -3)·2n +1+6.。
秋九年级数学上册 第2章 一元二次方程 2.5 一元二次方程的应用 第2课时 图形面积和动点几何问题

第2课时 图形面积和动点几何问题知|识|目|标1.通过讨论、探究,会用一元二次方程解决图形面积问题.2.在理解直角三角形面积计算的基础上,能够建立一元二次方程解决与动点有关的几何问题.目标一 能利用一元二次方程解决图形面积问题例1 教材例3针对训练如图2-5-2,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一块长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a 米.(1)用含a 的式子表示花圃的面积;(2)如果通道所占面积是整个长方形空地面积的38,求出此时通道的宽. 图2-5-2【归纳总结】利用图形的面积建立一元二次方程模型的步骤(1)设元;(2)用未知数表示各边的长度;(3)利用面积公式列一元二次方程;(4)解一元二次方程;(5)针对实际情况舍去负根和超X围的根,从而得出结果.目标二利用一元二次方程解决动点几何问题例2 教材补充例题在矩形ABCD中,AB=5 cm,BC=6 cm,点P从点A开始沿边AB向终点B以1 cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,当点Q运动到点C时,两点同时停止运动.设运动时间为t s(t>0).(1)填空:BQ=________ cm,PB=________ cm(用含t的代数式表示).(2)当t为何值时,PQ的长度等于5 cm?(3)是否存在t的值,使得五边形APQCD的面积等于26 cm2?若存在,请求出此时t的值;若不存在,请说明理由.【归纳总结】利用一元二次方程解决动点问题的方法(1)构造直角三角形法,利用勾股定理建立一元二次方程.(2)等线段法,利用三角形全等构造两线段相等,建立一元二次方程;(3)等面积法,利用三角形面积(或三角形高)的变化建立面积等式.实现将几何问题转化为代数问题,从而加以解决.知识点利用一元二次方程解几何图形问题常用的等量关系有:(1)勾股定理;(2)面积的等量关系.[点拨] 在建立一元二次方程模型解几何图形实际问题的过程中,必须检验方程的根的实际意义,所求得的根应该保证几何图形的存在.如图2-5-3,某农场有一块长40 m ,宽32 m 的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140 m 2,求小路的宽.图2-5-3解:解法1:设小路的宽为x m ,则东西方向小路的面积为40x m 2,南北方向小路的面积为32x m 2. 则40×32-40x -32x =1140,解得x =3518. 所以小路的宽为3518m. 解法2:设小路的宽为x m ,将4块种植地平移为一个矩形,其长为(40-x )m ,宽为(32-x )m.根据矩形面积公式,得(40-x )(32-x )=1140,整理得x 2-72x +140=0.解得x 1=2,x 2=70.答:小路的宽应是2 m 或70 m.以上两种解法正确吗?若不正确,出现错误的原因是什么?请给出正确的答案.详解详析【目标突破】例1 解:(1)由图可知,花圃的面积为(40-2a)(60-2a)平方米.(2)由已知可列方程:60×40-(40-2a)(60-2a)=38×60×40,解得a 1=5,a 2=45(舍去).答:此时通道的宽为5米.例2 解:(1)2t (5-t)(2)由题意得(5-t)2+(2t)2=52,解得t 1=0(不合题意,舍去),t 2=2.∴当t =2时,PQ 的长度等于5 cm .(3)存在.∵矩形ABCD 的面积是5×6=30(cm 2),五边形APQCD 的面积等于26 cm 2,∴△PBQ 的面积为30-26=4(cm 2),∴(5-t)×2t×12=4, 解得t 1=4(不合题意,舍去),t 2=1.即当t =1时,五边形APQCD 的面积等于26 cm 2.备选题型 用一元二次方程解决存在性问题例 用一根长22 cm 的铁丝,能不能恰好折成一个面积为32 cm 2的矩形?试分析你的结论.解:设折成的矩形的长为x cm ,则宽为(11-x)cm ,矩形的面积为x(11-x)cm 2,依题意,得x(11-x)=32,化简为x 2-11x +32=0, Δ=b 2-4ac =(-11)2-4×1×32=121-128=-7<0,因此方程无实数根,则用长为22 cm 的铁丝不能折成一个面积为32 cm 2的矩形.【总结反思】[反思] 解:两种解法都不正确,解法1多减去了两条小路交叉重叠的小正方形的面积,因此正确的方程是40×32-40x -32x +x 2=1140;解法2没有考虑方程的根是否符合实际意义,因为x<32,显然x=70不符合题意.正确的答案为x=2,即小路的宽为2 m.。
湘教版数学九年级上册_课时作业:第2课时_图形面积和动点问题

2.5第2课时图形面积和动点问题一、选择题1.王叔叔从市场上买了一块长80 cm、宽70 cm的矩形铁皮,准备制作一个工具箱.如图,他将矩形铁皮的四个角各剪掉一个边长为x cm的正方形后,剩余的部分刚好能围成一个底面积为3000 cm2的无盖长方体工具箱,根据题意可列方程为()A.(80-x)(70-x)=3000B.80×70-4x2=3000C.(80-2x)(70-2x)=3000D.80×70-4x2-(70+80)x=30002.如图,在宽为20米,长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551平方米,则修建的路宽应为()A.1米B.1.5米C.2米D.2.5米3.如图,将边长为2 cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′.若两个三角形重叠部分的面积为 1 cm2,则它移动的距离AA′的值为()A.0.5 cm B.1 cm C.1.5 cm D.2 cm4.如图,在△ABC中,AC=50 cm,BC=40 cm,∠C=90°,点P从点A开始沿AC边向点C以2 cm/s的速度匀速移动,同时另一点Q由点C开始以3 cm/s的速度沿着射线CB 匀速移动,当△PCQ的面积等于300 cm2时,运动时间为()A.5 s B.20 s C.5 s或20 s D.不确定二、填空题5.如图,用长度为32米的篱笆,一面利用墙(墙的最大可用长度为16米),围成一个面积为120平方米的长方形花圃.若设BC的长为x米,则根据条件能得到一个关于x的一元二次方程,该方程的一般形式为______________.(不用写出x的取值范围)6.如图所示,在Rt△ABC中,∠BAC=90°,AB=AC=16 cm,AD为BC边上的高,动点P从点A出发,沿AD方向以 2 cm/s的速度向点D运动.E为AC边上一点.设△ABP 的面积为S1,矩形PDFE的面积为S2,运动时间为t s,则t=________时,S1=2S2.三、解答题7.如图①,要设计一幅宽20 cm、长30 cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3.如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?分析:由横、竖彩条的宽度比为2∶3,可设每个横彩条的宽为2x cm,则每个竖彩条的宽为3x cm.为更好地寻找题目中的等量关系,将横、竖彩条分别集中,原问题转化为如图②的情况,得到矩形ABCD.(1)如图②,用含x的代数式表示:AB=________cm,AD=________cm,矩形ABCD的面积为_______________cm2;(2)列出方程并完成本题解答.8.图是一幅长20 cm 、宽12 cm 的图案,其中有一横两竖的彩条,横、竖彩条的宽度比为3∶2.设竖彩条的宽度为x cm ,图案中三条彩条所占面积为y cm 2.(1)试用含有x 的代数式表示y ,并确定x 的取值范围;(2)若图案中三条彩条所占面积是图案面积的25,求横、竖彩条的宽度.9.如图,在△ABC 中,∠B =90°,AB =6 cm ,BC =3 cm ,点P 从点A 开始沿AB 边向点B 以2 cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以1 cm/s 的速度移动,如果P ,Q 两点同时出发,点P 运动到C 时,P ,Q 两点同时停止运动.(1)几秒钟后,△APQ 是等腰三角形?(2)几秒钟后,△BPQ 的面积是四边形CQP A 的面积的1310.李明准备进行如下试验操作:把一根长40 cm 的铁丝剪成两段,并把每段首尾相连各围成一个正方形.(1)要使这两个正方形的面积之和等于58 cm 2,李明应该怎么剪这根铁丝?(2)李明认为这两个正方形的面积之和不可能等于48 cm 2,你觉得他的想法正确吗?请说明理由.方案设计某小区计划在一块长100 m 、宽60 m 的矩形荒地上修建一个配绿化带的活动区,要求整体布局既是轴对称图形,又是中心对称图形,且绿化率不低于35%(绿化率=绿化面积总面积×100%).(1)甲方案:如图①所示,设计两条互相垂直且宽度都为a m 的十字活动区域,周边四块为绿化带(图中阴影部分),若绿化面积为2100 m 2,求a 的值;(2)乙方案:如图K -16-10②所示(单位:m),场地正中央设计菱形绿化带(图中阴影部分),周边为活动区域,请通过计算说明该方案是否符合要求.详解详析[课堂达标] 1.[答案] C2.[解析] A 设修建的路宽为x m .依题意,得(30-x)(20-x)=551, 解得x 1=1,x 2=49(不合题意,舍去).3.[解析] B 设AC 交A′B′于点H.∵∠A =45°,∠AA′H =90°,∴△A′HA 是等腰直角三角形.设AA′=x cm ,则阴影部分的底A′H 的长为x cm ,高A′D =(2-x)cm ,∴x·(2-x)=1,∴x 1=x 2=1,即AA′=1 cm .4.[解析] C 设运动时间为t s ,则AP =2t ,CQ =3t ,∴PC =50-2t.∵12·PC·CQ =300,∴12·(50-2t)·3t =300,解得t =20或t =5,∴运动时间为20 s 或5 s 时,△PCQ 的面积等于300 cm 2.故选C .5.[答案] x 2-32x +240=0[解析] 依题意得12(32-x)x =120.整理,得x 2-32x +240=0.6.[答案] 6[解析] ∵在Rt △ABC 中,∠BAC =90°,AB =AC =16 cm ,AD 为BC 边上的高, ∴AD =BD =CD =8 2 cm .又∵AP =2t cm ,则S 1=12AP·BD =12×2×8 2t =8t ,PD =(8 2-2t)cm .∵PE ∥BC ,∴∠AEP =∠C =45°,∠APE =∠ADC =90°, ∴∠PAE =∠AEP =45°,∴PE =AP =2t cm ,∴S 2=PD·PE =(8 2-2t)·2t.∵S 1=2S 2,∴8t =2(8 2-2t)·2t ,解得t =6或t =0(舍去).故答案是6.7.[解析] 读懂题中的分析,利用已有的数量关系与面积公式列方程. 解:(1)(20-6x)(30-4x) (20-6x)(30-4x) (2)根据题意,得(20-6x)(30-4x)=(1-13)×20×30.整理,得6x 2-65x +50=0,解得x 1=56,x 2=10(不合题意,舍去),则2x =53,3x =52.答:每个横、竖彩条的宽度分别为53 cm ,52 cm .8.解:(1)根据题意可知,横彩条的宽度为32x cm ,∴⎩⎪⎨⎪⎧x>0,20-2x>0,12-32x>0,解得0<x <8.y =20×32x +2×12·x -2×32x·x =-3x 2+54x ,即y =-3x 2+54x(0<x <8).(2)根据题意,得-3x 2+54x =25×20×12,整理,得x 2-18x +32=0, 解得x 1=2,x 2=16(舍去),∴32x =3.答:横彩条的宽度为3 cm ,竖彩条的宽度为2 cm . 9.解:设运动时间为t s ,则AP =2t ,BP =6-2t ,BQ =t. (1)∵∠B =90°,∴∠APQ >90°. ∵△APQ 是等腰三角形,∴AP =PQ ,即2t =(6-2t )2+t 2,解得t 1=12-6 3,t 2=12+6 3>3(不合题意,舍去).答:(12-6 3)s 后,△APQ 是等腰三角形.(2)△BPQ 的面积是四边形CQPA 的面积的13,即△BPQ 的面积等于△ABC 面积的14.∵S △BPQ =12BP·BQ =12(6-2t)t =3t -t 2,S △ABC =12AB·BC =9,∴3t -t 2=94,即t 2-3t +94=0,解得t 1=t 2=32.答:32s 后,△BPQ 的面积是四边形CQPA 的面积的13.11.解:(1)设剪成的较短的铁丝长为x cm ,则较长的铁丝长为(40-x)cm . 由题意,得⎝⎛⎭⎫x 42+⎝⎛⎭⎫40-x 42=58, 解得x 1=12,x 2=28, 当x =12时,40-12=28(cm ),当x =28时,40-28=12(cm )<28 cm (舍去).答:李明应该把铁丝剪成12 cm 和28 cm 的两段.(2)正确.理由:设剪成的较短的铁丝长为m cm ,则较长的铁丝长为(40-m)cm , 由题意,得⎝⎛⎭⎫m 42+⎝⎛⎭⎫40-m 42=48. 整理,得m 2-40m +416=0. ∵Δ=(-40)2-4×416=-64<0, ∴原方程无实数根,∴这两个正方形的面积之和不可能等于48 cm 2,即李明的想法正确. [素养提升]解:(1)依题意有(100-a)(60-a)=2100, 解得a 1=30,a 2=130(不合题意,舍去). 答:a 的值是30.(2)100-5×2=100-10=90(m ), 60-5×2=60-10=50(m ), 90×50÷2=2250(m 2), 100×60=6000(m 2), 22506000×100%=37.5%. ∵37.5%>35%, ∴该方案符合要求.。
七年级数学上册第2章有理数的运算2.5有理数的乘方第2课时分层训练

2.5 有理数的乘方(第2课时)科学记数法:把一个数表示成a(1≤|a|<10)与____________相乘的形式,叫做科学记数法.A组基础训练1.地球半径约为6400000米,则此数用科学记数法表示为( )A.0.64×107 B.6.4×106 C.6.4×105 D.64×1052.下列各数是用科学记数法表示的是( )A.0.1×105 B.10.3×106 C.12×108 D.-7.13×1063.1.234×104是( )A.五位数 B.四位数C.三位数 D.两位数4.下列运输工具中,可将一批总质量为1.2×107kg的货物一次运走的是( )A.一艘万吨级巨轮 B.一辆汽车C.一辆拖拉机 D.一辆马车5.(福州中考)计算3.8×107-3.7×107,结果用科学记数法表示为( )A.0.1×107 B.0.1×106 C.1×107 D.1×1066.要把质量为1千克的物体送入太空,火箭需要消耗质量为62千克的燃料.”神舟6号”实验飞船质量达8吨,要把”神舟6号”送入太空,火箭需消耗燃料的质量用科学记数法表示为( )A.0.496×107千克 B.49.6×104千克C.4.96×106千克 D.4.96×105千克7.若5960000用科学记数法表示为a×10n,则a=____________,n=____________.8.下列用科学记数法记出的数转换为原数:(1)1×105=____________;(2)2.015×103=____________;(3)-7.04×106=____________;(4)5.83×108=____________.9.(1)我国陆地面积大约为9600000km2,用科学记数法表示9600000为____________.(2)全球每小时约有510000000t污水排入江河湖海,则510000000用科学记数法表示为____________.(3)截至2016年3月4日,全世界人口总数大约为7260000000人,则7260000000用科学记数法表示为____________.(4)水星与太阳的距离约为5.79×107km,则这个数的原数为____________km.(5)我国发射的”海洋1号”气象卫星,进入预定轨道后,若绕地球运行的速度为每秒7.9×103m,运行2×102s所走过的路程是____________米(用科学记数法表示).(6)我国研制的某种超级计算机每秒可做1.2×1012次运算,用科学记数法表示它工作8min可以运算____________次.10.比较大小:(1)9.523×1010____________1.002×1011;(2)-8.76×109____________-1.03×1010.11.计算(结果用科学记数法表示):(1)(2.4×109)÷(8×106);(2)(2.4×104)×(5.1×103);(3)(3×104)3.12.据测算,我国每天因土地沙漠化造成的经济损失为1.5亿元,若一年按365天计算,用科学记数法表示我国一年土地沙漠化造成的经济损失为多少元?。
部编版道德与法治五年级下册建立良好的公共秩序 第2课时 教案

2.5 建立良好的公共秩序第二课时教学设计教学目标1.通过视频观看、分享生活、感受交流等活动,认识到构建有序和谐的公共生活,要提高自身的守序意识,遵守社会公德、法律法规。
(教学重点)2.通过社会调查、案例分析、小组探究等活动,明确共建有序生活,需要汇聚社会各方面的力量,需要国家的支持、制度的保障。
(教学难点)教学过程课前导入同学们,上节课我们知道了公共生活需要秩序。
今天我们来学习《共同建设有序生活》(出示课题)一、规范自己行为1.出示教材“活动园”,分组讨论我们在不同公共场合应该怎么做小结作为一名小学生,社会生活的一份子,养成文明好习惯,为共建有序生活履行好小公民的义务尤为重要。
(板书:个人文明习惯)二、社会各方努力,构建有序生活不过,生活中的和谐有序,也会因为一些小状况而被打破。
比如说(出示问题)问题一:路口红绿灯坏了,车辆行人乱成一团。
问题二:工厂向河流排放污水,导致河流受到污染。
问题三:社会上出现感染性较强的流行病疫情。
2.课前我们对书本上的这些问题进行了调查。
(出示课前调查表)先在小组里交流下吧,(小组交流,播放录音)哪一组先来和我们分享?(一)交通出行问题预设:1.我调查的是路口红灯坏了的解决办法,我咨询了爸爸的交警朋友黄叔叔,我们一起去听听交警叔叔怎么说吧!(播放录音)当我们发现路口的信号灯发生故障时,我们应先拨打110报警。
2.同学们思考下,当路口的信号灯指示方向和交警叔叔的手势指挥不一致时,我们该听谁的呢?你说的真棒!答案是(出示图片)遇有交通警察现场指挥时,应当按照警察的指挥通行。
3.2020年4月25日,在我县百尺南路上出现了文明有序的一幕(播放45度让路视频)小结:个人自觉的规则意识,成就了一个个感动的瞬间!4.交通出行涉及千家万户,课前,同学们对家人的行车情况进行了调查。
(出示调查表)我们看到,虽然出行途中会碰到一些情况,但是形成良好的社会风气我们正在努力!(出示小红花)5.路口终于恢复了有序的通行,同学们这都是谁的功劳啊?(学生回答)6.小结:公共生活中的很多问题,不是一个人,某个部门,某一个团体就能解决的,需要凝聚社会各方力量。
苏科版初中数学七年级上册《2.5有理数的加法与减法》第二课时有理数的加法运算律教学课件

C.加法的交换律和结合律
D.以上都不对
能凑成整数的两个数先相加.
随堂练习
4.计算:
(1) 16+(-25)+24+(-35)
(2) (+0.7)+(-0.9)+(-1.8)+1.3+(-0.2)
解: (1) 16+(-25)+24+(-35)
=16+24+[(-25)+ (-35)]
单位,第三次向右跳3个单位,第四次向左跳4个单位,…,按这样的规律跳100次,
跳骚到原点的距离是多少?
-4
-3
-2
-1
0
1
2
3
4
解:+1+(-2)+(+3)+(-4)+(+5)+ …… +(+99)+(-100)
= [+1+(-2)]+[(+3)+(-4)]+ …… +[(+99)+(-100)]
=(-1)+(-1)+ …… +(-1)
计算:(-1)+(+2)+(-3)+(+4).
解:原式=(-1)+(-3)+(+2)+(+4)
=[(-1)+(-3)]+[(+2)+(+4)]
(
加法交换律
)
(
加法结合律
)
=(-4)+(+6)
=2.
2.用简便算法计算.
名师课堂--2.5 第2课时 科学记数法---七年级上册

2.5有理数的乘方第2课时科学记数法知识点1科学记数法的表示1.下列各数用科学记数法表示正确的是()A.0.58×1011B.12.3×107×104D.8.07×102C.342.[2019·宁波]宁波是世界银行在亚洲地区选择的第一个开展垃圾分类试点项目的城市,项目总投资为1526000000元.数1526000000用科学记数法表示为()A.1.526×108B.15.26×108C.1.526×109D.1.526×10103.[教材例3(1)变式]用科学记数法表示以下各数:(1)100000000=;(2)3080000=;(3)-780100=.4.纳米技术已经开始用于生产生活之中,已知1米=1000000000纳米,那么216.3米=纳米.(结果用科学记数法表示)知识点2还原用科学记数法表示的数5.用科学记数法表示的数是1.69×105,则原来的数是()A.169B.1690C.16900D.1690006.用科学记数法表示的数1.001×1025的整数位数有()A.23位B.24位C.25位D.26位7.[教材例3(2)变式]下列用科学记数法表示的数,原来各是什么数?(1)5.2×106;(2)1.07×104.8.某机构对30万人的调查结果显示,沉迷于手机上网的初中生大约占7%,则这部分沉迷于手机上网的初中生人数用科学记数法可表示为()A.2.1×105人B.21×103人C.0.21×105人D.2.1×104人9.[2018·义乌模拟]天文学里常用“光年”作为距离单位.规定“1光年”为光在一年内传播的距离,大约等于94600亿千米,94600亿千米用科学记数法可表示为千米.10.比较大小:(1)1.5×102020与9.8×102019;(2)-3.6×105与-1.2×106.11.[教材作业题第5题变式]计算(结果用科学记数法表示):(1)4.3×104-3.4×103;(2)(-3×105)3.12.先计算,然后根据计算结果回答问题:(1)计算:①(1×102)×(2×104)=;②(2×104)×(3×107)=;③(3×107)×(4×104)=;④(4×105)×(5×1010)=.(2)已知式子(a×10n)×(b×10m)=c×10p成立,其中a,b,c均为大于或等于1且小于10的数,m,n,p 均为正整数,你能说出m,n,p之间存在的等量关系吗?教师详解详析1.D2.C3.(1)1×108(2)3.08×106(3)-7.801×1054.2.163×10115.D6.D7.(1)5200000(2)107008.D9.9.46×101210.解:(1)1.5×102020>9.8×102019.(2)-3.6×105>-1.2×106.11.解:(1)原式=43000-3400=39600=3.96×104.(2)原式=(-300000)3=-27000000000000000=-2.7×1016.12.解:(1)①2×106②6×1011③1.2×1012④2×1016 (2)(a×10n)×(b×10m)=ab×10m+n=c×10p.∵a,b,c均为大于或等于1且小于10的数,∴当1≤ab<10时,p=m+n;当ab≥10时,p=m+n+1.。
2.5直线与圆的位置关系(第2课时)(同步课件)-九年级数学上册同步精品课堂(苏科版)

直线与圆的位置关系(2)
第2课时
圆的切线的判定
学习目标
1.探索直线与圆相切的条件,能判断一条直线是否为圆的切线
;
2.会用三角尺画过圆上一点的切线.
问题导学
知识回顾
有哪些方法可以判定直线与圆相切?
直线与圆的
位置关系
相 交
相 切
相 离
公共点个数
2
1
0
圆心到直线的距离
d与半径r的关系
d<r
d=r
心,则另一直角边与⊙ 的位置关系为( B )
A.相交
B.相切
C.相离
D.无法确定
当堂检测
基础过关
4.如图,在矩形中, = , = ,⊙ 是以为直径
的圆,则直线与⊙ 的位置关系是________.
相切
当堂检测
基础过关
5.如图,P是⊙ 的直径的延长线上一点,∠ = °,则当
即∠ = °,
∴ ⊥ ,
∵ 是⊙ 的半径,
∴直线与⊙ 相切.
D
C
A
O
B
新知巩固
6.如图,在△ 中,∠ = °.
(1)实践与操作:用尺规作图法作∠的平分线交于点D;
(保留作图痕迹,不要求写作法)
解:(1) 如图1,即为所作;
C
A
B
新知巩固
综合提升
4. 如图,CD是☉O的直径,BD是弦,延长DC到点A,使∠ABD=120°,
连接BC.若添加一个条件,使AB是☉O的切线,现有下列条件:
① AC=BC;② AC=OC;③ OC=BC;④ AB=BD当堂检测
综合提升
5.(2024·山东东营·中考真题)如图,△ 内接于⊙ ,是⊙ 的直径,点
绥化市实验中学九年级数学上册 第2章 一元二次方程2.5 一元二次方程的应用第2课时 用一元二次方程

解:(1)设 x 秒后,△PBQ 的面积等于 6 cm2,依题意,得12 (5-x)·2x=6, 解得 x1=2,x2=3.故 2 秒或 3 秒后,△PBQ 的面积等于 6 cm2; (2)设 x 秒后,PQ 的长度等于 5 cm,依题意,得(5-x)2+(2x)2=52, 解得 x1=0(舍,)x2=2.故 2 秒后,PQ 的长度等于 5 cm;
7 那么此直角三角形的面积是4____.
5.(4分)如下图 , 邻边不等的矩形花圃ABCD , 它的一边AD利用已有的 围墙 , 另外三边所围的栅栏的总长度是6 m.假设矩形的面积为4 m2 , 那么AB的长度是1 ____m.(可利用的围墙长度超过6 m)
6.(4分)一块四周镶有宽度相等的花边的地毯 , 如下图 , 它的长为8 m , 宽为5 m , 如果地毯中央长方形图案的面积为18 m2 , 那么花边的宽是1m____.
一平面内 , 从标杆DC退后123步的G处 , 可看到山峰
A和标杆顶端C在一直线上 , 从标杆FE退后127步的
H处 , 可看到山峰A和标杆顶端E在一直线上.求山
峰的高度AB及它和标杆CD的水平距离BD30750步,
(注意:KCDGAK,KEFH AK.)
CD
FE
7.(8分)如下图 , 有一长方形的地 , 该地块长为x米 , 宽为120米 , 建筑商将 它分成三部分 : 甲、乙、丙 , 甲和乙为正方形 , 现计划甲建设住宅区 , 乙建设 商场 , 丙开辟成公司.假设已知丙地的面积为3 200平方米 ,
你能算出x的值吗 ?
解 : 根据题意 , 得(x-120)【120-(x-120)]=3 200 , 即x2-360x+32 000=0 , 解得x1=200 , x2=160.故x的值为200或160.
2.5 第2课时 有理数加法运算律

第2课时 有理数加法运算律知识点 1 有理数的加法交换律与加法结合律1.运算过程5+(-3)+7+(-9)+12=(5+7+12)+[(-3)+(-9)]应用了( ) A .加法交换律 B .加法结合律C .分配律D .加法的交换律与结合律 2.计算314+⎝⎛⎭⎫-235+534+⎝⎛⎭⎫-725时,运算律用得恰当的是( ) A.⎣⎡⎦⎤314+⎝⎛⎭⎫-235+⎣⎡⎦⎤ 534+⎝⎛⎭⎫-725 B .(314+534)+⎣⎡⎦⎤⎝⎛⎭⎫-235+⎝⎛⎭⎫-725 C.⎣⎡⎦⎤314+⎝⎛⎭⎫-725+⎣⎡⎦⎤⎝⎛⎭⎫-235+534D.⎣⎡⎦⎤⎝⎛⎭⎫-235+534+⎣⎡⎦⎤314+⎝⎛⎭⎫-725 3.使用运算律计算⎝⎛⎭⎫-14+45+⎝⎛⎭⎫-34的结果是( ) A.95 B .-95 C.15 D .-15 4.-7,-12,2三个数和的绝对值是( )A .3B .7C .17D .21 5.在括号内填上每一步运算的依据: 22+(-6)+(-22)=(-6)+22+(-22) ( ) =(-6)+[22+(-22)] ( )=(-6)+0()=-6. ()6.计算:-200.95+28+0.95+(-8)=________.7.绝对值小于5的所有整数的和是__________.8.计算:(1)18+(-29)+52;(2)(-301)+125+301+(-75);(3)2018·省泰中附中月考(-26.54)+(-6.4)+18.54+6.4;(4)2018·黄桥月考-3.2+(-5.2)+(-2.8)+15.2;(5)2018·滨海县月考 (-0.125)+12+(-713)+218+623;(6)(+1317)+(-3.5)+(-6)+(+2.5)+(+6)+(+417).知识点 2 有理数加法运算律的应用9.某商店去年四个季度盈亏情况如下(盈余为正):+128.5万元,-140万元,-95.5万元,+280万元,这个商店的总盈亏情况是( ) A .盈余644万元 B .亏本173万元 C .盈余173万元 D .亏本644万元10.2018·宜兴月考某人用400元钱购买了8套儿童服装,准备以一定的价格出售,如果以每套55元的价格为标准,超出的记为正数,不足的记为负数,记录如下(单位:元):+2,-3,+2,-1,-2,+1,-2,0.(1)他卖完这8套服装后的总收入是多少?(2)盈利(或亏损)了多少元?11.若三个有理数的和为0,则下列结论正确的是()A.这三个数都是0B.最少有两个数是负数C.最多有两个数是正数D.这三个数互为相反数12.2018·楚水月考小红在写作业时,不慎将一滴墨水滴在数轴上,根据图2-5-3中的数据,请确定墨迹遮盖住的整数的和为________.图2-5-313.计算:(-1)+2+(-3)+4+(-5)+6+…+(-2017)+2018+(-2019)+2020.14.有一批水果,标准质量为每筐25千克,现抽取8筐样品进行检测,称重结果如下(单位:千克):27,24,23,28,21,26,22,27,为求得8筐样品的总质量,我们可以选取一个恰当的基准数进行简化运算.(1)你认为选取的一个恰当的基准数为________;(2)根据你选取的基准数,用正、负数填写上表(超出基准数记为正,不足基准数记为负);(3)这8筐水果的总质量是多少?15.2017·江阴校级月考 阅读材料:对于(-556)+(-923)+1734+(-312)可以如下计算:原式=[(-5)+(-56)]+[(-9)+(-23)]+(17+34)+[(-3)+(-12)]=[(-5)+(-9)+17+(-3)]+[(-56)+(-23)+34+(-12)]=0+(-114)=-114.上面这种方法叫拆数法,你看懂了吗?仿照上面的方法,请你计算:(-201956)+(-201823)+403834+(-112).教师详解详析1.D [解析] 本题运用了加法的交换律、加法的结合律进行运算.故选D. 2.B3.D [解析] 原式=⎝⎛⎭⎫-14+⎝⎛⎭⎫-34+45=-1+45=-15.故选D. 4.C [解析] (-7)+(-12)+2=(-7)+(-10)=-17,-17的绝对值是17.故选C. 5.加法交换律 加法结合律 互为相反数的两个数相加得0 一个数与0相加,仍得这个数6.-1807.0 [解析] 根据绝对值的意义,结合数轴,得绝对值小于5的所有整数为0,±1,±2,±3,±4,所以它们的和为0.8.解:(1)原式=18+52+(-29)=41. (2)原式=(-301)+301+125+(-75)=50. (3)原式=[(-26.54)+18.54]+[(-6.4)+6.4]=-8. (4)原式=[-3.2+(-2.8)]+[(-5.2)+15.2]=-6+10=4.(5)原式=⎣⎡⎦⎤(-0.125)+218+12+⎣⎡⎦⎤(-713)+623=2+12+(-23)=1313. (6)原式=⎣⎡⎦⎤(+1317)+(+417)+[(-3.5)+(+2.5)]+[(-6)+(+6)]=1+(-1)+0=0. 9.C [解析] 先将这些数相加,若和为正,则表示盈余;若和为负,则表示亏本.(+128.5)+(-140)+(-95.5)+280=(128.5+280)+[(-140)+(-95.5)]=408.5+(-235.5)=173.故选C.10.解:(1)+2+(-3)+2+(-1)+(-2)+1+(-2)+0=-3(元),8×55+(-3)=437(元). 答:他卖完这8套服装后的总收入是437元.(2)437-400=37(元).答:盈利37元.11.C[解析] A项,不能确定,例如:-2+2+0=0.B项,不能确定,例如:-2+2+0=0.C项,正确.D项,错误,因为三个数不能称作互为相反数.故选C.12.-5[解析] 被墨迹遮盖住的整数为-3,-2,-1,0,1,它们的和为(-3)+(-2)+(-1)+0+1=-5.13.[解析] 本题加数比较多,若一个一个地加,显然比较麻烦,而且容易算错,但注意到相邻两个加数相加得1或-1,所以可以简化计算.解:(-1)+2+(-3)+4+(-5)+6+…+(-2017)+2018+(-2019)+2020=[(-1)+2]+[(-3)+4]+[(-5)+6]+…+[(-2017)+2018]+[(-2019)+2020]=1+1+1+…+1+1,\s\do4(1010个))=1010.14.解:(1)(2)问答案不唯一,(1)25(2)+2-1-2+3-4+1-3+2(3)25×8+[(+2)+(-1)+(-2)+(+3)+(-4)+(+1)+(-3)+(+2)]=200+(-2)=198(千克).答:这8筐水果的总质量是198千克.[点评] 在求多个数值的和的时候,注意运算的技巧(如本题取25为基准数,结合正负数表示相反意义的量的知识),再应用有理数加法的法则,可使问题的解决过程显得简捷.15.解:原式=[(-2019)+(-56)]+[(-2018)+(-23)]+(4038+34)+[(-1)+(-12)]=[(-2019)+(-2018)+4038+(-1)]+[(-56)+(-23)+34+(-12)]=0+(-114)=-114.。
