山东省巨野县一中二轮专题复习(函数)检测

合集下载

巨野县第一中学2018-2019学年高二9月月考数学试题解析

巨野县第一中学2018-2019学年高二9月月考数学试题解析班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1．满足下列条件的函数)(x f 中，)(x f 为偶函数的是（）A.()||x f e x =B.2()x x f e e =C.2(ln )ln f x x = D.1(ln )f x x x=+【命题意图】本题考查函数的解析式与奇偶性等基础知识，意在考查分析求解能力.2．若圆226260x y x y +--+=上有且仅有三个点到直线10(ax y a -+=是实数）的距离为，则a =（）A ． 1±B ．± C． D．3．已知平面向量与的夹角为3π，且32|2|=+b a ，1||=b ，则=||a （） A ． B ．3 C ． D ．4．已知，y 满足不等式430,35250,1,x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩则目标函数2z x y =+的最大值为（）A ．3B ．132C ．12D ．155．设a ，b ∈R ，i 为虚数单位，若2＋a i1＋i ＝3＋b i ，则a －b 为（）A ．3B ．2C ．1D ．06． “p q ∨为真”是“p ⌝为假”的（）条件A ．充分不必要B ．必要不充分C ．充要D ．既不充分也不必要 7．如图在圆O 中，AB ，CD 是圆O 互相垂直的两条直径，现分别以OA ，OB ，OC ，OD 为直径作四个圆，在圆O 内随机取一点，则此点取自阴影部分的概率是（）DABCOA ．π1B ．π21C ．π121-D ．π2141-【命题意图】本题考查几何概型概率的求法，借助圆这个载体，突出了几何概型的基本运算能力，因用到圆的几何性质及面积的割补思想，属于中等难度． 8．直径为6的球的表面积和体积分别是（）A ．144,144ππB ．144,36ππC ．36,144ππD ．36,36ππ9．复数i iiz (21+=是虚数单位）的虚部为（） A ．1- B ．i - C ．i 2 D ．2【命题意图】本题考查复数的运算和概念等基础知识，意在考查基本运算能力． 10．已知函数⎩⎨⎧≤>=)0(||)0(log )(2x x x x x f ，函数)(x g 满足以下三点条件：①定义域为R ；②对任意R x ∈，有1()(2)2g x g x =+；③当]1,1[-∈x 时，()g x .则函数)()(x g x f y -=在区间]4,4[-上零点的个数为（）A ．7B ．6C ．5D ．4【命题意图】本题考查利用函数图象来解决零点问题，突出了对分段函数的转化及数形结合思想的考查，本题综合性强，难度大.11．函数2(44)xy a a a =-+是指数函数，则的值是（） A ．4 B ．1或3 C ．3 D ．112．将函数x x f ωsin )(=（其中0>ω）的图象向右平移4π个单位长度，所得的图象经过点 )0,43(π，则ω的最小值是（） A ．31 B ． C ．35D ．二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上） 13．1F ，2F 分别为双曲线22221x y a b-=（a ，0b >）的左、右焦点，点P 在双曲线上，满足120PF PF ⋅=，若12PF F ∆的内切圆半径与外接圆半径之比为12，则该双曲线的离心率为______________.【命题意图】本题考查双曲线的几何性质，直角三角形内切圆半径与外接圆半径的计算等基础知识，意在考查基本运算能力及推理能力．14．定义在R 上的可导函数()f x ，已知()f x y e=′的图象如图所示，则()y f x =的增区间是 ▲ ．15．已知向量,满足42=，2||=，4)3()(=-⋅+，则与的夹角为 .【命题意图】本题考查向量的数量积、模及夹角知识，突出对向量的基础运算及化归能力的考查，属于容易题. 16．若复数12,z z 在复平面内对应的点关于y 轴对称，且12i z =-，则复数1212||z z z +在复平面内对应的点在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【命题意图】本题考查复数的几何意义、模与代数运算等基础知识，意在考查转化思想与计算能力．三、解答题（本大共6小题，共70分。

2023年山东省菏泽市巨野县中考数学二模试题(含答案)

二〇二三年初中学业水平模拟考试（二）数学试题1.本试题共24个题，满分120分.考试时间120分钟.2.请把答案作答在答题卡上，选择题用2B 铅笔填涂，非选择题用0.5毫米的黑色签字笔书写在答题卡的指定区域内，答在其他位置上不得分.一、选择题（本大题共8个小题，每小题3分，共24分.在每小题给出的四个选项中，只有一个选项是正确的，请把正确选项的序号涂在答题卡的相应位置.）1.手机移动支付给生活带来便捷.图1是孙老师2023年4月6日微信账单的收支明细（正数表示收入，负数表示支出，单位：元），孙老师当天微信收支的最终结果是（）A.收入19元B.支出8元C.支出5元D.收入6元2.下列计算正确的是（）A. B. C. D.3.如图2，在数轴上A ，B ，C ，D 四个点所对应的数中是不等式组的解的是（）A.点A 对应的数B.点B 对应的数C.点C 对应的数D.点D 对应的数4.如图3，将一副三角板叠放在一起，使直角的顶点重合于点O ，，CD 与OA 交于点E ，已知，则的度数为（）A.45° B.60° C.70°D.75°()32528a a=29=3=844a a a -÷=-1202x x x -<⎧⎪⎨≤⎪⎩AB OC ∥30A ∠=︒DEO ∠5.图4是由4个大小相同的正方体搭成的几何体的俯视图，那么该几何体的主视图不可能是（）A. B. C. D.6.为了传承传统手工技艺，提高同学们的手工制作能力，某中学七年级一班的美术老师特地给学生们开了一节手工课，教同学们编织“中国结”，为了了解同学们的学习情况，便随机抽取了20名学生，对他们的编织数量进行统计，统计结果如下表：编织数量/个23456人数/人36542请根据上表，判断下列说法正确的是（）A.样本为20名学生B.众数是4个C.中位数是3个D.平均数是3.8个7.关于x 的一元二次方程的根的情况是（）A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.实数根的个数由m 的值确定8.如图5所示，边长为2的等边是三棱镜的一个横截面.一束光线沿着与边垂直的方向射入到边上的点D 处（点D 与B ，C 不重合），反射光线沿的向射出去，与垂直，且入射光线和反射光线使.设的长为x ，的面积为y ，则下列图象中能大致表示y 与x 的函数关系的（）A.B.C. D.二、填空题（本大题共6个小题，每小题3分，共18分，只要求把最后结果填写在答题卡的相应区域内.）9.地球的储水量是很丰富的，共有14.5亿立方千米之多。

2022年山东省菏泽市巨野县第一中学高二数学理期末试题含解析

2022年山东省菏泽市巨野县第一中学高二数学理期末试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 函数f(x)＝a x-b的图象如图所示，其中a、b为常数，则下列结论正确的是 ()A.a>1，b<0B. a>1，b>0C.0<a<1，b>0D.0<a<1，b<0参考答案：D2. 设函数，则有（）A．是奇函数，B．是奇函数，C．是偶函数D．是偶函数，参考答案：C 3. 已知x，y满足线性约束条件，则z = x – 2y的最大值和最小值分别是别（）A．0和– 4 B．2和– 4 C．2和–2.5 D．1和0参考答案：C4. 若命题，则是（）A．B．C．D．参考答案：D略5. 过两点(-1，1)和(0，3)的直线在x轴上的截距为( )．(A) (B)(C)-3 (D) 3参考答案：A6. 函数f(x)＝(x－3)e x的单调递增区间是()A．(1,4) B．(0,3) C．(2，＋∞)D．(－∞，2)参考答案：Cf′(x)＝ex＋(x－3)ex＝ex(x－2)，由f′(x)>0，得x>2.∴f(x)在(2，＋∞)上是递增的．7. 已知点在平面内，并且对空间任一点，则的值为（）A． B． C． D．参考答案：D略8. 曲线在处的切线斜率为参考答案：略9. 设集合，，则下列结论中正确的是( ) A ．B ． C．D．参考答案：C略10. 已知函数：①；②；③；④．其中对于定义域内的任意一个自变量都存在唯一个自变量，使得成立的函数是( ) Ａ．③Ｂ．②③Ｃ．①②④Ｄ．④参考答案：A略二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数的导函数为且满足，则．参考答案：,则，所以令x= ，，所以12. 若两平行直线3x–2y–1=0和6x+ay+c=0之间的距离是，则的值为 .参考答案：±113. 若从4名男生和3名女生中任选2人参加演讲比赛，则至少选出1名女生的概率为．（结果用分数表示）参考答案：从4名男生和3名女生中任选2人参加演讲比赛，则所有可能结果共有种，设事件A“所选2人都是男生”，则A事件“所选2人都是男生”包含的基本事件个数有种，∴，故至少选出1名女生的概率为.14. 复数z满足方程i＝1－i，则z＝________.参考答案：－1＋i15. 已知一个平面与正方体的12条棱的夹角均为，那么为 .参考答案：16. 在棱长为1的正方体ABCD﹣A1B1C1D1中，点P1，P2分别是线段AB，BD1（不包括端点）上的动点，且线段P1P2平行于平面A1ADD1，则四面体P1P2AB1的体积的最大值是．参考答案：【考点】棱柱、棱锥、棱台的体积．【分析】由题意可得△P1P2B∽△AD1B，设出P1B=x，则P1P2=x，P2到平面AA1B1B的距离为x，求出四面体的体积，通过二次函数的最值，求出四面体的体积的最大值．【解答】解：由题意在棱长为1的正方体ABCD﹣A1B1C1D1中，点P1，P2分别是线段AB，BD1（不包括端点）上的动点，且线段P1P2平行于平面A1ADD1，△P1P2B∽△AD1B，设P1B=x，x∈（0，1），则P1P2=x，P2到平面AA1B1B的距离为x，所以四面体P1P2AB1的体积为V=××1×x×（1﹣x）=（x﹣x2），当x=时，体积取得最大值：．故答案是：．17. 设是抛物线上两点，且满足OA⊥OB，则等于________．参考答案：略三、解答题：本大题共5小题，共72分。

山东省巨野县第一中学人教版数学必修一2章基本初等函数小结复习课课件

幂函数
定义图象和性质
第二页，编辑于星期日：九点分。
二.应用举例. zxxk
例1.计算
|
1
0.01| 2
(
5)0
3log3 2
(lg 2)2
lg 2 lg 5 lg 5
8
例2.已知函数f (x) loga (1 x) loga (x 3)
(a 0且a 1)
1)求函数f (x)的定义域;
2)求函数f (x)的单调区间;
3)当0 a 1时,求函数f (x)的最小值.
第三页，编辑于星期日：九点分。
应用举例.学科网
例3.已知 2(log 1 x)2 7 log1 x 3 0求2
f (x) (log2
x 4
)(log
2
2
x的)值域. 2
例4.
设a 0, f (x) ex a 是R上的偶函数.
第二章小结复习课
第一页，编辑于星期日：九点分。
一.知识结构及知识梳理. n次方根及其性质
指数与指数函数
指数
根式及其性质分数指数幂
有理数指数幂的运算性质
指数函数
定义图象和性质
基本初等函数
定义对数运算性质
对数与对数函数
对数换底公式
对数函数
定义图象和性质
a ex
1)求a的值;
2)证明f (x)在(0, )上是增函数.
第四页，编辑于星期日：九点分。
应用举例.组卷网
设函数f (x) lg 1 2x a (a R), 2
1)求函数f (x)的定义域; 2)如果当x (,1]时, f (x)有意义, 求a的取值范围.
第五页，编辑于星期日：九点分。

巨野县一中2018-2019学年高二上学期第二次月考试卷数学

巨野县一中2018-2019学年高二上学期第二次月考试卷数学班级__________ 姓名__________ 分数__________一、选择题1．已知函数，，若，则（）A1 B2 C3 D-12．设全集U=M ∪N=﹛1，2，3，4，5﹜，M ∩∁U N=﹛2，4﹜，则N=（） A ．{1，2，3}B ．{1，3，5}C ．{1，4，5}D ．{2，3，4}3．四棱锥的八条棱代表8种不同的化工产品，由公共点的两条棱代表的化工产品放在同一仓库是危险的，没有公共点的两条棱代表的化工产品放在同一仓库是安全的，现打算用编号为①、②、③、④的4个仓库存放这8种化工产品，那么安全存放的不同方法种数为（）A ．96B ．48C ．24D ．04．已知函数f （x ）是定义在R 上的偶函数，且对任意的x ∈R ，都有f （x+2）=f （x ）．当0≤x ≤1时，f （x ）=x 2．若直线y=x+a 与函数y=f （x ）的图象在[0，2]内恰有两个不同的公共点，则实数a 的值是（）A ．0B ．0或C ．或D ．0或5．设集合,,则( )A BCD6．在10201511x x ⎛⎫++ ⎪⎝⎭的展开式中，含2x 项的系数为（）（A ）10 （ B ） 30 （C ） 45 （D ） 1207．已知的终边过点()2,3，则7tan 4πθ⎛⎫+⎪⎝⎭等于（） A ．15- B ．15C ．-5D ．58．已知一元二次不等式f （x ）＜0的解集为{x|x ＜﹣1或x ＞}，则f （10x ）＞0的解集为（）A ．{x|x ＜﹣1或x ＞﹣lg2}B ．{x|﹣1＜x ＜﹣lg2}C ．{x|x ＞﹣lg2}D ．{x|x ＜﹣lg2}9．已知函数f （2x+1）=3x+2，且f （a ）=2，则a 的值等于（） A ．8B ．1C ．5D ．﹣110．已知三棱柱111ABC A B C - 的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（）A ．4 B ．4 C.4D ．3411．已知函数y=f （x ）的周期为2，当x ∈[﹣1，1]时 f （x ）=x 2，那么函数y=f （x ）的图象与函数y=|lgx|的图象的交点共有（）A ．10个B ．9个C ．8个D ．1个12．一个多面体的直观图和三视图如图所示，点M 是边AB 上的动点，记四面体FMC E -的体积为1V ，多面体BCE ADF -的体积为2V ，则=21V V （）1111] A ．41 B ．31 C ．21D ．不是定值，随点M 的变化而变化二、填空题13．设O 为坐标原点，抛物线C ：y 2=2px （p ＞0）的准线为l ，焦点为F ，过F 斜率为的直线与抛物线C相交于A ，B 两点，直线AO 与l 相交于D ，若|AF|＞|BF|，则= ．14．等比数列{a n }的前n 项和为S n ，已知S 3=a 1+3a 2，则公比q= ．15．定义)}(),(min{x g x f 为)(x f 与)(x g 中值的较小者，则函数},2min{)(2x x x f -=的取值范围是 16．阅读右侧程序框图，输出的结果i 的值为．17．正方体ABCD﹣A1B1C1D1中，平面AB1D1和平面BC1D的位置关系为．18．如图是正方体的平面展开图，则在这个正方体中①BM与ED平行；②CN与BE是异面直线；③CN与BM成60 角；④DM与BN是异面直线．以上四个命题中，正确命题的序号是（写出所有你认为正确的命题）．三、解答题19．为了培养学生的安全意识，某中学举行了一次安全自救的知识竞赛活动，共有800 名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100 分）进行统计，得到如下的频率分布表，请你根据频率分布表解答下列问题：（1）求出频率分布表中①、②、③、④、⑤的值；（2）为鼓励更多的学生了解“安全自救”知识，成绩不低于85分的学生能获奖，请估计在参加的800名学生中大约有多少名学生获奖？（3）在上述统计数据的分析中，有一项指标计算的程序框图如图所示，则该程序的功能是什么？求输出的S合计20．已知函数f（x）=|x﹣a|．（1）若不等式f（x）≤3的解集为{x|﹣1≤x≤5}，求实数a的值；（2）在（1）的条件下，若f（x）+f（x+5）≥m对一切实数x恒成立，求实数m的取值范围．21．（本小题满分12分）如图，在四棱锥ABCD S -中，底面ABCD 为菱形，Q P E 、、分别是棱AB SC AD 、、的中点，且⊥SE 平面ABCD .（1）求证：//PQ 平面SAD ；（2）求证：平面⊥SAC 平面SEQ .22．如图，在四边形ABCD 中，∠DAB=90°，∠ADC=135°，AB=5，CD=2，AD=2，求四边形ABCD 绕AD 旋转一周所成几何体的表面积．23．已知椭圆C ： +=1（a ＞b ＞0）的一个长轴顶点为A （2，0），离心率为，直线y=k （x ﹣1）与椭圆C 交于不同的两点M ，N ，（Ⅰ）求椭圆C 的方程；（Ⅱ）当△AMN 的面积为时，求k 的值．24．【常州市2018届高三上武进区高中数学期中】已知函数()()221ln f x ax a x x =+--，R a ∈．⑴若曲线()y f x =在点()()1,1f 处的切线经过点()2,11，求实数a 的值； ⑵若函数()f x 在区间()2,3上单调，求实数a 的取值范围； ⑶设()1sin 8g x x =，若对()10,x ∀∈+∞，[]20,πx ∃∈，使得()()122f x g x +≥成立，求整数a 的最小值．巨野县一中2018-2019学年高二上学期第二次月考试卷数学（参考答案）一、选择题1．【答案】A【解析】g（1）=a﹣1，若f[g（1）]=1，则f（a﹣1）=1，即5|a﹣1|=1，则|a﹣1|=0，解得a=12．【答案】B【解析】解：∵全集U=M∪N=﹛1，2，3，4，5﹜，M∩C u N=﹛2，4﹜，∴集合M，N对应的韦恩图为所以N={1，3，5}故选B3．【答案】B【解析】排列、组合的实际应用；空间中直线与直线之间的位置关系．【专题】计算题；压轴题．【分析】首先分析题目已知由公共点的两条棱代表的化工产品放在同一仓库是危险的，没有公共点的两条棱代表的化工产品放在同一仓库是安全的，现打算用编号为①、②、③、④的4个仓库存放这8种化工产品，求安全存放的不同方法的种数．首先需要把四棱锥个顶点设出来，然后分析到四棱锥没有公共点的8条棱分4组，只有2种情况．然后求出即可得到答案．【解答】解：8种化工产品分4组，设四棱锥的顶点是P，底面四边形的个顶点为A、B、C、D．分析得到四棱锥没有公共点的8条棱分4组，只有2种情况，（PA、DC；PB、AD；PC、AB；PD、BC）或（PA、BC；PD、AB；PC、AD；PB、DC）那么安全存放的不同方法种数为2A44=48．故选B．【点评】此题主要考查排列组合在实际中的应用，其中涉及到空间直线与直线之间的位置关系的判断，把空间几何与概率问题联系在一起有一定的综合性且非常新颖．4．【答案】D【解析】解：∵f （x ）是定义在R 上的偶函数，当0≤x ≤1时，f （x ）=x 2，∴当﹣1≤x ≤0时，0≤﹣x ≤1，f （﹣x ）=（﹣x ）2=x 2=f （x ），又f （x+2）=f （x ），∴f （x ）是周期为2的函数，又直线y=x+a 与函数y=f （x ）的图象在[0，2]内恰有两个不同的公共点，其图象如下：当a=0时，直线y=x+a 变为直线l 1，其方程为：y=x ，显然，l 1与函数y=f （x ）的图象在[0，2]内恰有两个不同的公共点；当a ≠0时，直线y=x+a 与函数y=f （x ）的图象在[0，2]内恰有两个不同的公共点，由图可知，直线y=x+a 与函数y=f （x ）相切，切点的横坐标x 0∈[0，1]．由得：x 2﹣x ﹣a=0，由△=1+4a=0得a=﹣，此时，x 0=x=∈[0，1]．综上所述，a=﹣或0 故选D ．5．【答案】C【解析】送分题,直接考察补集的概念,,故选C 。

山东省巨野一中高二数学下学期模块检测试题理(无答案)新人教A版

巨野一中2012-2013学年高二下学期模块检测数学（理）试题第I 卷（选择题）一、选择题（本大题共12小题，每小题5分，共60分） 1．复数2ii+-等于（）. A ．12i -+ B.12i - C. i 21+ D. 12i --2．从甲地去乙地有3班火车，从乙地去丙地有2班轮船，则从甲地去丙地可选择的旅行方式有（）A ．5种B ．6种C ．7种D ．8种3．一质点运动方程()212s t gt =（29.8 /g m s =），则 3 t s =时的瞬时速度为（） A . 20 B. 49.4 C . 29.4 D . 64.1 4．1(2)xex dx +⎰等于（）A. 1B. 1e -C. eD. 1e +5．已知f (x )＝x 3＋ax 2＋(a ＋6)x ＋1有极大值和极小值，则a 的取值范围为( )．A ．－1＜a ＜2B ．－3＜a ＜6C ．a ＜－1或a ＞2D ．a ＜－3或a ＞66．已知函数x e x f x 3)(1-=+，则=')0(f （）A.0B.2- C ．－3D ．3-e7．设()f x '是函数()f x 的导函数，()y f x '=的图象如图1所示，则()y f x =的图象最有可能的是（）8．函数ln y x x =的递减区间是（）A ．1(,)e +∞B ．1(,)-∞C ．1(0,)D ．(,)e +∞9r 为三角形内切圆的半径，利用类比推理，可得出四面体的体积为（）A C r 为四面体内切球的半径）D 10．用数学归纳法证明等式(1)(2)()213(21)()nn n n n n n N *++⋅⋅⋅+=⋅⋅⋅⋅⋅⋅-∈，从“k 到k+1”左端需增乘的代数式为（）A.2(21)k +B.21k +11．x y ln =与，e x =及x 轴围成图形的面积是（）A BC 12．对于R 上可导的函数)(x f ，若满足(1)'()0x f x ->，则必有（）A.(0)(2)2(1)f f f +< B ．(0)(2)2(1)f f f +> C. (0)(2)2(1)f f f +≤ D. (0)(2)2(1)f f f +≥ 第II 卷（非选择题）（共90分）二、填空题（本大题共4小题，每小题4分，共16分） 13．将三封信投入4个邮箱，不同的投法有种．14．已知函数()y f x =在0x x =处的导数为-216．右图是函数()y f x =的导函数()y f x '=的图象，给出下列命题：①2-是函数()y f x =的极值点； ②1不是函数()y f x =的极值点； ③()y f x =在0x =处切线的斜率小于零； ④()y f x =在区间(2,2)-上单调递减.则正确命题的序号是．（写出所有正确命题的序号）三、解答题（本大题共6个小题，共74分.）解答须写出文字说明、证明过程和演算步骤． 17．（本题满分12分）当m 取何实数时，复数i m m m m z )152()369(22--+--=，（1）是实数？（2）是虚数？（3）是纯虚数？ 18．（本题满分12分）用数学归纳法证：)(3)2)(1()1(433221*N n n n n n n ∈++=+⨯+⋅⋅⋅+⨯+⨯+⨯．19．（本题满分12分）已知曲线y=.34313+x （1）求曲线在x=2处的切线方程；（2）求曲线过点（2，4）的切线方程.20．（本题满分12分）某商场销售某种商品的经验表明，该商品每日的销售量（单位：千克）与销售价格（单位：元/千克）满足关系式，其中，为常数，已知销售价格为元/千克时，每日可售出该商品千克。

山东省巨野一中2010-2011学年高二“每周一练”数学试题

参考答案
ex (x a) ex 1 ex x (a 1)
1、解：函数 f (x) 的定义域为x | x a f '(x)
（3）若 f (x) 的最小值为 1，求 a 的取值范围．
ex
4．设函数 f (x)
x
（Ⅰ）求函数 f (x) 的单调区间；
（Ⅱ）若 k 0 ，求不等式 f ' (x) k(1 x) f (x) 0 的解集．
山东省巨野一中 2010—2011 学年度高二数学“每周
一练”系列试题（31）
（命题范围:导数及其应用 2）
ex
在 a,0 上的最小值小于或等于时，存在实数 x a,0 ，
2
1
使得不等式 f (x) 成立
2
a 2 (0,) f '(x) 0,
∴ 的单调增区间为
f (x) (0,).
②当 0 a 2 时，
2 a 2 a
1 '
若 k 0 ，则当 x , 时， f x 0 ，函数 f x 单调递减，
k
1 '
（2）若存在实数 x a,0 ，使得不等式 f (x) 成立，求 a 的取值范围。
2
2．设函数 f (x) xekx (k 0)
k
即 k 1 时，函数 f (x) 在 1,1 内单调递增，
综上可知，函数 f (x) 在区间 1,1 内单调递增时， k 的取值范围是 1,0 U0,1
若 a 1 0 即 a 1时
x (a, a 1) a 1 (a 1,0)
f '(x) 0 +

山东省菏泽市巨野县第一中学高二数学理上学期期末试题含解析

山东省菏泽市巨野县第一中学高二数学理上学期期末试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 设则与的关系是A. B. C. D. 且参考答案：B略2. 有下列关系：①人的年龄与他（她）拥有的财富之间的关系；②曲线上的点与该点的坐标之间的关系；③苹果的产量与气候之间的关系；④森林中的同一种树木，其横断面直径与高度之间的关系，其中有相关关系的是A．①③④B．①② C．②③D．①②③参考答案：A3. 若，则( )A. B.C. D. 或参考答案：D略4. 要从已编号（1—50）的50件产品中随机抽取5件进行检验，用系统抽样方法确定所选取的5件产品的编号可能是（）A．5,10,15,20,25 B．2,4,8,16,22C．1,2,3,4,5 D．3,13,23,33,43参考答案：D略5. 设不等式组表示的平面区域为，在区域内随机取一个点，则此点到坐标原点的距离大于等于2的概率是（）A． B． C． D．参考答案：A略6. 已知数列是等比数列，是它的前n项和，若 ,且与2的等差中项为 ,则=( )A ．35 B．33 C．31D．29参考答案：C7. 函数在处的切线方程为（）A. B. C.D.参考答案：D8. 函数的零点所在的一个区间是（）A．（﹣1，0）B．（0，1）C．（1，2）D．（2，3）参考答案：D【考点】函数零点的判定定理．【分析】判断函数值，利用零点定理推出结果即可．【解答】解：函数，可得：f（﹣1）=5＞0，f（0）=3＞0，f（1）=＞0，f（2）=＞0，f（3）=﹣0，由零点定理可知，函数的零点在（2，3）内．故选：D．9. 若复数满足，则实数a的取值范围是（）A. B. [－1,1]C. D. (－∞,－1]∪[1,+∞)参考答案：B【分析】利用复数模的公式即可求出实数的范围。

【详解】因为，所以，解得.故答案选B【点睛】本题考查复数乘法公式以及模的计算，不等式的解，属于基础题。

山东巨野县第一中学三角函数与解三角形多选题试题含答案

山东巨野县第一中学三角函数与解三角形多选题试题含答案一、三角函数与解三角形多选题1．在ABC 中，角,,A B C 所对的边分别为,,a b c ，下列命题正确的是（）A ．若::4:5:6a b c =，ABC 的最大内角是最小内角的2倍B ．若cos cos a B b A c -=，则ABC 一定为直角三角形 C ．若4,5,6a b c ===，则ABCD ．若()()()cos cos cos 1A B B C C A ---=，则ABC 一定是等边三角形【答案】ABD 【分析】对于A 选项，求得2A C =，由此确定选项正确.对于B 选项，求得2A π=，由此确定选项正确.对于C 选项，利用正弦定理求得ABC 外接圆半径，由此确定选项错误.对于D 选项，证得()()()cos cos cos 1A B B C C A -=-=-=，得到A B C ==，确定选项正确. 【详解】对于A 选项，A 角最小，C 角最大.由余弦定理得253616453cos 0256604A +-===>⨯⨯，16253651cos 0245408C +-===>⨯⨯，2231cos 22cos 12148A A ⎛⎫=-=⨯-= ⎪⎝⎭，cos2cos A C =.0,022A C ππ<<<<，则02A π<<，所以2A C =，所以A 选项正确.对于B 选项，cos cos a B b A c -=，由正弦定理得sin cos sin cos sin A B B A C -=，()sin cos cos sin sin sin cos cos sin A B A B A B A B A B -=+=+，cos sin 0=A B ，由于0,0A B ππ<<<<，所以2A π=，故B 选项正确.对于C 选项，16253651cos 245408C +-===⨯⨯，0C π<<，sin C ==，设三角形ABC 外接圆半径为R，则2sin 2sin c cR R C C=⇒===，故C 选项错误.对于D 选项，0,0,A B A B ππππ<<-<-<-<-<，故()1cos 1A B -<-≤，同理可得()()1cos 1,1cos 1B C C A -<-≤-<-≤，要使()()()cos cos cos 1A B B C C A ---=，则需()()()cos cos cos 1A B B C C A -=-=-=，所以0,0,0A B B C C A -=-=-=，所以A B C ==，所以D 选项正确. 故选：ABD 【点睛】利用正弦定理可求得三角形外接圆的半径R ，要注意公式是2sin aR A=，而不是sin aR A =.2．在单位圆O ：221x y +=上任取一点()P x y ，，圆O 与x 轴正向的交点是A ，将OA 绕原点O 旋转到OP 所成的角记为θ，若x ，y 关于θ的表达式分别为()x fθ=，()y g θ=，则下列说法正确的是（）A ．()x f θ=是偶函数，()y g θ=是奇函数；B ．()x f θ=在()0，π上为减函数，()y g θ=在()0，π上为增函数；C ．()()1fg θθ+≥在02πθ⎛⎤∈⎥⎝⎦，上恒成立；D ．函数()()22t f g θθ=+的最大值为2.【答案】ACD 【分析】依据三角函数的基本概念可知cos x θ=，sin y θ=，根据三角函数的奇偶性和单调性可判断A 、B ；根据辅助角公式知()()4f g πθθθ⎛⎫+=+ ⎪⎝⎭，再利用三角函数求值域可判断C ；对于D ，2cos sin2t θθ=+，先对函数t 求导，从而可知函数t 的单调性，进而可得当1sin 2θ=，cos 2θ=时，函数t 取得最大值，结合正弦的二倍角公式，代入进行运算即可得解．【详解】由题意，根据三角函数的定义可知，x cos θ=，y sin θ=，对于A ，函数()cos fθθ=是偶函数，()sin g θθ=是奇函数，故A 正确；对于B ，由正弦，余弦函数的基本性质可知，函数()cos f θθ=在()0,π上为减函数，函数()sin g θθ=在0,2π⎛⎫⎪⎝⎭为增函数，在,2ππ⎛⎫⎪⎝⎭为减函数，故B 错误；对于C ，当0θπ⎛⎤∈ ⎥2⎝⎦，时，3,444πππθ⎛⎤+∈ ⎥⎝⎦()()cos sin 4f g πθθθθθ⎛⎫+=+=+∈ ⎪⎝⎭，故C 正确；对于D ，函数()()222cos sin2t fg θθθθ=+=+，求导22sin 2cos22sin 2(12sin )2(2sin 1)(sin 1)t θθθθθθ'=-+=-+-=--+，令0t '>，则11sin 2θ-<<；令0t '<，则1sin 12θ<<， ∴函数t 在06,π⎡⎤⎢⎥⎣⎦和5,26ππ⎡⎤⎢⎥⎣⎦上单调递增，在5,66ππ⎛⎫⎪⎝⎭上单调递减，当6πθ=即1sin 2θ=，cos θ=时，函数取得极大值1222t =⨯=又当2θπ=即sin 0θ=，cos 1θ=时，212012t =⨯+⨯⨯=，所以函数()()22t f g θθ=+，故D 正确.故选：ACD. 【点睛】方法点睛：考查三角函数的值域时，常用的方法：（1）将函数化简整理为()()sin f x A x ωϕ=+，再利用三角函数性质求值域；（2）利用导数研究三角函数的单调区间，从而求出函数的最值.3．设函数g (x )=sinωx (ω＞0)向左平移5πω个单位长度得到函数f (x )，已知f (x )在[0，2π]上有且只有5个零点，则下列结论正确的是（）A ．f (x )的图象关于直线2x π=对称B ．f (x )在(0，2π)上有且只有3个极大值点，f (x )在(0，2π)上有且只有2个极小值点C ．f (x )在(0,)10π上单调递增 D ．ω的取值范围是[1229,510) 【答案】CD 【分析】利用正弦函数的对称轴可知，A 不正确；由图可知()f x 在(0,2)π上还可能有3个极小值点，B 不正确；由2A B x x π≤<解得的结果可知，D 正确；根据()f x 在3(0,)10πω上递增，且31010ππω<，可知C 正确. 【详解】依题意得()()5f x g x πω=+sin[()]5x πωω=+sin()5x πω=+， 2T πω=，如图：对于A ，令52x k ππωπ+=+，k Z ∈，得310k x ππωω=+，k Z ∈，所以()f x 的图象关于直线310k x ππωω=+(k Z ∈)对称，故A 不正确；对于B ，根据图象可知，2A B x x π≤<，()f x 在(0,2)π有3个极大值点，()f x 在(0,2)π有2个或3个极小值点，故B 不正确，对于D ，因为5522452525A x T ππππωωωω=-+=-+⨯=，22933555B x T ππππωωωω=-+=-+⨯=，所以2429255πππωω≤<，解得1229510ω≤<，所以D 正确；对于C ，因为1123545410T ππππωωωω-+=-+⨯=，由图可知()f x 在3(0,)10πω上递增，因为29310ω<<，所以33(1)0101010πππωω-=-<，所以()f x 在(0,)10π上单调递增，故C 正确；故选：CD. 【点睛】本题考查了三角函数的相位变换，考查了正弦函数的对称轴和单调性和周期性，考查了极值点的概念，考查了函数的零点，考查了数形结合思想，属于中档题.4．已知函数()()sin f x x ωϕ=+（其中，0>ω，||2ϕπ<），08f π⎛⎫-= ⎪⎝⎭，3()8f x f π⎛⎫≤ ⎪⎝⎭恒成立，且()f x 在区间,1224ππ⎛⎫- ⎪⎝⎭上单调，则下列说法正确的是（）A ．存在ϕ，使得()f x 是偶函数B ．3(0)4f f π⎛⎫=⎪⎝⎭C ．ω是奇数D ．ω的最大值为3【答案】BCD 【分析】根据3()8f x f π⎛⎫≤⎪⎝⎭得到21k ω=+，根据单调区间得到3ω≤，得到1ω=或3ω=，故CD 正确，代入验证知()f x 不可能为偶函数，A 错误，计算得到B 正确，得到答案. 【详解】08f π⎛⎫-= ⎪⎝⎭，3()8f x f π⎛⎫≤ ⎪⎝⎭，则3188242k T πππ⎛⎫⎛⎫--==+ ⎪ ⎪⎝⎭⎝⎭，k ∈N ，故221T k π=+，21k ω=+，k ∈N ， 08f π⎛⎫-= ⎪⎝⎭，则()s n 08i f x πωϕ⎛⎫=+= ⎪⎭-⎝，故8k πωϕπ+=-，8k ϕπωπ=+，k Z ∈，当,1224x ππ⎛⎫∈-⎪⎝⎭时，,246x k k ωπωπωϕππ⎛⎫+∈++ ⎪⎝⎭，k Z ∈，()f x 在区间,1224ππ⎛⎫-⎪⎝⎭上单调，故241282T πππ⎛⎫--=≤ ⎪⎝⎭，故4T π≥，即8ω≤，0243ωππ<≤，故62ωππ≤，故3ω≤，综上所述：1ω=或3ω=，故CD 正确；1ω=或3ω=，故8k ϕππ=+或38k ϕππ=+，k Z ∈，()f x 不可能为偶函数，A 错误；当1ω=时，(0)sin sin 8f k πϕπ⎛⎫==+⎪⎝⎭，33sin sin 4488f k k ππππππ⎛⎫⎛⎫⎛⎫=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故3(0)4f f π⎛⎫= ⎪⎝⎭；当3ω=时，3(0)sin sin 8f k πϕπ⎛⎫==+⎪⎝⎭， 393sin sin 4488f k k ππππππ⎛⎫⎛⎫⎛⎫=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故3(0)4f f π⎛⎫= ⎪⎝⎭，综上所述：3(0)4f f π⎛⎫= ⎪⎝⎭，B 正确；故选：BCD. 【点睛】本题考查了三角函数的性质和参数的计算，难度较大，意在考查学生的计算能力和综合应用能力.5．函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图象如图所示，则下列结论正确的是（）A ．1()2sin 36f x x π⎛⎫=-⎪⎝⎭ B ．若把()f x 的横坐标缩短为原来的23倍，纵坐标不变，得到的函数在[],ππ-上是增函数C ．若把函数()f x 的图像向左平移2π个单位，则所得函数是奇函数 D ．函数()y f x =的图象关于直线4x π=-对称【答案】ACD 【分析】根据函数的图象求出函数的解析式，得选项A 正确；求出213263x πππ--得到函数在[],ππ-上不是增函数，得选项B 错误；求出图象变换后的解析式得到选项C 正确；求出函数的对称轴方程，得到选项D 正确. 【详解】 A, 如图所示：1732422T πππ=-=， 6T π∴=，∴2163πωπ==，(2)2f π=，∴2(2)2sin()23f ππϕ=+=，即2sin()13πϕ+=， ∴22()32k k Z ππϕπ+=+∈， ∴2()6k k Z πϕπ=-∈，||ϕπ<，∴6πϕ=-，∴1()2sin()36f x x π=-，故选项A 正确；B, 把()y f x =的横坐标缩短为原来的23倍，纵坐标不变，得到的函数12sin()26y x π=-，[x π∈-，]π，∴213263x πππ--，∴12sin()26y x π=-在[π-，]π上不单调递增，故选项B 错误；C, 把()y f x =的图象向左平移2π个单位，则所得函数12sin[()]2sin 3223xy x ππ=-+=，是奇函数，故选项C 正确； D, 设1,,32,362x k k Z x k πππππ-=+∈∴=+当24k x π=-⇒=-，所以函数()y f x =的图象关于直线4x π=-对称，故选项D 正确.故选：ACD 【点睛】方法点睛：求三角函数的解析式，一般利用待定系数法，一般先设出三角函数的解析式sin()y A wx k ，再求待定系数,,,A w k ，最值确定函数的,A k ,周期确定函数的w ,非平衡位置的点确定函数的φ.6．已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，下列说法正确的是（）A ．函数()y f x =的周期为πB ．函数()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦单调递减C ．函数()y f x =的图象关于直线512x π=-对称 D ．该图象向右平移6π个单位可得2sin 2y x =的图象【答案】ACD 【分析】先根据图像求出()y f x =的解析式，再分别验证A 、B 、C 、D 是否正确. 对于A ：利用周期公式求周期；对于B ：利用复合函数“同增异减”求单调区间；对于C ：计算512f π⎛-⎫⎪⎝⎭，看512x π=-是否经过顶点；对于D ：利用“左加右减”判断. 【详解】由图像可知：A =2，周期24,2312T T ππππω⎛⎫=-=∴==⎪⎝⎭；由=2sin 2212122f ππϕπϕ⎧⎛⎫⎛⎫⨯+= ⎪ ⎪⎪⎪⎝⎭⎝⎭⎨⎪<⎪⎩解得：3πϕ=故函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭对于A ：4312T πππ⎛⎫=-= ⎪⎝⎭，故A 正确；对于B ：当236x ππ-≤≤- 时203x ππ-≤+≤，所以()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦上不单调.故B 错误；对于C ：当512x π=-时255s 2121232in f πππ⎛⎫⎛⎫=-=- ⎪ ⎭⎝-⎪⎭+⎝⨯，即直线512x π=-是()y f x =的一条对称轴.故C 正确；对于D ：()y f x =向右平移6π个单位得到2sin 222sin 263y x x ππ⎛⎫=-⨯+= ⎪⎝⎭，故D 正确. 故选：ACD 【点睛】求三角函数解析式的方法： (1)求A 通常用最大值或最小值； (2)求ω通常用周期；()求φ通常利用函数上的点带入即可求解.7．已知函数()22sin cos f x x x x =+，则下列结论中正确的是（）A ．()f x 的图象是由y= 2sin2x 的图象向左移3π个单位得到的 B ．()f x 在,03π⎡⎤-⎢⎥⎣⎦上单调递增C ．()f x 的对称中心的坐标是(),026k k Z ππ⎛⎫-∈⎪⎝⎭D ．函数()()g x f x =[]0,10内共有8个零点【答案】BCD 【分析】A.化简得()2sin(2)3f x x π=+，利用函数的图象变换得该选项错误；B.利用复合函数的单调性原理分析得该选项正确；C. 由2,3x k k Z ππ+=∈得该选项正确；D.解方程sin 232x π⎛⎫+= ⎪⎝⎭得该选项正确. 【详解】()2π2sin cos sin 222sin 22sin 236f x x x x x x x x π⎛⎫⎛⎫=+-=+=+=+ ⎪ ⎪⎝⎭⎝⎭，把2sin 2y x =的图象向左平移6π个单位，得到()f x ，所以选项A 不正确; 设23t x π=+，则t 在,03π⎡⎤-⎢⎥⎣⎦上单调增， ,03x π⎡⎤∈-⎢⎥⎣⎦2,333x πππ⎡⎤∴+∈-⎢⎥⎣⎦,,33t ππ⎡⎤∴∈-⎢⎥⎣⎦又sin y t =在,33ππ⎡⎤-⎢⎥⎣⎦上单调递增， ()2sin 23f x x π⎛⎫∴=+ ⎪⎝⎭在,03π⎡⎤-⎢⎥⎣⎦上单调递增，所以选项B 正确;由2,3x k k Z ππ+=∈得对称中心为(),062k k Z ππ⎛⎫-+∈ ⎪⎝⎭，所以选项C 正确；由sin 232x π⎛⎫+= ⎪⎝⎭得2233x k πππ+=+或222,33x k k Z πππ+=+∈解得x k π=或,6x k k Z ππ=+∈，又[]0,10,x ∈0,1,2,3k ∴=时，713190,,,,2,,3,6666x πππππππ=，共8个零点，所以选项D 正确. 故选：BCD 【点睛】方法点睛：函数的零点问题的研究，常用的方法有：（1）方程法（解方程即得解）；（2）图象法（直接画出函数的图象得解）；（3）方程+图象法（令()=0f x 得()()g x h x =，再分析函数(),()g x h x 的图象得解）. 要根据已知条件灵活选择方程求解.8．已知函数()()cos 22f x x πϕϕ⎛⎫=+<⎪⎝⎭，()()124F x f x f x π⎛⎫=+ ⎪⎝⎭为奇函数，则下述四个结论中说法正确的是（）A ．tan ϕ=B ．()f x 在[],a a -上存在零点，则a 的最小值为6π C ．()F x 在3,44ππ⎛⎫⎪⎝⎭上单调递增 D ．()F x 的图象可由()f x 的图象向左平移2π个单位得到【答案】ABC 【分析】首先得到()()124F x f x f x π⎛⎫=++ ⎪⎝⎭的解析式，再根据函数的奇偶性求出参数ϕ，最后结合三角函数的性质一一验证即可. 【详解】解：因为()cos(2)f x x ϕ=+，所以11()()+cos(2)sin(2)cos 2224223F x f x f x x x x ππϕϕϕ⎛⎫⎛⎫=+=+-+=++ ⎪ ⎪⎝⎭⎝⎭，因为()F x 为奇函数，则(0)0F =，即cos 03πϕ⎛⎫+= ⎪⎝⎭，所以32k ππϕπ+=+，k Z ∈，因为||2ϕπ<，所以6π=ϕ；对于A ，tan tan63πϕ==，故A 正确；对于B ，令()cos 206f x x π⎛⎫=+= ⎪⎝⎭，得26k x ππ=+，k ∈Z ，若()f x 在[,]a a -上存在零点，则0a >且a 的最小值为6π，故B 正确；对于C ，()cos 2sin 263F x x x ππ⎛⎫=++=- ⎪⎝⎭，当3,44x ππ⎛⎫∈ ⎪⎝⎭时，2,232x ππ⎛⎫∈ ⎪⎝⎭，则()F x 在3,44ππ⎛⎫⎪⎝⎭上单调递增，故C 正确. 对于D ，因为()cos 26f x x π⎛⎫=+⎪⎝⎭， ()cos 266F x x ππ⎡⎤⎛⎫=++⎪⎢⎥⎝⎭⎣⎦，根据“左加右减”，()F x 的图象可由()f x 的图象向左平移6π个单位得到，故D 错误.故选：ABC . 【点睛】关键点点睛：本题解答的关键是先根据()()1224F x f x f x π⎛⎫=++ ⎪⎝⎭为奇函数，确定参数ϕ的值，再结合三角函数的性质逐一判断即可.二、数列多选题9．设数列{}n a 的前n 项和为n S ，若存在实数A ，使得对任意*n N ∈，都有n S A <，则称数列{}n a 为“T 数列”.则以下结论正确的是（）A ．若{}n a 是等差数列，且10a >，公差0d <，则数列{}n a 是“T 数列”B ．若{}n a 是等比数列，且公比q 满足||1q <，则数列{}n a 是“T 数列”C ．若12(1)2n n n a n n ++=+，则数列{}n a 是“T 数列”D ．若2241n n a n =-，则数列{}n a 是“T 数列【答案】BC 【分析】写出等差数列的前n 项和结合“T 数列”的定义判断A ；写出等比数列的前n 项和结合“T 数列”的定义判断B ；利用裂项相消法求和判断C ；当n 无限增大时，n S 也无限增大判断D ．【详解】在A 中，若{}n a 是等差数列，且10a >，公差0d <，则2122n d d S n a n ⎛⎫=+- ⎪⎝⎭，当n 无限增大时，n S 也无限增大，所以数列{}n a 不是“T 数列”，故A 错误. 在B 中，因为{}n a 是等比数列，且公比q 满足||1q <，所以()11111112111111n nn n a q a a q a a q aS qq q q q q-==-+<------，所以数列{}n a 是“T 数列”，故B 正确. 在C 中，因为11211(1)22(1)2n n n n n a n n n n +++==-+⋅+⋅，所以122311111111111||122222322(1)22(1)22n n n n S n n n ++=-+-++-=-<⨯⨯⨯⨯⋅+⋅+⋅∣∣.所以数列{}n a 是“T 数列”，故C 正确.在D 中，因为22211141441n n a n n ⎛⎫==+ ⎪--⎝⎭，所以222111114342143141n S n n ⎛⎫=+++++⎪⨯-⨯--⎝⎭，当n 无限增大时，n S 也无限增大，所以数列{}n a 不是“T 数列”，故D 错误. 故选：BC. 【点睛】方法点睛：裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1)()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭；（2）1k=；（3）()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭；（4）()()122121n n n +--()()()()1121212121n n n n ++---=--1112121n n +=---；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.10．已知等差数列{}n a 的前n 项和为n S ，若831a =，10210S =，则（） A ．19919S a =B ．数列{}22n a是公比为8的等比数列C ．若()1nn n b a =-⋅，则数列{}n b 的前2020项和为4040D ．若11n n n b a a +=，则数列{}n b 的前2020项和为202024249【答案】CD 【分析】由等差数列性质可判断A ；结合已知条件可求出等差数列的公差，从而可求出通项公式以及22n a ，结合等比数列的定义可判断B ；写出n b ，由定义写出2020T 的表达式，进行分组求和即可判断C ；11144143n b n n ⎛⎫=- ⎪-+⎝⎭，裂项相消即可求和.【详解】由等差数列的性质可知，191019S a =，故A 错误；设{}n a 的公差为d ，则有811017311045210a a d S a d =+=⎧⎨=+=⎩，解得13a =，4d =，故41n a n =-，28122na n -=，则数列{}22n a是公比为82的等比数列，故B 错误；若()()()1141n nn n b a n =-⋅=-⋅-，则{}n b 的前2020项20203711158079410104040T =-+-+-⋅⋅⋅+=⨯=，故C 正确；若()()1111414344143n b n n n n ⎛⎫==- ⎪-+-+⎝⎭，则{}n b 的前2020项和2020111111120204377118079808324249T ⎛⎫=-+-+⋅⋅⋅+-=⎪⎝⎭，故D 正确．故选:CD ．【点睛】方法点睛:求数列的前n 项和常见思路有：1、对于等差和等比数列，直接结合求和公式求解；2、等差数列±等比数列时，常采取分组求和法；3、等差数列⨯等比数列时，常采取错位相减法；4、裂项相消法.。

山东巨野县第一中学函数的概念与基本初等函数多选题试题含答案

山东巨野县第一中学函数的概念与基本初等函数多选题试题含答案一、函数的概念与基本初等函数多选题1．若实数2a ≥，则下列不等式中一定成立的是（）A ．21(1)(2)a a a a +++>+B ．1log (1)log (2)a a a a ++>+C ．1log (1)a a a a ++< D ．12log (2)1a a a a +++<+ 【答案】ABD 【分析】对于选项A ：原式等价于()()ln 1ln 212a a a a ++>++，对于选项C ：1log (1)a a a a ++<()ln 11ln a a a a ++⇔<()ln 1ln 1a a a a+⇔<+，对于选项D ：变形为()()ln 2ln 121a a a a ++<++，构造函数()ln xf x x =，通过求导判断其在(),x e ∈+∞上的单调性即可判断；对于选项B ：利用换底公式：1log (1)log (2)a a a a ++>+()()()ln 1ln 2ln ln 1a a a a ++⇔>+，等价于()()2ln 1ln ln 2a a a +>⋅+，利用基本不等式22a b ab +⎛⎫≤ ⎪⎝⎭，再结合放缩法即可判断；【详解】令()ln x f x x =，则()21ln x f x x -'=0<在()3,x ∈+∞上恒成立，所以函数()ln xf x x=在(),x e ∈+∞上单调递减，对于选项A ：因为2a ≥，所以21(1)(2)a a a a +++>+()()()()2ln 11ln 2a a a a ⇔++>++，即原不等式等价于()()ln 1ln 212a a a a ++>++，因为12a a +<+，所以()()ln 1ln 212a a a a ++>++，从而可得21(1)(2)a a a a +++>+，故选项A 正确；对于选项C ：1log (1)a a a a ++<()ln 11ln a a a a ++⇔<()ln 1ln 1a a a a+⇔<+，由于函数()ln x f x x =在(),e +∞上单调递减，所以()()43f f <，即ln 4ln 343<，因为ln 42ln 2ln 2442==，所以ln 2ln 323<，取2a =，则()ln 1ln 1a a a a+>+，故选项C 错误；对于选项D ：12log (2)1a a a a +++<+()()ln 22ln 11a a a a ++⇔<++()()ln 2ln 121a a a a ++⇔<++，与选项A 相同，故选项D 正确.对于选项B ：1log (1)log (2)a a a a ++>+()()()ln 1ln 2ln ln 1a a a a ++⇔>+，因为2a ≥，所以等价于()()2ln 1ln ln 2a a a +>⋅+，因为()()2ln ln 2ln ln 22a a a a ++⎡⎤⋅+<⎢⎥⎣⎦，因为()()()()222222ln 2ln 21ln ln 2ln 1222a a a a a a a ⎡⎤⎡⎤+++++⎡⎤⎢⎥⎢⎥=<=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，所以不等式1log (1)log (2)a a a a ++>+成立，故选项B 正确；故选：ABD 【点睛】本题考查利用对数的换底公式、构造函数法、利用导数判断函数的单调性、结合基本不等式和放缩法比较大小；考查逻辑推理能力、知识的综合运用能力、转化与化归能力和运算求解能力；属于综合型强、难度大型试题.2．已知函数()sin sin xxf x e e=+，以下结论正确的是（）A ．()f x 是偶函数B ．()f x 最小值为2C ．()f x 在区间,2ππ⎛⎫-- ⎪⎝⎭上单调递减D ．()()2g x f x x π=-的零点个数为5【答案】ABD 【分析】去掉绝对值，由函数的奇偶性及周期性，对函数分段研究，利用导数再得到函数的单调性，再对选项进行判断. 【详解】∵x ∈R ，()()f x f x -=，∴()f x 是偶函数，A 正确；因为()()2f x f x π+=，由函数的奇偶性与周期性，只须研究()f x 在[]0,2π上图像变化情况.()sin sin sin 2,01,2x x x e x f x e x e πππ⎧≤≤⎪=⎨+<≤⎪⎩，当0x π≤≤，()sin 2cos xf x xe '=，则()f x 在0,2x π⎡⎤∈⎢⎥⎣⎦上单调递增，在,2ππ⎡⎤⎢⎥⎣⎦上单调递减，此时()[]2,2f x e ∈；当2x ππ≤≤时，()()sin sin cos xx f x x ee -'=-，则()f x 在3,2x ππ⎡⎤∈⎢⎥⎣⎦上单调递增，在3,22x ππ⎡⎤∈⎢⎥⎣⎦上单调递减，此时()12,f x e e ⎡⎤∈+⎢⎥⎣⎦，故当02x π≤≤时，()min 2f x =，B 正确. 因()f x 在,2x ππ⎛⎫∈ ⎪⎝⎭上单调递减，又()f x 是偶函数，故()f x 在,2ππ⎛⎫-- ⎪⎝⎭上单调递增，故C 错误. 对于D ，转化为()2f x x π=根的个数问题.因()f x 在0,2π⎛⎫ ⎪⎝⎭上单调递增，在,2ππ⎛⎫⎪⎝⎭上单调递减，在3,2ππ⎛⎫ ⎪⎝⎭上单调递增，在3,22ππ⎛⎫⎪⎝⎭上单调递减.当(),x π∈-∞时，()2f x ≥，22x π<，()2f x x π=无实根.()3,x π∈+∞时，()max 262x e f x π>>=，()2f x xπ=无实根，3,2x ππ⎡⎤∈⎢⎥⎣⎦，显然x π=为方程之根.()sin sin x xf x e e -=+，()()sin sin cos 0x x f x x e e -'=->，3123322f e e πππ⎛⎫=+>⨯=⎪⎝⎭，单独就这段图象，()302f f ππ⎛⎫'='=⎪⎝⎭，()f x 在3,2ππ⎡⎤⎢⎥⎣⎦上变化趋势为先快扣慢，故()g x 在3,2ππ⎛⎫⎪⎝⎭内有1个零点，由图像知()g x 在3,32ππ⎛⎫⎪⎝⎭内有3个零点，又5252f e π⎛⎫=> ⎪⎝⎭，结合图象，知D 正确.故选：ABD. 【点睛】方法点睛：研究函数性质往往从以下方面入手：（1）分析单调性、奇偶性、周期性以及对称性；（2）数形结合法：先对解析式变形，进而构造两个容易画出图象的函数，将两个函数的图象画在同一个平面直角坐标系中，利用数形结合的方法求解.3．函数1()()0()x f x x ⎧=⎨⎩为有理数为无理数，则下列结论正确的是（）A ．()f x 是偶函数B ．()f x 的值域是{0,1}C ．方程(())f f x x =的解为1x =D ．方程(())()f f x f x =的解为1x =【答案】ABC 【分析】逐项分析判断即可. 【详解】当x -为有理数时，x 也为有理数∴()1f x -=当x -为无理数时，x 也为无理数∴()0f x -= ∴1()()0()x f x x ⎧-=⎨⎩为有理数为无理数∴()()f x f x -=()f x ∴是偶函数，A 对；易知B 对；1x =时，()((1))11f f f ==∴C 对(())()f f x f x =的解为全体有理数∴D 错故选：ABC. 【点睛】本题综合考查分段函数的奇偶性判断、值域、解方程等，要求学生能灵活应用知识解题，难度较大.4．若()f x 满足对任意的实数a ，b 都有()()()f a b f a f b +=且()12f =，则下列判断正确的有（） A ．()f x 是奇函数B ．()f x 在定义域上单调递增C ．当()0,x ∈+∞时，函数()1f x >D ．()()()()()()()()()()()()2462016201820202020135201520172019f f f f f f f f f f f f +++⋅⋅⋅++= 【答案】BCD 【分析】利用新定义结合函数的性质进行判断．计算出(1)f 判断A ；先利用(1)21f =>证明所有有理数p ，有()1f p >，然后用任意无理数q 都可以看作是一个有理数列的极限，由极限的性质得()1f q >，这样可判断C ，由此再根据单调性定义判断B ，根据定义计算(2)(21)f n f n -（n N ∈），然后求得D 中的和，从而判断D ．【详解】令0,1a b ==，则(1)(10)(1)(0)f f f f =+=，即22(0)f =，∴(0)1f =，()f x 不可能是奇函数，A 错；对于任意x ∈R ，()0f x ≠，若存在0x R ∈，使得0()0f x =，则0000(0)(())()()0f f x x f x f x =+-=-=，与(0)1f =矛盾，故对于任意x ∈R ，()0f x ≠，∴对于任意x ∈R ，2()022222x x x x x f x f f f f ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+==> ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦， ∵(1)21f =>，∴对任意正整数n ，11111111121nn n f n n f f f f f n n n n n n n ⎛⎫ ⎪⎝⎭⎛⎫ ⎪⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫ ⎪+++===> ⎪ ⎪ ⎪ ⎪⎢⎥ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ⎪ ⎪⎝⎭个个，∴11f n ⎛⎫> ⎪⎝⎭，同理()(111)(1)(1)(1)21n f n f f f f =+++==>，对任意正有理数p ，显然有m p n=（,m n是互质的正整数），则1()1mm f p f fn n ⎡⎤⎛⎫⎛⎫==> ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，对任意正无理数q ，可得看作是某个有理数列123,,,p p p 的极限，而()1i f p >，i N ∈，∴()f q 与()i f p 的极限，∴()1f q >，综上对所有正实数x ，有()1f x >，C 正确，设12x x <，则210x x ->，∴21()1f x x ->，则21211211()(())()()()f x f x x x f x f x x f x =+-=⋅->，∴()f x 是增函数，B 正确；由已知(2)(211)(21)(1)2(21)f n f n f n f f n =-+=-=-，∴(2)2(21)f n f n =-，∴()()()()()()()()()()()()10102246201620182020222210102020135201520172019f f f f f f f f f f f f +++⋅⋅⋅++=+++=⨯=个，D 正确．故选：BCD ．【点睛】本题考查新定义函数，考查学生分析问题，解决问题的能力，逻辑思维能力，运算求解能力，对学生要求较高，本题属于难题．5．已知函数()()23,03,0x x x f x f x x ⎧--<⎪=⎨-≥⎪⎩，以下结论正确的是（）A ．()f x 在区间[]4,6上是增函数 B ．()()220204f f -+=C ．若函数()y f x b =-在(),6-∞上有6个零点()1,2,3,4,5,6i x i =，则619ii x==∑D ．若方程()1f x kx =+恰有3个实根，则{}11,13k ⎛⎫∈-- ⎪⎝⎭【答案】BCD 【分析】根据()f x 在[2-，0]上的单调性判断A ，根据(2020)(2)f f =-判断B ，根据图象的对称性判断C ，根据直线1y kx =+与()y f x =的图象有3个交点判断D ．【详解】解：由题意可知当3x -时，()f x 是以3为周期的函数，故()f x 在[4，6]上的单调性与()f x 在[2-，0]上的单调性相同，而当0x <时，239()()24f x x =-++，()f x ∴在[2-，0]上不单调，故A 错误；又(2020)(2)2f f =-=，故(2)(2020)4f f -+=，故B 正确；作出()y f x =的函数图象如图所示：由于()y f x b =-在(,6)-∞上有6个零点，故直线y b =与()y f x =在(,6)-∞上有6个交点，不妨设1i i x x +<，1i =，2，3，4，5，由图象可知1x ，2x 关于直线32x =-对称，3x ，4x 关于直线32x =对称，5x ，6x 关于直线92x=对称，∴613392229222iix==-⨯+⨯+⨯=∑，故C正确；若直线1y kx=+经过点(3,0)，则13k=-，若直线1y kx=+与23(0)y x x x=--<相切，则消元可得：2(3)10x k x+++=，令0∆=可得2(3)40k+-=，解得1k=-或5k=-，当1k=-时，1x=-，当5k=-时，1x=（舍)，故1k=-．若直线1y kx=+与()y f x=在(0,3)上的图象相切，由对称性可得1k=．因为方程()1f x kx=+恰有3个实根，故直线1y kx=+与()y f x=的图象有3个交点，113k∴-<<-或1k=，故D正确．故选：BCD．【点睛】本题考查了函数零点与函数图象的关系，考查函数周期性、对称性的应用，属于中档题．6．下列选项中a的范围能使得关于x的不等式220x x a+--<至少有一个负数解的是（）A．9,04⎛⎫- ⎪⎝⎭B．()2,3C．1,2D．0,1【答案】ACD【分析】将不等式变形为22x a x-<-，作出函数2,2y x a y x=-=-的图象，根据恰有一个负数解时判断出临界位置，再通过平移图象得到a的取值范围.【详解】因为220x x a+--<，所以22x a x-<-且220x，在同一坐标系中作出2,2y x a y x=-=-的图象如下图：当y x a =-与22y x =-在y 轴左侧相切时，22x a x -=-仅有一解，所以()1420a ∆=++=，所以94a =-，将y x a =-向右移动至第二次过点()0,2时，02a -=，此时2a =或2a =-（舍），结合图象可知：9,24a ⎛⎫∈- ⎪⎝⎭，所以ACD 满足要求. 故选：ACD. 【点睛】本题考查函数与方程的综合应用，着重考查数形结合的思想，难度较难.利用数形结合可解决的常见问题有：函数的零点或方程根的个数问题、求解参数范围或者解不等式、研究函数的性质等.7．已知函数()22,21ln 1,1x x f x x x e +-≤≤⎧=⎨-<≤⎩，若关于x 的方程()f x m =恰有两个不同解()1212,x x x x <，则()212)x x f x -（的取值可能是（） A ．3- B ．1-C ．0D ．2【答案】BC 【分析】利用函数的单调性以及已知条件得到1122,e ,(1,0]2m m x x m +-==∈-，代入()212)x x f x -（，令121(),(1,0]2x g x xe x x x +=-+∈-，求导，利用导函数的单调性分析原函数的单调性，即可求出取值范围. 【详解】因为()f x m =的两根为()1212,x x x x <，所以1122,e ,(1,0]2m m x x m +-==∈-，从而()()211212222m m m m x x f x e m me m ++-⎛⎫-=-=-+ ⎪⎝⎭．令121(),(1,0]2x g x xex x x +=-+∈-，则1()(1)1x g x x e x +'=+-+，(1,0]x ∈-．因为(1,0]x ∈-，所以1010,1,10x x e e x ++>>=-+>，所以()0g x '>在(1,0]-上恒成立，从而()g x 在(1,0]-上单调递增．又5(0)0,(1)2g g =-=-，所以5(),02g x ⎛⎤∈-⎥⎝⎦，即()()212x x f x -⋅的取值范围是5,02⎛⎤- ⎥⎝⎦，故选：BC ．【点睛】关键点睛：本题考查利用导数解决函数的范围问题.构造函数121(),(1,0]2x g x xe x x x +=-+∈-，利用导数求取值范围是解决本题的关键.8．若定义在R 上的函数()f x 满足()()0f x f x ，当0x <时，23()22f x x ax a =++(a ∈R )，则下列说法正确的是（）A ．若方程()2af x ax =+有两个不同的实数根，则0a <或48a << B ．若方程()2af x ax =+有两个不同的实数根，则48a << C ．若方程()2af x ax =+有4个不同的实数根，则8a > D ．若方程()2af x ax =+有4个不同的实数根，则4a > 【答案】AC 【分析】由题知()f x 是R 上的奇函数，则由0x <时的解析式可求出()f x 在R 上的解析式.先讨论特殊情况0x =为方程的根，则可求出0a =，此时方程化为()0f x =，而函数()f x 为R 上的减函数，则方程仅有一个根.当0x ≠时，由分段函数分类讨论得出0x <时，1(1)2(1)a x x =-+++-+，0x >时，4242a x x =-++-.利用数形结合思想，画出图象，则可得知方程()2af x ax =+不同的实数根个数分别为2个和4时，参数a 的取值范围. 【详解】因为()()0f x f x 所以()()f x f x -=-，所以()f x 是R 上的奇函数，(0)0f =，当0x >时，0x -<，23()22f x x ax a -=-+，所以23()()22f x f x x ax a =--=-+-，综上2232,02()0,032,02x ax a x f x x x ax a x ⎧++<⎪⎪==⎨⎪⎪-+->⎩，若0x =是方程()2af x ax =+的一个根，则0a =，此时()2af x ax =+，即()0f x =，而22,0()0,0,0x x f x x x x ⎧<⎪==⎨⎪->⎩，在R 上单调递减，当0a =时，原方程有一个实根. 当0x <时，23222a x ax a ax ++=+，所以20x ax a ++=，当1x =-时不满足，所以21(1)21(1)x a x x x =-=-++++-+，当0x >时，23222ax ax a ax -+-=+，所以220x ax a -+=，当2x =时不满足，所以242422x a x x x ==-++--，如图：若方程()2a f x ax =+有两个不同的实数根，则0a <或48a <<；若方程()2a f x ax =+有4个不同的实数根，则8a >. 故选：AC【点睛】关键点点睛：本题的关键是将方程()2a f x ax =+进行参数分离，再借助数形结合法，求出对应的参数的取值范围.二、导数及其应用多选题9．阿基米德是伟大的物理学家，更是伟大的数学家，他曾经对高中教材中的抛物线做过系统而深入的研究，定义了抛物线阿基米德三角形：抛物线的弦与弦的端点处的两条切线围成的三角形称为抛物线阿基米德三角形.设抛物线C ：2y x 上两个不同点,A B 横坐标分别为1x ，2x ，以,A B 为切点的切线交于P 点.则关于阿基米德三角形PAB 的说法正确的有（）A ．若AB 过抛物线的焦点，则P 点一定在抛物线的准线上B ．若阿基米德三角形PAB 33C ．若阿基米德三角形PAB 为直角三角形，则其面积有最小值14 D ．一般情况下，阿基米德三角形PAB 的面积212||4x x S -= 【答案】ABC【分析】设出直线AB 的斜截式方程、点,A B 的坐标，根据导数的几何意义求出切线,PA PB 的方程，进而求出点P 的坐标，将直线AB 的方程和抛物线方程联立，得到一元二次方程以及该方程两根的和、积的关系.A ：把抛物线焦点的坐标代入直线AB 的斜截式方程中，根据抛物线的准线方程进行判断即可；B ：根据正三角形的性质，结合正三角形的面积公式进行判断即可；C ：根据直角三角形的性质，结合直角三角形的面积公式进行判断即可；D ：根据点到直线距离公式、两点间距离公式进行求解判断即可..【详解】由题意可知：直线AB 一定存在斜率，所以设直线AB 的方程为：y kx m =+，由题意可知：点221122(,),(,)A x x B x x ，不妨设120x x <<，由2'2y x y x ，所以直线切线,PA PB 的方程分别为：221112222(),2()y x x x x y x x x x -=--=-，两方程联立得：211122222()2()y x x x x y x x x x ⎧-=-⎨-=-⎩，解得：12122x x x y x x +⎧=⎪⎨⎪=⎩，所以P 点坐标为：1212(,)2x x x x +，直线AB 的方程与抛物线方程联立得：2121220,y kx m x kx m x x k x x m y x=+⎧⇒--=⇒+==-⎨=⎩. A ：抛物线C ：2y x 的焦点坐标为1(0,)4，准线方程为 14y =-，因为AB 过抛物线的焦点，所以14m =，而1214x x m =-=-，显然P 点一定在抛物线的准线上，故本选项说法正确；B ：因为阿基米德三角形PAB 为正三角形，所以有||||PA PB =，= 因为 12x x ≠，所以化简得：12x x =-，此时221111(,),(,)A x x B x x -， P 点坐标为：21(0,)x -，因为阿基米德三角形PAB 为正三角形，所以有||||PA AB =，112x x =-⇒=，因此正三角形PAB，所以正三角形PAB的面积为11sin 602224︒==，故本选项说法正确；C ：阿基米德三角形PAB 为直角三角形，当PA PB ⊥时，所以1212121222121122122114PA PB x x x x x x k k x x x x x x x x ++--⋅=-⇒⋅=-⇒=---，直线AB 的方程为：14y kx =+所以P 点坐标为：1(,)24k-，点 P 到直线AB 的距离为：=||AB ===，因为12121,4x x k x x +==-，所以21AB k =+，因此直角PAB的面积为：2111(1)224k ⨯+=≥，当且仅当0k =时，取等号，显然其面积有最小值14，故本说法正确； D ：因为1212,x x k x x m +==-，所以1||AB x x ===-，点P 到直线AB 的距离为：212== 所以阿基米德三角形PAB的面积32121211224x x S x x -=⋅-=，故本选项说法不正确.故选：ABC【点睛】关键点睛：解决本题的关键就是一元二次方程根与系数关系的整体代换应用，本题重点考查了数学运算核心素养的应用.10．定义在R 上的函数()f x ，若存在函数()g x ax b =+（a ，b 为常数），使得()()f x g x ≥对一切实数x 都成立，则称()g x 为函数()f x 的一个承托函数，下列命题中正确的是（）A ．函数()2g x =-是函数ln ,0()1,0x x f x x >⎧=⎨⎩的一个承托函数 B ．函数()1g x x =-是函数()sin f x x x =+的一个承托函数C ．若函数()g x ax = 是函数()x f x e =的一个承托函数，则a 的取值范围是[0,]eD ．值域是R 的函数()f x 不存在承托函数【答案】BC【分析】由承托函数的定义依次判断即可.【详解】解：对A ，∵当0x >时，()ln (,)f x x =∈-∞+∞，∴()()2f x g x ≥=-对一切实数x 不一定都成立，故A 错误；对B ，令()()()t x f x g x =-，则()sin (1)sin 10t x x x x x =+--=+≥恒成立， ∴函数()1g x x =-是函数()sin f x x x =+的一个承托函数，故B 正确；对C ，令()x h x e ax =-，则()xh x e a '=-，若0a =，由题意知，结论成立，若0a >，令()0h x '=，得ln x a =，∴函数()h x 在(,ln )a -∞上为减函数，在(ln ,)a +∞上为增函数，∴当ln x a =时，函数()h x 取得极小值，也是最小值，为ln a a a -，∵()g x ax =是函数()x f x e =的一个承托函数，∴ln 0a a a -≥，即ln 1a ≤，∴0a e <≤，若0a <，当x →-∞时，()h x →-∞，故不成立，综上，当0a e 时，函数()g x ax =是函数()x f x e =的一个承托函数，故C 正确；对D ，不妨令()2,()21f x x g x x ==-，则()()10f x g x -=≥恒成立，故()21g x x =-是()2f x x =的一个承托函数，故D 错误.故选：BC .【点睛】方法点睛：以函数为载体的新定义问题，是高考命题创新型试题的一个热点，常见的命题形式有新概念、新法则、新运算等，这类试题中函数只是基本的依托，考查的是考生创造性解决问题的能力．。

2024年山东省菏泽市巨野县中考二模数学试题

2024年山东省菏泽市巨野县中考二模数学试题一、单选题1．二十四节气是中国劳动人民独创的文化遗产，能反应季节的变化，指导农事活动．下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是（） A ． B ． C ． D ．2．“燕山雪花大如席，片片吹落轩辕台．”这是诗仙李白眼里的雪花．单个雪花的重量其实很轻，只有0.00003kg 左右，0.00003用科学记数法可表示为（）A ．5310-⨯B ．4310-⨯C ．40.310-⨯D ．50.310-⨯ 3．实数a ，b 在数轴上对应点的位置如图所示，则b a -的结果可能是（）A ．-1B ．1C ．2D ．34．某几何体的三视图如图所示，则该几何体是（）主视图左视图俯视图A ．B ．C ．D ． 5．光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，所以在水中平行的光线，在空气中也是平行的．若水面和杯底互相平行，143,2122∠=︒∠=︒，则3∠与4∠的度数分别为（）A ．43︒与58︒B ．43︒与45︒C ．45︒与58︒D ．43︒与32° 6．下列等式从左到右的变形，属于因式分解的是（）A ．()22211x x x +-=-B ．()()22a b a b a b +-=-C ．()22442x x x ++=+D ．()2211x x x -+=- 7．反比例函数k y x=与二次函数()20y kx x k k =-+-≠在同一平面直角坐标系中的大致图像可能是（） A ． B ．C ．D ．8．如图，已知AOB ∠，以点O 为圆心，适当长为半径作圆弧，与角的两边分别交于,C D 两点，分别以点C D ，为圆心，大于12CD 长为半径作圆弧，两条圆弧交于AOB ∠内一点P ，连接OP ，过点P 作直线PE OA ∥，交OB 于点E ，过点P 作直线PF OB ∥，交OA 于点F ．若60AOB ∠=︒，8cm OP =，则四边形PFOE 的周长是（）A ．32cmB ．C D9．在平面直角坐标系中，等边AOB V 如图放置，点A 的坐标为()1,0-，每一次将AOB V 绕着点O 顺时针方向旋转60︒，同时每边扩大为原来的2倍，第一次旋转后得到11AOB △，第二次旋转后得到22A OB △，…，依次类推，则点2024A 的坐标为（）A ．(20232,2B ．()20232,0C ．(20242,2D ．()20232,0- 10．如图，已知菱形ABCD 的对角线AC ，BD 相交于点O ，6AC =，8BD =，点E 在AD 上，13AE DE =，点F 为AB 的中点，点G ，H 为BD 上的动点，1GH =，连接FH ，EG ，则+FH EG 的最小值为（）A ．4B ．174C ．194D ．5二、填空题1112．三角形的两边长分别为6和8，第二边长是方程212200x x -+=的一个实根，则第三边长为．13．ABC V 与111A B C △的位似比为2:1，原点O 为它们的位似中心．若点A 的坐标为()6,4，则对应点1A 的坐标可以为．14．已知关于的x方程21(1)02m x --=有两个实数根，则m 的取值范围是． 15．如图，在O e 内有一个平行四边形OABC ，点A ，B ，C 在圆上，点N 为边AB 上一动点(点N 与点B 不重合)，O e 的半径为1，则阴影部分面积为．16．规定：如果两个函数的图象关于y 轴对称，那么称这两个函数互为“Y 函数”．例如：函数3y x =+与3y x =-+互为“Y 函数”．若函数2(1)34k y x k x k =+-+-的图象与x 轴只有一个交点，则它的“Y 函数”图象与x 轴的交点坐标为．三、解答题17．（1）计算：101(1)tan 602π-⎛⎫+++-︒ ⎪⎝⎭．（2）解不等式组：()2132113x x x x ⎧+>-⎪⎨-+<⎪⎩18．甲、乙两班分别选5名同学组成代表队参加学校组织的“国防知识”选拔赛，现根据成绩（满分10分）制作如图统计图和统计表（尚未完成）甲、乙两班代表队成绩统计表请根据有关信息解决下列问题：（1）填空：a ＝，b ＝；（2）学校预估如果平均分能达8.5分，在参加市团体比赛中即可以获奖，现应选派代表队参加市比赛；（填“甲”或“乙”）（3）现将从成绩满分的3个学生中随机抽取2人参加市国防知识个人竞赛，请用树状图或列表法求出恰好抽到甲，乙班各一个学生的概率．19．如图1是一种手机支架，由托板、支撑板和底座构成，手机放置在托板上，图2是其侧面结构示意图，量得托板120mm AB =，支撑板110mm CD =，底座DE ，托板AB 固定在支撑板顶端C 处，且40mm CB =，托板AB 可绕点C 转动，支撑板CD 可绕点D 转动．(1)若70DCB ∠=︒，60CDE ∠=︒，求点A 到直线DE 的距离．（精确到0.1mm ）(2)为了观看舒适，在（1）的情况下，把AB 绕点C 逆时针旋转20︒后，再将CD 绕点D 顺时针旋转，使点B 落在直线DE 上，求CD 旋转的角度大约是多少度？参考数据：（sin 400.643︒≈，cos400.766︒≈，tan400.839︒≈，sin 200.342︒≈，cos200.940︒≈，tan 200.364︒≈ 1.732≈）．20．聚焦“绿色发展，美丽宜居”县城建设，围绕“老旧改造人人参与，和谐家园家家受益”的思路，某市从2021年起连续投入资金用于“建设美丽城市，改造老旧小区”，让小区“旧貌”换“新颜”．已知每年投入资金的增长率相同，其中2021年投入资金1000万元，2023年投入资金1440万元．(1)求该市改造小区投入资金的年平均增长率；(2)2023年小区改造的平均费用为每个80万元，2024年为提高小区品质，每个小区改造费用计划增加20%．如果投入资金年增长率保持不变，求该市2024年最多可以改造多少个小区？21．如图，AB 为O e 的直径，AC 和BD 是O e 的弦，连接,AD CD ．(1)若点C 为AP 的中点，且PC PD =，求B ∠的度数；(2)若点C 为弧AD 的中点，4PD =，PC =O e 的半径．22．如图，在平面直角坐标系中，菱形ABCD 的顶点C 与原点O 重合，点B 在y 轴的正半轴上，点A 在反比例函数()0ky x x=>的图象上，点D 的坐标为()4,3．（1）求k 的值．（2）设点M 在反比例函数图象上，连接MA ，MD ，若△MAD 的面积是菱形ABCD 面积的14，求点M 的坐标． 23．在数学综合实践课上，兴趣小组的同学用两个完全相同的矩形纸片展开探究活动，这两张矩形纸片的长为8cm ，宽为4cm ．将两个完全相同的矩形纸片ABCD 和EFGQ 摆成图1的形状，点A 与点E 重合，边AD 与边EF 重合，边AB ，QE 在同一直线上．(1)请判断ACG V 的形状，并说明理由；(2)如图2，在（1）的条件下，将矩形EFGQ 绕点A 顺时针旋转（转动的度数小于45︒），边EF 与边CD 相交于点M ．①当旋转度数为30︒，请求出点F 到CD 的距离；②连接BM ，当180AMB AMC ∠+∠=︒时，求CBM ∠的度数；(3)从图2开始，将长方形EFGQ 绕点A 旋转一周，若边EF 所在直线恰好经过线段BQ 的中点O 时，连接BF ，FQ ，请直接写出V BFQ 的面积．24．综合与探究抛物线()240y ax bx a =+-≠与x 轴交于点()2,0A -和()4,0B ，与y 轴交于点C ，连接BC ．点P 是线段BC 下方抛物线上的一个动点（不与点B ，C 重合），过点P 作y 轴的平行线交BC 于M ，交x 轴于N ，设点P 的横坐标为t ．(1)求该抛物线的解析式；(2)用关于t 的代数式表示线段PM ，求PM 的最大值及此时点M 的坐标；(3)若91,2P ⎛⎫- ⎪⎝⎭连接CP ，在y 轴上是否存在点Q ，使得CPQ V 为直角三角形，若存在，直接写出点Q 的坐标；若不存在，请说明理由．。

山东省菏泽市巨野县第一中学2024-2025学年高一上学期10月月考试题

山东省菏泽市巨野县第一中学2024-2025学年高一上学期10月月考试题一、单选题1．命题“2024x ∃≥，使得24048x >”的否定形式为（）A ．2024x ∃<，24048x ≤B ．2024x ∀≥，24048x <C ．2024x ∀<，24048x ≤D ．2024x ∀≥，24048x ≤2．设全集{}*|8U x x =∈<N ，集合{1,3,6},{3,5,7}A B ==，则()U A B ð的子集个数为（）A ．3B ．4C ．7D ．83．使不等式24430x x --<成立的一个充分不必要条件是（）A ．112x -<<B ．1322x -<<C ．1433x -<<D ．3522x -<<4．函数1()21f x x =++在[]0,1上的最小值为（）A ．2B ．52C ．D ．35．已知函数()2411f x x -=+，则函数()y f x =的解析式是（）A ．()222f x x x =++，0x ≥B ．()222f x x x =++，1x ≥-C ．()222f x x x =-+，0x ≥D ．()222f x x x =-+，1x ≥-6．若关于x 的不等式20ax b ->的解集是{}|2x x >，则关于x 的不等式()()20ax b x +->的解集是（）A ．{4x x <-或2}x >B ．{2x x <-或2}x >C ．{}42x x -<<D ．{}22x x -<<7．中国南宋大数学家秦九韶提出了“三斜求积术”，即已知三角形三边长求三角形面积的公式：设三角形的三条边长分别为a ，b ，c ，则三角形的面积S 可由公式S =求得，其中p 为三角形周长的一半，这个公式也被称为海伦—秦九韶公式，现有一个三角形的边长满足4a =，6b c +=，则此三角形面积的最大值为（）A ．B ．C ．D ．8．函数()()()252,2213,2a x x f x x a x a x ⎧---≥⎪=⎨+--<⎪⎩，若对任意()1212,R x x x x ∈≠，都有()()12120f x f x x x -<-成立，则实数a 的取值范围为（）A ．[]4,1--B ．[]4,2--C ．(]5,1--D ．[]5,4--二、多选题9．已知,,,a b c d ∈R ，则下列命题正确的是（）A ．若a b >，c d >，则ac bd >B ．若0bc ad ->，0bd >，则a b c db d++<C ．若0a b <<，则b aa b<D ．若a b >，11a b>，则0a >，0b <10．下列各组函数中，是同一个函数的有（）A ．()1f x x=与()2x g x x =B ．()2f x x =与()()21g x x =+C ．()2f x =与()||g x x =D ．()f x x =与()g x =11．若函数()f x =[0,)+∞，则a 的可能取值为（）A ．12B ．14C ．18D ．0三、填空题12．已知幂函数()()213m f x m x -=-在()0,∞+内是单调递增函数，则实数m =.13．已知(1)f x +的定义域为[1,2]-，则(21)f x -的定义域为．14．用()C A 表示非空集合A 中的元素的个数，定义()()*A B C A C B =-，若{}2870A x x x =--=，()(){}22360B x x ax x ax =+++=，若*1A B =，则a 的所有可能取值构成集合M ，则()C M =.四、解答题15．已知函数21,1()1,1x x f x x x ⎧-+<⎪=⎨-≥⎪⎩.(1)画出函数()f x 的图象；(2)求3(())2f f -的值；(3)写出函数()f x 的单调递减区间.16．已知全集U =R ，集合{}217A x x =-≤，{}2142B x m x m =-≤≤-.(1)若2m =，求A B ⋂和()U A B ⋃ð；(2)若A B A = ，求m 的取值范围.17．已知函数21()(12)()4f x x a x a =+-+∈R ．(1)若函数()f x 在[2,)+∞上单调递增，求a 的取值范围；(2)是否存在实数a ，使得函数12f x ⎛⎫- ⎪⎝⎭在区间[]1,1-上的最小值为2-?若存在，求出a 的值；若不存在，请说明理由．18．某保健厂研制了一种足浴气血生机的足疗盆，具体原理是：在足浴盆右侧离中心()018x x <<厘米处安装臭氧发生孔，产生的臭氧对双脚起保健作用.根据检测发现，该臭氧发生孔工作时会对泡脚的舒适程度起到干扰作用，已知臭氧发生孔工作时，对左脚的干扰度与2x 成反比，比例系数为2；对右脚的干扰度与21350x -成反比，比例系数为k ，且当10x =时，对左脚和右脚的干扰度之和为0.06.(1)求臭氧发生孔工作时对左脚和右脚的干扰度之和y 关于x 的表达式；(2)求臭氧发生孔对左脚和右脚的干扰度之和的最小值，并求此时x 的值.19．对于定义在D 上的函数()f x ，若存在实数m ，n 且m n <，使得()f x 在区间[,]m n 上的最大值为2m，最小值为2n ，则称[,]m n 为()f x 的一个“保值区间”．已知函数()g x 是定义在R 上的奇函数，当()0,x ∞∈+）时，()3g x x =-+．(1)求函数()g x 的解析式；(2)求函数()g x 在()0,∞+内的“保值区间”；(3)若以函数()g x 在定义域内所有“保值区间”上的图象作为函数()y h x =的图象，求函数()y h x =的值域．。

山东省巨野县一中高三第二次模拟考试新高考化学试卷及答案解析

山东省巨野县一中高三第二次模拟考试新高考化学试卷注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置． 3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效． 5．如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题（每题只有一个选项符合题意） 1、化学与生活密切相关。

下列说法错误的是A ．绿色净水消毒剂高铁酸钠有强氧化性，其还原产物水解生成Fe(OH)3胶体B ．电子货币的使用和推广符合绿色化学发展理念C ．检查酒驾时，三氧化铬(橙红色)被酒精氧化成硫酸铬(绿色)D ．自行车镀锌辐条破损后仍能抗腐蚀，是利用了原电池反应原理 2、下列说法不正确的是A ．石油分馏可获得汽油、煤油、石蜡等矿物油，煤焦油干馏可获得苯、甲苯等有机物B ．生活中常见的聚乙烯、聚氯乙烯、纶、有机玻璃、合成橡胶都是通过加聚反应得到的C ．按系统命名法，有机物可命名为2，2，4，4，5—五甲基—3，3—二乙基己烷D ．碳原子数≤6的链状单烯烃，与HBr 反应的产物只有一种结构，符合条件的单烯烃有4种(不考虑顺反异构) 3、W 、X 、Y 、Z 为原子序数依次增大的短周期主族元素，W 和Y 同族，X 和Z 同族，X 的简单离子和Y 的简单离子具有相同的电子层结构，W 和X 、Z 均能形成共价化合物，W 和X 、Y 分别形成的化合物溶于水均呈碱性。

下列说法错误的是A ．4种元素中Y 的金属性最强B ．最高价氧化物对应的水化物的酸性：Z>XC ．简单阳离子氧化性：W>YD ．W 和Y 形成的化合物与水反应能生成一种还原性气体 4、根据下列实验操作和现象得出的结论正确的是操作现象结论A将2SO 分别通人溴水和酸性高锰酸钾溶液中溴水和酸性高锰酸钾溶液均褪色2SO 具有漂白性A ．AB ．BC ．CD ．D5、下列我国科研成果所涉及材料中，主要成分为同主族元素形成的无机非金属材料的是 A ．AB ．BC ．CD ．D6、对下表鉴别实验的“解释”正确的是 A ．AB ．BC ．CD ．D7、中国传统诗词中蕴含着许多化学知识，下列分析不正确的是（）。

山东省巨野一中高二数学下学期期中测试题新人教A版

一、选择题1．若函数3()33f x x bx b =-+在(01)，内有极小值，则（）Ａ．01b <<Ｂ．1b < Ｃ．0b > Ｄ．12b <2．理想状态下，质量为5千克的物体按规律223S t t =+作直线运动，其中S 以厘米为单位，t 以秒为单位，则物体受到的作用力为（）Ａ．30牛Ｂ．5610-⨯牛Ｃ．0.3牛Ｄ．6牛3．已知1z i =+，2211z az b i z z +=--+，则实数a ，b 的大小关系为（）Ａ．a b > Ｂ．a b < Ｃ．a b = Ｄ．大小关系无法确定4．计算3π2π2cos xdx -⎰的结果是（）Ａ．4 Ｂ．2 Ｃ．0 Ｄ．π5．共轭的两个复数之和大于2的一个充要条件为（）Ａ．两复数的实部都大于1Ｂ．两复数的实部都大于2Ｃ．两复数的虚部都大于1Ｄ．两复数的虚部都大于26．()F n 是一个关于自然数n 的命题，若()F k 真，则(1)F k +真，现已知(20)F 不真，那么：①(21)F 不真；②(19)F 不真；③(21)F 真；④(18)F 不真；⑤(18)F 真．其中正确的结论为（）Ａ．②④Ｂ．①② Ｃ．③⑤ Ｄ．①⑤7．若函数32()39f x x x x a =-+++在区间[21]--，上的最大值为2，则它在该区间上的最小值为（）Ａ．5- Ｂ．7Ｃ．10 Ｄ．19-8．集合{}2212(25)(56)M m m m m i =--+++，，，{}310N =，，且M N φ≠，则实数m 的值为（）Ａ．2-Ｂ．2-或4 Ｃ．2-或3-Ｄ．2-或59．若函数3()y a x x =-的递减区间为33⎛⎫- ⎪ ⎪⎝⎭，，则a 的取值范围是（）Ａ．(0)+，∞ Ｂ．(10)-，Ｃ．(1)+，∞ Ｄ．(01)，10．下列四条曲线（直线）所围成的区域的面积是（）Ａ．sin y x =；Ｂ．cos y x =；Ｃ．π4x =-；Ｄ．π4x =．11．抛物线2y x bx c =++在点(12)，处的切线与其平行直线0bx y c ++=间的距离是（）Ａ．2 Ｂ．2 Ｃ．32 Ｄ．2二、填空题13．在等差数列{}n a 中，我们有()n m a a n m d =+-，类比等差数列，在等比数列{}n a 中n a 与m a 之间的关系为．14．周长为20cm 的矩形，绕一条边旋转成一个圆柱，则圆柱体积的最大值为．15.如果复数z 满足|z +i |+|z -i |=2，那么|z +i +1|的最小值是．16.设()y f x =是可导函数，则2(1y f x =+的导数为．三、解答题：本大题共5小题，共74分.解答应写出文字说明，证明过程或演算步骤.17.用数学归纳法证明：2222121(1)1234(1)(1)2n n n n n --+-+-++-=-··．18.如图，直线y kx =分抛物线2y x x =-与x 轴所围图形为面积相等的两部分，求k 的值.．20.设复数z 满足5z =，且(3+4i )z 在复平面上对应的点在第二、四象限的角平分线上，若252()z m m -=∈R ，求z 和m 的值.．21，已知函数f(x)=x3+ax2+bx+5,记f(x)的导数为f ′(x).(1)若曲线f(x)在点(1,f(1))处的切线斜率为3，且x=23时，y=f(x)有极值,求函数f(x)的解析式.(2)在(1)的条件下，求函数f(x)在［-4,1］上的最大值和最小值.,22，已知函数()2f x x |x a |,a R.=-∈（1）当0a ≤时，求证函数()()f x ,-∞+∞在上是增函数；（2）当a=3时，求函数()f x 在区间[0，b]上的最大值。

2022-2023学年山东省菏泽市巨野县第一中学高二上学期期末数学试题

2022-2023学年山东省菏泽市巨野县第一中学高二上学期期末数学试题1.是首项和公差均为3的等差数列，如果，则n等于（）．A．671 B．672 C．673 D．6742.设为等差数列的前项和，已知，，则（）A．7 B．8 C．9 D．103.阿波罗尼斯研究发现：如果一个动点P到两个定点的距离之比为常数（，且），那么点P的轨迹为圆，这就是著名的阿波罗尼斯圆．若点C到，的距离之比为，则点C到直线的最小距离为（）A．B．C．D．4.如图，某建筑物白色的波浪形屋顶像翅膀一样漂浮，建筑师通过双曲线的设计元素赋予了这座建筑以轻盈，极简和雕塑般的气质，该建筑物外形弧线的一段可以近似看成焦点在y轴上的双曲线上支的一部分.已知该双曲线的上焦点F到下顶点的距离为18，F到渐近线的距离为6，则该双曲线的离心率为（）.A．B．C．D．5.已知椭圆：的中心为，过焦点的直线与交于，两点，线段的中点为，若，则椭圆的方程为（）A．B．C．D．6.对于空间一点O和不共线三点A，B，C，且有，则（）A．O，A，B，C四点共面B．P，A，B，C四点共面C．O，P，B，C四点共面D．O，P，A，B，C五点共面7.已知直线与圆：交于，两点，且，则的值为（）D．2 A．B．C．8.已知椭圆的左、右焦点分别为、，点在椭圆上且在轴的下方，若线段的中点在以原点为圆心，为半径的圆上，则直线的倾斜角为（）A．B．C．D．9.(多选题) 已知在直三棱柱中，底面是一个等腰直角三角形，且，E、F、G、M分别为的中点．则（）A．与平面夹角余弦值为B．与所成角为C．平面EFB D．平面⊥平面10.已知椭圆的左、右焦点分别是，，为椭圆上一点，则下列结论正确的是（）A．的周长为6 B．的面积为C．的内切圆的半径为D．的外接圆的直径为11.过抛物线上一点A(1，-4)作两条相互垂直的直线，与C的另外两个交点分别为M，N，则（）A．C的准线方程是B．过C的焦点的最短弦长为8C．直线MN过定点(0，4)D．当点A到直线MN的距离最大时，直线MN的方程为12.已知，则下述正确的是（）A．圆C的半径B．点在圆C的内部C．直线与圆C相切D．圆与圆C相交13.已知P为抛物线上一个动点，Q为圆上一个动点，那么点P到点Q的距离与点P到直线的距离之和的最小值是___________.14.已知F为双曲线C：的右焦点，A为C的左顶点，B为C上的点，且BF垂直于x轴，若AB的斜率为2，则C的离心率为______．15.斐波那契数列（Fibonaccisequence）又称黄金分割数列，是数学史上一个著名的数列：1，1，2，3，5，8，13，21，34，…….已知在斐波那契数列中，，，，若，则数列的前2020项和为___________（用含m 的代数式表示）.16.已知抛物线的焦点为F，Q（2，3）为C内的一点，M为C上任意一点，且的最小值为4，则p＝______；若直线l过点Q，与拋物线C交于A，B两点，且Q为线段AB的中点，则的面积为______．17.已知空间三点，，．设，．(1)求，；(2)求与的夹角；(3)若向量与互相垂直，求实数k的值．18.记为数列的前n项和．已知．(1)证明：是等差数列；(2)若成等比数列，求的最小值．19.已知直三棱柱中，侧面为正方形，AB＝BC＝2，E，F分别为AC和的中点，D为棱上的点．.(1)证明：BF⊥DE；(2)当为何值时，面与面DFE所成的二面角的正弦值最小？20.如图，正四棱柱ABCD－A1B1C1D1中，AA1＝2AB，E为棱CC1的中点．(1)用向量法证明：平面B1ED1；(2)求直线B1D与平面B1ED1所成角的正弦值．21.已知P是离心率为的椭圆上任意一点，且P到两个焦点的距离之和为4．(1)求椭圆C的方程；(2)设点A是椭圆C的左顶点，直线AP交y轴于点D，E为线段AP的中点，在x轴上是否存在定点M，使得直线DM与OE交于Q，且点Q在一个定圆上，若存在，求点M的坐标与该圆的方程；若不存在，说明理由．22.已知椭圆的上､下焦点分别为，，左､右顶点分别为，，且四边形是面积为8的正方形.(1)求C的标准方程.(2)M，N为C上且在y轴右侧的两点，，与的交点为P，试问是否为定值？若是定值，求出该定值；若不是，请说明理由.。

2024年山东省菏泽市巨野县中考数学一模试卷

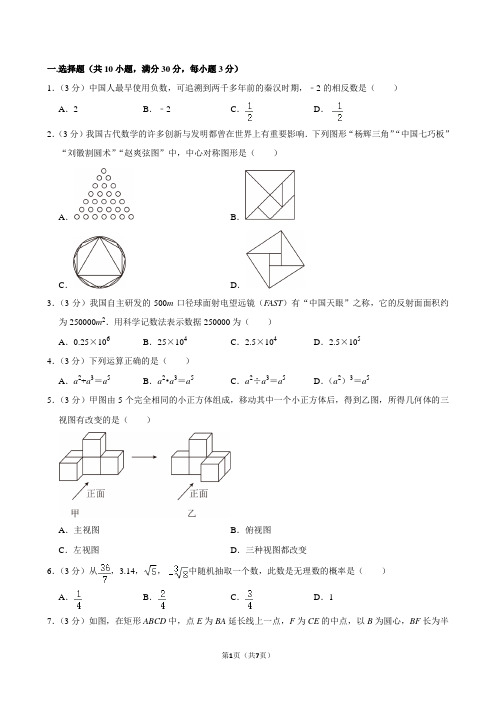
一.选择题（共10小题，满分30分，每小题3分）1．（3分）中国人最早使用负数，可追溯到两千多年前的秦汉时期，﹣2的相反数是（）A．2B．﹣2C．D．2．（3分）我国古代数学的许多创新与发明都曾在世界上有重要影响．下列图形“杨辉三角”“中国七巧板”“刘徽割圆术”“赵爽弦图”中，中心对称图形是（）A．B．C．D．3．（3分）我国自主研发的500m口径球面射电望远镜（F AST）有“中国天眼”之称，它的反射面面积约为250000m2．用科学记数法表示数据250000为（）A．0.25×106B．25×104C．2.5×104D．2.5×1054．（3分）下列运算正确的是（）A．a2+a3＝a5B．a2•a3＝a5C．a2÷a3＝a5D．（a2）3＝a55．（3分）甲图由5个完全相同的小正方体组成，移动其中一个小正方体后，得到乙图，所得几何体的三视图有改变的是（）A．主视图B．俯视图C．左视图D．三种视图都改变6．（3分）从，3.14，，中随机抽取一个数，此数是无理数的概率是（）A．B．C．D．17．（3分）如图，在矩形ABCD中，点E为BA延长线上一点，F为CE的中点，以B为圆心，BF长为半径的圆弧过AD与CE的交点G，连接BG．若AB＝4，CE＝10，则AG＝（）A．2B．2.5C．3D．3.58．（3分）如图，AB，AC是⊙O的弦，OB，OC是⊙O的半径，点P为OB上任意一点（点P不与点B 重合），连接CP．若∠BAC＝70°，则∠BPC的度数可能是（）A．70°B．105°C．125°D．155°9．（3分）将一副直角三角板作如图所示摆放，∠GEF＝60°，∠MNP＝45°，AB∥CD，则下列结论不正确的是（）A．GE∥MP B．∠EFN＝150°C．∠BEF＝60°D．∠AEG＝∠PMN10．（3分）直线y1＝ax+b和抛物线（a，b是常数，且a≠0）在同一平面直角坐标系中，直线y1＝ax+b经过点（﹣4，0）．下列结论：①抛物线的对称轴是直线x＝﹣2；②抛物线与x轴一定有两个交点；③关于x的方程ax2+bx＝ax+b有两个根x1＝﹣4，x2＝1；④若a ＞0，当x＜﹣4或x＞1时，y1＞y2.其中正确的结论是（）A．①②③④B．①②③C．②③D．①④二.填空题（共6小题，满分18分，每小题3分）11．（3分）若x+y＝3，xy＝2，则x2y+xy2的值为．12．（3分）关于x的不等式组有3个整数解，则实数m的取值范围是．13．（3分）甲、乙两船从相距150km的A，B两地同时匀速沿江出发相向而行，甲船从A地顺流航行90km 时与从B地逆流航行的乙船相遇．甲、乙两船在静水中的航速均为30km/h，则江水的流速为km/h．14．（3分）据《墨经》记载，在两千多年前，我国学者墨子和他的学生做了“小孔或像”实验，阐释了光的直线传播原理．小孔成像的示意图如图所示，光线经过小孔O，物体AB在幕布上形成倒立的实像CD（点A，B的对应点分别是C，D）．若物体AB的高为12cm，实像CD的高度为4cm，则小孔O的高度OE为cm．15．（3分）如图，在矩形ABCD中，以点D为圆心，AD长为半径画弧，以点C为圆心，CD长为半径画弧，两弧恰好交于BC边上的点E处，现从矩形内部随机取一点，若AB＝1，则该点取自阴影部分的概率为．16．（3分）如图，在边长为2的正方形ABCD中，点E为AD的中点，将△CDE沿CE翻折得△CME，点M落在四边形ABCE内．点N为线段CE上的动点，过点N作NP∥EM交MC于点P，则MN+NP 的最小值为．三.解答题（共8小题，满分72分）17．（8分）（1）计算：﹣4|sin60°|+﹣（2023﹣π）0；（2）先化简，再求值：，其中．18．（8分）如图，在平面直角坐标系中，一次函数y＝ax+b（a＜0）与反比例函数y＝（k≠0）交于A（﹣m，3m），B（4，﹣3）两点，与y轴交于点C，连接OA，OB．（1）求反比例函数和一次函数的表达式；（2）求△AOB的面积；（3）请根据图象直接写出不等式＜ax+b的解集．19．（8分）蹴鞠是起源于中国古代的一种足球运动，有着悠久的历史和丰富的文化内涵．在战国时期就开始流行，为发扬传统文化，唤醒中国礼仪，某学校开展足球射门比赛．随机从报名的学生中抽取了40人，每人射门30次，射中一次得1分，满分30分，得到这40名学生的得分（没有满分学生），将他们的成绩分成六组：A：0～5分；B：5～10分；C：10～15分；D：15～20分；E：20～25分；F：25～30分，绘制成如图所示的频数分布直方图（每组数据含最小值，不含最大值）．（1）若D组数据为：15，15，15，16，17，17，18，18，19，19，19，19，则这组数据的众数是，中位数是；（2）若将此直方图绘制成扇形统计图，B：5～10分所在扇形的圆心角的度数为°；（3）若用每组数据的组中值（如5≤x＜10的组中值是7.5）来代表该组同学的平均成绩；①请求出这40名同学的总成绩；②若此时再加上5名同学，要使总平均成绩不低于17分，求这5名同学的平均成绩至少为多少分？20．（8分）问题情境：筒车是我国古代发明的一种水利灌溉工具，既经济又环保．明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理（如图①）．假定在水流量稳定的情况下，筒车上的每一个盛水筒都按逆时针做匀速圆周运动，每旋转一周用时120秒．问题设置：把筒车抽象为一个半径为r的⊙O．如图②，OM始终垂直于水平面，设筒车半径为2米．当t＝0时，某盛水筒恰好位于水面A处，此时∠AOM＝30°，经过95秒后该盛水筒运动到点B处．问题解决：（1）求该盛水筒从A处逆时针旋转到B处时，∠BOM的度数；（2）求该盛水筒旋转至B处时，它到水面的距离．（结果精确到0.1米）（参考数据≈1.414，≈1.732）21．（8分）某商场销售A、B两种商品，每件进价均为20元．调查发现，如果售出A种20件，B种10件，销售总额为840元；如果售出A种10件，B种15件，销售总额为660元．（1）求A、B两种商品的销售单价；（2）经市场调研，A种商品按原售价销售，可售出40件，原售价每降价1元，销售量可增加10件；B 种商品的售价不变，A种商品售价不低于B种商品售价．设A种商品降价m元，如果A、B两种商品销售量相同，求m取何值时，商场销售A、B两种商品可获得总利润最大？最大利润是多少？22．（8分）如图，四边形ABCD是⊙O的内接四边形，AB是直径，C是的中点，过点C作CE⊥AD交AD的延长线于点E．（1）求证：CE是⊙O的切线；（2）若BC＝6，AC＝8，求CE，DE的长．23．（12分）综合与实践问题情境：如图1，在正方形ABCD中，对角线AC，BD相交于点O，M是线段OB上一点，连接AM．操作探究：将△MAB沿射线BA平移得到△M'A'B'，使点M的对应点M′落在对角线AC上，M'A'与AD边交于点E，连接M'D，A'D．（1）如图2，当M是OB的中点时，求证：AA'＝AB'．（2）如图3，当M是OB上任意一点时，试猜想△M'A'D的形状，并说明理由．拓展延伸：（3）在（2）的条件下，请直接写出AA'，AM'，AD之间的数量关系．24．（12分）【建立模型】（1）如图1，点B是线段CD上的一点，AC⊥BC，AB⊥BE，ED⊥BD，垂足分别为C，B，D，AB＝BE．求证：△ACB≌△BDE；【类比迁移】（2）如图2，一次函数y＝3x+3的图象与y轴交于点A、与x轴交于点B，将线段AB绕点B逆时针旋转90°得到BC，直线AC交x轴于点D．①求点C的坐标；②求直线AC的解析式；【拓展延伸】（3）如图3，抛物线y＝x2﹣3x﹣4与x轴交于A，B两点（点A在点B的左侧），与y轴交于C点，已知点Q（0，﹣1），连接BQ，抛物线上是否存在点M，使得tan∠MBQ＝，若存在，求出点M的横坐标．。