经纬度计算距离和方位角
计算距离方位角 的经纬度坐标

计算距离方位角的经纬度坐标随着全球定位系统(GPS)和地图定位技术的发展,人们在日常生活和工作中经常需要计算两点之间的距离和方位角。
而经纬度坐标则是描述地球上任意一点位置的常用方式。
在这篇文章中,我们将探讨如何利用经纬度坐标来计算两点之间的距离和方位角。
一、经纬度坐标的表示和计算1.1 经纬度坐标的表示经度和纬度分别用度(°)、分(′)和秒(″)来表示,例如北纬30°15′20″,东经120°59′36″。
在计算机编程中,经纬度通常用小数表示,例如东经120.xxx°、北纬30.xxx°。
1.2 经纬度坐标的计算计算两点之间的距离和方位角通常涉及地球的曲率和球面三角学的知识。
常见的计算方法包括球面三角学公式、Vincenty公式等。
二、计算两点之间距离的方法2.1 球面三角学公式球面三角学公式是最基本的计算地球表面两点之间距离的方法之一。
其基本原理是根据两点的经纬度坐标来计算它们之间的大圆弧距离。
2.2 Vincenty公式Vincenty公式是一种更精确的计算地球表面两点之间距离的方法,它考虑了地球的椭球体形状和扁率因素,因此在距离较大的情况下精度更高。
三、计算两点之间方位角的方法3.1 利用正弦定理在已知两点的经纬度坐标后,可以利用正弦定理来计算它们之间的方位角,即两点连线与正北方向的夹角。
3.2 利用方位角公式另一种计算方位角的方法是利用方位角公式,根据两点的经纬度坐标和球面三角学的知识来计算它们之间的方位角。
四、实际应用和注意事项4.1 在实际应用中,除了纯粹的数学计算外,还需要考虑地图投影方式、坐标系转换等因素。
4.2 在计算距离和方位角时,需要注意经纬度坐标的单位转换,比如将度分秒转换为小数表示。
4.3 对于距离较短的情况,可以采用简化的计算方法来近似计算两点之间的距离和方位角。
计算距离和方位角的经纬度坐标是一项涉及到地理信息和数学知识的复杂计算。
经纬网的应用-坐标、方向、距离

经纬网的应用-坐标、 方向、距离
https://
REPORTING
2023
目录
• 经纬网基本概念与原理 • 坐标系统及其在经纬网中应用 • 方向判断与导航技术在经纬网中运用 • 距离计算在经纬网中实践 • 经纬网在各行业领域应用案例分析 • 总结与展望:未来发展趋势和挑战
转换工具
为了方便进行坐标转换,可以使用一些专门的转换工具或软件,如GIS软件中的坐标转换 功能等。这些工具通常提供了多种坐标系统间的转换方法,能够满足不同需求。
2023
PART 03
方向判断与导航技术在经 纬网中运用
REPORTING
方位角计算及应用场景
01
02
03
方位角定义
方位角是从正北方向顺时 针量到目标方向线的水平 角,用于描述两点之间的 相对方向。
物流领域应用
在物流领域,计算两点之间的距离对于规划 运输路线、估算运输成本等具有重要意义。 例如,根据发货地和收货地的经纬度信息, 可以计算出两地之间的大圆距离或椭球面距 离,从而为物流公司提供参考。
交通领域应用
在交通领域,计算两点之间的距离可以帮助 规划交通路线、评估交通拥堵状况等。例如 ,根据起点和终点的经纬度信息,可以计算 出两点之间的实际距离,从而为驾驶员提供 导航服务。同时,交通管理部门也可以通过 分析不同路段的距离数据,来评估交通拥堵
应用场景局限性
目前经纬网的应用主要集中在导航、位置服务等少数领域,在其他 领域的应用相对较少。
技术标准和规范不统一
由于缺乏统一的技术标准和规范,不同系统之间的数据交换和共享 存在困难。
未来发展趋势预测及机遇挖掘
智能化发展
随着人工智能技术的不断发展,经纬网将实现更 高程度的智能化,包括智能定位、智能导航等。
关于坐标与坐标方位角的计算

关于坐标与坐标方位角的计算坐标与坐标方位角是地理学中经常涉及的两个概念。
坐标一般指的是其中一点在地球表面的位置,而坐标方位角是指其中一点相对于参考点的方向。
在地理信息系统、导航系统以及测量、航海等领域中,坐标与坐标方位角的计算是非常重要的。
首先,我们先来了解一下坐标的概念和表示方法。
坐标一般是由经度和纬度两个数值组成。
经度是指地球上其中一点与本初子午线的夹角,范围是从0°到180°东经或西经。
纬度是指地球上其中一点与赤道的夹角,范围是从0°到90°北纬或南纬。
经度和纬度的单位都是度(°)。
在计算坐标时,我们需要使用测量仪器(如GPS)来测定其中一点的经度和纬度数值。
这些数值可以直接使用,也可以根据仪器的输出进行转换。
例如,GPS通常会输出以度、分、秒或以十进制度表示的经纬度数值,我们可以根据需要进行转换。
将经度和纬度数值表示为十进制度,方便计算和比较。
接下来,我们来讨论坐标方位角的计算。
坐标方位角是指一个点相对于参考点的方向,也可以理解为一个点与参考点之间连线与正北方向之间的夹角。
坐标方位角的计算通常使用数学中的三角函数来实现。
首先,我们需要确定一个正北方向。
在地球表面上,通常使用地心纬度方向作为正北方向。
地心纬度是指与参考椭球体表面垂直的线所作的纬度,在地球上大致是从南向北逐渐增加的方向。
因此,我们可以将地心纬度方向作为正北方向。
其次,我们需要使用球面三角学中的公式来计算坐标方位角。
球面三角学是关于球面上的三角形的一门数学学科,可以用来解决地理测量和导航等问题。
在坐标方位角的计算中,主要使用到的公式有:1.余弦定理:可以用来计算一个球面三角形的边长,即两点之间的距离。
2.正弦定理:可以用来计算一个球面三角形的角度。
通过这些公式,我们可以计算出点A与参考点B之间的距离以及夹角。
然后,根据夹角的正负和大小,我们可以确定点A相对于参考点B的方向角。
需要注意的是,坐标方位角的计算要考虑地球的曲率。
起算方位角计算公式

起算方位角计算公式方位角是指一个点相对于另一个点的方向角度,通常以北方向为基准,顺时针方向为正角度,逆时针方向为负角度。
在地理测量、导航和工程测量等领域,方位角的计算是非常重要的。
在本文中,我们将介绍起算方位角的计算公式及其应用。
起算方位角的计算公式如下:tan(θ) = (sin(Δλ) cos(φ2)) / (cos(φ1) sin(φ2) sin(φ1) cos(φ2) cos(Δλ))。
其中,θ表示起算方位角,Δλ表示目标点经度与起始点经度的差值,φ1和φ2分别表示起始点和目标点的纬度。
在实际应用中,我们通常使用这个公式来计算两个点之间的方位角,以便进行导航、测量或定位。
首先,我们需要确定起始点和目标点的经纬度坐标。
然后,根据上述公式,计算出起算方位角。
这个角度可以帮助我们确定目标点相对于起始点的方向,从而进行导航或测量。
在地理测量中,起算方位角的计算也经常用于确定地表上两个点之间的距离和方向。
通过测量起算方位角,我们可以计算出两点之间的直线距离,从而进行地图绘制、土地测量等工作。
另外,起算方位角的计算还可以应用于航空导航和航海导航中。
飞行员和航海员可以利用起算方位角来确定飞行或航行的方向,从而确保航线的准确性和安全性。
在工程测量中,起算方位角的计算也是必不可少的。
工程师们可以利用这个公式来确定工程项目中各个点之间的方向和距离,从而进行工程测量和设计。
总之,起算方位角的计算公式是地理测量、导航和工程测量等领域中非常重要的工具。
通过这个公式,我们可以准确地计算出两个点之间的方向角度,从而进行导航、测量和定位工作。
希望本文对您有所帮助,谢谢阅读!。
地球经纬度求方位角和距离

计算指定经纬度的地点到地心的距离?假定地球是椭圆;赤道半径6378km 极地半径6357km 指定地点为E140度, N37度求该地点地心距离估算!假定地球是个以自转轴为旋转轴的旋转椭球体地心为旋转椭圆两焦点的中点则指定地点到地心的距离与经度无关仅与纬度有关以过该点的经度线和地心所在平面建立平面直角坐标系用椭圆的参数方程x=acosθ=6378*cosθy=bsinθ=6357*sinθ将θ=37°带入x=5093.70 y=3825.74 点(5093.70 , 3825.74)到原点(0,0)的距离d=√(x^2+y^2) =6370.41 km根据两点的经纬度求方位角和距离,等最近自己做的一个小东西要用到经纬度方面的计算,查遍中文网页见到的要么基本上是一帮惜字如金装大爷的“砖家”,要么就是像贴膏药一样,啪,一大堆代码往上一贴,一点说明都没有,让人看不懂,有的看了半天看懂了,结果他用的公式要么有使用局限(但没有半点声明)要么根本就是个错的。
所以现在将自己几天学习来的在这里总结一下,方便后来人少走弯路。
这里主要解决四个问题:1、已知两点经纬度,求一点相对于另一点方位角;2、已知两点经纬度,求两点间距离;3、已知一点经纬度及与另一点距离和方位角,求另一点经纬度;4、问题1与问题2的简化算法。
注:简化算法的运算量和对系统的运算精度要求都大大降低,但只在短距离内(高纬地区建议10km以下)可以保证精度,除简化算法之外的算法可适用于地球上任意两点。
这里只是出于便于理解的目的来解释“原理”,具体到不同的编程环境还要自己做化简和注意单位。
在求算前我们先对符号及单位进行约定:此处设定求B相对于A的方位角,即A为当前位置,B为目标位置Aj:A点经度Aw:A点纬度Bj:B点经度Bw:B点纬度北纬为正,南纬为负;东经为正,西经为负经纬度使用度,DDD.DDDDDD°,非度分或度分秒。
度数未加说明均采用角度制R:地球平均半径Azimuth:方位角,以真北为0度起点,由东向南向西顺时针旋转360度A,B,C表示球面上的三个点及球面上“弧线”在该点处所夹的角a,b,c表示A,B,C三点的对“弧”两端点与地心连线所夹的角(其实这里解释成ABC三点对弧的弧度更方便)O为球心L为AB两点间球面距离(注:因我考虑欠缺,没有注意字母C大小写较难分辨,所以此处提醒读者在后面的公式中注意C的大小写。
日期时间和当地经纬度计算太阳天顶角和方位角

日期时间和当地经纬度计算太阳天顶角和方位角太阳天顶角和方位角是与太阳相关的重要概念,通过日期、时间和当地的经纬度可以计算得出。
这两个概念在航海、天文学以及可再生能源等领域有着广泛的应用。
接下来,我将详细介绍如何通过日期、时间和当地经纬度来计算太阳天顶角和方位角。
首先,我们需要了解一些基本概念。
1. 太阳天顶角(Solar Zenith Angle):太阳天顶角是指太阳光线与垂直于地球表面的直线之间的夹角。
太阳天顶角越小,太阳光线越垂直于地球表面,到达地面的能量越大。
2. 方位角(Azimuth Angle):方位角是指太阳光线在地平面上的方向角度。
0度表示正北方向,90度表示正东方向,180度表示正南方向,270度表示正西方向。
接下来,我们来讨论如何通过日期、时间和当地经纬度来计算太阳天顶角和方位角。
1. 计算太阳时角(Solar Hour Angle):太阳时角是指太阳在当地经度上的角度,以正午为0度。
太阳时角的范围在-180度到180度之间。
太阳时角的计算公式如下:太阳时角=(时差+当前时间的时角)-(当地经度/15)其中,时差是指太阳时角和平太阳时角之间的差异,可以通过经纬度和日期来计算得出,具体的计算公式可以参考天文学的相关文献或者使用计算工具进行计算。
当前时间的时角的计算公式如下:当前时间的时角=15*(当前时间-12)注意,这里的时间以24小时制表示。
2. 计算太阳的高度角(Solar Altitude Angle):太阳的高度角是指太阳光线与地平面的夹角。
太阳高度角的计算公式如下:太阳高度角 = arcsin(sin(纬度) * sin(太阳赤纬) + cos(纬度) * cos(太阳赤纬) * cos(太阳时角))其中,纬度是指当地的纬度,太阳赤纬是根据日期和时间计算得出的赤纬。
3. 计算太阳的方位角(Solar Azimuth Angle):太阳的方位角是指太阳光线在地平面上的方向角度。
度量长度与角度的转换与换算

度量长度与角度的转换与换算长度和角度是我们日常生活中经常遇到的概念。
无论是在建筑、工程、地理测量还是日常生活中,我们都需要对长度和角度进行度量、转换和换算。
本文将探讨度量长度与角度的转换与换算的方法和技巧。
一、度量长度的单位与转换长度是物体的空间延伸大小,常用的长度单位有米(m)、千米(km)、厘米(cm)、毫米(mm)等。
在度量长度时,我们需要根据具体情况选择合适的单位。
在日常生活中,我们经常使用厘米和毫米来度量小物体的长度,如书本的厚度、钢笔的长度等。
而对于较大的物体,如房屋、道路等,我们则使用米和千米来度量。
在进行长度的转换时,我们需要掌握一些基本的换算关系。
1米等于100厘米,1米等于1000毫米,1千米等于1000米。
根据这些换算关系,我们可以进行不同单位之间的转换。
例如,如果我们需要将1000米转换为千米,只需将1000除以1000,得到1千米。
如果我们需要将2000毫米转换为米,只需将2000除以1000,得到2米。
二、度量角度的单位与转换角度是物体之间的夹角大小,常用的角度单位有度(°)、弧度(rad)等。
在度量角度时,我们需要选择合适的单位,并掌握角度的转换方法。
在日常生活中,我们常用度来度量角度,如直角为90°,圆周为360°。
而在数学、物理等学科中,我们使用弧度来度量角度。
度与弧度之间的转换关系是:1周角等于2π弧度,1弧度等于180/π度。
根据这些换算关系,我们可以进行度与弧度之间的转换。
例如,如果我们需要将60°转换为弧度,只需将60乘以π再除以180,得到约为1.047弧度。
如果我们需要将π/4弧度转换为度,只需将π/4乘以180再除以π,得到约为45°。
三、长度与角度的换算在实际应用中,我们有时需要将长度和角度进行换算。
例如,在地理测量中,我们常常需要根据地球上两点的经纬度计算两点之间的距离和方位角。
对于长度和角度的换算,我们可以利用三角函数来进行计算。
经纬度计算距离与方位角

经纬度计算距离与⽅位⾓距离根据经纬度计算距离是有固定公式的,按照公式写个函数很简单。
import mathdef cal_dis(lat1, lon1,lat2, lon2):latitude1 = (math.pi/180)*lat1latitude2 = (math.pi/180)*lat2longitude1 = (math.pi/180)*lon1longitude2= (math.pi/180)*lon2#因此AB两点的球⾯距离为:{arccos[sinb*siny+cosb*cosy*cos(a-x)]}*R#地球半径R = 6378.137d = math.acos(math.sin(latitude1)*math.sin(latitude2)+ math.cos(latitude1)*math.cos(latitude2)*math.cos(longitude2-longitude1))*Rreturn dif__name__ == '__main__':print cal_dis(23.0,101.1,23.06,113.34)注意,经纬度是⾓度,⽽三⾓函数的输⼊是弧度,⾓度与弧度的关系 180=pi有⼀次我在⼀个项⽬中发现 matlab 的计算距离和上⾯这个函数有些出⼊,虽然相差不⼤,但是确实不⼀样,当时也折腾了好久,后来发现python 有个⾃带的函数计算结果和 matlab 相同。
from geopy.distance import geodesicgeodesic((30.28708,120.12802999999997), (28.7427,115.86572000000001)).m⽅位⾓def calc_azimuth(lat1, lon1, lat2, lon2):lat1_rad = lat1 * math.pi / 180lon1_rad = lon1 * math.pi / 180lat2_rad = lat2 * math.pi / 180lon2_rad = lon2 * math.pi / 180y = math.sin(lon2_rad - lon1_rad) * math.cos(lat2_rad)x = math.cos(lat1_rad) * math.sin(lat2_rad) - \math.sin(lat1_rad) * math.cos(lat2_rad) * math.cos(lon2_rad - lon1_rad)brng = math.atan2(y, x) * 180 / math.pireturn float((brng + 360.0) % 360.0)所谓⽅位⾓是与正北⽅向、顺时针之间的夹⾓。
方位角的计算方法

方位角的计算方法(原创版2篇)目录(篇1)1.方位角的定义2.计算方位角的基本公式3.方位角的应用实例正文(篇1)方位角是一种用来描述物体位置和方向的度量方式,通常用于地图、导航和测量等领域。
在我们生活中,方位角是一个非常实用的工具,它能帮助我们更准确地找到目标位置。
那么,如何计算方位角呢?接下来,我将为大家详细介绍方位角的计算方法。
首先,我们来了解一下方位角的定义。
方位角是指从正北方向开始,逆时针旋转到目标方向的角度。
换句话说,就是从北往东、南、西旋转到目标方向的角度。
这个角度的范围是0°到360°,其中0°表示正北方向,90°表示正东方向,180°表示正南方向,270°表示正西方向,360°又回到了正北方向。
接下来,我们来介绍一下计算方位角的基本公式。
假设我们现在要计算从正北方向逆时针旋转到目标方向的角度,那么我们可以使用以下公式:方位角 = 目标方向角度 - 180°其中,目标方向角度是指从正北方向开始,逆时针旋转到目标方向的角度。
如果目标方向在正北方向的左侧,那么目标方向角度是正值;如果目标方向在正北方向的右侧,那么目标方向角度是负值。
举个例子,假设我们要计算从正北方向逆时针旋转到西南方向的方位角。
首先,我们需要确定西南方向相对于正北方向的角度。
在地图上,我们可以看到西南方向与正北方向的夹角大约是45°。
因此,目标方向角度为45°。
将这个值代入公式,我们可以得到:方位角= 45° - 180° = -135°这意味着,从正北方向逆时针旋转135°就可以到达西南方向。
方位角在实际应用中具有重要意义。
例如,在导航系统中,我们可以通过输入目标位置的经纬度和当前位置的经纬度,计算出目标相对于当前位置的方位角,从而为出行提供准确的方向指引。
此外,方位角还在地图制作、航空航天、地质勘探等领域发挥着重要作用。
工程测量坐标计算公式

工程测量坐标计算公式工程测量是工程建设的重要环节,准确的坐标计算是保证工程质量和施工安全的基础。
本文将介绍工程测量中常用的坐标计算公式,帮助读者更好地理解并应用于实践中。
一、坐标计算的基础知识在工程测量中,常用的坐标系统有直角坐标系和大地坐标系。
直角坐标系以某一点为原点,建立笛卡尔坐标系,用x、y、z三个轴线表示空间位置。
大地坐标系则以地球为基准,通过经度、纬度和高程来确定点的相对位置。
二、坐标计算公式1. 直角坐标系的坐标计算公式在直角坐标系中,常用的坐标计算公式有:- 两点间距离计算公式:设A点坐标为(x1, y1, z1),B点坐标为(x2, y2, z2)。
则两点间的距离d计算公式如下:d = √((x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2)- 点到直线距离计算公式:设点A的坐标为(x1, y1, z1),直线方程为Ax + By + Cz + D = 0。
则A点到直线的距离d计算公式如下:d = |Ax1 + By1 + Cz1 + D| / √(A^2 + B^2 + C^2)- 点到平面距离计算公式:设点A的坐标为(x1, y1, z1),平面方程为Ax + By + Cz + D = 0。
则A点到平面的距离d计算公式如下:d = |Ax1 + By1 + Cz1 + D| / √(A^2 + B^2 + C^2)2. 大地坐标系的坐标计算公式在大地坐标系中,常用的坐标计算公式有:- 两点间距离计算公式:根据两点的经纬度计算其球面距离,公式如下:d = R * arccos(sinφ1*sinφ2 + cosφ1*cosφ2*cos(λ2-λ1))其中,R为地球半径,φ为纬度,λ为经度。
- 两点间方位角计算公式:根据两点经纬度计算其中一点相对于另一点的方位角,公式如下:α = arctan((sinΔλ * cosφ2) / (cosφ1*sinφ2 -sinφ1*cosφ2*cosΔλ))其中,φ为纬度,λ为经度,Δλ为两点经度差。
方位角的计算方法

方位角的计算方法方位角是指在平面直角坐标系中,特定点与正方向x轴之间逆时针方向的夹角。
它在数学、地理、航空航天等领域中都有广泛的应用。
计算方位角的方法主要有以下几种:1.基于直角坐标系的计算:假设有两个点A(x1, y1)和B(x2, y2),首先需要计算出两点之间的直线斜率k = (y2 - y1) / (x2 - x1)。
然后利用反正切函数,通过求解arctan(k)得到弧度值θ。
最后利用单位换算,将弧度值θ转化为角度值α=θ * 180 / π,即为所求的方位角。
2.基于极坐标系的计算:在极坐标系中,一个点可以通过距离r和极角θ来表示。
假设有两个点A(r1,θ1)和B(r2,θ2),要计算两点之间的方位角,首先需要将两点的极角θ转化为弧度制,然后通过计算Δθ=θ2-θ1得到两点之间的相对角度。
最后利用单位换算,将相对角度Δθ转化为角度值α=Δθ*180/π,即得到方位角。
3.基于方向向量的计算:假设有两个点A(x1, y1)和B(x2, y2),可以将两点之间的连线看作一个方向向量。
首先需要计算出两点之间的方向向量V(x2 - x1, y2 - y1)。
然后利用反正切函数,通过求解arctan(Vy / Vx)得到弧度值θ。
最后利用单位换算,将弧度值θ转化为角度值α=θ * 180 / π,即为所求的方位角。
需要注意的是,在计算方位角时,可能会遇到特殊情况,例如:-当两点在同一直线上时,方位角为0或180度;-当两点重合时,方位角没有定义。
总结起来,方位角的计算方法有基于直角坐标系、极坐标系和方向向量三种方法,根据具体情况选择适合的方法进行计算。
坐标计算方法

坐标计算方法在地理信息系统(GIS)和地理定位领域,坐标计算是一个非常重要的环节。
通过坐标计算,我们可以精确地确定地理位置,进行地图绘制,进行导航定位等工作。
本文将介绍一些常见的坐标计算方法,帮助大家更好地理解和应用这些方法。
首先,我们来介绍一种常见的坐标计算方法——经纬度坐标计算。
经纬度坐标是地球表面上任意一点的地理坐标,通常用度、分、秒来表示。
经度是指地球表面上某一点与本初子午线的夹角,而纬度是指地球表面上某一点与赤道的夹角。
在实际应用中,我们常常需要根据已知的经纬度坐标来计算距离、方位角等信息。
这时,我们可以利用球面三角形的计算方法来进行经纬度坐标的计算。
其次,还有一种常见的坐标计算方法——平面坐标计算。
在地图绘制和工程测量中,我们通常需要将地球表面上的经纬度坐标转换为平面坐标,以便进行实际测量和绘图工作。
这时,我们可以利用投影变换的方法来进行平面坐标的计算。
常见的地图投影包括墨卡托投影、兰伯特投影、等距投影等,它们可以将地球表面上的经纬度坐标转换为平面坐标,以满足不同精度和应用需求。
另外,还有一种常见的坐标计算方法——空间坐标计算。
在地理定位和导航领域,我们通常需要根据已知的空间坐标来计算目标的位置和运动轨迹。
这时,我们可以利用三维空间几何计算的方法来进行空间坐标的计算。
通过三角测量、距离测量、角度测量等手段,我们可以精确地确定目标的空间位置和运动状态。
综上所述,坐标计算方法是地理信息系统和地理定位领域的重要内容,它涉及到经纬度坐标、平面坐标和空间坐标等多个方面。
通过合理地运用各种坐标计算方法,我们可以更准确地确定地理位置,进行地图绘制,进行导航定位等工作。
希望本文介绍的内容能够帮助大家更好地理解和应用坐标计算方法,提高工作效率和精度。
总结:本文介绍了坐标计算方法在地理信息系统和地理定位领域的重要性,以及经纬度坐标计算、平面坐标计算和空间坐标计算三种常见的坐标计算方法。
通过合理地运用这些方法,可以更准确地确定地理位置,进行地图绘制,进行导航定位等工作。
经纬度计算方位角

原文地址:根据两点的经纬度求方位角和距离,等作者:多乎哉不多也多亦不多乎实乃少也最近自己做的一个小东西要用到经纬度方面的计算,查遍中文网页见到的要么基本上是一帮惜字如金装大爷的“砖家”,要么就是像贴膏药一样,啪,一大堆代码往上一贴,一点说明都没有,让人看不懂,有的看了半天看懂了,结果他用的公式要么有使用局限(但没有半点声明)要么根本就是个错的。
所以现在将自己几天学习来的在这里总结一下,方便后来人少走弯路。
这里主要解决四个问题:1、已知两点经纬度,求一点相对于另一点方位角;2、已知两点经纬度,求两点间距离;3、已知一点经纬度及与另一点距离和方位角,求另一点经纬度;4、问题1与问题2的简化算法。
注:简化算法的运算量和对系统的运算精度要求都大大降低,但只在短距离内(高纬地区建议10km以下)可以保证精度,除简化算法之外的算法可适用于地球上任意两点。
这里只是出于便于理解的目的来解释“原理”,具体到不同的编程环境还要自己做化简和注意单位。
在求算前我们先对符号及单位进行约定:此处设定求B相对于A的方位角,即A为当前位置,B为目标位置Aj:A点经度Aw:A点纬度Bj:B点经度Bw:B点纬度北纬为正,南纬为负;东经为正,西经为负经纬度使用度,DDD.DDDDDD°,非度分或度分秒。
度数未加说明均采用角度制R:地球平均半径Azimuth:方位角,以真北为0度起点,由东向南向西顺时针旋转360度A,B,C表示球面上的三个点及球面上“弧线”在该点处所夹的角a,b,c表示A,B,C三点的对“弧”两端点与地心连线所夹的角(其实这里解释成ABC三点对弧的弧度更方便)O为球心L为AB两点间球面距离(注:因我考虑欠缺,没有注意字母C大小写较难分辨,所以此处提醒读者在后面的公式中注意C的大小写。
)一、方位角的求算已知A、B两点经纬度,如何求出B相对于A的方位角?——————————————————卖关子环节,可选择性跳过———————————————————说到这里,人们或许会首先想因为地球是个球体,如果AB两点足够近(如相距1Km)可以当做平面三角形已知两临边求夹角,把两点的经度、纬度各自做差,差值作为两边的长度,再用反正切函数一算就得到了角度,似乎很有道理,但是如果将计算结果与实际测量值做比较,就会发现比较大的误差,而这种误差在某些地区甚至能用普通的量角器测量出来,其实这已经不叫误差,而叫错误了。
日期、时间和当地经纬度计算太阳天顶角和方位角

根据日期、时间和当地经纬度计算太阳天顶角和方位角的原理转载中国气象科学研究院王炳忠研究员编写的《太阳辐射计算讲座》。
在开展野外试验的时候,经常需要知道当时的太阳天顶角和方位角,比如测量地物反射率时,需要知道太阳天顶角,来选择恰当的灰板反射率曲线。
进行地物BRDF测量时,更需要知道太阳天顶角。
太阳天顶角和方位角可以通过经纬仪实地测量得到,但是经纬仪携带不便。
只要知道当地经纬度和时间,就可以根据下文的原理,计算得到当时当地的太阳天顶角和方位角。
1日地距离地球绕太阳公转的轨道是椭圆形的,太阳位于椭圆两焦点中的一个。
发自太阳到达地球表面的辐射能量与日地间距离的平方成反比,因此,一个准确的日地距离值R就变得十分重要了。
日地平均距离R0,又称天文单位,1天文单位=1.496×108km或者,更准确地讲等于149597890±500km。
日地距离的最小值(或称近日点)为0.983天文单位,其日期大约在1月3日;而其最大值(或称远日点)为1.017天文单位,日期大约在7月4日。
地球处于日地平均距离的日期为4月4日和10月5日。
由于日地距离对于任何一年的任何一天都是精确已知的,所以这个距离可用一个数学表达式表述。
为了避免日地距离用具体长度计量单位表示过于冗长,一般均以其与日地平均距离比值的平方表示,即E R=(r/r0)2,也有的表达式用的是其倒数,即r0/r,这并无实质区别,只是在使用时,需要注意,不可混淆。
我们得到的数学表达式为E R=1.000423+0.032359sinθ+0.000086sin2θ-0.008349cosθ+0.000115cos2θ(1)式中θ称日角,即θ=2πt/365.2422(2)这里t又由两部分组成,即t=N-N0(3)式中N为积日,所谓积日,就是日期在年内的顺序号,例如,1月1日其积日为1,平年12月31日的积日为365,闰年则为366,等等。
N0=79.6764+0.2422×(年份-1985)-INT〔(年份-1985)/4〕(4)2太阳赤纬角地球绕太阳公转的轨道平面称黄道面,而地球的自转轴称极轴。
经纬度计算距离计算公式

经纬度计算距离计算公式经纬度计算距离计算公式1. Haversine公式Haversine公式是一种常用的计算地球上两点间距离的公式。
它基于球面三角学原理,通过经纬度计算出两点间的弧长,然后转换为实际距离。
公式:d=2rarcsin(√sin2((θ2−θ1)/2)+cos(θ1)⋅cos(θ2)⋅sin2((λ2−λ1)/2))其中,d为两点间距离,r为地球半径,θ1和λ1为第一个点的纬度和经度,θ2和λ2为第二个点的纬度和经度。
示例:假设第一个点的坐标为(, -),第二个点的坐标为(, -)。
采用地球半径r=6371千米(常用值),代入Haversine公式进行计算,可以得到两点之间的距离为约千米。
2. Vincenty公式Vincenty公式是一种更为精确的计算地球上两点间距离的公式。
它考虑了地球的椭球形状,通过迭代计算,可以得到更准确的结果。
公式:a=r1⋅r2⋅sin(θ2−θ1)2+r2⋅r3⋅sin(θ3−θ2)2b=r1⋅r2⋅cos(θ2−θ1)−r2⋅r3cos(θ3−θ2)c=r1⋅r3⋅cos(θ3−θ1)−r2⋅r3⋅cos(θ3−θ2) d=arctan(r2⋅r3sin(θ3−θ2)⋅cos(θ3−θ1)r1⋅r2⋅sin(θ2−θ1)⋅cos(θ3−θ2)+r1⋅r3⋅sin(θ3−θ1)⋅cos(θ2−θ1))latitude=θ1+c⋅cos(A)−b⋅sin(A)r2λ2=λ1+d r2d=r1⋅arcsin(sin(θ2−θ1)⋅cos(θ3)⋅sin(θ2−θ1)+cos(θ1)⋅cos(θ2)⋅sin2(λ3−λ2))其中,d为两点间距离,r1、r2、r3分别为两个点的纬度、经度对应的椭球半径,θ1和λ1为第一个点的纬度和经度,θ2和λ2为第二个点的纬度和经度,θ3和λ3为两点连线在球面上的方位角,A为初始猜测的方位角。
示例:以第一个点的坐标为(, -),第二个点的坐标为(, -),根据Vincenty公式进行计算,可以得到两点之间的距离为约千米。
计算经纬度、距离、方位角

计算经纬度、距离、⽅位⾓1.根据两点经纬度计算其间距离,发现有3种公式,结果区别不是很⼤。
2.根据⼀点的经纬度与到另外⼀点的距离、⽅位⾓,计算另⼀点的经纬度,误差不是很⼤。
1package com.zhs.util;23/**4 *5 * 计算经纬度、距离、⽅位⾓6 *7 * @author lillian.he8 * @time 2016-06-029 * */10public class CalculationLogLatDistance {11/**12 * 地球⾚道半径(km)13 * */14public final static double EARTH_RADIUS = 6378.137;15/**16 * 地球每度的弧长(km)17 * */18public final static double EARTH_ARC = 111.199;1920/**21 * 转化为弧度(rad)22 * */23public static double rad(double d) {24return d * Math.PI / 180.0;25 }2627/**28 * 求两经纬度距离29 *30 * @param lon131 * 第⼀点的经度32 * @param lat133 * 第⼀点的纬度34 * @param lon235 * 第⼆点的经度36 * @param lat237 * 第⼆点的纬度38 * @return两点距离,单位km39 * */40public static double GetDistanceOne(double lon1, double lat1, double lon2,41double lat2) {42double r1 = rad(lat1);43double r2 = rad(lon1);44double a = rad(lat2);45double b = rad(lon2);46double s = Math.acos(Math.cos(r1) * Math.cos(a) * Math.cos(r2 - b)47 + Math.sin(r1) * Math.sin(a))48 * EARTH_RADIUS;49return s;50 }5152/**53 * 求两经纬度距离(google maps源码中)54 *55 * @param lon156 * 第⼀点的经度57 * @param lat158 * 第⼀点的纬度59 * @param lon260 * 第⼆点的经度61 * @param lat262 * 第⼆点的纬度63 * @return两点距离,单位km64 * */65public static double GetDistanceTwo(double lon1, double lat1, double lon2,66double lat2) {67double radLat1 = rad(lat1);68double radLat2 = rad(lat2);69double a = radLat1 - radLat2;70double b = rad(lon1) - rad(lon2);71double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2)72 + Math.cos(radLat1) * Math.cos(radLat2)73 * Math.pow(Math.sin(b / 2), 2)));74 s = s * EARTH_RADIUS;75return s;76 }7778/**79 * 求两经纬度距离80 *81 * @param lon182 * 第⼀点的经度83 * @param lat184 * 第⼀点的纬度85 * @param lon286 * 第⼆点的经度87 * @param lat288 * 第⼆点的纬度89 * @return两点距离,单位km90 * */91public static double GetDistanceThree(double lon1, double lat1,92double lon2, double lat2) {93double radLat1 = rad(lat1);94double radLat2 = rad(lat2);95double radLon1 = rad(lon1);96double radLon2 = rad(lon2);97if (radLat1 < 0)98 radLat1 = Math.PI / 2 + Math.abs(radLat1);// south99if (radLat1 > 0)100 radLat1 = Math.PI / 2 - Math.abs(radLat1);// north101if (radLon1 < 0)102 radLon1 = Math.PI * 2 - Math.abs(radLon1);// west103if (radLat2 < 0)104 radLat2 = Math.PI / 2 + Math.abs(radLat2);// south105if (radLat2 > 0)106 radLat2 = Math.PI / 2 - Math.abs(radLat2);// north107if (radLon2 < 0)108 radLon2 = Math.PI * 2 - Math.abs(radLon2);// west109double x1 = Math.cos(radLon1) * Math.sin(radLat1);110double y1 = Math.sin(radLon1) * Math.sin(radLat1);111double z1 = Math.cos(radLat1);112113double x2 = Math.cos(radLon2) * Math.sin(radLat2);114double y2 = Math.sin(radLon2) * Math.sin(radLat2);115double z2 = Math.cos(radLat2);116117double d = Math.pow((x1 - x2), 2) + Math.pow((y1 - y2), 2)118 + Math.pow((z1 - z2), 2);119//// 余弦定理求夹⾓120// double theta = Math.acos((2 - d) / 2);121122 d = Math.pow(EARTH_RADIUS, 2) * d;123////余弦定理求夹⾓124double theta = Math.acos((2 * Math.pow(EARTH_RADIUS, 2) - d) 125 / (2 * Math.pow(EARTH_RADIUS, 2)));126127double dist = theta * EARTH_RADIUS;128return dist;129 }130131/**132 * 求两经纬度⽅向⾓133 *134 * @param lon1135 * 第⼀点的经度136 * @param lat1137 * 第⼀点的纬度138 * @param lon2139 * 第⼆点的经度140 * @param lat2141 * 第⼆点的纬度142 * @return⽅位⾓,⾓度(单位:°)143 * */144public static double GetAzimuth(double lon1, double lat1, double lon2, 145double lat2) {146 lat1 = rad(lat1);147 lat2 = rad(lat2);148 lon1 = rad(lon1);149 lon2 = rad(lon2);150double azimuth = Math.sin(lat1) * Math.sin(lat2) + Math.cos(lat1) 151 * Math.cos(lat2) * Math.cos(lon2 - lon1);152 azimuth = Math.sqrt(1 - azimuth * azimuth);153 azimuth = Math.cos(lat2) * Math.sin(lon2 - lon1) / azimuth;154 azimuth = Math.asin(azimuth) * 180 / Math.PI;155if (Double.isNaN(azimuth)) {156if (lon1 < lon2) {157 azimuth = 90.0;158 } else {159 azimuth = 270.0;160 }161 }162return azimuth;163 }164165/**166 * 已知⼀点经纬度A,和与另⼀点B的距离和⽅位⾓,求B的经纬度(计算结果有误) 167 *168 * @param lon1169 * A的经度170 * @param lat1171 * A的纬度172 * @param distance173 * AB距离(单位:⽶)174 * @param azimuth175 * AB⽅位⾓176 * @return B的经纬度177 * */178public static String GetOtherPoint(double lon1, double lat1,179double distance, double azimuth) {180 azimuth = rad(azimuth);181double ab = distance / EARTH_ARC;// AB间弧线长182 ab = rad(ab);183double Lat = Math.asin(Math.sin(lat1) * Math.cos(ab) + Math.cos(lat1)184 * Math.sin(ab) * Math.cos(azimuth));185double Lon = lon1186 + Math.asin(Math.sin(azimuth) * Math.sin(ab) / Math.cos(Lat));187 System.out.println(Lon + "," + Lat);188189double a = Math.acos(Math.cos(90 - lon1) * Math.cos(ab)190 + Math.sin(90 - lon1) * Math.sin(ab) * Math.cos(azimuth));191double C = Math.asin(Math.sin(ab) * Math.sin(azimuth) / Math.sin(a));192 System.out.println("c=" + C);193double lon2 = lon1 + C;194double lat2 = 90 - a;195return lon2 + "," + lat2;196 }197198/**199 * 已知⼀点经纬度A,和与另⼀点B的距离和⽅位⾓,求B的经纬度200 *201 * @param lon1202 * A的经度203 * @param lat1204 * A的纬度205 * @param distance206 * AB距离(单位:⽶)207 * @param azimuth208 * AB⽅位⾓209 * @return B的经纬度210 * */211public static String ConvertDistanceToLogLat(double lng1, double lat1,212double distance, double azimuth) {213 azimuth = rad(azimuth);214// 将距离转换成经度的计算公式215double lon = lng1 + (distance * Math.sin(azimuth))216 / (EARTH_ARC * Math.cos(rad(lat1)));217// 将距离转换成纬度的计算公式218double lat = lat1 + (distance * Math.cos(azimuth)) / EARTH_ARC;219return lon + "," + lat;220 }221222public static void main(String[] args) {223double lon1 = 121.469156;224double lat1 = 31.232307;225double lon2 = 121.469156;226double lat2 = 31.233205;227double distance = GetDistanceTwo(lon1, lat1, lon2, lat2);228double azimuth = GetAzimuth(lon1, lat1, lon2, lat2);229 System.out.println("经纬度为(" + lon1 + "," + lat1 + ")的点与经纬度为(" + lon2 230 + "," + lat2 + ")相距:" + distance + "千⽶," + "⽅位⾓:" + azimuth 231 + "°");232 System.out.println("距经纬度为(" + lon1 + "," + lat1 + ")的点" + distance 233 + "千⽶,⽅位⾓为" + azimuth + "°的另⼀点经纬度为("234 + ConvertDistanceToLogLat(lon1, lat1, distance, azimuth) + ")");235 }236 }。
gis计算点经纬度的公式

gis计算点经纬度的公式GIS计算点经纬度的公式在地理信息系统(GIS)中,经纬度是非常重要的地理坐标表示方式。
计算点的经纬度是GIS中的一项基本操作,以下是相关的公式和解释说明。
1. 经纬度的定义经度表示一个地点相对于参考子午线(如格林尼治子午线)的东、西位置,用度(°)来表示。
东经用正数表示,西经用负数表示。
纬度表示一个地点相对于赤道的北、南位置,同样用度(°)来表示。
北纬用正数表示,南纬用负数表示。
2. 经纬度的范围经度的合理范围为-180°至+180°,纬度的合理范围为-90°至+90°。
3. 经纬度的表示方式经纬度一般以以下方式表示:纬度在前,经度在后,用逗号(,)隔开。
例如,北京的经度°,纬度°可以表示为:, 。
4. 根据距离和方位角计算新点的经纬度如果已知一个点的经纬度、距离和方位角,可以通过计算得到另一个点的经纬度。
以下是用于计算的公式:纬度角度增量(Δφ)的计算公式:Δφ = Δd × sin(θ)其中,Δφ为纬度角度增量,Δd为距离,θ为方位角。
经度角度增量(Δλ)的计算公式:Δλ = (Δd × cos(φ)) / R其中,Δλ为经度角度增量,φ为起始点的纬度,Δd为距离,R为地球半径。
新点的纬度(φ₂)的计算公式:φ₂ = φ₁ + Δφ其中,φ₂为新点的纬度,φ₁为起始点的纬度,Δφ为纬度角度增量。
新点的经度(λ₂)的计算公式:λ₂ = λ₁ + Δλ其中,λ₂为新点的经度,λ₁为起始点的经度,Δλ为经度角度增量。
5. 举例说明以北京为例,已知其经度为°,纬度为°。
假设有一个航线长度为1000千米,方位角为45°,我们可以通过上述公式计算出新点的经纬度。
首先,计算纬度角度增量Δφ:Δφ = 1000 × sin(45°) ≈然后,计算经度角度增量Δλ:Δλ = (1000 × cos(°)) / R根据地球半径的取值不同,Δλ的计算结果会有所差别。
经纬度计算距离公式
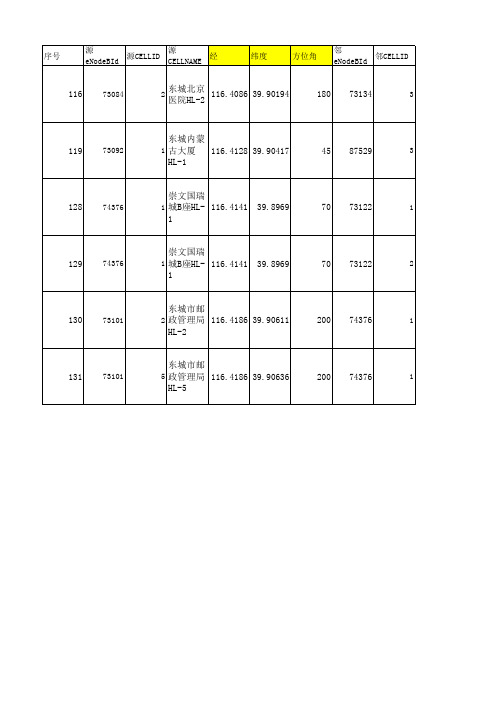
相距330
1月5日
米,方位 角相差20
°内
双向
叶秀全 张密密
相距330
1月5日
米,方位 角相差90
°内
双向
叶秀全 张密密
相距1100
1月5日
米,方位 角相差90
°内
双向
叶秀全 张密密
相距1100
1月5日
米,方位 角相差90
°内
40 加邻区
305.89
110 加邻区
1023.83 -130 加邻区
1044.67 -130 加邻区
单项/双向 调整原因
修改发起 人
操作人
双向
高慧
张密密
修改时间 漏配原因
相距720
12月16日
米,方位 角相差90
°内
双向
高慧
张密密
相距290
12月16日
米,方位 角相差
100°内
双向
叶秀全 张密密
城B座HL- 116.4141 39.8969
70 HL-2-崇 #N/A
1
文国瑞城
B座HL-1
东城市邮
崇文国瑞
政管理局
城B座HL- 116.4141 39.8969
70 HL-5-崇 #N/A
1
文国瑞城
B座HL-1
距离
方位角差 增加/删除
683.25
60 加邻区
261.56
265 加邻区
305.89
古大厦 310 HL-1-东
城同仁医
#N/A
院HL-3
崇文国瑞
崇文普仁 医院HL-1
116.4136 39.89389
城B座HL110 1-崇文普
大地方位角计算

大地方位角计算
在我们的日常生活中,往往会出现需要确定物体所在位置的情况。
对于一个物体在地球上的位置,我们可以用经度和纬度来描述,但是
对于一个观察者来说,需要确定的是物体相对于自己的位置,这时就
需要用到大地方位角。
大地方位角又叫地平方位角,是观察者所处位置与天空物体之间
的相对方位关系。
它是从南点开始,沿着地平线上的顺时针方向来测
量的,取值范围在0度到360度之间。
计算大地方位角需要用到观察者的经纬度以及物体的赤道坐标,
赤道坐标是根据星体在天球上的位置所确定的一个系统,用赤经和赤
纬来描述。
在计算过程中,需要将经纬度和赤道坐标转换为地平坐标系中的
坐标,可以通过如下公式进行转换:
sin(azimuth) = -sin(H)*cos(δ)/cos(φ)
cos(azimuth) = (sin(δ) - sin(φ)*sin(φ)) /
(cos(φ)*cos(δ))
其中,H为物体与本地子午圈距离(单位为度),δ为物体的赤
纬(单位为度),φ为观察者的纬度(单位为度),azimuth即为大
地方位角(单位为度)。
通过计算得到物体的大地方位角后,我们就能够确定物体相对于观察者的方位关系。
比如在夜晚观测星空时,可以通过大地方位角来确定某个星体的方位,从而更好地进行观测。
总的来说,掌握大地方位角的计算方法对于进行天文观测和导航定位都有很大的帮助,希望大家能够学好这个知识点,加强自己的观测能力和定位技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经纬度计算距离和方位角方位角(azimuthangle):从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角,叫方位角。
(一)方位角的种类由于每点都有真北、磁北和坐标纵线北三种不同的指北方向线,因此,从某点到某一目标,就有三种不同方位角。
(1)真方位角。
某点指向北极的方向线叫真北方向线,而经线,也叫真子午线。
由真子午线方向的北端起,顺时针量到直线间的夹角,称为该直线的真方位角,一般用A表示。
通常在精密测量中使用。
(2)磁方位角。
地球是一个大磁体,地球的磁极位置是不断变化的,某点指向磁北极的方向线叫磁北方向线,也叫磁子午线。
在地形图南、北图廓上的磁南、磁北两点间的直线,为该图的磁子午线。
由磁子午线方向的北端起,顺时针量至直线间的夹角,称为该直线的磁方位角,用Am表示。
(3)坐标方位角。
由坐标纵轴方向的北端起,顺时针量到直线间的夹角,称为该直线的坐标方位角,常简称方位角,用a表示。
方位角在测绘、地质与地球物理勘探、航空、航海、炮兵射击及部队行进时等,都广泛使用。
不同的方位角可以相互换算。
军事应用:为了计算方便精确,方位角的单位不用度,用密位作单位。
换算作:360度=6000密位。
(二)三种方位角之间的关系因标准方向选择的不同,使得一条直线有不同的方位角。
同一直线的三种方位角之间的关系为:A=Am+δA=a+γa=Am+δ-γ(三)坐标方位角的推算1.正、反坐标方位角每条直线段都有两个端点,若直线段从起点1到终点2为直线的前进方向,则在起点1处的坐标方位角a12称为直线12的正方位角,在终点2处的坐标方位角a21称为直线12的反方位角。
a反=a正±180°式中,当a正<180°时,上式用加180°;当a正>180°时,上式用减180°。
2.坐标方位角的推算实际工作中并不需要测定每条直线的坐标方位角,而是通过与已知坐标方位角的直线连测后,推算出各直线的坐标方位角。
因β2在推算路线前进方向的右侧,该转折角称为右角;β3在推算路线前进方向的左侧,该转折角称为左角。
从而可归纳出推算坐标方位角的一般公式为:a前=a后+180°+β左a前=a后+180°-β右如果计算的结果大于360?,应减去360°,为负值,则加上360?。
天文学方位角定义:在地平坐标系中,通过南点、北点的地平经圈称子午圈。
子午圈被天顶、天底等分为两个180°的半圆。
以北点为中点的半个圆弧,称为子圈,以南点为中点的半个圆弧,称为午圈。
在地平坐标系中,午圈所起的作用相当于本初子午线在地理坐标系中的作用,是地平经度(方位)度量的起始面。
方位即地平经度,是一种两面角,即午圈所在的平面与通过天体所在的地平经圈平面的夹角,以午圈所在的平面为起始面,按顺时针方向度量。
方位的度量亦可在地平圈上进行,以南点为起算点,由南点开始按顺时针方向计量。
方位的大小变化范围为0°~360°,南点为0°,西点为90°,北点为180°,东点为270°。
上述这种方位度量是在天文学中所用的方法。
磁偏角简介沈括在《梦溪笔谈》中记载与验证了磁针“常微偏东、不全南也”的磁偏角现象,比西欧记录早400年。
英国人罗伯特·诺曼(Robert Norman)发现一根磁针用绳子在半中间吊起来,跟水平形成一偏角,他将这称为磁偏角。
1581年,他在自己的《新奇的吸引力》一书中发表了他的发现。
各个地方的磁偏角不同,而且,由于磁极也处在运动之中,某一地点磁偏角会随之间而改变。
许多海洋动物可以感应到磁偏角并利用它来识途。
磁偏角是磁场强度矢量的水平投影与正北方向之间的夹角,变即磁子午线与地理子午线之间的夹角。
如果磁场强度矢量的指向偏向正北方向以东称东偏,偏向正北方向以西称西偏。
地磁要素磁偏角可以用磁偏测量仪测出来。
各地的磁倾角不同,在地磁极处,磁偏角是90度。
磁偏角的度数是测量出来的,不是计算出来的。
在绘图时,将此前对磁偏角的实际测量值标在地图(特别是海图,普通地图标磁偏角的少)上。
当然,磁偏角的变化呈现出一定的规律,我国东部地区磁偏角为西偏,甘肃酒泉以西多为东偏。
地磁极是接近南极和北极的,但并不和南极、北极重合,一个约在北纬72°、西经96°处;一个约在南纬70°、东经150°处。
磁北极距地理北极大约相差1500km. 在一天中磁北极的位置也是不停的变动,它的轨迹大致为一椭圆形,磁北极平均每天向北以40m。
磁北极大约于2005年进入俄罗斯境内。
东经25度地区,磁偏角在1-2度之间;北纬25度以上地区,磁偏角大于2度;若在西经低纬度地区,磁偏角是5-20度;西经45度以上,磁偏角为25-50度,在我国,正常情况下,磁偏角最大可达6度,一般情况为2-3度。
地图的方向:上北、下南、左西、右东是大多数地图的方向,但这可不是通用原则,如果地图上有方向标,可以通过方向标了解到这些。
磁偏角还是不断有规律变化的,地图上的磁偏角只是测图时的磁偏角(磁北比真北偏左,加上磁偏角;磁北比真北偏右,减去磁偏角;在我国一般是加上)。
使用地图本身所注的磁偏角要注意出版年限,地图太老误差较大。
计算方法关于用经纬度计算距离:地球赤道上环绕地球一周走一圈共40075.04公里,而@一圈分成360°,而每1°(度)有60,每一度一秒在赤道上的长度计算如下:=111.31955km40075.04km/360°111.31955km/60=1.8553258km=1855.3m 而每一分又有60秒,每一秒就代表1855.3m/60=30.92m 任意两点距离计算公式为十cosΦAcosΦBcos(λB—λA)]} 其中d=111.12cos{1/[sinΦAsinΦBA点经度,纬度分别为λA和ΦA,B点的经度、纬度分别为λB和ΦB,d为距离。
至于比例尺计算就不废话了也许上面的冗长又深奥的回复让你大头了吧? 简单地说,也就是 1.不同的地方地磁偏角也不同! 2.正常情况下,我国磁偏角最大可达6度,一般情况为2-3度 3.东经25度地区,磁偏角在1-2度之间;北纬25度以上地区,磁偏角大于2度;若在西经低纬度地区,磁偏角是5-20度;西经45度以上,磁偏角为25-50度,在我国,正常情况下,磁偏角最大可达6度,一般情况为2-3度。
地球磁场是在不断变化的。
它有长期变化和短期变化。
地球磁场的短期变化部分,即上述的地球变化磁场;除去短期变化部分,便是地球基本磁场,即上述的偶极磁场。
地磁要素的长期变化,来源于地球内部的物质运动。
它首先表现为地磁场的向西漂移。
例如,0°磁偏线与赤道的交点,近400 年来已西移95°。
其次,磁场强度有稳定的衰减,近百年来,基本磁场强度衰减了5%。
如果照此速度继续衰减下去,那么,基本磁场将会在 2 千年后消失。
另外,磁极也在移动,如地磁北极的纬度逐年递增0°.004;其经度每年向西增加0°.007。
关于分类地磁要素的短期变化,来源于电离层及太阳活动的影响,变化形态比较复杂,分平静变化和干扰变化。
平静变化是经常性和周期性的变化,有太阳日变化、太阴日变化和季节变化。
来自太阳的带电粒子,影响地球大气电离层的状况,从而造成各地的磁场以太阳日为周期的变化。
地磁强度的水平分量的太阳日变化,可达0. 03,约为水平分量的0. 5 %;地磁偏角的变化可达10′。
月——0.04μT球对于地球大气的潮汐作用,使得一部分大气以太阴日为周期,运行于地球各部分之间。
这种变化包括大气电离层的变化,因而造成各地磁场以太阴日为周期的变化。
它的变化幅度很小,磁场强度水平分量的变幅只有千分之几μ T,约为水平分量的0. 05%;地磁偏角的变幅不到40″。
太阳直射点的南北移动,以及随之而来的太阳辐射能在地球上的分布的季节变化,造成地磁要素的太阳日变化的幅度因季节而变化。
一般地说,夏季太阳日变化的幅度较大,冬季较小。
地磁要素的十扰变化要复杂得多。
小的干扰多半是区域性的,次数频繁,变幅很小。
大的干扰是全球性的,次数较少,平均每年10 次左右,变化幅度较大。
特大的干扰称磁暴。
磁暴发生时,磁针不安地扰动不止;在几小时到几日内,磁场强度的变化可达十分之几甚至几个μT。
磁暴的发生与太阳活动直接相关。
来自太阳的高能粒子,不仅干扰地球磁场,同时破坏大气电离层结构,中断无线电通讯,高纬度地区出现极光。
中国各地磁偏角地名磁偏角漠河11°00' 齐齐哈尔9°54' 哈尔滨9°39' 长春8°53' 满洲里8°40' 沈阳7°44' 旅大6°35' 北京5°50' 天津5°30' 济南5°01' 呼和浩特4°36' 徐州4°27' 上海4°26' 太原4°11' 包头4°03' 南京4°00' 合肥3°52' 郑州3°50' 杭州3°50' 许昌3°40' 九江3°03' 武汉2°54' 南昌2°48' 银川2°35' 台北2°32' 西安2°29' 长沙2°14' 赣州2°01' 衡阳1°56' 厦门1°50' 兰州1°44' 重庆1°34' 遵义1°26' 西宁1°22' 桂林1°22' 贵阳1°17' 成都1°16' 广州1°09' 柳州1°08' 东沙群岛1°05' 昆明1°00' 南宁0°50' 湛江0°44' 凭祥0°39' 海口0°29' 拉萨0°21'珠穆朗玛0°19' 西沙群岛0°10' 曾母暗沙0°24'(东)南沙群岛0°35'(东)乌鲁木齐2°44'(东)地质罗盘的使用方法地质罗盘地质罗盘又称“袖珍经纬仪”。
