2010MATLAB及控制系统仿真_1
控制系统MATLAB仿真基础

系统仿真§ 4.1控制系统的数学模型1、传递函数模型(tranfer function)2、零极点增益模型(zero-pole-gain)3、状态空间模型(state-space)4、动态结构图(Simulink结构图)一、传递函数模型(transfer fcn-----tf)1、传递函数模型的形式传函定义:在零初始条件下,系统输出量的拉氏变换C(S)与输入量的拉氏变换R(S)之比。
C(S) b1S m+b2S m-1+…+b mG(S)=----------- =- --------------------------------R(S) a1S n + a2S n-1 +…+ a nnum(S)= ------------den(S)2、在MATLAB命令中的输入形式在MATLAB环境中,可直接用分子分母多项式系数构成的两个向量num、den表示系统: num = [b1, b2, ..., b m];den = [a1, a2, ..., a n];注:1)将系统的分子分母多项式的系数按降幂的方式以向量的形式输入两个变量,中间缺项的用0补齐,不能遗漏。
2)num、den是任意两个变量名,用户可以用其他任意的变量名来输入系数向量。
3)当系统种含有几个传函时,输入MATLAB命令状态下可用n1,d1;n2,d2…….。
4)给变量num,den赋值时用的是方括号;方括号内每个系数分隔开用空格或逗号;num,den方括号间用的是分号。
3、函数命令tf( )在MATLAB中,用函数命令tf( )来建立控制系统的传函模型,或者将零极点增益模型、状态空间模型转换为传函模型。
tf( )函数命令的调用格式为:圆括号中的逗号不能用空格来代替sys = tf ( num, den ) [G= tf ( num, den )]其中,函数的返回变量sys或G 为连续系统的传函模型;函数输入参量num和den分别为系统的分子分母多项式的系数向量。
应用MATLAB控制系统仿真

01
根据系统性能要求,设计比例、积分、微分控制器参数,优化
系统性能。
状态反馈控制器设计
02
通过状态反馈控制器设计,实现系统的最优控制。
鲁棒控制器设计
03
针对不确定性系统,设计鲁棒控制器,提高系统对参数变化的
适应性。
04
控制系统仿真的动态行为,通过建立和求解微 分方程来模拟系统的动态响应。
性能等。
05
Matlab控制系统仿真实 例
一阶系统仿真
总结词:简单模拟
详细描述:一阶系统是最简 单的控制系统,其动态行为 可以用一个一阶微分方程描 述。在Matlab中,可以使用 `tf`函数创建一个一阶传递函 数模型,然后使用`step`函 数进行仿真。
总结词:性能分析
详细描述:通过仿真,可以 观察一阶系统的响应曲线, 包括超调和调节时间等性能 指标。使用Matlab的绘图功 能,可以直观地展示系统的 动态行为。
THANKS FOR WATCHING
感谢您的观看
适用于模拟数字控制系统、采样控制系统等。
实时仿真
01
在实际硬件上实时模拟控制系统的动态行为,通过将
控制算法嵌入到实际控制系统中进行实时仿真。
02
使用Matlab中的`real-time workshop`等工具箱进
行建模和仿真,可以方便地实现实时仿真。
03
适用于模拟实际控制系统、验证控制算法的正确性和
实时仿真
Matlab支持实时仿真,可以在实 际硬件上运行控制算法,进行系 统测试。
02
控制系统数学模型
线性时不变系统
线性时不变系统(LTI)是指系统的输出与输入之间的关系 可以用线性常数来描述的系统。在控制系统中,LTI系统是 最常见的系统类型之一。
Matlab控制系统仿真

一. 控制系统的模型与转换目前大多数控制系统的分析设计方法都要求系统的模型已知。
所以,控制系统的数学模型是控制系统分析和设计的基础。
获得数学模型的方法有两种:一种是从已知的物理规律出发,用数学推导的方法建立系统的数学模型,另外一种就是利用试验数据拟合。
前一种方法称为系统的物理建模方法,而后者称为系统辨识,两者各有优势和适用场合。
一般的分析研究中将控制系统分为连续系统和离散系统,描述连线性连续系统常用的方式是传递函数(传递函数矩阵)和状态空间模型,相应的离散系统可以用离散传递函数和离散状态方程表示。
各种模型之间还可以进行相互转换。
1.1 连续线性系统的数学模型连续线性系统一般可以用传递函数描述,也可以用状态方程描述。
前者是经典控制的常用模型,而后者是现代控制理论的基础。
它们是描述同一个系统的不同描述方式。
除此之外,还可以用零极点的形式表示连续线性系统模型。
本章着重介绍这些数学模型,并侧重介绍这些模型在控制系统的Matlab 环境下的表示方法。
高阶线性常微分方程通常是描述线性连续系统的最传统的方法,其基本表达式为:)()()()()()()()(111101111t u b dt t du b dt t u d b dt t u d b t y a dt t dy a dt t y d a dt t y d m m m m m m n n n n n n ++++=++++------ 其中)(t u ,)(t y 分别是控制系统的输入和输出信号,他们均是时间t 的函数,n 是系统的阶次。
利用Laplace 引入的积分变换(拉氏变换),可以在另初始条件下对该微分方程进行变换,得到控制系统的传递函数:nn n n m m m m a s a s a s b s b s b s b s G ++++++++=----1111110)( (n m ≤) 传递函数的引入使得控制系统的研究变得简单,它是控制理论中线性系统模型的一种主要描述方式。
基于MATLAB控制系统的仿真与应用毕业设计论文

基于MATLAB控制系统的仿真与应用毕业设计论文目录一、内容概括 (2)1. 研究背景和意义 (3)2. 国内外研究现状 (4)3. 研究目的和内容 (5)二、MATLAB控制系统仿真基础 (7)三、控制系统建模 (8)1. 控制系统模型概述 (10)2. MATLAB建模方法 (11)3. 系统模型的验证与校正 (12)四、控制系统性能分析 (14)1. 稳定性分析 (14)2. 响应性能分析 (16)3. 误差性能分析 (17)五、基于MATLAB控制系统的设计与应用实例分析 (19)1. 控制系统设计要求与方案选择 (20)2. 基于MATLAB的控制系统设计流程 (22)3. 实例一 (23)4. 实例二 (25)六、优化算法在控制系统中的应用及MATLAB实现 (26)1. 优化算法概述及其在控制系统中的应用价值 (28)2. 优化算法介绍及MATLAB实现方法 (29)3. 基于MATLAB的优化算法在控制系统中的实践应用案例及分析对比研究31一、内容概括本论文旨在探讨基于MATLAB控制系统的仿真与应用,通过对控制系统进行深入的理论分析和实际应用研究,提出一种有效的控制系统设计方案,并通过实验验证其正确性和有效性。
本文对控制系统的基本理论进行了详细的阐述,包括控制系统的定义、分类、性能指标以及设计方法。
我们以一个具体的控制系统为例,对其进行分析和设计。
在这个过程中,我们运用MATLAB软件作为主要的仿真工具,对控制系统的稳定性、动态响应、鲁棒性等方面进行了全面的仿真分析。
在完成理论分析和实际设计之后,我们进一步研究了基于MATLAB 的控制系统仿真方法。
通过对仿真模型的建立、仿真参数的选择以及仿真结果的分析,我们提出了一种高效的仿真策略。
我们将所设计的控制系统应用于实际场景中,通过实验数据验证了所提出方案的有效性和可行性。
本论文通过理论与实践相结合的方法,深入探讨了基于MATLAB 控制系统的仿真与应用。
实验一 指导书 MATLAB 在控制系统模型建立与仿真中的应用
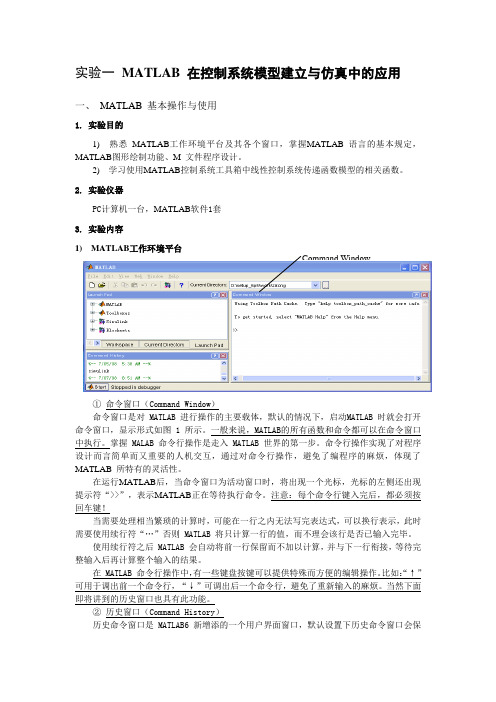
实验一MATLAB 在控制系统模型建立与仿真中的应用一、MATLAB 基本操作与使用1. 实验目的1) 熟悉MATLAB工作环境平台及其各个窗口,掌握MATLAB 语言的基本规定,MATLAB图形绘制功能、M 文件程序设计。
2) 学习使用MATLAB控制系统工具箱中线性控制系统传递函数模型的相关函数。
2. 实验仪器PC计算机一台,MATLAB软件1套3. 实验内容1) MATLAB工作环境平台Command Window图1 在英文Windows 平台上的MATLAB6.5 MATLAB工作平台①命令窗口(Command Window)命令窗口是对 MATLAB 进行操作的主要载体,默认的情况下,启动MATLAB 时就会打开命令窗口,显示形式如图 1 所示。
一般来说,MATLAB的所有函数和命令都可以在命令窗口中执行。
掌握 MALAB 命令行操作是走入 MATLAB 世界的第一步。
命令行操作实现了对程序设计而言简单而又重要的人机交互,通过对命令行操作,避免了编程序的麻烦,体现了MATLAB所特有的灵活性。
在运行MATLAB后,当命令窗口为活动窗口时,将出现一个光标,光标的左侧还出现提示符“>>”,表示MATLAB正在等待执行命令。
注意:每个命令行键入完后,都必须按回车键!当需要处理相当繁琐的计算时,可能在一行之内无法写完表达式,可以换行表示,此时需要使用续行符“…”否则 MATLAB 将只计算一行的值,而不理会该行是否已输入完毕。
使用续行符之后 MATLAB 会自动将前一行保留而不加以计算,并与下一行衔接,等待完整输入后再计算整个输入的结果。
在 MATLAB 命令行操作中,有一些键盘按键可以提供特殊而方便的编辑操作。
比如:“↑”可用于调出前一个命令行,“↓”可调出后一个命令行,避免了重新输入的麻烦。
当然下面即将讲到的历史窗口也具有此功能。
②历史窗口(Command History)历史命令窗口是 MATLAB6 新增添的一个用户界面窗口,默认设置下历史命令窗口会保留自安装时起所有命令的历史记录,并标明使用时间,以方便使用者的查询。
MATLAB控制系统各种仿真例题(包括simulink解法)

一、 控制系统的模型与转换1. 请将下面的传递函数模型输入到matlab 环境。
]52)1)[(2(24)(32233++++++=s s s s s s s G )99.02.0)(1(568.0)(22+--+=z z z z z H ,T=0.1s >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5));GTransfer function:s^3 + 4 s + 2------------------------------------------------------s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3>> num=[1 0 0.56];den=conv([1 -1],[1 -0.2 0.99]);H=tf(num,den,'Ts',0.1)Transfer function:z^2 + 0.56-----------------------------z^3 - 1.2 z^2 + 1.19 z - 0.992. 请将下面的零极点模型输入到matlab 环境。
请求出上述模型的零极点,并绘制其位置。
)1)(6)(5()1)(1(8)(22+++-+++=s s s s j s j s s G )2.8()6.2)(2.3()(1511-++=----z z z z z H ,T=0.05s>>z=[-1-j -1+j];p=[0 0 -5 -6 -j j];G=zpk(z,p,8)Zero/pole/gain:8 (s^2 + 2s + 2)--------------------------s^2 (s+5) (s+6) (s^2 + 1)>>pzmap(G)>> z=[0 0 0 0 0 -1/3.2 -1/2.6];p=[1/8.2];H=zpk(z,p,1,'Ts',0.05)Zero/pole/gain:z^5 (z+0.3125) (z+0.3846)-------------------------(z-0.122)Sampling time: 0.05>>pzmap (H )num=[0,7.1570,-6.4875 ];den=[1,-2.2326,1.7641,-0.4966];sysd=tf(num,den,0.05,'variable','z^-1')Transfer function:7.157 z^-1 - 6.487 z^-2-----------------------------------------1 - 2.233 z^-1 + 1.764 z^-2 - 0.4966 z^-3Sampling time: 0.05二、 线性系统分析1. 请分析下面传递函数模型的稳定性。
2010MATLAB及控制系统仿真_2_matlab_2

主讲教师:姜萍
1.2.2 MATLAB基本设计
1、变量
变量在使用前不需定义维数和大小。
命名规则:以字母打头、不含标点符号、最多不超过 19个字符,区分字母的大小写,如X1、 x1、 a、 A 等。另外要避免使用特殊变量。 变量可按需要定义成全局变量和局部变量:
• 典型 M函数文件的结构如下 :
函数申明行:位于函数文件的首行,以关键字 function 开头,函数名以及函数的输入输出变量都在 这一行被定义。 笫一注释行:紧随函数申明行之后以%开头笫一注释行。 该行供lookfor关键词查询和 help在线帮助使用 在线帮助文本区 :笫一注释行及其之后的连续以%开 头的所有注释行构成整个在线帮助文本。 编写和修改记录:与在线帮助文本区相隔一个“空”行, 也以%开头,标志编写及修改该M文件的作者日期等 。 函数体:为清晰起见,与前面的注释以“空”行相隔。 例:函数myguass.m 调用testguass.m
函数文件中定义的变量为局部变量,在函数内有效。
全局变量的定义: global 变量名
避免使用特殊变量:
特殊变量 取值 NaN 不定量 如0/0
ans
pi eps flops inf
结果的缺省变量名
圆周率 计算机的最小数 浮点运算数 无穷大 如1/0
ij
nargin
基本虚数单位
函数的输入变量数目
nargout 函数的输出变量数目 realmin 最小的可用正实数
矩阵块操作
可进行元素更改、插入子块、提取子块、重排子块、 扩大子块等。
冒号“:”的应用:代表全部
冒号“:”在列标位置:代表全部的列 冒号“:”在行标位置:代表全部的行
控制系统MATLAB仿真实验指导书

实验5. 控制理论仿真实验1 控制系统的建模一、实验目的1.学习在命令窗口建立系统模型的方法;2.学习如何在三种模型之间相互转换;3.学习如何用仿真工具建模。
二、相关知识1.传递函数模型设连续系统的传递函数为:nn n n m m m m a s a s a s a b s b s b s b s den s num s G ++++++++==----11101110)()()( 设离散系统的传递函数为:nn n n m m m m a z a z a z a b z b z b z b z den z num z G ++++++++==----11101110)()()( 则在中,都可直接用分子/分母多项式系数构成的两个向量与构成的矢量组[]表示系统,即],,,[10m b b b=],,,[10n a a a建立控制系统的传递函数模型(对象)的函数为 (),调用格式为:()()()()返回的变量为连续系统的传递函数模型。
()返回的变量为离散系统的传递函数模型,为采样周期,当1或[]时,系统的采样周期未定义。
()将任意的控制系统对象转换成传递函数模型。
离散系统的传递函数的表达式还有一种表示为1-z 的形式(即形式),转换为形式的函数命令为(),调用格式为:()()()函数用来建立一个采样时间未指定的形式传递函数。
()函数用来建立一个采样时间为的形式传递函数。
2.零极点增益模型设连续系统的零极点增益模型传递函数为:)())(()())(()(2121n m p s p s p s z s z s z s k s G ------= 设离散系统的零极点增益模型传递函数为:)())(()())(()(1010n m p z p z p z z z z z z z k z G ------= 则在中,都可直接用向量构成的矢量组[]表示系统,即],,[10m z z z],,[10n p p p][k在中,用函数()来建立控制系统的零极点增益模型,调用格式为:()()()()返回的变量为连续系统的零极点增益模型。
MATLAB语言与控制系统仿真_参考题答案_第3章

3.5 MATLAB 绘图实训3.5.1 实训目的1.学会MATLAB 绘图的基本知识;2.掌握MATLAB 子图绘制、图形注释、图形编辑等基本方法;3.学会通过MATLAB 绘图解决一些实际问题;4.练习二维、三维绘图的多种绘图方式,了解图形的修饰方法;5.学会制作简单的MATLAB 动画。
图3-46 炮弹发射示意图3.5.2 实训内容1. 炮弹发射问题〔1炮弹发射的基础知识炮弹以角度α射出的行程是时间的函数,可以分解为水平距离)(t x 和垂直距离)(t y 。
)cos()(0αtv t x = %水平方向的行程; 205.0)sin()(gt tv t y -=α %垂直方向的行程;其中,0v 是初速度;g 是重力加速度,为9.82m/s ;t 是时间。
〔2炮弹发射程序举例:分析以下程序以及图3-47各个图形的实际意义。
a=pi/4; v0=300; g=9.8;t=0:0.01:50; x=t*v0*cos<a>;y=t*v0*sin<a>-0.5*g*t.^2;subplot<221>;plot<t,x>;grid;title<‘时间-水平位移曲线'>; subplot<222>;plot<t,y>;grid;title<‘时间-垂直位移曲线'>; subplot<223>;plot<x,y>;grid;title<‘水平位移-垂直位移曲线'>; subplot<224>;plot<y,x>;grid;title<‘垂直位移-水平位移曲线'>; 图3-4745角发射曲线 〔3编程解决炮弹发射问题①假设在水平地面上以垂直于水平面的角度向上发射炮弹,即发射角90=α,假设初速度分别为[310,290,270]m/s,试绘制时间-垂直位移曲线,编程求取最高射程;绘图要求:◆ 标题设为"炮弹垂直发射问题";◆ 在图上通过添加文本的方式表明初速度; ◆ 在x 轴标注"时间";◆ 在y 轴上标注"垂直距离"; ◆ 添加网格线;◆ 将310m/s 的曲线改为线粗为2的红色实线; ◆ 将290m/s 的曲线改为线粗为3的绿色点划线;◆ 将270m/s 的曲线改为线粗为2的蓝色长点划线;a=pi/2; v1=310; g=9.8;t=0:0.01:50; x1=t*v1*cos<a>;y1=t*v1*sin<a>-0.5*g*t.^2;plot<t,y1>;grid; title<'炮弹垂直发射问题'>; xlabel<'时间'>; ylabel<'垂直距离'>; hold on; v2=290;x2=t*v2*cos<a>;y2=t*v2*sin<a>-0.5*g*t.^2; plot<t,y2>; v3=270;x3=t*v3*cos<a>;y3=t*v3*sin<a>-0.5*g*t.^2; plot<t,y3>;zgsc=[max<y1>; max<y2>; max<y3>] %三次发射的最高射程 运行结果如下: zgsc =1.0e+003 * 4.9031 4.29083.7194最高射程分别为:4903.1米,4290.8米,3719.4米。
《MATLAB及系统仿真》2010年课程简介

《MATLAB及系统仿真》2010年课程简介第一篇:《MATLAB及系统仿真》2010年课程简介课程编号:216317课程名称:MATLAB及系统仿真学分:2学分总学时:32学时其中授课学时:20学时上机学时:12学时先修课程:C语言、线性代数、信号与系统、通信原理开课部门:计算机与通信学院课程内容:本课程要求学生掌握:MATLAB基本语句结构,矩阵的基本运算,控制语句,M文件和M函数的编写与调用,绘图功能,数学函数库的调用,SIMULINK仿真。
通过本课程的学习,学生应能够在MATLAB 环境下解决常见的数学问题和工程问题,并且能利用MATLAB软件对通信系统里的各种调制和解调过程进行仿真分析。
选课对象:通信工程,计算机科学与技术、电子信息技术第二篇:电子信息MATLAB系统仿真与设计电子信息系统仿真与设计课程设计报告设计课题: 油价变化系统的模型姓名:学院: 机电与信息工程学院专业: 电子信息科学与技术班级: 09级 2班学号: 日期 2010-2011第三学期指导教师: 李光明张军蕊山东大学威海分校信息工程学院建模:1背景设某一星期的油价为p,其中n表示年份,它与上一星期的油价、油价升值速率以及新增资源所能满足的个体数目之间的动力学方程由如下的差分方程所描述:从此差分方程中可以看出,此油价变化系统为一非线性离散系统。
如果设油价初始值、油价升值速率、新增资源所能满足的个体数目,要求建立此油价动态变化系统的系统模型,并分析油价在未来100个星期内之间的变化趋势。
2 建立油价变化系统的模型(1)Discrete模块库Unit Delay模块:其主要功能是将输入信号延迟一个采样时间,它是离散系统的差分方程描述以及离散系统仿真的基础。
在仿真时只要设置延迟模块的初始值便可计算系统输出。
(2)Discrete模块库Zero-Order Hold模块:其主要功能是对信号进行零阶保持。
使用Simulink对离散系统进行仿真时,单位延迟是Discrete模块库中的Unit Delay模块来完成的。
控制系统仿真 计算机辅助设计 matlab simulink 2010版PPT 100510基传递函数模型的控制系统设计-Bode图法

Bode图法基本要求为了获得比较高的开环增益及满意的相对稳定性,必须改变开环频率特性响应曲线的形状,这主要体现为:1)在低频区和中频区增益应该足够大,2)且中频区的对数幅频特性的斜率应为-20dB/dec,并有足够的带宽,以保证适当的相角裕度;3)而在高频区,要使增益尽可能地衰减下来,以便使高频噪声的影响达到最小。
Bode图设计方法的频域指标为。
K c ,,ωγ基本思路在Bode图中的对数频率特性的低频区表征了闭环系统的稳态特性,中频区表征了系统的相对稳定性和响应性,而高频区表征了系统的抗干扰特性。
在大多数实际情况中,校正问题实质上是在稳态精度和相对稳定性之间取折衷的问题。
05101520M a g n i t u d e (d B )10-11010110210310403060P h a s e (d e g )Bode DiagramFrequency (rad/sec)串联超前校正描述:超前校正装置的主要作用是改变系统开环Bode 图中曲线的形状来产生足够大的超前相角,以补偿原系统中过大的相角滞后,从而提高系统的相对稳定性,致使闭环系统的频带扩宽。
设超前校正装置的传递函数为TsaTss G c ++=11)(1>a mm a φφsin 1sin 1−+=alg 10mφ串联超前校正Bode图的几何设计方法1.根据稳态指标要求确定未校正系统的型别和开环增益,并绘制Bode图;2.根据动态指标要求确定超前校正装置的参数;第一种情形:给出了的要求值(1)确定超前校正所应提供的最大超前相角(2)求解的值)20~5( ,)](180[0°°°=+′∠+−=εεωγφc m j G amm a φφsin 1sin 1−+=a j G m lg 10)(lg 200−=′ω(确定)m ωc ω)(0s G ′如果,说明值选择合理,能够满足相角裕度要求,否则按如下方法重新选择的值:c m ωω≈a a 2)(1c j G a ω′=a j G c lg 10)(lg 200−=′ω11sin 1+−=′−a a mφm mφφ≥′若,则正确,否则重新调整值。
2010MATLAB及控制系统仿真_matlab_3

例p50_1.m
五.数据的输入输出
1、数据不多时,可由FileSave Workspace As保存 工作空间当前所有变量(保存为***.mat)。类似地, 由File Import Data 可装载数据。 2、save、load命令:以二进制格式保存和读入 save 将工作空间所有变量以二进制格式存入matlab.mat save filename 将所有变量以二进制格式存入filename.mat save filename x y z 将变量x y z以二进制格式存入
Characteristic Polynomials 特征多项式
The poly function also computes the coefficients of the characteristic polynomial of a matrix. A = [1.2 3 -0.9; 5 1.75 6; 9 0 1]; poly(A) ans = 1.0000 -3.9500 -1.8500 -163.2750 The roots of this polynomial, computed with roots, are the characteristic roots, or eigenvalues, of the matrix A. (Use eig to compute the eigenvalues of a matrix directly.) A = [1.2 3 -0.9; 5 1.75 6; 9 0 1]; r1= roots(poly(A)) r2= eig(A)
function g=myguass(a)
%The Solution of Linear Systems AX=B by Guassian Elimination %input a=[A|B] is augmented matrix %output g=x is the result %It was edited in Mar 20,2002 and modified in May 3,2003 by JP
MATLAB与控制系统仿真实验指导书

《MATLAB与控制系统仿真》实验指导书(2011年第一版)西安邮电学院自动化学院2011年6月目录前言 (1)MATLAB语言实验项目 (3)实验一熟悉MATLAB集成环境与基础运算 (3)实验二 MATLAB的基本计算 (7)实验三 MATLAB图形系统 (9)实验四 MATLAB程序设计 (13)实验五 MATLAB函数文件 (15)实验六MATLAB数据处理与多项式计算 (17)实验七 SIMULINK仿真实验 (21)前言MATLAB 产品家族是美国 MathWorks公司开发的用于概念设计、算法开发、建模仿真、实时实现的理想的集成环境。
是矩阵实验室(Matrix Laboratory)的简称,是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和SIMULINK两大部分。
MATLAB由于其完整的专业体系和先进的设计开发思路,使得 MATLAB 在多种领域都有广阔的应用空间,特别是在科学计算、建模仿真以及系统工程的设计开发上已经成为行业内的首选设计工具,它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
MATLAB软件工具在自动化专业、测控技术与仪器和电气工程及其自动化等专业的本科生学习中,经常用来计算、仿真和设计,尤其是MATLAB软件的仿真功能,能使学生对所学知识有更加深入的理解和分析。
《MATLAB与控制系统仿真》课程,和《自动控制原理》、《现代控制理论》、《数字信号处理》、《电力电子技术》等重要的专业课程相互支撑、相辅相成,同时也有利于学生完成课程设计和毕业设计等实践教学环节。
自动控制原理MATLAB仿真实验指导书10-10解析

应)。本次实验从分析系统的性能指标出发,给出了在
MATLAB环境下获取系统时域响应和分析系统
的动态性能和稳态性能的方法。
用 MATLAB求系统的瞬态响应时, 将传递函数的分子、 分母多项式的系数分别以 s 的降幂排列写
为两个数组 num、 den。由于控制系统分子的阶次 m一般小于其分母的阶次 n,所以 num中的数组元
即可得到系统的单位阶跃响应曲线在 0-10s 间的部分,如图 2-2 所示。
脉冲响应
① 求系统脉冲响应的指令有:
impulse (num,den)
时间向量 t 的范围由软件自动设定,阶跃响应曲线随即绘出
impulse (num,den,t)
时间向量 t 的范围可以由人工给定(例如 t=0:0.1:10 )
R1 100 K , R2 200K , C1 1uf
其对应的模拟电路及 SIMULINK 图形如图 1-4 所示。
图 1-4 惯性环节的模拟电路及 SIMULINK 图形
3.积分环节 (I) 的传递函数为
G(s) Z 2 Z1
1 R1C1 s
1 R1 100K ,C1 1uf
0.1s
其对应的模拟电路及 SIMULINK 图形如图 1-5 所示。
5.比例 +微分环节( PD)的传递函数为
G( s)
Z2
Z1
R2 R1
( R1C1 s
1)
(0.1s 1)
R1 R2 100K , C1 10uf
C2
其对应的模拟电路及 SIMULINK 图形如图 1-7 所示。
C1 0.01uf
图 1-7 比例 +微分环节的模拟电路及 6.比例 +积分环节( PI )的传递函数为
MATLAB控制系统的仿真
C R
x1 x2
0 1
L
u
L
y [1
0]
x1 x2
[0]u
•
x Ax bu
y CT x du
• 没有良好的计算工具前:系统建立、变换、分析、设 计、绘图等相当复杂。
• MATLAB控制系统软件包以面向对象的数据结构为基 础,提供了大量的控制工程计算、设计库函数,可以 方便地用于控制系统设计、分析和建模。
Transfer function:
s+1 ------------s^2 + 5 s + 6
Matlab与系统仿真
22
应用——系统稳定性判断
系统稳定性判据: 对于连续时间系统,如果闭环极点全部在S平面左半平面,
则系统是稳定的;
若连续时间系统的全部零/极点都位于S左半平面, 则系统是——最小相位系统。
Matlab与系统仿真
38
4.2 动态特性和时域分析函数
(一)动态特性和时域分析函数表 (二)常用函数说明 (三)例子
Matlab与系统仿真
39
(一)动态特性和时域分析函数表 ——与系统的零极点有关的函数
表8.6前部分p263
Matlab与系统仿真
40
——与系统的时域分析有关的函数
Matlab与系统仿真
Matlab与系统仿真
8
4.1 控制工具箱中的LTI对象
Linear Time Invariable
(一)控制系统模型的建立 (二)模型的简单组合 (三)连续系统和采样系统变换(*略)
Matlab与系统仿真
9
(一)控制系统模型的建立
➢ MATLAB规定3种LTI子对象:
• Tf 对象—— 传递函数模型 • zpk 对象—— 零极增益模型 • ss 对象—— 状态空间模型
MATLAB与系统仿真实验手册2010

MATLAB与控制系统仿真实验指导书河北大学电子信息工程学院20010年9月目录实验一MATLAB基本操作与基本运算 (1)实验二M文件及数值积分仿真方法设计 (3)实验三MATLAB 的图形绘制 (4)实验四函数文件设计和控制系统模型的描述 (6)实验五控制系统的分析与设计 (7)实验六连续系统离散化仿真方法设计 (8)实验七SIMULINK 仿真 (9)实验八SIMULINK 应用进阶 (10)附录MATLAB常用函数 (12)实验一MATLAB基本操作与基本运算一、实验目的及要求:1.熟悉MATLAB6.5的开发环境;2.掌握MATLAB6.5的一些常用命令;3.掌握矩阵、变量、表达式的输入方法及各种基本运算。
二、实验内容:1.熟悉MATLAB6的开发环境:①MATLAB的各种窗口:命令窗口、命令历史窗口、启动平台窗口、工作空间窗口、当前路径窗口。
图1 MA TLAB界面窗口②路径的设置:建立自己的文件夹,加入到MA TLAB路径中,并保存。
设置当前路径,以方便文件管理。
③改变命令窗口数据的显示格式>> format short>> format long然后键入特殊变量:pi (圆周率),比较显示结果。
2.掌握MATLAB 常用命令>> who %列出工作空间中变量>> whos %列出工作空间中变量,同时包括变量详细信息 >>save test %将工作空间中变量存储到test.mat 文件中 >>load test %从test.mat 文件中读取变量到工作空间中 >>clear %清除工作空间中变量>>help 函数名 %对所选函数的功能、调用格式及相关函数给出说明 >>lookfor %查找具有某种功能的函数但却不知道该函数的准确名称如: lookfor Lyapunov 可列出与Lyapunov 有关的所有函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
主讲教师:姜萍
请大家先看一组图片
神州飞船模拟训练仓
模拟飞船监控室
模拟器是航天员进行航天飞行程序及操作训练的 专业技术训练场所,通过航天飞行模拟器的视景 软件把在太空中运行时飞行操作程序及异常处理 在地面进行仿真模拟,从而使航天员熟悉和适应 在太空的生活。 航天员们要在与真实飞船相同的训练模拟器上 按照航天飞行程序进行模拟飞行,从进入飞船到 发射升空、轨道运行及返回、着陆,熟悉太空往 返的全过程。
第一章 概述
第一节 计算机仿真的基本概念 第二节 计算机仿真的发展 本课程主要讲授内容
第一章 概述
计算机仿真技术是一门利用计算机软件模拟 实际环境进行科学实验的技术。 它具有经济、可靠、实用、安全、灵活、可 多次重复使用的优点,已成为对许多复杂系统进 行分析、设计、试验、评估的必不可少的手段。 计算机仿真技术是以数学理论为基础,以计 算机和各种物理设施为工具,利用系统模型对实 际的或设想的系统进行实验仿真研究的一门综合 技术。
可将不易建模的部分以实物形式参与仿真,从而避 免了建模的困难; 进一步检验系统数学模型的正确性和仿真的精确性
可检验构成真实系统的某些实物部件乃至整个系统 的性能指标及可靠性,准确调整系统的参数和控制规律。 在航空航天、电力系统等研究中十分重要。
C、按仿真时钟
与实际时钟 T 的比例分
T
(2)数字计算机仿真: 数字计算机仿真是基于数值计算原理的仿真, 它的主要工具是:数字计算机和相应的数字仿真 软件。 应用数字计算机仿真的首要步骤是必须把数 学模型离散化,因为数字计算机本身就是一个离 散系统。 (3)混合计算机仿真: 由模拟计算机和数字计算机通过一套A/D、 D/A接口组成,具有模拟计算机的快速性和数字 计算机的高精度和灵活性的优点。
(2)数学仿真: 首先建立系统的数学模型,并将数学模型转 换成仿真计算模型,通过仿真模型的运行达到研 究系统运行的目的。 特点是方便灵活、经济、通用,发展迅速。
(3)物理-数学(半实物)仿真 将系统的一部分用数学模型描述,用计算机 运行仿真计算模型,另一部分以实物(或物理模 型)方式引入仿真回路。 半实物仿真特点:
2、计算机仿真的三个基本要素: 系统、模型与计算机。
系统
数学模型建立 仿真实验
模型
计算机
仿真模型建立
计算机仿真的三要素及三个基本活动
3、系统仿真的三个基本活动
①数学模型建立:实际上是一个模型辩识的过程。 所建模型常常是忽略了一些次要因素的简化模型。
②仿真模型建立:即是设计一种算法,以使系统 模型能被计算机接受并能在计算机上运行。显然, 由于在算法设计上存在着误差,所以仿真模型对 于实际系统将是一个二次简化模型。 ③仿真实验:即是对模型的运算。需要设计一个 合理的、服务于系统研究的仿真软件。
4、系统分类
①静态系统和动态系统;
②确定系统和随机系统;
③连续系统和离散系统;
④其它分类: 线性系统和非线性系统;定常系统和时变系 统;单变量系统和多变量系统等。
二、系统模型
是系统某种特定性能的一种抽象形式。 模型的表达形式有物理模型和数学模型两类。
数学模型是系统的某种特征本质的数学表达式, 是用数学公式来描述所研究的客观对象或系统中 的某一方面的问题。
(3)混合系统仿真: 当系统的数学模型是由上述两类模型混合 构成时,称为混合系统仿真。其仿真方法是将 上述两类方法综合于一体。 (4)系统动力学仿真: 当对象的数学模型是用系统动力学方程式来 描述时,该系统的仿真称为系统动力学仿真。
B、按参与仿真的模型种类分:
(1)物理仿真 按照实际系统的性质构造系统的物理模型进 行试验研究,直观形象、逼真;但投资大、周期 长,又不易修改。
第一节 计算机仿真的基本概念
系统仿真是通过系统模型的试验去研究一个 已存在或正在研究设计的系统的过程。它不是系 统原型的复现,而是按研究的侧重面或实际需要 对系统简化提炼,以利于抓住问题的本质或主要 矛盾。 用物理模型来进行仿真一般称为物理仿真, 它主要是应用几何相似及环境条件相似来进行。
而由数学模型在计算机上进行实验研究的 仿真一般则称为数字仿真。又称计算机仿真。
2.仿真试验的执行控制; 3.资料结果的分析、显示及文档化; 4.模型、程序、数据、图形的存储、检索与管理
系统仿真技术是从50年代诞生的。近三十年来,随 着计算机技术的飞速发展,出现了许多优秀的计算机应 用软件,还有专用的仿真语言。
仿真软件发展的三个阶段:
1、软件包阶段 :一般由Basic语言或Fortran语言编成 某类仿真的软件包。仿真的早期工作集中在软件包的编 写上。 2、交互式语言阶段:60年代---70年代出现了一些专用 的仿真语言,虽然有了人机交互,但应用起来仍不是十 分方便,必须有严格的格式 。 3、面向对象的程序环境阶段:采用Visual C++等语言 开发出实用的、具有良好人机交互功能的软件。还有一
具备在不同工况条件下分析和改进机组运行操作方 案、方式,并加以优化的能力和手段。
具备对岗位运行人员、热控检修岗位和技术管理人 员进行定期轮训的能力,可作为上岗、晋升前的考 核手段,客观地反映被培训人员的实际操作能力和 分析判断能力,提供相应手段。 具备对机组的控制系统进行仿真研究以选择最佳的 控制方案和动态整定参数的能力和手段。 具备对机组的故障原因和结果进行分析,以便改进 运行操作和制定反事故对策的能力和手段。
4、系统仿真的分类
A、按系统的模量随时间连续变化的系统的仿真研 究,数学模型包括:连续模型(微分方程)、离 散时间模型(差分方程)及连续—离散混合模型。 仿真方法主要是微(差)分方程的数值求解方法。
(2)离散事件系统仿真: 对系统状态只在一些时间点上由随机事件的驱 动而发生变化的系统进行仿真称为离散事件系统 仿真。其数学模型多用流程图或网络图来描述。
5、系统仿真的一般步骤
①根据仿真目的确定仿真方案 ②建立系统的数学模型(一次建模); ③转换成仿真模型(二次建模); ④编写仿真程序; ⑤进行仿真实验:运行仿真程序,在不同的初始条件和参数下,
对系统进行反复分析和研究。
⑥仿真结果分析:对结果分析处理,修正数学模型、仿真模型
及程序。
实际系统 根据仿真目的确定仿真方案 系统描述 建立数学模型(一次建模) 建立仿真模型(二次建模) 编写仿真程序 进行仿真实验,分析结果 仿真结果是否达到要求 N Y 结束仿真 修改程序 Y 程序不正确 N Y 建模不正确 N Y 方案不正确 修改模型 修改方案
一、系统
1、定义:由相互联系、相互制约、相互依存 的若干部分结合在一起形成的具体特定功能和运 动规律的有机整体。 2、系统的三要素:
①实体——组成系统的具体对象;
②属性——实体所具有的每一种有效特性(状 态和参数); ③活动——系统内对象随时间推移而发生的状 态变化。
3、系统的性质 ①整体性 ②相关性 ③ 目的性
公司位于保定国家高新技术开发区火炬产业园内,主导产品—— 电力系统仿真机的技术水平一直处于国内领先、国际先进的水平。
公司自1989年研制成功我国第一台300MW火电厂全仿真机以来, 先后承接160多个火电厂、变电以及飞船的仿真项目,产品遍布 全国26个省、市、自治区,在国内的电力系统仿真领域,市场占 有率位居第一。 其中公司研制开发的国内第一台300MW火电机组仿真机,荣获 了全国十大科技成就奖、电力部科技进步一等奖。 利用公司技术开发的载人航天飞船训练模拟器助“神舟5号”飞 船飞天成功,为我国载人航天事业做出了重要贡献。
虚拟场景 Virtual Environment
第二节 计算机仿真的发展
因为仿真是一门综合性技术学科,它涉及 到系统分析、控制理论、计算方法和计算机技术 等,所以它的发展也是与其它技术的发展紧密相 连。主要看一下仿真软件的发展,一般分成三个 阶段。
系统仿真软件是一类面向仿真用途的计算机 应用软件,其主要功能: 1.模型描述的规范与处理;
6、系统仿真的应用
①系统分析与设计; ②系统理论研究; ③专职人员培训; 系统仿真的目的及其作用: 优化设计 经济性 安全性: 预测性
建模与仿真技术已成功地应用于航空航天、信息、 生物、材料、能源、先进制造等高新技术领域和 工业、农业、商业、教育、军事、交通、社会、 经济、医学、生命、生活服务和娱乐等众多领域 的系统论证、试验、分析、维护、辅助决策及人 员训练、教育等。 建模仿真技术已作为人们认识、改造客观世界的 重要手段。
大型火力发电厂
火电仿真机
火电仿真机
火电仿真机
火电仿真机
对电厂生产全过程进行仿真;额定参数的正常启动、停机; 滑参数的启动、运行、停机;机组带基本负荷的运行特性; 机组带调峰负荷的运行特性;冷态、温态及热态、极热态启 动运行;故障跳闸和各种操作以及其他扰动下的暂态特性。 所有的模型符合物理学、数学和电力科学的基本定律,而不 是用预定的关系曲线来代替,任何近似的假设和计算方法, 都不应该降低对模型逼真度的要求。 所有设备或系统的模型都能良好的反映其动态过程,具有较 高的静态精确度,能够实现对仿真对象的连续、实时的仿真, 仿真效果与实际机组运行工况一致,仿真环境应使受训人员 在感觉上视觉上与被仿真机组环境一致。 完善的运行人员培训功能,提供向受训人员展现正常和故障 情况的实际现场运行状态,有效地提高运行人员的专业知识、 操作技能、应变能力和熟练程度,使运行人员经培训后能熟 练地掌握机组启停过程和维持正常运行的全部操作,学会处 理异常、紧急事故的技能,提高实际操作能力和分析判断能 力,训练应急处理能力,确保机组安全、经济运行。
些专用软件,MATLAB就是其中一个成功的范例。
工程实际对仿真技术提出的新需求:
1、减少模型的开发时间; 2、提高模型建立的精度和实验的精度; 3、改进人与人、人与计算机的通信。 半个多世纪来,现代建模与仿真技术在各 类应用需求的牵引及有关学科技术的推动下, 已经发展形成了综合性的专业技术体系。在新 的世纪,建模与仿真技术正向现代化——网络 化、虚拟化、智能化、协同化方向发展。
