{品质管理品质知识}初三四次教学质量检测试卷
初三第四次教学质量检测试卷

初三第四次教学质量检测试卷
第一部分:选择题
1.学生应该以什么样的态度对待每一次教学质量检测? A. 随便应付 B. 认真对待 C. 玩手机 D. 睡觉
2.请简述对于学生来说,教学质量检测的意义是什么? A. 无所谓 B. 检测学习成果 C. 无聊 D. 得到高分
第二部分:填空题
3.课堂上,学生应该_______认真听讲,积极思考。
4.在准备考试时,学生应当做好复习________,勤奋努力。
第三部分:简答题
5.请简述你在这次教学质量检测中遇到的困难,并描述你是如何克服这些困难的。
6.你认为在学生学习过程中,老师和家长应该起到什么样的作用?请阐述你的观点。
第四部分:求解题
7.如果一个学生在数学、英语和物理三门课程中分别获得了80分、85分和88分,求这个学生的平均成绩。
8.假设教学质量检测总分为150分,小明获得了120分,求小明本次检测的得分率。
答题注意事项:
1.请确保在规定的时间内完成所有题目。
2.请将答案填写在指定的答题区域内。
3.答案写清楚、字迹工整。
九年级数学上学期第四次质量检测考试试题 试题

石化教育中心九年级第四次质量检测考试制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日数学试题考生注意:1、考试时间是是120分钟。
2、全卷一共分三局部,总分120分3、请将答案写在答题卡相应的位置上。
一、选择题:〔每一小题3分,一共30分〕 1.-5的相反数是〔 〕A.5B.-5C.51 512.不等式:-2x<4的解集是〔 〕A.x<-2B.x>-2C.x>2D.x<23.一个正方形的面积为28,那么它的边长为〔 〕A .3到4之间B 。
4到5之间C 。
5到6之间D 。
6到7之间。
4。
以下运算中,①x 2+x 3=2x 5②(x 2)3=x 6③30×2=5 ④-1-︳-5︳+3=8 ⑤1÷2·21=1正确的个数是〔 〕A.1B. 2C. 3D.4.5.百货大楼店庆期间,服装柜台推出全场打八折的优惠活动,持贵宾卡可在八折根底上继续小雨妈妈持贵宾卡买了标价为10000元的商品,一共节了2800元。
那么贵宾卡又享受的折数是〔A ,7.2折B 。
8折C 。
9折D 。
9.5折. 6.函数y=31+x 的自变量x 的取值范围是〔 〕 A .x.>-3 B. x<-3 C.x ≥-3 D. x ≠-3.7.如图,在矩形ABCD 中,AB=2,BC=1。
动点P 从点B 出发,沿道路B---C---D 做匀速运动,ABP 的面积S 与点P 的运动路程x 之间函数图象大致是〔 〕A8.如图左以下图,把一张长方形纸片沿EF 折叠后,点D ,E 分别落在D 1,C 1的位置,假设∠FE 那么∠AED 1等于〔 〕A .700B 。
650C 。
500D 。
250。
B 1A 1BOA D 1C 1E BDCF A9.如图右上图,∠AOB=900,∠B=300,△A 1OB 1可以看做是由△AOB 绕点O 顺时针旋转α角度得假设点A 1在AB 上,那么旋转角α的大小可以是〔 〕A .300B 。
九年级数学上学期第四次质检试卷(含解析) 新人教版

2015-2016学年辽宁省盘锦一中九年级(上)第四次质检数学试卷一、选择题1.实数,,,2.020020002,π,,tan30°,无理数有()个.A.2 B.3 C.4 D.52.明天数学课要学“勾股定理”.小敏在“百度”搜索引擎中输入“勾股定理”,能搜索到与之相关的结果个数约为12 500 000,这个数用科学记数法表示为()A.1.25×105B.1.25×106C.1.25×107D.1.25×1083.已知:如图,∠A0B的两边 0A、0B均为平面反光镜,∠A OB=35°,一束平行于OB的光线RQ经0A上的Q点反射后,反射光线与0B交于点P,则∠QPB的度数是()A.60° B.70° C.80° D.85°4.主视图、左视图、俯视图分别是下列三个图形的物体是()A.B.C.D.5.一个多边形的内角和是900°,则这个多边形的边数是()A.6 B.7 C.8 D.96.若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=cx+a的图象可能是()A.B.C.D.7.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为()A.4,5 B.5,4 C.4,4 D.5,58.如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是()A.B.C.D.二、填空题9.不等式组的所有整数解的和为.10.服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利50%,则这款服装每件的进价是.11.关于方程x2﹣ax﹣2a=0的两根的平方和是5,则a的值是.12.一个扇形的圆心角是120°,面积为3π cm2,那么这个扇形的弧长为cm.13.如图,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为.14.如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为.15.如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为.16.一组数据为0,3,8,15,24,…则第n个数据表示为.三、解答题17.先化简再求值:÷(a﹣2﹣),其中a=2+.18.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:(1)本次参加抽样调查的居民有多少人?(2)将两幅不完整的图补充完整;(3)若居民区有8000人,请估计爱吃D粽的人数.19.如图,四边形ABCD中,∠ADC=∠B=90°,∠C=60°,AD=,E为DC中点,AE∥BC.求BC的长和四边形ABCD的面积.20.在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, 1.7)21.已知反比例函数y=(m为常数)的图象经过点A(﹣1,6).(1)求m的值;(2)如图,过点A作直线AC与函数y=的图象交于点B,与x轴交于点C,且AB=2BC,求点C 的坐标.22.某商店经销一种T恤衫,4月上旬的营业额为2000元,为扩大销售量,4月中旬该商店对这种T恤衫打9折销售(原销售价格的90%),结果销售量增加20件,营业额增加700元.求该种T恤衫4月上旬的销售价格.23.如图所示,△ABC中,AC=BC,以BC为直径作⊙O交AB于点D,交AC于点G,作直线DF⊥AC交AC于点F,交CB的延长线于点E.(1)求证:直线EF四⊙O的切线;(2)若BC=6,AB=4,求DE的长.24.某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:(1)求张强返回时的速度;(2)妈妈比按原速返回提前多少分钟到家?(3)请直接写出张强与妈妈何时相距1000米?25.已知:在Rt△ABC,∠ABC=90°,∠C=60°,现将一个足够大的直角三角板的顶点P放在斜边AC上.(1)设三角板的两直角边分别交边AB、BC于点M、N.①当点P是AC的中点时,分别作PE⊥AB于点E,PF⊥BC于点F,得到图1,写出图中的一对全等三角形;②在①的条件下,写出与△PEM相似的三角形,并直接写出PN与PM的数量关系.(2)移动点P,使AP=2CP,将三角板绕点P旋转,设旋转过程中三角板的两直角边分别交边AB、BC于点M、N(PM不与边AB垂直,PN不与边BC垂直);或者三角板的两直角边分别交边AB、BC的延长线与点M、N.③请在备用图中画出图形,判断PM与PN的数量关系,并选择其中一种图形证明你的结论;④在③的条件下,当△PCN是等腰三角形时,若BC=3cm,则线段BN的长是.26.如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.(1)求抛物线解析式及点D坐标;(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平行四边形,求此时点P的坐标;(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.2015-2016学年辽宁省盘锦一中九年级(上)第四次质检数学试卷参考答案与试题解析一、选择题1.实数,,,2.020020002,π,,tan30°,无理数有()个.A.2 B.3 C.4 D.5【考点】无理数;特殊角的三角函数值.【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【解答】解:,π,tan30°是无理数,故选:B.【点评】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.2.明天数学课要学“勾股定理”.小敏在“百度”搜索引擎中输入“勾股定理”,能搜索到与之相关的结果个数约为12 500 000,这个数用科学记数法表示为()A.1.25×105B.1.25×106C.1.25×107D.1.25×108【考点】科学记数法—表示较大的数.【专题】存在型.【分析】根据用科学记数法表示数的方法进行解答即可.【解答】解:∵12 500 000共有8位数,∴n=8﹣1=7,∴12 500 000用科学记数法表示为:1.25×107.故选C.【点评】本题考查的是科学记数法的概念,即把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n是正整数,这种记数法叫做科学记数法.3.已知:如图,∠A0B的两边 0A、0B均为平面反光镜,∠AOB=35°,一束平行于OB的光线RQ经0A上的Q点反射后,反射光线与0B交于点P,则∠QPB的度数是()A.60° B.70° C.80° D.85°【考点】平行线的性质.【专题】跨学科.【分析】求出∠AQR=∠PQO,根据平行线性质求出∠AQR=∠AOB=35°=∠PQO,代入∠QPB=∠AOB+∠PQO 求出即可.【解答】解:∵∠A0B的两边 0A、0B均为平面反光镜,∴∠AQR=∠PQO,∵QR∥OB,∠A0B=35°,∴∠AQR=∠AOB=35°=∠PQO,∴∠QPB=∠AOB+∠PQO=70°,故选B.【点评】本题考查了平行线性质,三角形外角性质的应用,主要考查学生的推理和计算能力.4.主视图、左视图、俯视图分别是下列三个图形的物体是()A.B.C.D.【考点】由三视图判断几何体.【专题】几何图形问题.【分析】根据三视图想象立体图形,从主视图可以看出左边的一列有两个,左视图可以看出左边的一列后面一行有两个,俯视图中左边的一列有两排,综合起来可得解.【解答】解:从主视图可以看出左边的一列有两个,右边的两列只有一行(第二行);从左视图可以看出左边的一列后面一行有两个,左边的一列只有一行(第二行);从俯视图可以看出左边的一列有两排,右边的两列只有一排(第二排).故选D.【点评】本题考查由三视图想象立体图形.做这类题时要借助三种视图表示物体的特点,从主视图上弄清物体的上下和左右形状;从俯视图上弄清物体的左右和前后形状;从左视图上弄清楚物体的上下和前后形状,综合分析,合理猜想,结合生活经验描绘出草图后,再检验是否符合题意.5.一个多边形的内角和是900°,则这个多边形的边数是()A.6 B.7 C.8 D.9【考点】多边形内角与外角.【专题】计算题.【分析】本题根据多边形的内角和定理和多边形的内角和等于900°,列出方程,解出即可.【解答】解:设这个多边形的边数为n,则有(n﹣2)180°=900°,解得:n=7,∴这个多边形的边数为7.故选:B.【点评】本题主要考查多边形的内角和定理,解题的关键是根据已知等量关系列出方程从而解决问题.6.若实数a,b,c满足a+b+c=0,且a<b<c,则函数y=cx+a的图象可能是()A.B.C.D.【考点】一次函数图象与系数的关系.【专题】压轴题;存在型.【分析】先判断出a是负数,c是正数,然后根据一次函数图象与系数的关系确定图象经过的象限以及与y轴的交点的位置即可得解.【解答】解:∵a+b+c=0,且a<b<c,∴a<0,c>0,(b的正负情况不能确定),∵a<0,∴函数y=cx+a的图象与y轴负半轴相交,∵c>0,∴函数y=cx+a的图象经过第一、三、四象限.故选C.【点评】本题主要考查了一次函数图象与系数的关系,先确定出a、c的正负情况是解题的关键,也是本题的难点.7.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为()A.4,5 B.5,4 C.4,4 D.5,5【考点】众数;中位数.【分析】根据众数及中位数的定义,结合所给数据即可作出判断.【解答】解:将数据从小到大排列为:1,2,3,3,4,4,5,5,5,5,这组数据的众数为:5;中位数为:4.故选A.【点评】本题考查了众数、中位数的知识,解答本题的关键是掌握众数及中位数的定义.8.如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是()A.B.C.D.【考点】动点问题的函数图象.【专题】压轴题.【分析】这是分段函数:①点P在AC边上时,y=x,它的图象是一次函数图象的一部分;②点P在边BC上时,利用勾股定理求得y与x的函数关系式,根据关系式选择图象;③点P在边AB上时,利用线段间的和差关系求得y与x的函数关系式,由关系式选择图象.【解答】解:①当点P在AC边上,即0≤x≤1时,y=x,它的图象是一次函数图象的一部分;②点P在边BC上,即1<x≤3时,根据勾股定理得 AP=,即y=,则其函数图象是y随x的增大而增大,且不是一次函数.故B、C、D错误;③点P在边AB上,即3<x≤3+时,y=+3﹣x=﹣x+3+,其函数图象是直线的一部分.综上所述,A选项符合题意.故选:A.【点评】本题考查了动点问题的函数图象.此题涉及到了函数y=的图象问题,在初中阶段没有学到该函数图象,所以只要采取排除法进行解题.二、填空题9.不等式组的所有整数解的和为﹣2 .【考点】一元一次不等式组的整数解.【分析】先分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出符合条件的x的所有整数解相加即可求解.【解答】解:,由①得:x≥﹣2,由②得:x<2,∴﹣2≤x<2,∴不等式组的整数解为:﹣2,﹣1,0,1.所有整数解的和为﹣2﹣1+0+1=﹣2.故答案为:﹣2.【点评】本题考查的是解一元一次不等式组及求一元一次不等式组的整数解,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.10.服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利50%,则这款服装每件的进价是160元.【考点】一元一次方程的应用.【分析】设这款服装每件的进价为x元,根据利润=售价﹣进价建立方程求出x的值就可以求出结论.【解答】解:设这款服装每件的进价为x元,由题意,得300×0.8﹣x=50%x,解得:x=160.故答案是:160元.【点评】本题考查了列一元一次方程解实际问题的运用,销售问题的数量关系利润=售价﹣进价的运用,解答时根据销售问题的数量关系建立方程是关键.11.关于方程x2﹣ax﹣2a=0的两根的平方和是5,则a的值是 1 .【考点】根与系数的关系.【分析】设方程的两根分别为m、n,根据根与系数的关系得到m+n=a,mn=﹣2a,再由m2+n2=5得(m+n)2﹣2mn=5,所以a2﹣4a=5,解得a=﹣1,a2=5,然后根据判别式确定满足条件的a的值.1【解答】解:设方程的两根分别为m、n,则m+n=a,mn=﹣2a,∵m2+n2=5,∴(m+n)2﹣2mn=5,∴a2+4a=5,解得a1=1,a2=﹣5,当a=﹣5时,原方程变形为程x2+5x+10=0,△=25﹣4×10<0,方程没有实数解,∴a=1.故答案为1.【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=﹣,x1x2=.12.一个扇形的圆心角是120°,面积为3π cm2,那么这个扇形的弧长为2πcm.【考点】扇形面积的计算;弧长的计算.【专题】计算题.【分析】首先根据扇形的面积公式计算出扇形的半径,再根据弧长公式计算即可解答.【解答】解:设这个扇形的半径是rcm.根据扇形面积公式,得=3π,解得r=±3(负值舍去).故半径为3.弧长是:=2πcm.故答案为2π.【点评】本题主要考查扇形面积的计算以及弧长的计算,熟练运用公式进行计算是解答本题的关键.13.如图,在平面直角坐标系中,△ABC经过平移后点A的对应点为点A′,则平移后点B的对应点B′的坐标为(﹣2,1).【考点】坐标与图形变化-平移.【专题】压轴题;数形结合.【分析】先根据点A与A′确定平移规律,再根据规律写出点B的对应点B′的坐标即可.【解答】解:由图可得,点A(1,﹣1),A′(﹣3,3),所以,平移规律是:向左平移4个单位,再向上平移4个单位,∵点B的坐标为(2,﹣3),∴B′的坐标为(﹣2,1).故答案为:(﹣2,1).【点评】本题考查了平移与坐标与图形的变化,根据图形得到平移规律是解题的关键.14.如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为或.【考点】翻折变换(折叠问题).【专题】压轴题.【分析】连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P,先利用勾股定理求出MD′,再分两种情况利用勾股定理求出DE.【解答】解:如图,连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P∵点D的对应点D′落在∠ABC的角平分线上,∴MD′=PD′,设MD′=x,则PD′=BM=x,∴AM=AB﹣BM=7﹣x,又折叠图形可得AD=AD′=5,∴x2+(7﹣x)2=25,解得x=3或4,即MD′=3或4.在Rt△END′中,设ED′=a,①当MD′=3时,AM=7﹣3=4,D′N=5﹣3=2,EN=4﹣a,∴a2=22+(4﹣a)2,解得a=,即DE=,②当MD′=4时,AM=7﹣4=3,D′N=5﹣4=1,EN=3﹣a,∴a2=12+(3﹣a)2,解得a=,即DE=.故答案为:或.【点评】本题主要考查了折叠问题,解题的关键是明确掌握折叠以后有哪些线段是对应相等的.15.如图,在菱形ABCD中,AB=1,∠DAB=60°,把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′,其中点C的运动路径为,则图中阴影部分的面积为.【考点】菱形的性质;全等三角形的判定与性质;扇形面积的计算;旋转的性质.【分析】根据菱形的性质以及旋转角为30°,连接CD′和BC′,可得A、D′、C及A、B、C′分别共线,求出扇形面积,再根据AAS证得两个小三角形全等,求得其面积,最后根据扇形ACC′的面积﹣两个小的三角形面积即可.【解答】解:连接CD′和BC′,∵∠DAB=60°,∴∠DAC=∠CAB=30°,∵∠C′AB′=30°,∴A、D′、C及A、B、C′分别共线.∴AC=∴扇形ACC′的面积为: =,∵AC=AC′,AD′=AB∴在△OCD′和△OC'B中,∴△OCD′≌△OC′B(AAS).∴OB=OD′,CO=C′O∵∠CBC′=60°,∠BC′O=30°∴∠COD′=90°∵CD′=AC﹣AD′=﹣1OB+C′O=1∴在Rt△BOC′中,BO2+(1﹣BO)2=(﹣1)2解得BO=,C′O=﹣,∴S△OC′B=•BO•C′O=﹣∴图中阴影部分的面积为:S扇形ACC′﹣2S△OC′B=+﹣.故答案为: +﹣.【点评】本题考查了旋转的性质,菱形的性质,扇形的面积公式,勾股定理,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.16.一组数据为0,3,8,15,24,…则第n个数据表示为n2﹣1 .【考点】规律型:数字的变化类.【分析】设第n个是为a n(n为正整数),根据给定的部分数据找出变化规律“a n=n2﹣1”,此题得解.【解答】解:设第n个是为a n(n为正整数),观察,发现:a1=0=12﹣1,a2=3=22﹣1,a3=8=32﹣1,a4=15=42﹣1,a5=24=52﹣1,…,∴a n=n2﹣1.故答案为:n2﹣1.【点评】本题考查了规律型中数字的变化类,解题的关键是根据数的变化找出变化规律“a n=n2﹣1”.本题属于基础题,难度不大,解决该题型题目时,根据数的变化找出变化规律是关键.三、解答题17.(2015秋•盘锦校级月考)先化简再求值:÷(a﹣2﹣),其中a=2+.【考点】分式的化简求值.【分析】利用提取公因数、合并同类项等方法将原代数式化简为,代入a的值即可得出结论.【解答】解:÷(a﹣2﹣),=÷,=÷,=•,=,∵a=2+,∴÷(a﹣2﹣)===.【点评】本题考查了分式的化简求值,将原代数式化简为是解题的关键.18.“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:(1)本次参加抽样调查的居民有多少人?(2)将两幅不完整的图补充完整;(3)若居民区有8000人,请估计爱吃D粽的人数.【考点】条形统计图;用样本估计总体;扇形统计图.【分析】(1)根据B类有60人,占10%,据此即可求得抽查的总人数;(2)利用总数减去其它各组的人数即可求得C类的人数,然后求得百分比即可;(3)利用总数8000乘以对应的百分比即可求解.【解答】解:(1)本次参加抽样调查的居民的人数是:60÷10%=600(人);(2)C类的人数是:600﹣180﹣60﹣240=120(人),所占的百分比是:×100%=20%,A类所占的百分比是:×100%=30%.;(3)8000×40%=3200(人).【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.19.(2013•北京一模)如图,四边形ABCD中,∠ADC=∠B=90°,∠C=60°,AD=,E为DC中点,AE∥BC.求BC的长和四边形ABCD的面积.【考点】解直角三角形;矩形的判定与性质.【分析】过E作EF⊥BC于F,证明四边形 ABCD是矩形,在Rt△ADE中求出AE,DE的长度,根据E 是中点,求出EC的长度,继而求出CF,则可得出BC的长度,根据四边形ABCD的面积S四边形ABCD=S△+S梯形ABCE也可求出其面积.ADE【解答】解:过E作EF⊥BC于F,∵∠B=90°,∴AB∥EF,∵AE∥BC,∠B=90°,∴四边形 ABCD是矩形.∵AE∥BC,∴∠AED=∠C=60°.在Rt△ADE中,∠ADC=90°,AD=,∴DE==1,AE==2,又∵E为DC中点,∴CE=DE=1,在Rt△CEF中,∠CFE=90°,∠C=60°,则CF=CE•cos 60°=,EF=CE•sin 60°=,∴BC=BF+CF=AE+CF=2+=,∴四边形ABCD的面积S四边形ABCD=S△ADE+S梯形ABCE=AD•DE+(AE+BC)•EF=××1+×(2+)×=.【点评】本题考查了解直角三角形的知识,难度一般,在各直角三角形中利用解直角三角形的方法求出各边长是解答本题的关键.20.在中俄“海上联合﹣2014”反潜演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°,试根据以上数据求出潜艇C离开海平面的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, 1.7)【考点】解直角三角形的应用-仰角俯角问题.【专题】几何图形问题.【分析】过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,分别在Rt△ACD 中表示出CD和在Rt△BCD中表示出BD,从而利用二者之间的关系列出方程求解.【解答】解:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,根据题意得:∠ACD=30°,∠BCD=68°,设AD=x,则BD=BA+AD=1000+x,在Rt△ACD中,CD===,在Rt△BCD中,BD=CD•tan68°,∴1000+x=x•tan68°解得:x=≈≈308米,∴潜艇C离开海平面的下潜深度为308米.【点评】本题考查了解直角三角形的应用,解题的关键是从题目中抽象出直角三角形并选择合适的边角关系求解.21.已知反比例函数y=(m为常数)的图象经过点A(﹣1,6).(1)求m的值;(2)如图,过点A作直线AC与函数y=的图象交于点B,与x轴交于点C,且AB=2BC,求点C 的坐标.【考点】反比例函数综合题.【专题】计算题.【分析】(1)将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;(2)分别过点A、B作x轴的垂线,垂足分别为点E、D,则△CBD∽△CAE,运用相似三角形知识求出CD的长即可求出点C的横坐标.【解答】解:(1)∵图象过点A(﹣1,6),∴=6,解得m=2.故m的值为2;(2)分别过点A、B作x轴的垂线,垂足分别为点E、D,由题意得,AE=6,OE=1,即A(﹣1,6),∵BD⊥x轴,AE⊥x轴,∴AE∥BD,∴△CBD∽△CAE,∴=,∵AB=2BC,∴=,∴=,∴BD=2.即点B的纵坐标为2.当y=2时,x=﹣3,即B(﹣3,2),设直线AB解析式为:y=kx+b,把A和B代入得:,解得,∴直线AB解析式为y=2x+8,令y=0,解得x=﹣4,∴C(﹣4,0).【点评】由于今年来各地中考题不断降低难度,中考考查知识点有向低年级平移的趋势,反比例函数出现在解答题中的频数越来约多.22.某商店经销一种T恤衫,4月上旬的营业额为2000元,为扩大销售量,4月中旬该商店对这种T恤衫打9折销售(原销售价格的90%),结果销售量增加20件,营业额增加700元.求该种T恤衫4月上旬的销售价格.【考点】分式方程的应用.【分析】设该种T恤衫4月上旬的销售价为每件x元,则4月中旬的售价为每件0.9x元,根据总价÷单价=数量之间的关系建立方程求出其解即可.【解答】解:设该种T恤衫4月上旬的销售价为每件x元,则4月中旬的售价为每件0.9x元,根据题意得,解得:x=50.经检验,x=50是所得方程的解,且符合题意.答:该种T恤衫4月上旬的销售价格是每件50元.【点评】本题是一道销售问题的应用题,考查了列分式方程解实际问题的运用,分式方程的解法的运用,解答时运用销售数量之间的数量关系建立方程是解答本题的关键.23.如图所示,△ABC中,AC=BC,以BC为直径作⊙O交AB于点D,交AC于点G,作直线DF⊥AC交AC于点F,交CB的延长线于点E.(1)求证:直线EF四⊙O的切线;(2)若BC=6,AB=4,求DE的长.【考点】切线的判定.【专题】证明题.【分析】(1)连结OD,如图,通过证明OD∥AC,加上DF⊥AC,于是可得到DF⊥OD,然后根据切线的判定定理可得DF为⊙O的切线;,(2)连结CD,作DH⊥BC于H,如图,先利用圆周角定理得到∠BDC=90°,则根据等腰三角形的性质得BD=AD=AB=2,在Rt△BDC中可利用勾股定理计算出CD=2,再利用面积法克计算出DH=2,接着根据勾股定理计算出OH=1,然后证明Rt△ODH∽Rt△OED,利用相似比可计算出DE.【解答】(1)证明:连结OD,如图,∵AC=BC,∴∠A=∠ABC,∵OB=OD,∴∠ODB=∠OBD,∴∠ODB=∠A,∴OD∥AC,而DF⊥AC,∴DF⊥OD,∴DF为⊙O的切线;(2)解:连结CD,作DH⊥BC于H,如图,∵BC为直径,∴∠BDC=90°,而CA=CB,∴BD=AD=AB=2,在Rt△BDC中,CD==2,∵DH•BC=DE•CD,∴DH==2,在Rt△ODH中,OH==1,∵∠DOH=∠EOD,∴Rt△ODH∽Rt△OED,∴=,即=,∴DE=6.【点评】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理和相似三角形的判定与性质.24.某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:(1)求张强返回时的速度;(2)妈妈比按原速返回提前多少分钟到家?(3)请直接写出张强与妈妈何时相距1000米?【考点】一次函数的应用.【分析】(1)根据速度=路程÷时间,即可解答;(2)求出妈妈原来的速度,妈妈原来走完3000米所用的时间,即可解答;(3)分别求出张强和妈妈的函数解析式,根据张强与妈妈相距1000米,列出方程,即可解答.【解答】解:(1)3000÷(50﹣30)=3000÷20=150(米/分),答:张强返回时的速度为150米/分;(2)(45﹣30)×150=2250(米),点B的坐标为(45,750),妈妈原来的速度为:2250÷45=50(米/分),妈妈原来回家所用的时间为:3000÷50=60(分),60﹣50=10(分),妈妈比按原速返回提前10分钟到家;(3)如图:设线段BD的函数解析式为:y=kx+b,把(0,3000),(45,750)代入得:,解得:,∴y=﹣50x+3000,线段OA的函数解析式为:y=100x(0≤x≤30),设线段AC的解析式为:y=k1x+b1,把(30,3000),(50,0)代入得:解得:,∴y=﹣150x+7500,(30<x≤50)当张强与妈妈相距1000米时,即﹣50x+3000﹣100x=1000或100x﹣(﹣50x+3000)=1000或(﹣150x+7500)﹣(﹣50x+3000)=1000,解得:x=35或x=或x=,∴当时间为35分或分或分时,张强与妈妈何时相距1000米.【点评】本题考查了一次函数的应用,解决本题的关键是读懂函数图象,获取相关信息,并用待定系数法求函数解析式.25.已知:在Rt△ABC,∠ABC=90°,∠C=60°,现将一个足够大的直角三角板的顶点P放在斜边AC上.(1)设三角板的两直角边分别交边AB、BC于点M、N.①当点P是AC的中点时,分别作PE⊥AB于点E,PF⊥BC于点F,得到图1,写出图中的一对全等三角形;②在①的条件下,写出与△PEM相似的三角形,并直接写出PN与PM的数量关系.(2)移动点P,使AP=2CP,将三角板绕点P旋转,设旋转过程中三角板的两直角边分别交边AB、BC于点M、N(PM不与边AB垂直,PN不与边BC垂直);或者三角板的两直角边分别交边AB、BC的延长线与点M、N.③请在备用图中画出图形,判断PM与PN的数量关系,并选择其中一种图形证明你的结论;④在③的条件下,当△PCN是等腰三角形时,若BC=3cm,则线段BN的长是1cm或5cm .【考点】相似形综合题.【分析】(1)①求出∠AEP=∠B=∠PFC=90°,∠APE=∠C=60°,根据AAS推出两三角形全等即可.②求出AB=BC,求出PE=BC,PF=AB,推出==,求出∠EPM=∠NPF=90°﹣∠MPF,∠PEM=∠PFN=90°,根据相似三角形的判定推出△PFN∽△PEM,推出==,即可得出答案.(2)③过P作PE⊥AB于E,PF⊥BC于F,求出△AEP∽∠PFC,推出==2,设CF=x,则PE=2x,求出PF=x,证△PEM∽△PFN,推出==即可.④求出CP=2cm,分为两种情况:第一种情况:当N在线段BC上时,得出△PCN是等边三角形,求出CN=CP=2cm,代入BN=BC﹣CN求出即可;第二种情况:当N在线段BC的延长线上时,求出CN=PC=2cm,代入BN=BC+CN求出即可.【解答】(1)解:①△AEP≌△PFC,理由是:∵P为AC中点,∴AP=PC,∵PE⊥AB,PF⊥BC,∠B=90°,∴∠AEP=∠B=∠PFC=90°,∴PF∥AB,PE∥BC,∴∠APE=∠C=60°,在△AEP和△PFC中∴△AEP≌△PFC(AAS).。
初三第四次教学质量检测试卷

初三第四次教学质量检测试卷一、选择题(每题3分,共30分)1.下列各项中,哪一项是物质的属性?A. 颜色B. 化学变化C. 密度D. 温度2.在自行车上有一个钟。
当钟已走的路程与自行车已走的路程相同时,钟上的“走”字刚好归零。
这张钟是怎样制成的?A. 在钟上装一个碰撞复位装置B. 在钟上装一个计数器C. 在钟上装一个减法块D. 不需要其他装置3.一毫升的水,凝固成冰所产生的体积变化是多少?A. 0.1毫升B. 10毫升C. 1升D. 1毫升4.当有一种液态物质凝结为固态时,通常会 ______。
A. 吸收热量B. 释放热量C. 保持温度不变D. 温度会下降5.石头、水、氧气分别属于 __________ 。
A. 固体、液体、气体B. 液体、气体、固体C. 固体、气体、液体D. 气体、液体、固体6.铜是由哪两种元素构成的?A. 铜和铅B. 铜和氧C. 铜和硫D. 铜和锌7.印刷纸透光透气性的稠浆纸是由_______制成的。
A. 植物的纤维B. 金属长条C. 动物的皮毛D. 矿物质8.粒子在一个舞台上迅速描绘出一个平板波,这是因为_______。
A. 粒子具有传播性B. 粒子具有振动性C. 波动是由粒子传播而成的D. 波动既是粒子又是波9.电磁辐射是由__________而形成的。
A. 机械振动B. 电荷振动C. 密度的扰动D. 单摆的摆动10.一个物体第一次被水浸湿,然后被放在一旁等干燥。
第二次被浸湿,如其质量不变,则说明\\\\\_A. 有水向内部扩程B. 有水从物体内部流出C. 有水在物体外部定居D. 有水在物体外部晾干二、填空题(每题2分,共20分)1.在火山喷发中,来自于火山口的担子石属于气火山喷发中的 [ _________ ]。
2.热传导是指 [ _________ ]。
3.火山锥由火山爆发时喷出的 [ _________ ] 组成。
4.壮观的火山山体是由 [ _________ ] 构成的。
九年级物理第四次质检测试题

九年级物理第四次质检试题2011-2一、单项选择题(每小题4分,共40分;下列各题所列的四个选项中,只有一个是正确的,把正确的选项前的字母填在答卷相应的位置上)1.一架天平的砝码已经生锈,用它测物体的质量,其测量值与真实值相比较()A.偏大 B.偏小 C.一样大 D.无法比较2.一个物体受到均为2 0 N的一对平衡力作用做匀速直线运动,如果这一对力同时忽然减少到5 N,则该物体( )A.运动的速度逐渐减小 B.速度将减小,但仍做匀速直线运动C.仍按原来的速度做匀速直线运动 D.运动的速度逐渐增大3.下列说法中正确的是( )A.坐在沙发上比坐在板凳上舒服,是因为坐在沙发上,沙发对人的压力小B.人无论呼气还是吸气都是利用大气压C.拔河比赛时,获胜方对绳的拉力大D.人行道上的盲道是为了增大摩擦.使盲人不易滑倒4.有关家居装修,下列说法不正确的是()A.使用环保油漆可以减少分子扩散产生的刺激味B.用太阳能热水器替代燃气热水器更环保C.装修线路时,插座应串联在电路中D.新房装修后不能马上入住,是防止新家具中油漆扩散出的有害气体伤害人体5.小明在公路上骑自行车,若说他是静止的,则选择的参照物可能是()A.迎面走来的行人 B.路旁的树木C.小明骑的自行车 D.从身边超越的汽车6.“能源危机”和“环境污染”是当今世界面临的两大难题。
下列选项中,不利于解决这两大难题的是()A.煤和石油的开发.利用 B.氢气燃料的开发.利用C.太阳能的开发.利用 D.风能的开发.利用7.在如图所示的电路中,用滑动变阻器调节灯的亮度,若要求滑片P向右端滑动时灯逐渐变暗,则下列接法正确的是()A.M接C,N接B B.M接A,N接BC.M接C,N接D D.M接A,N接D8.如图所示是四冲程汽油机的一个工作循环示意图,其中属于做功冲程的是()9.把装满水的量筒,口朝下浸没在水中,如图所示,抓住筒底向上提,在筒口离开水面前量筒露出水面部分()A. 充满水B. 有水,但不满C. 没有水D. 依次出现上述现象10.如图,甲鱼缸注满水,相同的鱼缸乙注满水中浮有一只船,两个鱼缸分别放在台秤上,下列说法正确的是:1 / 5()A.甲重力大于乙的重力 B.甲.乙的重力相等C.乙的重力大于甲的重力 D.无法判断二、填空题(每空2分,共20分;请把下列各题的正确答案填写在答卷相应题目的答题位置上)11.如图所示的钢丝钳,它是(省力/费力)杠杆,钳口做成凹凸不平是为了。
{品质管理品质知识}九年级四次质量检测科学试题

{品质管理品质知识}九年级四次质量检测科学试题A.绳拉牛的力与牛拉绳的力是一对平衡力B.绳拉牛的力与地面对牛的摩擦力是一对平衡力C.绳拉牛的力小于牛拉绳的力D.绳拉牛的力小于地面对牛的摩擦力11、小红同学在一支铅笔的下端粘上一块橡皮泥,将它分别置于甲、乙两杯液体中观察到静止时的情形如图所示,下列说法正确的是:A.铅笔在甲杯液体中受到的浮力较大B.铅笔在乙杯液体中受到的浮力较大C.乙杯液体的密度较大D.甲杯液体的密度较大12、足球运动员用150牛的作用力,将重4.5牛的足球踢出,足球沿水平场地向前运动的最大距离为20米,则运动员对足球所做的功为:A.3000焦B.90焦C.0焦D.无法确定13、张红同学用吸管吸饮料时出现了一个怪现象,无论她怎么用力,饮料都吸不上来。
你认为出现这种现象的原因是:A.吸管有孔B.大气压偏小C.吸管太细D.吸管插得太深14、2008年北京奥运会成功举行,在奥运会比赛中,下列说法错误的是:A.3m跳板跳水运动员起跳时用力蹬跳板是要利用跳板的弹性势能B.赛艇比赛运动员用的船桨属于省力杠杆C.游泳比赛运动员向后划水是应用力的相互作用D.在4×lOOm接力赛中,交接棒时两运动员尽可能做到相对静止15、洗衣机、空调、电冰箱等家用电器都使用三孔插头、插座,如图所示,插座中有一个孔是用来接地的。
如果在你家中这个孔没有接地,将会发生的现象是:A.家用电器消耗的电能会增加B.人接触家用电器外壳时有可能发生触电事故C.家用电器的使用寿命会缩短D.家用电器不能正常工作16、“发面”是制作包子等食品过程中常见的工艺,是利用面粉中酵母菌大量繁殖产生的某些物质和随后加入的“苏打”反应产生的气体使面粉蓬松可口,在发酵后未加入“苏打”之前的面粉中滴加紫色石蕊试液,石蕊最有可能变成的颜色是:A.无色B.浅红色C.紫色D.蓝色17、《三国演义》中有这样一个故事:诸葛亮率领的汉军误饮了“哑泉”。
哑泉,“人若饮之,则不能言,不过旬日必死”。
九年级数学上册第四次质量检测试题

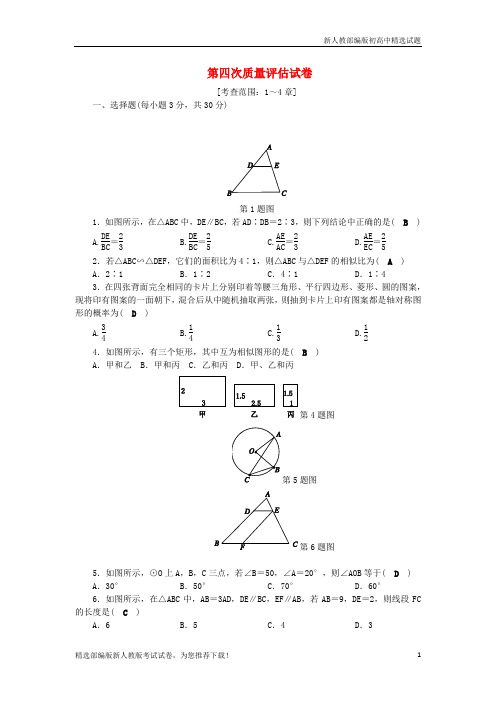
九年级数学上册第四次质量检测试题数 学 试 题(满分:150分,时间1)第I 卷(选择题,共30分)一、选择题(每小题3分,计30分) 1、在函数21-=x y 中,自变量x 的取值范围是( ) A 、0≠x B 、2>x C 、2≠x D 、2-<x 2、下列事件中,是必然事件的是( ) A 、购买一张彩票中奖一百万元 B 、购买电视机,任选一个频道,正在播新闻。
C 、要地球上,上抛出去的篮球会下落D 、掷两枚质地均匀的正方体骰子,点数之和一定大于63、如图,已知等腰梯形ABCD 的中位线EF 的长为6,腰AD 的长为5,则该等腰梯形的周长是( ) A 、11 B 、16 C 、17 D 、224、如图,身高为1.6m 的某学生想测量一棵大树的高度,她沿着树影BA 由B到A 走去,当走到C 点时,她的影子顶端正好与树影子顶端重合,测得BC=3.2m ,CA=0.8m ,则树的高度为( ) A 、4.8m B 、6.4m C 、8m D 、10m5、下列函数中。
既是轴对称图形,又是中心对称图形的是( ) A 、12+-=x y B 、xy 1=C 、)1(322<+-=x x x y D 、)900(sin 0<<=x x y6、在直角坐标系中,A (3,0)、B (0,4),以A 为圆心,2为半径作⊙A ,再以B 为圆心,4为半径作⊙B ,则⊙A 与⊙B 的位置关系是( ) A 、内含 B 、相交 C 、外离 D 、外切或内切7、关于02)1(2=-++-k x k x x 的一元二次方程的根情况是( ) A 、有两个相等的实数根 B 、有两个不相等的实数根 C 、没有实数根 D 、无法判断8、如图,在把易拉罐中的水倒入一个圆水杯中的过程中,若水杯中的水在点P 与易拉罐刚好接触,则此时水杯中的水深为( )A 、2cmB 、4cmC 、6cmD 、8cm9、如图,⊙A 、⊙B 、⊙C 两两不相交,且它们的半径都是1cm ,AB=AC=4cm ,BC=3cm ,则图中阴影部分图形的周长为( ) A 、11cm B 、(5+π)cm C 、(5+2π)cm D 、(6+π)cm10、如图所示,边长分别为1和2的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t ,大正方形内除去小正方形部分的面积为S (阴影部分),那么S 与t 的大致图象应为( )第II 卷(非选择题,共1二、填空题(每小题3分,计24分)11、某食品包装袋上标有“净含量385g ±5g ”,这包食品的合格净含量范围是________g 。
2019九年级数学上册 第四次质量评估试卷 (新版)浙教版

第四次质量评估试卷[考查范围:1~4章]一、选择题(每小题3分,共30分)第1题图1.如图所示,在△ABC中,DE∥BC,若AD∶DB=2∶3,则下列结论中正确的是( B)A.DEBC=23B.DEBC=25C.AEAC=23D.AEEC=252.若△ABC∽△DEF,它们的面积比为4∶1,则△ABC与△DEF的相似比为( A) A.2∶1 B.1∶2 C.4∶1 D.1∶43.在四张背面完全相同的卡片上分别印着等腰三角形、平行四边形、菱形、圆的图案,现将印有图案的一面朝下,混合后从中随机抽取两张,则抽到卡片上印有图案都是轴对称图形的概率为( D)A.34B.14C.13D.124.如图所示,有三个矩形,其中互为相似图形的是( B)A.甲和乙 B.甲和丙 C.乙和丙 D.甲、乙和丙第4题图5题图第6题图5.如图所示,⊙O上A,B,C三点,若∠B=50,∠A=20°,则∠AOB等于( D) A.30°B.50°C.70°D.60°6.如图所示,在△ABC中,AB=3AD,DE∥BC,EF∥AB,若AB=9,DE=2,则线段FC 的长度是( C)A.6 B.5 C.4 D.37.如图所示,在平面直角坐标系中,O 为坐标原点,点A 的坐标为(1,3),将线段OA 绕原点O 逆时针旋转30°,得到线段OB ,则点B 的坐标是( A )A .(0,2)B .(2,0)C .(1,-3)D .(-1,3)7题图8题图9题图8.如图所示,在△ABC 中,∠ACB =90°,AC +BC =8,分别以AB ,AC ,BC 为半径作半圆,若记图中阴影部分的面积为y ,AC 为x ,则下列y 关于x 的图象中正确的是( A )A B C D9.如图所示,在钝角三角形ABC 中,AB =6 cm ,AC =12 cm ,动点D 从点A 出发到点B 止,动点E 从点C 出发到点A 止,点D 运动的速度为1 cm/s ,点E 运动的速度为2 cm/s.如果两点同时运动,那么当以点A ,D ,E 为顶点的三角形与△ABC 相似时,运动的时间是( A )A .3 s 或4.8 sB .3 sC .4.5 sD .4.5 s 或4.8 s10.抛物线y =ax 2+bx +3(a≠0)过A(4,4),B(2,m)两点,点B 到抛物线对称轴的距离记为d ,满足0<d≤1,则实数m 的取值范围是( B )A .m ≤2或m≥3B .m ≤3或m≥4C .2<m <3D .3<m <4二、填空题(每小题4分,共24分)11.已知a b =52,则a +b a -b =__73__. 12.如图,∠DAB =∠CAE,请你再补充一个边条件,使得△ABC∽△ADE:__∠D=∠B(答案不唯一)__.13.圆内接四边形ABCD ,两组对边的延长线分别相交于点E ,F ,且∠E=40°,∠F =60°,则∠A=__40°__.第12题图13题图第15题图16题图 14.抛物线y =x 2+bx +c 与x 轴相交于A(-1,0),B(3,0)两点,写出y >-3时x的取值范围:__x <0或x >2__.15.如图所示,AD 是△ABC 的高,AE 是△ABC 的外接圆⊙O 的直径,且AB =42,AC =5,AD =4,则⊙O 的直径AE =.16.如图所示,在Rt △ABC 中,∠C =90°,AC =10,BC =30,动点P 从点B 开始沿边BC 向点C 以每秒2个单位长度的速度运动,动点Q 从点C 开始沿边CA 向点A 以每秒1个单位长度的速度运动,连结PQ ,点P ,Q 分别从点B ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t 秒(t≥0).(1)当t =__6__秒时,点P ,C ,Q 所构成的三角形与Rt △ABC 相似;(2)在整个运动过程中,线段PQ 的中点所经过的路程长为.三、解答题(共66分)17.(6分)有A ,B ,C 三种款式的帽子,E ,F 两种款式的围巾,穿戴时小婷任意选一顶帽子和一条围巾.(1)用合适的方法表示搭配的所有可能的结果;(2)求小婷恰好选中她所喜欢的A 款帽子和E 款围巾的概率.解:(1)根据题意,小婷任意选取一顶帽子和一条围巾,有A 、E ,A 、F ,B 、E ,B 、F ,C 、E ,C 、F ,6种情况,(2)小婷恰好选中她所喜欢的A 款帽子和E 款围巾的概率=16.第18题图18.(8分)“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图所示,矩形ABCD ,东边城墙AB 长9里,南边城墙AD 长7里,东门点E 、南门点F 分别是AB ,AD 的中点,EG ⊥AB ,FH ⊥AD ,EG =15里,HG 经过A 点,求FH 的长.解:∵EG⊥AB,FH ⊥AD ,HG 经过A 点,∴FA ∥EG ,EA ∥FH ,∴∠HFA =∠AEG=90°,∠FHA =∠EAG,∴△AFH ∽△GEA ,∴AF EG =FH EA. ∵AB =9里,AD =7里,EG =15里,∴FA =3.5里,EA =4.5里,∴3.515=FH 4.5,解得FH =1.05里.第19题图19.(8分)如图所示,正方形ABCD 的边长为1,其中弧DE 、弧EF 、弧FG 的圆心依次为点A ,B ,C.(1)求点D 沿三条弧运动到点G 所经过的路线长;(2)判断直线GB 与DF 的位置关系,并说明理由.解:(1)根据弧长公式,得所求路线长为90π×1180+90π×2180+90π×3180=3π. (2)GB⊥DF.理由如下:在△FCD 和△GCB 中,∵⎩⎪⎨⎪⎧CF =CG ,∠FCD =∠GCB,CD =CB ,∴△FCD ≌△GCB(SAS),∴∠G =∠F,∵∠F +∠FDC=90°,∴∠G +∠FDC=90°,∴∠GHD =90°,∴GB ⊥DF.第20题图20.(8分)如图所示,在矩形ABCD 中,BE ⊥AC 分别交AC ,AD 于点F ,E ,若AD =1,AB =CF ,求AE 的长.解:∵四边形ABCD 是矩形,∴BC =AD =1,∠BAE =∠ABC=90°,∴∠ABE +∠CBF=90°, ∵BE ⊥AC ,∴∠BFC =90°,∴∠BCF +∠CBF=90°,∴∠ABE =∠FCB,在△AB E 和△FCB 中,⎩⎪⎨⎪⎧∠EAB=∠BFC=90°,AB =CF ,∠ABE =∠FCB,∴△ABE ≌△FCB ,∴BF =AE ,BE =BC =1,∵BE ⊥AC ,∴∠BAF +∠ABF=90°,∵∠ABF +∠AEB=90°,∴∠BAF =∠AEB,∵∠BAE =∠AFB,∴△ABE ∽△FBA ,∴AB BF=BE AB ,∴AB AE =1AB,∴AE =AB 2, 在Rt △ABE 中,BE =1,根据勾股定理,得AB 2+AE 2=BE 2=1,∴AE +AE 2=1,∵AE >0,∴AE =5-12. 21.(8分)已知一次函数y 1=x +b 的图象与二次函数y 2=a(x 2+bx +3)(a≠0,a ,b 为常数)的图象交于A ,B 两点,且点A 的坐标为(0,3).(1)求出a ,b 的值;(2)求出点B 的坐标,并直接写出当y 1≥y 2时x 的取值范围;(3)设s =y 1+y 2,t =y 1-y 2,若n≤x≤m 时,s 随着x 的增大而增大,且t 也随着x 的增大而增大,求n 的最小值和m 的最大值.解:(1)把A(0,3)代入y 1=x +b 中,得b =3,∴y 1=x +3,y 2=a(x 2+3x +3),把A(0,3)代入y 2=a(x 2+3x +3)中,得3a =3,a =1,∴a =1,b =3. (2)由题意,得⎩⎪⎨⎪⎧y =x +3,y =x 2+3x +3, 解得⎩⎪⎨⎪⎧x 1=0,y 1=3或⎩⎪⎨⎪⎧x 2=-2,y 2=1.第21题答图∴B(-2,1),如图所示,当y 1≥y 2时x 的取值范围是-2≤x≤0.(3)s =y 1+y 2=x +3+x 2+3x +3=x 2+4x +6=(x +2)2+2,∵抛物线开口向上,∴当x≥-2时,s 随着x 的增大而增大,t =y 1-y 2=x +3-(x 2+3x +3)=-x 2-2x =-(x +1)2+1,∵抛物线开口向下,∴当x≤-1时,t 随着x 的增大而增大,∴当-2≤x≤-1时,s 随着x 的增大而增大,且t 也随着x 的增大而增大, ∵n ≤x ≤m ,s 随着x 的增大而增大,且t 也随着x 的增大而增大,∴n 的最小值-2,m 的最大值-1.第22题图22.(8分)有一块锐角三角形卡纸余料ABC ,它的边BC =120 cm ,高AD =80 cm ,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2∶5的矩形纸片EFGH 和正方形纸片PMNQ ,裁剪时,矩形纸片的较长边在BC 上,正方形纸片一边在矩形纸片的较长边EH 上,其余顶点均分别在AB ,AC 上,具体裁剪方式如图所示.(1)求矩形纸片较长边EH 的长;(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料△AEH 中与边EH 平行的中位线剪一刀,再沿过该中位线两端点向边EH 所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.解:(1)设EF =2x ,EH =5x ,∵矩形对边EH∥BC,∴△AEH∽△ABC,∴EH BC =AR AD ,即5x 120=80-2x 80,解得x =15,EH =5x =15×5=75 cm , 所以矩形纸片较长边EH 的长为75 cm.(2)小聪的剪法不正确.理由如下:设正方形的边长为a ,AR =AD -RD =80-2×15=50 cm ,AK =50-a ,由题意,知△APQ∽△AEH,∴PQ EH =AK AR ,即a 75=50-a 50,解得a =30,与边EH 平行的中位线=12×75=37.5 cm ,∵37.5≠30,∴小聪的剪法不正确.图(a) 图(b)第23题图23.(10分)(1)如图(a)所示,已知∠ACB=∠DCE=90°,AC =BC =6,CD =CE ,AE =3,∠CAE =45°,求AD 的长;(2)如图(b)所示,已知∠ACB=∠DCE=90°,∠ABC =∠CED =∠CAE=30°,AC =3,AE =8,求AD 的长.解:(1)如图(a)所示,连结BE ,∵∠ACB =∠DCE=90°,∴∠ACB +∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,又∵AC=BC ,DC =EC ,在△ACD 和△BCE 中,⎩⎪⎨⎪⎧AC =BC ,∠BCE =∠ACD,DC =EC ,∴△ACD ≌△BCE ,∴AD =BE ,∵AC =BC =6,∴AB =62,∵∠ACB =90°,AC =BC ,∴∠BAC =∠ABC=45°.∵∠BAC =∠CAE=45°,∴∠BAE=90°,在Rt △BAE 中,AB =62,AE =3,∴BE =9,∴AD =9.23题答图(a)23题答图(b)(2)如图(b)所示,连结BE ,∵∠ACB =∠DCE=90°,∠ABC =∠CED=30°,∴AC BC =CD CE=13,AB =2AC =6,∠BAC =60°.∵∠ACB =∠DCE=90°,∠ABC =∠CED=30°,∴Rt △ABC ∽Rt △DCE ,∴AC DC =BC CE,∴∠BCE =∠ACD,∴△ACD ∽△BCE ,∴AD BE =AC BC =33,∵∠BAC =60°,∠CAE =30°,∴∠BAE =90°,又AB =6,AE =8,∴BE =10,∴AD =1033. 24.(10分)在平面直角坐标系中,抛物线y =-14x 2+32x +4的图象与x 轴交于B ,C 两点(B 在C 的左侧),与y 轴交于点A.(1)求出点A ,B ,C 的坐标;(2)在抛物线上有一动点P ,抛物线的对称轴上有另一动点Q ,若以B ,C ,P ,Q 为顶点的四边形是平行四边形,直接写出点P 的坐标;(3)向右平移抛物线,使平移后的抛物线恰好经过△ABC 的外心,求出平移后的抛物线的解析式.解:(1)当x =0时,y =4,∴与y 轴交点A(0,4),当y =0时,-14x 2+32x +4=0,解得:x 1=-2,x 2=8,∴B(-2,0),C(8,0).(2)y =-14x 2+32x +4=-14(x -3)2+254,当P 在x 轴的上方时,即为抛物线的顶点P ⎝⎛⎭⎪⎫3,254时,可以构成平行四边形BPCQ ,如图1, 当P 在x 轴的下方时,∵BC =2+8=10,若四边形BPCQ 为平行四边形,则BC∥PQ,BC =PQ =10,有两种情况:①当P 在抛物线对称轴的左侧时,如图2,∴点P 的横坐标为-7,当x =-7时,y =-14×(-7)2+32×(-7)+4=-754,此时P ⎝⎛⎭⎪⎫-7,-754; ②当P 在抛物线对称轴的右侧时,如图3,∴点P 的横坐标为13,当x =13时,y =-14×132+32×13+4=-754,此时P ⎝⎛⎭⎪⎫13,-754; 综上所述,点P 的坐标为P ⎝⎛⎭⎪⎫3,254或⎝ ⎛⎭⎪⎫-7,-754或⎝ ⎛⎭⎪⎫13,-754. (3)如图3,∵A(0,4),B(-2,0),C(8,0),∴OA =4,OB =2,OC =8,∴OB OA =24=12,OA OC =48=12,∴OB OA =OA OC, ∵∠AOB =∠AOC=90°,∴△AOB ∽△COA ,∴∠BAO =∠ACO,∵∠ACO +∠OAC=90°,∴∠BAO +∠OAC=90°,∴∠BAC =90°,∴△ABC 是直角三角形,∴△ABC 的外心就是斜边AB 的中点E ,∵BC =10,∴BC 的中点E 的坐标为(3,0),即平移后的解析式经过E(3,0),∴相当于把原抛物线向右平移5个单位,∴平移后的解析式为y =-14(x -3-5)2+254=-14x 2+4x -394.24题答图第24题答图第24题答图。
{品质管理品质知识}九年级数学教学质量试题

{品质管理品质知识}九年级数学教学质量试题A.(x-)2=B.(x-)2=-C.(x-)2=D.(x-)2=17.关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0,则a的值() A.1B.-1C.±1D.28.已知一个圆锥的高是20,底面半径为10,则这个圆锥的侧面积展开图的圆心角等于()A.90o B.100o C.120o D.150o二、填空题(本大题共5小题,每小题4分,共20分)9.35÷7= .10.正方形的外接圆的半径为4cm,则正方形的边心距为cm.11.某次足球比赛中,每两个足球队之间要进行一次主场比赛和一次客场比赛,共有20场比赛活动,则这次足球比赛共有个足球队参加.12.已知点A(2,a)和点B(b,-1)关于原点对称,则a= ;b= .13.已知直角三角形的两直角边分别为5,12,则它的外接圆半径R= ,内切圆半径r= .三、解答题(本大题共有5小题,每小题7分,共35分,解答应写出文字说明、证明过程或演算步骤。
)14.计算:3--+(-2)(+2)15.解方程:x2+x=916.如图2,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=25o,求∠P的度数.C图217.一个袋子里有2个红色球,3个黄色球,4个绿色球,这些球除颜色外,它们的大小,形状都相同,从中随机摸出一个球,求这个球是红色或绿色的概率。
18.先化简后求值:(-)÷,其中x=-9四、解答题(本大题共3小题,每小题9分,共27分,解答过程要写出文字说明,证明过程或演算步骤)19.已知关于x的方程2x2-kx+1=0的一个解与方程=4的解相同(1)求k的值;(2)求方程2x2-kx+1=0的另一个解。
20.如图3,AB是直径,AC是弦,OD⊥AB交AC于点D,若∠A=30o,OD=20cm,求CD的长。
图321.小李为九年级(1)班毕业联欢会设计了一个“配紫色”的游戏,下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形。
2019九年级数学下册 第四次质量评估试卷 (新版)浙教版

第四次质量评估试卷[考查范围:九年级全册]一、选择题(每小题3分,共30分) 1.已知x 3=y 4,则xy的值是( B )A.43B.34C.47D.742.如图所示,已知∠ACB 是⊙O 的圆周角,∠ACB =50°,则圆心角∠AOB 是( D ) A .40° B .50° C .80° D .100°第2题图第3题图3.如图所示,在△ABC 中,点D ,E 分别在AB ,AC 边上,DE ∥BC.若AE∶EC=3∶1,AD =6,则BD 等于( A ) A .2 B .4 C .6 D .84.二次函数y =3x 2的图象向左平移2个单位,得到新的图象的二次函数表达式是( C )A .y =3x 2+2B .y =(3x +2)2C .y =3(x +2)2D .y =3(x -2)25.已知粉笔盒里只有2支黄色粉笔和3支红色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,则取出黄色粉笔的概率是( B )A.15B.25C.35D.236.如图所示,在ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF∶FC 等于( D ) A .3∶2 B .3∶1 C .1∶1 D .1∶26题图第7题图7.如图所示,△ABC 的三个顶点都在⊙O 上,∠BAC 的平分线交BC 于点D ,交⊙O 于点E ,则与△ABD 相似的三角形有( B )A .3个B .2个C .1个D .0个8.某同学在用描点法画二次函数y =ax 2+bx +c 的图象时,列出了下面的表格:由于粗心,他算错了其中一个y 值,则这个错误的数值是( B )A .-11B .-5C .2D .-29.定义符号min{a ,b}的含义为:当a≥b 时,min{a ,b}=b ;当a <b 时,min{a ,b}=a.如:min{1,-3}=-3,min{-4,-2}=-4.则min {}-x 2+1,-x 的最大值是( A ) A.5-12B.5+12C .1D .0第10题图10.如图所示,等边△ABC 和等腰Rt △DEF 均内接于⊙O,∠D =90°,EF ∥AC ,AC 分别交DE ,DF 于点P ,Q ,EF 分别交AB ,BC 于点G ,H ,则PQGH的值是( C )A.325B.233C.32D.23二、填空题(每小题4分,共24分)11.两个数3与27的比例中项是__±9__.12.在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机抽出一个球.记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.2,则估计盒子中大约有红球__16__个.13.如图所示,在菱形纸片ABCD 中,∠A =60°,将纸片折叠,点A ,D 分别落在A′,D ′处,且A′D′经过B ,EF 为折痕,当D′F⊥CD 时,CF FD 的值为2.14.如图所示,⊙O 的半径为2,点A ,C 在⊙O 上,线段BD 经过圆心O ,∠ABD =∠CDB=90°,AB =1,CD =3,则图中阴影部分的面积为__53π__.13题图14题图15题图15.如图所示,AB =5,P 是线段AB 上的动点,分别以AP 、BP 为边,在线段AB 的同侧作正方形APCD 和正方形BPEF ,连结CF ,则CF 的最小值是.16.如图所示,一块铁片边缘是由抛物线和线段AB 组成的,测得AB =20 cm ,抛物线的顶点到AB 边的距离为25 cm.现要沿AB 边向上依次截取宽度均为4 cm 的矩形铁皮,从下往上依次是第一块,第二块……如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第__6__块.三、解答题(共66分)图1 图2第17题图17.(6分)四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,将扑克牌洗匀后,如图2,背面朝上放置在桌面上.小亮和小明设计的游戏规则是两人同时抽取一张扑克牌,两张牌面数字之和为奇数时,小亮获胜;否则小明获胜.请问这个游戏规则公平吗?请说明理由.解:此游戏规则不公平,理由如下. 画树状图得:第17题答图共有12种等可能的结果,其中两张牌面数字之和为奇数的有8种情况, 所以P(小亮获胜)=812=23,P(小明获胜)=1-23=13.因为23>13,所以这个游戏规则不公平.18.(8分)已知二次函数y =ax 2+bx -2的图象经过点(-2,4),(-1,0). (1)求这个二次函数的表达式; (2)求函数的对称轴;(3)当-1≤x≤2时,求y 的范围.解:(1)根据题意,得⎩⎪⎨⎪⎧4a -2b -2=4,a -b -2=0,解得⎩⎪⎨⎪⎧a =1,b =-1,∴该二次函数的解析式为y =x 2-x -2.(2)∵y=x 2-x -2=⎝ ⎛⎭⎪⎫x -122-94,∴对称轴为直线x =12.(3)∵y=x 2-x -2=⎝ ⎛⎭⎪⎫x -122-94,∴顶点为⎝ ⎛⎭⎪⎫12,-94,二次函数的最小值为-94,设抛物线与x 轴的另一个交点为(m ,0),∴x =-1+m 2=12,∴m =2,∴另一个交点为(2,0),∴当-1≤x≤2时,-94≤y≤0.19.(8分)用工件槽[如图(a)]可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图(a)所示的A ,B ,E 三个接触点,该球的大小就符合要求.图(b)是过球心O 及A ,B ,E 三点的截面示意图,求这种铁球的直径.第19题图第19题答图解:连结OA ,OE ,设OE 与AB 交于点P ,如图所示.∵AC=BD ,AC ⊥CD ,BD ⊥CD ,∴四边形ACDB 是矩形.∵CD =16 cm ,PE =4 cm ,∴PA =8 cm ,BP =8 cm ,在Rt △OAP 中,由勾股定理得OA 2=PA 2+OP 2,即OA 2=82+(OA -4)2,解得OA =10.即这种铁球的直径为20 cm.第20题图20.(8分)如图所示,在矩形ABCD 中,AB =6,BC =10,点P 在边BC 上,点Q 在边CD 上, (1)如图(a)所示,将△ADQ 沿AQ 折叠,点D 恰好与点P 重合,求CQ 的长. (2)如图(b)所示,若CQ =2,且△ABP∽△PCQ 相似,求BP 的长.解:(1)由折叠可知,Rt △APQ ≌Rt △ADQ ,∴AP =AD =BC =10,DQ =PQ ,在Rt △ABP 中,AB =6,AP =10,∴BP =AP 2-AB 2=8,在Rt △PCQ 中,PC =BC -BP =2,设CQ =x ,则PQ =DQ =6-x ,由勾股定理可得x =83,即CQ =83.(2)∵CQ=2且△ABP∽△PCQ,设BP =x ,则PC =10-x.∴CQ BP =PC AB ,BP =CQ·AB PC ,即x =2×610-x ,解得x 1=5+13,x 2=5-13.∴BP =5+13或5-13.第21题图21.(8分)某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.(1)求y 与x 之间的函数关系式;(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克? (3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?解:(1)设函数的表达式为y =kx +b ,该一次函数过点(12,74),(28,66),得⎩⎪⎨⎪⎧12K +b =7428k +b =66,解得⎩⎪⎨⎪⎧k =-0.5b =80, ∴该函数的表达式为y =-0.5x +80,(2)根据题意,得(-0.5x +80)(80+x)=6750,解得x 1=10,x 2=70∵投入成本最低.∴x 2=70不满足题意,舍去.∴增种果树10棵时,果园可以收获果实6750千克.(3)根据题意,得w =(-0.5x +80)(80+x)=-0.5 x 2+40 x +6400=-0.5(x -40)2+7200 ∵a =-0.5<0,则抛物线开口向下,函数有最大值∴当x =40时,w 最大值为7200千克.∴当增种果树40棵时果园的最大产量是7200千克.第22题图22.(8分)【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sin α=13,求sin 2α的值.小娟是这样给小芸讲解的:构造如图1所示的图形,在⊙O 中,AB 是直径,点C 在⊙O 上,所以∠ACB =90°,作CD⊥AB 于点D.设∠BAC=α,则sin α=BC AB =13,可设BC =x ,则AB =3x ,……【问题解决】(1)请按照小娟的思路,利用图1求出sin 2α的值;(写出完整的解答过程) (2)如图2,已知点M ,N ,P 为⊙O 上的三点,且∠P=β,sin β=35,求sin 2β的值.第22题答图解:(1)在⊙O 中,AB 是直径,点C 在⊙O 上,∴∠ACB =90°,作CD⊥AB 于点D. 设∠BAC=α,则sin α=BC AB =13,可设BC =x ,则AB =3x.∴∠OAC =∠OCA=α,∴∠COB =2α,∴sin 2α=CO DC =429.(2)如图2,连结NO ,并延长交⊙O 于点Q ,连结MQ ,MO ,过点M 作MR⊥NO 于点R. 在⊙O 中,∠NMQ =90°.∵∠Q =∠P=β,∴∠MON =2∠Q=2β. 在Rt △QMN 中,∵ sin β=MN NQ =35,∴设MN =3k ,则NQ =5k ,易得OM =12NQ =52k. ∴MQ =QN 2-MN 2=4k.∵S △NMQ =12MN ·MQ =12NQ ·MR ,∴3k ·4k =5k·MR,∴MR =125k.在Rt △MRO 中,sin 2β=sin ∠MON =MR OM =125k 5k 2=2425.第23题图23.(10分)如图所示,直线l :y =3x +3与x 轴交于点A ,与y 轴交于点B.把△AOB 沿y 轴翻折,点A 落到点C ,抛物线过点B ,C 和D(3,0).(1)求直线BD 和抛物线的解析式;(2)点Q 是抛物线对称轴上一动点,是否存在点Q 使得|BQ -CQ|的值最大?若存在,请直接写出点Q 的坐标;若不存在,请说明理由;(3)在抛物线上是否存在点P ,使S △PBD =6?若存在,求出点P 的坐标;若不存在,说明理由. 解:(1)∵直线l :y =3x +3与x 轴交于点A ,与y 轴交于点B ,∴A(-1,0),B(0,3); ∵把△AOB 沿y 轴翻折,点A 落到点C ,∴C(1,0).设直线BD 的解析式为y =kx +b ,∵点B(0,3),D(3,0)在直线BD 上,∴⎩⎪⎨⎪⎧b =3,3k +b =0,解得k =-1,b =3,∴直线BD 的解析式为y =-x +3.设抛物线的解析式为y =a(x -1)(x -3),∵点B(0,3)在抛物线上,∴3=a×(-1)×(-3),解得a =1,∴抛物线的解析式为y =(x -1)(x -3)=x 2-4x +3.(2)∵B(0,3),C(1,0),∴直线BC 为y =-3x +3,∵抛物线对称轴为直线x =2,∴当x =2时,y =-3.∴Q(2,-3).第23题答图(3)假设存在点P ,使S △PBD =6,设点P 坐标为(m ,n). (Ⅰ)当点P 位于直线BD 上方时,如答图(a)所示. 过点P 作PE⊥x 轴于点E ,则PE =n ,DE =m -3. S △PBD =S梯形PEOB-S △BOD -S △PDE =12(3+n)m -12×3×3-12(m -3)n =6,化简,得m +n =7 ①,∵P(m ,n)在抛物线上,∴n =m 2-4m +3,代入①式,整理得m 2-3m -4=0,解得m 1=4,m 2=-1,∴n 1=3,n 2=8,∴P 1(4,3),P 2(-1,8).(Ⅱ)当点P 位于直线BD 下方时,如答图(b)所示:过点P 作PE⊥y 轴于点E ,则PE =m ,OE =-n ,BE =3-n.S △PBD =S 梯形PEOD +S △BOD -S △PBE =12(3+m)(-n)+12×3×3-12(3-n)m =6,化简,得:m +n =-1 ②,∵P(m ,n)在抛物线上,∴n =m 2-4m +3,代入②式,整理得m 2-3m +4=0,Δ=-7<0,此方程无解.故此时点P 不存在.综上所述,在抛物线上存在点P ,使S △PBD =6,点P 的坐标为(4,3)或(-1,8).第24题图24.(10分)如图所示,在△ABC 中,AC =BC ,∠ACB =Rt ∠,点P 是线段BC 延长线上任意一点,以AP 为直角边作等腰直角△APD,且∠APD=Rt ∠,连结BD.(1)求证:AC AP =ABAD.(2)在点P 运动过程中,试问∠PBD 的度数是否会变化?若不变,请求出它的度数;若变化,请说明它的变化趋势.(3)已知AB =2,设CP =x ,S △PBD =S.①试求S 关于x 的函数表达式;②当S =38时,求△BPD 的外接圆半径.解:(1)证明:如图,设AD 与PB 交于点K. ∵CA =BC ,∠ACB =90°,∴∠ABC =45°, ∵PA =PD ,∠APD =90°,∴∠PDK =∠PAD=∠ABK=45°,∵∠AKB =∠DKP,∴△AKB ∽△PKD ,∴AK PK =BKDK,∵∠AKP =∠BKD,∴△AKP ∽△BKD ,∴∠ADB =∠APK,∠PAK =∠DBK=45°, ∴∠ABD =∠ABK+∠DBK=90°, ∴∠ABD =∠ACP,∵∠ADB =∠APC, ∴△ABD ∽△ACP ,∴AC AP =ABAD.(2)结论:∠PBD 的度数是定值,∠PBD =45°.理由:由(1)可知△AKP∽△BKD,∴∠PAK =∠DBK=45°, ∴在点P 运动过程中,∠PBD 的度数是定值,∠PBD =45°. (3)①在Rt △ABC 中,∵AB =2, ∴BC =AC =1,在Rt △ACP 中,PA =AC 2+PC 2=1+x 2,∵△ABD ∽△ACP ,∴AC AB =PCBD ,∴12=xBD,∴BD =2x , ∴S =S △ABD +S △APD -S △ABP =12·2·2x +12·1+x 2·1+x 2-12(1+x)·1=12x 2+12x.第24题答图②取AD 的中点O ,连结OB ,OP.∵∠ABD =∠APD=90°,∴OB =OA =OP =OD , ∴点O 是△PBD 的外接圆的圆心, ∵S =38,∴12x 2+12x =38,解得x =12或-32(舍去),∴PC =12,由(2)可知BD =2x ,∴BD =22, 在Rt △ABD 中,AD =AB 2+BD 2=(2)2+⎝ ⎛⎭⎪⎫222=102,∴OD =12AD =104,∴△PBD 的外接圆的半径为104.。
九年级数学第四次质检课标 试题

2021--2021学年度九年级数学第四次质检考前须知:1.本卷满分是为120分,考试时间是是为120分钟.2.本卷是试题卷,不能答题,答题必须写在答题卡上,解题中的辅助线和标注角的字母、符号等必须添在答题卡的图形上.3.在答题卡上答题,选择题必须用2B黑色....签字笔或者黑色墨水..钢笔答题. ★ 祝 考 试 顺 利 ★一、选择题〔本大题一一共10小题,每一小题3分,一共30分.每一小题只有一个正确选项,请把正确选项的代号填在题后的括号内.〕1.-4的相反数等于〔 〕A. 4B. -4C. 41D. 41- 2.以下运算中,正确的选项是〔 〕A . 422x x x =+B . 22x x x =÷C . 4224)2(x x -=- D . 32x x x =⋅3.2008年11月26日,“中国红歌会〞在HY 成功举行. “中国红歌会〞自2021年以来连续举办三届,报名人数到达138000余人,用科学计数法表示为〔 〕A.人4108.13⨯B.人5108.13⨯C.人510381⨯. D .人610381⨯.4. 下面有4个汽车标志图案,其中是轴对称图形的是:〔 〕班级 学号 姓名………密……………封……………线………………内………………不…………………准…………………答……………题………① ② ③ ④A.②③④B.①③④C.①②④D.①②③542+-=x x y 的顶点坐标是( )A.( 2, 1 )B.( -2, 1 )C.( 2, 5 )D.( -2,5〕 6. 将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形, 这个新的图形可以是以下图形中的〔 〕。
A. 三角形B. 平行四边形C. 矩形D. 正方形7. 由几个小立方块所搭几何体的俯视图如下图,小正方形中的数字表示 在俯视图位置的小立方块的个数,这个几何体的主视图是〔 〕A .B .C .D .8.如图,矩形ABCD 内接于⊙O ,且AB =3,BC 中阴影局部所表示的扇形AOD 的面积为( ) A. 3π B. 4π C. 6π D.8π9.如图,小正方形的边长均为1,那么以下图中的三角形〔阴影局部〕与△ABC 相似的是〔 〕ABCDO 第(8)题第(6)题211110.在平面直角坐标系中,点A(-4,0),点B(2,0),假设点C在一次函数122y x=-+的图象上,且△ABC为等腰三角形,那么满足条件的点C有〔〕A. 2个B. 3个C. 4个D. 5二、填空题〔本大题一一共6小题,每一小题4分,一共24分〕y=中,自变量x的取值范围是 .12.分解因式:2222x y-=13、在由小正三角形组成的虚线网格中,那么tan∠AOB= 。
【考试重点】新九年级数学上册 第四次质量评估试卷 (新版)浙教版
第四次质量评估试卷[考查范围:1~4章]一、选择题(每小题3分,共30分)第1题图1.如图所示,在△ABC中,DE∥BC,若AD∶DB=2∶3,则下列结论中正确的是( B)A.DEBC=23B.DEBC=25C.AEAC=23D.AEEC=252.若△ABC∽△DEF,它们的面积比为4∶1,则△ABC与△DEF的相似比为( A) A.2∶1 B.1∶2 C.4∶1 D.1∶43.在四张背面完全相同的卡片上分别印着等腰三角形、平行四边形、菱形、圆的图案,现将印有图案的一面朝下,混合后从中随机抽取两张,则抽到卡片上印有图案都是轴对称图形的概率为( D)A.34B.14C.13D.124.如图所示,有三个矩形,其中互为相似图形的是( B)A.甲和乙 B.甲和丙 C.乙和丙 D.甲、乙和丙第4题图5题图6题图5.如图所示,⊙O上A,B,C三点,若∠B=50,∠A=20°,则∠AOB等于( D) A.30°B.50°C.70°D.60°6.如图所示,在△ABC中,AB=3AD,DE∥BC,EF∥AB,若AB=9,DE=2,则线段FC 的长度是( C)A.6 B.5 C.4 D.37.如图所示,在平面直角坐标系中,O 为坐标原点,点A 的坐标为(1,3),将线段OA 绕原点O 逆时针旋转30°,得到线段OB ,则点B 的坐标是( A )A .(0,2)B .(2,0)C .(1,-3)D .(-1,3)7题图8题图9题图8.如图所示,在△ABC 中,∠ACB =90°,AC +BC =8,分别以AB ,AC ,BC 为半径作半圆,若记图中阴影部分的面积为y ,AC 为x ,则下列y 关于x 的图象中正确的是( A )A B C D9.如图所示,在钝角三角形ABC 中,AB =6 cm ,AC =12 cm ,动点D 从点A 出发到点B 止,动点E 从点C 出发到点A 止,点D 运动的速度为1 cm/s ,点E 运动的速度为2 cm/s.如果两点同时运动,那么当以点A ,D ,E 为顶点的三角形与△ABC 相似时,运动的时间是( A )A .3 s 或4.8 sB .3 sC .4.5 sD .4.5 s 或4.8 s10.抛物线y =ax 2+bx +3(a≠0)过A(4,4),B(2,m)两点,点B 到抛物线对称轴的距离记为d ,满足0<d≤1,则实数m 的取值范围是( B )A .m ≤2或m≥3B .m ≤3或m≥4C .2<m <3D .3<m <4 二、填空题(每小题4分,共24分)11.已知a b =52,则a +b a -b =__73__.12.如图,∠DAB =∠CAE,请你再补充一个边条件,使得△ABC∽△ADE:__∠D=∠B(答案不唯一)__.13.圆内接四边形ABCD ,两组对边的延长线分别相交于点E ,F ,且∠E=40°,∠F =60°,则∠A=__40°__.第12题图13题图第15题图16题图14.抛物线y =x 2+bx +c 与x 轴相交于A(-1,0),B(3,0)两点,写出y >-3时x 的取值范围:__x <0或x >2__.15.如图所示,AD 是△ABC 的高,AE 是△ABC 的外接圆⊙O 的直径,且AB =42,AC =5,AD =4,则⊙O 的直径AE =.16.如图所示,在Rt △ABC 中,∠C =90°,AC =10,BC =30,动点P 从点B 开始沿边BC 向点C 以每秒2个单位长度的速度运动,动点Q 从点C 开始沿边CA 向点A 以每秒1个单位长度的速度运动,连结PQ ,点P ,Q 分别从点B ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t 秒(t≥0).(1)当t =__6__秒时,点P ,C ,Q 所构成的三角形与Rt △ABC 相似;(2)在整个运动过程中,线段PQ 的中点所经过的路程长为. 三、解答题(共66分)17.(6分)有A ,B ,C 三种款式的帽子,E ,F 两种款式的围巾,穿戴时小婷任意选一顶帽子和一条围巾.(1)用合适的方法表示搭配的所有可能的结果;(2)求小婷恰好选中她所喜欢的A 款帽子和E 款围巾的概率.解:(1)根据题意,小婷任意选取一顶帽子和一条围巾,有A 、E ,A 、F ,B 、E ,B 、F ,C 、E ,C 、F ,6种情况,(2)小婷恰好选中她所喜欢的A 款帽子和E 款围巾的概率=16.第18题图18.(8分)“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图所示,矩形ABCD ,东边城墙AB 长9里,南边城墙AD 长7里,东门点E 、南门点F 分别是AB ,AD 的中点,EG ⊥AB ,FH ⊥AD ,EG =15里,HG 经过A 点,求FH 的长.解:∵EG⊥AB,FH ⊥AD ,HG 经过A 点,∴FA ∥EG ,EA ∥FH ,∴∠HFA =∠AEG=90°,∠FHA =∠EAG,∴△AFH ∽△GEA ,∴AF EG =FHEA.∵AB =9里,AD =7里,EG =15里,∴FA =3.5里,EA =4.5里,∴3.515=FH4.5,解得FH=1.05里.第19题图19.(8分)如图所示,正方形ABCD 的边长为1,其中弧DE 、弧EF 、弧FG 的圆心依次为点A ,B ,C.(1)求点D 沿三条弧运动到点G 所经过的路线长; (2)判断直线GB 与DF 的位置关系,并说明理由.解:(1)根据弧长公式,得所求路线长为90π×1180+90π×2180+90π×3180=3π.(2)GB⊥DF.理由如下:在△FCD 和△GCB 中,∵⎩⎪⎨⎪⎧CF =CG ,∠FCD =∠GCB,CD =CB ,∴△FCD ≌△GCB(SAS),∴∠G =∠F,∵∠F +∠FDC=90°,∴∠G +∠FDC=90°,∴∠GHD =90°,∴GB ⊥DF.第20题图20.(8分)如图所示,在矩形ABCD 中,BE ⊥AC 分别交AC ,AD 于点F ,E ,若AD =1,AB =CF ,求AE 的长.解:∵四边形ABCD 是矩形,∴BC =AD =1,∠BAE =∠ABC=90°,∴∠ABE +∠CBF=90°, ∵BE ⊥AC ,∴∠BFC =90°,∴∠BCF +∠CBF=90°,∴∠ABE =∠FCB,在△AB E 和△FCB 中,⎩⎪⎨⎪⎧∠EAB=∠BFC=90°,AB =CF ,∠ABE =∠FCB,∴△ABE ≌△FCB ,∴BF =AE ,BE =BC =1,∵BE ⊥AC ,∴∠BAF +∠ABF=90°,∵∠ABF +∠AEB=90°,∴∠BAF =∠AEB,∵∠BAE =∠AFB,∴△ABE ∽△FBA ,∴ABBF =BE AB ,∴AB AE =1AB,∴AE =AB 2, 在Rt △ABE 中,BE =1,根据勾股定理,得AB 2+AE 2=BE 2=1,∴AE +AE 2=1,∵AE >0,∴AE =5-12. 21.(8分)已知一次函数y 1=x +b 的图象与二次函数y 2=a(x 2+bx +3)(a≠0,a ,b 为常数)的图象交于A ,B 两点,且点A 的坐标为(0,3).(1)求出a ,b 的值;(2)求出点B 的坐标,并直接写出当y 1≥y 2时x 的取值范围; (3)设s =y 1+y 2,t =y 1-y 2,若n≤x≤m 时,s 随着x 的增大而增大,且t 也随着x 的增大而增大,求n 的最小值和m 的最大值.解:(1)把A(0,3)代入y 1=x +b 中,得b =3,∴y 1=x +3,y 2=a(x 2+3x +3),把A(0,3)代入y 2=a(x 2+3x +3)中,得3a =3,a =1,∴a =1,b =3. (2)由题意,得⎩⎪⎨⎪⎧y =x +3,y =x 2+3x +3, 解得⎩⎪⎨⎪⎧x 1=0,y 1=3或⎩⎪⎨⎪⎧x 2=-2,y 2=1.第21题答图∴B(-2,1),如图所示,当y 1≥y 2时x 的取值范围是-2≤x≤0.(3)s =y 1+y 2=x +3+x 2+3x +3=x 2+4x +6=(x +2)2+2,∵抛物线开口向上,∴当x≥-2时,s 随着x 的增大而增大,t =y 1-y 2=x +3-(x 2+3x +3)=-x 2-2x =-(x +1)2+1,∵抛物线开口向下,∴当x≤-1时,t 随着x 的增大而增大,∴当-2≤x≤-1时,s 随着x 的增大而增大,且t 也随着x 的增大而增大, ∵n ≤x ≤m ,s 随着x 的增大而增大,且t 也随着x 的增大而增大, ∴n 的最小值-2,m 的最大值-1.第22题图22.(8分)有一块锐角三角形卡纸余料ABC ,它的边BC =120 cm ,高AD =80 cm ,为使卡纸余料得到充分利用,现把它裁剪成一个邻边之比为2∶5的矩形纸片EFGH 和正方形纸片PMNQ ,裁剪时,矩形纸片的较长边在BC 上,正方形纸片一边在矩形纸片的较长边EH 上,其余顶点均分别在AB ,AC 上,具体裁剪方式如图所示.(1)求矩形纸片较长边EH 的长;(2)裁剪正方形纸片时,小聪同学是按以下方法进行裁剪的:先沿着剩余料△AEH 中与边EH 平行的中位线剪一刀,再沿过该中位线两端点向边EH 所作的垂线剪两刀,请你通过计算,判断小聪的剪法是否正确.解:(1)设EF =2x ,EH =5x ,∵矩形对边EH∥BC,∴△AEH∽△ABC,∴EH BC =AR AD ,即5x120=80-2x80,解得x =15,EH =5x =15×5=75 cm , 所以矩形纸片较长边EH 的长为75 cm. (2)小聪的剪法不正确.理由如下:设正方形的边长为a ,AR =AD -RD =80-2×15=50 cm ,AK =50-a ,由题意,知△APQ∽△AEH,∴PQ EH =AK AR ,即a 75=50-a 50,解得a =30,与边EH 平行的中位线=12×75=37.5 cm ,∵37.5≠30,∴小聪的剪法不正确.图(a) 图(b)第23题图23.(10分)(1)如图(a)所示,已知∠ACB=∠DCE=90°,AC =BC =6,CD =CE ,AE =3,∠CAE =45°,求AD 的长;(2)如图(b)所示,已知∠ACB=∠DCE=90°,∠ABC =∠CED =∠CAE=30°,AC =3,AE =8,求AD 的长.解:(1)如图(a)所示,连结BE ,∵∠ACB =∠DCE=90°, ∴∠ACB +∠ACE=∠DCE+∠ACE,即∠BCE=∠ACD,又∵AC=BC ,DC =EC ,在△ACD 和△BCE 中,⎩⎪⎨⎪⎧AC =BC ,∠BCE =∠ACD,DC =EC ,∴△ACD ≌△BCE ,∴AD =BE ,∵AC =BC =6,∴AB =62,∵∠ACB =90°,AC =BC ,∴∠BAC =∠ABC=45°.∵∠BAC =∠CAE=45°,∴∠BAE=90°,在Rt △BAE 中,AB =62,AE =3,∴BE =9,∴AD =9.第23题答图(a)第23题答图(b)(2)如图(b)所示,连结BE ,∵∠ACB =∠DCE=90°,∠ABC =∠CED=30°,∴AC BC =CDCE =13,AB =2AC =6,∠BAC =60°.∵∠ACB =∠DCE=90°,∠ABC =∠CED=30°,∴Rt △ABC ∽Rt △DCE ,∴AC DC =BCCE ,∴∠BCE =∠ACD,∴△ACD ∽△BCE ,∴AD BE =AC BC =33,∵∠BAC =60°,∠CAE =30°,∴∠BAE =90°,又AB =6,AE =8,∴BE =10,∴AD =1033.24.(10分)在平面直角坐标系中,抛物线y =-14x 2+32x +4的图象与x 轴交于B ,C 两点(B 在C 的左侧),与y 轴交于点A.(1)求出点A ,B ,C 的坐标;(2)在抛物线上有一动点P ,抛物线的对称轴上有另一动点Q ,若以B ,C ,P ,Q 为顶点的四边形是平行四边形,直接写出点P 的坐标;(3)向右平移抛物线,使平移后的抛物线恰好经过△ABC 的外心,求出平移后的抛物线的解析式.解:(1)当x =0时,y =4,∴与y 轴交点A(0,4),当y =0时,-14x 2+32x +4=0,解得:x 1=-2,x 2=8,∴B(-2,0),C(8,0).(2)y =-14x 2+32x +4=-14(x -3)2+254,当P 在x 轴的上方时,即为抛物线的顶点P ⎝⎛⎭⎪⎫3,254时,可以构成平行四边形BPCQ ,如图1,当P 在x 轴的下方时,∵BC =2+8=10,若四边形BPCQ 为平行四边形,则BC∥PQ,BC =PQ =10,有两种情况:①当P 在抛物线对称轴的左侧时,如图2,∴点P 的横坐标为-7,当x =-7时,y =-14×(-7)2+32×(-7)+4=-754,此时P ⎝⎛⎭⎪⎫-7,-754; ②当P 在抛物线对称轴的右侧时,如图3,∴点P 的横坐标为13,当x =13时,y =-14×132+32×13+4=-754,此时P ⎝ ⎛⎭⎪⎫13,-754;综上所述,点P 的坐标为P ⎝ ⎛⎭⎪⎫3,254或⎝ ⎛⎭⎪⎫-7,-754或⎝ ⎛⎭⎪⎫13,-754.(3)如图3,∵A(0,4),B(-2,0),C(8,0),∴OA =4,OB =2,OC =8,∴OB OA =24=12,OA OC =48=12,∴OB OA =OA OC, ∵∠AOB =∠AOC=90°,∴△AOB ∽△COA ,∴∠BAO =∠ACO,∵∠ACO +∠OAC=90°,∴∠BAO +∠OAC=90°,∴∠BAC =90°, ∴△ABC 是直角三角形,∴△ABC 的外心就是斜边AB 的中点E , ∵BC =10,∴BC 的中点E 的坐标为(3,0), 即平移后的解析式经过E(3,0),∴相当于把原抛物线向右平移5个单位,∴平移后的解析式为y =-14(x -3-5)2+254=-14x 2+4x -394.第24题答图第24题答图第24题答图。
九年级化学第四次质检试题

九年级化学第四次质检测试题可能用到的相对原子质量:H -1 C -12 N -14 O -16一、选择题:(本题共10道小题,每题3分,共30分,每题各有一个正确答案。
) 1.当你站在电视机背后时,常能闻到一股特殊气味,散发出这种气味的物质是臭氧(O 3),氧气在放电的条件下可以转化为臭氧,下列与此相关的说法中正确的是( ) A .该变化是化学变化 B .氧气属于化合物 C .该变化是物理变化 D .臭氧是混合物 2.下列常见物质中,属于纯净物的是( ) A .可乐饮料 B .加碘食盐 C .蒸馏水 D .玻璃钢 3.生铁放入足量的硫酸铜溶液中,剩余的残渣是( )A .CuB .C C .FeD .C 和Cu 4.下列有关对自然界水的做法不合理...的是( ) A .水是最常用的溶剂 B .煮沸的汤比煮沸的水温度高 C .蒸发海水得到粗盐 D .用明矾溶液来区别硬水和软水 5.以下实验基本操作正确的是( )A B C D6.下列各组气体中,仅用燃着的木条不能区分出来的是( ) A .一氧化碳和二氧化碳 B . 氧气和空气 C . 甲烷和空气 D .二氧化碳和氮气 7.关于下列实验现象的描述,错误..的是( ) A .蜡烛在氧气里燃烧比在空气里燃烧更旺,发出白光,并放出热量 B .红磷在氧气中燃烧产生大量白雾C .镁带在空气中燃烧,发出耀眼的白光,生成白色固体D .细铁丝在氧气中剧烈燃烧,火星四射,生成黑色固体8.下列适量物质溶于水后,可以造成溶液温度显著降低的是( ) A .硝酸铵 B .蔗糖 C .氯化钠 D .浓硫酸9.元素周期表中铝元素的部分信息如右下图所示,下列说法正确的是( ) A .铝的元素符号是AgB .铝的原子序数是26.98C .铝的核内质子数是13D .铝在反应中易得到电子 10.已知白磷的着火点为40℃,下列实验中白磷能够燃烧的是( ) 二、(本小题共4小题35分) 11.(16分)用数字和化学符号填空:(1)氩气 ;(2)2个镁离子 ;(3)地壳中含量最高的金属元素 ; (4) 3 个二氧化碳分子 ;(5)五氧化二磷中磷元素为+5价 。
九年级数学下册 第四次质量评估试卷 (新版)浙教版

第四次质量评估试卷[考查范围:九年级全册]一、选择题(每小题3分,共30分) 1.已知x 3=y 4,则xy的值是( B )A.43B.34C.47D.742.如图所示,已知∠ACB 是⊙O 的圆周角,∠ACB =50°,则圆心角∠AOB 是( D ) A .40° B .50° C .80° D .100°第2题图第3题图3.如图所示,在△ABC 中,点D ,E 分别在AB ,AC 边上,DE ∥BC.若AE∶EC=3∶1,AD =6,则BD 等于( A )A .2B .4C .6D .84.二次函数y =3x 2的图象向左平移2个单位,得到新的图象的二次函数表达式是( C )A .y =3x 2+2B .y =(3x +2)2C .y =3(x +2)2D .y =3(x -2)25.已知粉笔盒里只有2支黄色粉笔和3支红色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔,则取出黄色粉笔的概率是( B )A.15B.25C.35D.236.如图所示,在ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF∶FC 等于( D )A .3∶2B .3∶1C .1∶1D .1∶26题图第7题图7.如图所示,△ABC 的三个顶点都在⊙O 上,∠BAC 的平分线交BC 于点D ,交⊙O 于点E ,则与△ABD 相似的三角形有( B )A .3个B .2个C .1个D .0个82A .-11B .-5C .2D .-29.定义符号min{a ,b}的含义为:当a≥b 时,min{a ,b}=b ;当a <b 时,min{a ,b}=a.如:min{1,-3}=-3,min{-4,-2}=-4.则min {}-x 2+1,-x 的最大值是( A )A.5-12B.5+12C .1D .0第10题图10.如图所示,等边△ABC 和等腰Rt △DEF 均内接于⊙O,∠D =90°,EF ∥AC ,AC 分别交DE ,DF 于点P ,Q ,EF 分别交AB ,BC 于点G ,H ,则PQGH的值是( C )A.325B.233C.32D.23二、填空题(每小题4分,共24分)11.两个数3与27的比例中项是__±9__. 12.在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机抽出一个球.记下颜色后再放回口袋中,通过大量重复摸球试验发现,摸到黄球的频率是0.2,则估计盒子中大约有红球__16__个.13.如图所示,在菱形纸片ABCD 中,∠A =60°,将纸片折叠,点A ,D 分别落在A′,D ′处,且A′D′经过B ,EF 为折痕,当D′F⊥CD 时,CF FD 的值为2.14.如图所示,⊙O 的半径为2,点A ,C 在⊙O 上,线段BD 经过圆心O ,∠ABD =∠CDB =90°,AB =1,CD =3,则图中阴影部分的面积为__53π__.13题图14题图15题图第16题图15.如图所示,AB =5,P 是线段AB 上的动点,分别以AP 、BP 为边,在线段AB 的同侧作正方形APCD 和正方形BPEF ,连结CF ,则CF 的最小值是.16.如图所示,一块铁片边缘是由抛物线和线段AB 组成的,测得AB =20 cm ,抛物线的顶点到AB 边的距离为25 cm.现要沿AB 边向上依次截取宽度均为4 cm 的矩形铁皮,从下往上依次是第一块,第二块……如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第__6__块.三、解答题(共66分)图1 图2第17题图17.(6分)四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图1,将扑克牌洗匀后,如图2,背面朝上放置在桌面上.小亮和小明设计的游戏规则是两人同时抽取一张扑克牌,两张牌面数字之和为奇数时,小亮获胜;否则小明获胜.请问这个游戏规则公平吗?请说明理由.解:此游戏规则不公平,理由如下. 画树状图得:第17题答图共有12种等可能的结果,其中两张牌面数字之和为奇数的有8种情况, 所以P(小亮获胜)=812=23,P(小明获胜)=1-23=13.因为23>13,所以这个游戏规则不公平.18.(8分)已知二次函数y =ax 2+bx -2的图象经过点(-2,4),(-1,0). (1)求这个二次函数的表达式; (2)求函数的对称轴;(3)当-1≤x≤2时,求y 的范围.解:(1)根据题意,得⎩⎪⎨⎪⎧4a -2b -2=4,a -b -2=0,解得⎩⎪⎨⎪⎧a =1,b =-1,∴该二次函数的解析式为y =x2-x -2.(2)∵y=x 2-x -2=⎝ ⎛⎭⎪⎫x -122-94,∴对称轴为直线x =12.(3)∵y=x 2-x -2=⎝ ⎛⎭⎪⎫x -122-94,∴顶点为⎝ ⎛⎭⎪⎫12,-94,二次函数的最小值为-94,设抛物线与x 轴的另一个交点为(m ,0),∴x =-1+m 2=12,∴m =2,∴另一个交点为(2,0),∴当-1≤x≤2时,-94≤y≤0.19.(8分)用工件槽[如图(a)]可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图(a)所示的A ,B ,E 三个接触点,该球的大小就符合要求.图(b)是过球心O 及A ,B ,E 三点的截面示意图,求这种铁球的直径.第19题图第19题答图解:连结OA ,OE ,设OE 与AB 交于点P ,如图所示.∵AC=BD ,AC ⊥CD ,BD ⊥CD ,∴四边形ACDB 是矩形.∵CD=16 cm ,PE =4 cm ,∴PA =8 cm ,BP =8 cm ,在Rt △OAP 中,由勾股定理得OA 2=PA 2+OP 2,即OA 2=82+(OA -4)2,解得OA =10.即这种铁球的直径为20 cm.第20题图20.(8分)如图所示,在矩形ABCD 中,AB =6,BC =10,点P 在边BC 上,点Q 在边CD 上,(1)如图(a)所示,将△ADQ 沿AQ 折叠,点D 恰好与点P 重合,求CQ 的长.(2)如图(b)所示,若CQ =2,且△ABP∽△PCQ 相似,求BP 的长.解:(1)由折叠可知,Rt △APQ ≌Rt △ADQ ,∴AP =AD =BC =10,DQ =PQ ,在Rt △ABP 中,AB =6,AP =10,∴BP =AP 2-AB 2=8,在Rt △PCQ 中,PC =BC -BP =2,设CQ =x ,则PQ =DQ =6-x ,由勾股定理可得x =83,即CQ =83.(2)∵CQ=2且△ABP∽△PCQ,设BP =x ,则PC =10-x.∴CQ BP =PC AB ,BP =CQ·ABPC ,即x=2×610-x,解得x 1=5+13,x 2=5-13. ∴BP =5+13或5-13.第21题图21.(8分)某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.(1)求y 与x 之间的函数关系式;(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克? (3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?解:(1)设函数的表达式为y =kx +b ,该一次函数过点(12,74),(28,66),得⎩⎪⎨⎪⎧12K +b =7428k +b =66,解得⎩⎪⎨⎪⎧k =-0.5b =80,∴该函数的表达式为y =-0.5x +80,(2)根据题意,得(-0.5x +80)(80+x)=6750,解得x 1=10,x 2=70∵投入成本最低.∴x 2=70不满足题意,舍去.∴增种果树10棵时,果园可以收获果实6750千克.(3)根据题意,得w =(-0.5x +80)(80+x)=-0.5 x 2+40 x +6400=-0.5(x -40)2+7200∵a =-0.5<0,则抛物线开口向下,函数有最大值∴当x =40时,w 最大值为7200千克.∴当增种果树40棵时果园的最大产量是7200千克.第22题图22.(8分)【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sin α=13,求sin 2α的值.小娟是这样给小芸讲解的:构造如图1所示的图形,在⊙O中,AB 是直径,点C 在⊙O 上,所以∠ACB=90°,作CD⊥AB 于点D.设∠BAC=α,则sin α=BC AB =13,可设BC =x ,则AB =3x ,…… 【问题解决】(1)请按照小娟的思路,利用图1求出sin 2α的值;(写出完整的解答过程)(2)如图2,已知点M ,N ,P 为⊙O 上的三点,且∠P=β,sin β=35,求sin 2β的值.第22题答图解:(1)在⊙O 中,AB 是直径,点C 在⊙O 上,∴∠ACB =90°,作CD⊥AB 于点D. 设∠BAC=α,则sin α=BC AB =13,可设BC =x ,则AB =3x.∴AC =AB 2-BC 2=(3x )2-x 2=22x ,∵12AC ·BC =12AB ·CD ,∴CD =223x ,∵OA =OC ,∴∠OAC =∠OCA=α,∴∠COB =2α,∴sin 2α=CO DC =429.(2)如图2,连结NO ,并延长交⊙O 于点Q ,连结MQ ,MO ,过点M 作MR⊥NO 于点R.在⊙O 中,∠NMQ =90°.∵∠Q =∠P=β,∴∠MON =2∠Q=2β. 在Rt △QMN 中,∵ sin β=MN NQ =35,∴设MN =3k ,则NQ =5k ,易得OM =12NQ =52k. ∴MQ =QN 2-MN 2=4k.∵S △NMQ =12MN ·MQ =12NQ ·MR ,∴3k ·4k =5k·MR,∴MR =125k.在Rt △MRO 中,sin 2β=sin ∠MON =MR OM =125k 5k 2=2425.第23题图23.(10分)如图所示,直线l :y =3x +3与x 轴交于点A ,与y 轴交于点B.把△AOB 沿y 轴翻折,点A 落到点C ,抛物线过点B ,C 和D(3,0).(1)求直线BD 和抛物线的解析式;(2)点Q 是抛物线对称轴上一动点,是否存在点Q 使得|BQ -CQ|的值最大?若存在,请直接写出点Q 的坐标;若不存在,请说明理由;(3)在抛物线上是否存在点P ,使S △PBD =6?若存在,求出点P 的坐标;若不存在,说明理由.解:(1)∵直线l :y =3x +3与x 轴交于点A ,与y 轴交于点B ,∴A(-1,0),B(0,3); ∵把△AOB 沿y 轴翻折,点A 落到点C ,∴C(1,0).设直线BD 的解析式为y =kx +b ,∵点B(0,3),D(3,0)在直线BD 上,∴⎩⎪⎨⎪⎧b =3,3k +b =0,解得k =-1,b =3,∴直线BD 的解析式为y =-x +3.设抛物线的解析式为y =a(x -1)(x -3),∵点B(0,3)在抛物线上,∴3=a×(-1)×(-3),解得a =1,∴抛物线的解析式为y =(x -1)(x -3)=x 2-4x +3.(2)∵B(0,3),C(1,0),∴直线BC 为y =-3x +3,∵抛物线对称轴为直线x =2,∴当x =2时,y =-3.∴Q(2,-3).第23题答图(3)假设存在点P ,使S △PBD =6,设点P 坐标为(m ,n). (Ⅰ)当点P 位于直线BD 上方时,如答图(a)所示. 过点P 作PE⊥x 轴于点E ,则PE =n ,DE =m -3.S △PBD =S 梯形PEOB -S △BOD -S △PDE =12(3+n)m -12×3×3-12(m -3)n =6,化简,得m +n =7 ①,∵P(m ,n)在抛物线上,∴n =m 2-4m +3,代入①式,整理得m 2-3m -4=0,解得m 1=4,m 2=-1,∴n 1=3,n 2=8,∴P 1(4,3),P 2(-1,8).(Ⅱ)当点P 位于直线BD 下方时,如答图(b)所示:过点P 作PE⊥y 轴于点E ,则PE =m ,OE =-n ,BE =3-n.S △PBD =S 梯形PEOD +S △BOD -S △PBE =12(3+m)(-n)+12×3×3-12(3-n)m =6,化简,得:m+n =-1 ②,∵P(m ,n)在抛物线上,∴n =m 2-4m +3,代入②式,整理得m 2-3m +4=0,Δ=-7<0,此方程无解.故此时点P 不存在.综上所述,在抛物线上存在点P ,使S △PBD =6,点P 的坐标为(4,3)或(-1,8).第24题图24.(10分)如图所示,在△ABC 中,AC =BC ,∠ACB =Rt ∠,点P 是线段BC 延长线上任意一点,以AP 为直角边作等腰直角△APD,且∠APD=Rt ∠,连结BD.(1)求证:AC AP =ABAD.(2)在点P 运动过程中,试问∠PBD 的度数是否会变化?若不变,请求出它的度数;若变化,请说明它的变化趋势.(3)已知AB =2,设CP =x ,S △PBD =S.①试求S 关于x 的函数表达式;②当S =38时,求△BPD 的外接圆半径.解:(1)证明:如图,设AD 与PB 交于点K. ∵CA =BC ,∠ACB =90°,∴∠ABC =45°, ∵PA =PD ,∠APD =90°,∴∠PDK =∠PAD=∠ABK=45°,∵∠AKB =∠DKP, ∴△AKB ∽△PKD ,∴AK PK =BKDK,∵∠AKP =∠BKD,∴△AKP ∽△BKD ,∴∠ADB =∠APK,∠PAK =∠DBK=45°, ∴∠ABD =∠ABK+∠DBK=90°, ∴∠ABD =∠ACP,∵∠ADB =∠APC, ∴△ABD ∽△ACP ,∴AC AP =ABAD.(2)结论:∠PBD 的度数是定值,∠PBD =45°.理由:由(1)可知△AKP∽△BKD,∴∠PAK =∠DBK=45°, ∴在点P 运动过程中,∠PBD 的度数是定值,∠PBD =45°. (3)①在Rt △ABC 中,∵AB =2, ∴BC =AC =1,在Rt △ACP 中,PA =AC 2+PC 2=1+x 2,∵△ABD ∽△ACP ,∴AC AB =PCBD,∴12=xBD,∴BD =2x , ∴S =S △ABD +S △APD -S △ABP =12·2·2x +12·1+x 2·1+x 2-12(1+x)·1=12x 2+12x.第24题答图②取AD 的中点O ,连结OB ,OP.∵∠ABD =∠APD=90°,∴OB =OA =OP =OD , ∴点O 是△PBD 的外接圆的圆心, ∵S =38,∴12x 2+12x =38,解得x =12或-32(舍去),∴PC =12,由(2)可知BD =2x ,∴BD =22, 在Rt △ABD 中,AD =AB 2+BD 2=(2)2+⎝ ⎛⎭⎪⎫222=102,∴OD =12AD =104,∴△PBD 的外接圆的半径为104.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{品质管理品质知识}初三四次教学质量检测试卷衢州华外2004学年第二学期初三第四次教学质量检测试卷初三语文命题:初三语文备课组一、语文知识积累与运用。
(25分)1.给加点字注音或按注音写出汉字。
(4分)(1)龙游为何多塔?今日依然众说纷纭,莫zhōng()一是,或曰镇邪扶正,避灾求吉,以俟.()风调雨顺,国泰民安;或曰长期异地任职的显赫官员欲借建塔光宗耀祖,流芳百世。
至于何说为上,还有待人们考证。
(2)亚灵两峰间的小弄仅5米宽,石梯长300米。
弄里风冽冽,凉嗖嗖,疲劳和暑气逃dùn()头贴峭壁,仰望苍穹.()浩渺天宇只有二三百米长眉毛月形的白光。
真是“名山罕见三爿石,胜景唯推一字天。
”2.按要求写出相关名句。
(8分)(选做其中八条横线的内容,若全做只改前面8道)(1),要留青白在人间。
(《石灰吟》明·于谦)(2),只缘身在此山中。
(宋·苏轼《题西林壁》)(3)长风破浪会有时,。
(《行路难》唐·李白)(4),各领风骚数百年。
(清·赵翼《论诗》)(5),千金散尽还复来。
(唐·李白《将进酒》)(6)纸上得来终觉浅,。
(《冬夜读书示子聿》宋·陆游)(7),柯烂不知归。
振衣独啸无人见,。
(8)食饱心自若,,,衢州人食人。
(9)海内存知已,。
(唐·王勃《送杜少府之任蜀川》)(10)为人性僻耽佳句,。
(唐·杜甫《江上值水如海势聊短述》)(11),一片冰心在玉壶。
(唐·王昌龄)《芙蓉楼送辛渐》(12)苏轼在《明月几时有》一词中表达美好祝愿的诗句是:,。
3.根据十二生肖排列顺序,在横线上补写出含有缺失生肖的成语。
(3分)首.鼠两端狐假虎.威守株待兔.龙.飞凤舞画蛇.添足羊.肠小道沐猴.而冠狗.尾续貂行同狗彘.(猪)4.修改下面句子的语病。
(2分)代表们对开发山区的经济交换了广泛的意见。
5.根据下面的语境仿照画线的句子写两个句子,使之语意连贯。
(4分)课外多读读文学名著不仅能拓宽我们的视野,增广见识,还能陶冶情操,得到许多有益的人生启示:读高尔基的《童年》,我们可以体会到旧俄时代下层人民生活的苦难;读茅盾的《子夜》,我们可以了解到“只有社会主义才能救中国的真理;,;,。
”6.仿照下面例句写两个句子。
(4分)例句:①宽容,是一束阳光,可以消融彼此间猜疑的积雪。
仿句:宽容,,。
例句:②大厦巍然屹立,是因为有坚强的支柱,理想和信念就是人生大厦的支柱。
仿句:,是因为,理想和信念就是。
二、现代文阅读(43分)(一)理性的阅读(12分)①世间许多事情都是经过不断地积累经验才会上升到一定的层次,读书也不例外。
对于读书,人们说得最多的话题不外乎多读、勤读。
多读、勤读固然能学到一些知识,但是读书倘若能够“深”入书中,即使读的书数量不是很多,也能尝到读书的滋味,领悟到更多的道理。
这就需要克服随意性,多一些理性。
②随着社会的发展,书籍的数量不断增多,在读书上人们只有进行一番选择,才能找到引起自己阅读兴趣又有阅读价值的书。
而不加选择的阅读,至少说明在读书上还不成熟。
一位学者把读书的艺术概括为不读的艺术,理由是:“书为无限,生命有限;以有限应无限,只能采用此策。
”所谓“不读”,实际上就是要有选择地阅读,多读经典著作,少读甚至不读流行作品,更不用说那些粗制滥造的文字垃圾。
从某种意义上说,读书的水平也反映在书籍的选择上,犹如在琳琅满目的货架上,就看谁有眼力拿到货真价实的东西。
而选择的对象,恰恰也能标明一个人的情趣、欣赏水平乃至人生追求。
因此,读什么书会像一面镜子,将人们的精神境界映照得一清二楚。
③同是一本书,有人读后没有留下什么印象,时间久了,脑海中只剩下一片空白;而有的人读后,不仅能记住书中的内容,甚至能背诵出精彩的语句,更能谈出自己对这本书的看法,读书的这种差异,就在于读书者是用眼读还是用心去读。
孔子说:“学而不思则罔,思而不学则殆。
”用“心”阅读,正在于读书的同时也伴随着不断的思考。
④记得杨绛先生曾把读书比作串门,串门总要有进有出,读书也如此。
认真地读一本书,就会情不自禁地进入一种环境之中;情感随着书中情节的变化而起伏,思想沿着作者的思路向前发展。
读书不仅应该能够读进去,重要的是能跳出书外,静观默想,分析对比,理清哪些是对的,哪些是错的。
这样的阅读会使人从欣赏水平到修养都得到提高,不读“死书”,意为不去读那些毫无生气的书;不死读书,还在于不可尽信书,而要有主见。
理性的阅读会引导人们在知识的台阶上攀得更高。
7.作者阐述的主要观点是什么?(2分)8.文章围绕主要观点从哪三个方面进行了具体阐述,它们分别阐述了什么?(3分)9.第④段中“串门总要有进有出,读书也如此。
”这里的“进.和出.”分别指什么?(3分) 10.就本文提出的读书经验,请你选择其中的一点,结合自己的实际谈谈看法。
(4分)(二)(20分)(一)⑴他和妻子驾驶着一辆满载生活用品和卡车奔驰在无边无际的热带草原上,他们要去处于草原深处的建筑公路的基地。
⑵就在这时,突然在他们的近前闪现出一头凶猛的狮子。
卡车加大马力狂奔,试图甩掉狮子。
狮子却紧追不放。
⑶他们越是心急,令他们恼火的事情偏偏发生:汽车陷进一个土坑,熄火了。
要想重新发动汽车,必须用摇把把车子摇醒。
可狮子就趴在车外,眈眈而视。
⑷大声吼吓,掷东西打,两个人办法施尽,狮子却丝毫没有想走开的意思。
无奈中,他拥着妻子在车里度过了漫长难耐的一夜。
可是狮子比他们还有耐心,第二天早上,这头猛兽还守在车外,向这两个要到口边的美味垂涎。
⑸太阳似火,空气仿佛都在燃烧,妻子已经开始脱水了。
在热带草原上,脱水是很可怕的,不用多久,人就会死亡。
他只有紧紧拥住妻子,似乎只有这样,才能不让狮子和死亡把她带走。
此时,他们内心的绝望比狮子还狰狞。
必须行动了,否则只能坐以待毙。
他说:“只有我下去和狮子搏斗,或许能取胜。
”其实两个人心里都很清楚,即使他们的力量加起来也未必抵得过那头猛兽。
妻子像在自言自语:“不能再呆下去,否则不是热死,也会筋疲力尽,最后连开车的力气也没有了。
很多人都在等我们回去,再不出去他们连饭都吃不上了。
”⑹车外,狮子一点都没有对他们失去兴趣,它欲耗尽对手的生命,以延续它的生命。
没有刀光剑影,生与死在沉寂中却铿锵相对。
⑺不知过了多久,妻子轻轻地说道:“我有一个办法。
”“什么办法?快说!”丈夫多么希望听到她能把他们引向生路啊!妻子默默伸出双手,眼里涌满泪水,嘴角禁不住地颤抖着。
他突然明白了妻子的所谓办法,抓住妻子肩膀吼道:“不行!不!”妻子扳开他的手:“你不能这样,不能冲动。
你下去。
谁开车?”她话没说完,就猛地推开他,打开车门,跳下车,拼命向远方跑去。
⑻狮子随之跃起,痴追而去。
⑼她这是将生命送进狮口,为丈夫铺设生还之路。
⑽他只觉热血冲头,欲爆欲裂。
他抓起摇把,跳下车,追向狮子。
他怎么能看着自己的妻子活活被猛兽吃掉呢?⑾妻子的声音从远处传来:“快把车开走!快开车!”他的心被撕扯着、刺扎着。
他在妻子的喊声中回到了车前,发动起汽车,疯了般地追向狮子。
⑿远远地,狮子撕咬妻子的情景也撕碎了他的心。
汽车撞向狮子,那猛兽才惊慌地逃了。
⒀草原上只留下响彻很远很远的哭声——凄惨、悲凉、断肠。
⒁这是1999年10月的一天,一个叫刘火根的看山老人讲述的故事。
老人就是那位丈夫,他和妻子是当年中国援建非洲一个国家的筑路队成员。
27年前,妻了用生命留给他的爱一直深刻在他的心里。
⒂去时是双,回来成单。
回国后,刘火根把妻子的骨灰绑在身上隐居在深山护林,直到今日。
他说,寂静的地方能让妻子睡得踏实,也能让他更清楚地听到妻子灵魂的声音。
他说,27年妻子的骨灰从未离开过他的身体,以后也不会。
哪怕死了,他也要和妻子相陪相伴、不离不分。
⒃凶残可以夺走生命,却夺不走永恒不变的一个字:爱!(二)儿子喜欢读书,可是他对写作没有兴趣。
我为此十分头痛。
有一次,几位文友在恭维我发表的一篇杂文。
没想儿子在旁边插嘴说:“我也能写出那样的作文来。
”我一听,立即鼓励他说:“我知道,你是优秀的。
只要你坚持每天练笔,你会写得比这更好!”晚上儿子还真的写了一篇记叙文。
尽管作文存在着很多缺点,水平在一般偏下,我还是给了儿子极高的评价,给他打了99分。
儿子一见,竟高兴得笑出声来。
这是他小学四年来作文得到的最高分。
高兴之余,他竟天真地问我:“爸爸,为什么不给我打,100分呢?”我给他指出因为有几个错误的标点符号,扣去了他一分。
儿子信服地点点头,表示以后要多注意,尽量得满分。
以后,在我的鼓励下,儿子每天坚持写作,可他始终没有得到他祈盼的那一分,因为这一分由原先的标点符号扩展到字词,到了句法,到了语法,到了写作技巧;练习的文种也从记叙文到应用文,到散文,到诗歌,到小说。
时间在儿子努力追求一分的过程中逝去了。
在他读初中时,已有不少的“豆腐块”散见于各报刊。
高考时,他如愿被北京师范大学录取。
起点高了,视野宽了,他的写作水平也有了很大提高。
每次发表作品,他都邮寄给我。
每次我都给他打99分,然后指出需要改进的地方。
大四那年,有一次,儿子突然回家了,原来他的一篇小说在全国大学生征文中获得了一等奖!他不惜奔波两千多里路,来与我共享他的成功。
他的这篇小说写得确实不错,可以说无懈可击。
可我还是给他打了99分。
儿子要走了。
我高伸胳膊搂住他的头,说:“儿子,以后就不用给我寄作品了,既麻烦又浪费钱财。
现在我把那一分的权利还给你。
”儿子一听,愣了一会儿,继而认真地对我说:“爸爸,不用了。
其实,我早已把它放在我的心里了。
每次做事,我都想尽办法去得到和超越这一分;在这苦苦的追求和超越中,我逐渐长大了。
”11.选文(一)、(二)都离不开一个“爱”,一个是爱夫爱妻,一个是爱父爱子,爱的方式不同,你认为哪一篇更真切、更感人,试说明,不超过50字。
(3分)12.分别用两个四字短语给选文(一)(二)概括内容或情节。
(4分)选文(一):选文(二):13.让刘火根老人27年来身背妻子骨灰隐居山林的原因,除了他自己讲述的两点,更重要的原因是什么?(3分)14.读完选文(一)(二)请分别给选文(一)(二)拟个好题(4分)选文(一):选文(二):15.假如你是刘火根的儿子,或是选文(二)中的父亲,请代他们各自说上一句得体的话。
结合选文内容回答。
(6分)选文(一):儿子对父亲说:。
选文(二):父亲对儿子说:。
(三)(11分)到太空“修炼”种子1987年8月5日,在我国发射第九颗返回式卫星时,中科院遗传所的科研人员首次将辣椒、小麦、水稻等一批种子搭载升空。
随着这批种子太空旅行的开始,我国开始了太空育种的尝试。
至今,我国已先后8次利用返回式卫星进行了51种植物、300多个品种的太空培育试验。
几年来,我国农业科学家将1987年经过太空“修炼”的青椒种子,在黑龙江省进行试种和选优,经过几个回合的培养、长势旺盛、高产优质、抗病性强的新品种诞生了。
