(完整版)阿波罗尼斯圆及其应用

阿波罗尼斯圆及其直接应用 (解析版)

1专题一：阿波罗尼斯圆介绍及其直接应用主干知识：1、阿波罗尼斯圆的定义在平面上给定两点,A B ，设P 点在同一平面上且满足PAPBλ=，当0λ>且1λ≠时，P 点的轨迹是个圆，称之为阿波罗尼斯圆．（1λ=时P 点的轨迹是线段AB 的中垂线）2、阿波罗尼斯圆的方程【定理1】设()()()1,,,0,,0P x y A a B a -．若PAPBλ=（0λ>且1λ≠），则点P 的轨迹方程是2222221211a x a y λλλλ⎛⎫+⎛⎫-+= ⎪ ⎪--⎝⎭⎝⎭，其轨迹是以221,01a λλ⎛⎫+ ⎪-⎝⎭为圆心，半径为221a r λλ=-的圆．例题讲解例1．（2022·河北盐山中学高二期中）已知两定点()2,1A -，()2,1B -，如果动点P满足PA =，则点P 的轨迹所包围的图形的面积等于___________.【分析】设(,)P x y ，根据题设条件，结合两点距离公式列方程并整理即可得P 的轨迹方程，即知轨迹为圆，进而求其面积即可.【详解】设(,)P x y ，由题设得：2222(2)(1)2[(2)(1)]x y x y ++-=-++，∴22(6)(3)40x y -++=，故P的圆，∴图形的面积等于40π.故答案为：40π例2．（2022四川涪陵月考）若ABC ∆满足条件4, 2 AB AC BC ==，则ABC ∆面积的最大值为__________．【分析】设BC x =，则2AC x =，由余弦定理得出cos B ，根据三角形任意两边之和大于第三边得出x 的范围，再由三角形面积公式，结合二次函数的性质得出答案.【详解】设BC x =，则2AC x =，由余弦定理可得22216(2)163cos 248x x x B x x+--==⨯⨯由三角形任意两边之和大于第三边得2442x x x x +>⎧⎨+>⎩，解得443x <<，即216169x <<14sin 222ABCS x B ∆∴=⋅⋅⋅===当2809x =时，ABC ∆面积取最大值163故答案为：163答案第2页，共3页例3．在平面直角坐标xOy 中，已知点()()1,0,4,0A B ，若直线0x y m -+=上存在点P 使得12PA PB =，则实数m 的取值范围是_______．【分析】根据12PA PB =得出点P 的轨迹方程，又点P 在直线0x y m -+=上，则点P 的轨迹与直线必须有公共点，进而解决问题.【详解】解：设(,)P x y则PA PB ==因为12PA PB ==，同时平方，化简得224x y +=，故点P 的轨迹为圆心在（0,0），半径2为的圆，又点P 在直线0x y m -+=上，故圆224x y +=与直线0x y m -+=必须有公共点，2≤，解得m -≤例4．阿波罗尼斯是古希腊著名数学家，与欧几里得、阿基米德被称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，阿波罗尼斯圆就是他的研究成果之一，指的是：已知动点M 与两个定点A ，B 的距离之比为λ（0λ>，且1λ≠），那么点M 的轨迹就是阿波罗尼斯圆.若平面内两定点A ，B 间的距离为2，动点P满足PA PB=22PA PB +的最大值为（）A．16+B．8+C．7+D．3【分析】设()()1,0,1,0A B -，(),P x y，由PA PB=P 的轨迹为以()2,0为圆心，半()222221PA PB x y +=++，其中22x y +可看作圆()2223x y -+=上的点(),x y 到原点()0,0的距离的平方，从而根据圆的性质即可求解.【详解】解：由题意，设()()1,0,1,0A B -，(),P x y ，因为PA PB=，即()2223x y-+=，所以点P 的轨迹为以()2,0因为()()()222222221121x y x y x y PA PB =++++-+=++，其中22x y +可看作圆()2223x y -+=上的点(),x y 到原点()0,0的距离的平方，所以()(222max27x y+=+=+，所以()22max2116x y ⎡⎤++=+⎣⎦22PA PB +的最大值为16+3故选：A.例5．（2022四川·成都外国语学校高二月考）古希腊数学家阿波罗尼奥斯（约公元首262~公元前190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，著作中这样一个命题：平面内与两定点距离的比为常数(0k k >且)1k ≠的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆，已知点()1,0A -，()2,0B ，圆()()()221:204C x y m m -+-=>，在圆上存在点P 满足2PA PB=，则实数m 的取值范围是（）A．22⎣⎦B．542⎡⎢⎣⎦C．2⎛ ⎝⎦D．2⎥⎣⎦【分析】设(),P x y ，根据2PA PB =求出点P 的轨迹方程，根据题意可得两个圆有公共点，根据圆心距大于或等于半径之差的绝对值小于或等于半径之和，解不等式即可求解.【详解】设(),P x y ，因为点()1,0A -，()2,0B ，2PA PB =，=22650x y x +-+=，所以()2234x y -+=，可得圆心()3,0，半径2R =，由圆()()221:24C x y m -+-=可得圆心()2,C m ，半径12r =，因为在圆C 上存在点P 满足2PA PB =，所以圆()2234x y -+=与圆()()221:24C x y m -+-=有公共点，所以112222-≤≤+，整理可得：2925144m ≤+≤，解得：22m ≤≤，所以实数m 的取值范围是2⎥⎣⎦，。

阿波罗尼斯圆性质及其应用探究

阿波罗尼斯圆性质及其应用探究背景展示阿波罗尼斯是古希腊著名数学家，与欧几里得、阿基米德被称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，主要研究成果集中在他的代表作《圆锥曲线论》一书，阿波罗尼斯圆是他的研究成果之一。

1.“阿波罗尼斯圆”：在平面上给定两点B A ,，设P 点在同一平面上且满足,λ=PBPA当0>λ且1≠λ时，P 点的轨迹是个圆，称之为阿波罗尼斯圆。

（1=λ时P 点的轨迹是线段AB 的中垂线）2.阿波罗尼斯圆的证明..角坐标系中点为原点建立平面直轴，所在的直线为证明：以AB x AB ()()()，不妨设y x P a B a A ,,0,,0,-()()22222222,,,,PA PA PB PA PB x a y x a y PBλλλ⎡⎤=∴==∴++=-+⎣⎦()()()()0112112222222=-++--+-∴a ax y x λλλλ()()2222222222221211,01112⎪⎭⎫ ⎝⎛-=+⎪⎪⎭⎫ ⎝⎛-+-∴=-+-+-+∴λλλλλλλa y a x a ax y x λλλλλ=⎪⎭⎫ ⎝⎛-=+⎪⎪⎭⎫ ⎝⎛-+-∴PB PA a y a x 的解都满足又以上过程均可逆，2222221211 .120,11222为半径的圆上运动为圆心，以在以综上，动点-=⎪⎪⎭⎫ ⎝⎛-+λλλλa r a C P 3.阿波罗尼斯圆的性质.性质1点A 、点B 在圆心C 的同侧；当1>λ时，点B 在圆C 内，点A 在圆C 外；当10<<λ时，点A 在圆C 内，点B 在圆C 外。

().,11,012111122222的右侧当然也在点的右侧，在点点所示，时，如图证明：当A B C a a a a a ∴>-+∴>-=--+>λλλλλλ.,1212112222222的内部在圆点的关系与圆、下面讨论点C B a a a a C A B ∴⎪⎭⎫⎝⎛-<⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+-λλλλλ.,12121122222222的外部在圆点C A a a a a ∴⎪⎭⎫ ⎝⎛->⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+--λλλλλλ()().,11,01211210222222的左侧当然也在点的左侧，在点点所示，时，如图当B A C a a a a a ∴-<-+∴<-=---+<<λλλλλλλ .,1212112222222的外部在圆点的关系与圆、下面讨论点C B a a a a C A B ∴⎪⎭⎫⎝⎛->⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+-λλλλλ .,12121122222222的内部在圆点C A a a a a ∴⎪⎭⎫⎝⎛-<⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-+--λλλλλλ.的同侧在圆心、综上可得定点C B A当1>λ时，点B 在圆C 内，点A 在圆C 外；当10<<λ时，点A 在圆C 内，点B 在圆C 外。

阿波罗尼斯圆及其应用阿波罗尼斯圆的逆用 (解析版)

阿波罗尼斯圆及其应用阿波罗尼斯圆的逆用阿波罗尼斯圆及其应用阿波罗尼斯圆的逆用【微点综述】当题目给了阿氏圆和一个定点，我们可以通过下述方法快速找到另一个定点，便于计算，令圆O 与直线OA 相交于M ，N 两点设点E 为OA 上一点，且满足PA PE =λ，由阿氏圆定理AN NE =λ，AMME=λ，则AN =λNE ⇒OA -R =λR -OE ，∴λOE =1+λ R -OA ①同理AM =λME ⇒R +OA =λOE +R ，∴λOE =1-λ R +OA ②由①②消OA 得：2λOE =2R ，即ROE=λ，即R =λOE ，由①②消R 得：OA =λ2OE ，因此，满足条件的点E 在阿氏圆的圆心和定点A 的连线上，且ROE=λ或OAOE=λ2．【典例刨析】1.(2022·湖南·临澧一中高二开学考试)阿波罗尼斯是古希腊著名数学家，他对圆锥曲线有深刻系统的研究，主要研究成果集中在他的代表作《圆锥曲线论》一书，阿波罗尼斯圆是他的研究成果之一，指的是：已知动点M 与两定点A ，B 的距离之比为λ(λ>0，λ≠1)，那么点M 的轨迹就是阿波罗尼斯圆．下面我们来研究与此相关的一个问题，已知圆O ：x 2+y 2=1上的动点M 和定点A -12,0 ，B (1，1)，则2|MA |+|MB |的最小值为( )A.6B.7C.10D.112.阿波罗尼斯是古希腊著名数学家，与欧几里得、阿基米德并称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，阿波罗尼斯圆是他的研究成果之一，指的是：已知动点M 与两定点A ，B 的距离之比为λ(λ>0,λ≠1)，那么点M 的轨迹就是阿波罗尼斯圆，简称阿氏圆．已知在平面直角坐标系中，圆O :x 2+y 2=1、点A -12,0 和点B 0,12 ，M 为圆O 上的动点，则2|MA |-|MB |的最大值为( )A.52B.172C.32D.223.古希腊数学家阿波罗尼斯(约前262-前190年)的著作《圆锥曲线论》是古代光辉的科学成果，著作中有这样一个命题：平面内与两定点距离的比为常数k k >0 且k ≠1 的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.已知O 0,0 ，A 3,0 ，圆C :x -2 2+y 2=r 2r >0 上有且仅有一个点P 满足PA =2PO ，则r 的取值为( )A.1B.5C.1或5D.不存在4.已知点P 是圆x -4 2+y -4 2=8上的动点，A 6,-1 ，O 为坐标原点，则PO +2PA 的最小值为______．5.已知圆C ：x -1 2+y -1 2=1，定点P 是圆C 上的动点，B 2,0 ，O 是坐标原点，则2PO +PB 的最小值为______．6.(2022江西·南昌八中高二月考)古希腊数学家阿波罗尼奥斯(约公元首262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果，著作中有这样一个命题：平面内与两定点距离的比为常数k (k >0且k ≠1)的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆．已知O (0,0)，A (3,0)，圆C :(x -2)2+y 2=r 2(r >1)上有且仅有一个点P 满足|PA |=2|PO |，则r 的取值为_______.【针对训练】7.阿波罗尼斯是古希腊著名数学家，与欧几里得､阿基米德并称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，主要研究成果集中在他的代表作《圆锥曲线》一书，阿波罗尼斯圆就是他的研究成果之一.指的是：已知动点M 与两定点Q ,P 的距离之比MQMP =λ(λ>0,λ≠1)，那么点M 的轨迹就是阿波罗尼斯圆.已知动点M 的轨迹是阿波罗尼斯圆，其方程为x 2+y 2=1，其中，定点Q 为x 轴上一点，定点P 的坐标为-13,0 ,λ=3，若点B 1,1 ，则3MP +MB 的最小值为( )A.10B.11C.15D.178.阿波罗尼斯是古希腊著名数学家，与欧几里得､阿基米德被称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，主要研究成果在他的代表作《圆锥曲线》一书，阿波罗尼斯圆是他的研究成果之一，指的是：已知动点M 与两个定点A ､B 的距离之比为λ(λ>0，λ≠1)，那么点M 的轨迹就是阿波罗尼斯圆.若已知圆O ：x 2+y 2=1和点A -12,0 ，点B (4，2)，M 为圆O 上的动点，则2|MA |+|MB |的最小值为___________9.(2022安徽·合肥六中高二期中)古希腊数学家阿波罗尼奥斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果，著作中有这样一个命题：平面内与两定点距离的比为常数k (k >0且k ≠1)的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.已知圆O :x 2+y 2=1和A -12,0 ，点B (1,1)，M 为圆O 上动点，则MA +12MB 的最小值为_______.10.(2022上海金山中学高二期末)古希腊数学家阿波罗尼斯在他的巨著《圆锥曲线论》中有一个著名的几何问题：在平面上给定两点A 、B ，动点P 满足PA |=λPB (其中λ是正常数，且λ≠1)，则P 的轨迹是一个圆，这个圆称之为“阿波罗尼斯圆”．现已知两定点M (-1,0)、N (2,1)，P 是圆O :x 2+y 2=3上的动点，则3PM +PN 的最小值为____________11.阿波罗尼斯证明过这样一个命题：平面内到两定点距离之比为常数k k >0,k ≠1 的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆．若平面内两定点A 、B 间的距离为2，动点P 满足PAPB=2，求PA 2+PB2的最小值．12.(2022·江苏省江阴高级中学高三开学考试)希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名他发现：“平面内到两个定点A ,B 的距离之比为定值λλ≠1 的点的轨迹是圆”.后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆.已知在平面直角坐标系xOy 中，A -2,1 ，B -2,4 ，点P 是满足λ=12的阿氏圆上的任一点，则该阿氏圆的方程为___________________；若点Q 为抛物线E :y 2=4x 上的动点，Q 在y 轴上的射影为H ，则12PB +PQ +QH 的最小值为______.参考答案1.【答案】C【分析】讨论点M 在x 轴上与不在x 轴上两种情况，若点M 不在x 轴上，构造点K (-2，0)，可以根据三角形的相似性得到|MK ||MA |=|OM ||OA |=2，进而得到2|MA |+|MB |=|MB |+|MK |，最后根据三点共线求出答案.【详解】①当点M 在x 轴上时，点M 的坐标为(-1，0)或(1，0)．若点M 的坐标为(-1，0)，则2|MA |+|MB |=2×12+1+1 2+12=1+5；若点M 的坐标为(1，0)，则2|MA |+|MB |=2×32+1-1 2+12=4．②当点M 不在x 轴上时，取点K (-2，0)，如图，连接OM ，MK ，因为|OM |=1，|OA |=12，|OK |=2，所以|OM ||OA |=|OK ||OM |=2．因为∠MOK =∠AOM ，所以△MOK ∽△AOM ，则|MK ||MA |=|OM ||OA |=2，所以|MK |=2|MA |，则2|MA |+|MB |=|MB |+|MK |．易知|MB |+|MK |≥|BK |，所以|MB |+|MK |的最小值为|BK |．因为B (1，1)，K (-2，0)，所以(2|MA |+|MB |)min =|BK |=-2-12+0-1 2=10．又10<1+5<4，所以2|MA |+|MB |的最小值为10．故选：C 2.【答案】B【分析】令2MA =MC ，则MA MC=12，由阿氏圆的定义可知：C (-2,0)，由数形结合可知2|MA |-|MB |=|MC |-|MB |的最大值.【详解】设M x ,y ，令2MA =MC ，则MA MC=12，由题知圆x 2+y 2=1是关于点A 、C 的阿波罗尼斯圆，且λ=12，设点C m ,n ，则MA MC =x +12 2+y 2x -m 2+y -n2=12，整理得：x 2+y 2+2m +43x +2n 3y =m 2+n 2-13，比较两方程可得：2m +43=0，2n 3=0，m 2+n 2-13=1，即m =-2，n =0，点C -2,0 ，当点M 位于图中M 1的位置时，2|MA |-|MB |=|MC |-|MB |的值最大，最大为BC =172.故选：B .【点睛】关键点点睛：本题主要考查直线和圆的位置关系，圆上动点问题，解题的关键是通过数形结合知两线段距离差的最值是在两端点为起点的的射线上，属于一般题.3.【答案】C【分析】直接设点P x ,y ，根据PA =2PO 可以求得点P 的轨迹为圆，根据题意两圆有且仅有一个公共点，则两圆外切或内切，可得CC 1 =r +r 1或CC 1 =r -r 1 ．【详解】设点P x ,y ∵PA =2PO 即x -32+y 2=2x 2+y 2整理得：x +1 2+y 2=4∴点P 的轨迹为以C 1-1,0 为圆心，半径r 1=2的圆，∵圆C :x -2 2+y 2=r 2的C 2,0 为圆心，半径r 的圆由题意可得：3=CC 1 =r +r 1或3=CC 1 =r -r 1 ∴r =1或r =5故选：C ．4.【答案】10【分析】解法1：借助阿波罗尼斯圆的逆用，得到PO +2PA =2PA +PA ，进而根据三点共线即可求出最值；解法2：将PO +2PA =x 2+y 2+2x -6 2+y +1 2转化为=2x -3 2+y -3 2+x -62+y +1 2 ，进而结合进而根据三点共线即可求出最值．【详解】解法1：阿波罗尼斯圆的逆用假设A m ,n ，使得PO =2PA ，则x 2+y 2=2x -m 2+y -n 2，从而可得3x 2-8mx +4m 2+3y 2-8ny +4n 2=0，从而可知圆心坐标为4m 3,4n3，所以4m 3=4，4n 3=4，解得m =n =4，即A 3,3 ．所以PO +2PA =2PA +PA ≥2A A =26-3 2+-1-3 2=10．即PO +2PA 的最小值为10．解法2：代数转逆法由x -4 2+y -4 2=8，得x 2+y 2=8x +8y -24．PO +2PA =x 2+y 2+2x -6 2+y +1 2=2x 2+y 24+x -62+y +1 2=2x2+y 2 -34x 2+y 2 +x -62+y +1 2=2x 2+y 2-6x +6y -18 +x -62+y +1 2=2x -3 2+y -3 2+x -62+y +1 2x -32+y -3 2+x -6 2+y +1 2表示的是动点x ,y 与3,3 和6,-1 之间的距离之和，当且仅当三点共线时，和最小，故PO +2PA ≥26-3 2+3+1 2=2×5=10．5.【答案】5【分析】解法1：阿波罗尼斯圆的逆用，设B m ,n ，使得PB =2PB ，利用两点间的距离公式化简可求得B 32,12 ，得直线BB 与圆C 相交，则2PO +PB =2PO +PB ≥2OB ，从而可求得其最小值，解法2：代数转逆法，2PO +PB =2x 2+y 2+x -2 2+y 2=2x 2+y 2+x -32 2+y -12 2 ，可得当点O ,P ,B 32,12 共线，且P 在OB 之间时取得最小值.【详解】解：解法1：阿波罗尼斯圆的逆用设B m ,n ，使得PB =2PB ，则x -2 2+y 2=2x -m 2+y -n 2 ，整理，得x 2-4m -1 x +y 2-4ny +2m 2+n 2-2 =0，即[x -2(m -1)]2+(y -2n )2=2m 2+2n 2-8m +8=2(m -2)2+2n 2所以2m -1 =1，2n =1，从而B 32,12．经验证，知直线BB 与圆C 相交．从而2PO +PB =2PO +PB ≥2OB =2⋅94+14=2⋅52=5．所以2PO +PB 的最小值为5．解法2：代数转逆法2PO +PB =2x 2+y 2+x -22+y 2=2x 2+y 2+12x 2+y 2-2x +2=2x 2+y 2+x2+y 2 -12x 2+y 2 -2x +2 =2x 2+y 2+x 2+y 2-122x +2y -1 -2x +2 =2x 2+y 2+x 2+y 2-3x -y +52=2x 2+y 2+x -322+y -122≥2⋅94+14=2⋅52=5．所以2PO +PB 的最小值为5．故答案为：5【点睛】关键点点睛：此题考查点与圆的位置关系，考查阿波罗尼斯圆的逆用，解题的关键是根据阿波罗尼斯圆，设B m ,n ，使得PB =2PB ，化简后将问题转化为2PO +PB =2PO +PB ≥2OB ，考查数学转化思想，属于较难题.6.【答案】5【分析】设动点P x ,y ，根据题意求出点P 的轨迹方程可知轨迹为圆，由题意可知两圆相外切，再讨论内切和外切列方程即可得求解.【详解】设动点P x ,y ，由PA =2PO ，得x -3 2+y 2=4x 2+4y 2，整理得x +1 2+y 2=4，即点P 的轨迹方程为：x +1 2+y 2=4，又因为圆C :(x -2)2+y 2=r 2(r >1)上有且仅有一个点P 满足x +1 2+y 2=4，所以两圆相切，圆x +1 2+y 2=4的圆心坐标为-1,0 ，半径为2，圆C ：x -2 2+y 2=r 2r >0 的圆心坐标为2,0 ，半径为r ，两圆的圆心距为3，当两圆外切时，r +2=3，得r =1，因为r >1，故r =1舍去，当两圆内切时，r -2 =3，r >1，得r =5．故答案为：5.7.【答案】D【分析】设Q a ,0 ，M x ,y ，根据|MQ ||MP |=λ和x 2+y 2=1求出a 的值，由3|MP |+|MB |=|MQ |+|MB |，两点之间直线最短，可得3|MP |+|MB |的最小值为BQ ，根据坐标求出BQ 即可.【详解】设Q a ,0 ，M x ,y ，所以MQ =x -a 2+y 2，由P -13,0 ，所以PM =x +13 2+y 2，因为|MQ ||MP |=λ且λ=3，所以x -a 2+y 2x +13 2+y2=3，整理可得x 2+y 2+3+a 4x =a 2-18，又动点M 的轨迹是x 2+y 2=1，所以3+a 4=0a 2-18=1，解得a =-3，所以Q -3,0 ，又MQ =3|MP |，所以3|MP |+|MB |=|MQ |+|MB |≥BQ ，因为B (1,1)，所以3|MP |+|MB |的最小值BQ =1+32+1-0 2=17，当M 在位置M 1或M 2时等号成立.故选：8.【答案】210【分析】设M (x ，y )，令2|MA |=|MC |，根据圆x 2+y 2=1是关于点A ､C 的阿波罗尼斯圆，且λ=12，求得点C 坐标，再连接BC ，由直线段最短求解.整理得：【详解】设M (x ，y )，令2|MA |=|MC |，则|MA ||MC |=12，由题知圆x 2+y 2=1是关于点A ､C 的阿波罗尼斯圆，且λ=12，设点C (m ，n )，则|MA ||MC |=x +12 2+y 2(x -m )2+(y -n )2=12，整理得：x 2+y 2+2m +43x +2n 3y =m 2+n 2-13，比较两方程可得：2m +43=0，2n 3=0，m 2+n 2-13=1，即m =-2，n =0，所以点C (-2，0)，如图所示：当点M 位于图中M 1､M 2的位置时，2|MA |+|MB |=|MC |+|MB |的值最小，最小为210.故答案为：2109.【答案】102【分析】根据阿波罗尼斯圆的性质，结合两点间线段最短进行求解即可.【详解】令2MA =MC ，则MA MC=12.由题意可得圆x 2+y 2=1是关于点A ，C 的阿波罗尼斯圆，且λ=12设点C 坐标为C m ,n ，则MA MC =x +12 2+y 2x -m 2+y -n2=12整理得x 2+y 2+2m +43x +2n 3y =m 2+n 2-13由题意得该圆的方程为x 2+y 2=1，所以2m +4=02n =0m 2+n 2-13=1 ，解得m =-2n =0 所以点C 的坐标为(-2,0)，所以2MA +MB =MC +MB ，因此当点M 、C 、B 在同一条直线上时，2MA +MB =MC +MB 的值最小，且为(1+2)2+(1-0)2=10，故MA +12MB 最小为102.故答案为：10210.【答案】26【分析】在x 轴上取S -3,0 ，由△MOP ∼△POS 可得PS =3PM ，可得3PM +PN ≥SN ，利用两点间距离公式可求得结果.【详解】如图，在x 轴上取点S -3,0 ，∵OM OP =OP OS =33，∠MOP =∠POS ，∴△MOP ∼△POS ，∴PS =3PM ，∴3PM +PN =PS +PN ≥SN (当且仅当P 为SN 与圆O 交点时取等号)，∴3PM +PN min =SN =-3-22+0-1 2=26.故答案为：26.11.【答案】36-242【分析】以经过A 、B 的直线为x 轴，线段AB 的垂直平分线为y 轴建立平面直角坐标系，设点P x ,y ，根据已知条件可得出点P 的轨迹方程，利用代数法可得出PA 2+PB 2=2OP 2+2，数形结合可求出OP 的最小值，即可得解.【详解】以经过A 、B 的直线为x 轴，线段AB 的垂直平分线为y 轴建立平面直角坐标系，则A -1,0 、B 1,0 ，设点P x ,y ，因为PA PB=2，即x +1 2+y 2x -12+y2=2，整理可得x 2+y 2-6x +1=0，即x -3 2+y 2=8，所以点P 的轨迹是以C 3,0 为圆心，22为半径的圆，则PA2+PB 2=x +1 2+y 2+x -1 2+y 2=2x 2+y 2 +2=2OP 2+2，当点P 为线段OC 与圆C 的交点时，OP 取得最小值，所以，PA 2+PB 2 min =2×3-22 2+2=36-24 2.12.【答案】x +2 2+y 2=4； 10-1##-1+10.【分析】设点P 坐标，根据题意写出关于x 与y 的关系式化简即可；由PA =12PB ，QH =QF -1，代入12PB +PQ +QH 中，即可取出最小值.【详解】设点P (x ,y )，∵λ=12，∴PA PB =12⇒(x +2)2+(y -1)2(x +2)2+(y -4)2=12⇒x +2 2+y 2=4.抛物线的焦点为点F ，由题意知F 1,0 ，QH =QF -1，∵PA =12PB ，∴12PB +PQ +QH min =PA +PQ +QF -1 min =AF -1=-2-1 2+12-1=10-1.故答案为：x +2 2+y 2=4；10-1.。

阿波罗尼斯圆及其应用

阿波罗尼斯及其应用
一、以教材为背景，引出阿波罗尼斯圆
1、定义：
已知点M与两个定点叫,“2距离的比是一个正数机，求点M的轨迹方程，并说明轨迹是什么图形(考虑机=1和〃 2 ≠ 1两种情形).
分析：当初=1时，表示线段2的垂直平分线.
下面我们只考虑机w 1时的情形
2、引例:已知点P(2,0),Q(8,0),点M与点用距离是它与点磔勺距离的(,用《几何画
板》探求M的轨迹,并给出轨迹方程.
(1)用几何画板进行动画演示
结论1：
(2)回顾求动点轨迹方程的一般步骤：建系、设点、列式、化简
(3)改变些的值进行动画演示.
MQ
结论2：
二、探究新知
1、阿波罗尼斯圆
(1)定义
(2)人物简介
(3)注意事项
三、阿波罗尼斯圆的方程推导
已知点M与两个定点M∣,M?距离的比是一个正数〃?，求点M的轨迹方程，并说明轨迹是什么图形(m≠l).
四、阿波罗尼斯圆的应用
例1(2008江苏卷13)若AB = 2,AC =√2BC,则SMBC最大值是. X
例2、（2013年江苏高考）在平面直角坐标系Xeyt l ,点A （0,3）,圆球半径为1,圆心C 在直
线 /： y=2x-4±,若圆C 上存在点使得MA=2MO,求圆心C 的横坐标疝勺取值范围.
例3、已知A(-2,0),P 为圆U(x + 4y +
练习:若48 = 2,8。

= 1,8 = 3,用为以瓦）为直径的圆上一点,则怨= MC
五、课堂小结
1、一个概念
2、两种思想：方程思想、转化思想
坐标为
V=16上任意一点,若点B 满足2∣ PAl = IPM ,则
5的
3、三类问题：轨迹、定点、定值。

完整版阿氏圆

中考数学压轴之阿氏圆模型专题训练阿氏圆（阿波罗尼斯圆）：已知平面上两定点一 B ,则所有满足PC k （ k 不等于1）的点P 的轨迹是一个圆，这个轨迹PB最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆。

在初中的题目中往往利用逆向思维构造" 斜A"型相似（也叫"母子型相似"）+两点间线段最短解决带系数两线段之和的最值问题。

在几何画板上观察下面的图形，当 P 在在圆A 上运动时，PC PB 的长在不断的发生变化，但 PC 的比值却始终保持不变。

PB解决阿氏圆问题，首先要熟练掌握母子型相似三角形的性质和构造方法。

如图，在△ APB 的边AB 上找一点C,使得AP AC ,贝吐匕时厶APS A ABPAB AP母子型相似（共角共边）A -C⑤计算AC 的长度即为最小值.②计算0P 的值，则k 0P 丄 OB OB 2的线段BP 的两端点, 半径 "圆心到定点的距离 OC ③计算OC 的长度，由一一k 得：OCOP④ 连接AC ,当A 、P 、C 三点共线时， 1OP （相似比X 半径）AP 1 -BP AP PC AC 2 那么如何应用"阿氏圆"的性质解答带系数的两条线段和的最小值呢 ?我们来看一道基本题目：①分别连接圆心0与系数不为1 即 OP 0B;实战练习：- 已知O O半径为1, AC BD为切线，AC=1, BD=2试求上2 PC PD的最小值25、(1)如图1,已知正方形ABC的边长为4,圆B的半径为2,点P是圆B上的一个动点，求PD -PC 的2、已知点3、已知点(1)-AP4 A(-3,0) , B( 0,3 ), C (1,0 ),若点P为。

C上一动点，且。

C与y轴相切, BP的最小值;(2)S VPAB的最小值.4、如图1,在平面直角坐标系xoy中，半O O交x轴与点A B(2,0)两点，AD BC均为半O O 的切线，AD=2 BC=7.(1)求OD的长；(2)如图2,若点P是半O O上的动点，Q为OD的中点.连接PO PQ.①求证：△OP GA ODP;②是否存在点P,使PD 2PC有最小值，若存在，试求出点P的坐标；若不存在，请说明理由•A(4, 0)，B(4最小值和PD - PC的最大值.2 2⑵如图2,已知正方形ABCD勺边长为9,圆B的半径为6,点P是圆B上的一个动点，那么PD - PC的最小值为；PD -PC的最大值为3 ----------- 3 --------------(3)如图3,已知菱形ABCD勺边长为4,/ B=60°,圆B的半径为2.点P是圆B上的一个1 1动点.那么PD 1 PC的最小值为；PD 1 PC的最大值为2 26、(2016年*济南28题)如图1,抛物线y = ax2+ (a+ 3)x+ 3 (0)与x轴交于点A (4, 0),与y轴交于点B,在x轴上有一动点E ( m, 0) (0v m v 4),过点E作x轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM丄AB于点M.(1)求a的值和直线AB的函数表达式；(2)设厶PMN的周长为AEN的周长为C2,若§ =-，求m的値；C25(3)如图2,在(2)的条件下，将线段OE绕点O逆时针旋转得到OE',旋转角为皿0 ° av 90°)，连2接E'A、E'B,求E'A+ ；E B的最小值.x7、(2017年*遵义27题)如图，抛物线y=ax2+bx-a - b (a v 0, a、b为常数)与x轴交于A、C两点，与y轴交于B 点，直线AB的函数关系式为y= 8x + 16.9 3(1)求该抛物线的函数关系式与C点坐标；(2)已知点M( m, 0)是线段OA上的一个动点，过点M作x轴的垂线I分别与直线AB和抛物线交于D、E两点，当m为何值时，△ BDE恰好是以DE为底边的等腰三角形？(3)在(2)问条件下，当厶BDE恰好是以DE为底边的等腰三角形时，动点M相应位置记为点M，将OM绕原点O顺时针旋转得到ON(旋转角在0°到90°之间)；NPi :探究：线段OB上是否存在定点P( P不与OB重合)，无论ON如何旋转，竺始终保持不变，若存在,NB试求出P点坐标；若不存在，请说明理由；ii :试求出此旋转过程中，(NA+?NB的最小值.4。

阿波罗尼斯圆及其应用(整理)

阿波罗尼斯圆的应用1.“阿波罗尼斯圆”：在平面上给定两点',A A ，设P 点在同一平面上且满足,'λ=PA PA当0>λ且1≠λ时，P 点的轨迹是个圆，称之为阿波罗尼斯圆。

（1=λ时P 点的轨迹是线段AB 的中垂线）2.阿波罗尼斯圆的相关性质性质1.当1>λ时，点'A 在圆O 内，点A 在圆O 外；当10<<λ时，点A 在圆O 内，点'A 在圆O 外。

性质2.所作出的阿波罗尼斯圆的半径为|AA'|1r λλ=-性质3：'OA rr OA ==λ λ越大，圆越小.例1：已知P 点在边长为2的正方形ABCD 的内切圆上运动，则BP AP 2+的最小值是_______ 解析:22',1,2,'=∴====OA r OA OA r r OA λ '2,2'PA PA PA PA=∴==λ,5'2)'(22=≥+=+B A BP PA BP PA练习1：已知P 在边长为2的正三角形ABC 的内切圆上运动，则BP AP 2+的最小值是_______27练习2：已知点P 在圆4:22=+y x O 上运动，)4,4(),0,4(B A ，求BP AP 2+的最小值例2：（06四川）已知两定点).0,1(),0,2(B A -如果动点P 满足PB PA 2=，则点P 的轨迹所围成的图形的面积是________________.练习1：满足条件BC AC AB 2,2==的ABC ∆面积的最大值是___________.练习2.在等腰ABC ∆中，BD AC AB ,=是腰AC 上的中线，且,3=BD 则ABC ∆面积的最大值是___________.例3：已知平面ABCD ⊥平面ADEF ，AB ⊥AD ，CD ⊥AD ，且AB=1，AD=CD=2，ADEF 是正方形，在正方形ADEF 内部有一点M ，满足MB ，MC 与平面ADEF 所成角相等，则点M 的轨迹长度为_________94π练习：在正方体1111D C B A ABCD -中，33=AB ，点E ，F 在线段1DB 上，且,1FB EF DE ==点M 是正方体表面上一个动点，点P,Q 是空间两个动点，若2||||||||==QF QE PF PE 且4||=PQ ，则MQ MP ⋅的最小值为____________38-练习2：已知△ABC 的面积为1，∠A 的角平分线交对边BC 于D ， AB=2AC ，且AD=kAC ，则当k=________时，边BC 的长度最短.5102=k 分析：面积为定值，AB=2AC ，所以A 的轨迹为阿氏圆，设圆交BC 和延长线为D 、E ，易得AD 即为∠A 的角平分线，且当AO 垂直BC 时BC 有最小值，设圆半径为r ，OC r r OB ===2λ,r r OB OD rOC r OB =-=∴==,2,2 r AD r 2,25AC ==勾股定理得： 5102252===∴r r ACADk 3、已知向量,a b 满足：||3,||2||,b a b a ==-若||3a b λ+≥恒成立，则实数λ的取值范围是_______.例4. （2015年高考数学湖北卷）如图，圆C 与x 轴相切于点(1,0)T ，与y 轴正半轴交于两点,A B （B 在A 的上方），且2AB =．（Ⅰ）圆C 的标准．．方程为；（Ⅱ）过点A 任作一条直线与圆22:1O x y +=相交于,M N 两点，下列三个结论：①NA MA NBMB=； ②2NB MA NAMB-=； ③2NB MA NAMB+=号是 .（写出所有正确结论的序号）解：（1）易知半径2r =，所以圆的方程为()(22122x y -+=；（2）易知()()21,21A B ，设(),P x y 为圆C 上任意一点，则()()()()()()()()222221422221221221422221221221x y yyPA PBy y x y +-+-----====+-++-+--，故①正确；())21212NB MANA MB-=-=，②正确；))212122NB MANA MB+=+=yxOTC NA MB5、已知点(0,2),(1,1)A B --，P 是圆C:222x y +=上的一个动点.求||||PB PA 的最大值. 6、已知向量||6,||||,2,b a a c b a c m ==--=是||()a tb t R +∈的最小值,求m 的最大值.。

微专题16 阿波罗尼斯圆问题梳理及其运用

在平面直角坐标系 xOy 中，已知圆 C 经过 A(0，2)，O(0，0)，D(t， 0)(t>0)三点，M 是线段 AD 上的动点，l1，l2 是过点 B(1，0)且互相垂直的两条直线，其中 l1 交 y 轴于点 E，l2 交圆 C 于 P，Q 两点． (1)若 t＝PQ＝6，求直线 l2 的方程； (2)若 t 是使 AM≤2BM 恒成立的最小正整数，求三角形 EPQ 的面积的最小值．
2
2
2
2
串讲 2 已知点 P 是圆 O：x2＋y2＝25 上任意一点，平面上有两个定点 13 1 M(10，0)，N( 2 ，3)，则 PN＋2PM 的最小值为
5
．
解析：设 x 轴上一定点 Q(m， 0)，记 PM∶PQ＝λ， P(x， y)，由 PM∶PQ ＝λ 得(x－10)2＋y2＝λ2[(x－m)2＋y2]，化简得(λ2－1)x2＋(λ2－1)y2＋(20 －2mλ2)x＋(λ2m2－100)＝0，因为 x2＋y2＝25，所以
2 解析：依题意，PA2＝PO2－12，PB2＝PO2 － 2 ，因为 PB＝2PA，所 1 2 2 2 2 以 PB2＝4PA2，所以 PO2 － 4 ＝ 4( PO － 1 ) ，可得 PO ＝ 4 PO ，设 P(x， 1 1
4 2 2 64 y)，可得(x－4 )＋y ＝4(x ＋y )化简得(x＋3) ＋y ＝ 9 .所以满足条件的
2 2 2 2
4 8 点 P 在以(－3，0)为圆心，3为半径的圆上，又因为点 P 在直线 x＋ 3y 4 |－3－b| 8 －b＝0 上，且恰有两个点，所以直线和圆应该相交，所以 <3， 1＋ 3 20 解得－ 3 <b<4.
变式 2 已知点 A(－2，0)，B(4，0)，圆 C：(x＋4) ＋(y＋b) ＝16，点 P PA 是圆 C 上任意一点，若PB为定值，则 b 的值为 0 ．

(完整版)阿氏圆问题归纳

阿氏圆题型的解题方法和技巧以阿氏圆(阿波罗尼斯圆)为背景的几何问题近年来在中考数学中经常出现，对于此类问题的归纳和剖析显得非常重要.具体内容如下：阿氏圆定理(全称：阿波罗尼斯圆定理)，具体的描述：一动点P 到两定点A 、B 的距离之比等于定比n m (≠1)，则P 点的轨迹，是以定比n m内分和外分定线段AB 的两个分点的连线为直径的圆．这个轨迹最先由古希腊数学家阿波罗尼斯发现，该圆称为阿波罗尼斯圆，简称阿氏圆．定理读起来和理解起来比较枯燥，阿氏圆题型也就是大家经常见到的PA+kPB ，(k ≠1)P 点的运动轨迹是圆或者圆弧的题型.PA+kPB,(k ≠1)P 点的运动轨迹是圆或圆弧的题型阿氏圆基本解法：构造母子三角形相似【问题】在平面直角坐标系xOy 中，在x 轴、y 轴分别有点C(m ，0)，D(0，n).点P 是平面内一动点，且OP=r ，求PC+kPD 的最小值.阿氏圆一般解题步骤：第一步：确定动点的运动轨迹(圆)，以点O 为圆心、r 为半径画圆；(若圆已经画出则可省略这一步) 第二步：连接动点至圆心O(将系数不为1的线段的固定端点与圆心相连接)，即连接OP 、OD ；第三步：计算出所连接的这两条线段OP 、OD 长度；第四步：计算这两条线段长度的比k ；第五步：在OD 上取点M ，使得OM:OP=OP:OD=k ；第六步：连接CM ，与圆O 交点即为点P ．此时CM 即所求的最小值.习题【旋转隐圆】如图，在Rt △ABC 中，∠ACB=90°，D 为AC 的中点，M 为BD 的中点，将线段AD 绕A 点任意旋转（旋转过程中始终保持点M 为BD 的中点），若AC=4，BC=3，那么在旋转过程中，线段CM 长度的取值范围是___________.1.Rt △ABC 中，∠ACB=90°，AC=4，BC=3，点D 为△ABC 内一动点，满足CD=2，则AD+32BD 的最小值为_______.2.如图，菱形ABCD 的边长为2，锐角大小为60°，⊙A 与BC 相切于点E ，在⊙A 上任取一点P ，则PB+23PD 的最小值为________.3.如图，已知菱形ABCD 的边长为4，∠B=60°，圆B 的半径为2，P 为圆B 上一动点，则PD+1PC 的最小值为_________.6.如图，边长为47.如图，边长为4的正方形，点P 是正方形内部任意一点，且BP=2，则PD+21PC 的最小值为______；2PD+4PC 的最小值为______.8.在平面直角坐标系xOy 中，A(2，0)，B(0,2)，C(4，0)，D(3，2)，P 是△AOB 外部的第一象限内一动点，且∠BPA=135°，则2PD+PC 的最小值是_______.9.在△ABC 中，AB=9，BC=8，∠ABC=60°，⊙A 的半径为6，P 是⊙A 上的动点，连接PB 、PC ，则3PC+2PB 的最小值为_______.10.如图，在Rt △ABC 中，∠A=30°，AC=8，以C 为圆心，4为半径作⊙C ． (1)试判断⊙C 与AB 的位置关系，并说明理由；(2)点F 是⊙C 上一动点，点D 在AC 上且CD=2，试说明△FCD ～△ACF ； (3)点E 是AB 上任意一点，在(2)的情况下，试求出EF+21FA 的最小值.11.(1)如图1，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求PD+21PC 的最小值和PD-21PC 的最大值； (2)如图2，已知正方形ABCD 的边长为9，圆B 的半径为6，点P 是圆B 上的一个动点，那么PD+32PC 的最小值为______，PD-32PC 的最大值为______． (3)如图3，已知菱形ABCD 的边长为4，∠B=60°，圆B 的半径为2，点P 是圆B 上的一个动点，那么PD+21PC 的最小值为______，PD-21PC 的最大值为________.2PA+PB 的最小值.【二次函数结合阿氏圆题型】13.如图1，抛物线y=ax ²+(a+3)x+3（a ≠0）与x 轴交于点A （4，0），与y 轴交于点B ，在x 轴上有一动点E （m ，0）（0＜m ＜4），过点E 作x 轴的垂线交直线AB 于点N ，交抛物线于点P ，过点P 作PM ⊥AB 于点M ．(1)求a 的值和直线AB 的函数表达式； (2)设△PMN 的周长为C1，△AEN 的周长为C2，若5621=C C ，求m 的值； (3)如图2，在（2）条件下，将线段OE 绕点O 逆时针旋转得到OE ′，旋转角为α（0°＜α＜90°），连接E ′A 、E ′B ，求E ′A+32E ′B 的最小值．问题背景：如图1，在△ABC中，BC=4，AB=2AC．问题初探：请写出任意一对满足条件的AB与AC的值：AB=_____，AC=_______．问题再探：如图2，在AC右侧作∠CAD=∠B，交BC的延长线于点D，求CD的长．问题解决：求△ABC的面积的最大值．1.小明的数学探究小组进行了系列探究活动．类比定义：类比等腰三角形给出如下定义：有一组邻边相等的凸四边形叫做邻等四边形．探索理解：(1)如图1，已知A、B、C在格点（小正方形的顶点）上，请你协助小明用两种不同的方法画出格点D，连接DA、DC，使四边形ABCD为邻等四边形；尝试体验：(2)如图2，邻等四边形ABCD中，AD=CD，∠ABC=120°，∠ADC=60°，AB=2，BC=1，求四边形ABCD的面积．解决应用：(3)如图3，邻等四边形ABCD中，AD=CD，∠ABC=75°，∠ADC=60°，BD=4．小明爸爸所在的工厂，需要裁取某种四边形的材料板，这个材料板的形状恰巧是符合如图3条件的邻等四边形，要求尽可能节约．你能求出这种四边形面积的最小值吗？如果能，请求出此时四边形ABCD面积的最小值；如果不能，请说明理由．2.我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．(1)如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．(2)如图2，等邻边四边形ABCD中，AB=AD，∠BAD+∠BCD=90°，AC、BD为对角线，AC=2 AB，试探究BC，BD的数量关系．(3)如图3，等邻边四边形ABCD中，AB=AD，AC=2，∠BAD=2∠BCD=60°，求等邻边四边形ABCD 面积的最小值.。

阿波罗尼斯圆介绍及其直接应用 (解析版)

阿波罗尼斯圆及其应用阿波罗尼斯圆介绍及其直接应用阿波罗尼斯圆及其应用阿波罗尼斯圆介绍及其直接应用【微点综述】动点的轨迹问题是高考中的一个热点和重点，尤其是阿波罗尼斯圆在高考中频频出现．处理此类问题的关键是通过建立直角坐标系，寻找动点满足的条件，得出动点的轨迹是一个定圆，从而把问题转化为直线和圆、圆和圆的位置关系问题，并在解决问题的过程中感悟转化与化归、化繁为简的数学思想方法．阿波罗尼斯(Apollonius 约公元前262~192)，古希腊数学家，与欧几里得、阿基米德并称为亚历山大时期数学三巨匠．阿波罗尼斯年青时到亚历山大城跟随欧几里得的后继者学习，和当时的大数学家合作研究．他对圆锥曲线有深刻而系统的研究，主要研究成果集中在他的代表作《圆锥曲线论》一书中，阿波罗尼斯圆是他的研究成果之一．1.阿波罗尼斯圆的定义在平面上给定两点A ,B ，设P 点在同一平面上且满足PAPB=λ，当λ>0且λ≠1时，P 点的轨迹是个圆，称之为阿波罗尼斯圆．(λ=1时P 点的轨迹是线段AB 的中垂线)2.阿波罗尼斯圆的证明【定理1】设P x ,y ,A 1-a ,0 ,B a ,0 ．若PA PB =λ(λ>0且λ≠1)，则点P 的轨迹方程是x -λ2+1λ2-1a 2+y 2=2aλλ2-1 2，其轨迹是以λ2+1λ2-1a ,0 为圆心，半径为r =2aλλ2-1的圆．证明：由PA =λPB 及两点间距离公式，可得x +a 2+y 2=λ2x -a 2+y 2 ，化简可得1-λ2 x 2+1-λ2 y 2+21+λ2 ax +1-λ2 a 2=0①，(1)当λ=1时，得x =0，此时动点的轨迹是线段AB 的垂直平分线；(2)当λ≠1时，方程①两边都除以1-λ2得x 2+y 2+2a 1+λ2 x 1-λ2+a 2=0，化为标准形式即为：x -λ2+1λ2-1a 2+y 2=2aλλ2-1 2，∴点P 的轨迹方程是以λ2+1λ2-1a ,0 为圆心，半径为r =2aλλ2-1的圆．图① 图② 图③阿波罗尼斯圆的另一种形式：【定理2】A ,B 为两已知点，M ,N 分别为线段AB 的定比为λλ≠1 的内外分点，则以MN 为直径的圆C 上任意点P 到A ,B 两点的距离之比为λ．证明：以λ>1为例．如图②，设AB =2a ，AM MB =AN NB =λ，则AM =2aλ1+λ,BM =2a -2aλ1+λ=2a1+λ，AN =2aλλ-1,BN =2aλλ-1-2a =2aλ-1．过B 作AB 的垂线圆C 交于Q ,R 两点，由相交弦定理及勾股定理得QB 2=MB ⋅BN =4a 2λ2-1,QA 2=AB 2+QB 2=4a 2λ2λ2-1，于是QB =2a λ2-1,QA =2aλ2-1,∴QA QB =λ．∵M ,Q ,N 同时在到A ,B 两点距离之比等于λ的圆上，而不共线的三点所确定的圆是唯一的，∴圆C 上任意一点P 到A ,B 两点的距离之比恒为λ．同理可证0<λ<1的情形．3.阿波罗尼斯圆的相关性质由上面定理2的证明可得如下的性质：性质1：当λ>1时，点B 在圆C 内，点A 在圆C 外；当0<λ<1时，点A 在圆C 内，点B 在圆C 外．性质2：因AQ 2=AM ⋅AN ，故AQ 是圆C 的一条切线．若已知圆C 及圆C 外一点A ，可以作出与之对应的点B ，反之亦然．性质3：所作出的阿波罗尼斯圆的直径为MN =4aλλ2-1 ，面积为4πa 2λ2λ2-12．性质4：过点A 作圆C 的切线AQ (Q 为切点)，则QM ,QN 分别为∠AQB 的内、外角平分线．性质5：阿波罗尼斯圆的直径两端是按比例内分AB 和外分AB 所得的两个分点，如图所示，M 是AB 的内分点，N 是AB 的外分点，此时必有PM 平分∠APB ，PN 平分∠APB 的外角．证明：如图①，由已知可得PA PB =MA MB =NA NB =λ(λ>0且λ≠1)，∵S ΔPAM S ΔPBM =MA MB=λ，又S ΔPAM =12PA ⋅PM sin ∠APM ,S ΔPBM =12PB ⋅PM sin ∠BPM ,∴PA ⋅PM sin ∠APMPB ⋅PM sin ∠BPM=λ，∴sin ∠APM =sin ∠BPM ,∴∠APM =∠BPM ,∴PM 平分∠APB ．由等角的余角相等可得∠BPN =∠DPN ，∴PN 平分∠APB 的外角．性质6：过点B 作圆C 不与QR 重合的弦EF ，则AB 平分∠EAF ．证明：如图④，连结ME ,MF ，由已知FA FB =EA EB =λ,∴EB FB =EA FA.∵S ΔABE S ΔABF =EBFB (λ>0且λ≠1)，又S ΔABE =12AB ⋅AE sin ∠BAE ,S ΔABF =12AB ⋅AF sin ∠BAF ,∴AB ⋅AE sin ∠BAE AB ⋅AF sin ∠BAF =EB FB =AEAF，∴sin ∠BAE =sin ∠BAF ,∴∠BAE =∠BAF ,∴AB 平分∠EAF ．∴sin ∠BAE =sin ∠BAF ,∴∠BAE =∠BAF ,∴AB 平分∠EAF ．【典例刨析】1.(2022·河北盐山中学高二期中)已知两定点A -2,1 ，B 2,-1 ，如果动点P 满足PA =2PB ，则点P 的轨迹所包围的图形的面积等于___________.2.(2022四川涪陵月考)若ΔABC 满足条件AB =4,AC =2BC ，则ΔABC 面积的最大值为__________．3.已知圆O ：x 2+y 2=9，点B -5,0 ，在直线OB 上存在定点A (不同于点B )，满足对于圆O 上任意一点P ，都有PAPB 为一常数，试求所有满足条件的点A 的坐标，并求PAPB．4.在平面直角坐标xOy 中，已知点A 1,0 ,B 4,0 ，若直线x -y +m =0上存在点P 使得PA =12PB ，则实数m 的取值范围是_______．5.阿波罗尼斯是古希腊著名数学家，与欧几里得、阿基米德被称为亚历山大时期数学三巨匠，他对圆锥曲线有深刻而系统的研究，阿波罗尼斯圆就是他的研究成果之一，指的是：已知动点M 与两个定点A ，B 的距离之比为λ(λ>0，且λ≠1)，那么点M 的轨迹就是阿波罗尼斯圆.若平面内两定点A ，B 间的距离为2，动点P 满足PAPB =3，则PA 2+PB 2的最大值为( )A.16+83B.8+43C.7+43D.3+36.(2022四川·成都外国语学校高二月考)古希腊数学家阿波罗尼奥斯(约公元首262~公元前190年)的著作《圆锥曲线论》是古代世界光辉的科学成果，著作中这样一个命题：平面内与两定点距离的比为常数k k >0 且k ≠1 的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆，已知点A -1,0 ，B 2,0 ，圆C :x -2 2+y -m 2=14m >0 ，在圆上存在点P 满足PA =2PB ，则实数m 的取值范围是( )A.22,62B.54,212C.0,212D.52,212【针对训练】7.在平面直角坐标系xOy 中，已知圆O :x 2+y 2=1，O 1:x -4 2+y 2=4，动点P 在直线x +3y -b =0上，过P 点分别作圆O ,O 1的切线，切点分别为A ,B ，若满足PB =2PA 的点P 有且只有两个，则实数b 的取值范围是________．8.已知A ,B 是平面上两个定点，平面上的动点C ,D 满足|CA |CB=|DA|DB =m ，若对于任意的m ≥3，不等式CD≤k AB 恒成立，则实数k 的最小值为______．9.已知点A (0,1)，B (1,0)，C (t ,0)，点D 是直线AC 上的动点，若|AD |≤2|BD|恒成立，则最小正整数t =__________.10.在平面直角坐标系xOy 中，已知圆O ：x 2+y 2=1，圆O 1：(x +4)2+y 2=4，动点P 在直线l ：x -22y +b =0上(b <0)，过P 分别作圆O ，O 1的切线，切点分别为A ，B ，若满足PB =2PA 的点P 有且只有一个，则实数b 的值为______.11.在平面直角坐标系xOy 中，M ,N 是两定点，点P 是圆O ：x 2+y 2=1上任意一点，满足：PM =2PN ，则MN 的长为.12.(2022辽宁·高二期中)古希腊著名数学家阿波罗尼斯与欧几里得､阿基米德齐名，他发现：“平面内到两个定点A ，B 的距离之比为定值λ(λ>0且λ≠1)的点的轨迹是圆”.后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆.在平面直角坐标系xOy 中，A (-2,0)，B (4,0)，动点P 满足|PA ||PB |=12.设点P 的轨迹为C 1.(1)求曲线C 1的方程；(2)若曲线C 1和⊙C 2:(x -4)2+(y -6)2=r 2(r >0)无公共点，求r 的取值范围.参考答案1.【答案】40π【分析】设P (x ,y )，根据题设条件，结合两点距离公式列方程并整理即可得P 的轨迹方程，即知轨迹为圆，进而求其面积即可.【详解】设P (x ,y )，由题设得：(x +2)2+(y -1)2=2[(x -2)2+(y +1)2]，∴(x -6)2+(y +3)2=40，故P 的轨迹是半径为40的圆，∴图形的面积等于40π.故答案为：40π2.【答案】163【分析】设BC =x ，则AC =2x ，由余弦定理得出cos B ，根据三角形任意两边之和大于第三边得出x 的范围，再由三角形面积公式，结合二次函数的性质得出答案.【详解】设BC =x ，则AC =2x ，由余弦定理可得cos B =16+x 2-(2x )22×4×x =16-3x 28x由三角形任意两边之和大于第三边得x +2x >4x +4>2x ，解得43<x <4，即169<x 2<16∴S ΔABC =12⋅4⋅x ⋅sin B =2x 1-cos 2B =2x 1-16-3x 2 264x 2=2569-916x 2-809 2当x 2=809时，ΔABC 面积取最大值163故答案为：163【点睛】本题主要考查了求三角形面积的最值，涉及余弦定理的应用，属于中档题.3.【答案】A -95,0 ，PA PB=35【分析】根据两点距离的坐标运算可得10λ2+2a x +34λ2-a 2-9=0，进而得10λ2+2a =034λ2-a 2-9=0 ，即可求解.【详解】设P (x ,y ),A (a ,0),a ≠-5，设PA PB=λ>0故PA PB=x -a 2+y 2x +52+y2=λ，且x 2+y 2=9，化简得：10λ2+2a x +34λ2-a 2-9=0，该式对任意的x ∈-3,3 恒成立，故10λ2+2a =034λ2-a 2-9=0 ，解得a =-95λ=35或a =-5λ=1 (舍去)，故PA PB=35，A -95,0 4.【答案】-22,22【分析】根据PA =12PB 得出点P 的轨迹方程，又点P 在直线x -y +m =0上，则点P 的轨迹与直线必须有公共点，进而解决问题.【详解】解：设P (x ,y )则PA =(x -1)2+(y -0)2,PB =(x -4)2+(y -0)2，因为PA =12PB ，所以有(x -1)2+(y -0)2=12(x -4)2+(y -0)2，同时平方，化简得x 2+y 2=4，故点P 的轨迹为圆心在(0,0)，半径2为的圆，又点P 在直线x -y +m =0上，故圆x 2+y 2=4与直线x -y +m =0必须有公共点，所以|m |1+1≤2，解得-22≤m ≤2 2.【点睛】本题考查了点的轨迹问题、直线与圆的位置关系的问题，解题的关键是能从题意中转化出动点的轨迹，并能求出点的轨迹方程.5.【答案】A【分析】设A -1,0 ,B 1,0 ，P x ,y ，由PA PB=3，可得点P 的轨迹为以2,0 为圆心，半径为3的圆，又PA 2+PB 2=2x 2+y 2+1 ，其中x 2+y 2可看作圆x -2 2+y 2=3上的点x ,y 到原点0,0 的距离的平方，从而根据圆的性质即可求解.【详解】解：由题意，设A -1,0 ,B 1,0 ，P x ,y ，因为PA PB=3，所以x +1 2+y 2x -12+y2=3，即x -2 2+y 2=3，所以点P 的轨迹为以2,0 为圆心，半径为3的圆，因为PA 2+PB 2=x +1 2+y 2+x -1 2+y 2=2x 2+y 2+1 ，其中x 2+y 2可看作圆x -2 2+y 2=3上的点x ,y 到原点0,0 的距离的平方，所以x 2+y 2 max =2+3 2=7+43，所以2x 2+y 2+1 max =16+83，即PA 2+PB 2的最大值为16+83，故选：A .6.【答案】D【分析】设P x ,y ，根据PA =2PB 求出点P 的轨迹方程，根据题意可得两个圆有公共点，根据圆心距大于或等于半径之差的绝对值小于或等于半径之和，解不等式即可求解.【详解】设P x ,y ，因为点A -1,0 ，B 2,0 ，PA =2PB ，所以x +12+y 2=2x -2 2+y 2即x 2+y 2-6x +5=0，所以x -3 2+y 2=4，可得圆心3,0 ，半径R =2，由圆C :x -2 2+y -m 2=14可得圆心C 2,m ，半径r =12，因为在圆C 上存在点P 满足PA =2PB ，所以圆x -3 2+y 2=4与圆C :x -2 2+y -m 2=14有公共点，所以2-12≤3-2 2+m 2≤2+12，整理可得：94≤1+m 2≤254，解得：52≤m ≤212，所以实数m 的取值范围是52,212，故选：D .7.【答案】-203,4.【分析】设出点的坐标，将原问题转化为直线与圆相交的问题，求解关于b 的不等式即可求得实数b 的取值范围.【详解】由题意O (0,0),O 1(4,0).设P (x ,y )，则∵PB =2PA ，∴x -42+y 2-4=2x 2+y 2-1，∴(x -4)2+y 2=4(x 2+y 2)，∴x 2+y 2+83x -163=0，圆心坐标为-43,0 ,半径为83，∵动点P 在直线x +3y -b =0上，满足PB =2PA 的点P 有且只有两个，∴直线与圆x 2+y 2+83x -163=0相交，∴圆心到直线的距离d =-43-b 1+3<83，∴-43-163<b <-43+163，即实数b 的取值范围是-203,4 .【点睛】本题主要考查圆的方程及其应用，等价转化的数学思想，直线与圆是位置关系的应用等知识，意在考查学生的转化能力和计算求解能力.8.【答案】34【分析】建立坐标系，得点C ,D 的轨迹方程，分离参量求范围即可求解【详解】不妨设AB =1，以A 为原点，AB 所在直线为x 轴建立直角坐标系，则A 0,0 ,B 1,0 ，设C x ,y ,∴x 2+y 2x -1 2+y2=m ⇒x -m 2m 2-1 2+y 2=m 2m 2-1 2故动点C ,D 的轨迹为圆，由CD≤k AB 恒成立，则k ≥CD max =2m m 2-1=2m -1m≥34故答案为34【点睛】本题考查圆的轨迹方程，平面问题坐标化的思想，是难题9.【答案】4【解析】设点D x ,y ,根据|AD |≤2|BD|列出关于D x ,y 的关系式,再数形结合分析即可.【详解】设点D x ,y ,因为点D 是直线AC 上的动点,故y -1x =-1t⇒x +ty -t =0.由|AD |≤2|BD |得x 2+y -1 2≤4x -1 2+y 2 ,化简得x -43 2+y +13 2≥89.依题意可知,直线AC 与圆x -43 2+y +13 2=89至多有一个公共点,所以43-43t 1+t 2≥89,解得t ≥2+3或t ≤2- 3.所以最小正整数t =4.故答案为：4【点睛】本题主要考查了直线与圆和向量的综合运用,需要设点的坐标表达所给的信息,再数形结合利用圆心到直线的距离列式求解.属于中档题.10.【答案】-283.【分析】根据圆的切线的性质和三角形全等，得到PO 1 =2PO ，求得点P 的轨迹方程，再根据直线与圆相切，利用圆心到直线的距离等于半径，即可求解．【详解】由题意得：O (0,0)，O 1(-4,0)，设P (x ,y )，如下图所示∵PA 、PB 分别是圆O ，O 1的切线，∴∠PBO 1=∠PAO =90°，又∵PB =2PA ，BO 1=2AO ，∴△PBO 1∽△PAO ，∴PO 1 =2PO ，∴PO 1 2=4PO 2，∴(x +4)2+y 2=4(x 2+y 2)，整理得x -43 2+y 2=649，∴点P (x ，y )的轨迹是以43,0 为圆心、半径等于83的圆，∵动点P 在直线l ：x -22y +b =0上(b <0)，满足PB =2PA 的点P 有且只有一个，∴该直线l 与圆x -43 2+y 2=649相切，∴圆心43,0 到直线l 的距离d 满足d =r ，即43+b 12+(22)2=83，解得b =203或-283，又因为b <0，所以b =-283．【点睛】本题主要考查了圆的切线的性质，以及直线与圆的位置关系的应用，其中解答中根据圆的切下的性质和三角形全等求得点P 的轨迹方程，再根据直线与圆相切，列出方程求解是解答的关键，着重考查了推理与运算能力，属于中档试题．11.【答案】32【分析】不妨就假设M ,N 在x 轴上，设M (m ,0),N (n ,0),P (x ,y )，由PM =2PN 可得x 2+y 2+2m -8n3x +4n 2-m 23=0，然后和方程x 2+y 2=1对比，就可以求出m ,n 【详解】由于M ,N 是两定点，不妨就假设M ,N 在x 轴上如图所示：设M (m ,0),N (n ,0),P (x ,y )，PM =2PN ，∴PM 2=4PN 2，∴(x -m )2+y 2=4(m -n )2+y 2 ，即x 2-2mx +m 2+y 2=4x 2-8nx +4n 2+4y 2，3x 2+(2m -8n )x +3y 2+4n 2-m 2=0，x 2+y 2+2m -8n 3x +4n 2-m 23=0与x 2+y 2=1表示同一个圆.∴2m -8n =0m 2-4n 23=1∴{m =2n =12或m =-2n =-12∴MN =32.故答案为：32.【点睛】本题考查的是圆的方程和点的轨迹方程的求法，较简单.12.【答案】(1)(x +4)2+y 2=16(2)(0,6)∪(14,+∞)【分析】(1)设P (x ,y )，然后根据|PA ||PB |=12列方程化简计算即可得曲线C 1的方程，(2)先求出两圆的圆心和半径，再由题意可得两圆外离或内含，从而可得C 1C 2 >4+r 或C 1C 2 <r -4，从而可求出r 的取值范围(1)设P (x ,y )，因为A (-2,0)，B (4,0)，动点P 满足|PA ||PB |=12，所以(x +2)2+y 2(x -4)2+y 2=12，化简得x 2+y 2+8x =0，即(x +4)2+y 2=16，所以曲线C 1的方程为(x +4)2+y 2=16，(2)曲线C 1的圆心为C 1(-4,0)，半径为4，⊙C 2:(x -4)2+(y -6)2=r 2(r >0)的圆心为C 2(4,6)，半径为r ，因为曲线C 1和⊙C 2:(x -4)2+(y -6)2=r 2(r >0)无公共点，所以两圆外离或内含，所以C 1C 2 >4+r 或C 1C 2 <r -4，所以(-4-4)2+(0-6)2=10>4+r 或(-4-4)2+(0-6)2=10<r -4，所以0<r <6或r >14，所以r 的取值范围为(0,6)∪(14,+∞)。

阿氏圆的性质及其应用

阿波罗尼斯圆的性质及其应用廖波定义：平面内到两定点的距离之比为常数()10≠>λλλ且的点的轨迹是圆，简称阿氏圆。

已知：点的轨迹。

求P PB AP a AB ,,2λ==解：以AB 为垂直平分线和AB 所在直线为坐标轴，建立如图所示坐标系。

令),(y x P 。

()()[]22222y a x y a x BP AP +-=++⇒=λλ 2222221211⎪⎭⎫ ⎝⎛-=+⎪⎪⎭⎫ ⎝⎛-+-⇒m ma y a x λλ性质①在内。

外，在时，在外。

内，在时，A B A O B ΘO <<Θ>101λλ②APB PP BP A P PB P A ∠⇒==平分'''λ③λ==∙=⇒∆∆BPAP OB OP OA OB OP POB AOP )2(,)1(2相似与一、在解三角形中的应用例1、已知：BC AC AB 2,2==的三角形ABC ，求其面积的最大值？解：由阿氏圆的性质可得，当C 点在圆的最高点时，面积最大。

22222212max max =⇒⎪⎭⎫ ⎝⎛+==∙=r r r r r h AB S ，而22max =S 例2、在____,2,2的最大值则边中，面积c b a S ABC ==∆解：如图所示：r c c r r r r OA 232121,212=⇒⎪⎭⎫ ⎝⎛+==r h c hc c S ==⇒=∙⨯=max h ,42h 21要最大。

最小，要使又666232232122=⇒=⇒=⎪⎭⎫ ⎝⎛⇒=∙∙∴c c r r r 二、在两点间距离的应用例3、在坐标系中，A(4,0),B(0,3),P 为422=+y x 上一个动点，则3AP+2BP 的最小值为_____解：方案①将B 点转移到圆内D 处，DP BP r OD BP DP OD OB OD r 23342=⇒=⇒=⇒∙=()104332323min ==+=⎪⎭⎫ ⎝⎛+∴AD DP AP DP AP 方案②将A 点转移到圆内C 处,使AP=2PC,将圆外线段变到圆内，系数变大，不能达到PC 与PB 系数一致的目的，所以，点在圆外变到圆内，系数变大，反之，系数变小.例4、已知：______y 6-13253,422的最小值为则+-==+x d y x 解：如图所示()()PB y x y PC y x x =-+=-=+-=22223613,3132-53接下来和例3如法炮制,化系数相同法则得：()102)34(4232322=+≥+=∴P A PD d 例5、已知l .05:l 2221，在直线若对圆上任意一点与直线：P y x r y x =-+=+ΘO 上均存在两点E 、F ，使_____,8,2的取值范围则且r EF PF PE ==解：因为定线段EF 是直线上的动线段，所以1ΘO 是半径一定的动圆。

阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤天地中，阿波罗尼斯圆是一个引人入胜且具有重要应用价值的概念。

它宛如一颗璀璨的明珠，闪耀着智慧的光芒，为解决众多几何问题提供了独特而有效的途径。

要理解阿波罗尼斯圆，首先得从它的定义说起。

阿波罗尼斯圆指的是：平面内到两个定点的距离之比为常数（不为 1）的点的轨迹是一个圆。

这个定义听起来或许有些抽象，但通过具体的例子就能清晰许多。

假设平面上有两个定点 A 和 B，点 P 满足｜PA|／｜PB| ＝ k（k 不为 1），那么点 P 的轨迹就是一个阿波罗尼斯圆。

当 k ＞ 1 时，点 P的轨迹是以线段 AB 的内分点为圆心的圆；当 0 ＜ k ＜ 1 时，点 P 的轨迹是以线段 AB 的外分点为圆心的圆。

那么，阿波罗尼斯圆有哪些独特的性质呢？其一，圆心一定在线段AB 的垂直平分线上。

这是因为圆的对称性，使得圆心必然位于这条对称轴上。

其二，圆与线段AB 的两个端点的连线所成的夹角是恒定的。

接下来，让我们看看阿波罗尼斯圆在实际问题中的应用。

在几何问题中，它常常能帮助我们快速找到满足特定条件的点的位置。

例如，已知三角形的两个顶点以及这两个顶点到第三个顶点的距离之比，我们就可以利用阿波罗尼斯圆来确定第三个顶点的可能位置。

在物理学中，阿波罗尼斯圆也有其用武之地。

比如在电场问题中，当两个等量同种电荷形成的电场中，等势线的形状就类似于阿波罗尼斯圆。

通过对阿波罗尼斯圆的理解和运用，我们能够更深入地分析电场的分布和性质。

在工程设计中，阿波罗尼斯圆也能发挥作用。

比如在道路规划中，如果需要设计一条弯道，使得车辆在通过时从两个特定点观察到的视线角度保持一定比例，就可以借助阿波罗尼斯圆来确定弯道的形状和位置。

在数学竞赛中，阿波罗尼斯圆更是常常成为解题的关键。

例如，在一些复杂的几何证明题中，巧妙地引入阿波罗尼斯圆的概念，能够化繁为简，找到解题的突破口。

再举一个具体的例子来说明。

假设有一个三角形 ABC，已知 A、B两点的坐标以及｜PA|／｜PB| ＝ 2，要求出点 P 的轨迹方程。

阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤天地中，阿波罗尼斯圆宛如一颗璀璨的明珠，闪耀着独特的光芒。

它不仅具有深刻的理论内涵，还在众多实际问题中有着广泛而重要的应用。

要理解阿波罗尼斯圆，首先得从它的定义说起。

阿波罗尼斯圆是指平面内到两个定点的距离之比为定值（不为 1）的点的轨迹所形成的圆。

简单来说，假如有两个定点 A 和 B，一个动点 P，并且满足｜PA|／｜PB| ＝定值 k（k ≠ 1），那么点 P 的轨迹就是一个圆。

这个圆有着一些有趣的性质。

比如说，圆心在线段AB 的中垂线上；而且，当两个定点之间的距离固定，以及比值 k 确定时，这个圆的大小和位置也就唯一确定了。

那么，阿波罗尼斯圆在实际中有哪些应用呢？让我们一起来看看。

在几何问题中，阿波罗尼斯圆常常能帮助我们巧妙地解决一些难题。

比如，在三角形中，如果已知某两条边的长度以及它们的比值，要求第三边的取值范围，这时就可以通过构建阿波罗尼斯圆来找到答案。

在物理学中，阿波罗尼斯圆也有它的身影。

例如，在研究两个点电荷之间的电场分布时，如果电荷的电荷量之比为定值，那么等势线的形状就类似于阿波罗尼斯圆。

在工程领域，阿波罗尼斯圆同样发挥着重要作用。

在建筑设计中，当需要确定一些特定的位置关系，以保证结构的稳定性和美观性时，阿波罗尼斯圆的知识能够提供有效的解决方案。

在数学竞赛中，阿波罗尼斯圆更是屡见不鲜。

很多看似复杂的竞赛题目，一旦引入阿波罗尼斯圆的概念，往往就能迎刃而解。

接下来，通过一个具体的例子来感受一下阿波罗尼斯圆的魅力。

假设在平面直角坐标系中，有两个定点 A(0, 0)和 B(4, 0)，动点 P 满足｜PA| ／｜PB| ＝ 1/2，求点 P 的轨迹方程。

首先，设点 P 的坐标为（x, y)。

则｜PA| ＝√（x²＋ y²)，｜PB| ＝√（x 4)²＋ y²。

因为｜PA| ／｜PB| ＝ 1/2，所以√（x²＋ y²) ／√（x 4)²＋ y²＝1/2。

阿波罗尼斯圆的轴对称性及其应用

阿波罗尼斯圆的轴对称性及其应用阿波罗尼斯圆是古希腊数学家阿波罗尼斯提出的一种特殊的椭圆曲线，具有许多独特的性质和应用。

其中，轴对称性是阿波罗尼斯圆最为重要的性质之一，本文将探讨阿波罗尼斯圆的轴对称性及其在几何学和工程学中的应用。

一、阿波罗尼斯圆的定义与性质阿波罗尼斯圆是由一个移动的点P和两个固定的焦点F1和F2组成的曲线。

其定义是点P到F1的距离与点P到F2的距离之比等于一个常数e的绝对值，即PF1/PF2 = e。

阿波罗尼斯圆是一种闭合曲线，其形状类似于椭圆，但焦点并不位于椭圆的中心点上。

阿波罗尼斯圆具有许多有趣的性质，其中最重要的是其轴对称性。

阿波罗尼斯圆是以一条直线(称为主轴)为对称轴，对称性质使得阿波罗尼斯圆在几何学和工程学中得到广泛的应用。

二、阿波罗尼斯圆的轴对称性阿波罗尼斯圆具有以主轴为对称轴的轴对称性质。

即对于任意一点P(x, y)在阿波罗尼斯圆上，如果其关于主轴的对称点为P'(-x, y)，那么P'也必然在阿波罗尼斯圆上。

通过阿波罗尼斯圆的轴对称性，我们可以得到一些关于曲线的重要结论。

首先，对称性保证了阿波罗尼斯圆上的点在主轴两侧以相等的距离分布，这对于研究曲线的几何性质具有重要意义。

其次，轴对称性也使得我们可以通过知道曲线上一部分的特性来推断另一部分的特性，从而简化问题的求解过程。

三、阿波罗尼斯圆的应用阿波罗尼斯圆作为一种特殊的椭圆曲线，在几何学和工程学中有许多应用。

以下介绍几个典型的应用。

1.设计与建筑阿波罗尼斯圆的轴对称性使得它成为建筑与设计中常用的几何形状。

例如，一些钟表和灯具的设计中常使用阿波罗尼斯圆的形状，给人以优雅和和谐的感觉。

此外，阿波罗尼斯圆的轴对称性也被广泛用于设计拱门、穹顶等建筑元素，提升建筑物的美感和结构强度。

2.物体运动轨迹在物理学和天文学中，阿波罗尼斯圆的轴对称性也有广泛的应用。

例如，负责控制和预测天体运动的天文学家经常使用阿波罗尼斯圆来描述天体的轨道。

阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤领域中，阿波罗尼斯圆是一个引人入胜且具有重要应用价值的概念。

它以古希腊数学家阿波罗尼斯的名字命名，展现了数学的深邃与美妙。

让我们先来了解一下阿波罗尼斯圆的定义。

给定平面内两个定点A、B，平面内一动点 P 满足 PA ／ PB ＝λ（λ 为非零常数且λ ≠ 1），则点 P 的轨迹是一个圆，这个圆就被称为阿波罗尼斯圆。

为了更直观地理解阿波罗尼斯圆，我们可以通过一个简单的例子来感受。

假设 A、B 两点的坐标分别为（－2, 0) 和（2, 0)，λ ＝ 2。

设点P 的坐标为（x, y)，根据距离公式，PA 的长度为√（x ＋ 2)＾2 ＋ y^2，PB 的长度为√（x 2)＾2 ＋ y^2。

因为 PA ／ PB ＝ 2，所以√（x ＋ 2)＾2 ＋ y^2 ／√（x 2)＾2 ＋ y^2 ＝ 2。

对等式两边进行平方并化简，最终可以得到一个圆的方程。

那么，阿波罗尼斯圆有哪些独特的性质呢？首先，圆心一定在线段AB 的中垂线上。

其次，当λ ＞ 1 时，点 P 的轨迹是一个以线段 AB 靠近 B 点的一侧为优弧的圆；当 0 ＜λ ＜ 1 时，点 P 的轨迹是一个以线段 AB 靠近 A 点的一侧为优弧的圆。

接下来，让我们探讨一下阿波罗尼斯圆在实际中的应用。

在物理学中，阿波罗尼斯圆可以用来分析带电粒子在电场中的运动轨迹。

例如，当两个等量同种电荷形成的电场中，一个带电粒子在其中运动，其轨迹可能就符合阿波罗尼斯圆的特征。

在工程设计中，阿波罗尼斯圆也有重要的作用。

比如在建筑设计中，要确定一些特定的支撑点位置，使得结构更加稳定，就可以运用阿波罗尼斯圆的原理来进行计算和规划。

在计算机图形学中，阿波罗尼斯圆可以用于生成特定形状的图形。

通过对阿波罗尼斯圆的参数进行调整，可以创造出丰富多样的视觉效果。

在数学竞赛和考试中，阿波罗尼斯圆也是一个常见的考点。

它常常与三角形、圆的相关知识结合，考察学生对几何图形的理解和运用能力。

阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤领域中，阿波罗尼斯圆是一个具有独特魅力和重要应用价值的概念。

它不仅在理论上丰富了我们对几何图形的理解，还在实际问题的解决中发挥着重要作用。

要理解阿波罗尼斯圆，首先得从它的定义说起。

阿波罗尼斯圆是指平面内到两个定点的距离之比为常数（不为 1）的点的轨迹。

简单来说，如果有两个固定的点 A 和 B，一个动点 P 到 A 和 B 的距离之比始终是一个定值 k（k 不等于 1），那么点 P 的轨迹就是一个阿波罗尼斯圆。

那么，如何来确定这个圆呢？假设两个定点 A 和 B 的坐标分别为（x1, y1) 和（x2, y2)，距离之比为 k，我们可以通过一系列的代数运算来找到这个圆的方程。

这其中涉及到距离公式以及一些代数变形，虽然过程可能稍显复杂，但最终得出的结果却能清晰地描述这个圆的特征。

阿波罗尼斯圆有着许多有趣的性质。

比如说，圆心一定在线段 AB的中垂线上。

而且，当两个定点之间的距离固定，比值 k 变化时，圆的大小和位置也会相应地改变。

接下来，让我们看看阿波罗尼斯圆在实际中的应用。

在物理学中，它可以用来研究带电粒子在电场中的运动轨迹。

当电场强度的分布满足一定条件时，粒子的运动轨迹可能就会是一个阿波罗尼斯圆。

这为我们分析粒子的运动规律提供了有力的工具。

在工程设计中，阿波罗尼斯圆也能大显身手。

例如在道路规划中，如果要设计一条曲线道路，使得车辆从一个固定点出发，到另一个固定点的行驶时间与距离之比保持恒定，就可以利用阿波罗尼斯圆的原理来进行规划。

在数学竞赛和高考中，阿波罗尼斯圆也常常作为考点出现。

它可能会隐藏在一些看似复杂的几何问题中，需要我们敏锐地发现并运用其相关知识来求解。

例如，给出一些点的位置关系和距离条件，让我们判断某个点是否在特定的阿波罗尼斯圆上，或者求与阿波罗尼斯圆相关的最值问题。

再举一个具体的例子，假设在一个平面直角坐标系中，有两点 A(－3, 0) 和 B(3, 0)，动点 P 满足｜PA| ＝ 2|PB|，我们可以通过计算得出点P 的轨迹方程，进而分析其性质和相关应用。

阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤领域中，阿波罗尼斯圆是一个引人入胜且具有重要应用价值的概念。

它以古希腊数学家阿波罗尼斯的名字命名，展现了几何图形与数学原理之间的精妙联系。

要理解阿波罗尼斯圆，首先得从它的定义入手。

阿波罗尼斯圆是指平面内到两个定点的距离之比为定值（不为 1）的点的轨迹。

也就是说，如果有两个定点 A 和 B，点 P 满足｜PA|／｜PB| ＝ k（k 为非 1 的常数），那么点 P 的轨迹就是一个阿波罗尼斯圆。

为了更直观地感受阿波罗尼斯圆，我们不妨通过一个简单的例子来看看它是如何形成的。

假设定点 A 的坐标为(－1, 0)，定点 B 的坐标为(1, 0)，且比值 k ＝ 2。

我们可以通过距离公式和等式｜PA|／｜PB| ＝2 来列出方程，经过一番计算和化简，就能得到点 P 的轨迹方程，从而描绘出这个阿波罗尼斯圆的图形。

那么，阿波罗尼斯圆在实际中有哪些应用呢？一个常见的应用是在物理学中的带电粒子在电场和磁场中的运动问题。

比如，当带电粒子在特定的电场和磁场中运动时，其轨迹可能会符合阿波罗尼斯圆的特征。

通过对阿波罗尼斯圆性质的深入理解，我们可以更好地分析带电粒子的运动路径、速度变化等关键信息，从而为相关的物理研究和实际应用提供有力的理论支持。

在工程领域，阿波罗尼斯圆也有着不可小觑的作用。

比如在建筑设计中，当需要规划一些具有特定比例关系的布局时，阿波罗尼斯圆的概念可以帮助设计师巧妙地安排空间，实现美观与实用的完美结合。

又比如在道路规划中，为了使车辆行驶更加流畅和安全，有时需要根据不同地点之间的距离比例关系来设计路线，阿波罗尼斯圆的原理就能在其中发挥指导作用。

在数学解题中，阿波罗尼斯圆更是常常成为巧妙解题的关键。

例如，在一些涉及到距离比值的几何问题中，如果能够敏锐地发现其隐藏的阿波罗尼斯圆结构，往往能够化繁为简，迅速找到解题的突破口。

我们来看一个具体的数学问题。

已知三角形 ABC 中，AB ＝ 4，AC ＝ 2，且点 P 满足｜PA| ＝ 2|PB|，求点 P 的轨迹。

阿波罗尼斯圆定理及应用

x
l
A
O
y
例2、(08年江苏，13题)若AB=2，AC= √2 BC，则三角形ABC的面积的最大值是____。
变式：
在等腰三角形ABC中，如图，AB=AC，BD 是腰AC的中线，且BD= √3 ，则三角形 ABC面积的最大值是________
A
D
B
C
课后巩固，检验定理
课后作业: 1、已知点P是圆O：x2+y2=25上任意一点，平面上有两个定点M（10，0），N（13/2,3）则PN+1/2PM的最小值为_____
特殊到一般，提出猜想
猜想：平面内到两个定点的距离之比为定值的动点轨迹是圆。
总结提炼，得到定理
阿波罗尼斯圆定理：在平面上给定两点A,B 设点 P 在同一平面上，且满足 PA/PB= λ ，当 λ>0且λ ≠1 时，点 P 的轨迹是一个圆。称之为阿波罗尼斯圆，简称“阿氏圆”。（当 λ=1 时，点 P 的轨迹是线段AB的垂直平分线）
2、一缉私艇巡航至距领海边界线l（一条南北方向的直线）3.8海里的A处，发现在其北偏东 30 °方向相距4海里的B处有一走私船正欲逃跑，缉私艇立即追击。已知缉私艇的最大航速是走私船最大航速的3倍。假设缉私艇和走私船均按直线方向以最大航速航行。问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由。
阿波罗尼斯圆定理及其应用
.
教材入手，奠定基础
问题1 （必修2 习题2.2（1）探究拓展第12题）已知点M（x,y）与两点O（0,0），A（3,0）的距离之比为 1/2 ，那么点M的坐标应满足什么关系？
教材入手，奠定基础
问题2 （选修2-1.2.6.2求曲线的方程例2）求平面内到两定点A，B的距离之比为2的动点M的轨迹方程。

(完整版)阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用数学理论1.“阿波罗尼斯圆”：在平面上给定两点B A ,，设P 点在同一平面上且满足,λ=PB PA 当0>λ且1≠λ时，P 点的轨迹是个圆，称之为阿波罗尼斯圆。

（1=λ时P 点的轨迹是线段AB 的中垂线）2.阿波罗尼斯圆的证明及相关性质定理：B A ,为两已知点，Q P ,分别为线段AB 的定比为)1(≠λλ的内外分点，则以PQ 为直径的圆O 上任意点到B A ,两点的距离之比为.λ证（以1>λ为例）设λ===QBAQ PB AP a AB ,，则 1,1,1,1-=-=+=+=λλλλλλa BQ a AQ a PB a AP . 由相交弦定理及勾股定理知,1,1222222222-=+=-=⋅=λλλa BC AB AC a BQ PB BC 于是,1,122-=-=λλλa AC aBC .λ=BCAC 而C Q P ,,同时在到B A ,两点距离之比等于λ的曲线（圆）上，不共线的三点所确定的圆是唯一的，因此，圆O 上任意一点到B A ,两点的距离之比恒为.λ性质1.当1>λ时，点B 在圆O 内，点A 在圆O 外；当10<<λ时，点A 在圆O 内，点B 在圆O 外。

性质2.因AQ AP AC ⋅=2，过AC 是圆O 的一条切线。

若已知圆O 及圆O 外一点A ，可以作出与之对应的点,B 反之亦然。

性质3.所作出的阿波罗尼斯圆的直径为122-=λλa PQ ，面积为.122⎪⎭⎫ ⎝⎛-λλπa 性质4.过点A 作圆O 的切线C AC (为切点），则CQ CP ,分别为ACB ∠的内、外角平分线。

性质5.过点B 作圆O 不与CD 重合的弦,EF 则AB 平分.EAF ∠数学应用1.（03北京春季）设)0)(0,(),0,(>-c c B c A 为两定点，动点P 到点A 的距离与到点B 的距离之比为定值),0(>a a 求点P 的轨迹.2.（05江苏）圆1O 和圆2O 的半径都是1，421=O O ，过动点P 分别作圆1O 和圆2O 的切线N M PN PM ,(,分别为切点），使得PN PM 2=，试建立适当坐标系，求动点P 的轨迹方程.3.（06四川）已知两定点).0,1(),0,2(B A -如果动点P 满足PB PA 2=，则点P 的轨迹所围成的图形的面积是________________.4.(08江苏)满足条件BC AC AB 2,2==的ABC ∆面积的最大值是___________.5.在等腰ABC ∆中，BD AC AB ,=是腰AC 上的中线，且,3=BD 则ABC ∆面积的最大值是___________.6.已知P A ),0,2(-是圆16)4(:22=++y x C 上任意一点，问在平面上是否存在一点B ，使得21=PB PA 若存在，求出点B 坐标；若不存在，说明理由.变式：已知圆16)4(:22=++y x C ，问在x 轴上是否存在点A 和点B ，使得对于圆C 上任意一点P ，都有?21=PB PA 若存在，求出B A ,坐标；若不存在，说明理由.7.在ABC ∆中，AD AC AB ,2=是A ∠的平分线，且.kAC AD =（1）求k 的取值范围；（2）若ABC ∆的面积为1，求k 为何值时，BC 最短.。

(完整版)阿氏圆问题归纳

阿氏圆题型的解题方法和技巧以阿氏圆(阿波罗尼斯圆)为背景的几何问题近年来在中考数学中经常出现，对于此类问题的归纳和剖析显得非常重要.具体内容如下：阿氏圆定理(全称：阿波罗尼斯圆定理)，具体的描述：一动点P 到两定点A 、B 的距离之比等于定比n m (≠1)，则P 点的轨迹，是以定比n m内分和外分定线段AB 的两个分点的连线为直径的圆．这个轨迹最先由古希腊数学家阿波罗尼斯发现，该圆称为阿波罗尼斯圆，简称阿氏圆．定理读起来和理解起来比较枯燥，阿氏圆题型也就是大家经常见到的PA+kPB ，(k ≠1)P 点的运动轨迹是圆或者圆弧的题型.PA+kPB,(k ≠1)P 点的运动轨迹是圆或圆弧的题型阿氏圆基本解法：构造母子三角形相似【问题】在平面直角坐标系xOy 中，在x 轴、y 轴分别有点C(m ，0)，D(0，n).点P 是平面内一动点，且OP=r ，求PC+kPD 的最小值.阿氏圆一般解题步骤：第一步：确定动点的运动轨迹(圆)，以点O 为圆心、r 为半径画圆；(若圆已经画出则可省略这一步) 第二步：连接动点至圆心O(将系数不为1的线段的固定端点与圆心相连接)，即连接OP 、OD ；第三步：计算出所连接的这两条线段OP 、OD 长度；第四步：计算这两条线段长度的比k ；第五步：在OD 上取点M ，使得OM:OP=OP:OD=k ；第六步：连接CM ，与圆O 交点即为点P ．此时CM 即所求的最小值.习题【旋转隐圆】如图，在Rt △ABC 中，∠ACB=90°，D 为AC 的中点，M 为BD 的中点，将线段AD 绕A 点任意旋转（旋转过程中始终保持点M 为BD 的中点），若AC=4，BC=3，那么在旋转过程中，线段CM 长度的取值范围是___________.1.Rt △ABC 中，∠ACB=90°，AC=4，BC=3，点D 为△ABC 内一动点，满足CD=2，则AD+32BD 的最小值为_______.2.如图，菱形ABCD 的边长为2，锐角大小为60°，⊙A 与BC 相切于点E ，在⊙A 上任取一点P ，则PB+23PD 的最小值为________.3.如图，已知菱形ABCD 的边长为4，∠B=60°，圆B 的半径为2，P 为圆B 上一动点，则PD+1PC 的最小值为_________.6.如图，边长为47.如图，边长为4的正方形，点P 是正方形内部任意一点，且BP=2，则PD+21PC 的最小值为______；2PD+4PC 的最小值为______.8.在平面直角坐标系xOy 中，A(2，0)，B(0,2)，C(4，0)，D(3，2)，P 是△AOB 外部的第一象限内一动点，且∠BPA=135°，则2PD+PC 的最小值是_______.9.在△ABC 中，AB=9，BC=8，∠ABC=60°，⊙A 的半径为6，P 是⊙A 上的动点，连接PB 、PC ，则3PC+2PB 的最小值为_______.10.如图，在Rt △ABC 中，∠A=30°，AC=8，以C 为圆心，4为半径作⊙C ． (1)试判断⊙C 与AB 的位置关系，并说明理由；(2)点F 是⊙C 上一动点，点D 在AC 上且CD=2，试说明△FCD ～△ACF ； (3)点E 是AB 上任意一点，在(2)的情况下，试求出EF+21FA 的最小值.11.(1)如图1，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求PD+21PC 的最小值和PD-21PC 的最大值； (2)如图2，已知正方形ABCD 的边长为9，圆B 的半径为6，点P 是圆B 上的一个动点，那么PD+32PC 的最小值为______，PD-32PC 的最大值为______． (3)如图3，已知菱形ABCD 的边长为4，∠B=60°，圆B 的半径为2，点P 是圆B 上的一个动点，那么PD+21PC 的最小值为______，PD-21PC 的最大值为________.2PA+PB 的最小值.【二次函数结合阿氏圆题型】13.如图1，抛物线y=ax ²+(a+3)x+3（a ≠0）与x 轴交于点A （4，0），与y 轴交于点B ，在x 轴上有一动点E （m ，0）（0＜m ＜4），过点E 作x 轴的垂线交直线AB 于点N ，交抛物线于点P ，过点P 作PM ⊥AB 于点M ．(1)求a 的值和直线AB 的函数表达式； (2)设△PMN 的周长为C1，△AEN 的周长为C2，若5621=C C ，求m 的值； (3)如图2，在（2）条件下，将线段OE 绕点O 逆时针旋转得到OE ′，旋转角为α（0°＜α＜90°），连接E ′A 、E ′B ，求E ′A+32E ′B 的最小值．问题背景：如图1，在△ABC中，BC=4，AB=2AC．问题初探：请写出任意一对满足条件的AB与AC的值：AB=_____，AC=_______．问题再探：如图2，在AC右侧作∠CAD=∠B，交BC的延长线于点D，求CD的长．问题解决：求△ABC的面积的最大值．1.小明的数学探究小组进行了系列探究活动．类比定义：类比等腰三角形给出如下定义：有一组邻边相等的凸四边形叫做邻等四边形．探索理解：(1)如图1，已知A、B、C在格点（小正方形的顶点）上，请你协助小明用两种不同的方法画出格点D，连接DA、DC，使四边形ABCD为邻等四边形；尝试体验：(2)如图2，邻等四边形ABCD中，AD=CD，∠ABC=120°，∠ADC=60°，AB=2，BC=1，求四边形ABCD的面积．解决应用：(3)如图3，邻等四边形ABCD中，AD=CD，∠ABC=75°，∠ADC=60°，BD=4．小明爸爸所在的工厂，需要裁取某种四边形的材料板，这个材料板的形状恰巧是符合如图3条件的邻等四边形，要求尽可能节约．你能求出这种四边形面积的最小值吗？如果能，请求出此时四边形ABCD面积的最小值；如果不能，请说明理由．2.我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．(1)如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件．(2)如图2，等邻边四边形ABCD中，AB=AD，∠BAD+∠BCD=90°，AC、BD为对角线，AC=2 AB，试探究BC，BD的数量关系．(3)如图3，等邻边四边形ABCD中，AB=AD，AC=2，∠BAD=2∠BCD=60°，求等邻边四边形ABCD 面积的最小值.。

阿氏圆介绍

在 OB 直线上，圆 O 即为阿氏圆！点拨：遇到两点一圆转化线段*k 时，当系数 k 不为 1 时，可以利用阿氏圆进行转化！
整理：长沙 huyoo 来源：网络
设a20b10且ap2bp则点的距离比都是定值k那么在证明过程中可以用这个原理就是说如果我们知道了圆上一点到直径上两定点的距离比那么我们就可以知道圆上另一点到两定点的距离比
阿氏圆定理介绍
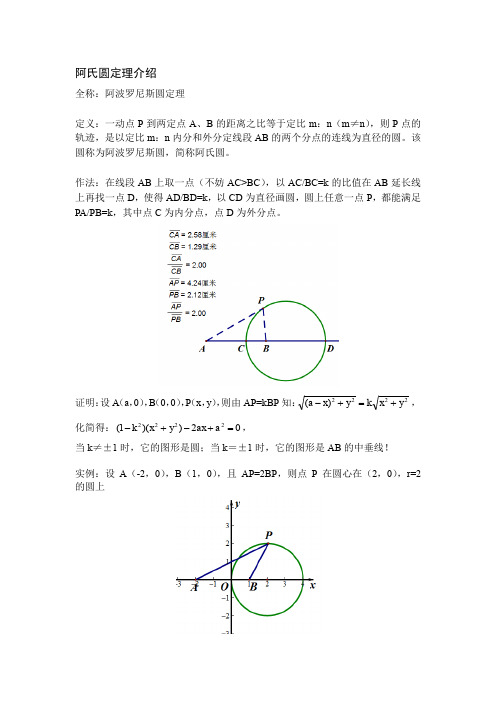
全称：阿波罗尼斯圆定理定义：一动点 P 到两定点 A、B 的距离之比等于定比 m：n（m≠n），则 P 点的轨迹，是以定比 m：n 内分和外分定线段 AB 的两个分点的连线为直径的圆。该圆称为阿波罗尼斯圆，简称阿氏圆。作法：在线段 AB 上取一点（不妨 AC>BC），以 AC/BC=k 的比值在 AB 延长线上再找一点 D，使得 AD/BD=k，以 CD 为直径画圆，圆上任意一点 P，都能满足 PA/PB=k，其中点 C 为内分点，点 D 为外分点。
证明：设A （a， 0）， B （0， 0）， P （x， y），则由 AP=kBP 知： (a x) 2 y 2 k x 2 y 2 ，化简得： (1 k 2 )( x 2 y 2 ) 2ax a 2 0 ，当 k≠±1 时，它的图形是圆；当 k＝±1 时，它的图形是 AB 的中垂线！实例：设 A（-2，0），B（1，0），且 AP=2BP，则点 P 在圆心在（2，0），r=2 的圆上
应用：可知阿氏圆上任意一点 P 到点 A 和点 B 的距离比都是定值 k，那么在证明过程中可以用这个原理，就是说如果我们知道了圆上一点到直径上两定点的距离比，那么我们就可以知道圆上另一点到两定点的距离比。
实战：Leabharlann 对于2 PE 2 ，且这个定点 PB 的转化，就是找到另外一个定点 E，使得： 2 PB 2

(完整版)阿波罗尼斯圆及其应用

阿波罗尼斯圆及其直接应用 (解析版)

阿波罗尼斯圆性质及其应用探究

阿波罗尼斯圆及其应用 阿波罗尼斯圆的逆用 (解析版)

阿波罗尼斯圆及其应用

完整版阿氏圆

阿波罗尼斯圆及其应用(整理)

微专题16 阿波罗尼斯圆问题梳理及其运用

(完整版)阿氏圆问题归纳

阿波罗尼斯圆介绍及其直接应用 (解析版)

阿氏圆的性质及其应用

阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用

阿波罗尼斯圆的轴对称性及其应用

阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用

阿波罗尼斯圆定理及应用

(完整版)阿波罗尼斯圆及其应用

(完整版)阿氏圆问题归纳

阿氏圆介绍

阿波罗尼斯圆及其应用阿波罗尼斯圆的逆用 (解析版)