【轨迹方程】--apollonius圆(阿波罗尼斯圆,简称“阿氏圆”)
【轨迹方程】--Apollonius圆 (阿波罗尼斯 圆,简称 “阿氏圆”)

1 Apollonius 圆 (阿波罗尼斯 圆,简称 “阿氏圆”)
例. 已知,两点坐标()()3,0,3,0A B -,若平面上一点P 满足
2PA PB
=,求P 点轨迹. 解:设P (),x y ,由题意
2= 化简得 ()22516x y ++=
一般地:若平面上P 和定点A 、B 满足PA PB
λ=,当0λ>且1λ≠时,P 的轨迹是一个圆
“阿氏圆”性质:
(1)等比:2PA MA A PB MB NB
N ===;(正弦定理推论) (2)平分:PM 平分APB ∠,
PN 平分APB ∠的外角
(3)性质逆用
(2011苏州市 一模)
18.已知椭圆E :22221x y a
b +=()0a b >>
的离心率为2,且过点(P ,设椭圆E 的右准线l 与x
轴的交点为A ,椭圆的上顶点为B ,直线AB 被以原点为圆心的圆O 所截得的弦长(1)求椭圆E 的方程及圆O 的方程;
(2)若M 是准线l 上纵坐标为t 的点,求证:存在一个异于M 的点Q ,对于圆O 上任意
一点N ,有
MN NQ 为定值;且当
M 在直线l 运动时,点Q 在一个定圆上.
(第18题图)。
阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤领域中,阿波罗尼斯圆是一个具有独特魅力和重要应用价值的概念。
它不仅在理论上丰富了我们对几何图形的理解,还在实际问题的解决中发挥着重要作用。
要理解阿波罗尼斯圆,首先得从它的定义说起。
阿波罗尼斯圆是指平面内到两个定点的距离之比为常数(不为 1)的点的轨迹。
简单来说,如果有两个固定的点 A 和 B,一个动点 P 到 A 和 B 的距离之比始终是一个定值 k(k 不等于 1),那么点 P 的轨迹就是一个阿波罗尼斯圆。
那么,如何来确定这个圆呢?假设两个定点 A 和 B 的坐标分别为(x1, y1) 和(x2, y2),距离之比为 k,我们可以通过一系列的代数运算来找到这个圆的方程。
这其中涉及到距离公式以及一些代数变形,虽然过程可能稍显复杂,但最终得出的结果却能清晰地描述这个圆的特征。
阿波罗尼斯圆有着许多有趣的性质。
比如说,圆心一定在线段 AB的中垂线上。
而且,当两个定点之间的距离固定,比值 k 变化时,圆的大小和位置也会相应地改变。
接下来,让我们看看阿波罗尼斯圆在实际中的应用。
在物理学中,它可以用来研究带电粒子在电场中的运动轨迹。
当电场强度的分布满足一定条件时,粒子的运动轨迹可能就会是一个阿波罗尼斯圆。
这为我们分析粒子的运动规律提供了有力的工具。
在工程设计中,阿波罗尼斯圆也能大显身手。
例如在道路规划中,如果要设计一条曲线道路,使得车辆从一个固定点出发,到另一个固定点的行驶时间与距离之比保持恒定,就可以利用阿波罗尼斯圆的原理来进行规划。
在数学竞赛和高考中,阿波罗尼斯圆也常常作为考点出现。
它可能会隐藏在一些看似复杂的几何问题中,需要我们敏锐地发现并运用其相关知识来求解。
例如,给出一些点的位置关系和距离条件,让我们判断某个点是否在特定的阿波罗尼斯圆上,或者求与阿波罗尼斯圆相关的最值问题。
再举一个具体的例子,假设在一个平面直角坐标系中,有两点 A(-3, 0) 和 B(3, 0),动点 P 满足|PA| = 2|PB|,我们可以通过计算得出点P 的轨迹方程,进而分析其性质和相关应用。
阿氏圆动点轨迹

阿氏圆动点轨迹
阿氏圆(Apollonian Circle)是由希腊数学家阿波罗尼乌斯(Apollonius)提出的一个几何概念,指的是通过三个给定的
圆的相切、交、外切和内切操作,生成的一系列互相相切的圆。
阿氏圆动点轨迹即指的是通过在阿氏圆中固定一个点,并不断改变其他两个固定点的位置,从而得到该点在运动过程中所生成的轨迹。
具体来说,设阿氏圆的三个给定圆分别为圆A、圆B、圆C,
其中圆A和圆B相切于点D,圆A和圆C相切于点E,圆B
和圆C相切于点F。
假设我们固定点D和点E,并改变点F的位置,那么圆B和
圆C的位置也会随之改变,从而生成一个阿氏圆。
同时,点F 的位置和阿氏圆的半径也会决定着点D和点E之间的距离。
因此,通过改变点F的位置,我们可以得到点D和点E之间
的各种距离,从而得到点F的轨迹。
通过类似的方式,我们也可以固定点D和点F,改变点E的
位置,得到点E的轨迹;或固定点E和点F,改变点D的位置,得到点D的轨迹。
总结起来,阿氏圆动点轨迹就是通过固定两个点,改变另外一个点的位置,并不断做阿氏圆运算,从而得到该点在运动过程中所生成的轨迹。
需要注意的是,阿氏圆动点轨迹的性质和形状会受到三个给定圆的位置和相对大小的影响,不同的参数组合会得到不同的结果。
这也是阿氏圆的研究领域之一。
阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤领域中,阿波罗尼斯圆是一个引人入胜且具有重要应用价值的概念。
它以古希腊数学家阿波罗尼斯的名字命名,展现了几何图形与数学原理之间的精妙联系。
要理解阿波罗尼斯圆,首先得从它的定义入手。
阿波罗尼斯圆是指平面内到两个定点的距离之比为定值(不为 1)的点的轨迹。
也就是说,如果有两个定点 A 和 B,点 P 满足|PA|/|PB| = k(k 为非 1 的常数),那么点 P 的轨迹就是一个阿波罗尼斯圆。
为了更直观地感受阿波罗尼斯圆,我们不妨通过一个简单的例子来看看它是如何形成的。
假设定点 A 的坐标为(-1, 0),定点 B 的坐标为(1, 0),且比值 k = 2。
我们可以通过距离公式和等式|PA|/|PB| =2 来列出方程,经过一番计算和化简,就能得到点 P 的轨迹方程,从而描绘出这个阿波罗尼斯圆的图形。
那么,阿波罗尼斯圆在实际中有哪些应用呢?一个常见的应用是在物理学中的带电粒子在电场和磁场中的运动问题。
比如,当带电粒子在特定的电场和磁场中运动时,其轨迹可能会符合阿波罗尼斯圆的特征。
通过对阿波罗尼斯圆性质的深入理解,我们可以更好地分析带电粒子的运动路径、速度变化等关键信息,从而为相关的物理研究和实际应用提供有力的理论支持。
在工程领域,阿波罗尼斯圆也有着不可小觑的作用。
比如在建筑设计中,当需要规划一些具有特定比例关系的布局时,阿波罗尼斯圆的概念可以帮助设计师巧妙地安排空间,实现美观与实用的完美结合。
又比如在道路规划中,为了使车辆行驶更加流畅和安全,有时需要根据不同地点之间的距离比例关系来设计路线,阿波罗尼斯圆的原理就能在其中发挥指导作用。
在数学解题中,阿波罗尼斯圆更是常常成为巧妙解题的关键。
例如,在一些涉及到距离比值的几何问题中,如果能够敏锐地发现其隐藏的阿波罗尼斯圆结构,往往能够化繁为简,迅速找到解题的突破口。
我们来看一个具体的数学问题。
已知三角形 ABC 中,AB = 4,AC = 2,且点 P 满足|PA| = 2|PB|,求点 P 的轨迹。
阿氏圆

到两点点的距离之和为定值(大于两定点距离)的点的轨迹是椭圆.到两点点的距离之差为定值(小于两定点距离)的点的轨迹是双曲线那么到两定点的距离之比为定值的点的轨迹是什么呢?没错就是阿氏圆.阿氏圆定理(全称:阿波罗尼斯圆定理),具体的描述:一动点P到两定点A、B的距离之比等于定比m:n,则P点的轨迹,是以定比m:n内分和外分定线段AB的两个分点的连线为直径的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,该圆称为阿波罗尼斯圆,简称阿氏圆.【分析】令B为坐标原点,A的坐标为(a,0).则动点P(x,y).满足PA/PB=k(为实数,且不为±1)得(k2-1)(x2+y2)+2ax-a2=0,当k不为±1时,它的图形是圆.当k为±1时,轨迹是两点连线的中垂线.【典型例题】问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP、BP,求AP+1/2BP的最小值.(1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使CD=1,则有CD/CP=CP/CB=1/2,又∵∠PCD=∠BCP,∴△PCD∽△BCP.∴PD/BP=1/2,∴PD=1/2BP,∴AP+1/2BP=AP+PD.请你完成余下的思考,并直接写出答案:AP +1/2BP 的最小值为.(2)自主探索:在“问题提出”的条件不变的情况下,1/3AP +BP 的最小值为.(3)拓展延伸:已知扇形COD 中,∠COD =90°,OC =6,OA =3,OB =5,点P 是弧CD 上一点,求2PA +PB 的最小值.10.(3分)(2015•贵港)如图,已知P 是⊙O 外一点,Q 是⊙O 上的动点,线段PQ 的中点为M ,连接OP ,OM .若⊙O 的半径为2,OP=4,则线段OM 的最小值是( )A . 0B . 1C . 2D . 318.如图,在ABC ∆中, 90,8,6ACB BC AC ∠=︒==,以点C 为圆心,4为半径的圆上有一个动点D .连接AD 、BD 、CD ,则12BD AD +的最小值是 .。
2022年中考数学专题复习:几何最值模型 第6讲阿氏圆问题

6、阿氏圆-例题精讲
例题1,如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,2为半径作圆C,分别交AC、BC于D、E两点,
1
13.
点P是圆C上的一个动点,则2 + 的最小值为________.
1
【分析】本题最大难点在于转化2 .此时P点
的轨迹是圆,注意圆C的半径为2,CA=4,连接
∵AB=BD=4,BD是切线,∴∠ABD=90d°,∠BAD=∠D=45°,
∵AB是直径,∴∠APB=90°,
∴∠PAB=∠PBA=45°,∴PA=PB,PO⊥AB,
∵AC=PO=2,AC//PO,∴四边形AOPC是平行四边形,
ห้องสมุดไป่ตู้
∴OA=OP,∠AOP=90°,∴四边形AOPC是正方形,
∴PM=
6、阿氏圆-模型总结
2
【模型建立】如图1所示,圆的半径为R,点A、B都在圆外,P为圆O上一动点,已知 = 5 ,
2
连接PA、PB,则当“ + 5 PB”的值最小时,P点的位置如何确定?
图1
解决办法:如图2,在线段OB上截取OC,使得OC=
2
图2
2
2
R,则可说明△BPO与PCO相似,则有
学无止境
中考数学几何最值模型
第(6)讲阿氏圆问题
苏科版九年级
模型汇总
6、阿波罗尼斯圆-人物介绍
人物介绍
阿波罗尼斯(Apollonius约公元前262-190年),古希腊数学家,与欧几里得,阿基米德齐名.
阿波罗尼斯圆定理及拓展及解题

R150 47
R40
L
A
R100
C
B
R57.14285714
120
R60
图 6 运用方法三两对圆法绘制阿氏圆
A
C
B
R57.14285714
D
120
图 7 阿波罗尼斯圆定理扩展 1——点到两圆切线定比
圆圆阿氏圆方程,见图 9。
Y
kL
P(x,y)
图 8 题目 1 题解
TA
RA
O OA
RB TB C OB OQ
X RD
a Xo
图 9 圆圆阿氏圆方程
3
根据已知条件列方程:
x2 y2 R A2 k 2L2
, x a2 y2 RB2 L2
x2 2ax a2 y2 RB2 L2
k 2 x2 2ak 2 x a2k 2 k 2 y2 k 2RB2 k 2L2
k2 1
x2 y2
心圆。见图 15。
2ak 2x
R
2 A
k
2
a2
RB2
0
此公式为圆方程式,证明了动点到两定圆切线长度为定比的轨迹是一个圆。
令 y 0 ,求 C 点 D 点的 x 坐标:
k2
1
x2
2ak 2x
R
2 A
k
2
a2
RB2
0
x
2
1 k2 1
2ak 2
2ak 2
2 4 k2 1
a2k 2
R
2 A
k
2
R
绘制阿氏圆的方法三,两对圆法,定比点三点圆法。几何原理,到两定点距离为定比的 点在阿氏圆上,三点定圆。见图 6。
在绘制阿氏圆的基础上解题,题目 1 题解见图 8。 阿波罗尼斯圆定理扩展 1:已知平面上一动点 P 到两定圆 OA(半径 RA)、OB(半径 RB)切线(切点为 TA 、TB)的长度之比为不等于 1 的定值(PTA/PTB =k,k≠1)则点 P 的运动轨迹是一个圆——阿氏圆。——点到两圆切线定比。见图 7。
阿氏圆(2018中考数学压轴热点)
--阿氏圆模型专题训练阿氏圆( 阿波罗尼斯圆) :已知平面上两定点A、B,则所有满足PA/PB=k(k 不等于1) 的点P 的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿氏圆。
在初中的题目中往往利用逆向思维构造斜屁型相似( 也叫母子型相似或美人鱼相似)+ 两点间线段最短解决带系数两线段之和的最值问题。
观察下面的图形,当P 在在圆上运动时,PA、PB的长在不断的发生变化,但它们的比值却始终保持不变。
解决阿氏圆问题,首先要熟练掌握母子型相似三角形的性质和构造方法。
ABD D,使得AD/AB=AB/AC,则此时△∽△ACB如图,在△ABC的边AC上找一点母子型相似(共角共边)BA CD: 我们来看一道基本题目的性质解答带系数的两条线段和的最小值呢?那么如何应用阿氏圆为圆上一动点 . CB=4,CA=6已知∠ACB=90°,,⊙C半径为2,PA1(1) AP 求BP 的最小值为 21AP 求(2) 的最小值为BP3PBC 实战练习:D 1 AB上一动点,,,为切线,AC、BD AC=1BD=2P 为弧,半径为、已知⊙O 1 2的最小值试求PC PDC 2PB AO1 AP),,(、已知点2 A4 0B 上运动,试求的⊙2 在半径为),点,(44 P O BP 的最小值 2yBPxO A-- --1 -- --轴相切,与y 为⊙C 上一动点,且⊙C P,B(0,3 ),C(1,0 ),若点3、已知点A(-3,0)1AP(1)y ; BP 的最小值 4B(2)S 的最小值 .PAB PO CxA4、如图1,在平面直角坐标系xoy 中,半⊙O交x 轴与点A、B(2,0) 两点,AD、BC均为半⊙O 的切线,AD=2,BC=7.(1)求OD的长;(2)如图2,若点P 是半⊙O上的动点,Q为OD的中点 . 连接PO、PQ.①求证:△OPQ∽△ODP;②是否存在点P,使PD 2PC 有最小值,若存在,试求出点P 的坐标;若不存在,请说明理由 .5、(1)如图1,已知正方形ABC的边长为4,圆B 的半径为2,点P 是圆B 上的一个动点,1 1求PD PC 的最小值和PD PC 的最大值 .2 2(2)如图2,已知正方形ABCD的边长为9,圆B 的半径为6,点P 是圆B 上的一个动点,那么2 2;PD PDPC 的最小值为PC 的最大值为3 3B 上的一个2. 点P 是圆4,已知菱形ABCD的边长为,∠B=60°,圆B 的半径为3(3)如图11PC 的最大值为PC 的最小值为PD PD动点. 那么;22巩固练习:----2----11、如图,在Rt△ABC中,∠ACB﹦90°,CB﹦4,CA﹦6,圆C 半径为2,P 为圆上一动点,连接AP,BP,AP BP2 最小值为()A、37B、6C、2 17D、4APC B2、如图,在△ABC中,∠B﹦90°,AB﹦CB﹦2,以点 B 为圆心作圆B 与AC 相切,点P 为圆B 上任一动点,2.PC 则PA 的最小值是2CPAB3E,在⊙相切于点60,锐角大小为的边长为 2 °,⊙A 与BC3、如图,菱形ABCDPD,则PB A 上任取一点P2的最小值为.PADB E C4、在平面直角坐标系中,A(2,0),B(0,2),C (4,0),D(3 ,2),P 是△AOB 外部的第一象限内一.动点,且∠BPA﹦135°,则2PD﹢PC的最小值是yx----3----12,点4,圆B 的半径为5、(1)如图1,已知正方形ABCD的边长为PC求PDP 是圆B 上的一个动点,21的最小值和PC 的最大值.PD 2上的一个动点,求,点P 是圆B 9,圆B 的半径为6,已知正方2(2)如图2PCPD 的边长为ABCD形3 2的最大值.PC PD 的最小值和3上的一个动是圆B ,2,点P,∠B﹦90°,圆B 的半径为(3)如图3,已知菱形ABCD的边长为41 PC PD点,求21PD 的最小值和PC 的最大值. 2DA D AADPPPBBC C3图1 图2 图套路总结阿氏圆基本解法:构造相似kPD PC 阿氏圆一般解题步骤:OD 、的线段的两个端点分别与圆心相连接)O (将系数不为1 ,则连接OP;第一步:连接动点至圆心OD 长度;、第二步:计算出所连接的这两条线段OP OPm ;第三步:计算这两条线段长度的OD比OM m ;,使OD 第四步:在上取点M OP 得交点即为点,与圆第五步:连接CM O P.----4----1.如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C 半径为2,P 为圆上一动点,连结AP,BP,AP+BP的最小值为()2.如图,半圆的半径为1,AB 为直径,AC、BD 为切线,P BD=2 AC=1 上一动点,求为,,的最小值.PC+PD5--。
专题阿氏圆——精选推荐

专题阿氏圆定义平面内到两个定点,A B 的距离之比为定值()1≠K K 的点的轨迹是圆证明:令B 为坐标原点,A 的坐标为(a,0).则动点P(x,y)1.(2017·武汉六校联考)阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果击中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M 与两定点A 、B 的距离之比为λ(0λ>,1λ≠),那么点M 的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆:221x y +=和点1(,0)2A -,点(1,1)B ,M 为圆O 上动点,则2||||MA MB +的最小值为()A .6B .7C .10D .112.(2020·肥城市第一高级中学高三月考)古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点,A B 的距离之比为定值()1λλ≠的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系xOy 中,()()2,0,4,0,A B -点12PA P PB =满足.设点P 的轨迹为C ,下列结论正确的是()A .C 的方程为()2249x y ++=B .在x 轴上存在异于,A B 的两定点,D E ,使得12PD PE =C .当,,A B P 三点不共线时,射线PO 是APB ∠的平分线D .在C 上存在点M ,使得2||MO MA =3.(2020·浙江省温岭中学高三一模)已知()2,0A -,()2,0B ,动点M 满足2MA MB =,则点M 的轨迹方程是___________;又若0MA MB ⋅=,此时MAB △的面积为___________.4.(2019·湖北省孝感高中高二月考)公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius )在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下结果:平面内到两定点距离之比等于已知数的动点轨迹为直线或圆.后世把这种圆称之为阿波罗尼斯圆.已知直角坐标系中(2,0),(2,0)A B -,则满足||2||PA PB =的点P 的轨迹的圆心为____________,面积为____________.5.(2020·湖南省高三期末(文))阿波罗尼斯与阿基米德、欧几里得被称为亚历山大时期数学三巨匠.“阿波罗尼斯圆”是他的代表成果之一:平面上一点P 到两定点,A B 的距离之满足||(01)||PA t t t PB =>≠且为常数,则P 点的轨迹为圆.已知圆O :221x y +=和1(,0)2A -,若定点(,0)B b (12b ≠-)和常数λ满足:对圆O 上任意一点M ,都有||||MB MA λ=,则=λ_________,=b ___________.5.(2019·浙江省高二期末)公元前3世纪,古希腊数学家阿波罗尼斯在前人的基础上写了一部划时代的著作《圆锥曲线论》,该书给出了当时数学家们所研究的六大轨迹问题,其中之一便是“到两个定点的距离之比等于不为1的常数的轨迹是圆”,简称“阿氏圆”.用解析几何方法解决“到两个定点(00)O ,,(30)A ,的距离之比为12的动点M 轨迹方程是:22230x y x ++-=”,则该“阿氏圆”的圆心坐标是______,半径是_____.6.(2020·江西省高二期末(文))阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数()0,1k k k >≠的点的轨迹是圆,后人将这个圆称为阿氏圆.若平面内两定点A B 、间的距离为2,动点P 满足3PA PB=,当,,P A B 不共线时,三角形PAB 面积的最大值是_______________.8.(2019·安徽省高二月考(理))若平面内动点P 到两定点,A B 的距离之比||||PA PB λ=(其中λ为常数,0,1λλ>≠),则动点P 的轨迹为圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现的,故称作阿波罗尼斯圆.若已知(1,0),(1,0),2A B λ-=,则此阿波罗尼斯圆的方程为_____.9.(2020·福建省高三月考(理))波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数k (0k >且0k ≠)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.现有ABC ∆,4,sin 2sin AC C A ==,则当ABC ∆的面积最大时,AC 边上的高为_______________.10.(2020·湖北襄阳四中高二期末)一动点到两定点距离的比值为非零常数λ,当1λ≠时,动点的轨迹为圆,后世称之为阿波罗尼斯圆已知两定点A 、B 的坐标分别为:()4,0A 、()10B ,,动点M 满足2AM BM =.(1)求动点M 的阿波罗尼斯圆的方程;(2)过()2,3P 作该圆的切线l ,求l 的方程.11.(2019·湖北省高二期中)阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数(0,1)k k k >≠的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点0,0,()()3,0O A ,动点P 满足12PO PA =.(1)求点P 的轨迹方程;(2)求22PO PA +的最大值.12.(2018·黑龙江省高一期末)平面内动点P 到两定点A ,B 距离之比为常数(0,1)λλλ>≠,则动点P 的轨迹叫做阿波罗尼斯圆.现已知定点()0,0A 、()6,0B -,圆心为C ,(1)求满足上述定义的圆C 的方程,并指出圆心C 的坐标和半径;(2)若12λ=,且经过点()4,2Q 的直线l 交圆C 于M ,N 两点,当CMN ∆的面积最大时,求直线l 的方程.7专题阿氏圆参考答案1.C2.BC3.223320120x y x +-+=;165.4.10,03⎛⎫ ⎪⎝⎭649π5.2λ=2b =-6.(1,0)-27.348.2210103x y x +-+=9.8310.(1)224x y +=;(2)2x =或12590x y -+=.11.(1)22(1)4x y ++=;(2)45.12.(2)60x y +-=.。
阿波罗尼斯圆定理及拓展及解题

图 29 运用方法七同心阿氏圆法绘制阿氏圆 4
题目 5 题解见图 30。
10
60 R50
73
R84 4a
7a
R50 120
R95.68082847
图 30 题目 5 题解
题目 6,点到点的距离与点到圆切 线的长度之比为定比。见图 31。
4a 7a
应用方法九点切距定比法绘制阿 氏圆,见图 32。
运用方法七同心阿氏圆法绘制阿 氏圆,见图 33、图 34。
40
R15
R20
60
图 10 题目 2 点到两圆切线定比
4
绘制阿氏圆的方法五, 定比切线点一对圆法,公切 线定比分点定比切线点三点 圆法。几何原理,到两定圆 切线长度为定比的点在阿氏 圆上,三点定圆。见图 12。
绘制阿氏圆的方法六, 定比切线点两对圆法,定比 切线点三点圆法。几何原理, 到两定圆切线长度为定比的 点在阿氏圆上,三点定圆。 见图 13。
, x2 2ax a2 y2 L2
k 2 x2 2ak 2x a2k 2 k 2 y2 k 2L2
k 2 1 x2 y2 2ak 2x a2k 2 0
此公式为圆方程式,证明了动点到两定点距离定比的轨迹是一个圆。
令 y 0 ,求 C 点 D 点的 x 坐标:
k 2 1 x2 2ak 2x a2k 2 0
图 28 扩展 3 扩展——同心阿氏圆
从前面的点点阿氏圆圆 心公式、圆圆阿氏圆圆心公 式和点圆阿氏圆圆心公式, 可以得知同比例的三个阿氏 圆圆心为同一个点,圆心的 x 坐标相同:
xQ
ak 2 k2 1
a
a k2 1
40
70
R50
R118.18181818
阿波罗尼斯圆的轨迹及其几何解释

阿波罗尼斯圆的轨迹及其几何解释阿波罗尼斯圆是一种特殊的数学曲线,其轨迹可以通过一系列几何解释来理解。
本文将介绍阿波罗尼斯圆的数学定义、轨迹特征以及几何解释。
一、阿波罗尼斯圆的数学定义阿波罗尼斯圆,又称为阿波罗尼斯曲线,是在平面上给定两个不相交的焦点F1和F2以及一个正实数a时的一个点P的轨迹。
具体而言,该点P到焦点F1和F2的距离之比等于常数e的值,即PF1 / PF2 = e。
二、阿波罗尼斯圆的轨迹特征1. 长轴和短轴:阿波罗尼斯圆的轨迹是一个闭合的曲线,它具有两个主要特征——长轴和短轴。
长轴是通过焦点F1和F2的直线段,并且它的长度等于2a。
短轴则是在长轴上垂直且通过焦点F1和F2中点的线段。
2. 弦:阿波罗尼斯圆上的任意两个焦点F1和F2之间的线段被称为弦。
该弦的长度与焦点到曲线的距离之比始终等于e。
3. 对称性:阿波罗尼斯圆具有对称性。
即圆上的任意一点P关于焦点F1和焦点F2的连线的中点都在曲线上。
即焦点到曲线的距离等于中点到曲线的距离。
三、几何解释阿波罗尼斯圆具有许多精妙的几何解释,下面我们将介绍其中两个重要的几何解释。
1. 离心率为1的椭圆切割阿波罗尼斯圆可以通过一个离心率为1的椭圆进行切割的方式得到。
具体而言,在一个离心率为1的椭圆上选择两个焦点F1和F2,并规定一个特定的长度2a作为切割线段的长度。
然后,将这个长度沿着椭圆的长轴移动,得到一系列与椭圆相切的曲线,即阿波罗尼斯圆的轨迹。
2. 螺旋线生成另一个几何解释是通过螺旋线的生成方式得到阿波罗尼斯圆的轨迹。
首先,选择一个固定的起始点P0和一个固定的角度θ0,然后按照一定的规则进行旋转和移动。
具体规则是每次旋转角度为θ0,然后向前移动固定距离d。
重复这个步骤直到达到一定条件,得到一系列点P1,P2,P3...,这些点组成的轨迹即为阿波罗尼斯圆。
总结:阿波罗尼斯圆是一种特殊的数学曲线,其轨迹可以通过离心率为1的椭圆切割和螺旋线的生成方式得到。
阿波罗尼斯圆轨迹方程

阿波罗尼斯圆轨迹方程稿子一嘿,亲爱的小伙伴们!今天咱们来聊聊超有趣的阿波罗尼斯圆轨迹方程。
你们知道吗?这个方程就像是一个神秘的魔法咒语,能揭开好多图形的秘密。
想象一下,在一个大大的数学世界里,有一些点按照特定的规律移动,然后就形成了阿波罗尼斯圆。
它可不是随便出现的哦,是有一套严格的规则在控制着。
这个方程看起来可能有点复杂,一堆字母和符号,但其实只要咱们耐心点,就能发现它的美妙之处。
比如说,当我们给定两个固定的点,然后通过这个方程,就能算出那个神奇的圆的位置和大小。
是不是感觉像在变魔术?而且哦,阿波罗尼斯圆在好多数学问题里都能派上用场。
比如解决几何图形的最值问题,一下子就能找到最巧妙的答案。
怎么样,是不是对这个阿波罗尼斯圆轨迹方程有点好奇啦?那就一起深入探索它的奇妙世界吧!稿子二嗨呀,朋友们!今天咱们要讲讲那个神奇的阿波罗尼斯圆轨迹方程。
一提到这个名字,是不是感觉有点高大上?但别被它吓到啦,其实它也没那么难理解。
你看啊,咱们先想象有两个固定的点,就像两个坚守岗位的小卫士。
然后呢,根据这个方程,就能找出一个特别的圆。
这个圆可有意思了,它的出现就像是数学天空中的一颗璀璨星星。
有时候,我们在解题的时候,被各种条件绕得晕头转向。
但是,只要想起阿波罗尼斯圆轨迹方程,就好像找到了一把万能钥匙,能打开难题的大门。
而且哦,它不仅仅在数学课本里有用,在现实生活中也有它的影子呢。
比如说建筑设计、工程规划,都可能用到它。
所以呀,别觉得数学枯燥无聊,像阿波罗尼斯圆轨迹方程这样的知识,其实充满了乐趣和惊喜。
让我们一起爱上数学,探索更多的奇妙之处吧!。
阿波罗尼斯圆和蒙日圆的问题 解析版

阿波罗尼斯圆和蒙日圆的问题一、知识点梳理一、阿波罗尼斯圆1.阿波罗尼斯圆的定义在平面上给定两点A ,B ,设P 点在同一平面上且满足PAPB=λ,当λ>0且λ≠1时,P 点的轨迹是个圆,称之为阿波罗尼斯圆.(λ=1时P 点的轨迹是线段AB 的中垂线)2.阿波罗尼斯圆的证明设P x ,y ,A 1-a ,0 ,B a ,0 .若PA PB =λ(λ>0且λ≠1),则点P 的轨迹方程是x -λ2+1λ2-1a2+y 2=2aλλ2-12,其轨迹是以λ2+1λ2-1a ,0为圆心,半径为r =2aλλ2-1的圆.证明:由PA =λPB 及两点间距离公式,可得x +a 2+y 2=λ2x -a 2+y 2 ,化简可得1-λ2 x 2+1-λ2 y 2+21+λ2 ax +1-λ2 a 2=0①,(1)当λ=1时,得x =0,此时动点的轨迹是线段AB 的垂直平分线;(2)当λ≠1时,方程①两边都除以1-λ2得x 2+y 2+2a 1+λ2 x 1-λ2+a 2=0,化为标准形式即为:x -λ2+1λ2-1a2+y 2=2aλλ2-12,∴点P 的轨迹方程是以λ2+1λ2-1a ,0为圆心,半径为r =2aλλ2-1的圆.图① 图② 图③【定理】A ,B 为两已知点,M ,N 分别为线段AB 的定比为λλ≠1 的内外分点,则以MN 为直径的圆C 上任意点P 到A ,B 两点的距离之比为λ.证明:以λ>1为例.如图②,设AB =2a ,AM MB =AN NB =λ,则AM =2aλ1+λ,BM =2a -2aλ1+λ=2a1+λ,AN =2aλλ-1,BN =2aλλ-1-2a =2aλ-1.过B 作AB 的垂线圆C 交于Q ,R 两点,由相交弦定理及勾股定理得QB 2=MB ⋅BN =4a 2λ2-1,QA 2=AB 2+QB 2=4a 2λ2λ2-1,于是QB =2aλ2-1,QA =2aλ2-1,∴QA QB =λ.∵M ,Q ,N 同时在到A ,B 两点距离之比等于λ的圆上,而不共线的三点所确定的圆是唯一的,∴圆C 上任意一点P 到A ,B 两点的距离之比恒为λ.同理可证0<λ<1的情形.3.阿波罗尼斯圆的相关结论【结论1】当λ>1时,点B 在圆C 内,点A 在圆C 外;当0<λ<1时,点A 在圆C 内,点B 在圆C 外.【结论2】因AQ 2=AM ⋅AN ,故AQ 是圆C 的一条切线.若已知圆C 及圆C 外一点A ,可以作出与之对应的点B ,反之亦然.【结论3】所作出的阿波罗尼斯圆的直径为MN =4aλλ2-1 ,面积为4πa 2λ2λ2-12.【结论4】过点A 作圆C 的切线AQ (Q 为切点),则QM ,QN 分别为∠AQB 的内、外角平分线.【结论5】阿波罗尼斯圆的直径两端是按比例内分AB 和外分AB 所得的两个分点,如图所示,M 是AB 的内分点,N 是AB 的外分点,此时必有PM 平分∠APB ,PN 平分∠APB 的外角.证明:如图①,由已知可得PA PB =MA MB =NA NB =λ(λ>0且λ≠1),∵S ΔPAM S ΔPBM =MA MB=λ,又S ΔPAM =12PA ⋅PM sin ∠APM ,S ΔPBM =12PB ⋅PM sin ∠BPM ,∴PA ⋅PM sin ∠APMPB ⋅PM sin ∠BPM=λ,∴sin ∠APM =sin ∠BPM ,∴∠APM =∠BPM ,∴PM 平分∠APB .由等角的余角相等可得∠BPN =∠DPN ,∴PN 平分∠APB 的外角.【结论6】过点B 作圆C 不与QR 重合的弦EF ,则AB 平分∠EAF .证明:如图③,连结ME ,MF ,由已知FA FB =EA EB =λ,∴EB FB =EA FA.∵S ΔABE S ΔABF =EBFB (λ>0且λ≠1),又S ΔABE=12AB ⋅AE sin ∠BAE ,S ΔABF =12AB ⋅AF sin ∠BAF ,∴AB ⋅AE sin ∠BAE AB ⋅AF sin ∠BAF =EB FB =AEAF,∴sin ∠BAE =sin ∠BAF ,∴∠BAE =∠BAF ,∴AB 平分∠EAF .∴sin ∠BAE =sin ∠BAF ,∴∠BAE =∠BAF ,∴AB 平分∠EAF .二、蒙日圆1.蒙日圆的定义在椭圆上,任意两条相互垂直的切线的交点都在同一个圆上,它的圆心是椭圆的中心,半径等于椭圆长半轴短半轴平方和的几何平方根,这个圆叫蒙日圆,如图1.证明:设椭圆的方程为x 2a 2+y 2b 2=1a >b >0 ,则椭圆两条互相垂直的切线PA ,PB 交点P 的轨迹是蒙日圆:x 2+y 2=a 2+b 2.①当题设中的两条互相垂直的切线PA ,PB 斜率均存在且不为0时,可设P x 0,y 0 (x 0≠±a 且y 0≠±b ),过P 的椭圆的切线方程为y -y 0=k x -x 0 k ≠0 ,由y -y 0=k x -x 0 ,x 2a2+y 2b2=1,得a 2k 2+b 2 x 2-2ka 2kx 0-y 0 x +a 2kx 0-y 0 2-a 2b 2=0,由其判别式值为0,得x 20-a 2 k 2-2x 0y 0k +y 20-b 2=0x 20-a 2≠0 ,∵k PA ,k PB 是这个关于k 的一元二次方程的两个根,∴k PA ⋅k PB =y 20-b2x 20-a2,由已知PA ⊥PB ,∴k PA ⋅k PB =-1,∴y 20-b 2x 20-a2=-1,∴x 20+y 20=a 2+b 2,∴点P 的坐标满足方程x 2+y 2=a 2+b 2.②当题设中的两条互相垂直的切线PA ,PB 有斜率不存在或斜率为0时,可得点P 的坐标为±a ,b 或a ,±b ,此时点P 也在圆x 2+y 2=a 2+b 2上.综上所述:椭圆x 2a 2+y 2b 2=1a >b >0 两条互相垂直的切线PA ,PB 交点P 的轨迹是蒙日圆:x 2+y 2=a 2+b 2.2.蒙日圆的几何性质【结论1】过圆x 2+y 2=a 2+b 2上的动点P 作椭圆x 2a 2+y 2b2=1a >b >0 的两条切线PA ,PB ,则PA ⊥PB .证明:设P 点坐标x 0,y 0 ,由x 2a 2+y 2b 2=1y -y 0=k x -x 0,得a 2k 2+b 2x 2-2ka 2kx 0-y 0x +a 2kx 0-y 0 2-a 2b 2=0,由其判别式的值为0,得x 20-a 2 k 2-2x 0y 0k +y 20-b 2=0x 20-a 2≠0 ,∵k PA ,k PB 是这个关于k 的一元二次方程的两个根,∴k PA ⋅k PB =y 20-b 2x 20-a 2,x 20+y 20=a 2+b 2,k PA ⋅k PB =y 20-b 2x 20-a2=-1,PA ⊥PB .【结论2】设P 为蒙日圆O :x 2+y 2=a 2+b 2上任一点,过点P 作椭圆x 2a 2+y 2b2=1的两条切线,交椭圆于点A ,B,O为原点,则OP,AB的斜率乘积为定值k OP⋅k AB=-b2a2.【结论3】设P为蒙日圆O:x2+y2=a2+b2上任一点,过点P作椭圆x2a2+y2b2=1的两条切线,切点分别为A,B,O为原点,则OA,PA的斜率乘积为定值k OA⋅k PA=-b2a2,且OB,PB的斜率乘积为定值k OB⋅k PB=-b2a2(垂径定理的推广).【结论4】过圆x2+y2=a2+b2上的动点P作椭圆x2a2+y2b2=1a>b>0的两条切线,O为原点,则PO平分椭圆的切点弦AB.证明:P点坐标x0,y0,直线OP斜率k OP=y0x0,由切点弦公式得到AB方程x0xa2+y0yb2=1,k AB=-b2x0a2y0,k OP⋅k AB=-b2a2,由点差法可知,OP平分AB,如图M是中点.【结论5】设P为蒙日圆O:x2+y2=a2+b2上任一点,过点P作椭圆x2a2+y2b2=1a>b>0的两条切线,交蒙日圆O于两点C,D,则OP,CD的斜率乘积为定值k OP⋅k CD=-b2a2.【结论6】设P为蒙日圆x2+y2=a2+b2上任一点,过点P作椭圆x2a2+y2b2=1a>b>0的两条切线,切点分别为A,B,O为原点,则OA,OB的斜率乘积为定值:k OP⋅k CD=-b4a4.【结论7】设P为蒙日圆x2+y2=a2+b2上任一点,过点P作椭圆x2a2+y2b2=1a>b>0的两条切线,切点分别为A,B,O为原点,则SΔAOB的最大值为ab2,SΔAOB的最小值为a2b2a2+b2.【结论8】设P为蒙日圆x2+y2=a2+b2上任一点,过点P作椭圆x2a2+y2b2=1a>b>0的两条切线,切点分别为A,B,则SΔAPB的最大值为a4a2+b2,SΔAPB的最小值为b4a2+b2.二、题型精讲精练1设A ,B 是平面上两点,则满足PA PB=k (其中k 为常数,k ≠0且k ≠1)的点P 的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿波罗尼斯圆,简称阿氏圆,已知A 6,0 ,B 62,0,且k =2.(1)求点P 所在圆M 的方程.(2)已知圆Ω:x +2 2+y -2 2=5与x 轴交于C ,D 两点(点C 在点D 的左边),斜率不为0的直线l 过点D 且与圆M 交于E ,F 两点,证明:∠ECD =∠FCD .【详解】(1)解:由题意可得,PA PB=2,即PA =2PB ,则x -6 2+y 2=2x -622+y 2,整理得x 2+y 2=3,即圆M 的方程为x 2+y 2=3.(2)证明:对于圆Ω,令y =0,得x =-1或x =-3,所以C -3,0 ,D -1,0 .设直线l 的方程为x =ty -1,E x 1,y 1 ,F x 2,y 2 .由x =ty -1,x 2+y 2=3,得1+t 2 y 2-2ty -2=0,则y 1+y 2=2t 1+t 2,y 1y 2=-21+t 2.k CE +k CF =y 1x 1+3+y 2x 2+3=y 1x 2+3 +y 2x 1+3 x 1+3 x 2+3=y 1y 2t +2 +y 2ty 1+2 x 1+3 x 2+3 =2×ty 1y 2+y 1+y 2x 1+3 x 2+3 =2×-2t 1+t 2+2t 1+t 2x 1+3 x 2+3 =0则直线EC 与FC 关于x 轴对称,即∠ECD =∠FCD .2已知椭圆C :x 2a 2+y 2b 2=1a >b >0 的一个焦点为5,0 ,离心率为53.(I )求椭圆C 的标准方程;(II )若动点P x 0,y 0 为椭圆外一点,且点P 到椭圆C 的两条切线相互垂直,求点P 的轨迹方程.【详解】(I )可知c =5,又e =c a =5a =53,∴a =3,b 2=a 2-c 2=9-5=4,故椭圆C 的标准方程为x 29+y 24=1.(II )设两切线为l 1,l 2,①当l 1⊥x 轴或l 1⎳x 轴时,对应l 2⎳x 轴或l 2⊥x 轴,可知P ±3,2 或P 3,±2 .②当l 1与x 轴不垂直且不平行时,x 0≠±3,设l 1的斜率为k ,则k ≠0,l 2的斜率为-1k,l 1的方程为y -y 0=k x -x 0 ,联立x 29+y 24=1,得9k 2+4 x 2+18k y 0-kx 0 x +9y 0-kx 0 2-4 =0,∵直线与椭圆相切,∴Δ=0,得18k 2y 0-kx 02-36y 0-kx 0 2-4 9k 2+4 =0,∴4y 0-kx 0 2-49k 2+4 =0,整理得x 20-9 k 2-2x 0y 0k +y 02-4=0(*),∴k 是方程(*)的一个根,同理-1k是方程(*)的另一个根,其中x 0≠±3,∴点P 的轨迹方程为x 2+y 2=13x ≠±3 ,又P ±3,2 或P 3,±2 满足上式.综上知:点P 的轨迹方程为x 2+y 2=13.【题型训练-刷模拟】1.阿波罗尼斯圆一、单选题1.(2023·全国·高三专题练习)我们都知道:平面内到两定点距离之比等于定值(不为1)的动点轨迹为圆.后来该轨迹被人们称为阿波罗尼斯圆.已知平面内有两点A -1,0 和B 2,1 ,且该平面内的点P 满足|PA |=2|PB |,若点P 的轨迹关于直线mx +ny -2=0(m ,n >0)对称,则2m +5n的最小值是()A.10B.20C.30D.40【答案】B【分析】点P 的轨迹为圆,直线mx +ny -2=0过圆心,得5m +2n =2,利用基本不等式求2m +5n的最小值.【详解】设点P 的坐标为x ,y ,因为PA =2PB ,则PA 2=2PB 2,即x +1 2+y 2=2x -2 2+y -1 2 ,所以点P 的轨迹方程为(x -5)2+(y -2)2=20,因为P 点的轨迹关于直线mx +ny -2=0m >0,n >0 对称,所以圆心5,2 在此直线上,即5m +2n =2,所以2m +5n =125m +2n 2m +5n =1220+4n m +25m n ≥10+12×24n m ⋅25m n=20,当且仅当4n m =25m n ,即m =15,n =12时,等号成立,所以2m +5n的最小值是20.故选:B .2.(2023·全国·高三专题练习)古希腊数学家阿波罗尼斯的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数k (k >0且k ≠1)的点的轨迹是圆,后人将之称为阿波罗尼斯圆.现有椭圆T :x 2a 2+y 2b 2=1(a >b>0),A ,B 为椭圆T 长轴的端点,C ,D 为椭圆T 短轴的端点,E ,F 分别为椭圆T 的左右焦点,动点M 满足ME MF=2,△MAB 面积的最大值为46,△MCD 面积的最小值为2,则椭圆T 的离心率为()A.63B.33C.22D.32【答案】A【分析】由题可得动点M 的轨迹方程x -5c 3 2+y 2=16c 29,可得12×2a ×43c =46,12×2b ×13c =2,即求.【详解】设M x ,y ,E -c ,0 ,F c ,0 ,由ME MF=2,可得x +c2+y 2=2x -c 2+y 2=2,化简得x -5c 3 2+y 2=16c 29.∵△MAB 面积的最大值为46,△MCD 面积的最小值为2,∴12×2a ×43c =46,12×2b ×13c =2,∴b 2=13a 2=a 2-c 2,即c 2=23a 2,∴e =63.故选:A .3.(2023秋·江西宜春·高三江西省丰城中学校考期中)阿波罗尼斯是古希腊著名的数学家,对圆锥曲线有深刻而系统的研究,阿波罗尼斯圆就是他的研究成果之一,指的是:已知动点M 与两定点Q ,P 的距离之比MQ MP=λλ>0,λ≠1 ,那么点M 的轨迹就是阿波罗尼斯圆.已知动点M 的轨迹是阿波罗尼斯圆,其方程为x 2+y 2=1,定点Q 为x 轴上一点,P -12,0 且λ=2,若点B 1,1 ,则2MP +MB 的最小值为()A.6B.7C.10D.11【答案】C【分析】根据点M 的轨迹方程可得Q -2,0 ,结合条件可得2MP +MB =MQ +MB ≥QB ,即得.【详解】设Q a ,0 ,M x ,y ,所以MQ =x -a2+y 2,又P -12,0 ,所以MP =x +122+y 2.因为MQ MP=λ且λ=2,所以x -a2+y 2x +122+y 2=2,整理可得x 2+y 2+4+2a 3x =a 2-13,又动点M 的轨迹是x 2+y 2=1,所以4+2a3=0a 2-13=1,解得a =-2,所以Q -2,0 ,又MQ =2MP ,所以2MP +MB =MQ +MB ,因为B 1,1 ,所以2MP +MB 的最小值为BQ =1+22+1-0 2=10.故选:C .4.(2023·广西·统考模拟预测)阿波罗尼斯是古希腊著名数学家,与阿基米德、欧几里得并称为亚历山大时期数学三巨匠,他研究发现:如果一个动点P 到两个定点的距离之比为常数λ(λ>0且λ≠1),那么点P 的轨迹为圆,这就是著名的阿波罗尼斯圆.若点P 到A 2,0 ,B -2,0 的距离比为3,则点P 到直线l :22x -y -2=0的距离的最大值是()A.32+23B.2+23C.43D.63【答案】A【分析】先由题意求出点P 的轨迹方程,再由直线和圆的位置关系求解即可.【详解】由题意,设点P x ,y ,则PA PB=x -22+y 2x +2 2+y2=3,∴x -22+y 2x +2 2+y 2=3,化简得点P 的轨迹方程为x +4 2+y 2=12,∴点P 的轨迹是以-4,0 为圆心,半径r =23的圆.圆心-4,0 到直线l :22x -y -2=0的距离d =-82-222 2+-12=32,∴点P 到直线l 最大距离为d +r =32+2 3.故选:A .5.(2023·湖北襄阳·襄阳四中校考模拟预测)数学家阿波罗尼斯证明过这样一个命题:平面内到两定点距离之比为常数λ(λ>0且λ≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系xOy 中,A -2,0 ,动点M 满足MA =2MO ,得到动点M 的轨迹是阿氏圆C .若对任意实数k ,直线l :y =k x -1 +b 与圆C 恒有公共点,则b 的取值范围是()A.-133,133B.-143,143C.-153,153D.-43,43【答案】C【分析】设点M x ,y ,求出动点M 的轨迹圆C 的方程,再求出直线l 过定点坐标,依题意点1,b 在圆C 的内部,即可得到不等式,解得即可.【详解】设点M x ,y ,∵MA =2MO ,∴(x +2)2+y 2=4x 2+4y 2,所以动点M 的轨迹为阿氏圆C :3x 2+3y 2-4x -4=0,又直线l :y =k x -1 +b 恒过点1,b ,若对任意实数k 直线l :y =k x -1 +b 与圆C 恒有公共点,∴1,b 在圆C 的内部或圆上,所以3+3b 2-8≤0,所以3b 2≤5,解得-153≤b ≤153,即b 的取值范围为-153,153.故选:C6.(2023·全国·校联考模拟预测)阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,阿波罗尼斯发现:平面内到两个定点A ,B 的距离之比为定值λ(λ>0,且λ≠1)的点的轨迹是圆,此圆被称为“阿波罗尼斯圆”.在平面直角坐标系xOy 中,A -2,0 ,B 4,0 ,点P 满足PA PB=12.设点P 的轨迹为曲线C ,则下列说法错误的是()A.C 的方程为(x +4)2+y 2=16B.当A ,B ,P 三点不共线时,则∠APO =∠BPOC.在C 上存在点M ,使得|MO |=2|MA |D.若D 2,2 ,则PB +2PD 的最小值为45【答案】C【分析】根据已知条件及两点之间的距离公式,利用三角形的角平分线定理及圆与圆的位置关系,结合三点共线时线段取得最短即可求解.【详解】设P x ,y ,由PAPB =12,得x +2 2+y 2x -42+y 2=12,化简得(x +4)2+y 2=16,故A 正确;当A ,B ,P 三点不共线时,OA OB =12=PA PB,所以PO 是∠APB 的角平分线,所以∠APO =∠BPO ,故B 正确;设M x ,y ,则x 2+y 2=2x +2 2+y 2,化简得x +832+y 2=169,因为-4+832+0-02=43<4-43,所以C 上不存在点M ,使得|MO |=2|MA |,故C 错误;因为PA PB=12,所以PB =2PA ,所以PB +2PD =2PA +2PD ≥2AD =45,当且仅当P 在线段AD 上时,等号成立,故D 正确.故选:C .7.(2023·四川成都·石室中学校考模拟预测)已知平面上两定点A ,B ,则所有满足PA PB=λ(λ>0且λ≠1)的点P 的轨迹是一个圆心在直线AB 上,半径为λ1-λ2⋅AB 的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称作阿氏圆.已知动点P 在棱长为6的正方体ABCD -A 1B 1C 1D 1的一个侧面ABB 1A 1上运动,且满足PA =2PB ,则点P 的轨迹长度为()A.8π3B.4π3C.3πD.15π2【答案】B【分析】根据阿氏圆的定义分析得P 点轨迹为球与侧面的交线,计算其弧长即可【详解】在图1中,以B 为原点建立平面直角坐标系xBy ,如图2所示,设阿氏圆圆心为O a ,0 ,半径为r .因为PA =2PB ,所以PA PB=2,所以r =21-22⋅AB =23×6=4.设圆O 与AB 交于点M .由阿氏圆性质,知MA MB=λ=2.又MB =4-BO =4-a ,所以MA =2MB =8-2a .又MA +MB =6,所以8-2a +4-a =6,解得a =2,所以O 2,0 ,所以点P 在空间内的轨迹为以O 为球心,半径为4的球.当点P 在侧面ABB 1A 1内部时,如图2所示,截面圆与AB ,BB 1分别交于点M ,R ,所以点P 在侧面ABB 1A 1内的轨迹为MR.因为在Rt △RBO 中,RO =4,BO =2,所以∠ROB =π3,所以MR=π3×4=4π3,所以点P 在侧面ABB 1A 1内部的轨迹长为4π3.故选:B.二、多选题8.(2023秋·云南保山·高三统考期末)古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名,他发现:平面内到两个定点A,B的距离之比为定值λ(λ>0且λ≠1)的点的轨迹是一个圆,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系xOy中,A-1,0,B2,0,点P满足PAPB=12,设点P的轨迹为曲线C,下列结论正确的是()A.曲线C的方程为(x+2)2+y2=4B.曲线C与圆C :x2+(y-2)2=4外切C.曲线C被直线l:x+y=0截得的弦长为22D.曲线C上恰有三个点到直线m:x+3y=0的距离为1【答案】ACD【分析】对于A,设点P x,y,由两点间距离公式代入化简判断;对于B,根据圆心距与两半径和的关系进行判断;对于C,先求出点到直线的距离,再结合勾股定理求出弦长;对于D,结合点到直线的距离以及圆C 的半径分析判断.【详解】对于A,设P x,y,由定义PAPB=12,得(x+1)2+y2(x-2)2+y2=12,化简整理得(x+2)2+y2=4,故A正确;对于B,C的圆心为-2,0,半径r1=2;C 的圆心为0,2,半径r2=2;圆心距CC =22≠r1+r2,故B错误;对于C,圆心C-2,0到直线l:x+y=0的距离d=22=2,所以弦长为2r12-d2=22,故C正确;对于D,圆心C-2,0到直线m:x+3y=0的距离d=22=1,半径r=2,所以圆C上恰有三个点到直线m的距离为1,故D正确.故选:ACD.9.(2024·全国·高三专题练习)古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名,他发现:“平面内到两个定点A,B的距离之比为定值λ(λ≠1)的点的轨迹是圆.”后来人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系xOy中,A(1,0),B(3,0),点P满足PAPB=2,点P的轨迹为曲线C,下列结论正确的是()A.曲线C的方程为x2+y2-10x+17=0B.直线3x+4y=0与曲线C有公共点C.曲线C被x轴截得的弦长为42D.△ABP面积的最大值为22【答案】ACD【分析】通过阿氏圆的定义结合PAPB=2,设P x,y,从而可以得到曲线C的方程;通过计算圆心到直线3x+4y=0的距离是否小于等于半径,从而判断B的正确性;计算圆心到x轴的距离d,结合d2+l22=r2,得到曲线C被x轴截得的弦长l,从而判断C的正确性;AB的长度确定,所以△ABP面积的最大值即为点P到AB距离的最大值,从而判断C的正确性.【详解】设P x,y,对于选项A,因为PAPB=2,所以x-12+y2x-32+y2=2,化简得x2+y2-10x+17=0,故A正确;对于选项B,因为曲线C为x2+y2-10x+17=0,所以圆心为5,0,半径为22,计算圆心5,0到直线3x +4y=0的距离为d=3>22,所以直线3x+4y=0与曲线C没有公共点,故B错误;对于选项C,曲线C的圆心在x轴上,所以被x轴截得的弦即为直径,所以曲线C被x轴截得的弦长为42,故C正确;对于选项D,因为A(1,0),B(3,0),所以AB=2,故S△ABP=12⋅AB⋅y p =y p ,而曲线C为x2+y2-10x+17=0,所以y p∈-22,22,即S△ABP的最大值为22,故D正确.故选:ACD10.(2023·全国·高三专题练习)古希腊著名数学家阿波罗尼斯发现:平面内到两个定点A,B的距离之比为定值λλ≠1的点的轨迹是圆,此圆被称为“阿波罗尼斯圆”.在平面直角坐标系xOy中,A-2,0,B4,0,点P满足PAPB=12.设点P的轨迹为C,则( ).A.轨迹C的方程为x+42+y2=9B.在x轴上存在异于A,B的两点D,E,使得PDPE=12C.当A,B,P三点不共线时,射线PO是∠APB的角平分线D.在C上存在点M,使得MO=2MA【答案】BC【分析】利用求轨迹方程的方法确定轨迹C的方程可判断A;设D m,0,E n,0,由两点间的距离公式结合轨迹C的方程可判断B;由角平分线的定义可判断C;设M x,y,由MO=2MA求出点M的轨迹方程与x2+y2+8x=0联立,可判断D.【详解】对于A,在平面直角坐标系xOy中,A-2,0,B4,0,点P满足PAPB=12,设P x,y,则x+22+y2x-42+y2=12,化简得x2+y2+8x=0,即x+42+y2=16,所以A错误;对于B,假设在x轴上存在异于A,B的两点D,E,使得PDPE=12,设D m,0,E n,0,则x-n2+y2=2x-m2+y2,化简得3x2+3y2-8m-2nx+4m2-n2=0,由轨迹C的方程为x2+y2+8x=0,可得8m-2n=-24,4m2-n2=0,解得m=-6,n=-12或m=-2,n=4(舍去),所以B正确;对于C,当A,B,P三点不共线时,OAOB =12=PAPB,可得射线PO是∠APB的角平分线,所以C正确;对于D,若在C上存在点M,使得MO=2MA,可设M x,y,则x2+y2=2x+22+y2,化简得x2+y2+163x+163=0,与x2+y2+8x=0联立,方程组无解,故不存在点M,所以D错误.故选:BC.11.(2023春·湖南长沙·高三湖南师大附中校联考阶段练习)阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,阿波罗尼斯发现:平面内到两个定点A,B的距离之比为定值λ(λ>0,且λ≠1)的点的轨迹是圆,此圆被称为“阿波罗尼斯圆”.在平面直角坐标系xOy中,A-2,0,B4,0,点P满足PAPB=12.设点P的轨迹为曲线C,则下列说法正确的是()A.C 的方程为x +4 2+y 2=16B.当A ,B ,P 三点不共线时,则∠APO =∠BPOC.在C 上存在点M ,使得MO =2MAD.若D 2,2 ,则PB +2PD 的最小值为45【答案】ABD【分析】对于A ,通过直接法求出点P 的轨迹方程即可判断;对于B ,由题意,结合三角形内角平分线定理进行判断即可;对于C ,由“阿波罗尼斯圆”定义,求点M 轨迹方程,用圆与圆的位置关系进行判断即可;对于D ,将PB +2PD 转化为2PA +2PD 进行判断即可.【详解】设P x ,y ,(P 不与A ,B 重合)∵A -2,0 ,B 4,0 ,∴PA =x +22+y 2,PB =x -42+y 2,∴PAPB=12,得x +2 2+y 2x -42+y 2=12,化简得x +4 2+y 2=16,∴点P 的轨迹曲线C 是以C -4,0 为圆心,半径r =4的圆,对于A ,曲线C 的方程为x +4 2+y 2=16,故选项A 正确;对于B ,由已知,OA =2,OB =4,∴OA OB=12=PA PB,∴当A ,B ,P 三点不共线时,由三角形内角平分线定理知,PO 是△APB 内角∠APB 的角平分线,∴∠APO =∠BPO ,故选项B 正确;对于C ,若MO =2MA ,则MO MA=2,由题意,M 点轨迹是圆,设M x ,y ,由MO MA=2得x 2+y 2x +22+y 2=2,化简得点M 轨迹方程为x +832+y 2=169,即点M 的轨迹是圆心为C -83,0 ,半径r =43的圆,圆C 与圆C 的圆心距CC =-4+832+0-0 2=43<r -r =83,∴圆C 与圆C 的位置关系为内含,圆C 与圆C 无公共点,∴C 上不存在点M ,使得MO =2MA ,故选项C 错误;对于D ,∵PA PB=12,∴PB =2PA ,∴PB +2PD =2PA +2PD =2PA +PD ≥2AD =2×-2-22+0-2 2=45,当且仅当P 在线段AD 上时,等号成立,故选项D 正确.故选:ABD .三、填空题12.(2023·全国·高三专题练习)阿波罗尼斯(约前262-前190年)证明过这样一个命题:平面内到两定点距离之比为常数k k >0,k ≠1 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点O 0,0 ,A 3,0 ,动点P 满足PO PA=12,则点P 的轨迹方程是.【答案】x +1 2+y 2=4【分析】直接设点P 的坐标,利用两点间距离公式代入化简整理可求点P 的轨迹方程.【详解】设P x ,y ,PO PA=12即x 2+y 2x -32+y 2=12,整理得:x 2+y 2+2x -3=0即x +1 2+y 2=4.故答案为:x +1 2+y 2=4.13.(2023春·上海闵行·高三上海市七宝中学校考开学考试)阿波罗尼斯证明过这样一个命题:平面内到两定点距离之比为常数的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点A ,B 间的距离为3,动点P 满足PA PB=2,则PA ⋅PB的范围为.【答案】-2,18【分析】以AB 中点为原点O ,以AB 所在直线为x 轴,以AB 的垂直平分线为y 轴,建立平面直角坐标系xOy ,则A -32,0 ,B 32,0 .设P x ,y ,由题可得点P 轨迹方程,后可得答案.【详解】以AB 中点为原点O ,以AB 所在直线为x 轴,以AB 的垂直平分线为y 轴,建立平面直角坐标系xOy ,因为AB =3,所以A -32,0 ,B 32,0 .设P x ,y ,因为PA PB=2,所以x +322+y 2=2⋅x -322+y 2,整理得x 2+y 2-5x +94=0,即x -522+y 2=4.y 2=4-x -522≥0⇒x ∈12,92.又PA =-32-x ,-y ,PB =32-x ,-y ,则PA ⋅PB =x 2+y 2-94=x 2+4-x -52 2-94=5x -92,则PA ⋅PB ∈-2,18 .故答案为:-2,1814.(2023·全国·高三专题练习)阿波罗尼斯的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数k (k >0且k ≠1)的点的轨迹是圆,后人将这个圆称为阿氏圆,现有△ABC ,BC =6,sin B =12sin C ,当△ABC 的面积最大时,则AC 的长为.【答案】25【分析】利用正弦定理将角化边,即可求得点A 的轨迹方程,然后确定三角形面积的最大值和点A 的坐标,最后求解AC 的长度即可.【详解】解:因为sin B =12sin C ,由正弦定理可得b =12c ,即c =2b ,因为BC =6,不妨令B (-3,0),C (3,0),建立如图所示的平面直角坐标系,设点A 的坐标为A x ,y y ≠0 ,点A 的轨迹方程满足:(x +3)2+y 2=2(x -3)2+y 2,整理可得:(x -5)2+y 2=16,y ≠0 ,即点A 的轨迹是以(5,0)为圆心,4为半径的圆(除与x 轴两交点外),当点A 的坐标A (5,4)或A (5,-4)时三角形的面积最大,其最大值为S =12×6×4=12,由勾股定理可得AC =22+42=25.故答案为:25.15.(2023·河北衡水·校联考二模)希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点A ,B 的距离之比为定值λλ≠1 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系xOy 中,A -3,1 ,B -3,6 ,点P 是满足λ=63的阿氏圆上的任一点,若抛物线y =16x 2的焦点为F ,过点F 的直线与此阿氏圆相交所得的最长弦与最短弦的和为.【答案】106+123【分析】由阿氏圆的定义得到点P 的轨迹方程,即阿氏圆的方程,然后由圆的性质即可求解.【详解】设P x ,y ,由阿氏圆的定义可得PA PB=63,即(x +3)2+(y -1)2(x +3)2+(y -6)2=23,化简得x 2+y 2+6x +18y -60=0.所以(x +3)2+(y +9)2=150,所以点P 在圆心为-3,-9 ,半径为56的圆上,因为抛物线C :y =16x 2的焦点为F .所以F 0,32,因为(0+3)2+32+92=4774<150.所以点F 在圆(x +3)2+(y +9)2=150内,因为点F 到与圆心的距离为4774=4772,所以过点F 的最短弦长为2150-4774=123,过点F 的最长弦长为2150=106,所以过点F 的最长弦与最短弦的和为106+123.故答案为:106+12316.(2023·湖南长沙·长沙市实验中学校考三模)已知平面上两定点A 、B ,则所有满足PA PB=λ(λ>0且λ≠1)的点P 的轨迹是一个圆心在直线AB 上,半径为λ1-λ2⋅AB 的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称作阿氏圆.已知棱长为3的正方体ABCD -A 1B 1C 1D 1表面上动点P 满足PA =2PB ,则点P 的轨迹长度为.【答案】43π+32π【分析】以B 为原点建立平面直角坐标系xBy ,结合题意可得点P 在空间内的轨迹为以O 1,0 为球心,半径为2的球.再根据球的性质求解即可.【详解】在图1中,以B 为原点建立平面直角坐标系xBy 如图2所示,设阿氏圆圆心为O a ,0 ,半径为r ,因为PA =2PB ,所以PA PB=2,所以r =21-22⋅AB =23×3=2,设圆O 与AB 交于点M ,由阿氏圆性质,知MA MB=λ=2,又MB =2-BO =2-a ,所以MA =2MB =4-2a ,又MA +MB =3,所以4-2a +2-a =3,解得a =1,所以O 1,0 ,所以点P 在空间内的轨迹为以O 为球心,半径为2的球,当点P 在面ABB 1A 1内部时,如图2所示,截面圆与AB ,BB 1分别交于点M ,R ,所以点P 在面ABB 1A 1内的轨迹为MR,因为在Rt △RBO 中,RO =2,BO =1,所以∠ROB =π3,所以MR=π3×2=2π3,所以点P 在面ABB 1A 1内部的轨迹长为2π3,同理,点P 在面ABCD 内部的轨迹长为2π3,当点P 在面BCC 1B 1内部时,如图3所示,因为OB ⊥平面BCC 1B 1,所以平面BCC 1B 1截球所得小圆是以B 为圆心,以BP 长为半径的圆,截面圆与BB 1,BC 分别交于点R ,Q ,且BP =OP 2-OB 2=4-1=3,所以点P 在面BCC 1B 1内的轨迹为RQ,且RQ=π2×3=32π,综上,点P 的轨迹长度为2π3+2π3+32π=43π+32π.故答案为:43π+32π.【点睛】方法点睛:求球与平面公共点轨迹长度时先求出平面截球所得圆面的半径,当截面为完整的圆时可直接求圆周长,当截面只是圆的一部分时先求圆心角的大小再计算弧长.四、解答题17.(2023·全国·高三专题练习)古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名,他发现:“平面内到两个定点A ,B 的距离之比为定值λ(λ>0且λ≠1)的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系xOy 中,A (-2,0),B (4,0),动点P 满足|PA ||PB |=12.设点P 的轨迹为C 1.(1)求曲线C 1的方程;(2)若曲线C 1和⊙C 2:(x -4)2+(y -6)2=r 2(r >0)无公共点,求r 的取值范围.【答案】(1)(x +4)2+y 2=16(2)(0,6)∪(14,+∞)【分析】(1)设P (x ,y ),然后根据|PA ||PB |=12列方程化简计算即可得曲线C 1的方程,(2)先求出两圆的圆心和半径,再由题意可得两圆外离或内含,从而可得C 1C 2 >4+r 或C 1C 2 <r -4,从而可求出r 的取值范围(1)设P (x ,y ),因为A (-2,0),B (4,0),动点P 满足|PA ||PB |=12,所以(x +2)2+y 2(x -4)2+y 2=12,化简得x 2+y 2+8x =0,即(x +4)2+y 2=16,所以曲线C 1的方程为(x +4)2+y 2=16,(2)曲线C 1的圆心为C 1(-4,0),半径为4,⊙C 2:(x -4)2+(y -6)2=r 2(r >0)的圆心为C 2(4,6),半径为r ,因为曲线C 1和⊙C 2:(x -4)2+(y -6)2=r 2(r >0)无公共点,所以两圆外离或内含,所以C 1C 2 >4+r 或C 1C 2 <r -4,所以(-4-4)2+(0-6)2=10>4+r 或(-4-4)2+(0-6)2=10<r -4,所以0<r <6或r >14,所以r 的取值范围为(0,6)∪(14,+∞)18.(2023·全国·高三专题练习)平面上两点A 、B ,则所有满足PA PB=k 且k 不等于1的点P 的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿氏圆.已知圆C 1上的动点P 满足:PO PA=2(其中O 为坐标原点,A 点的坐标为0,3 .(1)直线L ︰y =x 上任取一点Q ,作圆C 1的切线,切点分别为M ,N ,求四边形QMC 1N 面积的最小值;(2)在(1)的条件下,证明:直线MN 恒过一定点并写出该定点坐标.【答案】(1)4;(2)证明见解析,1,3 .【分析】(1)设点P 的坐标为x ,y ,求出点P 的轨迹方程为x 2+(y -4)2=4,求出S QMC 1N =2S △QMC 1=2QM ,QM =|C 1Q |2-4,求出|QM |最小值即得解;(2)设Q a ,a ,两圆方程相减可得MN 的方程为a x +y -4 -4y -12 =0,即得解.【详解】(1)解:设点P 的坐标为x ,y ,根据题设条件有P ∈P PO =2PA , 所以有x 2+y 2=2x 2+y -3 2,化简得x 2+(y -4)2=4. 所以S QMC 1N =2S △QMC 1=2×12C 1M ⋅QM =2QM QM =C 1Q |2- C 1M |2=|C 1Q |2-4,由题知,当C 1Q ⊥L 时,此时C 1Q =d =0-42=22,|QM |最小,即四边形QMC 1N 面积取得最小值4.(2)解;设Q a ,a ,由几何性质,可知M ,N 两点在以C 1Q 为直径的圆上,此圆的方程为x x -a +y -4 y -a =0,而直线MN 是此圆与圆C 1的相交弦所在直线,相减可得MN 的方程为a x +y -4 -4y -12 =0,所以直线MN 恒过定点1,3 .19.(2023秋·重庆沙坪坝·高三重庆南开中学校考期末)阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一,指的是已知动点M 与两定点Q ,P 的距离之比MQ MP=λλ>0,λ≠1 ,λ是一个常数,那么动点M 的轨迹就是阿波罗尼斯圆,圆心在直线PQ 上.已知动点M 的轨迹是阿波罗尼斯圆,其方程为x 2+y 2=4,定点分别为椭圆C :x 2a 2+y 2b2=1a >b >0 的右焦点F 与右顶点A ,且椭圆C 的离心率为e =12.(1)求椭圆C 的标准方程;(2)如图,过右焦点F 斜率为k k >0 的直线l 与椭圆C 相交于B ,D (点B 在x 轴上方),点S ,T 是椭圆C 上异于B ,D 的两点,SF 平分∠BSD ,TF 平分∠BTD .①求BS DS的取值范围;②将点S 、F 、T 看作一个阿波罗尼斯圆上的三点,若△SFT 外接圆的面积为81π8,求直线l 的方程.【答案】(1)x 28+y 26=1;(2)①13,1 ;②y =52x -102.【分析】(1)方法1,利用特殊值法,求得椭圆方程,方法2,利用定义整理得x 2+y 2+2x -2aλ2λ2-1x +λ2a 2-c 2λ2-1=0,再根据条件列式求得椭圆方程;方法3,利用定义进行整理,由MF MA为常数,求得系数,得到椭圆方程;(2)①首先由面积比值求得BS DS=BF DF,令BF DF=λ,则BF =λFD,利用坐标表示向量,求得λ=35-2x 0,再求范围;②由阿波罗尼斯圆定义知,S ,T ,F 在以B ,D 为定点得阿波罗尼斯圆上,由几何关系列式得BF DF=2r -BF 2r +DF,求得r ,再根据1BF-1DF=2-2x 0322-12x 0=229,求得x 0,y 0,即可计算直线方程.【详解】(1)方法(1)特殊值法,令M ±2,0 ,c -2a -2=c +2a +2,且a =2c ,解得c 2=2∴a 2=8,b 2=a 2-c 2=6,椭圆C 的方程为x 28+y 26=1方法(2)设M x ,y ,由题意MF MA=x -c2+y 2x -a 2+y2=λ(常数),整理得:x 2+y 2+2x -2aλ2λ2-1x +λ2a 2-c 2λ2-1=0,故2c -2aλ2λ2-1=0λ2a 2-c 2λ2-1=-4,又c a =12,解得:a =22,c =2.∴b 2=a 2-c 2=6,椭圆C 的方程为x 28+y 26=1.方法(3)设M x ,y ,则x 2+y 2=4.由题意MF MA=x -c 2+y 2x -a2+y2=x -c 2+4-x 2x -a2+4-x2=c 2+4-2cxa 2+4-2ax∵MF MA为常数,∴c 2+4a 2+4=c a ,又c a =12,解得:a 2=8,c 2=2,故b 2=a 2-c 2=6∴椭圆C 的方程为x 28+y 26=1(2)①由S △SBF S △SDF =12SB ⋅SF ⋅sin ∠BSF 12SD⋅SF ⋅sin ∠DSF =SB SD ,又S △SBF S △SDF =BF DF ,∴BS DS=BF DF(或由角平分线定理得)。
阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤天地中,阿波罗尼斯圆是一个引人入胜且具有重要应用价值的概念。
它宛如一颗璀璨的明珠,闪耀着智慧的光芒,为解决众多几何问题提供了独特而有效的途径。
要理解阿波罗尼斯圆,首先得从它的定义说起。
阿波罗尼斯圆指的是:平面内到两个定点的距离之比为常数(不为 1)的点的轨迹是一个圆。
这个定义听起来或许有些抽象,但通过具体的例子就能清晰许多。
假设平面上有两个定点 A 和 B,点 P 满足|PA|/|PB| = k(k 不为 1),那么点 P 的轨迹就是一个阿波罗尼斯圆。
当 k > 1 时,点 P的轨迹是以线段 AB 的内分点为圆心的圆;当 0 < k < 1 时,点 P 的轨迹是以线段 AB 的外分点为圆心的圆。
那么,阿波罗尼斯圆有哪些独特的性质呢?其一,圆心一定在线段AB 的垂直平分线上。
这是因为圆的对称性,使得圆心必然位于这条对称轴上。
其二,圆与线段AB 的两个端点的连线所成的夹角是恒定的。
接下来,让我们看看阿波罗尼斯圆在实际问题中的应用。
在几何问题中,它常常能帮助我们快速找到满足特定条件的点的位置。
例如,已知三角形的两个顶点以及这两个顶点到第三个顶点的距离之比,我们就可以利用阿波罗尼斯圆来确定第三个顶点的可能位置。
在物理学中,阿波罗尼斯圆也有其用武之地。
比如在电场问题中,当两个等量同种电荷形成的电场中,等势线的形状就类似于阿波罗尼斯圆。
通过对阿波罗尼斯圆的理解和运用,我们能够更深入地分析电场的分布和性质。
在工程设计中,阿波罗尼斯圆也能发挥作用。
比如在道路规划中,如果需要设计一条弯道,使得车辆在通过时从两个特定点观察到的视线角度保持一定比例,就可以借助阿波罗尼斯圆来确定弯道的形状和位置。
在数学竞赛中,阿波罗尼斯圆更是常常成为解题的关键。
例如,在一些复杂的几何证明题中,巧妙地引入阿波罗尼斯圆的概念,能够化繁为简,找到解题的突破口。
再举一个具体的例子来说明。
假设有一个三角形 ABC,已知 A、B两点的坐标以及|PA|/|PB| = 2,要求出点 P 的轨迹方程。
阿波罗尼斯圆及其应用

阿波罗尼斯圆及其应用在数学的广袤天地中,阿波罗尼斯圆宛如一颗璀璨的明珠,闪耀着独特的光芒。
它不仅是一个富有魅力的几何概念,更在众多领域有着广泛而重要的应用。
要理解阿波罗尼斯圆,首先得从它的定义说起。
阿波罗尼斯圆是指平面内到两个定点的距离之比为常数(不为 1)的点的轨迹所形成的圆。
不妨假设平面内有两个定点 A 和 B,点 P 满足|PA| /|PB| = k (k 为非 1 常数),那么点 P 的轨迹就是一个圆。
这个圆就被称为阿波罗尼斯圆。
为了更直观地感受阿波罗尼斯圆,我们可以通过一个简单的作图来描绘它。
以 A、B 两点所在直线为 x 轴,AB 中点为原点建立直角坐标系。
设 A(a,0),B(a,0),点 P(x,y),则根据距离公式和已知条件可以得到一个方程,经过一系列的推导和化简,就能得出阿波罗尼斯圆的方程。
阿波罗尼斯圆具有许多有趣的性质。
比如,圆心一定在线段 AB 的中垂线上;当两个定点 A、B 固定,比值 k 变化时,阿波罗尼斯圆的大小和位置也会相应改变。
那么,阿波罗尼斯圆在实际中有哪些应用呢?在物理学中,它可以用来解决带电粒子在电场中的运动问题。
例如,当存在两个等量异种电荷时,电场线的分布就与阿波罗尼斯圆有着密切的关系。
通过分析电场中某点到两个电荷的距离之比,结合阿波罗尼斯圆的性质,能够更加清晰地了解电场的分布情况,从而预测带电粒子的运动轨迹。
在工程设计中,阿波罗尼斯圆也大有用武之地。
比如在道路规划中,如果要设计一条公路,使得从两个固定地点出发的车辆到达公路上某一点的距离之比保持恒定,就可以利用阿波罗尼斯圆来确定公路的最佳位置,以实现资源的最优分配和效率的最大化。
在数学竞赛中,阿波罗尼斯圆更是常常成为解题的关键工具。
许多看似复杂的几何问题,一旦引入阿波罗尼斯圆的概念,往往就能迎刃而解。
例如,对于一些涉及到三角形边长比例关系、点到定点距离关系的问题,通过构造阿波罗尼斯圆,可以找到隐藏的几何关系,从而简化计算和推理过程。
阿波罗尼斯圆方程

阿波罗尼斯圆方程
生活中有许多有趣的东西,今天让我们来聊一聊阿波罗尼斯圆方程。
首先,我们需要了解阿波罗尼斯圆方程是什么。
简单来说,阿波罗尼斯圆方程是一个数学表达式,用来描述一个圆的特定属性,例如半径,中心位置以及方程的幂次。
这个方程的标准形式为:(x-a)² + (y-b)²=r²,其中a,b分别代表中心点的x,y位置,r代表半径。
阿波罗尼斯圆方程在几何或坐标系中有一些绝活。
例如,它可以被用来画出圆形的轮廓,可以用来描绘曲线等。
此外,它还可以用来处理圆形拟合技术,这也是近年来成像处理设备最常用的技术之一。
在此技术中,给定一系列离散的有限点,目标是在这些离散点尽可能少的情况下拟合出最佳的圆形,其半径和中心位置可以根据所给数据进行估算。
在生活中,阿波罗尼斯圆方程还可以应用于摄影技术上。
例如建筑物的大门,橱窗等都是圆形的,而用阿波罗尼斯圆方程进行拟合可以使它们的线条更加圆滑,让人们视觉上有更好的体验效果。
有了阿波罗尼斯圆方程,艺术作品的描绘效果也会有很大的改变。
例如画家在描绘一个圆时可以把阿波罗尼斯圆方程看成是一种技巧,用它可以精准地描绘出圆形的线条,而不需要拘泥于直线,给观众带来更多的视觉享受。
总之,阿波罗尼斯圆方程在几何、坐标系、拟合技术、摄影技术和艺术作品上都有大量的应用,使业余爱好者和专业人士都能够从中受益。
让我们一起欣赏圆形的美丽,期待未来它能给我们带来更多的惊喜。
阿波罗尼斯圆是什么。?

阿波罗尼斯圆是什么。
?阿波罗尼斯(Apollonius)圆,简称阿⽒圆。
[编辑本段]定义 在平⾯上给定相异两点A、B,设P点在同⼀平⾯上且满⾜PA/PB= λ,当λ>0且λ≠1时,P点的轨迹是个圆,这个圆我们称作阿波罗尼斯圆。
这个结论称作阿波罗尼斯轨迹定理。
设M、N分别为线段AB按定⽐λ分割的内分点和外分点,则MN为阿波罗尼斯圆的直径,且MN=[2λ/(λ^2-1)]AB。
[编辑本段]证明 我们可以通过公式推导出AN的长度:AN:BN=AP:BP ,其中BN=AN+AB,所以AN:(AN+AB)=AP:BP=>AN=AP×AB÷(BP-AP),以NP为直径的圆就是我们所求的轨迹圆。
[编辑本段]性质 由阿波罗尼斯圆可得阿波罗尼斯定理,即: 设三⾓形的三边和三中线分别为a、b、c、ma(a为下标,下同)、mb、mc,则有以下关系: b^2+c^2=a^2/2+2ma^2; c^2+a^2=b^2/2+2mb^2; a^2+b^2=c^2/2+2mc^2。
阿波罗尼斯圆:⼀动点P与两定点A、B的距离之⽐等于定⽐m:n,则点P的轨迹,是以定⽐m:n内分和外分定线段的两个分点的连线为直径的圆。
这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称阿⽒圆。
这个定理的证明⽅法很多。
下⾯是笔者的分析与证明,希望读者喜欢。
如图,P是平⾯上⼀动点,A、B是两定点,PA∶PB= m∶n ,M是AB的内分点(M在线段AB上),N是AB的外分点(N在AB的延长线上)且AM∶MB=AN∶NB=m∶n,则P点的轨迹是以MN为直径的圆。
下⾯先证明两个定理:⼀、如图⼀,已知M是BC上⼀点,且AB∶AC=BM∶MC,求证:AM平分∠BAC(三⾓形内⾓平分线定理的逆定理)证明:过C点作CD∥AM交BA的延长线于D,则AB∶AD=BM∶MC∵AB∶AC=BM∶MC,∴AB∶AD =AB∶AC,∴AC=AD,∴∠D=∠3,∵CD∥AM,∴∠1=∠D,∠2=∠3,∴∠1=∠2,∴AM平分∠BAC。
第17篇 阿氏圆在保护中的应用
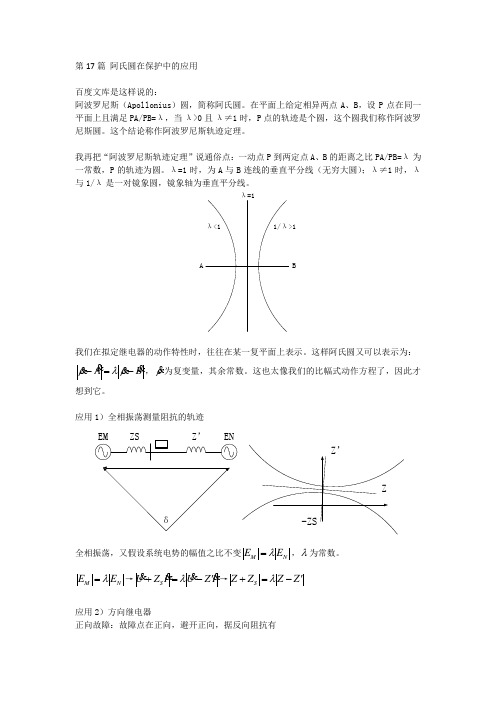
第17篇 阿氏圆在保护中的应用百度文库是这样说的:阿波罗尼斯(Apollonius )圆,简称阿氏圆。
在平面上给定相异两点A 、B ,设P 点在同一平面上且满足PA/PB=λ,当λ>0且λ≠1时,P 点的轨迹是个圆,这个圆我们称作阿波罗尼斯圆。
这个结论称作阿波罗尼斯轨迹定理。
我再把“阿波罗尼斯轨迹定理”说通俗点:一动点P 到两定点A 、B 的距离之比PA/PB=λ为一常数,P 的轨迹为圆。
λ=1时,为A 与B 连线的垂直平分线(无穷大圆);λ≠1时,λ与1/λ是一对镜象圆,镜象轴为垂直平分线。
A Bλ=1λ<11/λ>1我们在拟定继电器的动作特性时,往往在某一复平面上表示。
这样阿氏圆又可以表示为:B A -=-ρλρ,ρ 为复变量,其余常数。
这也太像我们的比幅式动作方程了,因此才想到它。
应用1)全相振荡测量阻抗的轨迹ZS Z ’EMEN全相振荡,又假设系统电势的幅值之比不变N M E E λ=,λ为常数。
N M E E λ=→I Z U I Z U S '-=+λ→Z Z Z Z S'-=+λ应用2)方向继电器正向故障:故障点在正向,避开正向,据反向阻抗有I Z U S ∆-=∆ 或0=∆+∆I Z U S(1) 反向故障:故障点在反向,避开反向,据正向阻抗有I Z U ∆'=∆ 或0=∆'-∆I Z U (2)显然,将(2)式为动作量、(1)式为制作量是一个理想的动作特性 ||||I Z U I Z U S∆+∆>∆'-∆或||||S Z Z Z Z +∆>'-∆ (3)应用3)差动继电器 NM N M I I I I ->+35.0λ→ρλρ ->+35.01Re分析ρ在复平面:区外故障,1-=ρ ;单电源区内故障,0=ρ 。
因此,我们可以假设ρ 的动作特性为红线所示的区域ρλρ ->+35.01或NM N M I I I I ->+35.0λ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Apollonius 圆 (阿波罗尼斯 圆,简称 “阿氏圆”)
例. 已知,两点坐标()()3,0,3,0A B -,若平面上一点P 满足2PA PB =,求P 点轨迹. 解:设P (),x y ,由题意 ()()22
22
323x y x y ++=-+ 化简得 ()22516x y ++=
一般地:若平面上P 和定点A 、B 满足PA PB
λ=,当0λ>且1λ≠时,P 的轨迹是一个圆
“阿氏圆”性质:
(1)等比:2PA MA A PB MB NB
N ===;(正弦定理推论) (2)平分:PM 平分APB ∠,
PN 平分APB ∠的外角
(3)性质逆用
(2011苏州市 一模)
18.已知椭圆E :22221x y a b +=()0a b >>的离心率为2,且过点()
2,2P ,设椭圆E 的右准线l 与x 轴的交点为A ,椭圆的上顶点为B ,直线AB 被以原点为圆心的圆O 所截得的弦长为455
. (1)求椭圆E 的方程及圆O 的方程;
(2)若M 是准线l 上纵坐标为t 的点,求证:存在一个异于M 的点Q ,对于圆O 上任意一
点N ,有
MN NQ
为定值;且当M 在直线l 运动时,点Q 在一个定圆上.
(第18题图)。
