2018-2019高三上文科数学12月考试卷
2019届高三12月月考数学(文)试卷

2019届高三12月月考试卷数学(文科)试题全卷满分150分,考试时间120分钟。
★祝考试顺利★注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题作答用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试卷和草稿纸上无效。
3.非选择题作答用0.5毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内。
答在试卷和草稿纸上无效。
考生必须保持答题卡的整洁。
考试结束后,只需上交答题卡。
第I卷(选择题, 共60分)一、选择题(共12小题,每小题5分,共60分,每小题只有一个正确答案)在每小题给出的四个选项中,只有一项是最符合题目要求的,选出正确的选项并将该选项在答题卡上涂黑。
一.选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合A={-2,0,1,3},B={-1,1,3},则元素的个数为()A.2B.4C.5.D.72.复数Z=的共轭复数的虚部为()A.iB.C. iD.3.已知p:a0;q:+a0,则p是q的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.在等差数列{}中,=9,且2=+6,则=()A.3B. 2C.0D.15.已知向量a,b满足=2,=3,a b=- 6,则向量a在向量b上的投影为()A.2B. 1C.1D.26.已知a=,b=,c,则a,b,c满足()A.a<b<cB.b<a<cC.c<a<bD.c<b<a 7.已知sin )=(0<),则sin2=( )A.B. C.D.8.函数f(x)=-2-1的大致图像为( )9.若函数f(x)=asinx+cosx 在[- ]为增函数,则实数a 的取值范围是( )A.[1,+) B.(, 1] C.[1,1] D. (, 1][1,+)10.在ABC 中,角A,B,C 的对边分别为a,b,c, =1,ABC 外接圆的半径为3,则a=( )A.2B.3C.. D.211. 2,)0,0(12222离心率为的左焦点为已知双曲线F b a by a x >>=-,若经过F 和(0,4)P 两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )1..22=-y x A 122.22=-y x B 144.22=-y x C 188.22=-y x D 12. 已知定义在R 上的可导函数)(x f 满足0)()('<+x f x f ,设)(2m m f a -=,)1(12f e b m m ⋅=+-,则b a 、的大小关系是( )A .b a <B .b a >C .b a =D .b a 、的大小与m 有关二. 填空题(本大题4小题 每小题5分,共20分.请将答案填写在答题卷中的横线上) 13.曲线y=(x+1)lnx 在点(1,0)处的切线方程为_____.14.若实数x,y 满足,则目标函数z=x+y 的最大值为___.15.若将函数f(x)=cos(2x+)(0<)的图像沿x 轴向左平移个单位长度所得的函数图像关于直线对称,则___.16.已知函数f(x)=-,则f()+f()= ___.三.解答题(共6小题,满分70分解答应写出必要的文字说明、证明过程或演算步骤)17. (12分) 在ABC 中,角A,B,C 的对边分别为a,b,c,且b=2asinB,tanA>0.(1)求角A 的大小;(2)若b=1,c=2.ABC 的面积为S,求.18. (12分)已知等差数列{}的前n 项和为,且=8,+=2+2. (1)求;(2)设数列{}的前n 项和为,求证:.19.(12分)如图,平行四边形ABCD 中,24BC AB ==,60ABC ∠=︒,PA ⊥平面ABCD ,2PA =, E ,F 分别为BC ,PE 的中点. (1)求证:AF ⊥平面PED ; (2)求点C 到平面PED 的距离.20.(12分)已知椭圆2222:1(0)x y D a b a b +=>>的离心率为e =,点(在椭圆D 上.(Ⅰ)求椭圆D 的方程; (Ⅱ)过椭圆内一点(0,)P t 的直线l 的斜率为k ,且与椭圆C 交于,M N 两点,设直线OM ,ON (O 为坐标原点)的斜率分别为12,k k ,若对任意k ,存在实数λ,使得12k k k λ+=,求实数λ的取值范围.21. (12分) 已知函数()21(1)ln 2f x x a x a x =-++. (1)当1a <时,讨论函数)(x f 的单调性;(2)若不等式e 12)1()(2-++≥++a x x x a x f 对于任意1e ,e x -⎡⎤∈⎣⎦成立, 求正实数a 的取值范围.(二)选考题:共10分。
高三数学12月月考试题文(含解析)

贵州省贵阳市第一中学2018届高三12月考数学文科试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分、在每小题给出的四个选项中,只有一项是符合题目要求的、1。
设集合,集合,则( )A、B。
C、 D。
【答案】B【解析】=,因此故选B2、在复平面中,复数的共轭复数,则对应的点在( )A、第一象限 B。
第二象限C、第三象限 D、第四象限【答案】A【解析】= 则对应的点为 ,此点在第一象限、故选A3、在等差数列中,已知,且公差,则其前项和取最小值时的的值为( )A。
B、或C。
D。
【答案】B【解析】等差数列中,可得,则,当时,最小,又,因此当n=8或n=7时前n项和取最小值,故选B。
4、下列命题正确的是( )A、存在,使得的否定是:不存在,使得B、对任意,均有的否定是:存在,使得C、若,则或的否命题是:若,则或D、若为假命题,则命题与必一真一假【答案】A【解析】A选项命题的否定是:对任意,均有,即:不存在,使得,因此A正确;B选项命题的否定是:存在,使得,因此B错;C选项否命题中“或”应是“且",因此C错;D选项命题A与B都是假,因此D错;故选A、5、在平面直角坐标系中,向量,,若,,三点能构成三角形,则( )A、 B、C。
D、【答案】B【解析】若M,A,B三点能构成三角形,则M,A,B三点不共线;若M,A,B三点共线,有:,。
故要使M,A,B三点不共线,则、故选B、6。
设函数,则“函数在上存在零点”是“”的( )A。
充分而不必要条件B、必要而不充分条件C、充分且必要条件D、既不充分也不必要条件【答案】B【解析】因为若函数在上存在零点,又,则在(2,8)上递增,则,则,故不一定;反过来,当,得,则函数在(2,8)上存在零点,故选B、7、若,满足约束条件,则的范围是( )A。
B。
C。
D、【答案】B【解析】作出不等式组表示的平面区域,如图所示,8。
如图,设网格纸上每个小正方形的边长为,网格纸中粗线部分为某几何体的三视图,那么该几何体的表面积为( )A、B。
2018—2019学年全国卷人教版高三月考(12月)考试试题数学(文)试卷 含答案

2018—2019学年全国卷人教版高三月考(12月)考试试题文科数学全卷满分150分,考试时间120分钟。
★祝考试顺利★注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题作答用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
答在试卷和草稿纸上无效。
3.非选择题作答用0.5毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内。
答在试卷和草稿纸上无效。
考生必须保持答题卡的整洁。
考试结束后,只需上交答题卡。
第I 卷 (选择题, 共60分)一、选择题(共12小题,每小题5分,共60分,每小题只有一个正确答案)在每小题给出的四个选项中,只有一项是最符合题目要求的,选出正确的选项并将该选项在答题卡上涂黑。
1.若下列不等式成立的是( )A. B. C. D.2.设{},2,1,0,1,2,{|1}U R A B x x ==--=≥ ,则U A C B ⋂=A. {}1,2B. {}1,0,1-C. {}2,1,0--D. {}2,1,0,1--3.已知向量,,若()∥(),则实数k 的值为( )A. B. C. D.4.若3sin 5α=-, α是第三象限角,则sin 4πα⎛⎫+= ⎪⎝⎭A.10 B. 10 C. 10- D. 10-5.下面是关于复数21z i=-+的四个命题: ①2z =;②22z i =;③z 的共轭复数为1i +;④z 的虚部为1-.其中正确的命题 ( ) A. ②③ B. ①② C. ②④ D. ③④ 6.已知向量1a =,b =,且()·23b a b +=,则向量a , b 的夹角的余弦值为( )A.4B. 4-C.4D. 47.若实数,满足约束条件则的取值范围是( )A.B.C.D.8.要得到函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象,只需将函数()cos 23g x x π⎛⎫=+⎪⎝⎭的图象 A. 向左平移2π个单位长度 B. 向右平移2π个单位长度 C. 向左平移4π个单位长度 D. 向右平移4π个单位长度9.在ABC ∆中,若sin :sin :sin 2:3:4A B C =,则ABC ∆是( )A. 直角三角形B. 钝角三角形C. 锐角三角形D. 等腰直角三角形 10.不等式282133x x --⎛⎫> ⎪⎝⎭的解集是 ( )A .{|24}x x -<< B. {|24}x x << C. {|4}x x <D.11.已知函数()f x x α=的图象过点()4,2,令()()11n a f n f n =++(*n N ∈),记数列{}n a 的前n 项和为n S ,则2017S =( )A.1 B.1C. 1D. 112.中国古代数学著作《算法统综》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”.其大意为:“有一个走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”.则该人第五天走的路程为( )A. 6里B. 12里C. 24里D. 48里第II 卷(非选择题)二、填空题(每题5分,共20分)13.若sin cos 1sin cos 2αααα+=-,则tan2α等于________.14.已知(,),则的最大值为__________.15.将全体正偶数排成一个三角形数阵:根据以上排列规律,数阵中第()3n n ≥行的从左至右的第3个数是__________.16.已知ABC ∆面积S 和三边c b a ,,满足:8,)(22=+--=c b c b a S ,则ABC ∆面积S 的最大值为 .三、解答题(共70分。
最新2018届高三12月月考数学(文)试题

(Ⅰ)求
的Hale Waihona Puke ;(Ⅱ)求 CD的长.18.(本题满分为 12 分)
已知 {a n} 是等比数列, a2 =2 且公比 q> 0,﹣ 2, a1, a3 成等差数列.
(Ⅰ)求 q 的值;
· 3·
(Ⅱ)已知 bn anan 1 nan 1(n=1,2,3,…),设 sn 是数列 { bn } 的前 n 项和.若 s1 s2 ,且 sk sk 1 (k=2,3,4,…), 求实数 λ 的取值范围.
11. 函数 y
x ln(
sin x ) 的图像大致是(
)
x sin x
D .92 cm3
12. 函数 f ( x) A sin(2 x )(
, A>0) 部分图像如图所示,且 2
f (a) f (b) 0 ,对不同的
x1, x2 a,b ,若 f ( x1) f ( x2 ) ,有 f ( x1 x2 ) 3 ,则( )
行 97 里,之后每天比前一天少行 0.5 里.良马到齐后,立刻返回去迎驽马,多少天后两马相遇.”
试确定离开长安后的第
天,两马相逢.
15.已知函数 f ( x)= x3+ax2+b2x+1,若 a 是从 1, 2, 3 三个数中任取的一个数, b 是从 0, 1,
2 三个数中任取的一个数,则该函数有两个极值点的概率为
A. 5 B . 4
,则目标函数 z=x+2y 的最大值为( )
C
.﹣ 1
D.
· 1·
9.已知函数 y=f ( x)的图象是由函数
的图象向左平移
个单位得到的, 则
=( )
A.
B.
C .0
D
2018届高三12月文科数学试题详细答案

高三12月月考试题(一)文科数学参考解答一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的).1. C 【解析】()()()[)020323.R A B C A B ==⇒=I ,,,, 2. D 【解析】()2,234,3,4,7.a bi b ai i i b a a b i+=--=-==-∴-=-由已知 3. C【解析】()()3|2|f x a x a =+-在()1+∞,上为增函数()()3023532.44812a a P a +>⎧--⎪⇔⇔-<≤⇒==⎨--≤⎪⎩4. A 【解析】1ln02a =<且正弦函数sin y x =是增函数,,即10sin 2∴<<1212122c -====,a b c ∴<<. 5. C【解析】由已知圆心322⎛⎫ ⎪⎝⎭,在直线0ax by -=上,所以35.44b e a =⇒= 6. C 【解析】()()()()22ln 1cos 222cos 24cos x f x e x x f x f x x x x x x =++⇒--=+=24cos .33333f f πππππ⎛⎫⎛⎫⇒--=⨯= ⎪ ⎪⎝⎭⎝⎭7. B 【解析】675,125,100,125,100100,NO c 125MOD10025,a 100,b 25a b c aMODb a b c ======⇒=⇒====否,100250,25,0,0,YES,a 25.c MOD a b c ======输出 8 C 【解析】图象过点()1110sin ,||;22226121262f x f k πππππϕϕϕωπ⎛⎫⎛⎫⇒=<⇒=≤⇒⨯+=+ ⎪ ⎪⎝⎭⎝⎭Q Q , min 244,(,0) 4.k k Z ωωω⇒=+∈>⇒=【解析】由题意满七进一,可得该图示为七进制数, 化为十进制数为321737276510.⨯+⨯+⨯+= 10. C 【解析】由题意知该几何体是放倒的圆柱,底面半径为1,高为2,右侧是一个半径为1的四分之一球组成的组合体,则该几何体的体积为2314712+1=433p pp 创创,故选C . 11. D 【解析】22=2+11x y x x =--的对称中心为()1,2 在抛物线上得2,p = 设221212,,,,44y y A y y ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭易得124y y =-,由抛物线定义得22221212212133 3.4442y y y y AF BF ⎛⎫+=+++=++≥= ⎪⎝⎭ 所以选D.12. C 【解析】画出函数()f x 的图象,如图所示,则221e x <<,且()()122222ln f x f x x x x x ==,记 函数2ln ()(1e )x g x x x =<<,则21ln ()xg'x x-=,令()0g'x =,得e x =,当(1,e)x Î时,()0g'x >;当2(e,e )x Î时,()0g'x <,故当e x =时,函数()g x 取到最大值,最大值为1e ,即()12f x x 的最大值为1e,故选C .第Ⅱ卷本试卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分) 13.[)898.14..15.7.16.36.3 ,--+?13.【解析】各组抽到的编号按从小到大构成公差为10的等差数列,其通项为()1011293103107132098.22n a a a n a ++=-=⇒==Q 抽到的个号码的中位数为14.【解析】()()()12||1;33AB AC AB AC AM BC AB BM AC AB AB AC AC AB ⎛⎫+=⇒⋅=-⋅=+-=+- ⎪⎝⎭u u u r u u u r u u u r u u u r u u u u r u u u r u u u r u u u u r u u u r u u u r u u u r u u u r u u u r u u u r221211818.3333333AB AC AB AC =-+-⋅=-++=u u u r u u u r u u u r u u u r15. 【解析】1222(log 3)(log 3)(log 3)f f f =-=-,因为2log 312(log 3)2f +=1+=2log 32217?=,故12(log 3)7.f =-16.【解析】由题知0)1(,0)1(==-f f ,因为函数)(x f 的图象关于直线3=x 对称,所以(7)(1)0f f =-=且(5)(1)0f f ==,即⎩⎨⎧=++⨯=++0)525(240)74948b a b a (,解得35,12=-=b a ,所以)(x f =)3512)(1(22+--x x x =)7)(5)(1)(1(---+x x x x =)76)(56(22--+-x x x x ,设162--=x x t (10-≥t ),则)(t f =)6)(6(-+t t (10-≥t )=362-t ≥-36,故函数)(x f 的值域为[-36,+∞).三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分) 【解析】(Ⅰ)由条件得1221(1)2n n a a n n +=+g ,又1n =时,21na n =,故数列2n a n ⎧⎫⎨⎬⎩⎭构成首项为1,公比为12的等比数列.从而2112n n a n -=,即212n n n a -=.……6分(Ⅱ)由22(1)21222n nn n n n n b ++=-=得 23521222n n n S +=+++L 231135212122222n n n n n S +-+⇒=++++L , 两式相减得:23113111212()222222n n n n S ++=++++-L ,所以2552n n n S +=-. ……12分18.【解析】 (Ⅰ)设这200名学生中男生对19大“比较关注”与“不太关注”的人数分别为,.x y 则女生对19大“比较关注”与“不太关注”的人数分别为85, 5.y y -+由题意110100,10.4853x y x y x y ì+=ï?=í=ï-ïî()22200100157510 2.597 6.6351752511090k 创-?=?创? ,所以没有99%的把握认为男生与女生对19大的关注有差异.(Ⅱ)该校学生会从对两19大“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,则男生抽取4人,记为,,,.a b c d 女生抽取3人,记为,,.x y z 从中选2人共有,,,,,,,,,,,,,,,,,,,,ab ac ad ax ay az bc bd bx by bz cd cx cy cz dx dy dz xy xz yz 共21种,其中全为男生的有,,,,,,ab ac ad bc bd cd 共 6种.所以全为男生的概率为62=.21719.(本小题满分12分) 【解析】(Ⅰ)因为,,,.PD PE PD PF PE PF P PD PEF EF PEF PD EF ⊥⊥=⇒⊥⊂⇒⊥I 平面平面 …….5分(Ⅱ)设EF 、BD 相交于O ,连结PO .1BF =,1PE PF ==,EF =2, 则222EF PE PF =+,所以△PEF 是直角三角形,……7分 易得,.EF PO EF PD EF PBD ⊥⊥⇒⊥平面,.PBD BEDF PBD BEDF BD ⇒⊥=I 平面平面平面平面则122OP EF ==,332,24OD BD PD ===,……9分 作PH BD H PH BEDF P BEDF d ⊥⇒⊥于平面,设到面的距离,比较关注 不太关注 合计 男生 100 10 110 女生 75 15 90 合计17525200则2.3PO PD OD PH d PH ⋅=⋅⇒==……11分 则四棱锥P BEDF -的体积`3111224.(3323189BEDF A BEDF V S d -=⋅=⋅⋅==四棱椎 …….12分. 20. (本小题满分12分)【解析】(Ⅰ)由题意椭圆C 的标准方程为12422=+y x ,所以42=a ,22=b ,从而224222=-=-=b a c ,所以22==a c e …….2分 (Ⅱ)直线AB 与圆222=+y x 相切.证明如下:设点),(00y x A ,)2,(t B ,其中00≠x ,因为OB OA ⊥,所以0=•,即0200=+y tx ,解得02x y t -=,…….4分 当t x =0时,220t y -=,代入椭圆C 的方程得2±=t ,此时直线AB 与圆222=+y x 相切. …….6分当t x ≠0时,直线AB 的方程为)(2200t x tx y y ---=-,即02)()2(0000=-+---ty x y t x x y ,…….8分 圆心到直线AB 的距离为202000)()2(|2|t x y ty x d -+--=,又422020=+y x ,02x y t -=, 故22168|4|4|22|20204002020202020020=+++=++-=x x x x x x y y x x y x d .故此直线AB 与圆222=+y x 相切. …….12分21. (本小题满分12分) 【解析】(Ⅰ)函数()f x 的定义域是()-+∞∞,,(),x f x e a =-‘.()0a > ……1分 ()'0ln f x x a >⇒>⇒()f x 的单调增区间是()ln ,;a +∞()'0ln f x x a <⇒<⇒()f x 的单调减区间是()-ln ;a ∞,……3分 ()()()()()()()()'''ln ln ln ,00,1;01,.g a f x f a a a g a a g a a g a a ===-⇒=->⇒∈<⇒∈+∞极小值所以()g a 在()0,1上单调递增,在()1,+∞上单调递减. ……5分所以1a =是函数()g a 在()0+∞,上唯一的极大值点,也是最大值点,所以()()()max =1 1.g a g a g ==极大值……6分(Ⅱ)由(Ⅰ)()()(]ln ln 0,f x f a a a a a e 极小值0==-≥⇒∈……8分()(]()()2''',0,22,a a a f a e a a e f a e a f a e Q =-∈⇒=-⇒=-()()()()()'''min 0ln ,ln ,ln 222ln 20f a a a e f a f 揶==->]Z在, ……10分()(]()()()(220011.e e f a e f f e e e f a e e ⎤∴⇒=<=-⇒-⎦Z 在,的范围是, ……12分请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.(本小题满分10分)选修4-4:坐标系与参数方程【解析】(Ⅰ)由2sin ρθ=,得22sin ρρθ=,又cos x ρθ=,sin y ρθ=, 所以曲线C 的直角坐标方程为2220x y y +-=.……5分 (Ⅱ)直线l 为经过点(1,0)P -倾斜角为α的直线,由1cos sin x t y t αα=-+⎧⎨=⎩代入2220x y y +-=,整理得22(sin cos )10t t αα-++=,由2[2(sin cos )]40αα∆=-+->,得|sin cos |1αα+>,设B A ,对应的参数分别为12,t t ,则122(sin cos )t t αα+=+,1210t t ⋅=>, 则12||||||||PA PB t t +=+12||2|sin cos |t t αα=+=+,又1|sin cos |αα<+≤2||||PA PB <+≤所以||||PA PB +的取值范围为(2,.……10分 23.(本小题满分10分)选修4-5:不等式选讲【解析】 (Ⅰ)要使不等式()|1|f x m ≥-有解,只需max ()|1|f x m ≥-. 又()|3||2|(3)(2)5f x x x x x =--+≤--+=,当且仅当2x ≤-时等号成立. 故15m -≤,46m ∴-≤≤,故实数m 的最小值4M =-;……5分 (Ⅱ)因为正数,a b 满足34a b M +=-=,313194()(3)()6612a b a b b a b a b a ∴+=++=++≥=313b a∴+≥.……10分。
2019届高三数学12月月考试题 文新 版新人教版

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……2019学年度月份考试 高三学年数学试题(文科)一、选择题(本大题共12小题,每小题5分,共60分。
在每題给出的四个选中,只有一项是符合题目要求)一、选择题:本大题共12小题,每小题5分,共60分。
1.已知全集={1,2,3,4,5}U ,集合={2,3,4}A ,{}3,1=B ,则(C A)B=U ( )A .{1}B .{1,5}C .{1,3,5}D .{1,4} 2.已知()2,a ib i a b R i+=+∈,其中i 为虚数单位,则a b +=( ) A. 1- B. 1 C. 2 D. 33.命题“2,320x R x x ∃∈-+=”的否定是 ( )A .2,320x R x x ∀∈-+=B .2,320x R x x ∃∈-+≠C .2,320x R x x ∃∈-+> D .2,320x R x x ∀∈-+≠4.已知0.6log 0.5a =,ln0.5b =,0.50.6c =.则( )A .>>a c bB .>>a b cC .>>c a bD .>>c b a5.某几何体的三视图如图所示,则该几何体的体积为( ) A .16+8πB .8+8πC .16+16πD .8+16π6.直线02=-+y x 与圆()()22122=-+-y x 相交于A ,B 两点,则弦|AB|=( )A .2B .2C .6D 7.执行右面的程序框图,若输出的结果是1516,则输入的a 为( ) A .3 B .4 C .5 D .68.设双曲线)0,0(12222>>=-b a bx a y 的渐近线与抛物线12+=x y是否相切,则该双曲线的离心率等于( ) A.25 B.5 C.6 D.26 9.要得到函数y =sin ⎝ ⎛⎭⎪⎫4x -π3的图象,只需将函数y =sin 4x 的图象( ) A .向左平移π12个单位 B .向右平移π12个单位 C .向左平移π3个单位 D .向右平移π3个单位10.函数)sin(ϕω+=x A y 在一个周期内的图象如下图所示,此函数的解析式为( )A .)(32sinπ+=x y B .)(654sin2π+=x y C .)(32sinπ-=x y D. )(322sin2π+=x y 11. 已知,a b 均为正数,且142a b+=,则使a b c +≥恒成立的c 的取值范围为( )A .9(,]2-∞ B .(0,1] C .(,9]-∞ D .(,8]-∞ 12.设()f x 是定义在R 上的函数, f(0)=2,对任意R x ∈,f(x)+f ’(x)>1,则1)(+>x x e x f e 的解集为( )A. (0,+∞)B. (-∞,0)C. (,1)(1)-∞-⋃+∞,D.(,1)(01)-∞-⋃, 二、 填空题(本大题共4小题,每小题5分,共20分) 13.已知函数()()()2200x x f x x x ≥⎧⎪=⎨<⎪⎩,则()[]=-3f f ________. 14.设变量,x y 满足约束条件0,0,220,x x y x y ≥⎧⎪-≥⎨⎪--≤⎩则32z x y =-的最大值为 .15.已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE →·DC →的最大值为 . 16.长方体1111ABCD A B C D -的各个顶点都在体积为323π的球O 的球面上,其中12AA =, 则四棱锥O-ABCD 的体积的最大值为 .三、解答题(本大题共5题,共70分,解答时应写出必要的文字说明证明过程或演算步骤) 17.(本小题满分10分)已知{}n a 为等差数列,且36a =-,60a =。
【高三数学试题精选】2018届高三数学上12月月考文科试题(带答案)

2018届高三数学上12月月考文科试题(带答案)
5 唐徕回民中学2)
c(2,+∞) D(-∞,-1)
第Ⅱ卷
二、填空题本大题共4小题,每小题5分.
13 在中,角所对应的边分别为,已知,则
14 已知是圆上的三点,若,则与的夹角为
15 设,向量,若,则 _______
16 如图,在平行四边形中,已知,
,则的值是.
三、解答题本大题共6小题,共计70分。
解答应写出字说明.证明过程或演算步骤。
17.(本小题满分12分)
在三角形中,内角所对的边分别是已知 ,
(1)求和的值;
(2)求的值
18.(本小题满分12分)
已知等差数列的前项和为 ),
(1) 求数列的通项式;
(2)设求数列的前项和
19.(本小题满分12分)
已知数列的前项和为,且 ),数列满足,且点 )在直线上(1)求数列、的通项式;
(2)求数列的前项和
20.(本小题满分12分)。
2018届高三上期12月文科数学月考试题和答案

2018届高三上期12月文科数学月考试题和答案D(Ⅱ)求函数y =f (x )在区间⎥⎦⎤⎢⎣⎡-0,2π内的单调性.20.(本小题满分12分)已知数列 的前项和为n S ,()*∈-=N n a S n n ,212 ,数列{}n b 满足,点()1,+n n b b P 在直线上.(Ⅰ)求数列{}n a ,{}n b 的通项n a 和n b ; (Ⅱ)令n n n b a c ⋅=,求数列{}n c 的前n 项和n T ;21.(本小题满分12分) 已知函数),(ln )(R ∈++=b a x bx ax f 在1=x 处的切线方程为0198=-+y x . (Ⅰ)求b a ,;(Ⅱ)如果函数k x f x g -=)()(仅有一个零点,求实数k 的取值范围.22.(本小题满分10分)选修4-5:不等式选讲已知函数()|1|2|1|f x m x x =---+.(Ⅰ)当5m =时,求不等式()2f x >的解集;(Ⅱ)已知函数()1212x g -++=x x ,若任意R x x ∈21,,有()()21x f x g >恒成立,求实数m 的取值范围.12月月考参考答案第Ⅰ卷 (选择题,共60分)题号 1 2 3 4 5 6 7 8 9 10 11 12 答案BDCDBBCD第Ⅱ卷 ( 非选择题,共90分)二、填空题: 本大题共4小题,每小题5分. 13.(-∞,-3]∪[7,+∞) 14.436654321a a a a a a a a = 15.1.6 16. ①②③三、解答题: 本大题共6小题. 解答应写出文字说明,证明过程或演算步骤. 17.解:(Ⅰ)设等差数列{a n }的公差d ,则a n =a 1+(n -1)d , 由题设,2d =4-1=3, 所以d =. 所以a n =1+(n -1)= -+, 所以a 11=16;(Ⅱ)设b n =,则数列{b n }是等差数列, b 1=,b 3=,b n =-(n -1)=,即=, 所以a n =.18. 解:(Ⅰ)f (x )的定义域为R .f '(x )=e x [x 2+(a +2)x +2a ]=e x (x +2)(x +a ) 令f '(x )=0,得x 1=-2,x 2=-a当-a =-2,即a =2时,f '(x )≥0恒成立,f (x )的单调增区间为(-∞,+∞),无单调减区间 当-a <-2,即a >2时,f '(x ),f (x )的变化情况如下表:x (-∞,-a ) -a (-a ,-2) -2 (-2,+∞) f '(x )+-+f (x ) ↗ 极大值 ↘ 极小值 ↗所以,f (x )的单调增区间为(-∞,-a ),(-2,+∞),单调减区间为(-a ,-2) 当-a >-2,即a <2时,f '(x ),f (x )的变化情况如下表: x(-∞,-2) -2(-2,-a )-a (-a ,+∞)f '(x ) + 0 - 0 +f (x ) ↗ 极大值 ↘ 极小值 ↗ 所以,f (x )的单调增区间为(-∞,-2),(-a ,+∞),单调减区间为(-2,-a ) (Ⅱ)由题知函数)(x f y =与m y =的图像有3个交点∵a =-1, ∴f (x )=e x (x 2-x -1).由(Ⅰ)题知f (x )的极大值为27)2(-=-e f ,极小值为0)1(<-=e f . 又2-<x 时,0)(>x f ,所以270-<<e m 所以,m 的范围是 270-<<e m 19. 解:(1)f (x )==,当时,,所以f (x )的值域为.(2)⎥⎦⎤⎢⎣⎡--12,2ππ单减,⎥⎦⎤⎢⎣⎡-0,12π单增20. 解:,当时,,,是首项为,公比为2的等比数列.因此 , 当时,满足, 所以.因为在直线上, 所以, 而, 所以.(2) ,③因此 ④③-④得:,.21. 解:(Ⅰ))0(1)()(2'>++-=x xb x a x f由题,⎪⎩⎪⎨⎧-=++-==+=811)1()1( 491)1(2'b a f b a f 解得⎪⎩⎪⎨⎧==129b a ……………4分 (Ⅱ)当29=a 时,x x x f ln )1(29)(++=,其定义域为),0(+∞ 22)1(2)2)(12(1)1(29)(+--=++-='x x x x x x x f ,令0)(='x f 得211=x ,22=x 因为当210<<x 或2>x 时,0)(>'x f ;当221<<x 时,0)(<'x f 所以函数)(x f 在)21,0(上递增,在)2,21(上递减,在),2(+∞上递增且)(x f 的极大值为2ln 3)21(-=f ,极小值为2ln 23)2(+=f又当+→0x 时,-∞→)(x f ;当+∞→x 时,+∞→)(x f 因为函数k x f x g -=)()(仅有一个零点,所以函数)(x f y =的图象与直线k y =仅有一个交点. 所以2ln 3->k 或2ln 23+<k ……………12分 22. 解:(Ⅰ)当5m =时,36(1)()2(11)43(1)x x f x x x x x + <-⎧⎪=-+ -≤≤⎨⎪- >⎩,……………3分由()2f x >易得不等式的解集为4{|0}3x x -<<;……………5分(Ⅱ)由题知()max min )(x f x g >.212121212=+-+≥-++x x x x 当且仅当2121≤≤-x 时,“=”成立, 所以2)(min =x g ……………8分 又()2)1(max -=-=m f x f所以22->m ,所以4<m即实数m 的取值范围是 4<m ……………10分。
2018-2019学年上学期12月月考试卷高三数学(基础卷)

2018-2019学年上学期12月月考试卷高三数学(基础卷)满分150分 时间120分钟班级: 姓名: 座号:一、选择题(共14个小题,每小题5分,共70分)1.若集合{}13A x x =≤≤,集合{}2B x x =<,则A B =I(A ){}12x x ≤< (B ){}12x x << (C ){}3x x ≤ (D ){}23x x <≤2.tan330︒=(A )3(B )3(C )3- (D )3-3.已知lg2=a ,lg3=b ,则3lg 2=(A )a -b (B )b -a (C )ba(D )a b4.函数()2sin cos f x x x =的最大值为(A )2(B )2-(C )1(D )1-5.下列函数中,在()0,+∞上是减函数的是A .1y x =B .21y x =+C .2xy = D .()()00x x y x x >⎧⎪=⎨-≤⎪⎩ 6.在等比数列{}n a 中,若32a =,则12345a a a a a = (A )8(B )16(C )32(D )427.已知点()0,0O 与点()0,2A 分别在直线y x m =+的两侧,那么m 的取值范围是(A )20m -<< (B )02m << (C )0m <或2m >(D )0m >或2m <-8.如果直线ax +2y +1=0与直线x +3y -2=0互相垂直,那么a 的值等于(A )6 (B )-32(C ) (D )-69.如果一个几何体的三视图中至少有两个三角形,那么这个几何体不可能...是(A )正三棱锥 (B )正三棱柱 (C )圆锥 (D )正四棱锥10. 如图,D 是△ABC 的边AB 的三等分点,则向量CD u u u r等于(A )23CA AB +u u u r u u u r (B )13CA AB +u u u r u u u r(C )23CB AB +u u u r u u u r(D )13CB AB+u u u r u u u r11.已知()1f x x x =+,那么下列各式中,对任意不为零的实数x 都成立的是(A )()()f x f x =- (B )()1f x f x ⎛⎫= ⎪⎝⎭(C )()f x x >(D )()2f x >12.如果执行右面的程序框图,那么输出的S 等于(A )45 (B )55 (C )90 (D )11013.下列几何体的下底面面积相等,高也相等,则体积最大的是DC B A14.△ABC 中,45A ∠=︒,105B ∠=︒,A ∠的对边2a =,则C ∠的对边c 等于(A )2(B )3(C )2(D )1二、填空题(共4道小题,每小题5分,共20分)15.函数()21f x x =-的定义域为________________________.16.在1-和4之间插入两个数,使这4个数顺次构成等差数列,则插入的两个数的和为____. 17. 命题03,2>+-∈∀x x R x 的否命题是 .18. 已知椭圆,它的长轴长为 .CADB开始 S =0 k ≤10S = S +k k = k +1结束输出S 是 否k =1永安九中2013-2014学年上学期12月月考试卷高三数学(基础卷)答题卷考试时间:120分钟 (2013年12月)一.选择题(本大题共14小题,每小题5分,共70分).题号 1 2 3 4 5 6 7 答案 题号 8 9 10 11 12 13 14 答案二.填空题(本大题共4小题,每小题5分,共20分).15. 16.17. 18. 三,解答题(本大题共6个小题,共60分) 19.(本小题8分)解不等式组的解集班级:姓名:号:20.(本小题8分)已知sin β= , β是锐角,求cos β,sin2β的值。
2018-2019学年广东省深圳市高级中学高三(上)12月模拟数学试卷(文科)

2018-2019学年广东省深圳市高级中学高三(上)12月模拟数学试卷(文科)一、选择题:本大题共 12小题,每小题5分,在每小题给出的四个选项中,只有一项是符 合题目要求的.2(5 分)已知集合 A={x|x -4x 3 :::0},B ={x|y =1 n(x 一2)},则(SB)" A 等于()C . • 5C . 3值范围是()1C . (0,-]9.( 5分)已知直线4x -3y ^0与LI C :x 2 y 2 4^0相交于A 、B 两点,且.AOB =120 ,2. A . {x| -2, x ::;1} B . {x| -2剟x 2}C. {x|1 :::x 2}{x|x :: 2}(5分) 已知i 是虚数单位,则复数1 3i1 —i的模为() 1. 3.(5分)抛两个各面上分别标有2, 3,4, 5, 6的均匀的正方体玩具,“向上的两个之和为 3”的概率是(1 184. (5分) F 列函数中,既是偶函数又在区间B . f (x)二x13C . f (x) = xf(x)=2」5.2(5分)过抛物线y =4x 的焦点F 的直线 交该抛物线于A , B 两点,点A 在第一象限, 6. 若| AF | =3,则直线 I 的斜率为2.2(5分)已知 |a|=1, b =(0,2),且 ai_b =1,则向量a 与b 夹角的大小为7. (5分) 设命题 p: _x :::1 ,■ 1,命题 q : x 0 , 2 ■0x (1,则下列命题中是真命题的 x 0(5分)已知■ 0,函数 (一P) qC . p (一q)D .(一卩)(一口)f (x)二sin(,x )在区间4,二]上单调递减,则实数-的取[1 3] [24]D . (0 , 2]则实数a 的值为( )则ABC 的面积为(题: ①当x 0时,f (x ) =e x(1 -x );②函数f (x )有2个零点;③f (x ) 0的解集为(-1 ,0)-(1 , 亦);④ P x , x ^ R ,都有 | f (xj - f (X 2) |<2 .其中正确命题个数是()A . 1B . 2C . 3D . 4二、填空题:本大题共 4小题,每小题5分,满分20分.3x13 . (5 分)若 f (x ) =1 n (e 1) ax 是偶函数,则 a 二 ____ . -■ 314 . (5 分)已知 cos ( ) ,则 sin 2二= _________ .4 5515.( 5分)已知点(x,y )在 ABC 所包围的阴影区域内(包含边界),若B (3,— )是使得z =ax -y2 取得最大值的最优解,则实数 a 的取值范围为 _B . 10C . 11 或 21D . 3 或 1310. ( 5分)如图,网络纸上正方形小格的边长为1,图中粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积为11':D . 12 二11 ( 5分)在ABC 中,设角A , B , C 的对边分别是 a , b , c ,已知 C =2A,cosA 二F,b =5 ,4 12 . ( 5分)已知函数 f (x )定义在R 上的奇函数,当x :::0时,f (x )=e x (x 1),给出下列命B . 6 二2相切,且椭圆C 的右焦点F (c ,0)关于直线y 冷X 的对称点E 在椭圆C 上,则,0EF 的面 积为 三、解答题(本大题共 5小题,满分60分•解答须写出文字说明、证明过程或演算步骤)217. ( 12分)已知正项数列{a n }的前n 项和为S n ,且S 是a n 和a n 的等差中项.(I )求数列{a n }的通项公式;(H )若a k n{a i ,a 2,...a n ,...},且a%,比2,…,a k n,…成等比数列,当k =2 , k ? =4时,求数列{k n }的前n 项和T n . 18. (12分)从某企业生产的某种产品中抽取 100件,测量这些产品的一项质量指标值,由 测量表得如下频数分布表: 质量指标值分组[75 , 85)[85 , 95) [95 , 105)[105 , 115)[115 , 125)频数62638228(I )在答题卡上作出这些数据的频率分布直方图: (n )估计这种产品质量指标值的众数、中位数及平均数(同一组中的数据用该组区间的中点值作代表);(川)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于 95的产品至少要占全部产品的 80% ”的规定?xOy 中,已知直线x ■ • 2y —2 •. 2 =0与椭圆C : —2 = 1(a b 0) a b16. (5分)在直角坐标系°75 S3 95 105 115 12$ 质量指标值19. (12分)如图,三棱柱ABC —AB’G中,平面AAB’B丄平面ABC , D是AC的中点.(I)求证:BQ//平面ABD ;(H)若N A AB =NACB =60©, AB =BB, , AC =2 , BC =1,求三棱锥A - ABD 的体积.20. (12分)设椭圆M :笃•冷=1(a b 0)的离心率与双曲线x2-y2=1的离心率互为倒a b数,且内切于圆x2 y2 =4 .(1) 求椭圆M的方程;(2) 已知A( -2, ■ 2) , F是椭圆M的下焦点,在椭圆M上是否存在点P,使AAFP的周长最大?若存在,请求出UAFP周长的最大值,并求此时.AFP的面积;若不存在,请说明理由.x21. (12分)已知f(x) =e acosx(e为自然对数的底数).(1 )若f(x)在x=0处的切线过点P(1,6),求实数a的值;TT(2 )当x・[0, ]时,f(x) --ax恒成立,求实数a的取值范围.2[选修4-4 :坐标系与参数方程]22. (10分)在平面直角坐标系中,直线l过点P(2,「3)且倾斜角为:-,以坐标原点为极点,频率4864IX3864864H864-,~2-oll 1 lo ooooCl223. 设函数 f (x) =|2x -7| 1 . (1 )求不等式f(x), X 的解集;(2)若存在X 使不等式f (x) 一2 I x _1|, a 成立,求实数a 的取值范围.X 轴的非负半轴为极轴,建立极坐标系,曲线与曲线C 相交于A , B 两点; (1) 求曲线C 的直角坐标方程;(2) 若| AB^ 13,求直线I 的倾斜角:.的值. [选修4-5:不等式选讲] C 的极坐标方程为]= 4cos 「…一),直线I3第6页(共20页)2018-2019学年广东省深圳市高级中学高三(上)12月模拟数学试卷(文科)参考答案与试题解析一、选择题:本大题共 12小题,每小题5分,在每小题给出的四个选项中,只有一项是符 合题目要求的.1.( 5 分)已知集合 A ={x|x ? _4x 3 :::0} , B={x|y=l n (x-2)},则(0R B )「| A 等于( )A . {x| -2, x ::;1}B . {x|—2 剟x2}C . {x|1:::x,2}D . {x|x :::2}【解答】 解:由 x 2 -4x 3 ::: 0,得(x _1)(x -3) ::: 0,即 1 ::: x ::: 3,故 A 二{x |1 ::: x ::: 3}, 由 x —2 .0 ,得 x 2,故 B ={x|x 2} , e.B ={x|x, 2}, 则 ©B )D A 二{x|1 :::x, 2} 故选:C .1 +3i2. ( 5分)已知i 是虚数单位,则复数 「的模为()1 -i(1,2)和(2,1)两种,21由古典概型知概率为 P =- 136 18故选:D .【解答】解:;复数口M1 3i )(1。
河南省洛阳市2018-2019学年高三(上)12月模拟数学试卷(文科)(解析版)
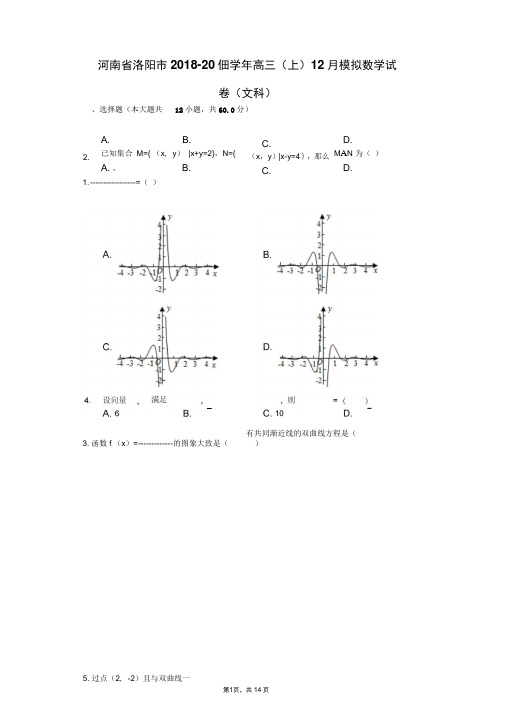
河南省洛阳市2018-20佃学年高三(上)12月模拟数学试卷(文科)、选择题(本大题共12小题,共60.0分)1. ----------------- =( )3. 函数f (x )=------------- 的图象大致是( )2.A.已知集合 M={ (x , y ) |x+y=2},N={A. ,B.B. C. (x ,y )|x-y=4},那么 C.D. M A N 为( )D.有共同渐近线的双曲线方程是(5. 过点(2, -2)且与双曲线一面积为()A. 一B.——C.-7. 《九章算术》中盈不足章中有这样一则故事:今有良马与驽马发长安,至齐•齐去长安三千里•良 马初日行一百九十三里,日增一十二里;驽马初日 行九十七里,日减二里.”为了计算每天良马和驽 马所走的路程之和,设计框图如下图•若输出的S的值为350,则判断框中可填()A. ?B. ?C. ?D.?8.微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为 8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62 元,5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低 于3元的概率是()A. —B. -C. -D.- 9.直三棱柱ABC-A 1B 1C 1中,AB 丄AC , AB=AC=AA 1,则直线A 1B 与AC 1所成角的大小 为( )A.B.C.D.10. 将函数v-图象上各点的横坐标伸长到原来的2倍(纵坐标 不变),再把得到的图象向左平移-个单位长度,所得函数图象关于-对称,则0 =( )A. -B. -C. -D.-11. 已知函数f (x )为定义在[-3 , t-2]上的偶函数,且在[-3, 0]上单调递减,则满足 f(-X 2+2X -3)v f ( x 2 -)的 x 的取值范围()A. —-B. --C. --D. --6.△\BC 的内角A , B , C 的对边分别为 a , b , c ,若 C=—, c=,b=3a ,则 A ABC 的A. B. C. D.12.已知F1, F2是椭圆C的两个焦点,P 是C 上的一点,若PF1IPF2,且/PF2F1=60 °则C的离心率为( )A. —B. "C.——D."二、填空题(本大题共4小题,共20.0分)213. 已知函数f (X) =lnx+2x-4x,则函数f (x)的图象在X=1处的切线方程为_________________14. 已知实数x, y满足,则目标函数u=x+2y的最大值是_________15. 已知sin a +cos 0 =1 ,贝U sin ( a +) = _____ .16. 直三棱柱ABC-A1B1C1的底面是直角三角形,侧棱长等于底面三角形的斜边长,若其外接球的体积为——,则该三棱柱体积的最大值为_________ .三、解答题(本大题共7小题,共82.0分)17. 设{a n}(n€N )是各项均为正数的等比数列,且a?=3, a4-a3=18.(I )求{a n}的通项公式;(n ) 若b n=a n+log3a n,求bi+ b2+…+b n.18. 设椭圆——(a> b> 0),离心率—,短轴―,抛物线顶点在原点,以坐标轴为对称轴,焦点为(0, 1),(1)求椭圆和抛物线的方程;(2)设坐标原点为0,A为抛物线上第一象限内的点,B为椭圆是一点,且有0A丄0B , 当线段AB的中点在y轴上时,求直线AB的方程.19. 已知函数f (x) =xlnx .(1)证明:f (x)耳<-1 ;(2)若当-时,f (x) Wx2-x+a-1,求实数a的取值范围.20. 已知平面直角坐标系xOy中,过点P (-1,-2)的直线I的参数方程为(t为参数),以原点0为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为p ?sin 0 ?tana9 =a> 0),直线I与曲线C相交于不同的两点M、N.(1)求曲线C的直角坐标方程和直线I的普通方程;(2)若|PM|=|MN|,求实数a的值.答案和解析1. 【答案】B【解析】解:•••-=二=」^=3,扑I -hi,故选:B.本题是一个复数的乘除运算,先进行复数乘法运算,在分子和分母上进行,再进行复数的除法运算,分子和分母同乘以分母的共轭复数,化简后得到结果.本题考查复数的乘除混合运算,是一个基础题,复数的加减乘除运算是比较简单的问题,在高考时有时会出现,若出现则是要我们一定要得分的题目.2. 【答案】D【解析】解:将集合M和集合N中的方程联立得:-r+^=2)d'①+②得:2x=6,解得:x=3,①-②得:2y=-2,解得:y=-1,『J-=l••方程组的解为::@二1,则Mn N={ 3, -1)}.故选:D.将集合M与集合N中的方程联立组成方程组,求出方程组的解即可确定出两集合的交集.此题考查了交集及其运算,以及二元一次方程组的解法,是一道基本题型,学生易弄错集合中元素的性质.3.【答案】A【解析】解:定义域为O, 0) U 0,+X),厂小I 7TJ'.■f -x)=f x),f x)为偶函数,。
2019届高三数学12月月考试题文(6)

和诚中学2018-2019学年度高三12月月考数学试题(文科)考试时间:120分钟满分:150分一、选择题(本大题共12小题,每小题5分,共60分)1.已知集合,集合,全集为U=R,则为A.B.C.D.2.设,,,,则的大小关系是()A.B.C.D.3.设,若函数在上的最大值是3,则其在上的最小值是()A.2B.1C.0D.4.函数的图象大致为A.B.C.D.5.将偶函数()的图象向右平移个单位长度后,得到的曲线的对称中心为()A.()B.()C.()D.()6.已知的三个内角A、B、C所对的边长分别为a、b、c,若,则该三角形一定是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形7.已知平面向量满足,且,则向量的夹角为()A.B.C.D.8.设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是()A.若α⊥β,m⊥α,则m∥βB.若m∥α,n⊂α,则m∥nC.若α∩β=m,n∥α,n∥β,则m∥nD.若α⊥β,且α∩β=m,点A∈α,直线AB⊥m,则AB⊥β9.若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示,则所截去的三棱锥......的外接球的表面积等于A.B.C.D.10.已知数列满足,且,其前n项之和为,则满足不等式的最小整数n是()A. 5 B. 6 C. 7 D. 811.若函数有两个极值点,则实数的取值范围是()A.B.C.D.12.设函数.若曲线与函数的图象有4个不同的公共点,则实数的取值范围是()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.在平行四边形中,,,,若 ,则的值为______.14.设变量满足约束条件,则的最大值是______.15.函数的部分图象如图所示,若,且,则_______ .16.在中,三内角所对的边分别是,若依次成等比数列,则的取值范围是____ .三、解答题(本大题共6小题,17题10分,18-22各12分,共70分.解答应写出文字说明,证明过程或演算步骤)17.已知集合,.(1)当m=8时,求;(2)若,求实数m的值.18.设数列的前项和为,且(1)求证:数列为等差数列;(2)设是数列的前项和,求.19.如图,在四棱锥中,底面为平行四边形,,,且底面.(1)证明:平面;(2)若为的中点,求三棱锥的体积.20.在△ABC中,已知.(1)求内角B的大小;(2)若,求的值.21.的内角所对的边分别为,且满足.(1)求的值;(2)若外接圆半径为,求的面积.22.已知函数(为自然对数的底数)(1)讨论函数的单调性;(2)当且时,在上为减函数,求实数的最小值.数学参考答案1.D【解析】∵,∴又∴故选:D2.D【解析】因为,所以可得因为,所以递减,所以可得,故选D.3.A【解析】设则.因为所以当时,;当时,,即于是4.C【解析】由,得为偶数,图象关于轴对称,排除;,排除;,排除,故选C.5.A【解析】∵()为偶函数,∴,∴.∴.令(),得().∴曲线的对称中心为()6.A【解析】由及余弦定理得,整理得,∴,∴为等腰三角形.故选A.7.D【解析】因为,解得,由,得,所以.故选D8.C【解析】A选项不正确,因为α⊥β,m⊥β时,可能有m⊂α;B选项不正确,因m∥α,n⊂α,则m∥n或异面.C选项正确,因为α∩β=m,n∥α,n∥β,则画图如下左图:必有m∥n,D选项不正确,画图如下右图:故选:C.9.A【解析】由三视图知几何体是底面为边长为3,4,5的三角形,高为5的三棱柱被平面截得的,如图所示,截去的是一个三棱锥,底面是边长为3,4,5的直角三角形,高为3,的棱锥,如图蓝色线条的图像是该棱锥,三棱锥上底面外接圆半径圆心设为M半径为r,球心到底面距离为设球心为O,由勾股定理得到故选A.10.C【解析】对3a n+1+a n=4 变形得:3(a n+1﹣1)=﹣(a n﹣1)即:故可以分析得到数列b n=a n﹣1为首项为8公比为的等比数列.所以b n=a n﹣1=8×a n=8×+1所以|S n﹣n﹣6|=解得最小的正整数n=7故选:C.11.B【解析】因为函数有两个极值点,所以有两个不同的正零点,因为,当时,在恒成立,则在上单调递增,不可能有两个正根(舍),当时,令,得,令,得,即在上单调递增,在上单调递减,若有两个不同的正根,则,解得.12.A【解析】由有,显然,在同一坐标系中分别作出直线和函数的图象,当直线与相切时,求出,当直线与相切时,求得,所以,又当直线经过点时,,此时与有两个交点,一共还是4个交点,符合。
甘肃省兰州一中2018-2019学年高三上学期12月月考数学(文)试卷(附解析)

【解析】
分析:因为为边上任意一点,故将中的化为得变形得。则,可得。
详解:因为为的中点,,
所以,
即
因为为边上任意一点,
所以,所以。
故选A。
点睛:由,求的值。注意结论的运用:若是一平面内四点,若,则。反之成立。
8.B
【解析】
【分析】
先求导数,而根据f(x)在R上存在极值便有f′(x)=0有两个不同实数根,从而这样即可得到这样由余弦函数的图象便可得出的范围,即得出结果.
7.2
7.4
(I)根据表中数据,建立关于的线性回归方程;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为:.
(参考数据:,计算结果保留小数点后两位)
15.如图,在长方形ABCD中,AB= ,AD=2,E,F为线段AB的三等分点,G、H为线段DC的三等分点.将长方形ABCD卷成以AD为母线的圆柱W的半个侧面,AB、CD分别为圆柱W上、下底面的直径.
选C.
点睛:空间几何体表面积的求法
(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.
(2)多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.
(3)旋转体的表面积问题注意其侧面展开图的应用.
10.D
【解析】
【分析】
由题意构造函数f(x)=x3+2018x,求出f′(x),判断出函数f(x)为单调递增函数且为奇函数,由已知的两等式得到f(a5﹣1)=1及f(a2014﹣1)=﹣1,由f(x)为奇函数得到f(1﹣a2014)=1,由函数的单调性得到a5﹣1与1﹣a2014相等即a5+a2014=2,然后根据等差数列的前n项和的公式表示出S2018,根据等差数列的性质化简后,将a5+a2014=2代入即可求出值,再根据单调性判断出a5>a2014.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三上文科 数学科12月月考答题卷 第 1页 共 4页 高三上文科数学科9月月考答题卷 第 2页 共 4 页
考号_____________ 班级_________ 座号______ 姓名_____________
厦门市翔安第一中学
2018~2019学年第一学期高三年12月月考试题卷
数学文科 满分150分
一.选择题(每小题5分,共60分.每小题有且只有一个正确的选项)
1.已知全集U =R ,集合{}
260A x x x =--≥,{}1B x x =≥,则()U C A B =( )
A.{}13x x ≤<
B.{}23x x ≤<
C.{}3x x >
D.∅
2. 在复平面内,复数和对应的点分别是和,则( )
A.
B.
C.
D.
3.已知3sin 24α=
,42
ππ
α<<,则sin cos αα-的值是( ) A .12 B .12- C .14 D .14
-
4.若变量,x y 满足约束条件0
20220x y x y x y +≥⎧⎪
-≤⎨⎪-+≥⎩
,则z x y =-的最小值等于( )
A .0
B .1-
C .72-
D .4
3
-
5.在ABC ∆中,3BD DC =,若12AD AB AC λλ=+,则12λλ的值为( )
A.
116 B. 12 C. 316 D. 10
9
6.已知三条直线l 1:2x-3y+1=0,l 2:4x+3y+5=0,l 3:mx-y-1=0不能构成三角形,则实数m 的取值集合为
( )
A.
B.
C.
D.
7.已知a >0,b >0,a +b =+,则+的最小值为( ) A. 4 B. 2 C. 8 D. 16
8. 已知n S 为数列{}n a 的前n 项和,且2log (1)1n S n +=+,则数列{}n a 的通项公式为( ) A .2n n a = B .312
2
n n
n a n =⎧=⎨
≥⎩ C .12n n a -= D .12n n a +=
9.圆C 与x 轴相切于点T (1,0),与y 轴正半轴交于A ,B 两点,且|AB|=2,则圆C 的标准方程为 ( )
A. (x-1)2+(y-)2=2
B. (x-1)2+(y-2)2=2
C. (x+1)2+(y+)2=4
D. (x-1)2+(y-)2=4
10. 函数(
,
,
)的部分图象如图所示,则该函数的图象可由函
数
的图象( )
A. 向左平移个单位得到
B. 向右平移个单位得到
C. 向左平移个单位得到
D. 向右平移个单位得到
11.如图,正三棱柱111ABC A B C -各条棱的长度均相等,D 为1AA 的中点,,M N 分别是线段1BB 和线段1CC 上的动点(含端点),且满足1BM C N =,当,M N 运动时,下列结论中不正确的是( )
A.在DMN △内总存在与平面ABC 平行的线段
B.平面DMN ⊥平面11BCC B
C.三棱锥1A DMN -的体积为定值
D.DMN △可能为直角三角形
12. 定义运算设函数,若函数在区间上有三个零
点,则实数的取值范围是( ) A. B.
C.
D.
高三上文科 数学科12月月考答题卷 第 3页 共 4页 高三上文科数学科9月月考答题卷 第 4页 共 4 页
二:填空题(共4题,每题5分共20分) 13.
,则使
成立的值是____________.
14. 甲、乙、丙、丁四人分别从一个装有编号为
的四个完全相同的小球的袋中依次取出一个
小球.现知道 :①甲取出的小球编号为偶数;②乙取出的小球编号比甲大;③乙、丙取出的小球编号差的绝对值比甲大.则丁取出的小球编号是________.
15.中国古代数学经典《九章算术》中,将四个面都为直角三角形的三棱锥称之为鐅臑.若三棱锥P ABC -为鐅臑,且PA ⊥平面ABC ,2PA =,3AB =,4BC =,AB BC ⊥,则该鐅臑的外接球
的表面积为__________. 16.已知数列中,
,
,且
.则数列
的前n 项_和为____________
三:解答题:(17、18、19题每题10分、20、21题每题13分,22题14分)
17.在直角坐标系xoy 中,直线l 的参数方程为⎩
⎨
⎧+=+=αα
sin 2cos 1t y t x (t 为参数),在极坐标系(与直角
坐标系xoy 取相同的长度单位,且以原点O 为极点,以x 轴非负半轴为极轴)中,圆C 的方程为
θρsin 6=.
(1)求圆C 的直角坐标方程;
(2)若点)2,1(P ,设圆C 与直线l 交于点B A ,,求||||PB PA +的最小值. 18.如图,在ABC ∆中, 3
B π
∠=
, D 为边BC 上的点, E 为AD 上的点,且8AE =,
AC = 4
CED π
∠=
.
(1)求CE 的长;
(2)若5CD =,求cos DAB ∠的值.
19.已知n S 是等差数列{}n a 的前n 项和,且12a =,520S =.n T 是数列{}n b 的前n 项和,且
()122n n T n N +*=-∈.
(Ⅰ)求数列{}n a ,{}n b 的通项公式;
(Ⅱ)求数列()21log n n a b ⎧⎫⎪⎪
⎨⎬⎪⎪⎩⎭
的前n 项和n U .
20.如图,四棱锥P ABCD -中,侧面PAB ⊥底面ABCD ,PA PB =,24CD AB ==,
CD AB ∥,90BPA BAD ∠=∠=︒.
(1)求证:PB ⊥平面PAD ;
(2)若三棱锥C PBD -的体积为2,求PAD ∆
的面积.
21.在平面直角坐标系xOy 中,曲线y=x 2-6x+1与两坐标轴的交点都在圆C 上.
(1)求圆C 的方程;
(2)若圆C 与直线x-y+a=0交于A ,B 两点,且OA ⊥OB ,求a 的值.
22.已知函数f(x)=
x
nx
a 1+在x =1处取得极值. (Ⅰ)求a 的值,并讨论函数f(x)的单调性; (Ⅱ)当[),1+∞∈x 时,f(x)
x m
+≥
1恒成立,求实数m 的取值范围.。
