年全国各地中考数学考点分类汇编相交线与平行线
中考数学真题分类汇编:相交线与平行线

相交线与平行线一.选择题1.(2012临沂)如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是()A.40°B.50°C.60°D.140°考点:平行线的性质;直角三角形的性质。
解答:解:∵AB∥CD,DB⊥BC,∠1=40°,∴∠3=∠1=40°,∵DB⊥BC,∴∠2=90°﹣∠3=90°﹣40°=50°.故选B.2.(2012张家界)如图,直线a、b被直线c所截,下列说法正确的是()A.当∠1=∠2时,一定有a∥b B.当a∥b时,一定有∠1=∠2C.当a∥b时,一定有∠1+∠2=90° D.当∠1+∠2=180°时,一定有a∥b考点:平行线的判定;平行线的性质。
解答:解:A.若∠1=∠2不符合a∥b的条件,故本选项错误;3.(2012中考)如图,直线a∥b,直线c与a,b相交,∠1=65°,则∠2=(B)A.115°B.65°C.35°D.25°4.(2012山西)如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于()A.35°B.40°C.45°D.50°考点:平行线的性质。
解答:解:∵∠CEF=140°,∴∠FED=180°﹣∠CEF=180°﹣140°=40°,∵直线AB∥CD,∴∠A∠FED=40°.故选B.5.(2012潜江)如图,AB∥CD,∠A=48°,∠C=22°.则∠E等于()6.(2012十堰)图,直线BD ∥EF ,AE 与BD 交于点C ,若∠ABC=30°,∠BAC=75°,则∠CEF 的大小为( D ) A .60° B .75° C .90° D .105° 【考点】平行线的性质;三角形内角和定理. 【专题】探究型.【分析】先根据三角形外角的性质求出∠1的度数,再由平行线的性质即可得出结论. 【解答】解:∵∠1是△ABC 的外角,∠ABC=30°,∠BAC=75°,∴∠1=∠ABC+∠BAC=30°+75°=105°, ∵直线BD ∥EF , ∴∠CEF=∠1=105°. 故选D .【点评】本题考查的是平行线的性质及三角形外角的性质,熟知两直线平行,同位角相等是解答此题的关键.7.(2012宜昌)如图,将三角尺与直尺贴在一起,使三角尺的直角顶点C (∠ACB=90°)在直尺的一边上,若∠1=60°,则∠2的度数等于( )8.(2012海南)小明同学把一个含有450角的直角三角板在如图所示的两条平行线m n ,上,测得0120α∠=,则β∠的度数是【 】A .450B .550C .650D .750【答案】D 。
2013-2022北京中考真题数学汇编:相交线与平行线

2013-2022北京中考真题数学汇编相交线与平行线一、单选题1.(2022·北京·中考真题)如图,利用工具测量角,则1∠的大小为( )A .30°B .60°C .120°D .150°2.(2021·北京·中考真题)如图,点O 在直线AB 上,OC OD ⊥.若120AOC ∠=︒,则BOD ∠的大小为( )A .30B .40︒C .50︒D .60︒3.(2020·北京·中考真题)如图,AB 和CD 相交于点O ,则下列结论正确的是( )A .∠1=∠2B .∠2=∠3C .∠1>∠4+∠5D .∠2<∠54.(2019·北京·中考真题)用三个不等式a b >,0ab >,11a b <中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题,组成真命题的个数为( )A .0B .1C .2D .35.(2017·北京·中考真题)如图所示,点P 到直线l 的距离是( )A .线段PA 的长度B .线段PB 的长度C .线段PC 的长度D .线段PD 的长度6.(2016·北京·中考真题)甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是轴对称的是( )A .B .C .D .7.(2015·北京·中考真题)如图,直线l 1,l 2,l 3交于一点,直线l 4∥l 1,若∠1=124°,∠2=88°,则∠3的度数为( )A .26°B .36°C .46°D .56°8.(2013·北京·中考真题)如图,直线a ,b 被直线c 所截,a ∥b ,∠1=∠2,若∠3=40°,则∠4等于A .40°B .50°C .70°D .80°二、填空题 9.(2020·北京·中考真题)如图是某剧场第一排座位分布图:甲、乙、丙、丁四人购票,所购票分别为2,3,4,5.每人选座购票时,只购买第一排的座位相邻的票,同时使自己所选的座位之和最小.如果按“甲、乙、丙、丁”的先后顺序购票,那么甲购买1,2号座位的票,乙购买3,5,7号座位的票,丙选座购票后,丁无法购买到第一排座位的票.若丙第一购票,要使其他三人都能购买到第一排座位的票,写出一种满足条件的购票的先后顺序______.10.(2018·北京·中考真题)用一组a ,b ,c 的值说明命题“若a b <,则ac bc <”是错误的,这组值可以是=a _____,b =______,c =_______。
中考数学复习----《相交线与平行线之平行线》知识点总结与专项练习题(含答案解析)

中考数学复习----《相交线与平行线之平行线》知识点总结与专项练习题(含答案解析)知识点总结1. 三线八角:同位角,内错角,同旁内角。
2. 平行线定义:两条永不相交的直线的位置关系是平行线。
3. 平行线性质:①两直线平行,同位角相等。
②两直线平行,内错角相等。
③两直线平行,同旁内角互补。
④同一平面内,过直线外一点有且只有一条直线与已知直线平行。
⑤平行于同一直线的两直线平行。
即c b b a ∥,∥,则c a ∥。
4. 平行线的判定:①同位角相等,两直线平行。
②内错角相等,两直线平行。
③同旁内角相等,两直线平行。
④垂直于同一直线的两直线平行。
即若c a b a ⊥⊥,,则c a ∥。
⑤平行于同一直线的两直线平行。
即若c b b a ∥,∥,则c a ∥。
5. 平行线间的距离:平行线间的距离处处相等。
练习题9.(2022•青海)数学课上老师用双手形象的表示了“三线八角”图形,如图所示(两大拇指代表被截直线,食指代表截线).从左至右依次表示()A.同旁内角、同位角、内错角B.同位角、内错角、对顶角C.对顶角、同位角、同旁内角D.同位角、内错角、同旁内角【分析】两条线a、b被第三条直线c所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角;两个角分别在截线的异侧,且夹在两条被截线之间,具有这样位置关系的一对角互为内错角;两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的一对角互为同旁内角.据此作答即可.【解答】解:根据同位角、内错角、同旁内角的概念,可知第一个图是同位角,第二个图是内错角,第三个图是同旁内角.故选:D.10.(2022•贺州)如图,直线a,b被直线c所截,下列各组角是同位角的是()A.∠1与∠2 B.∠1与∠3 C.∠2与∠3 D.∠3与∠4【分析】同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角.【解答】解:根据同位角、邻补角、对顶角的定义进行判断,A、∠1和∠2是对顶角,故A错误;B、∠1和∠3是同位角,故B正确;C、∠2和∠3是内错角,故C错误;D、∠3和∠4是邻补角,故D错误.故选:B.11.(2022•东营)如图,直线a∥b,一个三角板的直角顶点在直线a上,两直角边均与直线b相交,∠1=40°,则∠2=()A.40°B.50°C.60°D.65°【分析】先由已知直角三角板得∠4=90°,然后由∠1+∠3+∠4=180°,求出∠3的度数,再由直线a∥b,根据平行线的性质,得出∠2=∠3=50°.【解答】解:如图:∵∠4=90°,∠1=40°,∠1+∠3+∠4=180°,∴∠3=180°﹣90°﹣40°=50°,∵直线a∥b,∴∠2=∠3=50°.故选:B.12.(2022•资阳)将直尺和三角板按如图所示的位置放置.若∠1=40°,则∠2度数是()A.60°B.50°C.40°D.30°【分析】如图,易知三角板的∠A为直角,直尺的两条边平行,则可得∠1的对顶角和∠2的同位角互为余角,即可求解.【解答】解:如图,根据题意可知∠A为直角,直尺的两条边平行,∴∠2=∠ACB,∵∠ACB+∠ABC=90°,∠ABC=∠1,∴∠2=90°﹣∠1=90°﹣40°=50°,故选:B.13.(2022•襄阳)已知直线m∥n,将一块含30°角的直角三角板ABC(∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°.则∠2的度数为()A.30°B.40°C.60°D.70°【分析】根据平行线的性质求得∠ABD,再根据角的和差关系求得结果.【解答】解:∵m∥n,∠1=70°,∴∠1=∠ABD=70°,∵∠ABC=30°,∴∠2=∠ABD﹣∠ABC=40°,故选:B.14.(2022•锦州)如图,直线a∥b,将含30°角的直角三角板ABC(∠ABC=30°)按图中位置摆放,若∠1=110°,则∠2的度数为()A.30°B.36°C.40°D.50°【分析】根据平行线的性质可得∠3=∠1=110°,则有∠4=70°,然后根据三角形外角的性质可求解.【解答】解:如图,∵a∥b,∠1=110°,∴∠3=∠1=110°,∴∠4=180°﹣∠3=70°,∵∠B=30°∴∠2=∠4﹣∠B=40°;故选:C.15.(2022•六盘水)如图,a∥b,∠1=43°,则∠2的度数是()A.137°B.53°C.47°D.43°【分析】根据平行线的性质,得∠2=∠1=43°.【解答】解:∵a∥b,∠1=43°,∴∠2=∠1=43°.故选:D.16.(2022•济南)如图,AB∥CD,点E在AB上,EC平分∠AED,若∠1=65°,则∠2的度数为()A.45°B.50°C.57.5°D.65°【分析】根据平行线的性质,由AB∥CD,得∠AEC=∠1=65°.根据角平分线的定义,得EC平分∠AED,那么∠AED=2∠AEC=130°,进而求得∠2=180°﹣∠AED=50°.【解答】解:∵AB∥CD,∴∠AEC=∠1=65°.∵EC平分∠AED,∴∠AED=2∠AEC=130°.∴∠2=180°﹣∠AED=50°.故选:B.17.(2022•丹东)如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,过点A作AC ⊥l2,垂足为C,若∠1=52°,则∠2的度数是()A.32°B.38°C.48°D.52°【分析】根据平行线的性质求出∠ABC,根据三角形内角和定理求出即可.【解答】解:∵直线l1∥l2,∠1=52°,∴∠ABC=∠1=52°,∵AC⊥l2,∴∠ACB=90°,∴∠2=180°﹣∠ABC﹣∠ACB=180°﹣52°﹣90°=38°,故选:B.18.(2022•南通)如图,a∥b,∠3=80°,∠1﹣∠2=20°,则∠1的度数是()A.30°B.40°C.50°D.80°【分析】根据平行线的性质可得∠1=∠4,然后根据三角形的外角可得∠3=∠4+∠2,从而可得∠1+∠2=80°,最后进行计算即可解答.【解答】解:如图:∵a∥b,∴∠1=∠4,∵∠3是△ABC的一个外角,∴∠3=∠4+∠2,∵∠3=80°,∴∠1+∠2=80°,∵∠1﹣∠2=20°,∴2∠1+∠2﹣∠2=100°,∴∠1=50°,故选:C.19.(2022•西藏)如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为()A.46°B.90°C.96°D.134°【分析】根据平行线的性质定理求解即可.【解答】解:∵l1∥l2,∴∠1+∠3+∠2=180°,∵∠1=38°,∠2=46°,∴∠3=96°,故选:C.20.(2022•兰州)如图,直线a∥b,直线c与直线a,b分别相交于点A,B,AC⊥b,垂足为C.若∠1=52°,则∠2=()A.52°B.45°C.38°D.26°【分析】根据平行线的性质可得∠ABC=52°,根据垂直定义可得∠ACB=90°,然后利用直角三角形的两个锐角互余,进行计算即可解答.【解答】解:∵a∥b,∴∠1=∠ABC=52°,∵AC⊥b,∴∠ACB=90°,∴∠2=90°﹣∠ABC=38°,故选:C.21.(2022•通辽)如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠ABM=35°时,∠DCN的度数为()A.55°B.70°C.60°D.35°【分析】根据“两直线平行,同旁内角互补”解答即可.【解答】解:∵∠ABM=35°,∠ABM=∠OBC,∴∠OBC=35°,∴∠ABC=180°﹣∠ABM﹣∠OBC=180°﹣35°﹣35°=110°,∵CD∥AB,∴∠ABC+∠BCD=180°,∴∠BCD=180°﹣∠ABC=70°,∵∠BCO=∠DCN,∠BCO+∠BCD+∠DCN=180°,∴∠DCN=(180°﹣∠BCD)=55°,故选:A.22.(2022•潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB与CD平行,入射光线l与出射光线m平行.若入射光线l与镜面AB的夹角∠1=40°10',则∠6的度数为()A.100°40' B.99°80' C.99°40' D.99°20'【分析】先根据反射角等于入射角求出∠2的度数,再求出∠5的度数,最后根据平行线的性质得出即可.【解答】解:∵入射角等于反射角,∠1=40°10',∴∠2=∠1=40°10',∵∠1+∠2+∠5=180°,∴∠5=180°﹣40°10'﹣40°10'=99°40',∵入射光线l与出射光线m平行,∴∠6=∠5=99°40'.故选:C.23.(2022•新疆)如图,AB与CD相交于点O,若∠A=∠B=30°,∠C=50°,则∠D=()A.20°B.30°C.40°D.50°【分析】根据∠A=∠B=30°,得出AC∥DB,即可得出∠D=∠C=50°.【解答】解:∵∠A=∠B=30°,∴AC∥DB,又∵∠C=50°,∴∠D=∠C=50°,故选:D.24.(2022•柳州)如图,直线a,b被直线c所截,若a∥b,∠1=70°,则∠2的度数是()A.50°B.60°C.70°D.110°【分析】由两直线平行,同位角相等可知∠2=∠1.【解答】解:∵a∥b,∴∠2=∠1=70°.故选:C.25.(2022•雅安)如图,已知直线a∥b,直线c与a,b分别交于点A,B,若∠1=120°,则∠2=()A.60°B.120°C.30°D.15°【分析】本题要注意到∠1的对顶角与∠2同旁内角,并且两边互相平行,可以考虑平行线的性质及对顶角相等.【解答】解:∵∠1=120°,∴它的对顶角是120°,∵a∥b,∴∠2=60°.故选:A.26.(2022•宿迁)如图,AB∥ED,若∠1=70°,则∠2的度数是()A.70°B.80°C.100°D.110°【分析】根据两直线平行,同旁内角互补和对顶角相等解答.【解答】解:∵∠1=70°,∴∠3=70°,∵AB∥ED,∴∠2=180°﹣∠3=180°﹣70°=110°,故选:D.27.(2022•陕西)如图,AB∥CD,BC∥EF.若∠1=58°,则∠2的大小为()A.120°B.122°C.132°D.148°【分析】根据两直线平行,内错角相等分别求出∠C、∠CGF,再根据平角的概念计算即可.【解答】解:∵AB∥CD,∠1=58°,∴∠C=∠1=58°,∵BC∥EF,∴∠CGF=∠C=58°,∴∠2=180°﹣∠CGF=180°﹣58°=122°,故选:B.28.(2022•吉林)如图,如果∠1=∠2,那么AB∥CD,其依据可以简单说成()A.两直线平行,内错角相等B.内错角相等,两直线平行C.两直线平行,同位角相等D.同位角相等,两直线平行【分析】由平行的判定求解.【解答】解:∵∠1=∠2,∴AB∥CD(同位角相等,两直线平行),故选:D.29.(2022•台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是()A.∠2=90°B.∠3=90°C.∠4=90°D.∠5=90°【分析】根据平行线的判定逐项分析即可得到结论.【解答】解:A.由∠2=90°不能判定两条铁轨平行,故该选项不符合题意;B.由∠3=90°=∠1,可判定两枕木平行,故该选项不符合题意;C.∵∠1=90°,∠4=90°,∴∠1=∠4,∴两条铁轨平行,故该选项符合题意;D.由∠5=90°不能判定两条铁轨平行,故该选项不符合题意;故选:C.30.(2022•郴州)如图,直线a∥b,且直线a,b被直线c,d所截,则下列条件不能判定直线c∥d的是()A.∠3=∠4 B.∠1+∠5=180°C.∠1=∠2 D.∠1=∠4【分析】根据平行线的判定定理进行一一分析.【解答】解:A、若∠3=∠4时,由“内错角相等,两直线平行”可以判定c∥d,不符合题意;B、若∠1+∠5=180°时,由“同旁内角互补,两直线平行”可以判定c∥d,不符合题意;C、若∠1=∠2时,由“内错角相等,两直线平行”可以判定a∥b,不能判定c∥d,符合题意;D、由a∥b推知∠4+∠5=180°.若∠1=∠4时,则∠1+∠5=180°,由“同旁内角互补,两直线平行”可以判定c∥d,不符合题意.故选:C.。
中考数学复习解答题专项集训之相交线与平行线

中考数学复习解答题专项集训之相交线与平行线1.已知:如图,△ABC中,点D、E分别在AB、AC上,EF交DC于点F,∠3+∠2=180°,∠1=∠B.(1)求证:DE∥BC;(2)若DE平分∠ADC,∠3=3∠B,求∠2的度数.2.如图,AB∥CD,AB∥EF,AF平分∠BAE,∠DAE=10°,∠ADC=120°.求∠AFE 的度数.3.如图,在△ABC中,AD平分∠BAC交BC于点D,E为边AB上一点,AE=DE.(1)求证:AC∥DE.(2)若DE=2,BE=4,CD=32,求BC的长.4.如图,点F在线段AB上,点E,G在线段CD上,AB∥CD,∠1=∠2.(1)求证:FG∥AE;(2)若FG⊥BC于点H,BC平分∠ABD,∠D=120°,求∠1的度数.5.如图,在四边形ABCD中,AD∥BC,∠B=∠D,点E在BA的延长线上,连接CE.(1)求证:∠E=∠ECD;(2)若∠E=60°,CE平分∠BCD,请判断△BCE的形状,证明你的结论.6.如图是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面EF,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,∠AOE=∠BNM.(1)求证:OE∥DM;(2)若OE平分∠AOF,∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM的度数.7.已知AD∥BC,AB∥CD,E在线段BC延长线上,AE平分∠BAD.连接DE,若∠ADE =3∠CDE.(1)若∠AED=60°,求∠CDE的度数;(2)若∠AEB=60°,探究DE与BE的位置关系,并说明理由.8.已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;(1)求证:DE∥BA.(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.9.综合与实践问题情境:“综合与实践”课上,老师将一副直角三角板摆放在直线MN上(如图1,∠EDC=90°,∠DEC=60°,∠ABC=90°,∠BAC=45°).保持三角板EDC不动,老师将三角板ABC绕点C以每秒5°的速度顺时针旋转,旋转时间为t秒,当AC与射线CN重合时停止旋转.各小组解决老师给出的问题,又提出新的数学问题,请你解决这些问题.深入探究:①老师提出,如图2,当AC转到与∠DCE的角平分线重合时,∠ECB﹣∠DCA=15°,当AC在∠DCE内部的其他位置时,结论∠ECB﹣∠DCA=15°是否依然成立?请说明理由.②勤学小组提出:若AC旋转至∠DCE的外部,∠DCA与∠ECB是否还存在如上数量关系?若存在,请说明理由;若不存在,请写出∠DCA与∠ECB的数量关系,并说明理由.拓展提升:③智慧小组提出:若AC旋转到与射线CM重合时停止旋转.在旋转过程中,直线DE与直线AC是否存在平行的位置关系?若存在,请直接写出t的值;若不存在,请说明理由.10.如图,已知∠E=∠F,∠A=∠D.求证:∠1=∠2.11.如图,四边形ABCD中,点E,F分别在AD,BC上,G在AB的延长线上,若∠D+∠GBC=180°,AD∥BC,EF∥DC.求证:AB∥EF.12.如图,AB∥DG,∠1+∠2=180°.(1)试判断AD与EF的位置关系,并说明理由.(2)若DG是∠ADC的平分线,∠2=150°,求∠B的度数.13.如图,已知∠AGF=∠ABC,∠1+∠2=180°.(1)试判断BF与DE的位置关系,并说明理由;(2)若BF⊥AC,∠2=135°,求∠AFG的度数.14.图1为科研小组研制的智能机器,水平操作台为l,底座AB固定,高AB为50cm,始终与平台l垂直,连杆BC长度为60cm,机械臂CD长度为40cm,点B,C是转动点,AB,BC与CD始终在同一平面内.(1)转动连杆BC,机械臂CD,当张角∠ABC=120°且CD∥AB时(如图2),求机械臂臂端D到操作台l的距离.(2)转动连杆BC,机械臂CD,要使机械臂端D能碰到操作台l上的物体M,则物体M 离底座A的最远距离是多少?15.已知,如图所示,直线AB∥CD,∠AEP=∠CFQ.求证:∠EPM=∠FQM.16.课堂上同学们独立完成了这样一道问题:“如图,已知AB∥CD,AD∥BC,求证:∠1=∠2.”小莲同学解答如下:∵AB∥CD,∴∠1+∠BCD=180°,∵AD∥BC,∴∠2+∠BCD=180°,∴∠1=∠2.小莲的证法是否正确?若正确,请在框内打“√”;若错误,请写出你的证明过程.17.如图1是长方形纸带,∠DEF=28°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠DHF的度数是.18.如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.求证:AD∥BC.19.如图,△ABC中,D是AC上一点,过D作DE∥BC交AB于E点,F是BC上一点,连接DF.若∠1=∠AED.(1)求证:DF∥AB.(2)若∠1=50°,DF平分∠CDE,求∠C的度数.20.如图1,AB∥CD,E为AB与CD之间的一点,连接BE,过点E作EF⊥BE,与CD相交于点F.(1)求证:∠1+∠2=90°.(2)如图2,E为AB上方的一点,其他条件不变,(1)中的结论是否仍然成立?如果成立,请给予证明;如果不成立,请写出正确结论并证明.(3)如图3,E为AB下方的一点,其他条件不变,(1)中的结论是否仍然成立?如果成立,请给予证明;如果不成立,请直接写出正确结论.。
相交线与平行线考点及题型总结

相交线与平行线考点及题型总结-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII相交线与平行线考点及题型总结第一节相交线一、知识要点:(一)当同一平面内的三条直线相交时,有三种情况:一种是只有一个交点;一种是有两个交点,即两条直线平行被第三条直线所截;还有一种是三个交点,即三条直线两两相交。
(二)余角、补角、对顶角1、余角:如果两个角的和是直角,那么称这两个角互为余角.2、补角:如果两个角的和是平角,那么称这两个角互为补角.3、对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.4、互为余角的有关性质:①∠1+∠2=90°,则∠1、∠2互余;反过来,若∠1,∠2互余,则∠1+∠2=90°;②同角或等角的余角相等,如果∠l十∠2=90°,∠1+∠ 3=90°,则∠2=∠3.5、互为补角的有关性质:①若∠A+∠B=180°,则∠A、∠B互补;反过来,若∠A、∠B互补,则∠A+∠B=180°.②同角或等角的补角相等.如果∠A+∠C=180°,∠A+∠B=180°,则∠B=∠C.6、对顶角的性质:对顶角相等.(三)垂直:相交的一种特殊情况是垂直,两条直线交角成90 。
1、经过直线外一点,作直线垂线,有且只有一条;2、点到直线上各点的距离中,垂线段最短。
(四)两条直线被第三条直线所截,产生两个交点,形成了八个角(不可分的):1、同位角:没有公共顶点的两个角,它们在直线AB,CD的同侧,在第三条直线EF的同旁(即位置相同),这样的一对角叫做同位角;2、内错角:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的两旁(即位置交错),这样的一对角叫做内错角;3、同旁内角:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的同旁,这样的一对角叫做同旁内角;二、题型分析: 题型一:列方程求角例1:一个角的余角比它的补角的21少20°.则这个角为 ( ) A 、30° B 、40° C 、60° D 、75° 答案:B分析:若设这个角为x ,则这个角的余角是90°-x ,补角是180°-x ,于是构造出方程即可求解求解:设这个角为x ,则这个角的余角是90°-x ,补角是180°-x .则根据题意,得21(180°-x )-(90°-x )=20° ; 解得:x =40°. 故应选B . 说明:处理有关互为余角与互为补角的问题,除了要弄清楚它们的概念,通常情况下还要引进未知数,构造方程求解.习题演练:1、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30 ,那么这两个角是( )A 、42138 、B 、都是10C 、42138 、或4210 、D 、以上都不对 答案:A分析:两个条件可以确定两个角互补,列方程即可解得A 。
2020年中考数学必考专题15 相交线与平行线(解析版)

专题15 相交线与平行线一、相交线1.邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
邻补角的性质:邻补角互补。
2.对顶角:一个角的两边分别是另一个角的两边的反向延长线,像这样的两个角互为对顶角。
对顶角的性质:对顶角相等。
3.垂线:两条直线相交成直角时,叫做互相垂直,其中一条叫做另一条的垂线。
4.垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
5.同位角、内错角、同旁内角:同位角:∠1与∠5像这样具有相同位置关系的一对角叫做同位角。
内错角:∠2与∠6像这样的一对角叫做内错角。
同旁内角:∠2与∠5像这样的一对角叫做同旁内角。
二、平行线1.平行线概念:在同一平面内,两条不想交的直线叫做平行线。
记做a∥b2.两条直线的位置关系:平行和相交。
3.平行线公理及其推论:(1)经过已知直线外一点,有且只有一条直线与这条直线平行;(2)如果两条直线都与第三条直线平行,那么这两条直线平行.4.平行线的判定:判定方法1:两条直线被第三条直线所截,同位角相等,两直线平行;专题知识回顾判定方法2:两条直线被第三条直线所截,内错角相等,两直线平行;判定方法3:两条直线被第三条直线所截,同旁内角互补,两直线平行.5.平行线的性质:性质1:两直线平行,同位角相等。
性质2:两直线平行,内错角相等。
性质3:两直线平行,同旁内角互补。
6.平行线的判定:判定1:同位角相等,两直线平行。
判定2:内错角相等,两直线平行。
判定3:同旁内角相等,两直线平行。
7.证明的一般步骤(1)根据题意,画出图形。
(2)根据题设、结论、结合图形,写出已知、求证。
(3)经过分析,找出由已知推出求证的途径,写出证明过程。
专题典型题考法及解析【例题1】(2019•河北省)下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容则回答正确的是()A.◎代表∠FEC B.@代表同位角C.▲代表∠EFC D.※代表AB【答案】C.【解析】证明:延长BE交CD于点F,则∠BEC=∠EFC+∠C(三角形的外角等于与它不相邻两个内角之和).又∠BEC=∠B+∠C,得∠B=∠EF C.故AB∥CD(内错角相等,两直线平行).【例题2】(2019广西河池)如图,1120∠的大小是()a b,则2∠=︒,要使//A.60︒B.80︒C.100︒D.120︒【答案】D.【解析】平行线的判定如果21120a b.∠=∠=︒,那么//所以要使//∠的大小是120︒.故选:D.a b,则2【例题3】(2019广西省贵港市)如图,直线//∠=.∠=︒,则2a b,直线m与a,b均相交,若138【答案】142︒.【解析】知识点是平行线的性质如图,//Q,a b∴∠=∠,23Q,∠+∠=︒13180∴∠=︒-︒=︒.218038142一、选择题1.(2019•贵州省铜仁市)如图,如果∠1=∠3,∠2=60°,那么∠4的度数为()A.60°B.100°C.120°D.130°\【答案】C.【解答】∵∠1=∠3,∴a∥b,∴∠5=∠2=60°,∴∠4=180°﹣60°=120°,2.(2019广东深圳)如图,已知l1∥AB,AC为角平分线,下列说法错误的是()A.∠1=∠4 B.∠1=∠5 C.∠2=∠3 D.∠1=∠3【答案】B【解析】∵AC为角平分线,∴∠1=∠2.∵l1∥AB,∴∠4=∠2,∠3=∠2,∴∠1=∠4,∠1=∠3.故A、C、D正确.∵l1∥AB,∴∠5=∠1+∠2,故B错误.故选B.3.(2019•湖北省鄂州市)如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=35°,则∠1的度专题典型训练题数为()A.45°B.55°C.65°D.75°【答案】B【解析】根据平行线的性质和直角的定义解答即可.如图,作EF∥AB∥CD,∴∠2=∠AEF=35°,∠1=∠FEC,∵∠AEC=90°,∴∠1=90°﹣35°=55°4.(2019•海南省)如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长度为半径画弧,分别交直线l1、l2于B、C两点,连结AC、B C.若∠ABC=70°,则∠1的大小为()A.20°B.35°C.40°D.70°【答案】C【解析】根据平行线的性质解答即可.∵点A为圆心,适当长度为半径画弧,分别交直线l1、l2于B、C,∴AC=AB,∴∠CBA=∠BCA=70°,∵l1∥l2,∴∠CBA+∠BCA+∠1=180°,∴∠1=180°﹣70°﹣70°=40°5.(2019广西北部湾)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为。
2023中考数学复习:角、相交线与平行线

A.A点
B.B点
C.C点
D.D点
12
13
14
15
16
17
挑战高分
基础全练
中考创新练
15.(2022·山西)如图,Rt△ABC是一块直角三角板,其中∠C=90°,
∠BAC=30°.直尺的一边DE经过顶点A,若DE∥BC,则∠DAB的
度数为( B )
A.100°
B.120°
C.135°
D.150°
12
A.55°
B.25°
C.65°
D.75°
12
13
14
15
16
17
挑战高分
基础全练
中考创新练
14.(2022·山东威海)图1是光的反射规律示意图.其中,PO是入射光线,OQ
是反射光线,法线KO⊥MN,∠POK是入射角,∠KOQ是反射角,∠KOQ=
∠POK.图2中,光线自点P射入,经镜面EF反射后经过的点是( B )
则∠2=( C )
A.20°
B.80°
C.100°
1
D.120°
2
3
4
5
6
7
8
9
10
11
挑战高分
基础全练
中考创新练
10.(2022·湖南岳阳)如图,已知l∥AB,CD⊥l于点D,若∠C=40°,则∠1
的度数是( C )
A.30°
B.40°
C.50°
1
D.60°
2
3
4
5
6
7
8
9
10
11
挑战高分
基础全练
形纸条上,若∠1=28°,则∠2的度数为( D )
中考数学知识点(相交线、平行线)

七年级下册相交线、平行线9. (分类)9.1. 相交线(包含题目总数:4)七年级下册 相交线、平行线两条直线相交,可以得到四个角,我们把两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角叫做对顶角.如图1中的1∠与3∠就是对顶角.我们把两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角叫做邻补角.如图1中的1∠与2∠就是邻补角. 这样可以得到邻补角和对顶角的重要性质:邻补角互补,对顶角相等.图1 图2 如图2,直线AB 、CD 与EF 相交(或者说两条直线AB 、CD 被第三条直线EF 所截),构成八个角.其中像1∠与5∠,这两个角分别在AB 、CD 的上方,并且在EF 的右侧,像这样位置相同的一对角叫做同位角.如2∠与6∠,3∠与7∠,4∠与8∠都是同位角;3∠与5∠,这两个角都在AB 、CD 之间,并且3∠在EF 的左侧,5∠在EF 的右侧,像这样的角叫做内错角.如4∠与6∠是内错角;3∠与6∠在直线AB 、CD 之间,并且在EF 的同一旁,像这样的一对角叫做同旁内角.如4∠与5∠是同旁内角.七年级下册相交线、平行线9.2. 垂线(包含题目总数:3)两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直.其中一条直线叫另一条直线的垂线,它们的交点叫垂足.如图,直线AB、CD互相垂直,记作“CDAB ”(或CD⊥AB),读作“AB垂直于CD”.如果垂足是O,记作“AB垂直于CD,垂足为O”.七年级下册相交线、平行线垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直.性质2:直线外一点与直线上各点连结的所有线段中,垂线段最短.简称:垂线段最短.七年级下册相交线、平行线空间里也有垂直的情况.空间中垂直的判定方法有下面两种:(1)直线与平面垂直的判定方法:若一条直线垂直于一个平面内的两条相交直线,则这条直线与这个平面垂直.(2)平面与平面垂直的判定方法:若一个平面经过另一个平面的一条垂线,则这两平面互相垂直.9.3. 平行线(包含题目总数:8)008020;008030;008040;008050;008070;008090;008160;008170;9.3.1. 平行线的概念在同一个平面内,不相交的两条直线叫做平行线.平行用符号“//”表示,如图,直线AB 与CD是平行线,记作“AB//CD”,读作“AB平行于CD”.在同一个平面内,两条直线的位置关系只有两种:相交或平行.七年级下册相交线、平行线注意:①平行线是无限延伸的,无论怎样延伸也不相交.②今后遇到线段、射线平行时,特指线段、射线所在的直线平行.9.3.2. 平行公理及其推论平行公理:经过直线外一点,有且只有一条直线与这条直线平行.推论:如果两条直线都和第三条直线平行,那么这两条直线也相互平行.即:如果ba//,a//.c//,那么cb七年级下册相交线、平行线9.3.3. 平行线的判定平行线的判定公理:两条直线被第三条直线所截,如果同位角相等,那么两直线平行,简单的说成:同位角相等,两直线平行.平行线的两个判定定理:1、两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行.2、两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行.注意:上面的判定是由角的等量关系得到两直线的位置关系,判定直线平行还有下面三种判定方法:(1)平行于同一直线的两直线平行;七年级下册相交线、平行线(2)垂直于同一直线的两直线平行;(3)平行线的定义.9.3.4. 平行线的性质(1)两条平行线被第三条直线所截,同位角相等.(2)两条平行线被第三条直线所截,内错角相等.(3)两条平行线被第三条直线所截,同旁内角互补.9.3.5. 空间中的平行关系在空间里,既不相交也不平行的直线是异面直线.在空间里,如果一条直线与一个平面没有公共点,就说这条直线与这个平面互相平行.在空间里,如果两个平面没有公共点,就说这两个平面互相平行.直线与平面、平面与平面平行的判定:七年级下册相交线、平行线①不在平面内的一条直线,只要与平面内的某一条直线平行,那么这条直线与这个平面平行.②如果一个平面内两条相交直线都与另一个平面平行,那么这两个平面互相平行.9.4. 命题、定理、证明(包含题目总数:2)008140;008150;命题的概念:判断一件事情的语句,叫做命题.注意:命题的定义包括两层涵义:①命题必须是一个完整的句子;②这个句子必须对某件事情做出判断.例如:“直角都相等”,“相等的角是对顶角”等七年级下册相交线、平行线都是命题.“连结P、Q两点”、“过点p作直线l”等都不是命题.命题的一般形态:任一个命题都可以写成形式:“如果……,那么…….”有时也写成:“若……,则…….”“倘若……,那么…….”命题的题设(条件)部分,有时也可用“已知……”或者“若……”等形式表述;命题的结论部分,有时也可用“求证……”或“则……”等形式表述.七年级下册 相交线、平行线命题的分类(按正确、错误与否分):()()⎩⎨⎧错误的命题假命题正确的命题真命题命题所谓正确的命题就是:如果题设成立,那么结论一定成立的命题.所谓错误的命题就是:如果题设成立,不能保证结论总是成立的命题.注意:对于假命题并不要求:在题设成立时,结论一定错误,事实上,只要你不能保证结论一定成立,这个命题就是假命题了,因此,要说明一个命题是假命题,只要举出一个“反例”就可以了.公理:七年级下册相交线、平行线人们在长期实践中总结出来的得到人们公认的真命题,叫做公理,如“同位角相等,两直线平行”、“两直线平行,同位角相等”等.注意:①公理是通过长期实践反复验证过的,不需要再进行推理而都承认的真命题.②公理可以作为判定其它命题真假的根据.定理:用推理的方法判断为正确的命题叫做定理,如“内错角相等,两直线平行”、“两直线平行,内错角相等”等等.注意:定理都是真命题,但真命题不一定都是定理,一般选择一些最基本最常用的真命题作为定理,可以用它们为根据推证其它命题,这些被选作定理的真命题,在教科书中是用七年级下册相交线、平行线黑体字排印的.证明:判断一个命题的正确性的推理过程叫做证明.注意:在几何问题的研究上,必须经过证明,才能作出真实可靠的判断.如“对顶角相等”这个命题,如果只采用测量的方法,只能测量有限个对顶角是相等的,但采用推理方法证明了对顶角相等,那么就可以确信一切对顶角相等.证明的一般步骤:(1)根据题意,画出图形;(2)根据题设、结论、结合图形,写出已知求证;七年级下册相交线、平行线(3)经过分析,找出由已知推出求证的途径,写出证明过程.注意:①在一般情况下,分析的过程不要求写出来,有些题目中,已经画出了图形,写好了已知、求证,这时,只要写出“证明”一项就可以了.②证明中的每一步推理都要有根据,不能“想当然”,这些根据,可以是已知条件,也可以是定义、公理,已经学过的定理,在初学证明时,要求把根据写在第一步推理后面的括号内,其中像等量代换,利用等式性质加减乘除等代数运算可不注理由.。
2022年全国中考数学试题真题汇编 相交线与平行线(一)
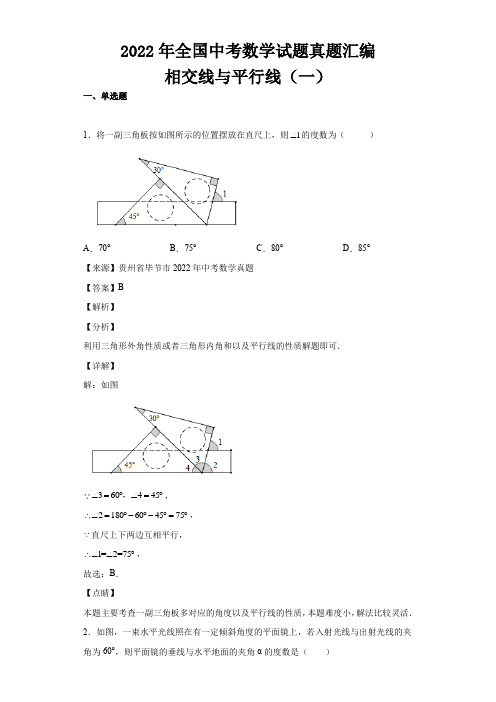
2022年全国中考数学试题真题汇编相交线与平行线(一)一、单选题1.将一副三角板按如图所示的位置摆放在直尺上,则1∠的度数为()A.70°B.75°C.80°D.85°【来源】贵州省毕节市2022年中考数学真题【答案】B【解析】【分析】利用三角形外角性质或者三角形内角和以及平行线的性质解题即可.【详解】解:如图,,∠=︒∠=︒360445∴∠=︒-︒-︒=︒,2180604575直尺上下两边互相平行,1=2=75∴∠∠︒,故选:B.【点睛】本题主要考查一副三角板多对应的角度以及平行线的性质,本题难度小,解法比较灵活.2.如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是()A.15°B.30°C.45°D.60°【来源】山东省潍坊市2022年中考数学真题【答案】B【解析】【分析】作CD⊥平面镜,垂足为G,根据EF⊥平面镜,可得CD//EF,根据水平线与底面所在直线平行,进而可得夹角α的度数.【详解】解:如图,作CD⊥平面镜,垂足为G,⊥EF⊥平面镜,⊥CD//EF,⊥⊥CDH=⊥EFH=α,根据题意可知:AG⊥DF,⊥⊥AGC=⊥CDH=α,⊥⊥AGC=α,⊥⊥AGC12=∠AGB12=⨯60°=30°,⊥α=30°.故选:B.【点睛】本题考查了入射角等于反射角问题,解决本题的关键是法线CG 平分⊥AGB . 3.如图,直线//,1130a b ∠=︒,则2∠等于( )A .70︒B .60︒C .50︒D .40︒【来源】山东省淄博市2022年中考数学试题【答案】C【解析】【分析】如图,由题意易得⊥2+⊥3=180°,⊥1=⊥3,然后问题可求解.【详解】解:如图所示:⊥//a b ,⊥⊥2+⊥3=180°,⊥31130∠=∠=︒,⊥250∠=︒;故选C .【点睛】本题主要考查平行线的性质及对顶角的定义,熟练掌握平行线的性质及对顶角的定义是解题的关键.4.如图,//m n ,其中140∠=︒,则2∠的度数为( )A .130︒B .140︒C .150︒D .160︒【来源】重庆市数学试题【答案】B【解析】【分析】根据两直线平行同旁内角互补,可求出2∠的对顶角即可.【详解】解:如图://m n ,13180∠+∠=︒,3140∴∠=︒,2,3∠∠互为对顶角;23140∴∠=∠=︒,故选:B .【点睛】本题考查了平行线的性质,对顶角、解题的关键是:利用平行线的性质得出同旁内角互补,再利用对顶角相等即可求解.5.如图,直线12l l //,直线3l 交1l 于点A ,交2l 于点B ,过点B 的直线4l 交1l 于点C .若350∠=︒,123240∠+∠+∠=︒,则4∠等于( )A .80︒B .70︒C .60︒D .50︒【来源】内蒙古包头市、巴彦淖尔市2022年中考数学真题【答案】B【解析】根据平行线性质计算角度即可.【详解】解:⊥12l l //,350∠=︒,⊥1=18050130∠︒-︒=︒,⊥123240∠+∠+∠=︒,⊥2=240-180=60∠︒︒,⊥4=1802180605070BAC ACB ∠∠=︒-∠-∠=︒-︒-︒=︒,故选:B .【点睛】本题主要考查平行线性质,熟练识别同位角、内错角,同旁内角是解决本题的关键. 6.如图,在ABC 中,50B ∠=︒,70C ∠=︒,直线DE 经过点A ,50DAB ∠=︒,则EAC ∠的度数是( )A .40°B .50°C .60°D .70°【来源】内蒙古呼和浩特市2022年中考数学真题【答案】D【解析】【分析】根据B DAB ∠=∠可判断//DE BC ,再利用两直线平行内错角相等即可得出结论.【详解】50,50B DAB ∠=︒∠=︒,直线DE 经过点A ,//DE BC ∴70C ∠=︒70C EAC ∴∠=∠=︒故选:D .本题考查了平行线的判定和性质,熟练掌握平行线的判定定理和性质定理是解题关键.7.如图,下列两个角是同旁内角的是( )A .1∠与2∠B .1∠与3∠C .1∠与4∠D .2∠与4∠【来源】广西贺州市2022年中考数学真题【答案】B【解析】【分析】根据同旁内角的概念求解即可.【详解】解:由图可知,⊥1与⊥3是同旁内角,⊥1与⊥2是内错角,⊥4与⊥2是同位角,故选:B .【点睛】本题考查了同旁内角的概念,属于基础题,熟练掌握同位角,同旁内角,内错角的概念是解决本题的关键.8.如图,//AB CD ,EF CD ⊥于点F ,若150BEF ∠=︒,则ABE ∠=( )A .30B .40︒C .50︒D .60︒【来源】山东省东营市2022年中考数学真题【解析】【分析】过点E 作EH ⊥CD ,由此求出90HEF ∠=︒,得到60BEH ∠=︒,根据平行线的推论得到AB ⊥EH ,利用平行线的性质求出答案.【详解】解:过点E 作EH ⊥CD ,如图,⊥180DFE HEF ∠+∠=︒,⊥EF CD ⊥,⊥90DFE ∠=︒,⊥90HEF ∠=︒,⊥150BEF ∠=︒,⊥60BEH ∠=︒,⊥EH ⊥CD ,//AB CD ,⊥AB ⊥EH ,⊥ABE ∠=60BEH ∠=︒,故选:D .【点睛】此题考查平行线的推论,平行线的性质,正确引出辅助线、熟记定理是解题的关键. 9.如图,//a b ,M ,N 分别在a ,b 上,P 为两平行线间一点,那么123∠+∠+∠= ( )A .180︒B .270︒C .360︒D .540︒【来源】初中数学【答案】C【解析】【分析】 首先过点P 作P A ⊥a ,构造三条平行线,然后利用两直线平行,同旁内角互补进行做题.【详解】解:过点P 作P A ⊥a ,则a ⊥b ⊥P A ,⊥⊥1+⊥MP A =180°,⊥3+⊥NP A =180°,⊥⊥1+⊥MPN +⊥3=360°.故选:C .【点睛】本题考查了平行线的性质,两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.10.如图,//a b ,160∠=︒,则2∠的度数为( )A .90︒B .100︒C .110︒D .120︒【来源】河南省2022年中考数学真题【答案】D【解析】【分析】先利用“两直线平行,同位角相等”求出⊥3,再利用邻补角互补求出⊥2.【详解】解:如图,⊥a ⊥b ,⊥⊥1=⊥3=60°,⊥⊥2=180°-⊥3=120°,【点睛】本题考查了平行线的性质和邻补角互补的性质,解决本题的关键是牢记相关概念,本题较基础,考查了学生的基本功.11.一把直尺与一块直角三角板按如图方式摆放,若⊥1=47°,则⊥2=()A.40°B.43°C.45°D.47°【来源】浙江省台州市2022年中考数学真题【答案】B【解析】【分析】过三角板的直角顶点作直尺两边的平行线,根据平行线的性质即可求解.【详解】解:如图,过三角板的直角顶点作直尺两边的平行线,⊥直尺的两边互相平行,∠=∠=︒,⊥3147∠=︒-∠=︒,⊥490343∠=∠=︒,⊥2443【点睛】本题考查平行线的性质,掌握平行线的性质是解题的关键.12.如图,将一块含有60︒角的直角三角板放置在两条平行线上,若145∠=︒,则2∠为( )A .15︒B .25︒C .35︒D .45︒【来源】湖北省随州市2022年中考数学真题【答案】A【解析】【分析】过60°角顶点作直线平行于已知直线,然后根据平行线的性质推出⊥1+⊥2=60°,从而求出⊥2即可.【详解】如图,已知//a b ,作直线//c a ,则//c b ,则⊥1=⊥3,⊥2=⊥4,⊥⊥3+⊥4=60°,⊥⊥1+⊥2=60°,⊥⊥2=60°-⊥1=15°,故选:A .【点睛】本题考查平行线的基本性质,理解平行线的性质定理是解题关键.13.一副三角板按如图方式放置,含45︒角的三角板的斜边与含30°角的三角板的长直∠的度数是()角边平行,则αA.10︒B.15︒C.20︒D.25︒【来源】山东省菏泽市2022年中考数学真题【答案】B【解析】【分析】利用两直线平行,内错角相等传递等角后计算即可【详解】如图,⊥AB∥DE,⊥⊥BAE=⊥E=30°,∠=⊥CAB-⊥BAE= 45°-30°=15°,⊥α故选B【点睛】本题考查了平行线的性质,三角板的意义,熟练掌握平行线的性质是解题的关键.14.如图,一束光线AB先后经平面镜OM,ON反射后,反射光线CD与AB平行,当∠的度数为()∠=︒时,DCN40ABMA .40︒B .50︒C .60︒D .80︒【来源】四川省达州市2022年中考数学真题【答案】B【解析】【分析】过点B 作BE OM ⊥,过点C 作CE ON ⊥,BE 与CE 相交于点E ;根据余角性质计算得CBE ∠;根据平行线性质,得BCD ∠,结合角平分线性质,计算得DCE ∠;再根据余角性质计算,即可得到答案.【详解】如下图,过点B 作BE OM ⊥,过点C 作CE ON ⊥,BE 与CE 相交于点E⊥40ABM ∠=︒,CBE ABE ∠=∠⊥9050CBE ABE ABM ∠=∠=︒-∠=︒⊥100ABC ABE CBE ∠=∠+∠=︒⊥CD 与AB 平行⊥18080BCD ABC ∠=︒-∠=︒⊥BCE DCE ∠=∠,BCE DCE BCD ∠+∠=∠ ⊥1402BCE DCE BCD ∠=∠=∠=︒ ⊥9050DCN DCE ∠=︒-∠=︒故选:B .【点睛】本题考查了平行线、角平分线、垂线、余角的知识;解题的关键是熟练掌握平行线的性质,从而完成求解.15.将一副直角三角板按如图方式摆放,若直线//a b ,则1∠的大小为( )A .45︒B .60︒C .75︒D .105︒【来源】湖南省岳阳市2022年中考数学真题【答案】C【解析】【分析】根据平行线的性质解题.【详解】⊥a ⊥b⊥()1+45+60=180∠︒︒︒(两直线平行,同旁内角互补)⊥1=75︒∠.故选:C .【点睛】本题考查平行线的性质.两直线平行,同旁内角互补.16.如图,设点P 是直线l 外一点,PQ l ⊥,垂足为点Q ,点T 是直线l 上的一个动点,连接PT ,则( )A .PT PQ ≥2B .PT PQ ≤2C .PT PQ ≥D .PT PQ ≤【来源】浙江省杭州市2022年中考数学真题【答案】C【解析】【分析】根据垂线段距离最短可以判断得出答案.【详解】解:根据点P 是直线l 外一点,PQ l ⊥,垂足为点Q ,PQ ∴是垂线段,即连接直线外的点P 与直线上各点的所有线段中距离最短, 当点T 与点Q 重合时有PQ PT =,综上所述:PT PQ ≥,故选:C .【点睛】本题考查了垂线段最短的定义,解题的关键是:理解垂线段最短的定义.17.如图,直线DE 过点A ,且//DE BC .若60B ∠=︒,150∠=︒,则2∠的度数为()A .50︒B .60︒C .70︒D .80︒【来源】新疆维吾尔自治区、生产建设兵团2022年中考数学试题【答案】C【解析】【分析】根据两直线平行同旁内角互补求出⊥BAE ,即可求出⊥2.【详解】⊥//DE BC ,⊥180B BAE ∠+∠=︒,⊥180120BAE B ∠=︒-∠=︒,即:12120∠+∠=︒,⊥2120170∠=︒-∠=︒,故选:C .【点睛】本题考查平行线的性质,熟记平行线的基本性质是解题关键.18.如图,//AB CD ,//BC DE ,若7228B '∠=︒,那么D ∠的度数是( )A .7228'︒B .10128'︒C .10732'︒D .12732'︒【来源】山东省济宁市2022年中考数学真题【答案】C【解析】【分析】先根据//AB CD 求出C ∠的度数,再由//BC DE 即可求出D ∠的度数.【详解】解:⊥//AB CD ,7228B '∠=︒,⊥7228C B '∠=∠=︒,⊥//BC DE ,⊥180D C ∠+∠=︒,⊥18010732D C '∠=︒-∠=︒,故选:C .【点睛】本题主要考查平行线的性质以及角度的计算,熟记平行线的性质定理是解题的关键. 19.如图,直线c 与直线a 、b 都相交.若//a b ,155∠=︒,则2∠=( )A .60︒B .55︒C .50︒D .45︒【来源】云南省2022年中考数学真题【答案】B【解析】【分析】直接利用平行线的性质:两直线平行,同位角相等,即可得出答案.【详解】解:如图,1=55∠︒,3=55,∴∠︒⊥a ⊥b ,⊥3=55°,⊥⊥2=⊥3=55°.故选B .【点睛】此题主要考查了平行线的性质,正确掌握平行线的基本性质是解题关键.20.如图,AB ⊥CD ⊥EF ,若⊥ABC =130°,⊥BCE =55°,则⊥CEF 的度数为()A .95°B .105°C .110°D .115°【来源】2022年山东省聊城市中考数学真题试卷【答案】B【解析】【分析】由//AB CD 平行的性质可知ABC DCB ∠=∠,再结合//EF CD 即可求解.【详解】解://AB CD130ABC DCB ∴∠=∠=︒1305575ECD DCB BCE ∴∠=∠-∠=︒-︒=︒//EF CD180ECD CEF ∴∠+∠=︒18075105CEF ∴∠=︒-︒=︒故答案是:B .【点睛】本题考查平行线的性质和角度求解,难度不大,属于基础题.解题的关键是掌握平行线的性质.21.如图,点O 在直线AB 上,OC OD ⊥.若120AOC ∠=︒,则BOD ∠的大小为( )A .30B .40︒C .50︒D .60︒【来源】北京市2022年中考数学真题试题【答案】A【解析】【分析】由题意易得60COB ∠=︒,90COD ∠=︒,进而问题可求解.【详解】解:⊥点O 在直线AB 上,OC OD ⊥,⊥180AOC COB ∠+∠=︒,90COD ∠=︒,⊥120AOC ∠=︒,⊥60COB ∠=︒,⊥9030BOD COB ∠=︒-∠=︒;故选A .【点睛】本题主要考查垂直的定义及邻补角的定义,熟练掌握垂直的定义及邻补角的定义是解题的关键.22.如图,在⊥ABC 中,⊥A =70°,⊥C =30°,BD 平分⊥ABC 交AC 于点D ,DE ⊥AB ,交BC 于点E ,则⊥BDE 的度数是( )A .30°B .40°C .50°D .60°【来源】江苏省宿迁市2022年中考数学真题【答案】B【解析】【分析】由三角形的内角和可求⊥ABC ,根据角平分线可以求得⊥ABD ,由DE //AB ,可得⊥BDE =⊥ABD 即可.【详解】解:⊥⊥A +⊥C =100°⊥⊥ABC =80°,⊥BD 平分⊥BAC ,⊥⊥ABD =40°,⊥DE ⊥AB ,⊥⊥BDE =⊥ABD =40°,故答案为B .【点睛】本题考查三角形的内角和定理、角平分线的意义、平行线的性质,灵活应用所学知识是解答本题的关键.23.阅读下列材料,其⊥~⊥步中数学依据错误的是( ) 如图:已知直线//b c ,a b ⊥,求证:a c ⊥.A .⊥B .⊥C .⊥D .⊥【来源】湖北省荆州市2022年中考数学真题【答案】C【解析】【分析】根据垂直的定义和平行线的性质进行判断即可【详解】解:证明:⊥⊥a b ⊥(已知)⊥190∠=︒(垂直的定义)⊥又⊥//b c (已知)⊥⊥12∠=∠(两直线平行,同位角相等)⊥2190∠=∠=︒(等量代换)⊥⊥a c ⊥(垂直的定义).所以错在⊥故选:C【点睛】本题考查了垂直的定义和平行线的性质,熟练掌握平行线的性质是解题的关键. 24.如图,将直角三角板放置在矩形纸片上,若148∠=︒,则2∠的度数为()A .42°B .48°C .52°D .60°【来源】四川省眉山市2022年中考数学真题【答案】A【解析】【分析】先通过作辅助线,将⊥1转化到⊥BAC ,再利用直角三角形两锐角互余即可求出⊥2.【详解】解:如图,延长该直角三角形一边,与该矩形纸片一边的交点记为点A ,由矩形对边平行,可得⊥1=⊥BAC ,因为BC ⊥AB ,⊥⊥BAC +⊥2=90°,⊥⊥1+⊥2=90°,因为⊥1=48°,⊥⊥2=42°;故选:A .【点睛】本题考查了矩形的性质、平行线的性质、直角三角形的性质等内容,要求学生能根据题意理解其中的隐含关系,解决本题的关键是对角进行的转化,因此需要牢记并能灵活应用相关性质等.25.如图,//AB CD ,EF 分别与AB ,CD 交于点G ,H ,100AGE ∠=°,则DHF ∠的度数为( )A .100︒B .80︒C .50︒D .40︒【来源】湖南省长沙市2022年中考试数学真题【答案】A【解析】【分析】先根据平行线的性质可得100CHE AGE ∠=∠=︒,再根据对顶角相等即可得.【详解】解://,100AB CD AGE ∠=︒,100CHE AGE ∴∠=∠=︒,100CHE DHF ∴∠=∠=︒(对顶角相等),故选:A .【点睛】本题考查了平行线的性质、对顶角相等,熟练掌握平行线的性质是解题关键. 26.如图,直线//,DE BF Rt ABC 的顶点B 在BF 上,若20CBF ∠=︒,则ADE ∠=()A .70︒B .60︒C .75︒D .80︒【来源】甘肃省武威市2022年中考数学试卷【答案】A【解析】【分析】先求出CBF ∠的余角⊥ABF ,利用平行线性质可求⊥ADE .【详解】解:⊥Rt ABC ,20CBF ∠=︒⊥⊥ABC =90°,⊥ABF =90°-⊥CBF =90°-20°=70°,⊥//DE BF ,⊥⊥ADE =⊥ABF =70°.故选择A .本题考查余角性质,平行线性质,掌握余角性质,平行线性质是解题关键. 27.某同学的作业如下框,其中⊥处填的依据是( )A .两直线平行,内错角相等B .内错角相等,两直线平行C .两直线平行,同位角相等D .两直线平行,同旁内角互补 【来源】浙江省金华市2022年中考数学真题【答案】C【解析】【分析】首先准确分析题目,已知12//l l ,结论是34∠=∠,所以应用的是平行线的性质定理,从图中得知⊥3和⊥4是同位角关系,即可选出答案.【详解】解:⊥12//l l ,⊥34∠=∠(两直线平行,同位角相等).故选C .【点睛】本题主要考查了平行线的性质的应用,解题的关键是理解平行线之间内错角的位置,从而准确地选择出平行线的性质定理.28.设a ,b ,c 为互不相等的实数,且4155b a c =+,则下列结论正确的是( ) A .a b c >> B .c b a >> C .4()a b b c -=- D .5()a c a b -=-【来源】安徽省2022年中考数学真题【答案】D【解析】举反例可判断A 和B ,将式子整理可判断C 和D .【详解】解:A .当5a =,10c =,41655b ac =+=时,c b a >>,故A 错误; B .当10a =,5c =,41955b ac =+=时,a b c >>,故B 错误; C .4()a b b c -=-整理可得1455b a c =-,故C 错误;D .5()a c a b -=-整理可得4155b ac =+,故D 正确; 故选:D .【点睛】本题考查等式的性质,掌握等式的性质是解题的关键.29.如图,直线a //b ,148∠︒=,则2∠等于( )A .24°B .42°C .48°D .132°【来源】2022年广西贺州市中考数学试卷【答案】C【解析】【分析】根据两直线平行,内错角相等求解即可.【详解】解:⊥直线a ⊥b ,⊥2148∠=∠=︒.故选:C .【点睛】本题考查了平行线的性质,用到的知识点为:两直线平行,内错角相等,解题关键是熟记平行线的性质,准确识图.二、填空题30.如图,直线l 1,l 2相交于点O ,⊥1=70°,则⊥2=_____°.【来源】2022年广西桂林市中考数学真题【答案】70【解析】【分析】根据对顶角的性质解答即可.【详解】解:⊥⊥1和⊥2是一对顶角,⊥⊥2=⊥1=70°,故答案为:70.【点睛】本题主要考查了对顶角,熟练掌握对顶角相等是解答本题的关键.31.如图,直线a⊥b,直线c与直线a,b相交,若⊥1=54°,则⊥3=________度.【来源】2022年湖北省孝感市中考数学试卷【答案】54【解析】【分析】根据对顶角相等和平行线的性质“两直线平行同位角相等”,通过等量代换求解.【详解】因为a⊥b,∠=∠,所以23所以31∠=∠,因为154∠=︒,所以354∠=︒,故答案为:54.【点睛】本题考查了平行线的性质和对顶角的性质,熟练掌握对顶角相等,两直线平行同位角相等、内错角相等,加以灵活运用求解相关角的度数是解题关键.32.请写出命题“如果a b >,那么0b a -<”的逆命题:________.【来源】2022年江苏省无锡市中考数学真题【答案】如果0b a -<,那么a b >【解析】【分析】根据逆命题的概念解答即可.【详解】解:命题“如果a b >,那么0b a -<”的逆命题是“如果0b a -<,那么a b >”, 故答案为:如果0b a -<,那么a b >.【点睛】此题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.33.如图,C 岛在A 岛的北偏东50︒方向,C 岛在B 岛的北偏西35︒方向,则ACB ∠的大小是_____.【来源】2022年湖北省宜昌市中考数学真题【答案】85︒##85度【分析】∥交AB于F,根据方位角的定义,结合平行线性质即可求解.过C作CF DA【详解】解:C岛在A岛的北偏东50︒方向,DAC∴∠=︒,50C岛在B岛的北偏西35︒方向,∴∠=︒,35CBE∥交AB于F,如图所示:过C作CF DADA CF EB∴∥∥,∴∠=∠=︒∠=∠=︒,50,35FCA DAC FCB CBEACB FCA FCB∴∠=∠+∠=︒,85故答案为:85︒.【点睛】本题考查方位角的概念与平行线的性质求角度,理解方位角的定义,并熟练掌握平行线的性质是解决问题的关键.34.如图6,已知直线a⊥b,⊥BAC=90°,⊥1=50°,则⊥2=______.【来源】2022年四川省乐山市中考数学真题【答案】40°##40度根据平行线的性质可以得到⊥3的度数,进一步计算即可求得⊥2的度数.【详解】解:⊥a ⊥b ,⊥⊥1=⊥3=50°,⊥⊥BAC =90°,⊥⊥2+⊥3=90°,⊥⊥2=90°-⊥3=40°,故答案为:40°.【点睛】本题考查平行线的性质,解答本题的关键是明确题意,利用数形结合的思想解答. 35.如图,已知a b ∥,1110∠=︒,则2∠的度数为________.【来源】2022年四川省眉山市中考数学真题【答案】110︒##110度【解析】【分析】根据题意,由平行线的性质“两直线平行,同位角相等”可知3=1∠∠,再借助3∠与2∠为对顶角即可确定2∠的度数.【详解】解:如下图,⊥a b ∥,1110∠=︒,⊥3=1110∠∠=︒,⊥3∠与2∠为对顶角,⊥2=3110∠∠=︒.故答案为:110︒.【点睛】此题考查了对顶角的性质和平行线的性质,熟记“两直线平行,同位角相等”是解题的关键.36.将一副三角板如图摆放,则______⊥______,理由是______.【来源】2022年甘肃省兰州市中考数学试卷(A 卷)【答案】 BC DE 内错角相等,两直线平行【解析】【分析】根据三角板的角度可知90BCA DEF ∠=∠=︒,根据内错角相等,两直线平行判断即可.【详解】解:一副三角板如图摆放,⊥90BCA DEF ∠=∠=︒,⊥//BC DE (内错角相等,两直线平行),故答案为:BC ;DE ;内错角相等,两直线平行.本题考查了平行线的判定,熟知平行线的判定定理是解本题的关键.37.如图,直线//a b ,若128∠=︒,则2∠=____.【来源】2022年四川省绵阳市中考真题数学试卷【答案】152︒【解析】【分析】利用平行线的性质可得3128∠=∠=︒,再利用邻补角即可求2∠的度数.【详解】解:如图,//a b ,128∠=︒,3128∴∠=∠=︒,21803152∴∠=︒-∠=︒.故答案为:152︒.【点睛】本题主要考查平行线的性质,解答的关键是结合图形分析清楚角与角之间的关系. 38.“如果a b =,那么a b =”的逆命题是___________.【来源】江苏省苏州市数学考试【答案】如果a b =,那么a b =【解析】【分析】把一个命题的条件和结论互换就得到它的逆命题,从而得出答案.【详解】解:“如果a b =,那么a b =”的逆命题是:“如果a b =,那么a b =”,故答案为:如果a b =,那么a b =.【点睛】本题考查命题与定理,解题的关键是理解题意,掌握逆命题的定义.39.如图,⊥ABC 沿BC 所在直线向右平移得到⊥DEF ,若EC =2,BF =8,则BE =___.【来源】辽宁省大连市数学试题【答案】3【解析】【分析】利用平移的性质解决问题即可.【详解】解:由平移的性质可知,BE =CF ,⊥BF =8,EC =2,⊥BE +CF =8﹣2=6,⊥BE =CF =3,⊥平移的距离为3,故答案为:3.【点睛】本题考查平移的性质,解题的关键是熟练掌握平移变换的性质,属于中考常考题型. 40.如图,直线a ,b 被直线c 所截,已知//a b ,1130∠=︒,则2∠为______度.【来源】湖南省湘潭市2022年中考数学真题【答案】50【解析】【详解】解:如图,⊥//a b ,1130∠=︒,⊥⊥3=130°,又⊥⊥2+⊥3=180°,⊥⊥2=180°-⊥3=180°-130°=50°.故答案为:50.【点睛】此题主要考查了平行线的性质以及邻补角,熟练掌握它们的性质是解答此题的关键. 41.如图,直线//AB CD ,一块含有30°角的直角三角尺顶点E 位于直线CD 上,EG 平分CEF ∠,则1∠的度数为_________°.【来源】辽宁省阜新市2022年中考数学试题【答案】60【解析】【分析】根据角平分线的定义可求出CEG ∠的度数,即可得到CEF ∠的度数,再利用平行线的性质即可解决问题.【详解】一块含有30°角的直角三角尺顶点E 位于直线CD 上,30FEG ∴∠=︒, EG 平分CEF ∠,30CEG FEG ∴∠=∠=︒,60∴∠=∠+∠=︒,CEF CEG FEGAB CD,//∴∠=∠=︒.CEF160故答案为:60.【点睛】本题考查了角平分线定义和平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.42.如图,直线a,b被直线c所截,当⊥1 ___⊥2时,a//b.(用“>”,“<”或“=”填空)【来源】2022年广西桂林市中考数学真题【答案】=.【解析】【分析】由图形可知⊥1 与⊥2是同位角,利用直线平行判定定理可以确定⊥1 =⊥2,可判断a//b.【详解】解:⊥直线a,b被直线c所截,⊥1与⊥2是同位角,⊥当⊥1 =⊥2,a//b.故答案为=.【点睛】本题考查平行线判定,掌握平行线判定判定定理是解题关键.43.如图,AB⊥CD,CB平分⊥ECD,若⊥B=26°,则⊥1的度数是________.【来源】广西贵港市2022年中考数学真题【答案】52︒【分析】根据平行线的性质得出26B BCD ∠=∠=︒,根据角平分线定义求出252ECD BCD ∠=∠=︒,再根据平行线的性质即可得解.【详解】解://AB CD ,26B ∠=︒,26BCD B ∴∠=∠=︒, CB 平分ECD ∠,252ECD BCD ∴∠=∠=︒,//AB CD ,152ECD ∴∠=∠=︒,故答案为:52︒.【点睛】本题考查了平行线的性质和角平分线定义的应用,能根据平行线的性质求出B BCD ∠=∠是解此题的关键.44.如图,直线//,160a b ∠=︒,则2∠的度数是______︒.【来源】广西柳州市2022年中考数学真题试卷【答案】60【解析】【分析】根据平行线的性质可得⊥1=⊥3,根据对顶角相等即可求得⊥2的度数.【详解】⊥a ⊥b ,如图⊥⊥3=⊥1=60゜⊥⊥2=⊥3故答案为:60【点睛】本题考查了平行线的性质、对顶角的性质,掌握这两个性质并熟练运用是关键. 45.如图,已知//AB CD ,BC 是ABD ∠的平分线,若264∠=︒,则3∠=________.【来源】湖南省张家界市2022年中考数学真题试题【答案】58°【解析】【分析】先根据对顶角的性质可得⊥BDC =264∠=︒,然后根据平行线的性质求得⊥ABC ,最后根据角平分线的定义求解即可.【详解】解:⊥⊥BDC 和⊥2是对顶角⊥⊥BDC =264∠=︒⊥//AB CD⊥⊥BDC +⊥ABD =180°,即⊥ABD =116°⊥BC 是ABD ∠的平分线 ⊥⊥3=⊥1=12⊥ABD =58°.故填:58°.本题主要考查了平行线的性质、对顶角相等以及角平分线的相关知识,掌握平行线的性质成为解答本题的关键.46.如图,AB 与CD 相交于点O ,OE 是AOC ∠的平分线,且OC 恰好平分EOB ∠,则AOD ∠=_______度.【来源】湖南省益阳市2022年中考数学真题【答案】60【解析】【分析】先根据角平分线的定义、平角的定义可得60COB ∠=︒,再根据对顶角相等即可得.【详解】解:设2AOC x ∠=, OE 是AOC ∠的平分线,12AOE EOC AOC x ∴∠=∠=∠=, OC 平分EOB ∠,COB EOC x ∴∠=∠=,又180AOE EOC COB ∠+∠+∠=︒,180x x x ∴++=︒,解得60x =︒,即60COB ∠=︒,由对顶角相等得:60AOD COB ∠=∠=︒,故答案为:60.【点睛】本题考查了角平分线的定义、平角的定义、对顶角相等,熟练掌握角平分线的定义是解题关键.47.如图,点O ,C 在直线n 上,OB 平分AOC ∠,若//m n ,156∠=︒,则2∠=_______________.【来源】广西贵港市2022年中考数学真题【答案】62°【解析】【分析】根据//m n 和OB 平分AOC ∠,计算出BOC ∠的度数,便可求解.【详解】解:如图:∵//m n∴156AON ∠=∠=, 2BOC ∠=∠180124AOC AON ∴∠=-∠=∵OB 平分AOC ∠1622BOC AOC ∴∠=∠= 62BOC ∴∠=故答案为62°【点睛】本题考查平行线性质,以及角平分线性质,属于基础题.三、解答题48.如图,在平行四边形ABCD 中,点E ,F 分别在AD ,BC 上,且ED BF =,连接AF ,CE ,AC ,EF ,且AC 与EF 相交于点O .(1)求证:四边形AFCE 是平行四边形;(2)若AC 平分8FAE AC ∠=,,3tan 4DAC ∠=,求四边形AFCE 的面积. 【来源】2022年广西贺州市中考数学真题【答案】(1)详见解析;(2)24.【解析】【分析】(1)根据一组对边平行且相等的四边形是平行四边形解答;(2)由平行线的性质可得EAC ACF ∠=∠,再根据角平分线的性质解得EAC FAC ∠=∠,继而证明AF FC =,由此证明平行四边形AFCE 是菱形,根据菱形的性质得到14,2AO AC AC EF ==⊥,结合正切函数的定义解得3EO =,最后根据三角形面积公式解答.(1) 证明:四边形ABCD 是平行四边形AD BC AE FC ∴=,∥ED BF =AD ED BC BF -=-,即AE FC =.∴四边形AFCE 是平行四边形.(2)解:AE FC ∥,EAC ACF ∴∠=∠. AC 平分FAE ∠,EAC FAC ∠=∠∴.ACF FAC ∴∠=∠.AF FC ∴=,由(1)知四边形AFCE 是平行四边形,∴平行四边形AFCE 是菱形.14,2AO AC AC EF ∴==⊥,在 Rt AOE △中,34,tan 4AO DAC =∠=, 3EO ∴=. 11S 43622AOE AO EO ∴=⋅=⨯⨯=△ 424AOE AFCE S S ==菱形.【点睛】本题考查平行四边形的判定、菱形的判定与性质、平行线的性质、角平分线的性质、正切函数的定义等知识,是重要考点,难度一般,掌握相关知识是解题关键. 49.如图,在四边形ABCD 中,AD BC ∥,80B ∠=︒.(1)求BAD ∠的度数;(2)AE 平分BAD ∠交BC 于点E ,50BCD ∠=︒.求证:AE DC ∥.【来源】2022年湖北省武汉市中考数学真题【答案】(1)100BAD ∠=︒(2)详见解析【解析】【分析】(1)根据两直线平行,同旁内角互补,即可求解;(2)根据AE 平分BAD ∠,可得50DAE ∠=︒.再由AD BC ∥,可得50AEB DAE ∠=∠=︒.即可求证.(1)解:⊥AD BC ∥,⊥180B BAD ∠+∠=°,⊥80B ∠=︒,⊥100BAD ∠=︒.(2)证明:⊥AE 平分BAD ∠,⊥50DAE ∠=︒.⊥AD BC ∥,⊥50AEB DAE ∠=∠=︒.⊥50BCD ∠=︒,⊥BCD AEB ∠=∠.⊥AE DC ∥.【点睛】本题主要考查了平行线的判定和性质,熟练掌握平行线的判定和性质定理是解题的关键 50.如图,//AB CD ,B D ∠=∠,直线EF 与AD ,BC 的延长线分别交于点E ,F .求证:DEF F ∠=∠.【来源】湖北省武汉市2022年中考数学真题【答案】见解析【解析】【分析】根据已知条件//AB CD ,B D ∠=∠,得到DCF D ∠=∠,从而得到//AD BC ,即可证明DEF F ∠=∠.【详解】证明:⊥//AB CD ,⊥DCF B ∠=∠.⊥B D ∠=∠,⊥DCF D ∠=∠.⊥//AD BC .⊥DEF F ∠=∠.【点睛】本题考查平行线的性质和判定.平行线的性质:两直线平行,内错角相等.平行线的判定:同位角相等,两直线平行.。
专题34相交线与平行线(1) 中考数学真题分项汇编系列2(学生版)

专题34相交线与平行线(1)(全国一年)学校:___________姓名:___________班级:___________考号:___________一、单选题1.(2020·浙江衢州中考真题)过直线l 外一点P 作直线l 的平行线,下列尺规作图中错误的是( ) A . B .C .D .2.(2020·广西河池中考真题)如图,直线a ,b 被直线c 所截,则∠1与∠2的位置关系是( )A .同位角B .内错角C .同旁内角D .邻补角3.(2020·贵州黔西中考真题)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1的度数为( )A .37°B .43°C .53°D .54°4.(2020·山东临沂中考真题)如图,在ABC 中,AB AC =,40A ︒∠=,//CD AB ,则BCD ∠=( )A .40︒B .50︒C .60︒D .70︒5.(2020·辽宁大连中考真题)如图,ABC 中,60,40,//A B DE BC ︒︒∠=∠=,则AED ∠的度数是( )A .50︒B .60︒C .70︒D .80︒6.(2020·辽宁鞍山中考真题)如图,直线l 1//l 2,点A 在直线l 1上,以点A 为圆心,适当长为半径画弧,分别交直线l 1、l 2于B 、C 两点,连结AC 、BC .若∠ABC =54°,则∠1的大小为()A .36°.B .54°.C .72°.D .73°.7.(2020·浙江金华中考真题)如图,工人师傅用角尺画出工件边缘AB 的垂线a 和b ,得到a ∥b ,理由是( )A .连结直线外一点与直线上各点的所有线段中,垂线段最短B .在同一平面内,垂直于同一条直线的两条直线互相平行C .在同一平面内,过一点有一条而且仅有一条直线垂直于已知直线D .经过直线外一点,有且只有一条直线与这条直线平行8.(2020·辽宁朝阳中考真题)如图,四边形ABCO 是矩形,点D 是BC 边上的动点(点D 与点B 、点C不重合),则BAD DOC ADO∠+∠∠的值为( )A .1B .12C .2D .无法确定9.(2020·内蒙古呼伦贝尔中考真题)如图,直线//,AB CD AE CE ⊥于点E ,若120EAB ︒∠=,则ECD ∠的度数是( )A .120°B .100°C .150°D .160°10.(2020·山东滨州中考真题)如图,AB//CD ,点P 为CD 上一点,PF 是∠EPC 的平分线,若∠1=55°,则∠EPD 的大小为( )A .60°B .70°C .80°D .100°11.(2020·四川绵阳中考真题)在螳螂的示意图中,AB ∥DE ,△ABC 是等腰三角形,∠ABC =124°,∠CDE =72°,则∠ACD =( )A .16°B .28°C .44°D .45°12.(2020·四川绵阳中考真题)如图,在四边形ABCD 中,∠A =∠C =90°,DF ∥BC ,∠ABC 的平分线BE 交DF 于点G ,GH ⊥DF ,点E 恰好为DH 的中点,若AE =3,CD =2,则GH =( )A .1B .2C .3D .413.(2020·江苏宿迁中考真题)如图,直线a ,b 被直线c 所截,a ∥b ,∠1=50°,则∠2的度数为( )A .40°B .50°C .130°D .150°14.(2020·辽宁沈阳中考真题)如图,直线//AB CD ,且AC CB ⊥于点C ,若35BAC ∠=︒,则BCD ∠的度数为( )A .65°B .55°C .45°D .35°15.(2020·四川眉山中考真题)一副三角板如图所示摆放,则α∠与β∠的数量关系为( )A .180αβ∠+∠=︒B .225αβ∠+∠=︒C .270αβ∠+∠=︒D .αβ∠=∠16.(2020·江苏南通中考真题)如图,已知AB ∥CD ,∠A =54°,∠E =18°,则∠C 的度数是( )A .36°B .34°C .32°D .30°17.(2020·辽宁营口中考真题)如图,AB ∥CD ,∠EFD =64°,∠FEB 的角平分线EG 交CD 于点G ,则∠GEB 的度数为( )A .66°B .56°C .68°D .58°18.(2020·山东淄博中考真题)如图,在四边形ABCD 中,CD ∥AB ,AC ⊥BC ,若∠B =50°,则∠DCA 等于( )A .30°B .35°C .40°D .45°19.(2020·甘肃金昌中考真题)如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节AE 间的距离,若AE 间的距离调节到60cm ,菱形的边长20AB cm =,则DAB ∠的度数是( )A .90︒B .100︒C .120︒D .150︒20.(2020·四川雅安中考真题)下列四个选项中不是命题的是( )A .对顶角相等B .过直线外一点作直线的平行线C .三角形任意两边之和大于第三边D .如果a b a c ==,,那么b c =21.(2020·山东威海中考真题)如图,矩形ABCD 的四个顶点分别在直线3l ,4l ,2l ,1l 上.若直线1234//////l l l l 且间距相等,4AB =,3BC =,则tan α的值为( )A .38B .34C .52D .151522.(2020·山东东营中考真题)如图,直线AB CD 、相交于点,O 射线OM 平分,BOD ∠若42AOC ∠=︒,则AOM ∠等于( )A .159B .161C .169D .13823.(2020·海南中考真题)如图,已知//,AB CD 直线AC 和BD 相交于点,E 若70,40ABE ACD ∠=︒∠=︒,则AEB ∠等于( )A .50︒B .60︒C .70︒D .80︒24.(2020·湖南永州中考真题)已知点()00,P x y 和直线y kx b =+,求点P 到直线y kx b =+的距离d 可用公式0021kx y b d k -+=+计算.根据以上材料解决下面问题:如图,C 的圆心C 的坐标为()1,1,半径为1,直线l 的表达式为26y x =-+,P 是直线l 上的动点,Q 是C 上的动点,则PQ 的最小值是( )A .355B .3515-C .6515-D .225.(2020·湖北荆州中考真题)将一张矩形纸片折叠成如图所示的图形,若30CAB ︒∠=,则ACB ∠的度数是( )A .45︒B .55︒C .65︒D .75︒26.(2020·宁夏中考真题)如图摆放的一副学生用直角三角板,3045F C ∠=∠=,,AB 与DE 相交于点G ,当//EF BC 时,EGB ∠的度数是( )A .135°B .120°C .115°D .105°27.(2020·贵州毕节中考真题)将一幅直角三角板(90A FDE ∠=∠=︒,45F ∠=︒,60C ∠=°,点D 在边AB 上)按图中所示位置摆放,两条斜边为EF ,BC ,且//EF BC ,则ADF ∠等于( )A .70︒B .75︒C .80︒D .85︒28.(2020·广西玉林中考真题)下列命题中,其逆命题是真命题的是( )A .对顶角相等B .两直线平行,同位角相等C .全等三角形的对应角相等D .正方形的四个角相等29.(2020·广西玉林中考真题)如图是A ,B ,C 三岛的平面图,C 岛在A 岛的北偏东35度方向,B 岛在A 岛的北偏东80度方向,C 岛在B 岛的北偏西55度方向,则A ,B ,C 三岛组成一个( )A .等腰直角三角形B .等腰三角形C .直角三角形D .等边三角形30.(2020·湖南郴州中考真题)如图,直线,a b 被直线,c d 所截下列条件能判定//a b 的是( )A .13∠=∠B .24180∠+∠=C .45∠=∠D .12∠=∠31.(2020·广东深圳中考真题)一把直尺与30°的直角三角板如图所示,∠1=40°,则∠2=( )A .50°B .60°C .70°D .80°32.(2020·湖南娄底中考真题)如图,将直尺与三角尺叠放在一起,如果128∠=︒,那么2∠的度数为( )A .62°B .56°C .28°D .72°33.(2020·四川宜宾中考真题)如图,M ,N 分别是ABC ∆的边AB ,AC 的中点,若65,45A ANM ∠=︒∠=︒,则B =( )A .20︒B .45︒C .65︒D .70︒34.(2020·湖北省直辖县级单位中考真题)将一副三角尺如图摆放,点E 在AC 上,点D 在BC 的延长线上,//,90,45,60EF BC B EDF A F ∠=∠=︒∠=︒∠=︒,则CED ∠的度数是( )A .15°B .20°C .25°D .30°35.(2020·湖南长沙中考真题)如图,一块直角三角板的60度的顶点A 与直角顶点C 分别在平行线,FD GH上,斜边AB 平分CAD ∠,交直线GH 于点E ,则ECB ∠的大小为( )A .60︒B .45︒C .30︒D .25︒36.(2020·江苏常州中考真题)如图,直线a 、b 被直线c 所截,//a b ,1140∠=︒,则2∠的度数是( )A .30°B .40°C .50°D .60°37.(2020·辽宁抚顺中考真题)一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若120∠=︒,则∠2的度数是( )A .15°B .20°C .25°D .40°38.(2020·四川内江中考真题)如图,已知直线//a b ,150∠=︒,则2∠的度数为( )A .140︒B .130︒C .50︒D .40︒39.(2020·湖北随州中考真题)如图,直线12//l l ,直线l 与1l ,2l 分别交于A ,B 两点,若160︒∠=,则2∠的度数是( )A .60︒B .100︒C .120︒D .140︒40.(2020·黑龙江齐齐哈尔中考真题)有两个直角三角形纸板,一个含45°角,另一个含30°角,如图①所示叠放,先将含30°角的纸板固定不动,再将含45°角的纸板绕顶点A 顺时针旋转,使BC ∥DE ,如图②所示,则旋转角∠BAD 的度数为( )A .15°B .30°C .45°D .60°41.(2020·湖北孝感中考真题)如图,直线AB ,CD 相交于点O ,OE CD ⊥,垂足为点O .若40BOE ∠=︒,则AOC ∠的度数为( )A .40︒B .50︒C .60︒D .140︒42.(2020·河北中考真题)如图,在平面内作已知直线m 的垂线,可作垂线的条数有( )A .0条B .1条C .2条D .无数条43.(2020·北京中考真题)如图,AB 和CD 相交于点O ,则下列结论正确的是( )A .∠1=∠2B .∠2=∠3C .∠1>∠4+∠5D .∠2<∠544.(2020·湖北鄂州中考真题)如图,//a b ,一块含45︒的直角三角板的一个顶点落在其中一条直线上,若165︒∠=,则2∠的度数为( )A .25︒B .35︒C .55︒D .65︒45.(2020·贵州贵阳中考真题)如图,直线a ,b 相交于点O ,如果1260∠+∠=︒,那么3∠是( )A .150︒B .120︒C .60︒D .3046.(2020·江西中考真题)如图,1265,335︒∠=∠=∠=︒,则下列结论错误的是( )A .//AB CD B .30B ∠=︒C .2C EFC ∠+∠=∠D .CG FG >47.(2020·湖北襄阳中考真题)如图,//AB CD ,直线EF 分别交AB ,CD 于点E ,F ,EG 平分BEF ∠,若64EFG ∠=︒,则EGD ∠的大小是( )A .132︒B .128︒C .122︒D .112︒48.(2020·河南中考真题)如图,1234//,//l l l l ,若170∠=︒,则2∠的度数为( )A .100︒B .110︒C .120︒D .130︒49.(2020·湖南岳阳中考真题)如图,DA AB ⊥,CD DA ⊥,56B ∠=︒,则C ∠的度数是( )A .154︒B .144︒C .134︒D .124︒50.(2020·湖南岳阳中考真题)下列命题是真命题的是( ) A .一个角的补角一定大于这个角 B .平行于同一条直线的两条直线平行 C .等边三角形是中心对称图形D .旋转改变图形的形状和大小51.(2020·湖南怀化中考真题)如图,已知直线a ,b 被直线c 所截,且//a b ,若40α︒∠=,则β∠的度数为( )A .140︒B .50︒C .60︒D .40︒52.(2020·四川广元中考真题)如图,a ∥b,M 、N 分别在a,b 上,P 为两平行线间一点,那么∠1+∠2+∠3=( ).A .180°B .360°C .270°D .540°53.(2020·山东聊城中考真题)如图,在ABC 中,AB =AC ,∠C =65°,点D 是BC 边上任意一点,过点D 作DF ∥AB 交AC 于点E ,则∠FEC 的度数是( )A .120°B .130°C .145°D .150°54.(2020·重庆中考真题)如图,在平面直角坐标系中,矩形ABCD 的对角线AC 的中点与坐标原点重合,点E 是x 轴上一点,连接AE .若AD 平分OAE ∠,反比例函数(0,0)ky k x x=>>的图象经过AE 上的两点A ,F ,且AF EF =,ABE △的面积为18,则k 的值为( )A .6B .12C .18D .2455.(2020·四川自贡中考真题)如图,a ∥b ,150∠=,则2∠的度数为 ( )A .40°B .50°C .55°D .60°56.(2020·四川攀枝花中考真题)如图,平行线AB 、CD 被直线EF 所截,过点B 作BG EF ⊥于点G ,已知150∠=︒,则B ∠=( ).A .20︒B .30︒C .40︒D .50︒二、填空题57.(2020·辽宁大连中考真题)如图,在平面直角坐标系中,正方形ABCD 的顶点A 与D 在函数(0)ky x x=>的图象上,AC x ⊥轴,垂足为C ,点B 的坐标为(0,2),则k 的值为______.58.(2020·云南中考真题)如图,直线c 与直线a 、b 都相交.若a ∥b ,154∠=︒,则2∠=___________度.59.(2020·四川绵阳中考真题)如图,四边形ABCD 中,AB ∥CD ,∠ABC =60°,AD =BC =CD =4,点M 是四边形ABCD 内的一个动点,满足∠AMD =90°,则点M 到直线BC 的距离的最小值为_____.60.(2020·四川凉山中考真题)如图,点C 、D 分别是半圆AOB 上的三等分点,若阴影部分的面积为32π,则半圆的半径OA 的长为__________.61.(2020·云南昆明中考真题)如图,点C 位于点A 正北方向,点B 位于点A 北偏东50°方向,点C 位于点B 北偏西35°方向,则∠ABC 的度数为_____°.62.(2020·四川雅安中考真题)如图,//a b c ,与a b ,都相交,150∠=︒,则2∠=_________.63.(2020·吉林中考真题)如图,某单位要在河岸l 上建一个水泵房引水到C 处,他们的做法是:过点C 作CD l ⊥于点D ,将水泵房建在了D 处.这样做最节省水管长度,其数学道理是_______.64.(2020·湖南益阳中考真题)如图,//AB CD ,AB AE ⊥,42CAE ∠=,则ACD ∠的度数为__________.65.(2020·湖南永州中考真题)已知直线//a b ,用一块含30°角的直角三角板按图中所示的方式放置,若125∠=︒,则2∠=_________.66.(2020·内蒙古通辽中考真题)如图,点O 在直线AB 上,531728AOC ︒'''∠=,则BOC ∠的度数是______.67.(2020·内蒙古中考真题)如图,在平行四边形ABCD 中,2,AB ABC =∠的平分线与BCD ∠的平分线交于点E ,若点E 恰好在边AD 上,则22BE CE +的值为______.68.(2020·陕西中考真题)如图,在正五边形ABCDE 中,DM 是边CD 的延长线,连接BD ,则∠BDM 的度数是_____.69.(2020·江苏盐城中考真题)如图,直线,a b 被直线c 所截,//,160a b ∠=.那么2∠=_______________________.70.(2020·湖北恩施中考真题)如图,直线12//l l ,点A 在直线1l 上,点B 在直线2l 上,AB BC =,30C ∠=︒,180∠=︒,则2∠=______.71.(2020·四川内江中考真题)如图,在矩形ABCD 中,10BC =,30ABD ∠=︒,若点M 、N 分别是线段DB 、AB 上的两个动点,则AM MN +的最小值为___________________.72.(2020·湖南邵阳中考真题)如图,在Rt ABC 中,90ACB ∠=︒,斜边2AB =,过点C 作//CF AB ,以AB 为边作菱形ABEF ,若30F ∠=︒,则Rt ABC 的面积为________.73.(2020·湖北黄冈中考真题)已知:如图,//,75,135AB EF ABC CDF ︒︒∠=∠=,则BCD ∠=_____________度.74.(2020·湖北咸宁中考真题)如图,请填写一个条件,使结论成立:∵__________,∴//a b .75.(2020·湖南湘西中考真题)如图,直线AE ∥BC ,BA AC ⊥,若54ABC ∠=︒,则EAC ∠=___________度.76.(2020·湖南张家界中考真题)如图,AOB ∠的一边OA 为平面镜,38AOB ︒∠=,一束光线(与水平线OB 平行)从点C 射入经平面镜反射后,反射光线落在OB 上的点E 处,则DEB ∠的度数是_______度.77.(2020·湖南湘潭中考真题)如图,点P 是AOC ∠的角平分线上一点,PD OA ⊥,垂足为点D ,且3PD =,点M 是射线OC 上一动点,则PM 的最小值为________.78.(2020·湖南衡阳中考真题)一副三角板如图摆放,且//AB CD ,则∠1的度数为_________.79.(2020·山东临沂中考真题)我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点(2,1)A 到以原点为圆心,以1为半径的圆的距离为_____.80.(2020·四川南充中考真题)如图,两直线交于点O ,若∠1+∠2=76°,则∠1=________度.81.(2020·江苏连云港中考真题)如图,正六边形123456A A A A A A 内部有一个正五形12345B B B B B ,且3344//A A B B ,直线l 经过2B 、3B ,则直线l 与12A A 的夹角α=________︒.三、解答题82.(2020·江苏镇江中考真题)如图,AC 是四边形ABCD 的对角线,∠1=∠B ,点E 、F 分别在AB 、BC 上,BE =CD ,BF =CA ,连接EF . (1)求证:∠D =∠2;(2)若EF ∥AC ,∠D =78°,求∠BAC 的度数.83.(2020·江苏宿迁中考真题)(感知)(1)如图①,在四边形ABCD 中,∠C =∠D =90°,点E 在边CD 上,∠AEB =90°,求证:AE EB =DECB. (探究)(2)如图②,在四边形ABCD 中,∠C =∠ADC =90°,点E 在边CD 上,点F 在边AD 的延长线上,∠FEG =∠AEB =90°,且EF EG =AEEB,连接BG 交CD 于点H .求证:BH =GH . (拓展)(3)如图③,点E 在四边形ABCD 内,∠AEB +∠DEC =180°,且AE EB =DEEC,过E 作EF 交AD于点F ,若∠EFA =∠AEB ,延长FE 交BC 于点G .求证:BG =CG .84.(2020·四川凉山中考真题)如图,AB 是半圆AOB 的直径,C 是半圆上的一点,AD 平分BAC ∠交半圆于点D ,过点D 作DH AC ⊥与AC 的延长线交于点H .(1)求证:DH 是半圆的切线; (2)若25DH =,5sin 3BAC ∠=,求半圆的直径. 85.(2020·黑龙江大庆中考真题)如图,AB ,CD 为两个建筑物,两建筑物底部之间的水平地面上有一点M .从建筑物AB 的顶点A 测得M 点的俯角为45°,从建筑物CD 的顶点C 测得M 点的俯角为75°,测得建筑物AB 的顶点A 的俯角为30°.若已知建筑物AB 的高度为20米,求两建筑物顶点A 、C 之间的距离(结果精确到1m ,参考数据:2 1.414≈,3 1.732≈)86.(2020·山东东营中考真题)如图,C 处是一钻井平台,位于东营港口A 的北偏东60方向上,与港口A 相距602海里,一艘摩托艇从A 出发,自西向东航行至B 时,改变航向以每小时50海里的速度沿BC 方向行进,此时C 位于B 的北偏西45方向,则从B 到达C 需要多少小时?87.(2020·湖北荆州中考真题)如图,将ABC 绕点B 顺时针旋转60度得到DBE ∆,点C 的对应点E 恰好落在AB 的延长线上,连接AD .(1)求证://BC AD ;(2)若AB=4,BC=1,求A ,C 两点旋转所经过的路径长之和.88.(2020·湖北黄石中考真题)如图,,//,70,40AB AE AB DE DAB E =∠=︒∠=︒.(1)求DAE ∠的度数;(2)若30B ∠=︒,求证:AD BC =. 89.(2020·山西中考真题)阅读与思考下面是小宇同学的数学日记,请仔细阅读并完成相应的任务.×年×月×日 星期日没有直角尺也能作出直角今天,我在书店一本书上看到下面材料:木工师傅有一块如图①所示的四边形木板,他已经在木板上画出一条裁割线AB ,现根据木板的情况,要过AB 上的一点C ,作出AB 的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢?办法一:如图①,可利用一把有刻度的直尺在AB 上量出30CD cm =,然后分别以D ,C 为圆心,以50cm 与40cm 为半径画圆弧,两弧相交于点E ,作直线CE ,则DCE ∠必为90︒.办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出M ,N 两点,然后把木棒斜放在木板上,使点M 与点C 重合,用铅笔在木板上将点N 对应的位置标记为点Q ,保持点N 不动,将木棒绕点N 旋转,使点M 落在AB 上,在木板上将点M 对应的位置标记为点R .然后将RQ 延长,在延长线上截取线段QS MN =,得到点S ,作直线SC ,则90RCS ∠=︒.我有如下思考:以上两种办法依据的是什么数学原理呢?我还有什么办法不用直角尺也能作出垂线呢? …… 任务:(1)填空;“办法一”依据的一个数学定理是_____________________________________; (2)根据“办法二”的操作过程,证明90RCS ∠=︒;(3)①尺规作图:请在图③的木板上,过点C 作出AB 的垂线(在木板上保留作图痕迹,不写作法); ②说明你的作法依据的数学定理或基本事实(写出一个即可)90.(2020·四川内江中考真题)如图,抛物线2y ax bx c =++经过A (-1,0)、B (4,0)、C (0,2)三点,点D (x ,y )为抛物线上第一象限内的一个动点. (1)求抛物线所对应的函数表达式;(2)当BCD ∆的面积为3时,求点D 的坐标;(3)过点D 作DE BC ⊥,垂足为点E ,是否存在点D ,使得CDE ∆中的某个角等于ABC ∠的2倍?若存在,求点D 的横坐标;若不存在,请说明理由.91.(2020·广东中考真题)如图,点B 是反比例函数8y x=(0x >)图象上一点,过点B 分别向坐标轴作垂线,垂足为A ,C ,反比例函数ky x=(0x >)的图象经过OB 的中点M ,与AB ,BC 分别相交于点D ,E .连接DE 并延长交x 轴于点F ,点G 与点O 关于点C 对称,连接BF ,BG .(1)填空:k =_________; (2)求BDF ∆的面积;(3)求证:四边形BDFG 为平行四边形.92.(2020·湖北宜昌中考真题)光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射,如图,水面AB 与水杯下沿CD 平行,光线EF 从水中射向空气时发生折射,光线变成FH ,点G 在射线EF 上,已知20,45HFB FED ∠=︒∠=︒,求GFH ∠的度数.93.(2020·湖北孝感中考真题)如图,在ABCD 中,点E 在AB 的延长线上,点F 在CD 的延长线上,满足BE DF =.连接EF ,分别与BC ,AD 交于点G ,H .求证:EG FH =.94.(2020·河北中考真题)如图1和图2,在ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速移动,到达点N 时停止;而点Q 在AC 边上随P 移动,且始终保持APQ B ∠=∠.(1)当点P 在BC 上时,求点P 与点A 的最短距离;(2)若点P 在MB 上,且PQ 将ABC ∆的面积分成上下4:5两部分时,求MP 的长;(3)设点P 移动的路程为x ,当03x ≤≤及39x ≤≤时,分别求点P 到直线AC 的距离(用含x 的式子表示);(4)在点P 处设计并安装一扫描器,按定角APQ ∠扫描APQ ∆区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若94AK =,请直接..写出点K 被扫描到的总时长. 95.(2020·湖北武汉中考真题)如图,直线EF 分别与直线AB ,CD 交于点E ,F .EM 平分BEF ∠,FN 平分CFE ∠,且EM ∥FN .求证:AB ∥CD .96.(2020·北京中考真题)已知:如图,ABC 为锐角三角形,AB=BC ,CD ∥AB . 求作:线段BP ,使得点P 在直线CD 上,且∠ABP=12BAC ∠. 作法:①以点A 为圆心,AC 长为半径画圆,交直线CD 于C ,P 两点;②连接BP .线段BP 就是所求作线段.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹) (2)完成下面的证明. 证明:∵CD ∥AB , ∴∠ABP= . ∵AB=AC , ∴点B 在⊙A 上. 又∵∠BPC=12∠BAC ( )(填推理依据) ∴∠ABP=12∠BAC97.(2020·江苏南京中考真题)如图,在ABC 和A B C '''中,D 、D 分别是AB 、A B ''上一点,AD A D AB A B ''=''.(1)当CD AC ABC D A C A B ==''''''时,求证:~ABC A B C '''△△ 证明的途径可以用如框图表示,请填写其中的空格 E '(2)当CD AC BCC D A C B C==''''''时,判断ABC 与A B C '''是否相似,并说明理由 98.(2020·江西中考真题)如图,Rt ABC 中,90ACB ∠=,顶点A ,B 都在反比例函数(0)ky x x=>的图象上,直线AC x ⊥轴,垂足为D ,连结OA ,OC ,并延长OC 交AB 于点E ,当2AB OA =时,点E 恰为AB 的中点,若45AOD ∠=,22OA =. (1)求反比例函数的解析式; (2)求EOD ∠的度数.99.(2020·山东菏泽中考真题)如图,在ABC 中,AB AC =,以AB 为直径的⊙O 与BC 相交于点D ,过点D 作⊙O 的切线交AC 于点E .(1)求证:DE AC ⊥;(2)若⊙O 的半径为5,16BC =,求DE 的长.。
相交线与平行线(优选真题60道)(2021-2023年)中考数学真题(全国通用)(解析版)

三年(2021-2023)中考数学真题分项汇编(全国通用)相交线与平行线(优选真题60道)一.选择题(共40小题)1.(2023•日照)在数学活动课上,小明同学将含30°角的直角三角板的一个顶点按如图方式放置在直尺上,测得∠1=23°,则∠2的度数是()A.23°B.53°C.60°D.67°【分析】利用平行线的性质即可求解.【解答】解:如图,三角板EFG与直尺ABCD分别交AB于点F、H.∵AB∥CD,∴∠2=∠FHG.又∵∠1+∠E=∠FHG,∴∠2=∠1+∠E=23°+30°=53°.故选:B.【点评】本题考查平行线的性质,比较简单.2.(2023•鄂州)如图,直线AB∥CD,GE⊥EF于点E.若∠BGE=60°,则∠EFD的度数是()A.60°B.30°C.40°D.70°【分析】过点E作AB的平行线,利用平行线的性质即可求解.【解答】解:过点E作直线HI∥AB.∵AB∥CD,AB∥HI,∴CD∥HI.∴∠BGE=∠GEH=60°,∴∠HEF=∠GEF﹣∠GEH=90°﹣60°=30°.∴∠EFD=∠HEF=30°.故选:B.【点评】本题考查了垂线及平行线的性质,正确作出辅助线是解决本题的关键.3.(2023•长沙)如图,直线m∥直线n,点A在直线n上,点B在直线m上,连接AB,过点A作AC⊥AB,交直线m于点C.若∠1=40°,则∠2的度数为()A.30°B.40°C.50°D.60°【分析】根据两直线平行,同旁内角互补得出∠1+∠BAC+∠2=180°,结合已知条件即可求出∠2的度数.【解答】解:∵直线m∥直线n,∴∠1+∠BAC+∠2=180°,∵AC⊥AB,∴∠BAC=90°,∵∠1=40°,∴40°+90°+∠2=180°,∴∠2=50°,故选:C.【点评】本题考查了平行线的性质和垂线的定义,熟知:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.4.(2023•大连)如图,直线AB∥CD,∠ABE=45°,∠D=20°,则∠E的度数为()A.20°B.25°C.30°D.35°【分析】由平行线的性质可得∠ABE=∠BCD,从而求出∠DCE,再根据三角形的内角和即可求解.【解答】解:∵AB∥CD,∴∠ABE=∠BCD=45°,∴∠DCE=135°,由三角形的内角和可得∠E=180°﹣135°﹣20°=25°.故选:B.【点评】本题考查平行线的性质和三角形的内角和定理,熟练掌握性质是解题关键.5.(2023•贵州)如图,AB∥CD,AC与BD相交于点E.若∠C=40°,则∠A的度数是()A.39°B.40°C.41°D.42°【分析】根据两直线平行,内错角相等即可求出∠A的度数.【解答】解:∵AB∥CD,∴∠A=∠C,∵∠C=40°,∴∠A=40°,故选:B.【点评】本题考查了平行线的性质,熟知:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.6.(2023•深圳)如图为商场某品牌椅子的侧面图,∠DEF=120°,DE与地面平行,∠ABD=50°,则∠ACB=()A.70°B.65°C.60°D.50°【分析】由平行线的性质可得∠D=∠ABD=50°,再利用三角形的外角性质可求得∠DCE的度数,结合对顶角相等即可求∠ACB的度数.【解答】解:∵DE∥AB,∠ABD=50°,∴∠D=∠ABD=50°,∵∠DEF=120°,且∠DEF是△DCE的外角,∴∠DCE=∠DEF﹣∠D=70°,∴∠ACB=∠DCE=70°.故选:A.【点评】三角形的外角性质,解答的关键是熟记平行线的性质并灵活运用.7.(2023•辽宁)如图,直线CD,EF被射线OA,OB所截,CD∥EF,若∠1=108°,则∠2的度数为()A.52°B.62°C.72°D.82°【分析】根据两直线平行,同旁内角互补,得出∠2+∠3=180°,由∠1=∠3,得出∠1+∠3=180°,即可得答案.【解答】解:如图:∵CD∥EF,∴∠2+∠3=180°,∵∠1=∠3,∴∠1+∠2=180°,∵∠1=108°,∴∠2=72°,故选:C.【点评】本题考查的是平行线的性质,熟知两直线平行,同旁内角互补,是解答此题的关键.8.(2023•张家界)如图,已知直线AB∥CD,EG平分∠BEF,∠1=40°,则∠2的度数是()A.70°B.50°C.40°D.140°【分析】由平角的定义可得∠BEF=140°,由角平分线的定义可得∠BEG=∠FEG=70°,再利用两直线平行,内错角相等即可求解.【解答】解:∵∠1=40°,∴∠BEF=180°﹣∠1=180°﹣40°=140°,∵EG平分∠BEF,∴∠BEG=∠FEG=70°,∵AB∥CD,∴∠2=∠BEG=70°.故选:A.【点评】本题主要考查平角的定义、角平分线的定义、平行线的性质,熟练掌握角平分线的定义和平行线的性质是解题关键.9.(2023•东营)如图,AB∥CD,点E在线段BC上(不与点B,C重合),连接DE.若∠D=40°,∠BED =60°,则∠B=()A.10°B.20°C.40°D.60°【分析】利用平行线的性质及外角计算即可.【解答】解:∵∠C+∠D=∠BED=60°,∴∠C=60°﹣∠D=60°﹣40°=20°.又∵AB∥CD,∴∠B=∠C=20°.故选:B.【点评】本题简单地考查了平行线的性质,知识点比较基础,一定要掌握.10.(2023•菏泽)一把直尺和一个含30°角的直角三角板按如图方式放置,若∠1=20°,则∠2=()A.30°B.40°C.50°D.60°【分析】由平行线的性质可得∠3=∠1=20°,从而可求∠2.【解答】解:如图,由题意得:∠CAD=60°,∵AB∥DE,∠1=20°,∴∠3=∠1=20°,∴∠2=∠CAD﹣∠3=40°.故选:B.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等.11.(2023•齐齐哈尔)如图,直线l1∥l2,分别与直线l交于点A,B,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=45°,则∠2的度数是()A.135°B.105°C.95°D.75°【分析】依据l1∥l2,即可得到∠1=∠3=45°,再根据∠4=30°,即可得出从∠2=180°﹣∠3﹣∠4=105°.【解答】解:如图,∵l1∥l2,∴∠1=∠3=45°,又∵∠4=30°,∴∠2=180°﹣∠3﹣∠4=180°﹣45°﹣30°=105°,故选:B.【点评】此题主要考查了平行线的性质,三角板的特征,角度的计算,解本题的关键是利用平行线的性质.12.(2023•绥化)将一副三角板按如图所示摆放在一组平行线内,∠1=25°,∠2=30°,则∠3的度数为()A.55°B.65°C.70°D.75°【分析】由题意可求得∠BAC=115°,再由平行线的性质可求得∠ACD的度数,结合平角的定义即可求∠3.【解答】解:如图,由题意可得:∠CAE=90°,∠ACF=45°,∵∠1=25°,∴∠BAC=∠1+∠CAE=115°,∵AB∥CD,∴∠BAC+∠ACD=180°,∴∠ACD=180°﹣∠BAC=65°,∴∠3=180°﹣∠ACD﹣∠ACF=70°.故选:C.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质并灵活运用.13.(2023•河南)如图,直线AB,CD相交于点O,若∠1=80°,∠2=30°,则∠AOE的度数为()A.30°B.50°C.60°D.80°【分析】由对顶角的性质得到∠AOD=∠1=80°,即可求出∠AOE的度数.【解答】解:∵∠AOD=∠1=80°,∴∠AOE=∠AOD﹣∠2=80°﹣30°=50°.故选:B.【点评】本题考查对顶角,关键是掌握对顶角的性质:对顶角相等.14.(2023•济宁)如图,a,b是直尺的两边,a∥b,把三角板的直角顶点放在直尺的b边上,若∠1=35°,则∠2的度数是()A.65°B.55°C.45°D.35°【分析】利用平角的定义及角的和差关系,先求出∠3,再利用平行线的性质求出∠2.【解答】解:∵∠BEF=90°,∠CED是平角,∠1=35°,∵a∥b,∴∠1=∠3=35°.∵∠BEC=180°﹣∠E﹣∠3=180°﹣90°﹣35°=55°故选:B.【点评】本题主要考查了平行线的性质,根据平角的定义求出∠3的度数是解决本题的关键.15.(2023•兰州)如图,直线AB与CD相交于点O,则∠BOD=()A.40°B.50°C.55°D.60°【分析】利用对顶角相等可得∠BOD=∠AOC,由量角器度量的方法可得结论.【解答】解:∵直线AB与CD相交于点O,∴∠BOD=∠AOC,∵∠AOC=50°,∴∠BOD=50故选:B.【点评】本题考查了对顶角相等和量角器的度量的方法,掌握这些知识点是解题的关键.16.(2023•广西)如图,一条公路两次转弯后又回到与原来相同的方向,∠A=130°,那么∠B的度数是()A.160°B.150°C.140°D.130°【分析】由平行线的性质,即可得到∠B=∠A=130°.【解答】解:∵公路两次转弯后又回到与原来相同的方向,∴AC∥BD,∴∠B=∠A=130°.故选:D.【点评】本题考查平行线的性质,关键是由题意得到AC∥BD.17.(2023•广东)如图,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD=()A.43°B.53°C.107°D.137°【解答】解:∵AB∥CD,∴∠ABC=∠BCD=137°,故选:D.【点评】本题考查平行线的性质,熟练掌握性质解解题关键.18.(2023•岳阳)已知AB∥CD,点E在直线AB上,点F,G在直线CD上,EG⊥EF于点E,∠AEF=40°,则∠EGF的度数是()A.40°B.45°C.50°D.60°【分析】由平角的定义可求得∠BEG=50°,再由平行线的性质即可求解.【解答】解:∵EG⊥EF,∴∠FEG=90°,∵∠AEF+∠FEG+∠BEG=180°,∠AEF=40°,∴∠BEF=180°﹣∠AEF﹣∠FEG=50°,∵AB∥CD,∴∠EGF=∠BEG=50°.故选:C.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等.19.(2023•荆州)如图所示的“箭头”图形中,AB∥CD,∠B=∠D=80°,∠E=∠F=47°,则图中∠G 的度数是()A.80°B.76°C.66°D.56°【分析】延长AB交EG于M,延长CD交FG于N,过G作GK∥AB,得到GK∥CD,推出∠KGM=∠EMB,∠KGN=∠DNF,得到∠EGF=∠EMB+∠DNF,由三角形外角的性质得到∠EMB=33°,∠DNF =33°,即可求出∠EGF的度数.【解答】解:延长AB交EG于,延长CD交FG于N,过G作GK∥AB,∵AB∥CD,∴GK∥CD,∴∠KGM=∠EMB,∠KGN=∠DNF,∴∠KGM+∠KGN=∠EMB+∠DNF,∴∠EGF=∠EMB+∠DNF,∵∠ABE=80°,∠E=47°,∴∠EMB=∠ABE﹣∠E=33°,同理:∠DNF=33°,∴∠EGF=∠EMB+∠DNF=33°+33°=66°.故选:C.【点评】本题考查平行线的性质,三角形外角的性质,关键是通过作辅助线,由平行线的性质,得到∠EGF =∠EMB+∠DNF,由三角形外角的性质求出∠EMB、∠DNF的度数,即可解决问题.20.(2023•陕西)如图,l∥AB,∠A=2∠B.若∠1=108°,则∠2的度数为()A.36°B.46°C.72°D.82°【分析】由对顶角相等可得∠3=∠1=108°,再由平行线的性质可求得∠A=72°,∠B=∠2,结合已知条件可求得∠B,即可求解.【解答】解:如图,∵∠1=108°,∴∠3=∠1=108°,∵l∥AB,∴∠3+∠A=180°,∠2=∠B,∴∠A=180°﹣∠3=72°,∵∠A=2∠B,∴∠B=36°,∴∠2=36°.故选:A.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补.21.(2023•随州)如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为()A.30°B.60°C.120°D.150°【分析】直接根据平行线的性质即可得出结论.【解答】解:∵直线l1∥l2,∠1=60°,∴∠2=180°﹣∠1=180°﹣60°=120°.故选:C.【点评】本题考查的是平行线的性质,熟知两直线平行,同旁内角互补是解题的关键.22.(2023•邵阳)如图,直线a,b被直线c所截,已知a∥b,∠1=50°,则∠2的大小为()A.40°B.50°C.70°D.130°【分析】根据对顶角相等,可得∠1=∠3,又由平行线的性质,求得∠2的度数.【解答】解:如图所示:∵a∥b,∴∠2=∠3,∵∠1=∠3,∠1=50°,∴∠1=∠2=50°.故选:B.【点评】此题考查了平行线的性质与对顶角的性质,注意掌握两直线平行,同位角相等是解此题的关键.23.(2023•金华)如图,已知∠1=∠2=∠3=50°,则∠4的度数是()A.120°B.125°C.130°D.135°【分析】由同位角相等两直线平行得到a与b平行,再由两直线平行同旁内角互补,求出∠5的度数,根据对顶角相等即可求出∠4的度数.【解答】解:∵∠1=∠3=50°,∴a∥b,∴∠5+∠2=180°,∵∠2=50°,∴∠5=130°,∴∠4=∠5=130°.故选:C.【点评】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.24.(2023•湖北)如图,Rt△ABC的直角顶点A在直线a上,斜边BC在直线b上,若a∥b,∠1=55°,则∠2=()A.55°B.45°C.35°D.25°【分析】由平行线的性质可得∠ABC=∠1=55°,再由三角形的内角和即可求∠2.【解答】解:∵a∥b,∠1=55°,∴∠ABC=∠1=55°,∵∠BAC=90°,∴∠2=180°﹣∠ABC﹣∠BAC=35°.故选:C.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等.25.(2023•枣庄)如图,一束太阳光线平行照射在放置于地面的正六边形上,若∠1=44°,则∠2的度数为()A.14°B.16°C.24°D.26°【分析】由多边形的外角和可求得∠BCD=60°,∠ABC=120°,再由平行线的性质可得∠BDC=∠1=44°,由三角形的外角性质可求得∠3的度数,即可求∠2的度数.【解答】解:如图,∵太阳光线平行照射在放置于地面的正六边形上,∴∠BCD=360°÷6=60°,EF∥BD,∠ABC=120°,∴∠BDC=∠1=44°,∵∠3是△BCD的外角,∴∠3=∠BDC+∠BCD=104°,∴∠2=∠ABC﹣∠3=16°.故选:B.【点评】本题主要考查平行线的性质,解答的关键熟记平行线的性质:两直线平行,同位角相等.26.(2023•宜昌)如图,小颖按如下方式操作直尺和含30°角的三角尺,依次画出了直线a,b,c.如果∠1=70°,则∠2的度数为()A.110°B.70°C.40°D.30°【分析】根据平行线的性质得到∠3=∠1=70°,三角形的外角的性质得到∠3=∠4+∠5=70°,由∠2=∠5即可解答.【解答】解:如图,由题意得,∠4=30°,a∥b,∴∠3=∠1=70°,∵∠3=∠4+∠5=70°,∴∠5=40°,∴∠2=∠5=40°,故选:C.【点评】本题考查了平行线的性质,对顶角的性质,三角形外角定理,掌握平行线的性质是解题关键.27.(2023•山西)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若∠1=155°,∠2=30°,则∠3的度数为()A.45°B.50°C.55°D.60°【分析】由平行线的性质求出∠OFB=25°,由对顶角的性质得到∠POF=∠2=30°,由三角形外角的性质即可求出∠3的度数.【解答】解:∵AB∥OF,∴∠1+∠OFB=180°,∵∠1=155°,∴∠OFB=25°,∵∠POF=∠2=30°,∴∠3=∠POF+∠OFB=30°+25°=55°.故选:C.【点评】本题考查平行线的性质,三角形外角的性质,对顶角的性质,关键是由平行线的性质求出∠OFB 的度数,由对顶角的性质得到∠POF的度数,由三角形外角的性质即可解决问题.28.(2023•苏州)如图,在正方形网格内,线段PQ的两个端点都在格点上,网格内另有A,B,C,D四个格点,下面四个结论中,正确的是()A.连接AB,则AB∥PQ B.连接BC,则BC∥PQC.连接BD,则BD⊥PQ D.连接AD,则AD⊥PQ【分析】根据平行的本质是平移,将线段AB、线段BC平移至线段PQ上,若重合则平行,若不重合则不平行.延长线段DB、线段DA与线段PQ相交,观察所成的角是否为直角判定是否垂直.【解答】解:连接AB,将点A平移到点P,即为向上平移3个单位,将点B向上平移3个单位后,点B 不在PQ直线上,∴AB与PQ不平行,选项A错误,连接BC,将点B平移到点P,即为向上平移4个单位,再向右平移1个单位,将点C按点B方式平移后,点C在PQ直线上,∴BC∥PQ,选项B正确,连接BD、AD,并延长与直线PQ相交,根据垂直的意义,BD、AD与PQ不垂直,选项C、D错误.故选:B.【点评】本题考查了学生在网格中的数形结合的能力,明确平行的本质是平移,将线段平移后观察是否重合从而判定是否平行是解决本题的关键.29.(2022•陕西)如图,AB∥CD,BC∥EF.若∠1=58°,则∠2的大小为()A.120°B.122°C.132°D.148°【分析】根据两直线平行,内错角相等分别求出∠C、∠CGF,再根据平角的概念计算即可.【解答】解:∵AB∥CD,∠1=58°,∴∠C=∠1=58°,∵BC∥EF,∴∠CGF=∠C=58°,∴∠2=180°﹣∠CGF=180°﹣58°=122°,故选:B.30.(2022•兰州)如图,直线a∥b,直线c与直线a,b分别相交于点A,B,AC⊥b,垂足为C.若∠1=52°,则∠2=()A.52°B.45°C.38°D.26°【分析】根据平行线的性质可得∠ABC=52°,根据垂直定义可得∠ACB=90°,然后利用直角三角形的两个锐角互余,进行计算即可解答.【解答】解:∵a∥b,∴∠1=∠ABC=52°,∵AC⊥b,∴∠ACB=90°,∴∠2=90°﹣∠ABC=38°,故选:C.【点评】本题考查了平行线的性质,垂线,熟练掌握平行线的性质是解题的关键.31.(2022•河南)如图,直线AB,CD相交于点O,EO⊥CD,垂足为O.若∠1=54°,则∠2的度数为()A.26°B.36°C.44°D.54°【分析】首先利用垂直的定义得到∠COE=90°,然后利用平角的定义即可求解.【解答】解:∵EO⊥CD,∴∠COE=90°,∵∠1+∠COE+∠2=180°,∴∠2=180°﹣∠1﹣∠COE=180°﹣54°﹣90°=36°.故选:B.【点评】本题主要考查了垂直的定义和平角的性质计算,要注意领会由垂直得直角这一要点.32.(2022•辽宁)如图,直线m∥n,AC⊥BC于点C,∠1=30°,则∠2的度数为()A.140°B.130°C.120°D.110°【分析】根据垂线的性质可得∠ACB=90°,进而得出∠ABC与∠1互余,再根据平行线的性质可得答案.【解答】解:∵AC⊥BC于点C,∴∠ACB=90°,∴∠ABC+∠1=90°,∴∠ABC=90°﹣30°=60°,∵m∥n,∴∠2=180°﹣∠ABC=120°.故选:C.【点评】本题主要考查平行线的性质,掌握两直线平行,同旁内角互补是解题的关键.33.(2022•常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是()A.垂线段最短B.两点确定一条直线C.过一点有且只有一条直线与已知直线垂直D.过直线外一点有且只有一条直线与已知直线平行【分析】根据生活经验结合数学原理解答即可.【解答】解:小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是垂线段最短,故选:A.【点评】本题主要考查了垂线段最短的性质,熟练掌握数学和生活密不可分的关系是解答本题的关键.34.(2022•潍坊)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面AB与CD平行,入射光线l与出射光线m平行.若入射光线l与镜面AB的夹角∠1=40°10',则∠6的度数为()A.100°40'B.99°80'C.99°40'D.99°20'【分析】先根据反射角等于入射角求出∠2的度数,再求出∠5的度数,最后根据平行线的性质得出即可.【解答】解:∵入射角等于反射角,∠1=40°10',∴∠2=∠1=40°10',∵∠1+∠2+∠5=180°,∴∠5=180°﹣40°10'﹣40°10'=99°40',∵入射光线l与出射光线m平行,∴∠6=∠5=99°40'.故选:C.【点评】本题考查了平行线的性质,能灵活运用平行线的性质定理推理是解此题的关键.35.(2022•襄阳)已知直线m∥n,将一块含30°角的直角三角板ABC(∠ABC=30°,∠BAC=60°)按如图方式放置,点A,B分别落在直线m,n上.若∠1=70°.则∠2的度数为()A.30°B.40°C.60°D.70°【分析】根据平行线的性质求得∠ABD,再根据角的和差关系求得结果.【解答】解:∵m∥n,∠1=70°,∴∠1=∠ABD=70°,∵∠ABC=30°,∴∠2=∠ABD﹣∠ABC=40°,故选:B.【点评】本题主要考查了平行线的性质,关键是熟练掌握平行线的性质.36.(2021•安徽)两个直角三角板如图摆放,其中∠BAC=∠EDF=90°,∠E=45°,∠C=30°,AB与DF交于点M.若BC∥EF,则∠BMD的大小为()A.60°B.67.5°C.75°D.82.5°【分析】首先根据直角三角形两锐角互余可算出∠F和∠B的度数,再由“两直线平行,内错角相等”,可求出∠MDB的度数,在△BMD中,利用三角形内角和可求出∠BMD的度数.【解答】解:如图,在△ABC和△DEF中,∠BAC=∠EDF=90°,∠E=45°,∠C=30°,∴∠B=90°﹣∠C=60°,∠F=90°﹣∠E=45°,∵BC∥EF,∴∠MDB=∠F=45°,在△BMD中,∠BMD=180°﹣∠B﹣∠MDB=75°.故选:C.法二、∵BC∥EF,∴∠EAC=∠C=30°,则∠MAE=120°,在四边形AMDE中,∠AMD =360°﹣120°﹣90°﹣45,∴∠BMD=180﹣∠AMD=75°.故选:C.【点评】本题主要考查三角形内角和,平行线的性质等内容,根据图形,结合定理求出每个角的度数是解题关键.37.(2021•宜昌)如图,将一副三角尺按图中所示位置摆放,点F在AC上,其中∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB∥DE,则∠AFD的度数是()A.15°B.30°C.45°D.60°【分析】利用三角板的度数可得∠A=30°,∠D=45°,由平行线的性质定理可得∠1=∠D=45°,利用三角形外角的性质可得结果.【解答】解:如图,∵∠ACB=90°,∠ABC=60°,∴∠A=180°﹣∠ACB﹣∠ABC=180°﹣90°﹣60°=30°,∵∠EFD=90°,∠DEF=45°,∴∠D=180°﹣∠EFD﹣∠DEF=180°﹣90°﹣45°=45°,∵AB∥DE,∴∠1=∠D=45°,∴∠AFD=∠1﹣∠A=45°﹣30°=15°,故选:A.【点评】本题主要考查了平行线的性质定理和外角的性质,求出∠A,∠D的度数是解本题的关键.38.(2021•娄底)如图,AB∥CD,点E、F在AC边上,已知∠CED=70°,∠BFC=130°,则∠B+∠D 的度数为()A.40°B.50°C.60°D.70°【分析】先由平行线的性质得出∠A+∠C=180°,再由三角形的内角和为180°,将△ABF和△CDE的内角和加起来即可得∠B+∠D的度数.【解答】解:∵∠BFC=130°,∴∠BF A=50°,又∵AB∥CD,∴∠A+∠C=180°,∵∠B+∠A+∠BF A+∠D+∠C+∠CED=360°,∴∠B+∠D=60°,故选:C.【点评】本题主要考查平行线的性质和三角形的内角和,这两个知识点中考基本都是放在一起考的,平行线的性质与判定要熟记于心.39.(2021•包头)如图,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于()A.80°B.70°C.60°D.50°【分析】由题意得,∠2=60°,由平角的定义可得∠5=70°,再根据平行线的性质即可求解.【解答】解:如图,∵l1∥l2,∴∠1+∠3=180°,∵∠1+∠2+∠3=240°,∴∠2=240°﹣(∠1+∠3)=60°,∵∠3+∠2+∠5=180°,∠3=50°,∴∠5=180°﹣∠2﹣∠3=70°,∵l1∥l2,∴∠4=∠5=70°,故选:B.【点评】此题考查了平行线的性质,熟记平行线的性质定理及平角的定义是解题的关键.需要注意的是,在有平行线的前提下,若要计算或求证的角与已知角不是两平行线被三条直线所截得的角,那么就需要借助一个中间量,将两者联系起来.本题就是先求的∠4的同位角,进而求出∠4的.40.(2021•营口)如图,EF与AB,BC,CD分别交于点E,G,F,且∠1=∠2=30°,EF⊥AB,则下列结论错误的是()A.AB∥CD B.∠3=60°C.FG=12FC D.GF⊥CD【分析】先根据平行线的判定可得AB∥CD,根据直角三角形的性质可得∠3,根据含30°的直角三角形的性质可得FG=12GC,再由平行线的性质得到GF⊥CD,即可得出结论.【解答】解:∵∠1=∠2=30°,∴AB∥CD,故A不符合题意;∵EF⊥AB,∴∠BEG=90°,∴∠3=90°﹣30°=60°,故B不符合题意;∵∠2=30°,∴FG=12GC,故C符合题意;∵AB∥CD,EF⊥AB,∴GF⊥CD,故D不符合题意.故选:C.【点评】本题考查的是垂线,平行线的判定,用到的知识点为:内错角相等,两直线平行.二.填空题(共20小题)41.(2023•通辽)将一副三角尺如图所示放置,其中AB∥DE,则∠CDF=度.【分析】利用平行线的性质和三角尺各角的度数进行计算即可.【解答】解:∵AB∥DE,∴∠BDE=∠B=30°.∴∠CDF=180°﹣∠EDF﹣∠BDE=180°﹣45°﹣30°=105°.故答案为:105.【点评】本题主要考查平行线的性质的简单运用.另外,一定要把一副三角尺各角的度数作为常识牢记于心.42.(2023•永州)如图,AB∥CD,BC∥ED,∠B=80,则∠D=度.【分析】首先由AB∥CD得出∠BCD=∠B=80°,再由BC∥ED得出∠D+∠BCD=180°,据此可得出此题的答案.【解答】解:∵AB∥CD,∠B=80,∴∠BCD=∠B=80°,∵BC∥ED,∴∠D+∠BCD=180°,∴∠D=100°.故答案为:100.【点评】此题主要考查了平行线的判定和性质,解答此题的关键是准确识图,熟练掌握平行线的判定及性质:两直线平行,同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补.43.(2023•杭州)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A=.【分析】由平行线的性质得到∠B=∠ADE=28°,由三角形外角的性质得到∠A=∠ACF﹣∠B=118°﹣28°=90°.【解答】解:∵DE∥BC,∴∠B=∠ADE=28°,∵∠ACF=∠A+∠B,∴∠A=∠ACF﹣∠B=118°﹣28°=90°.故答案为:90°.【点评】本题考查平行线的性质,三角形外角的性质,关键是由平行线的性质求出∠B的度数,由三角形外角的性质即可求出∠A的度数.44.(2023•台州)用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为.【分析】利用平行线的性质和各角之间的关系即可求解.【解答】解:如图,标注三角形的三个顶点A、B、C.∠2=∠BAC=180°﹣∠ABC﹣∠ACB.∵图案是由一张等宽的纸条折成的,∴AB=AC,∴∠ABC=∠ACB.又∵纸条的长边平行,∴∠ABC=∠1=20°,∴∠2=∠BAC=180°﹣2∠ABC=180°﹣2∠1=180°﹣2×20°=140°.故答案为:140°.【点评】本题比较简单,主要考查了平行线的性质的运用.45.(2023•威海)某些灯具的设计原理与抛物线有关.如图,从点O照射到抛物线上的光线OA,OB等反射后都沿着与POQ平行的方向射出.若∠AOB=150°,∠OBD=90°,则∠OAC=°.【分析】根据两直线平行,内错角相等可得∠POB=∠OBD=90°,那么∠AOP=∠AOB﹣∠POB=60°,再根据两直线平行,内错角相等可得∠OAC=∠AOP=60°.【解答】解:∵BD∥PQ,∴∠POB=∠OBD=90°,∵∠AOB=150°,∴∠AOP=∠AOB﹣∠POB=150°﹣90°=60°,∵AC∥PQ,∴∠OAC=∠AOP=60°.故答案为:60.【点评】本题考查了平行线的性质,是基础题,熟记性质是解题的关键.46.(2023•烟台)一杆古秤在称物时的状态如图所示,已知∠1=102°,则∠2的度数为.【分析】根据两直线平行,内错角相等得到∠2=∠BCD,由∠1的度数求出∠BCD的度数,即可得到∠2的度数.【解答】解:如图,由题意得:AB∥CD,∴∠2=∠BCD,∵∠1=102°,∴∠BCD=78°,∴∠2=78°,故答案为:78°.【点评】本题考查了平行线的性质,熟知:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.47.(2022•镇江)一副三角板如图放置,∠A=45°,∠E=30°,DE∥AC,则∠1=°.【分析】利用平行和对顶角相等求出∠DOA,根据三角形内角和求出∠D,根据外角性质求出∠1.【解答】解:如图,设DE交AB于O点,∵DE∥AC,∴∠A=∠BOE=45°,∴∠DOA=∠BOE=45°,∠D=90°﹣∠E=90°﹣30°=60°,∠1=∠D+∠DOA=60°+45°=105°.故答案为:105.【点评】本题考查平行线的性质、对顶角和三角形内角和定理,熟练运用平行线的性质是关键.48.(2022•扬州)将一副直角三角板如图放置,已知∠E=60°,∠C=45°,EF∥BC,则∠BND=°.【分析】由直角三角形的性质得出∠F=30°,∠B=45°,由平行线的性质得出∠NDB=∠F=30°,再由三角形内角和定理即可求出∠BND的度数.【解答】解:已知∠E=60°,∠C=45°,∠F=30°,∠B=45°,∵EF∥BC,∴∠NDB=∠F=30°,∴∠BND=180°﹣∠B﹣∠NDB=180°﹣45°﹣30°=105°,故答案为:105.【点评】本题考查了平行线的性质,熟练掌握平行线的性质,直角三角形的性质,三角形内角和定理是解决问题的关键.49.(2022•阜新)一副三角板如图摆放,直线AB∥CD,则∠α的度数是.【分析】根据题意可得:∠EBD=90°,∠BDE=45°,∠EDC=30°,然后利用平行线的性质可得∠ABD+∠BDC=180°,从而进行计算即可解答.【解答】解:如图:由题意得:∠EFD=90°,∠FDE=45°,∠EDC=30°,∵AB∥CD,∴∠AFD+∠FDC=180°,∴∠α=180°﹣∠EFD﹣∠FDE﹣∠EDC=180°﹣90°﹣45°﹣30°=15°,故答案为:15°.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.50.(2022•湖北)如图,直线a∥b,直线c与直线a,b相交,若∠1=54°,则∠3=度.【分析】根据两直线平行,同位角相等和邻补角的定义解答即可.【解答】解:∵a ∥b ,∴∠4=∠1=54°,∴∠3=180°﹣∠4=180°﹣54°=126°,故答案为:126.【点评】本题主要考查了平行线的性质以及邻补角互补的运用,解决问题的关键是掌握:两直线平行,同位角相等.51.(2022•西藏)如图,依下列步骤尺规作图,并保留作图痕迹:(1)分别以点A ,B 为圆心,大于12AB 的长为半径作弧,两弧相交于E ,F 两点,作直线EF ; (2)以点A 为圆心,适当长为半径画弧,分别交AB ,AC 于点G ,H ,再分别以点G ,H 为圆心,大于12GH 的长为半径画弧,两弧在∠BAC 的内部相交于点O ,画射线AO ,交直线EF 于点M .已知线段AB =6,∠BAC =60°,则点M 到射线AC 的距离为 .【分析】根据线段的垂直平分线和角平分线的作法可知:EF 是线段AB 的垂直平分线,AO 是∠AOB 的平分线,利用线段的垂直平分线的性质和角平分线的性质的求解即可.【解答】解:如图所示:根据题意可知:EF 是线段AB 的垂直平分线,AO 是∠BAC 的平分线,∵AB =6,∠BAC =60°,∴∠BAO =∠CAO =12∠BAC =30°,AD =12AB =3,∴AM=2MD,在Rt△ADM中,(2MD)2=MD2+AD2,即4MD2=MD2+32,∴MD=√3,∵AM是∠AOB的平分线,MD⊥AB,∴点M到射线AC的距离为√3.故答案为:√3.【点评】本题考查作图﹣基本作图,线段的垂直平分线的性质,角平分线的性质等知识,解题的关键是理解题意灵活运用基本作图的知识解决问题.52.(2022•乐山)如图,已知直线a∥b,∠BAC=90°,∠1=50°.则∠2=.【分析】根据直角三角形的两锐角互余求出∠ACB,再根据平行线的性质解答即可.【解答】解:在Rt△ABC中,∠BAC=90°,∠1=50°,则∠ACB=90°﹣50°=40°,∵a∥b,∴∠2=∠ACB=40°,故答案为:40°.【点评】本题考查的是平行线的性质、直角三角形的性质,掌握两直线平行、同位角相等是解题的关键.53.(2022•绵阳)两个三角形如图摆放,其中∠BAC=90°,∠EDF=100°,∠B=60°,∠F=40°,DE 与AC交于点M,若BC∥EF,则∠DMC的大小为.【分析】延长ED交CB的延长线于点G,利用三角形内角和定理可得求出∠E,∠C的度数,再利用平行线的性质可求出∠G的度数,然后利用三角形内角和定理进行计算即可解答.【解答】解:延长ED交CB的延长线于点G,∵∠BAC=90°,∠ABC=60°,∴∠C=90°﹣∠ABC=30°,∵∠EDF=100°,∠F=40°,∴∠E=180°﹣∠F﹣∠EDF=40°,∵EF∥BC,∴∠E=∠G=40°,∴∠DMC=180°﹣∠C﹣∠G=110°,故答案为:110°.【点评】本题考查了平行线的性质,三角形内角和定理,熟练掌握平行线的性质,以及三角形内角和定理是解题的关键.54.(2022•枣庄)光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,光线变成FH,点G在射线EF上,已知∠HFB=20°,∠FED=45°,则∠GFH的度数为.【分析】根据平行线的性质知∠GFB=∠FED=45°,结合图形求得∠GFH的度数.【解答】解:∵AB∥CD,∴∠GFB=∠FED=45°.∵∠HFB=20°,∴∠GFH=∠GFB﹣∠HFB=45°﹣20°=25°.故答案为:25°.【点评】本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.55.(2022•济宁)如图,直线l1,l2,l3被直线l4所截,若l1∥l2,l2∥l3,∠1=126°32',则∠2的度数是.【分析】由平行线性质即可解答.【解答】解:如图:∵l1∥l2,l2∥l3,∴l1∥l3,∴∠1=∠3=126°32',∴∠2=180°﹣∠3=180°﹣126°32'=53°28';故答案为:53°28'.【点评】本题考查平行线的性质及应用,解题的关键是掌握平行的传递性和平行线的性质.56.(2022•宜昌)如图,C岛在A50°方向,C岛在B岛的北偏西35°方向,则∠ACB的大小是.【分析】过点C作CF∥AD,根据平行线的性质,求得∠ACF与∠BCF,再由角的和差可得答案.【解答】解:过点C作CF∥AD,如图,∵AD ∥BE ,∴AD ∥CF ∥BE ,∴∠ACF =∠DAC ,∠BCF =∠EBC ,∴∠ACB =∠ACF +∠BCF =∠DAC +∠EBC ,由C 岛在A 岛的北偏东50°方向,C 岛在B 岛的北偏西35°方向,得∠DAC =50°,∠CBE =35°.∴∠ACB =50°+35°=85°,故答案为:85°.【点评】本题考查了方向角,平行线的性质,利用平行线的性质得出得出∠ACF =50°,∠BCF =35°是解题关键.57.(2021•大庆)如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有 个交点.【分析】由所给条件可得n 条直线相交最多有n(n−1)2个交点,令n =20即可求解. 【解答】解:2条直线相交有1个交点,3条直线相交最多有1+2=3个交点,4条直线相交最多有1+2+3=6个交点,……n 条直线相交最多有n(n−1)2个交点,∴20条直线相交最多有190个交点.故答案为190.【点评】本题考查相交线交点个数问题,直线两两相交时去掉重复交点是解题的关键.58.(2021•长春)将一副三角板按如图所示的方式摆放,点D在边AC上,BC∥EF,则∠ADE的大小为度.【分析】由“两直线平行,同位角性质”得到∠1=∠E=45°,再根据三角形的外角定理求解即可.【解答】解:如图,∠C=30°,∠E=45°,∵BC∥EF,∴∠1=∠E=45°,∴∠ADE=∠1+∠C=45°+30°=75°,故答案为:75.【点评】此题考查了平行线的性质,熟记平行线的性质定理及三角形的外角定理是解题的关键.59.(2021•益阳)如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD =度.【分析】根据角平分线的定义得出∠AOE=∠COE,∠COE=∠BOC,求出∠AOE=∠COE=∠BOC,根据∠AOE+∠COE+∠BOC=180°求出∠BOC,再根据对顶角相等求出答案即可.【解答】解:∵OE是∠AOC的平分线,OC恰好平分∠EOB,∴∠AOE=∠COE,∠COE=∠BOC,∴∠AOE=∠COE=∠BOC,∵∠AOE+∠COE+∠BOC=180°,∴∠BOC=60°,。
2023年中考数学真题分项汇编(全国通用):几何图形初步与三视图和相交线与平行线(原卷版)
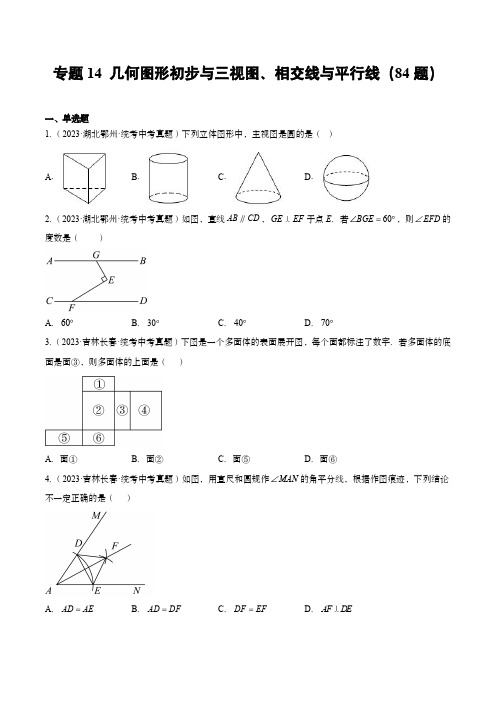
专题14几何图形初步与三视图、相交线与平行线(84题)一、单选题1.(2023·湖北鄂州·统考中考真题)下列立体图形中,主视图是圆的是()A .B .C .D .2.(2023·湖北鄂州·统考中考真题)如图,直线AB CD ,GE EF 于点E .若60BGE ,则EFD 的度数是()A .60B .30C .40D .703.(2023·吉林长春·统考中考真题)下图是一个多面体的表面展开图,每个面都标注了数字.若多面体的底面是面③,则多面体的上面是()A .面①B .面②C .面⑤D .面⑥4.(2023·吉林长春·统考中考真题)如图,用直尺和圆规作MAN 的角平分线,根据作图痕迹,下列结论不一定正确的是()A .AD AEB .AD DFC .DF EFD .AF D E5.(2023·甘肃兰州·统考中考真题)如图,直线AB 与CD 相交于点O ,则BOD ()A .40B .50C .55D .606.(2023·山东东营·统考中考真题)如图,AB CD ∥,点E 在线段BC 上(不与点B ,C 重合),连接DE ,若40D ,60BED ,则B ()A .10B .20C .40D .607.(2023·内蒙古·统考中考真题)几个大小相同的小正方体搭成几何体的俯视图如图所示,图中小正方形中数字表示对应位置小正方体的个数,该几何体的主视图是()A .B .C .D .8.(2023·内蒙古·统考中考真题)如图,直线a b ,直线l 与直线,a b 分别相交于点,A B ,点C 在直线b 上,且CA CB .若132 ,则2 的度数为()A .32B .58C .74D .759.(2023·全国·统考中考真题)图①是2023年6月11日吉林市全程马拉松男子组颁奖现场.图②是领奖台的示意图,则此领奖台的主视图是()A .B .C .D .10.(2023·黑龙江绥化·统考中考真题)将一副三角板按下图所示摆放在一组平行线内,125 ,230 ,则3 的度数为()A .55B .65C .70D .7511.(2023·黑龙江绥化·统考中考真题)如图是一个正方体,被切去一角,则其左视图是()A .B .C .D .12.(2023·黑龙江齐齐哈尔·统考中考真题)如图,若几何体是由六个棱长为1的正方体组合而成的,则该几何体左视图的面积是()A .2B .3C .4D .513.(2023·黑龙江齐齐哈尔·统考中考真题)如图,直线12l l ∥,分别与直线l 交于点A ,B ,把一块含30 角的三角尺按如图所示的位置摆放,若145 ,则2 的度数是()A .135B .105C .95D .7514.(2023·河南·统考中考真题)如图,直线AB ,CD 相交于点O ,若180 ,230 ,则AOE 的度数为()A .30B .50C .60D .8015.(2023·河南·统考中考真题)北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是()A .主视图与左视图相同B .主视图与俯视图相同C .左视图与俯视图相同D .三种视图都相同16.(2023·黑龙江·统考中考真题)一个几何体由若干大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为()A .4B .5C .6D .717.(2023·湖北·统考中考真题)如图是一个立体图形的三视图,该立体图形是()A .三棱柱B .圆柱C .三棱锥D .圆锥18.(2023·湖南张家界·统考中考真题)如图是由5个完全相同的小正方体组成的立体图形,其主视图是()A .B .C .D .19.(2023·辽宁大连·统考中考真题)如图,直线,45,20AB CD ABE D ∥,则E 的度数为()A .20B .25C .30D .3520.(2023·辽宁大连·统考中考真题)如图所示的几何体中,主视图是()A .B .C .D .21.(2023·广东·统考中考真题)如图,街道AB 与CD 平行,拐角137ABC ,则拐角BCD ()A .43B .53C .107D .13722.(2023·山东·统考中考真题)一把直尺和一个含30 角的直角三角板按如图方式放置,若120 ,则2 ()A .30B .40C .50D .6023.(2023·山东·统考中考真题)如图所示的几何体是由5个大小相同的小正方体组成的,它的主视图是()A .B .C .D .24.(2023·山东·统考中考真题)如图,,a b 是直尺的两边,a b ,把三角板的直角顶点放在直尺的b 边上,若135 ,则2 的度数是()A.65 B.55 C.45 D.3525.(2023·山东·统考中考真题)一个几何体的三视图如下,则这个几何体的表面积是()A.39πB.45πC.48πD.54π26.(2023·福建·统考中考真题)下图是由一个长方体和一个圆柱组成的几何体,它的俯视图是()A.B.C.D.27.(2023·湖北荆州·统考中考真题)观察如图所示的几何体,下列关于其三视图的说法正确的是()A .主视图既是中心对称图形,又是轴对称图形B .左视图既是中心对称图形,又是轴对称图形C .俯视图既是中心对称图形,又是轴对称图形D .主视图、左视图、俯视图都是中心对称图形28.(2023·湖北荆州·统考中考真题)如图所示的“箭头”图形中,AB CD ∥,80B D ,47E F ,则图中G 的度数是()A .80B .76C .66D .5629.(2023·山东聊城·统考中考真题)如图,分别过ABC 的顶点A ,B 作AD BE .若25CAD ,80EBC ,则ACB 的度数为()A .65B .75C .85D .9530.(2023·山东聊城·统考中考真题)如图所示几何体的主视图是()A .B .C .D .31.(2023·四川·统考中考真题)某几何体是由四个大小相同的小立方块拼成,其俯视图如图所示,图中数字表示该位置上的小立方块个数,则这个几何体的左视图是()A .B .C .D .32.(2023·广西·统考中考真题)如图,一条公路两次转弯后又回到与原来相同的方向,如果130A ,那么B 的度数是()A .160B .150C .140D .13033.(2023·湖南·统考中考真题)如图,直线,a b 被直线c 所截,已知,150a b ∥,则2 的大小为()A .40B .50C .70D .13034.(2023·湖北黄冈·统考中考真题)如图,Rt ABC △的直角顶点A 在直线a 上,斜边BC 在直线b 上,若155a b ,,则2 ()A .55B .45C .35D .2535.(2023·湖北黄冈·统考中考真题)下列几何体中,三视图都是圆的是()A .长方体B .图柱C .圆锥D .球36.(2023·湖南郴州·统考中考真题)下列几何体中,各自的三视图完全一样的是()A .B .C .D .37.(2023·湖北宜昌·统考中考真题)“争创全国文明典范城市,让文明成为宜昌人民的内在气质和城市的亮丽名片”.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,“城”字对面的字是().A .文B .明C .典D .范38.(2023·湖北宜昌·统考中考真题)如图,小颖按如下方式操作直尺和含30 角的三角尺,依次画出了直线a ,b ,c .如果170 ∠,则2 的度数为().A .110B .70C .40D .3039.(2023·湖北武汉·统考中考真题)如图是由4个相同的小正方体组成的几何体,它的左视图是()A .B .C .D .40.(2023·湖北十堰·统考中考真题)下列几何体中,三视图的三个视图完全相同的几何体是()A .B .C .D .41.(2023·四川内江·统考中考真题)如图是由5个完全相同的小正方体堆成的物体,其主视图是()A .B .C .D .42.(2023·山东滨州·统考中考真题)如图所示摆放的水杯,其俯视图为()A .B .C .D .43.(2023·湖北随州·统考中考真题)如图是一个放在水平桌面上的圆柱体,该几何体的三视图中完全相同的是()A .主视图和俯视图B .左视图和俯视图C .主视图和左视图D .三个视图均相同44.(2023·湖北随州·统考中考真题)如图,直线12l l ∥,直线l 与1l 、2l 相交,若图中160 ,则2 为()A .30B .60C .120D .15045.(2023·天津·统考中考真题)如图是一个由6个相同的正方体组成的立体图形,它的主视图是()A .B .C .D .46.(2023·山东枣庄·统考中考真题)榫卯是古代中国建筑、家具及其它器械的主要结构方式,是我国工艺文化精神的传奇;凸出部分叫榫,凹进部分叫卯,下图是某个部件“卯”的实物图,它的主视图是()A .B .C .D .47.(2023·山东临沂·统考中考真题)下图是我国某一古建筑的主视图,最符合视图特点的建筑物的图片是()A.B.C.D.的度数是()48.(2023·山东临沂·统考中考真题)下图中用量角器测得ABCA.50 B.80 C.130 D.15049.(2023·湖南永州·统考中考真题)下列几何体中,其三视图的主视图和左视图都为三角形的是()A.B.C.D.50.(2023·江苏苏州·统考中考真题)今天是父亲节,小东同学准备送给父亲一个小礼物.已知礼物外包装的主视图如图所示,则该礼物的外包装不可能...是()A .长方体B .正方体C .圆柱D .三棱锥51.(2023·湖南·统考中考真题)作为中国非物质文化遗产之一的紫砂壶,成型工艺特别,造型式样丰富,陶器色泽古朴典雅,从一个方面鲜明地反映了中华民族造型审美意识.如图是一把做工精湛的紫砂壶“景舟石瓢”,下面四幅图是从左面看到的图形的是()A .B .C .D .52.(2023·山东烟台·统考中考真题)如图,对正方体进行两次切割,得到如图⑤所示的几何体,则图⑤几何体的俯视图为()A .B .C .D .53.(2023·湖南岳阳·统考中考真题)已知AB CD ,点E 在直线AB 上,点,F G 在直线CD 上,EG EF 于点,40E AEF ,则EGF 的度数是()A .40B .45C .50D .6054.(2023·湖南岳阳·统考中考真题)下列几何体的主视图是圆的是()A .B .C .D .55.(2023·江苏扬州·统考中考真题)下列图形中是棱锥的侧面展开图的是()A.B.C.D.56.(2023·四川乐山·统考中考真题)下面几何体中,是圆柱的是()A.B.C.D.57.(2023·浙江绍兴·统考中考真题)由8个相同的立方体搭成的几何体如图所示,则它的主视图是()A.B.C.D.58.(2023·浙江台州·统考中考真题)如图是由5个相同的正方体搭成的立体图形,其主视图是().A.B.C.D.59.(2023·浙江温州·统考中考真题)截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是()A.B.C .D .60.(2023·湖南怀化·统考中考真题)如图,平移直线AB 至CD ,直线AB ,CD 被直线EF 所截,160 ,则2 的度数为()A .30B .60C .100D .12061.(2023·江西·统考中考真题)如图,平面镜MN 放置在水平地面CD 上,墙面PD CD 于点D ,一束光线AO 照射到镜面MN 上,反射光线为OB ,点B 在PD 上,若35AOC ,则OBD 的度数为()A .35B .45C .55D .6562.(2023·云南·统考中考真题)某班同学用几个几何体组合成一个装饰品美化校园.其中一个几何体的三视图(其中主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是()A .球B .圆柱C .长方体D .圆锥63.(2023·浙江宁波·统考中考真题)如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是()A .B .C .D .64.(2023·四川眉山·统考中考真题)由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的最少个数为()A .6B .9C .10D .1465.(2023·四川眉山·统考中考真题)如图,ABC 中,,40 AB AC A ,则ACD 的度数为()A .70B .100C .110D .14066.(2023·江苏连云港·统考中考真题)下列水平放置的几何体中,主视图是圆形的是()A .B .C .D .67.(2023·四川遂宁·统考中考真题)生活中一些常见的物体可以抽象成立体图形,以下立体图形中三视图形状相同的可能是()A.正方体B.圆锥C.圆柱D.四棱锥68.(2023·四川广安·统考中考真题)如图,由5个大小相同的小正方体搭成的几何体,它的俯视图是()A.B.C.D.69.(2023·浙江金华·统考中考真题)某物体如图所示,其俯视图是()A.B.C.D.70.(2023·浙江嘉兴·统考中考真题)如图的几何体由3个同样大小的正方体搭成,它的俯视图是()A.B.C.D.71.(2023·安徽·统考中考真题)某几何体的三视图如图所示,则该几何体为()A.B.C.D.72.(2023·浙江·统考中考真题)如图,箭头所指的是某陶艺工作室用于垫放陶器的5块相同的耐火砖搭成的几何体,它的主视图是()A.B.C.D.73.(2023·四川凉山·统考中考真题)光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,145,2120则34()A.165 B.155 C.105 D.9074.(2023·四川凉山·统考中考真题)如图是由4个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是()A .B .C .D .75.(2023·重庆·统考中考真题)如图,直线a ,b 被直线c 所截,若a b ,163 ,则2 的度数为().A .27B .53C .63D .11776.(2023·重庆·统考中考真题)四个大小相同的正方体搭成的几何体如图所示,从正面看到的视图是()A .B .C .D .77.(2023·四川泸州·统考中考真题)一个立体图形的三视图如图所示,则该立体图形是()A .圆柱B .圆锥C .长方体D .三棱柱78.(2023·四川泸州·统考中考真题)如图,AB CD ∥,若55D ,则1 的度数为()A .125B .135C .145D .155 79.(2023·四川自贡·统考中考真题)如图,某人沿路线A B C D 行走,AB 与CD 方向相同,1128 ,则2 ()A .52B .118C .128D .13880.(2023·四川自贡·统考中考真题)如图中六棱柱的左视图是()A .B .C .D .82.(2023·内蒙古通辽·统考中考真题)将一副三角尺如图所示放置,其中AB DE ∥,则CDF ___________度.83.(2023·山东烟台·统考中考真题)一杆古秤在称物时的状态如图所示,已知1102 ,则2 的度数为_____.84.(2023·浙江台州·统考中考真题)用一张等宽的纸条折成如图所示的图案,若120 ,则∠2的度数为________.。
(完整版)相交线与平行线考点及题型总结

相交线与平行线考点及题型总结第一节 相交线一、知识要点:(一)当同一平面内的三条直线相交时,有三种情况:一种是只有一个交点;一种是有两个交点,即两条直线平行被第三条直线所截;还有一种是三个交点,即三条直线两两相交。
(二)余角、补角、对顶角1、余角:如果两个角的和是直角,那么称这两个角互为余角.2、补角:如果两个角的和是平角,那么称这两个角互为补角.3、对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.4、互为余角的有关性质:①∠1+∠2=90°,则∠1、∠2互余;反过来,若∠1,∠2互余,则∠1+∠2=90°;②同角或等角的余角相等,如果∠l 十∠2=90°,∠1+∠ 3=90°,则∠2=∠3.5、互为补角的有关性质:①若∠A +∠B =180°,则∠A 、∠B 互补;反过来,若∠A 、∠B 互补,则∠A +∠B =180°.②同角或等角的补角相等.如果∠A +∠C =180°,∠A +∠B =180°,则∠B =∠C .6、对顶角的性质:对顶角相等.(三)垂直:相交的一种特殊情况是垂直,两条直线交角成90 。
1、经过直线外一点,作直线垂线,有且只有一条; 2、点到直线上各点的距离中,垂线段最短。
(四)两条直线被第三条直线所截,产生两个交点,形成了八个角(不可分的):1、同位角:没有公共顶点的两个角,它们在直线AB,CD 的同侧,在第三条直线EF 的同旁(即位置相同),这样的一对角叫做同位角;2、内错角:没有公共顶点的两个角,它们在直线AB,CD 之间,在第三条直线EF 的两旁(即位置交错),这样的一对角叫做内错角;3、同旁内角:没有公共顶点的两个角,它们在直线AB,CD 之间,在第三条直线EF 的同旁,这样的一对角叫做同旁内角;二、题型分析: 题型一:列方程求角例1:一个角的余角比它的补角的21少20°.则这个角为 ( ) A 、30° B 、40° C 、60° D 、75° 答案:B分析:若设这个角为x ,则这个角的余角是90°-x ,补角是180°-x ,于是构造出方程即可求解 求解:设这个角为x ,则这个角的余角是90°-x ,补角是180°-x .则根据题意,得21(180°-x )-(90°-x )=20° ; 解得:x =40°. 故应选B . 说明:处理有关互为余角与互为补角的问题,除了要弄清楚它们的概念,通常情况下还要引进未知数,构造方程求解.习题演练:1、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30 ,那么这两个角是( )A 、42138、 B 、都是10 C 、42138、或4210、 D 、以上都不对 答案:A分析:两个条件可以确定两个角互补,列方程即可解得A 。
2023年湖北省中考数学分类汇编:相交线与平行线
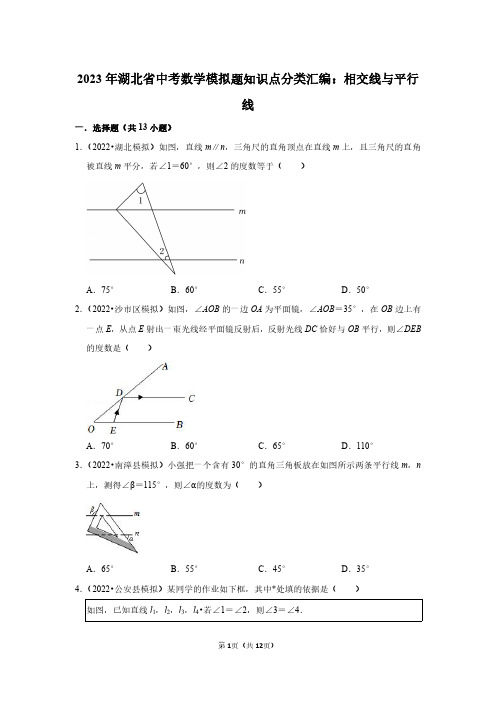
2023年湖北省中考数学模拟题知识点分类汇编:相交线与平行
线
一.选择题(共13小题)
1.(2022•湖北模拟)如图,直线m∥n,三角尺的直角顶点在直线m上,且三角尺的直角
被直线m平分,若∠1=60°,则∠2的度数等于(
)
A.75°B.60°C.55°D.50°2.(2022•沙市区模拟)如图,∠AOB的一边OA为平面镜,∠AOB=35°,在OB边上有一点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好与OB平行,则∠DEB 的度数是(
)
A.70°B.60°C.65°D.110°3.(2022•南漳县模拟)小强把一个含有30°的直角三角板放在如图所示两条平行线m,n 上,测得∠β=115°,则∠α的度数为(
)
A.65°B.55°C.45°D.35°4.(2022•公安县模拟)某同学的作业如下框,其中*处填的依据是()
如图,已知直线l1,l2,l3,l4•若∠1=∠2,则∠3=∠4.
第1页(共12页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相交线与平行线一、选择题1. (2013湖北黄冈,3,3分)如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF =()A.60° B.120° C.150° D.180°【答案】A.【解析】由AB∥CD,得∠BAC+∠C=180°,所以∠C=180°-∠BAC=180°-120°=60°.而AC∥DF,所以∠CDF=C=60°.【方法指导】本题考查平行线的性质,属于几何初步知识.识别∠BAC与∠C是同旁内角,∠C与∠CDF是内错角,进而根据两直线平行,同旁内角互补、内错角相等发现它们之间的数量关系是解题关键.2.(2013江苏扬州,5,3分)下列图形中,由AB∥CD能得到∠1=∠2的是().【答案】B.【解析】如图,由“对顶角相等”可得∠1=∠3,因为AB∥CD,所以∠2=∠3,所以∠1=∠2.所以应选B.【方法指导】本题考查对顶角和平行线的性质,用对顶角性质先得到∠1=∠3,再由“两直线平行,同位角相等”可得∠2=∠3.由“等量代换”可得∠1=∠2.【易错警示】本题容易出现的错误是错认为内错角相等而选C.3. (2013重庆市(A),2,4分)已知∠A=65°,则∠A的补角等于()A.125° B.105° C.115° D.95°【答案】C.【解析】如果两个角的和为180°,那么这两个角互为补角.根据定义可知,65°角的补角等于180°-65°=115°.【方法指导】本题考查补角的概念,属于几何初步知识.直接根据概念解答即可.4.(2013重庆市(A),5,4分)如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD 的度数为()A.40° B.35° C.50° D.45°【答案】A.【解析】思路1:∵AD 平分∠BAC ,∠BAD =70°,∴∠BAC =2∠BAD =140°.又∵AB ∥CD ,∴∠BAC +∠ACD =180°,则∠ACD =180°-∠BAC =180°-140°=40°.思路2:利用平行线的性质求出∠ADC =70°,利用角平分线求出∠CAD =70°,然后根据三角形的内角和是180°,求出∠ACD =40°.【方法指导】本题考查平行线的性质、角平分线和三角形的内角和是180°.平行线间的角离不开同位角、同旁内角、内错角等知识,另外还要和三角形的内角和定理,及外角等于与它不相邻的两内角和相联系. 5.(2013山东临沂,3,3分)如图,已知AB ∥CD ,∠2=135°,则∠1的度数是( ) A .35° B .45° C .55° D .65°【答案】B .【解析】∠2=1350,则它的对顶角与∠1是同旁内角,因为AB ∥CD ,所以∠1=450【方法指导】根据对顶角的性质和两直线平行,同旁内角互补计算求得. 【易错点分析】将两角当成同位角而导致错误.6.(2013山东德州,4,3分)如图,A B ∥CD ,点E 在BC 上,且CD=CE ,∠D=740,,则∠B的度数为A 、680B 、320C 、220D 、160 【答案】B.【解析】在△CDE 中,∵CD=CE ,∴∠D=∠DEF=74°, ∴∠C=180°-2×74°=32°. ∵AB ∥CD ,∴∠B=∠C=32°.【方法指导】本题考查了平行线性质、等腰三角形性质、三角形内角和.本题把平行线、三角形内角和、等腰三角形基础知识进行简单组合进行考查.注意“等边对等角”前提是在同一个三角形中,也就是是等腰三角形的重要性质.7.(2013湖南永州,4,3分)如图,下列条件中能判断直线1l ∥2l 的是A .∠1=∠2B . ∠1=∠5C . ∠1+∠3=180°D . ∠3=∠5A B CD12l 1【答案】C. 【解析】本题考查了平行线的判定,需要确定两个角是不是属于三线八角的基本图形。
∠1和∠2是直线3l 和直线4l 形成的三线八角中的同旁内角;∠1和∠5不是三线八角的基本图形;∠1和∠3是1l 和2l 被3l 所截形成的同旁内角,它们互补,则两直线平行;∠3和∠5是对顶角,不能用来判断两直线是否平行。
【方法指导】判断两直线平行,在直线型部分有以下方法: 1.同位角相等,两直线平行; 2.内错角相等,两直线平行; 3.同旁内角互补,两直线平行4.在同一平面内两条直线都和第三条直线平行,这两条直线也互相平行。
8.(2013浙江湖州,4,3分)如图,已知直线a 、b 被直线c 所截,a ∥b ,∠1=60°,则∠2的度数为( )A .30°B .60°C .120°D .150° 【答案】C【解析】因为a ∥b ,所以∠1=∠3(两直线平行,同位角相等),因为∠1=60°,所以∠3=60°,又因为∠2+∠3=180°,所以∠2=120°。
故选C 。
3【方法指导】本题考查了平行线的性质,邻补角的定义,是基础题,熟记性质是解题的关键.根据两直线平行,同位角相等求出∠3,再根据邻补角的定义解答. 9.(2013重庆,2,4分)如图,直线a ,b , c ,d ,已知c ⊥a ,c ⊥b ,直线b ,c ,d 交于一点,若∠1=50°,则∠2等于( )A .60°B .50°C .40°D .30°【答案】B【解析】∵a ⊥c ,b ⊥c ,∴a ∥b . ∴∠2=∠1=50°. 故选B . 【方法指导】本题考查了平行线的判定和性质,灵活运用平行线的判定和性质是解题的关键. 平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;反过来可得平行线的判定,即:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.10. (2013四川雅安,4,3分)如图,AB ∥CD ,AD 平分∠BAC ,且∠C =80°,则∠D 的度数为( )A .50°B .60°C .70°D .100° 【答案】A【解析】∵AB ∥CD ,∴∠C A B =180°-∠C =100°,∠D =∠B A D , 又∵AD 平分∠BAC ,∴∠B A D =12∠C A B =50°,∴∠D 的度数为50°.【方法指导】本题考查的知识点是平行线的性质、角平分线的定义,也考查了简单的逻辑推理.难度不大.11. (2013广东省,6,3分)如题6图,AC ∥DF ,AB ∥EF ,点D 、E 分别在AB 、AC 上,若0502=∠,则是1∠的大小是A . 030B . 040C . 050D . 060cab d12(第2题图)【答案】 C .【解析】因为AC ∥DF ,所以A ∠=1∠,又因为AB ∥EF ,所以A ∠=2∠,所以所以1∠=2∠,由0502=∠得0501=∠,答案选C .【方法指导】平行线的性质是初中几何内容的基础,命题者一般都会把这个考点设计为一道送分题,解决这类题的关键是找准同位角或内错角或同旁内角. 12.(2013白银,3,3分)如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )A . 15°B . 20°C . 25°D .30°考点: 平行线的性质. 分析: 根据两直线平行,内错角相等求出∠3,再求解即可. 解答:解:∵直尺的两边平行,∠1=20°, ∴∠3=∠1=20°,∴∠2=45°﹣20°=25°. 故选C .点评:本题考查了两直线平行,内错角相等的性质,是基础题,熟记性质是解题的关键. 13.(2013广东珠海,2,3分)如图两平行线a 、b 被直线l 所截,且∠1=60°,则∠2的度数为( )A . 30°B . 45°C . 60°D . 120°考点: 平行线的性质. 分析: 由a ∥b ,根据两直线平行,同位角相等,即可求得∠3=∠1=60°,又由对顶角相等,即可求得答案.解答:解:∵a∥b,∴∠3=∠1=60°,∴∠2=∠3=60°.故选C.点评:此题考查了平行线的性质.此题比较简单,注意掌握数形结合思想的应用.14.(2013湖北孝感,3,3分)如图,∠1=∠2,∠3=40°,则∠4等于()A.120°B.130°C.140°D.40°考点:平行线的判定与性质.分析:首先根据同位角相等,两直线平行可得a∥b,再根据平行线的性质可得∠3=∠5,再根据邻补角互补可得∠4的度数.解答:解:∵∠1=∠2,∴a∥b,∴∠3=∠5,∵∠3=40°,∴∠5=40°,∴∠4=180°﹣40°=140°,故选:C.点评:此题主要考查了平行线的性质与判定,关键是掌握同位角相等,两直线平行;两直线平行,同位角相等. 15.(2013湖北宜昌,8,3分)如图,已知AB ∥CD,E 是AB 上一点,DE 平分∠BEC 交CD 于D ,∠BEC=100°,则∠D 的度数是( )A . 100°B . 80°C . 60°D . 50°考点: 平行线的性质. 分析: 根据角平分线的性质可得∠BED=50°,再根据平行线的性质可得∠D=∠BED=50°.解答:解:∵DE 平分∠BEC 交CD 于D , ∴∠BED=∠BEC , ∵∠BEC=100°, ∴∠BED=50°, ∵AB ∥CD ,∴∠D=∠BED=50°, 故选:D . 点评:此题主要考查了平行线的性质以及角平分线定义,关键是掌握两直线平行,内错角相等. 16 .(2013湖南娄底,3,3分)下列图形中,由AB ∥CD ,能使∠1=∠2成立的是( ) A .B .C .D .考点: 平行线的性质. 分析: 根据平行线的性质对各选项分析判断后利用排除法求解. 解答:解:A 、由AB ∥CD 可得∠1+∠2=180°,故本选项错误; B 、∵AB ∥CD , ∴∠1=∠3,又∵∠2=∠3(对顶角相等),∴∠1=∠2, 故本选项正确;C 、由AC ∥BD 得到∠1=∠2,由AB ∥CD 不能得到,故本选项错误; D 、梯形ABCD 是等腰梯形才可以有∠1=∠2,故本选项错误. 故选B . 点评: 本题考查了平行线的性质,等腰梯形的性质,熟记性质并准确识图是解题的关键.17.(2013•东营,4,3分)如图,已知AB ∥CD ,AD 和BC 相交于点O ,∠A =50°,∠AOB =105°,则∠C 等于( )A . 20°B . 25°C . 35°D . 45°答案:B解析:因为50A ∠=°,105AOB ∠=°,所以18025B A AOB ∠=°−∠−∠=°,因为A B ∥CD ,所以25C B ∠=∠=°.18 . 2013浙江丽水3分)如图,AB ∥CD ,AD 和BC 相交于点O ,∠A =20°,∠COD =100°,则∠C 的度数是 A. 80° B. 70° C. 60° D. 50°19.(2013上海市,5,4分)如图1,已知在△ABC 中,点D 、E 、F 分别是边AB 、AC 、BC 上的点,DE ∥BC ,EF ∥AB ,且AD ∶DB = 3∶5,那么CF ∶CB 等于( ) (A ) 5∶8 ; (B )3∶8 ; (C ) 3∶5 ; (D )2∶5.20.(2013陕西,3,3分)如图,AB ∥CD ,∠CED=90°,∠AEC=35°,则∠D 的大小( )A . 65°B . 55°C .45°D . 35°考点:平行线的性质应用与互余的定义。
