连续系统的时域分析习题答案
信号与系统课后题解第二章

⑺
对⑺式求一阶导,有:
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中,有:
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ,则有:
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为:
由联立方程可得 故系统的零输入响应为:
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
(2)由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )
郑君里《信号与系统》(第3版)笔记和课后习题(含考研真题)详解-第2章 连续时间系统的时域分析【圣才

Ri(t) v1(t) e(t)
Ri(t)
1 C
t
i(
)d
v1 (t )
e(t)
vo (t) v1(t)
消元可得微分方程:
6 / 59
圣才电子书
十万种考研考证电子书、题库视频学习平
1
台
C
d
dt
vo (t)
1 R
vo (t)
R
e(t)
2-2 图 2-2-2 所示为理想火箭推动器模型。火箭质量为 m1,荷载舱质量为 m2,两 者中间用刚度系数为 k 的弹簧相连接。火箭和荷载舱各自受到摩擦力的作用,摩擦系数分 别为 f1 和 f2。求火箭推进力 e(t)与荷载舱运动速度 v2(t)之间的微分方程表示。
M
di1 (t ) dt
Ri2 (t)
0
化简方程组可得微分方程:
(L2
M
2
)
d4 dt 4
vo
(t)
2RL
d3 dt 3
vo
(t)
2L C
R2
d2 dt 2
vo
(t)
2R C
d dt
vo
(t)
1 C2
vo
(t)
MR
d2 dt 2
e(t)
(3)由图 2-2-1(c)所示列写电路方程,得:
C
dv1 (t ) dt
b.自由响应由两部分组成,其中,一部分由起始状态决定,另一部分由激励信号决 定,二者都与系统的自身参数有关;当系统 0-状态为零,则零输入响应为零,但自由响应 可以不为零。
c.零输入响应在 0-时刻到 0+时刻不跳变,此时刻若发生跳变,可能为零状态响应分 量。
信号与线性系统课后答案

解: (a) H ( p)
p
p p
1
2
p p2
2
1
1 2
1 4
2( 1 ) 2
p2 1
p
2
+ 1F
f
-
1F
+
1H u -
h(t
)
1 2
(t)
2 4
sin
t (t), 2
(a)
g(t)
t
h( )d
0_
1 2
(t
)
2 4
cos
2
t (t)
0
1 2
cos
t (t) . 2
+
(b) H ( p)
4j
ห้องสมุดไป่ตู้
2
(5) y(t) f1(t 1) f1(t 2) sinπ(t 1)[ε(t 1) ε(t 2)] sinπt[ε(t 2) ε(t 1)];
(6)
y(t)
n0
f2 (t
nT )
sinπ n0 T
(t
nT )ε(t
nT
)
sinπT tε(sinπT t)ε(t) .
p
2
p 1 p
1
;
Hi
f
( p)
i0 (t) f (t)
p
p2 2
p
p
1
.
2 -3 给定如下传输算子 H( p),试写出它们对应的微分方程。
( 1)
H ( p)
p p
3
;
(2) H ( p)
p p
3 3
;
(3)
H(
p)
p3 2p 3
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解
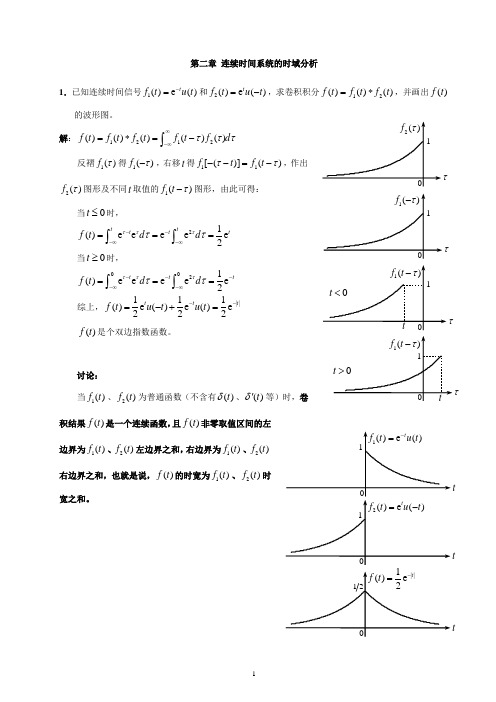
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。
(NEW)吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解

目 录第1章 信号与系统1.1 复习笔记1.2 课后习题详解1.3 名校考研真题详解第2章 连续系统的时域分析2.1 复习笔记2.2 课后习题详解2.3 名校考研真题详解第3章 离散系统的时域分析3.1 复习笔记3.2 课后习题详解3.3 名校考研真题详解第4章 傅里叶变换和系统的频域分析4.1 复习笔记4.2 课后习题详解4.3 名校考研真题详解第5章 连续系统的s域分析5.1 复习笔记5.2 课后习题详解5.3 名校考研真题详解第6章 离散系统的z域分析6.1 复习笔记6.2 课后习题详解6.3 名校考研真题详解第7章 系统函数7.1 复习笔记7.2 课后习题详解7.3 名校考研真题详解第8章 系统的状态变量分析8.1 复习笔记8.2 课后习题详解8.3 名校考研真题详解第1章 信号与系统1.1 复习笔记一、信号的基本概念与分类信号是载有信息的随时间变化的物理量或物理现象,其图像为信号的波形。
根据信号的不同特性,可对信号进行不同的分类:确定信号与随机信号;周期信号与非周期信号;连续时间信号与离散时间信号;实信号与复信号;能量信号与功率信号等。
二、信号的基本运算1加法和乘法f1(t)±f2(t)或f1(t)×f2(t)两信号f1(·)和f2(·)的相加、减、乘指同一时刻两信号之值对应相加、减、乘。
2.反转和平移(1)反转f(-t)f(-t)波形为f(t)波形以t=0为轴反转。
图1-1(2)平移f(t+t0)t0>0,f(t+t0)为f(t)波形在t轴上左移t0;t0<0,f(t+t0)为f(t)波形在t轴上右移t0。
图1-2平移的应用:在雷达系统中,雷达接收到的目标回波信号比发射信号延迟了时间t0,利用该延迟时间t0可以计算出目标与雷达之间的距离。
这里雷达接收到的目标回波信号就是延时信号。
3.尺度变换f(at)若a>1,则f(at)波形为f(t)的波形在时间轴上压缩为原来的;若0<a<1,则f(at)波形为f(t)的波形在时间轴上扩展为原来的;若a<0,则f(at)波形为f(t)的波形反转并压缩或展宽至。
信号与线性系统-白恩健书答案

第1章基本概念K第1章习题k1.1解:(1)x(t)为周期信号,周期为T=10。
(2)x(t)为非周期信号。
(3)x[n]为非周期信号。
(4)x[n]为周期信号,周期为N=2。
(5)x(t)为非周期信号。
(6)x[n]为周期信号,周期为N=2。
1.2解:(1)x(t)为功率信号。
(2)x(t)既不是能量信号也不是功率信号。
(3)x[n]为能量信号。
(4)x(t)为能量信号。
(5)x(t)为能量信号。
(6)x[n]为能量信号。
1.3略。
1.4略。
1.5(原题有误)一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。
用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统,即x[n−k]=S−k(x[n])。
写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。
解:提示:可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。
1.6解:(1)因果、无记忆、非线性、时不变、BIBO稳定系统。
(2)因果、无记忆、线性、时变和BIBO稳定系统。
(3)因果、无记忆、线性、时变和非稳定系统。
(4)因果、记忆、线性、时不变和BIBO稳定系统。
(5)因果、无记忆、线性、时变和BIBO稳定系统。
(6)因果、记忆、时不变、非稳定系统。
–2/48–第1章基本概念(7)因果、无记忆、线性、时不变和BIBO稳定系统。
(8)非因果系统、无记忆、线性、时不变、BIBO稳定系统。
1.7证明略。
1.8解:(1)x[n]的响应为{1,1,−1,2,n=0,1,2,3}。
(2)x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。
(3)x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。
1.9证明提示:根据微积分的极限定义证明。
1.10解:(1)x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。
(2)x(t)的响应为[2(t+e−t)−2]u(t)。
_第二章连续系统的时域分析习题解答

第二章 连续系统的时域分析习题解答2-1图题2・1所示各电路中,激励为于亿),响应为⑴和u 0(t)o 试列写各响应关于(“)(* + O.OO2" + £)"o(f)="詁=> (3p 4- 625)«0(/) = 375/(t);% =2xlO*o =>(3” + 625血=7.5x105;=>(/?2+p + l>0 =(/? + !)/; (/r+p + l)/0 =/.2・2求图题2」各电路中响应怙⑴和必⑴对激励/⑴的传输算子H(p)°鯉(、\H 375 .耳 5 J )⑴ _7.5x]0-” 解:(a)丹“心)一 口)一 3〃+ 625'"(")—/(/)一 3〃+ 625 '(b)- = 2P + i ; H (”)=鶴一 ------------------------------------ j (0 p + p + \ /(/) p +〃 + l给定如下传输算子H(p),试写岀它们对应的微分方程。
2-3(2)%)=锯;⑵第+ 2等+ 3广(4)兽+ 3器+2尸黑+ 3% —dr dr d r dr2-4已知连续系统的输入输岀算子方程及0-初始条件为:3"席篇:3)/(。
y (°H ,y'(oxi ;(2)w )=〃(;¥:;[8)m ),y (Q )= o, y'(0.) = i, y"(oj = o ;辺心洙為妙何皿…㈣".P 1 +P⑴心治 辺船;解:⑴器+7;辺 2需+3y = ^ + 3f;(b)如(/)=分1/F + p + 1试求系统的零输入响应y x (t)(t 0)o解:(1)/^ =-1, /A =-3, y(r) = ^e-z + A 2e-3f ,(2) p[ = 0,卩2.3 = 一2 ± j2, y(f) = A 】+ A 2e"2z cos(2r + A 3), Q = A { + A 2COS A^ 1 = -2A 2(COS A 3 +sin A 3)=> < 0 = 4A>2cos£A = 0 A 2 = 0.5 => y(/) = O.5e~2/ sin 2f, f MO ・心—90。
(NEW)吴大正《信号与线性系统分析》(第4版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】上册

【答案】
【解析】设f1(t)=ε(t)由LTI系统的线性和时不变性得(由于该题 没有给出系统的初始状态,所以这里不考虑)
f(t)=ε(t-1)-ε(t-2)=f1(t-1)-f1(t-2)
3.已知某LTI系统,当t>0时有: 当输入f(t)=(e-t+2e-2t)ε(t)时,输出响应为(e-t+5e-2t) ε(t); 当输入f(t)=(2e-t+e-2t)ε(t)时,输出响应为(5e-t+e-2t) ε(t); 当输入f(t)=(e-t+e-2t)ε(t)时,输出响应为(e-t+e-2t) ε(t); 则当输入为f(t)=(e-t-e-2t)ε(t)时,系统的输出响应为 ______。[长沙理工大学2006研]
【答案】
;
;稳定
【解析】由
可知,该系统任意两个相邻的输出值之差就是该
系统的输入值,即
,因此其逆系统的方程是
。
又因为
可知该逆系统的单位冲激响应为
为有限长序列,则其收敛域包含整个坐标平面。可见包含单位圆,则稳 定。
二、选择题 1.用下列差分方程描述的系统为线性系统的是( )。[西安电子科 技大学研] A.y(k)+y(k-1)=2f(k)+3 B.y(k)+y(k-1)y(k-2)=2f(k) C.y(k)+ky(k-2)=f(1-k)+2f(k-1) D.y(k)+2y(k-2)=2|f(k)| 【答案】C
图2-3 解:由框图可知,系统函数
令 因输入
,由于两共轭零点实部为1,可以求得 ,故 。
,即
时,系统全响应
,即
① 由此可知 的三个一阶极点分别为 , , ,分别代入传 递函数特征方程式
,从而可得
根据
可写出系统微分方程为
对方程两边取单边拉氏变换,将 由式①=②,可求得
实验三 线性时不变(LTI)连续系统的时域分析

执行结果
实验任务 1:LTI系统的微分方程y''(t)+2y'(t)+y(t)=f'(t)+2f(t),激励f (t)=e-2tε(t),
(1) 利用 impulse 函数获得冲激响应; (2) 利用 lsim 函数求取零状态响应; (3) 用卷积分析法计算其零状态响应; 要求:在一个图形窗口里以 3 个子图形式绘制冲激响应和两种方法得到的零状 态响应的波形。 (4)改变系统的 a 系数矩阵,观察冲激响应和零状态响应时域波形的变化情况。 建议 a 系数向量分别如下取值讨论。
用。
一、实验目的
1. 掌握系统时域分析常用函数的使用方法; 2. 理解系统特征根对系统时域特性的影响;
二、实验原理及内容 2.1 连续系统的时域分析 2.1.1 连续系统时域分析的几个常用函数
设 LTI 连续时间系统的微分方程为
a 2 y''(t)+a 1 y'(t)+a 0 y(t)=b 2 f''(t)+b 1 f'(t)+b 0 f(t)
将积分变量离散化即将用n替代d用替代只要时域取样间隔足够小上式可近似为再把观察响应时刻离散化即将t用k替换只要足够小通常将fn简记为fnhkn简记为hknyk简记为yk这样上式便可表示为因此两个连续信号ft和ht的卷积yt可用ft和ht的取样信号f均取整数
实验三 线性时不变(LTI)连续系统的时域分析
2.1.2 连续信号卷积的近似计算
连续系统的零状态响应 y(t)可通过输入信号 f(t)与系统冲激响应 h(t)的卷积求 得;但是计算机只能处理数字信号,不能直接处理模拟信号,因此,卷积积分不 能直接用计算机计算。为了解决这个问题,可以将连续信号用取样信号来近似表 示,利用卷积和近似求得卷积积分。下面就连续信号卷积积分的近似计算进行简 单推导。
吴大正《信号与线性系统分析》(第4版)名校考研真题(连续系统的时域分析)【圣才出品】

y(2t)
21
f ( )h(2t )d
f (21)h(2t 21)d 21 2
f
(21)h[2(t
1)]d1
2
f
(2t)
h(2t)。
另解:此题也可以使用傅里叶变换性质得到:
设 f t F ,ht H , y t Y
则Y F H ,由尺度变换特性得
y
2t
【答案】 (et 7e2t ) (t)
【解析】根据 LTI 系统的线性性质,这里给出的条件较多,所以要考虑系统的初始状态 (1)首先算出两组输入对应的零输入响应
f1(t) (et 2e2t ) (t) (2et e2t ) (t) (et e2t ) (t) 其零状态响应为: (et 5e2t ) (t) (5et e2t ) (t) 4(et e2t ) (t)
1 2
Y
1 2
1 2
F
1 2
H
1 2
2
1 2
F
1 2
1 2
H
1 2
则 y 2t 2 f 2t h 2t 。
2.已知某 LTI 系统,当输入为 f(t)=ε(t)时,其输出为 y(t)=e-tε(t)+ε(- 1-t);则当输入为 f(t)=ε(t-1)-ε(t-2)时,系统的响应 yf(t)=______。[长沙 理工大学 2006 研]
三、分析计算题
1.已知某系统的转秱函数 H ()
j
,系统的激励信号 e(t) etu(t) ,
2 j5 6
求系统的零状态响应
rzs (t) ,并标明受迫分量和自然分量。[天津工业大学 2006 研] 解: H ( j) 进行部分分式分解,可得:
H ( j)
信号与系统第2章 习题答案

第2章 线性时不变连续系统的时域分析2.1如题图2-1所示机械位移系统,质量为m 的刚体一端由弹簧牵引,弹簧的另一端固定在壁上,弹簧的刚度系数为k 。
刚体与地面间的摩擦系数为f ,外加牵引力为)(t F S ,求外加牵引力)(t F S 与刚体运动速度)(t v 间的关系。
题图2-1解:由机械系统元件特性,拉力k F 与位移x 成正比,即k F kx =又()()tx t v d ττ-∞=⎰所以,()()()tk F t kx t kv d ττ-∞==⎰刚体在光滑表面滑动,摩擦力与速度成正比,即()()f F t fv t = 根据牛顿第二定律以及整个系统力平衡的达朗贝尔原理,可得()()()()ts dF t fv t k v d mv t dtττ-∞--=⎰ 整理得22()()()()s d d dm v t fv t kv t F t dt dt dt--= 2.2题图2-2所示电路,输入激励是电流源)(t i s ,试列出电流)(t i L 及1R 上电压)(1t u 为输出响应变量的方程式。
题图2-2解:由电路的基尔霍夫电流定律可得:()()()C L S i t i t i t += (1) 根据电容特性,()()C C di t Cu t dt= (2) 由电路的基尔霍夫电压定律可得:12()()()()C C L L du t R i t L i t R i t dt+=+ (3) 将21()()()()C L L C du t Li t R i t R i t dt=+-代入(2)得 2212()()()()C L L C d d di t LC i t R C i t R C i t dt dt dt=+-(4)()()()C S L i t i t i t =-代入(4)得,22112()()()()()()S L L L S L d d d di t i t LC i t R C i t R C i t R C i t dt dt dt dt-=+-+整理得,21212()11()()()()()L L L S S R R R d d d i t i t i t i t i t dt L dt LC L dt LC+++=+ (5) 将111()()(()())C S L u t i t R i t i t R ==-,即11()()()L S u t i t i t R =-代入(5)得 21121112111()()()()11(())(())(())()()S S S S S u t R R u t u t R d d d i t i t i t i t i t dt R L dt R LC R L dt LC+-+-+-=+整理得,221211211122()()()()()()S S R R u t R R d d d u t u t R i t i t dt L LC dt L dt+++=-- 2.3某连续系统的输入输出方程为)(')(4)('3)("2t x t y t y t y =++已知)()(t u t x =,1)0(=-y ,1)0('=-y ,试计算)0(+y 和)0('+y 值。
第二章连续系统的时域分析

解得系数为 代入得
A1 2 A2 4
rzi (t) 2e2t 4et ,t 0
(3)零状态响应rzs(t) 满足 r”(t) + 3r’(t) + 2r(t) = 2δ(t) + 6u(t) 利用系数匹配法解得:
r'zs (0) r'zs (0) 2 2 rzs (0) rzs (0) 0 0
利用初始值解得: A1 1 A2 0
全响应为:
r(t)
e2t
3
t0
(2)零输入响应rzi(t), 激励为0 , rzi (0+)= rzi (0-)= rzi (0-)=2 rzi’(0+)= rzi’(0-)= rzi’(0-)=0
根据特征根求得通解为:
rzi (t) A1e2t A2et
四.系统响应划分
自由响应+强迫响应 (Natural+forced)
暂态响应+稳态响应 (Transient+Steady-state)
零输入响应+零状态响应 (Zero-input+Zero-state)
①自由响应:也称固有响应,由系统本身特性决定,与外加激励 形式无关。对应于齐次解。 强迫响应:形式取决于外加激励。对应于特解。
解得 A1 + B0 = 2 A2= –1
最后得微分方程的全解为
r(t) 2e2t e3t te2t
上式第一项的系数A1+B0= 2,不能区分A1和B0,因而也不能 区分自由响应和强迫响应。
二、关于 0- 和 0+ 初始值 1、0- 状态和 0+ 状态 0- 状态称为零输入时的初始状态。即初始值是由系统的储 能产生的; 0+ 状态称为加入输入后的初始状态。即初始值不仅有系统 的储能,还受激励的影响。 从 0- 状态到 0+ 状态的跃变 当系统已经用微分方程表示时,系统的初始值从0- 状态到 0+ 状态有没有跳变决定于微分方程右端自由项是否包含(t)及 其各阶导数。
郑君里信号与系统习题解答第二章

第二章 连续时间系统的时域分析经典法:双零法卷积积分法:求零状态响应求解系统响应→定初始条件满足换路定则起始点有跳变:求跳变量零输入响应:用经典法求解零状态响应:卷积积分法求解()()()()⎩⎨⎧==-+-+0000L L c c i i u u例题•例题1:连续时间系统求解(经典法,双零法) •例题2:求冲激响应(n >m ) •例题3:求冲激响应(n <m ) •例题4:求系统的零状态响应 •例题5:卷积 •例题6:系统互联例2-1分析在求解系统的完全响应时,要用到有关的三个量是: :起始状态,它决定零输入响应;()()()()()()()()()强迫响应。
状态响应,自由响应,并指出零输入响应,零,求系统的全响应,已知 系统的微分方程为描述某t u t e r r t e t t e t r t t r t t r =='=+=++--,00,206d d 22d d 3d d LTI 22()-0)(k r ⎩⎨⎧状态变量描述法输出描述法—输入建立系统的数学模型:跳变量,它决定零状态响应; :初始条件,它决定完全响应;这三个量之间的关系是 分别利用 求零状态响应和完全响应,需先确定微分方程的特解。
解:方法一:利用 先来求完全响应,再求零输入响应,零状态响应等于完全响应减去零输入响应。
方法二:用方法一求零输入响应后,利用跳变量 来求零状态响应,零状态响应加上零输入响应等于完全响应。
本题也可以用卷积积分求系统的零状态响应。
方法一1. 完全响应 该完全响应是方程 (1)方程(1)的特征方程为 特征根为 方程(1)的齐次解为因为方程(1)在t >0时,可写为 (2)显然,方程(1)的特解可设为常数D ,把D 代入方程(2)求得 所以方程(1)的解为下面由冲激函数匹配法定初始条件 由冲激函数匹配法定初始条件 据方程(1)可设代入方程(1),得匹配方程两端的 ,及其各阶导数项,得 所以,所以系统的完全响应为()+0)(k zsr ()+0)(k r ()()()+-+=-000)()()(k zs k k r r r ()()++00)()(k k zs r r ,()()代入原方程有将t u t e =()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()++'0,0r r ()()++''0,0zs zs r r ()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()的解且满足00,20='=--r r 0232=++αα2121-=-=αα,()t t e A e A t r 221--+=()()()()t u t r t t r tt r 62d d 3d d 22=++3=D ()3221++=--tt e A e A t r ()()()t u b t a t t r ∆+=δ22d d ()()t u a t t r ∆=d d ()无跳变t r ()()()()()()t u t t r t u a t u b t a 6223+=+∆+∆+δδ2=a ()t δ()()22000=+=+'='-+a r r ()()200==-+r r ()()代入把20,20=='++r r ()3221++=--t t e A e A t r 1,021-==A A 得()0 32≥+-=-t e t r t ()t r zi 再求零输入响应2.求零输入响应 (3)(3)式的特征根为 方程(3)的齐次解即系统的零输入响应为所以,系统的零输入响应为 下面求零状态响应零状态响应=完全响应—零输入响应,即 因为特解为3,所以强迫响应是3,自由响应是方法二(5)以上分析可用下面的数学过程描述 代入(5)式 根据在t =0时刻,微分方程两端的 及其各阶导数应该平衡相等,得 于是t >0时,方程为 齐次解为 ,特解为3,于是有所以,系统的零状态响应为方法一求出系统的零输入响应为()是方程响应因为激励为零,零输入t r zi ()()()02d 3d d 22=++t r dt t r t t r ()()()()()()的解.,且满足 0000 2000='='='===--+--+r r r r r r zi zi zi zi 2121-=-=αα,()t t zi e B e B t r 221--+=()()式解得,代入,由)4(0020='=++zi zi r r 2,421-==B B ()0 242≥-=--t e e t r t t zi ()0 342≥++-=--t e e t r t t zs t t e e 24--+-()是方程零状态响应t r zs ()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()的解且满足000='=--zs zs r r ()项由于上式等号右边有t δ()应含有冲激函数,,故t r zs "()将发生跳变,即从而t r zs '()()-+'≠'00zs zs r r ()处是连续的.在而0=t t r zs ()()()()()t u a t r t t u b t a t r tzs zs∆=+∆+=+d d ,d d 22δ()()()()()()t u t t r t u a t u b t a 6223+=+∆+∆+δδ()t δ2=a ()()()()002000===+'='-+-+zs zs zs zs r r a r r ()()()()t u t r t t r t t r 62d d 3d d 22=++ 221t t e D e D --+()3221++=--t t zi e D e D t r ()()得由初始条件0,200=='++zs zs r r 1,421=-=D D ()0) ( 342≥++-=--t e e t r t t zs ()0 242≥-=--t e e t r t t zi完全响应=零状态响应+零输入响应,即例2-2冲激响应是系统对单位冲激信号激励时的零状态响应。
《信号与系统》第二版第二章:LTI连续时间系统的时域分析
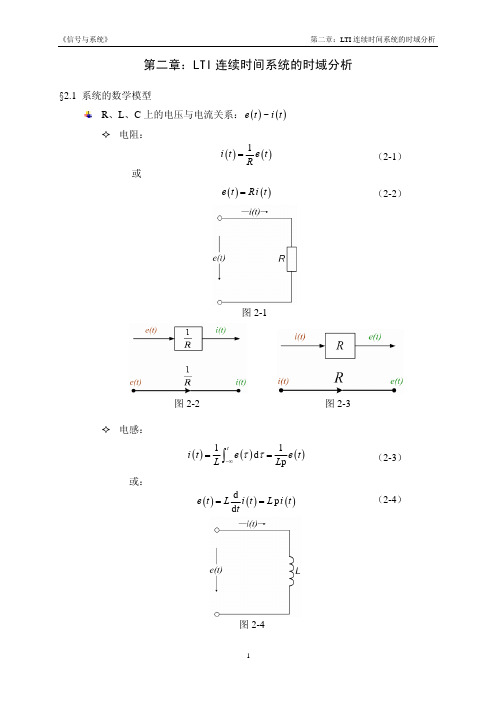
零状态(zero state)响应 yzs (t ) :不考虑起始时刻系统储能的作用,即Y(0-) ≡0,由系统的外加激励信号 v (t ) = v (t )u (t ) ≠ 0 所产生的响应。
零输入响应 yzi (t ) :
5
《信号与系统》
第二章:LTI 连续时间系统的时域分析
∏(p −αi )
i =1
(αi 为互异特征根)
= N (p) ⎡⎣eαnt ∗ ∗ eα1t ∗ v (t )⎤⎦
(2-19)
n
∑ yzs (t ) = 齐次解 Aieαit +特解 B (t ) i =1
(2-20)
特解 B (t ) 反映系统输入对输出的强迫。
非零状态线性系统: 定义(非零状态线性系统):系统 T 的初始状态为X(0-)≠0
令: D (p) pn + an−1pn−1 + ... + a1p + a0
N (p) bmpm + ... + b1p + b0
4
《信号与系统》
有:
第二章:LTI 连续时间系统的时域分析
y
(t)
=
N (p) D(p)
v(t
)
H (p)v(t)
(2-13)
其中,
H
(p)
=
N (p) D(p)
称为系统算子。
≤ ∫ ∫ f (τ ) g (t −τ ) dτ dt ΩΩ
= ∫ f (τ ) ∫ g (t −τ ) dtdτ
Ω
Ω
=∫
f (τ )
g (t ) dτ = 1
f (t) 1
g (t ) 1
信号与系统第三版课后习题答案

信号与系统第三版课后习题答案信号与系统第三版课后习题答案信号与系统是电子信息类专业中一门重要的基础课程,它是研究信号的产生、传输、处理和识别的学科。
在学习这门课程时,课后习题是非常重要的,它可以帮助我们巩固所学的知识,并且提高解决问题的能力。
下面是信号与系统第三版课后习题的答案。
第一章:信号与系统的基本概念1. 信号是指随时间、空间或其他独立变量的变化而变化的物理量。
系统是指能够对输入信号进行处理并产生输出信号的物理设备或数学模型。
2. 连续时间信号是在连续时间范围内定义的信号,可以用连续函数表示。
离散时间信号是在离散时间范围内定义的信号,可以用数列表示。
3. 周期信号是指在一定时间间隔内重复出现的信号,具有周期性。
非周期信号是指不具有周期性的信号。
4. 奇对称信号是指关于原点对称的信号,即f(t)=-f(-t)。
偶对称信号是指关于原点对称的信号,即f(t)=f(-t)。
5. 系统的线性性质是指系统满足叠加原理,即对于输入信号的线性组合,输出信号也是这些输入信号的线性组合。
6. 系统的时不变性质是指系统对于不同时间的输入信号,输出信号的特性是不变的。
7. 系统的因果性质是指系统的输出只依赖于当前和过去的输入信号,而不依赖于未来的输入信号。
第二章:连续时间信号与系统的时域分析1. 奇偶分解是将一个信号分解为奇对称和偶对称两个部分的过程。
奇偶分解的目的是简化信号的处理和分析。
2. 卷积是信号处理中常用的一种操作,它描述了两个信号之间的相互作用。
卷积的定义为:y(t) = ∫[x(τ)h(t-τ)]dτ。
3. 系统的冲激响应是指系统对于单位冲激信号的输出响应。
冲激响应可以用来描述系统的特性和性能。
4. 系统的单位阶跃响应是指系统对于单位阶跃信号的输出响应。
单位阶跃响应可以用来描述系统的稳定性和响应速度。
5. 系统的单位斜坡响应是指系统对于单位斜坡信号的输出响应。
单位斜坡响应可以用来描述系统的积分特性。
实验3连续系统的时域及复频域分析

实验三 连系统的时域及复频域分析一、实验目的1、熟悉LTI 连续时间系统的时域及复频域分析方法;2、熟悉系统的零输入响应、零状态响应及冲激响应的求解步骤;3、熟悉拉普拉斯变换的原理及性质,熟悉常见信号的拉氏变换。
3、学会用MA TLAB 进行部分分式展开,学会用MATLAB 进行Laplace 正、反变换。
4、学会用MA TLAB 分析LTI 系统的特性。
二、实验环境计算机,Matlab 软件三、实验原理(一)连续系统的时域分析LTI 连续时间系统以常系数微分方程描述,系统的零状态响应可通过求解初始状态为零的微分方程得到。
MATLAB 提供了专门用于求解零初始状态微分方程数值解的函数以及专门用于求连续系统冲激响应及阶跃响应并绘制其时域波形的函数,利用其可以方便的计算系统的响应。
1、连续时间系统零状态响应的求解LTI 连续时间以常系数微分方程描述,系统的零状态响应可通过求解初始状态为零的微分方程得到.在MATLAB 的控制系统工具箱提供了一个用于求解零初始状态微分方程数值解的函数lsim.其调用方式为: y=lsim(sys,f,t)式中,t 表示计算系统响应的抽样点向量;f 是系统输入信号向量;sys 是LTI 系统模型,用来表示微分方程、差分方程、状态方程。
在求解微分方程时,微分方程的LTI 系统模型sys 要借助tf 函数获得(Create transfer function model ),其调用方式为:sys=tf(b,a)式中,b 和a 分别为微分方程右端和左端各项的系数向量。
(注意:微分方程中为零的系数一定要写入向量a 和b 中。
)例1:系统的微分方程为:)()(100)('2)(''t x t y t y t y =++,已知输入信号)π2sin(10)(t t x =。
ts=0;te=5;dt=0.01;sys=tf([1],[1 2 100]);%注意系数与微分方程系数的对应关系t=ts:dt:te;f=10*sin(2*pi*t);y=lsim(sys,f,t); %LSIM Simulate time response of dynamic systems toarbitrary inputs. 注意调用格式。
管致中《信号与线性系统》(第5版)(课后习题 连续时间系统的时域分析)

8 / 43
圣才电子书
十万种考研考证电子书、题库视频学习平 台
2.6 已知电路如图 2-5 所示,电路未加激励的初始条件为:
(1) i10 2A,i'1 0 1A s ;(2) i10 1A,i'2 0 2A 。 求上述两种情况下电流 i1t及 i2t的零输入响应。
由②式可得:
③
由①式可得:
④
将式③代入式④可得:
用微分算子表示为: 即 (2)同理,将式①代入式③可得:
整理得: 用微分算子表示为:
1 / 43
圣才电子书
即
十万种考研考证电子书、题库视频学习平
台
。
2.2 H(p)。
写出图 2-2 中输入 e t 和输出 i1 t 之间关系的线性微分方程,并求转移算子
圣才电子书
十万种考研考证电子书、题库视频学习平
台
第 2 章 连续时间系统的时域分析
2.1 写出图 2-1 中输入 it 和输出 u1t 及 u2 t 之间关系的线性微分方程,并求转移
算子。
图 2-1 答:(1)利用节点法来分析电路,可得
对于节点 1:
①
对于节点 2:
②
(1)
d3 dt 3
r(t)
2
d2 dt 2
r(t)
d dt
r(t)
3
d dt
e(t)
e(t) ,
r0
r0
0,r0
1;
(2)
d3 dt 3
r(t)
3
d2 dt 2
r(t)
2
d dt
r(t)
《信号与系统》考研试题解答第二章连续系统的时域分析

第二章 连续系统的时域分析一、单项选择题X2.1(东南大学2002年考研题)一线性时不变连续时间系统,其在某激励信号作用下的自由响应为(e -3t +e -t )ε(t ),强迫响应为(1-e -2t )ε(t ),则下面的说法正确的是 。
(A )该系统一定是二阶系统 (B )该系统一定是稳定系统(C )零输入响应中一定包含(e -3t +e -t )ε(t ) (D )零状态响应中一定包含(1-e -2t )ε(t )X2.2(西安电子科技大学2005年考研题)信号f 1(t )和 f 2(t ) 如图X2.2所示,f =f 1(t )* f 2(t ),则 f (-1)等于 。
(A )1 (B )-1 (C )1.5 (D )-0.5图X2.2X2.3(西安电子科技大学2005年考研题)下列等式不成立的是 。
[])()(*)()()()(*)()()(*)()(*)()()(*)()(*)()(2121210201t f t t f D t f t t f C t f dt d t f dt d t f t f dt d B t f t f t t f t t f A ='='⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==+-δδ答案:X2.1[D],X2.2[C],X2.3[B]二、判断与填空题T2.1(北京航空航天大学2001年考研题)判断下列说法是否正确,正确的打“√”,错误的打“×”。
(1)若)(*)()(t h t f t y =,则)2(*)2(2)2(t h t f t y =。
[ ] (2)如果x (t )和y (t )均为奇函数,则x (t )*y (t )为偶函数。
[ ] (3)卷积的方法只适用于线性时不变系统的分析。
[ ] (4)若)(*)()(t h t f t y =,则)(*)()(t h t f t y --=-。
[ ](5)两个LTI 系统级联,其总的输入输出关系与它们在级联中的次序没有关系。
