二面角专题习题
二面角典型习题

二面角1.二面角的计算:1)定义法;2)三垂线定理法;3)垂面法;4)面积射影法;例1、已知P 是二面角AB αβ--棱上一点,过P 分别在αβ、内引射线PM ,PN ,且45,60BPM BPN MPN ∠=∠=︒∠=︒,求此二面角的度数。
例2、已知P 为锐二面角l αβ--棱上的点,,4530PQ PQ l αβ⊂︒︒与成,与成,则二面角l αβ--的度数是多少。
例3、已知二面角l αβ--的度数为θ,在面α内有一条射线AB 与棱l 成锐角δ,与面βγ成角,则必有( )(A )sin sin sin θδγ= (B )sin sin cos θδγ=(C )cos cos sin θδγ= (D )cos cos cos θδγ=例4、在120︒的二面角l αβ--的面α、β内分别有A 、B 两点,且A 、B 到棱l 的距离AC 、BD 分别长2、4,AB=10,求:(1)直线AB 与棱l 所成角的正弦值。
(2)直线AB 与平面β所成角的正弦值。
例5、已知二面角MN αβ--为60︒,,,A B BC AB αββ∈∈为在上的射影,且C 在棱MN 上,AB 与β所成角为60︒,且45AC MCB ∠=︒,求线段AB 的长。
例6、已知二面角DC αβ--的度数为θ,,,A B ADC αβ∈∈∆的面积为S ,且DC=m ,AB DC ⊥,AB 与平面β成30︒角,当θ变化时,求DBC ∆面积最大值。
例7、已知C 是以AB 为直径的圆周上的一点,30ABC ∠=︒,45PA ABC PBA ⊥∠=︒面,,求二面角A-PB-C 的正弦值。
例8、在正方体1111ABCD A BC D -中,利用cos S S θ=射影解下列各题1)P 、Q 分别为1,A A AB 的中点,求平面1C PQ 与底面ABCD 所成角的余弦值2)求二面角11C BD C --的大小;3)M 是棱BC 的中点,求二面角111D B M C --的余弦值。
二面角习题及答案

二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC 是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
解:DPCABEDBAS CSR NMO DPC4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =0120,求二面角 A-BD-C 的余弦值。
解:5.已知正方体 AC',M 、N 分别是BB',DD'的中点,求截面 AMC'N 与面ABCD ,CC'D'D 所成的角。
解:6.如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:DBAECD ’ B ’DAC ’B A ’CMNBFEACD7. 三棱锥 A-BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9. 如图所示,四棱锥P —ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD ,PC =a,E 是PA 的中点.(1)求证平面BDE ⊥平面ABCD.(2)求点E 到平面PBC 的距离.(3)求二面角A —EB —D 的平面角大小. 解析:10. 如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC 上,G在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.DOABC11. 如图,设ABC —A1B1C1是直三棱柱,E 、F 分别为AB 、A1B1的中点,且AB =2AA1=2a,AC =BC =3a. (1)求证:AF ⊥A1C(2)求二面角C —AF —B 的大小12.如图1111D C B A ABCD -是长方体,AB=2,11==AD AA ,求二平面C AB 1与1111D C B A 所成二面角的大小.13. 在正方体1111D C B A A B C D-中,1BB K ∈,1CC M ∈,且141BB BK =,143CC CM =..求:平面AKM 与ABCD 所成角的大小.14. 如图,将边长为a 的正三角形ABC 按它的高AD 为折痕折成一个二面角C AD C --'. (1)若二面角C AD C --'是直二面角,求C C '的长; (2)求C A '与平面CD C '所成的角;(3)若二面角C AD C --'的平面角为120°,求二面角D C C A -'-的平面角的正切值.参考答案解:由已知条件,D是BC的中点∴CD =BD =2 又△ADC是正三角形∴AD =CD =BD =2∴D是△ABC之外心又在BC上∴△ABC是以∠BAC为直角的三角形,∴AB⊥AC,又PC⊥面ABC∴PA⊥AB (三垂线定理)∴∠PAC即为二面角P-AB-C之平面角,DPCAB易求 ∠PAC =30°2、解:∵ BS =BC ,又DE 垂直平分SC ∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DC 则 ∠EDC 就是所要求的平面角 设 SA =AB =a ,则 BC =SB =2a 且 AC = 3易证 △SAC ∽△DEC ∴ ∠CDE =∠SAC =60°3、解:取OC 之中点N ,则 MN ∥PO ∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2,过 N 作 NR ⊥BD 于 R ,连MR , 则 ∠MRN 即为二面角 M-BD-C 的平面角过 C 作 CE ⊥BD 于S 则 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE ∴ 58BD BC CD CE =⋅=∴ 54RN =25RN MN MRN tan ==∠ ∴ 25a r c t a n M RN =∠EDBASCSR N MOBDPA C4. 解:过 A 作 AE ⊥CB 的延长线于E , 连结 DE , ∵ 面ABC ⊥面BCD ∴ AE ⊥面BCD∴ E 点即为点A 在面BCD 内的射影∴ △EBD 为△ABD 在面BCD 内的射影设 AB =a 则AE =DE =ABsin60°=a 23 ∴ AD =41ABD cos 26=∠, ∴ sin ∠ABD =415∴ 22A B D a 815415a 21S =⨯=∆ 又 a 21BE = ∴ 2B D E a 83a 21a 2321S =⋅⋅=∆ ∴ 55S S c o s A B D B D E ==θ∆∆ 5. 解:设边长为a ,易证 ANC'N 是菱形 且MN =a 2,A'C =a 3∴S□AMC'N = 2a 26'AC 21MN =⋅ 由于AMC'N 在面ABCD 上的射影即 为正方形ABCD ∴ S□ABCD =2a ∴ 36a 26a c o s 221==θ D ’ B ’DAC ’BA ’C MN∴ 36a r c c o s 1=θ 取CC'的中点M',连结DM'则平行四边形DM'C'N 是四边形AMC'N 在CC'D'D 上的射影,S□DM'C'M =2a 21 ∴ 66a 26a21c o s 222==θ ∴66arccos2=θ 6. 解:作DF ⊥AB 于F ,CE ⊥AB 于E , ∵ AC =CD =1 ∠ABC =30°∴ AD =2,BC =3 ,AB =2, BD =2在Rt △ABC 中,23231AB BC AC CE =⨯=⋅=,同理 1222AB BDAD DF =⨯=⋅= ∴ 1DF BD BF 22=-=21CE AC AE 22=-= ∴ 212112EF =--= ∴ θ⋅-++=cos DF EF 2EF DF CE CD 2222∴ 33cos =θ 即所求角的大小为33arccos。
二面角典型习题(可编辑修改word版)
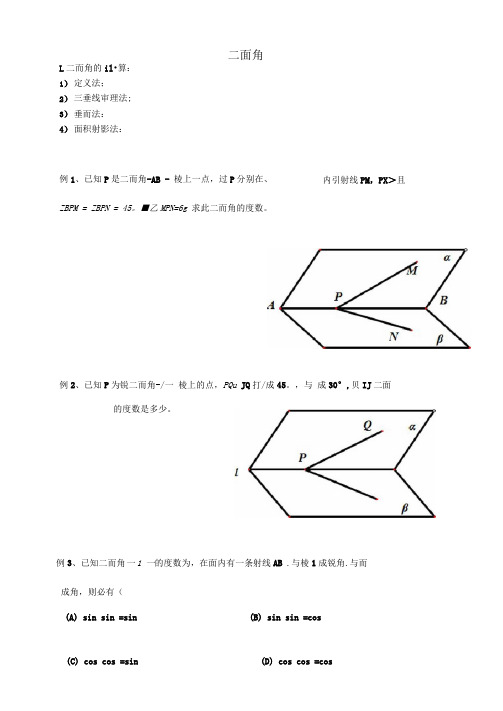
(C) cos cos =sin (D) cos cos =cosL 二而角的il •算:1) 定义法;2) 三垂线审理法;3) 垂而法:4) 面积射影法:例1、已知P 是二而角-AB - 棱上一点,过P 分别在、 ZBPM = ZBPN = 45。
■乙MPN=6g 求此二而角的度数。
例2、已知P 为锐二而角-/一 棱上的点,PQu JQ 打/成45。
,与 成30°,贝IJ 二面例3、已知二而角一1 一的度数为,在面内有一条射线AB .与棱1成锐角.与而成角,则必有(二面角内引射线PM ,PX >且的度数是多少。
(A) sin sin =sin (B) sin sin =cos例4、在120。
的二而角-/一的面、内分别有A、B两点.且A、B到棱1的距离AC、BD 分别长2、4, AB=1O,求J(1)直线AB .与棱1所成角的正弦值。
(2)直线AB •与平而所成角的正弦值.例5、已知二而角-MN-为60。
,Ae.Be为AB在上的射影,且C在棱MX 上,AB与所成角为60。
,且AC= JM Z MCB=45。
, 求线段AB的长。
例6、已知二而角一 DC —的度数为,A e ,B€ .MDC的而枳为S,且D(二m.AB丄DC , AB与平而成30。
角,当DMDi W — A- Di例是以AB 为直径的圆周上的一点,ZABC = 30。
,P4丄而ABC, ZPBA = 45。
,求二而角A-PB-C 的正弦值。
S 例8、在正方体ABCD - 中,利用cos =3■解下列各题S1)P. Q 分别为AyA.AB 的中点,求平而C,PQ 打底而ABCD 所成角的余弦值 2)求二而角Ci-BDi-C 的大小:3) M 是棱BC的中点,求二面角Q-BjM-G 的余弦值。
——・B例9.已知D 、E 分别是边长为a 的等边三角形ABC 的边AB 、AC 上的点,DE//BC.现沿DE 将三角形ADE 折起,是二面角A-DE-B 成60度角,当DE 在什么位置时,使折起后的顶点A 到BC 边距离最短?最短是多少?ZADC = ZBCA = 90°, AABC = 60。
完整版二面角练习题

周练六1.如图,已知在三棱柱ABC ABQ,中,三个侧棱都是矩形,点D为AB的中点+AC 3,BC 4, AB 5,AA, 4 ,(I)求证AC BC i;(n )求证AC1 P平面CDB1;(川)求异面直线AC i与B i C所成角的余弦值+2 .如图,已知正方形ABCD和正方形ABEF所在平面成60°的二面角,所成角的正弦值。
求直线BD与平面ABEF A —"DF3.如图,在棱长为a的正方体ABC—ABCD中,求:(1 )面AABB与面ABCD所成角的大小;(2)二面角C-BD-C的正切值(3)二面角B1 BC1 DP4•过正方形ABCD的顶点A作PA A平面ABCD ,设PA=AB=a , (1)求二面角B- PC- D的大小;(2)求二面角C-PD-AB C5.如图所示,四棱锥P —ABCD的底面ABCD是边长为1的菱形,/ BCD = 60°, E是CD的中点,PA丄底面ABCD , PA= .3•⑴证明:BE丄平面PAB;⑵求二面角A—BE—P的大小(3) PB与面PAC的角6如图,在底面为直角梯形的四棱锥P ABCD 中,AD//BC, ABC 90 ,PA 平面ABCD PA 3, AD 2, AB ^3 BC=6(1)求证:BD平面PAC;⑵求二面角P BD A的大小.(3)求二面角B-PC-A的大小7.如图,直二面角D —AB —E中,四边形ABCD是边长为2的正方形,AE=EB , F为CE 上的点,且BF丄平面ACE.(I)求证AE丄平面BCE;(H)求二面角B—AC —E的大小; (川)求点D到平面ACE的距离.8•如图,在四棱锥P ABCD中,底面ABCD是矩形•已知AB 3 , AD 2 ,PA 2 , PD 2近,/ PAB 60°.(I)证明AD 平面PAB ;(n)求异面直线PC与AD所成的角的大小;(川)求二面角P BD A的正切值.。
二面角习题含详细答案

又AP⊥PC,PB∩PC=P, ∴AP⊥平面PBC①.…………………………………………2分 又BC⊂平面PBC,∴AP⊥BC. 又AC⊥BC,AP∩AC=A, ∴BC⊥平面PAC①.
又BC⊂平面ABC,∴平面PAC⊥平面ABC.…………………4分
(2)∵PA⊥PC,且PA⊥PB,
∴∠BPC是二面角D-AP-C的平面角②. 由(1)知BC⊥平面PAC,则BC⊥PC, ∴sin∠BPC= BC 2 . ……………………………………8分
通过分析条件,鉴别已知角是否为二面角的 平面角,否则就需利用垂直关系作辅助线得 到其平面角. 证明且点明某平面角是所求二面角的平面角. 把角放在三角形内求值,要注意的是二面角 的范围.
作图
定性
求解
【典例训练】
1.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,
则二面角B-PA-C的大小为( )
证明
求值
【想一想】找二面角的平面角的方法有哪些?
提示:(1)垂面法:由二面角的平面角的定义,只需作与棱垂 直的平面,则该平面与两半平面所成交线构成的角就是二面角 的平面角. (2)平移法:先分别在两半平面内找一条垂直于棱的射线,然 后平移到一起找到二面角的平面角.
【规范解答】线面垂直的综合应用
【典例】(12分)如图所示,已知三
(A)90°
(B)60°
(C)45°
(D)30°
2.如图所示,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分 SC,且分别交AC,SC于点D,E,又SA=AB,SB=BC,求二面角
E-BD-C的大小.
【解析】1.选A.∵PA⊥平面ABC,BA,CA⊂平面ABC,
∴BA⊥PA,CA⊥PA,因此,∠BAC即为二面角B-PA-C的平面角.
二面角专项训练(人教A版)(含答案)

二面角专项训练(人教A版)一、单选题(共7道,每道10分)1.等于90°的二面角内有一点P,过P有PA⊥α于点A,PB⊥β于点B,如果PA=PB=a,则P 到交线的距离为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:与二面角有关的点、线、面间的距离计算2.如图,在三棱锥F-ABC中,FC⊥底面ABC,CA=CB=CF,∠ACB=120°,则二面角F-AB-C的正切值为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:二面角的平面角及求法3.如图,在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是腰长为的等腰三角形,则二面角V-AB-C的平面角为( )A.30°B.45°C.60°D.90°答案:C解题思路:试题难度:三颗星知识点:二面角的平面角及求法4.如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥AB,PA=AB=2,AC=1,则二面角A-PC-B的正弦值为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:二面角的平面角及求法5.如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,D是棱AA1的中点,则二面角B-DC1-C的余弦值为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:二面角的平面角及求法6.如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,D是棱AA1的中点,DC1⊥BD,则二面角A1-BD-C1的大小为( )A.30°B.45°C.60°D.90°答案:A解题思路:试题难度:三颗星知识点:二面角的平面角及求法7.如图,在直三棱柱ABC-A1B1C1中,AB1⊥A1C,AB=4,AC=BC=3,D为AB的中点,则二面角A1-CD-C1的平面角的余弦值为( )A. B. C. D.答案:D解题思路:试题难度:三颗星知识点:二面角的平面角及求法。
二面角典型习题

二面角1.二面角的计算:1)定义法;2)三垂线定理法;3)垂面法;4)面积射影法;例1、已知P 是二面角棱上一点,过P 分别在内引射线PM ,PN ,且AB αβ--αβ、,求此二面角的度数。
45,60BPM BPN MPN ∠=∠=︒∠=︒例2、已知P 为锐二面角棱上的点,,则二l αβ--,4530PQ PQ l αβ⊂︒︒与成,与成面角的度数是多少。
l αβ--例3、已知二面角的度数为,在面内有一条射线AB 与棱l 成锐角,与面l αβ--θαδ,则必有( )βγ成角(A ) (B )sin sin sin θδγ=sin sin cos θδγ=(C ) (D )cos cos sin θδγ=cos cos cos θδγ=例4、在的二面角的面、内分别有A 、B 两点,且A 、B 到棱l 的距离120︒l αβ--αβAC 、BD 分别长2、4,AB=10,求:(1)直线AB 与棱l 所成角的正弦值。
(2)直线AB 与平面所成角的正弦值。
β例5、已知二面角为,上的射影,且C 在棱MN αβ--60︒,,A B BC AB αββ∈∈为在MN 上,AB 与所成角为,且,求线段AB 的长。
β60︒45AC MCB =∠=︒例6、已知二面角的度数为,的面积为S ,且DC=m ,DC αβ--θ,,A B ADC αβ∈∈∆,AB 与平面成角,当变化时,求面积最大值。
AB DC ⊥β30︒θDBC ∆in例7、已知C是以AB为直径的圆周上的一点,,30ABC∠=︒,求二面角A-45PA ABC PBA⊥∠=︒面,PB-C的正弦值。
例8、在正方体中,利用解下列各题1111ABCD A B C D-cosSSθ=射影1)P、Q分别为的中点,求平面与底面ABCD所成角的余弦值1,A A AB1C PQ2)求二面角的大小;11C BD C--3)M是棱BC的中点,求二面角的余弦值。
111D B M C--例9、已知D 、E 分别是边长为a 的等边三角形ABC 的边AB 、AC 上的点,DE//BC ,现沿DE 将三角形ADE 折起,是二面角A-DE-B 成60度角,当DE 在什么位置时,使折起后的顶点A 到BC 边距离最短?最短是多少?例10、等腰Rt 和Rt 有公共边AC ,,ADC ∆BCA ∆90,60ADC BCA ABC ∠=∠=︒∠=︒以AC 为棱折起多少度的二面角时,有BD=BC ?两个平面垂直1、两个平面垂直的证明1)定义2)判定定理2、两个平面垂直的性质例1、已知ABCD 为矩形,E 为半圆CED 上一点,且平面ABCD 平面CDE ⊥1)求证DE 是AD 与BE 的公垂线2)若AD=DE=AB ,求AD 与BE 所成角的大小。
二面角习题及标准答案

二面角习题及答案————————————————————————————————作者:————————————————————————————————日期:二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
解:4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =0120,求二面角 A-BD-C 的余弦值。
解:DPC A BE DB ASCS R NMO B DPA CB A EC5.已知正方体 AC',M 、N 分别是BB',DD'的中点,求截面 AMC'N 与面ABCD ,CC'D'D 所成的角。
解:6.如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:7. 三棱锥 A-BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9. 如图所示,四棱锥P —ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD ,PC =a,E 是PA 的中点.(1)求证平面BDE ⊥平面ABCD.(2)求点E 到平面PBC 的距离.(3)求二面角A —EB —D 的平面角大小. 解析:D BD ACBAC M N B F E ACDDOA BC10. 如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC 上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.11. 如图,设ABC —A1B1C1是直三棱柱,E 、F 分别为AB 、A1B1的中点,且AB =2AA1=2a,AC =BC =3a. (1)求证:AF ⊥A1C(2)求二面角C —AF —B 的大小12.如图1111D C B A ABCD -是长方体,AB=2,11==AD AA ,求二平面C AB 1与1111D C B A 所成二面角的大小.13. 在正方体1111D C B A ABCD -中,1BB K ∈,1CC M ∈,且141BB BK =,143CC CM =..求:平面AKM 与ABCD 所成角的大小.14. 如图,将边长为a 的正三角形ABC 按它的高AD 为折痕折成一个二面角C AD C --'. (1)若二面角C AD C --'是直二面角,求C C '的长; (2)求C A '与平面CD C '所成的角;(3)若二面角C AD C --'的平面角为120°,求二面角D C C A -'-的平面角的正切值.参考答案解:由已知条件,D 是BC 的中点∴ CD =BD =2 又△ADC 是正三角形 ∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上 ∴ △ABC 是以∠BAC 为直角的三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC ∴ PA ⊥AB (三垂线定理)∴∠PAC 即为二面角 P-AB-C 之平面角, 易求 ∠PAC =30°2、解:∵ BS =BC ,又DE 垂直平分SC ∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC ∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DC 则 ∠EDC 就是所要求的平面角 设 SA =AB =a ,则 BC =SB =2a 且 AC = 3易证 △SAC ∽△DEC ∴ ∠CDE =∠SAC =60° 3、解:取OC 之中点N ,则 MN ∥PO ∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2, 过 N 作 NR ⊥BD 于 R ,连MR , 则 ∠MRN 即为二面角 M-BD-C 的平面角 过 C 作 CE ⊥BD 于S则 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE ∴ 58BD BC CD CE =⋅=DPCA BE DBASCS R N MO B DPA C∴ 54RN =25RN MN MRN tan ==∠ ∴ 25arctanMRN =∠ 4. 解:过 A 作 AE ⊥CB 的延长线于E , 连结 DE , ∵ 面ABC ⊥面BCD ∴ AE ⊥面BCD∴ E 点即为点A 在面BCD 内的射影∴ △EBD 为△ABD 在面BCD 内的射影设 AB =a 则AE =DE =ABsin60°=a 23 ∴ AD =41ABD cos 26=∠, ∴ sin ∠ABD =415∴ 22ABD a 815415a 21S =⨯=∆ 又 a 21BE = ∴ 2BDE a 83a 21a 2321S =⋅⋅=∆ ∴ 55S S cos ABD BDE ==θ∆∆ 5. 解:设边长为a ,易证 ANC'N 是菱形 且MN =a 2,A'C =a 3 ∴S□AMC'N = 2a 26'AC 21MN =⋅由于AMC'N 在面ABCD 上的射影即 为正方形ABCD ∴ S□ABCD =2aD B D AC BAC MN∴ 36a 26a cos 221==θ ∴ 36arccos1=θ 取CC'的中点M',连结DM'则平行四边形DM'C'N 是四边形AMC'N 在CC'D'D 上的射影,S□DM'C'M =2a 21 ∴ 66a 26a21cos 222==θ ∴66arccos2=θ 6. 解:作DF ⊥AB 于F ,CE ⊥AB 于E , ∵ AC =CD =1 ∠ABC =30° ∴ AD =2,BC =3 , AB =2, BD =2 在Rt △ABC 中, 23231AB BC AC CE =⨯=⋅=,同理 1222ABBDAD DF =⨯=⋅= ∴ 1DF BD BF 22=-=21CE AC AE 22=-= ∴ 212112EF =--= ∴ θ⋅-++=cos DF EF 2EF DF CE CD 2222∴ 33cos =θ BF E ACD即所求角的大小为33arccos。
高考数学二面角专题训练

高考数学二面角专题训练1.(06安徽卷)如图,P 是边长为1的正六边形ABCDEF 所在平面外一点,1PA =,P 在平面ABC 内的射影为BF 的中点O 。
(Ⅰ)证明PA ⊥BF ;(Ⅱ)求面APB 与面DPB 所成二面角的大小。
解:(Ⅰ)在正六边形ABCDEF 中,ABF 为等腰三角形,∵P 在平面ABC 内的射影为O ,∴PO ⊥平面ABF ,∴AO 为PA 在平面ABF 内的射影;∵O 为BF 中点,∴AO ⊥BF ,∴PA ⊥BF 。
(Ⅱ)∵PO ⊥平面ABF ,∴平面PBF ⊥平面ABC ;而O 为BF 中点,ABCDEF 是正六边形 ,∴A 、O 、D 共线,且直线AD ⊥BF ,则AD ⊥平面PBF ;又∵正六边形ABCDEF 的边长为1,∴12AO =,32DO =,BO =。
过O 在平面POB 内作OH ⊥PB 于H ,连AH 、DH ,则AH ⊥PB ,DH ⊥PB ,所以AHD ∠为所求二面角平面角。
在AHO 中,OH=7,1tan AOAHO OH ∠==。
在DHO中,3tan 7DO DHO OH ∠===;而tan tan()2AHD AHO DHO ∠=∠+∠== (Ⅱ)以O 为坐标原点,建立空间直角坐标系,P(0,0,1),A(0,12-,0),0,0),D(0,2,0),∴1(0,,1)2PA =--,3(1)PB =-,(0,2,1)PD =-设平面PAB 的法向量为111(,,1)n x y =,则1n PA ⊥,1n PB⊥,得11110210y x ⎧--=⎪⎪-=,123(2,1)3n =-;设平面PDB 的法向量为222(,,1)n x y =,则2n PD ⊥,2n PB ⊥,得22210102y x -=⎧-=⎩,2231(,1)32n =;121212cos ,||||n n n n n n ⋅<>==⋅2. (06北京卷)如图,在底面为平行四边表的四棱锥P ABCD -中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点.(Ⅰ)求证:AC PB ⊥;(Ⅱ)求证://PB 平面AEC ; (Ⅲ)求二面角E AC B --的大小.解法一:(Ⅰ)PA ⊥平面ABCD ,∴AB 是PB 在平面ABCD 上得射影, 又AB ⊥AC ,AC ⊂平面ABCD , ∴AC ⊥PB.(Ⅱ)连接BD ,与AC 相交与O ,连接EO , ABCD 是平行四边形 ∴O 是BD 的中点 又E 是PD 的中点, ∴EO PB.又PB ⊄平面AEC ,EO ⊂平面AEC , ∴PB 平面AEC ,(Ⅲ)取BC 中点G ,连接OG ,则点G 的坐标为,,022a b ⎛⎫ ⎪⎝⎭,0,,02b OC ⎛⎫= ⎪⎝⎭又(,0,0),OE AC a =b b=(0,-,),220,0,OE AC OG AC ∴==,,OE AC OG AC ∴⊥⊥EOG ∴∠是二面角E AC B -=的平面角。
文科立体几何线面角二面角专题_带答案解析

【解析】试题分析:(1)由题意,可取 中点 ,连接 ,则易知平面 ∥平面 ,由条件易证 平面 ,则 平面 ,又 平面 ,根据线面垂直的定义,从而问题可得证;(2)由题意,采用坐标法进行求解,可取 中点 为坐标原点,过 点作平行于 的直线为 轴, 为 轴, 为 轴,建立空间直角坐标系,分别算出平面 和平面 的法向量,结合图形,二面角 为锐角,从而问题可得解.
6.(1)见解析(2)见解析(3)
【解析】分析:(1)先证明 ,再证明 平面 .(2)先证明 面 ,再证明平面 平面 .(3)利用异面直线所成的角的定义求直线 与直线 所成角的正弦值为 .
详解:(1)证明:连接 ,
∵ 、 分别是 、 的中点,
∴ , ,
∵三棱柱 中,∴ , ,
又 为棱 的中点,∴ , ,
∴四边形 是平行四边形,∴ ,
又∵ 平面 , 平面 ,∴ 平面 .
(2)证明:∵ 是 的中点,∴ ,
又∵ 平面 , 平面 ,
∴ ,又∵ ,
∴ 面 ,又 面 ,
∴平面 平面 ;
(3)解:∵ , ,
∴ 为直线 与直线 所成的角.
设三棱柱 的棱长为 ,则 ,
∴ ,∴ .
即直线 与直线 所成角的正弦值为 .
8.(1)见解析;(2)
【解析】分析:(1)由题意得 是等边三角形,故得 ,于是 ,从而得 ,所以 ,然后根据线面平行的判定定理可得结论成立.(2)由 平面 可得 ,于是 平面 .又 ,所以直线 与平面 所成角即直线 与平面 所成角,从而得到 即为所求角,然后根据解三角形可得所求.
详解:(1)因为 , 为 的中点,所以 ,且 .
连结 .因为 ,所以 为等腰直角三角形,
且 , .
二面角练习题

二面角练习题1、在三棱锥P-ABC中,已知PB⊥底面ABC,AC⊥BC,PB=BC=AC,点E、F分别是PC、XXX的中点.我们需要证明两个结论:Ⅰ)PC⊥平面BEF;Ⅱ)二面角A-EB-F的大小等于120°。
为证明(Ⅰ),我们可以通过三角形的性质来解决。
首先连接PE、PF,因为PE、PF分别是三角形PBC、PAC的中线,所以PE=PF=1/2BC=1/2AC。
又因为PB=BC=AC,所以△PBE和△PBF是等腰三角形,∠PBE=∠PBF。
又因为EF是△PBE和△PBF的中线,所以EF⊥PB,即EF⊥平面ABC。
又因为BE⊥平面ABC,所以PC⊥平面BEF。
为证明(Ⅱ),我们可以利用向量的知识,设向量PA=a,向量PB=b,则向量PC=a+b。
由于PB⊥平面ABC,所以向量PB在平面ABC上的投影为0,即b在平面ABC的法向量上。
又因为AC⊥BC,所以向量AC在平面ABC的法向量上,且向量AC与向量b的夹角为60°。
因此,向量PC在平面ABC的法向量上的投影为a的模长乘以cos60°,即PC在平面ABC的法向量上的投影为1/2PA。
由于PE、PF分别是△PAC、△PBC的中线,所以PE=PF=1/2PA=1/2PC。
因此,向量PE和向量PF在平面BEF上的投影相等,即二面角A-EB-F的大小等于120°。
2、在正方体ABCD-A1B1C1D1中,已知O是AC、BD的交点,E、F分别是AB、AD的中点。
我们需要证明三个结论:1)直线OD1与直线A1C1垂直;2)异面直线EF与A1C1所成角的大小等于60°;3)二面角B-AC-D1的大小等于90°。
为证明(1),我们可以利用向量的知识。
设向量OA1=a,向量OC1=b,则向量OD1=a+b。
因为正方体ABCD-A1B1C1D1中,向量OA1和向量OC1垂直且长度相等,所以向量OA1和向量OC1的夹角为90°。
专题求二面角含答案

1、如图,在直三棱柱 ABC-A1B1C1 中,AC=3,BC=4,AB=5,AA1 =4,点 D 是 AB 的中点C1B1A1CBDA(1)求证:AC BC 1 ;(2)求证:AC 1 //平面 CDB 1 ; (3)求二面角 B-DC-B1 的余弦值.2、如图,在长方体 ABCD 一 A1B1C1D1 中,AA1=2, AD = 3, E 为 CD 中点,三棱 锥 A1-AB1E 的体积是 6. (1) 设 P 是棱 BB1 的中点,证明:CP//平面 AEB1; (2) 求 AB 的长; (3)求二面角 B—AB1-E 的余弦值.试卷第 1 页,总 3 页3、如图,正方形 与梯形 所在的平面互相垂直,,,,, 为 的中点.(1)求证: 平面 ;(2)求证:平面平面 ;(3)求平面 与平面 所成锐二面角的余弦值.4、如图所示,三棱柱 ABC﹣A1B1C1 的底面是边长为 2 正三角形,D 是 A1C1 的中点,且 AA1⊥平面 ABC,AA1=3. (Ⅰ)求证:A1B∥平面 B1DC; (Ⅱ)求二面角 D﹣B1C﹣C1 的余弦值.试卷第 2 页,总 3 页5 、 如 图 , 在 四 棱 锥 P-ABCD 中 ,PA⊥ 底 面 ABCD, 底 面 ABCD 为 直 角 梯 形,AD∥BC,∠BAD=90°,PA=AD=AB=2BC=2,过 AD 的平面分别交 PB,PC 于 M,N 两点.(1)求证:MN∥BC; (2)若 M,N 分别为 PB,PC 的中点, ①求证:PB⊥DN; ②求二面角 P-DN-A 的余弦值.6、如图,在正三棱柱 ABC A1B1C1 中,点 D 是棱 AB 的中点,BC 1, AA1 3 .AD CBA1 C1B1(1)求证: BC1 // 平面 A1DC ; (2)求二面角 D A1C A 的平面角的正弦值.试卷第 3 页,总 3 页1、【答案】(1)AC BC 1 ;参考答案(2)AC //平面 CDB ;113 34 (3)二面角 B-DC-B1 的余弦值为 34试题分析:(1)考虑到第三问要求二面角的大小,故需要在空间直角坐标系中用法向量 的方法求解,因此可提前建系,(1)(2)问也可方便证明,因为是直三棱柱可以以 C 为 坐标原点,直线 CA,CB,CC1 分别为 x 轴、y 轴、z 轴建立空间直角坐标系,利用向量证明 AC • BC1 0 即可得证;(2)要证明线面平行,必须证明线线平行;(3)分别求出平面 BDC 和平面 DCB1 的法向量,求出法向量的夹角的余弦值即为二面角 B-DC-B1 的余弦 值(注意值的正负判断) 试题解析:因为直三棱柱的底面三边长分别为 3、4、5 所以 AC, BC,CC1 两两垂直,以 C 为坐标原 点,直线 CA,CB,CC1 分别为 x 轴、y 轴、z 轴建立空间直角坐标系(1)因为 AC 3,0,0, BC1 0, 4, 4 ,所以 AC • BC1 0 ,即 AC BC1(2)设CB1C1BE,则E 0, 2,2,故DE 3 2, 0,2 ,AC13, 0,4所以DE1 2AC1,即DE//AC1因为 DE 平面 CDB1 , AC1 平面 CDB1 ,所以 AC 1 //平面 CDB 1(3)可求得平面 CDB1 的一个法向量为 n1 4,3,3 ,取平面 CDB 的一个法向量为n2 0,0,1 ,则 cosn1, n2 3 343 3434 ,由图可知,二面角 B-DC-B1 的余弦值为 34考点:1.直线与平面平行的判定及性质;2.利用空间直角坐标系求二面角的求法;答案第 1 页,总 9 页2、【答案】3、【答案】(1)证明过程详见解析;(2)证明过程详见解析;(3) . 试题分析:本题主要考查中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、 二面角等基础知识,考查学生的空间想象能力、逻辑推理能力、计算能力.第一问,作答案第 2 页,总 9 页出辅助线 MN,N 为 中点,在 中,利用中位线得到,且,结合已知条件,可证出四边形 ABMN 为平行四边形,所以,利用线面平行的判定,得 ∥平面 ;第二问,利用面面垂直的性质,判断 面 ,再利用已知的边长,可证出,则利用线面垂直的判定得 平面 BDE,再利用面面垂直的判定得平面平面 ;第三问,可以利用传统几何法证明二面角的平面角,也可以利用向量法 建立空间直角坐标系,求出平面 BEC 和平面 ADEF 的法向量,利用夹角公式计算即可.(1)证明:取 中点 ,连结.在△ 中, 分别为 的中点,所以 ∥ ,且.由已知 ∥ ,,所以∥ ,且.所以四边形 为平行四边形,所以 ∥ .又因为 平面 ,且 平面 ,所以 ∥平面 .4 分(2)证明:在正方形 中,.又因为平面平面 ,且平面平面,所以 平面 .所以.6 分在直角梯形 中,, ,可得.答案第 3 页,总 9 页在△ 中,,所以.7 分所以 平面 .8 分又因为 平面 ,所以平面平面 .9 分(3)(方法一)延长 和 交于 .在平面内过 作于 ,连结 .由平面∥,,平面平面 = ,得,于是.又, 平面 ,所以,于是 就是平面 与平面 平面角.12 分所成锐二面角的平面 ,由,得.又,于是有.在中,.所以平面 与平面 所成锐二面角的余弦值为 .14 分答案第 4 页,总 9 页(方法二)由(2)知 平面 ,且.以 为原点,所在直线分别为 轴,建立空间直角坐标系.易得.平面 的一个法向量为的一个法向量,因为,所以所以为平面 的一个法向量.12分设平面 与平面 所成锐二面角为 ..设为平面,令 ,得.则.所以平面 与平面 所成锐二面角的余弦值为. 【考点】中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角. 4、【答案】 证明:(1)连结 BC1,B1C,交于点 O,连结 OD, ∵三棱柱 ABC﹣A1B1C1 的底面是边长为 2 正三角形,D 是 A1C1 的中点, ∴OD∥A1B, ∵A1B?平面 B1DC,OD?平面 B1DC, ∴A1B∥平面 B1DC. (2)∵三棱柱 ABC﹣A1B1C1 的底面是边长为 2 正三角形,D 是 A1C1 的中点,且 AA1⊥平面 ABC,AA1=3. ∴以 D 为原点,DC1 为 x 轴,DB1 为 y 轴,过 D 作平面 A1B1C1 的垂线为 z 轴,建立空间直 角坐标系, 则 D(0,0,0),B1(0, ,0),C(1,0,3),C1(1,0,0),答案第 5 页,总 9 页=(﹣1, ,﹣3), =(﹣1,0,﹣3), 设平面 B1DC 的法向量 =(x,y,z),=(0,0,﹣3),则,取 z=1,得 =(﹣3,0,1),设平面 B1CC1 的法向量 =(a,b,c),则,取 b=1,得 =(),设二面角 D﹣B1C﹣C1 的平面角为 θ,则 cosθ===.∴二面角 D﹣B1C﹣C1 的余弦值为.5、【答案】(1)见解析;(2)见解析, 试题分析:(1)先证明 BC∥平面 ADNM,再证明 MN∥BC.(2)①先证明 PB⊥平面 ADNM, 再证明 PB⊥DN.②以 A 为坐标原点,直线 AB 为 x 轴,直线 AD 为 y 轴,直线 AP 为 z 轴,建立 空间直角坐标系 A-xyz,利用向量法求二面角 P-DN-A 的余弦值. 【详解】 (1)证明因为底面 ABCD 为直角梯形,所以 BC∥AD.因为 BC 平面ADNM, AD 平面ADNM ,所以 BC∥平面 ADNM. 因为 BC 平面 PBC,平面 PBC∩平面 ADNM=MN,所以 MN∥BC. (2)①证明因为 M,N 分别为 PB,PC 的中点,PA=AB,所以 PB⊥MA. 因为∠BAD=90°,所以 DA⊥AB.答案第 6 页,总 9 页因为 PA⊥底面 ABCD,所以 DA⊥PA. 因为 PA∩AB=A,所以 DA⊥平面 PAB. 所以 PB⊥DA. 因为 AM∩DA=A,所以 PB⊥平面 ADNM. 因为 DN 平面 ADNM,所以 PB⊥DN.②如图,以 A 为坐标原点,直线 AB 为 x 轴,直线 AD 为 y 轴,直线 AP 为 z 轴,建立空间直角 坐标系 A-xyz, 则 A(0,0,0),B(2,0,0),C(2,1,0),D(0,2,0),P(0,0,2).由①知,PB⊥平面 ADNM,所以平面 ADNM 的法向量为 =(-2,0,2). 设平面 PDN 的法向量为 n=(x,y,z),因为 =(2,1,-2), =(0,2,-2),所以令 z=2,则 y=2,x=1. 所以 n=(1,2,2),所以 cos<n, >=.所以二面角 P-DN-A 的余弦值为 . 【点睛】 (1)本题主要考查二面角的向量求法,考查空间线面位置关系的证明,意在考查学生对 该知识的掌握水平和空间想象分析推理转化能力.(2)二面角的求法方法一:(几何法)找 作(定义法、三垂线法、垂面法) 证(定义) 指 求(解三角形).方法二:(向量法)首先求出两个平面的法向量 ;再代入公式(其中 分别是两个平面的法向量, 是二面角的平面角.)求解.(注意先通过观察二面角的大小选择“ ” 号).6、【答案】(1)证明见解析;(2) 2 13 . 13答案第 7 页,总 9 页试题分析:(1)连结1AC 交1A C 于点G ,连结DG ,利用四边形11ACC A 是平行四边形,进而证明出DG ∥1BC ,即可利用线面平行的判定定理,证得//1BC 平面DC A 1;(2)分别以,,CB OE OA 所在的直线为x 轴,y 轴,z 轴建立空间直角坐标系,分别求解平面1DA C 和平面1A CA 的一个法向量,利用向量的夹角公式,即可求解二面角1DAC A的平面角的余弦值,进而求解其正弦值.试题解析:(Ⅰ)证明:连结1AC 交1A C 于点G ,连结DG . 在正三棱柱111C B A ABC -中,四边形11ACC A 是平行四边形,∴1AG GC =. ∵AD DB =,∴DG ∥1BC .∵DG ⊂平面1A DC ,1BC ⊄平面1A DC ,∴1BC ∥平面1A DC . (2)过点A 作AO BC ⊥交BC 于O ,过点O 作OE BC ⊥交11B C 于E .因为平面ABC ⊥平面11CBB C ,所以AO ⊥平面11CBB C .分别以,,CB OE OA 所在的直线为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示.因为11,3BCAA ,ABC ∆是等边三角形,所以O 为BC 的中点.则()0,0,0O ,B 0,0) (Ⅰ)设平面1A DC 的法向量为(),,n x y z =,则10,0.n CD n A C ⎧⋅=⎪⎨⋅=⎪⎩ ∵3(,0,CD =,11(A C =-⎪⎩,得平面1A DC 的一个法向量为(3,1,n =-1BC =(10)1BC ·n =0∴∴1BC ∥平面1A DC .(Ⅱ)可求平面1ACA 的一个法向量为(13,0,n =设二面角1D AC A 的大小为θ,则16,n n <>∵()0,θπ∈,213sin 13DEDFEDF 考点:直线与平面平行的判定与证明;二面角的求解.。
二面角专题训练

二面角专题训练一.解答题(共14小题)1.如图,在四棱锥S﹣ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,,求:(Ⅰ)点A到平面BCS的距离;(Ⅱ)二面角E﹣CD﹣A的大小.2.如图所示,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=,∠ABC=60°.(1)证明:AB⊥A1C;(2)求二面角A﹣A1C﹣B的余弦值.3.如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC,BE(Ⅰ)证明:C,D,F,E四点共面;(Ⅱ)设AB=BC=BE,求二面角A﹣ED﹣B的大小.4.如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,.沿它的对角线BD把△BDC0折起,使点C0到达平面ABC0D外点C的位置.(Ⅰ)证明:平面ABC0D⊥平面CBC0;(Ⅱ)如果△ABC为等腰三角形,求二面角A﹣BD﹣C的大小.5.如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1.(Ⅰ)求证:AB⊥BC;(Ⅱ)若AA1=AC=a,直线AC与平面A1BC所成的角为θ,二面角A1﹣BC﹣A的大小为φ,求证:θ+φ=.6.如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E 是PC的中点.(I)证明:CD⊥AE;(II)证明:PD⊥平面ABE;(III)求二面角A﹣PD﹣C的大小.7.如图,在四面体ABCD中,平面ABC⊥平面ACD,AB⊥BC,AC=AD=2,BC=CD=1(Ⅰ)求四面体ABCD的体积;(Ⅱ)求二面角C﹣AB﹣D的平面角的正切值.8.如图,在锥体P﹣ABCD中,ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=,PB=2,E,F分别是BC,PC的中点(1)证明:AD⊥平面DEF(2)求二面角P﹣AD﹣B的余弦值.9.如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2.(1)求直线AM与平面BCD所成的角的大小;(2)求平面ACM与平面BCD所成的二面角的正弦值.10.如图,在五面体ABCDEF中,AB∥DC,,CD=AD=2,四边形ABFE为平行四边形,FA⊥平面ABCD,,求:(Ⅰ)直线AB到平面EFCD的距离;(Ⅱ)二面角F﹣AD﹣E的平面角的正切值.11.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.(1)求证:BC⊥平面PAC;(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;(3)是否存在点E使得二面角A﹣DE﹣P为直二面角?并说明理由.12.如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.(I)设E是DC的中点,求证:D1E∥平面A1BD;(II)求二面角A1﹣BD﹣C1的余弦值.13.如图,在三棱锥A﹣BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=,BD=CD=1,另一个侧面是正三角形.(1)求证:AD⊥BC.(2)求二面角B﹣AC﹣D的大小.(3)在直线AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定E的位置;若不存在,说明理由.14.如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC.已知,求(Ⅰ)异面直线PD与EC的距离;(Ⅱ)二面角E﹣PC﹣D的大小.二面角专题训练参考答案与试题解析一.解答题(共14小题)1.如图,在四棱锥S﹣ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,,求:(Ⅰ)点A到平面BCS的距离;(Ⅱ)二面角E﹣CD﹣A的大小.中,,故所求二面角的大小为2.如图所示,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=AA1=,∠ABC=60°.(1)证明:AB⊥A1C;(2)求二面角A﹣A1C﹣B的余弦值.=ADB=,ADB=,的余弦值为3.如,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC,BE(Ⅰ)证明:C,D,F,E四点共面;(Ⅱ)设AB=BC=BE,求二面角A﹣ED﹣B的大小.BC得同理可得的平面角.的大小4.如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,.沿它的对角线BD把△BDC0折起,使点C0到达平面ABC0D外点C的位置.(Ⅰ)证明:平面ABC0D⊥平面CBC0;(Ⅱ)如果△ABC为等腰三角形,求二面角A﹣BD﹣C的大小.所以与的大小.由夹角公式求与,所以∠因此只有中,,的坐标为,所以与夹角的大小等于二面角,.5.如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1.(Ⅰ)求证:AB⊥BC;(Ⅱ)若AA1=AC=a,直线AC与平面A1BC所成的角为θ,二面角A1﹣BC﹣A的大小为φ,求证:θ+φ=.,即可得到结论.=D==.6.如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E 是PC的中点.(I)证明:CD⊥AE;(II)证明:PD⊥平面ABE;(III)求二面角A﹣PD﹣C的大小.,可得.中,.的大小是7.如图,在四面体ABCD中,平面ABC⊥平面ACD,AB⊥BC,AC=AD=2,BC=CD=1(Ⅰ)求四面体ABCD的体积;(Ⅱ)求二面角C﹣AB﹣D的平面角的正切值.=的坐标,同时易得,>,进而由同角三角函,=AC CD=AB==AB BC=V=×=,从而EF=;DEF=的平面角的正切值为,由⊥||=1或(舍),||=1|或(舍),)||=,||=1V=××|||h=(Ⅱ)由(Ⅰ)知(,,)设非零向量=的法向量,则由⊥可得,l+m=0⊥可得,m+,n==,﹣=<>=,>的平面角的正切值为8.如图,在锥体P﹣ABCD中,ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=,PB=2,E,F分别是BC,PC的中点(1)证明:AD⊥平面DEF(2)求二面角P﹣AD﹣B的余弦值.,PG=BG=,因此二面角的余弦值为9.如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2.(1)求直线AM与平面BCD所成的角的大小;(2)求平面ACM与平面BCD所成的二面角的正弦值.OB=MO=,则,,所以所以,所求二面角的正弦值是10.如图,在五面体ABCDEF中,AB∥DC,,CD=AD=2,四边形ABFE为平行四边形,FA⊥平面ABCD,,求:(Ⅰ)直线AB到平面EFCD的距离;(Ⅱ)二面角F﹣AD﹣E的平面角的正切值.的法向量,则直线=AB.的距离为,知中,,,从而,的平面角的正切值为点为坐标原点,的方向为)可得.即因,解得.②联立①,②解得,所以.得,.即.故,,,11.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.(1)求证:BC⊥平面PAC;(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;(3)是否存在点E使得二面角A﹣DE﹣P为直二面角?并说明理由.BCABAB==所成角的正弦值为12.如图,在直四棱柱ABCD﹣A1B1C1D1中,已知DC=DD1=2AD=2AB,AD⊥DC,AB∥DC.(I)设E是DC的中点,求证:D1E∥平面A1BD;(II)求二面角A1﹣BD﹣C1的余弦值.得,则为平面,,则的余弦值为13.如图,在三棱锥A﹣BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=,BD=CD=1,另一个侧面是正三角形.(1)求证:AD⊥BC.(2)求二面角B﹣AC﹣D的大小.(3)在直线AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定E的位置;若不存在,说明理由.=BC=ACAB=AC=BC=BM=,MN=CD=,BN=AD=BMN= BMN=arccos=x=CE=14.如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC.已知,求(Ⅰ)异面直线PD与EC的距离;(Ⅱ)二面角E﹣PC﹣D的大小.:PD=,,,的大小为.。
二面角习题与答案

∴ 又
∴
∴
5.解:设边长为a,易证ANC'N是菱形
且MN = ,A'C =
∴S□AMC'N=
由于AMC'N在面ABCD上的射影即
为正方形ABCD
∴S□ABCD=
∴
∴
取CC'的中点M',连结DM'
则平行四边形DM'C'N是四边形AMC'N在CC'D'D上的射影,
S□DM'C'M=
∴
5.已知正方体AC',M、N分别是BB',DD'的中点,求截面AMC'N与面ABCD,CC'D'D所成的角。
解:
6.如图AC⊥面BCD,BD⊥面ACD,若AC =CD =1,∠ABC =30°,求二面角 的大小。
解:
7.三棱锥A-BCD中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC = ,AD =4,求二面角A-BC-D的度数。
14.如图,将边长为a的正三角形ABC按它的高AD为折痕折成一个二面角 .
(1)若二面角 是直二面角,求 的长;
(2)求 与平面 所成的角;
(3)若二面角 的平面角为120°,求二面角 的平面角的正切值.
参考答案
解:由已知条件,D是BC的中点
∴CD =BD =2又△ADC是正三角形
∴AD =CD =BD =2
∴CE= a,OE= a,∴tan∠COE= =2.
∴二面角C—AF—B的大小是arctan2.
12、解析:∵ 平面ABCD∥平面 ,∴ 平面 与平面 的交线l为过点 且平行于AC的直线.直线l就是二平面 与 所成二面角的棱.又 ⊥平面 ,过 作AH⊥l于H,连结AH.则 为二面角 的平面角.可求得 .因此所求角的大小为 或
二面角专项训练

二面角专项训练1、已知正方体1111D C B A ABCD -中,O 1、O 是上下底面正方形的中心,E 是AB 棱上一点,且AE :EB=1:2,求二面角A 1-O 1O-E 的大小。
2、 如图,在四棱锥P —ABCD 中,底面ABCD 是矩形,已知AB = 3,AD = 2,PA = 2,︒=∠=60,22PAB PD . (1)证明:AD ⊥平面PAB ; (2)求二面角P —BD —A 的大小.3、如图,在四棱锥V-ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,二面角V-AD-B 是直二面角.(1)证明AB ⊥平面VAD ;(2)求面VAD 与面VDB 所成的二面角的大小.PAB CEOO 1ADDC 1BACB4、如图,AB ⊥平面BCD ,DC ⊥CB ,AD 与平面BCD 成30°的角,且AB=BC.(1)求AD 与平面ABC 所成的角的大小;(2)求二面角C-AD-B 的大小;5、 如图,ABCD 是直角梯形,∠ABC=900,SA ⊥底面ABCD ,SA=AB=BC=1,AD=0.5,求面SCD 与面SBA 所成二面角的大小。
6、如图,在底面为平行四边形的四棱锥P-ABCD中,AC AB ⊥,PA ⊥平面ABCD ,且AB PA =,点E 是PD 的中点。
(1)证明:PB AC ⊥; (2)证明:PB//平面AEC ; (3)求二面角E-AC-B 的大小。
EPDCBASDCBADCBA。
二面角专项练习

二面角专项练习班级_____________姓名_____________一、定义法:直接在二面角的棱上取一点,分别在两个半平面内作棱的垂线,得出平面角.例1 在四棱锥P-ABCD 中,ABCD 是正方形,PA ⊥平面ABCD ,PA=AB=a ,求二面角B-PC-D 的大小。
二、垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂逆定理作出二面角的平面角;例2在四棱锥P-ABCD 中,ABCD 是平行四边形,PA ⊥平面ABCD ,PA=AB=a ,∠ABC=30°,求二面角P-BC-A 的正切。
三、垂面法:作棱的垂直平面,则这个垂面与二面角两个面的夹的角就是二面角的平面角 例3 在四棱锥P-ABCD中,ABCD 是正方形,PA ⊥平面ABCD ,的大小。
四、投影面积法:一个平面α上的图形面积为S ,它在另一个平面β上S',这两个平面的夹角为θ,则S'=Scos θ或cos θ=/SS .例4 在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。
法(尤其要考虑射影法)。
例5、在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,与平面PDC 所成二面角的大小。
方法归纳:二面角的类型和求法可用框图展现如下:如图,已知在侧棱垂直于底面三棱柱ABC —A 1B 1C 1中AC=3,AB=5,.,4,53cos 1的中点是点AB D AA CAB ==∠。
(Ⅰ)求证:1BC AC ⊥;(Ⅱ)求证:AC 1//平面CDB 1; (Ⅲ)求三棱锥A 1—B 1CD 的体积.18. (本题满分14分) 如图所示, 四棱锥P -ABCD 底面是直角梯形,,,2,BA AD CD AD CD AB PA ⊥⊥=⊥底面ABCD , E 为PC 的中点, PA =AD =AB =1.(1)证明: //EB PAD 平面; (2)证明: BE PDC ⊥平面; (3)求三棱锥B -PDC 的体积V .如图,四棱锥P —ABCD 中,ABCD 为矩形,△PAD 为等腰直角三角形,∠APD=90°,面PAD ⊥面ABCD ,且AB=1,AD=2,E 、F 分别为PC 和BD 的中点. (1)证明:EF ∥面PAD ;(2)证明:面PDC ⊥面PAD ; (3)求四棱锥P —ABCD 的体积.18.(本小题满分14分) 如图4所示,四棱锥P ABCD -中,底面ABCD 为正方 形,PD ⊥平面ABCD ,2PD AB ==,E ,F ,G 分别为PC 、PD 、BC 的中点. (1)求证:PA P 平面EFG ; (2)求三棱锥P EFG -的体积.18.(本小题满分14分)如图,已知棱柱ABCD —A 1B 1C 1D 1的底面是菱形,且AA 1⊥面ABCD ,∠DAB=60°,AD=AA 1,F 为棱AA 1的中点,M 为线段BD 1的中点。
二面角习题及答案

二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC 是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解:由已知条件,D 是BC 的中点∴ CD =BD =2 又△ADC 是正三角形 ∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上 ∴ △ABC 是以∠BAC 为直角的三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC∴ PA ⊥AB (三垂线定理)∴∠PAC 即为二面角 P-AB-C 之平面角, 易求 ∠PAC =30°2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
解:∵ BS =BC ,又DE 垂直平分SC∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC ∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DC 则 ∠EDC 就是所要求的平面角 设 SA =AB =a ,则 BC =SB =2a 且 AC = 3易证 △SAC ∽△DEC ∴ ∠CDE =∠SAC =60°3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
AB解:取OC 之中点N ,则 MN ∥PO ∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2 过 N 作 NR ⊥BD于 R ,连MR ,则 ∠MRN 即为二面角 M-BD-C 过 C 作 CE ⊥BD 于S 则 RN =21CE 在 Rt △BCD 中, ∴ 58BD BC CD CE =⋅=∴ 54RN =25RN MN MRN tan ==∠ ∴ 25arctanMRN =∠ 4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =0120,求二面角 A-BD-C 的余弦值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求二面角专题
4
5
如何用空间向量求解二面角
求解二面角大小的方法很多,诸如定义法、三垂线法、垂面法、射影法、向量法等若干种。
而这些方法中最简单易学的就是向量法,但在实际教学中本人发现学生利用向量法求解二面角还是存在一些问题,究其原因应是对向量法的源头不尽了解。
本文就简要介绍有关这类问题的处理方法,希望对大家有所帮助。
在立体几何中求二面角可归结为求两个向量的夹角问题.对于空
间向量→a 、→b ,有cos <→a ,→
b >=
→
→→
→⋅⋅|
|||b a b
a .利用这一结论,我们可以
较方便地处理立体几何中二面角的问题.
例1 在四棱锥V-ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD .求面VAD 与面VDB 所成的二面角的大小.
证明: 建立如图空间直角坐标系,并设正方形边 长为1,依题意
得AB −−→
= (0,1,0),是面VAD 的法向量, 设n →
= (1,y ,z)是面VDB 的法向量,则
0,0.n VB n VB →−−→→−−→
⎧⋅=⎪⎨⎪⋅=⎩
⇒1,3y z =-⎧⎪
⎨=-
⎪⎩⇒n →= (1,-1
,-。
∴cos <AB −−→,n →
>
||||
AB n
AB n −−→→
−−→→
⋅⋅=
-
7
,
又由题意知,面VAD 与面VDB
所成的二面角为锐角,所以其大小为
例2如图,直三棱柱ABC —A 1B 1C 1中,∠ACB =90︒,AC=1,CB=2,侧棱AA 1=1,侧面AA 1B 1B 的两条对角线交点为D ,B 1C 1的中点为M .
⑴求证CD ⊥平面BDM ;
⑵求面B 1BD 与面CBD 所成二面角的大小. 解:⑴略
⑵如图,以C 为原点建立坐标系.设BD 中点为G ,连结B 1G ,则
依
G(4,14,14),BD −−→= (
-2,12,12
),
1B G −−→
= (
,-34,1
4
), ∴BD −−→
·1B G −−→
= 0,∴BD ⊥B 1G . 又CD ⊥BD ,∴CD −−→
与1B G −−→
的夹角θ等于所求二面角的平面角.
∴ cos θ=
11||||
CD B G CD B G −−→−−→
−−→
−−→
⋅⋅=
-
3
. 所以所求二面角的大小等于π-
arccos
3
. 例3如图,在四棱锥P —ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD=DC ,E 是PC 的中点,作EF ⊥PB 交PB 于点F .求二面角C —PB —D 的大小
y B
B 1
C 1
A 1
C
A
D
M
解:如图所示建立空间直角坐标系,D 为坐标原点,设a DC =
设点F 的坐标为000()x y z ,,,
PA −−→
=PB λ−−→
,则000()()x y z a a a a λ-=-,,,,.
从而000(1)x a y a z a λλλ===-,,.所以
PE −−→
=
00011
(,
,)(,(),())2222
a a x y z a a a λλλ---=---.
由条件EF ⊥PB 知,PE −−→·PB −−→
= 0,即0)2
1()21
(222=---+-a a a λλλ,解得3
1=λ.
∴点F 的坐标为2()333
a a a
,,,且()366a a a PE −−→=--,,,
2()333
a a a
FD −−→
=---,,,
∴PB −−→
·FD −−→
222
20333
a a a =--+
=,即FD PB ⊥,故EFD ∠是二面角C —PB —D 的平面角.
∵PE −−→
·FD −−→
=222291896a a a a =-+=
,且||6PE a −−→==
,
||FD −−→
==,
∴2
1cos 2||||
a PE FD
EFD PE FD −−→−−→
−−→−−→
⋅∠=
=
=
,∴3
π
=∠EFD . 所以,二面角C —PB —D 的大小为3
π.
例4 已知三棱柱OAB —1O A 1B 1中,平面11O OBB ⊥平面OAB ,∠
AOB =︒90,∠OB O 1=︒60,且OB =1OO = 2,OA =3,求二面角1O —AB —O 的大小.
解:以O 为原点,分别以OA ,OB 所在的直线为x ,y 轴,过O 点且与平面AOB 垂直的直线为z 轴,建立空间直角坐标系.如图,
则O (0,0,0),1O (0,1,3),A(3,0,0),1A (3,1,3),B(0,2,0).
∴−→
−1AO = (-3,1,3),−→
−AB = (-3,2,0).
显然−→
−OZ 为平面AOB 的法向量,取→
1n = (0,0,1),设平面AB O 1的法向量为→
2n = (x ,y ,z),则
→
2n ·−→−1AO = 0,→
2n ·−→
−AB = 0.
即⎪⎩⎪⎨⎧=+-=++-0
230
33y x z y x ,令y =3,x = 2,z = 1,则→2n = (2,3,1).
∴cos <→
1n ,
→
2n >=|
|||2121→
→
→
→⋅⋅n n n n =
2
21=
42,即<→1n ,→2n >= arccos 4
2
.
故二面角1O —AB —O 的大小为arccos
4
2
.。
