第8讲 IIR滤波器设计
《IIR滤波器设计》课件

带通滤波器的设计
1
数字域设计
2
展示数字域中带通IIR滤波器设计的流程
和实现步骤。
3
模拟域设计
介绍模拟域中带通IIR滤波器设计的基本 概念和方法。
加权最小二乘设计
讨论通过加权最小二乘法设计带通IIR滤 波器的优势和局限。
带阻滤波器的设计
频域设计
使用频域设计方法来设计带阻 IIR滤波器,解决特定频率范围 内的滤波需求。
时域设计
采用时域设计技术设计带阻IIR 滤波器,以满足特定时域条件 的滤波要求。
优化设计
讨论优化设计方法,帮助您设 计出最有效、最稳定的带阻IIR 滤波器。
IIR滤波器的实现
直接IIR滤波器
介绍直接形式I和II的IIR滤波器的 结构和特点,以及如何进行滤波 计算。
级联IIR滤波器
展示级联IIR滤波器的结构和实现 步骤,讨论级联滤波器的优点。
锐化滤波器的应用
深入探讨如何利用IIR滤波器设计锐化滤 波器,以提高信号处理的精度和准确性。
实例演示
MATLAB实现
使用MATLAB演示如何利用工具箱函数实现IIR滤波 器设计,并展示不码,演示如何自己实现 IIR滤波器,并比较不同实现方法的性能。
总结
IIR滤波器的优缺点
总结IIR滤波器的优势和局限 性,帮助您理解何时选择IIR 滤波器。
发展趋势
展望IIR滤波器和数字信号处 理未来的发展方向和趋势, 以及可能的创新。
应用场景
探索IIR滤波器在实际应用中 的广泛应用领域,从音频处 理到生物医学信号分析。
并联IIR滤波器
探讨并联IIR滤波器的结构和应用, 以及设计和调优方法。
IIR滤波器设计的常见问题与解决方案
iir数字滤波器设计原理

iir数字滤波器设计原理IIR数字滤波器设计原理IIR(Infinite Impulse Response)数字滤波器是一种常用的数字滤波器,其设计原理基于无限冲激响应。
与FIR(Finite Impulse Response)数字滤波器相比,IIR数字滤波器具有更低的计算复杂度和更窄的频率过渡带。
在信号处理和通信系统中,IIR数字滤波器被广泛应用于滤波、陷波、均衡等领域。
IIR数字滤波器的设计原理主要涉及两个方面:滤波器的结构和滤波器的参数。
一、滤波器的结构IIR数字滤波器的结构通常基于差分方程来描述。
最常见的结构是直接型I和直接型II结构。
直接型I结构是基于直接计算差分方程的形式,而直接型II结构则是通过级联和并联方式来实现。
直接型I结构的特点是简单直接,适用于一阶和二阶滤波器。
它的计算复杂度较低,但对于高阶滤波器会存在数值不稳定性的问题。
直接型II结构通过级联和并联方式来实现,可以有效地解决数值不稳定性的问题。
它的计算复杂度相对较高,但适用于高阶滤波器的设计。
二、滤波器的参数IIR数字滤波器的参数包括滤波器的阶数、截止频率、增益等。
这些参数根据实际需求来确定。
滤波器的阶数决定了滤波器的复杂度和性能。
阶数越高,滤波器的频率响应越陡峭,但计算复杂度也越高。
截止频率是指滤波器的频率响应开始衰减的频率。
截止频率可以分为低通、高通、带通和带阻滤波器。
根据实际需求,选择合适的截止频率可以实现对信号的滤波效果。
增益是指滤波器在特定频率上的增益或衰减程度。
增益可以用于滤波器的频率响应的平坦化或强调某些频率。
IIR数字滤波器的设计通常包括以下几个步骤:1. 确定滤波器的类型和结构,如直接型I或直接型II结构;2. 确定滤波器的阶数,根据要求的频率响应和计算复杂度来选择;3. 设计滤波器的差分方程,可以使用脉冲响应不变法、双线性变换法等方法;4. 根据差分方程的系数,实现滤波器的级联和并联结构;5. 进行滤波器的参数调整和优化,如截止频率、增益等;6. 对滤波器进行性能测试和验证,确保设计满足要求。
iir滤波器设计方法

iir滤波器设计方法IIR滤波器设计方法数字信号处理中的滤波器是一项重要的技术,用于滤除数字信号中的噪声和干扰,并对信号进行平滑处理。
IIR滤波器作为数字滤波器的一种,被广泛应用于音频处理、图像处理等领域。
下面将介绍IIR滤波器的设计方法。
一、数字滤波器的基本原理数字滤波器是一种按照某种规律改变信号频率和幅度的系统。
数字滤波器的基本原理是,将输入信号x(n)通过一定的滤波器系统后,得到输出信号y(n)。
滤波器系统可以是连续时域滤波器,也可以是离散时域滤波器。
其中,IIR滤波器是离散时域滤波器的其中一类。
二、IIR滤波器的分类IIR滤波器可以分为两类:低通滤波器和高通滤波器。
低通滤波器用于滤除高频噪声,保留低频信息,常用于音频等信号处理。
高通滤波器则用于滤除低频噪声,保留高频信息,常用于图像边缘检测等处理。
三、IIR滤波器设计方法1. 选择滤波器类型首先需要选择合适的滤波器类型,通常是根据所要处理的信号类型选择,“低通”或“高通”滤波器。
2. 确定滤波器参数在选定滤波器类型后,需要确定滤波器参数。
通常包括切-off频率、通带增益、阻带增益等。
其中,切-off频率是指信号经过滤波器后的频率处理效果,通带增益和阻带增益是指滤波器在信号传输过程中增益的波动程度。
3. 设计滤波器传递函数设计滤波器传递函数的目的是,确定在滤波器系统中所要使用的传递函数,以实现所要求的滤波效果。
根据IIR滤波器的设计方法,通常采用应用差分方程来实现传递函数。
4. 设置初始滤波器系数通过选择合适的初始滤波器系数,可以影响整个滤波器系统的滤波效果。
在确定了滤波器的传递函数后,设计人员可以根据所要求的滤波效果来选择合适的初始滤波器系数。
5. 优化滤波器系数通过不断的调节和优化滤波器系数,可以提高整个滤波器系统的滤波效果。
优化的过程通常需要根据实际的滤波效果进行多次调整和修改。
四、总结IIR滤波器是数字信号处理中一种常用的滤波器类型,其设计方法可以通过选择合适的滤波器类型、确定滤波器参数、设计滤波器传递函数、设置初始滤波器系数和优化滤波器系数等步骤来实现。
毕业设计IIR滤波器的设计与实现

毕业设计IIR滤波器的设计与实现IIR滤波器(Infinite Impulse Response Filter)是一种数字滤波器,具有无限冲击响应。
相比于FIR滤波器,IIR滤波器具有更高的效率和更快的计算速度。
本文将针对IIR滤波器的设计与实现展开讨论。
首先,我们将介绍IIR滤波器的基本原理。
IIR滤波器利用反馈连接来实现滤波操作,其输出信号是输入信号和过去输出信号的加权和。
这种结构可以实现滤波器的自适应性和相位响应的宽带特性。
常见的IIR滤波器类型包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
接下来,我们将介绍IIR滤波器的设计方法。
IIR滤波器的设计可以采用模拟滤波器的设计方法,然后通过模拟滤波器的转换来得到数字滤波器。
其中,模拟滤波器可以使用拉普拉斯变换或者频率域转换等方法进行设计。
设计过程中需要考虑要满足的频率响应要求、滤波器的阶数以及稳定性等因素。
根据不同的设计要求,可以选择适合的设计方法和滤波器类型。
接下来,我们将介绍IIR滤波器的实现方法。
一种常见的IIR滤波器实现方法是直接形态实现,即通过差分方程的形式实现滤波器。
通过差分方程可以将IIR滤波器的输入信号与过去输出信号进行运算,得到输出信号。
此外,还可以利用双边z变换或单边z变换等方法将差分方程转换为差分方程的系数表示形式。
这样可以方便地进行滤波器的实现和计算。
另一种常见的IIR滤波器实现方法是级联形态实现,即将滤波器的阶数分解为若干个一阶或二阶滤波器的级联。
通过级联形式可以降低滤波器的复杂度和计算量。
最后,我们将介绍IIR滤波器的应用领域。
IIR滤波器广泛应用于信号处理、通信系统、音频处理等领域。
在信号处理中,IIR滤波器常用于滤除噪声、滤波和频谱分析等任务。
在通信系统中,IIR滤波器常用于调制解调、信道均衡和解调等任务。
在音频处理中,IIR滤波器常用于音频均衡、音调调整等任务。
综上所述,IIR滤波器是一种高效、快速的数字滤波器。
IIR低通滤波器设计

IIR低通滤波器设计IIR低通滤波器(Infinite Impulse Response Low-pass Filter)是一种常见的数字信号处理滤波器,用于滤除高频信号,保留低频信号。
IIR滤波器的特点是具有无限长的脉冲响应,并且能够在频域中实现既定的频率响应。
IIR滤波器设计的基本原理是将一个连续时间的系统函数转换为差分方程,并通过对这个差分方程进行优化来设计滤波器。
IIR滤波器通常由二阶或更高阶的差分方程组成,每个阶段包含一个延迟线和一个系数。
通过调整各个系数的值,可以修改滤波器的频率响应。
1.确定滤波器的需求:首先需要确定滤波器的截止频率和通带衰减等参数。
这些参数决定了滤波器的性能和适用范围。
2. 选择滤波器结构:根据应用的需求和性能要求,选择合适的IIR 滤波器结构。
常见的结构包括Butterworth滤波器、Chebyshev滤波器和Elliptic滤波器等。
3.转换为频率响应函数:将低通滤波器的幅度响应转换为特定形式的频率响应函数。
常见的响应函数包括单位增益的低通滤波器响应和指定范围内的最小相位响应等。
4.选择滤波器阶数:通过调整滤波器的阶数,可以改变滤波器的频率响应特性。
增加阶数可以获得更陡峭的滚降特性,但也会增加计算和存储空间的需求。
5.设计滤波器系数:根据所选择的滤波器结构和阶数,使用合适的设计方法计算滤波器的系数。
常见的设计方法包括频率变换法、极点截断法和最优化设计等。
6. 实现滤波器:将滤波器的差分方程转换为数字信号处理器(DSP)或嵌入式系统中的实际滤波器。
可以使用直接形式、级联形式或者Lattice滤波器结构等不同的实现方式。
7.评估滤波器性能:使用测试数据对设计的滤波器进行评估,并根据需要对滤波器进行调整和优化。
可以使用频率相应曲线、群延迟响应和信号波形等多种方法进行性能评估。
总结来说,设计IIR低通滤波器的过程涉及滤波器需求的确定、结构的选择、频率响应函数的转换、阶数和系数的设定、滤波器实现和性能评估等多个方面。
8第八章 IIR滤波器设计
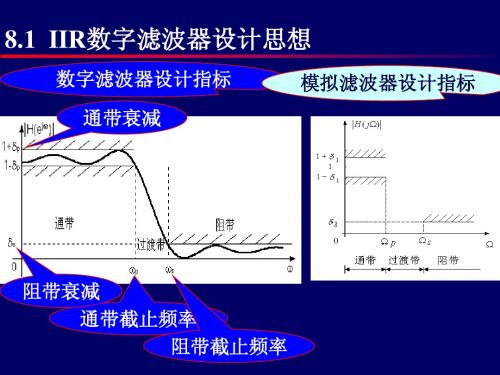
复频率拓广
2 1 e Ts s1 s Ts 1 e Ts s1
利用S1平面与Z平面之间的变换关系
z e s1Ts
2 1 z 1 2 z 1 s 1 Ts 1 z Ts z 1
8.3 双线性变换法
双线性变换,又称线性分式变换
2 1 z 1 2 z 1 s Ts 1 z 1 Ts z 1
j
M 1
低通到低通
(1 ) tan tan 2 (1 ) 2
(1 )(1 cos ) 2 arctan (1 ) sin
e
e j 1 e j
2 sin( ) 2
sin(
)
8.4 频带变换
s 2 1
Z平面极点 z1 e
H ( z) 0.5 1 e
0.5Ts
0.5Ts
z 2 e Ts
z
1
1 1 e Ts z 1
3 2.9928z 1 2 3.7121 1 1.7214z 2 z
8.2 冲激响应不变法:
例题
8.3 双线性变换法
Ap s sp
s平面上 的极点
s平面与z平面的关系
Ap 1 e
s pTs
s pTs
z
1
z (1 s s p ) e
s sp
z平面上 的极点
ze
sT s
z re
j
反映s平面的极点与z平面的极点有 对应关系,零点之间无对应。
re
j
1
M
z
1
i
1
| i | 1 极点在单位圆内
iir数字滤波器的设计步骤

IIR数字滤波器的设计步骤1.简介I I R(In fi ni te Im pu l se Re sp on se)数字滤波器是一种常用的数字信号处理技术,它的设计步骤可以帮助我们实现对信号的滤波和频率选择。
本文将介绍I IR数字滤波器的设计步骤。
2.设计步骤2.1确定滤波器的类型I I R数字滤波器的类型分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
根据信号的要求,我们需确定所需滤波器的类型。
2.2确定滤波器的规格根据滤波器的应用场景和信号特性,我们需确定滤波器的通带范围、阻带范围和衰减要求。
2.3选择滤波器的原型常用的I IR数字滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
根据滤波器的需求,我们需选择适合的滤波器原型。
2.4设计滤波器的传递函数根据滤波器的规格和选定的滤波器原型,我们需计算滤波器的传递函数。
传递函数表示了输入和输出之间的关系,可以帮助我们设计滤波器的频率响应。
2.5对传递函数进行分解将滤波器的传递函数进行分解,可得到II R数字滤波器的差分方程。
通过对差分方程进行相关计算,可以得到滤波器的系数。
2.6滤波器的稳定性判断根据滤波器的差分方程,判断滤波器的稳定性。
稳定性意味着滤波器的输出不会无限增长,确保了滤波器的可靠性和准确性。
2.7选择实现方式根据滤波器的设计需求和实际应用场景,我们需选择I IR数字滤波器的实现方式。
常见的实现方式有直接I I型、级联结构和并行结构等。
2.8优化滤波器性能在设计滤波器后,我们可以对滤波器的性能进行优化。
优化包括滤波器的阶数和抗混淆能力等方面。
3.总结I I R数字滤波器的设计步骤包括确定滤波器的类型和规格、选择滤波器的原型、设计滤波器的传递函数、对传递函数进行分解、判断滤波器的稳定性、选择实现方式和优化滤波器性能等。
通过这些步骤的实施,我们可以有效地设计出满足信号处理需求的II R数字滤波器。
IIR滤波器的设计与实现

IIR滤波器的设计与实现IIR滤波器(Infinite Impulse Response Filter)是一种数字滤波器,其特点是具有无限冲激响应。
与FIR滤波器不同,它的输出不仅与输入信号有关,还与历史输入信号有关。
这使得IIR滤波器在一些应用中具有更高的灵活性和效率。
设计一个IIR滤波器主要包括确定滤波器的传递函数和选择滤波器类型两个步骤。
在确定传递函数时,可以根据不同的要求选择不同的滤波器类型,如低通滤波器、高通滤波器、带通滤波器等。
常见的IIR滤波器设计方法包括脉冲响应不变法、双线性变换法和频率抽样法等。
在实际实现过程中,可以使用各种工具和软件进行设计和仿真。
其中一种常用的设计方法是MATLAB工具包中提供的函数,如butter、cheby、ellip等。
这些函数可以根据用户提供的设计参数生成IIR滤波器的系数。
通过调试和优化这些系数,可以得到满足要求的滤波器。
IIR滤波器的实现通常分为直接形式和间接形式两种。
直接形式实现简单直观,但会引入大量的计算和存储开销;间接形式在计算和存储方面更加高效,但会增加系统的复杂性。
选择哪种实现形式需要根据具体应用场景和性能需求来决定。
在进行IIR滤波器的实际设计和实现时,还需要注意一些常见的问题。
例如,滤波器的阶数和截止频率的选择需要根据信号的特性和要求来确定;如果滤波器存在共振或不稳定的问题,可以通过增加阶数或调整系数来解决;另外,在实际应用中,可能还需要考虑滤波器的滤波延迟、实时性和系统资源消耗等因素。
总之,IIR滤波器的设计和实现是一个综合考虑信号特性、要求和系统约束的过程。
通过选择合适的设计方法、优化滤波器系数和选择合适的实现形式,可以得到满足要求的高性能滤波器。
IIR数字滤波器的设计

归一化Butterworth滤波器的极点
条件:h(t)是实的 H( jw ) =H*( jw )
H (s)H (s) sjw H ( jw)H ( jw) H ( jw) 2
H (s)H (s)
1
1 ( js)2 N
极点:
sk (1)1/ 2 N j {e jπ2 πk }1/ 2 N j
零点为:
z1 1/ d* (1/ r)e j
b)一阶全通滤波器的频率响应
A1 (e
j
)
e j d 1 de j
e j
A1 ( z)
1 d e j 1 de j
z 1 d 1 dz 1
A1(e j ) 1
A1 (e
j
)
e j
1 1
re j e re j e
j j
( ) 2 tan1 r sin( ) 1 r cos( )
b)m阶全通滤波器的频率响应
由于: Am
( z ) Am
( z 1 )
z m DM ( z 1 ) Dm (z)
z m Dm ( z) Dm ( z 1 )
1
Am (e j ) 2 Am (z) Am (z 1) ze j 1
由于 : Am (e j0 ) 1
所以: (0) 0
m阶实系数全通系统可分解为m个一阶全通系统的积,由于 一阶全通系统相位是递减的
x(t)
A/D
x[k]
离散系统
y[k]
D/A
ys(t) Hr(jw)
yr(t)
T
T
1) h(t) wcewctu(t)
H
(z)
1
wc
ewcT
z
1
iir二阶滤波器参数

iir二阶滤波器参数IIR二阶滤波器参数的设计与应用引言:IIR滤波器是一种常见的数字滤波器,由于其具有稳定性好、设计灵活等优点,在信号处理领域得到了广泛应用。
本文将着重介绍IIR二阶滤波器的参数设计及其在实际应用中的一些特点和注意事项。
一、IIR二阶滤波器的基本结构IIR滤波器是指其系统函数(传递函数)的分母和分子都是多项式,且分母多项式的次数不小于分子多项式的次数。
而二阶IIR滤波器是指系统函数的分母和分子都是二次多项式。
二阶IIR滤波器的传递函数一般表示为H(z) = (b0 + b1z^(-1) + b2z^(-2)) / (1 + a1z^(-1) + a2z^(-2)),其中b0、b1、b2为前向系数,a1、a2为反馈系数。
这些系数的选择将直接影响滤波器的性能。
二、IIR二阶滤波器参数设计1. 频率响应要求:在设计滤波器时,首先需要明确所需的频率响应特性。
常见的频率响应要求有低通、高通、带通、带阻等。
根据不同的需求,可以选择不同的滤波器类型和参数。
2. 范围和阶数选择:根据所需的频率响应和性能要求,确定滤波器的阶数。
一般情况下,二阶滤波器已经能够满足大部分应用的要求。
3. 频率转换:将所需的频率响应特性转化为模拟滤波器的频率响应。
常用的方法有频率归一化和频率预畸。
这一步骤可以帮助确定滤波器的截止频率和通带增益。
4. 频率变换:将模拟滤波器的频率响应转化为数字滤波器的频率响应。
常用的方法有双线性变换、脉冲响应不变法等。
这一步骤可以帮助确定滤波器的数字化参数。
5. 系数计算:根据频率变换得到的数字滤波器的参数,通过一定的计算方法得到前向系数b0、b1、b2和反馈系数a1、a2的具体数值。
常用的计算方法有巴特沃斯、切比雪夫、椭圆等。
三、IIR二阶滤波器的应用特点1. 实时处理:IIR滤波器具有实时性好的特点,适用于需要对实时信号进行滤波处理的应用场景。
例如音频处理、图像处理等。
2. 相位响应:相比于FIR滤波器,IIR滤波器的相位响应更加复杂。
iir数字滤波器设计及c语言程序

iir数字滤波器设计及c语言程序IIR数字滤波器设计及C语言程序IIR(Infinite Impulse Response)数字滤波器是一种常用的数字信号处理技术,广泛应用于音频处理、图像处理、通信系统等领域。
本文将介绍IIR数字滤波器的设计原理,并给出相应的C语言程序实现。
一、IIR数字滤波器的设计原理IIR数字滤波器的设计基于差分方程,其输入信号和输出信号之间存在一定的差分关系。
相比于FIR(Finite Impulse Response)数字滤波器,IIR数字滤波器具有更窄的转换带宽、更高的滤波器阶数和更好的相位响应等特点。
IIR数字滤波器的设计主要包括两个关键步骤:滤波器规格确定和滤波器参数计算。
首先,根据实际需求确定滤波器的类型(低通、高通、带通或带阻)、截止频率、通带衰减和阻带衰减等规格。
然后,根据这些规格利用数字滤波器设计方法计算出滤波器的系数,从而实现对输入信号的滤波。
二、IIR数字滤波器的设计方法常见的IIR数字滤波器设计方法有脉冲响应不变法、双线性变换法和最小均方误差法等。
下面以最常用的脉冲响应不变法为例介绍设计方法。
脉冲响应不变法的基本思想是将模拟滤波器的脉冲响应与数字滤波器的单位脉冲响应进行匹配。
首先,根据模拟滤波器的传递函数H(s)确定其脉冲响应h(t)。
然后,将连续时间下的脉冲响应离散化,得到离散时间下的单位脉冲响应h[n]。
接下来,根据单位脉冲响应h[n]计算出数字滤波器的差分方程系数,从而得到滤波器的数字表示。
三、IIR数字滤波器的C语言程序实现下面给出一个简单的IIR数字滤波器的C语言程序实现示例,以低通滤波器为例:```c#include <stdio.h>#define N 100 // 输入信号长度#define M 5 // 滤波器阶数// IIR数字滤波器系数float b[M+1] = {0.1, 0.2, 0.3, 0.2, 0.1};float a[M+1] = {1.0, -0.5, 0.3, -0.2, 0.1};// IIR数字滤波器函数float IIR_filter(float *x, float *y, int n) {int i, j;float sum;for (i = 0; i < n; i++) {sum = 0;for (j = 0; j <= M; j++) { if (i - j >= 0) {sum += b[j] * x[i - j]; }}for (j = 1; j <= M; j++) { if (i - j >= 0) {sum -= a[j] * y[i - j]; }}y[i] = sum;}}int main() {float x[N]; // 输入信号float y[N]; // 输出信号int i;// 生成输入信号for (i = 0; i < N; i++) {x[i] = i;}// IIR数字滤波器滤波IIR_filter(x, y, N);// 输出滤波后的信号for (i = 0; i < N; i++) {printf("%f ", y[i]);}return 0;}```以上是一个简单的IIR数字滤波器的C语言程序实现示例。
IIR滤波器的原理与设计方法

IIR滤波器的原理与设计方法IIR(Infinite Impulse Response)滤波器是一种数字滤波器,其具有无限冲激响应的特点。
与FIR(Finite Impulse Response)滤波器相比,IIR滤波器具有更高的效率和更窄的频带特性。
本文将介绍IIR滤波器的原理和设计方法。
一、IIR滤波器的原理IIR滤波器是通过对输入信号和输出信号之间的差异进行递归运算而实现滤波的。
其核心原理是利用差分方程来描述滤波器的行为。
IIR滤波器可以被表达为如下形式:y[n] = b₀x[n] + b₁x[n-1] + ... + bₘx[n-ₘ] - a₁y[n-1] - ... - aₘy[n-ₘ]其中,x[n]表示输入信号的当前采样值,y[n]表示输出信号的当前采样值,a₁,...,aₘ和b₀,...,bₘ是滤波器的系数。
二、IIR滤波器的设计方法设计IIR滤波器需要确定滤波器的阶数、截止频率和系数等参数,以下介绍一种常用的设计方法:巴特沃斯滤波器设计方法。
1. 确定滤波器阶数滤波器的阶数决定了滤波器的复杂度和频率响应的形状。
阶数越高,频率响应越陡峭。
根据需要的滤波效果和计算复杂度,选择适当的滤波器阶数。
2. 确定截止频率截止频率是滤波器在频域上的边界,用于确定滤波器的通带和阻带。
根据信号的频谱分析以及滤波器的应用要求,确定合适的截止频率。
3. 求解滤波器系数根据巴特沃斯滤波器的设计方法,可以采用双线性变换、频率抽样和极点放置等技术求解滤波器的系数。
具体方法比较复杂,需要使用专业的滤波器设计软件或者数字信号处理工具包进行计算。
4. 评估设计结果设计完成后,需要评估滤波器的性能指标,如频率响应、相位响应、群延迟等。
可以通过频域分析和时域仿真等方法来评估滤波器的设计效果。
三、结论IIR滤波器是一种常用的数字滤波器,其具有无限冲激响应的特点。
通过对输入信号和输出信号进行递归运算,可以实现滤波效果。
设计IIR滤波器需要确定滤波器的阶数、截止频率和系数等参数,并通过专业的设计方法进行求解。
实验八 IIR数字滤波器的设计

0.9
1
直接设计数字滤波器的MATLAB函数: [N,wn]=buttord(wp,ws,Rp,Rs) %数字频率采用标 准化频率,取值范围为0~1之间,标准化频率1对 应的数字频率为π,对应的模拟频率为采样频率 的一半。设计带通滤波器时,wp=[wp1,wp2]; ws=[ws1,ws2] [b,a]=butter(N,wn) [b,a]=butter(N,wn,’ftype’) %N为滤波器的阶数, wn为滤波器的截止频率(0~1),“ftype”为滤 波器的类型:‘high’为高通,‘stop’为带阻, 截止频率为wn=[w1,w2];带通滤波时, wn=[w1,w2];缺省时为低通和带通滤波器
0
Magnitude (dB)
-50
-100
-150
0
0.1
0.2
0.3 0.4 0.5 0.6 0.7 0.8 Normalized Frequency ( rad/sample)
0.9
1
200
Phase (degrees)
100 0 -100 -200
0
0.1
0.2
0.3 0.4 0.5 0.6 0.7 0.8 Normalized Frequency ( rad/sample)
1. wp=0.2*pi; %digital Passband freq in rad
ws=0.3*pi; %digital Stopband freq in rad Fs=1000; wp1=2*Fs*tan(wp/2);ws1=2*Fs*tan(ws/2); Rp=1;Rs=15; [N,Wn]=buttord(wp1,ws1,Rp,Rs,'s'); %返回模拟滤波器的最小阶数和 截止频率 [Z,P,K]=buttap(N); %模拟低通滤波器原型 [Bap,Aap]=zp2tf(Z,P,K); [b,a]=lp2lp(Bap,Aap,Wn); [bz,az]=bilinear(b,a,Fs); [H,W]=freqz(bz,az); plot(W,abs(H)); grid xlabel('频率/弧度') ylabel('频率响应幅度') [H,W]=freqz(bz,az,50) figure stem(W,abs(H))
IIR滤波器设计解读

IIR滤波器设计解读IIR滤波器,即无限脉冲响应滤波器,是一种数字滤波器,其频率响应特性由其差分方程决定。
与FIR滤波器相比,IIR滤波器具有更少的滤波器系数和更高的滤波器阶数,可以实现更高的系统性能。
在本文中,我将解读IIR滤波器的设计过程和其性能特点。
首先,确定滤波器的类型是设计过程中的重要步骤之一、常见的IIR 滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。
根据具体的应用需求和信号特征选择适当的滤波器类型。
接下来,选择适当的滤波器规范是关键。
滤波器规范通常包括通频带的下限和上限、通频带的最大衰减及其相对于通频带的阻带衰减。
根据信号处理的要求和设计的实际情况选择适当的滤波器规范。
然后,设计滤波器的传递函数。
传递函数是滤波器频率响应的数学表示。
常见的IIR滤波器传递函数包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。
根据滤波器类型和规范选择适当的传递函数。
将传递函数转化为差分方程是设计过程中的下一步。
差分方程是IIR 滤波器频率响应特性的离散时间表示。
根据滤波器传递函数的形式和离散时间系统的特点,将传递函数转化为差分方程。
进行滤波器的实现是设计过程的关键。
根据差分方程的特点,可以采用直接形式实现或间接形式实现滤波器。
直接形式实现直接使用差分方程进行计算,而间接形式实现可以通过级联或并联结构实现滤波器。
最后,分析滤波器的性能是设计过程的重要一步。
滤波器的性能特点包括频率响应、相位响应和稳定性等。
通过分析滤波器的性能,评估滤波器的优劣以及是否满足设计要求。
总之,IIR滤波器设计是一个复杂且关键的过程,需要根据具体的应用需求和设计的实际情况选择适当的滤波器类型、滤波器规范和传递函数,并将传递函数转化为差分方程进行滤波器的实现,最后分析滤波器的性能。
通过合理的设计和实现,可以实现满足实际需求的高性能IIR滤波器。
《IIR滤波器的设计》课件

解释频率转换法,如低通到带通和高通 到带通的频率转换,以及其在滤波器设 计中的作用。
工程应用
语音信号处理中的应 用
探讨IIR滤波器在语音信号处理 中的应用,如降噪、语音增强 和语音识别等。
图像处理中的应用
介绍IIR滤波器在图像处理中的 应用,如图像增强、边缘检测 和图像去噪等。
音频信号处理中的应 用
讨论IIR滤波器在音频信号处理 中的应用,如均衡器、混响效 果和音频压缩等。
总结
IIR滤波器的优缺点
总结IIR滤波器的优点和缺点,讨论其在实际应 用中需要注意的问题。
IIR滤波器的应用前景
展望IIR滤波器的应用前景,探讨其在未来的发 展方向和创新应用。
滤波器的基本特征
讨论滤波器的基本特征,包 括传递函数、频率响应和滤 波器的稳定性。
IIR滤波器的概述
与FIR滤波器的区别
介绍IIR滤波器与FIR滤波器的传输函数和极点-零 点图
解释IIR滤波器的传输函数和极 点-零点图,以及如何通过调整 极点和零点来改变滤波器的性 质。
《IIR滤波器的设计》PPT 课件
介绍IIR滤波器的设计原理和应用。包括滤波器基础、IIR滤波器的概述、设计 方法和工程应用。
滤波器基础
数字信号处理的基 本概念
介绍数字信号处理的基本概 念,包括采样、量化和数字 信号的表示。
时间域与频率域分 析
解释时间域和频率域分析的 概念和方法,以及它们在滤 波器设计中的应用。
IIR滤波器的类型
介绍不同类型的IIR滤波器,如 低通、高通、带通和带阻滤波 器,以及它们的应用场景。
IIR滤波器的设计方法
1
变换方法
2
介绍变换方法,如模拟到数字转换和频
iir数字滤波器的设计

iir数字滤波器的设计什么是iir数字滤波器?iir(infinite impulse response)数字滤波器是一种数字滤波器,与fir(finite impulse response)数字滤波器不同。
与fir数字滤波器只要考虑最近的输入和输出有关,因此具有有限的冲击响应,iir数字滤波器具有无限的冲击响应,因为它们可以让输出与过去的输入有关。
在iir数字滤波器中,有反馈路径,这是与fir数字滤波器不同的。
这意味着,iir滤波器依赖于以前的输出和输入来计算当前的输出。
iir数字滤波器的应用iir数字滤波器在数码信号处理中得到了广泛应用,可以用于各种应用,包括:•音频处理:包括音频滤波器,均衡器和调音台等•通信:数字化通信和语音处理•生产控制:包括传感器计算和控制器如何设计iir数字滤波器?要设计iir数字滤波器,我们需要考虑几个步骤。
1. 确定数字滤波器的类型在设计iir数字滤波器之前,我们需要先确定所需的数字滤波器类型。
通常,数字滤波器可以分为以下两类:•低通滤波器(LPF)•高通滤波器(HPF)根据所需的应用程序和系统需求,您可以确定所需的滤波器类型。
2. 确定滤波器规格在设计iir数字滤波器之前,我们需要确定所需的滤波器规格。
这包括通带和阻带频率,通带和阻带增益等。
3. 选择设计工具在选择设计工具时,可以使用以下工具:•Matlab•Python4. 根据设计规格进行设计使用所选的设计工具,我们可以根据滤波器规格进行设计。
例如,我们可以使用Matlab中的dsp工具箱设计数字滤波器。
Fs = 1000; % 采样频率Fpass = 200; % 通带频率Fstop = 300; % 阻带频率Apass = 1; % 通带最大衰减Astop = 80; % 阻带最小衰减% 将数字滤波器设计为低通滤波器,并使用butterworth滤波器设计方法d = fdesign.lowpass('Fp,Fst,Ap,Ast',Fpass,Fstop,Apass,Astop,Fs);Hd = design(d,'butter');% 将数字滤波器设计为高通滤波器,并使用chebyshev滤波器设计方法d = fdesign.highpass('Fst,Fp,Ast,Ap',Fpass,Fstop,Astop,Apass,Fs);Hd = design(d,'cheby1');以上示例演示了如何使用Matlab中的dsp工具箱设计数字低通滤波器和数字高通滤波器。
《IIR滤波器》课件

电路实现
Elliptic滤波器的电路实现通常较 为复杂,但提供了较好的滤波性 能。
IIR滤波器的优缺点
1 优点
能够实现更复杂的频率响应和滤波效果,计算复杂度较低。
2 缺点
容易产生不稳定性问题,相位响应可能不是线性的。
应用示例与总结
音频处理
• 音频均衡器 • 音频压缩器 • 音频滤波
图像处理
• 图像增强 • 图像滤波 • 图像去噪
信号处理
• 生物医学信号处理 • 通信系统 • 雷达信号处理
Butterworth滤波器的设计
1
选择阶数
根据需要的频率响应特性选择合适的滤波器阶数。
2
计算截止频率
根据设计要求计算截止频率,并选择合适的滤波器类型。
3
设计滤波器
计算巴特沃斯滤波器的传递函数或差分方程。
Chebyshev滤波器的设计
设计要求
根据设计要求选择通带和阻带特性。
选择阶数
根据设计要求和通带纹波以及阻带衰减来选择适当的滤波器阶数。
设Hale Waihona Puke 滤波器使用Chebyshev I型或Chebyshev II型滤波器设计方法,计算传递函数或差分方程。
Elliptic滤波器的设计
通带纹波和阻带衰减
Elliptic滤波器允许在通带和阻带 中同时定义纹波和衰减,提供更 精确的频率选择。
设计方法
使用椭圆函数和拉塞尔函数进行 滤波器设计,以实现设计要求的 频率响应。
《IIR滤波器》PPT课件
IIR滤波器概述
IIR滤波器是一种数字滤波器,采用递归算法进行信号处理。它具有无限冲激响应特性,可以实现更复杂的频 率响应和滤波效果。
一阶和二阶IIR滤波器
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.用双线性变换法设计IIR数字滤波器
脉冲响应不变法的主要缺点是产生频率响应的混 叠失真。这是因为从S平面到Z平面是多值的映 射关系所造成的。为了克服这一缺点,可以采用 非线性频率压缩方法,将整个频率轴上的频率范 围压缩到-π/T~π/T之间,再用z=esT转换到 Z平面上。也就是说,第一步先将整个S平面压缩 映射到S1平面的-π/T~π/T一条横带里;第二 步再通过标准变换关系z=es1T将此横带变换到 整个Z平面上去。这样就使S平面与Z平面建立了 一一对应的单值关系,消除了多值变换性,也就 消除了频谱混叠现象,映射关系如图1-3所示。
IIR数字滤波器的设计
IIR数字滤波器的设计实际上是求解滤波器的系数ak 和bk。 利用MATLAB信号处理工具箱中的滤波器设计和分 析工具(FDATool)可以很方便地设计出符合应用要 求的未经量化的IIR滤波器。 示例:IIR低通滤波器设计要求: 低通巴特奥斯滤波器在其通带边缘1kHz处的增益为 -3dB,12kHz处的阻带衰减为30dB,采样频率为 25kHz。
H a ( jΩ )
2π T
-π o T
π T
2π T
H (eΒιβλιοθήκη j )… -3 -2 - o 2 3
…
= T
对某一模拟滤波器的单位冲激响应ha(t)进行采 样,采样频率为fs,若使fs增加,即令采样时间 间隔(T=1/fs)减小,则系统频率响应各周期 延拓分量之间相距更远,因而可减小频率响应的 混叠效应。
= 2 tan 2 T
-
o
由图看出,在零频率附近,模拟角频率Ω与数字频率ω之间的 变换关系接近于线性关系;但当Ω进一步增加时,ω增长得越 来越慢,最后当Ω→∞时,ω终止在折叠频率ω=π处,因而 双线性变换就不会出现由于高频部分超过折叠频率而混淆到 低频部分去的现象,从而消除了频率混叠现象。
j 3 / T jIm[z]
/ T o - / T -3 / T S平面 Z平面
-1
o
1
Re[z]
由(1-1)式,数字滤波器的频率响应和模拟滤 波器的频率响应间的关系为 1 2k (1-2) j H (e ) H j
T
k
a
T
用MATLAB的FDA Tools求取滤波器系数,步骤:
1)双击Launch pad窗口中的Filter Design Toolbox项 中的Filter Design & Analysis Tool(FDA Tool) 2)在Design Filter选项卡中选择Filter Type类型为 Lowpass 3)在Design Method里选择IIR(Butterworth) 4)在Filter Order中选择Minimum order即最小的阶数 5)Frequency specifications里的Units选择为Hz,输 入Fs(采样频率):25000,Fpass(通带截止频率): 1000,Fstop(阻带截止频率):12000
还可以直接用MATLAB的命令输入方法求系数: 如本文采用巴特沃斯滤波器,故需要在工具箱中调用 的两个函数buttord和butter的调用格式为: [N,Wc]=buttord(wp,ws,Rp,As) [b,a] =butter(N,Wc) 其中N为滤波器阶数:wp和ws分别为通带截止频率 矢量和阻带截止频率矢量,单位为π,一般需要模拟 频率指标对采样频率的一半作归一化;Rp和As分别 为通带最大衰减和阻带最小衰减,单位dB;wc为3 dB边缘频率矢量;b和a即为IIR公式中的系数矢量。
2 e e j j1T / 2 j1T / 2 T e e
j1T / 2
j1T / 2
将此关系解析延拓到整个S平面和S1平面,令jΩ=s, jΩ1=s1,则得
2 e s1T / 2 e s1T / 2 2 s1T 2 1 e s1T s s1T / 2 s1T / 2 tanh s1T T e e T 2 T 1 e
H (e ) Ha j T T
但是,任何一个实际的模拟滤波器频率响应都不是 严格限带的,变换后就会产生周期延拓分量的频谱 交叠,即产生频率响应的混叠失真,如图所示。这 时数字滤波器的频响就不同于原模拟滤波器的频响, 而带有一定的失真。当模拟滤波器的频率响应在折 叠频率以上处衰减越大、越快时,变换后频率响应 混叠失真就越小。这时,采用脉冲响应不变法设计 的数字滤波器才能得到良好的效果。
自行根据以上IIR数字滤波器设计方法,基于 MATLAB设计一个IIR带通滤波器,其中带通的 中心频率为ωp0=0.5π,;通带截止频率 ωp1=0.4π,ωp2=0.6π;通带最大衰减 αp=3dB;阻带最小衰减αs=15dB;阻带截止频 率ωs2=0.3π,ωs2=0.7π
(FDA Tool 或者直接命令输入)
(1-1) 则可看出,脉冲响应不变法将模拟滤波器的S平面变 换成数字滤波器的Z平面,这个从s到z的变换 z=esT是从S平面变换到Z平面的标准变换关系式。
X ( z)
z e
sT
1 T
1 X a ( s jk s ) T k
2 Xas j k T k
再将S1平面通过以下标准变换关系映射到Z平面 z=es1T 从而得到S平面和Z平面的单值映射关系为:
2 1 z 1 s T 1 z 1
(1-6)
T 2 1 s s 2 T z T 2 (1-7) 1 s s 2 T 式(1-6)与式(1-7)是S平面与Z平面之间的单 值映射关系,这种变换都是两个线性函数之比, 因此称为双线性变换
IIR数字滤波器的结构
任意阶的IIR滤波器可通过数学分解,表示为:
其中为如下的二阶形式:
一般有N≥M,称N为滤波器的阶数
这样就可以将任意阶的IIR滤波器通过若干二阶 网络(也称为滤波器的二阶基本节)级联起来构成, 其结构如图1所示。其中,代表第i级的二阶网络。
对于每一个二阶基本节,可以转置直接II型结构加 以实现,如图2所示。
其线性常系数差分方程为:
采用这种级联结构实现IIR滤波器的优点是每一 个基本节只是关系到滤波器的某一对极点和一对 零点,调整系数a0i、a1i、a2i,只单独地调整了 滤波器第i对零点而不影响其他任何零、极点。同 样,调整b1i、b2i系数、也只单独调整了第i对极 点。因此,这种结构便于准确地实现滤波器的零、 极点,也便于调整滤波器的频率响应性能。这种结 构的另一个优点是存储单元需要较少,在硬件实现 时,可以用一个二阶节进行时分复用,从而降低对 FPGA硬件资源的要求。
注意:如果要输入的是归一化频率(2π f/fs),则选择 Units为Normalized(0 to 1)
6)输入Apass(通带增益): -3 , Astop(阻带增益):30 7)设计好各参数后,点击最下面的按钮Design Filter,生 成滤波器及系数 8)查看系数:菜单Analysis->Filter Coefficitions 得到 的滤波器系数为 Numerator: (分子多项式系数) 0.3346 0.3346 Denominator: (分母多项式系数) 1.0 (注意:该项为a0,实际运算时用不着) -0.3308
这就是说,数字滤波器的频率响应是模拟滤波器 频率响应的周期延拓。正如采样定理所讨论的, 只有当模拟滤波器的频率响应是限带的,且带限 于折叠频率以内时,即 s (1-3)
H a ( j) 0 | |
T
2
才能使数字滤波器的频率响应在折叠频率以内重现 模拟滤波器的频率响应,而不产生混叠失真,即 |ω|<π (1-4) 1 j
脉冲响应不变法优缺点:
从以上讨论可以看出,脉冲响应不变法使得数字滤波器的单位 脉冲响应完全模仿模拟滤波器的单位冲激响应,也就是时域逼 近良好,而且模拟频率Ω和数字频率ω之间呈线性关系ω=ΩT。 因而,一个线性相位的模拟滤波器(例如贝塞尔滤波器)通过 脉冲响应不变法得到的仍然是一个线性相位的数字滤波器。 脉冲响应不变法的最大缺点是有频率响应的混叠效应。所以, 脉冲响应不变法只适用于限带的模拟滤波器(例如,衰减特性 很好的低通或带通滤波器),而且高频衰减越快,混叠效应越 小。至于高通和带阻滤波器,由于它们在高频部分不衰减,因 此将完全混淆在低频响应中。如果要对高通和带阻滤波器采用 脉冲响应不变法,就必须先对高通和带阻滤波器加一保护滤波 器,滤掉高于折叠频率以上的频率,然后再使用脉冲响应不变 法转换为数字滤波器。当然这样会进一步增加设计复杂性和滤 波器的阶数。
脉冲相应不变法设计和双线性变换法
求解滤波器的系数和 ,它是数学上的一种逼近问 题,即在规定意义上(通常采用最小均方误差准 则)去逼近系统的特性。如果在S平面上去逼近, 就得到模拟滤波器;如果在z平面上去逼近,就 得到数字滤波器。
1.用脉冲相应不变法设计IIR数字滤波器
利用模拟滤波器来设计数字滤波器,也就是使数 字滤波器能模仿模拟滤波器的特性,这种模仿可 以从不同的角度出发。脉冲响应不变法是从滤波 器的脉冲响应出发,使数字滤波器的单位脉冲响 应序列h(n)模仿模拟滤波器的冲激响应ha(t), 即将ha(t)进行等间隔采样,使h(n)正好等于 ha(t)的采样值,满足h(n)=ha(nT) 式中,T是采样周期。 如果令Ha(s)是ha(t)的拉普拉斯变换,H(z) 为h(n)的Z变换,利用采样序列的Z变换与模拟 信号的拉普拉斯变换的关系得
j
因此
| z |
2 2 T 2 2 T
2
2
由此看出,当σ<0时,|z|<1;当σ>0时, |z|>1。也就是说,S平面的左半平面映射到Z 平面的单位圆内,S平面的右半平面映射到Z平面 的单位圆外,S平面的虚轴映射到Z平面的单位圆 上。因此,稳定的模拟滤波器经双线性变换后所 得的数字滤波器也一定是稳定的。
