湖北孝感云梦上八年级上期中质量检测试卷
孝感市云梦县八年级上学期物理期中考试试卷

孝感市云梦县八年级上学期物理期中考试试卷姓名:________ 班级:________ 成绩:________一、单项选择题(每小题3分,共36分) (共12题;共36分)1. (3分)如图所示是小枫和同学们利用实验室的长方体木块做了“探究力的作用效果的影响因素”的实验,根据实验现象,他们得出了以下结论,其中正确的是()a.由(1)(4)说明力的大小会影响力的作用效果;b.由(2)(5)说明力的方向会影响力的作用效果;c.由(3)(6)说明力的作用点会影响力的作用效果.d.本实验运用的物理研究方法是转化法.A . abcdB . abcC . acdD . bc2. (3分)(2017·平邑模拟) 下列数据中最接近实际情况的是()A . 普通中学生的身高约为0.5mB . 正常工作中的冰箱冷冻室的温度约为20℃C . 长跑运动员的平均速度约为50m/sD . 两个鸡蛋的质量约为0.1kg3. (3分)下列现象中不能说明光在均匀介质中沿直线传播的是()A . 小孔成像B . 日食现象C . 一叶障目D . 平面镜成像4. (3分) (2018八上·南平期中) 下列所说的数据中,哪一个是符合客观实际的()A . 一名中学生的身高约为 1.65cmB . 中学生在1s内心跳约次70次C . 这张试卷的厚度大约为2mmD . 步行上学的速度约为1m/s5. (3分) (2019八上·中山期末) 关于错误和误差,下列说法正确的是()A . 误差就是错误B . 误差和错误都可以避免C . 误差只能减小,但不能消除D . 误差是在测量过程中不遵守测量规则造成的6. (3分) (2017八上·福建月考) PM2.5是指大气中直径小于或等于2.5 μm的颗粒物,单个PM2.5是隐藏在空气的浮尘中,容易被吸人人的肺部造成危害,下列关于PM2.5颗粒物直径的单位换算过程正确的是()A . 2.5µm=2.5µm×10-6mB . 2.5µm=2.5 ×10-5dmC . 2.5 µm=2.5×10-6cmD . 2.5 µm= 2.5 ×10-9m7. (3分)能区分不同歌手声音的主要依据是()A . 响度B . 音调C . 音色D . 振幅8. (3分)(2020·孝感) 下列有关声现象,说法正确的是()A . 声音的传播不需要介质,真空也能传声B . 频率的高低决定声音的音色C . 利用超声波给金属工件探伤,说明声能传递信息D . 从环境保护的角度来讲,优美的音乐一定不属于噪声9. (3分)下列四个现象中,有一个形成的原因与另外三个不同,这个现象是()A . 教室靠左前方的同学看到黑板上有一小块光斑B . 对着镜子梳妆时能看到镜中的自己C . 晴天树荫下地面上有许多的光斑D . 河水中映出了岸上柳树的倒影10. (3分) (2019八上·东莞月考) 如下图所示的四种现象中,与平面镜成像原理相同的是()A .B .C .D .11. (3分) (2018八上·鹤岗月考) 人站在平面镜前向平面镜靠拢时,他在镜中的像()A . 变大B . 变小C . 不变D . 无法判断12. (3分)(2017·菏泽) 关于声现象,下列说法正确的是()A . 声音在空气中传播比在水中传播的快B . 声音和光在空气中传播时,声音传播的较快C . 喇叭播放的歌曲都是乐音D . 声音是由物体的振动产生的二、填空题(每空1分,共16分) (共8题;共18分)13. (2分) (2019八上·梅江月考) 课堂上老师讲课的声音是由声带________产生的,它通过________传入我们耳朵;我们能分辨出不同老师的声音,这主要是因为他们发出声音的________不同。
湖北省孝感市云梦县八年级(上)期中物理试卷

湖北省孝感市云梦县八年级(上)期中物理试卷一、选择题(下列各小题中1-10题为单项选择题,每题2分,11-12题多多项选择题,每小题2分,共26分。
多项选择题选对但不全得2分,选错得零分。
请将正确答案填入上表的栏中)1.(2分)为了学好物理,小雨同学对自己提出了几个要求,你认为不合理的是()A.重视观察和实验B.只要死记硬背、多做题,就能学好物理C.重视科学探究的运用D.注意从生产和生活中寻找物理问题2.(2分)关于某中学生自身的数据,符合实际的是()A.静卧时脉搏跳动一次时间约为1sB.正常体温42℃C.步行速度5m/sD.身高1.65cm3.(2分)2017年7月30日上午9时,在朱日和训练基地举行庆祝中国人民解放军建军90周年阅兵;24架直升机绘出“90”字样匀速通过阅兵现场上空,象征着人民军队走过了90年光辉历程,下列关于24架直升机的运动说法正确的是()A.不论以什么为参照物直升机都是运动的B.以其中一架直升机为参照物其它直升机都是运动的C.以其中一架直升机为参照物其它直升机都是静止的D.以现场缓缓飘动的国旗为参照物其它直升机都是静止的4.(2分)下列现象属于机械运动是()A.秋虫鸣叫B.星光闪闪C.滴水成冰D.电梯上升5.(2分)如图所示,城市高架道路的部分路段,两侧设有3m左右高的板墙,安装这些板墙的目的是()A.保护车辆行使安全B.减小车辆噪声污染C.增加高架道路美观D.阻止车辆废气外泄6.(2分)使用拉伸了的软塑料尺测物体的长度,测量的结果将()A.比真实值偏大B.比真实值偏小C.不受影响D.和真实值完全一样7.(2分)牙科医生用来观察病人牙齿的小镜子,要放在火上烤一下才放进病人的口腔中,医生这样做是为了()A.消毒,防止将病毒带入口中B.把镜面上的水分烘干C.避免病人感觉镜子冷D.防止口腔中的水蒸气液化,便于观察8.(2分)为了节约用水,西宁市园艺工人利用滴灌的方法给道路两旁树木浇水,如图所示。
湖北省孝感市孝昌县2024-2025学年八年级上学期11月期中物理试题(含答案)

2024—2025学年度上学期初中期中质量监测八年级物理试卷一、选择题(共12题,每题2分,共24分,在每题给出的四个选项中,只有一项符合题目要求)1.3月12日植树节这一天,某学校组织九年级同学参加植树造林活动。
根据图片信息,对图中这棵小树的高度估测合理的是()第1题图第2题图A.2dm B.2km C.20mm D.2m2.在第十四届中国国际航空航天博览会上,歼-10、歼-20、歼-16、运油-20等飞机轮番表演,成为本次航展最靓的“仔”。
如图是歼-20飞行表演,飞行员感觉自己是静止的,则飞行员所选择的参照物是()A.地面B.机场C.歼-20战机D.坐在合上观看的观众3.某物体做匀速直线运动,由速度公式可知,物体的()A.速度大小恒定不变B.速度与路程成正比C.速度与时间成反比D.以上说法都对4.关于声现象,下列说法中正确的是()A.声音在空气中的传播速度为3×108 m/sB.无人机在空中飞行时,螺旋桨发出的声音是物体的振动产生的C.超声波可以在真空中传播D.北京天坛的回音壁,能产生奇妙的声学现象,不是声音反射形成的5.以下关于声的实验图片,说法正确的是()甲乙丙丁A.如图甲所示,放在发声音叉旁的小球弹跳起来,说明:发声的音叉在振动B.如图乙所示,随着真空罩内空气的减少,听到闹铃声越来越大C.如图丙所示,演奏古筝时用力拨动同一根琴弦,音调会升高D.如图丁所示,将瓶底去除蒙上薄膜,瓶口对着点燃的蜡烛,用力拍打薄膜,蜡烛熄灭。
说明:声可以传递信息6.央视《国家宝藏》节目中的贾湖骨笛是以鹤类鸟的翅膀骨头制成的,它是世界上最早的可吹奏的乐器(如图),比古埃及出现的笛子要早2000年。
关于骨笛的说法正确的是()A.吹奏的笛声是由笛骨振动发出的B.按住不同的笛孔发出声音的音调会不同C.笛声在空气中传播的速度越来越慢D.吹奏的笛声一定属于噪声7.下列选项对图中情景描述错误的是()甲:用手拨动尺子乙:两列声波的波形丙:摩托车的消声器丁:海豚表演A.甲图中钢尺伸出桌面长度越短,音调越高B.乙图中的两列声波的音色不同C.丙图中消音器是在声源处减弱噪声D.丁图中的海豚只能接收到超声波8.下列关于温度及温度计的说法正确的是()A.凭感觉也可以准确判断物体的冷热程度B.用温度计测温度时,要先观察量程和分度值,然后选用合适的温度计C.用温度计测量水温时,应等温度计的示数稳定后再拿出来读数D.不论是哪种温度计,其原理都是利用了液体的热胀冷缩这一性质9.关于物态变化现象,下列说法正确的是()A.冬天窗户上的冰花是水凝固形成的B.利用干冰制造的“烟雾”是干冰熔化形成的C.夏天吹风扇感到凉爽,是因为风加快了汗液的蒸发且蒸发要吸热D.与100℃的热水相比,100℃的水蒸气造成的烫伤更严重,是因为水汽化时要放热10.关于下列四幅图的说法正确的是()甲乙丙丁A .甲图中,温度计的示数为16℃B .乙图中,某晶体熔化图象是bc 段,晶体温度不变C .丙图中,花儿上的露珠是水蒸气凝华而成的D .丁图中,烈日下小狗伸出舌头降温,是因为水升华吸热11.在“探索厨房中的物态变化问题”跨学科实践活动中,下列说法不正确的是( )A .电壶里的水烧开后,壶嘴会冒“白气”,这种“白气”是小液滴而不是水蒸气B .打开冰箱,用打湿了的手去拿冷冻室的肉块时,手往往会被“粘”住C .厨房里使用的瓶装液化气,是用在一定温度下压缩体积的方法使气体液化的D .煮饺子时,当水沸腾后仍然用大火加热,这样饺子不仅熟得快且节省水和燃料12.周末,小丽陪妈妈一起到公园锻炼身体,1km 的圆形步道她们用90min 走了6圈,手机软件显示小丽步数为5500步。
2020-2021学年湖北省孝感市云梦县八年级(上)期中数学试卷(附答案详解)
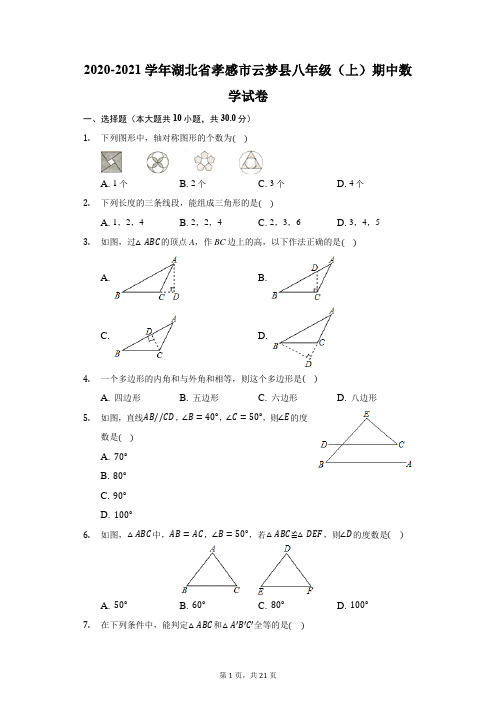
2020-2021学年湖北省孝感市云梦县八年级(上)期中数学试卷一、选择题(本大题共10小题,共30.0分)1.下列图形中,轴对称图形的个数为()A. 1个B. 2个C. 3个D. 4个2.下列长度的三条线段,能组成三角形的是()A. 1,2,4B. 2,2,4C. 2,3,6D. 3,4,53.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A. B.C. D.4.一个多边形的内角和与外角和相等,则这个多边形是()A. 四边形B. 五边形C. 六边形D. 八边形5.如图,直线AB//CD,∠B=40°,∠C=50°,则∠E的度数是()A. 70°B. 80°C. 90°D. 100°6.如图,△ABC中,AB=AC,∠B=50°,若△ABC≌△DEF,则∠D的度数是()A. 50°B. 60°C. 80°D. 100°7.在下列条件中,能判定△ABC和△A′B′C′全等的是()A. AB=A′B′,BC=B′C′,∠A=∠A′B. ∠A=∠A′,∠C=∠C′,AC=B′C′C. ∠A=∠A′,∠B=∠B′,∠C=∠C′D. AB=A′B′,BC=B′C′,∠B=∠B′.8.如图,∠B=∠C=90°,DM平分∠ADC,AM平分∠DAB,CB=10,则点M到AD的距离为()A. 5B. 6C. 7D. 89.如图,将长方形纸片ABCD折叠,使点D和点B重合,点C落在点C′处,折痕为EF,若AB=4,BC=8,则△ABE和△BC′F的周长之和为()A. 18B. 20C. 22D. 2410.如图,等腰△BC中,AB=AC=10,BC=16,△ABD是等边三角形,点P是∠BAC的角平分线上一动点,连接PC、PD,则PC+PD的最小值为()A. 8B. 10C. 12D. 16二、填空题(本大题共6小题,共18.0分)11.点P(−3,−4)关于y轴对称点的坐标是______.12.在△ABC中,∠A=38°,∠B=62°,则与∠C相邻的外角为______°.13.若a、b、c为三角形的三边,则√(a+b−c)2+√(b−c−a)2=______.14.如图,在△ABC中,∠B=90°,∠A=30°,分别以A,AC为半径画弧,两弧交于M,NC两点为圆心,大于12两点,直线MN交AB于点D,交AC于点E,若BD=4,则AB的长度为______.15.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm,则BE=______.16.平面直角坐标系中,已知点A(1,2),B(3,0),若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是______.三、解答题(本大题共8小题,共72.0分)17.一个多边形的内角和是它的外角和的5倍,求这个多边形的边数.18.如图,在△ABC中,∠C=∠ABC=2∠A,BD平分∠ABC,BE是AC边上的高,求∠DBE的度数.19.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.求证:(1)∠A=∠D;(2)AB//DE.20.如图,在△ABC中,AD,AE分别是边BC上的中线和高.(1)若AE=5cm,S△ABC=30cm2.求DC的长.(2)若∠B=40°,∠C=50°,求∠DAE的大小.21.如图,△ABC为等边三角形,点D,E分别在边BC,AC上,且AE=CD,AD与BE相交于点F.(1)求证:∠BFD的度数;(2)过点B作BH⊥AD于点H,若EF=3,FH=6,求出AD的长度.22.如图,在平面直角坐标系中,A(1,3),B(2,1),C(4,4).(1)计算△ABC的面积;(2)在图形中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1、B1、C1的坐标;(3)在x轴上画点P,使PA+PC最小(保留作图痕迹).23.如图,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE交于点H,连CH.(1)求证:△ACD≌△BCE;(2)求证:CH平分∠AHE;(3)求∠CHE的度数.(用含α的式子表示)24.如图,在直角坐标系中,△ABC的三个顶点都在坐标轴上,A,B两点关于y轴对称,点C是y轴正半轴上一个动点,AD是角平分线.(1)如图1,若∠ACB=90°,直接写出线段AB,CD,AC之间数量关系;(2)如图2,若AB=AC+BD,求∠ACB的度数;(3)如图2,若∠ACB=100°,求证:AB=AD+CD.答案和解析1.【答案】C【解析】解:第一个图形不是轴对称图形;第二个图形是轴对称图形;第三个图形是轴对称图形;第四个图形是轴对称图形;故选:C.根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴即可选出答案.此题主要考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.【答案】D【解析】解:A、1+2<4,不能构成三角形,不符合题意;B、2+2=4,不能构成三角形,不符合题意;C、2+3<6,不能构成三角形,不符合题意;D、3+4>5,能构成三角形,符合题意.故选:D.根据三角形的三边满足两边之和大于第三边来进行判断.此题主要考查了三角形的三边关系,在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.3.【答案】A【解析】【分析】本题考查了三角形的高线,熟记高线的定义是解题的关键.根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:△ABC中BC边上的高的是A选项.故选:A.4.【答案】A【解析】解:设此多边形是n边形,∵多边形的外角和为360°,∴180(n−2)=360,解得:n=4.∴这个多边形是四边形.故选:A.首先设此多边形是n边形,由多边形的外角和为360°,即可得方程180(n−2)=360,解此方程即可求得答案.此题考查了多边形的内角和与外角和的知识.此题难度不大,注意多边形的外角和为360°,n边形的内角和等于180°(n−2).5.【答案】C【解析】解:∵AB//CD,∴∠1=∠B=40°,∴∠E=180°−∠1=∠C=90°,故选:C.根据平行线的性质求出∠1,根据三角形内角和定理计算,得到答案.本题考查的是平行线的性质、三角形内角和定理,掌握两直线平行,同位角相等是解题的关键.6.【答案】C【解析】解:∵AB=AC,∠B=50°,∴∠C=∠B=50°,∴∠A=180°−50°−50°=80°,∵△ABC≌△DEF,∴∠D=∠A=80°,故选:C.根据等腰三角形的性质、三角形内角和定理求出∠A,根据全等三角形的性质解答即可.本题考查的是全等三角形的性质、三角形内角和定理,掌握全等三角形的对应角相等是解题的关键.7.【答案】D【解析】解:当AB=A′B′,BC=B′C′,∠A=∠A′时,不能判定△ABC和△A′B′C′全等,∠A与∠A′不是已知两边的夹角;当∠A=∠A′,∠C=∠C′,AC=B′C′时,不能判定△ABC和△A′B′C′全等,B′C′不是∠A′与∠C′的夹边;当∠A=∠A′,∠B=∠B′,∠C=∠C′时,不能判定△ABC和△A′B′C′全等,不存在AAA的方法;当AB=A′B′,BC=B′C′,∠B=∠B′时,能判定△ABC和△A′B′C′全等,依据是SAS.故选:D.三条边分别对应相等的两个三角形全等;两边及其夹角分别对应相等的两个三角形全等;两角及其夹边分别对应相等的两个三角形全等;两角及其中一个角的对边对应相等的两个三角形全等.依据上述方法进行判断即可.本题主要考查了全等三角形的判定,解题时注意:若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.8.【答案】A【解析】解:如图,过点M作ME⊥AD于E,则∠DEM=90°,∵DM平分∠ADC,∴∠MDE=∠MDC,在△DME和△DMC中,{∠DEM=∠C=90°∠MDE=∠MDCDM=DM,∴△DME≌△DMC(AAS),∴ME=MC,同理:ME=MB,∴MB=MC=ME,∵BC=10,∴ME=MB=12×10=5,即点M到AD的距离为5.故选:A.过点M作ME⊥AD于E,证△DME≌△DMC(AAS),得ME=MC,同理:ME=MB,则MB=MC=ME,即可得出结论.本题考查了全等三角形的判定与性质、角平分线的性质等知识;熟练掌握全等三角形的判定与性质,作出辅助线是解题的关键.9.【答案】D【解析】解:将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,∵∠ABE+∠EBF=∠C′BF+∠EBF=90°∴∠ABE=∠C′BF在△BAE和△BC′F中,{∠FC′B=∠EAB BC′=AB∠ABE=∠C′BF,∴△BAE≌△BC′F(ASA),∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=4+8=12,∴△ABE与△BC′F的周长和=2△ABE的周长=2×12=24.故选:D.由折叠特性可得CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,推出∠ABE=∠C′BF,所以△BAE≌△BC′F,根据△ABE和△BC′F的周长=2△ABE的周长求解.本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,折叠前后图形的形状和大小不变,如本题中折叠前后角边相等.10.【答案】B【解析】解:如图,连接BP,∵点P是∠BAC的角平分线上一动点,AB=AC,∴AP垂直平分BC,∴CP=BP,∴PD+PC=PD+PB,∴当B,P,D在在同一直线上时,BP+PD的最小值为线段BD长,又∵△ABD是等边三角形,AB=BD=10,∴PD+PC的最小值为10,故选:B.连接BP,根据AP垂直平分BC,即可得到CP=BP,再根据当B,P,D在在同一直线上时,BP+PD的最小值为线段BD长,即可得出PD+PC的最小值为10.本题主要考查了最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.11.【答案】(3,−4)【解析】解:首先可知点P(−3,−4),再由平面直角坐标系中关于y轴对称的点的坐标特点:横坐标相反数,纵坐标不变,可得:点P关于y轴的对称点的坐标是(3,−4).本题比较容易,考查平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点:关于y轴对称的点,纵坐标相同,横坐标互为相反数.解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.12.【答案】100【解析】解:∠C相邻的外角=∠A+∠B=38°+62°=100°.故答案是:100.根据三角形内角与外角的关系:外角等于不相邻的两个内角的和即可求得.主要考查了三角形的内角和外角之间的关系,即三角形的外角等于与它不相邻的两个内角和.13.【答案】2a【解析】解:∵a、b、c为三角形的三边∴a+b>c,c+a>b∴原式=|a+b−c|+|b−c−a|=a+b−c+c+a−b=2a故答案为:2a由a,b,c为三角形的三边,根据三角形三边关系,即可得a+b>c,c+a>b,又由√(a+b−c)2+√(b−c−a)2=|a+b−c|+|b−c−a|,即可求得答案.此题考查了二次根式的性质和三角形三边的关系.此题难度适中,注意掌握√a2=|a|.14.【答案】12【解析】解:由基本作图方法得出:MN垂直平分线段AC,则AD=DC,∵∠B=90°,∠A=30°,∴∠ACB=60°,∠A=∠ACD=30°,∴∠DCB=30°,∵BD=4,∴DC=2BD=8,∴AB=AD+BD=DC+BD=8+4=12.故答案为:12.直接利用基本作图方法结合线段垂直平分线的性质得出AD=DC,即可得出答案.此题主要考查了基本作图,正确得出DC的长是解题关键.15.【答案】0.8cm【解析】解:∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠EBC+∠BCE=90°.∵∠BCE+∠ACD=90°,∴∠EBC=∠DCA.在△CEB和△ADC中,{∠E=∠ADC∠EBC=∠DCA BC=AC,∴△CEB≌△ADC(AAS),∴BE=DC,CE=AD=2.5.∵DC=CE−DE,DE=1.7cm,∴DC=2.5−1.7=0.8cm,∴BE=0.8cm故答案为0.8cm.根据条件可以得出∠E=∠ADC=90°,进而得出△CEB≌△ADC,就可以得出BE=DC,就可以求出BE的值.本题考查了垂直的性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.16.【答案】7【解析】解:∵点A、B的坐标分别为(1,2)、B(3,0),∴AB=√(3−1)2+(0−2)2=2√2,①若AC=AB,以A为圆心,AB为半径画弧与坐标轴有3个交点(B点除外),即满足△ABC是等腰三角形的C点有3个;②若BC=AB,以B为圆心,BA为半径画弧与坐标轴有2个交点,即满足△ABC是等腰三角形的C点有2个;③若CA=CB,作AB的垂直平分线与坐标轴有2个交点,即满足△ABC是等腰三角形的C点有2个.综上所述:点C在坐标轴上,△ABC是等腰三角形,符合条件的点C共有7个.故答案为:7.由点A、B的坐标可得到AB=2√2,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数即可.本题主考查了等腰三角形的判定以及分类讨论思想的运用,分三种情况分别讨论是解题的关键.17.【答案】解:设多边形的边数为n,由题意得,(n−2)⋅180°=5×360°,解得n=12,所以,这个多边形是十二边形.【解析】根据多边形的内角和公式(n−2)⋅180°和外角和定理列出方程,然后求解即可.本题考查了多边形的内角与外角,熟记内角和公式和外角和定理并列出方程是解题的关键.18.【答案】解:在△ABC中,∠ABC+∠A+∠C=180°,∵∠C=∠ABC=2∠A,∴∠A=36°,∴∠C=∠ABC=72°,∵BD平分∠ABC,∠ABC=36°,∴∠CBD=12∵BE是AC边上的高,∴∠CBE=90°−∠C=18°,∴∠DBE=∠CBD−∠CBE=36°−18°=18°.【解析】根据三角形的内角和等于180°和已知条件求出∠A,∠ABC,再根据角平分线的定义表示出∠CBD,根据直角三角形两锐角互余表示出∠CBE,根据∠DBE=∠CBD−∠CBE即可得解.本题考查了等腰三角形的性质,三角形的内角和定理,角平分线的定义,直角三角形两锐角互余的性质,熟记定理与性质并准确识图理清图中各角度之间的关系是解题的关键.19.【答案】证明:(1)∵BE=CF,∴BE+EC=CF+EC,∴BC=EF,在△ABC和△DEF中,{BC=EF AB=DE AC=DF,∴△ABC≌△DEF(SSS),∴∠A=∠D;(2)由(1)得:△ABC≌△DEF,∴∠B=∠DEF,∴AB//DE.【解析】(1)先由BE=CF得BC=EF,再根据SSS定理得△ABC≌△DEF,即可得出结论;(2)先由全等三角形得∠B=∠DEF,再由平行线的判定定理得AB//DE即可.本题考查全等三角形的判定和性质,平行线的判定等知识;解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.20.【答案】解:(1)∵AD,AE分别是边BC上的中线和高,AE=5cm,S△ABC=30cm2,∴S△ADC=15cm2,∴12×AE×CD=15,∴12×5×CD=15,解得:CD=6(cm);(2)∵∠B=40°,∠C=50°,∴∠BAC=90°,又∵AD为中线,∴AD=12BC=BD,∴∠ADE=2∠B=80°,又∵AE⊥BC,∴∠DAE=10°.【解析】(1)利用三角形的中线平分三角形面积得出S△ADC=15cm2,进而利用三角形面积得出CD的长.(2)依据∠B=40°,∠C=50°,可知△ABC为直角三角形,再根据AD为中线,即可得到△ABD为等腰三角形,即可得到∠ADE的度数,进而得出∠DAE的度数.此题主要考查了三角形的面积以及三角形中线以及高线的性质,根据已知得出S△ADC是解题关键.21.【答案】(1)证明:∵△ABC是等边三角形,∴∠BAE=∠C=60°,AB=AC,在△ABE和△CAD中,{AE=CD∠BAE=∠C AB=CA,∴△ABE≌△CAD(SAS),∴∠ABE=∠CAD,BE=AD,∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAF=∠BAC=60°;(2)解:∵BH⊥AD,∴∠BHF=90°∴∠FBH=30°,∴FH=12BF,即BF=2FH,∵FH=6,EF=3,∴BF=12,BE=BF+EF=15,∴AD=BE=15.【解析】(1)根据SAS证明△ABE≌△CAD,得∠ABE=∠CAD,BE=AD,进而得出结论;(2)证明∠FBH=30°,再利用直角三角形的性质,推出BF=2FH,即可解决问题.本题考查全等三角形的判定和性质,等边三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.22.【答案】解:(1)△ABC的面积为3×3−12×1×2−12×2×3−12×1×3=72;(2)△A1B1C1如图所示,其中,A1(−1,3)、B1(−2,1)、C1(−4,4).(3)如图所示,点P即为所求.【解析】(1)利用割补法求解即可;(2)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可;(3)作出点A关于x轴的对称点A′,再连接A′C,与x轴的交点即为所求.本题主要考查作图−轴对称变换,解题的关键是掌握轴对称变换的定义和性质,并据此得出变换后的对应点.23.【答案】(1)证明:∵∠ACB=∠DCE=α,∴∠ACD=∠BCE,在△ACD和△BCE中,{CA=CB∠ACD=∠BCE CD=CE,∴△ACD≌△BCE(SAS);(2)证明:过点C作CM⊥AD于M,CN⊥BE于N,∵△ACD≌△BCE,∴∠CAM=∠CBN,在△ACM和△BCN中,{∠CAM=∠CBN∠AMC=∠BNC=90°AC=BC,∴△ACM≌△BCN,∴CM=CN,∴CH平分∠AHE;(3)∵△ACD≌△BCE,∴∠CAD=∠CBE,∵∠AMC=∠AMC,∴∠AHB=∠ACB=α,∴∠AHE=180°−α,∴∠CHE=12∠AHE=90°−12α.【解析】(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS,即可判定:△ACD≌△BCE;(2)首先作CM⊥AD于M,CN⊥BE于N,由△ACD≌△BCE,可证∠CAD=∠CBE,再证△ACM≌△BCN,(或证△ECN≌△DCM),可得CM=CN,即可证得CH平分∠AHE;(3)由△ACD≌△BCE,可得∠CAD=∠CBE,继而求得∠AHB=∠ACB=α,则可求得∠CHE的度数.此题考查了全等三角形的判定与性质以及角平分线的定义.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.24.【答案】解:(1)如图1,过D作DM⊥AB于M,∵A,B两点关于y轴对称,∴CA=CB,∵∠ACB=90°,AD是角平分线,∴CD=MD,∠ABC=45°,∴∠BDM=45°,∴BM=DM,∴BM=CD,在Rt △ADC 和Rt △ADM 中,{CD =MD AD =AD, ∴Rt △ADC≌Rt △ADM(HL),∴AC =AM ,∴AB =AM +BM =AC +CD ,即AB =AC +CD ;(2)设∠ACB =α,则∠CAB =∠CBA =90°−12α, 在AB 上截取AK =AC ,连结DK , ∵AB =AC +BD ,∴BK =BD ,∵AD 是角平分线,∴在△CAD 和△KAD 中,{AC =AK ∠CAD =∠KAD AD =AD,∴△CAD≌△KAD(SAS),∴∠ACD =∠AKD =α,∴∠BKD =180°−α,∵BK =BD ,∴∠BDK =180°−α,在△BDK 中,180°−α+180°−α+90°−12α=180°, ∴α=108°,∴∠ACB =108°;(3)如图2,在AB 上截取AH =AD ,连接DH ,∵∠ACB=100°,AC=BC,∴∠CAB=∠CBA=40°,∵AD是角平分线,∴∠HAD=∠CAD=20°,∴∠ADH=∠AHD=80°,在AB上截取AK=AC,连接DK,由(1)得,△CAD≌△KAD,∴∠ACB=∠AKD=100°,CD=DK,∴∠DKH=80°=∠DHK,∴DK=DH=CD,∵∠CBA=40°,∴∠BDH=40°,∴DH=BH,∴BH=CD,∵AB=AH+BH,∴AB=AD+CD.【解析】本题考查了全等三角形的判定和性质,轴对称的性质,等腰三角形的性质,角平分线的定义,三角形的内角和,正确的作出辅助线是解题的关键.(1)如图1,过D作DM⊥AB于M,根据轴对称的性质得到CA=CB,根据角平分线的性质得到CD=MD,∠ABC=45°,根据全等三角形的性质得到AC=AM,于是得到结论;α,在AB上截取AK=AC,连结DK,根(2)设∠ACB=α,则∠CAB=∠CBA=90°−12据角平分线的定义得到∠CAD=∠KAD,根据全等三角形的性质得到∠ACD=∠AKD=α,根据三角形的内角和即可得到结论;(3)如图2,在AB上截取AH=AD,连接DH,根据等腰三角形的性质得到∠CAB=∠CBA=40°,根据角平分线的定义得到∠HAD=∠CAD=20°,求得∠ADH=∠AHD= 80°,在AB上截取AK=AC,连接DK,根据全等三角形的性质得到∠ACB=∠AKD= 100°,CD=DK,根据等腰三角形的性质得到DH=BH,于是得到结论.第21页,共21页。
湖北省孝感市云梦县外国语学校2021—2022学年八年级上学期期中模拟测试语文卷

湖北省孝感市云梦县外国语学校2021—2022学年八年级上学期期中模拟测试语文卷学校:___________姓名:___________班级:___________考号:___________一、现代文阅读阅读《天空没有多余的星星》文段,完成下面小题。
①李忠义是一个工人。
②他没有值得炫耀的地方,活得也很艰难。
他从小患有腿疾,走起路来一跛一跛的。
个子不高,头发有些发白,近乎丑陋的脸上还有一块疤。
因为腿疾,单位安排他当收发员,无非是分发报纸信件。
李忠义是个闲不住的人,他把自己的本职工作做好后,就常到工地去转转。
技术活他插不上手,可他总能找到自己能干的活儿:道路坑洼他去填平,排水沟堵了他去疏通,散落的砂石他细心地堆积成方,散放的管材他整理成行。
他眼里总有活儿。
夏日,酷暑难当,他主动去食堂帮厨,吃力地把解暑的绿豆汤担到工地,自己渴了却忍着不喝。
冬日,他常常夜半巡夜,生怕工棚生火酿成事故。
每天清晨大家走出工棚,总会看到皑皑雪地上,有一串串高低不平的足印。
③他文化水平不高,却在工地醒目的地方立起一块黑板,用他笨拙的字迹,将每日新闻、安全警示和天气预报写在上面,虽然版面不很美观,却很受工友们的欢迎。
④别人有困难他跟着着急,别人高兴他跟着快乐,别人痛苦他也跟着痛苦。
一次,一个工友半夜发烧,他背着工友顶着风雪去医院,跛着腿跑来跑去,整整陪护了三天。
工友病愈出院了,他却病倒了,一病就是一星期。
⑤大凡地位卑微的人头就扬不起来,位尊显贵的人头就低不下去。
李忠义却在命运面前不低头,也从不抱怨生活对他的不公。
他充实地、忙忙碌碌地打发每一天,用他炽热的胸膛温暖冬天,用他辛勤的汗水融化冰雪。
一次,工会到工地放露天电影,放到一半时,风把银幕掀落,正在大家焦急之时,只见一个笨拙的身影,蹬着梯子攀上柱顶,吃力地把银幕重新拉好。
电影又重新放映,场内响起掌声。
⑥可就在那个冬季的一天,李忠义值了一宿夜班,不知是过于劳累,还是那天风雪太大,经过一个无人值守的铁路道口时,竟被呼啸而来的火车刮倒,被人发现送往医院,已经无救了。
孝感市云梦县八年级上学期物理期中考试试卷

孝感市云梦县八年级上学期物理期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)(2018·平邑模拟) 下列数据最接近实际情况的是()A . 100W的电冰箱正常工作一天耗电约为3kW•hB . 人体感觉舒适的温度约是38℃C . 一个初中生所受到的重力大约是500ND . 台灯正常工作时的电流是2A2. (2分)(2018·宝应模拟) 在科学实验时,为了减小误差或寻找普遍规律,经常需要进行反复多次实验:①“测量物体的长度”时,多次测量②“研究杠杆的平衡”时,改变动力(臂)和阻力(臂),多次测量③“研究串、并联电路的电流特点”时,换用不同定值电阻,多次测量④“用电压表和电流表测导体的电阻”时,多次测量电阻两端电压和通过电阻的电流值;上述实验中寻找普遍规律的是()A . ①②B . ①③C . ②④D . ②③3. (2分)德化南埕的漂流吸引了众多游客。
一叶扁舟,顺水而下,出没浪端谷底,惊险刺激。
我们说坐在橡皮艇上的游客静止不动,所选的参照物是()A . 两岸山上的树B . 橡皮艇C . 河岸上的摄影记者D . 水中四处游动的鱼4. (2分)(2017·菏泽模拟) 人工智能使得人们的生活越来越方便,华人青年王孟秋发明了一款功能强大的便携式家用“无人相机”,相机内装有多种高科技传感器,底部装有镜头和声呐(发射超声,同时能接受超声的装置),机身只有240克.你认为向下发射超声的“底部声呐”可能与下列相机的哪个功能有关()A . 用手机控制相机B . 相机能自动悬浮停在合适高度拍摄C . 相机水平位置运动时遇到障碍物会自动避开D . 笑脸抓拍5. (2分)(2019·连云港) 下列关于声音的说法正确的是()A . 发声的物体一定都在振动B . “脆如银铃”是指声音的响度大C . 我们调节电视机的音量改变的是声音的音调D . 开会时将手机调为静音是在传播过程中减弱噪声6. (2分)下列关于声的说法中是正确的是()A . 正在发声的物体都在振动B . 只要物体振动,就能听到声音C . 声音在各种物质中传播的速度是一样的D . 声音不能在固体物质中传播7. (2分) (2019八上·来宾期末) 为了减少高速行驶的车辆产生的噪声对公路两侧居民的干扰.常在高速公路的两侧架设具有一定高度的屏障。
上学期云梦县八年级数学期中质量检测题.doc

上学期云梦县八年级数学期中质量检测一、选择题(本大题共10小题,每小题3分,共计30分,请将唯一正确答案填入下表中)1.下列各曲线中不能表示y是x的函数的是:2.下列函数中,自变量x的取值范围是x≥2的是:A.y= B.y= C.y= D.y =3.关于函数y=x,下列结论正确的是:A.函数图像必须经过点(1,2) B.函数图像经过二、四象限C.y随x的增大而增大 D.y随x的增大而减小4.小明把自己一周的支出情况,用所示的统计图来表示,下面说法正确的是:A.从图中可以直接看出具体消息数额B.从图中可以直接看出总消费数额C.从图中可以直接看出各项消费数额占总消费额的百分比D.从图中可以直接看出各项消费数额在一周中的具体变化情况5.一个有50个数据的样本,落在某一小组内的频率是0.3,那么这50个数据中,在这一小组内的数据频数是:A.50 B.30 C.15D.36.在扇形统计图中,各扇形面积之比为5:4:3:2:1,其中最大扇形的圆心为:A.150° B.120° C.100°D.90°7.在下列条件中,不断判定△ABC≌△的是:A.∠A=∠,∠C=∠,AC= B.∠A=∠,AB=,BC=C.∠B=∠,∠C=∠,AC= D.BA=,BC=,AC=8.如图,△ABC≌△BAD,点A和点B、点C和点D是对应点,如果AB=8cm,BC=4cm,AC=6cm,那么BD+AD的长是:A.14cm B.12cm C.10cm D.10cm或12cm9.下列关于一次函数y=-2x+1的结论:①y随x的增大而减小.②图象与直线y=-2x平行.③图象与y轴的交点坐标是(0,1).④图象经过第一、二、四象限.其中正确的有:A.4个B.3个C.2个 D.1个10.如图所示,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠的度数为:A.80° B.100° C.6 0° D.45°二、填空题(每小题3分,共计30分)11.在△ABC≌△中,已知∠A=∠,AC=,请你添加一个条件,使△ABC≌△,你添加的条件是.12.一个正方形的边长为5cm,它的边长减少x cm后得到的新正方形的周长为y cm,则y与x的关系式是,自变量的取值范围是.13.若直线y=-x+a和直线y=x+b的交点坐标为(m,8),则a+b =.14.已知直线y=x-2与y=-x+2相交于点(2,0),则不等式x-2≥-x的解集是.15.如图所示,是对某班一次数学测验成绩进行统计分析,所得频数折线图,这次测验的优秀率(80分以上为优秀)为.16.一组数据中最大数为80,最小数为50,若取组距为5,那么这组数据应分成组.17.某中学对200名学生进行了关于“造成学生睡眠少的原因”的抽样调查,将调查结果制成扇形统计图(如图),由图中的信息可知,认为“造成学生睡眠少的主要原因是作业太多”的人数有名.18.如图是表示2006年多哈亚运会金牌分布的扇形统计图,已知日本获得金牌50枚,由扇形统计图估计中国获得金牌的数量是枚.19.如图,在△ABC中,AD=DE,AB=BE,∠CED=70°,则∠A=.20.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交于BC于点D,DE⊥AB于点E,若△DBE的周长是16cm,则边AB的长是.三、解答题(本大题共7小题,满分60分)21.(6分×2=12分)(1)已知一个一次函数的图像经过点(-4,8)和点(6,3),求这个函数的解析式.(2)画出函数y=2x-6的图象,并利用图象,若-6≤y≤0,求x的取值范围.22.(8分)如图,l1表示神风摩托车厂一天的销售收入与摩托车销售量的关系;l2表示摩托车厂一天的销售成本与销售量的关系.(1)写出销售收入与销售量之间的函数关系式;(2)写出销售成本与销售量之间的函数关系式;(3)当一天的销售量为多少辆时,销售收入等于销售成本?(4)当一天的销售超过多少辆时,工厂才能获利(利润=收入-成本)?23.(8分)某中学体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:(1)全班有多少同学?(2)组距是多少?组数是多少?(3)跳绳次数x达到100为及格,该班踏绳的及格率是多少?(4)画出适当的统计图表示上面的信息.24.(8分)如图,OC是∠AOB的角平分线,P是OC上一点,PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接OF,EF.求证:DF=EF.25.(8分)学校鼓励学生参加社会实践,小萌所在班级的研究性学习小组在假期对她们所在城市的一家晚报的读者进行一次问卷调查,以便了解读者对这种报纸四个版面的喜欢情况.她们调查了男女读者各500名,要求每个读者选出自己喜欢的一个版面,并将得到的数据绘制了下面尚未完成的统计图.(1)请将图补充完整;(2)计算男、女读者喜欢每个版面的总人数,并分别画出折线统计图.26.(8分)如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,请你用三角形全等的知识帮小明设计一个方案,测出A、B间的距离,并说明理由.27.(8分)某游乐场每天的盈利额y(元)与售出的门票数(张)之间的函数关系如图所示.(1)当0≤x≤200,且x为整数时,y关于x的函数解析式为.当200<x≤300,且x为整数时,y关于x 的函数解析式为.(2)要使游乐场一天的盈利额超过1000元,试问该天至少应售出多少张门票?(3)请思考并解释图象与y轴的交点(0,-1000)的实际意义.(4)根据图象请你再提供2条信息.2007—2008学年度上学期期中八年级数学参考答案及评分说明一、选择题(每小题3分)1.D 2.B 3.C 4.C5.C6.B 7.B 8.C 9.A10.A二、填空题(每小题3分)11.∠C=∠或∠B=∠或AB= 12.y=-4x+20,0≤x<13.16 14.x≥2 15.56% 16.6 17.8818.165 19.110° 20.16cm三、解答题21.①设一次函数的解析为y=kx+b 1分∵此一次函数的图象经过点(-4,8)、(6,3)∴ 3分解得: 5分即一次函数的解析式为y=-x+6 6分②画图象如图: 4分由图象知,若-6≤y≤0,则x的取值范围是0≤x≤3. 6分22.(1)y=x 2分(2)y=x+2 4分(3)4辆 6分(4)超过4辆 8分23.(1)全班有2+4+21+13+8+4+1=53(人) 2分(2)组距是20,组数为7. 4分(3)跳绳次数x≥100范围的同学有21+13+8+4+1=47(人),因此及格率为88.7%.6分(4)统计图如图所示8分24.证明:∵∠1=∠2,PD⊥OA,PE⊥OB∴PD=PE 2分∴Rt△ODP≌Rt△OEP∴OD=OE 4分在△ODF和△OEF中OD=OE∠1=∠2OF=OF∴△ODF≌△OEF7分∴DF=EF 8分25.(1)图略4分(2)新闻版:500×30%+500×32%=310(人);文娱版:500×10%+500×30%=200(人);体育版:500×48%+500×20%=340(人);生活版:500×12%+500×18%=150(人). 6分折线图略.8分26.说明:设计方案开放,仅提供2种方案.写出方案给3分,画图证明给5分,共8分.方案一、如图,先在地上了以一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC,连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,DE的长度就是A、B间的距离.证明:在△ABC和△EDC中BC=EC∴△ABC≌△EDC∴AB=DE方案二、如图,要测量A、B间的距离,可以在AB的垂线BF上.取两点C、D,使CD、BC,再过D点作出BF的垂线DG,并在DG上找一点E,使A、C、E在一条直线上,这时测得的DE的长就是A、B间的距离.证明:在△ABC和△EDC中BC=DC∴△ABC≌△EDC∴AB=DE27.(1)y=10x-1000,y=15x-25000. 2分(2)由题意知:15x-25000>1000,解得x>233,∵x为整数,∴x=234(张). 4分(3)游乐场停业一天(或一张票没卖),亏损1000元. 6分(4)游乐场每天售票100张时不亏不盈,游乐场每天售票最多为300张等.8分。
湖北省孝感市云梦县八年级(上)期中数学试卷

期中数学试卷题号一二三总分得分一、选择题(本大题共10小题,共30.0分)1.下面4个字中,是轴对称图形的是( )A. B. C. D.2.下列线段长,能构成三角形的是( )A. 3,4,8B. 7,8,15C. 5,12,13D. 6,6,133.下列图形具有稳定性的是( )A. 锐角三角形B. 正方形C. 五边形D. 六边形4.一个多边形的内角和是它的外角和的2倍,则这个多边形是( )A. 五边形B. 六边形C. 七边形D. 八边形5.下列各图中,a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )A. 甲和乙B. 只有乙C. 甲和丙D. 乙和丙6.如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=55°,从C处观测A,B两处的视角∠ACB的度数是( )A. 20°B. 25°C. 30°D. 35°7.等腰三角形的两边长分别为3、6,则该三角形的周长为( )A. 12或15B. 9C. 12D. 158.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,若AD=3.4cm,DE=2.7cm,则BE的长是( )A. 0.7cmB. 1.4cmC. 1.7cmD. 2.7cm9.如图,已知△ABC中,∠ABC=45°,H是高AD和BE的交点,∠CAD=30°,CD=6,则线段BH的长度为( )A. 8B. 10C. 12D. 1610.如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,EG⊥BC于点G,连接AG、FG.下列结论:①AE=GE;②△AEF 为等腰三角形;③△DFG为等腰直角三角形;④AG=BF其中正确结论的个数是( )A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共6小题,共18.0分)11.若点A与点B(4,3)关于x轴对称,则点A的坐标为______.12.如图,△ABC≌△DCB,∠DBC=36°,则∠AOB=______.13.已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为______.14.如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于O,∠BAC=50°,∠C=70°,则∠AOB的度数是______.15.如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了______ 米.16.如图,正方形ABCD的面积为25,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为____.三、解答题(本大题共8小题,共72.0分)17.如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=64°,∠ACD=36°,∠ABE=20°.求∠BDC和∠EFC的度数.18.如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点C,DF⊥EF于点F,AC=DF.求证:(1)△ABC≌△DEF;(2)AB∥DE.19.如图,利用关于坐标轴对称点的坐标的特点,分别画出△ABC关于x轴和y轴对称的图形,并在图上标出对称点的坐标.20.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,垂足为D,交AC于点E.(1)若∠ABE=50°,求∠EBC的度数;(2)若△ABC的周长为43cm,BC的长为11cm,求△BCE的周长21.如图,Rt△ABC中,∠ACB=90°,∠A=30°,一同学利用直尺和圆规完成如下操作:①以点B为圆心,以适当的长为半径画弧,交BC于点M,交AB的延长线于点N;②分别以点M、N为圆心,以大于MN的长为半径画弧,两弧交于点P,作直线BP交AC的延长线于点D.请你观察图形,根据操作结果解答下列问题;(1)线段BD与AB的大小关系是______(2)过点D作DE⊥AB交AB的延长线于点E,若AC=a,BC=b,求△ADE的面积.22.如图,△ABC关于y轴对称,点A的坐标为(-2,0),∠ACO=30°,点D的坐标为(5,0),连接CD,以CD为边,在CD上方作等边三角形CDE,连接BE(1)求∠EBD的度数;(2)求线段BE的长23.已知:点D到△ABC的两边AB、AC所在直线的距离相等,即DE⊥AB,DF⊥AC,DE=DF,且DB=DC.(1)如图1,若点D在BC上,求证:AB=AC;(2)如图2,若点D在△ABC的内部,求证:AB=AC;(3)若点D在△ABC外部,猜想:AB=AC还成立吗?如果成立,请画图,并加以证明;如果不成立,请画出反例示图,并证明.24.如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上运动,∠EDB=∠ACB,BE⊥DE,DE与AB相交于点F(1)如图1,当点D运动到与线段BC的端点C重合时,从探究线段BE与线段DF 的数量关系,并证明你的结论;(2)如图2,当点D在线段BC上运动时,探究线段BE与线段DF的数量关系,并证明你的结论.答案和解析1.【答案】A【解析】解:A、是轴对称图形,故本选项符合题意;B、不是轴对称图形,故本选项不合题意;C、不是轴对称图形,故本选项不合题意;D、不是轴对称图形,故本选项不合题意.故选:A.根据轴对称图形的概念求解.本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.2.【答案】C【解析】解:A、3+4<8,不能构成三角形,故此选项不合题意;B、7+8=15,不能构成三角形,故此选项不合题意;C、12+5>13,能构成三角形,故此选项符合题意;D、6+6<13,不能构成三角形,故此选项不合题意.故选:C.根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边即可求解.本题考查了能够组成三角形三边的条件,其实用两条较短的线段相加,如果大于最长的那条就能够组成三角形.3.【答案】A【解析】解:A、锐角三角形具有稳定性,故此选项正确;B、正方形不具有稳定性,故此选项错误;C、五边形不具有稳定性,故此选项错误;D、六边形不具有稳定性,故此选项错误;故选:A.根据三角形具有稳定性,可得答案.此题主要考查了三角形的性质,关键是掌握三角形具有稳定性.4.【答案】B【解析】解:设这个多边形是n边形,根据题意,得(n-2)×180°=2×360,解得:n=6.故这个多边形是六边形.故选:B.多边形的外角和是360°,则内角和是2×360=720°.设这个多边形是n边形,内角和是(n-2)•180°,这样就得到一个关于n的方程,从而求出边数n的值.本题考查了多边形的内角与外角,熟记内角和公式和外角和定理并列出方程是解题的关键.根据多边形的内角和定理,求边数的问题就可以转化为解方程的问题来解决.5.【答案】D【解析】解:根据“SAS”判断图乙中的三角形与△ABC全等;根据“AAS”判断图丙中的三角形与△ABC全等.故选:D.利用三角形全等的判定方法对各选项进行判断.本题考查了全等三角形的判定:灵活应用全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件.6.【答案】B【解析】解:∵∠CBD是△ABC的外角,∴∠CBD=∠CAD+∠ACB,∴∠ACB=∠CBD-∠ACB=55°-30°=25°.故选:B.因为∠CBD是△ABC的外角,所以∠CBD=∠CAD+∠ACB,则∠ACB=∠CBD-∠ACB.本题考查的是三角形外角与内角的关系,即三角形的外角等于与它不相邻的两个内角的和.7.【答案】D【解析】解:当等腰三角形的腰为3时,三边为3,3,6,3+3=6,三边关系不成立,当等腰三角形的腰为6时,三边为3,6,6,三边关系成立,周长为3+6+6=15.故选:D.求等腰三角形的周长,即是确定等腰三角形的腰与底的长求周长;题目给出等腰三角形有两条边长为3和6,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.本题考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.8.【答案】A【解析】解:∵∠ACB=90°,∴∠BCE+∠ACD=90°,又∵BE⊥CE,AD⊥CE,∴∠E=∠ADC=90°,∴∠BCE+∠CBE=90°,∴∠CBE=∠ACD,在△CBE和△ACD中,,∴△CBE≌△ACD(AAS),∴BE=CD,CE=AD=3.4(cm),∵DE=2.7(cm),∴CD=CE-DE=AD-DE=3.4-2.7=0.7(cm),∴BE=CD=0.7(cm),故选:A.可先证明△BCE≌△CAD,可求得CE=AD,结合条件可求得CD,则可求得BE.本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA 、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等).9.【答案】C【解析】解:∵AD⊥BC,∠CAD=30°,CD=6,∴AC=2CD=12,∵∠ABC=45°,AD⊥BC,∴∠ABC=∠BAD=45°,∴AD=BD,∵AD⊥BC,BE⊥AC,∴∠C+∠DAC=90°,∠C+∠CBE=90°,∴∠DAC=∠CBE,且AD=BD,∠ADB=∠ADC=90°,∴△ADC≌△BDH(ASA)∴BH=AC=12,故选:C.由直角三角形的性质可得AC=2CD=12,由“ASA”可证△ADC≌△BDH,可得BH=AC=12.本题考查了全等三角形的判定和性质,等腰三角形的性质,直角三角形的性质,证明△ADC≌△BDH是本题的关键.10.【答案】D【解析】解:∵BF平分∠ABC,∠BAC=90°,EG⊥BC∴AE=EG,故①符合题意,∵AE=EG,BE=BE∴Rt△ABE≌Rt△GBE(HL)∴AB=BG,∠AEB=∠BEG,∵AD⊥BC,EG⊥BC,∴AD∥EG,∴∠AFE=∠BEG=∠AEF,∴AE=AF,∴△AEF是等腰三角形,故②符合题意,∵等腰Rt△ABC中,∠BAC=90°,AD⊥BC,∴AD=BD=CD,∠DAC=∠C=45°,∵AB=BG,AE=EG,∴BE是AG的垂直平分线,∴AF=FG,且AE=EG,EF=EF,∴△AEF≌△GEF(SSS)∴∠AFE=∠GFE=∠FEG=∠AEF,∴AE∥FG,∴∠DFG=∠DAC=45°,∠DGF=∠C=45°,∴∠DFG=∠DGF,∴DF=DG,且∠ADC=90°,∴△DFG是等腰直角三角形,故③符合题意,∵BD=AD,∠ADB=∠ADG,DF=DG,∴△BDF≌△ADG(SAS)∴BF=AG,故④符合题意;故选:D.利用全等三角形的性质和等腰直角三角形的性质以及角平分线的性质定理一一判断即可.本题考查了全等三角形的判定和性质,角平分线的性质,线段垂直平分线的性质,熟练运用全等三角形的判定是本题的关键.11.【答案】(4,-3)【解析】解:∵点A与点B(4,3)关于x轴对称,∴点A的坐标为(4,-3).故答案为:(4,-3).根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答.本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.12.【答案】72°【解析】解:如图,∵△ABC≌△DCB,∠DBC=36°,∴∠ACB=∠DBC=36°.∴∠AOB=∠ACB-∠DBC=36°+36°=72°.故答案是:72°.由全等三角形的对应角相等和三角形外角定理求解.本题考查了全等三角形对应角相等的性质,三角形的一个外角等于与它不相邻的两个内角的和,熟记性质是解题的关键.13.【答案】3:2【解析】解:∵AD是△ABC的角平分线,∴点D到AB的距离等于点D到AC的距离,又∵AB:AC=3:2,则△ABD与△ACD的面积之比为3:2.故答案为:3:2.本题需先利用角平分线的性质可知点D到AB、AC的距离相等,即两三角形的高相等,观察△ABD与△ACD,面积比即为已知AB、AC的比,答案可得.本题考查了角平分线的性质;此题的关键是根据角平分线的性质,求得点D到AB的距离等于点D到AC的距离,即△ABD边AB上的高与△ACD边AC上的高相等.14.【答案】125°【解析】解:∵∠ABC=180°-∠BAC-∠C=180°-50°-70°=60°,∵AE,BF是角平分线,∴∠OAF=∠BAC=25°,∠FBC=∠ABC=30°,∴∠OFC=∠FBC+∠FCB=30°+70°=100°,∴∠AOB=∠AFO+∠OAF=100°+25°=125°,故答案为125°.利用三角形的内角和定理以及三角形的外角的性质解决问题即可.本题考查三角形内角和定理,三角形的外角的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.15.【答案】90【解析】解:由题意可知,小明第一次回到出发地A点时,他一共转了360°,且每次都是向左转40°,所以共转了9次,一次沿直线前进10米,9次就前进90米.利用多边形的外角和即可解决问题.本题考查根据多边形的外角和解决实际问题,多边形的外角和是360°.16.【答案】5【解析】解:∵正方形ABCD的面积为25,△ABE是等边三角形,∴BE=AB=5连接PB,则PD=PB,那么PD+PE=PB+PE,因此当P、B、E在一直线的时候,最小,也就是PD+PE=PB+PE=BE=AB=5此题考查轴对称,最短路线问题,可由两点之间线段最短再结合题意进行求解.熟练掌握轴对称的性质,理解两点之间线段最短的涵义.17.【答案】解:∵∠BDC是∠A和∠ACD的外角,∴∠BDC=∠A+∠ACD=64°+36°=100°.又在△BDF中:∠BDF+∠DBF+∠DFB=180°,∴100°+20°+∠DFB=180°,∴∠DFB=60°,又∵∠EFC=∠DFB,∴∠EFC=60°【解析】利用三角形内角和定理以及三角形的外角的性质解决问题即可.本题考查三角形内角和定理,三角形的外角的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.18.【答案】证明:(1)∵AC⊥BC于点C,DF⊥EF于点F,∴∠ACB=∠DFE=90°,在△ABC和△DEF中,,∴△ABC≌△DEF(SAS);(2)∵△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE.【解析】(1)由SAS容易证明△ABC≌△DEF;(2)由△ABC≌△DEF,得出对应角相等∠B=∠DEF,即可得出结论.本题考查了全等三角形的判定与性质、平行线的判定;熟练掌握全等三角形的判定与性质,证明三角形全等是解决问题的关键.19.【答案】解:如图所示,如图,△A′B′C′与△A″B″C″即为所求.【解析】依据轴对称的性质,分别作出三角形各顶点关于x、y轴的对称点,再顺次连接即可.此题主要考查了平面坐标系中点的对称性以及画三角形,作对称图形时关键是作出对应点.20.【答案】解:(1)∵DE垂直平分AB∴∠A=∠ABE=50°,又∵AB=AC,∴∠ABC=∠ACB,而∠A+∠ABC+∠ACB=180°,∴∠ABC=×(180°-50°)=65°,∴∠EBC=∠ABC-∠ABE=65°-50°=15°;(2)∵△ABC的周长为43cm,BC=11cm∴AB=AC=16cm,又∵DE垂直平分AB∴EA=EB,∴△BCE的周长为:BC+BE+CE=BC+AE+CE=BC+AC=16+11=27cm.【解析】(1)由DE是AB的垂直平分线,根据线段垂直平分线的性质得出AE=BE,则可求得∠ABE的度数,又由AB=AC,根据等边对等角与三角形内角和定理,即可求得∠ABC的度数,继而求得答案;(2)求出AC和BC的值,再根据线段垂直平分线的性质得出AE=BE,求出△BCE的周长=AC+BC,代入求出即可.此题考查了线段垂直平分线的性质与等腰三角形的性质,能求出AE=BE是解此题的关键,此题比较简单,注意数形结合思想的应用,注意:线段垂直平分线上的点到线段的两个端点的距离相等.21.【答案】BD=AB【解析】解:(1)BD=AB(见(2)中证明).故答案为BD=AB.(2)在Rt△ABC中,∠A=30°,AC=a,BC=b,∴∠ABC=60°,BA=2b,∴∠CBE=120°,由作图可知,BD是∠CBE的平分线∴∠CBD=∠EBD=∠CBE=60°,在△BAC和△BDC中,∴△BAC≌△BDC(ASA),∴CA=CD=a,BA=BD=2b∠BDC=∠A=30°,∵∠BCD=∠BED=90°,∠CBD=∠EBD,BD=BD,∴△DBE≌△DBC(AAS),∴DE=DC=a,BE=BC=b,∴S△ADE=•AE•DE=ab.(1)结论:BD=AB.利用全等三角形的性质即可证明.(2)求出AE.DE即可解决问题.本题考查作图-基本作图,全等三角形的判定和性质,直角三角形30度角的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.22.【答案】解:(1)∵△ABC关于y轴对称,∠ACO=30°,∴CA=CB,∠ACB=2∠ACO=60°,AO=BO=2,∴△ABC是等边三角形,∴∠AC=BC=AB=4,又∵△CDE是等边三角形,∴CD=CE,∠DCE=60°,∴∠ACB=∠DCE,∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,在△ACD和△BCE中,∴△ACD≌△BCE(SAS)∴∠CBE=∠CAD=60°,∴∠EBD=180°-∠ABC-∠CBE=60°;(2)由(1)知,△ACD≌△BCE,∴BE=AD,又∵点A的坐标为(-2,0),点D的坐标为(5,0),∴AD=7∴BE=7【解析】(1)由轴对称的性质可得CA=CB,∠ACB=2∠ACO=60°,AO=BO=2,可得△ABC 是等边三角形,由“SAS”可证△ACD≌△BCE,可得∠CBE=∠CAD=60°,由平角性质可求解;(2)由全等三角形的性质可求BE=AD=7.本题考查了翻折变换,全等三角形的判定和性质,等边三角形的判定和性质,证明△ACD≌△BCE是本题的关键.23.【答案】(1)证明:∵DE⊥AB,DF⊥AC∴△DBE和△DCF是直角三角形在Rt△DBE和Rt△DCF中,∴Rt△DBE≌Rt△DCF(HL)∴∠B=∠C,∴AB=AC;(2)证明:同理:Rt△DBE≌Rt△DCF(HL),∴∠DBE=∠DCF,又∵DB=DC,∴∠DBC=∠DCB,∴∠DBE+∠DBC=∠DCF+∠DCB,∴AB=AC.(3)解:若点D在△ABC外部,则AB=AC不一定成立.如图所示:连接AD,在Rt△ADE和Rt△ADF中,,∴Rt△ADE≌Rt△ADF(HL),∴AE=AF,又∵AB>AE,AF>AC,∴AB>AC.【解析】(1)先利用斜边直角边定理证明△DBE≌△DCF,根据全等三角形对应角相等得到∠B=∠C,再根据等角对等边的性质即可得到AB=AC;(2)证明Rt△DBE≌Rt△DCF,可得∠DBE=∠DCF,又DB=DC,可得∠DBC=∠DCB,则结论得证;(3)画出图形,连接AD,证明Rt△ADE≌Rt△ADF,可得AE=AF,可证得AB>AC.则AB=AC不一定成立.此题主要考查了全等三角形的判定,全等三角形对应角相等的判定与性质,等角对等边的性质,熟练掌握全等三角形的判定方法是解题的关键.24.【答案】解:(1)如图①,延长CA与BE交于点G,,∵∠EDB=∠ACB,∴∠EDG=∠BDG-∠BDE=∠ACB-∠ACB=∠ACB,∴∠BDE=∠EDG,即CE是∠BCG的平分线,又∵BE⊥DE,∴BE=EG=BG,∵∠BED=∠BAD=90°,∠BFE=∠CFA,∴∠EBF=∠ACF,在△ABG和△ACF中,∴△ABG≌△ACF(ASA),∴BG=CF=FD,又∵BE=BG,∴BE=FD.(2)结论仍然成立,理由如下:如图②,过点D作DG∥AC,与AB交于H,与BE的延长线交于G,,∵DG∥AC,∠BAC=90°,∴∠BDG=∠C,∠BHD=∠BHG=∠BAC=90°,又∵∠BDE=∠ACB,∴∠EDG=∠BDG-∠BDE=∠C-∠C=∠C,∴∠BDE=∠EDG,在△DEB和△DEG中,∴△DEB≌△DEG(ASA),∴BE=EG=BG,∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=∠GDB,∴HB=HD,∵∠BED=∠BHD=90°,∠BFE=∠DFH,∴∠EBF=∠HDF,即∠HBG=∠HDF,在△BGH和△DFH中,∴△BGH≌△DFH(ASA),∴BG=FD,又∵BE=BG,∴BE=FD.【解析】(1)首先延长CA与BE交于点G,根据∠EDB=∠ACB,BE⊥DE,判断出BE=EG=BG;然后根据全等三角形的判定方法,判断出△ABG≌△ACF,即可判断出BG=CF=FD,再根据BE=BG,可得BE=FD,据此判断即可.(2)首先过点D作DG∥AC,与AB交于H,与BE的延长线交于G,根据DG∥AC,∠BAC=90°,判断出∠BDE=∠EDG;然后根据全等三角形的判定方法,判断出△DEB≌△DEG,即可判断出BE=EG=BG;最后根据全等三角形的判定方法,判断出△BGH≌△DFH,即可判断出BG=FD,所以BE=FD,据此判断即可.本题考查了全等三角形的判定和性质,等腰直角三角形的性质,添加恰当辅助线构造全等三角形是本题的关键.。
湖北省孝感市云梦县2023-2024学年八年级上学期11月期中学情调研数学试卷(含解析)

云梦县2023—2024学年度上学期期中学情调研八年级数学温馨提示:1.答题前,考生务必将自已所在县(市、区)、学校、姓名、考号填写在指定的位置,并将条形码粘贴在答题卡上的指定位置。
2.选择题选出答案后,用2B铅笔在答题卡上将对应题号的字母代号涂黑;非选择题的答案必须写在答题卡的指定位置,在本卷上答题无效。
3.本练习满分120分,练习时间120分钟。
一、精心选一选(本大题共8小题,每小题3分,满分24分,在每小题给出的四个选项中只有一个正确选项,请在答题卡上把正确答案的代号涂黑)1.文明交通,平安回家.在下列交通标志中,是轴对称图形的是()A.B.C.D.2.以下生活现象不是利用三角形稳定性的是()A.B.C.D.3.在平面直角坐标系中,点关于轴对称的点的坐标是()A.B.C.D.4.若一个正多边形的一个内角是,则这个正多边表的边数为()A.8B.7C.6D.55.在中作边上的高,下列画法正确的是()A.B.C.D.6.如图,,,,则()A.3B.3.5C.4D.57.如图,在中,平分,于点,交于点,若,,则的面积为()A.B.C.D.8.如图,在中,,在上,将沿折叠,点落在边上的点处,若,则的度数为()A.B.C.D.二、细心填一填(本大题共8小题,每小题3分,满分24分。
请把答案填在答题卡相应题号的横线上)9.从六边形的一个顶点出发,可以画出条对角线,则的值为__________.10.已知三角形三边长均为整数,若其中两边长分别是3和5,则第三边的长可能为__________.(填一个你认为正确的结果)11.在中,,,则__________.12.若等腰三角形的周长为16cm,其中一边长4cm,则该等腰三角形的底边为__________cm.13.如图,在中,,,点,是中线上两点,,则图中阴影面积是__________.14.如图,在中,,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于,两点,连接,交于点,连接,若,则的长度为__________.15.如图,,点为内一点,点、分别在、上,当周长最小时,的度数是__________.16.如图,在中,,.点、、分别为边、、上的点,且为等边三角形,若.则的值为__________.三、专心解一解(本大题共8小题,满分72分,请认真读题,冷静思考,解答题应写出必要的文字说明、证明过程或演算步骤,请把解题过程写在答题卡相应题号的位置)17.(8分)一个多边形的内角和比五边形的内角和多,并且这个多边形的各内角都相等.这个多边形的每个内角等于多少度?18.(8分)如图,,平分角,求证:是等腰三角形.19.(8分)如图,点,在的边上,,.求证.20.(8分)如图,平分,,,.求的度数.21.(8分)在测量一个小口圆形容器的壁厚时(容器壁厚度均匀),小明用“型转动钳”按如图方法进行测量,其中,,只需测得,,就可以知道圆形容器的壁厚了.(1)请你利用所学习的数学知识说明;(2)若,,求出圆形容器的壁厚.22.(10)如图,在下列带有坐标系的网格中,的顶点都在边长为1的小正方形的顶点(即格点)上,它们的坐标分别为,,.运用所学的知识,利用无刻度直尺作图(不写作法,保留作图痕迹).(1)直接写出的面积为__________;(2)在图中作出关于轴对称的图形;(3)在图中作出的高线.23.(10分)如图,在平面直角坐标系中,为坐标原点,点,点,且实数,满足,是第三象限的一点,连接,过点作于,延长至点,使,连接,,.(1)直接写出点和点的坐标:__________,__________;(2)判断的形状,并说明理由;(3)若点的坐标为,求点的坐标.24.(12分)(1)问题呈现:如图①:在中,若,,点为边的中点,求边上的中线的取值范围.解决此问题常用倍长中线法:延长到点使,再连接,可证,从而把、,集中在中,利用三角形三边的关系即可判断中线的取值范围是__________;(2)探究应用:如图②,在中,点是的中点,于点,交于点,交于点,连接,判断与的大小关系并证明;(3)问题拓展:如图③,在四边形中,,与的延长线交于点,点是的中点,若是的角平分线.试探究线段,,之间的数量关系,并加以证明.图①图②图③云梦县2023—2024学年度上学期期中学情调研八年级数学参考答案1-4:BCDA,5-8:CCBA9.3 10.5(答案不唯一)11.10 12.4 13.14.20 15.60° 16.17.解:设这个多边形的边数为,依题可知:3分解得,5分因为这个多边形的各内角都相等,所以这个多边形的每个内角大小为:8分18.证明:2分平分角4分是等腰三角形.8分19.证明:2分在和中:6分(ASA).8分20.解:∵,,∴,2分∵平分,∴,4分∵是高,,∴,6分∴.8分21.解:(1)连接.在和中,,4分∴(SAS),∴;5分(2)∵,,∴圆形容器的壁厚为.8分22.解:(1)答案:12 3分(2)如图,关于轴对称的图形为6分(3)如图取格点,连接,根据网格特点可得,则,故,即为高线;10分23.解:(1),;2分(2)如图,设与轴交于点,,,又,在和中:∴(SAS)4分∴,即∴∴是等腰直角三角形.6分过点作轴于点,过点作轴于点;则由(2)可知:,在和中:∴(AAS)8分∴,点的坐标为,∴,;,∴点的坐标为.10分24.解:(1),3分延长至,使,连接,如图①所示,∵是边上的中线,∴,在和中,∵,∴(SAS),∴,在中,由三角形的三边关系得:,∴,即,∴(2);5分证明:延长至点,使,连接、,如图②所示.同(1)得:(SAS),∴,6分∵,,∴,7分在中,由三角形的三边关系得:,∴;8分.9分如图③,延长,交于点,∵,∴,在和中,,,∴(AAS),∴,10分∵是的平分线,∴,∴,∴,∵,∴.12分。
湖北省孝感市云梦县2020-2021学年八年级上学期期中考试数学试题
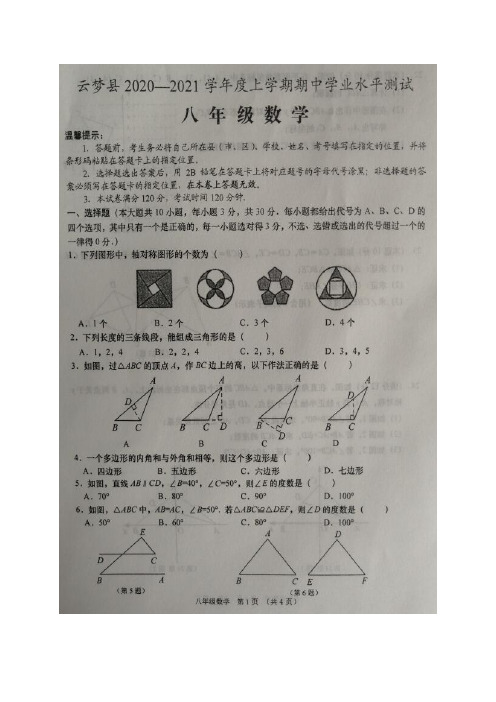
八年级数学参考答案
一、选择题
题号 1
2
3
4
5
6
7
8
9 10
答案 C D B A C C D A D B
二、填空题
11. (3, 4)
12.100
13. 2a
14.12
三、解答题
15.0.8
16.5
17. (n 2)180 5360 , n 12 ………………………………………………8 分
(3)若 ACB 100 , CAB CBA 40
∵AD 是角平分线
∴ BAD= 1 CAB 20 2
在 AB 上取点 N,使 AN=AD,连接 DN
∴ AND=80
∴ ABD BDN=80 A
而 ABD 40 ,∴ BDN =40 ∴ NB ND
y C D
O MN Bx
又∵ DMN 180 DMA 180 ACB 180 100 80
D
θ
A
O M Bx
又 AB AM BM
∴ BD BM
∴ BDM BMD 1 (180 ABC) 1 [180 (90 )] 45
2
2
2
4
又 AMD BMD 180
∴ (45 )=180 4
∴ =108
即 ACB 108 …………………………………..………………………….…7 分
2 B1 1 –5 –4 –3 –2 –1 O
–1
B 1 2P3 4 5 x
–2
–3
–4
–5
23.(1)∵ AC BC,ACD BCE,CD CE
∴△ACD ≌ △BCE (SAS)………………………………………………3 分
湖北省孝感市云梦县2022-2023学年八年级上学期期中数学试卷

湖北省孝感市云梦县2022-2023学年八年级上学期期中数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.下列图形是某几届冬奥会图标,其中是轴对称图形的是( )A .B .C .D . 2.一个三角形两边长分别为9cm 和4cm ,则第三边长可能为 ( )A .4cmB .9cmC .5cmD .13cm 3.如图,若BAD CAD ∠=∠,AB AC =,则ABD ACD △≌△的理由是( )A .SASB .AASC .ASAD .SSS4.如图,B 、C 、D 三点共线,∠B =56°,∠ACD =120°,则∠A 的度数为( )A .56°B .64°C .60°D .176°5.一个多边形的每个内角都等于120°,则这个多边形的边数为( )A .4B .5C .6D .7 6.如图,A 、B 、C 、D 在一条直线上,MB ND =,MBA D ∠=∠,添加下列某一条件后不能判定ABM ∠CDN △的是( )A .M N ∠=∠B .AB CD =C .AM CN =D .AM CN ∥ 7.如图,在ABC 中,AB AC =,AD DB =,DE AB ⊥于点E ,若3BC =,且BDC 的周长为8,则AE 的长为( )A .2B .2.5C .3D .3.5 8.如图,在等腰直角三角形ABC 中,90BAC ∠=︒,D 是AC 的中点,EC BD ⊥,交BD的延长线于点E ,BA 与CE 的延长线交于点F ,若12BF =,则FBC 的面积为( )A .40B .46C .48D .50二、填空题9.点()26P -,关于x 轴对称的点Q 的坐标是______. 10.如图,一名滑雪运动员沿着倾斜角为30°的斜坡,从A 滑行至B ,已知100m AB =,则这名滑雪运动员的高度下降了_______米.11.若一个等腰三角形的腰与底边长分别为4和6,则这个等腰三角形的周长为______. 12.如图:在Rt ABC 中,90B ,以顶点C 为圆心,适当长为半径画弧,分别交AC 、BC 于点E 、F ,再分别以点E 、F 为圆心,大于EF 的长为半径画弧,两弧交于点P ,作射线CP 交AB 于点D ,若BD 2=,6AC =,则ACD 的面积为____.13.如图,五边形ABCDE 中,125A ∠=︒,则1234∠+∠+∠+∠的度数是______.14.如图,在ABC 中,AD ,AE 分别是边CB 上的中线和高,6AE cm =,212ABD S cm =,则DC 的长是______cm .15.如图,在ABC 中,AB =AC ,BC =4,面积是10.AB 的垂直平分线ED 分别交AC ,AB 边于E 、D 两点,若点F 为BC 边的中点,点P 为线段ED 上一动点,则PBF 周长的最小值为__________.16.如图∠ABC 与∠CDE 都是等边三角形,且∠EBD =65°,则∠AEB 的度数是__________.三、解答题17.如果一个多边形的内角和与外角和之比是 13:2,求这个多边形的边数. 18.已知,如图,点D ,E 分别在AB ,AC 上,B C ∠=∠,AB AC =.求证:AEB ACD ≌△△. 19.如图,四边形ABCD 中,90A C ∠=∠=︒,BE 平分ABC ∠交AD 于E ,DF 平分ADC ∠交BC 于F .求证//BE DF .20.如图,点E 、F 在BC 上,BE =CF ,AB =DC ,∠B =∠C .求证:∠A =∠D .21.如图,在ABC 中,AB AC =,36A ∠=︒,AC 的垂直平分线DE 分别交AB 、AC 于D 、E 两点.(1)求证:BCD △是等腰三角形;(2)若BCD △的周长是26,10BC =,求ACD 的周长.22.∠ABC 在平面直角坐标系中的位置如图所示.(1)作出∠ABC 关于y 轴对称的三角形∠A 1B 1C 1;(2)在图中用无刻度的直尺画出既平分∠ABC 的周长又平分∠ABC 的面积的一条直线;(3)直接写出∠A 1B 1C 1的面积为 .23.如图1,在平面直角坐标系中,点(),0A a ,()0,B b ,a ,b 满足2(5)20a b ++-=.(1)直接写出A ,B 两点的坐标,A (______,______),B (______,______);(2)如图1,过点B 作BC AB ⊥,且BC AB =,求点C 的坐标;(3)如图2,过点A 作AD AB ⊥,且AD AB =,过点A 作AE AO ⊥,且AE AO =,连接DE 交x 轴于点P ,求AP 的长.24.在等腰ABC 中,AB AC =,点D 是AC 上一动点,点E 在BD 的延长线上且AB AE =,AF 平分CAE ∠交DE 于点F ,连接FC .(1)如图1,求证:ABE ACF ∠=∠;(2)如图2,当60ABC ∠=︒时,求证:AF EF FB +=;(3)如图3,当=45ABC ∠︒,且AE BC ∥时,请直接写出BD 和EF 之间的数量关系:(不用写证明过程).。
2021-2022学年湖北省孝感市云梦县八年级(上)期中数学试题及答案解析

2021-2022学年湖北省孝感市云梦县八年级(上)期中数学试卷一、选择题(本大题共8小题,共24.0分。
在每小题列出的选项中,选出符合题目的一项)1.下列各组长度的线段能组成三角形的是( )A. 3,3,8B. 6,6,11C. 5,5,11D. 4,4,82.下列倡导节约的图案中,是轴对称图形的是( )A. B. C. D.3.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定4.等腰三角形的底角为50°,则这个等腰三角形的顶角为( )A. 50°B. 80°C. 100°D. 50°或80°5.如图,在△ABC中,已知点D,E分别为BC,AD的中点,若S△AEC=1,则S△ABC=( )A. 2B. 3C. 4D. 66.若正多边形的一个外角是45°,则该正多边形的内角和为( )A. 1080°B. 900°C. 720°D. 540°7.如图,点F,B,E,C在同一条直线上,点A,D在直线BE的两侧,AC//DF,CE=FB,添加下列哪个条件后,仍不能判定出△ABC≌△DEF( )A. AB=DEB. AB//DEC. ∠A=∠DD. AC=DF8.如图,已知∠DCE=90°,∠DAC=90°,BE⊥AC于B,且DC=EC,若BE=7,AB=3,则AD的长为( )A. 3B. 5C. 4D. 不确定二、填空题(本大题共8小题,共24.0分)9.点A(2,1)关于y轴的对称点坐标是______.10.三角形三条中线的交点叫做三角形的______.11.九边形中过其中一个顶点有______条对角线.12.等边三角形有______条对称轴.13.在直角三角形ABC中,∠B=90°,∠A=60°,若AB=1,则AC=______.14.小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此反复,小林共走了108米回到点P,则角α的度数为______ .15.如图,已知:BD是∠ABC的平分线,DE⊥BC于E,S△ABC=36cm2;,AB=12cm,BC=18cm,则DE的长为______cm.16.如图,△ABC的面积为30cm2,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于1MN的长为半径画弧,两弧交于点P,作射线AP,过2点C作CD⊥AP于点D,连接DB,则△DAB的面积是______cm2.三、解答题(本大题共8小题,共72.0分。
湖北省孝感市八年级上学期语文期中质量检测试卷

湖北省孝感市八年级上学期语文期中质量检测试卷姓名:________ 班级:________ 成绩:________一、语文知识积累(15分) (共3题;共15分)1. (3分)改正下面诗句中的错字。
①几个世纪也不退色________②一声声沧凉________③带着岁月苍桑________2. (8分) (2017九上·芜湖期末) 默写古诗文中的名句名篇。
(1)请在下列横线上填写出古诗文名句。
(任选其中4句)①过尽千帆皆不是,________。
(温庭筠《望江南》)②浊酒一杯家万里,________。
(范仲淹《渔家傲·秋思》)③________,拾此充饥肠。
(白居易《观刈麦》④________,只有香如故。
(陆游《卜算子·咏梅》)⑤________,帘卷西风,人比黄花瘦。
(李清照《醉花阴》)⑥了却君王天下事,________。
(辛弃疾《破阵子·为陈同甫赋壮词以寄之》)(2)请写出《出师表》中诸葛亮自述身世、表达淡泊名利的句子。
________,________,________,________。
3. (4分) (2017七下·扬州月考) 杭州王大爷想去一趟南京,假设你已帮他买好了高铁车票,准备把车票交给王大爷。
请根据下面提供的车票,告诉王大爷主要的乘车信息,并提醒他带好身份证,提前半小时到达高铁车站。
请你写出这段话,50字左右。
二、阅读(45分) (共1题;共7分)4. (7.0分)孙悟空的第一个师傅是________,孙悟空的兵器原是大禹治水的________,又唤________,大闹天宫后被如来佛祖压在________下。
后皈依佛门,唐僧为他取名________。
为西天取经立下汗马功劳,后被封为________。
三、文学作品阅读(38分) (共4题;共38分)5. (13.0分)阅读理解职业汪曾祺①文林街一年四季,从早到晚,有各种吆喝叫卖的声音。
2022-2023学年湖北省孝感市云梦县八年级(上)期中物理试卷(附答案详解)

2022-2023学年湖北省孝感市云梦县八年级(上)期中物理试卷一、单选题(本大题共11小题,共33.0分)1.为了学好物理,小雨同学对自己提出了几个要求,你认为不合理的是( )A. 重视观察和实验B. 只要死记硬背、多做题,就能学好物理C. 重视科学探究的运用D. 注意从生产和生活中寻找物理问题2.生活处处有物理,留心观察皆学问。
下列几种估测中,最接近实际的是( )A. 人的正常体温约为40℃B. 珠穆朗玛峰的海拔高度约为8848kmC. 成年人正常步行的速度约为1.1m/sD. 老师正常讲课时声音的响度约为120dB3.锣鼓队表演时。
当队员用手按住正在发声的鼓面,鼓声就消失了,其主要原因是( )A. 手不能传播声音B. 手吸收了声波C. 手把声音反射回去D. 手使鼓面停止了振动4.如图所示的四种物态变化实例中,属于液化的是( )A. 水壶冒“白气”B. 干手器将手烘干C. 草上形成“白霜”D. 冰雪遇暖消融5.下列措施中,不能减弱噪声的是( )A. 摩托车的消声器B. 居民区旁高架桥上的隔音挡板C. 学校附近安装噪声监测装置D. 工厂用的防噪声耳罩6.甲、乙两支相同的体温计的示数都是38.0℃,若直接去测量两个体温分别是37.0℃和39.5℃的人,则下列判断正确的是( )A. 甲体温计的示数是38.0℃,乙体温计的示数是39.5℃B. 甲体温计的示数是38.0℃,乙体温计的示数是38.0℃C. 甲体温计的示数是37.0℃,乙体温计的示数是38.0℃D. 甲体温计的示数是37.0℃,乙体温计的示数是39.5℃7.物理老师演示了“金鱼的复活”实验,将一条活泼乱跳的金鱼放入空杯中,向杯中倒入液态氮(沸点为−196℃),观察到杯中液态氮“沸腾”,周围“烟雾缭绕”,金鱼变得硬邦邦的,把金鱼迅速放入水中,金鱼又活泼乱跳了,下列说法中正确的是( )A. 杯中液态氮“沸腾”是液化现象B. 看到的“烟雾缭绕”是汽化形成的C. 金鱼变得硬邦邦,其表面的冰主要是凝固形成的D. 金鱼在复活的过程中,其表面的冰全部发生了升华8.宋代诗人陈与义有诗“枫花两岸照船红,百里榆堤半日风,卧看满天云不动;不知云与我俱东。
湖北省孝感市云梦县2022-2023学年八年级上学期期中英语试卷

2022-2023学年湖北省孝感市云梦县八年级(上)期中英语试卷第一卷(共88分)一、听力理解(每小题5分,共25分)第一节:听下面5段材料,从下面6幅图片中选出相对应的图片。
每段材料读两遍。
1.(1)(2)(3)(4)(5)第二节:听下面6段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出一个最佳选项。
每段对话或独白读两遍。
2.(1)How many hours does Mr.Fat sleep every night?A.Ten.B.Nine.C.Eight.(2)How often does he eat junk food?A.Three times a week.B.Four times a week.C.Three or four times a week.3.(1)Who is Jenny going to Shanghai with?A.Her friends.B.Her parents.C.Her grandparents.(2)How are they going to get there?A.On foot.B.By ship.C.By taxi.4.(1)Who is taller,Alex or Paul?A.Jenny.B.Paul.C.We don't know.(2)What sport does Paul play three times a week?A.Baseball.B.Basketball.C.Tennis.5.(1)Where are they going for lunch?A.Mr Big's Fast Food.B.Mr Jack's Fast Food.C.Jason's Fast Food.(2)Why do they go there?A.Because it's close to school.B.Because it's expensive.C.Because its service is the best.(3)How are they going there?A.By bike.B.On foot.C.By bus.6.(1)Where are the speakers probably talking?A.In a coffee bar.B.At home.C.On the street.(2)Which bar has the most comfortable seats?A.Red Coffee Bar.B.Black Coffee Bar.C.Green Coffee Bar.(3)What CANT people do in Black Coffee Bar?A.Read books or magazines.B.Watch news on TV.C.Listen to the piano music. 7.(1)How does Tim like his weekend?A.He thinks it was great.B.He thinks it was OK.C.He thinks it was bad.(2)How was the road last weekend?A.Clean.B.Crowded.C.Dirty.(3)When did Tim get to the top of the mountain?A.In the morning.B.In the afternoon.C.At night.8.(1)What are they talking about? shows.B.Movies.C.News.(2)Which cartoon does Tony like?A.Snow White.B.Kung Fu Panda.C.Mickey Mouse.(3)How often does Danny watch action movies?A.Three times a week.B.Once a week.C.Once a month.(4)What does Lisa want to be?A.A writer.B.A teacher.C.An actress.(5)Who does Billy want to show his comedies to?A.His parents.B.His friends.C.His teachers.二、选择填空(每小题1分,共10分)9.﹣Can I get you something to drink,Ella?﹣()A.My pleasure.B.Yes,I can.C.It's very nice of you.D.Here you are. 10.—Do you usually go to the mountains?—No.I ________ climb mountains.I don't like it.()A.hardly ever B.often C.usually D.always11.I found ______ difficult to study English well.()A.it B.that C.its D.this12.﹣Jill,do you know which one is Mrs.Miller?()﹣Yes.She's the one ________ long curly hair.A.on B.for C.in D.with13.﹣﹣______do you go camping a year?﹣﹣Three times a year.()A.How often B.How many C.How long D.How soon14.﹣We expected Ben to show his talents in the competition,but he didn't .﹣Why?()A.mind B.show C.happened D.appear 15.—That's a nice model plane.—Yes,it is.My aunt ____________ it for me last birthday.()A.buy B.will buy C.is buying D.bought 16.—Who is ___________ at math,Sam or Tom?—Sam.He always gets the first in math tests.()A.good B.better C.bad D.worse17.﹣The films are all wonderful.I can't decide which one to choose.﹣Why not see My Motherland and Me?I think it's______of all.()A.educational B.the most educationalC.more educational D.most educational18.The teacher asked the students to ______ a story about a trip to the moon.()A.give up B.turn up C.cut up D.make up三、完形填空(每空1分,共15分)19.(15分)Thailand is home to thousands of wild monkeys.These monkeys are(1)with people.Many visitors enjoy(2)with these monkeys and giving them food. (3)the food is junk food.A wild (野生的)monkey eats too much junk food and becomes too fat.People call(4)"Uncle Fat".Uncle Fat is 26 kg.That is three times(5)than he should be.Uncle Fat always eats (6)that people give to him.It is very dangerous to be this fat.Uncle Fat may have a lot of health problems(7)heart disease(心脏病)and diabetes(糖尿病).Some zoo keepers think they should take the problem(8),so they decide to help him.They(9)him to the zoo and now Uncle Fat is going on a(10)diet(饮食).The zoo keepers only feed him fruit and(11)twice a day.Supakarn Kaewchot,a vet(兽医),believes Uncle Fat will be(12)in a few months.She also says people(13)feed monkeys junk food. "We think the monkey becomes too fat(14) a large number of people come here and feed them." Supakarn says. "But please don't feed them junk food.It is very bad for their (15)and the problem is really man﹣made."(1)A.popular B.angry C.enjoyable D.pleased(2)ughing B.fighting C.shouting D.playing(3)A.Most of B.Either of C.Both of D.None of(4) B.them C.him D.her(5)A.heavier B.thinner C.longer D.shorter(6)A.few B.both C.nothing D.everything(7)A.for example B.at least C.such as D.in fact(8)A.quietly B.hardly C.seriously D.clearly(9)A.take B.reach C.decide D.feed(10)A.easy B.strict C.enough D.similar(11)A.cola B.chocolate C.hamburgers D.vegetables(12)A.fat B.thin C.strong D.tall(13)A.shouldn't B.wouldn't C.should D.would(14)A.but B.however C.because D.so(15)A.fact B.health C.mind D.talent四、阅读理解(共两节,满分28分)第一节阅读下面三篇短文,根据短文内容,从所给的A、B、C、D四个选项中选出最佳选项。
湖北省孝感市云梦县八年级(上)期中数学试卷(解析版)
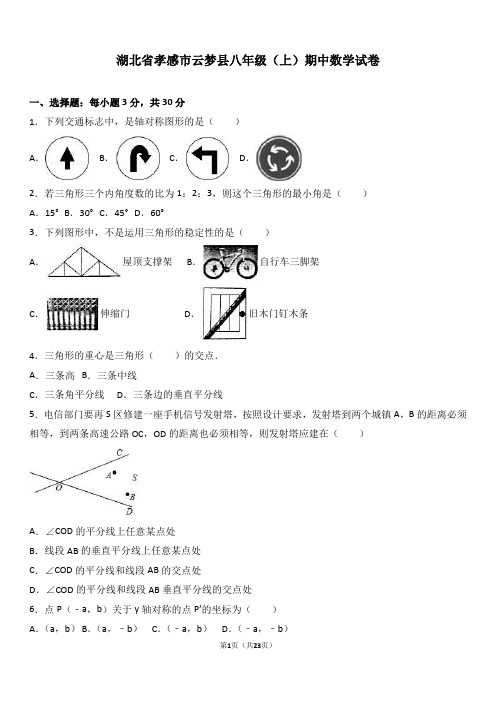
湖北省孝感市云梦县八年级(上)期中数学试卷一、选择题:每小题3分,共30分1.下列交通标志中,是轴对称图形的是()A.B.C.D.2.若三角形三个内角度数的比为1:2:3,则这个三角形的最小角是()A.15°B.30°C.45°D.60°3.下列图形中,不是运用三角形的稳定性的是()A.屋顶支撑架B.自行车三脚架C.伸缩门D.旧木门钉木条4.三角形的重心是三角形()的交点.A.三条高B.三条中线C.三条角平分线D.三条边的垂直平分线5.电信部门要再S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在()A.∠COD的平分线上任意某点处B.线段AB的垂直平分线上任意某点处C.∠COD的平分线和线段AB的交点处D.∠COD的平分线和线段AB垂直平分线的交点处6.点P(﹣a,b)关于y轴对称的点P′的坐标为()A.(a,b) B.(a,﹣b)C.(﹣a,b)D.(﹣a,﹣b)7.如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.135°B.270° C.300° D.315°8.如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是()A.45°B.48°C.50°D.72°9.如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是()A.15°B.25°C.30°D.10°10.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是()A.3 B.5 C.6 D.8二、填空题:共6道小题,每小题3分,共18分11.一个n边形的内角和是它外角和的3倍,则边数n=.12.点P(﹣2,3)关于x轴的对称点P′的坐标为.13.在等腰三角形中,它的一边长等于5,一边长等于6,则它的周长为.14.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=度.15.如图,这是由边长为1的等边三角形摆出的一系列图形,按这种方式摆下去,则第n个图形的周长是.16.如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上,则△PMN周长的最小值为.三、解答题(本大题共8小题,满分72分)17.如图,M,N为两个居民小区,公交部门要在公路l上建一个公共汽车站P(尺规作图,不写作法,保留作图痕迹).(1)如图1,请问这个公共汽车站P建在什么位置,能使两个小区到车站的路程一样长?(2)如图2,请问这个公共汽车站P建在什么位置,能使两个小区到车站的总路程最短?18.如图,已知△ABC的周长为24cm,AD是BC边上的中线,AD=AB,AD=5cm,△ABD的周长是18cm,求AC的长.19.如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的数是多少?20.如图,在正五边形ABCDE中,连接AC,求∠CAE的度数.21.如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.22.在平面直角坐标系中,已知点A(1,0),B(4,2),C(2,3).(1)画出△ABC关于y轴的对称图形△A1B1C1;(2)△A1B1C1三个顶点的坐标;(3)画出△ABC关于直线l(l上各点纵坐标都为1)的对称图形△A2B2C2,写出点C关于直线l的对称点C2的坐标.23.如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=50°时,求∠DEF的度数;(3)△DEF可能是等腰直角三角形吗?为什么?24.如图,在△ABC中,AD平分∠BAC,DF⊥AB,DM⊥AC,AB=18cm,AF=12cm,AC=16cm,动点E 以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.(1)求的值;(2)求证:在运动过程中,无论t取何值,都有=2;(3)当t取何值时,△DFE≌△DMG.湖北省孝感市云梦县八年级(上)期中数学试卷参考答案与试题解析一、选择题:每小题3分,共30分1.下列交通标志中,是轴对称图形的是()A.B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:A、是轴对称图形,故此选项正确;B、不是轴对称图形,故此选项错误;C、不是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项错误;故选:B.2.若三角形三个内角度数的比为1:2:3,则这个三角形的最小角是()A.15°B.30°C.45°D.60°【考点】三角形内角和定理.【分析】设这三个内角分别为x,2x,3x,根据三角形的内角和为180°,列方程求出角的度数即可.【解答】解:设这三个内角分别为x,2x,3x,由题意得,x+2x+3x=180°,解得:x=30°,即最小角为30°.故选B.3.下列图形中,不是运用三角形的稳定性的是()A.屋顶支撑架 B.自行车三脚架C.伸缩门D.旧木门钉木条【考点】三角形的稳定性.【分析】利用三角形的稳定性进行解答.【解答】解:伸缩的拉闸门是利用了四边形的不稳定性,A、B、D都是利用了三角形的稳定性,故选:C4.三角形的重心是三角形()的交点.A.三条高B.三条中线C.三条角平分线D.三条边的垂直平分线【考点】三角形的重心.【分析】根据三角形的重心的定义解答.【解答】解:三角形的重心是三角形的三条中线的交点.故选B5.电信部门要再S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在()A.∠COD的平分线上任意某点处B.线段AB的垂直平分线上任意某点处C.∠COD的平分线和线段AB的交点处D.∠COD的平分线和线段AB垂直平分线的交点处【考点】线段垂直平分线的性质;角平分线的性质.【分析】根据角平分线的性质:角平分线上的点到角两边的距离相等;线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等,可得答案.【解答】解:作∠COD的角平分线,作AB的垂直平分线,得∠COD的角平分线与AB的垂直平分线的交点即为所求得点.故选D.6.点P(﹣a,b)关于y轴对称的点P′的坐标为()A.(a,b) B.(a,﹣b)C.(﹣a,b)D.(﹣a,﹣b)【考点】关于x轴、y轴对称的点的坐标.【分析】根据平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点:关于y轴对称的点,纵坐标相同,横坐标互为相反数.【解答】解:∵平面直角坐标系中关于y轴对称的点的坐标特点:横坐标相反数,纵坐标不变,可得:点P(﹣a,b)关于y轴对称的点P′的坐标是(a,b).故选:A.7.如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.135°B.270° C.300° D.315°【考点】多边形内角与外角;三角形内角和定理.【分析】利用了四边形内角和为360°和直角三角形的性质求解.【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°,∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.故选B.8.如图,在△ABE中,∠A=108°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是()A.45°B.48°C.50°D.72°【考点】等腰三角形的性质;线段垂直平分线的性质.【分析】根据线段的垂直平分线的性质得到CA=CE,根据等腰三角形的性质得到∠CAE=∠E,根据三角形的外角的性质得到∠ACB=2∠E,根据三角形内角和定理计算即可.【解答】解:∵MN是AE的垂直平分线,∴CA=CE,∴∠CAE=∠E,∴∠ACB=2∠E,∵AB=CE,∴AB=AC,∴∠B=∠ACB=2∠E,∵∠BAE=108°,∴∠B+∠E=72°,∴∠B=48°,故选B.9.如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是()A.15°B.25°C.30°D.10°【考点】三角形的外角性质.【分析】先由三角形外角的性质求出∠BDF的度数,根据三角形内角和定理即可得出结论.【解答】解:∵Rt△CDE中,∠C=90°,∠E=30°,∴∠BDF=∠C+∠E=90°+30°=120°,∵△BDF中,∠B=45°,∠BDF=120°,∴∠BFD=180°﹣45°﹣120°=15°.故选A.10.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是()A.3 B.5 C.6 D.8【考点】旋转的性质;等边三角形的性质.【分析】先计算出OC=6,根据等边三角形的性质得∠A=∠C=60°,再根据旋转的性质得OD=OP,∠POD=60°,根据三角形内角和和平角定义得∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,利用等量代换可得∠2=∠3,然后根据“AAS”判断△AOP≌△CDO,则AP=CO=6.【解答】解:如图,∵AC=9,AO=3,∴OC=6,∵△ABC为等边三角形,∴∠A=∠C=60°,∵线段OP绕点D逆时针旋转60゜得到线段OD,要使点D恰好落在BC上,∴OD=OP,∠POD=60°,∵∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,∴∠1+∠2=120°,∠1+∠3=120°,∴∠2=∠3,在△AOP和△CDO中,∵,∴△AOP≌△CDO,∴AP=CO=6,故选:C.二、填空题:共6道小题,每小题3分,共18分11.一个n边形的内角和是它外角和的3倍,则边数n=8.【考点】多边形内角与外角.【分析】利用多边形的外角和是360度,一个n边形的内角和等于它外角和的5倍,则内角和是5×360°,而n边形的内角和是(n﹣2)180°,则可得到方程,解之即可.【解答】解:根据题意列方程,得:(n﹣2)180°=3×360°,解得:n=8,即边数n等于8.故答案为8.12.点P(﹣2,3)关于x轴的对称点P′的坐标为(﹣2,﹣3).【考点】关于x轴、y轴对称的点的坐标.【分析】让点P的横坐标不变,纵坐标互为相反数即可得到点P关于x轴的对称点P′的坐标.【解答】解:∵点P(﹣2,3)关于x轴的对称点P′,∴点P′的横坐标不变,为﹣2;纵坐标为﹣3,∴点P关于x轴的对称点P′的坐标为(﹣2,﹣3).故答案为:(﹣2,﹣3).13.在等腰三角形中,它的一边长等于5,一边长等于6,则它的周长为17或16.【考点】等腰三角形的性质;三角形三边关系.【分析】分别从若底边长为5,腰长为6与若底边长为6,腰长为5,去分析求解即可求得答案.【解答】解:若底边长为5,腰长为6,则它的周长为:5+6+6=17;若底边长为6,腰长为5,则它的周长为:6+5+5=16;故它的周长为17或16,故答案为17或16.14.如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=15度.【考点】等边三角形的性质;三角形的外角性质;等腰三角形的性质.【分析】根据等边三角形三个角相等,可知∠ACB=60°,根据等腰三角形底角相等即可得出∠E的度数.【解答】解:∵△ABC是等边三角形,∴∠ACB=60°,∠ACD=120°,∵CG=CD,∴∠CDG=30°,∠FDE=150°,∵DF=DE,∴∠E=15°.故答案为:15.15.如图,这是由边长为1的等边三角形摆出的一系列图形,按这种方式摆下去,则第n个图形的周长是2+n.【考点】规律型:图形的变化类.【分析】观察摆放的一系列图形,可得到依次的周长分别是3,4,5,6,7,…,从中得到规律,根据规律写出第n个图形的周长.【解答】解:由已知一系列图形观察图形依次的周长分别是:(1)2+1=3,(2)2+2=4,(3)2+3=5,(4)2+4=6,(5)2+5=7,…,所以第n个图形的周长为:2+n.故答案为:2+n.16.如图,∠AOB=30°,点P为∠AOB内一点,OP=8.点M、N分别在OA、OB上,则△PMN周长的最小值为8.【考点】轴对称﹣最短路线问题.【分析】分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,△PMN的周长=P1P2,然后证明△OP1P2是等边三角形,即可求解.【解答】解:分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,则OP1=OP=OP2,∠P1OA=∠POA,∠POB=∠P2OB,MP=P1M,PN=P2N,则△PMN的周长的最小值=P1P2∴∠P1OP2=2∠AOB=60°,∴△OP1P2是等边三角形.△PMN的周长=P1P2,∴P1P2=OP1=OP2=OP=8.故答案为:8.三、解答题(本大题共8小题,满分72分)17.如图,M,N为两个居民小区,公交部门要在公路l上建一个公共汽车站P(尺规作图,不写作法,保留作图痕迹).(1)如图1,请问这个公共汽车站P建在什么位置,能使两个小区到车站的路程一样长?(2)如图2,请问这个公共汽车站P建在什么位置,能使两个小区到车站的总路程最短?【考点】作图—应用与设计作图;线段垂直平分线的性质;轴对称﹣最短路线问题.【分析】(1)点P是线段MN的垂直平分线与直线l的交点.(2)先作点M关于直线l的对称点M′,再连接M′N,与直线l交于点P.【解答】解:(1)如图1,点P即为所求;(2)如图2,点P即为所求.18.如图,已知△ABC的周长为24cm,AD是BC边上的中线,AD=AB,AD=5cm,△ABD的周长是18cm,求AC的长.【考点】三角形的角平分线、中线和高.【分析】由AD=AB、AD=5cm,可求出AB的长度,结合△ABD的周长是18cm,可求出BD的长度,进而可求出BC的长度,再根据△ABC的周长为24cm,即可求出AC的长.【解答】解:∵AD=AB,AD=5cm,∴AB=8cm.又∵△ABD的周长是18cm,∴BD=5cm.又∵D是BC的中点,∴BC=2BD=10cm.又∵△ABC的周长为24cm,∴AC=24﹣8﹣10=6cm.19.如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的数是多少?【考点】线段垂直平分线的性质.【分析】由∠BAC=110°,即可求得∠B+∠C=70°,又由MP和NQ分别垂直平分AB和AC,即可得AP=BP,AQ=CQ,则可求得∠BAP+∠CAQ=∠B+∠C=70°,继而求得答案.【解答】解:∵∠BAC=110°,∴∠B+∠C=70°,∵MP和NQ分别垂直平分AB和AC,∴AP=BP,AQ=CQ,∴∠BAP=∠B,∠CAQ=∠C,∴∠BAP+∠CAQ=∠B+∠C=70°,∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=40°.20.如图,在正五边形ABCDE中,连接AC,求∠CAE的度数.【考点】多边形内角与外角.【分析】首先利用多边形的内角和公式求得正五边形的内角和,再求得每个内角的度数,利用等腰三角形的性质可得∠BAE的度数,易得∠CAE.【解答】解:正五边形内角和:(5﹣2)×180°=3×180°=540°∴∠ABC=∠BAE==108°,∴∠BAE===36°,∴∠CAE=∠BAE﹣∠BAC=108°﹣36°=72°.21.如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.【考点】全等三角形的判定与性质;角平分线的性质.【分析】过点D作DG⊥AB于G,由HL分别证明Rt△ADG≌Rt△ADF和Rt△DFN≌Rt△DGM,得MG=NF,AG=AF,再把AM+AN变形即可得出结论.【解答】证明:过点D作DG⊥AB于G,如图所示:∵AD平分∠BAC,DF⊥AC,∴DF=DG,在Rt△ADG和Rt△ADF中,,∴Rt△ADG≌Rt△ADF(HL),∴AG=AF,在Rt△DFN和Rt△DGM中,,∴Rt△DFN≌Rt△DGM(HL),∴MG=NF又∵AG=AF,∴AM+AN=AG+MG+AN=AF+NF+AN=2AF.22.在平面直角坐标系中,已知点A(1,0),B(4,2),C(2,3).(1)画出△ABC关于y轴的对称图形△A1B1C1;(2)△A1B1C1三个顶点的坐标;(3)画出△ABC关于直线l(l上各点纵坐标都为1)的对称图形△A2B2C2,写出点C关于直线l的对称点C2的坐标.【考点】作图﹣轴对称变换.【分析】(1)分别作出点A、B、C关于y轴的对称点,顺次连接即可;(2)根据(1)中所画图象可得;(3)分别作出点A、B、C关于直线x=﹣1的对称点,顺次连接即可.【解答】解:(1)如图,△A1B1C1即为所求.(2)由图可知点A1(﹣1,0)、B1(﹣4,2)、C1(﹣2,3);(3)如图,△A2B2C2即为所求,点C2(2,﹣5).23.如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=50°时,求∠DEF的度数;(3)△DEF可能是等腰直角三角形吗?为什么?【考点】全等三角形的判定与性质;等腰直角三角形.【分析】(1)根据AB=AC可得∠B=∠C,即可求证△BDE≌△CEF,即可解题;(2)根据全等三角形的性质得到∠CEF=∠BDE,于是得到∠DEF=∠B,根据等腰三角形的性质即可得到结论.(3)由(1)知:△DEF是等腰三角形,DE=EF,由(2)知,∠DEF=∠B,于是得到结论.【解答】(1)证明:∵AB=AC,∴∠B=∠C,在△BDE和△CEF中,∵∴△BDE≌△CEF,∴DE=EF,∴△DEF是等腰三角形;(2)解:∵∠DEC=∠B+∠BDE,即∠DEF+∠CEF=∠B+∠BDE,∵△BDE≌△CEF,∴∠CEF=∠BDE,∴∠DEF=∠B,又∵在△ABC中,AB=AC,∠A=50°,∴∠B=65°,∴∠DEF=65°;(3)解:由(1)知:△DEF是等腰三角形,DE=EF,由(2)知,∠DEF=∠B,而∠B不可能为直角,∴△DEF不可能是等腰直角三角形.24.如图,在△ABC中,AD平分∠BAC,DF⊥AB,DM⊥AC,AB=18cm,AF=12cm,AC=16cm,动点E 以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.(1)求的值;(2)求证:在运动过程中,无论t取何值,都有=2;(3)当t取何值时,△DFE≌△DMG.第21页(共23页)【考点】三角形综合题;三角形的面积;全等三角形的性质;角平分线的性质.【分析】(1)根据角平分线的性质,得出DF=DM ,再根据S △ABD =×AB ×DF ,S △ACD =×AC ×DM ,即可得出的值;(2)根据动点E 以2cm/s 的速度从A 点向F 点运动,动点G 以1cm/s 的速度从C 点向A 点运动,可得AE=2t ,CG=t ,而DF=DM ,再根据=进行计算求解即可;(3)分两种情况进行讨论:①当点G 在线段CM 上时,②当点G 在线段MA 上时,分别根据△DFE ≌△DMG ,得出EF=GM ,据此列出关于t 的方程,进行求解即可.【解答】解:(1)∵AD 平分∠BAC ,DF ⊥AB ,DM ⊥AC∴DF=DM ,又∵S △ABD =×AB ×DF ,S △ACD =×AC ×DM ,∴===;(2)证明:∵动点E 以2cm/s 的速度从A 点向F 点运动,动点G 以1cm/s 的速度从C 点向A 点运动, ∴AE=2t ,CG=t ,而DF=DM ,∴====2;(3)①如图1,当点G 在线段CM 上时,EF=AF﹣AE=12﹣2t,AM=AF=12,GM=CM﹣CG=(16﹣12)﹣t=4﹣t,∵△DFE≌△DMG,∴EF=GM,∴12﹣2t=4﹣t,∴t=8(舍去);②如图2,当点G在线段MA上时,EF=AF﹣AE=12﹣2t,GM=CG﹣CM=t﹣4,∵△DFE≌△DMG,∴EF=GM,∴12﹣2t=t﹣4,∴t=,综上所述:t=.第22页(共23页)第23页(共23页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省云梦县2009-2010学年度八年级上学期期中质量检测Ⅰ听力部分20分Ⅰ请听句子和对话,选择与图片内容意思一致的选项,每小题1分,共5分A go to the busB go there by carC take a piano lessonD cooking in the kitchenE have a toothache1__________2__________3_________4_________5____________Ⅱ听句子,选择适当的应答语,每小题1分,共5分6 A I‟m Chinese. B I‟m not well C I‟m a foreigner.7 A She walks much B She does every day C She walks to school.8 A I play basketball at 4 pm B I play basketball three times a weekC I play basketball for two hours9 A I‟d like some honey B No, you can‟t help me C Yes, you do.10 A Half an hour B At 1:00 pm C 2 kmsⅢ听对话,选择正确的答语,每小题1分,共5分11 A By bike B On foot C By bus12 A He has a headache B He has a stomachache C He has a sore throat13 A She is staying at home B She is going camping C She is visiting her aunt14 A Five weeks B Five days C Two days15 A Because she is meeting her aunt B Because she is studying for a testC Because she is relaxing at homeⅣ短文理解,根据所听短文内容,选择最佳答案,每小题1分,共5分16 How many tests did Sarah have last week ?A 1B 2C 317 What did Sarah really want to do last Saturday night?She wanted ______A to stay at home and watch TvB to work at the restaurantC to study until midnight18 Who did Sarah go to the movie with?A Her sisterB Her parentsC Her friend19 What did they think of the movie ?___________A It was exciting but so scaryB It was boringC It was old but boring20 Where does Sarah usually work on Saturday?A At schoolB In the libraryC At the restaurantⅡ笔试部分100分Ⅴ选择填空题,每小题1分,共15分21 Which of ______ two books is more interesting?A theB aC thisD /22 My little brother didn‟t want to walk to the park. There was something wrong with his ______ .A armsB headC teethD feet23 You look worri ed. What‟s your ____ ?I have trouble learning English.A nameB questionC problemD job24 How to read “6:10”in English ? It‟s ______A six past tenB ten to sixC six tenD ten six25 I didn‟t know you took a bus to school . Oh, I _ take a bus , but it is snowing today.A hardlyB neverC sometimesD usually26 I don‟t know to play computer games again. I‟d like to do ___A important somethingB something importantC important anythingD anything important27 How do you usually get to school? ______ABy the bus BBy bus C Take taxi D Take a walk28 What do you think of your English teacher? I love her. She is really ______.She always has a smile on her face.A outgoingB funnyC friendlyD serious29 Can you go to the park with me the weekend? Sorry, I can‟t. I ______visit my uncle.A shouldB canC have toD want30 In ____ parts of the world , things are difficult.A the othersB anotherC the otherD other31 My sister Lisa didn‟t finish her homework ____ ten o‟clock last night?A onB whenC tillD over32 Would you like some more soup? _______ . It is delicious . But I‟ve had enough.A Yes, pleaseB No,thanksC Nothing muchD I‟d like some.33 ___-is necessary for me to study English well.A ThatB ThisC ItD There34 ______ hours do you sleep every night? Nine hours .A How longB How oftenC How muchD How many35 Can you come to my birthday party? I(…d love to. But ______A I can‟tB I won‟tC I canD I‟m freeVI 补全对话, 每小题1份,共5 分从方框中选择适当的项完成对话,有一个多余,一项只用一次Bill: Hello! Mike? This is Bill.Mike: Today is my birthday.Bill: Today is my birthday.Mike: Is it? 36________________Bill: Thank you. I want to have a birthday party this evening. 37_______Mike: Sure, I‟d love to .38____________Bill: At six in the evening.Mike: 39___________________Bill: You can take the No111 bus.Mike: 40__________Bill: It takes about 15 minutes by bus.Mike: OK See you this evening !Bill: See you . Thanks very much.Ⅶ完形填空。
每小题1分,共10分A factory begins to make a new kind of dog food. They have a party to show the dog 41__ to the other people. People 42__ the newspaper and TV stations are there.There 43____ a dog at the party. It is going to eat the dog food and the people are going to take photos. The plan is to show everyone 44___ the dog likes the new dog food.When the time 45____ ,a man puts a plate of the dog food in front of 46____ .Everyone looks at the dog. But the dog 47___ eat any of it. The dog doesn‟t like it.The boss of the factory must 48___ something now. All of the people are 49____,and all of the people are laughing. So the boss 50____ the dog food.41 A drink B food C bread D milk42 A on B of C from D in43 A is B are C have D has44 A where B how C what D why45 A comes B goes C has D leaves46 A the boss B the dog C people D everyone47 A not B isn‟t C don‟t D doesn‟t48 A speak B answer C do D have49 A looking at B watching C seeing D listening50 A eat B eats C drink D drinksⅧ阅读理解。
