水力学课件-水跃
第七章 水跃

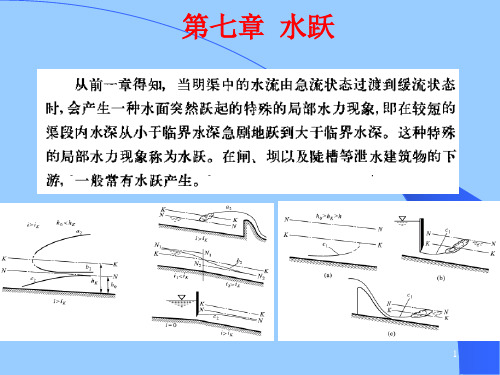
第七章 水跃考点一 水跃的基本概念1、水跃现象在明渠中水流由急流过渡到缓流时,会产生一种水面突然跃起的特殊局部水流现象,即在较短的渠段内水深从小于临界水深急剧的跃到大于临界水深,这种特殊的局部水流现象称为水跃。
2、相关概念(1)跃前断面、跃后断面(2)跃前水深、跃后水深、共轭水深 (3)跃高、跃长 3、.水跃的分类水跃可以按其位置和跃前断面的弗劳德数进行分类。
(1)按水跃跃首所处的位置,可以将水跃分为远驱水跃、临界水跃和淹没水跃。
其分类标准以坝址(或闸后收缩断面)处收缩断面水深'c h 的共轭水深"c h (即跃后水深)与下游水深t h 相比较:当t c h h >"为远驱水跃t c h h ="为临界水跃t c h h <"为淹没水跃。
(2)按跃前断面的弗劳德数Fr 可以将水跃分为波状水跃、弱水跃、不稳定水跃、稳定水跃和强水跃。
当7.11<<Fr 为波状水跃; 当5.27.1<<Fr 为弱水跃;当5.45.2<<Fr 为不稳定水跃,也叫颤动水跃; 当95.4<<Fr 为稳定水跃; 当9>Fr 为强水跃。
或当7.11<<Fr 为波状水跃; 当7.1>Fr 为完全水跃。
考点二 棱柱体水平明渠的水跃方程在水平明渠中,水跃的基本方程为22221112c c h A gA Q h A gA Q +=+ 式中Q 为流量;21A A 、分别表示水跃前、后断面的面积;21c c h h 、分别表示水跃前、后断面形心距水面的距离。
当明渠断面的形状、尺寸以及渠中的流量一定时,水跃方程的左右两边都是水深的函数。
此函数称为水跃函数,以符号c Ah gAQ h J +=2)(表示,则有 )()("'c c h J h J =上式表明,在棱柱体水平明渠中,跃前水深'c h 与跃后水深"c h 之间具有相同的水跃函数值,所以也叫这两个水深为共轭水深。
水力学第10章 明渠恒定急变流-水跃和水跌

第10章 明渠恒定急变流—水跃和水跌10.1知识要点10.1.1水跃—急流到缓流的过渡1.水跃现象在明渠中水流由急流过渡到缓流时,会产生一种水面突然跃起的特殊局部水流现象,即在较短的渠段内水深从小于临界水深急剧的跃到大于临界水深,这种特殊的局部水流现象称为水跃。
水跃发生的条件是跃前水深与跃后水深存在共轭水深的关系。
2.水跃的分类水跃可以按其位置和跃前断面的弗劳德数进行分类。
按水跃跃首所处的位置,可以将水跃分为远驱水跃、临界水跃和淹没水跃。
其分类标准以坝址(或闸后收缩断面)处收缩断面水深'c h 的共轭水深"c h (即跃后水深)与下游水深t h 相比较,当t c h h >"为远驱水跃、t c h h ="为临界水跃、t c h h <"为淹没水跃。
按跃前断面的弗劳德数Fr 可以将水跃分为波状水跃、弱水跃、不稳定水跃、稳定水跃和强水跃。
当7.11<<Fr 为波状水跃; 当5.27.1<<Fr 为弱水跃;当5.45.2<<Fr 为不稳定水跃,也叫颤动水跃;当95.4<<Fr 为稳定水跃; 当9>Fr 为强水跃。
10.1.2棱柱体水平明渠的水跃方程在水平明渠中,水跃的基本方程为22221112c c h A gA Qh A gA Q+=+ (10.1)式中Q 为流量;21A A 、分别表示水跃前、后断面的面积;21c c h h 、分别表示水跃前、后断面形心距水面的距离。
当明渠断面的形状、尺寸以及渠中的流量一定时,水跃方程的左右两边都是水深的函数。
此函数称为水跃函数,以符号)(h J 表示,则有)()("'c c h J h J = (10.2)上式表明,在棱柱体水平明渠中,跃前水深'c h 与跃后水深"c h 之间具有相同的水跃函数值,所以也叫这两个水深为共轭水深。
水跃讲义

§2.2 棱柱体水平明渠中水跃共轭水深的计算
当明渠断面的形状、尺寸和渠中的流量给定时,由已 知的一个共轭水深计算未知的一个共轭水深,称为共轭水 深的计算。
一、共轭水深计算的一般方法
第2章 水跃
本 §2.1 棱柱体水平明渠的水跃方程 章 主 §2.2 棱柱体水平明渠中水跃共轭水深的计算
要 §2.3 棱柱体水平明渠中水跃的能量损失 内 容 §2.4 棱柱体水平明渠中水跃跃长的确定
基本概念
1.水跃(hydraulic jump)的定义 在较短的区段内,水深从小于临界水深急剧地跃到大
本章重点:
1)什么是水跃?水跃产生的原因。
本章结束 2)水跃现象有何特点?
3)棱柱体水平明渠水跃方程及其推导思想。 4)共轭水深的计算方法。 5)水跃函数及水跃曲线的特点。 6)水跃能量损失的机理。 7)水跃类型及其与消能效率的关系(特点)。 8)水跃长度的确定。
hC
h 2
代入水跃方程,得
解之,得
q2 h12 q2 h22 gh1 2 gh2 2
h2
h1 2
1
8
q2 gh13
1
或
h1
h2 2
18 q2 gh23
1
§2.2 棱柱体水平明渠中水跃共轭水深的计算
三、矩形明渠共轭水深的计算
因为
Fr12
12
gh1
q2 gh13
公式又可写为
h2
h1 2
§2.4 棱柱体水平明渠中水跃长度确定
一、矩形断面明渠
Lj 10.8h1(Fr1 1)0.93
水力学第7章-1水跃

依据共轭水深方程,由一个共轭水深求另一个共 轭水深。
hc1 A1
1Q2
gA1
hc2 A2
2Q2
gA2
由于共轭水深方程是一个关于共轭水深的高次 方程,不便直接计算,常用的方法为试算法。
11
12
13
例7.2 棱柱形平底明渠,断面形状、尺寸、跃 前水深给定。问:水跃段中底槛的存在对跃后水 深有何影响?
效率越高。 通过实验资料分析,可知:
1 Fr1 1.7 ,为波状水跃,消能效果最差; 1.7 Fr1 2.5 ,为弱水跃, K j 20% ; 2.5 Fr1 4.5 ,为不稳定水跃,K j 20 45% ;
4.5 Fr1 9 ,为稳定水跃,K j 45 70% ; Fr1 9 ,为强水跃,K j 85% 。
b
q2 h12 q2 h22 gh1 2 gh2 2
17
q2 h12 q2 h22 gh1 2 gh2 2
2q 2 g
h1h22 h2h12
h1
h2 2
18 q2 gh23
1
h2 2
1 8Fr22 1
同样地
h2
h1 2
q2 1 8 gh13
1
h1 2
1 8Fr12 1
A1hc1
Q2 gA2
A2hc2
T
h
即
J
(h1 )
J
(h2
)
T
h2
可见,h1不变,有底槛时,
h1
h2 会减小。
J (h2) J (h1) J (h)
16
二、矩形明渠共轭水深的计算
共轭水深方程
Q2 gA1
A1hc1
水力学第七章课件 水跃

棱柱体水平明渠中,跃前和跃后水深不相等,但其水
跃函数值相等,h1 h2 互称为共轭水深 h1
h2
当断面形状尺寸、流量Q一定时,绘h J(h)曲线
h
J(h)
当h→0,J
h
Q2 gA
hc
A
当趋近于∞时, J h 也趋近于∞
当h∈[0,∞],J(h)有J(h)min
J (h)min
d[J (h)] dh
Ahc
Q2B gA2
d( Ahc dh
)
0
d(Ahc ) lim Δ(Ahc ) lim (A B Δ h) A
dh
Δh0 Δ h
Δ h0
2
Q 2 A3 Fr 1 gB
临界流方程
h
hk J min
J(h)
d[J (h)] dh
d dh
Q2 gA
Ahc
Q2B gA2
A
A(1
Q2B gA3
gA
hc A
J h1 J h2
1
2
a K
h1 FP1
v1
Ff i = 0
v2 FP2
K h2
x
1
Lj
2
Q2v2 1v1 P1 P2 Ff g hc1A1 g hc2 A2 0
式中,A过水断面的面积;
hc 相应于A上形心点水深 ; 1 ,2 对应跃前和跃后断面
Q2v2 1v1 P1 P2 Ff g hc1A1 g hc2 A2
)
A(1
Fr
2)
h
hk
:
d[J (h)] dh
A(1
Fr 2 )
0
h
hhk
:
《水力学》第七章水跃

加强与流体力学、环境科学、生物学等学科的交叉合作,从多角度揭 示水跃现象的规律和影响。
水跃研究面临的挑战和问题
水跃现象的复杂性和不确 定性
由于水跃现象受到多种因素的 影响,如流速、流量、水深、 地形等,其表现形式和特性具 有很大的不确定性,给研究带 来困难。
实验和观测的局限性
进行水跃实验和观测需要特定 的设备和条件,有时难以模拟 实际情况,同时观测结果可能 受到多种干扰因素的影响。
理论模型的发展和完善
虽然现有的水力学理论对水跃 现象有一定的解释能力,但仍 需要不断发展和完善理论模型 ,以适应各种复杂情况。
工程应用的需求
在实际工程中,需要准确预测 和控制水跃行为,以满足工程 安全、环境保护等方面的需求 ,因此需要加强水跃理论在实 际工程中的应用研究。
水跃研究对实际工程的指导意义
03
水跃的数值模拟和计算方法
数值模拟的基本原理
离散化
将连续的水流运动过程离散化,将连 续的空间离散为一系列的网格点或单 元。
建立方程
求解方程
利用数值计算方法,如有限差分法、 有限元法等,求解离散化后的水流运 动方程,得到各网格点的水动力参数 值。
根据水力学的基本原理,建立离散化 后的水流运动方程,如NavierStokes方程。
详细描述
根据形成原因的不同,水跃可分为跌水水跃和堰流水跃等类型。跌水水跃是由于河道中 存在落差而形成的水跃,堰流水跃则是由于水流遇到障碍物(如堰)而形成的水跃。此 外,根据水流形态和水位变化情况,水跃还可分为远驱式水跃、临界式水跃和淹没式水
跃等类型。
02
水跃形成的机理
水流流态的转变
急流到缓流的转变
的影响。
水跃在给水排水工程中的应用
课件:第七章 水跃、堰流及闸孔出流

水跃函数:当流量Q、渠道断面形状尺寸 一定时,J 为水跃函数
Q2 gA hc A J (h)
J h 水跃方程可化为
1
J h2
棱柱体水平明渠中,跃前和跃后水深不相等,但其水
跃函数值相等,h1 h2 互称为共轭水深 h1
h2
水跃函数曲线
当断面形状尺寸、
流量Q一定时,绘 h J(h)曲线
(2)确定流量系数 0.60 0.176 e 0.56
H
(3)设下游为自由出流,计算过闸流量
H0
H
V02 2g
0.82 5
19.6
5.03m
Q eb 2gH0 0.5613 19.65.03 16.68m3 / s
(4)判别出流是否淹没
由
e 0.2 H
查表8.8得 2 0.620
则收缩断面水深 hc 2 e 0.621 0.62m
Hd
4cos2
u2
;n 2
2g
uy
u
Bθ
ux
x
P1 y 克里格——奥菲采洛夫剖面
WES剖面
渥奇剖面
WES剖面的水力设计方法
1.85
y Hd
0.5
x Hd
Hd 0.75~ 0.95Hmax
曲线形实用堰系数
Q s1mb
2g
H3 2 0
WES堰 md=0.502; 克—奥堰 md=0.49;
1
1
B
H
b B
0.2,
b B
0.2
P1
H
3,
P1 H
3
(1)对单孔宽顶堰 b
边墩间宽度, B
堰上游水面宽度
(2)对于多孔宽顶堰
水力学课件-水跃

c c
K
K ht i1=0
设跃前水深为收缩断面水深hc, 即有h1 = hc,计算相应的跃后 水深h2,
棱柱体水平明渠中水跃跃长的确定
矩形明渠的跃长公式
L j = 10.8h1 ( Fr1 − 1)
0.93
10 L j = 0.32 (h2 − h1 ) Fr1
梯形明渠的跃长公式
B2 − B1 L j = 5h2 [1 + 4 ] B1
h2 q2 h1 = [ 1 + 8 3 − 1] 2 gh2
确定水跃发生位置
K N1 N2 h01 hk N1 i1>ik
h1 q2 1
N2 h02
c1
h02 i2<ik
h02
K
返回
泄水建筑物下游水跃发生位置的判别
若计算的h2= ht,则跃前断 面恰好在收缩断面处,称 为临界式水跃 若计算的h2> ht,则跃前断 面必在收缩断面的下游, 称为远离式水跃 若计算的h2> ht,则跃前断 面必在收缩断面的下游, 称为远离式水跃
前进
主要内容 水跃现象 棱柱体水平明渠的水跃方程式 棱柱体水平明渠中水跃共轭水深的计算 泄水建筑物下游水跃发生位置的判别 棱柱体水平明渠中水跃跃长的确定
结束
当明渠水流由急流流态过渡到缓流流态时 当明渠水流由急流流态过渡到缓流流态时,会产生一 急流流态过渡到缓流流态 种水面突然跃起的特殊的局部水力现象, 种水面突然跃起的特殊的局部水力现象,即在较短的渠段 内水深从小于临界水深的急剧地跃到大于临界水深, 内水深从小于临界水深的急剧地跃到大于临界水深,这种 特殊的局部水力现象称为水跃 水跃。 特殊的局部水力现象称为水跃。
1 2
水力学第七章

2
2 gh'' gh'
h'2h'' h'h''2 2q2 0 g
h
h 2
1
ቤተ መጻሕፍቲ ባይዱ
8q 2 gh3
1
h h'' 2
1 8Fr22 1
h
h 2
1
8q 2 gh3
1
h h 2
1 8Fr12 1
矩形断面渠道共轭水深与临界水深的关系
h2h hh2 2q2 0 g
h2h hh2 2hc3r 0
水跃的动量方程
′"
c
c
取1-1,2-2断面间水体为控制体 1)底坡水平; 2)忽略渠床对水体的摩擦力作用; 3)两个断面上的动量校正系数α01=α02=1; 4)1-1和2-2断面是渐变流断面。
水平方向的动量方程为
yc1 A1
yc2 A2
Q
g
v2
v1
′"
c
c
v1 Q / A1
v2 Q / A2
yc1 A1
Q2 gA1
yc2 A2
Q2 gA2
平底坡棱柱形渠道的水 跃基本方程
根据平底坡棱柱形渠道的水跃方程
yc1 A1
Q2 gA1
yc2 A2
Q2 gA2
由于y和A均是水深h的函数,定义水跃函数
yc
A
Q2 gA
J
h
J h' J h''
共扼水深h`和h``是使水跃函数值相等的两个水 深。
水跃函数曲线
• 共扼水深就是同一条铅垂线与水跃函数曲线相 交的两点所对应的水深。跃前水深愈小对应的跃 后水深愈大。
水跃的原理及应用

水跃的原理及应用水跃是指在受到外界力的作用下,水在接触面上产生瞬时的跃起现象。
这一原理被广泛应用于科学研究、工程设计和生活实践中。
水跃的原理主要涉及两方面:一是压电效应,即在外界力的作用下,水分子发生受压变形;二是斯维奇效应,即受到压力后的水分子在接触面上产生剧烈的震动,从而使水跃起来。
首先,压电效应是水跃产生的根本原因之一。
水分子是由氢原子和氧原子组成的,分子间存在着相互作用力。
当外界力作用于水分子上时,分子之间的相互作用力会改变。
如压力增大,水分子之间的距离变小,相互作用力增大,使水分子发生变形,由而产生压电效应。
其次,斯维奇效应是导致水跃现象的关键因素。
斯维奇效应是指当外界力作用于已经受压的水分子时,水分子之间的相互作用力会改变,从而使分子在接触面上发生剧烈的震动。
这种震动引起了水分子之间的排列和重组,进而产生了水的跃起现象。
水跃的应用非常广泛。
在科学研究中,水跃原理被用于研究液体的物理性质,如表面张力、分子间相互作用等。
通过观察和分析水跃现象,科学家可以推测出水分子的内部结构和行为。
在工程设计中,水跃原理可以应用于水力学相关领域,如水泵、水轮机等。
通过合理地设计水跃装置,可以提高水力机械的效率和性能,从而实现对水资源的高效利用。
此外,水跃还可以应用于生活实践中。
例如,马球运动中的水球比赛就是利用了水跃原理。
在比赛中,运动员需要喷射气流将水球从地面上射出,并用球杆接住水球。
通过控制气流的压力和方向,运动员能够使水球以特定的轨迹和高度跃起,增加游戏的难度和趣味性。
总之,水跃原理是水分子在受外界力作用下产生跃起现象的物理机制。
这一原理被广泛应用于科学研究、工程设计和生活实践中,为人们的工作和生活带来了诸多便利和创新。
水力学课件-水跃.44页PPT

60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
13、遵守纪律的风气的培养,只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致,是 取得最 后胜利 的保证 。——雨果
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
水力学课件-水跃.
11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
水力学课件-水跃

水跃
跃前水深h'——跃前断面(表面旋滚起点所在过 水断面)的水深;
水 力 学 讲 义
跃后水深h"——跃后断面(表面旋滚终点所在过
水断面)的水深; 水跃高度 a= h"- h' 水跃长度Lj——跃前断面与跃后断面之间的距离.
第七章
水跃
7.1 棱柱体水平明渠的水跃方程 一、推导
在推导水跃方程之前,先探讨一下推导的方 法。对于属于明渠急变流的水跃来讲,其中有较 大的能量损失。我们既不能将它忽略不计,又没 有一个独立于能量方程之外的,用来确定水跃能 量损失的公式。因此,在推导水跃方程时,不能 应用恒定总流的能量方程而必须采用恒定总流的 动量方程。因为对水跃段应用动量方程可以不涉 及水跃中地较大地能量方程。
计算,还可以应用一些特制的计算曲线。
第七章
水跃
三、矩形明渠共轭水深的计算
矩形断面明渠的共轭水深计算依据下列公式 :
水 力 学 讲 义
h1 2 h2 [ 18 Fr 1 1] 2
或
h2 2 h [ 1 8 Fr 1] 2 1 2
第七章
7.3
水跃
水跃方程的实验验证
水跃的共轭水深计算是以水跃方程为依据的。 在推导该理论方程时,曾作过一些假定。这些假 定是否正确,有待实验来证明。
α 2 v2 α 3 v3 Ejj (h2 ) ( h3 ) 2g 2g
近似地令h3= h2,v3= v2及 简化为:
2
2
α 3 =1,于是上式可
2
v2 Ejj (α 2 - 1 ) 2g
第七章
水跃
棱柱体矩形水平明渠地Ejj的计算公式:
水 力 学 讲 义
水力学课件07

h1
图解法
J(h1)=J(h2) J(h)
矩形明渠共轭水深的计算
确定水跃发生位置
h1
h2 2
[
1
8
q2 gh23
1]
h2
h1 2
[
18
q2 gh13
1]
K
N1 h01
hk
i1>ik
N2
N2
h02 h02
K
N1 c1 h02
i2<ik
返回
泄水建筑物下游水跃发生位置的判别
cK
K ht
c
i1=0
设跃前水深为收缩断面水深hc, 即有h1 = hc,计算相应的跃后 水深h2,
若计算的h2= ht,则跃前断 面恰好在收缩断面处,称 为临界式水跃
若计算的h2> ht,则跃前断 面必在收缩断面的下游, 称为远离式水跃
若计算的h2> ht,则跃前断 面必在收缩断面的下游, 称为远离式水跃
返回
棱柱体水平明渠中水跃跃长的确定
矩形明渠的跃长公式 Lj 10.8h1(Fr1 1)0.93
A1hc1
Q2 gA2
A2hc2
当明渠断面的形状、尺寸及渠中流量一定时,上式仅是水深
的函数,称为水跃函数,记为
J
(h)
Q2 gA
Ahc
即有 J (h1) J (h2 ) 故称跃前、跃后水深为共轭水深 图示
返回
h
Q2
Q2
h2
gA1 A1hc1 gA2 A2hc2
试算法
共轭水深的一般计算方法:
特殊的局部水力现象称为水跃。
1
2
h1Biblioteka 跃前水深h′1跃前断面
7 水跃
式中,1 = AhC1 + Q ,A =0.5 2b+(m +m )h ]h 式中, J [ 1 1 1 2 1 1
gA 1
(7.9) )
例7.3 一水跃产生于一棱柱体梯形水平渠段中。 一水跃产生于一棱柱体梯形水平渠段中。 已知: 已知:Q=6.0m3/s,b=2.0m,m=1.0,h1=0.355m。求h2。 , , , 。 解:
h 称为共轭水深比 从上式可以看出, 是随 共轭水深比。 式中 η = 2 称为共轭水深比。从上式可以看出,η是随 h 1
水跃方程的实验验证
以η为纵坐标,Fr1为横坐 为纵坐标, 根据上式绘出理论曲线, 标,根据上式绘出理论曲线, 如图所示。在同一坐标中, 如图所示。在同一坐标中, 也绘出了实验点。 也绘出了实验点。可以看出 理论曲线与实验点相当吻合。 理论曲线与实验点相当吻合。
∴
Q 2 A3 6.15b)相同。 )相同。
例7.2 当棱柱体水平明渠的流量、断面形状和尺寸以及跃前水深 当棱柱体水平明渠的流量、 一定时,试问水跃段中的低槛(见图)将对跃后水深有何影响? 一定时,试问水跃段中的低槛(见图)将对跃后水深有何影响?
解:对图示的水跃段列应用动量方程有
Q2 Q2 + A1hc1 = + A2 hc 2 gA1 gA2
棱柱体水平明渠的水跃方程 (7.2) )
8
当明渠断面的形状、 尺寸以及渠中的流量一定时, 当明渠断面的形状 、 尺寸以及渠中的流量一定时 , 水跃方程的左右两边都仅是水深的函数,称为水跃函数。 水跃方程的左右两边都仅是水深的函数,称为水跃函数。 水跃函数 令
第七章 水跃
1
1.水跃分区 水跃分区
2
2. 水跃的特性参数
7.水跃

第七章 水跃一、简答题1 什么叫水跃、波状水跃和完全水跃?2 实验槽中水流现象如图示,流量不变,如提高或降低一些尾门(尾门之前的水流始终为缓流),试分析水跃位置是否移动?向前移动还是向后移动?为什么?图7.23 为什么可以利用水跃来消除能量?什么形式的水跃消能效率最高?二、计算题 1、图示为一矩形断面平底明渠中的水跃,水跃底部有一低坎。
已知单宽流量 q = 6 m 2/s 。
跃前水深 h 1 =0.5m ,水流作用在单宽低坎上的总压力2/)(21gh R ρ='。
取动量校正系数为1。
(1)求跃后水深h 2; (m 55.3h 2=;无低坎时 h 2=m 59.3 ) ?大多少?2、已知梯形断面渠道的底宽 b =1m ,边坡系数 m =1。
在水平渠段上的水跃共轭水深为 h 1=0.2 m ,h 2=0.6 m ,求通过渠道的流量 q v 。
[梯形断面形心的深度 h c =)(6/)23(mh b bh b h ++] (/s m 849.0q 3v = )3、某矩形断面平底渠道,底宽 b =7 m ,通过流量 q v =40 m 3/s 。
若渠中发生水跃时,跃前水深 h 1=0.8 m 。
求该水跃的水头损失。
(v 2=40/(7⨯2.5)=2.28m/s ;m 64.0E =∆ )4、某矩形断面平坡渠道,底宽m b 8=,流量s /m Q 316=,设跃前水深m .h '60=,求跃后水深''h 和水跃长度。
( 0.867m; 1.84m )5、有一底宽为12m 的矩形断面渠道中发生水跃,已知渠底高程为120.43m ,流量s /m Q 360=,测得跃后水位高程为123.5m ,试求水跃中单位体积水体所消耗的能量和消能率。
(29.89KJ/m 3; 48.7%)6、一直径D =1.0m 的水平无压圆管中发生水跃,已知流量Q =1.0m 3/s ,跃前水深'h 为0.4m ,求跃后水深''h 。
第八章 3水跃及水面线分析

当明渠水流由急流流态过渡到缓流流态时,会产生一种水面突然跃起的 特殊的局部水力现象,即在较短的渠段内水深从小于临界水深的急剧地跃到 大于临界水深,这种特殊的局部水力现象称为水跃。
1
h1
跃前水深h′
1
跃前断面
跃长Lj
2
h2
2
跃后水深 h
跃后断面
返回
1.棱柱体水平明渠的水跃方程式 1
2
FP1=ρgA1hc1
有三种可能:
①、 h01 > h02 (远驱水跃)
说明下游段的水深 h02挡不住上游段的急流而被冲向下游。 在下游渠道中将发生 CⅠ型雍水曲线,称为远驱水跃。
②、h01 = h02(临界水跃)
水跃恰好发生在变坡处,称为临界水跃。
③、 h01 < h0( 2 淹没水跃)
水深由变坡处的 h02 向上游逐渐减小,直到水深等于
aQ2 (B dh A) gA3 ds s
在渐变流中,水流的边界和断面变化很缓慢,那么沿程水头损失可近似 地按均匀流中的公式来估算。
dhf ds
J
Q2 K2
Q2 A2c 2 R
代入得: i dh aQ2 (B dh A) Q2 0 ds gA3 ds s K 2
dh ds
i
Q2 K2
h01 的共轭水深 h01 为止,然后以水跃来联接 h01
和 h01,上游渠道中发生 aⅡ型雍水曲线。
变坡棱柱体渠道非均匀渐变流水面线的定性分析(四)
b0
K
hk
N2
i1=0
b2
h02 i2>ik
KN2
前进
明渠恒定非均匀渐变流水面曲线的计算 ——逐段试算法
dEs d (E z0 ) dE dz0 J (i) i J
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c c
Kht i1ຫໍສະໝຸດ 0K为临界式水跃若计算的h2> ht,则跃前断
设跃前水深为收缩断面水深hc,
即有h1 = hc,计算相应的跃后 水深h2,
面必在收缩断面的下游, 称为远离式水跃 若计算的h2> ht,则跃前断 面必在收缩断面的下游, 称为远离式水跃
返回
棱柱体水平明渠中水跃跃长的确定
矩形明渠的跃长公式
1
2
h1
h2
跃前水深h′ 跃前断面
1
跃长Lj
2
跃后水深 h
跃后断面
返回
棱柱体水平明渠的水跃方程式 1
FP1=ρgA1hc1
1
2
Ff=0
2
FP2=ρgA2hc2
沿流动方向列动量方程得: Q(V2 V1 ) gA 1hc1 gA 2 hc 2
Q2 Q2 A1hc1 A2 hc 2 代入连续性方程并整理得: gA1 gA2
试算法
h1
图解法
矩形明渠共轭水深的计算
h2 q2 h1 [ 1 8 3 1] 2 gh2
确定水跃发生位置
K N1 N2
h01 hk N1 i1>ik
h1 q2 h2 [ 1 8 3 1] 2 gh1
N2
h02
c1
h02
h02
K
i2<ik
返回
泄水建筑物下游水跃发生位置的判别
若计算的h2= ht,则跃前断 面恰好在收缩断面处,称
当明渠断面的形状、尺寸及渠中流量一定时,上式仅是水深 2 Q 的函数,称为水跃函数,记为 J (h) Ahc
gA
即有
J (h1 ) J (h2 )
故称跃前、跃后水深为共轭水深
图示
返回
h h2
Q2 Q2 A1hc1 A2 hc 2 gA1 gA2
共轭水深的一般计算方法:
J(h1)=J(h2) J(h)
前进
主要内容 水跃现象 棱柱体水平明渠的水跃方程式 棱柱体水平明渠中水跃共轭水深的计算 泄水建筑物下游水跃发生位置的判别 棱柱体水平明渠中水跃跃长的确定
结束
当明渠水流由急流流态过渡到缓流流态时,会产生一 种水面突然跃起的特殊的局部水力现象,即在较短的渠段 内水深从小于临界水深的急剧地跃到大于临界水深,这种 特殊的局部水力现象称为水跃。
Lj 10.8h1 (Fr1 1)0.93
10 L j 0.32 (h2 h1 ) Fr1
梯形明渠的跃长公式
B2 B1 L j 5h2 [1 4 ] B1
返回
