水力学课件 水静力学 考研剖析
合集下载
水力学流体静力学PPT课件
在水利工程中，液体相对平衡 的原理被广泛应用于水坝、水 库等水工建筑物的设计和施工 中。
在医学领域，液体相对平衡的 原理也被应用于血液动力学和 药物输送等方面的研究。
04
液体内部压强与浮力
Chapter
液体内部压强的计算
压强定义
单位面积上所受的压力，用p表示 ，单位为Pa。
计算公式
p = F/A，其中F为压力，A为受力 面积。
了解液体运动的描述方法和基本方程 ；
能够运用所学知识分析和解决工程实 际问题。
教学方法与手段
01
02
03
教学方法
采用讲授、讨论、案例分 析等多种教学方法相结合 的方式。
教学手段
使用PPT课件、动画演示 、实验演示等教学手段辅 助教学。
考核方式
采用平时成绩、期末考试 成绩和实验成绩相结合的 考核方式。
的气体量来调节浮力大小。
05
流体静力学在水利工程中的应 用
Chapter
水库水位与坝体稳定性分析
水库水位确定
根据水库地形、库容曲线 及入库流量等资料，确定 水库在不同运行条件下的 水位。
坝体稳定性分析
运用土力学、岩石力学等 原理，分析坝体在静水压 力、扬压力等作用下的稳 定性，确保大坝安全。
渗流控制
液体相对平衡是流体静力学研究的基础。
等压面的形成与性质
等压面是指在液体内部，压强相等的各点所组成的面。
在重力场中，等压面是一个水平面，因为在同一水平面上，各点受到的重力作用相 同，所以压强也相等。
等压面具有传递压强的性质，即等压面上的压强可以传递到液体内部的任意一点。
液体相对平衡的应用
液体相对平衡的原理可以应用 于测量液体的密度和深度。
水力学ppt课件
目录•水力学基本概念与原理•流体静力学分析•流体动力学基础知识•管内流动与损失计算•明渠恒定均匀流与非均匀流分析•堰流、闸孔出流和泄水建筑物设计原理水力学基本概念与原理水力学定义及研究对象水力学的定义研究液体在静止和运动状态下的力学规律及其应用的科学。
研究对象液体（主要是水）的平衡、运动规律及其与固体边界的相互作用。
液体性质与分类液体的性质易流动性、压缩性、黏性、表面张力等。
液体的分类按密度可分为轻质液体和重质液体；按黏性可分为牛顿液体和非牛顿液体。
静压力与动压力概念静压力静止液体作用在与其接触的某个平面上法向的总压力。
动压力运动液体作用在与其接触的某个平面上法向的总压力。
连续性方程与伯努利方程连续性方程单位时间内流入、流出控制体的质量流量之差，等于控制体内质量的变化率。
伯努利方程理想液体在重力场作稳态流动时，具有压力能、位能和动能三种形式，它们之间可以相互转化，且总和保持不变。
流体静力学分析液体内部压强随深度的增加而增大。
在同一深度，液体向各个方向的压强相等。
液体的压强与液体的密度和深度有关，密度越大、深度越深，压强越大。
静止液体中压强分布规律液体相对平衡时表面形状确定方法0102 03当液体处于相对平衡状态时，其表面形状由液面所受外力和液体内部分子间相互作用力共同决定。
若液面所受外力为重力，则液面为水平面；若液面所受外力为其他力，则液面为与该力相平衡的曲面。
通过测量液体表面形状，可以推断出液体所受外力的性质和大小。
浮力的大小等于物体排开的液体所受的重力，即F 浮=G排=m排g=ρ液gV排。
浮力的产生条件是物体必须浸没在液体中，且物体下表面必须与液体接触。
浮力是液体对浸在其中的物体向上和向下的压力差，方向竖直向上。
浮力产生条件及计算方法潜水艇、气球等浮沉原理分析潜水艇通过改变自身重力来实现浮沉。
当潜水艇需要下潜时，它会向水舱注水，使自身重力大于浮力而下潜；当需要上浮时，它会将水舱中的水排出，减小自身重力，使浮力大于重力而上浮。
水力学课件 第一章 水静力学
§1.1 静水压强及其特征
联立上面各式代入后得：
1 2
pxyz
1 2
pnyz
1 6
xyzf x
0
1 2
p y xz
1 2
pnxz
1 6
xyzf y
0
1 2
pz xy
1 2
pnxy
1 6
xyzf z
0
联立上面各式代入后得：
1 2
pxyz
1 2
pnyz
1 6
xyzf x
0
1 2
p y xz
1 2
pnxz
§1.4 等压面
一、等压面(Isobaric Surface)：在平衡的液体中， 由压强相等的各点所组成的面叫做等压面。 等压面的重要特性是： 1.在静止的或相对平衡的液体中，等压面同时也是
等势面(Isopotential Surface)。 dp dU
2.在相对平衡的液体中，等压面与质量力正交。
条件：只适用于静止、同种、连续液体
三、气体压强计算
p p0
§ 1.5几种质量力同时作用下的液体平衡
z
gm h z
zs
o
x
以z轴为对称轴的旋转抛物面方程：
R
o
r
x
m
F
y 1 2rBiblioteka gz C 2§ 1.5几种质量力同时作用下的液体平衡 平衡微分方程： dp ( fxdx f ydy fzdz) 质量力：离心惯性力和重力 F m 2r, mg 单位质量力： fx 2 x, f y 2 y, fz g 自由面上压强不变为大气压： dp 0
§ 1.5几种质量力同时作用下的液体平衡
2、圆筒中液体内任一点静水压强分布规律：
水力学课件(主讲人：华北水利水电学院孙东坡教授) (1)
对压强，B点的相对压强和
真空度，A、B两点的压强差。
解: A点 相对压强 绝对压强
∵P1>0,
p1= 8KN/m2 p1 = pa+p1=98+8
=106KN/m2
∴真空度不存在
解: B点
绝对压强 p2 = 78KN/m2 相对压强 p2 = p2-pa=78-98
= -20KN/m2
真空度 pv = p2
(四)液体的两种分类:
1.理想液体：忽略粘滞性的 液体
2.实际液体：存在粘滞性的 液体
（五）液体所受外力的分类：
1.表面力：压力、剪切力等 2.质量力 ：重力、离心惯性
力等
第二章 水静力学
(一)静水压强： 1．静水压强的两个特性：
（1）垂直指向受压面 （2）大小与受压面方向无关
（1）方向：垂直指向受压面 （2）大小：与受压面方位无关
水银
求A、B两点的
E
E
压强差?
0.3m 0.2m
解：计算如下
p
=
p
+g
×
B
0.5
. m
60
p = p -g 0.2 C
A
水
A
油
水
水
×
D
C
汞G
G
p = p +g 0.3 0.5mF
D
×D 0.4m
g g E
D
油
C
C
水银
p = p - E× 0.E4- × 0.6
B
E
泵
水
0.3m
0.2m
p = p +g ×0.5-g ×0.2
c
对铰O取矩
真空度，A、B两点的压强差。
解: A点 相对压强 绝对压强
∵P1>0,
p1= 8KN/m2 p1 = pa+p1=98+8
=106KN/m2
∴真空度不存在
解: B点
绝对压强 p2 = 78KN/m2 相对压强 p2 = p2-pa=78-98
= -20KN/m2
真空度 pv = p2
(四)液体的两种分类:
1.理想液体：忽略粘滞性的 液体
2.实际液体：存在粘滞性的 液体
（五）液体所受外力的分类：
1.表面力：压力、剪切力等 2.质量力 ：重力、离心惯性
力等
第二章 水静力学
(一)静水压强： 1．静水压强的两个特性：
（1）垂直指向受压面 （2）大小与受压面方向无关
（1）方向：垂直指向受压面 （2）大小：与受压面方位无关
水银
求A、B两点的
E
E
压强差?
0.3m 0.2m
解：计算如下
p
=
p
+g
×
B
0.5
. m
60
p = p -g 0.2 C
A
水
A
油
水
水
×
D
C
汞G
G
p = p +g 0.3 0.5mF
D
×D 0.4m
g g E
D
油
C
C
水银
p = p - E× 0.E4- × 0.6
B
E
泵
水
0.3m
0.2m
p = p +g ×0.5-g ×0.2
c
对铰O取矩
2024版年度水力学全套课件
实质
质量守恒定律在流体力学中的具体表述。
意义
反映了流体运动在空间上的连续性，即流体不可能在某一区域内 突然消失或出现。
应用
用于求解流体的密度、速度等物理量在空间和时间上的变化规律。
19
伯努利方程及其应用
2024/2/3
实质
能量守恒定律在不可压缩、无粘性流体定常流动中的具体表述。
意义
反映了流体在流动过程中压能、位能和动能之间的相互转化关系。
2024/2/3
27
05
有压管道中的恒定流
2024/2/3
28
有压管道的特点与分类
特点
水流受压，流速分布不均，存在水头损失；管道对水流有约束作用，水流方向 明确。
分类
根据管道材料可分为金属管、非金属管和复合材料管；根据管道用途可分为输 水管、配水管和排水管等。
2024/2/3
29
简单管道的水力计算
应用
用于求解流体的压力、流速等物理量在流动过程中的变化规律，如 水力学中的虹吸现象、文丘里管等。
20
动量方程及其应用
实质
牛顿第二定律在流体力学中的具体表述。
意义
反映了流体动量的变化与作用在流体上的外力之间的关系。
应用
用于求解流体的流速、流量等物理量在受到外力作用时的 变化规律，如水力学中的堰流、孔口出流等问题。
要点二
水力计算步骤
确定堰的类型和尺寸，测量堰上水头H，根据公式计算流量Q。
2024/2/3
42
实用堰流的水力计算
基本公式
实用堰流的流量系数m与堰的进口形状有关，常采用经验公式或实验数据确定。流量Q仍可按薄壁堰流公式计算， 但需对流量系数m进行修正。
水力计算步骤
水力学 流体静力学PPT课件
• 1).合力F的大小等于压强分布体 的体积，即 F = •b；
• 2).合力F的方向为垂直指向受压 面；
• 3).合力F的作用线通过压强分布 体的形心，作用线与受压面的交 点即为D点。
§2-2 流体静止的微分方程
一.流体静止的微分方程：
• 边长分别为dx,dy,dz的微元平行六面体受表面力和质量力的共同作用而保 持静止。
微元体的中心为A点，左表面的中 心为B点，右表面的中心为C点。 A 点的压强为p(x,y,z)。
x方向的静力平衡：
(p
1 2
p x
dx)dydz ( p
1 2
。 确定液体作用在平面上的总压力的大小、方向和作用点
一.解析法：
1.合力的大小：
dA上的相对压强：p γh γy sin θ dA上液体作用的合力为：dF pdA γy sin θdA
第34页/共72页
F dF y sin dA sin ydA
A
A
A
sin yc A hc A
计是一个水平倾角为的Π形管。
已知测压计两侧斜液柱读数的差值
为L=30mm，倾角 = 30°，试求压
强差p1 – p2 。 3)
(书上P29的例2-
解：
这里：z1 z2
p1 γ(z3 z1) γ(z4 z2 ) p2
p1 p2 γ(z3 z4 ) γL sin θ
第26页/共72页
dz
p0 p
R 0 T0 0.0065z
取：g = 9.807m/s²， = 0.0065K/m， R = 287 N•m/Kg•K，T0 = 288K。 则：
g
p p0
1
T0
R z
1
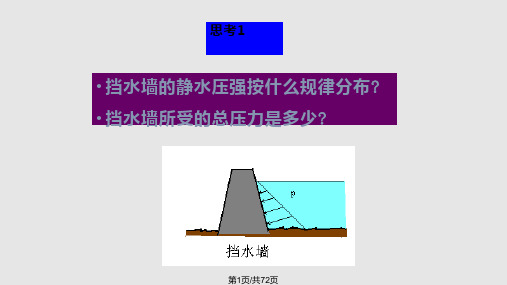
• 2).合力F的方向为垂直指向受压 面；
• 3).合力F的作用线通过压强分布 体的形心，作用线与受压面的交 点即为D点。
§2-2 流体静止的微分方程
一.流体静止的微分方程：
• 边长分别为dx,dy,dz的微元平行六面体受表面力和质量力的共同作用而保 持静止。
微元体的中心为A点，左表面的中 心为B点，右表面的中心为C点。 A 点的压强为p(x,y,z)。
x方向的静力平衡：
(p
1 2
p x
dx)dydz ( p
1 2
。 确定液体作用在平面上的总压力的大小、方向和作用点
一.解析法：
1.合力的大小：
dA上的相对压强：p γh γy sin θ dA上液体作用的合力为：dF pdA γy sin θdA
第34页/共72页
F dF y sin dA sin ydA
A
A
A
sin yc A hc A
计是一个水平倾角为的Π形管。
已知测压计两侧斜液柱读数的差值
为L=30mm，倾角 = 30°，试求压
强差p1 – p2 。 3)
(书上P29的例2-
解：
这里：z1 z2
p1 γ(z3 z1) γ(z4 z2 ) p2
p1 p2 γ(z3 z4 ) γL sin θ
第26页/共72页
dz
p0 p
R 0 T0 0.0065z
取：g = 9.807m/s²， = 0.0065K/m， R = 287 N•m/Kg•K，T0 = 288K。 则：
g
p p0
1
T0
R z
1
水力学吴持恭件 水静力学PPT课件
⑶、用液柱高度表示。
p = h
可写成
h= p
p 对于任一点的静水压强 可以用上式化为对任
何一种容重为 的液柱高度。
如：水柱、汞柱等
第33页/共102页
第二章 水静力学
三、静水压强的图示
1、方法
由 pabs = p0 h压强与水深成线性关系。
因而，在任一平面的作用面上，其压强分布为一 直线。只要算出作用面最上和最下两个点的压强后 ，即可定出整个压强的分布线。 2、原则 ⑴、每一点处的压强垂直于该点处的作用面。 ⑵、静水压强的大小随着距自由面的深度而增加 另外：对实际工程有用的是相对压强的图示。如欲
第二章 水静力学
若 P0<Pa
则：位于测压管中的水位高
度将低于容器内液面高度。
即 hA<h
P0
那么，真空高度为：
h
hB = h hA
A
pA = p0 h = pa hA
pa p0 = h hA = hB
hB
=
pa p0
第39页/共102页
Pa
hB hA ZA
第二章 水静力学
在水力学上，把任一点的相对压强高度（即测压管高 度）与该点基准面以上的位置之和称为测压管水头。
pn ΔAn ΔPn＝ 斜面压力
y
1 2
pz Δx Δy
x
ΔPz＝ 底面压力
7
第7页/共102页
第二章 水静力学
四面体的体积D V为
Z D Pn Px A Py
D
V=
1
6
Dx
• Dy
•Dz
C
O B Pz X
Y
总质量力在三个坐标方向的投影为
Fx
第二章水静力学水力学PPT课件
《水力学》精品课程多媒体课件
第二章
1
《水力学》精品课程多媒体课件
§2-1 静水压强及特性
一、静水压强定义
lim
A0
P A
N/m2 (Pa) KN/m2 (KPa)
二、特性
1、垂直指向作用面
Ⅰ
N
N
Ⅱ
Ⅱ
2、任意点上各方向p相等
用牛顿第二定律证明
F=0
① 说明该性质的含义（结合图形）
2
《水力学》精品课程多媒体课件
则该点存在真空，又称“负
压”真空度：pv pa p'
理论上：pv pa 实际中达不到。
真空高度：h v
pv
16
《水力学》精品课程多媒体课件
理论上：hv=10m；实际上：hv=7~8m 举例：
讨论分布规律：
p 2r2
（2-13）式变形为
z （2-14）
r 2g
等压面方程： 2r 2 z c
2g
可见等压面为旋转抛物面，自由面亦为等压
面，其上p=0。自由液面方程：
12
2r2
z
（2-15）
2g
《水力学》精品课程多媒体课件
由（2-15）式可知： 2 r 2
2g
表示A点处自由面高出x0y平面的
dpd(g)
积分得：
pzc（2-10）
d(z p) 0
积分得 :zp c
说明：在重力作用下，均质不可压缩液体中，各点的
(z p ) 值相等。
在自由面上：
zz0;pp0;cz0p0 9
pp0(z0 z)
pp0 h（2-11）
二、几种质量力同时作用
取坐标研究，液体相对于坐标及 处于平衡状态。属相对静止。
第二章
1
《水力学》精品课程多媒体课件
§2-1 静水压强及特性
一、静水压强定义
lim
A0
P A
N/m2 (Pa) KN/m2 (KPa)
二、特性
1、垂直指向作用面
Ⅰ
N
N
Ⅱ
Ⅱ
2、任意点上各方向p相等
用牛顿第二定律证明
F=0
① 说明该性质的含义（结合图形）
2
《水力学》精品课程多媒体课件
则该点存在真空，又称“负
压”真空度：pv pa p'
理论上：pv pa 实际中达不到。
真空高度：h v
pv
16
《水力学》精品课程多媒体课件
理论上：hv=10m；实际上：hv=7~8m 举例：
讨论分布规律：
p 2r2
（2-13）式变形为
z （2-14）
r 2g
等压面方程： 2r 2 z c
2g
可见等压面为旋转抛物面，自由面亦为等压
面，其上p=0。自由液面方程：
12
2r2
z
（2-15）
2g
《水力学》精品课程多媒体课件
由（2-15）式可知： 2 r 2
2g
表示A点处自由面高出x0y平面的
dpd(g)
积分得：
pzc（2-10）
d(z p) 0
积分得 :zp c
说明：在重力作用下，均质不可压缩液体中，各点的
(z p ) 值相等。
在自由面上：
zz0;pp0;cz0p0 9
pp0(z0 z)
pp0 h（2-11）
二、几种质量力同时作用
取坐标研究，液体相对于坐标及 处于平衡状态。属相对静止。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
y
p fz z
Yangzhou Univ
《水力学》
第一章 水静力学
§2 液体平衡的微分方程式
2 液体平衡的微分方程式
液体平衡状态时,作用于液体上各种力之间的关系式 形心点A的压强为p ( x, y, z ) 则
(p p dx p dx )dydz ( p )dydz f x dxdydz 0 x 2 x 2 p fx x
pA A g (s x) n g h = pA A g ( x h)= pB B g (s x) m g h
pB B g ( x h)
Yangzhou Univ
《水力学》
第一章 水静力学
§5 作用于平面上的静水总压力
5 作用于平面上的静水总压力
静水压强的分布规律是 由单位质量力所决定的
《水力学》
第一章 水静力学
§3 重力作用下静水压强的分布规律
3 重力作用下静水压强的分布规律 z
3.1 水静力学基本方程
只受重力作用：fx=0，fy=0，fz=-g
p0 h 1 Z Z0
dp ( f x dx f y dy f z dz) gdz
单位：N/㎡、kN/㎡ 、Pa 、kPa
Yangzhou Univ
《水力学》
第一章 水静力学
§1 静水压强定义及其特性
1 静水压强定义及其特性
静水压强垂直指向受压面
静水压强的特性
×
M
作用于同一点上各方向的 静水压强的大小相等
B
表明任一点的静水压强仅是空间坐标的函数， 压强p是一个标量，即p = p ( x, y, z )
(p
z
dz A dy dx
p dx p dx )dydz ( p )dydz f x dxdydz 0 x 2 x 2 p fx x
p fy y
p dx p dx ( p p )dydz x 2 x 2
整理化简得：
pp (
p dx p dx )dydz x x2 2
真空值（或真空压强）——指绝对压强小于大气压强的数值， 用pk来表示
pk pa p p
Yangzhou Univ
《水力学》
第一章 水静力学
§3 重力作用下静水压强的分布规律
3.3 压强的单位
应力单位 工程大气压单位 液柱高度 1个工程大气压=98kN/㎡ =10m水柱压
p 积分得： z c g p0 y 在液面上，z=z0，p=p0，则 c z0 g
x
p p0 g ( z0 z)
p p0 gh
Yangzhou Univ
《水力学》
第一章 水静力学
§3 重力作用下静水压强的分布规律
3 重力作用下静水压强的分布规律 z
水力学
熊亚南
扬州大学水利科学与工程技术学院
Yangzhou Univ
《水力学》
第二章 水静力学
水静力学的任务是研究液体平衡的规律
及其实际应用。 工程应用主要是确定水 对水工建筑物的表面上
的作用力。
Yangzhou Univ
《水力学》
第二章 水静力学
§1 静水压强定义及其特性 §2 液体的平衡微分方程式 §3 重力作用下静水压强的分布规律 §4 压强的测量
Yangzhou Univ
《水力学》
第一章 水静力学
§3 重力作用下静水压强的分布规律
3.5 等压面
由压强相等的点连成的面，称为等压面。 可以证明等压面必与质量力正交。 只受重力作用的连通的同一种液体内，等压面
为水平面；反之，水平面为等压面。
连通容器
Yangzhou Univ
连通容器
连通器被隔断
(p p dx p dx )dydz ( p )dydz f x dxdydz 0 x 2 x 2 p fx x
p fy y
整理化简得：
dp ( f x dx f y dy f z dz)
p fz z
Yangzhou Univ
方向向右→
h1 h FP右 2 3 3
可解得：e=1.56m
合力对任一轴的力矩等于各分 Yangzhou 力对该轴力矩的代数和。 Univ
《水力学》
第一章 水静力学
§5 作用于平面上的静水总压力
例题：某挡水矩形闸门，门宽b=2m， 一侧水深h1=4m，另一侧水深h2=2m， 求该闸门上所受到的静水总压力。
Yangzhou Univ
《水力学》
第一章 水静力学
§2 液体平衡的微分方程式
2 液体平衡的微分方程式
液体平衡状态时,作用于液体上各种力之间的关系式 形心点A的压强为p ( x, y, z ) 表面力： 质量力：
ρfxdxdydz ρfydxdydz ρfzdxdydz
p dx p dx ( p p )dydz x 2 x 2
§5 作用于平面上的静水总压力 §6 作用于曲面上的静水总压力
Yangzhou Univ
《水力学》
第一章 水静力学
§1 静水压强定义及其特性
1 静水压强定义及其特性
P P
静水压力：静止液体作用在与之接触的表面上力，用P表示。 面平均静水压强
P p A
静水压强
p lim
P A 0 A
5.1 静水压强分布图
静水压强分布图的绘制规则： 1.按一定比例，用线段长度代表该点静水压强的大小
2.用箭头表示静水压强的方向,并与作用面垂直
pa A
相对压强分布图
Yangzhou Univ
Pa+ρgh
B
《水力学》
第一章 水静力学
§5 作用于平面上的静水总压力
A
A
B
B
C
A
A
B
Yangzhou Univ
h1
e
h2
解法二：首先将两侧的压强分布图叠加，直接求总压力
(h2 h1 ) ( gh1 gh2 ) FP b b 117.6kN 方向向右 2 1 FP三角形 三角形b g (h1 h2 ) (h1 h2 ) b 39.2kN 2
Yangzhou Univ
《水力学》
第一章 水静力学
§3 重力作用下静水压强的分布规律
3 重力作用下静水压强的分布规律 z
3.1 水静力学基本方程
p0 h 1 Z 2 Z0
p p0 gh
压强由两 部分组成 液面上的气体压强p0
单位面积上高度为h的液柱重 y ρgh
x
若已知：液面气体压强p0=98kN/m2，水深h1=1m， 试计算：1点处的压强及同水深壁面上点的压强。
FP矩形 矩形 b g (h1 h2 ) h2 b 78.4kN
h1 h2 h2 ) FP矩形 依力矩定理： FP e FP三角形 (h2 3 2
Yangzhou Univ
可解得：e=1.56m
《水力学》
第一章 水静力学
§5 作用于平面上的静水总压力
4.3 解析法 ——适用于任意形状的平面 F
dFP ghdA gL sin dA
FP dFP gL sin dA
A A
P
O （b）
hc
h
dFP
α
D C
g sin LdA
A
dA L
M（b，L） C LC
b
其中
为平面对Ob轴的面积矩
p fy y
整理化简得：
Euler平衡微分方程式
p fz z
Yangzhou Univ
《水力学》
第一章 水静力学
§2 液体平衡的微分方程式
2 液体平衡的微分方程式
液体平衡状态时,作用于液体上各种力之间的关系式 形心点A的压强为p ( x, y, z ) 则
(p p dx p dx )dydz ( p )dydz f x dxdydz 0 x 2 x 2 p fx x
p fy y
整理化简得：
平衡液体中，静水压强沿某 一方向的变化率与该方向的 单位体积上的质量力相等。
p fz z
Yangzhou Univ
《水力学》
第一章 水静力学
§2 液体平衡的微分方程式
2 液体平衡的微分方程式
液体平衡状态时,作用于液体上各种力之间的关系式 形心点A的压强为p ( x, y, z ) 则
《水力学》
第一章 水静力学
§4 压强的测量
4 压强的测量
——利用静水力学原理设计的液体测压计
4.1
测压管
pa
h
A B A
L h α
pA pB g h
pA g h g L sin
Yangzhou Univ
《水力学》
第一章 水静力学
§4 压强的测量
B
《水力学》
第一章 水静力学
§5 作用于平面上的静水总压力
画出下列容器左侧壁面上的压强分布图
Yangzhou Univ
《水力学》
第一章 水静力学
§5 作用于平面上的静水总压力
5.2 图解法 ——适用于矩形平面
静水总压力的大小:
FP
A
FP b
e
B
b O
Ω为静水压强分布图形的面积； b为矩形受压面的宽度； 静水总压力的方向：垂直并指向受压面
dx A dy
z
dz
pp (