七年级下全等三角形练习题经典综合拔高题
(完整)全等三角形证明之能力拔高(经典题目)

全等三角形能力拔高题姓名:一、角度转化问题1.已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.2.已知:如图,AD=AE,AB=AC,∠DAE=∠BAC.求证:BD=CE.3.已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.4.如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l 的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,求证:EF=AE+BF.5.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.二、二次全等问题1.已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.2.已知:如图,AC与BD交于O点,AB∥DC,AB=DC.若过O点作直线l,分别交AB、DC于E、F两点,求证:OE=OF.3.如图,E在AB上,∠1=∠2,∠3=∠4,那么AC等于AD吗?为什么?4.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.MF E CBA5、已知:如图,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC 于F ,DB=DC , 求证:EB=FC【练习】1、已知∠B=∠E=90°,CE=CB ,AB ∥CD. 求证:△ADC 是等腰三角形。
2、如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
求证:MB=MCG FEDC BA3、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD4、如图:在△ABC 中,∠C =90°,AD 平分∠ BAC ,DE ⊥AB 交AB 于E ,BC=30, BD :CD=3:2,则DE= 。
5、如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。
北师七年级下册数学全等三角形的基础、判定、经典、精选拔高证明题

七年级下册数学全等三角形的基础,判定,经典,精选证明题(一)全等三角形的基础1、已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证:AC∥DF.2、如图,已知: AD是BC上的中线 ,且DF=DE.求证:BE∥CF.3、如图, 已知:AB⊥BC于B , EF⊥AC于G , DF⊥BC于D , BC=DF.求证:AC=EF.4、如图,在ΔABC中,AC=AB,AD是BC边上的中线。
求证:AD⊥BC,5、如图,已知AB=DE,BC=EF,AF=DC。
求证:∠EFD=∠BCA 6、如图,ΔABC的两条高AD、BE相交于H,且AD=BD,试说明下列结论成立的理由。
(1)∠DBH=∠DAC;(2)ΔBDH≌ΔADC。
7、已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
8、如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.9、在△ABC中,,AB=AC, 在AB边上取点D,在AC延长线上了取点E ,使CE=BD , 连接DE交BC于点F,求证DF=EF .(二) 全等三角形的判定1.已知∠BAC=∠DAE,∠1=∠2,BD=CE,问ABD≌⊿ACE.吗?为什么?ADEBC122.已知CD∥AB,DF∥EB,DF=EB,问AF=CE吗?说明理由。
ADCEFB3.已知BE=CF,AB=CD,∠B=∠C.问AF=DE吗?ACDBEF4.已知AD=CB,∠A=∠C,AE=CF,问EB∥DF吗?说明理由。
BADFEC5.已知,M是AB的中点,∠1=∠2,MC=MD,问∠C=∠D吗?说明理由。
MABCD126.已知,AE=DF,BF=CE,AE∥DF,问AB=CD吗?说明理由。
DCFEAB7.已知∠1=∠2,∠3=∠4,问AC=AD吗?说明理由。
ACDB12348.已知∠E=∠F,∠1=∠2,AB=CD,问AE=DF吗?说明理由。
全等三角形拔高题目附带答案

全等三角形提高练习1. 如下图,△≌△,的延长线过点E ,∠∠105°,∠10°,∠50°,求∠的度数。
2. 如图,△中,∠30°,将△绕点O 顺时针旋转52°,得到△A ′′,边A ′B ′与边交于点C 〔A ′不在上〕,那么∠A3. 如下图,在△中,∠90°,D 、E么∠C 的度数是多少?AB'C4. 如下图,把△绕点C 顺时针旋转35°,得到△A ′B ′C ,A ′假设∠A ′90°,那么∠5. ,如下图,,⊥于D ,且50,而40,那么是多少?6. 如图,△中,∠90°,,分别过点B 、C 作过点A 的垂线、,垂足分别为D 、E ,假设3,2,那么7. 如图,是△的角平分线,⊥,⊥,垂足分别是E 、F 垂直吗?证明你的结论。
A B8.如下图,在△中,为∠的角平分线,⊥于E,⊥于F,△的面积是28220,8,求的长。
9.,如图:,∠∠E,∠∠,∠∠,求证:⊥10.如图,,⊥于D,⊥于E,与相交于点HC B11. 如下图,,为△的高,E 为上一点,交于F ,且有,,求证:⊥12.△、△均是等边三角形,、分别与、交于点M 、N〔3〕△为等边三角形 〔4〕∥ 13.:如图1,点C 为线段上一点,△、△都是等边三角形,交于点E ,交于点F (1) 求证:BAB(2)求证:△为等边三角形14.∠60°;⑤△是等边三角形;⑥∥,其中正确的有〔A.3个 B. 4个 C. 5个 D. 6个15.:、是△的高,点F在上,,点G在的延长线上,16.如图:在△中,、分别是、两边上的高,在上截取,在的延长线上截取,连结、求证:〔1〕〔2〕与的位置关系如何AB B17.如图,E 是正方形的边的中点,点F 在上,且∠∠ 求证:18.如下图,△中,,D 是延长线上一点,∠60°,E 是上一点,且,求证:19.如下图,在△中,∠90°,平分∠,⊥,垂足为F ,,求证:D20.如图:,直线、相交于C ,∠∠180°,∥,交于F21.如图,是∠的平分线,P 是上一点,⊥于D ,⊥于E ,F 是上一点,连接和,求证:22.:如图,⊥于点F ,⊥于点E ,且,求证:〔1〕△≌△ 〔2〕 点D 在∠A 的平分线上B23.如图,∥,O 是∠与∠的平分线的交点,⊥于E距离是多少?24.如图,过线段的两个端点作射线、画∠、∠的平分线交于E 〔1〕∠是什么角?〔2〕过点E 作一直线交于D ,交于C ,观察线段、,你有何发现? 〔3〕无论的两端点在、如何移动,只要经过点E ,①;②谁成立?并说明理由。
七年级下全等三角形练习题经典综合拔高题

1..AB=DE,BE=CF.求证:AC∥DF,已知:如图点B,E,C,F在同一直线上,AB∥DE,且且 ,线已知: AD是BC上的中22.如图,.DF=DE.求证:BE∥CFBCB , EF⊥AC于G , DF⊥于23.如图, 已知:AB⊥BC F.D , BC=DF.求证:AC=EF 于AGCBDEBC,请说明理由。
,ABC中,AC=ABAD是BC边上的中线,则AD⊥Δ24.如图,在ACB D,请说明理由。
EFD=∠BCA,则∠,25.如图,已知AB=DEBC=EF,AF=DC E ADCF,AE=AC平分∠上一点,是边中,Δ26.如图,在ABCDBCADBACAB,在上截取B A - 1 -BC的长。
,已知DE=2cm,BD=3cm,求线段连结DE,试说明下列结论成立的AD=BDBE相交于H,且ABC27.如图,Δ的两条高AD、理由。
;)∠DBH=∠DAC(1A。
≌ΔADC(2)ΔBDH E HBCD上,、、、如图,已知为等边三角形,、分别在边28.CABC?ABCABEDF且也是等边三角形.DEF?除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的(1)猜想是正确的;你所证明相等的线段,可以通过怎样的变化相互得到?写出变化(2)A过程.EFCDBAD与BE相已知等边三角形ABC中,BD=CE,9,交于点P,求∠APE的大小。
AFBC边上的一点,是如图,在矩形10.ABCD中,F=,且于⊥,的延长线于的延长线交DCGDEAGEDE- 2 -,根据上述条件,请你在图中找出一对全等三角形,并证明你的结论。
DC AD在P的平分线,BD为∠ABCAB=BC,点11已知:如图所示,M的关系.,判断PM与PN于PM⊥AD于M,?PN⊥CDNBD上,PNC B°,∠OAP+∠OBP=180的平分线上一点,PC⊥OA于C,?12如图所示,P为∠AOB ,求AO+BO的值.若OC=4cmA C PODBEC=2.AD=4,CE⊥PB,若AD如图,13∠ABC=90°,AB=BC,BP为一条射线,⊥BP,DE的长。
全等三角形拔高题目附带答案

全等三角形提高练习1. 如图所示,△ABC ≌△ADE ,BC 的延长线过点E ,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF的度数。
2. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A ′OB ′,边A ′B ′与边OB 交于点C (A ′不在OB 上),则∠A ′CO 的度数为多少?3. 如图所示,在△ABC 中,∠A=90°,D 、E 分别是AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC ,则∠C 的度数是多少?4. 如图所示,把△ABC 绕点C 顺时针旋转35°,得到△A ′B ′C ,A ′B ′交AC 于点D ,若∠A ′DC=90°,则∠A=5. 已知,如图所示,AB=AC ,AD ⊥BC 于D ,且AB+AC+BC=50cm,而AB+BD+AD=40cm ,则AD 是多少?6. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B 、C 作过点A 的垂线BC 、CE ,垂足分别为D 、E ,若BD=3,CE=2,则DE=AB'CA7. 如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,连接EF ,交AD 于G ,AD 与EF 垂直吗?证明你的结论。
8. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 的面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长。
9. 已知,如图:AB=AE ,∠B=∠E ,∠BAC=∠EAD ,∠CAF=∠DAF ,求证:AF ⊥CD10. 如图,AD=BD ,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点H ,则BH 与AC 相等吗?为什么?11. 如图所示,已知,AD 为△ABC 的高,E 为AC 上一点,BE 交AD 于F ,且有BF=AC ,FD=CD ,求证:BE ⊥AC12. △DAC 、△EBC 均是等边三角形,AF 、BD 分别与CD 、CE 交于点M 、N ,求证:(1)AE=BD (2)CM=CN (3)△CMN 为等边三角形 (4)MN ∥BCBCBBAB C13. 已知:如图1,点C 为线段AB 上一点,△ACM 、△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN 于点F(1) 求证:AN=BM(2) 求证:△CEF 为等边三角形14. 如图所示,已知△ABC 和△BDE 都是等边三角形,下列结论:①AE=CD ;②BF=BG ;③BH 平分∠AHD ;④∠AHC=60°;⑤△BFG 是等边三角形;⑥FG ∥AD ,其中正确的有( ) A .3个 B. 4个 C. 5个 D. 6个15. 已知:BD 、CE 是△ABC 的高,点F 在BD 上,BF=AC ,点G 在CE 的延长线上,CG=AB ,求证:AG ⊥AF16. 如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG求证:(1)AD=AG(2)AD 与AG 的位置关系如何17.如图,已知E 是正方形ABCD 的边CD 的中点,点F 在BC 上,且∠DAE=∠FAE求证:AF=AD-CF18.如图所示,已知△ABC 中,AB=AC ,D 是CB 延长线上一点,∠ADB=60°,E 是AD 上一点,且DE=DB ,求证:AC=BE+BC19.如图所示,已知在△AEC 中,∠E=90°,AD 平分∠EAC ,DF ⊥AC ,垂足为F ,DB=DCA B B D20.已知如图:AB=DE ,直线AE 、BD 相交于C ,∠B+∠D=180°,AF ∥DE ,交BD 于F ,求证:CF=CD21.如图,OC 是∠AOB 的平分线,P 是OC 上一点,PD ⊥OA 于D ,PE ⊥OB 于E ,F 是OC 上一点,连接DF 和EF ,求证:DF=EF22.已知:如图,BF ⊥AC 于点F ,CE ⊥AB 于点E ,且BD=CD ,求证:(1)△BDE ≌△CDF (2) 点D 在∠A的平分线上23.如图,已知AB ∥CD ,O 是∠ACD 与∠BAC 的平分线的交点,OE ⊥AC 于E ,且OE=2,则AB 与CD 之间的距离是多少?24.如图,过线段AB 的两个端点作射线AM 、BN ,使AM ∥BN ,按下列要求画图并回答:画∠MAB 、∠NBA 的平分线交于E(1)∠AEB 是什么角?(2)过点E 作一直线交AM 于D ,交BN 于C ,观察线段DE 、CE ,你有何发现? (3)无论DC 的两端点在AM 、BN 如何移动,只要DC 经过点E ,①AD+BC=AB ;②AD+BC=CD 谁成立?并说明理由。
最全全等三角形练习题综合拔高题

全等三角形拔高题1.如图,在ΔABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知DE=2cm,BD=3cm,求线段BC的长。
2.已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
3.已知:如图所示,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,•PN⊥CD于N,判断PM与PN的关系.4.如图所示,P为∠AOB的平分线上一点,PC⊥OA于C,•∠OAP+∠OBP=180°,若OC=4cm,求AO+BO的值.5.如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别AB CDEPDACBMNPDACBO作DE•⊥AC ,BF ⊥AC ,若AB=CD ,可以得到BD 平分EF ,为什么?若将△DEC 的边EC 沿AC 方向移动,变为如图所示时,其余条件不变,上述结论是否成立?请说明理由.6. 如图,△ABC 中,D 是BC 的中点,过D 点的直线GF 交AC 于F ,交AC 的平行线BG 于G 点, DE ⊥DF ,交AB 于点E ,连结EG 、EF .(1) 求证:BG=CF;(2) 请你判断BE+CF 与EF 的大小关系,并说明理由。
7. 已知:如图E 在△ABC 的边AC 上,且∠AEB=∠ABC 。
(1) 求证:∠ABE=∠C ;(2) 若∠BAE 的平分线AF 交BE 于F ,FD ∥BC 交AC 于D ,设AB=5,AC=8,求DC 的长。
8. 如图,在△ABC 和△DCB 中,AB = DC ,AC = DB ,AC 与DB 交于点M .G D F A C B E G D F A C B E FE D C B AG(1) 求证:△ABC ≌△DCB ;(2)过点C 作CN ∥BD ,过点B 作BN ∥AC ,CN 与BN 交于点N ,试判 断线段BN 与CN 的数量关系,并证明你的结论.9. 已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,(1) 求证:△AED ≌△EBC .(2) 观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):10. 如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .(1) 求证:MB =MD ,ME =MF(2) 当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.B C A D M NO ED C B A11. 如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE ⊥BD 于E .(1) 若BD 平分∠ABC ,求证CE=12BD ;(2) 若D 为AC 上一动点,∠AED 如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由。
全等三角形拔高题目附带标准答案

全等三角形提高练习1. 如图所示,△AB C ≌△AD E,BC 的延长线过点E ,∠ACB =∠AE D=105°,∠CA D=10°,∠B=50°,求∠D EF的度数。
2. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A′OB′,边A ′B ′与边O B交于点C(A ′不在OB 上),则∠A ′CO 的度数为多少?3. 如图所示,在△AB C中,∠A=90°,D 、E 分别是AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC,则∠C 的度数是多少?4. 如图所示,把△ABC 绕点C 顺时针旋转35°,得到△A′B ′C ,A ′B′交AC 于点D,若∠A ′DC=90°,则∠A=5. 已知,如图所示,A B=AC ,A D⊥BC 于D ,且AB +AC+B C=50cm ,而AB+BD +AD=40cm ,则AD 是多少?6. 如图,R t△A BC中,∠BAC=90°,AB=AC ,分别过点B 、C作过点A 的垂线BC 、CE ,垂足分别为D 、E,若BD=3,CE=2,则DE=AB'CA7. 如图,AD 是△A BC 的角平分线,D E⊥AB ,D F⊥AC,垂足分别是E、F,连接EF,交AD于G,AD 与EF 垂直吗?证明你的结论。
8. 如图所示,在△AB C中,AD 为∠BAC 的角平分线,D E ⊥AB 于E,DF ⊥AC 于F ,△ABC 的面积是28cm2,AB=20cm ,AC=8cm ,求DE 的长。
9. 已知,如图:AB =AE ,∠B=∠E ,∠BAC=∠EAD ,∠CAF =∠DAF,求证:AF ⊥CD10. 如图,A D=BD ,A D ⊥BC 于D,BE ⊥AC 于E ,AD 与BE相交于点H ,则BH 与A C相等吗?为什么?11. 如图所示,已知,AD 为△AB C的高,E 为A C上一点,BE 交AD 于F ,且有BF=AC ,FD=CD,求证:BE⊥AC12. △DAC 、△E BC均是等边三角形,A F、BD 分别与CD 、CE 交于点M、N,求证:(1)A E=BD (2)CM=CN (3)△CMN 为等边三角形 (4)M N∥BCBCBBA B。
全等三角形证明之能力拔高(经典题目)
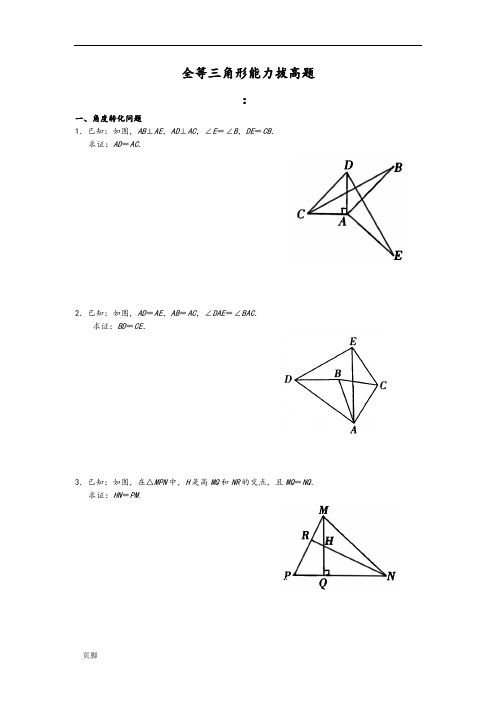
全等三角形能力拔高题:一、角度转化问题1.已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.2.已知:如图,AD=AE,AB=AC,∠DAE=∠BAC.求证:BD=CE.3.已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.4.如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,求证:EF=AE+BF.5.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.二、二次全等问题1.已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.2.已知:如图,AC与BD交于O点,AB∥DC,AB=DC.若过O点作直线l,分别交AB、DC于E、F两点,求证:OE=OF.3.如图,E在AB上,∠1=∠2,∠3=∠4,那么AC等于AD吗?为什么?4.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.5、已知:如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,DB=DC,MF E CBA求证:EB=FC【练习】1、已知∠B=∠E=90°,CE=CB ,AB ∥CD. 求证:△ADC 是等腰三角形。
2、如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
求证:MB=MCEAG FEDC BA 3、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD4、如图:在△ABC 中,∠C =90°,AD 平分∠ BAC ,DE ⊥AB 交AB 于E ,BC=30, BD :CD=3:2,则DE= 。
5、如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。
七年级下全等三角形练习题经典综合拔高题

1. 已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF.求证:AC ∥DF .2. 如图,已知: AD 是BC 上的中线 ,且DF=DE .求证:BE ∥CF .3. 如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC于D , BC=DF .求证:AC=EF .4. 如图,在ΔABC 中,AC=AB ,AD 是BC 边上的中线,则AD ⊥BC ,请说明理由。
5. 如图,已知AB=DE ,BC=EF ,AF=DC ,则∠EFD=∠BCA ,请说明理由。
FGEDCBAA BC D E F A B C DF E DCBA6. 如图,在ΔABC 中,D 是边BC 上一点,AD 平分∠BAC ,在AB 上截取AE=AC ,连结DE ,已知DE=2cm ,BD=3cm ,求线段BC 的长。
7. 如图,ΔABC 的两条高AD 、BE 相交于H ,且AD=BD ,试说明下列结论成立的理由。
(1)∠DBH=∠DAC ;(2)ΔBDH ≌ΔADC 。
8. 如图,已知ABC ∆为等边三角形,D 、E 、F 分别在边BC 、CA 、AB 上,且DEF ∆也是等边三角形.(1) 除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的;(2) 你所证明相等的线段,可以通过怎样的变化相互得到?写出变化过程.9,已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
A B C DE A BCDE H10.如图,在矩形ABCD 中,F 是BC 边上的一点,AF 的延长线交DC 的延长线于G ,DE ⊥AG 于E ,且DE =DC ,根据上述条件,请你在图中找出一对全等三角形,并证明你的结论。
11已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点P 在BD 上,PM ⊥AD 于M ,•PN ⊥CD 于N ,判断PM 与PN 的关系.12如图所示,P 为∠AOB 的平分线上一点,PC ⊥OA 于C ,•∠OAP+∠OBP=180°,若OC=4cm ,求AO+BO 的值.13如图,∠ABC=90°,AB=BC ,BP 为一条射线,AD ⊥BP ,CE ⊥PB ,若AD=4,EC=2.求DE 的长。
全等三角形拔高题目附带答案

全等三角形提高练习1. 如图所示,△A BC ≌△ADE,BC 的延长线过点E,∠ACB=∠AE D=105°,∠CA D=10°,∠B =50°,求∠DE F的度数。
2. 如图,△AO B中,∠B=30°,将△A OB 绕点O顺时针旋转52°,得到△A ′OB ′,边A ′B ′与边OB交于点C (A ′不在O B上),则∠A ′CO 的度数为多少?3. 如图所示,在△AB C中,∠A=90°,D 、E 分别是AC 、BC 上的点,若△ADB ≌△ED B≌△EDC,则∠C的度数是多少?4. 如图所示,把△A BC 绕点C 顺时针旋转35°,得到△A′B ′C,A ′B′交AC 于点D,若∠A ′DC=90°,则∠A=5. 已知,如图所示,A B=AC ,A D ⊥BC 于D,且AB+AC+BC=50cm,而AB+BD+AD =40cm,则AD 是多少?6. 如图,Rt △ABC 中,∠BA C=90°,AB=AC ,分别过点B 、C作过点A 的垂线B C、CE,垂足分别为D 、E ,若BD=3,C E=2,则DE =AB'CA7. 如图,AD 是△ABC 的角平分线,DE ⊥AB,DF ⊥AC ,垂足分别是E、F ,连接EF,交AD 于G ,AD 与EF垂直吗?证明你的结论。
8. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,DE ⊥AB 于E ,DF ⊥A C于F ,△ABC 的面积是28cm 2,AB=20cm,AC =8c m,求DE 的长。
9. 已知,如图:A B=AE,∠B=∠E,∠BAC=∠EAD ,∠CAF =∠DAF,求证:AF ⊥C D10. 如图,AD=BD,A D ⊥BC 于D ,BE ⊥AC 于E ,A D与BE 相交于点H,则BH 与AC 相等吗?为什么?11. 如图所示,已知,AD 为△A BC 的高,E 为AC 上一点,BE 交AD 于F ,且有BF =AC ,F D=CD ,求证:BE ⊥AC12. △DAC 、△EBC 均是等边三角形,A F、BD 分别与C D、CE 交于点M 、N,求证:(1)AE=B D (2)CM=CN (3)△CMN 为等边三角形 (4)MN ∥BCBCBBAB13. 已知:如图1,点C 为线段AB 上一点,△ACM 、△CB N都是等边三角形,A N交M C于点E,BM交CN 于点F(1) 求证:AN=BM(2) 求证:△CEF 为等边三角形14. 如图所示,已知△AB C和△BDE 都是等边三角形,下列结论:①AE=CD ;②BF=BG;③B H平分∠AHD ;④∠A HC =60°;⑤△B FG是等边三角形;⑥FG ∥A D,其中正确的有(A .3个 B. 4个 C . 5个 D. 6个15. 已知:BD 、CE 是△ABC 的高,点F在BD上,BF=AC ,点G 在C E的延长线上,CG=AB,求证:A G⊥AF16. 如图:在△AB C中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取B D=AC ,在CF 的延长线上截取CG=AB,连结AD 、AG求证:(1)A D=AG(2)AD 与AG 的位置关系如何17.如图,已知E 是正方形ABCD 的边CD 的中点,点F 在B C上,且∠DAE=∠FA E求证:AF =AD-CF18.如图所示,已知△ABC 中,AB=AC ,D 是CB 延长线上一点,∠ADB=60°,E是AD 上一点,且DE=DB,求证:AC=BE+BCA B B19.如图所示,已知在△AEC 中,∠E =90°,AD 平分∠EAC,DF ⊥AC,垂足为F ,DB=DC ,求证:BE=CF20.已知如图:AB=DE,直线AE 、BD 相交于C ,∠B+∠D=180°,A F∥DE ,交B D于F,求证:CF=CD21.如图,OC 是∠AOB 的平分线,P 是O C上一点,PD⊥OA 于D ,PE⊥O B于E ,F是O C上一点,连接DF和E F,求证:DF=E F22.已知:如图,BF ⊥AC 于点F ,CE ⊥AB 于点E,且B D=CD ,求证:(1)△BDE ≌△CD F (2) 点D在∠A 的平分线上23.如图,已知AB ∥CD ,O 是∠ACD 与∠BAC 的平分线的交点,OE ⊥AC 于E,且O E=2,则AB 与CD 之间的距离是多少?24.如图,过线段AB 的两个端点作射线A M、BN ,使AM ∥B N,画∠MAB 、∠N BA 的平分线交于E(1)∠AEB 是什么角?(2)过点E 作一直线交AM 于D,交BN 于C ,观察线段DE 、C E,你有何发现? (3)无论DC 的两端点在AM、BN 如何移动,只要DC经过点E,①A D+BC=AB;②A D+BC=CD 谁成立?并说B C明理由。
全等三角形证明之能力拔高(经典题目)

全等三角形能力拔高题(一)姓名:一、角度转化问题1.已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.2.已知:如图,AD=AE,AB=AC,∠DAE=∠BAC.求证:BD=CE.3.已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.4.如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,求证:EF=AE+BF.5.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.二、二次全等问题1.已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.2.已知:如图,AC与BD交于O点,AB∥DC,AB=DC.若过O点作直线l,分别交AB、DC 于E、F两点,求证:OE=OF.3.如图,E在AB上,∠1=∠2,∠3=∠4,那么AC等于AD吗?为什么?4.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.G FEDCB A5、已知:如图,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC 于F ,DB=DC , 求证:EB=FC【练习】1、已知∠B=∠E=90°,CE=CB ,AB ∥CD. 求证:△ADC 是等腰三角形。
2、如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
求证:MB=MC3、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD 4、如图:在△ABC 中,∠C =90°,AD 平分∠ BAC ,DE ⊥AB 交AB 于E ,BC=30, BD :CD=3:2,则DE=。
5、如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。
全等三角形练习题综合拔高题

1.如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC 于D , BC=DF .求证:AC=EF .2.如图,在ΔABC 中,D 是边BC 上一点,AD 平分∠BAC ,在AB 上截取AE=AC ,连结DE ,已知DE=2cm ,BD=3cm ,求线段BC 的长。
3.已知等边三角形ABC 中,BD =CE ,AD 与BE 相交于点P ,求∠APE 的大小。
4.如图所示,P 为∠AOB 的平分线上一点,PC ⊥OA 于C ,•∠OAP+∠OBP=180°,若OC=4cm ,求AO+BO 的值.5.如图所示,A ,E ,F ,C 在一条直线上,AE=CF ,过E ,F 分别作DE•⊥AC ,BF ⊥AC ,若AB=CD ,可以得到BD 平分EF ,为什么?若将△DEC 的边EC 沿AC 方向移动,变为如图所示时,其余条件不变,上述结论是否成立?请说明理由. 6.如图,△ABC 中,D 是BC 的中点,过D 点的直线GF 交AC 于F ,交AC 的平行线BG 于G 点,DE ⊥DF ,交AB 于点E ,连结EG 、EF.(1) 求证:BG=CF; (2) 请你判断BE+CF 与EF 的大小关系,并说明理由。
7.如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O.求证:(1) △ABC ≌△AED ; (2) OB =OE .8.如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D为AC 上一点,CE ⊥BD 于E .若BD 平分∠ABC ,求证CE=12BD ;PD A COFEDCBAGE9.如图所示,△ABC 中,∠ACB=90°,AC=BC,AE 是BC 边上的中线,过C 作CF ⊥AE, 垂足为F,过B 作BD ⊥BC 交CF 的延长线于D.求证:(1)AE=CD;(2)若AC=12cm,求BD 的长.10.如图,ABCD 是正方形,点G 是BC 上的任意一点,DE AG ⊥于E ,BF DE ∥,交AG 于F .求证:AF BF EF =+.DCBA EFG。
(整理)七级下册数学同步拔高(综合强化)北师版三角形全等基础

七年级下册数学同步拔高(综合+强化)北师版三角形全等基础一、单选题(共7道,每道15分)1.如图PD⊥AB于D,PE⊥AC于E,且PD=PE,则△APD与△APE全等的理由是()A.SASB.AASC.SSAD.HL2.木工师傅在制作门框时,需要在矩形门框的对角钉一根木条,他这样做的原因是()A.利用三角形的稳定性来改变矩形的不稳定性,以防变形B.更好看一些C.防盗能力更强D.以上都不正确3.如图,AC=DF,BC=EF,AD=BE,则下面说法不正确的是()A.△ABC≌△DEFB.∠C=∠FC.∠A=∠EDFD.∠EDF=∠CBA4.如图,D在AB上,E在AC上,且∠B=∠C,则在下列条件中,无法判定△ABE≌△ACD的是()A.AD=AEB.AB=ACC.BE=CDD.∠AEB=∠ADC5.已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,可补充的条件有()①AC=AE②∠C=∠E③∠B=∠D④∠BAC=∠DAEA.①②④B.①②③C.②③④D.①③④6.如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G,∠AED=105°,∠CAD=25°,∠B=30°,则∠1的度数为()A.60°B.70°C.80°D.85°7.如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD、BC交于点P,连接OP,则下列结论中正确的有()①△APC≌△BPD②△ADO≌△BCO③△AOP≌△BOP④△OCP≌△ODP.A.①②④B.①②③C.②③④D.①②③④。
七年级下册数学同步拔高(综合 强化)北师版 三角形全等基础

七年级下册数学同步拔高(综合+强化)北师版三角形全等基础一、单选题(共7道,每道15分)1.如图PD⊥AB于D,PE⊥AC于E,且PD=PE,则△APD与△APE全等地理由是()A.SASB.AASC.SSAD.HL2.木工师傅在制作门框时,需要在矩形门框地对角钉一根木条,他这样做地原因是()A.利用三角形地稳定性来改变矩形地不稳定性,以防变形B.更好看一些C.防盗能力更强D.以上都不正确3.如图,AC=DF,BC=EF,AD=BE,则下面说法不正确地是()A.△ABC≌△DEFB.∠C=∠FC.∠A=∠EDFD.∠EDF=∠CBA4.如图,D在AB上,E在AC上,且∠B=∠C,则在下列条件中,无法判定△ABE≌△ACD地是()A.AD=AEB.AB=ACC.BE=CDD.∠AEB=∠ADC5.已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,可补充地条件有()①AC=AE②∠C=∠E③∠B=∠D④∠BAC=∠DAEA.①②④B.①②③C.②③④D.①③④6.如图,△ABC≌△ADE,BC地延长线交DA于点F,交DE于点G,∠AED=105°,∠CAD=25°,∠B=30°,则∠1地度数为()A.60°B.70°C.80°D.85°7.如图,在∠AOB地两边上截取AO=BO,OC=OD,连接AD、BC交于点P,连接OP,则下列结论中正确地有()①△APC≌△BPD②△ADO≌△BCO③△AOP≌△BOP④△OCP≌△ODP.A.①②④B.①②③C.②③④D.①②③④。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,
且AB=DE,BE=CF.求证:AC ∥DF .
2. 如图,已知: AD 是BC 上的中线 ,且
DF=DE .求证:BE ∥CF .
3. 如图, 已知:AB ⊥BC 于B , EF ⊥AC 于G , DF ⊥BC
于D , BC=DF .求证:AC=EF .
4. 如图,在ΔABC 中,AC=AB ,AD 是BC 边上的中线,则AD ⊥BC ,请说明理由。
5. 如图,已知AB=DE ,BC=EF ,AF=DC ,则∠EFD=∠BCA ,请说明理由。
F
G
E
D
C
B
A
A B
C D E F A B C D
F E D
C
B
A
6. 如图,在ΔABC 中,D 是边BC 上一点,AD 平分∠BAC ,在AB 上截取AE=AC ,
连结DE ,已知DE=2cm ,BD=3cm ,求线段BC 的长。
7. 如图,ΔABC 的两条高AD 、BE 相交于H ,且AD=BD ,试说明下列结论成立的
理由。
(1)∠DBH=∠DAC ;
(2)ΔBDH ≌ΔADC 。
8. 如图,已知ABC ∆为等边三角形,D 、E 、F 分别在边BC 、CA 、AB 上,
且DEF ∆也是等边三角形.
(1) 除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的
猜想是正确的;
(2) 你所证明相等的线段,可以通过怎样的变化相互得到?写出变化
过程.
9,已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
A B C D
E A B
C
D
E H
10.如图,在矩形ABCD 中,F 是BC 边上的一点,AF 的延长线交DC 的延长线于G ,DE ⊥AG 于E ,且DE =DC ,根据上述条件,请你在图中找出一对全等三角形,并证明你的结论。
11已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点P 在
BD 上,PM ⊥AD 于M ,•PN ⊥CD 于N ,判断PM 与PN 的关系.
12如图所示,P 为∠AOB 的平分线上一点,PC ⊥OA 于C ,•∠OAP+∠OBP=180°,若OC=4cm ,求AO+BO 的值.
13如图,∠ABC=90°,AB=BC ,BP 为一条射线,AD ⊥BP ,CE ⊥PB ,若AD=4,EC=2.求DE 的长。
i.
14如图所示,A ,E ,F ,C 在一条直线上,AE=CF ,过E ,F 分别作DE•⊥AC ,BF ⊥AC ,若AB=CD ,可以得到BD 平分EF ,为什么?若将△DEC 的边EC 沿AC 方向移动,变为如图所示时,其余条件不变,上述结论是否成立?请说明理由.
P D A C M N P D A
C B O
15如图,OE=OF ,OC=OD ,CF 与DE 交于点A ,求证: AC=AD 。
16已知:如图E 在△ABC 的边AC 上,且∠AEB=∠ABC 。
(2) 求证:∠ABE=∠C ;
(3) 若∠BAE 的平分线AF 交BE 于F ,FD ∥BC 交AC 于D ,设AB=5,AC=8,求DC 的长。
17如图∠ACB=90°,AC=BC,BE ⊥CE,AD ⊥CE 于D ,AD=2、5cm ,DE=1.7cm,求BE 的长
18如图,在△ABE 中,AB =AE,AD =AC,∠BAD =∠EAC, BC 、DE 交于点O.求证:(1) △ABC ≌△AED ; (2) OB =OE .
G D
F
A
C
B
E
G
D
F
A
C
B
E
F E
D C
A
O
19如图,D 是等边△ABC 的边AB 上的一动点,以CD 为一边向上作等边△EDC ,连接AE ,找出图中的一组全等三角形,并说明理由.
20已知:如图,B 、E 、F 、C 四点在同一条直线上,AB =DC ,BE =CF ,∠B =∠C .
求证:OA =OD .
21如图,△ABC 中,∠BAC =90度,AB =AC ,BD 是∠ABC 的平分线,BD 的延长线垂直于过C 点的直线于E ,直线CE 交BA 的延长线于F .求证:BD =2CE .
22如图,,AB AC AD BC D AD AE AB DAE DE F =⊥=∠于点,,平分交于点,请你写出图中三对..全等三角形,并选取其中一对加以证明.
E D C B A
B
D
C
F A
E
F E D
C B
A
23如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M .
(3) 求证:MB =MD ,ME =MF
(4) 当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能
否成立?若成立请给予证明;若不成立请说明理由.
24如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE ⊥BD 于E .
(5) 若BD 平分∠ABC ,求证CE=1
2BD ;
(6) 若D 为AC 上一动点,∠AED 如何变化,
若变化,求它的变化范围;若不变,求出它的度数,并说明理由。
25、在△ABC 中,,AB=AC , 在AB 边上取点D ,在AC 延长线上了取点E ,使CE=BD , 连接DE 交BC 于点F ,求证DF=EF .
E D C
B
A
F
C B
A E
D
26、如图,△ABC 中,D 是BC 的中点,过D 点的直线GF 交AC 于F ,交AC 的平行线BG 于G 点,
DE ⊥DF ,交AB 于点E ,连结EG 、EF. (1) 求证:EG=EF;
(2) 请你判断BE+CF 与EF 的大小关系,并说明理由。
27、 如图△ABC ≌△A `B`C,∠ACB=90°,∠A=25°,点B 在A `B`上,
求∠ACA `的度数。
28、 如图:四边形ABCD 中,AD ∥BC ,AB=AD+BC ,E 是CD 的中点,求证:
AE ⊥BE 。
29、 如图所示,△ABC 中,∠ACB=90°,AC=BC,AE 是BC 边上的中线,过C 作CF
⊥AE, 垂足为F,过B 作BD ⊥BC 交CF 的延长线于D.
A`
B
B E F
E D C B A G
E
D
C
B
A
F
求证:(1)AE=CD;(2)若AC=12cm,求BD 的长.
30在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF=BE 。
i. 求证:CE=CF 。
ii. 在图中,若G 点在AD 上,且∠GCE=45° ,则GE=BE+GD 成立吗?
为什么?
31如图(1), 已知△ABC 中, ∠BAC=900, AB=AC, AE 是过A 的一条直线, 且B 、C 在A 、E 的异侧, BD ⊥AE 于D, CE ⊥AE 于E 试说明: BD=DE+CE.
32若直线AE 绕A 点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD 与DE 、CE 的关系如何? 为什么?
若直线AE 绕A 点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD 与DE 、CE 的关系如何? 请直接写出结果, 不需说明.
C
E G
E
D C B A
M
F 归纳前二个问得出BD 、DE 、CE 关系。
用简洁的语言加以说明。
33如图所示,已知D 是等腰△ABC 底边BC 上的一点,它到两腰AB 、AC 的距离
分别为DE 、DF,CM ⊥AB,垂足为M,请你探索一下线段DE 、DF 、CM 三者之间的数量关系, 并给予证明.
34在Rt △ABC 中,AB=AC ,∠BAC=90°,O 为BC 的中点. 写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系,并说明理由.
若点M 、N 分别是AB 、AC 上的点,且BM=AN ,试判断△OMN 形状,并证明你的结论. 35如图,ABCD 是正方形,点G 是BC 上的任意一点,DE AG ⊥于E ,BF DE ∥,交AG 于F .求证:AF=BF+EF .
36如图10,在四边形ABCD 中,AD ∥BC ,E 为CD 的中点,连结AE 、BE ,BE ⊥AE ,延长AE 交BC 的延长线于点F .
求证:(1)FC =AD ;
(2)AB =BC +AD .
如图①,将边长为4cm 的正方形纸片ABCD 沿EF 折叠(点E 、F 分别在边AB 、CD
D
C
B
A E
F
G
上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P,连接EP.
(1)如图②,若M为AD边的中点,
①,△AEM的周长=_____cm;
②求证:EP=AE+DP;
(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.。
