上海市各区2018届九年级中考二模数学试卷精选汇编:填空题专题
上海市黄浦区2018届中考二模数学试题--有答案

黄浦区2018年九年级模拟考数学试卷2018年4月(考试时间:100分钟总分:150分)一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】1.下列实数中,介于与之间的是()2332(A ;(B (C );(D ).3227π2.下列方程中没有实数根的是()(A );(B );210x x +-=210x x ++=(C );(D ).210x -=20x x +=3.一个反比例函数与一个一次函数在同一坐标平面内的图像如图示,如果其中的反比例函数解析式为,k y x=那么该一次函数可能的解析式是()(A );(B );y kx k =+y kx k =-(C );(D ).y kx k =-+y kx k =--4.一个民营企业10名员工的月平均工资如下表,则能较好反映这些员工月平均工资水平的是()人次1112113工资30321.51.220.8(工资单位:万元)(A )平均数;(B )中位数;(C )众数;(D )标准差.5.计算:()AB BA +=(A );(B );(C );(D )0.AB BA 06.下列命题中,假命题是()(A )如果一条直线平分弦和弦所对的一条弧,那么这条直线经过圆心,并且垂直于这条弦;(B )如果一条直线平分弦所对的两条弧,那么这条直线经过圆心,并且垂直于这条弦;(C )如果一条直线经过圆心,并且平分弦,那么该直线平分这条弦所对的弧,并且垂直于这条弦;(D )如果一条直线经过圆心,并且垂直弦,那么该直线平分这条弦和弦所对的弧.二、填空题:(本大题共12题,每题4分,满分48分)7=.21-8.因式分解:.212x x --=9.方程的解是.125x x +=+10.不等式组的解集是.12031302x x ⎧->⎪⎪⎨⎪-≤⎪⎩11.已知点P 位于第三象限内,且点P 到两坐标轴的距离分别为2和4,若反比例函数图像经过点P ,则该反比例函数的解析式为.12.如果一次函数的图像经过第一、二、四象限,那么其函数值y 随自变量x 的值的增大而.(填“增大”或“减小”)13.女生小琳所在班级共有40名学生,其中女生占60%.现学校组织部分女生去市三女中参观,需要从小琳所在班级的女生当中随机抽取一名女生参加,那么小琳被抽到的概率是.14.已知平行四边形相邻两个内角相差40°,则该平行四边形中较小内角的度数是.15.半径为1的圆的内接正三角形的边长为.16.如图,点D 、E 分别为△ABC 边CA 、CB 上的点,已知DE ∥AB ,且DE 经过△ABC 的重心,设,CA a =,则.(用、表示)CB b = DE = a b 17.如图,在四边形ABCD 中,,M 、N 分别是AC 、BD 的中902624ABC ADC AC BD ∠=∠=︒==,,点,则线段MN 的长为.(第16题)(第17题)(第18题)18.如图,将矩形ABCD 沿对角线AC 折叠,使点B 翻折到点E 处,如果DE ∶AC =1∶3,那么AD ∶AB =.三、解答题:(本大题共7题,满分78分)19.(本题满分10分)计算:.()()12322220182018323++---20.(本题满分10分)解方程组:.2222295x xy y x y ⎧-+=⎪⎨+=⎪⎩21.(本题满分10分)如图,AH 是△ABC 的高,D 是边AB 上一点,CD 与AH 交于点E .已知AB =AC =6,cos B =,23AD ∶DB =1∶2.(1)求△ABC 的面积;(2)求CE ∶DE .22.(本题满分10分)今年1月25日,上海地区下了一场大雪.这天早上王大爷去买菜,他先去了超市,发现蔬菜普遍涨价了,青菜、花菜和大白菜这两天的价格如下表.王大爷觉得超市的菜不够新鲜,所以他又去了菜市场,他花了30元买了一些新鲜菠菜,他跟卖菜阿姨说:“你今天的菠菜比昨天涨了5元/斤。
上海市各区2018届中考数学二模试卷精选汇编压轴题专题(有答案)
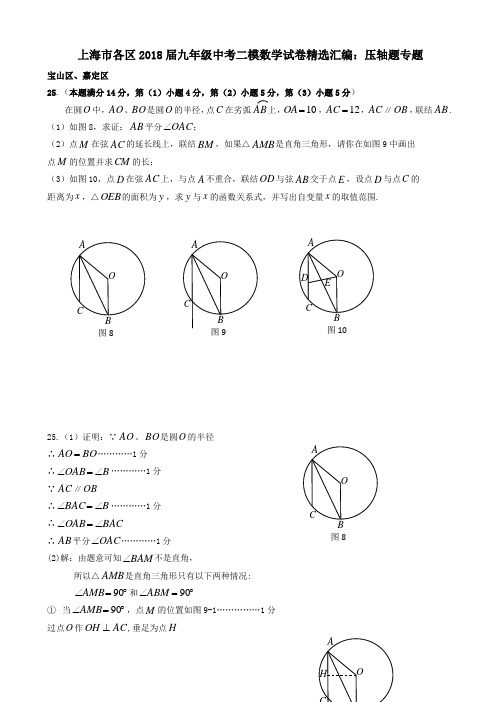
上海市各区2018届九年级中考二模数学试卷精选汇编:压轴题专题宝山区、嘉定区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)在圆O 中,AO 、BO 是圆O 的半径,点C 在劣弧AB 上,10=OA,12=AC ,AC ∥OB ,联结AB . (1)如图8,求证:AB 平分OAC ∠;(2)点M 在弦AC 的延长线上,联结BM ,如果△AMB 是直角三角形,请你在如图9中画出 点M 的位置并求CM 的长;(3)如图10,点D 在弦AC 上,与点A 不重合,联结OD 与弦AB 交于点E ,设点D 与点C 的 距离为x ,△OEB 的面积为y ,求y 与x 的函数关系式,并写出自变量x 的取值范围.25.(1)证明:∵AO 、BO 是圆O 的半径 ∴BO AO =…………1分 ∴B OAB ∠=∠…………1分 ∵AC ∥OB∴B BAC ∠=∠…………1分 ∴BAC OAB ∠=∠∴AB 平分OAC ∠…………1分 (2)解:由题意可知BAM ∠不是直角,所以△AMB 是直角三角形只有以下两种情况:︒=∠90AMB 和︒=∠90ABM① 当︒=∠90AMB ,点M 的位置如图9-1……………1分 过点O 作AC OH ⊥,垂足为点H图8图10图8∵OH 经过圆心 ∴AC HC AH 21== ∵12=AC ∴6==HC AH 在Rt △AHO 中,222OA HO AH =+ ∵10=OA ∴8=OH∵AC ∥OB ∴︒=∠+∠180OBM AMB ∵︒=∠90AMB ∴︒=∠90OBM ∴四边形OBMH 是矩形 ∴10==HM OB∴4=-=HC HM CM ……………2分 ②当︒=∠90ABM ,点M 的位置如图9-2 由①可知58=AB ,552cos =∠CAB 在Rt △ABM 中,552cos ==∠AM AB CAB∴20=AM8=-=AC AM CM ……………2分综上所述,CM 的长为4或8.说明:只要画出一种情况点M 的位置就给1分,两个点都画正确也给1分. (3)过点O 作AB OG ⊥,垂足为点G 由(1)、(2)可知,CAB OAG ∠=∠sin sin 由(2)可得:55sin =∠CAB ∵10=OA ∴52=OG ……………1分 ∵AC ∥OB ∴ADOBAE BE =……………1分 又BE AE -=58,x AD -=12,10=OB ∴xBEBE -=-121058 ∴x BE -=22580 ……………1分∴52225802121⨯-⨯=⨯⨯=xOG BE y ∴xy -=22400……………1分自变量x 的取值范围为120<≤x ……………1分图10长宁区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)在圆O 中,C 是弦AB 上的一点,联结OC 并延长,交劣弧AB 于点D ,联结AO 、BO 、AD 、BD . 已知圆O 的半径长为5 ,弦AB 的长为8.(1)如图1,当点D 是弧AB 的中点时,求CD 的长; (2)如图2,设AC =x ,y S S OBDACO=∆∆,求y 关于x 的函数解析式并写出定义域; (3)若四边形AOBD 是梯形,求AD 的长.25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分) 解:(1)∵OD 过圆心,点D 是弧AB 的中点,AB =8, ∴OD ⊥AB ,421==AB AC (2分) 在Rt △AOC 中,︒=∠90ACO Θ,AO =5, ∴322=-=AC AO CO (1分)5=OD Θ,2=-=∴OC OD CD (1分)(2)过点O 作OH ⊥AB ,垂足为点H ,则由(1)可得AH =4,OH =3 ∵AC =x ,∴|4|-=x CH在Rt △HOC 中,︒=∠90CHO Θ,AO =5, ∴258|4|322222+-=-+=+=x x x HC HO CO , (1分)∴525882+-⋅-=⋅=⋅==∆∆∆∆∆∆x x x x OD OC BC AC S S S S S S y OBD OBC OBC ACO OBD ACO O AC DBO BA C DBAOxx x x 5402582-+-= (80<<x ) (3分)(3)①当OB //AD 时, 过点A 作AE ⊥OB 交BO 延长线于点E ,过点O 作OF ⊥AD ,垂足为点F , 则OF =AE , AE OB OH AB S ABO ⋅=⋅=∆2121Θ ∴OF OB OH AB AE ==⋅=524 在Rt △AOF 中,︒=∠90AFO Θ,AO =5, ∴5722=-=OF AO AF ∵OF 过圆心,OF ⊥AD ,∴5142==AF AD . (3分) ②当OA //BD 时, 过点B 作BM ⊥OA 交AO 延长线于点M ,过点D 作DG ⊥AO ,垂足为点G , 则由①的方法可得524==BM DG , 在Rt △GOD 中,︒=∠90DGO Θ,DO =5, ∴5722=-=DG DO GO ,518575=-=-=GO AO AG , 在Rt △GAD 中,︒=∠90DGA Θ,∴622=+=DG AG AD ( 3分)综上得6514或=AD 崇明区25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)如图,已知ABC △中,8AB =,10BC =,12AC =,D 是AC 边上一点,且2AB AD AC =⋅,联结BD ,点E 、F 分别是BC 、AC 上两点(点E 不与B 、C 重合),AEF C ∠=∠,AE 与BD 相交于点G . (1)求证:BD 平分ABC ∠;(2)设BE x =,CF y =,求y 与x 之间的函数关系式; (3)联结FG ,当GEF △是等腰三角形时,求BE 的长度.25.(满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)(第25题图)A BCDGEF(备用图)ABCD(1)∵8AB =,12AC = 又∵2AB AD AC =g ∴163AD =∴16201233CD =-= ……………………………1分 ∵2AB AD AC =g ∴AD AB AB AC= 又∵BAC ∠是公共角 ∴ADB ABC △∽△ …………………………1分 ∴ABD C =∠∠,BD ADBC AB= ∴203BD =∴BD CD = ∴DBC C =∠∠ ………………………1分 ∴ABD DBC =∠∠ ∴BD 平分ABC ∠ ………………………1分 (2)过点A 作AH BC ∥交BD 的延长线于点H∵AH BC ∥ ∴16432053AD DH AH DC BD BC ==== ∵203BD CD ==,8AH = ∴163AD DH == ∴12BH = ……1分 ∵AH BC ∥ ∴AH HG BE BG = ∴812BG x BG -= ∴128xBG x =+…1分 ∵BEF C EFC =+∠∠∠ 即BEA AEF C EFC +=+∠∠∠∠ ∵AEF C =∠∠ ∴BEA EFC =∠∠ 又∵DBC C =∠∠∴BEG CFE △∽△ ……………………………………………………………1分∴BE BGCF EC= ∴12810x x x y x +=-∴228012x x y -++= …………………………………………………………1分(3)当△GEF 是等腰三角形时,存在以下三种情况:1° GE GF = 易证23GE BE EF CF == ,即23x y =,得到4BE = ………2分 2° EG EF = 易证BE CF =,即x y =,5BE =-+…………2分 3° FG FE = 易证 32GE BE EF CF == ,即32x y =3BE =-+ ………2分奉贤区25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)已知:如图9,在半径为2的扇形AOB 中,∠AOB=90°,点C 在半径OB 上,AC 的垂直平分线交OA 于点D ,交弧AB 于点E ,联结BE 、CD .(1)若C 是半径OB 中点,求∠OCD 的正弦值; (2)若E 是弧AB 的中点,求证:BC BO BE ⋅=2;(3)联结CE ,当△DCE 是以CD 为腰的等腰三角形时,求CD 的长.图9备用图ABO备用图ABO黄浦区25.(本题满分14分)如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;(2)当∠B=70°时,求∠AEC的度数;(3)当△ACE为直角三角形时,求边BC的长.25. 解:(1)过A作AH⊥BC于H,————————————————————(1分)由∠D=∠BCD=90°,得四边形ADCH为矩形.在△BAH 中,AB =2,∠BHA =90°,AH =y ,HB =1x -,所以22221y x =+-,——————————————————————(1分) 则()22303y x x x =-++<<.———————————————(2分)(2)取CD 中点T ,联结TE ,————————————————————(1分) 则TE 是梯形中位线,得ET ∥AD ,ET ⊥CD .∴∠AET =∠B =70°. ———————————————————————(1分) 又AD =AE =1,∴∠AED =∠ADE =∠DET =35°. ——————————————————(1分) 由ET 垂直平分CD ,得∠CET =∠DET =35°,————————————(1分) 所以∠AEC =70°+35°=105°. ——————————————————(1分)(3)当∠AEC =90°时,易知△CBE ≌△CAE ≌△CAD ,得∠BCE =30°, 则在△ABH 中,∠B =60°,∠AHB =90°,AB =2,得BH =1,于是BC =2. ——————————————————————(2分)当∠CAE =90°时,易知△CDA ∽△BCA ,又2224AC BC AB x =-=-,则2241174AD CAx x AC CBx -±=⇒=⇒=-(舍负)—————(2分) 易知∠ACE <90°.所以边BC 的长为2或117+.——————————————————(1分)金山区25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5 分)如图9,已知在梯形ABCD 中,AD ∥BC ,AB =DC =AD =5,3sin 5B =,P 是线段BC 上 一点,以P 为圆心,PA 为半径的⊙P 与射线AD 的另一个交点为Q ,射线PQ 与射线CD 相交于点E ,设BP =x .(1)求证△ABP ∽△ECP ;(2)如果点Q 在线段AD 上(与点A 、D 不重合),设△APQ 的面积为y ,求y 关于x 的函数关系式,并写出定义域; (3)如果△QED 与△QAP 相似,求BP 的长.25.解:(1)在⊙P 中,PA =PQ ,∴∠PAQ =∠PQA ,……………………………(1分)∵AD ∥BC ,∴∠PAQ =∠APB ,∠PQA =∠QPC ,∴∠APB =∠EPC ,……(1分) ∵梯形ABCD 中,AD ∥BC ,AB =DC ,∴∠B =∠C ,…………………………(1分) ∴△APB ∽△ECP .…………………………………………………………(1分) (2)作AM ⊥BC ,PN ⊥AD ,∵AD ∥BC ,∴AM ∥PN ,∴四边形AMPN 是平行四边形,∴AM =PN ,AN =MP .………………………………………………………(1分) 在Rt △AMB 中,∠AMB =90°,AB =5,sinB =35, ∴AM =3,BM =4,∴PN =3,PM =AN =x -4,……………………………………(1分) ∵PN ⊥AQ ,∴AN =NQ ,∴AQ = 2x -8,……………………………………(1分) ∴()1128322y AQ PN x =⋅⋅=⋅-⋅,即312y x =-,………………………(1分) 定义域是1342x <<.………………………………………………………(1分) (3)解法一:由△QED 与△QAP 相似,∠AQP =∠EQD ,①如果∠PAQ =∠DEQ ,∵△APB ∽△ECP ,∴∠PAB =∠DEQ ,又∵∠PAQ =∠APB ,∴∠PAB =∠APB ,∴BP =BA =5.………………………(2分)ABCD图9备用图②如果∠PAQ =∠EDQ ,∵∠PAQ =∠APB ,∠EDQ =∠C ,∠B =∠C ,∴∠B =∠APB ,∴ AB =AP ,∵AM ⊥BC ,∴ BM =MP =4,∴ BP =8.………(2分) 综上所述BP 的长为5或者8.………………………………………………(1分) 解法二:由△QAP 与△QED 相似,∠AQP =∠EQD , 在Rt △APN 中,AP PQ ===∵QD ∥PC ,∴EQ EPQD PC=, ∵△APB ∽△ECP ,∴AP EPPB PC=,∴AP EQ PB QD =, ①如果AQ EQ QP QD =,∴AQ AP QP PB =x=,解得5x =………………………………………………………………………(2分) ②如果AQ DQ QP QE =,∴AQ PBQP AP==解得8x =………………………………………………………………………(2分) 综上所述BP 的长为5或者8.…………………………………………………(1分)静安区25.(本题满分14分,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分) 如图,平行四边形ABCD 中,已知AB =6,BC =9,31cos =∠ABC .对角线AC 、BD 交于点O .动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .设BP = x .(1) 求AC 的长;(2) 设⊙O 的半径为y ,当⊙P 与⊙O 外切时, 求y 关于x 的函数解析式,并写出定义域; (3) 如果AC 是⊙O 的直径,⊙O 经过点E , 求⊙O 与⊙P 的圆心距OP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分) 解:(1)作AH ⊥BC 于H ,且31cos =∠ABC ,AB =6, A 第25题图B P OC DE · 第25题备用图ABOCDDA · POE那么2316cos =⨯=∠⋅=ABC AB BH …………(2分) BC =9,HC =9-2=7,242622=-=AH , ……………………(1分) 9493222=+=+=HC AH AC ﹒ ………(1分)(2)作OI ⊥AB 于I ,联结PO , AC =BC =9,AO =4.5 ∴∠OAB =∠ABC ,∴Rt △AIO 中, 31cos cos ==∠=∠AO AI ABC IAO∴AI =1.5,IO =2322=AI ……………………(1分) ∴PI =AB -BP -AI =6-x -1.5=x -29, ……………………(1分) ∴Rt △PIO 中,41539481918)29()23(2222222+-=+-+=-+=+=x x x x x OI PI OP ……(1分) ∵⊙P 与⊙O 外切,∴y x x x OP +=+-=415392 ……………………(1分) ∴y =x x x x x x -+-=-+-153364214153922…………………………(1分) ∵动点P 在边AB 上,⊙P 经过点B ,交线段PA 于点E .∴定义域:0<x ≤3…………(1分) (3)由题意得:∵点E 在线段AP 上,⊙O 经过点E ,∴⊙O 与⊙P 相交 ∵AO 是⊙O 半径,且AO >OI ,∴交点E 存在两种不同的位置,OE =OA =29① 当E 与点A 不重合时,AE 是⊙O 的弦,OI 是弦心距,∵AI =1.5,AE =3, ∴点E 是AB 中点,321==AB BE ,23==PE BP ,3=PI , IO =23 3327)23(32222==+=+=IO PI OP ……………………(2分)② 当E 与点A 重合时,点P 是AB 中点,点O 是AC 中点,2921==BC OP ……(2分) ∴33=OP 或29. 闵行区25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)如图,已知在Rt △ABC 中,∠ACB = 90o,AC =6,BC = 8,点F 在线段AB 上,以点B 为圆心,BF 为半径的圆交BC 于点E ,射线AE 交圆B 于点D (点D 、E 不重合).(1)如果设BF = x ,EF = y ,求y 与x 之间的函数关系式,并写出它的定义域;第25题图(2)(2)如果»»2EDEF =,求ED 的长; (3)联结CD 、BD ,请判断四边形ABDC 是否为直角梯形?说明理由.25.解:(1)在Rt △ABC 中,6AC =,8BC =,90ACB ∠=o∴10AB =.……………………………………………………………(1分) 过E 作EH ⊥AB ,垂足是H , 易得:35EH x =,45BH x =,15FH x =.…………………………(1分) 在Rt △EHF 中,222223155EF EH FH x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,∴(08)y x x =<<.………………………………………(1分+1分) (2)取»ED的中点P ,联结BP 交ED 于点G ∵»»2EDEF =,P 是»ED 的中点,∴»»»EP EF PD ==. ∴∠FBE =∠EBP =∠PBD .∵»»EPEF =,BP 过圆心,∴BG ⊥ED ,ED =2EG =2DG .…………(1分) 又∵∠CEA =∠DEB ,∴∠CAE =∠EBP =∠ABC .……………………………………………(1分)又∵BE 是公共边,∴BEH BEG ∆∆≌.∴35EH EG GD x ===.在Rt △CEA 中,∵AC = 6,8BC =,tan tan AC CECAE ABC BC AC∠=∠==, ∴66339tan 822CE AC CAE ⨯⨯=⋅∠===.……………………………(1分) (备用图)CBA (第25题图)CBEF DADEBACF∴9169782222BE =-=-=.……………………………………………(1分) ∴6672125525ED EG x ===⨯=.……………………………………(1分)(3)四边形ABDC 不可能为直角梯形.…………………………………(1分)①当CD ∥AB 时,如果四边形ABDC 是直角梯形, 只可能∠ABD =∠CDB = 90o. 在Rt △CBD 中,∵8BC =, ∴32cos 5CD BC BCD =⋅∠=, 24sin 5BD BC BCD BE =⋅∠==. ∴321651025CD AB ==,328153245CE BE -==; ∴CD CEAB BE≠. ∴CD 不平行于AB ,与CD ∥AB 矛盾.∴四边形ABDC 不可能为直角梯形.…………………………(2分) ②当AC ∥BD 时,如果四边形ABDC 只可能∠ACD =∠CDB = 90o. ∵AC ∥BD ,∠ACB = 90o, ∴∠ACB =∠CBD = 90o . ∴∠ABD =∠ACB +∠BCD > 90o. 与∠ACD =∠CDB = 90o矛盾.∴四边形ABDC 不可能为直角梯形.…………………………(2分)普陀区25.(本题满分14分)已知P 是O ⊙的直径BA 延长线上的一个动点,P ∠的另一边交O ⊙于点C 、D ,两点位于AB 的上方,AB =6,OP m =,1sin 3P =,如图11所示.另一个半径为6的1O ⊙经过点C 、D ,圆心距1OO n =.(1)当6m =时,求线段CD 的长;(2)设圆心1O 在直线AB 上方,试用n 的代数式表示m ;(3)△1POO 在点P 的运动过程中,是否能成为以1OO 为腰的等腰三角形,如果能,试求出此时n 的值;如果不能,请说明理由.DEBACFDC25.解:(1)过点O 作OH ⊥CD ,垂足为点H ,联结OC .在Rt △POH 中,∵1sin 3P =,6PO =,∴2OH =. ········· (1分) ∵AB =6,∴3OC =. ······················ (1分)由勾股定理得 CH = ····················· (1分)∵OH ⊥DC ,∴2CD CH == ················ (1分) (2)在Rt △POH 中,∵1sin 3P =, PO m =,∴3mOH =. ········ (1分) 在Rt △OCH 中,2293m CH ⎛⎫- ⎪⎝⎭=. ················ (1分)在Rt △1O CH 中,22363m CH n ⎛⎫-- ⎪⎝⎭=. ·············· (1分)可得 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭=,解得23812n m n -=. ········· (2分)(3)△1POO 成为等腰三角形可分以下几种情况:● 当圆心1O 、O 在弦CD 异侧时①1OP OO =,即m n =,由23812n n n-=解得9n =. ········· (1分)即圆心距等于O ⊙、1O ⊙的半径的和,就有O ⊙、1O ⊙外切不合题意舍去.(1分)②11O P OO =n =,解得23m n =,即23n 23812n n -=,解得n ·········· (1分) ● 当圆心1O 、O 在弦CD 同侧时,同理可得 28132n m n-=.∵1POO ∠是钝角,∴只能是m n =,即28132n n n-=,解得n . ·· (2分)综上所述,n .青浦区25.(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9-1,已知扇形MON,∠MON=90o,点B在弧MN上移动,联结BM,作OD⊥BM,垂足为点D,C为线段OD上一点,且OC=BM,联结BC并延长交半径OM于点A,设OA= x,∠COM的正切值为y.(1)如图9-2,当AB⊥OM时,求证:AM =AC;(2)求y关于x的函数关系式,并写出定义域;(3)当△OAC为等腰三角形时,求x的值.25.解:(1)∵OD⊥BM,AB⊥OM,∴∠ODM =∠BAM=90°.··········(1分)∵∠ABM +∠M =∠DOM +∠M,∴∠ABM =∠DOM.·········(1分)∵∠OAC=∠BAM,OC =BM,∴△OAC≌△ABM,······················(1分)∴AC =AM.·························(1分)(2)过点D作DE//AB,交OM于点E.················(1分)∵OB=OM,OD⊥BM,∴BD=DM.················(1分)∵DE//AB,∴=MD MEDM AE,∴AE=EM,∵OM,∴AE=)12x.················(1分)∵DE//AB,∴2==OA OC DMOE OD OD,···················(1分)∴2=DM OAOD OE,∴=y(0<≤x·················(2分)(3)(i)当OA=OC时,∵111222===DM BM OC x,O MNDCBA图9-1ONDCBA图9-2NMO备用图在Rt △ODM中,==OD =DM y OD,1=x=x=x .(2分) (ii )当AO =AC 时,则∠AOC =∠ACO ,∵∠ACO >∠COB ,∠COB =∠AOC ,∴∠ACO >∠AOC ,∴此种情况不存在. ····················· (1分) (ⅲ)当CO =CA 时,则∠COA =∠CAO=α,∵∠CAO >∠M ,∠M =90α︒-,∴α>90α︒-,∴α>45︒,∴290α∠=>︒BOA ,∵90∠≤︒BOA ,∴此种情况不存在. ·· (1分)松江区25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分)如图,已知Rt △ABC 中,∠ACB =90°,BC =2,AC =3,以点C 为圆心、CB 为半径的圆交AB 于点D ,过点A 作AE ∥CD ,交BC 延长线于点E.(1)求CE 的长;(2)P 是 CE 延长线上一点,直线AP 、CD 交于点Q.① 如果△ACQ ∽△CPQ ,求CP 的长;② 如果以点A 为圆心,AQ 为半径的圆与⊙C 相切,求CP 的长.25.(本题满分14分,第(1)小题4分,第(2)小题每个小题各5分) 解:(1)∵AE ∥CD∴BC DC BE AE=…………………………………1分 ∵BC=DC∴BE=AE …………………………………1分 设CE =x(第25题图)CBA DE(备用图)CBADECBA DE则AE =BE =x +2 ∵ ∠ACB =90°, ∴222AC CE AE +=即229(2)x x +=+………………………1分 ∴54x =即54CE =…………………………………1分 (2)①∵△ACQ ∽△CPQ ,∠QAC>∠P∴∠ACQ=∠P …………………………………1分 又∵AE ∥CD ∴∠ACQ=∠CAE∴∠CAE=∠P ………………………………1分 ∴△ACE ∽△PCA ,…………………………1分 ∴2AC CE CP =⋅…………………………1分 即2534CP =⋅ ∴365CP =……………………………1分 ②设CP =t ,则54PE t =- ∵∠ACB =90°,∴AP ∵AE ∥CD ∴AQ ECAP EP=……………………………1分5545454t t ==--∴AQ =1分若两圆外切,那么1AQ == 此时方程无实数解……………………………1分CBA DEPQ若两圆内切切,那么2595t AQ +== ∴21540160t t -+= 解之得2041015t ±=………………………1分又∵54t >∴2041015t +=………………………1分徐汇区25. 已知四边形ABCD 是边长为10的菱形,对角线AC 、BD 相交于点E ,过点C 作CF ∥DB 交AB 延长线于点F ,联结EF 交BC 于点H . (1)如图1,当EF BC ⊥时,求AE 的长;(2)如图2,以EF 为直径作⊙O ,⊙O 经过点C 交边CD 于点G (点C 、G 不重合),设AE 的长为x ,EH 的长为y ;① 求y 关于x 的函数关系式,并写出定义域;③ 联结EG ,当DEG ∆是以DG 为腰的等腰三角形时,求AE 的长.杨浦区25、(本题满分14分,第(1)小题4分,第(2)小题6分,第(3)小题4分)如图9,在梯形ABCD中,AD//BC,AB=DC=5,AD=1,BC=9,点P为边BC上一动点,作PH⊥DC,垂足H在边DC上,以点P为圆心PH为半径画圆,交射线PB于点E.(1)当圆P过点A时,求圆P的半径;(2)分别联结EH和EA,当△ABE△CEH时,以点B为圆心,r为半径的圆B与圆P相交,试求圆B的半径r的取值范围;(3)将劣弧沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值。
上海市2018年中考二模数学试卷含答案

2017-2018学年第二学期九年级质量调研考试数 学 试 卷(考试时间100分钟,满分150分)考生注意:1.本试卷含三个大题,共25题.2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答 题一律无效.3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证 明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分) 【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】 1.在下列各式中,二次单项式是 (A )21x +;(B )213xy ;(C )2xy ;(D )21()2-.2.下列运算结果正确的是 (A )222()a b a b +=+; (B )2323a a a +=; (C )325a a a ⋅=;(D )112(0)2a a a-=≠. 3.在平面直角坐标系中,反比例函数(0)ky k x=≠图像在每个象限内y 随着x 的增大而减小,那么它的图像的两个分支分别在 (A )第一、三象限; (B )第二、四象限; (C )第一、二象限;(D )第三、四象限.4.有9名学生参加校民乐决赛,最终成绩各不相同,其中一名同学想要知道自己是否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的 (A )平均数;(B )中位数;(C )众数;(D )方差. 5.已知四边形ABCD 是平行四边形,下列结论中不正确的是 (A )当AB = BC 时,四边形ABCD 是菱形; (B )当AC ⊥BD 时,四边形ABCD 是菱形; (C )当∠ABC = 90o 时,四边形ABCD 是矩形;(D )当AC = BD 时,四边形ABCD 是正方形.6.点A 在圆O 上,已知圆O 的半径是4,如果点A 到直线a 的距离是8,那么圆O 与直线a 的位置关系可能是(A )相交; (B )相离; (C )相切或相交; (D )相切或相离.二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:21+2-= ▲ .8.在实数范围内分解因式:243x -= ▲ . 91的解是 ▲ .10.已知关于x 的方程230x x m --=没有实数根,那么m 的取值范围是 ▲ .11.已知直线(0)y kx b k =+≠与直线13y x =-平行,且截距为5,那么这条直线的解析式为 ▲ .12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小杰过马路时,恰巧是绿灯的概率是 ▲ .13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.1,那么第六组的频数是 ▲ .14.如图,已知在矩形ABCD 中,点E 在边AD 上,且AE = 2ED .设B A a =u u r r ,BC b =uu u r r,那么CE =uu u r ▲ (用a r 、b r的式子表示). 15.如果二次函数2111y a x b x c =++(10a ≠,1a 、1b 、1c 是常数)与2222y a x b x c =++(20a ≠,2a 、2b 、2c 是常数)满足1a 与2a 互为相反数,1b 与2b 相等,1c 与2c 互为倒数,那么称这两个函数为“亚旋转函数”.请直接写出函数232y x x =-+-的“亚旋转函数”为 ▲ .16.如果正n 边形的中心角为2α,边长为5,那么它的边心距为 ▲ .(用锐角α的三角比表示)17.如图,一辆小汽车在公路l 上由东向西行驶,已知测速探头M 到公路l 的距离MN为9米,测得此车从点A 行驶到点B 所用的时间为0.6秒,并测得点A 的俯角为30o ,点B 的俯角为60o .那么此车从A 到B 的平均速度为 ▲ 米/秒.(结果保1.7321.414)18.在直角梯形ABCD 中,AB // CD ,∠DAB = 90o ,AB = 12,DC = 7,5cos 13ABC ∠=,点E 在线段AD 上,将△ABE 沿BE 翻折,点A 恰巧落在对角线BD 上点P 处,那么PD = ▲ .ABDC(第14题图)EABDC(第18题图)AMN (第17题图)l三、解答题:(本大题共7题,满分78分)19.(本题满分10分)120183(1)2cos45+8-+--o.20.(本题满分10分)解方程组:221;20.y xx xy y-=⎧⎨--=⎩21.(本题满分10分,其中第(1)小题4分,第(2)小题6分)已知一次函数24y x=-+的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o,tan ABC∠(1)求点C的坐标;(2)在第一象限内有一点M(1,m),且点MC位于直线AB的同侧,使得ABCABMSS∆∆=2求点M的坐标.22.(本题满分10分)为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多14小时,求自行车的平均速度?23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD 相交于点F,FG∥AC,联结DG.(1)求证:BF BC AB BD⋅=⋅;(2)求证:四边形ADGF是菱形.AB E G CFD(第23题图)(第21题图)24.(本题满分12分,其中每小题各4分)如图,已知在平面直角坐标系xOy 中,抛物线22y ax x c =-+与x 轴交于 点A 和点B (1,0),与y 轴相交于点C (0,3). (1)求抛物线的解析式和顶点D 的坐标; (2)求证:∠DAB=∠ACB ;(3)点Q 在抛物线上,且△ADQ 是以AD 为底的等腰三角形,求Q 点的坐标.25.(本题满分14分,其中第(1)小题4分,第(2)、(3)小题各5分)如图,已知在Rt △ABC 中,∠ACB = 90o ,AC =6,BC = 8,点F 在线段AB 上,以点B 为圆心,BF 为半径的圆交BC 于点E ,射线AE 交圆B 于点D (点D 、E 不重合). (1)如果设BF = x ,EF = y ,求y 与x 之间的函数关系式,并写出它的定义域; (2)如果2ED EF =,求ED 的长;(3)联结CD 、BD ,请判断四边形ABDC 是否为直角梯形?说明理由.(第24题图) (备用图)CA (第25题图) CB EF D A参考答案及评分标准一、选择题:(本大题共6题,每题4分,满分24分) 1.C ;2.C ;3.A ;4.B ;5.D ;6.D .二、填空题:(本大题共12题,每题4分,满分48分)7.5; 8.2x x (; 9.1x =; 10.94m <-; 11.153y x =-+;12.512; 13.8; 14.13a b -r r ; 15.2132y x x =+-; 16.5cot 2α(或52tan α);17.17.3; 18.12.三、解答题:(本大题共7题,满分78分) 19.解:原式112+……………………………………(2分+2分+2分+2分)2=.……………………………………………………………………(2分)20.解:由②得:20x y -=,+0x y =…………………………………………(2分)原方程组可化为120y x x y -=⎧⎨-=⎩,10y x x y -=⎧⎨+=⎩………………………………(2分)解得原方程组的解为21x y =-⎧⎨=-⎩,1212x y ⎧=-⎪⎪⎨⎪=⎪⎩…………………………………(5分)∴原方程组的解是21x y =-⎧⎨=-⎩,1212x y ⎧=-⎪⎪⎨⎪=⎪⎩……………………………………(1分)21.解:(1)令0y =,则240x -+=,解得:2x =,∴点A 坐标是(2,0).令0x =,则4y =,∴点B 坐标是(0,4).………………………(1分)∴AB .………………………………(1分)∵90BAC ∠=,1tan 2ABC ∠=,∴AC =过C 点作CD ⊥x 轴于点D ,易得OBA DAC ∆∆∽.…………………(1分) ∴2AD =,1CD =,∴点C 坐标是(4,1).………………………(1分) (2)11522ABC S AB AC ∆=⋅=⨯.………………………………(1分)∵2ABM ABC S S ∆∆=,∴52ABM S ∆=.……………………………………(1分)∵(1M,)m,∴点M在直线1x=上;令直线1x=与线段AB交于点E,2ME m=-;……………………(1分)分别过点A、B作直线1x=的垂线,垂足分别是点F、G,∴AF+BG = OA = 2;……………………………………………………(1分)∴111()222ABM BME AMES S S ME BG ME AF ME BG AF∆∆=+=⋅+⋅=+1152222ME OA ME=⋅=⨯⨯=…………………(1分)∴52ME=,522m-=,92m=,∴(1M,92).……………………(1分)22.解:设自行车的平均速度是x千米/时.………………………………………(1分)根据题意,列方程得7.57.51154x x-=+;……………………………………(3分)化简得:2154500x x+-=;………………………………………………(2分)解得:115x=,230x=-;…………………………………………………(2分)经检验,115x=是原方程的根,且符合题意,230x=-不符合题意舍去.(1分)答:自行车的平均速度是15千米/时.………………………………………(1分)23.证明:(1)∵AE平分∠BAC,∴∠BAC=2∠BAF=2∠EAC.∵∠BAC=2∠C,∴∠BAF=∠C=∠EAC.…………………………(1分)又∵BD平分∠ABC,∴∠ABD=∠DBC.……………………………(1分)∵∠ABF=∠C,∠ABD=∠DBC,∴ABF CBD∆∆∽.…………………………………………………(1分)∴AB BFBC BD=.………………………………………………………(1分)∴BF BC AB BD⋅=⋅.………………………………………………(1分)(2)∵FG∥AC,∴∠C=∠FGB,∴∠FGB=∠F AB.………………(1分)∵∠BAF=∠BGF,∠ABD=∠GBD,BF=BF,∴ABF GBF∆∆≌.∴AF=FG,BA=BG.…………………………(1分)∵BA=BG,∠ABD=∠GBD,BD=BD,∴ABD GBD∆∆≌.∴∠BAD=∠BGD.……………………………(1分)∵∠BAD=2∠C,∴∠BGD=2∠C,∴∠GDC=∠C,∴∠GDC=∠EAC,∴AF∥DG.……………………………………(1分)又∵FG∥AC,∴四边形ADGF是平行四边形.……………………(1分)∴AF=FG.……………………………………………………………(1分)∴四边形ADGF是菱形.……………………………………………(1分)24.解:(1)把B(1,0)和C(0,3)代入22y ax x c=-+中,得9603a cc++=⎧⎨=⎩,解得13ac=-⎧⎨=⎩.……………………………………(2分)∴抛物线的解析式是:223y x x =--+.……………………………(1分) ∴顶点坐标D (-1,4).……………………………………………(1分) (2)令0y =,则2230x x --+=,13x =-,21x =,∴A (-3,0)∴3OA OC ==,∴∠CAO =∠OCA .…………………………………(1分)在Rt BOC ∆中,1tan 3OB OCB OC ∠==.………………………………(1分)∵AC =DCAD =, ∴2220AC DC +=,220AD =;∴222AC DC AD +=,ACD ∆是直角三角形且90ACD ∠=,∴1tan 3DC DAC AC ∠==,又∵∠DAC 和∠OCB 都是锐角,∴∠DAC =∠OCB .…………………(1分) ∴DAC CAO BCO OCA ∠+∠=∠+∠,即DAB ACB ∠=∠.……………………………………………………(1分) (3)令(Q x ,)y 且满足223y x x =--+,(3A -,0),(1D -,4)∵ADQ ∆是以AD 为底的等腰三角形,∴22QD QA =,即2222(3)(1)(4)x y x y ++=++-,化简得:220x y -+=.………………………………………………(1分) 由222023x y y x x -+=⎧⎨=--+⎩,……………………………………………………(1分)解得11x y ⎧=⎪⎪⎨⎪=⎪⎩,22x y ⎧=⎪⎪⎨⎪⎪⎩. ∴点Q的坐标是⎝⎭,⎝⎭.…(2分)25.解:(1)在Rt △ABC 中,6AC =,8BC =,90ACB ∠=∴10AB =.……………………………………………………………(1分) 过E 作EH ⊥AB ,垂足是H ,易得:35EH x =,45BH x =,15FH x =.…………………………(1分)在Rt △EHF 中,222223155EF EH FH x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭,∴(08)y x =<<.………………………………………(1分+1分) (2)取ED 的中点P ,联结BP 交ED 于点G∵2ED EF =,P 是ED 的中点,∴EP EF PD ==. ∴∠FBE =∠EBP =∠PBD .∵EP EF=,BP过圆心,∴BG⊥ED,ED =2EG =2DG.…………(1分)又∵∠CEA =∠DEB,∴∠CAE=∠EBP=∠ABC.……………………………………………(1分)又∵BE是公共边,∴BEH BEG∆∆≌.∴35EH EG GD x===.在Rt△CEA中,∵AC = 6,8BC=,tan tan AC CECAE ABCBC AC∠=∠==,∴66339tan822CE AC CAE⨯⨯=⋅∠===.……………………………(1分)∴9169782222BE=-=-=.……………………………………………(1分)∴6672125525ED EG x===⨯=.……………………………………(1分)(3)四边形ABDC不可能为直角梯形.…………………………………(1分)①当CD∥AB时,如果四边形ABDC是直角梯形,只可能∠ABD =∠CDB = 90o.在Rt△CBD中,∵8BC=,∴32cos5CD BC BCD=⋅∠=,24sin5BD BC BCD BE =⋅∠==∴321651025CDAB==,32853245CEBE-==∴CD CE AB BE≠.∴CD不平行于AB,与CD∥AB矛盾.∴四边形ABDC不可能为直角梯形.…………………………(2分)②当AC∥BD时,如果四边形ABDC只可能∠ACD =∠CDB = 90o.∵AC∥BD,∠ACB = 90o,∴∠ACB =∠CBD = 90o.∴∠ABD =∠ACB +∠BCD > 90o.与∠ACD =∠CDB = 90o矛盾.∴四边形ABDC不可能为直角梯形.…………………………(2分)。
上海市各区2018届中考数学二模试卷精选汇编:解方程组不等式组及参考答案

静安区
x1 1
5 ,
x2 1
5
,…………………………………………(
y1 3 5
y2 3 5
4 分)
20.(本题满分 10 分)
x4 5
解方程:
x1 1x
20.(本题满分 10 分)
6x
.
x2 1
x4 5
6x
解方程:
x1 1x
x2 1
解: ( x 4)( x 1) 5( x 1) 6x
x2 3x 4 5x 5 6x 0 x 2 8x 9 0 x1 1, x2 9 经检验 x1 1是 增根,舍去 ∴原方程的根是 x 9 .
20.(本题满分 10 分)
解:方程①可变形为 (x 6 y)( x y) 0
得 x 6y 0或 x y 0
( 2 分)
将它们与方程②分别组成方程组,得(Ⅰ)
x 6y 0
xy0
或(Ⅱ)
( 2 分)
2x y 1
2x y 1
解方程组(Ⅰ)
6 x
13 , 1
y 13
解方程组(Ⅱ)
x1 y1
( 4 分)
所以原方程组的解是
所以原方程组可化为两个二元一次方程组:
x 2 y 3, 2x y 1;
x 2 y 3,
……………… 2 分
2x y 1;
分别解这两个方程组,得原方程组的解是
1
x1 1, x2
, 5 ………… 4 分
y1 1; y2
7 .
5
长宁区 20.(本题满分 10 分)
2
x
5 xy
6y2
0 , ①
解方程组:
2x y 1 . ②
2x 3 x x x 12
上海市各区2018届中考数学二模试卷精选汇编:填空题及答案

16.如图,在梯形ABCD中,AB//CD,∠C=90°,BC=CD=4, ,
若 , ,用 、 表示 ▲.
17.如果一个三角形有一条边上的高等于这条边的一半,
那么我们把这个三角形叫做半高三角形.已知直角三角形ABC
是半高三角形,且斜边 ,则它的周长等于▲.
二、填空题:(本大题共12题,每题4分,满分48分)
7. ;8. ;9. ;10. ;
11. ;12. ;13. ;14. ;
15. ;16. ;17. ;18. .
奉贤区
7.计算: .
8.如果 ,且 ,那么 的值是.
9.方程 的根是.
10.已知反比例函数 ,在其图像所在的每个象限内, 的值随 的值增大而减
17.如图2,点 、 、 在圆 上,弦 与半径 互相平分,那么 度数为▲度.
18.如图3,在△ 中, , ,点 在边 上,且 .
如果△ 绕点 顺时针旋转,使点 与点 重合,点 旋转至点 ,那么线段
的长为▲.
7. 2 8. 9. 10.
11. 12. 13. 400 14. 2.8 15.
16. 2 17. 120° 18.
上海市各区2018届中考二模数学试卷精选汇编 填空题专题
宝山区、嘉定区
二、填空题(本大题共12题,每题4分,满分48分)
7.计算: ▲.
8.一种细菌的半径是 米,用科学记数法把它表示为▲米.
9.因式分解: ▲.
10.不等式组 的解集是▲.
11.在一个不透明的布袋中装有 个白球、 个红球和 个黄球,这些球除了颜色不同之外,其余均相同.如果从中随机摸出一个球,摸到黄球的概率是▲.
上海市各区2018年中考二模数学试题_(2) 推荐

九年级数学试卷参考答案一、选择题:(本大题共6题,每题4分,满分24分)1.A ;2.D ;3.B ;4.D ;5. B ;6.C . 二、填空题:(本大题共12题,每题4分,满分48分)7.x ≠1; 8.1.37×109; 9.x =1; 10.()()2121+---x x ;11. 4;12.m >3; 13. 0.3; 14.6180120+=x x ; 15.)(21b a-; 16.内切; 17.4 ; 18.750或150. 三、解答题:(本大题共7题,满分78分)19.解:原式=333334+-++-…………………………………………………(8分)=133-………………………………………………………………………(2分)AF N第一个观点第一个观点①②③④⑤①②③④⑤①②③④⑤①②③④⑤⑤④③②①20. 解:由①得 x <1. …………………………………………………………………(3分) 由②得 1-≥x .…………………………………………………………………(3分) ∴ 原不等式组的解集为11<≤-x . …………………………………………(2分) 画图略………………………………………………………………………………(2分) 21.解:(1)过点B 作BF ⊥AD 于F 。
…………………………………………………(1分)在Rt ABF △中,∵35==AF BF i ,且10BF m =。
∴6AF m =………………(2分)∴AB = …………………………………………………………(2分)(2)如图,延长EC 至点M ,AD 至点N ,连接MN ,过点E 作EG ⊥AD 于G 。
在Rt △AEG 中,∵65==AG EG i ,且10BF m =, ∴AG =12m ,BE=GF=AG - AF =6 m 。
……………………………………………(2分)∴ABE CMND S S =△梯形 ………………(1()1122BE EG MC ND ∙∙=+。
上海市各区2018届中考数学二模试卷精选汇编填空题专题

上海市各区2018届九年级中考二模数学试卷精选汇编 填空题专题宝山区、嘉定区二、填空题(本大题共12题,每题4分,满分48分) 7.计算:=4 ▲ .8.一种细菌的半径是00000419.0米,用科学记数法把它表示为 ▲ 米. 9. 因式分解:=-x x 42 ▲ .10.不等式组⎩⎨⎧>+≤-063,01x x 的解集是 ▲ .11.在一个不透明的布袋中装有2个白球、8个红球和5个黄球,这些球除了颜色不同之外,其余均相同.如果从中随机摸出一个球,摸到黄球的概率是 ▲ . 12.方程23=+x 的根是 ▲ .13.近视眼镜的度数y (度)与镜片焦距x (米)呈反比例,其函数关系式为xy 120=.如果近似眼镜镜片的焦距3.0=x 米,那么近视眼镜的度数y 为 ▲ . 14.数据1、2、3、3、6的方差是 ▲ .15.在△ABC 中,点D 是边BC 的中点,=,=,那么=AD ▲ (用、表示). 16.如图1,在矩形ABCD 中,点E 在边CD 上,点F 在对角线BD 上,5:2:=DE DF ,BD EF ⊥,那么=∠ADB tan ▲ .17.如图2,点A 、B 、C 在圆O 上,弦AC 与半径OB 互相平分,那么AOC ∠度数为 ▲ 度. 18.如图3,在△ABC 中,5==AC AB ,6=BC ,点D 在边AB 上,且︒=∠90BDC .如果△ACD 绕点A 顺时针旋转,使点C 与点B 重合,点D 旋转至点1D ,那么线段1DD 的长为 ▲ .7. 2 8. 64.1910-⨯ 9. (4)x x - 10. 21x -<≤图2A BCD图3图111. 1312. 1x = 13. 400 14. 2.8 15. 2a b +r r16. 2 17. 120° 18. 4225长宁区二、填空题(本大题共12题, 每题4分, 满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7. 计算:=--︒0)3(30sin ▲ . 8. 方程6+=-x x 的解是 ▲ .9. 不等式组⎪⎩⎪⎨⎧≥-<+-1)12(303x x 的解集是 ▲ .10.已知反比例函数xky =的图像经过点(-2017,2018),当0>x 时,函数值y 随 自变量x 的值增大而 ▲ .(填“增大”或“减小”)11.若关于x 的方程032=--m x x 有两个相等的实数根,则m 的值是 ▲ . 12.在形状为等腰三角形、圆、矩形、菱形、直角梯形的5张纸片中随机抽取一张,抽到中心对称图形的概率是 ▲ .13.抛物线522++=mx mx y 的对称轴是直线 ▲ . 14.小明统计了家里3月份的电话通话清单,按通话时间画出频数分布直方图(如图所示),则通话时间不足10分钟的 通话次数的频率是 ▲ .15.如图,在四边形ABCD 中,点E 、F 分别是边AB 、AD 的中点,BC =15,CD =9,EF =6,∠AFE =50°,则∠ADC 的度数为 ▲ .16.如图,在梯形ABCD 中,AB //CD ,∠C=90°,BC =CD =4,52=AD , 若=,=,用a 、b 表示= ▲ . 17.如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC 是半高三角形,且斜边5=AB ,则它的周长等于 ▲ . 18.如图,在矩形ABCD 中,对角线BD 的长为1,点P 是线段BD上的一点,联结CP ,将△BCP 沿着直线CP 翻折,若点B 落在 边AD 上的点E 处,且EP //AB ,则AB 的长等于 ▲ .第14题图 A DEF第15题图 第16题图 DCBA 第18题图AB CD二.填空题:(本大题共12题,满分48分) 7.21-; 8.2-=x ; 9.3>x ; 10.增大; 11.43-=m ; 12.53; 13.1-=x ;14.7.0;15.︒140; 16.→→-a b 21; 17.255或535++; 18.215-.崇明区二、填空题(本大题共12题,每题4分,满分48分) 7.因式分解:29x -= ▲ .8.不等式组1023x x x -<⎧⎨+>⎩的解集是 ▲ .9.函数12y x =-的定义域是 ▲ . 103=的解是 ▲ .11.已知袋子中的球除颜色外均相同,其中红球有3个,如果从中随机摸得1个红球的概率为18,那么袋子中共有 ▲ 个球.12.如果关于x 的方程240x x k +-=有两个相等的实数根,那么实数k 的值是 ▲ . 13.如果将抛物线221y x x =+-向上平移,使它经过点(1,3)A ,那么所得新抛物线的表达式是▲ .14.某校组织了主题为“共建生态岛”的电子小报作品征集活动,先从中随机抽取了部分作品,按,,,A B C D 四个等级进行评分,然后根据统计结果绘制了如下两幅不完整的统计图,那么此次抽取的作品中等级为B 的作品数为 ▲ .15.已知梯形ABCD ,AD BC ∥,2BC AD =,如果AB a =,AC b =,那么DA = ▲ . (用,a b 表示).16.如图,正六边形ABCDEF 的顶点B 、C 分别在正方形AGHI 的边AG 、GH 上,如果4AB =,那么CH 的长为 ▲ .17.在矩形ABCD 中,5AB =,12BC =,点E 是边AB 上一点(不与A 、B 重合),以点A 为圆心,AE 为半径作A ⊙,如果C ⊙与A ⊙外切,那么C ⊙的半径r 的取值范围是 ▲ .18.如图,ABC △中,90BAC ∠=︒,6AB =,8AC =,点D 是BC 的中点,将ABD △沿AD 翻折得到AED △,联结CE ,那么线段CE 的长等于 ▲ .(第14题图)HDCIFGE (第18题图)DCBAE二、填空题:(本大题共12题,每题4分,满分48分)7.(3)(3)x x +-; 8.31x -<<; 9.2x ≠; 10.8x =; 11.24; 12.4-; 13.22y x x =+; 14.48;15.1122a b -; 16.6-; 17.813r <<; 18.145. 奉贤区 7.计算:=-aa 211 . 8.如果822=-b a ,且4=+b a ,那么b a -的值是 . 9.方程242=-x 的根是 . 10.已知反比例函数)0(≠=k xky ,在其图像所在的每个象限内,y 的值随x 的值增大而减 小,那么它的图像所在的象限是第 象限.11.如果将抛物线22y x =平移,使平移后的抛物线顶点坐标为(1,2),那么所得新抛物线的表达式是 .12.将6本相同厚度的书叠起来,它们的高度是9厘米.如果将这样相同厚度的书叠起来的高度是42厘米,那么这些书有 本.13.从1,2,3,4,5,6,7,8这八个数中,任意抽取一个数,这个数恰好是合数的概率是. 14.某校为了了解学生双休日参加社会实践活动的情况,随机抽取了100名学生进行调查,并绘成如图3所示的频数分布直方图.已知该校共有1000名学生,据此估计,该校双休日参加社会实践活动时间在2~2.5小时之间的学生数大约是全体学生数的 (填百分数) . 15.如图4,在梯形ABCD 中,AD //BC ,BC=2AD ,E 、F 分别是边AD 、BC 的中点,设a AD =, =,那么EF 等于 (结果用、的线性组合表示). 16.如果一个矩形的面积是40,两条对角线夹角的正切值是34,那么它的一条对角线长是 . 17.已知正方形ABCD ,AB =1,分别以点A 、C 为圆心画圆,如果点B 在圆A 外,且圆A与圆C 外切,那么圆C 的半径长r 的取值范围是 .18.如图5,将△ABC 的边AB 绕着点A 顺时针旋转)900(︒<<︒αα得到AB ’,边AC 绕着点A 逆时针旋转)900(︒<<︒ββ得到AC ’,联结B ′C ′.当︒=+90βα时,我们称△A B ′C ′ 是△ABC 的“双旋三角形”.如果等边△ABC 的边长为a ,那么它的“双旋三角形”的面 积是 (用含a 的代数式表示). 人数 AB ′二、填空题: 7、12a ; 8、2; 9、4; 10、一三; 11、22(1)2y x =-+; 12、28; 13、38; 14、28%; 15、12a b +; 16、10; 171r << 18、214a黄浦区 7= . 8.因式分解:212x x --= . 9.方程1x +=的解是 .10.不等式组12031302x x ⎧->⎪⎪⎨⎪-≤⎪⎩的解集是 .11.已知点P 位于第三象限内,且点P 到两坐标轴的距离分别为2和4,若反比例函数图像经过点P ,则该反比例函数的解析式为 .12.如果一次函数的图像经过第一、二、四象限,那么其函数值y 随自变量x 的值的增大而 . (填“增大”或“减小”)13.女生小琳所在班级共有40名学生,其中女生占60%.现学校组织部分女生去市三女中参观,需要从小琳所在班级的女生当中随机抽取一名女生参加,那么小琳被抽到的概率是 . 14.已知平行四边形相邻两个内角相差40°,则该平行四边形中较小内角的度数是 . 15.半径为1的圆的内接正三角形的边长为 .16.如图,点D 、E 分别为△ABC 边CA 、CB 上的点,已知DE ∥AB ,且DE 经过△ABC 的重心,设CA a =, CB b =,则DE = .(用a 、b 表示)17.如图,在四边形ABCD 中,902624ABC ADC AC BD ∠=∠=︒==,,,M 、N 分别是AC 、BD 的中点,则线段MN 的长为 .18.如图,将矩形ABCD 沿对角线AC 折叠,使点B 翻折到点E 处,如果DE ∶AC =1∶3,那么AD ∶AB = .图4A B DFE CBC二、填空题:(本大题共12题,每题4分,满分48分)71; 8.()()34x x +-; 9.2; 10.166x <≤; 11.8y x =; 12.减小; 13.124; 14.70; 1516.2233b a -.; 17.5; 18∶1. 金山区7.因式分解:2a a -= ▲ . 8.函数y =的定义域是 ▲ .9.方程21xx =-的解是 ▲ . 10.一次函数2y x =-+的图像不经过第 ▲ 象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是 ▲ . 12.如果关于x 的一元二次方程240x x k -+=有两个不相等的实数根,那么k 的取值范围是 ▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于 ▲ . 14.空气质量指数,简称AQI ,如果AQI 在0~50空 气质量类别为优,在51~100空气质量类别为良, 在101~150空气质量类别为轻度污染,按照某市最 近一段时间的AQI 画出的频数分布直方图如图3 所示,已知每天的AQI 都是整数,那么空气质量 类别为优和良的天数占总天数的百分比为 ▲ %. 15.一辆汽车在坡度为1:2.4的斜坡上向上行驶130米,那么这辆汽车的高度上升了 ▲ 米.16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是 ▲ . 17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d 的的取值范围是 ▲ .图318.如图4,Rt △ABC 中,∠C =90°,AC =6,BC =8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC , 那么点P 和点B 间的距离等于 ▲ .二.填空题:(本大题共12题,满分48分)7.()1a a -; 8.2x ≥; 9.2x =; 10.三; 11.12; 12.4k <; 13.4; 14.80; 15.50; 16.12; 17.3d 15<<; 18.52或10. 静安区二、填空题:(本大题共12题,每题4分,满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7.32)2(a a ⋅ = ▲ .8.分解因式:=+-xy y x 4)(2▲ . 9.方程组⎩⎨⎧=-=+62,3x y y x 的解是 ▲ .10.如果4-x x 有意义,那么x 的取值范围是 ▲ .11.如果函数x a y 12--=(a 为常数)的图像上有两点),1(1y 、),31(2y ,那么函数值1y ▲ 2y .(填“<”、“=”或“>”)12.为了解植物园内某种花卉的生长情况,在一片约有3000株此类花卉的园地内,随机抽测了200株的高度作为样本,统计结果整理后列表如下:(每组数据可包括最低值,不包括最高值)厘米的约为 ▲ 株.13.从1,2,3,4,5,6,7,8,9中任取一个数,这个数即是奇数又是素数的概率是 ▲ .14.如图,在△ABC中,点G 是重心,过点G 作DE ∥BC ,分别交AB 、AC 于点D 、E .已知b CBa AB ==, ,那么AE = ▲ .(用向量表示). 15.如图,已知⊙O 中,直径AB 平分弦CD ,且交CD 于点E , 如果OE =BE ,那么弦CD 所对的圆心角是 ▲ 度.16.已知正多边形的边长为a ,且它的一个外角是其内角的一半,那么此正图4AB E DCG·第14题图多边形的边心距是 ▲ .(用含字母a 的代数式表示). 17.在平面直角坐标系中,如果对任意一点(a ,b ),规定两种变换:),(),(b a b a f --=,),(),(a b b a g -=,那么[]=-)2,1(f g ▲ .18.等腰△ABC 中,AB =AC ,它的外接圆⊙O 半径为1,如果线段OB 绕点O 旋转90°后可与线段OC 重合,那么∠ABC 的余切值是 ▲ .7、54a . 8、2)(y x +. 9、⎩⎨⎧=-=41y x . 10、x > 4. 11、>. 12、960.13、31. 14、b a 3232-. 15、120. 16、a 23. 17、(2,1). 18、12±. 闵行区二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:21+2-= ▲ .8.在实数范围内分解因式:243x -= ▲ . 91的解是 ▲ .10.已知关于x 的方程230x x m --=没有实数根,那么m 的取值范围是 ▲ .11.已知直线(0)y kx b k =+≠与直线13y x =-平行,且截距为5,那么这条直线的解析式为 ▲ .12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小杰过马路时,恰巧是绿灯的概率是 ▲ .13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.1,那么第六组的频数是 ▲ .14.如图,已知在矩形ABCD 中,点E 在边AD 上,且AE = 2ED .设B A a =u u r r ,BC b =uu u r r ,那么CE =uu u r▲ (用a r 、b r的式子表示).15.如果二次函数2111y a x b x c =++(10a ≠,1a 、1b 、1c 是常数)与2222y a x b x c =++(20a ≠,2a 、2b 、2c 是常数)满足1a 与2a 互为相反数,1b 与2b 相等,1c 与2c 互为倒数,那么称这两个函数为“亚旋转函数”.请直接写出函数232y x x =-+-的“亚旋转函数”为 ▲ .16.如果正n 边形的中心角为2α,边长为5,那么它的边心距为 ▲ .(用锐角α的三角比表示) 17.如图,一辆小汽车在公路l 上由东向西行驶,已知测速探头M 到公路l 的距离MN 为9米,测得此车从点A 行驶到点B 所用的时间为0.6秒,并测得点A 的俯角为30o,点B 的俯角为60o.那么此车从A 到B 的平均速度为 ▲ 米/秒.1.732≈1.414≈) 18.在直角梯形ABCD 中,AB // CD ,∠DAB = 90o,AB = 12,DC = 7,5cos 13ABC ∠=,点E 在线段AD 上,将△ABE 沿BE 翻折,点A 恰巧落在对角线BD 上点P 处,那么PD = ▲ .AB DCEDCMl二、填空题:(本大题共12题,每题4分,满分48分)7.5; 8.2x x -(; 9.1x =; 10.94m <-; 11.153y x =-+; 12.512; 13.8; 14.13a b -r r ; 15.2132y x x =+-; 16.5cot 2α(或52tan α); 17.17.3; 18.12. 普陀区7.计算:xy x 3122⋅= ▲ . 8.方程x 的根是 ▲ .9.大型纪录片《厉害了,我的国》上映25天,累计票房约为402700000元,成为中国纪录电影票房冠军.402700000用科学记数法表示是 ▲ .10.用换元法解方程312122=+-+x x x x 时,如果设y xx =+21,那么原方程化成以y 为“元”的方程是 ▲ . 11.已知正比例函数的图像经过点M (2-)、),(11y x A 、),(22y x B ,如果21x x <,那么1y ▲ 2y .(填“>”、“=”、“<”)12.已知二次函数的图像开口向上,且经过原点,试写出一个符合上述条件的二次函数的解析式: ▲ .(只需写出一个)13.如果一个多边形的内角和是720,那么这个多边形的边有 ▲ 条.14.如果将“概率”的英文单词 probability 中的11个字母分别写在11张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母b 的概率是 ▲ .15.2018年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖的东南亚地区.据调查发现2018年春节期间出境游约有700万人,游客目的地分布情况的扇形图如图3所示,从中可知出境游东南亚 地区的游客约有 ▲ 万人.16. 如图4,在梯形ABCD 中,BC AD //,AD BC 3=,点E 、F 分别是边AB 、CD 的中点.设=,b DC =,那么向量EC 用向量a 、b 表示是 ▲ .17. 如图5,矩形ABCD 中,如果以AB 为直径的⊙O 沿着BC 滚动一周,点B 恰好与点C 重合,那么ABBC的值等于 ▲ .(结果保留两位小数)A东南亚欧美澳新16% 港澳台 15%韩日 11%其他13%图318. 如图6,在平面直角坐标系xOy 中,△ABC 的顶点A 、C 在坐标轴上,点B 的坐标是(22).将△ABC沿x 轴向左平移得到△111A B C ,点1B 落在函数6y x =-的图像上.如果此时四边形11AA C C 的面积等于552,那么点1C 的坐标是 ▲ .二、填空题:(本大题共12题,每题4分,满分48分)青浦区7.计算:32()=a a ÷- ▲ . 8.因式分解:24=a a - ▲ . 9.函数y 的定义域是 ▲ .010.不等式组1020.x x +≥⎧⎨->⎩,的整数解是 ▲ .11.关于x 的方程=2(1)ax x a +≠的解是 ▲ . 12.抛物线2(3)+1y x =-的顶点坐标是 ▲ .13.掷一枚材质均匀的骰子,掷得的点数为合数的概率是 ▲ .14.如果点1P (2,1y )、2P (3,2y )在抛物线2+2y x x =-上,那么1y ▲ 2y .(填“>”、 “<”或 “=”) 15.如图2,已知在平行四边形ABCD 中,E 是边AB 的中点,F 在边AD 上,且AF ︰FD=2︰1,如果AB a =,BC b =,那么EF = ▲ .16.如图3,如果两个相似多边形任意一组对应顶点P 、P '所在的直线都经过同一点O ,且有(0)OP k OP k '=⋅≠,那么我们把这样的两个多边形叫位似多边形,点O 叫做位似中心.已知ABC ∆与A B C '''∆是关于点O 的位似三角形,3OA OA '=,则ABC ∆与A B C '''∆的周长之比是 ▲ .17.如图4,在△ABC 中,BC=7,AC=,tan 1C =,点P 为AB 边上一动点(点P 不与点B 重合),以点P 为圆心,PB 为半径画圆,如果点C 在圆外,那么PB 的取值范围是 ▲ .18.已知,在Rt △ABC 中,∠C =90°,AC =9, BC =12,点D 、E 分别在边AC 、BC 上,且7.323x y ; 8. 3x =; 9. 810027.4⨯ ; 10. 32=-yy ; 11.>;12. 2y x =等; 13.6; 14.112; 15.315; 16.b a212+;17.3.14;18.(5-211). yxOABC图 6 A B CDEF图 4BCDO A 图5CD ︰CE =3︰4.将△CDE 绕点D 顺时针旋转,当点C 落在线段DE 上的点F 处时,BF恰好是∠ABC 的平分线,此时线段CD 的长是 ▲ .二、填空题:7.a ; 8.()4-a a ; 9.3≥-x ; 10.101、、-; 11. 21-a ; 12.(3,1); 13.13; 14.>; 15.2132-b a ; 16.1︰3; 17.3508<<PB ; 18.6. 松江区7.因式分解:34a a - = ▲ . 8x =的根是 ▲ . 9.函数32x y x-=的定义域是 ▲ . 10.已知方程240x x m -+=有两个不相等的实数根,则m 的取值范围是 ▲ . 11.把抛物线22y x =-向左平移1个单位,则平移后抛物线的表达式为 ▲ . 12.函数y kx b =+的图像如图所示,则当0y <时,x 的取值范围是 ▲ .13.一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,随机投掷这枚骰子,那么向上一面的点数为合数的概率是 ▲ .14.某区有4000名学生参加学业水平测试,从中随机抽取500名,对测试成绩进行了统计,统计结果见下表:那么根据上述数据可以估计该区这次参加学业水平测试成绩小于60分的有 ▲ 人.15. 如图,在△ABC 中,D 是AB 的中点,E 是AC 上一点,且AE =2EC ,如果AB a =uuu r r ,AC b =uuu r r ,那么DE uuu r=▲ .(用a r 、b r表示).图3A BCDEF 图2图4POP'ACDE (第15题图)B(第12题图)(第18题图)ADCB16.一个正n 边形的一个内角等于它的中心角的2倍,则n =▲ .17.平面直角坐标系xoy 中,若抛物线2y ax =上的两点A 、B 满足OA =OB ,且1tan 2OAB ∠=,则称线段AB 为该抛物线的通径.那么抛物线212y x =的通径长为 ▲ . 18.如图,已知平行四边形ABCD 中,AC =BC ,∠ACB =45°,将三角形ABC 沿着AC 翻折,点B 落在点E 处,联结DE ,那么DEAC的值为 ▲ . 二、填空题:(本大题共12题,每题4分,满分48分)7. (2)(2)a a a +-; 8. 2x =; 9. 0x ≠; 10. 4m <; 11.22(1)y x =-+;12. 1x <-; 13. 13; 14. 120; 15. 1223a b -+r r ;1 .徐汇区 7. 函数12y x =-的定义域是 8. 在实数范围内分解因式:22x y y -=9. 2=的解是 10. 不等式组2672x x -≥⎧⎨+>-⎩的解集是11. 已知点1(,)A a y 、2(,)B b y 在反比例函数3y x=的图像上,如果0a b <<,那么1y 与2y 的大小关系是1y 2y12. 抛物线2242y x x =+-的顶点坐标是13. 四张背面完全相同的卡片上分别写有0.3227四个实数,如果将卡片字面 朝下随意放在桌子上,任意取一张,那么抽到有理数的概率为14. 在ABC ∆中,点D 在边BC 上,且:1:2BD DC =,如果设AB a =,AC b =,那么BD 等于 (结果用a 、b 的线性组合表示)15. 如图,为了解全校300名男生的身高情况,随机抽取若干男生进行身高测量,将所得数据(精确到1cm )整理画出频数分布直方图(每组数据含最低值,不含最高值),估计该校男生的身高在170cm ~175cm 之间的人数约有 人16. 已知两圆相切,它们的圆心距为3,一个圆的半径是4,那么另一个圆的半径是17. 从三角形(非等腰三角形)一个顶点引出一条射线与对边相交,该顶点与该交点间的线段把这个三角形分割成两个小三角形,如果其中一个小三角形是等腰三角形,另一个与原三角形相似,那么我们把这条线段叫做这个三角形的完美分割线,如图,在ABC ∆中,1DB =,2BC =,CD 是ABC ∆的完美分割线,且ACD ∆是以CD 为底边的等腰三角形,则CD 的长为18. 如图,在Rt ABC ∆中,90C ∠=︒,5AB =,3BC =,点P 、Q 分别在边BC 、AC 上,PQ ∥AB ,把PCQ ∆绕点P 旋转得到PDE ∆(点C 、Q 分别与点D 、E 对应),点D 落在线段PQ 上,若AD 平分BAC ∠,则CP 的长为二. 填空题7. 2x ≠ 8. (y x x + 9. 7x = 10. 93x -<≤-11. > 12. (1,4)-- 13. 3414. 1133b a -r r15. 72 16. 1或7 17. 3218. 2 杨浦区二、填空题(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置上】 7、计算: 8、当时,化简:=9、函数中,自变量x 的取值范围是10、如果反比例函数 的图像经过点的值等于11、三人中至少有两人性别相同的概率是 12、25位同学10秒钟跳绳的成绩汇总如下表:那么跳绳次数的中位数是13、李明早上骑自行车上学,中途因道路施工推车步行了一段路,到学校共用时15分钟,如果他骑自行车的平均速度是每分钟250米,推车步行的平均速度是每分钟80米,他家离学校的路程是2900米,设他推车步行的时间为x分钟,那么可列出的方程是14、四边形ABCD中,向量=15、若正n边形的内角和为1400,则边数n为16、如图3,△ABC中,∠A=800,∠B=400,BC的垂直平分线交AB于点D,联结DC,如果AD=2,BD=6那么△ADC的周长为17、如图4,正△ABC的边长为2,点A、B的半径为的圆上,点C在圆内,将正△ABC绕点A逆时针旋转,当点C第一次落在圆上时,旋转角的正切值是18、当关于X的一元二次方程有实数根,且其中一个根为另一个根的2倍时,称之为“倍根方程”,如果关于X的一元二次方程是“倍根方程”,那么m的值为。
2018年年上海市中考数学二模试卷含答案

2018学年第二学期期中教学质量调研九年级数学试卷(满分150分,100分钟完成)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本调研卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个是正确的,旋转正确项的代号并填涂在答题纸的相应位置上]1.下列实数中,有理数是( )(A )2; (B (C (D 2.下列方程中,有实数根的是( )(Ax =; (B )2(2)10x +-=; (C )210x +=; (D 0. 3.如果a >b ,m <0,那么下列不等式中成立的是( )(A )am >bm ; (B )a b m m>; (C )a +m >b +m ; (D )-a +m >-b +m .4.如图,AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,EG 平分∠BEF ,如果∠EFG =64°,那么∠EGD 的大小是( ) (A )122°;(B )124°;(C )120°;(D )126°.5.已知两组数据:12345a a a a a 、、、、和123451a a a a a --1、-1、-1、-1、,下列判断中错误的是( )(A )平均数不相等,方差相等; (B )中位数不相等,标准差相等; (C )平均数相等,标准差不相等;(D )中位数不相等,方差相等. 6.下列命题中,假命题是( )(A )两组对角分别相等的四边形是平行四边形;(B )有一条对角线与一组邻边构成等腰三角形的平行四边形是菱形; (C )一组邻边互相垂直,两组对边分别平行的四边形是矩形; (D )有一组邻边相等且互相垂直的平行四边形是正方形.二、填空题:(本大题共12题,每题4分,满分48分) [在答题纸相应题号后的空格内直接填写答案] 7.计算:23(2)a a ⋅= ▲ .8.分解因式:2()4x y xy -+= ▲ .9.方程组3,26x y y x +=⎧⎨-=⎩的解是 ▲ .10有意义,那么x 的取值范围是 ▲ .11.如果函数21a y x--=(a 为常数)的图像上有两点1(1,)y ,21(,)3y ,那么函数值1y ▲2y (填“<”,“=”或“>”).12.为了解植物园的某种花卉的生长情况,在一片约为3000株此类花卉的园地内,随机检测了200株的高度作为样本,统计结果整理后列表如下:(每组数据可包括最低值,不包括最高值)试估计该园地内此类花卉高度小于55厘米且不小于45厘米的约为 ▲株. 13.从1,2,3,4,5,6,7,8,9中任取一个数,这个数既是奇数又是素数的概率是▲ .14.如图,在△ABC 中,点G 是重心,过点G 作DE ∥BC 分别交AB 、AC 于点D 、E ,已知,AB a CB b == ,那么AE =▲ (用向量表示). 15.如图,已知O 中,直径AB 平分弦CD ,且交CD 于点E ,如果OE =BE ,那么弦CD 所对的圆心角是▲ 度.16.已知正多边形的边长为a ,且它的一个外角是其内角的一半,那么此正多边形的边心距是 ▲ .(用含字母a 的代数式表示)17. 在平面直角坐标系中,如果对任意一点(a ,b ),规定两种变换:(,)(,),(,)(,)f a b a b g a b b a =--=-,那么g [f (1, -2)] ▲ .18.等腰△ABC 中,AB =AC ,它的外接圆O 半径为1,如果线段OB 绕点O 旋转90°后可与线段OC 重合,那么∠ABC 的余切值是 ▲ .三、解答题:(本大题共7题,满分78分)[将下列各题的解答过程,做在答题纸的相应位置上]19.(本题满分10分)201801(cot 45)(3)(sin 30)π--︒++--︒.20.(本题满分10分) 解方程:2456111x xx x x ++=+--.21.(本题满分10分,每小题满分5分)已知:如图,边长为1的正方形ABCD 中,对角线AC 、DB 交于点H ,DE 平分∠ADB ,交AC 于点E ,联结BE 并延长,交边AD 于点F . 求:(1)求证:DC =EC ; (2)求△EAF 的面积.今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价位10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:(1)求y与x之间的函数关系式;(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?(销售利润=销售价-成本价).23.(本题满分12分,第小题满分6分)已知,如图,在平行四边形ABCD中,AC、DB交于点E,点F在BC的延长线上,联结EF、DF,且∠DEF=∠ADC.求证:(1)求证:EF AB=;BF DB(2)如果22=⋅,求证:平行四边形ABCD是矩形.BD AD DF在平面直角坐标系xOy 中,已知点B (8,0)和点C (9,-3)抛物线28y ax ax c =-+(a 、c是常数,a ≠0)经过点B 、C ,且与x 轴的另一个交点为A ,对称轴上有一点M ,满足MA =MC . (1)求这条抛物线的表达式; (2)求四边形ABCM 的面积;(3)如果坐标系内有一点D ,满足三角形ABCD 是等腰梯形,且AD ∥BC ,求点D 的坐标.25.(本题满分14分,第(1)小题满分6分,第(2)小题满分8分)如图,平行四边形ABCD 中,已知AB =6,BC =9,cos ∠ABC =13,对角线AC 、BD 交于点O ,动点P 在边AB 上,P 经过点B ,交线段P A 于点E ,设BP =x ..(1)求AC 的长;(2)设O 的半径为y ,当P 与O 外切时,求y 关于x 的函数关系式,并写出定义域; (3)如果AC 是O 的直径,O 经过点E ,求O 与P 的圆心距OP 的长.九年级数学试卷参考答案及评分标准1、D ,2、B ,3、C ,4、A ,5、C ,6、B7、54a ,8、2()x y +,9、14x y =-⎧⎨=⎩,10、x >4,11、>,12、960,13、13,14、2233a b -,15、120,16,17、(2,1),18111920、x =9,21、(1)略(222、y =-2x +60,(2)15 23、略,24、(1)21833y x x =-+,(2)392,(3)1339(,)55D -,25、(1)9,(2)3)y x <≤,(3)。
上海市各区2018届中考数学二模试卷精选汇编:填空题

上海市各区2018届中考二模数学试卷精选汇编 填空题专题宝山区、嘉定区二、填空题(本大题共12题,每题4分,满分48分) 7.计算:=4 ▲ .8.一种细菌的半径是00000419.0米,用科学记数法把它表示为 ▲ 米. 9. 因式分解:=-x x 42 ▲ . 10.不等式组⎩⎨⎧>+≤-063,01x x 的解集是 ▲ .11.在一个不透明的布袋中装有2个白球、8个红球和5个黄球,这些球除了颜色不同之外,其余均相同.如果从中随机摸出一个球,摸到黄球的概率是 ▲ . 12.方程23=+x 的根是 ▲ .13.近视眼镜的度数y (度)与镜片焦距x (米)呈反比例,其函数关系式为xy 120=.如果近似眼镜镜片的焦距3.0=x 米,那么近视眼镜的度数y 为 ▲ . 14.数据1、2、3、3、6的方差是 ▲ .15.在△ABC 中,点D 是边BC 的中点,=,=,那么=AD ▲ (用、表示).16.如图1,在矩形ABCD 中,点E 在边CD 上,点F 在对角线BD 上,5:2:=DE DF ,BD EF ⊥,那么=∠ADB tan ▲ .17.如图2,点A 、B 、C 在圆O 上,弦AC 与半径OB 互相平分,那么AOC ∠度数为 ▲ 度. 18.如图3,在△ABC 中,5==AC AB ,6=BC ,点D 在边AB 上,且︒=∠90BDC .如果△ACD 绕点A 顺时针旋转,使点C 与点B 重合,点D 旋转至点1D ,那么线段1DD 的长为 ▲ .O AC图2A BCD图3B ACF图17. 2 8. 64.1910-⨯ 9. (4)x x - 10. 21x -<≤11. 1312. 1x = 13. 400 14. 2.8 15. 2a b +r r16. 2 17. 120° 18. 4225长宁区二、填空题(本大题共12题, 每题4分, 满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7. 计算:=--︒0)3(30sin ▲ . 8. 方程6+=-x x 的解是 ▲ .9. 不等式组⎪⎩⎪⎨⎧≥-<+-1)12(303x x 的解集是 ▲ .10.已知反比例函数xky =的图像经过点(-2017,2018),当0>x 时,函数值y 随 自变量x 的值增大而 ▲ .(填“增大”或“减小”)11.若关于x 的方程032=--m x x 有两个相等的实数根,则m 的值是 ▲ . 12.在形状为等腰三角形、圆、矩形、菱形、直角梯形的5张纸片中随机抽取一张,抽到中心对称图形的概率是 ▲ .13.抛物线522++=mx mx y 的对称轴是直线 ▲ . 14.小明统计了家里3月份的电话通话清单,按通话时间画出频数分布直方图(如图所示),则通话时间不足10分钟的 通话次数的频率是 ▲ .15.如图,在四边形ABCD 中,点E 、F 分别是边AB 、AD 的中点,BC =15,CD =9,EF =6,∠AFE =50°,则∠ADC 的度数为 ▲ .16.如图,在梯形ABCD 中,AB //CD ,∠C=90°,BC =CD =4,52=AD ,若a AD =,b DC =,用a 、b 表示=DB ▲ .第14题图 ABCDE F第15题图BA17.如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC 是半高三角形,且斜边5=AB ,则它的周长等于 ▲ . 18.如图,在矩形ABCD 中,对角线BD 的长为1,点P 是线段BD上的一点,联结CP ,将△BCP 沿着直线CP 翻折,若点B 落在 边AD 上的点E 处,且EP //AB ,则AB 的长等于 ▲ .二.填空题:(本大题共12题,满分48分) 7.21-; 8.2-=x ; 9.3>x ; 10.增大; 11.43-=m ; 12.53; 13.1-=x ;14.7.0;15.︒140; 16.→→-a b 21; 17.255或535++; 18.215-.崇明区二、填空题(本大题共12题,每题4分,满分48分) 7.因式分解:29x -= ▲ .8.不等式组1023x x x -<⎧⎨+>⎩的解集是 ▲ .9.函数12y x =-的定义域是 ▲ . 10.方程13x +=的解是 ▲ .11.已知袋子中的球除颜色外均相同,其中红球有3个,如果从中随机摸得1个红球的概率为18,那么袋子中共有 ▲ 个球.12.如果关于x 的方程240x x k +-=有两个相等的实数根,那么实数k 的值是 ▲ . 13.如果将抛物线221y x x =+-向上平移,使它经过点(1,3)A ,那么所得新抛物线的表达式是▲ .14.某校组织了主题为“共建生态岛”的电子小报作品征集活动,先从中随机抽取了部分作品,按,,,A B C D 四个等级进行评分,然后根据统计结果绘制了如下两幅不完整的统计图,那么此次抽取的作品中等级为B 的作品数为 ▲ .第18题图ABCD(第14题图)15.已知梯形ABCD ,AD BC ∥,2BC AD =,如果AB a =u u u r r ,AC b =u u u r r ,那么DA =u u u r▲ . (用,a b r r表示).16.如图,正六边形ABCDEF 的顶点B 、C 分别在正方形AGHI 的边AG 、GH 上,如果4AB =,那么CH 的长为 ▲ .17.在矩形ABCD 中,5AB =,12BC =,点E 是边AB 上一点(不与A 、B 重合),以点A 为圆心,AE 为半径作A ⊙,如果C ⊙与A ⊙外切,那么C ⊙的半径r 的取值范围是 ▲ .18.如图,ABC △中,90BAC ∠=︒,6AB =,8AC =,点D 是BC 的中点,将ABD △沿AD 翻折得到AED △,联结CE ,那么线段CE 的长等于 ▲ .二、填空题:(本大题共12题,每题4分,满分48分)7.(3)(3)x x +-; 8.31x -<<; 9.2x ≠; 10.8x =; 11.24; 12.4-; 13.22y x x =+; 14.48;15.1122a b -r r ; 16.623-; 17.813r <<; 18.145.奉贤区 7.计算:=-aa 211 . 8.如果822=-b a ,且4=+b a ,那么b a -的值是 . 9.方程242=-x 的根是 . 10.已知反比例函数)0(≠=k xky ,在其图像所在的每个象限内,y 的值随x 的值增大而减 小,那么它的图像所在的象限是第 象限.11.如果将抛物线22y x =平移,使平移后的抛物线顶点坐标为(1,2),那么所得新抛物线的表达式是 .(第16题图)HDCIFBAGE (第18题图)DCBAE12.将6本相同厚度的书叠起来,它们的高度是9厘米.如果将这样相同厚度的书叠起来的高度是42厘米,那么这些书有 本.13.从1,2,3,4,5,6,7,8这八个数中,任意抽取一个数,这个数恰好是合数的概率是.14.某校为了了解学生双休日参加社会实践活动的情况,随机抽取了100名学生进行调查,并绘成如图3所示的频数分布直方图.已知该校共有1000名学生,据此估计,该校双休日参加社会实践活动时间在2~2.5小时之间的学生数大约是全体学生数的 (填百分数) . 15.如图4,在梯形ABCD 中,AD //BC ,BC=2AD ,E 、F 分别是边AD 、BC 的中点,设=, =,那么EF 等于 (结果用、的线性组合表示). 16.如果一个矩形的面积是40,两条对角线夹角的正切值是34,那么它的一条对角线长是 . 17.已知正方形ABCD ,AB =1,分别以点A 、C 为圆心画圆,如果点B 在圆A 外,且圆A与圆C 外切,那么圆C 的半径长r 的取值范围是 .18.如图5,将△ABC 的边AB 绕着点A 顺时针旋转)900(︒<<︒αα得到AB ’,边AC 绕着点A 逆时针旋转)900(︒<<︒ββ得到AC ’,联结B ′C ′.当︒=+90βα时,我们称△A B ′C ′ 是△ABC 的“双旋三角形”.如果等边△ABC 的边长为a ,那么它的“双旋三角形”的面积是 (用含a 的代数式表示).二、填空题:7、12a ; 8、2; 9、4; 10、一三; 11、22(1)2y x =-+; 12、28; 13、38; 14、28%; 15、12a b +r r ; 16、10; 17212r << 18、214a黄浦区 721-= . 8.因式分解:212x x --= .9.方程125x x +=+的解是 .图4A B DFE C810 24 30 0.5 1 1.5 2 2.5 3 时间(小时)图3人数 BC图5AB ′C ′10.不等式组1203130 2xx⎧->⎪⎪⎨⎪-≤⎪⎩的解集是 .11.已知点P位于第三象限内,且点P到两坐标轴的距离分别为2和4,若反比例函数图像经过点P,则该反比例函数的解析式为.12.如果一次函数的图像经过第一、二、四象限,那么其函数值y随自变量x的值的增大而.(填“增大”或“减小”)13.女生小琳所在班级共有40名学生,其中女生占60%.现学校组织部分女生去市三女中参观,需要从小琳所在班级的女生当中随机抽取一名女生参加,那么小琳被抽到的概率是.14.已知平行四边形相邻两个内角相差40°,则该平行四边形中较小内角的度数是.15.半径为1的圆的内接正三角形的边长为.16.如图,点D、E分别为△ABC边CA、CB上的点,已知DE∥AB,且DE经过△ABC的重心,设CA a=u u u r r,CB b=u u u r r,则DE=u u u r.(用ar、br表示)17.如图,在四边形ABCD中,902624ABC ADC AC BD∠=∠=︒==,,,M、N分别是AC、BD的中点,则线段MN的长为.18.如图,将矩形ABCD沿对角线AC折叠,使点B翻折到点E处,如果DE∶AC=1∶3,那么AD∶AB= .二、填空题:(本大题共12题,每题4分,满分48分)721; 8.()()34x x+-; 9.2; 10.166x<≤;11.8yx=; 12.减小; 13.124; 14.70;153 16.2233b a-r r.; 17.5; 182∶1.金山区7.因式分解:2a a-=▲ .8.函数2y x =-的定义域是 ▲ .9.方程21xx =-的解是 ▲ . 10.一次函数2y x =-+的图像不经过第 ▲ 象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是 ▲ . 12.如果关于x 的一元二次方程240x x k -+=有两个不相等的实数根,那么k 的取值范围是 ▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于 ▲ . 14.空气质量指数,简称AQI ,如果AQI 在0~50空气质量类别为优,在51~100空气质量类别为良, 在101~150空气质量类别为轻度污染,按照某市最 近一段时间的AQI 画出的频数分布直方图如图3 所示,已知每天的AQI 都是整数,那么空气质量 类别为优和良的天数占总天数的百分比为 ▲ %. 15.一辆汽车在坡度为1:2.4的斜坡上向上行驶130米,那么这辆汽车的高度上升了 ▲ 米.16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是 ▲ . 17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d 的的取值范围是 ▲ .18.如图4,Rt △ABC 中,∠C =90°,AC =6,BC =8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC , 那么点P 和点B 间的距离等于 ▲ .二.填空题:(本大题共12题,满分48分)7.()1a a -; 8.2x ≥; 9.2x =; 10.三; 11.12; 12.4k <; 13.4; 14.80; 15.50; 16.12; 17.3d 15<<; 18.52或10.静安区10 14 6 天数图350.5 100.5 150.5A图4D二、填空题:(本大题共12题,每题4分,满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7.32)2(a a ⋅ = ▲ .8.分解因式:=+-xy y x 4)(2▲ .9.方程组⎩⎨⎧=-=+62,3x y y x 的解是 ▲ .10.如果4-x x 有意义,那么x 的取值范围是 ▲ .11.如果函数x a y 12--=(a 为常数)的图像上有两点),1(1y 、),31(2y ,那么函数值1y ▲ 2y .(填“<”、“=”或“>”)12.为了解植物园内某种花卉的生长情况,在一片约有3000株此类花卉的园地内,随机抽测了200株的高度作为样本,统计结果整理后列表如下:(每组数据可包括最低值,不包括最高值) 高度(cm ) 40~45 45~50 50~55 55~60 60~65 65~70 频数334222244336试估计该园地内此类花卉高度小于55厘米且不小于45厘米的约为 ▲ 株.13.从1,2,3,4,5,6,7,8,9中任取一个数,这个数即是奇数又是素数的概率是 ▲ .14.如图,在△ABC 中,点G 是重心,过点G 作DE ∥BC ,分别交AB 、AC 于点D 、E .已知b CB a AB ==, ,那么AE = ▲ .(用向量表示). 15.如图,已知⊙O 中,直径AB 平分弦CD ,且交CD 于点E , 如果OE =BE ,那么弦CD 所对的圆心角是 ▲ 度.16.已知正多边形的边长为a ,且它的一个外角是其内角的一半,那么此正多边形的边心距是 ▲ .(用含字母a 的代数式表示). 17.在平面直角坐标系中,如果对任意一点(a ,b ),规定两种变换:),(),(b a b a f --=,),(),(a b b a g -=,那么[]=-)2,1(f g ▲ .18.等腰△ABC 中,AB =AC ,它的外接圆⊙O 半径为1,如果线段OB 绕点O 旋转90°后可与线段OC 重合,那么∠ABC 的余切值是 ▲ .7、54a . 8、2)(y x +. 9、⎩⎨⎧=-=41y x . 10、x > 4. 11、>. 12、960.ABE DCG·第14题图ACE第15题图· EO13、31. 14、3232-. 15、120. 16、a 23. 17、(2,1). 18、12±. 闵行区二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:21+2-= ▲ .8.在实数范围内分解因式:243x -= ▲ . 9211x -的解是 ▲ .10.已知关于x 的方程230x x m --=没有实数根,那么m 的取值范围是 ▲ .11.已知直线(0)y kx b k =+≠与直线13y x =-平行,且截距为5,那么这条直线的解析式为 ▲ .12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小杰过马路时,恰巧是绿灯的概率是 ▲ .13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.1,那么第六组的频数是 ▲ .14.如图,已知在矩形ABCD 中,点E 在边AD 上,且AE = 2ED .设BA a =uu r r ,BC b =uu u r r ,那么CE =uu u r▲ (用a r 、b r的式子表示).15.如果二次函数2111y a x b x c =++(10a ≠,1a 、1b 、1c 是常数)与2222y a x b x c =++(20a ≠,2a 、2b 、2c 是常数)满足1a 与2a 互为相反数,1b 与2b 相等,1c 与2c 互为倒数,那么称这两个函数为“亚旋转函数”.请直接写出函数232y x x =-+-的“亚旋转函数”为 ▲ .16.如果正n 边形的中心角为2α,边长为5,那么它的边心距为 ▲ .(用锐角α的三角比表示) 17.如图,一辆小汽车在公路l 上由东向西行驶,已知测速探头M 到公路l 的距离MN 为9米,测得此车从点A 行驶到点B 所用的时间为0.6秒,并测得点A 的俯角为30o ,点B 的俯角为60o .那么此车从A 到B 的平均速度为 ▲ 米/秒.3 1.7322 1.414≈) 18.在直角梯形ABCD 中,AB // CD ,∠DAB = 90o,AB = 12,DC = 7,5cos 13ABC ∠=,点E 在线段AD 上,将△ABE 沿BE 翻折,点A 恰巧落在对角线BD 上点P 处,那么PD = ▲ .二、填空题:(本大题共12题,每题4分,满分48分)ABDC(第14题图)E ABD C(第18题图)BMN (第17题图)l7.5; 8.23)(23)x x +-(; 9.1x =; 10.94m <-; 11.153y x =-+; 12.512; 13.8; 14.13a b -r r ; 15.2132y x x =+-; 16.5cot 2α(或52tan α); 17.17.3; 18.12212-. 普陀区7.计算:xy x 3122⋅= ▲ . 8.方程32x x =+的根是 ▲ .9.大型纪录片《厉害了,我的国》上映25天,累计票房约为402700000元,成为中国纪录电影票房冠军.402700000用科学记数法表示是 ▲ .10.用换元法解方程312122=+-+x x x x 时,如果设y xx =+21,那么原方程化成以y 为“元”的方程是 ▲ . 11.已知正比例函数的图像经过点M (2-)、),(11y x A 、),(22y x B ,如果21x x <,那么1y ▲ 2y .(填“>”、“=”、“<”)12.已知二次函数的图像开口向上,且经过原点,试写出一个符合上述条件的二次函数的解析式: ▲ .(只需写出一个)13.如果一个多边形的内角和是720o ,那么这个多边形的边有 ▲ 条.14.如果将“概率”的英文单词 probability 中的11个字母分别写在11张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母b 的概率是 ▲ .15.2018年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖的东南亚地区.据调查发现2018年春节期间出境游约有700万人,游客目的地分布情况的扇形图如图3所示,从中可知出境游东南亚 地区的游客约有 ▲ 万人.16. 如图4,在梯形ABCD 中,BC AD //,AD BC 3=,点E 、F 分别是边AB 、CD 的中点.设a AD =,b DC =,那么向量EC 用向量a 、b 表示是 ▲ .17. 如图5,矩形ABCD 中,如果以AB 为直径的⊙O 沿着BC 滚动一周,点B 恰好与点C 重合,那么ABBC的值等于 ▲ .(结果保留两位小数)y BCADEFDO A A东南亚欧美澳新16%港澳台 15%韩日11% 其他13% 图318. 如图6,在平面直角坐标系xOy 中,△ABC 的顶点A 、C 在坐标轴上,点B 的坐标是(22).将△ABC 沿x 轴向左平移得到△111A B C ,点1B 落在函数6y x =-的图像上.如果此时四边形11AA C C 的面积等于552,那么点1C 的坐标是 ▲ .二、填空题:(本大题共12题,每题4分,满分48分)青浦区7.计算:32()=a a ÷- ▲ .8.因式分解:24=a a - ▲ . 9.函数3y x +的定义域是 ▲ .010.不等式组1020.x x +≥⎧⎨->⎩,的整数解是 ▲ .11.关于x 的方程=2(1)ax x a +≠的解是 ▲ . 12.抛物线2(3)+1y x =-的顶点坐标是 ▲ .13.掷一枚材质均匀的骰子,掷得的点数为合数的概率是 ▲ .14.如果点1P (2,1y )、2P (3,2y )在抛物线2+2y x x =-上,那么1y ▲ 2y .(填“>”、 “<”或 “=”) 15.如图2,已知在平行四边形ABCD 中,E 是边AB 的中点,F 在边AD 上,且AF ︰FD=2︰1,如果AB a =u u u r r ,BC b =u u u r r,那么EF =u u u r▲ .16.如图3,如果两个相似多边形任意一组对应顶点P 、P '所在的直线都经过同一点O ,且有(0)OP k OP k '=⋅≠,那么我们把这样的两个多边形叫位似多边形,点O 叫做位似中心.已知ABC ∆与A B C '''∆是关于点O 的位似三角形,3OA OA '=,则ABC ∆与A B C '''∆的周长之比是 ▲ .17.如图4,在△ABC 中,BC=7,AC =32,tan 1C =,点P 为AB 边上一动点(点P 不与点B 重合),以点P7.323x y ; 8. 3x =;9. 810027.4⨯ ; 10. 32=-yy ; 11.>;12. 2y x =等;13.6; 14.112; 15.315; 16.b a ρρ212+;17.3.14;18.(5-211).为圆心,PB 为半径画圆,如果点C 在圆外,那么PB 的取值范围是 ▲ . 18.已知,在Rt △ABC 中,∠C =90°,AC =9, BC =12,点D 、E 分别在边AC 、BC 上,且CD ︰CE =3︰4.将△CDE 绕点D 顺时针旋转,当点C 落在线段DE 上的点F 处时,BF恰好是∠ABC 的平分线,此时线段CD 的长是 ▲ .二、填空题:7.a ; 8.()4-a a ; 9.3≥-x ; 10.101、、-; 11. 21-a ; 12.(3,1); 13.13; 14.>; 15.2132-r r b a ; 16.1︰3; 17.3508<<PB ; 18.6.松江区7.因式分解:34a a - = ▲ . 8.方程2x x +=的根是 ▲ . 9.函数32x y x-=的定义域是 ▲ . 10.已知方程240x x m -+=有两个不相等的实数根,则m 的取值范围是 ▲ . 11.把抛物线22y x =-向左平移1个单位,则平移后抛物线的表达式为 ▲ . 12.函数y kx b =+的图像如图所示,则当0y <时,x 的取值范围是 ▲ .13.一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,随机投掷这枚骰子,那么向上一面的点数为合数的概率是 ▲ .14.某区有4000名学生参加学业水平测试,从中随机抽取500名,对测试成绩进行了统计,统计结果见下表:成绩(x ) x <6060≤x <7070≤x <8080≤x <90 90≤x ≤100 人数155978140208那么根据上述数据可以估计该区这次参加学业水平测试成绩小于60分的有 ▲ 人.15. 如图,在△ABC 中,D 是AB 的中点,E 是AC 上一点,且AE =2EC ,如果AB a =uu u r r ,AC b =uuu r r ,那么DE uuu r =▲ .(用a r 、b r表示).图3 ABCDE F图2图4POP'16.一个正n 边形的一个内角等于它的中心角的2倍,则n =▲ .17.平面直角坐标系xoy 中,若抛物线2y ax =上的两点A 、B 满足OA =OB ,且1tan 2OAB ∠=,则称线段AB 为该抛物线的通径.那么抛物线212y x =的通径长为 ▲ . 18.如图,已知平行四边形ABCD 中,AC =BC ,∠ACB =45°,将三角形ABC 沿着AC 翻折,点B 落在点E 处,联结DE ,那么DEAC的值为 ▲ . 二、填空题:(本大题共12题,每题4分,满分48分)7. (2)(2)a a a +-; 8. 2x =; 9. 0x ≠; 10. 4m <; 11.22(1)y x =-+;12. 1x <-; 13. 13; 14. 120; 15. 1223a b -+r r ;21 .徐汇区 7. 函数12y x =-的定义域是 8. 在实数范围内分解因式:22x y y -= 9. 32x -=的解是 10. 不等式组2672x x -≥⎧⎨+>-⎩的解集是11. 已知点1(,)A a y 、2(,)B b y 在反比例函数3y x=的图像上,如果0a b <<,那么1y 与2y 的大小关系是1y 2y12. 抛物线2242y x x =+-的顶点坐标是 13. 四张背面完全相同的卡片上分别写有0.3g92227四个实数,如果将卡片字面 朝下随意放在桌子上,任意取一张,那么抽到有理数的概率为14. 在ABC ∆中,点D 在边BC 上,且:1:2BD DC =,如果设AB a =u u u r r ,AC b =u u u r r ,那么BD u u u r等于 (结果用a r 、b r的线性组合表示)15. 如图,为了解全校300名男生的身高情况,随机抽取若干男生进行身高测量,将所得数据(精确到1cm )整理画出频数分布直方图(每组数据含最低值,不含最高值),估计该校男生的身高在170cm ~175cm 之间的ACDE (第15题图)B-1xy(第12题图)(第18题图)A DC人数约有 人16. 已知两圆相切,它们的圆心距为3,一个圆的半径是4,那么另一个圆的半径是17. 从三角形(非等腰三角形)一个顶点引出一条射线与对边相交,该顶点与该交点间的线段把这个三角形分割成两个小三角形,如果其中一个小三角形是等腰三角形,另一个与原三角形相似,那么我们把这条线段叫做这个三角形的完美分割线,如图,在ABC ∆中,1DB =,2BC =,CD 是ABC ∆的完美分割线,且ACD ∆是以CD 为底边的等腰三角形,则CD 的长为18. 如图,在Rt ABC ∆中,90C ∠=︒,5AB =,3BC =,点P 、Q 分别在边BC 、AC 上,PQ ∥AB ,把PCQ ∆绕点P 旋转得到PDE ∆(点C 、Q 分别与点D 、E 对应),点D 落在线段PQ 上,若AD 平分BAC ∠,则CP 的长为 二. 填空题7. 2x ≠ 8. (2)(2)y x x -+ 9. 7x = 10. 93x -<≤-11. > 12. (1,4)-- 13. 3414. 1133b a -r r15. 72 16. 1或7 17. 3218. 2 杨浦区二、填空题(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置上】 7、计算: 8、当时,化简:=9、函数 中,自变量x 的取值范围是10、如果反比例函数 的图像经过点的值等于11、三人中至少有两人性别相同的概率是 12、25位同学10秒钟跳绳的成绩汇总如下表:人数 1234510次数15 8 25 10 17 20那么跳绳次数的中位数是13、李明早上骑自行车上学,中途因道路施工推车步行了一段路,到学校共用时15分钟,如果他骑自行车的平均速度是每分钟250米,推车步行的平均速度是每分钟80米,他家离学校的路程是2900米,设他推车步行的时间为x分钟,那么可列出的方程是14、四边形ABCD中,向量=15、若正n边形的内角和为1400,则边数n为16、如图3,△ABC中,∠A=800,∠B=400,BC的垂直平分线交AB于点D,联结DC,如果AD=2,BD=6那么△ADC的周长为17、如图4,正△ABC的边长为2,点A、B的半径为的圆上,点C在圆内,将正△ABC绕点A逆时针旋转,当点C第一次落在圆上时,旋转角的正切值是18、当关于X的一元二次方程有实数根,且其中一个根为另一个根的2倍时,称之为“倍根方程”,如果关于X的一元二次方程是“倍根方程”,那么m的值为。
上海18年初三数学各区二模23题汇编(含答案)

18年 二模23题汇编求线段比值或者证明线段倍数关系:1. 构造“A ”字形或“8”字形,利用比例线段常见于背景为平行四边形、特殊平行四边形或者梯形等存在隐含平行的几何图形的题目,或者题目已知平行或比值,以及燕尾形中。
2. 利用相似,对应边成比例 3. 利用锐角三角比常见于以直角三角形,矩形、正方形为背景,或者本身已知垂直的题目,遇到等腰梯形或直角梯形也常添加垂直与锐角三角比结合23.(普陀)已知:如图9,梯形ABCD 中,AD ∥BC ,DE ∥AB ,DE 与对角线AC 交于点F ,FG ∥AD ,且FG EF =.(1)求证:四边形ABED 是菱形; (2)联结AE ,又知AC ⊥ED ,求证:212AE EF ED =.23.证明: (1)∵AD ∥BC ,DE ∥AB ,∴四边形ABED 是平行四边形. ·································· (2分) ∵FG ∥AD ,∴FG CFAD CA=. ············································································· (1分) 同理 EF CF AB CA =. ···························································································· (1分) 得FG AD =EF AB∵FG EF =,∴AD AB =. ·············································································· (1分) ∴四边形ABED 是菱形. ····················································································· (1分) (2)联结BD ,与AE 交于点H .∵四边形ABED 是菱形,∴,BD ⊥AE . ········································· (2分)得90DHE ∠= .同理90AFE ∠=. ∴DHE AFE ∠∠=. ························································································ (1分) 又∵AED ∠是公共角,∴△DHE ∽△AFE . ······················································ (1分) ∴EH DE EF AE =. ································································································ (1分) ∴12AE 2=EF i ED . ······················································································· (1分)12EH AE =ABCDEF G图923(崇明)如图,AM 是ABC △的中线,点D 是线段AM 上一点(不与点A 重合).DE AB ∥交BC 于点K ,CE AM ∥,联结AE .(1)求证:AB CMEK CK=; (2)求证:BD AE =.23.(本题满分12分,每小题6分) (1)证明:∵DE AB ∥∴ ABCEKC =∠∠ ……………………………………………………1分 ∵CE AM ∥∴ AMB ECK =∠∠ ……………………………………………………1分∴ABM EKC △∽△ ……………………………………………………1分∴AB BMEK CK=………………………………………………………1分 ∵ AM 是△ABC 的中线∴BM CM = ………………………………………………………1分 ∴AB CMEK CK=………………………………………………………1分 (2)证明:∵CE AM ∥∴DE CMEK CK =………………………………………………………2分 又∵AB CMEK CK=∴DE AB = ………………………………………………………2分 又∵DE AB ∥∴四边形ABDE 是平行四边形 …………………………………………1分 ∴BD AE = ………………………………………………………1分23.(奉贤)已知:如图7,梯形ABCD ,DC ∥AB ,对角线AC 平分∠BCD ,点E 在边CB 的延长线上,EA ⊥AC ,垂足为点A . (1)求证:B 是EC 的中点;(2)分别延长CD 、EA 相交于点F ,若EC DC AC ⋅=2,求证:FC AC AF AD ::=.(第23题图)ABK MCDEACDE图7B23.(本题满分12分,每小题满分各6分)证明:(1)∵DC ∥AB ,∴∠DCB =∠CAB . ……………………………………………1分 ∵AC 平分∠BCD ,∴∠DCB =∠BCA .∴∠CAB =∠BCA . ………………………………………………………………………1分 ∴BC =BA . ………………………………………………………………………………1分 ∵EA ⊥AC ,∴∠CAB +∠BAE=90°,∠BCA +∠E=90°. ∴∠BAE =∠E . …………1分 ∴BA =BE . …………………………………………………………………………………1分 ∴BC =BE ,即B 是EC 的中点. ………………………………………………………1分 (2)∵EC DC AC ⋅=2,∴AC EC DC AC ::=.∵∠DCA =∠ACE ,∴△DCA ∽△ACE . ………………………………………………2分 ∴EC AC AE AD ::=.……………………………………………………………………1分 ∵∠FCA =∠ECA ,AC=AC ,∠F AC =∠EAC ,∴△FCA ≌△ECA . …………………2分 ∴AE =AF ,EC =FC .∴FC AC AF AD ::=. …………………………………………………………………1分23.(黄浦)如图,点E 、F 分别为菱形ABCD 边AD 、CD 的中点. (1)求证:BE =BF ;(2)当△BEF 为等边三角形时,求证:∠D =2∠A .23. 证:(1)∵四边形ABCD 为菱形,∴AB =BC =AD =CD ,∠A =∠C ,——————————————————(2分) 又E 、F 是边的中点,∴AE =CF ,——————————————————————————(1分)∴△ABE ≌△CBF ———————————————————————(2分) ∴BE =BF . ——————————————————————————(1分)(2)联结AC 、BD ,AC 交BE 、BD 于点G 、O . ——————————(1分) ∵△BEF 是等边三角形, ∴EB =EF ,又∵E 、F 是两边中点, ∴AO =12AC =EF =BE .——————————————————————(1分) 又△ABD 中,BE 、AO 均为中线,则G 为△ABD 的重心, ∴1133OGAO BE GE ===, ∴AG =BG ,——————————————————————————(1分) 又∠AGE =∠BGO ,∴△AGE ≌△BGO ,———— ——————————————————(1分)∴AE =BO ,则AD =BD ,∴△ABD 是等边三角形,—— —————————————————(1分) 所以∠BAD =60°,则∠ADC =120°,即∠ADC =2∠BAD . ——— ——————————————————(1分)FEDCBAE G第23题图C A B DF23.(虹口)如图,四边形ABCD 是矩形,E 是对角线AC 上的一点,EB =ED 且∠ABE =∠ADE . (1)求证:四边形ABCD 是正方形;(2)延长DE 交BC 于点F ,交AB 的延长线于点G ,求证:EF AG BC BE ⋅=⋅.23. 证:(1)证明:联结BD …………………………………………………………………(1分)∵EB =ED ∴∠EBD =∠EDB …………………………………………………(2分)∵∠ABE =∠ADE ∴∠ABD =∠ADB …………………………………………(1分) ∴AB=AD …………………………………………………………………………(1分) ∵四边形ABCD 是矩形 ∴四边形ABCD 是正方形………………………(1分) (2)证明:∵四边形ABCD 是矩形∴AD ∥BC ∴EF ECDE EA =………………………………………………(2分)同理 DC EC AG EA =……………………………………………………………(2分)∵DE=BE∵四边形ABCD 是正方形 ∴BC=DC …………………………………………(1分) ∴EF BC BE AG =∴EF AG BC BE ⋅=⋅ ……………………………………………………………(1分)证明乘积式:1. 化成比例式找相似相似找法,一般为横看或者竖看比例式当中的线段,观察构成两条线段的三个顶点即为要找的三角形顶点2. 找中间量进行转化:1) 找中间比利用等比转化 2) 找中间积利用等积进行转化3. 特殊四边形的特性与判定条件,如对角线相互平分 23.(闵行)如图,已知在△ABC 中,∠BAC =2∠C ,∠BAC 的平分线AE 与∠ABC 的平分线BD 相交于点F ,FG ∥AC ,联结DG .(1)求证:BF BC AB BD ⋅=⋅; (2)求证:四边形ADGF 是菱形.23.证明:(1)∵AE 平分∠BAC ,∴∠BAC =2∠BAF =2∠EAC .∵∠BAC =2∠C ,∴∠BAF =∠C =∠EAC .…………………………(1分) 又∵BD 平分∠ABC ,∴∠ABD =∠DBC .……………………………(1分) ∵∠ABF =∠C ,∠ABD =∠DBC ,∴ABF CBD ∆∆∽.…………………………………………………(1分) ∴AB BF BC BD=.………………………………………………………(1分) ∴BF BC AB BD ⋅=⋅.………………………………………………(1分) (2)∵FG ∥AC ,∴∠C =∠FGB ,∴∠FGB =∠F AB .………………(1分)∵∠BAF =∠BGF ,∠ABD =∠GBD ,BF =BF ,∴ABF GBF ∆∆≌.∴AF =FG ,BA =BG .…………………………(1分) ∵BA =BG ,∠ABD =∠GBD ,BD =BD ,∴ABD GBD ∆∆≌.∴∠BAD =∠BGD .……………………………(1分) ∵∠BAD =2∠C ,∴∠BGD =2∠C ,∴∠GDC =∠C ,∴∠GDC =∠EAC ,∴AF ∥DG .……………………………………(1分) 又∵FG ∥AC ,∴四边形ADGF 是平行四边形.……………………(1分) ∴AF =FG .……………………………………………………………(1分) ∴四边形ADGF 是菱形.……………………………………………(1分)AB E GC F D(第23题图)23.(青浦)如图7,在梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点M ,点E 在边 BC 上,且DAE DCB ∠=∠,联结AE ,AE 与BD 交于点F .(1)求证:2DM MF MB =⋅; (2)联结DE ,如果3BF FM =,求证:四边形ABED 是平行四边形.23.证明:(1)∵AD //BC ,∴∠=∠DAE AEB , ············································· (1分)∵∠=∠DCB DAE ,∴∠=∠DCB AEB , ································ (1分) ∴AE //DC ,··········································································· (1分)∴=FM AMMD MC. ··································································· (1分) ∵AD //BC ,∴=AM DMMC MB, ··················································· (1分) ∴=FM DM MD MB, ··································································· (1分) 即2=⋅MD MF MB .(2)设=FM a ,则=3BF a ,=4BM a . ··········································· (1分)由2=⋅MD MF MB ,得24=⋅MD a a ,∴2=MD a , ········································································ (1分)∴3==DF BF a . ·································································· (1分) ∵AD //BC ,∴1==AF DFEF BF, ···················································· (1分) ∴=AF EF , ········································································· (1分) ∴四边形ABED 是平行四边形. ··················································· (1分)MFE DCBA图723.(松江)如图,已知梯形ABCD 中,AB ∥CD ,∠D =90°,BE 平分∠ABC ,交CD 于点E , F 是AB 的中点,联结AE 、EF ,且AE ⊥BE .求证:(1)四边形BCEF 是菱形;(2).证明:(1) ∵BE 平分∠ABC ,∴∠ABE =∠CBE …………………………………………………1分 ∵AE ⊥BE ∴∠AEB =90°∵F 是AB 的中点∴………………………………………………1分∴∠FEB =∠FBE …………………………………………………1分 ∴∠FEB =∠CBE …………………………………………………1分 ∴EF ∥BC …………………………………………………1分 ∵AB ∥CD∴四边形BCEF 是平行四边形…………………………1分 ∵∴四边形BCEF 是菱形……………………………………1分 (2) ∵四边形BCEF 是菱形, ∴BC =BF ∵ ∴AB =2BC ………………………………………………1分 ∵ AB ∥CD∴ ∠DEA =∠EAB ∵ ∠D =∠AEB∴ △EDA ∽△AEB ………………………………………2分∴ …………………………………………1分∴ BE ·AE =AD ·AB∴ …………………………………1分2BE AE AD BC ⋅=⋅12EF BF AB ==EF BF =12BF AB =AD AEBE AB =2BE AE AD BC ⋅=⋅(第23题图)FA CD EB23. (徐汇)在梯形ABCD 中,AD ∥BC ,AB CD =,BD BC =,点E 在对角线BD 上,且DCE DBC ∠=∠. (1)求证:AD BE =;(2)延长CE 交AB 于点F ,如果CF AB ⊥, 求证:4EF FC DE BD ⋅=⋅.23.(长宁)如图,在四边形ABCD 中,AD //BC ,E 在BC 的延长线,联结AE 分别交BD 、CD 于点 G 、F ,且AG GF BE AD =.(1)求证:AB //CD ;(2)若BD GD BC ⋅=2,BG =GE ,求证:四边形ABCD 是菱形.证明:(1)∵BC AD // ∴BGDG BE AD = (2分)∵AG GF BE AD = ∴AGGF BG DG = (1分) ∴ CD AB // (2分)(2)∵BC AD //,CD AB //∴四边形ABCD 是平行四边形 ∴BC=AD (1分)∵ BD GD BC ⋅=2∴ BD GD AD ⋅=2即ADGDBD AD =又 ∵BDA ADG ∠=∠ ∴ADG ∆∽BDA ∆ (1分)∴ABD DAG ∠=∠∵CD AB // ∴BDC ABD ∠=∠ ∵BC AD // ∴E DAG ∠=∠∵BG =GE ∴E DBC ∠=∠ ∴DBC BDC ∠=∠ (3分) ∴BC=CD (1分) ∵四边形ABCD 是平行四边形 ∴平行四边形ABCD 是菱形. (1分) 23.(宝山嘉定)如图6,在正方形ABCD 中,点M 是边BC 上的一点(不与B 、C 重合),点N 在CD 边的延长线上,且满足︒=∠90MAN ,联结MN 、AC ,MN 与边AD 交于点E . (1)求证:AN AM =;ACDEF GB第23题图(2)如果NAD CAD ∠=∠2,求证:AE AC AM ⋅=2.证明垂直:1. 所求角所在的三角形与已知直角三角形相似2. 三线合一,勾股定理,证明互余等3. 特殊的四边形特性与判定23.(金山)如图7,已知AD 是△ABC 的中线, M 是AD 的中点, 过A 点作AE ∥BC ,CM 的延 长线与AE 相交于点E ,与AB 相交于点F .(1)求证:四边形AEBD 是平行四边形;(2)如果AC =3AF ,求证四边形AEBD 是矩形.23.证明:(1)∵AE //BC ,∴∠AEM =∠DCM ,∠EAM =∠CDM ,…………………………(1分)又∵AM=DM ,∴△AME ≌△DMC ,∴AE =CD ,………………………………(1分) ∵BD=CD ,∴AE =BD .……………………………………………………………(1分) ∵AE ∥BD ,∴四边形AEBD 是平行四边形.……………………………………(2分)(2)∵AE //BC,∴AF AEFB BC=.………………………………………………………(1分) ∵AE=BD=CD ,∴12AF AE FB BC ==,∴AB=3AF .……………………………(1分)∵AC=3AF ,∴AB=AC ,…………………………………………………………(1分) 又∵AD 是△ABC 的中线,∴AD ⊥BC ,即∠ADB =90°.……………………(1分) ∴四边形AEBD 是矩形.…………………………………………………………(1分)E AF M B D图7C23.(静安)已知:如图,在平行四边形ABCD 中, AC 、DB 交于点E , 点F 在BC 的延长线上,联结EF 、DF ,且∠DEF =∠ADC . (1)求证:DBABBF EF =; (2)如果DF AD BD ⋅=22,求证:平行四边形ABCD 是矩形.23.(本题满分12分,第(1)小题6分,第(2)小题6分) 证明:(1)∵平行四边形ABCD ,∴AD //BC ,AB //DC∴∠BAD +∠ADC =180°,……………………………………(1分)又∵∠BEF +∠DEF =180°, ∴∠BAD +∠ADC =∠BEF +∠DEF ……(1分) ∵∠DEF =∠ADC ∴∠BAD =∠BEF , …………………………(1分) ∵AB //DC , ∴∠EBF =∠ADB …………………………(1分)∴△ADB ∽△EBF ∴DB ABBF EF =………………………(2分) (2) ∵△ADB ∽△EBF ,∴BFBEBD AD =, ………………………(1分) 在平行四边形ABCD 中,BE =ED =BD 21∴221BD BE BD BF AD =⋅=⋅∴BF AD BD ⋅=22, ………………………………………(1分) 又∵DF AD BD ⋅=22∴DF BF =,△DBF 是等腰三角形 …………………………(1分) ∵DE BE =∴FE ⊥BD , 即∠DEF =90° …………………………(1分) ∴∠ADC =∠DEF =90° …………………………(1分) ∴平行四边形ABCD 是矩形 …………………………(1分)C第23题图A B DEF11 / 1123. (杨浦)已知:如图7,在平行四边形ABCD 中,点G 为对角线AC 的中点,过点G 的直线EF 分别交边AB 、CD 于点E 、F ,过点G 的直线MN 分别交边AD 、BC 于点M 、N ,且AGE CGN .(1)求证:四边形ENFM 为平行四边形;(2)当四边形ENFM 为矩形时,求证:BE BN .(1)ABCD 是平行四边形∴BC AD CD AB ∥,∥∴ACB DAC ∠=∠在AMG △与CNG △中⎪⎩⎪⎨⎧∠=∠=∠=∠CGNAGM GC AG ACBDACCNG AMG ≌△△∴GN MG =同理CFG AEG ≌△△∴GF EG =∴EMFN 是平行四边形(2)EMFN 是矩形∴GN EG =在AEG △与CNG △中⎪⎩⎪⎨⎧=∠=∠=GNEG CGN AGE GCAGCNG AGE ≌△△∴NC AE GCN GAE =∠=∠,∴AC AB =∴BN EB =。
上海市各区2018届中考数学二模试卷精选汇编填空题专题20190128189

上海市各区2018届九年级中考二模数学试卷精选汇编 填空题专题宝山区、嘉定区二、填空题(本大题共12题,每题4分,满分48分) 7.计算:=4 ▲ .8.一种细菌的半径是00000419.0米,用科学记数法把它表示为 ▲ 米. 9. 因式分解:=-x x 42 ▲ . 10.不等式组⎩⎨⎧>+≤-063,01x x 的解集是 ▲ .11.在一个不透明的布袋中装有2个白球、8个红球和5个黄球,这些球除了颜色不同之外,其余均相同.如果从中随机摸出一个球,摸到黄球的概率是 ▲ . 12.方程23=+x 的根是 ▲ .13.近视眼镜的度数y (度)与镜片焦距x (米)呈反比例,其函数关系式为xy 120=.如果近似眼镜镜片的焦距3.0=x 米,那么近视眼镜的度数y 为 ▲ . 14.数据1、2、3、3、6的方差是 ▲ .15.在△ABC 中,点D 是边BC 的中点,=,=,那么= ▲ (用、表示).16.如图1,在矩形ABCD 中,点E 在边CD 上,点F 在对角线BD 上,5:2:=DE DF ,BD EF ⊥,那么=∠ADB tan ▲ .17.如图2,点A 、B 、C 在圆O 上,弦AC 与半径OB 互相平分,那么AOC ∠度数为 ▲ 度. 18.如图3,在△ABC 中,5==AC AB ,6=BC ,点D 在边AB 上,且︒=∠90BDC .如果△ACD 绕点A 顺时针旋转,使点C 与点B 重合,点D 旋转至点1D ,那么线段1DD 的长为 ▲ .ABCD图37. 2 8. 64.1910-⨯ 9. (4)x x - 10. 21x -<≤ 11.1312. 1x = 13. 400 14. 2.8 15. 2a b +16. 2 17. 120° 18. 4225长宁区二、填空题(本大题共12题, 每题4分, 满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7. 计算:=--︒0)3(30sin ▲ . 8. 方程6+=-x x 的解是 ▲ .9. 不等式组⎪⎩⎪⎨⎧≥-<+-1)12(303x x 的解集是 ▲ .10.已知反比例函数xky =的图像经过点(-2017,2018),当0>x 时,函数值y 随 自变量x 的值增大而 ▲ .(填“增大”或“减小”)11.若关于x 的方程032=--m x x 有两个相等的实数根,则m 的值是 ▲ . 12.在形状为等腰三角形、圆、矩形、菱形、直角梯形的5张纸片中随机抽取一张,抽到中心对称图形的概率是 ▲ .13.抛物线522++=mx mx y 的对称轴是直线 ▲ . 14.小明统计了家里3月份的电话通话清单,按通话时间画出频数分布直方图(如图所示),则通话时间不足10分钟的 通话次数的频率是 ▲ .15.如图,在四边形ABCD 中,点E 、F 分别是边AB 、AD 的中点,第14题图 ADE FBC =15,CD =9,EF =6,∠AFE =50°,则∠ADC 的度数为 ▲ .16.如图,在梯形ABCD 中,AB //CD ,∠C=90°,BC =CD =4,52=AD ,若=,b DC =,用、表示=DB ▲ . 17.如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC 是半高三角形,且斜边5=AB ,则它的周长等于 ▲ . 18.如图,在矩形ABCD 中,对角线BD 的长为1,点P 是线段BD上的一点,联结CP ,将△BCP 沿着直线CP 翻折,若点B 落在 边AD 上的点E 处,且EP //AB ,则AB 的长等于 ▲ .二.填空题:(本大题共12题,满分48分) 7.21-; 8.2-=x ; 9.3>x ; 10.增大; 11.43-=m ; 12.53; 13.1-=x ;14.7.0;15.︒140; 16.→→-a b 21; 17.255或535++; 18.215-. 崇明区二、填空题(本大题共12题,每题4分,满分48分) 7.因式分解:29x -= ▲ .8.不等式组1023x x x -<⎧⎨+>⎩的解集是 ▲ .9.函数12y x =-的定义域是 ▲ . 103=的解是 ▲ .11.已知袋子中的球除颜色外均相同,其中红球有3个,如果从中随机摸得1个红球的概率为18,那么袋子中共有 ▲ 个球.12.如果关于x 的方程240x x k +-=有两个相等的实数根,那么实数k 的值是 ▲ . 13.如果将抛物线221y x x =+-向上平移,使它经过点(1,3)A ,那么所得新抛物线的表达式第16题图D CBA 第18题图ABCD是▲ .14.某校组织了主题为“共建生态岛”的电子小报作品征集活动,先从中随机抽取了部分作品,按,,,A B C D 四个等级进行评分,然后根据统计结果绘制了如下两幅不完整的统计图,那么此次抽取的作品中等级为B 的作品数为 ▲ .15.已知梯形ABCD ,AD BC ∥,2BC AD =,如果AB a =,AC b =,那么DA = ▲ . (用,a b 表示).16.如图,正六边形ABCDEF 的顶点B 、C 分别在正方形AGHI 的边AG 、GH 上,如果4AB =, 那么CH 的长为 ▲ .17.在矩形ABCD 中,5AB =,12BC =,点E 是边AB 上一点(不与A 、B 重合),以点A 为圆心,AE 为半径作A ⊙,如果C ⊙与A ⊙外切,那么C ⊙的半径r 的取值范围是 ▲ . 18.如图,ABC △中,90BAC ∠=︒,6AB =,8AC =,点D 是BC 的中点,将ABD △沿AD翻折得到AED △,联结CE ,那么线段CE 的长等于 ▲ .二、填空题:(本大题共12题,每题4分,满分48分)7.(3)(3)x x +-; 8.31x -<<; 9.2x ≠; 10.8x =; 11.24; 12.4-; 13.22y x x =+; 14.48; 15.1122a b -; 16.623-; 17.813r <<; 18.145. (第14题图)(第16题图)HDCIFBAGE (第18题图)DCBAE奉贤区 7.计算:=-aa 211 . 8.如果822=-b a ,且4=+b a ,那么b a -的值是 . 9.方程242=-x 的根是 . 10.已知反比例函数)0(≠=k xky ,在其图像所在的每个象限内,y 的值随x 的值增大而减 小,那么它的图像所在的象限是第 象限.11.如果将抛物线22y x =平移,使平移后的抛物线顶点坐标为(1,2),那么所得新抛物线的表达式是 .12.将6本相同厚度的书叠起来,它们的高度是9厘米.如果将这样相同厚度的书叠起来的高度是42厘米,那么这些书有 本.13.从1,2,3,4,5,6,7,8这八个数中,任意抽取一个数,这个数恰好是合数的概率是. 14.某校为了了解学生双休日参加社会实践活动的情况,随机抽取了100名学生进行调查,并绘成如图3所示的频数分布直方图.已知该校共有1000名学生,据此估计,该校双休 日参加社会实践活动时间在2~2.5小时之间的学生数大约是全体学生数的 (填百分数) .15.如图4,在梯形ABCD 中,AD //BC ,BC=2AD ,E 、F 分别是边AD 、BC 的中点,设=, =,那么等于 (结果用、的线性组合表示). 16.如果一个矩形的面积是40,两条对角线夹角的正切值是34,那么它的一条对角线长是 .17.已知正方形ABCD ,AB =1,分别以点A 、C 为圆心画圆,如果点B 在圆A 外,且圆A与圆C 外切,那么圆C 的半径长r 的取值范围是 .18.如图5,将△ABC 的边AB 绕着点A 顺时针旋转)900(︒<<︒αα得到AB ’,边AC 绕 着点A 逆时针旋转)900(︒<<︒ββ得到AC ’,联结B ′C ′.当︒=+90βα时,我们称△AB ′C ′是△ABC 的“双旋三角形”.如果等边△ABC 的边长为a ,那么它的“双旋三角形”的面积是 (用含a 的代数式表示).A B DFE C人数 C图5AB ′C ′二、填空题: 7、12a ; 8、2; 9、4; 10、一三; 11、22(1)2y x =-+; 12、28; 13、38; 14、28%; 15、12a b +; 16、10; 171r << 18、214a黄浦区 7= . 8.因式分解:212x x --= . 9.方程1x +=的解是 .10.不等式组12031302x x ⎧->⎪⎪⎨⎪-≤⎪⎩的解集是 .11.已知点P 位于第三象限内,且点P 到两坐标轴的距离分别为2和4,若反比例函数图像经过点P ,则该反比例函数的解析式为 .12.如果一次函数的图像经过第一、二、四象限,那么其函数值y 随自变量x 的值的增大而 .(填“增大”或“减小”)13.女生小琳所在班级共有40名学生,其中女生占60%.现学校组织部分女生去市三女中参观,需要从小琳所在班级的女生当中随机抽取一名女生参加,那么小琳被抽到的概率是 .14.已知平行四边形相邻两个内角相差40°,则该平行四边形中较小内角的度数是 . 15.半径为1的圆的内接正三角形的边长为 .16.如图,点D 、E 分别为△ABC 边CA 、CB 上的点,已知DE ∥AB ,且DE 经过△ABC 的重心,设CA a =,CB b =,则DE = .(用a 、b 表示)17.如图,在四边形ABCD中,902624ABC ADC AC BD∠=∠=︒==,,,M、N分别是AC、BD的中点,则线段MN的长为.18.如图,将矩形ABCD沿对角线AC折叠,使点B翻折到点E处,如果DE∶AC=1∶3,那么AD∶AB= .二、填空题:(本大题共12题,每题4分,满分48分)721; 8.()()34x x+-; 9.2; 10.166x<≤;11.8yx=; 12.减小; 13.124; 14.70;153; 16.2233b a-.; 17.5; 182∶1.金山区7.因式分解:2a a-=▲ .8.函数2y x=-的定义域是▲ .9.方程21xx=-的解是▲.10.一次函数2y x=-+的图像不经过第▲象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是▲ .12.如果关于x的一元二次方程240x x k-+=有两个不相等的实数根,那么k的取值范围是▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于▲ .14.空气质量指数,简称AQI,如果AQI在0~50空气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最1014天数0 50.5 100.5 150.5近一段时间的AQI 画出的频数分布直方图如图3 所示,已知每天的AQI 都是整数,那么空气质量 类别为优和良的天数占总天数的百分比为 ▲ %. 15.一辆汽车在坡度为1:2.4的斜坡上向上行驶130米,那么这辆汽车的高度上升了 ▲ 米.16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是 ▲ . 17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d 的的取值范围是 ▲ .18.如图4,Rt △ABC 中,∠C =90°,AC =6,BC =8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC , 那么点P 和点B 间的距离等于 ▲ .二.填空题:(本大题共12题,满分48分)7.()1a a -; 8.2x ≥; 9.2x =; 10.三; 11.12; 12.4k <; 13.4; 14.80; 15.50; 16.12; 17.3d 15<<; 18.52或10. 静安区二、填空题:(本大题共12题,每题4分,满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7.32)2(a a ⋅ = ▲ .8.分解因式:=+-xy y x 4)(2▲ .9.方程组⎩⎨⎧=-=+62,3x y y x 的解是 ▲ .10.如果4-x x 有意义,那么x 的取值范围是 ▲ .11.如果函数x a y 12--=(a 为常数)的图像上有两点),1(1y 、),31(2y ,那么函数值图41y ▲ 2y .(填“<”、“=”或“>”) 12.为了解植物园内某种花卉的生长情况,在一片约有3000株此类花卉的园地内,随机抽测了200株的高度作为样本,统计结果整理后列表如下:(每组数据可包括最低值,不包括最高值)试估计该园地内此类花卉高度小于55厘米且不小于45厘米的约为 ▲ 株. 13.从1,2,3,4,5,6,7,8,9中任取一个数,这个数即是奇数又是素数的概率是 ▲ .14.如图,在△ABC 中,点G 是重心,过点G 作DE ∥BC ,分别交AB 、AC 于点D 、E .已知b CB a AB ==, ,那么AE = ▲ .(用向量表示).15.如图,已知⊙O 中,直径AB 平分弦CD ,且交CD 于点E , 如果OE =BE ,那么弦CD 所对的圆心角是 ▲ 度.16.已知正多边形的边长为a ,且它的一个外角是其内角的一半,那么此正多边形的边心距是 ▲ .(用含字母a 的代数式表示). 17.在平面直角坐标系中,如果对任意一点(a ,b ),规定两种变换:),(),(b a b a f --=,),(),(a b b a g -=,那么[]=-)2,1(f g ▲ .18.等腰△ABC 中,AB =AC ,它的外接圆⊙O 半径为1,如果线段OB 绕点O 旋转90°后可与线段OC 重合,那么∠ABC 的余切值是 ▲ .7、54a . 8、2)(y x +. 9、⎩⎨⎧=-=41y x . 10、x > 4. 11、>. 12、960.13、31. 14、3232-. 15、120. 16、a 23. 17、(2,1). 18、12±. 闵行区二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:21+2-= ▲ .8.在实数范围内分解因式:243x -= ▲ . 91=的解是 ▲ .10.已知关于x 的方程230x x m --=没有实数根,那么m 的取值范围是 ▲ .11.已知直线(0)y kx b k =+≠与直线13y x =-平行,且截距为5,那么这条直线的解析式为ABE DCG·第14题图第15题图▲ .12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小杰过马路时,恰巧是绿灯的概率是 ▲ .13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.1,那么第六组的频数是 ▲ .14.如图,已知在矩形ABCD 中,点E 在边AD 上,且AE = 2ED .设BA a =,BC b =,那么CE =▲ (用a 、b 的式子表示).15.如果二次函数2111y a x b x c =++(10a ≠,1a 、1b 、1c 是常数)与2222y a x b x c =++(20a ≠,2a 、2b 、2c 是常数)满足1a 与2a 互为相反数,1b 与2b 相等,1c 与2c 互为倒数,那么称这两个函数为“亚旋转函数”.请直接写出函数232y x x =-+-的“亚旋转函数”为 ▲ .16.如果正n 边形的中心角为2α,边长为5,那么它的边心距为 ▲ .(用锐角α的三角比表示)17.如图,一辆小汽车在公路l 上由东向西行驶,已知测速探头M 到公路l 的距离MN 为9米,测得此车从点A 行驶到点B 所用的时间为0.6秒,并测得点A 的俯角为30o,点B 的俯角为60o.那么此车从A 到B 的平均速度为 ▲ 米/秒.(结果保留三个有效数字,参考1.7321.414)18.在直角梯形ABCD 中,AB // CD ,∠DAB = 90o,AB = 12,DC = 7,5cos 13ABC ∠=,点E 在线段AD 上,将△ABE 沿BE 翻折,点A 恰巧落在对角线BD 上点P 处,那么PD = ▲ .二、填空题:(本大题共12题,每题4分,满分48分)7.5; 8.2x x +(; 9.1x =; 10.94m <-; 11.153y x =-+; 12.512; 13.8; 14.13a b -; 15.2132y x x =+-; 16.5cot 2α(或52tan α); 17.17.3; 18.12-. 普陀区ABD(第14题图)E ABD C(第18题图)AMN (第17题图)l7.计算:xy x 3122⋅= ▲ . 8.方程32x x =+的根是 ▲ .9.大型纪录片《厉害了,我的国》上映25天,累计票房约为402700000元,成为中国纪录电影票房冠军.402700000用科学记数法表示是 ▲ .10.用换元法解方程312122=+-+x x x x 时,如果设y xx =+21,那么原方程化成以y 为“元”的方程是 ▲ .11.已知正比例函数的图像经过点M (2-)、),(11y x A 、),(22y x B ,如果21x x <,那么1y ▲ 2y .(填“>”、“=”、“<”)12.已知二次函数的图像开口向上,且经过原点,试写出一个符合上述条件的二次函数的解析式: ▲ .(只需写出一个)13.如果一个多边形的内角和是720,那么这个多边形的边有 ▲ 条.14.如果将“概率”的英文单词 probability 中的11个字母分别写在11张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母b 的概率是 ▲ .15.2018年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖的东南亚地区.据调查发现2018年春节期间出境游约有700万人, 游客目的地分布情况的扇形图如图3所示,从中可知出境游东南亚 地区的游客约有 ▲ 万人.16. 如图4,在梯形ABCD 中,BC AD //,AD BC 3=,点E 、F 分别是边AB 、CD 的中点.设a AD =,b DC =,那么向量EC 用向量a 、b 表示是 ▲ .17. 如图5,矩形ABCD 中,如果以AB 为直径的⊙O 沿着BC 滚动一周,点B 恰好与点C 重合,那么ABBC的值等于 ▲ .(结果保留两位小数)y xO ABC图6ABCDEF图4BC DO A 图5A东南亚欧美澳新16%港澳台 15%韩日11%其他 13%图318. 如图6,在平面直角坐标系xOy 中,△ABC 的顶点A 、C 在坐标轴上,点B 的坐标是(22).将△ABC 沿x 轴向左平移得到△111A B C ,点1B 落在函数6y x=-的图像上.如果此时四边形11AA C C 的面积等于552,那么点1C 的坐标是 ▲ . 二、填空题:(本大题共12题,每题4分,满分48分) 青浦区7.计算:32()=a a ÷- ▲ . 8.因式分解:24=a a - ▲ . 9.函数y 的定义域是 ▲ .010.不等式组1020.x x +≥⎧⎨->⎩,的整数解是 ▲ .11.关于x 的方程=2(1)ax x a +≠的解是 ▲ . 12.抛物线2(3)+1y x =-的顶点坐标是 ▲ .13.掷一枚材质均匀的骰子,掷得的点数为合数的概率是 ▲ .14.如果点1P (2,1y )、2P (3,2y )在抛物线2+2y x x =-上,那么1y ▲ 2y .(填“>”、 “<”或 “=”)15.如图2,已知在平行四边形ABCD 中,E 是边AB 的中点,F 在边AD 上,且AF ︰FD=2︰1,如果AB a =,BC b =,那么EF = ▲ .16.如图3,如果两个相似多边形任意一组对应顶点P 、P '所在的直线都经过同一点O ,且有(0)OP k OP k '=⋅≠,那么我们把这样的两个多边形叫位似多边形,点O 叫做位似中心.已知ABC ∆与A B C '''∆是关于点O 的位似三角形,3OA OA '=,则ABC ∆与A B C '''∆的周长之比是 ▲ .7.323x y ; 8. 3x =;9. 810027.4⨯ ; 10. 32=-yy ; 11.>;12. 2y x =等;13.6; 14.112; 15.315; 16.b a212+;17.3.14;18.(5-211).17.如图4,在△ABC 中,BC=7,AC =32,tan 1C =,点P 为AB 边上一动点(点P 不与点B重合),以点P 为圆心,PB 为半径画圆,如果点C 在圆外,那么PB 的取值范围是 ▲ . 18.已知,在Rt △ABC 中,∠C =90°,AC =9, BC =12,点D 、E 分别在边AC 、BC 上,且CD ︰CE =3︰4.将△CDE 绕点D 顺时针旋转,当点C 落在线段DE 上的点F 处时,BF恰好是∠ABC 的平分线,此时线段CD 的长是 ▲ .二、填空题:7.a ; 8.()4-a a ; 9.3≥-x ; 10.101、、-; 11. 21-a ; 12.(3,1); 13.13; 14.>; 15.2132-b a ; 16.1︰3; 17.3508<<PB ; 18.6.松江区7.因式分解:34a a - = ▲ . 8.方程2x x +=的根是 ▲ . 9.函数32x y x-=的定义域是 ▲ . 10.已知方程240x x m -+=有两个不相等的实数根,则m 的取值范围是 ▲ . 11.把抛物线22y x =-向左平移1个单位,则平移后抛物线的表达式为 ▲ . 12.函数y kx b =+的图像如图所示,则当0y <时,x 的取值范围是 ▲ .13.一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,随机投掷这枚骰子,那么向上一面的点数为合数的概率是 ▲ .14.某区有4000名学生参加学业水平测试,从中随机抽取500名,对测试成绩进行了统计,统计结果见下表: 成绩(x ) x <6060≤x <7070≤x <8080≤x <90 90≤x ≤100 人数155978140208那么根据上述数据可以估计该区这次参加学业水平测试成绩小于60分的有 ▲ 人. 15. 如图,在△ABC 中,D 是AB 的中点,E 是AC 上一点,且AE =2EC ,如果AB a =,AC b =,图3 ABCDE F图2图4POP'那么DE =▲ .(用a 、b 表示).16.一个正n 边形的一个内角等于它的中心角的2倍,则n =▲ .17.平面直角坐标系xoy 中,若抛物线2y ax =上的两点A 、B 满足OA =OB ,且1tan 2OAB ∠=,则称线段AB 为该抛物线的通径.那么抛物线212y x =的通径长为 ▲ . 18.如图,已知平行四边形ABCD 中,AC =BC ,∠ACB =45°,将三角形ABC 沿着AC 翻折,点B落在点E 处,联结DE ,那么DEAC的值为 ▲ . 二、填空题:(本大题共12题,每题4分,满分48分)7. (2)(2)a a a +-; 8. 2x =; 9. 0x ≠; 10. 4m <; 11.22(1)y x =-+; 12.1x <-; 13.13; 14. 120; 15. 1223a b -+;16. 6; 17. 2; 18.1 .徐汇区 7. 函数12y x =-的定义域是 8. 在实数范围内分解因式:22x y y -= 9. 2=的解是 10. 不等式组2672x x -≥⎧⎨+>-⎩的解集是11. 已知点1(,)A a y 、2(,)B b y 在反比例函数3y x=的图像上,如果0a b <<,那么1y 与2y 的大小关系是1y 2y12. 抛物线2242y x x =+-的顶点坐标是ACDE(第15题图)B(第12题图)(第18题图)A DCB13. 四张背面完全相同的卡片上分别写有0.3、9、2、227四个实数,如果将卡片字面 朝下随意放在桌子上,任意取一张,那么抽到有理数的概率为14. 在ABC ∆中,点D 在边BC 上,且:1:2BD DC =,如果设AB a =,AC b =,那么BD 等于 (结果用a 、b 的线性组合表示)15. 如图,为了解全校300名男生的身高情况,随机抽取若干男生进行身高测量,将所得数据(精确到1cm )整理画出频数分布直方图(每组数据含最低值,不含最高值),估计该校男生的身高在170cm ~175cm 之间的人数约有 人16. 已知两圆相切,它们的圆心距为3,一个圆的半径是4,那么另一个圆的半径是 17. 从三角形(非等腰三角形)一个顶点引出一条射线与对边相交,该顶点与该交点间的线段把这个三角形分割成两个小三角形,如果其中一个小三角形是等腰三角形,另一个与原三角形相似,那么我们把这条线段叫做这个三角形的完美分割线,如图,在ABC ∆中,1DB =,2BC =,CD 是ABC ∆的完美分割线,且ACD ∆是以CD 为底边的等腰三角形,则CD 的长为18. 如图,在Rt ABC ∆中,90C ∠=︒,5AB =,3BC =,点P 、Q 分别在边BC 、AC 上,PQ ∥AB ,把PCQ ∆绕点P 旋转得到PDE ∆(点C 、Q 分别与点D 、E 对应),点D 落在线段PQ 上,若AD 平分BAC ∠,则CP 的长为 二. 填空题7. 2x ≠ 8. (2)(2)y x x -+ 9. 7x = 10. 93x -<≤- 11. > 12. (1,4)-- 13.3414. 1133b a -15. 72 16. 1或7 17. 3218. 2 杨浦区二、填空题(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置上】 7、计算:8、当时,化简: =9、函数中,自变量x的取值范围是10、如果反比例函数的图像经过点的值等于11、三人中至少有两人性别相同的概率是12、25位同学10秒钟跳绳的成绩汇总如下表:人数 1 2 3 4 5 10次数15 8 25 10 17 20那么跳绳次数的中位数是13、李明早上骑自行车上学,中途因道路施工推车步行了一段路,到学校共用时15分钟,如果他骑自行车的平均速度是每分钟250米,推车步行的平均速度是每分钟80米,他家离学校的路程是2900米,设他推车步行的时间为x分钟,那么可列出的方程是14、四边形ABCD中,向量=15、若正n边形的内角和为1400,则边数n为16、如图3,△ABC中,∠A=800,∠B=400,BC的垂直平分线交AB于点D,联结DC,如果AD=2,BD=6那么△ADC的周长为17、如图4,正△ABC的边长为2,点A、B的半径为的圆上,点C在圆内,将正△ABC绕点A逆时针旋转,当点C第一次落在圆上时,旋转角的正切值是18、当关于X的一元二次方程有实数根,且其中一个根为另一个根的2倍时,称之为“倍根方程”,如果关于X的一元二次方程是“倍根方程”,那么m的值为。
2018年浦东新区初三数学二模试卷及答案

2018 年浦东新区初三数学二模试卷(完卷时间: 100 分钟,满分: 150 分)2018.5 考生注意:1.本试卷含三个大题,共 25 题.答题时,考生务必按答题要求在答题纸...规定的位置上作答, 在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸...的相应位置上写出证明或计 算的主要步骤.一、选择题: (本大题共 6题,每题 4 分,满分 24分) 【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸 的相应位置上】 1.下列代数式中,单项式是(A) 1; x (B ) 0; (C ) x 1;(D ) x .2.下列代数式中,二次根式mn 的有理化因式可以是(A ) m n ;(Bm n ; (C ) m n ;(D ) mn23.已知一元二次方程 x 22x 1 0 ,下列判断正确的是(A )该方程有两个不相等的实数根; ( B )该方程有两个相等的实数根; (C )该方程没有实数根; (D )该方程的根的情况不确定. 4.某运动员进行射击测试,共射靶 6 次,成绩记录如下: 8.5, 9.0, 10, 8.0, 9.5, 10,在下列各统计量中,表示这组数据离散程度的量(C )方差; (D) 频率.(A )平均数; (B )众数; 5.下列 y 关于 x 的函数中, 当 x 0时,函数值 y 随 x 的值增大而减小的是2 x2 x1 (A ) y x 2; (B ) y ; (C ) y ; (D y2 3x6.已知四边形 ABCD 中,AB//CD ,AC=BD ,下列判断中正.确.的是(A )如果 BC=AD ,那么四边形 ABCD 是等腰梯形; (B )如果 AD//BC ,那么四边形 ABCD 是菱形; (C )如果 AC 平分 BD ,那么四边形 ABCD 是矩形; (D )如果 AC ⊥BD ,那么四边形 ABCD 是正方形. 二、填空题: (本大题共 12题,每题 4分,满分 48 分)228.因式分解: x 4y ▲7.计算:2b 3 a 2ab9.方程2x 1 3的解是▲10.如果将分别写着“幸福” 、“奋斗”的两张纸片,随机放入“■都是■出来的”中的两个■内(每个■只放一张纸片),那么文字恰好组成“幸福都是奋斗出来的” 概率是▲11. 已知正方形的边长为 2cm,那么它的半径长是▲cm.12.某市种植 60亩树苗,实际每天比原计划多种植 3 亩树苗,因此提前一天完成任务,求原计划每天种植多少亩树苗.设原计划每天种植 x亩树苗,根据题意可列出关于 x 的方程▲13.近年来,出境旅游成为越来越多中国公民的假期选择 .将 2017年某小区居民出境游的不同方式的人次情况画成扇形图和条形图 , 如图 1 所示.那么 2017年该小区居民出境游中跟团游的人数为▲图2 图314.如图 2,在□ABCD中,E是 BC中点,AE交BD于点 F,如果AE a,那么AF= ▲ (用向量a表示).15.在南海阅兵式上,某架“直 -8”型直升飞机在海平面上方 1200米的点 A处,测得其到海平面观摩点 B的俯角为 60 ,此时点 A、B之间的距离是▲ 米.16.如图 3,已知在梯形 ABCD 中, AD∥ BC, AD=AB=DC =3,BC=6,将△ABD 绕着点D逆时针旋转,使点 A 落在点 C 处,点 B落在点 B 处,那么 BB = ▲ .217.如果抛物线 C:y ax2bx c(a 0)与直线 l:y kx d(k 0)都经过 y 轴上一点 P,且抛物线 C的顶点 Q在直线 l上,那么称此直线 l 与该抛物线 C具有“点线和谐”关系.如果直线y mx 1与抛物线y x22x n具有“点线和谐”关系,那么m n ▲ .18. 已知l1 ∥ l2 ,l1 、l2之间的距离是 3cm,圆心 O到直线 l1的距离是 1cm,如果⊙O与直线 l1、 l 2有三个公共点,那么圆 O 的半径为▲ cm.三、解答题:(本大题共7题,满分78 分)19.(本题满分10分)20.(本题满分 10 分)3x x 6,解不等式组x 1 x 1 ,并把它的解集在数轴(如图 4)上表示出来.26–5 –4 –3 –2 –1 O 1 2 3 4 5 x 图421.(本题满分 10 分)如图 5,已知 AB 是⊙ O 的直径,弦 CD 交 AB 于点 E , CEA 30 ,OE=4,DE=5 3.求弦 CD 及⊙O 的半径长.22.(本题满分 10分,其中第( 1)小题 5 分,第( 2)小题 5分)某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费方米及以下为第一档;年用天然气量超出 310 立方米为第二档.某户应交天然气费 y (元)与年用天然气量 x (立方米)的关系如图 6 所示,观察图像并回答下列问题: (1)年用天然气量不超过 310 立方米时,求 y 关于 x 的函数解析式(不写定义域) ;计算: 8 11- 2 -27 3 (1)-1. 年用天然气量 310 立(2)小明家 2017 年天然气费为 1029 元,求小明家 2017年使用天然气量.23.(本题满分12 分,其中第( 1)小题 5 分,第( 2)小题 7分)已知:如图 7,在正方形 ABCD 中,点 E 为边AB 的中点,联结DE .点 F 在 DE 上,且CF=CD ,过点 F 作 FG⊥ FC 交 AD 于点G.( 1)求证: GF=GD ;24.(本题满分12 分,每小题 4 分)已知平面直角坐标系 xOy (如图 8),二次函数y=ax2+bx+4 的图图7像经过 A(-2,0)、图6B ( 4, 0)两点,与 y 轴交于点C 点. ( 1)求这个二次函数的解析式;(2)如果点 E 在线段 OC 上,且∠ CBE=∠ACO ,求点 E 的坐标;(3)点 M 在 y 轴上,且位于点 C 上方,点 N 在直线 BC 上,点 P 为上述二次函数图像的 对.称.轴.上的点,如果以 C 、M 、N 、P 为顶点的四边形是菱形,求点 M 的坐标 .y5 4 3 2 1–5 –4–3 –2 –1 O –1 –2 –31 2 3 4 5–5 图825.(本题满分 14分,其中第( 1)小题 4分,第( 2)小题 5分,第( 3)小题 5分)1如图 9,已知在 △ABC 中,AB=AC ,tanB ,BC=4,点 E 是在线段 BA 延长线上一点, 2以点E 为圆心, EC 为半径的圆交射线 BC 于点C 、F (点C 、F 不重合),射线 EF 与射线 AC 交于点 P .(1)求证: AE 2AP AC ;(2)当点 F 在线段 BC 上,设CF=x ,△PFC 的面积为 y ,求y 关于 x 的函数解析式及定义域;FP 1 (3)当 FP 1时,求 BE 的长.EF 2图9备用图2018 年浦东新区初三数学二模参考答案及评分标准一、选择(本大题共 6题,每题 4 分,满分 24分) 1. B ; 2. C ; 3.A ; 4.C ; 5.D ; 6.C . 二、填空题: (本大题共 12 题,每题 4分,满分 48 分) 7. 2ab 2;8. x 2y x 2y ; 9.x 5;10. 1;11. 2;12.60 60 1;2 x x3 213.24; 14. a ; 15. 800 3;16.9;17.0;18.2或 4.3 三、解答(本大题共 7题,满分 78 分) 19.解:原式 2 2 2 -1-3 2 . 8 分)3 2 -2 2 分) 3x x 6, ① 20. 解: x 1 x 1 2 6 .② 由①得: 2x 6 .⋯⋯ 解得 x 3.⋯⋯ 由②得: (3 x-1) x 1 . 2 分) ( 1 分) ( 1 分) 3x 3 x 1.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)2x 4 . 解得 x 2 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) ∴原不等式组的解集为 -3 x 2. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分) -4 -3 -2 -1 O 1 2 3 4 x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)21. 解: 过点O 作OM CD 于点M ,联结 OD . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1分)∵ CEA 30 ,∴ OEM CEA 30 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) 在 Rt △ OEM 中,∵ OE=4,13∴ OM OE 2 , EM OE cos30 4 2 3 .(2 分)22 ∵ DE 5 3 ,∴ DM DE EM 3 3 .⋯⋯⋯⋯( 1 分) ∵ OM过圆心, OM CD , ∴ CD 2DM . ⋯⋯⋯⋯( 2 分) ∴ CD 6 3 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) ∵ OM 2, DM3 3,∴在 Rt△ DOM 中, OD OM 2DM 222 3 3 231∴ 弦 CD 的长为 6 3 ,⊙ O 的半径长为 31 .⋯⋯⋯⋯⋯⋯⋯⋯⋯23.证明:(1)∵四边形 ABCD 是正方形 ,∴ ADC 90 . ⋯⋯⋯( 1分)∵FG ⊥FC , ∴∠ GFC= 90 .° ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (1 分) ∵CF CD ,∴∠CDF=∠CFD . ⋯⋯⋯⋯⋯⋯⋯⋯⋯ (1 分)∴∠GFC-∠CFD=∠ADC-∠CDE ,即∠GFD=∠GDF.(1 分) ∴GF =GD . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) 2)联结 CG.∵CF CD ,GF GD ,∴点G 、C 在线段FD 的中垂线上 . ⋯⋯( 1分) ∴GC ⊥ DE ,∴∠ CDF +∠DCG = 90°,∵∠ CDF +∠ADE = 90 °,∴∠ DCG=∠ADE.∵四边形ABCD 是正方形 ,∴ AD=DC ,∠DAE=∠CDG=90°, ∴△ DAE ≌△ CDG . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1分) ∴ AE DG . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (1 分) ∵点E 是边AB 的中点,∴点G 是边 AD 的中点,∴ AG GD GF . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) ∴ DAF AFG , GDF GFD ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵ DAF AFG GFD GDF 180 ,⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) ∴ 2 AFG 2 GFD180 ,∴∠ AFD = 90°,即 AF ⊥DE. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1分) ∵四边形 ABCD 是正方形 ,∴ ADC 90 . 1 分) ∵FG ⊥FC ,∴∠ GFC= 90 °. 1 分) 在 Rt △ CFG 与 Rt △ CDG 中, CF CD ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ CG CG. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分) ∴Rt △ CFG ≌Rt △CDG.1 分)22.解:(1)设 y kx (k 0). ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵ y kx (k 0) 的图像过点( 310, 930),⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) ∴ 930 310k ,∴ k 3. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 2 分) ∴ y 3x .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ (1 分) (2)设 y kx b (k 0). ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵ y kx b (k 0)的图像过点( 310,930)和( 320,963),∴310k b 930,∴320k b 963.∴ kb3.933,.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) ∴ y 3.3x 93. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)当 y 1029时,3.3x 93 1029,解得 x 340. ⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) 答:小明家 2017 年使用天然气量为 340 立方米 . ⋯⋯⋯⋯⋯⋯⋯⋯( 1分)∴ GF GD . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) 2)∵ CF CD, GFGD,∴点G、C在线段 FD的中垂线上. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1分)∴FH=HD ,GC⊥DE ,∴∠EDC +∠DCH = 90 °,∵∠ ADE+∠EDC= 90 °,∴∠ADE=∠DCH. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1分)∵四边形 ABCD是正方形,∴AD=DC =AB,∠ DAE=∠ CDG= 90 °,∵ ADE DCH ,AD DC, EAD GDC .△ ADE ≌△ DCG . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)AE DG . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)点E是边AB的中点,∴点G是边 AD的中点,点H是边FD的中点,∴GH是△AFD 的中位线. ⋯⋯⋯⋯⋯⋯( 1分)GH // AF ,AFD GHD ,GH⊥FD,∴∠ GHD= 90 °,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∠AFD= 90 °,即 AF⊥DE . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)224.解:(1)∵ 抛物线y ax2bx 4与 x轴交于点 A(-2,0),B(4,0),∴4a-2b 4 0;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯∴ 16a 4b 4 0.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯a - 1;解得 a -2;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯b 1.抛物线的解析式为y -1 x2x 4 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1分)2∵ EH BC ,∴ CH=EH .AO 1∴在 Rt△ ACO 中,tan ACO ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯CO 21 分)2 分)2)过点 E作EH BC于点 H .当 x 0 时,y 1 -x222x 4 4 ,OC=4,在 Rt△ COB 中,∵∠ COB=90OC=OB= 4,∴ OCB 45 ,BC 4 2 .1 分)在 Rt△ ACO 中,∵ A( -2,0),∴EH 1∵∠ CBE= ∠ACO,∴在 Rt△ EBH 中, tan EBHBH 2设 EH k(k 0),则BH 2k ,CH=k ,CE 2k .∴ CB CH HB 3k 4 2 . ∴抛物线的对称轴为直线 x=1. ① 当 MC 为菱形 MCNP 的边时,∴ CM // PN ,∴∠ PNC=∠NCO=45°. ∵点 P 在二次函数的对称轴上, ∴ 点P 的横坐标为 1,点N 的横坐标为 1.∴ CN 12 . sin45∵四边形MCNP 是菱形,∴ CM CN 2, ∴ OM OC CM 4 2, ∴ M (0,4 2) .③ 当MC 为菱形 MNCP 的对角线时, 设NP 交CM 于点Q ,CM 、 NP 互相垂直平分,∴ NQ QP 1. MQ QC ,∵点N 在直线 BC 上,∠ NCM =∠OCB= 45°.∴4 2,∴ k,⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 8, 3,⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4,∴ E (0,4). ⋯⋯⋯ 33 -2,0),B(4,0),∴ CE ∴ EO3)∵ A1 分) 1 分) 1 分)1 分)1 分) ②当MC 为菱形 MCPN 的边时,不存在 1 分)在 Rt△CQN 中,∴∠ NCQ=∠CNQ= 45°,∴ QN CQ 1,∴ MQ CQ 1,∴ CM 2,∴ OM OC CM 4 2 6,∴ M(0,6). ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1分)∴综上所述M (0,4 2)或 M(0,6).1)∵ AB AC,∴∠ B=∠ ACB.25.证明:∵ EF EC,∴∠EFC=∠ECF.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵ EFC BBEF ,又∵ ECF ACB ACE,∴∠ BEF =∠ACE. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵ EAC 是公共角,∴△ AEP∽△ ACE. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1分)AE AP 2∴,∴ AE 2AP AC . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)AC AE2)∵∠ B=∠ACB,∠ ECF=∠EFC,∴△ ECB∽△ PFC.2∴S PFC FC. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1分)CBSECB过点E做EH CF于点 H,∵ EH 经过圆心, EH CF,1 1 1∴ CH FC x. ∴ BH 4 x . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)2 2 2EH 1 1在 Rt△ BEH 中,∵ tan B ,∴ EH 2- x .BH 2 41 1 1 1∴ S ECB BC EH 4 (2 x) 4 x . ⋯⋯⋯⋯( 1 分)ECB2 2 424 1 x 42B M F H CPE PE 1EF EC 2 ∵△ AEP ∽△ ACE. ∴ AE PE ∴AC EC ,1∴ AE 1 AC . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)2过点 A 作AM BC ,垂足为点 M .∵ AB AC ,BC 4,∴ BM 1BC 2,23 5 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯②当点F 在线段 BC 延长线上时,∵∠EFC=∠ECF , EFC FCP P , ECF B BEC . 又∵ B ACB , ACB FCP ,∴∠ B =∠ FCP.在 Rt △ ABM 中, tan B 12∴ AM 1, AB AC 5 . ⋯( 1 分) 1 分)2BE∴∠ P =∠ BEC. ∵ EAC 是公共角, ∴△ AEP ∽△ ACE , AE AC PEECFP EFPE PE EF EC ∴ AE 3AC 35.22 55∴ BE . ⋯⋯⋯⋯⋯⋯( 1 分) 2 综上所述 , BE 3 5或 5 5.221 分)。
上海市各区2018届中考数学2模试卷精选汇编综合计算专题6

综共计算宝山区、嘉定区21. (本 分 10 分,第( 1)小 5 分,第( 2)小 5 分)如 4,在梯形 ABCD 中, AD ∥ BC , BAD 90 , ACAD .(1)假如 BACBCA10 ,求 D 的度数;(2)若 AC10 , cot D1 ABCD 的面 .BC,求梯形3A4D21. 解:( 1)∵ AD ∥ BC∴ BCA CAD∵ BAC BCA10∴ BACCAD 10∵ BAD 90∴BAC CAD 90⋯⋯⋯⋯⋯⋯⋯1 分BC⋯⋯⋯⋯⋯⋯⋯1 分A4HD∴CAD40⋯⋯⋯⋯⋯⋯⋯1 分∵ AC AD∴ ACD D ⋯⋯⋯⋯⋯⋯⋯ 1 分∵ ACD DCAD 180∴ D 70⋯⋯⋯⋯⋯⋯⋯ 1 分(2) 点C 作CHAD , 垂足 点 H ,在 Rt △ CHD中, cotD1 3HD1∴ cot D1 分CH⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3HDx , CH 3x ,∵ ACAD ,AC 10 ∴ AH 10 x在 Rt △ CHA 中, AH 2 CH 2AC 2∴ (10x) 2(3x)2 102∴ x 2 , x 0 (舍去)∴ HD2 ⋯⋯⋯⋯ 1分∴ HC6, AH8, AD 10 ⋯⋯⋯⋯⋯⋯ 1 分 ∵ BAD CHD90 ∴ AB ∥CH∵ AD ∥ BC ∴四边形 ABCH 是平行四边形 ∴ BC AH 81 分 ∴梯形 ABCD 的面积 S1(AD BC) CH1(108) 6 541分2 2长宁区21.(此题满分 10 分,第( 1)小题 4 分,第( 2)小题 6 分)如图,在等腰三角形中, = ,点 D 在 BA 的延伸线上,=24,ABCAB ACBCD5 .sin ABCA13( 1)求 AB 的长;( 2)若=6.5 ,求 DCB 的余切值.BCAD第 21题图21.(此题满分 10 分,第( 1)小题 4 分,第( 2)小题 6 分)解:( 1)过点 A 作 AE ⊥ BC ,垂足为点 E又∵ =∴1 ∵=24∴=12(1 分)BEBCAB ACBCBE2在 Rt ABE 中, AEB90 ,sinABCAE 5 (1 分)AB13设 AE=5k,AB=13k ∵ AB 2 AE 2 BE 2 ∴ BE 12k 12 ∴ k 1 , ∴ AE 5k5 ,AB 13k13(2 分)(2)过点 D 作 DF ⊥BC , 垂足为点 F∵AD=6.5, AB=13∴ BD=AB+AD=∵AE ⊥ BC ,DF ⊥ BC ∴ AEB DFB 90 ∴ AE // DF∴ AEBE AB 又 ∵ AE =5, BE =12, AB =13,DFBF BD∴ DF15,BF 18(4 分)2∴ CFBC BF即CF 2418 6(1 分)在 Rt DCF 中, DFCCF 6 4 ( 1 分)90 , cot DCB15 5DF2崇明区21.(本 分 10 分,第 (1)、 (2) 小 分各 5 分)已知 O 的直径 AB 12 ,点 C 是 上一点,且 ABC 30 ,点 P 是弦 BC 上一 点,点P 作PD OP交于点 .O D(1)如 1,当 PD ∥ AB ,求 PD 的 ;(2)如 2,当 BP 均分OPD ,求 PC 的 .CCDDPPABABOO(第 21 题图 1)(第 21 题图 2)21.( 本 分 10 分,每小5 分)( 1)解: OD∵直径 AB 12 ∴ OB OD 6 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分∵ PD ⊥ OP ∴ ∠DPO 90∵ PD ∥ AB ∴∠DPO∠ POB 180∴ ∠POB 90⋯⋯1 分又∵ ∠ABC30 ,OB6∴ OP OB tan302 3 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分2PD 22⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分∵在 Rt △POD 中, POOD ∴ (2 3)2PD 2 62∴ PD2 6 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分( 2) 点 O 作 OH ⊥ BC ,垂足 H∵ OH ⊥BC∴∠OHB ∠OHP 90∵∠ABC 30 ,OB 6∴ OH 1OB 3,BH OB cos30 3 3 ⋯⋯⋯⋯⋯⋯⋯⋯2 分2∵在⊙ O 中, OH⊥BC∴ CH BH 33 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∵ BP均分∠OPD ∴∠BPO 1∠DPO 45 2∴ PH OH cot 45 3 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分∴ PC CH PH 3 3 3 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分奉区21.(本分 10 分,每小分各 5 分)已知:如6,在△中,=13,8, 5 ,⊥ ,垂足点ABC AB AC= cos BAC 13 BD ACA 是 BD的中点, AE并延,交 BC于点 F.(1)求 EAD 的余切;(2)求BF的. E CFB F图 621、(1)5;(2)5;68黄浦区D, EDC21.(本分10 分)如, AH是△ ABC的高, D是 AB上一点, CD与 AH交于点 E.已知 AB=AC=6,cos B=2,3AD∶ DB=1∶2.(1)求△ABC的面积;(2)求CE∶DE.21.解:( 1)由AB=AC=6,AH⊥BC,得 =2 . —————————————————————————( 2 分)BC BH在△ ABH中, AB=6,cosB= 2,∠ AHB=90°,得 BH=26 4,AH32 22 5,————————————(2分)3 = 6 4则 BC=8,因此△ ABC面积= 1 2 5 8 8 5 .——————————————( 1 分)2(2)过D作BC的平行线交AH于点F,———————————————( 1 分)由 AD∶ DB=1∶2,得 AD∶AB=1∶3,则 CE CH BH AB 3 .——————————————(4 分)DE DF DF AD 1金山区21.(此题满分10 分,每题 5 分)如图 5,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥ AE,垂足为 F.A D( 1)求证:AF=BE;( 2)假如BE∶EC=2∶ 1,求∠CDF的余切值. FB E C图 521.解:( 1)∵四 形 ABCD 是矩形,∴ AD =BC ,AD ∥ BC ,∠ B =90°,∴∠ DAF=∠ AEB ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1分)∵, ⊥,∴ ,∠ ∠90°,⋯⋯⋯⋯⋯⋯⋯⋯⋯(2 分)AE=BC DF AE AD=AE AFD= EBA=∴△ ADF ≌△ EAB ,∴ AF =EB ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(2分)( 2) BE =2k , EC =k , AD =BC =AE =3k ,AF =BE =2k ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)∵∠ ADC =90°,∠ AFD =90°,∴∠ CDF +∠ ADF =90°,∠ DAF +∠ ADF =90°,∴∠ CDF =∠ DAF ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(2分)在Rt △ 中,∠=90°, =AD 2AF 25kADF AFDDF∴ cot ∠ CDF =cot ∠ DAF =AF2k 2 5 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(2DF5k5分) 静安区21.(本 分 10 分,第( 1)小 分 5 分,第( 2)小 分5 分)已知:如 , 1 的正方形 ABCD 中, AC 、 DB 交于点 H . DE 均分∠ ADB ,交 AC 于点 E . BE 并延 ,交 AD 于点 F .AF D( 1)求 : DC =EC ;E( 2)求△ EAF 的面 .HB第 21题图C21.(本 分10 分, 第( 1)小 5 分,第( 2)小 5 分)解:( 1)∵正方形ABCD ,∴, ∠ =∠ =∠=∠=90°AF DDC=BC=BA=AD BAD ADCDCB CBAAH=DH=CH=BH ,AC ⊥ BD ,E∴∠ ADH =∠ HDC =∠ DCH =∠DAE = 45 °.⋯⋯⋯⋯( 2 分)H又∵ DE 均分∠ AD B ∴∠ ADE =∠EDHBC∵∠ DAE +∠ ADE =∠ DEC , ∠ EDH +∠HDC =∠ EDC ⋯⋯⋯⋯( 1 分) 第 21题图∴∠ EDC =∠ DEC ⋯⋯⋯⋯( 1 分) ∴ DC =EC⋯⋯⋯⋯( 1 分)( 2)∵正方形 ABCD ,∴ AD ∥ BC ,∴△ AFE ∽△ CBE ∴SAEFAE2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)SCEB()EC∵ AB=BC=DC=EC =1, AC = 2 , ∴AE = 2 1 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)Rt △ BHC 中, BH =2BC = 2 ,22∴在△ BEC 中, BH ⊥EC ,SBEC1 12 2 ⋯⋯⋯⋯⋯⋯⋯⋯( 2 分)22 4∴SAEF( 2 1)2, ∴S AEF2(3 22)3 24 2 444⋯⋯⋯⋯( 1 分)行区21.(本 分 10 分,此中第( 1)小4 分,第( 2)小 6 分)已知一次函数y2 x 4 的 像与x 、y 分 交于点、 ,以AB 在第一象限A B内作直角三角形 ABC ,且∠ BAC = 90 o, tan ABC1 . y2B( 1)求点 C 的坐 ;( 2)在第一象限内有一点 M ( 1, m ),且点 M 与点C 位于直的同 ,使得2S ABM S ABC ,CAB求点 M 的坐 .OAx(第 21 题图)21.解:( 1)令 y 0 , 2 x 4 0 ,解得: x 2,∴点 A 坐 是( 2, 0).令 x 0 , y4 ,∴点 B 坐 是( 0, 4).⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)∴ AB222225 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)OA OB 2 4∵ BAC 90 , tanABC1,∴AC5 .2C 点作 CD ⊥ x 于点 D ,易得OBA ∽ DAC .⋯⋯⋯⋯⋯⋯⋯( 1 分) ∴ AD 2,CD 1 ,∴点 C 坐 是( 4, 1).⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)(2) S ABC1 AB AC1 2 5 55 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)22∵ 2S ABMSABC,∴ S ABM5.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)2∵ M (1 , m) ,∴点 M 在直 x1 上;令直 x 1 与 段 AB 交于点 E , ME m 2 ;⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)分 点、作直 x1 的垂 ,垂足分 是点、 ,A BF G∴+ = OA = 2 ;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)AF BG∴S ABM S BME S AME1ME BG1ME AF1ME(BG AF )2221 ME OA1 2 ME5⋯⋯⋯⋯⋯⋯⋯( 1 分)2 22∴ ME 5 5 , m 9 ,∴ M(1,9.⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)2 , m 22 )22普陀区21.(本 分 10 分)如 7,在 Rt △ ABC 中, C 90 ,点 D 在 BC 上,DE ⊥ AB ,点 E 垂足, AB 7 ,DAB 45 , tan B3.4CD( 1)求 DE 的 ;( 2)求 CDA 的余弦 .A E B图 721.解:(1)∵ DE ⊥ AB ,∴DEA 90又∵ DAB 45 ,∴ DE AE . ·················(1 分)在 Rt △ DEB 中,DEB 90 , tan B3 ,∴DE 3. ······· (1 分)4 BE 4设 DE 3x ,那么 AE 3x , BE 4x .∵ AB 7 ,∴ 3x 4x7 ,解得 x1 . · ·············· (2 分) ∴ DE3 . ··························(1 分)(2) 在 Rt △ ADE 中,由勾股定理,得 AD 3 2 . ··········· (1 分) 同理得 BD 5 . ························· (1 分)在 Rt △ ABC 中,由3 4 28 (1 分)tan B ,可得 cos B.∴ BC. ····455∴ CD3(1 分). ··························5∴cosCD 2(1 分)CDA. ···················AD10即 CDA 的余弦值为2 .10青浦区21. ( 此题满分 10 分,第( 1)、( 2)小题,每题 5 分)如图 5,在 Rt △ ABC 中,∠ C =90°, AC=3,BC =4,∠ ABC 的均分线交边 AC 于点 D ,延伸BD 至点 E ,且 BD=2DE ,联络 AE .( 1)求线段 CD 的长;AED( 2)求△ ADE 的面积 .BC图 521.解:( 1)过点 D 作⊥ ,垂足为点 . ················( 1 分)DH AB H ∵ BD 均分∠ ABC ,∠ C =90°,∴ DH = DC =x , · ·······················(1 分)则 AD =3 x .∵∠ C =90°, AC=3, BC =4,∴ AB =5. ·············· (1 分)∵ sin BACHDBC ,ADAB∴x4,························ (1 分)3 x 5∴ x 4( 1 分). ··························3(2) S ABD1AB DH1 5410 . ··············( 1 分)223 3∵ BD=2DE ,∴SABDBD 2 ,····················(3 分)SADEDE∴S ADE10 1 5(1 分)32. ····················3松江区21. (本 分 10 分, 每小 各 5 分)如 ,已知△ ABC 中,∠ B =45°, tan C1 ,2BC =6.( 1)求△ ABC 面 ;( 2) AC 的垂直均分 交 AC 于点 D ,交 BC 于点E. 求 DE 的 .ADBE C(第 21题图)21. (本 分 10 分, 每小 各 5 分)A解:( 1) 点 A 作 AH ⊥BC 于点 H ⋯⋯⋯⋯ 1 分D在 Rt ABC 中,∠ B =45°AH = x , BH =x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分EC(第 21题图)AH 1在 Rt AHC 中, tanC2HC∴HC=2x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分∵BC=6∴ 2 =6 得x =2x+ x∴=2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分AH ∴S ABC 1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分BCAH 62(2)由( 1)得AH=2,CH=4在 Rt AHC 中,AC AH 2 HC 2 2 5 ⋯⋯⋯⋯⋯⋯⋯ 2 分∵DE垂直均分 AC∴ CD 1AC 5 2ED⊥ AC ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分在 Rt EDC 中,tan C ED 1 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1 分CD 2∴ DE 1 5 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 1 分2徐区21.如,在Rt ABC 中, C 90 , AC 3 ,BC 4 ,AD均分BAC 交 BC 于点D. (1)求tan DAB;(2)若⊙O A、D两点,且点O在AB上,用尺作的方法确立点 O 的地点并求出的⊙ O 半径.(保存作迹,不写作法)杨浦区21、(此题满分10 分,第( 1)小题满分 3 分,第( 2)小题满分7 分)0 已知,如图5,在梯形ABCD中, DC//AB, AD=BC, BD均分∠ ABC,∠ A=60 求:( 1)求∠CDB的度数( 2)当AD=2 时,求对角线BD的长和梯形ABCD的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海市各区2018届九年级中考二模数学试卷精选汇编填空题专题宝山区、嘉定区二、填空题(本大题共12题,每题4分,满分48分) 7.计算:=4 ▲ .8.一种细菌的半径是00000419.0米,用科学记数法把它表示为 ▲ 米. 9. 因式分解:=-x x 42 ▲ . 10.不等式组⎩⎨⎧>+≤-063,01x x 的解集是 ▲ .11.在一个不透明的布袋中装有2个白球、8个红球和5个黄球,这些球除了颜色不同之外,其余均相同.如果从中随机摸出一个球,摸到黄球的概率是 ▲ . 12.方程23=+x 的根是 ▲ .13.近视眼镜的度数y (度)与镜片焦距x (米)呈反比例,其函数关系式为xy 120=.如果近似眼镜镜片的焦距3.0=x 米,那么近视眼镜的度数y 为 ▲ . 14.数据1、2、3、3、6的方差是 ▲ .15.在△ABC 中,点D 是边BC 的中点,=,=,那么= ▲ (用、表示). 16.如图1,在矩形ABCD 中,点E 在边CD 上,点F 在对角线BD 上,5:2:=DE DF ,BD EF ⊥,那么=∠ADB tan ▲ .17.如图2,点A 、B 、C 在圆O 上,弦AC 与半径OB 互相平分,那么AOC ∠度数为 ▲ 度. 18.如图3,在△ABC 中,5==AC AB ,6=BC ,点D 在边AB 上,且︒=∠90BDC . 如果△ACD 绕点A 顺时针旋转,使点C 与点B 重合,点D 旋转至点1D ,那么线段1DD 的长为 ▲ .图2A BCD图3图17. 2 8. 64.1910-⨯ 9. (4)x x - 10. 21x -<≤11. 1312. 1x = 13. 400 14. 2.8 15. 2a b +r r16. 2 17. 120° 18.4225长宁区二、填空题(本大题共12题, 每题4分, 满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7. 计算:=--︒0)3(30sin ▲ . 8. 方程6+=-x x 的解是 ▲ .9. 不等式组⎪⎩⎪⎨⎧≥-<+-1)12(303x x 的解集是 ▲ .10.已知反比例函数xky =的图像经过点(-2017,2018),当0>x 时,函数值y 随 自变量x 的值增大而 ▲ .(填“增大”或“减小”)11.若关于x 的方程032=--m x x 有两个相等的实数根,则m 的值是 ▲ . 12.在形状为等腰三角形、圆、矩形、菱形、直角梯形的5张纸片中随机抽取一张,抽到中心对称图形的概率是 ▲ .13.抛物线522++=mx mx y 的对称轴是直线 ▲ . 14.小明统计了家里3月份的电话通话清单,按通话时间画出频数分布直方图(如图所示),则通话时间不足10分钟的 通话次数的频率是 ▲ .15.如图,在四边形ABCD 中,点E 、F 分别是边AB 、AD 的中点,BC =15,CD =9,EF =6,∠AFE =50°,则∠ADC 的度数为 ▲ . 16.如图,在梯形ABCD 中,AB //CD ,∠C=90°,BC =CD =4,52=AD ,第14题图AB CDE F第15题图若=,=,用、表示= ▲ . 17.如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形ABC 是半高三角形,且斜边5=AB ,则它的周长等于 ▲ . 18.如图,在矩形ABCD 中,对角线BD 的长为1,点P 是线段BD上的一点,联结CP ,将△BCP 沿着直线CP 翻折,若点B 落在 边AD 上的点E 处,且EP //AB ,则AB 的长等于 ▲ .二.填空题:(本大题共12题,满分48分) 7.21-; 8.2-=x ; 9.3>x ; 10.增大; 11.43-=m ; 12.53; 13.1-=x ;14.7.0;15.︒140; 16.→→-a b 21; 17.255或535++; 18.215-.崇明区二、填空题(本大题共12题,每题4分,满分48分)7.因式分解:29x -= ▲ .8.不等式组1023x x x -<⎧⎨+>⎩的解集是 ▲ .9.函数12y x =-的定义域是 ▲ . 103=的解是 ▲ .11.已知袋子中的球除颜色外均相同,其中红球有3个,如果从中随机摸得1个红球的概率为18,那么袋子中共有 ▲ 个球.12.如果关于x 的方程240x x k +-=有两个相等的实数根,那么实数k 的值是 ▲ . 13.如果将抛物线221y x x =+-向上平移,使它经过点(1,3)A ,那么所得新抛物线的表达式是▲ .14.某校组织了主题为“共建生态岛”的电子小报作品征集活动,先从中随机抽取了部分作品,按,,,A B C D第16题图D CBA 第18题图AB CD(第14题图)四个等级进行评分,然后根据统计结果绘制了如下两幅不完整的统计图,那么此次抽取的作品中等级为B 的作品数为 ▲ .15.已知梯形ABCD ,AD BC ∥,2BC AD =,如果AB a =,AC b =,那么DA = ▲ . (用,a b 表示).16.如图,正六边形ABCDEF 的顶点B 、C 分别在正方形AGHI 的边AG 、GH 上,如果4AB =,那么CH 的长为 ▲ .17.在矩形ABCD 中,5AB =,12BC =,点E 是边AB 上一点(不与A 、B 重合),以点A 为圆心,AE为半径作A ⊙,如果C ⊙与A ⊙外切,那么C ⊙的半径r 的取值范围是 ▲ .18.如图,ABC △中,90BAC ∠=︒,6AB =,8AC =,点D 是BC 的中点,将ABD △沿AD 翻折得到AED △,联结CE ,那么线段CE 的长等于 ▲ .二、填空题:(本大题共12题,每题4分,满分48分)7.(3)(3)x x +-; 8.31x -<<; 9.2x ≠; 10.8x =; 11.24; 12.4-; 13.22y x x =+; 14.48; 15.1122a b -; 16.6-; 17.813r <<; 18.145. 奉贤区7.计算:=-aa 211 . 8.如果822=-b a ,且4=+b a ,那么b a -的值是 . 9.方程242=-x 的根是 . 10.已知反比例函数)0(≠=k xky ,在其图像所在的每个象限内,y 的值随x 的值增大而减 (第16题图)HDCIFBA GE (第18题图)DCBAE小,那么它的图像所在的象限是第 象限.11.如果将抛物线22y x =平移,使平移后的抛物线顶点坐标为(1,2),那么所得新抛物线的表达式是 .12.将6本相同厚度的书叠起来,它们的高度是9厘米.如果将这样相同厚度的书叠起来的高度是42厘米,那么这些书有 本.13.从1,2,3,4,5,6,7,8这八个数中,任意抽取一个数,这个数恰好是合数的概率是. 14.某校为了了解学生双休日参加社会实践活动的情况,随机抽取了100名学生进行调查,并绘成如图3所示的频数分布直方图.已知该校共有1000名学生,据此估计,该校双休日参加社会实践活动时间在2~2.5小时之间的学生数大约是全体学生数的 (填百分数) . 15.如图4,在梯形ABCD 中,AD //BC ,BC=2AD ,E 、F 分别是边AD 、BC 的中点,设a AD =, =,那么EF 等于 (结果用、的线性组合表示). 16.如果一个矩形的面积是40,两条对角线夹角的正切值是34,那么它的一条对角线长是 . 17.已知正方形ABCD ,AB =1,分别以点A 、C 为圆心画圆,如果点B 在圆A 外,且圆A与圆C 外切,那么圆C 的半径长r 的取值范围是 .18.如图5,将△ABC 的边AB 绕着点A 顺时针旋转)900(︒<<︒αα得到AB ’,边AC 绕 着点A 逆时针旋转)900(︒<<︒ββ得到AC ’,联结B ′C ′.当︒=+90βα时,我们称△A B ′C ′ 是△ABC 的“双旋三角形”.如果等边△ABC 的边长为a ,那么它的“双旋三角形”的面积是 (用含a 的代数式表示).二、填空题: 7、12a ; 8、2; 9、4; 10、一三; 11、22(1)2y x =-+; 12、28; 13、38; 14、28%; 15、12a b +; 16、10; 171r << 18、214a黄浦区图4A B DFE C图3人数 BC图5AB ′C ′7= . 8.因式分解:212x x --= . 9.方程1x +=的解是 .10.不等式组12031302x x ⎧->⎪⎪⎨⎪-≤⎪⎩的解集是 .11.已知点P 位于第三象限内,且点P 到两坐标轴的距离分别为2和4,若反比例函数图像经过点P ,则该反比例函数的解析式为 .12.如果一次函数的图像经过第一、二、四象限,那么其函数值y 随自变量x 的值的增大而 . (填“增大”或“减小”)13.女生小琳所在班级共有40名学生,其中女生占60%.现学校组织部分女生去市三女中参观,需要从小琳所在班级的女生当中随机抽取一名女生参加,那么小琳被抽到的概率是 . 14.已知平行四边形相邻两个内角相差40°,则该平行四边形中较小内角的度数是 . 15.半径为1的圆的内接正三角形的边长为 .16.如图,点D 、E 分别为△ABC 边CA 、CB 上的点,已知DE ∥AB ,且DE 经过△ABC 的重心,设CA a =,C B b =,则DE = .(用a 、b 表示)17.如图,在四边形ABCD 中,902624ABC ADC AC BD ∠=∠=︒==,,,M 、N 分别是AC 、BD 的中点,则线段MN 的长为 .18.如图,将矩形ABCD 沿对角线AC 折叠,使点B 翻折到点E 处,如果DE ∶AC =1∶3,那么AD ∶AB = .二、填空题:(本大题共12题,每题4分,满分48分)71; 8.()()34x x +-; 9.2; 10.166x <≤;11.8y x =; 12.减小; 13.124; 14.70; 1516.2233b a -.; 17.5; 18∶1.金山区7.因式分解:2a a -= ▲ . 8.函数y =的定义域是 ▲ .9.方程21xx =-的解是 ▲ . 10.一次函数2y x =-+的图像不经过第 ▲ 象限.11.有一枚材质均匀的正方体骰子,它的六个面上分别有1点、2点、…、6点的标记,掷这枚骰子,向上一面出现的点数是素数的概率是 ▲ . 12.如果关于x 的一元二次方程240x x k -+=有两个不相等的实数根,那么k 的取值范围是 ▲ .13.如果梯形的中位线长为6,一条底边长为8,那么另一条底边长等于 ▲ . 14.空气质量指数,简称AQI ,如果AQI 在0~50空 气质量类别为优,在51~100空气质量类别为良, 在101~150空气质量类别为轻度污染,按照某市最 近一段时间的AQI 画出的频数分布直方图如图3 所示,已知每天的AQI 都是整数,那么空气质量 类别为优和良的天数占总天数的百分比为 ▲ %. 15.一辆汽车在坡度为1:2.4的斜坡上向上行驶130米,那么这辆汽车的高度上升了 ▲ 米.16.如果一个正多边形的中心角等于30°,那么这个正多边形的边数是 ▲ . 17.如果两圆的半径之比为3:2,当这两圆内切时圆心距为3,那么当这两圆相交时,圆心距d 的的取值范围是 ▲ .18.如图4,Rt △ABC 中,∠C =90°,AC =6,BC =8,D 是AB 的中点,P 是直线BC 上一点,把△BDP 沿PD 所 在的直线翻折后,点B 落在点Q 处,如果QD ⊥BC , 那么点P 和点B 间的距离等于 ▲ .图3图4二.填空题:(本大题共12题,满分48分)7.()1a a -; 8.2x ≥; 9.2x =; 10.三; 11.12; 12.4k <; 13.4; 14.80; 15.50; 16.12; 17.3d 15<<; 18.52或10.静安区二、填空题:(本大题共12题,每题4分,满分48分) 【在答题纸相应题号后的空格内直接填写答案】 7.32)2(a a ⋅ = ▲ .8.分解因式:=+-xy y x 4)(2▲ .9.方程组⎩⎨⎧=-=+62,3x y y x 的解是 ▲ .10.如果4-x x 有意义,那么x 的取值范围是 ▲ .11.如果函数x a y 12--=(a 为常数)的图像上有两点),1(1y 、),31(2y ,那么函数值1y ▲ 2y .(填“<”、“=”或“>”)12.为了解植物园内某种花卉的生长情况,在一片约有3000株此类花卉的园地内,随机抽测了200株的高度作为样本,统计结果整理后列表如下:(每组数据可包括最低值,不包括最高值)试估计该园地内此类花卉高度小于55厘米且不小于45厘米的约为 ▲ 株.13.从1,2,3,4,5,6,7,8,9中任取一个数,这个数即是奇数又是素数的概率是 ▲ .14.如图,在△ABC 中,点G 是重心,过点G 作DE ∥BC ,分别交AB 、AC 于点D 、E .已知==, ,那么AE = ▲.(用向量b a 、表示). 15.如图,已知⊙O 中,直径AB 平分弦CD ,且交CD 于点E , 如果OE =BE ,那么弦CD 所对的圆心角是 ▲ 度.16.已知正多边形的边长为a ,且它的一个外角是其内角的一半,那么此正多边形的边心距是 ▲ .(用含字母a 的代数式表示). 17.在平面直角坐标系中,如果对任意一点(a ,b ),规定两种变换:ABE DCG·第14题图第15题图),(),(b a b a f --=,),(),(a b b a g -=,那么[]=-)2,1(f g ▲ .18.等腰△ABC 中,AB =AC ,它的外接圆⊙O 半径为1,如果线段OB 绕点O 旋转90°后可与线段OC 重合,那么∠ABC 的余切值是 ▲ .7、54a . 8、2)(y x +. 9、⎩⎨⎧=-=41y x . 10、x > 4. 11、>. 12、960.13、31. 14、3232-. 15、120. 16、a 23. 17、(2,1). 18、12±. 闵行区二、填空题:(本大题共12题,每题4分,满分48分) 7.计算:21+2-= ▲ .8.在实数范围内分解因式:243x -= ▲ . 91的解是 ▲ .10.已知关于x 的方程230x x m --=没有实数根,那么m 的取值范围是 ▲ .11.已知直线(0)y kx b k =+≠与直线13y x =-平行,且截距为5,那么这条直线的解析式为 ▲ .12.一个十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当小杰过马路时,恰巧是绿灯的概率是 ▲ .13.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、6,第五组的频率是0.1,那么第六组的频数是 ▲ .14.如图,已知在矩形ABCD 中,点E 在边AD 上,且AE = 2ED .设BA a =uu r r ,BC b =uu u r r ,那么CE =uu u r▲(用a r 、b r的式子表示).15.如果二次函数2111y a x b x c =++(10a ≠,1a 、1b 、1c 是常数)与2222y a x b x c =++(20a ≠,2a 、2b 、2c 是常数)满足1a 与2a 互为相反数,1b 与2b 相等,1c 与2c 互为倒数,那么称这两个函数为“亚旋转函数”.请直接写出函数232y x x =-+-的“亚旋转函数”为 ▲ .16.如果正n 边形的中心角为2α,边长为5,那么它的边心距为 ▲ .(用锐角α的三角比表示) 17.如图,一辆小汽车在公路l 上由东向西行驶,已知测速探头M 到公路l 的距离MN 为9米,测得此车从点A 行驶到点B 所用的时间为0.6秒,并测得点A 的俯角为30o ,点B 的俯角为60o .那么此车从A 到B 的平均速度为 ▲ 米/秒.1.7321.414) 18.在直角梯形ABCD 中,AB // CD ,∠DAB = 90o ,AB = 12,DC = 7,5cos 13ABC ∠=,点E 在线段AD 上,将△ABE 沿BE 翻折,点A 恰巧落在对角线BD 上点P 处,那么PD = ▲ .ABDC(第14题图)EA BDCAMN l二、填空题:(本大题共12题,每题4分,满分48分)7.5; 8.2x x -(; 9.1x =; 10.94m <-; 11.153y x =-+; 12.512; 13.8; 14.13a b -r r ; 15.2132y x x =+-; 16.5cot 2α(或52tan α);17.17.3; 18.12.普陀区7.计算:xy x 3122⋅= ▲ . 8.方程x 的根是 ▲ .9.大型纪录片《厉害了,我的国》上映25天,累计票房约为402700000元,成为中国纪录电影票房冠军.402700000用科学记数法表示是 ▲ .10.用换元法解方程312122=+-+x x x x 时,如果设y xx =+21,那么原方程化成以y 为“元”的方程是 ▲ . 11.已知正比例函数的图像经过点M (2-)、),(11y x A 、),(22y x B ,如果21x x <,那么1y ▲ 2y .(填“>”、“=”、“<”)12.已知二次函数的图像开口向上,且经过原点,试写出一个符合上述条件的二次函数的解析式: ▲ .(只需写出一个)13.如果一个多边形的内角和是720,那么这个多边形的边有 ▲ 条.14.如果将“概率”的英文单词 probability 中的11个字母分别写在11张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母b 的概率是 ▲ .15.2018年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖的东南亚地区.据调查发现2018年春节期间出境游约有700万人,游客目的地分布情况的扇形图如图3所示,从中可知出境游东南亚 地区的游客约有 ▲ 万人.A东南亚欧美澳新16%港澳台 15%韩日11%其他 13%图316. 如图4,在梯形ABCD 中,BC AD //,AD BC 3=,点E 、F 分别是边AB 、CD 的中点.设a AD =,b DC =,那么向量EC 用向量、表示是 ▲ .17. 如图5,矩形ABCD 中,如果以AB 为直径的⊙O 沿着BC 滚动一周,点B 恰好与点C 重合,那么ABBC 的值等于 ▲ .(结果保留两位小数)18. 如图6,在平面直角坐标系xOy 中,△ABC 的顶点A 、C 在坐标轴上,点B 的坐标是(22).将△ABC 沿x 轴向左平移得到△111A B C ,点1B 落在函数6y x =-的图像上.如果此时四边形11AA C C 的面积等于552,那么点1C 的坐标是 ▲ .二、填空题:(本大题共12题,每题4分,满分48分)青浦区7.计算:32()=a a ÷- ▲ . 8.因式分解:24=a a - ▲ . 9.函数y 的定义域是 ▲ .010.不等式组1020.x x +≥⎧⎨->⎩,的整数解是 ▲ .11.关于x 的方程=2(1)ax x a +≠的解是 ▲ . 12.抛物线2(3)+1y x =-的顶点坐标是 ▲ .13.掷一枚材质均匀的骰子,掷得的点数为合数的概率是 ▲ .7.323x y ; 8. 3x =;9. 810027.4⨯ ; 10. 32=-yy ; 11.>;12. 2y x =等;13.6; 14.112; 15.315; 16.b a212+; 17.3.14;18.(5-211). yxO ABC图 6ABCDEF图 4BCDO A 图514.如果点1P (2,1y )、2P (3,2y )在抛物线2+2y x x =-上,那么1y ▲ 2y .(填“>”、 “<”或 “=”) 15.如图2,已知在平行四边形ABCD 中,E 是边AB 的中点,F 在边AD 上,且AF ︰FD=2︰1,如果AB a =,BC b =,那么EF = ▲ .16.如图3,如果两个相似多边形任意一组对应顶点P 、P '所在的直线都经过同一点O ,且有(0)OP k OP k '=⋅≠,那么我们把这样的两个多边形叫位似多边形,点O 叫做位似中心.已知ABC ∆与A B C '''∆是关于点O 的位似三角形,3OA OA '=,则ABC ∆与A B C '''∆的周长之比是 ▲ .17.如图4,在△ABC 中,BC=7,AC=,tan 1C =,点P 为AB 边上一动点(点P 不与点B 重合),以点P 为圆心,PB 为半径画圆,如果点C 在圆外,那么PB 的取值范围是 ▲ . 18.已知,在Rt △ABC 中,∠C =90°,AC =9, BC =12,点D 、E 分别在边AC 、BC 上,且CD ︰CE =3︰4.将△CDE 绕点D 顺时针旋转,当点C 落在线段DE 上的点F 处时,BF 恰好是∠ABC 的平分线,此时线段CD 的长是 ▲ .二、填空题:7.a ; 8.()4-a a ; 9.3≥-x ; 10.101、、-; 11.21-a ; 12.(3,1); 13.13; 14.>; 15.2132-b a ; 16.1︰3; 17.3508<<PB ; 18.6.松江区7.因式分解:34a a - = ▲ . 8x =的根是 ▲ . 9.函数32x y x-=10.已知方程24x x m -+=m 的取值范围是 ▲ . 11.把抛物线22y x =-向左平移1个单位,则平移后抛物线的表达式为 ▲ . 12.函数y kx b =+的图像如图所示,则当0y <时,x 的取值范围是 ▲ .13.一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数,随机投掷这枚骰子,那么向上一面的点数为合数的概率是 ▲ .14.某区有4000名学生参加学业水平测试,从中随机抽取500名,对测试成绩进行了统计,统计结果见图3 ABCDE F图2图4POP'下表:那么根据上述数据可以估计该区这次参加学业水平测试成绩小于60分的有 ▲ 人.15. 如图,在△ABC 中,D 是AB 的中点,E 是AC 上一点,且AE =2EC ,如果AB a =uu u r r ,AC b =uuu r r ,那么DE uuu r =▲ .(用a r 、b r表示).16.一个正n 边形的一个内角等于它的中心角的2倍,则n =▲ .17.平面直角坐标系xoy 中,若抛物线2y ax =上的两点A 、B 满足OA =OB ,且1tan 2OAB ∠=,则称线段AB 为该抛物线的通径.那么抛物线212y x =的通径长为 ▲ . 18.如图,已知平行四边形ABCD 中,AC =BC ,∠ACB =45°,将三角形ABC 沿着AC 翻折,点B 落在点E处,联结DE ,那么DEAC的值为 ▲ . 二、填空题:(本大题共12题,每题4分,满分48分)7. (2)(2)a a a +-; 8. 2x =; 9. 0x ≠; 10. 4m <; 11.22(1)y x =-+;12. 1x <-; 13.13; 14. 120; 15. 1223a b -+r r ;16. 6; 17. 2; 18.1- .徐汇区7. 函数12y x =-的定义域是8. 在实数范围内分解因式:22x y y -=9. 2=的解是10. 不等式组2672x x -≥⎧⎨+>-⎩的解集是ACDE (第15题图)B(第12题图)(第18题图)A DC11. 已知点1(,)A a y 、2(,)B b y 在反比例函数3y x=的图像上,如果0a b <<,那么1y 与2y 的大小关系是1y 2y12. 抛物线2242y x x =+-的顶点坐标是13. 四张背面完全相同的卡片上分别写有0.3227四个实数,如果将卡片字面 朝下随意放在桌子上,任意取一张,那么抽到有理数的概率为14. 在ABC ∆中,点D 在边BC 上,且:1:2BD DC =,如果设AB a =,AC b =,那么BD 等于 (结果用a 、b 的线性组合表示)15. 如图,为了解全校300名男生的身高情况,随机抽取若干男生进行身高测量,将所得数据(精确到1cm )整理画出频数分布直方图(每组数据含最低值,不含最高值),估计该校男生的身高在170cm ~175cm 之间的人数约有 人16. 已知两圆相切,它们的圆心距为3,一个圆的半径是4,那么另一个圆的半径是17. 从三角形(非等腰三角形)一个顶点引出一条射线与对边相交,该顶点与该交点间的线段把这个三角形分割成两个小三角形,如果其中一个小三角形是等腰三角形,另一个与原三角形相似,那么我们把这条线段叫做这个三角形的完美分割线,如图,在ABC ∆中,1DB =,2BC =,CD 是ABC ∆的完美分割线,且ACD ∆是以CD 为底边的等腰三角形,则CD 的长为18. 如图,在Rt ABC ∆中,90C ∠=︒,5AB =,3BC =,点P 、Q 分别在边BC 、AC 上,PQ ∥AB ,把PCQ ∆绕点P 旋转得到PDE ∆(点C 、Q 分别与点D 、E 对应),点D 落在线段PQ 上,若AD 平分BAC ∠,则CP 的长为二. 填空题7. 2x ≠ 8. (y x x + 9. 7x = 10. 93x -<≤-11. > 12. (1,4)-- 13. 3414. 1133b a -r r15. 72 16. 1或7 17.3218. 2 杨浦区二、填空题(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置上】7、计算:8、当时,化简:=9、函数中,自变量x的取值范围是10、如果反比例函数的图像经过点的值等于11、三人中至少有两人性别相同的概率是12、25位同学10秒钟跳绳的成绩汇总如下表:那么跳绳次数的中位数是13、李明早上骑自行车上学,中途因道路施工推车步行了一段路,到学校共用时15分钟,如果他骑自行车的平均速度是每分钟250米,推车步行的平均速度是每分钟80米,他家离学校的路程是2900米,设他推车步行的时间为x分钟,那么可列出的方程是14、四边形ABCD中,向量=15、若正n边形的内角和为1400,则边数n为16、如图3,△ABC中,∠A=800,∠B=400,BC的垂直平分线交AB于点D,联结DC,如果AD=2,BD=6那么△ADC的周长为17、如图4,正△ABC的边长为2,点A、B的半径为的圆上,点C在圆内,将正△ABC绕点A逆时针旋转,当点C第一次落在圆上时,旋转角的正切值是18、当关于X的一元二次方程有实数根,且其中一个根为另一个根的2倍时,称之为“倍根方程”,如果关于X的一元二次方程是“倍根方程”,那么m的值为。
