新领航教育特供:天津市耀华中学2013届高三第一次月考 理科数学试题
天津高三数学理科试题分类汇编13导数

最新 2013 届天津高三数学理科试题精选分类汇编13:导数一、选择题1 .(天津市蓟县二中 2013 届高三第六次月考数学(理)试题)函数的图象与 x 轴所围成的封闭图形的面积为()()A .B .1 C. 2 D.2 .(天津市耀华中学2013 届高三第一次月考理科数学试题)已知函数 f (x)= x2 cos x,则f (0.6),f (0),f (-0.5) 的大小关系是()A .f (0)< f (0.6)< f (-0.5) B.f (0)< f (-0.5)< f (0.6)C.f (0.6)< f (-0.5)< f (0) D.f (-0.5)< f (0)< f (0.6)3 .(天津市天津一中2013 届高三上学期一月考理科数学). 定义在 R 上的可导函数 f(x), 且 f(x) 图像连续 , 当 x≠ 0 时 , f '( x) x 1 f ( x) 0 ,则函数 g( x) f (x) x 1的零点的个数为()A . 1B .2 C. 0 D.0或24 .(天津市新华中学2012 届高三上学期第二次月考理科数学)已知函数 f ( x)( x R) 满足 f (1) 1 ,且 f (x) 的导函数 f '( x) 1 x 1的解集为2,则 f ( x)22()A .x 1 x 1B .x x 1C .x x 1或 x 1D.x x 1二、填空题5 .(天津市六校 2013 届高三第二次联考数学理试题(WORD 版))若 f(x) 在 R上可2+2f ’(2)+3, 3导 ,f(x)=x 则 f (x)dx .6 .(天津南开中学2013 届高三第四次月考数学理试卷)若不等式 | ax3 ln x | 1 对任意 x (0,1] 都成立 , 则实数 a 取值范围是 ________.17 .(天津市耀华中学2013 届高三第一次月考理科数学试题)计算(2 x+e x )dx = ;-18 .(天津市天津一中2013 届高三上学期一月考理科数学)曲线 xy 1与直线y=x和y=3所围成的平面图形的面积为 _________.9 .(天津市天津一中20131 e 1dx , 则 m与n届高三上学期第二次月考数学理试题)设me x dx,n x0 1的大小关系为 ______.10.(天津耀华中学2013 届高三年级第三次月考理科数学试卷)已知函数 f ( x) x3 bx2 cx d 在区间 [ 1,2] 上是减函数,那么 b c的最大值为________________;三、解答题11.2013 届高三第六次月考数学(理)试题)已知函数(为自然(天津市蓟县二中对数的底数).(1)求的最小值;( 2)设不等式的解集为,若,且,求实数的取值范围(3)已知,且,可否存在等差数列和首项为公比大于0 的等比数列,使得 ?若存在,央求出数列 的通项公式.若不存在,请说明原由.12.2013 届高三第六次月考数学(理)试题)已知函数(天津市蓟县二中( ) .(1)若,试确定函数的单调区间;( 2)若函数在其图象上任意一点 处切线的斜率都小于 ,求实数 的取值范围 .(3)若,求 的取值范围 .13.(天津市十二区县重点中学2013 届高三毕业班联考(一)数学(理)试题)已知函数f xln 2ax 1x 3x 2 2ax a R3( Ⅰ) 若 x2 为 f x 的极值点 , 求实数 a 的值 ;( Ⅱ) 若 yf x 在 3,上为增函数 , 求实数 a 的取值范围 ;1 1 x 3b ( Ⅲ) 当 a时 , 方程 f 1 xx23有实根 , 求实数 b 的最大值 .2013 年天津市十二区县重点学校高三毕业班联考( 一14.(天津市六校 2013 届高三第二次联考数学理试题(WORD 版))已知函数 f( x )=2ln x +ax 2-1( a ∈ R)(1) 求函数 f(x) 的单调区间 ;(2) 若 a=1, 分别解答下面两题 ,(i) 若不等式 f(1+x)+f(1-x)<m 对任意的 0<x<1 恒成立 , 求 m 的取值范围 ;(ii) 若 x 1,x 2 是两个不相等的正数 , 且 f(x 1)+f(x 2)=0, 求证 x 1+x 2>2.15.(天津南开中学 2013 届高三第四次月考数学理试卷)已知函数 f (x) x ln( x a) 的最小值为 0,其中 a0 .(1) 求 a 的值(2) 若对任意的 x[0, ) , 有 f ( x)kx 2 成立 , 求实数 k 的最小值n2N * )(3) 证明2i ln( 2n 1) 2(ni 1116 .( 2012-2013-2 天津一中高三 年级数学第四次月考检测试卷(理))已知函数f x ln x ax 2 x 在 x 0 处获取极值 .(1) 求实数 a 的值;(2) 若关于 x 的方程f x5x b 在区间0,2上恰有两个不同样的实数根, 求实数b的取值范2围;(3) 证明 : 对任意的正整数3 4 n 1ln n 1 都成立. n ,不等式29 n2417.(天津市耀华中学 2013 届高三第一次月考理科数学试题)( 本小题满分14 分) 设函数f (x)=x2 +bln (x+1) ,其中b≠0。
天津市天津一中2013届高三上学期一月考 理科数学-推荐下载

na
,因为
a,
b,
c
中任意两个都不共线,则有
8.定义在 R 上的可导函数 f(x),且 f(x)图像连续,当 x≠0 时, f '(x) x1 f (x) 0 ,则函数
g(x) f (x) x1 的零点的个数为
A.1
B.2
【答案】C
【解析】由 f '(x) x1 f (x) 0 ,得 xf '(x) f (x) 0 ,当 x 0 时, xf '(x) f (x) 0 , x
天津一中 2012—2013 学年高三
数学一月考试卷(理科)
一、选择题:(共 40 分,每小题 5 分,每小题给出的四个选项中,只有一项符合题目要求) 1.有关下列命题的说法正确的是
A.命题“若 x2=1,则 x=1”的否命题为:若“x2=1 则 x≠1”
B.“ x 1 ”是“ x2 5x 6 0 ”的必要不充分条件 C.命题“ x∈R,使得 x2+x+1<0”的否定是:“ x∈R,均有 x2+x+1<0”
7
3 63
3
B.直角三角形 D.等腰或直角三角形
【解析】由 sin Acos A sin B cos B 得 sin 2A sin 2B sin( 2B) ,所以 2A 2B 或 2 A 2B ,即 A B 或 A B ,所以三角形为等腰或直角三角形,选 D. 2
B.b
C.c
C. z y x
x
,即
1,即 log2
log2
1,所以 0
【解析】因为 a b 与 c 共线,所以有 a b mc ,又 b c 与 a 共线,所以有 b c na ,即
天津耀华中学2013届高三模拟考试十二(理综)+解析+答案

天津耀华中学2013届高三模拟考试理科综合能力测试(十二)本试卷分第1卷(选择题)和第Ⅱ卷两部分,共300分,考试用时150分钟。
第Ⅰ卷1至4页,第Ⅱ卷5至14页。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷(选择题共21题每题6分共126分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考号、科目涂写在答题卡上,并在规定位置粘贴考试用条形码。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上的无效。
在下列各题的四个选项中,只有一个选项是最符合题目要求的。
以下数据可供解题时参考:相对原子质量: H1 C12 016 Na23 P 311.蛋白质分子能被肽酶降解,至于哪一肽键被断裂则决定于肽酶的类型。
肽酶P能断裂带有侧链R4的氨基酸和相邻氨基酸的氨基基团之间的肽键。
下列说法正确的是:A .肽酶P 可以催化3处的化学键断裂B .在肽酶P 的作用下,经过脱水缩合可以形成两条肽链C .上图所示肽链由四种氨基酸脱水缩合而成D .在有丝分裂间期的细胞核中不可能会发生1、3键的形成2.请仔细观察下图1中蔗糖水解为葡萄糖的机理,分析与图2所示化学反应无关的分子:A .AB .BC .CD .D3.如图所示,茎a 侧生长素在B 点以下的浓度范围内,下列对b 侧生长素浓度范围的描述哪项较为准确?步骤1 步骤2 步骤3A.在OA段范围内B.在BC段范围内C.在BD段范围内D.在BA段范围内4.当动物缺乏激素时,可以通过“饲喂法”或“注射法”对该激素进行人为补充,下列可通过“饲喂法”补充的是:①生长激素②甲状腺激素③胰岛素④性激素A.①② B.①③ C.②④ D.①④5.可以成为人体第三道防线的结构或物质是:①骨髓②扁桃体③淋巴细胞④抗体⑤红细胞⑥吞噬细胞⑦抗原决定簇A.①③④⑤⑥B.③④⑥⑦C.①②③④⑥D.①③⑤⑥6.右图中曲线Ⅱ表示的是牛被引入某孤岛后的种群数量变化。
最新2013届天津高三数学理科试题精选分类汇编3:三角函数

最新2013届天津高三数学试题精选分类汇编3:三角函数一、选择题1 .(天津市和平区2013届高三第一次质量调查理科数学)若f (x )a sin x b =+(a ,b 为常数)的最大值是5,最小值是-1,则ab的值为 ( )A .、23-B .、23或23-C .、 32-D .、322 .(天津市蓟县二中2013届高三第六次月考数学(理)试题)边长为的三角形的最大角与最小角的和是( ) ( )A .B .C .D .3 .(天津市十二区县重点中学2013届高三毕业班联考(一)数学(理)试题)在钝角△ABC 中,已知AB=3, AC=1,∠B=30°,则△ABC 的面积是( )A .23B .43 C .23 D .43 4 .(天津市六校2013届高三第二次联考数学理试题(WORD 版))设函数f(x)=Asin(ϕω+x )(A>0,ω>0,-2π<ϕ<2π)的图象关于直线x=32π对称,且周期为π,则f(x)( )A .图象过点(0,21) B .最大值为-AC .图象关于(π,0)对称D .在[125π,32π]上是减函数 5 .(天津市新华中学2013届高三寒假复习质量反馈数学(理)试题)设ω>0,函数y=sin(ωx+3π)+2的图像向右平移34π个单位后与原图像重合,则ω的最小值是( )A .23B .43C .32D .36 .(天津市新华中学2013届高三寒假复习质量反馈数学(理)试题)已知21)4tan (=+απ,则ααα2cos 1cos 2sin 2+-的值为( )7 .(天津南开中学2013届高三第四次月考数学理试卷)为了得到函数x x x y 2cos 21cos sin 3+=的图象,只需将函数x y 2sin =的图象( )A .向左平移12π个长度单位 B .向右平移12π个长度单位 C .向左平移6π个长度单位D .向右平移6π个长度单位8 .(2012-2013-2天津一中高三年级数学第四次月考检测试卷(理))在ABC ∆中,角,,A B C 所对边长分别为,,a b c ,若2222a b c +=,则cos C 的最小值为( )ABC .12D .12-9 .(天津市耀华中学2013届高三第一次月考理科数学试题)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,,且1+2cos(B+C)=0,则BC 边上的高等于( )ABC .D10.(天津市耀华中学2013届高三第一次月考理科数学试题)把函数=()y sin x x R ∈的图象上所有的点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是 ( )A .=(2-),R 3y sin x x π∈ B .=(+),R 26x y sin x π∈ C .=(2+),R 3y sin x x π∈D . 2=(2+),R 3y sin x x π∈11.(天津市天津一中2013届高三上学期一月考理科数学)在∆ABC 中,A,B,C 为内角,且sin cos sin cos A A B B =,则∆ABC 是( ) A .等腰三角形 B .直角三角形C .等腰直角三角形D .等腰或直角三角形A .35-B .56-C .-1D .212.(天津市天津一中2013届高三上学期一月考理科数学)设函数sin()3y x π=+(x ∈R),则f(x)( )A .在区间[-π,2π-]上是减函数B .在区间27[,]36ππ上是增函数 C .在区间[8π,4π]上是增函数 D .在区间5[,]36ππ上是减函数13.(天津市天津一中2013届高三上学期一月考理科数学)函数f(x)=sin2x-4sin 3xcosx(x ∈R)的最小正周期为 ( )A .8πB .4π C .2π D .π14.(天津市新华中学2012届高三上学期第二次月考理科数学)把函数sin(2)4y x π=+的图象向右平移8π个单位,再把所得图象上各点的横坐标缩短到原来的一半,则所得图象对应的函数解析式是( )A .y=sin (4x+83π) B .y=sin (4x+8π) C . y=sin4x D .y=sinx15.(天津市新华中学2012届高三上学期第二次月考理科数学)函数ln cos y x =⎪⎭⎫ ⎝⎛<<-22ππx 的图象是16.(天津市滨海新区五所重点学校2013届高三联考试题数学(理)试题)在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,其中120,1A b ==,且ABC ∆则sin sin a bA B+=+( )A B C .D .17.(天津市天津一中2013届高三上学期第二次月考数学理试题)函数2()3s i n 22s i n f x x x =-,(02x π≤≤)则函数f(x)的最小值为 ( )A .1B .-2C .√3D .-√318.(天津市天津一中2013届高三上学期第二次月考数学理试题)在∆ABC 中,tanA 是以-4为第三项,4为第七项的等差数列的公差,tanB 是以13为第三项,9为第六项的等比数列的公比,则这个三角形是( )A .钝角三角形B .锐角三角形C .等腰直角三角形D .以上都不对19.(天津市天津一中2013届高三上学期第三次月考数学理试题)△ABC 的三个内角C B A ,,所对的边分别为c b a ,,,a A b B A a 2cos sin sin 2=+,则=ab( )A .32B .22C .3D .220.(天津耀华中学2013届高三年级第三次月考理科数学试卷)将函数⎪⎭⎫⎝⎛+=42sin 2)(πx x f 的图像向右平移)0(>ϕϕ个单位,再将图像上每一点横坐标缩短到原来的21倍,所得图像关于直线4π=x 对称,则ϕ的最小正值为 ( )A .8πB .83πC .43π D .2π二、填空题21.(天津市蓟县二中2013届高三第六次月考数学(理)试题)已知函数,给出下列四个说法: ①若,则; ②的最小正周期是;③在区间上是增函数; ④的图象关于直线对称.其中正确说法的序号是______.22.(天津市耀华中学2013届高三第一次月考理科数学试题)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,若222+=2012a b c ,则(+)tan A tan BtanC tan A tan B 的值为 ;23.(天津市耀华中学2013届高三第一次月考理科数学试题)函数()=(+)(,,f x Asin x A ωϕωϕ为常数,A>0,ω>0)的部分图象如图所示,则f (0)的值是 ;24.(天津市天津一中2013届高三上学期一月考理科数学)函数()sin(2)3f x x π=-(x ∈R)的图象为C,以下结论中:①图象C 关于直线1112x π=对称; ②图象C 关于点2(,0)3π对称; ③函数f(x)在区间5(,)1212ππ-内是增函数;④由3sin 2y x =的图象向右平移3π个单位长度可以得到图象C. 则正确的是 .(写出所有正确结论的编号)25.(天津市天津一中2013届高三上学期一月考理科数学)已知3sin cos 8x x =,且(,)42x ππ∈,则cos sin x x -=_________.26.(天津市新华中学2012届高三上学期第二次月考理科数学)在△ABC 中,若sinA=2sinBcosC 则△ABC的形状为________。
天津市天津一中2013届高三零月考数学(理)试题(附答案)
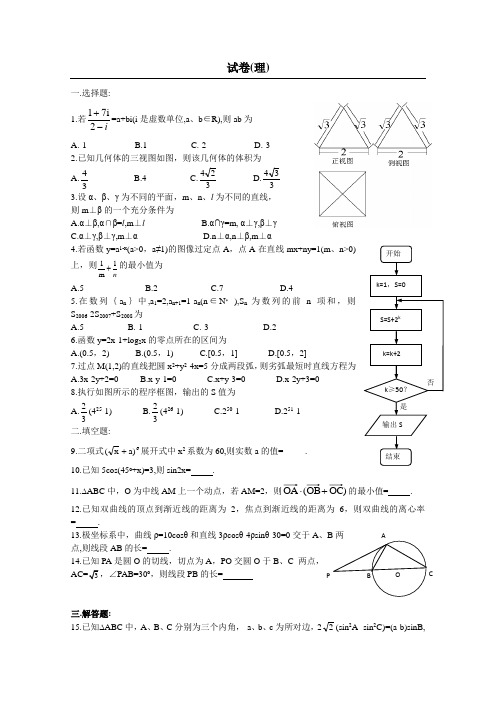
试卷(理)一.选择题: 1.若i-+2i71=a+bi(i 是虚数单位,a 、b ∈R),则ab 为 A.-1 B.1 C.-2 D.-3 2.已知几何体的三视图如图,则该几何体的体积为A.34B.4C.324D.334 3.设α、β、γ为不同的平面,m 、n 、l 为不同的直线, 则m ⊥β的一个充分条件为A.α⊥β,α∩β=l ,m ⊥lB.α∩γ=m, α⊥γ,β⊥γC.α⊥γ,β⊥γ,m ⊥αD.n ⊥α,n ⊥β,m ⊥α4.若函数y=a 1-x (a>0,a ≠1)的图像过定点A ,点A 在直线mx+ny=1(m 、n>0)上,则n1m1+的最小值为A.5B.2C.7D.45.在数列{a n }中,a 1=2,a n+1=1-a n (n ∈N ∗ ),S n 为数列的前n 项和,则S 2006-2S 2007+S 2008为 A.5 B.-1 C.-3 D.26.函数y=2x-1+log 2x 的零点所在的区间为A.(0.5,2)B.(0.5,1)C.[0.5,1]D.[0.5,2]7.过点M(1,2)的直线把圆x 2+y 2-4x=5分成两段弧,则劣弧最短时直线方程为 A.3x-2y+2=0 B.x-y-1=0 C.x+y-3=0 D.x-2y+3=0 8.执行如图所示的程序框图,输出的S 值为A.32(425-1)B.32(426-1) C.250-1 D.251-1 二.填空题:9.二项式6a)x (+展开式中x 2系数为60,则实数a 的值=_____. 10.已知5cos(45o +x)=3,则sin2x= .11.∆ABC 中,O 为中线AM 上一个动点,若AM=2,则)(+⋅的最小值= . 12.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则双曲线的离心率= .13.极坐标系中,曲线ρ=10cos θ和直线3ρcos θ-4ρsin θ-30=0交于A 、B 两点,则线段AB 的长= .14.已知PA 是圆O 的切线,切点为A ,PO 交圆O 于B 、C 两点,PAB=30o ,则线段PB 的长=三.解答题:15.已知∆ABC 中,A 、B 、C 分别为三个内角, a 、b 、c 为所对边,22(sin 2A- sin 2C)=(a-b)sinB,O B C P APA B CDE∆ABC 的外接圆半径为2,(1)求角C ;(2)求∆ABC 面积S 的最大值.16.右图为一多面体,其底面ABCD 为正方形,PD ⊥平面ABCD ,CE//DP ,且PD=2CE ,(1)求证:BE//平面PDA ;(2)若N 为线段PB 的中点,求证:EN ⊥平面PDB ;(3)若PD=2AD ,求平面PBE 与平面ABCD 所成的二面角的余弦值.17.设有编号为1,2,3,……,n 的n 个学生,编号为1,2,3,……,n 的n 个座位.规定每个学生坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为ξ,已知ξ=2时,共有6种坐法.(1)求n 的值; (2)求随机变量ξ的概率分布列和数学期望.18.数列{a n }的前n 项和S n ,点(a n ,S n )在直线y=2x-3n 上,(1)若数列{a n +c }为等比数列,求常数c 的值;(2)求数列{a n }的通项公式;(3) 数列{a n }中是否存在三项,使它们构成等差数列?若存在,求出一组适合条件的项;若不存在,说明理由.19.已知椭圆C 1:)0(12222>>=+b a b y a x 的离心率为33,直线l : y=x+2与以原点为圆心,以椭圆的短半轴长为半径的圆相切.(1)求椭圆C 1的方程;(2)设椭圆C 1的左、右焦点F 1、F 2,直线l 1过点F 1且垂直于椭圆长轴,动直线l 2垂直l 1于点P ,线段P F 2的垂直平分线交l 2于点M ,求点M 的轨迹C 2方程;(3)设C 2与x 轴交于Q 点,不同的两点R 、S 在C 2上,且满足⋅=0.,求∣QS ∣的取值范围.20.已知函数f(x)=ax 4lnx+bx 4-c (x>0),在x = 1处取得极值-3-c ,其中a,b,c 为常数.(1)试确定a,b 的值;(2)讨论函数f(x)的单调区间;(3)若对任意x>0,不等式f(x)+2c 2≥0恒成立,求c 的取值范围.答案:一、选择题: 1、D 2、C 3、D 4、D 5、C 6、B 7、D 8、A二、填空题: 9、±210、25711、-2 12、3 13、8 14、1三、解答题:15、解:(1))(sin 22)sin (sin )2(2222b a B C A -=-a 2-c 2=ab-b 2即a 2+b 2-c 2=ab ∴2abcosC=ab cosC=21 c=3π(2)S ΔABC =21absinC =21absin 3π=sinAsinB 32 =)32sin(sin 32A A -π=)sin 21cos 23(sin 32A A A + =3sinAcosA+3sin2A=23sin2A+23(1-cos2A) =23sin2A-23cos2A+23=3sin(2A-6π)+23当2A-6π=2π 即A=3π时,S ΔABCmax =233 16、解:(1)取PD 中点F ,则FD //EC ,∴□EFDC ∴EF //CD //AB ∴□EFAB ∴ BE//AF ∴BE//平面PDA AF ⊆面PDA(2)设AC ∩BD=O 则NO //CE ∴□NOCE ∴CO//EN ∵ PD ⊥面ABCD ∴ PD ⊥NE ∴NE ⊥平面PDB PD//CE//NO BD ⊥NE(3)设平面PBE 与平面ABCD 所夹角为α∵PD ⊥平面ABCD 于D ,CE ⊥平面ABCD 于C ,∴PBES ∆∆=BDCS cos αS ΔBDC =2a 2,在ΔPBE 中,PB=2a ,BE=a 26,PE=a 26S ΔPBE =22222)26(22121a a a a EN PB =-⋅⋅=⋅⋅ ∴22222cos 22==a a α 17、解:(1)由ξ=2可知有n-2学生对位,2个错位,选n-2个学生对位 ∴62-n n=C ,∴n=4(2)P(ξ=0)=241144=A ,P (ξ=2)=446A =41P (ξ=3)=3124414=⋅A C ,P (ξ=4)=31944=AE ξ334131201=⨯+⨯+⨯+⨯= 18、把(a n ;S n )代入y=2x-3n 中, S n =2a n -3nS n-1=2a n-1-3(n-1) (n ≥2) 两式相减:a n =2a n-1+3 即a n +3=2(a n-1+3)∴c=3,当n=1时,a 1=3(2)由{a n +3}是首项6公比2的等比数列 ∴a n +3=6·2n-1 ∴a n =3·2n -3(n ∈N*) (3)设0<<βα假设存在 则]323[2)323()323(-⋅=-⋅+-⋅βγα即βγα2222⋅=+222=+--βγβα事实上,0<-βα,0>-βγ∴ 0<12<-βα ∴222>+--βγβα 22>-βγ ∴假设存在不成立 ∴不存在 19、解:(1)由e=33可知 a=c 3 ∴2a 2=3b 2a 2=b 2+c 2由y=x+2与(x 2+y 2=b 2)相切b=22∴ b=2 123x 22=+y 为椭圆C 1的方程a=3(2)F 1(-1,0),F 2(1,0)由已知可知MF 2=MP即点M 到点F 2距离等于点M 到直线l 1:x=-1的距离点M 是焦点为F 2渐近线为x=-1的抛物线,p=2 ∴y 2=4x(3)由(2)可知Q 点为原点O ,设R (x 1,y 1) ,S (x 2,y 2)2221214y ,4y x x ==,由0=⋅RS OR即x 1(x 2-x 1)+y 1(y 2-y 1)=0 x 1x 2-21x +y 1y 2-21y =0, x 1x 2-21x -40x 4x x 121=-0)2(2)-x x (21221=+-x22-x x 121+=x 44112≥+=x x x ,当且仅当x 1=2时,x 2≥16而|QS|=|OS|=2222y x +=2224x x +≥815164162=⨯⨯∴|QS|∈[815,+∞) 另:设直线OR 方程 y=kx ⇒ R(k442,k ),不妨设k>0y 2=4x 直线RS 方程 y-k 4=-)44,)1(4()4(122k k k k s k x k --+⇒- y 2=4x ∴ |QS|=|OS|=4815)1()k 1(k 24≥+++kk (k+k1)2≥420、解:(1)f ’(x )=4ax 3lnx+ax 3+4bx 3 由 f ’(1)=0f(1)=-3-c 即⎩⎨⎧-==∴⎩⎨⎧==+312c --3c -b 04b a b a (2)f(x)=12x 4lnx-3x 4-cf ’(x)=48x 3lnx+12x 3-12x 3=48x 3lnx ,(x>0) f(x)增区间(1,+∞),减区间(0,1) (3)由对x>0,f(x)+2c 2≥0成立即:12x 4lnx-3x 4-c+2c 2≥0对x ∈R 成立 即:c-2c 2≤12x 4lnx-3x 4对x ∈R 成立 必须满足c-2c 2≤{12x 4lnx-3x 4}min设g(x)=12x 4lnx-3x 4 g ’(x)=48x 3lnx ,如图当x=1时,g(x)min =g(1)=-3 ∴c-2c 2≤3 即2c 2-c-3≥0 ∴c ≤-1或c ≥23。
天津市耀华中学高三数学第一次校模拟 理 新人教A版

天津市耀华中学2013届高三第一次校模拟考试理科数学试卷第I 卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟第Ⅰ卷(选择题共40分)本卷共8题,每题5分,共40分。
在每题给出的四个选项中,只有一项是最符合题目要求的,将答案涂在答题卡上。
1.复数3232.2323i i i i+--=-+( ) A.0 B.2 C.2i - D. 2i2.下列选项中,p 是q 的必要不充分条件的是( )A. :1p x = 2:q x x =B. :p m n +是无理数, :q m 和n 是无理数C. :p a c b d +>+, :q a b c d >>且D. :1p a >, :()log (0,1)a q f x x a a =>≠且在(0,)+∞上为增函数 3.如果执行右面的程序框图,那么输出的S=( )A.2652B.2550C.2500D.24504.设0ω>,函数sin 23y x πω⎛⎫=++ ⎪⎝⎭的图象向右平移43π个单位后与原图象重合,则ω的最小值是( ) A. 32 B. 43C. 23D. 3 5.一个等差数列第5项510a =,且1233a a a ++=,则有( )A. 12,3a d ==-B. 12,3a d =-=C. 13,2a d =-=D. 13,2a d ==6.已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F,由F 向其渐近线上引垂线,垂中为P,若线段PF 的中点在此双曲线上,则此双曲线的离心率为( ) A.2 B. 3 C.2 D. 5 7.在矩形ABCD 中,1,3AB AD ==, P 为矩形内一点,且32AP =,若(,)AP AB AD R λμλμ=+∈u u u r u u u r u u u r ,則3λμ+的最大值为( )A.62B. 32C. 334+D. 6324+ 8.高三年级有文科、理科共9个备课组,每个备课组的人数不少于4个,现从这9个备课组中抽出l2人,每个备课组至少1人,组成“年级核心组”商议年级的有关事宣。
无锡新领航教育特供:【2013备考】高考数学各地名校试题解析分类汇编(一)1 集合 理

小升初 中高考 高二会考 艺考生文化课 一对一辅导 /wxxlhjy QQ:157171090
- 1 - 无锡新领航教育特供:
各地解析分类汇编:集合与简易逻辑
1【云南省玉溪一中2013届高三第四次月考理】已知:p “,,a b c 成等比数列”,
:q “ac b =”,那么p 成立是q 成立的( )
A .充分不必要条件
B .必要不充分条件
C .充要条件
D . 既不充分又非必要条件 【答案】D
【解析】,,a b c 成等比数列,则有2b ac =,
所以b =所以p 成立是q 成立不充分条件.当==0a b c =时,有ac b =
成立,但此时,,a b c 不成等比数列,所以p 成立是q 成立既不充分又非必要条件,选D.
2【云南省玉溪一中2013届高三上学期期中考试理】设全集{}1,2,3,4,5U =,集合{}2,3,4A =,{}2,5B =,则()U B C A =( )
A.{}5
B. {}125, ,
C. {}12345, , , ,
D.∅
【答案】B
【解析】{1,5}U C A =,所以()={1,5}{2,5}={1,2,5}U B C A ,选B.
【解析】当k =0时,x =1;当k =1时,x =2;当k =5时,x =4;当k =8时,x =5,故选B.
4【云南师大附中2013届高三高考适应性月考卷(三)理科】已知条件2:340p x x --≤;条件22:690q x x m -+-≤ 若p 是q 的充分不必要条件,则m 的取值范围是( )
A .[]1,1-
B .[]4,4-
C .(][),44,-∞-+∞
D .(][),11,-∞-+∞ 【答案】C。
无锡新领航教育特供:【2013备考】高考数学各地名校试题解析分类汇编(一)11 复数与框图 理

小升初 中高考 高二会考 艺考生文化课 一对一辅导 /wxxlhjy QQ:157171090
- 1 - 无锡新领航教育特供:
各地解析分类汇编:复数与框图
1【云南省玉溪一中2013届高三第四次月考理】若复数2)1(ai +(i 为虚数单位)是纯虚数,则实数=a ( )
A.1±
B.1-
C.0
D.1
【答案】A
【解析】2222
(1)1212ai ai a i a ai +=++=-+,要使复数是纯虚数,则有210a -=且20a ≠,解得1a =±,选A.
2.【云南省玉溪一中2013届高三上学期期中考试理】复数z 1=3+i,z 2=1-i,则复数
2
1z z 的虚部为 ( )
A.2
B.-2i
C.-2
D.2i
【答案】A 【解析】123(3)(1)24=121(1)(1)2z i i i i i z i i i ++++===+--+,所以虚部为2,选A.
A .第四象限
B .第三象限
C .第二象限
D .第一象限 【答案】A
【解析】1i 22z =-对应的点是112
2⎛⎫- ⎪⎝⎭,,故选A. 4.【云南省玉溪一中2013届高三第三次月考 理】复数
12i i + (i 是虚数单位)的虚部是( ) A .15 B .25 C .5i D .5
i - 【答案】A
【解析】(12)22112(12)(12)555
i i i i i i i i -+===+++-,所以虚部是15,选A.。
天津市天津一中2013届高三(上)零月考数学理试题(WORD解析版)

天津一中2013届高三(上)零月考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.(3分)若=a+bi(i是虚数单位,a、b∈R),则ab为()A.﹣1 B.1C.﹣2 D.﹣3考点:复数代数形式的乘除运算;复数相等的充要条件.专题:计算题.分析:利用复数的代数形式的乘除运算,知==﹣1+3i=a+bi,由此能求出ab.解答:解:∵====﹣1+3i=a+bi,∴a=﹣1,b=3,∴ab=﹣3.故选D.点评:本题考查复数的代数形式的乘除运算,是基础题.解题时要认真审题,仔细解答.2.(3分)已知几何体的三视图如图,则该几何体的体积为()A.B.4C.D.考点:由三视图求面积、体积.专题:计算题.分析:根据已知的三视图可判断出该几何体是一个正四棱锥,且可得底面棱长为2,侧面高为,由此求出底面面积和棱锥的高,代入棱锥体积公式,可得答案.解答:解:由已知可得该几何体是一个底面棱长为2侧面高为的正四棱锥则棱锥的高h==∴棱锥的高V=Sh=×2×2×=故选C点评:本题考查的知识点是由三视图求体积,其中根据已知分析出几何体的形状是解答的关键.3.(3分)(2005•天津)设α、β、γ为平面,m、n、l为直线,则m⊥β的一个充分条件是()A.α⊥β,α∩β=l,m⊥l B.α∩γ=m,α⊥γ,β⊥γC.α⊥γ,β⊥γ,m⊥αD.n⊥α,n⊥β,m⊥α考点:直线与平面垂直的判定.专题:证明题;转化思想.分析:根据面面垂直的判定定理可知选项A是否正确,根据平面α与平面β的位置关系进行判定可知选项B和C是否正确,根据垂直于同一直线的两平面平行,以及与两平行平面中一个垂直则垂直于另一个平面,可知选项D正确.解答:解:α⊥β,α∩β=l,m⊥l,根据面面垂直的判定定理可知,缺少条件m⊂α,故不正确;α∩γ=m,α⊥γ,β⊥γ,而α与β可能平行,也可能相交,则m与β不一定垂直,故不正确;α⊥γ,β⊥γ,m⊥α,而α与β可能平行,也可能相交,则m与β不一定垂直,故不正确;n⊥α,n⊥β,⇒α∥β,而m⊥α,则m⊥β,故正确故选D点评:本小题主要考查空间线面关系、面面关系以及充分条件的判定等知识,考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力,属于基础题.4.(3分)若函数y=a1﹣x(a>0,a≠1)的图象过定点A,点A在直线mx+ny=1(m、n>0)上,则的最小值为()A.5B.2C.7D.4考点:基本不等式.专题:计算题.分析:函数y=a1﹣x(a>0,a≠1)的图象恒过定点A,知A(1,1),点A在直线mx+ny﹣1=0上,得m+n=1结合mn>0,可得m>0,n>0,利用1的变换构造出可以用基本不等式求最值的形式求最值解答:解:由已知定点A坐标为(1,1),由点A在直线mx+ny﹣1=0上,∴m+n=1,又mn>0,∴m>0,n>0,∴=()(m+n)=2当且仅当即m=n=时取等号故选D点评:本题主要考查了利用基本不等式求解最值,解题的关键是利用1的代换配凑基本不等式应用的条件5.(3分)在数列{a n}中,a1=2,a n+1=1﹣a n(n∈N∗),S n为数列的前n项和,则S2006﹣2S2007+S2008为()A.5B.﹣1 C.﹣3 D.2考点:数列的求和;等差数列.专题:计算题.分析:依题意,可求得a1=a3=…=a2n﹣1=2,a2=a4=…=a2n=﹣1.从而可求得答案.解答:解:∵数列{a n}中,a n+1=1﹣a n(n∈N∗),∴a n+a n+1=1.又a1=2,∴a2=﹣1,∴a3=2,同理可求,a4=﹣1,a5=﹣1,…∴a1=a3=…=a2n﹣1=2,a2=a4=…=a2n=﹣1.∴S2006=1003;同理可求得S2007=1005,S2008=1004,∴S2006﹣2S2007+S2008=﹣3.故选C.点评:本题考查数列的求和,分析出a1=a3=…=a2n﹣1=2,a2=a4=…=a2n=﹣1是关键,考查分析与计算能力,属于中档题.6.(3分)函数y=2x﹣1+log2x的零点所在的区间为()A.(0.5,2)B.(0.5,1)C.[0.5,1]D.[0.5,2]考点:函数的零点.专题:计算题.分析:判断函数在区间端点处函数值的符号,当它们异号时存在零点.解答:解:因为2×0.5﹣1+log20.5=log20.5<0,2×1﹣1+log21=1>0,又在(0.5,1)上函数y=2x﹣1+log2x的图象是连续不断的一条曲线,所以函数y=2x﹣1+log2x在区间(0.5,1)上存在零点.故选B.点评:本题考查函数零点存在的条件,须满足两条:①在区间上图象连续不断;②端点处函数值异号.7.(3分)过点M(1,2)的直线把圆x2+y2﹣4x=5分成两段弧,则劣弧最短时直线方程为()A.3x﹣2y+2=0 B.x﹣y﹣1=0 C.x+y﹣3=0 D.x﹣2y+3=0考点:直线与圆相交的性质.专题:计算题;直线与圆.分析:设已知圆的圆心为C,根据平面几何知识,得劣弧最短时相应的弦长也最短,所以求出过点M,且与CM垂直的直线l即可,根据垂直直线斜率之间的关系算出l的斜率,最后利用点斜式列式,再化成一般式方程,即得所求.解答:解:∵劣弧最短时,相应的弦长也最短∴过点M(1,2)的直线l截圆C:x2+y2﹣4x=5,所得短劣弧对应的直线与CM垂直∵圆x2+y2﹣4x=5的圆心C(2,0)∴CM的斜率k==﹣2,可得直线l的斜率k1=﹣=由此可得直线l方程为:y﹣2=(x﹣1),整理得x﹣2y+3=0故选:D点评:本题给出圆内一点M,求经过点M且被圆截得最短弧的直线l的方程,着重考查了直线的位置关系和直线与圆相交的性质等知识,属于基础题.8.(3分)(2013•甘肃三模)执行如图所示的程序框图,输出的S值为()A.(425﹣1)B.(426﹣1)C.250﹣1 D.251﹣1考点:程序框图.专题:计算题;等差数列与等比数列.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出等比数列的和.解答:解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S=0+2+23+…+249==(425﹣1)故选A.点评:本题主要考查了直到型循环结构,直到型循环是先循环后判断.对循环体每次循环需要进行分析并找出内在规律.本题属于基础题二.填空题:9.(3分)的展开式中x2项的系数为60,则实数a=±2.考点:二项式系数的性质.专题:计算题.分析:在的通项公式中,令x的指数等于2,求得r=2,从而得到展开式中x2项的系数为60=C62a2,解方程求得实数a的值.解答:解:的通项公式为T r+1=C6r a r,令=2可得r=2,展开式中x2项的系数为60=C62a2,∴a2=4,a=±2.故答案为:±2.点评:本题主要考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,得到60=C62a2,是解题的关键,属于中档题.10.(3分)已知5cos(45°+x)=3,则sin2x=.考点:二倍角的正弦.专题:三角函数的求值.分析:由题意可得cos(45°+x)=,再利用二倍角的余弦公式求得sin2x=﹣cos(90°+2x)的值.解答:解:由题意可得cos(45°+x)=,∴sin2x=﹣cos(90°+2x)=﹣cos[2(45°+x)]=﹣2cos2(45°+x)+1=﹣2×+1=,故答案为.点评:本题主要考查二倍角的余弦公式的应用,属于基础题.11.(3分)(2005•江苏)在△ABC中,O为中线AM上一个动点,若AM=2,则的最小值是﹣2.考点:平面向量数量积的运算.专题:计算题;压轴题.分析:利用向量的运算法则:平行四边形法则作出,判断出共线,得到的夹角,利用向量的数量积公式将转化成二次函数求出最小值,解答:解:以OB和OC做平行四边形OBNC.则因为M为BC的中点所以且反向∴=,设OA=x,(0≤x≤2)OM=2﹣x,ON=4﹣2x∴=2x2﹣4x(0≤x≤2)其对称轴x=1所以当x=1时有最小值﹣2故答案为﹣2点评:本题考查向量的运算法则、向量共线的充要条件、向量的数量积公式、二次函数最值的求法.12.(3分)(2007•海南)已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为3.考点:双曲线的简单性质.专题:计算题.分析:过双曲线的顶点A、焦点F分别向其渐近线作垂线,垂足分别为B、C,根据比例线段的性质可知进而求得a和c的关系,则离心率可得.解答:解:如图,过双曲线的顶点A、焦点F分别向其渐近线作垂线,垂足分别为B、C,则:故答案为3点评:本题主要考查了双曲线的简单性质.考查了比例线段的知识和双曲线的离心率问题.13.(3分)极坐标系中,曲线ρ=10cosθ和直线3ρcosθ﹣4ρsinθ﹣30=0交于A、B两点,则线段AB 的长=8.考点:简单曲线的极坐标方程;直线与圆相交的性质.专题:直线与圆.分析:先把曲线和直线的极坐标方程化为普通方程,再利用|AB|=2(d为圆心到直线的距离)即可得出答案.解答:解:∵曲线ρ=10cosθ,∴ρ2=10ρcosθ,化为普通方程:x2+y2=10x,即(x﹣5)2+y2=25,∴圆心C(5,0),半径r=5.∵直线3ρcosθ﹣4ρsinθ﹣30=0,∴普通方程为3x﹣4y﹣30=0.圆心C(5,0)到直线的距离d==3,∴|AB|===8.故答案为8.点评:充分理解|AB|=2(d为圆心到直线的距离)是解题的关键.当然也可以先把交点A、B的坐标求出来,再利用两点间的距离公式即可求出.14.(3分)(2010•怀柔区二模)已知PA是圆O(O为圆心)的切线,切点为A,PO交圆O于B,C两点,,则线段PB的长为1.考点:圆的切线方程.专题:压轴题.分析:利用直径上的圆周角是直角,切点与圆心连线与切线垂直,推出△OAB是正三角形,PB=AB=r (半径),然后求出结果.解答:解:PA是圆O(O为圆心)的切线,切点为A,PO交圆O于B,C两点,∠CAB=90°,又OA⊥AP,∠PAB=30°∴∠CAO=30°△OAB是正三角形,且∠ACO=30°,∠APO=30°∴AB=PB设圆的半径为r,则;PB=1故答案为:1.点评:本题考查圆的切线方程,平面几何知识,是中档题.三.解答题:15.已知△ABC中,A、B、C分别为三个内角,a、b、c为所对边,2(sin2A﹣sin2C)=(a﹣b)sinB,△ABC的外接圆半径为,(1)求角C;(2)求△ABC面积S的最大值.考点:余弦定理;正弦定理.专题:解三角形.分析:(1)利用正弦定理化简已知等式的右边,整理后再利用余弦定理变形,求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;(2)由C的度数求出A+B的度数,用A表示出B,利用三角形的面积公式列出关系式,利用正弦定理化简后,将sinC的值及表示出的B代入,利用两角和与差的正弦函数公式化简,整理后利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的图象与性质即可得出面积的最大值.解答:解:(1)利用正弦定理化简已知的等式得:2(sin2A﹣sin2C)=2sinB(a﹣b),整理得:a2﹣c2=ab﹣b2,即a2+b2﹣c2=ab,∵c2=a2+b2﹣2abcosC,即a2+b2﹣c2=2abcosC,∴2abcosC=ab,即cosC=,则C=;(2)∵C=,∴A+B=,即B=﹣A,∵==2,即a=2sinA,b=2sinB,∴S△ABC=absinC=absin=×2sinA×2sinB×=2sinAsinB=2sinAsin(﹣A)=2sinA(cosA+sinA)=3sinAcosA+sin2A=sin2A+(1﹣cos2A)=sin2A﹣cos2A+=sin(2A﹣)+,则当2A﹣=,即A=时,S△ABCmax=.点评:此题考查了正弦、余弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.16.如图为一多面体,其底面ABCD为正方形,PD⊥平面ABCD,CE∥DP,且PD=2CE.(1)求证:BE∥平面PDA;(2)若N为线段PB的中点,求证:EN⊥平面PDB;(3)若PD=AD,求平面PBE与平面ABCD所成的二面角的余弦值.考点:直线与平面平行的判定;二面角的平面角及求法.专题:综合题;空间角.分析:(1)取PD中点F,证明四边形EFAB为平行四边形,可得BE∥AF,利用线面平行的判定可得BE∥平面PDA;(2)设AC∩BD=O,证明CO∥EN,C0⊥平面PDB,即可得到NE⊥平面PDB;(3)设平面PBE与平面ABCD所夹角为α,利用即可求得结论.解答:(1)证明:取PD中点F,则FD∥EC,FD=EC∴四边形EFDC为长方形∴EF∥CD∥AB∴四边形EFAB为平行四边形∴BE∥AF∵BE⊄面PDA,AF⊂面PDA∴BE∥平面PDA;(2)证明:设AC∩BD=O,则NO∥CE,NO=CE∴四边形NOCE为长方形,∴CO∥EN∵PD⊥面ABCD,∴CO⊂面ABCD∴PD⊥CO,∵CO⊥BD,PD∩BD=D∴C0⊥平面PDB∴NE⊥平面PDB;(3)解:设平面PBE与平面ABCD所夹角为α∵PD⊥平面ABCD于D,CE⊥平面ABCD于C,∴在△PBE中,PB=2a,BE=,PE=,∴S△PBE=∵S△BDC=,∴点评:本题考查线面平行,线面垂直,考查面面角,考查学生分析解决问题的能力,属于中档题.17.(2007•深圳二模)有编号为1,2,3,…,n的n个学生,入坐编号为1,2,3,…n的n个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为ξ,已知ξ=2时,共有6种坐法.(1)求n的值;(2)求随机变量ξ的概率分布列和数学期望.考点:离散型随机变量及其分布列.专题:计算题.分析:(1)解题的关键是ξ=2时,共有6种坐法,写出关于n的表示式,解出未知量,把不合题意的舍去.(2)学生所坐的座位号与该生的编号不同的学生人数为ξ,由题意知ξ的可能取值是0,2,3,4,当变量是0时表示学生所坐的座位号与该生的编号都相同,当变量是2时表示学生所坐的座位号与该生的编号有2个相同,理解变量对应的事件,写出分布列和期望.解答:解:(1)∵当ξ=2时,有C n2种坐法,∴C n2=6,即,n2﹣n﹣12=0,n=4或n=﹣3(舍去),∴n=4.(2)∵学生所坐的座位号与该生的编号不同的学生人数为ξ,由题意知ξ的可能取值是0,2,3,4,当变量是0时表示学生所坐的座位号与该生的编号都相同,当变量是2时表示学生所坐的座位号与该生的编号有2个相同,当变量是3时表示学生所坐的座位号与该生的编号有1个相同,当变量是4时表示学生所坐的座位号与该生的编号有0个相同,∴,,,,∴ξ的概率分布列为:∴.点评:培养运用从具体到抽象、从特殊到一般的观点分析问题的能力,充分体现数学的化归思想.启发诱导的同时,训练了学生观察和概括归纳的能力.18.数列{a n}的前n项和为S n,S n=2a n﹣3n(n∈N*)(1)若数列{a n+c}成等比数列,求常数c值;(2)求数列{a n}的通项公式a n(3)数列{a n}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.考点:等差数列与等比数列的综合.专题:计算题;压轴题.分析:(1)利用递推公式可得a n=s n﹣s n﹣1,利用等比数列的定义可求c(2)由递推公式a n=s n﹣s n﹣1(n≥2),a1=s1求解(3)假设存在a s,a p,a r成等差数列,则2a p=a s+a r,结合(2)中的通项公式进行推理.解答:解:(1)由S n=2a n﹣3n及S n+1=2a n+1﹣3(n+1)得a n+1=2a n+3∴,∴c=3(2)∵a1=S1=2a1﹣3,∴a1=3,a n+3=(a1+3)•2n﹣1∴a n=3.2n﹣3(n∈N*)(3)设存在S,P,r∈N*,且s<p<r使a s,a p,a r成等差数列∴2a p=a s+a r即2(3•2p﹣3)=(3•2s﹣3)+(3•2r﹣3)∴2p+1=2s+2r∴2p﹣s+1=1+2r﹣s∵s,p,r∈N*且s<p<r∴2p﹣s+1、2r﹣s为偶数1+2r﹣s为奇数矛盾,不存在满足条件的三项点评:本题主要考查了数列的递推关系a n=s n﹣s n﹣1(n≥2),a1=s1的应用及等比数列的定义,而对存在性问题,一般是先假设存在,然后由假设结合已知条件进行推理,看是否产生矛盾,从而判断存在性.19.(2013•梅州二模)已知椭圆的离心率为,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆相切.(1)求椭圆C1的方程;(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于直线l1,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;(3)设C2与x轴交于点Q,不同的两点R,S在C2上,且满足,求的取值范围.考点:圆与圆锥曲线的综合;平面向量数量积的运算;轨迹方程;椭圆的标准方程.专题:计算题;压轴题.分析:(1)先由离心率为,求出a,b,c的关系,再利用直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆相切,求出b即可求椭圆C1的方程;(2)把题中条件转化为动点M的轨迹是以l1:x=﹣1为准线,F2为焦点的抛物线,即可求点M的轨迹C2的方程;(3)先设出点R,S的坐标,利用求出点R,S的坐标之间的关系,再用点R,S 的坐标表示出,利用函数求最值的方法即可求的取值范围.解答:解:(1)由得2a2=3b2,又由直线l:y=x+2与圆x2+y2=b2相切,得,,∴椭圆C1的方程为:.(4分)(2)由MP=MF2得动点M的轨迹是以l1:x=﹣1为准线,F2为焦点的抛物线,∴点M的轨迹C2的方程为y2=4x.(8分)(3)Q(0,0),设,∴,由,得,∵y1≠y2∴化简得,(10分)∴(当且仅当y1=±4时等号成立),∵,又∵y22≥64,∴当y22=64,即y2=±8时,∴的取值范围是.(13分)点评:本题是对圆与椭圆知识的综合考查.当直线与圆相切时,可以利用圆心到直线的距离等于半径求解.,也可以把直线与圆的方程联立让对应方程的判别式为0求解.20.(2007•重庆)已知函数f(x)=ax4lnx+bx4﹣c(x>0)在x=1处取得极值﹣3﹣c,其中a,b,c 为常数.(1)试确定a,b的值;(2)讨论函数f(x)的单调区间;(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求c的取值范围.考点:利用导数研究函数的极值;函数恒成立问题;利用导数研究函数的单调性.专题:计算题.分析:(1)因为x=1时函数取得极值得f(x)=﹣3﹣c求出b,然后令导函数=0求出a即可;(2)解出导函数为0时x的值讨论x的取值范围时导函数的正负决定f(x)的单调区间;(3)不等式f(x)≥﹣2c2恒成立即f(x)的极小值≥﹣2c2,求出c的解集即可.解答:解:(1)由题意知f(1)=﹣3﹣c,因此b﹣c=﹣3﹣c,从而b=﹣3又对f(x)求导得=x3(4alnx+a+4b)由题意f'(1)=0,因此a+4b=0,解得a=12(2)由(I)知f'(x)=48x3lnx(x>0),令f'(x)=0,解得x=1当0<x<1时,f'(x)<0,此时f(x)为减函数;当x>1时,f'(x)>0,此时f(x)为增函数因此f(x)的单调递减区间为(0,1),而f(x)的单调递增区间为(1,+∞)(3)由(II)知,f(x)在x=1处取得极小值f(1)=﹣3﹣c,此极小值也是最小值,要使f(x)≥﹣2c2(x>0)恒成立,只需﹣3﹣c≥﹣2c2即2c2﹣c﹣3≥0,从而(2c﹣3)(c+1)≥0,解得或c≤﹣1所以c的取值范围为(﹣∞,﹣1]∪点评:考查学生利用导数研究函数极值的能力,利用导数研究函数的单调性的能力,函数恒成立时条件的应用能力.。
【解析版】天津市耀华中学2013届高三第三次月考数学理试题

天津耀华中学2013届高三年级第三次月考 理科数学试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题目要求的. 1. 复数=++-ii i 111 A. i -B.C. i -1D. i +1【答案】D 【 解析】2211(1)1221(1)(1)12ii i i i i i i i i i i ++-++-++====+-+-,选D. 2. 条件甲:⎩⎨⎧<<<+<3042xy y x ;条件乙:⎩⎨⎧<<<<3210y x ,则甲是乙的A. 充要条件B. 充分而不必要条件C. 必要而不充分条件D. 既不充分也不必要条件【答案】C 【 解析】当⎩⎨⎧<<<<3210y x 能得到⎩⎨⎧<<<+<3042xy y x ,但当⎩⎨⎧<<<+<3042xy y x 时,不妨取21x y ==,满足⎩⎨⎧<<<+<3042xy y x ,但⎩⎨⎧<<<<3210y x 不满足,所以甲是乙的必要而不充分条件 选C. 3. 设x ,y 满足⎪⎩⎪⎨⎧≤--≥-≥+22142y x y x y x ,则y x z +=A. 有最小值2,最大值3B. 有最小值2,无最大值C. 有最大值3,无最小值D. 既无最小值,也无最大值【答案】B【 解析】由y x z +=得y x z =-+.做出不等式对应的平面区域阴影部分,平移直线y x z =-+,由图象可知当直线y x z =-+经过点C (2,0)时,直线的截距最小,此时z 最小,为202z x y =+=+=,无最大值,选B.4. 某程序框图如图所示,该程序运行后输出的k 的值是A. 4B. 5C. 6D. 7【答案】A【 解析】第一次循环为00,021,1S S k ==+==;第二次循环为11,123,2S S k ==+==;第三次循环为33,3211,3S S k ==+==;第四次循环为1111,112100,4S S k ==+>=;第五次循环,不满足条件,输出4k =.选A.5. 已知等比数列{a n }的首项为1,若1234,2,a a a 成等差数列,则数列⎭⎬⎫⎩⎨⎧n a 1的前5项和为 A.1631B. 2C.1633 D.3316 【答案】A【 解析】因为1234,2,a a a 成等差数列,所以13244a a a +=,即211144a a q a q +=,所以2440q q -+=,即2(2)02q q -==,,所以1112n n n a a q--==,所以111()2n n a -=,所以⎭⎬⎫⎩⎨⎧n a 1的前5项和55511(1())13122[1()]121612S -==-=-,选A. 6. 将函数⎪⎭⎫ ⎝⎛+=42sin 2)(πx x f 的图像向右平移)0(>ϕϕ个单位,再将图像上每一点横坐标缩短到原来的21倍,所得图像关于直线4π=x 对称,则ϕ的最小正值为 A.8πB.83πC.43π D.2π【答案】B【 解析】函数⎪⎭⎫ ⎝⎛+=42sin 2)(πx x f 的图像向右平移)0(>ϕϕ个单位得到2sin[2()]2sin(22)44y x x ππϕϕ=-+=+-,再将图像上每一点横坐标缩短到原来的21倍得到2sin(42)4y x πϕ=+-,此时 关于直线4π=x 对,即当4π=x 时,4242,4442x k k Z ππππϕϕπ+-=⨯+-=+∈,所以324k πϕπ=+,3,82k k Z ππϕ=+∈,所以当0k =时,ϕ的最小正值为38πϕ=,选B. 7. 设F 是抛物线)0(2:21>=p px y C 的焦点,点A 是抛物线与双曲线22222:by a x C -=1)0,0(>>b a 的一条渐近线的一个公共点,且x AF ⊥轴,则双曲线的离心率为A. 2B.3C.25D.5【答案】D【 解析】由题意知(,0)2p F ,不妨取双曲线的渐近线为b y x a =,由22b y x a y px⎧=⎪⎨⎪=⎩得222pa x b =.因为x AF ⊥,所以2A p x =,即2222pa p x b ==,解得224b a =,即22224b a c a ==-,所以225c a =,即25e =,所以离心率e = D.8. 若直角坐标平面内的两点P 、Q 满足条件:①P 、Q 都在函数)(x f y =的图像上;②P 、Q 关于原点对称,则称点对[P,Q]是函数)(x f y =的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数⎩⎨⎧≤-->=)0(4)0(log )(22x x x x x x f ,则此函数的“友好点对”有A. 0对B. 1对C. 2对D. 3对【答案】C【 解析】解:根据题意:当0x >时,0x -<,则22()()4()4f x x x x x -=---=-+, 若P 、Q 关于原点对称,可知,函数为奇函数,可有2()4()f x x x f x -=-+=-,即2()4,(0)f x x x x =->,则函数24,(0)y x x x =--≤的图象关于原点对称的函数是2()4,(0)f x x x x =->,由题意知,作出函数2()4,(0)f x x x x =->的图象,看它与函数2()log ,(0)f x x x =>交点个数即可得到友好点对的个数.由图象可知它们的图象交点个数为2个,所以此函数的“友好点对”有2对,选C.第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9. 某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为_______; 【答案】18【 解析】由题意知,中年职工和老年职工共有270人,则老年职工人数为90人.则抽出老年职工人数为x ,则3290160x =,解得18x =. 10. 一个几何体的三视图如图所示,则该几何体的体积为____________;【答案】80【 解析】解:由三视图可知该几何体为上部是一四棱锥,下部为正方体的组合体.四棱锥的高3,正方体棱长为4,所以正方体的体积为3464=.四棱锥的体积为1443163⨯⨯⨯=,所以该组合体的体积之和为641680+=.11. 若⊙5:221=+y x O 与⊙)(20)(:222R m y m x O ∈=+-相交于A 、B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长度是____________________; 【答案】4【 解析】由题知)0,(),0,0(21m O O ,且53||5<<m ,又21AO A O ⊥,所以有525)52()5(222±=⇒=+=m m ,所以452052=⋅⋅=AB . 12. 已知函数d cx bx x x f +++=23)(在区间[1,2]-上是减函数,那么b c +的最大值为________________; 【答案】215-【 解析】函数的导数为2'()32f x x bx c =++,因为函数d cx bx x x f +++=23)(在区间[1,2]-上是减函数,所以2'()320f x x bx c =++≤在[1,2]-上横成立.则有'(1)0'(2)0f f -≤⎧⎨≤⎩,即3201240b c b c -+≤⎧⎨++≤⎩,设z b c =+,则c b z =-+.做出不等式对应的平面区域BCD,如图,平移直线c b z =-+,由图象平移可知当直线c b z =-+经过点B 时,直线c b z =-+的截距最大,此时z 最大.由3201240b c b c -+=⎧⎨++=⎩,解得326b c ⎧=-⎪⎨⎪=-⎩,即3(,6)2B --,代入z b c =+得315(6)22z =-+-=-,即b c +的最大值为215-.13. 如图所示,在平行四边形ABCD 中,BD AP ⊥,垂足为P ,且3=AP ,则AC AP ⋅=_______;【答案】18 【 解析】设ACBD O =,则2()AC AB BO =+,AP AC = 2()AP AB BO +=22AP AB AP BO +222()2AP AB AP AP PB AP ==+=18=.14. 设{a n }是等比数列,公比2=q ,S n 为{a n }的前n 项和.记1217+-=n nn n a S S T ,*N n ∈,设0n T 为数列{T n }的最大项,则n 0=__________; 【答案】4【 解析】设首项为1a ,则1(2)12n n S =-,212(2)12n n S =-,11(2)n n a a +=,所以1217+-=n nn n a S S T 2111(2)(2)1212(2)n n na ---=2(2)17(2)12(2)n n n -=-[(2)17]12(2)n n=+--,因为16(2)2(2)8(2)(2)n nn n≥⨯=,当且仅当(2)(2)n n =,即2)4n =,4n =时取等号,此时[(2)17](817)12(2)1221n n n T =+-≤-=---,有最大值,所以04n =.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15. (本小题满分13分)已知函数)(1cos 2)62sin()(2R x x x x f ∈-+-=π(1)求)(x f 的单调递增区间;(2)在△ABC 中,三内角A,B,C 的对边分别为a,b,c ,已知21)(=A f ,b,a,c 成等差数列,且9=⋅AC AB ,求a 的值.16. (本小题满分13分)甲、乙、丙三人进行象棋比赛,每两人比赛一场,共赛三场.每场比赛胜者得3分,负者得0分,没有平局,在每一场比赛中,甲胜乙的概率为32,甲胜丙的概率为41,乙胜丙的概率为51. (1)求甲获第一名且丙获第二名的概率;(2)设在该次比赛中,甲得分为ξ,求ξ的分布列和数学期望.17. (本小题满分13分)在四棱锥P -ABCD 中,底面ABCD 是直角梯形,AB//CD ,︒90=ABC ∠,AB=PB=PC=BC=2CD ,平面PBC ⊥平面ABCD.(1)求证:AB ⊥平面PBC ;(2)求平面ADP 与平面BCP 所成的锐二面角的大小; (3)在棱PB 上是否存在点M 使得CM//平面PAD ?若存在,求PBPM的值;若不存在,请说明理由.18. (本小题满分13分)如图F 1、F 2为椭圆1:2222=+by a x C 的左、右焦点,D 、E 是椭圆的两个顶点,椭圆的离心率23=e ,2312-=∆DEF S .若点),(00y x M 在椭圆C 上,则点),(00b y a x N 称为点M 的一个“椭点”,直线l 与椭圆交于A 、B 两点,A 、B 两点的“椭点”分别为P 、Q.(1)求椭圆C 的标准方程;(2)问是否存在过左焦点F 1的直线l ,使得以PQ 为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.19. (本小题满分14分)已知函数x x ppx x f ln )(--=,)21(ln )(22p e e x p x x g -+-=,其中无理数e=2.71828….(1)若p=0,求证:x x f -≥1)(;(2)若)(x f 在其定义域内是单调函数,求p 的取值范围;(3)对于在区间(1,2)中的任意常数p ,是否存在00>x 使得)()(00x g x f ≤成立?若存在,求出符合条件的一个x 0;若不存在,请说明理由.20. (本小题满分14分)已知数列{a n }的前n 项和)(2)21(*1N n a S n n n ∈+--=-,数列{b n }满足n n n a b 2=.(1)求证数列{b n }是等差数列,并求数列{a n }的通项公式; (2)设数列⎭⎬⎫⎩⎨⎧+n a n n 1的前n 项和为T n ,证明:*N n ∈且3≥n 时,125+>n n T n ; (3)设数列{c n }满足n c a n n n n λ1)1()3(--=-(λ为非零常数,*N n ∈),问是否存在整数λ,使得对任意*N n ∈,都有n n c c >+1.数学发展性试题(理科):(15分)1. 若0,,>c b a 且324)(-=+++bc c b a a ,则c b a ++2的最小值为( )A.13-B.13+C. 232+D. 232-2. 对于各数互不相等的整数数组),,,,(321n i i i i ⋯(n 是不小于3的正整数),若对任意的p ,},,3,2,1{n q ⋯∈,当q p <时有q p i i >,则称q p i i ,是该数组的一个“逆序”.一个数组中所有“逆序”的个数称为该数组的“逆序数”,如数组(2,3,1)的逆序数等于2.若数组),,,,(321n i i i i ⋯的逆序数为n ,则数组),,,(11i i i n n ⋯-的逆序数为_________;3. 定义在)1,1(-上的函数⎪⎪⎭⎫⎝⎛--=-xy y x f y f x f 1)()(,当)0,1(-∈x 时0)(>x f .若)0(,21,11151f R f Q f f P =⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=,则P,Q,R 的大小关系为_____________.【试题答案】一、选择题:本大题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案DCBA ABDC二、填空题:本大题共6小题,每小题5分,共30分. 9. 1810. 80 11. 4 12. 215-13. 18 14. 4三、解答题:本大题共6小题,共80分. 15. 解:(1)x x x x x x f 2cos 2cos 212sin 231cos 2)62sin()(2+-=-+-=π)62sin(2cos 212sin 23π+=+=x x x 令)(226222Z k k x k ∈+≤+≤-πππππ )(x f 的单调递增区间为)](6,3[Z k k k ∈+-ππππ(2)由21)(=A f ,得21)62sin(=+πA ∵62626ππππ+<+<A ,∴6562ππ=+A ,∴3π=A 由b,a,c 成等差数列得2a=b+c∵9=⋅AC AB ,∴9cos =A bc ,∴18=bc由余弦定理,得bc c b A bc c b a 3)(cos 22222-+=-+= ∴183422⨯-=a a ,∴23=a16. 解:(1)甲获第一,则甲胜乙且甲胜丙,所以甲获第一的概率为614132=⨯ 丙获第二,则丙胜乙,其概率为54511=-, 所以甲获第一名且丙获第二名的概率为1525461=⨯ (2)ξ可能取的值为0,3,6.41)411)(321()0(=--==ξP127)321(41)411(32)3(=-+-==ξP614132)6(=⨯==ξP 所以ξ的分布列为ξ0 3 6P41 127 61 E ξ=4116161273410=⨯+⨯+⨯17. 解:(1)证明:因为o 90=∠ABC ,所以AB ⊥BC因为平面PBC ⊥平面ABCD ,平面PBC ∩平面ABCD=BC ,AB ⊂平面ABCD , 所以AB ⊥平面PBC. (2)如图,取BC 的中点O ,连接PO ,因为PB=PC ,所以PO ⊥BC.因为PB=PC ,所以PO ⊥BC ,因为平面PBC ⊥平面ABCD ,所以PO ⊥平面ABCD.以O 为原点,OB 所在的直线为x 轴,在平面ABCD 内过O 垂直于BC 的直线为y 轴,OP 所在直线为z 轴建立空间直角坐标系O -xyz.不妨设BC=2.由AB=PB=PC=BC=2CD 得,)0,2,1(),0,1,1(),3,0,0(A D P -.所以)0,1,2(),3,1,1(=-=DA DP , 设平面PAD 的法向量为),,(z y x m =.因为⎪⎩⎪⎨⎧=⋅=⋅0DA m DP m ,所以⎩⎨⎧=+=+-0203y x z y x令1-=x ,则3,2==z y .所以)3,2,1(-=m .取平面BCP 的一个法向量)0,1,0(=n ,所以22||||,cos =⋅>=<n m n m n m 所以平面ADP 与平面BCP 所成的锐二面角的大小为4π(3)在棱PB 上存在点M 使得CM//平面PAD ,此时21=PB PM .取AB 的中点N ,连接CM ,CN ,MN ,则MN//PA ,AN=21AB.因为AB=2CD ,所以AN=CD ,因为AB//CD ,所以四边形ANCD 是平行四边形,所以CN//AD. 因为MN ∩CN=N ,PA ∩AD=A ,所以平面MNC//平面PAD.因为CM ⊂平面MNC ,所以CM//平面PAD.18. 解:(1)由题意得23==a c e ,故a b a c 21,23==, 231)231(412)23(21)(2122-=-⨯=⨯-=⨯-⨯=∆a a a a b c a S DEF , 故42=a ,即a=2,所以b=1,c=3,故椭圆C 的标准方程为1422=+y x . (2)①当直线l 的斜率不存在时,直线l 的方程为3-=x联立⎪⎩⎪⎨⎧=+-=14322y x x 解得⎪⎩⎪⎨⎧=-=213y x 或⎪⎩⎪⎨⎧-=-=213y x ,不妨令)21,3(),21,3(---B A , 所以对应的“椭点”坐标)21,23(),21,23(---Q P .而021≠=⋅OQ OP . 所以此时以PQ 为直径的圆不过坐标原点.②当直线l 的斜率存在时,设直线l 的方程为)3(+=x k y联立⎪⎩⎪⎨⎧=++=14)3(22y x x k y ,消去y 得:041238)14(2222=-+++k x k x k 设),(),,(2211y x B y x A ,则这两点的“椭点”坐标分别为),2(),,2(2211y x Q y x P ,由根与系数的关系可得:14382221+-=+k k x x ,144122221+-=k k x x 若使得以PQ 为直径的圆经过坐标原点,则OP ⊥OQ , 而),2(),,2(2211y x OQ y x OP ==,因此0=⋅OQ OP , 即042221212121=+=+⨯y y x x y y x x 即141222+-k k =0,解得22±=k 所以直线方程为2622+=x y 或2622--=x y 19. 解:(1)证明:当p=0时,x x f ln )(-=.令)0(1ln )(>+-=x x x x m ,则xx x x m -=-='111)( 若10<<x ,则0)(>'x m ,)(x m 在区间)1,0(上单调递增;若1>x ,则0)(<'x m ,)(x m 在区间),1(+∞上单调递减.易知,当x=1时,)(x m 取得极大值,也是最大值.于是0)1()(=≤m x m ,即01ln ≤+-x x ,即x x -≥-1ln故若p=0,有x x f -≥1)((2)2221)(xp x px x x p p x f +-=-+=',令)0()(2>+-=x p x px x h ①当p=0,01)(<-='xx f ,则)(x f 在),0(+∞上单调递减,故当p=0时符合题意; ②若p>0,pp p p p x p p x px x h 4141)21()(22-≥-+-=+-= 则当041≥-pp ,即21≥p 时,0)(≥'x f 在x>0上恒成立,故当21≥p 时,)(x f 在),0(+∞上单调递增; ③若p<0,p p p x p p x px x h 41)21()(22-+-=+-=的图像的对称轴为021<=px ,0)0(<=p h ,则0)(<'x f 在x>0上恒成立,故当p<0时,)(x f 在),0(+∞上单调递减. 综上所述,),21[]0,(+∞-∞∈U p(3)令pxe e x px x g xf x F 2ln 2)()()(2-+-=-=,则原问题等价于是否存在x 0>0使得0)(0≤x F 成立,故只需满足0)]([min ≤x F 即可. 因为)2)(()2)((22)(2222p e x p e x xp px e px e px px e e x p x F ---=+--=---=' 而21,0<<>p x ,故02,0<->pe p e , 故当p e x <<0时,0)(<'x F ,则)(x F 在),0(p e 上单调递减;当pe x >时,0)(>'x F ,则)(x F 在),(+∞pe 上单调递增. 易知04ln 222ln 22)()(min >-+=-++-==p e e p e p e F x F 与上述要求的0)]([min ≤x F 相矛盾,故不存在00>x 使得)()(00x g xf ≤成立.20. 解:(1)在2)21(1+--=-n n n a S 中,令n=1,可得1121a a S n =+--=,即211=a 当2≥n 时,2)21(211+--=---n n n a S ,∴111)21(---++-=-=n n n n n n a a S S a , ∴11)21(2--+=n n n a a ,即12211+=--n n n n a a .∵n n n a b 2=,∴11+=-n n b b ,即当2≥n 时,11=--n n b b .又1211==a b ,∴数列{b n }是首项和公差均为1的等差数列.于是n n n a n n b 21)1(1==⋅-+=,∴n n n a 2=. (2)由(1)得n n n n a n n c )21)(1(1+=+=,所以 n n n T )21)(1()21(4)21(321232++⋯+⨯+⨯+⨯= ① 1432)21)(1()21(4)21(3)21(221+++⋯+⨯+⨯+⨯=n n n T ② 由①-②得132)21)(1()21()21()21(121++-+⋯+++=n n n n T 1112323)21)(1(211])21(1[411++-+-=+---+=n n n n n∴n n n T 233+-=)12(2)122)(3(125233125+--+=+-+-=+-n n n n n n n n T n n n n于是确定T n 与125+n n 的大小关系等价于比较n2与2n+1的大小由⋯⨯<+⨯<+⨯<+⨯<+⨯<;522;1422;1322;1222;11225432 可猜想当3≥n 时,122+>n n .证明如下:证法1:①当n=3时,由上验算显示成立.②假设n=k+1时1)1(2)12(1)1(224)12(22221++>-+++=+=+>=+k k k k k g k k 所以当n=k+1时猜想也成立综合①②可知,对一切3≥n 的正整数,都有122+>n n .证法2:当3≥n 时1222)11(21101210+>+=+++≥++⋯+++=+=--n n C C C C C C C C C nn n n n n n n n n n n n n n综上所述,当n=1,2时125+<n nT n ,当3≥n 时125+>n nT n(3)∵nn n nn n n a n c 2)1(3)1(311⋅-+⋅-+=--λλ∴]2)1(3[]2)1(3[1111n n n n n n n n c c ⋅-+-⋅-+=--+++λλ02)1(3321>⋅--⋅=-n n n λ ∴1123)1(--⎪⎭⎫⎝⎛<⋅-n n λ ①当n=2k -1,k=1,2,3,……时,①式即为2223-⎪⎭⎫⎝⎛<k λ ②依题意,②式对k=1,2,3……都成立,∴1<λ当n=2k,k=1,2,3,……时,①式即为1223-⎪⎭⎫⎝⎛->k λ ③依题意,③式对k=1,2,3……都成立, ∴23->λ ∴123<<-λ,又0≠λ∴存在整数1-=λ,使得对任意*N n ∈有n n c c >+1.数学发展性试题1. D2. 232n n -3. Q R P >>。
2023-2024学年天津市耀华中学高三上学期第一次月考物理试题及答案

天津市耀华中学2024届高三年级第一次月考物理试卷一、单项选择题(本题共5小题,每小题5分,共25分。
每小给出的四个选项中,只有一个选项是正确的)1. 下列说法中正确的是( )A. 光的衍射现象说明了光具有粒子性B. 在白光下观察竖直放置的肥皂液膜,呈现的彩色条纹是光的折射现象造成的C. 光从光疏介质射入光密介质时也可能发生全反射D. 清晨人们刚刚看到太阳从地平线上升起时,实际太阳还在地平线以下2. 某国产车型启用全新动力标识,新的命名方式直接与车辆的加速性能联系起来,如图,TFSI 前面的那组数字称为G 值,单位为2m /s ,计算公式为“10v G t∆=⨯∆”,式中v ∆为从静止加速到时速100公里的速度变化量,t ∆为不同车型的百公里加速时间。
则以下说法正确的是( )A. G 值越大,车辆的速度变化量越大B. G 值越大,车辆的动力越强劲C. 时速100公里是指车辆百公里加速的平均速度D. 标识为45TFSI 的车辆百公里加速时间约为7.3s3. 从固定斜面上的O 点每隔0.1 s 由静止释放一个同样的小球。
释放后小球做匀加速直线运动。
某一时刻,拍下小球在斜面滚动的照片,如图所示。
测得小球相邻位置间的距离x AB =4 cm ,x BC =8 cm 。
已知O 点距离斜面底端的长度为l =35 cm 。
由以上数据可以得出( )A. 小球的加速度大小为12 m/s 2B. 小球在A 点的速度为0C. 斜面上最多有5个小球在滚动D. 该照片是距A 点处小球释放后0.3 s 拍摄的4. 如图所示,细绳一端固定在A 点,跨过与A 等高的光滑定滑轮B 后在另一端悬挂一个沙桶Q .现有另一个沙桶P 通过光滑挂钩挂在AB 之间,稳定后挂钩下降至C 点,∠ACB=120°,下列说法正确的是A. 若只增加Q 桶的沙子,再次平衡后C 点位置不变B. 若只增加P 桶的沙子,再次平衡后C 点位置不变C. 若在两桶内增加相同质量的沙子,再次平衡后C 点位置不变D. 若在两桶内增加相同质量的沙子,再次平衡后沙桶Q 位置上升5. 现代的激光打印机都是自动进纸的,有一种进纸原理如图所示。
【解析版】天津市耀华中学2013年高考数学一模试卷(理科)

2013年天津市耀华中学高考数学一模试卷(理科)一、本卷共8题,每题5分,共40分.在每题给出的四个选项中,只有一项是最符合题目要求的,将答案涂在答题卡上.1.(5分)(2009•宁夏)复数﹣=()解:﹣﹣=﹣=i+i=2i,则m+n=n=3.(5分)(2007•海南)如果执行程序框图,那么输出的S=()×4.(5分)(2010•辽宁)设ω>0,函数y=sin(ωx+)+2的图象向右平移个单位后与原图象重合,B)个单位后为=,所以有=2k,即≥,6.(5分)已知双曲线=1(a>0,b>0)的右焦点为F,由F向其渐近线上引垂线,垂中为P,若B.y=的斜率为﹣,设,x=,))把中点坐标代入双曲线方程=7.(5分)在矩形ABCD中,AB=1,AD=,P为矩形内一点,且,若(λ,μ∈R),B.=)进行坐标变换得出)),得=∵即(y=,∴=,的最大值为.8.(5分)高三年级有文科、理科共9个备课组,每个备课组的人数不少于4个,现从这9个备课组中抽二、填空题:共6个小题,每小题5分,共30分,将答案填写在后面的答题卡上;9.(5分)(2011•山东)某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为16.每个个体被抽到的概率是=×10.(5分)某三棱锥的三视图如图所示,该三棱锥的表面积是30+6.=5AB==2BD==AD==ADB==ADB=××××=30+611.(5分)如图所示,直线PA切⊙O于点A,直线PO分别与⊙O相交子点B、C,已知,则线段AB长4.,,412.(5分)在直角坐标系xOy中,直线l的参数方程为(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为,设圆C与直线l交于点A、B,则弦AB长为.(=0的方程为ρ+,的圆.d==.13.(5分)已知实数x,y∈(0,),且tanx=3tany,则x﹣y的最大值是.)=,∵≥,当且仅当≤)的最大值为,﹣,则最大值为,故答案为:.14.(5分)函数f(x)=,若直线y=kx﹣1与函数y=f(x)有3个公共点,则实数k的取值范围是(0,1).三.解答题:共6个小题,总计80分,解答应写出必要的文字说明、证明过程或演算步骤.15.(13分)已知函数f(x)=tan(2x+)(I)求该函数的定义域,周期及单调区间;(II)若f(θ)=,求的值.”T=≠()得,)得,综上得,函数的周期是{x|单调增区间是()式子==①,∴),)﹣]=得,,得,=代入上式①得,=216.(13分)某中学校本课程共开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门课程课,现有该校的甲、乙、丙3名学生:(I)求恰有2门选修课没有被这3名学生选择的概率;(II)设3名学生选择A选修课的人数为ξ,求ξ的概率分布列及数学期望Eξ.(=,,=,=×+1×+2×+3×=(17.(13分)已知三棱柱A1B1C1﹣ABC中,三个侧面均为矩形,底面ABC为等腰直角三角形,C1C=CA=CB=2,点D为棱CC1的中点,点E在棱B1C1上运动.(I)求证A1C⊥AE;(II)当点E到达某一位置时,恰使二面角E﹣A1D﹣B的平面角的余弦值为,求;(III)在(II)的条件下,在平面ABC上确定点F,使得EF⊥平面A1DB?并求出EF的长度.可证⊥,只需证明=0的一个法向量,由两法向量夹角余弦值的绝对值等于,可知与平面||=,因为所以⊥,即==,即,取==,设=,即,取=,得||=所以;,且=,且,所以所以||=的长度为,此时点18.(13分)已知数列{a n}满足:(I)求a2,a3;(II)设,求证:数列{b n}是等比数列,并求其通项公式;(Ⅲ)求数列{a n}前20项中所有奇数项的和.)利用等比数列的定义证出=+1=﹣,且==,﹣++90+((18+﹣=﹣19.(14分)已知点D(0,﹣2),过点D作抛物线C1:x2=2py(p>0)的切线l,切点A在第二象限,如图(Ⅰ)求切点A的纵坐标;(Ⅱ)若离心率为的椭圆恰好经过切点A,设切线l交椭圆的另一点为B,记切线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.,且的斜率为,得的方程为,再)由得,由,所以椭圆方程为,由此能求出椭圆方程.,且的斜率为的方程为,又点∴,即点,切线斜率,由所以椭圆方程为,且过,∴,椭圆方程为.20.(14分)(2013•济南二模)设,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.(1)求a的值;(2)若∀x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求m的范围.(3)求证:.先将原来的恒成立问题转化为时,时,成立.不妨令,得由题设∴)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣时,时,方程﹣,综上所述,.时,时,不妨令所以,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣累加可得。
2023-2024学年天津市耀华中学高三上学期第一次月考数学试题及答案

天津市耀华中学2024届高三年级第一次月考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试用时120分钟.第Ⅰ卷(选择题 共45分)一、选择题:本大题共9小题,每小题5分,共45分,在每小题给出的四个选项中,有且只有一项是符合题目要求的,请把正确答案填涂在答题卡上.1 已知集合{}220A x x x =+-<,{}lg 1B x x =<,A B = ( )A. ()2,10-B. ()0,1C. ()2,1-D. (),10-∞2. 设x ∈R ,则“11||22x -<”是“31x <”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件3. 函数()3ln xf x x=的部分图象是A. B.C. D.4. 5G 技术在我国已经进入调整发展的阶段,5G 手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:.时间x12345销售量y (千只)0.50.81.01.21.5若x 与y 线性相关,且线性回归方程为 0.24y x a=+,则下列说法不正确的是( )A. 由题中数据可知,变量y 与x 正相关,且相关系数1r <B. 线性回归方程 0.24y x a=+中 0.26a =C. 当解释变量x 每增加1个单位时,预报变量 y 平均增加0.24个单位D. 可以预测6x =时,该商场5G 手机销量约为1.72(千只)5. 已知0.20.212log 0.5,0.5,log 0.4a b c ===,则a ,b ,c 的大小关系为( )A. a b c <<B. a c b<< C. b<c<a D. c<a<b6. 已知4log a a =,则2log a a +=( )A 11或238-B. 11或218-C. 12或238-D. 10或218-7. “送出一本书,共圆读书梦”,某校组织为偏远乡村小学送书籍的志愿活动,运送的卡车共装有10个纸箱,其中5箱英语书、2箱数学书、3箱语文书.到目的地时发现丢失一箱,但不知丢失哪一箱.现从剩下9箱中任意打开2箱都是英语书的概率为( )A.29B.18C.112D.588. 将函数()π2sin 23f x x ⎛⎫=- ⎪⎝⎭的图像上所有点横坐标变为原来的2倍,纵坐标不变,得到函数()g x 的图像,有下述四个结论:①()π2sin 6g x x ⎛⎫=-⎪⎝⎭②函数()g x 在π0,2⎛⎫⎪⎝⎭上单调递增③点4π,03⎛⎫⎪⎝⎭是函数()g x 图像的一个对称中心④当ππ,2x ⎡⎤∈-⎢⎥⎣⎦时,函数()g x 的最大值为2其中所有正确结论的编号是( )A. ①②③B. ②③C. ①③④D. ②④.9. 已知函数()()()()()()22121,1,11,1,1a x a x x f x a x ax x x ⎧-++-∈-⎪=⎨-++∉-⎪⎩有且只有3个零点,则实数a 的取值范围是( )A. ()0,1 B. ()(),80,1-∞- C. [)0,1 D. (][),80,1-∞- 第Ⅱ卷(非选择题 共105分)二、填空题:本大题共6小题,每小题5分,共30分,请将答案填写在答题卡上.10. 复数()21i 1iz -=+(i 为虚数单位),则z =______.11.在6的二项展开式中,2x 的系数为___________.12.若2sin sin αβ+=3π2αβ+=,则sin α=________;cos 2β=________.13. 某专业资格考试包含甲、乙、丙3个科目,假设小张甲科目合格的概率为34,乙、丙科目合格的概率均为23,且3个科目是否合格相互独立.设小张3科中合格的科目数为X ,则(2)P X ==___________;()E X =___________.14. 已知0a >,0b >的最大值为________.15. 设R ω∈,函数()2π2sin ,0,6314,0,22x x f x x x x ωω⎧⎛⎫+≥ ⎪⎪⎪⎝⎭=⎨⎪++<⎪⎩()g x x ω=.若()f x 在1π,32⎛⎫- ⎪⎝⎭上单调递增,且函数()f x 与()g x 图象有三个交点,则ω的取值范围是________.三、解答题:本大题共5小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤,请把解题过程写在答案卡上.16. 已知ABC 的内角A ,B ,C 的对边分别为a,b ,c ,满足22cos c b A =+.(1)求角B ;(2)若1cos 4A =,求sin(2)A B +的值;(3)若7c =,sin b A =b 的值.的17. 已知底面ABCD 是正方形,PA ⊥平面ABCD ,//PA DQ ,33PA AD DQ ===,点E 、F 分别为线段PB 、CQ 的中点.(1)求证://EF 平面PADQ ;(2)求平面PCQ 与平面CDQ 夹角的余弦值;(3)线段PC 上是否存在点M ,使得直线AM 与平面PCQ,若存在求出PM MC 的值,若不存在,说明理由.18. 已知{}n a 为等差数列,6,2,n n n a n b a n -⎧=⎨⎩为奇数为偶数,记n S ,n T 分别为数列{}n a ,{}n b 的前n 项和,432S =,316T =.(1)求{}n a 通项公式;(2)证明:当5n >时,n n T S >.19. 如图,已知椭圆E :22221(0)x y a b a b +=>>()F 且斜率为k 的直线交椭圆E 于,A B 两点,线段AB 的中点为M ,直线l :40x ky +=交椭圆E 于,C D 两点.(1)求椭圆E 的方程;(2)求证:点M 在直线l上;的(3)是否存在实数k ,使得3BDM ACM S S ∆∆=?若存在,求出k 的值,若不存在,说明理由.20 已知函数()()1211222x f x x ex x -=--++,()()24cos ln 1g x ax x a x x =-+++,其中a ∈R .(1)讨论函数()f x 的单调性,并求不等式()0f x >的解集;(2)用{}max ,m n 表示m ,n 的最大值,记()()(){}max ,F x f x g x =,讨论函数()F x 的零点个数..天津市耀华中学2024届高三年级第一次月考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试用时120分钟.第Ⅰ卷(选择题 共45分)一、选择题:本大题共9小题,每小题5分,共45分,在每小题给出的四个选项中,有且只有一项是符合题目要求的,请把正确答案填涂在答题卡上.1. 已知集合{}220A x x x =+-<,{}lg 1B x x =<,A B = ( )A. ()2,10-B. ()0,1C. ()2,1-D. (),10-∞【答案】B 【解析】【分析】根据解一元二次不等式的解法,结合对数函数的单调性、集合交集的定义进行求解即可.【详解】因为{}()2202,1A x x x =+-<=-,{}()lg 10,10B x x =<=,所以A B = ()0,1,故选:B2. 设x ∈R ,则“11||22x -<”是“31x <”的A. 充分而不必要条件B 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A 【解析】【详解】分析:首先求解绝对值不等式,然后求解三次不等式即可确定两者之间的关系.详解:绝对值不等式1122x -<⇔111222x -<-<⇔01x <<,由31x <⇔1x <..据此可知1122x -<是31x <的充分而不必要条件.本题选择A 选项.点睛:本题主要考查绝对值不等式的解法,充分不必要条件的判断等知识,意在考查学生的转化能力和计算求解能力.3. 函数()3ln xf x x =的部分图象是A. B.C. D.【答案】A 【解析】【分析】根据奇偶性排除B ,当1x >时,()3ln 0xf x x =>,排除CD ,得到答案.【详解】()()()33ln ln ,x xf x f x f x x x =-==--, ()f x 为奇函数,排除B 当1x >时,()3ln 0xf x x=>恒成立,排除CD 故答案选A【点睛】本题考查了函数图像的判断,通过奇偶性,特殊值法排除选项是解题的关键.4. 5G 技术在我国已经进入调整发展的阶段,5G 手机的销量也逐渐上升,某手机商城统计了最近5个月手机的实际销量,如下表所示:时间x12345销售量y (千只)0.50.8 1.0 1.2 1.5若x 与y 线性相关,且线性回归方程为 0.24y x a=+,则下列说法不正确的是( )A. 由题中数据可知,变量y 与x 正相关,且相关系数1r <B. 线性回归方程 0.24y x a=+中 0.26a =C. 当解释变量x 每增加1个单位时,预报变量 y 平均增加0.24个单位D. 可以预测6x =时,该商场5G 手机销量约为1.72(千只)【答案】ACD 【解析】【分析】根据已知数据,分析总体单调性,结合增量的变化判断A 选项;根据已知数据得到样本中心点,代入回归方程求解即可判断B 选项;根据回归方程判断CD 选项.【详解】从数据看y 随x 的增加而增加,故变量y 与x 正相关,由于各增量并不相等,故相关系数1r <,故A 正确;由已知数据得()11234535=++++=,()10.50.8 1.0 1.2 1.515y =++++=,代入ˆˆ0.24yx a =+中得到ˆ130.240.28a =-⨯=,故B 错;根据线性回归方程ˆ0.240.28yx =+可得x 每增加一个单位时,预报变量ˆy 平均增加0.24个单位,故C 正确.将6x =代入ˆ0.240.28yx =+中得到ˆ0.2460.28 1.72y =⨯+=,故D 正确.故选:ACD.5. 已知0.20.212log 0.5,0.5,log 0.4a b c ===,则a ,b ,c 的大小关系为( )A. a b c << B. a c b<< C. b<c<a D. c<a<b【答案】A 【解析】【分析】由指数函数与对数函数的单调性求解即可【详解】因为0.20.20.21log 0.5log log 2a ==<=,而150.2110.522b ⎛⎫==> ⎪⎝⎭,且0.20.51<,所以a b <.又12225log 0.4log log 212c ==>>,所以a b c <<,故选:A.6. 已知4log a a =,则2log a a +=( )A. 11或238-B. 11或218-C. 12或238-D. 10或218-【答案】A 【解析】【分析】对4log a a =43log 2a =或32-,讨论43log 2a =或32-时2log a a+的值,即可得出答案.【详解】由4log aa =()(4log 44log log aa=()49249log log4a ==,所以43log 2a =或32-.当43log 2a =时,33242a ===8,所以22log 8log 811a a +=+=;当43log 2a =-时,32148a -==,所以221123log log 888a a +=+=-,综上,a +2log 11a =或238-,故选:A.7. “送出一本书,共圆读书梦”,某校组织为偏远乡村小学送书籍的志愿活动,运送的卡车共装有10个纸箱,其中5箱英语书、2箱数学书、3箱语文书.到目的地时发现丢失一箱,但不知丢失哪一箱.现从剩下9箱中任意打开2箱都是英语书的概率为( )A.29B.18C.112D.58【答案】A 【解析】【分析】剩下9箱中任意打开2箱都是英语书的情况整体分为三种情况:丢失的英语书、数学书和语文书,计算出每种情况的概率即可.【详解】设事件A 表示丢失一箱后任取两箱是英语书,事件k B 表示丢失的一箱为,1,2,3k k =分别表示英语书、数学书、语文书.由全概率公式得()()()2223554222219999C C C 11382|2C 5C 10C C 9k k k P A P B P A B ===⨯+⨯+⨯==∑.故选:A8. 将函数()π2sin 23f x x ⎛⎫=- ⎪⎝⎭的图像上所有点横坐标变为原来的2倍,纵坐标不变,得到函数()g x 的图像,有下述四个结论:①()π2sin 6g x x ⎛⎫=-⎪⎝⎭②函数()g x 在π0,2⎛⎫⎪⎝⎭上单调递增③点4π,03⎛⎫⎪⎝⎭是函数()g x 图像的一个对称中心④当ππ,2x ⎡⎤∈-⎢⎥⎣⎦时,函数()g x 的最大值为2其中所有正确结论的编号是( )A. ①②③ B. ②③C. ①③④D. ②④【答案】B 【解析】【分析】根据图象变换可得()π2sin 3g x x ⎛⎫=-⎪⎝⎭,结合正弦函数的性质逐项分析判断.【详解】由题意可得:()π2sin 3g x x ⎛⎫=-⎪⎝⎭,故①错误;因为π0,2x ⎛⎫∈ ⎪⎝⎭,则πππ,336x ⎛⎫-∈- ⎪⎝⎭,且sin y x =在ππ,36⎛⎫- ⎪⎝⎭上单调递增,所以函数()g x 在π0,2⎛⎫⎪⎝⎭上单调递增,故②正确;因为4π4ππ2sin 2sin π0333g ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭,所以点4π,03⎛⎫⎪⎝⎭是函数()g x 图像的一个对称中心,故③正确;因为ππ,2x ⎡⎤∈-⎢⎥⎣⎦,则π4ππ,336x ⎡⎤∈-⎢⎥⎣⎦-,所以当π4π33x -=-,即πx =-时,函数()g x 的最大值为()4ππ2sin 3g ⎛⎫-=-= ⎪⎝⎭,故④错误;故选:B.9. 已知函数()()()()()()22121,1,11,1,1a x a x x f x a x ax x x ⎧-++-∈-⎪=⎨-++∉-⎪⎩有且只有3个零点,则实数a 的取值范围是( )A. ()0,1 B. ()(),80,1-∞- C. [)0,1 D. (][),80,1-∞- 【答案】B【解析】【分析】先求1a =时函数()f x 的零点,再考虑1a ≠时,函数()f x 在(][),11,-∞+∞ 的零点,由此确定函数()f x 在()1,1-上的零点个数,结合二次函数性质求a 的取值范围.【详解】当1a =时,()()[)(]31,1,1,1,0,,1x x f x x x x x ∞∞⎧-∈-⎪=+∈+⎨⎪∈--⎩,所以区间(],1-∞-内的任意实数和13都为函数()f x 的零点,不满足要求;当1a ≠时,若(],1x ∈-∞-,则()()21f x a x ax x =-+-,令()0f x =,可得0x =(舍去),或=1x -,所以=1x -为函数()f x 的一个零点;若[)1,x ∞∈+,则()()21f x a x ax x =-++,令()0f x =,则()210a x ax x -++=,所以11a x a +=-,若111a a+≥-,即01a ≤<,则函数()f x 在[)1,+∞上有一个零点;若1a >或a<0时,则函数()f x 在[)1,+∞上没有零点;当01a ≤<时,函数()f x 在(][),11,-∞-⋃+∞上有两个零点;当1a >或a<0时,函数()f x 在(][),11,-∞-⋃+∞上有一个零点,因为当01a ≤<时,函数()f x 在(][),11,-∞-⋃+∞上有两个零点;又函数()f x 在R 上有3个零点,所以函数()f x 在()1,1-上有且只有一个零点,即方程()()21210a x a x -++-=在()1,1-上有一个根,由()()()22418a a a a ∆=++-=+,当0a =时,方程()()21210a x a x -++-=的根为1x =(舍去),故0a =时,方程()()21210a x a x -++-=在()1,1-上没有根,矛盾当01a <<时,0∆>,设()()()[]2121,1,1g x a x a x x =-++-∈-,函数()()()2121g x a x a x =-++-的对称轴为2122a x a+=>-,函数()g x 的图象为开口向下的抛物线,由方程()()21210a x a x -++-=在()1,1-上有一个根可得()()10,10g g >-<,所以()()()()1210,1210a a a a -++->--+-<,所以01a <<,当1a >时,则函数()f x 在(][),11,-∞-⋃+∞上有一个零点;又函数()f x 在R 上有3个零点,所以函数()f x 在()1,1-上有且只有两个零点,即方程()()21210a x a x -++-=在()1,1-上有两个根,由()()()[]2121,1,1g x a x a x x =-++-∈-可得函数()g x 的图象为开口向上的抛物线,函数()()()2121g x a x a x =-++-的对称轴为222a x a+=-,则()()()224180a a a a ∆=++-=+>,21122a a+-<<-, ()()10,10g g >->,所以4a >,()()()()1210,1210a a a a -++->--+->,满足条件的a 不存在,当a<0时,则函数()f x 在(][),11,-∞-⋃+∞上有一个零点;又函数()f x 在R 上有3个零点,所以函数()f x 在()1,1-上有且只有两个零点,即方程()()21210a x a x -++-=在()1,1-上有两个根,由()()()[]2121,1,1g x a x a x x =-++-∈-可得函数()g x 的图象为开口向下的抛物线,函数()()()2121g x a x a x =-++-的对称轴为222a x a+=-,则()()()224180a a a a ∆=++-=+>,21122a a +-<<-, ()()10,10g g <-<,所以8a <-,a<0,()()()()1210,1210a a a a -++-<--+-<,所以8a <-,故实数a 的取值范围是()(),80,1-∞- .故选:B【点睛】关键点睛:含绝对值函数的相关问题的解决的关键在于去绝对值,将其转化为不含绝对值的函数,分段函数的性质的研究可以分段研究.第Ⅱ卷(非选择题 共105分)二、填空题:本大题共6小题,每小题5分,共30分,请将答案填写在答题卡上.10. 复数()21i 1iz -=+(i 为虚数单位),则z =______.【解析】【分析】先利用复数的运算化简复数,再利用模长的公式求解模长.【详解】()()()()()21i 2i 1i 2i i 1i 1i 1i 1i 1i 1i z ----====--=--+++-.所以z ==.11. 在6的二项展开式中,2x 的系数为___________.【答案】38-【解析】【详解】试题分析:因为6263166((1)2r r r r r r r r T C C x ---+==-,所以由32r -=得1r =,因此2x 的系数为1463(1)28C --=-考点:二项式定理【方法点睛】1.求特定项系数问题可以分两步完成:第一步是根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n 和r 的隐含条件,即n ,r 均为非负整数,且n≥r );第二步是根据所求的指数,再求所求解的项的系数.2.有理项是字母指数为整数的项.解此类问题必须合并通项公式中同一字母的指数,根据具体要求,令其为整数,再根据数的整除性来求解.12. 若2sin sin αβ+=3π2αβ+=,则sin α=________;cos 2β=________.【答案】 ①. ②. 35##0.6【解析】【分析】由2sin sin αβ+=3π2αβ+=,可得出2sin cos αα-=,再结合同角平方关系即可求出sin α=,从而算出sin β=3cos 25β=.【详解】 2sin sin αβ+=3π2αβ+=,3π2sin sin()2αα∴+-=2sin cos αα-=,cos 2sin αα∴=-,又22sin cos 1αα+= ,∴(22sin 2sin 1,αα+=解得sin α=∴2sin β+=,解得sin β=,23cos 212sin 5ββ∴=-=.综上,sin α=3cos 25β=.,35.13. 某专业资格考试包含甲、乙、丙3个科目,假设小张甲科目合格的概率为34,乙、丙科目合格的概率均为23,且3个科目是否合格相互独立.设小张3科中合格的科目数为X ,则(2)P X ==___________;()E X =___________.【答案】①. 49; ②. 2512##1212.【解析】【分析】根据独立事件概率的公式,结合数学期望的公式进行求解即可.【详解】3223223224(2)(1(1(1)4334334339P X ==-⨯⨯+⨯-⨯+⨯⨯-=;3221(0)(1)(1(1)43336P X ==-⨯-⨯-=,3223223227(1)(1(1)(1)(1)(1)(143343343336P X ==⨯-⨯-+-⨯⨯-+-⨯-⨯=,3221(3)4333P X ==⨯⨯=,所以174125()012336369312E X =⨯+⨯+⨯+⨯=,故答案为:49;251214. 已知0a >,0b >的最大值为________.【解析】【分析】利用基本不等式可得答案.【详解】因为0a >,0b >,所以=≤==,当且仅当2a a b=+即a b=等号成立..15. 设Rω∈,函数()2π2sin,0,6314,0,22x xf xx x xωω⎧⎛⎫+≥⎪⎪⎪⎝⎭=⎨⎪++<⎪⎩()g x xω=.若()f x在1π,32⎛⎫- ⎪⎝⎭上单调递增,且函数()f x与()g x的图象有三个交点,则ω的取值范围是________.【答案】23⎤⎥⎦.【解析】【分析】利用()f x在1π,32⎛⎫- ⎪⎝⎭上单调递增可得1243ω≤≤,函数()f x与()g x的图象有三个交点,可转化为方程23610x xω++=在(),0x∈-∞上有两个不同的实数根可得答案.【详解】当π0,2x⎡⎫∈⎪⎢⎣⎭时,πππ,626ωω⎡⎫++⎪⎢⎣⎭x,因为()f x在1π,32⎛⎫- ⎪⎝⎭上单调递增,所以()π0ππ2624133π12sin62ω⎧+≤⎪⎪⎪-≤-⎨⎪⎪≥⎪⎩,解得1243ω≤≤,又函数()f x与()g x图象有三个交点,所以在(),0x∈-∞上函数()f x与()g x的图象有两个交点,即方程231422x x xωω++=在(),0x∈-∞上有两个不同的实数根,即方程23610x xω++=在(),0x∈-∞上有两个不同的实数根,的所以22Δ3612003060102ωωω⎧=->⎪⎪-<⎨⎪⨯+⨯+>⎪⎩,解得ω>当0x ≥时,令()()π2sin 6ωω⎛⎫-=+- ⎪⎝⎭f xg x x x ,由0x =时,()()10f x g x -=>,当π5π66ω+=x 时,7π3ω=x ,此时,()()7π203-=-<f x g x ,结合图象,所以0x ≥时,函数()f x 与()g x 的图象只有一个交点,综上所述,23ω⎤∈⎥⎦.故答案为:233⎤⎥⎦.【点睛】关键点点睛:解题的关键点是转化为方程23610x x ω++=在(),0x ∈-∞上有两个不同的实数根.三、解答题:本大题共5小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤,请把解题过程写在答案卡上.16. 已知ABC 的内角A ,B ,C 的对边分别为a ,b ,c,满足22cos c b A =+.(1)求角B ;(2)若1cos 4A =,求sin(2)AB +的值;(3)若7c =,sin b A =b 的值.【答案】(1)6π.(2.(3【解析】【分析】(1)由正弦定理化边为角后,由诱导公式和两角和的正弦公式化简后可求得B ;(2)由二倍角公式求得sin 2,cos 2A A 后再由两角和的正弦公式可求值;(3)由正弦定理求得a ,再由余弦定理求得b .【详解】(1)∵22cos c b A =+,由正弦定理得,2sin 2sin cos C A B A=+∴2(sin cos cos sin )2sin cos A B+A B A B A =+,即2sin cos A B A =.∵sin 0A ≠,∴cos B =又0B π<<,∴6B π=(2)由已知得,sin A ==∴sin 22sin cos A A A ==,27cos 22cos 18A A =-=-∴sin(2)sin(2sin 2cos cos 2sin 666A B A A A πππ+++==.(3)由正弦定理sin sin a b A B =,得sin sin b A a B =.由(1)知,6B π=,∴a =由余弦定理得,2222cos 19b a c ac B =+-=.∴b =【点睛】本题考查正弦定理、余弦定理、考查两角和的正弦公式、二倍角公式、诱导公式,同角间的三角函数关系,考查公式较多,解题关键是正确选择应用公式的顺序.在三角形中出现边角关系时,常常用正弦定理进行边角转换.17. 已知底面ABCD 是正方形,PA ⊥平面ABCD ,//PA DQ ,33PA AD DQ ===,点E 、F 分别为线段PB 、CQ 中点.(1)求证://EF 平面PADQ ;(2)求平面PCQ 与平面CDQ 夹角的余弦值;(3)线段PC 上是否存在点M ,使得直线AM 与平面PCQ,若存在求出PM MC 的值,若不存在,说明理由.【答案】(1)证明见解析(2(3)存在;1PM MC =或15PM MC =【解析】【分析】(1)法一:分别取AB 、CD 的中点G 、H ,连接EG 、GH 、FH ,证明出平面//EGHF 平面ADQP ,利用面面平行的性质可证得结论成立;法二:以点A 为坐标原点,以AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量法可证得结论成立;(2)利用空间向量法可求得平面PCQ 与平面CDQ 夹角的余弦值;(3)假设存在点M ,使得PM PC λ= ,其中[]0,1λ∈,求出向量AM 的坐标,利用空间向量法可得出关于λ的方程,解之即可.【小问1详解】的证明:法一:分别取AB 、CD 的中点G 、H ,连接EG 、GH 、FH ,由题意可知点E 、F 分别为线段PB 、CQ 的中点.所以//EG PA ,//FH QD ,因为//PA DQ ,所以//EG FH ,所以点E 、G 、H 、F 四点共面,因为G 、H 分别为AB 、CD 的中点,所以//GH AD ,因为AD ⊂平面ADQP ,GH ⊄平面ADQP ,所以//GH 平面ADQP ,又因为//FH QD ,QD ⊂平面ADQP ,FH ⊄平面ADQP ,所以//FH 平面ADQP ,又因为FH GH H = ,FH 、GH Ì平面EGHF ,所以平面//EGHF 平面ADQP ,因为EF ⊂平面EGHF ,所以//EF 平面ADQP ;法二:因为ABCD 为正方形,且PA ⊥平面ABCD ,所以AP 、AB 、AD 两两互相垂直,以点A 为坐标原点,以AB 、AD 、AP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()0,0,3P 、()3,3,0C 、()0,3,1Q 、()3,0,0B 、33,0,22E ⎛⎫⎪⎝⎭、31,3,22F ⎛⎫ ⎪⎝⎭,所以()0,3,1EF =- ,易知平面PADQ 的一个法向量()1,0,0a = ,所以0a EF ⋅= ,所以E F a ⊥ ,又因为EF ⊄平面ADQP ,所以//EF 平面ADQP .【小问2详解】解:设平面PCQ 的法向量(),,m x y z = ,()3,3,3PC =- ,()3,0,1CQ =- ,则333030m PC x y z m CQ x z ⎧⋅=+-=⎪⎨⋅=-+=⎪⎩ ,取1x =,可得()1,2,3m = ,所以平面PCQ 的一个法向量为()1,2,3m = ,易知平面CQD 的一个法向量()0,1,0n = ,设平面PCQ 与平面CQD 夹角为θ,则cos cos ,m n m n m n θ⋅=====⋅ ,所以平面PCQ 与平面CQD【小问3详解】解:假设存在点M ,使得()3,3,3PM PC λλλλ==- ,其中[]0,1λ∈,则()()()0,0,33,3,33,3,33AM AP PM λλλλλλ=+=+-=- ,由(2)得平面PCQ 的一个法向量为()1,2,3m = ,由题意可得c os ,AM = ,整理可得212810λλ-+=.即()()21610λλ--=,因为01λ≤≤,解得16λ=或12,所以,15PM MC =或1PM MC=.18. 已知{}n a 为等差数列,6,2,n n na nb a n -⎧=⎨⎩为奇数为偶数,记n S ,n T 分别为数列{}n a ,{}n b 的前n 项和,432S =,316T =.(1)求{}n a 的通项公式;(2)证明:当5n >时,n n T S >.【答案】(1)23n a n =+;(2)证明见解析.【解析】【分析】(1)设等差数列{}n a 的公差为d ,用1,a d 表示n S 及n T ,即可求解作答.(2)方法1,利用(1)的结论求出n S ,n b ,再分奇偶结合分组求和法求出n T ,并与n S 作差比较作答;方法2,利用(1)的结论求出n S ,n b ,再分奇偶借助等差数列前n 项和公式求出n T ,并与n S 作差比较作答.【小问1详解】设等差数列{}n a 的公差为d ,而6,21,N 2,2n n n a n k b k a n k*-=-⎧=∈⎨=⎩,则112213316,222,626b a b a a d b a a d =-==+=-=+-,于是41314632441216S a d T a d =+=⎧⎨=+-=⎩,解得15,2a d ==,1(1)23n a a n d n =+-=+,所以数列{}n a 的通项公式是23n a n =+.【小问2详解】方法1:由(1)知,2(523)42n n n S n n ++==+,23,21,N 46,2n n n k b k n n k*-=-⎧=∈⎨+=⎩,当n 为偶数时,12(1)34661n n b b n n n -+=--++=+,213(61)372222n n n T n n ++=⋅=+,当5n >时,22371()(4)(1)0222n n T S n n n n n n -=+-+=->,因此n n T S >,当n 奇数时,22113735(1)(1)[4(1)6]52222n n n T T b n n n n n ++=-=+++-++=+-,当5n >时,22351(5)(4)(2)(5)0222n n T S n n n n n n -=+--+=+->,因此n n T S >,所以当5n >时,n n T S >.方法2:由(1)知,2(523)42n n n S n n ++==+,23,21,N 46,2n n n k b k n n k*-=-⎧=∈⎨+=⎩,当n 为偶数时,21312412(1)3144637()()222222n n n n n n n T b b b b b b n n --+--++=+++++++=⋅+⋅=+ ,当5n >时,22371()(4)(1)0222n n T S n n n n n n -=+-+=->,因此n n T S >,当n 为奇数时,若3n ≥,则为132411231144(1)61()()2222n n n n n n n T b b b b b b --+-++-+-=+++++++=⋅+⋅ 235522n n =+-,显然111T b ==-满足上式,因此当n 为奇数时,235522n T n n =+-,当5n >时,22351(5)(4)(2)(5)0222n n T S n n n n n n -=+--+=+->,因此n n T S >,所以当5n >时,n n T S >.19. 如图,已知椭圆E :22221(0)x y a b a b +=>>()F 且斜率为k 的直线交椭圆E 于,A B 两点,线段AB 的中点为M ,直线l :40x ky +=交椭圆E 于,C D 两点.(1)求椭圆E 的方程;(2)求证:点M 在直线l 上;(3)是否存在实数k ,使得3BDM ACM S S ∆∆?若存在,求出k 的值,若不存在,说明理由.【答案】(1)22141x y +=(2)详见解析(3)存在,且k =【解析】【分析】(1)根据离心率和焦点坐标列方程组,解方程组求得,a b 的值,进而求得椭圆E 的方程.(2)写出直线AB 的方程,联立直线的方程和椭圆的方程,求得中点M 的坐标,将坐标代入直线l 的方程,满足方程,由此证得点M 在直线l 上.(3)由(2)知,A B 到l 的距离相等,根据两个三角形面积的关系,得到M 是OC 的中点,设出C 点的坐标,联立直线l 的方程和椭圆的方程,求得C 点的坐标,并由此求得k 的值.【详解】解:(1)解:由c a c ⎧=⎪⎨⎪=⎩,解得2a =,1b =所以所求椭圆的标准方程为22141x y +=(2)设()11,A x y ,()22,B x y ,()00,M x y,(2244y k x x y ⎧=+⎪⎨+=⎪⎩,消x 得,()2222411240k x x k +-+-=,解得12012022x x x y y y ⎧+==⎪⎪⎨+⎪==⎪⎩将()00,M x y 代入到40x ky +=中,满足方程所以点M 在直线l 上.(3)由(2)知,A B 到l 的距离相等,若BDM ∆的面积是ACM ∆面积的3倍,得3DM CM =,有DO CO =,∴M 是OC 的中点,设()33,C x y ,则302y y =,联立224044x ky x y +=⎧⎨+=⎩,解得3y =,=解得218k =,所以k =.【点睛】本小题主要考查椭圆标准方程的求法,考查直线和椭圆的位置关系,考查根与系数关系,考查方程的思想,属于中档题.要证明一个点在某条直线上,那么先求得这个点的坐标,然后将点的坐标代入直线方程,如果方程成立,则这个点在直线上,否则不在这条直线上.20. 已知函数()()1211222x f x x e x x -=--++,()()24cos ln 1g x ax x a x x =-+++,其中a ∈R .(1)讨论函数()f x 的单调性,并求不等式()0f x >的解集;(2)用{}max ,m n 表示m ,n 的最大值,记()()(){}max ,F x f x g x =,讨论函数()F x 的零点个数.【答案】(1)增函数;()1,+∞;(2)答案见解析.【解析】【分析】(1)先对函数求导,得到()()()111x f x x e-'=--,根据导数的方法,即可判定其单调性,进而可求出不等式的解集.(2)1x >时,()0F x >恒成立,当11x -<<时,()0f x <恒成立,故()F x 的零点即为函数()g x 的零点,讨论()g x 在11x -<<的零点个数得到答案.【详解】(1)()()()()111111x x f x x e x x e --'=--+=--,当1x >时,10x ->,110x e -->,∴()0f x ¢>,当1x <时,10x -<,110x e --<,∴()0f x ¢>,当1x =时,()0f x '=,所以当x ∈R 时,()0f x '≥,即()f x 在R 上是增函数;又()10f =,所以()0f x >的解集为()1,+∞.(2))函数()F x 的定义域为(1,)-+∞由(1)得,函数()f x 在x ∈R 单调递增,()10f =当1x >时,()0f x >,又()max{(),()}F x f xg x =,所以1x >时,()0F x >恒成立,即1x >时,()0F x =无零点.当11x -<<时,()0f x <恒成立,所以()F x 零点即为函数()g x 的零点下面讨论函数()g x 在11x -<<的零点个数:1()214sin 1g x ax a x x '=--++,所以21()24cos (11)(1)g x a a x x x ''=---<<+①当0a >时,因为11x -<<,cos (cos1,1)x ∈又函数cos y x =在区间π0,2⎛⎫ ⎪⎝⎭递减,所以π1cos1cos 32>=即当11x -<<时,12cos 0x -<,21()2(12cos )0(1)g x a x x ''=--<+所以()g x '单调递减,由()00g '=得:当10x -<<时()0g x '>,()g x 递增的当01x <<时()0g x '<,()g x 递减当1x →-时ln(1)x +→-∞,()g x ∴→-∞,当0x =时(0)40g a =>又(1)14cos1ln 2g a a =-++,()10f =当1ln 2(1)014cos1g a ->⇒>+时,函数()F x 有1个零点;当1ln 2(1)014cos1g a -=⇒=+时,函数()F x 有2个零点;当1ln 2(1)0014cos1g a -<⇒<<+时,函数()F x 有3个零点;②当0a =时,()ln(1)g x x x =+-,由①得:当10x -<<时,()0g x '>,()g x 递增,当01x <<时,()0g x '<,()g x 递减,所以max ()(0)0g x g ==,(1)ln 210g =-<,所以当0a =时函数()F x 有2个零点③当a<0时,()2()4cos ln(1)g x a x x x x =+-++()24cos 0a x x +<,ln(1)0x x -++≤,即()0g x <成立,由()10f =,所以当a<0时函数()F x 有1个零点综上所述:当1ln 214cos1a ->+或a<0时,函数()F x 有1个零点;当1ln 214cos1a -=+或0a =时,函数()F x 有2个零点;当1ln 2014cos1a -<<+时,函数()F x 有3个零点.【点睛】思路点睛:导数的方法研究函数的零点时,通常需要对函数求导,根据导数的方法研究函数单调性,极值或最值等,有时需要借助数形结合的方法求解.。
天津耀华中学高一数学理联考试卷含解析

天津耀华中学高一数学理联考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 不等式的解集是:A. (-1,0)B.(-∞,-1)∪(0,+∞)C. (0,1)D. (-∞,0)∪(1,+∞)参考答案:C【分析】把不等式转化为不等式,即可求解,得到答案.【详解】由题意,不等式,等价于,解得,即不等式的解集为(0,1),故选C.【点睛】本题主要考查了一元二次不等式的求解,其中解答中熟记一元二次不等式的解法是解答的关键,着重考查了推理与运算能力,属于基础题.2. 已知函数f(x)=Asin(ωx+φ)(ω>0,﹣π<φ<0)的部分图象如图所示,则下列判断正确的是()A.函数f(x)的最小正周期为πB.函数f(x)的值域为[﹣,]C.函数f(x)的图象关于直线x=﹣对称D.函数f(x)的图象向右平移个单位得到函数y=Asinωx的图象参考答案:A【考点】正弦函数的图象.【分析】由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式;再利用函数y=Asin (ωx+φ)的图象变换规律,正弦函数的图象和性质,得出结论.【解答】解:根据函数f(x)=Asin(ωx+φ)(ω>0,﹣π<φ<0)的部分图象,可得==﹣,∴ω=π.再根据五点法作图可得π?+φ=0,∴φ=﹣,即f(x)=Asin(πx﹣),故函数的周期为=2,故排除A;由于A不确定,故函数f(x)的值域不确定,故排除B;令x=﹣,可得f(x)=﹣A,为函数的最小值,故函数f(x)的图象关于直线x=﹣对称,故C正确;把函数f(x)的图象向右平移个单位得到函数y=Asin[π(x﹣)﹣]=Asin(πx﹣)的图象,故D错误,故选:A.【点评】本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值;函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质,属于基础题.3. 已知M={0,1,2},N={x|x=2a,a M},则M N=()A {0,1}B {0,2}C {0,1,2}D {0,1,2,4}参考答案:B略4. 为了得到函数的图象,只需把函数的图象上所有( ).A.向右平移B.向右平移C.向左平移D.向左平移参考答案:B略5. 下列判断正确的是()A、 B、 C、 D、参考答案:D6. 设函数f(x)定义在实数集上,f(2﹣x)=f(x),且当x≥1时,f(x)=lnx,则有()A.B.C.D.参考答案:C【考点】对数值大小的比较.【分析】由f(2﹣x)=f(x)得到函数的对称轴为x=1,再由x≥1时,f(x)=lnx得到函数的图象,从而得到答案.【解答】解:∵f(2﹣x)=f(x)∴函数的对称轴为x=1∵x≥1时,f(x)=lnx∴函数以x=1为对称轴且左减右增,故当x=1时函数有最小值,离x=1越远,函数值越大故选C.7. 已知平面上直线的方向向量=(),点和在上的射影分别是和,则=,其中等于()A. B. C.2D.参考答案:D8. 数列{a n}的通项公式,其前n项和为S n,则等于()A. 1006B. 1008C. -1006D. -1008参考答案:B【分析】依据为周期函数,得到,并项求和,即可求出的值。
天津市耀华中学届高三第一次月考 理科数学试卷

天津市耀华中学2016届高三第一次月考理科数学试卷本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分共150分,考试用时120分钟.第I 卷(选择题共40分)一.选择题:本大题共8小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题目要求的,将答案涂在答题卡上.......... 1.已知集合**{|2,},{|2,}n A x x n N B x x n n N ==∈==∈,则下列不正确...的是 A .A B ⊆ B .A B A =I C .()Z B A =∅I ðD .A B B =U2.函数24sin 2cos ()33y x x x ππ=+≤≤的最大值和最小值分别是 A .,4741-B .,472-C .,241-D .,22-3.函数()ln f x x ax =+存在与直线20x y -=平行的切线,则实数a 的取值范围是 A .(,2]-∞ B .(,2)-∞ C .(2,)+∞ D .(0,)+∞4.要得到函数x y cos 3=的图象,只需将函数)62sin(3π-=x y 的图象上所有点 A.横坐标缩短到原来的21(纵坐标不变),所得图象再向左平移32π个单位B.横坐标缩短到原来的21(纵坐标不变),所得图象再向右平移6π个单位C.横坐标伸长到原来的2倍(纵坐标不变),所得图象向左平移32π个单位D.横坐标伸长到原来的2倍(纵坐标不变),所得图象向右平移6π个单位5.在ABC ∆中,如果边,,a b c 满足1()2a b c ≤+,则A ∠ A.一定是锐角B.一定是钝角C.一定是直角D.以上情况都有可能6.设02x π<<,则“2sin 1x x <”是“sin 1x x <”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件7.设方程()3lg x x =-的两个根为1x ,2x ,则 A.120x x < B.121x x = C.121x x > D.1201x x <<8.若函数3()3f x x x =-在区间2(12,)a a -上有最小值,则实数a 的取值范围是A .(-B .(1,4)-C .(1,2]-D .(1,2)-第II 卷(非选择题共110分)二.填空题:本大题共6小题,每小题5分,共30分,将答案填写在答题纸上........... 9.计算定积分的值:3211(2)x dx x-⎰= .10.已知234(0)9a a =>,则32log a =________.11.在ABC ∆中,60A =︒,1=b =++++CB A cb a sin sin sin .12.若函数2(2)1(0)()22(0)x f x x f x x +-+≥⎧=⎨-<⎩,则(2014)f = .13.当662sin cos y x x =+取得最小值时,cos 2x = .14.已知集合22{|30},{|1log (1)2}A x x ax B x x =-+≤=≤+≤,若A B ⊆,则实数a的取值范围是 .三.解答题:本大题共6小题,共80分,将解题过程及答案填写在答题纸上................ 15.(本小题满分13分)设函数()cos(2)22,(,)3f x x x m x R m R π=+++∈∈,(Ⅰ)求函数()f x 的最小正周期及单调增区间; (Ⅱ)当04x π≤≤时,()f x 的最小值为0,求实数m 的值.16.(本小题满分13分)某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分1AC 别为23和12,且各株大树是否成活互不影响.求移栽的4株大树中:(Ⅰ)两种大树各成活1株的概率;(Ⅱ)成活的株数ξ的分布列与期望.17.(本小题满分13分)如图,在直四棱柱1111ABCD A B C D-中,侧棱1AA的长为3,底面ABCD是边长为2的正方形,E是棱BC的中点.(Ⅰ)求证:1BD∥平面1C DE;(Ⅱ)求二面角1C DE C--的正切值;(Ⅲ)在侧棱1BB上是否存在点P,使得CP⊥平面1C DE?证明你的结论.18.(本小题满分13分)已知函数xaxxxf ln)(2-+=,.a R∈(Ⅰ)若0a=时,求曲线()y f x=在点(1,(1))f处的切线方程;(Ⅱ)令2)()(xxfxg-=,是否存在实数a,当∈x],0(e(e是自然常数)时,函数)(xg的最小值是3,若存在,求出a的值;若不存在,请说明理由.19.(本小题满分14分)已知曲线C的方程为24(0)y x x=>,曲线E是以()011,-F、()012,F为焦点的椭圆,点P 为曲线C 与曲线E 在第一象限的交点,且352=PF . (Ⅰ)求曲线E 的标准方程; (Ⅱ)直线与椭圆E 相交于A 、B 两点,若AB 的中点M 在曲线C 上,求直线的斜率k 的取值范围.20.(本小题满分14分)函数1()()2ln f x p x x x =--,2()eg x x=,p R ∈, (Ⅰ)若()f x 在2x =处取得极值,求p 的值;(Ⅱ)若()f x 在其定义域内为单调函数,求p 的取值范围;(Ⅲ)若在[]1,e 上至少存在一点0x ,使得00()()f x g x >成立,求p 的取值范围.天津市耀华中学2016届高三第一次月考(理科)数学参考答案9、223;10、3-;1112、1007;13、3-14、(-; 三、解答题:本大题共6小题,共80分。
天津市新华中学2013届高三上学期第一次月考数学(理)试题

天津新华中学2012-2013学年度第一学期高三年级第一次月考数学试卷(理科)一、选择题:(本大题共8小题,每小题4分,共32分.)在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合2A={|log <1},B={x|0<<c}x x x ,若=A B B ,则c 的取值范围是A. (0,1]B. [1,+)∞C. (0,2]D. [2,+)∞【答案】D【解析】2{log 1}{01}A x x x x =<=<<.因为AB B =,所以A B ⊆.所以1c ≥,即[1,)+∞,选B.2. 已知命题:"[1,2],-0"2p x x a ∀∈≥,命题:"R,+2+2=0"2q x x ax -a ∃∈使,若命题“p q 且”是真命题,则实数a 的取值范围是A. {|-2=1}a a a ≤或B. {|-2}a a ≤C. {|-22}a a a ≤≤≤或1D. {|-21}a a ≤≤ 【答案】A【解析】由20x a -≥,得2,[1,2]a x x ≤∈,所以1a ≤.要使q 成立,则有244(2)0a a ∆=--≥,即220a a +-≥,解得1a ≥或2a ≤-.因为命题“p q 且”是真命题,则,p q 同时为真,即112a a a ≤⎧⎨≥≤-⎩或,即2a ≤-或1a =,选A.3. 已知函数()()2531m f x m m x--=--是幂函数且是()0,+∞上的增函数,则m 的值为 A. 2 B. -1 C. -1或2D. 0【答案】B【解析】因为函数为幂函数,所以211m m --=,即220m m --=,解得2m =或1m =-.因为幂函数在(0,)+∞,所以530m -->,即35m <-,所以1m =-.选B. 4. 已知定义在区间[0,2]上的函数=()y f x 的图象如图所示,则=(2-)y f x 的图象为【答案】A【解析】当0x =时,(20)(2)1y f f =-==,排除B,C,D,选A.5. 给定函数①12=y x -,②23+3=2xx y -,③12=log |1-|y x ,④=sin2xy π,其中在(0,1)上单调递减的个数为A. 0B. 1 个C. 2 个D. 3个 【答案】C【解析】①为幂函数,102-<,所以在(0,1)上递减.②223333()24x x x -+=-+,在(0,1)上递减,所以函数23+3=2x x y -在(0,1),递减.③1122log 1log 1y x x =-=-,在(0,1)递增.④sin2y x π=的周期,4T =,在(0,1)上单调递增,所以满足条件的有2个,选C.6. 设3=2a log ,=2b ln ,12=5c -,则A. <<a b cB. <<b c aC. <<c a bD. <<c b a【答案】C【解析】321log 2log 3=,21ln 2log e =,125-=222log 3log 0e >>>>,所以22110log 3log e <<<,即c a b <<。
天津市耀华中学2013届高三第一次月考理科数学试题 Word版.pdf

耀华中学2013届高三年级第一次月考理科数学试卷 本试卷分第卷(选择题)和第卷(非选择题)两部分,共150分,考试用时l20分钟。
第卷(选择题共40分) 一、选择题:本大题共8小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题要求的, 1、i是虚数单位,复数等于A、iB、-iC、1213iD、12+13i 2、下列命题中是假命题的是 A、 B、 、 D、 3、在下区中,函数的零点所在的区间为A、,0)B、)C、,)D、,) 4、设,R,”是“”的 A、充分不必要条件 、必要不充分条件C、充要条件D、既不充分也不必要条件 5、把函数的图象上所有的点向左平行移动个单位度,再把所得图象上所有点的坐标缩短到原来的倍(纵坐标不变),得到的图象所表示的函数是 B、、D、 6、已知函数,的大小关系是 A、 B、 、D、 7、ABC中,,b,c分别是角A,B,C的对边,a=,b,且12cos(B+C)=0,则BC边上的高等于 A、B、、 D、 8、定义域为R的函数满足,当[,2)时, 时,恒成立,则实数A、[2,)(0,l)、[-2,) [l,+∞)、[2,lD、(,2] (0,l第卷(非选择题共分) 二、填空题:本大题共6小题,每小题5分,共30分。
请将答案填写在答题纸上. 9、计算=10、设集合(0,+∞)上的增函数, ,则=; 11、函数为常数,>0, >0)的部分图象如图所示,则f(0)的值是、1,若函数有最大值,则不筹式为13、A,B,C的对边,若,则 14、若关于的不等式对任意在恒成立,则实 常数的取值范围是; 耀华中学2013届高三年级第一次月考理科数学答题纸 二、填空题:本大题共6小题,每小题5分,共30分。
9、12、三、解答题;本大题共6小题,共8分。
解答应写出必要的文字说明、证明过程或演算步骤。
满分, (1)求函数的最正周期; (2)求使函数取得最大值的x集合; 若且,求的值。
名题精品解析天津市耀华中学2013届高三第一次月考(物理)

天津市耀华中学2013届高三第一次月考物理试卷一.选择题(1-8题为单选,每题3分,9-14题为多选,每题4分,共计48分)1.如图所示,物块在力F作用下向右沿水平方向匀加速运动,则物块受的摩擦力f与拉力的合力方向应该是A.水平向右B.竖直向上C.向右偏上D.向左偏上【答案】C【学优高考网解析】将拉力按照作用效果正交分解,如图所示,物体水平向右加速运动,故F1>f,即F1与f的合力向右,再与F2合成,合力斜向右上方.故选C。
2.物体沿一条直线作加速运动,从开始计时起,第1s内的位移是lm,第2s 内的位移是2m,第3s内的位移是3m,第4s内的位移是4m,由此可知A.此物体一定作匀加速直线运动B.此物体的初速度是零C.此物体的加速度是lm/s2D.此物体在前4s内的平均速度是2.5m/s 【答案】D【学优高考网解析】各时间段内位移随时间增加,但由题意无法确定各段时间内的具体运动形式,故无法判断物体是否做的匀加速直线运动;同时也无法得出物体的初速度及加速度;故ABC错误;由svt=可得,此物体在前4s内的平均速度为:12344v+++=m/s=2.5m/s;故D正确.3.作用于O点的三力平衡,设其中一个力的大小为F1,沿y轴正方向,力F2大小未知,与x轴负方向夹角为θ,如图所示,下列关于第三个力F3的判断正确的是A.力F3只能在第四象限B.力F3与F2夹角越小,则F2和F3的合力越小C.F3的最小值为F1cosθD.力F3可能在第一象限的任意区域【答案】C【学优高考网解析】三力平衡时,三个力中任意两个力的合力与第三个力等值、反向、共线;通过作图可以知道,当F1、F2的合力F与F2垂直时合力F最小,等于F1cosθ,故C正确;由于三力平衡,F2与F3的合力始终等于F1,故B错误;当F1、F2的合力F在第三象限时,力F3在第一象限,故A错误;通过作图可知,当F1、F2的合力F可以在F1与F2之间的任意方向,而三力平衡时,三个力中任意两个力的合力与第三个力等值、反向、共线,故力F3只能在F1与F2之间的某个方向的反方向上,故D错误;故选C.4.一条不可伸长的轻绳跨过质量可忽略不计的定滑轮,绳的一端系一质量m=15kg 的重物,重物静止于地面上,有一质量为10kg 的猴子,从绳子的另一端沿绳向上爬,如图所示,不计滑轮磨擦,在重物不离开地面的条件下,猴子向上爬的最大加速度为(g 取l0m/s 2)A .25 m/s 2B .10 m/s 2C .5 m/s 2D .15 m/s 2【答案】C【学优高考网解析】小猴以最大加速度向上爬行时,重物对地压力为零,故小猴对细绳的拉力等于重物的重力,即F=Mg ;小猴对细绳的拉力等于细绳对小猴的拉力F ′=F ;对小猴受力分析,受重力和拉力,根据牛顿第二定律,有F ′-mg=ma解得a=()M m g m -=5m/s 2 故选C .5.甲、乙两个物体分别从A 、C 两点由静止出发做匀加速直线运动,B 为A 、C 的中点,两物体在AB 段的加速度大小均为a l ,在BC 段的加速度均为a 2,且a l <a 2。
数学丨天津市耀华中学2025届高三上学期11月第一次月考数学试卷及答案

天津市耀华中学2025届高三年级第一次月考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷(选择题共45分)一.选择题:本大题共9小题,每小题5分,共45分,在每小题的4个选项中,只有一项是符合题目要求的,将答案涂在答题卡上..........1.全集U={1,2,3,4,5,6},集合A={1,3,5},B={2,4},则()A.U=A∪BB.U=(C U A)∪BC.U=A∪(C U B)D.U=(C U A)∪(C U B)2.“x-1<2成立”是“x(x-3)<0成立”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3.已知函数,则y=f的图象大致为().A. B.C. D.4.若函数y=co图象的一个对称中心是的最小值为()A.1B.2C.4D.85.函数y=(sin x+cos x)(sin x-cos x)是A.奇函数且在上单调递增「π7B.奇函数且在|,π|上单调递增「π7C.偶函数且在|0,|上单调减增D.偶函数且在「|π,π7|上单调递增6.在等差数列{a n }中,a 1=0,公差d ≠0,若a m =a 1+a 2+…+a 9,则m 的值为A.37B.36C.20D.197.记实数x 1,x 2,ⅆ,x n 中的最大数为max{x 1,x 2,…,x n },最小数为min {x 1,x 2,…,x n },则max {min {x +1,x -x +1,-x +6}}=A3B.1C.3D.7.428.已知函数f 若存在x 1,x 2∈R ,x 1≠x 2,使得f(x 1)=f (x 2)成立,则实数a 的取值范围是()A.a <-2或a >2B.a >2C.-2<a <2D.a <29.已知函数f 若对任意的c >1,存在实数a ,b 满足0<a <b <c ,使得f(c )=f (a )=g (b ),则k 的最大值为()A.3B.4C.5D.6第Ⅱ卷(非选择题共105分)二.填空题:本大题共6小题,每小题5分,共30分,将答案填写在答题纸上...........10.已知方程cos 2x +4sin x -a =0有解,则a 的范围是______.11.已知x >0,y >0,x +2y +2xy =8,则x +2y 的最小值为.12.已知sin α-sin β=-,cos α-cos β=,且α,β均为锐角,则tan (α-β)的值等于13.函数y =ln |x -1|的图象与函数y =-2cos πx ,(-2≤x ≤4)的图象所有交点的横坐标之和等于.___________14.将y =sin 2x 的图象向右平移φ单位(φ>0),使得平移后的图象仍过点(π,3),则φ的最小值为322L 2」L 2」L 2」___________.15.已知数列满足:a1=1,a2=,且a n+2=则数列{a n}的通项公式是三.解答题:本大题共5个小题,共计75分.请在解答时写出必要的文字说明、证明过程或演算步骤.答案写在答题卡的相应位置上.16.在V ABC中,角A,B,C的对边分别为a,b,c,且角A,B,C成等差数列.13,a=3,求边c的值;(Ⅱ)设t=sin A sin C,求t的最大值.17.已知函数f(x)=sin(①x+φ)(①>0,0<φ<π),其图象经过点,且与x轴两个相邻的交点的距离为π.(1)求f(x)的解析式;在V ABC中,a=13,f,求V ABC的面积.18.在三棱柱ABC﹣AB1C1中,侧面ABB1A1为矩形,AB=2,AA1=22,D是AA1的中点,BD与AB1交于点O,且CO⊥平面ABB1A1.(1)证明:BC⊥AB1;(2)若OC=OA,求直线CD与平面ABC所成角的正弦值.19.已知数列{a n}的前n项和为S n,且S n=2a n-1(n∈N*).}的通项公式;(1)求数列{a n(2)令b n=na n,求数列{b n}的前n项和T n;(3)记c n=3n-2.(-1)nλa n(λ≠0),是否存在实数λ使得对任意的n∈N*,恒有c n+1>c n?若存在,求出λ的取值范围;若不存在,说明理由.20.已知a为实数,函数f(x)=a.ln x+x2-4x.(1)是否存在实数a,使得f(x)在x=1处取极值?证明你的结论;(2)若函数f(x)在[2,3]上存在单调递增区间,求实数a的取值范围;设g=2a ln x+x2-5x-若存在x0∈[1,e],使得f(x)<g(x)成立,求实数a的取值范围.天津市耀华中学2025届高三年级第一次月考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷(选择题共45分)一.选择题:本大题共9小题,每小题5分,共45分,在每小题的4个选项中,只有一项是符合题目要求的,将答案涂在答题卡上..........【1题答案】【答案】D【2题答案】【答案】B【3题答案】【答案】A【4题答案】【答案】B【5题答案】【答案】C【6题答案】【答案】A【7题答案】【答案】D【8题答案】【答案】D【9题答案】【答案】A第Ⅱ卷(非选择题共105分)二.填空题:本大题共6小题,每小题5分,共30分,将答案填写在答题纸上...........【10题答案】【答案】[-4,4]【11题答案】【答案】4【12题答案】【答案】【13题答案】【答案】6【14题答案】【15题答案】三.解答题:本大题共5个小题,共计75分.请在解答时写出必要的文字说明、证明过程或演算步骤.答案写在答题卡的相应位置上.【16题答案】【答案】(I)4;(II).【17题答案】【答案】(1)f(x)=cos x(2)84【18题答案】【答案】(1)证明见解析;(2).【19题答案】a=2n—1;.2n+1;存在,且—<λ<1.【20题答案】【答案】(1)不存在,证明见解析;(2)a>—6(3)或a<—2天津市耀华中学2025届高三年级第一次月考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷(选择题共45分)一.选择题:本大题共9小题,每小题5分,共45分,在每小题的4个选项中,只有一项是符合题目要求的,将答案涂在答题卡上..........【1题答案】【答案】D【2题答案】【答案】B【3题答案】【答案】A【4题答案】【答案】B【5题答案】【答案】C【6题答案】【答案】A【7题答案】【答案】D【8题答案】【答案】D【9题答案】【答案】A第Ⅱ卷(非选择题共105分)二.填空题:本大题共6小题,每小题5分,共30分,将答案填写在答题纸上...........【10题答案】【答案】[-4,4]【11题答案】【答案】4【12题答案】【答案】【13题答案】【答案】6【14题答案】【15题答案】三.解答题:本大题共5个小题,共计75分.请在解答时写出必要的文字说明、证明过程或演算步骤.答案写在答题卡的相应位置上.【16题答案】【答案】(I)4;(II).【17题答案】【答案】(1)f(x)=cos x(2)84【18题答案】【答案】(1)证明见解析;(2).【19题答案】a=2n—1;.2n+1;存在,且—<λ<1.【20题答案】【答案】(1)不存在,证明见解析;(2)a>—6(3)或a<—2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初 中高考 高二会考 艺考生文化课 一对一辅导 (教师版) /wxxlhjy QQ:157171090 - 1 - 无锡新领航教育特供:耀华中学2013届高三年级
第一次月考
理科数学试卷
本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试用时l20分钟。
第I 卷(选择题共40分)
一、选择题:本大题共8小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题目要求的,请将答案涂在答题卡上。
1、i 是虚数单位,复数3+22-3i
i 等于
A 、i
B 、-i
C 、12-13i
D 、12+13i
【答案】A 【解析】3+223i
i -(3+2)(23)13=23(23)13i i i i i i +==-+(),选A. 2、下列命题中是假命题的是
A 、(0,),>2x x sin x π
∀∈ B 、000,+=2x R sin x cos x ∃∈
C 、 ,3>0x x R ∀∈
D 、00,=0x R lg x ∃∈
【答案】B
【解析】因为000+4sin x cos x x π+≤(),所以B 错误,选B.
3、在下列区间中,函数()=+43x f x e x -的零点所在的区间为
A 、(1
-4,0) B 、(0,1
4) C 、(1
4,1
2) D 、(1
2,3
4)
【答案】C 【解析】1114441
()=2=1604f e e --<
,1
21
()=102f e -->,所以函数的零点在11(,)42,选C.
4、设a ,b ∈R ,那么“>1a
b ”是“>>0a b ”的
A 、充分不必要条件
B 、必要不充分条件。
