一元一次方程思维导图
初中数学知识点思维导图

初中数学知识点思维导图1. 数与式1.1. 有理数- 定义:可以表示为两个整数的比的数。
- 性质:包括正有理数、负有理数和零。
- 运算:加法、减法、乘法、除法。
1.2. 无理数- 定义:不能表示为两个整数比的实数。
- 例子:π、√2等。
1.3. 代数式- 单项式:由数字和字母的乘积组成。
- 多项式:由多个单项式相加组成。
- 运算:合并同类项、分配律等。
2. 方程与不等式2.1. 一元一次方程- 形式:ax + b = 0。
- 解法:移项、合并同类项。
2.2. 二元一次方程组- 形式:ax + by = e, cx + dy = f。
- 解法:代入法、消元法。
2.3. 不等式- 性质:传递性、可加性、乘法性。
- 解法:移项、合并同类项、取交集。
3. 函数3.1. 一次函数- 形式:y = mx + b。
- 图像:直线。
3.2. 二次函数- 形式:y = ax^2 + bx + c。
- 图像:抛物线。
3.3. 反比例函数- 形式:y = k/x。
- 图像:双曲线。
4. 几何4.1. 点、线、面- 点:几何图形的基本元素。
- 线:由无数点组成。
- 面:由无数线组成。
4.2. 角- 锐角:小于90°。
- 直角:等于90°。
- 钝角:大于90°小于180°。
4.3. 三角形- 等边三角形:三边相等。
- 等腰三角形:两边相等。
- 直角三角形:一个角为90°。
4.4. 四边形- 正方形:四边相等且四个角都是直角。
- 矩形:对边相等且四个角都是直角。
- 平行四边形:对边平行。
4.5. 圆- 定义:所有点到中心点距离相等的点的集合。
- 性质:周长、面积、直径、半径。
5. 统计与概率5.1. 数据收集与处理- 收集:通过调查、实验等方式。
- 处理:数据整理、分类。
5.2. 统计图表- 条形图:表示数量的多少。
- 折线图:表示数量的变化趋势。
- 饼图:表示各部分占总体的比例。
初中数学知识结构图思维导图

公式 提公 法 因式 法
单项式除以单项式
同底数幂相除
除法
乘法公式
单项式与多项式 幂的乘法
乘法
运算
分母中 含字母、
分母 不为零
系数 相加 字母 不变
合并 同类项
加减 同类项
每个单项式 升降幂排列
项 次数
多项式
整式
最高项的次 数
意义
单项式
字母指数和
次数
系数
数字因 数
不改变 分式的值
公因式
通分化成同分 母
反比例函数
图象 性质
柱形储藏室轮船卸货 力学问题 电学问题
应用
一次函 数与反 比例函 数
解析式
形如y k x
(k为常数,k 0)
实际问题,图象在第 一象限
看图 象能 口述 性质
y
y
ox o
图象
1.开口方向 2.顶点坐标 3.对称轴 4.增减性 5.极值
性质
看式
子类
型能
口述
性质 ① yax2 ② yax2k
角平分线
条件
全等三角形
SSS
对应边、角、周长 面积、中线、高线、
角平分线相等
性质 表示方法
定义
两个三角形 用符号≌连接
完全重合 两个三角形
关系
位似变换
性质
两角对应 相等
相似三角形
判定
两边成比例 且夹角相等
全等 三角形 与 相似 三
角形
相似图形 形状相同
相似多边形
平行
比例线段
性质
ac bd
对应角相等, 周长的比=相似比 方
(3) a2 a
Y随 x的 增 大 而 增 大
一元一次方程及分式方程知识网络图
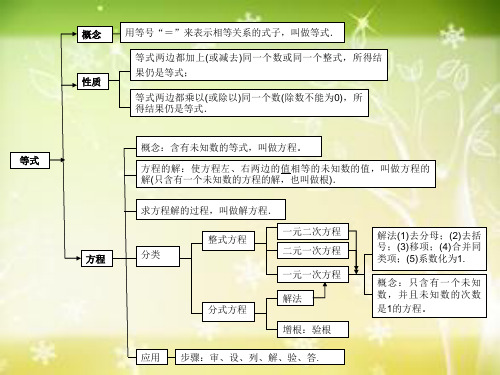
性质
概念:含有未知数的等式,叫做方程. 等式 方程的解:使方程左、右两边的值相等的未知数的值,叫做方程的 解(只含有一个未知数的方程的解,也叫做根). 求方程解的过程,叫做解方程. 整式方程 方程 分类 一元二次方程 二元一次方程 一元一次方程 解法 分式方程 增根:验根 应用 步骤:审、设、列、解、验、答. 解法(1)去分母; (2)去括 号;(3)移项; (4)合并同 类项;(5)系数化为1. 概念:只含有一个未知 数,并且未知数的次数 是1的方程.
一元一次方程知识结构图

7.工程问题:工作总量=工作效率×时间
盈亏问题:利润=售价-成本利率=利润÷成本×100%
售价=标价×折扣数×10%
储蓄利润问题:利息=本金×一个未知数未知数的次数都是1这样的方程叫做一元一次方程
一元一次方程知识结构图
知识结构图:
概念、定义:
1.含有一个未知数,未知数的次数都是1,这样的方程叫做一元一次方程。
3等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
5.等式的性质2:等式两边乘同一个数,或除以一个不为0的数,结果仍相等。
七年级数学上册知识点思维导图、考点梳理一元一次方程

七年级数学上册知识点思维导
图、考点梳理一元一次方程
七年级数学上册知识点思维导图、考点梳理——一元一次方程_问题
1.列方程时,要先设字母表示未知数,然后根据问题中的相等关系,写出还有未知数的等式——方程。
2.含有一个未知数(元素)且该未知数的次数为1的方程称为一元线性方程。
3.利用等价关系分析实际问题中的数量关系,列出方程,是用数学方法解决实际问题的一种方法。
4.等式1的性质:等式两边加(或减)相同的数(或公式),结果仍然相等。
5.等式的性质2:当等式两边都乘以同一个数,或者除以一个不为0的数,结果仍然相等。
6.将等式一边的变化符号移动到另一边叫做移项。
7.应用:行程问题:s=v×t
工程问题:工作总量=工作效率×时间
盈亏问题:利润=售价-成本利率=利润÷成本×100%
售价=标价×折扣数×10%储蓄利润问题:利息=本金×利率×时间本息和=本金+利息
end。
